|

REPUBLIQUE DEMOCRATIQUE DU
CONGO
ENSEIGNEMENT SUPERIEUR, UNIVERSITAIRE ET RECHERCHE
SCIENTIFIQUE
INSTITUT SUPERIEUR PEDAGOGIQUE

![]()
B.P. 854 BUKAVU
SECTION : SCIENCES COMMERCIALES, ADMINISTRATIVES
ET INFORMATIQUE
LA LIAISON AUTOMATIQUE DES PLUSIEURES PARTIES D'UNE
IMAGE PERCUE SUR UN SCANNER
DEPARTEMENT D'INFORMATIQUE ET GESTION
Présenté par
Jean-Marie MUNGUAKONKWA Biringanine
Travail présenté en vue de l'obtention du
diplôme de gradué en pédagogie
appliquée
Option : Informatique et Gestion
Année Académique 2007-2008
Directeur : Ass. Dieudonné KYENDA
S.
EPIGRAPHE
On naît homme, mais c'est patiemment et
progressivement qu'on devient vraiment homme. Devenir un homme demande un
effort de prise de conscience, de valorisation personnelle qui passe par le
chemin de l'être et de l'agir. Il faudra donc être à
l'écoute des autres, la réflexion critique et l'accueil de tout
ce qui peut enrichir. (Père G. Defour).
La paresse rend tout difficile, le travail rend tout
aisé, celui qui se lève tard, s'agite tout le jour est commence
à peine ses affaires quand il est déjà nuit.
Employez bien votre temps si vous voulez mériter le
repos et ne perdez pas une heure puisque vous n'êtres pas sûr
même d'une minute.
(Franklin)
IN MEMORIAM
A notre regretté petit frère SAMMY IRENGE
BIRINGANINE que la mort a fait rejoindre à nos ancêtres sans qu'il
ne savoure le fruit de nos labeurs,
A toutes les personnes qui sont mortes pour
rétablir la justice, la paix et la sécurité dans notre
pays.
Que le monde de nos ancêtres leur soit
agréable
MUNGUAKONKWA BIRINGANINE JM
DEDICACE
A l'éternel Dieu Tout Puissant pour nous avoir
protégé depuis les bas âges et toute notre vie.
A notre père BIRINGANINE NSIBULA,
A notre mère MASAWA CONCILIE M'MPALIZA,
A tous ceux qui nous sont chers
Je dédie ce travail
MUNGUAKONKWA BIRINGANINE JM
REMERCIEMENTS
A l'éternel Dieu Tout Puissant qui nous a
assisté tout au long de notre formation professionnelle.
A nos parents Deogratias BIRINGANINE NSIBULA et CONCILIE
M'MPALIZA pour vos sages conseils, vos encouragements et les multiples
interventions à mes problèmes, pour votre affection et votre
amour incomparable, vos efforts et les sacrifices inquantifiables vous avez
fait que je sois homme.
Que se travail vous soulage.
Nos remerciements s'adressent de tout coeur à notre
Directeur Dieudonné KYENDA SULIKA pour avoir accepté de diriger
ce travail malgré ses multiples occupations. Qu'il trouve ici
l'expression de notre reconnaissance
Aux Assistants et chefs de travaux de la Section Sciences
Commerciales Administratives et Informatique qui ont guidé nos
premiers pas à l'Université : ANNICET ITONGWA, TASHO
KASONGO, BULABULA KIZUNGU, Léandre KASELE W., Georges CHIHUNDA, NYONGOLO
LUWAWA, qu'ils trouvent ici le gain d'affection et le fruit de nos efforts.
Au chef de travaux Gervais CHIRHALWIRA pour ses conseils
A mes oncles paternels KAMUNTU NSIBULA, PASCAL NSIBULA,
A mes frères et soeurs Aimé BIRINGANINE,
Orthance BIRINGANINE, SHOKANO BIRINGANINE, YVETTE BIRINGANINE, ODILA
BIRINGANINE, MAYELE MIHIGO ANDRE.
A la famille MUHIGANYA: JC OMBENI MUHIGANYA, GASPARD, FILLE
MUHIGANYA, NEEMA MUHIGANYA, CHIMANUKA MUHIGANYA, BALEMBA MUHIGANYA,
EZECKIEL.
A nos amis SHABANI MUKELE, BAHAVU BIHANGO RUBEN,
MULUMEODERHWA SAGE, MWEZE MUGISHO BOB, LWABOSHI MAJOR, FRANCO HESHIMA MAJOR,
SAFARI MUNGANGA, PAPA JEAN MASEMO, DANNY MILENGE, JHO PATY MPADU KIZITO, JUSTIN
BYAMUNGU, MWATI NGENDO FABRICE,
A mes camarades ISHARA KIBASOMBA, BIRINGANINE NDAZI DANNY,
DIDIER MUTIKI, MULONGESHA MAZAMBI OLIVIER, LEON BYAMUNGU, DIEDO MUTUMAYI,
BULONGO TUKILINABO, MULAGANIRE NABINTU NYABA 2, OMARI MISSUMBA, LUSH MASONGA,
LUCIEN TCHIKO, LUCIEN MUBALAMA BADERHA, Roger YAMBAYAMBA, KARIMA TUDU.
Que ceux qui ne sont pas cité nominalement dans ce
travail ne se sentent pas oubliées mais qu'ils sachent que nous les
portons à coeurs.
MUNGUAKONKWA BIRINGANINE JM
SIGLES ET ABBREVIATIONS
B : Bleu
Comp. : Comparaison
DPI : Dots per inch
ISP : Institut Supérieur Pédagogique de
Bukavu
R : Rouge
V : Vert
Pixel : Picture Elément
PPP : Point Par Pouce
PUT : Look-Up Table
LZW : Lempel Ziv Welch
RLE : Run Length Encoded
RGB : Red Green Blue
0. INTRODUCTION
O.1. PROBLEMATIQUE
Le développement rapide des applications informatiques
s'est accompagné d'un accroissement important de l'utilisation des
images numériques, notamment dans le domaine des multimédias, des
jeux, des transmissions satellite ou de l'imagerie médicale.
En analyse d'images, l'exploitation de la donnée
chromatique permet de simplifier effectivement l'identification des objets et
leur extraction d'une scène. Jusqu'aux années 80, la plupart des
images « colorées » étaient en fait des
images pseudo-couleurs une couleur étant appliqué à une
intensité monochromatique particulière, ce n'est pas le cas des
images « couleur » dont nous disposons actuellement et dont
nous allons étudier.
Les images numérisées posent, par leur taille
importante, de nombreux problèmes quant à leur traitement. Aussi
bien lorsqu'il s'agit de numériser une image cartographique dont les
dimensions sont grandes, en utilisant un scanner.
Ces images cartographiques posent toujours de
problèmes pour être numérisée. Il apparaît
que ces images sont des grandes dimensions et lorsqu'il faut scanner une telle
image, le scanner n'est toujours pas apte à recevoir
l'intégralité de l'image.
Mais alors, si on n'arrive pas à scanner l'image en
plusieurs parties, et procéder à une liaison automatique de ces
différentes parties scannées, se posera un problème de la
traiter entièrement.
Ainsi, nous nous sommes penchés plus
précisément sur la liaison automatique des plusieurs parties
d'une image perçue sur un scanner.
· Comment peut-on arriver à déterminer les
limites des différentes parties d'une image cartographique
scannée de façon automatique ?
· comment peut-on arriver à lier automatiquement
les différentes parties de l'image scannée afin de reconstruire
l'image entière.
O.2. HYPOTHESE
Considérant le problème évoqué
ci-haut nous supposons que :
· L'utilisation d'algorithme de traitement d'image permet
de trouver les limites des différentes parties de l'image
scannée.
· L'utilisation d'Algorithmes de traitement d'image
permet une liaison automatique des différentes parties de l'image
scannée.
O.3. METHODOLOGIE ET
TECHNIQUES DU TRAVAIL
0.3.1 METHODOLOGIE
1. La méthode comparative
Cette méthode nous a permis de comparer les
différentes bandes des pixels extraites dans la première image
avec d'autres bandes des pixels extraites dans la deuxième image ligne
par ligne et de haut vers le bas à de pixels de mêmes couleurs.
2. Les calculs statistiques :
Cette méthode nous a permis de trouver le niveau de
ressemblance possible entre une bande extraite dans la première image et
une autre extraite dans la deuxième image. Elle nous a également
permis de trouver la moyenne de ressemblance après la comparaison.
0.3.2. TECHNIQUES
Pour mener à fin notre recherche nous avons recourus
à l'utilisation de différentes techniques de recherche et dont
les principales sont :
1. La technique documentaire
Cette technique nous a permis d'exploiter les
différentes documentations (ouvrages et articles) traitées par
nos prédécesseurs en rapport avec le problème que nous
souhaitons résoudre.
2. La technique de navigation sur internet
Cette technique nous a permis de faire des recherches sur
internet dans différents sites web et moteur de recherche, ce qui a
élargi notre champ de recherche.
0.4. CHOIX ET INTERET DU
SUJET
Notre intérêt attaché à ce sujet
orienté vers le traitement d'images et reconnaissance de formes,
s'explique d'une part par le fait que nous avons voulu nous familiariser au
domaine de traitement d'image. Ce domaine faisant aujourd'hui l'objet de
plusieurs recherches aussi bien dans le traitement des images cartographiques.
D'autre par nous avons voulu emboiter le pas de nos
prédécesseurs qui se sont intéressés à ce
domaine qui jusque là semble être négligé dans notre
milieu. Par conséquent disposer aux futurs étudiants une
documentation dans ce domaine de traitement d'image et de reconnaissance de
forme.
0.5. DIFFICULTES
RECONTREES
Tout au long de notre recherche, nous nous sommes
heurtés à des difficultés suivantes :
- Le Manque d'ouvrage orienté vers le traitement
d'image,
- Le Manque de moyen financier pour l'accès aux
données à l'intérêt.
CHAP I. GENERALITES SUR
LE TRAITEMENT D'IMAGES
I.1 INTRODUCTION
Avec la parole, l'image constitue
l'un des moyens les plus importants qu'utilise l'homme pour communiquer avec
autrui. C'est un moyen de communication universel dont la richesse du contenu
permet aux êtres humains de tout âge et de toute culture de se
comprendre.
C'est aussi le moyen le plus efficace pour communiquer, chacun
peut analyser l'image à sa manière, pour en dégager une
impression et d'en extraire des informations précises.
De ce fait, le traitement d'images est l'ensemble des
méthodes et techniques opérant sur celles-ci, dans le but de
rendre cette opération possible, plus simple, plus efficace et plus
agréable, d'améliorer l'aspect visuel de l'image et d'en extraire
des informations jugées pertinentes.
I.2 DEFINITION DE L'IMAGE
L'image est une représentation d'une personne ou d'un
objet par la peinture, la sculpture, le dessin, la photographie, le film, etc.
C'est aussi un ensemble structuré d'informations qui,
après affichage sur l'écran, ont une signification pour l'oeil
humain.
Elle peut être décrite sous la forme d'une
fonction I(x,y) de brillance analogique continue, définie dans un
domaine borné, Les x et y sont les coordonnées spatiales d'un
point de l'image et I est une fonction d'intensité lumineuse et de
couleur. Sous cet aspect, l'image est inexploitable par la machine, ce qui
nécessite sa numérisation [1(*)]
I.3 IMAGE NUMERIQUE
Contrairement aux images obtenues à l'aide d'un
appareil photo, ou dessinées sur du papier, les images manipulées
par un ordinateur sont numériques (représentées par une
série de bits).
L'image numérique est l'image dont la surface est
divisée en éléments de tailles fixes appelés
cellules ou pixels, ayant chacun comme caractéristique un niveau de gris
ou de couleurs prélevé à l'emplacement correspondant dans
l'image réelle, ou calculé à partir d'une description
interne de la scène à représenter [2(*)].
La numérisation d'une image est la conversion de
celle-ci de son état analogique en une image numérique
représentée par une matrice bidimensionnelle de valeurs
numériques f(x,y) où :
X, y : coordonnées cartésiennes d'un point
de l'image.
f(x, y) : niveau de gris en ce point
Pour des raisons de commodité de représentation
pour l'affichage et l'adressage, les données images sont
généralement rangées sous formes de tableau I de n lignes
et p colonnes. Chaque élément I(x, y) représente un pixel
de l'image et à sa valeur est associé un niveau de gris
codé sur m bits (2m niveaux de gris ; 0 = noir ;
2m-1 = blanc). La valeur en chaque point exprime la mesure
d'intensité lumineuse perçue par le capteur.
I.4 CARACTERISTIQUES
D'UNE IMAGE NUMERIQUE
L'image est un ensemble structuré d'informations
caractérisé par les paramètres suivants:
I.4.1
Pixel [3(*)]
Contraction de l'expression anglaise " Picture
Eléments ": éléments d'image, le pixel est le plus
petit point de l'image, c'est une entité calculable qui peut recevoir
une structure et une quantification. Si le bit est la plus petite unité
d'information que peut traiter un ordinateur, le pixel est le plus petit
élément que peuvent manipuler les matériels et logiciels
d'affichage ou d'impression. La lettre A, par exemple, peut être
affichée comme un groupe de pixels dans la figure ci-dessous :

La quantité d'information que véhicule chaque
pixel donne des nuances entre images monochromes et images couleurs. Dans le
cas d'une image monochrome, chaque pixel est codé sur un octet, et la
taille mémoire nécessaire pour afficher une telle image est
directement liée à la taille de l'image.
Dans une image couleur (R.V.B.), un pixel peut être
représenté sur trois octets : un octet pour chacune des
couleurs : rouge (R), vert (V) et bleu (B).
I.4.2 Dimension [4(*)]
C'est la taille de l'image. Cette dernière se
présente sous forme de matrice dont les éléments sont des
valeurs numériques représentatives des intensités
lumineuses (pixels). Le nombre de lignes de cette matrice multiplié par
le nombre de colonnes nous donne le nombre total de pixels dans une image.
I.4.3 Résolution[5(*)]
La résolution est définie par un nombre de
pixels par unité de longueur de l'image à numériser en dpi
(dots per inch) ou ppp (points par pouce)]. On parle de définition pour
un écran et de résolution pour une image.
Plus le nombre de pixels est élevé par
unité de longueur de l'image à numériser, plus la
quantité d'information qui décrit l'image est importante et plus
la résolution est élevée (et plus le poids de l'image est
élevé).
La résolution d'une image correspond au niveau de
détail qui va être représenté sur cette image. Pour
la numérisation il faut considérer les 2 équations
suivantes :
(X*résolution) = x pixels
(Y*résolution) = y pixels
où X et Y représentent la taille (pouce ou cm,
un pouce=2,54 centimètres) de la structure à numériser,
où résolution représente la résolution de
numérisation, et où x et y représentent la taille (en
pixels) de l'image.
I.4.4 La taille d'une
image
Pour connaître la taille d'une image, il est
nécessaire de compter le nombre de pixels que contient l'image, cela
revient à calculer le nombre des cases du tableau, soit la hauteur de
celui-ci que multiplie sa largeur. La taille de l'image est alors le nombre
des pixels que multiplie la taille (en octet) de chacun de ces
éléments.6(*)
Exemple : pour une image de 240 X 420 en True
Color :
Nombre de pixels :
240 X 420 = 100800
Taille de chaque pixel : 24 bits / 8 = 3 octets
Le poids de l'image est ainsi égal à :
100800 X 3 = 302.400 égal 302.400/1024 = 295 Ko
I.4.4 Bruit
Un bruit (parasite) dans une image est considéré
comme un phénomène de brusque variation de l'intensité
d'un pixel par rapport à ses voisins, il provient de l'éclairage
des dispositifs optiques et électroniques du capteur [7(*)].
I.4.5 Histogramme
L'histogramme des niveaux de gris ou des couleurs d'une image
est une fonction qui donne la fréquence d'apparition de chaque
niveau de gris (couleur) dans l'image. Pour diminuer l'erreur de
quantification, pour comparer deux images obtenues sous des éclairages
différents, ou encore pour mesurer certaines propriétés
sur une image, on modifie souvent l'histogramme correspondant[8(*)][9(*)] Il permet de donner un grand nombre d'information sur
la distribution des niveaux de gris (couleur) et de voir entre quelles bornes
est repartie la majorité des niveaux de gris (couleur) dans les cas
d'une image trop claire ou d'une image trop foncée.
Il peut être utilisé pour améliorer la
qualité d'une image (Rehaussement d'image) en introduisant quelques
modifications, pour pouvoir extraire les informations utiles de celle-ci.
I.4.6 Contours et textures
Les contours représentent
la frontière entre les objets de l'image, ou la limite entre deux pixels
dont les niveaux de gris représentent une différence
significative [GRA 91]. Les textures décrivent la structure de ceux-ci.
L'extraction de contour consiste à identifier dans l'image les points
qui séparent deux textures différentes [10(*)]
I.4.7 Luminance[11(*)]
C'est le degré de luminosité des points de
l'image. Elle est définie aussi comme étant le quotient de
l'intensité lumineuse d'une surface par l'aire apparente de cette
surface, pour un observateur lointain, le mot luminance est substitué au
mot brillance, qui correspond à l'éclat d'un objet. Une bonne
luminance se caractérise par :
1. Des images
lumineuses (brillantes);
2. Un bon contraste : il faut
éviter les images où la gamme de contraste tend vers le blanc ou
le noir; ces images entraînent des pertes de détails dans les
zones sombres ou lumineuses.
3. L'absence de parasites.
I.4.8 Contraste [12(*)]
C'est l'opposition marquée entre deux régions
d'une image, plus précisément entre les régions sombres et
les régions claires de cette image. Le contraste est défini en
fonction des luminances de deux zones d'images.
Si L1 et L2 sont les degrés de luminosité
respectivement de deux zones voisines A1 et A2 d'une image, le contraste C est
défini par le rapport :
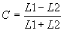
I.4.9 Images a niveaux de
gris[13(*)]
Le niveau de gris est la valeur de l'intensité
lumineuse en un point. La couleur du pixel peut prendre des valeurs allant du
noir au blanc en passant par un nombre fini de niveaux intermédiaires.
Donc pour représenter les images à niveaux de gris, on peut
attribuer à chaque pixel de l'image une valeur correspondant à la
quantité de lumière renvoyée. Cette valeur peut être
comprise par exemple entre 0 et 255. Chaque pixel n'est donc plus
représenté par un bit, mais par un octet. Pour cela, il faut que
le matériel utilisé pour afficher l'image soit capable de
produire les différents niveaux de gris correspondant.
Le nombre de niveaux de gris dépend du nombre de
bits utilisés pour décrire la " couleur " de chaque
pixel de l'image. Plus ce nombre est important, plus les niveaux possibles sont
nombreux.
I.4.10 Images en couleurs [14(*)]
Même s'il est parfois utile de pouvoir
représenter des images en noir et blanc, les applications
multimédias utilisent le plus souvent des images en couleurs. La
représentation des couleurs s'effectue de la même manière
que les images monochromes avec cependant quelques particularités. En
effet, il faut tout d'abord choisir un modèle de représentation.
On peut représenter les couleurs à l'aide de leurs composantes
primaires. Les systèmes émettant de la lumière
(écrans d'ordinateurs,...) sont basés sur le principe de la
synthèse additive : les couleurs sont composées d'un
mélange de rouge, vert et bleu (modèle R.V.B.).
La représentation en couleurs
réelles
Elle consiste à utiliser 24 bits pour chaque point de
l'image. Huit bits sont employés pour décrire la composante rouge
(R), huit pour le vert (V) et huit pour le bleu (B). Il est ainsi possible de
représenter environ 16,7 millions de couleurs différentes
simultanément. Cela est cependant théorique, car aucun
écran n'est capable d'afficher 16 millions de points. Dans la plus haute
résolution (1600 x 1200), l'écran n'affiche que 1 920 000 points.
Par ailleurs, l'oeil humain n'est pas capable de distinguer autant de couleurs.
La représentation en couleurs indexées
Afin de diminuer la charge de travail nécessaire pour
manipuler des images en 24 bits, on peut utiliser le mode de
représentation en couleurs indexée. Le principe consiste à
déterminer le nombre de couleurs différentes utilisées
dans l'image, puis à créer une table de ces couleurs en
attribuant à chacune une valeur numérique correspondant à
sa position dans la table. La table, appelée palette, comporte
également la description de chacune des couleurs, sur 24 bits.
Autres modèles de
représentation
Le modèle R.V.B. représentant toutes les
couleurs par l'addition de trois composantes fondamentales, n'est pas le seul
possible. Il en existe de nombreux autres. L'un d'eux est
particulièrement important. Il consiste à séparer les
informations de couleurs (chrominance) et les informations d'intensité
lumineuse (luminance). Il s'agit du principe employé pour les
enregistrements vidéo. La chrominance est représentée par
deux valeurs (selon des modèles divers) et la luminance par une valeur.
I.5 Qualité de
l'image numérique [15(*)]
Elle dépend, d'une part, de la qualité des
images d'origine et, d'autre part, des moyens mis en oeuvre pour convertir un
signal analogique en signal numérique. Elle dépend aussi
de :
1. La qualité des périphériques de
numérisation de l'image, du nombre de niveaux de gris ou de couleurs
enregistrées, etc.
2. La qualité de l'affichage à
l'écran : définition de l'écran, nombre de teintes
disponibles simultanément, calibrage de l'écran, etc.
Les critères d'appréciation de la qualité
d'une image, tels que cités succinctement ci-dessus, dépendent
largement de la structure même de l'image réaliste ou conceptuelle
et de son mode de représentation (bitmap ou vectorielle).
I.6 IMAGES BITMAP ET IMAGES
VECTORIELLES[16(*)]
Les images appartiennent à deux grandes familles :
bitmap (image-bit) et vectorielle.
Alors qu'une image vectorielle est décrite à
l'aide de courbes et d'équations mathématiques, une image bitmap
est constituée de pixels et se réduit donc à une matrice
de points.
Si les images vectorielles peuvent être
manipulées avec beaucoup de facilité, les modifications de
taille, par exemple, apportées à une image bitmap ne sont pas
sans incidence.
I.7 LES DIFFERENTS TYPES
D'IMAGES NUMERIQUES
Les images numériques sont classés selon le
format hors la multitude des formats vient de la volonté de chacun des
fabricants de logiciel d'imposer le sien car on trouve très peu de
différences hormis quelques-uns sont compressés et les autres ne
le sont pas mais aussi ce qui change, ce sont les en-têtes du fichier.
Parmi ces formats nous pouvons citer17(*) :
- le format vectoriel
- le format méta fichier
- le format bitmap
I.7.1 Les formats
vectoriels
Présentation :
Les formats vectoriels sont en fait une suite d'objets
géométriques (rond, carré, droite, image clipart)
défini par leurs coordonnées polaires. Le format les plus connus
sont : DXF (Autocad) ; SYLK ; Lotus PIC et Lotus DDIF ;
cependant, départ le fait qu'ils soient vectoriels ces formats
supportent les images de type de photo. Ainsi hormis dans le secteur du dessin
industriel avec le logiciel Autocad, les images vectorielles sont peu
utilisées, au profit des métas fichiers18(*).
Les avantages
Les fichiers vectoriels sont adaptés au stockage
d'images de forme géométrique (cercle, carré, droit...) ou
qui peuvent facilement être transformé en forme
géométrique comme texte et certains formats sophistiqués
s'intègrent des objets en 3 dimensions.
Les objets vectoriels peuvent aisément dimensionner
pour l'interface de sortie.
La plupart des formats sont en ASCII ce qui se permet de les
modifier directement avec un simple éditeur de texte.
Il est généralement facile d'effectuer un rendu
d'un fichier vectoriel puis de le convertir en bitmap. La qualité
restée est la bonne dans ce cas.
Les inconvénients
Les fichiers vectoriels peuvent difficilement stocker les
images complexes comme de photographie ou la couleur peut varier d'un point
à l'autre.
L'apparence d'une image vectoriel peut
énormément varier en fonction du logiciel qui l'interprète
ce la dépend en fait des algorithmes utilisés pour l'affichage.
La reconstitution d'une image à partir des vecteurs peut prendre
beaucoup de temps qu'une image bitmap de complexité égal.
I.7.2 Les formats
méta fichiers
Présentation
Les métas fichiers sont très vite rependus. Ils
offrent la possibilité d'intégrer à la fois des images
bitmap et des objets vectoriels. Les formats les plus connus sont : EPS
Mackintosh ; PICT RIF et WMF. Les métas fichiers ont la
facilités de les porter dune plate forme à une autre. Les
données étant stockées la plupart de temps, en ASCII, les
problèmes d'ordre de bit n'apparaissent pas. L'ASCCII offre aussi une
plus grande aptitude à la compression des fichiers19(*).
Les avantages
Les métas fichiers ont des avantages des fichiers
bitmap et des fichiers vectoriels.
La plupart des formats sont binaires quelques-uns sont
orientés, le partage d'un ordinateur à un autre se fait
généralement sans encombre.
Les métas fichiers peuvent généralement
être compressés avec un gain important.
Les inconvénients
Avec un nouveau format il y a risque de créer de
nombreux problèmes lors d'échange de données avec d'autres
logiciels.
L'exemple d'une image en méta fichier en format WMF.
Le format WMF est un méta format en effet, il est utilisé pour
stocker des images vectorielles, des images bitmap sur disque ou en
mémoire afin de les utiliser ultérieurement sans Windows.
Un fichier contient une suite d'objet chacun décrit par
un en-tête. Le format WMF peut contenir 65535 objets au maximum. Le
type possible pour chaque objet (cercle, carré, bitmap..) est
défini dans la librairie windows.h
I.7.3. Les formats
bitmap[20(*)]
BMP : format de Windows et d'OS/2 pour les PC
sous Dos et Windows.
Sa structure étant élémentaire, on
peut choisir un codage de 1 à 24 bits par pixel21(*), soit du noir et
blanc aux 16 millions de couleurs et, dans certains cas, appliquer une
compression sans pertes RLE22(*).
FPX (Flashpix) : développé par
Kodak, Hewlett-Packard, Live Picture et Microsoft.
L'idée est
d'obtenir avec un format Bitmap des possibilités de zoom comparables aux
formats vectoriels. Le fichier est en fait plusieurs mêmes images avec
des résolutions différentes. Dans les démos
proposées par
Live Picture, on charge d'abord une
image à faible résolution, et en cliquant sur n'importe quelle
zone, on zoome, c'est-à-dire que le navigateur va chercher un morceau de
la même image à plus haute résolution, et ainsi de suite.
Pour utiliser ce format sur le Web, il faut télécharger un
plug-in
chez
Live Picture. Ce format peut
être compressé en JPeg mais il reste plus lourd que le JPeg
seul.
Pour l'instant son usage est peu répandu et on a bien
du mal à faire fonctionner le plug-in à partir d'une image issue
de PSP.
GIF (Graphic lnterchange Format) :
développé par CompuServe.
Ce format très courant sur le
Web permet une très bonne compression non destructrice basé sur
l'algorithme LZW23(*). On
trouve actuellement deux formats (chez PSP par exemple), le GIF 87A, vieux, et
le GIF 89A qui a permis les GIF Animés, en fait une suite d'images GIF
à la durée d'affichage variables. GIF gère la
transparence, on le voit ici.
JPG (JPeg) Joint Photographic Expert Group.
C'est un format donnant de bons résultats pour la photographie, mais qui
utilise une compression destructrice sur 8 bits en niveaux de gris ou 24 bits
en couleurs. Il existe un format progressif optimisé.
PCD (Photo CD) : créé par
Kodak, Tout comme FlashPix, du même Kodak, il code l'image sous plusieurs
définitions. On ne le voit guère.
PCX (PiCture eXchange) le format
défini par PC Paintbrush de Zsof que tout le monde a sûrement
déjà manipulé. Il accepte les modes de couleur RVB,
indexées, niveaux de gris et N&B. De plus il veut bien qu'on le
compresse PCX prend en charge le mode de compression RLE.
PNG (Portable Network Graphic). Il
se veut le remplaçant de GIF sur lequel certains veulent mettre un
copyright. Il utilise comme GIF la compression LZW24(*). Mieux que
GIFounet, il gère les images 24 bits, comme le JPegounet, mais garde la
transparence plus l'entrelacement (affichage progressif), ne lui manque plus
que l'animation. De plus, il commence à être reconnu par de
nombreux programmes, dont mon IE 5.0 et mon PSP (quand même !)
PSD (Photoshop Document) le format de
Photoshop. Il gère tous les types d'images du N&B au CMJN,
même le multicouche et d'autres trucs d'enfer !
PSP : le format de Paint Shop Pro. Equivalent
de PSD.
TIF (Tagged Image File Format) le
format basique, récupérable partout même sur Mac (quoique
le passage de PC à Mac ne soit pas toujours évident). C'est
souvent le format par défaut donc récupéré à
la sortie d'un scanner. Pour ceux qui veulent tout compresser, on peut utiliser
la LZW
CHAP II LES IMAGES
BITMAP
II.1. BUT DE L'ANALYSE DE
L'IMAGE [24(*)]
Le but de l'analyse d'images est de fournir une description
quantitative de l'image nombre d'une certaine taille ou une reconnaissance de
forme, utile si les caractéristiques morphologiques de l'image sont
liées aux propriétés de l'objet. Elle trouve des
applications dans de nombreux domaines : cartographie, science de
matériaux, sciences de la vie, géologie, robotique...
II.2. DEFINITION
Les images bitmap sont des images où les données
sont représentées par un tableau à deux dimensions
(où "matrice") de pixels (points de couleur).
Le pixel (abréviation de "PICture
élément") représente le plus petit élément
constitutif d'une image numérique.
L'écran fournit une représentation visuelle de
l'image en la balayant de gauche à droite (largeur de l'image : axe des
abscisses) et de haut en bas (hauteur de l'image : axe des
ordonnées).
Le pixel est définit spatialement dans l'image par ses
coordonnées (X, Y).
Toute image à l'écran est matricielle.
II.3. CODAGE DES
COULEURS
A chaque pixel de l'image est attribuée une valeur
codée sur un certain nombre de bits (nommée "profondeur codage")
et correspondant à une couleur ou à l'intensité du pixel
(niveau de gris).
On distingue plusieurs standards de codage :
Bitmap noir et blanc
Le pixel est codé sur un bit (soit deux couleurs
possibles : noir/blanc) ·
Bitmap 16 ou 256 couleurs (ou "niveaux de gris")
Le pixel est codé sur 4 bits (soit 2 puissance 4
possibilités = 16 couleurs ou dégradés de gris possibles)
ou sur un octet (soit 2 puissance 8 possibilités = 256 couleurs ou
dégradés de gris possibles) ·
Codage "couleur vraie" ("true color"
ou "RGB")
La couleur est codée sur 3 octets (24 bits) par le
triplet RVB ou RGB (Rouge-Vert-Bleu /Red-Green-Blue), soit 256 x 256 x 256
possibilités (près de 16 millions de couleurs possibles).
Le mélange de ces trois couleurs à des
proportions diverses permet quasiment de reproduire à l'écran
toutes les couleurs du spectre visible.
Il est possible de rajouter une quatrième composante
(un 4e octet) permettant d'ajouter une information de transparence ou de
texture, chaque pixel est alors codé sur 32 bits.
Palette de couleur (ou "table des
couleurs" ou "colormap" ou "LUT" : Look-up table)
Cette solution offre l'avantage de réduire l'espace de
stockage. En effet, on considère alors que 256 couleurs sont suffisantes
sur les 16 millions de couleurs possibles.
Les 256 couleurs sont définies dans la palette (3
octets par couleur) et au pixel de l'image est attribuée la valeur de
l'indice (codé sur 8 bits) de la couleur dans la palette.
On parle alors d'"image en couleurs indexées".
Profondeur de l'image
(Ou "profondeur d'analyse" ou "résolution de
pixels")
Nombre de bits codant la couleur d'un pixel.
1 bit : 2 couleurs ·
8 bits (1 octet) : 256 couleurs ·
16 bits : 65 536 couleurs ·
24 bits : 16,7 millions de couleurs (ou couleurs vraies)
·
32 bits : 1,07 milliards de couleurs ·
Image bitmap ou matricielle
II.4. DEFINITION DE
L'IMAGE
Nombre de pixels constituant l'image (= nombre de lignes x
nombre de colonnes).
"Dimension informatique" de l'image.
II.5. RESOLUTION DE
L'IMAGE
Nombre de points par unité de surface, exprimé
en points par pouce (PPP, en anglais DPI pour Dots Per Inch), un pouce
représentant 2.54 cm. Plus la résolution est
élevée, plus la quantité d'information est grande, plus
l'image est détaillée et donc de qualité.
La résolution de l'écran est en moyenne de 72
dpi.
La résolution d'une imprimante est au moins de 300
dpi.
II.6. POIDS D'UNE IMAGE
Définition de l'image x nombre de bits codant chaque
pixel (poids en octets).
Cette valeur est à divisée par 1024 pour avoir
le poids en kilooctets (Ko).
II.6 TRANSPARENCE DE
L'IMAGE
Possibilité de voir à travers l'image des
éléments graphiques situés derrière celle-ci. Elle
peut se définir de 2 façons différentes :
Dans le cas d'une image indexée : une couleur est
définie comme transparente dans la palette de couleurs alpha-blending :
à chaque pixel de l'image est ajouté un octet définissant
son niveau de transparence (de 0 à 255).
II.7 LA
GESTION DES IMAGES BITMAP [25(*)]
Bitmap, ça veut plus ou moins dire littéralement
carte à points, ou carte à bit.
Et c'est bien ce genre
d'informations que contient un fichier de ce type. Chaque pixel est
enregistré dans le bitmap. Aucune compression, que ce soit du type LZW
ou par perte de données, n'est utilisée dans ce format.
C'est pourquoi la lecture et
l'interprétation de ce genre de fichier reste relativement simples. Un
fichier bitmap est composé de 4 choses :
les
informations générales,
les
informations d'en-tête,
la
palette et
les
données.
II.7.1 Les
informations générales
Les informations générales commencent avec le
début du fichier, c'est à dire de l'octet 0 et s'achèvent
à l'offset 10.
Voici ces informations :
|
Offset (position)
|
Longueur (en octets)
|
Signification
|
|
0
|
2
|
Normalement, il doit y avoir BM pour
confirmer que l'image
est bien un bitmap
|
|
2
|
4
|
Taille du fichier, sans la partie d'en-tête
|
|
6
|
2
|
Réservé. Normalement à zéro (0)
|
|
8
|
2
|
Réservé. Normalement à zéro (0)
|
|
10
|
4
|
Offset à partir du quel commencent les données.
|
Hormis la confirmation du type d'image (Offset 0), ces
informations sont rarement utilisées. On passe
généralement directement aux informations d'en-tête.
II.7.2. Les
informations d'en-tête
Ces informations suivent directement les informations
générales. Elles commencent donc au 14ème
octet.
|
Offset (position)
|
Longueur (en octets)
|
Signification
|
|
14
|
4
|
Taille des informations d'en-tête, soit 40, soit 12
|
|
18
|
4
|
Largeur de l'image, en pixels
|
|
22
|
4
|
Hauteur de l'image, en pixels
|
|
26
|
2
|
Nombre de plan, doit être à 1
|
|
28
|
2
|
Nombre de bits par pixels. Les valeurs peuvent
être 1, 4, 8 ou 24
|
|
30
|
4
|
Compression, doit normalement être à
zéro.
Sinon, c'est une image RLE
|
|
34
|
4
|
Taille de l'image, en octets
|
|
38
|
4
|
Largeur de l'image, dans une autre unité
|
|
42
|
4
|
Hauteur de l'image, dans une autre unité
|
|
46
|
4
|
Nombre de couleurs utilisées par l'image.
Si 0,
alors toutes les couleurs sont utilisées.
|
|
50
|
4
|
Nombre de couleurs importantes.
Si 0, alors toutes les
couleurs sont
importantes.
|
Elles donnent des renseignements sur l'image proprement dite :
largeur, hauteur, nombres de couleurs...
Explication du tableau
d'en-tête (en anglais file header) [26(*)]
La signature (sur 2 octets), indiquant qu'il s'agit d'un
fichier BMP à l'aide des deux caractères.
o BM, 424D : en hexadécimal, inique qu'il s'agit
d'un bitmap Windows.
o CI : indique qu'il s'agit d'une icône couleur
OS/2
o CP : indique qu'il s'agit d'un pointeur de couleur
OS/2
o IC : indique qu'il s'agit d'une icône OS/2
o PT : indique qu'il s'agit d'un pointeur OS/2
La largeur de l'image (sur 4 octets), c'est-à-dire le
nombre de pixels horizontalement (en anglais width)
La hauteur de l'image (sur 4 octets), c'est-à-dire le
nombre de pixels verticalement (en anglais height)
Le nombre plan (sur 2 octets). Cette valeur vaut toujours
1.
La profondeur de codage de la couleur (sur 2 octets)
c'est-à-dire le nombre de bits utilisés pour coder la couleur.
Cette valeur peut être égale à 1, 4, 8, 16, 24, ou 32
La méthode de compression (sur 4 octets). Cette
valeur vaut 0 lorsque l'image n'est pas compressée, ou bien 1,2 ou 3
suivant le type de compression utilisée :
o 1 pour un codage RLE de 8 bits par pixel
o 2 pour un codage RLE de 4 bits par pixel
o 3 pour un codage RLE bitfields, signifiant que la couleur
est codée par un triple masque représenté par la
palette.
La taille totale de l'image en octets (sur 4 octets)
La résolution verticale (sur 4 octets),
c'est-à-dire le nombre de pixels par mètre verticalement.
Le nombre de couleurs de la palette (sur 4 octets)
Ce nombre égale à 0 lorsque chaque couleur a
son importance.
II.7.3. La palette
La palette représente les couleurs utilisées par
l'image. Elles sont codées en RGB : Red, Green et Blue. Selon les
valeurs de ces composantes, on obtient différentes couleurs. Chaque
composante peut varier de 0 à 255. Attention ! Pour les fichiers
bitmap 24 bits, il n'y a pas de palette !
Voici comment obtenir ces couleurs :
|
Offset (position)
|
Longueur (en octets)
|
Signification
|
|
14 + Taille de l'en-tête
|
1
|
Intensité du Bleu de la couleur 0
|
|
14 + Taille de l'en-tête + 1
|
1
|
Intensité du Vert de la couleur 0
|
|
14 + Taille de l'en-tête + 2
|
1
|
Intensité du Rouge de la couleur 0
|
|
14 + Taille de l'en-tête + 3
|
1
|
Inutilisé. Doit être à zéro.
|
|
14 + Taille de l'en-tête + 4
|
1
|
Intensité du Bleu de la couleur 1
|
II.7.4. Les
données
Les données représentent l'index de la couleur
de chaque pixel de l'image.
Elles commencent dans le coin inférieur
gauche de l'image. Chaque donnée de plus est un pixel vers la droite.
Ensuite, tout dépend du nombre de bits par pixels de
l'image :
|
Bits par pixels
|
Représentation
|
|
1 (monochrome)
|
8 pixels (horizontaux) sont représentés dans un
octet.
Chaque bit de cet octet représente la couleur : 0 pour
noir
1 pour blanc.
|
|
4 (16 couleurs)
|
Un octet représente 2 pixels de l'image. Les 4 bits de
poids
fort représentent la 1ere couleur, et les 4 bits de
poids
faible la 2ème couleur de cet octet.
|
|
8 (256 couleurs)
|
Le plus simple. Chaque octet représente la couleur d'un
pixel.
|
|
24 (16777216
couleurs)
|
Comme dit plus haut, pour ce type d'image, il n'y a pas de
palette.
Chaque pixel est représenté par 3 octets. Chacun de
ces 3 octets
correspond à l'intensité d'une des 3 (!)
composantes RGB du pixel.
|
LA LECTURE DES IMAGES
BMP
Voici un exemple de gestion des images bitmap avec le langage
Java.
import java.io.*;
class LireImagebmp{
static int[][] r;
static int[][] v;
static int[][] b;
static int[] entete;
static void lireImagebmp1(String adresseImage){
int largeur=25;//19;
int hauteur=16;//15;
int position=54;
int complement=largeur % 4;
if (hauteur <0|| largeur<0){
System.out.println("image introuvable : "+ adresseImage
+"!");
}
r=new int[hauteur][largeur];
v=new int[hauteur][largeur];
b=new int[hauteur][largeur];
entete=new int[position];
try{
FileInputStream fis=new
FileInputStream(adresseImage);
BufferedInputStream bis=new
BufferedInputStream(fis);
DataInputStream dis=new DataInputStream(bis);
for (int i=0; i<position; i++){
entete[i]=dis.read();// entete de l'image
System.out.println(i+" : "+entete[i]);
}
for (int i=hauteur-1; i>=0; i--){
for(int j=0; j<largeur; j++){
b[i][j]=dis.read(); v[i][j]=dis.read();
r[i][j]=dis.read();//corps de l'image
//System.out.println("i="+i+"
j="+j+"\t"+r[i][j]+";"+v[i][j]+";"+b[i][j]);
}
for(int j=0; j<complement; j++)
dis.read();
}
dis.close();
for (int i=0; i<hauteur; i++){
for(int j=0; j<largeur; j++){
System.out.println("i="+ij="+j+"\t"+r[i][j]+";"+v[i][j]+";"+b[i][j]);
}
}
}catch(IOException e) {
System.out.println("Erreur dans la lecture de
l'image");
}
}
public static void main(String[] arg){
lireImagebmp1("jm1.bmp");
}}
CHAPITRE III. LA LIAISON
ET LA DETERMINATION DES LIMITES D'UNE IMAGE SCANNEE EN PLUSIEURES PARTIES
II.1. DEFINITION DE
QUELQUES CONCEPTS
III.1.1. Une bande
Une bande est une partie extraite d'une image quelconque, qui
a ses attributs bien définis. Elle constitue pour notre travail un
ensemble de lignes et colonnes, soit de la première image ou soit de la
deuxième image qu'il faut comparer.
III.1.2. La position
Une position est un niveau dans une image qui permet
d'identifier soit une ou plusieurs lignes dans une image, soit une ou plusieurs
pixels de même couleur ou de couleurs différentes.
III.1.3. Niveau de gris 27(*)
Le niveau de gris, en imprimerie, désigne la
concentration des points de trame et est donc directement en rapport avec le
rendu de l'image. Un niveau de gris va alors varier du blanc au noir. Ce la
est également valable pour toutes autres couleurs (cyan, magenta,
jaune). On fera alors varier la densité de cyan du blanc jusqu'au cyan
foncé.
Dans le cas d'une image numérique, le niveau de gris
représente l'intensité lumineuse d'un pixel, lorsque ses
composants de couleur sont identiques en intensité lumineuse.
Convertir une image couleur en niveau de
gris
Pour les images couleurs, un pixel dispose
généralement de trois composants RVB (en anglais Red, Green,
Blue). Un pixel gris a ses trois valeurs RGB identiques. Une méthode
simple pour convertir une image couleur en niveau de gris pourrait être
de calculer la moyenne des trois composantes RGB et d'utiliser cette valeur
moyenne pour chacune des composantes :
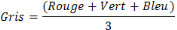
III.2. LA DETERMINATION DES
LIMITES D'UNE IMAGE SCANNEE EN PLUSIEURES PARTIES
III.2.1. Notions sur la
détermination des limites
La détermination des limites consiste à
identifier dans les différentes parties de l'image scannée, une
partie de l'une ou de l'autre image qui est commune. Il faudra alors
déterminer cette partie commune dans les deux images en questions.
Par exemple : soit une image quelconque scannée
en 2 parties de mêmes attributs, de hauteur=8, et de largeur=10.
Partie de la 1ère image qui se
répète dans la 2ème image
Bande commune

image1
image2

A partir de la position 0 (ligne) en partant de bas vers le
haut jusqu'à la position 4 de la 1ère image, cette
partie se retrouve dans la 2ème image de la
3ème position jusqu'à la 7ème
position en partant de bas vers le haut. C'est ces 2 parties montrer sur les
2 images qui sont communes dans les 2 images et qu'il faut extraire pour passer
à la liaison. Mais en attendant nous présentons d'abord la
méthode ressemblance.
III.2.2. La méthode
ressemblance
La méthode ressemblance qui a deux arguments et
retourne un nombre décimal. Les arguments sont :
- Le premier argument de type Bitmap est l'image129(*)
- Le second argument de type Bitmap est l'image2
Bitmap est une classe, qui nous a permis de construire un
nouvel objet de type Bitmap, à partir de l'adresse d'une image
d'extension .bmp, codée en 24 bits. Voici la signature de l'une de ces
méthodes qui nous a permis de créer cet objet.
Bitmap (java.lang.String adresse). Suivra ensuite le corps de
la méthode composé de la manière suivante :
- Deux arguments de type Pixel24bits30(*)
Pixel24bits est aussi une classe de manipulation des pixels
des images bitmap. Cette classe nous a permis de construire un objet de type
Pixel24bits auquel nous avons appliqué la méthode getPixels()
pour retourner une grille de pixels de l'image Bitmap sous forme d'un tableau
à deux dimensions d'objets de type Pixel24bits.
1. Extraction de la 1ère bande dans
la 1ère image
Dans 3 boucles qui sont définit comme suit :
Considérons une ligne des Pixels situé à
la même hauteur.
Pour un compteur qui varie de la hauteur de la
1ère image moins 1 à la hauteur de la bande moins 1,
décrémente le compteur en raison d'une unité. Dans cette
boucle le compteur parcours la hauteur de la 1ère image. Le
compteur est également la position de la ligne inférieure de la
bande.
Pour un compteur qui varie de 0 à la hauteur de la
bande incrémente le compteur en raison d'une unité. Cette boucle
parcours la hauteur de la bande.
Pour un compteur variant de 0 à la largeur de la
bande, incrémente le compteur d'une unité. Cette boucle
parcours la ligne de la bande.
Ces 3 boucles nous ont permis de parcourir la hauteur de la
1ère image, la hauteur de la bande1 et la largeur de la
bande1. Cela étant la 1ère bande a été
extraite. Le nombre des bandes à extraire dans la
1ère image est égal à la hauteur de la
1ère image moins la hauteur de la bande.
Cependant, à une position i1 de la hauteur de la bande
correspondra une position i moins la hauteur de la bande + (plus) i1, i
étant la hauteur de la 1ère image moins 1.
2. Extraction de la 2ème bande dans
la 2ème image
Dans deux boucles définit comme suit :
Pour un compteur qui varie de 0 à la hauteur de la
2ème image moins la hauteur de la bande incrémente le
compteur d'une unité. Le compteur est la position de la ligne
supérieure de la bande extraite de la 1ère image.
Pour un compteur variant de 0 à la largeur de la
2ème image incrémente le compteur d'une unité.
Le compteur parcours la ligne de la bande.
Ces deux boucles nous ont permis de parcourir d'abord la
hauteur de la 2ème image qui est évidemment la positon
de la ligne supérieure de la hauteur de la 1ère bande
(extraite de la 1ère image), ensuite la hauteur de la
2ème bande, enfin la largeur de la 2ème
bande. Finalement la 2ème bande a été extraite
de la deuxième image. Le nombre de bande extraite dans la
2ème image est égal à la hauteur de la
2ème image moins la hauteur de la bande.
Il faut signaler que pour une position i2 de la hauteur de la
2ème bande correspondra une position j plus (+) i2, j
étant la position de la ligne supérieure de la bande extraite de
la 1ère image (bande1) et j parcours la hauteur de la
2ème bande.
Ces deux bandes étant déjà extraites,
nous avons fait appel à la méthode compareTo qui sera
développé dans le point suivant pour comparer les 2 bandes (l'une
extraite de la 1ère image, l'autre de la
2ème image). Les résultants de cette comparaison
étant trop vastes. Nous avons cherché à déterminer
le maximum des résultats de la comparaison. Ce maximum est la valeur de
retour de cette méthode (méthode ressemblance).
3. Conclusion partielle
La méthode ressemblance nous a permis d'abord
d'extraire de la 1ère image différentes bandes
d'images ensuite extraire de la 2ème image différentes
autres bande, enfin ces deux bandes ont été comparées
entre elles en faisant appel à la comapreTo. Les résultats de
cette méthode étant vaste, nous avons cherché le maximum
des résultats. Cette méthode retourne le maximum de ressemblance
entre deux images de même hauteur et de même largeur.
Dans notre programme ces deux images sont des bandes
extraites des images plus vastes de mêmes largeurs, mais de longueurs
différentes.
III.2.3. La méthode
CompareTo
La méthode CompareTo qui a comme valeur de retour un
nombre décimal avec :
- Deux arguments de Pixel24bits31(*)
Cette méthode test premièrement si les deux
images ont la même largeur et la même hauteur. Cette
méthode comparera seulement les images de même hauteur, et de
même largeur.
Prenons l'exemple de deux bandes de hauteur=5.
 
Bande1 (extraite de la 1ère image) commune
Bande2 (extraite de 2ère image) commune
La première bande parcourt la 2ème
bande lors de la comparaison ligne par ligne de haut vers le bas pour de
comparaisons partielles. Chaque comparaison partielle calcul le nombre de
pixels identiques (c'est-à-dire de même couleur), située
à la même distance horizontale par rapport à la marge
gauche.
La comparaison partielle pour notre exemple est parfois
instable à cause des fluctuations sur des images supposées
identiques. Car l'échantillon des pixels prévus pour la
comparaison n'est pas suffisant. Il devient alors nécessaire
d'augmenter la taille de l'échantillon. Par conséquent la
comparaison partielle consistera à comparer un certain nombre fini des
lignes des pixels de la 1ère bande au même nombre de
lignes adjacentes de la 2ème bande.
Cette comparaison nous a permis de trouver la formule
suivante :
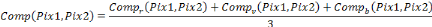
De cette formule notre souhait était de trouver soit 1
pour signifier qu'il y a eu nette ressemblance après comparaison, soit 0
pour signifier qu'il y a totalement dissemblance.
Pour tenir compte des valeurs intermédiaires comprises
entre 0 et 1, pour des bandes qui se ressemblent presque (effet dû aux
fluctuations sur des images supposées identiques). Nous avons
utilisé la formule suivante :
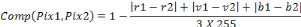
Avec r1 : niveau de gris du pixel rouge de la bande1
Avec r2 : niveau de gris du pixel rouge de la bande2
Avec v1 : niveau de gris du pixel vert de la bande1
Avec v2 : niveau de gris du pixel vert de la bande2
Avec b1 : niveau de gris du pixel bleu de la bande1
Avec r2 : niveau de gris du pixel bleu de la bande2
De cette formule nous comprenons que les résultats de
comparaison seront compris entre 0 et 1. Cette formule nous a permis de
trouver la ressemblance des différentes bandes de hauteur=5 extraites
l'une dans la 1ère image et l'autre dans la
2ème image.
Le nombre de ressemblance trouvé pour chaque bande.
Nous avons calculé aussi la moyenne de toutes ces ressemblances qui est
même la valeur de retour de cette méthode.
Cette moyenne égale à la somme de ressemblance
(nmbr) divisé par la hauteur de la 1ère image
multiplié par la hauteur de la 2ème image. La moyenne
de ressemblance que nous cherchons va nous permettre de trouver la position
dans la 1ère et la 2ème image où il
y a eu nette ressemblance. Et c'est le débit de cette position
où commence notre limite inférieure et la fin constitue notre
limite supérieure.
CONCLUSION PARTIELLE
La méthode CompareTo compare deux images de même
hauteur et de même largeur. Cette méthode nous a permis de
calculer le nombre de ressemblance possible entre la 1ère
bande et la 2ème bande, mais également à
calculer la moyenne de toutes ces ressemblances. C'est cette moyenne de
ressemblance qui est même la valeur de retour de cette méthode. A
partir de cette moyenne nous avons déterminé nos deux limites.
L'une correspondant au début où la moyenne de ressemblance est
nette (c'est-à-dire égal à 1) et l'autre sur la
deuxième image où la moyenne de ressemblance est égal
aussi à 1.
III.3. LA LIAISON
AUTOMATIQUE D'UNE IMAGE SCANNEE EN PLUSIEURES PARTIES
III.3.1. Notions sur la
liaison
Après avoir analysé la méthode CompareTo
et la méthode ressemblance vu précédemment qui nous ont
permis d'identifier la limite supérieure et inférieure de la
bande répétée dans les deux images auxquelles nous avons
fait allusion précédemment. Il importe de choisir une technique
de liaison.
La liaison va consister, soit à éliminer dans
la 1ère image la bande qui se trouve
répétée dans la 2ème image, ensuite
extraire le reste de la 1ère image et le coller dans une
image destination32(*),
soit également éliminer dans la 2ème image la
bande répétée dans la 1ère image et
extraire le reste de la deuxième image puis le coller dans l'image
destination.
Dans le cadre de notre travail nous allons utiliser la
technique qui consiste à éliminer de la 1ère
image la bande répétée, ensuite extraire le reste de la
1ère image et le coller dans l'image destination.
Voici les images auxquelles nous avons fait allusion dans
notre application informatique :
Limite inférieure dans l'image1
Limite supérieure dans l'image1
Bande commune
Image1
Image2
Bande commune
Image destination (construite après liaison)
Cette brève notion étant, nous pouvons
présenter la méthode liaison qui nous a permis de lier les 2
images.
III.3.2. La méthode
liaison
La méthode liaison sans valeur de retour
avec :
- Deux arguments de type entier,
- Quatre arguments de type Pixel24bits
Le premier argument de type entier (n) est la valeur de la
hauteur de l'image destination.
Le second argument (longueur) est la valeur de hauteur de la
partie de la 1ère image restée après
élimination de la bande répétée (commune) entre les
deux images dans la 1ère image.
Le premier argument de type Pixel24bits [][] (de la grille1)
est une grille de Pixel de la 1ère image, le second
(grille2) est une grille de Pixel de la 2ème image, le
troisième (monImage) est aussi une grille de Pixel, obtenue après
avoir éliminé dans la grille1(représentant la
1ère image) la bande commune ou répétée
entre les 2 images. Enfin le 4ème est aussi une grille de
Pixel où nous avons collés le reste de la 1ère
image (monImage) et la 2ème image (grille2). Il faut
souligner que cette dernière grille constitue notre image destination ou
image construite après liaison.
1. Elimination de la grille1 la bande commune ou
répétée entre les 2 images
Dans 3 boucles qui sont définit comme suit :
Pour un compteur qui varie de la hauteur de la
1ère image moins 1 à la limite supérieure de la
bande commune moins 1, décrémente le compteur en raison d'une
unité. Dans cette boucle le compteur parcours la hauteur de la
1ère image.
Pour un compteur variant de 0 à la limite
supérieure de la bande commune (longueur) dans la 1ère
image, incrémente le compteur d'une unité. Le compteur parcours
la hauteur de la band commune.
Pour un compteur variant de 0 à la largeur de la
1ère image, incrémente le compteur d'une unité.
Cette boucle parcours la ligne de la bande commune. Cela étant, dans
la grille1 la bande commune a été éliminée et nous
avons stocké le reste de la grille1 dans monImage.
2. Liaison proprement dit
Puisque dans la 1ère mage (grille1) nous avons
éliminé la bande commune, il reste maintenant de copier le reste
de cette grille1 (monImage) dans l'image destination, ensuite copier toute la
grille 2 dans l'image destination.
Pour un compteur variant de 0 à la limite
supérieur de la bande commune, incrémente le compteur en raison
d'une unité et copie monImage (qui est le reste de la
1ère image après élimination de bande commune)
dans l'image destination (ImageDest)33(*), incrémente le compteur en raison d'une
unité et copie la 2ème image (grille2) qui
représente la 2ème image) dans l'image destination.
Enfin on aura construit l'image destination.
3. Conclusion partielle
Au fait, la méthode liaison nous a aidé d'abord
à éliminer dans la 1ère image la bande commune (partie
commune aux deux images), ensuite extraire le reste de la 1ère image et
le coller dans la 1ère partie de l'image de destination
l'image destination.
Enfin copier toute la deuxième 2ème
image et la coller dans la deuxième partie de l'image destination pour
construire l'image finale qui est l'image destination.
III.4. GUIDE
D'UTILISATEUR
De prime à bord il est important de signaler que notre
application tourne en mode console.
1. Préparation des images :
Il s'agit ici de deux images d'extension .bmp (image1 et
image2), de même largeur et de hauteur quelconque.
2. De la compilation du fichier code
- Le fichier contenant le code doit être dans le
même répertoire avec les deux images à copier
- Sur la console DOS assurer-vous que vous êtes dans le
répertoire contenant le code (utilisez la commande CD)
- Sur le mode console de Ms Dos tapez la commande
javac TraitImage.java ou utilisez une commande pour compiler
dans un éditeur de code (il s'agit ici de JCreator pour notre
application)
3. De l'exécution du programme
- Sur la console Dos tapez la commande java TraitImage
image1.bmp image2.bmp
4. Résultats attendus
- Allez dans le répertoire contenant le code source et
vous allez y trouver une nouvelle image qui s'est créée
(imageDest), ouvrez - la. Elle est le résultat de notre application.
CONCLUSION
Au terme de ce travail de fin d'étude qui sanction la
fin de notre premier cycle de graduat. Il a été question de la
liaison automatique des plusieurs parties d'une image perçue sur un
scanner.
Nous avons développé d'une part la notion
portant sur la détermination des limites et d'autre part sur la liaison
automatique des plusieurs parties d'une image perçue sur un scanner.
Pour y arriver, nous avons fait recours à la
méthode comparative et aux calculs statistiques.
Deux algorithmes de traitement d'image ont marqué
notre étude :
- La détermination des limites
- La liaison automatique
Les résultats obtenus par notre application
informatique confirment bien nos hypothèses, car ces résultats
ont été réalisés grâces à ces deux
approches algorithmiques ci-haut.
Ce travail présente beaucoup d'approches pour
être développé, c'est pourquoi les algorithmes
utilisés sont loin d'apporter des solutions pour tout type d'image, mais
aussi pour l'interprétation de fluctuation apportée à des
images par le processus de scanning.
Le cas général de notre travail consistait
à scanner une image en plusieurs parties puis la reconstruire par un
algorithme de traitement d'image. Mais faute de temps nous avons pris un cas
un peu réduit qui consiste à scanner une image et avec le
logiciel Paint la diviser en partie. Et avec notre application on peut
rassembler ces parties et reconstruire l'image entière. Ce cas
général fera donc l'objet d'une étude approfondie pour
choisir un algorithme le plus performant et le mieux adapté. Il
constituera donc l'objet d'une autre recherche. Tant de problèmes
restent donc non résolus.
Le présent travail, étant réalisé
par un humain, il n'est pas exempté d'imperfection. Ainsi, les
remarques et suggestions pour son amélioration sont donc les
bienvenues.
BIBLIOGRAPHIE
A. OVRAGE
1. Laura LEMAY et Rogers CADERNHEAD, « Java
1.2 », la source d'or, 1998
2. M. André, « Introduction aux techniques de
traitement d'images », Eyrolles,
1987.
3. R.C. GONZALES et P. WINTZ, « Digital Image
Processing », Addition
Wessley », 1997
4. M. HADALLAH, « Codage des images fixes par
méthodes des hybride basée
sur la QV et les approximations fractales »,
PFE USTHB
5. MICROSOFT, « Encyclopédie
Encarta », 2005.
6. M. KUNT, « Traitement numérique des
images », vol.2, 1993
7. M. KUNT, « Traitement numérique des
images », vol.2, 1993
8. A. d'HARDANCOURT, « Fou du
multimédia » Sybex 1995
9. S. DEKKAR, « Compression des images fixes par la
méthode des fractales » PFE INI, 1996
B. TFC ET MEMOIRES
10. KAMPEMPE Kilimali, Séparation de l'image et du
fond, TFC/ISP Bukavu, 2005-2006
11. Martin NYONGOLO LUWAWA, Extraction des objets dans un
milieu hétérogène, mémoire ISP/ISP, 2005-2006
12. MOISE MWEZE, compression des images, TFC/ISP Bukavu,
2003-2004
13. SAMAMBA Tony, Reconnaissance des formes comme outil d'aide
aux traitements d'image. Cas des empreintes digitales, mémoire
ISP/Bukavu, 2005-2006.
C. WEBOGRAPHIE
- Http/www.artemis.jussieu.fr/la gestion des images bitmap
-
www.artemis.jussieu.fr/wwwos2/html/dess/memoire/promo95/muller/COMPRESS.HTM -
25k URL valide le 02/03/2008,
compression
d'image
- www.crdp.ac-grenoble.fr/image/index.htm - 8k URL valide le
02/03/2008,
les images numériques
- www.esiee.fr/~info/a2si/rapport1999-2003/node161.html - 14k
- URL valide le 02/03/2008,
compression
d'image
TABLE DES MATIERES
EPIGRAPHE
I
DEDICACE
III
REMERCIEMENTS
IV
SIGLES ET ABBREVIATIONS
V
0. INTRODUCTION
1
O.1. PROBLEMATIQUE
1
O.2. HYPOTHESE
2
O.3. METHODOLOGIE ET TECHNIQUES DU TRAVAIL
2
0.3.1 Methodologie
2
0.3.2. Techniques
2
0.4. CHOIX ET INTERET DU SUJET
2
0.5. DIFFICULTES RECONTREES
3
CHAP I. GENERALITES SUR LE TRAITEMENT D'IMAGES
4
I.1 INTRODUCTION
4
I.2 DEFINITION DE L'IMAGE
4
I.3 IMAGE NUMERIQUE
4
I.4 CARACTERISTIQUES D'UNE IMAGE NUMERIQUE
5
I.4.1 Pixel
5
I.4.2 Dimension
6
I.4.3 Résolution
6
I.4.4 La taille d'une image
7
I.4.4 Bruit
7
I.4.5 Histogramme
7
I.4.6 Contours et textures
8
I.4.7 Luminance
8
I.4.8 Contraste
8
I.4.9 Images a niveaux de gris
9
I.4.10 Images en couleurs
9
I.5 QUALITE DE L'image NUMERIQUE
10
I.6 IMAGES BITMAP ET IMAGES VECTORIELLES
11
I.7 LES DIFFERENTS TYPES D'IMAGES NUMERIQUES
11
I.7.1 Les formats vectoriels
11
I.7.2 Les formats méta fichiers
12
I.7.3. Les formats bitmap
13
CHAP II LES IMAGES BITMAP
15
II.1. BUT DE L'ANALYSE DE L'IMAGE []
15
II.2. DEFINITION
15
II.3. CODAGE DES COULEURS []
15
II.4. DEFINITION DE L'IMAGE
16
II.5. RESOLUTION DE L'IMAGE
16
II.6. POIDS D'UNE IMAGE
17
II.6 TRANSPARENCE DE L'IMAGE
17
II.7 LA GESTION DES IMAGES BITMAP]
17
II.7.1 Les informations générales
17
II.7.2. Les informations d'en-tête
18
II.7.3. La palette
19
II.7.4. Les données
20
LA LECTURE DES IMAGES BMP
21
CHAPITRE III. LA LIAISON ET LA DETERMINATION DES
LIMITES D'UNE IMAGE SCANNEE EN PLUSIEURES PARTIES
22
II.1. DEFINITION DE QUELQUES CONCEPTS
22
III.1.1. Une bande
22
III.1.2. La position
22
III.1.3. Niveau de gris
22
III.2. LA DETERMINATION DES LIMITES D'UNE IMAGE
SCANNEE EN PLUSIEURES PARTIES
23
III.2.1. Notions sur la détermination des
limites
23
III.2.2. La méthode ressemblance
23
III.2.3. La méthode CompareTo
25
III.3. LA LIAISON AUTOMATIQUE D'UNE IMAGE SCANNEE
EN PLUSIEURES PARTIES
28
III.3.1. Notions sur la liaison
28
III.3.2. La méthode liaison
29
III.4. GUIDE D'UTILISATEUR
30
1. De la préparation des
images.........................................................30
2. De la compilation du fichier code
30
3. De l'exécution du programme
30
4. Résultats attendus
30
CONCLUSION
31
BIBLIOGRAPHIE
32
TABLE DES MATIERES
33
* 1 M. André,
« Introduction aux techniques de traitement d'images »,
Eyrolles, 1987.
* 2 R.C. GONZALES et P.
WINTZ, « Digital Image Processing », Addition
Wessley » , 1997
* 3 M. HADALLAH,
« Codage des images fixes par méthodes des hybride
basée sur la QV et les approximations
fractales », PFE USTHB
* 4 MICROSOFT,
« Encyclopédie Encarta », 2005.
* 5 M. KUNT,
« Traitement numérique des images », vol.2, 1993
* 6 MOISE MWEZE, Compression Des
Images, TFC/ISP Bukavu, 2003-2004
* 7 R.C. GONZALES et P.
WINTZ, « Digital Image Processing », Addition
Wessley » , 1997
* 8 A. d'HARDANCOURT,
« Fou du multimédia » Sybex 1995
* 9 R.C. GONZALES et P.
WINTZ, « Digital Image Processing », Addition
Wessley » , 1997
* 10 M. KUNT,
« Traitement numérique des images », vol.2, 1993
* 11 A. d'HARDANCOURT,
« Fou du multimédia » Sybex 1995
* 12 SAMAMBA Tony,
Reconnaissance des formes comme outil d'aide aux traitements d'image. Cas des
empreintes digitales, mémoire ISP/Bukavu, 2005-2006.
* 13 MICROSOFT,
« Encyclopédie Encarta », 2005.
* 14 MICROSOFT,
« Encyclopédie Encarta », 2005.
* 15 S. DEKKAR,
« Compression des images fixes par la méthode des
fractales » PFE INI, 1996
* 16 MICROSOFT,
« Encyclopédie Encarta », 2006.
* 17 KAMPEMPE Kilimali,
séparation de l'image et du fond, TFC/ISP Bukavu, 2005-2006
* 18 KAMPEMPE Kilimali,
séparation de l'image et du fond, TFC/ISP Bukavu, 2005-2006
* 19 KAMPEMPE Kilimali,
séparation de l'image et du fond, TFC/ISP Bukavu, 2005-2006
* 20
www.artemis.jussieu.fr/wwwos2/html/dess/memoire/promo95/muller/COMPRESS.HTM -
25k URL valide
le 02/03/2008,
compression
d'image
* 21
www.crdp.ac-grenoble.fr/image/index.htm - 8k URL valide le 02/03/2008,
les images numériques
* 22
www.esiee.fr/~info/a2si/rapport1999-2003/node161.html - 14k - URL valide le
02/03/2008,
compression
d'image
* 23
www.artemis.jussieu.fr/wwwos2/html/dess/memoire/promo95/muller/COMPRESS.HTM -
25k URL valide
le 02/03/2008,
compression
d'image
* 24 KAMPEMPE Kilimali,
séparation de l'image et du fond, TFC/ISP Bukavu, 2005-2006
* 25
Http/www.artemis.jussieu.fr/la gestion des images bitmap
* 26 Martin NYONGOLO LUWAWA,
Extraction des objets dans un milieu hétérogène,
mémoire ISP/ISP, 2005-2006
* 27 28
Http/www.Wikipédia.fr/Niveau de gris/, URL valable
* 29 Dieudonné KYENDA
S., LRF, ISP/Bukavu, 2007.
* 30 Dieudonné KYENDA
S., LRF, ISP/Bukavu, inédit, 2007.
* 31 Dieudonné KYENDA
S., LRF, ISP/Bukavu, inédit,2007.
* 32 L'image destination c'est
l'image qu'on aura construit après la liaison.
* 33 La hauteur de l'image
destination est égale à la hauteur du reste de la
1ère image après avoir éliminé la bande
commune (longueur) plus la hauteur de la 2ème image.
| 


