Programmation d'un logiciel de résolution des problèmes d'équilibrage de bateaux en 3D par visual basic

RAPPORT DE STAGE

TECHNICIEN

P+R : YOUssEF MELLOUKI

"ENC+DRE" P+R : M. TILL+RD LOIC

+NNEE UNIVER'IT+IRE : 2005-2006

'UTET : Programmation d' un logiciel de résol ution des problèmes d'équilibrage des bateaux en 3D par Visual Basic.

A tous les ouvriers des entrepri ses

étrangères.

Monsieur Daniel Rodriguez, PDG du Chantier Naval Hésaro, m'ayant fait confiance en m'accueillant dans sa société.

Monsieur Tillard Loïc, responsable Qualité ISO, m'ayant accueilli dans son équipe au sein du bureau d'études.

Monsieur Giovanni Mazzeli, responsable de la motorisation et Monsieur Patrick De Paris, responsable du service d'achats dont les explications et les remarques ont largement élargi mes connaissances dans le domaine de la marine et de la construction navale.

Madame Karin Drieghe, responsable du service commercial, m'ayant fourni toute la documentation nécessaire à la présentation de la société.

Monsieur Houcine Haya, ouvrier à l'entreprise pour son esprit d'accueil dont il a fait preuve et en essayant de partager avec moi une expérience d'or acquise durant des années, m'a fait part d'une attention dont je le remercie vivement.

Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

I - Chantier Naval Hésaro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1 - Vocation et stratégie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

2 - Organigramme de la société . . . . . . . . . . . . . . . . . . . . 3

3 - Moyens de production . . . . . . . . . . . . . . . . . . . . . . . . . 3

a) Terrains et locaux . . . . . . . . . . . . . . . . . . . . . . . . . 3

b) Outillage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

II - Equilibrium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1 - Module de création de formes . . . . . . . . . . . . . . . . . . . . 4

a) Changement de repère et d'échelle . . . . . . . . . . 5

b) Créati on des segments de droites . . . . . . . . . . 7

c) Création des courbes de Bézi er . . . . . . . . . . 7

Définition des courbes de Bézier . . . . . 7
Créer une courbe de Bézier à l'aide du

module De création . . . . . . . . . . . . . . . 8

d) Gestion des objets . . . . . . . . . . . . . . . . . . . . . . . . . 10

e) Sélection des objets . . . . . . . . . . . . . . . . . . . . . . . . . 12

f) Enregistrement et chargement des objets . . . . . . . . . . 15

2 - Module de calcul . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

a) Affichage en 3D . . . . . . . . . . . . . . . . . . . . . . . . . 17

Modél isation mathématique . . . . . . . . . . 18

b) Génération des surfaces . . . . . . . . . . . . . . . . . . . . 20

c) Calculs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

Calcul d'aire . . . . . . . . . . . . . . . . . . . . 23

Conclusion. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

l y a 15 milliards d'années, la matière de l'univers était extrêmement dense et très chaude. Une gigantesque explosion, le Big Bang, a provoqué sa dissociation en des corps célestes. Le système solaire dont la planète terre fait partie ainsi formés à partir de ces corps célestes, l'apparition de l'homme date d'à peu près un million d'années.

L'homme préhistorique vivait dans des cavernes le protégeant de la pl uie et du froid. Il connus l'agriculture après avoir tenté la chasse et l'élevage, utilisant comme moyens de transport des animaux domestiqués tels que ânes et mules. Ses clans devinrent alors de plus en plus larges et la nécessité de moyens de transport plus efficaces s 'impose. La technologie avance, les chariots et les petites voitures tirées par des chevaux apparurent, jusqu'au jour où il décida de conquérir le bleu.

Le premier bateau que l'homme ait construit n'était rien d'autre qu'un tronc d'arbre coupé en deux, et vidé de l'intérieur. Le petit bateau s'est développé petit à petit jusqu'à atteindre plusieurs mètres de long avec des systèmes GPS et une longue li ste de gadgets de technologie de poi nte.

Chantier Naval Hésaro, l'entreprise où j 'ai passé mon stage technicien, est spécialisée dans la construction de bateaux et plus précisément les bateaux de plaisance de luxe et les navires de pêche. Les plans et les schémas de ces bateaux sont établis par des architectes navals espagnols et allemands. Ma mission moi, durant ce stage, était de résoudre un problème auquel sont confrontés souvent les constructeurs navals : les plans étant théoriques et établis sur microordinateur, ils ne présentent aucun défaut, autrement dits théoriquement, le bateau flotte parfaitement sur l'eau tout en gardant son toit horizontal. Mais la construction de ce dernier est loin d'être parfaite (le parfait n'existe que dans notre imagination), il en résulte ainsi des défauts d'inclinaison du bateau pouvant atteindre jusqu'à 28° qui peuvent facilement s'amplifier lors d'une tempête par exemple, et qui se corrigent par l'ajout de masses de l'autre côté du bateau.

Le sujet de mon stage est alors, la conception d'un logiciel qu'on a appelé Equilibrium, qui permet de créer tout d'abord la coque du bateau et en fonction de son angle d'inclinaison mesuré lors d'une première mise à l'eau dans un bassi n, il donne, après un simple clic, la masse qu'il faut ajouter de l'autre côté et sa distance par rapport à l'axe du bateau.

Ainsi, mon rapport de stage s'étalera sur deux parties : une première présentant l'entreprise et une deuxième expliquant le fonctionnement du logiciel et les pri nci pales étapes de sa programmation.

I - Chantier Naval Hésaro :

1 - Vocation et stratégie :

Créé en 1998, Chantier Naval Hésaro est une société anonyme française au capital de 3 000 000 Dh située au nouveau port d'Agadir, et est constituée de l'association de spécialistes en construction navale, Aluminium, Acier et Composite, et d'un savoir-faire local en ébénisterie. Elle aborde la fabrication de bateaux de plaisance de luxe, de service et des navi res de prche pouvant atteindre jusqu'à 50 m de long (chalutiers, sardiniers...).

Fig. 1 : Piripipao, bateau construit par CNH.
(Photo prise sur le port de M arsei lle)

La société intervient sur plusieurs marchés étrangers, notamment dans les

domaines de :

Pêche professionnelle : Afrique et Amérique du sud

Plaisance : M arché européen dans les domai nes

de construction de voiliers et M otors Yachts.

Navire garde côtes : Afrique, Amérique du sud, moyen orient.

2 - Organigramme de la société :

Direction

PDG : Daniel

Administrateur : Abdeslam

Qualité - ISO Loïc TILLARD

Informatique Hafid

Administration et Finance Abdeslam				Commercial Daniel				Coordination Alfred

Personnel
Farouk

Service Commercial
Karin

Production
Alfred

Service Compta
Sylvie

Service Achats Patrick

Chaudronnerie Houcine

Electricité
Driss

Peinture
Ali

Menuiserie Yazid

Tuyauterie
Brahim

Motorisation
Giovanni

3 - Moyens de production : a) Terrains et locaux :

Chantier Naval Hésaro est situé sur la zone portuaire d'Agadir avec un accès direct à la mer par élévateur de bateaux de 1000 tonnes. L'aménagement des locaux est organisé de la façon suivante :

2112 m^² d'usine.

360 m^² d'atelier de préparation. 336 m^² d'atelier de menuiserie. 276 m^² de magasi n et stockage. 510 m^² de bureaux.

b) Outillage :

La société possède un atelier de chaudronneri e doté de :

U ne presse pl ieuse hydraul ique numérique.

Un banc d'oxycoupage plasma numérique.

U ne presse à arcade.

U ne poi nçonneuse.

Tout l'appareillage de soudure.

Divers matériel de chaudronnerie.

Une cintreuse, une tronçonneuse, un compresseur à air, outillage à

main...

Elle possède aussi un atelier mécanique avec une perceuse radiale ainsi

qu'un atelier de menuiserie doté lui de :

Une scie à ruban. U ne sci e ci rcul ai re.

U ne raboteuse dégauchisseuse.

U ne mortaiseuse. U ne toupie.

U ne ponceuse.

Un bureau d'études et de coordination informatisées figure aussi parmi les locaux de l'entreprise, plus une administration bien évidemment.

II - Equilibrium :

Equilibrium, le logiciel qui va résoudre le problème d'inclinaison de bateaux nécessite un langage de programmation orienté objet dans un environnement Windows pour pouvoir mieux gérer ses composants, et vu que son interface doit être simple à utiliser, comme tout autre programme d'ailleurs, Microsoft Visual Basic est le langage adéquat pour cette réalisation.

Le programme conçu est composé de deux modules principaux : un module de création de formes pour dessiner les coques des bateaux et un module de calcul exploitant les dessins établis.

1 - Module de création de formes :

La coque d'un bateau a été toujours vu comme une baleine (l'homme n'a rien inventé). Elle est composée de couples jouant le rôle de squelette et de tôles couvrant ces couples comme une peau. Le premier module d'Equilibrium sert alors à dessiner ces couples qui ne peuvent, dans tous les cas, être composés que de deux éléments simples : des segments de droites et des courbes de Bézier.

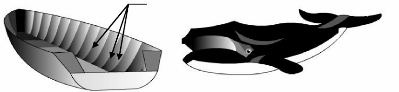
Couples de bateau (l'équivalent de squelette chez une baleine).

fig. 2 : Analogie entre la coque d'un bateau et une baleine.

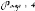
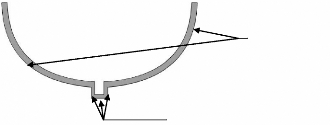
Courbes des Bézier

Segments de droites

fig. 3 : Décomposition d'un couple de bateau en des segments de droites et des courbes
de Bézier.

Pour faciliter l'utilisation du programme et surtout pour réduire au maximum le temps de dessin, on ne crée que la moitié des couples puisque aucun bateau dissymétrique n'a encore vu le jour et l'autre partie est générée par symétrie.

Commandes de traçage des segments de droites et des coubes de Bézier.

fig. 4 : Interface du module de création de formes Repère de dessin.

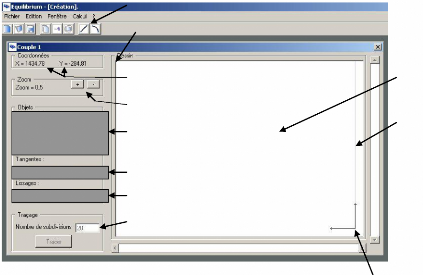
Coordonnées de la souris par rapport au repère de dessin exprimées en millimètre

Boutons de réglage du facteur de zoom.

Nombre des subdivisions des courbes de Bézier.

Coordonnées des extrémités des objets.

Angles des tangentes des courbes de Béziers.

Modules des vecteurs tangents des coibes de Bézier.

Origine de la fenêtre de dessin donnée par Visual Basic

Fenêtre
de
dessin.

Axe de symétrie

du
dessin.

a) Changement de repère et d'échelle :

Lors de l'exécution du programme, la fenrtre de dessin a des dimensions fixes, exprimées en pixel et ayant comme origine le point haut à gauche (voir figure cidessus) alors que l'idéal pour l'utilisateur, est d'avoir un repère et des dimensions en une unité plus pratique (le millimètre). D'autant plus que cette mrme fenrtre doit afficher les dessins avec des échelles d'affichages variables lors du changement de facteur de zoom. Donc surmonter cette difficulté, implique écrire une fonction qui change les coordonnées exprimées en pixels dans le repère lié à la fenêtre de dessin, en

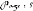
des coordonnées exprimées en millimètre dans le repère utilisateur et adaptables au facteur de zoom.

L'origine du nouveau repère est prise à une distance de 20 pixels des deux bords bas et droits de la fenêtre de dessin (ici la distance 20 pixels est prise uniquement pour des raisons d'esthétique mais on peut prendre n'importe quelle valeur du moment où on la juge utile).

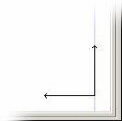
20 pixel

20 pixels

Fig. 5 : Position de l'origine du repère utilisateur
par rapport à la fenêtre de dessin

Soit L et H respectivement la l argeur et la hauteur de la fenêtre de dessi n

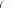
exprimées en pixel et Z le facteur de zoom écrit sous la forme

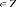
où .

On veut ici, et pour les mrmes raisons d'esthétique que la largeur de la fenrtre de dessin moins 20 pixels des deux côtés droit et gauche, soit équivalente à 5000 mm divisée par le facteur de zoom, et la hauteur de la fenêtre moi ns 20 pixels des deux côtés bas et haut

soit équivalente à mm, c'est-à-dire que quand le facteur de zoom est égale à 1 la

fenêtre affichera des distances de l'ordre de 5000 mm, et quand , lorsqu'on

Z

agrandit l'échelle d'affichage (respectivement quand lorsqu'on réduit l'échelle

d'affichage) la fenrtre affichera des distances de l'ordre de 2500 mm (respectivement 10 000 mm)

2

Remarque : Ici la distance à afficher dans le cas d'un facteur de zoom égale à 1, a été prise 5000 mm car en général les couples des bateaux ont des dimensions de l'ordre de 10 000 mm de largeur et donc 5000 mm pour la moitié qui va être affichée mais on peut, bien évidemment, là aussi, prendre n'importe quelle valeur puisque on peut changer l'échelle d'affichage.

Finalement, la fonction qui réalise ce changement de repère et d'échelle suivant l'axe X est :

mm

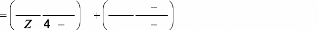
où X en pixels et en

0 1 ^f (X

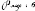
On remarque bien donc, que

000

0

De mrme la fonction qui réalise le changement de repère et d'échelle suivant l'axe Y est :

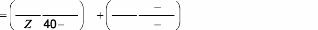
où X en pixels et en

0 1 (X

mm

et là aussi 000

f 0

Ainsi, nous avons un moyen facile de passage entre les coordonnées données par le langage de programmation et les coordonnées relatives aux dessins qu'on veut établir et pour le passage inverse (du mm au pixel), il suffit d'utiliser l'inverse de ces fonctions puisqu'elles sont linéaires et donc bijectives.

b) Création des segments de droites :

Lors de la création d'un segment de droite, les coordonnées des extrémités sont récupérées en pixels grâce aux fonctions données par Visual Basic (Fenêtre_MouseDown(Button As Integer, Shift As Integer, X As Single, Y As Single)), le segment de droite est dessiné et les coordonnées de ses extrémités sont converties en mm pour être stockées en mémoire comme un nouvel élément grâce aux fonctions définies dans le paragraphe précédent.

Création des courbes de Bézier : Définition des courbes de Bézier :

u = 0

u = 1

Fig. 6 : Modèle de courbe de Bézier.

Une courbe de Bézier est une courbe lisse obtenue à partir de n points appelés points de contrôle et permettant de changer facilement sa forme. Elle est défi nie par une expression paramétrique vectorielle, où chaque vecteur est modulé par une

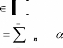
fonction du paramètre, avec telle que :

^f )

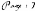
A l'origine les conditions suivantes sont imposées :

u

- la position correspondante à ce point est donnée par donc

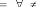
f ( 0

- la direction de la tangente en ce point est donnée par donc

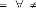
f ( 0

-

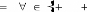
En général la dérivée ne dépend que des K vecteurs
ce qui impose

f k

(

(

A l'extrémité les conditions suivantes sont imposées :

u

-

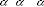
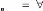
la position correspondante à ce point est donnée par la somme des vecteurs donc

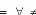
- la direction de la tangente en ce point est donnée par donc

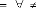
^f ()

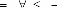
L'utilisation de ces conditions permet la détermination de familles de fonctions qu'on peut calculer directement à partir de l'expression :

i

		où
	Créer une courbe de Bézier à l'aide du module de création :

V ue la si mpl icité des formes des couples d'un bateau, les courbes de Bézier pouvant représenter un couple d'un bateau peuvent rtres créés à partir de 4 points seulement.

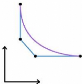
Fig. 7 : Obtention d'un couple à partir d'une
courbe de Bézier à 4 points.

Les deux premiers points sont les extrémités de la courbe et , comme les segments de droites, elles sont récupérées en pixel eux aussi. Quant au deux autres points restants ils sont déterminés par deux autres données précisées par l'utilisateur du programme, et qui sont les angles des tangentes et les lissages (notion exprimant la dérivée deuxième de la courbe).

,

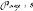
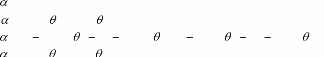
? ( ^{L C s L}

,? ( ^{x L Cos}

Exemple :

On veut tracer une courbe d'extrémités

et d'angles )

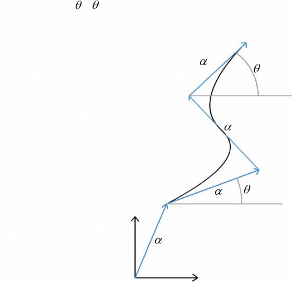
des tangentes : et de lissages.

^L

y

x

Fig. 8 : Obtention d'une courbe de Bézier à parti r de
deux points et quatre vecteurs.

La courbe de Bézier obtenue sera créée à partir des vecteurs et des points

suivants :

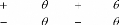
Théoriquement, dessiner une courbe de Bézier revient à parcourir l'intervalle [0,1] par une certaine variable u comme vu dans la définition des courbes de Bézier. En programmation parcourir un intervalle de R continuellement n'est pas possible pour la simple raison qu'il existe une infinité de points, donc subdiviser l'intervalle demeure la solution unique.

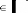
Ainsi, calculer P(u) où est ramené en un calcul de où
et N le nombre de subdivisions définis par l'utilisateur.

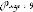
Finalement, la courbe de Bézier est décomposée en N segments de droites facilement programmables et les coordonnées de ses extrémités, les angles des tangentes et les lissages sont stockés en mémoire pour permettre leur traitement par la suite.

d) Gestion des objets :

Les objets que l'utilisateur du programme pourra créer, ne sont finalement que des traits dessinés sur l'écran loin d'être reconnaissables par l'ordinateur. Donc pour pouvoir gérer (supprimer, copier, coller, enregistrer, modifier...) ces objets, il est nécessaire de trouver une méthode permettant le passage entre les données des formes dessinées et l'image les représentant.

La méthode adoptée est alors une utilisation de tableaux : les données de tous les objets crées sont stockées en millimètre dans un tableau à deux dimensions qu'on va appeler T(ij). La première dimension sert à désigner les objets, ainsi, lorsqu'on écrit T(2,10) on sait directement qu'on a affaire au deuxième objet. Quant à la deuxième dimension, elle désigne les informations relatives aux objets (voir tableau cidessous). Contrairement à la première dimension pouvant être

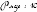
Où A (600,100), B (200,500), C (400,500), D (1000,1200) et E (2000,3000) (Voir Dessin).

C

D

E

A

B

Le tableau qui contiendra le dessin sera alors :

1	600	100	200	500	0	-	-	-	-	-
2	200	500	400	500	0	-	-	-	-	-
3	400	500	1000	1200	0	-	-	-	-	-
4	1000	1200	2000	3000	1	180	135	800	600	20

Maintenant, après avoir établi la méthode de stockage des objets, on sera souvent amené à actual iser le dessi n des objets crées : lors par exemple d'un agrandissement, ou encore lors d'une suppression d'un objet. Donc écrire une procédure qui réalise ceci, sera plus intelligent qu'écrire un bloc de 20 lignes pour chaque événement produit par l'utilisateur et qui nécessite l'actualisation du dessin.

La procédure qu'on va appeler Dessiner va naturellement parcourir le tableau T dans lequel sont stockés les objets. Et pour chaque i, elle testera d'abord si l'objet correspondant est une courbe de Bézier ou un simple segment de droite. (Autrement dits si ) si la procédure devra tracer un segment

( )

entre les point et sans oublier bien sur la conversion du

( ( ) ( ) ) ( ( ) ( 5 ) )

millimètre au pixel par l'intermédiaire de l'inverse des fonctions de changement de

repère : Jx et Jy défi nies dans la paragraphe II-1-a. et si (l'objet est une courbe

)

de Bézier), là il faudra dessiner un nombre de segments égale à T(i,11) et reliant les extrémités et .

Voici l'algorithme détaillé de la procédure Dessiner :

Soit N le nombre d'objets du dessin.

Dessiner

Début

Pour jusqu'à N faire

Si

alors

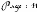
Tracer Segment

Si non

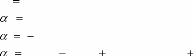
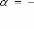
Pour à faire

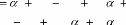
Tracer Segment

FPour.

FSi.

FPour.

Fin.

e) Sélection des objets :

Pour mieux manipuler les objets créés, il faut pouvoir les sélectionner et sélectionner un objet pour l'utilisateur, c'est cliquer sur ou proche de cet objet. M ais pour l'ordinateur cliquer en n'importe quel endroit de la fenrtre de dessin ne signifie rien, car la fenrtre de dessin n'est rien d'autre qu'une image au vrai sens du terme. Donc ce qu'il faut programmer dans cette phase, c'est lors d'un clic de souris il faut récupérer, les coordonnées du point, les convertir en mm, calculer la distance de ce point par rapport à tous les objets stockés dans le tableau T, trouver la plus petite distance, la convertir en pixels, tester s'elle est inférieure à quelques pixels. Si c'est le cas, l'objet est sélectionné si non la sélection a échoué. M ais avant de pouvoi r faire cel a, il faut d'abord définir la distance entre un point et un objet. Les objets qui peuvent exister sont des segments de droites et des courbes de Bézier formées elles aussi de petits segments. Donc finalement calculer la distance par rapport à un segment de droite devra suffire pour les deux types d'objets.

Exemple : Calcul de la distance d'un point par rapport à un segment.

Soit un segment [AB], un point M du plan, et N la projection de M sur

(AB).

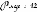
Il existe 3 cas possibles :

1er cas : le point N est compris entre A et B. Dans ce cas là la distance entre M et [AB] sera alors MN.

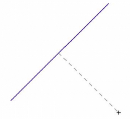
B

N

A

M

2ème cas : le point N n'est pas compris entre A et B, et situé du côté de A. Dans ce cas là alors, la distance entre M et [AB] sera MA.

B

A

N

M

3ème cas : le point N n'est pas compris entre A et B, et situé du côté de B. Dans ce cas, la distance entre M et [AB] sera MB.

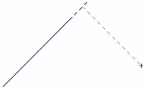
N B

A

M

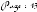
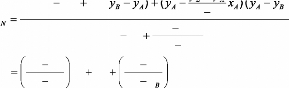
Algorithme de la fonction calculant la distance entre un point M et un segment de droite :

Distance

A

Début

Si alors

Si alors

Distance

FSi

Si alors

Distance

FSi

Si alors

Distance

FSi

Si non

Si alors

Distance

FSi

Si alors

Distance

FSi

Si alors

Distance

FSi

FSi

Fin

Algorithme de sélection d'objets :

Sélection

Début

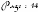
Pour à faire

Si alors

Si Distance

alors

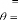
Distance

FSi

Si non

Pour à faire

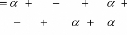
Si Distance

alors

Distance

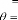
( P P

FSi

FSi

FPour

FPour

alors

Objet Sélectionné

Si

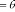
Si non

Objet Sélectionné

FSi

Fin

f) Enregistrement et chargement des objets :

L'enregistrement du dessin implique l'enregistrement du tableau T. Visual Basic offre la possibilité d'enregistrement dans des fichiers textes qui sont simples à utiliser et unidimensionnels.

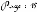
Le tableau T étant bidimensionnel, pour l'enregistrer il faut le transformer en un tableau unidimensionnel qu'on appellera S. Chaque ligne du tableau S doit contenir toutes les informations nécessaires pour identifier un objet. On prendra alors les données du tableau S comme des chaînes de caractères contentant les valeurs du tableau T suivant la direction j et séparées par le caractère

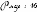
Position de chaque couple

importé

Génération de la coque

du bateau

Paramètres du calcul

Résultats du calcul

Liste des couples importés

Faire monter un couple vers le haut

Faire descendre un couple vers le bas

Supprimer un couple

Fenêtre de visualisation 3D

Ligne de flottaison

Paramétrage de la vue

Fig. 9 : Interface du module de calcul.

a) Affichage en 3D :

Lorsqu'on regarde un couloir infiniment long, on remarque qu'il y a une intersection à l'infini des traits représentant le couloir ce qui n'existe pas réellement puisque les bords du couloirs sont parfaitement parallèles. Cet effet n'est rien d'autre que l'effet de la vue en 3D réelle et c'est ce qui fera l'objet de l'étude suivante :

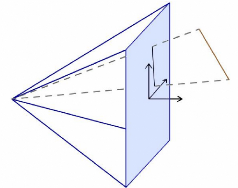
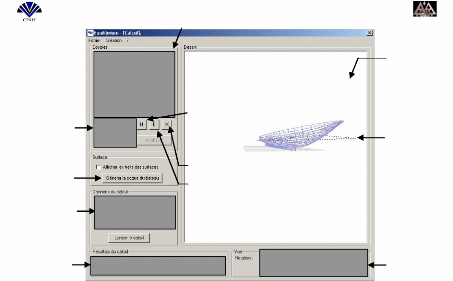
Z

C

O

P

M

Y

X

N

Fig. 10 : Affichage en 3D sur un écran assimilé à un plan.

On considère un écran qu'on assimilera à un plan auquel lié un repère (O,X,Y,Z) et un point C de coordonnées (0,0,-d) comme le centre de notre caméra virtuelle. Pour afficher un objet dans l'espace sur le plan P, il faudra le décomposer en éléments élémentaires (des segments de droites) et trouver les éléments élémentaires correspondants sur P à partir de l'intersection des droites (CM) où M est une extrémité

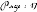
de l'objet élémentaire, et le plan P (voi r fig. 10), ainsi l'objet sera vue l'écran avec un effet de réal isme comme cité au début de ce paragraphe.

Modélisation mathématique :

Soit le segment [MN] dans l'espace où

,et

( x y z ( x y z 0 d

L'équation mathématique des deux droites (CM) et (CN) seront alors :

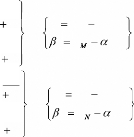
x_M

z_M

y_M

zd

M

x N

z N

y N

z_N

d

et

et

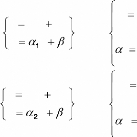
^{z b}

avec

^{z b}

avec

a₁

a₂

1

2

L'intersections des droites (CM) et (CN) avec le plan seront

alors :

et

.

Donc finalement afficher l'objet MN revient à dessiner un simple segment de droite >OJlJ] sur l'écran (P) et de la même manière on pourra afficher des objets beaucoup plus complexes tels que les couples d'un bateau.

Remarque :

Dans cette étude, on a considéré que le repère dans lequel sont exprimées les coordonnées des points M et N est le mrme que celui de l'écran ce qui ne permet pas un affichage dynamique en 3D. Autrement dits on ne peut pas survoler l'objet, l'approcher ou bien l'éloigner... donc il faut considérer un autre repère qu'on appellera LabsoluL et c'est dans ce repère que les coordonnées des objets seront expri mées. Et pour pouvoir changer l'angle de vue ou le rapprochement de l'affichage, il suffira de changer les coordonnées de la caméra vi rtuel le.

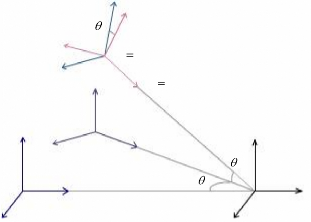
On considère maintenant deux repères, un repère absolu (O,X,Y,Z) dans lequel sont exprimées les coordonnées des objets y compris celles de la caméra et un

autre repère lié à la caméra permettant l'affichage des objets (voi r

( X Y Z

fig.1 1)

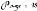
Y 4

Y

O

X

Z

Fig. 11 : Obtention du repère de la caméra
à parti r du repère absolu.

Il faut maintenant établir la matrice du changement de repère.

Soit un point M de coordonnées : (x,y,z) exprimées dans le repère absolu O(X,Y,Z). La position du repère lié à la caméra est obtenue à partir du repère absolu par 4 transformations simples :

Une translation suivant -Z : Une rotation suivant OY :

Une rotation suivant la droite passante par O et portée par :

Une rotation suivant :

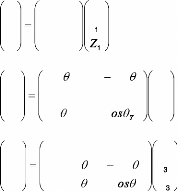
Ces transformations sont traduites par les équations suivantes :

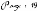
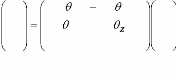
Donc :

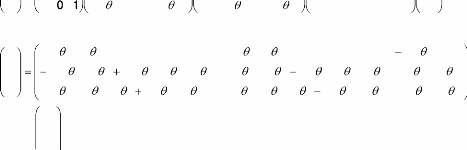
Y

ós Cos

Cos Sin

0

in SinSin,Cos

in Sin Sin ,Cos

0

Y

Donc pour obtenir les coordonnées du point M il suffit de les multiplier par la matrice A et là on procédera à l'affichage en 3D.

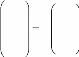
X '

Y M

Z M

X

Y Z

b) Génération des surfaces :

La génération de surface fait partie des principales fonctionnalités du module de calcul afin de pouvoir visualiser clairement la coque du bateau en 3 dimensions. Les surfaces générées sont des surfaces régl ées crées à parti r de courbes qui peuvent rtre soit des courbes de Bézier ou des segments. Lors de l'interpolation des courbes on distinguera 3 cas :

U ne interpolation entre 2 segments de droites.

Une interpolation entre 2 courbes de Bézier.

U ne interpolation entre un segment de droite et une courbe de Bézier.

Dans les trois cas les courbes sont divisées en un nombre N de subdivisions précisé par l'utilisateur.

Exemple :

Soit deux courbes AB et MN dont on veut dessiner la surface réglée et N le nombre de subdivisions des deux courbes.

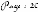
- 1^er cas : Si AB et MN sont des segments de droites. Algorithme :

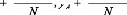
Pour à faire
Ligne

FPour.

Ici, comme pour A et B, M et N ont le même Z car le module de création dessine des courbes dans le plan et non pas dans l'espace.

- 2^ème cas : Si AB est un segment de droite et MN une courbe de Bézier d'angles de vecteurs tangents et, et de modules et.

Algorithme :

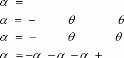
Pour à faire

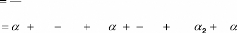
Ligne

( ^y )

FPour.

sont toutes les deux

et

- 3^ème cas :

des courbes de Bézier.

Algorithme :

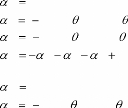
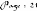
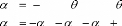
Pour à faire

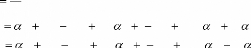
Ligne

( ^{P P} )

FPour.

c) Calculs :

La partie relative aux calculs (résolution de problème d'équilibre du bateau) est la partie la plus représentative du logiciel. Elle commence par fournir les données et finit bien sur, par afficher les résultats. La donnée fournie en plus de la forme géométrique de la coque du bateau, est l'angle d'inclinaison, et le résultat obtenu est en fait un couple physique qu'il faut raj outer (une masse fois sa distance par rapport à l'axe du bateau fois g).

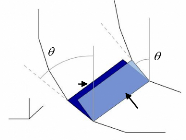
Lors de l'exécution du programme, la coque du bateau est décomposée en des petits éléments de surface plans tout en gardant dans la tête que la partie submergée sous l'eau d'un côté du bateau n'est pas la mrme que de l'autre côté puisque ce dernier est incliné. Les petits éléments de surface plans sont obtenus à partir de la décomposition des courbes (voir fig. 12.).

x

D

V

C1

S1

S2

Z B

A

C2

Fig. 12 : Interpolation de surfaces.

: Surface
générée à partir
d'un segment de
la courbe C1 en
atteignant C2.

: Surface générée à partir d'un segment de la courbe C2 en atteignant C1.

A partir d'un segment d'une courbe, on peut obtenir une petite surface plane 51 en atteignant une autre courbe et inversement on obtient une autre surface 52.

Remarques :

- Les surfaces 51 et 52 ne sont pas forcément les mêmes car les courbes à partir desquelles sont obtenues ces surfaces, peuvent être différentes et donc on peut

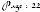
choisir pour le calcul de mécanique des f luides soit la surf ace S1 soit

n ?

(

la surf ace S2 ce qui engendra des erreurs de calcul assez considérables car la surf ace réelle n'est ni S1 ni S2, elle n'est peut rtre mrme pas plane. Donc pour minimiser ces erreurs de calculs on prendra une autre surf ace qui est la moyenne des surf aces S1 et S2

en angle et ainsi on aurait obtenu des erreurs beaucoup plus petites et

1 S

une surf ace plane générée à parti r de deux segments de courbes.

- L'élément de surface est obtenu ici à partir de deux petits segments de courbes donc pour faire le calcul sur toute la partie submergée sous l'eau de la coque du bateau, il suf f it de passer au autres éléments de courbes et ainsi, on aura la résultante du couple exercé par l'eau sur la coque du bateau. Il ne faut pas oublier aussi que la bateau est incliné donc les points f ormant les éléments de surf aces doivent subir une rotation d'angle (l'angle d'inclinaison du bateau).

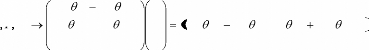
Calcul d'aire :

Contrairement aux surf aces S1 et _S2, la surf ace S plane, n'est pas rectangulaire d'autant plus qu'il s'agit d'un polygone avec un nombre de points variant entre 3 et 5 suivant les cas suivants :

1er cas : Si les quatre points f ormant les segments de courbes sont au dessous de la surf ace de l'eau appelée ligne de f lottaison, le nombre de points de la surf ace S sera alors 4.

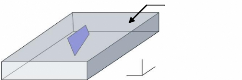
Li gne de f lottai son

0

B C

V

A

Z

X

2ème cas : Si un seul point est au-dessus de la ligne de f lottaison, le nombre de points f ormant la surf ace est 5 avec les points C' et D' (voir f igure ci-

dessous) obtenus par intersection de CD et BD avec la ligne de f lottaison.

^y

0

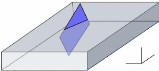
D' C
B

A

C'

X

V

Z

3ème cas : Si deux points de la même courbe sont au-dessus de la ligne de f lottaison, le nombre de points est alors 4 avec les points C' et D' obtenus par intersection de AC et BD avec la li gne de f lottaison .

y

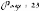
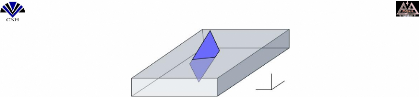
0

B

D' C'

A

C

X

V

Z

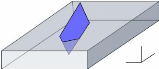
4ème cas : Si 3 points sont au-dessus de la ligne de flottaison, le nombre de points est alors 3 avec les points C' et B' obtenus par intersection de AC et

AB avec la ligne de flottaison.

^y

0

B

B'

A

C

C'

X

V

Z

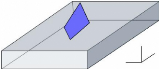
5ème cas : Si les 4 points sont au dessus de la li gne de fl ottaison, la surface sera alors formée de 4 points mais elle ne sera pas comptée puisque elle est audessus de l'eau et par la suite il n'y exerce aucun effort.

0

B

A

C

X

V

Z

0'après ces 5 cas on voit bien que l'élément de surface qui va être utilisé dans la relation : change en fonction de sa position par rapport à la

n ?

(

surface de l'eau, donc écrire une fonction qui calcule l'aire de sa partie submergée sous l'eau facilitera énormément la programmation du calcul de l'effort appliqué par l'eau sur la coque.

Posons l'équation de la surface de l'eau : Algorithme de la fonction : Fonction Aire
		`P1, P2, P3 et P4 sont les points formant l'élément de surface dS'
Fonction AireTriangle ^A 0ébut	`Fonction qui calcule l'aire d'un triangle ABC dans l'espace'

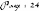
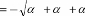
AireTriangle

²

Fin

Début	Si Alors ^y	`Permutation de P1 et P2 de telle manière à ce que P2 soit touj ours correspondant au point le plus haut du premier segment'

FSi

Si Alors

P2

P1

P4 _V

P3

x

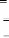
`De mrme permutation de P3 et P4 de telle manière à ce que P4 soit toujours correspondant au point le plus haut du deuxième segment'

FSi

Ligne de flottaison

Si et Alors

y y

Aire AireTriangle

( P P

AireTriangle

( ^{P P P}

V

P4

P2

Z

`1^er Cas'

P1 P3

FSi

Si et etAlors

^{y y}

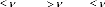
`2^ème Cas'

P4

P'2

P2

P1

P'3

P3

2

Aire AireTriangle

( P )

AireTriangle

( P P )

AireTriangle

^{P P P}

FSi

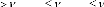
`2^ème Cas'

Si et etAlors

P2 P'4

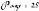
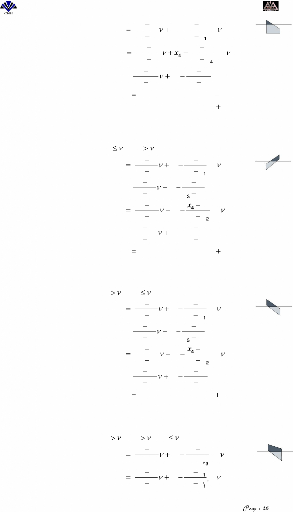
4

Aire AireTriangle

( P P P )

AireTriangle

( P P )

AireTriangle

^{P P P}

P'1

P1 P3

P4

FSi

Si et Alors

44 ₂

Aire AireTriangle

( P P )

AireTriangle

( P '

P P

FSi

Si et Alors

^{y y}

44 ₂

Aire AireTriangle

( P

AireTriangle

( ^{P P P}

FSi

Si et etAlors

^{y y}

`3^ème Cas'

P4

P1

P2

P'2

P3

P'1

`3^ème Cas'

y P3 3

P2

P1 P'4

P'3

P4

`4^ème Cas'

P3

P1

P2

P'1

P4

P'4

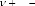
Aire AireTriangle

( ^{P P P}

FSi

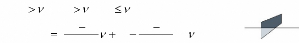
Si et etAlors

^{y y}

P2 P3

P'2 P'3

`4^ème Cas'

P1

P4

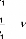
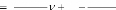
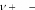
Aire AireTriangle

( ^{P P}

FSi

Si et Alors

y

Aire

FSi

`5^ème Cas'

P2

P4

P3

P1

Fin

Ai nsi l'aire de l'élément de surfacesubmergé est calculée, donc pour pouvoir appliquer la relation de mécanique des fluides il reste

.

n ?

(

encore le calcul deet

est la différence entre la hauteur de la ligne de flottaison et la moyenne des hauteurs des points formant le polygone correspondant à l'élément de surface.

Exemple :

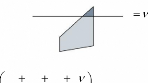
P2

P1

P3

P4

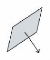
P3

P2

P4

P1

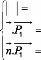
est le vecteur normal unitaire à l'élément de surfacedi rigé vers l'eau est obtenu en résolvant le système d'équations suivant :

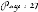
L'élément de forceainsi calculé, il reste maintenant à le traduire en

un couple physique élémentaire. Pour ce faire, on multipliepar la distance séparant l'origine du repère et la droite passante par le centre de l'élément de surface et portée par le vecteur tout en respectant les sens positifs et négatifs.

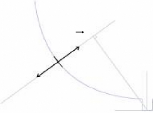
X

d V

On procède de cette manière pour touts les éléments de surface de la coque du bateau pour avoir le couple total résultant appliqué par l'eau sur le bateau, et à partir de ce couple trouvé, on saura systématiquement le couple qu'il faut rajouter pour équilibrer le bateau, qui n'est rien d'autre que son opposé.

Le couple nécessaire à l'équilibrage du bateau étant connu, on le traduit en un poids (une masse fois g) et une distance par rapport à l'axe du bateau où la masse va être posée tout en respectant la largeur maximale du bateau. C'est-à-dire qu'on ne pourra pas poser une masse à 15 mètres de l'axe alors que le bateau de fait que 8 mètres de largeur. Afin de résoudre ce problème, cette distance est prise de l'ordre de 80% de la moitié de la largeur maximale du bateau.

Exemple :

	où

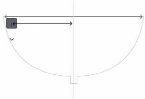
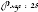
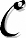
atia, le leader mondial des solutions 3D et de gestion du cycle de vie des produits (PLM Product Lifecycle Management) comprend un module de marine (Design Concept Marine) qui pourra résoudre facilement le problème d'équilibrage de bateaux. Donc finalement le stagiaire Ensamien n'a rien inventé, mais au lieu de se procurer une licence de Catia à 1 400 000 Dh de la part de l'entreprise, elle a pu résoudre le même problème au prix de deux mercis seulement : un merci de la part de l'encadrant et un autre merci de la part du patron, le patron pour qui, les seules raisons d'investir au Maroc sont avoir une main d'oeuvre moins chère et un pouvoir divin sur des ouvriers marocains terrifiés par un cauchemar appelé chômage.

Certaines améliorations du logiciel conçu peuvent aussi faire l'objet d'un nouveau stage pour un autre élève ingénieur, citons à titre d'exemple : une génération de la coque du bateau par des surfaces de Bézier au lieu des surfaces réglées ou encore un maillage triangulaire lors de l'interpolation des éléments de surface pour augmenter un petit peu plus la précision du calcul, même si les calculs actuels répondent largement aux exigences des constructeurs navals en matière de précision. Il reste maintenant un dernier stage avant le Projet Industriel de Fin d'Etudes, espérons qu'il soit si bénéfique lui aussi, que cela soit sur le niveau technique, humain ou culturel afin d'enrichir au maximum la formation d'ingénieur Arts et Métiers basée principalement sur les trois volets : savoir, savoir faire et savoir être.