Section 2 : ANALYSE
EXPLORATOIRE DES DONNEES
1. Les dépenses
gouvernementales
La série suivante nous montre que les dépenses
du gouvernement évoluent et s'élargissent dans le temps. C'est
ainsi que nous l'avons linéarisée.
Graphique 1: Série brute des
dépenses gouvernementales

Vu dans le corrélogramme, les dépenses du
gouvernement sont non stationnaires. C'est ainsi que nous allons appliquer le
test de racine unitaire de Dickey-Fuller Augmenté.
Graphique 2: Corrélogramme
de log de G

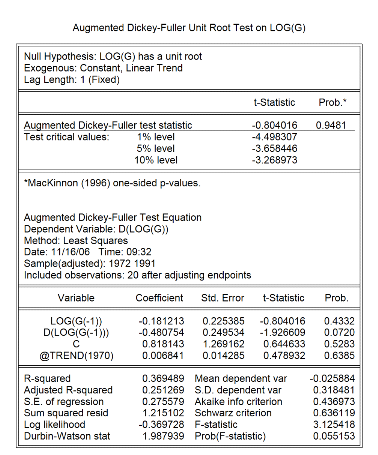
Le test de Dickey-Fuller appliqué sur le logarithme des
dépenses du gouvernement nous montre que la série est non
stationnaire. La deuxième partie du tableau nous montre que le
coefficient associé au trend est non significatif. Ainsi, nous sommes en
présence d'un DS sans dérive. Nous allons donc la stationnariser
par la différence première.
Tableau 1: ADF for log G
Selon le tableau suivant, la différence première
appliquée à cette série la rendue stationnaire.
Tableau 2: ADF for
dlG

2. Investissement
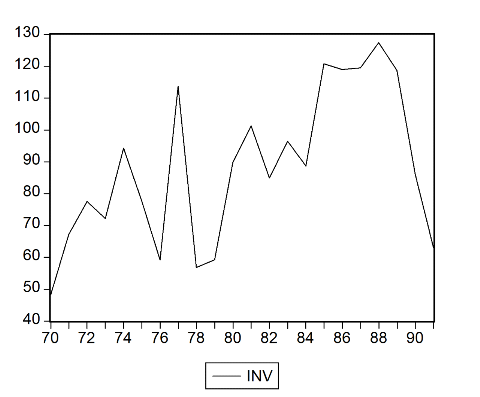
La série suivante nous montre que l'investissement
fluctue dans le temps. En 1978, le taux d'investissement a baissé. Cette
situation s'est aussi remarquée vers les années 1991 à
cause notamment des pillages et de l'insécurité qui a eu lieu
dans le pays. Par ailleurs, la série semble être non
stationnaire.
Graphique 3: Série
brute de Inv
Le logarithme appliqué à cette série nous
montre que la série est quasi stationnaire. Mais nous pensons pouvoir
confirmer cette intuition par le test de Dickey-Fuller.
Graphique 4:
Corrélogramme de Log(inv)

Le test de Dickey-Fuller nous montre que la série est
non stationnaire. Par ailleurs, le coefficient associé au trend est non
significatif. Nous sommes donc en présence d'un DS avec
dérive.
Tableau 3: ADF for
Log(inv)

La différence première appliquée à
la série la rendue stationnaire, comme nous le montre le tableau
suivant.
Tableau 4: ADF for
dlinv
|
Null Hypothesis: D(LOG(INV)) has a unit root
|
|
Exogenous: None
|
|
Lag Length: 1 (Fixed)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-4.758145
|
0.0001
|
|
Test critical values:
|
1% level
|
|
-2.692358
|
|
|
5% level
|
|
-1.960171
|
|
|
10% level
|
|
-1.607051
|
|
|
*MacKinnon (1996) one-sided p-values.
|
3. Taux d'intérêt
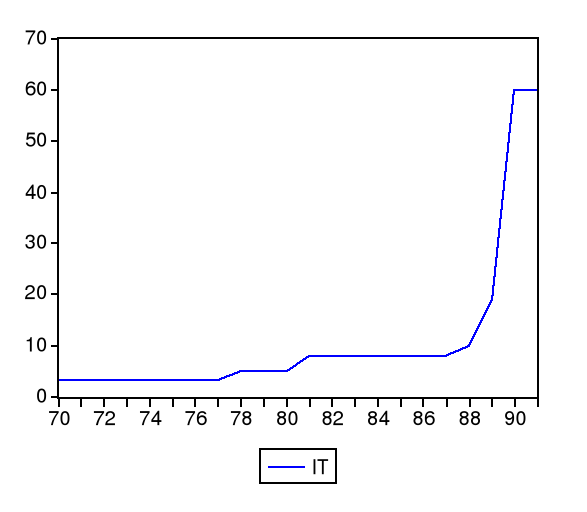
Le graphique suivant nous présente le taux
d'intérêt. Selon ce graphique, le taux d'intérêt a
grandement augmenté à partir de 1988. C'est le fait de la crise
qui a commencé avec les programmes d'ajustement structurels.
Graphique 5: Série
brute de It
La série en log du taux d'intérêt est
présentée dans le tableau suivant. Elle semble être non
stationnaire. Mais comme nous l'avons dit, nous devons confirmer cette
intuition par le test de Dickey-Fuller.
Graphique 6:
Corrélogramme de Log(it)

Le tableau suivant nous montre que la série est non
stationnaire. Par ailleurs, le coefficient associé au trend est
significatif. Nous sommes donc en présence d'un TS.
Tableau 5: ADF for
log(it)

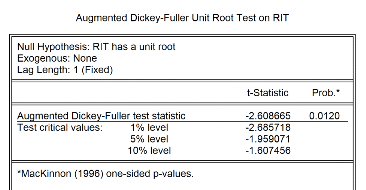
La série stationnarisée est RIT. Comme nous le
montre le tableau suivant, le test de ADF est concluant.
Tableau 6: ADF for
Rit
| 


