|
UNIVERSITE DE
KINSHASA

FACULTE DES SCIENCES ECONOMIQUES ET DE
GESTION
DEPARTEMENT DES SCIENCES ECONOMIQUES
CELLULE D'ECONOMIE MATHEMATIQUE
DEUXIEME LICENCE

Mémoire présenté et
défendu en vue de l'obtention du titre de Licencié en Sciences
Economiques
 OTCHIA SAMEN Christian OTCHIA SAMEN Christian
Directeur : Professeur KINTAMBU Emmanuel
ANNEE ACADEMIQUE 2005-2006
INTRODUCTION
Beaucoup de gens pensent que dans la conjoncture actuelle de
la RD Congo, l'objectif des études n'est plus la formation de l'esprit
mais l'acquisition du diplôme : c'est le minimum exigible qui
devient l'objet de la préoccupation des étudiants. C'est ainsi
que beaucoup d'étudiants ne se donnent plus à la lecture et
à la recherche.
Mais, nous, nous pensons que l'étudiant idéal
est celui qui apprend toujours parce qu'il doit solutionner les
problèmes qui se posent avec acuité.
En effet, ce n'est pas en apprenant par coeur la
définition d'un moteur à essence qu'on apprend à conduire
une voiture. On devient chauffeur en apprenant à mettre en marche le
moteur, à manipuler le levier de changement de vitesse, à
maîtriser la direction, ... et surtout en faisant beaucoup de
pratiques1(*). C'est dans
cette logique que le programme universitaire a prévu des séances
pratiques en vue de fidéliser les étudiants aux outils pratiques.
L'intérêt dans cette publication est d'assimiler les connaissances
théoriques et pratiques de l'économétrie, et de
s'appliquer sur le logiciel Eviews.
L'objectif de ce working paper est d'estimer un modèle
d'équations simultanées sur les données de la RD Congo de
1970 à 1991 d'une part et d'autre part, d'analyser les
caractéristiques dynamiques de ces équations en s'inspirant du
texte de KMENTA.
Avant de mettre un terme à cette introduction, il est
impérieux de remercier le professeur Emmanuel Gustave KINTAMBO MAFUKU
pour avoir fait de nous des économètres qualifiés. Nous
remercions par surcroît tout le corps professoral qui nous a aidé
à parfaire notre formation en économie mathématique.
Par ailleurs, nous remercions aussi les amis du groupe pour la
collaboration et la discussion tout au long de ce travail. Nous avons compris
ensemble que c'est du choc des idées que jaillit la lumière.
TABLE DES MATIERES
INTRODUCTION
1
TABLE DES MATIERES
2
LISTE DES TABLEAUX
2
LISTE DES FIGURES
2
Section 1 : MODELES A EQUATIONS
SIMULTANEES
3
Section 2 : ANALYSE EXPLORATOIRE DES
DONNEES
4
1. Les dépenses gouvernementales
4
2. Investissement
6
3. Taux d'intérêt
8
4. Offre de monnaie
10
5. Revenu
12
6. Consommation
14
Section 3 : IDENTIFICATION
15
Section 4 : ESTIMATION
17
1. L'équation de la consommation
17
2. L'équation de l'investissement
18
3. L'équation du taux
d'intérêt
18
ANNEXES
20
LISTE DES TABLEAUX
Tableau 1: ADF for log G
5
Tableau 2: ADF for dlG
6
Tableau 3: ADF for Log(inv)
7
Tableau 4: ADF for dlinv
8
Tableau 5: ADF for log(it)
9
Tableau 6: ADF for Rit
9
Tableau 7: ADF for Lmo
11
Tableau 8: ADF for Dlog
11
Tableau 9: ADF for Lpib
13
Tableau 10: ADF for Dlpib
13
Tableau 11: ADF for Lcons
15
Tableau 12: ADF for Rcons
15
Tableau 13: Estimation de l'équation de la
consommation par les doubles moindres carrés
17
Tableau 14: Estimation de l'équation de
l'investissement par les doubles moindres carrés
18
Tableau 15: Estimation de l'équation de
l'investissement par les doubles moindres carrés
19
LISTE DES FIGURES
Graphique 1: Série brute des dépenses
gouvernementales
4
Graphique 2: Corrélogramme de log de G
4
Graphique 3: Série brute de Inv
6
Graphique 4: Corrélogramme de Log(inv)
7
Graphique 5: Série brute de It
8
Graphique 6: Corrélogramme de Log(it)
8
Graphique 7: Série brute de mo
10
Graphique 8: Corrélogramme de Lmo
10
Graphique 9: Série brute du PIB
12
Graphique 10: Corrélogramme de Lpib
12
Graphique 11: Série brute de Cons
14
Graphique 12: Corrélogramme de Lcons
14
Section 1 : MODELES A
EQUATIONS SIMULTANEES
En fait, les phénomènes économiques de
quelque complexité sont décrits par un ensemble de variables, et
leur modélisation requiert en général plus d'une relation,
ou équation, reliant ces grandeurs, on parle alors de
modèles à équations
simultanées.
On distingue les variables endogènes, qui sont
déterminées par le modèle, et les variables
exogènes déterminées ou fixées en dehors de
celui-ci.
La modélisation opère en trois phases:
· la conception, c'est à dire l'écriture
ou la spécification du modèle
· l'estimation des équations du
modèle, selon des techniques appropriées
· la résolution du
modèle, préalable à son emploi pour la simulation ou la
prévision
Naturellement, dans la réalité, les choses ne
sont pas séquentielles et la mise au point d'un modèle
opère par allers et retours entre les trois étapes ci-dessus.
Cependant, dans le cadre de ce travail, nous allons
procéder par l'analyse exploratoire des données. Dans cette
étape, il va s'agir d'étudier l'évolution et le
comportement de nos variables dans le temps. Si elles sont non stationnaires,
les stationnariser selon leurs types de non stationnarité.
Ensuite, nous allons identifier nos équations. Cette
étape est nécessaire car elle nous permet de trouver la meilleure
méthode d'estimation pour chacune des équations du modèle.
Elle est par ailleurs suffisante parce que l'application aveugle de la
méthode de moindres carrés ordinaires peut conduire à des
résultats fallacieux dans la mesure où l'hypothèse de
l'indépendance entre la variable explicative et l'erreur n'est pas
respectée.
La troisième étape est l'estimation. On peut
estimer les paramètres de la forme structurelle du modèle lorsque
les équations sont exactement identifiées et
sur-identifiées. On distingue les méthodes à information
limitée et les méthodes à information complète. Les
premières consistent à estimer le modèle équation
par équation, sous l'hypothèse qu'il n'existe pas de
corrélations entre les aléas des différentes
équations. Les secondes considèrent le modèle dans sa
globalité et estiment les paramètres sous l'hypothèse
qu'il n'existe pas de corrélations entre les aléas
interéquations.
Enfin, la dernière étape va consiste à
écrire le modèle sous sa forme réduite et d'analyser les
caractéristiques dynamiques de ce modèle pour la simulation.
Section 2 : ANALYSE
EXPLORATOIRE DES DONNEES
1. Les dépenses
gouvernementales
La série suivante nous montre que les dépenses
du gouvernement évoluent et s'élargissent dans le temps. C'est
ainsi que nous l'avons linéarisée.
Graphique 1: Série brute des
dépenses gouvernementales

Vu dans le corrélogramme, les dépenses du
gouvernement sont non stationnaires. C'est ainsi que nous allons appliquer le
test de racine unitaire de Dickey-Fuller Augmenté.
Graphique 2: Corrélogramme
de log de G

Le test de Dickey-Fuller appliqué sur le logarithme des
dépenses du gouvernement nous montre que la série est non
stationnaire. La deuxième partie du tableau nous montre que le
coefficient associé au trend est non significatif. Ainsi, nous sommes en
présence d'un DS sans dérive. Nous allons donc la stationnariser
par la différence première.
Tableau 1: ADF for log G
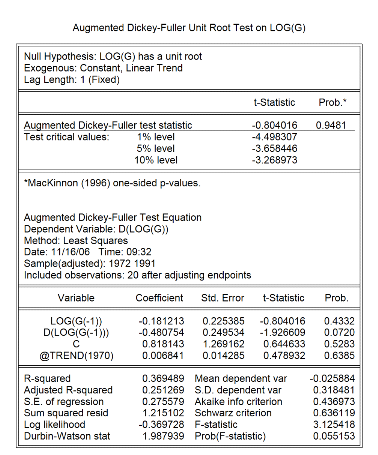
Selon le tableau suivant, la différence première
appliquée à cette série la rendue stationnaire.
Tableau 2: ADF for
dlG

2. Investissement
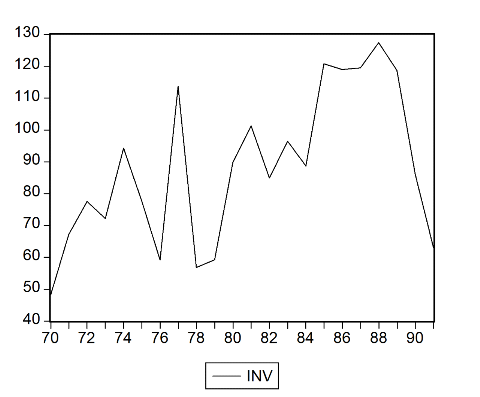
La série suivante nous montre que l'investissement
fluctue dans le temps. En 1978, le taux d'investissement a baissé. Cette
situation s'est aussi remarquée vers les années 1991 à
cause notamment des pillages et de l'insécurité qui a eu lieu
dans le pays. Par ailleurs, la série semble être non
stationnaire.
Graphique 3: Série
brute de Inv
Le logarithme appliqué à cette série nous
montre que la série est quasi stationnaire. Mais nous pensons pouvoir
confirmer cette intuition par le test de Dickey-Fuller.
Graphique 4:
Corrélogramme de Log(inv)

Le test de Dickey-Fuller nous montre que la série est
non stationnaire. Par ailleurs, le coefficient associé au trend est non
significatif. Nous sommes donc en présence d'un DS avec
dérive.
Tableau 3: ADF for
Log(inv)

La différence première appliquée à
la série la rendue stationnaire, comme nous le montre le tableau
suivant.
Tableau 4: ADF for
dlinv
|
Null Hypothesis: D(LOG(INV)) has a unit root
|
|
Exogenous: None
|
|
Lag Length: 1 (Fixed)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-4.758145
|
0.0001
|
|
Test critical values:
|
1% level
|
|
-2.692358
|
|
|
5% level
|
|
-1.960171
|
|
|
10% level
|
|
-1.607051
|
|
|
*MacKinnon (1996) one-sided p-values.
|
3. Taux d'intérêt
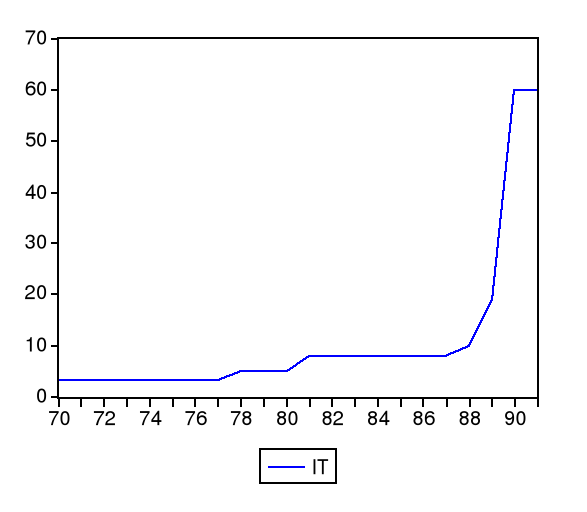
Le graphique suivant nous présente le taux
d'intérêt. Selon ce graphique, le taux d'intérêt a
grandement augmenté à partir de 1988. C'est le fait de la crise
qui a commencé avec les programmes d'ajustement structurels.
Graphique 5: Série
brute de It
La série en log du taux d'intérêt est
présentée dans le tableau suivant. Elle semble être non
stationnaire. Mais comme nous l'avons dit, nous devons confirmer cette
intuition par le test de Dickey-Fuller.
Graphique 6:
Corrélogramme de Log(it)

Le tableau suivant nous montre que la série est non
stationnaire. Par ailleurs, le coefficient associé au trend est
significatif. Nous sommes donc en présence d'un TS.
Tableau 5: ADF for
log(it)

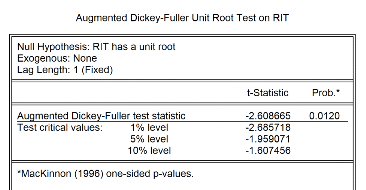
La série stationnarisée est RIT. Comme nous le
montre le tableau suivant, le test de ADF est concluant.
Tableau 6: ADF for
Rit
4. Offre de monnaie
La série suivante présente l'offre de monnaie.
Elle fluctue aussi à travers le temps.
Graphique 7: Série
brute de mo

Le corrélogramme de l'offre de monnaie exprimée
en logarithme nous renseigne que la série est non stationnaire.
Graphique 8:
Corrélogramme de Lmo

En outre, le test de ADF présenté dans le
tableau suivant nous confirme cette intuition. Par ailleurs, cette série
est un DS sans dérive.
Tableau 7: ADF for
Lmo

La série en différences premières est
stationnaire, comme nous le montre le tableau suivant :
Tableau 8: ADF for
Dlog
|
Null Hypothesis: D(LOG(MO)) has a unit root
|
|
Exogenous: None
|
|
Lag Length: 1 (Fixed)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-3.231219
|
0.0028
|
|
Test critical values:
|
1% level
|
|
-2.692358
|
|
|
5% level
|
|
-1.960171
|
|
|
10% level
|
|
-1.607051
|
|
|
*MacKinnon (1996) one-sided p-values.
|
5. Revenu
Le revenu fluctue aussi. Elle baisse surtout pendant les
périodes de crises, notamment pendant les périodes des PAS ou
pendant les pillages de 1991.
Graphique 9: Série
brute du PIB

La série en logarithme décroît un peu
rapidement. Mais nous allons le tester à l'aide du test de ADF.
Graphique 10:
Corrélogramme de Lpib

Le test de ADF nous renseigne que la série est non
stationnaire. Ainsi, nous sommes en présence d'un DS sans dérive.
Tableau 9: ADF for
Lpib

La série différenciée est donc
stationnaire.
Tableau 10: ADF for
Dlpib
|
Null Hypothesis: D(LOG(PIB)) has a unit root
|
|
Exogenous: None
|
|
Lag Length: 1 (Fixed)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-2.022679
|
0.0439
|
|
Test critical values:
|
1% level
|
|
-2.692358
|
|
|
5% level
|
|
-1.960171
|
|
|
10% level
|
|
-1.607051
|
|
|
*MacKinnon (1996) one-sided p-values.
|
6. Consommation
La série suivante présente la consommation. Elle
augmente au fil du temps.
Graphique 11: Série
brute de Cons

Le corrélogramme suivant nous montre que la
série est non stationnaire et le test d'ADF conduit également au
même résultat. En plus, la série est un TS. Nous l'avons
donc stationnarisé en faisant l'écart à la tendance.
Graphique 12:
Corrélogramme de Lcons

Tableau 11: ADF for
Lcons

Tableau 12: ADF for
Rcons
|
Null Hypothesis: RCONS has a unit root
|
|
Exogenous: None
|
|
Lag Length: 1 (Fixed)
|
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic
|
-2.241260
|
0.0274
|
|
Test critical values:
|
1% level
|
|
-2.685718
|
|
|
5% level
|
|
-1.959071
|
|
|
10% level
|
|
-1.607456
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
Section 3 :
IDENTIFICATION
Comme nous l'avions précisé ci-haut, cette
section consiste à présenter le modèle d'équations
simultanées et l'identifier.
Soit le modèle
Ct = á0 + á1
Yt + á2 Ct-1 + ì1t
(1)
It = â0 + â1
Rt + â2 It-1 + ì2t
(2)
Rt = ã0 + ã1
Yt + ã2 Mt + ì3t
(3)
Yt = Ct + It + Gt
(4)
D'après cette spécification, les variables
endogènes sont :
· Ct : consommation (Cons)
· Yt : revenu (PIB)
· It : Investissement (INV)
· Rt: Taux d'intérêt (It)
Et les variables endogènes sont :
· Mt: Offre de monnaie (Mo)
· Gt : Dépenses de gouvernement (G)
A partir du système d'équations
présenté ci-haut, nous allons isoler les termes du choc à
droite du signe d'égalité. Le modèle devient :
Ct - á0 - á1
Yt - á2 Ct-1 = ì1t
(1)
It - â0 - â1
Rt - â2 It-1 = ì2t
(2)
Rt - ã0 - ã1
Yt - ã2 Mt = ì3t
(3)
Yt - Ct - It - Gt=
0 (4)
|
Eq.
|
Ct
|
It
|
Rt
|
Yt
|
|
K**
|
G
|
G -1 -1
|
Décision
|
M.E
|
|
1
|
Mt
|
It-1
|
Ct-1
|
Gt
|
|
1
|
1
|
0
|
0
|
-á1
|
-á0
|
0
|
0
|
-á2
|
0
|
3
|
2
|
1
|
Sur.Id
|
DMC
|
|
2
|
0
|
1
|
-â1
|
0
|
- â0
|
0
|
-â2
|
0
|
0
|
3
|
2
|
1
|
Sur.Id
|
|
|
3
|
0
|
0
|
1
|
- ã1
|
- ã0
|
-ã2
|
0
|
0
|
0
|
3
|
2
|
1
|
Sur.Id
|
|
|
4
|
-1
|
-1
|
0
|
1
|
0
|
0
|
0
|
0
|
-1
|
|
|
|
|
|
Pour l'équation 1, on a :
 ö( ö( ) = 3
G=4 G-1=4-1=3 ) = 3
G=4 G-1=4-1=3
Par conséquent, l'équation 1 est
sur-identifiée.
Pour l'équation 2, on a :
 ö( ö( ) = 3
G=4 G-1=4-1=3 ) = 3
G=4 G-1=4-1=3
Par conséquent, l'équation 1 est
sur-identifiée.
Pour l'équation 3, on
a :
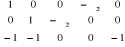 ö( ö( ) = 3
G=4 G-1=4-1=3 ) = 3
G=4 G-1=4-1=3
Par conséquent, l'équation 1 est
sur-identifiée.
Section 4 : ESTIMATION
1. L'équation de la
consommation
La commande incrémentée dans le logiciel Eviews 4.1
est :
TSLS rcons c dlpib rcons(-1) @ dlmo rcons(-1) dlinv(-1)
dlg
Tableau 13: Estimation de
l'équation de la consommation par les doubles moindres
carrés

Le tableau précédent présente
l'estimation de l'équation de la consommation par les Two-Stage Least
Squares. D'après ce tableau, seule la consommation de la période
précédente est statistiquement différente de zéro.
En outre, la consommation marginale est 0.77 et est positive. L'estimation est
en générale fiable, bien que les valeurs de R-squared n'aient
pas de signification dans un modèle d'équations
simultanées2(*).
2. L'équation de
l'investissement
La
commande incrémentée dans le logiciel Eviews 4.1 est :
TSLS DLINV c RIT DLINV(-1) @ dlmo rcons(-1) dlinv(-1)
dlg
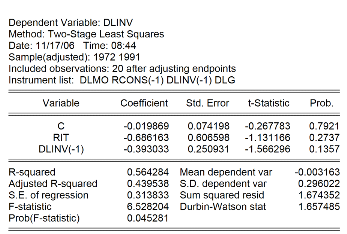
Le tableau suivant présente l'estimation de
l'équation de l'investissement par les Two-Stage Least Squares. Ce
tableau nous montre qu'aucune variable explicative n'est significative. Ainsi,
pendant cette sous période ce l'histoire de l'économie
congolaise, l'investissement n'est ni expliqué par le taux
d'intérêt, ni par les investissement de la période
précédente.
Tableau 14: Estimation de
l'équation de l'investissement par les doubles moindres
carrés
3. L'équation du taux
d'intérêt
La
commande incrémentée dans le logiciel Eviews 4.1 est :
TSLS rit c dlpib dlmo ar(1) ar(2) @ dlmo rcons(-1)
dlinv(-1) dlg
Le tableau suivant présente l'estimation de
l'équation du taux d'intérêt par les Two-Stage Least
Squares. Ce tableau nous montre également qu'aucune variable explicative
n'est significative. Ainsi, l'on peut conclure que pendant cette sous
période de l'histoire de l'économie congolaise, le taux
d'intérêt n'est ni expliqué par le revenu, ni l'offre de
monnaie.
Tableau 15: Estimation de
l'équation de l'investissement par les doubles moindres
carrés

ANNEXES
* 1 Otchia Samen
* 2 CADORET Isabelle et Al.,
Econométrie appliquée, 1ière éd.,
Bruxelles, De Boeck, 2004, p. 292
| 


