Modélisation et optimisation du système de production du champ de Zarzaitine par le gaz lift

Chapitre IV : Performances du réservoir et du puits

Introduction

Le point de fonctionnement d'un puits est le point d'intersection de deux courbes, la courbe de performance du réservoir (inflow) et la courbe de performance de tubing (outflow).

Les performances "internes et externes" du réservoir (Inflow and outflow performances) sont gouvernées par leurs propres lois physiques, mais doivent avoir la même valeur en un point situé au fond du puits. Ceci est l'application de la loi des noeuds» qui veut que tout ce qui entre dans le noeud est égal à ce qui sort (inflow = outflow).

IV.1 Inflow performance

IV.1.1 la perméabilité absolue

Les débits des fluides dans la roche dépendent des variables suivantes :

Les gradients de pression, la saturation des fluides, la viscosité des fluides, les propriétés des roches, et la plus importante c'est la perméabilité.

La perméabilité absolue est la capacité d'une roche à laisser passer une seule fluide à travers son milieu poreux. Elle est mesurée en millidarcies. Plus la valeur est grand plus l'écoulement de fluide est facile.

La perméabilité peut varier sensiblement dans les roches à quelques mètres écartés ou même avoir des valeurs différentes pour différentes directions à travers la même section de la roche, Cette propriété est anisotropie en raison des hétérogénéités du réservoir.

Comme on le voit dans l'équation de Darcy :

_q

_q

_A

? ?

_Kdp

?

_dl

(IV.1)

_A

35

: La vitesse d'écoulement de liquide à travers la section transversale dans une direction

_dl

_dp

donnée.

K : La perméabilité dans cette direction.

: Le gradient de pression.

u : La viscosité du liquide.

36

Chapitre IV : Performances du réservoir et du puits

IV.1.2 l'indice de la productivité

Les équations de l'écoulement nous disent que lorsque le puits est ouvert à la production, une onde de pression se déplace à travers le réservoir provoquant la pression dans la région touchée afin de diminuer continuellement avec le temps.

En vertu de ces passagères ou infini les conditions d'agir, les pressions en tout rayon donné diminue rapidement au début, puis se stabilise avec le temps.

La pression au fond du puits _Pwf, suit le même schéma pour une production constante.

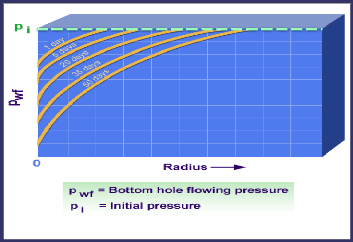
Figure IV 1: variation des pressions en tous rayons en fonction du temps

Peu de temps après le début de l'écoulement, la pression au fond du puits s'approche d'une valeur stable, et quand on utilise cette valeur stable dans nos calculs, nous pouvons l'utiliser comme une approximation des équations de l'écoulement à l'équilibre dans notre analyse.

La différence entre la pression du réservoir moyen et le fond du puits est appelée le pressure drawdown.

37

Chapitre IV : Performances du réservoir et du puits

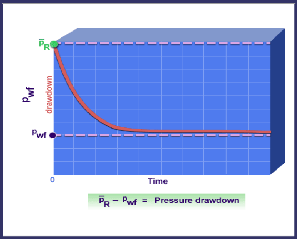
Figure IV 2:Évaluation de pressure drawdown

Pressure drawdown = Pr -Pwf.

Le drawdown entraîne un débit Q et définit l'indice de productivité J.

j ? Q

? P _r P wf

Indice de productivité :

(IV.2)

L'indice de productivité représente la réponse dynamique du réservoir et de ses propriétés du fluide dans la zone de drainage d'un puits. IL définit la relation qui existe entre le débit Q et la pression d'écoulement au fond du puits Pwf pour une pression donnée de réservoir P_r.

IV.1.3 Inflow performance Relationship - IPR

La construction de la courbe IPR (infow performance relationship) est très importante dans la production. Cette courbe représente la capacité d'un puits d'évacuer un fluide du réservoir jusqu'au fond du puits.

IV.1.3.1 La méthode de l'IP : (l'indice de productivité)

Quand la pression de fluide au fond du puits est au-dessus du point de bulle l'indice de la productivité sera constant.

Comme la pression tombe au-dessous du point de bulle, l'indice de productivité diminuera où fur et à mesure que le gas sort de la solution.

Gilbert (1954), le père de l'ingénierie de production moderne, il a été le premier à comprendre la pleine signification de cette baisse de l'indice de productivité.

38

Chapitre IV : Performances du réservoir et du puits

Il a tracé la courbe qui représente la pression d'écoulement au fond du puits Pwf en fonction du débit Q, c'est l'IPR.

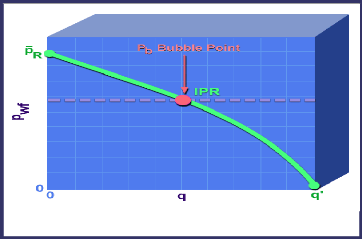
Figure IV 3:La courbe IPR

Parce que la pression du réservoir sera généralement depleté par la production, l'IPR sur la vie d'un puits est démontré par une famille de courbes diminue vers l'origine. Chaque courbe représente la relation entre la pression et le débit à une pression de réservoir donnée.

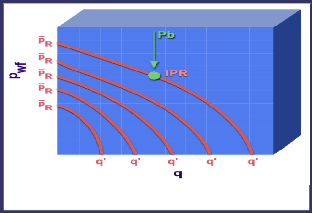
Figure IV 4:La variation de l'IPR sur la vie d'un puits

39

Chapitre IV : Performances du réservoir et du puits

Les extrémités des courbes IPR sont la pression du réservoir moyenne Pr à un débit compris entre zéro, et le débit maximal Q qui coule au fond du puits à une pression de zéro,

dans la pratique il n'est pas possible d'atteindre cette valeur, car la pression d'écoulement en fond du puits doit toujours avoir une certaine valeur finie.

Au-dessus du point de bulle, les courbes des IPR sont des lignes droite, car il y a une seule phase de fluide, et la perméabilité est une constante égale à la perméabilité absolue, l'indice de productivité est égale à la pente inverse de la courbe IPR.

Au-dessous du point de bulle, le gas sort de la solution et l'écoulement devient difficile qui provoque une diminution continue de l'indice de productivité.

_q ? p wf ? _p

? ?

^o _{1 0.2} ? _ ₀ . ₈ ?

_wf

= _ ? ?

_{o max} ? _r ? ? p _r ?

IV.1.3.2 La méthode de VOGEL

L'objectif principal de VOGEL était de simuler l'écoulement diphasique à travers un réservoir dans un trou foré.

Généralement on dit qu'un écoulement est diphasique lorsque la pression de réservoir est inférieure à la pression de bulle P_r < Pb .

VOGEL a établi une relation empirique qui caractérise ce type d'écoulement.

_{q p 2} IV3

: Le débit d'huile (STB/Day).

: La pression au fond du puits (psig).

Pression du réservoir moyenne ou la pression de bulle.

: Débit maximal qui correspond à , il peut être déterminé en utilisant les
données d'un test, c'est-à-dire pour un débit donné du test, nous avons :

?

qo

^ma^x

qo ?test?

¹ ? ⁰.² ? ? ? ⁰.⁸ ?

? p ? ?

? p^r? ? p^r ?

wf ? p

? wf ²

40

Chapitre IV : Performances du réservoir et du puits

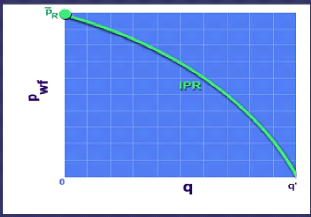
Figure IV 5:La courbe IPR de Vogel

Résultats de VOGEL sont seulement pour la partie incurvée dans la courbe IPR qui existe au-dessous du point de bulle.

Au-dessus du point de bulle, la courbe IPR est une ligne droite, nous pouvons obtenir sa forme, en tirant la tangente de la courbe à la pression de bulle, et l'étendant à la pression initiale moyenne du gisement.

IV.2 Vertical Lift Performance

La courbe de tubing (VLP) présente la capacité de l'installation et son influence sur l'écoulement en fonction des pertes de charge engendrées, elle a été tracée à partir des pressions de fond dynamiques calculées par l'une des corrélations de pertes de charge verticales pour différents débits liquides.

IV.2.1 Les régimes d'écoulements

Un certain nombre de différents régimes d'écoulement se produire lors de l'écoulement naturel dans les tubulures verticales. Afin de décrire chacun.

- liquide flow : Dans ce cas la pression à la base du tubing est supposée au-dessus du point de bulle, d'où le régime d'écoulement est monophasique.

- bubble flow : le mouvement montant du liquide est accompagné par réduction de pression, et que la pression descend au-dessous du point de bulle, les bulles de gas commencent à se former. Ces bulles glissés vers le haut dans la colonne.

- slug flow : Plus haut dans le tubing, la pression continue de baisser, plus le gas est libéré de solution et les plus grosses bulles croître régulièrement par les dépassements et coaliser avec les plus petits, comme ils se déplacent vers le haut, portent entre eux

41

Chapitre IV : Performances du réservoir et du puits

les gouttes d'huiles contenant des petites bulles de gas. C'est le régime le plus efficace.

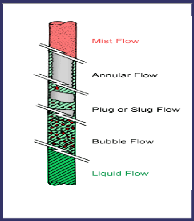
Figure IV 6:Les régimes d'écoulement

- annular flow : Plus élevé dans le tubing, à des pressions encore plus bas, le gas forme un canal continu dans le centre de la chaîne, et l'huile se déplace lentement vers le haut dans un anneau annulaire sur les parois internes du tube.

- mist flow : Enfin, si le tube a une longueur considérable de sorte qu'une baisse de pression importante a partir du bas vers le haut, l'annulaire de liquide se disparaître, ne laissant que le flux de gas entraînant un brouillard de gouttelettes de liquide.

IV.2.2 Les variables influençant sur les pertes de charges

Afin d'analyser et de concevoir nos systèmes de production, il est nécessaire de calculer la chute de pression qui existe entre le fond du puits et la surface lors de l'écoulement naturel. Le calcul de cette chute de pression pour toutes les conditions possibles est complexe.

Nous sommes obligés de compter sur des corrélations empiriques ou semi-empiriques. Ces corrélations tenir compte des sept variables importantes qui influent sur les pertes de charge d'un puits éruptif.

Ces variables sont : la taille de tubing, le débit, la viscosité du fluide, la densité du fluide, rapport gas-liquide (GLR), rapport eau-huile (WOR), et enfin, l'effet de glissement. Une autre variable est la déviation des puits verticaux.

Chapitre IV : Performances du réservoir et du puits

? taille de tubing

L'augmentation de diamètre provoque une diminution de perte de charge, Le schéma ci-dessous représente l'effet de taille de tubing sur les pertes de charge.

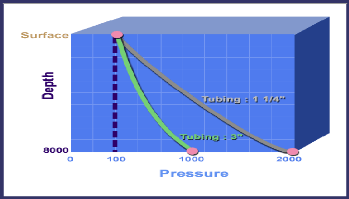
Figure IV 7:influence de la taille de tubing sur les pertes de charge

? la densité du fluide

L'augmentation de la densité du fluide faire augmenter les pertes de charge.

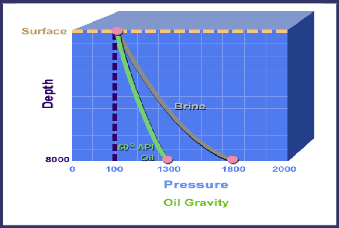
Figure IV 8:influence de la densité sur les pertes de charge

? La viscosité

Nous voyons que les grandes valeurs de la viscosité accorder une plus grande perte de charge, dû à l'augmentation de la pression de frottement.

42

43

Chapitre IV : Performances du réservoir et du puits

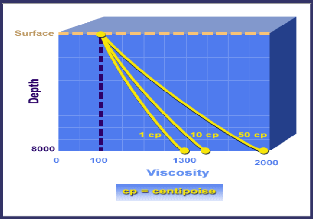
Figure IV 9:influence de la viscosité sur les pertes de charge.

? GLR :

L'augmentation de GLR accompagnée par une diminution des partes de charges.

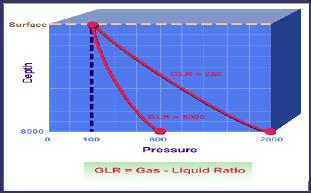
Figure IV 10: influence de GLR sur les pertes de charge

? WOR :

Comme le rapport eau-huile (WOR) croît, les pertes de pression dans le tubing augmentent également.

44

Chapitre IV : Performances du réservoir et du puits

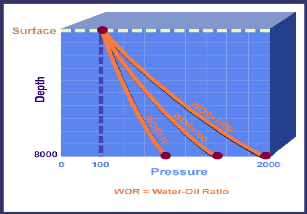
Figure IV 11:influence de WOR sur les pertes de charge

IV.2.3 Verticale corrélations flow

Maintenant que nous avons discuté les sept variables principales qui influent sur l'écoulement dans le tubing, nous devons examiner les différentes méthodes qui ont été développées pour calculer les pertes de charge, Il n'est pas surprenant que nos méthodes de prévision ne sont pas basés sur la solution exacte d'équations mathématiques, mais plutôt sur des relations empiriques ou semi-empirique.

Ces relations ont été développées en faisant certaines hypothèses sur les équations applicables à l'écoulement, et la collecte de données à partir d'un certain nombre du puits éruptifs dans des conditions contrôlées. Le résultat est la publication d'un ou plusieurs corrélations basées sur des bases mathématiques.

_{W ?qo .Pm}

IV.2.3.1 Corrélation de Poettman et Carpenter

Cette corrélation est développée à partir de l'équation générale de l'énergie, où le

mélange (huile, eau, gas) est considéré monophasique.

La corrélation de Poettman et Carpenter suppose que :

? L'effet de la viscosité est négligeable.

? Le terme d'accélération est négligeable (V= constante).

1) Une valeur moyenne pour le facteur de frottement le long du tubing.

La détermination des pertes de charge avec cette méthode est faite en utilisant des

abaques en termes de ñ et w.

(IV.4)

Chapitre IV : Performances du réservoir et du puits

Où : La masse volumique.

: Volume du mélange (huile, eau, gas). W : Débit massique du fluide.

_?1 ? _r

? ?? . ? ?

? ₁₄₄ ??

_{2 g.w.d}

_F ?

_{h ?h2?}

2) Le gradient de pression peut être exprimé comme suit :

_{10 5}

dP		?	F.W 2		? ?		(IV.5)
dh			7,413.10	.d ?

45

3) Le facteur de frottement :

(IV.6)

_4v

2?1

P1 : la pression à la profondeur h1.

P2 : la pression à la profondeur h2.

d : le diamètre de la conduite (tubing). V : la vitesse du fluide.

g : la gravité.

IV.2.3.2 Corrélation de Francher et Brown

Cette corrélation donne la plus petite valeur possible de VLP, car elle néglige les glissements de gas/liquide, il faut toujours prévoir une pression qui est inferieurs a la valeur mesuré.

Même si elle fait un bon match, Francher et Brown ne devrait pas être utilisée pour les travaux quantitatifs.

Chapitre IV : Performances du réservoir et du puits

q 1

? ?

_{q q}

l ? g

La procédure de calcul pour cette corrélation est la même que la méthode de Poettman et Carpenter, avec une petite modification sur la détermination de facteur de frottement.

Ils ont introduit l'effet de GLR sur le facteur de frottement pour :

300 < GLR < 1500 scf/bbl et 1500 < GLR < 3000 scf/bbl.

^FR g d

IV.2.3.3 Corrélation de Beggs et Brill

.

Beggs et Brill ont développé une corrélation de la perte de charge, qui est applicable pour les conduites horizontales de faibles diamètres 1" et 1"^1/2. Pour les problèmes d'écoulements inclinés et verticales, Beggs et Brill ont introduit un facteur qui prend en considération de l'inclinaison qui change de -90^° à +90^°

_N?

Elle surestime les chutes de pression dans les puits verticales et déviés.

Cette méthode est basée sur la détermination du régime d'écoulement qui dépend de :

1) hold-up des liquide sans frottement ë : .(IV.7)

2) nombre de Froude NFR :

Vm .(IV.8)

Où

V_m : vitesse superficielle de mélange. d : diamètre.

3) calcul des paramètres de correction :

L1 = 316. _ë0, 302 L2 = 0,1. ë-1,4516

L3 = 0,0009252. ë-2,4684 L4 = 0,5. ë-6,738 (IV.9)

4) sélection de régime d'écoulement :

Tableau IV 1:régime d'écoulement

Régime d'écoulement Limites

Ségrégation X < 0.01 et NFR = L1

ou X < 0.01 et NFR = L1

Transition X < 0.01 et L2 < NFR < L1

Intermittent 0.001 < X < 0.4 et L3 < NFR < L1

ou X < 0.4 et L3 < NFR < L4

Distribution X < 0.4 et NFR < L1

ou X > 0.4 et NFR > L4

46

Chapitre IV : Performances du réservoir et du puits

5) calcul de facteur de correction d'inclinaison :

(IV.10)

Avec :

Tableau IV 2:facteur de correction d'inclinaison

Ecoulement	d	e
Ségrégation	0.011	-3.768
Intermittent	2.960	0.3050

f g

3.5390 -1.614

_{0, 8725 ln Y+ 0, 01853 ln}

( )4

-0.4473 0.0978

_S

?

-

NB : pour l'écoulement de distribution C=O.

_{ln Y}

[ ( ) ]2

_{HL o}

6) Calcul des facteurs de correction du Hold-up :

ø = 1 + c x [ sin (1.8 xè ) - 0.333 sin ³ (1.8xè ) ] (IV.11).

Pour tubing vertical ø = 1 + 0.3X c

_{0,0523+ 3,182lnY-}

( ) 2

7) Calcul de liquide hold-up : HL(è) = HL(0) X ø .(IV.12)

8) Calcul le rapport de friction : FTP / FNS = e^s (IV.13)

Avec

_Y?

₂

_Y

9) 47

Calcul du facteur de frottement sans glissement : ₁

? _N ?

_{2 log} ? _{log N 3. 8215}

F TP = 2

₁

? _?(IV.14)

_j

?

?

?

? _{4, 5223} ?

F NS

_RE

RE _

_{F F}

_{NR TP}

10) Calcul du facteur de frottement pour les deux phases : _FTP ?

.

(IV.15)

Chapitre IV : Performances du réservoir et du puits

11) Le gradient de pression :

AP ?

^AH

.(IV.16)

^{F G V}

^{TP m m}

^1	^PTP ^V V	^m sg

^PTP +

²

^gd

48

^g.p

Où :

: vitesse superficielle.

IV.2.3.4 corrélation Hagedorn et Brown

La corrélation de Hagedorn et Brown est probablement la corrélation VLP la plus

largement appliquée. Elle fonctionne bien pour bubble et slug régimes d'écoulement dans une

large gamme d'applications. À des faibles débits, elle sous-prédit les pressions. Cela peut

entraîner des prévisions optimistes pour un minimum de débit stable.

Holdup=l'aire occupée par le liquide/la section de pipe.

? Hagedorn et Brown a constaté le holdup de liquide pourrait être corrélée à quatre

paramètres sans dimension :

_NLV ? _1.938 VSL?L ?4

_NGL ? _1.938 VSG L

? _?4

_Nd ? 120.872 L

d L

? _?2

_NL ? 0.15726 1 LL

_L ? _?4

_VsL ? _ft/sec

_L ? _lbm/ft3

₁

_L

Nombre de vitesse de liquide.

_VsG ? _ft/sec

₁

_L

Nombre de vitesse de gas.

₁

Nombre de diamètre de la pipe.

₁

₃

Nombre de viscosité liquide.

_L ? _dyne/cm

? Les expressions ci-dessus sont sans dimension lorsque les paramètres ci-dessous sont

exprimés en unités pratique suivants :

Vitesse superficielle du liquide

Vitesse superficielle du gas

Densité de Liquide

Tension Interfacial

Chapitre IV : Performances du réservoir et du puits

Viscosité de Liquide

Diamètre de Pipe

? Le liquide comprend à la fois l'huile et l'eau, donc la question qui se pose est du calculer les propriétés de mélange. Dans cette corrélation on utilise la moyenne pondérée approche :

? les débits fractionnaires de l'huile et de l'eau sont définis comme suit :

? _dP ? _g

? l ?

p _s =plhl +pg

? La fonction de corrélation est inscrite d'une valeur de CNL. Le nombre de liquide corrigé est lu à partir d'un graphique CNL vs NL.

? Une fois les facteurs de correction ont été déterminés, le holdup est calculé.

? À cause de changement d'altitude (terme de gravité) le gradient de pression est calculée à partir de :

?? ? ? _{l l}

_h ? ?

? _{dL ?g}

_{Gravity c}

₁ ? _h

_dP ? V ²

? ? _{f m}

?? ? _f

? _{dL ?2 g d}

_{Friction c}

p _n =plAl +pg(1_Al)

_VM ? _VSL ? VSG

^f p _g

- Le gradient de pression due à la friction est donné par :

.(IV.17)

?

_p

Où :

_p

49

(1--hl)

V SL

^l V

? ?

_M

Chapitre IV : Performances du réservoir et du puits

- Le gradient de friction est écrit en termes de débit massique (W) comme suit :

.(IV.18)
- Cette expression se simplifie en :

?

n

Vd _N? Re ? s

Où : (IV.19)

W= débit massique lbm/Day

s= densité basée sur le holdup de liquide lbm/ft3

d= diamètre intérieur de pipe feet

f=facteur de friction de deux phases dimension

- Le coefficient de frottement en deux phases est corrélé avec le nombre de Reynolds à

deux phases en utilisant le schéma standard de Moody.

_m

- Le nombre de Reynolds à deux phases est défini comme suit :

? _dP ( )

? _{p V}

_{s m}

??

? dL JAcceleration 2gdL

(IV.20)

Où :

L'accélération est donnée par :

_dL ? _dP ?

_p ( V ² )

_{s m}

₂

_A

_c

(IV.21)

g c

- Où Vm est la différence de la vitesse de mélange entre les extrémités de l'entrée et la sortie d'un élément de pipe. Le gradient d'accélération est appliqué comme une correction (Ek) à la somme de la gravité et des gradients de friction comme suit :

_E=

^K dP ?? dL ??

_{2 A dp} (IV.22)

? _dP ?

?? ?
? _{dL ?1 ?E}

_Total

(IV.23)

??

? dL ?Gravity

??

? dL ?Friction

- la chute de pression totale est calculée à partir de :

? _dP ?

? _dP ?

50

51

Chapitre IV : Performances du réservoir et du puits

Les améliorations suggérées par Brill et Hagedorn ont été mises en oeuvre dans PROSPER :

L'expérience a montré que Hagedorn et Brown donne d'excellents résultats pour les puits de pétrole en bubble et slug flow.

IV.2.3.5 Corrélation de Petroleum Experts

Cette corrélation combine les meilleurs caractéristiques des corrélations existant, il utilise la corrélation de Hagedorn-Brown dans le régime slug flow.

IV.3 Le point de fonctionnement du puits

Il suffit de tracer sur le même graphique, la réponse du réservoir, et la réponse du tubing. Ces deux courbes se coupent en un point qui est le point de fonctionnement du puits (couplage particulier d'un réservoir et d'une complétion) caractérisé par un débit et une pression de fond dynamique (Q, Pwf).

Il change selon un changement dû à l'un des paramètres qui caractérisent le réservoir ou le tubing, puisqu'il est sensible à certains paramètres.

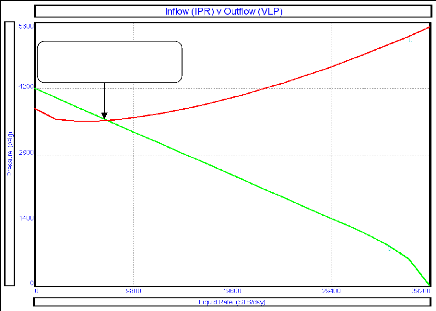
Le point de
fonctionnement

Figure IV 12:Inflow + Outflow performances

Chapitre IV : Performances du réservoir et du puits

IV.4 PETROLIUME EXPERT PROSPER

IV.4.1 Définition

Le PROSPER (PROduction and Systems PERformance) est un logiciel d'analyse de Performance des Systèmes de production.

PROSPER peut aider les ingénieurs de production ou de réservoir pour prédire l'écoulement et la température dans les tubings et les pipelines avec exactitude et vitesse. Les calculs de sensibilité que PROSPER nous offre permettent aux designs existants d'être optimisés, et l'influence des futurs changements sur les paramètres du système considéré.

En séparant la modélisation de chaque composant du système de production, PROSPER permet ainsi à l'utilisateur de vérifier chaque modèle de sous-système par le biais de la fonction matching, PROSPER assure que les calculs sont aussi exacts que possible. Une fois un modèle du système a été réglé aux vraies données de champ, PROSPER est utilisé avec confiance pour modeler le puits dans les différents scénarios, et faire les prédictions avancées de pression de réservoir basées sur les données de la production de surface.

52

Chapitre IV : Performances du réservoir et du puits

IV.4.2 L'organigramme de fonctionnement de PROSPER

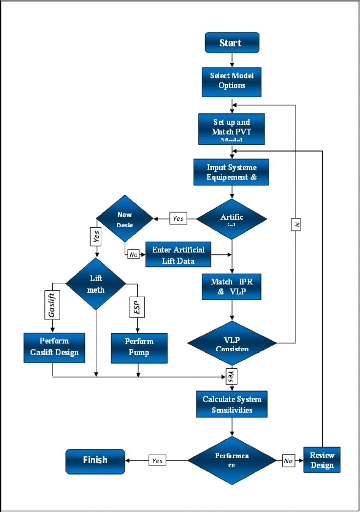
Figure IV 13:L'organigramme de fonctionnement de PROSPER

53

54

Chapitre V : Modalisation et Optimisation