Conception et dimensionnements d'un système porte source neutronique PuBe par le code de simulation Monte-Carlo (MCNP)

DEPARTEMENT : PHYSIQUE

MEMOIRE DE MASTER

DOMAINE : SCIENCE DE LA MATIERE
FILIERE : PHYSIQUE

SPECIALITE : PHYSIQUE DU RAYONNEMENT

Thème

Conception et dimensionnements d'un système porte source neutronique PuBe par le code de simulation Monte-Carlo

(MCNP)

Présenté par : Dirigé par :

SALHI ABIR Dr. MESSAI ADNANE
AZZOUZ NOUR EL HOUDA

Promotion : 2021/2022

Nous tenons avant tout à remercier Allah qui nous a donné la force et le courage pour la réalisation de ce mémoire.

Ce travail a été réalisé au sein du Centre de Recherche Nucléaire de Birine
(CRNB), à cet effet, nous tenons à remercier le Directeur Général du
centre, pour nous avoir donné l'occasion de réaliser ce stage et de mener à
terme nos travaux de mémoire.

Nous remercions notre encadreur Mr. Messai Adnane pour avoir dirigé
notre travail, pour tous ses précieux conseils, pour son écoute active et sa

disponibilité.

Nous remercions également madame Titouche Widad de nous avoir
toujours aidés depuis que nous sommes venus, nous la remercions de sa
patience, sa gentillesse et pour le temps qu'elle nous a accordé. Merci
beaucoup monsieur MAKOUDI Brahim pour toute l'aide et le discours
motivant Nous remercions particulièrement tous nos enseignants de
l'UFAS, et surtout notre responsable madame BOUKHENFOUF.

Nous remercions les membres du jury qui ont bien voulu examiner notre

travail.

Enfin, nous tenons à remercier tous ceux qui, de près ou de loin, ont
contribué à la réalisation de ce travail*

ABIR

Je dédie ce mémoire :

A ma grand-mère décédée « Salakji Zineb », qui était la raison pour laquelle je suis arrivé à ce jour, grâce à ses prières et ses voeux de succès.

A mon très cher père « Fayçal » Ton soutien fut une lumière dans tout mon
parcours. À ma chère mère « Houria » la lumière de mes yeux, qui était un
soutien pour moi et qui n'a jamais cessé de me soutenir, et de prier pour mon
succès dans tout ce que je veux

Aucune dédicace ne saurait exprimer l'amour l'estime et le respect que j'ai
toujours eu pour vous.

A mes soeurs « Riham et Ibtihel » et mon petit frère « Ahmed El Walid » pour leur tendresse, leur complicité et leur présence près de moi

A mes tantes et mes oncles de la famille Salhi et Aichour.

A mes proche « Hanine et Assala » pour leur amour et leur soutien constant, A « Habib Ramzi » qui m'as toujours encouragé, à faire de mon

mieux, son soutien m'a permis d'atteindre mes objectifs.

A tous mes collègues « Fouad, Amine, Zinedine, Nadjlaa, Sofia... ».

Avec l'expression de ma reconnaissance, je dédie ce modeste travail à
ceux qui, quels que soient les termes embrassés, je n'arriverais jamais
à leur exprimer mon amour sincère.

A l'Homme, mon précieux offre du dieu, qui doit ma vie, ma réussite
et tout mon respect : mon cher père « SACI ».

A la femme qui a souffert sans me laisser souffrir, qui n'a jamais dit
non à mes exigences et qui n'a épargné aucun effort pour me rendre
heureuse : mon mère « NOUARA ».

A vous mes frères « AYOUB et YOUNES » et ma grande
soeurs « WAHIBA » qui m'avez toujours soutenu et encouragé
durant ces années d'études.

A ma petite soeur « MARAM » la joie de mon coeur et la source de
bonheur, je te souhaite une vie pleine de joie de bonheur et de santé.

A tous mes amis de promotion de master en physique de rayonnement
toute personne qui occupe une place dans mon coeur.

Enfin et surtout, je tiens à me remercier pour tous les efforts que j'ai
fournis lors de ce stage et pour toutes les difficultés et pressions
auxquelles j'ai dû faire face.

Nour El Houda

Table de matière

INTRODUCTION GENERALE 1

CHAPITRE I : LES NOTIONS DE LA RADIOPROTECTION

I. INTRODUCTION 3

I. 1. Notions préliminaires 3

I.2. Les Principes de la radioprotection 4

I. 3. Les effets nocifs de la radioactivité 4

I. 4. Mesures et unités de la radioactivité 5

I. 5. Notion de dose et le débit de dose 5

I. 5. 1. La dose absorbée 6

I. 5. 2. Le débit de dose 6

I. 5. 3. La dose équivalente 6

I.5. 4. La dose ambiante 7

I. 6. Les limites de dose 7

I. 7. Les moyens de la radioprotection 8

I. 8. Conclusion 9

CHAPITRE II: INTERACTION NEUTRON-MATIERE

II. INTRODUCTION 10

II.1 Définitions et notions préliminaires 10

II. 2. Types d'interactions neutron-matière 11

II. 2. 1. Diffusions des neutrons 12

II. 2. 1. a. Diffusion élastique (n, n) 12

II. 2. 1. b. Diffusion inélastique (n, n') 12

II. 2. 2. Absorption des neutrons 13

II. 2. 2. a. Réactions de capture radiative (n, ã) 13

II. 2. 2. b. Réactions de transmutation (n, p) ou (n, á) 14

II. 2. 2. c. Réactions de type A (n, xn) A [x= 2, 3 ...] 14

II. 2. 2. d. Réaction de fission (n, fission) 14

II. 3. Notion de section efficace

............ . 15

II. 3. a. Section efficace microscopique 16

II. 3. b. Section efficace macroscopique 16

II. 4. Notion du libre parcours moyen ..... 18

II. 5. L'atténuation des neutrons...... 19

II. 6. Les sources des neutrons ...... 19

II. 6. a. Les réacteurs nucléaires 19

Table de matière

II. 6. b. Les sources radio-isotopiques 19

II. 6. c. Les accélérateurs de particules 22

‡U.7. Conclusion 22

CHAPITRE ‡V : CODE DE SIMULATION MONTE-CARLO (MCNP)

III. INTRODUCTION 23

III. 1 Aperçu général du code de simulation Monte Carlo 23

III. 2. Présentation du code MCNP 23

III. 2. 1. Structure du fichier d'entrée 23

III. 2. 1. a) Définition des cellules [23] 25

III. 2. 1. b) Définition des surfaces [23] 26

III. 2. 1. c) Données physiques [23] 28

III.5. Conclusion 30

CHAPITRE ‡W: MODELISATION DU DISPOSITIF PORTE-SOURCE NEUTRONIQUE

IV.INTRODUCTION 31

IV. 1. Présentation du dispositif Porte-source 31

IV. 2. La modélisation du système par le code MCNP5 32

IV. 2. 1. Elaboration du fichier d'entrée 32

IV. 2. 1. a) Modélisation Géométrique 32

IV. 2. 1. b) Données de matériaux dans MCNP5 34

IV. 2. 1. c) Paramètres de calculs 34

IV. 3. Etude de la dose par le code MCPN5 34

IV. 3. 1. Choix du matériau de la structure 34

IV. 3. 2. Dimensionnement du dispositif avec parois en Aluminium 35

IV. 4. Calcul du poids du dispositif porte source 37

IV. 5. Conclusion 38

CONCLUSION GENERALE 39

LES REFERENCES

Listes Des Figures

Figure 1: la pénétration des rayonnements ionisant 14

Figure 2: l'expérience de J. Chadwick 22

Figure 3 : les types d'interactions neutron-matière. 24

Figure 4 : Diffusion élastique . 24

Figure 5 : Diffusion inélastique 25

Figure 6 : Réactions d'absorption 25

Figure 7: La fission d'un noyau d'uranium 235 27

Figure 8 : Définition de la section efficace macroscopique 29

Figure 9 : schéma représente la source neutronique 32

Figure 10 : spectre d'énergie des neutrons de la source ²³⁸Pu-Be (á, n) 33

Figure 11 : Schématisation du fichier input du code MCNP 37

Figure 12 : interface Vised. 38

Figure 13 : Forme du dispositif pour une épaisseur de paraffine de 5 cm 46

Figure 14 : modèle MCNP5 du dispositif porte-source 47

Figure 15 : modèle de volume entourant le dispositif porte source. 47

Figure 16 : Débit de dose en fonction du matériau de structure. 49

Figure 17 : la dose en fonction la distance 50

Figure 18 : poids du dispositif en aluminium en fonction de l'épaisseur de la paraffine 52

Liste Des Tableaux

Tableau 1 : facteur de pondération radiologique (IAEA) 18

Tableau 2 : Classement des neutrons selon leur énergie cinétique 23

Tableau 3 : énergies seuils réactions (n, 2n). 26

Tableau 4 : comparaison du section efficace 29

Tableau 5 : récapitulatif de certaines surfaces. 40

Tableau 6 : les valeurs de Débit de dose en fonction du matériau de structure. 49

Introduction Générale

1

Introduction générale

Introduction Générale

L'une des sources énergétiques prometteuse de nos jours est l'énergie nucléaire. Celle-ci n'a cessé de susciter l'intérêt sur tous les plans de la vie courante à savoir : La génération d'électricité, la médecine nucléaire, l'agriculture, les opérations industrielles et l'alimentation, ...etc. Malgré cette multitude d'applications, l'utilisation de cette ressource reste néanmoins porteuse de risques et d'effets nocifs pour les individus et l'environnement si des mesures de précautions et de sureté ne sont pas prises.

En effet, les radiations qui émanent de la matière nucléaire, tels les rayonnements Gamma, les rayonnements X (RX), les neutrons, les particules chargées ou autres sont des radiations énergétiques ionisantes qui peuvent traverser le corps humain et ont des effets très nocifs sur la santé pour des durées d'exposition longues ou répétées et/ou pour de fortes intensités. Les lésions biologiques et effets néfastes ainsi provoqués varient selon le type et l'énergie de radiation considérée, elles sont généralement plus sévères avec les neutrons qu'avec, les RX ou les rayons gamma [1].

A partir de là, on voit bien que dans le domaine de l'industrie nucléaires, les travailleurs pouvant être soumis à ces rayonnements ionisants lors de leur activité, doivent impérativement se munir des dispositifs permettent leur protection contre toute dose supérieure à la norme tolérée. Cette protection peut être mise en oeuvre à travers plusieurs moyens et méthodes. L'une des méthodes la plus simple consiste par exemple en la mise d'un ou plusieurs écrans entre la source de rayonnements et les personnes concernées.

Le travail décrit dans ce mémoire, est une contribution pour la mise en oeuvre d'un moyen de protection du personnel, activant autour du réacteur sous-critique au CRNB, contre les effets néfastes du rayonnement neutronique provenant d'une source radioactive artificielle de type Pu-Be. Il sera question d'une étude à travers laquelle on va procéder au dimensionnement d'un dispositif porte source neutronique qui va permettre le déplacement de la source neutronique de son endroit de confinement vers le réacteur sous-critique, là où vont se dérouler les expériences de la physique nucléaire en toute sécurité. Suite à cela, ce manuscrit sera divisé en quatre chapitres différents.

Un premier chapitre sera dédié aux notions préliminaires de la radioprotection. Ces

notions nous ont été d'un grand apport lors du processus d'identification et de quantification des risques que peuvent engendrer les radiations et minimiser leurs conséquences sur le public

2

Introduction générale

et les opérateurs. Lors du deuxième chapitre, on présentera les notions théoriques de bases liées aux interactions du neutron avec la matière. Quant au troisième chapitre, celui-ci portera sur les outils de simulation de l'interaction du rayonnement ionisant avec la matière. L'accent sera particulièrement mis sur le code de simulation des processus nucléaires utilisé dans ce travail : MCNP. Le quatrième chapitre, sera consacré à la description et la modélisation du dispositif porte source neutronique. On exposera ainsi les résultats et les interprétations de simulations obtenus à l'issue du travail réalisé.

Le rapport sera clôturé par une conclusion générale lors de laquelle nous évaluerons les résultats finaux de l'ensemble des tâches menés au cours de ce projet de fin d'étude. Ladite conclusion inclura également un ensemble de propositions pour des améliorations et des extensions futures du système déjà réalisé.

Chapitre I : Les notions de la

Radioprotection

Chapitre I Les notions de la radioprotection

I. Introduction

Au cours de ce chapitre, nous essayerons de survoler les notions de base de la radioprotection ou protection contre les rayonnements ionisants et voir quelles sont les moyens de protection qui doivent permettre de réduire les expositions subies par les travailleurs et l'environnement au niveau le plus faible que l'on puisse raisonnablement atteindre. Les concepts qui seront acquis lors de ce chapitre nous permettrons d'assimiler le cahier des charges et les prérequis du système à réaliser au cours de ce PFE [2].

I. 1. Notions préliminaires

Tout équipement ou toute installation mettant en oeuvre de l'énergie nucléaire doit faire l'objet d'une approche de radioprotection. En effet, un tel milieu ionisant (voir figure 1) peut avoir des effets néfastes pour l'être humain et l'environnement. Prendre toutes les mesures et assurer le respect de toutes les précautions pour garantir la protection des personnes et de l'environnement constitue l'objectif de la radioprotection.

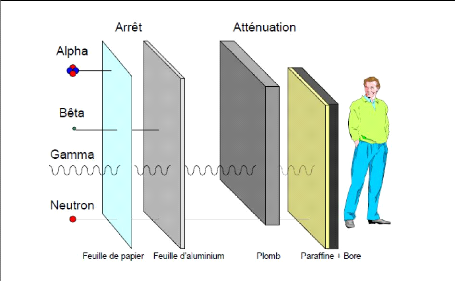
3

Figure 1: la pénétration des rayonnements ionisant [3].

Chapitre I Les notions de la radioprotection

4

‡T.2. Les Principes de la radioprotection

La radioprotection repose sur trois (03) principes fondamentaux, émis par la Commission Internationale de Protection Radiologique (CIPR), inscrits dans le code de la santé publique [4] :

a) Le Principe d'optimisation Le niveau des expositions des populations et des individus aux rayonnements ionisants doit être maintenu au plus bas niveau que l'on peut raisonnablement atteindre. Afin d'optimiser les expositions, on peut agir à la fois sur la source de rayonnements, les conditions de travail des intervenants et les conditions d'exposition [5].

b) Le Principe de justification Prévoit qu'une activité nucléaire ne peut être entreprise que si elle est justifiée par les avantages qu'elle procure, notamment en matière sanitaire, économique ou scientifique [6].

c) Le Principe de limitation Il faut éviter les effets dits déterministes, qui apparaissent à coup sûr au-dessus d'un certain seuil élevé d'exposition à la radioactivité [7].

Pour appliquer ces principes, la radioprotection met en oeuvre des moyens réglementaires et techniques spécifiquement adaptés à trois types de populations exposées : le public, les patients et les travailleurs.

I. 3. Les effets nocifs de la radioactivité

Lorsque nous parlons de la radioactivité et de ses conséquences sur l'homme, nous pensons directement à deux concepts importants : L'irradiation et la contamination.

a) L'irradiation Résulte directement d'une exposition externe à des rayonnements ionisants. Son effet s'arrête au moment où on s'éloigne de la source. Le rayonnement peut être mortel (létal) selon le niveau d'exposition.

b) La contamination Consiste à déposer ou à inhaler un produit radioactif. Dans ce cas, la radioactivité reste constante et durable jusqu'à l'élimination de la source de contamination. Les effets peuvent être plus ou moins néfastes pour la santé. On peut les classifier en deux catégories :

Ø Les effets déterministes

Ils se produisent dans le cas d'une exposition unique à fort débit de dose. Les rayonnements peuvent altérer le fonctionnement des tissus ou des organes et produire des effets aigus tels que rougeurs de la peau, perte des cheveux ou brûlures radiologiques. Ces effets deviennent plus sévères lorsque la dose augmente.

Ø Chapitre I Les notions de la radioprotection

5

Les effets à incidences aléatoires ou stochastiques

Ils se produisent dans le cas d'une exposition d'irradiation faible inférieure à la valeur seuil. Si la dose est faible et diffusée sur une longue période, le risque est considérablement plus faible car la probabilité de réparation des lésions est plus grande. Mais il y a toujours un risque d'effets à long terme, comme le cancer. Ces effets ne se produisent pas toujours, mais leur probabilité repose sur la dose.

I. 4. Mesures et unités de la radioactivité

Ø Le Becquerel (Bq) est l'unité de mesure de la radioactivité d'un corps. Elle caractérise le nombre de désintégrations spontanées de noyaux d'atomes instables qui s'y produit par seconde. Plus l'activité d'un élément instable est forte, plus sa radioactivité est puissante.

1Bq = 1 désintégration par seconde

Si une personne se trouve dans une pièce où sont présents des atomes instables, seule une partie de la radioactivité ambiante l'atteindra. Cette partie est exprimée par l'unité « Gray ». Le Gray (Gy) est l'unité qui permet de mesurer la quantité de rayonnement absorbé par un corps exposé à de la radioactivité.

Ø Le Sievert (Sv) est utilisé pour exprimer les effets biologiques des rayonnements ionisants sur la matière vivante.

Il est également nécessaire de comprendre que les effets de la radioactivité sur les tissus vivants, à dose absorbée égale (mesurée en Gray), varient significativement suivant la nature du rayonnement incident. Par exemple, l'impact du rayonnement alpha, à énergie égale, est le double de celui des rayonnements bêta et gamma.

I. 5. Notion de dose et le débit de dose

Lorsque les rayonnements ionisations traversent la matière, ils interagissent avec celle-ci en cédant tout ou une partie de leur énergie. Définir les quantités de rayonnement absorbées par la matière c'est définir la dose reçue par celle-ci.

Chapitre I Les notions de la radioprotection

6

‡T. 5. 1. La dose absorbée

On définit cette dose comme l'énergie déposée par les rayonnements dans un échantillon de matière [8].

dW??

D = d?? (En Gray ou Rad). (1)

Où Wa : est l'énergie déposée dans l'échantillon ; m : la masse de la matière considérée.

I. 5. 2. Le débit de dose

Lorsque le facteur temps est pris en compte, la mesure de la quantité de rayonnement absorbée est appelée « débit de dose » il est notéb.

?
·D= dd?D???? (En Gy/h) (2)

Où D : est l'énergie déposée dans l'échantillon, t : Le temps d'exposition. ‡T. 5. 3. La dose équivalente

Il faut savoir que tous les rayonnements ne produisent pas les mêmes effets. Si l'énergie est cédée dans un petit volume de tissu, la nuisance sera plus grande que si cette même énergie est cédée sur une plus grande distance. Le rayonnement alpha (a), dont le parcours moyen dans

la matière vivante est d'environ 40 um est a priori plus nocif que le rayonnement gamma (y) qui n'est que partiellement arrêté par l'homme. Le concept de dose équivalant permet d'exprimer ces deux effets, en tenant compte d'un facteur de nocivité de rayonnement R, et la dose équivalente est donnée par l'équation [9] :

HT,R= E_R WRDT,R (3)

Où DT,R : est la dose absorbée à l'organe T par l'irradiation R ;

WR : est le facteur de pondération du rayonnement.

Donc on dit que la dose équivalente totale est la somme de toutes les doses équivalentes ( HT, R) pour tous les types de rayonnements. Dans le tableau ci-dessous, on donne une idée sur l'ordre de grandeurs du facteur de pondération du rayonnement pour quelques particules ionisantes selon le type et la gamme d'énergie.

Chapitre I Les notions de la radioprotection

7

Type et gamme d'énergie	WR
Photons : toutes les énergies	1
Electron : toutes les énergies	1
Neutrons : énergie <10 KeV	5
Neutrons : énergie 10 KeV à 100 KeV	10
Neutrons :>100 KeV à 2 MeV	20

Tableau 1 : facteur de pondération radiologique (IAEA) [8].

?.5. 4. La dose ambiante

L'équivalent de dose ambiant est la quantité de dose dans une zone. Elle porte le symbole H* (10).

L'unité SI de H* (10) est le sievert (Sv).

?.6. Les limites de dose

Pour garantir la sûreté des travailleurs exerçant autour des installations nucléaires, leurs expositions aux rayonnements ionisants doit être surveillée de sorte que les limites de doses de dose admissibles ne doivent en aucun cas être dépassées. A titre d'exemple, si on veut surveiller les doses reçues par les individus durant une période assez importante, l'une des normes [10] stipule que les doses reçues ne doivent pas dépasser les limites suivantes :

§ Une dose efficace de 20 mSv par an en moyenne sur cinq années consécutives,

§ Une dose efficace de 50 mSv en une seule année,

Et dans le cas où on veut surveiller les travailleurs durant une heure de temps la limite de dose sera de 10uSv/h.

· dose équivalente au cristallin de 150 mSv en un an,

· dose équivalente aux extrémités (mains et pieds) ou à la peau de 500 mSv en un

an.

En ce qui concerne les apprentis âgés de 16 à 18 ans, et qui suivent une formation à un emploi comportant une exposition aux rayonnements ionisants, l'exposition professionnelle doit être maîtrisée de sorte que les limites ci-après ne soient pas dépassées :

§ dose efficace de 6 mSv en un an,

§ dose équivalente au cristallin de 50 mSv en un an,

Chapitre I Les notions de la radioprotection

8

Par contre l'exposition de personnes du grand public ne doit pas dépasser les limites suivantes :

· Une dose efficace de 1 mSv en un an.

Dans des circonstances particulières, une dose efficace allant jusqu'à 5 mSv en une seule année est admissible à condition que la dose moyenne sur cinq années consécutives ne dépasse pas 1 mSv par an.

Les limites de dose fixées ci-dessus ne s'appliquent pas aux personnes du public qui contribuent volontairement aux soins donnés à des patients subissant une exposition à visite. La dose reçue par ces personnes adultes doit néanmoins être maintenue à un niveau tel qu'il soit peu probable qu'elle dépasse 5 mSv pendant toute la durée de l'acte médical.

‡T. 7. Les moyens de la radioprotection

On sait déjà que la dose absorbée par un individu est le résultat du produit du débit de dose par le temps de présence aux alentours de la source considérée. Donc on voit bien que la protection contre l'exposition externe est en général garantie avec le respect d'une combinaison des trois paramètres suivants :

Ø Eloigner au maximum les personnes de la source des rayonnements,

Ø Diminuer autant que possible la durée d'exposition aux rayonnements,

Ø Placer entre la source et les personnes exposées un ou plusieurs écrans de protection appropriés à la nature des différents rayonnements ionisants. Ces paramètres peuvent être résumés de la manière suivante :

· La distance : S'éloigner de la source de rayonnements, car leur intensité diminuée avec la distance.

· Le temps : Plus la durée de l'exposition est courte, plus la dose de rayonnement est réduite.

· Le blindage : Le blindage permet d'arrêter ou atténuer les rayonnements ionisants. Il est utilisé pour protéger les personnels travailleurs des rayonnements ionisants. Les matériaux utilisés pour ce type de protections sont soit des absorbants soit des modérateurs de particules énergétiques.

Pour ce qui est du travail adressé dans ce mémoire, nous nous sommes basés sur le principe du blindage pour la mise au point du dispositif « porte source ». C'est ainsi que nous contribuerons à l'amélioration de l'aspect sûreté et protection des opérateurs et des

Chapitre I Les notions de la radioprotection

9

étudiants travaillant aux alentours de la source neutronique du réacteur sous-critique du CRNB.

I. 8. Conclusion

Lors de ce chapitre, on a abordé plusieurs notions de la radioprotection. Ces notions ainsi que les grandeurs qui leurs sont liées vont être abondamment utilisés pour le développement du travail à décrire tout au long de ce rapport.

Chapitre II : Interaction Neutron-

Matière

Chapitre II interaction Neutron-Matière

10

II. Introduction

Le but essentiel du travail à réaliser est de concevoir un dispositif qui puisse alléger voire arrêter un faisceau neutronique, provenant d'une source artificielle assez puissante. Ceci a pour effet d'éviter que ces neutrons atteignent les organes humains et provoques ainsi des lésions qui peuvent parfois être fatales pour le personnel exerçant aux alentours de cette source. Donc il apparait bien qu'un passage théorique sur les modes d'interaction du neutron avec la matière serait d'une grande utilité pour nous, surtout pour ce qui est du choix des matériaux qui vont être utilisés pour la construction du dispositif.

II.1 Définitions et notions préliminaires

Le neutron est une particule neutre qui compose le noyau des atomes avec les protons. C'est une particule dont la charge électrique totale est nulle et la masse est voisine de celle du proton (1.675×10^-27 kg). Il a été découvert dans l'une des expériences du chercheur britannique James Chadwick en 1932. Là où il a bombardé la cible du Béryllium (Be) par des particules alpha d'un émetteur radioactif. La réaction nucléaire mise en jeux dans cette expérience peut être exprimée par :

?? + ?????? ??

?? ???? ?? ? ????

???? + ???? (4)

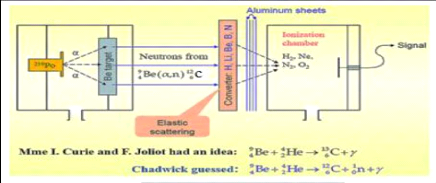
Figure 2: l'expérience de J. Chadwick [11].

Chapitre II interaction Neutron-Matière

11

Alors que le nombre de protons d'un noyau détermine son élément chimique, le nombre de neutrons détermine son isotope. Les neutrons liés dans un noyau atomique sont en général stables mais les neutrons libres sont instables : ils se désintègrent en un peu moins de 15 minutes.

j

jn

^?? ? ??p

?? + _ ??e (5)
Aussi, on ne peut aborder le contexte des neutrons et leurs modes d'interaction avec la matière sans passer par la notion de la classification énergétique de ceux-ci. En effet, les neutrons sont généralement classifiés selon leurs énergies cinétiques. Il existe Plusieurs classifications plus ou moins semblables. Le tableau suivant nous donne une idée sur le classement énergétique des neutrons :

catégorie		L'énergie cinétique	Les neutrons rapides
EC > 0.8 MeV		Les neutrons épi thermiques
1 eV < EC < 0.8 MeV		Les neutrons thermiques
EC < 1eV

Tableau 2 : Classement des neutrons selon leur énergie cinétique [12].

II. 2. Types d'interactions neutron-matière

Dépendant de la gamme des énergies considérées, les réactions des neutrons avec la matière sont souvent classifiées de la manière suivante :

Chapitre II interaction Neutron-Matière

12

Figure 3 : les types d'interactions neutron-

matière.

II. 2. 1. Diffusions des neutrons

La réaction de diffusion se produit lorsqu'un neutron vient heurter un noyau au repos. Ce dernier émet un neutron unique qui peut être diffèrent du neutron initial. La diffusion peut être élastique ou inélastique et dans les deux cas elle permet de ralentir les neutrons.

II. 2. 1. a. Diffusion élastique (n, n)

Dans une réaction de diffusion élastique entre un neutron et un noyau cible, il n'y a pas d'énergie transmise pour une excitation nucléaire. Le moment et l'énergie cinétiques sont conservés.

?? + ???? ??

??n ?? ? ??n

?? + ???? (6)

Figure 4 : Diffusion élastique [13].

II. 2. 1. b. Diffusion inélastique (n, n')

Dans une réaction de diffusion inélastique, le neutron incident est absorbé par le noyau cible pour former un noyau composé. Ce dernier va se désexciter en émettant un nouveau neutron moins énergétique, et un photon ã. La somme de l'énergie cinétique du neutron émis, celle du noyau cible et de l'énergie du photon gamma est égale à l'énergie cinétique du neutron

Chapitre II interaction Neutron-Matière

13

incident.

????

?? + ????

?? -- ????'

?? + ??*

?? -- ????'

?? + ????

?? +y (7)

??

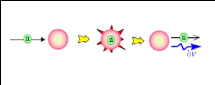
Figure 5 : Diffusion inélastique [13].

Il souligner le fait que durant la diffusion les neutrons perdent de l'énergie et ralentissent dans la matière. Cet aspect s'avère être très intéressant dans le contexte de ce travail. Nous cherchons à ralentir les neutrons à travers un obstacle physique afin que celui-

ci n'atteigne pas les personnes opérant autour des sources radioactives. De ce fait, il apparait très clair que l'utilisation les personnes opérant autour des sources radioactives. De ce fait, il apparait très clair que l'utilisation des matériaux diffuseurs de neutrons pour la construction du dispositif est un choix adéquat à prendre en charge.

II. 2. 2. Absorption des neutrons

La plupart des réactions d'absorption résultent de la capture d'un neutron accompagnée de l'émission d'une particule chargée, d'un ou plusieurs neutrons, ou d'un rayonnement y.

Figure 6 : Réactions d'absorption [13].

II. 2. 2. a. Réactions de capture radiative (n, ã)

Lorsqu'un neutron est capturé par un noyau, il apparaît un noyau composé qui sera dans la plupart du temps dans un état excité (avec une énergie supérieure). Lors de la collision inélastique, un neutron d'une énergie plus faible est expulsé immédiatement, le noyau reste dans un état excité. A la place de l'expulsion d'un neutron on peut avoir un noyau composé qui désintègre par un autre processus. Par exemple, le noyau peut céder son énergie sous la forme

Chapitre II interaction Neutron-Matière

14

d'un rayonnement gamma, ou des particules béta ou alpha, c'est ce procédé que l'on appelle la capture neutronique ou absorption neutronique. Ce type d'interaction est fréquent et aura dans la plupart des cas une plus grande probabilité de se produire pour des neutrons de basse énergie. ????

?? + ????

?? ? ??*

??+?? ? ??+???? ? ?+ã (8)

??

II. 2. 2. b. Réactions de transmutation (n, p) ou (n, á)

Un noyau peut absorber un neutron pour former un noyau composé qui se désexcitera en émettant une particule chargée (un proton ou une particule á), et un élément pouvant être stable, radioactif, ou dans un état excité. Ces réactions sont dites réactions à seuils, elles ne se produisent qu'à partir d'une certaine énergie spécifique au type du noyau cible.

II. 2. 2. c. Réactions de type A (n, xn) A [x= 2, 3 ...]

Dans le cas où l'énergie des neutrons incidents supérieures à 10 MeV, la désexcitation du noyau composé s'effectue par l'émission de deux neutrons ou plus.

?? + ???? ??-(??-??) (10)
???? ?? ? ?? ????

?? + ????

Ce phénomène de production de neutrons peut devenir important avec certains noyaux légers ou lourds. Le tableau ci-dessous indique quelques énergies seuils, relativement faibles, pour les réactions (n, 2n) :

Noyau	D	Li	Be	Bi	Th		238U	E (MeV)
3.34	6.2	1.85	7.4	6.44	6

Tableau 3 : énergies seuils réactions (n, 2n). II. 2. 2. d. Réaction de fission (n, fission)

La fission est la cassure d'un noyau lourd en deux fragments (en général), avec la production simultanée de x (entre 2.5 et 3) neutrons rapides. Pour un certain nombre de noyau N impair, la fission aura lieu pour les neutrons de faible énergie (thermiques). C'est le cas de nucléides ²³⁵U, ²³³U, ²³⁹Pu, ²⁴¹Am dont les trois premiers sont les combustibles utilisés actuellement dans les réacteurs nucléaires. Pour les autres noyaux lourds, la fission n'aura lieu que si l'énergie du projectile dépasse une valeur de seuil. Dans les réacteurs à neutrons thermiques l'énergie produite par fission est de l'ordre de 200Mev. L'énergie cinétique des fragments de fission en représente 75% [14].

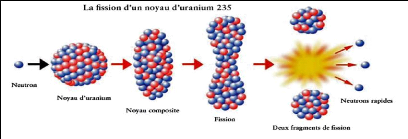
Chapitre II interaction Neutron-Matière

15

Figure 7: La fission d'un noyau d'uranium 235 [15].

Le neutron absorbé apporte son énergie cinétique, l'énergie mise en jeu par les forces nucléaires de liaison (cette énergie de liaison du dernier neutron est pour les noyaux lourds plus faible

que l'énergie moyenne de liaison par nucléon). Si l'énergie d'excitation ainsi acquise par le noyau composé est suffisante, on peut avoir une fission, ou désexcitation par un autre processus (rémission d'un neutron, éjection d'une particule chargée ou d'un photon Gamma) [14].

Le mécanisme de cette réaction correspond à une absorption totale du neutron incident par le noyau. Cette réaction s'effectue en plusieurs phases. L'absorption du neutron provoque tout d'abord une excitation résonnante de tous les nucléons. Puis le noyau se déforme et se scinde en 2 (parfois plus) fragments de fission (autres noyaux). Quasi simultanément et instantanément à la fission, 2 à 3 neutrons rapides et des photons gamma sont émis. Ils sont appelés neutrons prompts et gamma prompts de fission. Enfin, quelques microsecondes à quelques dizaines de secondes après la réaction de fission, certains produits de fission émis à l'état excité se désexcitent par décroissance â^- suivie de l'émission de neutrons dits retardés ou différés.

II. 3. Notion de section efficace

Les interactions décrites lors des paragraphes précédents ne peuvent être quantifiés qu'en utilisant des termes spécifiques telle la section efficace. La donnée fondamentale des interactions neutroniques est donnée par l'ensemble des probabilités d'interactions des neutrons avec les différents noyaux. La section efficace est la grandeur caractéristique de ces probabilités.

Chapitre II interaction Neutron-Matière

16

Une section efficace peut être microscopique (caractéristique d'une cible individuelle), ou macroscopique (caractéristique d'un matériau contenant un grand nombre de cibles) [16] :

II. 3. a. Section efficace microscopique

La probabilité qu'un neutron interagisse avec un noyau selon une réaction donnée dépend non seulement du type de noyau mais aussi de l'énergie du neutron. La probabilité qu'une réaction ait lieu entre un neutron et un noyau est appelée section efficace microscopique, notée ó. Elle s'exprime le plus souvent en barn tel que [16] :

1 barn =10^-24cm²

‡U. 3. b. Section efficace macroscopique

La section efficace macroscopique est la probabilité qu'un neutron interagisse avec la matière pour une unité de longueur, et au nombre de noyaux par unité de volume. Elle Est donnée par la relation suivante [16] :

E = N. a = ( P NA/M ). a (11)

Là où :

E : section efficace macroscopique (cm^-1) ;

N : nombre de noyaux par unité de volume (cm^-3) ;

a : section efficace microscopique (barn) ;

p : densité du matériau (g.cm^-3) ;

Na : nombre d'Avogadro (6.022 x10²³ mol^-1) ;

M : masse atomique du matériau (g/mol).

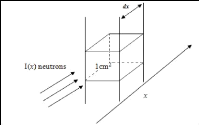
Chapitre II interaction Neutron-Matière

17

Figure 8 : Définition de la section efficace macroscopique.

La section efficace macroscopique Ó a les dimensions de l'inverse d'une longueur (cm^-1), c'est la probabilité par unité de parcours pour le processus spécifique décrit par la section efficace microscopique ó. Pour une combinaison de tous les processus, on ajoute les sections efficaces pour chaque interaction individuelle, c'est la section efficace totale et qui est donnée par [16] : Ótot= Ó diffusion + Ó capture + ...

Cette notion de section est très importante pour le choix du matériau de la structure du dispositif porte-source. Et comme le dispositif est principalement utilisé pour ralentir les neutrons émis par une source de neutrons, il doit être réalisé dans un matériau à section efficace de diffusion et/ou d'absorption assez importante.

Le tableau ci-dessous montre une petite comparaison du section d'absorption et de diffusion entre quelques matériaux :

Noyau	Masse	Section de diffusion		Section d'absorption	Hydrogène
1.00	20.4	0.332		Deutérium
2.00	3.40	0.0051		Béryllium
8.93	6.00	0.0076		Carbone
12.01	4.74	0.00337		Oxygène
15.86	3.89	0.000191

Tableau 4 : comparaison du section efficace [17].

Grâce à cette étude comparative des matériaux pouvant être utilisés comme matériaux de construction, nous avons choisi l'hydrogène (la paraffine ou l'eau) comme un matériau de remplissage et l'aluminium comme matériau de structure.

Chapitre II interaction Neutron-Matière

].

18

Figure 9 : Section Efficace des matériaux ralentisseurs/Diffuseurs de neutrons

Caractéristique des matériaux hydrogénés :

· Un coût pratiquement nul.

· Des propriétés thermodynamiques intéressantes et bien maîtrisées par les industriels.

· Un pouvoir modérateur exceptionnel : ce paramètre, qui caractérise la capacité d'un matériau à ralentir les neutrons, est le produit. En effet, pour un bon matériau ralentissement.

Ø Un autre critère doit également être considéré, à savoir le prix et la disponibilité des

matériaux sélectionnés.

‡U. 4. Notion du libre parcours moyen

L'inverse de la section efficace macroscopique, 1/s, est le libre parcours moyen des Neutrons, c'est-à-dire la valeur moyenne de la distance X à laquelle se produit la première Collision. Il est donné par :

ë (cm)= 1/s (12)

Là où :

s : section efficace macroscopique (????-??)

Chapitre II interaction Neutron-Matière

‡U. 5. L'atténuation des neutrons

Si un faisceau de neutrons traverse un matériau (absorbant ou diffusant), l'intensité du faisceau de neutrons détectés, décroît exponentiellement avec l'épaisseur de ce dernier selon la loi exponentielle suivante [19] :

I = Jo??-????????? (13)

Avec :

I : Intensité du faisceau transmis ;

Jo: Intensité du faisceau incident ;

Ótot : Section efficace macroscopique totale.

II. 6. Les sources des neutrons

Les neutrons peuvent être générés par plusieurs méthodes et moyens. Parmi ceux-ci on peut citer :

a) Les réacteurs nucléaires.

b) Les sources radio-isotopique.

c) Les accélérateurs de particule.

II. 6. a. Les réacteurs nucléaires

Un réacteur nucléaire est un système dans lequel est entretenue une réaction en chaîne

de fission. Les noyaux fissiles d'uranium sont bombardés avec des neutrons de faible énergie, cette réaction s'accompagne d'une libération d'énergie et de 2 ou 3 neutrons par noyau fissionné [20].

II. 6. b. Les sources radio-isotopiques

Dans le cas des sources radio-isotopiques, les neutrons sont obtenus à partir des réactions (ã, n) et (á, n) [20].

· 19

Les sources de type (á, n)

Chapitre II interaction Neutron-Matière

20

Les sources (á, n) sont produites à partir de la combinaison d'un radionucléide émetteur de particule alpha Comme : ²¹⁰Po, ²²⁶Ra ou ²³⁹Pu avec un élément léger comme : Be ou B. Les neutrons sont obtenus à partir des réactions : ⁹Be (a, n) 12C, ¹⁰B (a, n) ¹³N, 11B (a,n) ¹⁴N. Les éléments légers sont choisis selon l'importance de la section efficace de leur interaction avec les particules alpha.

2???? ? ??2 U

???? ???? 2???? + ₂He

??

????e

?? + ^2?? He ? ????

??2 + ????

??

Pour ce qui est de notre projet, on avoir à faire à une source de neutrons de ce type. C'est une source ²³⁸Pu-⁹Be dont les caractéristiques comprennent, entre autres :

· Une forme cylindrique dont les dimensions sont fournies aux chapitre IV.

Figure 10 : schéma représente la source neutronique [19].

· Un taux d'émission de neutrons de 3,4*10⁶ n/s,

· Une énergie moyenne de 4,5 MeV,

· Une demi-vie de 24360 ans,

· Une densité de 3,78 g/cm³,

· Une activité de 2 Ci.

Chapitre II interaction Neutron-Matière

21

Le spectre énergétique des neutrons produits par cette source est continu et est donné par la courbe de la Figure 11.

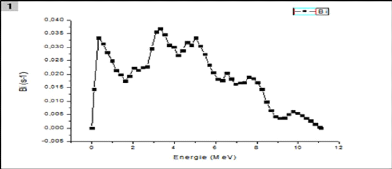
Figure 11 : spectre d'énergie des neutrons de la source ²³⁸Pu-Be (á, n).

· Les sources de type (y, n)

Les sources « photo neutronique » sont produites par les réactions (y, n). Ces sources sont obtenues à partir de la combinaison d'éléments radioactifs, émetteur y mono énergétiques, avec des éléments légers, le Béryllium et Deutérium. Les neutrons sont obtenus par la réaction du rayonnement y avec ces éléments légers, et ils sont mono-énergétiques [19].

· La fission spontanée

Les sources de fission spontanée peuvent également être employées comme générateurs de neutrons. Certains noyaux lourds, comme : ²⁵⁴Cf, ²⁵²Cf, ²⁴⁴Cm, ²⁴²Cm, ²³⁸Pu ²³³U, fissionnent d'une manière spontanée où des neutrons rapides sont émis. Cependant, dans la plupart des cas, la demi-vie de la fission spontanée est beaucoup plus grande que celle de la

désintégration alpha. Les neutrons émis ont une large gamme d'énergie avec une énergie la plus probable ~ 1 MeV et une énergie moyenne ~ 2.3 MeV [19].

Chapitre II interaction Neutron-Matière

22

II. 6. c. Les accélérateurs de particules

Les accélérateurs de particules permettent d'accélérer à de très grandes vitesses des particules chargées (électrons et protons par exemple). Les particules accélérées sont dirigées vers des noyaux cibles pour produire des neutrons. Les réactions nucléaires qui peuvent être utilisées dans les accélérateurs sont les suivantes [21] :

?? + ?? ? ?? + ?? ???? + ??.???? ??????

?? ?? ??

???? ?? ??

?? ?? + ?? ? ????

?? ?? + ?? ???? + ???? ??????
??

?? ??

?? ?? + ??????

?? ? ?? + ?? ?? - ??. ???? ??????

?? ??

?? ??
?? ??+

?? ?? ???? ? ?? ??+

?? ?? - ??.???? ??????
????

^??

‡U.7. Conclusion

Lors de ce chapitre, nous nous sommes attardés sur les modes d'interaction des neutrons avec la matière. On avait surtout mis l'accent sur les phénomènes susceptibles de ralentir les neutrons et les stopper dans la matière.

La notion de section efficace et ses applications nous a permis de faire un choix préliminaire des matériaux à utiliser pour la construction du dispositif porte-source neutronique.

Chapitre ‡V : Code de simulation

Monte-Carlo (MCNP)

Chapitre III Code Simulation Monte-Carlo

23

III. Introduction

Au cours du présent chapitre nous essayerons de donner un bref aperçu sur quelques aspects du code de simulation MCNP5 (Monte Carlo N-Particules). Nous essayerons de mettre l'accent sur les fonctionnalités les plus utilisées dans nos travaux de simulations décrites dans ce mémoire.

III. 1 Aperçu général du code de simulation Monte Carlo

Le code MCNP (Monté Carlo N-Particules) a été développé initialement par le Laboratoire de Los Alamos aux Etats Unis. Ses domaines d'application sont divers, qu'il s'agisse de la radioprotection, de la dosimétrie, des calculs de réacteurs, de l'imagerie médicale. Il est couramment utilisé pour la simulation du transport des neutrons thermiques et rapides, des photons et des électrons dans des géométries ou des configurations tridimensionnelles complexes constituées de divers matériaux [22]. Il consiste en une méthode probabiliste qui permet l'étude du comportement des particules par une méthode de tirage aléatoire. Il permet également d'estimer des grandeurs physiques telles que les flux et les doses de rayonnements. Pour ce faire, il suit l'histoire des particules depuis leur naissance jusqu'à leur disparition en tenant compte des probabilités d'interactions avec les différents matériaux rencontrés, représentées par les sections efficaces [23].

Aussi, ce code permet de modéliser des géométries simples et complexes. Pour cela un fichier d'entrées (input file) est préparé par l'utilisateur, dans lequel sont définies les cellules, les surfaces, les matériaux, du modèle ainsi que le type de réponses souhaitées [24].

III. 2. Présentation du code MCNP

Une présentation exhaustive du code MCNP sort du cadre de ce manuscrit, on se contentera plutôt de la description et la présentation du fichier d'entrée "Input". C'est le fichier à travers lequel on arrive à introduire nos commandes et nos directives pour obtenir la simulation requise.

III. 2. 1. Structure du fichier d'entrée

Tout utilisateur du code doit tout d'abord écrire un fichier d'entrée (input file) qui sera lu par le simulateur MCNP. Le contenu du fichier d'entrée MCNP nécessite plusieurs

Chapitre III Code Simulation Monte-Carlo

24

paramètres décrits à l'aide de cartes réparties en bloc. Sa structure est constituée de trois grands

blocs séparés par une ligne vide : les cartes des cellules, les cartes des surfaces et les cartes des

données dont y existent :

- Les données pour la source,

- Les données pour le matériau,

- Les données pour la grandeur à calculer ou tally.

La structure du fichier d'entrée est la suivante :

Figure 12 : Schématisation du fichier input du code MCNP.

Une autre caractéristique du code MCNP5, c'est que celui-ci permet la préparation des fichiers input moyennant une interface graphique appelée « Vised ». Ceci permet de visualiser instantanément le modèle introduit dans l'input (Figure 12).

Chapitre III Code Simulation Monte-Carlo

25

Figure 13 : interface Vised.

III. 2. 1. a) Définition des cellules [23]

Ce sont des boîtes constituant la géométrie à simuler. Elles se constituent des différents paramètres que sont : les numéros de cellule et de matériau attribués par l'utilisateur, la densité de matériau, les numéros des surfaces désignant la cellule avec les signes adéquats et les importances pour chaque particule. Un numéro de surface muni d'un signe (-) indique l'intérieur de la cellule, sinon son extérieur. Un zéro à la place du numéro de matériau et de la densité indique une cellule vide. La cellule peut être définie par deux opérateurs d'intersection et d'union. Ils sont représentés respectivement par un espace et le caractère (:) entre deux numéros de surface dans la carte cellule. Il est aussi possible d'exclure une cellule d'un espace par l'opérateur symbolisé par (#). Les cellules sont définies verticalement et se déclarent de la manière suivant :

j m d geom imp: x= params

Avec :

j : est un nombre compris entre 1 et 99999 (colonne 1-5) et définit le numéro de la cellule.

m : désigne la matière constituant cette cellule. Si on choisit m=0, la cellule est déclarée vide ;

si m?0, ce paramètre indique le matériau constituant la cellule.

d : densité du matériau de la cellule :

o

Chapitre III Code Simulation Monte-Carlo

26

Pas valeur de densité pour le vide donc égal zéro,

o Valeur positive = densité atomique (atoms /cm³),

o Valeur négative = densité de masse (g/cm³),

geom : spécifie la géométrie de la cellule par les surfaces qui la délimitent. imp:x : importance de la cellule pour la particule x. params : paramètres optionnels de la cellule.

Par exemple

Commentaire

C Cell card

4 1 1.234 E-3 -1 2 -3 imp : n=1

Numéro de la cellule densité surface paramètres (importance de la

particule dans le calcul)

Numéro du matériau de la cellule

III. 2. 1. b) Définition des surfaces [23]

C'est dans ce bloc que sont définies la géométrie et les dimensions du matériau à simuler. Les surfaces peuvent être représentées, par des équations (tableau 5), des points ou des macrostructures. Dans ce travail, c'est la méthode des macrostructures qui a été principalement utilisée. Ces dernières, déjà prêtes à l'utilisation, représentent une façon alternative de définir les cellules et les surfaces. Les formes prédéfinies sont : BOX (boîte), RPP (parallélépipède), SPH (sphère), RCC (cylindre), HEX (hexagone), REC (cylindre elliptique), TRC (cône), ELL (ellipsoïde), WED (cale, coin), ARB (polyèdre). Ces géométries sont décomposées par MCNPX en équations de surface et les facettes sont assignées des numéros individuels sélectionnés par l'utilisateur en vue de leur exploitation dans les différents tallies.

Chapitre III Code Simulation Monte-Carlo

27

Les surfaces qui délimitent les cellules sont définies comme suit :

j a List

Là où :

j : est un nombre compris entre 1 et 99999 désignant le numéro de la surface, a : mnémonique de surface (plan, cylindre, sphère, etc.).

List = caractéristiques de la surface : dimensions, rayons, ..., etc. en cm. (Voir le tableau qui suit)

Tableau 5 : récapitulatif de certaines surfaces [23].

Par exemple

Commentaire

C surfaces card

1 cz 20.0 $ infinité z cylindre

Numéro de la surface rayon en cm

commentaire pour information

Mnémonique qui indique une surface de

cylindre infini sur l'axe des z

Chapitre III Code Simulation Monte-Carlo

28

III. 2. 1. c) Données physiques [23]

Ce bloc permet de fournir les spécifications des problèmes physiques autres que la géométrie. En effet, il y est décrit les propriétés physiques des matériaux et y est précisé la source de rayonnement et le résultat attendu.

Ø Définition des matériaux

Les cartes de cette section précisent les compositions isotopiques des matériaux auxquels un numéro a déjà été attribué dans les cellules. Les matériaux se déclarent comme suit :

mn ZAID1 fraction1 ZAID2 fraction2 ...

Avec :

· mn= nom de la carte matériau (m), suivit par le numéro du matériau (n), entre les colonnes 1 et 5.

· zaid= numéro atomique suivit par la masse atomique de l'isotope. Il a la forme ZZZAAA.nnX.

· ZZZ numéro atomique.

· AAA masse atomique.

· nn identifiant des SE dans la librairie.

· X la classe de données : C pour les énergies continues, T thermal, P proton. Fraction= fraction de l'isotope.

Par exemple

mn zaid1 fraction1 zaid2 fraction2

m1 94239.66 c 2.442E-2 94240.66c 1.673E-3

Mn ZZZ numéro atomique

AAA masse atomique

nn identifiant des SE dans la librairie X la classe de données

Ø Chapitre III Code Simulation Monte-Carlo

29

Définition des sources [23]

La source est principalement définie par la commande SDEF. Celle-ci permet de décrire toutes ses caractéristiques (type de particule émise, son énergie, la position et la répartition géométrique de l'émission) et n'est autorisée qu'une seule fois dans le fichier d'entrée. Certains des paramètres à déclarer sont :

SDEF PAR POS ERG VEC DIR WGT

Avec :

Variable		Signification	PAR
Type de particule (N=1, P=2, E=3)		POS
la position de particule		ERG
énergie des particules		VEC
vecteur directeur de la source sinon isotrope		DIR
cosinus directeur de la source sinon isotrope		WGT
le poids statistique des particules

Il existe d'autres paramètres supplémentaires permettant à une variable de prendre plusieurs valeurs. Pour pouvoir les introduire, il faut inscrire la distribution Dn (n étant le numéro de la distribution) à la place d'une valeur numérique. Chaque distribution utilisée est paramétrée par une ou plusieurs cartes : SIn (Source Information) qui spécifie la forme de la distribution (discrète, continue...) et les valeurs variables prises par la source, SPn (Source Probability) qui décrit les probabilités correspondantes à la distribution décrite avec la source.

Ø Définition des tallies [24]

Les compteurs (tallies) sont des observables permettant de spécifier la grandeur physique que l'on veut obtenir à la fin du calcul MCNP. Défini par la carte Fn (n indique le type de tally), un tally se présente par F ou *F précédé de certains paramètres (numéro de cellule, numéro de surface...). Le tableau si dessous représente les différents types de tally disponibles dans MCNP. Les tallies peuvent être associes à d'autres cartes afin d'avoir un résultat autre que celui spécifié par la carte Fn. Dans ce travail, la carte Fn a été associée aux cartes DE (Dose Energy) et DF (Dose Function). Ces dernières permettent d'avoir directement l'équivalent de

Chapitre III Code Simulation Monte-Carlo

30

dose associé à une fluence en introduisant les coefficients de conversion. Elle se présente comme suit :

Fkn : X S1 S2 ...Sn tallie sur une surface

Fkn : X C1 ...Cn tallie sur une cellule

Avec :

k : un nombre entre 0 et 99 destiné à différentier les tallies de même type. n : un chiffre entre 1 et 8 destiné à indiquer le type de tally.

X: le type de particule.

Si : une surface sur laquelle on veut calculer le tally. Ci : une cellule dans laquelle on veut calculer le tally.

Mnémonique	Description	Unite F		Unite *F	F1
Nombre de particules traversant une surface	-	MeV		F2
Fluence de particules à travers une surface	1/cm^2	MeV /cm^2		F4
Fluence de particules dans une cellule	1/cm^2	MeV/cm^2		F5
Fluence de particules en un point détecteur	1/cm^2	MeV/cm^2		F6
Energie déposée par unité de masse	MeV/g	jerks/g		F7
Energie de fission déposée à travers une cellule	MeV/g	MeV		F8
Energie déposée	Evénement	MeV

III.5. Conclusion

Dans ce chapitre on a introduit l'outil de simulation utilisé pour la mise en oeuvre du travail décrit dans ce manuscrit. On s'est concentré beaucoup plus sur la structure et le contenu du fichier d'entrée "Input file". Les définitions des cartes que contient ce fichier sera tous utilisés dans le chapitre suivant pour décrire le travail réalisé.

CHAPITRE ‡W : Modélisation du

dispositif Porte-source neutronique

Chapitre IV modélisation du dispositif porte source neutronique

31

IV. Introduction

Dans ce chapitre nous décrirons l'ensemble des travaux de simulation entrepris dans le cadre de ce projet de fin d'étude. D'une manière abstraite, et du point de vue géométrie, le problème à traiter a pu être réduit en un ensemble de cylindres concentriques de matériaux différents. Ceci est dû au fait que la forme de la source neutronique est cylindrique. Donc, tout ce qui va être construit autour, comme dispositif porte-source, va suivre la géométrie de base et sera cylindrique. Tout le dispositif ainsi formé, y compris la source neutronique, va être simulé par le code de simulation MCNP5. Les résultats de cette simulation vont être présentés sous forme de tableau de doses de neutrons autour de ce dispositif porte-source. C'est ainsi et pour avoir des valeurs de dose en dessus des seuils admissibles on augmentait à chaque fois le rayon du dispositif, d'où la quantité de la paraffine autour de la source. Il est à noter ici que cette opération ne pouvait pas être refaite indéfiniment parce qu'une autre contrainte était également là : c'était la contrainte du poids du dispositif. Car si on augmentait indéfiniment le rayon du dispositif, le poids augmentera en conséquence et on aura un grand problème pour soulever et déplacer ce système. C'est pour cela qu'une étude parallèle portant sur la structure et le poids du dispositif a été également entreprise.

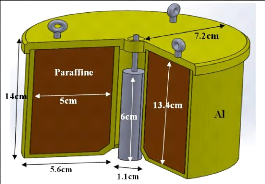
IV. 1. Présentation du dispositif Porte-source

Comme on l'avait déjà énoncé en haut, le dispositif à simuler peut-être réduit en un ensemble de cylindres concentriques de matériaux différents. Un cylindre creux représentant la structure mécanique en Aluminium, le cylindre relativement plein correspondant à la paraffine comme matériau de ralentissement des neutrons. Et en fin, le cylindre plein correspondant à la source neutronique. Un aperçu sur cette géométrie sous forme de cylindres imbriqués est représenté par la figure ci-dessous (Figure 14). Les dimensions mentionnées sont à titre indicatif seulement.

Chapitre IV modélisation du dispositif porte source neutronique

32

Figure 14 : Forme du dispositif pour une épaisseur de paraffine de 5cm.

IV. 2. La modélisation du système par le code MCNP5

IV. 2. 1. Elaboration du fichier d'entrée

IV. 2. 1. a) Modélisation Géométrique

L'élaboration du fichier input a été une étape importante dans le travail qu'on avait réalisé. Après avoir identifié les constituants du dispositif, leurs géométries et les dimensions (fixes et variables) associées, nous avons reporté ces données dans le fichier input MCNP5.

Les parois du dispositif, qui vont être soit en aluminium ou en acier, sont modélisées par un ensemble de quatre cellules (Figure 15). A ces dernières sont associées les surfaces qui les délimitent.

Ces parois métalliques entourent une couche de paraffine. Et afin d'étudier l'effet de cette paraffine sur la dose de neutron autour du dispositif porte source, nous avons préparé plusieurs fichiers d'entrés MCNP5, là où l'épaisseur de la paraffine a été variée de 5cm à 20cm avec un pas de 1cm.

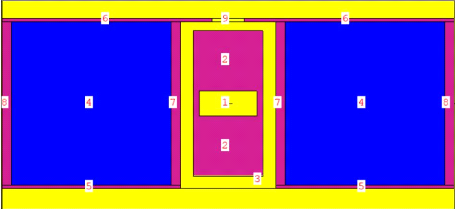
Chapitre IV modélisation du dispositif porte source neutronique

33

Figure 15 : modèle MCNP5 du dispositif porte-source.

Et pour avoir des mesures de dose dans le volume d'air qui entoure le dispositif, dans un cylindre de 2 m de rayon, celui-ci, i. e. l'air, a été subdivisé en quatre-vingts cellules (figure 16). Chacune de ces cellules a pour dimensions 10cm x 10cm.

Figure 16 : modèle de volume entourant le dispositif porte source.

Chapitre IV modélisation du dispositif porte source neutronique

34

Etant donné qu'il y a une grande symétrie dans la géométrie du système considéré, la dose a été déterminée en considérant un quart (20 cellules) seulement, la valeur de doses dans les autres cellules pourrait être déduite par symétrie.

Aussi, et du point de vue matériaux de structure, la simulation a été faite pour deux types de matériaux. Nous avons déterminé les doses ambiantes pour un dispositif en aluminium puis, on refait la même chose pour un dispositif de même géométrie mais en acier et ceci afin qu'on puisse voir l'effet des deux matériaux sur la dose environnante.

IV. 2. 1. b) Données de matériaux dans MCNP5

En utilisant les bibliothèques et les bases de données du code MCNP5, Nous avons choisi les matériaux qui composent le dispositif, à savoir, l'aluminium ou l'acier, la paraffine et l'air. Ces données ont été introduites dans les endroits réservés dans le fichier d'entrée.

IV. 2. 1. c) Paramètres de calculs

Dans cette partie du fichier d'entré, il y a lieu de définir quelques données spécifiques du programme sa simulation à savoir les caractéristiques de la source neutronique. Pour cela, nous avons défini une source ponctuelle isotrope avec une distribution d'énergie allant de 0 à 11 MeV et positionnée au centre du dispositif. Les données relatives à cette source ont été obtenues à travers la norme [10].

Sachant que cette étude a pour but le calcul de dose, nous avons utilisé le tally « F4 » pour calculer le flux volumique et le facteur de conversion « de4/dF4 » pour convertir ce flux vers des valeurs de doses.

IV. 3. Etude de la dose par le code MCPN5

IV. 3. 1. Choix du matériau de la structure

Pour la conception et le dimensionnement du dispositif porte-source on doit tout d'abord choisir le matériau de la structure mécanique (l'enveloppe). Au premier abord, deux choix différents s'offraient à nous : Soit l'Aluminium ou l'Acier. Chacun de ces deux métaux avait ses avantages et ses inconvénients, mais dans ce cas de figure ce qui importait le plus c'était le taux de ralentissement des neutrons induit par chacun. Et pour faire un choix judicieux, on a opté pour des simulations séparées pour chaque élément. Pour chaque matériau, nous avons choisi trois épaisseurs de la paraffine (5, 10 et 20cm), Les valeurs de doses obtenues sont reportées dans le tableau qui suit :

Chapitre IV modélisation du dispositif porte source neutronique

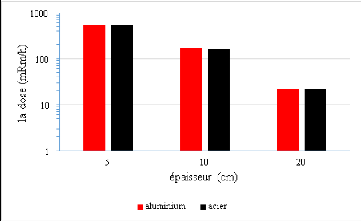
35

La dose (mRm/h)

L'épaisseur (cm)	Aluminium	Acier		Distance (cm)	5
538.752	527.882	17.1		10
168.354	164.119	22.1		20
21.0195	21.0195	32.1

Tableau 6 : les valeurs de Débit de dose en fonction du matériau de structure.

Une illustrions plus claire est donnée sous forme d'histogramme dans la figure ci-dessous.

Figure 17 : Débit de dose en fonction du matériau de structure.

Ø A partir cette figure, on voit bien que l'effet du matériau de structure sur le débit de dose est négligeable. Dans ce cas de figure, et puisque l'Aluminium est plus léger et moins corrosif que l'Acier (Densité de l'acier et plus importante que celle de l'aluminium), notre choix s'est fixé pour l'Aluminium comme matériau de structure.

IV. 3. 2. Dimensionnement du dispositif avec parois en Aluminium

Après avoir fixé le choix du matériau de la structure, l'étape suivante était le dimensionnement du dispositif porte source. Le terme dimensionnement peut être remplacé par : détermination de l'épaisseur de la paraffine correspondant au plus faible débit de dose possible. Pour cela, et au cours des simulations, on avait augmenté à chaque fois le rayon du dispositif, d'où la quantité de la paraffine autour de la source, et on avait calculé le débit de

Chapitre IV modélisation du dispositif porte source neutronique

36

dose correspondant autour du dispositif. C'est une sorte de balayage physique de l'épaisseur

de la paraffine considérée. On a commencé par une épaisseur initiale de 5cm, et on augmentait ainsi cette épaisseur pour chaque simulation à un pas de 01cm. Les résultats de la simulation MCNP sont donnés à chaque fois dans un fichier output, où les valeurs de doses sont obtenues en fonction de la distance entre les cellules étudiées et l'épaisseur de la paraffine.

Les résultats obtenus à l'issue de cette opération sont regroupés dans la figure suivante :

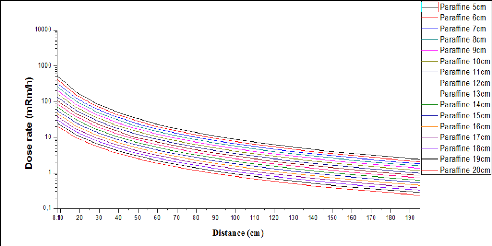
Figure 18 : la dose en fonction la distance.

Au premier coup d'oeil, on remarque que les 15 courbes de débit de doses ont la même allure de décroissance. Ce qui veut dire que la dose diminue progressivement au fur et à mesure que la distance augmente.

On constate également que le débit de dose diminue considérablement avec l'augmentation de l'épaisseur de la paraffine.

A travers ces résultats on constate par exemple que lorsque l'épaisseur de paraffine est de 5 cm, la dose reçue par le travailleur à une distance de 200 cm de la source est aux environs de 2.33 mRm/h. Ceci dépasse clairement la dose recommandée au niveau international qui est de 1 mRm/h.

Et lorsque l'épaisseur de paraffine passe à 20 cm, la dose reçue par le travailleur à une distance de 112.1 cm est inférieure à 1mRm/h. Ceci représente une amélioration palpable des conditions de travail et de radioprotection des opérateurs de réacteurs sous-critique du CRNB.

Chapitre IV modélisation du dispositif porte source neutronique

37

On voit bien que l'augmentation de la couche de la paraffine abaisse d'une manière considérable le débit de dose reçu par le personnel travaillant aux alentours de la source neutronique. La question qui se pose ici est la suivante : Est-ce qu'on peut aller au-delà de 20cm pour ce qui est de l'épaisseur de la paraffine ? Pour répondre à une telle question, on devait prendre en considération l'aspect poids du dispositif parce que le système de soulèvement et de déplacement de ce dispositif a des limites mécaniques et ne peut soulever des poids qui dépassent les 30Kg.

IV. 4. Calcul du poids du dispositif porte source

Cette dernière partie de notre étude porte sur la détermination du poids du dispositif porte-source. Il est à rappeler que ce dispositif est porté par un bras dont la charge maximale définie en haut. Nous allons déterminer le poids du dispositif lorsque ses parois sont en aluminium. L'épaisseur de la paraffine sera augmentée à chaque fois.

Pour calculer le poids, on utilisera l'équation suivante :

ñ= ^m /_v m= ñ * V

Là où :

ñ : la densité volumique en (g/cm³) ; m : La masse en (g) ;

V : Le volume en (cm³).

On a les dimensions du dispositif pour chaque épaisseur de la paraffine. Ceci va nous permettre d'avoir le volume de chaque élément et en fin on peut facilement avoir le poids correspondant. Les résultats obtenus à l'issue de cette phase sont résumés dans la courbe suivante :

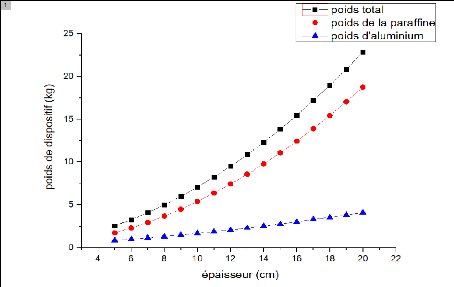
Chapitre IV modélisation du dispositif porte source neutronique

38

Figure 19 : poids du dispositif en aluminium en fonction de l'épaisseur de la paraffine.

En examinant de près cette courbe, on voit bien que le poids total du dispositif augmente d'une manière considérable en fonction de l'épaisseur de la couche de la paraffine. Pour une épaisseur de 20cm, ce poids dépasse clairement les 20Kg. Donc, pour les matériaux utilisés jusqu'ici on et les contraintes mécaniques du dispositif de soulèvement, on gardera la donnée de 20cm comme épaisseur de la couche de paraffine.

IV. 5. Conclusion

Au cours de ce chapitre, et en utilisant les données et le savoir exhibés dans les chapitres précédents, nous avons pu ressortir les données nécessaires à la conception du dispositif porte source adressé dans ce PFE. Nos études et nos simulations nous ont permis ainsi en premier lieu de choisir le matériau de structure. Nous avons également défini l'épaisseur optimale de la couche de la paraffine à travers une série de simulation bien étudiées. Ces données sont maintenant exploitables et peuvent dès à présent servir pour la fabrication de ce dispositif.

39

Conclusion Générale

Conclusion Générale

En partant du principe stipulant que les risques liés aux rayonnements émis par les sources radioactives en particulier les sources de neutrons, sont très élevées et représentent un danger pour les travailleurs autour des installations utilisant ces sources. Et voulant protéger cette catégorie de travailleurs au sein du réacteur sous-critique du CRNB contre tout danger de ce genre, on s'est proposé la réalisation d'un dispositif protecteur porte-source neutronique.

Ce dispositif jouera son rôle de radioprotection durant le déplacement de la source depuis son lieu de rangement vers le coeur du réacteur et inversement. La fabrication effective de ce dispositif doit impérativement passer par les étapes de conception et de dimensionnement. Cette dernière a fait l'objet du travail réalisé dans le cadre de ce projet de fin d'étude.

Comme outil de travail, nous avons utilisé le code de simulation Montre Carlo MCNP5. Une utilisation parallèle de ce code avec les règles et les normes de radioprotections nous a permis de réalisé tous les aspects du travail demandé. En premier lieu, les travaux de simulation accomplie nous ont permis de choisir le matériau de structure qui était l'Aluminium. Une fois cette phase franchie, on est passé à la phase du dimensionnement proprement dite. Ceci a été fait via une série de simulations bien élaborées et qui ont débouché sur un choix optimal de l'épaisseur de la couche de la paraffine à utiliser. Ce choix a été renforcé par la suite à travers une étude sur le poids admissible du dispositif porte-source.

Les données de simulation ainsi obtenues sont très probantes et peuvent être exploité pour la fabrication de ce dispositif.

Comme extension future visant à augmenter l'efficacité de ce dispositif et à réduire son poids, on se propose d'ajouter d'autres matériaux neutrophages au modèle actuel. De telle manière à ce que l'effet de la paraffine sur les neutrons (ralentisseur) sera renforcé par d'autres effets (absorbants) et ce en ajoutant par exemple de la poudre du cadmium, du bore ou du gadolinium à la paraffine déjà existante. Et suite aux critères de disponibilité et du prix de ces matériaux, une étude de simulation par MCNP5 serait d'un grand apport pour déterminer les doses et les rapports de concentration des matériaux à ajouter.

Par cette fin, nous tenons à signaler que la réalisation de ce projet au sein du CRNB nous a été bénéfique sur plusieurs plans. Entre autres, nous avons pu enrichir notre savoir dans le domaine des réacteurs nucléaires et des sources neutroniques. Nous avons également pu acquérir un esprit de travail d'équipe et de méthodologie pour faire aboutir un projet donné.

Les références

Les références

[1] de la Santé, Organisation Mondiale. « Rayonnements ionisants, effets sur la santé et mesures de protection. » Repéré à http://www. Who. Int/mediacentre/factsheets/fs371/fr (2016).

[2] AURENGO, ANDRE, and ROLAND MASSE. "Chapitre 3 La radioprotection : un guide sur les objectifs à atteindre." Sciences du démantèlement des installations nucléaires. EDP Sciences, 2021. 101-116.

[3] TITOUCHE WIDAD, « Notions de base de la radioactivité », COMENA, université des sciences et technologie HOUARI BOUMEDIEN, Mars 2022.

[4] HAUSMANN, EMILIE. Pour une meilleure radioprotection : une coopération entre manipulateurs en électroradiologie et infirmiers de bloc opératoire. Diss. Université de Lorraine, 2013.

[5] AUBERT, B. "Organisation de la radioprotection en France." Journal de Radiologie 91.11 (2010) : 1201-1206.

[6] BRENAUT, CHRYSTEL. « La radioprotection dans le nucléaire de proximité-Identification des activités et caractérisation du risque radiologique », 2004

[7] GRANGER, JEAN ERIC. "LA RADIOPROTECTION AU SERVICE DE MÉDECINE NUCLÉAIRE DE L'HÔPITAL IBN SINA." (2021).

[8] Gérard MAREY, « radioprotection, rayonnements, dosimétrie, protection », 2014

[9] METIVIER, HENRI. "Radioprotection et ingénierie nucléaire [Radiation shielding and nuclear engineering]." EDP Sciences-INSTN, Paris (2006).

[10] Art. 17-JOURNAL OFFICIEL DE LA REPUBLIQUE ALGERIENNE N°27-13 avril 2005

[11] OURED ILHEM, BENSAADALLAH KHAOULA, « Modélisation du canal horizontal de neutronographie par la méthode de Monte Carlo » mémoire pour l'obtention de diplôme master en physique. Option : physique des rayonnements, université Ferhat Abbas Sétif, 2020

[12] J.P. CUSSONNEAU, « INTERACTION RAYONNEMENTS MATIERE », Ecole des Mines de Nantes

[13] DUSSEAU, PR LAURENT. "Interactions Rayonnements-Matière." Institut d'Électronique du Sud (IES) (2009).

[14] BARRÉ BERTRAND, « Maîtriser l'énergie nucléaire, Encyclopédie de l'Environnement, (2022), [en ligne ISSN 2555-0950]

Les références

[15] B. AISSA et B. TARIQ, "Caractérisation de la résolution spatiale d'image induite par différents systèmes de détection utilisés en imagerie neutronique", mémoire d'ingéniorat en génie nucléaire, université Ferhat Abbas, Sétif, Algérie, 2009

[16] KNOLL, GLENN F. Radiation detection and measurement. JOHN WILEY & SONS, 2010.

[17] BERGMAN, A.A., ISAKOV, A.I., KAZARNOVSKIJ, M.V., POPOV, JU.P., & SHAPIRO, F.L. (1965). Moderation of Neutrons Emitted by a Pulsed Source and Neutron Spectrometry Based on Slowing-Down Time. International Atomic Energy Agency (IAEA): IAEA

[18] UPMC M2 Ingénierie pour le Nucléaire Neutronique 01. Introduction Générale Rappels

[19] LAMARSH, J. "Introduction to nuclear reactor theory/JOHN R. LAMARSH." SERBIULA (sistema Librum 2.0) (2020).

[20] MARGUET, SERGE. La physique des réacteurs nucléaires. Lavoisier, 2011.

[21] MUSTAPHA GUERRACHE, « Caractérisation d'un système de détection d'images utilisé en tomographie neutronique : Évaluation de la résolution et du contraste », université Ferhat Abbas Sétif, Mémoire de fin d'étude, 2015/2016.

[22] X-5 Monte Carlo Team. "MCNP-A General Monte Carlo N-Particle Transport Code, Version 5, LANL Report LA-UR-03-1987." (2003).

[23] SWEEZY, J. E. Los Alamos National Laboratory : MCNP-A general Monte Carlo N-Particle transport code, version 5. Vol. 2. LA-CP-03-0245, 2008.

[24] BRIESMEISTER, JUDITH F. "MCNPTM-A general Monte Carlo N-particle transport code." Version 4C, LA-13709-M, Los Alamos National Laboratory 2 (2000).