Le contrôle par PID est la méthode la plus
simple à programmer sur un processeur et elle est souvent
employée pour les asservissements [16].
Cette méthode est basée sur une structure qui
délivre un signal de commande à partir de l'erreur existante
entre la référence et la mesure de son intégrale et de sa
dérivée Figure 3.28.
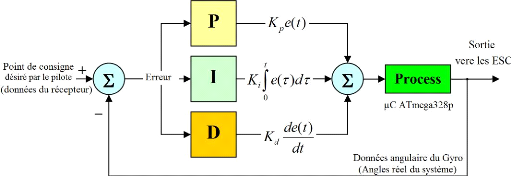
Figure 3.28 : Schéma de la boucle de
contrôleur PID.
53
Chapitre III Conception et mise en oeuvre du
fonctionnement
54
Chapitre III Conception et mise en oeuvre du
fonctionnement
Le contrôle par PID est souvent utiliser dans
l'industrie car il est très simple à mettre en place et
s'avère efficace à réduire les erreurs pour la plupart des
systèmes réels non linéaires. Dans notre cas le principe
de base du contrôleur PID est simple, lorsque le drone se trouve
déséquilibré à cause du vent ou de la turbulence,
l'algorithme envoie une commande vers les ESC qui provoque une réaction
dont le sens est opposé à celui qui a conduit au
déséquilibre, afin que le drone retrouve l'état
souhaité. Plus précisément, il faut garder les valeurs
mesurées du Gyro (données angulaires réel du
système) identique au point de consigne désiré par le
pilote (données d'entrée du récepteur de la routine
d'interruption) Figure 3.29.
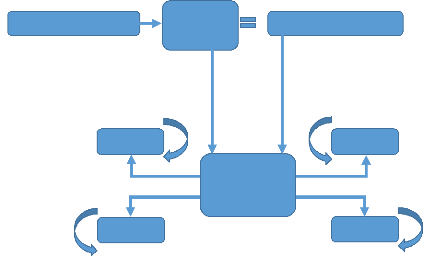
Données d'entrées du récepteur
Données d'entrée du Gyro
(Reciver_input 1, 2 et 3) (Taux angulaire)
Sens antihoraire
Données du Récepteur
Sens horaire Sens antihoraire
Moteur 4
Moteur 3
Conversion en °/ sec
Contrôleur PID
Données du Gyroscope
Moteur 1
Moteur 2
Sens horaire
Figure 3.29 : Schéma montre le principe du PID
utilisé dans ce contrôleur de vol.
Par exemple si le pilote ne veut aucun mouvement, le taux
angulaire Gyro doit être également nul, donc l'erreur du
système « ???? » pour un axe de mouvement est la
différence :
???? = (Données d'entrée du Gyro -
Données d'entrées du récepteur).
Le contrôleur PID calcule les corrections
nécessaires pour les trois axes (Pitch, Roll et Yaw), Les consignes pour
le contrôleur PID sont les signaux d'entrée du récepteur et
les variables des mouvements angulaires mesurées par le gyroscope, Les
sorties du contrôleur PID sont destinées pour contrôler la
vitesse des moteurs du quadrotor afin d'assurer l'équilibre.
L'utilisation des opérateurs mathématiques (Proportionnel,
Intégrateur et Dérivateur) permet de produire une sortie de
commande adéquate pour le système. Le modèle
mathématique du contrôleur PID est décrit comme suit :
????????????(????)
????(????) = ????????????(????) +
???????? ? ????(????)???????? + ????????
???????? , Tel que :
0
55
????(????) : L'erreur du système.
????(????) : Variable de sortie du PID.
???????? : Gain proportionnel.
???????? : Gain d'intégration. ???????? : Gain de
dérivation.
· Effet proportionnel ???????? ???? (????)
: Ce terme est proportionnel à l'erreur, il contribue
à la stabilité et
à la réactivité et permet une
augmentation du temps de réponse du système, en fait le
contrôleur seul n'est pas tout à fait suffisant pour stabiliser le
drone [17].
????
· Effet d'intégral ???????? ?
????(????)???????? : Ce terme est proportionnel à
l'intégrale de l'erreur, il permet au ????
système d'atteindre le point de consigne
désiré, permet aussi d'éliminé l'erreur statique du
système et de diminuer l'impact des perturbations [17], il en
résulte un système précis.
????????(????)
· Effet de la dérivée
???????? : Ce terme est proportionnel à la
dérivée de l'erreur, il permet
????????d'accéléré la
réponse du système et d'éliminé les oscillations
autours du point de consigne [17].
· Saturation du contrôleur PID et choix des
gains [18] :
Pour empêcher le PID de devenir incontrôlable, il
est nécessaire de limiter la sortie PID à une valeur critique qui
est le point de saturation du système et ça se détermine
selon les caractéristiques du système et l'algorithme du
contrôleur PID utilisé. Cette limitation est souvent
appliquée pour la sortie globale du contrôleur PID. Chaque
quadrotor est caractérisé par ces propres gains PID,
généralement les gains PID varis d'un drone à l'autre en
fonction du poids et du hardware utilisé. La
mise en oeuvre de la commande PID exige d'abord une
sélection adéquate des gains ???????? , ???????? et ???????? car
la réponse de la sortie PID sera influencée en agissant sur ces
trois gains. Pour notre système les gains seront
déterminés expérimentalement.
· Algorithme PID du contrôleur de vol
:
Dans le programme du contrôleur de vol, trois
contrôleurs PID sont utilisés pour les trois axes de mouvement
essentiels (Pitch, Roll et Yaw). Au début, il est nécessaire de
transférer les variables des canaux d'entrée du récepteur
(de la routine d'interruption) en degrés / seconde pour avoir les trois
points de consigne de mouvement, identiques en grandeurs que les données
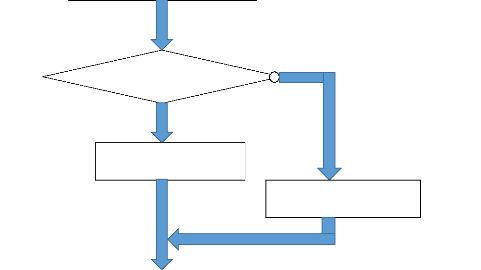
d'entrée du Gyro. L'organigramme suivant explique l'étape de
conversion des variables du récepteur en degrés / seconde pour un
axe de mouvement « Roll », la même routine se
répète pour les deux autres axes «Pitch et Yaw ».
Chapitre III Conception et mise en oeuvre du
fonctionnement
Initialiser la variable flottante point
de consigne Roll
à zéro :
Pid_Roll_consigne = 0
Du récepteur par 3 Permet d'obtenir
Un taux de Roll max Approximatif à 166 ° / s
Roll max = (2000 - 1500) ~ 3
La division de signal
166 ° / s
Reciver_input 1 >= 1500 ?
Pid_Roll_consigne =
(Reciver_input 1
-1500) ~ 3
Oui
1500 (en décimal) est la valeur centrale du
Reciver_input 1 Qui correspond à la position centrale du joystick "canal
Roll"
Non
Reciver_input 1 < 1500
Pid_Roll_consigne =
(Reciver_input 1
-1500) ~ 3
Roll max = (1000 - 1500) ~ 3
-166 ° / s
Les entrées du contrôleur PID {données du
récepteur : (Pid_Roll_consigne, Pid_Pitch_consigne, Pid_Yaw_consigne) et
les données angulaires du Gyro : (angle_roll, angle_pitch, angle_yaw)}
sont connues, reste à déterminer les variables de sortie PID pour
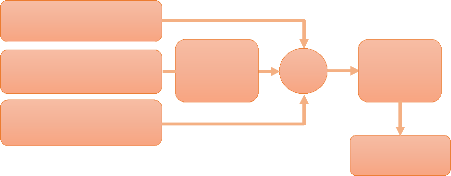
les mouvements (Pitch, Roll et Yaw). Dans le sous-programme PID les trois
parties (proportionnel, intégral et dérivé) sont
calculées simultanément et combinées à un seul
signal de sortie pour chaque axe de mouvement Figure 3.30.
Intégral
Sortie (I) = Sortie (I) + [E ×
Gain (I)]
Sortie (D) = (E -
E????????é????é) ×
Gain (D)
Proportionnel
Sortie (P) = E
× Gain (P)
Dérivé
Limiter la
sortie au point
de saturation
+
Sortie PID pour un axe de mouvement
Limiter la
sortie au point
de saturation
56
Figure 3.30 : L'algorithme utilisé dans le
sous-programme PID du contrôleur de vol pour un axe de
mouvement.
·
L'organigramme suivant explique le calcul du sorties PID pour un
axe de mouvement « Roll ».
La même routine se répète dans le
sous-programme PID du contrôleur de vol pour les deux autres axes
«Pitch et Yaw ».
Eprécé = e L'erreur actuelle e devienne l'erreur
précédente Eprécé Pour le prochain calcule.



