2.18. 2.2. Présentation de la méthode
d'estimation
Ici, nous présentons d'abord les variables
utilisées dans notre étude ainsi que leurs définitions
sont consignées dans le tableau ci-après. Il s'agit
principalement des variables du capital humain et d'autres déterminants
qui sont susceptibles d'influencer les variables de la transformation
structurelle. Ensuite la méthode d'estimation utilisée pour
l'analyse économétrique.
Présentation de la méthode des Moments
Généralisées (GMM)
Par définition le GMM est une
méthode générique pour estimer les paramètres d'un
modèle statistique qui se base sur un certain nombre de conditions sur
les moments du modèle. Elle est dit méthode a information
limitée, elle a été introduite par Hansen (1982) dans un
article « Large sample properties of generalized méthode of
moments estimators » puis généralisée par
Arellano, Bond (1991) ; Arellano et Bover (1995) ; sans oublier
Godman (2009). Parmi l'ensemble des développements opérés
récemment, la méthode des moments
généralisés (MMG) a eu un impact considérable en
économétrie. Du point de vue de la théorie
économétrique, elle a donné lieu à un vaste
programme de recherche, tant du point de vue des propriétés
statistiques de l'estimateur des moments généralisés que
de celui de 1'inférence statistique. Concernant les applications
économétriques, un nombre impressionnant d'études
empiriques est apparu depuis le début des années quatre-vingt
suite à la critique de Lucas (1976). Les modélisateurs ont
cherché à estimer des paramètres structurels restant
invariants aux modifications de la politique économique. La GMM a permis
l'estimation de tels paramètres, notamment dans le cadre des
modèles non linéaires à anticipations rationnelles. Du
point de vue statistique, cette méthode a fourni un traitement
unifié de nombreuses classes d'estimateurs. Les estimateurs de
référence du GMM sont l'estimateur du GMM en différence et
l'estimateur du GMM en système.
a) L'estimateur de la Méthode des Moments
Généralisés en différence
Elle se caractérise par deux grands
avantages spécifiques à savoir au niveau de la nature des
données en panel (le nombre d'individus soit supérieur au nombre
de période) ainsi qu'au niveau des solutions apportées. Cette
méthode permet de contrôler à la fois les effets
spécifiques individuels et temporels et de pallier à
d'éventuel biais d'endogéneité des variables surtout qu'il
existe dans le modèle un ou plusieurs retards de la variable. Ce dernier
se résume en quelques conditions d'application :
La condition (i) exprime la possible
corrélation des variables explicatives avec l'effet individuel, le terme
d'erreur autorégressif et l'erreur de mesure. La condition (ii)
établit que l'effet individuel, l'erreur autorégressive et
l'erreur de mesure sont de moyenne nulle et les termes d'erreurs sont non
corrélés avec l'effet individuel. La condition (iii) implique que
l'erreur de mesure n'est pas autocorrélée. La condition (iv)
suppose que l'erreur autorégressive et l'erreur de mesure ne
sont pas corrélées. La condition (v) signifie que les
deux erreurs ne sont pas corrélées entre les individus
du panel. Enfin, la condition (vi) impose que les conditions
initiales pour la variable dépendante et les variables
explicatives sont prédéterminées. De ce fait, Arellano et
Bond (1991) Suggèrent ainsi que, pour éliminer les effets fixes
individuels il faut passer de l'équation de référence
à une équation en différence première donc en
d'autres termes, les variables en niveau correctement retardées
servent d'instruments dans les équations en première
différence. Mais la difficulté est que celle-ci pose
problème dans la mesure où le terme d'erreur est par conception
corrélé avec la variable endogène retardée et les
instruments sont moins pertinents si le processus autorégressif va
au-delà de l'ordre 1.
b) L'estimateur de la Méthode des Moments
Généralisés en système
Ce dernier vient combler la limite du premier suite aux
travaux de Blundell et Bond(1998) qui ont utilisé les variables
retardées mais différenciées comme instruments. Ils
montrent que l'estimateur GMM en différence peut être
sévèrement biaisé, sur la base de simulations de
Monte-Carlo, lorsque le nombre d'individu est fini et la période
faible ; le nombre de moments est relativement grand par rapport
à la dimension individuelle et que les instruments sont faibles
au sens de Staiger et Stock (1997). Leurs résultats concernent
un modèle autorégressif simple sans variable explicative.
L'inclusion de variables explicatives peut réduire ce biais. Dans le
même temps, lorsque les variables explicatives (et la
variable dépendante) sont fortement persistantes (suivent
éventuellement une marche aléatoire), Blundell et Bond
(2000) mettent en évidence le biais et l'imprécision de
l'estimateur GMM en différence.
Néanmoins, la difficulté est de
mettre en évidence l'importance de ce biais à distance finie. Une
méthode simple consiste à comparer les estimations de la
méthode des moments généralisés en
première différence avec ceux de l'estimateur standard des
moindres carrés ordinaires (MCO) et l'estimateur Within. Dans le
cadre d'un modèle autorégressif d'ordre un (sans variable
explicative), Hsiao (1986) montre que l'estimateur MCO est biaisé vers
le haut tandis que Anderson et Hsiao (1981) et Nickell (1981) mettent
en évidence que l'estimateur Within est biaisé vers le bas
(lorsque la dimension temporelle est petite). Aussi, un estimateur consistent
du terme autorégressif devrait se situer entre ces deux cas limites.
Dès lors, si on observe que les estimations GMM en
différence sont proches ou inférieures aux résultats
de l'estimateur Within, on pourrait en conclure que les estimations
sont biaisées en raison par exemple d'instruments faibles.
Sevestre et Trognon (1996) montrent que ces résultats sont
encore valides en présence de régresseurs (à
l'exception de la variable dépendante retardée) non
corrélés avec l'effet individuel et strictement exogènes
par rapport à l'estmateur within. Blundell, Bond et Windmeijer
(2000) montrent que l'estimateur GMM en système améliore
très significativement les gains de précision mais aussi
réduit de manière importante le biais
d'échantillonnage par rapport à l'estimateur du GMM en
différence lorsque les régresseurs sont faiblement
exogènes et corrélés avec l'effet individuel.
Les travaux de Teixeira (2016), B. Amar (2014) ont
pertinemment fait usage de cette méthode d'estimation. Dans le cas de
notre étude, les équations (4) et (5) s'estimeront en
différence première et les variables endogènes sont sous
forme logarithmique. Cette transformation permet d'atténuer l'ampleur
des fluctuations et stabiliser les variances.
Cependant, se soulève un autre problème
puisque la variable dépendante retardée est par construction
corrélée avec le terme d'erreur. Comme solution les auteurs
postulent deux hypothèses à savoir l'absence
d'autocorrélation des termes d'erreurs ainsi que la faible
exogéneité des variables explicatives (aucune relation avec les
réalisations futures des termes d'erreurs). Dès lors Arellano et
Bond(1991) proposent les conditions des moments suivantes :
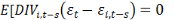 Pour s=2, t=3.......T
(8) Pour s=2, t=3.......T
(8)
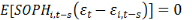 Pour s=2, t=3.......T
(9) Pour s=2, t=3.......T
(9)
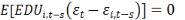 Pour s=2, t=2.......T
(10) Pour s=2, t=2.......T
(10)
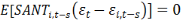 Pour s=2, t=2.......T
(11) Pour s=2, t=2.......T
(11)
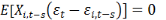 Pour s=2, t=2.......T
(12) Pour s=2, t=2.......T
(12)
Les conditions (8) à (12) soulignent
l'absence de corrélation entre les variables explicatives
retardées ainsi que les variables endogènes retardées avec
les variations du terme d'erreur. De ce fait, ses conditions ci-dessus
permettent d'utiliser des variables retardées en niveau comme
instruments pour estimer les équations.
| 


