Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
(a)

(c)
Figure 3.13. Données réelles
:(a) signal brut (canal 26), (b) représentation temps-
fréquence.
La figure 3.13 est une représentation temporelle puis
fréquentielle du 26ème canal du signal de l'IEEG
réel. Le plan temps-fréquence indique que ce canal
représente plus des événements HFOs que des pointes ce qui
justifie notre choix de travailler sur ce canal afin de reconstruire les pures
HFO.
La figure 3.14 est une représentation temporelle puis
fréquentielles des oscillations HFOs reconstruites par la technique de
la SWT.
GUESMI Thouraya
Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
(a)

(b)
Figure 3.14. Reconstruction d'oscillation :
(a)représentation temporelle, (b)
plan temps-fréquence.
La représentation temporelle dans la figure 3.14 (a)
illustre l'existence des événements HFOs avec quelques
éléments des pointes. Dans le plan temps-fréquence
à la figure 3.14 (b) nous remarquons quelques blobs qui
représentent les événements transitoires (pointes) par
rapport à la dominance des pics qui sont les oscillations HFO. Elles
sont alors des fausses HFO.
GUESMI Thouraya
GUESMI Thouraya
Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
(a)
(b)
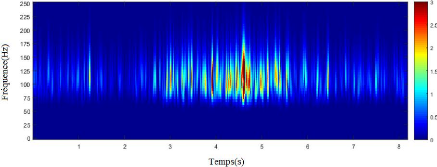
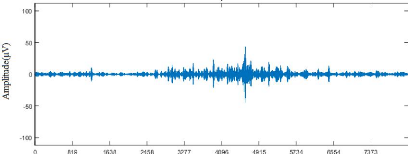
Figure 3.15. Signal réel
filtré : (a) représentation temporelle, (b) plan
temps-fréquence.
La figure 3.15 représente le signal réel
filtré et son plan temps-fréquence qui montre le spectre du
signal. Ce spectre s'étale entre affiche la représentation
situé dans la bande de fréquence de 80-250 Hz, il affiche alors
que des pures événements HFO (oscillation HFO sans les
éléments des pointes). Ces pures oscillations HFOs ont
été reconstruites par la SWT et représentées
à la figure 3.16.
GUESMI Thouraya
Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
(a)
(b)
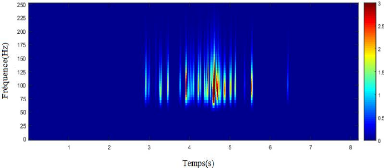
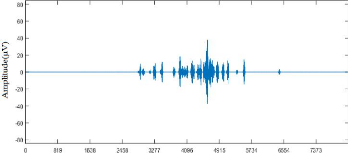
Figure 3.16. Reconstruction des pures HFO :
(a) représentation temporelle
(b) plan temps-fréquence.
La figure 3.16 (a) est les reconstructions des pures HFOs dans
le domaine temporelle mais son spectre est représenté dans la
figure 3.16(b) qui affiche seuls des pics situé dans la bande de
fréquence [80 250] Hz , nous avons alors arrivé de reconstruire
que les pures HFOs de notre signal IEEG réel par a méthode de
SWT.
Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
3.4. Conclusion
Dans ce chapitre, nous avons évalué la
performance de la méthode de la SWT pour la reconstruction des pures
oscillations HFOs pour des données simulées puis réelles.
Pour les signaux simulés (inspirés de l'enregistrement IEEG),
nous avons étudié la robustesse de la SWT dans la reconstruction
des HFOs tout en variant différents paramètres lors de la
simulation du signal [53]. En effet, et sur toute une plage de
fréquences (Ripples et Fast ripples), nous avons commencé par la
variation du rapport d'amplitude relative entre les oscillations HFOs et les
événements transitoires, ensuite le changement du taux de
chevauchement entre ces deux formes (du non chevauché jusqu'à une
superposition totale) et enfin le rapport signal / bruit (d'un signal non
bruité vers un signal noyé dans le bruit). A partir de nos
résultats obtenus et pour toutes les contraintes étudiées,
la reconstruction SWT du HFO révèle un bon taux du GOF [52].
Pour les données réelles, nous avons
évalué les performances de la SWT pour la reconstruction des HFOs
en utilisant la représentation temps-fréquence. La SWT, comme
pour les données simulées, elle donne de bons résultats
pour la reconstruction des pures
oscillations HFOs [54].
GUESMI Thouraya
52
| 


