Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
La phase de reconstruction se fait par l'application de la
fonction MATLAB nommé `iswt', mais avant tout
nous devrons assurer l'étape de seuillage dont nous avons projeté
sur les coefficients un masque rectangulaire ou triangulaire.
Pour la technique de SWT dans Matlab nous avons employé
la fonction Matlab `swt' et nous avons sélectionné 6 niveaux de
la décomposition. Ce choix est justifié pour les oscillations
à haute fréquence dont ses coefficients se propagent au point de
6 niveaux de décomposition [28]. Pour la famille
d'ondelettes, nous avons choisi l'ondelette symlets, le fait qu`elles sont
presque symétriques avec l'oscillation, cette famille d'ondelette se
caractérise encore par son orthogonalité ce qui rend
l'étape de reconstruction plus simple.
La figure suivante décrit les étapes à
suivre afin d'appliquer la technique de transformée d'ondelette
stationnaire (SWT).
Ces différentes étapes de la technique SWT vont
être appliquées sur nos données simulées puis
réelles afin de les évaluer pour la reconstruction des pures
HFO.
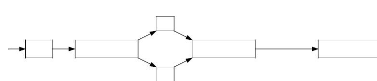
Signal
d'approximations
Décomposition
cAj
cDj
Seuillage
Reconstruction
SWT
cAj: coefficients
Masque (rectangulaire ou
Figure 3.1. Etapes de la transformée
d'ondelette stationnaire (SWT).
Dans les figures 3.2 et 3.3et 3.4 nous représentons les
résultats obtenus suite à
l'application de toutes les étapes mentionnées dans
la figure 3.1.
(a) (b)
cDj: coefficients de détails
GUESMI Thouraya
Chapitre 3 : Evaluation de la SWT en reconstruction
des HFOs
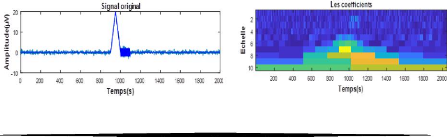
Figure 3.2. Signal original et sa
décomposition :(a)signal original bruité


(pointe+oscillation), (b) les coefficients d'approximations
et de détails.



Figure 3.3. Etape de seuillage.
Figure 3.4. Etape de reconstruction
3.3.2 Evaluation de la SWT en reconstruction des HFOs pour
les données simulées
GUESMI Thouraya
| 


