Détection automatique des oscillations corticales épileptiques à haute fréquence.

Année Universitaire 2018/2019

République Tunisienne
Ministère de l'enseignement supérieur et de
la recherche scientifique

Université de Gabès Institut Supérieur d'Informatique et de Multimédia de Gabès

Département Informatique Industrielle Année Universitaire 2018-2019 Code mémoire :

MEMOIRE DE MASTERE

Présenté en vue de l'obtention du

DIPLOME DE MASTERE DE RECHERCHE EN ELECTRONIQUE ET TELECOMMUNICATION - LMD

Sujet

Détection automatique des oscillations corticales

épileptiques à haute fréquence

Réalisé par

Thouraya GUESMI

Sous la direction de

Mme.Nawel JMAIL

Mme.Abir HADRICHE

Soutenu publiquement le 10 Mars 2020 devant le jury

Président : Mr. Mohamed BEN SLIMA Maitre de conférences à l'ENET'com.

Rapporteur : Mme. Ines NJEH Maitre assistante à l'ISIMG.

Membre : Mme. Nawel JMAIL Maitre assistante à l'ESCS.

Membre : Mme. Abir HADRICHE Maitre assistante à l'ISIMG.

Dédicace

A ma très chère mère

Quoi que je fasse ou que je dise, je ne saurai point te remercier comme il se
doit. Ton affection me couvre, ta bienveillance me guide et ta présence à
mes côtés a toujours été ma source de force pour affronter les différents
obstacles.

A mon très cher père

Tu as toujours été à mes côtés pour me soutenir et m'encourager. Que ce
travail traduit ma gratitude et mon affection.

Al `âme de mon grand frère

Je dédie cet événement marquant de ma vie à la mémoire de mon frère
disparu trop tôt. J'espère que, du monde qui est sien maintenant, il apprécie
cet humble geste comme preuve de reconnaissance de la part d'une soeur
qui a toujours prié pour le salut de son âme. Puisse Dieu, le tout puissant,
l'avoir en sa sainte miséricorde !

A mes très chers frères et mes belles soeurs.
A mon fiancé.
A mes petites nièces.
A tous mes amis.

G.Thouraya

Remerciements

C'est avec un réel plaisir que je tiens à remercier tous ceux, qui d'une façon ou d'une autre, ont contribué à la réalisation de ce mémoire.

Le travail, est réalisé dans le cadre du mémoire de mastère pour l'obtention du diplôme en mastère de recherche en Électroniques et Télécommunications.

Au terme de ce travail, j'adresse mes plus sincères remerciements à mes encadreurs, Mme. Hadriche Abir et Mme.Jmail Nawel, qui m'ont honoré tout au long de projet par leurs encadrements de qualité ainsi que leurs soutiens, pour être à la hauteur d'un tel projet.

Je remercie les membres du jury M.Ben Slima Mohamed et Mme.Njeh Ines d'avoir accepté d'évaluer ce travail.

Enfin, je tiens à remercier tous ceux qui, de près ou de loin, ont contribué à la réalisation de ce travail.

Chapitre 3. Evaluation de la transformée d'ondelette stationnaire en reconstruction

des pures oscillations à hautes fréquences (HFO) 33

Table des matières

Liste des Figures iii

Liste des Tableaux v

Abréviations vi

Introduction générale 1

Chapitre 1. Etat de l'art 3

1.1. Introduction 4

1.2. Système nerveux et activités cérébrales 4

1.2.1. Système Nerveux 4

1.2.2. Encéphale 4

1.2.3. Neurone 5

1.2.4. Potentiel de repos 6

1.2.5. Potentiel d'action : 7

1.3. Techniques d'acquisitions 8

1.3.1. Méthodes non invasives 8

1.3.1.1. Electroencéphalographie EEG 8

1.3.1.2. MagnétoEncéphaloGraphie MEG 9

1.3.2. Méthodes invasives 10

1.3.2.1. Stéréo-Electro-Encéphalo-Graphie SEEG (L'EEG intracérébral): 10

1.3.2.2. ElectroCorticoGraphie (ECoG) 11

1.3.3. Classification des ondes cérébrales humaines 12

1.3.4. Oscillations à hautes fréquences 13

1.4. Maladies neurologiques 13

1.4.1. Maladie de Parkinson 13

1.4.2. Maladie d'Alzheimer 14

1.4.3. Epilepsie 15

1.5. Conclusion 16

Chapitre 2. Les techniques de filtrages 18

2.1. Introduction 20

2.2. Etat de l'art : 20

2.3. Transformée de Fourier(TF) : 20

2.4. La Transformée en ondelette : 23

2.4.1. La transformée en ondelette continue (CWT) 24

2.4.2. La transformée en ondelette discrète (DWT) : 25

2.4.3. Transformée en ondelette stationnaire (SWT) : 26

2.5. Le Matching Pursuit (MP) : 28

2.6. Qualité de l'ajustement: Goodness of fit (GOF) 30

2.7. Analyse temps-fréquence des activités cérébrales épileptiques. 31

2.8. Conclusion 32

3.1. Introduction 34

3.2. Bases des données 35

3.3. Evaluation de la transformée d'ondelette stationnaire (SWT) en reconstruction des
HFOs : 36

3.3.1 Principe de la technique du SWT: 36

3.3.2 Evaluation de la SWT en reconstruction des HFOs pour les données simulées 38

3.3.3 Evaluation de la SWT en reconstruction des HFO pour les données réelles 46

3.4. Conclusion 51

Conclusion générale Erreur ! Signet non défini.

Références Erreur ! Signet non défini.

Liste des Figures

Figure 1.1. Les grandes divisions du système nerveux. 4

Figure 1.2. Le cerveau humain 5

Figure 1.3. Organisation d'un neurone. 6

Figure 1.4. Synapse. 6

Figure 1.5. Différentes phases du potentiel d'action (Scappaticci, 2007). 8

Figure 1.6. Placement des électrodes selon le système international '10-20', [Jasper,

1958]. 9

Figure 1.7. Système MEG au centre de Marseille [Jmail N., 2012]. 10

Figure 1.8. Tracés de SEEG [Jmail N., 2012]. 11

Figure 1.9. Différentes ondes cérébrales d'un signal EEG [Picot et al.,2009]. 13

Figure 1.10. Destruction massive des neurones (maladie de parkinson) [ICM, 2014]. 14

Figure 2.1. La Transformée de Fourier 21

Figure 2.2. La Transformée de Fourier par fenêtre glissante. 22

Figure 2.3. La transformée en ondelette. 23

Figure 2.4. Exemple des niveaux de composition de SWT (4 niveaux) 28

Figure 3.1. Etapes de la transformée d'ondelette stationnaire (SWT). 37

Figure 3.2. Signal original et sa décomposition :(a)signal original bruité

(pointe+oscillation), (b) les coefficients d'approximations et de détails. 38

Figure 3.3. Etape de seuillage. 38

Figure 3.4. Etape de reconstruction 38

Figure 3.5. Plan temps-fréquence de pic simulé et oscillations HFOs. Représentation
temporelle d'une (a) seule oscillation, (b) d'une seule pointe, (c) d'une pointe suivie d'une oscillation et d'un spectre d'une (d) seule oscillation, (e) d'une pointe, (f) d'une pointe suivie

d'une oscillation. 39

Figure 3.6. Deux ensembles de reconstruction des HFO par SWT (80 Hz et 200 Hz). 40

Figure 3.7. Deux ensembles de reconstruction de HFO par SWT pour différents rapport

d'amplitudes entre la pointe et l'oscillation. 41

Figure 3.8. Valeurs de GOF pour différents rapport d'amplitude entre la pointe et les

événements HFO. 42

Figure 3.9. Reconstruction des HFOs par SWT pour différents taux de chevauchement.
43

Figure 3.10. Valeurs du GOF pour différents taux de chevauchement temporel entre

HFO et pointes. 44
Nous étudions ici l'effet de bruit (variation de SNR) sur la reconstruction des pures

oscillations HFO par la SWT (Voir tableau 3.3). 44

Figure 3.11. Reconstruction des HFO par SWT pour différents SNR (-5db et 20 db). 45

Figure 3.12. GOF de la reconstruction du HFO pour différents taux du SNR. 46

Figure 3.13. Données réelles :(a) signal brut (canal 26), (b) représentation temps-

fréquence. 47

Figure 3.14. Reconstruction d'oscillation : (a)représentation temporelle, (b) plan temps-

fréquence. 48

Figure 3.15. Signal réel filtré : (a) représentation temporelle, (b) plan temps-fréquence. 49

Figure 3.16. Reconstruction des pures HFO : (a) représentation temporelle (b) plan

temps-fréquence 50

Liste des Tableaux

Tableau 1 Variation d'amplitude de la pointe par rapport à l'oscillation. 40

Tableau 2 Taux du chevauchement entre pointe et oscillation(%). 42

Tableau 3 Variation du SNR. 44

Abréviations

SNC Système Nerveux Centrale.

SNP Système Nerveux Périphérique.

EEG Electroencéphalographie.

IEEG Electroencéphalographie Intracérébral.

MEG Magnétoencepahlographie.

SEEG Stéréoélectroencéphalographie.

ECoG Electrocorticograpgie.

HFO Oscillation à Haute Fréquence.

R Ripple.

FR Fast Ripple.

TF Transformée de Fourier.

STFT Transformée de Fourier Fenêtrée.

WT Transformée d'ondelette.

CWT Transformée d'ondelette Continue.

DWT Transformée d'ondelette Discrète.

SWT Transformée d'ondelette Stationnaire.

MP Matching Pursuit.

GOF Goodness of Fit.

SNR Rapport signal / bruit.

1

Introduction générale

Introduction générale

Le cerveau est considéré comme l'organe le plus complexe pour l'être humain et les animaux. Il représente le centre du système nerveux sous forme d'une unité centralisée chargée de contrôler tous les autres organes du corps [1], il était et sera toujours très intéressant de comprendre et surveiller l'activité du cerveau humain pour des raisons médicales et comportementales.

Avec l'évolution des techniques de traitement des données, les neurologues disposent aujourd'hui d'une grande quantité d'outils puissants qui leur permettent de saisir l'activité cérébrale et de diagnostiquer ces fonctions.

Pour acquérir ces activités cérébrales différentes techniques d'enregistrement ont été utilisées telles que l'électroencéphalographie EEG, l'électroencéphalographie Intracérébrale (IEEG) qui assure l'enregistrement de l'EEG par des électrodes implantés à l'intérieur du cerveau. Le traitement de ces signaux enregistrés permet de diagnostiquer diverses maladies neurologiques comme l'épilepsie.

Cette maladie s'impose principalement sur l'analyse de ces signaux .Leur pré traitement justifie la présence de oscillations (onde : alpha, beta, delta, gamma et haute fréquence(HFO)) et des activités transitoires.

L'objectif de cette étude est d'évaluer la méthode de transformée d'ondelette stationnaire pour la reconstruction des pures HFO.

Nous établissons cette voie en acquérant les enregistrements de signaux IEEG et en les traitant dans le but d'obtenir une meilleure analyse corticale. Par conséquent, nous présentons notre projet en trois étapes :

Nous commençons dans le premier chapitre par une introduction au cerveau, la classification des ondes cérébrales, les principales maladies neurologiques spécialement l'épilepsie et les différentes techniques d'enregistrement des activités cérébrales.

Dans le deuxième chapitre, nous comparons différentes techniques de filtrage et leurs avantages dans le traitement des signaux IEEG, nous définissons la méthode

2

Introduction générale

d'évaluation(GOF) et enfin nous mettons l'accent sur l'analyse en temps-fréquences pour les activités cérébrales d'épilepsie.

La troisième et la dernière étape décrit les paramètres choisis pour la technique de filtrage SWT et les résultats obtenus pour la reconstruction des pures HFOs.

3

Chapitre 1 : Etat de l'art

Chapitre 1.

Etat de l'art

4

Chapitre 1 : Etat de l'art

Chapitre 1. Etat de l'art

1.1. Introduction

Le domaine médical en collaboration avec les chercheurs en neurologies ont connu un grand développement technologique au cours du temps. Néanmoins l'étude du cerveau humain persiste un sujet de grande importance en raison de la compréhension incomplète de ses fonctions, malgré la disponibilité croissante des systèmes informatiques avec l'évaluation des techniques d'enregistrement des activités cérébrales. Dans ce contexte les chercheurs s'investiguent pour mieux comprendre les mécanismes de ce dispositif suite à la compréhension des mécanismes neuronaux et différentes interactions entre neurones qui entraînent des courants électriques et des impulsions nerveuses.

Au cours de ce chapitre, nous allons introduire premièrement l'organisation du système nerveux puis détailler les principales techniques d'acquisitions des activités cérébrales et nous présentons par la suite les ondes cérébrales, leurs bandes fréquentielles et leurs tâches cognitives correspondantes.

En deuxième lieu, nous allons indiquer les principales maladies neurologiques les plus fréquentes tout en se focalisant sur l'épilepsie qui va être le sujet de ce mémoire.

1.2. Système nerveux et activités cérébrales

Dans cette section nous allons décrire la composition du système nerveux et révéler l'origine des interactions des signaux électriques cérébraux.

1.2.1. Système Nerveux

Le système nerveux chez l'être humain assure l'échange (l'envoi et la réception) des influx nerveux et leurs traitements, il est donc l'unité fonctionnelle du corps humain afin d'assurer la supervision de ses réactions.

De point de vue anatomie, le système nerveux se décompose en deux sous-systèmes :

? Le système nerveux central (SNC) comprenant l'encéphale en sa partie supérieure et la moelle épinière formant sa partie inférieure. Son rôle est de

4

Chapitre 1 : Etat de l'art

· recevoir, enregistrer, interpréter les signaux qui parviennent de la périphérie, et organiser la réponse à envoyer.

· Le système nerveux périphérique (SNP) qui comprend les voies nerveuses situées en dehors du SNC et qui fait véhiculer l'information émise et reçue au SNC. Il est composé des nerfs rachidiens qui sont les récepteurs des messages sensoriels, et les nerfs crâniens qui forment les unités sensorielle et motrice.

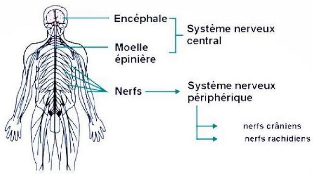
Figure 1.1. Les grandes divisions du système nerveux.

1.2.2. Encéphale

L'encéphale est le responsable de la commande du corps puisqu'il accueille et analyse

constamment les signaux nerveux du corps et envoie de nouveaux signaux montrant ces informations. Il est regroupé en trois parties placées dans la cavité de la boîte crânienne qui sont le cerveau, le cervelet et le tronc cérébral.

Le cerveau humain est l'unité centrale responsable des actions humaines, des réactions et du lien entre la perception interne et externe.

Dans sa définition atomique il se comporte comme la surface des deux hémisphères qui se divisent en quatre lobes montrés par la figure 1.2.

· le lobe frontal : commande la motricité volontaire, involontaire et la concentration.

· Le lobe temporal : assure la reconnaissance faciale et des fonctions auditives.

· Le lobe pariétal : est responsable de la conscience corporelle et le traitement des informations sensorielles.

· Le lobe occipital : est responsable au mécanisme de la vision.

5

Chapitre 1 : Etat de l'art

Le cervelet est responsable de la coordination et des fonctions motrices, il assure la régulation des activités musculaires puisqu'il traite les informations émises par le système nerveux central.

Sous le cerveau et en avant du cervelet se trouve le tronc cérébral composé de la substance blanche, et la substance grise, il est responsable au transfert des informations sensitives et motrices.

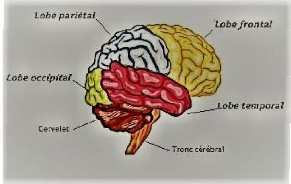
Figure 1.2. Le cerveau humain

Le cerveau comporte plus que huit milliards de neurones, qui sont organisés en deux catégories : un réseau de communication global afin d'unir les diverses régions corticales entre elles et un réseau local pour traiter les informations qui se trouvent dans la même masse neuronale.

1.2.3. Neurone

Le neurone est l'une des principales cellules du système nerveux central. Il permet de recevoir, propager, et transmettre les signaux électriques constituant l'influx nerveux [2].

Le neurone possède une structure de base qui est le corps cellulaire (Soma) et les prolongements (tels que l'axone et les dendrites) qui vont assurer la connexion entre les neurones eux-mêmes ou entre un neurone et une autre cellule.

6

Chapitre 1 : Etat de l'art

Figure 1.3. Organisation d'un neurone.

La conduction de l'influx nerveux se fait comme suit : le signal est reçu au niveau de dendrite qu'il achemine vers le soma ; ce signal est ensuite propagé à travers l'axone vers le neurone suivant grâce à la synapse qui est le point de communication entre les neurones. En effet, au niveau de synapse, des molécules chimiques appelées neurotransmetteurs sont libérées pour se fixer sur la cellule afin de transmettre le message nerveux. Lorsque les neurones sont connectés, le neurone qui transfère le signal est appelé un neurone pré-synaptique (situé avant la synapse) et le neurone qui le reçoit est appelé un neurone post-synaptique (situé après la synapse) (voir figure 1.4) [3].

L'influx nerveux se propage électriquement le long du neurone et chimiquement au niveau de la synapse.

Figure 1.4. Synapse.

1.2.4. Potentiel de repos

Le potentiel de repos est caractérisé par la polarisation électrique de la membrane plasmique d'un neurone.

7

Chapitre 1 : Etat de l'art

A l'état du repos, le neurone est à l'état de polarisation électrique où la polarisation membranaire est au delà de -70 millivolts et qui reste la même au cours du temps, tant que le neurone n'est pas sollicité sur ses entrées dendritiques par des neurones situés en amont dans le réseau.

La répartition des ions d'un coté à l'autre de la membrane plasmique est différent : on trouve de moins les ions Na+, Ca++ et Cl- dans la cellule qu'en dehors, par contre les ions K+ sont plus présents à l'extérieur. Ces gradients de concentration qui existent pour chaque espèce ionique entraînent des transports passifs par diffusion [4] .

1.2.5. Potentiel d'action :

Le potentiel d'action est un courant électrique qui se déplace au niveau de l'axone du neurone pour diffuser un signal à un ou plusieurs neurones, ou autres cellules excitables.

Lorsque la dépolarisation du neurone atteint un seuil suffisant, le neurone produit le potentiel d'action qui est une dépolarisation transitoire de la membrane plasmique des neurones répondant à la loi du « tout ou rien » [5] .

L'état d'action comporte trois phases successives :

? La première phase est une dépolarisation transitoire et locale de l'état précédent définie par une variation de la membrane interne de -70 mV à environ +30 mV. Cette transition est due à l'ouverture progressive des canaux sodiques dépendants de la tension, permettant à un nombre croissant d'ions Na + dans le milieu intracellulaire d'entrer selon le gradient électrochimique.

? La deuxième phase de repolarisation consiste à restaurer l'état de la membrane interne à -70 mV. Cette phase est due à la perméabilité de la membrane au potassium, laissant les ions K + en dehors pour rééquilibrer le milieu.

? La troisième phase d'hyperpolarisation représente une diminution du potentiel de la membrane interne, qui lui-même diminue plus que l'état d'immobilité où elle revient à -70mV.

Pour les neurones humains, le potentiel d'action se propage entre 50 et 100 m/s[6]. Lorsque le potentiel d'action atteint une synapse, il libère des neurotransmetteurs lors de la phase de dépolarisation post-synaptique et atteindre une hyperpolarisation.

Chapitre 1 : Etat de l'art

8

Figure 1.5. Différentes phases du potentiel d'action (Scappaticci, 2007).

1.3. Techniques d'acquisitions

L'activité cérébrale à l'état de repos ou à différents états cognitifs ou suite à une stimulation extérieure est enregistrée par différents dispositifs sophistiqués, dont nous pouvons les classer en techniques invasives et non invasives.

Les techniques non invasives sont principalement:

? L'Électroencéphalographie: EEG.

? La Magnéto-encéphalographie: MEG.

Et les techniques invasives sont:

? La Stéréoélectroencéphalographie (SEEG). ? L'Électrocorticographie (ECoG).

Que ce soit la méthode d'acquisition, ces techniques permettent d'étudier à la fois les processus cognitifs et aussi des activités pathologiques.

1.3.1. Méthodes non invasives

Les méthodes non invasives garanties une résolution spatiale intensifiée du signal acquis et un bon rapport signal sur bruit, ces techniques sont simples à exécuter et possèdent une excellente précision à l'échelle temporelle. Mais elles sont sensibles au bruit causé par divers artefacts.

1.3.1.1. Electroencéphalographie EEG

En 1929, l'EEG numérisé est décrit par le chercheur Hans Berger, ce travail a était corroboré par Adrian et Matthews à Cambridge et Jasper aux États-Unis [7].

9

Chapitre 1 : Etat de l'art

L'électroencéphalographie est une technique non invasive illustrée comme un tracé : c'est l'électroencéphalogramme (EEG) qui permet d'évaluer les activités électriques corticales.

Les signaux de l'EEG sont captés par des électrodes placées sur le scalp utilisées pour collecter les informations du signal du cuir chevelu en question et qui ne sont pas polarisées.

Le système international de l'emplacement des électrodes est `10-20' (à base de 19 électrodes) ou `10-10' (à base de 64 électrodes). les points de référence sont le nasion (haut du nez) et l'inion (point saillant à la base arrière du crâne) [8]. Ces points permettent d'avoir un bon emplacement des électrodes qui est déterminé par des intervalles de 10% et 20% de périmètre du crâne.

Une électrode est identifiée par une lettre et un chiffre. La lettre précise la région (F : frontale ; T : temporale ; C : centrale ; P : pariétale ; O : occipitale), les chiffres pairs représentent la partie droite de l'hémisphère droit et les chiffres impairs représentent sa partie gauche. Le z fait référence aux électrodes placées sur la ligne centrale.

Figure 1.6. Placement des électrodes selon le système international '10-20',

[Jasper, 1958].

1.3.1.2. MagnétoEncéphaloGraphie MEG

La magnétoencéphalogramme (MEG) est une technique de neuroimagerie basée sur la réflexion du champ magnétique sur le courant électrique [9]. La différence entre cette méthode et l'EEG réside dans le fait que l'os du crâne et les couches successives de peau et de tissu n'influencent pas beaucoup au champ magnétique de la MEG par rapport à la mesure du courant électrique comme principe de l'EEG. Cette technique garantit une précision spatiale élevée par rapport aux autres techniques tout en conservant la même précision temporelle.

10

Chapitre 1 : Etat de l'art

L'autre utilité de la MEG est quelle est plus perceptible aux oscillations corticales et aux activités de plus petit calibre. Cependant, l'EEG est moins coûteux que la MEG c'est pour quoi cette dernière est réservée aux cas difficiles du dépistage médical. L'amplitude du champ magnétique mesurée est extrêmement faible, ce qui nécessite des étapes de traitement supplémentaires à exploiter.

Figure 1.7. Système MEG au centre de Marseille [Jmail N., 2012].

1.3.2. Méthodes invasives

Les techniques invasives sont réalisées par l'implémentation des électrodes en profondeur dans le cerveau contrairement aux techniques non invasives qui remplacent les électrodes sur la superficie du scalp.

1.3.2.1. Stéréo-Electro-Encéphalo-Graphie SEEG (L'EEG intracérébral):

L'EEG intracérébral (IEEG ou SEEG) est une technique invasive développée en France par Bancaud et Talairach à la fin des années 50 [10]. Elle a été utilisée en neurologie par l'implantation des électrodes sous le crâne et à proximité des neurones du cortex cérébral afin d'enregistrer l'activité électrique en profondeur.

Le SEEG a un avantage par rapport aux enregistrements de surface puisqu'il permet d'avoir les activités neuronales directement depuis le générateur même situé en profondeur. Il permet également d'enregistrer des signaux de faible intensité de façon très focale et donne

11

Chapitre 1 : Etat de l'art

des renseignements très spécifiques lors du diagnostic pathologique. Par exemple et pour l'épilepsie, le SEEG peut nous informer sur la profondeur de la zone épileptogène [11] et le réseau impliqué dans les décharges épileptiques [12].

Cette technique est traumatisante puisqu'elle exige une exploration chirurgicale pour l'implémentation des électrodes. En revanches, elle demeure toujours dépendante aux méthodes non invasives qui fournissent une vue globale de l'activité cérébrale afin de déterminer la planification de la région à implanter et à explorer [13].

Figure 1.8. Tracés de SEEG [Jmail N., 2012].

1.3.2.2. ElectroCorticoGraphie (ECoG)

L'ElectroCorticoGraphie (ECoG) est une méthode invasive et une technique d'enregistrement intracrânienne qui utilise une grille d'électrode placée directement sur le cortex après ouverture de plusieurs cm² dans le crâne pour obtenir des signaux cérébraux électriques.

La grille ECoG est placée dans le cortex mais au-dessus du cerveau contrairement au SEEG [14].

12

Chapitre 1 : Etat de l'art

Cette technique peut considérer comme un péril sur la santé du patient puisqu'elle nécessite une opération chirurgicale dans le but d'ouvrir le crâne. En outre, elle ne permet pas l'enregistrement des activités creux des neurones.

Afin de collecter les données essentielles, il faut retenir le patient dans un milieu confiné qui peut durer quelques jours.

Le majeur bénéfice de l'ECoG par rapport aux autres méthodes non invasives, se trouve au niveau de l'élimination du facteur d'atténuation du signal à travers le crâne. En effet, c'est une activité de la structure interne contrairement à la technique de l'IEEG.

1.3.3. Classification des ondes cérébrales humaines

Chaque onde cérébrale est disséminée sur une bande fréquentielle bien précise et enregistrée suite à une tâche cognitive particulière :

? Onde Delta [0.5-4] Hz: spécifie le sommeil profond, elle possède une grande amplitude.

? Onde Thêta [4-8] Hz. : caractérise l'envie à dormir chez les enfants et l'état du repos chez les adultes, cette onde est moins fréquente chez les adultes que chez les enfants.

? Onde Alpha [8-13] Hz : correspond à la situation de relaxation (cas des yeux fermés), elle caractérise l'état du repos.

? Onde Beta [14-26] Hz: correspond à l'état de l'éveil, de la réflexion active ainsi de la concentration.

? Onde Gamma [30-45] Hz: apparait lors des tâches cognitives et des fonctions motrices. Elle est aussi présente en épilepsie avec des oscillations dans le lobe temporale [15].

13

Chapitre 1 : Etat de l'art

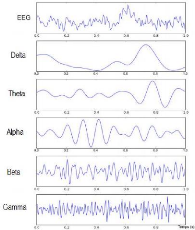
Figure 1.9. Différentes ondes cérébrales d'un signal EEG [Picot et al.,2009].

1.3.4. Oscillations à hautes fréquences

Les oscillations à haute fréquence (HFO) sont des activités cérébrales classées en deux catégories : les oscillations Ripples (R) qui se caractérisent par une bande fréquentielle entre 80 est 250 Hz ; et les oscillations Fast Ripples (FR) qui sont entre 250 et 500 HZ. En fait les FR ont été plus étroitement liées à l'activité pathologique et à la localisation de la zone responsable à la crise épileptique (SOZ :seizure onest zone) [16]. Les recherches sur les enregistrements intracrâniens humains indiquent que les R et les FR apparaissent dans les régions épileptogènes lors d'une acquisition des activités cérébrales épileptiques [17].

Au cours de la dernière décennie, les HFO pathologiques (80 - 500 Hz) [18] se sont émergées comme biomarqueurs d'une survenue d'une crise épileptique pour l'identification du tissu épileptogène et l'amélioration du diagnostic pré chirurgical et des résultats chirurgicaux des patients épileptiques [19].

1.4. Maladies neurologiques

1.4.1. Maladie de Parkinson

La maladie de Parkinson est décrite avec précision en 1817 par Parkinson, elle est la deuxième maladie neurodégénérative la plus représentée (après l'Alzheimer).

14

Chapitre 1 : Etat de l'art

Cette maladie se manifeste par la dégénérescence des neurones dopaminergiques responsables à la fabrication d'une espèce du neurotransmetteur appelée dopamine. Ce dernier est un produit chimique qui émet des signaux afin de contrôler les mouvements automatiques.

Figure 1.10. Destruction massive des neurones (maladie de parkinson) [ICM, 2014].

Les traitements de cette maladie ne permettant pas de le guérir corriger juste elles Contribuent à une amélioration de l'état du patient : elle est une affection chronique.

Dans certains cas la maladie de Parkinson peut être causée par des gènes héréditaires, le vieillissement ou facteur alimentaire, de même aucun facteur de risque n'est connu avec certitude.

Les symptômes essentiels de cette maladie sont :

? Le tremblement qui affecte les lèvres, visage, les mains.

? Raideur des organes moteurs.

? Absence dynamique du mouvement.

? Difficulté de la marche.

? Mal équilibration de conscience.

1.4.2. Maladie d'Alzheimer

La maladie d'Alzheimer est décrite en 1906 par Alzheimer, c'est une dégénérescence des neurones de l'hippocampe qui forment la zone de surveillance du mémoire. Cette maladie se manifeste sous forme des lésions qui touchent le cerveau ce qui provoquent la mort des neurones par l'accumulation de protéines bêta-amyloïdes dans certaines régions du cerveau. [20] .Généralement, il n'y a pas des traitements qui permettent de guérir l'Alzheimer .En

15

Chapitre 1 : Etat de l'art

outre, il ne se trouve pas des causes certaines pour son déclenchement, probablement elle apparaître en cas de vieillissement.

Les principaux symptômes de la maladie d'Alzheimer sont :

· Perturbation de cognition.

· Perdre du mémoire provisoirement (pendant quelques jours).

· Difficulté de concertation.

· Déséquilibre d'humeur.

· Troubles des gestes.

· Problème au langage.

1.4.3. Epilepsie

L'épilepsie, qui est définie comme étant une maladie neurologique traduisant un fonctionnement anormal, aigu et transitoire de l'activité électrique du cerveau, se manifeste par des phénomènes paroxystiques [21].

Cette maladie peut être une maladie héréditaire ou causé par les tumeurs, les malformations corticales ou les traumatismes.

Le phénomène d'épilepsie se manifeste en des crises de courte durée qui traduisent des activités anormales des neurones.

Des traitements médicamenteux peuvent être prescrits pour éviter et stopper ces crises, efficaces dans 70% des situations. Dans les autres cas, ils n'arrivent pas à la remédier et on parle alors d'épilepsie pharmaco résistante [22] qui exige une opération chirurgicale.

La localisation de la zone épileptogène responsable aux crises suite à des décharges neuronaux successifs, se base sur un ensemble de modalités très diverses, telles que l'observation du comportement du patient pendant une crise EEG_video, l'étude de son IRM et de ces signaux électro physiologiques (MEG/EEG, SEEG) [23].

En 1981 la ligue internationale contre l'épilepsie a classé la saisie d'épilepsie en trois types qui sont :

16

Chapitre 1 : Etat de l'art

? Les crises généralisées : correspondent au décharge corticale complet, elles peuvent être elles-mêmes classer en deux sous types : tonique clonique (crise convulsive) et crise non convulsive.

? Les crises partielles ou focales : affectent une zone corticale limitée avec des épisodes simples (ne pas affecter la conscience) ou des épisodes complexes (avoir une légère influence sur la conscience du patient).

? Les crises inclassables : qu'elles ne possèdent pas beaucoup d'informations cliniques.

Les différentes études se concentrent sur la connaissance des outils derrière le développement de cette maladie (causes, manifestations, ses effets sur le fonctionnement du cerveau).

La recherche clinique porte principalement sur l'application des techniques modernes de diagnostic et de traitement. En effet, ces techniques permettent aux scientifiques de mieux diagnostiquer ce type de maladie telles que l'électroencéphalographie (EEG), l'électroencéphalographie Intracérébral (IEEG) et la magnétoencéphalographie (MEG).

Le principal objectif de la technique d'enregistrement est de déterminer la zone épileptogène.

Les pointes épileptiques sont connues comme des indicateurs classiques de l'épilepsie . Cependant, les oscillations pathologiques épileptiques peuvent se produire dans différentes bandes de fréquences (alpha, bêta et gamma, les HFO) et peuvent être une preuve significative de la zone épileptogène. Alors la détection des Oscillations à haute fréquence (HFO) peut être considérée comme un nouveau biomarqueur de la zone épileptogéne dont nous allons se focaliser au cours de ce mémoire.

1.5. Conclusion

Dans ce chapitre, nous avons étudié la composition du cerveau humain et du système nerveux, la fonctionnalité de chaque organe de ce système et la tâche de chaque région cérébrale.

Nous avons détaillé le rôle des neurones pour la génération du potentiel d'action, les transmissions post-synaptiques et la création du courant ionique. Ces courants sont causés par des transferts ioniques pouvant être mesurés par différentes techniques d'acquisition.

17

Chapitre 1 : Etat de l'art

A ce stade nous avons présenté les principales techniques d'enregistrement des activités électriques tout en mettant l'accent sur leurs avantages et leurs inconvénients.

Nous avons également classifié les ondes cérébrales humaines générées et nous avons aussi montré l'existence des oscillations à haute fréquence HFO pour des activités cérébrales épileptiques.

Au cours de ce mémoire, nous allons détecter ces oscillations comme étant des biomarqueurs de la survenue d'une crise épileptique.

18

Chapitre 2.

Les techniques de filtrages

pour la détection des

biomarqueurs épileptiques

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Chapitre 2 : Les techniques de filtrages

2.1. Introduction

Dés l'apparition des diverses techniques d'enregistrement des activités cérébrales, les chercheurs ont continuellement investi du temps et de l'effort pour améliorer la qualité des signaux enregistrés. Grâce à ces recherches différents problèmes d'acquisition de détection et de traitement des données neurologiques sont en cours de résolution. En effet, améliorer le diagnostic des patients souffrant une pathologie neurologique est le premier défis des ingénieurs et des traiteurs des signaux (et/ou images). Ces derniers sont entrain de mettre en place des approches de traitement et de filtrages des signaux enregistrés et ne cessent pas de les améliorer pour récupérer le maximum des informations médicales apportées par les enregistrements. Reste la performance de ces approches pour une meilleure récupération et aussi une bonne compréhension des informations retenues dans les signaux enregistrés est un dilemme à confronter et à le résoudre correctement.

Dans ce chapitre, nous allons détailler les différentes techniques de filtrages temps fréquence basées sur la transformation d'ondelette. Par la suite nous allons montrer l'importance de ces techniques pour la détection et la reconnaissance des biomarqueurs pathologiques lors du traitement des activités cérébrales maladives tout en se focalisant sur l'épilepsie et leurs oscillations à hautes fréquences(HFO).

2.2. Etat de l'art :

L'analyse de Fourier était énoncée en 1807 par le physicien français Joseph Fourier qui a montré que n'importe quel signal peut être représenté par la somme des sinusoïdes.

La déclaration de Fourier a contribué dans le développement des idées existantes sur les fonctions. Il a ouvert la porte à un nouvel univers fonctionnel.

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Malgré la progression du domaine d'ondelette entre 1930 et 1970, l'essentielle progression dérive des études de Jean Morlet, vers 1975, où il a été le premier chercheur qui a décrit ses fonctions par les ondelettes. Plus précisément, elles ont été appelées "les ondelettes de pente constante."

Avant l'année 1975, le physicien Denis Gabor a offert l'idée à ajouter une fenêtre glissante à l'analyse de Fourier [24]. Cette technique permet d'éditer la représentation en temps et en fréquence.

La transformée en ondelettes (TW) a mis des paramétres en considération comme le choix d'ondelette mère, le choix du type de famille de TW et la sélection du facteur de niveau de décomposition. N. Al-Qazzaz et ses collaborateurs [25] donnent une ligne directrice au niveau de la sélection de l'ondelette mère.

Q. Tieng et ses collaborateurs [26] ont employé la transformée d'ondelette continue (CWT) pour la détection des pointes EEG de souris, pendant que, Amin et ses collaborateurs [27] ont opté la transformée d'ondelette discrète (DWT) pour l'extraction et la classification des caractéristiques des signaux EEG. Ces études ont offert des bons résultats malgré le chevauchement entre les bandes de fréquences au niveau du CWT et le problème de la décimation binaire (invariance de translation) dans le cas du DWT.

N. Jmail et ses collaborateurs [28] dans ses travaux ont utilisé la transformée d'ondelette stationnaire (SWT) pour séparer les transitions et les oscillations des signaux de l'EEG épileptiques. Il y avait un paradigme de recherche majeur qui nous a inspiré dans le processus d'évaluation de cette technique sur les oscillations HFO.

2.3. Transformée de Fourier(TF) :

Cette méthode permet d'exprimer une fonction périodique en une somme d'une séquence de sinus et de cosinus à différentes phases et amplitudes

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Figure 2.1. La Transformée de Fourier

Cette méthode est un moyen qui assure le passage du domaine temporel vers le domaine fréquentiel selon la formule:

?? (??) = ?~??(??). ??^-2??^????^?????? (2.1)

Néanmoins, la transformée de Fourier n'est pas capable de déterminer les phases du signal reconstruit à l'inverse malgré qu'elle peut extraire les informations sur le temps par la transformée de Fourier inverse :

??(??) = ? ??(??). ??²??^????^??????

8 (2.2)
-8

La transformée de Fourier est appliquée pour retirer les informations fréquentielles d'un signal, mais le grand inconvénient de cette transformation est son absence de résolution temporelle. Cela désigne la capacité du TR de révéler les fréquences dans le signal par contre elle est inapte d'identifier à quel instant elles se produisent dans le signal.

Il existe une transformée de Fourier plus « locale » donnant des informations mieux localisées, il s'agit de la transformée de Fourier Fenêtrée [29]

La transformée de Fourier Fenêtrée (STFT) est introduite afin de corriger les limites de la TF. Elle emploi une « Fenêtre glissante ».

Le principe général de la technique de la STFT pour l'analyse d'un signal est le suivant : il s'agit d'utiliser un masque sous forme d'une fenêtre glissante où le signal est stationnaire au niveau local puis il se décale le long du signal.

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

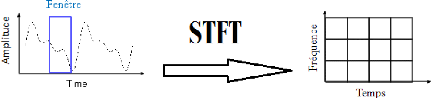
Figure 2.2. La Transformée de Fourier par fenêtre glissante.

La figure 2.2 indique que les sinus de la transformée de Fourier (TF) sont remplacés par des sinus multipliés dans une fenêtre temporellement glissante.

La STFT est définie par:

????????(??,??) = ?[x(t).??^*(t - s)].??^-??^2????^????t (2.3)

Avec :

· x (t) : signal d'origine.

· ??* : le conjugué de la fonction fenêtrée (t) .

· ?? : la fréquence.

· s : l'échelle temporelle.

Comme l'équation suggère, cette méthode est la multiplication de la TF avec une fonction fenêtrée. Cette technique garantit une résolution invariable pendant toute la durée du signal aussi la fenêtre g est invariante qui ne dépend pas de l'échelle s c'est-à-dire l'enveloppe de la fenêtre glissante est stable.

En outre, la taille de l'enveloppe définit la précision d'interprétation du signal avec la STFT :

· En cas de petite fenêtre : les harmoniques basses fréquences n'y seront pas contenues.

· En cas de grande fenêtre : les renseignements sur les harmoniques à haute fréquence sont inclus dans les informations sur la période complète de la fenêtre.

Alors le majeur désavantage de cette méthode est l'invariance de la taille de la fenêtre, ce qui entraine la nécessité d'une méthode où la fenêtre s'adapte avec le changement de fréquence dans le signal à analyser, cette technique est appelée analyse en ondelette.

Chapitre 2 : Les techniques de filtrages

2.4. La Transformée en ondelette :

L'importance dans le traitement d'un signal donné est d'obtenir le plus d'informations possibles dans son domaine temporel et/ou son domaine fréquentiel. Il est donc nécessaire que le signal se décompose en des fonctions bien localisées en temps et en fréquence.

Alex Grosmann et Jean Morlet [30] ont proposé la transformation en ondelette en tant qu'outil d'analyse temps-fréquence, les signaux sont alors représentés en mettant en évidence des informations temporelles et fréquentielles (temps-fréquence).

GUESMI Thouraya

Figure 2.3. La transformée en ondelette.

L'échelle est un paramètre servit en analyse par ondelette. Par analogie avec la fréquence, les basses fréquences, similaires à la grande échelle, donnent une information générale sur le signal et les hautes fréquences, semblables à la faible échelle, fournissent des informations profondes sur un motif masqué dans le signal.

L'analyse en ondelette dépend d'une fonction de paradigme d'ondelettes qui s'appelle une « ondelette mère ». La fonction mère se caractérise par sa limitation dans le domaine temporel, elle est normalisée, ayant une moyenne nulle. Cette spécificité se traduit mathématiquement par les équations (2.4) et (2.5).

???(t)??² = f ?(t)?^*(t)dt = 1

8 (2.4)
-8

f ?(t)

8 -8 dt=0 (2.5)
Selon les propriétés de translation et dilatation, l'ondelette mère capable de déterminer un ensemble de noyau indiqué selon l'équation (2.6).

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

(P??,u (t) = _v?1?(P(^t-u

?? ) (2.6)

Avec :

· ?? : Opérateur de translation.

· ?? : Opérateur de dilatation.

· v?1? : Opérateur de normalisation de l'énergie (l'énergie du signal résultant de la transformée est constante sur toutes les échelles).

Si ??> 1 : La plage de temps accroît : c'est une dilatation.

Si ??< 1 : La plage de temps décline : c'est une compression. La translation est démontrée par la localisation de l'ondelette dans le domaine temporelle.

2.4.1. La transformée en ondelette continue (CWT)

La transformée en ondelette continue est utilisée en cas d'appliquer une fonction continue afin d'obtenir les coefficients détaillés d'un signal continu. Conceptuellement, Elle est le coefficient de la base_(P??,u (t).

En outre, soit W la transformée en ondelette continue (CWT) d'un signal x(t), W est calculé selon l'équation (2.7).

Wx(??, ??) =< x(t), (P??,u > (2.7)

= ?_7₈ x(t)_(P??,u* (t)dt = ? mx(t) V_??(P^*(^t_??^u)dt

Avec :

· (P??,u est l'ondelette mère et * représente le complexe conjugué.

Grâce à cette transformation, nous pouvons affecter un signal unidimensionnel x(t) à un coefficient bidimensionnel Wx(??, ??). Les deux variables (??, ??) peuvent effectuer l'analyse de la fréquence temporelle.

La transformation en ondelette inverse est calculée afin de récupérer la fonction x(t), selon l'équation (2.8).

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

x(t)= ??p 1 ? ? ????(??, ??)

8 8 v?1 ? p (t-??

?? ) ???? ???? (2.8)

0 -8 ??²

Avec ??_p est déterminé par l'équation (2.9).

??_p = ? |p(??)|2

8 ???? < 8 (2.9)

0 ??

Où p(??) : est la TF de l'ondelette mére p(t).

Cette équation est nommée condition d'admissibilité et ??_p désigne la constante d'admissibilité.

L'inconvénient majeur de la CWT est la redondance, cela est expliqué par la translation de l'ondelette de façon continue, la transformée en ondelette discrète est la solution à utiliser pour diminuer cette redondance.

2.4.2. La transformée en ondelette discrète (DWT) :

La transformée en ondelette discrète (DWT) est assurer afin de surmonter la redondance chez la transformée en ondelette continue (CWT), tant que cette redondance augmente le temps et les ressources matérielles du calcul. En effet, la DWT donne les informations nécessaires et suffisantes afin d'analyser et rétablir le signal d'origine. Cela traduise la simplicité et la facilité d'implémentation du DWT par rapport à la CWT.

Le principe du DWT est la translation et la dilatation de l'ondelette en fonction des calibres discrets. En effet les paramètres d'échelle et de dilatation sont alors discrétisés par l'équation suivante :

?? = ?? 0 ?? , ??0 > 1

(2.10)

?? = ????0?? 0

?? ,??₀ > 0

??, ?? ? ??

Avec :

· ?? 0 ?? : est l'opérateur d'échelle.

· ??0 : est l'opérateur de translation.

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Les ondelettes mères sont également définies par l'équation (2.11):

??

???0,??0(??) =

é ?

(t-k ooeo) (2.11)

,

Soit ?? la Transformée en ondelette discrète du signal ??(??), S est calculé selon l'équation (2.12) suivante.

1 +8 0??ô

??(??0, ??0) = ???? J₈??(??) ? (t-?? ??ô ) dt (2.12)

0

Pour assurer l'analyse discrète, Meyer et al. ont montré que les valeurs ??₀ et ??₀ doivent être fixées par les grandeurs ??₀ = 2 ??????₀ = 1[????]. [31]. Donc l'ondelette mère est obtenue selon :

1

???0,??0(??) = _??(2jt-k) (2.13)

2.4.3. Transformée en ondelette stationnaire (SWT) :

La technique de SWT est considérée comme une diversité de la DWT avec l'avantage de surmonter la décimation du DWT, cela nous aide à concevoir les caractéristiques réelles du signal. Elle est encore plus performante que la CWT en dépassant le chevauchement des bandes de fréquences.

La transformée en ondelette stationnaire (SWT) est une fonction inversible qui ne varie pas en temps-fréquence, avec l'autorisation d'usage des masques dans ce plan (temps-fréquence). Sa caractéristique stationnaire assure la stabilité dans le domaine temporel c'est à dire la translation d'un signal provoque une translation de sa transformation.

Le principe de cette méthode est de décrire le signal dans le domaine temps-échelle ainsi la reconstruction des signaux par des coefficients sélectionnés [32].

Nous pouvons utiliser cette technique dans divers domaines d'application comme le filtrage et la détection [33]. Elle est avéré très utile dans l'analyse du signal de l'EEG [28].

Des coefficients de détails et d'approximations sont obtenus par la convolution du signal x(t) avec un filtre passe-bas puis passe-haut. En fait la SWT décompose le signal par ces coefficients, puis elle passe au seuillage qui se fait par l'application des masques afin de détecter les régions du signal souhaitées par la transformée en ondelette inverse « iswt» [34].

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Soit ??(??) un signal décomposé par SWT à la ??ième itération et à chaque échelle j, x(t) est calculé selon l'équation (2.14).

+8 +8 +8 +8

??(??) = ? ? ??????(??)????,?? (??)???? ???? + ? ? ??????(??)????,?? (??)???? ???? (2.14)

??=0 ??=0 ??=0 ??=0

Avec :

· ?? ???? : sont les coefficients de détails.

· ?????? : sont les coefficients d'approximation.

Les coefficients de détails et d'approximation sont acquis par la formule suivante :

??????(??) = ? ??(??)????,??(??)????

+8

??=0

??(??, ??) { (2.15)

+8

??????(??) = ? ??(??)????,??(??)????

??=0

Où :

· ????,??(??) = 2^-???? (2^-??(?? - ??)) : sont les fonctions de décalage.

· ????,??(??) = 2^-???? (2^-??(?? - ??)) : sont les fonctions d'échelle.

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Figure 2.4. Exemple des niveaux de composition de SWT (4 niveaux)

2.5. Le Matching Pursuit (MP) :

La technique de Matching Pursuit est utilisée en traitement du signal, elle était proposée par Mallat et Zhang en 1993: Il s'agit de la description du signal par un groupe d'ondes élémentaires, nommé atomes [35]. Ces atomes forment un dictionnaire.

L'un des principaux avantages du MP, est la prédispose en filtrage temps-fréquence, et l'approximation parcimonieuse, c'est-à-dire la possibilité de décrire le signal par un petit nombre d'atomes. Ces atomes ont certains paramètres dans les domaines temps fréquence [36].

Le MP est une technique optimale pour réduire le nombre des atomes ????(??) utilisés depuis le dictionnaire pour reconstruire correctement le signal s(t).

??(??) = ? ???? * ????(??)

?? (2.16)
0

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

Avec :

· a_n : est l'amplitude de l'atome 9_n(t) .

· 9_n(t) : est l'atome modélisé par la fonction de Gabor. Cette fonction est une oscillation modulée par une fonction Gaussienne translatée dans le temps [37] selon l'équation (2.17).

(t k) 2

9_y(t) = L(y) * e-Ðl _sc ) sin(2rcf (t - k) + (p) (2.17)

II9_yII = 1

Avec :

· sc : est l'enveloppe temporelle Gaussienne de l'atome qui détermine le nombre d'oscillation de la fonction de Gabor.

· k : est la position dans le temps.

· f : est la fréquence de la fonction sinus.

· (p : est la phase.

L'autre manière de déterminer l'étalement dans le temps de l'oscillation est par l'emploi de la grandeur d'oscillation :

æ= /%2rcf . sc (2.18)

Le dictionnaire D comprend une quantité importante de fonctions de Gabor (atomes), qui sont changées via la variation de ces grandeurs (sc, k, f, (p).

La méthode de MP fait une projection des atomes de Gabor sur le signal d'origine sur, il faut alors choisir à chaque itération l'atome qui offre l'excellence ressemblance avec le signal de départ s(t) en maximisant le produit scalaire<s, 9y0)9y0.

5 = (s, _9y0)9y0 + R_s (2.19)

Avec R_s est le reste du signal s(t) non encore reconstruit. A chaque itération, l'atome 9y, qui a le meilleur accord avec le signal est retenu, et le résidu Rns qui est le résultat de soustraction du signal reconstruit est calculé selon l'équation (2.20).

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

R???? = <R????,????0>?????? + R(??+1)?? (2.20)

Certains critères sont introduits pour délimiter le nombre des itérations parmi les quels nous pouvons introduire une métrique pour calculer le taux de reconstruction du signal. Ce taux de reconstruction est à gérer par l'utilisateur selon les exigences des processus.

2.6. Qualité de l'ajustement: Goodness of fit (GOF)

La qualité de l'ajustement (GOF) est employée dans différents domaines afin de l'utiliser comme une moyenne d'évaluation. En traitement du signal, cette méthode est dédiée à l'évaluation des performances du processus de filtrage de nombreux signaux physiologiques [38].

Le test de GOF utilisé dans notre étude est le test du chi-carré de Pearson [39]. En effet il s'agit d'un test statique qui compare entre la distribution de fréquence et la distribution théorique.

Ce test statique est la puissance du signal par rapport à la puissance théorique, définit par l'équation (2.21).

(2.21)

Avec

? ??(??) : est le signal d'origine.

? ????(??) : est le signal reconstruit.

Dans ce travail, nous avons calculé le GOF pour la méthode de filtrage SWT selon différentes valeurs de SNR et différentes amplitudes pour les oscillations à haute fréquence (entre 80 et 250 Hz) reconstruites à partir des enregistrements des activités cérébrales épileptiques.

GUESMI Thouraya

Chapitre 2 : Les techniques de filtrages

2.7. Analyse temps-fréquence des activités cérébrales épileptiques.

Pour diagnostiquer des différentes maladies neurologiques comme l'épilepsie nous pouvons exploiter différentes techniques d'acquisition des signaux électrophysiologiques (EEG, IEEG, MEG) .Afin de désigner ces troubles neurologiques, il est nécessaire d'examiner ces signaux à cause du comportement non-stationnaire. A ce propos, l'analyse en temps-fréquence des activités cérébrales épileptiques était considérée comme la vérité du terrain, comme cela a été fait dans plusieurs études.

C. Tallon-Baudry est ses collaborateurs [40], ont montré que les ondelettes de Morlet sont généralement recommandées car elles offrent un compromis idéal entre la résolution temporelle et fréquentielle.

P. Aguera et ses collaborateurs [41], ont adopté l'analyse en ondelettes sur des enregistrement MEG pour étudier les activités cérébrales oscillatoires. En effet ils utilisent la transformation de Gabor pour la détection des activités oscillatoires évoquées et induites comme réponses aux stimuli auditifs.

K. Gadhoumi et ses collaborateurs [42], ont utilisées l'analyse en ondelette (l'analyse de l'activité haute fréquence) pour identifier les caractéristiques distinctives cohérentes entre les périodes préictale et interictale dans l'EEG. Ils ont confirmées que cette méthode était utile soit pour distinguer ces deux états soit pour la prédiction des crises.

S.Burnos et ses collaborateurs [43], arrivent à déterminer que l'analyse des données IEEG dans le domaine temps-fréquence élimine les détections parasites causées par des artefacts ou par une forte activité épileptique et améliore la détection des HFOs.

P. Puranik et ses collaborateurs [44], ont recommandé que l'analyse temps-fréquence des signaux EEG permette de visualiser correctement ces signaux pour extraire les différents rythmes de fréquences comme les ondes alpha, bêta et gamma et les ondes à haute fréquence. Ici la transformée d'ondelette est exploitée afin d'assurer l'analyse des enregistrements EEG.

N.Jmail et all ont été utilisé à l'analyse temps-fréquence des signaux EEG, IEEG, MEG épileptique dans des plusieurs travaux. Ils ont Séparé entre les pointes et les oscillations par la transformée d'ondelette stationnaire(SWT) implémentée sur une architecture embarquée

Chapitre 2 : Les techniques de filtrages

[45].Ils ont également intégré la SWT sur une architecture embarqué pour détecter le temps précis et la localisation de l'accumulation de crises [46].

A.hadriche et ses collaborateurs ont employé l'analyse temps-fréquence par l'application de la méthode du Mtaching Pursuit (MP) pour détecter le potentiel évoqué [47].

Les approches d'analyse en temps-fréquence peuvent être regroupées selon différentes représentations : la représentation linière (TF, STFT, WT et la décomposition de Gabor), et la représentation quadratique comme le spectrogramme, la fonction d'ambigüité et la distribution de Winger-ville.

Sachant que la transformée en ondelettes s'appui sur une couverture par des translations en domaine temporel et par des dilatations en domaine fréquentiel, par conséquent cela mène à un pavage du plan temps-fréquence qui se change en fréquence et qui éventuellement représente significativement les propriétés d'un signal en temps et fréquence.

2.8. Conclusion

Au niveau de ce chapitre, nous avons montré les différentes techniques de filtrage référés à la transformation d'ondelette. Ainsi, nous avons montré les performances de la transformée d'ondelette stationnaire (SWT) vis-à-vis les autres techniques d'ondelettes. La SWT va être appliquée sur notre base de données des signaux de l'IEEG épileptiques (simulées et réelles). Nous avons aussi établit le critère d'évaluation (GOF) qui sera aussi utilisé afin d'évaluer cette technique de transformée d'ondelette stationnaire (SWT) pour la détection et la reconnaissance des oscillations épileptiques à haute fréquence (HFO).

GUESMI Thouraya

GUESMI Thouraya

Chapitre 3.

Evaluation de la transformée

d'ondelette stationnaire en

reconstruction des pures

oscillations à hautes

fréquences (HFO)

34

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

Chapitre 3 : Evaluation de la transformée

d'ondelette stationnaire (SWT) en

reconstruction des pures oscillations à hautes

fréquences (HFO).

3.1. Introduction

L'analyse des données de l'IEEG est une tâche délicate, qui exige l'exactitude dans chaque détail et à chaque étape du processus.

L'utilisation des techniques de filtrages peut être une épée à double tranchant; elle peut tirer le meilleur du signal en le nettoyant et en le purifiant des interférences indésirables, comme elle peut rendre les données inexactes et erronées en supprimant suite au filtrage certaines propriétés du signal électrophysiologique réel, et cela peut risquer un diagnostic erroné des maladies neurologiques ou même une mauvaise compréhension des tâches cognitives.

Par conséquent, le choix de ces techniques de filtrage et l'évaluation de leur robustesse vis-à-vis des données neurologiques est une opération sensible. À ce propos, N.Jmail est ses collaborateurs [28], ont prouvé l'efficacité de la transformation stationnaire en ondelettes dans la détection et la séparation entre les pointes et les oscillations gamma. Par conséquent, nous proposons d'étudier au niveau de ce chapitre les performances de cette transformation en ondelettes dans la reconstruction des HFOs purs pour des données de l'IEEG simulées et réelles.

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

3.2. Bases des données

Toutes les simulations réalisées dans ce projets ont été exécutées à l'aide du logiciel Matlab (Mathworks, Natick, MA) avec la boite à outils EEGlab. C'est un environnement de programmation structuré qui permette d'accéder, de stocker, de manipuler, de mesurer, et de visualiser les données de l'EEG, de l'IEEG et de la MEG [46].

Au cours de notre étude, nous avons appliqué des bases de données épileptiques pharmaco résistantes. En effet, nous avons utilisé deux bases de données qui sont simulées et réelles.

3.2.1 Données simulées

Les signaux simulés sont modélisés suite à une combinaison d'une pointe et des oscillations à haute fréquence (HFO) comme notre véritable signal IEEG, échantillonnés à 1000 Hz.

Entre les simulations nous avons changé le paramétrage de nos signaux : l'amplitude relative de la pointe par rapport l'oscillation, la fréquence d'oscillation, le rapport signal sur bruit (SNR) et le chevauchement entre les oscillations et la pointe.

Nous avons augmenté l'amplitude de la pointe de 2, 4, 6,8 et 10 fois par rapport à l'amplitude oscillante. Nous avons également fait varier la fréquence des oscillations dans cette plage [80 150 100 200 250] Hz (Ripples et Fast Ripples). Le chevauchement entre les oscillations HFO et la pointe a été modifié à pas égaux via la taille de la fenêtre d'oscillations: aucun chevauchement (pointe et oscillation sont complètement séparées) jusqu'à ce que nous atteignions un chevauchement de 100% lorsque les événements de la pointe et les oscillatoires sont superposés. Le pas de chevauchement est égal à 25%. Enfin, nous avons modifié le rapport signal/bruit (SNR de -5 dB à 20 dB).

( _{énergiedusignal} ?

_SNR = 10x _log10 ?

? _{énergiedubruit} ?

L'équation (3.1) définit le rapport signal/bruit (SNR) :

(3.1)

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

3.2.2 Données réelles :

Notre signal réel adopté dans ce projet est l'enregistrement d'un sujet pharmaco-résistant.

Ces données sont des enregistrements d'électroencéphalogramme de profondeur (IEEG) où les étapes d'acquisition et de prétraitement ont été affectées au service de neurophysiologie clinique de l'hôpital de La Timone à Marseille [48] et validées par un neurologue expert. En outre ces données ont été enregistrées sur un système Deltamed, et échantillonnées à 1000 Hz avec un filtre passe-bas. Cet enregistrement de l'IEEG particulier a été sélectionné grâce à sa présentation qui comprend des motifs HFO avec des oscillations épileptiques visibles et des pointes régulières.

Notre ensemble de données de 117 canaux est constitué d'un seul événement et une seule époque [51].

3.3. Evaluation de la transformée d'ondelette stationnaire (SWT) en reconstruction des HFOs :

3.3.1 Principe de la technique du SWT:

Pour faire une étude sur les oscillations à haute fréquence(HFO), nous avons utilisé dans cette partie la technique de transformée d'ondelette stationnaire (SWT) qui s'appuie sur une analyse en temps-fréquence. Elle est accessible de sélectionner des masques afin de reconstruire uniquement des parties particulières du plan temps-fréquence.

Cette méthode sert à exprimer le signal dans le plan temps-échelle par des coefficients d'approximation et de détails ensuite reconstruire la partie oscillatoire pure à travers les coefficients choisis [49].

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

La phase de reconstruction se fait par l'application de la fonction MATLAB nommé `iswt', mais avant tout nous devrons assurer l'étape de seuillage dont nous avons projeté sur les coefficients un masque rectangulaire ou triangulaire.

Pour la technique de SWT dans Matlab nous avons employé la fonction Matlab `swt' et nous avons sélectionné 6 niveaux de la décomposition. Ce choix est justifié pour les oscillations à haute fréquence dont ses coefficients se propagent au point de 6 niveaux de décomposition [28]. Pour la famille d'ondelettes, nous avons choisi l'ondelette symlets, le fait qu`elles sont presque symétriques avec l'oscillation, cette famille d'ondelette se caractérise encore par son orthogonalité ce qui rend l'étape de reconstruction plus simple.

La figure suivante décrit les étapes à suivre afin d'appliquer la technique de transformée d'ondelette stationnaire (SWT).

Ces différentes étapes de la technique SWT vont être appliquées sur nos données simulées puis réelles afin de les évaluer pour la reconstruction des pures HFO.

^Signal

^{d'approximations}

^{Décomposition}

^cAj

^cDj

^Seuillage

^{Reconstruction}

^SWT

^{cAj: coefficients}

^{Masque (rectangulaire ou}

Figure 3.1. Etapes de la transformée d'ondelette stationnaire (SWT).

Dans les figures 3.2 et 3.3et 3.4 nous représentons les résultats obtenus suite à

l'application de toutes les étapes mentionnées dans la figure 3.1.

(a) (b)

^{cDj: coefficients de détails}

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

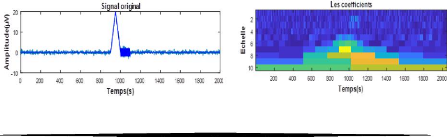
Figure 3.2. Signal original et sa décomposition :(a)signal original bruité

(pointe+oscillation), (b) les coefficients d'approximations et de détails.

Figure 3.3. Etape de seuillage.

Figure 3.4. Etape de reconstruction

3.3.2 Evaluation de la SWT en reconstruction des HFOs pour les données simulées

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

^{(d) (e) (f)}

(a) (c)

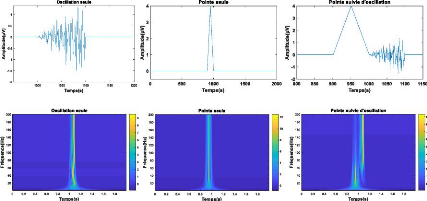
Figure 3.5. Plan temps-fréquence de pic simulé et oscillations HFOs. Représentation temporelle d'une (a) seule oscillation, (b) d'une seule pointe, (c) d'une pointe suivie d'une oscillation et d'un spectre d'une (d) seule oscillation, (e) d'une pointe, (f) d'une pointe suivie d'une oscillation.

^(b)

Nous représentons dans la figure 3.5 trois formes des données simulées. La première ligne est une représentation temporelle d'une oscillation de 150 Hz (Ripples), une pointe et les deux ensembles (pointe suivie d'oscillation). La deuxième ligne représente le plan de fréquence des trois événements étudiés. Nous remarquons que la combinaison de HFO et d'une pointe produit une forme complexe. Distinguer les éléments de base de chaque événement dans cette forme complexe est une tache assez difficile à accomplir.

Dans la figure 3.6, nous avons illustré la reconstruction temporelle des oscillations HFO par la technique de filtrage SWT pour deux configurations de fréquence (80 Hz et 200 Hz).

GUESMI Thouraya

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

(a) (b)

^(d)

^(c)

Figure 3.6. Deux ensembles de reconstruction des HFO par SWT (80 Hz et 200

Hz).

3.3.2.1 Résultats de la variation d'amplitude de la pointe par rapport à

l'oscillation:

Le tableau 3.1 regroupe les différentes valeurs d'amplitude de la pointe par rapport à l'oscillation. Pour chaque valeur nous avons appliqué la SWT pour la reconstruction des pures oscillations HFOs.

Tableau 1 Variation du rapport d'amplitude de la pointe par rapport à l'oscillation.

Rapport d'amplitude pointe et oscillation	entre	Fréquences (Hz)
2		80-100-150-200-250
4		80-100-150-200-250

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

6	80-100-150-200-250
8	80-100-150-200-250
10	80-100-150-200-250

La figure 3.7 illustre deux exemples de reconstruction des HFOs par la SWT pour deux rapports d'amplitudes : 4 puis 10 tout en gardant la même fréquence d'oscillations (égale à 100Hz), le même chevauchement (égale à 0% : une séparation complète entre la pointe et les HFOs) et le même SNR (SNR=5dB).

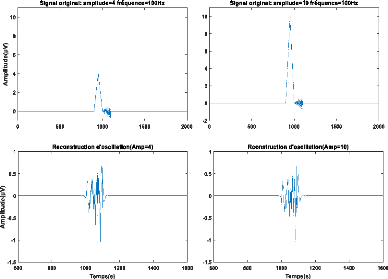
Figure 3.7. Deux ensembles de reconstruction de HFO par SWT pour

différents rapport d'amplitudes entre la pointe et l'oscillation.

La figure 3.8 montre les différentes valeurs du GOF mesurées suite à l'application de la SWT sur chaque signal simulé tout en faisant varier le rapport d'amplitude en fonction des différents HFOs qui sont variées de 80 jusqu'à 250 Hz en gardant les autres paramètres constants (SNR=10dB, chevauchement entre pointe et oscillation=0%).

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

Figure 3.8. Valeurs de GOF pour différents rapport d'amplitude entre la pointe et les événements HFO.

Depuis figure 3.8 nous remarquons que pour tous les rapports d'amplitude le résultat de reconstruction du HFO est au-delà de 78%. Le GOF atteint 97% pour un rapport d'amplitude qui est égale à 4. Par conséquent, nous pouvons annoter que les SWT ont de bonnes performances dans la reconstruction du HFO même pour une amplitude comparable des pointes et des oscillations HFO.

3.3.2.2 Résultats de la variation du chevauchement temporel entre la

pointe et l'oscillation

Au niveau de cette phase nous allons évaluer la performance de SWT pour la reconstruction des HFOs suite à la variation du chevauchement temporel entre la pointe et l'événement HFO, pour chaque fréquence nous allons chevaucher la pointe et l'oscillation avec des pas identiques égales à 25%(tableau 2).

Tableau 2 Taux du chevauchement entre pointe et oscillation(%).

Taux de chevauchement entre pointe et oscillation(%)	Fréquence (Hz)
0	80-100-150-200-250
25	80-100-150-200-250

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

50	80-100-150-200-250
75	80-100-150-200-250
100	80-100-150-200-250

La figure 3.9 montre la reconstruction des oscillations HFOs pour deux différents signaux obtenus suite à la variation du taux de chevauchement entre pointe et oscillation (pas de chevauchement versus un chevauchement total). Pour ces deux signaux nous avant gardé la même fréquence des oscillations (égale à 250hz) le même taux de SNR égale à 0dB et un rapport d'amplitude égale à 10.

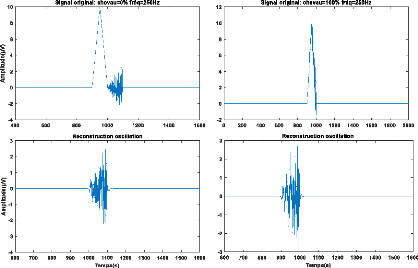
Figure 3.9. Reconstruction des HFOs par SWT pour différents taux de

chevauchement.

Nous représentons dans la figure 3.10 le résultat du GOF lors de la reconstruction des pures oscillations HFOs par la méthode SWT suite à la variation du taux de chevauchement temporel entre la pointe et les événements HFO.

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

GUESMI Thouraya

Figure 3.10. Valeurs du GOF pour différents taux de chevauchement temporel entre

HFO et pointes.

Nous constatons que pour toutes les configurations de chevauchement, le GOF est supérieur à 80% pour un faible taux de chevauchement et un chevauchement total, mais cette mesure diminue pour un taux de chevauchement entre 50% et 75%.

3.3.2.3 Résultats de la variation du SNR

Nous étudions ici l'effet de bruit (variation de SNR) sur la reconstruction des pures oscillations HFO par la SWT (Voir tableau 3).

En effet, nous avons ajouté un bruit blanc aléatoire à notre signal simulé, ce bruit a un spectre de 1/F qui correspond bien au spectre du bruit physiologique contaminant les enregistrements des activités cérébrales.

Tableau 3 Variation du SNR.

SNR (dB)	Fréquence (Hz)
-5	80-100-150-200-250
0	80-100-150-200-250
5	80-100-150-200-250

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

10	80-100-150-200-250
20	80-100-150-200-250

Nous représentons dans la figure 3.11 deux exemples de la reconstruction des HFO par la SWT. Nous avons varié la SNR (-5dB puis 20dB) et nous avons maintenu égale la fréquence des oscillations (=150 Hz), le taux de chevauchement (égale à 0%) et le rapport d'amplitude entre pointe et oscillation (égale à 6).

Figure 3.11. Reconstruction des HFO par SWT pour différents SNR (-5db et

20 db).

Dans la figure 3.11, nous avons regroupé les valeurs du GOF calculées lors de la reconstruction des pures HFO tout en variant le SNR du signal simulé.

GUESMI Thouraya

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

Figure 3.12. GOF de la reconstruction du HFO pour différents taux du SNR.

Nous constatons que le meilleur taux de GOF est obtenu pour un SNR> 10 dB, ce qui dépasse 85%, mais les résultats du GOF sont plus faibles pour un SNR faible qui est autour de 50%.

3.3.3 Evaluation de la SWT en reconstruction des HFO pour les données réelles

Notre objectif dans cette partie était d'évaluer la robustesse SWT de la reconstruction HFO sur un signal de l'IEEG réel en utilisant l'analyse temps-fréquence. C. G. Bénar et ses collaborateurs [50], ont affirmé qu'au niveau du plan temps-fréquence une oscillation HFO est représentée par un pic (limité en fréquence) située dans la bande fréquentielle 80-500 Hz tandis qu'un événement transitoire génère une goutte allongée (blob), étendue en fréquence.

La méthode SWT a été appliquée sur les données réelles ayant 117 canaux. Nous avons gardé les mêmes paramètres des données simulées où nous avons adopté l'ondelette `Symlets', décomposée à 6 niveaux et échantillonnée à 1000Hz.

Nous avons défilé les représentations de tous les 117 canaux pour les examiné afin de déterminer les canaux ayant le maximum des événements HFOs assez claires.

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

(a)

(c)

Figure 3.13. Données réelles :(a) signal brut (canal 26), (b) représentation temps-

fréquence.

La figure 3.13 est une représentation temporelle puis fréquentielle du 26^ème canal du signal de l'IEEG réel. Le plan temps-fréquence indique que ce canal représente plus des événements HFOs que des pointes ce qui justifie notre choix de travailler sur ce canal afin de reconstruire les pures HFO.

La figure 3.14 est une représentation temporelle puis fréquentielles des oscillations HFOs reconstruites par la technique de la SWT.

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

^(a)

^(b)

Figure 3.14. Reconstruction d'oscillation : (a)représentation temporelle, (b)

plan temps-fréquence.

La représentation temporelle dans la figure 3.14 (a) illustre l'existence des événements HFOs avec quelques éléments des pointes. Dans le plan temps-fréquence à la figure 3.14 (b) nous remarquons quelques blobs qui représentent les événements transitoires (pointes) par rapport à la dominance des pics qui sont les oscillations HFO. Elles sont alors des fausses HFO.

GUESMI Thouraya

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

(a)

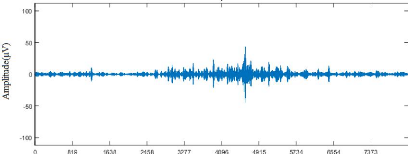
(b)

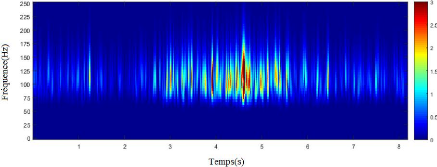
Figure 3.15. Signal réel filtré : (a) représentation temporelle, (b) plan

temps-fréquence.

La figure 3.15 représente le signal réel filtré et son plan temps-fréquence qui montre le spectre du signal. Ce spectre s'étale entre affiche la représentation situé dans la bande de fréquence de 80-250 Hz, il affiche alors que des pures événements HFO (oscillation HFO sans les éléments des pointes). Ces pures oscillations HFOs ont été reconstruites par la SWT et représentées à la figure 3.16.

GUESMI Thouraya

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

(a)

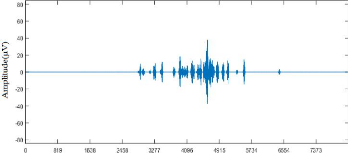
(b)

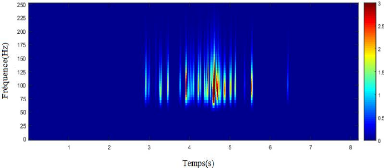
Figure 3.16. Reconstruction des pures HFO : (a) représentation temporelle

(b) plan temps-fréquence.

La figure 3.16 (a) est les reconstructions des pures HFOs dans le domaine temporelle mais son spectre est représenté dans la figure 3.16(b) qui affiche seuls des pics situé dans la bande de fréquence [80 250] Hz , nous avons alors arrivé de reconstruire que les pures HFOs de notre signal IEEG réel par a méthode de SWT.

Chapitre 3 : Evaluation de la SWT en reconstruction des HFOs

3.4. Conclusion

Dans ce chapitre, nous avons évalué la performance de la méthode de la SWT pour la reconstruction des pures oscillations HFOs pour des données simulées puis réelles. Pour les signaux simulés (inspirés de l'enregistrement IEEG), nous avons étudié la robustesse de la SWT dans la reconstruction des HFOs tout en variant différents paramètres lors de la simulation du signal [53]. En effet, et sur toute une plage de fréquences (Ripples et Fast ripples), nous avons commencé par la variation du rapport d'amplitude relative entre les oscillations HFOs et les événements transitoires, ensuite le changement du taux de chevauchement entre ces deux formes (du non chevauché jusqu'à une superposition totale) et enfin le rapport signal / bruit (d'un signal non bruité vers un signal noyé dans le bruit). A partir de nos résultats obtenus et pour toutes les contraintes étudiées, la reconstruction SWT du HFO révèle un bon taux du GOF [52].

Pour les données réelles, nous avons évalué les performances de la SWT pour la reconstruction des HFOs en utilisant la représentation temps-fréquence. La SWT, comme pour les données simulées, elle donne de bons résultats pour la reconstruction des pures

oscillations HFOs [54].

GUESMI Thouraya

52

Conclusion générale

Conclusion générale

L'épilepsie constitue une peine sur la santé publique, elle est la deuxième maladie neurologique après les accidents vasculaires cérébraux, où les plus parts des patients souffrent d'épilepsie pharmaco-résistante.

Au cours des 15 dernières années, les chercheurs ont montré l'utilité de l'activité intracérébrale épileptique au-dessus de 70 Hz: les oscillations à hautes fréquences (HFO) en tant que un biomarqueur efficace pour l'épileptogénicité, elle a été considéré comme un indice de déclanchement de la crise et apparaît pendant la période ictale.

Dans ce contexte s'articule notre travail de mastère de recherche dont nous avons pu détecter et reconnaitre automatiquement des pures oscillations à hautes fréquences.

Pour se faire, nous avons évalué la robustesse de la technique de la transformée d'ondelette stationnaire SWT sur des données de l'IEEG simulées et réelles.

En effet, cette technique de filtrage a été assez performante pour la détection et la reconnaissance des oscillations gamma pré ictales. Elle a été aussi employée pour la détection du temps précis et la localisation de l'accumulation de crises.

Comme résultats obtenus, nous avons trouvé un bon taux de ressemblance GOF entre les oscillations HFOs reconstruites et celles de départ. Ce taux a été calculé pour des centaines de signaux simulés tout en faisant varier à chaque fois un parmi les paramètres suivants : rapport d'amplitude entre oscillation et pointe, fréquences d'oscillations, rapport signal sur bruit SNR et chevauchement entre les deux formes.

Idem pour les données réelles, la SWT donne des bons résultats dans la reconstruction des HFOs non contaminé par un élément transitoire.

Ces résultats s'ajoutent à ceux trouvés en avance pour montrer la robustesse de la technique de la SWT pour la reconstruction et la détection non seulement des oscillations gamma épileptiques mais aussi pour des oscillations à haute fréquence. Cette technique peut être adéquate pour la détection des oscillations préictales sur toute la gamme de fréquence oscillatoire.

53

Conclusion générale

Les aboutissements que nous avons obtenus sont très prometteurs dans une perspective d'étude plus approfondie des HFOs purs pour définir la connectivité de ces réseaux afin de chercher les zones épileptogènes. Ces informations auraient un impact important pour l'aide à la décision suite à une intervention chirurgicale d'un patient pharmacorésistant pour délimiter le tissu épileptogène et la saisie libre.

GUESMI Thouraya

Références

[1] BLESSING, Bill et GIBBINS, Ian. Autonomic Nervous System. In: Scholarpedia of
Touch. Atlantis Press, Paris, 2016. p. 467-477.

[2] Speckman D, Marvin D, Nocerino J. 2005. Dendrite growth and degradation in multi-junction solar cells. s.l. : Progress in Photovoltaics Research and Applications 13:157-163, 2005.

[3] A. Hutt, «Etude de l ' activité neuronale: optimisation du temps de simulation et
stabilité des modèles,» 2013.

[4] M.-A. De Menorval, «Etude de la perméabilisation de la membrane plasmique et des
membranes des organites cellulaires par des agents chimiques et physiques,» no. Umr 8203, 2013.

[5] P. D. Action and E. T. Propagation, «Ontogénèse des canaux transmembranaires,» pp.
1-15.

[6] O. Rossel, «Dispositifs de mesure et d ' interpr ' etation de l ' activit ' e d ' un nerf,»
2013.

[7] Jasper HH. 1958. Report of the committee on methods of clinical examination in
electroencephalography. . s.l. : Electroencephalography and Clinical Neurophysiology 10:370-375 , 1958.

[8] American electroencephalographic society guidelines for standard electrode position
nomenclature. Sharbrough F, Chatrian G-E, Lesser RP, Lüders H, Nuwer M, Picton TW,. 1991. 1991, Journal of Clinical Neurophysiology , pp. 8:200-202.

[9] COHEN, David. Magnetoencephalography: evidence of magnetic fields produced by alpha-rhythm currents. Science, 1968, vol. 161, no 3843, p. 784-786.

[10] N. Jmail, «Séparation des activités cérébrales phasiques et oscillatoires en MEG, EEG et EEG intracérébral.»

[11] Talairach J, Bancaud J. (1973). Stereotaxic approach to epilepsy. Methodology of anatomofunctional stereotaxic investigations. . s.l. : Progress In Neurological Surgery 5:297354, (1973).

GUESMI Thouraya

Références

[12] Wendling F, Ansari-Asl K, Bartolomei F, Senhadji. 2009. From EEG signals to brain connectivity: a model-based evaluation of interdependence measures. s.l. : Journal of neuroscience methods 183:9-18, 2009.

[13] J. Bancaud et al., «`Generalized' epileptic seizures elicited by electrical stimulation of the frontal lobe in man,» Electroencephalogr. Clin. Neurophysiol., vol. 37, no. 3, pp. 275- 282, 1974, doi: 10.1016/0013-4694(74)90031-5.

[14] YANG, Tong, HAKIMIAN, Shahin, et SCHWARTZ, Theodore H. Intraoperative
ElectroCorticoGraphy (ECog): indications, techniques, and utility in epilepsy surgery. Epileptic Disorders, 2014, vol. 16, no 3, p. 271-279.

[15] Uchida S, Maehara T, Hirai N, Okubo Y, Shimizu H (2001) Cortical oscillations in
human medial temporal lobe during wakefulness and all-night sleep. Brain Research 891:719.

Hirai N, Uchida S, Maehara T, Okubo Y, Shimizu H (1999) Enhanced gamma (30-150 Hz) frequency in the human medial temporal lobe. Neuroscience 90:1149-1155

[16] Bragin, A., Mody, I., Wilson, CL, Engel, J. Local generation of rapid ripples in the epileptic brain. J Neurosci . 22 , (5), 2012-2021 (2002).

[17] Worrell, GA, Gardner, AB, et al. High frequency oscillations in the human temporal lobe: simultaneous recordings of microfilm and clinical macroelectrodes. Cerveau . 131 , (4), 928-937 (2008).

[18] Bragin, A., Engel, J., Wilson, C., Fried, I., Buzsáki, G. High frequency oscillations in the human brain. Hippocampe . 9 , (2), 137-142 (1999).

Bragin, A., Engel, J., Wilson, C., Fried, I., Mathern, G. Hippocampal and high frequency oscillations of the entorhinal cortex (100-500 Hz) in the human epileptic brain and in rats treated with kainic acid with chronic crises. L'épilepsie . 40 , (2), 127-137 (1999).

[19] Crépon, B., Navarro, V., et al. Mapping of interictal oscillations greater than 200 Hz recorded with intracranial macroelectrodes in human epilepsy. Cerveau . 133 , (1), 33-45 (2010).

[20] D. Anne-laure, «La Maladie d ' Alzheimer et ses thérapeutiques Remerciements,» 2019.

GUESMI Thouraya

Références

[21] Institut du Cerveau et de la Moelle Epinière, 2014.

[22] Witte H, Iasemidis LD, Litt B (2003) Special issue on epileptic seizure prediction.
IEEE Transactions on Biomedical Engineering 50:537-539.

[23] Adam C, Rouleau I, Saint-Hilaire JM (2000) Postictal aphasia and paresis: a clinical and intracerebral EEG study. The Canadian journal of neurological sciences Le journal canadien des sciences neurologiques 27:49-54.

[24] B. Bhusan, Principles and Applications of Tribology, New York: Widely, 1999.

[25] AL-QAZZAZ, Noor Kamal, HAMID BIN MOHD ALI, Sawal, AHMAD, SitiAnom, et al. Selection of mother wavelet functions for multi-channel eeg signal analysis during a working memory task. Sensors, 2015, vol. 15, no 11, p. 29015-29035.

[26] TIENG, Quang M., KHARATISHVILI, Irina, CHEN, Min, et al. Mouse EEG spike detection based on the adapted continuous wavelet transform. Journal of neural engineering, 2016, vol. 13, no 2, p. 026018.

[27] AMIN, HafeezUllah, MALIK, Aamir Saeed, AHMAD, Rana Fayyaz, et al. Feature extraction and classification for EEG signals using wavelet transform and machine learning techniques. Australasian Physical & Engineering Sciences in Medicine, 2015, vol. 38, no 1, p. 139-149.

[28] JMAIL, Nawel, GAVARET, Martine, WENDLING, Fabrice, et al. A comparison of methods for separation of transient and oscillatory signals in EEG. Journal of neuroscience methods, 2011, vol. 199, no 2, p. 273-289.

[29] ftp://ftp-developpez.com/smilesoft/wt.pdf.

[30] A. Grossmann and J. Morlet, «Decomposition of Hardy Functions Into,» SIAM J. Math. Anal., vol. 15, no. 4, 1984.

[31] Y. Meyer, Ondelettes et Opérations, Tome 1, Hermann, Editeurs des sciences et des arts, 1990.

[32] Wang XH, Istepanian RSH, Member S, Song YH (2003) Microarray Image Enhancement by Denoising Using Stationary Wavelet Transform. 2:184-189.

GUESMI Thouraya

Références

[33] Dai M, Peng C, Chan AK, Loguinov D (2004) Bayesian wavelet shrinkage with edge detection for SAR image despeckling. IEEE Transactions on Geoscience and Remote Sensing 42:1642-1648.

[34] Wang XH, Istepanian RSH, Member S, Song YH (2003) Microarray Image Enhancement by Denoising Using Stationary Wavelet Transform. 2:184-189.

[35] Mallat S, Zhang Z (1993) Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 41:3397-3415.

[36] Malinowska U, Piotr.J D, A Katarzyna J, Blinowska, Waldemar S, And Andrezej W (2006) Micro and Macrostructure of Sleep EEG. Clinical neuriengineering:26-31.

Suffczynski P, Wendling F, Bellanger J-jacques, Lopes FH, Silva DA (2006) Some Insights Into Computational Models of ( Patho ) Physiological Brain Activity. Brain 94.

[37] Durka PJ (2004) Adaptive time-frequency parametrization of epileptic spikes. Physical Review E- Statistical, Nonlinear and Soft Matter Physics 69:051914.

[38] HADRICHE, Abir, JMAIL, Nawel, KACHOURI, Abdennaceur, et al. The detection of Evoked Potential with variable latency and multiple trial using Consensus matching pursuit. In: Advanced Technologies for Signal and Image Processing (ATSIP), 2014 1st International Conference on. IEEE, 2014. p. 316-321.

[39] ZHANG, Xiufeng, SONG, Huifang, LIU, Yongliang, et al. Localizing percentages of interictal 18F-fluorodeoxyglucose (FDG)-PET and magnetoencephalography (MEG) in presurgical evaluation of 107 consecutive patients with non-lesional epilepsy. International Journal of Clinical & Experimental Medicine, 2016, vol. 9, no 12.

[40] C. Tallon-Baudry et O. Bertrand, «Activité gamma oscillatoire chez l'homme et son rôle dans la représentation des objets», Trends in Cognitive Sciences , vol. 3, non. 4, pp. 151-162, 1999.

[41] P. Aguera, K. Jerbi, A. Caclin, and O. Bertrand, «ELAN: A Software Package for Analysis and Visualization of MEG , EEG , and LFP Signals,» vol. 2011, 2011, doi: 10.1155/2011/158970.

[42] K. Gadhoumi, J. Lina, and J. Gotman, «Clinical Neurophysiology Discriminating preictal and interictal states in patients with temporal lobe epilepsy using wavelet analysis of

GUESMI Thouraya

Références

intracerebral EEG,» Clin. Neurophysiol., vol. 123, no. 10, pp. 1906-1916, 2012, doi: 10.1016/j.clinph.2012.03.001.

[43] Burnos S, Hilfiker P, Sueruecue O, Scholkmann F, Krayenbuehl N. Human intracranial High Frequency Oscillations (HFOs) detected by automatic time- frequency analysis. PLoS ONE 2014;9:1-12.

[44] P. Puranik, R. V Kshirsagar, and S. Motdhare, «EAI Endorsed Transactions Elementary Time Frequency Analysis of EEG Signal Processing,» vol. 4, no. 14, pp. 1-6, 2018.

[45] N. Jmail, R. Jarray, A. Hadrich, T. Frikha, and C. Benar, «Separation between spikes and oscillation by stationary wavelet transform implemented on an embedded architecture,» J. Neurol. Sci., vol. 381, no. October, p. 542, 2017, doi: 10.1016/j.jns.2017.08.3735.

[46] N. Jmail, M. Zaghdoud, A. Hadriche, T. Frikha, C. Ben Amar, and C. Bénar, «Integration of stationary wavelet transform on a dynamic partial reconfiguration for recognition of pre-ictal gamma oscillations,» Heliyon, vol. 4, no. 2, 2018, doi: 10.1016/j.heliyon.2018.e00530.

[47] Abir Hadriche, Nawel Jmail, Ridha Elleuch, Laurent Pezard, Different methods for partitioning the phase space of a dynamic system,2014 , pp 88-95.

[48] Delorme A., Makeig S. EEGLAB: une boîte à outils open source pour l'analyse de la dynamique d'EEG à essai unique, y compris l'analyse de composants indépendants. J. Neurosci.Méthodes. 2004; 134 (1): 9-21.

[49] JMAIL, Nawel, GAVARET, Martine, BARTOLOMEI, F., et al. Despiking SEEG signals reveals dynamics of gamma band preictal activity. Physiological measurement, 2017, vol. 38, no 2, p. N42.

[50] C. G. Bénar, L. Chauvière, F. Bartolomei, and F. Wendling, «Pitfalls of high-pass filtering for detecting epileptic oscillations: A technical note on `false' ripples,» Clin. Neurophysiol., vol. 121, no. 3, pp. 301-310, 2010, doi: 10.1016/j.clinph.2009.10.019.

[51] N Jmail, M Gavaret, F Bartolomei, C-G Bénar, Despikifying SEEG signals using a temporal basis set, IEEE International Conference on Intelligent Systems Design and Applications,2015, pp 580-584.

Références

[52] T Frikha, A Hadriche, R Khemakhem, N Jmail, M Abid, Adaptive architecture for medical application case study: evoked Potential detection using matching poursuit consensus, IEEE International Conference on Intelligent Systems Design and Applications,2015, pp 575-579.

[53] N Abdennour, A Hadriche, T Frikha, N Jmail , Extraction and Localization of Non-contaminated Alpha and Gamma Oscillations from EEG Signal Using Finite Impulse Response, Stationary Wavelet Transform, and Custom FIR, International Conference on Artificial Neural Networks, 2018, pp 511-520.

[54] Abir Hadriche, Nawel Jmail, Jean-Luc Blanc, Laurent Pezard ,Using centrality measures to extract core pattern of brain dynamics during the resting state, Computer Methods and Programs in Biomedicine, 2019, pp210-235.

GUESMI Thouraya

60

Détection automatique des oscillations corticales
épileptiques à haute fréquence

Thouraya GUESMI

ÊÇäÇíÈáá

ÇðíÆÇÞáÊ ÇåíáÚ ÑÚÊáÇæ (HFOs) ÉíÞäáÇ ÏÏÑÊáÇ ÉíáÇÚ

ÊÇÈÐÈÐÊáÇ ÇÔÊßÇ äã ÇäßãÊ ËÍÈáÇ

ÇÐå

í :

ÉÕáÇÎáÇ

ãÄáÇÊáÇ

äÓÍ ÇäÈÓÍ ËíÍ (SWT) ÉÊÈÇËáÇ ÊÇÌíæãáÇ áíæÍÊ ÇäÞÈØ

.)ÛÇãÏáá ÞíãÚáÇ íÆÇÈÑåßáÇ ØíØÎÊáÇ ÉÑÇÔÅ

)ÉíáÚáÇ

æ ÉÇßÇÍãáÇ

ÊÇäÇíÈáá

áÎÇÏÊáÇæ ÁÇÖæÖáÇ ÉÈÓä ÏÏÑÊáÇ

ÉíÈÓäáÇ

ÉÚÓáÇ

ÊÇáÇÊÎáÅ ÉíÞäáÇ ÏÏÑÊáÇ ÉíáÇÚ ÊÇÈÐÈÐÊáÇ

ÁÇäÈ ÉÏÇÚáÅ (GOF)

.HFOs äã SWT ÁÇäÈ ÉÏÇÚÅ ÉäÇÊã ãííÞÊá íäãÒáÇ

ÏÏÑÊáÇ ÞÇØä ÇäãÏÎÊÓÇ

ÉíáÚáÇ ÊÇäÇíÈáá

ÉÈÓäáÇÈ

Çã

. ÉÇßÇÍãáÇ

.ãÄáÇÊáÇ äÓÍ ÏÏÑÊáÇ ÉíáÇÚ ÊÇÈÐÈÐÊáÇ ÉÊÈÇËá ÊÇÌíæãáÇ

áíæÍÊÚÑÕáÇ ÛÇãÏáá

ÞíãÚáÇ íÆÇÈÑåßáÇ

ØíØÎÊáÇ

:

ÍíÊÇãáÇ

Résumé : Dans ce mémoire de recherche nous avons pu détecter et reconnaître automatiquement des pures oscillations à hautes fréquences(HFOs) pour des données épileptiques simulées et réelles (signal IEEG). Pour ce faire, nous avons appliqué la transformée d'ondelette stationnaire (SWT) où nous avons calculé le GOF de reconstruction des HFOs pour des différentes contraintes (amplitude relative, fréquence, SNR et chevauchement). Pour les données réelles, nous avons utilisé le domaine temps-fréquence pour évaluer la robustesse de la reconstruction des HFOs par la SWT.

Motsclés: IEEG, Épilepsie, HFOs, SWT, GOF.

.

61