Section 3. Opérationnalisation des
Modèles
I. la construction du modèle
économétrique
Un modèle peut être défini comme la
représentation schématique et partielle d'un
phénomène sous forme d'équation dont les variables sont
des grandeurs économiques. Ainsi un modèle bien construit permet
de valider la théorie économique à partir de l'observation
empirique des résultats suivant un processus bien défini. A ce
titre, il ressort que la modélisation constitue une étape
indispensable pour notre étude puisqu'elle nous permettra de confirmer
ou d'infirmer notre
hypothèse à partir d'un modèle
économétrique. Mais avant de mettre en place notre modèle
de base de travail, il est nécessaire de le présenter.
II. Généralités sur le
modèle
La démarche méthodologique utilisée dans
la littérature économique, pour la détermination de la
partie stable des dépôts à vue, repose essentiellement sur
deux approches : structurelle et équation en équilibre partiel.
L'approche en équilibre partiel est basée sur l'utilisation d'un
modèle économétrique avec des variables dépendantes
qui reflètent l'activité économique et le comportement
individuel des agents économiques en termes de consommation
d'investissement. (Abdelmoumni M., Cohen M., Dupré D., El Karoui N., et
Simoneau G; (1996)).
Sur la base des paramètres du modèle
estimé, les banques peuvent fixer des hypothèses
d'évolution des montants des dépôts. Toutefois,
l'incertitude liée à l'horizon de prévision amène
naturellement à considérer plusieurs scénarii. Par
ailleurs, la prévision des variables exogènes peut
nécessiter d'autres modèles explicatifs. Ce type
d'équation est donc surtout utile pour la prévision à
court terme. La deuxième approche repose sur une démarche
structurelle avec un modèle dont les coefficients sont
interprétables (Denis Dupré, 1996). Le modèle
estimé par Dupré est basé sur la dynamique ci-après
:
dDt/Dt = (á -âRt )dt + ådWt Avec Dt :
Encours des dépôts à la date t ; Rt : Taux
d'intérêt ;
á : Tendance moyenne du comportement non financier des
déposants ;
â : Taux de collecte supplémentaire pour un point de
diminution de taux.
DWt : un bruit blanc.
Sur la base de l'estimation des paramètres á
etâ, l'évolution de l'encours des dépôts est
estimée sous l'hypothèse que le bruit blanc est nul.
La méthode de Box et Jenkins consiste à
étudier systématiquement les séries chronologiques
à partir de leurs caractéristiques, afin de déterminer
dans la famille des modèles ARIMA, celui qui est le plus adapté
à représenter le phénomène étudié.

Elle procède par étapes successives dont trois
étapes principales qui sont définies ci-après : Recherche
de la représentation adéquate :
l'identification ; Estimation des paramètres Test
d'adéquation du modèle et prévision.
v Modèle ARMA
La méthode ARMA représente la Moyenne Mobile
Intégrée Autorégressive.
Dans le modèle ARMA, l'objectif recherché est la
détermination de chaque valeur de la série en fonction des
valeurs qui la précèdent (y1 = f(yt-1, yt-2, ...)). Un
modèle ARIMA est étiqueté comme modèle ARMA
(p,d,q), dans lequel :
· p est le nombre de termes auto régressifs ;
· d est l'ordre d'intégration de la série
modélisée ;
· q est le nombre de moyennes mobiles.
v Pour ce qui est du modèle statistique Durbin et
Watson (DW) :
Il est compris entre zéro et quatre. L'hypothèse
nulle d'absence d'autocorrélation des erreurs est acceptée
lorsque la valeur de cette statistique est proche de deux. Des valeurs
critiques au seuil de 5% (resp. d 1 et d 2 , avec d 1
>d 2 ) ont été tabulées. L'interprétation
du test de Durbin et Watson est alors la suivante :
1. Si la valeur calculée de la statistique DW est
inférieure à la valeur tabulée d1 alors il existe une
autocorrélation positive (ou p>0).
2. Si la valeur calculée de la statistique DW est
comprise entre d2 et 4-d2 , il n'est pas possible de rejeter l'hypothèse
nulle d'absence d'autocorrélation des résidus (ou p=0). Cet
intervalle est autrement dit l'intervalle pour il n'existe pas
d'autocorrélation des erreurs.
3. Si la valeur calculée de la statistique DW est
supérieure à la valeur tabulée 4-d1 alors il existe une
autocorrélation négative (ou p<0).
Les autres situations correspondent à des zones
d'indétermination. La figure qui suit résume
l'interprétation du test de Durbin et Watson.
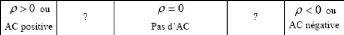

25
Note : pour les relations considérées, les
valeurs critiques sont respectivement de 1,16 et 1,39 au seuil de 5%.
L'utilisation de ce type de modèle nécessite la
disponibilité de données individuelles sur le comportement des
épargnants. Ces informations n'étant pas disponibles au
Sénégal, nous utiliserons dans notre démarche, une
approche semi structurelle qui est basée sur l'étude des
propriétés stochastiques des séries statistiques sur les
tableurs Excel et stata ou eviews.
Nous aborderons la partie suivante de notre étude
consacrée à l'aspect pratique qui, scindera le travail en
différents chapitres avec des sections : résultats descriptifs et
la discussion des résultats.
| 


