Biologie et écologie des rapaces sympatriques malgache accipiter madagascariensis et falco zoniventris dans la forêt sèche de Mangily, sud-ouest de Madagascar

I.5.1. Moyen et écart-type

Certains résultats sont présentés sous forme de moyenne accompagnée de l'écart-type (moyenne#177; écart-type) selon les formules suivantes :

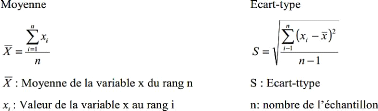
33

I.5.2. Test de Chi-deux (÷2)

Le test de ÷2 sert à tester l'homogénéité des faits observés avec ceux à espérer pour deux ou plus d'échantillons (Jonshon, 1992). Ce test est le plus utilisé et conseillé pour les ornithologues (Fowler & Cohen, 1985). Dans cette étude, il a été utilisé afin de comparer la distribution des effectifs de population dans les zones protégées et non protégées. Ce test est employé pour vérifier les hypothèses suivantes :

Hypothèse 1 :

H01 : « La distribution des effectifs des populations dans les zones protégées et non protégées est homogène ».

Ha1 : « La distribution des effectifs des populations dans les zones protégées et non protégées est hétérogène ».

34

Hypothèse 2 :

H02 : L'effectif de ces deux rapaces dans la zone étudiée est égal Ha2 : L'effectif de ces deux rapaces dans zone étudiée est différent La valeur de ÷2 est obtenue par la formule suivante (Jonshon, 1992) :

K X^2=? C=1	(oi-ci)^2
	Ci

Où : Oi : valeur observée et Ci : valeur calculée (théorique) Calcul de la fréquence calculée

Les données initiales étaient groupées dans un tableau de "l" lignes et de "c" colonnes. L'effectif calculé d'une case est le produit du total de la ligne par le total de la colonne, divisé par le total général.

Le degré de liberté (d.d.l) est obtenu par :

d.d.l = (Nombre de ligne - 1) (Nombre de colonne - 1).

Dans le cas où d.d.l = 1, il faudrait passer à la correction de Yates (Fowler et Cohen, 1985) pour chaque variable considérée dont :

(/0-C/-0,5)²

C

X2 yate =

La valeur de ÷2 à la fin de la correction de Yates sera 2 X ÷2yate.

Pour évaluer le tes de Chi-deux, la valeur de ÷2 ainsi obtenue (÷2cal) est comparée à celle donnée par la table (÷2tab). La probabilité de risque est de 5% avec l'hypothèse nulle H0 : « Il n'y a pas de différence significative entre les variables testés », donc :

- Si ÷2cal >÷2tab la différence est significative donc H0 rejetée

- Si ÷2cal < ÷2tab H0 acceptée