Fréquence optimale et fréquence de 5 minutes: Une comparaison des volatilités réalisées journalières à partir du modèle HAR-RV

16/04/2013

Université de Montréal

Rapport de recherche

Fréquence optimale et fréquence de 5 minutes : Une comparaison
des Volatilités Réalisées journalières à partir du modèle HAR-RV.

Rédigé par:

GUERRIER Joseph Junior

Dirigé par:

KALNINA Ilze

Département des sciences économiques
Faculté des arts et des sciences

1

Sommaire

I. Résumé du projet 2

II. Introduction et motivation 3

III. Revue de la littérature 4

Corsi (2009) 4

Corsi, Pirino et Reno (2010) 5

Bandi et Russell (2007) 7

IV. Statistiques descriptives et analyse des données 9

Volatilité réalisée du CHK stock: données regroupées par fréquences de 5 minutes 10

Volatilité réalisée du CHK stock: données regroupées par fréquences de 9 minutes 11

Volatilité réalisée, fréquences de 5 minutes et de 9 minutes : comparaison 11

Auto-corrélation des volatilités réalisées pour les séries journalières 13

V. Estimation et prévision 15

Test de stationnarité et relation de long terme 15

Estimation 17

Prévision hors échantillons 18

VI. Conclusion 24

VII. Annexe 25

VIII. référence ,.33

I- Résumé du projet

2

La réalisation de cet ouvrage s'appuie essentiellement sur les travaux de Corsi (1999) et de Bandi et Russell (2007). En effet notre modèle de base, pour les fins d'estimation et de prévision, est le modèle HAR(3)-RV présenté par Corsi. Notre analyse se portera sur le `CHK Stock' pour l'année 2010 avec des données journalières à hautes fréquences. Dans un premier temps on va regrouper les données en des fréquences de 5 minutes puis, en utilisant les même principes que Bandi et Russell (2007), on va déterminer une fréquence optimale<sup>1</sup> `M' pour chaque journée de transaction et prendre leur moyenne arithmétique simple sur les 252 jours ouvrables de l'année en question, afin d'avoir une seule et même fréquence optimale `M*'.

Le présent document commencera par une revue de littérature où principalement les travaux de Corsi (1999), Corsi, Pirino et Reno (2010) et Bandi et Russell (2007) seront présentés et sur lesquels on s'appuiera pour faire notre travail. Ensuite, la sélection, la manipulation et la transformation des données sur le CHK Stock (données allant du 4 janvier 2010 au 31 décembre 2010) permettront de déterminer la variable sous études qui est la RV² et de présenter les différents graphes et tableaux de statistiques descriptives relatifs aux diverses transformations qu'on aura opérées sur la variable de base pour les besoins d'analyse. En troisième lieu, on se prêtera à un exercice d'estimation des coefficients du modèle pour les deux séries en question³ en prenant soin de corriger les écarts-types selon Newey-West en vue de pallier de possibles problèmes d'auto corrélations des erreurs. Finalement, des prévisions hors échantillons seront effectuées pour les deux séries et leurs erreurs quadratiques moyennes seront comparées afin de déterminer laquelle donne un meilleur résultat.

1 La fréquence optimale M* selon Bandi et Russell (2007), est celle qui minimise la perte quadratique conditionnelle de la volatilité réalisée estimée.

2 Le RV se réfère à Realized volatility ou volatilité réalisée en français.

3 On fait référence à la série regroupée par fréquences de 5 minutes et celle regroupée par M* qui est la fréquence optimale de Bandi et Russell (2007)

II- Introduction et motivation

3

Le comportement des données financières hautes fréquences occupe une place importante dans la littérature économique depuis un certain temps. De nombreuses études ont été réalisées en vue de déterminer des méthodes d'estimation et de prévision appropriées. Des études comme celle réalisée par Corsi (1999), tentent de trouver un modèle dit à mémoire courte qui puisse donner d'assez bons résultats comparés à ceux de modèles plus complexes dits de long mémoire. L'analyse de ces types de données (données à hautes fréquences) pose souvent des problèmes dits de « microstructure noise» qui affectent les résultats d'analyse en biaisant les résultats d'estimation et de prévision. Bandi et Russell (2007) se sont donnés pour tâche de déterminer le regroupement des données en fréquences optimales en vue d'un arbitrage entre minimiser la `microstructure noise' et avoir une meilleure estimation de la variance intégrée pendant que d'autres utilisent par convention un regroupement des données par intervalles de 5 minutes. Notre travail consiste de ce fait à déterminer, pour le CHK Stock (Chesapeake Energy Coorporation⁴) la pertinence de la fréquence optimale, proposée par Bandi et Russell (2007), par rapport à la fréquence de 5 minutes conventionnellement utilisée. Nous allons donc estimer et faire la prévision pour deux bases de données⁵ différentes du CHK Stock (données allant du 4 janvier 2010 au 31 décembre 2010) en utilisant le modèle HAR(3)-RV de CORSI (1999) et déterminer, en analysant les erreurs quadratiques moyennes, laquelle des deux fréquences permet d'avoir un meilleur résultat.

4 Le Chesapeake Energy Corp est une compagnie de d'exploitation et de production de gaz naturel. Cette compagnie explore, développe et fait acquisition de propriétés en vue de la production de gaz naturel et de pétrole non raffiné.

5 Les données regroupées par fréquences de 5 minutes et celles regroupées en fréquence optimale selon Bandi et Russell (2007)

4

III- Revue de la littérature

Dans le cadre de ce travail, trois articles ont été retenus et utilisés comme base. Le premier est «A Simple Approximate Long-Memory Model of Realized Volatility» et a été réalisé par Corsi (1999). Le second intitulé « Thershold bipower variation and the impact of jumps on volatility forecasting» par Corsi, Pirino et Reno (2010) et finalement le dernier «Microstructure Noise, Realized variance, and optimal sampling» de Bandi et Russell (2007).

Corsi (2009)

Dans ce papier l'auteur présente le modèle `Heterogeneous Autoregressive model of realized Volatility' (HAR-RV) qui conduit à un modèle de type Auto-regressif (AR). Il montre que malgré la simplicité de la structure de ce dernier et, l'absence de propriété « long mémoire », il donne de très bons résultats de prévisions dans et hors échantillons.

A travers un survol de la littérature sur les problèmes que posent les séries financières, (notamment les auto- corrélations des carrés des rendements et les rendements absolus montrent de fortes persistances pour les longues périodes) l'auteur présente le modèle GARCH standard et les modèles de volatilités stochastiques à mémoire courte comme ayant des limitations dans la reproduction de certaines caractéristiques des données. Quant aux volatilités à mémoires longs, elles sont généralement obtenues grâce aux modèles FIGARCH de rendements ou les modèles ARFIMA de volatilité réalisée. Ces derniers ont de bonnes astuces mathématiques mais ont un manque quand à leur interprétation économique. D'un autre côté, une autre approche montre que, si le niveau d'intégration n'est pas assez large comparé à la fréquence la plus faible du modèle, de vraies modèles à mémoire courte peuvent être pris asymptotiquement pour des modèles à mémoire longue comme le montre LeBaron (2001). Finalement, Corsi propose un modèle additif en cascade de différentes composantes de volatilités générées par les actions de différents types de participants sur le marché. Ce modèle est le « Autorégressive modèle of Realized Volatility (HAR-RV) et selon ce dernier, il est capable de reproduire la même persistance de la volatilité observée dans les données empiriques.

5

La construction du modèle HAR-RV part du processus temporel standard continue suivant: dp(t) =u(t)dt +ó(t)dw(t) où p(t) est le logarithme des prix instantanés; u(t) est un processus aléatoire fini; w(t) est un mouvement brownien continue et ó(t) est processus stochastique indépendant de w(t). La variance intégrée (IV) est l'intégrale de la variance instantanée sur un

?

intervalle d'une journée IVt (d)= ? ?2(?)?? et la volatilité intégrée est noté ?? (?)= (IVt (d))1/2.
????

La variance intégrée (IVt ^(d)) peut être approximée par la somme des carrés des rendements à l'intérieur d'une journée et la volatilité réalisée sur un intervalle d'une journée est

???

??? (?)= (? r

??? ???.?'

? )1/2 avec Ä=1d/M et rt-j.Ä=p(t-j.Ä)-p(t-(j+1))⁶. La construction de ce modèle a été influencée par les Hypothèses d'hétérogénéité des marchés présentées par Muller et al (1983).

Dans le cadre de cet article Corsi considère un modèle hiérarchisé avec trois composantes de volatilité correspondant aux horizons d'un jour, une semaine et un mois (??^(d)1, ??^(w)1_, ??^(m)1) et la composante journalière de la volatilité permet de déterminer le rendement haute fréquence du processus suivant la relation rt= ?? (?) ?t avec ?t ~ N I D(0,1). Apres manipulations il obtient la représentation série temporelle très simple suivante ??????

(?) = c+ f3^(d) ??? (?)+ f3^(w) ??? (?)+ f3^(m) ??? ^(?)+ùt+1d qui est un HAR(3)-RV⁷. Les résultats de simulations avec ce modèle confirment de sa capacité à reproduire, avec efficacité, les volatilités et les rendements observés dans les données empiriques. En même temps, le critère d'information de Akaike traduit une préférence du HAR(3) à celui d'un AR(22) pendant que les résultats de prévisions comparés à ceux d'un ARFIMA (5,d,0) montrent que les deux modèles sont comparables.

Corsi, Pirino et Reno (2010)

La littérature sur l'importance des sauts en économie financière est vaste. Les auteurs de ce présent papier en citent quelques uns. Certains comme Ait-Sahalia (2004), Jiang et Oomen (2008), Barndorf-Nielsen et Shephard (2006), Lee et Mykland (2008) et Ait-Sahalia et Jacob

6 Anderson,Bollerslev, Diebold et Labys (2001), Anderson,Bollerslev, Diebold et Ebens (2001) et Barnadorff-Nielsen et Shephard (2002a,2002b) cités par Corsi (2009).

7 Corsi 2009

6

(2009) sont venus avec les tests de spécification. D'autres comme Bandi et Nguyen (2003) et Johannes (2004) ont réalisé des estimations non paramétriques en présence de sauts. Contrairement au travail de Corsi (2009) qui considérait les séries financières comme des variables continues, les auteurs de ce présent article ont surtout mis l'accent sur les sauts dont peuvent faire l'objet les variables financières. En clair, leur travail s'évertue à montrer que les sauts ont un impact positif significatif sur les volatilités futures ce qui leur permet du coup de prendre le contrepied des travaux de Andersen et al (2007), Forsberg et Ghysels (2007), Giot et Laurent (2007) qui eux ont trouvé un impact des sauts sur la volatilité qui est négatif ou nul. Ils procèdent en décomposant la volatilité en sa composante continue et en sa composante non continue en utilisant des estimateurs consistants. Les auteurs introduisent de ce fait l'estimateur « Thershold bipower variation (TBV)» ou seuil de variation à deux puissances qui se base sur l'utilisation combinée de la variation à deux puissances et l'estimation du seuil. La contribution leur papier est triple. D'abord, à travers des estimations réalistes, ils montrent qu'en présence de sauts, la variation à deux puissances ( Bipower Variation) a un biais plus important et ceci a pour conséquence une sous estimation de la composante du saut. Ensuite, ils proposent un estimateur alternatif de la puissance intégrée de la volatilité en présence de saut. Enfin, un nouveau test « C-Tz »⁸ permettant la détection de sauts est introduit et est une correction du test statistique « Z » de Barndorff-Nielsen et Stephard (2006)⁹.

Des estimations ont été faites en vue de montrer qu'en échantillon fini, la variation à deux puissances est un estimateur biaisé de la volatilité intégré en présence de sauts tandis que les estimateurs basés sur un seuil sont moins sensibles aux sauts et de ce fait sont moins biaisés. Les résultats des simulations ont permis de tirer les conclusions suivantes :

1- La mesure de la volatilité intégrée montre que les estimateurs de variations à deux puissances (bipower variation) contiennent plus de biais que ceux se basant sur un seul seuil.

8 Voir sa construction et son expression dans Threshold bipower variation and the impact of jumps on volatility forecasting page 279

9 Threshold bipower variation and the impact of jumps on volatility forecasting page 277.

7

2- Dans la détermination de la variance intégrée, la TBV¹⁰ est presque insensible au choix d'un seuil pour une certaine valeur d'une constante CO¹¹ tandis que la variance réalisée avec un seul seuil l'est d'avantage.

En conclusion, il a été montré dans ce papier que la décomposition de la volatilité en sauts et variation continue, améliore considérablement la projection de la volatilité à cause de l'impact positif des sauts sur la volatilité future. Les résultats empiriques obtenus à partir des `US stock index', des `stocks individuels' et des `Bonds du trésor' ont permis de montrer que les sauts peuvent être détectés grâce au test C-Tz basé sur les estimateurs TMPV¹².

Bandi et Russell (2007)

L'attention de ces auteurs s'est surtout portée vers les « Microstructure noise, realized variance and optimal sampling ». Leur objectif était de montrer comment la « microstructure noise» affectait la variance réalisée qui dans ce cas ne permettait pas d'identifier le prix d'équilibre sans friction. Aussi, ils se sont évertués à montrer comment le biais induit par la « Microstructure noise » des données à hautes fréquences pouvait faire l'objet d'un arbitrage avec la réduction de variance. Ils en dérivent une erreur quadratique moyenne (MSE¹³) optimale pour l'échantillon. Leur travail leur a aussi permis de déterminer la valeur optimale du nombre d'observations (ou fréquence) leur permettant d'obtenir le MSE minimal. Leur approche a ensuite été appliquée sur un échantillon de IBM ce qui leur a permis de confirmer sa justesse et la précision des résultats de projection.

Le modèle théorique qu'ils utilisent considère une période de temps fixe « h » et le prix observé à la i-ème période est: ?^?ih=pihOih.

Pih est le prix à l'équilibre sans friction et Oih est la « microstructure noise ». La transformation algorithmique des prix donne l'équation suivante:

ln(??ih) - ln (?^?(i-1)h) = ln(pih) - ln(p(i-1)h) + çih - ç(i-1)h i= 1,2,3 n, et ç = ln O

10 TBV fait référence à Threshold bipower variation

11 CO = 3. Voir Threshold bipower variation and the impact of jumps on volatility forecasting page 278

12 Threshold multipower variation

13 Dans la suite du travail, l'erreur quadratique moyenne sera notée MSE

8

ln(??ih) - ln (?^?(i-1)h) = ?Þi ; ln(pih) - ln(p(i-1)h) = ri çih - ç(i-1)h = åi

En divisant maintenant les périodes en « M » sous périodes (fréquences) ils obtiennent l'équation du rendement comme suit :

?^Þji = ln(?^?(i-1)h+jS) - ln (?^?(i-1)h+ (j-1)S) j= 1,2,3 M, et S= h/M

= ?^?_?rj+ ?j~_?åJ + 2 ?M?rjåj¹⁴

L'un des intérêts de leur travail est de caractériser les propriétés en échantillon fini et les propriétés asymptotiques de l'estimateur de la variance réalisée ?? = ?M_? ?Þ Cette expression de la variance réalisée n'est correcte que si le véritable processus de prix est observé, dans le cas contraire, V?

En échantillon fini, Bandi et Russel ont montré que le minimum du MSE de la variance réalisée est atteint pour une valeur spécifique de M soit M*¹⁵. Sous certaines hypothèses données¹⁶ ils

montrent que E_u(?^? -V)² = 2 ?? (Q+ o(1)) +Mb + M²a +c¹⁷. E_u est l'espérance conditionnelle à la

fréquence de la volatilité sur la période et sera notée tout simplement `E' quand l'espérance n'est pas conditionnelle. Ils montrent par la suite que la valeur de M, soit M* (fréquence optimale) qui permet de minimiser la MSE est : M* (h?/(?(?)<sup>2</sup>)<sup>2</sup>)<sup>1/3</sup>. Dans le document les auteurs considèrent également des extensions de M* pour des cas comme la `correction de biais de la variance réalisée', les `fonctions non linéaires de la variance intégrée' et les `bruits dépendants'¹⁸.

14 Voir Bandi et Russell (2007), page 9.

15 M* est la fréquence permettant d'avoir un MSE minimal

16 Voir les hypotheses dans Bandi et Russell (2007), page 11 et 12

17 Q?= _????M? r?4j ; a= (E(å2))2; b= E(å4) + 2E(å2å2-1)- 3(E(å2))2 ; c= 4E(å2)V- 2E(å2å2-1)+ 2(E(å2))2 et h est la durée en seconde d'une journee

d'activité. Voir les démonstrations dans Bandi et Russell (2007), appendis A.

18 Bandi et Russell (2007), page 14 à 18.

9

IV- Statistiques descriptives et analyse des données

Les données recueillies dans le cadre de ce travail sont des données de très hautes fréquences collectées pratiquement à la seconde. Une journée d'activité de trading commence de 9:30 am et se termine a 16 :00 PM du lundi au vendredi pour les jours non fériés de l'année en question¹⁹. Nous avons donc dans un premier temps regroupé les données en fréquences de 5 minutes ce qui nous donne 78 observations de prix pour chaque journée. Dans un second temps on a calculé la fréquence optimale à partir de la formule de Bandi et Russel M* (h?/(?(?)²)²)^1/3 où `h' est l'unité de période en secondes (dans notre cas `h' correspond a une journée d'activité de trading soit 23,400 secondes),`Q<sup>20</sup>' est appelé `integreted quarticity' et est généralement remplacé par

son estimateur Q?

??? ? ?r ? 4 21 et `?' est la microstructure noise. Pour arriver à la fréquence ??? j

optimale, on a choisit dans un premier temps, pour le calcul de r?⁴ et de ^?Q, une fréquence relativement basse de 15 minutes qui permette de rendre négligeable l'effet de la « microstructure noise du marché » sur leur calcul. Ensuite, on calcul un Mj²² pour chacun des 252 jours d'activités de l'année 2010 et on détermine sa valeur moyenne de sorte qu'on ait une valeur unique M*. Dans le cadre de ce travail on a trouvé une valeur M* avoisinant les 9 minutes et de ce fait, pour la simplicité des calculs on a considéré M*=9 minutes.

Le modèle HAR(3)-RV consiste à faire la régression ??????

(?) = c+ â^(d) ???(?)+ â^(w) ???(?)+

â(m) ???^(?)+ùt+1d.. Dans ce modèle, ??????

(?) est la volatilité réalisée journalière au temps t+1, ???(?) est la volatilité réalisée journalière au temps t, ???(?) est la volatilité réalisée hebdomadaire obtenue en faisant la moyenne arithmétique simple de la volatilité réalisée pour 5 jours ouvrables consécutifs et ??_?^(?)est la volatilité réalisée mensuelle obtenue en faisant la moyenne arithmétique simple de 20 jours ouvrables consécutifs. De ce fait, on a pu déterminer les volatilités réalisées ???(?) en prenant la racine carrée de la somme des carrés du logarithme

? )1/2.

des pris par intervalles de 5 minutes et de 9 minutes ???(?)= (? r

???

??? ???.?'

19 Cete consideration d'un journee d'activité est selon le New York Stock Exchange (NYSE).

20 `Q' est considéré comme la variance du signal

21 Pour le calcul le calcul de Q? on a pris M=15 minutes afin d'éviter la microstructure noise contamination.

22 Mj est une valeur journalière

10

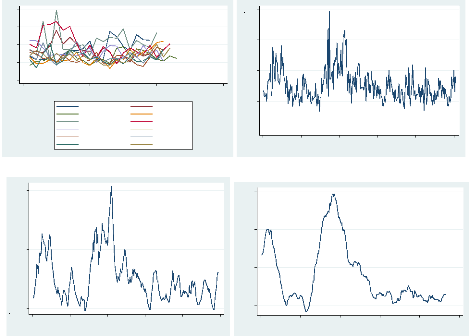
Volatilité Réalisée du CHK stock: Données regroupées par fréquences de 5 minutes

Les graphiques présentés dans cette partie du travail font ressortir les tendances des volatilités réalisées regroupées par fréquences de 5 minutes. La comparaison de ces dernières, mois par mois (de janvier 2010 à décembre 2010), laisse ressortir une certaine consistance dans les données sauf pour les mois de Février, Mai et Juin où il y a certaine hausse à leur début. Cette variation peut également être observée quand un graphique chronologique annuelle est réalisé et également en observant les volatilités hebdomadaires et mensuelles.

.01 .02

0

0 10 20 30

days 2

Jan freq 5 Fev freq 5
Mars freq 5 AVRIl freq 5
MAY freq 5 JUIN freq 5

JUILLET freq 5 AOUT freq 5
SEPT freq 5 OCT freq 5
NOV freq 5 DEC freq 5

.02

.015

.01

.005

0

0 50 100 150 200 250

days

.015

.01

.005

0 50 100 150 200 250

Weeks

.012

.01

.006 .008

0 50 100 150 200 250

Months

Figure 1 : Volatilités réalisées des données regroupées en fréquence de 5 minutes

11

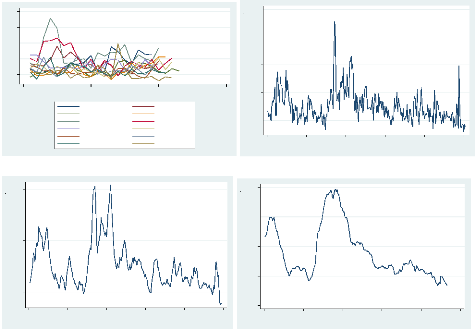
Volatilité Réalisée du CHK stock: Données regroupées par fréquences optimale de 9 minutes

A peu près les mêmes tendances sont observées quand les volatilités réalisées sont regroupées par fréquences de 9 minutes que quand elles le sont par fréquences de 5 minutes. Les graphiques suivant en attestent cette similitude.

Figure 2 : Volatilités réalisées des données regroupées en fréquence de 9 minutes

.01 .02

0 10 20 30

days 2

Jan freq 9 Fev freq 9
Mars freq 9 AVRIl freq 9
MAY freq 9 JUIN freq 9

JUILLET freq 9 AOUT freq 9
SEPT freq 9 OCT freq 9
NOV freq 9 DEC freq 9

.025

.02

.015

.01

.005

0 50 100 150 200 250

days

.015

.01

.005

0 50 100 150 200 250

Weeks

.012

.01

.004 .006 .008

0 50 100 150 200 250

Months

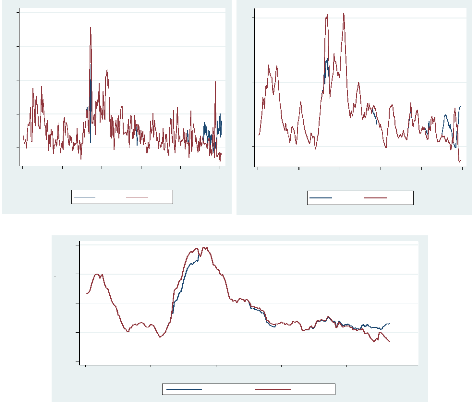
Volatilité Réalisée, fréquences de 5 minutes et de 9 minutes : Comparaison

En dehors des similitudes observées au niveau de leur tendance, on a jugé bon de mettre sur un même repère les volatilités réalisées de même type. Ce faisant, on peut remarquer que les graphes sont presque toujours confondus dans le cas des volatilités journalières et hebdomadaires, sauf à quelques rares endroits. En ce qui concerne leurs volatilités réalisées

12

considérées mensuellement, les données regroupées en fréquence de 9 minutes attestent de volatilités généralement plus élevées que ceux regroupées en fréquence optimale de 5 minutes.

Figure 3 : Volatilités réalisées : graphiques comparés des données de 5 minutes et de 9 minutes

.01

. 0 1 . 0 2

.0 1

0 50 100 150 200 250

days

0 50 100 150 200 250

Weeks

RV(d)5 RV(d)9

RV(w)5 RV(w)9

0 50 100 150 200 250

Months

RV(m)5 RV(m)9

Une analyse descriptive des donnés journalières permet de tirer les même conclusions que précédemment.

13

Tableau 1 : Statistiques descriptives

. tabstat rvd5 rvd9 rvw5 rvw9 rvm5 rvm9, statistics( mean sd skewness kurtosis ) columns(variables)

stats	rvd5	rvd9	rvw5	rvw9	rvm5	rvm9
mean	.0075705	.0075156	.0075754	.0075559	.0079124	.0076104
sd	.0025741	.0028641	.0019837	.00223	.0018749	.0017779
skewness	1.404292	1.650738	1.191229	1.299055	1.317743	.9857251
kurtosis	5.802221	7.374368	4.238651	4.662374	3.685027	2.791721

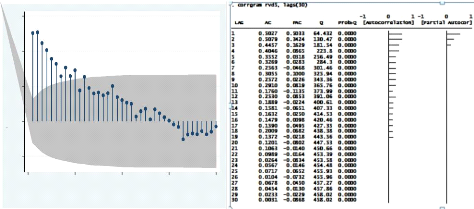
Auto-Corrélation des Volatilités réalisées pour les séries journalières

L'analyse des graphiques et tableaux d'auto-corrélations pour les séries de volatilités réalisées attestent d'une éventuelle stationnarité (sous l'hypothèse que la variable en question est homoskedastique) pour les deux séries (Volatilités réalisées journalières regroupées en fréquences de 5 minutes et en fréquences de 9 minutes) quand on fait le calcul avec 30 retards pour les deux séries. En effet, l'auto-corrélation des erreurs tend vers 0 à partir de 19^ème retard pour la série RV(d)5 et à partir du 22^ème retard pour la série RV(d)9.

14

Figure 4 : Auto-corrélation des volatilités réalisées journalières : fréquence de 5 minutes

0.00 0 . 2 0 0 . 4 0 0 . 6 0

-0.20

0 10 20 30 40

Lag

Bartlett's formula for MA(q) 95% confidence bands

0 . 0 0 0 . 2 0 0 . 4 0 0 . 6 0

- 0 . 2 0

0 10 20 30 40

Lag

Bartlett's formula for MA(q) 95% confidence bands

Figure 5 : Auto-corrélation des volatilités réalisées journalières : fréquence de 9 minutes

15

V- Estimation et prévision

Les variables en questions sont toutes les volatilités calculées à partir du logarithme du prix du stock CHK, considérées de manière journalières, hebdomadaires ou mensuelles pour des données regroupés en fréquences de 5 et de 9 minutes. Dans le cadre de l'estimation et pour la prévision, les variables dépendantes sont notées RV(d)5 et RV(d)9 et se réfèrent respectivement aux volatilités réalisées journalières pour la période « t+1 » des séries regroupées en fréquences de 5 et 9 minutes. Les variables explicatives RV(d)5t, RV(w)5t, RV(m)5t, RV(d)9t, RV(w)9t, RV(m)9t sont respectivement les volatilités réalisées journalières, hebdomadaires et mensuelles pour la période « t » respectivement pour les séries regroupés en fréquences de 5 et 9 minutes. Le modèle HAR utilisé régresse la volatilité journalière sur la volatilité journalière retardée ainsi que sur les volatilités hebdomadaire et mensuelle, également retardées, c'est-à-dire de la période « t ». Cette partie du travail présente dans un premier temps les testes de stationnarité puis les estimations ensuite les prévisions pours les deux séries sous études.

Test de Stationnarité et relation de long terme

Avant de procéder à l'estimation des paramètres du modèle, nous allons utiliser les tests Dickey-Fuller Augmenté (ADF) et Phillips-Perron (PP) pour déterminer si les séries de volatilités réalisés journalières, hebdomadaires et mensuelles sont stationnaires à travers le temps. L'hypothèse nulle de ces tests stipule que la variable contient une racine unitaire, tandis que l'hypothèse alternative indique que la série est générée par un processus stationnaire. Pour choisir le nombre optimal de retards à inclure dans la régression, nous avons utilisé le critère d'information AIC²³ (Akaike Information Criteria).

23 Voir tableau # 9 à tableau #14 en annexe.

16

Tableau# 2 Test de stationnarité ADF et PP

Augmented Dickey-Fuller

Test Stat

5% critical Value

RV(d)5t -4.284 -2.881

RV(w)5t -2.182 -2.882

RV(m)5t -2.349 -2.881

RV(d)9t -3.912 -2.881

RV(w)9t -2.084 -2.882

RV(m)9t -2.306 -2.882

Phillips-Perron Test

Test Stat

5% critical Value

RV(d)5t -9.017 -2.881

RV(w)5t -3.006 -2.881

RV(m)5t -1.313 -2.881

RV(d)9t
RV(w)9t
RV(m)9t

-6.849	-2.881
-3.004	-2.881
-1.024	-2.881

Source : Calculs effectués à partir de Stata

Le tableau ci-haut présente les résultats des deux tests (ADf et PP) pour les différentes séries utilisées dans l'estimation des volatilités réalisées journalières regroupées en fréquences de 5 et de 9 minutes. Selon le test ADF seulement les séries de volatilités réalisées journalières (fréquences de 5 et 9 minutes) sont stationnaires tandis que le test PP dénote la stationnarité des séries de volatilités hebdomadaires également en plus. Ceci est assez juste car le test PP est habituellement plus puissant que celui d'ADF. Michael et al (1997), soutiennent que ces problèmes peuvent être dus soit à des erreurs de mesure dans les données soit à cause de la faible puissance des tests, ou tout simplement à cause de l'absence de linéarité dans les séries. Toutefois on suppose que toutes les variables sont stationnaires pour pouvoir poursuivre notre étude.

17

Estimation

L'estimation des paramètres du modèle HAR(3)-RV est faite par la méthode des moindres carrés ordinaires (MCO)²⁴. On considère toutes les variables de l'équation ??????

(?) = c+ â^(d) ??? (?)+ â(w) ??? (?)+ â(m) ??? ^(?)+ùt+1d comme étant observées et on estime les paramètres. Cependant, dans le but de palier d'éventuels problèmes d'auto-corrélation des erreurs dans les données, on a appliqué la méthode de correction de covariance pour les séries corrélées de Newey-West. Le tableau suivant présente les résultats obtenus de l'estimation.

Tableau# 3 HAR(3)-RV estimation

Source : Calculs effectués à partir de Stata

Le seuil critique pour un niveau d'erreur de 5% est de 1,812²⁵ et en comparant les « t » statistiques (les valeurs entre parenthèses) à ce seuil on remarque que pour le modèle avec fréquences de 5 minutes, seulement le coefficient de la volatilité réalisée hebdomadaire est significativement différent de 0 tandis que pour le modèle avec fréquences de 9 minutes seulement le coefficient de la volatilité réalisée journalière l'est. Cette non significativité de la plus part des paramètres peut être du au fait que certaines séries ne sont pas stationnaires ou bien à cause d'une présence importante de « microstructure noise» dans les séries. Comme expliqué par Corsi 2009, la non significativité des paramètres en question peut être due au fait

24 Le principe des MCO est d'estimer les coefficients de façon à minimiser l'erreur d'estimation.

25 Valeur tirée de Hamilton, page 755.

18

de l'estimation de séries fortement affectées par la microstructure noise. En effet c'est possiblement le cas des séries RV(d)5t; RV(w)5t; RV(d)9t et RV(w)9t qui sont toutes stationnaires selon les résultats du test PP a 5%.

Une analyse d'un modèle AR(5)²⁶ sur les volatilités journalières regroupées suivant les deux fréquences utilisées, nous permet de soutenir l'hypothèse d'un possible problème de microstructure noise au niveau des données. En effet l'estimation des modèles AR(5), avec la correction de Newey West, nous montre que seulement les coefficients des volatilités réalisées avec un seul retard sont significativement différents de « 0 ».

Afin de pouvoir continuer avec notre travail et réaliser les prévisions, on va supposer que toutes les séries sont stationnaires et que les résultats d'estimations sont concluants.

Prévisions hors échantillons

Dans cette partie du travail on va procéder des exercices de prévisions hors échantillon afin de déterminer lequel des séries du CHK stock, regroupées soit en fréquences de 5 minutes soit en fréquences optimales de 9 minutes de Bandi et Russell (2007), est plus performant en utilisant le model HAR(3)-RV de Corsi (2009). En effet, l'une des utilités principales de l'estimation de volatilités est la réalisation de prévisions pouvant servir à la prise de décision.

Pour évaluer et comparer les prévisions du modèle HAR(3)-RV appliqué aux séries de CHK stock regroupées en fréquences de 5 minutes et en fréquences optimale de 9 minutes, on priorise dans le cadre de ce travail la méthode de fenêtre récursive. On a choisit de faire la prévision sur deux mois soit 40 jours ouvrables, selon notre définition d'un mois, dans le cadre de notre travail. Soit R le nombre d'observations pour l'estimation et P celui pour la prévision, on a donc a R=192 et P=40 pour les deux variables sous études (séries de volatilités réalisées journalières regroupées en fréquences de 5 minutes et de 9 minutes). Le principe de la fenêtre récursive est la suivante: On estime le modèle sur les observations de 1 à R et on fait une prévision pour R + h²⁷. On ajoute alors une nouvelle observation à l'échantillon et on ré-estime le modèle pour les

26 Voir tableau # 23 et 24 en annexe

27 ` h' varie de 1 à P

19

observations 1 à R+1et on fait une prévision pour R+1+h. L'échantillon avec lequel nous faisons l'estimation augmente à chaque fois.

Le processus de prévision hors échantillon se fera donc comme suit:

Premièrement on estime le modèle ??????

(?) = c+ â^(d) ??? (?)+ â(w) ??? (?)+ â(m) ??? ^(?)+ùt+1d en utilisant les données pour les jours de 1 à 192 et on détermine â^? (d)(192), â? (w)( 192), â? (m)( 192), ?^?28(192). Ensuite on produit la prévision de RV(d, 193) et on la note ??? (d, 193). Ensuite on estime à nouveau le même modèle mais en considérant maintenant les données se 1 à 193 pour déterminer â^? (d)(193), â? (w)( 193), â? (m)( 193), ?^?(193) puis produire la prévision de RV(d, 194)

qu'on note ???

(d, 194). On continue ainsi jusqu'à la prévision de RV(d, 232) qu'on note

?

?? (d, 232).

L'objectif de ce travail étant de comparer l'efficacité d'un regroupement des volatilités réalisées , journalières, hebdomadaires et mensuelles ,en fréquence de 5 minutes et en fréquence optimale ( qui est de 9 minutes dans notre cas), on va calculer le « Heteroskedasticity adjusted root meam square error (HRMSE) » tel que proposé par Corsi, Pirino et Renò (2010) pour chacune des deux projections et ensuite les comparer. Le modèle qui produira le HRMSE le plus faible sera considéré comme étant le meilleur dans le cadre bien précis du CHK stock. L'expression du

?

HRMSE est ?? ? ? ? ????????? ??? ? .

???

Les projections et calculs des HRMSE se trouvent dans les deux tableaux suivants.

28 C? eslt la valeur estimée de la constante C du modèle.

20

Tableau # 4 Prévisions des volatilités réalisées journalières regroupées en fréquences de 5 minutes

Jour

Volatilites Observees

Constante et Coefficients estimes du modele

Valeures projetees et Calcul du HRMSE

RV(d)5tf RV(w)5tf RV(m)5tf c" b1" b2" b3" Y" Y Y-Y" (Y-Y")/Y ((Y-Y")/Y)"2 (1/40)* ((Y-Y")/Y)"2

0.0018459	0.1563002		0.6018683		0.0076421
0.0017772	0.1645432		0.5858661		0.0220828
0.0017479	0.1651393		0.5815531		0.0286278
0.0017428	0.1636357		0.5827547		0.0293956
0.0018368	0.1725239		0.5702962		0.0236012
0.0018747	0.1720189		0.5685132		0.0220048
0.0018578	0.1713607		0.5704522		0.0224127
0.0018637	0.1709753		0.5706345		0.0220171
0.001829	0.1722678		0.5700312		0.0248247
0.0018153	0.172427		0.5704733		0.0256084
0.0018023	0.172894		0.5701506		0.0268075
0.0017804	0.170913		0.5728039		0.0283278
0.0018097	0.1709216		0.5725243		0.0255466
0.0018138	0.1705714		0.5728131		0.0251709
0.00177	0.1675821		0.5783849		0.0270914
0.0017913	0.1670175		0.5782288		0.0255592
0.0017537	0.1658684		0.5773317		0.0315081
0.001782	0.1648022		0.5784558		0.0284316
0.0017729	0.1662356		0.5770919		0.0293317
0.0016938	0.1664063		0.5707775		0.0434201
0.0016851	0.1641059		0.5723782		0.0449302
0.0017792	0.1501784		0.5898017		0.0314926
0.0017234	0.1566712		0.5798423		0.0407615
0.0016855	0.1530694		0.5807374		0.0471365
0.0017167	0.1557225		0.577874		0.0442253
0.0017442	0.158738		0.5723437		0.0439705
0.0017771	0.1592116		0.568745		0.0436602
0.001772	0.1588429		0.5698252		0.0434721
0.0017849	0.1586889		0.5685018		0.0435955
0.0017709	0.1595789		0.5691348		0.0435511
0.0017296	0.1586224		0.5742235		0.0437012
0.0017297	0.1586182		0.5742241		0.0436986
0.0016885	0.1566861		0.5787317		0.045387
0.0016946	0.1562236		0.5792334		0.044698
0.0016601	0.159206		0.5747735		0.049852
0.0016252	0.1613872		0.5690936		0.0569481
0.0016141	0.1629218		0.5662217		0.0594351
0.0015826	0.1594892		0.5661395		0.0659914
0.0016092	0.1587013		0.5688399		0.061456
0.0016032	0.1579979		0.5692925		0.0622881
		0.005868819
0.007035562		0.004248532		-0.00278703			-0.655998308		0.43033378	0.010758345
0.007520017		0.00634207		-0.001177947			-0.185735409		0.034497642	0.000862441
0.007776141		0.007737261		-3.88804E-05			-0.005025087		2.52515E-05	6.31287E-07
0.008009672		0.010947599		0.002937927			0.268362687		0.072018532	0.001800463
0.006985544		0.007909681		0.000924137			0.116836185		0.013650694	0.000341267
0.006452743		0.005889717		-0.000563026			-0.09559475		0.009138356	0.000228459
0.006601513		0.006711692		0.000110179			0.016415996		0.000269485	6.73712E-06
0.006485142		0.005281377		-0.001203766			-0.227926485		0.051950483	0.001298762
0.006743892		0.006047966		-0.000695926			-0.115067763		0.01324059	0.000331015
0.006618745		0.006172305		-0.000446441			-0.072329678		0.005231582	0.00013079
0.006692729		0.005999666		-0.000693063			-0.115516972		0.013344171	0.000333604
0.006958394		0.007826758		0.000868364			0.110948083		0.012309477	0.000307737
0.006712663		0.006497243		-0.00021542			-0.033155529		0.001099289	2.74822E-05
0.00634954		0.004813758		-0.001535782			-0.319040104		0.101786588	0.002544665
0.006578762		0.007142242		0.00056348			0.078893986		0.006224261	0.000155607
0.006362125		0.005652878		-0.000709247			-0.125466593		0.015741866	0.000393547
0.007227727		0.007616882		0.000389155			0.051091075		0.002610298	6.52574E-05
0.006574		0.005820431		-0.000753568			-0.129469527		0.016762358	0.000419059
0.006147081		0.003517128		-0.002629953			-0.747755821		0.559138768	0.013978469
0.007344819		0.00738077		3.59509E-05			0.004870885		2.37255E-05	5.93138E-07
0.007900158		0.010424015		0.002523858			0.242119517		0.05862186	0.001465547
0.006648317		0.004473709		-0.002174608			-0.486086137		0.236279733	0.005906993
0.006931213		0.005434635		-0.001496579			-0.275377982		0.075833033	0.001895826
0.007524139		0.008566717		0.001042578			0.121700962		0.014811124	0.000370278
0.007040897		0.007886634		0.000845737			0.107236784		0.011499728	0.000287493
0.006588018		0.007531939		0.000943922			0.125322541		0.015705739	0.000392643
0.006161541		0.005886214		-0.000275327			-0.046774834		0.002187885	5.46971E-05
0.006103207		0.006475832		0.000372625			0.057540904		0.003310956	8.27739E-05
0.005936236		0.005228465		-0.000707771			-0.135368821		0.018324718	0.000458118
0.005791484		0.004346462		-0.001445021			-0.332459157		0.110529091	0.002763227
0.00617182		0.006004133		-0.000167686			-0.027928441		0.000779998	1.94999E-05
0.006012499		0.004565474		-0.001447025			-0.316949503		0.100456987	0.002511425
0.006472666		0.006708174		0.000235507			0.035107493		0.001232536	3.08134E-05
0.006480789		0.005215601		-0.001265188			-0.242577562		0.058843874	0.001471097
0.006717458		0.005446289		-0.001271169			-0.233400871		0.054475967	0.001361899
0.007243671		0.006585228		-0.000658443			-0.099987956		0.009997591	0.00024994
0.007190466		0.005662202		-0.001528263			-0.269906167		0.072849339	0.001821233
0.007718061		0.008778895		0.001060834			0.120839166		0.014602104	0.000365053
0.007274014		0.006955459		-0.000318555			-0.045799325		0.002097578	5.24395E-05
0.007452727		0.008403169		0.000950442			0.113105178		0.012792781	0.00031982
0.004248532		0.007437029		0.006477798
0.00634207		0.007765266		0.006786572
0.007737261		0.00783919		0.006693154
0.010947599		0.007348013		0.006578023
0.007909681		0.006368086		0.006458978
0.005889717		0.006020611		0.006457826
0.006711692		0.006042601		0.006539937
0.005281377		0.006265614		0.006498663
0.006047966		0.006508787		0.006558386
0.006172305		0.006261946		0.006517411
0.005999666		0.006455934		0.006426119
0.007826758		0.006386576		0.006426342
0.006497243		0.006344601		0.006263278
0.004813758		0.006209238		0.006273825
0.007142242		0.005949912		0.006293917
0.005652878		0.005997618		0.006209119
0.007616882		0.006951845		0.006255737
0.005820431		0.006323211		0.006158003
0.003517128		0.006246051		0.006305926
0.00738077		0.007255969		0.006477842
0.010424015		0.007357142		0.006528962
0.004473709		0.006778727		0.00632396
0.005434635		0.007061228		0.006426751
0.008566717		0.007269467		0.006485111
0.007886634		0.006601817		0.006355011
0.007531939		0.005893783		0.006252902
0.005886214		0.005588221		0.006161543
0.006475832		0.005324073		0.006182722
0.005228465		0.005370542		0.006158296
0.004346462		0.005367969		0.006242826
0.006004133		0.005587934		0.006432462
0.004565474		0.005704153		0.006480055
0.006708174		0.005923499		0.006719377
0.005215601		0.006337643		0.006720978
0.005446289		0.006685615		0.006971874
0.006585228		0.007276991		0.007276991
0.005662202		0.007437161		0.007449931
0.008778895		0.007426378		0.008045841
0.006955459		0.007188374		0.007679314
0.008403169		0.007023501		0.008403169

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

Ó 0.055865745

HRMSE 0.027932873

Tableau réalisé à partir de donnés tirées de Stata

21

Tableau # 5 Prévisions des volatilités réalisées journalières regroupées en fréquences optimales de 9 minutes

Jour

Volatilites Observees

Constante et Coefficients estimes du modele

Valeures projetees et Calcul du HRMSE

RV(d)9tf RV(w)9tf RV(m)9tf c" b1" b2" b3" Y" Y Y-Y" (Y-Y")/Y ((Y-Y")/Y)"2 (1/40)* ((Y-Y")/Y)"2

0.004248532			0.007437029		0.006379598
0.00634207			0.007765266		0.006688372
0.007737261			0.00783919		0.006594954
0.010947599			0.007348013		0.006479822
0.007909681			0.006368086		0.006360778
0.005889717			0.006020611		0.006359626
0.006711692			0.006042601		0.006441737
0.005281377			0.006265614		0.006400463
0.006047966			0.006508787		0.006460186
0.006172305			0.006261946		0.006419211
0.005999666			0.006455934		0.006327919
0.007826758			0.006386576		0.006328142
0.006497243			0.0059518		0.006165078
0.004813758			0.005816437		0.006175624
0.007142242			0.005557111		0.006195717
0.005652878			0.005604817		0.006110919
0.005652878			0.006559044		0.006157536
0.005820431			0.006323211		0.006158003
0.003517128			0.006246051		0.006150091
0.00738077			0.007255969		0.006249331
0.010424015			0.007357142		0.006165095
0.004473709			0.006778727		0.005901533
0.005434635			0.007061228		0.005921585
0.008566717			0.007269467		0.00596387
0.007886634			0.006601817		0.005856193
0.007531939			0.005893783		0.005650987
0.005886214			0.005588221		0.005539465
0.006475832			0.005324073		0.00544073
0.005228465			0.005370542		0.00532952
0.004346462			0.005367969		0.005465916
0.006004133			0.005587934		0.005594856
0.004565474			0.005704153		0.005472397
0.006708174			0.005923499		0.005982961
0.005215601			0.005714305		0.005984453
0.005446289			0.00577157		0.005911916
0.006585228			0.005821523		0.00582443
0.005662202			0.005535032		0.005701916
0.005662202			0.00537754		0.005634773
0.00550193			0.005501166		0.005500463
0.005696053			0.005683414		0.005436699
0.005152772			0.005300706		0.005347576
0.0016343	0.4988372			0.2190531		0.0789913
0.0015735	0.5045644			0.2082028		0.0900205
0.0015446	0.5049687			0.2049135		0.0957035
0.0015167	0.4983139			0.2097454		0.1001111
0.001601	0.5046873			0.2017939		0.0933165
0.0016411	0.5041005			0.2007061		0.0909254
0.0016186	0.5034672			0.2024683		0.0920309
0.0016335	0.5026033			0.2029615		0.0908822
0.0016023	0.5036406			0.2022821		0.0936587
0.0015894	0.5038038			0.2024889		0.0945826
0.0015807	0.5040811			0.2022566		0.0954257
0.0015481	0.5016975			0.2050819		0.0982425
0.0015793	0.5022696			0.2034937		0.0960373
0.0015993	0.5011631			0.2038083		0.0947347
0.001548	0.4973144			0.2111833		0.0964418
0.0015752	0.4971371			0.2099546		0.0950001
0.0015571	0.4981234			0.2086602		0.0971989
0.0015386	0.4987583			0.2080517		0.0991009
0.0015557	0.4964643			0.210267		0.097359
0.0014701	0.4965922			0.2038865		0.1123259
0.0014411	0.4912439			0.2064881		0.1179327
0.0015748	0.4764531			0.2275757		0.0971853
0.0015246	0.4806918			0.2199227		0.1059929
0.001468	0.4772629			0.2182951		0.1169314
0.0014982	0.4789231			0.2177648		0.1126093
0.0015219	0.4804558			0.2161432		0.1101519
0.001563	0.4805763			0.2153835		0.1062996
0.0015474	0.4799933			0.2163888		0.1075804
0.0015695	0.479653			0.216393		0.1054701
0.0015643	0.479908			0.2162551		0.1059211
0.0015111	0.479429			0.2177645		0.1106778
0.0015249	0.4786584			0.2185117		0.1091777
0.0014766	0.4770252			0.2213892		0.1129838
0.0014959	0.4763711			0.2212694		0.1117119
0.0014761	0.4768629			0.2213596		0.1132328
0.0014494	0.4760472			0.2227128		0.1155342
0.0014636	0.4760072			0.2223139		0.1144428
0.0014548	0.4759681			0.2226839		0.1150718
0.0014474	0.4760374			0.2227438		0.1157511
0.0014323	0.4761774			0.2226057		0.117418
		0.005868819
0.005886663		0.004248532			-0.001638131			-0.385575644		0.148668577	0.003716714
0.006992323		0.00634207			-0.000650253			-0.102530152		0.010512432	0.000262811
0.007689191		0.007737261			4.80704E-05			0.006212839		3.85994E-05	9.64984E-07
0.009161955		0.010947599			0.001785644			0.163108302		0.026604318	0.000665108
0.007471522		0.007909681			0.000438159			0.055395276		0.003068637	7.67159E-05
0.006396734		0.005889717			-0.000507017			-0.086085187		0.007410659	0.000185266
0.006813991		0.006711692			-0.000102299			-0.015241876		0.000232315	5.80787E-06
0.006141304		0.005281377			-0.000859927			-0.162822564		0.026511187	0.00066278
0.006569965		0.006047966			-0.000521999			-0.086309872		0.007449394	0.000186235
0.006574151		0.006172305			-0.000401846			-0.065104711		0.004238623	0.000105966
0.006514619		0.005999666			-0.000514954			-0.085830403		0.007366858	0.000184171
0.007406229		0.007826758			0.00042053			0.053729729		0.002886884	7.21721E-05
0.006645899		0.006497243			-0.000148656			-0.022879823		0.000523486	1.30872E-05
0.005782262		0.004813758			-0.000968504			-0.201194949		0.040479407	0.001011985
0.006871035		0.007142242			0.000271207			0.037972274		0.001441894	3.60473E-05
0.00614275		0.005652878			-0.000489873			-0.086658975		0.007509778	0.000187744
0.006340048		0.005652878			-0.00068717			-0.12156115		0.014777113	0.000369428
0.006367407		0.005820431			-0.000546976			-0.093975088		0.008831317	0.000220783
0.005213934		0.003517128			-0.001696806			-0.482440679		0.232749009	0.005818725
0.007316689		0.00738077			6.40813E-05			0.008682194		7.53805E-05	1.88451E-06
0.008808063		0.010424015			0.001615953			0.155022097		0.024031851	0.000600796
0.005822528		0.004473709			-0.001348819			-0.301499105		0.090901711	0.002272543
0.006317555		0.005434635			-0.00088292			-0.162461691		0.026393801	0.000659845
0.007840829		0.008566717			0.000725888			0.084733511		0.007179768	0.000179494
0.007372396		0.007886634			0.000514238			0.065203718		0.004251525	0.000106288
0.007037032		0.007531939			0.000494907			0.06570784		0.00431752	0.000107938
0.006184229		0.005886214			-0.000298014			-0.050629231		0.002563319	6.4083E-05
0.006393142		0.006475832			8.26904E-05			0.012769079		0.000163049	4.07623E-06
0.005801601		0.005228465			-0.000573137			-0.109618529		0.012016222	0.000300406
0.005390009		0.004346462			-0.001043546			-0.240090933		0.057643656	0.001441091
0.006225736		0.006004133			-0.000221602			-0.036908287		0.001362222	3.40555E-05
0.00555409		0.004565474			-0.000988616			-0.21654188		0.046890386	0.00117226
0.006663944		0.006708174			4.42294E-05			0.006593367		4.34725E-05	1.08681E-06
0.005913397		0.005215601			-0.000697796			-0.133790128		0.017899798	0.000447495
0.006020249		0.005446289			-0.000573959			-0.105385377		0.011106078	0.000277652
0.006553728		0.006585228			3.14999E-05			0.004783421		2.28811E-05	5.72028E-07
0.006041907		0.005662202			-0.000379704			-0.067059493		0.004496976	0.000112424
0.005995723		0.005662202			-0.00033352			-0.058902939		0.003469556	8.67389E-05
0.00592856		0.00550193			-0.00042663			-0.077541879		0.006012743	0.000150319
0.006048158		1.00550193			0.999453771			0.993984936		0.988006053	0.024700151

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

Ó 0.046503711

HRMSE 0.023251856

Tableau réalisé à partir de donnés tirées de Stata

22

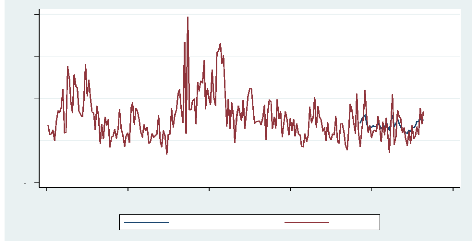
Figure 6 : Prévision à partir du 193^ème jour de RV(d)5

.01 .02

0

0 50 100 150 200 250

date

Prevision RV(d)5 RV(d)5

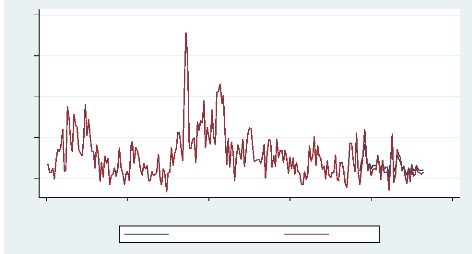
.01 .02

0 50 100 150 200 250

date

Prevision RV(d)9 RV(d)9

Figure 7 : Prévision à partir du 193^ème jour de RV(d)9

'

23

La réalisation d'une prévision hors échantillon suivant le principe de la fenêtre récursive nous a permis de calculer le HRMSE pour les deux modèles. Dans les tableaux précédents `??

représente la projection de la volatilité réalisée journalière pour les 2 modèles et `Y' est la volatilité réalisée observée. Les dernières colonnes des mêmes tableaux ont servi au calcul du HRMSE au fin de comparaison de la performance des deux modèles. En terme de HRMSE on peut remarquer que le modèle HAR(3)-RV regroupée suivant la fréquence optimum de 9 minutes et appliqué à la série CHK Stock du 4 janvier 2010 au 31 décembre 2010 donne une meilleure performance que si la série est regroupée en fréquence de 5 minutes. Le HRMSE de ce dernier qui est 0,027932873 est en effet supérieur à celui du précédent qui est de 0,023251856 pour une des prévisions hors échantillons sur 40 jours suivant le principe de la fenêtre récursive.

24

VI- Conclusion

Ce rapport de recherche a permis de comparer les résultats de prévision du modèle HAR(3)-RV de Corsi (2009) appliqué à des séries de hautes fréquences du CHK stock regroupées en fréquence de 5 minutes et en fréquence optimale selon Bandi et Russell (2007) qui est de 9 minutes dans le cadre de ce travail. L'analyse descriptive des deux séries à partir de leur auto-corrélogramme laisse présager une certaine stationnarité des séries journalière ce que le test de Philippes et Perron (PP) confirme. Cependant l'estimation des modèles complets ne permet pas conclure que certains coefficients du modèle HAR(3)-RV sont statistiquement différents de zéro. On procède quand même à des prévisions hors échantillons pour 40 jours en utilisant le principe de la fenêtre récursive. La comparaison de la performance des deux séries est faite sous la base de comparaison de leur HRMSE. Cette étude a donc permis ( malgré certains anomalies rencontrée au niveau de certains résultats) de confirmer que la fréquence optimale proposée par Bandi et Russell (2007) permet d'effectuer une meilleure prévision que la fréquence de 5 minutes généralement utilisée.

25

VII- Annexe

Newey-West estimation Tableau # 1

. newey rvd5 rvd5t rvw5t rvm5t, lag(10)

Regression with Newey-West standard errors Number of obs = 232

maximum lag: 10 F( 3, 228) = 101.88

Prob > F = 0.0000

		Newey-West
rvd5	Coef.	Std. Err.	t	P>|t|	[95% Conf.	Interval]
rvd5t	.1588765	.1706757	0.93	0.353	-.1774269	.4951799
rvw5t	.568678	.1450324	3.92	0.000	.2829028	.8544532
rvm5t	.0599194	.1630507	0.37	0.714	-.2613594	.3811983
_cons	.0016249	.0005843	2.78	0.006	.0004736	.0027761

Tableau # 2

. newey rvd9 rvd9t rvw9t rvm9t, lag(10)

Regression with Newey-West standard errors Number of obs = 232

maximum lag: 10 F( 3, 228) = 76.50

Prob > F = 0.0000

		Newey-West
rvd9	Coef.	Std. Err.	t	P>|t|	[95% Conf.	Interval]
rvd9t	.4761764	.100971	4.72	0.000	.2772208	.6751319
rvw9t	.2226054	.1906846	1.17	0.244	-.153124	.5983348
rvm9t	.1174122	.1856543	0.63	0.528	-.2484053	.4832297
_cons	.0014324	.0005998	2.39	0.018	.0002504	.0026143

Test de Philippes et Perron

Tableau # 3

. pperron rvd5, notrend

Phillips-Perron test for unit root Number of obs = 231

Newey-West lags = 4

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(rho) -126.933 -20.237 -13.962 -11.175

Z(t) -9.017 -3.466 -2.881 -2.571

MacKinnon approximate p-value for Z(t) = 0.0000

Tableau # 4

. pperron rvw5t, notrend

Phillips-Perron test for unit root Number of obs = 231

Newey-West lags = 4

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(rho) -17.647 -20.237 -13.962 -11.175

Z(t) -3.006 -3.466 -2.881 -2.571

MacKinnon approximate p-value for Z(t) = 0.0343

Tableau # 5

. pperron rvm5t, notrend

Phillips-Perron test for unit root Number of obs 231

Newey-West lags 4

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(rho) -3.407 -20.237 -13.962 -11.175

Z(t) -1.313 -3.466 -2.881 -2.571

MacKinnon approximate p-value for Z(t) 0.6233

Tableau # 6

. pperron rvd9t, notrend

Phillips-Perron test for unit root Number of obs 231

Newey-West lags 4

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(rho) -77.259 -20.237 -13.962 -11.175

Z(t) -6.849 -3.466 -2.881 -2.571

MacKinnon approximate p-value for Z(t) 0.0000

Tableau # 7

. pperron rvw9t, notrend

Phillips-Perron test for unit root Number of obs 231

Newey-West lags 4

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(rho) -18.226 -20.237 -13.962 -11.175

Z(t) -3.004 -3.466 -2.881 -2.571

MacKinnon approximate p-value for Z(t) 0.0346

Tableau # 8

. pperron rvm9t, notrend

Phillips-Perron test for unit root Number of obs 231

Newey-West lags 4

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(rho) -2.605 -20.237 -13.962 -11.175

Z(t) -1.024 -3.466 -2.881 -2.571

26

MacKinnon approximate p-value for Z(t) 0.7442

27

Critere d'information AIC Tableau # 9

. varsoc rvd5, maxlag(19)

Selection-order criteria

Sample: 20 - 232 Number of obs = 213

lag	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	965.643				6.8e-06	-9.05768	-9.0513	-9.0419
1	996.071	60.856	1	0.000	5.2e-06	-9.334	-9.32124	-9.30243
2	1012.19	32.233	1	0.000	4.5e-06	-9.47593	-9.4568	-9.42859*
3	1014.18	3.9842*	1	0.046	4.4e-06*	-9.48525*	-9.45974*	-9.42213
4	1014.55	.74868	1	0.387	4.5e-06	-9.47938	-9.44749	-9.40047
5	1014.79	.47742	1	0.490	4.5e-06	-9.47223	-9.43396	-9.37754
6	1015.1	.61668	1	0.432	4.5e-06	-9.46573	-9.42109	-9.35527
7	1015.43	.65334	1	0.419	4.6e-06	-9.45941	-9.40839	-9.33316
8	1017.12	3.3774	1	0.066	4.5e-06	-9.46588	-9.40848	-9.32385
9	1017.25	.2765	1	0.599	4.6e-06	-9.45779	-9.39401	-9.29998
10	1018.09	1.6796	1	0.195	4.6e-06	-9.45628	-9.38613	-9.28269
11	1019.54	2.8946	1	0.089	4.6e-06	-9.46048	-9.38395	-9.27111
12	1020.6	2.1162	1	0.146	4.6e-06	-9.46103	-9.37812	-9.25588
13	1020.62	.0468	1	0.829	4.6e-06	-9.45186	-9.36257	-9.23093
14	1021.25	1.2501	1	0.264	4.6e-06	-9.44834	-9.35267	-9.21163
15	1021.3	.0956	1	0.757	4.7e-06	-9.4394	-9.33736	-9.1869
16	1021.3	.00606	1	0.938	4.7e-06	-9.43003	-9.32162	-9.16176
17	1021.51	.42539	1	0.514	4.7e-06	-9.42264	-9.30785	-9.13859
18	1022.08	1.1473	1	0.284	4.8e-06	-9.41864	-9.29747	-9.1188
19	1022.19	.20466	1	0.651	4.8e-06	-9.41021	-9.28266	-9.0946

Endogenous: rvd5 Exogenous: _cons

Tableau # 10

. varsoc rvw5t, maxlag(19)

Selection-order criteria

Sample: 20 - 232 Number of obs = 213

lag	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	1022.14				4.0e-06	-9.58814	-9.58176	-9.57235
1	1285.78	527.28	1	0.000	3.4e-07	-12.0542	-12.0415	-12.0227
2	1291.72	11.897	1	0.001	3.3e-07	-12.1007	-12.0816	-12.0534
3	1301.56	19.676	1	0.000	3.0e-07	-12.1837	-12.1582	-12.1206
4	1301.69	.24757	1	0.619	3.0e-07	-12.1755	-12.1436	-12.0966
5	1301.69	.00871	1	0.926	3.0e-07	-12.1661	-12.1278	-12.0714
6	1327.41	51.44	1	0.000	2.4e-07	-12.3982	-12.3536	-12.2878
7	1334.2	13.572	1	0.000	2.3e-07	-12.4525	-12.4015	-12.3263*
8	1334.38	.37296	1	0.541	2.3e-07	-12.4449	-12.3875	-12.3029
9	1335.46	2.1555	1	0.142	2.3e-07	-12.4456	-12.3819	-12.2878
10	1336.53	2.1364	1	0.144	2.3e-07	-12.4463	-12.3761	-12.2727
11	1343.75	14.441	1	0.000	2.2e-07*	-12.5047*	-12.4282*	-12.3153
12	1344.06	.62431	1	0.429	2.2e-07	-12.4982	-12.4153	-12.2931
13	1344.57	1.0094	1	0.315	2.2e-07	-12.4936	-12.4043	-12.2726
14	1344.59	.05235	1	0.819	2.2e-07	-12.4844	-12.3888	-12.2477
15	1344.68	.16865	1	0.681	2.2e-07	-12.4758	-12.3738	-12.2233
16	1346.51	3.6635	1	0.056	2.2e-07	-12.4836	-12.3752	-12.2154
17	1346.74	.46974	1	0.493	2.2e-07	-12.4765	-12.3617	-12.1924
18	1347.91	2.3321	1	0.127	2.2e-07	-12.478	-12.3568	-12.1782
19	1350.62	5.4272*	1	0.020	2.2e-07	-12.4941	-12.3666	-12.1785

Endogenous: rvw5t Exogenous: _cons

28

Tableau # 11

. varsoc rvm5t, maxlag(19)

Selection-order criteria

Sample: 20 - 232 Number of obs = 213

lag	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	1072.92				2.5e-06	-10.065	-10.0586	-10.0492
1	1540.51	935.19	1	0.000	3.1e-08	-14.4461	-14.4334	-14.4146
2	1553.12	25.225	1	0.000	2.8e-08	-14.5552	-14.536	-14.5078
3	1569.27	32.288	1	0.000	2.4e-08	-14.6974	-14.6718	-14.6342
4	1572.56	6.5848	1	0.010	2.4e-08*	-14.7189*	-14.687*	-14.64*
5	1573.06	.98896	1	0.320	2.4e-08	-14.7141	-14.6759	-14.6195
6	1573.06	.00256	1	0.960	2.4e-08	-14.7048	-14.6601	-14.5943
7	1573.33	.54111	1	0.462	2.4e-08	-14.6979	-14.6469	-14.5717
8	1573.59	.52426	1	0.469	2.4e-08	-14.691	-14.6336	-14.549
9	1573.73	.28101	1	0.596	2.5e-08	-14.6829	-14.6191	-14.5251
10	1575.54	3.6228	1	0.057	2.4e-08	-14.6905	-14.6204	-14.5169
11	1576.61	2.1275	1	0.145	2.4e-08	-14.6911	-14.6146	-14.5018
12	1576.95	.69892	1	0.403	2.5e-08	-14.685	-14.6021	-14.4799
13	1578.15	2.3871	1	0.122	2.5e-08	-14.6868	-14.5976	-14.4659
14	1580.27	4.2526*	1	0.039	2.4e-08	-14.6974	-14.6018	-14.4607
15	1580.33	.11598	1	0.733	2.4e-08	-14.6886	-14.5865	-14.4361
16	1580.42	.1785	1	0.673	2.5e-08	-14.68	-14.5716	-14.4117
17	1580.46	.08172	1	0.775	2.5e-08	-14.671	-14.5562	-14.387
18	1580.46	3.6e-05	1	0.995	2.5e-08	-14.6616	-14.5404	-14.3618
19	1580.46	.00116	1	0.973	2.5e-08	-14.6522	-14.5247	-14.3366

Endogenous: rvm5t Exogenous: _cons

Tableau # 12

. varsoc rvd9t, maxlag(19)

Selection-order criteria

Sample: 20 - 232 Number of obs = 213

lag	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	949.137				8.0e-06	-8.90269	-8.89631	-8.88691
1	1009.51	120.75	1	0.000	4.6e-06	-9.46022	-9.44747*	-9.42866*
2	1010.16	1.2945	1	0.255	4.6e-06	-9.45691	-9.43778	-9.40957
3	1012.47	4.6123*	1	0.032	4.5e-06	-9.46918	-9.44367	-9.40605
4	1013.56	2.1938	1	0.139	4.5e-06*	-9.47009*	-9.4382	-9.39118
5	1014.2	1.2639	1	0.261	4.5e-06	-9.46663	-9.42837	-9.37195
6	1014.2	.0144	1	0.904	4.6e-06	-9.45731	-9.41267	-9.34684
7	1014.5	.58938	1	0.443	4.6e-06	-9.45069	-9.39967	-9.32444
8	1016.01	3.0151	1	0.082	4.6e-06	-9.45545	-9.39805	-9.31343
9	1016.02	.02056	1	0.886	4.6e-06	-9.44616	-9.38238	-9.28835
10	1016.61	1.181	1	0.277	4.6e-06	-9.44231	-9.37216	-9.26873
11	1017.36	1.5134	1	0.219	4.7e-06	-9.44003	-9.3635	-9.25066
12	1017.51	.28995	1	0.590	4.7e-06	-9.432	-9.34909	-9.22685
13	1017.68	.34479	1	0.557	4.7e-06	-9.42423	-9.33494	-9.2033
14	1017.74	.12329	1	0.725	4.8e-06	-9.41542	-9.31976	-9.17871
15	1017.76	.02975	1	0.863	4.8e-06	-9.40617	-9.30413	-9.15368
16	1018.69	1.873	1	0.171	4.8e-06	-9.40557	-9.29715	-9.1373
17	1018.71	.02515	1	0.874	4.9e-06	-9.3963	-9.28151	-9.11225
18	1019	.57995	1	0.446	4.9e-06	-9.38963	-9.26846	-9.0898
19	1019.21	.42082	1	0.517	4.9e-06	-9.38222	-9.25467	-9.06661

Endogenous: rvd9t Exogenous: _cons

Tableau # 13

. varsoc rvw9t, maxlag(19)

Selection-order criteria

Sample: 20 - 232 Number of obs = 213

lag	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	998.66				5.0e-06	-9.3677	-9.36132	-9.35192
1	1270.74	544.16	1	0.000	3.9e-07	-11.913	-11.9003	-11.8815
2	1303.6	65.72	1	0.000	2.9e-07	-12.2122	-12.1931	-12.1648
3	1303.61	.01622	1	0.899	2.9e-07	-12.2029	-12.1774	-12.1397
4	1303.61	.00657	1	0.935	3.0e-07	-12.1935	-12.1616	-12.1146
5	1304.81	2.4097	1	0.121	3.0e-07	-12.1954	-12.1572	-12.1008
6	1321.53	33.431	1	0.000	2.6e-07	-12.343	-12.2984	-12.2325
7	1331.06	19.053	1	0.000	2.4e-07	-12.4231	-12.372	-12.2968*
8	1331.18	.25189	1	0.616	2.4e-07	-12.4149	-12.3575	-12.2728
9	1333.55	4.7365	1	0.030	2.3e-07	-12.4277	-12.3639	-12.2699
10	1333.73	.36485	1	0.546	2.4e-07	-12.42	-12.3499	-12.2464
11	1337.78	8.0918	1	0.004	2.3e-07*	-12.4486*	-12.3721*	-12.2593
12	1338.1	.64604	1	0.422	2.3e-07	-12.4423	-12.3594	-12.2371
13	1338.32	.44029	1	0.507	2.3e-07	-12.4349	-12.3457	-12.214
14	1338.39	.13826	1	0.710	2.3e-07	-12.4262	-12.3305	-12.1895
15	1340.31	3.8444	1	0.050	2.3e-07	-12.4349	-12.3328	-12.1824
16	1342.65	4.6721*	1	0.031	2.3e-07	-12.4474	-12.339	-12.1791
17	1343.48	1.6598	1	0.198	2.3e-07	-12.4458	-12.331	-12.1618
18	1343.79	.62957	1	0.428	2.3e-07	-12.4394	-12.3182	-12.1395
19	1345.5	3.4093	1	0.065	2.3e-07	-12.446	-12.3184	-12.1304

Endogenous: rvw9t Exogenous: _cons

29

Tableau # 14

. varsoc rvm9t, maxlag(19)

Selection-order criteria

Sample: 20 - 232 Number of obs 213

lag	LL	LR	df	p	FPE	AIC	HQIC	SBIC
0	1047.82				3.2e-06	-9.8293	-9.82293	-9.81352
1	1539.21	982.78	1	0.000	3.2e-08	-14.4339	-14.4212	-14.4024
2	1575.19	71.947	1	0.000	2.3e-08	-14.7623	-14.7432	-14.715*
3	1576.18	1.9946	1	0.158	2.3e-08	-14.7623	-14.7368	-14.6992
4	1580.04	7.7022*	1	0.006	2.2e-08	-14.7891	-14.7572*	-14.7102
5	1580.29	.50968	1	0.475	2.2e-08	-14.7821	-14.7438	-14.6874
6	1582.11	3.634	1	0.057	2.2e-08*	-14.7897*	-14.7451	-14.6793
7	1582.11	.00551	1	0.941	2.2e-08	-14.7804	-14.7294	-14.6541
8	1582.16	.10225	1	0.749	2.3e-08	-14.7715	-14.7141	-14.6294
9	1583.15	1.9731	1	0.160	2.3e-08	-14.7713	-14.7076	-14.6135
10	1583.89	1.483	1	0.223	2.3e-08	-14.7689	-14.6988	-14.5953
11	1584.4	1.0261	1	0.311	2.3e-08	-14.7643	-14.6878	-14.575
12	1585.6	2.3981	1	0.121	2.3e-08	-14.7662	-14.6833	-14.5611
13	1585.93	.66061	1	0.416	2.3e-08	-14.7599	-14.6706	-14.539
14	1586.66	1.4592	1	0.227	2.3e-08	-14.7574	-14.6617	-14.5207
15	1586.75	.18685	1	0.666	2.3e-08	-14.7489	-14.6468	-14.4964
16	1586.83	.15594	1	0.693	2.3e-08	-14.7402	-14.6318	-14.4719
17	1588.11	2.5604	1	0.110	2.3e-08	-14.7428	-14.628	-14.4588
18	1588.68	1.1275	1	0.288	2.3e-08	-14.7387	-14.6176	-14.4389
19	1588.68	.01461	1	0.904	2.3e-08	-14.7294	-14.6019	-14.4138

Endogenous: rvm9t Exogenous: _cons

Test ADF Tableau # 15

. dfuller rvd5t, regress lags(2) notrend

Augmented Dickey-Fuller test for unit root Number of obs 229

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(t) -4.284 -3.467 -2.881 -2.571

D.rvd5t Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvd5t

L1. -.2809236 .0655763 -4.28 0.000 -.4101457 -.1517014

LD. -.4417156 .075837 -5.82 0.000 -.5911573 -.2922739

L2D. -.1580934 .0657674 -2.40 0.017 -.2876922 -.0284946

_cons .0021674 .0005222 4.15 0.000 .0011384 .0031963

MacKinnon approximate p-value for Z(t) 0.0005

Tableau # 16

. dfuller rvw5t, regress lags(10) notrend

Augmented Dickey-Fuller test for unit root Number of obs 221

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(t) -2.182 -3.470 -2.882 -2.572

MacKinnon approximate p-value for Z(t) 0.2127

D.rvw5t Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvw5t

L1. -.0397431 .0182099 -2.18 0.030 -.0756417 -.0038444

LD. .2802849 .0657874 4.26 0.000 .150593 .4099769
L2D. .2182326 .0682612 3.20 0.002 .0836639 .3528013 L3D. .0981402 .0692491 1.42 0.158 -.0383759 .2346564 L4D. .1255755 .0686311 1.83 0.069 -.0097225 .2608734 L5D. -.6483546 .0677782 -9.57 0.000 -.781971 -.5147381 L6D. .1924941 .0662076 2.91 0.004 .0619738 .3230144 L7D. -.0106351 .0668405 -0.16 0.874 -.142403 .1211329 L8D. .1361763 .0664534 2.05 0.042 .0051715 .2671812 L9D. .1340599 .066091 2.03 0.044 .0037694 .2643504 L10D. -.2457259 .06465 -3.80 0.000 -.3731756 -.1182763

_cons .0002955 .0001432 2.06 0.040 .0000133 .0005778

Tableau # 17

. dfuller rvm5t, regress lags(3) notrend

Augmented Dickey-Fuller test for unit root Number of obs 228

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(t) -2.349 -3.467 -2.881 -2.571

MacKinnon approximate p-value for Z(t) 0.1566

D.rvm5t Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvm5t

L1. -.014036 .0059746 -2.35 0.020 -.0258099 -.002262 LD. .2322732 .0641551 3.62 0.000 .1058452 .3587011 L2D. .2218274 .0645003 3.44 0.001 .0947193 .3489355 L3D. .2194213 .0643873 3.41 0.001 .0925359 .3463067

_cons .0001009 .0000464 2.18 0.031 9.48e-06 .0001922

Tableau # 18

. dfuller rvd9t, regress lags(3) notrend

Augmented Dickey-Fuller test for unit root Number of obs 228

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(t) -3.912 -3.467 -2.881 -2.571

D.rvd9t Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvd9t

L1. -.2425242 .061996 -3.91 0.000 -.3646972 -.1203512 LD. -.184317 .0764362 -2.41 0.017 -.3349467 -.0336873 L2D. -.2233121 .0708373 -3.15 0.002 -.3629083 -.0837159 L3D. -.1155613 .0664932 -1.74 0.084 -.2465968 .0154742

_cons .0018751 .0004997 3.75 0.000 .0008904 .0028599

30

MacKinnon approximate p-value for Z(t) 0.0019

Tableau # 19

. dfuller rvw9t, regress lags(10) notrend

Augmented Dickey-Fuller test for unit root Number of obs 221

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(t) -2.084 -3.470 -2.882 -2.572

MacKinnon approximate p-value for Z(t) 0.2508

D.rvw9t Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvw9t

L1. -.0359766 .0172596 -2.08 0.038 -.0700019 -.0019513 LD. .5437895 .0670889 8.11 0.000 .4115318 .6760473 L2D. -.028812 .0770943 -0.37 0.709 -.1807942 .1231701 L3D. .0903163 .076735 1.18 0.241 -.0609575 .2415901 L4D. .1134796 .0757622 1.50 0.136 -.0358765 .2628356 L5D. -.6179893 .0736328 -8.39 0.000 -.7631474 -.4728312 L6D. .2863941 .0721614 3.97 0.000 .1441366 .4286517 L7D. -.0459403 .0743459 -0.62 0.537 -.1925044 .1006237 L8D. .1350603 .0742259 1.82 0.070 -.0112672 .2813877 L9D. .0574387 .0742832 0.77 0.440 -.0890017 .203879 L10D. -.1859631 .066097 -2.81 0.005 -.3162655 -.0556608

_cons .0002637 .0001373 1.92 0.056 -7.06e-06 .0005344

Tableau # 20

. dfuller rvm9t, regress lags(5) notrend

Augmented Dickey-Fuller test for unit root Number of obs 226

Interpolated Dickey-Fuller

Test 1% Critical 5% Critical 10% Critical

Statistic Value Value Value

Z(t) -2.306 -3.468 -2.882 -2.572

31

MacKinnon approximate p-value for Z(t) 0.1700

D.rvm9t Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvm9t

L1. -.0132747 .0057565 -2.31 0.022 -.0246199 -.0019295

LD. .4335723 .0664152 6.53 0.000 .3026775 .5644671

L2D. -.0120557 .0725996 -0.17 0.868 -.1551389 .1310275

L3D. .1579577 .0716084 2.21 0.028 .016828 .2990874

L4D. .0148142 .072402 0.20 0.838 -.1278797 .157508

L5D. .1269073 .0663026 1.91 0.057 -.0037656 .2575801

_cons .0000926 .000045 2.06 0.041 3.95e-06 .0001812

NEWey West Tableau # 21

. newey rvd5 rvd5t rvw5t rvm5t, lag(10)

Regression with Newey-West standard errors Number of obs 232

maximum lag: 10 F( 3, 228) 102.46

Prob > F 0.0000

Newey-West

rvd5 Coef. Std. Err. t P>|t| [95% Conf. Interval]

rvd5t .1575747 .17043 0.92 0.356 -.1782444 .4933938 rvw5t .5831836 .1446845 4.03 0.000 .298094 .8682733 rvm5t .0385385 .1626678 0.24 0.813 -.281986 .359063 _cons .0016846 .0005856 2.88 0.004 .0005307 .0028384

. *(1 variable, 22 observations pasted into data editor) . *(1 variable, 22 observations pasted into data editor)

32

Tableau # 22

. newey rvd9 rvd9t rvw9t rvm9t, lag(10)

Regression with Newey-West standard errors Number of obs = 232

maximum lag: 10 F( 3, 228) = 76.50

Prob > F = 0.0000

		Newey-West
rvd9	Coef.	Std. Err.	t	P>|t|	[95% Conf.	Interval]
rvd9t	.4761764	.100971	4.72	0.000	.2772208	.6751319
rvw9t	.2226054	.1906846	1.17	0.244	-.153124	.5983348
rvm9t	.1174122	.1856543	0.63	0.528	-.2484053	.4832297
_cons	.0014324	.0005998	2.39	0.018	.0002504	.0026143

AR(5)

Tableau # 23 Optimal frequency (9mn)

. newey rvd91 rvd9t1 rvd9t2 rvd9t3 rvd9t4 rvd9t5, lag(22)

Regression with Newey-West maximum lag: 22		standard errors		Number of obs = F( 5, 226) = Prob > F =		232 147.65 0.0000
rvd91	Coef.	Newey-West Std. Err.	t	P>|t|	[95% Conf.	Interval]
rvd9t1	.5665762	.0890361	6.36	0.000	.3911292	.7420232
rvd9t2	-.0443474	.0912277	-0.49	0.627	-.224113	.1354183
rvd9t3	.1114792	.0787403	1.42	0.158	-.0436798	.2666383
rvd9t4	.0850122	.0828578	1.03	0.306	-.0782604	.2482848
rvd9t5	.0516655	.0511692	1.01	0.314	-.0491642	.1524952
_cons	.0017742	.0002681	6.62	0.000	.0012459	.0023025

Tableau # 24

. reg rvd91 rvd9t1 rvd9t2 rvd9t3 rvd9t4			rvd9t5
Source	SS	df MS		Number of obs	= 247
				F( 5, 241)	= 34.12
Model	.000825439	5 .000165088
				Prob > F	= 0.0000
Residual	.001166175	241 4.8389e-06		R-squared	= 0.4145
				Adj R-squared	= 0.4023
Total	.001991614	246 8.0960e-06
				Root MSE	= .0022
rvd91	Coef.	Std. Err. t	P>|t|	[95% Conf.	Interval]
rvd9t1	.5179317	.0642906 8.06	0.000	.3912884	.644575
rvd9t2	-.0240526	.0723328 -0.33	0.740	-.1665379	.1184327
rvd9t3	.1429031	.071643 1.99	0.047	.0017767	.2840295
rvd9t4	.0589587	.0722263 0.82	0.415	-.0833167	.2012341
rvd9t5	.0569715	.0640357 0.89	0.375	-.0691697	.1831127
_cons	.0018899	.0004975 3.80	0.000	.0009098	.00287

33

VIII- Références

Adrian, T. and J. Rosenberg (2008). Stock returns and volatility: Pricing the short-run and long-run components of market risk. Journal of Finance 63 (6), 2997-3030.

Ait-Sahalia, Y, and L. Mancini. 2008. «Out of sample forecasts of quadratic variation.» Journal of Econometrics 147: 17-33.

Andersen, T.G., and T. Bollerslev. 1997. «Heterogeneous information arrivals and return volatility dynamics: Uncovering the long run in high frequency data.» Journal of Finance 52: 975-1005.

Andersen, T. G., T. Bollerslev, F. X. Diebold, and H. Ebens. 2001. «The distribution of stock returns volatilities.» Journal of Financial Economics 61: 43-76.

Andersen, T, G., Dobrev, D and Schaumburg, E. 2010. «Jump-Robust Volatility estimation using nearest truncation». Federal Reserve Bank of New York Staff Reports. 38.

Alexander, C . 2008. «Market Analysis Vol1, Quantitative Methods in Finance». John Wiley and Sons Inc. 320.

Bandi, F. and B. Perron 2008. «Long-run risk-return trade-offs». Journal of Econometrics 143, 349-374.

Bandi, F and Russel, J. 2007. «Microstructure Noise, Realized Variance, and Optimal Sampling».

Bollerslev, T., C. Gallant, U. Pigorsch, C. Pigorsch, and G. Tauchen. 2006. «Statistical assessment of models for very high frequency financial price dynamics». Unpublished Manuscript.

Bollerslev, T., G. Tauchen, and H. Zhou. 2008. «Expected stock returns and variance risk premia». Review of Financial Studies 22 (11), 4463-4492.

Casas, I. and J. Gao. 2008. «Econometric estimation in long-range dependent volatility models: Theory and practice». Journal of econometrics 147 (1), 72-83.

Corsi, F. 2005. «Measuring and Modelling Realized Volatility: from tick-by-tick to long memory.» Ph. D. thesis, PhD in Finance, University of Lugano.

Corsi, F. 2009. «A simple approximate long-memory model of realized volatility». Journal of Financial Econometrics, Vol 7, No. 2,174-196.

Corsi, F, Pirino, D and Reno R. 2010. « Thershold bipower variation and the impact of jumps on volatility forecasting». Journal of Econometrics 159: 276-288.

34

Dacorogna, M. M., R. Genay, U. A. M· uller, R. B. Olsen, and O. V. Pictet. 2001. «An Introduction to High-Frequency Finance». San Diego, CA: Academic Press.

Corsi, F and Reno R. 2012. « Discrete-Time Volatility forecasting with persistent leverage effect and the link with continuous-time modeling». 31.

Granger, C. 1980. «Long memory relationships and the aggregation of dynamic models.» Journal of Econometrics 14: 227-238.

Hamilton, J, D 1994. « Time series Analysis». Princeton Universiti. 799.

Liu, L., Patton, A. J and Sheppard, K. 2012.» Does anything beat 5 Minutes RV? A comparison of Realized Measures Across Milti Asset Classes». Duke University and University of Oxford. 50.

Lynch, P., and G. Zumbach. 2003. «Market heterogeneities and the causal structure of volatility.» Quantitative Finance 3: 320-331.

Rossi, A., and G. Gallo. 2006. «Volatility estimation via hidden Markov models.» Journal of Empirical Finance 13: 203-230.

Rossi, E. and F. Spazzini (2010). «Finite sample results of range-based integrated volatility estimation». Working Paper.

Tsay, R, S.. 2005. «Analysis of Financial Time Series». John Wiley &Sons Inc. 638.

Visser, M. (2008). «Forecasting S&P 500 Daily Volatility using a Proxy for Downward Price Pressure». Working Paper.

Zhang, L., P. A. Mykland, and Y. A·ýt-Sahalia (2005). «A tale of two time scales: Determining integrated volatility with noisy high-frequency data». Journal of the American Statistical Association 100, 1394-1411.