3.1.3.1.2. Estimation des déchets
générés jusqu'à l'horizon 2034
La quantité moyenne par personne est de 0,55
kg/hab/jr
La quantité des déchets
générés par année = la population de chaque
année x 0,55 x 365
Q2019 = 34668 x 0,55 x 365 = 6959601 kg/an
Q2020 = 35708 x 0,55 x 365 = 7168381 kg/an
Q2021 = 36779 x 0,55 x 365 = 7383384,25 kg/an
Q2022 = 37 883 x 0,55 x 365 = 7605012,25 kg/an
Q2023 = 39 019 x 0,55 x 365 = 7833064,25 kg/an
Q2024 = 40 190 x 0,55 x 365 = 8068142,5 kg/an
Q2025 = 41 395 x 0,55 x 365 = 8310046,25 kg/an
Q2026 = 42 637 x 0,55 x 365 = 8559377,75 kg/an
Q2027 = 43 916 x 0,55 x 365 = 8816137 kg/an
Q2028 = 45 234 x 0,55 x 365 = 9080725,5 kg/an
Q2029 = 45 591 x 0,55 x 365 = 9152393,25 kg/an
Q2030 = 47 989 x 0,55 x 365 = 9633791,75 kg/an
Q2031 = 49 428 x 0,55 x 365 = 9922671 kg/an
Q2032 = 50 911 x 0,55 x 365 = 10220383,25 kg/an
Q2033 = 52 438 x 0,55 x 365 = 10526928,5 kg/an
Q2034 = 54 012 x 0,55 x 365 = 10842909 kg/an
La quantité des déchets cumuléedurant les
15 annéesde notre projet est 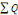 
Q15ans= 140 082 948,5 kg
La production des déchets ménagers solides
évoluant aussi avec la croissance économique d'un milieu nous
avons adopté un coefficient de majoration de 15%,
recommandé pour les villes des pays d'Afrique subsaharienne
(Memento de l'assainissement, 2012).
Q15ans = 140 082 948,5 + (140 082 948,5 x 0,15) =
161 095 390,775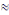 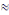 161 095 391 kg 161 095 391 kg
La fraction à enfouir représente 14,45%
de déchets, le reste étant valorisé
La quantité à enfouir sera donc de : 161
095 391 x 0,1455 = 23 439 379,39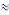  23 439 380 kg ; 23 439 380 kg ;
La masse volumique à la décharge après
compactage étant de 500 kg/m3 ;
Le volume à enfouir sera de 23 439 380 ÷ 500 =
46 878,76 m3 ;
Le volume du casier sera la somme du volume des déchets
à enfouir et le volume de la couverture de terre.
La couverture de terre (Ct) est une couche de terre
utilisée pour couvrir les déchets compactés. Cette
couverture représente 20% du volume de déchets
compactés.
Ct = V à enfouir x 0,2 = 46 878,76 x 0,20 = 9 375,752
m3 de terre
Volume du casier = Volume à enfouir + Ct = 46 878,76 +
9 375, 752 =56 254,512 m3
3.1.3.2. La forme du casier
Notre casier sera de forme rectangulaire avec une longueur de
130 m et une profondeur de7m.
3.1.3.2.1. Aménagement de la pente des talus
Les talusdevront être stables par eux-mêmes. Une
pente de 1V/3H (équivalant à 33,3% ou 15°) est
généralement considérée comme plus stable pour les
casiers devant contenir les déchets ménagers solide (Galvez R.,
2012).
Donc :1m de haut 3m de profondeur
7m de haut (3 ÷ 1) x 7m
7m de haut 21 m de profondeur
D'après le théorème de Pythagore, pour un
triangle rectangle, le carré de la longueur de l'hypoténuse
équivaut à la somme des carrés des longueurs de deux
autres cotés.
C2 = a2 + b2 avec a2
= 72 et b2 = 212
C2 = 72 + 212
C = 22,13 m

Nous savons que le volume à enfouir est de 56 254,512
m3 ;
Nous avons fixé une longueur à la surface du
casier de 130 m ;
Nous avons fixé une profondeur (hauteur) de 7 m ;
Connaissant la pente du talus, la longueur à la base du
casier sera de =130 - (2x21) = 88 m ;
Nous allons maintenant déterminer la largeur haute du
casier, autrement dit la distance qui sépare les deux longueurs du
casier.
| 


