Vérification empirique de la courbe de Philips
en RD du Congo : Relation inflation-chômage de 1988-2015
Hardy-Meshac. Biaya
Résumé
Existe-il une relation de long terme entre l'inflation et le
chômage en République démocratique du Congo(RDC) entre
1988 et 2015 ?cette relation si elle existe témoigne-t-elle
l'efficacité de la politique économique en République
démocratique du Congo(RDC) en période sous revue ? Pour
répondre à ces questions, nous évoluons de la
manière suivante : Premièrement nous mettons en revue la
littérature sur la courbe de Philips, Dixièmement nous
considérons une série longue des données allant de
1988-2015.En dernier lieu nous appliquons le modèle à correction
d'erreur avec l'apport de la cointégration pour nous rassurer de
l'existence d'une relation de long terme entre les deux variables et voir leurs
effets réciproques. Ici nous évaluons dans quelle mesure les
mesures économiques appliquées en RD du Congo affectent la
relation inflation-chômage. Les résultats de notre étude
montrent que la relation inflation-chômage existe, mais elle est positive
mais de faible ampleur, c'est-à-dire que l'inflation agit de
façon positive sur le chômage.
|
Mots- clés :
Relationinflation-chômage, RDC
|
INTRODUCTION
Depuis plusieurs décennies, le chômage et
l'inflation font l'objet d'une grande attention à la recherche en
science économique .l'attention portée à ces deux
variables (taux de chômage et inflation) est qu'elles constituent les
maux majeurs auxquels font face nos sociétés .Pour ce faire, les
autorités fournissent beaucoup d'efforts pour maitriser l'inflation et
propulser l'activité économique en recourant aux instruments de
leurs politiques économique.
Traditionnellement retenu comme objectifs de la politique
économique parmi les quatre depuis les travaux de Nicolas Kaldor(1971),
le carré magique. La courbe de Philips demeure une
référence incontournable dans l'étude de la relation entre
le taux de chômage et l'inflation .les travaux de A. William Philips sur
l'économie Britannique(1958), et certaines études qui ont suivis
sur l'économie américaine Paul Samuelson et Robert Solow(1960),
trouvent une relation empirique négative entre le taux de chômage
et l'inflation. Ces derniers ont interprété cette relation
négative comme offrant une possibilité d'arbitrage aux
responsables de la politique économique. Ceux-ci pourraient choisir
librement entre une inflation faible associée à un taux de
chômage élevé et une inflation élevée
associée à un taux de chômage faible en fonction de
l'importance qu'ils accordent à la stabilité des prix et à
l'activité1(*). Ce
qui par le suite a donné lieu à un certain nombre
d'interprétations.
En effet, les économistes et experts des années
1970, ont tenté effectivement à exploiter cette
possibilité d'arbitrage c'est-à-dire réduire le
chômage par une montée forte d'inflation, il s'est
révélé que le chômage ne reculait pas alors que
l'inflation ne cessait de monter, ce qui du point de vue empirique traduit un
déplacement vers le haut de la courbe de Philips. De ce fait, la
relation entre le taux de chômage et l'inflation s'est retrouvée
au centre de débats relevant des évolutions des certaines
économies de la moitié du XXe siècle qui prouvaient la
coexistence pendant une période assez longue d'un chômage
élevé et d'une forte inflation.
L'histoire récente de l'économie congolaise
fournit un bon exemple pour la vérification de la courbe de Philips.
Depuis un temps, nous avons constaté que l'économie congolaise a
enregistrée une forte inflation et qui malgré cette montée
inflationniste le chômage élevé persiste toujours. Le
gouvernement congolais, dans la recherche de l'amélioration des
conditions de vie des populations congolaises, a élaboré et mis
en oeuvre depuis 2001 des mesures de stabilisation dans le cadre de programme
Intérimaire Renforcé (PIR), du programme économique
soutenu par la facilité pour la réduction de la pauvreté
et la croissance(FRPC), et la Facilité Elargie des
Crédits(FEC)2(*) ,
ces mesurent ont contribué à maintenir le pays sur le chemin de
croissance économique positif et ont permis de ramener les taux
d'inflation annuels à des niveaux tolérables pour inciter
l'épargne et l'investissement. Force est cependant de constater qu'en
dépit du taux de croissance affiché et de la baisse des
pressions inflationnistes, plus de 70% de la population congolaise est au
chômage. Reste à savoir si la politique économique
appliquée par les autorités est-elle inefficace dans le contexte
congolais.
L'étude de la relation entre le taux de chômage
et l'inflation fait l'objet de notre travail. Nous voudrions à travers
cette étude saisir le comportement de chaque variable compte tenu de la
politique économique.
Notre étude vise un objectif principal qui est celui de
vérifier empiriquement la relation de long terme entre le taux de
chômage et l'inflation en République Démocratique du Congo
et en saisir les effets réciproques.
Pour atteindre notre objectif principal nous nous fixons les
objectifs spécifiques suivants :
· Etudier l'évolution de chacune de ces deux
variables pendant la période en revue
Notre grande préoccupation dans cette recherche est
d'identifier la nature du lien de long terme entre le taux de chômage et
l'inflation en RD du Congo. Notre étude suppose qu'il existe une
relation de long terme entre les deux variables. Ainsi, dans cet ordre
d'idée une série des questions est proposée pour analyser
la relation inflation-chômage telle que soutenue par Philips. Les
questions auxquelles, nous devons répondre sont les suivantes :
La relation entre le taux de chômage et l'inflation dans
le contexte congolais est-elle positive ou négative ?
Cette relation témoigne-t-elle l'efficacité de
la politique économique?
Deux hypothèses méritent d'être
testées :
Hypothèse 1. La relation entre le taux
de chômage et l'inflation est positive mais faible.
Hypothèse 2. Cette relation
témoigne l'inefficacité de la politique économique en RD
du Congo.
Le présent travail s'assigne un champ d'investigation
précis. Il se limitera essentiellement à la vérification
empirique de la relation à long terme entre le taux de chômage et
l'inflation en RD du Congo pour la période 1988-2015
L'intérêt qui est porté à ce sujet
se trouve d'une part être dans le souci de voir comment le taux de
chômage et le l'inflation se comportent à long terme surtout
compte tenu des mesures économiques prises par les autorités,
d'autre part amener les autorités dans la mesure du possible à
une politique économique ambitieuse.
Les statistiques que nous utilisons couvrent la période
1988-2015 et sont celles publiées dans les différents rapports
annuels par la Banque Centrale du Congoet le condensé d'information
statistiques de la BCC. Ces sont les séries annuelles. Pour
apprécier la relation qui existe entre les deux variables de notre
série et d'en avoir les effets réciproques, nous avons
estimé le modèle à correction d'erreur avec l'apport de la
cointegration par le logiciel eviews .nous partons d'une relation
théorique supposée exister à long terme
Outre l'introduction et la conclusion. Le présent
travail s'organise autour de deux chapitres. Le premier chapitre passe en
revue, la littérature relative aux interactions entre le taux de
chômage et l'inflation. Il s'agit de présenter l'origine de la
courbe de Philips, les fondements économiques de cette courbe ainsi que
ses différentes interprétations et enfin le deuxième et
dernier chapitre porte sur l'analyse économétrique et
l'interprétation des données.
CHAPITRE I. REVUE DE LA LITTERATURE DE LA COURBE DE
PHILIPS
Dans ce chapitre, nous présentons de manière
brève l'évolution de la courbe de Philips depuis son apparition.
Dans la première section nous présentons l'origine de la courbe
de Philips ainsi que les différentes modifications qu'elle a subies,
dans la deuxième nous parlons La courbe de Philips additionnée
des anticipations et en fin la troisième section présente la
courbe de Philips de long terme.
I.1. Origine de la courbe de Philips
L'histoire remonte des années 58, où
l'Economiste Néo-Zélandais du nom d'Alban William Philips, avait
publié un article intitulé « The Relation
Between Unemployement and the Rate of Change of Money Wage Rates in the United
Kindgdom, 1861-1957 ». Dans cet article Philips examinait la
relation entre le chômage et la croissance des salaires nominaux sur 97
observations de données Britanniques. Il avait constaté que le
chômage avait tendance à être faible quand la croissance des
salaires nominaux s'avère rapide, et à
êtreélevé quand la croissance des salaires nominaux est
lente.
Par la suite, les économistes qui ont utilisé la
courbe de Philips ont souvent favorisé l'utilisation du taux
d'inflation au lieu de la croissance des salaires nominaux dans l'examen du
lien avec le chômage3(*). Vers les années 60, plusieurs études
furent exécutées dont l'objectif était d'analyser la
relation inflation-chômage. L'un des travaux effectués est celui
dePaul Samuelson et Robert Slow en 1960 utilisant les données
américaines couvrant la période de 1900-1960, lequel travail va
aboutir à l'existence d'une relation négative entre les deux
variables.Ce fut le début de plusieurs débats sur une relation
portant le nom de « courbe de Philips » celle-cioffrant
une possibilité d'arbitrage aux responsables de la politique
économique. Ceux-ci pourraient choisir librement entre une inflation
faible associée à un taux de chômage élevé et
une inflation élevée associée à un taux de
chômage faible en fonction de l'importance qu'ils accordent à la
stabilité des prix et à l'activité.
Cette relation sera par la suite mis en cause par les
économistes et experts Américains des années 1970(Friedman
et Phelps en 1968), qui ont tenté effectivement à exploiter
cette possibilité d'arbitrage c'est-à-dire réduire le
chômage par une montée forte d'inflation, il s'est
révélé que le chômage ne reculait pas alors que
l'inflation ne cessait de monter, ce qui du point de vue empirique traduit un
déplacement vers le haut de la courbe de Philips.
I.2 La courbe de Philips additionnée des
anticipations
En 1968, les économistes Friedman et Phelps avaient
chacun publié un article qui mettait en question la logique
intrinsèque de la courbe de Philips. Sur la base d'un raisonnement
théorique, ils affirmaient avant même que des études
empiriques le montrent, qu'il ne devrait donc pas y avoir de relation
négative stable entre le chômage et l'inflation, mais plutôt
entre l'inflation anticipée et le chômage cyclique.
L'argument de Friedman reposait sur la possibilité
d'une erreur de prévision des prix de la part des travailleurs. Dans une
économie où le niveau général des prix est
stable(ou augmente de façon prévisible), l'offre et le demande de
travail déterminent un niveau de salaire réel et d'emploi en
équilibre. Mais, dit Friedman si la banque centrale crée une
expansion monétaire qui fait augmenter les prix. Celles les entreprises
auront des anticipations exactes et vont percevoir immédiatement la
hausse des prix et voir leur rentabilité s'améliorer au taux de
salaire courant. Le salaire réel baisse et la demande de travail
augmente. Par contre les travailleurs ayant des anticipations mauvaises parce
que ayant un raisonnement rétrospectif, vont continuer à
travailler et ils se rendront compte de la hausse de prix que après un
temps4(*). La concurrence
accrue entre employeurs leur procure des salaires nominaux et réels
perçus plus élevés. Ce qui les amène à
offrir plus de travail. La seule raison de cette hausse d'emploi c'est de la
perception des travailleurs.
I.3 La courbe de Philips de long terme
Nous pouvons bien voir à partir de l'argument de
Friedman sur la courbe de Philips additionnée des anticipations, qu'il
existe une relation négative entre l'inflation non anticipée et
le chômage cyclique. Il Ya cependant possibilité de comprendre
que cette situation ne peut pas se reproduire indéfiniment.
En effet, les travailleurs qui se laissent tromper par une
augmentation non anticipée du niveau général des prix
s'aperçoivent de leur bévue un jour ou l'autre. Selon la
théorie des anticipations rationnelles, les travailleurs vont prendre en
compte les nouvelles informations dans leurs prochaines anticipations de sorte
qu'à long terme le niveau d'emploi retournera à son niveau
d'équilibre initial. Selon cette même théorie, à
long terme l'inflation est parfaitement anticipée. L'offre et la demande
agrégée s'ajustent donc pour se trouver au niveau de production
optimal5(*).
CHAPITRE II. ANALYSE ECONOMETRIQUE ET INTERPRETATION DES
RESULTATS
Dans cette partie de notre travail, nous allons par le
modèle à correction d'erreur analyser les interactions de la
relation inflation-chômage et voir à l'issue de cette analyse si
la politique économique de la RD du Congo est elle efficace.
II.1 Etude de la stationnarité de la série
(tests formels et informels)
Nous servons des tests formels et informels pour
étudier la stationnarité de nos séries (taux d'inflation
et taux de chômage), si elles sont non stationnaire, les stationnariser
par les MCO ou l'écart à la tendance(TS), soit par la
différenciation ou les filtres aux différences(DS).pour
éviter le problème de régressions fallacieuses pour
lesquelles les résultats apparient significatifs alors qui ne le sont
pas en réalité .
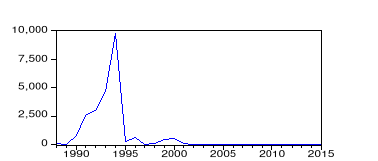
Note : la serie taux de change semble non stationnaire en
moyenne.

Note : la série taux de chômage semble non
stationnaire en moyenne.
Constat : après
vérification par les tests précités (Dickey-Fuller), nos
deux séries semblent non stationnaires du type DS
(intégrées d'ordre 1). cfr les tableaux en annexei. Ce qui
constitue pour nous la première condition nécessaire pour
conclure à l'existence d'une relation de cointégration.
II.2 Estimation de la relation de long terme et test de
stationnarité sur les résidus qui en découlent
Dans cette section, nous allons estimer la relation cointegrante
par la méthode de moindres carrés ordinaire, voir si la
série des résidus qui en découle est stationnaire en
niveau .ce qui est également l'une des conditions nécessaires.
Notre équation structurelle de long terme se
présente de la manière suivante:
LTXCH = C(1) + C(2)*LTXINF + åt
Nous avons générer :
· ltxinf= txinf-txinf(-1) c(1) : le terme
constant
· ltxch=txch-txch (-1) c(2) : la pente de long
terme qui explique la variation du taux de chômage, induit à une
variation à priori du taux d'inflation et åt represente le residu
de long terme.
txinf : série de taux d'inflation non stationnaire en
niveau de 1988-2015 ;
txch : série de taux de chômage non
stationnaire en niveau de 1988-2015 ;
ltxinf : série de taux d'inflation stationnaire
après la 1ér différence de 1998-2015 ;
ltxch : série de taux de chômage
stationnaireaprès la 1erdifférence de 1988-2015.
Les résultats de l'estimation se présentent comme
suit :
LTXCH = -0.433140624985 +
4.31257804858e-05*LTXINF
Les résidus du modèle estimé à long
terme étant stationnaires en niveau avec trend et intercepte, cfr annexe
ii c'est la condition suffisante pour conclure à l'existence d'une
relation de cointergration entre nos deux séries.
II.3 Estimation du modèle à correction
d'erreur
L'utilisation de ce modèle, nous aide à montrer la
relation commune de cointergration et d'en déduire les interactions
entre les variables6(*).
Ø Spécification du modèle
Le modèle se présente comme suit :
Txcht=co+c1txinft+c2txinft-1+c3txinft-2
Avec:
§ Txcht: taux de chômage au temps t
§ Txinft : taux d'inflation au temps t
§ Txinft-1 : taux d'inflation décalé
d'une période
Conformément à la spécification à la
Hendry, notre modèle se présente comme suit :
DLTXCH = C(1)*DLTXINF + C(2)*LTXCH(-1) + C(3)*LTXINF(-1)
c2 :c'est la force de rappel ou coefficient
d'équilibre, il doit être inférieur à l'unité
et statistiquement significatif, donc négatif .il
implique la vitesse d'ajustement de la variable endogène (ltxch), pour
retourner à l'équilibre de long terme suite à un choc.
Après estimation du modèle à correction
d'erreur, les résultats se présentent comme suit :
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
DLTXINF
|
0.000336
|
0.000654
|
0.514078
|
0.6121
|
|
LTXCH(-1)
|
-1.053270
|
0.213264
|
-4.938807
|
0.0001
|
|
LTXINF(-1)
|
0.001088
|
0.001052
|
1.034686
|
0.3116
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.535558
|
Mean dependent var
|
-0.053846
|
|
Adjusted R-squared
|
0.495171
|
S.D. dependent var
|
9.156341
|
|
S.E. of regression
|
6.505699
|
Akaike info criterion
|
6.691401
|
|
Sum squared resid
|
973.4549
|
Schwarz criterion
|
6.836566
|
|
Log likelihood
|
-83.98822
|
Hannan-Quinn criter.
|
6.733204
|
|
Durbin-Watson stat
|
2.166671
|
|
|
|
Remarque : la force de rappel (-1.053270) est
statistiquement significative.
II.4 Inférence et Interprétation des
résultats du modèle estimé
Les résultats de l'estimation du modèle à
correction d'erreur se présentent comme suit :
DLTXCH = 0.000336003437849*DLTXINF - 1.05327040086*LTXCH(-1) +
0.00108841425209*LTXINF(-1)
R²= 53.55%
DW= 2.16
A présent, le modèle estimé doit être
soumis aux différents tests(les résultats des différents
tests sont en annexiii).
ü le test de normalité des erreurs (Jarque-Bera) qui
vérifie si la série est normalement distribuée vaut
2.580705 avec une probabilité de 0.275174 ;
ü Le test d'absence d'autocorrélation
(Breusch-Godfrey), permet de tester une autocorrélation d''ordre
supérieur à 1. Ici l'hypothèse à tester est celle
de l'absence d'autocorrélation des erreurs. Ainsi la statistique F vaut
3.181203, avec une probabilité de 0.0621.ce qui affirme une absence
d'autocorrélation des erreurs ; on ne rejette donc pas
l'hypothèse nulle au seuil de confiance de 5% ;
ü Le test d'absence
d'hétéroscédasticité (Breusch-Pagan-Godfrey),
permet de tester le risque d'hétéroscédasticité. Sa
statistique F est 0.559197 avec une probabilité critique de 0.647. Donc
nous rejetons l'hétéroscédasticité au seuil de
5% ;
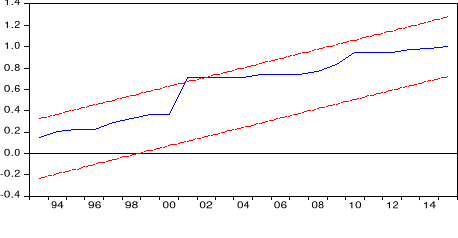
ü Le test de stabilité(CUSUM),
généralement utilisé pour détecter
d'éventuels mouvements systématiques dans la valeur des
coefficients reflétant une possible instabilité structurelle et
le test (CUSUM CARRE), qui est similaire au précèdent, il est
utilisé pour détecter les mouvements aléatoires
c'est-à-dire les mouvements ne provenant pas forcement d'une
modification structurelle7(*). Ainsi avec l'application du test cusum au seuil de
5%, nous constatons que la série de la somme cumulée des
résidus récursifs reste à l'intérieure de
l'intervalle formé des droites, suggérant l'absence de
l'instabilité de la relation sur la période
considérée. De même avec le test de cusum carré
hormis en 2001, où nous constatons franchissement cela du l'adoption
des nouvelles mesures économiques avec l'arrivée de Joseph Kabila
au pouvoir.
Tous les paramètres sont statistiquement significatifs, et
le modèle spécifié explique 54% de variation de
chômage en RD du Congo.
· l'ensemble de tests diagnostiques du modèle prouve
qu'il est globalement bon. Cfr annexe
· Elasticité à court terme : A
court terme, si l'inflation augmente de 10%, le chômage augmente de
0.0033%. nous constatons que le chômage est peu sensible à la
variation de l'inflation .l'amplitude de la sensibilité du chômage
fasse à la variation de l'inflation est très faible voir
négligeable.
· Elasticité à long terme :A long
terme, si l'inflation augmente de 10%, alors le chômage varie dans le
même sens pour 0.01%. donc les effets croissent à petit feu avec
le temps.
Nous constatons que les Elasticités sont faibles, à
court tout comme à long terme, cela veut dire que le chômage est
moins sensible à la variation de l'inflation.
CONCLUSION
Ce papier a utilisé le modèle à
correction d'erreur avec l'apport de la cointégration pour
vérifier empiriquement la courbe de Philips en République
démocratique du Congo(RDC) : relation inflation-chômage.Pour
ce faire, nous avons préalablementpassé en revue, la
littérature relative aux interactions entre le taux de chômage et
l'inflation, et nous avons considéré une période longue
allant de 1988 à 2015. Après l'estimation, il ressort
l'existence d'une relation positive inflation-chômage de long
termecaractérisée par une faible ampleur.
Les résultats montrent que les mesures
économiques (politique économique) prises par les
autorités avec l'arrivé de Joseph Kabila au pouvoir en 2001, ont
certes contribué à maintenir le pays sur le chemin de croissance
économique positif et ont permis de ramener les taux d'inflation annuels
à des niveaux tolérables pour inciter l'épargne et
l'investissement, mais elles n'ont pas réussi à répondre
aux objectifs de plein emploi.
Suite à la vérification empirique de la relation
inflation-chômage, il s'est également dégagé que la
politique d'austérité (rigueur) influence positivement
l'activité économique mais de manière inefficace.
C'est-à-dire que malgré la variation de l'inflation comme
phénomène monétaire, le chômage semble
répondre avec une ampleur négligeable. Cela dû, du fait
que le chômage observé dans le contexte congolais est du type
structurel. Les autorités devraient trouver d'autres mesures efficaces
susceptibles de faire face au problème de chômage qui se pose en
RD du Congo.
Bibliographie
Bourbonnais R. (2006), « Econométrie
manuel et exercices corrigés » DUNOD
Mathieu M, Courbe de Philips melchior
Bonsonga F. (2017), « Econométrie
manuel et exercices corrigés »
Pnud.(2013), « Rapports Socioécomique
2011-2012 et perspectives 2013 »
Mukunda. (2019), Politique économique
Karine D, courbe de Philips de long terme et la
rigidité salariale : un test de la conjecture de Tobin
ANNEXE I
Tableau 1 : Evolution du taux d'inflation en RD du
Congo
|
Null Hypothesis: TXINF has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 0 (Automatic - based on SIC, maxlag=0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-3.573475
|
0.0514
|
|
Test critical values:
|
1% level
|
|
-4.339330
|
|
|
5% level
|
|
-3.587527
|
|
|
10% level
|
|
-3.229230
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(TXINF)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 09/10/19 Time: 19:33
|
|
|
|
Sample (adjusted): 1989 2015
|
|
|
|
Included observations: 27 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
TXINF(-1)
|
-0.667998
|
0.186932
|
-3.573475
|
0.0015
|
|
C
|
1785.559
|
850.3519
|
2.099788
|
0.0464
|
|
@TREND(1988)
|
-85.97701
|
49.46084
|
-1.738284
|
0.0950
|
|
|
|
|
|
|
|
|
|
|
Tableau 2 : Evolution de chômage en RD du Congo
|
Null Hypothesis: TXCH has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 0 (Automatic - based on SIC, maxlag=0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-2.466245
|
0.3406
|
|
Test critical values:
|
1% level
|
|
-4.339330
|
|
|
5% level
|
|
-3.587527
|
|
|
10% level
|
|
-3.229230
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(TXCH)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 09/10/19 Time: 19:39
|
|
|
|
Sample (adjusted): 1989 2015
|
|
|
|
Included observations: 27 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
TXCH(-1)
|
-0.397305
|
0.161097
|
-2.466245
|
0.0212
|
|
C
|
25.27082
|
9.890348
|
2.555099
|
0.0174
|
|
@TREND(1988)
|
-0.300395
|
0.156590
|
-1.918354
|
0.0670
|
|
|
|
|
|
|
|
|
|
|
ANNEXE II
Tableau II.1 : Série dtxinf (taux d'inflation
stationnaire), en différence première.
|
Null Hypothesis: DTXINF has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 0 (Automatic - based on SIC, maxlag=0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-6.793082
|
0.0000
|
|
Test critical values:
|
1% level
|
|
-4.356068
|
|
|
5% level
|
|
-3.595026
|
|
|
10% level
|
|
-3.233456
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(DTXINF)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 09/10/19 Time: 19:50
|
|
|
|
Sample (adjusted): 1990 2015
|
|
|
|
Included observations: 26 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
DTXINF(-1)
|
-1.334710
|
0.196481
|
-6.793082
|
0.0000
|
|
C
|
288.7883
|
929.1660
|
0.310804
|
0.7587
|
|
@TREND(1988)
|
-20.27504
|
56.93616
|
-0.356101
|
0.7250
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau II.2 :Série dtxch (taux de chomage
stationnaire), en différence première.
|
Null Hypothesis: DTXCH has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 0 (Automatic - based on SIC, maxlag=0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-5.086783
|
0.0019
|
|
Test critical values:
|
1% level
|
|
-4.356068
|
|
|
5% level
|
|
-3.595026
|
|
|
10% level
|
|
-3.233456
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(DTXCH)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 09/10/19 Time: 19:58
|
|
|
|
Sample (adjusted): 1990 2015
|
|
|
|
Included observations: 26 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
DTXCH(-1)
|
-1.052569
|
0.206922
|
-5.086783
|
0.0000
|
|
C
|
2.223211
|
2.812184
|
0.790564
|
0.4373
|
|
@TREND(1988)
|
-0.179932
|
0.173207
|
-1.038831
|
0.3097
|
Tableau II.3 : Série des résidus
stationnaire en niveau(e)
|
Null Hypothesis: E has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 0 (Automatic - based on SIC, maxlag=0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-6.848402
|
0.0000
|
|
Test critical values:
|
1% level
|
|
-4.356068
|
|
|
5% level
|
|
-3.595026
|
|
|
10% level
|
|
-3.233456
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(E)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 09/10/19 Time: 20:01
|
|
|
|
Sample (adjusted): 1990 2015
|
|
|
|
Included observations: 26 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
E(-1)
|
-1.341935
|
0.195949
|
-6.848402
|
0.0000
|
|
C
|
279.6580
|
926.6031
|
0.301810
|
0.7655
|
|
@TREND(1988)
|
-19.27099
|
56.77558
|
-0.339424
|
0.7374
|
|
|
|
|
|
|
|
|
|
|
ANNEXE III
o test de normalité des erreurs
o test d'absence d'autorrélation des erreurs
|
Breusch-Godfrey Serial Correlation LM Test:
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic
|
3.181203
|
Prob. F(2,21)
|
0.0621
|
|
Obs*R-squared
|
5.967815
|
Prob. Chi-Square(2)
|
0.0506
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o Test d'absence
d'hétéroscédasticité
|
Heteroskedasticity Test: Breusch-Pagan-Godfrey
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic
|
0.559197
|
Prob. F(3,22)
|
0.6475
|
|
Obs*R-squared
|
1.842138
|
Prob. Chi-Square(3)
|
0.6058
|
|
Scaled explained SS
|
2.199090
|
Prob. Chi-Square(3)
|
0.5321
|
|
|
|
|
|
|
|
|
|
|
o Test de bruit blanc (résidus)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Autocorrelation
|
Partial Correlation
|
|
AC
|
PAC
|
Q-Stat
|
Prob
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. *| . |
|
. *| . |
|
1
|
-0.100
|
-0.100
|
0.2885
|
0.591
|
|
.**| . |
|
.**| . |
|
2
|
-0.290
|
-0.303
|
2.8465
|
0.241
|
|
. |* . |
|
. |* . |
|
3
|
0.167
|
0.110
|
3.7287
|
0.292
|
|
. | . |
|
. *| . |
|
4
|
-0.039
|
-0.108
|
3.7786
|
0.437
|
|
. *| . |
|
. *| . |
|
5
|
-0.129
|
-0.070
|
4.3597
|
0.499
|
|
. |* . |
|
. | . |
|
6
|
0.131
|
0.062
|
4.9877
|
0.545
|
|
. | . |
|
. | . |
|
7
|
0.005
|
-0.020
|
4.9886
|
0.661
|
|
***| . |
|
***| . |
|
8
|
-0.409
|
-0.386
|
11.768
|
0.162
|
|
. |* . |
|
. |* . |
|
9
|
0.169
|
0.087
|
12.995
|
0.163
|
|
. |* . |
|
. *| . |
|
10
|
0.131
|
-0.081
|
13.782
|
0.183
|
|
.**| . |
|
. *| . |
|
11
|
-0.211
|
-0.075
|
15.938
|
0.143
|
|
. | . |
|
. *| . |
|
12
|
0.025
|
-0.077
|
15.970
|
0.193
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o Test de stabilité (CUSUM)

o Test de stabilité (CUSUM CARRE)
§ Base de données
|
ANNEE
|
INFLATION
|
CHOMAGE
|
|
1988
|
121.5
|
51.2
|
|
1989
|
95.8
|
49.1
|
|
1990
|
874.5
|
52.6
|
|
1991
|
2641.9
|
49.4
|
|
1992
|
2989.6
|
56.3
|
|
1993
|
4651.7
|
68.7
|
|
1994
|
9796.9
|
67
|
|
1995
|
370.3
|
69.2
|
|
1996
|
693
|
62.8
|
|
1997
|
13.7
|
53.6
|
|
1998
|
134.8
|
57.2
|
|
1999
|
483.7
|
64.2
|
|
2000
|
511.21
|
66.9
|
|
2001
|
135.09
|
49
|
|
2002
|
15.8
|
49.1
|
|
2003
|
4.44
|
48.5
|
|
2004
|
9.22
|
45.4
|
|
2005
|
21.27
|
49.4
|
|
2006
|
18.2
|
48.2
|
|
2007
|
9.96
|
47.2
|
|
2008
|
23.5
|
53.2
|
|
2009
|
53.4
|
60.8
|
|
2010
|
9.84
|
50.1
|
|
2011
|
15.43
|
51.4
|
|
2012
|
2.72
|
51.4
|
|
2013
|
1.07
|
46.1
|
|
2014
|
1.26
|
43
|
|
2015
|
0.85
|
39.5
|
Source : différents rapports de la
banque Centrale du Congo et le condensé d'information statistique(BCC)
2007.
* 1 Mathieu mucherie, courbe de
philips melchior
* 2 Rapports
socioéconomique 2011-2012 et perspectives 2013
* 3 Voir Karine Dumont, Courbe
de Philips de long terme et la rigidité salariale : un test de la
conjecture de Tobin, janvier 2000 pp.5-6 revue économique
* 4 Voir Mukunda , Politique
Economique 2019
* 5 Voir Karine
* 6 Voir Bourbonnais R.
(2006), « Econométrie manuel et exercices
corrigés »DUNOD
* 7 Voir Bonsonga
(2017), « Econométrie manuel et exercices
corrigés »
| 


