3.3. Forme fonctionnelle du
modèle VAR utilisé
Le modèle VAR utilisé dans ce travail s'appuie
sur un modèle à quatre variables, mettant en relation la
Croissance du PIB, le taux de Scolarisation primaire, taux de Scolarisation
Secondaire et les dépenses Publiques d'investissement en
éducation dans les dépenses publiques totales.
Construisons le modèle suivant à q
décalages :
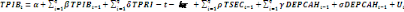 (4) (4)
 (5) (5)
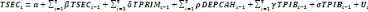 (6) (6)
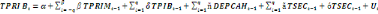 (7) (7)
La première équation postule que la croissance
économique est fonction de ses valeurs décalées de taux de
scolarité primaire, secondaire et des dépenses publiques en
éducation et des valeurs courantes de taux de scolarité primaire,
secondaire et des dépenses publiques en éducation.
La deuxième équation postule quant à elle
que les dépenses publiques en éducation est fonction des valeurs
décalées de la croissance économique, de ses propres
valeurs décalées, de taux de scolarité primaire,
secondaire et enfin des valeurs courantes de la croissance économique,
de taux de scolarité primaire, secondaire.
La troisième équation postule quant à
elle que Le taux de scolarité secondaire est fonction des valeurs
décalées de la croissance économique, de ses propres
valeurs décalées, de taux de scolarité primaire,
dépenses publiques en éducation et enfin des valeurs courantes de
la croissance économique, de taux de scolarité primaire,
dépenses publiques en éducation.
La quatrième et la dernière équation
postule quant à elle que Le taux de scolarité primaire est
fonction des valeurs décalées de la croissance
économique, de ses propres valeurs décalées, de taux de
scolarité secondaire, dépenses publiques en éducation et
enfin des valeurs courantes de la croissance économique, de taux de
scolarité secondaire, dépenses publiques en éducation.
Donc, les quatre équations constituent la forme
fonctionnelle de notre modèle VAR. Il sied de rappeler que le
décalage optimal sera déterminé en passant par les
critères d'Akaike et Schwartz.
3.4. Estimation du modèle et interprétation des
résultats
Une fois représentée par la forme fonctionnelle
adéquate ; la relation théorique c'est-à-dire le
modèle, peut être confrontée aux données
observées, il s'agit de vérifier leur caractère explicatif
de la réalité et de mesurer concrètement la valeur de
leurs paramètres. Il est alors possible de calculer le taux de
réaction des variables.
Les données observées peuvent être des
séries temporelles, des données en coupe instantanée ou
des données de panel. Mais en ce qui nous concerne, nos données
sont belles et bien des séries temporelles ou séries
chronologiques.
3.4.1. Présentation et traitement des
données.
Un processus peut être défini comme étant
une collection des variables aléatoires ordonnées dans le temps.
Ainsi des séries temporelles telles que la Croissance du PIB en %
annuel, le taux de Scolarisation primaire, taux de Scolarisation Secondaire et
les dépenses Publiques d'investissement en éducation en % des
dépenses publiques totales de la RDC couvrant la période 1980
à 2012 peuvent être considérées comme les
réalisations d'un processus aléatoire.
Le processus aléatoire qui intéresse tout
particulièrement les analystes des séries chronologiques est
« le processus stationnaire «, c'est-à-dire le processus
dans lesquels les données fluctuent autour de la moyenne constante
indépendamment du temps ;
Si une série chronologique ou
temporelle est stationnaire au sens défini ci-haut alors sa moyenne, sa
variance et son auto-covariance sur différents décalages restent
constantes quelque soit le moment où ces valeurs sont calculées.
La série chronologique qui ne vérifie pas ces conditions est dite
non stationnaire. Etant donné que c'est le processus stationnaire qui
retient l'attention des analystes, nous allons dans ce point procéder
par la stationnarisation de nos séries temporelles notamment la
Croissance du PIB en % annuel, le taux de Scolarisation primaire, taux de
Scolarisation Secondaire et les dépenses Publiques d'investissement en
éducation en % des dépenses publiques totales.
De tout ce qui précède, nous disons que la
résolution de nos séries temporelles par le modèle
« VAR » se fera à travers les étapes
suivantes :
· Vérification de la
stationnarité ;
· Détermination du nombre de retard
(décalage) optimal du modèle VAR ;
· Estimation des paramètres du
modèle ;
· Teste de la causalité de Granger ;
· Analyse de dynamique du VAR ;
· Prévision du modèle.
3.4.1.1. Stationnarité Des Variables
Cette étude se fera variable par variable. Pour ce faire,
nous allons recourir à l'analyse de leur graphique et au test de racine
unitaire ou de Dickey Fuller.
a) Le taux de croissance du PIB (TPIB)
Nous avons choisi d'utiliser le taux de croissance du PIB en %
comme indicateur de la croissance tels que récoltés dans les
différents rapports annuels de la Banque Centrale du Congo et de la
Banque Mondiale.
| 


