2.2 Méthodes d'analyse
A. Spécification des modèles
économétriques
Pour estimer la relation entre l'APD et les réformes
économiques, nous allons invoquer divers modèles
économétriques. Nous nous inspirons des travaux de Giuliano,
Mishra, et Spilimbergo (2009) sur les réformes et la démocratie
et postulons le modèle suivant :
???é????????????,??= á
??é????????????,??_1 + â ????????,??_1 + ?
X??,??_1 + ????,?? (2)
Dans cette équation, ???é????????????,??
est la variable dépendante capturant les réformes
économiques. Il faut noter que ??é????????????,?? est
obtenue à partir des indices de réforme sectorielle par l'une des
méthodes d'agrégation décrite plus haut.
??é????????????,??_1 est le niveau de l'indice
de réforme au cours de l'année ?? - 1. ????????,??_1
est le proxy mesurant l'APD. Pour les estimations, nous utiliseront trois
différents proxys à savoir; l'aide en proportion du Produit
National Brute (PNB), l'aide en proportion du Produit Intérieur Brute
(PIB), et l'aide par tête. X??,??_1 est un vecteur de variable
de contrôle qui comprend des variables comme le niveau de réforme
dans les pays voisins pour capturer l'effet de contagion des réformes,
le PIB par tête pour capturer l'effet du niveau de développement
sur la capacité à reformer. Les autres variables de
contrôle sont la qualité des institutions ; le taux de
scolarisation au secondaire; l'existence de dévaluation de la
monnaie, et l'existence d'un programme du FMI et/ou de la Banque
Mondiale.
Mémoire de fin de formation ISIA 30
Rédigé par : Marius KOUNOU
L'aide au développement stimule-t-elle des
réformes économiques?
B. Méthodes d'estimation des modèles
économétriques
Nous commençons l'analyse en examinant
l'équation (2) par les Moindres Carrés Ordinaire (MCO). Dans
cette estimation l'unité d'observations est la paire (pays,
année). Les hypothèses sur les résidus sont entre autres,
l'homoscédasticité, l'absence d'autocorrélation, et la
non-corrélation entre les résidus et les variables
explicatives.
Cependant, étant donné la nature des
données qui sont de panel, la méthode des MCO pose un
problème. En particulier, l'hypothèse d'absence
d'autocorrélation sera probablement violer car les données
étant répétées pour un même pays. Par
ailleurs, les MCO ne capturent adéquatement
l'hétérogénéité non observée entre
les pays et leurs facteurs spécifiques qui affectent la relation entre
aide et réformes. Pour analyser plus en détail la relation entre
l'aide et les réformes, nous étendons l'analyse empirique en
utilisant les méthodes d'estimation sur donnée de panel. Cette
approche a l'avantage d'aborder, au moins dans une certaine mesure, le
problème de l'hétérogénéité non
observée (Green 2012).
Mémoire de fin de formation ISIA 31
Rédigé par : Marius KOUNOU
L'aide au développement stimule-t-elle des
réformes économiques?
Test d'homogénéité sur
données de panel
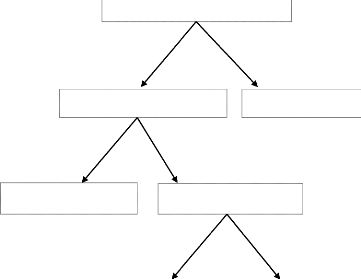
Figure 3 : Procédure générale du
test d'homogénéité
????,??= ái + ??'??????,?? + ??????
3 Vrai
??0 3 Rejetée ??0
??01 Rejetée
??01 Vrai
????,??= á + â'????,?? + ??????
2 Vrai
??0 2 Rejetée ??0
Test ??01 : ???? = á ???? = â
? i ? [1,N]
Test ??03 ái = á ?i ? [1,
N]
Test ??02 : ???? = â ,? i ? [1, N]
|
????,??= á + â'????,?? + ??????
|
????,??= ái + ??'??????,?? + ??????
|
|
Sources : Hurlin (2003)
|
|
Avant de présenter ces méthodes, il est d'usage
dans des données de panel de s'assurer de la spécification
homogène ou hétérogène du processus
générateur des données. Pour ce faire, le test
d'homogénéité de Fisher encore appelé test
d'empilage peut être utilisé. Le principe du test est
exposé dans l'encadré ci-dessous. Sur le plan
économétrique, il s'agit de tester l'égalité des
coefficients du modèle étudié dans la dimension
individuelle. Sur le plan économique, il permet de vérifier si on
est en droit d'admettre que le modèle théorique
étudié est parfaitement identique pour tous les
Mémoire de fin de formation ISIA 32
Rédigé par : Marius KOUNOU
L'aide au développement stimule-t-elle des
réformes économiques?
individus ou s'il existe des spécificités
propres à chaque individu. Le principe du test est exposé dans
l'encadre ci-dessus.

(3)
F1 =
SCR1,c-SCR1 (N-1)(k+1)
SCR1
NT-N(K+1)
) On considère le test de l'hypothèse
d'homogénéité totale. L'hypothèse nulle
associée s'écrit : Hô : âi = 13 ; ái =
á,V i = 1...N La statistique de Fisher F1 associée au
test d'Homogénéité totale Hô s'écrit sous la
forme suivante et suit un Fisher avec (N-1)(k+1) et NT-N(K+1)
degrés de liberté :
Où SCR1 désigne la somme des
carrés des résidus du modèle et SCR1,c la somme des
carrés des résidus du modèle contraint.
La somme des carrés des résidus du modèle
non contraint est simplement définie comme la somme des carrés
des résidus obtenus pour les N équations individuelles. Soit
SCR1 = EN1 SCRi Avec SCRi = YiYi -
(Xi'Yi ) Xi'Xi )-1 (Xi'Yi )
(4)
Les conclusions de ce test sont les suivantes : si l'on
accepte l'hypothèse nulle d'homogénéité globale, on
obtient alors un modèle pooled totalement homogène. Par contre si
on rejette l'hypothèse nulle, on passe à la seconde étape
qui consiste à déterminer si
l'hétérogénéité provient des
paramètres.
) Elle consiste à tester l'égalité pour tous
les individus des K composantes des vecteurs
Soit donc Hô : âi = 13, V i = 1...N. La
statistique de Fisher F2 associée au test
d'homogénéité totale Hô dans le modèle (3.4)
s'écrit sous la forme suivante :
SCR1,c'-SCR1 (N-1)k SCR1
NT-N(K+1)
(5)
F2 =
Encadré 1 : Les différentes étapes
du Test d'Homogénéité
Mémoire de fin de formation ISIA 33
Rédigé par : Marius KOUNOU
L'aide au développement stimule-t-elle des
réformes économiques?

(7)
F3 =
SCR1,c-SCR1,c' (N-1)
SCR1,c'
F2 suit un Fisher avec (N-1)k et NT-N(K+1)
degrés de liberté et SCR1,c'est la somme des carrés des
résidus du modèle contraint. Elle est donnée par la
formule suivante :
SCR1, c' = ?i=1 N Yi' Yi - (? i = 1 N
Xi'Yi )' ( ?i=1 N Xi'Xi )-1 (? i = 1 N
Xi'Yi ) (6)
Les conclusions de ce deuxième test sont les suivantes
: si on rejette l'hypothèse nulle d'égalité des
paramètres, on rejette alors la structure de panel et l'estimation se
fait en considérant N modèles individu par individu. Si en
revanche, on accepte l'hypothèse Hô , on retient la structure de
panel et l'on passe à la troisième étape consistant
à déterminer si les constantes ont une dimension individuelle.
? Elle consiste à tester l'égalité des N
constantes individuelles sous l'hypothèse de paramètres communs
`à tous les individus. On a donc Hô : ái = á, Vi =
1...N La statistique de Fisher F3 associée au test
d'Homogénéité totale Hô dans le modèle (3.4)
suit un Fisher avec (N-1) et N(T-1)-K degrés de liberté. Elle se
calcule par :
N(T-1)-K
Les conclusions de ce dernier test sont les suivantes : si
l'on rejette Hô , on obtient un modèle de panel avec effets
individuels. Dans le cas ou` l'on accepte Hô, on retrouve une structure
de panel totalement homogène (modèle pooled). Ce dernier test ne
sert alors qu'a confirmer ou infirmer les conclusions du premier test.
Sources : Hurlain (2003)
Mémoire de fin de formation ISIA 34
Rédigé par : Marius KOUNOU
L'aide au développement stimule-t-elle des
réformes économiques?
Modèles à effet fixe et à effet
aléatoire
Pour prendre en compte adéquatement la dimension panel
des données, le modèle spécifié à
l'équation (2) est légèrement altéré en
décomposant le terme d'erreur en une composante spécifique
à chaque pays, une composante spécifique à chaque
année et une composante aléatoire. On obtient l'équation
ci-dessous :
???é f ormei,t= á
??é f ormei,t-1 + â ??????i,t-1 + ?
??i,t-1 +ui + ??t + ??i,t (8)
L'estimation de l'équation (8) dépend de
l'hypothèse sur ui qui pourrait être soit fixe ou
aléatoire. Un modèle à effet fixe traite ui comme
une constante supplémentaire qui varie selon les pays et peut être
corrélée avec les variables explicatives. Dans un modèle
à effet aléatoire ui est supposé être une
partie des erreurs et est distribué indépendamment des variables
explicatives. Nous considérons à la fois le modèle
à effet fixe et le modèle à effet aléatoire, et
utilise un test de Hausman pour tester formellement le meilleur
modèle.
Le modèle à effet fixe peut être
estimé en utilisant une méthode d'estimation des effets qui
exploite les écarts des moyennes de groupe (ou période).
L'équation à estimer est écrit comme suit.
???é f ormei,t - ???é f orme
i = ??0 + ??(??????-????) + ?????? -
???? (9)
Le modèle à effet aléatoire estime les
équations suivantes:
|
???é f orme??,?? - ??^???é f orme
i = (1 - ??^)??0 +
??(??it-??i) + vit
vit = (1 - ??^)??i + ??it - ??^??i
??^ = 1 - ????
v???? 2+????2
|
(10)
|
Mémoire de fin de formation ISIA 35
Rédigé par : Marius KOUNOU
L'aide au développement stimule-t-elle des
réformes économiques?
Modèles de panel dynamique
Aussi bien les réformes et l'aide sont très
persistants au cours du temps en ce sens que les valeurs au cours d'une
année sont fortement corrélées aux valeurs des
années subséquentes. Cela explique pourquoi dans notre
spécification, le niveau de réformes au cours de l'année
t-1 est inclus dans le modèle. Cette dynamique dans le modèle
introduit une complication supplémentaire dans l'estimation des
modèles. En fait, en raison de la présence du lag de la variable
dépendante dans le côté droit de l'équation, les
résidus obtenus en prenant la première différence pour
éliminer l'effet fixe sont corrélés et l'estimation par
effet fixe ou aléatoire reste inconsistante (Arellano et Bond, 1991).
Pour résoudre le problème, nous comptons sur le
développement récent des estimations par Méthodes de
Moments Généralisée (GMM) suggérées par
Arellano et Bond (1991), Arellano et Bover (1995) et Blundell et Bond (1998).
Le principe est d'utiliser les retards d'ordre 2 et plus de la variable
dépendante combinés avec les retards de la première
différence des variables de contrôle comme des instruments.
| 


