III.3. Dimensionnement en couverture
III.3.1. Objectif du dimensionnement
Le dimensionnement d'un réseau UMTS permet d'assurer la
minimisation du coût de la liaison radio et de l'infrastructure du
réseau, en tenant compte de la couverture
35
radio et des tailles des cellules sous réserve de
contraintes de la QoS. Le dimensionnement en couverture d'un réseau UMTS
permet essentiellement de déterminer les tailles des cellules, le rayon
de cellule est obtenu suite à la réalisation d'un bilan de
liaison qui permet de déterminer l'affaiblissement maximal
alloué. Cette valeur du modèle de propagation est utile pour
déterminer le rayon de cellule.
Sachant la taille de la cellule, on pourra donc
déterminer pour la zone à planifier le nombre de stations de base
nécessaires en fonction du nombre d'utilisateurs dans la cellule suivant
les Indications de Jaana Laiho and Achim Wacker dans leur ouvrage «
Radio Network planning and optimisation for UMTS page190
». Notre dimensionnement suivra la démarche suivante
:
Prise de connaissance et introduction
de la Superficie
à couvrir qui peut une
ville ou un village
Introduction du Nombre d'usagers
actifs de la ville ou du
village
Introduction Nombre d'usagers dans
une cellule
Génération de mobiles dans une
cellule
fictive
Contrôle de puissances
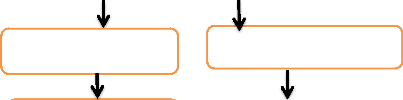
Mesure du niveau
d'interférence des mobiles
Détermination du Rayon d'une cellule
Distance entre deux sites
Couverture d'une cellule
36
Nombre de sites
Figure 15:Objectifs du dimensionnement
III.3.2. L'angle ö et distance MS et la station de
base
Pour calculer p, nous allons représenter le site (ou
station de base) par un point S de coordonnées (Xs, Ys, H) et la station
mobile par un point M de
37
coordonnées (Xm, Ym, 0). Puisque l'angle ö est
l'angle horizontal que fait le mobile avec l'antenne, il suffit de projeter ces
deux points sur le plan horizontal (OXY), ensuite, puisque cet angle
dépend de l'azimut de l'antenne, nous devons le calculer pour chaque
antenne i à part, avec :
? azimut=0° pour i=1,
? azimut=120° pour i=2,
? azimut=240° pour i=3.
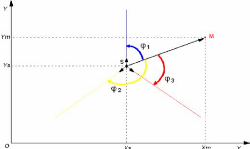
Figure 16:Calcul de l'angle ö [8]
On pose D = la distance entre la MS et la station de base:
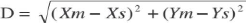
On pose:
S1 = vecteur unitaire indiquant le sens du secteur ayant un
azimut nul, de coordonnée (0,1) dans le plan horizontal.
S2 = vecteur unitaire indiquant le sens du secteur ayant un
azimut de 120°, donc de coordonnées ( cos(ð / 6), sin( ð/
6)) dans le plan horizontal.
S3 = vecteur unitaire indiquant le sens de secteur ayant un
azimut de 240°, donc de coordonnées (cos(ð / 6), sin(ð /
6)) dans le plan horizontal.
D'après la figure 19, on peut déduire les
valeurs des angles
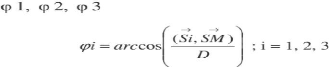
respectivement en fonction des vecteurs S1, S2, S3
38
Avec:
(Si, SM) est le produit scalaire entre Si, et SM égal
à : (Xi*(Xm-Xs) + Yi*(Ym-Ys)) où (Xi, Yi) sont les
coordonnées du vecteur Si [8].
| 


