Compression d'images fixes: comparaison des méthodes par transformations en ondelettes et celle par curvelets

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page i

DEDICACES

DEDICACES

A
NOS PARENTS
Monsieur et Madame TEGUEU
Et
Monsieur et Madame OTTOU

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page ii

REMERCIEMENTS

REMERCIEMENTS

Le présent travail a été réalisé grâce aux efforts conjugués de plusieurs personnes à qui nous aimerons exprimer notre profonde gratitude :

> Au Pr FOGUE MEDARD directeur de l'établissement pour sa disponibilité et la supervision générale des cours.

> Au Pr TCHINDA RENE vice-directeur de l'établissement, pour sa rigueur et sa discipline. > A Dr KAPCHE chef de département, pour ses conseils, sa franchise et surtout les efforts consentis pour la satisfaction de tous ses étudiants.

> A nos encadreurs : M.DJIMELI Alain et Dr TCHIOTSOP pour leur disponibilité et conseils qui nous ont permis d'améliorer d'avantage ce rapport et surtout d'atteindre les objectifs définis dans le cahier des charges.

> Aux enseignements du département de Génie des Télécommunications et Réseaux pour leur disponibilité, soutient et encadrement tout au long des ces trois années de formations.

Merci à tous ceux qui de près ou de loin ont contribué à la réussite de ce rapport de projet de

fin d'études.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page iii

AVANT-PROPOS

AVANT-PROPOS

L'institut Universitaire de Technologie FOTSO Victor de BANDJOUN en abrégé IUT-FV est l'établissement de l'Université de Dschang, né de la reforme Universitaire de 1993, suivant l'arrêté présidentiel N° 008/CAB/PR du 19 Janvier 1993, ayant pour vocation principale de dispenser en formation initiale un enseignement dans les domaines industriels et commerciaux.

> L'IUT-FV forme en deux ans, les étudiants qui obtiendront par la suite, sous réussite, un diplôme universitaire de technologie(DUT) dans les domaines de :

· Génie électrique (option électronique et électrotechnique)

· Génie des Télécommunications et Réseaux(GTR)

· Informatique de Gestion(IG)

· Maintenance Industrielle et Productrice(MIP)

· Génie civil(GC)

> L'IUT-FV prépare les candidats au Brevet de Technicien Supérieur(BTS). Pour cela, dispose dans ce cycle les domaines suivants :

· Génie électrique (option électronique et électrotechnique)

· Génie Civil(GC)

· Secrétariat de Direction(SD)

· Action Commercial(AC)

· Comptabilité et Gestion d'Entreprise(CGE)

> L'IUT-FV forme également les étudiants en cycle de licence technologique dans les domaines :

· Ingénierie des Télécommunications et Réseaux (ITR)

· Génie électrique

· Informatique et Réseaux

· Maintenance Industrielle et Productique

· Génie Civil

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page iv

AVANT-PROPOS

> L'IUT-FV forme également les étudiants en cycle de licence professionnelle dans les domaines :

· Gestion Comptable et Financier

· Gestion Administrative et Management des Organisations

· Marketing Manager Opérationnel

· Banque Gestionnaire des Relations Clientèles

> L'IUT-FV forme également les certifiés réseaux grâce à l'académie CISCO

En somme, l'IUT-FOTSO Victor avec son administration entreprenante, des enseignants dotés d'une conscience professionnelle et ses étudiants bénéficiant de son lotissement très propice à l'enseignement, à un avenir promoteur.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page v

CAHIER DES CHARGES

CAHIER DES CHARGES

Thème : Compression d'images fixes : comparaison de la méthode de curvelets et celle par ondelettes

Les candidats doivent utiliser la boîte à outils matlab d'ondelette et de curvelet pour compresser quatre images tests et comparer les résultats.

Travaux préliminaires :

> Les candidats doivent faire une revue des différentes méthodes de compression d'image.

> Les candidats doivent faire une étude théorique de la décomposition en ondelette et ressortir les avantages par rapport à la décomposition de fourrier.

> Les candidats doivent faire une étude théorique de la décomposition en curvelet et trouver les avantages par rapport à la décomposition en ondelette.

> Les candidats doivent se familiariser avec la boîte à ondelette et de curvelet de Matlab (l'installer si elle n'existe pas, faire une décomposition d'image, manipuler les coefficients ...)

Fonctionnalités attendues :

> Quatre images de test choisies au hasard doivent être compressées par les ondelettes en premier et par les curvelets avant de pouvoir faire une comparaison.

Encadreurs : M. DJIMELI, Dr TCHIOTSOP

Étudiants : SIMO TEGUEU Armel Francklin, EMBOLO Aurelien

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page vi

EPIGRAPHIE

EPIGRAPHIE

« Nos expériences quotidiennes-notamment nos sensations auditives-imposent une description en termes de temps et de fréquences. »

Gabor (1900-1979)

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page vii

LISTES DES FIGURES ET TABLEAUX

LISTES DES FIGURES ET TABLEAUX

Figure 1 F et sa série pour n=3 (rouge) et n=10 (bleu) 10

Figure 2 Série de Fourier de F pour n =2000 10

Figure 3 Quelques exemples d'ondelettes : Morlet, Daubechies et Meyer 20

Figure 4 Atome de la Wavelet Transform 22

Figure 5 Compression d'un signal 1D sous MATLAB selon l'algorithme de Haar 29

Figure 6 Analyse Multirésolution 30

Figure 7 Décomposition et approximation de l'image de lenna sous MATLAB selon Haar 31

Figure 8 Schéma de construction de la transformée en Curvelets d'une image 33

Figure 9 Pavage du plan fréquentiel de l'image de Lenna sous MATLAB dans le domaine

discret 35

Figure 10 Décomposition et approximation d'une image par pavage du plan fréquentiel dans

le domaine discret sous MATLAB 36

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page viii

SOMMAIRE

SOMMAIRE

DEDICACES............................................................................................................................................. i REMERCIEMENTS................................................................................................................................. ii AVANT-PROPOS ................................................................................................................................... iii CAHIERDES CHARGES ........................................................................................................................ v EPIGRAPHIE.......................................................................................................................................... vi LISTES DES FIGURES ET TABLEAUX ............................................................................................... vii SOMMAIRE.......................................................................................................................................... viii INTRODUCTION GENERALE ................................................................................................................. 1

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES.

I. METHODES DE COMPRESSION AVEC PERTE OU IRREVERSIBLE 2

I.1 LES METHODES SPATIALES 3

I.2 LES METHODES PAR TRANSFORMATION 4

II. METHODES DE COMPRESSION REVERSIBLES OU SANS PERTE 4

II.1 METHODES DIFFERENTIELLES ET PREDICTIVES 5

II.2 METHODES PAR PLAGES 5

II.3 CODAGE DE SHANNON-FANO : 6

II.4 CODAGE DE HUFFMAN : 6

II.5 METHODES PAR DICTIONNAIRE ADAPTATIF (LEMPEL-ZIV) : 6

II.6 CODAGE ARITHMETIQUE : 6

CHAPITRE II : DE L'ANALYSE DE FOURIER A L'ANALYSE PAR ONDELETTES.

I. L'ANALYSE DE FOURIER 9

I.1 DECOMPOSITION EN SERIE DE FOURIER DES FONCTIONS PERIODIQUES 9

I.2 LA TRANSFORMEE DE FOURIER 11

II. L'ANALYSE PAR ONDELETTES 18

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page ix

SOMMAIRE

CHAPITRE III : BASES D'ONDELETTES ORTHOGANALES DE HAAR : APPLICATION A LA

COMPRESSION D'UNE IMAGE FIXE

I. ANALYSE MULTIRESOLUTION 26

I.1 APPLICATION DE L'AMR A L'ALGORITHME D'ANALYSE DE HAAR POUR DECOMPOSITION

D'UNE IMAGE 27

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS APPLICATION A LA
COMPRESSION D'IMAGES FIXES

I. LA TRANSFORMEE EN CURVELETS 33

I.1 TRANSFORMEE EN CURVELETS DICRETES 34

I.2 COMPRESSION D'UNE IMAGE SOUS MATLAB SELON L'ALGORITHME FCDT 36

CHAPITRE V: IMPLEMENTATION ET EVALUATION EXPERIMENTALE

I MESURES DE PERFORMANCE DE LA COMPRESSION D'UNE IMAGE 37

I.1 TAUX DE COMPRESSION 37

I.2 MESURES DE DISTORSION 37

I.3 RAPIDITE DE COMPRESSION 38

II. PRESENTATION DES RESULTATS OBTENUS 38

CONCLUSIONGENERALE .................................................................................................................... a

BIBLIOGRAPHIE....................................................................................................................................

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 1

INTRODUCTION GENERALE

INTRODUCTION GENERALE

La compression d'image est un domaine de recherche déjà riche d'une longue histoire. Trouvant ses racines théoriques dans la théorie de l'information initiée par C. Shannon en 1948, elle a depuis fait appel à de nombreux outils mathématiques de plus en plus sophistiqués. La problématique est cependant d'actualité et découle des applications de stockages des données ou de transmission à travers les canaux à bande passante limitée. Malgré les développements technologiques considérables ces dernières années, l'être humain, insatiable, déclare indispensable ce qu'hier il considérait superflu, et nous sommes sans cesse confrontés à de nouveaux besoins exigeant l'accès à toujours plus d'information : les intérêts de la compression sont d'une grande importance et indispensables pour de nombreuses applications.

La compression d'image met en jeu différentes techniques. On peut grossièrement les diviser en quelques grandes familles. Certaines ont pour but de structurer la redondance présente dans l'image que l'on souhaite compresser. C'est le cas par exemple de la transformation, qui cherche à concentrer l'information dans un petit nombre d'éléments en changeant de domaine, et de la prédiction, qui calcule un estimateur de l'information courante à partir d'une information passée. Nous allons dans une chaîne de compression d'images fixes accorder notre réflexion à l'étape de transformation des coefficients en vue d'un changement d'espace en exploitant les outils de transformée en ondelettes et en curvelets puis en évaluant comparativement chacune leur performance en terme de taux de compression, qualité d'image et rapidité de compression grâce au logiciel MATLAB.

Ce rapport est composé de quatre chapitres. Les trois premiers présentent le contexte théorique des travaux réalisés corrélativement au cahier des chargés et sont parfaitement dépendants, décrivent et présentent les limites et avantages respectivement des transformées Fourrier, Ondelettes et Curvelets dans un cadre général et puis particulièrement dans le domaine de la compression d'images fixes. Le dernier chapitre présentera à travers une plate forme dynamique les résultats des compressions obtenues par ces deux transformées et une étude comparative basée sur les critères de performances en termes de taux de compression, qualité de l'image compressée et la rapidité de compression.

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES

CHAPITRE I REVUE SUR 9UE59UES TECHNI9UES DE COMPRESSION

9

~"~~~~~~

Introdu&tion

Les méthodes de compression et de codage réduisent le nombre moyen de bits par pixel à stocker ou à transmettre, en exploitant la redondance informationnelle de l'image. A cet effet, plusieurs recherches scientifiques ont contribué à la naissance de diverses méthodes de compression. Notons que la compression d'images est divisée en deux axes principaux : compression sans perte et celle avec perte. Le premier type de compression, utilise uniquement le principe de la réduction de l'information et n'engendre pas de perte, le deuxième type, quand à lui, définit une représentation approximative de l'information.

Ce chapitre se limite aux cas particuliers des images fixes, et à faire l'inventaire des méthodes disponibles, en vue de comprendre le principe et de tracer les grandes lignes prévisibles dans ce domaine.

I, METHODES DE COMPRESSION AVEC PERTE OU IRREVERSI75E

Le schéma général souvent utilisé pour décrire le fonctionnement des algorithmes de compression avec pertes est celui présenté dans la figure1.

Image Originale

Changement de représentation

Quantification

Codage des symboles(Entropique)

Image Compressée

Figure 1 Etapes principales de compression d'images avec perte

Dans ce modèle, le codeur, qui reçoit en entrée l'image, réduit les redondances et produit en sortie un code binaire. On distingue trois blocs :

> Transformation ou décorrélation : la dépendance existante entre chacun des pixels et ses voisins (la luminosité varie très peu d'un pixel à un pixel voisin) traduit une corrélation très forte sur l'image. La décorrélation consiste à transformer les pixels initiaux en un ensemble de coefficients moins corrélés pour réduire le volume d'information, c'est une opération réversible.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 2

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 3

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES

> Quantification : réalise une réduction du nombre de valeurs représentées, qui fait partie uniquement des algorithmes irréversibles (consiste à réduire les redondances psychovisuelles, elle peut être scalaire ou vectorielle).

> Le codage entropique : le codage entropique effectue un codage sans perte sur les valeurs quantifiées. Cette dernière étape est nécessaire dans les méthodes sans perte, mais elle est souvent présente aussi dans les algorithmes irréversibles, puisque les valeurs transformées et quantifiées contiennent davantage de redondances.

Contrairement aux méthodes de compression sans perte d'informations, ce type comporte une perte de données pendant le processus de codage/décodage. Le résultat qu'on peut en obtenir est une version altérée de l'image originale . Le but de ce type de compression est d'éliminer le plus d'information possible sans atténuer la qualité de l'image perçue par le système visuel humain. Avec ces méthodes, on peut aussi distinguer :

> Les méthodes spatiales (ou directes) qui agissent directement sur les échantillons d'une image dans le domaine spatial.

> Les méthodes par transformation qui reposent sur une transformée (en général linéaire) de l'image originale.

I.1 LES METHODES SPATIALES

a. Sous-échantillonnage

Le sous-échantillonnage consiste à ne conserver qu'une partie des données. Par exemple, si on ne stocke qu'un pixel de l'image sur deux, on obtient un TC de 4:1. L'image reconstruite s'obtient par interpolation, par exemple en remplaçant chaque pixel manquant par la moyenne de deux pixels adjacents. Cette méthode extrêmement simple est à employer avec précaution car la distorsion n'est pas contrôlée.

b. Le codage par troncature des blocs (BTC) :

BTC est une technique simple de compression des images au niveau de gris développé par Delp et Mitchell.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 4

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES

I.2 LES METHODES PAR TRANSFORMATION

Les méthodes par transformation figurent parmi les techniques de compression les plus employées, elles n'agissent pas directement sur l'image numérique dans sa représentation canonique, mais sur le domaine de sa transformée. Elles permettent d'obtenir des taux de compression élevés tout en conservant une bonne qualité d'image. Ce sont des méthodes qui font appel successivement à plusieurs principes de compression. Elles sont utilisées par des standards internationaux pour le codage des images fixes et de la vidéo (JPEG et MPEG). En général, les schémas de codage par transformation subdivisent l'image de taille NxN en sous-images de taille plus petite avant de faire subir à chacune de ces sous-images une transformation. L'objectif de ces transformations est double: Il s'agit de décorréler les données, c'est-à-dire d'obtenir des coefficients transformés moins corrélés que les pixels de l'image d'origine ; Concentrer l'énergie sur un nombre réduit de coefficients, les coefficients ayant une valeur plus importante aux basses fréquences qu'aux hautes fréquences. Dans ce cas, on obtiendra une compression effective en codant finement les coefficients des basses fréquences, et grossièrement, voire en supprimant, les coefficients des hautes fréquences. On peut citer entre autre :

> La transformation de Fourrier (DFT)

> La transformation en Cosinus Discrète (DCT)

> La transformation par ondelettes discrètes (DWT)

II. METHODES DE COMPRESSION REVERSIBLES OU SANS PERTE

Les méthodes sans perte peuvent s'appliquer dans le domaine spatial, mais plus difficilement dans le domaine fréquentiel. Ce type de compression n'occasionne aucune perte de données. Il est utilisé dans des applications comme l'archivage des images médicales, l'imagerie satellitaire (le coût des images est élevé et les détails sont importants), les textes, les programmes et tout autre type de données nécessitant une conservation intégrale. Dans ce cas, les compromis liés à ce mode de compression sont :

> Efficacité du codage, ceci peut être mesuré en bit par pixel, elle est limitée par l'entropie de la source. Plus l'entropie de la source est grande plus il est difficile à compresser.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 5

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES

> Temps de codage, celui-ci est lié à la complexité du processus de codage ou de décodage. Il peut être réduit si on augmente la capacité de calcul du composant de traitement. Pour certaines applications ce temps est contraint, ce qui impose le choix de la technique de codage.

> Complexité du codeur, elle peut être mesurée à l'aide de la quantité de ressources utilisées en termes de mémoire et du nombre d'opérations arithmétiques. Cette famille d'algorithmes est essentielle dans nos ordinateurs, la totalité des programmes d'archivage sont bâtis sur cette technique de compression sans perte d'information.

Il existe de nombreux types d'algorithmes de compression d'images sans perte. Voici les plus répandus.

II.1 METHODES DIFFERENTIELLES ET PREDICTIVES

Ces méthodes exploitent la redondance entre un pixel et ses voisins, qui en général se ressemblent beaucoup. Par exemple, on code le premier pixel, on calcule la différence avec le second pixel et on code cette différence. Cette dernière nécessite moins de bits que les pixels eux mêmes car cette différence est souvent faible. On code ensuite la différence entre le deuxième pixel et le troisième, etc...

Dans des systèmes plus complexes et performants, on établit une fonction de prédiction qui permet d'estimer la valeur d'un pixel en fonction des valeurs des pixels voisins. On code alors l'erreur de prédiction, qui est l'écart entre la vraie valeur du pixel et la valeur prédite. La façon de coder les erreurs de prédiction est souvent basée sur la quantification scalaire. Le codage prédictif ainsi décrit correspond à la modulation par impulsion et codage différentielle (MICD, ou DPCM en anglais).

II.2 METHODES PAR PLAGES

Le Codage par plage (Run length Encoding) :

Le principe de compression RLE est assez simple à mettre en oeuvre. Il repose sur le fait que dans une image, il existe de nombreuses répétitions d'un même pixel, ou d'une même séquence de pixels, tous juxtaposés. Ainsi, au lieu de coder chaque pixel d'une image, le RLE regroupe les valeurs voisines identiques et ne transmet une valeur qu'une seule fois, précédée

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 6

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES

par le nombre de répétitions. Il est clair que cette approche fonctionne bien s'il y a beaucoup de répétitions dans l'image. Cet algorithme très simple, peut aboutir à des taux de compression plus élevés.

II.3 CODAGE DE SHANNON-FANO

C. Shannon du laboratoire Belis et R. M. Fano du MIT ont développé à peu près en même temps une méthode de codage basée sur la simple connaissance de la probabilité d'occurrence de chaque symbole dans le message. Le procédé de Shannon-Fano consiste à construire une arborescence partant de la racine, et procédant par divisions successives. Le classement des fréquences se fait par ordre décroissant, ce qui suppose une première lecture du fichier et la sauvegarde de l'en-tête.

II.4 CODAGE DE HUFFMAN

L'imminent mathématicien, David Huffman, a proposé en 1952 une méthode statistique qui permet d'attribuer un mot de code binaire aux différents symboles à compresser (pixels ou caractères par exemple). La longueur de chaque mot de code n'est pas identique pour tous les symboles: les symboles les plus fréquents (qui apparaissent le plus souvent) sont codés avec de petits mots de code, tandis que les symboles les plus rares reçoivent de plus longs codes binaires. Le codeur de Huffman est très couramment employé en compression d'image. Il constitue très souvent l'étape finale produisant le flot binaire dans les méthodes par transformations.

II.5 METHODES PAR DICTIONNAIRE ADAPTATIF (LEMPEL-ZIV)

C'est une technique de codage qui utilise un dictionnaire. On cherche dans le fichier les chaînes qui se répètent en les mémorisant dans un dictionnaire. Ensuite, le codage consiste à remplacer les chaînes mémorisées par leurs adresses (ou indice) construite dans le

dictionnaire.

II.6 CODAGE ARITHMETIQUE

Contrairement aux algorithmes de Huffman et de Shannon-Fano qui associent à des symboles des motifs binaires dont les tailles dépendent de leurs distributions. Le codeur arithmétique traite le fichier dans son ensemble, en lui associant un unique nombre décimal

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 7

CHAPITRE I : REVUE SUR QUELQUES TECHNIQUES DE COMPRESSION D'IMAGES

rationnel. Ce code de sortie est un nombre à virgule flottante compris entre 0 et 1, dont le nombre de chiffres après la virgule correspond au nombre de symboles. Le codeur arithmétique est plus performant que le codeur de Huffman, mais il est plus complexe à implémenter.

CONCLUSION

Dans ce chapitre, nous avons présenté plusieurs techniques de compression d'images fixes sans et avec perte. Nous allons dans la suite de ce document nous intéresser précisément à deux méthodes de compression qui sont : la méthode de compression par ondelettes et celle par curvelets appartenant à la famille des méthodes de compression avec pertes par transformées.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 8

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

CHAPITRE II : DE L'ANALYSE DE FOURIER A L'ANALYSE PAR

ONDELETTES.

INTRODUCTION

L'idéal lors du traitement numérique d'une image en vue d'une compression ou d'un tatouillage d'informations, est de conserver d'avantage le caractère agréable de l'image. Par contre, dès lorsque l'on veut réduire d'avantage le poids d'une image pour répondre aux limites des systèmes de transmissions ou de stockages ou encore pour un éventuel tatouillage d'informations, il est indispensable de trouver un compromis optimal et satisfaisant. En effet l'on observe dans les détails d'une image plus de régions (zones lisses ou basses fréquences) que de frontières (zones à brusque variations ou hautes fréquences ou contours), il est donc évident de penser que si l'on veut compresser l'image, une transformée affectant de faibles valeurs aux zones lisses de l'image et de fort coefficients là ou l'intensité varie beaucoup sera bien adaptée : il suffira alors de garder les plus gros coefficients.

Un outil mathématique s'est avéré particulièrement efficace aussi bien pour le débruitage, que pour la compression, ou encore pour la détection de contours : il s'agit de la transformée en ondelette. L'analyse par ondelette découle tout naturellement de l'analyse de Fourier. Il est donc naturel de commencer par celle-ci afin de saisir les bases de cette nouvelle technique.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 9

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

I. L'ANALYSE DE FOURIER

I.1 DECOMPOSITION EN SERIE DE FOURIER DES FONCTIONS PERIODIQUES

Beaucoup d'équations physiques n'avaient pas de solution sous forme de fonctions simples. Ces solutions ont été représentées sous formes de séries de fonctions trigonométriques. En reprenant cette méthode, Fourier a montré que l'on pouvait ainsi représenter une large classe de fonctions.

Si x(t) est une fonction complexe de variable complexe périodique de période T on a :

8

f(x)=2a₀+/ (a_n cos

~ ~ ~~ sin ~~~~

~ ~

n-_1

Les coefficients sont calculés donc par :

2 T

~~ ~~~ ~~~~ cos ~~~~ ~ ~

~ dx ~ ~ ~~~~ sin ~~~~
et ~~ ~

~ ~ ~ dx

Interprétation

Cela peut paraître bizarre de recomposer une fonction en sommant en l'infini les intégrales de produit de celle-ci avec les sinus et les cosinus. C'est en réalité exactement équivalent à ce que l'on fait en algèbre vectoriel, à savoir exprimer un vecteur dans une base et pouvoir chaque coefficient en utilisant le produit scalaire. Le principe reste le même, le plus difficile est de faire abstraction de la notion habituelle de fonction pour se les représenter dans un espaces fonctionnels comme étant des vecteurs, autrement dit, les points ! De plus, le facteur

n sur lequel a lieu la sommation nous indique que pour une fonction de fréquence í= T

donnée, les sinus et cosinus de sa série de Fourier ont une fréquence de ní ; c'est-à-dire une fréquence multiple entier de la fréquence du signal analysé.

Voici un exemple de série de Fourier. Soit la fonction périodique suivante

F : R-) R telle que : F(x)= (2 !"#$ -- % & x & 0

2 !"#$ 0 & x & %

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 10

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Figure 2 F et sa série pour n=3 (rouge) et n=10 (bleu)

Bien entendu, la représentation d'un signal par sa série de Fourier est optimale pour une sommation sur un grand nombre de coefficients, comme le montre la figure Figure2.

Figure3 Série de Fourier de F pour n =2000 Limites de la série de Fourier

Les séries de Fourier sont, dans certains cas limitées. Tout d'abord,

> Un phénomène curieux apparaît aussi : les oscillations de Gibbs. Autour des points de discontinuité, la valeur de la série oscille légèrement et la valeur au point de discontinuité est supérieure (ou inférieure) de 9% à la valeur de F en ce même point.

> La présence des oscillations de Gibbs crée une incertitude au niveau des points de discontinuité du signal qui pour une image représente un contour qui est la partie de l'image qui devrait être transparente à la transformation. Donc la série de Fourier n'est pas adaptée à la compression d'images.

> la fonction F doit être périodique. Elle est en effet exprimée par une somme de sinusoïde qui est des fonctions périodiques, et on peut montrer qu'une somme quelconque de fonction est encore une fonction périodique.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 11

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Le fait que la série permette uniquement la représentation des fonctions périodiques, est ce qui motive la section suivante. En effet pour représenter d'autres fonctions sur R, on doit avoir besoin d'un outil.

I.2 LA TRANSFORMEE DE FOURIER

Introduction

Les transformations mathématiques sont appliquées aux signaux bruts pour obtenir d'avantages d'informations qui sont disponibles dans ces signaux. Dans la pratique, la plupart des signaux sont des signaux dépendant du temps (du domaine temporel) sous leur format brut. La représentation du signal est une représentation temps-amplitude. Cette représentation n'est pas toujours la meilleure pour la plupart des applications de traitement du signal. Dans beaucoup de cas, l'information la plus pertinente est cachée dans la composante de fréquence du signal. Le spectre de fréquence d'un signal est constitué par les composantes de fréquence de ce signal. Le spectre de fréquence d'un signal indique quelles sont les fréquences contenues dans ce signal. Intuitivement, nous savons que la fréquence est liée au régime de changement d'une variable physique ou mathématique. Si cette variable change

> Rapidement : changement à haute fréquence

> Lentement : changement à base fréquence, et

> Si elle ne change pas du tout, elle est de fréquence zéro.

Comment allons-nous mesurer la fréquence, comment allons trouver le contenu en fréquence d'un signal ? La réponse est la Transformée de Fourier (TF). Si on prend la TF d'un signal dans le domaine temporel, on obtient la représentation fréquence-amplitude de ce signal.

I.2.1 Transformée de Fourier à temps continu directe et inverse

)(f) =f ⁰¹ ~~*~+,-~~./ 2* (1), ~~*~ ~ ~ 01 )~~~+-~~./ 2f (2)

^,1 ^,1

Interprétation de l'équation (1):

Le signal x(*), est multiplié avec un terme exponentiel, à certaines fréquences « f» qui peut être écrit : cos (2%f*)+ jsin (2%f*) (3) et puis intégrer (additionner tous les termes de produit) sur tout le temps.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 12

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

> Si le résultat de cette intégration est une grande valeur, alors nous disons que le signal x(t) a une composante spectrale dominante à la fréquence « f ». Ceci signifie que la majorité de ce signal est composé de la fréquence «f ».

> Si le résultat de cette intégration est une petite valeur, alors nous disons que le signal x(t) n'a pas de composante spectrale dominante et majoritaire à la fréquence « f».

> Si ce résultat est nul, alors le signal ne contient pas du tout de fréquence « f ».

Le signal est multiplié avec le terme sinusoïdal de la fréquence « f ». Si le signal a une composante de la fréquence « f » d'amplitude élevée alors, cette composante et le terme sinusoïdal coïnciderons et leur produit donnera (relativement) une grande valeur. Ceci montre que le signal possède une fréquence majoritaire de « f ». Cependant, si le signal n'a pas une composante de fréquence de « f », le produit sera zéro, c'est-à-dire le signal n'a pas une composante de fréquence de « f ». Si la fréquence « f» n'a pas une composante importante du signal « x(t) », alors le produit donnera (relativement) une petite valeur. Ceci signifie que, la composante de fréquence « f» dans le signal « x(t) », a une petite amplitude, c'est-à-dire elle n'est pas une composante importante de « x(t) ».

L'information fournie par l'intégrale, correspond à tous les instants de temps, puisque l'intégrale est de --00 à +00 sur le temps. Il suit qu'à n' importe quel instant du temps, la composante avec la fréquence « f » apparaît, elle affectera également aussi bien le résultat de l'intégration. En d'autres termes, si la composante « f » de fréquence apparaît au temps T1 ou au temps T2, il y aura le même effet sur l'intégration.

C'est pourquoi la transformée de Fourier n'est pas appropriée si le signal a une fréquence variable dans le temps (non stationnaire). Si uniquement, le signal a une composante de fréquence « f » a tout moment (pour toutes les valeurs de « f » (stationnaire), alors le résultat obtenu par la transformée de Fourier a un sens.

Voici un exemple de la Transformée de Fourier :

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 13

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Exemple d'Application de la transformée de Fourier continue

Souvent, l'information qui ne peut pas être distinguée dans le domaine temporel est facilement visible dans le domaine fréquentiel. Prenons un exemple dans le secteur des signaux biologiques et supposons que nous observions un signal d'électrocardiographie (ECG), la forme typique du signal ECG d'un coeur sain est bien connu des cardiologues, tout écart avec cette forme est considéré comme le syndrome d'une possible pathologie. Ce signe de pathologie, cependant, n'est pas toujours très évident dans le signal, du domaine temporel, original. Les cardiologues utilisent jusqu'à présent les enregistrements de ces signaux dans le domaine temporel, ils figurent sur les bandes de papier pour analyser les ECG. Récemment, les nouveaux analyseurs ECG informatisés utilisent l'information de fréquence pour décider de l'existence d'une pathologie. Un symptôme de maladie peut parfois être mieux diagnostiqué quand on analyse les composantes fréquentielles du signal.

Inconvénients de la Transformée de Fourier continue

Malgré son immense succès, cette technique a un immense défaut, en particulier

> Son manque évident de localisation temporelle : une analyse globale

La FT, comme la WT est une transformation réversible, c'est-à-dire qu'elle permet le « aller-retour » entre le signal brut et le signal traité (transformé). Cependant, seulement l'un des deux est disponible à un instant donné. Aucune information de fréquence n'est disponible dans le domaine temporel et aucune information temporelle n'est disponible dans la FT du signal. En effet, l'analyse de Fourier permet de connaître les différentes fréquences excitées dans un signal, c'est-à-dire son spectre, mais ne permet pas de savoir à quel instant ces fréquences ont été émises. Cette analyse donne une information globale et non locale car les fonctions d'analyse utilisées sont des sinusoïdes qui oscillent indéfiniment sans s'amortir.

Cette perte de localité n'est pas un inconvénient pour analyser les signaux dont la structure n'évolue pas ou peu (statiquement stationnaire), mais devient un problème pour l'étude de signaux non stationnaires.

> Pertes d'informations temporelles : elle ne peut permettre de détecter la présence d'une singularité dans le signal analysé.

> L'analyse de Fourier ne permet pas l'analyse de signaux dont la fréquence varie dans le temps. De tels signaux nécessitent la mise en place d'une analyse temps-fréquence qui permettra une localisation de périodicité dans le temps et qui indiquera donc si la

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 14

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

période varie d'une façon continue, si elle disparaît puis réapparait par la suite, etc. Elle est donc adaptée aux signaux stationnaires.

> La non causalité de la transformée de Fourier. Il est clair que le calcul de X(f) nécessite la connaissance de f sur IR tout entier. Une analyse en temps réel est donc impossible. On ne peut pas connaitre le spectre d'une fonction f si on ignore la fonction. Par exemple deux fonctions identiques sur un même intervalle peuvent être de transformée de Fourier très différente.

> Un autre inconvénient de la TFC est la complexité de son implémentation algorithmique due à la fonction de décomposition continue sur IR. En effet la transformée de Fourier permet d'obtenir le spectre d'un signal dépendant du temps : on passe d'une étude temporelle du signal à une étude fréquentielle de celui-ci avec sa transformée. Seulement, il existe une différence cruciale entre une fonction mathématique continue et un signal physique. L'information que nous avons d'un signal physique est nécessairement discrète, on ne peut en effet enregistrer celui-ci avec une fréquence infinie, en prenant tous les points ! C'est cette discrétisation qui va permettre l'utilisation de la Fast Fourier Transform (ou FFT).

I.2.2 Transformée de Fourier Rapide (FFT)

Cette transformée de Fourier rapide est un algorithme de calcul, une recette qui va permettre de minimiser le nombre d'opérations nécessaires pour l'établissement de la transformée de Fourier d'un signal discret. L'analyse par FFT découle tout naturellement de l'analyse par TFD (Transformée de Fourier Discrète). Il est donc naturel de commencer par celle-ci afin de saisir les bases de cette nouvelle technique.

Transformée de Fourier Discrète

Depuis C. Shannon, il est possible d''echantillonner correctement un signal et donc de représenter celui-ci. Mais comment obtenir le spectre d'un signal physique ? Rappelons que la différence entre une fonction mathématique et l'information que nous possédons d'un signal physique réside dans le fait que cette dernière est discrète ! Remarquons au passage qu'un signal discret périodique possède un spectre discret. La première étape dans le calcul de la transformée de Fourier discrète (T.F.d.) de ce signal va donc être l'échantillonnage de ce

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 15

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

signal. Considérons un signal analogique de fréquence maximale f0, on va devoir échantillonner 2f0 fois ce signal pour pouvoir représenter celui-ci. Dans ce cas-ci, on prélève 2N échantillons (le nombre d'échantillons est une puissance de 2 pour un calcul optimal de l'algorithme) du signal. Pour une fréquence particulière, on multiplie les valeurs échantillonnées par l'exponentielle de la fréquence considérée, on additionne ces valeurs et on divise le total par le nombre d'échantillons. On réitère ce processus pour l'ensemble des fréquences discrètes du signal pour obtenir la transformée de Fourier de ce signal. Pour un meilleur fonctionnement de l'algorithme, on se restreint à un nombre de fréquences égales au nombre d'échantillons. D'un point de vue mathématique, la T.F.d. s'écrit :

)~~~ = 4 ~ ? ⁶

^4, 78 9

4 ₊:⁴ (3) f= 0, 1, 2, ..., 2^N -1 ; N est tel que 2^N > 2f0

6

)(f) désigne le coefficient de Fourier du signal x(*) à la fréquence f ; ce nombre reflète l'importance de cette fréquence dans le signal. Pour rappel, la fréquence est reliée à la pulsation ù par un facteur 2%.

Un bref coup d'oeil sur cette transformée discrète nous indique que d'un point de vue calculatoire, cette méthode nécessite N1² calculs, ou N1 est le nombre d'échantillons. En effet, il faut réaliser pour chaque fréquence N1 produits. Et comme il y a N1 fréquences . . . Cette méthode devient très vite longue et ennuyeuse. Une autre méthode s'avère plus efficace : la FFT

Lorsque l'on considère une fonction continue sur [0, 2 %], on peut tout d'abord la discrétiser à l'aide de N points. La plupart du temps, cette discrétisation est faite sur un mode dichotomique, c'est à dire que N est une puissance de 2. Après avoir fait cette discrétisation, on obtient une nouvelle fonction que l'on peut noter fN et le calcul de ses N coefficients de Fourier nécessite N² opérations élémentaires. La transformée de Fourier rapide est un algorithme permettant de calculer ceux-ci avec une complexité de O(N logN). L'idée étant, à chaque calcul d'un nouveau coefficient, de réutiliser les calculs faits pour calculer les coefficients précédents.

La transformée de Fourier rapide (FFT)

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 16

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Nous n'allons pas dans ce document détailler l'algorithme FFT. La transformée rapide utilise une version matricielle de la formule de la TFD. Le calcul matriciel n'est en soi pas très compliqué. Il y a des règles, il faut les appliquer. L'idée de cet algorithme rapide est de ranger les nombres qu'il faut multiplier de sorte qu'on évite de faire deux fois les mêmes calculs. C'est Carl Friedrich Gauss (1777-1855) qui le premier eut l'intuition de cet algorithme. Bien entendu, celui-ci n'a pas utilisé des matrices pour écrire son algorithme ; les matrices étant apparues pour la première fois en 1858 dans un article d'Arthur Cayley. Précisons encore que ce raccourci mathématique qu'est la FFT fut publié en 1965 par James Cooley et John Tukey. Aujourd'hui, cette transformée est la forme exploitable de la transformée de Fourier vu la taille en fréquence limitée des processeurs.

Voilà ainsi présentée une technique de calcul rapide permettant d'optimiser les temps d'évaluation d'une transformée de Fourier de signaux discrets venant ainsi résoudre le problème de modélisation algorithmique de la TFC.

Nous avons également vu que la TF n'était pas adaptée aux signaux non stationnaires or la plupart des signaux du monde réel ne sont pas stationnaires, et c'est justement dans l'évolution de leurs caractéristiques (statistiques, fréquentielles, temporelles, spatiales) que réside l'essentiel de l'information qu'ils contiennent. Les signaux vocaux et les images sont à ces titres exemplaires. Or l'analyse de Fourier propose une approche globale du signal, les intégrations sont faites de moins l'infini à plus l'infini, et toute notion de localisation temporelle (ou spatiale pour des images) disparaît dans l'espace de Fourier ; il faut donc trouver un compromis, une transformation qui renseigne sur le contenu fréquentiel tout en préservant la localisation afin d'obtenir une représentation temps/fréquence ou espace/échelle du signal. La première solution qui vient naturellement à l'esprit est de limiter le domaine d'intégration temporel (ou spatial) à l'aide d'une fonction «fenêtre» que l'on pourra faire glisser pour explorer le signal ; on obtient ainsi la transformée de Fourier à fenêtre glissante.

I.2.3 Transformée de Fourier à fenêtre glissante

La transformée de Fourier fenêtrée cherche à rendre locale l'analyse de Fourier en s'aidant de fenêtres. Une fenêtre est une fonction régulière, lentement variable et bien localisée. Cette fenêtre est donc nulle en dehors d'une certaine zone que l'on appelle son support. En multipliant la fonction étudiée par une fenêtre, on obtient une version locale dont on peut déterminer le contenu par une analyse de Fourier classique. On renouvelle alors l'opération en

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 17

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

déplaçant la fenêtre d'analyse. L'ensemble de ces transformées de Fourier localisées forme la transformée de Gabor du signal. On obtient donc une analyse du signal à la fois en temps et en fréquence. Les coefficients de cette transformée qui dépendront donc des deux paramètres que sont la fréquence ë _?et la position de la fenêtre b sont donnés par l'équation.

Wf (ë,b) = ~ ~(*) co(* -- b)e^-2ti'^l/d* '

où la fonction w est la fenêtre choisie pour analyser le signal.

Le principe de cette transformée s'exprime dans la figure ci-dessous :

Il consiste à observer le signal par intervalles de durée 250ms où on suppose le signal comme stationnaire et on fait une étude globale de cette portion par la TF permettant d'en déduire les 4 fréquences qui le composent et surtout leur cadence temporelle.

Inconvénients de la Transformée de Fourier fenêtrée

· Taille fixe de la fenêtre

On peut cependant noter que c'est un inconvénient majeur de la méthode de Gabor. En effet, la fenêtre est de longueur fixe, ce qui est un handicap important lorsqu'on veut traiter des signaux dont les variations peuvent avoir des ordres de grandeur très variables. En particulier, l'attaque d'une note de musique est une phase siège de hautes fréquences. Bien qu'étant très brève, cette phase est caractéristique de l'instrument et de l'interprétation. Elle est donc tout aussi importante que la phase de maintien de la note qui contient en général des fréquences plus basses. Ce pendant, le fait de garder constante la taille de la fenêtre d'analyse implique un sérieux

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 18

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

compromis. Avec une fenêtre étroite, on localise plutôt bien les composantes transitoires de hautes fréquences mais on devient alors aveugle aux composantes de longue durée, donc de basse fréquence, car la période du phénomène observé est trop grande pour rentrer dans une petite fenêtre. A l'inverse, quand une fenêtre est trop large, on ne peut préciser l'instant où se produit un changement brutal dans le signal (pic ou discontinuité) : cette information est noyée dans la totalité de l'information correspondant à l'intervalle de temps sélectionné par la fenêtre. Ce compromis peut être relié au principe d'incertitude d'Heisenberg concernant la dualité onde-corpuscule. Dans son papier « Uncertainty paper » (1927), Heisenberg écrit qu'une particule élémentaire n'a simultanément une position et une quantité de mouvement précise. Cet énoncé, rapporté au domaine du traitement du signal, signifie qu'un signal n'a pas simultanément une localisation précise en temps et en fréquence.

L'analyse par gaborettes a pour objet de déployer le signal dans le plan temps-fréquence. Cela résout le problème de la dictée musicale (qui consiste à écrire la partition en entendant la musique), mais toutes les notes ont alors la même durée puisque la taille de la fenêtre reste constante.

Nous venons donc de voire que garder constante la taille de la fenêtre durant l'analyse d'un signal ne nous donnait pas la totalité des informations : il faut faire un choix entre la localisation des hautes fréquences ou la localisation des basses fréquences. Il a donc fallu trouver un outil induisant une méthode de reconstruction qui soit indépendante de l'échelle d'analyse. Ce nouvel outil s'appelle les ondelettes.

II. L'ANALYSE PAR ONDELETTES

Introduction

En 1983, Morlet en travaillant sur l'analyse de signaux sismiques s'est retrouvé confronté à la Rigidité imposée par la taille fixe de la fenêtre de la transformée de Fourier à fenêtre glissante. Il décide alors d'utiliser une fenêtre de taille dilatée ou contractée selon les besoins. L'idée des ondelettes était née.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 19

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Principe

L'idée de l'ondelette est de pouvoir faire varier les largeurs en temps et en fréquences d'une fonction tout en la translatant le long du signal comme dans la transformée de Fourier fenêtrée. Pour rappel, le but de l'analyse à fenêtres est de pouvoir analyser localement les propriétés spectrales d'un signal. La transformée en ondelette d'une fonction f en un point (t ;ù) du plan temps-fréquences ne dépend donc que des valeurs de f(t) et f(ù) dans le rectangle de Heisenberg centré en (t ;ù). L'avantage de faire varier ces largeurs devient alors évident : on minimise le nombre de translations en temps et en fréquences de la fenêtre en optimisant la largeur de celle-ci. Ainsi dans les basses fréquences, une grande largeur en fréquences n'est pas nécessaire, on peut donc utiliser des rectangles plus larges en temps. Aux hautes fréquences, on va utiliser des rectangles plus larges en fréquences et plus localisés en temps. On peut voir cela comme une adaptation de l'ondelette à l'échelle qu'on lui impose : plus la fenêtre est petite dans le temps, plus l'ondelette va être compressée et osciller rapidement. Le contraire se produira lorsque la fenêtre est dilatée. Ainsi, les petites et grandes fenêtres enregistreront respectivement les variations rapides et moyennes du signal.

La transformée

Une ondelette mère 1)b est une fonction de base que l'on va translater et dilater pour recouvrir le plan temps-fréquences et analyser le signal. L'ondelette doit être une fonction de moyenne nulle ; en d'autres termes, ø doit être une onde ! Ce qui s'écrit mathématiquement :

>

+8 1)b(t)dt = 0 ,8

C'est la condition d'amissibilité. Elle doit vérifier aussi une autre condition celle de régularité qui consiste à faire décroître la transformée en ondelettes le plus rapidement possible à mesure que l'échelle décroît.

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Figure 4 Quelques exemples d'ondelettes : Morlet, Daubechies et Meyer

Il est à noter qu'il existe de nombreuses ondelettes. Certaines ont des formules mathématiques explicites alors que d'autres sont construites à partir de propriétés mathématiques plus complexes. Chaque famille d'ondelettes générée par une ondelette appelée ondelette mère possède les qualités bien spécifiques, comme par exemple :

> La symétrie : utile pour éviter le déphasage,

> Le nombre de moments nuls : c'est-à-dire le nombre d'oscillations ; utile pour la compression,

> La régularité : utile pour obtenir des signaux reconstruits lisses et réguliers

Le logiciel MATLAB grâce à ses fonctions wavenames et waveinfo présente une variété d'ondelettes et leurs caractéristiques. Le tableau ci-après présente quelques ondelettes les plus couramment utilisées.

	Haar	Daubechies	Meyer	Gaussian
Orthogonal	yes	yes	yes	no
Biorthogonal	yes	yes	yes	no
Compact Support	yes	yes	no	no
DWT	possible	possible	possible but without FWT FIR based approximation provides FWT	no
CWT	possible	possible	Possible	possible
Support width	1	2N-1	infinite	infinite
Filters length	2	2N
Regularity	Not continuous	about 0.2 N for large N	indefinitely derivable

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 20

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

Symmetry	yes	far from	yes	yes
Number of vanishing moments for psi	I	N
Effective support	[0 I]		[-8 81	[-5 51

Tableau 1 Tableau de comparaison de quelques ondelettes les plus courantes

A partir de l'ondelette mère =, on introduit alors les facteurs de translation u et d'échelle s :

=@,B (t) = ~v@ø (/,@

B ) qui est la famille d'ondelettes liée à =,

La transformée en ondelette d'une fonction f continue s'écrit donc comme décomposition en

01 01

fonctions ø@,B de f : E#, F ~ ~ ,1 ~~*~ =^Gu,s(t) 2* = ~ ~~*~ ~ =G~^/,H ~ 2*

^,1 vB B

On se déplace sur le plan temps-fréquence en faisant varier s et u. La valeur que l'on obtient est alors la décomposition spectrale locale de f. L'énergie de =@,B est concentrée autour de u sur une largeur s ó_J ou K_/ est la largeur du rectangle de l'ondelette mère. On peut évaluer aussi la transformée de Fourrier =@,B , pour voir la localisation et la largeur du rectangle en fréquences.

1

u,s(ù) = f ₊₁ =_u,s(t)+^,78/ 2*

= vB ~ f =^/,H

01 +,78/ 2* or

,1 ^B

Fø^L~F;~ ~ ~ =

,1 ~ /

01 B )+,78/ 2* donc, en posant t' = t - u, on obtient :

ø^Lu,s(ù) = vB ~ ~ =^/M

01 B~+,78~/M0H~ 2*N
^,1

= vB1 ~f =~^/M

01 B ~ +,78/M _2*N~ ₊^,78H
^,1

vB ~ ø

(sù)e,QRS

=

L

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 21

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 22

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

On voit donc que ø^Lu,s est obtenu en dilatant øL

par ~ . Donc l'énergie de ø^Lu,s est concentrée B

autour d'une fréquence centrale sur un intervalle proportionnel à ¹. En conclusion, les

B

rectangles de Heisenberg sont, dans l'analyse par ondelette, de largueur temporelle s a_t et de

largeur fréquentielle ¹ a_w , ou a_t et óT correspondent respectivement aux largeurs du rectangle

B

de Heisenberg de l'ondelette Mère.

Figure 5 Atome de la Wavelet Transform

Il est à noter que la transformée inverse se déduit facilement :

01 01

fC*~ = > > UE~~#, F~V=H,B ~*~ 2# 2F

^,1 ^,1

Avantages

Le fait que la transformée utilise des fonctions bien localisées dans le plan temps-fréquence lui donne beaucoup d'avantages :

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 23

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

> La résolution en fréquence de la transformée dépend du facteur de dilatation s par le principe d'Heisenberg, on peut donc choisir arbitrairement celle-ci suivant ce que l'on désire analyser.

> Pour des signaux physiques présentant des variations très rapides, des sauts, des marches, bref des discontinuités ; l'analyse en ondelettes est adaptée car l'ondelette va détecter ces variations et analyser celles-ci. Cette particularité rend l'analyse en ondelettes complémentaire à l'analyse de Fourier. En effet, avec l'analyse de Fourier, les discontinuités d'un signal ne sont pas facilement analysables, car les coefficients des fréquences correspondantes sont étalés dans toute la transformée.

> La localisation en temps est précieuse pour nombre d'applications. La transformée en ondelettes peut représenter complètement et efficacement un signal quelconque en peu de coefficients.

Inconvénients

> L'inconvénient majeur de la TOC est qu'elle est très redondante et par conséquent très lourde pour une implémentation algorithmique.

Il existe aussi une version discrète de la transformation en ondelettes qui correspond au cas où les paramètres d'échelle et de translation appartiennent à des ensembles discrets. L'on montre que le choix d'une base d'ondelettes discrètes Orthogonales produira un effet moins redondant et plus souple pour une implémentation d'un algorithme de calcul rapide (FWT: Fast Wavelet Transform).

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 24

CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR ONDELETTES

CONCLUSION

Nous avons vu comment, de l'analyse de Fourrier, en passant par l'analyse de Gabor, nous sommes aboutis à l'analyse par ondelettes. La transformée de Fourrier malgré ses inconvénients a connu un succès dans plusieurs domaines d'applications (compression des images à travers la norme JPEG, le débruitage des signaux et plusieurs autres domaines) et, doit son succès à sa capacité à bien décrire un grand nombre de signaux (tous les signaux stationnaires en fait) et à être implantée dans un système réel très efficacement. La transformation en ondelettes, elle aussi, a connu un grand succès qui repose sur le même type d'arguments. Précisons ici que la transformée en ondelettes a une ambition bien plus grande que celle de la transformée de Fourrier car la classe des signaux qu'elle vise à décrire, c'est-à-dire les signaux non stationnaires, est d'une bien plus grande diversité mais demeure dans certains cas moins efficace. Une particularité fondamentale pour classer les ondelettes est leur degré de redondance. La transformée en ondelettes continue est par construction très redondante mais la transformée en ondelettes discrète peut ne pas l'être et l'absence de redondance est même recherchée dans des applications comme la compression d'images.

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

~~~~~~~~

~~~~~~~~

~~~ :

7ASES D"ONDE5ETTES ORTHOGANA5ES DE HAAR

7 5 5 ~~ ~~~~

5 ~ 5 ~~~~~~~~~~~ ~"~~~ ~~~~~ 68

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 25

Nous avons vu au chapitre précédent qu'il existe plusieurs familles d'ondelettes caractérisées chacune par l'ondelette mère ip(t). Le tableau1 présente les plus courantes et leurs spécificités. Pour évaluer la transformée en ondelettes dans le domaine de la compression d'images fixes, notre choix porte sur l'analyse par ondelettes de Haar.

Le choix de l'ondelette résulte en fait d'un compromis entre son support et son nombre de moments nuls ; plus son support est petit, moins nombreux seront les gros coefficients affectées par une irrégularité d'un signal. D'un autre côté, prendre une ondelette avec beaucoup de moments nuls permet d'avoir des coefficients de petites échelles sur les parties régulières du signal. Or favoriser l'une de ses propriétés se fait au détriment de l'autre.

INTRODUCTION

Dans ce chapitre, nous nous restreignons à l'étude des ondelettes orthogonales qui sont un cas particulier des ondelettes discrètes. Ce type d'ondelettes est extrêmement utile en pratique car les ondelettes orthogonales sont non redondantes (la non redondance est à la fois bénéfique pour la rapidité de calcul de la transformation et pour les performances en terme de taux de compression) et leur inversibilité est assurée. Dans le chapitre précédent nous avons vu qu'il est "facile" de construire une transformation en ondelettes continue puisqu'il il suffit de trouver une fonction de moyenne nulle (l'ondelette mère). Par contre, il est beaucoup plus difficile de trouver des ondelettes orthogonales. Les travaux pionniers dans cette recherche sont ceux de J. Strömberg (1981) et ceux de Y. Meyer (1985). Dans ces travaux, des exemples de bases d'ondelettes orthogonales sont proposées mais aucune méthode générique pour trouver de telles bases n'a alors été proposée. C'est précisément là que l'analyse multirésolution (AMR) entre en scène. L'une des vertus de l'analyse multirésolution est de produire "facilement" des bases d'ondelettes orthogonales. C'est en voulant expliciter le lien entre les algorithmes pyramidaux du traitement d'image et la théorie des ondelettes que Stéphane Mallat a mis au point l'analyse multirésolution. Deux autres vertus de l'AMR est qu'elle est très adaptée à décrire certaines situations physiques telles que celles rencontrées en

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 26

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

traitement d'image où l'information est répartie à des échelles qui peuvent être très différentes, et elle se prête naturellement à une implantation rapide.

I. ANALYSE MULTIRESOLUTION

Soit un ensemble de sous-espaces de L²(R) (l'ensemble des signaux à énergie finie) tel que : ...c V2 c V1 c V0c V-1c...c _Vj+1 c Vjc...

GGGGGGGG_j = L² (f)

U J Ev Vn ; E` V j = 0

V j E Z , f (x) E Vj = f (2^-1 x) E Vj+1

V k E Z , f (x) E V0 = f ( x -- k) E V0

Ces propriétés définissent une analyse multirésolution sur L²(R).

L'analyse multirésolution a été définie par Mallat. L'idée est de projeter un signal f(t) E L²(R) appartenant à un espace Vj sur un sous-espace _Vj+1 et un sous-espace _Wj+1 dans le but de réduire la résolution de moitié. Le schéma est donné en figure ci-dessous. Il existe donc deux opérateurs de projection Aj et Dj qui projettent respectivement le signal f(t) sur _Vj+1 ^et Wj+1. Vj+1 est le sous-espace d'approximation et _Wj+1 le sous-espace de détails. On peut démontrer qu'il existe une fonction d'échelle =(t) E L²(R) qui engendre par dilatation et translation une base orthonormée de _Wj+1. Les espaces obtenus ne sont pas quelconques, ils possèdent des propriétés intéressantes. Par construction, les espaces d'approximation _Vj+1 et de détails Wj+1 sont supplémentaires : Vj = Vj+1g Wj+1.

V0

V1		W1
V2	W2

V3 W3

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

Les fonctions de bases dilatées sont données par les relations : (Di_,n(t)=2^-i/2(D(2^-it-n) avec nEZ et yri_,n(t)=2^-i/2yr(2^-it-n) avec nEZ .

On a donc Aif= < f, (Di,n> (Di,n et Dif=?_n < f, yrin > yri,n où < f(t), g(t) > désigne le produit scalaire n de f(t) par g(t) : < f(t), g(t) > = f00 ₀₀₀₀ f(t)g(t)^GGGGGGd_t

Puisque les fonctions utilisées appartiennent toutes à L²(R), on a g(t)^GGGGGG=g(t). On pose

ai,n= < f, (Di,n> ^et di,n= < f, _-th,n >. _ai,n ^et _di,n sont respectivement les coefficients d'approximation et de détails de la transformation en ondelettes de la fonction f.

I.1 APPLICATION DE L'AMR A L'ALGORITHME D'ANALYSE DE HAAR POUR

DECOMPOSITION D'UNE IMAGE

Les ondelettes de Haar

Considérons un signal échantillonné régulièrement sur [0;1] en 2^P points, on note ces points

xk =	z On associe à cet échantillon une fonction f définie par f (x)= (fk si x E [xk; xk+1[ k 0 sinon

Quand cet échantillonnage varie, la fonction f décrit l'ensemble E_p des fonctions constantes sur chacun des intervalles, et nulles en dehors de l'intervalle [0,1[. E_p est un sous-espace vectoriel de l'espace vectoriel des fonctions réelles à valeurs réelles. De plus, quand on fait varier p, les espaces E_p sont emboîtés, c'est à dire que E0 c E1 c...c _EP+1 c.... Leur réunion est donc encore un sous-espace vectoriel E de l'espace vectoriel des fonctions réelles à valeurs réelles.

On munit l'espace vectoriel E du produit scalaire définit par : (fIg) = fô f(x)g(x)dx Pour obtenir une base de E_p, il suffit de considérer les fonctions (p_p,kdéfinies par :

(pp,k :l (pp,k(x) = 0 sinon

(pp,k(x) = 1 si x E [xk ; xk+1]

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 27

En effet, par définition même de E_p, toute fonction f de E_p se décompose de façon unique sous la forme. f = _EXp o1 fk(pp,k. Ces fonctions (pp,k peuvent s'écrire sous la forme (pp,k (x) ⁼(p(2pX - K), où (p est définie par (p :

(p(x) = 1 si x E [0;1[

(p(x) = 0 sinon

Cette base est orthogonale, en effet on remarque que ((pp,kI(pp,k^')=⁰ si k ? k' et

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 28

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

}vw,l~vw,l^'= m ~ et. Il s'ensuit que la base des vw,lest orthogonale. Les espaces E_p sont alors

des espaces euclidiens. On considère le supplémentaire orthogonal F_p de E_p dans _Ep+1. Ainsi on a E_p = E1 € F0 € ...€ _Fp-1 pour tout p. Cette décomposition sert à définir la tendance grossière d'un signal E0, et ses détails à des résolutions de plus en plus fines (F0,F1,...).

Algorithme de calcul des coefficients des ondelettes de Haar

L'ondelette mère de Haar est la fonction définie par :

~

1 si x \ p0 ; ~É

Ø(x)=-1 si x \ ~ ;1{

~

0 sinon

A partir de cette fonction, on définit les fonctions Øp,k par Øp,k = Ø(2px-k) De même que dans le paragraphe précédent, }vw,l~øw,l^à = 0 si k ? k' et, }vw,l~øw,l = 0 car f_o^l (2wx - e) ø(2x - k)dx = 0. On en déduit que la famille qui réunit les vw,let ^lesøw,l(0 OE e OE 2w - 1) est une base orthogonale de _Ep+1, donc les Øp,k forment une base orthogonale de l'espace F_p de E_p dans _Ep+1 et on a le résultat fondamental suivant :Pour tout pç 1, la famille ~øw,l~~élé~m0~est une base orthogonale de F_p. De plus, }øw,l~øw,l = ~ 2m. Nous pouvons désormais calculer les coefficients d'ondelettes associés à un signal s_p y E_p. Il

se décompose sous la forme s(p) = ? Fw,lvw,l

m, . Puisque E_p = Ep-1 € Fp-1, s_p se décompose
l^,~

_~mèê _~mèê

en s_p = sp-1+ dp-1 ^avec sp-1 = ? Fw^,~,lvw^,~,l et dp-1 = ? Fw^,~,lvw^,~,l

l l

Pour les mêmes raisons, }vw,l~vw,1,l' = 0 et }vw,l~øw,1,l' = 0 si x ' «2k^N, 2k^N + 1» et

}vw,l~vw,~,l' = m ~ et }vw,l~øw,~,l' ~ m ~,~~ï si x ' «2k^N, 2k^N + 1».

Ceci permet de déterminer facilement la décomposition de s_p y E_p sur la base des vw^,1,l et øw^,1,l. En effet, si s_p = sp-1+ d_p alors l'orthogonalité de la base implique

~mèê ,~

}sw~vw^,~,l = -èê,

~èê et }sw~øw^,~,l = ™èê,

~èê . La décomposition s(p) = ? Fw,lvw,l et les

l^,~

valeurs des produits scalaires donnent alors }sw~vw^,1,l = -,:0-,:ê

~ et

-,:^,-,:ê_'-,:0-,:ê -,:,-,:ê

}v,z~ø^,1,z = 2 , doù s^,1,z = 2 et d^,1,z = 2

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 29

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

L'intérêt est que l'on passe d'un échantillon de taille 2^p à un échantillon principal de taille 2p-1 et un échantillon de taille 2^p-1 en utilisant que des sommes ou des différences.

Compression ou Approximation d'un signal 1D selon l'algorithme de Haar

Principe

Si le signal est régulier, les valeurs des échantillons successifs seront proches. Les coefficients de détails issus de la différence de deux valeurs consécutives de l'échantillon seront donc petits. En s'imposant une précision F, on ne gardera que les coefficients d'ondelettes supérieurs en valeur absolue à F.Ceci permet une compression du signal.

Voici l'algorithme utilisé : on reçoit un signal de la forme s(p) = ? Fw,lvw,l

m, , on le
l^,

décompose en s_p = sp-1+ dp-1 et on transforme _dp-1 ^en d^Gp-1, d^Gp-1 = ? ~m^èê,~ dG p-1,køw,1,l avec d^Gp-

l^,~

1,k = dp-1,k si ~d^,l,z~ ç F et dp-1,k = 0 sinon . On recommence ensuite le procédé avec le signal sp-1.

87.015% de coef à zéro

70.736% de coef à zéro

Figure 6 Compression d'un signal 1D sous MATLAB selon l'algorithme de Haar

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 30

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

Décomposition et approximation d'une image selon l'algorithme de Haar Présentation de l'algorithme

Une image en noir et blanc peut être considérée comme un ensemble de pixels, chaque pixel représentant un niveau de gris. On peut modéliser cette image par une matrice carré de taille égale à la résolution de l'image. Pour une image en couleur, il suffit de considérer trois images, chacune représentant le niveau de rouge, de vert et de bleu de l'image originale.

Pour mettre en application la méthode de Haar on pourrait considérer la matrice comme un échantillonnage en mettant ses lignes bout à bout. Cependant on perd le lien avec les colonnes. Il est donc plus efficace d'appliquer l'algorithme de Haar aux lignes de la matrice puis à ses colonnes. Cet algorithme de différentiation-sommation se traduit par la multiplication matricielle à l'aide d'une matrice contenant beaucoup de 0.

La décomposition d'un signal 2D tel qu'une image selon l'AMR ce présente comme suit :

Figure 7 Analyse Multirésolution

CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR : APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE

Figure 8 Décomposition et approximation de l'image de lenna sous MATLAB selon Haar

CONCLUSION

L'utilisation des ondelettes de Haar permet donc de nombreuses applications au niveau de la compression d'images et de signaux. D'autres familles d'ondelettes sont utilisées actuellement, elles offrent de meilleurs résultats de compression. Elles sont suffisantes pour comprendre le principe de compression par ondelettes. L'algorithme que nous avons utilisé est plus performant que le standard JPEG, qui compresse la taille d'une image par 20 en moyenne alors que la méthode par ondelettes compresse en moyenne par 50 : cas du JPEG 2000

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 31

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

~~~~~~~~

~~~~~~~~ IV ~~~~~~~~~~~

~~~~~~~~ ~~~~~ ~"~~

~"~~ ~5

~IGNA5 EN 5

5

5

~~~~~~~~ ~~~~~ 68,

~"~~~~~~

~ 5 ~~~~~~~~~~~ ~"~~~~~~

⁶⁸

INTRODUCTION

Depuis leur introduction au début des années 1980, les ondelettes ont fait l'objet de beaucoup d'attention dans des domaines aussi diversifiés que le débruitage, la compression, la détection des discontinuités et des pics, l'imagerie médicale ou satellitaire . . . Elles y ont démontré leur force, mais les ondelettes séparables sont isotropes et ne peuvent donc pas capturer, par exemple, la régularité d'un contour dans une image. Ceci est du au fait que les ondelettes sont des outils adaptés à la description des discontinuités de signaux mono dimensionnels et que cette propriété n'est plus vraie pour des dimensions supérieures. En particulier, l'orthogonalité de la décomposition et l'échantillonnage critique font apparaitre des effets d'aliasing visibles autour des contours. De plus, le nombre d'orientations est limité et fixe, et les contours sont redondants d'un niveau de résolution à un autre, ce qui requiert un grand nombre de coefficients d'ondelettes pour les représenter.

Afin de pallier à ce problème, de nouvelles décompositions multi-résolutions mieux adaptées à la représentation de tels signaux ont été introduites. Nous présenterons dans ce chapitre la description de l'une d'entre elle qu'est la transformée en Curvelets en vue d'une compression d'images fixes.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 32

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 33

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

I. LA TRANSFORMEE EN CURVELETS

Dans le domaine du discret et en particulier pour le cas des images, on peut considérer que de manière locale, on trouve des contours rectilignes. C'est ce qui conduit à la création de la transformée en Curvelets. Cette transformée est obtenue en deux grandes étapes. Tout d'abord on partitionne l'image en carrés de tailles variables avec recouvrement pour éviter les effets de bord. Ces carrés sont obtenus grâce à une fenêtre de Fourrier à support fini. Au sein de ces carrés on applique une transformée en Ridgelets discrète avec une dilatation de la fonction d'onde de 1/a². Les contours non capturés par l'analyse en ondelettes séparables se retrouvent dans les sous-bandes de détails. Un partitionnement suffisamment fin des sous-bandes permet alors d'obtenir des blocs où ces contours forment des lignes droites et sont donc adaptés à l'analyse en Ridgelets. La transformée en Curvelets est inversible mais redondante car l'analyse en Ridgelets discrète sous-jacente est réalisée au moyen d'une FFT2 du plan polaire, nécessitant plus de points que ceux disponibles dans la grille rectangulaire. Le choix d'utilisation de la FFT provient essentiellement du théorème de la projection de Fourrier (Fourier Slice Theorem). En effet, celui-ci indique que la transformée de Radon peut être obtenue en appliquant une transformée de Fourier inverse 1-D le long des lignes radiales passant par l'origine dans le domaine de Fourier 2-D de l'image.

Toutes ces étapes sont illustrées sur la figure suivante :

Figure 9 Schéma de construction de la transformée en Curvelets d'une image

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 34

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

I.1 TRANSFORMEE EN CURVELETS DICRETES

Nous allons aborder le fonctionnement de la transformée en Curvelets de façon plus détaillée que le point de vue présenté ci-dessus.

Dans le domaine continu, et donc dans notre cas si l'on travaille dans R², il faut considérer deux fenêtres pour décrire les Curvelets. La première fenêtre est une fenêtre radiale W(r), la seconde est une fenêtre angulaire avec les coordonnées polaires r et t dans le plan fréquentiel. Ces fenêtres sont des fonctions régulières à valeurs réelles strictement positives. Les ensembles de départs de ces fonctions sont respectivement r y [1/2,2] pour W et t y [-1,1] pour V. Ces fenêtres doivent toujours respecter les conditions d'admissibilité suivantes :

?01 E -,1 (2-$) = 1 ,$ \ p oeù, 2 {

?01 Y ú~,1 ~*~·~~1,*\ ~ ~ ~ , ~ ~ É ;

Nous pouvons alors définir une fenêtre fréquentielle Uj pour tout j ç j0 dans le domaine de Fourier.

-($,) = 2,

cents£ EU2^,-$VY~^~£/: ~~ )

qui dépend à la fois de l'échelle et de la direction. En rendant symétrique l'Erreur : source de la référence non trouvée afin de couvrir toutes les orientations possibles, C'est-à-dire Uj(r,?)+Uj(r,?+%), on obtient des valeurs réelles de Curvelets. Ces bases posées, il faut transférer ces différents résultats dans le domaine du discret. Le problème est que la fenêtre Uj fournit une analyse fréquentielle régulière le long de la couronne dyadique 2- OE $ OE 2-⁰¹ et de l'angle - %. 2,-/2 OE OE %.2^,-/² et que cela s'adapte difficilement sur les grilles Cartésiennes. Candès et al. proposent donc une nouvelle formulation de la couronne basée non pas sur des cercles comme sur la Figure (a) mais sur des carrés concentriques et des cisaillements comme sur la Figure (b). Dans cette nouvelle formulation l'analogue Cartésien de la famille ( E- )-«o telle que

E-(;) = E(2,-;) serait une fenêtre de la forme E#172; b(;) = v-0

~ ~;~ -- v-(;), b ç 0 où

v est définie par le produit de deux fenêtres passe-bas mono-dimensionnelles.

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

Ceci nous permet de séparer les échelles dans le domaine Cartésien ; il nous reste alors à étudier le cas de la séparation angulaire. En supposant que la fenêtre V respecte la condition d'admissibilité de l'Erreur : source de la référence non trouvée, on peut poser :

£

Y-(;) = Y(²

:8:) La fenêtre Cartésienne recherchée sera alors :

8_ê

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 35

®

(;) = E®

(;)Y-(;)

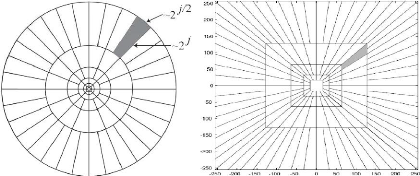
(a) Pavage du plan fréquentiel (b) Pavage du plan fréquentiel

dans le domaine continu dans le domaine discret

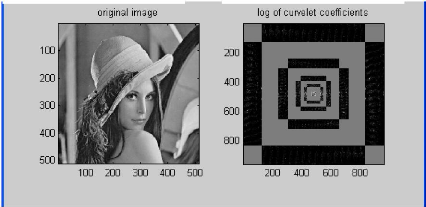
Figure 10 Pavage du plan fréquentiel de l'image de Lenna sous MATLAB dans le

domaine discret

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 36

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

I.2 COMPRESSION D'UNE IMAGE SOUS MATLAB SELON L'ALGORITHME FCDT

L'idée est de déterminer les coefficients de décomposition de l'image en curvelets en utilisant le script FCDT_usfft_matlab de la boîte à outils Curvelab développée récemment par l'université Stanford, leur appliquer un seuillage dont le coefficient dépend du taux de compression espéré. Nous avons à cet effet développé une interface ergonomie d'appréciation des résultats.

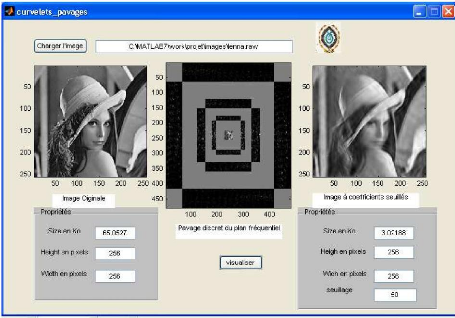
Figure 11 Décomposition et approximation d'une image par pavage du plan fréquentiel

dans le domaine discret sous MATLAB

CHAPITRE V : IMPLEMENTATION ET EVALUATION EXPERIMENTALE

CHAPITRE V: IMPLEMENTATION ET EVALUATION EXPERIMENTALE Introduction

Nous allons dans ce chapitre présenter à travers une plate forme développée sous MATLAB permettant de charger quatre images prises au hasard et compressées par ondelettes puis par curvelets les résultats d'une évaluation comparative en s'appuyant sur les critères de performances tels que le taux de compression, la distorsion et la rapidité de compression.

I MESURES DE PERFORMANCE DE LA COMPRESSION D'UNE IMAGE

I.1 TAUX DE COMPRESSION

Ce critère est très important puisqu'il dépend directement de la technique de compression

utilisée et peut être représenté soit comme une formule °#177; = 23 où u~ est la taille de l'image

2_'

originale et u la taille de l'image compressée, soit comme le nombre moyen de bits par pixels

(bpp) ou encore par le ratio ·²

2') :1 avec E la fonction partie entière.

I.2 MESURES DE DISTORSION

Deux techniques sont utilisées pour évaluer la distorsion : subjective et objective

> Les méthodes subjectives, nécessitent des tests psychovisuels de l'oeil humain. Les tests sont réalisés à plusieurs échelles avec des groupes de personnes.

> Les méthodes objectives, s'agissant de définir des quantités permettant d'évaluer numériquement la qualité de l'image reconstruite.

La distorsion (D) est l'erreur introduite par l'opération de compression, due au fait qu'éventuellement l'image reconstruite n'est pas exactement identique à l'image originale. La mesure de distorsion utilisée généralement en compression d'image, est l'erreur quadratique moyenne MSE (Mean Square Error). Cette grandeur est définie par la moyenne des écarts au carré entre le pixel I(m,n) de l'image originale et le pixel u¹(m ,n) de l'image reconstruite

~ 1/4, comme suit : °»· ~ 1/4.1/2 ? ? 1/2, pu3/4, j ~ u3/4, j{ 6 ~~~

~

. Une autre mesure répandue dans

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 37

ce but est peak signal noise ratio (PSNR) défini par À»Áf = 20·"i10(ÂÄ ÅÆ

v1/4ÇÈ ) avec À7

l'ensemble des pixels constituant l'image originale.

CHAPITRE V : IMPLEMENTATION ET EVALUATION EXPERIMENTALE

I.3 RAPIDITE DE COMPRESSION

Elle définit le temps de calcule de la transformée. Elle est importante pour évaluer la technique de compression dans les applications en temps réel.

II. PRESENTATION DES RESULTATS OBTENUS

Le résultat de mesures de performances de compression par ondelettes et par curvelets est présent sur l'image ci-dessous.

Figure 12 Interface dynamique présentant les résultats de mesures de performances de compression de quatre images par ondelettes et curvelets.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 38

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 39

CHAPITRE V : IMPLEMENTATION ET EVALUATION EXPERIMENTALE

Interprétation et Conclusion

Dans ce chapitre, il était question de présenter les résultats du dernier point des travaux à réaliser comme défini dans le cahier des charges qui consiste à charger quatre images prises au hasard et leur appliquer tout abord une compression par ondelettes puis par curvelets et comparer les résultats. Pour cela, nous nous sommes appuyés sur quelques critères : le taux de compression exprimé en ratio, le temps d'exécution exprimé en seconde(s), l'erreur quadratique moyenne sans unité mesurant la distorsion entre l'image originale et celle compressée (troisième colonne) et enfin dans la dernière colonne le Peak signal noise ratio PSRN exprimé en db renseignant également sur la distorsion de l'image et généralement utilisé par les développeurs pour apprécier la qualité de compression. Pour comparer les résultats, nous avons ainsi procédé : Pour chaque image et pour chaque transformée, grâce à l'outil slider de MATLAB, nous avons fixé une valeur seuil qui, par un seuillage dur devra fournir pour les deux transformées un taux de compression identique. Les résultats obtenus sont celles observées sur la figure 12 montrant que

· Ondelette est en moyenne vingt fois plus rapide que curvelets dans la compression d'une image et semble mieux adaptée pour les applications en temps réel.

· Les mesures de distorsion sont fonctions de l'image compressée et ne renseignement pas toujours directement sur la qualité visuelle de l'image mais sur la corrélation entre l'image originale et celle compressée, néanmoins les résultats sont flagrants et montrent que pour un même taux de compression le PSNR est plus élévé pour une compression suivant curvelets que celle suivant ondelettes.

· Une évaluation statistique basée sur une analyse psycho-visuelle montre que la compression par curvelets fourni un taux moyen de compression plus élevée que celle par ondelettes.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page a

BIBLIOGRAPHIE

CONCLUSION GENERALE

Le projet de fin d'études intitulé «Compression d'images fixes : comparaison de la méthode de curvelets et celle par ondelettes » proposé par M. DJIMELI Alain et Dr. TCHIOTSOP Daniel est celui auquel nous avons accordé un crédit intellectuel dont l'atteinte des objectifs était conditionnée par le respect fidèle des prescriptions qui nous ont été soumises à travers le cahier des charges consistant dans un premier temps à présenter une revue des différentes méthodes de compression d'image où nous avons à travers le chapitre I présenté pour chaque classe de compression sans et avec perte les méthodes qu'y sont rattachées, dans un second temps à faire une étude théorique de la décomposition en ondelettes et ressortir les avantages par rapport à la décomposition de Fourrier où nous avons à travers le chapitre II retenu que l'analyse par ondelettes est adaptée à une plus grande diversité d'applications et de signaux à l'instar des signaux stationnaires mais que l'analyse de Fourrier reste une alternative parfois plus satisfaisante, dans un troisième temps à faire une étude théorique de la décomposition en curvelets et trouver les avantages par rapport à la décomposition en ondelettes, où il ressortait du chapitre IV que les ondelettes séparables sont isotropes et ne peuvent donc pas capturer, par exemple, la régularité d'un contour dans une image et le nombre d'orientations est limité et fixe, les contours sont redondants d'un niveau de résolution à un autre, dans un quatrième temps se familiariser avec la boîte à ondelette et de curvelets de Matlab (l'installer si elle n'existe pas, faire une décomposition d'image, manipuler les coefficients ...), ce qui a été fait et s'exprime à travers les figures 8, 10 et 12 et enfin quatre images de test choisies au hasard doivent être compressées par les ondelettes en premier et par les curvelets avant de pouvoir faire une comparaison , où nous avons développé sous Matlab une plate forme dynamique présentant les critères d'appui de comparaisons tels que le taux de compression, la durée de compression, le PSNR et le MSE et donc les résultats et leurs interprétations sont présentés au chapitre V.

Au terme de ce projet, retenons que malgré les réussites des divers étapes indispensables à la réalisation de ce rapport nous avons concentré un maximum d'énergie pour surmonter certaines difficultés telles que tout d'abord le concept d'Analyse Multiresolution, ensuite la modélisation d'une décomposition en ondelettes en bancs de filtres numériques favorisant ainsi sa gestion algorithmique à l'instar de celui de haar et enfin la conception modulaire de la plate forme dynamique pour l'appréciation des résultats.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page b

BIBLIOGRAPHIE

BIBLIOGRAPHIE

TRAVAUX UNIVERSITAIRES

[11 P. Legai. Impact de l'imagerie spatiale commerciale haute résolution sur la sécurité internationale dans sa dimension de défense - Perspectives pour l'Europe de la défense. Thèse de doctorat, Université de Marne La Vallée, Janvier 2003.

[21 C. Lambert Nebout, C. Latry et G. Moury. La compression embarquée d'images pour les systèmes optiques d'observation spatiale. Dans GRETSI '01. 2001.

[3] X. Delaunay, C. Thiebaut et V. Charvillat. Compression embarquée d'images satellites : vers l'exploitation de la géométrie. Dans COmpression et REpresentation des Signaux Audiovisuels, p. 12-17. France Telecom R&D, Caen, France, novembre 2006.

E. J. Candès et D. L. Donoho. Curvelets - a surprisingly effective nonadaptive

representation for obJects with edges. Dans L. S. et al., rédacteur, Curves and Surfaces, p. 105-120. Vanderbilt University Press, Nashville, TN, 2000.

[51

[41

E. Le Pennec. Bandelettes et représentation géométrique des images. Thèse de doctorat,

École Polytechnique, décembre 2002.

[61

CANDÉS (E.), DONOHO (D.), Curvelets : A Surprisingly Effective Nonadaptive Representation of ObJects with Edges, in Schumaker L. L., Cohen A. and Rabut C., Curves and Surfaces fitting, Vanderbilt University Press (1999)

ARTICLES ET REVUES

[71 Brian C. Smith et Lawrence A. Rowe. Algorithms for manipulating compressed images. IEEE Computer Graphics and Applications, pages 34-42, 1993.

[81 M. Rabbani et R. Joshi. An overview of the JPEG2000 still image compression standard. Signal Processing : Image Communication Journal, 17(1), Janvier 2002.

[91 T. A. Welch. A technique for high-performance data compression. Computer Magazine of the Computer Group News of the IEEE Computer Group Society, 17(6), 1984.

LIENS INTERNETS

[101 University of British Columbia et Inc. Image Power. Power JBIG-2 coder. http://spmg. ece.ubc.ca/Jbig2.

[111 R. Victor Klassen. U.s. patent US2001/0016075 A1 : Rotated read-out of JPEG compressed images, aug 2001.