Etude par spectroscopie Raman et modélisation d'une résine composite rtm

IV.3.1.4. Analyse cinétique

Plusieurs modèles sont utilisés pour la description de la cinétique de réaction du système époxy amine. La vitesse de réaction est donnée en général par les équations suivantes :

r =

dt

(3)

da =kf(a)=Aexp(-E RT)f(a)

Où r : Vitesse de réaction,

á : Taux de conversion,

t : Temps,

k : Constante d'Arrhenius k = A exp (-E/RT)

A : Facteur pré-exponentiel,

E : l'Energie d'activation,

R : Constante des gaz,

T : Température absolue.

Chapitre IV Résultats et discussion

Les modèles les plus fréquemment utilisés sont les modèles cinétiques d'ordre n et la combinaison des modèles autocatalytique est d'ordre n sont décrit par les équations suivantes :

da

r= = k ( 1 - )n

a

d

(Modèle d'ordre n) (3)

t

Page 68

da r = = dt

( ^m)( )n k k 1 + 2 1 - a a

(Modèle autocatalytique) (4)

Où k, k₁ et k₂ sont des constantes,

m et n : Ordre de réaction.

Le taux de conversion et la vitesse de réaction sont déterminés directement à partir des thermogrammes de DSC par les relations suivantes :

a	=	DH t		(5)

da 1 dDH t dt D H dt Tot

(6)

Où MH_t : l'enthalpie isotherme au temps t

MHTot : l'enthalpie totale de réticulation obtenue par le test subséquent en dynamique.

Les figures (IV.12), (IV.13) et (IV.14) montrent la variation de la vitesse de réaction obtenues à partir des courbes DSC et des équations précédentes.

Nous remarquons pour les différentes formulations que la vitesse réactionnelle (dá/dt) augmente en général avec la température. Pour toutes les formulations étudiées, nous constatons que le temps au maximum du pic (t_p) diminue avec l'augmentation de la température, alors que la conversion augmente en fonction de la température et du temps.

Chapitre IV Résultats et discussion

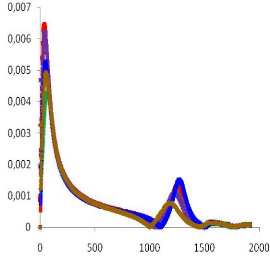
d /dt (1/°C)

Temps (s)

Figure IV.12 : Vitesse de réaction en fonction du temps pour la RTM6 à 100°C

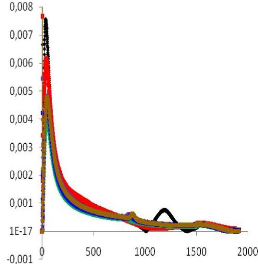
d /dt (1/°C)

Temps (s)

Page 69

Figure IV.13 : Vitesse de réaction en fonction du temps pour la RTM6 à 135°C

Chapitre IV Résultats et discussion

d /dt (1/°C)

Temps (s)

Page 70

Figure IV.14 : Vitesse de réaction en fonction du temps pour la RTM6 à 150°C

Les courbes de la vitesse de réaction en fonction du temps sont ajustées à l'aide de l'équation cinétique (4). Cette équation est modifiée pour tenir compte de l'effet de la diffusion, qui apparaît lorsque la résine passe de l'état caoutchoutique à l'état vitreux.

Dans cette équation modifiée _ámax, le maximum de conversion obtenue à chaque température remplace le nombre 1 dans le membre de droite de l'équation. D'autre part _ámax est calculée à partir des enthalpies de réaction et des enthalpies résiduelles obtenues par DSC. Les variations observées en DSC sont ajustées à l'aide de l'équation de Karkanas et Partridge.

da

dt

k 1 ( 1 - ) ^1+ ^nk ^m 2 ( 1 ) 2 n a a - a

(7)

Le tableau (IV.5), résume les paramètres obtenues par ajustement des données expérimentales à l'aide des équations (4) et (7). Les valeurs des facteurs pré-exponentiels et l'énergie d'activation sont calculées à partir de la température de chauffage qui dépend des constantes k₁ et k₂ en utilisant l'équation d'Arrhenius.

La constante k₁, correspond aux réactions entre la fonction époxy et les groupements amines, catalysées par des impuretés. Quant à k₂, elle correspond aux réactions entre la fonction époxy et les groupements amines, catalysées par les groupements hydroxyles initialement présents et formés durant la réaction de cuisson.

Les valeurs de E₁ et E₂ pour des cuissons des échantillons conventionnellement sont obtenue par Karkanas et Partridge.

L'évaluation des paramètres cinétiques est faite par une méthode analytique de régression des moindres carrés non-linéaire.

Chapitre IV Résultats et discussion

Page 71

Température
de chauffage
(°C)

Equation (4) 100°C 135°C 150°C Equation (7) 100°C 135°C 150°C	k1 (10^-5 s^-1)	k2 (10^-3 s^-1)	m	n	n1	n2
		da = k (	m )( )n k a 1 - a + 2 (4)
		1 dt
	2,21	0,53	0,95	0,59	-	-
	3,52	0,92	1,09	0,66	-	-
	4,30	1,35	1,11	0,79	-	-
	da n ^n k ^m = k1 (1 - ) 1 a + a - a 2 ( 1 ) 2 (7) dt
	2,15	0,51	0,95	-	0,52	0,66
	3,43	0,89	1,07	-	0,58	0,73
	4,11	1,28	1,05	-	0,71	0,86

Tableau IV.5 : Estimation des paramètres cinétiques à partir des modèles cinétiques déterminés par DSC Equation (4) : A₁ = 22420 s^-1 E₁ = 71,l kJ.mol^-1 A₂ = 10256 s^-1 E₂ = 55,65 kJ.mol^-1

Equation (7) : A₁ = 25820 s^-1 E₁ = 73,6 kJ.mol^-1 A₂ = 25460 s^-1 E₂ = 61,84 kJ.mol^-1

Dans cette partie, nous avons étudié la résine RTM6 pure par la DSC, méthode qui nous a permis de déduire le taux de réticulation de la résine pure et de procéder à l'analyse cinétique.

L'étude calorimétrique détaillée de la RTM6 à pour but d'étudier la cinétique de cuisson du système époxy-amine. Plusieurs modèles cinétiques sont utilisés dont le but de décrire le processus de cuisson par DSC. Le taux de réaction des groupes époxydes avec les amines sont déterminés et fités par le modèle cinétique autocatalytique. L'amélioration de ce modèle permet et pour des limitations du phénomène de diffusion entre les valeurs expérimentales et la prédiction du taux de réaction.

En comparant entre les données expérimentaux et le modèle prédit pour le mode dynamique à différentes vitesses de chauffes allant de 1 à 30°C.min^-1 (Figures 2 et 3) et en accord aux premiers stages de réactions mais la divergence apparaît vers la fin de la cuisson. Le modèle initial est modifié en utilisant deux ordres de réactions différents n pour les deux schémas de réactions précédemment mentionnés