|
Ministère de l'Enseignement Supérieur
et de la Recherche Scientifique
Université des Sciences et de la
Technologie d'Oran Mohamed Boudiaf
Faculté des Sciences
Département de Physique
Spécialité : physique
Option : Traitement de Surface et Structure
des Matériaux
Mr : BENDIEMRAD MANSOUR KAMAL
Soutiendra publiquement un
mémoire de Magister intitulé :
|
Réalisation d'un capteur de gaz
|
le : / 11/ 2009
|
Devant le jury composé de :
Président : Saïd HIADSI
Rapporteur : Saad HAMZAOUI Examinateur : Ahmed BELASSRI
Examinateur : Moustafa BOUDERBALA Membre invité : Zoubida BELGHOMARI
|
Professeur Professeur Professeur
Maitre de conférence Maitre assistante
|
U.S.T.O (M.B) U.S.T.O (M.B) U.S.T.O (M.B) U.S.T.O (M.B)
U.S.T.O (M.B)
|

Je tiens à remercier prioritairement le professeur Saad
HAMZAOUI pour m'avoir accueilli au sein du laboratoire de microscopie
électronique et sciences des matériaux (LME&SM),
encadré, orienté, assisté, et guidé sur les travaux
objet de mon mémoire. Les remerciements hors protocolaires s'expriment
loyalement et sincèrement pour ses qualités tant humaines que
scientifiques, qu'il trouve ici l'expression de toute ma gratitude pour avoir
mis à ma disposition tous les moyens disponibles au laboratoire et pour
n'avoir jamais cesser de me prodiguer conseils, assistances et aides.
Je souhaite remercier le professeur S. HIADSI pour avoir bien
voulu me faire l'honneur de présider le jury.
Je tiens également à témoigner ma
reconnaissance à Mr A. BELASSRI et Mr M. BOUDERBALA qui ont
accepté d'être membres du jury, ainsi que Mme Z. BELGHOMARI qui a
bien voulue examiner ce travail et participer au jury.
Mes remerciements s'adressent également à
l'ensemble des personnes que j'ai fréquemment sollicitées dans le
cadre de mon travail.
Enfin je tien à remercier l'ensemble de mes amis et de mes
connaissances pour leur aides et soutien morale, tendant à faciliter mes
tâches.
Merci à tous et toutes.
Résumé
L'objectif de ce travail est la réalisation de capteurs
à gaz à base de couches minces d'oxyde de zinc (ZnO)
dopées et non dopées, avec un mini four intégré
(conçu avec une double couche de nickel plus tungstène) sur un
wafer de Si poly cristallin, afin de contrôler et de réguler
à plus au moins un degré Celsius (1°C) de
précision.
Nous avons obtenu quatre types de capteurs : ZnO pur, ZnO
dopé Al 1% et 3 % et ZnO dopé Cu 1%.
Les mesures électriques effectuées sur ses
capteurs ont montré une grande sensibilité au gaz
d'éthanol pour celui dope Cu (S = 250), une sensibilité
moyenne pour le non dopé (S = 28) et une faible
sensibilité pour le dopé Al (S = 3).
L'état de surface observe par MEB présente une
structure colonnaire pour toutes les

couches avec des tailles de grains observé par DRX
correspondant à de la taille des
colonnes.
L'échantillon dope Cu présente des tailles de
grains et de colonne double de celle des autres.
Cette sensibilité ne peut par consequent pas être
expliquee par l'effet morphologique. L'explication serait dans un effet
catalytique du Cu ?
Mots clés : capteur de gaz MOX, oxyde de zinc, mini-four,
couches minces, sensibilité, détection.

Table des matières
Introduction générale 14

Chapitre I Les capteurs de gaz (chimiques)
Partie 1 : Rappel sur les capteurs de gaz et capteur
à base d'oxyde métallique
(MOX), cas de l'oxyde de Zinc ;
propriétés et application pour la détection des
gaz.
I.1 Introduction 19
I.2 Définition d'un capteur de gaz .. 19
I.3 Principales familles de capteurs 19
I.3.1 Capteur Direct . 21
I.3.1.1 Capteur à transistors à effet de champs
(GASFET ou ChemFET) .. 21
I.3.1.2 Capteur Electrochimique 21
I.3.1.3 Capteur à base d'oxyde métallique .. 22
I.3.2 Capteur Indirect (Complexe) ... 22
I.3.2.1 Capteur à microbalance de quartz 22
I.3.2.2 Capteur à onde acoustique de surface 23
I.3.2.3 Capteur à fibre optique 24
I.4 Caractéristique d'un capteur de gaz . 24
I.4.1 Sensibilité . 24
I.4.2 Sélectivité . 25
I.4.3 Stabilité 25
I.4.4 Température de fonctionnement .. 25
I.4.5 Temps de réponse . 25
I.5 Capteurs de gaz à base d'oxyde métallique (MOX)
26
I.5.1 Matériaux sensibles 26
I.5.2 Structure d'un capteur MOX ... 26
I.5.3 Principe de fonctionnement 27
I.5.3.1 Conductivité du ZnO 27
I.5.3.2 Interaction gaz - solide .. 27
I.5.3.3 Adsorption à la surface d'un oxyde
métallique 28
I.5.3.3.1 Chimisorption dans un semiconducteur 28
I.5.3.4 Mécanisme mise en jeu dans un oxyde
métallique pour la déviation du type
Semiconducteur .. 36
I.5.3.4.1 Mécanisme de la non stoechiométrie a
conductivité n 36
I.5.3.4.2 Mécanisme de la non stoechiométrie a
conductivité p 36
I.5.3.4.3 Effet de la morphologie sur les
propriétés électrique des oxydes
métalliques .. 37
I.5.3.4.4 A propos des joints de grains . 37
I.5.3.4.5 Rôle d'état de surface dans les oxydes
métalliques 38
I.5.3.5 Rôle de l'oxygène et principe de
détection 39
I.6 L'oxyde de zinc (ZnO) .. 41
I.6.1 Propriété de l'oxyde de zinc (ZnO) . 41
I.6.2 Structure cristalline du ZnO 41
I.6.3 Structure Electronique du ZnO 43
I.6.4 Propriété électrique de l'oxyde de
zinc 44

Partie 2 : Phénomène de chauffage dans
une couche mince métallique et transfert
de chaleur.

I.7 Introduction 47
I.8 Propriétés générales des
matériaux métalliques on couche mince à usage
thermique 47
I.9 Conductivité électrique dans une couche mince
métallique . 48
I.10 Dissipation de la chaleur par effet joule dans une couche
mince métallique 50
I.11 Phénomène de transfert de chaleur . 53
I.11.1 Phénomène de diffusion de la chaleur :
métal/isolant 54

Chapitre II Procédure expérimentale et
Techniques de caractérisation
Partie 1 : Réalisation du capteur de gaz et
process

II.1 Introduction . 58
II.2 Généralité sur les méthodes de
dépôt de couches minces 58
II.2.1 les méthodes de dépôts physiques
58
II.2.1.1 Dépôt par évaporation 59
II.2.1.2 Evaporation par effet Joule 59
II.2.1.3 Evaporation par bombardement électronique 59
II.2.1.4 Evaporation par un faisceau Laser 60
II.2.1.5 Dépôt par pulvérisation cathodique
.. 61
II.2.1.5.1 Pulvérisation DC (direct curent) 61
II.2.1.5.2 Pulvérisation RF (radio
fréquence) 62
II.2.1.5.3 Pulvérisation à magnétron 62
II.2.2 les méthodes de dépôt chimique 63
II.2.2.1 Dépôt en phase vapeur chimique (CVD) ..
63
II.3 Aspect physique de l'oxydation thermique du silicium ..
65
II.4 Procédure expérimentale . 69
II.4.1 Préparation des plaquettes de silicium
polycristallin . 69
II.4.1.1 Nettoyage .. 70
II.4.1.2 oxydation thermique des plaquettes de Si
(polycristallin) 70
II.4.1.3 découpage des plaquettes de Si (polycristallin)
71
II.4.2 Réalisation du capteur de gaz 71
II.4.2.1 Description du montage expérimentale 71
II.4.2.2 Conception du four intégré 72
II.4.2.2.1 Dépôt de couche mince de Nickel .. 72
II.4.2.2.2 Dépôt de couche mince de Tungstène
73
II.4.2.2.3 Dépôt de couche mince diélectrique
73
II.4.2.3 Réalisation de couches minces d'oxyde de zinc non
dopée et dopée 74
II.4.2.3.1 Dépôt de ZnO non dopé et
dopé 74

Partie 2 : caractérisation du capteur de gaz

II.5 Introduction .. 77
II.6 caractérisation structurelle et morphologique ..
77
II.6.1 Diffraction des rayons X 77
II.6.2 Caractérisation morphologique des
échantillons par microscope électronique à
balayage (MEB) . 78
II.7 caractérisation électrique . 79
II.7.1 Méthode de la pointe chaude pour la
détermination du type de conductivité dans
un semiconducteur .. 79
II.7.2 Mesure de l'épaisseur des couches minces
métalliques par la méthode des quatre pointes . 81
II.8 Banc
d'essai et de mesure de la réponse du capteur au gaz
d'éthanol 84
II.8.1 Gaz utilisé .. 84
II.8.2 Concentration du gaz débité dans le
dispositif de détection 84
II.8.3 Banc de caractérisation électrique du
capteur de gaz 86

Chapitre III Résultats expérimentaux et
discussion

89
89
89
III.1 Introduction
III.2 Dimension du capteur de gaz obtenu
III.2.1 Mesures d'épaisseur et de résistance des
couches minces métalliques
III.2.2 mesure d'épaisseur des
couches minces d'oxyde de silicium formé par
90
90 92 94 97
oxydation thermique
III.2.3 Mesure d'épaisseur des couches minces d'oxyde de
zinc non dopé et dopé
III.3 Mesure thermique effectué sur le mini four du
capteur .
III.3.1 Relation résistance épaisseur de couches
.
III.4 Type de conductivité dans l'oxyde zinc non
dopé et dopé .
97
III.5 Résultat des caractérisations structurelles
et morphologiques des oxydes de zinc (ZnO) et oxyde de silicium (SiO2)
.
III.5.1 Diagramme de diffraction de rayon X des couches minces de ZnO non
dopé et
97
99
99
100 103 103 103 103 118
dopé
III.5.1.1 Taille des grains
III.5.2 Morphologie des surfaces obtenues sur le SiO2
III.5.3 Morphologie de surfaces obtenues sur le ZnO non
dopé et dopé
III.6 Etude de la réponse du capteur envers le gaz
d'éthanol .
III.6.1 système de barbotage
III.6.2 Etape de la détection .
III.6.3 Protocole de la manipulation
III.6.3.1 Mesure de sensibilité des capteurs CG1, CG2, CG3
et CG4 ..

127
131

Annexe
Références bibliographiques

Figure I.1. Dispositif Direct .. 20
Figure I.2. Dispositif complexe 20
Figure I.3. Schéma d'un capteur de gaz de
type GASFET ... 21
Figure I.4. Capteur Electrochimique à
électrode .. 22
Figure I.5. Structure d'un capteur à
ondes acoustiques de surface 23
Figure I.6. Capteur de gaz à fibre
optique 24
Figure I.7. Structure d'un microcapteur MOX
développé par la société Microsens. ..
26
Figure I.8. Diagramme d'énergie d'un
semiconducteur type n et d'un adsorbat
avant la chimisorption 29
Figure I.9. Schéma du champ
électrique à l'intérieur de la Z.C.E 30
Figure I.10. Schéma de l'énergie
potentiel à l'intérieur de la Z.C.E 32
Figure I.11. Diagramme de bande
énergétique pour la chimisorption d'un
semiconducteur type (n) . 32
Figure I.12. Schéma du champ
électrique à l'intérieur de la Z.C.E .. 34
Figure I.13. Schéma de l'énergie
potentiel à l'intérieur de la Z.C.E 35
Figure I.14.
Diagramme de bande énergétique pour la chimisorption
d'un
semiconducteur type (p) . 35
Figure I.15. Représentation d'une
schématique de joint de grain 38
Figure I.16. Différentes structures de
l'oxyde de zinc .. 42
Figure I.17. Structure de bande de
ZnO en utilisant la méthode du pseudo
potentiel .. 43
Figure I.18. Phénomène de la non
stoechiométrie de ZnO 45
Figure I.19. Structure cristalline du nickel et
tungstène 48
Figure I.20. La sphere de Fermi qui englobe les
états occupés dans l'espace k dans l'état
fondamentale du gaz électronique 50
Figure I.21.
L'influence d'une force constante F agissant pendant
l'intervalle de
temps t 50
Figure I.22. Simulation de l'évolution du
temps de chauffage du micro four conçue
en cuivre par rapport à des puissances d'alimentations
différentes . 52
Figure I.23. Diffusion du flux de
chaleur à travers le substrat de silicium et les
différentes couches de SiO2 55
Figure I.24.
Représentation d'une simulation de la diffusion de la chaleur
du micro
four vers les deux régions isolatrice en SiO2 55
Figure II.1. Méthodes
générales de dépôt de couches minces sous vide ..
58
Figure II.2. Schéma de principe d'un
système de chauffage par un faisceau
d'électrons 60
Figure II.3. Schéma conventionnelle de
l'ablation Laser 60
Figure II.4. Schéma de principe de la
pulvérisation cathodique 61
Figure II.5. Système de
pulvérisation DC 62
Figure II.6. Schéma de principe de
dépôt en phase vapeur chimique (CVD) dans un
réacteur à parois chaudes 64
Figure II.7. Représentation de
l'épaisseur de SiO2 et de Si consommé .. 65
Figure II.8. Représentation de
l'oxydation thermique du Si 67
Figure II.9. Schéma de principe du four
servant à l'oxydation de Si . 70
Figure II.10. Les dimensions des substrats de Si
utilisé . 71
Figure II.11. Représentation de la
configuration finale du four . 74
Figure II.12. Configuration finale de notre
capteur de gaz, intégrant à la fois les
éléments chauffants et sensibles aux gaz . 75
Figure II.13. Géométrie de
diffraction (èhkl -2èhkl) et la loi de Bragg . 77
Figure II.14. Pouvoir thermoélectrique en
fonction de la température dans le
silicium n et p 80
Figure II.15. Schéma de principe de
technique de la pointe chaude 81
Figure II.16. Configuration des quatre pointes
alignées 82
Figure II.17. Schéma de principe du
barbotage suivi au LMESM pour contrôlé la variation du
Débit d'éthanol .. 85
Figure II.18. Schéma de principe du
dispositif pour le test du capteur 87
Figure III.1.
Géométrie du capteur de gaz réalisé en
technologie des couches
minces .. 89
Figure III.2. Image MEB de
l'épaisseur de la couche de SiO2 coté face du substrat
de Si, im x 300 .. 90
Figure III.3. Image MEB de l'épaisseur de
la couche de ZnO avec grossissement
de 10k 91
Figure III.4. Image MEB de
l'épaisseur de la couche de ZnO : 3% Al avec
grossissement de 10k 91
Figure III.5. Image
MEB de l'épaisseur de la couche de ZnO : 1% Al avec
grossissement de 10k 91
Figure III.6. Image
MEB de l'épaisseur de la couche de ZnO : 1% Cu avec
grossissement de 10k 91
Figure III.7.
Évolution de la température d'équilibre Tf de la
plaque chauffante en
fonction de la puissance fournie 92
Figure III.8.
Représente la variation de la résistance des couches
minces métallique
en fonction du temps de dépôt . 95
Figure
III.9. Représente le caractère ohmique des plaques
chauffantes des séries S1
et S2 .. 96
Figure III.10. Spectres de
diffraction de rayon X des couches minces de ZnO non
dopé et dopé . 98
Figure III.11.
Image MEB d'une couche de SiO2 formé par pulvérisation
rf, avec
un grossissement de 4k . 100
Figure III.12.
Image MEB d'une couche de SiO2 formé par oxydation thermique
de
Si polycristallin, avec un grossissement de 10k
100
Figure III.13. Image MEB d'une couche de ZnO
dopé Al 1%, avec un
grossissement de 10k 101
Figure III.14.
Image MEB d'une couche de ZnO dopé Al 3%, avec un
grossissement de 10k 101
Figure III.15.
Image MEB d'une couche de ZnO dopé Cu 1%, avec un
grossissement de : 4k (a) et 10k (b) . 101
Figure
III.16. Image MEB d'une couche de ZnO non dopé, avec un
grossissement
de : 4k (a) et 10k (b) . 101
Figure III.17. Ensemble ZnO non dopé SiO2
et Si IM x 340 102
Figure III.18. Représente la
variation de la résistance de trois capteurs (CG1) en
fonction de la température pour une concentration C1= 337
ppm 104
Figure III.19. Représente la variation de
la résistance de capteurs CG1 en fonction
de la température (pour une concentration C1 = 337 ppm) :
(a) échantillons soumis
à un recuit à 500 °C avant exposition au gaz
d'éthanol, (b) échantillon testé directement après
dépôt de la couche sensible . 105
Figure III.20.
Représente la variation de la résistance de capteurs CG1
en fonction
de la température (pour une concentration d'éthanol
C1 = 337 ppm) . 106
Figure III.21. Représente la
variation de la résistance de capteurs CG1 en fonction
de la température (pour une concentration d'éthanol
= 194 ppm) . 107
Figure III.22. Représente la
variation de la résistance de capteurs CG2 en fonction
de la température (pour une concentration d'éthanol
C1 = 337 ppm) . 109
Figure III.23. Représente la
variation de la résistance de capteurs CG2 en fonction
de la température (pour une concentration d'éthanol
= 194 ppm) . 110
Figure III.24. Représente la
variation de la résistance de capteurs CG3 en fonction
de la température (pour une concentration d'éthanol
C1 = 337 ppm) . 112
Figure III.25. Représente la
variation de la résistance de capteurs CG3 en fonction
de la température (pour une concentration d'éthanol
= 194 ppm) . 113
Figure III.26. Représente la
variation de la résistance de capteurs CG4 en fonction
de la température (pour une concentration d'éthanol
C1 = 337 ppm) . 115
Figure III.27. Représente la
variation de la résistance de capteurs CG4 en fonction
de la température (pour une concentration d'éthanol
= 194 ppm) . 116
Figure III.28. Evolution de la
Sensibilité de deux capteurs CG1 : (a) élément sensible
(ZnO non dopé) soumis à un recuit à 500 °C avant
exposition au gaz d'éthanol, (b) élément sensible (ZnO non
dopé) testé directement après dépôt de la
couche sensible, pour une concentration d'éthanol : C1 =
337 ppm 118
Figure III.29. Evolution de la
Sensibilité d'un capteur CG1 durant trois tests, pour
une concentration d'éthanol : (a) C1 = 337 ppm, (b) = 194
ppm 119
Figure III.30. Evolution de la Sensibilité
d'un capteur CG2 durant trois tests, pour
une concentration d'éthanol : (a) C1 = 337 ppm, (b) = 194
ppm 120
Figure III.31. Evolution de la Sensibilité
d'un capteur CG3 durant trois tests, pour
une concentration d'éthanol : (a) C1 = 337 ppm, (b) = 194
ppm 121
Figure III.32. Evolution de la Sensibilité
d'un capteur CG4 durant trois tests, pour
une concentration d'éthanol : (a) C1 = 337 ppm, (b) = 194
ppm 122
Tableau I.1. Classification des capteurs de gaz
selon leur principe de détection 20
Tableau I.2. Propriétés
générales de l'oxyde de zinc en couche mince .. 44
Tableau I.3. Propriétés
générales du Nickel et Tungstène .. 47
Tableau II.1. Propriété
générales des plaquettes de Si utilisés 69
Tableau II.2. Présentation de principales
caractéristiques et performances du
pulvérisateur cathodique radiofréquence RFS 200 ..
72
Tableau II.3. Paramètre de
dépôt de nickel 73
Tableau II.4. Paramètre de
dépôt de Tungstène . 73
Tableau II.5. Paramètre de
dépôt de SiO2 .. 74
Tableau II.6. Paramètre de
dépôt de ZnO pur et dopé 75
Tableau III.1. Mesure des épaisseurs des
couches minces métallique 89
Tableau III.2. Mesure des épaisseurs de
l'oxyde de silicium . 90
Tableau III.3. Mesure des épaisseurs de
l'oxyde de zinc 91
Tableau III.4. Les valeurs des puissances et
des températures de fonctionnement,
sous tension et courant continu
concernant les mesures effectuées sur les
échantillons S1 et S2 93
Tableau III.5. Résultat des mesures de
conductivité .. 97
Tableau III.6. Représente la taille des
grains des films d'oxyde de zinc non dopé et dopé obtenus .
99
Tableau III.7. Représente la taille moyenne des
colonnes des films d'oxyde de zinc
non dopé et dopé obtenus . 102

Le monde dans lequel nous vivons est en transformation
permanente et rapide, dominé par une biodiversité aux
phénomènes physiques prépondérants quant à
la qualité de notre environnement.
Ainsi, les avancées technologiques s'identifient par
des améliorations, des corrections et des ajouts de
procédés et moyens à l'effet de contrôler,
réguler et répondre au mieux à nos besoins quotidiens.
A l'heure actuelle ces transformations sont marquées
principalement par l'élaboration de capteurs qui ne cessent de se
développer, formant une interface entre le monde réel dans lequel
nous vivons et celui des systèmes modernes industriels et
environnementaux [1]. A telle enseigne qu'il nous est
dorénavant possible d'obtenir des informations en temps réel sur
des aspects physiques et chimiques de substance nocives ou
bénéfiques pour notre survie [2].
L'objectif fixer par nos travaux au sein du laboratoire de
microscopie électronique et sciences des matériaux est de
présenter l'état d'avancement de nos recherches dans le domaine
des dispositifs [3, 4, 5].
Pour cela nous avons focalisé notre travail sur le
développement d'une nouvelle méthodologie d'apports
énergétiques, pour la réalisation d'un capteur de gaz
à base de couches minces d'oxyde de zinc (ZnO) dopées (Al «
1% et 3% » et Cu « 1% ») et non dopées, avec un mini four
intégré (conçu avec une double couche de nickel plus
tungstène) sur un wafer de Si poly cristallin, afin de contrôler
et de réguler à plus au moins un demi degré Celsius
(0.5°C) de précision.
Notre mémoire s'articulera autour de trois chapitres. A
ce titre le chapitre un sera scindé en deux volets :
- le premier constituera en un rappel des capteurs de gaz,
ainsi que leurs principes de détections, dont ceux à base d'oxyde
métallique présentement il concernera l'oxyde de zinc (ZnO).
- Le second consacrera le principe de chauffage par effet joule
dans les couches minces
métalliques, ainsi que les
phénomènes de transfert de chaleur dans les corps solides.
Le chapitre deux présentera les démarches
expérimentales entreprises pour la réalisation de notre capteur
de gaz, ainsi que les différentes méthodes de le
caractériser (électriquement, structurellement et
morphologiquement).
Enfin, dans le chapitre trois, nous exposerons l'ensemble des
résultats et performances obtenus, pour le mini four d'une part, et
d'autre part les analyses conséquentes à l'élément
sensible.
Références bibliographiques :
[1] J. FRADEN, Handbook of Modern Sensors
Physics, Designs, and Applications, 3rd Edition Springer, 2004.
[2] Pavel Ripka et Alois Tipek, Modern Sensors
Handbook, 1st edition ISTE, 2007.
[3] M. K Bendimerad, Réalisation d'un
capteur de gaz à base de couches mince d'oxyde de zinc avec un micro
four intégré, Mémoire d'ingéniorat,
Université d'U.S.T.O.M.B, 2007.
[4] Y. BAKHA, Adsorption des gaz sur des
couches d'oxyde de zinc préparées par la technique pyrolyse
spray, Mémoire de magister, Université d'U.S.T.O.M.B, 2007.
[5] D. Cherrad, Élaboration et Etude
technologique des couches minces T.C.O de type « n »et « p
» par micro pipetage et procédé rf, Application : à
la détection des polluants, radiations ultraviolettes, jonction «
pn >>, Mémoire de magister, Université d'U.S.T.O.M.B,
2008.
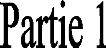

I.1 Introduction
Au titre de cette partie du chapitre (I), nous nous
étalerons sur un bref rappel des capteurs de gaz, déterminerons
les définitions et performances, pour entamer par la suite leur principe
de détection dans ceux à base d'oxyde métallique et dans
notre cas l'oxyde de zinc (ZnO).
I.2 Définition d'un capteur de gaz
Un capteur de gaz est défini comme un composant dont au
moins une de ses propriétés physiques change quand il est soumis
à un changement d'environnement gazeux. D'une manière
générale, un capteur est composé de deux
éléments principaux : l'élément sensible et le
transducteur :
- L'élément sensible est le coeur du capteur,
sur lequel se passe la réaction avec l'espèce gazeuse.
- Le dispositif permettant la conversion du résultat de
la réaction entre le gaz et l'élément sensible en un
signal facilement mesurable (signal électrique, optique ou
acoustique) L1].
I.3 Principales familles de capteurs
Tous les capteurs de gaz peuvent être classés en
fonction de leur principe de détection, basé sur un
phénomène physique ou chimique, ils peuvent êtres aussi
classés par la méthode de mesure effectuée. Pour cela Nous
allons séparer les capteurs de gaz (chimiques) en deux grands groupes
:
- les capteurs de gaz à mesure direct (simple) : ou la
réaction chimique affecte directement une mesurable
caractérisée électriquement par une résistance, un
potentiel, un courant ou bien une capacité (figure I.1).
- les capteurs de gaz à mesure indirecte (complexe) :
ou la réaction chimique n'affecte pas une caractéristique
électrique mesurable directement et on aura besoin de faire appelle
à un transducteur (rôle d'interface) pour convertir le
phénomène détecté en un signal électrique
mesurable (figure I.2) L2].

Capteur
Phénomène
Signal électrique
Figure I.1. Dispositif Direct
[2].

Signal électrique
Phénomène
Capteur
Transducteur
indicateur
Figure I.2. Dispositif complexe
[2].
Basé sur cette classification, le tableau I.1
présente les principaux types de capteurs. Et suit après un
aperçu du principe de détection de quelques types de capteurs.
Tableau I.1. Classification des capteurs de gaz
selon leur principe de détection [1].
|
PRINCIPE
|
GRANDEUR MESUREE
|
EXEMPLE DE CAPTEUR
|
|
Potentiométrique
|
Tension
|
Cellule électrochimique
|
|
Ampérométrique
|
Courant
|
Cellule électrochimique
|
|
capacitif
|
Capacité / charge
|
Capteur d'humidité
|
|
Calorimétrique
|
Température
|
pellistor
|
|
Gravimétrique
|
Masse
|
Capteur à microbalance
|
|
Résonance
|
Fréquence
|
Capteur à onde de surface
|
|
optique
|
Pic d'absorption
|
Détecteur infrarouge
|
|
Résistif
|
résistance
|
Capteur MOX
|
|
Fluorescence
|
Intensité lumineuse
|
Fibre optique
|
I.3.1 Capteur Direct
I.3.1.1 Capteur à transistors à effet de
champs (GASFET ou ChemFET)
Les capteurs de gaz de ce type ont la structure classique d'un
transistor MOS à effet de champs sauf que la grille est remplacée
par un oxyde métallique sensible au gaz. L'interaction de l'oxyde
métallique avec le gaz à détecter se traduit par une
variation de la tension de seuil du transistor [1]. La figure
I.3 présente une structure typique de ce capteur. En gardant les
polarisations drain-source VDS et grille-source VGS
constantes, la nature et la quantité du gaz adsorbé
conduisent à une variation du courant drain-source IDS
facilement mesurable. Ce type de capteur est principalement utilisé
pour la détection de l'hydrogène.
|
Figure I.3. Schéma d'un
capteur de
gaz de type
GASFET [1].
|
I.3.1.2 Capteur Electrochimique
Le principe de fonctionnement est basé sur les
réactions d'oxydoréduction. La structure la plus simple comprend
une membrane semi-perméable jouant un rôle de barrière de
diffusion, un électrolyte et deux électrodes entre lesquelles est
appliquée une différence de potentiel. L'absorption du gaz
à détecter donne lieu à une réaction
électrochimique spécifique, ce qui induit une force
électromotrice liée au transfert de charges entre le gaz et la
cellule. Ces capteurs sont sensibles et possèdent une bonne
sélectivité aux gaz [1]. Cependant, leur
durée de vie est limitée.

Figure I.4. Capteur Electrochimique à
électrode L2]. I.3.1.3 Capteur à base
d'oxyde métallique
Les capteurs de gaz à base d'oxydes métalliques
(capteur MOX) ont été développés par Seiyama et
Taguchi dans les années soixante L3]. Ils utilisaient
ZnO et SnO2 comme matériaux sensibles pour la détection des gaz
de pétroles liquéfiés LPG (liquid petroleum gases).
Depuis, de nombreux travaux de recherches ont été
réalisés et le sont encore à ce jour pour améliorer
leurs performances. Le principe de détection repose sur la variation de
conductivité électrique d'un oxyde métallique quand
celui-ci est mis en contact avec un nouvel environnement gazeux. Ce type de
capteur étant utilisé dans ce mémoire, nous allons
l'étudier en détail au paragraphe 5 de ce chapitre.
I.3.2 Capteur Indirect (Complexe)
I.3.2.1 Capteur à microbalance de quartz
Le dispositif est constitué d'un matériau
piézoélectrique de géométrie simple (disque ou
plaque rectangulaire) utilisé dans un oscillateur. Le principe de
fonctionnement repose sur la
variation de la fréquence de résonance du
matériau sensible quand une espèce s'adsorbe à sa
surface [2]. Cette variation est décrite par
l'équation de Sauerbrey :
|
(1.1)
|
|
Figure I.5. Structure
d'un capteur à
ondes
acoustiques de surface
[2].
|
Où mf est la masse du film par unité de
surface, ñq la masse volumique,
fq la fréquence propre de résonance du
quartz, fc la fréquence de résonance du
quartz en présence de l'espèce à détecter et
íq la vitesse de propagation de l'onde dans le
quartz.
Ce type de capteur est utilisé pour détecter les
composés organiques volatiles [2]. Ses avantages sont
une bonne sensibilité (de l'ordre de quelques ppm avec les hydrocarbures
halogénés), un fonctionnement à la température
ambiante. Cependant, il n'est pas sélectif et, de plus, il est sensible
à la température.
I.3.2.2 Capteur à onde acoustique de surface
Le principe de fonctionnement est proche de celui des capteurs
à microbalance à quartz. Sur un matériau
piézo-électrique sont déposées deux paires
d'électrodes interdigitées (figure I.5) l'une pour l'excitation
des ondes, l'autre pour leur détection après propagation.
Une couche sensible est déposée sur le trajet de
l'onde entre les deux électrodes. Elle permet l'adsorption de la
substance à détecter. Cette adsorption modifie la propagation de
l'onde et donc sa fréquence. Ces capteurs sont très sensibles, de
l'ordre du ppm pour l'ammoniac [4]. Notre laboratoire
s'intéresse à se type de capteur (M. ZERDALI).
I.3.2.3 Capteur à fibre optique
Le principe de fonctionnement est basé sur la
modification de la propagation de la lumière en présence du gaz
à détecter. Il existe deux principaux types de capteurs de gaz
à fibres optiques: les capteurs extrinsèques et les capteurs
intrinsèques. Dans les capteurs extrinsèques,
l'élément sensible se trouve au bout de la fibre, tandis que la
surface de la fibre constitue elleméme l'élément sensible
dans le cas des capteurs intrinsèques. La particularité de ces
capteurs est qu'ils permettent de déporter la mesure dans les
environnements difficiles à atteindre ou perturbés (par exemple,
dans le cas de pollution radioélectrique) L5].

Figure I.6. Capteur de gaz à fibre
optique L2].
I.4 Caractéristique d'un capteur de gaz
Les performances des capteurs sont souvent différentes
les unes des autres selon plusieurs paramètres à savoir : le type
du matériau utilisé pour la détection, les conditions de
travail du capteur et la technique de mesure effectuée.
I.4.1 Sensibilité
La première qualité que l'on recherche pour un
capteur est sa sensibilité aux gaz, c'est-à- dire son aptitude
à déceler de faibles concentrations avec une réponse
électrique mesurable. Dans la plupart des cas, la sensibilité
n'est pas la problématique principale dans l'utilisation d'un capteur
à base d'un semi-conducteur L6].
La sensibilité (S) est définie comme étant
le rapport entre la résistance du capteur sous air
(Rair) et sa résistance en présence d'une
certaine concentration de gaz (Rgaz). La sensibilité change
d'un matériau à un autre, et elle est définie comme suit
:
C'est-à-dire que pour un gaz réductif S >1,
tendit que pour un gaz oxydant S<1. I.4.2
Sélectivité
La sélectivité est définie comme
étant la capacité d'un capteur à répondre à
un certain gaz en présence des gaz interférents. C'est le
paramètre le plus important car le capteur est souvent utilisé
pour détecter un gaz dans une atmosphère contenant plusieurs gaz.
Actuellement, les capteurs à base d'oxydes métalliques souffrent
d'un manque important de sélectivité et de nombreuses
méthodes sont étudiées pour résoudre ce
problème [7].
I.4.3 Stabilité
Ce paramètre est utilisé pour
caractériser la dérive du signal du capteur dans le temps. Il
existe un vieillissement du capteur, ce qui limite son utilisation à
long terme. Différentes solutions sont proposées pour y
remédier, notamment par un traitement préalable de la couche
sensible [7].
I.4.4 Température de fonctionnement
Le processus d'adsorption et de désorption des
molécules de gaz à la surface du capteur dépend fortement
de sa température de fonctionnement. Afin de garantir une bonne
réversibilité des phénomènes d'adsorption et de
désorption, les capteurs MOX fonctionnent à température
élevée, typiquement entre 300°C et 500°C
[1].
I.4.5 Temps de réponse
Le temps de réponse est défini comme étant
le temps nécessaire pour que la réponse du capteur atteigne 90%
de son amplitude maximale lorsqu'il est exposé au gaz.
Ce temps dépend de plusieurs paramètres tels que
la température de fonctionnement du
capteur et la cinétique de
réponse au gaz. Pour les capteurs MOX, le temps de réponse est
|
Figure I.7. Structure d'un microcapteur
MOX
développé par la société
Microsens
L5].
|
relativement court, en particulier avec des capteurs à
base de couches minces constituées de grains de taille
nanométrique L1].
I.5 Capteurs de gaz à base d'oxyde
métallique (MOX) I.5.1 Matériaux sensibles
La plupart des oxydes métalliques présentent des
variations de conductivité lorsqu'ils sont soumis à un changement
de l'environnement gazeux. Les oxydes métalliques sont utilisés
en couches minces ou épaisses qui peuvent être
élaborées par des techniques de dépôt
différentes (pulvérisation cathodique, spin-coating,
évaporation, spray, etc....). Un matériau a une
sensibilité maximum à un gaz pour une température de
fonctionnement donnée L1].
I.5.2 Structure d'un capteur MOX
Du fait que les capteurs MOX fonctionnent à
température élevée (typiquement entre 300°C et
500°C), ils nécessitent une structure comportant une couche
sensible (dans notre cas l'oxyde de zinc) associée à un
élément de chauffage formé par une couche mince de Nickel
et Tungstène, présentement, notre cas qui sera
détaillé dans la deuxième partie de ce chapitre. La figure
I.7 montre une structure d'un capteur MOX proposé actuellement par
l'industrie.
I.5.3 Principe de fonctionnement
La conductivité des capteurs MOX est le
paramètre mesuré. Pour les oxydes métalliques de type n,
par exemple ZnO, la conductivité augmente en présence d'un gaz
réducteur alors qu'elle diminue en présence d'un gaz oxydant.
Ceci résulte d'un ensemble de réactions physico-chimiques entre
la couche sensible du capteur et les molécules de gaz adsorbées
à sa surface. Dans ce qui suit, nous détaillons quelques points
importants à prendre en compte pour comprendre ce qui se passe lorsqu'un
oxyde métallique est mis en contact avec un environnement gazeux
L1].
I.5.3.1 Conductivité du ZnO
La conductivité d'un semiconducteur est définie par
l'équation suivante :
Où q est la charge de l'électron, n
et p les concentrations en électrons libres et en trous,
ìn et ìp la mobilité des
électrons et des trous.
L'oxyde de zinc est un semiconducteur extrinsèque de
conductivité de type n (les porteurs électroniques majoritaires
sont les électrons). Le nombre d'électrons libres est très
supérieur à celui de trous. Sa conductivité peut donc
s'écrire :
Comme dans tous les semiconducteurs, l'augmentation de la
température entraîne un passage des électrons de la bande
de valence vers la bande de conduction. Le nombre de porteurs de charges libres
croît de façon exponentielle avec la température. D'autre
part, la conductivité de ZnO dépend également de la
morphologie de la couche sensible (conduction dans les grains et aux joints de
grains, état de surface que nous allons les détaillés au
paragraphe I.5.3.4.4 et I.5.3.4.5).
I.5.3.2 Interaction gaz - solide
Les interactions gaz- solide peuvent être classées
en quatre catégories L1].
· Les chocs entre les
molécules gazeuses et le solide : le matériau est insensible au
gaz dans ce type d'interaction.
· L'adsorption : il y a
fixation d'une fraction de la phase gazeuse sur la surface du solide. On peut
subdiviser l'adsorption en deux catégories : la physisorption et la
chimisorption ; nous allons les détaillés dans le sous chapitre
suivant.
· La réaction : adsorption
du gaz dans le solide suivie d'une réaction qui crée un nouveau
matériau.
· La désorption :
l'adsorption des molécules gazeuses est suivie de la création
d'une espèce gazeuse.
I.5.3.3 Adsorption à la surface d'un oxyde
métallique
Les molécules les ions ou bien les atomes formant la
surface d'un solide sont soumis à des forces qui se traduisent par un
champ attractif. La propriété que possède ce champ est
suffisante pour attirer les molécules de gaz ou de liquide situer au
voisinage de l'interface. Les forces qui provoque l'attraction à la
surface définissent tous simplement l'adsorption.
Dans le cas des oxydes métalliques, il est possible de
distinguer deux phénomènes intervenant dans l'adsorption des gaz
: la physisorption et la chimisorption.


La physisorption fait intervenir des forces d'origine
électrostatique de type VanderWaals. Avec une énergie de liaison
inférieure à 0.1 eV.
La chimisorption fait intervenir des forces de liaison de l'ordre
de grandeur de 1 eV, impliquant une combinaison chimique de la molécule
et du solide.
Lors de la physisorption la molécule adsorbée et
l'adsorbant peuvent étre considérés comme deux
système indépendants, alors que lors d'une chimisorption on se
trouve en présence d'un seul système.
Ces phénomènes d'adsorption vont modifier la
structure énergétique des bandes par l'apparition en surface
d'états accepteur ou donneur L8].
Par la suite nous allons démontrer l'effet
apporté par l'adsorption chimique (chimisorption) d'une molécule
de gaz créant ainsi des états de surface accepteur
Ea ou Ed donneur suivant que l'oxyde
métallique soit un semiconducteur de type (n) ou de type (p).
I.5.3.3.1 Chimisorption dans un semiconducteur
Pour étudier les phénomènes de transfert
d'électrons dans une interface gaz - semiconducteur, on a pris les deux
cas d'un semiconducteur de type (n) et (p) en contact d'un
gaz ayant un niveau accepteur, en présence de ce niveau
Ea situé sous le niveau de Fermi Ef du
semiconducteur, on constate un transfert d'électron que les
équations suivantes traduisent comme suit :

Adsorbat
Semiconducteur
NV Ec
Ef
Ea
Ev
Energie
Eg
Figure I.8. Diagramme d'énergie
d'un
semiconducteur type n et d'un
adsorbat avant la chimisorption.
a) Etude du phénomène lors du contact
(adsorbat / semiconducteur (n)) Pour cela nous allons faire appel
à l'équation de Poisson :
Ou V est le potentiel, ñ la
densité et år å0 sont respectivement la
constante diélectrique du matériau et la permittivité du
vide.
L'expression de la densité de charge de façon
générale en tenant compte de tous les paramètres est :
ñ = - e [p(x) - n(x) + D+(x) -
A-(x)] (1.6)
Où e est la charge électrique, p,
n la densité des porteurs (trous, électrons), et
D+, A- la densité des donneurs et
accepteurs.
Du fait qu'on est dans le cas d'un SC type n, on peut
réduire la relation (1.6) à : ñ = - e [- n(x) +
D+(x)], puisque les électrons sont majoritaire et en
considérant une ionisation complète des donneurs -
D+ (x) = D+ = cst.
On à un transfert d'électrons du semiconducteur
vers le niveau accepteur créant en surface une charge d'espace
positive.
On a:
Avec :
On remplace (1.8) dans (1.7) :
En intégrant la relation (1.9) on peut calculer le champ
électrique E :
Sachant que n(x) = 0 dans la zone de charge d'espace
(ZCE) et n(x) = D+ en volume.
Où D est la longueur de Debye (largeur de la ZCE).
Pour cause de neutralité, le champ électrique dans
la ZCE est nul - la charge dans la ZCE = la charge à la surface.
D+D = Ns (1.13)
Où Ns est le nombre de charge des
molécules adsorbé/unité d'aire.

E(x)
ZCE
D
-(eD+D/årå0)
x
30
Figure I.9. Schéma du
champ
électrique à l'intérieur de la Z.C.E
[9].
- Calcul du potentiel
1- Dans la zone de charge d'espace (ZCE) :
Pour trouver la variation du potentiel dans la ZCE, on
intègre une deuxième fois la relation (1.12).
2- A la surface :
Si on défini que le potentiel vaut zéro dans le
volume de l'échantillon et en utilisant la relation 1.13 pour
éliminé D ; le potentiel de surface peut s'écrire :
- Calcul de l'énergie potentiel :
Ep = -eV(x) (1.17)
Pour :
x = 0 - V(0) = - Ep = (1.18)




x = D- V(D) = 0 - Ep = 0 (1.19)
Ep(x)
Adsorbat Semiconducteur

Figure I.10. Schéma
de
l'énergie potentiel à l'intérieur
de la Z.C.E.

Adsorbat Semiconducteur

Ec
Ef

Ea
Ea
Ec
Ef
Ev
Energie

0


D
x
0
x
a) Avant chimisorption b) Après chimisorption
Figure I.11. Diagramme de bande
énergétique pour la chimisorption
d'un semiconducteur type
(n).
b) Etude du phénomène lors du contact
(adsorbat / semiconducteur (p))
De la méme manière on fait appel à
l'équation de Poisson : Champ et potentiel électrique
Dans le deuxième cas ou on considère un SC type
p, on peut réduire la relation (1.6) à : ñ = e [p(x) -
A- (x)], puisque les trous sont majoritaire et en
considérant une ionisation complète des accepteurs -
A- (x)= A- = cst [9].
On a:
Avec :
On remplace (1.22) dans (1.21) :
En intégrant la relation (1.23) on peut calculer le champ
électrique E :
Sachant que p(x) = 0 dans la zone de charge d'espace
(ZCE) et p(x) = A- en volume.
Où D est la longueur de Debye (largeur de la ZCE).
Pour cause de neutralité, le champ électrique dans
la ZCE est nul - la charge dans la ZCE = la charge à la surface
[9].
A- D = Ns (1.27)
Où Ns est le nombre de charge des
molécules adsorbé/unité d'aire.

E(x)
ZCE
D
x
Figure I.12. Schéma du
champ
électrique à l'intérieur de la
Z.C.E
L9].
- Calcul du potentiel
1- Dans la zone de charge d'espace (ZCE) :
Pour trouver la variation du potentiel dans la ZCE, on
intègre une deuxième fois la relation (1.26).
2- A la surface :
Si on défini que le potentiel vaut zéro dans le
volume de l'échantillon et en utilisant la relation 1.27 pour
éliminé D L9] ; le potentiel de surface peut
s'écrire :
- Calcul de l'énergie potentiel :
Ep = -eV(x) (1.31)
Pour :
x = 0 -9 V(0) = -9 Ep = - (1.32)




x = D-9 V(D) = 0 -9 Ep = 0 (1.33)

Ep(x)

0

x

D
-
Figure I.13. Schéma
de
l'énergie potentiel à l'intérieur
de la Z.C.E.

Adsorbat Semiconducteur
a) Avant chimisorption b) Après chimisorption
0
x
0
Energie
D
x
Ev
Adsorbat Semiconducteur
Ec
Ea
Energie
Ec
Ef
Ea
Ef
Ev
Figure I.14. Diagramme de bande
énergétique pour la chimisorption
d'un semiconducteur type
(p).
En présence d'un gaz oxydant tel que l'oxygène
nous aurons, en règle générale, un transfert
d'électrons du solide vers l'adsorbat et donc l'apparition d'une couche
appauvrie en en électrons qui se traduira par une augmentation de la
résistivité, à l'inverse, en présence d'un gaz
réducteur nous aurons un transfert d'électron de l'adsorbat vers
le semiconducteur et donc une diminution de la résistivité de la
couche. Ce sont ces deux conséquences de l'oxydoréduction d'une
couche solide qui constitue la mesurande pour les capteurs de gaz
L8].
I.5.3.4 Mécanisme mise en jeu dans un oxyde
métallique pour la déviation du type Semiconducteur
Généralement les oxydes métalliques sont
de type n et se composent d'un grand nombre de grains et de joints de grains.
La densité d'électrons en volume, ou à l'intérieur
des grains est constante et égale à la densité des ions
Nd (par unité de volume), là où tous les donneurs
sont ionisés aux températures opérationnelles
Lb0].
Wagner a mis en évidence l'existence de quatre types de
structures mettant en jeu ce type de conduction. Ces composés
présentent soit des lacunes soit des ions interstitiels. La
stoechiométrie n'est pas conservée mais la neutralité
électrique est assurée par la présence d'électrons
ou de trous.
I.5.3.4.1 Mécanisme de la non stoechiométrie
a conductivité n
- Soit M le métal et O l'oxygène :

Ces composés possèdent une sous
stoechiométrie due à des lacunes anioniques MO1-x (cas du ZnO,
TiO2) ou d'une insertion cationique M1+xO (cas du SnO2, PbO2,
CeO2).
I.5.3.4.2 Mécanisme de la non stoechiométrie
a conductivité p
|
Les composés qui possèdent une
conductivité de type p sont des oxydes métalliques avec des
lacunes cationique M1-xO (cas du NiO, Cu2O, MnO) ou d'une insertion
anionique MO1+x (cas du UO2).
|
L'existence des états accepteurs dans un oxyde
métallique de type n non dopé est une
vérité mais la classification stoechiométrique
mentionnée ci haut est la plus dominante à propos de
l'identification du type semiconducteur.
Housten et al [11] ont proposé un
modèle des bandes d'énergie et ont recensé pour des
monocristaux d'SnO2 de type n des niveaux accepteurs situés au
dessus de la bande de valence BV, le plus proche a été distant de
0,33 eV de la BV.
Egalement pour le ZnO de type n, K. S Weibenrieder et
al [12] ont proposé un model statistique pour calculer
les niveaux d'énergie localisés à la bande interdite et
ils ont montré l'existence des états accepteurs de type lacune de
zinc dont la distance énergétique entre ces niveaux et la BV
dépend des conditions d'élaboration par conséquent le taux
de ces états accepteurs explique l'état de compensation du ZnO et
non le type du semiconducteur.
I. 5.3.4.3 Effet de la morphologie sur les
propriétés électrique des oxydes métalliques
En effet touts oxydes métalliques possèdent une
agglomération polycristalline, la hauteur des barrières de
potentiel qui existe entre les grains dépend de la Morphologie du
matériau de départ et des conditions de synthèse, à
cet effet on constate que la taille des grains, rapport surface volume,
porosité, sauront joués le rôle prédominant et
important sur les propriétés électriques d'un oxyde
métallique semiconducteur.
De manière générale, les travaux
menés par beaucoup de chercheur s'accordent sur le fait que les
matériaux constitués de cristallites de très petites
dimensions sont les plus sensibles à l'action des gaz
[13].
I.5.3.4.4 A propos des joints de grains
Les joints de grains sont la région inter faciale entre
deux grains d'orientations cristallographiques différentes, elles sont
dues essentiellement à un désaccord entre les différentes
distributions atomiques des deux grains de contact. Chaque grain contribue
à la conductivité lors d'interaction du gaz avec le film qui peut
être modelé avec les barrières de potentiel, l'existence
des états de surface provoque une charge électrique Sur les
surfaces des grains. Ceci produit les deux potentiels de surface et de joint de
grains, aussi bien beaucoup d'auteur considère que les joints de grains
comme des régions de recombinaison - passages vis-à-vis des
porteurs minoritaires / majoritaire [11][12][14].

Figure I.15. Représente une
schématique de joint de grain a x = 0 et les bandes
d'énergies correspondantes. Un piégeage d'un électron de
conduction est illustré. Les largeurs d'épuisement dans les
grains sont xd1 et xd2,
respectivement. Ec et le bas de la bande de conduction,
Ev du dessus de la bande de valence, Ef est le
niveau de Fermi, q est la charge d'électron, et Vb est
la hauteur de la barrière de potentielle respectivement
L9].
Pour le potentiel VB de joint de grain, il joue le
rôle d'une barrière pour les électrons de conduction
qu'elles limitent leur mouvement considérablement. Le pliage de bande
provoque l'épuisement des électrons de conduction prés des
surfaces des grains et les joints de grains. La densité de charge
à la surface des joints de grains est représenté
NB (par unité de surface). La courbure de bande de la structure
montrée sur la figure I.15 s'appelle souvent Schottky dos à dos
ou double barrière de Schottky L9].
I.5.3.4.5 Rôle d'état de surface dans les
oxydes métalliques
Les états de surface sont les forces localisées
dans la bande interdite. Des électrons libres du film peuvent être
emprisonnés sur les surfaces des joints de grains ou des grains dans
deux genres d'état de surface ; intrinsèque et
extrinsèque.
a) Etat intrinsèque
Des états intrinsèques se composent d'états
qui sont crées par l'existence de la surface elle-même,
résultante des états rompus de surface.
b) Etat extrinsèque
Des états extrinsèque se composent
d'états qui sont crées par les impuretés
extérieurs, et dopage. Les états extrinsèques sont
crées par les atomes ou les molécules adsorbés sur la
surface.
L'existence des états extérieurs provoque des
procédés électroniques de piégeage. Si
l'électron est emprisonné dans un atome ou une molécule
adsorbé (états extrinsèque) créant un ion, ce
procédé s'appelle ionisation. En d'autres termes le
piégeage des électrons et l'ionisation de l'oxygène est le
méme phénomène.
L'oxygène chimisorbe dissociativement sur la surface
des oxydes métalliques résistifs dans des températures de
fonctionnement typique d'environ 300 ~ 400 °C, l'ion d'oxygène
O- est l'espèce dominante sur la surface.
I.5.3.5 Rôle de l'oxygène et principe de
détection
L'oxygène joue un rôle primordial dans la
détection des gaz par les oxydes métalliques. Les
molécules d'oxygène peuvent être adsorbées à
la surface d'un oxyde métallique lorsque celui-ci est mis en contact
avec l'oxygène selon les réactions suivantes
L1]:



Adsorption physique de l'oxygène :
O2 (gaz) = O2 (adsorbé) (1.34)
Adsorption chimique de l'oxygène :
O2 (adsorbé) + e- = (1.35)
Dissociation de l'oxygène :
O- + e-= O2- (1.37)
L'adsorption chimique de l'oxygène à la surface
du ZnO conduit à un transfert des électrons libres du
réseau vers les molécules adsorbées. Il résulte
donc une diminution de la conductivité électrique.
Quand le ZnO est exposé à des gaz autres que
l'oxygène présent dans l'air, il peut y avoir
une
réaction chimique avec les espèces
préadsorbées, notamment les espèces
oxygénées. Les
réactions qui ont lieu sont essentiellement des
réactions d'oxydoréduction. Par exemple, pour un gaz
réducteur comme l'éthanol que nous avons traité dans ce
mémoire, la réaction chimique suivante se produit :
1/ selon les travaux mené par : D R Patil, L A Patil et D
P Amalnerkar [15] où ils décrivent la
réaction d'adsorption de l'éthanol sur la surface du ZnO.
C2H5OH(gaz) + 6O2- (surface) -
2CO2(gaz) + 3H2O(gaz) + 12e- (band cond)
(1.38)
2/ aussi selon les travaux mené par : N Hongsith, S
Choopun, P Mangkorntong et N Mangkorntong [16].

2C2H5OH + - 2CH3CHO + 2H2O + 2 e (1.39)
2C2H5OH + - 2CH3CHO + 2H2O + 1 e (1.40)
Dans ce cas, le nombre des porteurs majoritaires augmente, ce
qui conduit à une augmentation de la conductivité
électrique. Inversement, pour un gaz oxydant comme O3, la
réaction suivante se produit :

O3 (gaz) + e- = + O2 (gaz) (1.41)
Le nombre de porteurs majoritaires diminue ce qui conduit
à une diminution de la conductivité électrique.
La variation de la résistance du capteur à base
d'oxyde métallique en fonction de la concentration de gaz est
décrite par la formule suivante :
R = K.[C]á (1.42)
Où K et á sont des constantes
et [C] la concentration d'un gaz dans l'air. Selon la nature du matériau
de la couche sensible, de sa structure et du gaz, la valeur de á
est comprise entre 0,2 et 0,8.
I.6 l'oxyde de zinc (ZnO)
I.6.1 Propriété de l'oxyde de zinc (ZnO)
L'oxyde de zinc, appelé blanc de zinc ou blanc de
neige, est une poudre blanche préparée par combustion de la
vapeur de zinc. Elle est employée comme pigment dans les peintures, et
comme charge dans les pneus en caoutchouc L17].
Les couches minces d'oxydes sont transparentes dans le
visible, réflectives dans l'IR et bonnes conductrices, ont connues
depuis quelques années un développement important, notamment a
cause de leur propriété électrique et optique
particulière. Et parmi ces oxydes nous citerons l'oxyde zinc qui
à prouvé depuis plusieurs années sa parfaite adaptation
aux différentes caractéristiques cité ci-dessus
L18]. Donc très approprié pour des applications dans
différents domaines t'elle que l'électronique,
l'optoélectronique, la conversion photovoltaïque et les capteurs de
gaz MOX.
I.6.2 Structure cristalline du ZnO
Le ZnO est un semiconducteur de la famille II-VI, il se
compose de Zinc (Zn) et d'Oxygène (O). Il se cristallise sous trois
formes, cubique, rocksalt et hexagonale wurtzite (figure I.16)
L19].
La structure de ZnO la plus stable thermodynamiquement est
hexagonal wurtzite L20]L21]. Elle cristallise selon la
structure hexagonale compacte, ou Chaque atome de zinc est entouré de
quatre atomes d'oxygène situés aux sommets d'un
tétraèdre (figure I.16. (b)).
Cette disposition est caractéristique des liaisons
covalentes de type sp3, mais ZnO a aussi à 50% un
caractère ionique. Les paramètres de maille de ZnO Würtzite
sont a = 3.2495A, c = 5.2069A, et c/a =
1.6022 L22].
Le ZnO peut aussi avoir une structure Rocksalt (NaCl) sous une
pression hydrostatique (p = 10GPa) avec réduction de la maille
en faveur des interactions coulombiennes L17], et une
structure zinc-blende métastable par hétéroépitaxie
par jet moléculaire (MBE) sur des substrats cubiques tels que : ZnS,
GaAs/ZnS, et Pt/TiSiO2.
Chapitre I Les capteurs de gaz (chimiques)

b)
C
d
a)
c) d)
Figure I.16. Différentes structures de
l'oxyde de zinc. A) hexagonal compact de type wurtzite, b)
maille conventionnelle de la structure wurtzite, c) structure zinc blende et d)
structure rocksalt.
I.6.3 Structure Electronique du ZnO
On rappelle que les structures électroniques de bande de
l'oxygène et du zinc sont :
O: 1s2 2s2 2p4
Zn: 1s2 2s2 2p6 3s2
3p6 3d10 4s2

Figure I.17. Structure de bande de ZnO en
utilisant la méthode du pseudo potentiel L22].
Les états 2p de l'oxygène forment la bande de
valence et les états 4s du zinc constituent la zone de conduction du
semi-conducteur du ZnO.
La figure I.17 illustre l'allure de la structure de bande du ZnO
de type wurtzite.
Il existe en réalité six bandes
résultantes des états 2p de l'oxygène, et les plus bas des
bandes de conduction ont une forte contribution des états 4s du Zinc.
La structure électronique de bandes montre que le ZnO
est un semi-conducteur à gap direct, le minimum de la bande de
conduction et le maximum de la bande de valence sont situés au
point . La largeur de la bande interdite est de l'ordre de 3,3
eV L22].
Tableau I.2. Propriétés
générales de l'oxyde de zinc en couche mince
L19].
|
Propriétés
|
valeurs
|
|
Paramètre du réseau à 300°K
a0
(nm)
c0 (nm)
a0/c0
|
0,32495
0,52069
1.602 (structure idéale)
|
|
Densité (Kg/m3)
|
5606
|
|
Phase stable à 300°K
|
Wurtzite
|
|
Point de fusion (°C)
|
1975
|
|
Conductivité thermique
|
0.6 - 1.2 W cm-1 °K-1
|
|
L'énergie de Gap (eV)
|
3.0 -3.3
|
|
Concentration d'électron intrinsèque
(/cm3)
|
type n : >1020 électrons
;
intrinsèque : 106 électrons ;
type p : <
1017 trous.
|
|
L'énergie de liaison d'exciton (meV)
|
60
|
|
Masse effective de l'électron
|
0.24
|
|
Masse effective du trou
|
0.59
|
|
Mobilité de Hall des électrons à
300°K
|
200 cm2/V/s
|
|
Mobilité de Hall des trous à 300°K
|
5 - 50 cm2/V/s
|
|
Valence
|
2
|
|
Résistivité intrinsèque à
300°K (Ù cm)
|
1010
|
|
Dopants type n
|
Ga , Al, , In,
|
|
Résistivité type n (Ù cm)
|
10-4 10-1
|
|
Dopants type p
|
Li, Cu, N
|
|
Résistivité type p (Ù cm)
|
106 - 1012
|
I.6.4 Propriété électrique de l'oxyde
de zinc
Le ZnO Est un semi-conducteur
dégénéré, de conductivité de type n, due
notamment à un excès de zinc en position interstitielle et/ou
à une déficience en oxygène L10]. Ses
propriétés électriques peuvent être modifiées
par la présence d'un changement en procédé de sa
synthèse chimique ou largement modifié par traitement thermique
sous hydrogène ou sous oxygène ou
par dopage, en particulier par substitution cationique Dans ce
dernier cas, des atomes de zinc sont substitués par des atomes
trivalents, si l'on veut augmenter la conductivité, ou par des atomes
monovalents, si l'on veut la réduire ; par conséquent, la
résistivité du ZnO peut aller dans une marge respective allant de
1012 a 10-4 .cm ce qui fait le
principal paramètre dont l'objet de l'étude des
propriétés électriques des couches minces de ZnO.
La réaction de formation de ZnO stoechiométrique
est :
Zn++ + 2e- + 1/2 O2 - ZnO
(1.43)
La composition élémentaire quantitative des
filmes minces ZnO a été faite à l'aide d'un
spectromètre dispersif d'énergie et son analyse a montré
que les compositions massiques de Zn et O sont respectivement 80,34 et
19,66 [10].
Atome de Zinc
en position
interstitielle
Zn2+ O2-
Zn2+
Zn2+ O2- Zn2+
e-

Zn2+ O2- Zn2+ O2- Zn2+
Zn2+ O2- Zn2+ O2- Zn2+
Lacune
d'oxygène

Electron libre
de zinc
O2- Zn2+ O2-
Zn2+
e

2-
Zn2+ O2- Zn2+ O2- Zn2+
Figure I.18. Phénomène de la non
stoechiométrie de ZnO [6].


I.7 Introduction
L'étude de cette seconde partie du chapitre (I)
consiste à constater le phénomène de chauffage dans une
couche mince métallique, ainsi que les principaux
phénomènes de conduction de la chaleur.
I.8 Propriétés générales
des matériaux métalliques on couche mince à usage
thermique
Tous les capteurs à oxyde métallique
fonctionnent sur le principe d'un élément sensible au gaz,
chauffé par une résistance métallique, à ce titre
le métal adéquat induira un bon fonctionnement du capteur en
général. Se basant sur cet axiome, notre choix s'est porté
sur le nickel et le tungstène.
Tableau I.3. Propriétés
générales du Nickel et Tungstène [23].
TUNGSTENE NICKEL
|
Général
|
|
|
|
Nom, Symbole, Numéro
|
Tungstène, W, 74
|
Nickel, Ni, 28
|
|
Masse volumique
|
19 250 kg/m3
|
8908 kg/m3
|
|
Propriétés atomiques
|
|
|
|
183.84 uma
|
|
|
Masse atomique
|
58,69 uma
|
|
Structure cristalline
|
Cubique centré
|
Cubique face centrée
|
|
Propriétés physiques
|
|
|
|
Etat de la matière
|
Solide
|
Solide ferromagnétique
|
|
Température de fusion
|
3695 °K
|
1728 °K
|
|
Température de vaporisation
|
5828 °K
|
3186 °K
|
|
Volume molaire
|
9.47 x 10-6 m3/mol
|
6.59 x 10-6 m3/mol
|
|
Energie de vaporisation
|
824 kJ/mol
|
370.4 kJ/mol
|
|
Energie de fusion
|
35.4 kJ/mol
|
17.47 kJ/mol
|
|
Pression de la vapeur
|
4.27 Pa à 3407 °C
|
237 Pa à 1452.9 °C
|
|
Vélocité du son
|
5174 m/s
|
4970 m/s
|
Divers
|
Chaleur massique
|
130 J/(kg.°K)
|
440 J/(kg.°K)
|
|
Conductivité électrique
|
8.9 106 S/m
|
14.3 106 S/m
|
|
Conductivité thermique
|
174 W/(m . °K)
|
90.7 W/(m . °K)
|
|
Résistivité électrique à
295
°K
|
5.3 10-6 ? cm
|
7.0 10-6 Ù cm
|

Atome de Nickel (Ni) Atome de Tungstène (W)
(a) (b)
Figure I.19. Structure cristalline : a)
cubique face centrée du Nickel, b) cubique centrée
du
Tungstène.
I.9 Conductivité électrique dans une couche
mince métallique
La quantité de mouvement total de N
électrons libres dans un métal «le nickel ou
tungstène » dans notre cas est reliée au vecteur d'onde par
:
Mouvement qui peut être décrit par la
deuxième loi de Newton tenant compte uniquement du champ
électrique E. La force s'écrit :
(1.45)
En l'absence de collision, la sphere de Fermi (figure
I.20 et figure I.21) de l'espace k est déplacée à
vitesse constante sous l'effet d'un champ électrique constant. En
intégrant la relation 1.65, nous obtenons :
k (t) - k (0) = -e E t / ê (1.46)
Si on applique un champ à l'instant t = 0 au
gaz d'électrons qui remplit la sphere de Fermi centrée
à l'origine de l'espace k, à l'instant t, la sphere est
déplacée en bloc et sont centre est en :
äk = -e E t / ê (1.47)
A cause des collisions des électrons avec les
impuretés, les défauts du réseau et les phonos, la
sphère déplacée peut être maintenue stationnaire
dans un champ électrique. Si le temps entre deux collisions est
ô, le déplacement de la sphère de Fermi
en régime continu est donné par la relation
précédente. L'incrément de vitesse est í =
-eEô/m. S'il y a, dans un champ électrique E
constant, n électrons de charge q = -e par
unité de volume la densité de courant électrique est :
= n q í = ne2ôE/m (1.48)
Ceci est la loi d'Ohm. La conductivité électrique
dans ce cas est définie par j = ó E, d'où
= n e2 ô / m (1.49)
la résistivité électrique ñ
est, par définition, l'inverse de la conductivité,
d'oüñ= m / n e2 ô (1.50)
Le libre parcourt moyen lm d'un
électron de conduction est défini par :
(1.51)
Où vF est la vitesse de l'électron
à la surface de fermi [23].
|
Sphère de Fermi
ky
En t = 0 F ky
|
Sphère de Fermi
En t
|
|
kx
|
|
ky
|
Figure I.20. La sphère de Fermi
englobe les états occupés dans l'espace k dans
l'état fondamentale du gaz électronique. La quantité de
mouvement résultante est nulle, car pour chaque état
occupé k il y a un état occupé en
-k [23].
Figure I.21. Sous l'influence d'une force
constante F agissant pendant l'intervalle de temps t chaque
état voit son vecteur k augmenté de äk
=Ft/ê ceci est équivalent à une translation de äk
de toute la sphère de Fermi. La quantité de mouvement totale est
N ê äk s'il y a N électrons en
présence. L'application de la force augmente l'énergie du
système d'une quantité N (ê äk)2 / 2
m [23].
I.10 Dissipation de la chaleur par effet joule dans
une couche mince métallique
Le passage d'un courant dans une couche mince métallique
(ou résistance), entraîne la délivrance d'une puissance de
la forme :
P = V2/ R (1.52)
Où P représente la puissance en Watt,
V représente la tension d'alimentation de la
résistance,
R représente la résistance ou bien
l'élément chauffant,
Dans un laps de temps dt, cette puissance créera
une énergie dE qui est donnée par la relation 1. 53.
dE = P dt = (V2/ R) dt (1.53)
Qui par la suite engendrera le dégagement d'une
quantité de chaleur dQ proportionnelle à la variation de
température dT, subit à l'intérieur de la
résistance métallique. La relation 1.54 représente la
variation entre la quantité de chaleur dégagée et
l'énergie du système (la résistance).
dQ = Cm M dT = V2/ R dt (1.54)
C M
Où Cm représente la chaleur
massique du matériau,
M représente la masse du matériau.
Si on intègre la relation 1.54, on trouvera la
corrélation qui lie la température au temps.
Où T représente la température de
fonctionnement dans un temps donné, V dt
C MdT k T T dt
( )
T0 représente la température initiale.
R
On remarque que si le temps t - , T - , hors ce n'est pas
exactement juste en effectuant les mesures. Pour cela il faudrait ajouter le
terme d'énergie perdue par conduction thermique due au contact entre le
métal et les oxyde de silicium des deux cotés. Dans ce cas la
relation 1.54 devient :
Où k est une constante de perte thermique
(W.k-1) qui relie la conductivité thermique K du
matériau (Nickel + Tungstène) à l'épaisseur
e de l'oxyde de silicium des deux cotés. Selon la relation
suivante :
k = KNi+W eSiO2 (1.57)
Pour résoudre cette équation de second
degré, nous allons procéder de la façon suivante.
1- imposé une condition aux limites suivantes : à
t = 0 T = T0.
2- Intégré l'équation 1.76 qui lie la
variation de la température en fonction du temps. Après tout
calcul fait en aboutit à l'expression suivante :
On remarque que pour :
t ? T ? TF,
Où TF est la température de fonctionnement
de notre micro four, et à pour expression
TF = T0 + V2/(R k) (1.59)
Donc la température de notre micro four dépend
essentiellement de la puissance électrique que du temps
[6].
Un exemple est illustré sur la figure I.22 à
l'aide du logiciel Mathematica où notre micro four a été
conçue en cuivre (ou la constante k vaut 0.02 W/°K), et
alimenté par des puissances différentes.

Figure I.22. Simulation de l'évolution
du temps de chauffage du micro four conçue en cuivre
par rapport
à des puissances d'alimentations différentes
[6].
I.11 Phénomène de transfert de chaleur
C'est un processus par lequel de l'énergie est
échangée sous forme de chaleur entre des corps ou des milieux aux
températures différentes. De nos jours trois types de transfert
de chaleur sont connus : par conduction, par rayonnement ou bien par
convection [24].
+ Transfert de chaleur par conduction : il
reste le seul mécanisme qui permet un transfert de chaleur efficace
à travers les solides opaques. C'est lorsque l'on chauffe l'une des
extrémités d'une barre métallique, la chaleur se transmet
par conduction à l'autre extrémité plus froide. Le
mécanisme exact de la conduction dans les solides n'est toujours pas
totalement élucidé, mais découle surtout du mouvement des
électrons libres dans le corps, enclenché dès que s'y
établit une différence de température. Ainsi, les bons
conducteurs de chaleur sont en général de bons conducteurs
électriques.
+ Transfert de chaleur par convection : dans
un champ de gravitation, toute différence de température dans un
liquide ou un gaz, modifie sa densité, sous le mouvement se produisant
alors au sein du fluide du fait de la poussée d'Archimède. Ce
mouvement de brassage, dans lequel les parties les plus chaudes du fluide ont
tendance à s'élever et les parties froides et denses à
descendre, s'appelle convection. Le mouvement du fluide peut être
naturel ou forcé. Les mouvements dus uniquement
à des différences de température du fluide constituent la
convection naturelle. La convection forcée est obtenue en soumettant le
fluide à une augmentation de pression, le mouvement se
déclenchant alors selon les lois de la mécanique des fluides.
+ Transfert de chaleur par rayonnement : il
est fondamentalement différent des deux autres types de transfert de
chaleur, en ce sens que les substances qui échangent de la chaleur n'ont
pas besoin d'être en contact l'une avec l'autre. Elles peuvent même
être séparées par le vide. Le rayonnement est
l'émission d'ondes électromagnétiques par un corps
chauffé, une explication générale du
phénomène étant fournie par la théorie quantique.
Les surfaces opaques peuvent absorber ou réfléchir les
rayonnements incidents. En général, les surfaces mates et
rugueuses absorbent mieux le rayonnement que les surfaces brillantes et polies.
À l'inverse, les surfaces brillantes réfléchissent mieux
le rayonnement que les surfaces mates.
Les corps dotés d'un bon pouvoir d'absorption sont
également de puissants émetteurs de chaleur, alors que les bons
réflecteurs sont de mauvais émetteurs.
I.11.1 Phénomène de diffusion de la chaleur :
métal/isolant
La diffusion de la chaleur dans un matériau donné,
à l'exemple de la silice (SiO2), est régie par l'équation
différentielle suivante :

Avec : (1.61)

Où D diffusivité thermique (m2
s-1)
k conductivité thermique (W m-1
k-1)

masse volumique (kg m-3)
Cm chaleur spécifique (J
kg-1 k-1)
La diffusion de la chaleur opère toujours dans des milieux
tri dimensionnels, cependant quand T x t
( , ) T x t
( , )
D
les conditions expérimentales conduisent à des
isothermes plans et parallèles, les flux
2
t x
thermiques sont parallèles à l'axe des x (figure
I.23) alors, le problème se ramène à un traitement
unidimensionnel, où on retrouve l'équation différentielle
I-8 sous la forme suivante.

L'équation 1.82 admet comme solution (Suivant les
conditions aux limites choisies) la relation suivante :
T (0,0) = T0
T (x,0) = 0
Où T0 température initiale à t = 0.
Direction du flux de

Wafer (Si polycristallin) Plaque chauffante
Direction du flux de chaleur
chaleur
Elément sensible aux gaz
Figure I.23. Diffusion du flux de chaleur
à travers le substrat de silicium et les différentes couches de
SiO2.

Figure I.24. Représente une simulation
de la diffusion de la chaleur du micro four vers les
deux régions
isolatrice en SiO2, a) substrat (SiO2 + Si), b) couche de protection en
SiO2 [6].




II.1 Introduction
La première partie de ce chapitre (II) abordera trois
principaux volets. Le premier concernera un rappel des différentes
méthodes de dépôt des couches minces, pour entamer par la
suite la partie technologie d'oxydation du silicium et enfin terminer par la
réalisation du capteur.
II.2 Généralité sur les
méthodes de dépôt de couches minces
Il existe principalement deux méthodes pour
l'élaboration des couches minces, soit par des procédés
physiques ou bien chimiques, comme indiqué sur la figure II.1.
|
|
Processus chimique
CVD
|
|
|
|
|
|
Processus physique
PVD
|
Dépôt chimique en phase vapeur (CVD)
Dépôt à basse pression (LPCVD)
Dépôt assisté plasma (PECVD) L'oxydation
anodique
Méthodes générales
pour déposer
des
couches minces.
Évaporation sous vide
Pulvérisation cathodique (sputtering) Dépôt
laser pulsé (PLD)
Canon à électron
Epitaxie par jet moléculaire MBE
Figure II.1. Méthodes
générales de dépôt de couches minces sous
vide [18]. II.2.1 les méthodes de
dépôts physiques
Généralement les couches minces
métalliques ou isolantes (diélectriques ou semiconductrices) sont
déposées par les procédés PVD qui souvent utilisent
l'évaporation, la sublimation ou la pulvérisation par
bombardement ionique, ces techniques s'effectuent dans une chambre, sous vide.
On transforme la matière à déposer en phase vapeur, ces
vapeurs sont ensuite condensées sur les surfaces pour aboutir finalement
à des couches minces.
II.2.1.1 Dépôt par évaporation
Les films métalliques ou semi-conducteurs dans cette
déposition par évaporation sont assurés par la
condensation de la vapeur métallique sur un substrat, tous les types des
métaux sont évaporés, quand ils sont chauffés
à des températures suffisamment hautes, le chauffage dans
l'évaporation s'effectue par plusieurs méthodes
[10].
- chauffage résistif : évaporation par effet
Joule.
- chauffage par faisceau d'électron : bombardement
électronique.
- chauffage par faisceau laser : appelé évaporation
par ablation laser.
II.2.1.2 Evaporation par effet Joule
Ce type d'évaporation consiste à déposer
le matériau désiré par évaporation par un filament,
nacelle ou creuset, généralement fabriqué à base de
métaux réfractaires (tungstène, tantale, molybdène,
ou en alumine) dans une chambre sous vide de l'ordre 10-6
à 10-7 Torr [25]. La vitesse de
dépôt dépend de la température de la source, de la
distance entre le creuset et le substrat mais aussi du coefficient de collage
des espèces évaporées sur le substrat. Elle varie
classiquement de 1 nanomètre par minute à 10 nanomètre par
minute.
Parmi les inconvénients de cette technique, on cite :
- La difficulté d'atteindre de très hautes
températures d'évaporation pour le dépôt des
métaux réfractaires.
- Les contaminations dues aux chauffages des nacelles et des
creusets.
II.2.1.3 Evaporation par bombardement
électronique
Cette technique consiste à porter un filament
généralement en tungstène ou tantale, à une haute
tension négative pour l'accélération des électrons,
et les focalises par voie électromagnétique ou
électrostatique vers la cible à évaporer. Ainsi
l'énergie cinétique des électrons est convertie en
énergie thermique pour évaporer le matériau. Cette
méthode est très utilisée pour les dépôts des
métaux de transition et spécialement les métaux
réfractaires parce qu'elle utilise une grande puissance de chauffage
avec une très haute efficacité de contrôle de
vitesse [25]. L'inconvénient de cette technique
résulte du faite de l'impossibilité à travailler à
haute pression ainsi qu'à la difficulté d'évaporer des
matériaux composés tels que les oxydes et les nitrures.

Faisceau d'électrons
Figure II.2. Schéma de principe d'un
système de chauffage par un faisceau d'électrons
[26].
II.2.1.4 Evaporation par un faisceau Laser
Le principe de cette technique consiste à irradier la
surface du matériau à évaporer placédans
un creuset, par un faisceau laser avec condensation sur le substrat;
l'élévation de la
température très rapide d'une zone de
très petite surface du matériau donne une évaporation
instantané, et donc une reproduction de la stoechiométrie du
matériau de source dans le flux de vapeur et en général
dans la couche déposée [25]. Cette technique
donne de bons résultats pour les dépôts des
supraconducteurs, alliages ferroélectriques et les mélanges des
matériaux composés. Elle permet de donner une
stoechiométrie des couches déposées celle des
matériaux massif [25,26]. L'évaporation par un
faisceau laser nécessite de mettre la source du laser à
l'extérieur de la chambre à vide et de transmettre le faisceau
laser au travers d'une fenétre (hublot) transparente à
la longueur d'onde du laser utilisé, mais dans le méme temps
compatible avec la bande d'absorption du matériau à
évaporer [26].

Figure II.3. Schéma conventionnelle de
l'ablation Laser [26].
60
II.2.1.5 Dépôt par pulvérisation
cathodique
La pulvérisation est un processus qui peut se
définir comme étant l'éjection des atomes superficiels
d'un matériau à déposer par des atomes ionisés d'un
gaz, en général inerte, et le transfert de ces atomes
éjectés sur un substrat que l'on désire recouvrir d'une
couche mince. Ce processus s'effectue dans une chambre sous vide ; après
pompage dans l'enceinte jusqu'à 10-4 - 10-7
Torr [26], on introduit un gaz généralement
de l'argon, à la pression 10-3 à
10-1 Torr [27]. Le plasma est crée
par l'application d'une tension électrique sur la cible, variant
entre 500 et 5000 Volts
[26]. Ce plasma apparaît sous forme d'un nuage luminescent
localiséentre les deux électrodes (cible et substrat).
Au méme instant, un courant électrique s'établit
entre l'anode et la cathode. Les électrons sont
attirés par l'anode (substrat), et les ions positifs sont attires par la
cathode (cible). Les atomes superficiels de la cible sont expulsés de
celle-ci sous l'effet de l'impact des ions positifs contenus dans le gaz
luminescent, et sont ensuite déposés sur le substrat. Ce dernier
se recouvre progressivement d'une couche du méme matériau que
celui de la cible ; on distingue trois différents types de
pulvérisation dont la diode DC, radio fréquence et à
magnétron [28].

Figure II.4. Schéma de principe de la
pulvérisation cathodique [10].
II.2.1.5.1 Pulvérisation DC (direct curent)
La technique DC consiste en l'application d'une tension
continue de l'ordre de 3 a 5 KeV. Généralement cette
technique est utilisée pour les dépôts des couches minces
conductrices.
Au cours du dépôt, la cible est chargée
positivement sous l'impact des ions positifs, si cette cible est isolante, la
charge positive qui y apparaît ne peut s'écouler. Par
conséquent, le plasma s'éteint et le dépôt ne peut
plus se produire, ce qui explique la restriction de l'utilisation de la
pulvérisation DC aux dépôts des
conducteurs [28].

Figure II.5. Système de
pulvérisation DC [10].
II.2.1.5.2 Pulvérisation RF (radio fréquence)
La technique RF est utilisée pour le
dépôt des conducteurs ainsi que ceux des couches minces isolantes
et semiconductrices. A cet effet le problème rencontré dans le
cas d'une cible isolantes en pulvérisation DC peut être
évité, puisque la tension appliquée aux bornes des
électrodes est un signal alternatif, le plasma contenant autant d'ions
que d'électrons, la polarisation alternative de la cible fait que
pendant l'alternance négative, la cathode attire les ions qui la
pulvérisent, en la chargeant positivement. Pendant l'alternance
positive, elle attire les électrons qui la déchargent
[28].
II.2.1.5.3 Pulvérisation à magnétron
Cette technique consiste à utiliser un aimant permanant
sous la cible, ce dernier permet d'obtenir un bon confinement du plasma. Le
champ magnétique constitue un piège à électron, les
électrons se déplacent suivant une trajectoire cycloïdale
dans une direction qui est à la fois perpendiculaire au champ
électrique et au champ magnétique. Par conséquent, ils
acquièrent une énergie plus grande et surtout ils parcourent des
distances beaucoup plus grandes que dans la technique rf. Les
collisions ionisantes sont donc plus nombreuses induisant, des densités
de courant ionique sur la cible plus importantes. Le plasma intense ainsi
créé permet
des vitesses de pulvérisation élevées
à des pressions assez basses. Cette technique de pulvérisation
peut être en mode RF ou DC [28].
|
Les avantages de la pulvérisation sont
|
|
- Le dépôt de n'import quel film (simple,
composé, réfractaire) est rendu possible sur n'importe quel
substrat (isolant, semi-conducteur).
- La composition d'une couche mince déposée par
pulvérisation tend à être la méme que celle de la
cible.
- L'obtention de couches stoechiométriques et
reproductibles.
- L'élimination des interférences de la couche
d'oxyde natif à l'interface.
- Les atomes pulvérisés sont
éjectés de la surface cible avec des énergies
cinétiques considérables, 5 à 100 fois
supérieures à celles des atomes obtenus en évaporation;
ceci est un facteur très important pour l'amélioration de la
structure des films et de leur adhésion au substrat.
II.2.2 les méthodes de dépôt
chimique
II.2.2.1 Dépôt en phase vapeur chimique
(CVD)
Le dépôt en phase vapeur chimique (CVD) est une
méthode dans laquelle le ou les constituants d'une phase gazeuse
réagissent pour former un film solide déposé sur un
substrat. Les composés volatils du matériau à
déposer sont éventuellement dilués dans un gaz porteur et
introduits dans une enceinte où sont placés les substrats. Le
film est obtenu par réaction chimique entre la phase vapeur et le
substrat chauffé. Dans certains cas, une élévation de
température est nécessaire pour maintenir la réaction
chimique. Le CVD est un domaine interdisciplinaire, il comprend un ensemble de
réactions chimiques, un processus thermodynamique et cinétique,
un phénomène de transport [28]. La
réaction chimique est au centre de ces disciplines: elle
détermine la nature, le type et les espèces présentes. Il
existe deux types de réacteurs: le réacteur à paroi chaude
et le réacteur à paroi froide.
- Dans le cas du réacteur à paroi chaude, ce
dernier est chauffé directement, ce qui permet d'opérer à
plus faible pression: à peu près 75 mtorr, pour lesquels des
dépôts se produisent bien sur les substrats, mais aussi sur les
parois (technique LPCVD : Low-Pressure Chemical Vapor Deposition)
[28].
- Dans le cas du réacteur à paroi froide, seul
le substrat est chauffé, si bien que la réaction n'est effective
qu'au niveau du substrat chauffé; elle se produit à pression
atmosphérique. Le principe de cette méthode de dépôt
est présenté dans la figure II.6, dans le cas de la paroi
chaude.


Figure II.6. Schéma de principe de
dépôt en phase vapeur chimique (CVD) dans un
réacteur
à parois chaudes [28].
La réaction chimique peut être activée
à l'aide d'un plasma. Cette méthode s'appelle ( PECVD : Plasma
Enhanced Chemical Vapor Deposition). Dans ce cas, il y a création de
particules énergétiques en plus [28].
La fabrication de couches minces métalliques grâce
à ces méthodes s'est particulièrement
développée ces dernières années.
Les avantages de ce procédé sont les suivants :
- La facililité d'obtenir un assez grand nombre
d'éléments ou de composés chimiques. - La présence
d'une bonne qualité des couches.
- Un excellent recouvrement des marches.
- Une bonne adaptabilité dans une chaîne de
production.
- Elle offre la possibilité de réaliser des
dépôts sélectifs, permettant d'éliminer une
étape de gravure et de planarisation de la surface.
Les inconvénients sont les suivants :
- Les films sont peu denses, souvent contaminés par des
gaz très réactifs issus de la réaction chimique
(hydrogène, fluor, chlore...).
- Tous les matériaux ne peuvent être
déposés par CVD.
- Le système de dépôt est relativement lourd
à mettre en oeuvre.
II.3 Aspect physique de l'oxydation thermique du silicium
Le Silicium (Si) peut être oxydé thermiquement
comme nous avons fait dans notre travail mais aussi par anodisation
électrochimique et par réaction chimique dans un plasma.
L'oxydation thermique est le procédé le plus important et le plus
utilisé en technologie des dispositifs en silicium.
L'oxydation thermique de Si est réalisée dans
des fours cylindriques entre 900 et 1200 °C par voie
humide dans un flux de vapeur d'eau pure ou par voie sèche dans un flux
d'oxygène pur sec, les flux étant de l'ordre de
10-2 ms-1. Les réactions de base sont
:
Si + O2 - SiO2 (2.1)
Si + 2H2O - SiO2 + 2H2 (2.2)
Néanmoins, le processus d'oxydation est
compliqué. Les paramètres thermiques, géométriques,
et hydrodynamiques doivent être sous contrôle précis.
Pendant l'oxydation, l'interface SiO2-Si se déplace progressivement dans
le silicium en consommant une épaisseur de silicium égale environ
à la moitie de la couche d'oxyde produite (figure II.7). L'oxyde
formé est amorphe avec une structure relativement ouverte propice
à la diffusion de l'espèce oxydante.
eSi épaisseur de Si consommé

eox épaisseur de l'oxyde formé
Si polycristallin
Figure II.7. Représentation de
l'épaisseur de SiO2 et de Si consommé.
Pour estimer l'épaisseur de Si consommé, tout
d'abord on calcul la masse de celui-ci comme suit :
mSi = dSi VSi = dSi S eSi (2.3)
Ainsi, on peut évaluer la masse de SiO2 formé
à partir du substrat de Si :

(2.4) - (2.5)

(2.5) - (2.6)
Avec :
dSi : masse volumique de Si égale à 2.33
g/cm3. MSi : masse molaire de Si égale à
28.08 g/mole. dSiO2 : masse volumique de SiO2 égale à
2.3 g/cm3.
MSiO2 : masse molaire de SiO2 égale à
60.08 g/mole. CSi : concentration de Si égale à 5 x
1022 atomes/cm3.
CSiO2 : concentration de SiO2 égale à 2.3
x 1022 molécules/cm3.
N : nombre d'Avogadro égale à 6.023 x
1023. eSi : épaisseur de Si consommé.
eSiO2 : épaisseur de SiO2 formé.
Nous présenterons un modèle cinétique de
l'oxydation thermique qui rend compte de certains mécanismes et
propriétés prédominants. Comme cela est
représenté à la figure II.8, on considère la couche
oxydé en régime de croissance. Elle sépare le milieu
oxydant où la concentration d'équilibre à la surface vaut
C0 de la surface du silicium où la concentration Ci
est déterminée par la diffusion de l'agent oxydant à
travers la couche d'oxyde. Dans le gaz
oxydant, la concentration d'équilibre à la surface
de l'oxyde est proportionnelle à la pression partielle
[29].
Gaz
oxydant oxyde silicium

Concentration C
C0 Ci

Concentration C
C0
Figure II.8. Représente l'oxydation
thermique du Si : a) modèle cinétique, b) croissance de l'oxyde
thermiquement dans les deux cas limites controlés par respectivement la
réaction de surface et la diffusion.
0 di d épaisseur x


a)
b)
k -* 0 (limité par la réaction de
surface)
D -*0 (limité par la diffusion)
La diffusion des molécules oxydantes à travers la
couche d'oxyde est caractérisée par un coefficient de diffusion
D. pour une épaisseur de couche x, le flux F1
peut s'écrire :
Et en tenant compte de l'hypothèse qu'a l'interface SiO2 -
Si, le taux de réaction est proportionnel aux concentrations des
réactants de sorte que le flux à l'interface s'écrit :
F2 = k Ci (2.8)
Où k est la constante de taux de réaction
chimique de surface pour l'oxydation. A l'état stationnaire, F = F1
= F2 et Ci peut être éliminé :
Le nombre volumique N de molécules de SiO2
dans l'oxyde de silicium vaut 2.2 x 1028 m-3. On
admet que l'on incorpore à chaque molécule de SiO2 une
molécule O2 ou deux molécules H2O. Ainsi, le nombre volumique de
molécules oxydantes N1 dans l'oxyde vaut 2.2 x 1028 m-3
pour l'oxydation sous oxygène sec et le double pour l'oxydation
dans la vapeur d'eau.
L'équation de continuité permet d'écrire
pour le flux oxydant atteignant l'interface oxydesilicium :
C'est une équation différentielle pour le taux
de croissance de la couche d'oxyde. Compte tenu d'une épaisseur d'oxyde
initiale di (due à la formation naturelle sur le silicium), la
solution de l'équation différentielle (2.10) est de la forme :
x2 + Ax = B (t + ô) (2.11)
où A = 2D/k, B = 2DC0/N1 et B/A =
kC0/N1. La constante ô = (di 2 + 2D di/k)Ni/DC0
exprime le changement d'origine de l'échelle de temps qui tient compte
de la couche d'oxyde initiale d'épaisseur di. La solution de
l'équation (2.11) pour exprimer la variation de l'épaisseur de la
couche d'oxyde en fonction du temps est standard.
Deux comportements asymptotiques s'en dégagent et
décrivent le début de l'oxydation. (t petit) d'une part
et la croissance d'une couche d'oxyde déjà épaisse,
(t grand) d`autre part. Pour t petit, le terme
linéaire dans la relation (2.11) est le plus important. La solution est
de la forme :
B/A est appelé constante de taux de croissance
linéaire. L'épaisseur de la couche d'oxyde augmente
proportionnellement au temps de réaction t. la croissance est
limitée par le taux de réaction chimique à l'interface
k. c'est le mécanisme le plus lent (k -)0 dans la
figure II.8. (b)). Pour des couches épaisses, t est grand ; le
terme parabolique dans la relation (2.11) prédomine ; la solution est de
la forme :
Où B est la constante de taux de croissance
quadratique. L'épaisseur de la couche d'oxyde augmente comme la racine
du temps de réaction . C'est la diffusion qui limite la croissance de
l'oxyde (D - 0 dans la figure II.8. (b)).
Dans tous les cas, l'oxydation thermique est un processus
activé thermiquement. La constante de taux de croissance linéaire
dépend de l'orientation cristalline de la surface de silicium
oxydée. L'énergie d'activation de l'ordre de 2 eV pour
l'oxydation sèche et humide est comparable à l'énergie de
la liaison chimique Si - Si qui doit être rompue.
La constante de taux de croissance quadratique est
indépendante de l'orientation de la surface de silicium.
L'énergie d'activation vaut 1,24 eV pour l'oxydation
sèche et 0,71 eV pour l'oxydation humide.
Les propriétés électriques de l'oxyde
thermique produit sous oxygène sec sont supérieures à
celles de l'oxyde fait sous vapeur d'eau. Les oxydes minces, comme les oxydes
de grille, sont donc préparés par oxydation sèche, tandis
que pour les oxydes de champ d'isolation ou de passivation qui exige des
couches d'oxyde épaisse, elles sont faites par voie humide
[29].
II.4 Procédure expérimentale
II.4.1 Préparation des plaquettes de silicium
polycristallin
Pour les besoins de réalisation de notre capteur de gaz,
notre choix s'est porté sur des substrats (plaquettes de Si
polycristallin), présentant les caractéristiques suivantes.
Tableau II.1. Propriétés
générales des plaquettes de Si utilisés.
|
Propriété
|
Valeur
|
|
Si
|
Polycristallin
|
|
Masse volumique
|
2330 kg.m-3
|
|
Chaleur massique
|
700 J / (kg.°K)
|
|
Conductivité thermique
|
148 W / (m.°K)
|
|
Résistivité à 300 °K
|
1.6 x 103 ?.cm
|
|
Dimension des plaquettes
|
(L x l x e) = (80 x 0 x 0.24) mm
|
Remarque 1 :
Avant de nettoyer les substrats de Si, on découpe la
plaquette à l'aide d'un coupe silicium spécialement conçue
en quatre substrats identiques ayant les dimensions suivantes : (L x
l x e) = (40 x 40 x 0,24) mm.
II.4.1.1 Nettoyage
Pour éviter toute mauvaise adhérence des couches
minces sur le substrat de Si, il doit être nettoyé pour
éliminer toutes traces d'impuretés (poussière,
humidité...). Dans un bac ultrason contenant de l'eau distillée
(voir annexe) on trempe ces derniers dans des béchers contenant chacun
de l'acétone, de l'éthanol pendant 15 min à une
température de 40 °C, puis dans de l'eau distillée
à une température de 50 °C pendant 15 min. Et enfin
ils sont séchés par l'intermédiaire d'un flux d'azote
comprimé à l'aide d'un générateur d'azote avec un
débit d'écoulement de 15 L/min (voire annexe).
II.4.1.2 oxydation thermique des plaquettes de Si
(polycristallin)
L'oxydation thermique de silicium à était
réalisée dans un four à moufle (voir annexe), à une
température de 1100 °C par voie humide (en présence de
vapeur d'eau (humidité ambiante 70%) et d'oxygène).
L'opération a duré six heures (6h) jusqu'à obtenir sur les
deux faces de Si une couleur violette.
Système de chauffage

Interrupteur d'allumage
Commande de contrôle de température
Circuit d'entrée d'air
Système d'entrée d'air
Substrat de Si
Support en quartz
Figure II.9. Schéma de principe du four
servant à l'oxydation de Si.
II.4.1.3 découpage des plaquettes de Si
(polycristallin)
Après oxydation de silicium, on passe à la
dernière étape avant les dépôts des
différentes couches minces. Mené d'un coupe silicium
spécialement conçu pour ca, nous découpons le substrat de
Si en plusieurs petits substrats ayant la dimension suivante : (L x
l) = (5 x ) mm.
Couche de SiO2 formée par oxydation thermique.
Wafer de silicium polycristallin comme substrat
Couche de SiO2 formée par oxydation thermique.

2 mm
5 mm
Figure II.10. Les dimensions des substrats de Si
utilisé.
II.4.2 Réalisation du capteur de gaz
II.4.2.1 Description du montage expérimentale
Pour aboutir à la réalisation de notre capteur
de gaz, nous avons opté pour une méthode physique de
dépôt des couches minces, à savoir la pulvérisation
cathodique rf. Ou un système de pulvérisation
radiofréquence RFS 200 « radio frequency sputtering » (voir
annexe), disponible au sein de notre laboratoire LMESM, présentant les
caractéristiques et les performances suivantes (voir tableau II.2).
Tableau II.2. Présentation de
principales caractéristiques et performances du
pulvérisateur
cathodique radiofréquence RFS 200
[6].
|
Alimentation radiofréquence
|
Puissance variable de : 0 ~ 200 W.
Fréquence radio :
13,56 MHz.
|
|
Système de vide
|
Pompe mécanique (pour assuré le
vide
primaire).
Pompe à diffusion (pour assuré le
vide
secondaire).
|
|
Dimensions et poids
|
(L x l x p) = (1625,5 x 0 x ) mm, ~
200kg
|
|
Alimentation électrique
Alimentation
électrique pour le générateur rf
|
Monophasé 100V (50Hz/60Hz) 1,8 kW
Monophasé
100V/200V (50Hz/60Hz) 490W
|
|
Condition de l'eau de refroidissement
|
Débit 5L/min, au dessous de 25 °C avec
une
pression (200 ~ 300 kPa).
|
Performance du pulvérisateur cathodique
radiofréquence RFS 200
10-5 Pa -* 10-8 Torr
Pression finale ou du vide secondaire
Pression du vide primaire
9 10-1 Pa -* 6,7 10-3 Torr
Pression de travail ou de pulvérisation
~ 10-3 Torr pour un gaz d'Argon (Ar).
II.4.2.2 Conception du four intégré
Une fois que les substrats de Si sont préts à
l'utilisation, vient la deuxième démarche pour la
réalisation de notre capteur, à savoir le dépôt de
couches minces métalliques (Ni, W), celui du diélectrique (SiO2)
pour une face du substrat de Si et de la couche sensible semiconductrice (ZnO
non dopé, ZnO :1%Al, ZnO :3%Al et ZnO :1%Cu) pour l'autre face par
pulvérisation cathodique rf.
II.4.2.2.1 Dépôt de couche mince de Nickel
Nous avons utilisé dans nos dépôt une cible
de nickel (Ni), avec une pureté de 99,99 %, présentant les
dimensions suivantes : diamètre = 80 mm, épaisseur = 1mm.
Pour obtenir des dépôts de Ni avec les
propriétés physiques désirées dans notre travail,
nous avons opté pour les paramètres de dépôt
indiqués dans le tableau II.3 :
Tableau II.3. Paramètre de
dépôt de nickel.
|
Pression du vide primaire
|
1.6 Pa
|
|
Pression du vide secondaire
|
3.4 10-3 Pa
|
|
Distance cible-substrat
|
3 cm
|
|
Pression d'argon
|
1.0 Pa - 7 mTorr
|
|
Puissance fournie
|
80 Watts
|
|
Temps de dépôt
|
De 1/4 heures à 1/2 heures
|
|
Température du substrat
|
Entre 64 et 72 °C
|
II.4.2.2.2 Dépôt de couche mince de
Tungstène
Nous avons aussi utilisé dans nos dépôts une
cible de Tungstène (W), avec une pureté de 99,95 %,
présentant les dimensions suivantes : (L x l x e) = (100 x100 x ) mm
Pour obtenir des dépôts de W avec les
propriétés physiques désirées dans notre travail,
nous avons choisi les paramètres de dépôt indiqués
dans le tableau II.4 :
Tableau II.4. Paramètre de
dépôt de Tungstène.
|
Pression du vide primaire
|
1.6 Pa
|
|
Pression du vide secondaire
|
3.0 10-3 Pa
|
|
Distance cible-substrat
|
3 cm
|
|
Pression d'argon
|
1.3 Pa - 9 mTorr
|
|
Puissance fournie
|
80 Watts
|
|
Temps de dépôt
|
De 1/4 heurs à 1/2 heurs
|
|
Température du substrat
|
Entre 74 et 81 °C
|
II.4.2.2.3 Dépôt de couche mince
diélectrique
La cible diélectrique amorphe du dioxyde de silicium
SiO2 qu'on a utilisée est en verre pur 99.99% et donc
relativement seuls les atomes de silicium et de l'oxygène contribuent
à la formation de la couche. Sont rôle est de protéger la
plaque chauffante formée par la couche mince de nickel et
Tungstène.
Pour réussir notre dépôt nous avons
adopté les paramètres indiqués dans le tableau II.5.
Tableau II.5. Paramètre de
dépôt de SiO2.
|
Pression du vide primaire
|
1.7 Pa
|
|
Pression du vide secondaire
|
6.0 10-3 Pa
|
|
Distance cible-substrat
|
3 cm
|
|
Pression d'argon
|
1.4 Pa - 10 mTorr
|
|
Puissance fournie
|
90 Watts
|
|
Temps de dépôt
|
1/2 heures
|
|
Température du substrat
|
Entre 96 et 100 °C
|
Couche d'isolation formée par le SiO2
Wafer de silicium polycristallin comme substrat

1mm 3mm
1mm
Couche d'isolation formée par le SiO2
Couche mince métallique formée par (Ni+W) comme
mini four intégré
Couche d'isolation formée par le SiO2
Figure II.11. Représentation de la
configuration finale du four.
II.4.2.3 Réalisation de couches minces d'oxyde
de zinc non dopée et dopée II.4.2.3.1
Dépôt de ZnO non dopé et dopé
Pour les besoins d'élaboration de la couche sensible de
notre capteur de gaz nous avons choisie quatre cibles de ZnO non dopé,
ZnO dopé 1% et 3% d'Aluminium et ZnO dopé 1% de Cuivre. Tous
ayant une pureté de 99,99%.
Les paramètres de dépôt sont indiqués
dans le tableau II.6.
Remarque 2 :
La cible de ZnO non dopé a été soumise
à un recuit sous air à la température de 300 °C, afin
de rétablir la stoechiométrie en surface de la cible qui avait
déjà été utilisée auparavant.
Tableau II.6. Paramètre de
dépôt de ZnO non dopé et dopé.
|
Pression du vide primaire
|
|
1.4 Pa
|
|
Pression du vide secondaire
|
|
4.8 10-3 Pa
|
|
Distance cible-substrat
position
|
|
3 cm
position //
|
|
Pression d'argon
|
|
2 Pa - 15 mTorr
|
|
Puissance fournie
|
|
120 Watts
|
|
Temps de dépôt
|
|
3 heurs
|
|
Température du substrat
|
ZnO
153 °C
|
ZnO : 3% Al
127 °C
|
ZnO : 1% Al
126 °C
|
ZnO : 1% Cu
133 °C
|
|
Couche sensible aux gaz formée par le ZnO non dopé
et dopé Couche d'isolation formée par le SiO2
Wafer de silicium polycristallin comme substrat
Couche d'isolation formée par le SiO2
Couche mince métallique formée par (Ni+W) comme
mini four intégré
Couche d'isolation formée par le SiO2
|
Figure II.12. Configuration finale de notre
capteur de gaz, intégrant à la fois les
éléments
chauffants et sensibles aux gaz.


II.5 Introduction
Au titre de cette seconde partie du chapitre (II), nous
aborderons les différentes méthodes de caractérisation
effectuées au sein et hors de notre laboratoire pour mener à bien
nos différents travaux.
II.6 caractérisation structurelle et
morphologique II.6.1 Diffraction des rayons X
La diffraction des rayons X (DRX) est une technique de
caractérisation qui permet de déterminer la structure
cristalline, et l'orientation cristalline des échantillons
étudiés. Cette dernière information est très utile
dans le cas de dépôt de couche mince sur un substrat.
Les techniques de diffraction des rayons X ont pris un essor
à partir de 1912. La technique a évolué très
rapidement, et les premières structures cristallines simples ont
été déterminées d'après l'expérience
de Laue, W. H. Bragg et W. L. Bragg [19].
Son principe repose sur l'interaction d'un faisceau de rayons
X avec la matière qui donne naissance au phénomène de
diffusion cohérente dans toutes les directions. Lorsque la distribution
des atomes est périodique, les ondes diffusées peuvent conduire
à des interférences si elles sont en phase. Les directions des
ondes émises en phase, correspondent à la condition de
diffraction, définie par la relation de Bragg [18] :
2 dhkl sin(è)= n ë (2.14)
dhkl distance inter-réticulaire d'une famille de
plan (hkl).

Rayons X incidents Rayons X diffractés
dhkl
èhkl
èhkl
2èhkl
d : distance inter-réticulaire 2
èhkl : angle de diffraction ë : longueur d'onde du RX
n : ordre de diffraction
Figure II.13. Géométrie de
diffraction (èhkl -2èhkl) et la loi de Bragg
[23].
Les mesures de diffraction X sont effectuées avec un
diffractomètre à poudre, utilisant un faisceau incident, la raie
Ká du cuivre (ë = 1.54 ?) obtenue par
un monochromateur germanium.
Le diffractomètre est utilisé en mode
è-2è. Dans ce mode, le détecteur est
positionné en permanence de façon à ne recevoir que les
faisceaux diffractés par les plans réticulaires parallèles
à la surface de l'échantillon.
Cette technique permet de savoir si les couches sont
cristallisées ou non, elle fournit de précieuses informations sur
les phases présentes dans les couches minces observées
[19] et leurs orientations. Ainsi on peut estimer la taille des grains
présents dans cette couche mince et cela grâce à la formule
de Scherer :
Où :
D représente la taille moyenne des cristallites
(grains).
ë la longueur d'onde de rayon X.
Äèhkl largeur a mi-hauteur du pic de
diffraction de Bragg avec un angle èhkl. k : constante
qui vaut = 0.9.
II.6.2 Caractérisation morphologique des
échantillons par microscope électronique à balayage (MEB)
Un microscope électronique à balayage de type
HITACHI S2500 (voir annexe) est disponible au sein de notre laboratoire de
microscopie électronique et sciences des matériaux, pour
étudier la morphologie et la texture de la surface de nos
échantillons.
Sont principe de fonctionnement repose sur l'émission
des électrons produits par un filament et la détection de signaux
provenant de l'interaction des ces derniers avec l'échantillon en
question sous vide, ces électrons qui irradient la surface de
l'échantillon pénètrent dans le matériau est
effectuent une interaction pour former ce qu'on nomme habituellement «
poire d'interaction ». Le volume de cette poire va dépendre du
numéro atomique moyen de l'échantillon et de l'énergie des
électrons incidents. Dans ce volume d'interaction, les électrons
du faisceau vont perdre leurs énergies par collision multiples avec les
atomes du matériau, générant ainsi de nombreux
phénomènes secondaires à savoir : l'émission des
électrons et photon, l'absorption des électrons, le
courant induit, le potentiel électrique, l'élévation de
température locale et la vibration du réseau
[6].
II.7 caractérisation électrique
II.7.1 Méthode de la pointe chaude pour la
détermination du type de conductivité dans un semiconducteur
C'est une technique qui repose sur le principe de l'effet
thermoélectrique, elle est rapide, fiable et très utilisée
pour déterminer le type de conductivité d'un semiconducteur.
L'outillage nécessaire est simple, il consiste simplement en une source
de chaleur (fer à souder comme exemple) et un
Milliampèremètre. Le fer à souder va jouer le rôle
d'une source de chaleur pour l'électrode positive du
milliampèremètre et l'électrode négative va jouer
le rôle d'une pointe froide (figure II.14) [30]. Le
milliampèremètre va indiquer une valeur positive ou
négative qui indique le type des porteurs majoritaires ; sens positif
type n, sens négatif type p. En effet, l'application de la pointe chaude
donne de l'énergie aux électrons du semiconducteur, ce qui
crée des électrons libres, la concentration des porteurs
majoritaires alors augmente, ces derniers sous l'effet du gradient de leur
concentration diffusent de la pointe chaude (qui leur donne naissance) vers la
pointe froide. Le courant électrique qui en résulte est
bouclé à travers le milliampèremètre
extérieur. Le courant qui résulte de cette diffusion est
défini par la première loi de Fick :
Pour un SC type n :
Pour un SC type p :
Avec :
q : la charge des électrons.
n, p : nombre de porteur des électrons et des
trous respectivement.
ìn, ìp : mobilité des
électrons et trou respectivement.
E : champ électrique.
Ou le champ électrique E produit par un gradient de
température est dit par définition le pouvoir
thermoélectrique absolu (Q) suivant l'expression :
On remplace (2.18) dans les deux relations (2.16) et (2.17) :
Pour un SC type n
Et pour un SC type p
Qn, Q,, : pouvoir thermoélectrique
absolu ; Qn < 0, Q,, > 0. dT/dx : gradient
de température.

Figure II.14. Pouvoir thermoélectrique
en fonction de la température dans le silicium n et p. au-dessus de 600
°K, les échantillons deviennent intrinsèque. Les ont
été calculées et les points représentent les
mesures expérimentales [23].
Chapitre II Procédure expérimentale et
Techniques de caractérisation

Pointe froide
Pointe chaude
-V+
0
Déplacement
d'électrons
pour
équilibré
la région
e-
SC type n

Pointe froide
Pointe chaude
-V+
0
Déplacement
de trou
pour
équilibré
la région
p-
SC type p

Pointe froide
Pointe chaude
Zone
chargée (-)
Zone
chargée (+)
-V+
Champ électrique SC type n

Pointe froide
Pointe chaude
Zone
chargée (+)
Zone
chargée (-)
-V+
Champ électrique SC type p
(a) (b)
Figure II.15. Schéma de principe de
technique de la pointe chaude : (a) SC type n, (b) SC
type p
L30].
II.7.2 Mesure de l'épaisseur des couches minces
métalliques par la méthode des quatre pointes
La méthode des quatre pointes est utilisée pour
la mesure de la résistivité des semi conducteurs épais ou
en couche déposée sur un isolant dans la majorité des
cas L22]. Mais, elle peut aussi être sollicitée
pour mesuré l'épaisseur de couches minces métalliques la
ou la résistivité ne varie pas beaucoup. Cette technique a deux
variantes :
v' La méthode des quatre pointes alignées (ou de
Wenner).
v' La méthode des quatre pointes carrées (ou de Van
der Pauw).
Nous avons utilisé la méthode des quatre pointes
alignées pour la mesure de l'épaisseur de nos
échantillons. Les quatre pointes conductrices (A B C D de gauche
à droite respectivement) et disposées en ligne droite de
méme espacement sont appliquées à l'échantillon
comme le montre la figure II.14 par simple pression (voir annexe). Un courant I
est injecté au point A. les équipotentielles sont des cylindres
de rayons r, et de hauteur e, avec une surface : S = 2 ð r e. les lignes de
courant sont parallèles à la surface entre deux cylindres
séparés d'une distance dr [6].

Ampère mètre
Surface équipotentielle V=cte
I
Ligne de courant
dr
Générateur de
tension
V
Échantillon
Figure II.16. a)Configuration des quatre
pointes alignées, b) Lignes de courant et
surfaces
équipotentielles pour couche mince.
La résistance entre deux cylindres est donnée par
:
dR = ñ dr / (2 ð r e) (2.21)
Où ñ c'est la résistivité, e
l'épaisseur et r le rayon du cylindre équipotentielle.
La différence de potentielle (ddp) ainsi crée entre
les deux cylindres B et C est donnée selon la loi d'Ohm :
dV = I dR = I ñ dr / (2 ð r e) (2.22)
Entre les pointes B et C distantes de rAB
et rAC, on pourra calculer la chute de tension on
intégrant la relation II.19.
(2.23)
Dans le cas ou rAC = 2rAB l'équation 2.20 devient :
VBC = ñ I ln(2)/ (2 ð e) (2.24)
On déduit que la résistivité s'écrit
:
ñ = (e 2 ð /ln (2)) VBC/I (2.25)
en tenant en compte des effets d'interactions entre les lignes de
courants et de la forme géométrique de l'échantillon, la
résistivité ñ tiens compte du facteur de forme F(
a/d, d/s, e/s).
ñ = (e 2 ð /ln (2)) VBC/I F(a/d, d/s,
e/s) (2.26)
donc l'expression de la résistivité devient:
ñ = 4,53 e VBC/I F(a/d, d/s, e/s)
(2.27)
Dans l'approximation ou les couches minces sont
considérées comme des matériaux bidimensionnels dont
l'épaisseur l est suffisamment petite devant la distance entre les
pointes, l'expression (2.27) devient :
ñ = e Rsheet (2.28)
avec
Rsheet = VBC/I F(a/d, d/s, e/s) 4.53 (2.29)
F(a/d, d/s) F(a/d) et F(e/s) = 1 (2.30)
II.8 Banc d'essai et de mesure de la réponse du
capteur au gaz d'éthanol II.8.1 Gaz utilisé
Le choix de gaz à détecter dépend des
applications visées. Dans ce travail, nous avons utilisé le gaz
d'éthanol C2H5OH.
L'éthanol ou alcool éthylique est un alcool
possédant la structure semi-développée suivante :
CH3-CH2-OH. C'est un liquide incolore, miscible dans l'eau en toutes
proportions. Produit pour la première fois par fermentation de sucres
naturels, actuellement on le fabrique industriellement par hydratation de
l'éthylène.
L'éthanol est utilisé comme intermédiaire
de synthèse dans l'industrie chimique et comme solvant.
Présentement on l'utilise comme source d'énergie motrice
alternative aux hydrocarbures. S'agissant d'un produit volatile qui passe de
l'état liquide à l'état gazeux à température
ambiante, son large champ d'application touche tant les unités à
prévenir des risques que ceux relatifs au contrôle de
qualité alimentaire (station service, silos à grain, chambre
froide de stockage, etc....).
II.8.2 Concentration du gaz débité dans le
dispositif de détection
Nous avons eux recours à une technique
développée dans notre laboratoire (LMESM) (voir annexe) depuis
déjà quelques années, pour calculer la concentration de la
vapeur d'éthanol générée à partir de sa
phase liquide sous l'influence d'un flux d'azote N2 (comme gaz
vecteur) de débit fixé à 5 (l/min) maintenu
durant toute l'opération du barbotage (figure II.17).
Chapitre II Procédure expérimentale et
Techniques de caractérisation

8
7
1
2
3
4
6
5
Figure II.17. Schéma de principe du
barbotage suivi au LMESM pour contrôlé la variation
du
Débit d'éthanol. 1. Entrée d'Azote
N2, 2. Sel gemme pour éliminer l'humidité,
3. Sortie du
gaz N2 sans humidité, 4.
Bocal en verre, 5. Support métallique,
6. Ethanol liquide, 7. Sortie de
gaz
Ethanol + N2, 8. Seringue pour contrôler le volume
d'éthanol.
Nous nous basons sur le développement des
paramètres chimiques fondamentaux de la solution utilisée
(l'éthanol liquide dans notre cas) :
Avec :
Déthanol = 0,7896,
ñéthanol La masse volumique de
l'éthanol, ñeau La masse volumique de l'eau
= 1g/cm3 (CGS).
En premier lieu, il faut calculer le volume de l'éthanol
gazeux V':
Est le nombre de moles de C2H5OH contenues dans le
volume V. avec :
N, D, M, m sont respectivement Le
nombre de moles, la densité de l'éthanol, la masse molaire de
l'éthanol, la masse d'éthanol.
donc :
Le débit d'éthanol gazeux s'écrit donc comme
suit :

Finalement, la concentration de l'éthanol gazeux
porté par l'azote se fait évaluer à partir du rapport
comme suit :
Et pour une concentration donnée en multiplie par
106 pour trouver sa valeur en ppm (partie par million).
II.8.3 Banc de caractérisation électrique du
capteur de gaz
Nous avons mis en place un dispositif expérimental,
conçu spécialement dans notre laboratoire (LMESM) (voir annexe)
pour tester nos capteurs de gaz. Il est constitué d'une part d'un
système d'alimentation du four, et d'autre part d'un système pour
effectuer les mesures électriques, en l'occurrence la
résistance.
On met notre capteur dans sont emplacement. La partie
chauffage sera reliée avec un générateur de tension
accordé avec deux multimètres, un pour mesurer le courant qui
passe à travers le mini four et l'autre pour contrôler la tension
d'alimentation de ce dernier, tandis que la partie exposé aux gaz, sera
reliée à un multimètre numérique d'une grande
résolution, ou on suivra la variation de sa résistance pendant
:
- Le cycle d'échauffement sous air.
- Le cycle d'introduction du gaz d'éthanol (cf. la
réponse du capteur).
6 7

3
2
4
1
5
9
8
Figure II.18. Schéma de principe du
dispositif pour le test du capteur. 1. Entré de
gaz
(éthanol + N2). 2. Contact métallique (W)
pour mesurer la résistance de l'oxyde de zinc.
3.
Capteur de gaz. 4. Support en
céramique. 5. Contact métallique (en W) pour
mini four. 6.
Ampèrmètre. 7.
Générateur de tension pour l'alimentation du mini four.
8. Voltmètre. 9.
Digimètre
pour mesurer la résistance de ZnO non dopé et dopé.


III.1 Introduction
Au titre du chapitre (III), nous verrons les principaux
résultats retrouvés durant nos travaux qui ont conduit à
la réalisation de notre capteur de gaz. A savoir les performances du
mini four, ainsi que l'élément sensible aux gaz formé par
l'oxyde de zinc non dopé et dopé à l'aluminium (1 et 3%)
et au cuivre (1%).
III.2 Dimension du capteur de gaz obtenu
Selon le motif proposé au départ, nous avons obtenu
un capteur de gaz possédant la dimension indiquée sur la figure
III.1.
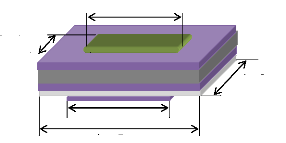
L" = 3 mm
l = 1 mm
l = 2 mm
L' = 3 mm
L = 5 mm
Figure III.1. Géométrie du capteur
de gaz réalisé en technologie des couches minces.
III.2.1 Mesures d'épaisseur et de résistance des
couches minces métalliques
A partir de la technique dite des quatre pointes aligné
(ou Wanner) décrites dans le chapitre précédent, et selon
le temps de dépôt, nous avons obtenus les résultats
suivants :
Tableau III.1. Mesure des épaisseurs
des couches minces métallique.
|
Echantillons
|
Temps de dépôt
(min)
|
Epaisseur des plaques
chauffantes (nm)
|
Résistance des mini
fours (?)
|
|
S1
|
15 min (Ni) +
15min (W)
|
eNi 37 nm, eW 14 nm
~ 51 nm
|
R0 (Ni/W) = 72 ?
|
|
S2
|
30 min (Ni) +
30 min (W)
|
eNi 78 nm, eW 27 nm
~ 105 nm
|
R0 (Ni/W) = 7 ?
|
Remarque 1 :
Les valeurs des résistances ont été
mesurées par la méthode directe à partir du dispositif de
test du capteur décri dans le chapitre précédent.
III.2.2 mesure d'épaisseur des couches minces
d'oxyde de silicium formée par oxydation thermique
Le microscope électronique à balayage (MEB) nous
a permis d'estimé l'épaisseur de l'oxyde de silicium (SiO2)
formé par oxydation thermique. Comme l'indique la figure III.2 et dont
les valeurs sont indiquées dans le tableau III.2.
Tableau III.2. Mesure des épaisseurs de
l'oxyde de silicium.
|
Si poly + SiO2
|
Epaisseur
|
|
Substrat de Si poly pur
|
230
|
~ 240 um
|
|
Substrat de Si poly pur restant
|
|
160 um
|
|
SiO2 face du substrat
|
|
80 um
|
|
SiO2 dos du substrat
|
|
30 um
|
|
Si + SiO2
|
300 um
|

Si poly-cristallin
e = 80 um
16 um
ZnO
Figure III.2. Image MEB
de
l'épaisseur de la couche de SiO2 coté
face du substrat
de Si, IM x 300.
III.2.3 Mesure d'épaisseur des couches minces
d'oxyde de zinc non dopé et dopé
Le microscope électronique à balayage (MEB) nous
a permis aussi d'estimer l'épaisseur de l'oxyde de zinc (ZnO) non
dopé et dopé déposé par pulvérisation
cathodique rf. Comme l'indique les figure III.3, III.4, III.5, III.6 et dont
les valeurs sont indiquées dans le tableau III.3.
Tableau III.3. Mesure des épaisseurs de
l'oxyde de zinc.
|
Echantillon
|
Temps de dépôt
|
Epaisseur des couches minces
|
|
ZnO non dopé
|
3h
|
1.5 um
|
|
ZnO : 3%Al
|
3h
|
1 um
|
|
ZnO : 1%Al
|
3h
|
1.5 um
|
|
ZnO : 1%Cu
|
3h
|
1 um
|

e = 1.5 Lm
1.5 Lm
e = 1 Lm
1.5 Lm
Figure III.3. Image MEB
de
l'épaisseur de la couche de ZnO avec
grossissement de 10k.
Figure III.4. Image MEB
de
l'épaisseur de la couche de ZnO : 3%
Al avec grossissement de
10k.
e = 1,5 Lm e = 1 Lm
1.5 Lm
1.5 Lm
Figure III.5. Image MEB
de
l'épaisseur de la couche de ZnO : 1%
Al avec grossissement de
10k.
Figure III.6. Image MEB
de
l'épaisseur de la couche de ZnO : 1%
Cu avec grossissement de
10k.
Nous observons d'après les figures III.3, III.4, III.5 et
III.6 que l'épaisseur des couches minces de ZnO non dopé et
dopé aluminium 1% sont plus importante que celles des couches minces de
ZnO dopé Al 3% et dopé cuivre 1%.
III.3 Mesure thermique effectué sur le mini four du
capteur
Les mesures thermiques ont été
réalisées suivant le montage décrit au chapitre
précédent, et afin d'obtenir l'effet joule dans le mini four,
nous avons utilisé une source de tension continue ou le courant maximale
que peut délivrer ce générateur est de 1 A, jouant le
rôle d'une batterie.
Le principe de la technique réside à faire
varier la tension d'alimentation et enregistrer à l'aide d'un
thermocouple la température d'équilibre ou de fonctionnement
atteint après un temps de stabilisation très court, environs 10
s.
Les valeurs mesurées sont indiquées sur les
courbes représentatives ci-dessous figure III.7, ou on a conservé
la même géométrie, et varie uniquement le temps de
dépôt des couches minces métalliques.

· Mini Four S1 -)dépôt (15 min Ni + 15 min
W) R0 = 72 ?
Mini Four S2 -)dépôt (30 min Ni + 30 min W) R0 = 7
?

Figure III.7. Évolution de la
température d'équilibre Tf du mini four en fonction de
la
puissance fournie.
On remarque selon les courbes obtenues que la
température d'équilibre TF est
proportionnelle
à la puissance fournie. Ce résultat concorde
exactement avec l'analyse théorique énumérer
dans le chapitre premier ; où on a trouvé que la
température d'équilibre était donnée par la
relation (1.59) :
Avec :
T0 : température ambiante.
V : la tension appliqué aux bornes de la plaque
chauffante.
R : la résistance de la plaque
chauffante.
k : c'est une constante de perte thermique qui
dépend du métal utilisé, elle caractérise les
pertes dues à la conduction thermique. Ainsi on peut la
déterminer à partir des courbes en calculant la pente des ces
dernières.
Pour les séries S1, on trouve une valeur de k = 0.0083
W/°K, tendit que pour les séries S2 on trouve une valeur de
k = 0.012 W/°K.
Comparé à la valeur théorique (relation
1.57) de k = 0.0080 W/°K, on peut conclure que les mesures
opérées sur les échantillons S1 et S2 ont donnée de
bon résultats.
Les mesures thermiques réalisées sur les
échantillons S1 et S2 révèlent une valeur de Tf = 400
°C pour une puissance de P = 3,2 Watts pour la série
S1et P = 4.6 Watts pour la série S2 comme indiqué dans
le tableau III.4.
Tableau III.4. Les valeurs des puissances et
des températures de fonctionnement, sous
tension et courant continu
concernant les mesures effectuées sur les échantillons S1 et
S2.
|
S1
|
S2
|
|
Température de
fonctionnement Tf
|
400 °C
Ou 673 °K
|
400 °C
Ou 673 °K
|
|
Puissance consommé P
|
3.2 Watts
|
4.6 Watts
|
|
Tension d'alimentation V
|
13 volts
|
7 Volts
|
|
Intensité électrique I
|
243 mA
|
650 mA
|
NB :
Nos expériences ont été
élaborées et conduites avec succès grace à l'apport
du mini four de la série S1 (72 ?) qui a contribué par
ses performances supérieur à ceux du S2 (7 ?) à
devenir l'agent principal dans l'ensemble de nos démarches
expérimentaux.
III.3.1 Relation résistance épaisseur de
couches
La variation du temps de dépôt (augmentation de
l'épaisseur des couches minces métalliques), va se
répercuter sur la résistance du mini four, puisque la relation
qui relie la résistance à l'épaisseur s'écrit comme
suit :
= ñ L / l e (3.1)
R, ñ, L, l et e sont respectivement la
résistance, la résistivité, la longueur et la largeur de
l'échantillon et l'épaisseur de l'échantillon.
Si le temps de dépôt est plus long - il y'aura plus
d'atomes qui arriverons sur la surface du substrat donc un accroissement de
l'épaisseur, ce qui conduit à une diminution de la
résistance.
Par conséquent, si on remplace les valeurs des
épaisseurs trouvées dans le tableau III.1 dans la relation (3.1),
on trouve les résistances suivantes :
- Pour la série S1 : R0 = 3.2 ?.
- Pour la
série S2 : R0 = 1.5 ?.
Ces deux résultats ne concordent pas avec les valeurs
mesurées expérimentalement, la raison est que probablement au
cours de l'élaboration des couches minces métallique pour des
temps de dépôt relativement court on aura la formation d'une
couche d'oxyde parasite qui fait augmenter la résistance de ces
couches.
Figure III.8. Représente la variation
de la résistance des couches minces métallique en
fonction du
temps de dépôt. (a) Nickel, (b) Tungstène.
Remarque 2 :
Les couches minces métalliques que nous avons
élaborées (dépôt de Ni plus dépôt de W)
présentent un caractère ohmique dans la relation qui relie
courant à la tension comme indiqué sur la figure III.9.
Figure III.9. Représente le
caractère ohmique des plaques chauffantes des séries :
(a) S1, (b)
S2.
Discussion :
Pour des raisons objectifs et techniques et en
préambule de notre expérimentation, notre choix s'est
porté sur le nickel (Ni) en temps qu'élément chauffant ;
alors nous avons constaté qu'au bout du deuxième essai,
nonobstant la présence d'une couche de SiO2 isolatrice, la plaque
chauffante à grillée.
Des lors, obligation nous est faite de trouver un métal
présentant une bonne conductivité avec un coefficient de
température de la résistance positive, et dont les
caractéristiques avoisines ceux du Nickel [31]. Notre
choix s'est porté sur le Tungstène (W).
III.4 Type de conductivité dans l'oxyde de zinc non
dopé et dopé
La détermination thermoélectrique du type de
conductivité de nos couches minces d'oxyde de zinc non dopé et
dopé par la technique de l'électrode chauffée nous a
permis de confirmer que nos couches minces de ZnO non dopé et
dopé à l'aluminium présentent une conductivité de
type n (conductivité dues aux électrons). Tendis que la
couche mince de ZnO dopé de cuivre présente une
conductivité de type p (conductivités dues aux trous).
Comme indiqué dans le tableau III.5.
Tableau III.5. Résultat des mesures de
conductivité.
|
Couche mince d'oxyde de zinc
|
Type de conductivité
|
|
ZnO non dopé
|
n
|
|
ZnO : 3% Al
|
n+
|
|
ZnO : 1% Al
|
n+
|
|
ZnO : 1% Cu
|
p
|

III.5 Résultat des caractérisations
structurelles et morphologiques des oxydes de zinc (ZnO) et oxyde de silicium
(SiO2)
III.5.1 Diagramme de diffraction de rayon X des
couches minces de ZnO non dopé et dopé
On a pu déterminer les propriétés
structurelles des couches minces de ZnO grâce un diffractomètre de
RX à poudres avec détecteur linéaire et chambre en
température 100-400 k (Bruker). Dont les diagrammes sont présents
sur la figure III.9.


Figure III.10. Spectres de diffraction de
rayon X des couches minces de : ZnO non dopé (a),
ZnO dopé Cu
1% (b) et ZnO dopé Al 1% (c).
Les pics du spectre DRX indiquent que tous les films obtenus
sont poly cristallins avec une structure hexagonale wurtzite
[32] et une orientation préférentielle d'axe c
perpendiculaire au substrat.
On n'a pas observé une grande différence
significative pour les couches minces non dopées et dopées Al et
Cu. Les trois spectres représentent le pic dominant (002) qui est
situé à 2è = 34.11° pour le ZnO non dopé,
à 34.26° pour le ZnO dopé Cu 1% et à 34.41° pour
le ZnO dopé Al 1%, respectivement. Des auteurs attribuent ce
décalage à la substitution de zinc par l'aluminium et le cuivre
dans la structure hexagonale [33] [34] [35].
La croissance selon les plans (002) est à l'origine de la
phase stable du ZnO, correspondant au minimum d'énergie (-5.416
eV)/mol [22].
III.5.1.1 Taille des grains
La taille des grains des différents films d'oxyde de
zinc a été déterminée à partir des spectres
de diffraction X de chaque échantillon, et la relation de Scherer
(relation (2.11)), dont les résultats sont résumés dans le
tableau III.6.
Tableau III.6. Représente la taille
moyenne des grains des films d'oxyde de zinc non dopé et
dopé
obtenus.
|
Échantillon
|
Taille des grains en nm
|
|
ZnO non dopé
|
30
|
|
ZnO dopé Cu 1%
|
58
|
|
ZnO dopé Al 1%
|
27
|
III.5.2 Morphologie des surfaces obtenues sur le SiO2
La morphologie des films de SiO2 obtenu par oxydation
thermique et pulvérisation rf ont été observée par
microscope électronique à balayage. Cet appareille nous renseigne
sur la rugosité des surface et la morphologie des couches.
Les figures III.11 et III.12 montre la texture des couches
observés en fonction de la méthode de dépôt.

3 um

1.5 um 1.5 um

13 um
Figure III.11. Image MEB d'une couche de SiO2
formé par pulvérisation rf, avec un
grossissement de 4k.

1.5 um
Figure III.12. Image MEB d'une couche de SiO2
formé par oxydation thermique de Si
polycristallin, avec un
grossissement de 10k.
Nous constatons que les couches d'SiO2 présentent des
rugosités différentes suivant la méthode de
dépôt ; ainsi, il a été observé par MEB que
par pulvérisation des multi grains disparates apparaissent, tendis que
par oxydation thermique, la formation des grains est plus volumineuse.
III.5.3 Morphologie de surfaces obtenues sur le ZnO non
dopé et dopé
La morphologie des différentes couches de ZnO non
dopé et dopé a été observée au microscope
électronique à balayage, cet appareille nous renseignera sur la
rugosité des surfaces, la morphologie des couches et leur structure
(colonnaire).
Figure III.13. Image MEB d'une Figure
III.14. Image MEB d'une
couche de ZnO dopé Al 1%, avec couche de ZnO dopé
Al 3%, avec
un grossissement de 10k un grossissement de 10k
(a) (b)

3 um
1.5 um
Figure III.15. Image MEB d'une couche de ZnO
dopé Cu 1%, avec un
grossissement de : 4k (a) et 10k (b).

3 um
1.5 um
(a) (b)
Figure III.16. Image MEB d'une couche de ZnO
non dopé, avec un
grossissement de : 4k (a) et 10k (b).
Figure III.17. Ensemble ZnO non dopé
SiO2 et Si IM x 340.
L'état de surface pour les quatre échantillons
présente un aspect granulaire du fait qu'ils sont épais. Aussi,
à quelques taux et types de dopages, le MEB fait ressortir pour
l'ensemble de nos échantillons des formations colonnaires avec de
multitudes grains englobant leurs joins.
Le MEB nous permis aussi de déterminer la taille moyenne
des colonnes, dont les valeurs sont indiquées dans le tableau III.7.
Tableau III.7. Représente la taille
moyenne des colonnes des films d'oxyde de zinc non dopé
et
dopé obtenus.
|
Échantillon
|
Taille moyenne des colonnes en
nm
|
|
ZnO non dopé
|
340
|
|
ZnO dopé Cu 1%
|
600
|
|
ZnO dopé Al 1%
|
260
|
Remarque 3 :
Nous avons remarqué que la taille des grains
trouvés par DRX correspond au dixième

( ) de la taille des colonnes mesurée par MEB. Et
ca pour l'ensemble des échantillons de
ZnO (dopé et non dopé) élaborés par
pulvérisation rf.
III.6 Etude de la réponse du capteur envers le
gaz d'éthanol III.6.1 système de barbotage
Grace au système de barbotage décrit
précédemment au chapitre II, nous avons pu déterminer et
contrôler les différentes concentrations d'éthanol
utilisé dans la détection par notre capteur.
Selon les études menées au sein de notre
laboratoire, on a montré que la concentration de la vapeur
d'éthanol décroit avec sa position dans la seringue principale.
Ceci s'explique par le transport de l'azote des molécules
d'éthanol se trouvant à la surface de la seringue ; plus le
niveau d'éthanol baisse plus la difficulté d'entrainement est
grande.
III.6.2 Etape de la détection
Au cours de cette étude, nous avons analysé la
réponse électrique de quatre séries de capteur à
savoir :
- Série CG1 : capteur de gaz à base d'oxyde de zinc
non dopé.
- Série CG2 : capteur de gaz à base d'oxyde de zinc
dopé Al 3%. - Série CG3 : capteur de gaz à base d'oxyde de
zinc dopé Al 1%. - Série CG4 : capteur de gaz à base
d'oxyde de zinc dopé Cu 1%.
Pour des concentrations d'éthanol fixé
respectivement à :

C1 = 337 ppm
C2 = 194 ppm
III.6.3 Protocole de la manipulation
La détection ne se fait qu'une fois la température
de 300 °C est atteinte, elle ne peut se faire à
température ambiante, ceci est démontré sur la figure
III.18.
Ceci est dü au faite que la réaction d'adsorption de
l'éthanol sur la surface de ZnO n'est activée qu'une fois cette
température est atteinte.
Figure III.18. Représente la variation
de la résistance de trois capteurs (CG1) en fonction de
la
température pour une concentration C1= 337 ppm.
Figure III.19. Représente la variation
de la résistance de capteurs CG1 en fonction de la
température
(pour une concentration C1 = 337 ppm) : (a) échantillons soumis
à un recuit à
500 °C avant exposition au gaz
d'éthanol, (b) échantillon testé directement après
dépôt de la
couche sensible.
(0 4 MO)
Cette expérience nous permet de montrer que les couches
minces de ZnO doivent être
Sous air R= 13 MOhm
soumises à un recuit sous air (adsorption d'une grande
quantité d'oxygène O2) avant d'être
ous ga Ethanol 3 test
employées dans la détection.



Figure III.20. Représente la variation
de la résistance de capteurs CG1 en fonction de la
température
(pour une concentration d'éthanol C1 = 337 ppm).



Figure III.21. Représente la variation
de la résistance de capteurs CG1 en fonction de la
température
(pour une concentration d'éthanol = 194 ppm).
Remarque 4 :
Trois cycles sous air sont nécessaires avant
détection, quelque soit la concentration de gaz d'éthanol
utilisée.
Il faut avoir une saturation en O2 de la couche de ZnO.



Figure III.22. Représente la variation
de la résistance de capteurs CG2 en fonction de la
température
(pour une concentration d'éthanol C1 = 337 ppm).



Figure III.23. Représente la variation
de la résistance de capteurs CG2 en fonction de la
température
(pour une concentration d'éthanol = 194 ppm).
Remarque 5 :
Le premier test effectué sur le capteur CG2 montre une
allure croissante de la résistance avec la température, due
notamment à l'adsorption d'O2 du faite qu'il est conducteur par dopage
d'Al 3%. Par la suite les deuxième et troisième tests suivent
l'allure de l'effet semiconducteur pendant le chauffage. Par la suite on
obtient une meilleure réponse au troisième essai.
L'effet devient reproductible par la suite, dans la gamme de
mesure 220 °C à 300 °C.



Figure III.24. Représente la variation
de la résistance de capteurs CG3 en fonction de la
température
(pour une concentration d'éthanol C1 = 337 ppm).



Figure III.25. Représente la variation
de la résistance de capteurs CG3 en fonction de la
température
(pour une concentration d'éthanol = 194 ppm).
Remarque 6 :
Le même aspect toujours trois cycles sont
nécessaires pour avoir une stabilité du capteur.



Figure III.26. Représente la variation
de la résistance de capteurs CG4 en fonction de la
température
(pour une concentration d'éthanol C1 = 337 ppm).



Figure III.27. Représente la variation
de la résistance de capteurs CG4 en fonction de la
température
(pour une concentration d'éthanol = 194 ppm).
Remarque 7 :
De loin le capteur CG4 (ZnO : 1% Cu) présente les
meilleurs performances, puisque au premier test, il donne une réponse
envers le gaz d'éthanol.
Bien que la taille des grains de l'échantillon
dopé Cu soit plus grande que celle des autres échantillons, la
réponse dans ce cas ci est meilleur. Alors qu'en principe de petits
grains induisent des surfaces spécifiques plus grandes et par
conséquent un pouvoir de détection plus important.
Ceci ne peut pas être expliqué par l'effet
morphologique. Mais serait dû probablement à un effet catalytique
du Cu ?
III.6.3.1 Mesure de sensibilité des capteurs CG1,
CG2, CG3 et CG4

Figure III.28. Evolution de la
Sensibilité de deux capteurs CG1 : (a) élément sensible
(ZnO
non dopé) soumis à un recuit à 500
°C avant exposition au gaz d'éthanol, (b)
élément sensible
(ZnO non dopé) testé
directement après dépôt de la couche sensible, pour une
concentration
d'éthanol : C1 = 337 ppm.
Remarque 8 :
L'échantillon recuit à 500 °C donne
une meilleure sensibilité (S = 90) que l'échantillon
tester directement après dépôt (S = 10).
Figure III.29. Evolution de la
Sensibilité d'un capteur CG1 durant trois tests, pour
une
concentration : (a) C1 = 337 ppm, (b) = 194 ppm.
Figure III.30. Evolution de la
Sensibilité d'un capteur CG2 durant trois tests, pour
une
concentration : (a) C1 = 337 ppm, (b) = 194 ppm.
Figure III.31. Evolution de la
Sensibilité d'un capteur CG3 durant trois tests, pour
une
concentration : (a) C1 = 337 ppm, (b) = 194 ppm.
Figure III.32. Evolution de la
Sensibilité d'un capteur CG4 durant trois tests, pour
une
concentration : (a) C1 = 337 ppm, (b) = 194 ppm.
Les mesures de sensibilité des quatre capteurs de gaz
envers le gaz d'éthanol montrent
1er
une piètre sensibilité du ZnO dopé
aluminium, une très forte sensibilité (la plus importante)
2éme test
éme
du ZnO dopé cuivre et une forte sensibilité du ZnO
pur essentiellement celui recuit à 500 °C.
3ém test 3éme test
Remarques générales :

Taille des grains = 1/10 taille d'une colonne.
En montée de température il n'y a pas de
réponse du capteur pour le gaz d'éthanol, par contre en descente
il y a une réponse électrique.
Les grains dans le ZnO dopé Al sont petites mais ne
donnent pas une bonne réponse au gaz d'éthanol, tendis que le ZnO
dopé Cu et non dopé donne une meilleur réponse.

Ce travail effectué au laboratoire de microscopie
électronique et sciences des matériaux, nous a permis à
travers plusieurs démarches de réaliser des capteurs de gaz
à base d'oxyde de zinc dopé (Al et Cu) et non dopé, avec
un mini four intégré (conçu avec une double couche de
nickel plus tungstène) sur un wafer de Si poly cristallin.
L'objectif visé était de faire en sorte qu'une
fois le capteur finalisé, il puisse fonctionner, et donc pouvoir
détecter différents gaz ayant un impact sur l'environnement (dans
notre cas le gaz d'éthanol).
Pour cela, nous avons conçu un banc de test
spécifique, ou il comprend d'une part un système d'alimentation
du mini four (plateforme chauffante du capteur), et d'autre part un
système de mesure de la réponse de l'élément
sensible du capteur.
Le travail expérimental à comporté deux
approches.
- La première procédure consiste à
réaliser le capteur. A savoir la préparation du wafer de Si
poly-cristallin comme plateforme d'intégration d'une partie du capteur,
suivi de son oxydation sous un flux constant d'air (humidité plus
oxygène) dans un four à moufle, ensuite le découpage en
dimension égale selon la disposition des contacts de mesures mises en
place (L x l) = (2 x 5) mm, et en fin la dernière étape
celle du dépôt des différents couches minces
métalliques (nickel plus tungstène ) d'une face et
semiconductrices (ZnO pur et dopé (Al :1%, 3% et Cu :1%) de l'autre
face.
- La deuxième procédure fait intervenir son
aptitude à détecter le gaz d'éthanol.
Nous avons obtenus quatre types de capteurs : ZnO pur, ZnO
dopé Al 1% et 3 % et ZnO dopé Cu 1%.
Nous avons aussi put atteindre les 400 °C
grace à l'apport du mini four en (Nickel plus Tungstène) avec une
précision de 0.5 °C, pour un courant de 243 mA et une tension de 13
Volts.
L'état de surface observé par MEB présente
une structure colonnaire pour toutes les

couches avec des tailles de grains observé par DRX
correspondant à de la taille des
colonnes.
L'échantillon dopé Cu présente des tailles
de grains et de colonne double de celle des autres.
Les mesures électriques effectuées sur ses
capteurs ont montré une grande sensibilité au gaz
d'éthanol pour celui dopé Cu (S = 250), une
sensibilité moyenne pour le non dopé (S = 28) et une
faible sensibilité pour le dopé Al (S = 3).
Cette sensibilité ne peut, par conséquent
être expliquée par l'effet morphologique, l'explication serait
plutôt dans un effet catalytique du Cu ?
En perspective une étude plus détaillée sur
ce dernier effet doit être entreprise.
La puissance fournie au capteur reste toujours importante (3
Watts), nous espérons par des techniques de gravures atteindre des
puissances beaucoup plus petite (de l'ordre du dixième de Watts).
Dans le cas des mini-capteurs, les problèmes de contact se
posent de façon cruciale. Une étude appropriée doit
être aussi poursuivie.

[1] K. An NGO, Etude d'un système
multicapteur pour la détection sélective des gaz, Thèse de
Doctorat, UNIVERSITE PAUL CEZANNE AIX-MARSEILLE III, 2006.
[2] J. FRADEN, Handbook of Modern Sensors
Physics, Designs, and Applications, 3rd Edition Springer, 2004.
[3] N. Taguchi, Japanese Patent Application No.
45-38200, 1962.
[4] M. Penza, E. Milella and V. I. Anisimkin,
Monitoring of NH3 gas by LB polypyrrolebased SAW sensor,
Sensors and Actuators B 47 (1998) 218-224.
[5] Pavel Ripka et Alois Tipek, Modern Sensors
Handbook, 1st edition ISTE, 2007.
[6] M. K Bendimerad, Réalisation d'un
capteur de gaz à base de couches mince d'oxyde de zinc avec un micro
four intégré, Mémoire d'ingéniorat,
Université d'U.S.T.O.M.B, 2007.
[7] H. BAHA, Conception d'un capteur de gaz
intelligent, Mémoire de magister, Université de Batna, 2007.
[8] Y. BAKHA, Adsorption des gaz sur des
couches d'oxyde de zinc préparées par la technique pyrolyse
spray, Mémoire de magister, Université d'U.S.T.O.M.B, 2007.
[9] Matthias Batzill, Ulrike Diebold, The
surface and materials science of tin oxide, progress in surface science, 79
(2005) 47-154.
[10] D. Cherrad, Élaboration et Etude
technologique des couches minces T.C.O de type « n »et « p
» par micro pipetage et procédé rf, Application : à
la détection des polluants, radiations ultraviolettes, jonction «
pn », Mémoire de magister, Université d'U.S.T.O.M.B,
2008.
[11] J.E.Housten, Kohnke, J.Appl.phys,
36(12) (1965) 3931-3938.
[12] K-S Weibenrieder; j Muller, Thin solid
films, 30-41 (1997) 300.
[13] M. Gaidi, Films minces de SnO2
dopés au platine ou au palladium et utilisés pour la
détection des gaz polluants : analyses in situ des corrélations
entre la réponse électrique et le Comportement des
agrégats métalliques, Thèse de doctorat de l'INP de
Grenoble, 1999.
[14] A. Varpula et al, Sensors and Actuators: B
(2007) 12-013.
[15] D R PATIL, L A PATIL et D P AMALNERKAR,
Ethanol gas sensing properties of Al2O3-doped ZnO thick film resistors, Bull.
Mater. Sci, 30-6 (2007) 553-559.
[16] N. Hongsith, S. Choopun, P. Mangkorntong et N.
Mangkorntong, Ethanol Sensing Properties of Zinc Oxide Nanobelts
Prepared by RF Sputtering, Department of Physics, Faculty of Science, Chiang
Mai University, Chiang Mai 50200, Thailand.
[17] K. Ellmer, A. Klein and B. Rech,
Transparent Conductive Zinc Oxide basics and applications in thin film solar
cells, Materials Science, Springer, 2008.
[18] F. Boutaba, Réalisation d'un
transducteur à base de couches minces d'oxyde de zinc dopé
cuivre, Mémoire de magister, Université d'U.S.T.O.M.B, 2005.
[19] AEK. Safou, Réalisation d'un
transducteur piézoélectrique IDT miniature à base d'une
couche mince de ZnO dopé cuivre, mémoire de magister,
Université d'U.S.T.O.M.B, 2009.
[20] U. Özgür, Ya. I. Alivov, C. Liu, A.
Teke, M. A. Reshchikov, S. Doðan,c_ V. Avrutin, S.J. Cho, and H.
Morkoçd, A comprehensive review of ZnO materials and devices,
Journal of Applied Physics, 98 (2005) 041301.
[21] Y. Min, Properties and sensor performance
of ZnO thin films, thèse de doctorat, Massachusetts Institute of
Technology MIT, 2003.
[22] M. Zerdali, Etude et Réalisation de
Transducteur SAW à base de Couches Minces de type II-VI ZnO,
thèse de doctorat, Université d'U.S.T.O.M.B, 2007.
[23] C. Kittel, physique de l'état
solide, 7e édition Dunod, Paris, 1998.
[24] S. Bories, M. Prat, transfert de chaleur
dans les milieux poreux, Techniques d'ingénieur (2000), Traité
génie énergétique B 8 250.
[25] A. Richardt, I. Richardt, les
évaporations sous vide, Edition INFINE Paris 2000.
[26] A. Richardt, A. M Durand, Le vide- les
couches minces-les couches dures, Edition INFINE Paris ,1994.
[27] J. J. Béssot, Dépôt
par pulvérisation cathodique, Technique de l'ingénieur M 1 (1985)
657-1.
[28] Geraldine C. Schwartz, Kris V.
Srikrishnan, Handbook of semiconductor interconnection technology,
2nd edition Taylor & Francis Group, 2006.
[29] Francis Lévy, Physique et
technologie des semiconducteurs, Traité des matériaux, presses
polytechniques et universitaires Romandes, 1995.
[30] DIETER K. SCHRODER, Semiconductor material
and device characterization, 3rd edition IEEE press and Wiley-Interscience,
2006.
[31] Weiping Yan, Henan Li, Yongbian Kuang, Liqun Du,
Jihong Guo, Nickel membrane temperature sensor in micro-flow
measurement, Journal of Alloys and Compounds 449 (2008) 210-213.
[32] M. Sahal, B. Hartiti, B. Mari, A. Ridah1, M.
Mollar, Etude des propriétés physiques des couches
minces de ZnO dopées Al, préparées par la méthode
de « sol-gel » associée au « spin coating », Afrique
SCIENCE 02(3) (2006) 245 - 254.
[33] H. Kin, A. Pique, JSHorwitz, H. Murata, Z.H.
Kafafi, C.M. Gilmore, D.B. Chresey, Thin Solid Films, 377-378 (2000)
798.
[34] P. P. SAHAY, Zinc oxide thin film gas
sensor for detection of acetone, JOURNAL OF MATERIALS SCIENCE 40
(2005) 4383 - 4385.
[35] M. Graf, A. Gurlo, N. Barsan, U. Weimar2 et A.
Hierlemann, Microfabricated gas sensor systems with sensitive
nanocrystalline metal-oxide films, Journal of Nanoparticle Research (2006)
8:823-839.

131
a) Bac ultrasons de type BRANSON YAMATO 3200.
b) Générateur d'azote N2.
c) Substrat de Silicium polycristallin avant oxydation.
|
d) Four d'oxydation thermique de Si.
|
|
|
|
|
e) Substrat de Silicium polycristallin après oxydation
thermique.
|
|
f) Système de pulvérisation cathodique
radiofréquence de type ULVAC KIKO RFS 200.
|
|

h) Microscope électronique à balayage de type
HITACHI S2500.
i) Montage utilisé pour la mesure de la
résistivité électrique des couches
minces semiconductrice et
d'épaisseur des couches minces
métalliques.

|
a)
b)
c)
d)
e)
|
g) Différents capteur de gaz élaborés au
laboratoire.
A. capteur à base de ZnO.
B. capteur à base de ZnO : 3%Al.
C. capteur à base de ZnO : 1%Al.
D. capteur à base de ZnO : 1%Cu.
E. système de chauffage.
|

j) Montage expérimentale pour tester le capteur de
gaz.
| 


