1.2. CAUSALITÉ DANS LE
CAS DE VARIABLES COINTÉGRÉES
Depuis plus d'une vingtaine d'années, de nombreux
articles révèlent que la majorité des séries
macroéconomiques sont non stationnaires, en particulier l'article de
Nelson et Plosser (1982). Ceci suppose qu'avant d'appliquer une quelconque
méthode d'estimation, une analyse approfondie des
propriétés des séries est indispensable. L'objectif
principal visé est celui de repérer l'éventuel non
stationnarité des séries. C'est en quelque sorte, l'étape
de la détermination de leur ordre.
Engle et Granger (1991) ont montré que si les variables
sont intégrées, le test classique de Granger, basé sur le
VAR, n'est plus approprié. Ils recommandent pour ce faire d'utiliser le
modèle à correction d'erreur. En outre, le test de
causalité basé sur le modèle vectoriel à correction
d'erreur présente l'avantage de fournir une relation causale même
si aucun coefficient estimé des variables d'intérêt
décalées n'est significatif. Les équations (1) et (2) sont
réécrites de la manière suivante :
Modèle vectoriel à correction
d'erreur
 (3) (3)
 (4) (4)
Où zt-1 est le terme à correction
d'erreur issu de l'estimation de la relation de la cointégration, Ä
l'opérateur de différence.
En utilisant le modèle vectoriel à correction
d'erreur (équation (3) et (4)), PIBt ne cause pas
CKWht au sens de Granger si  i= i= i=0 ; CKWht ne cause pas
PIBt si i=0 ; CKWht ne cause pas
PIBt si 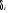 = = =0. =0.
Les tests classiques de Fisher et de Student permettront de
valider le modèle.
| 


