Memoire Online - Determinants de la fixation du prix des maisons d'habitation a Bukavu

Ce chapitre comprend cinq sections : la première présente les caractéristiques de l'échantillon ; la deuxième fait une étude exploratoire sur les relations entre certaines variables; la troisième, nous présente les résultats des estimations et interprétation des résultats et la quatrième nous montre les implications des résultats; et enfin, la cinquième présente les limites de ce travail et les perspectives de recherche.

Nous avons mené une enquête de terrain auprès 193 ménages du 4 au 18 Janvier 2015, soit pendant 14 jours, au cours de laquelle nous avons individuellement interrogé au moyen d'un questionnaire implémenté dans le téléphone portable ; en utilisant l'application Android ODK Collect 1.4.4 et ses différents outils afin de réduire le temps de l'enquête avec la rapidité de remplissage des formulaires, et la réduction du temps et des erreurs liés à l'encodage, ainsi que de permettre d'obtenir les coordonnées géographiques( longitude et latitude) des maisons enquêtées avec une précision moyenne de 5 mètres. Ce qui permet d'avoir un taux de réponse de 100%.

Les données présentées à cette section portent sur les caractéristiques socioprofessionnelles et démographiques des personnes enquêtées.

L'objectif de cette analyse est de faire une présentation plutôt informative sur le profil des personnes enquêtées (le sexe, l'état-civil et la profession).

Au regard de ce tableau nous remarquons que les femmes sont plus représentées dans notre échantillon que les hommes, soit 61,7% contre 38,3%. Ceci s'explique par le fait que le questionnaire était administré de manière aléatoire aux ménages sans distinction de sexe.

	Etat-civil					Total
	Célibataire	Marié	Divorc é	Veuf	Union libre	Total
Ibanda	10,0%	43,1%	11,1%	27,3%	32,7%	33,7%
Kadutu	30,0%	33,8%	22,2%	54,5%	49,0%	42,0%
Bagira	60,0%	23,1%	66,7%	18,2%	18,4%	24,4%
Total	100,0%	100,0%	100,0%	100,0%	100,0%	100,0%
	5,2%	33,7%	4,7%	5,7%	50,8%	100,0%

Aussi, de ce tableau il s'observe que notre échantillon est majoritairement constitué des personnes en union libre représentant 50,8% des enquêtés, suivi des personnes mariées constituant 33,7% alors que les célibataires, les veufs ainsi que les divorcés ne représentent ensemble que 15,6% des personnes enquêtées.

	Profession					Total
	Agriculteurs, Paysans et Sans emploi	Prestatair es des services	Salarié s	Commerçan ts	Autres	Total
Ibanda	34,5%	45,7%	30,8%	20,9%	58,3%	33,7%
Kadutu	45,5%	32,6%	53,8%	47,8%	16,7%	42,0%
Bagira	20,0%	21,7%	15,4%	31,3%	25,0%	24,4%
Total	100,0%	100,0%	100,0%	100,0%	100,0%	100,0%
	28,5%	23,8%	6,7%	34,7%	6,2%	100,0%

On peut constater de ce tableau ci-dessus que, les personnes exerçant du commerce sont plus représentées que d'autres avec 34,7% des enquêtés suivi des agriculteurs, paysans et sans emploi constituant 28,5%. Les salariés et autres ne forment ensemble que 12,9% des personnes enquêtées.

Les déterminants de la fixation du prix des immobiliers résidentiels comprend plusieurs dimensions, notamment les caractéristiques physiques, celles liées à la localisation de la maison, les caractéristiques de voisinage ainsi que les caractéristiques du propriétaire.

Dans cette section, on va mener une étude au moyen des tableaux croisés permettant de valider et d'expliquer les constats des analyses des caractéristiques. Ensuite l'étude statistique en termes d'analyse de corrélation, permet d'identifier les relations qui existent entre les variables étudiées et constitue ainsi le point de départ de la démarche de la modélisation dans ce travail.

Pour mesurer la corrélation entre deux variables qualitatives, on peut utiliser soit le coefficient de contingence (pour les variables nominales), soit le coefficient Tau-B de Kendall ou le coefficient de corrélation de Spearman (pour les variables ordinales), coefficients qui sont les analogues pour le cas des variables qualitatives du coefficient de corrélation R de Pearson pour les variables quantitatives. Tous ces coefficients prennent des valeurs comprises entre -1 et 1 (à l'exception du coefficient de contingence, qui prend des valeurs entre 0 et 1); un coefficient avec une valeur absolue proche de 1 indique une corrélation forte (positive ou négative, en fonction de son signe) entre les deux variables, et une valeur proche de 0 indique que la corrélation entre les variables est faible.

Nous traitons dans cette section, au premier point des caractéristiques physiques et de localisation des ménages et deuxième les caractéristiques socioprofessionnelles et démographiques des propriétaires.

L'objectif de cette partie est de faire une présentation descriptive des variables quantitative jugées pertinentes sur la fixation du prix des maisons d'habitation notamment le prix au mètre carré de la surface de la parcelle, la somme de différentes constructions se trouvant sur la parcelle ainsi le prix moyen d'une pièce comportant la maison dans chacune des communes. Cette analyse sera soutenue par la mesure de la corrélation R de Pearson entre la variable étudiée et le prix de la maison.

Le comportement du consommateur est résumé par le terme « hédonisme » selon lequel les individus cherchent à maximiser leur satisfaction par la recherche et le choix des attributs d'utilité qui composent le bien. Le prix d'un bien immobilier est dérivé du nombre et de la qualité de ces attributs d'utilité jugés par les individus supposés être rationnels. Il en découle donc que la connaissance de la surface de la parcelle d'une propriété immobilière demeurent importante car continue à régler les dynamiques des marchés immobiliers.

	Moyen	Média	Ecart-	Mini	Maxi	Prix	Prix au	N
	ne	ne	type	mum	mum	moyen	mètre carré
Ibanda	230,20	221,00	121,188	56	455	43092,31	187,195	65
Kadutu	147,47	96,00	117,22	36	640	19037,04	129,0909	81
Bagira	403,13	380,00	154,04	108	810	16276,60	40,37556	47
Total	237,59	212,00	162,66	36	810	26 466,32	111,3949	193

Il s'observe du tableau 3.4 que le prix moyen de la parcelle au mètre carré est plus élevé dans la commune d'Ibanda soit 187,195 $, suivi de la commune de Kadutu 129,0909 $ et 40,37556 et pourtant les maisons localisées dans la commune de Bagira présentent une surface moyenne plus élevée suivies par celle de la commune d'Ibanda.

L'analyse de la corrélation permettra de comprendre le lien existant entre la surface de la parcelle avec la valeur de la maison.

Tableau 3.5 : Corrélation surface de la parcelle (surfpcl)-prix de la maison (prms)

Ce tableau ci-dessus montre, par la corrélation de Pearson, qu'il existe une relation positive et significative au seuil de 1% de 24,2% entre la surface de la parcelle et le prix moyen de la maison, ce qui traduit que l'augmentation de la surface de la parcelle en moyenne est suivie par l'augmentation du prix de la maison.

III.2.1.2 La somme des surface de différentes constructions se trouvant sur la parcelle (surfms) La connaissance du niveau d'occupation de la parcelle est un élément important, car cela dans une certaine mesure peut permettre de comprendre les préférences des ménages en termes d'espace libre.

	Moyen ne	Médi ane	Ecart- type	surfms/s urfpcl	Prix moyen	Prix au mètre carré	N
Ibanda	193,41	190,00	105,923	84,40%	43092,31	222,8029	65
Kadutu	120,71	75,00	97,396	81,85%	19037,04	157,70889	81
Bagira	85,70	90,00	14,863	21,25%	16276,60	189,92	47
Total	136,67	90,00	97,870	57,52%	26 466,32	193,6512	193

Au regard du tableau 3.6 nous remarquons qu'un mètre carré construit est plus valorisé dans la commune d'Ibanda 228,8$ que dans d'autres, suivie par la commune de Bagira 189,92$ et 157,7$ dans la commune de Kadutu. Ensuite le rapport

surfms/surfpcl fait constater un niveau d'occupation de la parcelle très élevée dans la commune d'Ibanda représentant 84,40%, suivi par la commune de Kadutu soit 81,85% et 21,25% dans la commune de Bagira, ce qui fait voir qu'il y a une forte probabilité de trouver une maison avec un jardin ou une terrasse à Bagira plutôt que dans les deux autres communes. Ensuite on s'intéresserait à savoir le lien qui unit la surface construite et la valeur de la maison.

Tableau 3.7 : Corrélation bilatérale surface construite (surfms)-prix de la maison (prms)

Au regard du tableau 3.7 nous remarquons on trouve ainsi une corrélation positive et significative au seuil de 1% entre le prix de la maison et la somme des surfaces construites sur la parcelle de 53,6% signifiant qu'une augmentation des constructions sur la parcelle permet d'augmenter le prix de la maison.

Outre l'évidence que le prix des maisons est une fonction croissante de la surface de la parcelle ou de la somme de différentes constructions se trouvant sur la parcelle, il apparait que les acheteurs ont une préférence très nette pour les maisons disposant de plusieurs pièces.

A travers le tableau 3.8 nous constatons que les maisons de la commune d'Ibanda ont une moyenne élevée de nombre des pièces, soit 7,38 pièces suivie de la commune de Bagira ayant 7,02 et 5,67 pour la commune de Kadutu. Dans l'ensemble la moyenne s'élève à 6,58 et la médiane à 6, une moyenne supérieure à la médiane montre que plus de 50% des maisons dans l'ensemble ont un nombre des pièces inférieur à la moyenne, soit 6,58 pièce.

Tableau 3.9 : Corrélation de Pearson nombre des pièces (nbrepc)-prix de la maison (prms)

L'analyse de la corrélation montre un lien positif entre le nombre de pièces et le prix de la maison significative au seuil de 1% suggérant que l'augmentation d'une pièce entraine l'augmentation du prix. Cela implique qu'à logement de superficie égale, celui offrant plus de pièces est plus cher et donc plus demandé. Ce résultat serait la conséquence d'un territoire qui en moyenne propose un nombre d'individus par ménages relativement important.

III.2.2 Caractéristiques socioprofessionnelles et démographiques des propriétaires

Certains économistes considèrent que le niveau de vie, reflété par le profil socioéconomique des ménages, est déterminant dans leurs choix en matière de localisation résidentielle et pouvant influencer les niveaux de prix. Alonso (1964), Mills (1967) et Muth (1969) soutiennent en effet cette idée et montrent que l'offre et la demande sur le marché résidentiel expliquent la localisation des ménages aisés et des ménages pauvres dans des lieux différents, et pour Tiebout (1956) le jeu d'attraction et de répulsion entre différentes catégories de ménages structure l'espace résidentiel selon le niveau de vie.

Les tableaux 1.1 au 1.9 de l'annexe 1 nous montrent qu'en moyenne la distance par rapport au point central est plus grande pour les ménages localisés à Bagira suivi par ceux de la commune de Kadutu, de même pour le cout total de transport qui est en moyenne très élevé pour la commune de Bagira et influençant en général, négativement le prix des maisons, ce qui concorde avec les résultats du modèle urbain néoclassique proposé par Alonso (1964), puis étendu par Muth (1969) et Mills (1967, 1972) qui considèrent la ville comme circulaire, mono centrique et implantée sur une plaine isotrope et dont toute augmentation du prix unitaire de l'immobilier implique un rapprochement du centre afin de bénéficier d'une baisse de cout de transport.

L'analyse du statut du propriétaire des ménages montre une relation négative avec le prix. Ce qui signifie que les maisons appartenant aux personnes mariées coutent en moyenne plus cher que celles appartenant aux personnes célibataires.

Le niveau d'étude et la profession montrent qu'il existe une relation positive entre ces variables avec le prix des maisons ce qui signifie que le plus souvent, les ménages prennent la décision d'effectuer leur localisation résidentielle suite à l'occurrence d'un évènement d'ordre professionnel (obtention ou perte d'un emploi, changement de lieu de travail, fin d'activité, etc.), ou d'étude (réussite à un concours) et de ce fait ces variables influencent de manière positive les prix des maisons, cela s'inscrit dans la logique que l'option la plus courante étant de se rapprocher autant que possible de son groupe de référence.

Dans cette section, nous présentons dans une première étape les résultats de l'estimation par la méthode du moindre carré ordinaire, ensuite l'introduction de l'espace qui nous conduit à la deuxième étape qui consiste à prendre en compte l'hétérogénéité spatiale avec l'estimation du modèle par moindre carré ordinaire corrigé de l'hétéroscédasticité par la méthode de White et le recours à l'analyse de la variance (ANOVA spatiale). La troisième étape va consister à prendre en compte l'autocorrélation spatiale en estimant le modèle autorégressif spatial(SAR) et le modèle d'erreur spatial (SEM) par la méthode du maximum de vraisemblance et en quatrième étape le choix du modèle optimal entre ces quatre modèles estimé au moyen du test de ratio de vraisemblance. Et la cinquième étape va porter sur l'interprétation et discussion des résultats finals.

Cette sous-section présente la synthèse des résultats de l'estimation par la méthode de moindre carré ordinaire. Ces résultats sont obtenus grâce au logiciel STATA 12.

Tableau 3.10 : Résultats de la première estimation par moindre carré ordinaire (mco1)

Variables	Coefficients
Commune de Bagira	-1654.714	(0.810)
Commune de Kadutu	-12241.11	(0.000*)
Surface de la parcelle	10.69862	(0.351)
Surface des éléments construits	8.507277	(0.617)
Nombre des pièces	2146.049	(0.000*)
Etats des murs	2182.212	(0.459)
Nombre d'étage	12414.64	(0.000*)
Ancienneté de la maison	204.0747	(0.775)
Type de la maison	2010.463	(0.499)
Présence de plus de deux toilettes	4561.473	(0.053***)
Présence de garage	2229.419	(0.259)
Distance avec le centre-ville	-4.337581	(0.007**)
Distance avec l'axe principal	60.18355	(0.742)
Distance avec la route la plus proche	-48.03356	(0.333)
Distance avec l'infrastructure de transport	-2.632062	(0.989)
Distance avec le centre médical	161.6571	(0.415)
Distance avec un établissement d'enseignement	-112.6833	(0.753)
Niveau d'étude	3929.772	(0.000*)
Profession	3232.878	(0.000*)
Cout total de transport	-4.45861	(0.066***)
Constante	7328.84	(0.243)
F(20,172)=57,05 Prob>F =0,000 R-Squared=0,8690 Adj. R-squared=0,8538
significative à 1%, significative à 5%, **significative à 10%

Le test F de Fisher montre que la qualité du modèle est globalement bonne et le coefficient de détermination permet de montrer que les variables indépendantes expliquent à 86,9% les prix des maisons d'habitation dans la ville de Bukavu. Cependant, l'examen des T-student de significativité individuelle des variables révèlent que seules huit variables sont significatives au seuil de 1%, 5% ou 10%. Il s'agit de la localisation de la maison si elle est située à Kadutu(Commkad), le nombre des pièces(Nbrepc), la presence des 2 toilettes/salles de bain ou plus (Pres2toilslb), la distance avec le centre-ville (Distcentvil), le niveau d'étude (Nivetd) et la profession du propriétaire de la maison(Profess) ainsi que le cout total de transport (Ctttransp).

Ces résultats montrent qu'en majeur partie les variables pour lesquelles on attendait un signe à priori a été retrouvé, à l'exception de la variable distance de la maison avec la route principale (Distaxepripl) et de la distance entre la maison et un centre médical le plus proche(Distcentmedcl). Ainsi une maison d'habitation pourrait avoir une valeur supérieure grâce à sa proximité à l'axe principal ou d'un centre médical mais les résultats de l'étude montrent que les nuisances associées à ces variables l'emportent sur les avantages qu'elles apportent en termes d'accessibilité.

Gallo (2002) montre que sous la condition nécessaire que les résidus de l'estimation sont des variables aléatoires indépendantes et identiquement distribuées (la variance est constante et non corrélée), la méthode des moindres carrés ordinaires (MCO) permet d'obtenir les coefficients non biaisés, mais cette régression hédonique globale est susceptible de masquer des différences importantes dans l'espace.

Pour cette raison il est introduit la notion de l'espace dans ce modèle initial en faisant recours aux techniques de l'économétrie spatiale visant précisément à prendre en compte les deux grandes spécificités des données géographiques qui caractérisent les immobiliers résidentiels : l'hétérogénéité spatiale qui est liée à la différenciation des variables et des comportements dans l'espace et l'autocorrélation spatiale qui se réfère à l'absence d'indépendance entre observations géographiques.

Cette sous-section porte sur la prise en compte de l'instabilité dans l'espace des relations économiques appelée hétérogénéité spatiale. Le premier point porte sur la

détection de l'hétéroscédasticité et sa prise en compte dans le modèle initial et le deuxième sur l'analyse de la variance spatiale.

L'hétéroscédasticité provient des variables manquantes ou de toute autre forme de mauvaise spécification.

Plusieurs méthodes de vérification de l'homogénéité des résidus sont proposées dans la littérature. On peut citer entre autres le test de White et le test de Breusch-Pagan. Le test de Breusch-Pagan est plus spécifique à la vérification de l'hypothèse d'homogénéité que celui de White qui est plus général en détectant des formes d'anomalie des résidus autres que l'hétéroscédasticité (non-normalité par exemple).

Ce tableau montre qu'au seuil de 0,05 l'hypothèse nulle H0 est rejetée au profit de l'hypothèse alternative H1 permettant de conclure que le modèle est hétéroscedastique.

Dans ces conditions, White a fourni un estimateur convergent de la matrice des variances-covariances de l'estimateur des Moindres Carrés Ordinaires (MCO) en présence d'hétéroscédasticité de forme inconnue pour que l'inférence statistique basée sur les MCO soit asymptotiquement fiable.

Tableau 3.12 : Résultats de la deuxième régression par moindre carré ordinaire corrigé de l'hétéroscedasticité par la méthode de white. (mod2)

Variables	Acronyme	Coefficients
Commune de Bagira	Commbag	-1654.714 (0.816)
Commune de Kadutu	Commkad	-12241.11 (0.000*)
Surface de la parcelle	Surfpcl	10.69862 (0.446)
Surface des éléments construits	Surfms	8.507277 (0.674)
Nombre des pièces	Nbrepc	2146.049 (0.000*)
Etats des murs	Etmurs	2182.212 (0.223)
Nombre d'étage	Nbreetg	12414.64 (0.000 *)
Ancienneté de la maison	Ancms	204.0747 (0.807)
Type de la maison	Typems	2010.463 (0.289)
Présence de plus de deux toilettes	Pres2toilslb	4561.473 (0.063***)
Présence de garage	Presgarg	2229.419 (0.197)
Distance avec le centre-ville	Distcentvil	-4.337581 (0.006**)
Distance avec l'axe principal	Distaxepripl	60.18355 (0.762)
Distance avec la route la plus proche	Distrtproch	-48.03356 (0.206)
Distance avec l'infrastructure de	Distinfrtrppro	-2.632062 (0.990)
transport	ch
Distance avec le centre médical	Distcentrmdicl	161.6571 (0.411)
Distance avec un établissement d'enseignement	Distetensgmt	-112.6833 (0.749)
Niveau d'étude	Nivetd	3929.772 (0.003**)
Profession	Profess	3232.878 (0.001**)
Cout total de transport	Ctttransp	-4.45861 (0.177)
Constante	_cons	7328.84 (0.265)
F(20,172) = 64,66 Prob>F=0,000 R-squared=0,8690 ,
significative à 1%, * à 5% et ***significative à 10%

Au regard de ce tableau la qualité du modèle reste globalement bonne selon le test de Fisher et l'ensemble des variables expliquent toujours à 86,90% la fixation du prix. En

comparaison avec les résultats précèdent du Tableau 3.12, la variable cout total de transport (Ctttransp) n'est plus significative au seuil maximal de 10% tout comme la variable profession(Profess) et niveau d'étude (Nivetd) du propriétaire qui ne sont plus significatives à 1% mais seulement à partir de 5%. Ce qui implique que la correction du modèle de l'hétéroscedasticité nous permet de conserver un modèle avec sept variables significatives au seuil de 1%, 5% ou 10%. Il s'agit de la localisation de la maison si elle est située à Kadutu(Commkad), le nombre des pièces(Nbrepc), la presence des 2 toilettes/salles de bain ou plus (Pres2toilslb), la distance avec le centre-ville (Distcentvil), le niveau d'étude (Nivetd) ainsi que la profession du propriétaire de la maison(Profess).

Dans le cas de l'étude immobilière, il est possible que l'impact spatial ne soit pas homogène. Can (1990) pose la question : « la valeur des caractéristiques des biens immobiliers varie-t-elle selon la localisation du bien ? ». On s'intéresse alors à savoir la variabilité spatiale de la moyenne dans chaque étendue.

Ce point présente la réponse à la question que l'on peut se poser cherchant à savoir dans quelle mesure la moyenne des prix des maisons d'habitation varie entre les trois communes.

Il ressort du tableau 2.1 de l'annexe 2 que la moyenne totale est de 26 466,32 $ avec un écart-type de 28 180,040 et le prix minimum est de 4 000$. La commune d'Ibanda présente une moyenne des prix la plus élevée de 43 092,31$ contre 19 037,04$ pour la commune de kadutu et 16 276,60 $ dans la commune de Bagira.

Ces résultats peuvent également être visualisés sous forme de graphiques afin de comparer les moyennes des prix des maisons selon les communes et selon les quartiers.

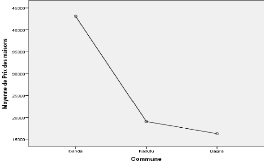
Ce graphique montre que la moyenne des prix est plus élevée dans la commune d'Ibanda, suivie de la commune de Kadutu

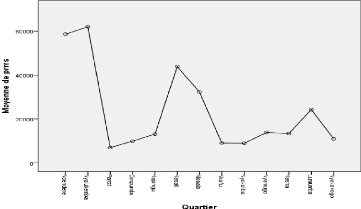
Ce graphique montre que la moyenne des prix des maisons est très élevées dans le quartier Nyalukemba suivi successivement du quartier Ndendere, Kasali, Mosala, Lumumba, Nyamugo, Kasha, Kajangu, Nyakavogo, Nkafu, Nyakaliba , Cimpunda.

Dans le but de pouvoir traiter ces différences de moyennes des prix des communes afin de savoir si au moins une des moyennes diffère significativement des autres, nous faisons recours à l'ANOVA spatiale qui sert à tester l'hypothèse d'égalité des moyennes des prix dans les trois communes. Pour s'assurer de sa faisabilité les deux conditions principales, l'hypothèse d'homogénéité de la variance (Test de Levene

=0,000<0,005 du tableau 3.13) et l'hypothèse de normalité (Kolmogorov et Shapiro = 0,000<0,05 du tableau 3.14) ne sont pas vérifiées d'où les conclusions de l'ANOVA ne seront pas valides pour ce travail à cause de hétérogénéité des variances ou d'une forte asymétrie des prix dans les trois communes.

Le test de Levene rejette de manière très significative l'hypothèse l'homogénéité des variances et ne permet donc pas de valider les résultats de l'analyse de la variance. Tableau 3.14 : Tests de normalité

De ce tableau on observe que l'hypothèse de normalité des résidus est rejetée. Les valeurs des maisons ne sont donc pas normalement distribuées dans les trois communes de la ville de Bukavu.

Carricano et Poujol (2008) montre que si les données ne sont pas appropriées à une ANOVA (hétérogénéité des variances ou données fortement asymétriques), il convient d'utiliser des tests non paramétriques qui ne supposent ni homogénéité de la variance,

ni une distribution normale comme le test de Kruskall-Wallis, qui est l'équivalent non paramétrique de l'ANOVA.

Le test de Kruskal-Wallis rejette de manière significative l'égalité des prix dans les trois communes. Les prix des maisons diffèrent donc significativement selon la commune de localisation ou il existe donc au moins une moyenne des prix qui diffère significativement des autres.

Cette conclusion ne faisant qu'indiquer que les prix différent globalement selon la localisation par commune ne précise donc pas laquelle diffère significativement des autres. D'où nous allons poursuivre l'étude afin d'isoler les différences entre des sous-ensembles afin de voir celle qui diffère des autres. Etant donné, la non homogénéité des variances et de la normalité, le test de Games-Howell de comparaison multiple est appliqué afin de déterminer les communes qui sont homogène pour les prix des maisons. Il porte sur la comparaison de toutes les moyennes prises deux à deux.

	(J) Commune de localisation	Différence de moyennes (I-J)	Signification	Intervalle de confiance à 95%
	(J) Commune de localisation	Différence de moyennes (I-J)	Signification	Borne inférieure	Borne supérieure
Ibanda	Kadutu	24055,271^*	,000	11845,49	36265,05
Ibanda	Bagira	26815,712^*	,000	15342,00	38289,42
Kadutu	Ibanda	-24055,271^*	,000	-36265,05	-11845,49
Kadutu	Bagira	2760,441	,548	-3486,78	9007,66
Bagira	Ibanda	-26815,712^*	,000	-38289,42	-15342,00
Bagira	Kadutu	-2760,441	,548	-9007,66	3486,78
*la différence moyenne est significative au niveau de 0,05

Ce tableau permet de détecter des différences significatives entre d'une part des prix des maisons de la commune d'Ibanda et d'autre part avec ceux de la commune de Bagira et de Kadutu. Mais les prix des maisons de la commune de Kadutu ne diffèrent pas significativement en moyenne de ceux de la commune de Bagira.

En effet, toutes choses étant égales par ailleurs, à une maison présentant des caractéristiques physiques identiques, une maison située dans la commune d'Ibanda serait vendue en moyenne plus chère que celle située à Bagira ou à Kadutu. Cette survalorisation du prix dans cette commune serait la conséquence de la dotation des caractéristiques externes demandées par les ménages en grand nombre, notamment la qualité de l'infrastructure (transports, institutions, réseau de commerce et de services), la proximité des lieux stratégiques, le cadre paysager, le niveau de richesse des habitants, l'intensité de la desserte en transports en commun, la sécurité, et même la présence de service public.

Pour déterminer la valeur de son bien, le propriétaire peut se renseigner, soit auprès de l'expert immobilier qui donne une estimation du prix basée sur la valeur des transactions sur les biens voisins, soit directement auprès des propriétaires des biens voisins. Il existe donc un processus d'interaction entre les valeurs des biens. Lorsque les prix immobiliers sont spatialement corrélés, une hausse de la valeur d'un bien se diffuse sur les biens voisins en passant par le processus d'évaluation (effet de

diffusion). Cela signifie qu'une observation a une influence très forte sur son proche voisin et que cette influence se diffuse dans le voisinage lointain. De plus des biens voisins ont souvent été construits à la même période, ils ont fréquemment la même structure, le même style et la même taille. Par ailleurs, ces biens doivent faire face aux mêmes variables d'externalité, positive ou négative, qui affectent le prix. Il peut s'agir de la qualité de l'environnement, le projet de construction de nouvelles routes, le problème d'inondation dans certains quartiers, les nuisances sonores, la vue, etc. Ces deux phénomènes, l'effet de la diffusion ou celui des externalités, montrent qu'il existe une corrélation spatiale qui influence les prix et en présence de corrélation spatiale, le modèle hédonique classique utilisant les moindres carrées ordinaires fournit des estimations biaisées et non efficientes. Cette particularité des données immobilières nécessite alors de prendre en compte la dépendance spatiale dans le modèle d'évaluation des biens immobiliers.

L'autocorrélation spatiale est définie comme la corrélation, positive ou négative, d'une variable avec elle-même provenant de la disposition géographique des données. Cette sous-section porte en première étape sur le diagnostic de l'existence de la dépendance spatiale dans le modèle hédoniste traditionnel des prix, en deuxième étape sur l'estimation du modèle autorégressif spatial (SAR ou LAG) pour lequel nous supposons que la valeur d'un bien immobilier dépend de la valeur des autres biens voisins traduit par l'effet de diffusion , et enfin la troisième étape sur l'estimation de l'erreur spatiale (SEM) pour la prise en compte l'influence des externalités dans le modèle traditionnel.

III.3.3.1 Tests de l'autocorrélation spatiale dans la régression par moindre carré ordinaire L'indice de Moran est à cet effet un indicateur principal utilisé en économétrie spatiale mais exige a priori de déterminer la structure de l'autocorrélation spatiale. Dans le présent travail, la matrice de voisinage avec la condition de distance de séparation maximale de 400 mètres sont choisis afin que chaque observation contienne au moins un voisin et l'inverse de la distance comme pondération. Ce choix est justifié par Srikhum (2012) qui montre que l'inverse de la distance permet de mesurer l'accessibilité qui est une des caractéristiques principales en évaluation immobilière.

De ce tableau ci-haut, il s'observe que la statistique de l'indice de Moran (Moran's I) est de 3,615 avec un P-value de 0,000 qui conduit au rejet de l'hypothèse nulle d'absence de dépendance spatiale. Le modèle est donc mal spécifié et il y a omission de l'autocorrélation spatiale.

Comme tous les deux tests du multiplicateur de Lagrange (LAGLM et ERRLM) sont significatifs et que le premier test (LAGLM ) est plus significatif que le test de l'autocorrélation des erreurs (ERRLM )¹⁹, Anselin et Rey (1991) et Florax et Folmer (1992) cités par Gallo (2002) propose de choisir le modèle autorégressif (SAR) comme le meilleur modèle. Ces tests indiquent donc la prédominance de l'effet de la diffusion sur la valeur des maisons que celui des externalités. Pour confirmer ce résultat, les deux modèles économétriques spatiaux sont estimés et seront vérifiés par le test du rapport de vraisemblance pour lequel le meilleur modèle sera celui qui minimise le critère d'information d'Akaïke.

¹⁹ Pour lequel au seuil 0,001 il devient impossible de rejeter l'hypothèse nulle.

Tableau 3.18 : Comparaison des résultats de Moindre ordinaire corrigé de l'hétéroscédasticité avec celui du modèle SAR et SEM

Modèles	Modèle simple		Modèle SAR		Modèle SEM
Estimation	MCO robustes)	(écart-types	MV		MV
Commbag	-1654.714	(0.816)	-4449,363	(0,473)	-2442,031	(0,744
Commkad	-12241.11	(0.000*)	-8578,381	(0.000*)	-12458,13	(0,000*
Surfpcl	10.69862	(0.446)	11,9539	(0,244)	7,919039	(0,448
Surfms	8.507277	(0.674)	-4,663611	(0,764)	8,468029	(0,587
Nbrepc	2146.049	(0.000*)	1933,98	(0.000*)	2042,781	(0,000*
Etmurs	2182.212	(0.223)	484,4737	(0,856)	1768,914	(0,518
Nbreetg	12414.64	(0.000 *)	13039	(0.000*)	12281,55	(0,000*
Ancms	204.0747	(0.807)	-554,0863	(0,402)	438,7111	(0,531
Typems	2010.463	(0.289)	2084,561	(0,434)	1776,533	(0,510
Pres2toilslb	4561.473	(0.063***)	4330,604	(0,039**)	3822,411	(0,078***
Presgarg	2229.419	(0.197)	2777,891	(0,117)	1993,099	(0,262
Distcentvil	-4.337581	(0.006**)	-2,929442	(0,046*)	-4,370257	(0,020**
Distaxepripl	60.18355	(0.762)	-89,82816	(0,591)	-28,60059	(0,863
Distrtproch	-48.03356	(0.206)	-65,50055	(0,142)	-55,83225	(0,231
Distinfrtrpproch	-2.632062	(0.990)	145,5518	(0,389)	76,3005	(0,45
Distcentrmdicl	161.6571	(0.411)	146,803	(0,408)	195,2044	(0,310
Distetensgmt	-112.6833	(0.749)	27,94557	(0,931)	-112,8768	(0,732
Nivetd	3929.772	(0.003**)	3527,593	(0,000*)	3468,528	(0,000*
Profess	3232.878	(0.001**)	3126,715	(0,000*)	3357,859	(0,000*
Ctttransp	-4.45861	(0.177)	-3,10503	(0,155)	-3,351624	(0,173
_cons	7328.84	(0.265)	62,706222	(0,991)	7979,884	(0,215
Rhô (??)			0,2182205	0,000*
Lambda (À)					0,2972573	0,005***

De ce tableau il s'observe que pour tous ces trois modèles sept variables sont significatives au seuil maximum de 10%. Il s'agit de la localisation de la maison dans la commune de Kadutu(Commkad), du nombre des pièces(Nbrepc), nombre d'étage(Nbreetg), la présence de plus de 2 toilettes/salles de bain (Pres2toilslb), la distance par rapport au centre-ville (Distcentvil) ainsi que le niveau d'étude(Nivetd) et la profession du propriétaire de la maison (Profess).

Pour le modèle SAR tous les signes à priori attendus ont été retrouvés à l'exception de la sommes des surfaces occupées sur la parcelle (Surfms), l'ancienneté de la maison(Ancms), et de la distance par rapport à l'accès à l'infrastructure de transport en commun la plus proche(Distinfrtrpproch). Cela signifierait que l'augmentation du niveau d'occupation de la parcelle entraine la diminution de la valeur de la maison pour la variable Surfms, ensuite pour l'ancienneté de la maison (Ancms) les maisons plus neuves valent moins que les maisons anciennes et enfin pour la variable de la proximité par rapport à un accès à l'infrastructure de transport en commun la plus proche (Distinfrtrpproch) avec un signe positif signifie que l'augmentation de la distance avec la maison influence positivement la valeur des immobiliers. Ce qui implique que les nuisances l'emportent sur les avantages procurés par cette proximité.

Généralement, l'autocorrélation spatiale peut être négative ou positive, les résultats de l'estimation du modèle SAR font apparaitre une autocorrélation spatiale positive et significative au seuil de 1% de 21,82%(Rhô=0,2182). Lorsqu'il y a autocorrélation spatiale pour une variable, cela signifie qu'il y a une relation fonctionnelle entre ce qui se passe en un point de l'espace et ce qui se passe ailleurs. Tobler (1979) avait souligné en suggérant la première loi de la géographie: « Everything is related to everything else, but closer things more so » cela signifie que dans un voisinage de 400 mètres considérés

dans ce travail des lieux proches se ressemblent davantage que les lieux éloignés²⁰. Cela traduit qu'une observation a une influence très forte sur son proche voisin et que cette influence se diffuse dans le voisinage lointain signifiant qu'une hausse du prix d'un bien a une influence sur les prix de biens voisins. Par exemple, le passage pour un immeuble d'un étage à cinq étages a une influence directe positive sur le prix de vente de cet immeuble et grâce à l'effet de diffusion, cette hausse du prix a une influence positive indirecte sur les prix des biens voisins en passant par le processus d'évaluation des biens. Ainsi, l'impact de ce prix se diffuse mais son importance dépend négativement de la distance avec d'autres biens.

Et pour le modèle SEM seules les variables distances par rapport à un établissement d'enseignement le plus proche(Distetensgmt) et la variable de la distance par rapport à l'accès à l'infrastructure de transport en commun la plus proche (Distinfrtrpproch) n'ont pas donné les signes attendus. Nos investigations montrent une autocorrélation spatiale des erreurs positive traduisant un impact positif des externalités sur la valeur des maisons 29,72%(Lambda=0,2972) mais non significative au seuil de 5% mais significative à 10%.

Ainsi pour vérifier la conclusion de Anselin et Rey (1991) et Florax et Folmer (1992) cités par Gallo (2002) basée sur les tests du multiplicateur de Lagrange pour lequel le meilleur modèle serait le modèle SAR, il est procédé au test moyen du test du ratio de vraisemblance pour lequel le meilleur modèle devrait être celui qui minimise le critère d'information Akaïke(AIC).

Si plusieurs modèles restent encore en compétition, Gallo (2002) propose de faire le choix entre modèles avec les critères traditionnels tels que les critères d'information d'Akaïke(AIC) en passant par le test du rapport de vraisemblance.

²⁰ L'augmentation de la distance de voisinage entraine l'augmentation du niveau de la corrélation.

Modèle	Observation	Ll(null)	Ll	Ddl	AIC	BIC
MCO (Mod1)	193	-2250,903	-2054,756	21	4151,51	4220,028
MCO (robuste) (Mod2)	193	-2250,903	-2054,756	21	4151,21	4220,028
SAR (Mod3)	193	-2054,756	-2054,758	23	4137,516	4212,558
SEM (Mod4)	193	-2054,756	-2051,369	23	4148,738	4223,78
Likelihood-ratio test LR chi2(5) = 24.77 Prob > chi2 = 0.0002

Ces résultats montrent que le modèle SAR est le modèle qui minimise le critère d'information d'Akaïke (AIC) suivi du modèle SEM. Ce résultat converge avec celui d'Anselin et Rey (1991) et Florax et Folmer (1992) cités par Gallo (2002) basées sur le test du multiplicateur de Lagrange pour lequel le modèle SAR est le meilleur²¹. Ce qui montre que l'effet de la diffusion (spillover effect) l'emporte sur l'effet des externalités sur la valeur des maisons dans la ville de Bukavu. Cela signifie que la valeur d'une maison a une influence très forte sur son proche voisin et que cette influence se diffuse dans le voisinage lointain. La moyenne pondérée des prix de vente des biens voisins est utilisée comme prix de référence pour déterminer la valeur de son bien. Il existe donc un processus d'interaction entre les valeurs des biens.

L'hypothèse du modèle classique de la régression multiple pour laquelle les variables explicatives du modèle soient indépendantes les unes des autres et que dans le cas contraire, il y a présence de multicolinéarité. Le tableau 3.1 de l'annexe 3 portant le test VIF réalisé après la régression par moindre carré ordinaire permet de montrer qu'il existe une multicolinéarité forte( c'est-à-dire VIF de la variable supérieur 10) pour certaines variables, il s'agit de la distance avec l'infrastructure de transport la plus

²¹ Ce résultat reste valable sous deux conditions suivantes : la première est basée sur « la matrice de voisinage » permettant de déterminer l'ensemble des voisins et la deuxième sur « la matrice de poids » pour déterminer les poids associés à chaque voisin où on peut donner des poids identiques pour le voisinage ou accorder des poids important aux voisins proches et des poids faibles aux voisins éloignés. Pour la première condition l'on a utilisé « la condition de distance » de séparation maximale de 400 mètres tout en sachant qu'on pourrait aussi utiliser « la condition de contiguïté » pour déterminer l'ensemble des voisinages ou d'augmenter la séparation. Et pour la deuxième « la matrice de poids standardisée » où on pourrait aussi utiliser « la matrice des poids binaires » ou « la matrice de poids binaire générale ». Ces résultats seraient différents si l'on modifiait l'une ou l'autre de ces deux conditions.

proche (Distinfrtransprch) avec un VIF de 208,96 ; de la distance avec l'axe principale la plus proche avec un VIF de 203.76 ainsi que de la localisation de la maison dans la commune de Bagira (Commbag) avec un VIF de 14,50.

La suppression de la variable Distinfrtransprch et Commbag a permis d'améliorer le modèle en obtenant un premier modèle optimal ne souffrant plus du problème de multicolinéarité, avec aucune variable avec un VIF = 10 (cfr tableau 3.2 de l'annexe 3) et pour lequel le test du rapport de vraisemblance montre une diminution du critère d'information d'Akaike pour tous les modèles et concluant toujours le modèle SAR étant le meilleur parce qu'il minimise le critère d'information d'Akaïke (AIC) de tous suivi du modèle SEM(cfr tableau 3.3 de l'annexe 3).

Pour raisons d'amélioration du modèle, nous avons fait une dernière estimation avec les variables significatives corrigés de la multicolinéarité de ces quatre différents modèle (MCO, MCO robuste, SAR et SEM) et avons obtenu les résultats ci-après :

Modèles	Modèle simple	Modèle SAR	Modèle SEM	VIF
Estimation	MCO robustes	MV	MV	VIF
Commkad	-13230.36 0.000*	-9146.249 0.000*	-13402.02 0,000*	1.64
Nbrepc	2811.991 0.000*	2301.876 0.000*	2588.56 0,000*	2.15
Nbreetag	11108.01 0.000*	12065.43 0.000*	11192.12 0,000*	1.76
Pres2toilslb	6018.483 0.07***	4855.249 0,019**	4921.392 0,022***	1.40
Distcentvil	-4.263679 0.000*	-3.030583 0,001*	-4.844167 0,000**	3.62
Distaxepripl	32.89461 0.000*	25.72392 0,059***	23.16502 0,187	1.32
Nivetd	4306.285 0.000*	3382.211 0,000*	3626.046 0,000*	1.22
Profess	4137.927 0.000*	3693.194 0,000*	4027.183 0,000*	1.38
Ctttransp	-4.948924 0.056***	-3.650898 0,055***	-3.592527 0,116	3.79
_cons	9400.736 0.024**	2464.794 0,540	11626.34 0,215
AIC	4140.864	4125.412	4136.734
Rhô (??)		0,20551 0,000*

Le modèle SAR étant donc le meilleur en termes de critère d'information, Il apparaît donc bien que ce modèle soit la spécification la plus adéquate, il fera alors l'objet

Le modèle nous indique aussi qu'à toutes choses égales par ailleurs, l'accroissement du nombre des pièces (Nbrepc) augmente le prix de la maison de manière significative. Le passage d'une pièce à deux pièces augmente le prix en moyenne de 2 301,876$. Ensuite, L'augmentation d'un niveau d'étage (Nbreetg) augmente significativement le prix de la maison de 12 065,43$ en moyenne.

Les résultats montrent aussi qu'une salle de bain ou toilette supplémentaire (Pres2toilslb) accroit la valeur de la maison de manière significative d'une valeur de 4 855,249$ au seuil de 5%.

L'impact global de la localisation sur la valeur de la maison est bien entendu lié à tout ce que sa proximité peut offrir.

La commune de référence dans cette recherche est la commune d'Ibanda, les coefficients négatifs associés à la variable pour la localisation d'une maison dans la commune de Kadutu(Commkad) indiquent que cette commune valorise plus faiblement les maisons d'habitation que la commune d'Ibanda.

La distance moyenne par rapport à la poste(Distcentcil) est très élevée pour les maisons situées à Bagira, suivie par celle de Kadutu et Ibanda, cette distance influence significativement la valeur des maisons de 3,92$ de manière négative.

Ce résultat concorde avec les hypothèses du modèle urbain néoclassique proposé par Alonso (1964), Mills (1967) et Muth (1969), postulant que la structure d'équilibre d'utilisation du sol est déterminée par l'arbitrage effectué par les ménages entre la rente foncière et l'accessibilité au centre de la ville, lieu de concentration des activité. Le succès de ce modèle monocentrique vient du fait qu'il parvient, à partir de développements relativement simples, à rendre compte de certaines régularités

concernant la répartition spatiale des populations, des activités économiques et des valeurs foncières.

La distance avec l'axe principale (Distaxepripl) influence négativement la valeur des maisons de manière significative. Cela implique que les inconvénients associés à sa proximité l'emportent sur ses avantages, d'où l'augmentation de cette distance influence positivement la valeur des maisons. Ce qui ne permet pas de vérifier notre hypothèse.

IIII.3.4.3 Impact des caractéristiques de voisinages sur le prix de la maison

L'accroissement de la distance avec un centre médical(Distcentrmdicl) et celle d'un établissement d'enseignement le plus proche(Distetensgmt) n'ont pas été retenu dans le modèle optimal car elles n'étaient pas significative. Ainsi, la présence de ces aménités qui ne sont pas toujours localisées dans le centre-ville et recherchées par les ménages telles que les hôpitaux ou les universités pourraient permettre de contrebalancer la force d'attraction du centre-ville (Straszheim, 1987) et d'expliquer, dans une certaine mesure, le phénomène d'étalement urbain, mais cette hypothèse n'a pas été vérifiée. Ce qui permettrait d'expliquer que la délocalisation des deux éléments dans les périphéries ne permettrait d'atteindre les objectifs d'étalement urbain.

IIII.3.4.4 Impact des caractéristiques socioprofessionnelles et démographiques sur la valeur des maisons

Enfin, les analyses portant sur la localisation résidentielle des différentes catégories socio-professionnelles et démographiques permettent à analyser la ségrégation résidentielle dans la ville de Bukavu en lien avec les déterminants des valeurs des maisons d'habitation et du choix résidentiel des ménages. Le niveau d'étude (Nivetd) et la profession (Profess) d'un côté permettant d'évaluer les préférences en termes d'environnement social pour lesquelles le modèle d'offre de biens publics locaux de Tiebout(1956), ou les modèles avec effets de voisinage (Durlauf, 2004) par le cout total de transport de l'autre côté permettent de mesurer les poids relatifs des préférences pour un environnement périurbain (distance au centre) du modèle urbain monocentrique d'Alonso (1964), puis (1969) et Mills (1967, 1972)

Les résultats montrent que le niveau d'étude(Nivetd) et la profession (Profess) du propriétaire des ménages influencent significativement la valeur de la maison, d'un montant respectif de 3 382,211$ et de 3 693,194 de manière positive, ce qui vérifie nos hypothèses basées sur ces variables. Cela implique que la composition en termes d'environnement social influence la valeur de la maison. De ce point de vue, il s'observe donc que l'étude des déterminants de la fixation du prix des maisons d'habitation peut être conçue comme une analyse des transformations sociales, démographiques, politiques, économiques qui affectent le milieu urbain. Cela se vérifie de part plusieurs études antérieures. On peut évoquer dans ce sens les apports d'Alonso (1964), Mills (1967) et Muth (1969), qui soutiennent l'idée que l'offre et la demande sur le marché immobilier expliquent la localisation des ménages aisés et des ménages pauvres dans des lieux différents, ou ceux de Tiebout (1956), selon lequel le jeu d'attraction et de répulsion entre différentes catégories de ménages structure l'espace résidentiel selon le niveau de vie, comme Zenou (2002) qui conclut que la composition sociale d'un quartier peut conditionner d'autres décisions prises par les ménages en terme du choix de localisation à travers les relations de voisinage qui peuvent avoir une influence sur la formation du capital humain en mesure même d'influencer sur les chances que les habitants accèdent à l'emploi.

Ensuite les résultats portant sur le cout total de transport aller-retour pouvant supporter le chef du ménage (Ctttansp) vérifie notre hypothèse émise ainsi que le modèle de Wingo(1961) pour lequel dans son approche donne un rôle central aux transports dans le fonctionnement urbain, en considérant que le marché foncier est conditionné par les transports urbains. Dans son modèle il prend en compte d'un coût généralisé de transport (comme dans ce présent travail) au lieu d'un coût de transport fonction linéaire de la distance au centre. Ce coût généralisé reflète l'ensemble des dépenses monétaires de transport et la valeur attribuée au temps de trajet. Il arrive à la conclusion que l'amélioration du réseau de transport entraîne une diminution des valeurs foncières et des densités résidentielles et une extension de la ville.

Cette section a pour objet d'identifier les implications induites de cette étude. Les résultats de cette analyse ont fait ressortir les facteurs pertinents des déterminants de la fixation du prix des maisons d'habitation dans la ville de Bukavu. De ces résultats, les implications suivantes peuvent être tirées par les décideurs publics en vue d'entrainer une baisse du prix des immobiliers résidentiels et pouvoir bien mener une politique d'étalement urbain :

- Dans une logique alternative, dans laquelle les complémentarités entre espaces urbains et ruraux soient utilisées au maximum, la délocalisation des activités ou des certains services publics (le parquet, la prison centrale,...) doit permettre de contrebalancer la force d'attraction du centre-ville et dans une certaine mesure, d'atteindre les objectifs actuels d'étalement urbain.

- Diminuer le temps dédié aux déplacements quotidiens de la population en assurant une cohérence entre la répartition de l'habitat et des emplois/activités sur le territoire en développant le réseau de transport public dans tous les territoires.

- Renforcer les infrastructures de transports et favoriser l'urbanisation autour des noeuds de transport public : stations de transport collectif en site propre, parking public, gares si possible... ;

- Lutter contre la ségrégation sociale dans le territoire à travers des dessertes plus importantes dans les quartiers périurbains en créant des centres commerciaux, des hôpitaux ou des écoles dans ces zones.

- limiter aussi possible l'étalement urbain et favoriser les modes d'urbanisation moins consommateurs d'espace en protégeant certaines zones, en limitant l'espace à occuper par une seule personne, en proposant des modèles des maisons à construire dans une zone.

Bien que cette recherche ait fait des avancées dans la compréhension des facteurs déterminants de la fixation du prix des maisons d'habitation dans la ville de Bukavu, elle rencontre cependant des limites. Tout d'abord, la petitesse de la taille de l'échantillon suite à une marge d'erreur et un seuil de signification égale à 5%. Ensuite la répartition de l'échantillon en commune et en quartier masque certaines informations. De ce fait une autre approche serait d'élargir la taille de l'échantillon et de le repartir en pôle urbain et périurbain en approfondissant la répartition en commune, quartier et avenu.

Ensuite, introduire dans un modèle hédonique une variable de centre-ville consiste de ce fait à agréger en un seul « bouquet » l'ensemble des éléments qui composent le centre urbain et donc à considérer que ces derniers se localisent en un même point géographique, alors que dans la réalité ces éléments se dispersent sur une zone géographique centrale plus ou moins étendue selon la ville considérée. Cependant, une étude permettant de désagréger la variable de centre-ville entre ses éléments composants, et d'en calculer des distances par rapport à l'immeuble permettrait d'améliorer cette étude. Cette limité a été observée aussi lors de l'introduction dans le modèle économétrique d'un ensemble d'indicateurs caractérisant l'environnement socio-économique du logement. Nombre de ces caractéristiques sociodémographiques étant corrélées, la plupart n'apparaissent pas dans le modèle économétrique, sans pour autant que cela signifie qu'elles ne jouent pas sur les choix résidentiels des ménages. Ainsi une étude incluant un bon nombre des variables sociodémographique permettraient d'améliorer le travail.

Au niveau des modèles spatiaux la condition de poids standardisée, utilisée dans ce travail, est la plus simple à appliquer mais elle présente un biais car dans la régression, cette condition accorde une importance plus grande aux observations ayant peu de voisins. D'où nous suggérons une recherche future utilisant différentes matrices de poids (Matrice de poids binaire, Matrice de poids binaire générale) et comparer ainsi les différents résultats.

Determinants de la fixation du prix des maisons d'habitation a Bukavu

CHAPITRE III : PRESENTATION ET ANALYSE DES DONNEES