|

REPUBLIQUE DEMOCRATIQUE DU CONGO
ENSEIGNEMENT SUPERIEUR ET
UNIVERSITAIRE
UNIVERSITE CATHOLIQUE DE BUKAVU
B.P 285 BUKAVU
FACULTE DES SCIENCES ECONOMIQUES ET DE GESTION
DETERMINANTS DE LA FIXATION DU PRIX DES
MAISONS
D'HABITATION A BUKAVU
Mémoire présenté et défendu par :
KAJEMBA WA KAJEMBA François
En vue de l'obtention du diplôme de licencié en
Sciences de gestion Option : Gestion
financière
Directeur : Professeur Docteur Christian KAMALA
KAGHOMA Co-directeur : Chef de Travaux Eugène LUBULA
MUMBERE
Mars 2015
EPIGRAPHE
« Ce n'est pas à dire que nous soyons par
nous- mêmes capables de concevoir quelque chose comme venant de
nous-même. Notre capacité, au contraire, vient de Dieu
»
2 corinthiens 3: 5
« Le disciple n'est pas plus que le maître; mais
tout disciple accompli sera comme son maître »
Luc 6 :40

DEDICACE
A mon Dieu, l'auteur et le consommateur de ma foi,
A la mémoire de ma mère, Fatuma ZANONA, et de
mon père, Ngekema KAJEMBA,
A mes futurs enfants et toute ma descendance à qui je
souhaite de faire ce que je n'ai pas pu faire,
A tous ceux qui me portent dans leurs coeurs.
II
REMERCIEMENT
Nous voulons, avant toute chose, rendre grâce à
l'Eternel Dieu pour sa protection qu'il ne cesse de nous garantir et de nous
permettre d'arriver à rédiger ce travail.
Aux autorités académiques de l'Université
Catholique de Bukavu, en général, et à celles de la
Faculté des Sciences Economiques et de Gestion, en particulier, pour
leur contribution à notre formation intellectuelle.
Je remercie le Professeur Docteur Christian KAMALA KAGHOMA
pour avoir accepté d'assurer l'encadrement de ce travail. Je lui exprime
ici ma reconnaissance la plus profonde pour le soutien, la confiance et
l'encouragement qu'il m'a témoignés tout au long de ce
travail.
Je remercie, de manière particulière, le Chef
des travaux Eugene LUBULA MUMBERE d'avoir encadré ce travail. Il a
significativement contribué à l'amélioration de cette
recherche. Son amour pour le travail bien fait me marquera à jamais dans
ma carrière de chercheur. Je lui exprime ici ma reconnaissance la plus
profonde pour la confiance qu'il m'a témoignée tout au long de ce
travail.
Je remercie affectueusement ma famille, avec toutes les
difficultés que nous avons dépassées ensemble, ce travail
constitue la meilleure occasion de montrer une reconnaissance profonde à
leur égard : ma grande soeur Ainsi, mes deux petites soeurs Esther et Ma
Fille et mon petit frère Danny. Pasteur Victor et Oncle David et
à toute la famille élargie dont l'amour me poussait jours et
nuits à plus d'efforts.
Nous ne pouvons pas terminer cette partie sans pour autant
reconnaitre l'apport de nos camarades avec qui nous avons mené cette
lutte et aux amis qui ont fortement contribué à la
rédaction de ce travail : Christophe MUGANGU, Oscar CHOKOLA, Fabrice
NGERENGO, Franck KINGOMBE, Joseph MUKULU, Issa KABANGE, Doudou DUNIA,
Chanceline ANGALIKIYANA, Bienvenu MATUNGULU, Samantha MALU MIMPE, Kefc
NDIRHUHIRWE, Oreste KABANDA, Dan MUKALAY, Guillain MALEKERA, Fabrice
BABWINE...
KAJEMBA WA KAJEMBA
III
SIGLES ET ABREVIATIONS
- AIC : Akaike Information Criterion
- ANOVA : Analysis Of Variance.
- Ddl : degré de liberté
- ERRLM : test du multiplicateur de Lagrange de l'erreur
spatiale
- ERRRLM : test robuste du multiplicateur de Lagrange de
l'erreur spatiale
- FGS2SLS : Feasible Generalized Spatial Two Least Squares
- G2SLS :Generalized Spatial Two stage least square
- IITA : International Institute of Tropical Agriculture
- LAGLM : test du multiplicateur de Lagrange de
l'autocorrélation spatiale
- LAGRLM : test du robuste du multiplicateur de Lagrange de
l'autocorrélation
spatiale
- MCMC : Markov Chain Monte Carlo
- MCO : Moindres Carrées Ordinaires
- Moran's I : Indice de Moran
- ODK : Open Data Kit
- SAR : Spatial Autoregressive Model
- SEM : Spatial Erreur Model
- SLX : Spatial Lagged X Model
iv
LISTE DES TABLEAUX
- Tableau 2.1 : Répartition de la population de Bukavu par
commune
- Tableau 2.2 : Répartition de la population par
ménages
- Tableau 2.3 : Répartition de l'échantillon pour
l'enquête proprement dite
- Tableau 2.4 : Définition des variables et
présentation des signes attendus
- Tableau 3.1 : correspondance commune-sexe des personnes
enquêtées
- Tableau 3.2 : Tableau croisé commune-Etat-civil des
enquêtés
- Tableau 3.3 : Tableau commune-Profession des personnes
enquêtées
- Tableau 3.4 : Tableau commune-surface de la parcelle
(surfpcl)-prix de la
maison (prms)
- Tableau 3.5 : Corrélation bilatérale surface de
la parcelle (surfpcl) -prix de la
maison (prms)
- Tableau 3.6 : commune-surface construite-prix par mètre
construit
- Tableau 3.7 : Corrélation bilatérale surface
construite (surfms)-prix de la maison
(prms)
- Tableau 3.8 : commune-nombre des pièces (nbrepc)
- Tableau 3.9 : Corrélation de Pearson nombre des
pièces (nbrepc) -prix de la
maison (prms)
- Tableau 3.10 : Résultats de la première
estimation par moindre carré ordinaire
(mod1)
- Tableau 3.11 : Résultat du test de Breusch-Pagan de
l'hétéroscedasticité
- Tableau 3.12 : Résultats de la deuxième
régression par moindre carré
ordinaire corrigé de
l'hétéroscedasticité par la méthode de white.
(mod2)
- Tableau 3.13 : Test d'homogénéité de la
variance
- Tableau 3.14 : Tests de normalité
- Tableau 3.15 : Résultat du test de Kruskal-Wallis
- Tableau 3.16 : Test de Games-Howell de comparaisons
multiples
- Tableau 3.17 : Diagnostic de la dépendance spatiale
- Tableau 3.16 : Comparaison des résultats de Moindre
ordinaire corrigé de
l'hétéroscédasticité avec celui du
modèle SAR et SEM
- Tableau 3.17 : Résultat du test du rapport de
vraisemblance
V
LISTE DES GRAPHIQUES
Graphique 3.1 : Diagramme des moyennes des prix selon les
communes Graphique 3.2 : Diagramme des moyennes des prix selon les quartiers
VI
TABLE DES MATIERES
EPIGRAPHE i
DEDICACE ii
REMERCIEMENT iii
SIGLES ET ABREVIATIONS iv
LISTE DES TABLEAUX v
LISTE DES GRAPHIQUES vi
TABLE DES MATIERES vii
INTRODUCTION 1
CHAPITRE I : REVUE DE LA LITTERATURE 6
I.1 REVUE THEORIQUE 6
I.1.1 Théorie de la valeur et du prix 6
I.1.2 Choix résidentiel des ménages 9
I.1.2.1 La théorie de la microéconomie urbaine 9
I.1.2.2 La théorie de l'utilité aléatoire
12
I.1.2.3 Déterminants du choix résidentiel des
ménages 14
I.1.3 La méthode hédonique 19
I.1.3.1 Théorie traditionnelle de la consommation 20
I.1.3.2 Théorie de Lancaster 20
I.1.3.3 Modèle de S. Rosen sur la demande de
caractéristique 21
I.2 REVUE EMPIRIQUE 23
CHAP. II APPROCHE METHODOLOGIQUE 27
II.1. TECHNIQUES DE COLLECTE DES DONNEES 27
II.1.1 Pré-enquête : détermination de la
taille de l'échantillon 27
II.1.2 L'enquête proprement dite 30
II.2 TECHNIQUE DE TRAITEMENT DES DONNEES 32
II.2.1 Fondement théorique et spécification du
modèle 32
II.2.1.1 Choix de la forme du modèle 33
II.2.1.2 Description des variables 38
II.2.2 Méthodes d'estimation 42
II.2.2.1 La méthode de moindre carré ordinaire
(MCO) 42
II.2.2.2 Prise en compte de
l'hétérogénéité spatiale 44
II.2.2.3 Prise en compte et mesures de l'autocorrélation
spatiale 47
vii
II.2.3. Choix du modèle optimal 55
II.2.4. Présentation des outils de traitement des
données 56
CHAPITRE III : PRESENTATION ET ANALYSE DES DONNEES 58
III.1 Caractéristiques de l'échantillon 58
III.2 Etude exploratoire sur les relations entre certaines
variables 60
II.2.1 Caractéristiques physiques et de localisation des
ménages 61
III.2.1.1 La surface de la parcelle 61
III.2.1.2 La somme des surface de différentes
constructions se trouvant sur la
parcelle (surfms) 62
III.2.1.3 Le nombre des pièces 63
III.2.2 Caractéristiques socioprofessionnelles et
démographiques des
propriétaires 65
III.3 Résultats des estimations et interprétation
66
III.3.1 Les résultats de la méthode de moindre
carré ordinaire 66
III.3.2 Prise en compte de
l'hétérogénéité spatiale 68
III.3.2.1 Hétéroscedasticité 69
III.3.2.2 ANOVA Spatiale 71
III.3.3 Prise en compte de l'autocorrélation spatiale
76
III.3.3.1 Tests de l'autocorrélation spatiale dans la
régression par moindre carré
ordinaire 76
III.3.3.3 Choix du Modèle optimal : le test du rapport de
vraisemblance 80
III.3.4 Interprétation et discussion des résultats
83
III.3.4.1 Impact des caractéristiques physiques sur le
prix de la maison 83
III.3.4.2 Rôles de la localisation sur la valeur de la
maison 83
IIII.3.4.3 Impact des caractéristiques de voisinages sur
le prix de la maison 84
IIII.3.4.4 Impact des caractéristiques
socioprofessionnelles et démographiques
sur la valeur des maisons 84
III.4 Implication des résultats 86
III.5 Limites et perspectives de recherche 87
CONCLUSION 88
BIBLIOGRAPHIE 91
ANNEXES NNNN
VIII
INTRODUCTION
Dans de nombreux pays, l'immobilier a un rôle moteur
dans l'économie comme c'est le cas aux Etats Unis, en Espagne et au
Royaume Uni (Clévenot, 2011). Plusieurs études montrent que
l'évolution de ce secteur est souvent fortement corrélé
avec celle de la croissance économique et parfois
considéré comme un indicateur de la situation économique,
étant donné que son impact est aussi important en période
de récession comme en celle d'expansion.
Leamer (2007) étudie la contribution de
l'investissement résidentiel à la croissance du PIB afin de
montrer le rôle que peut jouer cette composante avant et durant les
phases de récession. Il estime que ce secteur est un indicateur fiable
de la situation économique car lorsque l'immobilier est en
difficulté et les dépenses de logement sont en baisse, une
potentielle récession se prépare. De ce résultat il
conclut à la nécessité de prise en compte de
l'évolution du secteur immobilier dans la détermination de la
politique monétaire. Dufrénot et Malik (2010), à leur
tour, mettent en évidence le rôle des prix de l'immobilier dans le
déclenchement des récessions. Étant donné que le
secteur immobilier est l'une des plus importantes composantes de
l'économie et qu'il est fortement lié à l'évolution
de la conjoncture économique, il peut en conséquence
déclencher une crise en cas d'effondrement : la crise des «
subprime »1 en est la preuve.
L'immobilier occupe une place prépondérante dans
les choix d'investissement des ménages. Afin de réaliser un
investissement immobilier, une bonne évaluation du bien est une
étape indispensable pour les investisseurs (Shrikhum, 2012).
La ville de Bukavu a été créée en
1925 et son aménagement pour être une ville était
planifiée. On y distinguait les quartiers résidentiels, les
centres commerciaux, le centre Administratif, les zones industrielles et
portuaires, les espaces stratégiques, les sites de
récréation et les lieux culturelles(Mairie de Bukavu, 2014 ; et
Baissac et al., 2012; IFDP, 2013) .Après l'indépendance, la ville
a crû rapidement sur les plans
1 Elle est la crise qui s'est déclenché
au deuxième semestre 2006 avec le krach des prêts immobiliers
à risque aux Etats-Unis, que les emprunteurs, souvent dans des
conditions modestes, n'étaient plus capables de rembourser,
déclenchant la crise financière de 2007-2011.
1
démographique et spatial avec un taux de croissance
97,23% entre 1962 et 2001 et 59,2% entre 2001 et 2013 traduisant une
densité moyenne de 5 728 à 14 048 habitants/Km2 entre
2001 et 2013(IFDP, 2013; Baissac et al.(2012) montrent que le secteur
immobilier bukavien connait de ce fait une très forte expansion.
En considérant les caractéristiques
spécifiques d'un bien immobilier telles que son caractère
indivisible, sa valeur unitaire très élevée, sa faible
liquidité, sa grande hétérogénéité et
son immobilité physique, on est conduit à distinguer ce type de
bien des autres biens. Or, dans un marché de concurrence pure et
parfaite le prix du marché pour un bien est identique à la valeur
de celui-ci alors qu'en réalité, le marché des biens
immobiliers s'écarte de ces conditions idéales en raison de ses
caractéristiques propres. Une question se pose alors : quels sont les
facteurs qui permettent de fixer le prix des maisons ?
Van Lierop et Rima (1982) montre que le marché
immobilier comme tel n'existe pas : « ce que nous appelons le
marché des immobilier résidentiels est un phénomène
complexe d'éléments et de sous marchés
corrélés et mutuellement influençant. Parmi les facteurs,
les forces et les composantes qui interagissent pour former le marché
des immobiliers résidentiels, on peut inclure une multitude d'acteurs
individuels et groupés avec des intérêts et des
références contradictoires, une multitude de motifs individuels
et attributs de comportement résidentiel, une multitude de
possibilités de choix, une multitude d'effets de débordements
social et spatial et externalités, une multitude de processus dynamiques
associés avec le développement économique et
géographique d'un système spatial». Ses méthodes
d'estimation doivent donc être aussi différentes de celles des
autres biens et doivent pouvoir prendre en compte les caractéristiques
propres aux biens immobiliers.
Rosen (1974) fonde l'approche hédonique qui permet
d'intégrer l'hétérogénéité des biens
immobiliers. La méthode des prix hédonistes permet d'estimer le
prix des différentes caractéristiques : le prix de marché
consiste en la somme des prix implicites attachés aux
caractéristiques du bien. Cependant, comme son nom l'indique, le bien
immobilier ne peut pas être déplacé ; sa valeur
dépend donc aussi partiellement
2
de sa localisation. La méthode d'estimation de sa
valeur immobilière se doit aussi de prendre en compte cette
caractéristique spatiale.
Le modèle de prix hédoniste standard peut
être amélioré en intégrant des
caractéristiques spatiales comme variables explicatives du modèle
(Travels et al.,2013 ; Srikhum,2012; Gallo,2002). Mais, malgré le nombre
important des variables locales que l'on peut rajouter, en
général les régressions n'aboutissent pas à des
résidus spatialement non corrélés. Afin de
déterminer le modèle qui permet d`analyser plus finement cette
dépendance spatiale, il faut identifier précisément le
mode d'influence de la caractéristique spatiale sur le prix
immobilier.
Le processus d'évaluation d'une maison par un
particulier par lequel pour déterminer la valeur de son bien, le
propriétaire peut se renseigner, soit auprès de l'expert du
quartier qui donne une estimation de prix basée sur la valeur de
transaction des biens voisins, soit directement auprès des
propriétaires des biens proches. Cela traduit un lien entre l'effet de
diffusion (spillover effect) et la corrélation spatiale des prix
immobiliers. En effet, des biens voisins ont souvent été
construits à la même période, ils ont fréquemment la
même structure, le même style et la même taille. Par
ailleurs, ces biens doivent faire face aux mêmes variables
d'externalité. Cette ressemblance locale crée donc un
problème de corrélation spatiale dans le modèle des prix
hédonistes. Si cette dépendance spatiale n'est pas prise en
considération lors de la spécification du modèle, les
résidus du modèle hédonique seront dépendants. Le
modèle hédonique ne peut pas corriger à lui seul cette
dépendance d'où la prise en compte de
l'autocorrélation spatiale.
Dans le cas de l'étude immobilière, il
paraît aussi possible que l'impact spatial ne soit pas homogène.
Can (1990) pose la question : « la valeur des caractéristiques des
biens immobiliers varie-t-elle selon la localisation du bien ? ».
L'étude des marchés immobiliers dans les espaces
urbains fait souvent apparaître une segmentation de ces marchés:
les caractéristiques et les prix des maisons diffèrent
substantiellement selon leurs localisations. Cette segmentation provient entre
autres de l'inélasticité de la demande des ménages pour
certaines caractéristiques des logements ou encore de diverses
barrières institutionnelles. Elle conduit à des
3
variations persistantes et significatives des
caractéristiques des logements et de leurs prix dans les
différents sous marchés. Dans ces conditions, estimer une
relation "globale" entre le prix du logement et ses caractéristiques,
relation s'appliquant de la même façon sur toute l'aire urbaine
étudiée, est susceptible de masquer des différences
importantes dans l'espace. Cette instabilité dans l'espace du prix des
immobiliers conduit à la prise en compte de
l'hétérogénéité spatiale.
Ainsi, en nous inspirant du modèle de base de choix
résidentiel, développé notamment par les travaux d'un
côté d'Alonso (1964), Mills (1967) et Muth (1969), postulant que
la structure d'équilibre d'utilisation du sol est
déterminée par l'arbitrage effectué par les ménages
entre la rente foncière et l'accessibilité au centre de la ville,
lieu de concentration des activité, et d'autre part de Straszheim (1987)
pour lequel la présence d'aménités non localisées
dans le centre-ville et recherchées par les ménages permettrait
de contrebalancer la force d'attraction du centre-ville et d'expliquer, dans
une certaine mesure, le phénomène actuel d'étalement
urbain. L'objet de ce présent travail est alors d'analyser
l'efficacité de la mise en oeuvre d'une politique d'habitat,
d'étalement urbain, par la connaissance des préférences
des ménages en termes de localisation en vue d'une croissance urbaine
par une logique alternative, dans laquelle les complémentarités
entre espaces urbains et ruraux soient utilisées au maximum.
Pour atteindre cette fin, les données sont recueillies
dans la ville de Bukavu sur une population de 145 158 ménages de la
ville de Bukavu. De cet effectif total, un échantillon est extrait par
un tirage aléatoire stratifié proportionnellement au nombre des
ménages de chacune des communes(Bagira, Ibanda, Kadutu). Les
données utilisées sont collectées en deux étapes,
la première étape est constituée de la
préenquête effectuée auprès de 30 ménages
avec comme objectif de pouvoir déterminer la taille
d'échantillon. La deuxième étape est constituée de
l'enquête proprement dite. Un questionnaire d'enquête
inspiré des études antérieures, implémenté
dans le téléphone portable en utilisant l'application Android ODK
Collect 1.4.4 et ses différents outils, a été
adressé à 193 ménages de la ville de Bukavu. Le traitement
des données est obtenu en recourant successivement aux
méthodes
4
statistiques (moyenne, variances et écart-types),
à la méthode de moindre carré ordinaire(MCO), la prise en
compte de l'hétérogénéité spatiale par
l'estimation du modèle hédoniste par la méthode de moindre
carré ordinaire corrigé de
l'hétéroscedasticité par la méthode de White et
l'analyse de la variance spatiale de Kruskal-Wallis ensuite la prise en compte
de l'autocorrélation spatiale en comparant le modèle
autorégressif spatial (SAR) mesurant les effets de la diffusion des prix
et le modèle d'erreur spatial(SEM) mesurant les effets des
externalités sur la valeur des maisons d'habitation, en utilisant le
logiciel STATA 12 et SPSS 20.
Hormis l'Introduction et la conclusion générale,
ce présent travail est subdivisé en trois chapitres. Le premier
est consacré à la revue de la littérature où nous
présentons en premier la revue théorique dans laquelle nous
discutons de la théorie de la valeur et du prix, ensuite du choix
résidentiel des ménages et de la présentation de la
méthode hédonique et en second d'une revue empirique
commentée et discutée. Le deuxième chapitre est
consacré à la méthodologie utilisée. Il
décrit les techniques utilisées pour la collecte et le traitement
des données, les variables retenues ainsi que les outils
utilisés. Enfin, le troisième chapitre présente et discute
les résultats (statistiques et économétriques) et donne
les recommandations et les limites du travail.
5
CHAPITRE I : REVUE DE LA LITTERATURE
Ce chapitre est articulé autour de deux sections. La
première porte sur la revue théorique et la deuxième sur
les études empiriques relatives à l'objet de l'étude.
I.1 REVUE THEORIQUE
Cette section présente différentes
théories dans lesquelles nous pouvons envisager les hypothèses et
les propositions des déterminants de la fixation du prix des maisons
d'habitations.
I.1.1 Théorie de la valeur et du prix
L'évaluation d'un bien immobilier diffère selon
qu'il s'agit de la réalisation immédiate d'une vente, soit de sa
valorisation pour être inscrit au bilan d'une entreprise ou d'y appliquer
un impôt ou une assurance pour les particuliers. Ceci fait supposer
à priori qu'il n'existe pas un seul prix mais plusieurs pour un immeuble
déterminé.
Cette question de la valeur plurale des actifs fait distinguer
deux blocs où pour certains la signification du prix et celle de la
valeur diffère et d'autres soulignant que le prix obtenu sur un
marché est le seul indicateur fiable de la valeur.
D'un côté, c'est avec Adam Smith(1776), puis
David Ricardo(1817) que se constitue une véritable théorie de la
valeur dont le but est de parvenir à construire une explication des
prix. La difficulté d'une entreprise, comme le rappelle Mouchot (1994),
sera alors double, d'une part, il s'agira d'expliquer la distinction entre
valeur d'usage et valeur d'échange, et, d'autre part de répondre
à la question : quelle est la source de la valeur : la rareté, le
travail, ou les deux à la fois ?
Adam Smith(1776) émet une double hypothèse sur
cette origine. La première s'applique à un état primitif
où il n'y a pas accumulation des capitaux et appropriation du sol, et
c'est uniquement la quantité de travail incorporée dans la
production d'un bien qui déterminera sa valeur. La seconde concerne un
état avancé de la société, où certains
individus ont accumulé des capitaux et sont devenus propriétaires
terriens, la valeur devra tenir compte de la rémunération de
l'ensemble des facteurs de production. En d'autres termes, la valeur d'un bien
équivaudra à la somme des salaires
6
(prix du travail), des profits (rémunération du
capital) et de la rente (loyer de la terre). Parallèlement, il
différencie le « prix naturel » qui est le point central vers
lequel gravitent continuellement les prix de toutes les marchandises et le
« prix de marché », prix actuel auquel une marchandise se vend
communément. Ce dernier peut être au-dessus, en dessous ou
précisément au niveau du prix naturel.
De ce fait, Smith(1776) reconnaît que le bien
économique peut être appréhendé de manière
subjective par la satisfaction qu'il procure, et c'est la notion de valeur
d'usage, ou de manière objective à partir de la quantité
de bien échangé qui détermine la notion de valeur
d'échange. Mais du fait de son caractère subjectif « donc
non-communicable en un langage intelligible» (Walras, 1874), la valeur
d'usage ne sera donc pas prise en compte dans la théorie de la
valeur.
Dans le but de pouvoir mesurer la valeur du Produit National
Brut anglais que David Ricardo(1817) élabore sa théorie de la
valeur en opposant les biens rares des biens non rares. S'agissant des premiers
leur valeur dépend surtout de leur rareté. Pour les seconds dont
la quantité peut s'accroître par « l'industrie de l'homme et
dont la production est encouragée par une concurrence libre de toute
entrave », la valeur ne dépendra pas seulement d'un échange
particulier, mais surtout de la quantité de travail nécessaire
à la production de ce bien. Tout en reconnaissant l'importance du
marché, il estime que le profit et la rente sont des connaissances de la
valeur et non pas des causes de celle-ci et que par conséquent il ne
faut pas en tenir compte pour son calcul.
De l'autre côté, Léon Walras(1874) et les
théoriciens de la rareté montre que la valeur d'échange se
détermine sur le marché. Pour eux, c'est la demande qui est
essentielle car elle « doit être considérée comme le
fait principal, et l'offre comme un fait accessoire. On n'offre pas pour
offrir, on offre que parce qu'on ne peut pas demander sans offrir; l'offre
n'est qu'une conséquence de la demande». Le prix résulte
d'un état d'équilibre général, c'est-à-dire
au moment où le profit pur est nul, où l'entrepreneur
disparaît. « Ils subsistent alors non comme entrepreneurs mais comme
propriétaires fonciers, travailleurs ou capitalistes dans leurs propres
entreprises ou dans d'autres ».
7
Plus précisément d'un côté, Smith
précise que la valeur se mesure par le travail commandé, ou
travail que la possession d'un bien permet d'acheter ; Ricardo par le travail
incorporé dans le processus de production ; ou encore par le temps de
travail socialement nécessaire à sa production pour Marx. Sous
cet angle la valeur d'un bien mesurée en travail correspond alors
à son prix naturel, prix reflétant le véritable coût
de production. Le prix naturel est alors distinct du prix de marché ou
prix effectif, observable dans l'échange. Et de l'autre
côté Walras et Pareto s'accordent à la théorie de la
richesse sociale qui rassemble toutes les choses, matérielles ou
immatérielles, qui sont susceptibles d'avoir un prix parce qu'elles sont
rares, c'est-à-dire à la fois utiles et limitées en
quantité. Ainsi donc la valeur d'un bien, pour ces derniers,
dépendra de son niveau de rareté et c'est cette dernière
qui exprimera le prix du bien considéré.
Il s'observe alors que L'analyse de la valeur d'un bien se
réduit à celle de sa forme phénoménale,
c'est-à-dire de son prix effectif observable dans l'échange.
Le courant néo-classique propose une théorie de
la formation des prix, résumée par Debreu (1959), qui est
directement fondé sur l'utilité que les agents retirent de la
consommation des différents biens il s'agit de la valeur-utilité:
les goûts ou préférences de chaque individu sont
représentés par une fonction permettant à ce dernier de
classer des ensembles de biens selon l'utilité qu'ils lui procurent. Il
détermine alors sa demande de chaque bien en maximisant cette
utilité. C'est ensuite la confrontation de la demande globale qui somme
des demandes individuelles avec l'offre globale qui permettra alors
l'établissement du prix.
Ainsi, la distinction entre valeur d'usage et valeur
d'échange, introduite initialement par Smith est abandonnée : la
valeur d'échange d'un bien est identifiée à son prix alors
que la valeur d'usage renvoie au concept d'utilité; avec le
développement de la théorie néo-classique et l'ancrage de
la détermination des prix dans la notion d'utilité, l'opposition
entre les deux notions perd toute pertinence.
8
I.1.2 Choix résidentiel des ménages
Le terme « choix résidentiels »
désigne la stratégie adoptée par le ménage en vue
de prendre une décision de mobilité et de localisation
résidentielle. Le prix du foncier et le choix de localisation sont
étroitement liées, étant données que les
interactions entre les marchés urbains, et l'examen des
accessibilités relie ces deux questions en discussion (Homocianu,
2009).
L'objectif de cette section est donc d'analyser le
comportement des ménages comme principal facteur de la fixation des prix
des maisons, analyse qui va nous amener vers l'étude du fondement de
l'approche hédonique qui permet de comprendre le caractère
hétérogène des biens immobiliers.
I.1.2.1 La théorie de la microéconomie
urbaine
La théorie de la microéconomie urbaine offre des
éléments très intéressants pour la
compréhension des interactions dans le cadre du fonctionnement urbain
global. Les contributions de Von Thünen (1826), Wingo (1961) et Alonso
(1964) constituent les travaux fondateurs de ce champ, et cette direction a
été continuée et développée par le courant
de la Nouvelle Economie Urbaine. Cette approche se préoccupe notamment
des comportements des ménages en termes de choix de localisation
résidentielle et de formation du prix foncier.
Alonso (1964) propose une transposition de la théorie
de la localisation agricole de Von Thünen à la localisation
résidentielle et des firmes urbaines, pour expliquer le fonctionnement
interne de la ville. Pour cela, il construit une approche économique
dans laquelle il cherche à relier la rente foncière à
l'utilisation des sols.
Le modèle d'Alonso (1964) se base sur un certain nombre
d'hypothèses ayant un caractère très réducteur.
Ainsi, la ville est considérée circulaire, mono centrique et
implantée sur une plaine isotrope2. Le modèle mono
centrique s'appuie sur l'hypothèse de base selon laquelle dans la ville,
le centre attire la plupart de l'activité
2 Terme qualifiant les corps, les milieux, dont les
propriétés sont semblables quelles que soient les directions.
9
(l'emploi) de sa région et le résidentiel est
situé autour de ce centre. Une autre hypothèse de cette
théorie est que les décisions de localisation
résidentielle et le prix des immobiliers sont une fonction de
l'accessibilité - coût de transport, du coût du terrain et
du revenu du ménage.
Selon la logique proposée par Alonso, dans le jeu du
marché résidentiel, les résidents sont en
compétition pour les différentes zones, en accord avec leur
disponibilité à payer pour accéder à ces zones
(« bid rent theory »). La localisation des différents groupes
relativement homogènes de la population doit être en accord avec
le gradient de leur courbe« bid rent ». Les valeurs foncières
résultent d'un arbitrage entre les coûts de transport et
l'accessibilité. Les coûts de transport augmentent avec la
distance au centre d'emploi (« central business district ») et sont
identiques pour l'ensemble des ménages suburbains, et donc les rentes et
les densités diminuent avec la distance au centre. L'augmentation des
coûts de transport entraîne un accroissement de la pente de la
rente de marché et une réduction de la taille de la ville.
Inversement, lorsque les coûts de transport diminuent, la pente de la
rente s'aplati, et la taille de la ville de la ville augmente,
l'amélioration des transports abaissant les valeurs foncières au
centre tout en les augmentant à la périphérie, ce qui
favorise l'urbanisation de nouvelles surfaces.
Wingo (1961) dans son approche donne aussi un rôle
central aux transports dans le fonctionnement urbain, en considérant que
le marché foncier est conditionné par les transports urbains. Son
apport essentiel c'est la prise en compte dans le modèle d'un coût
généralisé de transport au lieu d'un coût de
transport fonction linéaire de la distance au centre. Ce coût
généralisé reflète l'ensemble des dépenses
monétaires de transport et la valeur attribuée au temps de
trajet. Il arrive à la conclusion que l'amélioration du
réseau de transport entraîne une diminution des valeurs
foncières et des densités résidentielles et une extension
de la ville.
Face au caractère réducteur des
hypothèses de ces modèles, divers auteurs ont tenté
d'apporter des améliorations, enlevant certaines hypothèses,
comme Mills (1967) qui a introduit dans son modèle le secteur des
transports en tant que secteur de
10
production, ensuite Anas et Shyong Duann (1985) ont
essayé d'intégrer l'effet de capitalisation du réseau de
transport dans les biens fonciers et immobiliers, dans un modèle qui
avait comme objectif de rendre compte de l'impact d'une amélioration des
transports sur les valeurs des biens immobiliers en milieu urbain, Ryan (1999)
à son tour a souligné aussi que les hypothèses faites sur
les coûts de transport et les distances dans le modèle initial
sont valables que si les villes sont supposées mono centriques, et que
les villes polycentriques génèrent des schémas de
déplacement difficilement prévisibles dans la mesure où
les dessertes offertes par l'infrastructure peuvent ne pas satisfaire les
besoins de certaines catégories de ménages ou de firmes. Dans ce
cas, il est possible que les coûts de transport et la distance à
l'infrastructure ne soient pas corrélés.
De la Barra(1989) a identifié certaines limites des
hypothèses simplificatrices évoquées ci-haut de l'approche
de la microéconomie. Pour lui, les consommateurs et les producteurs sont
supposés disposer d'une information parfaite sur les conditions du
marché, ils ont une mobilité à faible coût et
peuvent apparaître et disparaître sans coûts, les fonctions
d'utilité sont supposées déterministes, l'approche est
trop agrégée (on raisonne sur un individu moyen) et a un
caractère statique.
Les études de Boyce et alii (1972), Dornbusch (1976) et
Lerman (1977) ont montré que le facteur transport a une influence
relativement réduite, mais statistiquement significative sur le prix de
l'immobilier. D'autre part, les études empiriques de Mayo (1973),
Friedman (1975) et Pollakowski (1975) cités par Homocianu(2009), qui ont
examiné l'impact des facteurs socio-économiques et du niveau des
services publics sur les décisions de localisation des ménages,
ont conclu que le niveau des services d'éducation et
récréation ont, généralement, une moindre
importance sur les choix de localisation que l'accessibilité à
l'emploi, et que l'effet de l'accessibilité est conditionné par
des attributs comme la taille et le revenu des ménages. Ils ont aussi
montré que le degré de motorisation des ménages a une
influence sur les décisions de localisation résidentielle
11
Malgré cela, les éléments de cette
approche constituent, dans une mesure plus ou moins importante, les fondements
théoriques pour les analyses et les modèles interactifs
transport-urbanisme. Les modèles de la microéconomie urbaine
apportent des éclairages essentiels sur le comportement des agents
économiques dans la ville, sur les déterminants des choix de
localisation des ménages ou sur l'impact des transports sur les formes
urbaines relatif à la formation des prix immobiliers.
Une autre approche alternatives à celle d'Alonso, qui
avait un caractère déterministe et faisait l'hypothèse
d'une ville mono centrique a été proposée par McFadden
(1978) et Anas (1982) et elle est fondée sur la théorie de
l'utilité aléatoire.
I.1.2.2 La théorie de l'utilité
aléatoire
L'approche de l'utilité aléatoire, qui est
apparue suite aux travaux sur la théorie des fonctions d'utilité
aléatoire et des choix discrets est, en fait, l'adaptation de la
théorie classique du consommateur au champ des choix discrets, et vise
à donner un caractère plus réaliste aux modèles de
la microéconomie urbaine.
Dans les modèles standards, on considère une
fonction d'utilité de l'individu (consommateur) représentant ses
préférences qui est de type déterministe, en accord avec
la théorie économique néoclassique, qui suppose que
l'individu dispose d'un pouvoir discriminant parfait qui lui permet de
déterminer sa préférence de manière certaine et
cohérente. On fait aussi l'hypothèse qu'il existe une
règle de décision de l'individu qui est stable.
Or, en réalité, même si les individus sont
dans des situations identiques, leurs choix ne sont pas uniformément
rationnels, ni répétitifs. Il est nécessaire donc de
prendre en compte la dispersion des préférences individuelles,
qui est à l'origine de la variabilité des choix.
Une approche alternative proposée par McFadden (1978)
et Anas (1982) considère la probabilité qu'un ménage
choisisse un type de maison comme une fonction des
12
caractéristiques du bien, des caractéristiques
du ménage et des caractéristiques du voisinage où le bien
est localisé, y compris l'accessibilité.
Cette approche vise à construire des modèles
plus réalistes, cherchant à dépasser les hypothèses
trop simplificatrices des modèles de la microéconomie urbaine,
comme celle d'une information parfaite des consommateurs et producteurs sur le
marché, le caractère déterministe de la fonction
d'utilité des demandeurs, le caractère trop agrégé
de ces modèles.
Les modèles de choix discrets sont des modèles
probabilistes, qui permettent de prendre en compte l'existence d'une
diversité de préférences individuelles.
La logique de ces modèles est la suivante : un
individu, qui doit choisir une zone de localisation résidentielle parmi
un ensemble d'alternatives, attribue à chaque localisation une fonction
d'utilité, définie comme une fonction des attributs de la zone
(accessibilité, environnement), et sélectionne la localisation
qui maximise l'utilité. L'utilité d'un agent face à une
alternative contient donc une composante déterministe, exprimée
par les attributs de la zone et les caractéristiques de l'agent, et une
composante aléatoire, reflétant les éléments de
subjectivité des agents.
Dans cette approche McFadden(1978) montre que l'ensemble de la
population est partitionnée en segments en fonction de
différentes caractéristiques socio-économiques, dans
chaque segment, les individus étant supposés statistiquement
identiques. L'utilité de l'individu face à une alternative de
choix parmi plusieurs a deux composantes : une composante déterministe,
reflétant les caractéristiques de l'alternative et de l'individu,
et une composante aléatoire, reflétant les éléments
de subjectivité du décideur et les erreurs d'évaluation
dues au manque d'information ou à la rationalité limitée
de celui-ci.
Ces modèles permettent de calculer la
probabilité de choix d'une alternative et donc de prévoir le
comportement des décideurs, sur la base de certaines hypothèses
sur la distribution de la composante aléatoire. Ils se basent sur le
principe de la maximisation de l'utilité, selon lequel l'individu prend
la décision en choisissant l'alternative qui lui
13
procure la plus forte utilité. La probabilité
qu'un consommateur particulier choisisse une alternative est celle que
l'utilité de cette alternative pour ce consommateur soit la plus
élevée (plus élevée que pour toutes les autres
alternatives).
De ces théories précédentes il s'observe
que l'étude de la mobilité et de la localisation
résidentielle doit être conçue comme une analyse des
transformations sociales, démographiques, politiques, économiques
qui affectent le milieu urbain. De ce point de vue la connaissance des facteurs
déterminants des comportements résidentiels des ménages
permet de comprendre comment l'homme s'adapte aux changements de la
société concernant l'activité économique, la vie
privée, le progrès technique, les formes d'urbanisation,... et
constitue une étape essentielle dans la modélisation de la
formation du prix des maisons d'habitation.
I.1.2.3 Déterminants du choix résidentiel des
ménages a. La mobilité résidentielle
La mobilité résidentielle est fortement
liée à des événements familiaux, comme les
naissances, les mises en union, les séparations, la retraite
professionnelle ou le décès. La fonction principale de la
mobilité est le processus par lequel une famille ajuste son logement
à ses besoins qui sont générés par les variations
de la composition familiale accompagnant le cycle de vie. Par exemple,
l'apparition des enfants est un événement, qui fait que le
ménage peut avoir besoin de posséder un logement avec une plus
grande surface, et ensuite de chercher la proximité à une
école.
L'ensemble de ces caractéristiques du cycle de vie
constitue la base d'un système dynamique résidentiel, et
l'élaboration d'une typologie des ménages selon celles-ci va
permettre de mettre en évidence ses mécanismes, logiques et
interactions internes, qui gouvernent les choix résidentiels des
ménages.
Un changement de logement peut être aussi motivé
par un changement d'emploi (et parfois l'inverse). Le comportement rationnel
des ménages consiste à choisir leur lieu de résidence en
fonction de la localisation de l'emploi de chacun des membres. Mais
Homocianu(2009) montre que la perte ou le changement d'emploi d'un ou de
14
plusieurs membres ne sera pas forcément
accompagné par une décision de changement de logement.
b. La localisation résidentielle
Dans la prise de décision concernant la localisation de
leur résidence, les ménages cherchent à maximiser leur
satisfaction - ou utilité. Mais cette utilité ressentie par les
ménages est en réalité une résultante de plusieurs
facteurs : les facteurs subjectifs, qui tiennent des caractéristiques
socio-démo-économiques spécifiques à chaque
ménage ou catégorie de ménages et des comportements et
préférences de ceux-ci en matière de localisation
résidentielle, et les facteurs objectifs, qui relèvent des
caractéristiques physiques de l'environnement résidentiel
(logement, aménités, accessibilités).
1° La relation entre le profil
socio-démo-économique des ménages et la localisation
résidentielle
Concernant le premier groupe de facteurs, qui visent les
caractéristiques subjectives, spécifiques aux différents
ménages, on va analyser les relations qui existent entre les
comportements de localisation des ménages et les variables les
caractérisant, comme la catégorie socioprofessionnelle, le
revenu, le niveau d'études, la taille du ménage ou le nombre
d'enfants, l'âge (comme indicateur du cycle de vie). Ce sont des
variables qui pourraient être utilisées pour stratifier les
ménages en vue de l'estimation de leurs préférences de
localisation.
Homocianu(2009) a montré que le comportement des
ménages en matière de localisation varie significativement avec
la catégorie socioprofessionnelle des individus qui les composent. Dans
cette logique, les choix résidentiels des ménages seraient donc
de se rapprocher autant que possible de son groupe de
référence.
La typologie par catégories socioprofessionnelles
traduit souvent le statut socioéconomique, synthétisé par
deux variables corrélées : le revenu et le niveau
d'études. La variable clé, qui est le revenu, est certainement
une variable explicative
15
de la décision de localisation résidentielle,
que ce soit par le jeu du marché du logement, ou bien par l'influence
des interactions sociales.
Certains économistes considèrent que le niveau
de vie, reflété par le profil socioéconomique des
ménages, est déterminant dans leurs choix en matière de
localisation résidentielle.
On peut évoquer dans ce sens les apports d'Alonso
(1964), Mills (1967) et Muth (1969), qui soutiennent l'idée que l'offre
et la demande sur le marché du logement expliquent la localisation des
ménages aisés et des ménages pauvres dans des lieux
différents, ou ceux de Tiebout (1956), selon lequel le jeu d'attraction
et de répulsion entre différentes catégories de
ménages structure l'espace résidentiel selon le niveau de vie.
Par contre, Homocianu (2009) considèrent que ce n'est
pas le niveau de vie qui influence le choix du lieu de résidence, mais
plutôt l'inverse. Celui-ci accorde une très grande importance aux
caractéristiques socio-économiques du quartier, ces
dernières influençant, selon eux, plus le revenu des agents que
toute considération relative à l'accessibilité aux zones
d'emploi.
Travers et al. (2013) fait remarquer qu'en France, comme aux
Etats-Unis, l'homogénéité des ménages au sein des
quartiers est très visible dans le paysage urbain. Ainsi, il est
possible de réaliser une typologie des quartiers, séparant les
zones dans des classes selon le profil des ménages qui y habitent.
Les extensions apportées au modèle standard de
l'économie urbaine permettent d'introduire une différenciation
dans les caractéristiques des agents économiques, en tenant
compte de la composition du ménage (taille ou nombre d'enfants du
ménage). Les premiers modèles de localisation, comme celui
d'Alonso, Muth et Mills, ne tenaient pas compte de la structure
démographique du ménage. Or, un ménage composé d'un
nombre important de membres, par exemple, est plus susceptible de choisir une
résidence en périphérie, afin de bénéficier
d'une plus grande superficie à moindre coût qu'un ménage
composé d'un nombre plus réduit de personnes.
16
Hochman et Ofek(1977) vont dans ce sens, en soulignant
l'existence d'une corrélation positive entre la taille du ménage
et la distance entre le lieu de résidence et le centre.
2° Le lien entre les caractéristiques de
l'environnement résidentiel et les choix de localisation
résidentielle des ménages
La nouvelle théorie du consommateur de Lancaster(1964)
met en évidence que le logement (ou la résidence) peut être
vu comme un bien multidimensionnel différencié en un ensemble
d'attributs variant en quantité et en qualité. Il peut ainsi se
décomposer en trois dimensions : ses caractéristiques
intrinsèques, les aménités et l'accessibilité, il
s'agit de la méthode hédonique3.
Lorsqu'un ménage choisit un logement, il tient compte
de multiples variables structurelles, soit quantitatives, comme la superficie
ou le nombre de pièces de la résidence, ou qualitatives, comme
l'âge de l'immeuble (neuf ou ancien). Ces caractéristiques d'un
logement se reflètent, en général, dans son prix sur le
marché immobilier, ce prix étant également un
critère en fonction duquel les ménages font leurs choix
résidentiels. L'approche hédonique du prix immobilier repose sur
cette hypothèse que le logement est un bien complexe, dont les
caractéristiques sont les facteurs déterminants de son prix.
Le choix de la localisation résidentielle
effectué par les ménages est lié à la
qualité de l'environnement social, économique et physique de la
zone de résidence. En retour, ces choix individuels déterminent
une dynamique de cet environnement.
La théorie du flight-from-blight(en français,
esquive des externalités négatives) explique la structuration,
dans le contexte américain, d'une aire urbaine selon le niveau de
revenu, à la lumière des externalités produites par la
coexistence sur un territoire donné des ménages appartenant
à des classes de revenu différentes. En fait, les interactions
entre les différents groupes de ménages dotés de niveaux
de revenu différents, qu'elles passent par la fiscalité ou plus
généralement par les relations de proximité, sont
susceptibles de structurer l'aire urbaine en fonction du niveau de vie
3 Cette approche sera développée dans le point
suivant.
17
des ménages. Ainsi, la cohabitation, au centre-ville,
entre les classes aisées et les classes à bas revenu,
génère des externalités qui incitent les classes
aisées à établir leur lieu d'habitation dans la
périphérie et ce afin de se soustraire à ces
externalités. Il apparaît une représentation de l'aire
urbaine qui prend la forme d'une juxtaposition de communes qui sont
protégées les unes des autres par l'élaboration de
barrières à l'entrée. Les ménages à bas
revenu se retrouvent ainsi concentrés dans les villes-centres et
isolés du reste de la population. Cette isolation aggrave
généralement leur situation en amoindrissant le niveau et/ou la
qualité des aménités endogènes dont ils peuvent
bénéficier. Ainsi, les ménages à bas revenus sont
confrontés à un cercle vicieux, car leur situation de
pauvreté est confortée et accentuée par les
caractéristiques du quartier dans lequel ils résident.
Dans son étude, Zenou (2002) a cherché à
prendre en compte l'influence des aménités afin d'expliquer la
ségrégation résidentielle. Il conclut que les
ménages aisés donnent une plus grande importance à la
présence d'aménités que les ménages disposant d'un
revenu plus faible.
Homocianu(2009) note également que les
caractéristiques socio-économiques des quartiers sont en mesure
d'influencer les chances que les habitants accèdent à l'emploi,
le quartier de résidence, à travers les relations de voisinage,
peut conditionner d'autres décisions prises par les ménages ou
que les ressources du voisinage peuvent avoir une influence sur la formation du
capital humain.
Le choix de la localisation des ménages dépend
aussi de leurs préférences concernant la qualité de
l'environnement résidentiel, traduite en termes de présence
d'espaces verts et de loisir et de niveau de pollution de l'air.
Thériault, Kestens et Des Rosiers (2002), ont mis en évidence la
relation positive qui existe entre des variables comme la présence de la
végétation, ou d'un hôtel sur la valeur d'une maison.
Les choix de localisation des ménages, mais aussi la
valeur des logements, dépendent également de leur
proximité aux différentes activités et services de la
ville. La présence dans la zone de résidence d'activités
économiques, d'établissements d'enseignement ou commerciaux, la
proximité au centre et aux grandes infrastructures
18
de transport, le niveau de la densité de la population,
sont des facteurs qui vont guider les décisions des ménages de se
localiser dans une zone ou une autre, en fonction de leurs besoins et
préférences.
L'hypothèse de capitalisation des avantages
retirés de la localisation résidentielle, tels que les
aménités de voisinage ou l'accessibilité aux
différents services découlent de nombreux travaux
théoriques et empiriques en économie urbaine qui convergent vers
l'idée que sur un marché immobilier concurrentiel, les
consommateurs enchérissent pour les localisations selon leur propension
à payer pour les attributs de localisation et c'est l'enchère
maximale qui l'emporte et détermine le prix du marché. La valeur
d'un bien est le résultat de l'interaction entre l'offre, et la demande
qui reflète les caractéristiques des consommateurs (leurs
préférences, revenus).
Ainsi de ces théories du choix résidentiel des
ménages il s'observe que le logement est en effet un lieu de vie
où les individus dorment, mangent, s'instruisent ou encore cohabitent
avec d'autres membres de la famille. Bien localisé, il permet aux
individus d'avoir accès ou non aux pôles d'emplois, aux services,
aux espaces naturels, aux transports collectifs, etc. chaque logement est
constitué d'une série des caractéristique internes
(nombres des chambres, ...) et externe (accessibilité
générale, voisinage,...) et il est ainsi difficile, voire
impossible, de trouver deux logements parfaitement identiques. De ce fait, le
logement est considéré comme un bien
hétérogène et la méthode la plus utilisée
pour évaluer le prix de chaque caractéristique est la
méthode hédonique, utilisée principalement dans le domaine
de l'immobilier pour calculer le rôle des caractéristiques des
maisons dans la construction de leur prix.
I.1.3 La méthode hédonique
La détermination d'un prix à partir de l'offre
et de la demande d'un bien suppose qu'il existe des quantités
homogènes de ce bien. Lorsqu'on est en présence de biens par
nature hétérogènes, comme les immobiliers, la question se
pose de savoir si toute la théorie micro-économique
traditionnelle peut s'appliquer. Le problème réside dans la prise
en compte de la différenciation des biens dans l'analyse du comportement
du
19
consommateur et le débat porte notamment sur la
permanence ou la transformation dans le temps de ses
préférences.
I.1.3.1 Théorie traditionnelle de la
consommation
Les biens sont les objets que le consommateur considère
comme tels, c'est-à-dire ceux dont il souhaite posséder
davantage. Le bien économique ainsi conçu n'a d'existence qu'en
tant qu'équivalent d'une certaine quantité d'autres biens, deux
quantités quelconques étant équivalentes ou
échangeables si elles ont la même valeur. La pauvreté du
concept, notamment l'incapacité à prendre naturellement en compte
l'apparition de biens nouveaux ou les variations de qualité des biens
existants aboutit à l'impossibilité de construire une
théorie de la demande tant qu'on ne précise pas de quelle
manière les biens participent à la satisfaction de ces
besoins.
I.1.3.2 Théorie de Lancaster
L'hypothèse d'homogénéité des
biens est particulièrement réductrice, notamment lorsqu'on
s'intéresse aux biens durables. Aussi, la reformulation de la
théorie de la consommation dite « Nouvelle Théorie du
Consommateur » a ouvert de nouvelles perspectives. C'est à
Lancaster(1964) que revient le mérite de cette reformulation à
partir de la synthèse d'un certain nombre de questions posées par
la prise en compte de l'hétérogénéité des
biens dans l'analyse du comportement du consommateur. Cette nouvelle
théorie repose sur la prise en considération des attributs, ou
caractéristiques des biens déterminant leur qualité.
Lancaster propose de renouveler la notion de bien, en posant
que les consommateurs tirent leur utilité des
caractéristiques des biens, et non pas des biens eux-mêmes,
ce qui signifie aussi que les biens ne sont pas
désirés pour eux-mêmes, mais pour les services qu'ils
rendent. Dès lors, ce n'est plus l'offre et la demande
d'un bien qui détermine son prix, mais l'offre et la demande pour les
caractéristiques qu'il contient. L'analyse hédoniste ou
hédonique des prix, dont l'objet est d'étudier la formation du
prix des biens complexes, exploite cette hypothèse, et explique le prix
des biens par leurs caractéristiques.
20
I.1.3.3 Modèle de S. Rosen sur la demande de
caractéristique
Rosen (1974) a permis le développement des analyses
hédonistes en définissant les hypothèses et en proposant
un modèle d'équilibre sur un marché de biens
hétérogènes explicitant les fonctions d'offre et de
demande pour les caractéristiques de ces biens.
Les hypothèses sont les suivantes :
? Les caractéristiques sont objectivement mesurables et
les biens en nombre suffisant pour que les transactions portent sur l'ensemble
de ces caractéristiques, le bien étant un ensemble « non
dénouable » de caractéristiques. En effet, si les
caractéristiques sont définies de façon « objective
», elles se présentent de façon identique pour tous les
consommateurs, ce qui permet de les définir comme des biens.
? La structure des prix est un paramètre,
c'est-à-dire une grandeur mesurable, pour les acheteurs comme pour les
vendeurs.
L'équilibre de marché est atteint lorsque le
prix permet de faire correspondre pour l'ensemble des caractéristiques
les quantités demandées aux quantités offertes. Mais le
modèle de Rosen permet aussi d'établir que la fonction
hédonique des prix ne peut être assimilée à une
fonction de demande et indique la voie à suivre pour parvenir à
déduire les fonctions de demande recherchées des informations
fournies par le marché. Cela signifie que dans la composition du
modèle n'entrent que des caractéristiques du bien et non celles
qui correspondent à la demande tels : le revenu, la taille du
ménage ou les préférences des acquéreurs.
Pour identifier les fonctions de demande de
caractéristiques deux étapes sont nécessaires. La
première consiste à estimer la fonction hédonique des
prix, d'où l'on déduit, pour chaque observation de
l'échantillon, les prix marginaux des caractéristiques. La
seconde conduit à l'identification des fonctions de demande en
introduisant les prix marginaux comme variables dépendantes dans les
fonctions d'enchère pour les différentes caractéristiques.
Suivant Alonso, une courbe d'enchères sur deux caractéristiques
du logement comme la quantité de sol et la distance au centre,
correspondra à « l'ensemble des prix du sol que l'individu accepte
de payer à différentes distances du centre, en laissant son
niveau de satisfaction constant »
21
Plusieurs études ont utilisé cette
méthode dans l'estimation des prix en se basant sur les
différentes caractéristiques du bien.
22
I.2 REVUE EMPIRIQUE
Cette section présente quelques études analogues
à notre recherche et dont les résultats nous sont d'une
importance incommensurable. Partant toujours du modèle initial
théorique d'Alonso (1964) proposant une transposition de la
théorie de la localisation agricole de Von Thünen (1826) à
la localisation résidentielle et des firmes urbaines, pour expliquer le
fonctionnement interne de la ville. En se basant sur deux hypothèses, la
première portant sur le modèle mono centrique selon laquelle dans
la ville, le centre attire la plus part de l'activité (l'emploi) de sa
région et le résidentiel est situé autour de ce centre.
Une autre hypothèse montrant que les coûts de transport augmentent
avec la distance au centre d'emploi et sont identiques pour l'ensemble des
ménages suburbains, et donc les rentes et les densités diminuent
avec la distance au centre.
Pour Ryan (1999) les hypothèses faites sur les
coûts de transport et les distances dans le modèle initial
d'Alonso sont valables que si les villes sont supposées mono centriques.
Les villes polycentriques génèrent des schémas de
déplacement difficilement prévisibles dans la mesure où
les dessertes offertes par l'infrastructure peuvent ne pas satisfaire les
besoins de certaines catégories de ménages ou de firmes. Dans ce
cas, il est possible que les coûts de transport et la distance à
l'infrastructure ne soient pas corrélés.
Travers et al(2013) voulant dépasser le modèle
urbain proposé par Alonso(1964) qui n'était pas adapté aux
villes polycentriques comme la France, introduisent le rôle des
aménités4 urbaines permettant d'améliorer la
compréhension du choix résidentiel des ménages. Dans la
ville d'Angers, sur base de 1 016 appartement vendus en 2004 et 2005, par la
méthode hédonique des prix et la méthode des moindres
carrés ordinaires corrigée de la méthode
FGS2SLS5 ( Feasible Generalized Spatial Two Least Squares) qui tient
compte du double caractère spatial et endogènes des
caractéristiques des logements, montre que la proximité d'un
logement par rapport à un axe routier majeur (autoroute, rocade, etc)
agit négativement et de manière significative sur le
4 Une aménité est une caractéristique
géographiquement localisée agissant de manière positive
sur les agents économiques, il s'agit entre autres de : la forêt,
la qualité de l'air, des services publics de qualités, espaces
verts, monuments historiques, présence d'un restaurant ou d'un
hôtel, le charme du quartier, etc.
5 FGS2SLS est une méthode combinant à la fois la
méthode des variables instrumentales pour prendre en compte
l'autocorrélation spatiale de la variable expliquée et des
variables endogènes et la méthodes des moments
généralisés pour corriger l'autocorrélation
spatiale des erreurs.
23
prix par rapport à cette distance, c'est-à-dire
que les nuisances associées à ces infrastructures
routières l'emportent sur les avantages qu'elles apportent en termes
d'accessibilité. Et enfin les caractéristiques
extrinsèques agissent globalement positives et significatives sur le
prix du logement. Mais ce modèle ne tient pas compte de la
présence des aménités non localisées en ville et
pourtant recherchées par les ménages telles que les
forêts.
Ces résultats coïncident avec ceux de Dantas et
al(2010) qui ont mené une étude dont l'objectif était de
relever les effets du zonage6 sur le prix immobilier, dans le bassin
d'Arcachon (Sud-ouest de la France), qui connait une forte attractivité
résidentielle et touristique. Sur base de 2 287 transactions de logement
entre 2000 et 2006, ont estimé un modèle hédoniste par la
méthode des moindres carrés ordinaires avec correction de
l'autocorrélation spatiale, et de l'héteroscedasticité
spatiale corrigée à l'aide des méthodes de simulation
bayésiennes, montrent que les zones d'urbanisation futures ont un effet
dépréciatif sur le prix des immobiliers et la proximité
aux aménités renchérissent les prix des immobiliers; les
aménités naturelles protégées ont un effet
appréciatif, à condition de ne pas servir de support à une
exploitation agricole ou forestière. Mais cette étude ne montre
pas la relation inverse, c'est-à-dire l'influence du prix immobilier sur
le type de zonage.
Ainsi Brossard et al(2005) dans leur étude dont l'objet
était d'évaluer le paysage qui s'offre depuis une maison et son
impact sur le prix global de cette dernière, montre, au moyen d'une
régression multiple du type logarithmique et de la méthode
à effet aléatoire et des doubles différences avec deux
groupes, le groupe appartenant à un lotissement et le groupe hors
lotissement; ainsi que des images satellites et un modèle
numérique de terrain afin de reconstituer le champ de vision et les
objets qui s'y trouvent par des méthodes trigonométriques et
multi- échelles, que les prix hédonistes obtenus à partir
de 4 050 transactions immobilières de la région de Dijon entre
1995 et 2002 diffèrent avec celui de sa banlieue où ils sont
souvent voisins de zéro, avec la ceinture périurbaine d'une
quarantaine de kilomètres. Dans cette dernière les
résultats
6 Le zonage est la règlementation organisant la
répartition d'un territoire en zones et fixant pour chacune d'elles le
genre et les conditions de l'utilisation du sol.
24
montrent que les forêts et l'agriculture ont des prix
positifs et celui des routes est négatif lorsque ces objets sont
à proximité immédiate des maisons, mais ces prix sont
voisins de zéro lorsque ces objets sont situés au-delà de
quelques dizaines ou centaines de mètres, ainsi que lorsqu'ils existent
près des habitations mais qu'ils ne sont pas visibles. La composition
paysagère dans des formes complexes ou fragmentées a
également un prix positif dans la ceinture périurbaine.
Au-delà de 100 à 200 mètres, l'existence de plans des
visions ou leur contenu n'influencent pas les prix des maisons.
Aussi Loung et Boucq(2011) dans leur une étude visant
à évaluer l'impact d'une politique de transport en commun sur les
prix des immobiliers résidentiels dans la ville de Paris, au moyen d'un
échantillon de 162 032 transactions réalisées entre 2002
et 2008, Après une analyse descriptive et la modélisation
hédonique par la MCO de forme linéaire et logarithmique ainsi que
la régression logistique7 du type logit multinomial ,
montrent une valorisation de 5% des immeubles situés entre 200 et 400
mètres de l'infrastructure induite par le transport en commun mais qui
n'est pas significativement différente de zéro. Ne montrant pas
la décision des ménages situés à moins de 200
mètres qui cette politique peut constituer une
désaménité et par conséquent la baisse du prix.
Shrikhum(2012) à son tour dans son étude visant
à évaluer les biens immobiliers en présence d'une
dépendance spatiale des prix avec le traitement de
l'autocorrélation spatiale dans douze plus agglomérations
urbaines de France afin de relever le quartier dominant8 de chaque
ville comme déterminant de choix de l'investissement immobilier. Au
moyen de 216 664 transactions des appartements entre 1998 et 2007
analysée avec la statistique descriptive en menant une méthode
comparative dans l'analyse entre la géostatique et
l'économétrie spatiale par le modèle hédonique des
prix, conclut que le centre-ville apparait comme la zone dominante du
marché immobilier de 9 villes sur 12 de France. Montre encore que le
prix moyen au mètre carré ne peut pas caractériser le
quartier dominant, et ce n'est le cas ni pour le
7 Issu du programme de maximisation de l'utilité à
se déplacer
8 Ce travail définit le quartier dominant en fonction du
degré de corrélation spatiale des prix immobiliers, ainsi donc si
les données de tel quartier sont enlevées de la base de
données, le degré de corrélation spatiale baisse
sensiblement, alors ce quartier présente un rôle directif dans
l'effet de diffusion des prix immobiliers, dans ce cas ce quartier est donc
considéré comme un quartier dominant.
25
revenu des habitants, ni pour le taux de criminalité.
Mais si que les variables quantitatives ne caractérisent pas de
manière significatives les quartiers dominants quelles sont les
variables qualitatives principales qui caractérisent les quartiers
dominants.
26
CHAP. II APPROCHE METHODOLOGIQUE
Ce chapitre se subdivise en trois sections. La première
section expose les différentes techniques utilisées pour
collecter les données, la deuxième essaye de donner les
différentes techniques qui nous ont permis de traiter les
données. Enfin, la dernière section présente les outils
utilisés pour collecter et traiter les données
sous-étude.
II.1. TECHNIQUES DE COLLECTE DES DONNEES
Nous avons utilisé deux techniques principales pour
collecter les données : la préenquête et l'enquête
proprement dite.
Nous avons utilisé deux techniques principales pour
collecter les données : la préenquête et l'enquête
proprement dite.
II.1.1 Pré-enquête : détermination de la
taille de l'échantillon
Notre population cible est constituée des maisons
d'habitation de la ville de Bukavu. Pour améliorer la précision
de nos estimateurs et face à une population à enquêter non
homogène, nous avons optés pour un sondage stratifié avec
comme strates les communes de Kadutu, Ibanda et Bagira dont l'ensemble de la
population s'élève à 870 944 habitants (Mairie de Bukavu,
2013) présentée dans le Tableau 2.1.
Tableau 2.1 : Répartition de la population de Bukavu par
commune
|
BAGIRA
|
IBANDA
|
KADUTU
|
TOTAL
|
|
Habitants
|
215 088
|
297 560
|
358 306
|
870 944
|
|
Pourcentage
|
24,7
|
34,2
|
41,1
|
100
|
Source : Mairie de la ville de Bukavu, 2013
De ce tableau on observe que la commune de Kadutu est la plus
peuplée avec une proportion de 41,1% du total de la ville, suivie par la
commune d'Ibanda avec 34,2% et enfin 24,7% pour la commune de Bagira.
Le Tableau 2.2 montre le nombre des ménages que
comprend chaque commune en nous basant sur le rapport du PNUD(2009) montrant
qu'au sud-Kivu un ménage est constitué en moyenne par 6
personnes, d'où :
Nombre des ménages dans la ville de Bukavu= 870
944
6 = 1 45 157,33 soit 145 158
27
Tableau 2.2 : Répartition de la population par
ménages
|
BAGIRA
|
IBANDA
|
KADUTU
|
TOTAL
|
|
Habitants
|
215 088
|
297 560
|
358 306
|
870 944
|
|
Pourcentage
|
24,7
|
34,2
|
41,1
|
100
|
|
Ménages
|
35 848
|
49 593
|
59 717
|
145 158
|
De ce tableau ci-dessus, il s'observe que dans la commune de
Kadutu le nombre des ménages s'élève à 59 717, 49
593 dans la commune d'Ibanda et 35 848 dans la commune de Bagira et l'ensemble
à 145 158.
A défaut de temps et des moyens, nous ne pouvons pas
mener l'étude sur l'ensemble de ces 145 158 ménages d'où
nous extrayons un échantillon représentatif de cette population
(ensemble des ménages) en utilisant la formule (Ardilly, 2006).
????/2
2 x V?? 2
n = ??2 (Eq. 2.1)
Avec :
- n: la taille de l'échantillon
- ????/2 : est le coefficient de fiabilité, Il est
égal à 1,96 pour un intervalle de
confiance à 95%.
- å : la marge d'erreur voulue par le chercheur
(fixée à 5% dans cette étude).
- V2X : est la variance relative pour la variable X
donnée par la formule suivante : ??X 2 = (N-1
N ) . ??2
??2 (Eq.2.2)
Avec N : la taille de la population qui est le nombre des
ménages. ó = est l'écart-type de la population cible. Plus
la population est différenciée par rapport au facteur
étudié, plus grandes seront la variance et la taille de
l'échantillon.
Toutefois, un problème majeur se pose dans
l'application de cette formule, car le plus souvent on ne dispose pas cet
écart-type de la population. Anderson, D. et al. (2001)
préconisent trois solutions suivantes :
28
? Si l'on dispose les résultats d'une étude
similaire effectuée dans le passé récent, on utilise
l'écart-type observé à cette époque ;
? Possibilité d'organiser un pré-test ou une
étude pilote sur une trentaine d'individus de la population cible et
estimer l'écart-type sur cette base ;
? Si les valeurs extrêmes de la variable
étudiée (maximum et minimum) sont connues dans la population et
si la règle d'approximation normale est acceptable, l'écart-type
peut être estimé à partir de la différence entre les
deux valeurs extrêmes divisée par quatre.
D'où, la formule suivante : ?? = ??aleur ma??imale -
??aleur mi??imale
4
Pour notre travail, nous avons opté pour l'organisation
d'une pré-enquête auprès de 30 ménages de la ville
de Bukavu. La question a consisté à savoir le nombre des
pièces que porte la maison. Le résultat trouvé montre une
moyenne de 3,36 une médiane de 4 ainsi qu'un écart-type de
1,19.
En remplaçant dans l'Eq2.2 et Eq2.1 les différentes
valeurs susmentionnées.
Dans l'équation (2.2) ???? 2 = (145 157
145 158) . 1,192
3,362 = 0,1254 (1)
(1) Dans l'équation (2.1) donne n = 1,962 x
0,1254
0,052 = 192,69 ~ 193 ménages.
Une fois qu'on a déterminé la taille n de
l'échantillon total (193 ménages pour cette étude) et que
l'on a décidé de stratifier (3 strates pour notre cas comprenant
les trois communes :Bagira, Ibanda, et Kadutu), la prochaine décision
importante est celle de savoir combien d'unités prendre au sein de
chaque strate sous la contrainte de ne pas avoir une taille inférieure
à celle de n donnée. C'est le problème d'allocation
La répartition de l'échantillon total dans les
différentes states est importante dans la mesure où elle peut
avoir un impact considérable sur les écarts-types au sein des
strates et sur le total.
A partir des informations obtenues auprès de la Mairie
de Bukavu(2013), le tableau 2.3 montre la répartition de
l'échantillon stratifié proportionnellement à la taille de
chaque
29
commune en utilisant un taux de sondage f ( ?? ?? ) de 0,0013
identique au sein de chaque
state.
Tableau 2.3 : Répartition de l'échantillon pour
l'enquête proprement dite
|
COMMUNE
|
Ménages
|
Echantillon
|
Quartier
|
Sous-
échantillon
|
Pourcentage
|
|
BAGIRA
|
35 848
|
47
|
Kasha
|
16
|
24,7
|
|
Lumumba
|
16
|
|
Nyakavogo
|
15
|
|
IBANDA
|
49 593
|
65
|
Ndendere
|
22
|
34,2
|
|
Nyalukemba
|
22
|
|
Panzi
|
21
|
|
KADUTU
|
59 717
|
81
|
Cimpunda
|
12
|
41,1
|
|
Kajangu
|
12
|
|
Kasali
|
12
|
|
Mosala
|
12
|
|
Nkafu
|
11
|
|
Nyakaliba
|
11
|
|
Nyamugo
|
11
|
|
TOTAUX
|
145 158
|
193
|
|
193
|
100
|
Source : Mairie de la ville de Bukavu, 2013 et notre
confection
II.1.2 L'enquête proprement dite
L'enquête porte sur l'ensemble des maisons d'habitation
de la ville de Bukavu dont le nombre est estimé à 145 158 comme
démontré ci-haut et dont un échantillon de 193 maisons a
été extrait et reparti dans les trois communs et
différents quartiers de la ville de Bukavu.
Les données utilisées ont été
collectées après une brève introduction auprès de
nos enquêtés en leur expliquant le bien fondé de notre
recherche. Le questionnaire d'enquête implémenté dans le
téléphone Android en utilisant l'application ODK Collect 1.4.4 et
ses différents outils afin de d'éviter les erreurs liées
à l'encodage ainsi
30
que de permettre d'obtenir les coordonnées
géographiques( longitude et latitude) des maisons enquêtées
avec une grande précision( précision moyenne de 5 mètres)
nous a permis de réduire la durée de l'enquête que nous
avons ainsi réalisée pendant 14 jours, du 4 au 18 Janvier 2015,
d'une manière continue. S'ils estimaient être capables de
répondre immédiatement, nous les attendions jusqu'à ce
qu'ils terminent et cela pendant en moyenne 10 minutes, sinon ils nous allions
ailleurs. Cela nous a permis d'avoir un taux de réponse de 100%.
La fiabilité des informations récoltées
dépendait fortement du degré d'engagement des responsables et
leur volonté à pouvoir répondre convenablement à
toutes les questions posées. Cependant nous avons rencontré
certains problèmes dont les plus majeurs sont les suivants
:
- Certains des enquêteurs ne nous livraient pas
d'informations fiables au juste titre qu'ils estimaient que nous nous sommes
déguisés en étudiant mais dans le fonds on travaillait
pour le compte de l'Etat. Vu qu'il n'y avait pas moyen de surmonter cet
obstacle, nous étions obligé de présenter d'abord la carte
d'étudiant et s'il y avait toujours de la résistance on
décidait de ne pas enquêter le ménage en question.
- Réticence de certains ménages de pouvoir
donner une valeur proche de la réalité sur la valeur de leur
maisons par crainte d'être surtaxés par le service immobilier ou
l'inverse, c'est-à-dire le cas où certains ménages
surestimaient la valeur de leur maison. Lorsqu'on remarquait ce comportement
nous changions la façon de poser la question et nous leur demandions de
nous donner la valeur de transaction d'une maison proche et de pouvoir estimer
la valeur de sa maison sur base de cette valeur.
31
II.2 TECHNIQUE DE TRAITEMENT DES DONNEES
II.2.1 Fondement théorique et spécification du
modèle
La spécification du modèle
économétrique dépend du but poursuivi par le chercheur et
de la théorie économique sous-tendant. Ainsi le présent
travail vise à déterminer les différentes composantes
permettant de déterminer les prix des maisons d'habitation dans la ville
de Bukavu en se basant sur des modèles théoriques urbains pour
lesquels l'ensemble des activités était situé au
centre-ville conditionnant ainsi le choix résidentiel et dont les effets
sont contrebalancés par la recherche des aménités par les
ménages.
Ainsi, ce présent travail s'inspire du modèles
des prix hédoniques utilisé par Srikhum( 2012) ainsi que celui de
Basu et Thibodeau (1998) donnant les détails assez complets des
caractéristiques qui contribuent à donner une estimation du prix
d'un bien résidentiel et qui doivent être prises en compte dans le
modèle d'évaluation :
· les caractéristiques de l'immeuble (la taille
de l'immeuble, la forme, la topographie, la façade, etc.),
· les caractéristiques physiques des biens (la
surface en mètre carré, le nombre de pièces, le nombre de
salles de bain, l'étage, le nombre de garages, la présence de
piscine, les équipements, etc.),
· les caractéristiques de voisinage (le
pourcentage de terrains améliorés dans le voisinage, le
pourcentage de maisons occupées de propriétaire, le pourcentage
de propriétés non résidentielles, le pourcentage de
propriétés non développées, le temps de
réponse des pompiers ou des policiers, l'indice de criminalité,
etc.),
· les variables d'accessibilité (la distance au
quartier central des affaires, la distance à une école, aux
supermarchés, à un transport en commun, à des autoroutes
importantes, etc.),
· les variables d'externalité (le bruit, la
pollution, la congestion, etc.),
· les variables de zoning (la division de quartier en
différentes zones : industrielle, résidentielle, loisir),
· et la date de transaction.
32
Pour traduire les particularités de cette étude,
nous nous inspirons du modèle énoncé ci-haut afin d'avoir
un modèle adapté à l'objectif du travail.
II.2.1.1 Choix de la forme du modèle
Pour estimer les modèles hédoniques, plusieurs
formes fonctionnelles sont disponibles(voir Terra, 2005). En l'absence de
consensus sur la meilleure forme fonctionnelle, chacun est donc libre à
déterminer, en fonction des données dont il dispose, la forme
fonctionnelle la plus adaptée.
Ainsi la forme du modèle choisie pour cette
étude est la forme linéaire car elle est la plus simple à
interpréter et la plus utilisée dans l'estimation
hédonique. Elle relie le prix de vente aux différentes variables
explicatives. Le coefficient associé à chaque variable correspond
au prix implicite de cette caractéristique. Une augmentation d'une
unité d'une caractéristique donnée entraîne une
variation (en dollars) du prix de vente égale au coefficient de cette
variable.
En se référant au travail de Basu et Thibodeau
(1998) énoncé ci-haut, nous retenons une décomposition en
quatre parties de la valeur immobilière comme présentée
par Srikhum (2012):
???? = a??+ X1??+ X2??+ X3??+ X4??+ e?? (Eq. 2.3)
Avec ???? le vecteur des prix des biens immobiliers.
??, ??, ??, ?? Les coefficients de la
régression correspondant à X1
la matrice des caractéristiques physiques, X2
la
matrice des caractéristiques de localisation, X3
la matrice des caractéristiques de voisinage et X4 la
matrice des catégories socioprofessionnelles et démographiques du
propriétaire, a et e sont les vecteurs des constantes
et des résidus de l'estimation.
Le modèle retenu pour le présent travail est tel
que :
PRMS= â0 + â1SURFPCL + â2SURFMS +
â3NBREPC + â4NBREETG + â5ANCMS + â6TYPEMS +
â7ETMURS + â8PRES2TOILSLB + â9PRESGARG + â10COMMBAG +
â11COMMKAD +â12DISTCENTVIL + â13DISTAXPRIPL +
â14DISTRTPROCH + â15DISTINFRTRPPROCH + â16 DISTCENTRMEDICL +
â17 DISTETENSGMT +
â18NIVETD + â19 PROFESS + â20CTTRANSP Eq.
2.3
33
Tableau 2.4 : Définition des variables et
présentation des signes attendus
|
Variables
|
Acronymes
|
Modalités
|
Signes attendues
|
|
Variable dépendante
|
|
Prix des maisons
|
PRMS
|
Quantitative
|
|
|
Variables indépendantes
|
|
Caractéristiques physiques
|
Surface de la parcelle
|
SURFPCL
|
Quantitative : il s'agit de la surface en mètre
carré obtenue par la multiplication de la longueur fois la largeur de la
parcelle.
|
+
|
|
Surface de la maison
|
SURFMS
|
Quantitative : c'est la somme des surfaces des
différentes constructions se trouvant sur la parcelle.
|
+
|
|
Nombre des pièces
|
NBREPC
|
Quantitative : nombre des pièces à vivre de la
maison (à l'exception des pièces dites « humides » :
salle de bain, toilette, cuisine.
|
+
|
|
Etat des murs
|
ETMURS
|
Dichotomique :=1 si les murs sont peints, en bon état
et pas des fissures et =0 sinon.
|
+
|
34
|
Nombre d'étage
|
NBREETG
|
Quantitative : nombre des niveaux
comportant la maison
|
+
|
|
Ancienneté de la
maison
|
ANCMS
|
Catégorielle : =0 si avant 1980, =1 si entre
1980 et 1990, =2 si 1991 et 2000, =3 si 2001 et 2010 et =4 si
après 2010
|
+
|
|
Présence d'au moins 2 toilettes ou salles de bain
|
PRES2TOILSLB
|
Dichotomique
=1 si la maison a plus de 2 toilettes ou salle des bains et =0
sinon.
|
+
|
|
Présence d'un garage
|
PRESGARG
|
Dichotomique :=1 s'il y a un garage =0 sinon.
|
+
|
|
Type de la maison
|
TYPEMS
|
Dichotomique : =1 si la maison est en matériaux durable
et =0 sinon
|
+
|
|
Caractéristique de
localisation
|
Commune de bagira
|
COMMBAG
|
Dichotomique :=1 si la maison se trouve à Bagira et =0
sinon
|
-
|
|
Commune de
Kadutu
|
COMMKAD
|
Dichotomique :=1 si la maison se trouve à Kadutu et =0
sinon
|
-
|
|
Distance avec le
centre-ville
|
DISTCENTVIL
|
Quantitative : Il s'agit de la distance en mètre entre
la poste centrale (considérée comme le point du centre-ville) et
la maison.
|
-
|
|
Distance avec l'axe routier principal
|
DISTAXPRIPL
|
Quantitative : la distance en mètre entre la route
principale avec la maison.
|
-
|
35
|
Distance avec la
route la plus proche
|
DISTRTPROCH
|
Quantitative : Il s'agit distance en mètre de marche
à pied entre la maison et la route la plus proche.
|
-
|
|
Distance avec
l'infrastructure de
transport la plus
proche
|
DISTINFRTRPPROCH
|
Quantitative : distance avec l'axe routier le plus proche
où l'on peut obtenir facilement le transport en commun en
mètre.
|
-
|
|
Caractéristique de
voisinage
|
Distance avec un
centre médical le
plus proche
|
DISTCENTRMEDICL
|
Quantitative : distance entre le centre
médical le plus proche avec la maison en mètre.
Elle est exprimée en minute de marche à pied.
|
-
|
|
Distance avec un
établissement
d'enseignement le
plus proche
|
DISTETENSGMT
|
Quantitative : Elle est exprimée en minute de marche
à pied ; c'est la distance séparant la
maison avec un établissement
d'enseignement le plus
proche.
|
-
|
|
Catégorie
socioprofessionnelle et démographique
|
Niveau d'étude
|
NIVETD
|
Catégorielle :=0 Analphabète, =1 Primaire, =2
Secondaire, =3 Universitaire
|
+
|
|
Profession du chef
du ménage
|
PROFESS
|
Catégorielle :=0 si agriculteur, paysans et sans aucune
activité, =1 si prestataire des
|
+
|
36
|
|
|
services, =2 si salarié, =3 si commerçant et =4
si autres.
|
|
|
Cout de transport
journalier
|
CTTRANSP
|
Quantitative : il s'agit d'une estimation du cout de transport
que peut supporter le chef du ménage pour se rendre aux activités
habituelles.
|
-
|
37
II.2.1.2 Description des variables
1° La variable dépendante : le prix de la maison
C'est une variable quantitative notée PRMS. Cette
valeur peut être le prix de transaction, le prix annoncé ou la
valeur estimée du bien. Par manque de bases des données, les prix
des biens étudiés seront des valeurs estimées de ces biens
par le propriétaire. (Srikhum, 2012) montre que les maisons voisines ont
souvent été construites à la même période,
elles ont fréquemment la même structure, le même style et la
même taille. L'estimation de la valeur d'une maison peut se faire soit
auprès de l'expert du quartier ou soit auprès du
propriétaire, qui pourra donner une estimation du prix basée sur
la valeur de transaction des maisons voisines.
2° Les variables indépendantes
Les variables indépendantes vont se résumer en
quatre grandes catégories :
a. Les variables relatives aux
caractéristiques physiques
- Surface de la parcelle : elle est une variable quantitative
notée SURFPRCL. Elle est la surface en mètre carré obtenue
par la multiplication de la longueur de la largeur de la parcelle sur laquelle
se trouve la maison. Plus grande est cette surface plus élevé est
supposé être le prix de la maison (Srikhum, 2012).
- Surface de la maison : c'est une variable quantitative
notée SURFMS. Cette variable permet de comprendre le niveau d'occupation
de la parcelle. Elle est la somme des surfaces en mètre carré de
différentes constructions se trouvant sur la parcelle. Il s'agit de la
surface de maison principale, surface des maisons annexes, surface de la
toilette si elle est à l'extérieur de la maison principale, et la
surface des autres constructions se trouvant sur la parcelle par exemple une
boutique. Cette variable permet d'augmenter davantage la maison de la maison
Homocianu(2009).
- Nombre des pièces : il est une variable quantitative
notée NBREPC. Il s'agit du nombre des pièces à vivre de la
maison (y compris ceux des annexes s'ils existent) à l'exception des
pièces dites « humides » ; notamment salle de bain et
toilette. Cette variable est attendue avec un signe positif Travels et
al.(2013).
- Nombre d'étage : c'est une variable quantitative
notée NBREETG, il s'agit des nombre des niveaux que comporte la maison.
Le nombre des niveaux influence positive le prix de la maison Travels et
al.(2013).
- Ancienneté de la maison : Variable
catégorielle notée ANCMS. Elle prend successivement 5
modalités : elle sera égale à 0 si la maison a
été construite avant 1980, 1 si elle a été
construite entre 1980 et 1990, 2 si elle a été construite entre
1991 et 2000, 3 si elle a été construite entre 2001 et 2010 et 4
si c'est après 2010. Les maisons plus jeunes sont supposée
coutée plus chères que les autres Travels et al.(2013).
- Type de la maison : elle est une variable qualitative
notée TYPEMS. Elle présente deux modalités (soit 1 si la
maison est en matériaux durables et 0 sinon. Cette variable influence
positivement le prix du ménage si la maison en question est en
matériaux durables Travels et al. (2013).
- Etat des murs : c'est une variable qualitative notée
ETMURS basée sur son aspect intérieur et extérieur. Elle
prend deux valeurs, sera égale à 1 si la maison est en bon
état, c'est à dire lorsqu'elle a des murs bien vernis et n'ayant
pas des fissures dans ses murs. Une maison coutera plus cher que ses murs sont
en bon état Travels et al.(2013).
- Présence d'au moins deux salles de bains ou deux
toilettes : c'est une variable qualitative notée PRES2TOILSLB. Comprend
1 si la maison est dotée d'au moins deux salles de bains ou toilettes et
0 sinon Travels et al.(2013).
- Présence d'un garage : variable qualitative
notée PRESGARG avec deux modalités : 1 si la maison comporte un
garage et 0 sinon (Des Rosiers, 2001), b. Les variables
relatives aux caractéristiques de localisation
Les données spatiales doivent être
référencées par une localisation précise afin de
pouvoir calculer la distance entre les observations et permettre de
déterminer la matrice de poids9. La distance
euclidienne10 découlant du théorème de
Pythagore est
9 Le calcul de la matrice de poids permettra de
mesurer le niveau de dépendance des prix des maisons, ce point est
développé au niveau du calcul de l'autocorrélation
spatiale
10 La distance euclidienne est la ligne droite, la
plus courte, qui relie deux points dans l'espace à deux dimensions
(Srikhum, 2012).
39
la plus utilisée pour calculer la distance entre deux
points. Les coordonnées géographiques (les couples latitude et
longitude) sont les informations les plus convenables pour calculer la
distance. A partir de la latitude et la longitude, les coordonnées
cartésiennes sont obtenues en projetant les coordonnées
sphériques dans un espace cartésien à deux dimensions et
pouvant s'exprimer en n'importe quelle unité (mètres,
kilomètres, yards...) permettant ainsi de calculer des
différences. Les coordonnées géographiques11
sont récoltées au moyen d'un téléphone en utilisant
l'application Android ODK Collect.
- Commune de Bagira/Kadutu : C'est une variable dichotomique
notée COMMBAG/COMMKAD. Etant donné que nous avons posé la
commune d'Ibanda comme la commune de référence le coefficient
négatif associé à la variable COMMBAG/COMMKAD signifiera
le montant dépréciatif en unité monétaire de la
valeur d'une maison lorsqu'elle est située à Bagira/Kadutu en
référence à la commune d'Ibanda.
- Distance avec le centre-ville : c'est une variable
quantitative notée DISTCENTVIL mesurant la distance euclidienne entre la
maison et la poste de la ville de Bukavu considérée comme le
point central de la ville de Bukavu en mètre. Cette distance sera
calculée automatiquement au moyen de la différence des
coordonnées géographiques de la poste centrale avec celle de
chaque observation.
- Distance avec l'axe routier principal : variable
quantitative notée DISTAXPRIPL mesurant la distance euclidienne en
mètre entre la maison et la route principale. Plus cette distance est
grande avec la maison moins élevée sera la valeur de la maison
(Srikhum, 2012).
- Distance avec la route la plus proche : variable
quantitative notée DISTRTPROCH. Permet de mesurer distance de marche
à pied en mètre entre la maison et la route la plus proche afin
de rendre compte du
11 Les coordonnées géographiques sont
récoltées au format degré décimal (exemple
28,866399 et -2,501115) qui ensuite sont converties au format de la projection
traverse de Mercator(UTM) qui a permis d'exprimer le couple (longitude,
latitude) en mètre afin de pouvoir calculer les distances.
40
niveau d'accessibilité de la maison. Plus le niveau de
l'accessibilité sera difficile (c'est-à-dire la distance est
grande) moins élevée sera la valeur de la maison (Srikhum,
2012).
- Distance avec l'infrastructure de transport la plus proche :
c'est une variable quantitative notée DISTINFRTRPPROCH. Elle permet de
calculer la distance euclidienne en mètre entre la maison et
l'infrastructure permettant d'accéder facilement au transport en commun.
Cette distance influence négativement la valeur de la maison (Srikhum,
2012).
c. Les variables relatives aux caractéristiques de
voisinage
- Distance avec un établissement d'enseignement le
plus proche : variable quantitative notée DISTETENSGMT établit la
durée de marche à pied en minute estimée entre la maison
et un établissement d'enseignement le plus proche Homocianu(2009).
- Distance avec un centre médical le plus proche :
variable quantitative notée DISTCENTRMEDICL permettant de mesurer la
durée en minute de marche à pied estimée entre un centre
médical ou un hôpital le plus proche avec la maison.
d. Les variables relatives aux catégories
socioprofessionnelles et démographiques - Niveau d'étude :
Variable catégorielle comprenant 4 modalités : 0 si
analphabète, 1 si niveau primaire, 2 si niveau secondaire et 3 si niveau
universitaire. Cette variable est supposée influencer positivement la
valeur d'une maison. Homocianu(2009).
- Profession du chef du ménage : c'est une variable
catégorielle notée PROFESS avec 0 si agriculteur, paysans et sans
aucune activité, 1 si prestataire des services (salon de coiffure,
menuisier, restaurant,...), 2 si salarié, 3 si commerçant et 4 si
autres. Cette variable permet de capter l'activité principale dans
laquelle le propriétaire de la maison tire son revenu habituellement,
elle influencera positivement la valeur de la maison.
41
- Cout de transport journalier : Variable quantitative
notée CTTRANSP. Wingo (1961) donne un rôle central aux transports
dans le fonctionnement urbain, en considérant que le marché
foncier est conditionné par les transports urbains. Il prend en compte
dans le modèle d'un coût généralisé de
transport au lieu d'un coût de transport fonction linéaire de la
distance au centre comme Alonso(1964) le considérait. Ce coût
généralisé reflète l'ensemble des dépenses
monétaires de transport et la valeur attribuée au temps de
trajet. Cette variable comprendra la somme des couts de transport en commun
aller-retour que pourrait supporter le chef du ménage pour se rendre
à la poste centrale( nous avons considéré le marché
de Nyawera comme référence car c'est le centre commercial le plus
proche), pour se rendre à son travail( en nous inspirant du
modèle d'Alonso(1964) pour lequel le ménage effectue arbitrage
cout de transport travail- cout de foncier), pour se rendre au marché
central de Kadutu.
II.2.2 Méthodes d'estimation
II.2.2.1 La méthode de moindre carré ordinaire
(MCO)
Cherchant à mesurer la valeur que les ménages
accordent à une caractéristique donnée de la maison, la
méthode des prix hédoniques est l'une des principales
méthodes permettant d'estimer de telles valeurs et faisant ainsi recours
à la méthode d'estimation par Moindre Carré Ordinaire
(MCO) (Travers et al., 2013 et Srikhum, 2012).
Sous la condition nécessaire que les résidus de
l'estimation sont des variables aléatoires indépendantes et
identiquement distribuées (la variance est constante et non
corrélée), la méthode des moindres carrés
ordinaires (MCO) permet d'obtenir les coefficients non biaisés de l'Eq.
2.3. Mais Cette régression hédonique standard ne permet pas de
prendre en compte l'interaction existante entre les prix des maisons
voisines.
Le processus de détermination de la valeur des maisons
d'habitation pour lequel le propriétaire se renseigne sur les prix des
maisons voisines dans la détermination de la
42
valeur de sa maison crée localement une
dépendance spatiale des prix. De plus, des maisons voisines ont souvent
été construites à la même période, elles ont
fréquemment la même structure, le même style et la
même taille. Ces maisons doivent faire face aux mêmes variables
d'externalité. Cette ressemblance locale crée donc un
problème de corrélation spatiale des variables explicatives du
modèle des prix hédonistes.
Srikhum (2012) montre que si cette dépendance spatiale
n'est pas prise en considération lors de la spécification du
modèle, les résidus du modèle hédonique seront
dépendants.
De ce qui précède il s'observe qu'en
réalité la valeur d'une maison a une influence sur la valeur des
autres maisons situés proches de lui, d'où le problème de
l'autocorrélation spatiale entre les prix immobiliers.
Dans ce cas la méthode des moindres carrés
ordinaires est insuffisante et inadaptée(Travels et al.,2013 ;
Srikhum,2012; Gallo,2002) et les paramètres estimés de la
régression sont biaisés et non efficients.
Ensuite, Gallo (2002) montre que l'étude des
marchés immobiliers dans les espaces urbains fait souvent
apparaître une segmentation de ces marchés: les
caractéristiques et les prix des maisons diffèrent
substantiellement selon leurs localisations12. Cette segmentation
provenant entre autres de l'inélasticité de la demande des
ménages pour certaines caractéristiques des maisons ou encore de
diverses barrières institutionnelles conduit à des variations
persistantes et significatives des caractéristiques des logements et de
leurs prix dans les différents sous marchés. Dans ces conditions,
estimer une relation "globale" entre le prix des maisons et ses
caractéristiques, relation s'appliquant de la même façon
sur toute l'aire urbaine étudiée, est susceptible de masquer des
différences importantes dans l'espace.
L'instabilité dans l'espace des relations
économiques illustrée ci-haut est appelée
hétérogénéité spatiale (Gallo,2002) qui peut
s'observer sur plusieurs niveau: les comportements et les
phénomènes économiques ne sont pas les mêmes dans le
centre
12 Une maison située à Muhumba n'aura
pas la même valeur que celle située à Cimpunda, toutes
choses restant égales par ailleurs.
43
d'une ville et dans sa périphérie, dans une
région urbaine et dans une région rurale, dans les
différentes communes, quartiers, avenu, etc. cela peut se traduire dans
une régression économétrique de deux façons : par
des variances différentes ou par des coefficients différents.
Dans le premier cas, on est confronté à un problème
d'hétéroscédasticité, et dans le second cas, on
parle d'instabilité des paramètres de la régression qui
varient systématiquement avec la localisation.
Ces deux grandes particularités des données
spatiales, l'autocorrélation spatiale qui se réfère
à l'absence d'indépendance entre observations
géographiques et l'hétérogénéité
spatiale liée à la différenciation dans l'espace des
variables et des comportements, ont été souvent prises en compte
dans la littérature, comme par exemple dans le cadre de l'analyse des
espaces urbains: étude de la variation des densités de population
(Kau, Lee et Sirmans, 1986; McMillen et McDonald, 1998) et des
caractéristiques des logements ( Dubin et Sung, 1987; Can, 1990, 1992)
ou étude de la segmentation des marchés immobiliers (Goodman et
Kawai, 1982; Bender et Hwang, 1985).
A cet égard le recours aux méthodes de
l'économétrie spatiale visant à traiter les deux grandes
particularités des données spatiales : l'autocorrélation
spatiale et de l'hétérogénéité spatiale
devient incontournable.
II.2.2.2 Prise en compte de
l'hétérogénéité spatiale
L'hétérogénéité spatiale
est un phénomène lié à la différenciation
dans l'espace des variables et des comportements. Gallo (2002) indique qu'en
pratique, ces différences peuvent se traduire de deux façons dans
une régression: par des variances des termes d'erreurs
différentes qui correspondent au problème de
l'hétéroscédasticité ou par des coefficients
différents qui renvoie à l'instabilité des
paramètres de la régression.
Dans le cas de l'étude immobilière, il
paraît possible que l'impact spatial ne soit pas homogène. Can
(1990) pose la question : « la valeur des caractéristiques des
biens immobiliers varie-t-elle selon la localisation du bien ? ». Si cette
valeur varie, une seule estimation hédonique ne suffit pas pour estimer
l'ensemble des observations. Il faut un ou des outils qui permettent de
vérifier cette variation selon la
44
localisation des biens13. Par conséquent,
les caractéristiques de localisation prises en compte dans le
modèle d'évaluation doivent varier selon la segmentation de
marché14.
1°. Hétéroscédasticité
Une hypothèse du modèle de régression
linéaire est que la variance des perturbations soit constante. Lorsque
cette hypothèse est violée, il y a
hétéroscédasticité. La principale
conséquence de l'hétorescédasticité est que les
estimateurs restent linéaires et sans biais, mais ils ne sont plus de
variance minimum parmi tous les estimateurs. Les t-students seront aussi
artificiellement élevés, suggérant que les variables
explicatives sont significatives alors que non (Bourbonnais, 2009).
En général,
l'hétéroscédasticité provient des variables
manquantes ou de toute autre forme de mauvaise spécification. En outre,
lorsqu'on travaille sur des données localisées, les unités
spatiales utilisées ne sont généralement ni
régulières, ni homogènes : elles peuvent avoir des formes
et des aires différentes, des niveaux de développement variables,
des populations plus ou moins importantes etc.
Cette forme des erreurs conduit au test de Breusch-Pagan
(1979) basé sur le multiplicateur de Lagrange.
H0 : ái =0, i =1 ... T : le modèle est
homoscedastique H1 : Sinon : le modèle est
hétéroscedastique.
Dans le cas de l'hétéroscedasticité,
White (1980) a fourni un estimateur convergent de la matrice des
variances-covariances de l'estimateur des Moindres Carrés Ordinaires
(MCO) en présence d'hétéroscédasticité de
forme inconnue pour que l'inférence
13 Plusieurs exemples peuvent être évoqués
pour confirmer cette remarque. La caractéristique de localisation «
vue sur le lac Kivu » est une variable qui a une influence possible sur le
prix uniquement pour les maisons situées au bord du lac Kivu ou pouvant
avoir une vue au lac Kivu. En revanche, cette caractéristique n'a aucune
influence sur le prix des maisons situées à côté du
Marché central de Kadutu. La caractéristique « vue sur lac
Kivu» influence le prix uniquement pour les maisons situées
à coté ou au bord du lac et non pas pour ceux situés
à côté du marché de Kadutu. Les
caractéristiques de localisation des biens immobiliers diffèrent
selon leurs environnements. Un seul modèle d'évaluation avec les
mêmes caractéristiques pour toutes les segmentations donne des
résultat biaisé.
14 Prenons l'exemple de la distance jusqu'au transport en
commun. Etre situé près d'un accès à un transport
en commun augmente la valeur d'une maison grâce à la
facilité de déplacement, mais peut avoir une influence moins
importante voire même négative sur la valeur d'une maison. Les
acheteurs de maison disposant souvent de voiture, la localisation près
d'un accès de transport en commun peut être perçue, pour
eux, comme un inconvénient du fait de la nuisance sonore ou de la
fréquentation des passagers.
45
statistique basée sur les MCO soit asymptotiquement
fiable. Stata permet de corriger de
l'hétéroscédasticité la methode de moindre
carré ordinaire par la méthode de White afin corriger les
écarts-types au moyen de l'option robust (exemple : regress y
x1 x2 x3, robust).Toutes les interprétations et les tests
s'effectuent comme auparavant avec les nouveaux écarts-types.
2°. Instabilité des paramètres
L'instabilité des paramètres provient de
l'absence de stabilité dans l'espace des comportements ou des relations
économiques : les paramètres d'une régression varient
selon leurs localisations. L'on peut chercher à savoir dans quelle
mesure la moyenne d'une variable varie entre différents sous-groupes
d'observations localisées. Par exemple, on peut se demander si la
moyenne des prix des maisons d'habitation est la même à Ibanda,
Kadutu et Bagira ou si la moyenne des prix est la même dans tous les
quartiers de la ville de Bukavu. D'où l'on fera recours à
l'analyse de la variance spatiale.
? ANOVA Spatiale
Dans cette étude, il est question d'une analyse de
variance spatiale univariée vu que nous étudions l'effet d'une
variable indépendante qualitative (commune) sur une variable
dépendante (prix des maisons) quantitative avec l'objectif de tester si
la commune influence la valeur de la maison.
H0 :X1 = X2=X3
Par l'hypothèse nulle, on admet que les moyennes de
prix sont égales pour toutes les communes
H1 :X1 ? X2?
X3
L'hypothèse alternative avance qu'il y a au moins une
moyenne qui diffère des autres.
Afin de s'assurer que nos données acceptent l'analyse
de la variance, deux conditions principales sont nécessaires pour que
les conclusions soient valides : l'homogénéité de la
variance intragroupe et la normalité des données. Le test de
Levene (> 0,05) est
46
utilisé pour accepter l'hypothèse
d'homogénéité de la variance et le test de
normalité (test Kolmogorov ou de Shapiro > 0,05) qui doit accepter
l'hypothèse de normalité.
Si les données ne sont pas appropriées à
une ANOVA (hétérogénéité des variances ou
données fortement asymétriques) Carricano et Poujol (2008)
propose d'utiliser des tests non paramétriques qui ne supposent ni
homogénéité de la variance, ni une distribution normale.
Si cela est le cas nous ferons recours à l'alternative non
paramétrique de l'ANOVA15, le test de
Kruskall-Wallis16. Concernant l'efficacité du test de
Kruskal-Wallis, Rakotomalala(2008) montre que si l'hypothèse alternative
est vraie, là où il faudrait 95 observations pour que l'ANOVA
détecte la réponse correcte, il en faudrait 100 pour le test de
Kruskal-Wallis.
Srikhum (2012) montre que la prise en compte du
problème d'hétérogénéité spatiale
paraît important pour une analyse des données spatiales mais il
est beaucoup moins mentionné que l'autocorrélation spatiale par
la littérature dans l'étude immobilière.
II.2.2.3 Prise en compte et mesures de
l'autocorrélation spatiale
Les données spatiales sont normalement supposées
indépendantes alors que cette hypothèse est rarement
justifiée et devrait être systématiquement testée.
Comme précédemment indiqué, l'autocorrélation
spatiale se réfère à la ressemblance des observations en
fonction de leur localisation géographique. Ainsi les prix des biens
immobiliers sont spatialement corrélés parce que les biens
voisins sont semblables. L'objet de cette partie est de présenter
certains outils utilisés pour tester la présence de
l'autocorrélation spatiale, différentes sources de
l'autocorrélation spatiale ainsi que les modèles et
méthodes retenues pour ce présent travail pour redéfinir
la régression hédonique afin d'obtenir un estimateur non
biaisé et efficient du prix des maisons d'habitation à Bukavu.
15
http://en.wikipedia.org/wiki/Kruskal-Wallis_one-way_analysis_of_variance
16 Il existe des tests paramétriques qui sont
utilisés en cas d'absence de l'homogénéité de la
variance, notamment le test de « Welch » et de «
Brown&Forsythe » mais à notre connaissance nous n'avons pas
trouvé des tests qui puissent prendre en compte simultanément
l'absence de la normalité et celle de l'homogénéité
raison pour laquelle notre choix s'est orienté aux tests non
paramétriques, comme proposé Carricano et Poujol (2008), pour
lesquels ni la condition de normalité ni celle
d'homogénéité de la variance n'est posée à
l'avance.
47
1°. Tests de l'autocorrélation spatiale
Les mesures d'autocorrélation spatiale permettent
d'estimer la dépendance spatiale entre les valeurs d'une même
variable en différents endroits de l'espace. Pour la mettre en
évidence, les indices prennent en compte deux critères : la
proximité spatiale et la ressemblance ou la dissemblance des valeurs de
cette variable dans les unités spatiales de la zone d'étude.
Les indices les plus utilisés sont l'indice de Moran et
l'indice de Geary. Dans la littérature, le coefficient de Moran est
souvent préféré à celui de Geary en raison d'une
stabilité générale plus grande (Upton et Fingleton, 1985).
Dans cette étude nous allons utiliser seulement l'indice de Moran
(Moran's I). Avant de calculer cet indice, il est nécessaire de
définir les interactions spatiales prises en compte.
La matrice d'interactions spatiales est une matrice
carrée qui permet de mesurer les interactions entre les unités
spatiales, indépendamment de la variable étudiée. Sa
valeur est d'autant plus élevée que la « proximité
» spatiale entre les unités est forte. La matrice est
intégrée à l'équation de régression afin
d'estimer les coefficients non biaisés du modèle de prix
hédoniste.
Pour utiliser cette matrice, il est nécessaire de
donner a priori une forme fonctionnelle spécifique aux interactions
spatiales. Trois formes sont plus utilisées dans la
littérature:
- La matrice de contiguïté :
généralement, les éléments de la
matrice
de contigüité d'ordre k sont définis comme
le nombre minimal de frontières qu'il faut franchir pour aller d'une
unité spatiale à l'autre. La matrice de contiguïté la
plus utilisé est d'ordre 1 : les éléments de la matrice
sont égaux à 1 si deux unités sont voisines et sont nuls
dans le cas contraire. Cette forme est plus utilisée si on ne dispose
pas des coordonnées géographiques des
observations.
- La matrice des distances est une mesure
d'intensité spatiale
qui peut être utilisée
quand les données sont spatialisées sous forme de points. Elle
prend en compte le poids du voisinage (des valeurs 0 ou 1).
- Une autre manière plus détaillée de
décrire les interactions
spatiales consiste à prendre en
compte non seulement le voisinage (des valeurs
48
0 ou 1), mais de tenir compte aussi de l'intensité de
cette proximité spatiale, qui dépend de l'importance de la
frontière commune.
Une fois l'ensemble des voisinages défini, dans une
deuxième étape, il faut déterminer les poids
associés à chaque voisin. A cet effet on peut citer la matrice de
poids standardisée (Row-standardized weight matrix), la matrice de poids
binaire (Binary weight matrix) et la matrice de poids binaire
générale (General binary weight matrix).
Dans ce présent travail nous choisissons la matrice de
voisinage avec la condition de distance de séparation maximale de 400
mètres afin que chaque observation contienne au moins un voisin et
l'inverse de la distance comme pondération. Ce choix est justifié
par Srikhum (2012) qui montre que l'inverse de la distance permet de mesurer
l'accessibilité qui est une des caractéristiques principales en
évaluation immobilière.
? L'indice I de Moran
L'indice de Moran (Moran 1950) permet de mesurer le niveau
d'autocorrélation spatiale d'une variable et de tester sa
significativité. L'indice a des valeurs comprises entre -1 (indiquant
une dispersion parfaite) à 1 (corrélation parfaite). Une valeur
nulle signifie que la distribution spatiale de la variable
étudiée est parfaitement aléatoire dans le territoire. Les
valeurs négatives (positives) de l'indice indiquent une
autocorrélation spatiale négative (positive).
Pour le test d'hypothèse statistique, l'indice I de
Moran peut être transformé en Z-scores, pour lesquels les valeurs
plus grandes que le seuil de significativité positive ou plus petites
que le seuil de significativité négative indiquent une
autocorrélation spatiale significative, avec un taux d'erreur
correspondant au seuil (hypothèse de loi normale). Une
interprétation de l'indice de Moran peut être faite avec l'aide du
diagramme de Moran, qui représente, sous la forme d'un nuage de points,
les couples de valeurs correspondant à la valeur de la variable dans
chaque unité spatiale (en abscisse) et la moyenne des valeurs des zones
contiguës (en ordonnée) définies par la matrice
d'interactions spatial.
49
|
???????????? =
|
?? ? ? ??????(???? - ??)(???? - ??)
?? ??
??=1 ??=1
|
|
? ??? ??????(???? - ??)2
??
??=1 ??=1
|
où i,j = unité spatiale ; n = nombre
d'unités spatiales ; x est la valeur de la variable dans l'unité
i ; ?? est la moyenne de x ; et ?????? sont les éléments de la
matrice d'interactions spatiales, définie sous la forme de la
contigüité, les distances ou les frontières communes.
Pour le test d'hypothèse statistique nulle (pas
d'autocorrélation spatial), l'indice I de Moran peut être
transformé en Z-scores (les valeurs critiques) et p-value (la
significativité).L'espérance mathématique de l'indice de
Moran (hypothèse de non autocorrélation spatiale) est:
|
?? (????????????) =
|
1
|
|
??- 1
|
Et la variance est égale à :
??(????????????) = ??(???????????? 2) -
(??(??????????))2
Ainsi, la valeur critique z-score est égale à :
???? = ???????????? - ??( ????????????)
v?? (????????????) La valeur de p-value est l'approximation
numérique de la superficie au-dessous de la courbe de
la distribution de moyenne et variances connues.
2°. Sources de l'autocorrélation spatiale et
methodes d'estimation Basées sur différents travaux (Basu et
Thibodeau (1998); Bowen, Mikelbank et Prestegaard (2001); Dunse et Jones
(1998); LeSage et Pace (2009); Tu, Yu et Sun (2004)), trois sources
d'autocorrélation spatiale sont souvent citées : la ressemblance
des biens voisins, le processus de détermination des prix immobiliers et
la mauvaise définition du modèle d'estimation.
Les prix des biens immobiliers sont spatialement
corrélés parce que les biens voisins sont semblables. Cette
ressemblance apparait dans les caractéristiques physiques, dans les
caractéristiques de localisation et aussi dans les
50
caractéristiques de l'environnement. Les biens voisins
sont souvent construits à la même période. Par
conséquent, ils ont souvent la même structure, le même style
et la même taille. Les immeubles voisins ont souvent la même
qualité. Il est donc normal que la qualité d'un immeuble ait une
influence sur le prix des immeubles situés à côté de
lui. La dépendance des caractéristiques physiques est, par
conséquent, une source d'autocorrélation spatiale des prix
immobiliers. En outre, les biens voisins se confrontent normalement aux
mêmes caractéristiques de localisation (la qualité de
l'environnement, la présence de transports en commun, la distance
jusqu'au centre-ville, etc.) et aux mêmes externalités,
appelées aussi les caractéristiques de l'environnement (la
qualité de l'air, la vue, la nuisance sonore, etc.). La non prise en
compte de la dépendance des caractéristiques de localisation
cause le problème de corrélation des résidus de
l'estimation hédonique.
Une raison souvent employée pour expliquer la
dépendance spatiale des prix immobiliers est le processus de
valorisation du bien par le vendeur. Pour déterminer la valeur à
la vente de son bien, le propriétaire peut se renseigner, soit
auprès de l'expert de quartier qui donne une estimation de prix
basée sur la valeur de transaction des biens voisins, soit directement
auprès de propriétaires de biens voisins. La valeur du bien
immobilier dépend donc de la valeur de transaction des biens voisins.
Dans le cas où la dépendance spatiale des prix immobiliers est
causée par le processus de valorisation du bien, la dépendance se
présente donc dans la partie des variables endogènes du
modèle de régression hédonique. Lesage et Pace (2009)
redéfinissent un modèle hédonique plus avancé (par
rapport à l'Eq. 2.3) qui permet de prendre en compte la
dépendance des variables endogènes de la façon suivante
:
y = a + Xfi + pWy + e (Eq. 2.4)
Wy la matrice qui permet de prendre en compte la
valeur à la vente des biens voisins, p permet de mesurer le
degré de dépendance entre les biens voisins, fi
comportent les coefficients de la regression, X est la matrice des
caractéristiques physiques inclues dans la régression,
l'équation suppose bien qu'il n'y ait pas de dépendance spatiale
des caractéristiques physiques du bien. Les vecteurs a et e
respectivement les vecteurs des constantes et des résidus de
l'estimation.
51
La dépendance spatiale entre les valeurs de biens
immobiliers peut aussi être expliquée par les variables omises qui
ne sont pas prises en compte dans le modèle de l'estimation. Cela peut
correspondre aux variables non observables liées à la
préférence individuelle, aux infrastructures (le projet de
construction de nouvelles routes), aux nouvelles externalités (le
problème d'inondation d'un certain quartier). Cette variable manquante
crée donc un problème de dépendance spatiale des prix des
biens situés autour d'elle. La prise en compte de la valeur des biens
voisins dans le modèle d'évaluation des biens immobiliers permet
donc d'améliorer le pouvoir explicatif du modèle.
Supposons que l'Eq. 2.3 soit décomposée en deux
parties :
y = a + ???? + 8Z + e (Eq. 2.6)
Avec ???? et 8Z representant la valeur
correspondant aux deux groupes des variables explicatives. X et Z sont
indépendants mais Z subit le problème de dépendance
spatiale. Si l'information sur Z est omise, l'Eq. 2.3 va devenir y = a +
???? + e et la dépendance se présente dans les
résidus de l'estimation e avec :
e= 8??e+ ?
La variable non observable ne cause pas uniquement un
problème de corrélation spatiale, mais peut générer
un problème d'hétérogénéité
spatiale.
3° Modèles retenus pour ce travail
Étant donné que les sources de la
dépendance spatiale sont variées, soit dans la partie variable
à expliquer (modèle autorégressif spatial - SAR), soit
dans la partie des variables explicatives(modèle de variables
exogènes décalées - SLX), ou soit dans la partie des
résidus de l'estimation (modèle d'erreurs spatiales - SEM),
Srikhum(2012) montre que le choix d'un modèle de régression
linéaire prenant en compte l'autocorrélation spatiale
dépend des données étudiées, de leur distribution
dans l'espace, la source de l'autocorrélation spatiale prise en compte
dans l'étude, de l'information de localisation, du logiciel disponible
et de l'objectif de l'étude.
Ainsi comme l'objectif principal de ce travail est de
déterminer les facteurs explicatifs du prix des maisons d'habitations
dans la ville de Bukavu, parmi les différents
52
modèles spatiaux disponibles, nous retenons deux
modèles comme le montre Srikhum(2012) que seul le modèle
autorégressif spatial (modèle SAR : Spatial Autoregressive Model)
dans lequel la source de l'autocorrélation spatiale choisie est le
processus d'évaluation des biens et le modèle d'erreurs spatial
(modèle SEM : Spatial Error Model) où la dépendance est
causée par les erreurs de spécification du modèle de
l'estimation sont les plus utilisés.
? Modèle SAR (Spatial Autoregressive Spatial)
Le modèle spatial le plus basique est le modèle
autorégressif spatial (SAR) où l'autocorrélation spatiale
de la variable endogène est prise en compte. Cressie (1991) indique que
le modèle SAR est utilisé dans le cas où l'effet de
diffusion (spillover effect) cause la dépendance spatiale de la variable
endogène ; un changement a une influence directe sur une observation et
crée une influence indirecte sur les observations voisines. Le
modèle SAR est le modèle le plus utilisé en étude
immobilière car le processus d'évaluation de bien immobilier
crée la dépendance des prix. Le vendeur se renseigne notamment
auprès de ses voisins pour déterminer le prix de vente de son
bien. Quant à l'acheteur, il s'intéresse à la valeur des
biens localisés autour du bien qu'il veut acheter afin d'estimer le prix
d'achat le plus raisonnable. La valeur d'un bien est donc calculée en
prenant en compte la valeur estimée des biens voisins comme
référence et y ajoutant un surplus correspondant aux
caractéristiques spécifiques du bien ainsi qu'une plus-value
liée à la préférence de l'acheteur. Ainsi, par
exemple l'impact de l'existence d'un hôtel sur le prix immobilier se
diffuse mais l'importance de cet impact dépend négativement de la
distance entre cet hôtel et les maisons.
Le modèle autorégressif spatial (SAR) se
présente donc comme le modèle de régression
linéaire simple tout en intégrant le terme pWy qui
contient les poids des observations voisines intégrées dans
l'estimation.
Ce modèle s'écrit donc : y = a + Xf3 + pWy +
e
53
? Le modèle d'erreurs spatial (SEM)
Le modèle SEM est un autre modèle souvent
utilisé en étude immobilière. Ce modèle prend en
compte la dépendance spatiale due aux effets des externalités.
Deux motivations souvent mentionnées pour expliquer
l'autocorrélation des erreurs sont la variable omise lors de la
définition de modèle et
l'hétérogénéité spatiale.
Premièrement, lors de la définition du
modèle de régression, certaines variables ne sont pas prises en
compte comme variable explicative. Cela peut être dû à un
manque d'information ou à une mauvaise spécification du
modèle. Si cette variable explicative omise ne présente pas de
dépendance spatiale, ce modèle donnera des estimateurs non
biaisés. Mais si cette variable présente la dépendance
spatiale, les erreurs de l'estimation seront corrélées.
Deuxièmement, LeSage et Pace(2009) soulignent que le
modèle SEM peut aussi être développé pour
résoudre le problème
d'hétérogénéité comme justifié
précédemment.
Ce modèle s'écrit donc :y = a + ???? + 8Z +
e
X et Z sont indépendants mais Z subit le
problème de dépendance spatiale. Si l'information sur Z est
omise, cette équation va devenir
y = a + ???? + e Et la dépendance se
présente dans les résidus de l'estimation e avec :
e= 8??e+ ?
4°. Méthodes d'estimation
En présence de dépendance spatiale, l'estimation
par les moindres carrées ordinaires (MCO) donne des estimateurs
biaisés et non efficients. Srikhum(2012) montre que ni les MCO ni les
MCG ne permettent d'obtenir un estimateur non biaisé, convergent et
efficient.
Plusieurs méthodes sont proposées par la
littérature pour estimer la variable en présence de
dépendance spatiale. Gallo (2002) utilise la méthode du maximum
de vraisemblance. LeSage et Pace (2009) proposent le maximum de
vraisemblance
54
concentré et la méthode bayésienne qui
est basée sur le « Markov Chain Monte Carlo (MCMC) ». Kelejian
et Prucha (1998) et Drukker, Prucha et Raciborski (2011) proposent la
méthode de moindres carrés généralisés en
deux étapes. Ce présent travail ne portera que sur le maximum de
vraisemblance qui est la méthode la plus souvent utilisée en
étude immobilière.
II.2.3. Choix du modèle optimal
Si plusieurs modèles significatif sont en
compétition et comportant des variables explicatives différentes,
Gallo (2002) propose de faire le choix entre modèles avec les
critères traditionnels tels que les critères d'information
d'Akaïke(AIC) en passant par le test du rapport de vraisemblance pour
lequel le modèle optimal à retenir est celui qui minimise la
fonction d'Akaike (Akaike Information Criterion).
Après avoir choisi un modèle optimal, une des
hypothèses du modèle classique de la régression multiple
est que les variables explicatives du modèle soient indépendantes
les unes des autres. Dans le cas contraire, il y a présence de
multicolinéarité, problème généralement
rencontré dans la mise en oeuvre du modèle hédonique
(Gallo, 2002 ; Srikhum, 2012) traduisant de l'instabilité et
d'incohérence des coefficients de régression; des tests
statistiques de significativité individuelle des variables
invalidés par ce qu'on ne sait pas séparer leurs effets pour
évaluer leur importance.
La solution au problème passe par l'élimination
de la ou des variables qui sont à la source de la
colinéarité, par la substitution d'une variable interactive aux
deux variables fortement corrélées ou par l'application de la
procédure de régression par étape (Stepwise
Regression17), permettant d'éliminant de l'équation
toute caractéristique dont la contribution marginale à la valeur
réelle n'est pas suffisamment significative après avoir
appliqué des tests statistiques de la multicolinéarité
recommandés(Farrar et Glauber, VIF...).
17 A cet effet, Bourbonnais (2009) distingue 5
méthodes qui peuvent être utilisées pour retenir le
meilleur modèle. Il s'agit soit de considérer toutes les
régressions possibles, soit d'utiliser l'élimination progressive
(« Bachward Elimination »), soit la sélection progressive
(« Forward Regression »), soit la régression pas à pas
(« Stepwise Regression) et la régression par étage («
Stagewise Regression »). Les 3 dernières méthodes
étant appropriées pour les variables explicatives quantitatives,
la méthode Stepwise Regression est utilisée dans cette
étude.
55
Dans le cas de ce présent travail les VIFs, ou facteurs
d'inflation de la variance, étant, à ce jour, l'indicateur le
plus fiable de ce phénomène et plus utilisé (Travels et
al.,2013) indiquant, dans quelle mesure, chaque variable indépendante du
modèle est expliquée par l'ensemble des autres variables
explicatives, sera utilisé pour détecter la
multicolinéarité excessive. Le VIF prendra la valeur « 10
» si la variable en question est expliquée par les autres dans une
proportion de 90 %, « 5 » si le pouvoir explicatif est de 80 %,
« 2 »s'il n'est que de 50 %, etc. Dans la littérature
économétrique, les problèmes sérieux de
multicolinéarité ne surviennent que si le VIF atteint ou
excède la valeur « 10 ».
II.2.4. Présentation des outils de traitement des
données
Les traitements des données ainsi collectées par
les outils de ODK Collect 1.1.4 ont été faits en utilisant
conjointement le tableur d'Excel, et le logiciel SPSS 20 ainsi que le logiciel
STATA 12. Le premier nous a servi pour réorganiser la base des
données obtenues de l'application ODK, le deuxième nous a servi
aux analyses descriptives et l'analyse de la variance et le dernier pour les
régressions.
Ainsi pour la prise en compte de la dépendance spatiale
plusieurs logiciels n'intègrent pas ces analyse dans sa mémoire,
y compris même STATA 12, mais certains logiciels statistiques proposent
un package qui permet d'analyser le modèle avec la dépendance
spatiale et d'estimer le degré de corrélation spatiale. Drukker,
Prucha et Raciborski (2011) proposent le package spmat et gs2sls attaché
sur Stata. La fonction spmat est destinée à construire la matrice
de poids et la fonction gs2sls permet d'estimer le modèle spatial avec
la méthode de moindres carrés généralisés en
deux étapes (A Generalized Spatial Two-Stage Least Squares - GS2SLS).
Bivand (2012) propose le package spdep attaché à R qui permet de
construire la matrice de poids (avec le fonction knearneigh et dnearneigh) et
d'estimer les paramètres de corrélation spatiale avec plusieurs
méthodes possibles. LeSage et Pace (2009) donnent les codes Matlab pour
analyser les données spatiales. Comme chaque logiciel dispose d'une
mémoire interne différente, le choix du logiciel dépendra
non seulement de l'objectif de l'étude mais aussi de la taille de la
base de données et d'autres contraintes comme le niveau de la
familiarité avec l'analyste. C'est cette dernière raison a permis
d'orienté notre choix pour le logiciel Stata 12 avec trois principaux
packages qui ont
56
été téléchargés et
installés: spatwmat permettant de déterminer la matrice de poids,
spatdiag pour le diagnostic de la dépendance spatiale ainsi que le
package spatreg pour l'estimation par la méthode du maximum de
vraisemblance du modèle SAR ainsi que du modèle SEM.
57
CHAPITRE III : PRESENTATION ET ANALYSE DES DONNEES
Ce chapitre comprend cinq sections : la première
présente les caractéristiques de l'échantillon ; la
deuxième fait une étude exploratoire sur les relations entre
certaines variables; la troisième, nous présente les
résultats des estimations et interprétation des résultats
et la quatrième nous montre les implications des résultats; et
enfin, la cinquième présente les limites de ce travail et les
perspectives de recherche.
III.1 Caractéristiques de l'échantillon
Nous avons mené une enquête de terrain
auprès 193 ménages du 4 au 18 Janvier 2015, soit pendant 14
jours, au cours de laquelle nous avons individuellement interrogé au
moyen d'un questionnaire implémenté dans le
téléphone portable ; en utilisant l'application Android ODK
Collect 1.4.4 et ses différents outils afin de réduire le temps
de l'enquête avec la rapidité de remplissage des formulaires, et
la réduction du temps et des erreurs liés à l'encodage,
ainsi que de permettre d'obtenir les coordonnées géographiques(
longitude et latitude) des maisons enquêtées avec une
précision moyenne de 5 mètres. Ce qui permet d'avoir un taux de
réponse de 100%.
Les données présentées à cette
section portent sur les caractéristiques socioprofessionnelles et
démographiques des personnes enquêtées.
L'objectif de cette analyse est de faire une
présentation plutôt informative sur le profil des personnes
enquêtées (le sexe, l'état-civil et la profession).
Tableau 3.1 : correspondance commune-sexe des personnes
enquêtées
|
Sexe
|
Total
|
|
Homme
|
Femme
|
|
Ibanda
|
27,0%
|
37,8%
|
33,7%
|
|
Kadutu
|
35,1%
|
46,2%
|
42,0%
|
|
Bagira
|
37,8%
|
16,0%
|
24,4%
|
|
Total
|
100,0%
|
100,0%
|
100,0%
|
|
38,3%
|
61,7%
|
100,0%
|
Source : notre confection
58
Au regard de ce tableau nous remarquons que les femmes sont
plus représentées dans notre échantillon que les hommes,
soit 61,7% contre 38,3%. Ceci s'explique par le fait que le questionnaire
était administré de manière aléatoire aux
ménages sans distinction de sexe.
Tableau 3.2 : Tableau croisé commune-Etat-civil des
enquêtés
|
Etat-civil
|
Total
|
|
Célibataire
|
Marié
|
Divorc é
|
Veuf
|
Union libre
|
|
Ibanda
|
10,0%
|
43,1%
|
11,1%
|
27,3%
|
32,7%
|
33,7%
|
|
Kadutu
|
30,0%
|
33,8%
|
22,2%
|
54,5%
|
49,0%
|
42,0%
|
|
Bagira
|
60,0%
|
23,1%
|
66,7%
|
18,2%
|
18,4%
|
24,4%
|
|
Total
|
100,0%
|
100,0%
|
100,0%
|
100,0%
|
100,0%
|
100,0%
|
|
5,2%
|
33,7%
|
4,7%
|
5,7%
|
50,8%
|
100,0%
|
Source : notre confection
Aussi, de ce tableau il s'observe que notre échantillon
est majoritairement constitué des personnes en union libre
représentant 50,8% des enquêtés, suivi des personnes
mariées constituant 33,7% alors que les célibataires, les veufs
ainsi que les divorcés ne représentent ensemble que 15,6% des
personnes enquêtées.
Tableau 3.3 : Tableau commune-Profession des personnes
enquêtées
|
Profession
|
Total
|
|
Agriculteurs, Paysans et Sans emploi
|
Prestatair
es des
services
|
Salarié s
|
Commerçan ts
|
Autres
|
|
Ibanda
|
34,5%
|
45,7%
|
30,8%
|
20,9%
|
58,3%
|
33,7%
|
|
Kadutu
|
45,5%
|
32,6%
|
53,8%
|
47,8%
|
16,7%
|
42,0%
|
|
Bagira
|
20,0%
|
21,7%
|
15,4%
|
31,3%
|
25,0%
|
24,4%
|
|
Total
|
100,0%
|
100,0%
|
100,0%
|
100,0%
|
100,0%
|
100,0%
|
|
28,5%
|
23,8%
|
6,7%
|
34,7%
|
6,2%
|
100,0%
|
Source :notre confection
59
On peut constater de ce tableau ci-dessus que, les personnes
exerçant du commerce sont plus représentées que d'autres
avec 34,7% des enquêtés suivi des agriculteurs, paysans et sans
emploi constituant 28,5%. Les salariés et autres ne forment ensemble que
12,9% des personnes enquêtées.
III.2 Etude exploratoire sur les relations entre certaines
variables
Les déterminants de la fixation du prix des immobiliers
résidentiels comprend plusieurs dimensions, notamment les
caractéristiques physiques, celles liées à la localisation
de la maison, les caractéristiques de voisinage ainsi que les
caractéristiques du propriétaire.
Dans cette section, on va mener une étude au moyen des
tableaux croisés permettant de valider et d'expliquer les constats des
analyses des caractéristiques. Ensuite l'étude statistique en
termes d'analyse de corrélation, permet d'identifier les relations qui
existent entre les variables étudiées et constitue ainsi le point
de départ de la démarche de la modélisation dans ce
travail.
Pour mesurer la corrélation entre deux variables
qualitatives, on peut utiliser soit le coefficient de contingence (pour les
variables nominales), soit le coefficient Tau-B de Kendall ou le coefficient de
corrélation de Spearman (pour les variables ordinales), coefficients qui
sont les analogues pour le cas des variables qualitatives du coefficient de
corrélation R de Pearson pour les variables quantitatives. Tous ces
coefficients prennent des valeurs comprises entre -1 et 1 (à l'exception
du coefficient de contingence, qui prend des valeurs entre 0 et 1); un
coefficient avec une valeur absolue proche de 1 indique une corrélation
forte (positive ou négative, en fonction de son signe) entre les deux
variables, et une valeur proche de 0 indique que la corrélation entre
les variables est faible.
Nous traitons dans cette section, au premier point des
caractéristiques physiques et de localisation des ménages et
deuxième les caractéristiques socioprofessionnelles et
démographiques des propriétaires.
60
II.2.1 Caractéristiques physiques et de localisation
des ménages
L'objectif de cette partie est de faire une
présentation descriptive des variables quantitative jugées
pertinentes sur la fixation du prix des maisons d'habitation notamment le prix
au mètre carré de la surface de la parcelle, la somme de
différentes constructions se trouvant sur la parcelle ainsi le prix
moyen d'une pièce comportant la maison dans chacune des communes. Cette
analyse sera soutenue par la mesure de la corrélation R de Pearson entre
la variable étudiée et le prix de la maison.
III.2.1.1 La surface de la parcelle
Le comportement du consommateur est résumé par
le terme « hédonisme » selon lequel les individus cherchent
à maximiser leur satisfaction par la recherche et le choix des attributs
d'utilité qui composent le bien. Le prix d'un bien immobilier est
dérivé du nombre et de la qualité de ces attributs
d'utilité jugés par les individus supposés être
rationnels. Il en découle donc que la connaissance de la surface de la
parcelle d'une propriété immobilière demeurent importante
car continue à régler les dynamiques des marchés
immobiliers.
Tableau 3.4 : Tableau commune-surface de la parcelle - prix de la
maison
|
Moyen
|
Média
|
Ecart-
|
Mini
|
Maxi
|
Prix
|
Prix au
|
N
|
|
ne
|
ne
|
type
|
mum
|
mum
|
moyen
|
mètre
carré
|
|
|
Ibanda
|
230,20
|
221,00
|
121,188
|
56
|
455
|
43092,31
|
187,195
|
65
|
|
Kadutu
|
147,47
|
96,00
|
117,22
|
36
|
640
|
19037,04
|
129,0909
|
81
|
|
Bagira
|
403,13
|
380,00
|
154,04
|
108
|
810
|
16276,60
|
40,37556
|
47
|
|
Total
|
237,59
|
212,00
|
162,66
|
36
|
810
|
26 466,32
|
111,3949
|
193
|
Source : notre confection
Il s'observe du tableau 3.4 que le prix moyen de la parcelle
au mètre carré est plus élevé dans la commune
d'Ibanda soit 187,195 $, suivi de la commune de Kadutu 129,0909 $ et 40,37556
et pourtant les maisons localisées dans la commune de Bagira
présentent une surface moyenne plus élevée suivies par
celle de la commune d'Ibanda.
L'analyse de la corrélation permettra de comprendre le
lien existant entre la surface de la parcelle avec la valeur de la maison.
61
Tableau 3.5 : Corrélation surface de la parcelle
(surfpcl)-prix de la maison (prms)
|
Surfpcl
|
Prms
|
|
Surfpcl
|
Corrélation de
Pearson
|
1
|
,242**
|
|
Sig. (bilatérale)
|
|
,001
|
|
N
|
193
|
193
|
|
Prms
|
Corrélation de
Pearson
|
,242**
|
1
|
|
Sig. (bilatérale)
|
,001
|
|
|
N
|
193
|
193
|
|
**. La corrélation est significative au niveau 0.01
|
Source : notre confection
Ce tableau ci-dessus montre, par la corrélation de
Pearson, qu'il existe une relation positive et significative au seuil de 1% de
24,2% entre la surface de la parcelle et le prix moyen de la maison, ce qui
traduit que l'augmentation de la surface de la parcelle en moyenne est suivie
par l'augmentation du prix de la maison.
III.2.1.2 La somme des surface de différentes
constructions se trouvant sur la parcelle (surfms) La connaissance du
niveau d'occupation de la parcelle est un élément important, car
cela dans une certaine mesure peut permettre de comprendre les
préférences des ménages en termes d'espace libre.
Tableau 3.6 : commune-surface construite-prix par mètre
construit
|
Moyen ne
|
Médi ane
|
Ecart- type
|
surfms/s urfpcl
|
Prix moyen
|
Prix au
mètre carré
|
N
|
|
Ibanda
|
193,41
|
190,00
|
105,923
|
84,40%
|
43092,31
|
222,8029
|
65
|
|
Kadutu
|
120,71
|
75,00
|
97,396
|
81,85%
|
19037,04
|
157,70889
|
81
|
|
Bagira
|
85,70
|
90,00
|
14,863
|
21,25%
|
16276,60
|
189,92
|
47
|
|
Total
|
136,67
|
90,00
|
97,870
|
57,52%
|
26 466,32
|
193,6512
|
193
|
Source : notre confection
Au regard du tableau 3.6 nous remarquons qu'un mètre
carré construit est plus valorisé dans la commune d'Ibanda 228,8$
que dans d'autres, suivie par la commune de Bagira 189,92$ et 157,7$ dans la
commune de Kadutu. Ensuite le rapport
62
surfms/surfpcl fait constater un niveau d'occupation de la
parcelle très élevée dans la commune d'Ibanda
représentant 84,40%, suivi par la commune de Kadutu soit 81,85% et
21,25% dans la commune de Bagira, ce qui fait voir qu'il y a une forte
probabilité de trouver une maison avec un jardin ou une terrasse
à Bagira plutôt que dans les deux autres communes. Ensuite on
s'intéresserait à savoir le lien qui unit la surface construite
et la valeur de la maison.
Tableau 3.7 : Corrélation bilatérale surface
construite (surfms)-prix de la maison (prms)
|
Prms
|
Surfms
|
|
Prms
|
Corrélation de Pearson
|
1
|
,536**
|
|
Sig. (bilatérale)
|
|
,000
|
|
N
|
193
|
193
|
|
Surf ms
|
Corrélation de Pearson
|
,536**
|
1
|
|
Sig. (bilatérale)
|
,000
|
|
|
N
|
193
|
193
|
|
**. La corrélation est significative au niveau 0.01
(bilatéral).
|
Source : notre confection
Au regard du tableau 3.7 nous remarquons on trouve ainsi une
corrélation positive et significative au seuil de 1% entre le prix de la
maison et la somme des surfaces construites sur la parcelle de 53,6% signifiant
qu'une augmentation des constructions sur la parcelle permet d'augmenter le
prix de la maison.
III.2.1.3 Le nombre des pièces
Outre l'évidence que le prix des maisons est une
fonction croissante de la surface de la parcelle ou de la somme de
différentes constructions se trouvant sur la parcelle, il apparait que
les acheteurs ont une préférence très nette pour les
maisons disposant de plusieurs pièces.
63
Tableau 3.8 : commune-nombre des pièces (nbrepc)
|
Commu ne
|
Moyenne
|
Média ne
|
Ecart- type
|
Minimu m
|
Maximu m
|
N
|
|
Ibanda
|
7,38
|
6,00
|
3,490
|
3
|
17
|
65
|
|
Kadutu
|
5,67
|
5,00
|
2,811
|
3
|
14
|
81
|
|
Bagira
|
7,02
|
7,00
|
1,310
|
6
|
12
|
47
|
|
Total
|
6,58
|
6,00
|
2,895
|
3
|
17
|
193
|
Source : notre confection
A travers le tableau 3.8 nous constatons que les maisons de la
commune d'Ibanda ont une moyenne élevée de nombre des
pièces, soit 7,38 pièces suivie de la commune de Bagira ayant
7,02 et 5,67 pour la commune de Kadutu. Dans l'ensemble la moyenne
s'élève à 6,58 et la médiane à 6, une
moyenne supérieure à la médiane montre que plus de 50% des
maisons dans l'ensemble ont un nombre des pièces inférieur
à la moyenne, soit 6,58 pièce.
Tableau 3.9 : Corrélation de Pearson nombre des
pièces (nbrepc)-prix de la maison (prms)
|
Nbrepc
|
prms
|
|
Nbrepc
|
Corrélation de Pearson
|
1
|
,761**
|
|
Sig. (bilatérale)
|
|
,000
|
|
N
|
193
|
193
|
|
Prms
|
Corrélation de Pearson
|
,761**
|
1
|
|
Sig. (bilatérale)
|
,000
|
|
|
N
|
193
|
193
|
|
**. La corrélation est significative au niveau 0.01
(bilatéral).
|
Source : notre confection
L'analyse de la corrélation montre un lien positif
entre le nombre de pièces et le prix de la maison significative au seuil
de 1% suggérant que l'augmentation d'une pièce entraine
l'augmentation du prix. Cela implique qu'à logement de superficie
égale, celui offrant plus de pièces est plus cher et donc plus
demandé. Ce résultat serait la conséquence d'un territoire
qui en moyenne propose un nombre d'individus par ménages relativement
important.
64
III.2.2 Caractéristiques socioprofessionnelles et
démographiques des propriétaires
Certains économistes considèrent que le niveau
de vie, reflété par le profil socioéconomique des
ménages, est déterminant dans leurs choix en matière de
localisation résidentielle et pouvant influencer les niveaux de prix.
Alonso (1964), Mills (1967) et Muth (1969) soutiennent en effet cette
idée et montrent que l'offre et la demande sur le marché
résidentiel expliquent la localisation des ménages aisés
et des ménages pauvres dans des lieux différents, et pour Tiebout
(1956) le jeu d'attraction et de répulsion entre différentes
catégories de ménages structure l'espace résidentiel selon
le niveau de vie.
Les tableaux 1.1 au 1.9 de l'annexe 1 nous montrent qu'en
moyenne la distance par rapport au point central est plus grande pour les
ménages localisés à Bagira suivi par ceux de la commune de
Kadutu, de même pour le cout total de transport qui est en moyenne
très élevé pour la commune de Bagira et influençant
en général, négativement le prix des maisons, ce qui
concorde avec les résultats du modèle urbain néoclassique
proposé par Alonso (1964), puis étendu par Muth (1969) et Mills
(1967, 1972) qui considèrent la ville comme circulaire, mono centrique
et implantée sur une plaine isotrope et dont toute augmentation du prix
unitaire de l'immobilier implique un rapprochement du centre afin de
bénéficier d'une baisse de cout de transport.
L'analyse du statut du propriétaire des ménages
montre une relation négative avec le prix. Ce qui signifie que les
maisons appartenant aux personnes mariées coutent en moyenne plus cher
que celles appartenant aux personnes célibataires.
Le niveau d'étude et la profession montrent qu'il
existe une relation positive entre ces variables avec le prix des maisons ce
qui signifie que le plus souvent, les ménages prennent la
décision d'effectuer leur localisation résidentielle suite
à l'occurrence d'un évènement d'ordre professionnel
(obtention ou perte d'un emploi, changement de lieu de travail, fin
d'activité, etc.), ou d'étude (réussite à un
concours) et de ce fait ces variables influencent de manière positive
les prix des maisons, cela s'inscrit dans la logique que l'option la plus
courante étant de se rapprocher autant que possible de son groupe de
référence.
65
III.3 Résultats des estimations et
interprétation
Dans cette section, nous présentons dans une
première étape les résultats de l'estimation par la
méthode du moindre carré ordinaire, ensuite l'introduction de
l'espace qui nous conduit à la deuxième étape qui consiste
à prendre en compte l'hétérogénéité
spatiale avec l'estimation du modèle par moindre carré ordinaire
corrigé de l'hétéroscédasticité par la
méthode de White et le recours à l'analyse de la variance (ANOVA
spatiale). La troisième étape va consister à prendre en
compte l'autocorrélation spatiale en estimant le modèle
autorégressif spatial(SAR) et le modèle d'erreur spatial (SEM)
par la méthode du maximum de vraisemblance et en quatrième
étape le choix du modèle optimal entre ces quatre modèles
estimé au moyen du test de ratio de vraisemblance. Et la
cinquième étape va porter sur l'interprétation et
discussion des résultats finals.
III.3.1 Les résultats de la méthode de moindre
carré ordinaire
Cette sous-section présente la synthèse des
résultats de l'estimation par la méthode de moindre carré
ordinaire. Ces résultats sont obtenus grâce au logiciel STATA
12.
66
Tableau 3.10 : Résultats de la première estimation
par moindre carré ordinaire (mco1)
|
Variables
|
Coefficients
|
|
|
Commune de Bagira
|
-1654.714
|
(0.810)
|
|
Commune de Kadutu
|
-12241.11
|
(0.000*)
|
|
Surface de la parcelle
|
10.69862
|
(0.351)
|
|
Surface des éléments construits
|
8.507277
|
(0.617)
|
|
Nombre des pièces
|
2146.049
|
(0.000*)
|
|
Etats des murs
|
2182.212
|
(0.459)
|
|
Nombre d'étage
|
12414.64
|
(0.000*)
|
|
Ancienneté de la maison
|
204.0747
|
(0.775)
|
|
Type de la maison
|
2010.463
|
(0.499)
|
|
Présence de plus de deux toilettes
|
4561.473
|
(0.053***)
|
|
Présence de garage
|
2229.419
|
(0.259)
|
|
Distance avec le centre-ville
|
-4.337581
|
(0.007**)
|
|
Distance avec l'axe principal
|
60.18355
|
(0.742)
|
|
Distance avec la route la plus proche
|
-48.03356
|
(0.333)
|
|
Distance avec l'infrastructure de transport
|
-2.632062
|
(0.989)
|
|
Distance avec le centre médical
|
161.6571
|
(0.415)
|
|
Distance avec un établissement
d'enseignement
|
-112.6833
|
(0.753)
|
|
Niveau d'étude
|
3929.772
|
(0.000*)
|
|
Profession
|
3232.878
|
(0.000*)
|
|
Cout total de transport
|
-4.45861
|
(0.066***)
|
|
Constante
|
7328.84
|
(0.243)
|
|
F(20,172)=57,05 Prob>F =0,000 R-Squared=0,8690 Adj.
R-squared=0,8538
|
|
*significative à 1%, **significative à 5%,
***significative à 10%
|
|
Source : notre confection
67
Le test F de Fisher montre que la qualité du
modèle est globalement bonne et le coefficient de détermination
permet de montrer que les variables indépendantes expliquent à
86,9% les prix des maisons d'habitation dans la ville de Bukavu. Cependant,
l'examen des T-student de significativité individuelle des variables
révèlent que seules huit variables sont significatives au seuil
de 1%, 5% ou 10%. Il s'agit de la localisation de la maison si elle est
située à Kadutu(Commkad), le nombre des pièces(Nbrepc), la
presence des 2 toilettes/salles de bain ou plus (Pres2toilslb), la distance
avec le centre-ville (Distcentvil), le niveau d'étude (Nivetd) et la
profession du propriétaire de la maison(Profess) ainsi que le cout total
de transport (Ctttransp).
Ces résultats montrent qu'en majeur partie les
variables pour lesquelles on attendait un signe à priori a
été retrouvé, à l'exception de la variable distance
de la maison avec la route principale (Distaxepripl) et de la distance entre la
maison et un centre médical le plus proche(Distcentmedcl). Ainsi une
maison d'habitation pourrait avoir une valeur supérieure grâce
à sa proximité à l'axe principal ou d'un centre
médical mais les résultats de l'étude montrent que les
nuisances associées à ces variables l'emportent sur les avantages
qu'elles apportent en termes d'accessibilité.
Gallo (2002) montre que sous la condition nécessaire
que les résidus de l'estimation sont des variables aléatoires
indépendantes et identiquement distribuées (la variance est
constante et non corrélée), la méthode des moindres
carrés ordinaires (MCO) permet d'obtenir les coefficients non
biaisés, mais cette régression hédonique globale est
susceptible de masquer des différences importantes dans l'espace.
Pour cette raison il est introduit la notion de l'espace dans
ce modèle initial en faisant recours aux techniques de
l'économétrie spatiale visant précisément à
prendre en compte les deux grandes spécificités des
données géographiques qui caractérisent les immobiliers
résidentiels : l'hétérogénéité
spatiale qui est liée à la différenciation des variables
et des comportements dans l'espace et l'autocorrélation spatiale qui se
réfère à l'absence d'indépendance entre
observations géographiques.
III.3.2 Prise en compte de
l'hétérogénéité spatiale
Cette sous-section porte sur la prise en compte de
l'instabilité dans l'espace des relations économiques
appelée hétérogénéité spatiale. Le
premier point porte sur la
68
détection de
l'hétéroscédasticité et sa prise en compte dans le
modèle initial et le deuxième sur l'analyse de la variance
spatiale.
III.3.2.1 Hétéroscedasticité
L'hétéroscédasticité provient des
variables manquantes ou de toute autre forme de mauvaise
spécification.
Plusieurs méthodes de vérification de
l'homogénéité des résidus sont proposées
dans la littérature. On peut citer entre autres le test de White et le
test de Breusch-Pagan. Le test de Breusch-Pagan est plus spécifique
à la vérification de l'hypothèse
d'homogénéité que celui de White qui est plus
général en détectant des formes d'anomalie des
résidus autres que l'hétéroscédasticité
(non-normalité par exemple).
Tableau 3.11 : Résultat du test de Breusch-Pagan de
l'hétéroscedasticité
|
Chi2(1)
|
Prob>chi2
|
|
13,19
|
0,0003
|
Source : notre confection
Ce tableau montre qu'au seuil de 0,05 l'hypothèse nulle
H0 est rejetée au profit de l'hypothèse alternative H1 permettant
de conclure que le modèle est hétéroscedastique.
Dans ces conditions, White a fourni un estimateur convergent
de la matrice des variances-covariances de l'estimateur des Moindres
Carrés Ordinaires (MCO) en présence
d'hétéroscédasticité de forme inconnue pour que
l'inférence statistique basée sur les MCO soit asymptotiquement
fiable.
69
Tableau 3.12 : Résultats de la deuxième
régression par moindre carré ordinaire corrigé de
l'hétéroscedasticité par la méthode de white.
(mod2)
|
Variables
|
Acronyme
|
Coefficients
|
|
Commune de Bagira
|
Commbag
|
-1654.714 (0.816)
|
|
Commune de Kadutu
|
Commkad
|
-12241.11 (0.000*)
|
|
Surface de la parcelle
|
Surfpcl
|
10.69862 (0.446)
|
|
Surface des éléments construits
|
Surfms
|
8.507277 (0.674)
|
|
Nombre des pièces
|
Nbrepc
|
2146.049 (0.000*)
|
|
Etats des murs
|
Etmurs
|
2182.212 (0.223)
|
|
Nombre d'étage
|
Nbreetg
|
12414.64 (0.000 *)
|
|
Ancienneté de la maison
|
Ancms
|
204.0747 (0.807)
|
|
Type de la maison
|
Typems
|
2010.463 (0.289)
|
|
Présence de plus de deux toilettes
|
Pres2toilslb
|
4561.473 (0.063***)
|
|
Présence de garage
|
Presgarg
|
2229.419 (0.197)
|
|
Distance avec le centre-ville
|
Distcentvil
|
-4.337581 (0.006**)
|
|
Distance avec l'axe principal
|
Distaxepripl
|
60.18355 (0.762)
|
|
Distance avec la route la plus proche
|
Distrtproch
|
-48.03356 (0.206)
|
|
Distance avec l'infrastructure de
|
Distinfrtrppro
|
-2.632062 (0.990)
|
|
transport
|
ch
|
|
|
Distance avec le centre médical
|
Distcentrmdicl
|
161.6571 (0.411)
|
|
Distance avec un établissement
d'enseignement
|
Distetensgmt
|
-112.6833 (0.749)
|
|
Niveau d'étude
|
Nivetd
|
3929.772 (0.003**)
|
|
Profession
|
Profess
|
3232.878 (0.001**)
|
|
Cout total de transport
|
Ctttransp
|
-4.45861 (0.177)
|
|
Constante
|
_cons
|
7328.84 (0.265)
|
|
F(20,172) = 64,66 Prob>F=0,000 R-squared=0,8690 ,
|
|
*significative à 1%, ** à 5% et ***significative
à 10%
|
Source : notre confection
Au regard de ce tableau la qualité du modèle
reste globalement bonne selon le test de Fisher et l'ensemble des variables
expliquent toujours à 86,90% la fixation du prix. En
70
comparaison avec les résultats précèdent
du Tableau 3.12, la variable cout total de transport (Ctttransp) n'est plus
significative au seuil maximal de 10% tout comme la variable
profession(Profess) et niveau d'étude (Nivetd) du propriétaire
qui ne sont plus significatives à 1% mais seulement à partir de
5%. Ce qui implique que la correction du modèle de
l'hétéroscedasticité nous permet de conserver un
modèle avec sept variables significatives au seuil de 1%, 5% ou 10%. Il
s'agit de la localisation de la maison si elle est située à
Kadutu(Commkad), le nombre des pièces(Nbrepc), la presence des 2
toilettes/salles de bain ou plus (Pres2toilslb), la distance avec le
centre-ville (Distcentvil), le niveau d'étude (Nivetd) ainsi que la
profession du propriétaire de la maison(Profess).
Dans le cas de l'étude immobilière, il est
possible que l'impact spatial ne soit pas homogène. Can (1990) pose la
question : « la valeur des caractéristiques des biens immobiliers
varie-t-elle selon la localisation du bien ? ». On s'intéresse
alors à savoir la variabilité spatiale de la moyenne dans chaque
étendue.
III.3.2.2 ANOVA Spatiale
Ce point présente la réponse à la
question que l'on peut se poser cherchant à savoir dans quelle mesure la
moyenne des prix des maisons d'habitation varie entre les trois communes.
Il ressort du tableau 2.1 de l'annexe 2 que la moyenne totale
est de 26 466,32 $ avec un écart-type de 28 180,040 et le prix minimum
est de 4 000$. La commune d'Ibanda présente une moyenne des prix la plus
élevée de 43 092,31$ contre 19 037,04$ pour la commune de kadutu
et 16 276,60 $ dans la commune de Bagira.
Ces résultats peuvent également être
visualisés sous forme de graphiques afin de comparer les moyennes des
prix des maisons selon les communes et selon les quartiers.
71
Graphique 3.1 : Diagramme des moyennes des prix selon les
communes
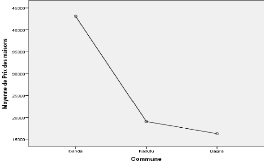
Ce graphique montre que la moyenne des prix est plus
élevée dans la commune d'Ibanda, suivie de la commune de
Kadutu
Graphique 3.2 : Diagramme des moyennes des prix selon les
quartiers
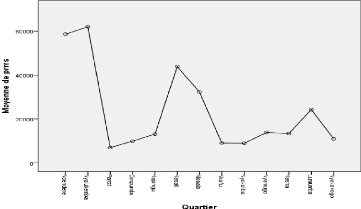
Ce graphique montre que la moyenne des prix des maisons est
très élevées dans le quartier Nyalukemba suivi
successivement du quartier Ndendere, Kasali, Mosala, Lumumba, Nyamugo, Kasha,
Kajangu, Nyakavogo, Nkafu, Nyakaliba , Cimpunda.
Dans le but de pouvoir traiter ces différences de
moyennes des prix des communes afin de savoir si au moins une des moyennes
diffère significativement des autres, nous faisons recours à
l'ANOVA spatiale qui sert à tester l'hypothèse
d'égalité des moyennes des prix dans les trois communes. Pour
s'assurer de sa faisabilité les deux conditions principales,
l'hypothèse d'homogénéité de la variance (Test de
Levene
72
=0,000<0,005 du tableau 3.13) et l'hypothèse de
normalité (Kolmogorov et Shapiro = 0,000<0,05 du tableau 3.14) ne
sont pas vérifiées d'où les conclusions de l'ANOVA ne
seront pas valides pour ce travail à cause de
hétérogénéité des variances ou d'une forte
asymétrie des prix dans les trois communes.
Tableau 3.13 : Test de Levene d'homogénéité
de la variance
|
Test d'homogénéité de la variance
|
|
Statistique de
Levene
|
ddl1
|
ddl2
|
Significatio n
|
|
Prix des
maisons
|
Basé sur la moyenne
|
26,734
|
2
|
190
|
,000
|
|
Basé sur la médiane
|
18,178
|
2
|
190
|
,000
|
|
Basé sur la médiane et avec ddl ajusté
|
18,178
|
2
|
139,8 97
|
,000
|
|
Basé sur la moyenne tronquée
|
23,619
|
2
|
190
|
,000
|
Source : notre confection
Le test de Levene rejette de manière très
significative l'hypothèse l'homogénéité des
variances et ne permet donc pas de valider les résultats de l'analyse de
la variance. Tableau 3.14 : Tests de normalité
|
Commune
|
Kolmogorov-Smirnov (K-S)
|
Shapiro-Wilk (S-W)
|
|
Statistique
|
Ddl
|
Signification
|
Statistique
|
Ddl
|
Signification
|
|
Ibanda
|
,172
|
65
|
,000
|
,875
|
65
|
,000
|
|
Kadutu
|
,245
|
81
|
,000
|
,683
|
81
|
,000
|
|
Bagira
|
,195
|
47
|
,000
|
,855
|
47
|
,000
|
Source : notre confection
De ce tableau on observe que l'hypothèse de
normalité des résidus est rejetée. Les valeurs des maisons
ne sont donc pas normalement distribuées dans les trois communes de la
ville de Bukavu.
Carricano et Poujol (2008) montre que si les données ne
sont pas appropriées à une ANOVA
(hétérogénéité des variances ou
données fortement asymétriques), il convient d'utiliser des tests
non paramétriques qui ne supposent ni homogénéité
de la variance,
73
ni une distribution normale comme le test de Kruskall-Wallis, qui
est l'équivalent non paramétrique de l'ANOVA.
Tableau 3.15 : Résultat du test de
Kruskal-Wallis18
|
Prix des maisons
|
|
Khi-deux
|
19,267
|
|
Ddl
|
2
|
|
Signification asymptotique
|
,000
|
Source : notre confection
Le test de Kruskal-Wallis rejette de manière
significative l'égalité des prix dans les trois communes. Les
prix des maisons diffèrent donc significativement selon la commune de
localisation ou il existe donc au moins une moyenne des prix qui diffère
significativement des autres.
Cette conclusion ne faisant qu'indiquer que les prix
différent globalement selon la localisation par commune ne
précise donc pas laquelle diffère significativement des autres.
D'où nous allons poursuivre l'étude afin d'isoler les
différences entre des sous-ensembles afin de voir celle qui
diffère des autres. Etant donné, la non
homogénéité des variances et de la normalité, le
test de Games-Howell de comparaison multiple est appliqué afin de
déterminer les communes qui sont homogène pour les prix des
maisons. Il porte sur la comparaison de toutes les moyennes prises deux
à deux.
18 Le tableau relatif au calcul des rangs se trouve
à l'annexe 2-tableau2.2
74
Tableau 3.16 : Test de Games-Howell de comparaisons multiples
|
(J) Commune de
localisation
|
Différence de
moyennes (I-J)
|
Signification
|
Intervalle de confiance à 95%
|
|
Borne inférieure
|
Borne
supérieure
|
|
Ibanda
|
Kadutu
|
24055,271*
|
,000
|
11845,49
|
36265,05
|
|
Bagira
|
26815,712*
|
,000
|
15342,00
|
38289,42
|
|
Kadutu
|
Ibanda
|
-24055,271*
|
,000
|
-36265,05
|
-11845,49
|
|
Bagira
|
2760,441
|
,548
|
-3486,78
|
9007,66
|
|
Bagira
|
Ibanda
|
-26815,712*
|
,000
|
-38289,42
|
-15342,00
|
|
Kadutu
|
-2760,441
|
,548
|
-9007,66
|
3486,78
|
|
*la différence moyenne est significative au niveau de
0,05
|
Source : notre confection
Ce tableau permet de détecter des différences
significatives entre d'une part des prix des maisons de la commune d'Ibanda et
d'autre part avec ceux de la commune de Bagira et de Kadutu. Mais les prix des
maisons de la commune de Kadutu ne diffèrent pas significativement en
moyenne de ceux de la commune de Bagira.
En effet, toutes choses étant égales par
ailleurs, à une maison présentant des caractéristiques
physiques identiques, une maison située dans la commune d'Ibanda serait
vendue en moyenne plus chère que celle située à Bagira ou
à Kadutu. Cette survalorisation du prix dans cette commune serait la
conséquence de la dotation des caractéristiques externes
demandées par les ménages en grand nombre, notamment la
qualité de l'infrastructure (transports, institutions, réseau de
commerce et de services), la proximité des lieux stratégiques, le
cadre paysager, le niveau de richesse des habitants, l'intensité de la
desserte en transports en commun, la sécurité, et même la
présence de service public.
Pour déterminer la valeur de son bien, le
propriétaire peut se renseigner, soit auprès de l'expert
immobilier qui donne une estimation du prix basée sur la valeur des
transactions sur les biens voisins, soit directement auprès des
propriétaires des biens voisins. Il existe donc un processus
d'interaction entre les valeurs des biens. Lorsque les prix immobiliers sont
spatialement corrélés, une hausse de la valeur d'un bien se
diffuse sur les biens voisins en passant par le processus d'évaluation
(effet de
75
diffusion). Cela signifie qu'une observation a une influence
très forte sur son proche voisin et que cette influence se diffuse dans
le voisinage lointain. De plus des biens voisins ont souvent été
construits à la même période, ils ont fréquemment la
même structure, le même style et la même taille. Par
ailleurs, ces biens doivent faire face aux mêmes variables
d'externalité, positive ou négative, qui affectent le prix. Il
peut s'agir de la qualité de l'environnement, le projet de construction
de nouvelles routes, le problème d'inondation dans certains quartiers,
les nuisances sonores, la vue, etc. Ces deux phénomènes, l'effet
de la diffusion ou celui des externalités, montrent qu'il existe une
corrélation spatiale qui influence les prix et en présence de
corrélation spatiale, le modèle hédonique classique
utilisant les moindres carrées ordinaires fournit des estimations
biaisées et non efficientes. Cette particularité des
données immobilières nécessite alors de prendre en compte
la dépendance spatiale dans le modèle d'évaluation des
biens immobiliers.
III.3.3 Prise en compte de l'autocorrélation
spatiale
L'autocorrélation spatiale est définie comme la
corrélation, positive ou négative, d'une variable avec
elle-même provenant de la disposition géographique des
données. Cette sous-section porte en première étape sur le
diagnostic de l'existence de la dépendance spatiale dans le
modèle hédoniste traditionnel des prix, en deuxième
étape sur l'estimation du modèle autorégressif spatial
(SAR ou LAG) pour lequel nous supposons que la valeur d'un bien immobilier
dépend de la valeur des autres biens voisins traduit par l'effet de
diffusion , et enfin la troisième étape sur l'estimation de
l'erreur spatiale (SEM) pour la prise en compte l'influence des
externalités dans le modèle traditionnel.
III.3.3.1 Tests de l'autocorrélation spatiale dans
la régression par moindre carré ordinaire L'indice de Moran
est à cet effet un indicateur principal utilisé en
économétrie spatiale mais exige a priori de déterminer la
structure de l'autocorrélation spatiale. Dans le présent travail,
la matrice de voisinage avec la condition de distance de séparation
maximale de 400 mètres sont choisis afin que chaque observation
contienne au moins un voisin et l'inverse de la distance comme
pondération. Ce choix est justifié par Srikhum (2012) qui montre
que l'inverse de la distance permet de mesurer l'accessibilité qui est
une des caractéristiques principales en évaluation
immobilière.
76
Tableau 3.17 : Diagnostic de la dépendance spatiale
|
Tests
|
Statistic
|
Ddl
|
p-value
|
|
Indice de Moran
|
3,615
|
1
|
0,000
|
|
Modèle SAR ou LAG
|
|
Multiplicateur de Lagrange ( LAGLM )
|
20,443
|
1
|
0,000
|
|
Multiplicateur robuste de Lagrange ( LAGRLM )
|
14,245
|
1
|
0,000
|
|
Modèle SEM
|
|
Multiplicateur de Lagrange ( ERRLM )
|
6,304
|
1
|
0,012
|
|
Multiplicateur robuste de Lagrange ( ERRRLM )
|
0,106
|
1
|
0,745
|
De ce tableau ci-haut, il s'observe que la statistique de
l'indice de Moran (Moran's I) est de 3,615 avec un P-value de 0,000 qui conduit
au rejet de l'hypothèse nulle d'absence de dépendance spatiale.
Le modèle est donc mal spécifié et il y a omission de
l'autocorrélation spatiale.
Comme tous les deux tests du multiplicateur de Lagrange (LAGLM
et ERRLM) sont significatifs et que le premier test (LAGLM ) est plus
significatif que le test de l'autocorrélation des erreurs (ERRLM
)19, Anselin et Rey (1991) et Florax et Folmer (1992) cités
par Gallo (2002) propose de choisir le modèle autorégressif (SAR)
comme le meilleur modèle. Ces tests indiquent donc la
prédominance de l'effet de la diffusion sur la valeur des maisons que
celui des externalités. Pour confirmer ce résultat, les deux
modèles économétriques spatiaux sont estimés et
seront vérifiés par le test du rapport de vraisemblance pour
lequel le meilleur modèle sera celui qui minimise le critère
d'information d'Akaïke.
19 Pour lequel au seuil 0,001 il devient impossible de
rejeter l'hypothèse nulle.
77
Tableau 3.18 : Comparaison des résultats de Moindre
ordinaire corrigé de l'hétéroscédasticité
avec celui du modèle SAR et SEM
|
Modèles
|
Modèle simple
|
Modèle SAR
|
Modèle SEM
|
|
|
Estimation
|
MCO robustes)
|
(écart-types
|
MV
|
MV
|
|
|
Commbag
|
-1654.714
|
(0.816)
|
-4449,363
|
(0,473)
|
-2442,031
|
(0,744
|
|
Commkad
|
-12241.11
|
(0.000*)
|
-8578,381
|
(0.000*)
|
-12458,13
|
(0,000*
|
|
Surfpcl
|
10.69862
|
(0.446)
|
11,9539
|
(0,244)
|
7,919039
|
(0,448
|
|
Surfms
|
8.507277
|
(0.674)
|
-4,663611
|
(0,764)
|
8,468029
|
(0,587
|
|
Nbrepc
|
2146.049
|
(0.000*)
|
1933,98
|
(0.000*)
|
2042,781
|
(0,000*
|
|
Etmurs
|
2182.212
|
(0.223)
|
484,4737
|
(0,856)
|
1768,914
|
(0,518
|
|
Nbreetg
|
12414.64
|
(0.000 *)
|
13039
|
(0.000*)
|
12281,55
|
(0,000*
|
|
Ancms
|
204.0747
|
(0.807)
|
-554,0863
|
(0,402)
|
438,7111
|
(0,531
|
|
Typems
|
2010.463
|
(0.289)
|
2084,561
|
(0,434)
|
1776,533
|
(0,510
|
|
Pres2toilslb
|
4561.473
|
(0.063***)
|
4330,604
|
(0,039**)
|
3822,411
|
(0,078***
|
|
Presgarg
|
2229.419
|
(0.197)
|
2777,891
|
(0,117)
|
1993,099
|
(0,262
|
|
Distcentvil
|
-4.337581
|
(0.006**)
|
-2,929442
|
(0,046*)
|
-4,370257
|
(0,020**
|
|
Distaxepripl
|
60.18355
|
(0.762)
|
-89,82816
|
(0,591)
|
-28,60059
|
(0,863
|
|
Distrtproch
|
-48.03356
|
(0.206)
|
-65,50055
|
(0,142)
|
-55,83225
|
(0,231
|
|
Distinfrtrpproch
|
-2.632062
|
(0.990)
|
145,5518
|
(0,389)
|
76,3005
|
(0,45
|
|
Distcentrmdicl
|
161.6571
|
(0.411)
|
146,803
|
(0,408)
|
195,2044
|
(0,310
|
|
Distetensgmt
|
-112.6833
|
(0.749)
|
27,94557
|
(0,931)
|
-112,8768
|
(0,732
|
|
Nivetd
|
3929.772
|
(0.003**)
|
3527,593
|
(0,000*)
|
3468,528
|
(0,000*
|
|
Profess
|
3232.878
|
(0.001**)
|
3126,715
|
(0,000*)
|
3357,859
|
(0,000*
|
|
Ctttransp
|
-4.45861
|
(0.177)
|
-3,10503
|
(0,155)
|
-3,351624
|
(0,173
|
|
_cons
|
7328.84
|
(0.265)
|
62,706222
|
(0,991)
|
7979,884
|
(0,215
|
|
Rhô (??)
|
|
|
0,2182205
|
0,000*
|
|
|
|
Lambda (À)
|
|
|
|
|
0,2972573
|
0,005***
|
78
|
Likelihood ratio test of rho
|
|
17.996
|
0.000*
|
|
|
|
Likelihood ratio test of lambda
|
|
|
|
6.774
|
0.009**
|
Source : notre confection
De ce tableau il s'observe que pour tous ces trois
modèles sept variables sont significatives au seuil maximum de 10%. Il
s'agit de la localisation de la maison dans la commune de Kadutu(Commkad), du
nombre des pièces(Nbrepc), nombre d'étage(Nbreetg), la
présence de plus de 2 toilettes/salles de bain (Pres2toilslb), la
distance par rapport au centre-ville (Distcentvil) ainsi que le niveau
d'étude(Nivetd) et la profession du propriétaire de la maison
(Profess).
Pour le modèle SAR tous les signes à priori
attendus ont été retrouvés à l'exception de la
sommes des surfaces occupées sur la parcelle (Surfms),
l'ancienneté de la maison(Ancms), et de la distance par rapport à
l'accès à l'infrastructure de transport en commun la plus
proche(Distinfrtrpproch). Cela signifierait que l'augmentation du niveau
d'occupation de la parcelle entraine la diminution de la valeur de la maison
pour la variable Surfms, ensuite pour l'ancienneté de la maison (Ancms)
les maisons plus neuves valent moins que les maisons anciennes et enfin pour la
variable de la proximité par rapport à un accès à
l'infrastructure de transport en commun la plus proche (Distinfrtrpproch) avec
un signe positif signifie que l'augmentation de la distance avec la maison
influence positivement la valeur des immobiliers. Ce qui implique que les
nuisances l'emportent sur les avantages procurés par cette
proximité.
Généralement, l'autocorrélation spatiale
peut être négative ou positive, les résultats de
l'estimation du modèle SAR font apparaitre une autocorrélation
spatiale positive et significative au seuil de 1% de 21,82%(Rhô=0,2182).
Lorsqu'il y a autocorrélation spatiale pour une variable, cela signifie
qu'il y a une relation fonctionnelle entre ce qui se passe en un point de
l'espace et ce qui se passe ailleurs. Tobler (1979) avait souligné en
suggérant la première loi de la géographie: «
Everything is related to everything else, but closer things more so »
cela signifie que dans un voisinage de 400 mètres
considérés
79
dans ce travail des lieux proches se ressemblent davantage que
les lieux éloignés20. Cela traduit qu'une observation
a une influence très forte sur son proche voisin et que cette influence
se diffuse dans le voisinage lointain signifiant qu'une hausse du prix d'un
bien a une influence sur les prix de biens voisins. Par exemple, le passage
pour un immeuble d'un étage à cinq étages a une influence
directe positive sur le prix de vente de cet immeuble et grâce à
l'effet de diffusion, cette hausse du prix a une influence positive indirecte
sur les prix des biens voisins en passant par le processus d'évaluation
des biens. Ainsi, l'impact de ce prix se diffuse mais son importance
dépend négativement de la distance avec d'autres biens.
Et pour le modèle SEM seules les variables distances
par rapport à un établissement d'enseignement le plus
proche(Distetensgmt) et la variable de la distance par rapport à
l'accès à l'infrastructure de transport en commun la plus proche
(Distinfrtrpproch) n'ont pas donné les signes attendus. Nos
investigations montrent une autocorrélation spatiale des erreurs
positive traduisant un impact positif des externalités sur la valeur des
maisons 29,72%(Lambda=0,2972) mais non significative au seuil de 5% mais
significative à 10%.
Ainsi pour vérifier la conclusion de Anselin et Rey
(1991) et Florax et Folmer (1992) cités par Gallo (2002) basée
sur les tests du multiplicateur de Lagrange pour lequel le meilleur
modèle serait le modèle SAR, il est procédé au test
moyen du test du ratio de vraisemblance pour lequel le meilleur modèle
devrait être celui qui minimise le critère d'information
Akaïke(AIC).
III.3.3.3 Choix du Modèle optimal : le test du rapport
de vraisemblance
Si plusieurs modèles restent encore en
compétition, Gallo (2002) propose de faire le choix entre modèles
avec les critères traditionnels tels que les critères
d'information d'Akaïke(AIC) en passant par le test du rapport de
vraisemblance.
20 L'augmentation de la distance de voisinage entraine
l'augmentation du niveau de la corrélation.
80
Tableau 3.19 : Résultat du test du rapport de
vraisemblance
|
Modèle
|
Observation
|
Ll(null)
|
Ll
|
Ddl
|
AIC
|
BIC
|
|
MCO (Mod1)
|
193
|
-2250,903
|
-2054,756
|
21
|
4151,51
|
4220,028
|
|
MCO (robuste) (Mod2)
|
193
|
-2250,903
|
-2054,756
|
21
|
4151,21
|
4220,028
|
|
SAR (Mod3)
|
193
|
-2054,756
|
-2054,758
|
23
|
4137,516
|
4212,558
|
|
SEM (Mod4)
|
193
|
-2054,756
|
-2051,369
|
23
|
4148,738
|
4223,78
|
|
Likelihood-ratio test LR chi2(5) = 24.77 Prob > chi2 =
0.0002
|
Source : notre confection
Ces résultats montrent que le modèle SAR est le
modèle qui minimise le critère d'information d'Akaïke (AIC)
suivi du modèle SEM. Ce résultat converge avec celui d'Anselin et
Rey (1991) et Florax et Folmer (1992) cités par Gallo (2002)
basées sur le test du multiplicateur de Lagrange pour lequel le
modèle SAR est le meilleur21. Ce qui montre que l'effet de la
diffusion (spillover effect) l'emporte sur l'effet des externalités sur
la valeur des maisons dans la ville de Bukavu. Cela signifie que la valeur
d'une maison a une influence très forte sur son proche voisin et que
cette influence se diffuse dans le voisinage lointain. La moyenne
pondérée des prix de vente des biens voisins est utilisée
comme prix de référence pour déterminer la valeur de son
bien. Il existe donc un processus d'interaction entre les valeurs des biens.
L'hypothèse du modèle classique de la
régression multiple pour laquelle les variables explicatives du
modèle soient indépendantes les unes des autres et que dans le
cas contraire, il y a présence de multicolinéarité. Le
tableau 3.1 de l'annexe 3 portant le test VIF réalisé
après la régression par moindre carré ordinaire permet de
montrer qu'il existe une multicolinéarité forte(
c'est-à-dire VIF de la variable supérieur 10) pour certaines
variables, il s'agit de la distance avec l'infrastructure de transport la
plus
21 Ce résultat reste valable sous deux
conditions suivantes : la première est basée sur « la
matrice de voisinage » permettant de déterminer l'ensemble des
voisins et la deuxième sur « la matrice de poids » pour
déterminer les poids associés à chaque voisin où on
peut donner des poids identiques pour le voisinage ou accorder des poids
important aux voisins proches et des poids faibles aux voisins
éloignés. Pour la première condition l'on a utilisé
« la condition de distance » de séparation maximale de 400
mètres tout en sachant qu'on pourrait aussi utiliser « la condition
de contiguïté » pour déterminer l'ensemble des
voisinages ou d'augmenter la séparation. Et pour la deuxième
« la matrice de poids standardisée » où on pourrait
aussi utiliser « la matrice des poids binaires » ou « la matrice
de poids binaire générale ». Ces résultats seraient
différents si l'on modifiait l'une ou l'autre de ces deux conditions.
81
proche (Distinfrtransprch) avec un VIF de 208,96 ; de la
distance avec l'axe principale la plus proche avec un VIF de 203.76 ainsi que
de la localisation de la maison dans la commune de Bagira (Commbag) avec un VIF
de 14,50.
La suppression de la variable Distinfrtransprch et Commbag a
permis d'améliorer le modèle en obtenant un premier modèle
optimal ne souffrant plus du problème de multicolinéarité,
avec aucune variable avec un VIF = 10 (cfr tableau 3.2 de l'annexe 3) et pour
lequel le test du rapport de vraisemblance montre une diminution du
critère d'information d'Akaike pour tous les modèles et concluant
toujours le modèle SAR étant le meilleur parce qu'il minimise le
critère d'information d'Akaïke (AIC) de tous suivi du modèle
SEM(cfr tableau 3.3 de l'annexe 3).
Pour raisons d'amélioration du modèle, nous
avons fait une dernière estimation avec les variables significatives
corrigés de la multicolinéarité de ces quatre
différents modèle (MCO, MCO robuste, SAR et SEM) et avons obtenu
les résultats ci-après :
Tableau 3.20 : Modèles optimaux
|
Modèles
|
Modèle simple
|
Modèle SAR
|
Modèle SEM
|
VIF
|
|
Estimation
|
MCO robustes
|
MV
|
MV
|
|
Commkad
|
-13230.36 0.000*
|
-9146.249 0.000*
|
-13402.02 0,000*
|
1.64
|
|
Nbrepc
|
2811.991 0.000*
|
2301.876 0.000*
|
2588.56 0,000*
|
2.15
|
|
Nbreetag
|
11108.01 0.000*
|
12065.43 0.000*
|
11192.12 0,000*
|
1.76
|
|
Pres2toilslb
|
6018.483 0.07***
|
4855.249 0,019**
|
4921.392 0,022***
|
1.40
|
|
Distcentvil
|
-4.263679 0.000*
|
-3.030583 0,001*
|
-4.844167 0,000**
|
3.62
|
|
Distaxepripl
|
32.89461 0.000*
|
25.72392 0,059***
|
23.16502 0,187
|
1.32
|
|
Nivetd
|
4306.285 0.000*
|
3382.211 0,000*
|
3626.046 0,000*
|
1.22
|
|
Profess
|
4137.927 0.000*
|
3693.194 0,000*
|
4027.183 0,000*
|
1.38
|
|
Ctttransp
|
-4.948924 0.056***
|
-3.650898 0,055***
|
-3.592527 0,116
|
3.79
|
|
_cons
|
9400.736 0.024**
|
2464.794 0,540
|
11626.34 0,215
|
|
|
AIC
|
4140.864
|
4125.412
|
4136.734
|
|
|
Rhô (??)
|
|
0,20551 0,000*
|
|
|
82
|
Lambda (À)
|
|
|
0, 3175548
|
0,002*
|
|
Le modèle SAR étant donc le meilleur en termes de
critère d'information, Il apparaît donc bien que ce modèle
soit la spécification la plus adéquate, il fera alors l'objet
d'interprétation.
III.3.4 Interprétation et discussion des
résultats
III.3.4.1 Impact des caractéristiques physiques sur le
prix de la maison
Le modèle nous indique aussi qu'à toutes choses
égales par ailleurs, l'accroissement du nombre des pièces
(Nbrepc) augmente le prix de la maison de manière significative. Le
passage d'une pièce à deux pièces augmente le prix en
moyenne de 2 301,876$. Ensuite, L'augmentation d'un niveau d'étage
(Nbreetg) augmente significativement le prix de la maison de 12 065,43$ en
moyenne.
Les résultats montrent aussi qu'une salle de bain ou
toilette supplémentaire (Pres2toilslb) accroit la valeur de la maison de
manière significative d'une valeur de 4 855,249$ au seuil de 5%.
III.3.4.2 Rôles de la localisation sur la valeur de la
maison
L'impact global de la localisation sur la valeur de la maison
est bien entendu lié à tout ce que sa proximité peut
offrir.
La commune de référence dans cette recherche est
la commune d'Ibanda, les coefficients négatifs associés à
la variable pour la localisation d'une maison dans la commune de
Kadutu(Commkad) indiquent que cette commune valorise plus faiblement les
maisons d'habitation que la commune d'Ibanda.
La distance moyenne par rapport à la poste(Distcentcil)
est très élevée pour les maisons situées à
Bagira, suivie par celle de Kadutu et Ibanda, cette distance influence
significativement la valeur des maisons de 3,92$ de manière
négative.
Ce résultat concorde avec les hypothèses du
modèle urbain néoclassique proposé par Alonso (1964),
Mills (1967) et Muth (1969), postulant que la structure d'équilibre
d'utilisation du sol est déterminée par l'arbitrage
effectué par les ménages entre la rente foncière et
l'accessibilité au centre de la ville, lieu de concentration des
activité. Le succès de ce modèle monocentrique vient du
fait qu'il parvient, à partir de développements relativement
simples, à rendre compte de certaines régularités
83
concernant la répartition spatiale des populations, des
activités économiques et des valeurs foncières.
La distance avec l'axe principale (Distaxepripl) influence
négativement la valeur des maisons de manière significative. Cela
implique que les inconvénients associés à sa
proximité l'emportent sur ses avantages, d'où l'augmentation de
cette distance influence positivement la valeur des maisons. Ce qui ne permet
pas de vérifier notre hypothèse.
IIII.3.4.3 Impact des caractéristiques de
voisinages sur le prix de la maison
L'accroissement de la distance avec un centre
médical(Distcentrmdicl) et celle d'un établissement
d'enseignement le plus proche(Distetensgmt) n'ont pas été retenu
dans le modèle optimal car elles n'étaient pas significative.
Ainsi, la présence de ces aménités qui ne sont pas
toujours localisées dans le centre-ville et recherchées par les
ménages telles que les hôpitaux ou les universités
pourraient permettre de contrebalancer la force d'attraction du centre-ville
(Straszheim, 1987) et d'expliquer, dans une certaine mesure, le
phénomène d'étalement urbain, mais cette hypothèse
n'a pas été vérifiée. Ce qui permettrait
d'expliquer que la délocalisation des deux éléments dans
les périphéries ne permettrait d'atteindre les objectifs
d'étalement urbain.
IIII.3.4.4 Impact des caractéristiques
socioprofessionnelles et démographiques sur la valeur des
maisons
Enfin, les analyses portant sur la localisation
résidentielle des différentes catégories
socio-professionnelles et démographiques permettent à analyser la
ségrégation résidentielle dans la ville de Bukavu en lien
avec les déterminants des valeurs des maisons d'habitation et du choix
résidentiel des ménages. Le niveau d'étude (Nivetd) et la
profession (Profess) d'un côté permettant d'évaluer les
préférences en termes d'environnement social pour lesquelles le
modèle d'offre de biens publics locaux de Tiebout(1956), ou les
modèles avec effets de voisinage (Durlauf, 2004) par le cout total de
transport de l'autre côté permettent de mesurer les poids relatifs
des préférences pour un environnement périurbain (distance
au centre) du modèle urbain monocentrique d'Alonso (1964), puis (1969)
et Mills (1967, 1972)
84
Les résultats montrent que le niveau
d'étude(Nivetd) et la profession (Profess) du propriétaire des
ménages influencent significativement la valeur de la maison, d'un
montant respectif de 3 382,211$ et de 3 693,194 de manière positive, ce
qui vérifie nos hypothèses basées sur ces variables. Cela
implique que la composition en termes d'environnement social influence la
valeur de la maison. De ce point de vue, il s'observe donc que l'étude
des déterminants de la fixation du prix des maisons d'habitation peut
être conçue comme une analyse des transformations sociales,
démographiques, politiques, économiques qui affectent le milieu
urbain. Cela se vérifie de part plusieurs études
antérieures. On peut évoquer dans ce sens les apports d'Alonso
(1964), Mills (1967) et Muth (1969), qui soutiennent l'idée que l'offre
et la demande sur le marché immobilier expliquent la localisation des
ménages aisés et des ménages pauvres dans des lieux
différents, ou ceux de Tiebout (1956), selon lequel le jeu d'attraction
et de répulsion entre différentes catégories de
ménages structure l'espace résidentiel selon le niveau de vie,
comme Zenou (2002) qui conclut que la composition sociale d'un quartier peut
conditionner d'autres décisions prises par les ménages en terme
du choix de localisation à travers les relations de voisinage qui
peuvent avoir une influence sur la formation du capital humain en mesure
même d'influencer sur les chances que les habitants accèdent
à l'emploi.
Ensuite les résultats portant sur le cout total de
transport aller-retour pouvant supporter le chef du ménage (Ctttansp)
vérifie notre hypothèse émise ainsi que le modèle
de Wingo(1961) pour lequel dans son approche donne un rôle central aux
transports dans le fonctionnement urbain, en considérant que le
marché foncier est conditionné par les transports urbains. Dans
son modèle il prend en compte d'un coût
généralisé de transport (comme dans ce présent
travail) au lieu d'un coût de transport fonction linéaire de la
distance au centre. Ce coût généralisé
reflète l'ensemble des dépenses monétaires de transport et
la valeur attribuée au temps de trajet. Il arrive à la conclusion
que l'amélioration du réseau de transport entraîne une
diminution des valeurs foncières et des densités
résidentielles et une extension de la ville.
85
III.4 Implication des résultats
Cette section a pour objet d'identifier les implications
induites de cette étude. Les résultats de cette analyse ont fait
ressortir les facteurs pertinents des déterminants de la fixation du
prix des maisons d'habitation dans la ville de Bukavu. De ces résultats,
les implications suivantes peuvent être tirées par les
décideurs publics en vue d'entrainer une baisse du prix des immobiliers
résidentiels et pouvoir bien mener une politique d'étalement
urbain :
- Dans une logique alternative, dans laquelle les
complémentarités entre espaces urbains et ruraux soient
utilisées au maximum, la délocalisation des activités ou
des certains services publics (le parquet, la prison centrale,...) doit
permettre de contrebalancer la force d'attraction du centre-ville et dans une
certaine mesure, d'atteindre les objectifs actuels d'étalement
urbain.
- Diminuer le temps dédié aux
déplacements quotidiens de la population en assurant une
cohérence entre la répartition de l'habitat et des
emplois/activités sur le territoire en développant le
réseau de transport public dans tous les territoires.
- Renforcer les infrastructures de transports et favoriser
l'urbanisation autour des noeuds de transport public : stations de transport
collectif en site propre, parking public, gares si possible... ;
- Lutter contre la ségrégation sociale dans le
territoire à travers des dessertes plus importantes dans les quartiers
périurbains en créant des centres commerciaux, des hôpitaux
ou des écoles dans ces zones.
- limiter aussi possible l'étalement urbain et
favoriser les modes d'urbanisation moins consommateurs d'espace en
protégeant certaines zones, en limitant l'espace à occuper par
une seule personne, en proposant des modèles des maisons à
construire dans une zone.
86
III.5 Limites et perspectives de recherche
Bien que cette recherche ait fait des avancées dans la
compréhension des facteurs déterminants de la fixation du prix
des maisons d'habitation dans la ville de Bukavu, elle rencontre cependant des
limites. Tout d'abord, la petitesse de la taille de l'échantillon suite
à une marge d'erreur et un seuil de signification égale à
5%. Ensuite la répartition de l'échantillon en commune et en
quartier masque certaines informations. De ce fait une autre approche serait
d'élargir la taille de l'échantillon et de le repartir en
pôle urbain et périurbain en approfondissant la répartition
en commune, quartier et avenu.
Ensuite, introduire dans un modèle hédonique une
variable de centre-ville consiste de ce fait à agréger en un seul
« bouquet » l'ensemble des éléments qui composent le
centre urbain et donc à considérer que ces derniers se localisent
en un même point géographique, alors que dans la
réalité ces éléments se dispersent sur une zone
géographique centrale plus ou moins étendue selon la ville
considérée. Cependant, une étude permettant de
désagréger la variable de centre-ville entre ses
éléments composants, et d'en calculer des distances par rapport
à l'immeuble permettrait d'améliorer cette étude. Cette
limité a été observée aussi lors de l'introduction
dans le modèle économétrique d'un ensemble d'indicateurs
caractérisant l'environnement socio-économique du logement.
Nombre de ces caractéristiques sociodémographiques étant
corrélées, la plupart n'apparaissent pas dans le modèle
économétrique, sans pour autant que cela signifie qu'elles ne
jouent pas sur les choix résidentiels des ménages. Ainsi une
étude incluant un bon nombre des variables sociodémographique
permettraient d'améliorer le travail.
Au niveau des modèles spatiaux la condition de poids
standardisée, utilisée dans ce travail, est la plus simple
à appliquer mais elle présente un biais car dans la
régression, cette condition accorde une importance plus grande aux
observations ayant peu de voisins. D'où nous suggérons une
recherche future utilisant différentes matrices de poids (Matrice de
poids binaire, Matrice de poids binaire générale) et comparer
ainsi les différents résultats.
87
CONCLUSION
Dans ce travail intitulé déterminants de la
fixation du prix des maisons d'habitation dans la ville de Bukavu la
préoccupation majeure était de ressortir les différents
facteurs qui permettent de déterminer la valeur des maisons d'habitation
dans la ville de Bukavu afin de comprendre les éléments que l'on
pourrait utiliser en vue d'une politique publique efficace d'étalement
de la ville.
En effet, L'immobilier occupe une place de plus en plus
prépondérante dans les choix d'investissement des ménages.
Une forte croissance démographique et un secteur immobilier en pleine
expansion dans la ville de Bukavu sont des éléments qui exigent
l'intervention des décideurs en vue de bien mener une politique publique
efficace d'étalement urbain. Les caractéristiques
spécifiques d'un bien immobilier telles que son caractère
indivisible, sa valeur unitaire très élevée, sa faible
liquidité, sa grande hétérogénéité et
son immobilité physique, conduisent à le distinguer des autres
biens. C'est ainsi que cette étude portant sur une évaluation des
immobiliers résidentiels à Bukavu a été
structurée en trois chapitres essentiels hormis l'introduction et la
conclusion.
Dans le premier chapitre, la revue de la littérature
renseigne que plusieurs approches abordent la question de la valeur des
immobiliers résidentiels. Une des approches stipule qu'elle
résulte des comportements des ménages en termes de choix de
localisation des ménages basés sur l'arbitrage des ménages
entre les coûts de localisation et les coûts de déplacements
entre le domicile et le lieu de travail supposé se situer au
centre-ville, alors qu'une autre montre la nécessité de la
présence d'aménités recherchées par les
ménages permettant de contrebalancer la force d'attraction du
centre-ville et le dernier point fait la présentation de la
théorie de Lancaster de l'analyse hédoniste ou hédonique
des prix, dont l'objet est d'étudier la formation du prix des biens
complexes, expliquant le prix des biens par leurs caractéristiques.
Le deuxième chapitre, expose l'approche
méthodologique qui, faisant ressortir les hypothèses du travail,
décrit toutes les étapes dès la récolte des
données aux procédures de traitement, successivement la
méthode de moindre carré ordinaire,
88
ensuite la prise en compte de
l'hétérogénéité spatiale par la correction
du modèle de l'hétéroscédasticité et
l'analyse de la variance spatiale et enfin la prise en compte de
l'autocorrélation spatiale en comparant le modèle
autorégressif spatial du modèle d'erreur spatial.
Les données utilisées provenant de
l'enquête ont été collectées dans les trois communes
basée sur une stratification proportionnelle avec un questionnaire,
implémenté dans le téléphone en utilisant
l'application Android ODK Collect, adapté des études
antérieures. Un total de 193 ménages ont été
enquêté ayant en moyenne 297,59 mètres carrés de
surface de parcelle avec 111,39$ comme prix au mètre carré, et
des maisons comportant en moyenne 7 pièces.
Enfin, le troisième chapitre présente et discute
les résultats. Pour vérifier les hypothèses, les
données ont été traitées sur SPSS Ver. 20 et STATA
12. La méthode de moindre carré a été
utilisée en premier pour estimer le modèle hédoniste,
ensuite le modèle a été amélioré par la
prise en compte de l'hétérogénéité spatiale
et de l'autocorrélation spatiale.
Les résultats de la méthode de moindre
carré ont montré que seules huit variables sont significatives au
seuil maximum de 10%. Il s'agit de la localisation de la maison si elle est
située à Kadutu(Commkad), le nombre des pièces(Nbrepc), la
presence des 2 toilettes/salles de bain ou plus (Pres2toilslb), la distance
avec le centre-ville (Distcentvil), le niveau d'étude (Nivetd) et la
profession du propriétaire de la maison(Profess) ainsi que le cout total
de transport (Ctttransp). Le test F de Fisher montre que la qualité du
modèle est globalement bonne avec un coefficient de détermination
de 86,9 %. La prise en compte de
l'hétérogénéité spatiale par la prise en
compte de l'hétéroscédasticité, le test de
Breusch-Pagan révèle que le modèle est
hétéroscedastique, la correction du modèle par la
méthode de White a permis de rejeter la variable cout total de transport
(Ctttransp) du modèle de MCO ce qui permet de conserver un modèle
avec sept variables explicatives significatives. Les résultats de
l'analyse de la variance spatiale n'a pas été valide à
cause de l'hétérogénéité de la variance et
la non normalités des erreurs, le recours au test non
paramétrique de Kruskal-Wallis fait rejeter de manière
significative l'égalité des prix dans les trois
89
communes. Les prix des maisons diffèrent donc
globalement selon la commune de localisation, le test de Games-Howell de
comparaisons multiples a révélé qu'il existe des
différences significatives du prix en moyenne entre d'un
côté les maisons de la commune d'Ibanda avec de l'autre
côté celles de la commune de Bagira et de Kadutu. Mais celles de
la commune de Kadutu ne diffèrent pas significativement en moyenne de
celles de la commune de Bagira.
Les résultats obtenus par l'introduction de la
dimension spatiale dans le modèle hédonique montrent qu'il existe
une dépendance spatiale dans les valeurs immobilières de
manière significative à Bukavu. Cette présence de
dépendance spatiale est d'abord confirmée par le test de Moran
ainsi que par la significativité élevée de ?? et de
À. Les signes de ces derniers montrent la présence d'une
autocorrélation spatiale positive sur le prix des biens. La comparaison
du modèle d'erreur spatiale avec le modèle autorégressif
spatial montre que le modèle autorégressif spatial est le
meilleur et permet de retenir sept variables significatives notamment la
localisation de la maison si elle est située à Kadutu(Commkad),
le nombre des pièces(Nbrepc), la presence des 2 toilettes/salles de bain
ou plus (Pres2toilslb), la distance avec le centre-ville (Distcentvil), le
niveau d'étude (Nivetd) et la profession du propriétaire de la
maison(Profess). Le test VIF de la multicolinéarité et le
critère d'information d'Akaike ont permis d'avoir un modèle
optimale grâce à la méthode Stepwise Regression en
conservant toujours le modèle SAR étant le modèle optimal
avec huit variables significatives en ajoutant la variable coût total de
transport au modèle précédent.
Il est dommage de constater que ce présent travail ne
puisse pas être très complet sur le problème du prix des
immobiliers résidentiels à Bukavu, n'ayant analysé que
certains aspects, une recherche future prenant en comptant plus des dimensions
liées à la résidence des ménages permettrait de
compléter cette étude.
90
BIBLIOGRAPHIE
1. Alonso, W.(1964), Location and land use,
Harvard University Press, Cambridge Press.
2. Anas, A., Shyong , D. L. (1985), Dynamic
forecasting of travel demand, residential location and land development :
policy simulation with the Chicago area transportation/land use
system, Papers, Regional Science Association, 56.
3. Anas, A. (1982), Residential location markets and
urban transportation, New York : academic Press.
4. Anderson, D. et al. (2001), Statistiques pour
l'économie et la gestion, Ed. De Boeck, Paris
5. Baissac, C. et Al. (2012), La Contribution des
Villes à la Croissance Économique et à la Réduction
de la Pauvreté, dans Johannes Herderschee, Daniel Mukoko Samba
et Moïse Tshimenga Tshibangu (éditeurs), Résilience
d'un Géant Africain : Accélérer la Croissance et
Promouvoir l'Emploi en République Démocratique du
Congo, Volume II : Etudes sectorielles, MÉDIASPAUL, Kinshasa,
pages 185-257.
6. Basu, Sabyasachi, et Thomas G. Thibodeau (1998),
«Analysis of spatial autocorrelation in house prices», The
Journal of Real Estate Finance and Economics 17, 61-85.
7. Bender B., Hwang H., (1985), Hedonic house price
indices and secondary employment centers, « Journal of Urban
Economics , 17, 90-107 ».
8. Bivand, Roger (2012), Spatial dependence: Weighting
schemes, statistics and model, Package Spdep in R.
9. Bourbonnais, R. (2009), Econométrie : manuel
et exercices, Université de ParisDauphine, 2ème
édition, Dunod, Paris
10. Bowen, William M. et, Brian A. Mikelbank, et Dean M.
Prestegaard, (2001), Theoretical and empirical considerations regarding
space in hedonic housing price model applications, Growth and Change
32.
11. Boyce, D., Allien, B., Mudge, R.R., Stater, P.B.,
Isserman, A.M. (1972), The impact of rapid transit on suburban
residential property values and land development analysis of the Philadelphia
high speed line, Regional Science Department, University of
Pennsylvania, NTIS n° PB 220 693, 1972.
91
12. Brossard, T. et al (2005), analyse
géographique et évaluation économique des paysages
périurbains, centre d'économie et de sociologie
appliquée à l'agriculture et aux espaces ruraux, France.
13. Can A., (1990), The measurement of neighborhood
dynamics in urban house prices, Economic Geography, 66, 254-272.
14. Carricano et Poujol (2008), Analyse des
données avec SPSS, Collection Synthex , Pearson Education
France.
15. Clévenot, M. (2011), les prix immobiliers
en France : une évolution singulière
16. Cressie, Noel A. C.(1991), Statistics for spatial
data (J. Wiley, New York).
17. De La Barra, T. (1989), Integrated land use and
transport modelling - Decision chains and hierarchies, Cambridge Urban
and Architectural Studies. Cambridge University Press.
18. Dornbusch, D.M. (1976), Bart-induced changes in
property values and rents. Land use and urban development project, phase
1, BART, Working papers WP 21-5-76, US Department of
Transportation and US Housing and Urban Development.
19. Drukker, D. M., I. R. Prucha, et R. Raciborski, (2011),
An ml and gs2sls estimator for the spatial autoregressivemodel,
Technical report, Stata.
20. Dubin R.A., Sung R.A., 1987, Spatial variation in
the price of housing : rent gradients in nonmonocentric cities, «
Urban Studies , 24, 193-204 »
21. Dufrénot, G. et Malik, SH. (2010), The
changing role of house price dynamics over the business cycle.
22. Dunse, Neil, et Colin Jones, (1998), A hedonic
price model of office rents, Journal of Property Valuation and
Investment 16, 297-312.
23. Durlauf, S.N., (2004), Neighborhood
effects, in Henderson, J.V. et Thisse, J.-F. (ed.) Handbook of
Regional and Urban Economics, vol. 4, Elsevier, 2173-2242.
24. Gallo, Julie Le (2002), Économétrie
spatiale : L'autocorrélation spatiale dans les modèles de
régression linéaire, Economie & prévision
155, 139-157
25. Goodman A.C., Kawai M., (1984), Functional form
and rental housing market analysis, Urban Studies, 21, 367-376.
26. Hochman, O., Ofek, H. (1977), The value of time in
consumption and residential location in urban cities, American
Economic Review, December, pp. 996-1004.
92
27. Homocianu, G. M. (2009), modélisation de
l'interaction transport urbanisme - choix résidentiels des
ménages dans l'aire urbaine de Lyon, thèse,
Université Lumière Lyon 2, laboratoire d'économie des
transports, France.
28. IFDP (2013), Gestion des terres urbaines et de
l'environnement à Bukavu : opinion de la société
civile.
29. Jayet, Hubert, (1993). Analyse spatiale
quantitative une introduction (Économica, Paris)
30. Kau J., Lee C, Sirmans C. (1986), Urban
Econometrics : Model Developments and Empirical Results, Greenwich,
JAI Press
31. Kelejian, Harry H., et Ingmar R. Prucha, (1998), A
generalized spatial twostage least squares procedure for estimating a spatial
autoregressive model with autoregressive disturbances, « The
Journal of Real Estate Finance and Economics 17, 99-121 ».
32. Lancaster, K. (1964), new approch of consummer
theory, journal of political economy.
33. Leamer, E. (2007), Housing is the business
cycle, NBER working papers 13428.
34. Lerman, S. (1977), The effect of the
Washingtonmetro on urban property values, CS Report n° 77-18,
Centre of Transportation Studies, Massachusetts Institute of Technology,
Cambridge.
35. LeSage, James P., et R. Kelley Pace(2009).
Introduction to spatial econometrics (CRC Press, Boca Raton ;
London).
36. Luong, D. et Boucq, E. (2011), Évaluation
de l'impact du T3 sur les prix de l'immobilier résidentiel,
Institut d'Aménagement et d'Urbanisme de la Région
d'Île-de-France (IAU îdF), Paris, France.
37. Mc Fadden, D. (1978), Modelling the Choice of
Residential Location, in Spatial Interaction Theory and Planning
Models, edited by A. Karlkvist et al., Amsterdam: Nord Holland
Publishers.
38. McMillen D.P., McDonald J.F. (1998), Population
density in Chicago: a bid rent approach, Urban Studies , 7,
1119-1130.
39. Mills, E. (1967), An aggregative model of
ressource allocation in metropolitan areas, American Economic Reviews
- Papersand proceedings, Vol. 57, pp. 197-210.
93
40. Moran, P. (1950), A test for serial independence
of residuals, « Biometrika, 37, 178181 ».
41. Muth, R. (1969), Cities and housing,
Chicago : University of Chicago Press.
42. Rakatomalala, R. (2008), comparaison des
populations : Tests non paramètriques, version 1.0,
Université Lumière Lyon 2.
43. Ricardo, D. (1817), les principes de
l'économie politique et de l'impot.
44. Rosen, S. (1974), Hedonic prices and implicit
markets: Product differentiation in pure competition, Journal of
Political Economy 82, 34-null.
45. Ryan, S. (1999), Property values and
transportation facilities : Finding the transportation - land -use
connection, Journal of Planning Literature, 13(4), pp. 412-427
46. Smith, A. (1776), la richesse des
nations.
47. Srikhum, P. (2012), Statistiques spatiales et
Etude immobilière, thèse, université
Paris-Dauphine, école doctorale de dauphine, Paris, France.
48. Straszheim, M. (1987), The Theory of Urban
Residential Location, in Handbook of Regional and Urban Economics, E.
S. Mills (ed.), vol. 2, chap. 18, pp. 717757
49. Sun, Hua, Yong Tu, et Shi-Ming Yu, (2005), A
spatio-temporal autoregressive model for multi-unit residential market
analysis, The Journal of Real Estate Finance and Economics 31,
155-187.
50. Theriault, M., Kestens, Y., Des Rosiers, F. (2002),
The impact of mature trees on house values and on residential location
choices in Quebec City, Université Laval.
51. Tiebout, C. (1956), A pure theory of local
expenditures, Journal of Political Economy, 64, pp. 416-424.
52. Tobler W., 1979, Cellular geography, in S. Gale et G.
Olsson (Eds), Philosophy in Geography, 379-386, Reidel,
Dordrecht.
53. Travers, M. et al (2013), Évaluation des
aménités urbaines par la méthode des prix
hédoniques : une application au cas de la ville d'Angers, «
économie et statistique n°460-461, 2013 », France.
54. Upton, G. et, Fingleton, B. (1985), Spatial Data
Analysis by Example. John Wiley, New York.
94
55. Van Lierop, W.F.J., Rima, A. (1982), Towards an
operational disaggregate model of choice for the housing market,
Collaborative Paper, IIASA, Laxenburg.
56. Walras, L. (1874), Eléments d'économie
politique.
57. Wingo, L. (1961), Transportation and urban
land, Ressource for the future, Inc. Washington D.C., 1961.
58. Zenou, Y. (2002), How do firms redline
workers?, Journal of Urban Economics, n° 52, pp. 391-408.
95
96
ANNEXES
Annexe 1 : Caractéristiques socioprofessionnelles et
démographiques des propriétaires Calcul de la distance par
rapport au centre (Poste centrale de Bukavu) Tableau 1.1 : La distance des
ménages avec le centre-ville (Distcentvil)
|
Commune
|
Moyenne
|
Médiane
|
Minimum
|
Maximum
|
Ecart-type
|
N
|
|
Ibanda
|
1727,4606
|
1804,60673
|
462,246731
|
3507,31087
|
872,351471
|
65
|
|
3
|
|
|
|
|
|
|
Kadutu
|
1870,5351
|
1759,09594
|
1139,30660
|
3384,47039
|
586,677468
|
81
|
|
6
|
|
|
|
|
|
|
Bagira
|
4996,1514
|
5027,90638
|
3697,33356
|
5278,40567
|
236,963178
|
47
|
|
Total
|
2583,5098
|
1988,1742
|
462,24673
|
5278,4056
|
1515,9048
|
193
|
Source : notre confection 1.2 Statut des propriétaires
Tableau 1.2 : Statut du propriétaire(Statutprop)-Prix de
la maison (prms)
|
Prms
|
Statutprop
|
|
Rho de
Spearman
|
Corrélation de
Spearman
|
1,000
|
-,315**
|
|
Sig. (bilatérale)
|
.
|
,000
|
|
N
|
193
|
193
|
|
Prms
|
Rho de Spearman
|
-,315**
|
1,000
|
|
Sig. (bilatérale
|
,000
|
|
|
N
|
193
|
193
|
|
**. La corrélation est signifiacative au niveau 0.01
(bilatéral)
|
Source : notre confection
Tableau 1.3 Statut du propriétaire-Prix de la maison
|
Moyenne
|
Médiane
|
Minimu m
|
Maximum
|
Ecart- type
|
N
|
|
Célibataires
|
33761,36
|
16500,00
|
5000
|
150000
|
37269,211
|
44
|
|
Mariés
|
31531,58
|
24000,00
|
4000
|
120000
|
26597,949
|
95
|
B
|
Divorcés
|
9531,25
|
9000,00
|
5000
|
14000
|
3639,912
|
16
|
|
Veuf
|
21833,33
|
12000,00
|
8000
|
75000
|
26095,338
|
6
|
|
Union libre
|
10734,38
|
8000,00
|
5000
|
80000
|
12980,124
|
32
|
|
Total
|
26466,32
|
14000,00
|
4000
|
150000
|
28180,040
|
193
|
Source : notre confection
C
1.3 Niveau d'étude
Tableau 1.4 : Corrélation de Spearman entre le niveau
d'étude(Nivetd) et le prix de la maison (prms)
|
Prms
|
Nivetd
|
|
Rho de
Spearman
|
Corrélation de
Spearman
|
1,000
|
,504**
|
|
Sig. (bilatérale)
|
,
|
,000
|
|
N
|
193
|
193
|
|
Prms
|
Rho de Spearman
|
,504***
|
1,000
|
|
Sig. (bilatérale
|
,000
|
,
|
|
N
|
193
|
193
|
|
**. La corrélation est significative au niveau 0.01
(bilatéral)
|
Source : notre confection
Tableau 1.5 : Niveau d'étude-prix de la maison
|
Moyenne
|
Médiane
|
Minimum
|
Maximum
|
Ecart-type
|
N
|
|
Analphabètes
|
6730,77
|
6500,00
|
4000
|
9000
|
1739,437
|
13
|
|
Primaires
|
15000,00
|
9500,00
|
5000
|
90000
|
17568,784
|
38
|
|
Secondaires
|
22853,57
|
14000,00
|
4000
|
120000
|
23164,573
|
84
|
|
Universitaires
|
43634,48
|
32500,00
|
6000
|
150000
|
34596,545
|
58
|
|
Total
|
26466,32
|
14000,00
|
4000
|
150000
|
28180,040
|
193
|
Source : notre confection
1.4 Profession des propriétaires
Tableau 1.6 : Corrélation de Spearman profession du
propriétaire(Profess)-prix de la maison (prms)
|
|
|
Prms
|
Profess
|
|
Rho
Spearman
|
de
|
Corrélation Spearman
|
de
|
1,000
|
,687**
|
|
Sig. (bilatérale)
|
|
,
|
,000
|
D
|
N
|
193
|
193
|
|
Prms
|
Rho de Spearman
|
,687**
|
1,000
|
|
Sig. (bilatérale
|
,000
|
,
|
|
N
|
193
|
193
|
|
**. La corrélation est significative au niveau 0.01
(bilatéral)
|
Source : notre confection
Tableau 1.7 : Comparaison des moyennes des prix selon les
catégories socioprofessionnelles des propriétaires
|
Moyenn e
|
Médian e
|
Minimu m
|
Maximu m
|
Ecart- type
|
N
|
|
Agriculteurs, Paysans et Sans
emploi
|
9472,22
|
7000,00
|
4000
|
45000
|
10159,404
|
36
|
|
Prestataires des services
|
10710,00
|
6250,00
|
4000
|
32200
|
9012,442
|
20
|
|
Salariés
|
18255,56
|
14000,00
|
6000
|
72000
|
12728,525
|
54
|
|
Commerçants
|
28380,95
|
24000,00
|
6000
|
73000
|
19192,164
|
42
|
|
Autres
|
57926,83
|
50000,00
|
9000
|
150000
|
39965,229
|
41
|
|
Total
|
26466,32
|
14000,00
|
4000
|
150000
|
28180,040
|
193
|
Source : notre confection 1.5 Transports privés
Tableau 1.8 : Tableau de corrélation de Pearson cout de
transport total (ctttransp)-prix des maisons
|
Prms
|
ctttransp
|
|
Prms
|
Corrélation de Pearson
|
1
|
-,260**
|
|
Sig. (bilatérale)
|
|
,000
|
|
N
|
193
|
193
|
E
|
Ctttransp
|
Corrélation de Pearson
|
-,260**
|
1
|
|
Sig. (bilatérale)
|
,000
|
|
|
N
|
193
|
193
|
|
**. La corrélation est significative au niveau 0.01
(bilatéral).
|
Source : notre confection
Tableau 1.9 : Comparaison des moyennes du cout total de transport
journalier selon la
commune
|
Moyenne
|
Médiane
|
Minimum
|
Maximum
|
Ecart- type
|
N
|
|
Ibanda
|
1721,85
|
1600,00
|
1600
|
2600
|
229,721
|
65
|
|
Kadutu
|
1712,35
|
1800,00
|
800
|
2600
|
549,177
|
81
|
|
Bagira
|
3157,45
|
3000,00
|
3000
|
4000
|
297,632
|
47
|
|
Total
|
2067,46
|
1800,00
|
800
|
4000
|
740,910
|
193
|
Source : notre confection
F
Annexe 2 : ANOVA Spatial
Tableau 2.1 : Analyse descriptive des prix dans les communes
|
Moyenne
|
Médiane
|
Minimum
|
Maximum
|
Ecart-type
|
Asymétrie
|
N
|
|
Ibanda
|
43092,31
|
35000,00
|
4000
|
150000
|
37112,882
|
1,045
|
65
|
|
Kadutu
|
19037,04
|
9000,00
|
4500
|
90000
|
20322,060
|
2,034
|
81
|
|
Bagira
|
16276,60
|
14000,00
|
5000
|
45000
|
9279,951
|
1,490
|
47
|
|
Total
|
26466,32
|
14000,00
|
4000
|
150000
|
28180,040
|
1,988
|
193
|
Source : notre confection
Tableau 2.2 : tableau des rangs pour le test de Kruskal-Wallis
|
Rangs
|
|
|
|
|
Commune
localisation
|
de
|
N
|
Rang moyen
|
|
Prix maisons
|
des
|
Ibanda
|
|
65
|
121,00
|
|
Kadutu
|
|
81
|
80,80
|
|
Bagira
|
|
47
|
91,73
|
|
Total
|
|
193
|
|
Source : notre confection
G
Annexe 3 : Résultats des estimations
Tableau 3.1 : Test VIF réalisé après la
régression par moindre carré ordinaire
|
Variable
|
VIF
|
|
Distinfrtr-h
|
208.96
|
|
Distaxepripl
|
203.76
|
|
Commbag
|
14.50
|
|
Distcentvil
|
9.72
|
|
Distrtproch
|
5.93
|
|
Surfpcl
|
5.72
|
|
Ctttransp
|
5.27
|
|
Surfms
|
4.56
|
|
Nbrepc
|
3.45
|
|
Typems
|
3.02
|
|
Etmurs
|
2.92
|
|
Nbreetg
|
2.60
|
|
Profess
|
2.27
|
|
Distcentrm-l
|
2.03
|
|
Commkad
|
1.92
|
|
Ancms
|
1.73
|
|
Distetensgmt
|
1.55
|
|
Pres2toilslb
|
1.55
|
|
Nivetd
|
1.41
|
|
Presgarg
|
1.30
|
|
Moyenne VIF
|
24.21
|
Source : notre confection
Tableau 3.2 : Test VIF amélioré après
suppression de la variable Distinfrtr-h et Commbag
|
Variable
|
VIF
|
|
Distrtproch
|
5.76
|
|
Distaxepripl
|
5.58
|
|
Distcentvil
|
5.54
|
|
Surfpcl
|
4.83
|
|
Ctttransp
|
4.38
|
|
Surfms
|
3.70
|
|
Nbrepc
|
3.34
|
|
Typems
|
3.00
|
|
Etmurs
|
2.86
|
|
Nbreetg
|
2.53
|
|
Profess
|
2.20
|
|
Distcentrm-l
|
1.99
|
|
Commkad
|
1.91
|
|
Ancms
|
1.72
|
|
Pres2toilslb
|
1.54
|
H
|
Nivetd
|
1.35
|
|
Presgarg
|
1.26
|
|
Moyenne des VIF
|
3.06
|
Source : notre confection

Tableau 3.3 : test du rapport de vraisemblance du premier
modèle optimal
|
Modèle
|
Observatio n
|
Ll(null)
|
Ll(modèl e)
|
Dd l
|
AIC
|
BIC
|
|
MCO (écart-types robustes)
|
193
|
-
|
-2060.432
|
10
|
4140.8
|
4173.4
|
|
(Mod2)
|
|
2250,903
|
|
|
64
|
91
|
|
SAR (Mod3)
|
193
|
-2060.43
|
-2050.706
|
12
|
4125.4
|
4164.5
|
|
|
|
|
|
12
|
64
|
|
SEM (Mod4)
|
193
|
-
|
-2056.367
|
12
|
4136.7
|
4175.8
|
|
|
2060.432
|
|
|
34
|
86
|
|
Likelihood-ratio test LR chi2(4) = 27.58 Prob > chi2 =
|
|
0.0000
|
Source : notre confection
Annexe 4 : Les cartes relatives aux enquêtes
réalisées dans la ville de Bukavu produites par Google Maps
Carte 1 : Les points enquêtés

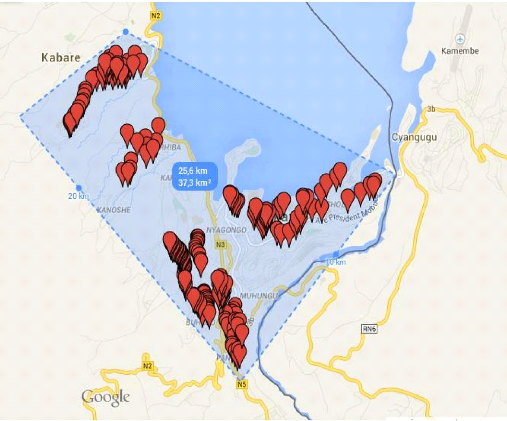
Carte 2 : Commune d'Ibanda
K
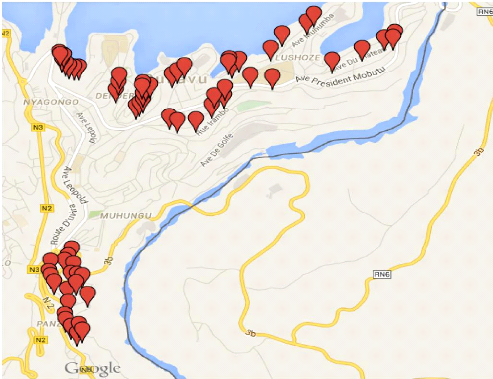
L
Carte 3 : Commune de Kadutu
M
Carte 3 : Commune de Bagira
N
Commune :
Quartier
Longitude :
Latitude
C'est avec une immense satisfaction que nous vous adressons ce
présent questionnaire dont le sujet est : « Déterminants de
la fixation du prix des maisons
d'habitation à Bukavu » et nous comptons sur la
sincérité de vos réponses.
I. Identité de l'enquêteur :
KAJEMBA WA KAJEMBA François
Etudiant en deuxième année de licence en Gestion
Financière
Université Catholique de Bukavu
Sexe et âge : Masculin/24 ans
Etat-civil : célibataire
Adresse : Av. Pesage II, N° 436, Ibanda/Bukavu
Contact : 0974242142/
kajembafranc@yahoo.fr
II. Identité de l'enquêté
:
1. Sexe :
a. Masculin
b. Féminin
2. Etat-civil
a. Célibataire
b. Marié(e)
c. Divorcé
d. Veuf/veuve
e. Union libre
3. Profession
a. Agriculteur, paysans et sans aucune activité
b. Prestataire des services (salon de coiffure, menuisier,
restaurant,...)
c. Salarié
O
d. Commerçant
e. Autres.
III. Questionnaire proprement dit
1. Caractéristiques physiques
1. Quelle est la surface de votre Parcelle
o Longueur ... ... ........ mètres
o Largeur mètres
o Surface :... ... mètres carrés
2. Quelle est la surface des éléments construits
sur la parcelle :
· Maison principale : Longueur ...X... Largeur ...=
...mètres carrés
· Annexes : Longueur ..........X Largeur .......=
......mètres carrés
· Toilettes : Longueur .........X... Largeur......... ...=
...mètres carrés
· Autres : Longueur ......X... Largeur =
..............mètres carrés
3. Combien de pièces habitables porte votre maison :
nombre des chambres + salons
· Maison principale
· Annexe :
4. Combien d'étage porte votre
maison...........................................................
5. A quelle période votre maison a-t-elle
été construite :
a. Avant 1980
b. Entre 1980 et 1990
c. Entre 1991 et 2000
d. Entre 2001 et 2010
e. Après 2010
6. Votre maison est-elle peinte
o Oui
o Non
7. De quels matériaux est construite votre maison
o Durable (brique)
o Semi-durable (ciment et sable)
o Planche
o Autres
8. Combien des toilettes et salles de bain porte votre maison
:
P
o Toilette
o Salles de bain
9. Votre maison a-t-elle un garage privé
o Oui
o Non
2. Caractéristique de localisation et
d'accessibilité
a. Quelle est la distance en mètre avec l'axe principal
la plus proche la plus
proche de chez vous
b. A combien estimez-vous la durée en minute de marche
à pied entre
votre maison avec la route la plus proche de la maison...
...................
c. Quelle est la distance en mètre avec l'infrastructure
de transport en
commun la plus proche de chez vous
3. Caractéristique de voisinage
a. Quelle est la durée en minute de marche à pied
entre la maison et un
centre médical le plus proche de la maison
b. Quelle est la durée en minute de marche à pied
avec un établissement
d'enseignement le plus proche
c. Y a-t-il déjà eu au moins une attaque dans
un rayon de 500 mètres de la maison :
o Oui
o Non
d. Existe-t-il un restaurant ou un hôtel de prestige
dans un rayon de 200mètres de la maison :
o Oui
o Non
4. Caractéristiques sociodémographiques
a. Quelle est le niveau d'étude du propriétaire de
la maison:
o Analphabète
o Primaire
o Secondaire
o Universitaire
b. Quelle est la profession du propriétaire de la maison
:
o Célibataire
Q
o
R
Marié(e)
o Divorcé
o Veuf/veuve
o Union libre
c. Avez-vous un véhicule ou un autre moyen de transport
privé
o Oui
o Non
Si oui, à combien pouvez-estimer en franc congolais le
coût journalier de carburant................
d. Combien peut couter en franc congolais le transport en commun
pour vous rendre :
o Au travail
o Au Marché de Kadutu...... ..........
o Au marché le plus proche................
o A la poste centrale (Marché de Nyawera)
e. Vous est-il déjà arrivé de vous
référer sur la valeur des maisons voisines pour estimer la valeur
de votre maison
o Oui
o Non
f. A combien pouvez-vous estimer la valeur de votre maison pour
la revente(en se basant sur une vente précédente dans votre
quartier)
g. A combien peut couter votre maison si elle était
donnée en location
| 


