|
REPUBLIQUE DU BENIN
***********
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA
RECHERCHE SCIENTIFIQUE
***********
UNIVERSITE D'ABOMEY-CALAVI (UAC)
***********
ECOLE NATIONALE D'ECONOMIE
APPLIQUEE ET DE MANAGEMENT
(ENEAM)
***********
MEMOIRE DE LICENCE (DTS)
***********
Filière : Statistique Option :
Statistiques Economique et Sectorielle
37ème PROMOTION
ANNEE ACADEMIQUE : 2018-2019
Etude des déterminants de
la production de l'igname dans le département du
Borgou/Bénin
Fariane A. ADJIBADE & Christian A.
M'PESSI
|
Maître de stage
|
Directeur de mémoire
|
|
Dr Ayi Yves Césaire AJAVON
|
Firmin VLAVONOU
|
|
Statisticien Géographe
|
Ingénieur Statisticien Economiste, Ph.D.
|
|
Directeur de la Statistique Agricole
|
Enseignant chercheur à l'UAC/ENEAM
|
Février 2020
AVERTISSEMENT
L'Ecole Nationale d'Economie Appliquée et de
Management (ENEAM) n'entend donner ni approbation, ni improbation aux opinions
émises dans ce mémoire. Ces opinions doivent être
considérées comme propres à leurs auteurs.
Identification du jury
Président du Jury :
Vice-Président :
Approbation
« Nous, soussignés,Firmin VLAVONOU, Ph.D.et DrAyi
Yves Césaire AJAVON respectivement directeur de mémoire et
maître de stage, certifions que le présent mémoire a
été effectivement réalisé par ses auteurs à
la suite d'un stage académique effectué à la Direction de
la Statistique Agricole. Ledit mémoire est arrivé à terme
et peut être soutenu devant un jury ».
Cotonou, le ...... /...... / 2020
|
Maître de stage
|
Directeur de mémoire
|
|
Dr Ayi Yves Césaire AJAVON
|
Firmin VLAVONOU
|
|
Statisticien Géographe
|
Ingénieur Statisticien Economiste, Ph.D.
|
|
Directeur de la Statistique Agricole
|
Enseignant chercheur à l'UAC/ENEAM
|
DEDICACES
À
Mes chers parents Sikiratou FAYOMI et Ganiou ADJIBADE, en
témoignage de ma gratitude pour tous leurs sacrifices quotidiens, leur
amour, leurs encouragements permanents et leurs prières ;
Mes frères et soeurs pour leur amour et leur
soutien.
Fariane Achamou ADJIBADE
Je dédie ce travail à :
Mes chers parents Comlan M'PESSI et Kossouwa SALIFOU, pour
tous leurssacrifices, leur soutien et leurs encouragements ;
Mes frères et soeurs, pour leur affection et leur
soutien indéfectible ;
Tous ceux qui, de près ou de loin m'ont aimé,
soutenu et respecté.
Christian Aurel M'PESSI
Remerciements
La réalisation de ce mémoire a été
possible grâce au concours de plusieurs personnes à qui nous
voudrions témoigner toute notre reconnaissance. Nous tenons à
exprimer notre profonde gratitude à :
Rosaline D.
WOROU-HOUNDEKON, Ph.D., Professeur Agrégée des Sciences
de Gestion, Directrice de l'ENEAM ;
Théophile K. DAGBA,
Ph.D., Maître de conférences, Directeur-adjoint,
Chargé des affaires académiques de l'ENEAM ;
Firmin
VLAVONOU, Ph.D., Enseignant chercheur à l'ENEAM, notre
Directeur de mémoire qui a accepté d'encadrer ce
mémoire ;
Dr. Ayi Yves Césaire AJAVON, notre
Maître de stage qui nous a acceptés dans sa structure, nous a
suivis, nous a assistés et nous a accordés les
éléments nécessaires pour l'élaboration de ce
document ;
Gilles GOHY, Ph.D., Chef du
Département de la Statistique à l'ENEAM ;
Dr. Jean-Marie V. KIKI, Chef Adjoint du
Département de la Statistique à l'ENEAM, chargé des
Statistiques Economique et Sectorielle ;
Barthélémy SENOU, Ph.D., Chef
Adjoint du Département de la Statistique à l'ENEAM, chargé
des Statistiques Démographique et Sociale ;
Tout le personnel
enseignant et administratif de l'ENEAM ;
Monsieur RémyHOUNGUEVOU, Chef Service
Etat et Perspectives de la population à l'INSAE ;
Messieurs Nourou ADJIBADE et Mamam ALOKI
Tous les cadres et fonctionnaires de la Direction de la
Statistique Agricole pour leurs conseils et soutien ;
Tous nos camarades de la 37èmepromotion de la
filière Statistique de l'ENEAM ;
Tous les stagiaires de la DSA ;
Tous ceux qui, de près ou de loin ont contribué
à la réalisation de ce travail.Sigles et abréviations
ADF: AugmentedDickey-Fuller
AIC: Akaike Information Criterion
al. : Alliés
AZ : Andrews et Zivot
ARDL: Auto RegressiveDistributedLag
CT: Court Terme
DSA : Direction de la Statistique
Agricole
ECT: Error Correction Term
EEAS: EuropeanExternal Action Service
HQ : Hannan-Quinn Information
Criterion
INRAB : Institut National des Recherches
Agricoles du Bénin
INSAE : Institut National de la Statistique et
de l'Analyse Economique
KPSS: Kwiatkowski, Phillips, Schmidt et
Shin
LT : Long Terme
MAEP : Ministère de l'Agriculture,
de l'Elevage et de la Pêche
MCE : Modèle à Correction
d'Erreur
PDRT : Programme de Développement
des Plantes à Racines et Tubercules
PIB : Produit Intérieur Brut
PP : Phillips-Perron
PSRSA : Plan Stratégique de Relance
du Secteur Agricole
RGPH : Recensement Général
de la Population et de l'Habitation
SC : Schwarz Criterion
VAR : Vecteur Autorégressif
Liste des tableaux
|
Tableaux
|
Titres
|
Pages
|
|
Tableau 1
|
Informations sur les données brutes
|
11
|
|
Tableau 2
|
Conditions de confirmation des hypothèses
|
17
|
|
Tableau 3
|
Statistiques descriptives des variables
|
18
|
|
Tableau 4
|
Résultats de l'analyse de la saisonnalité des
séries
|
21
|
|
Tableau 5
|
Résultats des tests de stationnarité des
séries
|
22
|
|
Tableau 6
|
Modèle ARDL(4,4,4,0,4)
|
23
|
|
Tableau 7
|
Résultats des tests diagnostiques du modèle ARDL
estimé
|
24
|
|
Tableau 8
|
Valeurs des coefficients du modèle ARDL(4,4,4,0,4)
|
24
|
|
Tableau 9
|
Résultats du test de cointégration de Pesaran et
al. (2001)
|
25
|
|
Tableau 10
|
Résultats d'estimation des coefficients de CT
|
25
|
|
Tableau 11
|
Résultats d'estimation des coefficients de LT
|
26
|
|
Tableau 12
|
Confirmation des hypothèses
|
28
|
Liste des figures
|
Figures
|
Titres
|
Pages
|
|
Figure 1
|
Boîtes à moustaches des variables
|
19
|
|
Figure 2
|
Evolution de la production de l'igname et de la superficie
emblavée
|
19
|
|
Figure 3
|
Evolution de la pluviométrie
|
20
|
|
Figure 4
|
Evolution du prix aux producteurs
|
20
|
|
Figure 5
|
Allure de la série « Prix aux producteurs »
après désaisonnalisation
|
21
|
|
Figure 6
|
Retards optimaux des séries selon le Critère
d'Information d'Akaike
|
22
|
SOMMAIRE
INTRODUCTION
3
CHAPITRE 1 : CADRE INSTITUTIONNEL DE
L'ETUDE
3
1.1. Présentation de la Direction de la
Statistique Agricole (DSA)
3
1.2. Déroulement du stage
5
CHAPITRE 2 : CADRE THEORIQUE ET METHODOLOGIQUE DE
L'ETUDE
6
2.1. Enjeux de l'étude
6
2.2. Revue de littérature et
méthodologie
8
2.3. Limites de l'étude
17
CHAPITRE 3 : PRESENTATION ET INTERPRETATION DES
RESULTATS
18
3.1. Analyse descriptive
18
3.2. Analyse explicative
20
3.3. Synthèse des résultats et
vérifications des hypothèses
27
3.4. Préconisations
opérationnelles
28
CONCLUSION
29
REFERENCES BIBLIOGRAPHIQUES
30
ANNEXE
a
1 Résumé
Le présent mémoire a pour objectif d'analyser
les déterminants de la production de l'igname dans le département
du Borgou au Bénin. Les données utilisées dans le cadre de
cette étude couvrent conjointement la période de 2010 à
2018 et proviennent de la Direction de la Statistique Agricole (DSA) et de
l'Institut National de la Statistique et de l'Analyse Economique (INSAE). Pour
manque d'observations nécessaires à une analyse
économétrique, nous avons trimestrialisé les
données annuelles disponibles à l'aide de l'algorithme de
Golstein et Kahn (1976). Deux types d'analyse ont été faits.
D'abord l'analyse descriptive au cours de laquelle nous avons produit les
statistiques et les courbes des différentes variables en jeu. Ensuite
l'analyse explicative qui a permis d'analyser successivement la
saisonnalité et la stationnarité des variables, d'estimer un
modèle ARDL et d'évaluer les effets à court et à
long termes après avoir testé la cointégration de ces
variables grâce à la méthode de Pesaran, Shin et Smith
(2001). Des résultats obtenus, il ressort que la superficie et les prix
aux producteurs ont des effets positifs à court et à long termes
sur la production de l'igname dans le département du Borgou. La
croissance démographique et la hauteur des pluies par contre n'ont pas
des effets significatifs sur la production de l'igname du Borgou à court
terme. Ces résultats s'inversent dans le temps : à long
terme, la croissance démographique et la hauteur des pluies affichent
des effets significativement positifs.
Mots clés : Igname, production,
ARDL, cointégration, algorithme, trimestrialisation
2 Abstract
The purpose of this study is to analyze the determinants of
yam production in the Borgou department in Benin. The data used for this study
jointly cover the period from 2010 to 2018 and come from the Direction of
Agricultural Statistics (DSA) and the National Institute of Statistics and
Economic Analysis (INSAE). Due to a lack of observations required for
econometric analysis, we have quartered the annual data available using the
algorithm of Golstein and Kahn (1976). Two types of analysis were done. First,
the descriptive analysis during which we produced the statistics and curves of
the different variables involved. Then the explanatory analysis that made it
possible to successively analyze the seasonality and stationarity of the
variables, to estimate an ARDL model and to evaluate the short and long run
effects after having tested the cointegration of these variables using the
method of Pesaran, Shin and Smith (2001). The results obtained show that the
area and producer prices have positive short and long run effects on the
production of yams in the Borgou department. Population growth and the height
of the rains, on the other hand, have no significant effects on the production
of Borgou yam in the short run. These results are reversed over time : in
the long run, population growth and the height of the rains show significantly
positive effects.
Keywords: Yam, production, ARDL,
cointegration, algorithm, quarterly
3 INTRODUCTION
Au Bénin, il continue d'exister malgré
l'autosuffisance alimentaire globale constatée, quelques zones à
risque d'insécurité alimentaire. Bien que le Plan
Stratégique de Relance du Secteur Agricole(PSRSA) adopté en 2008
ait pris en compte l'igname dans le lot des treize filières porteuses de
l'agriculture, les politiques agricoles pour assurer la sécurité
alimentaire sont généralement axées sur le manioc et les
céréales en particulier le maïs. Ces cultures ont longtemps
et continuent de faire parties des préoccupations des institutions
nationales de recherche ainsi que des services de vulgarisation agricoles. Mais
l'igname jusque-là, n'a jamais ou presque jamais figurée parmi
les préoccupations réelles de l'Etat béninois aussi bien
dans sa politique agricole que dans sa stratégie de
sécurité alimentaire, et pourtant nul n'ignore le rôle
traditionnel que joue l'igname dans l'alimentation notamment dans la
sécurité alimentaire et sa forte insertion dans l'économie
marchande (MAEP, 2016).
L'igname constitue pourtant l'une des cultures
vivrières les plus importantes du Bénin. Sa production nationale
a été estimée à 3 191 385 tonnes au cours de la
campagne 2014-2015. Cette importante quantité fait du Bénin le
quatrième producteur mondial après le Nigéria, la
Côte d'Ivoireet le Ghana, et de l'igname la seconde culture
vivrière la plus importante au plannational juste après le manioc
(Padonou, 2011). Sur le plan économique, il se développe suite
à l'augmentation de la demande de ce produit par la création d'un
marché intérieur principalement dans la ville de Cotonou qui
offre un excellent débouché pour la production nationale (MAEP,
2016), le commerce de l'igname indépendamment de l'appui de l'Etat. En
plus de ces facteurs extérieurs de la filière et qui limitent le
développement de la culture de l'igname, sa production est aussi
handicapée par des contraintes endogènes. L'igname est en effet
une culture très exigeante que ce soit en main d'oeuvre, en terre
fertile et matériel de plantation pour la reconduction de la culture
(INRAB, 2001).
Cette situation n'épargne guère le
département du Borgou confronté à l'épuisement des
terres dû lui-même à la disparition des jachères de
longue durée dont les sols encore riches en matières organiques
sont favorables à l'igname. De même, on note dans la zone une
quasi-absence de nouvelles défriches pour la production de l'igname
à cause de l'épuisement des sols et de la pression
démographique très élevée. Les paysans compensent
le recul de ces cultures par des cultures de soja, d'arachide, de maïs, de
manioc et du coton qui occupent un vaste espace.
Le département du Borgou est situé dans la
partie septentrionale, à l'est. Il est limité au Nord par le
département de l'Alibori, au Sud par les départements des
collines et de la Donga, à l'Est par la République
Fédérale du Nigéria, et à l'Ouest par le
département de l'Atacora. Il s'étend sur une superficie de
25 856 km² (23% du territoire national) dont 13 962 km² de
terres cultivables (54% de la superficie totale du département).
Administrativement, le département du Borgou est subdivisé en
huit (8) communes. Il s'agit de Kalalé, N'dali,
Pèrèrè, Nikki, Sinendé,
Bembèrèkè, Parakou et Tchaourou. Ces communes sont
subdivisées en quarante-trois (43) arrondissements et trois cent
dix(310) villages et quartiers de ville.
Le département du Borgou bénéficie du
climat de type soudanien avec une saison sèche et une saison des pluies.
La pluviométrie annuelle varie entre 900 et 1 300 mm par an. La saison
des pluies commence en avril et dure sept (7) mois environ. La
température moyenne annuelle s'établit autour de 26°C avec
un maximum de 35°C en mars et redescend aux environs de 23°C en
décembre-janvier. L'humidité relative varie entre 30 et 70%. Les
principaux types de sols rencontrés dans ce département sont
surtout les sols ferrugineux tropicaux, des sols ferralitiques, des sols
sablonneux argileux ou argilo sableux et les sols granito gneissiques à
caractère très varié. Sur ces sols sont
développées, presque dans toutes les communes du
département, trois principales cultures à savoir : l'igname,
le maïs et le soja. La végétation du Borgou est une savane
à physionomie diversifiée où la densité des arbres
diminue vers le Nord. On y distingue quatre (4) types de
végétation qui se rencontrent dans toutes ces communes : la
savane herbeuse, la savane arborée et arbustive, la savane boisée
et la forêt galerie.
La population du département du Borgou est
passée de 724 171 habitants en 2002 à 1 214 249 habitants en
2013, dont 607 013 hommes contre 607 236 femmes (RGPH4, 2013). C'est un
département à fort taux de croissance : 4,68% contre 3,52%
pour le niveau national et un poids démographique de 14% selon le RGPH4.
Le Borgou est un département fortement agricole car environ 66% de sa
population s'occupe de l'agriculture répartie en 83 275 ménages
de type agricole. Les groupes sociolinguistiques les plus rencontrés
sont : les Bariba et apparentés 37,6%, les Peulh ou Peul dans une
proportion de 33,0% et dans une moindre mesure les Gua ou Otamari et
apparentés 7,6%.
Malgré les potentialités agro-écologiques
importantes dont dispose le département du Borgou, la production de
l'igname semble ne pas donner les résultats escomptés de
façon récurrente. Les prix aux producteurs, les faibles
précipitations, la forte température sont-ils les facteurs qui
inhibent la production de l'igname dans cette zone du Bénin ?
Pour répondre à cette préoccupation et
dans la perspective de mieux connaître et de faire connaître la
filière igname pour relever le défi de la sécurité
alimentaire, il est indispensable de mener une étude sur les facteurs
influençant la production d'igname.
Intitulé « Etude des
déterminants de la production de l'igname dans le département du
Borgou/Bénin », le présent mémoire
s'articule autour de trois (3) chapitres. Le premier chapitre présente
le cadre institutionnel de l'étude ; le deuxième chapitre
porte sur le cadre théorique et méthodologique. Le
troisième quant à lui, est consacré à la
présentation et à l'interprétation des
résultats.
CHAPITRE 1
Cadre institutionnel de l'étude
4 CHAPITRE 1 : CADRE INSTITUTIONNEL DE L'ETUDE
Ce chapitre présente le cadre institutionnel de la
Direction de la Statistique Agricole (DSA), structure d'accueil de notre stage.
Il est reparti en deux sections. La première section aborde la
présentation de la DSA et la deuxième se réfère au
déroulement de notre stage.
4.1.1 1.1. Présentation de la Direction de la
Statistique Agricole (DSA)
4.1.2 1.1.1. Bref historique de la DSA
La Direction de la Statistique Agricole (DSA), placée
sous la tutelle du Ministère de l'Agriculture, de l'Elevage et de la
Pêche (MAEP), a été créée par
l'arrêté n°013/MAEP/DC/SGM/DRH/SA du 27 janvier 2014 portant
attributions, organisation et fonctionnement de la DSA. Devenue
opérationnelle le 03 février 2014 par l'arrêté
n°022/MAEP/DC/SGM/DRH/SA, elle fait partie des sept (07) directions
techniques que compte la Direction Générale du
Développement Agricole, de l'Alimentation et de la Nutrition (DGDAN).
Depuis sa création, la DSA a connu deux directeurs dont l'actuel est Dr
Ayi Yves Césaire AJAVON.
4.1.3 1.1.2. Mission et attributions de la DSA
La Direction de la Statistique Agricole, conformément
aux dispositions de l'article 63 du décret n°2016-422 du 20 juillet
2016 portant attributions, organisation et fonctionnement du Ministère
de l'Agriculture, de l'Elevage et de la Pêche, a pour mission de
constituer une base informationnelle durable permettant d'orienter les
décisions et de mesurer l'impact des actions pour le
développement agricole et rural. Elle assure pour l'ensemble du
ministère et en relation avec les directions techniques de la DGDAN et
la Direction de la Programmation et de la Prospective (DPP), la conception, la
réalisation et le suivi de toutes les actions de collecte, de
traitement, d'analyse et de diffusion des statistiques dans le domaine de la
production végétale, de l'élevage et de la pêche. A
ce titre, elle est chargée entre autres de :
ü Réaliser des enquêtes et recensements pour
obtenir des données de référence fiables sur le secteur
agricole et l'alimentation ;
ü Assurer la tenue des statistiques agricoles de
production, de transformation et de commercialisation ;
ü Concevoir un système d'information
intégré des statistiques et connaissances, l'actualiser et le
diffuser auprès des acteurs publics et privés ;
ü Assurer pour l'ensemble du ministère, la mission
de centralisation, de synthèse et d'analyse des informations sur le
secteur agricole et rural ;
ü Elaborer des normes statistiques et une
présentation type par secteur d'activités, par département
et par commune, des données statistiques, en collaboration avec les
autres administrations compétentes ;
ü Assurer la collecte des statistiques agricoles,
alimentaires, nutritionnelles et rurales ;
ü Participer à la surveillance de la situation
alimentaire, nutritionnelle et à l'identification des zones à
risque ;
ü Gérer une banque de données agricoles
nationales ;
ü Assurer la mise à jour et la fiabilité
des statistiques agricoles et alimentaires ;
ü Réaliser les études statistiques et
économiques dans les domaines agricole et rural ;
ü Elaborer des comptes économiques du secteur
agricole ;
ü Publier périodiquement les statistiques
agricoles, alimentaires et nutritionnelles ;
ü Apprécier les méthodologies à
utiliser pour toutes les autres structures dans le cadre des études
statistiques et économiques dans le secteur agricole ;
ü Animer les activités du Système National
Intégré de Statistiques Agricoles (SNISA) ;
ü Animer le système d'information du secteur
agricole ;
ü Représenter le secteur au sein du Conseil
National de la Statistique et dans les réunions nationales et
internationales ;
ü Promouvoir l'activité statistique au sein des
structures du MAEP et des partenaires agréés ;
ü Vulgariser les lois statistiques au niveau du secteur
agricole.
4.1.4 1.1.3. Organisation administrative (environnement
interne) de la DSA
La Direction de la Statistique Agricole a pour mission de
concevoir, de réaliser et de suivre toutes les actions de collecte, de
traitement, d'analyse et de diffusion des statistiques dans le domaine de
l'agriculture, de l'élevage et de la pêche. Dans l'accomplissement
de cette mission, la DSA dispose d'une équipe pluridisciplinaire
composée d'Ingénieurs Statisticiens Economistes, d'Economistes,
d'Ingénieurs des Travaux Statistiques, de Cartographes, d'Agronomes,
d'Informaticiens (analystes-programmeurs, programmateurs, pupitreurs),
d'Attachés des services administratifs, de Contrôleurs de services
financiers et de Secrétaires adjoints des services financiers. La
gestion de carrière de cette suite d'Agents Permanents de l'Etat et
d'Agents Contractuels est assurée par le Service Administratif et
Financier conformément aux lois en vigueur. La DSA comprend six (06)
services qui sont :
ü Le Secrétariat (Se) ;
ü Le Service Administratif et financier (SAF) ;
ü Le Service des Statistiques et Enquêtes de
Production Végétale (SSEPV) ;
ü Le Service des Statistiques et Enquêtes de
Production Animale (SSEPA) ;
ü Le Service des Statistiques et Enquêtes de
Production Aquacole (SSEPA) ;
ü Le Service du Traitement, de l'Information et des
Publications (STIP).
Les chefs de ces services sont appuyés dans l'exercice
de leurs fonctions par des chefs Division et des Collaborateurs.
4.1.5 1.1.4. Macro environnement (environnement externe) de la
DSA
Le macro-environnement désigne l'ensemble des forces
sociétales qui s'imposent à la DSA. On distingue :
l'environnement juridique, l'environnement économique, l'environnement
démographique et l'environnement technologique.
· Environnement juridique
Il regroupe les dispositions et les lois propres à la
DSA
· Environnement économique
C'est l'ensemble des enquêtes et recensements
réalisés par la DSA pour obtenir des données de
référence fiables sur le secteur agricole. Plusieurs structures
du MAEP sollicitent l'aide de la DSA pour la collecte de leurs informations.
· Environnement démographique
Pour la collecte des données sur le terrain, la DSA
procède au recrutement des agents enquêteurs. Ce recrutement se
fait suivant plusieurs critères à savoir : le lieu de
résidence, la ou les langues parlées et la disponibilité.
La direction exige des agents de résider sur les lieux de
déroulement de l'enquête, de comprendre et de savoir parler la
langue de la région dans laquelle ils sont affectés.
· Environnement technologique
L'environnement technologique de la DSA évolue et
permet de réaliser la collecte et le traitement des données
grâce à l'usage des machines de nouvelle génération
et des logiciels statistiques tels que Excel, Cspro, Stata, Eviews, SPSS, etc.
L'usage des smartphones dans les enquêtes avec la plateforme AKVO Flow,
l'existence d'une salle informatique et la formation sur les logiciels
existants, permettent d'obtenir des résultats fiables.
4.1.6 1.2. Déroulement du stage
Suite à notre demande de stage académique de
trois (3) mois en date du 24 septembre 2019, adressée au Directeur de la
Statistique Agricole, une autorisation nous a été
accordée. Ainsi, du 28 Octobre 2019 au 28 janvier 2020 nous avons
passé trois (3) mois à la Direction de la Statistique Agricole en
qualité de stagiaires académiques dans une ambiance conviviale,
professionnelle et instructive. Au cours de ce séjour, nous avons
noué d'excellentes relations avec le personnel et tous les stagiaires
professionnels de la DSA. Toutes les fois que nous avions eu des
préoccupations, nous avons, la plupart du temps
bénéficié de l'assistance de certains cadres de cette
institution. Nous avons par ailleurs approfondi nos connaissances
antérieures et acquis de nouvelles notions. En effet, sous l'impulsion
des chefs services en général et du Chef Service des Statistiques
et Enquêtes de Production Végétale (C/SSEPV) en
particulier, nous avons amélioré notre niveau dans l'utilisation
de deux logiciels de traitement de données dont SPSS et Excel. En somme,
la DSA nous a offert un cadre idéal de travail pour l'application de nos
connaissances théoriques acquises en classe et surtout a facilité
notre insertion progressive dans la vie professionnelle.
Cependant, nous avons rencontré une difficulté
particulière au cours de ces trois mois passés à la DSA.
Il s'agit de l'absence d'une prise électrique dans l'espace où
nous étions installés.
CHAPITRE 2
Cadre théorique et méthodologique de
l'étude
5 CHAPITRE 2:CADRE
THEORIQUE ET METHODOLOGIQUE DE L'ETUDE
Ce chapitre présente le cadre théorique et
méthodologique de l'étude à travers l'énoncé
du problème, l'intérêt de l'étude, les objectifs et
les hypothèses de recherche, la revue de littérature et
enfin la méthodologie.
5.1.1 2.1. Enjeux de l'étude
5.1.2 2.1.1. Problématique
· Enoncé du problème
L'agriculture est le socle de la plupart des économies
en Afrique subsaharienne. Au Bénin, en 2017, elle a contribué
à environ 20% du PIB, à plus de 50% aux emplois, à 75% aux
recettes d'exportation (EEAS, 2018). Sur une superficie totale de 11,47
millions d'hectares, 2,6 millions d'hectares représentent les terres
cultivables. L'agriculture vivrière contribue et surtout assure la
sécurité alimentaire. C'est le secteur agricole dont la
production n'est destinée ni à l'industrie agroalimentaire ni
à l'exportation ; elle sert essentiellement à la
consommation des producteurs eux-mêmes (Diagne et al., 2004).
De part sa production en igname, le Bénin occupe la
quatrième place après le Nigéria, la Côte d'Ivoire
et le Ghana avec une production annuelle estimée à 4% de la
production totale de la ceinture « yam belt » (Baco, Biaou
et Lescure, 2007a). C'est le deuxième produit vivrier après le
maïs et reste l'aliment de base des populations du centre et du nord du
pays (Auriole et Aboudou, 2006). Selon l'INSAE (2018), deux millions sept cent
trente-neuf mille quatre-vingt-huit (2 739 088) tonnes de tubercules
d'ignames ont été produites en 2012. Seulement 200 tonnes ont
été exportées principalement vers le Gabon, la
Géorgie et le Royaume-Unis. Cela montre que l'igname est un tubercule
très prisé par les populations, surtout dans la partie
septentrionale et centrale du pays. Pour certaines villes du pays comme
Savalou, la consommation de la nouvelle igname fait office d'une
célébration grandiose qui réunit les différents
groupes sociaux de la localité et d'ailleurs.
Le département du Borgou est le grenier national de
l'igname avec une production moyenne d'environ 884 928 tonnesdepuis la
campagne 1995-1996 (DSA/MAEP, 2018). En effet, le département du Borgou
est majoritairement composé de l'ethnie Bariba qui produit et a le
monopole de plus de variétés d'igname que les autres ethnies
(Baco et al.,2004). La production de l'igname,dans le Borgou, a atteint 1 446
128 tonnes pendant la campagne 2013-2014,soit 45,51% de la production nationale
de l'igname. Cependant, cette performance réalisée n'a pas pu
être maintenue pendant les campagnes suivantes. En effet, au cours de la
campagne 2014-2015, la production de l'igname dans le Borgou a connu une chute
de 8 187 tonnes par rapport à la campagne précédente.
La régression devient plus grande pendant la campagne de
2015-2016 ; soit 471 163 tonnes en moins par rapport à la
production annuelle de 2013-2014. Au cours de la campagne 2016-2017, on note
une augmentation de 70 750 tonnes par rapport à la campagne
précédente. On constate à cet effet que la production de
l'igname dans le Borgou n'est pas stable : elle évolue de
façon sinusoïdale.
Vu l'importance que revêt ce tubercule dans la
cohésion des groupes sociaux et dans l'affirmation identitaire des
ethnies du Bénin et surtout des ethnies du Borgou et compte tenu de
l'évolution en dent de scie de cette culture, une étude sur les
facteurs de la production de l'igname s'avère indispensable. C'est
justement dans cette logique que s'inscrit le thème de notre recherche
: Etude des déterminants de la production de l'igname dans le
département du Borgou/Bénin.
Pour répondre à cette préoccupation, il
s'agira pour nous d'apporter des éléments de réponses aux
questions ci-après :
Existe-t-il une relation entre la superficie emblavée
et la production de l'igname ?
La hauteur des pluies a-t-elle un impact sur la production de
l'igname dans le Borgou ?
La production de l'igname est-elle influencée par la
croissance démographique en milieu rural ?
· Intérêt de l'étude
L'igname joue aujourd'hui un rôle capital dans les
habitudes culinaires des populations du Bénin. Les mets issus de
l'igname (igname pilée, ignames frites, le wassa-wassa, la pâte de
cossettes d'igname, ...) sont consommés et beaucoup
appréciés par les populations sur toute l'étendue du
territoire national. Les multiples efforts des autorités locales et
gouvernementales pour promouvoir la filière igname et accroitre sa
productivité sont parfois limités, faute d'informations utiles
sur cette filière. Ainsi, la présente étude permettra de
déterminer les facteurs qui influencent la production de l'igname. Les
résultats de notre étude permettront à l'Etat et aux
autorités communales de disposer d'un certain nombre d'informations sur
ces facteurs, afin d'engager des actions spécifiques en faveur de la
filière igname, visant à améliorer la productivité
agricole et par ricochet, accroitre le PIB et contribuer à la
sécurité alimentaire.
5.1.3 2.1.2. Objectifs et hypothèses de recherche
· Objectifs de recherche
L'objectif général de cette étude est
d'analyser les déterminants de la production de l'igname dans le
département du Borgou au Bénin. De façon
spécifique, il s'agira de :
ü évaluer l'effet de la superficie emblavée
sur la production de l'igname ;
ü déterminer l'impact des fluctuations
pluviométriques sur la production de l'igname et
ü estimer l'influence de la croissance
démographiquesur la production de l'igname dans le département du
Borgou.
· Hypothèses de recherche
Sur la base de ces facteurs et compte tenu des objectifs
spécifiques que nous avons énumérés ci-haut, nous
formulons les hypothèses suivantes :
Hypothèse 1 : une hausse de la
superficie emblavée entraine une augmentation de la production de
l'igname dans le Borgou.
Hypothèse 2 : les
précipitations annuelles ont un impact sur la production de l'igname.
Hypothèse 3 : la croissance
démographique du Borgou a un effet significatif sur sa production de
l'igname.
5.1.4 2.2. Revue de littérature et
méthodologie
5.1.5 2.2.1. Définitions, Revues théorique et
empirique
Les ignames, de la famille des Dioscoreaceae, est un tubercule
très varié et cultivé dans toutes les régions
tropicales du globe terrestre. Le mot « igname » se traduit
par « Yam » en anglais. Cela vient d'une racine africaine
« nyam » qui signifie manger. En Bariba igname a pour
appellation « tassou », en Dendi,
« doundou ». L'igname est produite de façon
extensive dans trois régions du monde : L'Afrique occidentale, les
Caraïbes et l'Asie du Sud-Est, à l'exception de la Chine populaire
(PDRT, 2003). Quatre-vingt-quinze pour cent (95%) de la production mondiale
provient de l'Afrique occidentale et particulièrement de la zone
comprise entre la Côte d'Ivoire et le Cameroun (Mémento de
l'Agronome, 1993). Les pays de l'Afrique subsaharienne détiennent
95% des superficies mondiales et interviennent à hauteur de 95,8% des
superficies mondiales de l'igname. L'Afrique de l'Ouest, y compris le
Bénin et le Nigeria, assurent plus de 90% de la production mondiale
d'igname (Terry et al., 1997).
L'igname est une tige grimpante, volubile dextrorse
(Hénin, 1976). Ce sont des tiges souterraines, renflouées,
remplies de matières de réserves. Ses feuilles sont cordiformes.
C'est une plante monoïque à fleurs unisexuées (Simmons,
1988). Les tubercules d'ignames de forme variable, ovoïde à
oblongue, parfois aplatie ou en forme de massue allongée, peuvent
atteindre 1m de longueur et leur poids, généralement de 3
à 5 kg, aller jusqu'à 15 kg. La peau est
généralement jaune mais peut être presque blanche ou plus
foncée de brunâtre à noirâtre.
La culture de l'igname exige des régions à
pluviométrie importante, généralement supérieur
à 1500 mm, des températures moyennes de 23 à 30° C
avec une Saison sèche distincte ne dépassant pas cinq (5) mois et
une saison pluvieuse d'au moins cinq (5) mois (PDRT, 2003). L'igname exige des
sols sablo-argileux au pH de 5 à 7, riches notamment en potasse et en
matières organiques, profonds, ameublis et perméables (PDRT,
2003).
La production de l'igname est un long processus qui commence
traditionnellement par le défrichage des savanes boisées par
brûlis en préservant les essences utiles telles que le
karité, le néré. Très intensive en main-d'oeuvre,
la culture de l'igname a un cycle végétatif d'environ 200
à 350 jours selon les variétés. En effet, il existe
plusieurs variétés d'igname. Les noms locaux des
variétés sont différents d'une variété
à l'autre, d'une région à l'autre pour la même
variété. Ainsi, la variété
« Lamboko » désignée par les populations du
Zou, Collines, Ouémé, Plateau, prend la dénomination
« Danwaré » dans les régions du Borgou et de
l'Alibori. Ces noms, sous forme proverbiale, traduisent le rôle social ou
économique que joue la plante ou le nom de celui qui a introduit la
variété dans le milieu (PDRT, 2003). Dans le département
du Borgou, les variétés d'igname sont : Moroko,
Danwaré, Kokoro, Susinin, Asuru, Tokokorou,Sakunu, ....
Le tubercule d'igname se développe au fond d'une butte
de petite ou de grande taille selon la variété d'igname. PDRT
(2003) a montré que dans le département du Borgou, certains
paysans font des champs d'igname avec des buttes de grande taille dans les
bas-fonds : cette technique a été introduite dans le Borgou
par les migrants venus de l'Atacora où, par manque de terres fertiles,
les paysans sont obligés d'utiliser ce mode de culture exigeant en
main-d'oeuvre.
En démographie, la croissance (démographique)
est l'évolution de la taille d'une population donnée.Le taux
d'accroissement démographique décrit le rythme de cette
évolution c'est-à-dire l'augmentation ou la diminution. La
croissance démographique provoque une hausse des besoins humains dont la
satisfaction a un impact sur l'environnement et sur la production des produits
agricoles. La croissance continue de la population, avec l'augmentation de la
concentration démographique, la dégradation environnementale et
l'épuisement des ressources qui s'ensuivent, pourraient réduire
la productivité de l'agriculture (Nerlove, 1993).
Nerlove fut le premier à développer en 1956 et
1958 une théorie que l'on connaît sous le nom de « the
Nerlovian models of supply response » qui a permis d'expliquer la
réaction des producteurs agricoles américains face aux
changements perpétuels des prix des récoltes, des politiques
macroéconomiques et bien d'autres facteurs. Pour élaborer sa
théorie, Nerlove part de deux constats classiques. Les producteurs
réagissent par rapport aux prix actuels sur le marché.
Habituellement, les prix observés sont les prix du marché ou les
prix effectifs des producteurs après la récolte alors que les
décisions de production doivent être basées sur les prix
escomptés que des agriculteurs projettent plusieurs mois avant la
récolte. En raison du décalage temporaire qui intervient dans le
processus de production agricole, modéliser la formation des
anticipations est ainsi une importante question pour analyser l'offre du
secteur agricole. Les quantités observées peuvent différer
des quantités désirées en raison du retard d'ajustement
dans la réallocation des facteurs. Quand le prix du produit change,
plusieurs années peuvent s'écouler avant que les producteurs ne
puissent ajuster leur production ordinaire désirée au nouveau
prix.
Les travaux de Nerlove (1956) ont joué un rôle
prépondérant et ont apporté un souffle nouveau à la
modélisation de l'offre du secteur agricole face aux risques y
afférents et bien d'autres facteurs (tels que les politiques
macroéconomiques, les politiques commerciales, les changements
technologiques, les aléas climatiques, etc.). Les études
empiriques de ces modèles ont permis aux agroéconomistes (surtout
américains) de développer les outils adéquats de
politiques agricoles. Ceci a considérablement amélioré le
rôle du secteur agricole dans le développement économique
et a mis en relation l'Etat et les producteurs à travers les politiques
macroéconomiques et commerciales.
Cependant, la réaction de l'offre du secteur agricole
aux mouvements des prix a été l'objet de longues et vigoureuses
discussions se référant au traitement classique de
l'élasticité de l'offre de long terme de Nerlove (1956) pour le
blé, le coton, et le maïs aux Etats-Unis (Askari etCumming,
1976 et 1977). L'estimation des élasticités d'offre (de
court et long terme) varie largement d'une culture à l'autre, et d'une
région à l'autre. Ceci a conduit certains auteurs à dire
que les modèles « Nerloviens » sont inadéquats pour
décrire la réaction de longterme. Boussard et Saïd (2000)
soulignent que la politique agricole de l'ajustement structurel de long terme
peut ne pas être discernable avec l'analyse de la régression,
particulièrement dans les modèles avec un retard structurel comme
c'est le cas dans les modèles Nerloviens.Zonon (1996) confirme que des
prix agricoles très bas ne permettent pas une incitation et une
motivation des agriculteurs à produire davantage. Selon lui, les
producteurs réagissent plutôt à une augmentation des prix.
Le prix est considéré comme un facteur déterminant dans la
décision des paysans et dans l'offre agricole.
Les études de l'offre agricole dérivent
essentiellement des travaux de Nerlove (1956) sur la réaction de l'offre
des paysans américains face aux prix sur les marchés agricoles.
Le modèle de Nerlove est fondé sur les prix anticipés et
l'ajustement des superficies emblavées. Le modèle montre que les
ménages agricoles (producteurs) sont réceptifs et
réagissent positivement au prix. Des études dans les pays en voie
de développement montrent que les paysans intègrent toujours les
préoccupations de prix dans la production agricole et les revenus issus
de cette production (Bond, 1983 ; Koffi-Tessio, 2000 et Yotopoulos, 1973).
Ce résultat semble s'opposer à celui de plusieurs études
et auteurs, qui ont plutôt montré l'influence des autres facteurs
autres que les prix (Katembo, 2004). Celui-ci souligne que le débat sur
les incitations de l'offre agricole est partagé entre deux courants de
pensée : les défenseurs des facteurs prix (pricistes) et les
défenseurs des facteurs non prix (structuralistes). Les pricistes
pensent que l'accroissement des prix au producteur et la dévaluation
constituent des mesures incitatives àla production. Lipton (1987),
cité par Adimi et Dairo (2014) est l'un des pricistes qui pense que
cette politique est une solution à la crise agraire en Afrique (Kouakou,
2009 ; Nyemecketal, 2009). Ils concluent donc que, même si le
crédit permet aux producteurs d'accroître leurs
opportunités d'investir dans les intrants modernes, il n'y a aucune
garantie que ceux-ci soient utilisés de façon efficiente pour
accroître la production. Il existe une relation positive entre la
production et le niveau d'éducation. Quant aux études relatives
à la relation entre l'expérience et la production, plusieurs
auteurs comme Timmer (1971) aux Etats Unis, trouvent une relation positive mais
non significative entre la production et l'expérience du chef de
l'exploitation.
Idrissa (2007) montre que la pluviométrie est l'un des
déterminants pour les productions céréalières et
vivrières. L'impact des variations pluviométriques est lié
au fait qu'elles peuvent hypothéquer la réussite des
récoltes. Il notifie par ailleurs, que la régularité des
précipitations est souvent la garantie d'une bonne récolte plus
que ne l'est le total de la pluviométrie. Dans cette même
étude, il montre qu'une forte variation de la pluviométrie est
souvent responsable du déficit de la production agricole.
5.1.6 2.2.2. Méthodologie de
collecte des données et Traitement
5.1.7 2.2.2.1. Collecte des
données
En statistique, la pertinence des analyses repose sur la
qualité et la fiabilité des données collectées. Au
Bénin, ces données sontdifficiles à collecter etla plus
part du temps, elles sont quasi-inexistantes. Les données sur la
production de l'igname, la superficie emblavée et la hauteur des pluies,
consacrées à l'analyse économétrique faite dans ce
mémoire, initialement annuelles, couvrent la période de 2010
à 2018, ce qui fait neuf (09) observations. Pour plus de pertinence du
modèle économétrique, il a fallu procéder à
une trimestrialisation afin de disposer de plus d'une trentaine d'observations.
Cette trimestrialisation a été réalisée à
l'aide de l'algorithme de Goldstein et Kahn (1976). Ce traitement
d'épuration des données est bien entendu susceptible d'introduire
un biais dans les résultats. Cependant, toutes choses étant
égales par ailleurs, les estimations ont une marge d'erreur acceptable
pour la qualité de l'analyse faite dans cette étude.
Les données sur les prix aux producteurs couvrant la
période de 2010 à 2018 sont des données mensuelles. Nous
avons donc pu obtenir les données trimestrielles en calculant la moyenne
pour chaque trois (03) mois.
La variable « taux de croissance
démographique » a été exceptionnellement
traitée. Le RGPH a été réalisé en 1979,
1992, 2002 et 2013 ; ce qui fait que nous ne disposons pas de
données sur les années transitaires. De 2010 à 2012, nous
avons utilisé les données issues des projections
révisées du RGPH3. Ces projections ont été
révisées en 2008 après l'Enquête
Démographique et de Santé du Bénin, 3ème
édition (EDSB-III) réalisée en 2006. La population de 2013
est celle issue des résultats définitifs du RGPH4. Les
données de2014 à 2018 sont les projections faites à base
du RGPH4. Nous avons ensuite calculé le taux annuel de croissance
démographique avant de faire la trimestrialisation.
De façon globale, les données collectées
sont des séries temporelles de 2010 à 2018 sur la production de
l'igname, la superficie emblavée, le prix aux producteurs, les
précipitations annuelles et le taux de croissance
démographique.
Le tableau suivant résume les informations sur les
données brutes :
Tableau 1 : Informations sur les
données brutes
|
Variables
|
Unité
|
Abréviation
|
Source
|
|
Production de l'igname
|
Tonnes
|
Prod_ign
|
DSA
|
|
Superficie emblavée
|
Hectare
|
Sup_emb
|
DSA
|
|
Prix aux producteurs
|
F CFA
|
Prix_prod
|
INSAE
|
|
Taux de croissance démographique
|
%
|
Croi_demo
|
INSAE
|
|
Hauteur des pluies
|
mm
|
Haut_Pluie
|
INSAE
|
Source : Etabli par les auteurs, 2020
Algorithme de Goldstein et Kahn (1976)
Considérons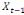 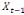 , , 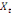 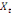 , ,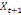 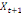 trois observations annuelles successives de la variable X. Si la
fonction quadratique qui passe par ces trois points (cf.
THEOREMED'EUCLIDE) est telle que : trois observations annuelles successives de la variable X. Si la
fonction quadratique qui passe par ces trois points (cf.
THEOREMED'EUCLIDE) est telle que :
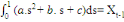 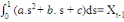 (1) (1)
 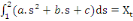 (2) (2)
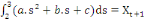 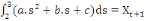 (3) (3)
Alors, on peut déterminer les paramètres a, b et
c, en calculant d'abord les intégrales de (1) à (3), puis en
résolvant le système d'équations suivant :
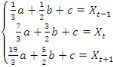 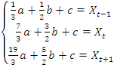 (4) (4)
La résolution de ce système conduit au
résultat suivant :
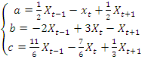 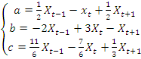 (5) (5)
A partir des valeurs des paramètres de la fonction
quadratique ainsi obtenues, les quatre observations trimestrielles de
l'année t peuvent être calculées en utilisant les formules
d'interpolation suivantes :
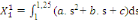 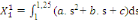 (6) (6)
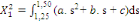 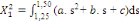 (7) (7)
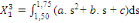 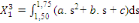 (8) (8)
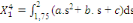 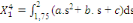 (9) (9)
Les calculs algébriques effectués sur les
expressions (6) à (9) ci-dessus dans lesquelles l'on aurait au
préalable remplacé les paramètres a, b et c par leur
expression de (5), conduisent enfin aux données d'interpolation
trimestrielles suivantes :
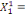 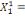 0 ,05468 0 ,05468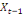 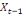 + 0,23438 + 0,23438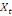 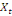 - 0,039067 - 0,039067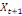 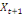 (10) (10)
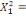 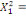 0,00781 0,00781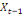 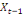 + 0,26563 + 0,26563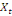 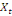 - 0,02344 - 0,02344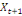 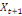 (11) (11)
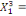 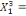 -0,02344 -0,02344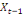 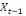 + 0,26562 + 0,26562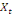 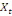 + 0,00781 + 0,00781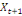 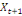 (12) (12)
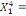 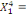 -0,03910 -0,03910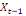 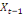 + 0,23437 + 0,23437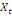 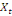 + 0,05469 + 0,05469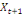 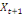 (13) (13)
La série trimestrielle obtenue peut être
ramenée à une série annuelle par sommation des
observations des quatre trimestres de chaque année. En effet,
d'après la relation de Chasles, l'on a :
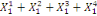 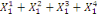 = = 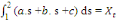 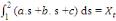 (14) (14)
5.1.8 2.2.2.2. Outils et modèle
d'analyse
Les méthodes utilisées dans cette étude
sont à la fois descriptives et explicatives. Pour décrire
l'évolution des variables, nous employons les méthodes
descriptives. Par contre, pour tester les hypothèses émises, nous
utilisons les méthodes explicatives.
5.1.9 2.2.2.2.1. Méthodes
descriptives
Toutes les variables intervenant dans le cadre de cette
étude sont des séries temporelles. C'est pourquoi, après
avoir donné leurs caractéristiques descriptives (moyenne,
écart-type, variance, ...) et réalisé la boîte
à moustaches, nous avons analysé successivement, à l'aide
du logiciel Excel, l'évolution au cours du temps de la production
d'igname, de la superficie emblavée, des prix aux producteurs, de la
hauteur des pluies, de la température et de la population rurale dans le
département du Borgou.
Boîte à moustaches
La boîte à moustaches, une traduction de Box
& Whiskers Plot, est une invention de TUKEY (1977) pour représenter
schématiquement la distribution d'une variable.
Cette représentation graphique peut être un moyen
pour approcher les concepts abstraits de la statistique, si l'on pratique son
usage sur différents jeux de données.
Le terme spécifique Box & Whiskers
Plot et le terme générique Box Plot recouvrent
une grande variété de diagrammes en forme de boîtes qui se
différencient par leur construction, leurs interprétations, et
leurs usages. E. HORBER qui a effectué des recherches bibliographiques
sur ce thème a repéré une soixantaine de formes et de
constructions différentes.
Dans le cadre de notre étude, nous avons
réalisé les boîtes à moustaches sur eviews 9.
Chacune de ces boîtes comprend :
· les quartiles Q1, Q2 (médiane) et Q3 ;
· les extrémums (minimum et maximum) de la
distribution ;
· la moyenne ;
· les moustaches inférieure et
supérieure ;
· l'extrémité de la moustache
inférieure notée Front.Basse
(Front.Basse=Q1-1,5*(Q3-Q1)) ;
· l'extrémité de la moustache
supérieure notée Front.Haute
(Front.Haute=Q3+1,5*(Q3-Q1))
· l'écart interquartile
Q3-Q1 ;
· les valeurs dites extrêmes, atypiques,
exceptionnelles, (outliers) situées au-delà des frontières
et représentées par des marqueurs (carré, ou
étoile, etc.).
5.1.10 2.2.2.2.2.
Méthodes explicatives
Détection de la saisonnalité
Pour détecter une éventuelle saisonnalité
de chaque série, nous avons procédé d'abord au test de
Buys Ballot qui permet de voir si le modèle de la variable
considérée est additif ou multiplicatif. Pour cela, on
procède à une régression, pour chaque variable, de son
écart-type sur sa moyenne. Si le coefficient de la moyenne n'est pas
significativement différent de zéro (0), on accepte
l'hypothèse d'un modèle additif. Dans le cas contraire, le
modèle est multiplicatif.
Une fois le choix du type de modèle fait, pour
vérifier la saisonnalité de la série, on admet les
hypothèses suivantes :
H0 : Pas de
saisonnalité
H1 :
Présence de saisonnalité
On calcule alors la statistique de Fisher :
F=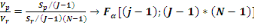 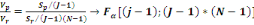
Où 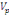 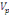 désigne la variance des périodes et désigne la variance des périodes et 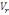 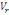 la variance des résidus. la variance des résidus.
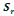 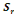 = =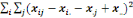 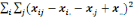
Règle de décision : Si
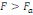 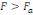 , on rejette l'hypothèse nulle H0 et donc il y a
saisonnalité. , on rejette l'hypothèse nulle H0 et donc il y a
saisonnalité.
Désaisonnalisation
Dans le cas d'une série affectée d'un mouvement
saisonnier, il convient de la retirer préalablement à tout
traitement statistique. Cette saisonnalité est ajoutée à
la série prévue à la fin du traitement afin d'obtenir une
prévision en terme brut.
Les tests de stationnarité
Une série temporelle dont la moyenne (mobile) et/ou la
variance dépendent du temps est dite non stationnaire. Cette non
stationnarité (du type déterministe ou stochastique), si elle
n'est pas traitée (stationnarisation), peut conduire à des
régressions « fallacieuses ». Plusieurs tests aident à
vérifier le caractère stationnaire ou non (existence d'une racine
unitaire) d'une série : test d'Augmented Dickey-Fuller/ADF, test de
Phillips-Perron/PP, test d'Andrews et Zivot/AZ, test Ng-Perron, KPSS,
Ouliaris-Park-Perron, Eliott-Rothenberg-Stock, etc. De tous ces tests, les
trois premiers sont faciles d'application et couramment utilisés. En
fait, le test ADF est efficace en cas d'autocorrélation des erreurs, le
test PP est adapté en présence
d'hétéroscédasticité, et le test AZ est
utilisé pour une série qui accuse une rupture de structure ou
changement de régime identifié de façon endogène.
Dans cette étude, nous avons fait recours aux tests ADF,PP et AZ.
Le modèle Auto Régressif à
Décalage Temporel (ARDL) de Pesaran et al. (2001)
Les modèles « AutoRegressive Distributed Lag/ARDL
», ou « modèles autorégressifs à
retards
échelonnés ou distribués/ARRE » en français,
sont des modèles dynamiques. Ces
derniers ont la particularité
de prendre en compte la dynamique temporelle (délai
d'ajustement,
anticipations, etc.) dans l'explication d'une variable (série
chronologique),
améliorant ainsi les prévisions et
efficacité des politiques (décisions, actions, etc.),
contrairement au modèle simple (non dynamique) dont l'explication
instantanée (effet
immédiat ou non étalé dans le
temps) ne restitue qu'une partie de la variation de la variable
à
expliquer. S'il est soulevé une certaine incertitude en ce qui a trait
à l'ordre réel d'intégration des variables soit à
cause de la présence de ruptures structurelles, soit pour une raison, la
méthodologie ARDL Bound testing et le modèle à correction
d'erreur qui y est dérivé va être utilisé (USAI,
Haïti, 2017). Pesaran et al.(2001)ont défini l'approche Auto
Regressive Distributed Lag (ARDL) en prenant en compte les insuffisances du
modèle VAR. Cette approche a été utilisée dans de
nombreuses études (Wolde Rufael, 2006 ; Squalli, 2007 ;
Akinlo, 2008 ; Odhiambo, 2009 ; Ouedrago, 2010).
Un ARDL est une régression des moindres carrés
contenant des retards de la variable dépendante et des variables
indépendantes. Habituellement, on note ARDL (p, q1, ...,
qk), où p désigne le nombre de retards de la variable
dépendante, qk le nombre de retards de la k-ième
variable explicative. Dans le cadre de notre étude, le modèle
ARDL où chaque variable est supposée stationnaire se
spécifie comme suit :
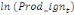 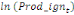 = =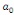 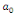 + +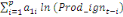 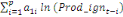 + +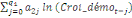 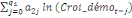 + +
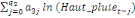 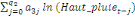 + +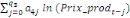 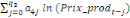 + +
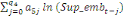 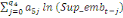 + +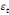 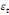 (a) (a)
Par ailleurs, Pesaran et al. (2001) ont
développé une nouvelle approche pour tester l'existence d'une
relation de long terme entre des variables caractérisées par un
ordre d'intégration différent. Il s'agit du test des limites
« bounds tests » pour une relation de long terme dans un
modèle autorégressif à retards échelonnés
(ARDL). A cause de la flexibilité qu'elle offre, cette technique est de
plus en plus utilisée comme alternative aux tests de
cointégration usuels (test de cointégration d'Engle et Granger
(1987) et de Johansen (1988, 1991) en raison de son caractère
contraignant. En effet, le test développé par Pesaran et al.
(2001) ne nécessite pas que les variables du modèle soient
purement I (0) ou I (1).Cette technique est mieux adaptée aux petits
échantillons et offre la possibilité de traiter conjointement la
dynamique de long terme et les ajustements de court terme. On utilise la
statistique de Wald ou la statistique de Fisher pour tester la
significativité de retards des variables en prenant en
considération la contrainte d'un Modèle à Correction
d'Erreur (MCE). L'approche de Pesaran et al. Se fait en plusieurs
étapes.
Dans un premier temps, on estime un Modèle à
Correction d'Erreur (MCE).
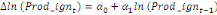 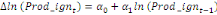 + +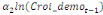 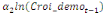 + +
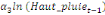 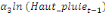 + +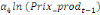 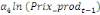 + +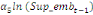 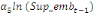
+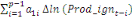 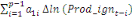 + +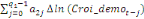 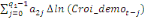 + +
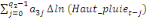 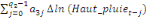 + +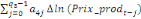 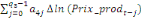
+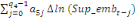 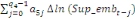 + +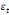 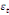 (b) (b)
Où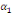 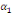 , ,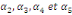 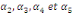 sont les multiplicateurs de long terme ; sont les multiplicateurs de long terme ; 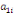 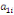 , , 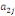 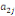 , ,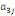 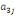 , ,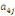 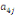 et et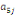 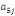 sont les coefficients de la dynamique de court terme ; les
paramètres sont les coefficients de la dynamique de court terme ; les
paramètres  , ,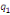 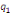 , ,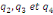 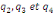 sont les ordres du modèle ARDL et sont les ordres du modèle ARDL et 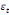 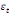 est un bruit blanc non autocorrélé avec est un bruit blanc non autocorrélé avec 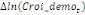 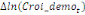 , ,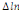 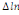 ( (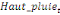 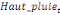 ), ), 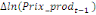 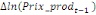 , , 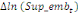 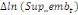 et avec les valeurs retardées de et avec les valeurs retardées de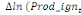 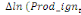 ), ),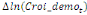 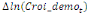 , ,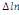 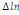 ( (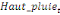 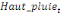 ), ), 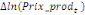 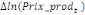 , ,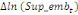 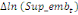 . .
Après avoir vérifié l'absence
d'autocorrélation des résidus, on procède au test de
significativité jointe des multiplicateurs de long terme 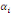 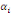 en utilisant le test de Fisher. en utilisant le test de Fisher.
  = =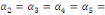 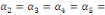 0 (Absence de cointégration) 0 (Absence de cointégration)
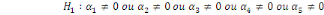 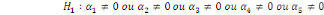 (Présence de cointégration). (Présence de cointégration).
Pesaran et al. (2001) montrent que la statistique
calculée ne suit pas une loi standard.Ils ont simulé deux
ensembles de valeurs critiques pour cette statistique, avec plusieurs cas
(selon qu'on introduit une constante et/ ou une tendance) et différents
seuils. Le premier ensemble correspond au cas où toutes les variables du
modèle sont stationnaires c'est-à-dire I(0) et représente
la borne inférieure ; le second ensemble correspond au cas
où toutes les variables du modèle sont intégrées
d'ordre un I(1) et représente la borne supérieure. Pour conclure
le test, on compare la statistique du test de Fisher aux deux bornes. Si les
F-statistiques calculées se trouvent au-dessus de la valeur critique
supérieure, l'hypothèse nulle d'absence de cointégration
est rejetée. Si les F-statistiques calculées se trouvent
au-dessous de la valeur critique inferieure, le test échoue donc
à rejeter l'hypothèse nulle traduisant une absence de
cointégration. Si les F-statistiques font partie de la bande, alors le
test est non conclusif. Ici nous utiliserons la table des valeurs critiques
proposées par Narayan (2005) pour des tailles d'échantillons
réduits pour plus de précision.
En présence de cointégration, les relations de
long terme sont obtenues par annulation des variables en différences
(Morley, 2006 ; Antonis, Katrakilidis et Persefoni, 2013).
Sur la base de l'équation (b), nous déduisons
qu'elles sont représentées par l'équation :
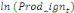 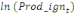 =- =-  - -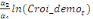 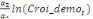 - -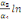 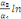 ( (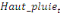 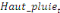 )- )- 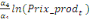 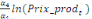
- 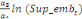 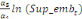 (c) (c)
A partir de cette relation de longue période, le terme
de correction d'erreur (ECT) peut être calculé.
Pour l'équation (c), il est égal à :
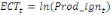 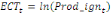 - [- - [-  - -  - -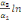 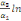 ( (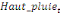 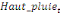 ) )
-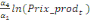 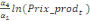 - -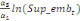 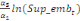 ] ]
L'inclusion de l'ECT retardée d'une période dans
l'équation des effets de court terme permet d'obtenir des estimations
non biaisées et de rendre compte de la vitesse d'ajustement de la
variable dépendante vers sa valeur d'équilibre (Engle et Granger,
1987). En présence de cointégration, les effets de court terme
seront par conséquent examinés sur la base de l'équation
suivante :
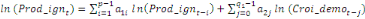 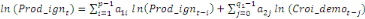 + +
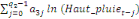 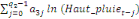 + +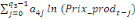 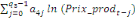 + +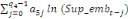 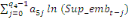
+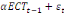 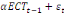 (d) (d)
où 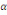 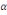 est un coefficient associé au terme ECT et qui
représente, en effet, la vitesse d'ajustement du modèle vers son
équilibre de long terme. Lorsque l'hypothèse de
cointégration est rejetée, les effets ne seront testés que
dans le court terme et les estimations seront basées sur la
modélisation VAR où p sera le retard optimal,
déterminé par de différents critères : est un coefficient associé au terme ECT et qui
représente, en effet, la vitesse d'ajustement du modèle vers son
équilibre de long terme. Lorsque l'hypothèse de
cointégration est rejetée, les effets ne seront testés que
dans le court terme et les estimations seront basées sur la
modélisation VAR où p sera le retard optimal,
déterminé par de différents critères :
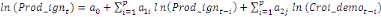 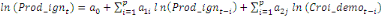 + +
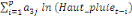 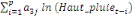 + +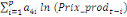 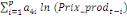 + +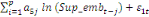 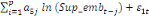
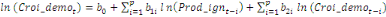 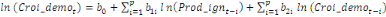 + +
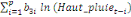 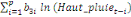 + +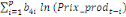 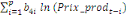 + +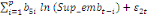 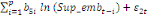
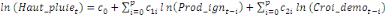 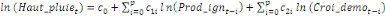 + +
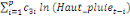 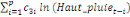 + +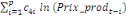 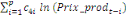 + +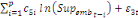 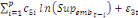
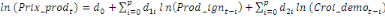 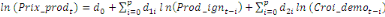 + +
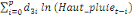 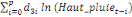 + +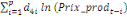 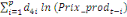 + +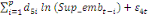 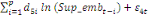
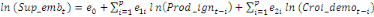 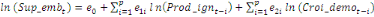 + +
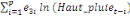 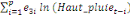 + +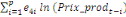 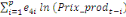 + +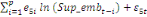 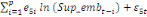
Ce test de cointégration de Pesaran et al. (2001) est
utilisé pour déterminer les relations de long terme entre la
production de l'igname et la population rurale, la hauteur des pluies, le prix
aux producteurs et la superficie emblavée.
Tests de validation ou de robustesse du
modèle
Il s'agit de vérifier notamment que les résidus
du modèle ARDL estimé vérifient les
propriétés requises pour que l'estimation soit valide. Les tests
appropriés sont les tests d'absence d'autocorrélation, de
normalité, d'hétéroscédasticité et de
stabilité.
Vérification des hypothèses
Les hypothèses formulées dans le cadre de cette
étude seront confirmées lorsque les coefficients des variables
considérées du modèle ARDL estimé remplissent
certaines conditions, comme l'indique le tableau suivant :
Tableau 2 : Conditions de confirmation des
hypothèses
|
Hypothèses
|
Conditions
|
Décision
|
|
Hypothèse 1
|
si la probabilité associée au coefficient de la
superficie emblavée est supérieure à 5% et le coefficient
de la superficie emblavée est positif
|
Confirmée
|
|
Hypothèse 2
|
si la probabilité associée au coefficient de la
hauteur des pluies est supérieure à 5%
|
Confirmée
|
|
Hypothèse 3
|
si la probabilité associée au coefficient de la
croissance démographique est supérieure à 5%
|
Confirmée
|
Source : Etabli par les auteurs, 2020
5.1.11 2.3. Limites de l'étude
Pour manque de données sur une longue période,
nous avons dû procéder à une trimestrialisation des
données annuelles de la période allant de 2010 à 2018.
Cela constitue la principale limite de notre étude. L'autre limite
réside dans le fait que nous n'avons pas pu avoir des données sur
la mécanisation agricole et la température qui sont pourtant des
variables pertinentes quand on veut expliquer la production de l'igname.
CHAPITRE 3
Présentation et interprétation des
résultats
6 CHAPITRE 3 :
PRESENTATION ET INTERPRETATIONDES RESULTATS
Ce chapitre présente les résultats des analyses
descriptive et explicative ainsi que les préconisations
opérationnelles qui découlent de la présente
étude.
6.1.1 3.1. Analyse
descriptive
6.1.2 3.1.1. Statistiques
descriptives
Il ressort du tableau ci-dessous que la production de l'igname
est la variable la plus volatile. Elle varie de 182 187 tonnes à 386 950
tonnes avec en moyenne 260 012 tonnes du 1er trimestre 2010 au
4ème trimestre 2018. On constate contrairement à la
production de l'igname, une faible dispersion autour de la moyenne (1,268183)
de la croissance démographique. Aussi, l'on note que les variables
production de l'igname, hauteur des pluies, prix aux producteurs et superficie
emblavée sont normalement distribuées (Prob. Jarque-Bera >
5%), sauf pour la croissance démographique.
Tableau 3 : Statistiques descriptives des
variables
|
|
PROD_IGN
|
CROI_DEMO
|
HAUT_PLUIE
|
PRIX_PROD
|
SUP_EMB
|
|
Mean
|
260012,3
|
1,268183
|
272,0912
|
203,9514
|
17935,16
|
|
Median
|
251821,3
|
0,733656
|
275,0672
|
199,7768
|
17473,75
|
|
Maximum
|
386950,3
|
5,592154
|
316,3175
|
282,5
|
21923,86
|
|
Minimum
|
182187,1
|
0,021462
|
212,6484
|
136,0945
|
13929,75
|
|
Std. Dev.
|
61393,89
|
1,483658
|
29,56342
|
39,58378
|
2275,266
|
|
Skewness
|
0,763329
|
2,295635
|
-0,35542
|
0,186449
|
0,042117
|
|
Kurtosis
|
2,497124
|
6,670777
|
2,215522
|
1,993221
|
2,063988
|
|
Jarque-Bera
|
3,875351
|
51,83154
|
1,681048
|
1,728986
|
1,324822
|
|
Probability
|
0,144038
|
0.000000
|
0,431484
|
0,421265
|
0,515607
|
|
Sum
|
9360443
|
45,65459
|
9795,283
|
7342,251
|
645665,7
|
|
Sum Sq. Dev.
|
1,32E+11
|
77,04341
|
30589,85
|
54840,65
|
1,81E+08
|
|
Observations
|
36
|
36
|
36
|
36
|
36
|
Source : Etabli par les auteurs, 2020
6.1.3 3.1.2. Boîte à
moustaches des variables
Sur la boîte à moustaches de la production de
l'igname, on note que 50% des productions trimestrielles de l'igname sont
inférieures à 251821 tonnes et 50% également de ces
productions sont supérieures à 251821 tonnes. Du premier
trimestre de 2010 au quatrième trimestre de 2018, 25% des productions
sont inférieures à 211156 tonnes. La moitié (50%) des
productions trimestrielles de l'igname est comprise entre251821 et 267518
tonnes. Le dernier quart (25%) de ces productions est supérieur à
267518 tonnes. On note aussi des productions atypiques (outliers) dont les
valeurs excèdent 350 000 tonnes.
Toutes les valeurs atypiques de la production de l'igname sont
situées au-delà de la frontière haute (352061). Aucune
valeur atypique ne se trouve au-delà de la frontière basse
(126613). Cependant, on constate que les valeurs atypiques de la croissance
démographique sont situées de part et d'autres des deux
frontières. Les autres variables ne présentent pas des valeurs
atypiques.
Figure 1 : Boîtes à moustaches des
variables
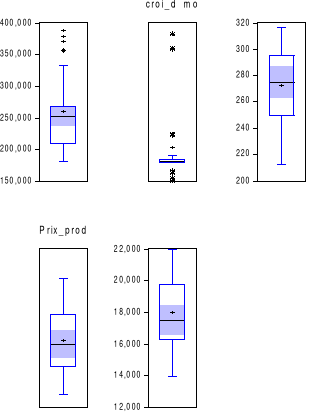
Source : Etabli par les
auteurs, 2020
6.1.4 3.1.2. Evolution graphique des
variables
6.1.5 3.1.2.1. Evolution de la
production de l'igname et de la superficie emblavée
La figure 2 présente l'évolution de la
production de l'igname et de la superficie emblavée dans le
département du Borgou pendant la période allant du 1er
trimestre de l'année 2010 au dernier trimestre de 2018. Il n'est pas
observé une grande variation dans les séries. Il y a un genre de
pallier ou de bosses dans les données de production. En effet, les deux
courbes évoluent sensiblement de façon parallèle durant la
période de 2010 à 2018. De 2010 au dernier trimestre de
l'année 2012, on note une légère tendance à la
hausse. La production de l'igname ainsi que la superficie emblavée vont
connaitre un déclin en 2013 avant de grimper de façon
exponentielle jusqu'à atteindre leurs points culminants respectifs
pendant le 4ème trimestre de l'année 2014. Les deux
courbes connaitront par la suite une tendance à la baisse jusqu'en
2018.
Figure 2 : Evolution de la production de l'igname
et de la superficie emblavée
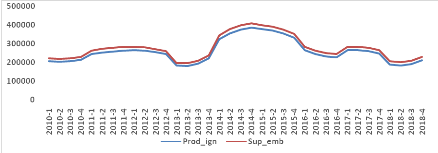
Source : Etabli par les auteurs, 2020
6.1.6 3.1.2.2. Evolution de la
pluviométrie
Le Borgou a connu d'importantes fluctuations
pluviométriques dans le temps. En effet, du 1er trimestre
2010 au dernier trimestre 2015, on note, de façon globale, une tendance
à la baisse et une oscillation de la hauteur des pluies. Par contre,
à partir de 2016, elle (la hauteur des pluies) devient de plus en plus
importante au fur et à mesure que les années évoluent.
Elle a atteint son seuil maximal au troisième trimestre de
l'année 2010 avec une estimation de 316,3175169 mm.
Figure 3 : Evolution de la
pluviométrie
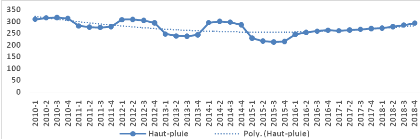
Source : Etabli par les auteurs, 2020
6.1.7 3.1.2.3. Evolution du prix aux
producteurs
Le prix aux producteurs a connu une évolution
saisonnière sur toute la période de l'étude. Le prix
maximum estimé à 283 F CFA a été obtenu pendant le
troisième trimestre de l'année 2015, le prix le plus bas
estimé à 136 F CFA a été obtenu au quatrième
trimestre de 2012.
Figure 4 : Evolution du prix aux
producteurs
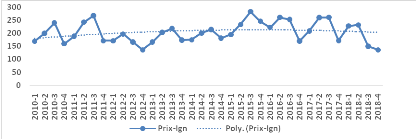
Source : Etabli par les auteurs, 2020
6.1.8 3.2. Analyse
explicative
6.1.9 3.2.1. Analyse de la
saisonnalité
Les données entrant en jeu dans cette étude sont
infra-annuelles (trimestrielles). Il est donc primordial de faire le test de
saisonnalité et, au cas où on détecterait une
éventuelle saisonnalité, procéder à leur
désaisonnalisation. Les résultats du test de saisonnalité
sont consignés dans le tableau suivant :
Tableau 4 : Résultats de l'analyse de la
saisonnalité des séries
|
Variables
|
p-value
|
Type de modèle
|
F-test (%)
|
Saisonnalité
|
|
LPROD_IGN
|
0,0771
|
Additif
|
68,17
|
Absence de saisonnalité
|
|
LCROI_DEMO
|
0,7064
|
Additif
|
65,05
|
Absence de saisonnalité
|
|
LHAUT_PLUIE
|
0,525
|
Additif
|
94,86
|
Absence de saisonnalité
|
|
LPRIX_PROD
|
0,2305
|
Additif
|
0,00
|
Présence de saisonnalité
|
|
LSUP_EMB
|
0,766
|
Additif
|
98,36
|
Absence de saisonnalité
|
Source : Etabli par les auteurs, 2020
Au seuil de 5%, la régression pour chaque variable, de
l'écart-type sur la moyenne révèle que le schéma
à utiliser pour tester la saisonnalité de ces séries, est
celui de type additif. Les tests effectués montrent qu'à
l'exception du prix aux producteurs, toutes les quatre (4) autres variables ne
présentent aucun aspect saisonnier. Nous avons donc
procédé à la désaisonnalisation de la série
« prix aux producteurs ». Ainsi, nous utiliserons pour la
suite de notre analyse, les variables LProd_ign, LCroi_demo, LHaut_pluie,
LSup_emb et LPrix_prod_sa (série désaisonnalisée).
La figure ci-après montre l'allure de la série
désaisonnalisée LPrix_prod_sa
Figure 5 : Allure de la série
« Prix aux producteurs » après
désaisonnalisation
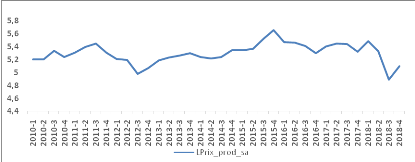
Source : Etabli par les auteurs, 2020
6.1.10 3.2.2.
Analyse de la stationnarité des séries
L'analyse de la stationnarité des séries a
été faite grâce aux tests d'Augmented Dickey-Fuller/ADF, de
Phillips-Perron/PP et d'Andrews et Zivot/AZ. Les résultats de ces tests
sont récapitulés dans le tableau 4. L'on note que les
séries production de l'igname, croissance démographique, prix aux
producteurs et superficie emblavée sont intégrées d'ordre
1 (stationnaire après la première différence), alors que
la série hauteur des pluies reste stationnaire à niveau (sans
différenciation). Les séries sont ainsi intégrées
à des ordres différents ; ce qui rend inefficace le test de
cointégration de Engle et Granger (applicable à deux
séries intégrées de même ordre) et celui de Johansen
(applicable à plusieurs séries intégrées de
même ordre) et rend opportun le test de cointégration aux bornes
(Pesaran,2001).
Tableau5 : Résultats des tests de
stationnarité des séries
|
Variables
|
Niveau
|
Différence première
|
Différence deuxième
|
Constat
|
|
ADF
|
PP
|
AZ
|
ADF
|
PP
|
AZ
|
ADF
|
PP
|
AZ
|
|
LPROD_IGN
|
-1,4689
|
-1,8742
|
-4,9215
|
-1,6737
|
-3,6189**
|
-5,0553
|
-3,05674
|
-
|
-6,8971**
|
I(1)
|
|
(0,8143)
|
(0,6463)
|
(0,0930)
|
(0,7339)
|
(0,0430)
|
(0,0693)
|
(0,0528)
|
(0,01)
|
|
LCROI_DEMO
|
-3,0246
|
-3,059447
|
-4,7479
|
-6,6086*
|
-6,6309*
|
-6,8224**
|
-
|
-
|
-
|
I(1)
|
|
(0,1402)
|
(0,1315)
|
(0,1407)
|
(0,0000)
|
(0,0000)
|
(0,01)
|
|
LHAUT_PLUIE
|
1,2188
|
-2,1236
|
-5,1921**
|
-1,9836
|
-4,1005**
|
-
|
-4,0602**
|
-
|
-
|
I(0)
|
|
(0,9999)
|
(0,5153)
|
(0,0481)
|
(0,5827)
|
(0,0144)
|
(0,0191)
|
|
LPRIX_PROD
|
-2.3882
|
-2,3984
|
-3,7128
|
-5,4861*
|
-6,1424*
|
-5,8901**
|
-
|
-
|
|
I(1)
|
|
(0.3789)
|
(0,3739)
|
(0,6998)
|
(0,0005)
|
(0,0001)
|
(0,01)
|
|
|
LSUP_EMB
|
-2,2433
|
-2,2866
|
-3,9748
|
-1,8427
|
-3,3068
|
-8,6217**
|
-5,2608*
|
-7,3585*
|
-
|
I(1)
|
|
(0,4478)
|
-0,4298
|
(0,5392)
|
(0,6545)
|
(0,0822)
|
(0,01)
|
(0,0013)
|
(0,0000)
|
Source : Etabli par les auteurs, 2020
NB : (.) : Probabilités ; * :
Stationnaires à 1% ; ** : Stationnaires à 5%
6.1.11 3.2.3.
Estimation du modèle ARDL
6.1.12 3.2.3.1.
Spécification du modèle ARDL
La modélisation par l'approche ARDL exige pour chaque
variable, la détermination du retard optimal. Nous nous sommes servis du
Critère d'Information d'Akaike (AIC) pour sélectionner le
modèle ARDL optimal, celui qui offre des résultats
statistiquement significatifs. Ci-dessous, les vingt (20) meilleurs
modèles parmi les deux mille cinq cent(2500) modèles
évalués :
Figure 6 : Retards optimaux des séries
selon le Critère d'Information d'Akaike
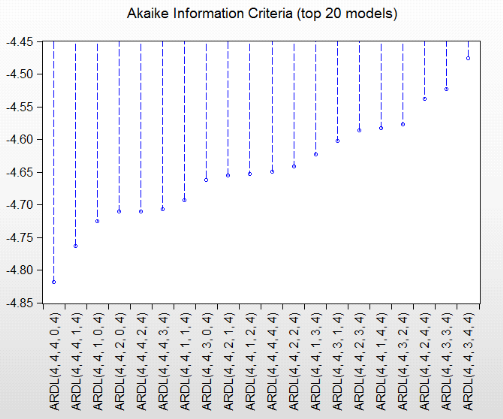
Source : Etabli par les auteurs, 2020
Comme on peut le voir, le modèle ARDL (4,4,4,0,4) est
le plus optimal parmi les 20 présentés, car il offre la plus
petite valeur du AIC.
6.1.13 3.2.3.2.
Estimation du modèle ARDL(4,4,4,0,4)
Les résultats d'estimation révèlent que
les coefficients dont les probabilités sont en gras sont
significativement différents de zéro (0) au seuil de 5%. Avec une
qualité d'ajustement meilleure, la production de l'igname dans le
département du Borgou est expliquée à hauteur de 97% par
les variables mis en jeu. La probabilité de la Statistique de Fisher
(0,0000) révèle qu'au seuil de 5%, le modèle
ARDL(4,4,4,0,4) est globalement significatif. Par ailleurs, le R2
(0,991511) est inférieur à la statistique de Durbin-Watson
(1,26632). D'après la règle de Granger, le modèle est de
bonne régression et toutes les variables utilisées dans cette
étude sont effectivement stationnaires.
Tableau 6 : Modèle
ARDL(4,4,4,0,4)
|
Variable dépendante : DLPROD_IGN
|
|
Variables
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
DLPROD_IGN(-1)
|
0 ,064360
|
0,053424
|
1,204691
|
0,2561
|
|
DLPROD_IGN(-2)
|
0,019151
|
0,054918
|
0,348723
|
0,7345
|
|
DLPROD_IGN(-3)
|
0,018592
|
0,052612
|
0,353372
|
0,7311
|
|
DLPROD_IGN(-4)
|
-1,543464
|
0,091120
|
-16,93879
|
0,0000
|
|
DLCROI_DEMO
|
-0,032270
|
0,009264
|
-3,483481
|
0,0059
|
|
DLCROI_DEMO(-1)
|
-0,011607
|
0,011131
|
-1,042756
|
0,3216
|
|
DLCROI_DEMO(-2)
|
-0,004771
|
0,010051
|
-0,474723
|
0,6452
|
|
DLCROI_DEMO(-3)
|
-0,000614
|
0,009557
|
-0,064282
|
0,9500
|
|
DLCROI_DEMO(-4)
|
0,024060
|
0,006550
|
3,673370
|
0,0043
|
|
LHAUT_PLUIE
|
-1,390484
|
0,158660
|
-8,763935
|
0,0000
|
|
LHAUT_PLUIE(-1)
|
1,371894
|
0,205427
|
6,678245
|
0,0001
|
|
LHAUT_PLUIE(-2)
|
-0,011249
|
0,132359
|
-0,084988
|
0,9339
|
|
LHAUT_PLUIE(-3)
|
-0,212337
|
0,144371
|
-1,470771
|
0,1721
|
|
LHAUT_PLUIE(-4)
|
0,209146
|
0,132851
|
1,574290
|
0,1465
|
|
DLPRIX_PROD_SA
|
-0,004504
|
0,039887
|
-0,112923
|
0,9123
|
|
DLSUP_EMB
|
1,600459
|
0,124269
|
12,87898
|
0,0000
|
|
DLSUP_EMB(-1)
|
-0,240322
|
0,100433
|
-2,392853
|
0,0378
|
|
DLSUP_EMB(-2)
|
-0,157039
|
0,097723
|
-1,606985
|
0,1391
|
|
DLSUP_EMB(-3)
|
-0,274448
|
0,113471
|
-2,418653
|
0,0361
|
|
DLSUP_EMB(-4)
|
2,499742
|
0,185316
|
13,48908
|
0,0000
|
|
C
|
0,174851
|
0,396457
|
0,441033
|
0,6686
|
|
R-carré
|
0,991511
|
F-statistic
|
58,39657
|
|
R-carré ajusté
|
0,974532
|
Prob(F-statistic)
|
0,000000
|
|
|
|
Durbin-Watson stat
|
1,26632
|
Source : Etabli par les auteurs, 2020
Le tableau suivant est le récapitulatif des tests de
robustesse du modèle ARDL(4,4,4,0,4) ainsi estimé :
Tableau 7 : Résultats des tests
diagnostiques du modèle ARDL estimé
|
Hypothèse du test
|
Tests
|
Valeurs (probabilité)
|
|
Autocorrélation
|
Breusch-Godfrey
|
2,203453 (0,1729)
|
|
Hétéroscédasticité
|
Breusch-Pagan-Godfrey
|
0,468866 (0,9283)
|
|
Normalité
|
Jarque-Bera
|
0,649362 (0,7228)
|
|
Spécification
|
Ramsey (Fisher)
|
0,125214 (0,7316)
|
Source : Etabli par les auteurs, 2020
L'hypothèse nulle est acceptée pour tous ces
tests. De ce fait, l'on note l'absence d'autocorrélation des erreurs,
l'absence d'hétéroscédasticité, la normalité
des erreurs, et la bonne spécification du modèle. Notre
modèle est ainsi validé sur le plan statistique.
Le modèle ARDL(4,4,4,0,4) estimé est globalement
bon et explique à 97% la production de l'igname dans le
département du Borgou, de 2010 à 2018.La spécification du
modèle est la suivante :
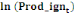 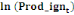 = =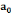 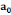 + +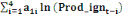 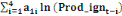 + +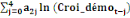 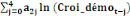 + +
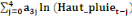 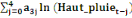 + +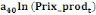 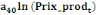 + +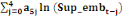 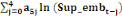 + +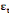 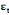
Où les valeurs des coefficients sont consignées
dans le tableau suivant :
Tableau 8 : Valeurs descoefficients du
modèle ARDL(4,4,4,0,4)
|
Coefficients
|
Valeurs
|
|
Coefficients
|
Valeurs
|
|
Coefficients
|
Valeurs
|
|
0,174851
|
|
|
-0,004771
|
|
|
0,209146
|
|
0,064360
|
|
|
-0,000614
|
|
|
-0,004504
|
|
0,019151
|
|
|
0,024060
|
|
|
1,600459
|
|
0,018592
|
|
|
-1,390484
|
|
|
-0,240322
|
|
-1,543464
|
|
|
1,371894
|
|
|
-0,157039
|
|
-0,032270
|
|
|
-0,011249
|
|
|
-0,274448
|
|
-0,011607
|
|
|
-0,212337
|
|
|
2,499742
|
Source : Etabli par les auteurs, 2020
6.1.14 3.2.3.3.
Test de cointégration aux bornes
Le test de cointégration de Pesaran et al. (2001) exige
que le modèle ARDL soit estimé au préalable. La
statistique du test calculée, soit la valeur F de Fisher, sera
comparée aux valeurs critiques (qui forment des bornes). Si la
statistique de Fisher est supérieure à la borne
supérieure, il y a cointégration. Il n'existe pas de
cointégration lorsque la statistique de Fisher est inférieure
à la borne supérieure. Cependant, on ne saurait conclure lorsque
la statistique de Fisher est strictement comprise entre les deux bornes.
Les résultats du test de cointégration aux
bornes confirment, au seuil de 1%, 2,5%, 5% et 10%, l'existence d'une relation
de cointégration entre les séries sous étude (la
valeur de F-stat est supérieure à celle de la borne
supérieure), ce qui donne la possibilité d'estimer les
effets de long terme delprod_ign, lcroi_demo, lhaut_pluie, lprix_prod,
lsup_emb.
Tableau 9 : Résultats du test de
cointégration de Pesaran et al. (2001)
|
Variables
|
Dlprod_ign, Dlcroi_demo, lhaut_pluie, Dlprix_prod,
Dlsup_emb
|
|
F-stat calculée
|
116,9155
|
|
K
|
4
|
|
Seuil critique
|
Borne inférieure
|
Borne supérieure
|
|
10%
|
2,45
|
3,52
|
|
5%
|
2,86
|
4,01
|
|
2.5%
|
3,25
|
4,49
|
|
1%
|
3,74
|
5,06
|
Source : Etabli par les auteurs, 2020
6.1.15 3.2.3.4.
Coefficients de Long terme et dynamique de court terme
6.1.16 3.2.3.4.1.
Coefficients de court terme (CT)
Comme on peut le lire sur le tableau 10 ci-dessous, le
coefficient d'ajustement ou force de rappel est statistiquement significatif et
négatif, ce qui garantit un mécanisme de correction d'erreurs, et
donc l'existence d'une relation de long terme (cointégration) entre
variables. Par ailleurs, le coefficient associé à la superficie
emblavée ainsi que celui associé aux prix aux producteurs sont
significativement différents de zéro (0) à court terme.
Par contre, la hauteur des pluies et la croissance démographique
présentent des coefficients non significatifs à court terme.
Aussi, l'on note ce qui suit :
§ les prix aux producteurs ont un impact positif sur la
production de l'igname dans le département du Borgou à CT :
une augmentation des prix aux producteurs de 1% entraine une hausse de 0,58% de
la production de l'igname. Mais un an en arrière les prix aux
producteurs constituaient un frein à la production de l'igname dans le
Borgou.
§ La superficie emblavée exerce un effet positif
sur la production de l'igname à court terme : un accroissement de la
superficie emblavée de 1% accélère la production de
l'igname de 3,08% à CT. Ces effets s'inversent plutôt dans le
temps : l'accroissement de la superficie il y a 3 ans a été un
frein à la production de l'igname dans le Borgou.
Tableau 10 :Résultats d'estimation
des coefficients de CT
|
Variable dépendante : LPROD_IGN
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
D(LPROD_IGN(-1))
|
2,248975
|
0,469416
|
4,791008
|
0,0020
|
|
D(LPROD_IGN(-2))
|
1,906765
|
0,456285
|
4,178889
|
0,0041
|
|
D(LPROD_IGN(-3))
|
1,268771
|
0,334243
|
3,795955
|
0,0068
|
|
D(LCROI_DEMO)
|
0,142368
|
0,066277
|
2,148073
|
0,0688
|
|
D(LCROI_DEMO(-1))
|
-0,079584
|
0,086065
|
-0,924697
|
0,3859
|
|
D(LCROI_DEMO(-2))
|
-0,184529
|
0,090298
|
-2,043565
|
0,0803
|
|
D(LCROI_DEMO(-3))
|
0,105825
|
0,059504
|
1,778457
|
0,1186
|
|
D(LHAUT_PLUIE)
|
-0,532717
|
0,427411
|
-1,246381
|
0,2527
|
|
D(LHAUT_PLUIE(-1))
|
-1,767428
|
0,621398
|
-2,844277
|
0,0249
|
|
D(LPRIX_PROD_SA)
|
0,577667
|
0,233537
|
2,473561
|
0,0426
|
|
D(LPRIX_PROD_SA(-1))
|
-0,828726
|
0,342173
|
-2,421949
|
0,0460
|
|
D(LPRIX_PROD_SA(-2))
|
-0,023188
|
0,259251
|
-0,089442
|
0,9312
|
|
D(LPRIX_PROD_SA(-3))
|
0,286015
|
0,206509
|
1,384998
|
0,2086
|
|
D(LSUP_EMB)
|
3,082190
|
0,630200
|
4,890815
|
0,0018
|
|
D(LSUP_EMB(-1))
|
-0,309545
|
0,624181
|
-0,495922
|
0,6351
|
|
D(LSUP_EMB(-2))
|
0,270879
|
0,643757
|
0,420779
|
0,6865
|
|
D(LSUP_EMB(-3))
|
-4,200060
|
1,099041
|
-3,821568
|
0,0065
|
|
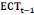 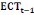
|
-2,82833
|
0,549047
|
-5,151343
|
0,0000
|
Source : Etabli par les auteurs, 2020
6.1.17 3.2.3.4.2.
Coefficients de long terme (LT)
Le tableau 11 ci-dessous nous fournit les coefficients ou
élasticités de long terme estimés. Tous ces coefficients
sont significativement différents de zéro (probabilités
associées inférieures à 5%). Comme à court terme,
les effets de la superficie emblavée dans le Borgou restent positifs
à long terme et se montrent plutôt moins que proportionnels : un
accroissement de la superficie emblavée de 1% accélère la
production de l'igname de 2,47% à LT. Les prix aux producteurs exercent
toujours une influence positive sur la production de l'igname dans le Borgou
à LT.
Par ailleurs, contrairement aux résultats à CT,
la croissance démographique et la hauteur des pluies affichent l'effet
escompté (positif) à LT.
Tableau 11 : Résultats d'estimation des
coefficients de LT
|
Variable dépendante : LPROD_IGN
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
LCROI_DEMO
|
0,145101
|
0,042182
|
3,439840
|
0,0108
|
|
LHAUT_PLUIE
|
0,735979
|
0,274305
|
2,683063
|
0,0314
|
|
LPRIX_PROD_SA
|
0,654265
|
0,214318
|
3,052783
|
0,0185
|
|
LSUP_EMB
|
2,467856
|
0,250405
|
9,855456
|
0,0000
|
|
C
|
-19,283474
|
4,813194
|
-4,006378
|
0,0051
|
Source : Etabli par les auteurs, 2020
6.1.18 3.3. Synthèse des résultats et
vérifications des hypothèses
6.1.19 3.3.1.
Synthèse des résultats
Au vu des résultats de nos différentes analyses,
il ressort que la superficie emblavée a un effet positif sur la
production de l'igname dans le département du Borgou aussi bien à
court terme qu'à long terme, mais dans une moindre proportion. En effet,
un accroissement de 1% de la superficie emblavée accélère
la production de l'igname de 3,08% à court terme et de 2,47% à
long terme. Cette décroissance de l'impact de la superficie
emblavée sur la production de l'igname au fil du temps pourrait
s'expliquer par le fait que la terre perd sa fertilité d'année en
année. La jachère s'avère alors indispensable.
Ensuite, les résultats montrent que l'accroissement de
la population du Borgou a un effet positif sur la production de l'igname
à long terme et un effet négatif à court terme. Même
si cela semble être un peu ambigu, il faut noter que la population
considérée dans le cadre de cette étude englobe toutes les
tranches d'âge. Les personnes constituant ces différentes tranches
d'âge sont actives à une certaine époque de leur vie et
inactives au début et au soir (pour la plupart) de leur vie. Par
ailleurs, les mets issus de l'igname sont très appréciés
par les populations du Borgou. Ainsi, lorsque la population augmente, la
demande de l'igname est forte. Les agriculteurs doivent donc hausser la
production pour équilibrer l'offre et la demande à long terme.
En outre, on note que les prix aux producteurs exercent des
effets positifs sur la production de l'igname dans le Borgou aussi bien
à court terme qu'à long terme mais dans différentes
proportions. Une hausse des prix de 1% entraine une augmentation de la
production de l'igname dans le département du Borgou de 0,58% à
court terme et de 0,65% à long terme. Il est clair qu'il y a une
légère augmentation de 0,07% de la production de l'igname
à long terme. Cette augmentation minime qu'elle soit, traduit le
comportement des producteurs de l'igname face à la variation des prix.
Ils ont tendance à revoir leur production à la hausse lorsque
qu'ils constatent que les prix actuels du marché sont bons. Ils
espèrent ainsi augmenter leurs revenus à long terme.
Enfin, la variable hauteur des pluies n'a pas un effet
significatif sur la production de l'igname dans le Borgou à court terme.
Mais à long terme, elle affiche un effet positif sur cette production.
La production de l'igname augmente de 0,74% lorsque la hauteur des pluies
augmente de 1%. Ce résultat bien qu'il soit positif, n'est pas assez
significatif au vu de l'importance de la pluie dans la production des cultures
vivrières. Les agriculteurs n'arrivent pas à cerner avec
exactitude la période des pluies. Dr Nestor Ahoyo Adjovi, Directeur
Adjoint de l'INRAB souligne qu'avec les changements climatiques, on ne sait
exactement quand commence la saison pluvieuse. Et de ce fait, le nombre de
jours de pluies pour certaines variétés d'igname est parfois
insuffisant. Par manque d'informations suffisantes sur ces changements
climatiques, lesagriculteurs mettent parfois tôt ou même tard les
semences d'igname en terre. Dans l'un ou l'autre des deux cas, il y a toujours
une répercussion sur la santé des plantes qui vont germer ou
carrément certains tubercules pourrissent à cause de
l'intensité de la chaleur. Il apparait clairement que la
pluviométrie pourrait constituer une entrave à la production de
l'igname aussi longtemps que les producteurs ne seront pas informés et
adaptés à ce mécanisme.
6.1.20 3.3.2.
Vérification des hypothèses
Les hypothèses émises dans le cadre de cette
étude sont confirmées conformément aux conditions que
chacune d'elles doit remplir, comme l'indique le tableau 12.
Tableau 12 : Confirmation des
hypothèses.
|
Hypothèses
|
Conditions
|
Décision
|
|
Une hausse de la superficie emblavée entraine une
augmentation de la production de l'igname dans le Borgou
|
prob(coef.Sup_emb)=0,0000<0,05
|
Confirmée
|
|
coef.Sup_emb=1,600459>0
|
|
Les précipitations annuelles ont un impact sur la
production de l'igname
|
prob(coef.Haut_pluie)=0,0000<0,05
|
Confirmée
|
|
La croissance démographique du Borgou a un effet
significatif sur sa production de l'igname
|
prob(coef.Croi_demo)=0,0059<0,05
|
Confirmée
|
Source : Etabli par les auteurs, 2020
6.1.21 3.4. Préconisations opérationnelles
Au vu des différents résultats obtenus à
l'issue de cette étude, il est primordial de formuler des
recommandations dans le but d'améliorer le niveau de la production de
l'igname dans le département du Borgou et de promouvoir la
filière sur toute l'étendue du territoire national. C'est
pourquoi nous recommandons aux autorités de :
- Promouvoir la mécanisation agricole pour faciliter
les labours et accroitre les surfaces de terres cultivées sans pour
autant porter atteinte à l'environnement ;
- Mettre à la disposition des groupements villageois,
des services météorologiques afin de les informer à temps
sur l'évolution du climat ;
- Maintenir le niveau de la population agricole (ou même
à la hausse) en mettant en place une politique de motivation des
producteurs de l'igname.
7 CONCLUSION
L'objectif de notre mémoire est d'analyser les
déterminants de la production de l'igname dans le département du
Borgou. Mais, vu l'importance de l'igname en matière nutritionnelle,
culturelle, économique et surtout de la lutte contre
l'insécurité alimentaire, il y a d'intérêt à
promouvoir sa culture et sa filière en général.
Les résultats ont montré que la production de
l'igname dans le département du Borgou dépend de la croissance
démographique, de la superficie emblavée, de la
pluviométrie et du prix aux producteurs. En effet, la superficie
emblavée et les prix aux producteurs entretiennent une relation positive
avec la production de l'igname à court et à long termes.
Cependant, les effets de la superficie emblavée sont moins
proportionnels à long terme, contrairement aux prix aux producteurs qui
exercent une influence légèrement importante sur la production de
l'igname dans le département du Borgou à long terme. Par
ailleurs, la croissance démographique ainsi que la hauteur des pluies
n'affichent aucun effet significatif à court terme sur la production de
l'igname. A long terme par contre, ces deux variables affichent l'effet
escompté (positif) sur la production de l'igname dans le Borgou. Alors,
la production de la filière igname doit passer par une attention
particulière sur chacun de ces facteurs qui, lorsqu'ils ne sont pas
suivis de près, arrièrent son développement.
Pour pérenniser et améliorer cette production de
l'igname dans le département du Borgou, nous suggérons aux
autorités de promouvoir la mécanisation agricole pour faciliter
les labours et accroitre les surfaces de terres cultivées sans pour
autant porter atteinte à l'environnement. Aussi faut-il mettre
à la disposition des groupements villageois, des services
météorologiques afin de les informer à temps sur
l'évolution du climat. Enfin, il faut maintenir le niveau de la
population agricole (ou même à la hausse) en mettant en place une
politique de motivation des producteurs de l'igname. Ces préconisations
sont d'ordre général et loin d'être opérationnelles
uniquement dans le département du Borgou, peuvent être
appliquées sur l'ensemble des pôles de développement de la
filière igname. Bien entendu, il ne faudrait pas croire, loin s'en faut,
que la filière igname est une panacée qui peut régler tous
les problèmes liés à l'insécurité
alimentaire. Elle ne pourra pas à elle seule, assurer la
sécurité alimentaire. Une réflexion globale prenant en
compte les cultures vivrières pourrait être d'une aide importante
dans le secteur agricole et dans la lutte contre l'insécurité
alimentaire.
REFERENCES BIBLIOGRAPHIQUES
1. Adimi, S et Dairo, J. (2014). Analyse des
déterminants de la production du maïs dans lacommune de
Savè. Mémoire de Licence en Economie Agricole (EA).
Faculté des
Sciences Economiques et Gestion (FASEG).
Université de Parakou (UP). Bénin.
2. Agbo, A. et Hounkpehedji, N. (2008). Analyse des
déterminants de la production des cultures vivrières au
Bénin : cas du maïs et de l'igname. Mémoire
soutenu à l'Ecole Nationale d'Economie Appliquée et de Management
(ENEAM).
3. ASECNA (2008). Rapports sur les pluviométries
décennales au Bénin, 1978-2007.
4. Askari, H. et Cumming, J.T. (1976).
Agricultural Supply Response: A survey of the
Econometric
Evidence.
5. Askari, H. et Cumming, J.T. (1977). Estimating
agricultural supply response with the
Nerlove model; a
survey.International Economy Review, 18 (2): 257-292.
6. Auriole, L. et Aboudou, R. (2006). Impacts de la
croissance urbaine sur les filières agricoles en Afrique de
l'Ouest : cas de l'igname à Parakou, Bénin. Ifeas, Lares,
document de travail Ecocité 13 :1-51.
7. Base de données de la DSA,2019
8. Baco, M. N., Biaou, G. et Lescure, J-P. (2007a).
Complementarity betwen Geographical and Social Patterns in the Preservation
of Yam (Dioscorea sp.) Diverty in Northern Benin. EconomicBotany61 :
385-393.
9. Baco, M. N., Tostain, S., Mongbo, R. L.,Dainou, O. et
Agbangla, C. (2004). Gestion dynamique de la diversité
variétale des ignames cultivées (Dioscorea cayenensis- D.
rotundata) dans la commune de Sinendé au nord Bénin.
PGRNewletters ; 139 : 18-24.
10. Bond, M. (1983). Les réactions de l'offre aux
variations des prix dans le secteur agricole en Afrique Subsaharienne.
Washington DC, FMI, mai 1983, Staff Papers, Vol. 30,4.
11. Boussard, J.M. et Saïd, S. (2000). Faut-il
encore des politiques agricoles.In Déméter
2001,
Économie et Stratégies Agricoles, Paris, A. Colin 2000, 303 p.
12. Diagne, A., Koné, M., Sylla, K. et Touré, A.
(2004). Politique rizicole et impact de la libéralisation de la
filière riz en Côte d'Ivoire. Contribution
présentée au « Séminaire de formation sur les
NERICA », Abidjan, 27-29 janvier 2004.
13. Engle, R.F. et Granger C.W.J. (1987). Cointegration
and error correction
representation : Estimation and testing.
In Econometrica, vol.55, n°2, pp. 251-276.
14. EuropeanExternal Action Service (2018).
Bénin : Revue sectorielle agricole, gestion 2017.
(Disponible à
https://eeas.europa.eu,
consulté le 18 Novembre 2019 à 16 heures).
15. Idrissa, D. (2007). Impact des fluctuations
pluviométriques sur la production agricole dansla région de
Thionck-Essy en Basse Casamance. Certificat d'aptitude
à
l'enseignement Moyen, Université Cheikh Anta Diop, Dakar.
16. INSAE. (2018). Production agricole 2008-2012.
(Disponible à
https://www.insae-bj.org,
consulté le 04 Novembre 2019 à 10 heures).
17. Johansen, S. (1988). Statistical Analysis of
Cointegrating Vectors. Journal of
Economic Dynamic and Control, Vol.12,
pp. 231-254.
18. Johansen, S. (1991). Estimation and Hypothesis Testing
of Cointegration Vectors
in Gaussian Vector Autoregressive Models.
Econometrica, Vol.59, pp. 1551-1580.
19. Katembo, P. (2004). Analyse de l'offre de café
au Nord-Kivu (République Démocratique du Congo).
Mémoire d'étude spécialisé en Economie Rurale,
Université Catholiquede Louvain, 71p.
20. Koffi-Tessio, E. M. (2000). Incitation et offre du
coton au Togo : une estimation
Econométrique. Revue
Economie Rurale 257, 7887.
21. Kouakou, S. (2009). Analyse de l'offre et de la
demande du bissap au Bénin : étude de cas dela ville de Cotonou.
Mémoire de maîtrise en Science économique
(FASEG).
Université d'Abomey-Calavi.
22. Mémento de l'Agronome (1993).
23. Morley, B. (2006). Causality between Economic Growth
and Immigration: An ARDL Bounds Testing Approach. Economics, Vol. 37, p.
1979- 1990.
24. Narayan, P. K. (2005). The saving and investment nexus
for China: evidence for cointégration tests. Applied Economics,
Vol. 37, p. 139- 162.
25. Nerlove, M. (1956). Estimates of supply of selected
agricultural commodities. Journal ofFarm economics, vol. 32 n°2.
26. Nerlove, M. (1993). Procreation, Fishing and Hunting:
Problems in the Economies of Renewable Resources and Dynamic Planar System.
American Journal of Agricultural Economies, 75:59- 71.
27. Nyemecketal, S. D. (2009). Analyse des
déterminants de l'efficacité technique
des
producteurs du riz pluvial dans le centre Ouest de la
Côte d'Ivoire.Analyse des
déterminants de la production
agricole en Afrique de l'Ouest n°2, p.67-97.
28. PDRT. (2003). Etude de la filière igname au
Bénin.
29. Pesaran M.H., Shin Y. et Smith R.J. (2001). Bounds
Testing Approaches to the
Analysis of Level Relationships.
Journal of Applied Econometrics, Vol.16, n°3, pp.289-326.
30. Timmer, C. P. (1971). Using a probabilistic frontier
production to measure technical
efficiency, Food Research Institute
Studies.
31. Toda, H.Y. et Yamamoto, T. (1995). Statistical
Inference in Vector Autoregressions
with Possibly Integrated
Processes. Journal of Econometrics, Vol. 66, pp. 225-250.
32. Yotopoulos, L. (1973). A test for relative efficiency:
some Further Result. American
EconomicReview, 63, p. 214-223.
33. Zonon, F. (1996). Analyse comparée de
l'efficacité de la production céréalière au
Burkina-Faso : cas de quatre zones agro-alimentaire. Thèse de
Doctorat 3e cycle en
économie rurale, Cires, Abidjan.
ANNEXE
8 ANNEXE
Annexe 1 : Tests de saisonnalité
- Production de l'igname
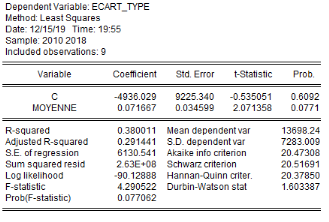

- Croissance démographique
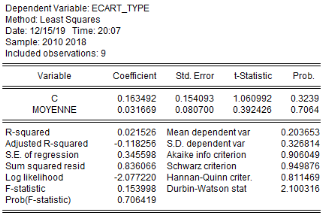

- Hauteur des pluies
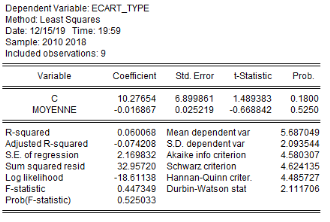

- Prix aux producteurs
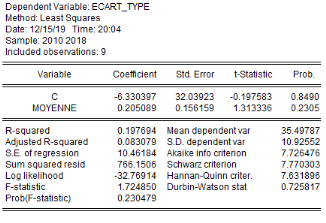

- Superficie emblavée
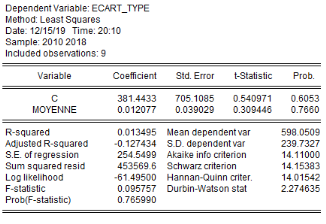
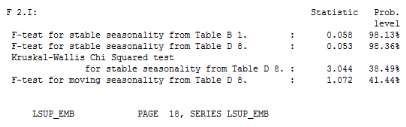
Annexe 2 : tests de stationnarité
- Production de l'igname
ADF Test
NIVEAU
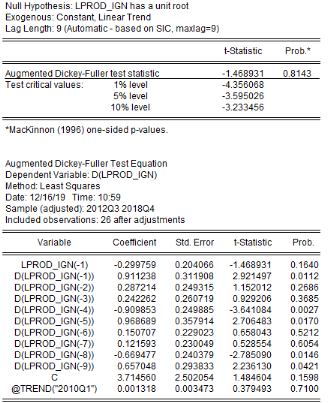 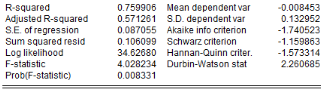
DIFFERENCE PREMIERE
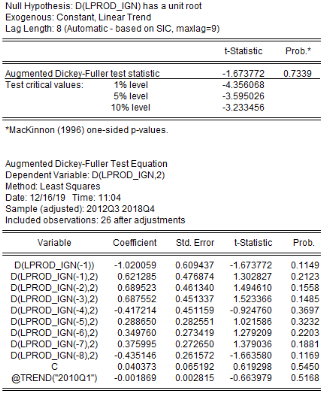 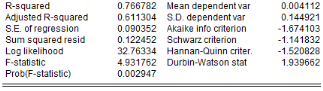
DIFFERENCE DEUXIEME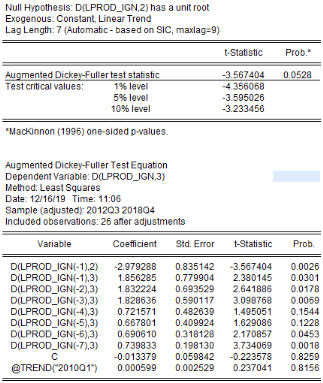 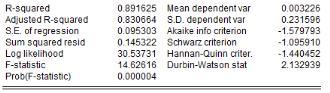
PP test
NIVEAU
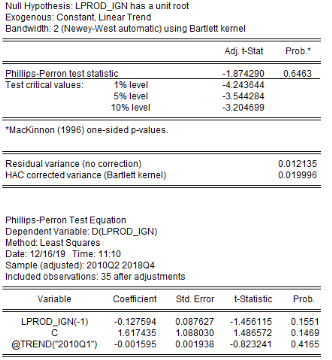 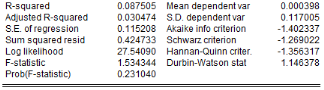
DIFFERENCE PREMIERE
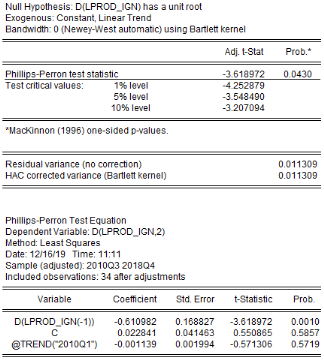 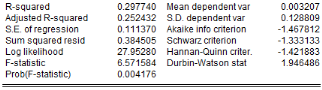
AZ Test
NIVEAU
 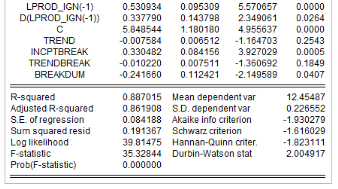
DIFFERENCE PREMIERE
 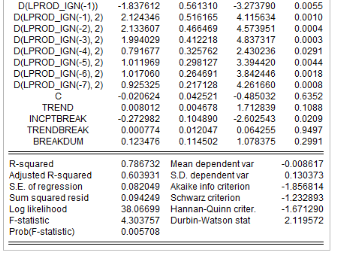
DIFFERENCE DEUXIEME
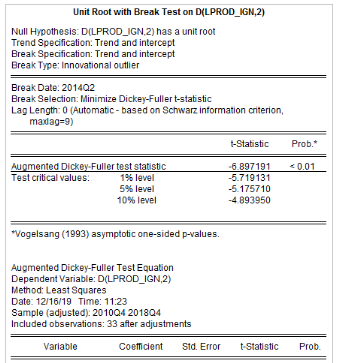 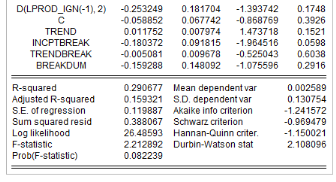
- Croissance démographique
ADF Test
NIVEAU
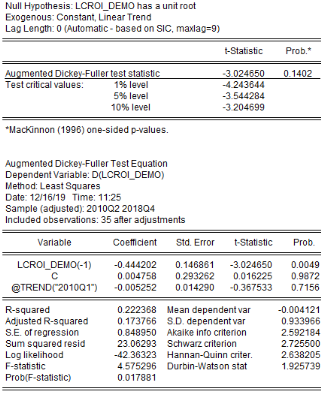
DIFFERENCE PREMIERE
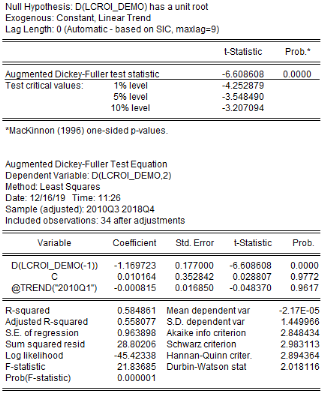
PP TEST
NIVEAU
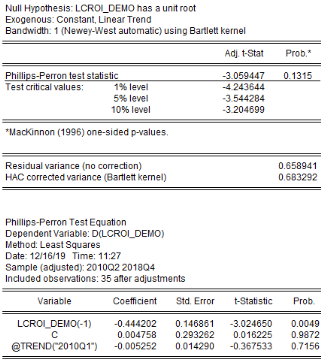 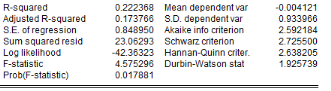
DIFFERENCE PREMIERE
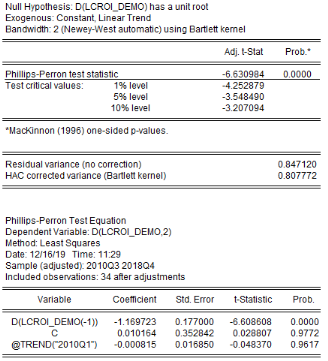 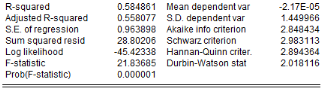
AZ TEST
NIVEAU
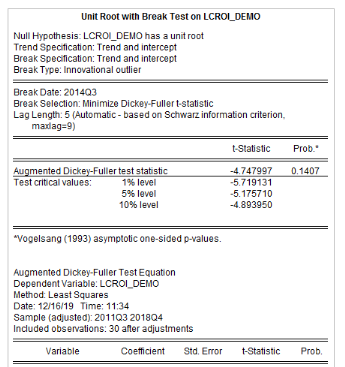 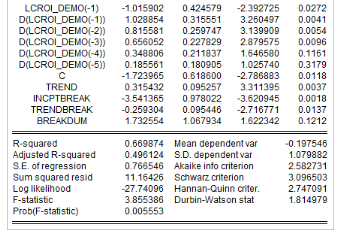
DIFFERENCE PREMIERE
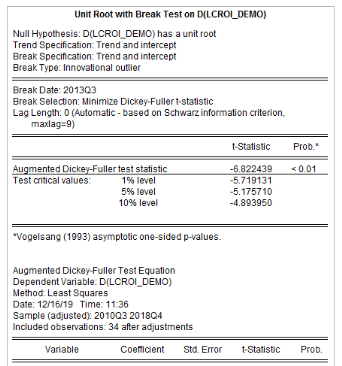 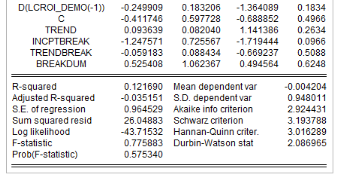
- Hauteur des pluies
ADF test
NIVEAU
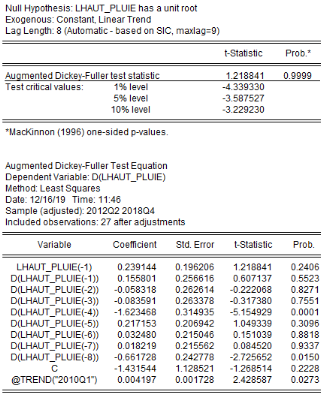 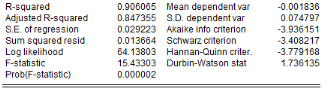
DIFFERENCE PREMIERE
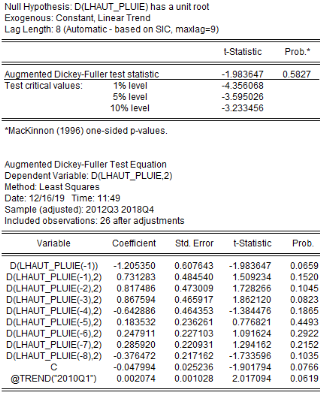 
DIFFERENCE DEUXIEME
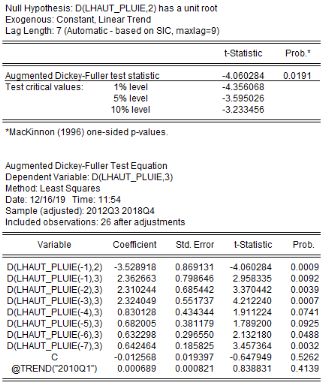 
PP test
NIVEAU
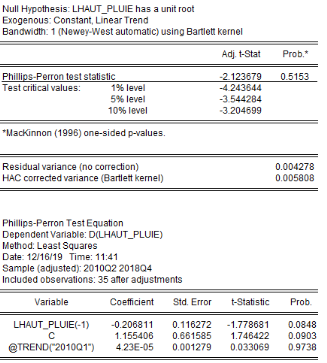 
DIFFERENCE PREMIERE
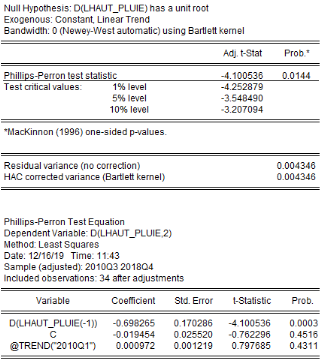 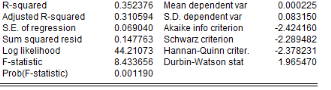
AZ test
NIVEAU

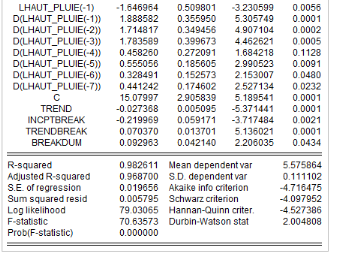
- Prix aux producteurs
ADF test
NIVEAU
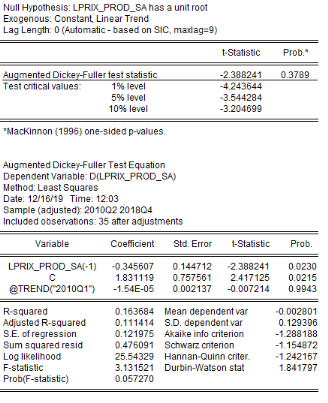
DIFFERENCE PREMIERE
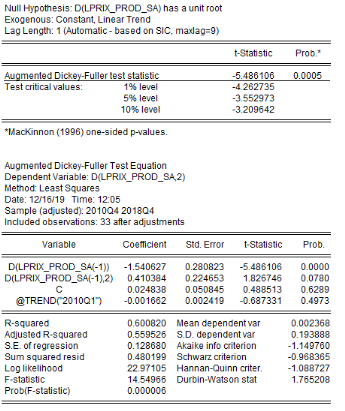
PP test
NIVEAU
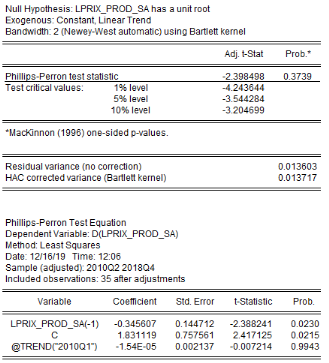 
DIFFERENCE PREMIERE
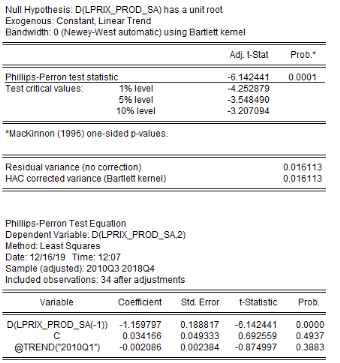 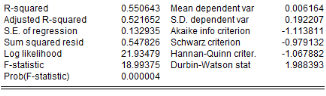
AZ test
NIVEAU
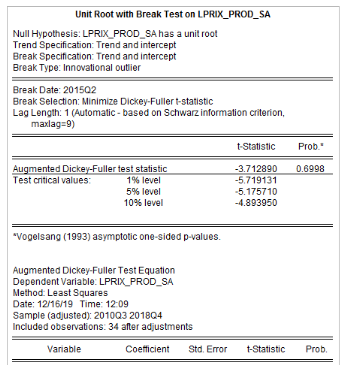 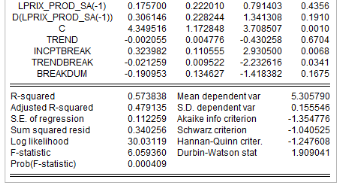
DIFFERENCE PREMIERE
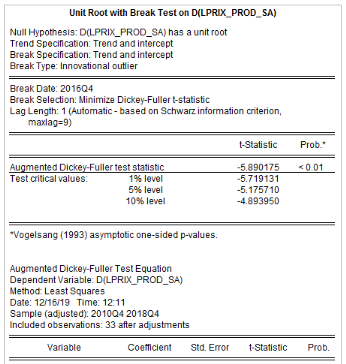 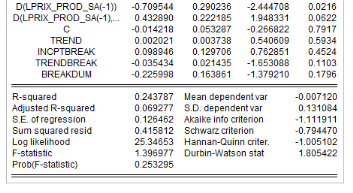
- Superficie emblavée
ADF test
NIVEAU
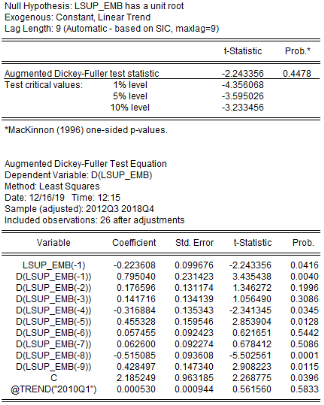 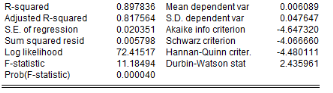
DIFFERENCE PREMIERE
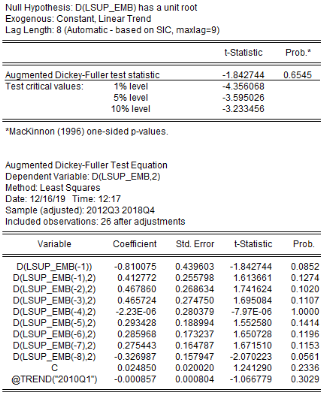 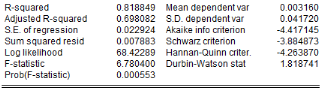
DIFFERENCE DEUXIEME
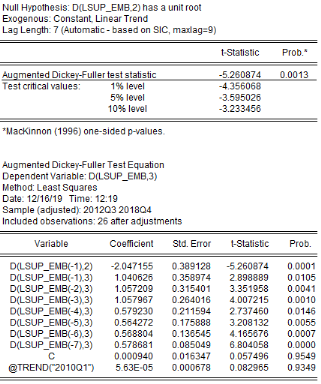 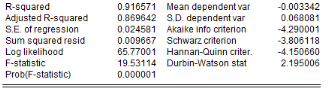
PP test
NIVEAU
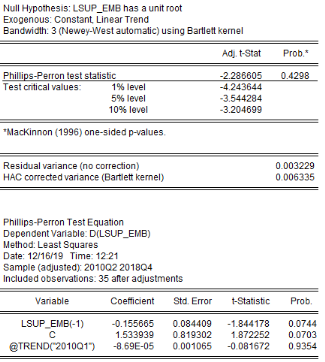 
DIFFERENCE PREMIERE
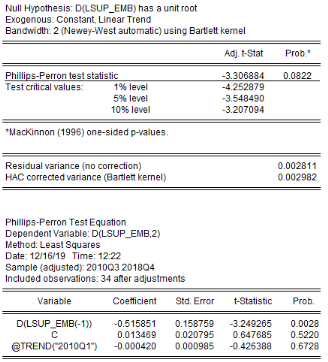 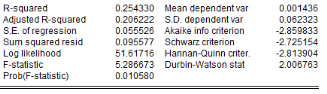
DIFFERENCE DEUXIME
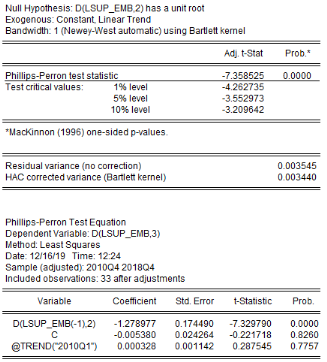 
AZ test
NIVEAU
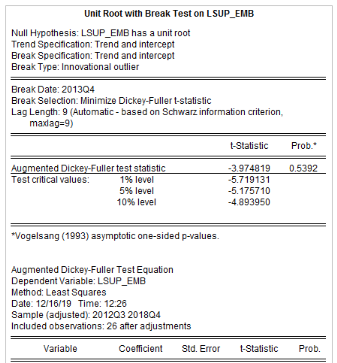
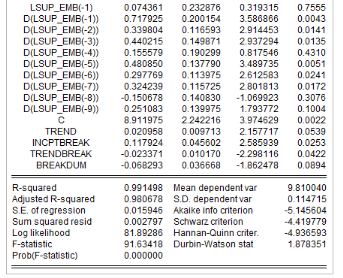
DIFFERENCE PREMIERE
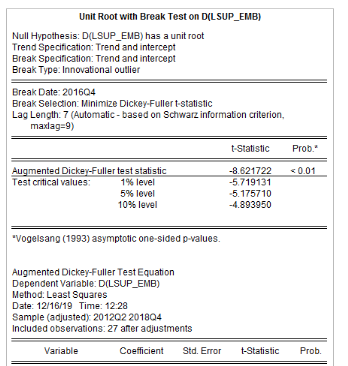 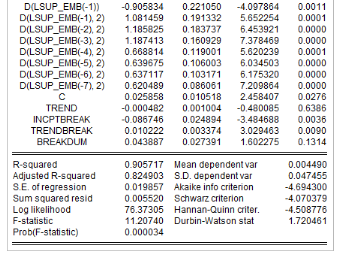
Annexe 3 : valeur des critères ayant permis
la détermination du meilleur modèle
|
Modèle
|
LogL
|
AIC*
|
BIC
|
HQ
|
Adj. R-sq
|
Specification
|
|
21
|
95.692006
|
-4.818839
|
-3.847428
|
-4.502183
|
0.974532
|
ARDL(4, 4, 4, 0, 4)
|
|
16
|
95.835771
|
-4.763598
|
-3.745930
|
-4.431864
|
0.971963
|
ARDL(4, 4, 4, 1, 4)
|
|
96
|
91.236576
|
-4.724940
|
-3.892303
|
-4.453521
|
0.973885
|
ARDL(4, 4, 1, 0, 4)
|
|
71
|
92.009733
|
-4.710305
|
-3.831410
|
-4.423807
|
0.973085
|
ARDL(4, 4, 2, 0, 4)
|
|
11
|
96.004352
|
-4.709958
|
-3.646032
|
-4.363145
|
0.968800
|
ARDL(4, 4, 4, 2, 4)
|
|
6
|
96.958774
|
-4.707018
|
-3.596834
|
-4.345126
|
0.966472
|
ARDL(4, 4, 4, 3, 4)
|
|
91
|
91.744519
|
-4.693195
|
-3.814299
|
-4.406697
|
0.972621
|
ARDL(4, 4, 1, 1, 4)
|
|
46
|
92.260102
|
-4.661942
|
-3.736789
|
-4.360365
|
0.971109
|
ARDL(4, 4, 3, 0, 4)
|
|
66
|
92.157955
|
-4.655352
|
-3.730199
|
-4.353775
|
0.970918
|
ARDL(4, 4, 2, 1, 4)
|
|
86
|
92.113692
|
-4.652496
|
-3.727343
|
-4.350919
|
0.970835
|
ARDL(4, 4, 1, 2, 4)
|
|
1
|
97.068101
|
-4.649555
|
-3.493114
|
-4.272584
|
0.961159
|
ARDL(4, 4, 4, 4, 4)
|
|
61
|
92.942249
|
-4.641435
|
-3.670025
|
-4.324780
|
0.969588
|
ARDL(4, 4, 2, 2, 4)
|
|
81
|
92.657523
|
-4.623066
|
-3.651655
|
-4.306410
|
0.969024
|
ARDL(4, 4, 1, 3, 4)
|
|
41
|
92.341407
|
-4.602671
|
-3.631261
|
-4.286016
|
0.968386
|
ARDL(4, 4, 3, 1, 4)
|
|
56
|
93.094635
|
-4.586751
|
-3.569082
|
-4.255016
|
0.966539
|
ARDL(4, 4, 2, 3, 4)
|
|
76
|
93.035727
|
-4.582950
|
-3.565282
|
-4.251216
|
0.966412
|
ARDL(4, 4, 1, 4, 4)
|
|
36
|
92.951573
|
-4.577521
|
-3.559852
|
-4.245786
|
0.966229
|
ARDL(4, 4, 3, 2, 4)
|
|
51
|
93.335686
|
-4.537786
|
-3.473860
|
-4.190973
|
0.962938
|
ARDL(4, 4, 2, 4, 4)
|
|
31
|
93.103040
|
-4.522777
|
-3.458851
|
-4.175963
|
0.962377
|
ARDL(4, 4, 3, 3, 4)
|
|
26
|
93.370105
|
-4.475491
|
-3.365307
|
-4.113598
|
0.957737
|
ARDL(4, 4, 3, 4, 4)
|
Annexe 4 : Estimation du modèle ARDL(4, 4, 1,
0, 4)
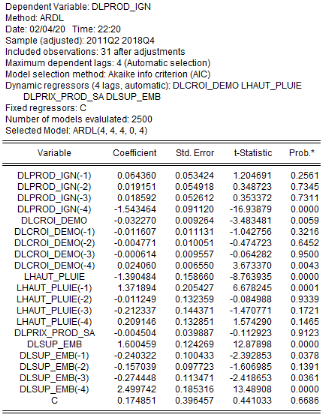
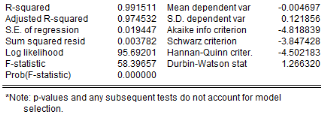
Annexe 5 : Tests diagnostiques du modèle ARDL
estimé
- Autocorrélation
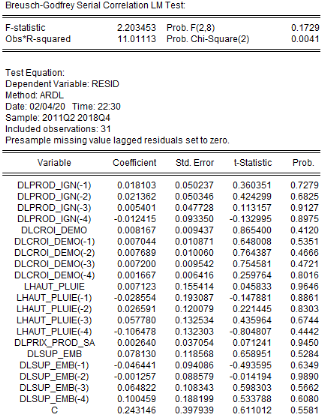 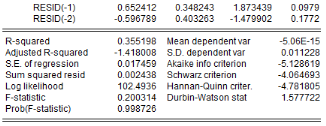
-
Hétéroscédasticité
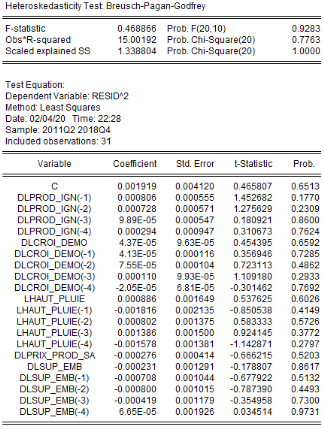
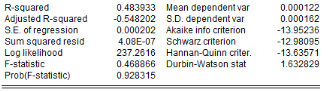
- Normalité
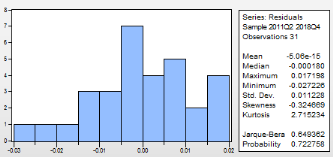
- Spécification

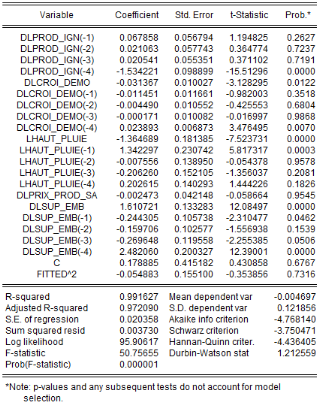
Annexe 6 : Résultats du test de
cointégration aux bornes (Bounds test)
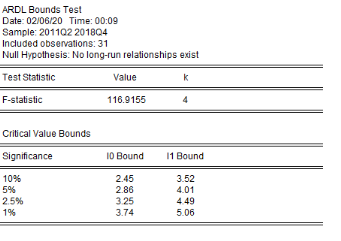
Annexe 7 : Test de cointégration et
estimation du long terme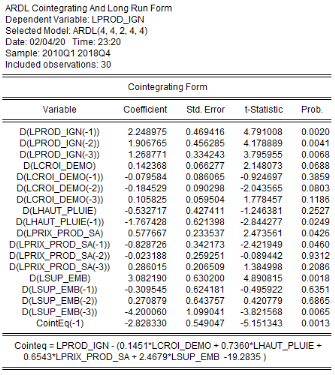 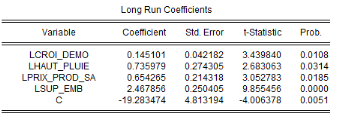
Table des matières
DEDICACES
iii
Remerciements
vi
Liste des tableaux
viii
Liste des figures
viii
Résumé
x
Abstract
xi
INTRODUCTION
1
CHAPITRE 1 : CADRE INSTITUTIONNEL DE
L'ETUDE
3
1.1. Présentation de la Direction de la
Statistique Agricole (DSA)
3
1.1.1. Bref historique de la DSA
3
1.1.2. Mission et attributions de la DSA
3
1.1.3. Organisation administrative (environnement
interne) de la DSA
4
1.1.4. Macro environnement (environnement externe)
de la DSA
4
1.2. Déroulement du stage
5
CHAPITRE 2 : CADRE THEORIQUE ET METHODOLOGIQUE DE
L'ETUDE
6
2.1. Enjeux de l'étude
6
2.1.1. Problématique
6
2.1.2. Objectifs et hypothèses de
recherche
7
2.2. Revue de littérature et
méthodologie
8
2.2.1. Définitions, Revues théorique
et empirique
8
2.2.2. Méthodologie de collecte des
données et Traitement
10
2.2.2.1. Collecte des données
10
2.2.2.2. Outils et modèle d'analyse
12
2.2.2.2.1. Méthodes descriptives
12
2.2.2.2.2. Méthodes explicatives
13
2.3. Limites de l'étude
17
CHAPITRE 3 : PRESENTATION ET INTERPRETATION DES
RESULTATS
18
3.1. Analyse descriptive
18
3.1.1. Statistiques descriptives
18
3.1.2. Boîte à moustaches des
variables
18
3.1.2. Evolution graphique des variables
19
3.1.2.1. Evolution de la production de l'igname et
de la superficie emblavée
19
3.1.2.2. Evolution de la pluviométrie
20
3.1.2.3. Evolution du prix aux producteurs
20
3.2. Analyse explicative
20
3.2.1. Analyse de la saisonnalité
20
3.2.2. Analyse de la stationnarité des
séries
21
3.2.3. Estimation du modèle ARDL
22
3.2.3.1. Spécification du modèle
ARDL
22
3.2.3.2. Estimation du modèle
ARDL(4,4,4,0,4)
23
3.2.3.3. Test de cointégration aux bornes
24
3.2.3.4. Coefficients de Long terme et dynamique de
court terme
25
3.2.3.4.1. Coefficients de court terme (CT)
25
3.2.3.4.2. Coefficients de long terme (LT)
26
3.3. Synthèse des résultats et
vérifications des hypothèses
27
3.3.1. Synthèse des résultats
27
3.3.2. Vérification des hypothèses
28
3.4. Préconisations
opérationnelles
28
CONCLUSION
29
REFERENCES BIBLIOGRAPHIQUES
30
ANNEXE
a
|
|



