|
CENTRO UNIVERSITÁRIO DE LINS -
UNILINS
ENGENHARIA ELÉTRICA
LINS/SP
2020
ACIONAMENTO DE MOTORES DE INDUÇO ATRAVÉS DE
INVERSORES DE
FREQUÊNCIA
Donatien Nsiangani Ngamuba
Johnson Emanuel Cavunji Roques
LINS/SP
2020
Donatien Nsiangani Ngamuba
Johnson Emanuel Cavunji Roques
ACIONAMENTO DE MOTORES DE INDUÇO ATRAVÉS DE
INVERSORES DE
FREQUÊNCIA
Trabalho de conclusão de curso, no formato de
Monografia, apresentado perante Banca Avaliadora do Centro Universitário
de Lins - UNILINS, como requisito parcial para obtenção do grau
de bacharel em Engenharia Elétrica.
Orientador: Prof. Me. Milton Léo.


Dedicamos este trabalho a todos que contribuíram
direta ou indiretamente em nossa formação
acadêmica.
AGRADECIMENTOS
Agradeço em primeiro lugar a Deus, por tudo quanto tem
feito pela minha vida, pela minha família, por todas as
bênçãos e livramentos que ele tem proporcionado para todos
nôs, por nos renovar a cada dia e nos oferecendo a oportunidade de
crescer em todos aspectos, principalmente espiritualmente.
Agradeço aos meus Pais (Astrid Mbulu Nene e Edgard
Nsiangani celane) que muito
fizeram e têm feito por mim, para nunca me
falte nada, por todas as lutas que eles já
enfrentaram e enfrentam
diariamente para proporcionar o bem-estar para mim e
para a nossa
família de modo geral.
Agradeço o nosso orientador Prof. Msc. Milton Léo
pela oportunidade,
ensinamentos, incentivos e apoio ao longo desses anos.
«Donatien Nsiangani Ngamuba»
«Johnson Emanuel»
AGRADECIMENTOS
Quando as coisas fluem da maneira que planejamos nos sentimos
bem, mas, é
quando elas apertam que sentimos quem nos tem algum
carinho.
Este período de minha trajetória cá no
Brasil, tem sido de muito aprendizado e
crescimento, e tudo isso só
me é possível pois Deus e minha família
sempre
estiveram comigo, ajudando a enfrentar tudo e continuar a seguir.
Agradeço a Deus pela vida, direção e
despertar, obrigado a minha família, em
especial aos meus pais Rita
Mauricio Cavunji e Salvador Manuel De Barros, pelos
ensinamentos e amor.
Obrigado ao meu colega e amigo Donatien Ngamuba, com quem muito
aprendo ao
longo desses anos de convívio, e pela oportunidade de
cooperar neste trabalho.
Obrigado a minha filha Serena Ekumbi por iluminar meus dias e
dar mais significado
a eles, a minha namorada Emelyn Fernanda, pelo amor,
companheirismo e por me
dar uma filha incrível, e pela sua
família por ser minha também.
E a todos os meus amigos e companheiros ao longo desses anos de
faculdade.
Obrigado
RESUMO
Neste trabalho pretente-se apresentar as possíveis
informações necessárias dos inversores de frequência
no controle de um motor de indução.
Os motores elétricos são responsáveis por
uma grande parcela do consumo mundial de energia, por isso existe uma
preocupação muito grande sobre sua eficiência. Até
algumas décadas atrás, os sistemas de controle para motores de
indução trifásicos, eram mais custosos e, por isso, em
várias aplicações não se fazia o uso de
técnicas de controle desses motores.
Com o desenvolvimento de teorias de controle e do
desenvolvimento tecnológico dos semicondutores esse contexto se alterou,
e assim viabilizou a aplicação de controle nos motores de
indução trifásica.
O presente trabalho de conclusão de curso tem por
finalidade apresentar o embasamento teórico básico para o projeto
de um inversor de frequência e, para isso, são apresentados os
principais conceitos relacionados aos inversores de frequência.
Palavras-chaves: Motor Elétrico. Inversor
de frequência.
ABSTRACT
In this work, we intend to present the possible necessary
information of the frequency inverters in the control of an induction motor.
Electric motors are responsible for a great share of the
world's energy consumption, so the efficiency of electric motors receives great
attention. Up until a few decades ago, control systems for tree-phase induction
motors were very expensive, and in several applications no control techniques
were used.
With the development of control theories and the technological
advancements in semiconductors, this situation has changed, therefore making it
affordable to apply control to three-phase induction motors.
This course completion project has the objective to present
the basic theoretical foundation for the design of a frequency inverter, and
for this the main concepts of frequency inverters will also be presented.
Keywords: Electric motor. Frequency inverter.
LISTA DE FIGURAS
Figura 1 - Mostra como os motores elétricos
podem ser divididos 19
Figura 2 - Motor de indução
19
Figura 3 - Diagrama de blocos de um inversor
25
Figura 4 - Diagrama de blocos de um Inversor de
Tensão Imposta 26
Figura 5 - Circuito básico de um Inversor de
Tensão Imposta Trifásico em
Ponte 27
Figura 6 - Retificador monofásico de ponte
completa 28
Figura 7 - Comparação entre
tensão de entrada e saída do retificador
monofásico com carga resistiva 28
Figura 8 - (a) Retificador com carga capacitiva
29
Figura 8 - (b) Comparação entre
tensão de entrada e saída de um retificador
com carga capacitiva 29
Figura 9 - Retificador trifásico de onda
completa não controlado 29
Figura 10 - Formas de onda de um retificador
trifásico de onda completa na
controlado 30
Figura 11 - Ação do filtro
31
Figura 12 - Inversor monofásico 32
Figura 13 - Transistor com proteção a
diodo 33
Figura 14 - Conversor CC-CA trifásico
34
Figura 15 - Forma de onda das fases na saída do
conversor trifásico 35
Figura 16 - (a) Princípio de
Operação da MLP senoidal 36
Figura 16 - (b) Pulsos oriundos da
comparação do sinal de referência e da
portadora 36
Figura 17 - Inversor de frequência alimentando
uma carga trifásica 40
Figura 18 - Inversor de frequência representando
o estado 40
Figura 19 - Todas as oito possíveis
combinações dos interruptores de um
inversor de frequência trifásico
41
Figura 20 - Vetores espaciais de tensão do
inverso trifásico 43
Figura 21 - Sequência de chaveamento para os
seis setores do plano
complexo 45
Figura 22 - Algoritmo básico para
implementação da modulação
vetorial 46
Figura 23 - Curva V/f do controle escalar
48
Figura 24 - Região de enfraquecimento de campo
49
Figura 25 - Motor de indução de 5 CV
50
Figura 26 - Inversor de frequência
50
Figura 27 - Circuito equivalente do motor de
indução 51
Figura 28 - Representação do IHM da WEG
54
LISTA DE TABELAS
Tabela 1 - Sinais de comutação
32
Tabela 2 - Sequência de acionamento dos
transistores 34
Tabela 3 - Relação V/F colhida
51
SUMÁRIO
|
1.
2.
3.
3.1.
3.2.
4.
|
INTRODUÇO
JUSTIFICATIVA
OBJETIVOS
Objetivo Geral
Objetivo específico
METODOLOGIA DA PESQUISA
|
11
13
14
14
14
15
|
|
5.
|
MOTOR DE INDUÇO
|
16
|
|
5.1.
|
Parâmetros do motor de indução
trifásico
|
19
|
|
5.2.
|
Acionamento elétrico para motores de
indução
|
20
|
|
5.2.1.
|
Partida direta
|
21
|
|
5.2.2.
|
Partida estrela - triângulo
|
21
|
|
5.2.3.
|
Partida com autotansformador
|
21
|
|
5.2.4.
|
Partida Soft Starter
|
22
|
|
5.2.5.
|
Inversores de frequência
|
22
|
|
6.
|
INVERSOR DE FREQUÊNCIA
|
23
|
|
6.1.
|
Retificador
|
25
|
|
6.1.1.
|
Retificador monofásico não controlado
|
25
|
|
6.1.2.
|
Retificador trifásico não controlado
|
27
|
|
6.2.
|
Barramento CC
|
28
|
|
6.3.
|
Inversor de tensão
|
29
|
|
6.3.1.
|
Conversor CC-CA monofásico
|
29
|
|
6.3.2.
|
Conversores CC-CA trifásicos
|
31
|
|
6.4.
|
Técnicas de modulação
|
33
|
|
6.4.1.
|
Modulação Senoidal
|
34
|
|
6.4.2.
|
Modulação Vetorial (SVPWM)
|
35
|
|
6.5.
|
Tipos de controles
|
44
|
|
6.5.1.
|
Controle escaler
|
45
|
|
6.5.2.
|
Controle vetorial
|
49
|
|
7.
|
PARAMETRIZAÇO
|
51
|
|
8.
|
INVERSORES NA PRÁTICA
|
54
|
|
9.
|
CONCLUSO
|
55
|
10. PROPOSTAS PARA TRABALHOS FUTUROS 56
11. REFERÊNCIAS 57
11
1. INTRODUÇO
Os motores estão presentes nos mais diversos setores da
vida humana, quer nas simples residências domiciliares, até as
indústrias e meios de transportes, fornecendo e tornando a vida mais
simples e simplificando processos ligados a vida cotidiana, com isso se tem uma
maior economia de tempo e outros recursos. («Controle e
Automação», Prof. Michel Robert Veiga, USP; 2018).
Atualmente, quase 100% da carga elétrica industrial
instalada no mundo é de acionamento de cargas motrizes. Na maioria dos
casos, esses acionamentos exigem um controle de velocidade, que vai desde a
partida até a velocidade nominal.Nas zonas industriais principalmente,
faz-se o usos de inversores de frequência para o acionamento e controle
de motores (principalmente de corrente alternada CA).Normalmente, o motor
utilizado é o de indução trifásico - MIT, que tem
como característica uma velocidade praticamente constante, em regime
permanente. («Controle e Automação», Prof. Michel
Robert Veiga, USP; 2018).
Um dos métodos utilizados para obter uma
operação com velocidade variável nos MIT é
através da variação da frequência de
alimentação. O equipamento capaz de promover uma
variação desse parâmetro é o inversor de
frequência.
Os inversores de freque^ncia, saÞo usados normalmente,
em motores eleìtricos de inducaÞo trifaìsicos para
substituir alguns dos sistemas de variacaÞo de velocidades meca^nicos,
tais como polias e variadores hidraìulicos e de velocidades, e que
exigem manutencaÞo (seja preventiva ou preditiva todas com elevado grau
de controle), assim como os custosos motores de corrente contiìnua pelo
conjunto motor assiìncrono e inversor, mais barato, de manutencaÞo
mais simples e reposicaÞo simplificada pela grande variedade de
componentes existentes no mercado.
12
Portanto, devido a sua importância na atividade
produtiva, esse equipamento é sempre muito estudado com o objetivo de
aumentar a sua eficiência.
Os conhecimentos adquiridos nas disciplinas Circuitos
Elétricos, Eletrônica Digital, Eletrônica de Potência
e Máquinas elétricas foi essencial para a
realização deste trabalho.
13
2. JUSTIFICATIVA
Com aumento da demanda por parte das induìstrias tanto
de processo quanto de manufaturas, tais como linha de montagem
automobiliìstica, bebidas, alimentiìcias, papel, celulose e
petroquiìmicas, que necessitam cada vez mais de processos produtivos e
eficientes, a forma para controlar a velocidade de motores de inducaÞo
trifaìsicos tem sido mudada para atender melhor o mercado, visando um
custo baixo de manutencaÞo e um lucro alto na producaÞo (AHMED,
2000).
Devido a essas e inúmeras razões para o uso de
dispositivos de controle nas diversas aréas, principalmente na
indústria do papel e celulose que não podem operar sem o controle
de velocidade, já outras áreas como bombas centrifugas e outras
que podem ser beneficiadas com a redução de energia, o uso de
dispositivos para controle de velocidade em motores tem uma extensa
aplicação na indústria.
Os inversores de frequência cada vez mais se destacam em
diferentes áreas principalmente no meio industrial, no controle de
velocidade, torque, economia de energia e etc, o que gera um interesse de nossa
pare acerca do funcionamento e uso desta ferramenta que muito tem a
contribuir.
14
3. OBJETIVOS
3.1. Objetivo Geral
Dada a evolução da humanidade e sua demanda por
produtos e trabalhos com mais rendimento e menos esforço, surgiram os
motores para alavancar o desenvolvimento e melhora de seus processos de
trabalhos e vida, e com o tempo surgiram os inversores de frequência para
facilitar o controle e o uso desses motores a fim de entregar mais
eficiência e rendimento, e com esse trabalho desejamos estudar os
inversores e suas aplicações em motores de
indução.
3.2. Objetivo específico
? Estudar o inversor, suas características e melhorias nos
processos de aplicação;
? Estudar o acionamento, controle de motores usando inversores
de frequência;
? Estudar as melhorias que os inversores trazem aos sistemas
aplicados.
15
4. METODOLOGIA DA PESQUISA
Para a realização desse trabalho teve-se a
necessidade de uma base teórica acerca do tema, por meio da
elaboração de uma revisão bibliográfica, com base
em pesquisas feitas em portais de informação, artigos
acadêmicos (revistas, teses, livros), dados coletados em entrevistas
orais com professores da Unilins, pesquisas de campo. Em harmonia com essa
fundamentação, será feita a análise dos dados e
elaborado o projeto: «ACIONAMENTO DE MOTORES DE INDUÇO
ATRAVÉS DE INVERSORES DE FREQUÊNCIA» aqui proposto
como solução para o problema apresentado.
16
5. MOTOR DE INDUÇO
O motor de indução foi, de forma apropriada,
patenteado primeiramente por Nikola Tesla em 1888. Esses motores têm sido
usados em larga escala nas indústrias devido a sua confiabilidade,
simplicidade e eficiência.
Os motores de indução são assim chamados
porque apenas o estator é alimentado com energia elétrica e o
rotor recebe energia através da indução
eletromagnética. Os motores de indução são motores
de corrente alternada que podem ser divididos tanto quando número de
fases quanto ao modo de enrolamento do rotor.
As máquinas rotativas de corrente alternada dividem-se
em dois grandes grupos: Máquinas Síncronas e
Máquinas Assíncronas.
Uma máquina diz-se síncrona quando roda à
velocidade de síncronismo, isto é, à velocidade que
resulta da aplicação da expressão:
Onde f, frequência da tensão de
alimentação e p, número de pares de pólos da
máquina.
Uma máquina diz-se assíncrona quando roda a uma
velocidade diferente da velocidade de síncronismo.
Para este trabalho foi escolhido o tipo de motor
assíncrono trifásico também chamado de motor de
indução trifásico com rotor de gaiola. Este rotor se torna
mais viável se considerar as aplicações de baixa
potência, que é o foco deste trabalho. A
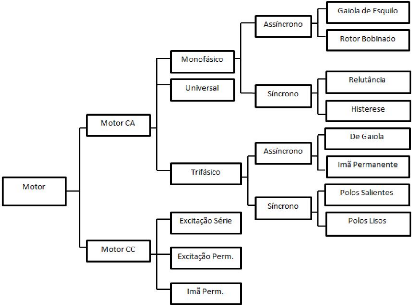
Figura 1 - Mostra como os motores elétricos podem ser
divididos. (Fonte: VAZ, 2010)
Na Figura 2 é possível identificar os principais
elementos que constituem um motor de indução, e como eles
são conectados em sua montagem.
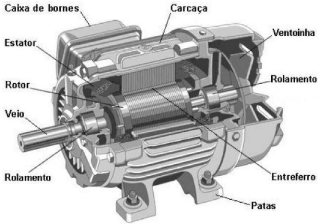
Figura 2 - Motor de indução. 17
18
Abaixo segue uma pequena descrição de cada parte de
um motor de indução:
· Estator: Parte fixa da
máquina, é constituído por chapas ferromagnéticas
empilhadas e isoladas entre si. As chapas possuem pequenas cavidades nas quais
são colocados enrolamentos de fios de cobre que são alimentados
pela rede elétrica.
· Rotor : Parte móvel do motor,
é constituído por um núcleo ferromagnético, que
pode ser um conjunto de enrolamento (motor de rotor bobinado) ou um conjunto de
condutores paralelos (motor de rotor em curto circuito ou também chamado
de rotor emgaiola de esquilo).
· Veio: Também conhecido como
eixo, faz parte do rotor e é o responsável por fornecer energia
mecânica a uma determinada aplicação.
· Rolamentos: São utilizados
para fazer o contato entre as partes girantes e fixas do motor.
· Patas: São usadas para a
fixação do motor.
· Caixa de bornes: Nesta caixa é
feita a ligação elétrica do motor com a rede.
· Entreferro: É um pequeno
espaçamento entre o rotor e o estator. Quanto menor for esse
espaçamento melhor será o fluxo magnético entre o rotor e
o estator.
· Ventoinha: Tem a função de
refrigeração do estator e do rotor.
· Carcaça: A carcaça acopla
o estator e serve de proteção contra o meio externo.
19
5.1. Parâmetros do motor de indução
trifásico
Para o entendimento do funcionamento e para o projeto de
sistemas controladores dessas máquinas, alguns parâmetros
são de extrema importância. Os parâmetros listados abaixo
proporcionam um entendimento básico sobre os motores de
indução trifásicos.
. Velocidade Síncrona (????): É a velocidade do
campo magnético girante.
Não é a velocidade
mecânica do motor, mas sim a velocidade do fluxo magnético gerado
pelo enrolamento do estator.
Ela é dada pela Equação (1):
120??
????= (1')
??
Onde:
ns --* velocidade síncrona ou velocidade do campo
magnético girante, (rpm); f --* freqüência da corrente do
estator ou freqüência da rede (alimentação), Hz; p --*
número total de pólos.
. Velocidade Mecânica (????) : É a velocidade no
eixo do motor ou
velocidade de funcionamento do motor e é dada pela
Equação 2
????= (1 - ??)???? (2)
Onde S é o escorregamento e pode ser calculado pela
Equação 3.
???? - ????
??(%) = * 100 (3)
????
Onde:
S(%) --* escorregamento percentual, %;
????--* velocidade síncrona (ou velocidade do campo
girante), rpm;
????--* velocidade de funcionamento do motor (ou velocidade do
rotor), rpm.
. Fluxo magnético (????) : É o fluxo que gera a
indução magnética no
motor de indução. Este fluxo é proporcional
à tensão aplicada no estator e inversamente proporcional à
frequência aplicada, como mostrado na equação 4. ??
???? ? (4)
??
20
Onde:
????? fluxo magnético, Wb;
V ? tensão aplicada no estator, V.
? Torque (T): é um esforço de torção,
ou torcional, produzido pelo motor.
O Torque do motor é proporcional
ao produto da corrente no rotor e do fluxo
magnético.
T ? IR.öm (5)
Sendo:
T: torque do motor (N.m);
IR: corrente no rotor (A);
öm: fluxo de magnetização (Wb).
O torque pode ser positivo ou negativo, dependendo da
direção de rotação.
? Potência (P): a potência de saída é
proporcional ao produto do torque e da velocidade ????.
??? ??.???? (6)
Sendo:
P: potência mecânica (W)
T: torque (N.m)
????: velocidade do rotor (rpm)
5.2. Acionamento elétrico para motores de
indução
Um dos grandes problemas nos motores é a corrente de
partida, cerca de seis vezes a corrente nominal. Devido ao fato dos motores
exigirem correntes altas na partida, pode ocorrer queda de tensão na
rede, e assim afetar os demais equipamentos ligados a mesma rede.
21
Para evitar estas altas correntes na partida, existem
métodos de acionamentos de motores elétricos que proporcionam uma
redução no valor da corrente de partida dessas máquinas,
tais como:
5.2.1. Partida direta
A partida direta para motores trifásicos é
relativamente a ligação mais simples dentre todas as partidas
usadas para acionar os motores trifásicos, pois o motor recebe a
alimentação diretamente da fonte de energia trifásica, e
dependem apenas de dispositivos de seccionamento para interferirem diretamente
no seu funcionamento, como por exemplo os disjuntores, relés
térmicos ou contatores.
Esta técnica pode ser considerada a mais simples, pois
necessita apenas de contatores, disjuntores e chaves para manobras. A partida
direta é utilizada para motores abaixo de 5CV desde que a corrente de
partida seja menor que a corrente suportada pela rede. (CAMARGO, 2011, p.26)
5.2.2. Partida estrela - triângulo
A partida estrela-triângulo é utilizada em
motores de elevada potência com o intuito de diminuir a corrente na
partida. Trata-se de uma técnica bastante utilizada, pois a sua
implementação é de baixo custo. (CAMARGO, 2011, p.26)
Nesta técnica, o motor parte na
configuração estrela e, após uma determinada velocidade,
passa para triângulo, e assim operando em suas condições
nominais.
Neste tipo de partida, a corrente e o torque são
reduzidos a 1/3, ou aproximadamente entre 25% e 33% da corrente de partida
nominal. (CAMARGO, 2011, p.27)
5.2.3. Partida com autotansformador
É utilizada na partida de motores maiores, de
até 15CV. A função do autotransformador é diminuir
a tensão na partida, podendo assim, diminuir a corrente de pico.
22
Essa técnica de partida tem um custo mais elevado
quando comparado com a técnica de partida estrela-triângulo, o que
faz com que sua aplicação seja mais limitada a casos
especiais.
5.2.4. Partida Soft Starter
O funcionamento de um soft starter, se dá
através de uma ponte tiristorizada, que fazem o chaveamento da
tensão para que ela possa ser disponibilizada para o motor de forma
crescente, ou seja, irá aumentar gradativamente, garantindo uma partida
suave e sem a presença da corrente de pico. Este chaveamento feito pela
ponte é controlado através do sistema de controle e disparo, que
é um modulo onde é possível realizar as
programações desejadas por meio de parâmetros, que
são identificados um a um pelo fabricante e disponibilizadas em um
manual.
5.2.5. Inversores de frequência
Além do controle de partida de motores de
indução, a indústria necessita do controle de velocidade
variável ao longo do processo. Esses controles que antes eram feitos por
motores de corrente contínua, agora passam a ser realizados por motores
de indução, cujo processo é possível graças
aos conversores de frequência.
Devido ao baixo custo, economia de energia, fácil
instalação e parametrização, os inversores de
frequência, como também são chamados, são utilizados
amplamente no meio industrial. (WEG, 2010, p.45).
23
6. INVERSOR DE FREQUÊNCIA
Antes de ser inventado, o grande problema era como cessar a
passagem da energia dentro do
mesmo. Com esse advento muitas coisas
foram possíveis, como por exemplo o não superaquecimento do motor
(consequentemente não queimando) com uma corrente contínua,
é quase que impossível realizar o controle de giro dos motores
elétricos, porém hoje já é possível realizar
esta alternância na energia recebida pelo motor, utilizando um inversor
de frequência. Assim auxiliando no processo de transformar a corrente
contínua em uma corrente alternada. Esse processo é muito
semelhante ao sistema dos interruptores de energia simples que temos em nossas
casas. E além disso, ainda tem a possibilidade de ser utilizado na
idealização de novos e mais potentes motores elétricos,
tanto para indústria de ventilação, como para
indústrias metalúrgicas. Atualmente existem várias
empresas especializadas na fabricação de inversores, como a
Siemens, a Weg, a Yaskawa, a Allen Bradley e a ABB, entre outras.
A ideia básica de um inversor de frequência
é transformar a tensão de entrada, geralmente corrente alternada
fornecida pela rede elétrica, em corrente contínua, e depois
transformar novamente em corrente alternada, mas agora com um sinal modulado,
onde é possível alterar tanto a amplitude como a frequência
deste sinal de saída.
Um inversor de frequência é formado basicamente
por um retificador, acoplado a um inversor trifásico através de
um elo de corrente contínua, como mostrado na Figura 3.
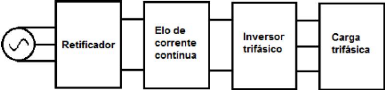
Figura 3 - Diagrama de blocos de um inversor (Fonte: BORBA,
2009)
O elo de corrente contínua tem a função
de fornecer corrente contínua, que geralmente é fornecida por um
retificador, ao inversor trifásico.
24
Este elo é constituído por componentes capazes
de armazenar energia elétrica, capacitores ou indutores, fator este que
depende da configuração do inversor. A configuração
que utiliza o capacitor é chamada de Inversor de Tensão Imposta
e, para a configuração com um indutor, é chamada de
Inversor de Corrente Imposta. (BORBA, 2009, p. 242)
O Inversor de Tensão Imposta, a tensão de
entrada do inversor é mantida constante pelo capacitor do elo CC como
mostrado na Figura 4.
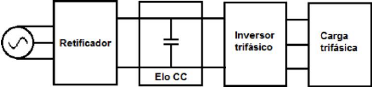
Figura 4 - Diagrama de blocos de um Inversor de Tensão
Imposta (Fonte: BORBA, 2009)
O bloco do retificador de tensão é
responsável por tratar o sinal CA da rede e fornecer um sinal
contínuo para o elo CC ou também chamado de barramento CC. O elo
tem por objetivo melhorar o sinal de tensão CC fornecido pelo
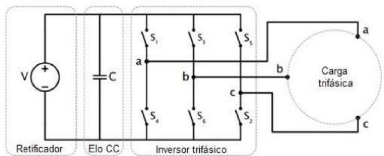
retificador, ou seja, torna o sinal mais regular para o inversor. Na Figura 5
é mostrado o circuito básico de um Inversor de Tensão
Imposta Trifásico alimentando uma carga trifásica. O inversor
transforma a tensão contínua fornecida pelo barramento CC em uma
tensão alternada com frequência modulada. Isso é muito
importante, pois algumas técnicas de controle de velocidade de motores
elétricos são baseadas na modulação da
frequência da tensão fornecida para o motor. A
modulação do sinal de saída é feita através
de técnicas da comutação dos interruptores S1, S2, S3, S4,
S5 e S6.
25
Figura 5 - Circuito básico de um Inversor de
Tensão Imposta Trifásico em Ponte. (Fonte:
BORBA, 2009)
6.1. Retificador
Como fornecimento de energia elétrica é feito,
essencialmente, a partir de uma rede de distribuição em corrente
alternada e muitas aplicações exigem uma tensão
contínua, a solução para essa adaptação de
alternado para contínuo é feita por conversores CA-CC, ou
também chamados de retificadores.
Os retificadores podem ser classificados de duas maneiras,
controlados e não controlados, de acordo com o número de fases da
tensão alternada de entrada (monofásico, trifásico,
hexafásico, etc.); em função do tipo de conexão dos
elementos retificadores (meia ponte x ponte completa). (EMERICH, 2005,
p.65).
6.1.1. Retificador monofásico não
controlado
Os retificadores não controlados são aqueles que
utilizam diodos como elementos de retificação, portanto,
não há a possibilidade de atuar no chaveamento desses
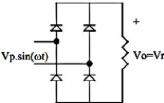
semicondutores. Um retificador monofásico de ponte completa com carga
puramente resistiva tem o esquema representado pela Figura 6.
26
Figura 6 - Retificador monofásico de ponte completa.
(Fonte: EMERICH, 2005)
A Figura 7 compara as formas de onda da tensão na entrada
do retificador com a forma de onda que será aplicada a essa carga
resistiva.
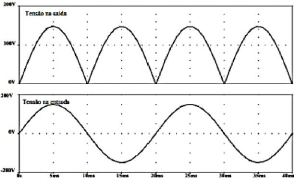
Figura 7 - Comparação entre tensão de
entrada e saída do retificador monofásico com carga
resistiva. (Fonte: EMERICH, 2005)
Percebe-se que a tensão de saída passa a ser
contínua, ou seja, em nenhum momento ela tem a sua polaridade
alterada.
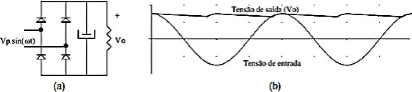
Um retificador com carga capacitiva, Figura 8 (a), faz com que a
tensão de saída seja alisada e assim eleva seu valor médio
quando comparado com a carga resistiva do caso anterior, efeito que pode ser
observado na Figura 8 (b).
27
Figura 8 - (a) Retificador com carga capacitiva, (b)
Comparação entre tensão de entrada e saída deum
retificador com carga capacitiva. (Fonte: EMERICH, 2005)
6.1.2. Retificador trifásico não
controlado
O retificador trifásico de onda completa não
controlado é assim chamado por usar um sistema trifásico, e onda
completa, pois aproveita todo o ciclo da onda, tanto positivo quanto negativo.
Na Figura 9 é ilustrado o esquema de retificador trifásico de
onda completa não controlado.
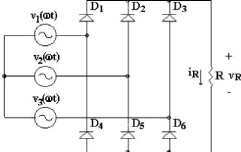
Figura 9 - Retificador trifásico de onda completa
não controlado. (Fonte: EMERICH, 2005)
Esta topologia conduzirá o diodo que estiver no momento
com a tensão mais positiva e o que estiver com a tensão mais
negativa. Cada par de diodos conduzirá por 60° e cada diodo
conduzirá por 120°. A frequência da tensão retificada
é igual a 6 vezes a frequência das tensões de
alimentação. Pode-se observar na Figura 10 que, a partir de
30°, os diodos D1 e D5 estão, respectivamente, nas tensões
mais positiva e mais negativa. Eles conduzirão até o
próximo cruzamento em que o diodo D6 fica na tensão mais negativa
e assim conduzirá no lugar de D5 e assim será até o
próximo cruzamento. (EMERICH, 2005, p.65)
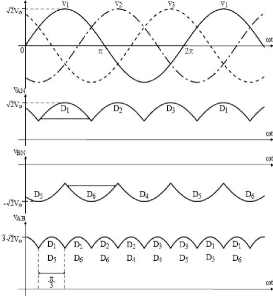
28
Figura 10 - Formas de onda de um retificador trifásico de
onda completa na controlado. (Fonte: EMERICH, 2005)
Esse retificador é mais eficiente do que o retificador
trifásico de meia onda, pois fornece seis pulsos enquanto o de meia onda
fornece apenas três, e assim fornece uma saída com menos
ondulação. Como a frequência de saída é mais
alta, a filtragem é simplificada. (EMERICH, 2005, p.65)
6.2. Barramento CC
Após a tensão de entrada ser retificada,
é necessário que essa tensão passe por um filtro, pois a
tensão fornecida pelo retificador contém certas
ondulações não desejadas.
O filtro pode ser formado basicamente por um capacitor ou
banco de capacitores. O capacitor é carregado com a tensão de
pico da entrada e, a partir do momento em que a tensão de entrada se
torna menor que a tensão no capacitor, os diodos são bloqueados e
a tensão passa a ser fornecida pelo capacitor. Assim, se o
projeto do filtro for realizado corretamente, a tensão
de saída do filtro é uma tensão sem
ondulações. A Figura 11 ilustra a ação de um filtro
ideal.
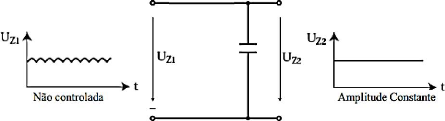
29
Figura 11 - Ação do filtro. (Fonte: EMERICH,
2005)
6.3. Inversor de tensão
O inversor é um conversor CC-CA, ou seja, este
conversor transforma a tensão contínua em tensão
alternada. Estes conversores CC-CA podem ser ligados a qualquer tipo de fonte
contínua, como por exemplo:
? Bancos de bateria;
? Células combustíveis;
? Rede de painéis solares.
No entanto, na indústria é mais comum os
conversores CC-CA serem conectados em circuitos com retificador e filtro.
(RANIEL, 2011, p.128)
A conversão de CC-CA é feita através da
comutação dos transistores. Para um melhor entendimento de como
é feito essa conversão, será apresentado primeiramente o
funcionamento de um circuito inversor monofásico.
6.3.1. Conversor CC-CA monofásico
Um modelo de inversor monofásico está
representado pela Figura 12. Para que a conversão seja feita de maneira
correta, os sinais S1, S2, S3 e S4 que
30
acionam os transistores devem ser comutados de forma
específica. Cada transistor irá receber no gate um sinal que pode
ser representado pelos níveis lógicos 1 ou 0 e, de forma a evitar
que os dois transistores de um mesmo braço conduzam em simultâneo,
os interruptores debaixo recebem os sinais complementares dos transistores de
cima, correspondentes.
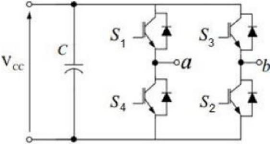
Figura 12 - Inversor monofásico. (Fonte: RANIEL, 2011)
Uma vez que o inversor é controlado por dois sinais
binários, onde esses sinais são referentes aos estados dos
transistores S1 e S3, o sinal binário 0 significa que o transistor
está bloqueado e o 1 significa que o transistor está conduzindo.
Na Tabela 1 são apresentados os estados de comutação
correspondentes a este modelo.
|
Sinal do Gate S1
|
Sinal do Gate S3
|
Saída de Tensão (??????)
|
|
1
|
0
|
Vcc
|
|
1
|
1
|
0
|
|
0
|
1
|
-Vcc
|
|
0
|
0
|
0
|
Tabela 1 - Sinais de comutação (Fonte: CONSTANTINO,
2013)
Nota-se que dois dos estados, (1,1) e (0,0), geram uma
tensão de 0V. Esta característica é chamada de
nível de tensão de redundância e pode ser utilizada para
outros propósitos de controle, desde que não afete o nível
de tensão da carga.
Em aplicações com cargas indutivas, podem
aparecer tensões inversas elevadas. Os transistores devem ser protegidos
dessas tensões e, para isso, um
31
diodo pode ser conectado entre o coletor e o emissor do
transistor, como mostrado na Figura 13. (BARBI, 2007)
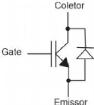
Figura 13 - Transistor com proteção a diodo.
6.3.2. Conversores CC-CA trifásicos
O conversor CC-CA trifásico de tensão, é
uma das estruturas mais empregadas na indústria, normalmente aplicado em
altas potências. Sua popularidade deve-se à sua eficiência
em obter tensões trifásicas com frequência
controlável (BARBI, 2005, p.394).
Como cada tensão de entrada dos motores de
indução é defasado em 120°, é
necessário que a lógica aplicada para a comutação
dos transistores também resulte em uma defasagem de 120° em cada
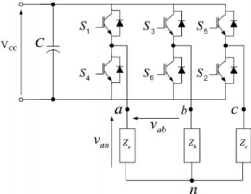
fase na saída do conversor CC-CA trifásico. Um conversor CC-CA
trifásico pode ser representado pela Figura 14.
32
Figura 14 - Conversor CC-CA trifásico. (Fonte:
CONSTANTINO, 2013)
Uma sequência possível de comutação
dos sinais de entrada do gate dos transistores é a que está
representada na Tabela 2.
|
Intervalo
|
S1
|
S2
|
S3
|
S4
|
S5
|
S6
|
|
0 - 60°
|
1
|
0
|
0
|
0
|
0
|
1
|
|
60° - 120°
|
1
|
1
|
0
|
0
|
0
|
0
|
|
120° - 180°
|
0
|
1
|
1
|
0
|
0
|
0
|
|
180° - 240°
|
0
|
0
|
1
|
1
|
0
|
0
|
|
240° - 300°
|
0
|
0
|
0
|
1
|
1
|
0
|
|
300° - 360°
|
0
|
0
|
0
|
0
|
1
|
1
|
Tabela 2 - Sequência de acionamento dos transistores.
(Fonte: CONSTANTINO, 2013)
Esta lôgica de acionamento faz com que um sinal
alternado e com 120? seja aplicado ao motor. Para que
não ocorra curto circuito nas fases, os transistores devem ser ativados
dois de cada vez, um do grupo S1, S3 e S5 e outro do grupo S4, S5 e S6. As
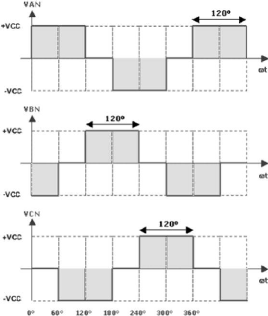
formas de onda das fases A, B e C para este tipo de lôgica são
mostradas na Figura 15.
33
Figura 15 - Forma de onda das fases na saída do conversor
trifásico. (Fonte: CLUBE DA ELETRÔNICA, 2009)
Tanto para o caso em que é usado um inversor
monofásico ou trifásico a forma de onda na saída do
inversor é retangular. Para que o sinal na saída se comporte como
um sinal senoidal é necessário que o os transistores sejam
acionados obedecendo algumas das técnicas de acionamento dos
transistores mais avançadas. No próximo item serão
estudadas duas das técnicas de modulação.
6.4. Técnicas de modulação
O acionamento dos transistores pode ser feito através
de técnicas de modulação por largura de pulso (MLP), seja
do tipo senoidal, histerese, modulação vetorial,
modulação ótima, modulação aleatória,
entre outras.
34
Dentre as principais técnicas de
modulação, a modulação vetorial tem-se tornado
bastante popular devido às seguintes características (NICOLAU,
2007, p.17):
? Alto aproveitamento da tensão do elo CC;
? Faixa de operação linear maior;
? Operação na faixa de sobre
modulação;
? Baixa distorção harmônica;
? Perdas de chaveamento são passíveis de
otimização.
A seguir serão apresentadas duas técnicas de
modulação, a modulação senoidal e a
modulação vetorial.
6.4.1. Modulação Senoidal
A modulação senoidal é a mais popular,
difundida e discutida na literatura, e comumente utilizada em
aplicações industriais.
Na MLP senoidal, um sinal senoidal de referência chamado
de moduladora é comparado com uma portadora triangular, e assim gera os
pulsos que acionam os transistores. A Figura 16 (a) mostra a
comparação entre o sinal da moduladora e a portadora, e a Figura
16 (b) apresenta o resultado da comparação, ou seja, o sinal PWM
que irá ativar um determinado transistor.
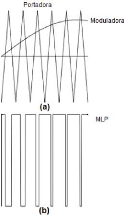
Figura 16 - (a) Princípio de Operação da MLP
senoidal. (b) Pulsos oriundos da comparação do sinal de
referência e da portadora.
(Fonte: NICOLAU, 2007)
35
6.4.2. Modulação Vetorial (SVPWM)
Com o intuito de diminuir o conteúdo harmônico e
melhorar o aproveitamento do barramento CC, em 1986, Van der Broek propôs
uma técnica baseada na teoria de vetores espaciais para máquinas
de corrente alternada, chamada de Modulação Vetorial ou SVPWM -
Space Vector Pulse Width Modulation (CORTÉS, 2005, p. 97). Nesta
técnica, a comutação dos interruptores é feita
através do cálculo de seus tempos de aplicação e
não mais através da comparação dos sinais de uma
moduladora com uma onda
triangular. Com isso, foi
possível um aumento de 15 % do aproveitamento do barramento CC.
Além de aumentar o aproveitamento do barramento CC, a
modulação vetorial também diminui o conteúdo
harmônico, minimiza as comutações dos interruptores e
também é adequada para implementação digital.
(FLORES, 2009, p.24)
O conceito de vetores espaciais é derivado do campo
girante da máquina CA a qual é acionada por um inversor de
saída modulada. Neste tipo de modulação, as grandezas
trifásicas podem ser transformadas para equivalentes bifásicas em
componentes síncronas com referencial girante ou estacionário.
(GIFFONI, 2008, p.142)
Considerando-se um sistema de tensões balanceadas
trifásicas representadas pelo conjunto das equações
abaixo:
???? = ??????????(????)
???? = ?????????? (???? - 3 2?? )
(7)
????=??????????(????+ 3 2?? )
Para análise do controle vetorial é
preferível expressar o sistema trifásico em função
do cosseno, como mostrado pelas equações a seguir:
|
????
????
|
????
=
=
|
= ??????????(????)
?????????? (???? -
??????????(???? +
|
3 2?? )
2?? )
|
(8)
|
|
3
|
36
Quando as tensões descritas pelas
Equações 8 são aplicadas a uma máquina CA é
gerado um fluxo girante no entreferro que pode ser representado como um vetor
que gira com velocidade síncrona. A amplitude e o ângulo deste
vetor podem ser encontrados pela transformada de Clarke, conforme mostrado pela
Equação 9.
|
|
??????? ?? = ???? + ???? = 23 (???? + ?????? +
??2????)
|
(9)
|
Sendo que:
|
|
|
|
|
|
|
|
|
??2??
|
|
|
|
|
|
|
??= ?? 3
|
|
|
|
(10)
|
|
|
??4??
|
|
|
|
|
|
|
??2 = ?? 3
|
|
|
|
(11)
|
|
|
|????????? | = v????2 +
????2
|
|
|
|
(12)
|
|
|
?? = ??????-1 (????
????)
|
|
|
|
(13)
|
? 2 3
???????? =
|
[(????
|
+ ?????? 32?? ???? + ?????? 32?? ????) + ??
|
(??????32?????? - ??????
|
32??
|
????)]
|
(14)
|
|
Separando-se a Equação 14 em partes reais e
imaginárias, obtém-se as equações
15 e 16, respectivamente.
2
???? = 3 (???? + ?????? 32?? ???? + ??????
2 2?? ????-??????
(??????
|
32?? ????)
????)
????
.[???? ]
????
|
(15)
(16)
(17)
|
|
32??
???? = 3
3
Passando-se agora para a forma matricial.
2?? 2??
1
|
|
??????3 ??????
[???? 3
2?? 2??
0
????] = 2 3 [ ]
|
|
?????? 3 -??????
3
|
1 -1 -1 [????
???? = 2 2 2 ????] (18)
???? 3 0 v3 - v3.??
2 2 ??
A Equação 18 representa a equação
de Clarke que torna possível representar um sistema de tensões
trifásico em seu equivalente bifásico.
Reescrevendo-se as funções
trigonométricas na forma exponencial através da seguinte
identidade trigonométrica de Euler:
????????+??-??????
??????(????) =2 (19)
Substituindo-se a Equação 19 na
Equação 9 se obtêm as equações 20, 21 e
22.
???????? + ??-??(????+4?? ???????? +
??-??(????+8??
3 ???? [???????? + ??-??????
2 3 ) 3)
?
???????? =

+ +
2 2
2 ] (20)
3 ???????? (21)
2
2
3 ????.
????????? =
37
??????? ?? = ???????????? (22)
Percebe-se que o vetor de referência ?? ??????gira em
plano complexo com módulo e velocidade síncrona constante, ou
seja, a transformada de Clarke não alterou as características
fundamentais do sistema trifásico, como amplitude e frequência.
Considerando, agora, o inversor trifásico alimentando
uma carga conforme ilustrado na Figura 17, é possível identificar
que para um inversor de três braços existem apenas oito
possibilidades de combinação de comutação, a saber
que os interruptores de um mesmo braço são complementares.
38
Figura 17 - Inversor de frequência alimentando uma carga
trifásica
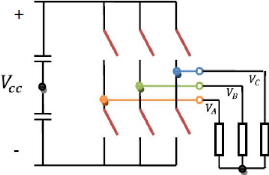
Fonte: FLORES, 2009.
Para identificar um estado específico de
comutação é necessário observar os estados dos
interruptores superiores do inversor da Figura 18, onde 1 significa que o
interruptor está conduzindo e 0 indica que o interruptor está
bloqueado. O estado da Figura 18 será chamado de ??1 =
100.
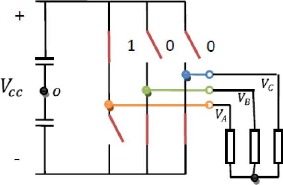
Figura 18 - Inversor de frequência representando o estado
(Fonte: FLORES, 2009.)
Escrevendo-se as equações das tensões
aplicadas à carga, tomando-se como refere^ncia o ponto «o»
para o estado contram-se as equações abaixo.
39
|
??????
????= + 2
??????
????= - 2
??????
????= - 2
|
(23)
|
Substituindo-se as equaçôes 23 na
Equação 9, resulta no vetor espacial no plano complexo para o
estado ??1 = 100, conforme pode ser observado pela
Equação 24.
2 3 - ??????
??1 = 3 (???2 ??? - ???2 ??? ????2?? 2
????4?3 ? ) = 23 ?????? (24)
Analisando-se os estados dos interruptores nas oito
combinaçôes possíveis da Figura 19 e realizando-se o mesmo
procedimento anterior, obtêm-se as equaçôes para os demais
estados.
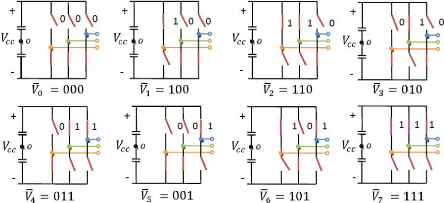
Figura 19 - Todas as oito possíveis
combinaçôes dos interruptores de um inversor de frequência
trifásico (Fonte: FLORES, 2009.)
As equaçôes para todas as oito
combinaçôes estão descritas abaixo:
2 3 - ??????
??0 = 3(- ??????
2- ???2 ??? ????2?? 2????4?_ ? )=0 (25)
22
????4??
??1 = 3(+??????
2 -???2 ???????2?3 ? -?????? 3)= 2 3??????
(26)
40
2 3 - ??????
??2 = 3(+ ??????
2 + ??????
2 ????2?? 2 ????4?3 ? )= 2
3???????????? 3 (27)
2 2 ????4??
??3 = 3(- ??????
2+ ???2 ??? ????2?3 ? - ?????? 3)= 2 3??????
????2?3 ? (28)
2 2 ????4??
??4 = 3(- ??????
2+ ???2 ??? ????2?3 ? + ?????? 3)= 2 3??????
?????? (29)
2 3 + ??????
??5 = 3(- ??????
2 - ???2 ??? ????2?? 2 ????4?3 ? )= 2 3??????
????4?3 ? (30)
2 3 + ??????
??6 = 3(+ ??????
2 - ???2 ??? ????2?? 2 ????4?3 ? )= 2 3??????
????5?3 ? (31)
2 2 ????4??
??7 = 3(+ ??????
2+ ???2 ??? ????2?3 ? + ?????? 3)=0 (32)
Pelas equaçôes de 25 a 32 é
possível perceber que seis combinaçôes resultam em
transferência de energia da fonte para a carga. Essas
combinaçôes recebem o nome de vetores ativos. As duas outras
combinaçôes nâo resultam em transferência de energia,
entâo sâo chamadas de vetores nulos (??0 = 000 ??
??7 = 111).
Os oitos vetores resultantes das combinaçôes dos
interruptores sâo os únicos vetores possíveis de gerar com
um inversor trifásico. Esses sâo vetores fixos em um plano
complexo, conforme representado pela Figura 20. Os vetores nulos sâo
representados no centro do plano, pois nâo possuem magnitude. Os seis
vetores ativos têm a mesma magnitude e estâo defasados em 60
formando um hexágono. Cada parte do hexágono é chamada de
setores, e assim entâo formando-se entâo seis setores. O vetor de
referência tem seu valor máximo na interseçâo do
hexágono com o círculo inscrito no mesmo. Tomando-se o primeiro
setor como referência, o vetor de referência é máximo
para um ângulo de 30, como mostrado na Figura 20.
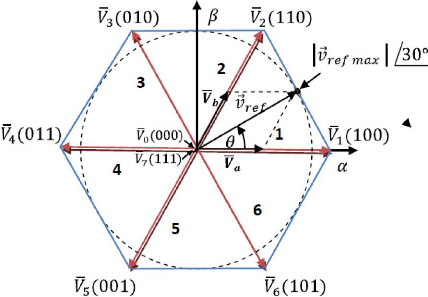
Figura 20 - Vetores espaciais de tensão do inverso
trifásico (Fonte: FLORES, 2009.)
Para que a modulação vetorial seja corretamente
aplicada, é preciso que o vetor de refere^ncia circule pelos seis
setores do plano complexo á-â. Para que isso seja realizado, o
inversor deverá aplicar à carga os vetores ativos
Va e Vb e os vetores nulos
V0 e V7 em um
período de amostragem T??. A aplicação
desses vetores deve ser tal que corresponda exatamente ao vetor de
referência. A Equação 33 apresenta uma forma de determinar
o vetor de referência através dos vetores ativos e nulos em um
período de amostragem.
1
???????? = T?? (V??.??a + V??.??b +
V0.??0 + V7.??7) (33)
?
41
A soma dos tempos deve ser igual ao período de
amostragem conforme mostrado na Equação 34.
??a+ ??b+ ??0 + ??7 = T?? (34)
Sabendo-se que V0 =
V7 = 0 e então reescrevendo-se a
Equação 33, obtém se a Equação 35.
42
????????? = ???? + ???? = ???? (???? ) + ????
(????) (35)
???? ????
Agora separando-se o vetor de referência em parte real e
parte imaginária no plano complexo obtêm-se as
equações 36 e 37, respectivamente.
2 1 2
????: ??????? ??. ??????(??). ???? = (3??????).???? +
2 . (3 ??????) . ???? (36)
2
????: ??????? ??. ??????(??). ???? = 0 + 23 .
(3 ??????) . ???? (37)
Assim entâo é possível solucionar as
equações e determinar os tempos. As equações abaixo
foram solucionadas para 0 < ?? < 60°.
v3. ????????? .????. ?????? (??
???? = 3 - ??) (38)
?? ????
v3.?????????
???? = . ????. ??????(??) (39)
??????
???? + ???? - ????
??0 = (40)
2
Agora que já é possível calcular os
tempos e, identificar em qual setor o vetor de referência se encontra,
deve-se determinar a ordem em que será aplicada aos interruptores.
Embora a sequência de aplicaçâo dos vetores nâo altere
o valor médio, ela tem grande influência nas perdas por
potência por comutaçâo e no conteúdo harmônico.
(NICOLAU, 2007, p.27)
A Figura 21 mostra uma possível sequência de
comutaçâo dos interruptores e como deve ser feito a
comutaçâo em cada setor.
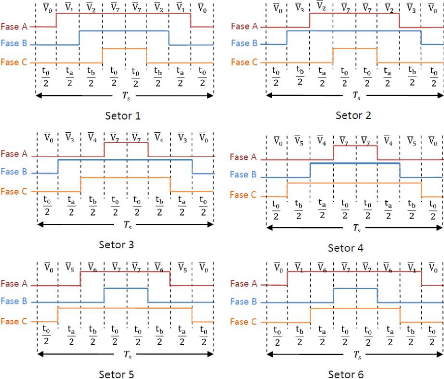
43
Figura 21 - Sequência de chaveamento para os seis setores
do plano complexo (Fonte: FLORES,
2009.)
O padrão de comutação dos interruptores
da Figura 22 propicia uma melhor distribuição das componentes
harmônicas, pelo fato de existir uma simetria na forma de onda e,
também, reduz o número de comutações dos
interruptores o que aumenta a vida útil dos mesmos. (CHILET, 2003, p.
17)
Enquanto o vetor de referência estiver em um setor, o
inversor deverá repetir a sequência de comutação dos
interruptores deste setor até que o vetor mude para o próximo
setor.
A técnica de modulação vetorial
irá aplicar uma tensão muito semelhante à tensão
obtida com a modulação senoidal. No entanto, ao se analisar o seu
espectro (tensão de fase), nota-se a presença de uma componente
de terceira harmônica, o que não ocorre na modulação
senoidal. (FLORES, 2009, p.33)
44
A Figura 22 mostra a representação do algoritmo
básico para a implementação da modulação
vetorial.
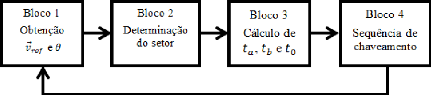
Figura 22 - Algoritmo básico para
implementação da modulação vetorial (Fonte: FLORES,
2009.)
Seguindo-se a Figura 22, a modulação vetorial
pode ser realizada da seguinte forma para cada período de amostragem:
1. Obter o módulo da tensão de referência e
seu ângulo com o eixo;
2. Identificar, com a informação do ângulo,
em qual setor o vetor de referência se encontra;
3. Calcular os tempos, e;
4. Aplicar a sequência de comutação dos
interruptores correspondente ao setor onde o vetor de referência se
encontra.
6.5. Tipos de controles
Na maioria das aplicações com inversores de
frequência, o controle de partida e a variação de
velocidade são suficientes. Para estas características, os
chamados inversores de frequência com controle escalar satisfazem estas
condições. Porém, algumas limitações
são impostas neste tipo de controle, como o limite de torque quando
operando com baixas frequências. Este tipo de controle opera em malha
aberta.
A fim de se conseguir um ajuste de torque com
baixíssimas frequências, através do equacionamento da
máquina elétrica e de modelos matemáticos, o inversor de
frequência com controle vetorial foi
desenvolvido. Com isso,
máquinas que antes tinham que ser controladas por motores C.C, agora
passam a ser operadas por motores de indução, devido a este tipo
de controle.
45
6.5.1. Controle escaler
Um método de controle de velocidade de motores de
indução com relativa simplicidade, que leva em conta apenas a
relação tensão/frequência, é chamado de
controle
escalar. Com o controle escalar
não é possível alcançar uma elevada precisão
em determinadas aplicações, mas o custo para a
implementação é baixo e sua simplicidade fazem com que
essa técnica de controle de velocidade seja muito utilizada.
No controle escalar, é possível obter uma
precisão de velocidade de até 0,5 % da rotação
nominal do motor sem que haja variação na carga e de 3 a 5%,
quando houver variação mecânica, de 0 a 100% do conjugado
nominal (PAIXO, 2009, p. 41).
A relação tensão/frequência
representa o fluxo magnético, como pode ser visto na
Equação 41, onde é a tensão no estator e é a
frequência.
V
???? = (41)
??
Em aplicações onde se deseja que o torque do
motor seja mantido constante, é necessário manter o fluxo
magnético também constante. Quando a tensão for variada a
frequência também deve ser variada na mesma
proporção (BENEDITO, 2011, p.121), como mostrado na Figura 23.
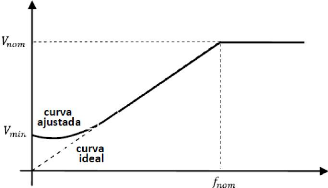
Figura 23 - Curva V/f do controle escalar. (Fonte: FLORES,
2009.)
46
Em condições ideais, a variação da
frequência neste tipo de controle é feita linearmente até
que seja obtida a tensão nominal do motor, mas, para frequências
baixas, a curva é ajustada a fim de compensar a queda de tensão
na impedância da estator, como mostrado na Figura 23.
Percebe-se também pela Figura 23, que o é
possível aumentar a frequência acima da frequência da rede,
mas, no entanto, a tensão não é aumentada acima da
nominal; essa limitação de tensão pode ser tanto pelas
características do motor ou pela capacidade de fornecimento da rede.
Considerando também que não é interessante o motor
trabalhar acima das condições nominais.
Como existem várias configurações em que
a razão V/f é mantida constante, é possível
trabalhar com várias curvas para o torque, o que torna possível
mantê-lo constante em várias velocidades, como mostrado na Figura
24.
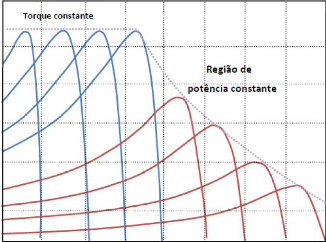
Figura 24 - Região de enfraquecimento de campo (Fonte:
FLORES, 2009.)
O inversor de frequência com controle escalar tem por
finalidade controlar a velocidade dos motores de indução. A
relação tensão/frequência possui curvas
predeterminadas e, com isso, é possível utilizar este modelo na
maioria dos controles de velocidade. É importante salientar que neste
tipo de controle, quando um grau de precisão e torque é exigido,
o modo escalar não consegue manter uma
47
relação precisa, ficando limitado a
aplicações em que não necessita da rotação
próxima de zero (BENEDITO, 2011, p.117).
Com o objetivo de estudar o controle escalar foi feito uma
montagem prática. Para isso utilizou-se um motor de
indução de 5 CV Figura 25 e um inversor de frequência WEG
CFW 09 Figura 26.

Figura 25 - Motor de indução de 5 CV (Fonte:
Autores)

48
Figura 26 - Inversor de frequência (Fonte: Autores)
Após a montagem foi configurado o inversor para o controle
escalar e obtidos os pontos representados na Tabela 3
|
Tensão (V)
|
Frequência (Hz)
|
Relação V/f
|
|
380
|
60
|
6,33
|
|
190
|
30
|
6,33
|
|
96
|
15
|
6,4
|
|
21
|
3
|
7
|
Tabela 3 - Relação V/F colhida
Logo, pode-se verificar que a relação V/f com a
frequência muito baixa vai aumentando. Assim caracterizando o
enfraquecimento de fluxo mostrado na Figura 23 na curva ajustada.
Para explicar melhor a questão do enfraquecimento de
fluxo para baixas frequência recorre-se ao circuito equivalente do motor
de indução apresentado na Figura 27.
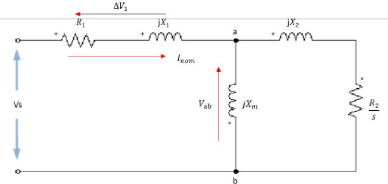
49
Figura 27 - Circuito equivalente do motor de
indução (Fonte: Autores)
Na Equação 41 a relação que o
fluxo tem entre a tensão e a frequência é constante, como
já elucidado anteriormente. Porém, essa informação
pode ser expressada de forma mais detalhada através da
Equação 42.
????-???1
???? = (42)
??
Conforme ???? vai diminuindo a subtração com
???1 começa a fazer diferença na divisão. Formalizando em
palavras, a queda de tensão em baixas frequências é alta,
afetando assim, significativamente a magnitude da corrente de
produção de fluxo magnetizante.
6.5.2. Controle vetorial
Os inversores de frequência com controle vetorial
são destinados a aplicações em que são
necessários além do controle preciso de velocidade, o controle de
torque elevado para mínimas rotações. Bobinadeiras,
guinchos, máquinas operatrizes são alguns exemplos de cargas que
utilizam este tipo de controle.
A lógica empregada no controle vetorial baseia-se nas
equações dinâmicas da máquina de
indução. Com isso, os
parâmetros são mais complexos do que o do controle escalar e o
resultado obtido é muito superior.
50
Para QUEIROZ (2008), os motores assíncronos apresentam
alto desempenho tanto em regime permanente como no período
transitório quando a técnica de controle vetorial é
aplicada.
Este tipo de controle utiliza a estratégia de matrizes
de transformação do sistema de 3 eixos para um sistema de 2
eixos, consistindo em decompor a corrente do motor em 2 vetores:
? O que produz fluxo magnetizante;
? O que produz torque.
Com isso, a regulagem do fluxo e do torque é realizada
de forma independente.
A ideia do controle vetorial foi imposta por Blaschke em 1972
e, também, é conhecida como «controle por orientacaÞo
de fluxo». (QUEIROZ, 2008, p. 4)
Ao contrário do controle escalar, em que é
necessária a queda de velocidade para aumentar o torque, neste tipo de
controle, uma tensão e uma frequência serão impostas de
modo a compensar a queda de velocidade e impor o torque necessário,
então, na saída de um inversor vetorial tem-se uma tensão
trifásica e frequência que são controladas de forma
independente, não se comportando como uma curva V/f linear.
7. PARAMETRIZAÇO
Para que o inversor funcione a contento, não basta
instalá-lo corretamente. É preciso «informar» a ele em
que condicaÞo de trabalho iraì operar. Essa tarefa é
justamente a parametrização do inversor.
Quanto maior o número de recursos que o inversor
oferece, tanto maior será o número de parâmetros
disponíveis.
A parametrização acontece no IHM (interface
Homem máquina). É através desse dispositivo que podemos
visualizar o que está ocorrendo no inversor (display), e
configurá-lo de acordo com a aplicação (teclas), Figura
28.

51
Figura 28 - Representação do IHM da WEG
52
Em um inversor há mais de 500 paramentos, a seguir
serão apresentados os de leitura, que são aqueles apenas a
título de acompanhamento.
PARÂMETRO 001:
Tensão nominal do motor.
Esse parâmetro existe na maioria dos inversores
comerciais, lembrando que não necessariamente como P 001, serve para
informarmos ao inversor qual é a tensão nominal em que o motor
irá operar.
Suponha que o motor tenha tensão nominal 380 VCA. Como
vamos introduzir essa informação (parâmetro) no
inversor?
Tomando uma base a Figura 25 (IHM) vamos observar a
sequência de «teclas». O display deveraì estar 0.0 (pois
só podemos parametrizar o inversor com o motor parado).
1° passo
Acionamos a tecla P e as setas ?? para
acharmos o para^metro. Ex: P e ? ateì achar o parâmetro
respectivo. No nosso caso, é logo o 1° 0 0 0 1
2° passo
Agora se aciona P novamente e o valor mostrado
no display será o valor do parâmetro e não mais a ordem em
que ele está. Ex: 0 2 2 0
3° passo
Como no exemplo a tensão desse parâmetro está
em 220 VCA e nosso motor funciona com 380 VCA, acionamos P e ?
ateì chegar nos 380. Ex: 0 3 8 0
4° passo
Basta acionar P novamente e o parâmetro
estará programado. Cerca de 90% dos inversores comerciais funcionam com
essa lógica. Todos os demais parâmetros são programados de
forma análoga.
Parâmetro 002:
Frequência máxima de saída.
53
Esse parâmetro determina a velocidade máxima do
motor. Parâmetro 003:
Frequência mínima de saída.
Esse parâmetro determina a velocidade mínima do
motor. Parâmetro 004:
Tempo de Partida («rampa de subida»).
Esse parâmetro indica em quanto tempo deseja-se que o
motor chegue á velocidade programada, estando ele parado.
Parâmetro 005:
Tempo de parada (rampa de descida).
O inversor pode produzir uma parada gradativa do motor. Essa
facilidade pode ser parametrizada.
Parâmetro 006: Tipo de
frenagem
Parâmetro = 1- parada por rampa
Parâmetro = 0 - parada por CC
No inversor, o para^metro 006 pode assumir dois estados:
«1» ou «0». Caso esteja em 1, a parada do motor
obedecerá a rampa programada no P 005. Caso esteja em 0 o motor
teraì sua parada através da «injecaÞo» de
corrente contiìnua em seus enrolamentos.
Em um motor CA, quando submetemos seus enrolamentos a uma
tensão CC, o rotor para imediatamente, como se uma trava mecânica
atuasse em seu eixo. Portanto, o projetista de máquinas deve pensar
muito bem se é assim mesmo que ele deseja que a parada ocorra.
Normalmente esse recurso é utilizado para cargas mecânicas
pequenas (leves), e que necessitam de resposta rápida (ex: eixos das
máquinas -ferramentas).
54
8. INVERSORES NA PRÁTICA
Para calcularmos a potência do inversor, temos de saber
qual motor (e qual carga) ele acionará. Normalmente, a potência
dos motores é dada em CV ou HP. Basta fazer a conversão para
watts. A seguir um exemplo prático:
Rede elétrica= 380 VCA Motor = 5 CV
Cálculos:
1 CV = 736 W
Portanto, como a rede elétrica é de 380 V, e os
inversores (normalmente) possuem um fator de pote^ncia= 0,8 (cos t= 0,80),
teremos:
P (W)
??= (43)
??.cos Ö
Onde:
I: corrente de Inversor
P: Potência em Watt. = 5 CV V: Tensão rede = 380
V
cos t: fator de potência = 0,80 Teremos:
5.736
?? = = 12,1 A (44)
380.0,80
Corrente nominal = 12,5 A (arredondando 12,10 para cima).
55
9. CONCLUSO
Este trabalho foi desenvolvido com a finalidade de oferecer
informações necessárias para o conhecimento básico
do funcionamento de um inversor de frequência. Para isso, foi apresentada
uma descrição sobre cada um dos estágios que constitui um
inversor de frequência.
A topologia de um inversor de frequência mostra que
é possível transformar uma tensão contínua em uma
tensão alternada. Esta conversão baseada no controle, ajuste da
frequência e nível da tensão de saída do inversor,
levam a excelentes resultados, desde que sejam utilizadas técnicas
especificas de modulação, levando o inversor de frequência
a um status importante dentro da família dos conversores.
Por fim, conclui-se, que o controle vetorial se mostra mais
eficiente que o controle escalar em acionamentos, em que é
necessária uma maior precisão na velocidade e no torque. E isso
pode ser conseguido realizando somente a alteração de no
próprio do inversor.
56
10. PROPOSTAS PARA TRABALHOS FUTUROS
Em relação a trabalhos futuros, recomenda-se a
implementação da modulação vetorial na
região de sobremodulação, pois assim é
possível aproveitar melhor a tensão do barramento CC e, por
conseguinte, diminuir a região de enfraquecimento de campo.
57
11. REFERÊNCIAS
Prof. Michel Robert Veiga, Disciplina «Controle e
Automação», Acionamentos Elétricas, USP,
2018.
NICOLAU, P.F. Técnica de
Modulação por Largura de Pulso Vetorial para Inversores Fonte de
Tensão. Itajubá: Universidade Federal de Itajubá,
Pós-Graduação em Engenharia Elétrica; 2007.
BORBA, J. L. Sistema de Transmissão
Elétrica. 2009. 242 p. Programa de especialização
profissional (Curso de Pós-Graduação em Engenharia
Ferroviária) - Pontifícia Universidade Católica, Minas
Gerais, 2009.
Zaparoli, I. O. Monitoramento de motor de
indução acionados com inversor de frequência. 2018.
Universidade Federal de Uberlândia, Minas Gerais, 2018.
BROCKVELD, S. L. Embasamento teórico para o
projeto de um inversor de frequência. 2015. 118 p. Trabalho de
Conclusão de Curso (Curso de engenharia mecatrônica) -
Universidade federal de santa catarina, Santa Catarina, 2015.
WEG EQUIPAMENTOS ELÉTRICOS S.A.. Motores de
indução alimentados por inversores de frequência
PWM. Jaraguá do Sul, SC. 2010.
CAMARGO, C.B. Acionamentos De Motores De
Indução Através das Técnicas de Controle Escalar e
Vetorial. Sorocaba: Faculdade de Engenharia de Sorocaba, Trabalho de
Conclusão de Curso em Engenharia Elétrica; 2011.
FRANCISCO, A. M. S. Motores de Indução
Trifásico. Viseu: [s.n.], 2006. 250 p. ELETROTÉCNICA
SANTO AMARO. Inversor de Frequência. Disponivel em:
www.esaeletrotecnica.com.br/inversor-frequencia.html.
Acesso em: 14 de Abril de 2020.
FLORES, D. C.; Estudo e implementação de um
inversor de frequência baseado em processador de sinais.
Pelotas: Centro politécnico da Universidade Católica de
Pelotas, Trabalho de Conclusão de curso em Engenharia Elétrica;
2009.
CLUBE DA ELETRÔNICA. Clube da Eletrônica. Clube da
Eletrônica, 08 Setembro
2009. Disponivel em:
58
http://www.clubedaeletronica.com.br/Eletricidade/PDF/Inversor%20de%20frequencia
.pdf . Acesso em: 19 Junho 2020.
| 


