1.5.1.1. TEST BASÉ SUR LE CORRÉLOGRAMME
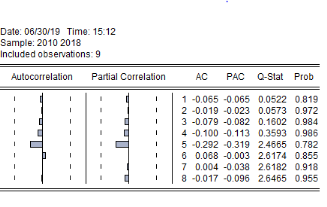
Aucune valeur des coefficients de la fonction
d'autocorrélation simple partielle ne sortent pas du boulevard de leur
intervalle de confiance : le résidu est un bruit blanc. (Voir
annexe 5)
1.5.1.2. TEST DE NORMALITÉ DES RÉSIDUS
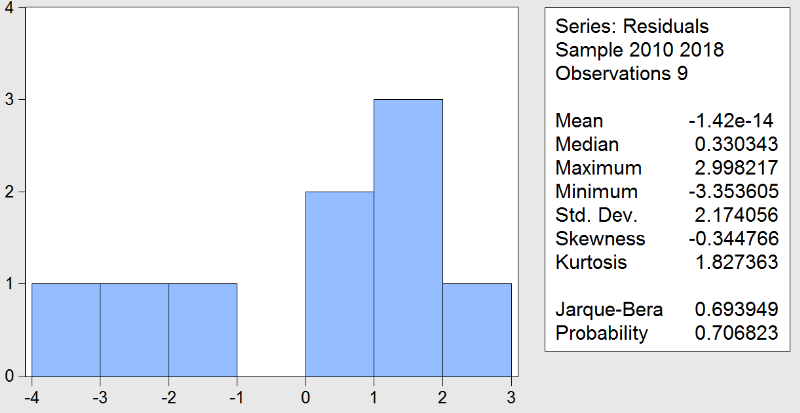
La probabilité critique de la statistique de
Jarque-Bera est supérieure au seuil de significativité de 5%,
soit 70.68% : les résidus sont normalement et indépendamment
distribués (Les résidus suivent une loi normale).
1.5.1.3. TEST D'AUTOCORRÉLATION DES ERREURS (TEST
LM)
|
Breusch-Godfrey Serial Correlation LM Test:
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic
|
0.919872
|
Prob. F(2,4)
|
0.6592
|
|
Obs*R-squared
|
2.835346
|
Prob. Chi-Square(2)
|
0.6423
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation:
|
|
|
|
|
Dependent Variable: RESID
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/30/19 Time: 14:47
|
|
|
|
Sample: 2010 2018
|
|
|
|
Included observations: 9
|
|
|
|
Presample missing value lagged residuals set to zero.
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C
|
0.837392
|
1.578449
|
0.530516
|
0.6238
|
|
SX2C
|
0.008196
|
0.017736
|
0.462131
|
0.6680
|
|
X1C
|
-2.179193
|
2.921562
|
-0.745900
|
0.5972
|
|
RESID(-1)
|
-0.449937
|
0.729739
|
-0.616573
|
0.5709
|
|
RESID(-2)
|
-0.951948
|
0.707593
|
-1.345334
|
0.9997
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.315038
|
Mean dependent var
|
-1.42E-14
|
|
Adjusted R-squared
|
-0.369923
|
S.D. dependent var
|
2.174056
|
|
S.E. of regression
|
2.544597
|
Akaike info criterion
|
5.006002
|
|
Sum squared resid
|
25.89989
|
Schwarz criterion
|
5.115571
|
|
Log likelihood
|
-17.52701
|
Hannan-Quinn criter.
|
4.769552
|
|
F-statistic
|
0.459936
|
Durbin-Watson stat
|
1.848610
|
|
Prob(F-statistic)
|
0.764787
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La probabilité critique du chi-carré à
deux degrés de liberté est supérieure à 5%, soit
64% : il y a absence d'autocorrélation des erreurs. (Voir annexe 7)
1.5.1.4. TEST
D'HÉTÉROSCÉDASTICITÉ DES ERREURS (TEST ARCH
D'HÉTÉROSCÉDASTICITÉ CONDITIONNELLE
AUTORÉGRESSIVE)
|
Heteroskedasticity Test: ARCH
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic
|
0.004975
|
Prob. F(1,6)
|
0.9461
|
|
Obs*R-squared
|
0.006628
|
Prob. Chi-Square(1)
|
0.9351
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation:
|
|
|
|
|
Dependent Variable: RESID^2
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/30/19 Time: 14:50
|
|
|
|
Sample (adjusted): 2011 2018
|
|
|
|
Included observations: 8 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C
|
3.408413
|
1.766458
|
1.929518
|
0.0019
|
|
RESID^2(-1)
|
-0.024349
|
0.345195
|
-0.070536
|
0.9461
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.654829
|
Mean dependent var
|
3.320688
|
|
Adjusted R-squared
|
-0.665700
|
S.D. dependent var
|
3.286244
|
|
S.E. of regression
|
3.548079
|
Akaike info criterion
|
5.583007
|
|
Sum squared resid
|
75.53317
|
Schwarz criterion
|
5.602868
|
|
Log likelihood
|
-20.33203
|
Hannan-Quinn criter.
|
5.449057
|
|
F-statistic
|
0.004975
|
Durbin-Watson stat
|
1.698528
|
|
Prob(F-statistic)
|
0.946060
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La probabilité critique de la statistique de ARCH est
supérieure à 5%, soit 93% : il y a absence
d'hétéroscédasticité conditionnelle
autorégressive. (Voir annexe 8).
Après vérification de toutes les
hypothèses, nous pouvons valider notre modèle.
| 


