Lasers - production et applications

7

Chapitre 2

La base théorique du laser

2.1 Introduction

Selon le modèle atomique de Bohr (1911), qui repose sur des études spectroscopiques, les transitions entre les niveaux d'énergies discrets d'un atome peuvent conduire à l'émission ou à l'absorption d'un rayonnement dont la fréquence correspond à la relation énergie-fréquence de Bohr. Dans un processus d'absorption, un photon est absorbé. Dans un processus d'émission, un photon est émis. Einstein a découvert que l'émission d'un photon est possible par deux processus différents : l'émission spontanée et l'émission stimulée, et que les coefficients décrivant les trois processus, absorption, émission stimulée et spontanée, sont liés les uns aux autres (relations d'Einstein).

En utilisant la loi du rayonnement de Planck, nous dérivons les relations d'Einstein. Nous montrons également que l'émission stimulée du rayonnement est un processus qui se produit en permanence autour de nous.

Les coefficients d'Einstein peuvent être extraits des résultats des études expérimentales des propriétés optiques de la matière à l'équilibre thermique. Dans ce chapitre, nous considérons un ensemble de systèmes à deux niveaux en équilibre thermique déterminé par la statistique de Maxwell-Boltzmann.

2.2 Processus de fonctionnement du laser 2.2.1 La lumière et les atomes dans une cavité

Comment la lumière interagit-elle avec un système atomique à deux niveaux? Nous étudierons cette question en trois étapes :

-- Nous décrivons l'équilibre thermique entre le rayonnement dans une cavité et les parois de la cavité.

-- Nous décrivons l'équilibre thermique entre un ensemble de systèmes atomiques à deux niveaux dans une cavité et les parois de la cavité.

-- Nous considérons une cavité qui contient un ensemble de systèmes atomiques à deux niveaux et un rayonnement.

Une cavité (fig. 2.1 gauche) contient le rayonnement d'un corps noir. La distribution spectrale de la densité d'énergie ñ(í) du rayonnement dépend de la température T des parois de la cavité.

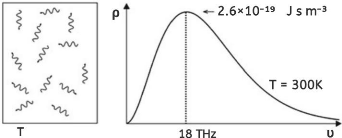
FIGURE 2.1 - Une cavité et une distribution Planckienne du rayonnement La densité spectrale d'énergie est déterminée par la loi de rayonnement de Planck :

8ðU^2 ñ(U) = c3 où k est la constante de Boltzmann.

1 (2.1) ehí/kT - 1

La distribution de fréquence est représentée sur la (fig. 2.1 droit). La fréquence _Umax du maximum de la distribution est directement proportionnelle à la température selon la relation :

hUmax 2.8 kT (2.2)

Si les parois sont à température ambiante (T = 300 K), le maximum de la distribution se situe dans l'infrarouge (Umax = 1.8 x 10¹³ Hz). La densité spectrale augmente comme U² à petite fréquence (U « Umax) et diminue comme ^U3e-hí/kT à grande fréquence (U » Umax). L'équilibre thermique s'établit par l'absorption du rayonnement par les parois de la cavité et par l'émission du rayonnement des parois dans la cavité. La densité d'énergie du rayonnement dans l'intervalle de fréquence [U , U + dU] est :

u(U) = ñ(U)dU (2.3)

Nous traitons maintenant une cavité contenant un ensemble de systèmes atomiques à deux niveaux en équilibre thermique qui est déterminé par les statistiques de Boltzmann,

N2 = e N1

-(E2-E1)/kT (2.4)

8

Le rapport de population est proche de l'unité si E2 - E1 » kT. Il décroît exponentiellement avec la différence d'énergie E2 - E1. L'équilibre thermique est établi par les collisions des systèmes atomiques à deux niveaux entre eux et avec les parois de la cavité.

Les ions d'impureté dans un solide ont des emplacements fixes. Les populations des niveaux d'énergie des différents ions sont en équilibre thermique avec le solide en raison de l'absorption et de l'émission de phonons. Les populations sont régies par les statistiques de Boltzmann.

Einstein a montré que l'équilibre thermique dans un gaz d'atomes peut également être établi par l'interaction directe du rayonnement avec les atomes et que trois processus d'interaction entre le rayonnement et les atomes doivent se produire : absorption, émission spontanée et émission stimulée.

En utilisant la relation énergie-fréquence de Bohr,

hv0 = E2 - E1 (2.5)
Où v0 est la fréquence de transition, nous pouvons écrire

N2 = e N1

-hí0/kT (2.6)

Nous allons maintenant caractériser les trois processus par les trois coefficients d'Einstein.

2.2.2 Émission spontanée

Les atomes excités (fig. 2.2) peuvent émettre des photons spontanément, c'est-à-dire sans cause extérieure.

Le rayonnement émis spontanément est incohérent et l'émission se produit dans toutes les directions de l'espace. La variation dN2 de la population N2 du niveau supérieur, à l'intérieur d'un intervalle de temps dt, est proportionnelle à N2 et à dt,

dN2 = A21N2dt (2.7)

A21 est le coefficient d'Einstein de l'émission spontanée. La population du niveau supérieur décroît exponentiellement

N2(t) = N2(0)e^-A21t = N2(0)e^-t/^ô87 (2.8)

N2(0) est la densité des systèmes atomiques à deux niveaux excités à t = 0 et _r5p est la durée de vie moyenne d'un système atomique à deux niveaux excité par rapport à l'émission spontanée ou bien la durée de vie spontanée.

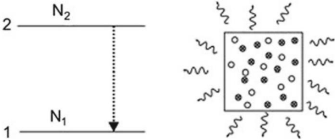
9

FIGURE 2.2 - Émission spontanée

Nous avons la relation simple :

A21 = 1/r5p (2.9)

Le coefficient d'Einstein _A21 est égal à l'inverse de la durée de vie spontanée.

2.2.3 Absorption

Les photons d'un champ lumineux peuvent être absorbés par des transitions 1 ? 2 (fig. 2.3a). La variation dN1 de la population N1 de l'état fondamental, dans un intervalle de temps

10

dt, est proportionnelle à la population de l'état fondamental lui-même, à la densité spectrale d'énergie ñ du champ de rayonnement et à dt

dN1 = _B12ñ(í0)N1dt (2.10)

B12 est le coefficient d'absorption d'Einstein et ñ(í0) est la densité spectrale d'énergie du rayonnement aux fréquences autour de í0. L'absorption n'est possible qu'en présence d'un champ, alors l'absorption est un processus stimulé.

FIGURE 2.3 - Transitions stimulées. (a) Absorption et (b) émission stimulée

2.2.4 Emission stimulée

L'émission stimulée (fig. 2.3b), par des transitions 2 --+ 1, est provoquée (stimulée, induite) par un champ de rayonnement. La variation dN2 de la population d'atomes dans l'état excité, dans un intervalle de temps dt, est proportionnelle à la population N2, à la densité spectrale d'énergie du rayonnement aux fréquences autour de í0 et à dt.

dN2 = _B21ñ(í0)N2dt (2.11)

B21 est le coefficient d'Einstein de l'émission stimulée. Le rayonnement créé par l'émission stimulée a les mêmes fréquences , direction, polarisation et phase que le rayonnement de stimulation.

2.3 Les relations d'Einstein

Nous recherchons des relations entre les coefficients d'Einstein. Comme nous l'avons vu, l'interaction d'un système atomique à deux niveaux avec le rayonnement se produit (fig. 2.4) par absorption, émission stimulée et spontanée. Nous décrivons ces trois processus par des équations de taux qui correspondent à des équations différentielles du premier ordre :

· La variation de la population N1 dû à l'absorption est donné par:

idN1 ~

abs = _B12 ñ(í0) N1 (2.12)

dt

la variation temporelle de la population N1 due à l'absorption est proportionnelle à ñ(í0) et à N1.

· La variation de la population N2 dû à l'émission stimulée est égal à :

idN2 ~

stim = _B21 ñ(í0) N2 (2.13)

dt

la variation temporelle de la population N2 due à l'émission stimulée est proportionnelle à ñ(í0) et à N2.

· 11

La variation de la population N2 dû à l'émission spontanée est :

fdN2 ~ dt sp

= -A21 N2 (2.14)

la variation temporelle de la population N2 due à l'émission spontanée de rayonnement est proportionnelle à N2.

FIGURE 2.4 - Modèle d'Einstein. Les flèches ondulées désignent des photons. L'atome en grisé, après la transition, vient augmenter la population d'atomes « blancs ».

Nous considérons une cavité avec un ensemble de systèmes atomiques à deux niveaux et un rayonnement en équilibre thermique. Dans la moyenne temporelle, le rapport _N2/N1 est une constante. Par conséquent, le taux d'absorption doit être égal au taux d'émission,

fdN1 ~ _fdN2 ~ _fdN2 ~

abs = stim + (2.15)

dt dt dt sp

Cela conduit à la relation suivante :

B12 ñ(u0) N1 = A21 N2 + B21 ñ(u0) N2 (2.16)

Il s'ensuit que

A21/B21

ñ(u0) = (2.17)

(B12/B21)N1/N2 - 1

Le facteur de Boltzmann détermine le rapport N1/N2. La comparaison avec la loi de rayonnement de Planck fournit les relations d'Einstein :

B21 = B12 (2.18)

8ðu²

A21 = c3 hu B21 (2.19)

La fréquence u (qui remplace u0) découle de la relation de Bohr hu = E2 - E1. On a le résultat :

* Le même coefficient d'Einstein régit l'absorption et l'émission stimulée. * Il existe un lien entre les coefficients d'émission spontanée et stimulée. * Le coefficient d'Einstein _A21 augmente fortement avec la fréquence.

La figure (fig. 2.5) montre la durée de vie spontanée pour différentes fréquences de transition u = (E2 - E1)/h à une valeur fixe de _B21 (= 1018 _m3 J-1 s^-2); la durée de vie spontanée est de l'ordre de 10^-6 s à une fréquence de transition (5 x 10¹⁴Hz) dans le visible, de 100s à une fréquence de transition (10¹² Hz) dans l'infrarouge lointain, et de 10^-15 s à une fréquence de transition (10¹⁷ Hz) dans le domaine des rayons X (fig. 2.5). Les durées de vie spontanées aux

FIGURE 2.5 - Durée de vie naturelle

fréquences de transition des rayons X sont très courtes. Par conséquent, l'exploitation d'un laser à rayons X est difficile.

Si les niveaux d'énergie sont dégénérés, la statistique de Boltzmann donne les résultats suivants

-(E2-E1)/kT (2.20)

N2 g2 = e N1 g1

12

où g1 est le degré de dégénérescence du 1^er niveau et g2 le degré de dégénérescence du 2eme niveau. Le traitement de l'équilibre entre les populations atomiques et le rayonnement dans une cavité conduit aux relations suivantes :

et (comme dans le cas non dégénéré)

g2 B12 = g1

B21 (2.21)

8ðí²

A21 = c3 hí B21 (2.22)

Dans le cas de systèmes atomiques à deux niveaux noyés dans un milieu d'indice de réfraction n, la vitesse de la lumière dans le vide doit être remplacée par la vitesse de la lumière dans le milieu. Les relations d'Einstein sont alors :

g1B21 = g2B12 (2.23)

8ðí²

(c/n)

A21 = ₃ hí B21 (2.24)

Sous cette forme, les relations d'Einstein sont valables si un milieu est optiquement isotrope. Si un milieu est optiquement anisotrope, la relation entre _A21 ^et _B21 doit être modifiée.

Si la densité spectrale d'énergie est donnée à l'échelle de la fréquence angulaire, ñ = ñ(ù) , le coefficient d'Einstein _Bù21 est plus petit du facteur 2ð, B^ù₂₁ = B21/2ð. Les relations d'Einstein sont alors :

g1B^ù21 = g2B^ù (2.25)

12

hù³

A21 =ð2c3 Bù (2.26)

21

Le tableau (tab. 2.1) présente les valeurs des coefficients d'Einstein déterminées par l'utili-sation de méthodes expérimentales ou théoriques. Quelques méthodes sont mentionnées dans ce qui suit :

· La mesure de _ô21 (par une expérience de luminescence) fournit également _A21 et (via les relations d'Einstein) _B21. Exemple : Nd :YAG.

· La mesure du coefficient d'absorption fournit _B21 et (via les relations d'Einstein) A21.

· Une analyse du spectre de luminescence donne A21 ; Exemple : des lasers bipolaires à semi-conducteurs.

· Les études théoriques des taux de transition fournissent B21 ; Exemple : QCL

13

TABLE 2.1 - Les coefficients d'Einstein

Laser	À	n	ôsp	A21(s^-1)		B21(m3 J^-1s^-2)	HeNe
633nm	1	100ns	10^7	1.5 x 10^20		CO2
10.6,im	1	5s	0.2	1.4 x 10^16		Nd :YAG
1.06,im	1.82	230 ,is	5.1 x 10^16	4.3 x 10^3		TiS (E || c)
830nm	1.74	3.8,is	1.7 x 10^18	4.3 x 10^3		Fibre
1,5,im	1.5	10ms	10^2	6.6 x 10^15		Semiconducteur
810nm	3.6	-	3 x 10^9	3.7 x 10^21		QCL
5,im	3.6	-	-	4 x 10^21

2.4 Conditions d'Amplification - Inversion de populations

2.4.1 Les conditions d'amplification

Si le système est en équilibre, les niveaux les plus bas sont toujours les plus peuplés. Si nous calculons la différence entre la population du niveau inférieur et celle du niveau placé juste au-dessus, elle est positive. La réponse impulsionnelle à l'arrivée d'un signal sera une absorption.

-- l'énergie absorbée par le milieu est : g1B12 p(u)N1 hu

-- l'énergie gagnée par le rayonnement est : g1B12 p(u)N2 hu d'où la variation d'énergie est :

dE = g1B12 p(u) (N1 - N2) hu (2.27)

A l'équilibre thermodynamique, dE < 0 puisque N2 < N1 d'après la loi de Boltzmann.

Si maintenant nous considérons que nous avons pu déplacer cet équilibre et peupler le niveau supérieur de façon telle que sa population soit nettement supérieure à celle du niveau inférieur, l'arrivée du même signal provoquera une émission stimulée. Il y a amplification du signal incident. Cette condition est appelée l'inversion de population (il faut que N2 > N1). Ainsi si :

· N2 < N1 : le rayonnement incident est absorbé;

· N2 = N1 : c'est le phénomène de saturation;

· N2 > N1 : le rayonnement incident est amplifié (le système est donc hors équilibre thermodynamique).

Pour obtenir l'amplification, premier pas vers l'effet laser, il faut donc déjà avoir réalisé deux conditions :

· disposer d'un milieu actif,

· avoir obtenu une inversion de population.

2.4.2 Les modes de transfert pour les transitions atomiques

Il faut arriver à stocker des électrons sur le niveau supérieur. Pratiquement, ce mécanisme de stockage se fait de plusieurs façons différentes.

2.4.2.1 Pompage optique

Le pompage optique est l'excitation du milieu actif par la lumière. C'est le mode de pompage des lasers à solides. On distingue généralement les systèmes à 3 niveaux et ceux à 4 niveaux. Le système à trois niveaux (fig. 2.6) a été proposé par Blömbergen en 1956. On amène, par un dispositif optique, les atomes sur le niveau E3 légèrement supérieur à E2. Le niveau E2 doit être métastable. Cela signifie que la durée de vie des atomes sur cet état est longue. C'est ce niveau qui va permettre de réaliser une inversion de populations.

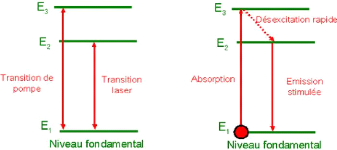
14

FIGURE 2.6 - Exemple d'un système à trois niveaux avec un pompage optique.

2.4.2.2 Pompage électronique

Ce type de pompage est généralement utilisé dans les lasers à gaz. Comme le gaz est en principe isolant, il faut d'abord envoyer une décharge pour ioniser le milieu et le rendre conducteur. Ensuite, en appliquant un champ électrique entre deux électrodes plongées dans le gaz, on obtient un courant. Les électrons qui circulent cèdent leur énergie cinétique aux atomes du milieu actif et provoquent l'inversion de population cherchée. Par exemple : le laser HeNe se fait par un pompage électronique (fig. 2.7).

FIGURE 2.7 - Exemple de HeNe avec un pompage électronique.

15

2.4.2.3 Pompage chimique

On utilise des réactions chimiques qui, en se produisant, fournissent directement des molécules ionisées. L'avantage de ce type de laser est qu'il ne nécessite pas de source d'électricité. Pratiquement, ces techniques, qui permettent d'obtenir de très grandes puissances, sont réservées aux applications militaires. On peut citer les lasers au fluorure d'hydrogène (HF) ou au fluorure de deutérium (DF) dans l'infrarouge moyen.

2.4.2.4 Pompage par injection de porteurs

C'est le pompage des lasers à semi-conducteur, qui est produit par le courant direct qui traverse une jonction de type P-N.

2.5 Cavité résonante

Il n'est pas suffisant de provoquer une inversion de population pour obtenir l'effet laser, il faut obliger les photons à partir en majorité dans une direction bien définie, ce qui va permettre d'augmenter considérablement leur flux par l'émission stimulée. C'est le rôle que joue la cavité.

La cavité est formée par deux miroirs parallèles (fig. 2.8), qui encadrent le milieu actif et qui définissent une direction privilégiée : leur normale. Le miroir arrière est totalement réfléchissant alors que le miroir avant laisse passer une partie du rayonnement, ce qui autorise l'émission laser.

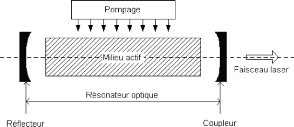
FIGURE 2.8 - Cavité résonante du laser.

Au départ, l'émission spontanée produit les premiers photons, qui peuvent se diriger dans n'importe quelle direction. Seuls ceux qui sont émis suivant l'axe normal aux deux miroirs rencontrent un grand nombre d'atomes excités. A la fin du premier passage, les photons en phase sont déjà assez nombreux. Ils se réfléchissent sur les miroirs et viennent encore entraîner d'autres photons, par émission stimulée. On imagine facilement qu'un gain important puisse être obtenu. Il faut enfin noter que le phénomène est rapide, étant donné la vitesse de la lumière et que l'émission spontanée ne joue qu'un rôle négligeable, limité à l'initialisation du phénomène.

Si le gain obtenu sur un aller et retour est supérieur aux pertes rencontrées, le seuil est franchi : un faisceau laser est émis.

La cavité joue de plus un rôle de filtre optique très sélectif. Il s'agit d'un interféromètre à ondes multiples qui ne fournit des interférences constructives que si (dans le cas de l'incidence normale) :

ë

nL = p (2.28)
2

16

L étant la longueur de la cavité, n l'indice de réfraction et p un nombre entier.

Les longueurs d'onde sont donc émises d'une façon régulière à l'intérieur de la largeur de raie totale, la raie de fluorescence : c'est ce que l'on appelle un peigne. L'écartement de deux fréquences successives est donné par :

Lë Lu = c ë2

c = (2.29) 2L

On peut voir que cet écartement est inversement proportionnel à la longueur de la cavité L. Si l'on veut avoir peu de modes, ou même un seul, il faudra prendre une cavité très courte.

Il est enfin primordial que l'absorption intrinsèque de ces filtres soit la plus faible possible. Dans les cavités laser, comme ils jouent un rôle fort important, ils sont réalisés à partir de matériaux dont les propriétés optiques sont compatibles avec toutes ces exigences.

Tout ceci montre que les sources laser ont pour spécificité : un rayonnement émis très pur (mono-chromaticité) grâce à leur cohérence temporelle et une grande directivité due à leur cohérence spatiale.

2.6 Conclusion

Pour conclure, nous n'avons vu dans ce chapitre juste la base théorique du fonctionnement des lasers, mais il y a en fait toute une branche de la physique qui est très compliquée, et que les physiciens et les ingénieurs continuent à développer jusqu'à aujourd'hui d'autre type de laser très avancés.