Lasers - production et applications

DéPARTEMENT DE PHYSIQUE APPLIQUéE

FILIèRE : SMP

PARCOURS : PHYSIQUE FONDAMENTALE

RAPPORT DE PROJET DE FIN D'ETUDES

Lasers

Production et Applications

Présenté Par :

Amine ALIDA Encadré Par :

Ayoub MAALAISSE Pr. Jamal EL QARS

Brahim ALAHYANE

Soutenu le 06/06/2022 devant les membres du jury :

Pr. Youssef Essediq EL YAKOUBI FSA-AM Examinateur

Pr. Jamal EL QARS FSA-AM Encadrant

Année Universitaire : 2021 - 2022

II

Remerciements

Nous tenons à remercier toute l'équipe pédagogique de la Faculté des Sciences Appliquées Ait Melloul et en particulier tout le corps professoral intervenant dans la filière « Science de la Matière Physique » pour l'effort fourni pour réussir notre formation et mieux atteindre tous les objectifs attendus des différentes matières.

Nos remerciements les plus distingués sont adressés à notre encadrant, Monsieur Jamal El QARS, qui en tant que professeur, a bien voulu accepter de suivre notre travail, nous diriger, afin de pouvoir mener ce projet à terme.

Nous tenons aussi à remercier le professeur Youssef Essediq EL YAKOUBI pour ses conseils lors de la préparation, son ouverture d'esprit, son engagement et son soutien ainsi que pour la pertinence de ses remarques. Et également en tant que membre du jury, de nous avoir honoré en acceptant de juger ce travail.

Nous tenons à remercier toutes les personnes, qui, de près ou de loin, se sont impliquées dans la réalisation de ce rapport, tant par le soutien opérationnel, que professionnel.

Nous adressons également nos sincères remerciements aux membres de nos familles qui n'ont jamais hésité à nous offrir le meilleur d'eux-mêmes, et surtout nos parents qui ont supporté les frais de nos études.

III

Résumé

Un laser est un dispositif qui émet de la lumière par un processus d'amplification optique basé sur l'émission stimulée de rayonnement électromagnétique. Le terme "laser" est à l'origine l'acronyme de "amplification de la lumière par émission stimulée de rayonnement". Le premier laser a été construit en 1960 par Theodore H. Maiman aux Hughes Research Laboratories, sur la base des travaux théoriques de Charles Hard Townes et Arthur Leonard Schawlow.

Un laser diffère des autres sources de lumière en ce qu'il émet de la lumière de manière cohérente. Les lasers peuvent également avoir une cohérence temporelle élevée, ce qui leur permet d'émettre de la lumière avec un spectre très étroit, c'est-à-dire qu'ils peuvent émettre une seule couleur de lumière.

Il existe de nombreux types de lasers, dont les plus importants sont les lasers à semiconducteurs, par exemple les lasers GaAs, et les lasers à gaz, comme les lasers à argon ionisé Ar⁺, mais il en existe également d'autres, comme les lasers chimiques, les lasers à fibres et les lasers à électrons libres.

Le laser a beaucoup d'applications, comme dans le domaine de la recherche scientifique, nous avons trouvé la fusion nucléaire par laser, le refroidissement des atomes, la détection des ondes gravitationnelles, etc. Et aussi dans les autres domaines comme le domaine industriel, médicale, dans la télécommunication et d'autre.

IV

Abstract

A laser is a device that emits light by an optical amplification process based on the stimulated emission of electromagnetic radiation. The term "laser" is originally an acronym for "light amplification by stimulated emission of radiation". The first laser was built in 1960 by Theodore H. Maiman at Hughes Research Laboratories, based on the theoretical work of Charles Hard Townes and Arthur Leonard Schawlow.

A laser differs from other light sources in that it emits light coherently. Lasers can also have high temporal coherence, which allows them to emit light with a very narrow spectrum, i.e., they can emit a single color of light.

There are many types of lasers, the most important of which are semiconductor lasers, such as GaAs lasers, and gas lasers, such as Ar⁺ ionized argon lasers, but there are also others, such as chemical lasers, fiber lasers and free electron lasers.

The laser has many applications, as in the field of scientific research, we found the nuclear fusion by laser, the cooling of atoms, the detection of gravitational waves etc. And also in other areas such as the industrial field, medical, in telecommunications and others.

V

Table des matières

Introduction Générale 1 Généralités sur les lasers			1 3
	1.1	Introduction	3
	1.2	Qu'est-ce qu'un laser?	3
	1.3	Le laser et l'ampoule	3
	1.4	Gammes spectrales et liste de quelques lasers	4
	1.5	Les propriétés du laser	4
	1.6	Conclusion	6
2	La base théorique du laser		7
	2.1	Introduction	7
	2.2	Processus de fonctionnement du laser	7
		2.2.1 La lumière et les atomes dans une cavité	7
		2.2.2 Émission spontanée	9
		2.2.3 Absorption	9
		2.2.4 Emission stimulée	10
	2.3	Les relations d'Einstein	10
	2.4	Conditions d'Amplification - Inversion de populations	13
		2.4.1 Les conditions d'amplification	13
		2.4.2 Les modes de transfert pour les transitions atomiques	13
		2.4.2.1 Pompage optique	14
		2.4.2.2 Pompage électronique	14
		2.4.2.3 Pompage chimique	15
		2.4.2.4 Pompage par injection de porteurs	15
	2.5	Cavité résonante	15
	2.6	Conclusion	16
3	Types et principe de fonctionnement		17
	3.1	Introduction	17
	3.2	Lasers à semi-conducteur	17
		3.2.1 Histoire	17
		3.2.2 Principe de fonctionnement	17
		3.2.3 La longueur d'onde du rayonnement	18
		3.2.4 Principaux avantages	19
		3.2.5 Exemple : Laser (Al)GaAs	19
	3.3	Lasers à gaz	20
		3.3.1 Principe de fonctionnement	20
		3.3.2 Exemple: Laser à argon ionisé (Ar^+)	20
	3.4	Autres types	21
		3.4.1 Lasers chimiques	21

VI

3.4.2 Lasers à fibre 22

3.4.3 Lasers à électrons libre 22

3.5 Conclusion 22

4 Quelques applications du laser 23

4.1 Introduction 23

4.2 Applications dans le domaine de la recherche scientifique 23

4.2.1 La télémétrie 23

4.2.2 La spectroscopie 24

4.2.3 La détection des ondes gravitationnelles 24

4.2.4 Vélocimétrie Doppler 25

4.2.5 La fusion nucléaire 25

4.2.6 Le refroidissement des atomes 26

4.3 Applications dans les autres domaines 27

4.3.1 Dans la vie quotidienne 27

4.3.2 Domaine industriel 28

4.3.3 Domaine médicale 28

4.3.4 Télécommunication 29

4.3.5 Les armes laser 29

4.4 Conclusion 29

Conclusion Générale 30

Bibliographie 31

VII

Table des figures

1	Theodore Maiman avec le premier laser.	2
1.1	Laser à onde continue (cw), laser femtoseconde (fs) et ampoule électrique . . . .	3
1.2	Gammes spectrales des lasers	5
2.1	Une cavité et une distribution Planckienne du rayonnement	8
2.2	Émission spontanée	9
2.3	Transitions stimulées. (a) Absorption et (b) émission stimulée	10
2.4	Modèle d'Einstein. Les flèches ondulées désignent des photons. L'atome en grisé,
	après la transition, vient augmenter la population d'atomes « blancs ».	11
2.5	Durée de vie naturelle	12
2.6	Exemple d'un système à trois niveaux avec un pompage optique	14
2.7	Exemple de HeNe avec un pompage électronique. 14
2.8	Cavité résonante du laser. 15
3.1	Représentation schématique des bandes d'énergie dans un semi-conducteur. . . .	18
3.2	Transitions radiatives de bande à bande dans les semi-conducteurs. 18
3.3	Choix du laser à semi-conducteur en fonction de la longueur d'onde	19
3.4	Illustration schématique de l'interaction matière-rayonnement. La fréquence du rayonnement émis ou absorbé dépend du type de la résonance mise en jeu : (a)
	atomique, (b) vibrationnelle, (c) rotationnelle. 20
3.5	Niveaux d'énergie du laser dans l'argon ionisé	21
3.6	Structure de base d'un laser à électrons libres. 22
4.1	Le laser utilisée pour mesurer la distance terre-lune	23
4.2	L'interféromètre VIRGO, Santo Stefano a Macerata, Pisa, Italie	24
4.3	Schéma des étapes de la fusion laser. 26
4.4	Les trois étapes du ralentissement d'un atome par un photon. En (a), un atome absorbe un photon se propageant en sens inverse; en (b), l'atome excité est
	ralenti; en (c), le photon est réémis dans une direction aléatoire	27

VIII

Liste des tableaux

1.1 Longueurs d'onde, fréquences et des quantum d'énergies des lasers 4

2.1 Les coefficients d'Einstein 13

1

Introduction Générale

Le laser est l'acronyme de Light Amplification by Stimulated Emission of Radiation, c'est à-dire amplificateur de lumière par émission stimulée de rayonnement électromagnétique. S'est peu à peu imposé dans notre vie sans que nous en soyons forcément conscients. Incontournable dans la fabrication d'objets aussi divers que les smart phones, les écrans LCD, les cellules photovoltaïques ..., il est tout aussi indispensable au fonctionnement d'Internet et joue un rôle crucial en médecine. Toute l'industrie du numérique - musique, vidéo, informatique - repose sur les lasers. De plus en plus utilisé pour l'analyse des matériaux, on le trouve dans les laboratoires de police scientifique, dans les usines de l'agroalimentaire, ou même sur Mars!. En 2021, plus de 1,8 milliards de lasers ont été fabriqués dans le monde. Il s'agit pour l'essentiel de lasers à semi-conducteur : moins de 800 000 autres lasers, notamment des lasers à gaz, des lasers à fibre et des lasers à état solide, sont fabriqués chaque année.

Malgré cette production massive, le laser fait encore l'objet de recherches intenses, pour atteindre des puissances plus élevées, des impulsions plus courtes, des caractéristiques spectrales meilleures, des rendements plus importants, ou tout simplement de nouvelles longueurs d'onde. Par exemple, en 2012, l'un des plus importants chalenges de la recherche industrielle dans le domaine des lasers a été la réalisation d'un laser à semi-conducteur émettant dans le vert. L'objectif est de compléter les lasers bleus et rouges déjà largement maîtrisés, afin de produire des images vidéo couleur, et de réaliser ainsi des petits vidéoprojecteurs puissants. La conception de nouveaux lasers est donc toujours d'actualité, et les questions que se posent aujourd'hui les chercheurs, ainsi que les problèmes auxquels ils sont confrontés pour concevoir ces lasers, sont les mêmes que ceux rencontrés par les pionniers de la discipline, il y a plus de 50 ans.

La première brique : l'émission stimulée

C'est le 16 mai 1960 qu'un chercheur américain, Theodore Maiman (fig. 1), réussit à produire le premier rayon laser. Mais l'histoire du laser commence 43 ans plus tôt avec Albert Einstein. Dans un article de 1917 intitulé « Zur Quant en theorie der Strahlung », il donne une interprétation de la loi du rayonnement du corps noir de Planck. Pour résoudre ce problème, il décrit les échanges d'énergie entre matière et rayonnement par les processus connus à l'époque, c'est à-dire l'émission spontanée et l'absorption. Mais ces processus ne suffisent pas, et il a l'idée lumineuse d'ajouter un nouveau processus : l'émission stimulée.

La deuxième brique : l'inversion de population

Mais pour obtenir cette lumière cohérente, il faut exciter massivement les atomes. En fait, nous verrons qu'il faut que dans un échantillon, la population d'atomes excités devienne supérieure à la population d'atomes non excités. On appelle cela réalisé une inversion de population. C'est la découverte du pompage optique, en 1950, par le physicien français Alfred Kastler, qui donne une première méthode pour réaliser cette inversion de population. Le pompage optique permet d'exciter un grand nombre d'atomes, et ouvre ainsi la porte à la réalisation d'un rayonnement cohérent.

2

FIGURE 1 - Theodore Maiman avec le premier laser.

Le Maser

Maser est l'acronyme de Microwave Amplification by Stimulated Emission of Radiation, c'est-à-dire amplification d'un rayonnement micro-onde par émission stimulée. Dès lors, deux groupes de physiciens se lancent dans la réalisation d'une source de lumière cohérente, le maser. Ces deux groupes ne communiquent pas entre eux et travaillent indépendamment, pour la simple raison qu'ils sont de part et d'autre du rideau de fer. Charles Townes, de l'université de Columbia, à New-York, affirme avoir eu l'idée du maser dès 1951, mais ce n'est qu'en 1954 qu'il construisit le premier maser avec deux de ses collaborateurs, J. P. Gordon et H. J. Zeiger. Ces résultats furent publiés en juillet 1954. Au contraire, à l'Institut de Physique Lebedev, à Moscou, Nikolay G. Basov et Aleksandr M. Prokhorov présentent publiquement le principe du maser dès 1952, lors d'une conférence organisée par l'Académie des Sciences, à Moscou. Leurs résultats théoriques furent publiés en septembre 1954, et ils réalisèrent leur premier maser en 1955.

De nombreux prix Nobel

En conclusion, on ne peut omettre d'évoquer le rôle central joué par le laser dans les avancées de la science au cours des 50 dernières années. On peut ainsi dénombrer au moins douze prix Nobel attribués à la fois pour les travaux fondateurs du laser et pour des résultats obtenus grâce au laser. Parmi les inventeurs du laser, Charles H. Townes, Nicolay G. Basov et Aleksandr M. Prokhorov reçurent le prix Nobel en 1964, pour des travaux fondamentaux dans le domaine de l'électronique quantique, conduisant à la construction d'oscillateurs et d'amplificateurs basés sur le principe du maser-laser. Deux ans plus tard, Alfred Kastler reçut aussi le prix Nobel, pour la découverte et le développement de méthodes optiques pour l'étude des résonances hertziennes dans les atomes. En 1981, Arthur L. Schawlow partage la même récompense avec Nicolaas Bloembergen, pour le développement de la spectroscopie laser. Theodore Maiman fut sélectionné deux fois pour le prix Nobel, mais jamais retenu. Il reçut cependant d'autres prix prestigieux, notamment le prix Wolf et le Japan Prize. Gordon Gould, dont le rôle réel dans l'invention du laser est toujours contesté par une partie de la communauté scientifique, a été élu au National Inventors Hall of Fame, une organisation américaine qui honore les plus grands inventeurs. C'est la plus haute récompense qu'il reçut, si l'on exclut les millions de dollars qu'il a gagné grâce à ses brevets, dont la validité a été reconnue à la suite d'une longue bataille judiciaire qui dura 30 ans.

Chapitre 1

Généralités sur les lasers

1.1 Introduction

Dans ce chapitre, nous allons poser quelques questions et y répondre en partie. Qu'est-ce qu'un laser? Quelle est la différence entre un laser et une ampoule électrique? Dans quelles gammes de fréquences sont disponibles les lasers? Et quelles sont ses propriétés?.

1.2 Q

u'est-ce qu'un laser?

Les lasers sont des dispositifs qui produisent un rayonnement cohérent pour des longueurs d'ondes situées dans les domaines infrarouge (IR), visible, ultraviolet (UV) du spectre électromagnétique. Les masers émettent sur le même principe dans le domaine Hertzien. On se limitera dans ce projet de fin d'étude aux lasers. Ces dispositifs emploient une variété extraordinaire de matériaux et de méthodes d'amplification, et ont d'innombrables applications réalisées ou potentielles.

1.3 Le laser et l'ampoule

La cohérence spatiale et temporelle fait la différence entre un laser et une ampoule électrique (fig. 1.1).Alors qu'une lampe émet des trains d'ondes non corrélés dans toutes les directions spatiales, un laser génère des ondes cohérentes dont elles peuvent avoir une forte directionnalité. Quelles sont les possibilités de génération d'ondes cohérentes dans l'espace et dans le temps?

3

FIGURE 1.1 - Laser à onde continue (cw), laser femtoseconde (fs) et ampoule électrique

Un laser peut générer une onde continue cohérente ou un train d'impulsions cohérentes. Les cas extrêmes de génération d'un rayonnement visible sont les suivants :

-- Le laser à onde continue (laser CW) émet une onde électromagnétique continue. Le champ est cohérent dans l'espace et dans le temps.

4

-- Le laser femtoseconde (laser FS) émet une onde électromagnétique constituée d'un train d'impulsions. La durée d'une seule impulsion d'un train peut être aussi courte que 5 fs (1 fs = 1 femtoseconde = 10^-15 s). Le champ d'un train d'impulsions est également cohérent dans l'espace et dans le temps.

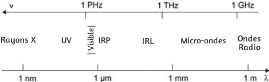
1.4 Gammes spectrales et liste de quelques lasers

La figure (fig. 1.2) représente les longueurs d'ondes et les fréquences des gammes spectrales du spectre électromagnétique - des rayons X aux micro-ondes et aux ondes radio en passant par l'ultraviolet (UV), le visible, la proche infrarouge (PIR) et l'infrarouge lointain (IRL), les micro-ondes et les ondes radio. La fréquence í d'une onde électromagnétique dans le vide obéit

à la relation suivante:

c

í = (1.1)
ë

avec c (= 3×10⁸ m.s^-1) est la vitesse de la lumière et ë la longueur d'onde.

Le domaine spectral visible correspond à une gamme de fréquences d'environ 430-750 THz (gamme de longueurs d'onde d'environ 400-700 nm). L'optique et la lumière font référence aux ondes électromagnétiques dont la longueur d'onde dans le vide est inférieure à environ 1 mm, c'est-à-dire dont la fréquence est supérieure à 300 GHz. Les lasers sont disponibles dans les régions de l'ultraviolet, du visible, du proche infrarouge, de l'infrarouge lointain et des mi-croondes. Des lasers de la gamme des rayons X sont en cours de développement. Les gammes spectrales dans lesquelles les lasers sont disponibles s'étendent de la gamme des GHz à la région supérieure à 1 000 THz.

Le tableau (Tab. 1.1) présente les données de quelques lasers à ondes continues. Les données concernent : ë = longueur d'onde du laser; í = fréquence du laser; hí = énergie quantique des photons d'un champ laser; h = 6.626 × 10^-34 J.s; Psort = puissance de sortie.

TABLE 1.1 - Longueurs d'onde, fréquences et des quantum d'énergies des lasers

Laser	ë	í(THz)	hí(10^-19J)	Psort
HeNe	633nm	474	3.1	1-10 mW
CO2	10.6um	28	0.18	1W à 1 kW
Nd :YAG	1.06u	283	1.9	2W
TiS	830nm	360	2.4	100 mW à 5W
Fibre	1.5 um	200	1.3	1W
Semiconducteur	840 nm	357	2.4	10-100 mW
QCL	1.5um	60	0.25	10-100 mW

1.5 Les propriétés du laser

Le rayonnement laser est caractérisé par un degré extrêmement élevé de (1) monochroma-ticité, (2) cohérence et (3) directionnalité. Nous allons maintenant comprendre la signification

5

FIGURE 1.2 - Gammes spectrales des lasers

de chacun de ces termes.

· Monochromaticité

L'énergie d'un photon détermine sa longueur d'onde par la relation d'énergie de Planck. Dans le cas idéal, le laser émet tous les photons avec la même énergie, et donc la même longueur d'onde, on dit qu'il est monochromatique. La lumière d'un laser provient généralement d'une transition atomique avec une seule longueur d'onde précise. Le laser a donc une seule couleur spectrale et est presque la lumière monochromatique la plus pure qui soit.

Cependant, dans tous les cas pratiques, le laser n'est pas vraiment monochromatique. Une onde vraiment monochromatique nécessite un train d'ondes d'une durée infinie. La ligne d'émis-sion spectrale d'où elle provient a une largeur finie, en raison de l'effet Doppler des atomes ou des molécules en mouvement dont elle provient. Par rapport aux sources ordinaires de lumière, la gamme de fréquences du laser est extrêmement réduite. Cette plage est appelée largeur de ligne ou bande passante.

· Cohérence

Avant d'aller plus avant, il faut insister sur ce point : c'est parce que la lumière laser est cohérente que l'action du laser sur la matière est si particulière, et peut transporter une importante quantité d'énergie lumineuse sur de longues distances.

La cohérence de la lumière laser traduit le fait que les ondes lumineuses transportées sont « en phase ». Les sources de lumières naturelles (étoiles), ou artificielles (ampoules électriques) émettent une lumière polychromatique et non cohérente. L'émission de photons s'effectuent de manière désordonnée : les photons de même longueur d'onde ne sont pas en phase.

Au contraire, la lumière laser est cohérente : les photons émis par la source laser ne sont pas distinguables : ils ont la même phase, même polarisation (angle formé par la vibration du champ électrique avec la direction de propagation). La cohérence de la lumière laser est à la fois spatiale et temporelle.

1. Cohérence spatiale : à un instant donné, tous les points situés dans un même plan perpendiculaire au faisceau laser sont dans le même état de phase (même valeur et orientation du champ électromagnétique).

2. Cohérence temporelle : elle traduit le fait que plusieurs ondes lumineuses émises successivement par un même point de la source demeurent en phase : cette caractéristique et bien sûr liée de près à l'aspect (presque) monochromatique de la lumière laser.

· Directionnalité

L'une des propriétés importantes d'un laser est sa grande directionnalité. Les miroirs placés aux extrémités opposées d'une cavité laser permettent au faisceau d'aller et venir afin de gagner en intensité par l'émission stimulée d'un plus grand nombre de photons à la même longueur

6

d'onde, ce qui entraîne une amplification plus importante en raison de la longueur du trajet dans le milieu. Les réflexions multiples produisent également un faisceau bien collimaté, car seuls les photons se déplaçant parallèlement aux parois de la cavité seront réfléchis par les deux miroirs. Si la lumière est une intensité faible sur l'axe, elle sera perdue dans le faisceau. La cavité résonante permet donc de garantir que seules les ondes électromagnétiques se déplaçant le long de l'axe optique peuvent être soutenues, ce qui permet d'augmenter le gain.

1.6 Conclusion

Dans ce chapitre, nous avons vu la définition d'un laser et certaines de ses propriétés, mais ce n'est pas suffisant pour comprendre complètement comment il fonctionne. Il est nécessaire de parler de certaines bases de sa théorie, et c'est ce que nous allons faire dans le prochain chapitre.

7

Chapitre 2

La base théorique du laser

2.1 Introduction

Selon le modèle atomique de Bohr (1911), qui repose sur des études spectroscopiques, les transitions entre les niveaux d'énergies discrets d'un atome peuvent conduire à l'émission ou à l'absorption d'un rayonnement dont la fréquence correspond à la relation énergie-fréquence de Bohr. Dans un processus d'absorption, un photon est absorbé. Dans un processus d'émission, un photon est émis. Einstein a découvert que l'émission d'un photon est possible par deux processus différents : l'émission spontanée et l'émission stimulée, et que les coefficients décrivant les trois processus, absorption, émission stimulée et spontanée, sont liés les uns aux autres (relations d'Einstein).

En utilisant la loi du rayonnement de Planck, nous dérivons les relations d'Einstein. Nous montrons également que l'émission stimulée du rayonnement est un processus qui se produit en permanence autour de nous.

Les coefficients d'Einstein peuvent être extraits des résultats des études expérimentales des propriétés optiques de la matière à l'équilibre thermique. Dans ce chapitre, nous considérons un ensemble de systèmes à deux niveaux en équilibre thermique déterminé par la statistique de Maxwell-Boltzmann.

2.2 Processus de fonctionnement du laser 2.2.1 La lumière et les atomes dans une cavité

Comment la lumière interagit-elle avec un système atomique à deux niveaux? Nous étudierons cette question en trois étapes :

-- Nous décrivons l'équilibre thermique entre le rayonnement dans une cavité et les parois de la cavité.

-- Nous décrivons l'équilibre thermique entre un ensemble de systèmes atomiques à deux niveaux dans une cavité et les parois de la cavité.

-- Nous considérons une cavité qui contient un ensemble de systèmes atomiques à deux niveaux et un rayonnement.

Une cavité (fig. 2.1 gauche) contient le rayonnement d'un corps noir. La distribution spectrale de la densité d'énergie ñ(í) du rayonnement dépend de la température T des parois de la cavité.

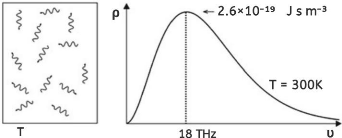
FIGURE 2.1 - Une cavité et une distribution Planckienne du rayonnement La densité spectrale d'énergie est déterminée par la loi de rayonnement de Planck :

8ðU^2 ñ(U) = c3 où k est la constante de Boltzmann.

1 (2.1) ehí/kT - 1

La distribution de fréquence est représentée sur la (fig. 2.1 droit). La fréquence _Umax du maximum de la distribution est directement proportionnelle à la température selon la relation :

hUmax 2.8 kT (2.2)

Si les parois sont à température ambiante (T = 300 K), le maximum de la distribution se situe dans l'infrarouge (Umax = 1.8 x 10¹³ Hz). La densité spectrale augmente comme U² à petite fréquence (U « Umax) et diminue comme ^U3e-hí/kT à grande fréquence (U » Umax). L'équilibre thermique s'établit par l'absorption du rayonnement par les parois de la cavité et par l'émission du rayonnement des parois dans la cavité. La densité d'énergie du rayonnement dans l'intervalle de fréquence [U , U + dU] est :

u(U) = ñ(U)dU (2.3)

Nous traitons maintenant une cavité contenant un ensemble de systèmes atomiques à deux niveaux en équilibre thermique qui est déterminé par les statistiques de Boltzmann,

N2 = e N1

-(E2-E1)/kT (2.4)

8

Le rapport de population est proche de l'unité si E2 - E1 » kT. Il décroît exponentiellement avec la différence d'énergie E2 - E1. L'équilibre thermique est établi par les collisions des systèmes atomiques à deux niveaux entre eux et avec les parois de la cavité.

Les ions d'impureté dans un solide ont des emplacements fixes. Les populations des niveaux d'énergie des différents ions sont en équilibre thermique avec le solide en raison de l'absorption et de l'émission de phonons. Les populations sont régies par les statistiques de Boltzmann.

Einstein a montré que l'équilibre thermique dans un gaz d'atomes peut également être établi par l'interaction directe du rayonnement avec les atomes et que trois processus d'interaction entre le rayonnement et les atomes doivent se produire : absorption, émission spontanée et émission stimulée.

En utilisant la relation énergie-fréquence de Bohr,

hv0 = E2 - E1 (2.5)
Où v0 est la fréquence de transition, nous pouvons écrire

N2 = e N1

-hí0/kT (2.6)

Nous allons maintenant caractériser les trois processus par les trois coefficients d'Einstein.

2.2.2 Émission spontanée

Les atomes excités (fig. 2.2) peuvent émettre des photons spontanément, c'est-à-dire sans cause extérieure.

Le rayonnement émis spontanément est incohérent et l'émission se produit dans toutes les directions de l'espace. La variation dN2 de la population N2 du niveau supérieur, à l'intérieur d'un intervalle de temps dt, est proportionnelle à N2 et à dt,

dN2 = A21N2dt (2.7)

A21 est le coefficient d'Einstein de l'émission spontanée. La population du niveau supérieur décroît exponentiellement

N2(t) = N2(0)e^-A21t = N2(0)e^-t/^ô87 (2.8)

N2(0) est la densité des systèmes atomiques à deux niveaux excités à t = 0 et _r5p est la durée de vie moyenne d'un système atomique à deux niveaux excité par rapport à l'émission spontanée ou bien la durée de vie spontanée.

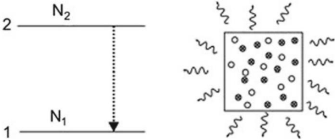
9

FIGURE 2.2 - Émission spontanée

Nous avons la relation simple :

A21 = 1/r5p (2.9)

Le coefficient d'Einstein _A21 est égal à l'inverse de la durée de vie spontanée.

2.2.3 Absorption

Les photons d'un champ lumineux peuvent être absorbés par des transitions 1 ? 2 (fig. 2.3a). La variation dN1 de la population N1 de l'état fondamental, dans un intervalle de temps

10

dt, est proportionnelle à la population de l'état fondamental lui-même, à la densité spectrale d'énergie ñ du champ de rayonnement et à dt

dN1 = _B12ñ(í0)N1dt (2.10)

B12 est le coefficient d'absorption d'Einstein et ñ(í0) est la densité spectrale d'énergie du rayonnement aux fréquences autour de í0. L'absorption n'est possible qu'en présence d'un champ, alors l'absorption est un processus stimulé.

FIGURE 2.3 - Transitions stimulées. (a) Absorption et (b) émission stimulée

2.2.4 Emission stimulée

L'émission stimulée (fig. 2.3b), par des transitions 2 --+ 1, est provoquée (stimulée, induite) par un champ de rayonnement. La variation dN2 de la population d'atomes dans l'état excité, dans un intervalle de temps dt, est proportionnelle à la population N2, à la densité spectrale d'énergie du rayonnement aux fréquences autour de í0 et à dt.

dN2 = _B21ñ(í0)N2dt (2.11)

B21 est le coefficient d'Einstein de l'émission stimulée. Le rayonnement créé par l'émission stimulée a les mêmes fréquences , direction, polarisation et phase que le rayonnement de stimulation.

2.3 Les relations d'Einstein

Nous recherchons des relations entre les coefficients d'Einstein. Comme nous l'avons vu, l'interaction d'un système atomique à deux niveaux avec le rayonnement se produit (fig. 2.4) par absorption, émission stimulée et spontanée. Nous décrivons ces trois processus par des équations de taux qui correspondent à des équations différentielles du premier ordre :

· La variation de la population N1 dû à l'absorption est donné par:

idN1 ~

abs = _B12 ñ(í0) N1 (2.12)

dt

la variation temporelle de la population N1 due à l'absorption est proportionnelle à ñ(í0) et à N1.

· La variation de la population N2 dû à l'émission stimulée est égal à :

idN2 ~

stim = _B21 ñ(í0) N2 (2.13)

dt

la variation temporelle de la population N2 due à l'émission stimulée est proportionnelle à ñ(í0) et à N2.

· 11

La variation de la population N2 dû à l'émission spontanée est :

fdN2 ~ dt sp

= -A21 N2 (2.14)

la variation temporelle de la population N2 due à l'émission spontanée de rayonnement est proportionnelle à N2.

FIGURE 2.4 - Modèle d'Einstein. Les flèches ondulées désignent des photons. L'atome en grisé, après la transition, vient augmenter la population d'atomes « blancs ».

Nous considérons une cavité avec un ensemble de systèmes atomiques à deux niveaux et un rayonnement en équilibre thermique. Dans la moyenne temporelle, le rapport _N2/N1 est une constante. Par conséquent, le taux d'absorption doit être égal au taux d'émission,

fdN1 ~ _fdN2 ~ _fdN2 ~

abs = stim + (2.15)

dt dt dt sp

Cela conduit à la relation suivante :

B12 ñ(u0) N1 = A21 N2 + B21 ñ(u0) N2 (2.16)

Il s'ensuit que

A21/B21

ñ(u0) = (2.17)

(B12/B21)N1/N2 - 1

Le facteur de Boltzmann détermine le rapport N1/N2. La comparaison avec la loi de rayonnement de Planck fournit les relations d'Einstein :

B21 = B12 (2.18)

8ðu²

A21 = c3 hu B21 (2.19)

La fréquence u (qui remplace u0) découle de la relation de Bohr hu = E2 - E1. On a le résultat :

* Le même coefficient d'Einstein régit l'absorption et l'émission stimulée. * Il existe un lien entre les coefficients d'émission spontanée et stimulée. * Le coefficient d'Einstein _A21 augmente fortement avec la fréquence.

La figure (fig. 2.5) montre la durée de vie spontanée pour différentes fréquences de transition u = (E2 - E1)/h à une valeur fixe de _B21 (= 1018 _m3 J-1 s^-2); la durée de vie spontanée est de l'ordre de 10^-6 s à une fréquence de transition (5 x 10¹⁴Hz) dans le visible, de 100s à une fréquence de transition (10¹² Hz) dans l'infrarouge lointain, et de 10^-15 s à une fréquence de transition (10¹⁷ Hz) dans le domaine des rayons X (fig. 2.5). Les durées de vie spontanées aux

FIGURE 2.5 - Durée de vie naturelle

fréquences de transition des rayons X sont très courtes. Par conséquent, l'exploitation d'un laser à rayons X est difficile.

Si les niveaux d'énergie sont dégénérés, la statistique de Boltzmann donne les résultats suivants

-(E2-E1)/kT (2.20)

N2 g2 = e N1 g1

12

où g1 est le degré de dégénérescence du 1^er niveau et g2 le degré de dégénérescence du 2eme niveau. Le traitement de l'équilibre entre les populations atomiques et le rayonnement dans une cavité conduit aux relations suivantes :

et (comme dans le cas non dégénéré)

g2 B12 = g1

B21 (2.21)

8ðí²

A21 = c3 hí B21 (2.22)

Dans le cas de systèmes atomiques à deux niveaux noyés dans un milieu d'indice de réfraction n, la vitesse de la lumière dans le vide doit être remplacée par la vitesse de la lumière dans le milieu. Les relations d'Einstein sont alors :

g1B21 = g2B12 (2.23)

8ðí²

(c/n)

A21 = ₃ hí B21 (2.24)

Sous cette forme, les relations d'Einstein sont valables si un milieu est optiquement isotrope. Si un milieu est optiquement anisotrope, la relation entre _A21 ^et _B21 doit être modifiée.

Si la densité spectrale d'énergie est donnée à l'échelle de la fréquence angulaire, ñ = ñ(ù) , le coefficient d'Einstein _Bù21 est plus petit du facteur 2ð, B^ù₂₁ = B21/2ð. Les relations d'Einstein sont alors :

g1B^ù21 = g2B^ù (2.25)

12

hù³

A21 =ð2c3 Bù (2.26)

21

Le tableau (tab. 2.1) présente les valeurs des coefficients d'Einstein déterminées par l'utili-sation de méthodes expérimentales ou théoriques. Quelques méthodes sont mentionnées dans ce qui suit :

· La mesure de _ô21 (par une expérience de luminescence) fournit également _A21 et (via les relations d'Einstein) _B21. Exemple : Nd :YAG.

· La mesure du coefficient d'absorption fournit _B21 et (via les relations d'Einstein) A21.

· Une analyse du spectre de luminescence donne A21 ; Exemple : des lasers bipolaires à semi-conducteurs.

· Les études théoriques des taux de transition fournissent B21 ; Exemple : QCL

13

TABLE 2.1 - Les coefficients d'Einstein

Laser	À	n	ôsp	A21(s^-1)		B21(m3 J^-1s^-2)	HeNe
633nm	1	100ns	10^7	1.5 x 10^20		CO2
10.6,im	1	5s	0.2	1.4 x 10^16		Nd :YAG
1.06,im	1.82	230 ,is	5.1 x 10^16	4.3 x 10^3		TiS (E || c)
830nm	1.74	3.8,is	1.7 x 10^18	4.3 x 10^3		Fibre
1,5,im	1.5	10ms	10^2	6.6 x 10^15		Semiconducteur
810nm	3.6	-	3 x 10^9	3.7 x 10^21		QCL
5,im	3.6	-	-	4 x 10^21

2.4 Conditions d'Amplification - Inversion de populations

2.4.1 Les conditions d'amplification

Si le système est en équilibre, les niveaux les plus bas sont toujours les plus peuplés. Si nous calculons la différence entre la population du niveau inférieur et celle du niveau placé juste au-dessus, elle est positive. La réponse impulsionnelle à l'arrivée d'un signal sera une absorption.

-- l'énergie absorbée par le milieu est : g1B12 p(u)N1 hu

-- l'énergie gagnée par le rayonnement est : g1B12 p(u)N2 hu d'où la variation d'énergie est :

dE = g1B12 p(u) (N1 - N2) hu (2.27)

A l'équilibre thermodynamique, dE < 0 puisque N2 < N1 d'après la loi de Boltzmann.

Si maintenant nous considérons que nous avons pu déplacer cet équilibre et peupler le niveau supérieur de façon telle que sa population soit nettement supérieure à celle du niveau inférieur, l'arrivée du même signal provoquera une émission stimulée. Il y a amplification du signal incident. Cette condition est appelée l'inversion de population (il faut que N2 > N1). Ainsi si :

· N2 < N1 : le rayonnement incident est absorbé;

· N2 = N1 : c'est le phénomène de saturation;

· N2 > N1 : le rayonnement incident est amplifié (le système est donc hors équilibre thermodynamique).

Pour obtenir l'amplification, premier pas vers l'effet laser, il faut donc déjà avoir réalisé deux conditions :

· disposer d'un milieu actif,

· avoir obtenu une inversion de population.

2.4.2 Les modes de transfert pour les transitions atomiques

Il faut arriver à stocker des électrons sur le niveau supérieur. Pratiquement, ce mécanisme de stockage se fait de plusieurs façons différentes.

2.4.2.1 Pompage optique

Le pompage optique est l'excitation du milieu actif par la lumière. C'est le mode de pompage des lasers à solides. On distingue généralement les systèmes à 3 niveaux et ceux à 4 niveaux. Le système à trois niveaux (fig. 2.6) a été proposé par Blömbergen en 1956. On amène, par un dispositif optique, les atomes sur le niveau E3 légèrement supérieur à E2. Le niveau E2 doit être métastable. Cela signifie que la durée de vie des atomes sur cet état est longue. C'est ce niveau qui va permettre de réaliser une inversion de populations.

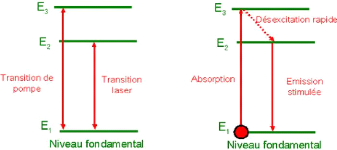
14

FIGURE 2.6 - Exemple d'un système à trois niveaux avec un pompage optique.

2.4.2.2 Pompage électronique

Ce type de pompage est généralement utilisé dans les lasers à gaz. Comme le gaz est en principe isolant, il faut d'abord envoyer une décharge pour ioniser le milieu et le rendre conducteur. Ensuite, en appliquant un champ électrique entre deux électrodes plongées dans le gaz, on obtient un courant. Les électrons qui circulent cèdent leur énergie cinétique aux atomes du milieu actif et provoquent l'inversion de population cherchée. Par exemple : le laser HeNe se fait par un pompage électronique (fig. 2.7).

FIGURE 2.7 - Exemple de HeNe avec un pompage électronique.

15

2.4.2.3 Pompage chimique

On utilise des réactions chimiques qui, en se produisant, fournissent directement des molécules ionisées. L'avantage de ce type de laser est qu'il ne nécessite pas de source d'électricité. Pratiquement, ces techniques, qui permettent d'obtenir de très grandes puissances, sont réservées aux applications militaires. On peut citer les lasers au fluorure d'hydrogène (HF) ou au fluorure de deutérium (DF) dans l'infrarouge moyen.

2.4.2.4 Pompage par injection de porteurs

C'est le pompage des lasers à semi-conducteur, qui est produit par le courant direct qui traverse une jonction de type P-N.

2.5 Cavité résonante

Il n'est pas suffisant de provoquer une inversion de population pour obtenir l'effet laser, il faut obliger les photons à partir en majorité dans une direction bien définie, ce qui va permettre d'augmenter considérablement leur flux par l'émission stimulée. C'est le rôle que joue la cavité.

La cavité est formée par deux miroirs parallèles (fig. 2.8), qui encadrent le milieu actif et qui définissent une direction privilégiée : leur normale. Le miroir arrière est totalement réfléchissant alors que le miroir avant laisse passer une partie du rayonnement, ce qui autorise l'émission laser.

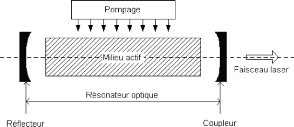
FIGURE 2.8 - Cavité résonante du laser.

Au départ, l'émission spontanée produit les premiers photons, qui peuvent se diriger dans n'importe quelle direction. Seuls ceux qui sont émis suivant l'axe normal aux deux miroirs rencontrent un grand nombre d'atomes excités. A la fin du premier passage, les photons en phase sont déjà assez nombreux. Ils se réfléchissent sur les miroirs et viennent encore entraîner d'autres photons, par émission stimulée. On imagine facilement qu'un gain important puisse être obtenu. Il faut enfin noter que le phénomène est rapide, étant donné la vitesse de la lumière et que l'émission spontanée ne joue qu'un rôle négligeable, limité à l'initialisation du phénomène.

Si le gain obtenu sur un aller et retour est supérieur aux pertes rencontrées, le seuil est franchi : un faisceau laser est émis.

La cavité joue de plus un rôle de filtre optique très sélectif. Il s'agit d'un interféromètre à ondes multiples qui ne fournit des interférences constructives que si (dans le cas de l'incidence normale) :

ë

nL = p (2.28)
2

16

L étant la longueur de la cavité, n l'indice de réfraction et p un nombre entier.

Les longueurs d'onde sont donc émises d'une façon régulière à l'intérieur de la largeur de raie totale, la raie de fluorescence : c'est ce que l'on appelle un peigne. L'écartement de deux fréquences successives est donné par :

Lë Lu = c ë2

c = (2.29) 2L

On peut voir que cet écartement est inversement proportionnel à la longueur de la cavité L. Si l'on veut avoir peu de modes, ou même un seul, il faudra prendre une cavité très courte.

Il est enfin primordial que l'absorption intrinsèque de ces filtres soit la plus faible possible. Dans les cavités laser, comme ils jouent un rôle fort important, ils sont réalisés à partir de matériaux dont les propriétés optiques sont compatibles avec toutes ces exigences.

Tout ceci montre que les sources laser ont pour spécificité : un rayonnement émis très pur (mono-chromaticité) grâce à leur cohérence temporelle et une grande directivité due à leur cohérence spatiale.

2.6 Conclusion

Pour conclure, nous n'avons vu dans ce chapitre juste la base théorique du fonctionnement des lasers, mais il y a en fait toute une branche de la physique qui est très compliquée, et que les physiciens et les ingénieurs continuent à développer jusqu'à aujourd'hui d'autre type de laser très avancés.

17

Chapitre 3

Types et principe de fonctionnement

3.1 Introduction

Dans ce chapitre, nous présentons en détail le fonctionnement des lasers les plus utilisés aujourd'hui. Ce sont tout d'abord les lasers à semi-conducteur, notamment grâce à leur utilisation pour les télécommunications. Puis les lasers à gaz, les plus utilisés dans l'industrie avec l'exemple de laser Ar⁺. Enfin nous réservons un paragraphe aux autres types du laser comme le laser chimique, les lasers à fibre et finalement le laser à électrons libres.

3.2 Lasers à semi-conducteur 3.2.1 Histoire

L'année même où Theodore Maiman réalisait le premier laser, les français Georges Duraf-fourg et Maurice Bernard du CNET, déterminaient théoriquement les conditions nécessaires au fonctionnement d'un laser à semi-conducteur.

De nombreux laboratoires, aux États-Unis vont alors se lancer dans la course à la réalisation de ce laser. L'équipe de Robert Hall, des laboratoires aux États Unis, parvient la première, en novembre 1962, à réaliser un laser émettant des impulsions infrarouges. Il faudra attendre encore 8 ans pour obtenir le premier laser continu.

3.2.2 Principe de fonctionnement

Le fonctionnement du laser à semi-conducteur basait sur l'insertion dans une cavité un milieu amplificateur, dans lequel on réalise une inversion de population grâce d'un mécanisme de pompage. Ici, le milieu amplificateur est un semi-conducteur, c'est-à-dire un matériau possédant une conductivité électrique intermédiaire entre un isolant et un métal.

Dans un semi-conducteur, les électrons peuvent occuper deux ensembles de niveaux d'énergie distincts, séparés par une région inoccupée. La bande inférieure, regroupant les niveaux non excités, est la bande de valence. La bande supérieure, celle des niveaux excités, est la bande de conduction.

La zone intermédiaire porte le nom: La bande interdite, La largeur E_g de la bande interdite joue un rôle analogue à la distance entre deux niveaux discrets d'un atome, et elle fixe donc la longueur d'onde du rayonnement.

Réaliser l'inversion de population permet donc à peupler la bande de conduction en dépeuplant la bande de valence. Autrement dit, l'électron, lorsqu'il est dans la bande de valence, est lié à la structure cristalline. Lorsqu'il est excité, il devient un électron libre et laisse un trou libre dans la structure cristalline. Pour se désexciter, un électron doit nécessairement trouver un trou pour reprendre sa place autour d'un atome : on dit qu'il se recombine avec un trou.

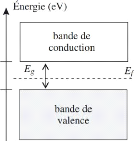
FIGURE 3.1 - Représentation schématique des bandes d'énergie dans un semi-conducteur.

Si l'on applique une différence de potentiel directe aux bornes de la jonction, les électrons et les trous vont migrer vers la zone de contact. Le nombre des électrons et des trous augmente et la recombinaison électron-trou est favorisée. Les photons ainsi créés constituent une source de lumière non cohérente : c'est le principe des LED. Pour obtenir un rayonnement cohérent, c'est-à-dire un laser, il suffit de placer la jonction P-N dans une cavité et de s'assurer que le pompage - soit le courant électrique - est suffisant pour compenser les pertes : c'est le principe de fonctionnement de la diode laser.

3.2.3 La longueur d'onde du rayonnement

La largeur E_g de la bande interdite joue un rôle analogue à la distance entre deux niveaux discrets d'un atome, et elle fixe donc la longueur d'onde du rayonnement (fig. 3.2).

18

FIGURE 3.2 - Transitions radiatives de bande à bande dans les semi-conducteurs.

hc

E_g = hí = (3.1)
ë

hc

ë =

(3.2)

E_g

avec E_g est le gap énergétique et ë la longueur d'onde du rayonnement.

On remarque que la longueur d'onde est inversement proportionnelle à l'énergie du gap.

Donc on peut varier la gamme spectrale de fonctionnement, qui peut être large, entre 0,3 et 30 um suivant le type de matériau semi-conducteur retenu (fig. 3.3). On peut ajuster la largeur de la bande interdite en utilisant des alliages et/ou des structures à puits quantiques.

19

FIGURE 3.3 - Choix du laser à semi-conducteur en fonction de la longueur d'onde.

3.2.4 Principaux avantages

· Le rendement élevé qui peut atteindre 50

· La puissance. Dans l'infrarouge proche, on obtient facilement plusieurs centaines de mW avec un courant de l'ordre de grandeur de 1A.

· Fonctionnement à la température ambiante. Aujourd'hui, la plupart des lasers à semiconducteur fonctionnent à température ambiante ~ 24^°C. Toutefois certains d'entre eux, notamment ceux à bande interdite étroite qui émettent à des longueurs d'onde plus élevées, sont maintenus à basse température, entre 10 et 20 K, pour limiter le peuplement de la bande de conduction par simple excitation thermique.

3.2.5 Exemple : Laser (Al)GaAs

(Al)GaAs est le système de matériaux semi-conducteurs composés le plus étudié et aussi le plus utilisé. La raison principale en est le faible décalage de réseau ?a/a de seulement 1.3x10^-3 entre AlAs et GaAs. Cela rend la fabrication d'hétéro structures facile puisque les contraintes de contrôle de la composition ne sont pas très strictes. Alors que les dispositifs électroniques ne nécessitent généralement que des couches minces _d'AlxGa1-xAs à faible teneur en Al (x < 0.3) où le décalage de réseau peut facilement être adapté de manière élastique, la notion d'AlGaAs dont le réseau est adapté à celui de GaAs n'est clairement pas vraie pour les lasers à diodes ayant des couches épaisses de gaine et de guide d'ondes à forte teneur en Al.

L'épaisseur critique de la couche au-delà de laquelle la formation de dislocations mal adaptées est attendue pour _{l'Al0.5Ga0.5As} n'est que de 500 nm et pour l'AlAs de 220 nm. Ce fait doit être gardé à l'esprit, bien que l'AlGaAs se révèle être plus résistant à la relaxation de la déformation que prévu théoriquement. Une autre raison de la prédominance de l'AlGaAs est le fait que l'As est beaucoup plus facile à manipuler que le P, qui a une pression de vapeur beaucoup plus élevée et se présente sous différentes modifications, dont certaines peuvent s'enflammer spontanément.

20

3.3 Lasers à gaz

3.3.1 Principe de fonctionnement

Le milieu actif gazeux d'un laser peut être constitué d'ions, d'atomes, ou encore des molécules.

-- Lorsque les atomes actifs sont neutres ou ionisés, le pompage réalise l'inversion de population entre deux niveaux électroniques (fig. 3.4) et la transition est typiquement située dans l'ultraviolet, le visible ou encore l'infrarouge proche (0, 2um < ë < 1um).

-- Par contre, si le milieu est moléculaire, la gamme spectrale peut être beaucoup plus étendue. Elle dépend du type de transition impliquée dans l'effet laser : transitions électroniques (0, 2um < ë < 1um), vibrationnelles (5um < ë < 50um) ou enfin rotationnelles (20um < ë < 1000um).

FIGURE 3.4 - Illustration schématique de l'interaction matière-rayonnement. La fréquence du rayonnement émis ou absorbé dépend du type de la résonance mise en jeu: (a) atomique, (b) vibrationnelle, (c) rotationnelle.

Un laser à gaz est typiquement formé d'un tube renfermant le mélange gazeux, placé entre les miroirs d'une cavité résonante. C'est une décharge électrique qui réalise le pompage du milieu actif dans la plupart des cas. Cependant, certains lasers sont optiquement pompés. C'est le cas, en particulier, des lasers émettant dans l'infrarouge lointain comme par exemple le laser à difluorométhane (CH2F2).

On distingue principalement deux types d'excitation :

· l'excitation directe : les électrons produits et accélérés dans la décharge électrique, transmettent par collision une partie de leur énergie cinétique aux atomes du milieu actif qui atteignent ainsi le niveau supérieur de la transition laser;

· l'excitation indirecte : on ajoute au milieu actif des atomes plus facilement excitables que ceux qui sont à l'origine de l'émission laser, mais qui n'y participent pas directement. Les collisions assurent ensuite le transfert de l'énergie acquise.

3.3.2 Exemple : Laser à argon ionisé (Ar⁺)

Dans le laser à ions d'argon, les collisions électroniques ultérieures conduisent à l'ionisation des atomes d'argon et à l'excitation des ions d'argon. Les configurations des électrons sont les

21

suivantes :

· L'Argon Ar : 1s² 2p⁶ 3s² 3p⁶ .

· L'ion d'Argon Ar⁺ : 1s² 2p⁶ 3s² 3p⁵ .

· L'ion d'Argon excité (Ar⁺)* : 1s² 2p⁶ 3s² 3p⁴ 4p .

Différentes transitions 4p ? 4s entre les niveaux 3p⁴4p et 3p⁴4s (divisés en raison de l'in-teraction spin-orbite) donnent lieu à une émission laser cw (laser à onde continue) dans le bleu et le vert, avec de fortes lignes d'émission à 488 et 514 nm.

Une décharge gazeuse dans un tube en céramique (diamètre 1-2mm; longueur 1m; refroidi à l'eau) contenant le gaz argon (pression 0,1 mbar) pompe le laser à ions argon. En raison de la double excitation, l'efficacité du laser à ions argon est proportionnelle au carré de la densité de courant dans la décharge gazeuse. A une puissance électrique élevée (courant 10 A; tension 5 kV), la puissance de sortie est grande (20W). L'efficacité du laser est faible (= 0.1 %).

FIGURE 3.5 - Niveaux d'énergie du laser dans l'argon ionisé.

Niveaux d'énergie du laser dans l'argon ionisé.

Le pompage comporte deux étapes : les atomes subissent d'abord une ionisation par collision, puis les ions sont excités vers des niveaux élevés. Plusieurs collisions sont toutefois nécessaires pour atteindre les niveaux 3p⁴4p de l'ion (fig. 3.5). Les deux niveaux de la transition laser étant très élevés par rapport au fondamental, ceux-ci sont pratiquement vides à température ambiante en absence de pompage. L'inversion de population est alors très facile à réaliser, d'autant que le niveau inférieur de la transition laser a une durée de vie courte.

3.4 Autres types 3.4.1 Lasers chimiques

Certaines liaisons chimiques permettent d'accumuler une quantité d'énergie qui peut être libérée au cours de leurs réaménagements. Les lasers chimiques permettent de convertir une partie de l'énergie stockée en rayonnement optique cohérent. Ils fonctionnent sur des transitions de rotation et vibration de molécules dont la plus connue est H(D)F. En restant sur le plan qualitatif, le principe de l'excitation consiste ici à provoquer la formation de molécules diatomiques vibrationnellement excitées (*) :

F+H2 ? H+(HF)^*
F2+H ? F+(HF)^*

22

Il faut fournir de l'énergie pour initier la réaction c'est-à-dire pour obtenir les agents chimiquement actifs H et F. Ces molécules se désexcitent en émettant des photons.

3.4.2 Lasers à fibre

Les lasers à fibre optique sont des lasers en verre. En comparaison avec d'autres lasers à l'état solide, les lasers à fibre sont flexibles et simples. Le milieu actif d'un laser à fibres est un verre qui est dopé avec des ions de terres rares. Les lasers à fibre optique ont de nombreuses applications dans les domaines de traitement des matériaux, la chimie, la médecine, la biologie.

3.4.3 Lasers à électrons libre

Dans un laser à électrons libres (FEL), un faisceau d'électrons se déplaçant à une vitesse proche de la vitesse de lumière est faite pour passer à travers le champ magnétique (fig. 3.6) généré par une structure périodique (appelé le onduleur). Le processus d'émission stimulé se produit l'interaction du champ électromagnétique du faisceau laser avec ces électrons relativistes se déplaçant dans la structure magnétique périodique. Comme dans tout autre laser, deux miroirs d'extrémité sont utilisés pour fournir pour l'oscillation laser. Le faisceau d'électrons est injecté dans la cavité laser, puis dévié la cavité à l'aide d'aimants de pliage appropriés.

FIGURE 3.6 - Structure de base d'un laser à électrons libres.

3.5 Conclusion

Dans ce chapitre, nous avons parlé de certains types de lasers comme les lasers à semi conducteurs et les lasers à gaz et de leur fonctionnement. Nous avons également parlé d'autres types mais sans détails. Parce que si vous voulez détailler les choses, vous aurez besoin d'un chapitre pour chaque type, en particulier pour le laser à électrons libres car il est trop difficile à traiter. Vous devez tenir compte ses effets quantiques et relativistes qui rendent sa physique trop compliquée.

23

Chapitre 4

Quelques applications du laser

4.1 Introduction

Le laser, depuis son invention, a toujours été un dispositif utile qui a rendu notre vie plus facile en raison de ses propriétés uniques. Dans ce chapitre, nous allons parler de certaines applications du laser dans la vie quotidienne et aussi de ses applications dans le domaine de la recherche scientifique.

4.2 Applications dans le domaine de la recherche scientifique

4.2.1 La télémétrie

On désire ici mesurer la distance entre deux points avec une grande précision. Depuis 1983, le mètre est défini par rapport à la vitesse de la lumière dans le vide, qui est fixée à exactement 299 792 458 m/s, la seconde étant elle-même définie comme 9 192 631 770 fois la période de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental du césium. L'utilisation de la lumière est donc particulièrement adaptée à la mesure d'une longueur, puisque c'est finale ment sa vitesse qui définit maintenant l'étalon de longueur.

FIGURE 4.1 - Le laser utilisée pour mesurer la distance terre-lune.

La méthode de télémétrie la plus simple est d'émettre vers l'objet dont on veut mesurer la distance une impulsion de lumière, puis de mesurer le temps ?t qu'elle met pour revenir à son point de départ. Si l'impulsion se propage avec une vitesse de groupe v_g, la distance recherchée est d = v_g?t/2 . La directivité du laser joue ici un rôle crucial, puisque l'intensité

24

détectée au retour dépend de la divergence du faisceau. Si les cibles sont relativement proches ou suffisamment réfléchissantes, c'est la lumière rétrodiffusée qui est utilisée pour faire la mesure. Les télémètres employés dans les métiers du bâtiment et des travaux publics exploitent cette technique, tout comme les jumelles laser qui, grâce à plusieurs mesures successives, permettent d'obtenir la vitesse d'un véhicule.

4.2.2 La spectroscopie

La spectroscopie consiste à identifier l'ensemble des niveaux d'énergie d'une molécule, ce qui donne d'innombrables informations sur sa structure interne et permet de plus d'en constituer une « signature ». Celle-ci peut ensuite servir à détecter la molécule, y compris dans les endroits les plus extrêmes : fours, moteurs à explosion, atmosphère terrestre, espace intersidéral pour n'en citer que quelques-uns.

Le laser permet de réaliser des spectres sur des temps très courts, en utilisant des impulsions femtosecondes. La spectroscopie femtoseconde permet notamment de suivre à cette échelle de temps l'évolution des réactifs dans une réaction chimique, ce qui améliore considérablement nos connaissances du domaine. Ces techniques développées par Ahmed Zewail lui ont valu le prix Nobel de Chimie en 1999.

4.2.3 La détection des ondes gravitationnelles

Les ondes gravitationnelles sont des oscillations de la courbure de l'espace-temps prédites par la théorie de la relativité générale. Elles n'ont jamais été observées, et c'est la raison pour laquelle des instruments destinés à détecter ces ondes ont été construits. Des détecteurs terrestres d'ondes gravitationnelles utilisant l'interférométrie laser sont mis en service pour des campagnes scientifiques. Actuellement, deux instruments comparables sont en service : LIGO aux États-Unis, et l'instrument franco-italien VIRGO (fig 4.2). Ils s'appuient tous les deux sur le même principe : comme la lumière suit les courbures de l'espace-temps, le passage d'une impulsion gravitationnelle peut être détecté par un interféromètre optique, car elle modifiera la longueur apparente des bras de l'interféromètre. Les deux bras étant perpendiculaires, ces modifications seront différentes dans les deux bras, et le passage d'un train d'ondes gravitationnelles se traduira donc par une oscillation périodique des franges d'interférence. Les impulsions gravitationnelles les plus puissantes sont générées par des évènements gravitationnels exceptionnellement violents, comme l'effondrement du coeur d'une supernova juste avant son explosion, ou la coalescence de deux trous noirs. Plus l'interféromètre est sensible, plus le nombre d'évè-nements détectables est important.

FIGURE 4.2 - L'interféromètre VIRGO, Santo Stefano a Macerata, Pisa, Italie.

25

Les sensibilités obtenues permettront de suivre des événements cosmiques d'un grand intérêt scientifique. La détection des événements, l'analyse quantitative et la localisation dans le ciel fourniront des informations vitales qui ne peuvent être obtenues par la fenêtre du rayonnement électromagnétique.

Le laser utilisé est un laser à néodyme de 20 W, avec une stabilité relative en fréquence de

v

10^-21 Hz sur une échelle de temps de 100 ms, et un bruit en fréquence de 2×10^-21 Hz/ Hz. Une amélioration de ces performances est déjà prévue, afin d'augmenter le nombre d'évènements détectables.

4.2.4 Vélocimétrie Doppler

L'objectif est ici de mesurer la vitesse d'un objet. On réalise une mesure interférométrique de la distance entre l'objet mobile et le laser fixe. On pourrait mesurer la vitesse de défilement des franges d'interférence et obtenir ainsi la vitesse de l'objet. On peut plus simplement mesurer directement la valeur du décalage de fréquence Doppler de l'onde retour.

Le principe est le même que celui exploité dans les radars qui jalonnent nos routes. Si une onde incidente de fréquence vi est rétro-réfléchie par un objet en mouvement, l'onde retour voit sa fréquence U_r modifiée : c'est l'effet Doppler. Le décalage 8v dépend de la vitesse v? de l'objet : 8v = -vv/c , où v est la composante de vitesse parallèle à la direction de propagation de la lumière. En mélangeant les ondes aller et retour, on observe un battement à la fréquence 8v qui nous renseigne directement sur la vitesse de l'objet. La précision de la mesure de la vitesse est limitée par la largeur spectrale du laser. Pour un laser YAG, un calcul simple donne 1 mm/s de précision pour une largeur spectrale de 1 kHz.

4.2.5 La fusion nucléaire

La réaction de fusion nucléaire entre le deutérium ²D et le tritium ³T est :

^3D + ²T ? ⁴He + m + 17.6 MeV

où n est un neutron. L'énergie produite (17.6 MeV = 2.8×10¹² J) est dix fois supérieure à l'énergie nécessaire pour provoquer la réaction. Elle rend donc la fusion très compétitive en termes de production d'énergie. Outre le fait que le mélange D-T est quatre fois plus énergétique que la même masse d'uranium, les avantages cités sont l'absence de déchets nucléaires à longue durée de vie et la quantité quasi illimitée de matière première (le deutérium est extrait de l'eau de mer, et le tritium est produit dans la réaction nucléaire à partir du lithium, qui est un élément abondant sur Terre). Outre son intérêt en termes de production d'énergie, la fusion nucléaire contrôlée est très attendue par de nombreux scientifiques, comme les astrophysiciens, qui espèrent reproduire les conditions qui règnent au coeur des étoiles. La fusion contrôlée est également au coeur du programme de simulation destiné à remplacer les essais nucléaires.

En 2009, au Lawrence Livermore National Laboratory, aux États-Unis, le National Ignition Facility (NIF), le plus grand dispositif de fusion thermonucléaire jamais construit, a été lancé. Sa partie principale est un laser à faisceaux multiples dont l'énergie en impulsion nanoseconde dépasse 1MJ (10⁶J). Sa tâche consiste à comprimer le combustible DT à une densité plus de quelques milliers de fois supérieure à celle du DT à l'état solide et à le chauffer à 100 millions de K degrés. Dans ce cas, le processus de compression et de chauffage du combustible est réalisé de manière indirecte - le rayonnement laser (dans la gamme des UV) est converti dans ce qu'on appelle le hohlraum (cylindre de 1 cm contenant une pastille sphérique de DT) en un rayonnement X doux très intense illuminant symétriquement la pastille de DT. Pour la première fois, les paramètres énergétiques du dispositif de fusion sont suffisants pour permettre l'allumage et la combustion auto-entretenue d'un combustible thermonucléaire à une échelle permettant de générer une énergie bien supérieure à celle fournie au combustible (fig. 4.3).

L'objectif principal de la campagne expérimentale actuelle du NIF est de réaliser, dans les deux ou trois prochaines années, un "big bang" thermonucléaire contrôlé dans lequel l'énergie de fusion sera au moins dix fois supérieure à l'énergie fournie par le laser. Le "big bang" attendu serait le résultat de cinquante ans d'efforts internationaux visant à démontrer la faisabilité physique et technique de la production, de manière contrôlée, de l'énergie de fusion nucléaire dans un plasma confiné par inertie et ouvrirait la voie à la réalisation pratique du réacteur thermonucléaire piloté par laser.

FIGURE 4.3 - Schéma des étapes de la fusion laser.

4.2.6 Le refroidissement des atomes

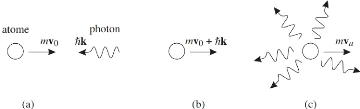
L'objectif est ici de ralentir, c'est-à-dire refroidir, les atomes avec de la lumière. Le principe repose sur l'échange d'impulsion entre des photons et des atomes. Considérons le cas d'un atome se déplaçant à la vitesse ?v0 dans une onde laser de fréquence í résonante avec une de ses transitions et se propageant en sens inverse (fig. 4.4a). L'impulsion de l'atome est alors m?v0 et celle d'un photon h^?k, où m est la masse de l'atome et k ? le vecteur d'onde du champ laser. Lors de l'absorption d'un photon par l'atome (fig. 4.4b), la conservation de l'impulsion implique que la vitesse de l'atome excité après absorption soit :

^?vexc = ?v0 +		h m	k? = ?v0 + ?vr (4.1)
vexc = v0 -		h m	k (4.2)
?vr =	h^?k/m est appelée vitesse de recul. Après absorption, l'atome est dans un état excité et

sa vitesse a diminué. Au bout d'un temps dépendant de la durée de vie de ce niveau excité, l'atome se désexcite par émission spontanée ou stimulée. Dans le cas de l'émission stimulée, on retrouve l'état initial. Dans le cas de l'émission spontanée, le photon est émis dans une direction aléatoire (fig. 4.4c) et la vitesse finale ?v_a de l'atome est :

?va = ?v0 +

h m

k?

h m

^?ks (4.3)

où ^?k_s est le vecteur d'onde du photon émis spontanément. ^?k_s a une direction aléatoire mais a toujours le même module : ^?k_s = ^?k . Si le processus est répété n fois, la vitesse finale de l'atome est :

?va = ?v0 + n	h m	k?	h X m i	^?ksi = ?v0 + n	h m	k? (4.4)
va = v0 - n	h m	k (4.5)

26

puisque _?ksi a une direction aléatoire et est donc nul en moyenne. Le module de la vitesse finale est donc :

27

FIGURE 4.4 - Les trois étapes du ralentissement d'un atome par un photon. En (a), un atome absorbe un photon se propageant en sens inverse; en (b), l'atome excité est ralenti; en (c), le photon est réémis dans une direction aléatoire.

Ce processus peut-il être efficace pour ralentir des atomes? Pour répondre à cette question, prenons l'exemple de l'atome de césium. La vitesse des atomes de césium dans une vapeur diluée à température ambiante est typiquement de 300 m.s^-1. Pour la raie du césium située à 852 nm, la vitesse de recul est v_r = 3.5×10^-3 m.s^-1, ce qui semble ridiculement faible pour ralentir un atome se déplaçant à 300 m.s^-1. Cependant, la durée de vie du niveau excité du césium est de 3×10^-7 s, ce qui fait que le processus peut se répéter jusqu'à 3 millions de fois par seconde! L'atome peut donc être complètement arrêté en quelques dixièmes de seconde. Réduire la vitesse des atomes par cette méthode est donc parfaitement réalisable.

L'équation (4.5) n'aboutit pas à un ralentissement de l'atome : une fois le sens de la vitesse inversé (nhk/m > v0), l'atome est accéléré. Pour éviter cela, on plonge l'atome dans deux ondes contra-propageantes de fréquence inférieure à la fréquence de résonance atomique V_a. Par effet Doppler, l'atome voit toujours l'onde se propageant dans le sens opposé au sien avec une fréquence plus proche de V_a que l'onde se propageant dans le même sens que lui. L'onde de sens opposé (plus résonante) le freine donc toujours davantage que l'onde de même sens (moins résonante) ne l'accélère. Quel que soit son sens de propagation, l'atome ralentit donc : c'est le refroidissement Doppler.

Dans la pratique, de nombreux processus interdisent de réduire indéfiniment la vitesse des atomes. Par exemple, en utilisant la méthode décrite ci-dessus, on peut ralentir des atomes alcalins jusqu'à des vitesses de l'ordre de 10 cm.s^-1, ce qui correspond à une température de quelques centaines de uK.

En utilisant des méthodes plus sophistiquées, des températures de l'ordre du nK ont été atteintes. Une des applications les plus spectaculaires des atomes refroidis est l'obtention de la condensation de Bose-Einstein, un état de la matière où les atomes se retrouvent dans un même état quantique. Prédite par Bose et Einstein en 1924, elle fut observée pour la première fois en 1995.

4.3 Applications dans les autres domaines 4.3.1 Dans la vie quotidienne

Le pointeur laser

Le pointeur laser l'utilisation la plus répandue du laser par le grand public est sans nul doute le pointeur laser. Mais ce dernier est aussi utilisé par les professionnels pour matérialiser une ligne droite : les applications sont nombreuses, depuis la matérialisation des lignes de niveau dans les métiers du bâtiment, jusqu'au guidage des tunneliers. Il y a longtemps que les lasers sont

28

utilisés dans les théodolites, ces instruments qui permettent aux géomètres et aux ingénieurs d'établir des relevés topographiques. Les scientifiques aussi utilisent dans leurs laboratoires des pointeurs laser pour aligner d'autres lasers. Les lasers utilisés dans les pointeurs sont assez simples. Il s'agit en général d'une diode laser (pointeur rouge) ou d'un laser à néodyme doublé (pointeur vert), d'une puissance de quelques mW, ce qui suffit à créer un faisceau parfaitement visible, même en plein jour. Les optiques de collimation doivent cependant être adaptées à l'usage, et notamment aux distances sur lesquelles le pointeur doit être utilisé.

Le lecteur des codes barres

Le code barre est un système d'identification d'objets; il est constitué d'une série de barres et d'espaces d'épaisseur variable. Le lecteur fournit une information électrique reproduisant la série de barres.

Le principe retenu est le suivant : un faisceau laser balaye le code barre et un détecteur collecte la lumière diffusée. Le signal temporel obtenu est une image du code barre. Compte tenu du cahier des charges décrit plus haut, le type de laser et l'optique utilisés jouent un rôle primordial dans la réalisation du lecteur. Les premiers lecteurs utilisaient des lasers He-Ne à 632 nm. Ils ont été progressivement remplacés par des diodes laser à 670 nm. Celles-ci émettent des faisceaux elliptiques dans le plan perpendiculaire à leur axe de propagation. Cette propriété est ici mise à profit pour limiter les risques d'erreurs de lecture du code barre.

4.3.2 Domaine industriel

Dans l'industrie, le laser est omniprésent : il façonne, découpe, soude, marque, grave, nettoie les matériaux les plus divers. Le laser est en général employé à puissance élevée, afin d'exploiter l'absorption du faisceau par le matériau. On amène ainsi localement le matériau à une température de quelques centaines ou quelques milliers de degrés, provoquant sa fusion, voire sa vaporisation. Grâce à la rapidité des changements de phase, la chaleur n'a pratiquement pas le temps de se propager, laissant les zones périphériques à l'usinage dans leur état d'origine : on peut ainsi obtenir des découpes ou des soudures plus propres qu'avec les autres procédés.

Soudage : Il s'agit en pratique ici de soudage de métaux, bien que cette méthode soit aussi appliquée sur des composés plastiques. Des tôles métalliques peuvent être soudées sur plusieurs millimètres d'épaisseur (par exemple 1 cm avec un laser CO2 de 5 kW) avec des vitesses de plusieurs mètres par minute (par exemple 6 m/mn pour une tôle d'acier de 1.5 mm d'épaisseur). La soudure est fine et propre, mais elle est aussi très précise, et l'on trouve donc aussi des applications de soudage de précision en micro-mécanique. Le rôle du laser est ici de chauffer le métal afin d'atteindre son point de fusion. Les intensités nécessaires sont de l'ordre de 10⁵ à 10⁷ W.cm^-2 . On utilise des lasers continus, typiquement le laser CO2 et le YAG, et c'est la vitesse de déplacement du faisceau le long de la zone à souder qui fixe la durée de l'interaction et donc la profondeur de pénétration.

Découpe et perçage : Le laser permet de découper ou percer toutes sortes de matériaux, depuis les aciers les plus durs jusqu'au papier, en passant par le verre, les tissus,....La découpe est rapide, nette, sans trace de brûlure ou d'échauffement, et peut être facilement automatisée et pilotée par ordinateur. En montant le laser sur des systèmes à plusieurs axes, on peut ainsi façonner des pièces avec des géométries complexes.

4.3.3 Domaine médicale

La plupart du temps, on utilise le laser en médecine pour détruire ou altérer des tissus de façon très localisée et précise. En ce sens, la directivité, la focalisation et la puissance du laser jouent un rôle important. Mais toutes ces caractéristiques seraient inutiles si l'on n'était

29

pas capable de détruire les tissus de façon sélective, grâce aux propriétés spectrales des lasers. Les coefficients d'absorption des molécules constituantes de l'organisme varient en effet avec la longueur d'onde. En choisissant judicieusement cette dernière, on peut donc exciter avec un laser un matériau sensible à cette longueur d'onde, par exemple du sang, situé derrière un autre matériau qui y est insensible (ou moins sensible), par exemple la surface de la peau.

4.3.4 Télécommunication

L'échange d'informations numériques fait maintenant partie de notre vie quotidienne, qu'il s'agisse de téléphoner, de regarder la télévision ou de naviguer sur Internet. Que ce soit à l'échelle de la planète, ou entre deux pièces d'un même bâtiment, le transport de ces informations est essentiellement optique.

Le dispositif de transmission par fibre optique est constitué d'un émetteur qui convertit le signal électrique en signal optique, d'une fibre optique qui propage le signal optique, de répéteurs éventuels qui l'amplifient, et finalement d'une photodiode qui reconvertit le signal optique en signal électrique.

L'émetteur est un laser à semi-conducteur à 1,3 um, et plus récemment à 1,55 um. À ces longueurs d'onde correspondent respectivement un minimum de dispersion et d'atténuation du signal dans les fibres. Le signal électrique numérique est transformé en signal lumineux en modulant directement l'intensité émise par le faisceau laser, le bit 0 correspondant à une absence d'émission. Les fréquences de modulation sont de l'ordre du GHz, et même davantage. Elles sont directement liées au débit d'informations transmis. C'est d'ailleurs un des avantages majeurs des fibres optiques par rapport aux traditionnels fils de cuivre que de pouvoir atteindre des débits très élevés. Pour fixer les idées, prenons l'exemple du téléphone. Les normes internationales fixent la bande passante des communications téléphoniques entre 300 Hz et 3400 Hz. En général, les opérateurs fixent la fréquence haute à 4 kHz, correspondant à un débit de 64 kbps (bps = bits par seconde) pour un signal numérique codé sur 8 bits. Sur une fibre optique de 1Gbps de débit, on peut donc faire passer simultanément plus de 15 000 conversations téléphoniques.

4.3.5 Les armes laser

Depuis les années 2000, plusieurs fabricants d'armes développent de véritables « rayons de la mort ». Il s'agit de lasers extrêmement puissants destinés à la destruction en vol de roquettes, d'obus, voire de missiles. Ces armes sont destinées à être embarquées sur des bateaux, des avions ou des véhicules terrestres, et ne peuvent donc pas disposer de ressources électriques importantes. C'est la raison pour laquelle elles utilisent souvent des lasers chimiques. Parmi les réalisations connues, on peut citer le THEL (Tactical High Energy Laser) embarqué sur un navire. Il utilise un laser HF émettant 1 MW en continu à 2,8 um. En 2004, une démonstration a montré qu'il était capable de détruire en vol des obus de mortier lancés en rafale. Citons également le Boeing YAL-1, qui a démontré en février 2010 sa capacité à détruire des missiles balistiques en vol. Il utilise lui aussi un laser chimique, à l'iodure d'oxygène. En fin, le SSHCL (Solid State Heat Capacity Laser), un laser néodyme de « seulement » 67 kW, permet d'avoir une idée des capacités de destruction de ce type d'armes : cette arme est capable de percer un trou carré de 13 cm de coté dans une plaque d'acier de 2,5 cm d'épaisseur, en 2 secondes.

4.4 Conclusion

Dans ce chapitre, nous avons parlé de certaines applications du laser dans notre vie quotidienne, puis de ses applications dans la recherche scientifique, tout en détaillant le fonctionnement du refroidissement par laser et de la fusion nucléaire par laser.

30

Conclusion Générale

Pour conclure, et après tout ce que nous avons vu, le développement du laser par les scientifiques est toujours en cours, la question est : quelle puissance les lasers pourraient-ils avoir? Le laser le plus puissant construit était de l'ordre de 25 PW (2.5x10¹⁶ W), mais le problème ici est qu'il y a une limite, appelée la limite de Schwinger, un champ critique dans l'électrodynamique quantique. La limite est typiquement rapportée comme un champ électrique ou magnétique maximum avant la non-linéarité de vide, à l'ordre de E r' 1.32 x 10¹⁸V/m et B r' 4.41 x 10⁹T.

À la limite de Schwinger, le champ électrique est suffisamment fort pour séparer les paires électron-positron qui sont créées spontanément par les fluctuations quantiques du vide. La conversion d'électrons et de positrons virtuels en électrons et positrons réels absorbe l'énergie du champ, ce qui rend difficile toute augmentation supplémentaire de ce dernier. La limite devrait être atteinte à une intensité laser critique d'environ 10²⁹ W.cm^-2. Mais il a été suggéré récemment que les effets de collision survenant au point focal d'un ou de plusieurs faisceaux laser pourraient conduire à la production de paires à des intensités inférieures de deux ordres de grandeur à la limite de Schwinger. S'appuient sur cette suggestion pour examiner ce qui se passe immédiatement après la création d'une paire.

Ils soulignent que les électrons et les positrons ne sont pas seulement créés par le champ laser, mais qu'ils sont rapidement accélérés à des vitesses relativistes extrêmes par celui-ci. Leur collision inévitable avec les photons du champ entraîne l'émission de particules gamma d'une énergie suffisante pour se désintégrer en d'autres paires électron-positron et en d'autres particules exotiques de haute énergie. Cela conduit à une cascade électrodynamique quantique similaire aux processus d'avalanche qui limitent les intensités laser supportées par les diélectriques classiques.

Les calculs des auteurs suggèrent que cette rupture du vide pourrait devenir un problème à des intensités laser focalisées d'environ 10²⁶ W.cm^-2 - bien en dessous de la limite de Schwinger, et juste quelques ordres de grandeur au-dessus des intensités qui devraient être atteintes par plusieurs installations laser actuellement en construction.

Est-il vraiment possible de fabriquer un laser dépassant la limite de Schwinger? Nous attendons qu'un futur prix Nobel réponde à cette question.

31

Bibliographie

[1] J. Badziak. Laser nuclear fusion : Current status, challenges and prospect. Bulletin of the Polish Academy of Sciences, 60(4) :1, 2012.

[2] S. Blin. Composants optoélectroniques - Lasers. UMR CNRS, 2010.

[3] J. Cornillaut. Compagnie industrielle des lasers (cilas). < https://dossier.
univ-st-etienne.fr/ltsi/www/slaser/PFfemto/principe/Cestquoi2.htm/>, 2022. [En Ligne; accédé 30-Mars-2022].

[4] J. Derouard. Physique Atomique et Moléculaire, Spectroscopie. Université Joseph Fourier, 2006.

[5] R. Diehl. High-Power Diode Lasers Fundamentals, Technology, Applications. Springer, 2000.

[6] M. Premasundaran et A.L. Dawar. Lasers : Basic characterstics. < https://www. worldoflasers.com/laserproperties.htm/>, 2011. [En Ligne; accédé 23-Avril-2022].

[7] F.Bretenaker et C. Drag. Cours de Physique des Lasers. Laboratoire Aimé Cotton, CNRS, 2008.

[8] A. Aspect; G. Grynberg et C. Fabre. Optique quantique : Lasers (Tome I et II). PHY551A, 2006.

[9] F. Balembois et S. Forget. Le laser : Fondamentaux. < http://www.optique-ingenieur. org/fr/cours/OPI_fr_M01_C01/co/Contenu_08.html/>, 2007. [En Ligne; accédé 03-Avril-2022].

[10] D. Hennequin et V. Zehnlé et D. Dangoisse. Les lasers, Cours et exercices corrigés. Dunod, Paris, 2013.

[11] E. Gerstner. Lasing at the limit. Nature Phys, 6(638), 2010.

[12] J. Jolly. Étude et réalisation d'un laser à argon ionisé stabilisé par des parois à haute température. Revue de Physique Appliquée, Société française de physique, 12(4) :2, 1973.

[13] H. Najib. Cours de Physique Atomique. FSK UIT, 2013.

[14] K.L. Renk. Basics of Laser Physics. Springer, 2017.

[15] A. Rüdiger. Gravitational Wave Detection by Laser Interferometry on Earth. Max-Planck-Institut für Gravitationsphysik, Teilinstitut Hannover, 23(2) :3, 2003.

[16] D. Zoubeida. Cours et Travaux dirigés de Physique des lasers. FS Bizerte, University of Carthage, 2010.

32