Analyse vibratoire des machines sur un banc d'essai - cas d'un disque tournant

ÊÜÜÜÜíÈÚÔáÇ ÊÜÜíØÇÑÞãíÏáÇ ÊÜÜÜíÑÆÇÓÜÜÜÜÌáÇ ÊÜÜÜíÑìåãÌáÇ

RÉPUBLIQUE ALGÉRIENNE DÉMOCRATIQUE ET POPULAIRE

íÜÜÜÜãáÚáÇ ËÜÜÜÜÍÈáÇ æ íÜÜÜáÇÚáÇ ãÜÜÜÜíáÚÊáÇ ÉÑÇÒæ

MINISTÈRE DE L'ENSEIGNEMENT SUPÉRIEUR ET DE LA RECHERCHE SCIENTIFIQUE

ØÇìÜÜÛáÇÈ ÌíáË ÑÇãÚ ÊÜÜÜÜÚãÇÌ

UNIVERSITÉ AMAR TELIDJI LAGHOUAT

ÇíÜÜÜÌìáìäßÊáÇ ÊÜÜÜíáß

FACULTÉ DE TECHNOLOGIE

DEPARTEMENT D'ELECTROTECHNIQUE

MÉMOIRE DE FIN D'ÉTUDES

Présentée en vue de l'obtention du diplôme de
Master Académique En Électrotechnique
Spécialité : Machines électriques

THÈME

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -
Présenté par : Said KOUIDRI Kouider GHRIS	Proposé par : M. SAROUTE Dirigé par : M. SAROUTE & M. HAMIDAT Suivi pratique par : K. HACHANI

Soutenue le : 05/06/ 2022
Devant le Jury composé de :

Président Prof. M. BIRAME Université de AMAR TELIDJI

Examinateur Prof. S. BESSEDDIK Université de AMAR TELIDJI

Encadreur Prof. M. SAROUTE Université de AMAR TELIDJI

Co-Encadreur M. HAMIDAT Université de AMAR TELIDJI

Année universitaire 2021 / 2022

I

REMERCIEMENTS

Nous remercions Allah de nous avoir donné la force et le courage pour réaliser ce modeste travail.

Nous tenons à remercier en premier lieu, mon directeur de thèse, Monsieur Mohammed SAROUT pour la confiance dont il nous a gratifié, pour ses conseils, sa disponibilité ainsi que son soutien, quand tout allait bien, mais surtout quand ça allait moins bien, qui au-delà d'être un excellent mentor, auprès de qui nous avons fait nos premiers pas en vibration. Merci de nous offrir la possibilité d'orienter nos recherches avec une grande liberté. C'est pour cela que nous avons eu la motivation de faire une recherche dans les vibrations.

Nous tenons à remercier Monsieur M. HAMIDAT le Co-encadreur.

Nous remercions également les membres du jury pour avoir accepté d'y siéger et d'examiner ce mémoire.

Nous remercions Monsieur Khaled HACHANI l'ingénieur pour son dévouement, ses conseils et son soutien moral et les informations utiles et le suivi pratique tout le long de l'élaboration de ce travail.

Nous remercions l'équipe de service mécanique (cellule de vibration) à DML pour leur accueil et leur disponibilité pendant la durée de notre stage.

Toutes ces personnes ont contribué, par leur disponibilité et leur bonne humeur, à rendre notre stage enrichissant et motivant.

Enfin, nous tenons à exprimer notre reconnaissance à Monsieur Mohamed KHADROUNE et le bureau de formation au DML et l'équipe d'administration commun PFE (Université - Société DML SONATRACH).

II

DEDICACES

A tous les étudiants de sciences et les ingénieurs musulmans dans le monde islamique ...

Nous dédions ce travail à tous les centres de traduction en arabe ...

III

ÕÜÎáã

ÉäÇíÕÇÇ äí áíáÞÇÇ ÈáØÊí æå ÉäíÊáÏÇ æÕÆÇÕáÎ ÇðÑß Ùä ÉáÊÎáÏÇ ÉíÚÇäÕÇÇ ÊáÇÇáãÌÇ í áÇÇãÚÊÓ Ç Ñß ËßáÇ æì íÇãÇÊÒÇÇ ÇÑß áãÍÇ ÉÏÚ ÖÑß Ç ÉÌÇáÍÇ äÅ ÇÐáÐæ .ÉíßíäÇßíí æ ÉíÆÇÈÑß åß ÉáÊãÎ ÚÇæä äí áÇØÚáÖÑß ÚÊí ä äßíã æäßÇæ ìÑß ÎáÇ ÊÇßÑß áãÍÇÈ ÉäÑÇÞí ÉáíÞËÇÇ ÉäÇíÕÇÇ ÊÇÇÇÑß Ìá ì á ÉÇÇÅÖÇÈ áÇØÚáÇ åÐì ÈääÊÇ .ÉÇáÂÇ åÐì ÉäÇíÕæ áÇØÚáÇ ÇÔÊßÇæ ãßÍÊÇÇ ÉÓÇÑÏÇ ÉíËÈÍ ÚíÑÇÔí .ÊÇÒÇãÊìáÇÇ áíáÊÍ ãÇÏÎÊÓÇÈ ÉíÆÇÞæÇÇ ÉäÇíÕÇÇ ãæåí ËÍÈÇÇ ÇÐì í ÓÑÏäÓ ÉáßáÏÇæ æ ÉÑÇæÏÜÇÇ ÊáÇáÂÇ í ÑæÜìÏÜÊÇÇ æ áÇØÜÚáÇ äÚ Ôß ÜáÇ ÊÇÒÇãÊìáÇÇ áíáÊÍ ãÏÎÜÊÜÓí ÉíÆÇíãÜíÜ ßÑÜìÇæÜÙ íÜ ì ÊÇÒÇãÜÊÜìÇáÇ .ÇåÊÇÇáÍáÖÜ ÇÜÓð ÇÜíÞí ßÑÜæÜí íÑÎáÇ ÇÐìÉäÒÇæíæ ÉíÒÇãÊìáÇÇ ÊÇÑÇÔÅÖÇ áÊÒÛÊÓÇ ÞíÑß Ø äÚ ÑÇæÏÇÇ Ñß ÕäÚÇÇ í ááÎ ÕíÎÔÊÇ ËÍÈÇÇ ÇÐì ÓíÑß ßÇ Êã ÉíÇÇÚ ÇäÊÈË ÉíáãÚÇÇ ÇääÆÇÊä áÊÒÎ äíæ ÉíÒÇãÊìÇ ÉÈÇäÊÓÇ ËæÏÍ ì á ÑÇæÏÇÇ Ñß ÕäÚáÇ íßííÇäíÏÇÇ ÇæáÓÇÇ í äÒÇæÊÇÇ ãÏÚ ìÏ .ÉäÒÇæáÏÇ ÉíäÞÇ ÇÖíæ ÇÇØÎáÇ ÕíÎÔÇ í ÊÇÒÇãÊìáÇÇ áíáÊÍ

ÉíÜÍÇÜÊã ÊÇãÜáß

.íÑíÇÚí ÉäÒÇæí ÊÒÇÇãÊì ÇáÇ áíáÊÍ äÒÇæÊÇÇ ãÏÚ áÇØÚáÇÇÔÊßÇæ ÕíÎÔÇ ÉíÆÇÞæ ÉäÇíÕ íÇãÇáÇ ÇÑß ãÍ

IV

Abstract

The asynchronous motor is the most used in the various industrial fields. For its excellent robustness quality, it requires a little maintenance comparaed to other motors, but can present failures of various natures that could be electrical or mechanical. thus, the need imposes several research projects to study the control, the detection of the defects and the maintenance of this machine. To avoid these breakdowns as well as heavy and expensive maintenance actions, we will study in this research the concept of preventive maintenance by using the vibration analysis.

Vibrations are physical phenomena where vibration analysis is used to highlight the defects of the operation or degradation of a rotating machine and give a better measure of its condition.

This work has been dedicated to the diagnosis of a defect of the rotor by the exploitation of vibratory signals and balancing of this latter. The imbalance in the dynamic behavior of the rotor has generated a vibratory response, and through our practical results we have proven the effectiveness of vibration analysis in the diagnosis of defects and also the balancing technique.

Keywords

Asynchronous motor, Preventive maintenance, Diagnosis and fault detection, Unbalance, Vibration analysis, Balancing, Standards.

V

RÉSUMÉ

Le moteur asynchrone est le plus utilisé dans les différents domaines industriels, car bien considéré par ses qualités de robustesse, il nécessite peu de maintenance comparable à d'autres moteurs, mais peut présenter des pannes de diverses natures, électriques ou mécaniques. Pour cela, la nécessité impose plusieurs projets de recherche pour l'étude de la commande, la détection des défauts et la maintenance de cette machine. Pour éviter ces pannes ainsi que des actions de maintenance lourdes et coûteuses, nous étudierons dans cette recherche le concept de maintenance préventive en utilisant l'analyse vibratoire.

Les vibrations sont des phénomènes physiques,l'analyse vibratoire est utilise pour mettre en évidence les défauts de fonctionnement ou de dégradation d'une machine tournante et donnent une meilleure mesure de son état.

Ce travail a été dédié au diagnostic d'un défaut du rotor par l'exploitation de signaux vibratoires et l'équilibrage de ce dernier . Le déséquilibre dans le comportement dynamique du rotor a généré une réponse vibratoire, et grâce à nos résultats pratiques nous avons prouvé l'efficacité de l'analyse vibratoire dans le diagnostic des défauts et aussi la technique d'équilibrage.

Mots-clés

Moteur asynchrone, Maintenance préventive, Diagnostic et détection de défaut, Balourd, Analyse vibratoire, Équilibrage, Normes.

VI

LISTE DES FIGURES

CHAPITRE I : Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Fig.I.1. Les composants d'un moteur asynchrone 5

Fig.I.2. Le stator 6

Fig.I.3. Structure d'un rotor bobiné 8

Fig.I.4. Structure d'un rotor à cage d'écureuil 8

Fig.I.5. Types de maintenance 10

Fig.I.6. Seuil de maintenance 11

Fig.I.7. Répartition des défauts rencontrés dans les entrainements asynchrones 14

Fig.I.8. Répartition des défauts rencontrés dans les applications entrainées par les moteurs asynchrones de la gamme Leroy Somer selon l'enquête menée auprès d'une filiale de

maintenance. 14

Fig.I.9. Exemple de roulement. (a) Défauts localisés. (b) Défauts distribués. 16

Fig.I.10. Différents types de défauts statorique 17

Fig.I.11. Rupture d'un anneau. 18

Fig.I.12. Positions du rotor et du stator dans une machine parfaite. 18

Fig.I.13. Types d'excentricités statiques (a), dynamique (b) et mixte (c) 19

Fig.I.14. Alignement parfait. 19

Fig.I.15. Désalignement angulaire (pas de décalage) 20

Fig.I.16. Désalignement parallèle. 20

Fig.I.17. Désalignement combiné. 21

Fig.I.18. Flexion d'arbre due à un défaut d'alignement ou de concentricité des paliers. 21

Fig.I.19. Modes élastiques d'un rotor flexible. 21

Fig.I.20. Déséquilibre du rotor. 22

Fig.I.21. Le déséquilibre, la vélocité de vibration et la force centrifuge en fonction de la

vitesse de rotation 23

Fig.I.22. Sources de déséquilibre 24

Fig.I.23. Déséquilibrage statique. 25

Fig.I.24. Déséquilibre de couple 25

Fig.I.25. Équilibre statique, déséquilibre du couple 26

Fig.I.26. Déséquilibre dynamique 26

CHAPITRE II : l'Analyse Vibratoire, Captures et Identification des Défauts

Fig.II.1. Composants de l'architecture de système de détection de défaut. 29

VII

Fig.II.2. Caractéristiques d'un signal vibratoire. 30

Fig.II.3. Signal sinusoïdal de déplacement 32

Fig.II.4. Signal sinusoïdal de vitesse 33

Fig.II.5. Signal sinusoïdal d'accélération 33

Fig.II.6. Capteurs de vibrations et les types de mesures. 34

Fig.II.7. Capteur de déplacement pour les paliers lisses. 35

Fig.II.8. Schéma de fonctionnement d'un capteur de déplacement 35

Fig.II.9. Capteur de vitesse à bobine mobile 37

Fig.II.10. Capteur de vitesse photoélectrique 38

Fig.II.11. Schéma d'un accéléromètre. 39

Fig.II.12. Schéma d'un accéléromètre à préamplificateur intégré. 41

Fig.II.13. Positionnement des accéléromètres sur un palier. 42

Fig.II.14. Plans de mesure 42

Fig.II.15. Les positions de placement d'un accéléromètre 42

Fig.II.16. Gamme dynamique et gamme de fréquences des capteurs. 43

Fig.II.17. Influence de la grandeur utilisée. 44

Fig.II.18. Harmoniques pour 1500 tr/min. 44

Fig.II.19. Illustration temporal-fréquentiel d'un signal oscillant 46

CHAPITRE III : Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Fig.III.1. Analyse d'ordre (résonance) de démarrage d'un rotor classe 2, 3, 4 ou 5 54

Fig.III.2. Interface d'objets de la base de données 58

Fig.III.3. Interface des signaux et analyses. 59

Fig.III.4. Analyseur de spectre FFT 59

Fig.III.5. Kit simulateur. 60

Fig.III.6. Plaque Signalétique du moteur de lancement. 60

Fig.III.7. Carte d'acquisition. 61

Fig.III.8. Capteur de vitesse (photoélectrique). 61

Fig.III.9. Un accéléromètre (piézoélectrique) 61

Fig.III.10. Création d'un balourd. 62

Fig.III.11. La masse de boulon. 62

Fig.III.12. Trends de démarrage Amplitude / Phase. 63

Fig.III.13. Signal FFT d'un capteur accéléromètre position vertical. 63

Fig.III.14. Signal indique un déphasage entre le capteur vertical et le capteur horizontal 64

Fig.III.15. Signal indique un balourd initial avec un phase ö0 = 0,20° 64

VIII

Fig.III.16. Poids de la masse d'essai. 66

Fig.III.17. Signal FFT d'un capteur accéléromètre position vertical 67

Fig.III.18. Signal indique un balourd résultant avec un phase ö1 = - 8,77 ° 67

Fig.III.19. Diagramme vectoriel de V0 , V1 et Ve pour l'unité : 1mm x = 0.05 mm y 69

Fig.III.20. Diagramme vectoriel de V0 , V1 et Ve pour l'unité : 1mm x = 1 mm y 69

Fig.III.21. Diagramme vectoriel de V0 , V1 , Ve , Ve' et Vc pour l'unité : 1 mm x=0,05 mm y

70

Fig.III.22. Diagramme vectoriel de V0 , V1 , Ve , Ve' et Vc pour l'unité : 1 mm x=1 mm y 70

Fig.III.23. Détermination de la position de la masse de correction 71

Fig.III.24. Par méthode numérique ( Un logiciel ) 71

Fig.III.25. Poids et positionnement de la masse de correction. 72

Fig.III.26. Signale FFT après l'équilibrage d'amplitude d'accélération. 72

Fig.III.27. Montage de la masse de correction à un rayon différent du rayon de montage de la

masse d'essai 73

IX

LISTE DES TABLEAUX

CHAPITRE I : Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Tab.I.1. Terminologie & définitions 12

CHAPITRE II : l'Analyse Vibratoire, Captures et Identification des Défauts

Tab.II.1. Niveaux vibratoires admissibles sur les machines tournantes 48

Tab.II.2. Les fréquences des vibrations et leurs causes probables 49

Tab.II.3. Identification des vibrations 50

CHAPITRE III : Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Tab.III.1. Comparaison les résultats de la masse de correction entre un logiciel et le un

programme sur MATLAB. 74

X

LISTE DES SYMBOLES ET ABREVIATIONS

A0 amplitude de vibration causée par le balourd (amplitude initiale)

AA amplitude d'accélération de la vibration absolue

AV amplitude de vitesse de la vibration absolue

Ac amplitude crête

Acc amplitude double (crête à crête)

Aeff, RMS amplitude efficace

a accélération

a_s enroulement d'un phase statorique

f.? angle de contact de la bille avec les bagues

C centre de masse

C.G Centre de Gravité

CPM Cycle Par Minute

CCV Coût du Cycle de Vie

Db diamètre d'une bille

D_c diamètre de la cage

d déplacement

eadm balourd spécifique

e déplacement du centre de la masse

F force due au déséquilibre

f fréquence d'alimentation

FFT Fast Fourier Transform (transformée de Fourier rapide)

f,- fréquence de rotation de l'arbre

fba.ex fréquence de défaut de bague externe

fba.in fréquence de défaut de bague interne

fbi fréquence de défaut de billes

f a fréquence de défaut de cage

ö0 angle de phase du signal vibratoire par rapport à l'impulsion du capteur

tachymétrique

g glissement

H champ magnétique

I_s courant statorique

M masse du rotor

XI

m masse du balourd

mess masse d'essai

m_r masse équivalente de balourd résiduel (la masse résiduelle)

m_c masse de correction

N vitesse nominale

Ns vitesse de synchronisme

???? nombre de billes

vitesse angulaire

p nombre de paires de pôles

R_c rayon du lieu de la masse de correction

Ress rayon du lieu de la masse de d'essai

RPM Rotation Par Minute

r distance entre le centre du rotor et centre de gravité du la masse "m" de

balourd

rf résistance de défaut

ô durée d'une période

U déséquilibre du rotor

Uadm balourd résiduel admissible

V0 vecteur représentant le balourd initial

V1 vecteur représentant le balourd résultant

V_e vecteur représente la contribution de la masse d'essai seule sur la nouvelle

condition de déséquilibre du rotor.

V_c vecteur représente la position et la valeur du balourd nécessaires pour
annuler le balourd initial

v vitesse

X vitesse de rotation en tr/min ou RPM

XII

Table des matières

REMERCIEMENTS I

DEDICACES II

RÉSUMÉ (Ar-En-Fr) V

LISTE DES FIGURES VI

LISTE DES TABLEAUX IX

LISTE DES SYMBOLES ET ABREVIATIONS X

INTRODUCTION GÉNÉRALE 1

CHAPITRE I : Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

I.1. Introduction 4

I.2. Principe de fonctionnement 4

I.3. Construction de la machine asynchrone 5

I.3.1. Stator 5

I.3.2. Rotor 6

I.3.2.1. Rotor bobiné 7

I.3.2.2. Rotor cage d'écureuil 8

I.3.3. Les organes mécaniques 8

I.3.3.1. Les roulements 9

I.4. Maintenance 9

I.4.1. Maintenance curative 10

I.4.2. Maintenance systématique 10

I.4.3. Maintenance prévisionnelle 10

I.4.4. Maintenance préventive 10

I.4.5. Maintenance conditionnelle 10

I.4.6. L'importance de la maintenance 11

I.5. Terminologie dédiée au diagnostic 12

I.6. Généralités sur les défauts des machines électrique 13

I.6.1. Défaut des roulements 15

I.6.1.1. Fréquences caractéristiques des défauts du roulement 16

I.6.2. Défauts au stator 16

I.6.3. Défauts au rotor 17

I.6.4. Défaut d'excentricité 18

XIII

I.6.5. Alignement d'arbres 19

I.6.5.1. Alignement parfait 19

I.6.5.2. Désalignement angulaire ou frontal (le délignage ou défaut de lignage) 20

I.6.5.3. Désalignement décalé ou parallèle 20

I.6.5.4. Désalignement combiné ou oblique 20

I.6.6. Flexion du rotor 21

I.6.7. Défaut de déséquilibre (balourd) 21

I.6.7.1. Les paramètres de déséquilibre 22

I.6.7.2. Déséquilibre et vitesse 23

I.6.7.3. Sources du déséquilibre 23

I.6.7.4. Déséquilibrage statique 24

I.6.7.5. Déséquilibre de couple 25

I.6.7.6. Déséquilibre dynamique 26

I.7. Conclusion 26

CHAPITRE II : l'Analyse Vibratoire, Captures et Identification des Défauts

II.1. Introduction 28

II.2. Analyse vibratoire 28

II.2.1. Définition d'une vibration 29

II.2.2. Vibration Caractéristiques 29

II.2.3. Intérêt du mesurage des vibrations 31

II.2.4. Techniques de mesurage 31

II.2.4.1. Le déplacement 31

II.2.4.2. La vitesse 32

II.2.4.3. L'accélération 33

II.2.4.4. Relations entre les grandeurs 34

II.3. Captures de vibrations 34

II.3.1. Capteur de déplacement 34

II.3.1.1. Principe de fonctionnement 35

II.3.1.2. Avantages 36

II.3.1.3. Inconvénients 36

II.3.2. Capteur de vitesse (Vélocité) 36

II.3.2.1. Capteur à bobine mobile (Classique) 36

II.3.2.1.1. Principe de fonctionnement d'un capteur de vitesse à bobine mobile 36

II.3.2.1.2. Avantages 37

XIV

II.3.2.1.3. Inconvénients 37

II.3.2.2. Capteur photoélectrique (Moderne) 38

II.3.3. Accéléromètre 38

II.3.3.1. Principe de fonctionnement 39

II.3.3.2. Avantages 40

II.3.3.3. Inconvénients 40

II.3.3.4. Accéléromètre à préamplificateur intégré 40

II.3.3.5. Montage de l'accéléromètre 41

II.3.4. Choix du capteur de vibrations 42

II.3.5. Influence de la grandeur utilisée 43

II.4. Harmoniques (Ordres) 44

II.5. Spectre FFT (Fast Fourier Transform) 45

II.6. Tendances et lignes de base en matière de vibrations 46

II.7. Normes et limites de vibration 47

II.8. Identification les défauts et leurs vibrations 48

II.9. Conclusion 51

CHAPITRE III : Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

III.1. Introduction 53

III.2. Importance de l'équilibrage 53

III.3. Technique de la réparation 53

III.4. L'équilibrage (La correction) 55

III.4.1. Types d'équilibrage 56

III.5. Logiciel VIB360 STUDIO 57

III.5.1. Représentation « objets » 57

III.5.2. La base de données 57

III.5.3. Les analyse 58

III.6. Simulation un défaut du balourd sur kit simulateur 59

III.6.1. Procédure d'équilibrage 62

III.6.1.1. Lancement 1 : Analyse d'ordre et analyse spectral (FFT) de balourd initial 62

III.6.1.2. Lancement 2 : Avec une masse d'essai 65

III.6.1.2.1. Choix d'une masse d'essai 65

III.6.1.3. Lancement 3 : Avec une masse de correction 68

III.6.1.3.1 Par méthode graphique ( Diagramme vectoriel ) 68

III.6.1.3.2 Par méthode numérique ( Un logiciel ) 71

XV

III.6.2. Résultat final (Vibration résiduelle) 72

III.6.3. Rayon de correction 73

III.6.4. Interprétation 74

III.6.5. Comparaison entre les programmes de calcule 74

III.7. Conclusion 75

CONCLUSION GÉNÉRALE 76

ANNEXES 78

Annexe En : Illustrated Vibration Diagnostic Chart 79

Annexe Fr : Tableau illustré de diagnostic des vibrations 84

Annexe En : Balance quality grades for various groups of representative rigid rotors (From

ISO 1940/1) 104

Annexe En : B.Maximum permissible residual unbalance, eper (Imperial values adapted

from ISO 1940/1) 105

Annexe Fr : Degrés de qualité d'équilibrage pour différents groupes de rotors rigides

representatives ( ISO 1940/1-1986 (F) ) 106

Annexe Fr : Valeur du balourd spécifique résiduel maximal admissible correspondant à

divers degrés de qualité d'équilibrage ( ISO 1940/1-1986 (F) ) 107

Programme en Matlab de l'équilibrage plan 1 pour les rotor rigide et les rotors quasi-

flexible 108

BIBLIOGRAPHIE 110

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 1

Introduction Générale

INTRODUCTION GÉNÉRALE

Dans le monde industriel et universitaire, le moteur asynchrone gagne en popularité. Il a progressivement supplanté la machine à courant continu et concurrencé son homologue synchrone dans une gamme de puissance allant de quelques watts à quelques mégawatts grâce à sa facilité de mise en oeuvre, sa petite taille, son bon rendement, son faible coût et son excellente fiabilité. Elle ne nécessite pas d'entretien fréquent, ce qui lui permet de fonctionner dans des environnements difficiles et à des niveaux de puissance élevés, tout en conservant une grande efficacité.

La dépendance totale vis-à-vis des machines asynchrones a conduit à l'apparition de certains problèmes tels que les vibrations. Le sujet de ce travail désigné pour résoudre ou bien éliminer ces problèmes. La méthode présentée est basée sur les analyses vibratoires extraites de ces machines.

Ce travail a donc été aidé par les agents mécaniciens de la société DML (direction maintenance Laghouat), Les travaux ont été menés au sein du Laboratoire de l'unité de vibration dans DML qui a une convention avec l'université de Laghouat.

Afin de répondre aux objectifs énoncés précédemment, le manuscrit est divisé en chapitres suivants :

Au premier chapitre, on commence par une discussion autour les machines asynchrones, cette étape est primordiale car elle permet non seulement une meilleure connaissance de la machine mais aussi prépare efficacement le terrain à l'application des stratégies de maintenance. Puis en situer la problématique des défauts des machines électriques, donc cette partie est consacrée aux principaux défauts et leurs causes et conséquences sur les machines asynchrones.

Au deuxième chapitre, on présentera l'analyse vibratoire concernons les différents nature des défauts lesquels se situe notre travail. Afin d'observer ces phénomènes apparaissent sur la machine, Nous allons montrer les capteurs leur contextes, types, caractéristiques et principes de fonctionnements.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 2

Introduction Générale

Le troisième chapitre, fera l'objet du principe d'équilibrage avec les différentes techniques de réparation d'un cas du balourd et son application sur les moteurs asynchrones. Afin de valider la théorie de l'équilibrage étudié, nous allons effectuer un test par simulation sur le kit simulateur.

Enfin, nous donnerons une conclusion générale qui met en évidence les résultats de notre recherche et les implications de nos résultats.

CHAPITRE I

Principaux Défauts de la Machine

Asynchrone, Causes et Conséquences

I.1. Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 4

Introduction

Selon le vocabulaire électrotechnique international, `'Une machine asynchrone est une machine à courant alternatif dont la vitesse en charge et la fréquence du réseau, auquel elle est reliée, ne sont pas dans un rapport constant`' Ce vocable est le seul utilisé en français, alors que les pays anglo-saxons désignent par machine à induction (induction machine) `'une machine asynchrone dont le circuit magnétique est associé à deux ou plus de deux circuits électriques se déplaçant l'un par rapport à l'autre et dans laquelle l'énergie est transférée de la partie fixe à la partie mobile, ou inversement par induction électromagnétique`'. [1]

Le moteur à induction se caractérise par sa simplicité, sa fiabilité et son faible coût, associés à une capacité de surcharge raisonnable, des exigences de service minimales et un bon rendement. Un moteur à induction utilise directement le courant alternatif fourni au stator. Le rotor reçoit la puissance par effet d'induction. [2]

Cependant, en raison de la durée de vie de ces machines électriques, des défauts de fabrication, d'alignement, mal fonctionnement ou d'autres problèmes d'origine électrique, de nombreux types de défauts sont inévitables dans les machines électriques et peuvent se produire dans leurs différents composants.

I.2. Principe de fonctionnement

Les moteurs fonctionnent selon un principe commun qui est celui de l'induction. Il y a une relation entre le stator, qui génère le champ magnétique et le rotor, qui transmet la force motrice, avec un isolement galvanique entre les deux éléments. L'alimentation du bobinage du stator génère une induction magnétique à laquelle est associé un champ magnétique à partir duquel est créée la force motrice. Pour produire un mouvement de rotation, le rotor doit être soumis à deux flux alternatifs qui ne sont pas synchronisés dans le temps et qui sont appliqués en deux endroits distincts, décalés selon la direction du mouvement souhaité. [3]

Le rotor. Celui-ci est constitué de conducteurs (des bobinages ou carrément des barres métalliques) disposés le long du rotor et court-circuités. Lorsque le champ tournant balaye ces conducteurs, il induit des courants qui entrent en interaction avec le champ et permettent à un couple moteur de se créer. Le rotor se met alors à tourner et se stabilise à une vitesse toujours légèrement inférieure à la vitesse de synchronisme. Il est impossible pour le rotor de tourner à la vitesse de synchronisme puisqu'il serait alors baigné dans un champ fixe, et donc parcouru par un courant nul. En l'absence de courant, le couple serait nul, et la machine décélèrerait. La légère différence de vitesse justifie le terme de « glissement » du rotor par rapport au champ tournant. [4]

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

I.3. Construction de la machine asynchrone

La machine asynchrone (figure.I.1) comporte un stator muni d'un enroulement triphasé et d'un rotor portant un enroulement triphasé ou une cage. C'est un transformateur à champ tournant dont le primaire est le stator et dont le secondaire, mis en court-circuit et libre de tourner.

Deux composantes principales constituent le moteur asynchrone, souvent appelé moteur d'induction. Elles sont faites de tôles d'acier au silicium et comportent des encoches dans lesquelles on place les enroulements. L'une des composants, appelée le stator, est fixe ; on y trouve les enroulements reliés à la source. L'autre composante nommée le rotor, est montée sur un axe et libre de tourner. Selon que les enroulements du rotor sont accessibles de l'extérieur ou sont fermés sur eux-mêmes en permanence, on reconnait deux types de rotor : le rotor bobiné et le rotor à cage d'écureuil. [5]

Ventilateur

Stator

Rotor à cage

Flasque palier

Roulement

Roulement

Boite de

raccordement Flasque

palier

Capot de ventilation

L'arbre du rotor

Enroulement statorique

Fig.I.1. Les composants d'un moteur asynchrone [3].

I.3.1. Stator

Est une partie fixe, composé par trois enroulements (bobines) régulièrement reparties et possédant deux pôles`2p'. Ils peuvent être couplés en étoile ou en triangle selon la règle suivante :

- Si la tension supportée par chaque enroulement est égale á la tension simple du réseau, le Stator doit être couplé en étoile.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 5

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 6

- Si la tension supportée par chaque enroulement est égale á la tension composée du réseau, le stator doit être couplé en triangle.

Les enroulements sont logés dans des encoches d'une armature cylindrique constituée d'un matériau ferromagnétique feuilleté afin de limiter les pertes par courant de Foucault. Le stator est fixé au corps du moteur et se compose d'un empilage de tôles très fines et de trois enroulements. En réseau triphasé, chaque enroulement est bobiné autour d'un noyau statorique et forme un électroaimant (une paire de pôles) lorsqu'il est relié à une phase du réseau. Le moteur asynchrone triphasé alternatif est le seul à fonctionner grâce à l'alternance des phases du réseau électrique.

L'explication physique est la suivante : La circulation d'un courant dans une bobine crée un champ magnétique H. Ce champ est dans l'axe de la bobine, sa direction et son intensité sont fonction du courant I_s. Si le courant est alternatif, le champ magnétique varie en sens et en direction à la même fréquence que le courant. Si deux bobines sont placées à proximité l'une de l'autre, le champ magnétique résultant est la somme vectorielle des deux autres.

Dans le cas du moteur triphasé, les trois bobines sont positionnées dans le stator à 120° les unes des autres, ce qui crée trois champs magnétiques. Compte-tenu de la nature du courant sur le réseau triphasé, les trois champs sont déphasés. Ainsi alimenté, le stator génère un champ magnétique, dit champ statorique tournant à une vitesse qui est dite de synchronisme (Ns). La fréquence de rotation de ce champ est liée à la fréquence du réseau et au nombre de paires de pôles de l'enroulement. Ns = 60f / p en nombre de tours par minute (RPM). [3]

Fig.I.2. Le stator [6].

I.3.2. Rotor

Est un partie en mouvement, et en court-circuit, Il y a deux types : bobine ou à cage d'écureuil. Il est composé d'un empilage de fines tôles métalliques isolées entre elles (afin d'éviter la circulation des courants de Foucault), d'enroulements et de conducteurs qui sont en

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 7

court-circuit. Sa particularité est de réagir au champ magnétique généré par le stator, (le champ statorique). Selon la loi de Lenz, le courant induit dans le rotor s'oppose, par son champ magnétique aux effets du champ inducteur. Les variations de flux entre les enroulements statoriques et rotoriques se traduisent par l'apparition d'une force : le couple. Le rotor entre ainsi en rotation à une vitesse nominale (N) qui se rapproche de la vitesse de synchronisme (Ns) qui est la vitesse maximale de rotation liée à la fréquence de l'alimentation.

La différence de vitesse entre Ns et N est nommée vitesse de glissement, d'où l'emploi de l'appellation « moteur asynchrone » qui traduit cette différence de vitesse. Le glissement g est exprimé en % de la vitesse de synchronisme et se calcule selon la formule suivante :

g =

(I.1)

Quand le moteur est en phase de démarrage, la vitesse du rotor est nulle et la différence de vitesse de rotation du champ magnétique et celle du rotor est maximale, ce qui génère l'induction de forts courants rotoriques par l'absence de force contre électromotrice (c'est l'origine du fort courant d'appel). Quand le rotor accélère, la différence de vitesse se réduit et les courants rotoriques diminuent. La vitesse du rotor se stabilise à sa vitesse N. [3]

I.3.2.1. Rotor bobiné

Il n'est relié à aucune alimentation électrique, il est muni d'un enroulement triphasé, composé des bobines. L'enroulement généralement couplée en étoile et connecté à trois bagues conductrices isolées les unes des autres sur lesquelles frottent des balais en graphite.

L'extrémité libre de chaque enroulement est reliée à une bague tournant avec l'arbre. Ces bagues permettent, par l'intermédiaire de trois balais, d'insérer une résistance extérieure en série avec chacun des trois enroulements lors du démarrage du moteur. En fonctionnement normal, les trois balais sont court-circuités. [7]

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

L'arbre du rotor

Enroulement de rotor

Encoches
oblique de
rotor

Brosses / Bagues

Fig.I.3. Structure d'un rotor bobiné [3] [8].

I.3.2.2. Rotor cage d'écureuil

Dans le type le plus utilisé, connu sous le nom de rotor à cage d'écureuil, des barres de cuivre ou d'aluminium sont placées dans des fentes découpées dans le fer laminé, les extrémités des barres étant soudées ou brasées dans un lourd anneau conducteur (figure I.4). Les conducteurs sont placés dans des fentes du noyau du rotor en fer laminé. Si les fentes sont inclinées, on obtient un meilleur démarrage et un fonctionnement plus silencieux. Ce type de rotor n'a pas de connexion externe, ce qui signifie que les bagues collectrices et les balais ne sont pas nécessaires. Le moteur à cage d'écureuil est bon marché, fiable et efficace.[9]

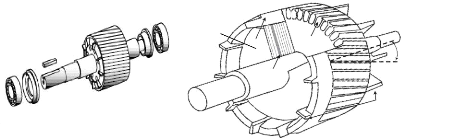
Bague
d'extrémité

Tôles

Encoche Angle

d'inclinaison

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 8

Fig.I.4. Structure d'un rotor à cage d'écureuil [3] [8]. I.3.3. Les organes mécaniques

La carcasse sert de support, elle joue le rôle d'enveloppe et assure la protection contre l'environnement extérieur.

L'arbre est un organe de transmission. Il comprend une partie centrale qui sert de support au corps du rotor et un bout d'arbre sur lequel est fixé un demi-accouplement. Il est généralement constitué en acier moulé ou forgé. Son dimensionnement est fonction des efforts de flexion (force centrifuge qui s'exerce sur lui, attraction magnétique radial, etc....), des efforts radiaux et tangentiels dus aux forces centrifuges, des efforts de torsion (couple

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 9

électromagnétique transmis en régime permanent, transitoire). Il est supporté par un ou plusieurs paliers. Ces paliers soutiennent le rotor et assurent la libre rotation. Le second palier est libre pour assurer les dilatations thermiques de l'arbre. Une isolation électrique de l'un des paliers assure l'élimination des courants dans l'arbre dû aux dissymétries des réluctances du circuit magnétique. Ils sont généralement à roulements pour les machines de petite et moyenne puissance.[10]

I.3.3.1. Les roulements

Éléments roulants ou antifriction Les roulements à éléments roulants sont l'un des types les plus courants utilisés dans les machines. Les roulements sont basés sur un mouvement de roulement, par opposition au mouvement de glissement des paliers lisses. L'utilisation d'éléments roulants entre les surfaces tournantes et stationnaires réduit le frottement à une fraction de celui résultant de l'utilisation de paliers lisses. L'utilisation de roulements est déterminée par de nombreux facteurs, notamment la charge, la vitesse, la sensibilité au désalignement, les limitations d'espace et le désir de positionnement précis de l'arbre. Ils supportent des charges radiales et axiales et sont généralement utilisés dans des applications à vitesse modérée à élever.

Contrairement aux paliers lisses à film fluide, les roulements à éléments roulants ont la capacité supplémentaire de supporter la charge totale de l'ensemble du rotor à n'importe quelle vitesse. Alors que les paliers à film fluide doivent avoir un engrenage tournant pour supporter le poids du rotor à basse vitesse, les roulements à éléments roulants peuvent maintenir l'axe central de l'arbre sur toute la plage de vitesse de la machine.[11]

I.4. Maintenance

Dans le milieu industriel le maintien de la continuité de service nécessite un effort de la part des exploitants de production. Le maillon faible est principalement la machine électrique, car sa panne paralyse immédiatement la production et entraîne une perte financière très importante. Une maintenance dite « prédictive » doit donc être assurée afin de prévenir à temps les défauts susceptibles de se produire dans les moteurs.

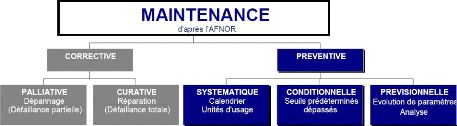
Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Fig.I.5. Types de maintenance [12]

.

I.4.1. Maintenance curative

Après un arrêt par défauts ou bien malle fonctionnement :

- Nécessite une équipe d'entretien surdimensionnée

- Ne permet pas de maîtriser la disponibilité des équipements

I.4.2. Maintenance systématique Selon un échéancier préétabli :

- Engendre le remplacement prématuré de composants

- Ne permet pas de prendre en compte l'évolution réelle de leur état I.4.3. Maintenance prévisionnelle

Maintenance préventive subordonnée à l'analyse de l'évolution surveillée de paramètres significatifs de la dégradation du bien, permettant de retarder et planifier les interventions.

I.4.4. Maintenance préventive

Maintenance exécutée à intervalles prédétermines ou selon des critères prescrits et destinée à réduire la probabilité de défaillance ou la dégradation du fonctionnement d'un bien.

I.4.5. Maintenance conditionnelle

Maintenance préventive qui comprend une combinaison de surveillance en fonctionnement et/ou d'essais, d'analyse et les actions qui en découlent.

La maintenance conditionnelle est basée sur l'analyse de l'évolution dans le temps de paramètres significatifs.

Note : Les définitions des types de maintenance selon les normes EN NF 13306 , AFNOR X60-010) .

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 10

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 11

Fig.I.6. Seuil de maintenance [13] I.4.6. L'importance de la maintenance

Les enjeux économiques liés à la maintenance des systèmes industriels, dont ceux entrainés par des moteurs asynchrones, sont très importants pour les entreprises. Cette remarque est d'autant plus vraie aujourd'hui en raison de l'automatisation, de la complexification et de l'interdépendance des machines et des lignes de production. Cependant, ce poste de dépense a longtemps été considéré comme inéluctable et faisant partie des frais généraux de fonctionnement.

La maintenance industrielle constitue pourtant un gisement de compétitivité élevé pour beaucoup d'entreprises. Les coûts directement ou indirectement associés à la maintenance représentent en effet un pourcentage élevé dans l'analyse du coût du cycle de vie (CCV) des systèmes industriels et peuvent être diminués en optimisant la stratégie de maintenance adoptée. [14]

Les coûts de maintenance, tels qu'ils sont définis par les procédures comptables normales des usines, représentent normalement une part importante des coûts d'exploitation totaux dans la plupart des usines. Aux États-Unis, les coûts d'entretien traditionnels (c'est-à-dire la main-d'oeuvre et les matériaux) ont augmenté à un rythme effréné au cours des dix dernières années. En 1981, les usines nationales ont dépensé plus de 600 milliards de dollars pour entretenir leurs systèmes critiques. En 1991, les coûts avaient augmenté à plus de 800 milliards de dollars, et on prévoyait qu'ils atteindraient 1,2 billion de dollars en l'an 2000. Ces évaluations indiquent qu'en moyenne, un tiers, soit 250 milliards de dollars, de tous les dollars consacrés à la maintenance sont gaspillés en raison de méthodes de gestion de la maintenance inefficaces. L'industrie américaine ne peut absorber ce niveau incroyable d'inefficacité et espérer être compétitive sur le marché mondial.

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 12

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

En raison de la nature exorbitante des coûts de maintenance, ils représentent le plus grand potentiel d'amélioration à court terme. Les retards, les rejets de produits, les temps d'arrêt prévus pour la maintenance et les coûts de maintenance traditionnels (tels que la main-d'oeuvre, les heures supplémentaires et les pièces de rechange) sont généralement les principaux facteurs contribuant aux coûts de maintenance anormaux dans une usine.

Jusqu'à récemment, les cadres moyens et supérieurs n'ont pas tenu compte de l'impact des opérations de maintenance sur la qualité des produits, les coûts de production et, surtout, les bénéfices nets. L'opinion générale était que "la maintenance est un mal nécessaire" ou que "rien ne peut être fait pour améliorer les coûts de maintenance". Ces affirmations étaient peut-être vraies il y a 10 ou 20 ans. Cependant, le développement de microprocesseurs ou d'instruments informatiques pouvant être utilisés pour surveiller l'état de fonctionnement des équipements, des machines et des systèmes de l'usine a fourni les moyens de gérer les opérations de maintenance. Ils ont permis de réduire ou d'éliminer les réparations inutiles, de prévenir les pannes catastrophiques des machines et de réduire l'impact négatif des opérations de maintenance sur la rentabilité des usines de fabrication et de production.[11]

I.5. Terminologie dédiée au diagnostic

Le tableau ci-dessous défier les étapes de la terminologie dédiée au diagnostic. Tab.I.1. Terminologie & définitions [15].

Terminologie	Définitions
Défaut	Déviation non permise d'au moins d'une propriété ou d'un paramètre caractéristique du système par rapport aux conditions normales de fonctionnement.
Panne ou défaillance	Interruption permanente de la capacité du système à remplir une fonction requise dans des conditions d'opérations spécifiées.
Dysfonctionnement	Exécution d'une fonction du système au cours de laquelle le service rendu n'est pas délivré ou est délivré de manière incomplète.
Symptôme	Changement d'une quantité observable par rapport à un comportement normal.
Perturbation	Signal d'entrée non contrôlé dont la présence est non souhaitable mais considérée comme normale.
Suivi	Fonction maintenant en permanence un historique des traitements effectués par le système de commande/supervision et une trace des événements que perçoit le système.
Détection de défauts	Détermination de la présence de défauts et de l'instant d'occurrence de ces défauts.
Localisation de défauts	Détermination du type, de la localisation et de la date d'un défaut détecté. Elle consiste à remonter d'un ensemble de symptômes à un

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 13

	ensemble de composants défaillants.
Identification de défauts	Détermination de la taille et du comportement temporel d'un défaut. C'est une fonction qui suit la localisation.
Diagnostic	Détermination du type, de la taille, de la localisation et de l'instant d'occurrence d'un défaut. C'est une fonction qui suit la détection et inclut les fonctions de localisation et d'identification.
Surveillance	Ensemble de fonctions s'exécutant en temps réel ayant pour but de reconstituer l'état réel du procédé au sein des modèles utilisés par le système de conduite du procédé. Elle consiste à l'enregistrement de l'information ainsi qu'à la reconnaissance et l'indication des comportements anormaux.
Supervision	Représente la surveillance d'un système physique et la prise de décisions appropriées en vue de maintenir son opération face à des défaillances.

I.6. Généralités sur les défauts des machines électrique

Il existe deux types de défauts principaux : internes et externes. Nous pouvons ainsi remarquer que les défauts internes de la machine sont causés par les constituants de la machine (circuit magnétique rotorique et statorique, bobinage statorique, entrefer mécanique, cage rotorique, ...) alors que les défauts externes sont provoqués, soit par les tensions d'alimentation et la charge mécanique, soit par l'environnement de l'utilisation de la machine. [16]

Nous citerons à titre indicatif des origines de type :

- Mécaniques: mauvaise fabrication, vibrations de la machine, force électromagnétiques

déséquilibrées, force centrifuge, fluctuations de la charge.

- Electriques: dégradations d'isolement, décharges partielles, étincelles.

- Thermiques: pertes dans le cuivre, manque de refroidissement général ou localisé.

- Environnementales: humidité, température, poussière.

Afin d'orienter notre étude vers la détection d'une ou plusieurs catégories de défaillances, il est nécessaire de connaitre les défauts se produisant le plus régulièrement dans les systèmes d'entrainement asynchrones et également ceux dont les conséquences sont les plus graves. Dans la littérature, plusieurs études ont été menées à grande échelle sur des moteurs asynchrones aux caractéristiques fortement différentes afin de connaitre la répartition des défaillances survenant dans ces systèmes [17], [18], [19] . Les résultats obtenus à l'issue de ces différentes études sont représentés sur la figure I.7 en classant les défauts selon 4 catégories : roulements, stator, rotor et autres.

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

[17] [18] [19]

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 14

Fig.I.7. Répartition des défauts rencontrés dans les entrainements asynchrones [14]
selon les études [17], [18] et [19].

Ces études statistiques nous informent que la majorité des défaillances rencontrées concernent les roulements à billes. Les défaillances au stator (majoritairement liées à l'isolation des bobinages) constituent également un pourcentage important des dégradations observées. Enfin, les défauts au rotor (arbre, accouplement, etc.) semblent se produire moins fréquemment.

Une étude a été menée auprès d'une filiale de service de Leroy Somer spécialisée dans la maintenance des systèmes d'entrainement. Cette étude n'est pas quantitative comme celles présentées dans [17], [18] et [19] mais se base sur l'expérience acquise au cours des phases de maintenance réalisées. Les chiffres fournis par la suite ne sont donc probablement pas strictement fidèles à la réalité mais fournissent une vision globale de la répartition des défaillances observées dans les systèmes entrainés par les moteurs asynchrones ciblés par notre étude. Les résultats obtenus sont illustrés par la figure I.8.

Fig.I.8. Répartition des défauts rencontrés dans les applications entrainées par les
moteurs asynchrones de la gamme Leroy Somer selon l'enquête menée auprès d'une
filiale de maintenance. [14]

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 15

I.6.1. Défaut des roulements

Les roulements sont des composants typiques des moteurs qui sont utilisés pour permettre la rotation de l'arbre. La majorité des pannes de moteur sont dues à un mauvais fonctionnement des roulements. Les roulements sont constitués de billes, d'une cage et de bagues intérieure et extérieure. Plusieurs éléments roulants (billes) sont placés entre ces deux bagues. La cage est utilisée pour maintenir les billes à égale distance les unes des autres. Les contraintes développées dans le moteur provoquent une fatigue des bagues des roulements, qui entraîne des défauts localisés (défauts uniques tels que l'écaillage, les piqûres, les bosses ou les trous) et des défauts répartis (rugosité de surface généralisée) dans les roulements du moteur.

Les défauts localisés sont induits principalement par l'usure opérationnelle (fatigue de contact) des roulements. Si les roulements sont correctement installés, exempts de contamination et bien lubrifiés pendant le fonctionnement, la défaillance des roulements ne se produira qu'après la durée de vie prédéterminée (millions de cycles) des roulements.

Ce type de défaillance commence initialement dans un sous-sol à un niveau microscopique en un seul point, puis, en raison des cycles de contrainte continus, elles peuvent finir par provoquer une rupture du matériau. Ces défauts ponctuels sont caractérisés comme des écaillages ou des piqûres, ou des défauts localisés. La défaillance des roulements peut également se produire en raison de leur température élevée.

La température des roulements ne doit pas augmenter au-delà de certains degrés dans des conditions nominales.

Degrés spécifiques dans les conditions nominales. Par exemple, dans les industries pétrolières et chimiques, la norme IEEE 841 spécifie que l'augmentation de la température des roulements, sous une charge nominale, ne doit pas dépasser 45°. L'augmentation de la température du bobinage, une mauvaise lubrification, la répartition de la température dans le moteur et la vitesse de fonctionnement du moteur sont les principaux facteurs d'augmentation de la température des roulements.[20]

Par conséquent, les mesures de la température des roulements peuvent fournir des données utiles pour estimer l'état de santé des roulements ainsi que celui du moteur.

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

(a) Défaut localisé sur extérieur du roulement

(b) Défauts distribués sur la bague intérieure

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 16

Fig.I.9. Exemple de roulement. (a) Défauts localisés. (b) Défauts distribués. [20] I.6.1.1. Fréquences caractéristiques des défauts du roulement

Nous pouvons distinguer quatre types de défauts de roulement, en fonction de leur localisation :

· Défaut de bague externe,

· Défaut de bague interne,

· Défaut de billes,

· Défaut de cage.

Chaque type de défaut cité ci-dessus est caractérisé par une fréquence fondamentale calculée à partir des dimensions du roulement et de la fréquence de rotation de l'arbre (????). Les expressions de ces fréquences pour les défauts de bague externe, de bague interne, de billes et de cage sont données respectivement, où ???? et ???? sont les diamètres d'une bille et de la cage, ?? est l'angle de contact de la bille avec les bagues et ???? est le nombre de billes.[21]

y' Défaut de bague externe

?? ?? ??

?? ?? ??

?? ??

??

y' Défaut de bague interne

?? ??

??

y' Défaut de billes

y' Défaut de cage

?? ?? ?? ?? ?? ??

?? ?? ?? ?? ?? ??

I.6.2. Défauts au stator

Les défauts qui sont les plus récurrents, localisés au niveau du stator, peuvent être définis comme suit : défaut d'isolant, court-circuit entre spires, court-circuit entre phases, court-

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

circuit entre phase et bâti, déséquilibre d'alimentation, défaut de circuit magnétique. Ces défauts sont habituellement liés à une dégradation de l'isolement.

Le court-circuit entre spires de la même phase est l'un des défauts les plus fréquents, qui peut être modélisé par une résistance connectant deux points de la bobine, sa valeur dépend de la gravité du défaut. La figure I.10 montre le bobinage du stator de la machine avec défaut entre spires. Le défaut est survenu sur l'enroulement de la phase a_s avec une résistance de défaut rf. Lorsque le défaut évolue vers un court-circuit franc, la résistance diminue vers zéro. A un stade avancé, un défaut de court-circuit entre spires peut s'aggraver et évoluer vers un court-circuit phase-phase ou phase-terre. L'augmentation de la température engendrée entraîne par la suite la destruction progressive des isolants et par effet cumulatif, la destruction complète de la machine. En général, un défaut de court-circuit engendre des vibrations et des oscillations de couple synonymes de présence de nouvelles composantes dans le couple électromagnétique. En effet, la résistance de court-circuit forme un nouveau bobinage qui induit un champ magnétique additionnel dans la machine.[22]

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 17

Fig.I.10. Différents types de défauts statorique [22] [23] I.6.3. Défauts au rotor

Dans une machine asynchrone avec un rotor à cage d'écureuil, les défauts se résument à la rupture de barres ou à la rupture d'anneaux de court-circuit. Ils sont souvent causés par les mauvaises conditions d'opérations essentiellement par des hautes températures ou les fortes charges surtout aux démarrages. En effet, une rupture partielle ou totale d'une de ces composantes peut être considérée comme un défaut. En conséquence, l'évolution du défaut réduit la valeur moyenne du couple électromagnétique, provoque des oscillations de la vitesse de rotation et engendre des vibrations mécaniques. L'augmentation de ces phénomènes accélère la dégradation de la cage rotorique. Les barres cassées peuvent alors s'ouvrir à l'extérieur en raison des forces centrifuges et endommager de façon catastrophique les enroulements statoriques.[22]

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Une portion d'anneau Deux portion d'anneaux

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 18

Fig.I.11. Rupture d'un anneau. [24]

I.6.4. Défaut d'excentricité

Dans une machine idéale, le centre du rotor est aligné sur celui du stator et l'axe de rotation du rotor est le même que l'axe du stator, comme illustré dans la figure I.12. Toutefois, les conséquences des défauts mécaniques peuvent se manifester au niveau de l'entrefer par un décentrement du rotor, se traduisant par des oscillations de couple . Ce phénomène est appelé excentricité défini comme une asymétrie dans l'entrefer entre le stator et le rotor. Ce défaut existe en général dans la machine, mais avec un faible niveau, dès sa fabrication et évolue avec le temps. Certains utilisateurs et fabricants spécifient un niveau d'excentricité maximal admissible de 5% alors que d'autres permettent un niveau maximal de 10% de la largeur de l'entrefer .Tout niveau d'excentricité supérieur à 60% nécessite une intervention immédiate afin d'éviter un frottement entre le rotor et le stator [21], ce qui peut mener à une panne très grave de la machine.

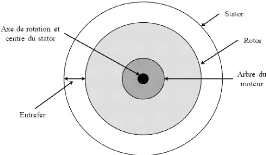
Fig.I.12. Positions du rotor et du stator dans une machine parfaite. [21]

Trois catégories d'excentricité peuvent être identifiées dans la littérature et sont illustrées dans la figure I.13 :

- Excentricité statique (figure I.13 (a)) : le rotor est déplacé du centre de l'alésage du stator mais il tourne toujours autour de son axe. Elle est due généralement soit à une imperfection de

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

l'alésage du stator, soit à un mauvais positionnement du rotor ou du stator à l'étape de mise en service.

- Excentricité dynamique (figure I.13 (b)) : le rotor est positionné au centre de l'alésage du stator mais il ne tourne plus autour de son axe. Ce type peut être provoqué par divers facteurs tels que l'usure des roulements, les résonnances mécaniques à la vitesse critique et le désalignement.

- Excentricité mixte (figure II.13 (c)) : la combinaison des deux cas cités précédemment.

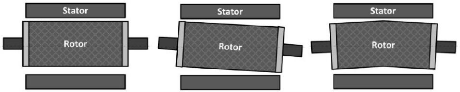
(a) (b) (c)

Fig.I.13. Types d'excentricités statiques (a), dynamique (b) et mixte (c) [21] I.6.5. Alignement d'arbres

L'alignement des arbres est le positionnement correct des axes des arbres des composants d'entraînement et des composants entraînés (c'est-à-dire les pompes, les boîtes de vitesses, etc.) qui constituent la chaîne cinématique de la machine. L'alignement est réalisé soit en calant, soit en déplaçant un composant de la machine, soit les deux. Son objectif est d'obtenir un axe de rotation commun à l'équilibre de fonctionnement pour deux arbres couplés ou un train d'arbres couplés. [11]

I.6.5.1. Alignement parfait

Deux arbres parfaitement alignés sont colinéaires et fonctionnent comme un arbre solide lorsqu'ils sont couplés. Cette condition est illustrée à la figure I.14 Cependant, il est extrêmement rare que deux arbres soient parfaitement alignés sans qu'une procédure d'alignement ne soit effectuée sur eux. En outre, l'état de l'alignement doit être contrôlé régulièrement pour maintenir la condition d'alignement parfait.

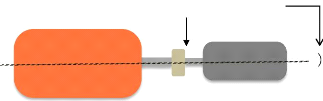
D = 0 mm et Äö = 0 °

Charge

Moteur

Fig.I.14. Alignement parfait. [S. Kouidri et K. Ghris]

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 19

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 20

I.6.5.2. Désalignement angulaire ou frontal (le délignage ou défaut de lignage)

Une bonne connaissance de l'alignement angulaire, également appelé désalignement frontal, est nécessaire pour comprendre les conditions d'alignement et effectuer les tâches associées à l'alignement des machines et des trains, telles que le dessin des graphiques d'alignement, le calcul des corrections de pied, la spécification de la croissance thermique, l'obtention des spécifications cibles et la détermination de l'alignement des arbres d'espacement. Le désalignement angulaire fait référence à la condition dans laquelle les arbres ne sont pas parallèles mais se trouvent dans le même plan sans décalage. Ce cas est illustré à la figure I.15 Notez qu'en cas de désalignement angulaire, il est possible que les arbres correspondants soient dans le même plan à l'intersection de la face de l'accouplement mais qu'ils aient une relation angulaire telle qu'ils ne sont pas colinéaires.[11]

D = 0 mm et Äö > 0 °

Moteur

Fig.I.15. Désalignement angulaire (pas de décalage) [S. Kouidri et K. Ghris] I.6.5.3. Désalignement décalé ou parallèle

Le désalignement décalé, également appelé désalignement parallèle, fait référence à la distance entre deux axes d'arbres et se mesure généralement en millièmes de pouce. Le décalage peut être présent dans le plan vertical ou horizontal. La figure I.16 illustre le décalage, montrant deux arbres appariés qui sont parallèles l'un à l'autre mais non colinéaires. Théoriquement, le décalage est mesuré au niveau de l'axe de l'accouplement.

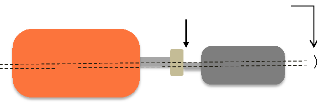
D > 0 mm et Äö = 0 °

Moteur

Charge

Fig.I.16. Désalignement parallèle. [S. Kouidri et K. Ghris] I.6.5.4. Désalignement combiné ou oblique

Un désalignement combiné ou oblique se produit lorsque les arbres ne sont pas parallèles (c'est-à-dire angulaires) et ne se croisent pas au niveau de l'accouplement (c'est-à-dire

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

décalés). La figure I.17 montre deux arbres obliques, ce qui est le type de problème de désalignement le plus courant. Ce type de désalignement peut se produire dans le plan horizontal ou vertical, ou dans les deux plans (horizontal et vertical).

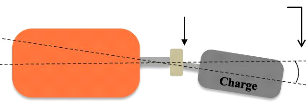
D > 0 mm et Äö > 0 °

Moteur

Fig.I.17. Désalignement combiné. [S. Kouidri et K. Ghris]

I.6.6. Flexion du rotor

Deux paliers du même arbre d'une machine : les axes des deux paliers d'un même corps de machine ne sont pas concentriques. Cette anomalie peut être la conséquence d'un défaut de montage d'un palier, mais également d'un mauvais calage des pattes de fixation ou d'une déformation de chassis (par exemple, sous l'effet de contraintes thermiques), qui se traduit par une flexion de l'arbre du rotor.

Fig.I.18. Flexion d'arbre due à un défaut d'alignement ou de concentricité des paliers.

[29]

Ill y a 3 modes élastiques d'un rotor flexible :

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 21

Fig.I.19. Modes élastiques d'un rotor flexible. [25] I.6.7. Défaut de déséquilibre (balourd)

Le balourd est le résultat d'un ensemble de forces engendrées par les écarts existant entre les centres de gravité des différents éléments constituant le rotor et son axe de rotation. Cette force centrifuge, issue de ces défauts de « non-concentricité » ou d'ajustage, est proportionnelle à la masse de matière qui crée ce déséquilibre et au carré de la vitesse. Elle génère des efforts tournants qui vont agir sur les différents éléments constitutifs du rotor, les ancrages de la machine et les paliers jusqu'à entraîner leur dégradation. Le défaut de balourd

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 22

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

est l'une des principales causes de réduction de la durée de vie des équipements et il constitue l'un des principaux risques pour la sécurité. C'est pour cette raison sans doute qu'il fait l'objet de normes importantes, tant pour son évaluation que pour sa correction. Ainsi, pour une classe d'équilibrage donnée, comparer l'amplitude de la vibration induite à des seuils fixes dans des normes ou à des spécifications de constructeurs, permettra de statuer sur le caractère acceptable ou non du déséquilibre et sur la nécessité de procéder ou non à un équilibrage suivant une procédure bien définie.

Le balourd, déséquilibre massique, peut provenir de défauts d'usinage, d'assemblage et de montage, mais aussi :

- D'une altération mécanique (perte d'ailette, érosion ou encrassement...),

- D'une altération thermique ou d'une déformation suite à des dilatations différentes des matériaux constituant le rotor ou encore à des différences de température localisées (balourd thermique).[29]

I.6.7.1. Les paramètres de déséquilibre

Les paramètres ci-dessous est paramètres de déséquilibrage :

"M" - Masse du rotor

"m" - Masse du balourd

"C" - Centre de masse

"e" - Déplacement du centre de la masse

"r" - Distance entre le centre du rotor et C.G

du la masse "m" de balourd

"F" - Force due au déséquilibre

"U" - Déséquilibre du rotor

"N" - Vitesse du rotor (RPM)

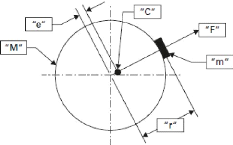
Fig.I.20. Déséquilibre du rotor. [26]

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 23

Et nous avons :

I.6.7.2. Déséquilibre et vitesse

De nombreuses personnes pensent que le déséquilibre s'aggrave avec l'augmentation de la vitesse. Nous savons que ce n'est pas le cas. Ce graphique montre que le balourd est une constante - c'est une propriété de masse du rotor.

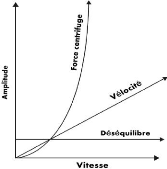
Fig.I.21. Le déséquilibre, la vélocité de vibration et la force centrifuge en fonction de

la vitesse de rotation [26]

Le déséquilibre est une propriété du rotor et ne change pas avec la vitesse de rotation. La vélocité de vibration change en rapport direct avec la vitesse de rotation.

La force centrifuge change en fonction de (RPM)².

Si un rotor avec un balourd "nul" est utilisé à n'importe quelle vitesse, il n'y aura pas de vibrations ni de forces sur les paliers. Il ne s'agit bien sûr que d'une situation théorique. Si un poids d'une masse de 1 gramme est ajouté au rotor à un rayon de 100 mm, lorsqu'il tourne, il y aura des vibrations et des forces d'appui qui changeront avec la vitesse, mais le déséquilibre est fixé à 100 g.mm - à moins que nous tournions assez vite pour que le poids s'approche de la vitesse de la lumière, auquel cas il deviendrait plus court et plus massif - mais c'est un autre problème.

I.6.7.3. Sources du déséquilibre

La plupart des fabricants de moteurs électriques standardisent l'équilibrage de leurs éléments rotatifs avec la totalité de la rainure de clavette remplie d'une demi-clavette. C'est-à-

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 24

dire que l'arbre est totalement rempli. Les fabricants d'accouplements pratiquent les mêmes procédures lorsqu'ils équilibrent leurs accouplements. Lors de l'assemblage de ces deux éléments, une clavette en L ou en T doit être utilisée pour maintenir l'équilibre d'origine. La figure I.22 montre certaine des sources les plus courantes de déséquilibre associées à l'installation d'un accouplement. Chacune de ces conditions peut entraîner une défaillance prématurée dans les roulements, des accouplements ou des joints.[27]

Rondelle supplémentaire

Rondelle manquante/ absente

Matériel clé

Manquant de matériel clé

Moyeu desserré sur l'arbre

Boulon en arrière

Boulon trop long

Fig.I.22. Sources de déséquilibre [27] I.6.7.4. Déséquilibrage statique

Imaginons un rotor parfaitement en équilibre. Ajoutons en un endroit de ce rotor une masse M. Le rotor présentera un déséquilibre. Même à l'arrêt, le rotor reviendra à une position d'équilibre. Il s'agit d'un déséquilibrage statique. Dès que le rotor sera en rotation, la masse M exercera une force radiale proportionnelle à la vitesse de rotation selon la relation

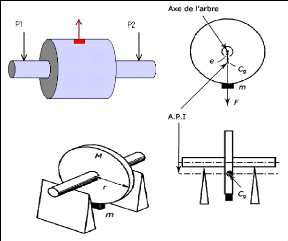
Force centrifuge

??

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 25

Chapitre I Principaux Défauts de la Machine Asynchrone, Causes et Conséquences

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 26

Fig.I.23. Déséquilibrage statique. [31] [28]

On mesure l'amplitude de l'accélération du signal vibratoire au point P1 et P2. Au point P1, l'amplitude vibratoire sera maximale lorsque la masse sera en haut du rotor. Elle sera minimale lorsqu'elle sera en bas du rotor, et ainsi de suite, à chaque tour du rotor. Il se passe la même chose au point P2. On voit que les efforts exercés sont en phase. Le signal vibratoire a donc une période de 1 tour. Pour trouver la fréquence de ce signal, il faut répondre à la question suivante :

Combien de fois ce signal sera-t-il au maximum en 1 seconde ?

Si on tourne à 1500 tours / minute, le signal sera à son maximum 1500 fois par minute. La fréquence du signal sera :

N

f		r

I.6.7.5. Déséquilibre de couple

Reprenons l'exemple précédent en remplaçant la masse M par 2 masses identiques mais décalées de 180° et placées à chaque extrémité du rotor. L'analyse temporelle des amplitudes du signal vibratoire montre que les signaux en P1 et P2 sont déphasés, En effet, les deux paliers supportant le rotor vont subir des efforts centrifuges de façon alternée. Le déphasage est en théorie de 180°.

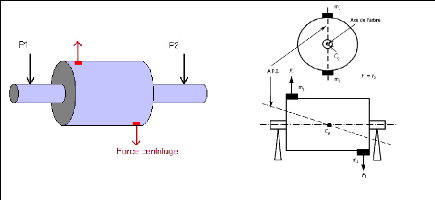
Fig.I.24. Déséquilibre de couple [31] [28]

La différence entre l'équilibre statique et l'équilibre de couple est illustrée à la figure I.25. On peut voir que lorsque le rotor est immobile, les masses d'extrémité s'équilibrent mutuellement. Cependant, lorsqu'il tourne, un fort déséquilibre se produit.

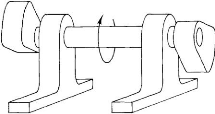
Fig.I.25. Équilibre statique, déséquilibre du couple [28] I.6.7.6. Déséquilibre dynamique

Il est la combinaison d'un déséquilibre statique et d'un déséquilibre de couple et constitue le type de déséquilibre le plus courant dans les rotors. Pour corriger le déséquilibre dynamique, il est nécessaire d'effectuer des mesures de vibrations pendant que la machine est en marche et d'ajouter des masses d'équilibrage dans deux plans.

Fig.I.26. Déséquilibre dynamique [28]

I.7. Conclusion

Dans ce premier chapitre nous avons vu quelques généralités sur les machines asynchrones qui sont largement utilisées dans le domaine industriel en raison de leur fiabilité, leur robustesse, le peu de maintenance qu'elles nécessitent et leur prix. Mais "Rien n'est parfait" comme le dit le psychologue australien Hugh Mackay, pour cela nous avons présenté les principaux défauts qui se produisent dans les machines asynchrones qu'ils soient internes ou externes, ces défauts ont une cause directe ou indirecte de vibrations.

Pour résoudre ces problèmes, il faut réduire les vibrations, dans le Chapitre suivant nous allons discuter l'analyse vibratoire des machines électriques.

CHAPITRE II

l'Analyse Vibratoire, Captures et

Identification des Défauts

II.1. Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 28

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Introduction

Dans ce chapitre nous aborderons à l'analyse vibratoire des machines électriques pour éliminer les causes de vibrations ou bien de développer la robustesse de ces machines. D'autre part, il est bien connu que la correcte maintenance réside dans un bon diagnostic, donc nous allons discuter les différents capteurs de vibrations qui nous aider d'obtenu bien estimation l'état de la machine et découvre l'étendue des dommages au moteur.

II.2. Analyse vibratoire

l'Analyse vibratoire était la boule de cristal de la maintenance dans laquelle un « initié » pourrait identifier tous les futurs dysfonctionnements d'une machine, cela se saurait et les unités de production se disputeraient à prix d'or les faveurs des meilleurs « médiums ». Néanmoins, cette technique, extrêmement puissante lorsqu'elle est utilisée avec des moyens appropriés à chaque problème, en fonction de sa complexité et de son enjeu économique, est un outil devenu aujourd'hui indispensable à tout service Maintenance pour assurer la surveillance efficace de machines dont les pannes ou les marches en dégradé présentent un risque majeur pour la sécurité du personnel, la production ou la qualité du produit fini.[29]

Une machine se compose d'un ensemble de mécanismes et d'organes combinés destinés à transformer une énergie ou à transmettre un mouvement. Ces mécanismes, mobiles entre eux, ne peuvent fonctionner sans jeux, contraintes, efforts dynamiques et chocs dont les effets se manifestent principalement sous forme de vibrations et de bruits. Tout changement dans l'importance de ces jeux, de ces contraintes, efforts ou chocs, se traduit immanquablement par une modification de l'intensité ou des fréquences de ces vibrations. Or, cette modification de comportement vibratoire constitue souvent la première manifestation physique d'une anomalie affectant la machine, cause potentielle à terme de dégradations, voire de pannes.

Cette particularité fait de l'analyse des vibrations un outil d'investigation indispensable à l'assise d'une maintenance moderne. Cet outil occupe une place privilégiée parmi les techniques de surveillance. Il permet, par la génération d'alarmes plus ou moins précoces, de signaler la présence d'un dysfonctionnement, de dépister l'apparition d'une dégradation et d'en suivre la progression, d'éviter une casse ou une dérive de la qualité du produit fabriqué, tout en permettant une action corrective programmée à bon escient au regard des impératifs de production.

La surveillance vibratoire des machines tournantes a sans doute toujours existé avec des moyens empiriques tels le toucher de la main ou l'utilisation de la pièce de monnaie dont l'équilibre sur la tranche garantissait le bon fonctionnement de la machine ou encore avec des

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 29

moyens un peu plus techniques tels le vibromètre à lamelles qui permettaient, dans les cas simples, d'identifier la fréquence de la vibration d'amplitude prépondérante.

Aujourd'hui, la nécessité de communiquer, non plus avec des impressions ou des sensations subjectives, mais avec des données objectives, reproductibles et fiables, a rendu indispensable de quantifier globalement les vibrations d'une machine par une mesure d'amplitude. Le besoin est ensuite rapidement apparu de fixer des seuils à ces valeurs et de connaître les amplitudes et les fréquences des composantes prépondérantes. Enfin, la possibilité de relier les fréquences de chaque composante vibratoire aux différentes forces dynamiques engendrées par le fonctionnement normal ou anormal de la machine et d'en interpréter les évolutions est devenue une réalité avec l'intégration à faible coût, dans les appareils de mesures de vibrations, de convertisseurs analogiques numériques et de coprocesseurs dédiés aux calculs de transformées de Fourier. [29]

Source de vibration

Dispositif de mesure de vibration

Carte d'acquisition

Traitement de signal

Affichage

Fig.II.1. Composants de l'architecture de système de détection de défaut. [30] II.2.1. Définition d'une vibration (selon la norme NFE 90-001)

Une vibration est une variation avec le temps d'une grandeur caractéristique du mouvement ou de la position d'un système mécanique lorsque la grandeur est alternativement plus grande et plus petite qu'une certaine valeur moyenne ou de référence.

Les phénomènes vibratoires sont des phénomènes périodiques ou apériodiques plus ou moins complexes.

II.2.2. Vibration Caractéristiques

Une vibration se caractérise principalement par sa fréquence, son amplitude et sa phase.

a)

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 30

Amplitude : Aide à détecter la sévérité du problème ou du défaut.

b) Fréquence : Aide à indiquer la cause du défaut.

c) Phase : Aide à déterminer la cause du défaut.

On appelle amplitude d'une onde vibratoire la valeur de ses écarts par rapport au point d'équilibre. On peut définir :

? L'amplitude maximale par rapport au point d'équilibre appelée également amplitude crête (Ac).

? L'amplitude double, aussi appelée amplitude crête à crête (Acc) ou « peak to peak » en anglais.

? L'amplitude efficace (Aeff), aussi appelée RMS (Root Mean Square en anglais).

L'amplitude des vibrations peut être mesurée en termes de déplacement, de vitesse et d'accélération. Le déplacement est mesuré de crête à crête et généralement en mils ou microns. La vitesse peut être mesurée en crête ou en valeur efficace et généralement en pouces (inch)/seconde ou en mm/seconde. L'accélération est exprimée en crête et généralement mesurée en g. La phase indique comment une machine se déplace par rapport à une référence de sa partie. La relation entre le mouvement d'une partie d'une machine et une référence - par exemple la position des deux extrémités de l'arbre lorsqu'il tourne.[31]

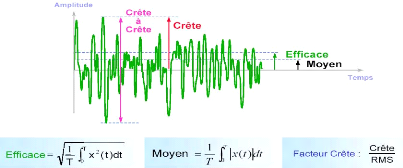
Fig.II.2. Caractéristiques d'un signal vibratoire. [31]

1 Hz = 1 cycle par seconde, Exemple pour un moteur tournant à 1500 tr/mn, la fréquence de rotation est égale à 1500/60=25 Hz

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 31

				??

Sur les machines tournantes industrielles, on utilise souvent le tour par minute pour exprimer une vitesse de rotation, parfois noté CPM (cycle par minute) ou RPM (rotation par minute).

II.2.3. Intérêt du mesurage des vibrations

Le but est évidemment de préserver et prolonger la durée de vie des machines stratégiques.

Pratiquement ces dernières peuvent être affectées par les facteurs suivants :

? Les machines elles-mêmes ne sont pas parfaites :

- Finition insuffisante,

- Jeux de fonctionnement trop importants,

- Mauvais équilibrages qui provoquent des balourds.

? Un mauvais montage :

- Mauvais alignements fréquents,

- Des serrages mal faits, des boulons déforment les pièces,

- Les fondations ne sont pas suffisamment résistantes.

? En marche :

- Les variations de température provoquent des dilatations,

- Les charges conduisent à des torsions, des flexions,

- L'usure accroît les jeux.

II.2.4. Techniques de mesurage

Trois paramètres (reliés entre eux) sont caractéristiques des vibrations : II.2.4.1. Le déplacement

Le Déplacement quantifie l'amplitude maximale du signal vibratoire. Historiquement, c'est la grandeur qui fut utilisée en premier car cette mesure était la seule possible avec les moyens de l'époque. Le Déplacement est inversement proportionnel au carré de la fréquence : Plus la

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 32

fréquence augmente, plus le Déplacement diminue : Son utilisation est réservée aux très basses fréquences : F < 100 Hz

Un signal vibratoire sinusoïdal généré par un balourd simple s'exprimera par la relation :

d(t) = D.sin (2. F. t + (p) (II.2)

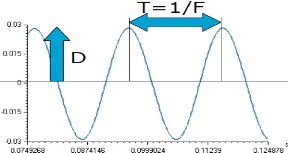
Fig.II.3. Signal sinusoïdal de déplacement [32] L'unité utilisée pour la mesure des déplacements est le micron (um). II.2.4.2. La vitesse

La Vitesse d'un mobile correspond à la variation de sa position par unité de temps. Mathématiquement, la vitesse s'exprime comme la dérivée du déplacement par rapport au temps :

d[d(t)]

d

La Vitesse est inversement proportionnelle à la fréquence : Plus la fréquence augmente, plus la Vitesse diminue : Son utilisation est réservée aux basses fréquences F < 1000 Hz.

Un signal vibratoire sinusoïdal généré par un balourd simple s'exprimera par la relation :

(II.4)

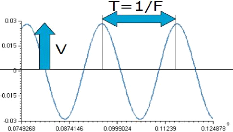
Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 33

Fig.II.4. Signal sinusoïdal de vitesse [32] L'unité utilisée est le mm/s.

II.2.4.3. L'accélération

L'Accélération d'un mobile correspond à la variation de sa vitesse par unité de temps. Mathématiquement, l'accélération s'exprime comme la dérivée de la vitesse par rapport au temps.

d[ v(t)]

d

L'Accélération représentative des forces dynamiques, ne dépend pas de la fréquence : C'est le paramètre privilégié en analyse vibratoire sur un large domaine de fréquences.

0 = F = 20000 Hz

Un signal vibratoire sinusoïdal généré par un balourd simple s'exprimera par la relation :

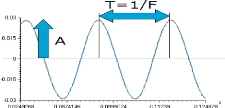
Fig.II.5. Signal sinusoïdal d'accélération [32] L'unité utilisée est le g , 1g = 9.80665 m/s².

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 34

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

II.2.4.4. Relations entre les grandeurs

Il existe une relation mathématique entre les grandeurs comme suit :

D'au :

??

II.3. Captures de vibrations

La première étape conduisant à l'obtention d'une lecture de vibrations consiste à convertir la vibration mécanique produite par une machine en un signal électrique équivalent. Cette opération est réalisée au moyen des capteurs de vibrations. On retrouve parmi les capteurs les plus couramment utilisés le capteur de déplacement, le capteur de vitesse et l'accéléromètre.

II.3.1. Capteur de déplacement

Le capteur de déplacement est un instrument qui produit un signal électrique directement proportionnel au déplacement relatif de la vibration d'un arbre ou d'un rotor. Il est monté en permanence à l'intérieur du palier. Il s'agit d'un capteur "non-contact", c'est-à-dire que le capteur n'entre jamais en contact avec la surface en vibration. Les capteurs de vibrations se divisent en deux catégories caractérisées par le type de mesure à effectuer, mesure de vibration absolue ou bien d'une mesure de vibration relative. Dans le premier cas, le capteur de vibrations est monté en un point quelconque sur la machine (figure II.6 ).[33]

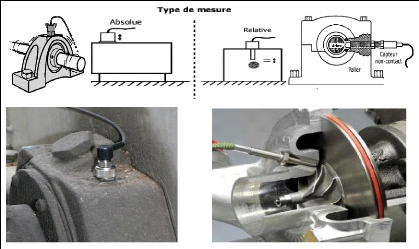
Accéléromètre

Capteur de déplacement

Fig.II.6. Capteurs de vibrations et les types de mesures. [33][34][35][36]

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 35

La mesure effectuée tient alors compte de tous les phénomènes vibratoires transmis par la structure de la machine au point de montage du capteur. Dans le deuxième cas, seule la vibration produite par le mouvement de l'arbre ou du rotor par rapport à une position de référence est mesurée. (figure II.7)

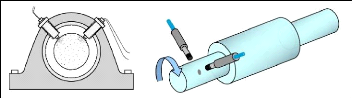
Fig.II.7. Capteur de déplacement pour les paliers lisses. [37] [34]

Le capteur de déplacement est utilisé pour toutes les applications où la surveillance des jeux entre les arbres et les paliers s'avère essentielle. C'est pourquoi l'on retrouve des capteurs de déplacement installés sur la plupart des turbines hydroélectriques et des turbomachines.

II.3.1.1. Principe de fonctionnement

Un oscillateur (appareil qui génère un signal oscillatoire) envoie un signal d'amplitude constante à très haute fréquence au capteur. Le signal, appelé signal porteur, produit un champ magnétique en passant au travers de la petite bobine située à l'extrémité du capteur.

L'arbre situé à proximité absorbe une partie de l'énergie du champ magnétique qui, à son tour, produit une réduction proportionnelle de l'amplitude du signal porteur (modulation).

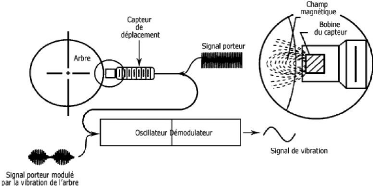
Fig.II.8. Schéma de fonctionnement d'un capteur de déplacement. [33]

Plus l'arbre se rapproche du capteur, plus l'amplitude du signal s'en trouve affectée. La modulation du signal porteur traduit donc l'importance du déplacement relatif de l'arbre par

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 36

rapport au palier. Le signal est ensuite démodulé et la vibration, déplacement de crête- à-crête, est mesurée.

L'unité utilisée est le um (10^-6 m) ou le mils (10^-3 pouce) : 1 mils = 25,4 um.

II.3.1.2. Avantages

Les principaux avantages associés à l'emploi du capteur de déplacement sont :

· la mesure directe du mouvement de l'arbre ;

· l'absence d'usure (aucun élément mobile) ;

· la mesure faite directement en unités de déplacement ;

· le fonctionnement jusqu'à des fréquences extrêmement faibles.

II.3.1.3. Inconvénients

Les principaux désavantages associés à l'emploi du capteur de déplacement sont :

· la mauvaise qualité du signal occasionnée par la présence d'irrégularités à la surface des arbres ;

· l'installation minutieuse requise ;

· la très faible gamme dynamique du capteur (la gamme dynamique est le rapport de l'amplitude la plus élevée à l'amplitude la plus faible qui puisse être mesurée) qui est de l'ordre de 100/1 ;

· la gamme de fréquences limitée du capteur qui n'excède pas en pratique 200 Hz. II.3.2. Capteur de vitesse (Vélocité)

Le capteur de vitesse produit un signal électrique directement proportionnel à la vitesse de la vibration absolue mesurée. On l'utilise pour la surveillance générale des vibrations sur les machines industrielles. Il existe plusieurs types de capteurs de vitesse, par exemple capture à bobine mobile, capture à une sonde photo-électrique et capture à une lumière stroboscopique.

II.3.2.1. Capteur à bobine mobile (Classique)

Pendant de nombreuses années, les seuls types de capteurs de vitesse disponibles pour la surveillance des machines étaient ceux utilisant une conception à bobine mobile.

II.3.2.1.1. Principe de fonctionnement d'un capteur de vitesse à bobine mobile

Ce capteur compose essentiellement d'une bobine supportée par des ressorts et d'un aimant permanent fixé au boîtier du capteur (figure II.9). L'aimant fournit un puissant champ

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 37

magnétique autour de la bobine suspendue. Lorsque le capteur est fixé sur une machine qui vibre, l'aimant permanent suit le mouvement de la vibration pendant que la bobine demeure stationnaire. Dans ces conditions, le mouvement du champ magnétique qui traverse la bobine génère une tension dont l'amplitude est proportionnelle à la vitesse de la vibration. Le signal est ensuite transmis du capteur au mesureur de vibrations.[33]

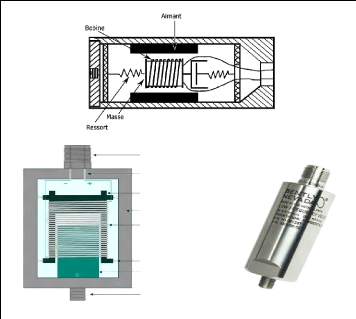
Connecteur

Broches de connecteur

Masse inertielle suspendue (cadre de la bobine)

Boîtier du capteur Bobine

Ressorts de suspension Aimant

Boulon de

Fig.II.9. Capteur de vitesse à bobine mobile [33][38] L'unité utilisée est le mm/s ou pouce/s.

1 po/s = 25,4 mm/s.

II.3.2.1.2. Avantages

Les principaux avantages associés à l'emploi du capteur de vitesse sont :

· un signal électrique de sortie généré sans avoir recours à une source d'alimentation externe ;

· la simplicité de l'instrumentation requise pour la mesure du signal.

II.3.2.1.3. Inconvénients

Les principaux désavantages associés à l'emploi du capteur de vitesse sont :

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 38

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

- l'usure des éléments mobiles,

- la grande dimension du capteur,

- une faible gamme dynamique de l'ordre de 1000/1,

- la sensibilité du capteur aux champs magnétiques,

- la sensibilité du capteur à son orientation,

- la limite élevée dans les basses fréquences (> 10 Hz).

II.3.2.2. Capteur photoélectrique (Moderne)

Les capteurs photoélectriques sont constitués d'un émetteur ou source lumineuse, dont les rayons lumineux sont détectés par un récepteur. La différence de signal lumineux, acquise lors de l'interruption de ce rayon, est transformée en un signal électrique, et est mesurée et utilisée par un circuit électrique. La lumière utilisée est soit infrarouge, soit rouge. En utilisant cette lumière, on peut créer différents types de capteurs photoélectriques. Il existe des modèles de capteurs à réflexion avec réflecteur ou réflexe. Ce type est également équipé d'un émetteur et d'un récepteur proches l'un de l'autre. La réflexion de la lumière émise est acquise à l'aide d'un ou plusieurs réflecteurs.

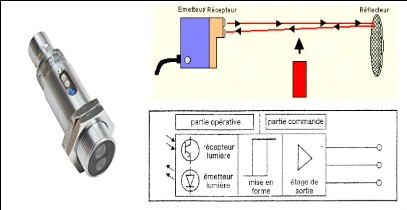
Fig.II.10. Capteur de vitesse photoélectrique [39] [40] [41] II.3.3. Accéléromètre

L'accéléromètre produit un signal électrique directement proportionnel à l'accélération de la vibration absolue mesurée. L'accéléromètre est le type de capteur le plus répandu aujourd'hui pour les mesures de vibrations des machines. Sa conception permet de mesurer efficacement non seulement l'accélération, mais aussi la vitesse et le déplacement (absolue).

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 39

En effet, les instruments de mesure qui utilisent un accéléromètre comportent des circuits électroniques (intégrateurs) permettant de sélectionner le paramètre de vibration requis.

II.3.3.1. Principe de fonctionnement

Le coeur de l'accéléromètre est constitué de petits éléments d'un matériau piézoélectrique. On qualifie un matériau de piézoélectrique quand une déformation du matériau, par compression ou par cisaillement, produit un signal électrique.

La figure suivante vous montre le schéma d'un accéléromètre où une masse est rattachée à chacun des éléments piézoélectriques. Le mouvement vibratoire de la base de l'accéléromètre est transmis à la masse qui agit à son tour sur chaque élément piézoélectrique avec une force égale au produit de la masse par sa propre accélération.

Ceux-ci produisent alors une charge électrique proportionnelle à la force appliquée. Les masses étant constantes, la charge produite par les éléments est également proportionnelle à l'accélération des masses.

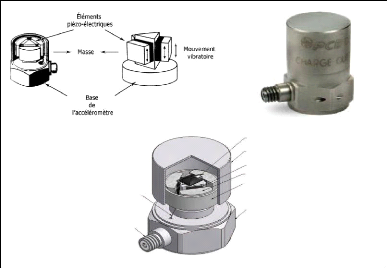
Fil conducteur

Connecteur électrique

Circuit du capteur ICP ®

Couverture

Matériau piézoélectrique Masse séismique

Bague de précharge

Base avec trou de montage taraudé

Fig.II.11. Schéma d'un accéléromètre. [33][35]

Le signal fourni par un accéléromètre possède un niveau si faible qu'il doit passer par un préamplificateur de charge dans le but d'en faciliter la mesure et l'analyse. Le rôle du préamplificateur consiste essentiellement à convertir la charge produite par la déformation des éléments piézoélectriques en un signal de tension équivalente.

L'unité utilisée est le m s^-2 ou le g :

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 40

1 g = 9,81 m/s².

II.3.3.2. Avantages

Les principaux avantages associés à l'emploi d'un accéléromètre sont :

· Une gamme dynamique très grande,

· Une gamme de fréquences très large,

· Un signal électrique de sortie généré sans avoir recours à une source d'alimentation externe,

· L'absence d'éléments mobiles,

· Un montage possible dans n'importe quelle direction,

· Une excellente performance dans les conditions environnementales les plus sévères,

· La faible dimension des capteurs.

II.3.3.3. Inconvénients

Les principaux désavantages associés à l'emploi de l'accéléromètre sont :

· l'impossibilité d'effectuer des mesures à des fréquences extrêmement faibles (< 0,1 Hz),

· le traitement du signal provenant de l'accéléromètre qui requiert une technologie plus sophistiquée, et donc plus dispendieuse, que celles utilisées par les deux autres types de capteurs.

II.3.3.4. Accéléromètre à préamplificateur intégré

Un nombre croissant d'accéléromètres sont équipés aujourd'hui d'un préamplificateur intégré (figure II.12). Ils nécessitent une source d'alimentation externe à courant constant qui est beaucoup plus facile à construire qu'un préamplificateur de charge conventionnel.

Néanmoins, l'électronique intégrée aux accéléromètres restreint les gammes dynamiques et thermiques de ceux-ci. Par exemple, la gamme des températures typiques d'un accéléromètre est de - 70 à 250°C, alors qu'elle est limitée à une plage allant de - 50 à 125°C pour un accéléromètre à préamplificateur intégré.[33]

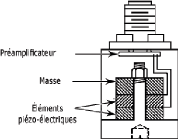
Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 41

Fig.II.12. Schéma d'un accéléromètre à préamplificateur intégré. [33] II.3.3.5. Montage de l'accéléromètre

Dans toutes les mesures de vibration, la qualité et la fiabilité du signal d'entrée ont une importance cruciale. En effet, l'instrument de mesure le plus sophistiqué ne peut pas produire des résultats fiables à partir de données qui ne le sont pas. Aussi, comme la nature des vibrations varie selon le type de défauts rencontrés sur les machines, le capteur de vibrations doit fonctionner dans une gamme très étendue et de façon sûre.

En ce sens, le montage même de l'accéléromètre aura un effet significatif sur le résultat des mesures et c'est pourquoi vous devez y accorder une attention toute particulière.

Le choix de l'emplacement de montage de l'accéléromètre doit être fait en considérant une position qui reflète la direction du phénomène vibratoire visé par la mesure. De plus, l'accéléromètre doit toujours être monté, chaque fois que cela est possible, dans une position qui assure un chemin de transmission court et rigide vers la source des vibrations.

Comme les forces internes d'une machine sont transmises à l'ensemble de la structure par l'entremise des paliers, ceux-ci sont considérés comme de bons emplacements pour le montage d'un accéléromètre.

La figure II.13 montre le schéma d'un palier sur lequel les accéléromètres ont été placés en vue d'assurer un trajet direct aux vibrations provenant du roulement.

L'accéléromètre (A) mesure directement les vibrations radiales du roulement, tandis que l'accéléromètre (B) mesure des vibrations qui sont modifiées par leur transmission à travers un joint superposé aux vibrations des autres composants de la machine. De façon similaire, l'accéléromètre (C) est placé sur un trajet de vibration plus direct que l'accéléromètre (D).

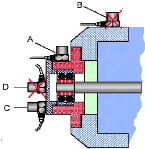
Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 42

Fig.II.13. Positionnement des accéléromètres sur un palier. [34]

Vous aurez compris que les positions B et D ne sont pas recommandées et que le choix entre les positions A et C dépend uniquement de l'objectif visé par la mesure.

Il existe 3 plans de mesure : 1) Radial - V vertical - H horizontal - O oblique 2) Axial A

O

Fig.II.14. Plans de mesure [42]

L'accéléromètre : doit être situé au-dessus du palier d'intérêt. Évitez autant que possible les espaces d'air dans les boîtiers. Les espaces d'air fausseronts les mesures des vibrations.

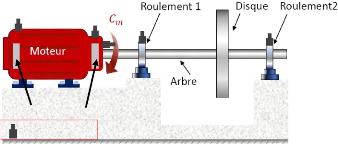
Roulements 3 et 4 interne de moteur

Accéléromètre

Fig.II.15. Les positions de placement d'un accéléromètre [43] II.3.4. Choix du capteur de vibrations

Si les capteurs de déplacement relatif sont tout indiqués pour certaines applications spécifiques de surveillance d'arbres, les capteurs sismiques, sensibles aux vibrations absolues, sont mieux adaptés à la surveillance générale des machines.

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Bien que les capteurs de déplacement relatif aient une gamme de fréquences pouvant aller (théoriquement) jusqu'à 10 000 Hz, ils ne peuvent détecter efficacement que les composantes fréquentielles en basses fréquences. Leur gamme dynamique ne peut habituellement pas couvrir les harmoniques supérieurs de la vitesse de rotation de l'arbre ou du rotor.

Les capteurs sismiques les plus courants sont le capteur de vitesse et l'accéléromètre piézoélectrique. L'accéléromètre est de loin le plus utilisé en raison de sa grande gamme dynamique, de l'étendue de sa gamme fréquentielle, de ses dimensions réduites, de sa fiabilité et de sa robustesse.

En effet, comme beaucoup de situations de surveillance nécessitent un gamme de mesures en fréquences bien supérieures à 1000 Hz et une détection d'amplitudes dans un rapport dépassant largement 1000/1, le choix de l'accéléromètre piézoélectrique s'impose de lui-même.

Une comparaison visuelle de la gamme dynamique et de la gamme de fréquences des capteurs de vibrations vous est montrée à la figure II.16. [33]

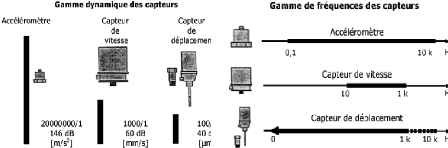
Fig.II.16. Gamme dynamique et gamme de fréquences des capteurs. [33] II.3.5. Influence de la grandeur utilisée

Les capteurs associés transforment la vibration mécanique en un signal électrique : capteur de proximité, capteur de vitesse, accéléromètres. La mesure de déplacement s'effectue à l'aide de capteur de proximité (champs magnétiques) , la mesure de vitesse s'effectue à l'aide de capteur de vitesse (courant induit dans une bobine ; Cette technique est peu utilisée).

Les capteurs de mesure de l'accélération les plus utilisés sont les accéléromètres piézoélectriques. A partir de l'accélération, on peut calculer par intégration successive la vitesse et le déplacement.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 43

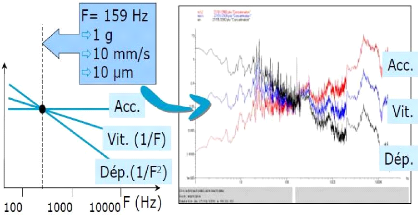
Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 44

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Fig.II.17. Influence de la grandeur utilisée. [32]

II.4. Harmoniques (Ordres)

Les signaux vibratoires sont difficiles à analyser du fait de leur contenu riche en pics.

Cependant un signal périodique complexe peut toujours être décomposé en une somme de signaux sinusoïdaux appelés harmoniques ou ordres.

Le but est de faire apparaître le fondamental et les harmoniques qui ont une fréquence multiple de ce dernier. harmoniques: relation entre une fréquence et la fréquence de rotation.

Exemple : pour 1500 tr/min , donc H= 1500/60 = 25 Hz

Fig.II.18. Harmoniques pour 1500 tr/min. [44]

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 45

II.5. Spectre FFT (Fast Fourier Transform)

L'invention de l'algorithme FFT (transformée de Fourier rapide) au milieu des années 1960 a rendu possible l'analyseur de spectre moderne en temps réel, qui transforme les signaux variant dans le temps du domaine temporel au domaine fréquentiel et fournit ainsi une image actualisée en permanence de la composition fréquentielle d'un signal. Avant l'apparition des analyseurs de spectre FFT, la principale visualisation en temps réel sur place des signaux de vibration se faisait dans leur domaine temporel naturel, généralement à l'aide d'un oscilloscope.

La base mathématique de l'analyse spectrale est l'intégrale de Fourier, qui a été fournie par le mathématicien Joseph Fourier au début des années 1800, bien avant les machines rotatives modernes. Cependant, avant l'algorithme FFT, qui utilise les méthodes de calcul numérique modernes, la transformation d'un signal mesuré dans le domaine temporel en un signal dans le domaine fréquentiel nécessitait un traitement "hors ligne" coûteux et lent. Plus précisément, un enregistrement du signal analogique était traité à travers plusieurs filtres analogiques à bande étroite dont les fréquences de la bande centrale couvraient la gamme de fréquences concernée. Les analyseurs de spectre pré-FFT étaient des équipements électroniques encombrants à utiliser avec succès, nécessitant un technicien expérimenté dans la façon d'accorder et d'ajuster les filtres de largeur de bande pour obtenir des résultats optimaux pour un enregistrement de signal de base de temps donné. Il est compréhensible que l'analyse spectrale pré-FFT ait été très peu utilisée. Les détails mathématiques des séries de Fourier, des intégrales de Fourier et des FFT font désormais partie intégrante de la composante mathématique des programmes universitaires d'ingénierie et sont bien traités dans de nombreux manuels et guides d'analyse mathématique et technique. Dans l'intérêt de l'espace et de la brièveté, ces détails mathématiques ne sont pas couverts ici. Au lieu de cela, une explication plus heuristique de l'analyse spectrale est donnée ici pour aider le praticien de la vibration des machines à comprendre la connexion directe entre un signal de base de temps et son spectre de fréquence.

L'idée pratique sous-jacente de la transformée de Fourier est qu'une fonction (par exemple, un signal de base de temps) peut être construite à partir d'une somme de fonctions sinusoïdales avec une distribution continue de la fréquence de zéro à une fréquence de coupure appropriée.

Pour un signal se répétant périodiquement ou une période définie, une version plus simple et plus restrictive de ceci (la série dite de Fourier) est applicable et additionne les composantes

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 46

sinusoïdales uniquement à un ensemble discret de fréquences qui sont les multiples entiers (n_1, 2, ...) d'une fréquence de base désignée Ù1 = 2ð/t, où t durée d'une période. Bien que les signatures de vibrations de machines ne contiennent souvent qu'un nombre limité de composantes harmoniques significatives, leurs fréquences ne sont souvent pas toutes des multiples entiers d'une seule fréquence de base, et par conséquent la transformée de Fourier, et non la série de Fourier, est l'outil approprié pour cartographier les signaux de vibrations de machines tournantes du domaine temporel au domaine fréquentiel.

La figure II.19 fournit un lien visuel entre une fonction du temps, X(t), et sa transformée de Fourier ou spectre de fréquence. Comme l'illustre la figure, quelques harmoniques additionnées produisent facilement une trace temporelle à partir de laquelle il est difficile de visualiser ou d'identifier directement les composants individuels qui y contribuent. En transformant le signal dans le domaine des fréquences, les composantes contributives sont facilement identifiées.[45]

?

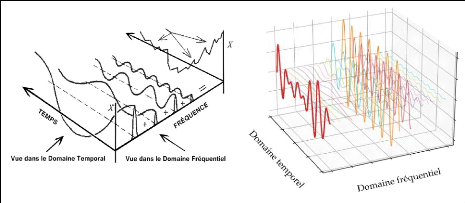
X(t)

Fig.II.19. Illustration temporal-fréquentiel d'un signal oscillant. [45][46] II.6. Tendances et lignes de base en matière de vibrations

Même dans les machines les plus saines, les signaux de vibration surveillés peuvent avoir tendance à migrer en amplitude et en angle de phase, tout en restant dans une "enveloppe" de base de niveaux de vibration acceptables. Ces changements bénins sont des effets normaux des changements des conditions de fonctionnement, par exemple, les transitoires thermiques, les changements de charge, l'usure normale et les fluctuations de l'environnement global de la machine. D'autre part, lorsque les signaux de vibration surveillés

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 47

commencent à augmenter en amplitude au-delà des niveaux de base établis pour une machine donnée, cette tendance doit être suivie attentivement par les opérateurs de l'usine afin d'évaluer en permanence la nécessité potentielle de :

? Modifier temporairement les conditions de fonctionnement de la machine.

? Programmer un arrêt anticipé de la machine pour des actions correctives.

? Procéder à un arrêt immédiat dicté par une augmentation rapide des amplitudes de

vibration.

Lorsque les niveaux de vibration d'une machine commencent à augmenter au-delà des niveaux de base établis, un problème à l'intérieur de la machine commence à émerger et l'augmentation des niveaux de vibration n'est souvent pas le seul symptôme du problème sous-jacent. Une fois que l'attention est portée sur une machine qui commence à montrer une tendance à la hausse des niveaux de vibration, divers outils d'analyse des signaux de vibration sont maintenant couramment utilisés pour chercher à identifier la ou les causes profondes.[45]

II.7. Normes et limites de vibration

La norme la plus largement utilisée comme indicateur de la sévérité des vibrations est la norme ISO 2372. Cette norme peut être utilisée pour déterminer les niveaux de vibration acceptables pour diverses classes de machines. Ainsi, pour utiliser cette norme ISO, il est nécessaire de commencer par classer la machine concernée. En lisant le tableau, nous pouvons établir une corrélation entre la sévérité de l'état de la machine et les vibrations. La norme utilise le paramètre de la vitesse efficace pour indiquer la sévérité. Les numéros 1, 2, 3 et 4, comme le montre (tableau II.1), classent la sévérité [47] :

Classe 1 : Parties individuelles de moteurs et de machines reliées intégralement à une machine complète dans son état normal de fonctionnement (les moteurs électriques de production d'une puissance maximale de 15 kW sont des exemples typiques de machines de cette catégorie).

Classe 2 : Machines de taille moyenne (généralement des moteurs électriques d'une puissance de 15 à 75 kW) sans fondations spéciales, moteurs ou machines montés de manière rigide (jusqu'à 300 kW) sur des fondations spéciales.

Classe 3 : Grands moteurs et autres grandes machines à masses rotatives montés sur des fondations rigides et lourdes, qui sont relativement rigides dans la direction des vibrations.

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 48

Classe 4 : Grands moteurs et autres grandes machines avec des masses rotatives montées sur des fondations, qui sont relativement souples dans la direction de la mesure des vibrations (par exemple - groupes turbogénérateurs, en particulier ceux avec des sous-structures légères).

Tab.II.1. Niveaux vibratoires admissibles sur les machines tournantes [48]

Norme ISO 2372
Niveaux vibratoires admissibles (RMS mm/s)			Classe 1	Classe 2	Classe 3	Classe 4
Amplitude efficace de la Vitesse Vibratoire en RMS dans la [10 ; 1000]	mm/s bande Hz		Mauvais	Mauvais	Mauvais	Mauvais
		18.0				18.0
						Limite
		11.2			11.2
					Limite
		7.1		7.1		7.1
				Limite		Moyen
		4.5	4.5		4.5
			Limite		Moyen
		2.8		2.8		2.8
				Moyen		Bon
		1.8	1.8		1.8
			Moyen		Bon
		1.12		1.12
				Bon
		0.71	0.71
			Bon

II.8. Identification les défauts et leurs vibrations

James E. Berry, P.E., de Associés techniques de Charlotte, N.C., a développé et finement réglée un "tableau mural illustré de diagnostic des vibrations" en anglais , mesurant 38 pouces de haut sur 54 pouces de large. Ce tableau est un outil très polyvalent pour une analyse précise des vibrations dans le cadre d'un programme structuré de maintenance conditionnelle [49] (Annexe) Il a été reproduit en français par GROUPE IMPEDANCE - MACHINES à Paris[50] (Annexe), le tableau affiche des spectres de vibrations typiques qui aident à déterminer l'état de fonctionnement des machines tournantes.

Il convient de noter que le tableau mural de diagnostic des vibrations de Associés techniques (Annexe) comprend des éléments clés tels que :

- Des illustrations de spectres de vibrations typiques ;

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

Chapitre II l'Analyse Vibratoire, Captures et Identification des Défauts

- Des remarques élaborant les symptômes qui accompagnent normalement chacun des 44 problèmes de machine couverts.

- Des dessins illustrant la façon dont la phase réagit lorsque ces problèmes sont prédominants.

Tab.II.2. Les fréquences des vibrations et leurs causes probables [50]

Fréquence en termes de RPM (X)	Cause les plus probables	Autres causes possibles et remarques
1 X rpm	Déséquilibre	1) Tourillons, engrenages ou poulies excentriques. 2) Mauvais alignement ou arbre tordu - si vibration axiale élevée 3) Courroies défectueuses si le régime de la courroie est élevé. 4) Résonance 5) Forces réciproques 6) Problèmes électriques
2 X rpm	Desserrage Mécanique	1) Mauvais alignement si vibrations axiales élevées 2) Forces réciproques 3) Résonance 4) Mauvaises courroies si 2 X rpm de courroie
3 X rpm	Désalignement	En général, est une combinaison de désalignement et de jeux axiale excessifs (desserrage).
Moins de 1 X rpm	Tourillon d'huile (Moins de 1/2 RPM)	1) Mauvaises courroies d'entraînement 2) Vibrations de fond 3) Résonance subharmonique 4) Vibration du "siège"
Synchrone (fréquence de ligne C.A.)	Problèmes électriques	Les problèmes électriquesLI courants comprennent les barres de rotor cassées, le rotor excentrique, les phases déséquilibrées dans les systèmes polyphasés, l'entrefer inégal.
2 X Fréquence de Synch.	Impulsions de couple	Rarement un problème à moins que la résonance est excitée
Plusieurs fois rpm (Fréquence Harmoniquement Reliée)	Mauvais engrenages Forces aérodynamiques Forces hydrauliques Mauvais serrage mécanique ForcesLIréciproque s	Nombre de dents de l'engrenage par rapport au régime de l'engrenage défectueux Nombre de pales du ventilateur par rapport au nombre de tours/minute Nombre d'aubes de la roue multiplié par le nombre de tours/minute Peut se produire à 2, 3, 4 harmoniques et parfois plus si desserrage important
Haute fréquence (non		1) La vibration du roulement peut être instable amplitude et

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 49

liée à l'harmonique)	Mauvais	fréquence.
	antifriction	2) La cavitation, la recirculation et la turbulence du flux
Roulements	provoquent des vibrations aléatoires à haute fréquence.
	3) Lubrification inadéquate des paliers lisses (vibration par frottement)
	4) Frottement

Tab.II.3. Identification des vibrations [50]

Cause	Amplitude	Fréquence	Phase	Remarques
Déséquilibre	Proportionnel au déséqui- libre. Le plus grand dans le sens radiale.	1 x rpm	Marque de référence unique.	Cause la plus fréquente de vibration.
Désalignement des accouplements ou des roulements et arbre tordu.	Large dans le sens axial direction axiale 50 % ou plus de vibrations radiales	1 x rpm habituel 2 et 3 x rpm parfois	Simple double ou triple	La meilleure façon de le découvrir est d'observer une vibration axiale importante. Utilisez des indicateurs à cadran ou une autre méthode pour un diagnostic positif. Si la machine est équipée de paliers lisses et qu'il n'y a pas de désalignement de l'accoup- lement équilibrez le rotor.
Mauvais roulements de type anti-friction	Instable - utiliser la mesure de la vitesse si possible	Très élevé plusieurs fois rpm	Erratique	Le roulement responsable est probablement celui qui est le plus proche du point de la plus grande vibration haute fréquence
Tourillons excentriques	Généralement pas grand	1 x rpm	Marque unique	Si sur des engrenages, la vibration la plus importante se situe dans l'axe des engrenages. Si sur un moteur ou un géné- rateur, la vibration disparaît lorsque l'alimentation est coupée. Si sur une pompe ou un ventilateur, essayer d'équilibrer.
Mauvais engrenages ou bruit d'engrenages	Faible - utiliser la mesure de la vitesse si possible	Nombre de dents de l'engrenage très élevé par rapport au nombre de tours/minute	Erratique
Desserrage		2 x rpm	Deux marques	Généralement accompagné d'un

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 50

mécanique			de référence. Légèrement erratique.	déséquilibre et/ou d'un désalignement.
Courroies d'entraînement défectueuses	Erratique ou pulsation	1,2,3, & 4 x rpm de courroies	Un ou deux selon la fréquence de la fréquence. Généralement instables.	La lumière stroboscopique est le meilleur outil pour figer une courroie défectueuse.
Électrique	Disparaît lorsque l'alimentation est coupée.	1 x rpm ou 1 ou 2 x fréquence synchrone fréquence.	Marque simple ou double rotative.	Si l'amplitude de la vibration chute instantanément lorsque l'alimentation est coupée la cause est électrique.
Aérodynamique hydraulique forces hydrauliques aérodynamiques		1 x rpm ou nombre de pales sur le ventilateur ou roue x rpm		Rare comme cause de troubles, sauf en cas de résonance.
Réciproque forces		1 x 2 et ordres supérieurs x rpm		Inhérents aux machines à mouvement alternatif, ils ne peuvent être réduits qu'en modifiant la conception ou en les isolant. modification de la conception ou l'isolation.

II.9. Conclusion

Dans ce chapitre, nous avons présenté les différentes grandeurs qui peuvent aider de contrôler et surveiller en permanence les machines en service. Nous avons aussi discuté sur la vibration et son influence sur l'activité des machines et comment observé ce phénomène avec les différents capteurs.

Après avoir collecté ces informations autours les moteurs asynchrone et les différents défauts de vibrations et les capteurs à travers les deux chapitres précédents, maintenant on peut de étudier un cas réelle d'un problème de vibration d'un machine électrique ou bien de simuler sur un banc d'essai, ce qui fera l'objet du dernier chapitre.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 51

CHAPITRE III

Contrôle et Equilibrage d'un Défaut

de Balourd sur un Banc d'Essai

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 53

III.1. Introduction

L'équilibrage est le procédé par lequel on tente d'améliorer la répartition de la masse d'un rotor de façon que le rotor tourne dans ses paliers sans créer de forces centrifuges non compensées. L'équilibrage des rotors contribue à prolonger la durée de vie des équipements. Il peut être réalisé sur une machine à équilibrer (fixe, équilibrage en atelier) ou encore à l'aide d'un analyseur de vibrations (portatif, équilibrage sur site).

Dans ce chapitre, nous allons simuler un problème de balourd sur un banc d'essai et apprendre à résoudre ce problème. Enfin, interprétons les résultats.

III.2. Importance de l'équilibrage

Les vibrations produites par un rotor déséquilibré créent une surcharge sur les paliers et sur la structure de la machine en général. L'équilibrage du rotor s'avère nécessaire pour éviter une ou plusieurs des situations suivantes

· Une diminution de la vie utile de la machine, de la durée de vie des roulements et de l'intégrité de la structure.

· Un accroissement de la fréquence des entretiens requis par la machine.

· Une production de moins bonne qualité par les équipements tels que les machines-outils et les rectifieuses, les machines à papier, les laminoirs, etc.

· Une détérioration de la qualité de vie au travail en ce qui a trait au bruit, à la sécurité et au confort (vibrations transmises au corps par le plancher par exemple).

L'équilibrage ne doit surtout pas se limiter aux seules machines dont la condition de déséquilibre est telle qu'il y a imminence de bris. [51]

III.3. Technique de la réparation

L'organisation internationale de normalisation (ISO) (1973) a publié des documents sur la classification des rotors et la qualité de l'équilibre des corps rigides en rotation, qui sont également abordés par Rieger (1986).

Les rotors peuvent être classés en systèmes rigides ou flexibles en fonction de leur comportement dynamique aux vitesses de fonctionnement. La classification d'un rotor peut être facilement déterminée en effectuant une analyse de la vitesse critique du système. Si la déformation ou l'énergie potentielle dans les roulements représente plus de 80 % de l'énergie de déformation totale du système, le rotor peut être classé comme rigide. Un rotor à corps rigide est un rotor qui peut être équilibré dans deux plans arbitraires. Le rotor semble maintenir l'équilibre dans toute sa gamme de vitesse de fonctionnement.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 54

D'autre part, si l'énergie de déformation de l'arbre commence à dépasser 20 % de l'énergie de déformation du système et que le rotor fonctionne à une ou plusieurs vitesses critiques, il peut être considéré comme un rotor flexible ou quasi-flexible. Dans ces circonstances, un équilibre du corps rigide à deux plans peut ne pas être adéquat, et des poids de compensation supplémentaires peuvent devoir être placés le long de l'arbre pour minimiser l'amplitude des vibrations à la vitesse.

Un rotor rigide est un rotor dont la vitesse de service est inférieure à 50% de sa première vitesse critique. Au-dessus de cette vitesse, le rotor est dit flexible. Un rotor rigide peut être équilibré en effectuant des corrections dans deux plans quelconques choisis arbitrairement. La procédure d'équilibrage des rotors flexibles est plus compliquée, en raison des déviations élastiques du rotor.[28] , par exemple .cas d'un rotor classe 2, 3,4 ou 5 :

Marge de séparation

Amplitude de vibration

1ère vitesse

qe

Généralement 10 % ou plus

2ème vitesse critique

Vitesse de
fonctionnement

Fig.III.1. Analyse d'ordre (résonance) de démarrage d'un rotor classe 2, 3, 4 ou 5

[42]

L'ISO a classé les rotors afin de décrire le type et la qualité de l'équilibrage nécessaire pour chaque cas particulier. Cinq classifications de base sont présentées par l'ISO [52] :

Classe 1 : Rotors rigides : Elle couvre 90% de toutes les applications [26] .Ces rotors peuvent être équilibrés dans deux plans axiaux arbitraires et resteront équilibrés dans toute la gamme des vitesses de fonctionnement.

Classe 2 : Rotors quasi-flexibles : Ces rotors ne sont pas parfaitement rigides mais peuvent être équilibrés de manière adéquate dans une machine à équilibrer à basse vitesse et conserveront un fonctionnement régulier dans toute la gamme de vitesses.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 55

Peuvent être équilibrés à l'aide d'une technique d'équilibrage modifiée (le choix des plans de correction est ici essentiel).[26]

Classe 3 : Rotors flexibles : Ces rotors ne peuvent pas être équilibrés dans une machine à équilibrer à basse vitesse et nécessitent une ou plusieurs corrections du plan de compensation à haute vitesse.

Classe 4 : Rotors à fixation flexible : Ces rotors peuvent être classés dans la classe 1, la classe 2 ,ou la classe 3 : rotors mais ont des composants en eux-mêmes ou attachés de manière flexible.

Classe 5 : Rotors flexibles à une vitesse : Ces rotors peuvent être classés comme les rotors flexibles de classe 3 mais sont équilibrés pour fonctionner à une seule vitesse.

III.4. L'équilibrage (La correction)

Pour régler l'équilibreuse. Une fois l'équilibreur réglé, le rotor est chargé et mesuré. Lorsqu'il n'est pas dans la tolérance, nous devons effectuer une correction. Jusqu'à présent, le processus a été simple, la machine est conçue de cette façon.

La correction est souvent difficile à réaliser. Les concepteurs ne prennent pas toujours des dispositions (adéquates) pour corriger les déséquilibres lors de la conception des rotors. Parfois, il n'y a aucun moyen d'enlever ou d'ajouter suffisamment de matériau, le matériau disponible ne se trouve pas dans des zones efficaces (petit rayon, proches les unes des autres, non séparées du centre de masse) ou le problème réside dans la précision nécessaire à l'enlèvement de la masse - par exemple, dans le cas d'un meulage à main levée, où la compétence de l'opérateur est essentielle pour une opération efficace sans endommager les pièces, la correction du déséquilibre est un domaine où la variabilité est immense. Les corrections peuvent ne représenter que quelques milligrammes sur un petit rotor à grande vitesse ou plusieurs kilogrammes sur une grande hélice de navire. L'équilibrage a souvent lieu sur des assemblages presque finis et l'apparence après l'équilibrage est importante. Le débit de production peut signifier qu'il ne reste que quelques secondes pour effectuer la correction. Dans de nombreux cas, un système d'équilibrage de production peut impliquer une ligne de transfert multiposte.

Afin d'obtenir une correction efficace du déséquilibre, nous devons décomposer le problème en une série de petites décisions. Il n'existe que trois choix pour la correction [26] :

Choix n° 1 - Ajouter de la masse -

Boulonner un bloc, ajouter une vis, ajouter une rondelle sous une vis, mélanger du mastic époxy et l'appliquer ou souder un bloc en place. Attention : obstruction qui empêchera le rotor

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 56

de tourner. Assurez-vous que le poids ne peut pas s'envoler et n'affaiblissez pas le rotor en perçant et en taraudant un trou pour appliquer un poids.

Choix n° 2 - Enlever la masse -

Percez, fraisez, rectifiez, enlevez le poids d'équilibre (peut-être une rondelle sous un boulon). Il faut faire attention à : couper trop profondément, affaiblir une partie du rotor qui pourrait se déformer à la vitesse de fonctionnement, endommager les enroulements de l'armature et laisser des copeaux sur les tourillons qui pourraient endommager la machine ou le rotor lors de la prochaine mesure.

Choix n° 3 - Redistribuer la masse -

Bagues asymétriques qui tournent, variation de la longueur des boulons maintenant la poulie sur l'arbre, rotation de la poulie sur l'arbre ou ouverture d'un alésage sous-dimensionné avec un décalage radial pour corriger le déséquilibre (centrage de la masse). Attention au serrage excessif des pièces réglables, à un décalage trop important des excentriques (limite la précision) ou à un décalage trop faible (limite la correction maximale).

Il est essentiel de s'assurer que les pièces réglables ne bougent pas en service, car cela peut entraîner un déséquilibre important ou un contact avec des composants non rotatifs, avec des résultats catastrophiques.

En examinant un rotor spécifique, nous décidons d'abord lequel des trois choix est le plus approprié. Dans le cadre de ce choix, nous décomposons ensuite les options et examinons les volumes de production. Parmi les autres considérations, citons l'entretien et la sécurité.

Si l'enlèvement de matière est utilisé, il se peut que des copeaux doivent être aspirés. Avec n'importe quel outil de coupe, il est nécessaire d'utiliser des protections pour protéger l'opérateur.

III.4.1. Types d'équilibrage

Il y a plusieurs types d'équilibrage lié au les plans de balourd :

1) Équilibrage 1 ou 2 plans des structures rigides:

-Équilibrage 1 plan (dit statique): équilibrage des forces de translation -Équilibrage 2 plans (dit dynamique): équilibrage des moments de rotation.

2) Équilibrage multi-plans des structures flexibles: on ajoute 1 plan par fréquence de résonance inférieure à la fréquence de rotation.[53]

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 57

III.5. Logiciel VIB360 STUDIO

Ce logiciel est utilisé dans laboratoire de de l'unité de vibration dans l'entreprise de DML pour l'analyse vibratoire des machines tournants. Les utiles de l'analyseur diagnostic vibratoire & gestion des mesures et comme suite :

-Gestion des résultats et sauvegarde des signaux temporels longs dans une base de données. -Automatisation et personnalisation des analyses, aide à l'interprétation directe.

-Traçabilité, généralisation des possibilités de contrôle et de modification.

-Installation sur PC Windows permettant l'acquisition, l'analyse, la gestion et l'édition. III.5.1. Représentation « objets »

Un organigramme permet l'organisation des points de mesure suivant la structure de l'objet étudié, cette structure est représentée par deux fenêtres interactives

- Sous forme d'organigramme. - Sous forme de tableau.

L'organigramme peut être facilement modifié et étendu grâce aux fonctions copié, collé, glissé, renommé, changé de niveau même après chargement des données.

La création d'une nouvelle étude crée automatiquement les fichiers nécessaires pour les données, la structure, et les rapports édités. [54]

III.5.2. La base de données

Avec une interface permet d'accéder rapidement aux informations, de sécuriser l'administration, et d'échanger des données standardisées (norme MIMOSA). Les signaux peuvent être enregistrées directement depuis le R (pilotage du PC pilotage de carte d'acquisition) ou transférés depuis tout système d'acquisition (formats. Bin ou. Wav). Les signaux temporels et les conditions d'essai sont archivés et attachés à chaque point de mesure. Les paramètres sont choisis dons un menu ; des voleurs particuliers peuvent être créés à la demande.

L'historique des mesures et des analyses est conservé pour l'étude de l'évolution et assurer la traçabilité des opérations. Il est toujours possible de corriger les paramètres, de modifier les analyses et même de créer une nouvelle série.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 58

Fig.III.2. Interface d'objets de la base de données

III.5.3. Les analyse

Elles sont programmées par l'utilisateur, individuellement ou par groupe de points de mesure. Il est toujours possible de visualiser le signal, d'en explorer les propriétés directement et de choisir les zones sur lesquelles on fait porter les analyses. Une large gamme d'outils d'analyse paramétrables et sauvegardée individuellement est intégrée au logiciel [54] :

- FFT (bandes fines et bandes l / l et 1 / 3 d'octaves, Zoom)

- Démodulation d'amplitude, phase, fréquence

- Enveloppe,

- Cepstre,

- Calcul d'orbite,

- Filtre de Gilbert, Filtre temporel Iong.

- GDE (diagnostic des engrènements)

- Fonction de transfert

- Kurtosis, Crête par bandes

- Toute fonction mathématique

Selon la sélection par cases à cocher, les points de mesure peuvent être affectés des mêmes analyses qui peuvent être traitées en même temps. Les graphes d'analyse peuvent toujours être associés à un tableau d'identitcation des pics, de visualisation des harmoniques etc. Le graphisme est paramétrable.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 59

Fig.III.3. Interface des signaux et analyses.

Fig.III.4. Analyseur de spectre FFT

III.6. Simulation un défaut du balourd sur kit simulateur

On faits des essais pour apprendre les effets d'un balourd sur notre kit-simulateur (figure III.4). Ce kit simulateur est une machine de classe 1 car la puissance qui demande est inférieure à 15 KW et considérant la taille. Le kit simule quelques défauts qui se produisent dans les machines asynchrones et toutes les machines tournantes.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Boîtier de contrôle

Moteur de lancement

Courroie

Accéléromètre

Accouplements

Roulements

Disque

Capteur de vitesse

Fig.III.5. Kit simulateur des défauts au laboratoire de l'unité de vibration DML
(SONATRACH - Laghouat 2022)

Th. Zürrer CH 8055 Zürich

Type : E P V 65 TG

190 V	E1 E2	160 V		A1 A2
0.13 A		2.0 A
220 W			4000 tr/min

Nbr S : 480262

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 60

Fig.III.6. Plaque Signalétique du moteur de lancement.

Les différents capteurs (accéléromètre et capteur de vitesse) sont connectés sur l'ordinateur à partir la carte d'acquisition.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 61

Fig.III.7. Carte d'acquisition.

La mesure de la phase, essentielle pour localiser la "partie lourde" dans le rotor à équilibrer, requiert l'emploi d'un capteur tachymétrique. Le capteur tachymétrique, monté à une distance appropriée de la surface du rotor.

Les figures suivantes montrent le montage de l'accéléromètre et de la sonde photoélectrique de même que celui d'une bande réfléchissante fixée sur le rotor. Le passage de la bande réfléchissante déclenche la sonde photo-électrique une fois par tour et une impulsion est envoyée à l'analyseur de vibrations.

Fig.III.8. Capteur de vitesse (photoélectrique).

La mesure de l'amplitude vibratoire, proportionnelle à la force produite par le balourd, requiert l'emploi d'un accéléromètre monté sur le palier du roulement.

Fig.III.9. Un accéléromètre (piézoélectrique)

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

D = 100 mm

Point de
référence (0°) de
l'accéléromètre
( le même
référence
d'équilibrage )

Boulon pour
crée un
balourd

M = 1.2 kg

Ruban adhésif
réfléchissent

comme un point

de référence pour
le capteur de

vitesse

Fig.III.10. Création d'un balourd.

Mesure le poids de boulon pour créer le balourd, poids de boulon est 1.7g.

Fig.III.11. La masse de boulon. III.6.1. Procédure d'équilibrage

Le boulon à crée le balourd, pour équilibrer le rotor, nous devons placer une masse de correction d'une certaine grosseur à un endroit où elle annule le balourd du rotor, c'est-à-dire en un point qui lui est diamétralement opposé. Pour ce faire, il faut déterminer la valeur et la position de la masse de correction.

III.6.1.1. Lancement 1 : Analyse d'ordre et analyse spectral (FFT) de balourd initial

Analyse d'ordre : Avec un démarrage monté en vitesse pour voir les ordres dominants (0-3000 tr/min).

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 62

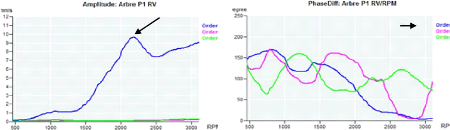
Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Fig.III.12. Trends de démarrage Amplitude / Phase.

La vitesse de service 3000 tr/min, en observe qui la première vitesse critique et 2200 tr/min.

- Le rotor est dans la classe 2 (quasi-flexible), Parce que la vitesse de fonctionnement du rotor au-dessus de sa première vitesse critique.

- Ordre 1 dominant et la rotation de la phase 180° au 0° explique clairement un problème du balourd.

La procédure d'équilibrage consiste d'abord à mesurer la vibration causée par le déséquilibre du rotor.

Analyses spectral (FFT) : à vitesse de fonctionnement de 3091 RPM (51,52 Hz)

On choisit 3000 RPM comme vitesse de fonctionnement, pour préserver les composants de l'émulateur car ils sont anciens (moteur, courroie).

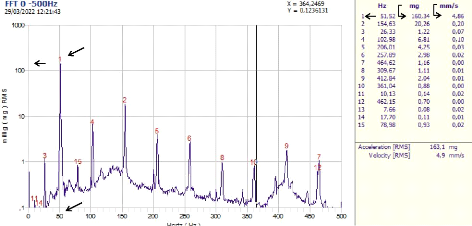
Fig.III.13. Signal FFT d'un capteur accéléromètre position vertical.

On prendre cette révèle d'un problème de balourd signifier par la présence 1X=51.52 Hz (3091 RPM) d'amplitude d'accélération de AA0 = 160.34 mg avec une amplitude de vitesse de la vibration absolue mesurée _AV0= 4,86mm/s.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 63

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Un rotor déséquilibré : Le déphasage entre un capteur position vertical et horizontal doit être #177; (90° --> 30°)

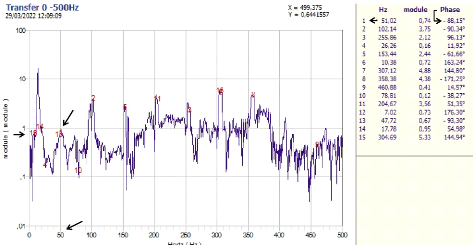
Fig.III.14. Signal indique un déphasage entre le capteur vertical et le capteur horizontal

Le déphasage indiqué entre le capteur vertical et le capteur horizontal est de - 88.15°.

Fig.III.15. Signal indique un balourd initial avec un phase ö0 = 0,20°

Donc, le balourd initial d'amplitude _AV0= 4,86 mm/s avec un angle ö0 = 0,20 ° de phase du signal vibratoire par rapport à l'impulsion du capteur vitesse.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 64

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 65

III.6.1.2. Lancement 2 : Avec une masse d'essai III.6.1.2.1. Choix d'une masse d'essai

Les calculs de correction du déséquilibre sont basés sur les changements que produit la masse d'essai sur l'état initial du rotor. Il est donc important de choisir une masse qui permette d'obtenir de bons résultats. Un sélectionnent d'une masse trop petite ne donne aucun changement d'amplitude ou de phase, par ailleurs le sélectionnent d'une masse trop grande peut endommager la machine.

La valeur du balourd résiduel admissible _Uadm peut servir à donner une valeur appropriée de la masse d'essai mess.

Le balourd résiduel admissible Uadm est obtenu en multipliant le balourd spécifique eadm par la masse du rotor M, soit :

??

On trouve le balourd spécifique _eadm à l'aide de l'abaque ISO 1940 (Annexe) en fonction du degré de qualité d'équilibrage requis et de la vitesse maximale de fonctionnement du rotor.

On choisit la vitesse de fonctionnement (rotation ou service) Nr = 3000 RPM comme point dans l'axe X et on dépose-le sur la line de classe de rotor G (dans notre cas G 6.3), L'intersection à partir de laquelle on obtient le point _eadm dans l'axe Y. On trouve que :

?? ?? ??

Donc :

??

La norme ISO 1940 recommande de choisir une masse d'essai équivalente à 5 à 10 fois la masse équivalente m_r le balourd résiduel admissible Uadm . On peut convertir le balourd résiduel Uadm en une masse équivalente (appelée aussi une masse résiduelle m_r), Pour obtenir la masse résiduelle m_r nous divisons le balourd résiduel Uadm par le rayon de correction Rc, soit la distance entre l'axe de l'arbre et l'emplacement de la masse la masse de correction. Sur de nombreux rotors, le rayon de correction Rc et le rayon _Ress de pose de la masse d'essai sont identiques. Par conséquent :

??

?? (III.2)

?? ?? (III.3)

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 66

Avec les unités suivantes :

eadm : (g · mm/kg)

M : (kg)

Ress : (mm)

m_r : (g)

mess : (g)

Il arrive que la masse d'essai calculée de cette façon soit trop petite. Toutefois, il vaut mieux avoir une masse d'essai trop faible plutôt que de risquer d'endommager le rotor. Avec l'expérience, nous en viendrons à estimer la masse d'essai adéquate.

Après avoir établi l'état initial du rotor sous la forme des valeurs AV0 et ö0, on placer une masse d'essai connue sur le rotor. La masse d'essai a pour effet de modifier l'amplitude et l'angle de phase de la vibration. On obtient alors les mesures suivantes : AV1 et ö1, soit l'amplitude et la phase de la vibration avec la masse d'essai.

On choisit une masse d'essai mess=1,6 g selon l'expérience de l'ingénieur et sans calcule, parce que nous connaissons déjà la masse du boulon qui a créé le balourd. La masse d'essai situé à öess = 0° (le lieu de la masse d'essai est comme un référence d'équilibrage).

Mesure le poids de la masse d'essai, mess =1.6g.

Fig.III.16. Poids de la masse d'essai.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyses spectral (FFT) : A vitesse de fonctionnement de 3122.4 RPM (52.04 Hz)

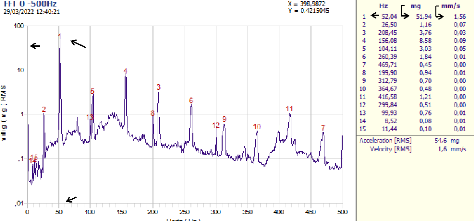
Fig.III.17. Signal FFT d'un capteur accéléromètre position vertical

Le capteur accéléromètre position vertical révèle un problème de balourd signifier par la présence 1X=52.04 Hz (3122.4 RPM) d'amplitude d'accélération de AA1 =51.94 mg avec une amplitude de vitesse de la vibration absolue mesurée AV1= 1,56 mm/s.

Fig.III.18. Signal indique un balourd résultant avec un phase ö1 = - 8,77 °

Donc, le balourd résultant (après avoir ajouté une masse d'essai) est d'amplitude AV1=1,56 mm/s avec une phase ö1 = - 8,77 °.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 67

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 68

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

III.6.1.3. Lancement 3 : Avec une masse de correction

L'étape suivante consiste à calculer la masse et l'angle de correction requis. Il existe deux méthodes pour trouver ces valeurs : par le tracé d'un diagramme vectoriel ou par le recours à un programme d'équilibrage.

III.6.1.3.1 Par méthode graphique ( Diagramme vectoriel )

La méthode par le tracé d'un diagramme vectoriel a l'avantage de visualiser les forces en jeu. Elle peut aussi d'aider à mieux comprendre comment on parvient à réaliser la correction du balourd dans un rotor déséquilibré.

Les mesures sont effectuées :

- AV0= 4,86mm/s et ö , °, soit l'amplitude et l'angle de phase du balourd initial.

- AV1= 1,56 mm/s et ö - 8,77 °, soit l'amplitude et l'angle de phase du balourd avec la

masse d'essai.

On déterminer les valeurs de la masse et de l'angle de correction en représentant d'abord les mesures sous la forme de vecteur. Le diagramme vectoriel des valeurs mesure, montré à la figure III.22, est construit selon la procédure suivante :

1. Traçage de vecteur V0 représentant le balourd initial. La longueur de V0 est égale à l'amplitude AV0 et sa direction est donnée par l'angle de phase ö0 (figure III.19).

2. Traçage d'autre vecteur V1 représentant le balourd résultant (amplitude AV1 et

angle de phase ö1) mesuré avec la masse d'essai (Fig.III.19).

V1= AV1(cos(ö1) + j*sin(ö1))

Application numérique:

V1=1,56 (cos(- 8,77) + j x sin(- 8,77)) =1.5418 - 0.2379i

3. Traçage de vecteur de la pointe de V0 à celle de V1 en prenant soin de lui donner la direction indiquée (figure III.19). Le nouveau vecteur V_e représente la contribution de la masse d'essai seule sur la nouvelle condition de déséquilibre du rotor.

Application numérique:

Ve=V1-V0 = (1.5418 - 0.2379i ) - (4.8600 + 0.0170i) = -3.3182 - 0.2549i

Ve = C(1.5418 , 0.2379) - B(4.8600 , 0.0170 )

Cette information permet de localiser avec précision la position de la masse de déséquilibre à l'origine du balourd initial et de calculer la masse de correction nécessaire pour l'éliminer sinon pour le réduire à une valeur acceptable.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 69

Les valeurs mesurées étant représentées sur le diagramme vectoriel, les calculs, se font comme suit :

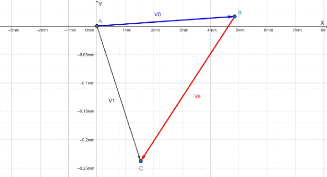
Fig.III.19. Diagramme vectoriel de V0, V1 et Ve pour l'unité : 1mm x = 0.05 mm y
[S. Kouidri et K. Ghris]

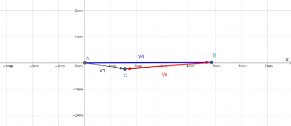
Fig.III.20. Diagramme vectoriel de V0, V1 et Ve pour l'unité : 1mm x = 1 mm y

[S. Kouidri et K. Ghris]

1. Traçage de nouveau vecteur Ve' parallèle au vecteur V_e' existant, suivant la même direction mais à partir de l'origine. (Figure III.21).

Application numérique:

Ve'= Ve' = -3.3182 - 0.2549i = E(-3.3182 , 0.2549 ) - A(0, 0 )

2. On reproduirons le vecteur V0 de l'autre côté de l'origine mais dans une direction opposée. Le nouveau vecteur appelé V_c représente la position et la valeur du balourd nécessaires pour annuler le balourd initial V0 et ainsi équilibrer le rotor (figure III.21).

Application numérique:

V_c = - V0 = - (4.8600 + 0.0170i) = - 4.8600 - 0.0170i

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 70

Fig.III.21. Diagramme vectoriel de V0 , V1 , Ve , Ve' et Vc pour l'unité : 1 mm

x=0,05mm y [S. Kouidri et K. Ghris]

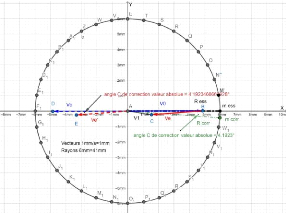
Fig.III.22. Diagramme vectoriel de V0 , V1 , Ve , Ve' et Vc pour l'unité : 1 mm

x=1mmy [S. Kouidri et K. Ghris]

Note : les figures III.19 - III.22 crée et disponible sur internet [55]

Connaissant l'effet de la masse d'essai, l'étape suivante consiste à augmenter ou à réduire cette masse de façon à la rendre égale au balourd et au besoin, à la déplacer angulairement jusqu'à ce qu'elle soit diamétralement opposée au balourd. Ce calcul, normalement fait au moyen d'un programme d'équilibrage ou d'un diagramme vectoriel, on donne la valeur m_c de la masse de correction et l'angle de correction c :

' g (III.6)

- '

° (III.7)

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 71

On place la masse de correction à la position indiquée par l'angle de correction. Un angle de correction positif indique que l'angle doit être mesuré dans le sens de la rotation. Pour un angle de correction négatif, l'angle doit être mesuré dans le sens inverse de la rotation. La masse de correction doit être montée au même rayon que la masse d'essai.

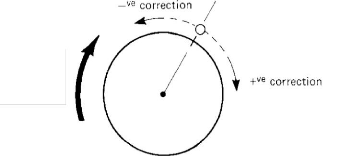
Position de la masse d'essai

Direction de rotation

Fig.III.23. Détermination de la position de la masse de correction [28] III.6.1.3.2 Par méthode numérique ( Un logiciel )

Maintenant, nous allons montrer les résultats d'équilibrage à l'aide d'un logiciel de calcule d'équilibrage.

Fig.III.24. Interface de logiciel d'équilibrage

On déplacer la masse d'essai et placer une masse de correction mc= 2,4 g a situé à öc = -4 °.

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Fig.III.25. Poids et positionnement de la masse de correction. III.6.2. Résultat final (Vibration résiduelle)

Il reste maintenant de poser la masse de correction à l'endroit approprié sur le rotor et à mesurer de nouveau l'amplitude de la vibration. Si la vibration résiduelle ne se trouve pas en deçà d'un seuil acceptable, on reprendre le cycle d'équilibrage.

Analyses spectral (FFT) : A vitesse de fonctionnement de 3024 RPM (50.40 Hz)

Fig.III.26. Signale FFT après l'équilibrage d'amplitude d'accélération.

L'équilibrage d'amplitude d'accélération de AA2 =25.29 mg avec une amplitude de vitesse de la vibration absolue mesurée AV2= 0,78 mm/s.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 72

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 73

III.6.3. Rayon de correction

Il est parfois impossible de monter la masse de correction au même rayon que la masse d'essai, en raison de la structure du rotor (figure III.27).

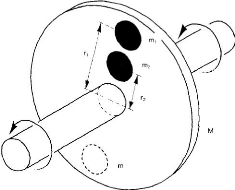
Fig.III.27. Montage de la masse de correction à un rayon différent du rayon de

montage de la masse d'essai [28]

Dans ce cas, pour corriger le déséquilibre, on utilise la relation suivante :

?

r

?

e

D'au :

e? = Balourd spécifique ;

= Masse résiduelle (masse équivalent) ; e^? = Rayon de la masse de correction ; = Masse de rotor.

On peut écrire aussi : Donc :	? e			? r
? e		? r	?? r		?? r

Donc, si le rayon, r2, auquel la masse de correction doit être montée, est différent du rayon, r1, auquel la masse d'essai était montée, il suffit de changer la valeur de la masse de correction, m2, pour que le produit (m)(r) reste constant, c'est-à-dire de manière à ce que :

?? r

?? r

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 74

III.6.4. Interprétation

Avant l'équilibrage, le balourd donne une amplitude d'accélération AA0 = 160.34 mg. Avec une amplitude de vitesse de la vibration absolue mesurée AV0 = 4,86mm/s. Maintenant, la valeur de vibration après l'équilibrage est d'amplitude d'accélération de AA2 = 25.29 mg avec une amplitude de vitesse de la vibration absolue mesurée AV2 = 0,78 mm/s au niveau moyen de vibration admissible, donc la procédure d'équilibrage est

effective.

III.6.5. Comparaison entre les programmes de calcule

Nous avons créé un programme sous MATLAB (Annexe) qui permet d'effectuer une

opération d'équilibrage plan 1 pour rotor class 1 et 2, qui :

- Estime une gamme pour sélectionner une masse d'essai

- Calcule la masse de correction

- Calcule l'angle de la masse de correction

- En plus, donner une possibilité de choisir un nouveau rayon pour la masse de correction.

Le tableau ci-dessous présente une comparaison des résultats de la masse de correction

entre un logiciel et le programme MATLAB pour les mêmes donnes :

Tab.III.1. Comparaison les résultats de la masse de correction entre un logiciel et le un

programme sur MATLAB.

		Amplitude (mm/s)	Phase (°)
Essai initial	Logiciel	4.86	0°
	Programme MATLAB	4.86	0°
		Masse (g)
Masse d'essai (0°)	Logiciel	1.6
	Programme MATLAB	1.6
		Amplitude (mm/s)	Phase (°)
Essai avec masse d'essai	Logiciel	1.56	- 8
	Programme MATLAB	1.56	- 8
		Masse (g)	Angle de masse d'essai (°)
Masse de correction	Logiciel	2.34	- 4
	Programme MATLAB	2.3404	- 3.7469

Chapitre III Contrôle et Equilibrage d'un Défaut de Balourd sur un Banc d'Essai

III.7. Conclusion

Dans ce chapitre, nous avons présenté le kit simulateur avec ses organes .et logiciel de traitement et visualisation les signaux de chaque essai. Nous avons également présenté les principes de la réparation et les techniques d'équilibrage parmi eux l'insertion d'une masse d'essai pour trouver la masse de correction.

Ensuite, nous avons appliqué avec succès cette technique d'équilibrage pour l'équilibrage du rotor du kit simulateur. Les résultats des essais obtenus ont montré que cette stratégie d'équilibrage permet de bien réinitialiser l'état d'équilibre du moteur.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 75

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 76

CONCLUSION GENERALE ET PERSPECTIVES

CONCLUSION GÉNÉRALE

Dans ce travail, nous avons étudié par simulation à partir un kit simulateur, l'analyse vibratoire moteur asynchrone. Pour atteindre ce but, nous avons présenté au début le préambule général, la méthodologie et les idées principales de ce travail, ses principes ainsi que les différentes stratégies de maintenance.

Plus précisément, le travail réalisé dans le cadre de ce mémoire présente une étude d'analyse vibratoire et une tentative d'équilibrage d'un cas de balourd du moteur asynchrone. En effet, on a présenté les techniques et la philosophie d'identification des défauts et leurs solutions de maintenance sur un MAS.

Notons que l'analyse vibratoire ne concerne pas seulement aux défauts mécaniques elles concernent aussi avec les défauts électriques, et chacun défaut à leur méthodes de reconnaissances et leur techniques de réparations.

Nous avons commencé dans le premier chapitre par présentation de la machine asynchrone comprend tous les organes que ça soit électriques ou bien mécaniques. Cette étape permet de mieux comprendre le matériel, aussi cette étape nous a également permis de nous préparer efficacement le terrain pour les techniques de maintenance à mettre en oeuvre.

Ensuite, afin de situer le problème des défaillances des machines électriques, ce chapitre est consacré aux l'analyse vibratoire des multiples natures des failles dans lesquelles se situe notre travail. Nous avons présenté aussi aux capteurs leur contexte, leurs types, leurs caractéristiques et leurs principes de fonctionnement afin de témoigner de ces occurrences sur les machines.

Dans le troisième chapitre, nous avons abordé l'objectif des principes d'équilibrage, ainsi que les différentes approches de correction des déséquilibres et leur application aux moteurs asynchrones. Nous avons réalisé avec succès un test de simulation sur le kit de simulation afin de valider la théorie de l'équilibrage étudiée.

Nous avons pu conclure, sur la base des résultats de ce projet, que la performance de l'équilibrage d'un balourd des machines tournantes doit être ajustée efficacement afin de produire de meilleurs résultats.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 77

CONCLUSION GENERALE ET PERSPECTIVES

Finalement, nous proposons comme perspectives du présent travail, une comparaison expérimentale -sur un moteur asynchrone- d'un capteur d'accélération fait maison avec un capteur d'accélération préfabriqué par des entreprises de premier plan pour trouver les coefficients de correction des niveaux de signal. Afin d'utiliser le logiciel d'accompagnement de celui-ci. Parce que ce sont des programmes pour les entreprises avec plus de 30 ans d'expérience dans le domaine de la fabrication des capteurs et l'analyse des vibrations.

ANNEXES

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 79

ANNEXES

Annexe EN : Illustrated Vibration Diagnostic Chart

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

80

ANNEXES

PROBLEM TYPICAL PHASE SOURCE SPECTRUM RELATIONSHIP REMARKS

MECHANICAL LOOSENESS

RADIALBASE Mechanical Looseness is indicated by aimer Type A, B or C vexation PLATE ^ee spectra. lx len_yA ion, e Type A its Caused by Structural loosenesstweakness of machine Witt,

· TYPE A ~ 4EAt]4nE FOOT · baseplate Or IOundatipn. BISri by pelerpreled grpr!ng,~oose hUd ·dOwn

ei. .... bons et the ease, and distortion o1 fie trame or base Ire., Ste toot) Phase

ii sir 6701. x RADIALstructure X C'.l X~yc TYPE B \ ir1 t7 , -

;_TLi.

analysis may reveal approv 90 · to 180* phase deerence between vertical measurements on bort, machine foot, basedale or base utselt. Type B rs generally caused by loose prllowbiock bolts, cracks in trame or in bearing pedestal_ Typa C is normally generated by improper le between component parts which win cause many harmonics due to nonlinear response of loose pans 10 dynarniC iOrces mom rotor Causes a truncation of time waveform and a raised nose floor in the spectrum. Type Cis often caused by a bearing liner

loose in es cap. a bearing loose and turning on es Shah, excessive clearance in either a sleeve or rotting element bearing, a loose impeller on TYPE C eiellem a shat;, etc Type C Prince aoften unstable and may vary widely morn one X ', /L. rnea5urement to nest. part..-ula ·ly d race shpts position on shalt horn one

NOTE RAMSED NOISE FLOOR

isa h

Xycxx X x< startup to ned Mechanical Looseness rs orten highly directional and may tear nr0 mho If · cause very Cillement read rigs when comparing levels at 30' incrernenls in Lr~

INDICATING LOOSENESS

n ~ fir,' radial direction all the way around one bearing housing. Alao, note that f 1 ^1looseness will ohen cause subharrnomc multiples at exactly 1/2 Or 1/35

Min

RPM (.5X, I.55, 2.5X, etc )

ROTOR RUB FLATTENED WAVEFORM

TRUNCATEDX

Rotor Rub produces similar spectra to Mechanical Looseness when rag parts Contact stanonary o0mpnnents Rue may be arther partial or throughout the entire shah revoluton. Usually^-venerates a series of RADIAL X frequencies, ohen eroding one or more resonances Grien excites integer traction Subharmonl s of running speed (1/2, 1/3, 1/4, 1/5,...1/n), x ?c X depending On location rubon of rotor natural frequencies Rotcan excite X~ is X many high ereouenc.es (similar to wide-band noise when chalk ea drug u1 o ',tong blackboard). h cari be very serious and of short duration if caused X Ni1i\i ry by shah conteceng bearing babbitt A luit annular rub throughout an entire shah revo(Wron can induce 'reverse precession · with the rotor whirling at

critical speed In a direction opposite shah rotation (inherently unstable

which can lead to catastrophic lalure)

JOURNAL BEARINGSSX A. WEAR!CLEARANCE PROBLEMS

1X y( N

RADIAL Latter stages of ve rnnie bearing wear are normally ev dented by presence of wnole series 01 running speed harmonies (up to 10 or 20)- Wroed ^4X5X lownai bearvrgs ohlen van allow large venicai amplitudes compared to 6X 7X nordontal. but. may show only one pronounced peek a! IX RPM- Journal bearings ver" excessive clearance may allow a minor unbalance and/or a misalignment Io cause high vioration which be H would much lower

NOTE MUSED NOL,E F1005 iNOICATeeG CLEARAwcEROOSE NESS !searing clearances were Set to spec.

B. OIL WHIRL INSTABILITY

· [_(ix RADIAL

/ I 40 ·.48 X RPM)Considered cm Whorl Instability occurs at .40 · .48X RPI/ and is often quite severe. excessive when emptitube exceeds 40% Of bearing clearances. Oit Whirl rs an c.1 lam excited vioration where deviations in normal operating conditions (attitude angle and eccentricity ratio) cause oit 4` wedge to 'push' Shatt arOund within ari beng. Destabilizing force in l ° direction or rotation reSu's in a whit (or forwards precession) Ge W flit is unstable since it increases cenrnlugal farces 'Mach increase whrd forces Can Cause oit to no longer support shah and can become unstable when

venirl frequency coincides wrai a rotor natural Irequency. Changes in oil viscosity, lube pressure and 6aternel pretoadS tan affect oit whirl.

C. OIL WHIP

oaf eaS4 weALAect · Oil Whip °LYnar ro.cT'ravie may occur if machine operated at Or above 2X rotor critical

^Ir`^onlev uenCy. When rotor up to twice critical speed, whirl win be very âet

INSTABILITY

~~~~ ° dose I rotor critical and cause a:passive vibration tISa1 al Alm may

-. wuwwayar seray

lose mat.x no longer Cie capable of supporting Ma speed will actually lock ortto

- eoioasmec. · r'el 2x, wear rotor critira! and this peak rail not pass through it aven i1 maceine is

brought to high higher and speeds Produces a laterai forward

~ ·q~

precessional subharrnonic vibration at rotor critical frequency. Inherently CRITICAL SPEED

' FAEoucNcy unlade which can lead to catastrophic (allure.

ROLLING ELEMENT BEARINGS (4 Failure Stages) 1,.. - Natural Frequencies of Installed Bearin Components and Support Structure

TOREA x_ i

DOMINANT FAILURE ZONE a B ARINO OEFrlcr $EeRrNC MEC REGION INATURAI STAGE I

SCENARIO ZONE C COMPON, FRED REGION

4 ROLLING ELEMENT BEARING FAILURE STAGES STAGE 7: Eames: rndicaboes of bearing problems appear ^inultrasonic kequencres ranging from shout 250,000 · 350,000 Hz; later, as wear increases, usually drops to approximately 20,000. 60.000 Hz (1,200,000 · ZONE^-D 3,600,000 CPU). These are mequenoes evaluated by Spike Energy (gSE). SPxf HFD(g) and Snook Pulse (d$) For example, spike energy may Ant fNENGT appear at about 25 gSE in Stage + actuel value depending on INlo1 measurement location and macnine speed). Acquiringhigh Ire ency n g R LL enveloped spectra confirms weather or net beaming is in Failure Stage 1. V STAGE 2: Slight bearing defects begin to 'ring' bearing component natural Irecluen:ies ff,1 which credominantly occur in 30K · 120K CPM range Such natural bequences may also be resonances of bearing 11-11-

BEARraiG DEFECT FREQUENCIES sail · N /I u, CDsa a RPM l P aero. Ne f ^141, WS el. RNA 2 ^1Pe /

l 'o; STAGE 2

n. rZ: ica m (~~ a

support structures- S'deband frequencies appear above And below naturel hequeriCy peak at end of Stage 2 Overall Spike energy grows (Ion example, from 25 to 50 gSE)- = SiOEAANO FRED STAGE 3: Roaring detect freq. encies and harmonics appear. Wnen wear ÎI progresses, more defect Irequeney narmOruCS appear end number of sidebands grow. boue around these and bearing Component natural II-11-

ear · PQ I.. 12 (COS 01^21. aqui ~e l ^ba^tJ FTF · I re Pa COS aI' aoU 1 1 Where.^-

STAGE 3 OLL Cr $ m f^l m N _

.~ le P 1

frequencies, Overall spike energy Continuel to increase (for example, tram .5 ho over I gSE). Wear rs now usually visible and may addend throughout periphery of Dearing, particularly wean many wen Iprmed sidebands accompany bearing deleCt Irequency harrnoni High frequency demodulated end enveloped spectre het n cofirm g Replace bearings now! (inWpendent of bearing defect frequency arepbtudea In vibration spectre).

BPFI a Inner Race frequency ReFO. Our Reea Hequeruy 55F . Ball SpinFreeu$ncy FTC .Fund. Train (Cepa) Treq N. · N.fabN N llMa Or Roars P. · Beanrig P4Ui 0.am ·le. (n or mm} e · Cmsacl Angle (degrees)

x x n at n 1.

B, - BaNlloar Domeier fin or mm(SICNIfr('AYrLY STAGE 4 RAN i ell{ FRED.

~~~ HIGH IBRATIOH

I JI

(F Of /MM STAGE 4: Towards the end, amplitude Of IX RPM 4 etta Pk is even O arrn . h usrs grows, and normally causes growth of many running Speed harmonics. ArfM21, Discrete bearing [mica: and component natural Irequencies actuallybegin ri"Ci ew2 to 'disappear and are replaced by random, broadband high frequency noise tOOr' . In addition, amplitudes of born high frequency noise 1100) AT END and Spike energy may in l= decrease; but j'AS: prior to ftilure, spike energy and HFD will usually grow Ici excessive amplitudes

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

81

ANNEXES

PROBLEM TYPICAL . SOURCE SPECTRUM REMARKS

HYDRAULIC AND AERODYNAMIC FORCES A. BLADE PASS & VANE PAS S

1 X v(

BPF BPF . 2BPF

IX 0 BLADES X RPM (IPM0,^41^111011111116idiffusers sIpEBM1bs \ _ ` i i

i

~+ Blade Pass Frequency (BPF) . No. of Blades (or Vanes) X RPM. This w frequency is inherent m pumps, fans and compressors, and normally does not present a problem. However, large amplitude 9PF (and harmonies) can be generated In pump i1 gap between rotating vanes and stationary is not equal all the way around. Arse, BPF (b harmonie) sometimes can coincide Min a system natural frequency causing high vibration. High BPF can be generated it impeller wear nog seizes on shaft, or i1 welds fastening drtluser vanes lad. Also. high BPF Can Cie Caused by abrupt bends in pipe (or duel), obstrvclrons which disturb flow, damper settings or if pump Or tan rotor is positioned ac0entrically within housing

RANDOM Flow Turbulence oten occurs blowers due to variations in pressure VIBRATION ar velocity of the air passing IMu Mea Or COnneeted ductwork flow

B. FLOW TURBULENCE

tan This BPF = BLADE OR disruption causes turbulence which wiu generate random, ^lowhequency 1 X BPF VANE PASS vibration, typically in the range O1 50 to 2000 CPM. If surging occurs FREQUENCY within a compressor, random broaduand high frequency vibration Can occur. Excessive turbulence can also ascite broadband high frequency

C. CAVITATIONGaation Cavitation normally generates random, higher frequency broadband RANDOM HIGH energy which is sometimes superimposed with blade pass frequency FREQ, VIBRATION harmonies. Normally indicates insuffipem suction pressure (starvation) vft can be quite Left e destructive ro pump internals uncorrected. Il

can particularly erode impeller varies.n of When present. ten sounds as it 1X B J. II 120KM 'gravel' is passing thru pump, Cavitation is usually caused by insufflaient Ai CA inlet flow. Car occur durrlg one survey, and be absent the next survey ( d

changes ^insuction valve settings are made),

GEARS A. NORMAL SPECTRUM

Q GMF. aT xq NT X Normal Spectrum shows Gear & Pinion Speeds. along with Gear Mesh = a tea' r RPUe Frequency (GMF) and very small OUF harmonics. OUF harmonics its common) will have running speedsidebands around them. Al-K yrig peaks are tier of law amplitude, and no natural frequencies of gears are excited FA,,,r 7GkiF sour ofat 3.25X OUF (minimum) when · teeth are known If loath

3.25X GMF count a not known. set F, at 200X RPM on ascii shah

B. TOOTH WEAR 51 T/26T Y \~,. n^''-

EAR ,J r ~ ^0 , E

NATUgAL FREOUENCv ur sour Tour ++ l~

Key indicator al Tooth Wear is excitation o/ Gear Natural Frequency ^(1,,),.S, along with sidebands wound it spaced at the running speed of trie bad gear. Gear Mash Frequency (GMF) may or may not change in amplitude, atmough high amplitude sidebands and number of sidebands surrounding GMF usually occur when wear is noticeable. Sitleband5 may be better 1 wear indicator than GMF frequencies themselves Also. high amplitudes ! commonly Occur at either 2XGMF or at 3XGMF (esp. 3XGMF). even when

i \

3,25X OUF GMF amplitude is acceptable.

C. TOOTH LOAD

. g

GMF- GMF Gear Mesn Frequencies are often very sensitive to load, High OUF amplitudes do nor necessarily indicate a problem, paritularty if sideband frequencies remain foie level, and no gear natural hequenCies tour 3sare excited. Each Analysis should be perlormed with system at Maximum operating load for meaningful spectral comparisons

D. GEAR ECCENTRICITY AND BACKLASH · ï

g i~ rs x f y 0 x p

76MF

sour 3.25X GMF Fairly high amplitude sidebands around OUF harmonies often suggest gear eccentricity, backlash, or nonparallel shafts which allow the rotation of one gear to 'modulate either the GMF amplitude or the running speed of the other gear. The gear with the problem is indicated by the spacing al the sideband frequenciea,Alsso, 1X RPM level of eccentric gear wet normally be hign if eccentricity is the dominant problem Improper backlash normally excites OUF harmonics and Gear Naturel Frequency. both of which will be srdebanded at 1 X RPM. OUF amplitudes will often

3.25X OUF decrease with increasing bad it backlash is the problem.

E. GEAR MISALIGNMENT

g GMF

msharmonies Gear Misalignment almost always excites second order or mgher OUF which are sidebanded at running speed Often will show only small amplitude 1x OUF, but much higher levels at 2X Or 3X GMF. Important to set Fuky high enough to capture at least 3 GMF narmomcs, 3GUF Also. sidebands around 2XGMF will often be spaces at 2X RPM Note that sideband amplitudes Olten are riot equal on left and right side el OUF and

3.25X GMF OUF harmonies due to the tooth misalignment_ Causes uri an weer peaem.

F. CRACKED/BROKENI A Cracked or Broken Tooth will generate a high amplitude at IX RPM of this gear only n Me tine waveform plus it will excite ~I+-~,k--WÂF~M r gear

TOOTH

cG ie iii

naturale r If II IF f^requency (Id sidebanded at as running speed. His best detected in Time Waveform wr4Gh will show apronounced spike every lime the problem i ·e · ^II

y G .1-4-11-1 0 U G A r A tooth trios 10 mesh with teeth on^tthe mating gear. Time between impaCt$ K 1 or ocaa vnTR BROKiN (p) will correspond l0 1/RPM of gear with the problem. Amplitudes of ` t AL OR cwtocEo morn Impact Spikes in Time Waveform often will be lOX to 205 higher than that

^-°-i at 1X RPM in the FFT t

G. GEAR 600 pPyl ,

PHASE cue ASSEMBLY PROBLEMS W.T est. s i tsT.T' 1sT.it3 -^.11030 N^.s RPM ~ · ue 15.000

GAPF. GMF o. Gear Assembly Phase Freq. (GAPF) can result in Fractional Gear Mesh ^~ · 1 Frequencies (if NA,> 1). It literally moans (TOIN) gear teeth vela contact Z ,e (TF(N) pinion teeth and will generate I4 wear patterns, where N, in a given p pp _ K. , 7G 100th combination equates Ire product of prime factors Common to the ^x + 1 $ r GMF number of teeth on the gear and pinion (NA a Assembly Pnase Factor) GAPF + + + GAPF (Or harmonies) Can show up right from the beginning it there were 1GAPF eCr,+tP manufacturing problems. Also, its sudden appearance in a periodic survey t I spectrum can indicate damage if contaminate particles pass inrougn trie

N E 4 mesh. resuming in damage IO the teeth in mesh at trie rime of ingestion just uhPF. 6000 CPM . 020X GMT (FRACTIONAL DMF) as they enter and leave meshing or trial gears have been reoriented

H. HUNTING TOOTH M Hunting TOOth Frequency (I,.,) OCCMS when (auks are present on DOM Me PROBLEMS + + iNT = (GMF)(N) gear and pinion which might have Occurred dunng the manufacturing

DRNER DRIVEN 1000 RPM a a57 RPM a + }

-m 3 ^170EAR TeirriON) process, due to mishandling, or in the field h can carne quite high RI ys + t SteANOs r` vibration, but since h Occurs al low frequencies predominately less then ço ^ 1- 600 CPM. it is Often missed, A gear set with this tooth repeat problem / \ normally emits t 'growling sound from the drive. The maximum affect 1:."...,....^---,...,..,..... ~: occurs when the faulty pinion and gear teeth bath enter mesh et me same

e NA . 1 is the ideal assembly lime (on same drives. this may occur only 1 of every lO to 20 revolutions, 8`17(2X31 · depending an the t,,, formula). Note that T,,,,,, and T4 refer to number of 7.1X7 J NA.1 phase lapor in geai design teeth on thegear endpinion, r (6X loopj (1) 1000 respectively N, is the Assembly Phase Factor 1,,,= 143 Pulse

CPM (One Per 7 Pinion Revolteions) defined above- Wilt often modulate both OUF and Gear RPM peaks le)(7) 7

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

82

ANNEXES

PROBLEM TYPICAL SOURCE SPECTRUM REMARKS

GEARS (CONTINUED) I. LOOSE BEARING FIT

^(-4 O ^a-â K Q GMF ^22GMF

Excessive Clearance of bearings supporting the gears can not only excite many running speed hamnonica. but will orlon cause high amplitude response al GMF, 2GMF and/or 3GMF Tnese high GMF amplitudes are actually a response to. and not the cause o1, loosenesswatt: in the bearings supporting the gearing Such excessive clearance can be Caused limner

~~ GMF

by extensive bearing wear or by improper beanng fit onto the toumai during installation, Left uncorrected, n can cause excessive gear wear ano damage to other components

AC INDUCTION MOTORS A. STATOR ECCENTRICITY SHORTED LAMINATIONS OR LOOSE IRONt^x

3200 UNE RADIAL 2% A Ai.

2FL Stator problems generate high vibration al 2X tine frequency (2F,). Stator FFT eccenlhei ry produces uneven stationary arc gap between rotor and stator which produces very directional vib ahon Differential Air Gap should not exceed 5% for induction motors and 109: for synchronous motors, Sot Fl . UNE FREO loot and warped bases can produce an eccentric Stator. Loose eon is due to stator SuPpen weakness ^orlooseness. Shorted stator laminations Can cause uneven, N which Oalized heating can distort the stator itself. This produces thermaey.ind-ced vibration which can significantly grow with

12K CPM operating time reusing stator distortion and static air gap problems.

B. ECCENTRIC ROTOR (Variable Air Gap) F, w Electrical L rte Freq. N, s Synch, Speed = 120F, F, = Slip Freq_ = N,- RPM F. = Pote Pass Freq. - F, X P

Eccentric Rotors produce a rotating vanable arr gap between the rotor and 3200 UNE FFT stator which induces pulsating vibration (normally between 2F, and closest - runn am nispectrum ng speed hnoc). Olten requires 'zoom' to separate 2F. RADIAL and running speed harmonic. Eccentric rotors generate 2F., surrounded by ^2FL Fp SIDEBANDS Pole Pass frequency Sidebands (F,j, aS well as F, sidebands around t X 2X AROUND 2FL rur'+ning speed. F, appears itself al tow frequency (Pole Pass Freq cy uen - LL Slip Frequency x *Poles) Common velues of F, range from about 20 to 120 CPM (0.3 -20 Hz), Soft loot or misakgnment Olten induces a variable

P w *Poles

12% CPM air gap due to distortion (actually a mechanical problem_ rot electrical).

C. ROTOR PROBLEMS Stalag ~~ Rotor Bars Ns · ·~ ·

R.oIAL 3200 UNE FFT Broken or Cracked roter bars or Snorting rings: bad loints between rotor r,slocawosw.ouNoO.ta seers NAKNONtC,5 bars and shorting rings: or shelled rotor !ampnations will produce hrgn IX 1x zx Sa +% running speed vbrahon with pole pass frequency sideoands (F,) In F · SX ex addition, these problems will Often generate F, sidebands around trie second, third, (birth and filth running speed harmonics Loose Or Open

2 Pole Motor Air-Gap Conductors

Rota ,-- ·'^·1500 · l: ~: · `~

UNE FFT rotor bars are indicated by 2X line heq (2F,) srdebands surrounding Rotor em....oronsxwssraeo ..mix are Bar Pass Frequency (RBPF) andlor its harmonics (RBPF . Number of a, sswea^,Os rabl.oriber *^,mete wile.* Bars X RPM) Often wilt cause high levels al 2X RBPF, wan only a smelt ,x RBPF 2X RBPF amplitude at IX RBPF Electrically induced arcing between loose rotor

Magnetic Field ._s

!! Ix 1 .I. bas and end rings will chan show high lests et 2)c RBPF (with 2f, 1 J.1 11111

SioebandS), but Imre or no increase in amplitudes a! I X RBPF 3eox CPM

(Loose Connector)

D. PHASING PROBLEMRADIALPhasing prabtems due to [pose or broken connectors can cause excessive vibration a; 2X Line Freq (2F,) whrth Wilt have erdebands around it spaced 2F, al f/S Line Free (1(3 F,: Levels el 2F can exceed 10 in/sec d tee I l,1 F, SQEBANDE 1% r A.t., ARddNQ uncorrected This is part ci-larly a prCbtem it !ne detective connector is Only i A ` sporadically making contact. Loose or broken connectors must be repai ·ed

to prevent catins:rophlc fartufe

AC SYNCHRONOUS MOTORS (Loose Stator Coils)

1600 LINE Fri Loose Stator Cols in synchronous motors will generate fairly high vibration al Coil Pass Freq. (CPF) which equals the number 01 stator toits X RPM COIL PASS FREO fa ^StatorColts w lereISS X eCoils/Pole). The Coil Pass Frequency will be surrounded by IX RPM sidebands Synchronous motor problems may 1x - lx ReM also be indicated by high amplitude peaks al approx. 60.000 To 90,000 2% SIOEBANDS CPM, accompanied by 2F, aidebands. Take at least one spectrum up to

90.000 CPM on each motor bearing housing

DC MOTORS AND CONTROLS A. NORMAL SPECTRUM

SCR FRE0=6F, (Full-Wave Reddiedi Many DC Motor and Control Problems can be detected by vibration i 2 ·3F, (HarNweve Rectit,ed; analysis- Fultwave rectited, motors (6 SCR's( generate a Signal at 6X ,' Une Frequency (6F1-360 Hz-21,600 CPM): white hall-wave rectified DC " SCR FRED motors (3 SCR's( generate 3X Line Freq (3FL-t60 Hz= 10,600 CPM). The SCR firing Frequency is normally present in a OC Motor Soeclrum, but at

low amplitude. Note the absence 01 Other peaks at multiples of F,

B. BROKEN ARMATURE WINDINGS, GROUNDING PROBLEMS OR FAULTY SYSTEM TUNING

Z =`âSCR a i`

When OC Motor spectra are dominated by high levels a! SCR or 2X SCR. mis normally indicates either Broken Motor Winnings or Faulty Tuning of FRED the Electrical Contrai System. Proper tuning atone can lower vibration at SCR and 2X SCR sigrtibcanily if control problems predominate. High ampleudas at these Irequennes would normally be above approximately

10 insect peak at t X SCR and about 04 in/sec at 2 X SCR Finng Freq

C. FAULTY FIRING CARD OR BLOWN FUSE

cents rcIr3XSCR offA~o 2r3X SCR

When one Icing card laits to lire, then 112 OI power is lost. and can cause SCR repeated momentary speed Changes in the motor. This Can lead to high amplitudes a! trSX and 2/3X SCR Frequency fl /3X SCR Freq, = 1X F, for half-wave hie-Wied, but 2X FL for a tue.wave rectified SCR) Cau67t: Card/SCR configuration Should be known before troubleshooting

motor (*SCRs, *Finng Cards, etc.).

D. FAULTY SCR, SHORTED CONTROL CARD, LOOSE CONNECTIONS AND/OR BLOWN FUSE

1 =` â N :

Fautry SCR's. Shorted Contrai Cards and%or Loose Connections can 5CR generate noticeable amplitude peaks at many combinations of line FRED frequency (FJ and SCR firing frequency. Nomlauy, 1 bbd SCR can cause high levels et FL and/or 511, in 6 SCR motors. The point to be made is that neither F,. 2FL, 4F1, nor SF atlould be present in DC Motor spectra.

E. FAULTY COMPARITOR CARD

SrcEaANDsuELrEOuti >{ TO sPEEo WAATiON5 C 3200 UNE SPECTRUM

-~` Faulty Comparator Cards cause probtenu with RPM fluctuation or 'hunting'. This causes a constant conapsinq and regenerating of Ins magnetic herd. These sidebands often approximate the RPM fluctuation SCR FREI]. and require e high resoluppn FFT to even detect them Such sidebands COuld also be due to generation end regeneration et the magnetic field.

F. ELECTRICAL CURRENT PASSAGE TH R U DC MOTOR BEARINGS

aereacNce FA£OUENUrs 7 Nit usLerCoueLCPro _ c IF Ft11m~~`esen' N spç LINE SPf GTRl1/1

ENetni~l rig tyby N-in~~ Flub a norm detected e series of dilterence frequencies with the spacing most often at the outer race dereaf frequency (BPFO). aven II sum suing is present on both the outer and inns, races They most often show up in a range centered et about 100,000 to t 50,000 CPM A 180K CPM Spectrum with 1600 Ines ^isrecommended lui

teOK GPM defection with measurements on both the OB and lB OC motor bearings

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

83

ANNEXES

PROBLEM TYPICAL^· SOURCE SPECTRUM REMARKS

BELT DRIVE PROBLEMS BELT FRED - ] 142 x PULLEY RPM It PITCH Dom.

A. WORN, LOOSE ORz MISMATCHED BELTS^Ecr VERT. PERPENDICULAR TO BELT TENSfON HORIZ. PULLEv 4 n ,( o VERT

Ô m û

Û 3 Z ^x1 ^rp 1

BELT LENGTH TIMING BELT FRED - BELT FRED XPBELTTEETH · . pum.EV RPM X /PULLEY TEETH x E Witt frequencies are below the RPM of er the motor or the driven machine. When they are worn, loose or mismatched, they normally cause 110 ^4multiples 01 ben frequency, Olten 2X belt Ireq. is the dominant peek, RADIAL IN UNE Amplitudes are normally unsteady, sometimes pulsing with attiser driver or WITH BELTS driven RPM, On timing belt drives.. wear or pulley misalignment to

NSION PUL.EY ·2 ^4t+o Oo BELT TENSION _ HORIZ.

PITCH QIAM, X RPM,

p / PARALLEL TEl indiEated by high amplitudes at the Timing Belt Frequency. Chain drives will indicate problems at Chain Pass Frequency which equals e'Sprbdke1 . PITCH OMAM, X APM., Teeth X RPM.

B. BELT/PULLEY 3)ff11~, OFF PIGEON 'f~ANGLE SET ~~ TOE

MISALIGNMENTin AXIAL

IX DRIVER

Misalignment of pulley produces high vibration et lx RPM predominantly the axial direction. The ratio of amplitudes of driver to driven RPM OR DRIVEN depends on where the data is taken, as well as on relative mass and trame stillness. Often with pulley misalignment, the highest axial vibration on the motor null be at tan RPM, or vice verse- Can be connrmed by phase measurements by selling Phase Filter at RPM o1 pulley with highest axis! emptilude: then compare at this frequency phase panicular on each rotor

-~ I-

in the aural direction.

C. ECCENTRIC PULLEYS e 02[41

RADIAL IX RPM ECCENTRIC Ji

Eccentric pulleys cause high vibration al 1X RPM oEfhe eccentric pulley The amplitude is normally highest in line with the belts. end should show upon both driver and driven bearings. It aS sOmebme5 possible to balance PULLEY eccentric pulleys by alaching washers to taper Lock bolts. However, even ds in int eber!. ty mil still induce vibration be andreversible it a di by fatig^uepphase stresses in the bort. Pulley eccentricity can be Confirmed by phase analysis showing honzonta & vanical phase differences of nearly 0e or

180'.

D. BELT RESONANCEtXRPM OX.

RADIAL ii BELT RESONANCE ^1

Belt Resonance Can cause high amplitudes It the belt natural frequency should happen to approach, or coincide with, either the motor or driven RPM Bet1 natural frequency can be altered by changing eerier the bent belt length Or cross i Can be detectedonll tensioning and tension.releasing leen releasing ben while measuring Ilia response pulleys or bearings, However, when bell natural frequencies

operating. will lend 10 De Slightly higher on the tignt side and lower on the slack side.

l

EAT v ~BR~i7I ~N TWO FREQUENCIES 100' OUT OF PHASE Iwo SMILE Hs uotloulSOF D IFFERENT

P

"~

HARMONICcommonly TWO IN

PHASE

FREQUENCIES

A Beat Frequency is the result of two cioseiy spaced frequencies equenes going into and out of syncttronizalion with one another. The wideband spectrum normally will show One pear pulsating up and down. Wien you 200m +nib this peas (lower spectrum below(, it actually shows two closely spaced peaks. Trie difference in these two peaks (F2.Fi) is Me beat frequency which appears rtsell in the widebend spectrum. The beat frequency is not seen in normal frequency range measurements since it is inherently low frequen, usually ranging from only approximately 5 to 100 cy.

FREOUENCY

CPM.

Fi AND Frl. BEAT FREQUENCY GENERATED BY TWO FREQUENCIES ABOVE

Fe= \

F2 /

· F1

t =

BEAT r

\

FREQUENCY

-

Maximum anWatiOn (F,( comes into Minimum vibration up 180' out of ° F

wAf result when the lime waveform of one frequency phase with the waveform of the other frequency (F2)_ occurs when waveforms of these two frequencies tine phase. PULSATinG }F- I AMPLITL DES WIDEBAND SPECTRUM

MINIMUM VIBRATION OCCURS WHEN

/ 2

\ \

_ L

MAXIMUM VIBRATION

\

OCCURS

F, r2 p. BEAT FREQUENCT ZOOM SPECTRUM

FREQUENCIES ARE 1130" OUT OF PHASE

WHEN 2 FREQUENCIES ARE IN PHASE

SOFT FOOT, SPRUNG FOOT AND FOOT-RELATED RESONANCE a`

B.!! Mn'Foot ·Relafed 'Soft Foor occurs when a machines f00; Or frame deflects greatly when a hold-down boll is loosened to hand tightness, causing the fool to Ise more than approximately .002..003 inch This does not always Cause a great vibration increase. However, it can da so if the Soft loot affects alignment or motor air gap concentricity 'Sprung Foor can cause great trame distortion, resulting in increased wbration, force and stress w the treme, bearing housing, etc. This can RADIAL DcEur when a hold ·duwe bolt is forceably torqued down on the sprung 1 X RPM (Typ,) foot in an attempt to level the foot. Resonance' ran cause dramatic amplitude increases from

_"

when e bolt (or combinations Of 5X to 15X or more. as compared with thatatVi i bons) is loosened to hand tightness. When tight, this bolt can notably _

change the natural frequency of trie foot or machine trame itself.

Solt Foot, Sprung Foot or Fool.Related Resonance most open affects vibration at 1X RPM, but can also do so at 2X RPM, 3X RPM, 2X line frequency, blade pass frequency, etc. (particularly Foot-Related Resonance).

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 84

ANNEXES

Annexe Fr : Tableau illustré de diagnostic des vibrations

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 85

ANNEXES

le desequilihre fcar. est en phase et stable. l'arnpLitude qui ea résulte

augrnerite etiionort,i=n du lkt~ de la vii .
· Js la 1=renlibria v i1 --'- P C: ri Y

du =Cor (augmentaticn de 3X cb le vit=e = augientaticrk de 9X de la vi_l raticn) .

Usa regi3Tec 1X est t 13eurs i_IL /t et domine habitoellement le spectre. La.

situatic peut "être ccrerigife i_n ta_1 L nt i e il1 masselotte sur un pian au

centre de gravité (CG) du retc n . Is dés e entre les axas ^hori itaazx et

vert.ioaux rculerrentsEX (ext^.éi^..-ie z_r) e IN (int&ieur) idTzutiit c 0' en1.4 -r -_n

t, cn rote . un déphasage de 90' envi= entre les lectures
}mizr^-rrtales et tAErticalesc chezit. rculayerit cïs rot en dâcpi T i 1 e (#177; 30
· ) .

lin bela.rd dynamique se traduit par- v iiritrverrient' de 180' du né re

arbre Un régime dr 1X mat teilleurs presle lot.Et dbnire:tx.e leme t: le.~., .

L' cx, i y.x1_i tu varie en p _p L ien du u zt 0 de I ' aax3rrentat#177;cn. de` vit, l,a

ptrarnierevitF== critique du =ter- . zt p°"' t viliatiEn ar^,tial et

t aticri r t d m r ~ ,mei 11E1-

entre le= a borizentaux et L' ti c o asr _r1=S Yr^-» 1 E ErtitS EX (e rie r)
et 7N

(intérieur) ci=smait être de 180' ariv#177;mn - Ncirrnalerrent _ cri rte -i Un

de 90' er rn eitre 1 l.eci,.ni hori z-nta 1.. et Mica 1F d ch ,e
rca ler t (#177; 30') _

le l i }-a e risme n e (le plus oO..Ir rt) est ure a iî_r -ri nai .mar cchsequilihre

d fore et de I lo...ad dynamique. Un zE g1Ne IX dEraire le spa^-ta^-e et i r r it
the ccerr t]im zr dE II3 plans le clAdiasec -radial entre les rcLi~1tS i nta.'#177;e r

(Di) et (EX) mit varier Enta 0 et 180' . Ceperdarit, leder

horimmtc l devrait t être nsib1 e re t id'aitigte au déphasage taartical ? .e

1 can =pare les mesures d a? ts . intéri etir (#177;- 30' ) . Si le

désécruiliinreit r rrr r i r,arit , cri note habi_tuelles^-,rait un d rha c 90^-

envi= entL

0^-

en i=entL 1i--ti lacztures tir r 1i E hcro_i_rit..R (#177; 40` ) .

Un d iiliI ire de rotor ect porta à ac pi^-cd/Lit un régin^-ie 1X élevé dans les

dire=ticns axiale et radiale Ti-- lecturEs axiales ta J t à êt:r phase tandis rn_ lc. Lectures radiales peutarat êttra instables. met, ^-le dephasase

1 -i rit el [ L habituellexrent identicie au déphasas vertical du =bar en

(#177; 30* ) . les icters en.perteàf reitàlafr-ri txid

ries forc et un balourd dynami g. qui r i i t. nal ituelltFrs it être tous diELEE

iiaLL igës. Etins la plupart cies cas, en de,_r.xA irsta1l er des riesselottes sur Lbi..12z

pl ÇDJrne. tna i r 1^-effet- ri=ir d .7i Iihres.

L`e itx cité melte d' un r 1a9^,- ei *xe le cire ds zctatinz et le ceritr

d' tme pou1 ie_ d " un ensren Nsm, d' un rr^-u 1 t, d' un irr#177; i t de
moteur, etc T vibratictls les plr, mar. s produisent au x i.me IX de la

1^-ri ^-1="^, ri M ptCpEgEnt lafecentral des oLidL1IAg _r I#177; 1

u~r~ txti; ries phashorizentalr et -5;=iir-FaI d_iffent habitt ck

O' eu de 180* (chacune indiquant un mi.ivar tt stx tkli.gl . s
destintiEs àé xi 1 ibrr =hale,

~ naltri, telt ~ra'cl sire: lavi8tian
d 1.re ~eCticz21EcI ale. m s 1' augretabveicm JJ'eut:rie dir f. r_nj d a1P. (

l' i rrâ rrta r c1 1 ri+c té) _

Ch az fausse' pr que tue vilaCaticn ale élevée ainsi qu'un dethasage

axial de l'arbre qui tend vers 180` . Tr t'#177;zratiiQ d rnina tes- it atx

régime IX si. 1' ads faa l prés du centre et au rue+ 2X s^- il est fax Pres

de 1'acoa ],arent (s'assurer de teniroony.te ^-Drientaticn Ihr â

chaQue nr i axiale si le senzs de lascalde est inverse^- ) . Se ri`r de

ccrnporateu r t lLrTL jr1 rr^- =if Mcr- la g de I "cstJ

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 86

ANNEXES

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 87

ANNEXES

le t^-iFtlignayrent angulaire se ri- par une viboetic n az-rirî1e élevée et un

deéphasaz de 180' à 1' ecocuplerient . ;?n général, la vihreticn. est élevÉe tant au ré irrie 2X qu'au régime IX. Il n'est pas inhabitupl qu' =^,111^, sait prÉectriinante ai régimes 1X. 2X cu 3X CEs sy ptran peuvent aussi être Signe de prchlsres

d' ao 7t . tin désalignement angulaire aigu peut aussi être un facteur
d' €itation harTricnics ara régime IX. Contrairement au jeu mécaniqtede

type 3, multiples ne se mit hab i tuel lDrcnt pas per un

sazil salaire plus éla.51.m le e.

Ia désalignerent parallèle te des smptZ:rr s similaires à ceux du

l ignerent angulaire mais aussi ure vibraticn radiale iale é1e app rock nt tua Irlphasesge de 180' a 1 ` a000up.Lement . Ia vilirat icn au régime 2X est sament plus margi qu'au regirre 1X, mais cri arrgalituzb est =vent dictÉe per le

type cl" a=o t et sa oarçositicn I ,' un desalignement angulaire
au radialient aigu, il peut gérén r c r *c à rIharrtcniquas heauDoup plus élcvre (4X-8X) ou rrserre rine s ~ie d' har nc iqu à hautdo fréquacnoe

à mi 1 f d' un jeu méoeniqus. Ia type d' acockiplemerit ainsi i c 1

matériaux qui le aorpcsent inf lu rit solvent largement m .1' enserkile du spectre

en ces cdiEilignerrent important _ En g -nal tcutef oci s, ].,e sail rue n'est pes plus éle4é.

Un

riouliernent coincé produit une vih 3 t lcn axiale cci i reb e . Il provogtae également tua rno xve rent de torsion s i rue ao , ri d ` un déph5sage vertical l hauu t-

bes et/au latex' al d' envircn 180*, me~are' dans l'axe du 1 L 'î tir. du r ulemE nt
Ce problème re peut être réglé per Un alignement des accouplements au un

e'lquilibrage du otor. le rciaerrent duit Gl leréinstallé a t.

lin jeu rreceniiqi. est per un si=i-tie de vibraticrs de type À_ e au. C.

7j A- Causé per Lire fiai hi Fi^=s au un reit di~s pi d'tme

machine, de soi sci-le ou de szn as ;ise ; peut at i être causé per une dét4riczraticn du ciment, un desserrement des boulms de la tese o une rWormaticn du chîssis eu ce la. Mese. Une analwc r phio= peut 18 ler un déphasage de 90' à 180' e nviic n entre .1eR yes venti,aall r 1,n Tr r , des

pieds de 1 ` a}_}, ei 1, du srrl e ou de l' 2:
·7521=^,

mâr~e.

7377 B- GérAral.ertent causé par un des gr xj i1 hoLarns de I N I ier à cb
cu ure fi.s uratticn du chgssis ou d'un s. ortdepa1 ier-

Tpj C- Normalerrent causé par un ajustement inonirrect de certaines pièces
qui Traduit de namhIrtEUS harrreniqtÉs causées per la répznse ncta-l;reeire

des pièces lâches aux forces dynamiques e.gercÉes per le xrDtor. l vitraticrs

de type C s nt sa_zuetat GE112Sée per un ^.jeun la garniture d' un aa. rE t dans scn chapeau., un roulement lâche qui torare sur scn acrhre, le dégagerrent ticessif d'un palier à coussiret-+i^-ui i le eu d'un =alertent a rouleaux, le jeu

d'un rotor sur arbre, etc . Une plias? de type C t szuv Ent instable et peut
vari _ert d' mere à L'autre, perticuliAremmt si le ta déplace sur 1 ` arbre entre deux derma.7rages _ le jeu mécanique est sauvent

h uterter7t directicnrel et 6 7--1 it do~ er- Li 1=1/ à rir^-r; ]xx_i ta s di f ft reutes .lr rsgt
I

'cn ef f 'motte une ccmparaisontle nivf eu per incréments de 30' dans le

radial tcut autour du l r iî ti r du raulerre nt . A rotor égalerrtalt qi' un jeu produit
sauveit rir--s mul t i plcs de sous-harmonique à exac tememat 1/2 ou 1/3X FFI{ (0,5X, 1"SX, 2, SIC, etc.)

ANNEXES

PROBLÈMES DE COURROIE

A. COURROIES USÉES,

w W

t U

⁰ K

x2 2

O RADIAL EN LIGNE

v AVEC LE:

COURROIES

W

_DUw aWô

02 â4.0

DIA PRIMETIF₁ X RPM , = DIA PRIMITIF, X RPM₂

DÉTENDUES OU

DÉPAREILLÉES

VERT.

HO RIZ. POULIE 1

PERPENDICULAIREA
LA TENSION DE LA
COURROIE

t(

PARAI 111 FA LA TENSION DE LA COURROIE

PODUE 2 'V

HORIZ.

B. DÉSALIGNEMENT COURROIES/POULIES

AXIAL 1 X MOTRICE OU COMMANDÉE

7DÉ^CALAGE
		CONVERGENCE

C POULIES EXCENTRIQUES

			RADIAL POULIE EXCENTRIQUE. IX RPM
				RESONANCE DE COURROIE
D. RÉSONANCE DES COURROIES					RADIAL	IX RPM

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 88

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

89

ANNEXES

FRÉQ. COURROIE = 3,142 X RPM POULIE X DIA. PRIMITIF

LONGUEUR DE LA COURROIE

FRÉQ. COURROIE DE RÉGLAGE = FRÉQ. COURROIE )f NB DENTS

RPM POULIE X NB !DENTS

Les fréquences de courroie se situent sous le régime du moteur cou de la machine entraînée. Des courroies usées, détendues ois dépareillées peuvent générer des fréquences 3 A4 fois supérieures à la normale. Une fréquence de 2X est souvent la crête dominante. Les amplitudes sont habituellement instables et pulsent parfois à la cadence du régime moteur ou commandé. Dans le cas des entraînements des counties de réglage, l'usure ou le désalignement d'une poulie sont indiqués par de-fortes amplitudes de la fréquence de fia courroie de réglage. Pour ce qui est des entraînements à chaîne la présence d'un problème sera signalée à la fréquence de passage de la chaîne, qui est égale au nombre de dents du pignon X RPM.

Le désalignement des poulies génère de fortes vibrations à 1X RPM, principalement dans le sens axial. Le ratio de,i amplitudes des régimes moteur et commandé dépend de l'endroit où les mg-sures sont prises ainsi que de la rigidité relative de la masse et du châssis. Lorsqu'on a affaire à un désalignement de poulie, il arrive souvent que la vibration ax iale la plus élevée du moteur soit au régime du ventilateur et inversement. Cela peut être confirmé par des mesures de phase, en réglant le filtre de phase au régime de la poulie présentant fa plus forte amplitude axiale, puis en comparant la phase à cette fréquence particulière sur chaque rotor dans le sens axial.

Les poulies excentriques provoquent de fortes vibrations â 1X RPM. L'amplitude est normalement plus forte dans l'axe des couirroles et devrait être présente aux roulements moteur et commandé. Il est parfois possible c'équilibrer des poulies excentriques en munissant les boulons de blocage coniques de rondelles. Cependant, même lorsque les poulies sont équilibrées, leur excentricité continuera de causer de lavibration etde soumettre les courroies à une fatigue réversible. L'excentricité des poulies peut ê:re confirmée par une analyse de phase montrant les différences de phase horizontale et verticale proches de 0⁰

ou 180°.

La résonance d'une courroie peut provoquer de fortes amplitudes s'il arrive que sa fréquence naturelle approche le régime moteur ou commandé, ou coïncide avec ceux-ci. !_a fréquence naturelle de la courroie peut être modifiée en changeant soit latension de la courroie, soit sa longueur, soit son profil. La fréquence naturelle peut être détectée en tendant puis en détendant lacourroie et en mesurant la réaction de ces manoeuvres sur les poulies ou les roulements. Cependant, lorsque la courroie est en mouvement, sa fréquence naturelle a tendance à être légèrement supérieure sur le cité tendu et légèrement inférieure

sur le côté qui a du jeu.

PALIERS/ROULEMENTS

DES ELEMENTS MOBILES SCÉNARIO DE DÉFAILLANCE PRÉPONDÉRANT

(4phasesde défaillance) ZONE B ZON C ZONE {7

PÉFALJJS DE PALIER COMPOSANT ÉNERGIE

ZONE A MAGE 17E ERE DE PM TER BE fil iii

PLAGE DE

f14'ÉQ.
NAIIIRELLES

Fréquences naturelles des our posants nts du pal ezimuiarien't

et de sa structure d'appui .

PHASE 1

(HD)

u

1~

FR$QÜENCES DES DÉFAUTS DE PALIER BFFI = Nb I + _P COS 9) x RPM

d

BPFO = -- 1- ,,, cos O) x RPM

_ ^Pd Irl- (84 ⁴(C[ 50~²¹ x RPM

2Bd I t1/470

T^, TF 2 r 1- - F_d COS 0) X RPM

:

BPFI = Fréquence de la voie de roulement

intérim .°

BPFO Fréquence de la voie de roulement

extérieure

HSF ⁿ Fréquence de rotation des billes

FIF = Fréq. fond, de la cage

N_b = Nombre de billes/rouleaux

B_d = Dia. des billes/radeaux (nm ou tu)

P_d a Dia. d'embrassement du Palier (n'n ou ,pa)

0 ç Angle de contact (degres)

= R_itQUE1+ CE DE

N! BANDE r 4TA.E

PHASE 4

VIBRATIONS ALÉATOIRES
 HAUTE FRÉQUENCE

II

014,

DL U/A1 Au

yrs

A.lGHMN?E

· D'^L FAQ ct ramEz Elv

C
I-

C

PHASE 2

4-r

PHASE 3

o

H w 2

H w

aI I

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

90

ANNEXES

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 91

ANNEXES

FillIEFS-POOMIIEVIE DES triXDITS l'ORTIES
I REMSES DE DÉ⁴74.11.LIKF

The' I- Its premiers signes de problenEs de palier apparaissent dans la

gamme de 250 000 - 35O 000 Hz de frequc ul . A mesure que
l' usure augmente, les problèves se fcnt sultir dans la gamme de 20 000 à 60 000 lf envi= (1 200 000 -- 3 600 000 OEM) . CFs f rëqua^-ces sut éveluees per I' &ergie de crête _(9EC) , la vale r HFD (g) et le siç 1 cie d (dB) . Par aurple, l' érErgiede crête paut apparaîtra d' ah dàamiran 0,25 91E dans la phase 1 (la valeur réelle dta d cie I ` emplacemEnt de la mesure et du régime

cle I' il } . la pt d . t chmees filiquErces permet
de oanf Cher si le palier est à la premiàe yhaee de cëfaillanze.

2- Es défauts de palier m_ir x ; commencent à faire e entenddre les

fru re errEs naturelles (f_n) des . i ts cu palier.. qui ° t su iut
dans la plage de 3OK à 12O1< OEl . es f rkpences peuvunt aussi étre des z anarr es des siruztures d`aPpai des p l.iets. s Vines de h ri e latérale apparaissait at -d s i et en--dszus ch la ctête de frhIE naturelle à la fin

la. phase 2 et l'énacgie de crête glc le c. rte (p.EK. , de 0,25 â 0,50 ger)

T 3 ts frégences et des hanyalicitEs de dhf aut de palier t

Dultipait à mesure cite l'usure , les friÉrzioens berb herb latérale

aligniaitent aussi autan- de ces frac; et des f roes naturelles des

OErstitu3ntsdEspaliErs L'& ech crêtecf lPQntirled`a gent (p.e r.
de 0 , 5 à plus de 1 ge) . A ce stade, l'usuye est numaLement visible et peut

s`éLerd e surtcuVa lai . 'ie du j lii . t1J'L t denanbrozes
rbuavel les frécitiences de bande latéral€3 bien n fc rri E accompagnent les

de défaut de palier lèssetres cle hautes fréquernes démodulés et a lc `' permettait de ccnf i rmer 1, atteinte de la tr i siene phase . Ficeplaoar les palm Deintermt (cp.P.11Birimmit 1'a li.tui das fréquarEs de ddaxt roineatée per les Ade vilr3tir)

I` .1--Vers la fin, ure amplittrh de fl I I est Ireine présente. Celle-ci augmente et entraîne normalement un15 augmentation de nombreuses de régime de Wicie. I.es frécitences naturelles discrete~ des

défauts de palier et des ccnstituants cc mi it à c4:liqparai txe > pour être
remplacées per un <csaai1 sur à large ban& re plus, 1'amplitude de ce seuil smireà huts frequa ces et de l' étimgie de crète path déc:roitre, mais tont juste awnt cite re surviEnre la df'aillamae, l'énalgie de arête et la valeur HFD au :sentent séréralelerit pax atteindre ute amplitttie snmsive.

ANNEXES

FERD

2FERD

3FERD

3. 'SX FERD

E. DÉSALIGNEMENT DES ROUES DENTÉES

F. DENTS FISSURÉES OU CASSÉES			*4+4+ ONC F. DE AUREE n e e n A - _L DE LA ROUE DENTE COMP'1RTANT RPM UNE DENT FISSURÉE OU CAS 3 E

G. PROBLÈMES DE PHASE D'ENGRENAGE

FPE = FERD 0.11 x Ne

x

250 - DE 15D = Dp 1000 RPM

25D - 5 .. II

153) ⁿ X 3 z ^°_o o

= 5

â . °

·

FERD

FPE 2FPE 3FFPE

4FPE

FP& FERD 15 000

NE 5

FPE = 3000 CPM = 0.20x FERD (FERD FRAcTIDNNAIRE)

H. PROBLÈMES CAUSÉS PAR UNE DENT ADDITIONNELLE

ROUE MOTRICE ROUE MENÉE

1000 RPM 857 RPM

6-1X2X3 7-1X7

1X RPM x-1000

(FERD) (NE)

(DRov ).) (I)elaaor+)

â P.1

n.

f_n BANDES LATÉRALES

= 1 est le facteur de phase d'engrenage Idéal pour la conception des eslgnena es

(6X 100) (1) _ 1000 - 143 CPM (UNE IMPULSION PAR 7 TOURS DU PIGNON)

(6)6) (7) 7

3FERD

2FERD

FERD

I. AJUSTEMENT D'UN ROULEMENT LÂCHE

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 92

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 93

ANNEXES

Ce problème produit presque toujours des harmoniques de FERD de rang 2 ou

supérieure qui se retrouvent en bande latérale en régime de fonctiorui rent . Ne
présente souvent qu'une faible amplitude à 1X FQu. mais des niveaux beaucoup plus élevés à 2X ou 3X bue. Il importe de régler la F . suf fisarmient haut pour capturer au moins le harmoniques de 3X t-hHD. Aussi, les hndos latérales autour de 2X FERD sont souvent espacées à 2X RPM. On notera que l'amplitude des bandes latérales ne sont souvent vent pas identique de part et d'autre de la 1-hi-1.) et de

harmoniques en raison du désalignement des dents. Cause une usure inégale.

U dant f issuree cu cassée produit une amplitude élevée à IX REM de la roue

en cause etcà.te la f_n de 'EnsgrEnaGe, qui se
ret/CIIVie en bande latérale en régime de fcrcticnnement _ Il se détecte plus facilement , rr- une gendede durée, qui pre te Line crête prcncrcée chaque nue

fais ^-la tt*p lerre tente de s e m- avec la rose qui 1-ai. est j+ ar elte

le ten s écoulé entre les iirçec (A) 1 l xri à 1 de la rc K tant
un prcblèm _ L'amplitude rig= s c rctc d' ire de 1 ' crtie de durée'est souvent de 10 à 20 fois pluts élevée que celle qui s= prcduit à 1X R dans la FUT.

Une f réquence de phase d' engrenage (FPE) peut engendrer des FERD

fxecticnnais (si N_E >1) _ Autierrait dit, les dEnts d' _ (IVIV tc t
aux dEnts du çagren (4, M_E) et gériit des prof ils d' u ure N_E , oü N_E clans ure ocumliinalsonde da-its deur e est égal au pn )Juit de facteurs premiers o rrrru.ms

au nombre de dents de la rue et du pigr n ( phase d'engrenage) .

Une rPE (cu d e ha ) peut apperaî ,.re ds le départ s' il s'agit d' lm
prih1 i,s de fabricaticn. l plus, em appe riticn soudaire dans un spectre de

omtcrôl' ,_ccl ~ q p peut &Lu aru si t l-^, parii culres aontaanrin ntes

paissent à trac 1^- t et endcm3E ait les deits pot leur

Une fréquence de dant add i.ticnr elle (f_m) s mit Î * e la roue d téc et le pigne/1 présentent tcus deux un r axe, cp Ikt p (fa(fahricaticn, namip.iJ aticn au autre) _ CF I le -ci peat entraîner- vibre tic ticns assez i part ntes, mais came e] ] se _rrrr od ai r t surtcut à ti fr q Ences -inférieu à 600 CFM, el 1. p3sse nt

scuvent ' _ Un engrenage qui pr ente ce genre de prcialicre érirt
seuvent un grcnderrent sourd.. L' ef f et Ire s imv un se produit lorgque les dents

déf de la roue et du pâ grtn s` e Yt au jrârr mirent (sur certaines
nes r 4 pet se produise à t us les 7.0 a 20 teors, s lai la formule F_EE) C i notera a las tArr D et D_{pi i} s' _pp1iqit au rinllrre de dents de la rue et cli pig n. tandis que N_E est le facteur t de phase d'engrenage déf ini plus haut . 11:dule souvent les crêtes de NFhL et de rotaticn (F f) de l'engra

Un jeu excessif des paliers d' Engrenag. peut ncn seulement produire de harmcniqur- de r(c)gime de fucticnnemEnt . 7nai s peuvent ei s i

aitreîr.er- suvEnt Lme it _is de forte a-rE litude à FERD, 1~4l 1D cra 3EMD.
C_ette r rrse est un cf f et et nen u re caLle du jeu des paliers Ili jeu eocessif

peut 6342.^-F3 at tribuabable â une f crte ut .ue da pe 'L cu à s ii instaLlaticn i noorre tte
' m 1' arlm . Si 1 "cri re cs rr7.ga p3s la si tua r i cn. celle-ci Peut causer une usuare Eticessive de l'Engrenage et eniennoger d^- autres conposant

ANNEXES

EPP = Nb DE PALES X RPM

FORCES HYDRAULIQUES ET AÉRODYNAMIQUES

A.

2FPP

BANDE LAIERA 1 RPM

FPP

PASSAGES DE PALES ET D'AUBES

B. TURBULENCE DE L'ÉCOULEMENT

C. CAVITATION ENGRENAGES

A. SPECTRE NORMAL

2

VIBRATIONS ALÉATOIRES

~YY = FRÉQUENCE DE PASSAGE DE PALES OU DES AH F.S

VIBRATIONS A HAUTES FRÉQUENCES ALÉATOIRES

1

II 120K
A FPP

^A.v F D=ltbT_EXRPl = NbT_p X 0 RPM

~ z P

FERD	2FERD	3FERD 3.2 X PERD

C P M

3 2',X FERD

FERD

3FERD

2FERD

B. USURE DES DENTS

FRÉQUENCE NATURELLE DES ROUES D]NTÉES

ra qi

â FERD 3FERD

7 Z

O t7

D. CHARGE DES DENTS

3 2:,X FERD

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 94

EXCENTRICITÉ DES ROUES DENTÉES ET JEU ENTRE-DENTS

3, X FERD

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

95

ANNEXES

Frequence de p .ge des pales &#177;F ') = nb de pas Lou 0^- annes x relia. 11 s agit

d ' une fréquence inhérente aux parafa . aux ven t i l a teurs et aux compresseurs qui ne présente normalement pas de problèmes Cependant, une FPP (et des harmoniques) de forte arpl itude pe tt se produire si 1 ' écart entre les pa 1 es et le di f fuseur

n'est égal sir tett le périmètre. Par la 1,YY (cu l' harn*~nique) peut
par fois coïncider avec la fréquence naturelle du systàrp et causer ainsi. d'im-portantes^-

'im-

portante - vibrations. Une 1-1-1" éle<' ? peut 'être pit v suite lorsque la bague d' etre

de la roue grippe sur 1 ' arbre . en ras de rupture des soudures des a Fbr ; du di f fureur ou encore par une conduite trop fortement cintr, . une obstruction quelconque. un mauvais réglage du registre ou une excentricité du rotor dans le corps de la panes ou du ventilateur.

Une turbulence de l'écoulent se produit souvent dans les ventilateurs en raison d'une r iaticn de la prPssic t c i de le vélocité de l'air dars le ,. .tilat ~r ou les conduits qui y sont reliés. Cela provoque une turbulence qui produit une vibration aléatoire à basse fréquence. normalement dans la plage de 50 à 2 000 caDM, Un phénomène de pompage se produisant dans un compresseur petit donner lieu à des vibrations aléatoires à haute fréquence. We turbulence excessive peut a -si engendrer dc- ha_ut_es fréquenc s à large bande.

We cavitation produit habitué^-liement une énergie aléatoire à haute fréquence

sur laquelle superposent par fois des Frermoniqur s dei #177;' . Cela peut dénoter

une pL1 ion d'aspiration i.rusuffi nte (étrangl rt ) . : -=avitation peut avoir un
effet destructeur important. toit pa^-rticulièrlarent sur les aubes de roue, si l'on ne corrige pas la situation. La cavitation produit souvent un bruit sc nblable à du gravier qui circulerait dans la palpe. Elle est habituell€rrent causée par un débit d'entité: trop faible. Elle peut être présente lors d'une inspection et éLre absente à la suivante (si l'on a effectué une modification des réglages de la soupape

d'aspiraticn) .

le spectre normal mrrttree la vitesse icia et des ragnons ai rt i que la

fréquence d' erxgrenement des roues denté (FERD) et de très faibles

harucniques de lihh1D _ C sant gt *a1 errent ercadrées de bandes

Latérales Tcutes les crêtes aznt da faible ,zsrt.x; ifi x a frégc lze net U
des rue= dentees n' este i tôc . F recx :minamdée à 3, SX F1 0 (minimum) Î p le rue de dents est ccnnu sin régi mar- F à 200X MI sem- chaque arlm.

le prirr=ipal in ter d'usure r i dans est l 'e r itaticn de la f~~ c 1'

et la c c latérales c30.1régi n'e dem xe de la r défectue se.
I ' angpl i tude de la F EFD peut lohangecr cu n n bien que âcs Lendes 1at ral,es de

farte amplitude ainsi qu'un certain rznbre de Ixk1iis lat&ales en=edreint la

FERD a ar a ,t babituellan u t lorsqte l'itaure t t L perceptible Ces bandes

pe vEnt mâne être de rreille us indicateurs d' usure qt I f= Fat

de fartes amplitudes rit soLzvent préserites à 2X au 3X FERD (surtout à
3X FERD) . mâne lorsque 1'ainplitu e est dtxrptable.

Tes Ft sn'xt scuTamrit tz s ibl c à l a charc . Ee fortes amplitu3s ne It

pas 116ZESSSixerrimit, sgr>e de prablerfe, su tout de lzEracb latérale
dere it fel hli= et qu' auoure f13 ria.^-a fatl+xell,e d'ersgrenarge n'est ac tôc.

Chaque analyse devrait être ef fe tuée à la charge rn rtaLe de fcancti rient

si 1' da3ire roarparei=ls i -ales sic firati _

Das bandes latere des d'assez farte .=xn pl itUi autour rif= hanrcniquE5sde FERD

sant so mit signe d" emzentricité ri -r roues, da jeu entre-derits ou ch

mn-pavai-

léliurre des arbres, la rotaticn d'une roue ci itee <module» akar 1` uplituda
ch la MW ou la ^-vi.te e rctaticn cia l'autre !nie_ (1 =.1 présen rt zri hlâre

est ida-ttif i rr pr r 1^. emEnt fréquies de bende latérale lin régime de

IX FEM d' une xci. e
·icen.tricr est n=malerrent élevé si 1' ztr rité est le

irohlArre dcritinant _ Un jeu Entre-czt, rent i.te habituellement cies
harir rnaes c3e FERD ainsj. que la f d"e .grtr.^- . qui seretrouvent en banch

latérale à IX Rai_ Ics amplituues + F dim u aant .,eit icirsciLe la cl

ar lte si_ le nrci l _{rre ts}t ta z rai- Un jeu ia^-ttre -dents.

ANNEXES

RÉSONANCE

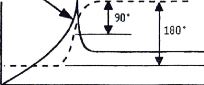
180°

Amp! i ti rr; Phase

1e f réquare cr ï tigtie

,AS]

₃₁

2e frikpErim critique e `_

FROTTEMENT DU ROTOR

RADIAL 5c

sr

ONDE TRONQUÉE APLATIE

COUSSINETS DE TOURILLON

A. PROBLÈMES D'USURE I

ET DE JEU

_3X RADIAL

².X _I 4_.X

N T ER LE SEUIL SCNCRE PLUS ÉLEVÉ, SIGNE DE JEU.

(0,40-0.48XFEN)

1x RADIAL

B. INSTABILITÉ DUE À UN TOURBILLON D'HUILE

DINEQUILIEff DE LÀ KARcE

c srala
ace trast un tcu 1Lr nulle se 1m€oisant ant

Pr', VI les_ tik DU ~ ss-if az meut

_ ROTOR =oie1 vitesiaüe~

insizbilité due

+.. vite9eacriniq

,m gutiu,pse ZC

reatrepwca la

TOURBILION

D'HUILEEXCESSIF

GRAISSAGE

VITESSE TIQUE

FRCQt1E4 CE

C. INSTABILITÉ DUE Â UN GRAISSAGE

EXCESSIF

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 96

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

97

ANNEXES

Un ir-xijttri de réscnan=ese produit la s frine frécruenme f coin

r avec une fréquence naturelle du s9stàrre et peut alca^-s causer ure ampli-
f icaticn importante de l ' aerspl it^-t i- qui lm ut traduire par lire dhfai Llarae pré-

. Voirec tta r ii_ LL peut s' d' ure fx6quarcenaturelle du_,
qua _peut aussi provenir. fréquErroment du d____ de 1^- i . de la bzâte d'engrenages c

'en-

c u mr e ,1- o u xcn rs de traalsm issicn Si un rotor a atteint le 1 nt

Cu le s5LEL1 de r6Ecnanze, ii 1. faatiquaent impossible dW I "è ' 1 itr r- en rai

sc i du diethasege important qu' il s nl--ri t ; 90 ecu point de mescnanze et près de 180* passé ce point) . Cela. nécessite sr:Livait ure baisse sse cu une hausse de la

fxëqaernenaturelle. Fn hal, 1 fr6q: naturelles ne changant POE lnrs-
q re le iégiirt=t modifie, ce qui en fa^- i 1 i tel` id ntif ioaticn. (sag dEns le cas das

appareils à g r= paliers lisses ou c ruL_IL fortement en porte à faux) .

Uri f c tterrent de rcxtcir gendwe un spectre similaire à --1 ui d` un jeu mécani.gt r-l=p[iJèc= rotatives s t u#177; t à c s piècesf i " le Luittetrent geut se pioduire sur une partie seulement Cu sur I a <sup>frit</sup> I té c:la rotettien da 1 ` archre il bre I habittleraerit uzserie de froquences qui e i_tent sQsvit tu7e cu

plusieurs réscneono ainsi que frac;ii:ns Entirrc c

x pire de m n#177; (1/2 l/3, 1./4, 1/S ... 1r:i) saïirn I"r igire fréquEnces natu-

relles

atu-rellie s du =toi-. Te frottement du rotai^-- _p a..it aussi i.tam~ de rimbrEuses hautes f ré (similaires s aou bruit 3i t de beaic lige prorlait par le fro terrent d^-ure

craie ^aie .r' un tableau) CP1 iii-ci peut être très grave et de eaute ckiô s' il est

causé per le ocrit r t de 1 ` iir.e sur le m=tal blanc (^-1= paliers. Un frotterrent

annilai e =si. la rotaticn cmp_t e de 1^. arbre peut EnGendrer ure «préoessicn inverse., oû le rot= tournerait à ure vita criticee dans le sEns =traire de la rotaticn c1 1^-arbre (ure cc diticn fc r daire tale ent instable susceptible r

prcyvoquer ure détaillai= ca a) .

Tr derniers stades de 1' usure d^- un couiret, de tcurillcn s nt habitLellerrent

f i _per 1'r-r~_r T t iic i l mei" ure ._e . 1' 1 z^^r.~Z=i ff.' 10 .^....i 20) . Un.

ccussinet essuyé ¹prcd it i ^-it L `r aliplitlldes elevdes viertical.ernent par

1.cr'r'
· L. 1 aLa ..;
·1~, mais~io~.cvâ La ₁ ûc~~iti,ca.~ iZ.~i

1X RFM. Les coussinets â,?ant tai j r t _e r i£ it r_lt _çe t talai m éy

di s qui 1 ilire et/ou. un ril.¹ ignar ent pouvant porcrvcquar une importante

cji1~rsMti~r~ i a~~ai t 1 t pl te ci l_e j_ea

ccllfcrrmérrent aux spdi=ifij aticcns.

Cette inst hilité'- produit entre 0.40 et 0.48 REM. Elle est souvent as a grave et

est j ug c ive lorsque ï ' amplitude clérza. e 40 % du jeu cio 9acznets . Le
tourbillon d'huile Pest une vibration induite par le film d'huile, où une déviation des conditions normales de marche (angle d'attitude et rapport d'excenn tri cite ) fcnt en sorte que le min d'huile fait t.balla:ter» 1' vraie dans le coussinet . La force déstabilint.e. produite dans le s de la r_otation engendoe un tourbillon instable

(ou pre' ion directe) parce qu'il augrmnte la force centrifuge qui. à son tour,
accroît la force de tourbi Ilonn nt _ L' h-_a i l e ri e alors de ne plus supporter l'arbre et de devenir instable lorsque la fréquence du tourbillon coïncide avec une

fi.f,_q ,_{enoe r}ats mal 1 e du rotor. r ir, f#177;,a _{g n}tr tin cfr~ci t de l'huile, de la pr xi ion
de lubrification Cu des précharges peut agir Mme incidence sur le ta.irbilion d' huile.

the instabilité dus à un graissage exces f ^Iv ztj r ite lcri' un anlareil

ut ^-i 1 i cp à r}__? r?fo i s r ^, _i ius laf ` ~' ~r-_i t _jte n zctcr. A _e le

t.ct bi.11ci d' huile = L très prod'e de la vitesse critigi et peit causer ure
ci.braticn emcessive qte le film cl huile re a plus ' irere d" absorb=ir la vitt du tcurbiil se crifcr:i a zrr à la nitr- critique du xr tem- et n'en

err pas TE esi .1' cri fait fci' ti rue ^-appareil a.tri réj]sedeplusenrh
élevé C = I a mit ure vibraticn sub-har rcniiqteprezeive Lataale directe à

la fr q > crit igue du rotor, un phE3vr> 1C [ci-dament-9i 1& ent instable
susar=ptiblice causer ser L.Tr rV..fa^-' lance cat

ANNEXES

MOTEURS c.a. INDUCTION A. EXCENTRICITÉ DU STATOR, TÔLES COURT-CIRCUITÉES OU FER LÂCHE							FFT DE 3200 LIGNES
					RADIAL ]X		2 FA FA = FRÉQUENCE D'ALIMENTATION
									12K MI

RADIAL

lx

2F BANDES LATÉI ALES F_p

AUTOUR DE

12K CPI7,7

B. EXCENTRICITÉ DU ROTOR (entrefer variable)

F_A = Fréq. d'alimentation (conducteur)

N_S = Vitesse de synchr. - i 20

--

P

F_c = Fréq. de glissement - N_s -- RPM

Fp = Fréq. de passage des pâles = F_G X P

P - Nb de pâles

Stator

Barres de rotor

Rotor

Moteur , bipolaire--~!

Entrefer

Conducteurs

Champ magnétique

RADIAL

BANDES LATÉRALES F AUTOUR DES HARMONICI FS DE

LA VFTESSE DE RÉGIM'

IX 2x 3X 4X

5X EX

FPBR = F RÉQ, DE PASSAGE DES BARRES DE ROTC F = NB DE BARRES X RPM, BANDES LATÉRALES 2 F_A AUTC IR OE

LA FPBR ET/(OU DE 2X FPBR.

_Ix FPBR

2X

2XFFBR

C PROBLÈMES DE ROTOR

360E: CPM

RADIAL

BANDES LATE}ALES

I /3F_AAUTOUF DE 2F_A

IX

D. PROBLÈMES DE PHASE (connecteurs desserrés)

FREQ. DE PASSAGE DE BOBINE

BANDES LATÉRALES â IX RPM

MOTEURS c.a. ASYNCHRONES (bobines de stator lâches)

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant -

98

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 99

ANNEXES

Les problèmes de stator produisent des vibrations élevées à 2fois la fréquence d'alimentation (F_A). Une excentricité produit un entrefer fixe inégal entre le rotor et le stator, qui produit des vibrations très orientées. La différence d'entrefer ne doit pas dépasser 5 %pour les moteurs à induction et 10 % pour les moteurs synchrones. Un socle «spongieux» ou un socle déformé peuvent provoquer une excentricité du stator. Un fer de stator lâche est attribuable au relâchement structurel ou à la faiblesse du :support de stator. Un court-circuit des tôles du stator peut entraîner une surchauffe inégale localisée qui risque de déformer le stator. Cette surchauffe produit une vibration susceptible d'augmenter considérablement avec le temps, provoquant ainsi un gauchissement du stator et des problèmes d'entrefer statique.

L'excentricité du rotor produit entre celui-1:i et le stator un entrefer inégal en rotation qui induit une vibration pulsa ite (normalement entre 2F_A et l'harmonique de vitesse de régime la plus proche). Cette situation nécessite souvent un spectre «zoom» afin de distinguer la vibration 2F_A del'harmonique de vitesse de régime. Un rotor excentrique g'ànère une vibration à 2F encadrée par des bandes latérales à la fréquence de passage des pôles (l=_e) ainsi que des bandes latérales F de part et d'autre de la vitesse de regime. La F apparat à basse fréquence (f = fréquence de glissement X nb de pôles). tes valeurs courantes de la F se situent entre 20 et 120CPM (0,3 - 2,0Hz) environ. Un pied de machine Fp

ou un désalignernent sont souvent lacause d'un entrefer variable cause par la distorsion (il ;'agit ici d'un problème d'origine mécanique et non électrique).

Des barres de rotor ou des anneaux de court-circuitage cassés ou fissurés, des joints défectueux entre les barres de rotor e- les anneaux de court-circuita9e, ou encore des disques de rotor cou rt-ci rcuitO produisent des vibrations élevees

à la vitesse de régime, accompagnées de 1-andel latérales de fréquence de passage de pôle (Fp). Ces problèmespeuventaussi générer des bandes latérales de F_p de part et d'autre des deuxieme, troisième, quatrième et cinquième harmoniques de vitesse de régime. La présence de barres de rotor desserrées ou ouvertes est indiquée par des bandes latérales à 2F encadrant la fréquence de passage des barres de rotor (FPBR) et/ou ses harmoniques (FPBR = nb de barres X RPM). Cette situation se traduit souvent par des niveaux élevés à 2X FPBR, avec une faible amplitude seulement: à 1X FPBR. Des arcs électriques entre des barres de rotor desserres et les anneaux d'extrémité produisent souvent des niveaux élevés à 2X FPBR (avec des Dandes latérales de 2F_A), mais

pratiquement aucune augmentation de l'amplitude à 1 X FPBR. A

Les problèmes de phase causés pardes connecteurs desserrés ou cassés peuvent provoquer des vibrations excessives à 2F_A, accompagnées de bandes latérales espacées del/3F _A. Des niveaux à2F_A peuvent dépasser 1 ,Opo/sec s'ils ne sont pas corrigés. Ce problème est particulièrenmerj t aigu si le connecteur défectueux ne fait contact que sporadiquement. Les con lecteurs défectueux doivent être réparés afin d'éviter tout risque de panne catastrophique. ,

Une bobine de stator de moteur synchrone qui a du jeu génère des vibrations assez élevées à la fréquence de passage de bobine (FPB); celle-ci est égale au nombreide bobines X RPM (nb bobines = nb pôles X nb bobines/pôles). La FPB est encadrée de bandes latérales à 1 X RPM. Un problème de moteur synchrone peut aussi être signalé par des crêtes de forte amplitude entre 60000 et 90000 CPM, accompagnées de bandes latérales A2 F_A. On doit prendre au moins une lecture de spectre. jusqu'à 90000 CPM sur chaque boîtier de roulement.

ANNEXES

MOTEURS c.c. ET COMMANDES

A. SPECTRE NORMAL

B. ENROULEMENTS CASSÉS,

PROBLÈMES DE MISE Â LA

MASSE OU RÉGLAGE

DÉFECTUEUX

FRÉQ. SCR = 6F_A (REDR. A 2 ALTERNANCES) 3 F_A (REDR. A 1 ALTERNANCE)

x~

a.

X FRÉC.SCR

N t

FRÉQ. SCR

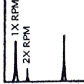
1 /3XSCR

213XSCR

FRÉQ. SCR

C. CIRCUIT D'ALLUMAGE

DÉFECTUEUX OU FUSIBLE

GRILLÉ

FRÉQ. 'SCR

Ln

D. SCR DÉFECTUEUX, CIRCUIT

DE COMMANDE COURT-

CIRCUITÉ, CONNEXIONS

DESSERRÉES ET/OU FUSIBLE

GRILLÉ

BANDES LATÉRALES NORMALEMENT ÉGALES AUX VARIATIONS DE RÉGIME

SPECTRE DE.3200 LIGNES FRÉQ.

5CR

X

E. CIRCUIT DE

COMPARAISON

DÉFECTUEUX

F. PASSAGE DE COURANT À

TRAVERS LES ROULEMENTS

DU MOTEUR

FRÉQUENCES DIFFÉRENCES NORMALEMENT ÉGALES A LA I3'4O EN PRÉSENCE OE CANNELURES

X ce

x SPECTRE DE 1600 LIGNES

180 < CPM

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 100

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 101

ANNEXES

De nombreux problèmes de moteur c.c. et c e commandes peuvent être décelés par une analyse des vibration s. Les moteurs àà redresseurs à 2alternances (6SCR) génèrent un signal à 6X la fréquence, d'alimentation 6F_A = 360KHz = 21600CPM), tandis que les moteurs c.c. a redresseurs à 1 alternance (3SCR) génèrent des signaux à 3X la fréquence d'alimentation (3F_A = 180Hz = 10800CPM). La fréquence d'allumage des !;CR apparaît normalement dans le spectre d'un moteur c.c. mais à faible amplitude. Â noter la présence d'autres crêtes à des multiples de la F_A.

Lorsque le spectre d'un moteurc.c. est dominé par des niveaux élevés à 1 X ou 2X SCR, cela dénote habituellement un enrot.lement cassé ou un mauvais réglage du système de commande électrique. Ur bon réglage peut diminuer considérablement la vibration s'il s'agit avant tout d'un problème de commande. A ces fréquences, les amplitudes sont assez fortes, soit de l'ordre 0,10po/sec avec des crêtes à 1 X SCR et de 0,04po/sec à la fréquence d'allumage de 2XSCR.

Lorsqu'un circuit d'allumage fait défaut, 1 /3 de la puissance est alors perdue, ce qui peut occasionner des variations de régime répétées du moteur et des amplitudes élevées Al/3X et 2 /3X de la frécuence SCR (1 /3X fréq. SCR = 1X F_A pour les SCR à 1 alternance et 2X F _A pour les SCR â 2alternances).

Attention: la configuration des circuits et ces SCR doit être connue avant de procéder à la réparation du moteur(nbde SCR, nb de circuits d'allumage, etc.)

Les SCR défectueux, les circuits de comrande court-circu ités et/ou les connexions desserrées peuvent générer des crêtes d'amplitude perceptibles à de nombreuses combinaisons de fréquence d'alimentation (F_A) et de fréquence d'allumage SCR. Normalement, un SCR défectueux peut générer des niveaux élevés à la F_A, et/ou à 5F_A dans les moteurs à SSCR. Le spectre d'un moteur c.c. ne devrait jamais présenter de F_A ni de 2F_A,'4F_A ou SF_A.

Un circuit de comparaison défectueux peut causer des problèmes de fluctuation de régime ou d'oscillations longitudinales qui provoquent un cycle d'affaiblissement et de régénération constant du champ magnétique. Ces bandes latérales se rapprochent souvent des variati ans de régime et nécessitent une FFTà haute définition pour les déceler. Elles peuvent aussi être causées parla génération-régénération du champ magnétique.

Les cannelures induites électriquement sont normalement décelées par une série de fréquences différences dont l'espacement est le plus souvent présent à la fréquence de défectuosité de la voie de ra.ilement extérieure, même si des cannelures sont présentes sur les voies de roulement intérieure et extérieure. Celles-ci se cantonnent habituellement dans une plage située entre 100000 et 150000 CPM. Un spectre de 1600lignes â 18OK CPM est recommandé pour les besoins de détection, avec des mesures sur les roulements intérieur et extérieur des moteurs c.c.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 102

ANNEXES

SPECTRE DE^-BANDE L^-RGE

AMPLITUDES PULSATOIRES

u:

LL

VIBRATION DE BATTEMENT

i1= FRÉQUENCE DE BATTEMENT

SPECTRE ZOOM

DEUX FRÉQUENCES DEUX FRÉQUENCES

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 103

ANNEXES

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 104

ANNEXES

Annexe EN : Balance quality grades for various groups of representative rigid rotors (From ISO

1940/1)

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 105

ANNEXES

Annexe EN : B.Maximum permissible residual unbalance, eper (Imperial values adapted from ISO

1940/1)

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 106

ANNEXES

Annexe Fr : Degrés de qualité d'équilibrage pour différents groupes de rotors rigides representatives
( ISO 1940/1-1986 (F) )

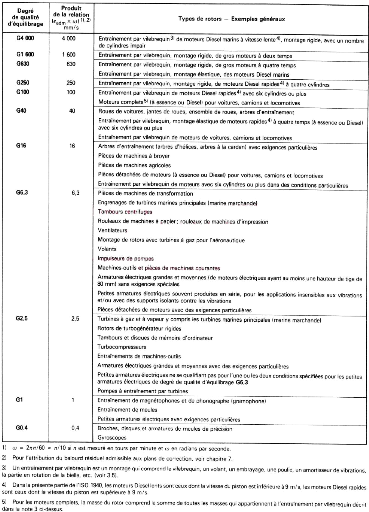
Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 107

ANNEXES

Annexe Fr : Valeur du balourd spécifique résiduel maximal admissible correspondant à divers
degrés de qualité d'équilibrage ( ISO 1940/1-1986 (F) )

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 108

ANNEXES

Programme en Matlab de l'équilibrage plan 1 pour les rotor rigide et les rotors quasi-flexibles :

clc

clear all

disp('Matlab-balancing program plan 1 for rigid rotors and quasi-flexible rotors ') disp('This program was created by Said KOUIDRI and Kouider GHRIS')

disp('This field of research is under motivation and orientation of prof:Mohammed SAROUTE')

disp(' ')

disp('Matlab-programme équilibrage plan 1 pour les rotor rigide et les rotors quasi-

flexibles')

disp('Ce programme a été créé par Said KOUIDRI et Kouider GHRIS')

disp('Ce domaine de recherche est sous la motivation et l_orientation du

prof:Mohammed SAROUTE')

disp('Contact : [e-mail]')

disp(' ')

disp('éntrez l_amplitude de vitesse de la "vibration absolue" de balourd initial')

disp('en mm/s ,Example Av_0=4.86')

Av_0=input('Av_0=') ;

disp('éntrez la phase de balourd initial en degree,Example phi_0=0.2 ')

phi_0=input('phi_0=');

disp('Connaissez-vous la valeur de la masse du rotor ? si vous savez, écrivez oui')

disp('si non écrivez non')

oui=1;

non=0;

reponse=input('reponse=');

if reponse==oui

disp('éntrezla valure de la masse du rotor M en kg,Example M=1.2')

M=input('M=');

disp('éntrez la valure de balourd spécifique e_adm en g.mm/kg ,à l_aide de l_abaque')

disp('ISO 1940 ,Nous choisissons la vitesse de fonctionnement (rotation ou service)

')

disp('Nr comme point dans laxe X et et déposezle sur la line de classe de rotor G .')

disp('L_intersection à partir de laquelle on obtient le point e_adm dans laxe Y')

disp('Examp: classe de rotor =G6.3,la vitesse de fonctionnement =3000 RPM')

disp('L_intersection donne e_adm =20 g.mm/kg ')

e_adm=input('e_adm=');

disp('le balourd résiduel admissible U_adm en g.mm est: ')

U_adm=e_adm*M

disp('éntrez la valeur du rayon du lieu que vous souhaitez placer la masse d_essai ')

disp('en mm,R_ess=41 ')

R_ess=input('R_ess=');

disp('la masse équivalente ,appelée aussi une masse résiduelle m_r en g est: ')

m_r=U_adm/R_ess

disp('La norme ISO 1940 recommande de choisir une masse d_essai m_ess en g enter ')

disp('m_ess_min et m_ess_max')

m_ess_min=m_r*5

m_ess_max=m_r*10

disp('éntrez une masse d_essai m_ess en g,Example m_ess=1.6 ')

m_ess=input('m_ess=');

else if reponse==non

disp(' choisir une masse d_essai m_ess en g en utilisant votre expérience,Example

m_ess=1.6 ')

m_ess=input('m_ess=');

disp('éntrez la valeur R_ess du rayon du lieu que vous souhaitez placer la masse

d_essai')

disp('en mm ,Example R_ess=41')

R_ess=input('R_ess=');

end

end

disp('le lieu de la masse d_essai comme un référence d_équilibrage ,angle

angle_m_ess=0^°')

disp('éntrez l_amplitude de vitesse de la "vibration absolue" de balourd

résultant(après ')

disp('avoir ajouté une masse d_essai)en mm/s ,Example Av_1=1.56')

Av_1=input('Av_1=');

disp('éntrez la phase de balourd résultant en degree,Example phi_1=-8.77 ')

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 109

ANNEXES

phi_1=input('phi_1=');

V0=Av_0*(cosd(phi_0)+j*sind(phi_0));

phi_V0_rad=angle(V0);

phi_V0_deg=rad2deg(phi_V0_rad);

V1=Av_1*(cosd(phi_1)+j*sind(phi_1)) ;

phi_V1_rad=angle(V1);

phi_V1_deg= rad2deg(phi_V1_rad);

Ve_prime=V1-V0 ;

phi_Ve_prime_rad=angle(Ve_prime);

phi_Ve_prime_deg= rad2deg(phi_Ve_prime_rad);

Vc=-V0;

phi_Vc_rad=angle(Vc);

phi_Vc_deg= rad2deg(phi_Vc_rad);

if (imag(Vc)< 0) && (imag(Ve_prime)< 0)

angle_C_de_correction=phi_Vc_deg-phi_Ve_prime_deg

end

if (phi_Vc_deg == 180)&& (imag(Ve_prime)< 0);

phi_Vc_deg=phi_Vc_deg*phi_Ve_prime_deg/abs(phi_Ve_prime_deg);

angle_C_de_correction=phi_Vc_deg-phi_Ve_prime_deg

end

if phi_Vc_deg == phi_Ve_prime_deg;

angle_C_de_correction=0

end

if (phi_Vc_deg) > 0 && (phi_Ve_prime_deg < 0);

if real(Ve_prime)< 0

phi_Vc_deg=-360+phi_Vc_deg;

angle_C_de_correction=phi_Vc_deg-phi_Ve_prime_deg else if real(Ve_prime)> 0 angle_C_de_correction=phi_Vc_deg-phi_Ve_prime_deg end

end

end

if (phi_Vc_deg) > 0 && (phi_Ve_prime_deg > 0); angle_C_de_correction=phi_Vc_deg-phi_Ve_prime_deg

end

disp('la masse de correctione avec un angle en degree angle_C_de_correction :')

angle_C_de_correction

disp('la masse de correctione m_corr en g:')

m_corr=m_ess*abs(V0)/abs(Ve_prime)

disp('le rayon de du lieu de la masse de correctione R_corr en mm est:')

R_corr=R_ess

disp('Si vous souhaitez extraire des valeurs par méthode graphique')

disp('( diagramme vectoriel) utilise le site https://www.geogebra.org/m/whh7jnmb ')

V0

phi_V0_deg

V1

phi_V1_deg

Ve_prime

phi_Ve_prime_deg

Vc

phi_Vc_deg

disp('Si vous shouaitez modifier le rayon du lieu de la masse de correctione')

disp('en gardant l_angle de correction,éntrez le nouveau rayon de votre choix

R_corr_New en mm')

R_corr_New=input('R_corr_New=');

disp('la nouvelle masse de correction m_corr_New en g est :')

m_corr_New=m_corr*R_corr/R_corr_New

BIBLIOGRAPHIE

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 111

BIBLIOGRAPHIE

BIBLIOGRAPHIE

[1] J. Chatelain,"Machines Electriques," dans Traité d'Électricité ,Vol. 10, J. Neirynck, Suisse: Presses
polytechninques romandes, 1983.

[2] M. E. El-Hawary, Electrical Energy Systems, Florida, USA: CRC Press LLC, 2000.

[3] Guide technique :Protection et contrôle des moteurs triphasés asynchrones, France: Legrand, 2020, Accédé: Mar.5.2022. [en ligne]. Disponible : https://export.legrand.com/guide-technique-protection-et-controle-des-moteurs-triphases-asynchrones

[4] L. Lasne, Exercices et problèmes d'électrotechnique :notions de base et machines électriques, Paris, France: Dunod, 2005.

[5] R. P . Bouchard et G. Olivier ,Conception de moteurs asynchrones triphasés, Canada: Éditions de l'Ecole Polytechnique de Montréal, 1997.

[6] C. Müssener et R. Linnertz ,Cours UniTrain :Machines asynchrones, Lucas Nülle LabSoft, ( Ver 1.0.0.5 ), exe.

[7] T. Wildi et G. Sybille, Électrotechnique, 4e Éd, Canada: De Boeck, 2005.

[8] J. Faiz, V. Ghorbanian et G. Joksimoviæ, "Fault Diagnosis of Induction Motors," dans IET Energy Engineering Series, Vol. 108, London, UK: The Institution of Engineering and Technology, 2017.

[9] J. Bird, Electrical and Electronic Principles and Technology, 2nd Ed ,Oxford, UK: Newnes, 2003.

[10] M. Guerguer, " Diagnostic de la machine asynchrone par analyse vibratoire ", Mémoire de Master,
Dépt.Gén.Élect, Univ Constantine 1, Constantine , Algérie, 2013.

[11] R. K. Mobley, "Maintenance Fundamentals," dans Plant Engineering Maintenance Series, Vol. 3, 2nd Edi, Oxford, UK: Elsevier Inc, 2004.

[12] Réunion technique :Les Contrôles Non Destructifs, France : CIMI.Cellule de Diffusion Technologique, 2012, Accédé:Fév.22.2022. [en ligne]. Disponible : https://www.cimi.fr/images/stories/cdt/CDT_Controle_non_destructif_201203.pdf

[13] F. Champavier, "La Maintenance Conditionnelle," dans Formation : Analyse vibratoire des machines tournantes, Chap.1 ,01db MetraVib Technologies,2008, Accédé: Mar.16.2022. [en ligne]. Disponible : https://archive.org/details/AnalyseVibratoireDesMachinesTournantesPdf

[14] E. Fournier, "Protocole de diagnostic des entrainements asynchrones par references: application a la detection des desequilibres mecaniques et des defauts de courroie ", Thèse de Doctorat, Dépt.Gén.Élect, Univ Toulouse, Toulouse, France, 2015.

[15] A. Medoued, "Surveillance et diagnostic des defauts des machines electriques : Applications aux moteurs asynchrones ", Thèse de Doctorat, Dépt.Gén.Élect, Univ 20 Août 1955, Skikda, Algérie, 2012.

[16] A. Chahmi, "Identification paramétrique de la machine asynchrone dédiée au diagnostic,", Thèse de Doctorat, Dépt.Gén.Élect, Univ Mohamed Boudiaf, Oran, Algérie, 2017.

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 112

BIBLIOGRAPHIE

[17] P. O'donnell, Report of large motor reliability survey of industrial and commercial installations, Part I, IEEE Transactions on industry applications, Vol. 21, no. 4, 1985.

[18] P. F. Albrecht, J. C. Appiarius, R. M. McCoy, E.L. Owen et D.K. Sharma, Assesment of the reliability of motors in utility applications - updated, IEEE Transactions on energy conversion, Vol. 1, no. 1, 1986.

[19] O. V. Thorsen et M. Dalva, Failure identification and analysis for highvoltage induction motors dans the petrochemical industry, IEEE Transactions on industry applications, Vol. 35, no. 4, 1999.

[20] S. Nordin, I.Muhammad et I. Rosdiazli, Condition Monitoring and Faults Diagnosis of Induction Motors: Electrical Signature Analysis, Boca Raton, FL :CRC Press, 2019.

[21] K. Alameh, "Contribution au diagnostic et à l'analyse de défauts d'une machine synchrone à aimants permanents ", Thèse de Doctorat, Dépt.Automatique, Univ Rouen Normandie, Rouen, France, 2017.

[22] Y. Imaouchen, "Mesure et analyse des vibrations des machines électriques tournantes", Thèse de Doctorat, Dépt.Gén.Élect, Univ Abderrahmane Mira, Bejaia, Algérie, 2015.

[23] M. Bensmaine, "Réalisation d'un banc d'essai destiné au diagnostic des défauts d'excentricité", Mémoire de Magistère, Dépt.Gén.Élect, Univ Mohamed Boudiaf, Oran, Algérie, 2012.

[24] M. Houioua, "Etude comparative des différents facteurs de sévérité de défauts dans un moteur asynchrone triphasé ", Mémoire de Master, Dépt.Gén.Élect, Univ Mohamed Khider, Biskra, Algérie, 2019.

[25] F. Champavier, "Les Outils de Traitement du Signal," dans Formation :Analyse vibratoire des machines tournantes, Chap. 5, 01db MetraVib Technologies, 2008, Accédé: Mar.16.2022. [en ligne]. Disponible : https://archive.org/details/AnalyseVibratoireDesMachinesTournantesPdf

[26] D. Norfield, Practical Balancing of Rotating Machinery, Oxford, UK: Elsevier, 2006.

[27] R. B. McMillan, Rotating machinery :Practical solutions to unbalance and misalignment, Lilburn, Georgia: The Fairmont Press Inc, 2004.

[28] M. Camhaoil, A. C. Nielsen et C. N. Aonghusa, Application notes: Static and Dynamic Balancing of Rigid Rotors, Denmark :Brüel & Kjaer, (n.d).

[29] A. Boulenger et C. Pachaud, Aide-mémoire : Surveillance des machines par analyse des vibrations, Paris, France:Dunod, 2009.

[30] K. Merah, "Diagnostic des défauts de roulement d'un moteur par analyse vibratoire (Etude comparative avec l'analyse du courant statorique)", Mémoire de Magistère, Dépt.Gén.Élect, Univ Mohamed Boudiaf, Oran, Algérie, 2016.

[31] H. Faigner, Analyse vibratoire des machines tournantes: Strategies de maintenance, Chap. 24, BTS MI, Accédé: Avr.5.2022. [en ligne]. Disponible : https://hubertfaigner.fr/wp-content/uploads/2021/04/S51-Approche-Systemique-dun-Bien.docx

[32] F. Champavier, "L'Analyse Vibratoire," dans Formation :Analyse vibratoire des machines tournantes, Chap. 2, 01db MetraVib Technologies, 2008, Accédé: Mar.16.2022. [en ligne]. Disponible : https://archive.org/details/AnalyseVibratoireDesMachinesTournantesPdf

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 113

BIBLIOGRAPHIE

[33] B. Magnard et E. Pasquier, Maxicours :Méthode d'équilibrage, France: Educlever, 2021,

Accédé: Avr.25.2022. [en ligne]. Disponible : https://www.maxicours.com/se/cours/methode-d-equilibrage-1/

[34] Acoustics & Vibration Research Group, Mechanical Engineering, The Free University of Brussels, Belgium: Brüel & Kjaer, 2001, Accédé: Avr.29.2022. [en ligne]. Disponible

: https://slideplayer.com/slide/5021409

[35] IMI Sensors Product Catalog : Industrial Vibration Sensors Switches & Instrumentation, USA: PCB Group Inc, 2012, Accédé: Mar.14.2022. [en ligne]. Disponible : https://www.pcb.com/Contentstore/mktgcontent/Linkeddocuments/IMI_Downloads/IMICat_Low Res.pdf

[36] Capteurs inductifs (à courants de Foucault) pour le déplacement, la distance & la position, Accédé: Mai.23.2022. [en ligne]. Disponible : https://www.usinenouvelle.com/expo/capteurs-inductifs-a-courants-de-fouca-p132893620.html

[37] F. Champavier, "La Surveillance des Machines," dans Formation :Analyse vibratoire des machines tournantes, Chap. 4, 01db MetraVib Technologies, 2008, Accédé: Mar.16.2022. [en ligne]. Disponible : https://archive.org/details/AnalyseVibratoireDesMachinesTournantesPdf

[38] C. Mcmillen, ARTICLE : Accelerometers: What do I use ,Baker Hughes, 2021, Accédé: Mai.23.2022. [en ligne]. Disponible : https://www.bakerhughes.com/bently-nevada/orbit-home/orbit-article/accelerometers-what-do-i-use

[39] Capteurs intelligents, Accédé: Mai.23.2022. [en ligne]. Disponible : https://www.andromediatech.com/capteurs-intelligents/

[40] Les détecteurs tout ou rien, Accédé: Mai.23.2022. [en ligne]. Disponible : http://lycees.ac-rouen.fr/maupassant/site2/BEPME/sujet04_05/comm_%20tech/Presentation/Doc_eleve/12_dete cteurs.pdf

[41] Capteurs et détecteurs , Accédé: Mai.23.2022. [en ligne]. Disponible : https://formation-bp-melec-89.webself.net/file/si309268/download/T-BP-TD6-fi5157762.pdf

[42] D. Stilp, "Vibration Analysis Services ", FES Systems Inc and GEA Refrigeration Division, 2008, [Modifié par S. Kouidri et K. Ghris], Accédé: Avr.13.2022. [en ligne]. Disponible : https://cupdf.com/document/rt-2008-principles-and-practices-of-vibrational-analysis-keefer.html?page=25

[43] E. Sghaier, "Dynamique des rotors à très hautes vitesses en régime non stationnaire :Identification par le filtre de Kalman", Thèse de Doctorat, Dépt.Gén.Méc, Univ Paris-Saclay, France, 2020, [Modifié par S. Kouidri et K. Ghris].

[44] E. Boulai, "Vibrations,"dans Acoustique industrielle Vibrations, Chap. 1, Moteurs Leroy Somer, 2015, p. 16, Accédé: Mar.31.2022. [en ligne]. Disponible : https://slideplayer.fr/slide/12015305

[45] L. Maurice et J. Adams, "Rotating machinery vibration :From analysis to troubleshooting," dans Mechanical Engineering Series, Vol. 130, L. L. Faulkner, New York, USA: Marcel Dekker Inc, 2001.

[46] Transformation de Fourier : rappels, Mai.25.2022. [en ligne]. Disponible : https://glq2200.clberube.org/chapitres/docs/signal-fourier

Analyse Vibratoire des Machines sur un Banc d'Essai - Cas d'un Disque Tournant - 114

BIBLIOGRAPHIE

[47] P. Girdhar et C. Scheffer, Practical Machinery Vibration Analysis and Predictive Maintenance,

Oxford, UK: Newnes, 2004.

[48] Niveaux vibratoires admissibles sur les machines tournantes, Norme ISO 2372, Accédé: Mai.15.2022. [en ligne]. Disponible

: http://www.vibraconseil.fr/normes/norme%20ISO%202372.htm

[49] Analyse vibratoire des machines tournantes :Initiation , France: Impédance machines, (n.d). http://www.impedance.fr

[50] H. P. Bloch et F. K. Geitner, Machinery Failure Analysis and Troubleshooting :Practical Machinery
Management for Process Plants, Vol. 2, 4th Ed, Oxford, UK :Elsevier, 2012.

[51] B. Magnard et E. Pasquier, Maxicours : Phenomene de desequilibre et equilibrage, France: Educlever, 2021, Accédé: Avr.25.2022. [en ligne]. Disponible : https://www.maxicours.com/se/cours/phenomene-de-desequilibre-et-equilibrage-2

[52] E. J. Gunter et C. Jackson. Balancing of rigid and flexible rotors. F. F. Ehrich, Malabar, Florida : Krieger Publishing Company, 1999.

[53] M. Thomas, "Équilibrage et alignement des machines," dans Vibrations expérimentales, École de Technologie supérieure, 2003, Accédé: Mar.29.2022. [en ligne]. Disponible : http://acversailles.free.fr/documentation/08~Documentation_Generale_M_Suire/Vibrations/Balo urd/Equilibrage_et_alignement_des_machines.pdf

[54] VIB360 Studio :Analyse et traitement des vibrations, France: Impédance, 2013, Accédé: Avr.12.2022. [en ligne]. Disponible : https://www.vib360.fr/pdf/vib360-4pages-aout2013.pdf

[55] S. Kouidri et K. Ghris, Diagramme vectoriel d'équilibrage plan 1, 2022, Accédé: Mai.6.2022. [en ligne]. Disponible : https://www.geogebra.org/m/whh7jnmb