IV.1.1.2 Comparaison des moyennes au
pré-test
Vérification de l'égalité des variances
(test de Snedecor)
a - Hypothèse Ho :
Il n'y a pas de différence significative entre les deux
variances dans les deux groupes.
b - Définir le risque :
On choisit = 5 % d'où Ftable = F0,95 ;14;14 = 2,44
c - Calculer la valeur du test :
On calcule le quotient de la plus grande des deux variances sur
la plus petite : Ftest = 0,283 / 0,222 = 1,27
d - Comparer Ftest et Ftable
1,27 < 2,44
L'hypothèse H0 est acceptée. On peut donc conclure
à l'égalité des variances des deux groupes. Cette
vérification concernant l'égalité des variances
étant réalisée, on peut comparer les variances des
moyennes des échantillons.
103
a - Emettre l'hypothèse Ho
:
Il n'y a pas d'écart significatif entre les moyennes des
deux populations ( = 5 %). Cela revient à choisir une valeur de
différence égale D = 0.
b - Choix du risque
Le risque bilatéral est de 5 %.
Le nombre de degrés de liberté (DDL) est v = 15 +
15 - 2 = 28 La valeur de t table est donc t0,975;28 = 2,1048
c - Calculer la valeur t du test.
On calcule tout d'abord l'écart-type des
différences des moyennes d'échantillons :
Sd=
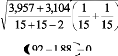
= 0,18
t calc = = 0,22
d - Comparaison de t test et t table
0,22 < 2,101
Conclusion : on accepte l'hypothèse Ho ce qui revient
à admettre que les deux échantillons sont issus de deux
populations dont les moyennes sont égales. On peut aussi
considérer qu'ils sont issus de la même population puisque l'on a
aussi vérifié que les variances étaient égales.
IV.1.1.3 Comparaison des moyennes au post-test
En appliquant le même raisonnement, on abouti aux
résultats suivants :
a - Hypothèse Ho :
Il n'y a pas de différence significative entre les deux
variances dans les deux groupes.
b - Définir le risque :
On choisit = 5 % d'où Ftable = F0,95;14;14 = 2,44
c - Calculer la valeur du test :
On calcule le quotient de la plus grande des deux variances sur
la plus petite :
104
Ftest = 1,871/ 0,960 = 1,948
d - Comparer Ftest et Ftable
1,948 < 2,44
L'hypothèse Ho est acceptée. On peut donc conclure
à l'égalité des variances des deux groupes. Cette
vérification concernant l'égalité des variances
étant réalisée, on peut comparer les variances des
moyennes des échantillons.
a - Emettre l'hypothèse Ho :
Il n'y a pas d'écart significatif entre les moyennes des
deux populations ( = 5 %). Cela revient à choisir une valeur de
différence égale D = 0.
b - Choix du risque
Le risque bilatéral est de 5 %.
Le nombre de degrés de liberté (DDL) est v = 15 +
15 - 2 = 18
La valeur de t table est donc t0,975;28 = 2,1048
1 3,437 26,1 97
15 2
5,8867 4,6133
0
c - Calculer la valeur t du test.
On calcule tout d'abord l'écart-type des
différences des moyennes d'échantillons :
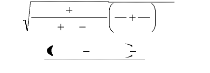
Sd=
15
1
1
15
= 0,43
15
t calc =
0,43
= 2,96
d - Comparaison de t test et t table
t calc > t tab
2,96 > 2,101
Conclusion : on rejette l'hypothèse Ho ; ce qui revient
à admettre qu'il y a une différence significative entre les
moyennes des deux groupes au post-test. Cette différence étant
significative prouve une augmentation des scores et constitue un indicateur
d'amélioration de l'apprentissage par le didacticiel. Nous passons
à la deuxième catégorie des résultats de
l'étude.
105
| 


