2. Algorithme
Entrées : ensemble d'attributs A;
échantillon E; classe c
Début
Initialiser à l'arbre vide;
Si tous les exemples de E ont la même classe
c
Alors étiqueter la racine par c;
Sinon si l'ensemble des attributs A est vide
Alors étiqueter la racine par la classe majoritaire
dans E;
Si non soit au meilleur attribut choisi dans A;
Étiqueter la racine par a;
Pour toute valeur v de a
Construire une branche étiquetée par
v;
Soit Eav l'ensemble des exemples tels que e(a) =
v;
Ajouter l'arbre construit par ID3(A-{a}, Eav,
c);
Fin pour
Fin sinon
Fin sinon
Retourner racine;
Fin
3. Exemple
Pour introduire et exécuter "à la main"
l'algorithme ID3 nous allons tout d'abord considérer l'exemple
ci-dessous: Une entreprise possède les informations suivantes sur ses
clients et souhaite pouvoir prédire à l'avenir si un client
donné effectue des consultations de compte sur Internet.
|
Client
|
Moyenne des montants
|
Age
|
Lieu de Résidence
|
Etudes supérieures
|
Consultation par internet
|
|
1
|
Moyen
|
Moyen
|
Village
|
Oui
|
oui
|
|
2
|
Elevé
|
Moyen
|
Bourg
|
non
|
non
|
|
3
|
Faible
|
Age
|
Bourg
|
non
|
non
|
|
4
|
Faible
|
Moyen
|
Bourg
|
oui
|
oui
|
|
5
|
Moyen
|
Jeune
|
Ville
|
oui
|
Oui
|
|
6
|
Elevé
|
Agé
|
Ville
|
oui
|
non
|
|
7
|
Moyen
|
Agé
|
Ville
|
oui
|
non
|
|
8
|
Faible
|
Moyen
|
Village
|
non
|
non
|
Tableau II.2. Exemples
pratiques
Ici, on voit bien que la procédure de
classification à trouver qui à partir de la description d'un
client, nous indique si le client effectue la consultation de ses comptes par
Internet, c'est-à-dire la classe associée au client.
- Le premier client est décrit par (M : moyen, Age
: moyen, Résidence : village, Etudes : oui) et a pour classe
Oui.
- Le deuxième client est décrit par (M :
élevé, Age : moyen, Résidence : bourg, Etudes : non) et a
pour classe Non.
Pour cela, nous allons construire un arbre de
décision qui classifie les clients. Les arbres sont construits de
façon descendante. Lorsqu'un test est choisi, on divise l'ensemble
d'apprentissage pour chacune des branches et on réapplique
récursivement l'algorithme.
Choix du meilleur attribut : Pour cet algorithme deux
mesures existent pour choisir le meilleur attribut : la mesure d'entropie et la
mesure de fréquence:
L'entropie : Le gain (avec pour
fonction i l'entropie) est également appelé l'entropie de Shannon
et peut se réécrire de la manière suivante :
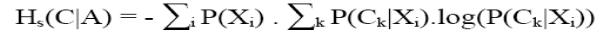
Pour déterminer le premier attribut test (racine de
l'arbre), on recherche l'attribut d'entropie la plus faible. On doit donc
calculer H(C|Solde), H(C|Age), H(C|Lieu), H(C|Etudes), où la classe C
correspond aux personnes qui consultent leurs comptes sur Internet.
H(C|Solde) = -P (faible).(P (C|faible) log(P (C|faible)) +
P (C |faible)log(P (C|faible)))-P (moyen).(P (C|moyen) log(P (C|moyen)) + P
(C|moyen) log(P (C|moyen)))-P (eleve).(P (C|eleve) log(P (C|eleve)) + P
(C|eleve) log(P(C|eleve)))H(C|Solde)
H(C|Solde) = -3/8(1/3.log(1/3) +
2/3.log(2/3)-3/8(2/3.log(2/3) + 1/3.log(1/3)-2/8(0.log(0) + 1.log(1)
H(C|Solde) = 0.20725
H(C|Age) = -P (jeune).(P (C|jeune) log(P (C|jeune)) + P (C
|jeune)log(P (C|jeune)))-P (moyen).(P (C|moyen) log(P (C|moyen)) + P (C |moyen)
log(P (C|moyen)))-P (age).(P (C|age) log(P (C|age)) + P (C|age) log(P
(C|age)))
H(C|Age) = 0.15051
H(C|Lieu) = -P (bourg).(P (C|bourg) log(P (C|bourg)) + P
(C |bourg)log(P (C|bourg)))-P (village).(P (C|village) log(P (C|village)) + P
(C |village) log(P (C|village)))-P (ville).(P (C|ville) log(P (C|ville)) + P
(C|ville)log(P (C|ville)))
H(C|Lieu) = 0.2825
H(C|Etudes) = -P (oui).(P (C|oui) log(P (C|oui)) + P (C
|oui) log(P (C|oui)))-P (non).(P (C|non) log(P (C|non)) + P (C|non) log(P
(C|non)))
H(C|Etudes) = 0.18275
Le premier attribut est donc l'âge (attribut dont
l'entropie est minimale). On obtient l'arbre suivant :
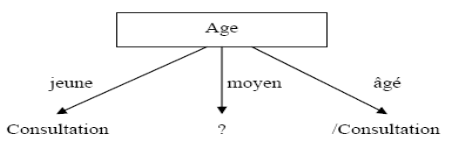
Figure II.1Arbre de
décision construit à partir de l'attribut Age
Pour la branche correspondant à un âge moyen,
on ne peut pas conclure, on doit donc recalculer l'entropie sur la partition
correspondante.
H(C|Solde) = -P (faible).(P (C|faible) log(P (C|faible)) +
P (C |faible) log(P (C|faible)))-P (moyen).(P (C|moyen) log(P (C|moyen)) + P
(C|moyen)log(P (C|moyen)))-P (eleve).(P (C|eleve) log(P (C|eleve)) + P
(C|eleve) log(P (C|eleve)))
H(C|Solde) = -2/4(1/2.log(1/2) + 1/2.log(1/2)-1/4(1.log(1)
+ 0.log(0)-1/4(0.log(0) + 1.log(1)
H(C|Solde) = 0.15051
H(C|Lieu) = -P (bourg).(P (C|bourg) log(P (C|bourg)) + P
(C |bourg) log(P (C|bourg)))-P (village).(P (C|village) log(P (C|village)) + P
(C |village) log(P (C|village)))-P (ville).(P (C|ville) log(P (C|ville)) + P
(C|ville) log(P (C|ville)))
H(C|Lieu) = 0.30103
H(C|Etudes) = -P (oui).(P (C|oui) log(P (C|oui)) + P (C
|oui) log(P (C|oui)))-P (non).(P (C|non) log(P (C|non)) + P (C|non) log(P
(C|non)))
H(C|Etudes) = 0
L'attribut qui a l'entropie la plus faible est «
Etudes ».
L'arbre devient alors :
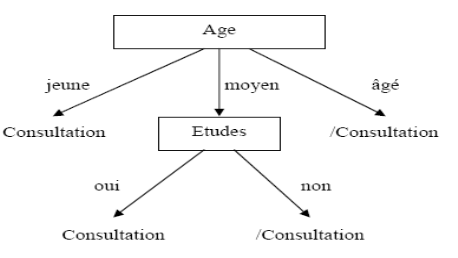
Figure II.2. Arbre de
décision finale
L'ensemble des exemples est classé et on constate
que sur cet ensemble d'apprentissage, seuls deux attributs sur les quatre sont
discriminants.
| 


