3.2. Analyse de la dynamique de la forêt
La période considérée pour l'analyse de
la dynamique de la forêt de Maâmora est de 1987 à 2014. Ce
choix est directement lié à la disponibilité des images
satellitaires de la zone. Pour évaluer la dynamique de la
végétation, on a procédé par une détection
du changement de la végétation après avoir
cartographié la répartition des principales espèces de la
forêt.
La figure ci-après donne un aperçu
général sur la méthode d'analyse de la dynamique de la
forêt.
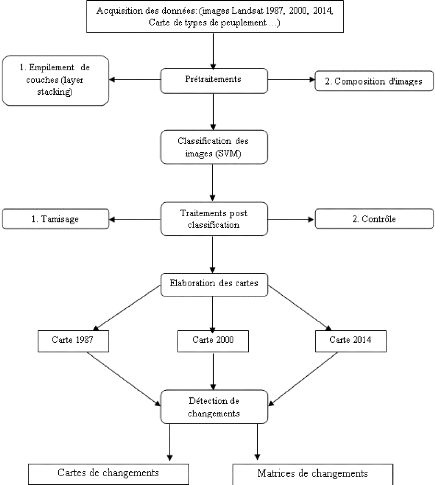
Figure 7. Méthodologie de l'Analyse de
la dynamique de la forêt.
26
3.2.1. Cartographie de la répartition des
principales espèces
3.2.1.1. Choix des classes
A partir d'une carte de type de peuplement établie lors
de la dernière révision d'aménagement de la forêt de
Maâmora (HCEFLCD, 2012), on a identifié 12 classes en tenant
compte d'une part des principales espèces de la forêt (Chêne
liège, Eucalyptus, Pins et Acacia) et d'autre part de la faculté
de discernement entre les classes de densité vu que la définition
des zones d'entrainement pour la classification ainsi que le contrôle de
la classification sont faits par interprétation visuelle.
On a ainsi distingué les classes suivantes: Quercus
suber dense (Qs1), moyennement dense (Qs2), clair (Qs3), épars
(Qs4); Eucalyptus dense (Eu1), moyennement dense (Eu2), clair (Eu3),
épars (Eu4); Acacia, Pin, Quercus suber en mélange avec
les résineux (QsR) et enfin les vides. Les classes de densité
« dense », « moyennement dense », « clair » et
« épars » correspondent respectivement aux taux de
recouvrement (R) suivant : R > 75%, 50% < R < 75%, 25% < R < 50%
et R < 25%.
3.2.1.2. Classification des images
L'algorithme de classification adopté est le SVM pour
Support Vector Machine. Cet algorithme a été adopté pour
son efficacité à classifier les données complexes et en
tirer de bons résultats.
Principe de la méthode :
La méthode SVM est une méthode de classification
supervisée qui permet de résoudre des problèmes de
discrimination et de régression. Elle passe par un entrainement sur un
jeu de données duquel elle détermine de façon optimale un
plan de séparation comme indiqué dans la figure 8. Pour les
données non linéaires, Il y a d'abord une transformation à
l'aide de fonctions Kernel. Le plan déterminé n'est pas absolu vu
qu'il y a plusieurs plans qui permettent de séparer entre les jeux de
données. Pour des questions d'optimisation, une marge sépare les
données de 2 classes. Par exemple, dans la figure ci-après, la
distance (d+)+(d-) constitue cette marge. A cause de cette marge, cette
méthode est également appelée Séparateur à
vaste marge. Les points situés sur les plans H1 et H2 sont
appelés les vecteurs de support.
27
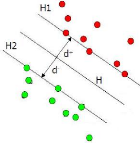
Figure 8. Séparateurs à vaste
marge (Source : Berwick, 2003).
Dans le cas de la classification d'images satellites, des ROIs
sont fournis et l'algorithme fait un apprentissage sur ces données.
Pendant l'entrainement de l'algorithme, la séparation entre les pixels
des classes fournies en ROIs se fait sur la base de l'information spectrale.
Les plans ainsi que les marges de séparation sont
déterminés donnant lieu à un modèle. Pendant la
classification de l'entièreté de l'image, chaque pixel est
classé dans une catégorie en fonction de son information
spectrale à l'aide du modèle déterminé lors de
l'entrainement.
Définition des ROIs : le SVM est un
algorithme de classification supervisée, et comme toutes les autres
méthodes de classification supervisée, il a
nécessité la définition des zones d'entrainements ou ROI
(Regions Of Interest). Disposant d'un shapefile des types de peuplements, on a
alors procédé à la délimitation des ROIs en
visualisant le shapefile sur l'image. Ce ne fut pas un travail automatique car
il a fallu s'assurer de la correspondance entre la classe donnée par le
shapefile et celle obtenue par interprétation visuelle de l'image
satellitaire.
Le problème majeur est celui de la classification des
images plus anciennes. Pour pallier à ce problème, on a
commencé par l'image la plus récente avant de remonter
progressivement aux plus anciennes permettant ainsi de s'habituer aux
signatures spectrales des différentes classes pendant
l'interprétation visuelle.
Dans QGIS, la définition des ROIs n'est rien d'autre
que la création d'une couche de polygones des différentes
classes.
Calcul des statistiques de l'image : C'est
l'étape qui suit la définition des ROIs. Il s'agit du calcul de
la moyenne et de l'écart-type de chaque bande de l'image. Le fichier
résultant est stocké dans un fichier XML et utilisé dans
les étapes suivantes.
28
Apprentissage de l'algorithme : A partir des
ROIs fournis ainsi que les statistiques de l'image, l'algorithme produit un
modèle qui servira à classifier dans la suite les autres pixels
non inclus dans les ROIs.
Classification proprement dite : C'est ici
que, sur la base du modèle produit précédemment, l'image
est classifiée donnant lieu aux classes prédéfinies dans
les ROIs.
Tamisage de l'image classifiée :
L'algorithme "sieve" permet de tamiser l'image afin de ne pas avoir
des pixels isolés. Pour cela, il est à fournir la taille de la
plus petite entité à
considérer ou MMU (Minimum Mapping Unit) qui est de 1ha
au moins en matière de cartographie forestière (ONF, 2014). On a
considéré environ 2ha soit 20 pixels d'une image Landsat 30m.
Contrôle et validation de la classification :
Vu que la qualité de la classification est tributaire de
plusieurs facteurs comme par exemple le choix des classes, la qualité
des
ROIs définis pour ne citer que ceux-ci, il convient de
contrôler la classification. La
méthode de contrôle adoptée est en partie
celle proposée par l'ONF. Après le tamisage de l'image
classifiée, on a procédé à la
génération aléatoire de 60 points de contrôle par
classe. Ensuite, par interprétation visuelle, on a
renseigné dans un champ la classe à
laquelle devrait appartenir le point. Ceci a servi plus tard
de vérité terrain pour le calcul de la matrice de confusion. Une
fois la classe de chaque point renseignée, on procède au
calcul de la matrice de confusion qui permettra de calculer le
coefficient Kappa via une
table de calcul excel. Selon Landis et Koch (1977), le
coefficient Kappa permet d'apprécier la qualité de la
classification et dire qu'elle est excellente si K > 0,8, bonne si
0,8 > K > 0,6, modérée quand 0,6 > K
> 0,2 et mauvaise quand K < 0,2. Dans notre cas, la classification est
validée si le coefficient Kappa excède 80%. Faute de quoi, il a
fallu soit redéfinir les ROIs dans le cas où il y a trop de
confusion entre les classes, ou soit redéfinir les classes si elles ne
sont pas bien définies dans le choix des classes jusqu'à
l'obtention d'une précision de classification satisfaisante.
Pour l'image de 2014 où il a été possible
d'effectuer un contrôle sur terrain, un second contrôle basé
sur des vérités terrain (polygones) recueillies sur quelques
sites en forêt de Maâmora a été
réalisé. Ces polygones ont été utilisés pour
un second calcul du coefficient Kappa.
| 


