Chapitre 1
- Les trois composantes du champ de déplacement A =
(u, v, w) :
( )
( )
( )
- les six composantes du tenseur de petites
déformations :
( )
( )
( )
- les six composantes du tenseur des contraintes :
Pour résoudre un tel problème, nous devons
disposer de 15 équations. Ces équations sont :
|
Les trois équations d'équilibre [2]
:
|
|
|
|
|
|
|
Sur V :
9 /176
10 /176
Chapitre 1
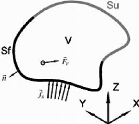
Figure 1.3: Solide de domaine V soumis à des
chargements
Les six relations géométriques de Cauchy
[2] :
Ces équations assurent que les déformations
dérivent d'un champ de déplacement
( )
( )
( )
La loi de Hooke sous forme directe pour un
matériau isotrope, élastique et linéaire [2] :
( )
( )
( )
Ces équations sont assorties de conditions aux limites
en pression ou en déplacement :
11 /176
Chapitre 1
Sur Sf : {
Sur Su :
1.5.2. Les différentes méthodes de
résolution
La résolution des équations de la théorie
de l'élasticité peut être menée de plusieurs
manières en fonction des quantités prises comme inconnues et on
distingue généralement trois grandes méthodes de
résolution :
- La résolution du problème en fonction des
déplacements : dans ce cas, on considère que les fonctions
inconnues sont les composantes : u, v, w du vecteur déplacement ;
- La résolution en fonction des contraintes : dans ce
cas, on considère que les fonctions inconnues sont les composantes des
contraintes normales et tangentielles ;
- La résolution du problème sous forme mixte :
dans ce cas, on considère comme fonctions inconnues, une partie des
fonctions déplacements et l'autre partie des fonctions contraintes.
En théorie de l'élasticité, l'on
est souvent conduit à résoudre les équations de
Lamé qui constituent un modèle décrivant le comportement,
en déformation, d'un solide sous des conditions de chargement et de
fixation connues (conditions aux limites).
La résolution du problème de la théorie
de l'élasticité consiste à déterminer en tout point
des coordonnées cartésiennes un vecteur de composantes u, v, w
caractérisant un petit déplacement de ce point au cours de la
déformation du milieu.
Nous proposerons dans la suite la méthode de GALERKIN
pour la résolution des équations de Lamé, afin de simuler
le comportement d'un solide à surface lisse, sous des conditions aux
limites en déplacement et soumis à un chargement volumique.
12 /176
Chapitre 1
| 


