Modélisation et simulation par éléments finis. Cas d'un tablier de pont.

REPUBLIQUE DU BENIN

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE

LA RECHERCHE SCIENTIFIQUE
UNIVERSITE D'ABOMEY-CALAVI

ECOLE POLYTECHNIQUE D'ABOMEY-CALAVI

DEPARTEMENT DE GENIE CIVIL
OPTION : Bâtiments et Travaux Publics

MEMOIRE DE FIN DE FORMATION

Présenté et soutenu par :
Boris Sèdjro S. KAGBO

En vue de l'obtention du diplôme

d'Ingénieur de Conception en Génie-Civil

MODELISATION ET SIMULATION PAR ELEMENTS FINIS : CAS

D'UN TABLIER DE PONT

Thème du mémoire :

Devant le jury composé de :

Dr. SAVY Mathias Président

Dr. HOUINOU Agathe Examinateur

Dr. OLODO Emanuel Rapporteur 1

Pr. ADANHOUNME Villevo Rapporteur 2

Sous la direction de :

Dr. Ing. Emmanuel OLODO

Maître Assistant du CAMES,

Enseignant à l'EPAC / UAC

&

Pr. Villevo ADANHOUNME

Maître de conférences du CAMES, Professeur,

Enseignant à la CIPMA / UAC

Novembre 2014

Certification

Certification

Nous certifions que ce mémoire a été conduit et réalisé sous notre direction par Monsieur Boris Sèdjro S. KAGBO au Département de Génie Civil de l'Ecole Polytechnique d'Abomey-Calavi (EPAC) avec la collaboration de la Chaire Internationale en Physiques Mathématiques et Applications (CIPMA).

i /176

Sous la direction de :

Dr. Ing. Emmanuel OLODO
Maître Assistant du CAMES,
Enseignant à l'EPAC / UAC
&
Pr. Villevo ADANHOUNME
Maître de conférences du CAMES, Professeur,
Enseignant à la CIPMA / UAC

ii /176

Dédicaces

Dédicaces

Je dédie ce mémoire à :

Ma mère, qui a oeuvré pour ma réussite, par son amour, son soutien, tous les sacrifices consentis et ses précieux conseils, pour toute son assistance et sa présence dans ma vie, reçois à travers ce travail aussi modeste soit-il, l'expression de mes sentiments et de mon éternelle gratitude.

Mon père, qui peut voir à travers ce travail le résultat de longues années de sacrifices et de privations pour m'aider à avancer dans la vie. Puisse Dieu faire en sorte que ce travail porte son fruit ; merci pour les valeurs nobles, l'éducation et pour ton attachement exceptionnel au sens de la responsabilité parentale.

Mes frères et soeurs qui n'ont cessé d'être pour moi des exemples de persévérance, de courage et de générosité.

Mes professeurs de l'EPAC qui doivent voir dans ce travail la fierté d'un savoir bien acquis.

Boris Sosthène S. KAGBO

iii /176

Remerciements

Remerciements

« Tout ce qui est conçu et construit dans ce monde peut être amélioré

par la simulation. »

L'élaboration du présent mémoire a été possible grâce au soutien indéfectible et à la franche collaboration de plusieurs personnes. Je tiens donc à exprimer mes sincères remerciements et ma profonde gratitude à :

Dr. Ing. Emmanuel OLODO, Maître Assistant du CAMES, mon maître de mémoire, pour avoir accepté d'encadrer ce travail et de le conduire jusqu'au bout. Ce document n'aurait pu être réalisé sans ses conseils, son esprit d'écoute, son soutien sans pareils et surtout cette confiance qu'il a placée en moi ;

Pr. Villevo ADANHOUNME, Maître de Conférences du CAMES, Professeur, mon co-maître de mémoire, pour ses apports, son enthousiasme, ses conseils, ses analyses fort pertinentes, son implication personnelle malgré ses multiples occupations et pour avoir effectué avec moi un travail d'une rare qualité à l'occasion de la préparation de ce mémoire ; je lui dis : « Merci !!! » ;

Pr. Mohamed GIBIGAYE, Maître de Conférences du CAMES, Enseignant-Chercheur à l'EPAC/UAC, mon professeur. Pour nous avoir enseigné avec tant de dévotion ; pour nous avoir inculqués constamment, la rigueur au travail et la persévérance dans toutes nos entreprises ;

Ing. Zinsou Côme AHOUANSOU, mon parrain, « Aux âmes bien nées, la valeur n'attend point le nombre d'années ». Vous êtes si jeune, mais déjà si riche d'expériences. Merci d'avoir accepté spontanément de travailler avec moi ;

Ing. Thomas Dèkandji EKPO, Directeur Général du bureau d'étude PERS-BTP, pour m'avoir encadré lors de mon stage, pour

iv /176

Remerciements

votre promptitude quand il s'est agi de mettre à ma disposition un projet réel et pour m'avoir prodigué des encouragements personnels très utiles dans les périodes de doute. Vos conseils, au-delà de cela, m'ont été d'une grande utilité ;

Pr. Gérard GBAGUIDI AISSE, Maître de Conférences du CAMES, Enseignant-Chercheur à l'EPAC/UAC, mon professeur. Pour tous les conseils qu'il nous a procurés lors de notre cursus à l'EPAC ;

Pr. Victor GBAGUIDI, Maître de Conférences du CAMES, Enseignant-Chercheur à l'EPAC/UAC, mon professeur. Pour nous avoir enseigné avec tant de dévotion ;

M. François TOLLO, mon oncle, je n'essaierai pas de chercher des formules pour exprimer ma gratitude, je n'en trouverai sûrement pas. Simplement, merci pour tout ;

Pr. Norbert HOUNKONNOU, Professeur Titulaire, Président de la Chaire Internationale en Physiques Mathématiques et Applications (CIPMA-Chaire UNESCO) / UAC. Pour votre grande disponibilité et vos conseils très instructifs ;

À tous les enseignants de l'EPAC et en particulier ceux du département de génie civil, pour la qualité de l'enseignement. Nous voulons citer :

? Pr. ADJOVI Edmond, Maître de Conférences en Sciences et Techniques de Génie-Civil, Professeur Titulaire, Enseignant à l'EPAC, Directeur de l'ESTBR-Abomey ;

? Dr. Ing. ALLOBA Ezéchiel, Maître Assistant du CAMES, Enseignant à l'EPAC ;

? Dr. Ing. BACHAROU Taofick, Maître Assistant du CAMES, Enseignant à l'EPAC ;

v /176

Remerciements

> Pr. CODO François de Paule, Maitre de Conférences du CAMES, Professeur, Enseignant à l'EPAC ;

> Dr. Ing. CHAFFA Gédéon, Maître Assistant du CAMES, Enseignant à l'EPAC ;

> Dr. Ing. DEGBEGNON Léopold, Maître Assistant du CAMES, Enseignant à l'EPAC, Enseignant à l'EPAC ;

> Dr. Arch. DIOGO Noël, Docteur architecte, Enseignant à l'EPAC ;

> Dr. HOUINOU Agathe SOUROU, Docteur Ingénieur en Mécanique des sols, Enseignant à l'EPAC ;

> Dr. HOUINOU Gossou Jean, Maître Assistant du CAMES, Enseignant à l'EPAC ;

> Dr. SAVY Mathias, Maître Assistant du CAMES, Enseignant à l'EPAC ;

> Dr. TCHEHOUALI Adolphe, Maître Assistant du CAMES, Enseignant à l'EPAC ;

> Dr. WANKPO Tonalémi Epiphane Sonon, Docteur Ingénieur en Hydraulique, Enseignant à l'EPAC ;

> Dr. ZEVOUNOU Crépin, Maître Assistant du CAMES, Enseignant à l'EPAC ;

> Dr. ZINSOU Codjo Luc, Docteur Ingénieur en Mécanique des sols, Enseignant à l'EPAC ;

> Ing. ZOHOUNGBOGBO Prosper ; > Ing. Maximin d'ALMEIDA.

Au Professeur Félicien AVLESSI, Directeur de L'Ecole Polytechnique d'Abomey-Calavi et au Professeur Martin AINA chef du Département de Génie Civil.

A tout le personnel du bureau d'étude PERS-BTP pour leur soutien.

vi /176

Remerciements

A tous les camarades de la 7^ème promotion et plus particulièrement mes amis Ibrahim, Imeldo, Gildas, Samson, Loïc avec qui nous avons passé cinq (5) mémorables années de notre vie et pour les nostalgiques moments d'entraide, de solidarité et de joie.

A mes amis Eric, Hermann avec qui j'ai passé de très bons moments durant ces cinq années.

Je ne voudrais en aucun cas oublier, mon Père KAGBO Alain, ma Mère MIGAN Denise, mon frère Roland, ma soeur Alena, pour tout leur soutien.

vii /176

Résumé

Résumé

Dans l'ingénierie civile, la modélisation permet de comprendre les variables qui influencent une structure conçue, afin de l'optimiser techniquement et de procéder à des vérifications de stabilité, rigidité et résistance.

Le présent travail de recherche s'intéresse aux techniques de modélisation et de simulation numérique par la méthode des éléments finis. Il est principalement structuré en quatre grandes parties. La première partie, qui tient lieu de généralités, présente les méthodes d'approximations en physiques et aborde la construction pratique d'un problème variationnel à travers l'étude de la déformation, d'un solide, décrit par les équations de lamé que nous reformulons par les équations de Poisson et de Laplace. Avec la prise en compte des conditions aux limites et l'utilisation de la méthode de GALERKIN, nous résolvons les équations de Lamé et déterminons le tenseur des contraintes et des déformations.

La deuxième partie traite de la construction d'un modèle élément fini, nous exposons la méthode d'approximation par élément fini et les principes de maillage d'un domaine. Les concepts de transformation géométrique et d'élément de référence simplifient la construction des fonctions d'interpolation et des matrices de rigidités élémentaires. Nous développons également la technique d'assemblage des matrices élémentaires pour la résolution du système d'équations global.

La troisième partie constitue une étude de certains types d'éléments finis et porte une attention particulière à l'élément fini tétraédrique à 12 degrés de liberté. Nous proposons un programme développé en FORTRAN pour calculer sa matrice de rigidité élémentaire.

Dans la dernière partie, nous utilisons le logiciel Autodesk Robot SAP 2012, pour modéliser par éléments finis, les éléments d'un tablier de pont ; il s'agit du pont à construire sur le tronçon 1 : Frontière TOGO-TCHETTI SAVALOU, au PK 23 + 200. Nous effectuons une simulation numérique sur le tablier, pris dans son ensemble, et aboutissons à un dimensionnement de chacun de ses éléments.

Mots clés : modélisation, simulation, éléments finis, équations de Lamé, GALERKIN, maillage, éléments de référence, fonctions d'interpolations, matrice de rigidité, degré de liberté, assemblage.

viii /176

Abstract

Abstract

In civil engineering, modeling makes it possible to understand the variables that influence a structure designed to optimize technically and conduct audits of stability, stiffness and strength.

This research work focuses on modeling techniques and numerical simulation by finite element method. It is mainly divided into four main parts.

The first part, which takes the place of generality, these approximation methods in physics and discusses the practical construction of a variational problem through the study of the deformation of a solid, described by the Lame's equations by reformulating the Laplace and Poisson's equations. With the consideration of the boundary conditions and the use of the GALERKIN method, we solve the Lame's equations and determine the stress tensor and deformation.

The second part deals with the construction of a finite element model, we present the method of approximation by finite element mesh and the principles of a domain. The concepts of geometrical transformation and for reference simplify the construction of the interpolation function and elementary stiffness matrices. We are also developing the assembly of the elementary matrices to the technical resolution of the overall system of equations.

The third part is a study of certain types of finite elements and pays particular attention to the finite element tetrahedral 12 degrees of freedom. We propose a system developed in FORTRAN to calculate the elementary stiffness matrix program.

In the last part, we use the Autodesk Robot 2012 SAP software for finite element model, the elements of a bridge deck; it is the bridge to be built on the section 1: TOGO-Tchetti SAVALOU Frontier, PK 23 + 200. We perform a numerical simulation on the apron, taken as a whole, and end up with a design for each of its elements.

ix /176

Sommaire

Sommaire

Certification i

Dédicaces ii

Remerciements iii

Résumé vii

Abstract viii

Sommaire ix

Liste des figures xii

Liste des tableaux xviii

Liste des symboles et abréviations xix

Avant-propos xxi

Introduction générale 1

Chapitre 1 : Méthodes d'approximations en physiques 3

1.1. Modélisation et Simulation 4

1.2. Classification des systèmes physiques 4

1.3. Processus d'analyse d'un problème physique 5

1.4. Méthodes d'approximations 7

1.5. Définition d'un problème de l'élasticité linéaire 8

1.6. Méthode de GALERKIN pour la résolution des équations de Lamé 12

Chapitre 2 : Méthode des Eléments finis 28

2.1. Processus d'analyse par la méthode des éléments finis 29

2.2. Discrétisation géométrique (maillage) 32

2.3. Approximation nodale 39

2.4. Approximation par éléments finis 41

2.5. Définition de la géométrie des éléments 43

x /176

Sommaire

2.6. Approximation sur un élément de référence 49

2.7. Construction des fonctions d'interpolations et de transformations

géométriques 53

2.8. Matrice élémentaire 59

2.9. Assemblage et conditions aux limites 60

Chapitre 3 : Etude de quelques exemples d'éléments finis 62

3.1. Elément fini linéaire à deux noeuds 63

3.2. Elément fini triangulaire plan à trois noeuds 64

3.3. Elément fini tétraédrique à quatre noeuds 66

Chapitre 4 : Modélisation et Simulation numérique d'un tablier de pont 90

4.1. Matériels employés pour la simulation 91

4.2. Présentation générale de l'ouvrage 92

4.3. Caractéristiques du Tablier 94

4.4. Définition des charges et actions appliquées à la structure 99

4.5. Définition du flux de travail 109

4.6. Définition de la structure 110

4.7. Construction du modèle éléments finis (EF) 116

4.8. Introduction des conditions de fixations (Appuis) 118

4.9. Choix des normes et règlements à utiliser 119

4.10. Définitions des charges 120

4.11. Lancement des calculs de la structure 128

4.12. Résultats de calcul 129

4.13. Définition des combinaisons d'actions 134

4.14. Exploitation des résultats 136

xi /176

Sommaire

Conclusion et perspectives 157

Références bibliographiques 158

Table des matières 162

Annexes 167

xii /176

Liste des figures

Liste des figures

Figure 1.1: Processus d'analyse utilisant un modèle numérique 6

Figure 1.2: Vue synthétique des méthodes d'approximation 8

Figure 1.3: Solide de domaine V soumis à des chargements 10

Figure 1.4 : Représentation 3D du domaine Q 16

Figure 1.5 : Courbe de simulation de la composante _åxx du tenseur des

déformations 25

Figure 1.6 : Courbe de simulation de la composante _åyy du tenseur des

déformations 25

Figure 1.7 : Courbe de simulation de la composante _åzz du tenseur des

déformations 26

Figure 1.8 : Courbe de simulation de la composante _åxy du tenseur des

déformations 26

Figure 1.9 : Courbe de simulation de la composante _åyz du tenseur des

déformations 27

Figure 1.10: Courbe de simulation de la composante _åzx du tenseur des

déformations 27

Figure 2.1 : Organigramme descriptif de la démarche de résolution MEF 30

Figure 2.2 : (a) - Solide (Poutre en I) ; (b) Modèle éléments finis 31

Figure 2.3 : Maillage d'un pont de type Bow-string en vue d'une simulation 33

Figure 2.4 : (a) maillage en 2D (poutre I) ; (b) maillage en 3D (poutre I) 33

Figure 2.5 : (a) maillage raffiné (plaque) ; (b) maillage grossier (plaque) 34

Figure 2.6 : Formes géométriques 1D 34

Figure 2.7 : Formes géométriques 2D 35

Figure 2.8 : Formes géométriques 3D 35

Figure 2.9 : Connexions inadéquates entre éléments 36

xiii /176

Liste des figures

Figure 2.10 : Connexions adéquates entre éléments 37

Figure 2.11 : Exemple de maillage à exclure 38

Figure 2.12 : Discrétisation géométrique des frontières courbes 38

Figure 2.13 : Méthodes d'approximation 43

Figure 2.14 : Transformation d'un élément de référence en élément réel 44

Figure 2.15 : Transformation d'un même élément de référence en tous les

éléments réels 45

Figure 2.16 : Exemple d'éléments de référence à une dimension 47

Figure 2.17 : Exemple d'éléments de référence à deux dimensions 47

Figure 2.18 : Exemple d'éléments de référence à trois dimensions 48

Figure 3.1 : Elément de Poutre plan. 63

Figure 3.2 : Elément fini de poutre avec deux degrés de liberté par noeuds. 63

Figure 3.3 : Elément fini de poutre avec trois degrés de liberté par noeuds. 64

Figure 3.4 : Elément triangulaire plan à trois noeuds. 65

Figure 3.5 : Elément triangulaire plan avec deux degrés de liberté par noeuds.65

Figure 3.6 : Elément de référence de forme tétraédrique. 66
Figure 3.7 : Capture d'écran des données en Input du programme matrice_K 88 Figure 3.8 : Capture d'écran des données en Output du programme matrice_K

89

Figure 4.1 : Vue aérienne du pont 93

Figure 4.2 : Trottoir équipé de garde-corps 93

Figure 4.3 : Vue de dessus du tablier 94

Figure 4.4 : Vue de dessous du tablier 94

Figure 4.5. Vue en plan générale 96

Figure 4.6 : Coupe longitudinale axiale 97

xiv /176

Liste des figures

Figure 4.7 : Coupe transversale du tablier 98

Figure 4.8 : Convoi de charges du système Bc 103

Figure 4.9 : système Bc en vue transversale et en plan 103

Figure 4.10 : Système Bt en vue transversale, longitudinale et en plan 104

Figure 4.11 : Axes de construction créés dans Autocad 110

Figure 4.12 : Importation des Axes de constructions 110

Figure 4.13 : - Boite de dialogue - Importation des fichiers dwg/dxf 111

Figure 4.14 : Axes de constructions importés dans Robot 111

Figure 4.15 : Définition des poutres et entretoises 112

Figure 4.16 : - Boite de dialogue - Panneaux 112

Figure 4.17 : - Boite de dialogue - Paramètre de ferraillage, Onglets Général et

Matériaux 113

Figure 4.18 : - Boite de dialogue - Paramètre de ferraillage, Onglets Paramètre

ELS et Ferraillage 114

Figure 4.19 : - Boite de dialogue - Nouvelle épaisseur 115

Figure 4.20: - Boite de dialogue - Modèle de Calcul du panneau 115

Figure 4.21 : Définition de la structure du Tablier dans Robot 116

Figure 4.22 : - Boite de dialogue - Options de maillage 117

Figure 4.23 : - Boite de dialogue - Options de maillage avancées 117

Figure 4.24 : Maillage du tablier 118

Figure 4.25 : - Boite de dialogue - Appuis 118

Figure 4.26 : Système d'appuis du tablier 119

Figure 4.27 : - Boite de dialogue - Préférence de l'affaire, choix de la norme de

conception 120

Figure 4.28 : - Boite de dialogue - Cas de charge 121

xv /176

Liste des figures

Figure 4.29 : - Boite de dialogue - Charges roulantes 122

Figure 4.30 : - Boite de dialogue - Charges roulantes 123

Figure 4.31 : - Boite de dialogue - Polyligne-contour 124

Figure 4.32 : - Boite de dialogue - Paramètres de la route 124

Figure 4.33 : Cas 3 - Q_trottoir : Charge d'exploitation des trottoirs 125

Figure 4.34 : Cas 5 - A(L) : Surcharge A(L) 125

Figure 4.35 : Cas 6 - G_garde_corps : Poids propre des Garde-corps 126

Figure 4.36 : Cas 7 - G Trottoir : Poids propre des trottoirs 126

Figure 4.37 : Cas 8 - G_coucheR+etanch : Poids propre Couche de roulement

& étanchéité 126

Figure 4.38 : Cas 9 - 2 File Bc Poutres : deux files du convoi de camions Bc 127

Figure 4.39 : Cas 10 - 2 File Bc Dalle : deux files du convoi de camions Bc 127

Figure 4.40 : Cas 11 - 2 File Bt Dalle : groupes de deux essieux-tandems 127

Figure 4.41 : Cas 12 - 2 File Bc Dalle, deux files du convoi de camions Bc 127

Figure 4.42 : - Boite de dialogue - Calcul 128

Figure 4.43 : Cartographie des contraintes _æyy relatives au système de charges

A (Travées 1, 2 et 3) 129

Figure 4.44 : Cartographie des contraintes _æyy relatives aux convois de charges

Bc (Travée 2) 129

Figure 4.45 : Cartographie des contraintes _æyy relatives aux convois de charges

Bc (Travée 3) 130

Figure 4.46 : Cartographie des contraintes _æyy relatives aux groupes d'essieux-

tandems (Travée 2) 130

Figure 4.47 : Cartographie des contraintes _æyy relatives aux groupes d'essieux-

tandems (Travée 3) 130

xvi /176

Liste des figures

Figure 4.48 : Moment fléchissant _myy dû aux systèmes de charge A (Travées 1,

2 et 3) 131

Figure 4.49 : Moment fléchissant _myy dû aux convois de charges Bc aux

convois de charges Bc (Travée 2) 131

Figure 4.50 : Moment fléchissant _myy dû aux convois de charges Bc (Travée 3)

132

Figure 4.51 : Moment fléchissant _myy dû aux groupes d'essieux-tandems

(Travée 2) 132

Figure 4.52 : Moment fléchissant _myy dû aux groupes d'essieux-tandems

(Travée 2) 132

Figure 4.53 : Moment fléchissant maximum dans la poutre de rive gauche

(Travée 3) 133

Figure 4.54 : Moment fléchissant maximum dans la poutre intermédiaire

gauche (Travée 3) 133

Figure 4.55 : Moment fléchissant maximum dans l'entretoise d'about (Travée 3)

134

Figure 4.56 : - Boite de dialogue - composante du cas 134

Figure 4.57 : - Boite de dialogue - Combinaison 135

Figure 4.58 : Cartographie des sections d'aciers réels dans la direction

principale de portance (lit inférieur) 136

Figure 4.59 : Cartographie des sections d'aciers réels dans la direction

secondaire (lit inférieur) 137

Figure 4.60 : Cartographie des sections d'aciers réels dans la direction

principale de portance (lit supérieur) 137

Figure 4.61 : Cartographie des sections d'aciers réels dans la direction

secondaire (lit supérieur) 138

Figure 4.62 : Schéma de ferraillage dalle sous chaussée (1/4) 139

Figure 4.63 : Schéma de ferraillage dalle sous chaussée (2/4) 140

xvii /176

Liste des figures

Figure 4.64 : Schéma de ferraillage dalle sous chaussée (3/4) 141

Figure 4.65 : Schéma de ferraillage dalle sous chaussée (4/4) 142

Figure 4.66 : Schéma de ferraillage poutres de rives (1/4) 144

Figure 4.67 : Schéma de ferraillage poutres de rives (2/4) 145

Figure 4.68 : Schéma de ferraillage poutres de rives (3/4) 146

Figure 4.69 : Schéma de ferraillage poutres de rives (4/4) 147

Figure 4.70 : Schéma de ferraillage poutres intermédiaires (1/4) 149

Figure 4.71 : Schéma de ferraillage poutres intermédiaires (2/4) 150

Figure 4.72 : Schéma de ferraillage poutres intermédiaires (3/4) 151

Figure 4.73 : Schéma de ferraillage poutres intermédiaires (4/4) 152

Figure 4.74 : Schéma de ferraillage entretoises (1/3) 154

Figure 4.75 : Schéma de ferraillage entretoises (2/3) 155

Figure 4.76 : Schéma de ferraillage entretoises (3/3) 156

xviii /176

Liste des tableaux

Liste des tableaux

Tableau 2.1 : Nombre de monômes nécessaire pour construire des polynômes

complets 54

Tableau 2.2 : Bases polynomiales complètes et incomplètes 55

Tableau 3.1 : Tableau des valeurs de la matrice de rigidité élémentaire de

l'élément tétraédrique à 4 noeuds (douze degrés de liberté). 84

Tableau 3.2 : Valeurs d'essai pour le test du programme matrice_K 88

Tableau 4.1 : Charges permanentes 99

Tableau 4.2 : Classe de pont en fonction de la largeur roulable 100

Tableau 4.3 : Coefficient de dégressivité transversale de la charge A(L) 101

Tableau 4.4 : Coefficients a1 et a2 102

Tableau 4.5 : Coefficient de dégressivité transversale b_c 104

Tableau 4.6 : Coefficient de dégressivité transversale bt 104

Tableau 4.7 : Tableau de détermination de la longueur L pour le calcul de 61 106 Tableau 4.8 : Tableau de détermination de la valeur de G pour le calcul de 61

106

Tableau 4.9 : Tableau de détermination de la valeur de G pour le calcul de 62

107

Tableau 4.10 : Tableau récapitulatif des valeurs de 6 108

Tableau 4.11 : Tableau récapitulatif des valeurs du produit de coefficients 6*b

109

xix /176

Liste des symboles et abréviations

Liste des symboles et abréviations

[ ] . Matrice quelconque (carrée ou rectangulaire)

{ } . Vecteur (matrice colonne)

< > . Matrice ligne

[ ]^t . Matrice transposée

[ ]^-1 . Matrice inverse

V . Volume du solide

S . Surface du solide

. Contour

IV . Intégrale sur le volume

IS . Intégrale sur la surface

I . Intégrale sur le contour

Ó . Somme

{u} . Champ de déplacement en un point quelconque

{E} ou [E] . Champ de déformation en un point quelconque

{æ} ou [æ] . Champ de déformation en un point quelconque

[H] . Matrice des constantes d'élasticité

{u_n} . Déplacements nodaux pour un élément

{f^V} . Champ de forces de volume

{f^S} . Champ de forces de surface

Ni . Fonction de forme attachée au noeud i

[N] . Matrice des fonctions d'interpolation

[B] . Matrice des fonctions de déformation

[D] . Matrice des opérateurs de dérivation

[K] . Matrice de rigidité de la structure

[K_e] . Matrice de rigidité élémentaire

xx /176

Liste des symboles et abréviations

{F^V} . Forces nodales de volume

{F^S} . Forces nodales de surface

{F} . Forces nodales pour la structure

x, y, z . Coordonnées dans le repère réel (global)

x . Notation simplifiée des coordonnées : x=< x, y, z >

î, ç, æ . Coordonnées dans le repère de référence (local)

î . Notation simplifiée des coordonnées : î=< î, ç, æ >

A . Section de la poutre

I . Inertie de la poutre

L . Longueur d'un élément

ö . Fonction de pondération

A, p . Coefficients de Lamé

E . Module d'élasticité longitudinale

G . Module d'élasticité transversale

í . Coefficient de Poisson

EDP . Equation aux dérivées partielles

DDL . Degrés de libertés

EF . Eléments finis

MEF . Méthode des éléments finis

xxi /176

Avant-propos

Avant-propos

L

'idée fondamentale derrière la méthode des éléments finis remonte loin en arrière. Les Grecs par exemple avaient reconnu que l'on peut approcher la solution d'un problème complexe en le divisant en problèmes plus simples. On peut par exemple approcher le périmètre d'un cercle en calculant le périmètre d'un polygone à n côtés, pourvu que n soit suffisamment grand. Il suffit alors de connaitre la longueur d'un segment de droite, problème beaucoup plus simple que celui de la longueur d'un arc de cercle.

Le présent travail se veut être une base solide de restitution de connaissances techniques et pratiques indispensables à la construction d'un modèle élément fini, en vue d'une simulation numérique.

Nous poursuivrons ainsi deux objectifs. Bien sûr, nous souhaitons une description relativement classique des principales étapes de mise en oeuvre de la méthode sur un ordinateur et passer directement à une illustration à travers notre étude de cas, mais notre objectif est d'en dégager aussi les bases mathématiques les plus fondamentales.

On peut se demander s'il y a vraiment besoin de s'attarder autant sur les aspects plus mathématiques. La réponse nous est apparue de plus en plus évidente au vu des applications énormes de cette méthode en ingénierie et des contraintes de sécurité de plus en plus sévères qui entrent en jeu de compte.

Les logiciels modernes utilisant la méthode des éléments finis bénéficient d'une interface graphique rendant leur utilisation relativement simple. Par ailleurs, un certain nombre de tâches sont automatisables. On peut donc quasiment lancer un calcul sur ordinateur sans connaître la méthode.

Cependant, le modèle utilisé risque d'être inadapté au problème, on aura donc un résultat très éloigné de la réalité. L'utilisateur doit avoir des connaissances suffisantes pour être en mesure de :

? maîtriser le modèle, c'est-à-dire utiliser les options permettant de représenter le plus fidèlement possible la réalité ;

xxii /176

Avant-propos

· contrôler la qualité du résultat, détecter les résultats manifestement erronés et juger de la fiabilité des calculs qui leur sont présentés ;

· interpréter les résultats, et éventuellement les post-traités, c'est-à-dire utiliser les résultats pour faire d'autres calculs.

L'utilisation d'un logiciel de résolution par la méthode des éléments finis est donc faussement simple, ce qui n'est pas sans poser problème :

Car la manipulation de plus en plus fréquente de ce genre de technologie par des personnels non spécialistes ou inadéquatement formés commence à être une source d'inquiétude très sérieuse, compte tenu des enjeux de sécurité sous-jacents. De manière générale, utiliser un logiciel quelconque pour résoudre un problème d'ingénierie sans en comprendre le fonctionnement est très dangereux.

Le 1^er chapitre est consacré à la résolution théorique par l'approche variationnelle du système d'équations de lamé qui est un cas particulier des équations stationnaires, de l'élasticité linéaire, modélisant les déformations d'un solide sous l'hypothèse de petites déformations et de petits déplacements. Nous illustrons ainsi l'une des méthodes étant à la base des bases de la méthode des éléments finis.

Le 2^ème chapitre est dédié à l'étude des principes de bases de modélisation par éléments finis ; il fait notamment ressortir les notions de :

· discrétisation d'un domaine en éléments de formes connues ;

· matrice des fonctions d'interpolations ;

· matrice de rigidité élémentaire ;

· assemblage des matrices élémentaires.

Le 3^ème chapitre aborde l'étude des propriétés de quelques éléments finis, il s'est achevé par l'élaboration d'un programme de calcul de la matrice de rigidité élémentaire pour l'élément fini tétraédrique à 12 DDL. Ce programme, loin d'être un programme de résolution complet, est destiné principalement à être utilisé en tant que routine (sous-programme), dans un programme global de résolution de modèles éléments finis.

xxiii /176

Avant-propos

Le 4^ème chapitre étudie un cas pratique de simulation numérique effectué sur un tablier de pont.

Nous insistons notamment sur le fait que notre travail ne consiste pas en une étude technique détaillée du pont, mais à construire un modèle numérique, élément fini, du tablier et à effectuer une simulation numérique sur ce modèle.

Le modèle élément fini, ainsi construit, fait alors office de maquette numérique sur laquelle on observera l'influence, en temps réel, des différentes actions agissant sur la structure.

Le travail consistera, en tenant compte de plusieurs essais de cas de charges, à définir les cas produisant les effets les plus défavorables et à partir de ces considérations pour proposer un dimensionnement des éléments du tablier.

Aussi, le présent travail a permis d'expliquer en détail la manière dont le logiciel Autodesk ROBOT SAP 2012 doit être utilisé pour conduire des essais de simulation numérique.

1 /176

Chapitre 1

Introduction générale

Le développement de l'informatique a conduit à de grands changements dans les approches traditionnelles des calculs d'ingénierie. La méthode de premier plan de résolution numérique pour une grande variété de problèmes physiques est la méthode des éléments finis (MEF).

Les particularités de la MEF qui la placent en position dominante face à d'autres méthodes telles que : la méthode des différences finies, la méthode des volumes finis, les méthodes des éléments de frontière ... etc. ; sont ces qualités inhérentes telles que:

- la versatilité : la méthode est appropriée pour résoudre toutes sortes de problèmes physiques et mathématiques;

- Bonne algorithmisation : l'aptitude à développer des suites logicielles qui couvrent un large champ d'applications;

- Bonne stabilité numérique des algorithmes MEF.

Le point central de la méthode des éléments finis est dans le remplacement de la structure d'origine, de forme complexe, par un modèle numérique discrétisé qui représente de manière appropriée l'essence physique et les propriétés de la structure d'origine. L'élément le plus important dans ce modèle est la discrétisation par les éléments finis. Ce qui suppose la construction d'un ensemble de volumes élémentaires de formes déterminées (les éléments finis), combiné en un système uni (appelé maillage d'éléments finis).

La structure, de forme géométrique complexe, est représentée comme une union des éléments finis. Les éléments finis sont considérés comme reliés les uns aux autres par l'intermédiaire des noeuds, dans lesquels chacun des trois degrés de liberté de translation et de rotation est présenté. Les charges extérieures appliquées à la structure sont converties en forces équivalentes appliquées aux noeuds des éléments finis. Les restrictions des mouvements de la structure (Appuis) sont également transférées aux éléments finis.

2 /176

Chapitre 1

En écrivant un système d'équations pour chaque élément fini qui est impliqué dans le rapprochement du système physique d'origine, nous les étudions ensemble et obtenons un système d'équations pour l'ensemble de la structure. L'ordre de ce système d'équations est égal au produit du nombre de noeuds dans la structure et du nombre de degrés de liberté introduits dans un noeud. Dans un logiciel EF, cela revient généralement à des dizaines ou des centaines de milliers d'équations algébriques.

En construisant le système d'équations pour l'ensemble de la structure et en le résolvant, nous obtenons les valeurs de la mesure physique recherchée (par exemple, les déplacements) dans les noeuds du maillage d'éléments finis, ainsi que des mesures physiques supplémentaires, par exemple, les déformations et les contraintes.

3 /176

Chapitre 1

Chapitre 1 : Méthodes

d'approximations en physiques

Sommaire

1.1. Modélisation et Simulation 4

1.2. Classification des systèmes physiques 4

1.3. Processus d'analyse d'un problème physique 5

1.4. Méthodes d'approximations 7

1.5. Définition d'un problème de l'élasticité linéaire 8

1.6. Applications de la méthode de GALERKIN pour la résolution des

équations de Lamé 12

4 /176

Chapitre 1

1.1. Modélisation et Simulation 1.1.1. Modélisation

La modélisation est une opération par laquelle on établit le modèle d'un système complexe. Un modèle est une représentation mathématique d'un phénomène complexe auquel on affecte des informations dans le but d'utiliser les lois de la mécanique générale pour faire des vérifications de résistance et de rigidité.

1.1.2. Simulation

La simulation est l'un des outils d'aide, de prise de décision les plus efficaces, à la disposition des concepteurs et des gestionnaires des systèmes complexes. Elle consiste à construire un modèle d'un système réel et à conduire des expériences sur ce modèle afin de comprendre le comportement de ce système et d'en améliorer les performances.

1.2. Classification des systèmes physiques

Un système physique est caractérisé par un ensemble de variables qui peuvent dépendre des coordonnées d'espace (x, y, z) et du temps t. Le système est dit stationnaire si ses variables ne dépendent pas du temps. Certaines variables d du système sont connues à priori : propriétés physiques, dimensions du système, sollicitations, conditions aux limites, etc.

D'autres variables u sont inconnues : déplacements, vitesses, températures, contraintes, etc.

Un modèle mathématique du système permet d'écrire des relations entre u et d en utilisant des lois physiques. Ces relations constituent un système d'équations en u qu'on est souvent amené à résoudre, le nombre de degrés de liberté du système est le nombre de paramètres nécessaires pour définir u à un instant t donné.

Un système est discret s'il possède un nombre de degrés de liberté fini, un système est continu s'il possède un nombre de degrés de liberté infini.

Le comportement d'un système discret est représenté par un système d'équations algébriques, celui d'un système continu est le plus souvent représenté par un système d'équations aux dérivées partielles ou

5 /176

Chapitre 1

intégro-différentielles associé à des conditions aux limites en espace et en temps.

Les équations algébriques des systèmes discrets peuvent être résolues par les méthodes numériques. Par contre, les équations des systèmes continus ne peuvent en général pas être résolues directement. Il est nécessaire de discrétiser ces équations, c'est-à-dire de les remplacer par des équations algébriques. La méthode des éléments finis est l'une des méthodes qui peuvent être utilisées pour faire cette discrétisation.

1.3. Processus d'analyse d'un problème physique

De façon générale, les différentes étapes d'analyse d'un problème physique s'organisent suivant le processus schématisé par la figure 1.1. Nous partons d'un problème physique ; le cadre précis de l'étude est défini par les hypothèses simplificatrices qui permettent de définir un modèle mathématique. La difficulté pour l'ingénieur est de savoir choisir parmi les lois de la physique celles dont les équations traduiront avec la précision voulue la réalité du problème physique. Un bon choix doit donner une réponse acceptable pour des efforts de mise en oeuvre non prohibitifs.

Le choix du modèle mathématique est un compromis entre le problème posé à l'ingénieur « quelles grandeurs veut-on calculer et avec quelle précision ? » et les moyens disponibles pour y répondre. Les équations du modèle retenu sont soumises à un certain nombre d'hypothèses basées sur les sciences de l'ingénieur. Il faut connaître le domaine de validité de ces hypothèses pour pouvoir vérifier que la solution obtenue est satisfaisante.

Si le modèle mathématique n'admet pas de solution analytique, il faut chercher une solution approchée de ce modèle. La discrétisation du problème correspond au choix d'un modèle numérique permettant de traiter les équations mathématiques.

6 /176

Chapitre 1

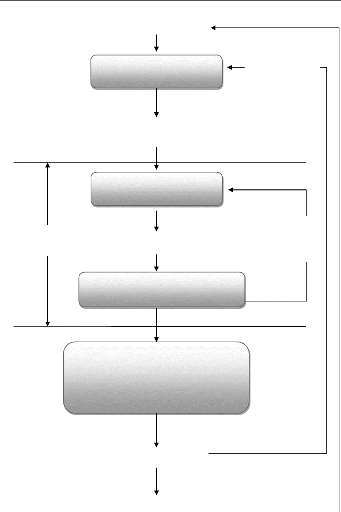
Modèle numérique

Problème

Hypothèses de modélisation

Modèle
mathématique

Evolution du
modèle
mathématique

Discrétisation du problème

Réponse obtenue

Vérification des hypothèses de
modélisation (analyse du modèle
mathématique)

Interprétation des résultats

Estimation de la précision du modèle numérique

Procédure numérique

Evolution du
modèle
numérique

(Nouveau modèle physique)

Figure 1.1: Processus d'analyse utilisant un modèle numérique

7 /176

Chapitre 1

1.4. Méthodes d'approximations

Pour discrétiser les modèles complexes de phénomènes physiques, l'ingénieur dispose à l'heure actuelle de méthodes d'approximation permettant de résoudre la plupart des problèmes pour lesquels il n'existe pas de solution formelle.

Toutes les méthodes d'approximation ont un même objectif, remplacer un problème mathématique (équations différentielles ou intégrales) par un problème mathématique discret (équation matricielle), problème de dimension finie que l'on sait résoudre numériquement.

La classification que nous proposons sur la figure 1.2 n'est pas unique, elle permet simplement de distinguer la méthode, en fonction de la démarche utilisée pour obtenir une forme intégrale. La transformation puis la discrétisation de cette forme intégrale conduisent à une équation matricielle que l'on sait résoudre analytiquement ou numériquement. Il est important de noter qu'un problème physique peut être formulé de façon équivalente en un système d'équations différentielles ou sous une formulation variationnelle. Nous montrons un peu plus loin comment passer de l'une à l'autre. Les méthodes d'approximations sont :

Méthode des résidus pondérés (ou annulation d'erreur) : Elle utilise comme point de départ les équations locales et les conditions aux limites du problème. Ces équations sont des équations différentielles définies, d'une part sur l'intérieur du domaine ce sont les équations locales, et d'autre part sur la frontière du domaine ce sont les conditions aux limites.

Méthodes variationnelles : Le point de départ de ces méthodes est un principe variationnel qui est une formulation mathématique du problème basée sur des considérations énergétiques. La formulation obtenue dépend bien entendu des hypothèses de modélisation du problème physique.

Chapitre 1

Système physique continu

Mise en équations

Méthodes
variationnelles

Formes différentielles

8 /176

Méthodes des résidus pondérés

Formes

Méthodes

d'approximation

Discrétisation

Formes matricielles

Figure 1.2: Vue synthétique des méthodes d'approximation

1.5. Définition d'un problème de l'élasticité linéaire

1.5.1. Equations fondamentales de la théorie de l'élasticité

En Théorie de l'élasticité, et sous l'hypothèse des petites déformations, le nombre d'inconnus pour un problème de mécanique des milieux continus est égal à 15.

En effet, l'objectif est de déterminer :

Chapitre 1

- Les trois composantes du champ de déplacement A = (u, v, w) :

( )

( )

( )

- les six composantes du tenseur de petites déformations :

( )

( )

( )

- les six composantes du tenseur des contraintes :

Pour résoudre un tel problème, nous devons disposer de 15 équations. Ces équations sont :

Les trois équations d'équilibre [2] :

Sur V :

9 /176

10 /176

Chapitre 1

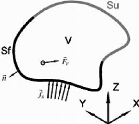
Figure 1.3: Solide de domaine V soumis à des chargements

Les six relations géométriques de Cauchy [2] :

Ces équations assurent que les déformations dérivent d'un champ de déplacement

( )

( )

( )

La loi de Hooke sous forme directe pour un matériau isotrope, élastique et linéaire [2] :

[	(	)]
[	(	)]
[	(	)]

( )

( )

( )

Ces équations sont assorties de conditions aux limites en pression ou en déplacement :

11 /176

Chapitre 1

Sur Sf : {

Sur S_u :

1.5.2. Les différentes méthodes de résolution

La résolution des équations de la théorie de l'élasticité peut être menée de plusieurs manières en fonction des quantités prises comme inconnues et on distingue généralement trois grandes méthodes de résolution :

- La résolution du problème en fonction des déplacements : dans ce cas, on considère que les fonctions inconnues sont les composantes : u, v, w du vecteur déplacement ;

- La résolution en fonction des contraintes : dans ce cas, on considère que les fonctions inconnues sont les composantes des contraintes normales et tangentielles ;

- La résolution du problème sous forme mixte : dans ce cas, on considère comme fonctions inconnues, une partie des fonctions déplacements et l'autre partie des fonctions contraintes.

En théorie de l'élasticité, l'on est souvent conduit à résoudre les équations de Lamé qui constituent un modèle décrivant le comportement, en déformation, d'un solide sous des conditions de chargement et de fixation connues (conditions aux limites).

La résolution du problème de la théorie de l'élasticité consiste à déterminer en tout point des coordonnées cartésiennes un vecteur de composantes u, v, w caractérisant un petit déplacement de ce point au cours de la déformation du milieu.

Nous proposerons dans la suite la méthode de GALERKIN pour la résolution des équations de Lamé, afin de simuler le comportement d'un solide à surface lisse, sous des conditions aux limites en déplacement et soumis à un chargement volumique.

12 /176

Chapitre 1

1.6. Méthode de GALERKIN pour la résolution des équations de Lamé

1.6.1. Modèle mathématique étudié

Supposons qu'un solide élastique occupe dans l'espace à trois dimensions un domaine 0 délimité par une surface fermée S.

Nous obtenons les équations de Lamé, caractérisant le comportement, sous la forme suivante [2] :

(A+u) V ( divA) (1.1)

Avec la condition aux limites en déplacement (condition de type Dirichlet) :

(1.2)

Où A et u sont les coefficients de lamé tels que :

(1 + v)(1 -- 2v)

(1 + v) , 2 (À. + u)

(y étant le coefficient de poisson et E le module de Young)

A = A(x, y, z) = ( u(x, y, z) , v(x, y, z) , w(x, y, z)) E R³ sont les

composantes du vecteur déplacement en chaque point du solide de 0 délimité par la surface S.

Ao = (uo, _vo,wo) est le vecteur déplacement imposé à la surface du solide ; p est la densité du solide.

P = ( P₁, P₂, P₃) la charge constante.

1.6.2. Transformation du modèle mathématique L'équation vectorielle (1.1) peut alors s'écrire sous la forme :

Chapitre 1

( ) ( )

( ) ( ) (1.3)

( ) ( )

Nous allons chercher la solution de ces équations sous la forme

,

Où est un vecteur harmonique c'est-à-dire : ,

???????????

est le gradient d'une fonction scalaire c'est-à-dire : Nous adoptons les hypothèses suivantes :

13 /176

{ (1.4)

Soit ( ) ; alors {

(1.5)

(1.6)

Puisque ( ), on a :

{

En substituant (1.6) dans (1.3) on a :

(		, (		(		(
	)		)		)		)-
(
	)	, (	)	(	)	(	)-
(		, __ (		(		(
	)		__)		)		)-

(1.7)

En prenant en compte (1.5), le système d'équations (1.7) devient :

Chapitre 1

( ) , ( ) ( ) ( )-

( ) , ( ) ( ) ( )-

( ) , ( ) ( ) ( )-

(1.8)

En réorganisant le système d'équations ci-dessus, on aboutit au système suivant :

, ( )-

0 ( )1 (1.9)

{ , ( )-

(1.9)		,(	)	(	)
		,(	)	(	)
	{	,(	)	(	)

-

- (1.10)
-

14 /176

L'intégration de ce système d'équations nous donne :

( ) ( ) ( ) ( ) ( ) .. ( )

(1.11)

Où f1, f2, f3 sont des fonctions arbitraires.

Sans perdre la généralité et pour la compatibilité du système, nous supposons que :

( ) ( )

( ) ( ) (1.12)

( ) .. ( )

15 /176

Chapitre 1

En substituant (1.12) dans (1.11), on ramène le système (1.11) sous forme de l'équation de Poisson:

( ) ( ) (1.13)

En remplaçant dans cette équation le coefficient de Poisson par son expression, on obtient :

( ) , ( ) (1.14)

			Ou , ( )- ( )	(1.15)

1.6.3. Résolution de l'équation de Poisson par l'approche variationnelle de GALERKIN

1.6.3.1. Méthode de GALERKIN

La méthode de GALERKIN consiste en ce qui suit :

Nous cherchons une solution de l'équation de Poisson (1.15) sous la forme d'une combinaison linéaire de fonctions linéairement

indépendantes vérifiant la condition aux limites (1.4), c'est-à-dire Ø/S=0.

On substitue la solution approchée dans (1.15) et on multiplie par les fonctions linéairement indépendantes ; ensuite on intègre par partie suivant le domaine 0 pour obtenir une relation intégrale à partir de laquelle on détermine les coefficients de la combinaison linéaire.

1.6.3.2. Application de la méthode de GALERKIN En multipliant l'équation (1.14) par une fonction non nulle on a : ( ( ) , ( )-) En intégrant suivant 0, on obtient :

(1.16)

? ( ( ) , ( )-) (1.17)

16 /176

Chapitre 1

? ( )

( ) ? , ( )-

(1.18)

Par une intégration par parties, on a :

? ( ) ? , (

( )

)- pour ö/S = 0. En posant , on a : ? (. / ( ) ? , ( . / . / ) )-

(1.19) (1.20)

Pour l'application, nous considérons le domaine d'intégration 0 défini par :

* ( )

+

Figure 1.4 : Représentation 3D du domaine 0

17 /176

Chapitre 1

Considérons la partie S1 de la surface S définit par :

* ( ) +

La condition se présente alors comme un cas particulier de

la condition aux limites (1.4)

Les conditions aux limites (1.4) et (1.5) sont équivalentes aux conditions suivantes :

{ (1.21)

{ (1.22)

{ (1.23)

Choisissons un point arbitraire ( )

( ) ( ) les fonctions prennent les valeurs

suivantes :

( ) les fonctions prennent les valeurs suivantes :

( )

( ( ) ) ( ) ( ) ( )

( )( )

( )

18 /176

Chapitre 1

( ) ( )( )

En posant ( ) ( ) ( )

Nous avons :

Posons ( ) ( )( )

Prenons dans un premier temps, le premier membre de l'égalité (1.20) :

?(( ) ( ) ( ) )

? ? ? (( ) ( ) ( ) )

( ) ( )( )

( ) ( )

( ) ( )

( ) ( )( )

Le calcul de l'intégrale nous donne :

? ? ? (( ) ( ) ( ) )

? ? ? (( ( ) ) ( ( ) )

( ( )( )) )

Chapitre 1

? ? ? (( ) ( ) ( ) )

(

)

? ? ? (( ) ( ) ( ) )

( )

(

( ) ( )

( )

)

En posant :

( ( )

( ) ( )

( )

)

On a alors ? ? ? ( )

19 /176

En prenant le deuxième membre de l'égalité (1.20), on a :

20 /176

Chapitre 1

	?, ( )-
( )
		?, ( )- n
( )

L'intégration sur le domaine Ù nous donne :

( ) ?, ( )-

( )

( ) ,( ) (

( ) ( )

)

-

( )

( ) ?, ( )-

( )

( ) , ( ) ( ( )

( ) ( )

) -

En posant :

, ( ( ) ( ) )

( )

( ) ( )

-

Nous avons :

( ) ?, ( )-

( )

21 /176

Chapitre 1

( )

1

En substituant chaque membre de la relation (1.20) par son expression, nous pouvons écrire :

( ) ( )

La fonction de l'équation différentielle peut alors s'écrire :

( ) ( )( )

( )

Avec :

( ( )

( ) ( )

( )

)

( ) ( )

,( ) ( )

( ) ( )

-

( ) ( ) ( )

Les composantes du vecteur déplacement s'écrivent alors:

Chapitre 1

( )

+ ( ( )

)

( )

( ) ( ) ( ) + (

)

. ( ) /

22 /176

	( ) ( )	+ ( ( )( ) )

(1.24)

1.6.3.3. Détermination du tenseur des déformations Le calcul du tenseur des déformations nous donne :

( )

( )

( )

( )

( )( )

( )

( ( ) )

( ) ( )

( ( ) )		( )
( )		( )

( )

( )

1.6.3.4. Détermination du tenseur des contraintes Le calcul du tenseur des contraintes donne :

23 /176

Chapitre 1

* )(

(

)(

)

(

(

)

(

)

)

(

)(

(

)

(

(

) +

)

)

)

( (

) )

)

(

* * )(

(

)(

(

)(

(

)

( )+

(

(

) )

(

)

) (

) )

(

(

)

)(

)

)

(

)(

(

)

(

(

)

)

(

)

( )

(

) ( (

)

)+

*( *( *(

) ) )

(

(

+ )

(

)(

)

(

(

) )

)

( ( )+ )+

)

)

(

)(

)

(

(

) (

(

)(

)

(

)

(

(

)

)

24 /176

Chapitre 1

1.6.3.5. Simulation du tenseur des déformations

Afin de visualiser aisément la déformation du domaine, fixons des valeurs pour certains paramètres entrant dans les calculs.

, _Y ,

Choisissons le point 01, ,n^Z + ^Z) E S\S1, tel que : n = 1, Nous avons alors :

Définissons comme matériau de la structure, un béton ayant les caractéristiques suivantes :

Module de Young : E = 32000 MPa

Coefficient de Poisson : =0.

Module de cisaillement : G = 16300.00 MPa

Densité : p = 24.53 KN/m³

Pour la valeur z=15, l'état de déformation se présente comme suit :

La courbe représentative de _Exx à une allure parabolique comme le montre la figure 1.5

Chapitre 1

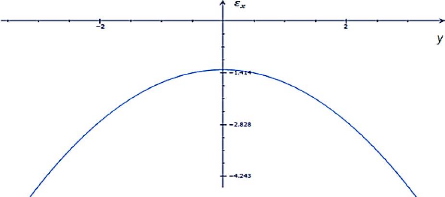
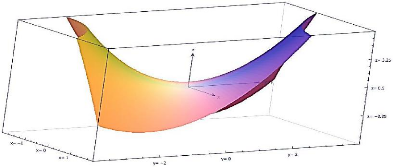
Figure 1.5 : Courbe de simulation de la composante _åxx du tenseur des déformations

Figure 1.6 : Courbe de simulation de la composante _åyy du tenseur des déformations

25 /176

( )( )

Chapitre 1

Figure 1.7 : Courbe de simulation de la composante _åzz du tenseur des déformations

Figure 1.8 : Courbe de simulation de la composante _åxy du tenseur des déformations

26 /176

( )

Chapitre 1

Figure 1.9 : Courbe de simulation de la composante _åyz du tenseur des déformations

(y² --16)

27 /176

Figure 1.10: Courbe de simulation de la composante _åzx du tenseur des déformations

28 /176

Chapitre 2

Chapitre 2 : Méthode des Eléments

finis

Sommaire

2.1. Processus d'analyse par la méthode des éléments finis 29

2.2. Discrétisation géométrique (maillage) 32

2.3. Approximation nodale 39

2.4. Approximation par éléments finis 41

2.5. Définition de la géométrie des éléments 43

2.6. Approximation sur un élément de référence 49

2.7. Construction des fonctions d'interpolations et de transformations

géométriques 53

2.8. Matrice élémentaire 59

2.9. Assemblage et conditions aux limites 60

29 /176

Chapitre 2

2.1. Processus d'analyse par la méthode des éléments finis

2.1.1. Analyse des problèmes physiques modélisés par une équation

Un certain nombre de problèmes physiques sont décrits par des équations aux dérivées partielles (EDP) sur un domaine spatial, un volume.

Il s'agit d'une généralisation des équations différentielles aux fonctions de plusieurs variables. Par exemple, si l'on a une fonction de trois

variables f(xi, x₂, x3), l'équation suivante :

Notons que

· la fonction É peut être une fonction vectorielle ;

· l'équation fait souvent intervenir des dérivées secondes 3²É/3x² _i ou 3²É/3xixj (voire d'ordres plus élevés) ;

· les coefficients ai et A ne sont pas nécessairement des constantes, mais peuvent être des fonctions.

La résolution exacte, analytique, de telles équations devient vite impossible manuellement. Par contre, si l'on découpe le domaine spatial en petites cellules, appelées « éléments finis » (EF), on peut résoudre simplement l'EDP sur chaque élément.

La méthode des éléments finis (MEF) consiste donc à [24]:

· découper le modèle spatial en éléments finis : c'est le maillage ;

· écrire une version simplifiée de l'EDP sur chaque élément fini (notons que les conditions limites d'un élément ne sont pas connues, on ne connaît que les conditions globales) ;

· rassembler les expressions des EDP locales pour appliquer les conditions aux limites du problème.

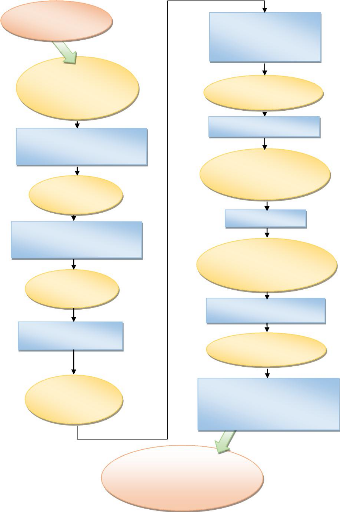
On retrouve dans l'organigramme suivant la démarche générale de la méthode des éléments finis (MEF).

30 /176

Chapitre 2

Formulation intégrale Méthodes des résidus pondérés

Problème d'ingénierie

Hypothèse de
GALERKIN Ö=äu

Formules de Green
(Intégration par partie)

Equations aux dérivées partielles

Conditions aux limites

Formulation intégrale faible

Formulation
intégrale faible
avec

Formulation intégrale forte

Champs de
déplacements

Déformations

Interpolation

Déplacement-Déformations Loi de HOOKE

Vecteurs de localisation

Transformation du système de résolution

Matrice de rigidité et
vecteur force globaux.
Système [??][????) = [F)

Maillage

Elément de référence Interpolation

Matrice de rigidité et
vecteur force locaux
expansés

Matrice de rigidité et vecteur force

Déplacements et
réactions aux noeuds

Assemblage

Figure 2.1 : Organigramme descriptif de la démarche de résolution MEF

Chapitre 2

2.1.2. Principe des éléments finis en calcul des structures

Partant des hypothèses de petits déplacements et petites déformations, la mécanique des solides déformable a permis d'établir deux types d'équations régissant l'équilibre d'un corps : les équations d'équilibre des forces et la compatibilité des déplacements.

L'intégration de ces équations n'étant pas aisée, l'une des méthodes les plus utilisées pour les résoudre est celle dite des éléments finis qui revient à remplacer le système continu par un système discret.

Le solide est alors divisé en un certain nombre de sous-domaines dont l'assemblage permet la reconstitution de la géométrie initiale.

Le processus de division du solide en un ensemble de sous-domaine s'appelle le maillage, on parle également de discrétisation géométrique du solide.

Chacun de ces sous-domaines porte le nom d'éléments et ces éléments sont dits finis parce qu'ils sont de forme et de dimension connue. Ils sont reliés entre eux par des noeuds dont les degrés de liberté (DDL) constituent les inconnues du problème.

Noeuds Eléments

31 /176

Figure 2.2 : (a) - Solide (Poutre en I) ; (b) Modèle éléments finis

Considérant un champ de déplacement cinématiquement admissible sur l'élément, la méthode consiste le plus souvent à approximer celui-ci au moyen d'une fonction polynomiale formée d'un nombre fini de paramètres et à l'exprimer en fonction des déplacements nodaux (les

32 /176

Chapitre 2

déplacements associés aux degrés de liberté), on aboutit à une approximation nodale du champ de déplacement.

Les principales étapes de construction d'un modèle éléments finis sont les suivantes [24]:

y' Discrétisation du milieu continu en sous-domaines (maillage) ;

y' Construction de l'approximation nodale par sous-

domaine (approximation par éléments finis) ; y' Calcul des matrices élémentaires correspondant à la forme

intégrale du problème ;

y' Assemblage des matrices élémentaires - Prise en compte des conditions aux limites ;

y' Résolution du système d'équations.

La résolution du problème nécessite alors une profonde maitrise :

y' des règles de maillage ;

y' du principe de construction de l'approximation nodale ;

y' du processus de calcul des matrices élémentaires ;

y' et de la notion d'assemblage.

Nous expliciterons chacune de ses étapes dans la suite.

2.2. Discrétisation géométrique (maillage) 2.2.1. Définition du maillage

Un maillage est la discrétisation spatiale d'un milieu continu, ou aussi, une modélisation géométrique d'un domaine par des éléments proportionnés finis et bien définis. L'objet d'un maillage est de procéder à une simplification d'un système par un modèle représentant ce système et, éventuellement, son environnement (le milieu), dans l'optique de simulations de calculs ou de représentations graphiques.

On parle également dans le langage commun de pavage du domaine. Un maillage est défini par [19] :

y' son repère ;

Chapitre 2

? les points (noeuds) le constituant, caractérisés par leurs coordonnées ;

? les cellules (éléments finis) reliant n de ces points ;

Figure 2.3 : Maillage d'un pont de type Bow-string en vue d'une simulation

2.2.2. Caractérisation d'un maillage

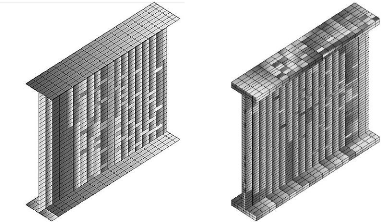
Un maillage se caractérise par [19] :

- sa dimension : typiquement 1D, 2D ou 3D ;

33 /176

Figure 2.4 : (a) maillage en 2D (poutre I) ; (b) maillage en 3D (poutre I)

34 /176

Chapitre 2

- son volume (dimension totale couverte) ;

?

: Volume de l'élément fini i

Nombre d'éléments dans le maillage

- sa finesse : surface ou volume moyen des cellules composant le maillage ;

Figure 2.5 : (a) maillage raffiné (plaque) ; (b) maillage grossier (plaque)

- la géométrie des cellules : en 1D segments ; en 2D triangles,

polygones, carrés ; en 3D polyèdres, parallélépipèdes, cubes.

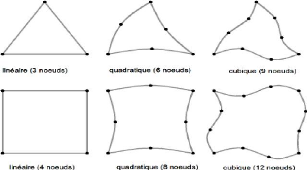
Figure 2.6 : Formes géométriques 1D

35 /176

Chapitre 2

Figure 2.7 : Formes géométriques 2D

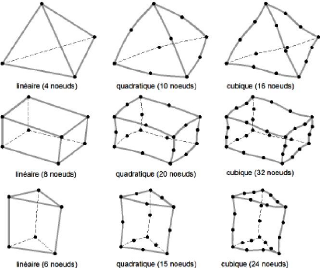
Figure 2.8 : Formes géométriques 3D

2.2.3. But et rôle du maillage

Le but principal d'un maillage d'éléments finis est de rapprocher adéquatement la géométrie issue de la modélisation, de la géométrie de l'objet réel.

L'étape du maillage est d'une importance capitale et la qualité de la solution du problème étudié y est étroitement liée.

Premièrement, la qualité d'une solution dépend de la forme des éléments finis utilisés pour mailler le domaine. Les meilleurs résultats de la modélisation par éléments finis sont atteints si les éléments (par exemple : tétraèdres et triangles) formant le modèle maillé sont proches de ceux qui sont équilatéraux [19].

Deuxièmement, outre les formes des éléments finis, la qualité de la solution est directement affectée par le degré de discrétisation du modèle géométrique original, la « densité » du maillage d'éléments finis [19].

Chapitre 2

Dans les logiciels éléments finis, l'utilisateur peut contrôler ce paramètre du générateur de maillage en spécifiant une taille moyenne relative ou absolue des éléments finis se rapprochant de la géométrie du corps, ou par les paramètres qui influencent la génération du maillage. Habituellement, une division plus fine donne de meilleurs résultats en termes de précision. Néanmoins, on doit garder à l'esprit qu'en faisant usage d'un grand nombre d'éléments de très petite taille, on augmente la taille du système d'équation à résoudre, ce qui ralentit la vitesse de calcul.

2.2.4. Règles de partition du domaine en éléments

La partition du domaine V en éléments V^e doit respecter les deux règles suivantes:

? Deux éléments distincts ne peuvent avoir en commun que des points situés sur leur frontière commune, si elle existe. Cette condition exclut le recouvrement de deux éléments. Les frontières entre éléments peuvent être des points, des courbes ou des surfaces [5]:

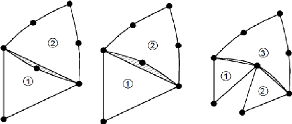
36 /176

Figure 2.9 : Connexions inadéquates entre éléments

37 /176

Chapitre 2

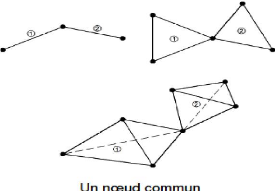
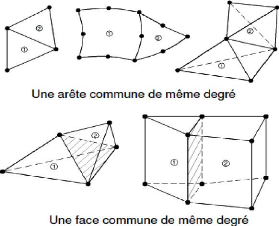
Figure 2.10 : Connexions adéquates entre éléments

? L'ensemble de tous les éléments V^e doit constituer un domaine aussi proche que possible du domaine donné V, nous excluons en particulier les « trous » entre éléments [5]:

38 /176

Chapitre 2

1

2

Trou inadmissible entre éléments

Figure 2.11 : Exemple de maillage à exclure

Lorsque la frontière du domaine V est constituée par des courbes ou des surfaces plus complexes que celles qui définissent les frontières des éléments, une erreur est inévitable. Cette erreur est appelée erreur de discrétisation géométrique, elle peut être réduite en diminuant la taille des éléments, ou en utilisant des éléments à frontières plus complexes :

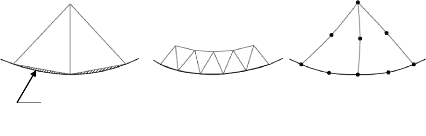
Erreur de
discrétisation
géométrique

Augmentation du
nombre
d'éléments

Utilisation d'éléments à frontières courbées

Figure 2.12 : Discrétisation géométrique des frontières courbes

Les deux règles précédentes sont respectées si les éléments sont construits de la manière suivante :

- Chaque élément est défini de manière unique à partir des coordonnées des noeuds géométriques situés sur cet élément. Le plus souvent ces noeuds géométriques sont situés sur les frontières de l'élément et sont communs à plusieurs éléments ;

- La frontière d'un élément à deux ou trois dimensions est formée par un ensemble de courbes ou de surfaces. Chaque portion de

Chapitre 2

frontière doit être définie de manière unique à partir des coordonnées des seuls noeuds géométriques situés sur cette portion de frontière. Ainsi les portions de frontière communes à deux éléments sont définies de manière identique pour l'un ou l'autre élément.

2.3. Approximation nodale

Un modèle mathématique d'un système physique fait intervenir plusieurs

variables ou fonctions dites exactes ( ) : températures, vitesses,
épaisseurs, déplacements, etc.

Celles-ci sont représentées par des fonctions « approchées» ( ) telles que la différence :

( ) ( )

soit assez « petite» pour l'objectif visé.

La fonction approchée u est le plus souvent linéaire en ái :

( ) ( ) ( ) ( )

( ) < ( ) ( ) ( )> { }

où : P1,P2,...,P_n sont des fonctions connues linéairement

indépendantes (chaque fonction ne peut pas être construite par combinaison linéaire des autres fonctions), telles que des polynômes ou des fonctions trigonométriques, ces fonctions sont indépendantes des ái

á1, á 2, ..., á _n sont les paramètres de l'approximation.

39 /176

Les paramètres á1, á 2, ..., á _n n'ont pas en général de sens physique.

40 /176

Chapitre 2

Cependant nous pouvons choisir comme paramètres á, les valeurs de la fonction ( ) en n points appelés noeuds de coordonnées

Imposons de plus que la fonction approchée coïncide avec la fonction exacte ( ) en ces noeuds:

( ) ( )

( ) ( )

( ) ( )

La fonction approchée s'écrit alors:

( ) ( ) ( ) ( )

u_n

( ) < ( ) ( ) ( )> { }

ü La relation ci-dessus définit une approximation nodale ;

ü Les paramètres ái, sont les paramètres généraux de l'approximation ;

ü Les paramètres ui, sont les paramètres nodaux ou variables nodales de l'approximation ;

ü Les fonctions N(x) sont les fonctions d'interpolation.

L'approximation nodale possède les deux propriétés suivantes :

Comme ( ) les fonctions Ni vérifient

( ) {

L'erreur d'approximation définie par:

41 /176

Chapitre 2

( ) ( )

s'annule en tous les noeuds xi :

La méthode d'approximation nodale d'une fonction d'une variable u(x) s'étend directement à l'approximation d'une fonction de plusieurs variables; par exemple dans le cas d'une fonction de 3 variables:

( ) ( )

où :

x appartient à un domaine V,

La fonction approchée u(x) s'écrit sous la forme :

( ) ( ) < ( ) ( ) ( )> { }

et doit vérifier la relation ( ) ( )

où i=1, 2, ..., n sont les coordonnées des noeuds.

2.4. Approximation par éléments finis

La construction d'une fonction approchée u(x) est difficile lorsque le nombre n de noeuds et donc de paramètres ui, devient important. Le problème se complique encore si le domaine V a une forme complexe et si la fonction u(x) doit satisfaire des conditions aux limites sur la frontière de V.

La méthode d'approximation nodale par sous-domaines simplifie la reconstruction de u(x) et s'adapte très bien au calcul sur ordinateur

Elle consiste à [4] :

? identifier un ensemble de sous-domaines V^e du domaine V;

42 /176

Chapitre 2

y' définir une fonction approchée u^e(x) différente sur chaque sous-domaine V^e par la méthode d'approximation nodale.

La méthode d'approximation par éléments finis est une méthode particulière d'approximation par sous-domaines qui présente les particularités suivantes [4] :

y' L'approximation nodale sur chaque sous-domaine V^e ne fait intervenir que les variables nodales attachées à des noeuds situés sur V^e et sur sa frontière ;

y' Les fonctions approchées u^e(x) sur chaque sous-domaine V^e sont construites de manière à être continues sur V^e et elles satisfont des conditions de continuité entre les différents sous-domaines.

2.4.1. Définitions

y' Les sous-domaines V^e sont appelés des éléments ;

y' Les points en lesquels la fonction approchée u^e(x) coïncide avec la fonction exacte u_ex(x) sont les noeuds d'interpolation ou points nodaux ;

y' Les coordonnées x, de ces noeuds sont les coordonnées nodales ;

y' Les valeurs ui = u^e(xi) = uex(xi) sont les variables nodales.

L'approximation par éléments finis présente deux aspects distincts :

- Il faut tout d'abord définir analytiquement la géométrie de tous les éléments, ce qui est plus ou moins compliqué selon leurs formes ;

- Il faut ensuite construire les fonctions d'interpolation Ni(x) correspondant à chaque élément.

Chapitre 2

Expression typique de u :

		x appartient à V			Approximation sur le domaine

Partition en sous-

domaine Ve

x appartient à Ve

Approximation
par sous-
domaines

u( ) < ( )>*á+

Approximation
non nodale

u( ) <N( )>*????+

Approximation
nodale

????( ) <??^e( )>*á+

????( ) <????( )>*????+

Approximation
générale par
sous-domaines
(non nodale
et/ou nodale)

????( ) <????( )>*??????+

Approximation
par éléments
finis

43 /176

Figure 2.13 : Méthodes d'approximation

2.5. Définition de la géométrie des éléments 2.5.1. Eléments de référence

De manière à simplifier la définition analytique des éléments de forme complexe, nous utiliserons la notion d'élément de référence: un élément

de référence y^r est un élément de forme très simple, repéré dans un

espace de référence, qui peut être transformé en chaque élément réel Ve par une transformation géométrique [4]. Par exemple dans le cas d'un triangle:

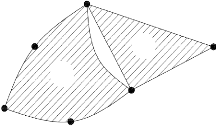
Chapitre 2

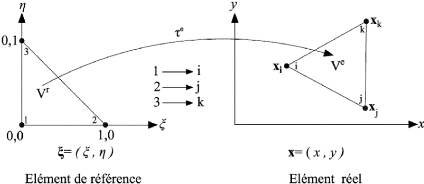
Figure 2.14 : Transformation d'un élément de référence en élément réel

Afin d'alléger les notations, les écritures x et seront respectivement

adoptés en lieu et place des notations classiques (x,y) pour les coordonnées des noeuds dans l'espace réel et (î,ç) dans l'espace de référence. La différence pourra se faire aisément avec l'utilisation de la forme italique pour les notations classiques.

La transformation ??e définit les coordonnées x=(x,y) de chaque point de

l'élément réel à partir des coordonnées =( ) du point correspondant de l'élément de référence.

La transformation ??e dépend de la forme et de la position de l'élément réel, donc des coordonnées des noeuds géométriques qui le définissent. Il y a donc une transformation ??e différente pour chaque élément réel :

e e( )

où sont les coordonnées des noeuds géométriques qui

appartiennent à l'élément e.

44 /176

Elément 1 ( )

45 /176

Chapitre 2

Elément 2 T²: k x²=x²(, x1, x5, x3 )

Elément 3 T³: k x³=x³(, x5, x4, x3 )

Chaque transformation Te est choisie de manière à présenter les propriétés suivantes :

ü Elle est bijective en tout point k situé sur l'élément de référence ou

sur sa frontière : à tout point V^r correspond donc un point de Ve et un seul, et inversement ;

ü Les noeuds géométriques de l'élément de référence correspondent aux noeuds géométriques de l'élément réel ;

ü Chaque portion de frontière de l'élément de référence, définie par les noeuds géométriques de cette frontière, correspond à la portion de frontière de l'élément réel définie par les noeuds correspondants.

Soulignons qu'un même élément de référence V^r (par exemple un triangle à 3 noeuds) se transforme en tous les éléments réels Ve de même type (triangles à 3 noeuds) par des transformations Te différentes :

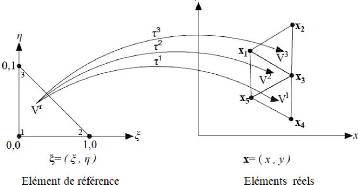
Figure 2.15 : Transformation d'un même élément de référence en tous les éléments

réels

Pour simplifier la notation, l'indice supérieur e, caractéristique d'un élément, sera supprimé, nous utiliserons une transformation r linéaire

46 /176

Chapitre 2

par rapport aux coordonnées des noeuds géométriques de l'élément réel V^r.

( ) , ( )-* +

De plus les fonctions de transformation sont choisies identiques pour les trois coordonnées :

( ) < ( )>* +

( ) < ( ) >* +

( ) < ( ) >* +

Par exemple pour un triangle à 3 noeuds xi, xj, xk :

( ) ( ) ( ) ( ) < ( )> {

( ) ( ) ( ) ( ) < ( )>{

<N > < ( ) ( ) ( )>

Où ( ) appartient à Vr

Les fonctions , sont habituellement des polynômes en appelées

fonctions de transformation géométrique.

Elles sont construites de la même manière que les fonctions d'interpolation N( ).

Grâce à la transformation géométrique ?? nous remplaçons la définition analytique de chaque élément Ve dans l'espace des x par la définition analytique, plus simple, de son élément de référence V^r dans l'espace

Chapitre 2

des . Par la suite nous travaillerons systématiquement dans l'espace des .

2.5.2. Formes d'éléments de référence classiques

Nous présentons ci-dessous la forme et la définition analytique des éléments de référence correspondant aux éléments classiques [4] :

Elément de référence à une dimension :

47 /176

Figure 2.16 : Exemple d'éléments de référence à une dimension

Elément de référence à deux dimensions :

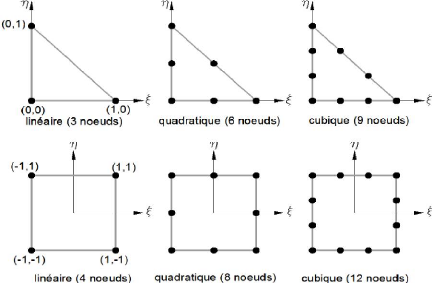
Figure 2.17 : Exemple d'éléments de référence à deux dimensions

48 /176

Chapitre 2

Elément de référence à trois dimensions :

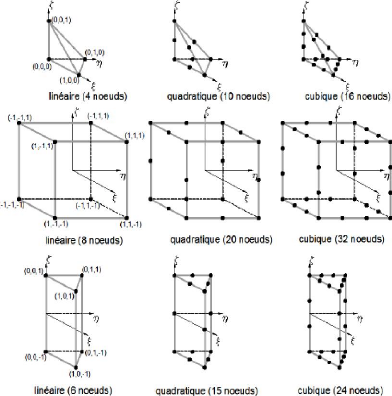
Figure 2.18 : Exemple d'éléments de référence à trois dimensions

- Dans les éléments de référence quadratiques, les noeuds situés sur les côtés sont aux milieux ( ) de ceux-ci. Dans les éléments cubiques, ils sont situés au tiers (1/3) et aux deux tiers (2/3) des côtés ;

- Les fonctions de transformation géométrique ( ) n'ont pas été données explicitement pour les éléments de référence ci-dessus. En effet la construction de ces fonctions est identique à celle des

49 /176

Chapitre 2

fonctions d'interpolation N( ) qui sera détaillée dans les lignes à suivre.

2.6. Approximation sur un élément de référence

2.6.1. Expression de la fonction approchée ( )

Nous choisissons sur le domaine V un ensemble de n noeuds

d'interpolation de coordonnées xi confondues ou non avec les noeuds géométriques.

Sur chaque élément Ve nous utilisons une approximation nodale de la

fonction exacte ( ).

( ) ( ) < ( ) ( ) ( ) > { < ( )>* +

où : x appartient à Ve,

sont les valeurs de aux ^e noeuds d'interpolation de
l'élément, ou variables nodales,

( ) sont les fonctions d'interpolation sur l'élément réel.

e ( ) ( ) < ( )>* +

Avec :

( ) , ( )-* +

où : * + sont les variables nodales de l'élément ;

( ) sont les fonctions d'interpolation sur l'élément de référence. Remarque :

? En général les fonctions N(x) ne sont utilisées que pour des éléments simples. Elles sont le plus souvent remplacées par les fonctions N( ) où x et sont liés par la transformation ?? ;

Chapitre 2

? Les mêmes fonctions N( ) peuvent être utilisées pour tous les éléments possédant le même élément de référence caractérisé par

:

· sa forme ;

· ses noeuds géométriques;

· ses noeuds d'interpolation.

2.6.2. Propriétés de la fonction approchée ( )

2.6.2.1. Propriété fondamentale de l'approximation nodale

La fonction approchée ( ) coïncide avec la fonction exacte ( ) en

tous Les noeuds d'interpolation de l'élément, de coordonnées xi :

( ) ( ) < ( ) ( ) > {

}

De même, en utilisant l'approximation sur l'élément de référence

D'où:

U_ne

( ) ( ) < ( ) ( ) > { }

D'où :

50 /176

( ) {

51 /176

Chapitre 2

Continuité sur l'élément

Si nous désirons obtenir une fonction approchée (x) continue sur l'élément, ainsi que ses dérivées jusqu'à l'ordre s, nous devons utiliser des fonctions ( ) continues et à dérivées continues jusqu'à l'ordre s.

Continuité entre éléments

Si nous désirons que (x) et ses dérivées jusqu'à l'ordre soient

continues sur une frontière commune à deux éléments, il faut que (x)

et ses dérivées jusqu'à l'ordre s dépendent de manière unique des seules variables nodales associées aux noeuds de cette frontière. Considérons d'abord la continuité de (x) sur une frontière (continuité

) :

( ) < ( ) ( ) > { }

Les produits ( ) , doivent être nuls si , n'est pas une variable

nodale associée à un noeud de cette frontière.

D'où :

( ) ,

Lorsque x est situé sur une frontière et , n'est pas une variable nodale de cette frontière.

De même sur l'élément de référence :

( ) ,

Lorsque est situé sur une frontière et , n'est pas une variable nodale de cette frontière.

u( )

La condition pour que soit continue sur une frontière s'écrit de

manière similaire :

52 /176

Chapitre 2

u

u( ) ( ) ( ) u

< }

> {

u

où :

( )

Lorsque x est situé sur une frontière et , n'est pas une variable nodale de cette frontière.

La condition précédente s'écrit sur l'élément de référence, à deux dimensions:

( ) ( )

La notion de continuité sur les frontières entre les éléments est une notion clé de la méthode des éléments finis. Elle est liée à la notion d'élément conforme ou non conforme. Le type de continuité qu'il faut assurer dépend du problème traité.

Si la fonction ( ) est seule continue sur les frontières entre les

éléments, l'approximation est de type (ou classe ). Si ( ) et ses

dérivées premières sont continues, l'approximation est de type . Si
( ) et ses dérivées jusqu'à l'ordre n sont continues, l'approximation est de type .

Un élément est dit isoparamétrique si les fonctions de transformation

géométrique N ( ) sont identiques aux fonctions d'interpolation N ( ). Ceci implique que les noeuds géométriques soient confondus avec les noeuds d'interpolation.

53 /176

Chapitre 2

Nous dirons qu'un élément est pseudo-isoparamétrique si ses fonctions N ( ) et N ( ) sont des polynômes différents utilisant les mêmes monômes.

Si l'ordre des polynômes N ( ) est inférieur à l'ordre des polynômes

N ( ), l'élément est sub-paramétrique. Il est super-paramétrique dans le cas contraire.

Le nombre de variables nodales ; associées à l'ensemble des noeuds d'interpolation de l'élément est appelé nombre de degrés de liberté de

l'élément et noté .

2.7. Construction des fonctions d'interpolations et de transformations géométriques

2.7.1. Construction des fonctions N ( ) et Ni( )

Les fonctions de transformation géométrique N ( ) et les fonctions

d'interpolation sur l'élément de référence Ni( ) ont les mêmes propriétés.

Ceux-ci sont souvent des polynômes classiques de type Lagrange ou Hermite; cependant il n'existe pas de technique manuelle systématique pour les construire.

Nous proposerons dans les paragraphes suivants une méthode numérique générale valable pour tous les types d'éléments.

2.7.1.1. Méthode générale de construction

Choix de la base polynomiale :

Exprimons ( ) sur l'élément de référence sous la forme d'une

combinaison linéaire de fonctions connues indépendantes P1( ), P2( ), ..., qui sont le plus souvent des monômes indépendants. Le choix des fonctions Pi( ) est l'une des opérations de base de la méthode des éléments finis:

Nombre de dimensions

Bases complètes

1

1

Degré du polynôme r

2

1

Base polynomiale < >

<1 î> (linéaire)

<1 î î²> (quadratique)

2

3

54 /176

Chapitre 2

( ) < ( ) ( ) ( )> { } < ( )>* +

L'ensemble des fonctions ( ) constitue la base polynomiale de l'approximation, son nombre de termes doit être égal au nombre de

variables nodales ou nombre de degrés de liberté de l'élément. Nous
utilisons le plus souvent une base polynomiale complète; ceci n'est

possible que pour certaines valeurs de , Le tableau suivant précise le
nombre de monômes nécessaires pour construire des polynômes complets.

Degré du polynôme r	1 dimension	2 dimensions	3 dimensions
1	2	3	4
2	3	6	10
3	4	10	20
4	5	15	35
5	6	21	56

Tableau 2.1 : Nombre de monômes nécessaire pour construire des polynômes

complets

Bases polynomiales complètes et incomplètes

55 /176

Chapitre 2

2 2	1 2	<1 î q> (linéaire) <1 î q î^2 îq q^2 > (quadratique)	3 6
3 3	1 2	<1 î q æ > (linéaire) <1 î q æ î^2 îq q^2 qæ æ^2 îæ > (quadratique)	4 10
Bases non complètes
2 3	2 3	<1 î q îq > (bi-linéaire) <1 î q æ îq qæ îæ îqæ > (tri-linéaire)	4 8

Tableau 2.2 : Bases polynomiales complètes et incomplètes

Pour construire les fonctions de transformation géométrique ,

choisissons de la même manière des expressions de x de la forme :

(	)	<	(	)>*	+
(	)	<	(	)>{	}
(	)	<	(	)>*	+

56 /176

Chapitre 2

Le nombre de fonctions ( ) et de coefficients * +, { } et * + est égal au nombre de noeuds géométriques de l'élément.

Définitions :

ü Les coefficients * + sont appelés variables généralisées de l'élément par opposition aux variables nodales *u + ;

ü La relation ( ) < ( )>* + définit l'approximation généralisée

par opposition à l'approximation nodale ( ) < ( )>*u + ;

ü les coefficients * +, { } et * + sont appelés parfois coordonnées généralisées de l'élément par opposition aux coordonnées nodales * +, * +, * + des noeuds géométriques.

Relations entre variables généralisées et variables nodales :

Exprimons qu'en chaque noeud d'interpolation de coordonnées * +, la

fonction u( ) prend la valeur nodale ( ) :

<

(

)

(

)

(

)>

U 2 } * + {

<

(

)

(

)

(

)>

*

+

<

(

)

(

)

(

)>

En posant :

<

(

)

(

)

(

)>

, -

<

(

)

(

)

(

)>

<

(

)

(

)

(

)>

Chapitre 2

nous pouvons écrire :

* + , -* +

Soit en inversant la matrice nodale , - d'ordre

* + , - *u +

Pour passer de *u + , -* + à la relation * + , - *u + il ne faut

pas que , - soit singulière. Ceci dépend du choix de la base polynomiale et des coordonnées * + des noeuds de l'élément de référence. Puisque , - est indépendante de la géométrie de l'élément

réel, la propriété de singularité de , - est une caractéristique de l'élément de référence et non de l'élément réel.

De la même manière, nous écrivons les relations aux noeuds géométriques:

*	+	,	-*		+	*
+	,	-{	}		*
+	,	-*	+

Soit après inversion de , -

*	+	,	- *		+	{
}	,	- *	+		*
+	,	- *	+

57 /176

? Expression des fonctions Net N :

58 /176

Chapitre 2

Reportons * + , - *u + dans

( ) < ( ) ( ) ( )> { } < ( )>* +

Nous avons :

( ) < ( )>, - * +

Soit :

( ) , ( )-* +

D'où :

( ) < ( )>, -

Nous obtenons de la même manière dans le cas des fonctions N :

( ) < ( )>* +

( ) < ( )>* +

( ) < ( )>* +

Où :

< ( )> < ( )>, -

? Dérivation de la fonction ( ) :

Les fonctions dérivées s'obtiennent comme suit :

< > < >

{ < >

< >

} , - *u +

*u + [ ]*u +

[ < >] [ < >]

Résumé des opérations de construction de <N>

59 /176

Chapitre 2

ü Choix de la base polynomiale < ( )>

;

ü Evaluation de la matrice nodale , - [ ( )] ;

ü Inversion de la matrice nodale , - ;

ü Calcul de <N> aux points désirés :

( ) < ( )>, -

Il est important de noter que ces opérations ne doivent être effectuées qu'une seule fois pour l'ensemble des éléments réels qui possèdent le même élément de référence.

2.8. Matrice élémentaire

2.8.1. Matrice de rigidité élémentaire

Pour un élément de domaine , la matrice de rigidité élémentaire vaut :

?, - , -, -

, - représente la matrice des fonctions de déformation ; , - représente la matrice des constantes d'élasticité.

2.8.2. Matrice des forces équivalentes de volume

Pour un élément, la matrice des forces équivalentes de volume se détermine par la formule ci-dessous:

* + ?, - * +

, - représente la matrice des fonctions d'interpolations * + représente le vecteur des forces volumiques.

2.8.3. Matrice des forces équivalentes de surface

Le calcul est conduit de la même manière que pour la matrice des forces équivalentes de volume , les forces nodales équivalentes aux forces de surface sont :

Chapitre 2

* + ?, - * +

* + représente le vecteur des forces surfaciques.

2.9. Assemblage et conditions aux limites 2.9.1. Définition de l'assemblage

L'assemblage est l'opération qui consiste à construire la matrice globale , - et le vecteur global des sollicitations * + à partir des matrices élémentaires , - et des vecteurs élémentaires des sollicitations * +.

2.9.2. Les règles et étapes de l'assemblage

Les règles d'assemblage sont définies par la relation :

?

les matrices élémentaires étant initialement exprimées dans le repère local propre à chaque élément, on les exprime dans le repère global avant de procéder à leur sommation étendue au domaine maillé.

La procédure qui consiste à exprimer une matrice élémentaire en repère global s'appelle l'expansion de matrice

Ainsi donc nous avons :

, - ?, -

* + ? * +

avec * +=* + * +

, -, * +, * + sont les matrices et vecteurs élémentaires expansés.

60 /176

L'assemblage se déroule donc principalement en deux étapes :

61 /176

Chapitre 2

? construction des matrices étendues par expansion des matrices et vecteurs élémentaires [ k_e], tf }, tf } ;

? addition des matrices et des vecteurs étendus.

62 /176

Chapitre 3

Chapitre 3 : Etude de quelques

exemples d'éléments finis

Sommaire

3.1. Elément fini linéaire à deux noeuds 63

3.2. Elément fini triangulaire plan à trois noeuds 64

3.3. Elément fini tétraédrique à quatre noeuds 66

Chapitre 3

3.1. Elément fini linéaire à deux noeuds 3.1.1. Définition

Il s'agit d'un élément de type poutre pour le calcul des réseaux de poutre chargés.

Figure 3.1 : Elément de Poutre plan.

Soit E, A, I, L ses caractéristiques mécaniques et géométriques. 3.1.2. Matrice de rigidité élémentaire

3.1.2.1. Poutre en flexion simple

Pour une poutre qui travaille en flexion simple, l'élément fini utilisé possède deux degrés de liberté par noeuds (1 degré de liberté en déplacement, 1 degré de liberté en rotation), soit au total quatre degrés de liberté.

63 /176

Figure 3.2 : Elément fini de poutre avec deux degrés de liberté par noeuds.

Chapitre 3

La matrice de rigidité élémentaire utilisée dans les calculs est :

12	6L	--12	6L
El 6L	4L^2	--6L	2L^2
[K ] = L3 --12	--6L	12	--6L
6L	2L^2	--6L	4L^2

3.1.2.2. Poutre en flexion composée

Cet élément possède trois degrés de liberté par noeuds (2 degrés de liberté en déplacement et 1 degré de liberté en rotation), soit au total six degrés de liberté.

Figure 3.3 : Elément fini de poutre avec trois degrés de liberté par noeuds.

La matrice de rigidité élémentaire utilisée dans les calculs est :

[K ]

64 /176

--

L2 L L² L

3.2. Elément fini triangulaire plan à trois noeuds 3.2.1. Définition

Il s'agit d'un élément à trois noeuds, utilisés pour les problèmes de contrainte plane, de déformations planes ou d'axisymétrie.

65 /176

Chapitre 3

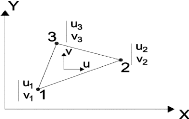
Figure 3.4 : Elément triangulaire plan à trois noeuds.

3.2.2. Matrice de rigidité élémentaire

Cet élément possède deux degrés de liberté en déplacement par noeuds.

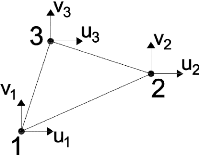
Figure 3.5 : Elément triangulaire plan avec deux degrés de liberté par noeuds.

La matrice de rigidité élémentaire utilisée dans les calculs est :

eE

[K l 4A( 1 -- v²)

Sym

x1₁ + Cyi_z

Avec :

66 /176

Chapitre 3

3.3. Elément fini tétraédrique à quatre noeuds 3.3.1. Définition

Le tétraèdre à champ linéaire est l'élément tridimensionnel le plus simple, son élément de référence se présente comme suit :

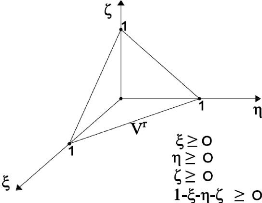
Figure 3.6 : Elément de référence de forme tétraédrique.

Celui-ci est construit par extension du triangle isoparamétrique à trois noeuds. Il possède trois degrés de liberté en déplacement par noeud, ce qui correspond à un total de douze degrés de liberté (DDL).

3.3.2. Construction de la matrice des fonctions d'interpolation

Choix de la base polynomiale (P())

La base polynomiale utilisée est celle-ci : (P()) = ( 1 f i 0 Evaluation de la matrice nodale [P_a]

Calcul de la matrice [P_a] :

[ ]

67 /176

Chapitre 3

, -	( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) < > < > < > < >

Le calcul de , - donne :

, -

[

]

Inversion de la matrice nodale , -

Le calcul de , - donne :

, -

( ) < ( )>, -]

( ) < > [

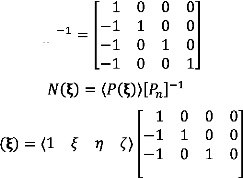
10 0

--1 1

--1 0 0

< ( )> < >

Chapitre 3

L'élément de référence tétraédrique à 4 noeuds ayant 12 DDL, la matrice des fonctions d'interpolation se présente comme suit :

, ( )-

[

]

Avec :

3.3.3. Calcul de la matrice jacobienne de la transformation géométrique

< >

, - [< > ] [* + * + * + ]

< >

, - [ ] [

68 /176

, - [

69 /176

Chapitre 3

(J) = (x₂ -- x₁)(Y₃ -- Y₁)(z₄ -- z₁) + (Y₂ -- Y₁)(z₃ -- z1)(x_,,4^-- x₁) + (z₂ -- z₁)(x₃ -- x₁)(Y₄ -- Y₁) -- (x₂ -- x₁)(z₃ -- z₁)(y₄-- Y₁) -- (Y₂ -- Y₁)(x₃ -- x₁)(z₄ -- z₁) -- (z₂ -- z₁)(Y₃ -- Y₁)(x₄ -- x₁)

det(J) = 6V^e

Ve représente le volume du tétraèdre défini par l'élément dans l'espace réel.

Champ de déplacement

Le champ de déplacement se calcule par la relation :

u(k) = [ N(k)]{u_n}

Champs de déformation

Il est défini par la relation { E} = [ B]{u_n}

La matrice [ B] est obtenue par application de l'opérateur dérivée sur le champ de déplacement, donc par la relation :

[ B] = [ D][ N( k)]

[ B (x)] = [[ B₁(x)] [ B₂ (x)] [ B₃ (x)] [ B₄(x)]]

[ Bi (x)]

o

aY ax

70 /176

Chapitre 3

, -

, - , - [

, - [ ]

Avec :

V représente le volume du tétraèdre
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)
(	)(	)	(	)(	)

Chapitre 3

[

71 /176

}{

Calcul de , ( )-On a :

{

}

, ( )-

Calcul de , ( )-

Chapitre 3

{

}

, ( )-

Calcul de , ( )-

72 /176

{

}

Chapitre 3

[B₃ ( k)]

f f 0

Calcul de [B4(k)]

73 /176

aN4 {f33

aZ

[B₄ ( k)]

f

23 f13⁰

La matrice [ B] se présente comme suit :

[ B( k)] = [[ B₁( k)] [B₂(k)] [ B₃ ( k)] [ B₄ ( k)]]

Avec :

74 /176

Chapitre 3

f

, ( )-

f

,B (0- V			f f f f f f f
,B (0- V	f f f f f f f [ f f o 12	,B (??)- V		f f f f f f f [ f f

3.3.4. Construction de la matrice de rigidité élémentaire

La matrice de rigidité élémentaire se calcule grâce à la formule suivante :

, - ? , ( )- , -, ( )-

En ramenant l'intégral sur l'espace des éléments de référence, on a :

, - ? e ( ) , ( )- , -, ( )- e ( )

Chapitre 3

,

- ?, ( )- , -, ( )-
e ( ) Comme la matrice des fonctions de déformation, dans le cas l'élément

finis tétraédrique à 4 noeuds, est indépendante des coordonnées , on peut écrire :

, - e ( ) ,

, - ,

(	)- ,	-, (	)-
(	)- ,	-, (	)-

75 /176

, - , ( )- , -, ( )-

76 /176

Termes de la matrice de

rigidité , -

Expression :

((

( )

)

(

)(

)

(

)(

)

)

((

)

(

)(

)

(

)(

))

((

)

(

)(

)

(

)(

))

(

(

)(

)

(

)(

)

(

) (

))

(

(

) (

)

(

))

(

(

) (

)

(

))

(

(

)(

)

(

)(

)

(

)(

))

(

(

) (

)

(

))

77 /176

(

(

) (

)

(

))

( (

)(

)

(

)(

)

(

)(

))

(

(

) (

)

(

))

(

(

) (

)

(

))

((

)(

)

(

)(

)

(

)(

)

)

((

)

(

)(

)

(

)(

))

(

(

) (

)

(

))

(

)(

)

(

)(

)

(

)(

)

(

) (

)

(

)

(

) (

)

(

)

78 /176

(

)

(

)

(

)(

)

(

) (

)

(

) (

)

(

)

(

) (

)

(

)

(

)

(

)

(

)(

)

(

) (

)

(

) (

)

(

)

(

)(

)

(

)(

)

(

)(

)

(

) (

)

(

)

(

) (

)

(

)

(

)

(

)

(

) (

)

(

)(

)

(

) (

)

(

)

79 /176

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

80 /176

					(		)
		(		)		(		)		(	)
					(		)
					(		)
	(		)		(		)		(	)
					(		)
		(		)		(		)		(	)
					(		)

81 /176

					(		)
		(		)		(		)		(	)
					(		)
	(		)		(		)		(	)
					(		)
					(		)
		(		)		(		)		(	)

82 /176

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

83 /176

					(	)
		(		)		(	)		(	)
					(	)
	(		)		(	)		(	)
					(	)
					(	)
		(		)		(	)		(	)
	(		)		(	)		(	)

84 /176

	(	)	(	)	(	)
	(	)	(	)	(	)

Tableau 3.1 : Tableau des valeurs de la matrice de rigidité élémentaire de l'élément tétraédrique à 4 noeuds (douze degrés de

liberté).

85 /176

Chapitre 3

3.3.5. Programme (matrice_K) de Calcul de la matrice de rigidité élémentaire pour un élément tétraédrique à 4 noeuds

3.3.5.1. Structure du programme

? Données du problème (Input)

- Module de Young E ;

- Coefficient de Poisson y ;

- Coordonnées des noeuds de l'élément réel (xi, yi, zi).

? Résultat (Output):

- Matrice de rigidité élémentaire Ke

3.3.5.2. Code source en FORTRAN

Program matrice_k

implicit none

integer, parameter :: n=3 ! dimension du tableau

real, dimension(1:3,1:12) ::B1,B2,B3,B4

real, dimension(1:3,1:3):: jacb_inv

integer :: i,j,lin,col,lin1,col1

real, dimension(1:12,1:12)::Ke

real, dimension(1:6,1:12)::B,res1,res2,res3,res4

real, dimension(1:12,1:6)::Bt,res5

real, dimension(1:6,1:3)::B_1,B_2,B_3,B_4

real, dimension(1:6,1:6)::H !!!!!!! matrice des constantes d'élasticté

real::x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3,x_4,y_4,z_4,vol,det_jab,nu,E

real,dimension(1:3,1:4)::c_noeud

lin=6;col=12;;lin1=6;col1=6

!!! Entrer des donnees

26 write(*,*)"Entrer le module de young E et le coefficient de POISSON v"

read(*,*,err=26)E,nu

!!!!!! Verification de la valeur de E et nu

if ((E.le.0).or.((nu.lt.0).or.(nu.gt.0.4999))) then

write(*,28)

write(*,*)" Veuillez entrer des valeurs convenables pour E et v (E>0)

(0<v<0.5) "

write(*,28)

goto 26

endif

do j=1,4

27 write(*,24)"Entrer les coordonnees du noeud ",j 24 format(x,A,2x,I1)

read(*,*,err=27)c_noeud(1,j),c_noeud(2,j),c_noeud(3,j) enddo

write(*,28)

!!! Affectation des coordonnées

x_1=c_noeud(1,1);y_1=c_noeud(2,1);z_1=c_noeud(3,1) x_2=c_noeud(1,2);y_2=c_noeud(2,2);z_2=c_noeud(3,2) x_3=c_noeud(1,3);y_3=c_noeud(2,3);z_3=c_noeud(3,3) x_4=c_noeud(1,4);y_4=c_noeud(2,4);z_4=c_noeud(3,4) !!!!!!! vérification de la singularité de J if ((det_jab(x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3,x_4,y_4,z_4)).eq.0) then write(*,*)" la matrice jacobienne de transformation est singuliere " write(*,*)" cela peut etre du a une grande distorsion de l'element " write(*,*)" Veuillez changer svp les coordonnees des noeuds"

write(*,28);28 format(/:)

86 /176

Chapitre 3

goto 27 endif

11111111111111111111111111

jacb_inv(1,1)=(y_3-y_1)*(z_4-z_1)-(z_3-z_1)*(y_4-y_1) jacb_inv(1,2)=(z_2-z_1)*(y_4-y_1)-(z_4-z_1)*(y_2-y_1) jacb_inv(1,3)=(y_2-y_1)*(z_3-z_1)-(y_3-y_1)*(z_2-z_1) jacb_inv(2,1)=(z_3-z_1)*(x_4-x_1)-(z_4-z_1)*(x_3-x_1) jacb_inv(2,2)=(x_2-x_1)*(z_4-z_1)-(x_4-x_1)*(z_2-z_1) jacb_inv(2,3)=(z_2-z_1)*(x_3-x_1)-(x_2-x_1)*(z_3-z_1) jacb_inv(3,1)=(x_3-x_1)*(y_4-y_1)-(y_3-y_1)*(x_4-x_1) jacb_inv(3,2)=(y_2-y_1)*(x_4-x_1)-(x_2-x_1)*(y_4-y_1) jacb_inv(3,3)=(x_2-x_1)*(y_3-y_1)-(y_2-y_1)*(x_3-x_1)

1111111111111111111111111111111

B_1=reshape((/-jacb_inv(1,1)-jacb_inv(1,2)-jacb_inv(1,3),0.,0.,0.,& &-jacb_inv(2,1)-jacb_inv(2,2)-jacb_inv(2,3),0.,0.,0.,& &-jacb_inv(3,1)-jacb_inv(3,2)-jacb_inv(3,3)& &,0.,-jacb_inv(3,1)-jacb_inv(3,2)-jacb_inv(3,3),-jacb_inv(2,1)-jacb_inv(2,2)& &-jacb_inv(2,3),-jacb_inv(3,1)-jacb_inv(3,2)-jacb_inv(3,3),0.,-jacb_inv(1,1)-& &jacb_inv(1,2)-jacb_inv(1,3),-jacb_inv(2,1)-jacb_inv(2,2)-jacb_inv(2,3),& &-jacb_inv(1,1)-jacb_inv(1,2)-jacb_inv(1,3),0./),(/6,3/),order=(/2,1/)) B_2=reshape((/jacb_inv(1,1),0.,0.,0.,jacb_inv(2,1),0.,0.,0.,jacb_inv(3,1),0 .,jacb_inv(3,1)& &,jacb_inv(2,1),jacb_inv(3,1),0.,jacb_inv(1,1),jacb_inv(2,1),jacb_inv(1,1), 0./),(/6,3/),order=(/2,1/)) B_3=reshape((/jacb_inv(1,2),0.,0.,0.,jacb_inv(2,2),0.,0.,0.,jacb_inv(3,2),0 .,jacb_inv(3,2)& &,jacb_inv(2,2),jacb_inv(3,2),0.,jacb_inv(1,2),jacb_inv(2,2),jacb_inv(1,2), 0./),(/6,3/),order=(/2,1/)) B_4=reshape((/jacb_inv(1,3),0.,0.,0.,jacb_inv(2,3),0.,0.,0.,jacb_inv(3,3),0 .,jacb_inv(3,3)& &,jacb_inv(2,3),jacb_inv(3,3),0.,jacb_inv(1,3),jacb_inv(2,3),jacb_inv(1,3), 0./),(/6,3/),order=(/2,1/)) H=reshape((/1-nu,nu,nu,0.,0.,0.,nu,1-nu,nu,0.,0.,0.,nu,nu,1-nu,0.,0.,0.,0.,0.,0.,(1-2*nu)/2,0.,0.,0.,0.,& &0.,0.,(1-2*nu)/2,0.,0.,0.,0.,0.,0.,(1-2*nu)/2/),(/6,6/),order=(/2,1/)) 111 function pour calculer le coefficient multiplicateur de Ke vol=36*((1/6.)*det_jab(x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3,x_4,y_4,z_4))*(1 -2*nu)*(1+nu)

11111111111111 appel des procedures

call table_Bi(1.,B1);call table_Bi(2.,B2);call table_Bi(3.,B3);call
table_Bi(4.,B4)

call produit(B_1,B1,lin,3,3,col,res1);call produit(B_2,B2,lin,3,3,col,res2) call produit(B_3,B3,lin,3,3,col,res3);call produit(B_4,B4,lin,3,3,col,res4) B=res1+res2+res3+res4;Bt=transpose(B)

call produit(Bt,H,12,6,6,6,res5);call produit(res5,B,col,lin1,lin,col,ke) call system('mkdir c:\matrice_K_B')

open(unit=20,file=' c:\matrice_K_B\metrice_K.txt',status='unknown')

write(20,15)"+

+"

write(20,15)"| Matrice de rigidité élémentaire d'un élément tétraédrique à 4 noeuds|"

write(20,15)"+

+"

15 format(A)

write(20,16);16 format(/:)

11111111111 écriture des noeuds

write(20,18)"+ +"
write(20,18)"| Coordonnées des noeuds (x, y, z) |"

write(20,25)"+ +"
18 format(x,A);25 format(x,A,/:)

do i=1,4

write(20,19)"Noeud ",i,"|"

87 /176

Chapitre 3

19 format(A,x,I1,2x,A,x,$)

do j=1,3

write(20,21)c_noeud(j,i),"|"

21 format(F8.4,x,A,$)

enddo

write(20,22);22 format(2/:)

enddo

!!!!!!!!!!!! écriture la matrice Ke

write(20,23)"Ke =",E/vol,"*"

23 format(A,x,F18.4,x,A)

do i=1,12

write(20,11)"|"

11 format(x,A,x,$)

do j=1,12

write(20,12)ke(i,j)

12 format(F8.4,x,"|",$)

enddo

write(20,13);13 format(/:)

enddo

close(20)

call system('start c:\matrice_K_B\metrice_K.txt')

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

end program

!

!procédure pour la table de localisation pour les matrices Bi

!cette sous routine permet d'insérer la matrice identité à la

!place de Bi

!

subroutine table_Bi(col,tab)

integer i,j

real::col

real, dimension(1:3,1:12)::tab

tab=0;j=3*col-2

do i=1,3

tab(i,j)=1;j=j+1

enddo

return

end

!procédure pour calculer les termes ji la matrice jacobienne inverse

!

! procédure pour calculer le déterminant de la matrice

! de la matrice jacobienne de transformation

!warning: cette procédure est pour ce cas spécificique

!il ne peut être utilisé pour calculer le déterminant d'1e autre matrice

function det_jab(x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3,x_4,y_4,z_4)

real:: x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3,x_4,y_4,z_4,det_jab

det_jab=((x_2-x_1)*(y_3-y_1)*(z_4-z_1)+(y_2-y_1)*(z_3-z_1)*(x_4-x_1)+&

&(z_2-z_1)*(x_3-x_1)*(y_4-y_1)-(x_2-x_1)*(z_3-z_1)*(y_4-y_1)-(y_2-&

&y_1)*(x_3-x_1)*(z_4-z_1)-(z_2-z_1)*(y_3-y_1)*(x_4-x_1))

return

end function det_jab

!

subroutine produit(mat1,mat2,n,c,n1,c1,res)

integer::i,j,k,n,c,n1,c1

real, dimension(1:n,1:c1)::res

real, dimension(1:n,1:c)::mat1

real, dimension(1:n1,1:c1)::mat2

do i=1,n

do j=1,c1

res(i,j)=0.

do k=1,c

res(i,j)=res(i,j)+mat1(i,k)*mat2(k,j)

enddo

enddo

Chapitre 3

enddo

end subroutine produit

3.3.5.3. Exemple de l'exécution du programme Input :

,

Noeu n°	x	y	z
1	0.75	0.33	0.1
2	1.01	0.1	0.05
3	0.02	1.11	0.12
4	0.105	0	1.2

Tableau 3.2 : Valeurs d'essai pour le test du programme matrice_K

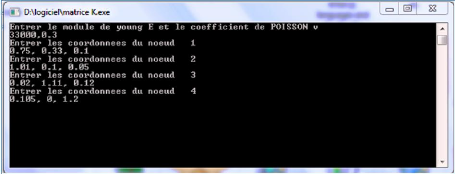
Figure 3.7 : Capture d'écran des données en Input du programme matrice_K

88 /176

Output :

Chapitre 3

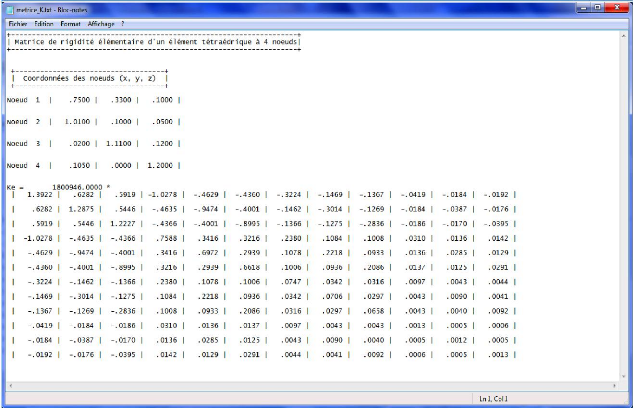
89 /176

Figure 3.8 : Capture d'écran des données en Output du programme matrice_K

90 /176

Chapitre 4

Chapitre 4 : Modélisation et Simulation

numérique d'un tablier de pont

Sommaire

4.1.	Matériels employés pour la simulation	91
4.2.	Présentation générale de l'ouvrage	92
4.3.	Caractéristiques du Tablier	94
4.4.	Définition des charges et actions appliquées à la structure	99
4.5.	Définition du flux de travail	109
4.6.	Définition de la structure	110
4.7.	Construction du modèle éléments finis (EF)	116
4.8.	Introduction des conditions de fixations (Appuis)	118
4.9.	Choix des normes et règlements à utiliser	119
4.10.	Définitions des charges	120
4.11.	Lancement des calculs de la structure	128
4.12.	Résultats de calcul	129
4.13.	Définition des combinaisons d'actions	134
4.14.	Exploitation des résultats	136

91 /176

Chapitre 4

4.1. Matériels employés pour la simulation

La conduite de la simulation numérique a été possible grâce à l'utilisation d'un ordinateur et de certains logiciels

4.1.1. Ordinateur

L'ordinateur utilisé est un Acer Aspire 5742. Ces caractéristiques sont les suivantes :

Processeur : Intel® CoreTM i5 CPU M480 @ 2.67GHz 2.97 GHz
Mémoire installée (RAM) : 4 Go (3.68 Go utilisable)

Type du système : Système d'exploitation 64 bits

Disque dur : 450 Go

4.1.2. Logiciel Autodesk AutoCAD 2012

Le logiciel Autodesk AutoCAD 2012 a été utilisé pour représenter les axes de notre structure. Le fichier des axes sera ensuite importé, en fond, dans le logiciel Autodesk Robot SAP 2012 pour procéder à la modélisation numérique de la structure.

4.1.3. Logiciel Autodesk Robot SAP 2012

Le logiciel Autodesk Robot SAP 2012 a été choisi pour modéliser, simuler le comportement, analyser et dimensionner notre structure, car son code de calcul est basé sur la méthode des éléments finis.

4.1.3.1. Description générale du logiciel Autodesk Robot SAP 2012

A

utodesk Robot SAP est une plate-forme logicielle destinée aux ingénieurs. Elle permet de modéliser, de concevoir, d'analyser n'importe quel type de structure.

Il effectue plusieurs types d'analyses :

· l'analyse statique

· l'analyse harmonique

· l'analyse temporelle (linéaire et non-linéaire)

· l'analyse Push-over

· l'analyse élasto-plastique des barres

· l'analyse Footfall

92 /176

Chapitre 4

? l'analyse Frequency Response Functions

Dans notre étude, seule l'analyse statique sera effectuée. Bien que le logiciel robot soit un outil souple de calcul en ingénierie, l'utilisateur doit être capable de générer un modèle adéquat et fonctionnel d'éléments finis de la structure, de l'analyser, d'interpréter correctement les résultats de l'analyse et d'exploiter les résultats pour le dimensionnement de la structure.

Pour effectuer toute analyse statique, l'équation caractéristique que le programme établit et résout est du type de [ K]( U) = ( F) qui relie le vecteur des forces généralisées et les déplacements aux noeuds, de la structure maillée, par l'intermédiaire de la matrice de rigidité globale.

Pour l'analyse des structures de types plaques et coques, les modèles éléments finis sont construits en utilisant des éléments triangulaires à 3 ou 6 noeuds ou quadrangulaires à 4 ou 8 noeuds.

4.2. Présentation générale de l'ouvrage

La réalisation de l'ouvrage, objet de la présente étude, s'inscrit dans le cadre des travaux d'aménagement et de bitumage des tronçons « frontière TOGO - TCHETTI - SAVALOU (42 km) » et « LOGOZOHE - GLAZOUE (17 KM) ».

Il s'agit d'un pont à poutre, à 3 travées indépendantes, d'une longueur totale de 50 m, à construire sur le tronçon 1 : « frontière TOGO-TCHETTI SAVALOU » au PK 23+200.

Le pont reposera sur des fondations superficielles par l'intermédiaire des piles, et de deux culées aux extrémités, comme le montre le rendu photo-réaliste suivant :

93 /176

Chapitre 4

Figure 4.1 : Vue aérienne du pont

Le profil en travers du pont suit la disposition ci-contre :

? Largeur de la chaussée : 7.00 m (2 voies de circulation). La chaussée est déversée en toit, à 2.5% de pente.

? 2 trottoirs de 1.15 m de largeur chacun, équipés de garde-corps métalliques en encorbellements latéraux, soit une largeur totale de 9.00 m.

Figure 4.2 : Trottoir équipé de garde-corps

Notre étude ne consiste pas en une étude technique détaillée du pont, mais en une simulation numérique de son tablier.

94 /176

Chapitre 4

4.3. Caractéristiques du Tablier

Le Tablier de longueur totale 50 m est constitué de :

? Une dalle sous chaussée ;

? Des nervures, associées à la dalle sous chaussée, appelées

poutres ;

? Des entretoises solidaires des poutres et de la dalle sous

chaussée.

Figure 4.3 : Vue de dessus du tablier

Figure 4.4 : Vue de dessous du tablier

95 /176

Chapitre 4

4.3.1. Les poutres

Le pont comportera 4 poutres (40 cm x 150 cm), par travée, espacées de 2.00 m chacune et un encorbellement de part et d'autre de 75 cm.

Sur les 1^ère et 3^ème travées, les poutres possèdent une longueur totale de 16.805 m et portent sur 16.48 m ; tandis que sur la travée du milieu, elles possèdent une longueur totale de 16.27 m et portent sur 15.96 m.

Des joints de dilatations de 3 cm sont insérés au début et à la fin de chaque travée.

4.3.2. Les entretoises

Les entretoises (30 cm x 140 cm) ont pour but de solidariser les poutres entre elles. Elles reportent l'effet des charges sur les différentes poutres.

La Longueur de chaque entretoise est 7.80m. Le nombre d'entretoises de chaque travée sera de 2 avec un espacement entre nus d'entretoise de 16.18 m.

4.3.3. La dalle sous chaussée

Une dalle en Béton Armé sera coulée sur place. Il est supporté par un réseau de poutres et d'entretoise qui le découpent en dalle de côté a et b avec :

? a=2.60 m et b=16.48 m sur les 1^ère et 3^ème travées ; ? a=2.60 m et b=16.27 m sur la 2^ème travée.

La dalle possède une épaisseur ht= 20 cm.

96 /176

Chapitre 4

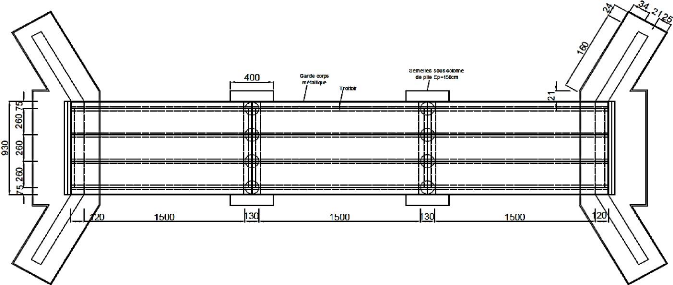
Figure 4.5. Vue en plan générale

Chapitre 4

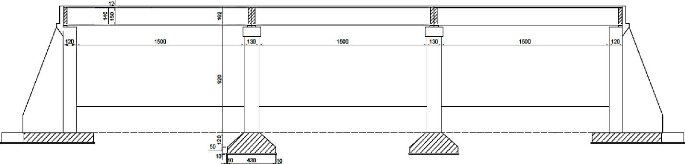
97 /176

Figure 4.6 : Coupe longitudinale axiale

Chapitre 4

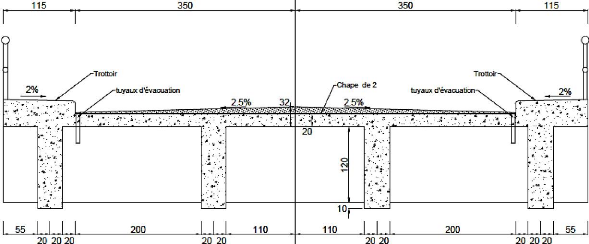
98 /176

Figure 4.7 : Coupe transversale du tablier

99 /176

Chapitre 4

4.4. Définition des charges et actions appliquées à la structure 4.4.1. Charges permanentes

Elles résultent du poids propre :

? des éléments du tablier

- dalle sous chaussée ;

- entretoises ;

- poutres ;

? des revêtements du tablier :

- couche d'étanchéité (à base d'asphalte) ;

- couche de roulement (béton bitumineux) ;

? des autres équipements portés par le tablier :

- trottoir ;

- dispositifs de retenue.

Les poids propres des éléments du tablier sont pris en compte directement lors de la modélisation dans le logiciel Autodesk Robot SAP.

Les valeurs des autres charges permanentes peuvent être estimées comme suit :

Equipements	ép(cm)	g			Étanchéité
2	0.44	KN/m^2		Couche de roulement
10	2.5
31	7.75
-	0.5	KN/m

Tableau 4.1 : Charges permanentes

100 /176

Chapitre 4

4.4.2. Charges d'exploitations

4.4.2.1. Charges sur les trottoirs

D'après le fascicule 61 titre II du Cahier des Prescriptions Communes (CPC), une charge uniforme de 1.5 kN/m² est supportée par chaque trottoir du pont.

4.4.2.2. Charges de chaussée

Elles sont directement liées aux charges routières ; Le Fascicule 61 Titre II du Cahier des Prescriptions Communes (CPC) définit deux « systèmes », distincts et indépendants, de charges routières à caractère normal : le système A et le système B.

Nos justifications, après comparaison, ne feront état que du système dont les effets sont les plus importants.

Le pont à construire sur le tronçon 1 : « frontière TOGO-TCHETTI SAVALOU » au PK 23+200, possède une largeur roulable LR = 7.00 m ;

La chaussée étant encadrée par deux bordures, la largeur chargeable (L_c) se retrouve confondue avec la largeur roulable. Nous avons alors :

L_c = LR = 7.00 m

On distingue trois classes de ponts, en fonction de leur largeur roulable :

Classe		Largeur roulable	I II III
= 7 m 5.50 m < LR < 7 m = 5.50 m

Tableau 4.2 : Classe de pont en fonction de la largeur roulable

Il apparait alors, au vu de la classification précédente, que le pont, objet de notre étude, est de 1^ère classe.

101 /176

Chapitre 4

4.4.2.3. Système A

Le système A se compose d'une charge uniformément répartie dont l'intensité dépend de la longueur chargée suivant la loi :

(L)

L étant la longueur chargée, exprimé en m.

Nous disposerons les charges entre zéros de ligne d'influence de façon à obtenir le maximum de l'effet recherché et on l'appliquera, moyennant certains coefficients pondérateurs, sur toute la partie de la largeur chargeable de chaque travée.

Tout d'abord, la densité A(L) est multipliée par un coefficient a1, assimilable à un coefficient de dégressivité transversale, donné dans le tableau ci-dessous :

Classe		Nombre de voies chargées					du pont
1		2	3	4	5	I
1		1	0.9	0.75	0.75	II
2		0.9	-	-	-	III
0.9		0.8

Tableau 4.3 : Coefficient de dégressivité transversale de la charge A(L)

La densité de charge effective q(L) peut être mise sous la forme :

q(L) = Sup( a₁A(L) ; ( 4 -- 0.002L)} KN/m²

La charge de calcul est :

Q = Y * * q (L) KN/m

Avec : a2=v0/v, v étant la largeur d'une voie

v0=3.50 m pour les ponts de 1^ère classe

v0=3.00 m pour les ponts de 2^ème classe

v0=2.75 m pour les ponts de S^ème classe

102 /176

Chapitre 4

Le coefficient pondérateur vaut 1.20 à l'ELS et 1.07 x 1.5 à l'ELU.

Dans le cadre de notre simulation, nous évaluerons les charges de calcul sans pondérations ; en effet, les coefficients de pondération seront pris en compte lors de la définition des combinaisons d'actions dans le logiciel Autodesk Robot SAP.

? Evaluation de la charge de calcul pour le pont

a1	a2				1
3.5/3.5	=	1

Tableau 4.4 : Coefficients a1 et a2

Pour les 1^ère et 3^ème travées, la charge de calcul prend la valeur suivante :

* ( ) ( )+

Pour la 2^ème travée :

* ( ) ( )+

4.4.2.4. Système B

Le système de charges B comprend trois sous-systèmes distincts :

- le sous-système B_c qui se compose de camion type ;

- le sous-système B_r qui se compose d'une roue isolée ;

- et le sous-système Bt qui se compose de groupes de deux

essieux dénommés essieux tandems.

Pour la simulation, on s'intéressera essentiellement aux effets provenant

des sous-systèmes B_c et Bt.

103 /176

Chapitre 4

? Sous-système B_c

Le sous-système B_c se compose de camions de poids individuel égal à 30 t, soit 300 kN.

On disposera autant de files de deux camions au maximum que de voies de circulation, soit au total deux files de camions pour notre ouvrage.

Le convoi de charges du système B_c se représente schématiquement comme suit :

Figure 4.8 : Convoi de charges du système Bc

Figure 4.9 : système Bc en vue transversale et en plan

Il est affecté d'un coefficient de pondération b_c (dégressivité transversale) donné dans le tableau ci-dessous :

Chapitre 4

Classe du		Nombre de voies chargées					pont
1		2	3	4	5	I
1.2		1.1	0.95	0.80	0.70	II
1		1	-	-	-	III
1		0.8

Tableau 4.5 : Coefficient de dégressivité transversale b_c ? Sous-système Bt

Le sous-système Bt se compose de deux tandems à deux essieux de quatre roues chacun, le poids de chaque essieu étant de 16 t, soit 160 kN :

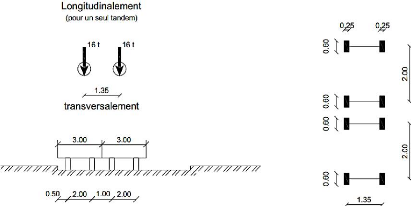
104 /176

Figure 4.10 : Système Bt en vue transversale, longitudinale et en plan

Il est affecté d'un coefficient de pondération bt choisi selon le tableau suivant :

Classe du pont	Première		Deuxième	Coefficient
1.0	0.9

Tableau 4.6 : Coefficient de dégressivité transversale bt

105 /176

Chapitre 4

Qu'il s'agisse du sous-système B_c ou du sous-système Bt, la charge de calcul vaut :

b = b_c ou bt selon le cas

6 = coefficient de majoration dynamique :

Le coefficient vaut 1.20 à l'ELS et 1.07 x 1.5 à l'ELU.

? Calcul du coefficient de majoration dynamique applicable aux poutres (61)

Avec :

L : Longueur de la travée étudiée ;

G : poids total de ladite travée ;

S : poids total maximal des essieux du système B (B_c ou Bt).

De manière à uniformiser la charge de calcul à prendre en compte, lors du processus de simulation, pour toutes les travées du pont, nous maximiserons le coefficient 61 en prenant la plus petite valeur possible pour L et la valeur de G qui lui correspond.

Cela revient à définir L tel que :

L = Min (L1, L2, L3)

Avec:

Li: Longueur de la travée i

106 /176

Chapitre 4

- Calcul de L :

L1		16.805 m	L2
16.27 m		L3
16.805 m		Min (L1, L2, L3)
16.27 m

Tableau 4.7 : Tableau de détermination de la longueur L pour le calcul de ä1

L= 16.27 m

- Calcul de G :

Poutre		976,20 kN	Entretoise
163,80 kN		Dalle sous chaussée
756,56 kN		Couche de roulement
284,73 kN		Étanchéité
51,76 kN		Garde-corps
16,27 kN		Trottoir
290,01 kN		G
2615,73 kN

Tableau 4.8 : Tableau de détermination de la valeur de G pour le calcul de ä1

G= 2615,73 kN

- Calcul de S

Sbc = 2*(120+120+60+120+120) = 540 kN
Sbt = 720 kN

Chapitre 4

( ⁶¹bC' ⁶1b )

Calcul du coefficient de majoration dynamique applicable à la dalle sous chaussée (62)

- Longueur L à considérer :

Largeur roulable : LR=7.00 m

Distance entre plans moyens des poutres de rive :

L= 7.80 m.

- Calcul de G

Dalle sous chaussée		362,70 kN	Couche de roulement
136,50 kN		Étanchéité
24,02 kN		Garde-corps
7,80 kN		Trottoir
139,04 kN		G
670,06 kN

Tableau 4.9 : Tableau de détermination de la valeur de G pour le calcul de 62

107 /176

- Calcul de S

108 /176

Chapitre 4

Sbc = 2*(120+120) = 480 kN
Sbt = 720 kN

( ⁶²bC' ⁶2b )

Nous résumons les différentes valeurs du coefficient de majoration dynamique dans le tableau ci-dessous :

Eléments	Poutres		Dalle sous chaussée	6
1,134	1.285

Tableau 4.10 : Tableau récapitulatif des valeurs de 6

Les valeurs des charges du système B seront multipliées, dans un premier temps, par le produit de coefficients 6*b, puis par le coefficient y selon l'état limite considéré.

Pour des raisons de commodité, nous choisissons de ne tenir compte, à l'étape actuelle, que du produit de coefficients 6*b dont les valeurs se résument dans le tableau suivant.

109 /176

Chapitre 4

	Sous-système Bc		Sous-système Bt	Poutres
1.247	1.134		Dalle sous chaussée
1.414	1.285

Tableau 4.11 : Tableau récapitulatif des valeurs du produit de coefficients ä*b

Le coefficient pondérateur y sera introduit lors de la définition des combinaisons d'actions dans le logiciel Autodesk Robot SAP 2012.

4.5. Définition du flux de travail

La modélisation et la simulation du tablier, du pont, se feront en complétant les différentes étapes ci-dessous :

· Définition de la structure

· Construction du modèle éléments finis (EF)

· Introduction des conditions de fixations (Appuis)

· Choix des normes et règlements à utiliser

· Définitions des charges

· Lancement des calculs de la structure

· Résultats de calcul

· Définition des combinaisons d'actions

· Exploitation des résultats

Chapitre 4

4.6. Définition de la structure

Les lignes de construction forment une grille auxiliaire qui facilite la définition des différents éléments de la structure et permet de se référer aux composants de cette structure (c'est-à-dire de les sélectionner).

4.6.1. Création des lignes de construction dans Autocad

Il est parfois plus aisé de crée les lignes de construction dans Autocad en vue d'une importation dans Robot. Cette procédure sera utilisée pour implanter les axes de la structure de notre Tablier.

Figure 4.11 : Axes de construction créés dans Autocad

4.6.2. Importation des lignes de construction dans Robot SAP

menu Fichier/Importer/Fonds DXF, DWG

110 /176

Figure 4.12 : Importation des Axes de constructions

Chapitre 4

Après la sélection du fichier dwg/dxf, la boite ci-dessous permet de définir les paramètres d'insertion du fichier dwg/dxf.

Figure 4.13 : - Boite de dialogue - Importation des fichiers dwg/dxf

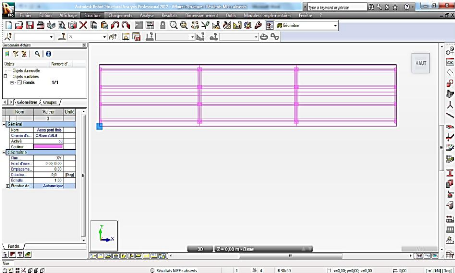
111 /176

Figure 4.14 : Axes de constructions importés dans Robot

112 /176

Chapitre 4

4.6.3. Création de la géométrie

4.6.3.1. Définition des poutres et entretoises

Pour des raisons de concisions, nous ne décrirons pas la procédure de définitions de ces éléments.

La géométrie, après la définition des poutres et entretoises, se présente comme suit :

Figure 4.15 : Définition des poutres et entretoises

4.6.3.2. Modélisation des dalles sous-chaussées

Pour la définition de ces éléments, la procédure suivante est adoptée :

? Choix de l'outil Panneaux : Structure/Panneaux

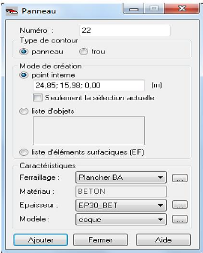
Figure 4.16 : - Boite de dialogue - Panneaux

113 /176

Chapitre 4

? Clic sur le bouton panneau dans type de contour

? Définition des caractéristiques :

- Clic sur le bouton dans

(On définit les paramètres dans chaque onglet conformément aux figures suivantes

et on clique sur le bouton )

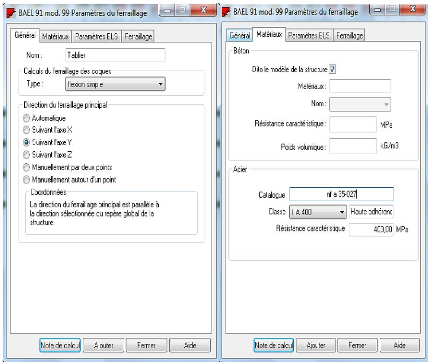
Figure 4.17 : - Boite de dialogue - Paramètre de ferraillage, Onglets Général et

Matériaux

114 /176

Chapitre 4

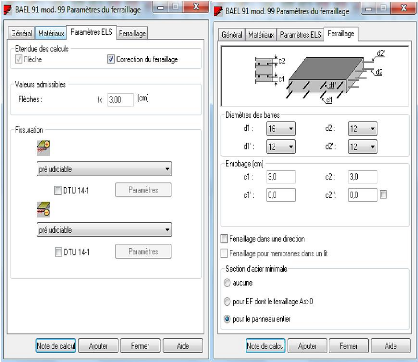
Figure 4.18 : - Boite de dialogue - Paramètre de ferraillage, Onglets Paramètre ELS

et Ferraillage

- Clic sur le bouton dans

(on définit les paramètres comme sur la figure suivante et on clique sur

)

115 /176

Chapitre 4

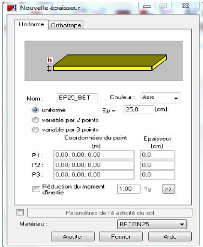
Figure 4.19 : - Boite de dialogue - Nouvelle épaisseur

- Clic sur le bouton dans

(on définit les paramètres comme sur la figure suivante et on clique sur

)

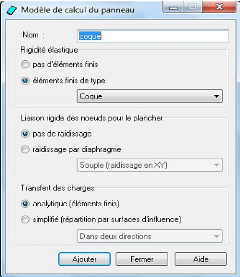
Figure 4.20: - Boite de dialogue - Modèle de Calcul du panneau

116 /176

Chapitre 4

? Choix d'un point interne

(on choisit les points dans les contours importés pour crées les dalles
sous-chaussées)

La définition géométrique de la structure du Tablier se présente comme

suit :

Figure 4.21 : Définition de la structure du Tablier dans Robot

4.7. Construction du modèle éléments finis (EF)

Le modèle EF est défini par le maillage de la structure du Tablier.

Le maillage de la structure, dans le logiciel Robot, nécessite de compléter les étapes suivantes :

? Sélectionner les panneaux à mailler

? Choix de l'outil option de maillage : Analyse/Maillage/Options de

maillage

La boite de dialogue Options de maillage permet de définir les paramètres du maillage.

117 /176

Chapitre 4

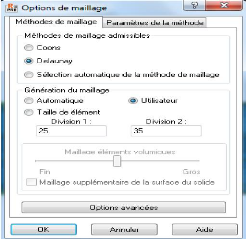
Figure 4.22 : - Boite de dialogue - Options de maillage

La procédure de paramétrage se présente comme suit :

? Clic sur le bouton dans la boite de

dialogue option de maillage (figure 4.23)

(on définit les paramètres comme sur la figure suivante)

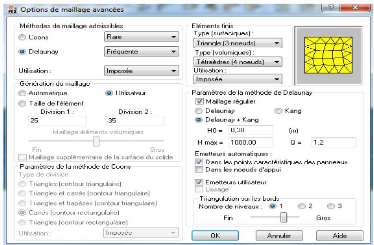
Figure 4.23 : - Boite de dialogue - Options de maillage avancées

118 /176

Chapitre 4

? Clic sur le bouton pour valider le modèle

? Clic sur le bouton Génération de maillage

sur la barre

d'outils Options de génération de maillage

Le maillage de la structure du Tablier se présente comme suit :

Figure 4.24 : Maillage du tablier

4.8. Introduction des conditions de fixations (Appuis)

La procédure suivante est adoptée pour introduire les appuis dans la structure modélisée :

? Ouverture de la boite de dialogue Appuis

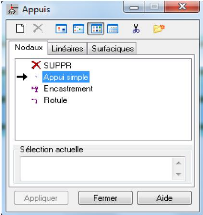
Figure 4.25 : - Boite de dialogue - Appuis

119 /176

Chapitre 4

? Mise en surbrillance du type d'appuis à affecter

? Sélection des noeuds concernés dans le champ Sélection

actuelle

? Clic sur le bouton pour affecter les appuis aux noeuds

concernés

La figure suivante présente le système d'appuis utilisé pour la structure de notre tablier :

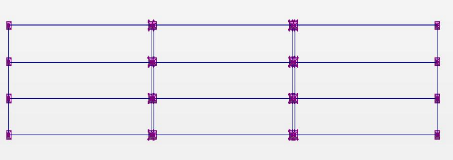
Figure 4.26 : Système d'appuis du tablier

4.9. Choix des normes et règlements à utiliser

? Sélection de Préférence de l'affaire : menu Outils /Préférence de

l'affaire

(on définit les paramètres conformément à la figure 4.28 et on clique sur

pour valider le choix)

120 /176

Chapitre 4

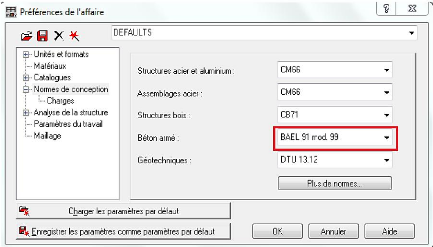
Figure 4.27 : - Boite de dialogue - Préférence de l'affaire, choix de la norme de

conception

4.10. Définitions des charges

4.10.1. Création des Cas de Charges

La boite de dialogue cas de charge sert à créer/modifier les cas de charges.

Le processus de création des cas de charge se présente comme suit :

? Ouverture de la boite de dialogue cas de charges : menu Chargement/cas de charge

? Choix du nom de la charge

? Choix de la nature de la charge dans le champ Nature

121 /176

Chapitre 4

? Clic sur le bouton pour créer le cas de charges

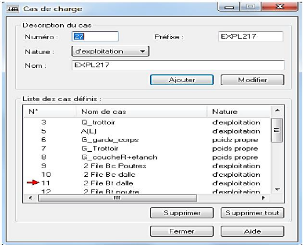
Figure 4.28 : - Boite de dialogue - Cas de charge

4.10.2. Définition des charges 4.10.2.1. Charges statiques

La boîte de dialogue Charge sert à définir les charges pour les cas de charge créés.

Remarque : Au moins un cas de charge doit être défini avant d'utiliser cette boite de dialogue.

Le processus de création des cas de charge se présente comme suit : ? Ouverture de la boite de dialogue charge :

menu Chargement/Définir charge .

La partie supérieure de la boîte de dialogue affiche deux informations : le cas de charge sélectionné (nom et numéro) pour lequel la charge sera définie le type de charge appliquée aux barres/noeuds de la structure.

? Saisie de la valeur de la charge

? Saisie des numéros des éléments de structure (barres, noeuds,

panneaux), auxquels la charge sera affectée, dans le champ

Chapitre 4

? Clic sur le bouton pour procéder à l'affectation de la

charge définie aux éléments dont les numéros ont été saisis dans le champ Appliquer à

4.10.2.2. Charges roulantes

L'option permettant de définir des charges roulantes permet d'analyser une structure avec un déplacement des charges appliquées.

Le processus de création et de définition des charges roulantes se présente comme suit :

:

? Ouverture de la boite de dialogue charges roulantes

menu Chargement/autres charges/Roulantes

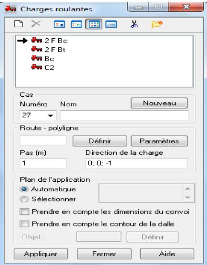
Figure 4.29 : - Boite de dialogue - Charges roulantes

Les charges roulantes sont définies par la description du convoi et de sa route sur la structure. Le convoi est un ensemble de force à directions, valeurs et positions données. Pour chaque pas, le convoi est déplacé d'une position vers la position suivante ; l'ensemble de forces appliquées aux éléments est créé pour chaque position. Par conséquent, le cas de charge roulante est considéré comme un ensemble de plusieurs cas de charge statiques (un cas de charge pour chaque position du convoi).

122 /176

? Sélection ou création du convoi qui sollicitera la structure

123 /176

Chapitre 4

Pour sélectionner le convoi, on le met en surbrillance sur la liste de types de convois actifs

Pour créer un nouveau convoi, on ouvre la boite de dialogue suivante par un clic sur

l'icône

, et procède au paramétrage nécessaire

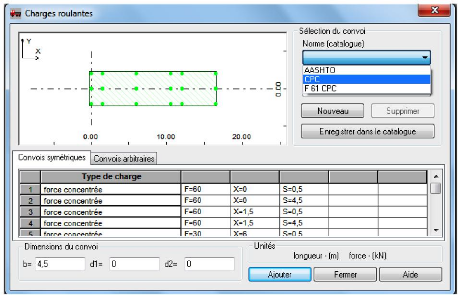
Figure 4.30 : - Boite de dialogue - Charges roulantes

La définition du convoi peut être composée de forces concentrées, linéaires ou surfaciques au contour rectangulaire.

Dans cette boîte de dialogue, on sélectionne le convoi qui sera ajouté à la liste active des convois affichée dans la boîte de dialogue Charges roulantes.

Dans notre cas, la définition du convoi est uniquement composée de forces concentrées.

? Définition de l'itinéraire/route du convoi

124 /176

Chapitre 4

Pour définir la route du convoi, on clique sur le bouton ,

(- Boite de dialogue - Charges roulantes), qui ouvre la boîte de dialogue Polyligne - contour.

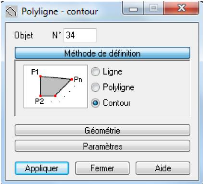
Figure 4.31 : - Boite de dialogue - Polyligne-contour

Un clic sur le bouton Paramètres , (- Boite de

dialogue - Charges roulantes), ouvre une boîte de dialogue supplémentaire dans laquelle vous pourrez définir les coefficients multiplicateurs : coefficient de majoration dynamique, coefficient de frottement des pneus.

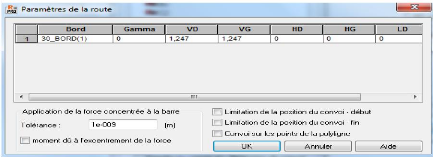
Figure 4.32 : - Boite de dialogue - Paramètres de la route

Les paramètres suivants , (- Boite de dialogue -

Charges roulantes), définissent un déplacement de charge :

- Pas : indique la valeur du pas pris pour le mouvement du convoi.

- Direction de la charge : indique la direction des efforts définissant le convoi.

125 /176

Chapitre 4

? Clic sur le bouton

Un clic sur ce bouton crée un nouveau cas de charge roulante.

La structure du tablier est sollicitée par plusieurs cas de charges dont certains sont représentés sur les figures ci-dessous :

Les numéros - noms attribués à ces cas sont conformes à ceux définis dans Robot.

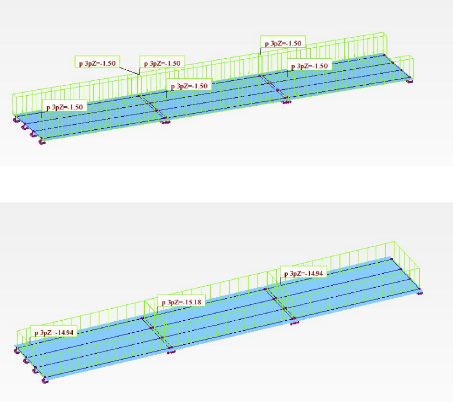
Figure 4.33 : Cas 3 - Q_trottoir : Charge d'exploitation des trottoirs

Figure 4.34 : Cas 5 À A(L) : Surcharge A(L)

126 /176

Chapitre 4

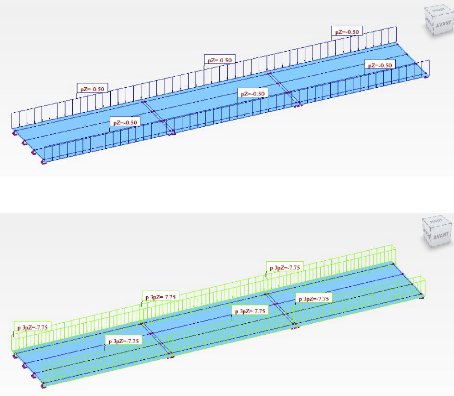
Figure 4.35 : Cas 6 -- G_garde_corps : Poids propre des Garde-corps

Figure 4.36 : Cas 7 -- G Trottoir : Poids propre des trottoirs

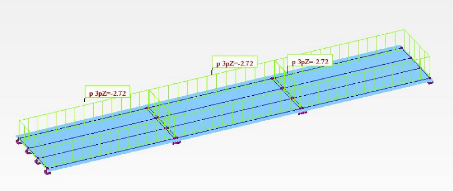
Figure 4.37 : Cas 8 -- G_coucheR+etanch : Poids propre Couche de roulement &

étanchéité

127 /176

Chapitre 4

Nous créons deux variantes, pour chaque sous-système de charge B, qui diffèrent l'une de l'autre par leur disposition transversale. Nous avons donc les cas suivants :

Figure 4.38 : Cas 9 - 2 File Bc Poutres : deux files du convoi de camions Bc
(disposition adoptée pour les poutres)

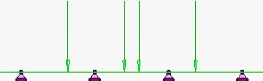
Figure 4.39 : Cas 10 - 2 File Bc Dalle : deux files du convoi de camions Bc
(disposition adoptée pour la dalle)

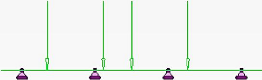
Figure 4.40 : Cas 11 - 2 File Bt Dalle : groupes de deux essieux-tandems
(disposition adoptée pour les poutres)

Figure 4.41 : Cas 12 - 2 File Bc Dalle, deux files du convoi de camions Bc
(disposition adoptée pour la dalle)

128 /176

Chapitre 4

4.11. Lancement des calculs de la structure On procède au lancement des calculs en sélectionnant l'outil menu Analyse/Calcul La boite de dialogue suivante apparait

Figure 4.42 : - Boite de dialogue - Calcul

La zone statistique, encadrée en rouge, de la boite de dialogue Calcul fournit les informations relatives au modèle EF étudié et le nombre d'équations résolu dans les calculs.

On peut lire ainsi que, le modèle EF de notre tablier, comporte 3064 noeuds et 5697 éléments finis. En outre, le système d'équations résolu par le logiciel comporte 18336 équations.

129 /176

Chapitre 4

4.12. Résultats de calcul

4.12.1. Panneaux

4.12.1.1. Cartographies des panneaux

A travers un processus itératif de recherche des effets les plus défavorables, basé sur l'observation des valeurs de la contrainte normale _ayy dans la direction principale de portance des panneaux de dalles, nous avons faire ressortir les cartographies des contraintes ayy suivantes :

La 1^re travée et la 3^e travée étant identiques, les résultats obtenus pour la 3^e travée sont valables pour la 1^re travée.

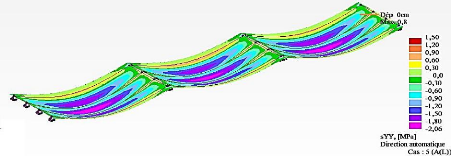
Figure 4.43 : Cartographie des contraintes _ayy relatives au système de charges A
(Travées 1, 2 et 3)

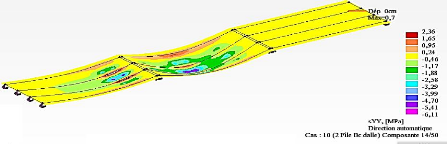
Figure 4.44 : Cartographie des contraintes _ayy relatives aux convois de charges Bc

(Travée 2)

130 /176

Chapitre 4

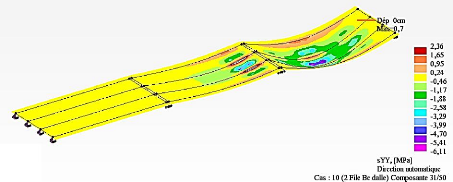
Figure 4.45 : Cartographie des contraintes _æyy relatives aux convois de charges Bc

(Travée 3)

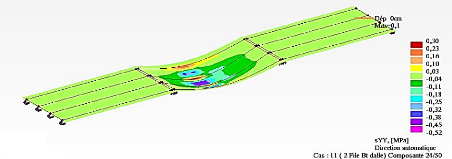
Figure 4.46 : Cartographie des contraintes _æyy relatives aux groupes d'essieux-
tandems (Travée 2)

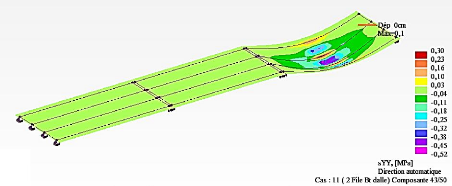
Figure 4.47 : Cartographie des contraintes _æyy relatives aux groupes d'essieux-
tandems (Travée 3)

131 /176

Chapitre 4

Une observation des cartographies des contraintes nous permet de déduire que le système composé de deux files de convois de camions Bc est prépondérant.

Nous procèderons à des vérifications supplémentaires en observant les valeurs du moment fléchissant en des coupes effectuées sur les panneaux de dalles.

4.12.1.2. Coupes sur panneaux

Une Coupe longitudinale a été effectuée sur l'axe des panneaux, afin de visualiser les valeurs maximales, suivant les travées et les cas de charges, du moment fléchissant _myy en kN.m

Figure 4.48 : Moment fléchissant _myy dû aux systèmes de charge A (Travées 1, 2 et

3)

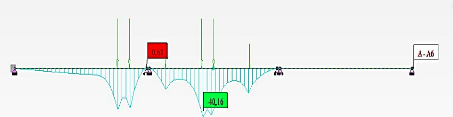
Figure 4.49 : Moment fléchissant _myy dû aux convois de charges Bc aux convois de
charges Bc (Travée 2)

Chapitre 4

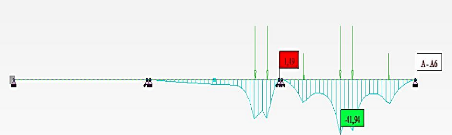
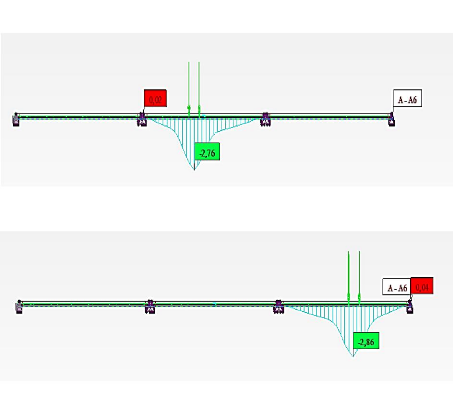
Figure 4.50 : Moment fléchissant _myy dû aux convois de charges Bc (Travée 3)

Figure 4.51 : Moment fléchissant _myy dû aux groupes d'essieux-tandems (Travée 2)

Figure 4.52 : Moment fléchissant _myy dû aux groupes d'essieux-tandems (Travée 2)

132 /176

L'observation des diagrammes du moment fléchissant permet de déduire que le système de charges défini par deux files de convois de camions Bc est prépondérant sur les autres systèmes. En outre, pour un même système de charge, les moments sont plus importants dans la 3^e travée que la 2^e travée.

133 /176

Chapitre 4

Pour nos justifications, nous utiliserons la composante du cas de charge qui engendre les moments les plus importants dans la 3^e travée.

Les résultats obtenus pour cette travée seront automatiquement adoptés pour les autres travées.

4.12.2. Barres

Les résultats les plus importants, étant obtenus dans la 3^e travée et relative aux systèmes de charges composés de deux files de camions Bc, nos analyses se concentreront sur les effets de ce système de charge sur les barres de structures disposées dans cette travée.

En outre, la symétrie du système de structure nous permet de nous limiter aux poutres situées d'un même côté du plan de symétrie du tablier et à l'une des entretoises de la travée.

4.12.2.1. Analyse détaillée des barres ? Poutre de rive gauche

Figure 4.53 : Moment fléchissant maximum dans la poutre de rive gauche (Travée 3)

? Poutre intermédiaire gauche

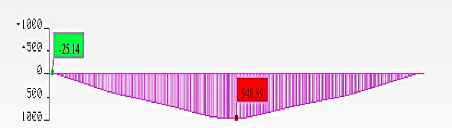
Figure 4.54 : Moment fléchissant maximum dans la poutre intermédiaire gauche

(Travée 3)

? Entretoise d'about

134 /176

Chapitre 4

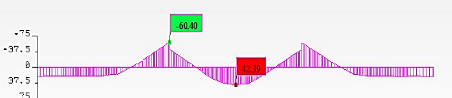
Figure 4.55 : Moment fléchissant maximum dans l'entretoise d'about (Travée 3)

4.13. Définition des combinaisons d'actions

4.13.1. Création des composantes de cas charges

Pour chacune des positions du système de charges composées de deux files de convois de camions Bc, nous générons des cas de charges correspondant à ces positionnements.

Ces cas de charges varieront d'un type d'élément du tablier à l'autre, et leur utilisation, pour les justifications, ne sera réservée que pour les types d'éléments de structure pour lesquels ils ont été générés.

Le processus de création de composantes de cas de charges se présente comme suit :

? Sélection du cas de convoi de charges dans la barre de sélection des cas de charges

? Ouverture de la boite de dialogue composante du cas

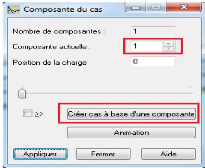
Figure 4.56 : - Boite de dialogue - composante du cas

Chapitre 4

? Sélection, dans le champ composante actuelle, de la position du convoi de charge

? Clic sur le bouton Créer cas à base d'une composante. 4.13.2. Génération des combinaisons d'actions

L'outil combinaisons manuelles , menu chargement sert à définir des

coefficients pondérateurs spécifiques à chaque type d'actions agissant sur la structure, selon l'Etat Limite considéré.

La boite de dialogue suivante donne une illustration du cas combinaison ELU générer pour le calcul de la dalle sous-chaussée.

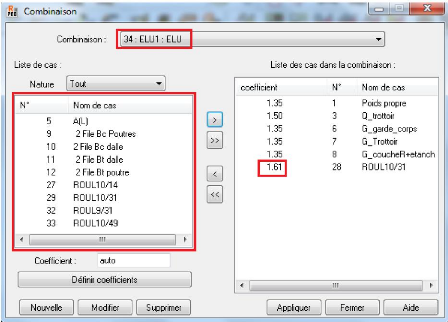
Figure 4.57 : - Boite de dialogue - Combinaison

Au niveau des zones en rouges :

135 /176

? Dans le champ combinaison :

136 /176

Chapitre 4

- Il est indiqué le numéro correspondant au cas de charges défini par la combinaison (exp : 34) ;

- Le nom de la combinaison (exp : ELU1) ; - L'Etat Limite considéré (exp : ELU).

? Dans le champ Nature, tous les cas de charges définis dans le logiciel sont listés

? Dans le champ Liste des cas de la combinaison, tous les cas de charges entrant dans la combinaison sont présents.

Chaque cas de charges porte devant lui, le coefficient qui le pondère.

4.14. Exploitation des résultats

4.14.1. Dalle sous chaussée

4.14.1.1. Cartographies et plans d'exécution

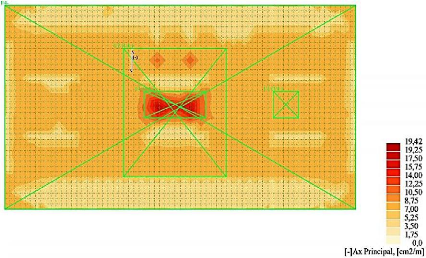
Figure 4.58 : Cartographie des sections d'aciers réels dans la direction principale de
portance (lit inférieur)

137 /176

Chapitre 4

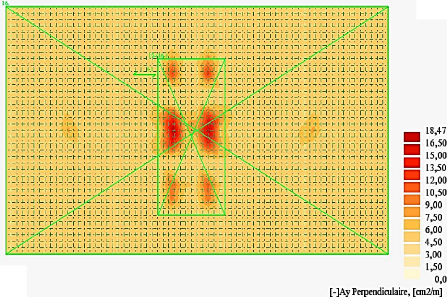
Figure 4.59 : Cartographie des sections d'aciers réels dans la direction secondaire (lit

inférieur)

Figure 4.60 : Cartographie des sections d'aciers réels dans la direction principale de
portance (lit supérieur)

138 /176

Chapitre 4

Figure 4.61 : Cartographie des sections d'aciers réels dans la direction secondaire (lit

supérieur)

Les plans de ferraillage de la dalle sous chaussée se présentent comme suit :

139 /176

Chapitre 4

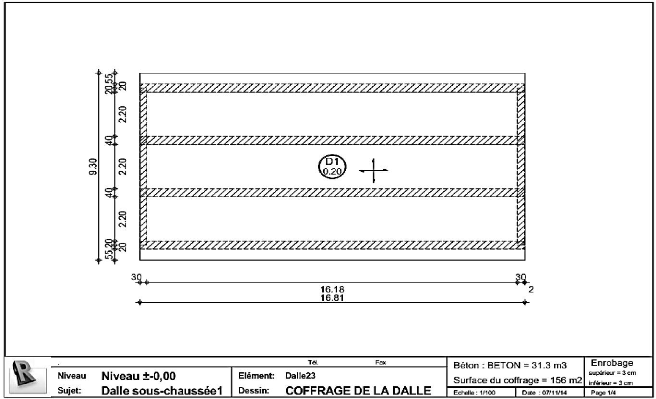
Figure 4.62 : Schéma de ferraillage dalle sous chaussée (1/4)

140 /176

Chapitre 4

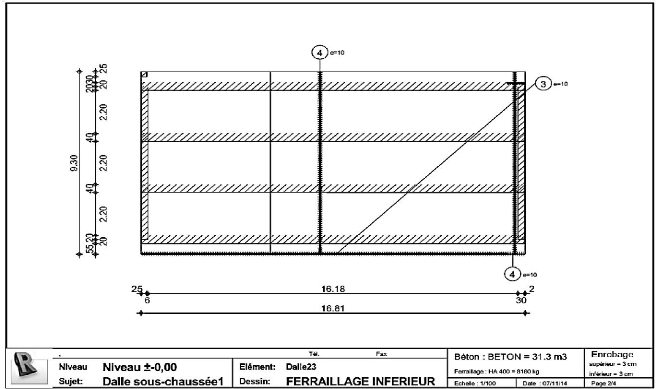
Figure 4.63 : Schéma de ferraillage dalle sous chaussée (2/4)

141 /176

Chapitre 4

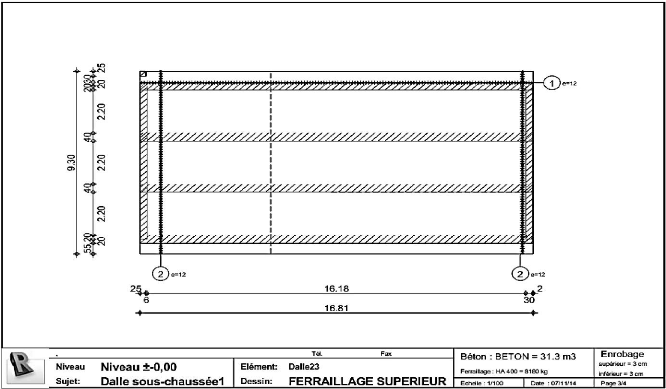
Figure 4.64 : Schéma de ferraillage dalle sous chaussée (3/4)

142 /176

Chapitre 4

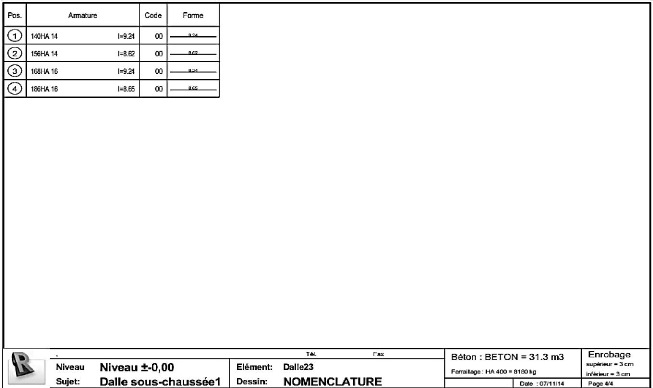
Figure 4.65 : Schéma de ferraillage dalle sous chaussée (4/4)

143 /176

Chapitre 4

4.14.2. Poutres de rives

4.14.2.1. Plans d'exécutions Pages suivantes

144 /176

Chapitre 4

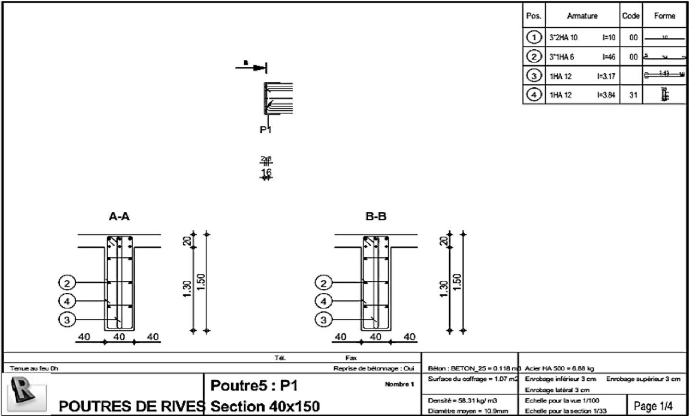
Figure 4.66 : Schéma de ferraillage poutres de rives (1/4)

145 /176

Chapitre 4

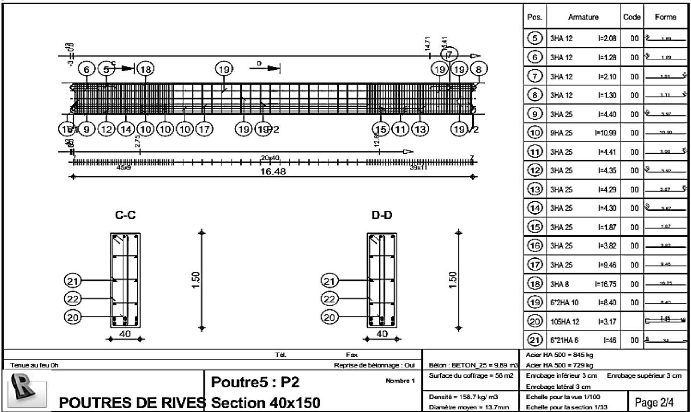
Figure 4.67 : Schéma de ferraillage poutres de rives (2/4)

146 /176

Chapitre 4

Figure 4.68 : Schéma de ferraillage poutres de rives (3/4)

147 /176

Chapitre 4

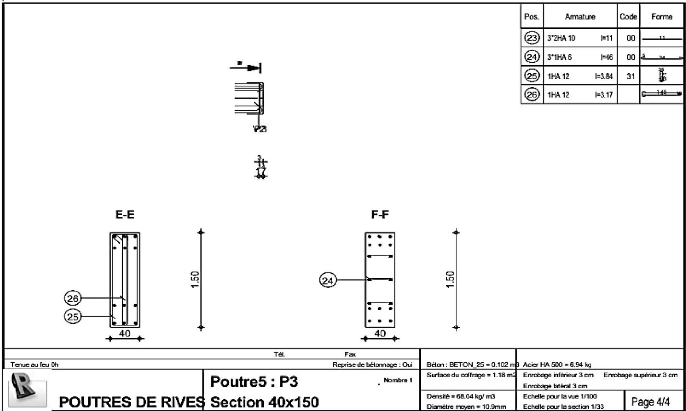
Figure 4.69 : Schéma de ferraillage poutres de rives (4/4)

148 /176

Chapitre 4

4.14.3. Poutres intermédiaires 4.14.3.1. Plans d'exécutions Pages suivantes

149 /176

Chapitre 4

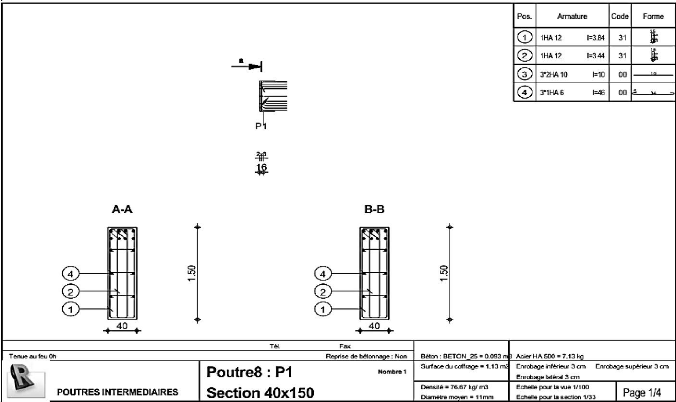
Figure 4.70 : Schéma de ferraillage poutres intermédiaires (1/4)

150 /176

Chapitre 4

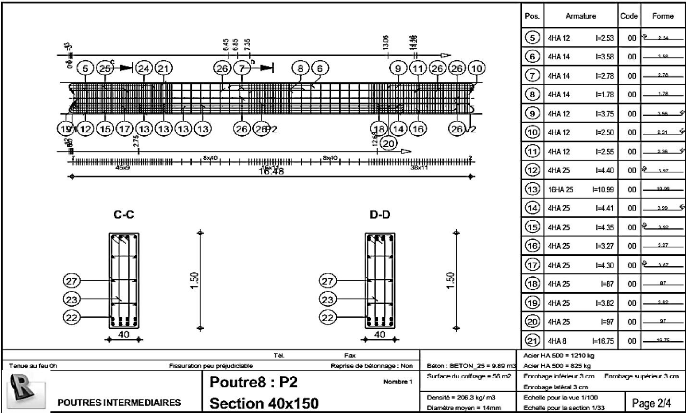
Figure 4.71 : Schéma de ferraillage poutres intermédiaires (2/4)

151 /176

Chapitre 4

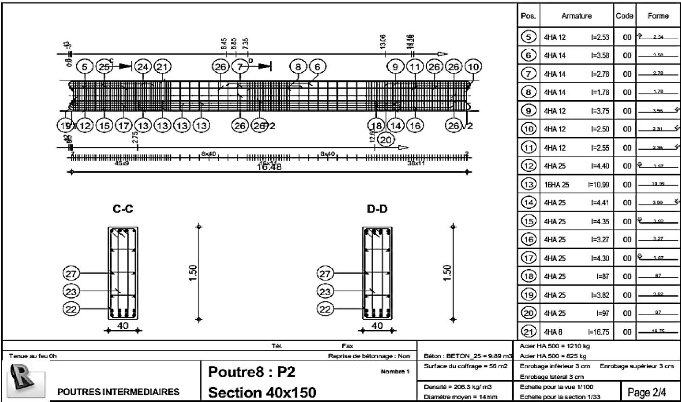
Figure 4.72 : Schéma de ferraillage poutres intermédiaires (3/4)

152 /176

Chapitre 4

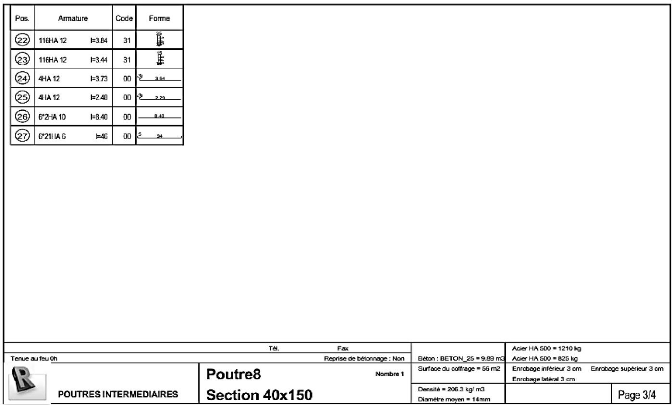
Figure 4.73 : Schéma de ferraillage poutres intermédiaires (4/4)

153 /176

Chapitre 4

4.14.4. Entretoises

4.14.4.1. Plans d'exécutions Pages suivantes

154 /176

Chapitre 4

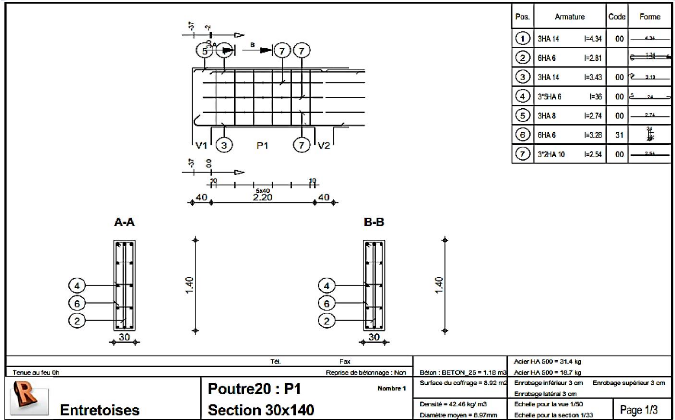
Figure 4.74 : Schéma de ferraillage entretoises (1/3)

155 /176

Chapitre 4

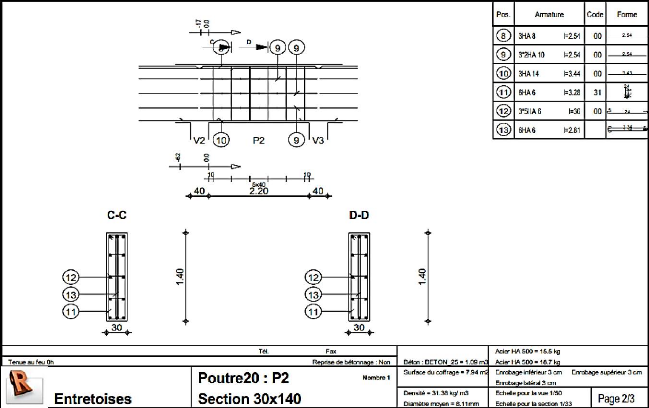
Figure 4.75 : Schéma de ferraillage entretoises (2/3)

156 /176

Chapitre 4

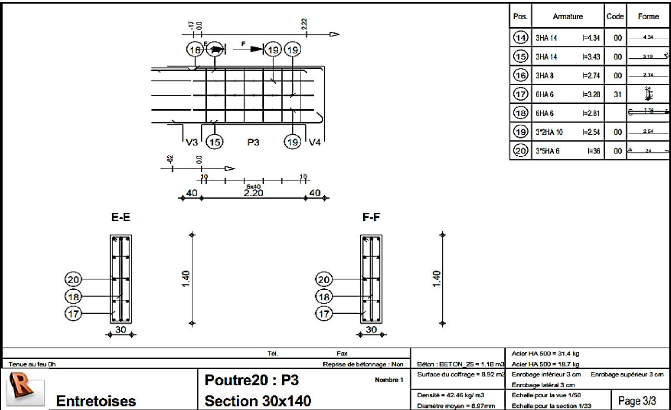
Figure 4.76 : Schéma de ferraillage entretoises (3/3)

157 /176

Conclusion et perspectives

Conclusion et perspectives

La modélisation par éléments finis est une discipline relativement récente qui mêle étroitement les mathématiques, la mécanique et l'analyse numérique.

La présente étude a permis, d'une part, de cerner les bases mathématiques fondamentales sur lesquelles se fonde la méthode des éléments finis et d'autre part de comprendre le processus de mise en oeuvre de la méthode sur ordinateur à travers l'utilisation du logiciel Autodesk Robot SAP 2012 pour les simulations réalisées sur notre tablier de pont ; ainsi, tous les objectifs assignés à cette étude ont été atteints.

Nous déduisons aussi, qu'un travail d'étude efficace, sur la structure d'un ouvrage ne peut être conduit que par un ingénieur expérimenté, possédant une solide culture technique dans les domaines de la modélisation des structures, des normes de conception et de calcul, des propriétés physiques et mécaniques des matériaux utilisables dans des conditions économiques acceptables et des méthodes d'exécutions.

Nous ambitionnons d'aborder ultérieurement d'autres problèmes plus complexes dépassant le simple cadre de l'analyse statique et qui ferait intervenir d'autres types d'analyses telles que : l'analyse harmonique, l'analyse temporelle (linéaire et non-linéaire) et l'analyse élasto-plastique des barres.

158 /176

Références bibliographiques

Références bibliographiques

[1] BATOZ, Jean-Louis., DHATT, Gouri. Modélisation des structures
par éléments finis. Vol 2, Paris : Hermès, 1995, 483 p.

[2] PARTON, V., PERLINE, P. Equations intégrales de la théorie de
l'élasticité. Editions MIR-Moscou, 1983V.

[3] TRENOGUINE. Analyse fonctionnelle. Editions MIR-Moscou,
1985.

[4] DHATT, Gouri., TOUZOT, Gilbert. Une présentation de la
méthode des éléments finis. Paris : Edition des Universités de Laval, 1986, 544 p. (ISBN 2.224-00700-0)

[5] CUILLIERE, Jean-Christophe. Introduction à la méthode des
éléments finis À Cours et exercices corrigés. Paris : Dunod, 2011. (ISBN 978-2-10-056438-5)

[6] OUDIN, Hervé. Introduction à la méthode des éléments finis.
Nantes : Ecole centrale de Nantes, Laboratoire Mécanique et Matériaux, division Mécanique des structures, 65 p.

[7] DOMISSY, E. Formulation et évaluation d'éléments finis volumiques modifiés pour l'analyse linéaire et non linéaire des coques. France : UT Compiègne, Thèse, 1997.

[8] WANG, Chu-Kia. Matrix methods of structural analysis.
International Textbook Co. 2^e edition, 1970. (ISBN 0700222677)

[9] HUEBNER, Kenneth H., THORHTON, Earl A., BYROM, Ted G.

159 /176

Références bibliographiques

The finite element method. Third edition, 1995. 627 p.

[10] CHASKALOVIC, J. Méthode des éléments finis pour les sciences de l'ingénieur. Lavoisier, 2004. (ISBN 2-7430-0708-7)

[11] CRAVEUR, Jean-Charles. Modélisation des éléments finis. 3ème édition. Paris : Dunod, 2008, 328 p. (ISBN 978-2-10-053983-3)

[12] GUIRANDE, Valdiodio Diouf. Modélisation par éléments finis appliquée au calcul des ponts courbes. Sénégal : Ecole Polytechnique de Thiès, Projet de fin d'études, 2002, 119 p.

[13] POUYE Ibrahima. Modélisation par éléments finis des poutres courbes. Sénégal : Ecole polytechnique de Thiès, Projet de fin de formation, 2008-2009, 57 p.

[14] KEITA Boubacar. Modélisation par éléments finis type P des ponts courbes. Sénégal : Projet de fin d'études, Ecole Polytechnique de Thiès, 2005.

[15] CIARLET, Patrick., LUNEVILLE, Eric. La méthode des éléments finis : de la théorie à la pratique : Tome 1. Concepts généraux, DUNOD.

[16] QUANG HUY, Nguyen. Modélisation du comportement des poutres mixtes acier-béton. Ed Paf.

[17] ERN, Alexandre., GUERMOND, Jean-Luc. Éléments Finis : Théorie, Applications, Mise en OEuvre (Mathématiques et Applications 36). (French Edition)

160 /176

Références bibliographiques

[18] NOUY, Anthony. Méthodes éléments finis stochastiques. Nantes : Institut de Recherche en Génie Civil et Mécanique, Université de Nantes, Ecole Centrale Nantes.

[19] CIARLET, Patrick., LUNEVILLE, Eric. La méthode des éléments finis : de la théorie à la pratique : Tome 1. Concepts généraux, DUNOD.

[20] P. Jean Frey., P-L. George, Maillages : Applications aux
éléments finis. HERMES, Science Publications, 1999.

[21] GRUAU, Cyril. Thèse : Génération de métriques pour l'adaptation anisotrope de maillages, applications à la mise en forme des matériaux ». Mécanique numérique. Paris : Ecole des mines supérieures des mines de paris, 2004.

[22] CALGARO, Jean-Armand. Projet et construction des ponts. Paris : Presses de l'école nationale des ponts et chaussées, 457 p. (ISBN 2-85978-327-X)

[23] MILLENIUM., R., Manuel d'utilisation ROBOT Béton Armé. 2004. 18: p. 220.

[24] Anonyme. http://fr.wikipedia.org/w/index.php?title=Méthode_des_él éments_finis&oldid=101572723, consulté le 23 juillet 2014.

[25] Anonyme. http://fr.wikibooks.org/w/index.php?title=Méthode_des_é léments_finis/Présentation_générale&oldid=434214, consulté le 23 juillet 2014.

[26] F. Hecht, O. Pironneau, J. Morice, A. Le Hyaric, and K. Ohtsuka.

161 /176

Références bibliographiques

Freefem++. http://www.freefem.org/ff++/index.htm, consulté le 20 Août 2014.

162 /176

Table des matières

Table des matières

Certification i

Dédicaces ii

Remerciements iii

Résumé vii

Abstract viii

Sommaire ix

Liste des figures xii

Liste des tableaux xviii

Liste des symboles et abréviations xix

Avant-propos xxi

Introduction générale 1

Chapitre 1 : Méthodes d'approximations en physiques 3

1.1. Modélisation et Simulation 4

1.1.1. Modélisation 4

1.1.2. Simulation 4

1.2. Classification des systèmes physiques 4

1.3. Processus d'analyse d'un problème physique 5

1.4. Méthodes d'approximations 7

1.5. Définition d'un problème de l'élasticité linéaire 8

1.5.1. Equations fondamentales de la théorie de l'élasticité 8

1.5.2. Les différentes méthodes de résolution 11

1.6. Méthode de GALERKIN pour la résolution des équations de Lamé 12

1.6.1. Modèle mathématique étudié 12

1.6.2. Transformation du modèle mathématique 12

163 /176

Table des matières

1.6.3. Résolution de l'équation de Poisson par l'approche variationnelle

de GALERKIN 15

1.6.3.1. Méthode de GALERKIN 15

1.6.3.2. Application de la méthode de GALERKIN 15

1.6.3.3. Détermination du tenseur des déformations 22

1.6.3.4. Détermination du tenseur des contraintes 22

1.6.3.5. Simulation du tenseur des déformations 24

Chapitre 2 : Méthode des Eléments finis 28

2.1. Processus d'analyse par la méthode des éléments finis 29

2.1.1. Analyse des problèmes physiques modélisés par une équation 29

2.1.2. Principe des éléments finis en calcul des structures 31

2.2. Discrétisation géométrique (maillage) 32

2.2.1. Définition du maillage 32

2.2.2. Caractérisation d'un maillage 33

2.2.3. But et rôle du maillage 35

2.2.4. Règles de partition du domaine en éléments 36

2.3. Approximation nodale 39

2.4. Approximation par éléments finis 41

2.4.1. Définitions 42

2.5. Définition de la géométrie des éléments 43

2.5.1. Eléments de référence 43

2.5.2. Formes d'éléments de référence classiques 47

2.6. Approximation sur un élément de référence 49

2.6.1. Expression de la fonction approchée ( ) 49

2.6.2. Propriétés de la fonction approchée ( ) 50

2.6.2.1. Propriété fondamentale de l'approximation nodale 50

2.7. Construction des fonctions d'interpolations et de transformations

géométriques 53

164 /176

Table des matières

2.7.1. Construction des fonctions N ( ) et Ni( ) 53

2.7.1.1. Méthode générale de construction 53

2.8. Matrice élémentaire 59

2.8.1. Matrice de rigidité élémentaire 59

2.8.2. Matrice des forces équivalentes de volume 59

2.8.3. Matrice des forces équivalentes de surface 59

2.9. Assemblage et conditions aux limites 60

2.9.1. Définition de l'assemblage 60

2.9.2. Les règles et étapes de l'assemblage 60

Chapitre 3 : Etude de quelques exemples d'éléments finis 62

3.1. Elément fini linéaire à deux noeuds 63

3.1.1. Définition 63

3.1.2. Matrice de rigidité élémentaire 63

3.1.2.1. Poutre en flexion simple 63

3.1.2.2. Poutre en flexion composée 64

3.2. Elément fini triangulaire plan à trois noeuds 64

3.2.1. Définition 64

3.2.2. Matrice de rigidité élémentaire 65

3.3. Elément fini tétraédrique à quatre noeuds 66

3.3.1. Définition 66

3.3.2. Construction de la matrice des fonctions d'interpolation 66

3.3.3. Calcul de la matrice jacobienne de la transformation géométrique 68

3.3.4. Construction de la matrice de rigidité élémentaire 74

3.3.5. Programme (matrice_k) de Calcul de la matrice de rigidité

élémentaire pour un élément tétraédrique à 4 noeuds 85

3.3.5.1. Structure du programme 85

3.3.5.2. Code source en FORTRAN 85

165 /176

Table des matières

3.3.5.3. Exemple de l'exécution du programme 88

Chapitre 4 : Modélisation et Simulation numérique d'un tablier de pont 90

4.1. Matériels employés pour la simulation 91

4.1.1. Ordinateur 91

4.1.2. Logiciel Autodesk AutoCAD 2012 91

4.1.3. Logiciel Autodesk Robot SAP 2012 91

4.1.3.1. Description générale du logiciel Autodesk Robot SAP 2012 91

4.2. Présentation générale de l'ouvrage 92

4.3. Caractéristiques du Tablier 94

4.3.1. Les poutres 95

4.3.2. Les entretoises 95

4.3.3. La dalle sous chaussée 95

4.4. Définition des charges et actions appliquées à la structure 99

4.4.1. Charges permanentes 99

4.4.2. Charges d'exploitations 100

4.4.2.1. Charges sur les trottoirs 100

4.4.2.2. Charges de chaussée 100

4.4.2.3. Système A 101

4.4.2.4. Système B 102

4.5. Définition du flux de travail 109

4.6. Définition de la structure 110

4.6.1. Création des lignes de construction dans Autocad 110

4.6.2. Importation des lignes de construction dans Robot SAP 110

4.6.3. Création de la géométrie 112

4.6.3.1. Définition des poutres et entretoises 112

4.6.3.2. Modélisation des dalles sous-chaussées 112

4.7. Construction du modèle éléments finis (EF) 116

4.8. Introduction des conditions de fixations (Appuis) 118

166 /176

Table des matières

4.9. Choix des normes et règlements à utiliser 119

4.10. Définitions des charges 120

4.10.1. Création des Cas de Charges 120

4.10.2. Définition des charges 121

4.10.2.1. Charges statiques 121

4.10.2.2. Charges roulantes 122

4.11. Lancement des calculs de la structure 128

4.12. Résultats de calcul 129

4.12.1. Panneaux 129

4.12.1.1. Cartographies des panneaux 129

4.12.1.2. Coupes sur panneaux 131

4.12.2. Barres 133

4.12.2.1. Analyse détaillés des barres 133

4.13. Définition des combinaisons d'actions 134

4.13.1. Création des composantes de cas charges 134

4.13.2. Génération des combinaisons d'actions 135

4.14. Exploitation des résultats 136

4.14.1. Dalle sous chaussée 136

4.14.1.1. Cartographies et plans d'exécution 136

4.14.2. Poutres de rives 143

4.14.2.1. Plans d'exécutions 143

4.14.3. Poutres intermédiaires 148

4.14.3.1. Plans d'exécutions 148

4.14.4. Entretoises 153

4.14.4.1. Plans d'exécutions 153

Conclusion et perspectives 157

Références bibliographiques 158

Table des matières 162

Annexes 167

Annexes

Annexes

Annexe : Note de calcul Dalle sous-chaussée Dalle : Dalle23 - panneau n° 23

A.1. Ferraillage :

Type : Tablier

Direction armatures principales : 90°

Classe armatures principales : HA 400; résistance caractéristique = 400,00 MPa

Diamètres des barres inférieures d1 = 1,6 (cm) d2 = 1,6 (cm)

supérieures d1 = 1,4 (cm) d2 = 1,4 (cm)

Enrobage inférieur c1 = 3,0 (cm)

supérieur c2 = 3,0 (cm)

A.2. Béton

Classe : BETON; résistance caractéristique = 25,00 MPa

Densité : 2549,29 (kG/m3)

A.3. Hypothèses

Calculs suivants : BAEL 91 mod. 99

Méthode de calcul de la section d'acier : Analytique

Fissuration

- lit supérieur : préjudiciable

- lit inférieur : préjudiciable

Flèche admissible : 3,0 (cm)

Vérification du poinçonnement : oui

Type de calcul : flexion

A.4. Géométrie de la dalle Epaisseur 0,20 (m)

Contour :

bord début fin longueur

x1

1	0,00	-9,30
2	16,81	-9,30
3	16,81	0,00
4	0,00	0,00

Appui :

n° Nom dimensions

5 linéaire 0,40 / 16,81

11 linéaire 0,40 / 16,81

17 linéaire 0,40 / 16,81

23 linéaire 0,40 / 16,81

33 linéaire 7,80 / 0,30

35 linéaire 7,80 / 0,30

coordonnées (m)	bord x y
8,40	-0,75 --
8,40	-3,35 --
8,40	-5,95 --
8,40	-8,55 --
0,16	-4,65 --
16,64	-4,65 --

167 /176

y1

	x2	y2 (m)
16,81	-9,30	16,81
16,81	0,00	9,30
0,00	0,00	16,81
0,00	-9,30	9,30

168 /176

Annexes

0 linéaire 0,50 / 0,50 0,00 0,00 --

A.5. Résultats des calculs :

A.5.1. Moments maximaux + ferraillage pour la flexion

Ax(+) Ax(-) Ay(+) Ay(-)

Ferraillage réel (cm2/m): 0,00	0,00	0,00	0,00
Ferraillage théorique modifié (cm2/m): 8,04	8,04	4,52	4,52
Ferraillage théorique primaire (cm2/m): 0,00	0,00	0,00	0,00

A.5.2. Moments maximaux + ferraillage pour la flexion

Ax(+) Ax(-) Ay(+) Ay(-)

Symboles :

section théorique/section réelle

Ax(+) (cm2/m)	8,04/0,00	8,04/0,00	8,04/0,00	8,04/0,00
Ax(-) (cm2/m)	8,04/0,00	8,04/0,00	8,04/0,00	8,04/0,00
Ay(+) (cm2/m)	4,52/0,00	4,52/0,00	4,52/0,00	4,52/0,00
Ay(-) (cm2/m)	4,52/0,00	4,52/0,00	4,52/0,00	4,52/0,00

A.5.3. Poinçonnement

Appui N°/ Point Position (m) Géométrie : (m)

x y a b

P1 0,00 0,00 force 0,50 0,50

Appui N°/ Point Chargements : (kN) Périmètre critique (m)

Q Qadm u Qadm / Q

P1 400,00 100,0 3,38 4,00 > 1

A.5.4. Flèche

|f(+)| = 0,1 (cm) <= fdop(+) = 3,0 (cm) |f(-)| = 1,9 (cm) <= fdop(-) = 3,0 (cm)

A.7 Chargements :

Cas Type Liste Valeur

1 poids propre 3A23 PZ Moins

6 (EF) linéaire sur les bords FZ= Aucun [kN]

6 (EF) linéaire 2p (3D) FZ1=-0,50[kN/m] FZ2= -

0,50[kN/m] N1X=0,03[m] N1Y=9,20[m] N1Z=0,0[m] N2X=16,84[m] N2Y=9,20[m]
N2Z=0,0[m]

6 (EF) linéaire 2p (3D) FZ1=-0,50[kN/m] FZ2= -

0,50[kN/m] N1X=16,86[m] N1Y=9,20[m] N1Z=0,0[m] N2X=33,13[m] N2Y=9,20[m]
N2Z=0,0[m]

169 /176

Annexes

6 (EF) linéaire 2p (3D) FZ1=-0,50[kN/m] FZ2=-

0,50[kN/m] N1X=33,16[m] N1Y=9,20[m] N1Z=0,0[m] N2X=49,97[m] N2Y=9,20[m]
N2Z=0,0[m]

6 (EF) linéaire 2p (3D) FZ1=-0,50[kN/m] FZ2=-

0,50[kN/m] N1X=0,03[m] N1Y=0,10[m] N1Z=0,0[m] N2X=16,84[m] N2Y=0,10[m]
N2Z=0,0[m]

6 (EF) linéaire 2p (3D) FZ1=-0,50[kN/m] FZ2=-

0,50[kN/m] N1X=16,86[m] N1Y=0,10[m] N1Z=0,0[m] N2X=33,13[m] N2Y=0,10[m]
N2Z=0,0[m]

6 (EF) linéaire 2p (3D) FZ1=-0,50[kN/m] FZ2=-

0,50[kN/m] N1X=33,16[m] N1Y=0,10[m] N1Z=0,0[m] N2X=49,97[m] N2Y=0,10[m]
N2Z=0,0[m]

5 P1(0.03, 5 P1(16.9, 5 P1(33.2,	(EF) surfacique 3p (contour) 21 8.15, 0) P2(0.03, 1.15, 0) P3(16.8, 1.15, 0) P4(16.8, 8.15, 0) (EF) surfacique 3p (contour) 22 8.15, 0) P2(16.9, 1.15, 0) P3(33.1, 1.15, 0) P4(33.1, 8.15, 0) (EF) surfacique 3p (contour) 23 8.15, 0) P2(33.2, 1.15, 0) P3(50, 1.15, 0) P4(50, 8.15, 0)			PZ1=-14,94[kN/m2] PZ1=-15,18[kN/m2] PZ1=-14,94[kN/m2]
3	(EF) surfacique 3p (contour)		22	PZ1=-1,50[kN/m2]
P1(16.8,	9.3, 0) P2(16.8, 8.15, 0) P3(0.03, 8.15, 0) P4(0.03,	9.3,	0)
3	(EF) surfacique 3p (contour)		22	PZ1=-1,50[kN/m2]
P1(0.03,	1.15, 0) P2(0.03, 0, 0) P3(16.8, 0, 0) P4(16.8, 1.15,	0)
3	(EF) surfacique 3p (contour)		23	PZ1=-1,50[kN/m2]
P1(16.9,	9.3, 0) P2(16.9, 8.15, 0) P3(33.1, 8.15, 0) P4(33.1,	9.3,	0)
3	(EF) surfacique 3p (contour)		23	PZ1=-1,50[kN/m2]
P1(16.9,	1.15, 0) P2(16.9, 0, 0) P3(33.1, 0, 0) P4(33.1, 1.15,	0)
3	(EF) surfacique 3p (contour)			PZ1=-1,50[kN/m2]
P1(33.2,	1.15, 0) P2(33.2, 0, 0) P3(50, 0, 0) P4(50, 1.15, 0)
3	(EF) surfacique 3p (contour)			PZ1=-1,50[kN/m2]
P1(33.2,	9.3, 0) P2(33.2, 8.15, 0) P3(50, 8.15, 0) P4(50, 9.3,	0)
7	(EF) surfacique 3p (contour)		21	PZ1=-7,75[kN/m2]
P1(0.03,	9.3, 0) P2(0.03, 8.15, 0) P3(16.8, 8.15, 0) P4(16.8,	9.3,	0)
7	(EF) surfacique 3p (contour)		22	PZ1=-7,75[kN/m2]
P1(16.9,	9.3, 0) P2(16.9, 8.15, 0) P3(33.1, 8.15, 0) P4(33.1,	9.3,	0)
7	(EF) surfacique 3p (contour)		23	PZ1=-7,75[kN/m2]
P1(33.2,	9.3, 0) P2(33.2, 8.15, 0) P3(50, 8.15, 0) P4(50, 9.3,	0)
7	(EF) surfacique 3p (contour)		23	PZ1=-7,75[kN/m2]
P1(33.2,	1.15, 0) P2(33.2, 0, 0) P3(50, 0, 0) P4(50, 1.15, 0)
7	(EF) surfacique 3p (contour)		22	PZ1=-7,75[kN/m2]
P1(16.9,	1.15, 0) P2(33.1, 1.15, 0) P3(33.1, 0, 0) P4(16.9, 0,	0)

170 /176

Annexes

7 (EF) surfacique 3p (contour) 21 PZ1=-7,75[kN/m2]

P1(0.03, 1.15, 0) P2(16.8, 1.15, 0) P3(16.8, 0, 0) P4(0.03, 0, 0)

8 (EF) surfacique 3p (contour) 21 PZ1=-2,72[kN/m2]

P1(0.03, 8.15, 0) P2(16.8, 8.15, 0) P3(16.8, 1.15, 0) P4(0.03, 1.15, 0)

8 (EF) surfacique 3p (contour) 22 PZ1=-2,72[kN/m2]

P1(16.9, 8.15, 0) P2(33.1, 8.15, 0) P3(33.1, 1.15, 0) P4(16.9, 1.15, 0)

8 (EF) surfacique 3p (contour) 23 PZ1=-2,72[kN/m2]

P1(33.2, 8.15, 0) P2(33.2, 1.15, 0) P3(50, 1.15, 0) P4(50, 8.15, 0)

27 (EF) force dans le point FZ=-84,84[kN]
X=13,03[m] Y=4,40[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=13,03[m] Y=4,90[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=13,03[m] Y=2,40[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=13,03[m] Y=6,90[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=14,53[m] Y=4,40[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=14,53[m] Y=4,90[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=14,53[m] Y=2,40[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=14,53[m] Y=6,90[m]

27 (EF) force dans le point FZ=-42,42[kN]
X=19,03[m] Y=4,40[m]

27 (EF) force dans le point FZ=-42,42[kN]
X=19,03[m] Y=4,90[m]

27 (EF) force dans le point FZ=-42,42[kN]
X=19,03[m] Y=2,40[m]

27 (EF) force dans le point FZ=-42,42[kN]
X=19,03[m] Y=6,90[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=23,53[m] Y=4,40[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=23,53[m] Y=4,90[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=23,53[m] Y=2,40[m]

27 (EF) force dans le point FZ=-84,84[kN]
X=23,53[m] Y=6,90[m]

171 /176

Annexes

27		(EF) force dans le point	FZ=-84,84[kN]
X=25,03[m]	Y=4,40[m]
27		(EF) force dans le point	FZ=-84,84[kN]
X=25,03[m]	Y=4,90[m]
27		(EF) force dans le point	FZ=-84,84[kN]
X=25,03[m]	Y=2,40[m]
27		(EF) force dans le point	FZ=-84,84[kN]
X=25,03[m]	Y=6,90[m]
27		(EF) force dans le point	FZ=-42,42[kN]
X=29,53[m]	Y=4,40[m]
27		(EF) force dans le point	FZ=-42,42[kN]
X=29,53[m]	Y=4,90[m]
27		(EF) force dans le point	FZ=-42,42[kN]
X=29,53[m]	Y=2,40[m]
27		(EF) force dans le point	FZ=-42,42[kN]
X=29,53[m]	Y=6,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=4,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=4,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=2,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=6,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=4,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=4,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=2,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=6,90[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=4,40[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=4,90[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=2,40[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=6,90[m]

172 /176

Annexes

28		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=4,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=4,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=2,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=6,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=4,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=4,90[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=2,40[m]
28		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=6,90[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=4,40[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=4,90[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=2,40[m]
28		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=6,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=4,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=4,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=2,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=30,03[m]	Y=6,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=4,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=4,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=2,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=31,53[m]	Y=6,90[m]

173 /176

Annexes

29		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=4,40[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=4,90[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=2,40[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=36,03[m]	Y=6,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=4,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=4,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=2,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=40,53[m]	Y=6,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=4,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=4,90[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=2,40[m]
29		(EF) force dans le point	FZ=-84,84[kN]
X=42,03[m]	Y=6,90[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=4,40[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=4,90[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=2,40[m]
29		(EF) force dans le point	FZ=-42,42[kN]
X=46,53[m]	Y=6,90[m]
32		(EF) force dans le point	FZ=-74,82[kN]
X=30,03[m]	Y=5,40[m]
32		(EF) force dans le point	FZ=-74,82[kN]
X=30,03[m]	Y=5,90[m]
32		(EF) force dans le point	FZ=-74,82[kN]
X=30,03[m]	Y=3,40[m]
32		(EF) force dans le point	FZ=-74,82[kN]
X=30,03[m]	Y=7,90[m]

174 /176

Annexes

32			(EF) force dans le point		FZ=-74,82[kN]
X=31,53[m]	Y=5,40[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=31,53[m]	Y=5,90[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=31,53[m]	Y=3,40[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=31,53[m]	Y=7,90[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=36,03[m]	Y=5,40[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=36,03[m]	Y=5,90[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=36,03[m]	Y=3,40[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=36,03[m]	Y=7,90[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=40,53[m]	Y=5,40[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=40,53[m]	Y=5,90[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=40,53[m]	Y=3,40[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=40,53[m]	Y=7,90[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=42,03[m]	Y=5,40[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=42,03[m]	Y=5,90[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=42,03[m]	Y=3,40[m]
32			(EF) force dans le point		FZ=-74,82[kN]
X=42,03[m]	Y=7,90[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=46,53[m]	Y=5,40[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=46,53[m]	Y=5,90[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=46,53[m]	Y=3,40[m]
32			(EF) force dans le point		FZ=-37,41[kN]
X=46,53[m]	Y=7,90[m]

175 /176

Annexes

33		(EF) force dans le point	FZ=-84,84[kN]
X=48,03[m]	Y=4,40[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=48,03[m]	Y=4,90[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=48,03[m]	Y=2,40[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=48,03[m]	Y=6,90[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=49,53[m]	Y=4,40[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=49,53[m]	Y=4,90[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=49,53[m]	Y=2,40[m]
33		(EF) force dans le point	FZ=-84,84[kN]
X=49,53[m]	Y=6,90[m]

Combinaison / Composante Définition

ELU/34 (1+6+7+8)*1.35+3*1.50+28*1.61

ELS/37 (1+3+6+7+8)*1.00+28*1.20

A.8 Résultats théoriques - disposition des armatures

Liste de solutions : Ferraillage par barres

Solution n° Armatures Poids total

Diamètre / Poids (kG)

1 Résultats pour la solution n° 1			-		8083,86
Zones de ferraillage
Ferraillage inférieur
Nom	coordonnées				Armatures adoptées	At Ar
	x1	y1	x2	y2	? [mm] / [cm]	[cm2/m] [cm2/m]
1/5- Ax Principal	16,81	-9,30	0,00	-0,00	16,0 / 10,0	19,42 < 20,11
1/9- Ay Perpendiculaire	16,81	-9,30	0,00	-0,00	16,0 / 10,0	18,47 < 20,11

176 /176

Annexes

Ferraillage supérieur
Nom	coordonnées			Armatures adoptées	At Ar
	x1 y1	x2	y2	? [mm] / [cm]	[cm2/m] [cm2/m]
1/1+ Ax Principal	16,81 -9,30	0,00	-0,00	14,0 / 12,0	8,04 <12,83
1/2+ Ay Perpendiculaire	16,81 -9,30	0,00	-0,00	14,0 / 12,0	4,52 <12,83

4. Quantitatif

· Volume de Béton = 31,26 (m3)

· Surface de Coffrage = 156,29 (m2)

· Périmètre de la dalle = 52,21 (m)

· Superficie des réservations = 0,00 (m2)

· Acier HA 400

· Poids total = 8180,71 (kG)

· Densité = 261,72 (kG/m3)

· Diamètre moyen = 15,1 (mm)

· Liste par diamètres :

Diamètre Longueur Poids

(m) (kG)

14 2637,93 3188,80

16 3161,69 4991,91