3- Techniques de traitement des données
L'analyse et le traitement des données sont
effectués manuellement. Après la collecte, nous avons
regroupé les données selon leur nature afin d'établir des
statistiques y afférentes. Les résultats issus du traitement sont
présentés sous forme de tableau et/ou de graphe, suivies de brefs
commentaires. En outre, certaines statistiques ont fait objet d'analyse
à partir des ratios.
4- Le modèle théorique d'analyse
Dans une première phase, nous allons montrer par le
modèle de régression linéaire simple que le montant annuel
des recettes budgétaires est assis sur les recettes fiscales.
Dans la deuxième phase, nous allons reprendre le
même modèle avec le montant trimestriel des recettes fiscales et
des recettes budgétaires puis tester par la suite le paramètre
associé à la variable explicative par le test de Fisher. Ce test
nous permettra de juger de manière globale si la régression
effectuée est significative.
a- Première phase
Il s'agit de la phase de la détermination d'un
coefficient de corrélation (r1) entre la variable à
expliquer yt (montant annuel des recettes budgétaires) et la
variable explicative xt (montant annuel des recettes fiscales).
Soit : r1 = 
n1 : nombre d'observations qui
représente ici le nombre d'années ;
 : la moyenne de la variable explicative ; : la moyenne de la variable explicative ;
 : la moyenne de la variable à expliquer ; : la moyenne de la variable à expliquer ;
- Si r1 est proche de 1, alors il existe une forte
corrélation entre les deux variables ;
- Si 0  alors il existe une mauvaise corrélation entre les deux
variables. alors il existe une mauvaise corrélation entre les deux
variables.
b- Deuxième phase
Cette phase, la plus longue, vient certifier la
première.
En effet, il s'agira de reprendre le modèle de
régression linéaire simple avec les montants trimestriels des
recettes fiscales et budgétaires. Deux étapes sont à
suivre :
1ère Etape : La
détermination du coefficient de corrélation (r2) entre
la variable à expliquer yt (montant trimestriel des recettes
budgétaires) et la variable explicative xt (montant
trimestriel des recettes fiscales).
Soit : r2 = 
n2 : nombre d'observations qui
représente ici le nombre de trimestres ;
 : la moyenne de la variable explicative ; : la moyenne de la variable explicative ;
 : la moyenne de la variable à expliquer ; : la moyenne de la variable à expliquer ;
2ème Etape :
Elle consiste à tester le paramètre associé
à la variable explicative en tenant compte du nombre d'observations
n2 = 32.
Soit le modèle suivant :
 = a = a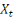 + b + + b +  avec: avec:
 : Variable à expliquer à la période t; : Variable à expliquer à la période t;
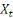 : Variable explicative à la période t; : Variable explicative à la période t;
 b : paramètres du modèle ; b : paramètres du modèle ;
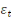 : erreur de spécification. : erreur de spécification.
Soit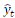 les valeurs ajustées de la variable à expliquer les valeurs ajustées de la variable à expliquer  = =  + + 
En effet, E =0 c'est-à-dire l'erreur moyenne est nulle ; avec
E( =0 c'est-à-dire l'erreur moyenne est nulle ; avec
E( l'espérance mathématique de termes d'erreur. l'espérance mathématique de termes d'erreur.
 - est l'estimateur sans biais de a et - est l'estimateur sans biais de a et
 - est l'estimateur sans biais de b. - est l'estimateur sans biais de b.
Ces estimateurs sont obtenus en
minimisant le carré de la distance entre chaque point nuage et de la
droite d'ajustement.
Détermination des estimateurs sans biais
 et et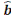
On sait que et = yt
-  - - 
Si  = 0 alors = 0 alors  = 0 donc = 0 donc  = 0 = 0
Appliquer la méthode des MCO revient à minimiser
la somme des carrés des écarts c'est-à-dire : min = 0 = 0
En considérant que les conditions du second ordre sont
vérifiées on a :
 
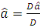 et et  avec avec
 = = - -  (Déterminant Général) (Déterminant Général)
 = = 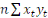 - -  (Déterminant associé à (Déterminant associé à ) )
 = = 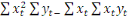 (Déterminant associé à (Déterminant associé à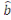 ) )
Finalement on a :
 = Y - = Y -  X X
Ainsi, le modèle de régression
devient :   + + 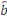
Test de Fisher
Ce test est fondamental et permettra de juger de
manière globale si la régression effectuée jusque
là est significative.
Le test d'hypothèse se fait par rapport au
paramètre  (la pente ou la propension marginale). Est-il significativement
différent de zéro (0) ? (la pente ou la propension marginale). Est-il significativement
différent de zéro (0) ?
On pose : et on pose le ratio de Fisher sous l'hypothèse et on pose le ratio de Fisher sous l'hypothèse 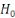 . Cette statistique de Fisher est déterminée à
partir d'un tableau d'analyse de la variance. Tout se résume en
réalité à l'analyse de la qualité de la
régression. Cette analyse qui se fait sur la base de la variance et
permet d'avoir des informations sur la proportion de variable explicative
(montant trimestriel des recettes fiscales) qui contribue à
l'explication de la variable à expliquer (montant trimestriel des
recettes budgétaires). L'analyse de la qualité de la
régression est rendue possible grâce au tableau suivant : . Cette statistique de Fisher est déterminée à
partir d'un tableau d'analyse de la variance. Tout se résume en
réalité à l'analyse de la qualité de la
régression. Cette analyse qui se fait sur la base de la variance et
permet d'avoir des informations sur la proportion de variable explicative
(montant trimestriel des recettes fiscales) qui contribue à
l'explication de la variable à expliquer (montant trimestriel des
recettes budgétaires). L'analyse de la qualité de la
régression est rendue possible grâce au tableau suivant :
|
Source de variation
|
Somme des carrés
|
ddl
|
Carrés moyens
|
|
X
|
|
1
|
|
|
Résidus
|
|
|
|
|
Total
|
|
|
-
|
La statistique de Fisher est :
 = =
Plus la variabilité expliquée va tendre vers la
variabilité totale, plus la régression effectuée serait
qualifiée de bonne. Ceci fait appel au coefficient R2
appelé coefficient de détermination.
Soit :  = = 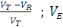 = =  et et 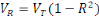
Donc :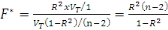 or or  avec 0 avec 0 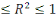
Ainsi :
Validité des
hypothèses :
Pour confirmer ou infirmer la 1ère
Hypothèse, nous allons nous baser sur les résultats de l'analyse
sur la connaissance des dispositions fiscales en vigueur par les contribuables
et son impact sur le recouvrement des recettes fiscales. Nous estimons au moins
que 50 % des contribuables ne devraient pas maîtriser les dispositions
fiscales en vigueur.
Quant à la 2ème Hypothèse, on
compare 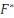 calculé à calculé à  valeur fictive, avec valeur fictive, avec  la probabilité de rejeter la probabilité de rejeter  bien qu'elle soit vraie à bien qu'elle soit vraie à degré de liberté. degré de liberté.
v Si   , alors on dira que la régression est globalement bonne et que
les recettes fiscales contribuent faiblement à l'amélioration des
recettes budgétaires. , alors on dira que la régression est globalement bonne et que
les recettes fiscales contribuent faiblement à l'amélioration des
recettes budgétaires.
v Si   , alors la régression effectuée n'est pas bonne. Par
conséquent, les recettes fiscales ne contribuent pas faiblement à
l'amélioration des recettes budgétaires. , alors la régression effectuée n'est pas bonne. Par
conséquent, les recettes fiscales ne contribuent pas faiblement à
l'amélioration des recettes budgétaires.
| 


