IV.7.9.2 Influence du coefficient de frottement
Nous allons maintenant, nous intéresser à
l'étude de sensibilité des résultats par rapport au
coefficient de frottement ; pour cette raison ; on faisant varier ce
paramètre de 0,2 jusqu'à 0,4 au niveau de la zone de contact
disque-plaquette à chaque simulation. La figure IV.97 montre
différentes configurations de la déformée totale du
modèle en phase finale du freinage. Nous pouvons clairement identifier
l'effet du frottement dans cette nouvelle simulation.
En l'absence de rotation, les résultats varient
très peu avec le coefficient de frottement. En revanche, avec la
rotation du disque, les déplacements, la surface réelle de
contact mais surtout les efforts tangentiels subissent une forte variation.

-a- : =0,25 -b- :
=0,30 -e- : =0,35
103
Fig.IV.97: Déformée
totale à la fin de freinage.
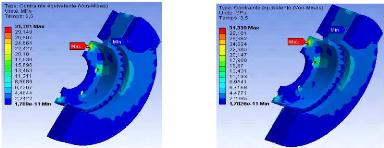
La figure IV.98 donne la répartition du champ des
contraintes de Von mises à l'instant t=3,5 [s] pour deux valeurs du
coefficient de friction. On constate que le coefficient de frottement n'exerce
aucune influence sur la contrainte.
Chapitre IV Résultats et Discussions
104
-a- : =0,25 -b- :
=0,35
Fig.IV.98: Contraintes de Von
Mises à l'instant t=3,5 [s].

-a- : =0,20 -b- :
=0,30 -e- : =0,40
Fig.IV.99: Champs de pression de
contact d'interface à l'instant t = 2 [s].
La figure IV.99 montre que l'augmentation de coefficient de
frottement s'accompagne par une diminution des pressions de contact des
plaquettes.
Dans les figures IV.100 et 101, on a présenté
respectivement l'évolution de la contrainte et la distance de glissement
en fonction du temps pour différentes valeurs du coefficient de
frottement. On note une augmentation de la contrainte de frottement avec
l'accroissement du coefficient de frottement. La distance de glissement est par
contre inversement proportionnelle au coefficient de frottement.
Chapitre IV Résultats et Discussions

Contrainte de frottement [MPa]
0 .4 5
0 .4 0
0 .3 5
0 .3 0
0 .2 5
0 .2 0
0 .1 5
0 .1 0
0 .0 5
0 .0 0
u = 0 ,2 u = 0 ,2 5 u = 0 ,3 u = 0 ,3 5 u = 0 ,4
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
105
Temps [ s]
Fig. IV.100:Evolution de
contrainte de frottement pour différentes valeurs de .
Distance de glissement [um]
4
3
2
1
0

u = 0 ,2 u = 0 ,2 5 u = 0 ,3 u = 0 ,3 5 u = 0 ,4
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [ s ]
Fig. IV.101: Evolution de distance
de glissement pour différentes valeurs de . IV.7.9.3
Influence de la vitesse de rotation du disque
La figure IV.102 représente le champ de pressions de
contact à l'instant t=45 [s] où les pressions maximales sont
atteintes pour ce type de freinage en fin de freinage. On constate que la
répartition de la pression est quasiment identique dans les trois cas et
elle augmente avec l'accroissement de la vitesse angulaire du disque [44], la
localisation de cette dernière se situe sur le bord inférieur de
la plaquette. On observe que cette augmentation peut créer l'usure des
plaquettes où elles peuvent laisser des dépôts sur le
disque, donnant lieu à ce qu'on appelle « le troisième corps
». On note que la pression maximale de contact dans la plaquette est
produite à l'entrée et descend vers la sortie de la région
de frottement.

Chapitre IV Résultats et Discussions
106
-a- : w =60 rad/s -b- :
w =90 rad/s -c- : w =120 rad/s
Fig. IV.102: Distributions de
pression de contact d'interface.
La figure IV.103 représente la distribution du champ de
contraintes de frottement à l'instant t=45[s], on note qu'à
mesure que la distribution de ce champ est symétrique par rapport
à la rainure et sa valeur augmente légèrement quand la
vitesse de rotation du disque augmente.
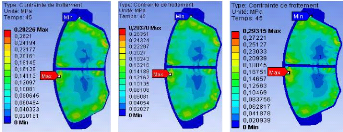
-a- : w =60 rad/s -b- :
w =90 rad/s -c - : w =120 rad/s
Fig. IV.103: Distributions de
contrainte de frottement d'interface.
La figure IV.104 donne la répartition du champ des
contraintes équivalentes de Von Mises à la fin de freinage
lorsqu'on varie la vitesse angulaire du disque. On observe que la
densité de distribution des contraintes augmente au niveau des
plaquettes intérieures avec l'accroissement de la vitesse du disque.

-a- : w =60 rad/s -b- :
w =90 rad/s -c - : w =120 rad/s
Fig. IV.104: Champs de contrainte
Von Mises de frottement d'interface.
Chapitre IV Résultats et Discussions
107
L'évolution des contraintes de Von Mises de surface du
disque pour différentes valeurs de vitesse de rotation est
présentée par la figure IV.105. On note que la contrainte du
disque reste quasi-identique et elle est inversement proportionnelle à
la vitesse de rotation.
3 5
3 0
2 5
2 0
1 5
1 0
5
Contrainte de Von Mises [MPa]
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
ro ta
|
tio n
|
6 0 ra
|
d /s
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
rotation
|
|
9 0 ra
|
d /s
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
rotation
|
|
1 2 0
|
ra d
|
/s
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
rotation
|
|
1 5 7
|
,8 9
|
ra d /s
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [s]
Fig. IV.105: Influence de la
vitesse de rotation sur la distribution du champ de contrainte de
Von Mises.
| 


