III.4.3.1.1 Flux de chaleur
Pendant le freinage, les énergies cinétiques et
potentielles pour un véhicule mobile sont converties en énergie
thermique par la chaleur de friction entre le disque de frein et les
plaquettes. La chaleur de friction est générée sur la
surface du disque et les plaquettes de frein. Dans le présent travail,
nous considérons la quantité de génération de la
chaleur par l'usure est très petit relativement à la chaleur
produite par frottement, ainsi l'effet de l'usure
Chapitre III Modélisation Thermomécanique du
Problème
51
matériel est négligé. Le flux de chaleur par
friction produit dans l'interface du disque et de la plaquette peut être
exprimé comme suit [33] :
Où est le coefficient de frottement, P est la
pression de contact, v la vitesse de glissement,
qui est définie par la vitesse angulaire du disque et le
rayon du disque de frein r.
Toute la chaleur produite sur le contact de frottement
l'interface q est la somme du
flux de la chaleur dans le disque et le flux de la chaleur dans
la plaquette .L'énergie
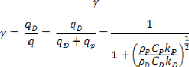
relative de freinage qui est absorbé par le disque de
frein est :
Dans l'équation ci-dessus, est la chaleur
spécifique de plaquette, est la
conductivité thermique de plaquette, est la densité
de plaquette, est la chaleur
spécifique de disque de frein, est la conductivité
thermique du disque de frein, et est la
densité de disque de frein. La génération
totale de la chaleur absorbée par le rotor est dedans limites des
propriétés matérielles du disque de frein et plaquette
[34, 35].
III.4.3.2 Problème élastique
La contrainte mécanique est liée à l'effort
par une équation constitutive suivante [31] :
Où [D] est la matrice de propriété
matérielle
La contrainte totale, somme des contraintes mécaniques et
thermiques, est donnée par :
Où les indices supérieurs mé et
th dénotent des contraintes mécaniques et thermiques,
respectivement,
L'équation (III.44) devient :
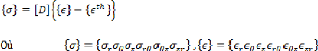
Pour un matériau isotrope, le changement de
température a comme conséquence une expansion de corps ou un
rétrécissement mais aucune déformation. En d'autres termes
le changement de température affecte les contraintes normales sans
contraintes de cisaillement. Le vecteur thermique de contrainte est
exprimé ainsi :
Chapitre III Modélisation Thermomécanique du
Problème
Dans lequel est le coefficient de la dilatation thermique et AT
indique l'écart de température. La contrainte totale est
exprimée en termes de déplacements nodaux comme :
Dans laquelle [B] est la matrice de cinématique
Substituons III.47 dans III.46, nous avons :
On applique la technique des moments résiduelle à
l'équation (III.48) on trouve les résultats dans
l'équation suivante :
Où la matrice de rigidité élémentaire
pour l'élasticité est donnée sous la forme :
et les vecteurs thermiques et mécaniques de force qui sont
dénotés comme suit :
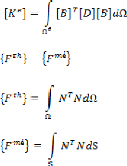
Le problème élastique est résolu en
employant l'équation constitutive .pendant la modélisation
numérique, une particulière attention est exigée pour
satisfaire la continuité des déplacements normaux sur la surface
de contact et les conditions de recouvrement [30].
Les conditions suivantes des déplacements et des
efforts sont imposées à chaque paire de noeuds sur
l'interface.
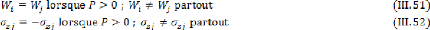
Les conditions suivantes de contrainte de la
température et de flux de chaleur sont imposées à chaque
paire de noeuds sur l'interface
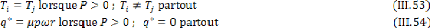
52
| 


