|
Année universitaire 2011/2012
UNIVERSITE DES SCIENCES ET DE LA TECHNOLOGIE
D'ORAN
Mohamed Boudiaf
FACULTE DE GENIE MECANIQUE
DEPARTEMENT de GENIE
MECANIQUE
THÈSE
Présentée par
BELHOCINE
ALI
Pour l'obtention du Diplôme de
DOCTORAT EN
SCIENCES
Spécialité : GENIE
MECANIQUE
Thème
ETUDE THERMOMECANIQUE DES DISQUES DE
FREIN
Application du Code de Calcul ANSYS v11.0
Membres du jury :
Président : YOUCEFI Abdelkader Pr
USTOMB
Directeur de thèse : BOUCHETARA
Mostefa Pr. USTOMB
Examinateurs :
BENGUEDIAB Mohamed Pr. U.de Sidi Belabbes
BENAMAR Ali Pr. ENSET Oran
TAMINE Tewfik MCA USTOMB
OULD CHIKH Bahri MCA U. de Mascara
Dédicace
Je dédie ce modeste travail à mes
chers
parents (ma mère et mon
père)
Mes chers frères et chères
soeurs
Atous mes amis
i
Remerciements
REMERCIEMENTS
J'aimerais remercier vivement mon directeur de recherche,
Monsieur BOUCHETARA Mostefa, Professeur à l'Université de
Sciences et de la Technologie -Mohamed Boudiaf d'Oran qui a assuré la
direction, le suivi et le bon déroulement de ce travail de recherche. Je
tiens à le remercier encore une fois pour son encouragement et ses
précieux conseils et critiques.
Je remercie messieurs les membres de jury d'avoir
accepté de juger ce travail.
Mes remerciements les plus chaleureux vont à tous mes
amis.
Enfin, je voudrais exprimer mes profonds remerciements
à mes parents et à toute ma famille par leur soutien permanent
durant les trois années que j'ai investi dans la recherche.
ii
Résumé
L'objet de cette thèse est de présenter une
étude du comportement thermomécanique des disques de frein
automobiles pour la prédiction de leur tenue en fatigue. La
stratégie de calcul numérique est repose sur le code de calcul
Ansys v.11. Ce dernier qui est basé sur la méthode des
éléments finis et qui possède des algorithmes de gestion
du contact avec frottement est utilisé pour simuler dans l'application
du freinage le comportement du mécanisme malgré son
complexité.
Dans un premier temps, est présentée une analyse
des phénomènes thermiques opérant dans un disque de frein
en service (flux de chaleur généré par frottement,
gradients thermiques élevés, élévation de
température). Cette modélisation est effectuée en tenant
compte l'influence d'un certains nombre de paramètre tel que le type de
freinage, le mode de refroidissement, les matériaux de conceptions.
Ensuite, une étude purement mécanique du contact
sec entre le disque et plaquettes est développée avec une bonne
prédiction devient un enjeu majeur pour les industriels tout en
modélisant le chargement et les conditions aux limites autours du
disque. Nous avons utilisé le même code de calcul pour visualiser
les déplacements, les déformations globales dans le disque, les
contraintes de cisaillement, les contraintes de Von Mises et les outils de
contact des plaquettes tout en effectuant une étude paramétrique
telle que ( le module de Young des plaquettes, le coefficient de frottement ,
le type de chargement , la vitesse de rotation du disque ,..) pour voir sa
sensibilité sur les résultats de calcul.
Ainsi, les analyses faites sur le comportement thermique et
mécanique que de ces prototypes montrent que ces types de solutions
technologiques représentent de réelles pistes
d'amélioration qui répond au besoin de l'ingénieur en
charge de la conception des disques de frein.
Mots clés :
Ansys 11.0- Contact sec-Méthode des
éléments finis (MEF)-disque de frein ventilé -Disque de
frein plein- Fonte Grise- Plaquettes -Etrier- Analyse transitoire-Coefficient
de transfert thermique-CFX-Etude paramétrique-Contraintes
thermiques-Flux de chaleur--Température-Maillage-Frottement-Chargement
mécanique-Conditions aux limites-Déformée
totale-Contraintes équivalentes de Von Mises-Contraintes de cisaillement
-Déformations-Distribution de pression de contact-Fissure-Usure.
iii
Abstract
The object of this thesis is to present a study of
thermomechanical behavior of the automobile discs brake for the prediction of
their resistance to fatigue. The numerical strategy of calculation is rests on
computer code Ansys v. 11. This last which is based on the finite element
method and which has management algorithms frictional contact is used to
simulate in the braking application, the behavior of mechanism in spite of its
complexity.
At first, presented an analysis of thermal phenomena operating
in a disk brake on (heat flux generated by friction, high thermal gradients,
temperature rise).This modeling is carried out by holding account the influence
of certain number parameters such as the type of braking, cooling mode,
materials designs.
Then, a study of purely mechanical dry contact between the
disc and pads is developed with a good prediction becomes a major stake for the
industrialists while modeling the loading and the boundary conditions around
the disc .We used the same computer code to visualize displacements, total
deformations in the disc, shear stresses, Von Mises stresses and, the tools of
contact pads while carrying out a parametric study such as (Young's modulus
pads, coefficient of friction, loading type, rotational speed of the disc..) to
see its sensitivity on the calculation results.
Thus, the analyzes done on the thermal and mechanical behavior
of these prototypes that show that these types of technological solutions
represent real areas for improvement that meets the need of the engineer in
charge of the design of the brake discs.
Keywords :
Ansys 11.0- Drying contact -Finite element method
(FEM)-Ventilated disc brake-Plain disc brake- Gray cast iron - Pads -Caliper
-Transient analysis -Heat transfer coefficient-CFX-Parametric study- Thermal
stress-Heat flux -Temperature-Mesh-Friction- Mechanical loading -Boundary
conditions -Total distortion-Stress equivalent of Von Mises-Shear
stress-Deformation- Contact pressure distribution -Crack-Wear.
iv
Table des matières
TABLE DES MATIERES
Dédicace
Remerciements i
Résumé ii
Abstract iii
Table des matières iv
Liste des figures et des tableaux viii
Nomenclature xiv
Introduction générale .1
Chapitre I : Etude Bibliographique 3
I.1. Introduction 3
I.2. Structure générale d'un système de
freinage 3
I.3. Frein travaillant par frottement 4
I.3.1. Frein à tambour 4
I.3.1.1 Principe de fonctionnement 4
I.3.2. Frein à disque . 6
I.3.2.1. Description d'un disque .7
I.4. Eléments d'un frein à disque 8
I.5. Types des étriers ..8
I.5.1. Frein à étrier coulissant ..9
I.5.2. Frein à étrier fixe 9
I.6. Les types de disque frein ..10
I.7. Autres types de disques et leurs caractéristiques .
11
I.7.1. Les disques rainurés ..11
I.7.2. Les disques percés 12
I.8. Comparaison entre disque et tambour . 12
I.8.1. Avantages ..12
I.8.2. Inconvénients 12
I.9. Les plaquettes . ..13
I.10. Problème du disque de frein . ..14
I.11. Les matériaux du disque de frein . 14
I.11.1. Le disque 15
I.11.2. Les garnitures .15
1.11.3. Les supports 16
I.12. Critère d'évaluation d'un système de
freinage 16
I.12.1. Efficacité 16
I.12.2. Confort 17
I.12.3. Endurance ..17
I.12.4 .Autres critères 19
I.13. Phénomènes thermiques dans le disque 19
v
Table des matières
I.14. Phénomènes mécaniques dans le disque
..19
I.15. Matériaux conventionnels : Aciers,Fontes, .20
I.15.1. Acier .20
I.15.2. Fontes 20
I.15.3 .Carbone .21
I.15.4 .Conditions d'utilisation 21
Chapitre II : Transfert de Chaleur 22
II.1. Introduction 22
II.2. Définitions .22
II.2.1. Champ de température 22
II.2.2 . Gradient de température 23
II.2.3 . Flux de chaleur 23
II.3. Modes de transfert de chaleur 23
II.3.1. Conduction 24
II.3.1.1 .Résistance thermique 24
II.3.1.2 ..Les régimes permanents .25
II.3.1.3. Les régimes transitoires 26
II.3.2. Convection .26
II.3.2.1. Le nombre de Reynolds 27
II.3.2.2. Le nombre de Nusselt ..27
II.3.2.3 .Le nombre de Prandtl ..27
II.3.3. Rayonnement .27
II.4 . Stockage d'énergie ..28
II.5 .Les équations gouvernantes du transfert de chaleur
transitoire par conduction .....28
II.6. Calcul de flux de chaleur entrant dans le disque . 29
II.6.1. Introduction 29
II.6.2. Les efforts agissant aux roues lors du freinage .30
II.6.3 .Puissance de freinage totale .31
II.6.4 . Expression du flux thermique initial 33
Chapitre III : Modélisation Thermomécanique
du Problème 34
III.1. Introduction 34
III.2. La modélisation thermique du problème
..34
III.2.1 .Equation de la chaleur 34
III.2.2. Forme différentielle 35
III.2.3 .Forme intégrale faible . 35
III.2.4. Forme discrétisé : éléments
finis 36
III.2.4.1. Représentation élémentaire (ou
locale) du champ de températures 36
III.2.4.2 .Représentation globale du champ de
températures 37
III.2.4.3. Partition des degrés de liberté 37
III.2.4.4 .Discrétisation de la forme intégrale
faible 38
III.2.4.4.1 .Conditions initiales et conditions aux limites 39
III.3. Etude mécanique du contact plaquette de
frein/disque 40
III.3.1 .Introduction 40
III.3.2 .Simulation du problème en ANSYS .....40
III.3.3. Création du modèle sur ANSYS Workbench
41
vi
Table des matières
III.3.4 .Choix du maillage 42
III.3.5 .Détermination de la pression de contact 43
III.3.6. Modélisation du modèle de contact de frein
à disque 45
III.3.6.1. Modélisation du chargement et des conditions
aux limites 45
III.3.6.1.1. Conditions aux limites appliquées au disque
45
III.3.6.1.2. Conditions aux limites et chargement
appliquées aux plaquettes 46
III.3.7 .Gestion du contact 47
III.3.8 .Lancement de calcul 47
III.4. Modélisation du couplage thermomécanique
47
III.4.1. Introduction 47
III.4.2. Méthode de la résolution 48
III.4.3. Formulation du problème .....48
III.4.3.1. Problème thermique 49
III.4.3.1.1.Flux de chaleur .....50
III.4.3.2. Problème élastique 51
III.4.4. Analyse en ANSYS Multiphysics .....52
Chapitre IV : Résultats et Discussions .
55
IV.1. Introduction 55
IV.2. Fiche technique du véhicule choisi 55
IV.3. Description du disque de frein ventilé et plein et
des plaquettes 56
IV.4. Détermination du coefficient d'échange par
convection (h) ....57
IV.4.1. Introduction 57
IV.4.2 . Modélisation en ANSYS CFX .58
IV.4.3 . Préparation de la géométrie et du
maillage 59
IV.4.3.1. Domaine fluide ..59
IV.4.3.1.1. Préparation du Maillage 59
IV.4.3.2. Disque de frein 60
IV.4.3.3 . Etude du maillage 61
IV.4.4. Flux d'air en mécanique des fluides 61
IV.4.5. Equations caractérisant un domaine fluide .62
IV.4.6. Modèle physique .62
IV.4.6.1. Etat stationnaire .62
IV.4.6.1.1 . Initialisation de la turbulence 62
IV.4.6.1.2. Définition du modèle matériau
63
IV.4.6.1.3. Définition du modèle Conditions Limites
63
IV.4.6.1.4 . Application des interfaces de domaine 63
IV.4.6.1.5. Méthode de résolution transient 63
IV.4.6.2 . Etat instationnaire ..64
IV.4.7 . Condition temporelles 64
IV.4.8. Lancement du calcul et affichage écran des
données 64
IV.5 . Analyse des résultats 64
IV.5.1 .Cas stationnaire .64
IV.5.2. Cas instationnaire 67
IV.6. Evolution transitoire de la température du disque
....70
IV.6.1. Introduction 70
IV.6.2 .Description paramétrique du freinage 71
IV.6.3 .Maillage ou discrétisation . 71
vii
Table des matières
IV.6.4. Chargement et conditions aux limites 72
IV.6.5 .Résultats et corrélation 73
IV.6.5.1. Disque plein 73
IV.6.5.2. Disque ventilé .73
IV.6.6 .Comparaison et interprétation 75
IV.6.6.1 . Comparaison entre les trois types de fonte 75
IV.6.6.2 . Comparaison entre disque plein et ventilé
76
IV.6.7 Influence du mode de freinage 80
IV.6.7.1 Freinage répété . 80
IV.7 .Résultats de calcul mécanique et discussions
83
IV.7.1. Maillage du modèle 83
IV.7.2. La déformée totale 83
IV.7.3. Contraintes équivalentes de Von Mises 85
IV.7.4 .Champs de contraintes sur les plaquettes de frein 87
IV.7.4.1 . Plaquette intérieure 87
IV.7.4.1.1. Répartition du champ des contraintes
équivalentes de Von Mises 87
IV.7.4.1.2 .Répartition du champ de pression de contact
88
IV.7.4.2 . Plaquette extérieure . 90
IV.7.4.2.1 . Répartition du champ des contraintes
équivalentes de Von Mises ....90
IV.7.4.2.2. Répartition du champ de pression de contact
91
IV.7.5 . Contraintes traction/compression et contraintes de
cisaillement dans le disque 92
IV.7.6 . Cas d'un disque sans rotation 93
IV.7.7.Cas d'un étrier à double piston 97
IV.7.8 Résultats des modèles maillés 98
IV.7.8.1. Influence de la finesse du maillage 100
IV.7.9 .Influence du matériau des plaquettes 101
IV.7.9.1. Influence du module de Young des plaquettes 101
IV.7.9.2. Influence du coefficient de frottement 103
IV.7.9.3. Influence de la vitesse de rotation du disque . 105
IV.7.9.4 .Cas d'un disque en Acier Inoxydable 107
IV.7.9.4.1. Comparaison entre le champ des déplacements
107
IV.7.9.4.2.Comparaison entre le champ des contraintes 108
IV.7.9.5 .Etude de l'influence de la rainure 109
IV.8 .Résultats du calcul thermoélastique 111
IV.8.1. Déformée totale et contraintes de Von Mises
du modèle . 111
IV.8.2. Champs des contraintes de Von Mises dans la plaquette
intérieure 113
IV.8.3. Pression de contact 115
IV.8.4. Déformation du disque 117
IV.8.5. L'effet parapluie 117
Conclusion générale et perspectives
..119
Bibliographie . .122
viii
Listes des figures et des tableaux
LISTE DES FIGURES ET DES TABLEAUX
Liste des
figures
Fig .I.1 : Schéma
d'implantation du système de freinage............
..............................3
Fig. I.2 : Frein à
tambour........................................................................................4
Fig. I.3 : Vue 3D d'un frein à
tambour.......................................................................4
Fig.I.4 : Différentes
technologies...............................................................................5
Fig. I.5 : Désignation des principaux
éléments............................................................6
Fig. I.6 : Exemples de freins à
disque.........................................................................7
Fig. I.7 : Le disque
plein..........................................................................................7
Fig. I.8 : Gorge
calorifique......................................................................................8
Fig. I.9 : Les éléments d'un frein
avant......................................................................8
Fig. I.10 : Types
d'étriers.........................................................................................9
Fig. I.11 : Le système
à étrier flottant .......................................
.................. 9
Fig. I.12 : Le système
à étrier à chape
flottante.............................................. 9
Fig. I.13 : Le système
à étrier
fixe................................................................ ...
9
Fig. I.14 : Exemple de disque
plein.........................................................................10
Fig. I.15 : Exemple de disque ventilé.
.....................................................................10
Fig. I.16 : Différentes géométries
d'ailettes. .............................................................11
Fig. I.17 : Disques ventilés : différentes
conceptions...................................................11
Fig. I.18 : Circulation de l'air
dans les canaux d'un disque ventilé.....................
......11
Fig. I.19 : Disque
rainuré........................................................................
..........12
Fig. I.20 : Disque
percé.....................................................................
...............12
Fig. I.21 : Plaquette de
frein...................................................................................13
Fig. I.22 : Disque
carbone-céramique......................................................................15
Fig. I.23 : Observation d'une fissure radiale de la bordure
extérieure du
disque jusqu'au
bol................................................................................18
Fig. I.24 : Faïençage sur les pistes de frottement
......................................................18 Fig. I.25 :
Fissure radiale sur les pistes de
frottement................................................18 Fig. I.26
: Fissure en pied d'ailette
.........................................................................18
Fig. I.27 : Rupture dans la gorge du
bol...................................................................18
Fig. I.28 : Section de disque fissuré
........................................................................18
Fig. I.29 : Fissure dans la
gorge............................................................
............18
Fig. I.30 : Usure des pistes
....................................................................................19
Fig. I.31 : Usure
non-uniforme................................................................................19
Fig. I.32 : Dépôts
de matière sur les pistes du disque..................
........................19
Fig. I.33 : Usure excessive des
plaquettes.............................................
...............19
Fig. I.34 : Mise en cône
d'un disque de frein......................................................
20
Fig.II.1 : Gradient de
température...........................................................
23
Fig.II.2 : Lois de Fourier
24
Fig.II.3 : Résistance
thermique............................................................... ...
24
Fig.II.4 : Définition
d'un élément de surface d'échange 26
Fig.II.5 : Elément en
rayonnement 28
Fig.II.6 : Définition des
forces agissant sur une automobile lors du freinage 30
Fig.II.7 : Efforts agissant sur
une voiture freinée, freinage d'arrêt sur plat 32
Fig.III.1 : Bilan thermique.
.........................................................................
34
Fig.III.2 : Organigramme principal
de résolution de système d'équations
parla M.E.F.
.................................................................................
39
ix
Listes des figures et des tableaux
Fig.III.3 : Création du
modèle sur ANSYS WB11.
......................................................42
Fig.III.4 : Elément
tétraèdre quadratique isoparamétrique à 10
noeuds......... .......42
Fig.III.5 : Maillage d'un disque
Noeuds 33256 éléments 17393 ............................
42
Fig.III.6 : Maillage d'une
plaquette rainurée Noeuds 2669 éléments 1266.........
...42
Fig.III.7 : Zone de contact
sélectionnée en ANSYS
1 Face : Aire ( Approx.)= 35797
mm2.......................................................43
Fig.III.8 : 2 Faces Aire = 5246,3
mm2 ................................................ 44
Fig.III.9 : 1 Corps : Volume= 85534
mm3...................................................... 44
Fig.III.10 : Modèle FE d'un
ensemble disque-plaquette.............................. 44
Fig.III.11 : Zone de
contact........................................................................
45
Fig.III.12: Conditions aux limites
et chargement imposées au disque-plaquette...... 46
Fig.III.13: Conditions aux limites
et chargement imposées au disque-plaquette
àdeux
pistons........................................................................
47
Fig.III.14 : Schéma du
couplage thermomécanique ..........................................
48
Fig.III.15 : Modèle de
disque de frein et plaquettes..........................................
49
Fig.III.16 : Modèle
élastique en élément fini de disque et plaquette
49
Fig.III.17 : Modèle
élément fini élastique pour l'analyse
thermoélastique transitoire
................................................... .... 49
Fig.III.18 : Modèle de
simulation d'un disque frein ventilé-plaquette.....................
53
Fig.III.19 : Organigramme de calcul
thermomécanique en ANSYS Multiphysics 54
Fig.III.20 : L'analyse du couplage
thermoélastique en ANSYS Multiphysics........... 54
Fig.IV.1 : Ensemble
disque-plaquette....................................................
...55
Fig.IV.2 : Application du
flux........................................................................
...55
Fig.IV.3 : Disque ventilé
(vue en contour).................................... ............
.......56
Fig.IV.4 : Caractéristiques
géométriques du disque
ventilé..........................................56
Fig.IV.5 : Disque
plein...................................................
........................ 57
Fig.IV.6 : Plaquettes de frein pour
Citroën...................................................... 57
Fig.IV.7 : Caractéristiques
géométriques des plaquettes de frein.........................
57
Fig.IV.8 : Modèle de CFD de
disque de frein.................................................... 58
Fig.IV.9 : Définition des
surfaces du domaine fluide........................... ... 59
Fig.IV.10 : Domaine fluide (Vue de
surface solide)............................................ 59
Fig.IV.11 : Domaine fluide (Vue de
surface transparente) 59
Fig.IV.12 : Maillage du domaine
fluide................................................... ....60
Fig.IV.13 : Définition des
surfaces du disque plein..................... ............... .......60
Fig.IV.14 : Définition des
surfaces du disque ventilé..................... .........
.......60
Fig.IV.15 : Disque
plein...........................................................................
.........61
Fig.IV.16 : Disque
ventilé........................................................................
....61
Fig.IV.17 : Maillage du disque
plein. Nombre d'éléments 272392..................... 61
Fig.IV.18 : Maillage du disque
ventilé. Nombre d'éléments 272392......... ...
61
Fig.IV.19: Répartition de coefficient de
transfert de chaleur sur
un disque plein dans le cas stationnaire (FG 15 )
65
Fig.IV.20 : Répartition de coefficient de
transfert de chaleur sur un disque
ventilé dans le cas stationnaire (FG 25
AL)..................................... 65
Fig.IV.21 :
Répartition de coefficient de transfert de chaleur sur un
disque
ventilé dans le cas stationnaire (FG
20)........................................ 65
Fig.IV.22 :
Répartition de coefficient de transfert de chaleur sur un
disque
ventilé dans le cas stationnaire (FG
15).................................... ....66
Fig.IV.23:
Variation du coefficient de transfert de chaleur (h) des
différentes
surfaces pour un disque plein dans le cas instationnaire (FG
15)... ...67
x
Listes des figures et des tableaux
Fig. IV.24 : Variation du
coefficient de transfert de chaleur (h) des différentes
surfaces pour un disque ventilé dans le cas
instationnaire (FG 25 AL).. 67
Fig.IV.25 : Variation du
coefficient de transfert de chaleur (h) des différentes
surfaces pour un disque ventilé dans le cas
instationnaire (FG 20)... ...68
Fig.IV.26: Variation du
coefficient de transfert de chaleur (h) des différentes
surfaces pour un disque ventilé dans le cas
instationnaire (FG 15)...... 68
Fig.IV.27: Variation du
coefficient de transfert de chaleur (h) sur la surface
( SPV2) et en fonction du temps pour un disque
ventilé (FG 15).....................69 Fig.IV.28:
Variation du coefficient de transfert de chaleur (h) sur la
surface
(SV1) et en fonction du temps pour un disque ventilé
(FG 15).................. ...70
Fig.IV.29 : Vitesse de freinage en
fonction du temps (freinage du type 0)... ... 71
Fig.IV.30 : Flux de chaleur en
fonction du temps.......................................... .......71
Fig.IV.31: Maillage d'un disque
plein................................................... ...72
Fig.IV.32 : Maillage d'un disque
à faces mappées.......................................
72
Fig.IV.33 : Maillage d'un disque
ventilé...................................................
...72
Fig.IV.34 : Variation de la
température du disque plein
en fonction du temps (FG
15)................................................... ...73
Fig.IV.35 : Répartition de
la température pour un disque plein
d'un matériau (FG
15)............................................................
....73
Fig.IV.36 : Variation de la température du
disque ventilé
en fonction du temps (FG
25AL)...................................................
73
Fig.IV.37 : Répartition de la température
pour un disque ventilé
d'un matériau (FG
25AL).........................................................
...73
Fig.IV.38 : Variation de la température du
disque ventilé en fonction
du temps (FG
20)............................................................... .......
74
Fig.IV.39 : Répartition de la température
pour un disque ventilé
d'un matériau (FG
20)............................................................
.........74
Fig.IV.40 : Variation de la température
du disque ventilé
en fonction du temps (FG
15).................................................................74
Fig.IV.41 : Répartition de la température pour
un disque ventilé
d'un matériau (FG
15).........................................................
74
Fig.IV.42: Variation de la température en
fonction de l'épaisseur pour
les trois type de fontes (FG 25 AL, FG 20 et FG
15).................. 75
Fig.IV.43 : Variation de la
température en fonction de rayon pour
les trois type de fontes (FG 25 AL, FG 20 et FG 15)
76
Fig.IV.44: Répartition de la température
pour un disque plein
d'un matériau FG
15...................................................................
77
Fig.IV.45: Répartition de flux de chaleur total
pour un disque plein
d'un matériau FG
15..................................................................
77
Fig.IV.46: Répartition de flux de chaleur
directionnel à l'instant t= 1.8839 [s]
selon les trois axes (X, Y, Z) pour un disque plein d'un
matériau FG 15......78 Fig.IV.47: Répartition de
la température pour un disque ventilé
d'un matériau FG
15..................................................................
78
Fig.IV.48: Répartition de flux de chaleur total
pour un disque ventilé
d'un matériau FG
15...............................................................
79
Fig.IV.49: Répartition de flux de chaleur
directionnel à l'instant t= 1.8506 [s]
selon les trois axes (X,Y,Z) pour un disque ventilé
d'un matériau FG 15... 79
Fig.IV.50 : Variation de
la température en fonction de l'épaisseur pour
les deux conceptions avec le même matériau
(FG15)........................ 79
xi
Listes des figures et des tableaux
Fig.IV.51 : Variation de la
température en fonction de rayon pour
les deux conceptions avec le même matériau
(FG15)... 80
Fig. IV.52 : Cycle avec quatorze
freinages successifs (mode 1).......... ...... ... 81
Fig. IV.53 : Cycle de freinage avec
phase de ralenti après chaque freinage (mode 2)... 81
Fig.
IV.54 : Carte thermique du disque en mode de freinage 1
à l'instant t=131,72
[s].............................................................
82
Fig. IV.55 : Carte thermique du disque en mode de
freinage 2
à l'instant t=130,45 [s].
................................................... ... ... 82
Fig.
IV.56 : Evolution de la température des deux modes de
freinage en fonction du temps
.......................................................
82
Fig.IV.57 : Maillage volumique du disque et
plaquettes
Noeuds 39208 ,Eléments
20351................................................... 83
Fig.IV.58 : La variation de la
déformée totale du modèle ( échelle
réelle)............... 84
Fig.IV.59 : La
déformée totale de la plaquette intérieure à la fin
de freinage t=45 [s] 84
Fig.IV.60 : La
déformée totale du disque à la fin de freinage t=45
[s].................. 84
Fig.IV.61 : La
déformée totale de la plaquette extérieure à la fin
de freinage t=45 [s] 84
Fig.IV.62: Variation de la
déformée totale en fonction du temps.....................
...85
Fig.IV.63 : Concentration des
contraintes de. Von Mises dans les trous de fixation .........85
Fig.IV.64 : Détail de
concentration des Contraintes..........................................
...85
Fig.IV.65 : Distribution des contraintes de Von Mises
dans le modèle
disque-plaquette...........................................................................
....86
Fig.IV.66 : Évolution des
contraintes de Von Mises selon le temps de simulation... 86
Fig.IV.67 : Distribution des
contraintes de Von Mises dans la plaquette intérieure... 87
Fig.IV.68 : Variation des
contraintes Von Mises en fonction de l'angle circulaire
dans la plaquette
intérieure.........................................................
88
Fig.IV.69 : Distribution des
pressions de contact dans la plaquette intérieure...... ......89
Fig.IV.70 : Variation des pressions
de contact en fonction de l'angle circulaire
dans la plaquette
intérieure......................................................
89
Fig.IV.71: Répartition de la
contrainte de frottement........................ ...... 90
Fig.IV.72: Répartition de la
distance de glissement.......................................... 90
Fig.IV.73 : Distribution des
contraintes de Von Mises dans la plaquette extérieure 91
Fig.IV.74: Distribution des
pressions de contact dans la plaquette extérieure 91
Fig.IV.75 : Variation des pressions
de contact en fonction de l'angle circulaire
dans la plaquette
extérieure...............................................................
92
Fig.IV.76: Répartition de
contrainte de frottement........................ ... 92
Fig.IV.77: Répartition de la
distance de glissement.......................................... 92
Fig.IV.78: Contraintes normales et
contraintes de cisaillement à t=45 [s] 93
Fig.IV.79: Contraintes de Von
Mises............................................. ....... 93
Fig.IV.80: Déformée
totale
...............................................................................
93
Fig.IV.81: Déplacements sur le rayon
extérieur moyen et sur la couronne
extérieure du disque en fonction de l'angle 94
Fig.IV.82: Variation de l'effort de
réaction sur le disque en fonction du temps... ... 94
Fig.IV.83: Forces de
réaction sur la piste intérieure du disque .....................
95
Fig.IV.84: Contraintes normales et
contraintes de cisaillement à t=45 [s].......... 95
Fig.IV.85: Effet de rotation du
disque sur les déplacements.............................. 97
Fig.IV.86: Effet de rotation du
disque sur le champ des contraintes 97
Fig.IV.87: Contraintes de Von
Mises...................................................... 98
Fig.IV.88 : Détail de
concentration des contraintes..............................
.........98
Fig.IV.89: Déformées
totales......................................................................
...98
xii
Listes des figures et des tableaux
Fig.IV.90 : Maillage volumique du
disque Noeuds 39208 , Eléments 20351...... 99
Fig.IV.91 : Maillage à
éléments quadrilatères Noeuds 90680 ,Eléments
31879... 99
Fig.IV.92 :Maillage à
éléments hexaédriques Noeuds 103098 , Eléments
36901...... 99
Fig.IV.93: Maillage fin. Noeuds
160918 ,Eléments 88625................................. 99
Fig.IV.94 : Maillage plus
raffiné, Noeuds 185901 , Eléments 113367... ......
.........100
Fig.IV.95: Comportement de la
plaquette intérieure........................... ............ 101
Fig.IV.96: Résultats des
contraintes en fonction du module de Young......................
102
Fig.IV.97: Déformée totale à la
fin de
freinage.........................................................103
Fig.IV.98: Contraintes de Von Mises
à l'instant t= 3,5 [s]............... ............ 104
Fig.IV.99: Champs de pression de
contact d'interface à l'instant t = 2[s] 104
Fig.IV.100:Evolution de contrainte
de frottement pour différentes valeurs de 105
Fig.IV.101: Evolution de distance
de glissement pour différentes valeurs de 105
Fig.IV.102: Distributions de
pression de contact d'interface..................... ... 106
Fig.IV.103: Distributions de
contrainte de frottement d'interface 106
Fig.IV.104: Champs de contrainte
Von Mises de frottement d'interface 106
Fig.IV.105: Influence de la vitesse
de rotation sur la distribution du champ
de contrainte de Von
Mises................................................ 107
Fig.IV.106: Déformée
totale à la fin de simulation 108
Fig.IV.107: Contraintes Von Mises
à la fin de simulation 108
Fig.IV.108: Variation de la
déformée totale en fonction du temps
pour les deux disques ....................................
109
Fig.IV.109: Variation de la contrainte de Von Mises en
fonction du temps pour les deux
disques..........................................................................109
Fig.IV.110: Plaquette sans rainure
110
Fig.IV.111: Plaquette avec rainure
110
Fig.IV.112: Influence de la rainure
sur la variation du champ
de contrainte de Von Mises 110
Fig.IV.113: Influence de la rainure
sur la variation de la déformée totale 110
Fig.IV.114: Distribution de la
température du disque
et plaquettes à l'instant t=1,7271
[s]....................................... 111
Fig. IV.115:
Déplacements du rayon moyen et la couronne
extérieure
du disque en fonction de la position angulaire à
l'instant t=3.5 [s] 112
Fig.IV.116: variation des
déplacements de piste en fonction du rayon
pour différentes positions angulaires à
l'instant t=3.5 [s]............ 112
Fig. IV.117:
Comparaison pour les résultats des déplacements
entre les deux modèles
traités..................................... 113
Fig.
IV.118: Comparaison pour les résultats des contraintes Von
Mises
entre les deux modèles traités
113
Fig.IV.119 : Distribution des contraintes de Von Mises
dans la plaquette intérieure.
simple piston (à gauche et au centre) , à
double piston ( à droite) 115
Fig. IV.120:
Distribution de pression de contact le long des bords
inférieur , supérieur et moyen de la plaquette
à l'instant t= 1.7271 [s] 116
Fig.IV.121 : Variation
de contrainte de Von Mises en fonction du temps
dans le couplage thermomécanique
116
Fig.IV.122 : Contrainte de frottement et distance de
glissement
de la plaquette intérieure à l'instant t= 3.5
[s]......... ......... 117
Fig. IV.123: Déformée
totale maximale en couplage thermomécanique... ......... 117
Fig. IV.124: L'effet parapluie d'un
disque 118
xiii
Listes des figures et des tableaux
Liste des tableaux
Tableau. I.1 : Composition et
résistance des 03 sortes de fontes pour la conception des
disques..................................................................20
Tableau .III.1 : Tableau des caractéristiques
mécaniques des deux pièces......................41
Tableau .III.2 : Caractéristiques de conception des
deux pièces....................................41
Tableau.III.3 : Données de
véhicule................................................................
...43
Tableau III.4 : Résultats d'un maillage d'un
type d'éléments tétraèdre
quadratique à 10
noeuds............................................................
44
Tableau III.5 : Résumé des types
d'éléments.............................................................45
Tableau III.6 : Propriétés
thermo-élastiques utilisées dans la
simulation........................53
Tableau. IV.1 : Fiche technique du
véhicule Citroën de type CX GTi Turbo 2..
55
Tableau. IV.2 : Nombre
d'éléments des différents maillage........................
.... 61
Tableau IV.3 : Valeur du coefficient de transfert
de chaleur de différentes
surfaces dans le cas stationnaire pour un disque plein (FG 15
) 65
Tableau IV.4 : Valeur du coefficient de transfert de
chaleur de Différentes
surfaces dans le cas stationnaire pour un disque
ventilé
(FG 25 AL, FG 20 et
FG15)................................................... 66
Tableau. IV.5 : Statistiques de
maillage calculées par le Multiphysics [Ansys WB] 72
Tableau. IV.6 : Résultats de
la simulation numérique 96
Tableau. IV.7 : Résultats
des différents cas de maillage 99
Tableau. IV.8 : Contraintes de Von
Mises et déformées totales....................................100
Tableau. IV.9 : Comparaison entre les résultats du
maillage
fin et maillage raffiné ...100
Tableau.
IV.10 : Propriétés mécaniques des plaquettes de
frein..................................101
Tableau. IV.11 : Influence du
matériau de plaquette de frein (valeurs extrêmes) ...102
Tableau. IV.12 : Tableau des
caractéristiques mécaniques des deux pièces..............
107
xiv
Nomenclature
NOMENCLATURE
a : Décélération
(m2/s)
Ad : Surface de disque balayée par une plaquette
(mm2)
Ac : Surface de plaquette en contact avec le disque
(mm2)
c : Chaleur massique ( J
kg-1°C-1)
C : Carbone
: Capacité thermique massique (J/(kgK))
: Coefficient de forme
[C] : Matrice de capacité thermique (J/K)
d : Diamètre, ou distance (m)
E : Le module d 'Young (GPa)
fh : Facteur de
répartition de l'effort de freinage , essieu arrière
fv : Facteur de répartition de l'effort de freinage , essieu
avant : Coefficient de résistance au roulement
F : Force (N)
: Vecteur des flux nodaux (W)
FD : Force motrice (N)
FFH : Effort de freinage rapporté à l'essieu
arrière (N)
FFV : Effort de freinage rapporté à l'essieu avant
(N)
FG : Effort de pesanteur (N)
FP : Effort exercé par le conducteur (N)
FR : Force de frottement (N)
FRA : Force de résistance de l'air (N)
FRP : Force de résistance due à la pente (N)
FRRH : Force de résistance au roulement de la roue
arrière (N)
FRRV : Force de résistance au roulement de la roue avant
(N)
FQH : Charge statique rapportée à l'essieu
arrière (N)
FQV : Charge statique rapportée à l'essieu avant
(N)
FS : Effort de freinage (N)
g : Accélération de la pesanteur
(ms-2)
h : Coefficient d'échange (
Wm-2K-1)
k : Conductivité thermique du matériau (
Wm-1K-1)
[K] :Matrice de conductivité thermique (W/K)
L : Distance entre l'essieu avant et l'essieu arrière
LH : Distance entre l'axe du l'essieu avant et le centre de
gravité du véhicule LV : Distance entre l'axe du l'essieu
arrière et le centre de gravité du véhicule
m : Masse du véhicule ( kg)
Mn : Manganèse
Mo : Molybdène

n : Nombre de noeuds de l'élément. :
Vecteur unitaire de la normale
: Fonctions d'interpolation ou fonctions de forme.
Ni : Nickel
P : Pression hydraulique (MPa)
P : Phosphore
xv
Nomenclature
PF : Puissance de freinage (W)
PFVI : Puissance de freinage rapporté au disque de frein
(W)
PR :Puissance de freinage due au roulement (W)
Q : Puissance thermique (W)
QV : Flux de chaleur (W)
Q'V : Flux de chaleur par unité de surface
(W/m2)
R : Résistance thermique ( W-1 K)
R : Rayon (m)
Rm :Résistance à la rupture
(N/mm2)
S : Surface (mm2)
: L'indice de saturation du carbone
Sf :Surface frontale du véhicule (mm2)
Si :
Silicium
t : Temps (s)
T : Champ de température (°C)
: Vecteur des températures nodales (K)
Ti :Titane
|
T0 : Température initiale (°
: Température de la surface (°
|
C) C)
|
(°
C)
:Température du milieu environnant la surface
um : Vitesse moyenne (m/s)
v : Vitesse (m/s)
v0 : Vitesse initiale (m/s)
: Volume (m3)
x : Coordonnées cartésiennes
y : Coordonnées cartésiennes
z : Coordonnées cartésiennes, ou
cylindriques
Caractères grecs
: Symbole de Kronecker
: Facteur d'émission de la surface
: Facteur d'exploitation
: Conductivité thermique (
Wm-1K-1)
è : Coordonnées angulaires, ou angle :
Coefficient de frottement
u : Viscosité dynamique du fluide (kg
m-1s-1)
: Coefficient de Poisson
: Viscosité cinématique du fluide (m2
s-1)
: Densité (kg/m3)
:Masse volumique de l'air (kgm-3)
: Constante de Stephan = 5,67×10-8
(Wm-2K-4)
óxx : Contrainte normale dans la direction x
óxy : Contrainte de cisaillement dans le plan xy
xvi
Nomenclature
óxz : Contrainte de cisaillement dans le plan
xz óyy : Contrainte normale dans la direction y óyz
: Contrainte de cisaillement dans le plan yz ózz :
Contrainte normale dans la direction z
: Flux de chaleur ( W)
: Densité de flux de chaleur ( W/m2)
w : Vitesse de rotation (rad/s)
Opérateurs mathématiques
: Gradient
div : Divergence d'un vecteur

Nombres sans dimensions
Nu : Le nombre de Nusselt Pr : Le nombre de
Prandtl Re : Le nombre de Reynolds
Exposants*
(e) : élastique (m) : mécanique (th) : thermique
Abréviation
ABS : Système antiblocage
FG : Fonte grise
ECE : Commission économique européenne
1
Introduction générale
INTRODUCTION GENERALE
Lorsque deux corps entrent en contact avec frottement, il y a
dissipation d'énergie et donc de la chaleur produite au niveau du
contact, ce qui entraîne une dilatation pouvant accroître le champ
de pression, ... . Ce phénomène s'accroît si les
contraintes tangentielles ainsi que les vitesses relatives de glissement entre
les deux corps sont importantes .Ces effets thermomécaniques se
traduisent la plus part du temps par la formation de zones localisées
à très forts gradients thermiques, les points chauds. Il y a
apparition de déformations thermiques et des concentrations de
contraintes pouvant générer des fissures, des vibrations, etc.
Avec le développement des nouvelles technologies dans
l'industrie automobile, les véhicules sont devenus de plus en plus
performants. Les systèmes de freinage doivent suivre ce même
rythme. Le frein, comme organe majeur de sécurité, succite
constamment un grand intérêt pour les ingénieurs. Outre la
concurrence dans le domaine de l'automobile de plus en plus rude s'ajoute les
soucis d'efficacité, de fiabilité, de confort, du coût et
du délai de fabrication. L'objectif de l'ingénieur est donc de
trouver le meilleur compromis entre ces exigences de sécurité et
de ces contraintes technico-économiques. Pour pouvoir réaliser
une conception optimale, il convient de mettre en oeuvre des techniques
numériques complétant les études expérimentales.
Dans l'industrie aéronautique et automobile, de
nombreuses pièces sont soumises simultanément à des
sollicitations thermiques et mécaniques. Les sollicitations
thermomécaniques peuvent provoquer des déformations et
mêmes des endommagements .Par exemple, le frottement dans un
système de freinage génère de la chaleur dans le disque
laquelle peut engendrer des déformations et des vibrations.
Dans cette étude, on s'intéressera à la
modélisation numérique du comportement thermomécanique des
disques de frein des véhicules en appliquant le code de calcul ANSYS
11.0. Ainsi, on établit le champ de température du disque et des
plaquettes de frein en fonction des conditions aux limites thermiques et
mécaniques.
Le disque de frein automobile peut subir des
dégradations dont l'origine réside dans les sollicitations
couplées mécaniques (pression des garnitures sur le disque et
serrage du disque sur le moyeu) et thermiques (échauffement par
frottement). En raison de la complexité du système, les
modélisations numériques ne sont envisageables que si on se base
sur des hypothèses simplificatrices. L'hypothèse
d'axisymétrie est communément adoptée ce qui
2
Introduction générale
implique que la rotation du disque et les
phénomènes tridimensionnels seront négligés. Ces
simplifications ne permettent qu'une prédiction quantitative
approximative de la réponse thermomécanique du disque.
L'objectif de cette thèse est de présenter une
modélisation du comportement thermomécanique des disques de frein
pour la prédiction de leur tenue en fatigue.
Cette étude est réalisée à l'aide
du logiciel ANSYS v 11.0 qui est basé sur la méthode des
éléments finies. Ce code de calcul est développé
principalement pour la résolution des problèmes physiques
complexes. Le calcul est divisé en trois étapes, la
première comporte un calcul thermique qui détermine
l'évolution du champ de la température dans le disque, la seconde
un calcul statique, qui détermine les champs de contraintes et les
déformations globales ainsi les pressions de contact du modèle et
la troisième présente les résultats du couplage
thermomécanique.
La présentation de ce travail s'articule autour de quatre
chapitres.
Le chapitre I présente une
étude bibliographique fondée sur les disques de frein, la
composition et les matériaux utilisés, ainsi que les
différents phénomènes thermiques et mécaniques
rencontrés.
Le chapitre II est consacré à
la formulation analytique de l'équation de chaleur tout en
décrivant les modes de transfert thermique y intervenant. Une
méthode de calcul est illustrée dans ce sens pour évaluer
la quantité du flux thermique de friction entrant dans le disque.
Le chapitre III porte sur la
modélisation numérique du problème thermomécanique
du disque de frein et la mise en ouvre du logiciel ANSYS v 11.0 utilisé
dans cette modélisation.
Le chapitre IV est consacré à
la présentation et à l'interprétation des
différents résultats thermomécaniques obtenus à
l'aide du code de calcul.
Enfin, ce travail se termine par une conclusion
générale présentant une synthèse des
résultats de simulation obtenus et par des perspectives dans le domaine
du contact sec glissant.
Chapitre I Etude Bibliographique
3
I.1 INTRODUCTION
Grâce aux continuels progrès technologiques dans
l'industrie du transport, les véhicules sont devenus plus puissants et
plus rapides. De ce fait, les systèmes de freinage doivent aussi suivre
cette progression pour assurer un fonctionnement adéquat avec les
dernières améliorations. Le frein, organe de
sécurité, reste ainsi un sujet d'étude très actuel
pour les ingénieurs. L'apparition de nouveaux matériaux (alliages
divers, céramique, etc.) et de nouveaux procédés de
fabrication ou de traitement de surface (grenaillage, trempe par induction,
etc. ) génère de nouveaux types de frein et donc la
nécessité de nouvelles études. De plus, avec la
concurrence industrielle toujours croissante, les problématiques
changent : en plus du souci d'efficacité, de fiabilité et de
confort, s'ajoute ceux du moindre coût et du délai de fabrication.
L'objectif pour l'ingénieur est de trouver le meilleur compromis entre
ces exigences. Il s'agit alors remplacer, du moins, compléter les essais
expérimentaux par des analyses numériques afin de tester plus de
possibilités pour mieux s'approcher du meilleur compromis,
réduire les coûts en fabriquant moins de prototypes et minimiser
les durées d'étude en limitant le nombre d'essais.
I.2 STRUCTURE GENERALE D'UN SYSTEME DE FREINAGE
La structure ci-dessous (Fig .I.1) représente une
structure de base que l'on retrouve dans tous les véhicules de tourisme
dit bas de gamme. On pourra cependant trouver des variantes telles que la
disposition de freins à disque sur l'essieu arrière, ou bien la
mise en place de système tels que l'ABS ou bien ESP [1].

Fig .I.1 : Schéma
d'implantation du système de freinage.
Dans un système de freinage, on distingue deux parties
:
· Partie commande
· Partie opérative.
Chapitre I Etude Bibliographique
4
I.3 FREINS TRAVAILLANT PAR FROTTEMENT I.3.1 Frein
à tambour
Il se compose d'un tambour en fonte solidaire de la roue, de
mâchoires solidaires du châssis, garnies d'un matériau
à haute résistance au frottement et à
l'échauffement et d'un cylindre qui presse les mâchoires contre le
tambour (Fig.I.2). Les mâchoires sont en acier recouvert d'une garniture
d'un matériau composite ayant un bon coefficient de frottement (0,35
à 0,40) avec le matériau du tambour et s'usant plus vite. L'usure
peut être rattrapée par un mécanisme de réglage
accessible de l'extérieur (non automatique) [2].

Fig. I.2 : Frein à
tambour.
I.3.1.1 Principe de fonctionnement
Le tambour est solidaire du moyeu de roue et tourne avec lui.
Les segments et les composants qui génèrent la force de freinage
sont généralement montés sur un plateau circulaire en
tôle emboutie nommé flasque qui ferme le tambour et est
fixé rigidement au porte-moyeu. Des ressorts hélicoïdaux
travaillant en traction connectent les deux segments et les empêchent de
frotter contre la couronne du tambour lorsque les freins ne sont pas
actionnés (Fig.I.3).
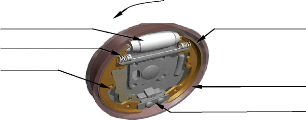
Piston hydraulique
Ressorts de rappel
Segment primaire
Tambour
Sens de rotation Segment secondaire
Axes
Fig. I.3 : Vue 3D d'un frein
à tambour.
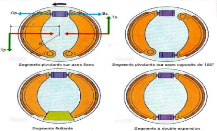
Chapitre I Etude Bibliographique
5
Fig. I.4 : Différentes
technologies.
Différentes façons d'articuler et de commander
les deux segments sont possibles. suivant la configuration adoptée,
l'effet d'auto-serrage est plus ou moins fort, obtenu dans un seul sens de
rotation ou dans les deux, sur une seule des mâchoires ou sur les deux
(Fig. I.4). Les deux segments sont actionnés par un piston qui
génère une force de serrage
. Une force tangentielle due à la rotation du tambour qui
agit sur le segment
amont (primaire) engendre un moment sur son axe de pivotement
qui est dans le même sens
que la force de serrage : c'est l'auto-serrage. Sur le segment
aval (ou secondaire), la force
tangentielle s'oppose à l'action de la force de serrage :
c'est l'auto-desserrage. Le
serrage de la mâchoire secondaire est donc plus faible
que le serrage de la mâchoire primaire ce qui entraîne une usure
inégale puisque les freins sont généralement
utilisés en marche avant. Ainsi il existe d'autres configurations
permettant de rendre l'usure égale et une puissance de freinage accrue.
Si les axes des segments sont intervertis, l'auto-serrage agit sur les deux
mâchoires, mais n'est effectif que dans un seul sens de rotation du
tambour. On peut également remplacer les pivots des deux segments par un
palier flottant. Au freinage, l'extrémité aval du segment
primaire s'appuie sur le palier et pousse l'extrémité amont du
segment secondaire, qui devient auto-serrant lui aussi. Ce montage est valable
pour les deux sens de rotation et est la technique la plus répandue
aujourd'hui. Une autre configuration consiste également à serrer
les deux mâchoires à l'aide de deux cylindres hydrauliques
à leur extrémité, mais ce type de frein est très
peu employé en raison de son rapport efficacité/prix peu
favorable.
Les tambours actuels montés sur l'essieu
arrière sont généralement en fonte. Quant aux
mâchoires, elles sont en tôle d'acier soudée ou en
aluminium, et revêtues d'une garniture de frottement à base de
laine d'acier, de cuivre et de coke en poudre ou encore d'oxyde de fer. La
principale caractéristique requise est un coefficient de frottement
relativement constant
Chapitre I Etude Bibliographique
6
avec la température et assez élevé, de
l'ordre de 0,5. Les freins à tambour sont encore bien
répandus aujourd'hui sur l'essieu arrière des véhicules
légers, aux performances modestes. I.3.2 Frein à
disque
Le frein à disque est un système de freinage
performant pour les véhicules munis de roues en contact avec le sol :
automobile, avion, train,
etc. et pour diverses machines. Ce
système transforme l'énergie cinétique du véhicule
en chaleur.
Le frein à disque (Fig. I.5) est composé de :
· un disque généralement
en fonte lié à la roue par l'intermédiaire du moyeu et qui
lui est intérieur ;
· deux plaquettes de part et d'autre du
disque, composées chacune d'une garniture en matériau composite
collée ou rivetée sur un support métallique ;
· un étrier en acier, solidaire
de l'essieu (par l'intermédiaire du pivot par exemple), qui supporte les
plaquettes ; en forme de chape, il recouvre un secteur du disque ;
· un piston hydraulique dans le cas
d'un étrier flottant ou coulissant ou deux pistons dans le cas d'un
étrier fixe posés contre les supports des plaquettes.

Fig. I.5 : Désignation
des principaux éléments.
Les disques sont des composants soumis à de fortes
températures. De manière générale, on trouve sur
les véhicules de série des disques pleins. Afin d'augmenter
l'échange thermique entre le disque et l'air environnant, on peut
utiliser des disques ventilés. En diminuant ainsi la température,
on garantit un meilleur frottement des garnitures sur les disques [1].
Si les systèmes de frein à disque sont
utilisés dans tous les domaines du transport (automobile, ferroviaire et
aéronautique), les caractéristiques techniques dépendent
des exigences de freinage ce qui donne des technologies différentes
(Fig.I.6).
Chapitre I Etude Bibliographique

-a- : Frein à disque
automobile. -b- : Frein à disque
aéronautique.
Fig. I.6 : Exemples de freins
à disque. I.3.2.1 Description d'un disque
Le disque est constitué d'un anneau plein avec deux
pistes de frottement (Fig. I.7), d'un bol qui est fixé sur le moyeu et
sur lequel est fixée la jante et d'un raccordement entre les pistes et
le bol. Ce raccordement est nécessaire car l'anneau et la partie du bol
qui est fixée au moyeu ne sont pas sur un même plan pour des
questions d'encombrement et de logement des plaquettes et de l'étrier.
La jonction entre le bol et les pistes est souvent usinée en forme de
gorge pour limiter le flux de chaleur issu des pistes vers le bol afin
d'éviter un échauffement excessif de la jante et du
pneumatique.
Les pistes de frottement sont dites extérieures quand
elles se situent du côté de la jante et intérieures quand
elles se situent du côté de l'essieu.
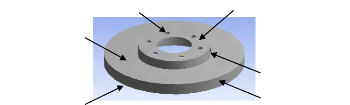
Trou de fixation Bol
Couronne extérieure
Piste intérieure
Piste extérieure
Gorge
7
Fig. I.7 : Le disque
plein.
La région de la gorge du bol est aussi très
sévèrement sollicitée. En effet, le disque tend à
se mettre en cône à cause des dilatations des pistes chaudes, mais
ce déplacement est retenu par la présence du bol qui est moins
chaud et par celle de l'étrier. De ce fait, de grandes concentrations de
contraintes naissent dans cette zone. Lors d'essais très
sévères sur banc dynamométrique, on peut parfois voir
apparaître une fissure circonférentielle (du côté
externe et/ou du côté interne du disque) qui se propage et
provoque la rupture brutale du bol.
Les gradients dans la gorge du bol s'expliquent de la
même manière. En début de freinage, la température
du bol est à 20° C tandis que celle des pistes est de
quelques centaines de degrés. De plus, dans le but d'éviter que
la température du moyeu ne soit trop
Chapitre I Etude Bibliographique
élevée (ce qui engendrerait des
élévations de température du pneu, très critique
pour son comportement), la gorge est usinée de manière à
ne pas transmettre trop de chaleur au bol (Fig.I.8). Avec cet usinage, la
température du bol baisse effectivement, mais les gradients thermiques
augmentent conséquemment dans cette zone. Ceux-ci engendrent des
contraintes thermiques qui expliquent les ruptures de bol observées lors
d'essais expérimentaux sévères.
8
Fig. I.8 : Gorge
calorifique
I.4 ELEMENTS D'UN FREIN Á DISQUE
Le disque de frein est un organe de friction fortement
sollicité, il doit résister à des températures de
600° C à 800° C dont les éléments sont
illustrés sur la figure .I.9 :

1. Disque 2. Plaquettes 3. Protections de disque de
frein
4. Support d'étrier 5. Colonnette 6. Etrier 7. Vis de
purge 8. Capuchon.
Fig. I.9 : Les éléments
d'un frein avant.
I.5 TYPES DES ETRIERS
On peut distinguer principalement, dans le secteur
automobile, deux types de réalisations. Les freins à
étriers coulissants ou à étriers fixes (Fig I.10). Les
premiers sont les plus répandus. Les étriers fixes sont surtout
utilisés dans le domaine des motocycles [1].
Naturellement, les étriers, comme tous les composants
non suspendus, doivent être le plus léger possible. Ils sont
habituellement coulés en alliage d'aluminium, parfois en alliage de
magnésium ou en fonte. Le porte-étrier peut être en fonte
et l'étrier en alliage léger.
Le diamètre des pistons récepteurs hydrauliques
dans les étriers est plus grand que celui des pistons actionnant les
segments des freins à tambour et la pression dans le circuit hydraulique
peut dépasser 100 bars alors que 15 bars suffisent avec des freins
à tambour.

Chapitre I Etude Bibliographique
-a- : Etrier flottant de la C6.
-b- : Etrier fixe.
Fig. I.10 : Types
d'étriers.
I.5.1 Frein à étrier coulissant
Lorsque le véhicule est en mouvement, le disque est en
rotation. Dans le cas d'un système à étrier coulissant
(Fig. I.11), pendant la phase de freinage, un circuit hydraulique
commandé par la pédale de frein actionne le piston qui presse la
première plaquette (plaquette interne) contre le disque. Lorsque
celle-ci est en contact avec le disque, l'étrier se déplace par
réaction grâce à un système de coulissage et
entraîne la seconde plaquette contre le disque. On pourra
également trouver des freins à chape coulissante au
fonctionnement quasi identique que les freins à étriers
coulissants [1] (Fig. I.12).

9
Fig. I.11 : Le système
à étrier flottant. Fig. I.12 : Le système
à étrier à chape flottante.
I.5.2 Frein à étrier fixe
Dans le cas de l'étrier fixe, qui est rigidement
attaché à l'essieu et qui comporte deux
pistons opposés alimentés par un même
circuit hydraulique, les deux pistons viennent presser les deux plaquettes sur
le disque lors de la mise en pression (Fig. I.13). L'avantage de ce dispositif
par rapport à l'étrier coulissant est la moindre quantité
de liquide mise en jeu (puisque chaque piston ne parcourt qu'une
demi-distance).

Fig. I.13 : Le système
à étrier fixe.
Chapitre I Etude Bibliographique
I.6 LES TYPES DE DISQUE FREIN
Il existe deux types de disque : les disques pleins et les
disques ventilés. Les disques pleins, de géométrie simple
et donc de fabrication simple, sont généralement placés
sur l'essieu arrière de la voiture. Ils se composent tout simplement
d'une couronne pleine reliée à un »bol» qui est
fixé sur le moyeu de la voiture (Fig. 1.14). Les disques
ventilés, de géométrie plus complexe, sont apparus plus
tardivement. Ils se trouvent la plupart du temps sur le train avant. Toutefois,
ils sont de plus en plus à l'arrière et à l'avant des
voitures de haut de gamme. Composés de deux couronnes - appelées
flasques - séparées par des ailettes (Fig. 1.15), ils
refroidissent mieux que les disques pleins grâce à la ventilation
entre les ailettes qui, en plus, favorisent le transfert thermique par
convection en augmentant les surfaces d'échange. Le disque
ventilé comporte plus de matière que le disque plein ; sa
capacité d'absorption calorifique est donc meilleure. Le nombre, la
taille et la forme (ailettes radiales, incurvées, pions circulaires...)
des ailettes sont variables (Fig. 1.16).

10
Fig. I.14 : Exemple de disque
plein. Fig. I.15 : Exemple de disque ventilé.

Chapitre I Etude Bibliographique
11
Fig. I.16 : Différentes
géométries d'ailettes.

-a- -b-
Fig. I.17 : Disques
ventilés : différentes conceptions [3].
La figure I.17 représente deux types de disque
ventilé. Le modèle « a » présente une moins
bonne ventilation que le « b », mais possède une meilleure
rigidité. La figure I.17 montre également la déformation
du deuxième type de disque soumis à un fort gradient de
température. La rotation du disque entraîne une circulation d'air
dans les canaux [3], d'où une amélioration du refroidissement
(Fig. I.18).

Fig. I.18 : Circulation de l'air
dans les canaux d'un disque ventilé [3]. I.7
AUTRES TYPES DE DISQUES ET LEURS CARACTERISTIQUES I.7.1 Les disques
rainurés
La raison pour laquelle on rainure les disques est trop
souvent mal comprise. Les gens croient généralement que les
rainures sont là pour améliorer le refroidissement. Il n'en est
rien. Elles sont là pour nettoyer la surface de la plaquette et briser
la couche gazeuse qui peut se former entre la plaquette et le disque quand les
hautes températures sont atteintes [4] . En pratique, la chaleur
crée des poussières et des gaz entre le disque et la surface de
la plaquette, réduisant ainsi l'efficacité, (Fig. I.19).

Chapitre I Etude Bibliographique
12
Fig. I.19 : Disque
rainuré.
I.7.2 Les disques percés
Le perçage des disques permet en plus du refroidissement,
le nettoyage des disques, (Fig. I.20). Les trous sont plus efficaces avec le
temps car ils sont plus ou moins autonettoyants. Mais l'augmentation du nombre
de trous réduit la surface de friction, un disque avec une masse
insuffisante (diamètre trop petit ou trop fin) a tendance à
craqueler et casser [4].

Fig. I.20 : Disque
percé.
I.8 COMPARAISON ENTRE TAMBOUR ET DISQUE I.8.1
Avantages
Par rapport aux freins à tambour, les freins à
disque se distinguent par les avantages suivants [5] :
· Meilleur refroidissement.
· La dilatation n'affecte pas la qualité de
freinage.
· Jeu de fonctionnement faible, action rapide.
· Bonne progressivité.
· Répartition uniforme de la pression.
· Absence de déformation.
· Puissance de freinage identique en marche avant et en
marche arrière.
· Pas de réglage (rattrapage de jeu automatique.
· Remplacement des garnitures plus rapide. I.8.2
Inconvénients
Les inconvénients des freins à tambour se
résument comme suit [5] :
· Mauvaise répartition de l'effort.
·
Chapitre I Etude Bibliographique
Moins bonne tenue à chaud.
· Dilatation et déformation du tambour.
· Usure plus prononcée sur le segment primaire
(comprimé).
I.9 LES PLAQUETTES
Les plaquettes de frein sont composées d'une plaque en
métal relativement rigide sur laquelle est collée une garniture,
semblable à celle que l'on peut trouver dans les freins à
tambour. Elle est toutefois soumise à des pressions plus
élevées, la surface de contact étant plus réduite.
La garniture est l'élément d'usure d'un système de frein
et sa périodicité de changement est plus courte que celle du
disque. La surface d'une garniture est très réduite
comparativement à la puissance de freinage qu'elle doit fournir. Elle
doit avoir de bonnes propriétés thermomécaniques et
également fournir un coefficient de frottement relativement stable avec
la température afin d'assurer un freinage le plus constant possible. Si
la rigidité de la garniture est relativement faible, de l'ordre de
quelques GPa, la plaque métallique au dos de la garniture se
doit d'être relativement rigide d'une part pour transmettre l'effort
provenant du piston hydraulique et d'autre part pour répartir la
pression le plus uniformément possible sur l'ensemble de la surface de
la garniture. Cela permet une usure uniforme de la garniture, rendant le
freinage constant au cours du temps et une répartition optimale du flux
de chaleur.
Les plaquettes sont les pièces les plus essentielles
de l'étrier, elles assurent le pincement du disque et de ce fait
l'arrêt du véhicule. Elles doivent supporter des
températures importantes liées aux frottements contre le disque
(ces températures peuvent atteindre les 800°C) [6] . Les plaquettes
de frein automobile comportent des rainures (Fig.I.21). Outre leurs
caractères d'évacuation des poussières et de l'eau, ces
rainures influent elles sur le comportement thermique de la plaquette. Cette
dernière doit présenter :
· Une bonne résistance à l'usure, non
agressivité des pistes de frottement.
· Absence de bruit.
· Haute résistance thermique. La
température des garnitures peut atteindre 600°C à
700°C.
13
Fig. I.21 : Plaquette de
frein.
Chapitre I Etude Bibliographique
14
Une température trop élevée peut
entraîner une perte d'efficacité presque totale du freinage
appelée : évanouissement ou fading.
La fabrication de la plaquette nécessite l'application de
plusieurs techniques [7]:
· support métallique : obtenu par
découpage (découpage fin pour la première monte), il subit
des opérations de nettoyage et de grenaillage.
· matériau de friction : pesage
mélange (et remélange).
· l'ensemble : cuisson,
cautérisation (pour la première monte), rectification et
peinture.
· personnalisation : plaque antibruit,
marquage
I.10 PROBLEME DU DISQUE DE FREIN
L'analyse bibliographique des phénomènes de
freinage montre que la principale sollicitation vient des fortes variations de
température induites par le frottement des plaquettes contre le disque.
En effet, la température peut varier de 20° C à plus de
700° C en quelques secondes seulement. Ces brusques variations ne
permettent pas à la température de s'homogénéiser.
De ce fait, le disque est le lieu de très forts gradients thermiques
dans l'épaisseur des pistes de frottement, mais aussi dans la direction
circonférentielle. Ces derniers gradients sont dus au fait que le flux
de chaleur qui entre dans le disque est localisé sous les plaquettes de
frein et que le disque tourne. Parfois, il apparait ce qu'on appelle des
points chauds; ce sont des zones circulaires
régulièrement espacées sur les pistes où la
température est localement plus élevée. Soumis à de
tels cycles thermiques, le disque subit des déformations
anélastiques (plastiques voire même viscoplastiques) qui sont
elles aussi homogènes dans la pièce. La prédiction
numérique des champs thermomécaniques qui s'établissent
dans le disque, a été mise en place la méthode de calcul
fondamental qui prenne en compte les couplages essentiels entre les
différents phénomènes, le caractère transitoire de
l'histoire thermique du disque, le comportement anélastique du
matériau, les gradients thermomécaniques orthoradiaux et la
rotation du disque. Dans cette étude, On se rend vite compte que la
simulation d'un freinage par une méthode classique par
éléments finis engendrerait des temps de calcul exorbitants.
I.11 LES MATERIAUX DU DISQUE DE FREIN
Les matériaux des composants du système de
freinage sont choisis selon les critères suivants : la fonction de la
pièce, le coût de la matière première et sa
facilité de fabrication, la masse.
Chapitre I Etude Bibliographique
15
Chapitre I Etude Bibliographique
I.11.1 Le disque
Afin d'assurer un bon comportement thermique et
mécanique, le matériau idéal pour le disque de frein doit
pouvoir emmagasiner beaucoup de chaleur et supporter un effort mécanique
important, sur une large gamme de température de fonctionnement (dans
l'automobile, les températures d'utilisation varient entre 0
°C et 800 °C ; dans l'aviation les températures
peuvent atteindre les 3000°C). De plus, il doit être bon
marché et être de fabrication relativement facile.
Ainsi, s'il existe des matériaux à meilleur
comportement thermomécanique, la fonte grise à graphite
lamellaire est la plus communément utilisée dans l'industrie
automobile. En effet, la fonte est peu chère, se fabrique
aisément et peut être coulée facilement. Elle
présente également une bonne conductivité, une assez bonne
résistance mécanique, et une faible usure. Les proportions de
carbone et les ajouts de différents types d'éléments
d'addition (phosphore, potassium, silicium, manganèse, cuivre, soufre,
nickel, chrome, molybdène, aluminium, autres éléments
d'alliages et des impuretés diverses) permettent de faire varier
légèrement les propriétés thermomécaniques
de la fonte qui reste ainsi en perpétuelle évolution [8][9][10].
On rappelle que plus la teneur en carbone est élevée, plus la
résistance mécanique de la fonte est mauvaise. Par contre, la
conductivité augmente, ce qui diminue les contraintes thermiques.
Il existe néanmoins dans le cas de véhicules
à hautes performances des disques bi-matière avec un moyeu (ou
bol) en aluminium ou acier et une piste de freinage (couronne) en
carbone-céramique vissée ou rivetée (Fig.I.22). Ces
disques sont particulièrement coûteux mais plus légers et
plus résistants à l'usure, à la corrosion et aux hautes
températures.

Fig. I.22 : Disque
carbone-céramique.
I.11.2 Les garnitures
Pour les garnitures, on cherche un matériau qui
génère un bon coefficient de frottement (le plus
élevé possible et le plus constant possible, quelles que soient
les variations de températures, de pression ou de vitesse). Il faut
cependant souligner que le comportement
16
de friction dépend aussi du matériau qui compose
l'autre structure frottante, à savoir le disque, des conditions d'appui
de la plaquette, etc. On veut aussi limiter les problèmes d'usure, de
corrosion et de bruit (qui est un problème classique de pièces
frottantes sur des solides en mouvement). Bien sûr, il y a aussi des
contraintes de coût.
Les garnitures sont faites de matériaux dits de
friction. Ceux-ci sont composés d'abrasifs et de lubrifiants,
d'élastomères, de poudre de métaux et autrefois,
d'amiante. Leur composition est souvent mal connue, restant confidentielle chez
les équipementiers.
1.11.3 Les supports
Les supports sont fabriqués avec un acier doux. Leur
rôle est de répartir l'effort exercé par le piston
hydraulique sur la totalité de la surface des garnitures, dans le but
d'obtenir une surface de contact disque/plaquette la plus large et la plus
homogène possible. Cela constitue un des critères de bon
fonctionnement du frein.
Le support est la pièce intermédiaire entre les
garnitures et le piston. Elle transmet donc la chaleur des garnitures (qui peut
être élevée) vers le liquide dans le piston. Afin
d'éviter ce phénomène, on utilise parfois des sous-couches
qui servent d'isolant thermique. Ces sous-couches permettent aussi d'absorber
une partie des bruits et des vibrations engendrés par le système
de frein à disque.
I.12 CRITERES D'EVALUATION D'UN SYSTEME DE
FREINAGE
Le frein à disque doit répondre à
différents types d'exigence, dont les principaux sont :
l'efficacité de freinage, l'endurance du système et le confort
d'utilisation.
I.12.1 Efficacité
L'efficacité du frein se mesure par son aptitude
à arrêter un véhicule en mouvement, sur une distance
minimale, quelles que soient les conditions extérieures. L'effort qui
sert à ralentir la rotation du disque doit donc être le plus
élevé possible. En d'autres termes, il faut optimiser l'effort
tangentiel issu du frottement des plaquettes sur le disque. Ainsi, plusieurs
paramètres interviennent : la pression de contact, la surface de
frottement et le coefficient de frottement. Plus ces
valeurs sont élevées, plus la distante d'arrêt du
véhicule est faible.
La pression de contact disque/garnitures dépend
essentiellement de la pression hydraulique dans le piston. Celle-ci varie entre
0 bar et 80 bars pour une voiture particulière. La
pression de contact dépend aussi de l'état de surface des deux
pièces frottantes, de l'usure, des rigidités des
matériaux, des dilatations thermiques, etc.
Chapitre I Etude Bibliographique
17
Le coefficient de frottement, noté , doit aussi rester le
plus stable possible, afin
d'assurer un freinage constant, quelles que soient les
conditions de freinage. Or, une fois les matériaux choisis, va
dépendre de la pression de contact, de la vitesse de rotation mais
aussi
de l'hygrométrie et de la température de
fonctionnement. En effet, la valeur de baisse par temps de pluie. De
même, quand la température atteint 400° C environ,
chute brutalement.
C'est ce qu'on appelle le fading.
Kennedy et Ling [11] pour l'aéronautique puis Day [12]
pour l'automobile ont mis en évidence que la surface réelle de
contact peut être très différente de la surface potentielle
de contact (surface totale des garnitures) avec des variations permanentes dues
au couplage entre les dilatations thermiques, les pressions de contact et
l'usure. Ces investigations ont été menées pour des
géométries simples de type annulaire avec l'hypothèse de
matériaux à comportement élastique linéaire.
I.12.2 Confort
Les problèmes de confort rencontrés avec le
frein à disque résident dans l'apparition de bruits et de
vibrations dans certaines configurations de freinage. Théoriquement, les
vibrations et les bruits sont reliés puisque le bruit est toujours
engendré par des vibrations. Cependant, on appelle communément
vibrations les vibrations qui sont ressenties autrement que
par les bruits. Dans le problème du frein, il s'agit principalement des
vibrations de la pédale de frein et du volant. Elles sont
essentiellement dues aux chocs entre le disque et les plaquettes et sont donc
liées à la vitesse de rotation de la roue. Les fréquences
de ces vibrations varient de quelques hertz à quelques centaines de
hertz.
Les bruits sont générés
par les instabilités du frottement des plaquettes contre le disque. Le
frottement est donc ce qu'on appelle l'excitation du bruit. Le
résonnateur (la pièce vibrante) est le plus souvent le disque,
mais il peut arriver que ce soit la plaquette ou l'étrier ou encore une
autre pièce de l'assemblage
I.12.3 Endurance
Un autre critère d'évaluation d'un frein
à disque est son endurance. Plus précisément, il s'agit de
garantir dans la durée l'ensemble des fonctions du système,
éviter toute avarie dangereuse et définir un seuil d'usure
à partir duquel les pièces doivent être changées.
Pour dimensionner un disque de frein, il faut alors connaître les avaries
susceptibles d'apparaître. Les observations expérimentales
permettent d'établir la liste des endommagements suivants
Chapitre I Etude Bibliographique
(certains peuvent se manifester sur un véhicule en
clientèle, d'autres ne surviennent que lors d'essais sur banc) :
· du faïençage sur les pistes de frottement
(Fig.I.24) ;
· des fissures radiales sur les pistes de frottement
(Fig.I.25) ;
· des fissures au pied des ailettes (Fig.I.26) ;
· une fissure circulaire (Fig.I.28), (Fig.I.29) au niveau
de la gorge qui peut aboutir à la rupture du disque (Fig.I.27) ;
· de l'usure (Fig.I.30), (Fig.I.31).
Le disque s'use par frottement contre les plaquettes. En
réalité, celles-ci sont fabriquées dans l'optique de
s'user davantage que le disque (Fig.I.33). Le frottement des deux pièces
engendre des problèmes de dépôt (Fig.I.32) et d'arrachement
de matière qui modifient la nature du contact.

Fig. I.23 : Observation d'une
fissure radiale de la bordure extérieure du disque jusqu'au bol

Fig. I.24 : Faïençage
sur les pistes Fig. I.25 : Fissure radiale sur les
pistes
de frottement de frottement

Fig. I.26 : Fissure en pied
d'ailette Fig. I.27 : Rupture dans la gorge du bol

18
Fig. I.28 : Section de disque
fissuré Fig. I.29 : Fissure dans la gorge
Chapitre I Etude Bibliographique

Fig. I.30 : Usure des
pistes Fig. I.31 : Usure non-uniforme
I.12.4 Autres critères
D'autres critères entrent en ligne de compte lors de
la conception d'un frein : son coût (matière première,
facilité de fabrication, etc.), son encombrement (on veut le
réduire au minimum), son poids (plus un véhicule est
léger, plus la vitesse maximale est élevée, et plus la
consommation de carburant par kilomètre est faible).

19
Fig. I.32 : Dépôts de
matière sur les Fig. I.33 : Usure excessive des
plaquettes
pistes du disque
I.13 PHENOMENES THERMIQUES DANS LE DISQUE
Lors de la phase de freinage, il existe des gradients
thermiques qui apparaissent dans le disque qui causent son
endommagement. En effet, le disque tend à se dilater dans les zones
chaudes, mais il est finalement »maintenu» par les zones froides.
Cela donne lieu à des contraintes de compression avec plastification.
Lors du refroidissement, il y a apparition de contraintes résiduelles de
traction. Le disque subit donc des cycles de contraintes traction/ compression
qui s'apparentent à des cycles de fatigue thermique. Il existe
différents types de gradients thermiques :
· les gradients dans l'épaisseur des pistes ;
· les gradients surfaciques (radiaux et surtout
orthoradiaux) ;
· les gradients dans la gorge du disque.
I.14 PHENOMENES MECANIQUES DANS LE DISQUE
Les phénomènes mécaniques peuvent
être classés en trois catégories :
· le chargement (pression et couple), les conditions aux
limites (serrage du disque sur le moyeu, contact avec la jante, présence
de l'étrier) et la géométrie du disque qui donnent la
déformation globale du disque, La dissymétrie de dilatations
engendrée favorise la mise en cône du disque (Fig.I.34) ;
·
Chapitre I Etude Bibliographique
20
le contact entre le disque et les plaquettes ;
· l'usure.

Fig. I.34 : Mise en cône
d'un disque de frein. I.15 MATERIAUX CONVENTIONNELS : ACIERS
,FONTES I.15.1 Acier
L'acier et la fonte sont les matériaux utilisés
le plus couramment de nos jours dans l'industrie automobile. Les aciers sont
des aciers inoxydables austénitiques tel que un X2 Cr Ni Mo 17-12
(ancienne désignation : Z2 CND 17-12 soit 0,02% de carbone, 17% de
chrome et 12% de nickel ainsi que des traces de molybdène). Les
propriétés mécaniques de ces aciers sont une grande
ductilité ainsi qu'une grande résilience, en particulier à
haute température [13].
I.15.2 Fontes
Les fontes à forte teneur en carbone sont aussi les
matériaux les plus couramment utilisés dans l'industrie
automobile, le tableau ci-après donne les compositions des alliages en
fontes (FG) destinés à la fabrication des disques de frein.
Eléments de l'alliage
|
FG 25 alliée
|
FG 20 HC
|
FG 20 HC
|
C%
|
3.0 à 3.5
|
3.62 à 3.68
|
3.7 à 3.9
|
Si%
|
1.9 à 2.4
|
max 2.1
|
1.8 à 2.2
|
Mn%
|
0.6 à 0.9
|
0.65 à 0.80
|
0.5 à 0.8
|
P%
|
max 0.12
|
max 0.085
|
max 0.12
|
S%
|
max 0.10
|
max 0.095
|
max 0.10
|
Cr%
|
0.2 à 0.4
|
0.18 à 0.3
|
....0.1
|
Mo%
|
0.3 à 0.5
|
0.3 à 0.45
|
-
|
Cu%
|
0.2 à 0.3
|
0.3 à 0.45
|
....0.25
|
Ni%
|
0.1 à 0.3
|
-
|
-
|
Ti%
|
-
|
0.03 à 0.05
|
-
|
Sc%
|
0.82 à 1.01
|
1.0 à 1.03
|
1.01 à 1.10
|
Dureté HB 30,750/5
|
-
|
180 à 225
|
160 à 200
|
Rm N/mm
|
250 à 300
|
.....200
|
.....150
|
|
Tableau. I.1 : Composition et
résistance des 03 sortes de fontes pour la conception des disques
[14].
Chapitre I Etude Bibliographique
21
L'indice de saturation du carbone a été
calculé par la formule de Jungbluth :

C : teneur en carbone. Si : teneur en silicium. P : teneur en
phosphore.
I.15.3 Carbone
Le matériau composite qu'est le carbone a
été découvert en 1958, à la suite de la pyrolyse
d'une fibre composite avec une matrice organique. Ce matériau,
composé d'un renforcement de carbone et d'une matrice carbone, ont
été développés dans un premier temps pour une
application dans le domaine aéronautique [13].
Les disques en carbone sont dotés des
propriétés suivantes :
Un coefficient de frottement exceptionnel quelle que soit la
température.
· Ils possèdent une grande stabilité
physico-chimique, même à des températures
supérieures à 1000°C.
· Ils ne sont pas sensibles aux chocs thermiques
(dilatation négligeable) ou à la fatigue mécanique.
· Ils sont invulnérables à l'oxydation
jusqu'à 500°C. Une couche antioxydation permet une protection
à plus haute température.
· Ils ont une capacité d'absorption thermique
double de l'acier
· Ils ont des caractéristique mécaniques
spécifiques (comparable, quelle que soit la température, à
l'aluminium quand il est froid) qui augmentent avec la température
jusqu'à 2000° C.
I.15.4 Conditions d'utilisation
De façon à fonctionner avec le meilleur
rendement et durer le plus longtemps possible, les températures des
disques doivent être correctes et équilibrées. En
général, les disques d'un véhicule devraient tous
fonctionner à des températures identiques [13]. La
température maximale du disque doit être accordée avec la
qualité des plaquettes utilisées. Les faces du disque ne doivent
pas dépasser les températures maximales recommandées pour
chaque type de plaquette. Avec une qualité CM 83 la température
du disque doit être entre 400° C et 600°C.
Chapitre II Transfert de Chaleur
22
II.1 INTRODUCTION
De tous temps, les problèmes de transmission
d'énergie, et en particulier de la chaleur, ont eu une importance
déterminante pour l'étude et le fonctionnement d'appareils tels
que les générateurs de vapeur, les fours, les échangeurs,
les évaporateurs, les condenseurs, etc., mais aussi pour des
opérations de transformations chimiques. Les problèmes de
transfert de chaleur sont nombreux, et on peut essayer de les
différencier par les buts poursuivis dont les principaux sont [15] :
· l'augmentation de l'énergie transmise ou
absorbée par une surface,
· l'obtention du meilleur rendement d'une source de
chaleur,
· la réduction ou l'augmentation du passage d'un
débit de chaleur d'un milieu à un autre.
Le transfert de chaleur au sein d'une phase ou, plus
généralement, entre deux phases, se fait de trois façons
:
· Par conduction,
· Par rayonnement,
· Par convection.
Un système de freinage a pour fonction principale de
transformer une énergie mécanique en une énergie
calorifique. Cette énergie se caractérise par un
échauffement global du disque et des plaquettes lors d'une phase de
freinage. Il est d'autant plus intéressant de simuler ce
phénomène à plusieurs titres. Pour cela et afin
modéliser ce problème précisément, nous nous
intéressons dans cette partie par le calcul du flux de la chaleur
initial entrant dans le disque au niveau de la zone de contact.
II. 2 DEFINITIONS
II.2.1 Champ de température
Les transferts d'énergie sont déterminés
à partir de l'évolution dans l'espace et dans le temps de la
température : T= f(x, y, z, t). La valeur instantanée de
la température en tout point de l'espace est un scalaire appelé
champ de température. On distingue deux cas [16] :
· Champ de température indépendant du
temps : le régime est dit permanent ou stationnaire.
· Evolution du champ de température avec le temps
: le régime est dit variable ou instationnaire.
Chapitre II Transfert de Chaleur
II.2.2 Gradient de température
Si l'on réunit tous les points de l'espace qui ont la
même température, on obtient une surface dite isotherme. La
variation de température par unité de longueur est maximale le
long de la normale à la surface isotherme. Cette variation est
caractérisée par le gradient de température [16]:
Isotherme

23
Fig.II.1 : Gradient de
température.
Avec : vecteur unitaire de la normale
II.2.3 Flux de chaleur

La chaleur s'écoule sous l'influence d'un gradient de
température par conduction des hautes vers les basses
températures. La quantité de chaleur transmise par unité
de temps et par unité d'aire de la surface isotherme est appelée
densité de flux de chaleur, elle est exprimée en [16]:
Où S est l'aire de la surface (m2).
On appelle flux de chaleur la quantité de chaleur
transmise sur la surface S par unité de temps, elle est exprimée
en W :

II.3 MODES DE TRANSFERT DE CHALEUR
Lorsque deux systèmes sont à des
températures différentes, le système le plus chaud
cède de la chaleur au plus froid. Il y a échange thermique ou
encore transfert thermique entre ces deux systèmes. Cette situation se
rencontre dans de nombreuses situations industrielles (moteurs thermiques ou
même électriques, centrales électriques au fuel au gaz,
etc...,
Chapitre II Transfert de Chaleur
électronique) ou domestique (chauffage de
l'habitat)[17]. Un transfert d'énergie donne lieu à un flux de
chaleur qui correspond à un déplacement de l'énergie du
plus chaud vers le plus froid. Il existe trois modes essentiels de transferts
de chaleur : la conduction, le rayonnement et la convection.
II.3.1 Conduction
C'est le transfert de chaleur au sein d'un milieu opaque,
sans déplacement de matière, sous l'influence de
différence de température. La propagation de la chaleur par
conduction à l'intérieur d'un corps s'effectue selon deux
mécanismes distincts : une transmission par les vibrations des atomes ou
molécules et une transmission par les électrons libres.
Le transfert de chaleur par conduction s'appuie sur la loi de
Fourier [16]:
qui relie la densité de puissance (unité
Wm-2) et le gradient local de température. k est
la conductivité thermique du matériau
considéré (unité Wm-1K-1).

a
ds
®
j
® n
®
grad T
Fig.II.2 : Lois de
Fourier.
II.3.1.1 Résistance thermique
On considère deux surfaces isothermes S1 et S2 de
températures et . Ces deux
surfaces sont correspondantes c'est à dire que toute
ligne de flux quittant la surface S1 atteint la surface S2. Pour un
milieu conductif en régime permanent sans source interne, le bilan
thermique s'écrit :

T1
S1
Surfaces isothermes
Lignes de flux
S2
0 T2
24
Fig.II.3 : Résistance
thermique [18]
Chapitre II Transfert de Chaleur
Appliquons, sur le volume fermé délimité
par les deux surfaces isothermes S1 et S2 et la surface latérale
constituée de toutes les lignes de flux s'appuyant sur le contour
fermé délimitant les deux surfaces isothermes, le
théorème d'Ostrogradsky [18],

Entre surfaces isothermes correspondantes le flux de chaleur est
conservé. Pour une surface isotherme quelconque S du tube de
courant

Le calcul de la circulation de suivant une ligne de flux
quelconque joignant les

surfaces isothermes S1 et S2 conduit à :
La multiplication de par un coefficient quelconque
entraîne la multiplication par le
même coefficient de .
On obtient donc la relation :
(II.9)
R est appelée résistance
thermique, c'est l'analogue thermique de la résistance
électrique. Elle est inversement proportionnelle à la
conductivité du milieu et augmente avec
la longueur des lignes de flux.
Résistance thermique relative à un
coefficient d'échange h se calcule comme suit :

II.3.1.2 Les régimes permanents


Il s'agit de résoudre le système
d'équations linéaires

: Représente la surface de la frontière
extérieure j, l'indice j est au maximum égal
à 6.
25
Ce sont les régimes pour lesquels la température
en tout point du milieu est indépendante du temps, le
déséquilibre est entretenu par les sources de chaleur [18].
Chapitre II Transfert de Chaleur
II.3.1.3 Les régimes transitoires
Les régimes transitoires correspondent à
l'évolution d'un système d'un état initial (permanent ou
en équilibre) vers un état final (permanent ou en
équilibre) provoquée par un changement à l'instant initial
des sources; le champ de température T ( M ,t ) dépend
du champ de température initial T ( M ,0 ) mais l'influence de
celui-ci s'estompe avec le temps. A l'instant initial, au moins une source
change, par contre elles demeurent constantes ensuite. Les régimes
transitoires ne doivent pas être confondus avec les
régimes variables pour lesquels les sources
évoluent au cours du temps [18]

Le champ de températures est régi par le
système d'équations

26
La méthode générale de résolution
par les fonctions de Green ne peut être envisagée sans
posséder une bonne maîtrise préalable de la technique de
séparation de variables avec développement en série de
fonctions orthogonales.
II.3.2 Convection
La convection est un transfert de chaleur dans un milieu
matériel avec mouvement de matière. Ce mode de transfert ne
concerne donc que les fluides ou les échanges entre un solide et un
fluide. Ce mécanisme de transfert est régi par la loi de Newton
[16]:
(II.16)

Fluide à
S
Fig.II.4 : Définition d'un
élément de surface d'échange.
Avec : Flux de chaleur transmis par convection (W)
Coefficient de transfert de chaleur par convection
(Wm-2°C-1)
°
C)
(
Température de la surface
Chapitre II Transfert de Chaleur
°
C)
(
27
Température du milieu environnant la surface
S Aire de la surface de contact solide / fluide
(m2)
La transmission de chaleur par convection est
désignée, selon le mode d'écoulement du fluide, par
convection libre et convection forcée. Lorsqu'il se produit au sein du
fluide des courants dus simplement aux différences de
température, on dit que la convection est naturelle ou
libre. Par contre si le mouvement du fluide est provoqué par une action
externe, telle une pompe ou un ventilateur, le processus est appelé
convection forcée.
II.3.2.1 Le nombre de Reynolds
Ce nombre joue un rôle fondamental dans la
caractérisation de l'écoulement ,il est définit par
l'expression suivante [19] :

avec est la viscosité cinématique du fluide
· Si Re < 2400 on est en régime laminaire.
· Pour des vitesses plus élevées, Re >>
2400, le régime turbulent apparaît
II.3.2.2 Le nombre de Nusselt
Ce nombre caractérise l'échange thermique entre
le fluide et la paroi, il est définit comme suit [19] :

II.3.2.3 Le nombre de Prandtl
Ce nombre est entièrement caractéristique du
fluide considéré [19]. L'inverse du nombre de Prandtl est
appelé par les « thermiciens » français : le nombre de
Stanton (S) . Dans le cas des gaz, Pr est sensiblement constant avec la
pression et la température et ne varie
qu'avec les changements thermiques de .

II.3.3 Rayonnement
C'est un transfert d'énergie
électromagnétique entre deux surfaces (même dans le vide).
Dans les problèmes de conduction, on prend en compte le rayonnement
entre un solide et le milieu environnant et dans ce cas, nous avons la relation
[16]:
Chapitre II Transfert de Chaleur
28
(II.20)

Milieu environnant à
S
Fig.II.5 : Elément en
rayonnement.
Avec : : Flux de chaleur transmis par rayonnement (W)
: Constante de Stephan ( 5,67×10-8
Wm-2K-4)
: Facteur d'émission de la surface
: Température de la surface (K)
: Température du milieu environnant la surface (K)
S : Aire de la surface (m2)
II.4 Stockage d'énergie
Le stockage d'énergie dans un corps correspond
à une augmentation de son énergie interne au cours du temps
d'où (à pression constante) [16] :

Avec : : Flux de chaleur stocké (W)
: Masse volumique (kg m-3)
: Volume (m3)
c : Chaleur massique ( J
kg-1°C-1)
C)
T : Température (°
t : Temps (s)
, V,c sont supposés constants, le produit est
appelé la capacitance thermique du corps.
II.5 Les équations gouvernantes du transfert de
chaleur transitoire par conduction
Considérons un matériau isotrope dans le
système tridimensionnel dans un domaine ?. Si l'écoulement de la
chaleur dans les directions x, y et z par
unité de surface et par unité de
Chapitre II Transfert de Chaleur
29
temps , et respectivement, la différence entre le flux
sortant et le flux entrant pour
un élément de volume dxdydz est
donnée comme suit [20],

Pour la conservation de la chaleur, cette quantité
doit être égale à la somme de la chaleur produite dans
l'élément dans le temps d'unité Qdxdydz et la
chaleur gagnée dans un temps d'unité dû au changement de
température, à savoir,

où c est la capacité de la chaleur
spécifique, est la densité, et T (x, y, z, t ) est la
distribution de la température.
La condition de l'égalité mène au rapport
différentiel :

Les flux de la chaleur dans les directions x , y et z sont :

La substitution de ces flux de la chaleur dans
l'équation (II.24) mène à une équation d'ordre plus
supérieur dans une variable indépendante simple T,

D'une manière semblable, l'équation
tridimensionnelle de la conduction de la chaleur peut être obtenue. On
peut également la écrire dans la notation vectorielle comme,

II.6 CALCUL DE FLUX DE CHALEUR ENTRANT DANS LE
DISQUE
II.6.1 Introduction
Les performances en freinage des véhicules sont de
toute évidence une des caractéristiques cruciales pour la
sécurité. Dans la perspective d'accroître la
sécurité, des efforts importants ont été consentis
ces dernières années pour améliorer le freinage. Des
normes réglementent le freinage dans la plupart des pays.
Chapitre II Transfert de Chaleur
30
II.6.2 Les efforts agissant aux roues lors du
freinage

FRA
B
FFH
FQH
h
A
FG
FFV
X
Y
FG cosá
FD
FRP
FRRH
FRRV
FQV
LH
LV
L
Fig. II.6 : Définition des
forces agissant sur une automobile lors du freinage
En observant la situation décrite à la Figure
II.6, on peut écrire l'équilibre longitudinal et transversal du
véhicule selon les axes x, y locaux de la voiture.

.
Avec

Chapitre II Transfert de Chaleur
Pour un véhicule routier, la force au roulement est
due au plat
formé par un pneumatique sur la route, est le
coefficient de résistance au roulement. Pour
un pneu haut pression
La force aérodynamique est donnée par :


Avec coefficient de forme, égal à : 0,3 à
0,4 sur voiture
surface frontale ; en première approche, pour un
véhicule routier de tourisme, on
peut prendre : S
masse volumique de l'air
II.6.3 Puissance de freinage totale

31
Dans le cas d'un freinage sur plat, on néglige les
résistances dues au roulement et à la
pente ( et ,la pénétration dans l'air est
généralement négligeable, pour
cette raison on prend ( .
Chapitre II Transfert de Chaleur
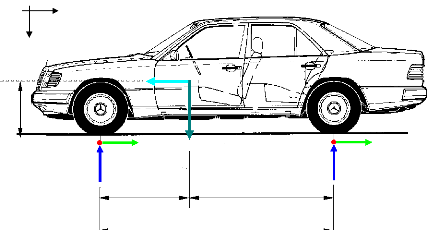
FQV
FQH
X
Y
FD
h
FG
A
B
FFV FFH
LV
LH
L
Fig. II.7 : Efforts agissant sur
une voiture freinée, freinage d'arrêt sur plat.
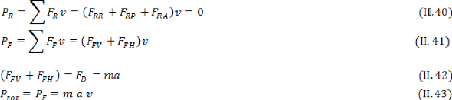

Soit le coefficient qui représente la proportion de
l'effort de freinage rapportée aux
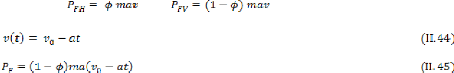
roues arrière alors si a est constante, on a
:
32
La puissance de freinage apportée au disque de frein
est égale à la moitié de la puissance totale :
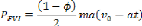
A l'instant t=0, on a donc

Chapitre II Transfert de Chaleur
On définit alors l'efficacité du freinage par le
rapport entre la décélération (a) et
l'accélération (g) :

33
II.6.4 Expression du flux thermique initial
Les disques de frein ont pour but de dissiper
l'énergie mécanique en chaleur. Pour les trains ou les voitures,
c'est l'énergie cinétique du véhicule qui est
dissipée par le frottement des patins sur les disques. L'ensemble patin
- disque s'échauffe sous cette action et refroidit à l'air
ambiant. Ces freinages étant répétés, les disques
de frein sont soumis à de la fatigue thermomécanique. Dans
l'automobile, de nombreuses études ont montré que les freinages
pouvaient engendrer des températures pouvant dépasser 700°C
en quelques secondes.
Si on considère que le disque de frein peut absorber
totalement la quantité de chaleur produite.
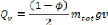
L'expression de la puissance de frottement transformée
par unité de surface est donc :
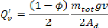
La grandeur caractérise le flux de chaleur injecté
dans le disque, Il doit donc être
uniquement localisé sur la surface réelle de
contact. Où la surface de disque balayé par une
plaquette de frein.
Si on introduit le facteur d'exploitation de la surface
frottante
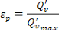
On obtient ainsi, l'équation du flux thermique initial
de friction entrant dans le disque, qui est se calcule comme suit :

Chapitre III Modélisation Thermomécanique du
Problème
34
III.1 INTRODUCTION
Un système de freinage a pour fonction principale de
transformer une énergie mécanique en une énergie
thermique. Cette énergie se caractérise par un
échauffement du disque et des plaquettes lors de la phase de freinage.
La modélisation du comportement thermique de l'ensemble disque
-plaquettes permet d'analyser l'évolution et la répartition des
températures au niveau des zones de contact. Grâce aux
résultats obtenus à partir du modèle
développé, il devient possible d'optimiser le système. La
modélisation des écoulements et des échanges de chaleur
permet de comprendre et de quantifier les phénomènes physiques
sans avoir recours à des essais expérimentaux.
III.2 LA MODELISATION THERMIQUE DU PROBLEME III.2.1
Equation de la chaleur
Soit v une partie quelconque de V
limitée par la surface s.

S
V
v
s
Fig.III.1 : Bilan
thermique.

La puissance thermique stockée dans v est
égale à la somme de la puissance thermique
générée par les sources volumiques contenues dans v
et de la puissance thermique reçue sous forme de flux à
travers la surface s [21] :
: la masse volumique du matériau (kg/m3)

: la capacité thermique massique (J/ kg K)
: la normale unitaire à s dirigée vers
l'extérieur de v
En transformant la relation (III.1) en intégrale de
volume à l'aide du théorème d'Ostrogradski, il en
résulte :

De l'équation (III.2), on déduit l'équation
de chaleur suivante:

Chapitre III Modélisation Thermomécanique du
Problème

Pour un matériau homogène et isotrope,
l'équation (III.3) dans le repère orthonormé
s'écrit :
III.2.2 Forme différentielle
Résoudre un problème thermique consiste
à chercher un champ de températures T(x, y, z,
t) à partir de l'équation (III.4) en tenant compte des
conditions aux limites et initiales suivantes [21] :
~ les conditions aux limites :


où
S est la surface du solide et la normale unitaire
à S dirigée vers l'extérieur de V.
~ la condition initiale à l'instant t =
t0 :

La quantité r(T), appelée
résidu de l'équation (III.3), est définie par :

III.2.3 Forme intégrale faible
Pour résoudre le problème définit par le
système d'équations (III.4, III.5, III.6) par la méthode
des éléments finis, on utilise la méthode des
résidus pondérés dans la formulation de Galerkin
[22, 23,24]. Multiplions l'équation (III.3) par une fonction
arbitraire et intégrons sur le domaine V :

: Fonction de pondération (ou fonction test).
En utilisant la relation :
35
Chapitre III Modélisation Thermomécanique du
Problème
l'équation (III.8) s'écrit :

Transformons la deuxième intégrale de cette
équation en intégrale de surface à l'aide du
théorème d'Ostrogradski :

et posons la condition T* = 0 sur ST,
d'où annulation de la dernière intégrale.
En utilisant la relation (III.11), les conditions aux limites
(III.5) et l'équation (III.10), on obtient la formulation
intégrale faible d'un problème thermique :

avec
- la condition aux limites : T = Tp
sur ST et
-
III.2.4 Forme discrétisée :
éléments finis
La solution analytique du système d'équations
(III.12, III.13) est en général inaccessible. On est donc conduit
à chercher une solution approchée par une méthode
numérique : la méthode des éléments finis. Cette
méthode est un cas particulier de la méthode de Galerkin
: le champ de températures et les fonctions test appartiennent
au même espace de dimension finie.
III.2.4.1 Représentation
élémentaire (ou locale) du champ de températures
Le champ de températures dans l'élément
(e) a pour expression [21]:
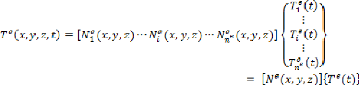
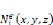
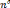
36
Chapitre III Modélisation Thermomécanique du
Problème
: Le nombre de noeuds de l'élément
: Les fonctions d'interpolation élémentaires
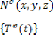
: La matrice d'interpolation élémentaire
: Le vecteur de température des noeuds de
l'élément (e). III.2.4.2 Représentation globale du
champ de températures
Le champ de températures sur l'ensemble du domaine V
a pour
expression:
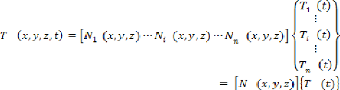
n : Le nombre de noeuds du maillage
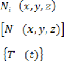
: Les fonctions d'interpolation (ou fonctions de forme) : La
matrice d'interpolation
: Le vecteur des températures nodales
Les fonctions d'interpolation vérifient les relations
:
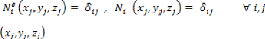
: Coordonnées du noeud j.
III.2.4.3 Partition des degrés de
liberté
Effectuons une partition des degrés de liberté
en températures inconnues
et connues [23] :
où le vecteur regroupe les températures (connues)
des noeuds situées sur la surface .
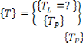
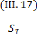
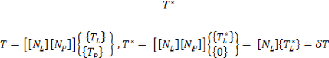
D'où l'expression de T et
37
Cette partition induit une partition de la matrice
d'interpolation :
Chapitre III Modélisation Thermomécanique du
Problème
III.2.4.4 Discrétisation de la forme
intégrale faible De l'expression du champ de températures T :
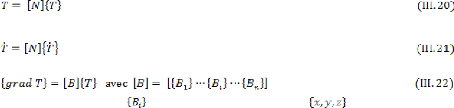
on déduit
Et
Pour un problème spatial, s'écrit dans le
repère orthonormé :
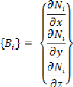
De même :
En remplaçant ces relations dans l'équation
(III.12 ), il vient [21]:
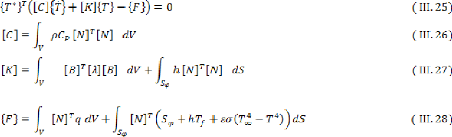
38
[C] : La matrice de capacité thermique (J/K)
[K] : La matrice de conductivité thermique (W/K)
: Le vecteur des flux nodaux (W)
: Le vecteur des températures nodales (K)
La discrétisation en espace du problème par la
méthode des éléments finis conduit à la
résolution d'un système d'équations en temps, en
général du premier ordre. La figure III.2 représente
l'organigramme principal par la M.E.F en utilisant la méthode des
substitutions successives.
Chapitre III Modélisation Thermomécanique du
Problème
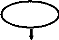
Début
Lire les données de contrôle
Evaluation pour chaque élément : La
matrice de capacité thermique La matrice de conductivité Vecteur
de flux
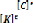
Assemblage des matrices
élémentaires
Pour la construction des matrices
globales
C T+K U = q

K T = q
Application de la méthode de
substitution
successive
39
Test de convergence

Fin
Fig.III.2 : Organigramme
principal de résolution de système d'équations par la
M.E.F.
III.2.4.4.1 Conditions initiales et conditions aux
limites
· La température du disque est constante est
égale :
· Dans notre cas, il s'agit d'un problème
thermique transitoire avec deux conditions aux limites :
V' Un flux de chaleur entrant dans le disque (conduction)
localisé dans la zone de contact disque-plaquette dans les deux
côtés,
V' Un échange de chaleur par convection sur toute la
surface du disque.
Chapitre III Modélisation Thermomécanique du
Problème
40
III.3 ETUDE MECANIQUE DU CONTACT PLAQUETTE DE
FREIN/DISQUE
III.3.1 Introduction
La complexité des systèmes physiques ou
technologiques destinés à être conçus ou
étudiés a conduit à employer des méthodes
numériques basées sur le principe d'approcher une solution
nominale le plus possible, mais celles-ci exigent de grands calculs
nécessitant des calculateurs efficaces.

Une étude du contact entre le disque et les plaquettes
de frein est nécessaire pour l'évaluation des pressions contact
et des efforts de cisaillement ainsi les contraintes équivalentes de Von
Mises et les déformations qui représentent le chargement
mécanique imposé au disque. De plus, le flux de chaleur qui est
engendré par le frottement est dépendant du contact. Son
expression théorique est [25] :
est le coefficient de frottement local, V la vitesse
de glissement du point considéré et P la
pression de contact.
Dans cette étude, on a modélisé le
disque et la plaquette en utilisant le logiciel d'élément finis
Multiphysics ANSYS 11 en caractérisant pour chaque
pièce les propriétés mécaniques des
matériaux. Le type d'analyse choisi est structurale statique
.La simulation a lieu pour durée totale de freinage t=45 [s] et
en adoptant le pas de temps pour les mêmes conditions du cas thermique
:
· Pas du temps initial = 0,25 [s]
· Pas du temps initial minimal = 0,125 [s]
· Pas du temps initial maximal = 0,5 [s]
III.3.2 Simulation du problème en ANSYS
Le code d'éléments finis ANSYS 11 (3D) est
utilisé dans cette partie pour simuler le comportement du
mécanisme de contact par frottement des deux corps (plaquette et disque)
lors d'un freinage d'arrêt. Ce code possède des algorithmes de
gestion du contact avec frottement basés sur la méthode des
multiplicateurs de Lagrange, ou la méthode de pénalisation. Le
module d'Young du disque étant environ 138 fois plus élevé
que celui de la plaquette, les simulations présentées dans notre
étude considèrent le contact avec frottement d'une plaquette
déformable sur un disque rigide. L'application de la pression de contact
sur la plaquette de frein vient mettre celle-ci en contact frottant avec le
disque dont la vitesse de
Chapitre III Modélisation Thermomécanique du
Problème
41
rotation est maintenue constante durant toute la simulation.
le matériau choisi du disque est le Fonte Grise FG 15 à haute
teneur en carbone et la plaquette de frein a un comportement élastique
isotrope dont les caractéristiques mécaniques des deux
pièces sont récapitulées dans le tableau III.1. Des
caractéristiques de conception des pièces sont également
fournies directement par le code Ansys 11 ; données dans le tableau
III.2 [26].
Le coefficient de frottement est égal à 0,2 au
niveau de la zone de contact. Dans le
cas avec frottement, cette dernière se situe de
l'interface de contact, les contraintes de cisaillement provoquées par
le frottement à ce niveau là sont à l'origine de ce
phénomène. Le coefficient de frottement dépend de beaucoup
de paramètres (pression, vitesse de glissement, température,
humidité, etc.). Nous rappelons que l'ANSYS peut, au choix, utiliser une
méthode de multiplicateurs de Lagrange ou bien une méthode de
Lagrangien augmenté, une méthode de pénalisation pour
résoudre le problème de contact [27]. C'est cette dernière
qui a été sélectionnée dans ce travail.
|
Disque
|
Plaquette
|
Module de Young E (Gpa)
|
138
|
1
|
Coefficient de Poisson
|
0 ,3
|
0,25
|
Masse volumique
|
7250
|
1400
|
Coefficient de frottement
|
0 ,2
|
0,2
|
|
Tableau .III.1 : Tableau des
caractéristiques mécaniques des deux pièces.
|
Disque
|
Plaquette
|
Volume ( )
|
9,5689e-004
|
8,5534e-005
|
Surface ( )
|
0 ,24237
|
1,8128 e-002
|
Masse (kg)
|
6,9375
|
0,44975
|
Faces
|
205
|
35
|
Arêtes
|
785
|
96
|
Sommets
|
504
|
64
|
Noeuds
|
34799
|
2165
|
Eléments
|
18268
|
1014
|
Moment d'inertie Ip1(kg·m2)
|
3,5776e-002
|
2,7242e-005
|
Moment d'inertie Ip2 (kg·m2)
|
6,9597e-002
|
1,5131e-004
|
Moment d'inertie Ip3 (kg·m2)
|
3,5774e-002
|
1,2863e-004
|
|
Tableau .III.2 :
Caractéristiques de conception des deux pièces.
III.3.3 Création du modèle sur ANSYS
Workbench
Pour commencer l'étude, on a créé une
structure sur ANSYS Wb qui représente le disque de
frein avec la plaquette. Puis, on a fait le maillage et on a défini les
conditions aux limites pour le mettre ensuite sur l'ANSYS Multiphysics et
initialiser le calcul.

Chapitre III Modélisation Thermomécanique du
Problème
Fig.III.3 : Création du
modèle sur ANSYS WB11.
III.3.4 Choix du maillage
Un fois la structure est créée, on a fait le
maillage. Il s'agit d'un maillage progressif. Le modèle disque-plaquette
a été maillé par des éléments volumiques
tétraédriques et quadratiques à 10 noeuds
(fig.III.4).

R
2
P
3
O
K
I
Q
N
J
Z
X
L
4
Y
M
1
Les noeuds: I, J, K, L, M, N, O, P, Q, R
Les faces: 1(J-I-K), 2(I-J-L), 3(J-K-L), 4(K-I-L)
Fig.III.4 : Elément
tétraèdre quadratique isoparamétrique à 10
noeuds.
L'ANSYS Workbench effectue un maillage automatique (par
défaut) .Si on aurait besoin de le raffiner, on doit intervenir dans le
changement des paramètres choisis par défaut. Les figures III.5,
6 donnent respectivement un maillage volumique d'un disque et une plaquette de
frein rainurée.

42
Fig.III.5 : Maillage d'un disque
Fig.III.6 : Maillage d'une plaquette rainurée
Noeuds 33256 éléments 17393. Noeuds 2669
éléments 1266.
Chapitre III Modélisation Thermomécanique du
Problème
43
III.3.5 Détermination de la pression de
contact
Le principe du modèle généralement dans
la littérature prendre en compte à chaque instant
l'évolution du contact disque-plaquette. Cette répartition du
contact permet de calculer et d'appliquer le flux de chaleur crée par
frottement. Dans cette étude, le calcul mécanique initial vise
à déterminer la valeur de la pression de contact (supposée
constante) entre le disque et la plaquette. On suppose que 60% des forces de
freinage est soutenu par les freins avant (les deux rotors), soit 30 % pour un
seul disque [28]. La force de rotor pour un véhicule typique est
calculée en utilisant les données de véhicule contenues
dans le tableau III.3, ayant pour résultat :
Masse du véhicule- M [kg]
|
|
1385
|
La vitesse initiale - [m/s]
|
|
60
|
Le temps d'arrêt-
|
|
45
|
Le rayon effectif du disque - [mm]
|
|
100,5
|
Le rayon de la roue -[mm]
|
|
380
|
Le coefficient de frottement disque/plaquette
|
[/]
|
0 ,2
|
Surface de plaquette [mm2]
|
|
5246,3
|
|
Tableau.III.3 : Données de
véhicule. Les forces travaillant au disque de frein [28] :

La vitesse de rotation du disque se calcule comme suit :

Surface totale du disque en contact avec les plaquettes =
35797 mm2 (Fig.III.7)

Fig.III.7 : Zone de contact
sélectionnée en ANSYS
1 Face : Ac = 35797
mm2
Chapitre III Modélisation Thermomécanique du
Problème

La pression extérieure entre le disque et les
plaquettes se calcule par la force appliquée au disque ; pour une voie
plate, la pression hydraulique est [29] :
Où est l'aire de surface de la plaquette en contact avec
le disque et le coefficient
de frottement. L'aire de zone en contact de la plaquette en
mm2 avec le disque est donnée directement en ANSYS en
sélectionnant cette surface comme indique la couleur vert dans la figure
III.8. Dans le cas d'une plaquette de frein sans rainure, le calcul de la
pression hydraulique exercée est obtenu de la même
manière.

44
Fig.III.8 : 2 Faces Aire = 5246,3
mm2 Fig.III.9 : 1 Corps : Volume= 85534
mm3
Après la visualisation des différends maillages
; en sélectionnant sur les tâches de l'applet du maillage, on
ouvre l'ensemble disque-plaquette sur le modèle FE, on
obtient le résumé de cette importation, ce qui
représenté sur les figures III.10, 11

Fig.III.10 : Modèle FE
d'un ensemble disque-plaquette.
Nom du corps
|
Noeuds
|
Eléments
|
Disque
|
34799
|
18268
|
Plaquette 1
|
1446
|
650
|
Plaquette 2
|
1461
|
660
|
Zone de contact 1
|
0
|
914
|
Zone de contact 2
|
0
|
83
|
|
Tableau III.4 : Résultats
d'un maillage d'un type d'éléments
tétraèdre
quadratique à 10 noeuds.
Chapitre III Modélisation Thermomécanique du
Problème

Contact
Triangulaire
Quadratique
Cible
Triangulaire
Quadratique
45
Fig.III.11 : Zone de
contact.
Nom de type d'élément générique
|
Nom ANSYS
|
Description
|
Tétraèdre quadratique à 10 noeuds
|
Mesh200
|
Meshing Facet
|
Contact triangulaire quadratique
|
Conta174
|
3D 8 Node Surface to Surface Contact
|
Cible triangulaire quadratique
|
Targe170
|
3D Target Segment
|
|
Tableau III.5 :
Résumé des types d'éléments.
III.3.6 Modélisation du modèle de contact de frein
à disque
Pour appliquer le modèle mécanique
d'élément finis avec un rotor, nous considérons les
hypothèses suivantes :
· La pression de freinage est uniformément
répartie sur la zone de contact du disque et les plaquettes.
· Le coefficient de frottement reste constant pendant le
freinage.
· Les matériaux du disque et des plaquettes sont
homogènes et leurs propriétés sont invariables avec la
température.
III.3.6.1 Modélisation du chargement et des
conditions aux limites
Les différentes conditions aux limites imposées
au modèle éléments finis du disque et de la plaquette en
configurations encastrées, compte tenu de son environnement direct, sont
les suivantes (Figure III.12) :
III.3.6.1.1 Conditions aux limites appliquées
au disque
· La rotation du disque est prise en compte, en tenant
sa vitesse angulaire imposée et constante w=157,89 rad/s
suivant y [30].
· Les noeuds du diamètre intérieur sont
bloqués suivant la direction radiale et axiale en laissant la direction
tangentielle libre (support cylindrique).
· Le disque est encastré par les 6
perçages au niveau du bol de fixation qui permettent de maintenir le
disque sur le moyeu dans les trois directions de l'espace.
Chapitre III Modélisation Thermomécanique du
Problème
46
III.3.6.1.2 Conditions aux limites et chargement
appliquées aux plaquettes
Les conditions aux limites appliquées aux plaquettes
sont définies en fonction des mouvements autorisés par
l'étrier. En effet, un des rôles de l'étrier est de retenir
les plaquettes qui ont la tendance naturelle à suivre le mouvement du
disque lorsque les deux structures sont en contact. L'étrier maintient
aussi les plaquettes dans la direction z.
Ainsi, les conditions imposées aux plaquettes sont :
· La plaquette est encastrée sur ses bords dans
le plan orthogonal à la surface de contact, autorisant ainsi un
mouvement de corps rigide dans la direction normale au contact tel que l'on
peut le trouver dans un montage de frein automobile [30].
· Un support fixe dans la plaquette
extérieure.
Le chargement mécanique est représenté
par les plaquettes qui viennent presser le disque et qui engendrent des
frottements dus à la rotation de ce dernier. L'effort de serrage des
plaquettes provient de la pression d'un piston hydraulique cylindrique sur la
plaquette où on a seulement une condition de chargement :
· Une pression P de 1 MPa
appliquée sur la plaquette intérieure.
Sans oublier la création des interactions de contact
(frottement ...) entre les deux pièces. On introduit un coefficient de
frottement u pour définir le frottement. Celui-ci dépend
de beaucoup de paramètres (pression, vitesse de glissement,
température, humidité, etc.) et varie donc au cours d'un
freinage. Pour des raisons de simplicité, il est pris constant et
égal à u = 0,2 dans les calculs.

Fig.III.12: Conditions aux
limites et chargement imposées
au disque-plaquette.
Gardant pour ce but le même chargement et même
conditions aux limites qu'au par avant, comme le montre la figure III.13.
Essayons maintenant, le cas d'un étrier fixe à deux pistons

Chapitre III Modélisation Thermomécanique du
Problème
47
Fig.III.13: Conditions aux
limites et chargement imposées
au disque-plaquette à deux
pistons.
III.3.7 Gestion du contact
Nous avons dit que le code de calcul ANSYS repose sur des
formulations telles que (méthode Lagrangien augmenté,
méthode par pénalité, MPC, Lagrangien normal) pour la
résolution numérique du problème de contact.
Dans notre étude, nous considérons une
méthode de pénalité pour la gestion du contact
plutôt que l'utilisation des multiplicateurs de Lagrange. Plusieurs
arguments motivant ce choix En premier lieu, c'est une méthode simple
à adapter et elle ne génère pas d'inconnues
supplémentaires [30]. D'autre part, les mesures
considérées de compression de la plaquette sur un support rigide
montrent un comportement non-linéaire, principalement dû aux
aspérités des surfaces de contact et/ou au comportement
élastique non-linéaire du matériau de plaquette. Une loi
de Signorini (et donc l'utilisation des multiplicateurs de Lagrange) simule un
contact "dur" entre les aspérités, la méthode de
pénalité non-linéaire simule un contact plus souple entre
les aspérités et la véracité d'une méthode
plutôt qu'une autre est difficilement évaluable tant que l'on ne
dispose pas de données expérimentales de
référence.
III.3.8 Lancement de calcul
Une fois les données sont installées, il ne
reste qu'à lancer la résolution. Le choix d'un résultat
parmi tant d'autres obtenus se fait selon le besoin de l'étude à
effectuer. Une fois les résultats obtenus, il ne reste qu'à
varier certains paramètres (caractéristiques physiques) par
rapport à certains autres afin de déterminer les plus influents.
Par exemple de notre étude (le module de Young, la vitesse de rotation
du disque, le coefficient de frottement ...etc.)
III.4 MODELISATION DU COUPLAGE THERMOMECANIQUE III.4.1
Introduction
Dans le cadre de notre étude, nous allons
particulièrement nous intéresser à la
thermoélasticité dans des cas où les problèmes
thermique et mécanique sont découplés.
Chapitre III Modélisation Thermomécanique du
Problème
48
Avant d'aller plus loin, insistons sur le fait que si la
résolution du problème thermoéIastique dans son aspect
couplé, requiert l'analyse simultanée de la température et
des déformations, la résolution dans un cas
découplé se fait en deux étapes distinctes :
· Déterminer le champ de température
indépendamment des conditions mécaniques.
· Evaluer les déformations produites par ce champ de
température.
III.4.2 Méthode de la résolution
Un calcul de structure prenant en compte les deux influences
(mécanique et thermique) est souvent difficile à réaliser
(temps de calcul long, problème de convergence). Au contraire de ce
couplage fort, lorsqu'on parvient à négliger les deux influences,
le couplage devient faible et le calcul devient plus aisé. On peut
distinguer deux types de couplage faible :
1) la loi de comportement dépend peu de la
température. Dans ce cas, le problème mécanique est
indépendant du problème thermique.
2) les sources de chaleur dues aux déformations
mécaniques sont négligeables devant les sources externes. Dans ce
cas, le problème thermique est indépendant du problème
mécanique.
Dans le cas d'un changement d'état, la quantité
d'énergie mise en jeu est telle qu'on néglige les sources de
chaleur interne.

t+?t
Equation de Fourier Champ de
température
Equation d'équilibre
Loi de
comportement
Déformation Contrainte
Fig.III.14 : Schéma du
couplage thermomécanique.
III.4.3 Formulation du problème
La présente étude a pour but d'analyser le
problème de contact thermo élastique des freins à disque
avec la génération de friction de la chaleur en employant la
méthode des éléments finis [31]. La simulation
numérique pour le comportement thermo élastique du frein
Chapitre III Modélisation Thermomécanique du
Problème
à disque est d'être obtenue pour l'état
d'arrêt simple. Il implique deux types de problème, un
problème thermique et un problème élastique.
III.4.3.1 Problème thermique
Ce module implique de trouver la distribution de la
température et la distribution de flux de la chaleur dans le disque
à de divers endroits. Il peut être trouvé en
résolvant l'équation en état instationnaire de conduction
de la chaleur dans les coordonnées cylindriques avec les conditions aux
limites appropriés.
L'équation en état instationnaire de conduction
de la chaleur d'état est donnée par [31]:

Plaquette
Plaquette
Disque
S1
S2
Si
FS1
FS2
Pression hydraulique
49
Fig.III.15 : Modèle de
disque de frein Fig.III.16 : Modèle élastique en
élément fini
et plaquettes de disque et plaquette.

Plaquette
Plaquette
Disque
Fig.III.17 : Modèle
élément fini élastique
pour l'analyse
thermoélastique transitoire [32].
La figure III.16 montre le modèle élément
fini du disque et plaquettes avec des conditions aux limites [32]. La pression
hydraulique est appliquée à la frontière le long du
Chapitre III Modélisation Thermomécanique du
Problème
rayon de la plaquette du côté de piston et la
condition d'immobilité dans la direction axiale est appliquée
à la frontière le long du rayon de côté de doigt.
Le modèle en élément fini thermique du
disque de frein avec les conditions aux limites est représenté
sur la figure III.17. Les conditions aux limites de convection sont
imposées sur toutes les frontières pour considérer des
états plus réalistes de la chaleur.
Température initiale est T0 = 20° C dans
cette étude.
Le disque entièrement et la partie latérale des
plaquettes sont soumis à la convection. Après l'application de la
méthode de Galerkin, on obtient les matrices d'élément
:

Où


Où et les fonctions de forme qui sont définies pour
le mode iso paramétrique
nodal de l'élément en coordonnées
cylindriques, N est le nombre des surfaces du disque. En employant la
technique de différence finie en arrière pour le terme
dérivatif

Et par substitution dans, nous avons

50
Pour résoudre l'équation (III.41), la technique
finie d'élément transitoire est employés, pendant la
simulation, les flux de la chaleur sont assignés à
l'élément dans la zone de contact à chaque pas de
temps.
III.4.3.1.1 Flux de chaleur
Pendant le freinage, les énergies cinétiques et
potentielles pour un véhicule mobile sont converties en énergie
thermique par la chaleur de friction entre le disque de frein et les
plaquettes. La chaleur de friction est générée sur la
surface du disque et les plaquettes de frein. Dans le présent travail,
nous considérons la quantité de génération de la
chaleur par l'usure est très petit relativement à la chaleur
produite par frottement, ainsi l'effet de l'usure
Chapitre III Modélisation Thermomécanique du
Problème
51
matériel est négligé. Le flux de chaleur par
friction produit dans l'interface du disque et de la plaquette peut être
exprimé comme suit [33] :
Où est le coefficient de frottement, P est la
pression de contact, v la vitesse de glissement,
qui est définie par la vitesse angulaire du disque et le
rayon du disque de frein r.
Toute la chaleur produite sur le contact de frottement
l'interface q est la somme du
flux de la chaleur dans le disque et le flux de la chaleur dans
la plaquette .L'énergie
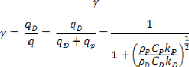
relative de freinage qui est absorbé par le disque de
frein est :
Dans l'équation ci-dessus, est la chaleur
spécifique de plaquette, est la
conductivité thermique de plaquette, est la densité
de plaquette, est la chaleur
spécifique de disque de frein, est la conductivité
thermique du disque de frein, et est la
densité de disque de frein. La génération
totale de la chaleur absorbée par le rotor est dedans limites des
propriétés matérielles du disque de frein et plaquette
[34, 35].
III.4.3.2 Problème élastique
La contrainte mécanique est liée à l'effort
par une équation constitutive suivante [31] :
Où [D] est la matrice de propriété
matérielle
La contrainte totale, somme des contraintes mécaniques et
thermiques, est donnée par :
Où les indices supérieurs mé et
th dénotent des contraintes mécaniques et thermiques,
respectivement,
L'équation (III.44) devient :
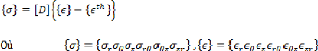
Pour un matériau isotrope, le changement de
température a comme conséquence une expansion de corps ou un
rétrécissement mais aucune déformation. En d'autres termes
le changement de température affecte les contraintes normales sans
contraintes de cisaillement. Le vecteur thermique de contrainte est
exprimé ainsi :
Chapitre III Modélisation Thermomécanique du
Problème
Dans lequel est le coefficient de la dilatation thermique et AT
indique l'écart de température. La contrainte totale est
exprimée en termes de déplacements nodaux comme :
Dans laquelle [B] est la matrice de cinématique
Substituons III.47 dans III.46, nous avons :
On applique la technique des moments résiduelle à
l'équation (III.48) on trouve les résultats dans
l'équation suivante :
Où la matrice de rigidité élémentaire
pour l'élasticité est donnée sous la forme :
et les vecteurs thermiques et mécaniques de force qui sont
dénotés comme suit :
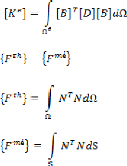
Le problème élastique est résolu en
employant l'équation constitutive .pendant la modélisation
numérique, une particulière attention est exigée pour
satisfaire la continuité des déplacements normaux sur la surface
de contact et les conditions de recouvrement [30].
Les conditions suivantes des déplacements et des
efforts sont imposées à chaque paire de noeuds sur
l'interface.
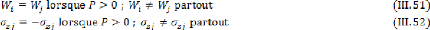
Les conditions suivantes de contrainte de la
température et de flux de chaleur sont imposées à chaque
paire de noeuds sur l'interface
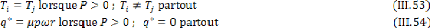
52
III.4.4 Analyse en ANSYS Multiphysics
Dans cette étape et à l'aide du code de calcul
élément fini ANSYS, nous allons faire une modélisation du
contact sec du disque et plaquette tout en montrant l'effet de la
Chapitre III Modélisation Thermomécanique du
Problème
53
température dans son comportement (contraintes et
déformations globales du modèle). La première étape
consiste à déterminer le champ de la température en 3 D
à l'aide d'une analyse thermique sous ANSYS , ensuite une analyse
mécanique structurale statique comme nous l'avons vu
précédemment , le couplage thermique s'effectuera par condition
thermique à une température non uniforme tout en prend
l'environnement thermique du modèle, Pour cette raison, la commande
« condition thermique » sera utilisée pour traiter le
problème couplé thermomécanique et gérer le
régime transitoire.
Pour étudier le comportement thermo élastique
transitoire du disque de frein, la simulation en ANSYS est obtenue dans la
durée totale de freinage ( t= 45 s). Réellement la variation de
la vitesse tournante pendant l'opération de freinage doit être
déterminée la dynamique de véhicule [36]. Cependant, dans
cette étude la vitesse tournante du disque a été
considérée comme une valeur connue ( =157.89 rd/s), la pression
hydraulique Ph est
assumée linéairement grimper jusqu'à
1 MPa. Les propriétés matérielles adoptées
dans cette simulation sont récapitulées dans le tableau III.6.
|
Propriétés matérielles
|
Plaquette
|
Disque
|
|
Conductivité thermique, k (w/m.°C)
|
5
|
57
|
|
Densité, (kg/m3)
|
1400
|
7250
|
|
La chaleur spécifique, c (J/Kg. °C)
|
1000
|
460
|
|
Coefficient de Poisson,
|
0,25
|
0,28
|
|
Dilatation thermique, (10-6 / °C)
|
10
|
10,85
|
|
Module élastique, E (GPa)
|
1
|
138
|
|
Coefficient de frottement
|
0,067
|
0,2
|
|
Conditions d'opération
|
|
|
|
Vitesse angulaire (rd/s)
|
|
157.89
|
|
Pression hydraulique, P (MPa)
|
|
1
|
Tableau III.6 :
Propriétés thermo-élastiques
utilisées dans la simulation.

Fig.III.18 : Modèle de
simulation d'un disque frein ventilé-plaquette [37].
Selon la vraie dimension du disque freinant et les plaquettes,
la modélisation pour l'accouplement thermique-structure transitoire
tridimensionnel de pendant le processus de freinage est établi. Il est
basé sur l'effet de la source de chaleur mobile avec la variation
Chapitre III Modélisation Thermomécanique du
Problème
54
coulissante relative et l'accouplement de l'écoulement
thermique de friction entre le disque et la plaquette. En employant le champ
non linéaire de multiphysics du logiciel d'Ansys, le processus freinant
du frein à disque est simulé [38]. La distribution de la
contrainte dans le disque et les pressions de contact d'interface sont
analysés..La période variationnelle du
température/contrainte augmente avec le temps freinant prolongé.
Et la raison de la rupture de fatigue thermique radiale du disque est
discutée.
Environnement
Solution
t+?t
Température
Conditions initiales et aux limites
Analyse thermique
Pression
Environnement
Solution
t+?t
Conditions initiales et aux limites
Contraintes et déformations
Condition thermique
Début
Analyse structurale statique
Fig.III.19 : Organigramme de
calcul thermomécanique en ANS VS Multiphysics.
Fig.III.20 : L'analyse du
couplage thermoélastique en ANS VS Multiphysics.
Chapitre IV Résultats et Discussions
IV.1 INTRODUCTION
Dans cette étude, on essaye de mettre en évidence
un problème d'échauffement excessif du disque, et de visualiser
les résultats pour pouvoir en tirer les modifications qui s'imposent sur
la conception du disque de frein du point de vue des matériaux et du
profile.
Notre travail consiste à étudier le comportement
thermique d'un disque de frein en trois dimensions, lequel inclut le flux de
chaleur généré à l'intérieur de celui-ci,
les températures maximales et minimales etc. Le scénario
analysé est un freinage d'arrêt. En pratique, le système de
freinage baigne dans un flux d'air, plus ou moins forcée selon le
système, qui participe au refroidissement du disque et des plaquettes.
Ce flux d'air est régi par les lois de l'aérodynamique. A l'aide
du code ANSYS CFX, on calcule alors les valeurs du coefficient d'échange
thermique h en fonction du temps .Ces valeurs seront utilisés
pour déterminer le comportement thermique du disque en régime
transitoire.
Dans cette modélisation, seul le disque est pris en
compte, les plaquettes sont remplacées par leur effet,
représenté par un flux de chaleur généré
à l'interface disque-plaquette qui est l'aire totale de contact (les
deux côtés du disque) (Fig.IV.2).

55
Fig.IV.1 : Ensemble
disque-plaquette. Fig.IV.2 : Application du flux de
chaleur
L'exemple traité est un disque de frein d'un
véhicule particulier (Fig.IV.1). Le mode de freinage choisi est
du type 0 imposé par les normes européennes
(ECE-13).
IV.2 FICHE TECHNIQUE DU VEHICULE CHOISI
Dans cette étude, on a choisi le véhicule
Citroën de type CX GTi Turbo 2
dont les caractéristiques techniques sont indiquées
dans le tableau IV.1 :
|
Type du moteur
|
4 cylindres en ligne
|
Freins avant
|
Disques
|
|
Energie
|
Essence
|
Longueur
|
465 cm
|
|
Disposition
|
Longitudinal avant
|
Largeur
|
177 cm
|
|
Cylindrée
|
2500 cc
|
Hauteur
|
136 cm
|
|
Puissance
|
168 chevaux à 5000 tr/min
|
Poids
|
1385 kg
|
|
Couple
|
30.0 mkg à 3250 tr/min
|
Poids/Puissance
|
8.24 kg/cv
|
|
Boite de vitesse
|
5 rapports
|
Vitesse max
|
223 km/h
|
Tableau. IV.1 : Fiche technique
du véhicule Citroën CX GTi Turbo 2.
Chapitre IV Résultats et Discussions
IV.3 DESCRIPTION DU DISQUE DE FREIN VENTILE ET PLEIN ET
DES PLAQUETTES
L'étude porte sur un disque de frein ventilé en
fonte grise FG à haute teneur en carbone ; il s'agit du disque (262 29
mm) qui équipe certaines versions des véhicules

Fig.IV.3 : Disque ventilé
(vue en contour).
Citroën CX GTi Turbo 2 (Fig.IV.3). V' Disque
ventilé :
Diamètre extérieur A = 262 mm Diamètre
intérieur B = 66 mm Epaisseur TH = 29 mm
Hauteur totale C = 51 mm
Nombre de trous = 06
Nombre d'ailette = 36
Matériaux/Composition = Fonte Grise Type de disque =
Ventilé à l'intérieur
Ailettes Trou de fixation

6
10°
TH
C
B
A
56
Fig.IV.4 :
Caractéristiques géométriques du disque
ventilé.
Chapitre IV Résultats et Discussions
57
y' Disque plein :
Pour faciliter la comparaison des résultats de
simulation, les dimensions géométriques des deux variantes de
disques, disque plein et disque ventilé sont les mêmes
(Fig.IV.5).

Fig.IV.5 : Disque plein.
|
Plaquettes de frein :
y' Épaisseur : 15 mm
y' Largeur : 61 mm
y' Hauteur : 139 mm
y' Largeur de la rainure : 3 mm
y' Profondeur de rainure : 6 mm
|
|
Fig.IV.6 : Plaquettes de frein
pour Citroën.

5
15
3
6
139
61
Fig.IV.7 :
Caractéristiques géométriques des
plaquettes de frein.
IV.4 DETERMINATION DU COEFFICIENT D'ECHANGE PAR
CONVECTION (H) IV.4.1 Introduction
L'analyse thermique du système de freinage exige une
détermination précise de la chaleur totale de friction produite
ainsi que la distribution de cette énergie entre le disque et les
garnitures. Lors d'un freinage d'urgence, toute la chaleur produite à
l'interface est égale à la chaleur absorbée par le disque
et les garnitures.
Lorsqu'un véhicule freine, une partie de la
température de friction s'échappe dans l'air grâce à
la convection et au rayonnement. Par conséquent, la détermination
des coefficients de transfert de chaleur est très importante. Il est,
cependant, très difficile de les calculer avec précision, car ils
dépendent de la forme du système de freinage, de la vitesse de
déplacement du véhicule et par conséquent de la
circulation de l'air [39]. Ici
Chapitre IV Résultats et Discussions
58
la modélisation de la convection se révèle
être le problème principal car elle est liée aux conditions
aérodynamiques du disque. On s'intéresse dans cette partie au
calcul du coefficient d'échange thermique (h).
Ce paramètre doit être exploité pour visualiser la
distribution tridimensionnelle de la température du disque.
IV.4.2 Modélisation en ANSYS CFX
La première étape de l'étude consiste
à créer le modèle CFD qui contient les
domaines à étudier en Ansys Worbench. Dans notre
cas, on a pris seulement un quart du disque puis on a définit le domaine
de l'air entourant ce disque .Dans cette étape, l'ANSYS ICEM CFD
va préparer les différentes surfaces pour les deux
domaines afin de faciliter le maillage, lesquelles seront exportée vers
cfx à l'aide de la commande « Output to cfx
». Après avoir obtenu le modèle sur CFX Pre et
avoir spécifié les conditions aux limites à l'aide de
l'option « boundary conditions », on définit
ses paramètres principaux sur CFX. Le disque est attaché à
quatre surfaces adiabatiques et deux surfaces de symétrie dans le
domaine fluide dont la température ambiante de l'air est égale
à 20 °C [40].
La figure (IV.8) montre le modèle CFD
élaboré qui sera utilisé dans ANSYS cfx
Pre.
Parois symétriques de l'air

Sortie
Disque
Paroi adiabatique de l'air
Air à 20 C°
Entrée
Fig.IV.8 : Modèle de CFD
de disque de frein.
IV.4.3 Préparation de la géométrie
et du maillage
IV.4.3.1 Domaine fluide :
Vu la symétrie dans le disque, on a pris uniquement le
quart de la géométrie du domaine fluide (Fig.IV.09, Fig.IV.10,
Fig.IV.11) en utilisant le logiciel ANSYS ICEM CFD.
Chapitre IV Résultats et Discussions
Sortie de l'air

Entrée 1 de l'air
DR1
DSYM1
DV1
Domaine interface fluide-solide
Entrée 2 de l'air
Fig.IV.9 : Définition des
surfaces du domaine fluide.

59
Fig.IV.10 : Domaine fluide
Fig.IV.11 : Domaine fluide
(Vue de surface solide). (Vue de surface
transparente).
IV.4.3.1.1 Préparation du Maillage :
Cette étape consiste à préparer le
maillage du domaine fluide. Dans notre cas, on a utilisé un
élément tétraédrique linéaire avec 30717
noeuds et 179798 éléments (Fig.IV.12).

Fig.IV.12 : Maillage du domaine
fluide.
Chapitre IV Résultats et Discussions
IV.4.3.2 Disque de frein
Pour des raisons de symétrie du disque , on a pris
uniquement le quart de la géométrie dans le cas du disque
ventilé et plein ; on a gardé la forme tétraédrique
pour générer le maillage des disques (Fig.IV.17 , Fig.IV.18) .

SV23
SF1
SF3
SV4
SYM2
SC3
ST3
SYM3
ST4 ST2 S
SV22
SV21
SC4
SC1
Fig.IV.13 : Définition des
surfaces du disque plein.

SC3 SF2
ST2 SV4
ST3
SF2
SPV4
SV21
SPV3
ST4 SYM2 SC1 SYM3
SV22
SV23
SC3
SF1
Fig.IV.14 : Définition des
surfaces du disque ventilé.

60
Fig.IV.15 : Disque plein.
Fig.IV.16 : Disque ventilé.

Chapitre IV Résultats et Discussions
61
Fig.IV.17 : Maillage du disque
plein Fig.IV.18 : Maillage du disque ventilé
(Nombre d'éléments 272392). (Nombre
d'éléments 27691).
IV.4.3.3 Etude du maillage
On a exécuté un raffinement sur le disque et sur le
domaine fluide. Le tableau IV.2 donne le nombre d'éléments pour
le maillage grossier et raffiné pour les types de disque de frein. Plus
le maillage est raffiné, plus la qualité de la solution est
meilleure.
|
Domaine
|
Disque plein
|
Disque ventilé
|
|
Nombre d'éléments
|
Nombre d'éléments
|
Nombre d'éléments
|
|
Maillage 1
|
167736
|
272392
|
27691
|
|
Maillage 2
|
1387512
|
253148
|
252994
|
Tableau.IV.2 : Nombre
d'éléments des différents maillage.
IV.4.4 Flux d'air en mécanique des fluides
L'écoulement dans le sillage des véhicules
automobiles peut-être séparé en deux structures ; la
première issue d'une ligne de séparation bidimensionnelle
génère un écoulement de base avec une pression statique
constante et une vitesse de transport voisine de zéro et la seconde est
issue d'une séparation tridimensionnelle de l'écoulement et
engendre des zones tourbillonnaires [39].
Ces deux effets produisent la traînée de forme
à laquelle s'ajoute une traînée de pression
résultant de la distribution de pression sur la géométrie
du véhicule et une traînée de frottement due au
cisaillement du fluide dans la couche limite. L'ensemble constitue la
traînée aérodynamique globale du véhicule. En
aérodynamique automobile, les écoulements fluides sont de nature
turbulente et dans les conditions courantes d'utilisation, le
déplacement du véhicule s'effectue à un nombre de Mach
inférieur à 0,3.
Chapitre IV Résultats et Discussions
IV.4.5 Equations caractérisant un domaine
fluide
Les équations qui régissent un domaine
d'écoulement sont comme suit [39]:

62
La première équation est l'équation de
continuité pour un fluide incompressible, la seconde représente
l'équation de Navier-Stockes pour un fluide Newtonien et la
troisième est l'équation de l'énergie pour un nombre de
Mach petit .
Dans notre cas, l'écoulement d'air (inflow) est
laminaire jusqu'au moment où il rencontre le disque. Une partie de ce
flux devient turbulente.
IV.4.6 Modèle physique
Après le maillage, on définit dans cette
étape les paramètres des différents modèles afin de
commencer l'analyse. Pour notre cas, on définit le domaine fluide qui
est l'air à 20 ° C et le domaine solide.
IV.4.6.1 Etat stationnaire
Dans un premier temps, on valide les modèles choisis et
on procède à une analyse en régime stationnaire
(Steady State). On doit activer le calcul du transfert de
chaleur : « Heat Transfer » dans Thermal
Energy Options. Dans le domaine de l'air, on prend la pression de
référence égale à 1 atmosphère et la
pression relative à la sortie est nulle.
IV.4.6.1.1 Initialisation de la turbulence
On choisit un écoulement turbulent de type k-å.
Ceci nous permet d'observer la turbulence autour du disque. Pour entamer
l'analyse du comportement thermique, on ajoute les paramètres suivants
pour produire et éditer les expressions en ANSYS CFX PRE :
V' Domaine fluide
Vitesse de l'air à l'entrée : V ent = 28 [m/s],
V' Domaine disque
Flux entrant : FLUX ent = 4197027.47 [W/m2].
FLUX ent : Flux entrant stationnaire.
Ve : Vitesse d'entrée de l'air stationnaire.
Chapitre IV Résultats et Discussions
63
Chapitre IV Résultats et Discussions
IV.4.6.1.2 Définition du modèle
matériau
On introduit les matériaux nécessaires au
modèle. Ainsi pour le disque, nous avons introduit dans la
bibliothèque les 03 sortes de fontes (FG 25 AL, FG 20, FG 15) en
spécifiant leurs caractéristiques physiques.
IV.4.6.1.3 Définition du modèle
Conditions Limites
La première étape consiste à
sélectionner les faces d'entrée et de sortie du flux de la
boîte. Ces options se trouvent dans le menu insert «
Boundary condition » dans le CFX Pre. La face d'entrée du
flux (Inlet).
La face de sortie du flux (Outlet).
Des conditions aux limites sont également
nécessaires sur les deux domaines. On utilise les conditions «
Wall » et « Symmetry ». Ceci
est obligatoire, car on peut régler un certain nombre de
paramètres sur ces C.L., tels que le flux entrant dans le disque, ou une
source de chaleur.
IV.4.6.1.4 Application des interfaces de domaine
Les domaines interfaces sont utilisés
généralement pour la connexion ou l'assemblage des domaines. Les
surfaces situées entre la région d'interaction (air-disque) sont
déclarées comme interface fluide-solide.
IV.4.6.1.5 Méthode de résolution
transient
Pour résoudre le problème, la méthode
dite transitoire ou du « transient » est
appliquée. Pendant la simulation de freinage, les différentes
valeurs du flux thermique sont assignées aux éléments
dépendants de la zone de contact à chaque pas de temps dans le
modèle. Le problème de convection peut être
considéré comme un problème tridimensionnel de transfert
thermique à plusieurs reprises, en utilisant un incrément de
temps plus petit tout en incluant la distribution initiale de la
température. Le pas de temps est régi par la variation de la
vitesse de rotation de disque. La méthode du transient en
éléments finis permet de simuler le transfert thermique dans un
disque tridimensionnel avec une vitesse variable et un flux variable .
IV.4.6.2 Etat instationnaire
D'une manière analogue, on ajoute les paramètres
suivants pour produire et éditer les expressions en ANSYS CFX PRE afin
d'entamer l'analyse thermique:
y' Domaine fluide
Vitesse à l'entrée : V ent inst = Vent - Va t,
64
V' Domaine disque
Flux entrant : FLUX inst = (CF) (V ent inst),
CF = 149893,838.
. V ent inst = Vent - Va t
FLUX inst : Flux entrant instationnaire.
V ent inst : Vitesse d'entrant de l'air instationnaire.
IV.4.7 Conditions temporelles
Pour les deux régimes (stationnaire et instationnaire),
on a pris les mêmes conditions
temporelles :
Temps total = 3,5 [s],
Pas du temps = 0,01 [s],
Temps initial = 0 [s],
Avant de lancer le calcul et l'analyse en ANSYS CFX PRE , on
doit vérifier tout le
modèle pour s'assurer que le modèle ne contient pas
d'erreurs.
IV.4.8 Lancement du calcul et affichage écran
des données
Après vérification du modèle et des
conditions aux limites, on démarre le calcul en ouvrant le menu
File puis en cliquant sur Write solver file
[41] . Les résultats sont stockés dans un fichier.
IV.5 ANALYSE DES RESULTATS
IV.5.1 Cas stationnaire
a. Disque plein
Dans ce régime, on considère que le comportement du
disque ne varie pas avec le temps. La figure IV.19 montre la distribution du
coefficient de transfert (h) dans un disque plein.

Fig.IV.19: Répartition de
coefficient de transfert de chaleur sur
un disque plein dans le cas
stationnaire (FG 15).
Chapitre IV Résultats et Discussions
65
|
FG 15
|
|
Surface
|
hmoy= [W m-2 k-1]
|
|
SC1
|
25,29168
|
|
S
|
5,18003
|
|
SC3
|
2,922075
|
|
SC4
|
11,77396
|
|
SF1
|
111,20765
|
|
SF3
|
53,15547
|
|
ST2
|
23,22845
|
|
ST3
|
65,6994
|
|
ST4
|
44,26725
|
|
SV1
|
81,37535
|
|
SV2
|
71,75842
|
|
SV3
|
41,83303
|
|
SV4
|
65,82545
|
Tableau IV.3 : Valeur du
coefficient de transfert de chaleur de différentes
surfaces dans le
cas stationnaire pour un disque plein (FG 15).
b. Disque ventilé

Fig.IV.20 : Répartition de
coefficient de transfert de chaleur sur un disque
ventilé dans le cas
stationnaire (FG 25 AL).

Fig. IV.21 : Répartition
de coefficient de transfert de chaleur sur un disque
ventilé dans le
cas stationnaire (FG 20).

Fig.IV.22 : Répartition de
coefficient de transfert de chaleur sur un disque
ventilé dans le cas stationnaire (FG 15).
Chapitre IV Résultats et Discussions
66
Les figures (IV.20, IV.21, IV.22) montrent les champs de
distribution du coefficient d'échange (h) pour les trois types
de matériaux. On constate que le comportement de (h) dans le
disque ne dépend pas du matériau choisi. La distribution de
(h) dans le disque n'est pas la même que celle existante dans la
littérature.
|
Matériau
|
FG 25
|
FG 20
|
FG15
|
|
Surface
|
hmoy= [W m-2 k-1]
|
|
SC1
|
54,1623
|
53,92603
|
53,8749
|
|
S
|
84,6842
|
83,7842
|
83,6516
|
|
SC3
|
44,4171
|
44,3485
|
44,32945
|
|
SF1 et 2
|
135,403
|
135,0584
|
135,0006
|
|
SF3
|
97,1709
|
95.0479
|
94,8257
|
|
SPV1
|
170,647
|
171.4507
|
171,5695
|
|
SPV2
|
134,081
|
134.3285
|
134,3615
|
|
SPV3
|
191 ,244
|
191.9436
|
192,0391
|
|
SPV4
|
175,166
|
176,1339
|
176,2763
|
|
ST1
|
113,609
|
114,3962
|
114,3915
|
|
ST2
|
35,0993
|
34,47225
|
34,3473
|
|
ST3
|
68,3315
|
66,33155
|
66,0317
|
|
ST4
|
75,0944
|
72,1235
|
71,6642
|
|
SV1
|
135,529
|
131,1182
|
131,2074
|
|
SV2
|
119,257
|
118,4648
|
118,2039
|
|
SV3
|
46,7022
|
44,8195
|
44,52635
|
|
SV4
|
111,576
|
108,5044
|
108,1817
|
Tableau IV.4: Valeur du
coefficient de transfert de chaleur de Différentes
surfaces dans le
cas stationnaire pour un disque ventilé
(FG 25 AL, FG 20 et FG15).
Le tableau (IV.4) montre les valeurs moyennes du coefficient
d'échange de chaleur (h) calculées par les valeurs
minimales et maximales des différentes surfaces du disque
ventilé. On constate que le type du matériau n'a pas une grande
influence sur la variation du coefficient d'échange thermique
(h). Contrairement au premier cas, on constate que la valeur du
coefficient d'échange thermique (h) est fortement
influencée par le système de ventilation pour le même
matériau (FG 15).
IV.5.2 Cas instationnaire
Les figures IV.23 et 24 montrent respectivement la variation
du coefficient ( h) en régime transitoire des
différences faces du disque plein et ventilé .
Chapitre IV Résultats et Discussions

67
120
Coefficient de transfert h [W m-2
°C-1]
110 100 90 80 70 60 50 40 30 20
SC1
S
SC3
SC4 SF1 SF3
ST2
ST3
ST4
SV1
SV2
SV3
SV4
10
0
-0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Temps [s]
Fig.IV.23: Variation du
coefficient de transfert de chaleur (h) des différentes
surfaces pour
un disque plein dans le cas instationnaire (FG 15).
0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0

Coefficient de transfert h [W m--2
°C-1]
260
240
220
200
180
160
140
120
100
40
20
80
60
0
SC1
S
SC3 SF1 SF3
SPV1
SPV2
SPV3
SPV4
ST1
ST2
ST3
ST4
SV1
SV2
SV3
SV4
Temps [s]
Fig. IV.24 : Variation du
coefficient de transfert de chaleur (h) des différentes
surfaces pour
un disque ventilé dans le cas instationnaire (FG 25 AL).
Chapitre IV Résultats et Discussions

SC1
S
SC3 SF1 SF3
SPV1
SPV2
SPV3
SPV4
ST1
ST2
ST3
ST4
SV1
SV2
SV3
SV4
260
240
Coefficient de transfert h [W m-2
°C-1]
220
200
180
160
140
120
100
80
60
40
20
0
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
68
Temps [s]
Fig. IV.25 : Variation du
coefficient de transfert de chaleur (h) des différentes
surfaces pour
un disque ventilé dans le cas instationnaire (FG 20).
Coefficient de transfert h [W m-2
°C-1]
260
240
220
200
180
160
140
120
100
40
20
80
60
0

SC1
S
SC3 SF1 SF3
SPV1
SPV2
SPV3
SPV4
ST1
ST2
ST3
ST4
SV1
SV2
SV3
SV4
0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0
Temps [s]
Fig. IV.26: Variation du
coefficient de transfert de chaleur (h) des différentes surfaces pour un
disque ventilé dans le cas instationnaire (FG 15).
Les figures IV.24 , 25 , 26 montrent la variation du
coefficient de transfert de chaleur (h) en régime transitoire
des différences faces du disque ventilé avec un matériau
différent.
La comparaison des figues IV.23 et 26 pour les deux
conceptions , disque ventilé et plein ayant le même
matériau (FG 15 ) , montre une très nette diffférence due
uniquement au système de ventilation.
Chapitre IV Résultats et Discussions
69
Les figures IV.27 et 28 montrent à titre d'exemple
l'évolution du coefficient d'échange (h) respectivement
pour la surface SPV2 et SV1 pour chaque pas de temps

Figure IV.27: Variation du
coefficient de transfert de chaleur (h) sur la surface ( SPV2) et
en
fonction du temps pour un disque ventilé (FG 15).

Chapitre IV Résultats et Discussions
70
Figure IV.28: Variation du
coefficient de transfert de chaleur (h) sur la surface (SV1) et en
fonction
du temps pour un disque ventilé (FG 15).
IV.6 EVOLUTION TRANSITOIRE DE LA TEMPERATURE DU
DISQUE
IV.6.1 Introduction
Les gradients thermiques établis dans un disque de frein
contribuent à sa déformation et à l'apparition de
fissures. La perte d'efficacité du frein et l'usure
accélérée sont à l'origine de la surchauffe du
disque et des plaquettes [42].
Chapitre IV Résultats et Discussions
71
Dans cette partie, une modélisation numérique en 3
D est développée pour déterminer le champs de
température du disque de frein. La modélisation est
effectuée en régime transitoire simulant un freinage
d'arrêt.
IV.6.2 Description paramétrique du freinage
La vitesse de véhicule décroit linéairement
avec le temps jusqu'à la valeur 0 (freinage d'arrêt), figure
IV.29.
|
Vitesse [ m s - 1 ]
|
|
-1
Vitesse [m s]
|
3 0 2 0 1 0 0
|
0 1 0 2 0 3 0 4 0
Temps [ s ]
Fig. IV.29 : Vitesse de freinage
en fonction du temps
(Freinage du type 0).
|
-2
Flux de chaleur [W m ]
|
5 x 1 0 6 4 x 1 0 6 3 x 1 0
6 2 x 1 0 6 1 x 1 0 6
0
|
La figure IV.30 représente la variation de flux de chaleur
pendant le temps de simulation.

Flux d e chaleur
0 1 0 2 0 3 0 4 0
T e m p s [ s ]
Fig. IV.30 : Flux de chaleur en
fonction du temps.
IV.6.3 Maillage ou discrétisation
La méthode des éléments finis repose sur
un découpage de l'espace selon un maillage. Plus ce maillage est
resserré plus la solution par la MEF sera précise. Les deux types
de disque sont modélisés par un maillage tridimensionnel à
éléments tétraédriques (TE 10) à 10 noeuds.
Ce dernier a été obtenu automatiquement à l'aide des
options d'ANSYS WB. On note que ce maillage est raffiné dans la zone de
contact disque - plaquettes. Les résultats du maillage sont
présentés dans le tableau IV.5 et les figures IV.31, 32 et 33.

Chapitre IV Résultats et Discussions
72
Fig. IV.31: Maillage d'un disque
plein Fig. IV.32 : Maillage d'un disque à faces
mappées.

-a- : Simple -b- :
Raffinement 1 -c- : Raffinement 2
Fig.IV.33 : Maillage d'un disque
ventilé.
|
Disque plein
|
Disque ventilé
|
|
Noeuds
|
Eléments
|
Noeuds
|
Eléments
|
|
Maillage simple
|
79963
|
46025
|
137289
|
77891
|
|
Raffinement
|
392366
|
256613
|
565662
|
369777
|
|
Raffinement 2
|
963156
|
649417
|
1274836
|
863743
|
|
Faces mappées
|
105308
|
62919
|
170717
|
101088
|
Tableau.IV.5 : Statistiques de
maillage calculées par le Multiphysics [Ansys WB]. IV.6.4
Chargement et conditions aux limites
Le calcul thermique avec ANSYS Workbench,
sera effectué en choisissant le régime de simulation transitoire
et en introduisant les conditions initiales et aux limites et les
propriétés physiques des matériaux. Le chargement
thermique est un flux de chaleur entrant dans le disque au niveau des
plaquettes de frein sur la surface réelle de contact (les deux
côtés du disque). La distribution du flux de chaleur due à
la friction des plaquettes de frein sur les pistes de frottement est
supposée uniforme.
Les conditions aux limites imposées au disque sont la
convection sur toutes les surfaces libres du disque. Les valeurs
imposées de (h) sur chaque surface sont importées
à l'aide de code de calcul CFX.
· Régime transitoire. temps total de freinage = 45
[s]
· Pas du temps initial = 0,25 [s]
· Pas du temps initial minimal = 0,125 [s]
· Pas du temps initial maximal = 0,5 [s]
· Température initiale du disque = 60 [C O]
· Matériau : les trois types de Fonte (FG 25 AL, FG
20, FG 15).
·
Chapitre IV Résultats et Discussions
73
Application de convection de chaleur sur toutes les surfaces
du disque en important les résultats du coefficient d'échange
(h) obtenus en fonction du temps sous forme de courbe dans la
simulation.
· Application du flux sur la surface de contact disque/
plaquettes et on introduit les valeurs obtenus dans le code CFX.
IV.6.5 Résultats et corrélation
IV.6.5.1 Disque plein
La courbe de la température en fonction du temps pour
le disque se distingue par une élévation rapide de
température jusqu'à l'instant t= 1,8839 s et atteint sa valeur
maximale T= 401,55 °C puis elle chute rapidement jusqu'à t= 4,9293
s. Après cet instant, la variation de la température devient
moins importante, Fig.IV.34.

Fig.IV.34 : Variation de la
température Fig.IV.35 : Répartition de la
température
du disque plein en fonction pour un disque plein
d'un
du temps (FG 15). matériau (FG 15).
IV.6.5.2 Disque ventilé

Fig.IV.36: Variation de la
température Fig.IV.37 : Répartition de la
température
du disque ventilé en fonction pour un disque
ventilé d'un
du temps (FG 25 AL). matériau (FG 25 AL).

Chapitre IV Résultats et Discussions
74
Fig. IV.38: Variation de la
température Fig. IV.39: Répartition de la
température
du disque ventilé en fonction pour un disque
ventilé d'un
du temps (FG 20). matériau (FG 20).

Fig. IV.40 : Variation de la
température Fig. IV.41 : Répartition de la
température
du disque ventilé en fonction pour un disque
ventilé d'un
du temps (FG 15). matériau (FG 15).
Les figures IV.36, 38, 40 donnent la variation de la
température en fonction du temps pendant la simulation du freinage. Les
valeurs les plus élevées de température sont sur la
surface de contact entre le disque de frein et les plaquettes. Cette forte
croissance est due à la rapidité du phénomène
physique pendant le freinage à savoir frottement,
microdéformation des surfaces de contact...etc. On note l'influence de
la rotation du disque sur l'évolution de la température qui
correspond à l'alternance échauffement/refroidissement au cours
d'une rotation. Cette alternance échauffement/refroidissement est due au
flux entrant décroissant. Il arrive un instant où le
refroidissement prend le dessus et conduit à la diminution du niveau de
température.
Pour le matériau FG 25 AL , la température
atteint une valeur maximale de T= 380, 7 °C à l'instant t=1,6067 s,
pour le matériau FG 20 Tmax= 351,56 °C à t=
1,8052 s, et pour FG 15 Tmax= 345,44 °C à t= 1,8506 s,
puis elle décroît rapidement jusqu'à l'instant t= 4,8315 s
pour FG 25 AL , pour FG 20 à t=4,9015 s et pour FG 15 à t= 4,8878
s , après lequel , l'écart de température dans le disque
devient moins important jusqu'à l'instant t=10,446 s pour FG
Chapitre IV Résultats et Discussions
75
25 AL , pour FG 20 à t=10,284 s et pour FG 15 à
t=10 ,195 s. L'intervalle de temps [ 0-3,5] correspond à la phase de
convection forcée. A partir de ce temps, on se trouve dans le champ de
la convection naturelle jusqu'à la fin de la simulation.
IV.6.6 Comparaison et interprétation
IV.6.6.1 Comparaison entre les trois types de
fonte
La figure IV.42 montre la comparaison de la variation de la
température en fonction de l'épaisseur à l'instant
où elle atteint sa valeur maximale. Pour les trois types de fonte, on
remarque que l'allure des courbes est presque la même. On constate que
plus on augmente l'épaisseur, plus la température diminue vers le
plan médian du disque. Ceci est dû au stockage d'énergie au
début de freinage qui augmente avec l'épaisseur. Suivant
l'épaisseur du disque, on a une symétrie de couleurs sur les deux
parties. Sur les côtés latéraux, on a une seule couleur
rouge qui correspond au phénomène de la conduction ; par contre
les dégradations des couleurs correspondent au phénomène
de convection. La partie éloignée de la surface de contact en
couleur bleu est complètement refroidi. Plus la conductivité
thermique du matériau est faible, plus la température est
élevée. La fonte FG 15 a une température plus petite que
les deux autres fontes FG 20 et FG AL 25.

Température [°C]
4 00
3 50
3 00
2 50
2 00
1 50
1 00
50
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u e v e n tilé
u e v e n tilé
u e v e
n tilé
|
F G 2 5
F G 2 0
F G 1 5
|
A L
|
|
|
|
|
|
D isq
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 5 1 0 1 5 2 0 2 5 3 0
E p a iss eu r [ m m ]
Fig. IV.42: Variation de la
température en fonction de l'épaisseur pour les trois type de
fontes (FG 25 AL, FG 20 et FG 15).
Chapitre IV Résultats et Discussions
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(D i s q u e v
(D i s q u e v
(D i s q u e v
|
e n tilé F G
e n tilé F G
e n
tilé F G
|
2 5 A L ) 2 0)
1 5 )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 0
3 8 0
3 6 0
3 4 0
3 2 0
Température [°C]
3 0 0
2 8 0
2 6 0
2 4 0
2 2 0
2 0 0
1 8 0
1 6 0
1 4 0
76
7 0 8 0 9 0 1 0 0 1 1 0 1 2 0 1 3 0 1 4 0
R a y o n [ m m ]
Fig. IV.43 : Variation de la
température en fonction de rayon pour les trois type de fontes (FG 25
AL, FG 20 et FG 15).
Sur la figure IV.43, qui représente le profil des
températures en fonction du rayon pour les trois matériaux (FG 25
AL, FG 20, FG 15), on observe que l'allure est la même, la
température maximale se trouve au rayon moyen ce qui correspondant aux
résultats expérimentaux.
D'après les résultats des figures
précédentes, on constate que le FG 15 possède un meilleur
comportement thermique dans la conception des disques de frein.
IV.6.6.2 Comparaison entre disque plein et
ventilé
Dans cette partie, on présente les cartographies de
flux de chaleur total et directionnel ainsi que la distribution de la
température dans un disque ventilé et plein en fonte FG 15 pour
chaque instant de freinage. La distribution de la température du disque
au début freinage (à t=0,25 s) est inhomogène. Selon les
essais expérimentaux effectués par [43], le freinage
débute souvent par la formation de cercles chauds en surfaces du disque
relativement uniformes dans la direction circonférentielle, se
déplaçant radialement sur le disque et se transformant ensuite en
points chauds ((hot spot)). L'apparition du phénomène
des points chauds est due à la dissipation non uniforme de flux de
chaleur.
Concernant le flux de chaleur, on constate d'après les
figures IV.45 et IV.48 que la valeur maximale du flux de chaleur total se
localise au niveau de la gorge calorifique à la fin du freinage (t=3,5
s) ; ceci s'explique par l'augmentation des gradients et les concentrations
thermiques dans cette zone. La gorge calorifique est usinée de
manière à limiter le flux de chaleur provenant des pistes de
frottement et se dirigeant vers le bol du disque de frein afin d'éviter
l'échauffement excessif de la jante et du pneumatique. Lors du
l'échauffement, le disque se tend à se dilater dans les zones
chaudes d'où naissance de contraintes de compression avec
plastification. Par contre, lors du refroidissement, il y a apparition de
Chapitre IV Résultats et Discussions
77
contraintes résiduelles de traction. Le disque est donc
soumis au cours de sa rotation à des contraintes traction
/compression.
a. Disque plein

-a- : à l'instant t=
0,25[s] -b- : à l'instant t= 1,8839[s] -c-
: à l'instant t= 3,5[s]
-d- : à l'instant t= 5 [s]
-e- : à l'instant t= 20 [s] -f- :
à l'instant t= 45[s]
Fig. IV.44: Répartition
de la température pour un disque plein d'un matériau FG
15.

-a- : à l'instant t= 0,25
[s] -b- : à l'instant t= 1,8839 [s] -c- :
à l'instant t= 3,5[s]

-d- : à l'instant t= 5 [s]
-e- : à l'instant t= 20 [s] -f- :
à l'instant t= 45 [s]
Fig. IV.45: Répartition
de flux de chaleur total pour un disque plein d'un matériau FG
15.

Chapitre IV Résultats et Discussions
78
-a- : Selon l'axe X -b- :
Selon l'axe Y -c- : Selon l'axe Z
Fig. IV.46: Répartition
de flux de chaleur directionnel à l'instant t= 1,8839 [s] selon les
trois
axes (X, Y, Z) pour un disque plein d'un matériau FG
15.
b. Disque ventilé

-a - : à l'instant t= 0,25
[s] -b- : à l'instant t= 1,8506 [s] -c- :
à l'instant t= 3,5 [s]
-d- : à l'instant t= 5 [s]
-e- : à l'instant t= 20 [s] -f- :
à l'instant t= 45 [s]
Fig. IV.47: Répartition
de la température pour un disque ventilé d'un matériau FG
15.

-a- : à l'instant t= 0,25
[s] -b- : à l'instant t= 1,8506 [s] -c- :
à l'instant t= 3,5[s]

Chapitre IV Résultats et Discussions
79
-d- : à l'instant t= 5 [s]
-e- : à l'instant t= 20 [s] -f- :
à l'instant t= 45 [s]
Fig. IV.48: Répartition de
flux de chaleur total pour un disque ventilé d'un matériau FG
15

-a- : Selon l'axe X -b- :
Selon l'axe Y -c- : Selon l'axe Z
Fig. IV.49: Répartition
de flux de chaleur directionnel à l'instant t= 1,8506 [s] suivant
les
trois axes (X, Y, Z) pour un disque ventilé d'un matériau
FG 15.

Température [°C]
400
350
300
250
200
150
100
50
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
plein F G ventilé F G
|
15
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Disque plein Disque ventilé
0 5 10 15 20 25 30
Epaisseur [mm ]
Fig. IV.50 : Variation de la
température en fonction de l'épaisseur pour
les deux
conceptions avec le même matériau (FG15).
Chapitre IV Résultats et Discussions

Température [°C]
4 2 0
4 0 0
3 8 0
3 6 0
3 4 0
3 2 0
3 0 0
2 8 0
2 6 0
2 4 0
2 2 0
2 0 0
1 8 0
1 6 0
1 4 0
D i s q u e plein F G 1 5 Disque v e n tilé F G 1
5
80
7 0 8 0 9 0 1 0 0 1 1 0 1 2 0 1 3 0 1 4 0
Rayon [ m m ]
Fig. IV.51 : Variation de la
température en fonction de rayon pour
les deux conceptions avec le
même matériau (FG15).
Les figures IV.50 et 51 représentent respectivement la
variation de la température en fonction de l'épaisseur et du
rayon. Au milieu du disque, la température est minimale ; au niveau du
rayon moyen, elle est par contre maximale.
L'écart de température dans les deux
conceptions (disque plein et disque ventilé) est important (?T = 60
°C). L'influence de la ventilation sur la répartition de la
température apparaît clairement en fin freinage (à
l'instant t=3,5).
IV.6.7 Influence du mode de freinage
Le disque de frein et la roue sont dimensionnés en
fonction des performances et des impératifs économiques du
véhicule. Ils doivent supporter des sollicitations mécaniques et
thermiques de plus en plus grandes à des vitesses moyennes de marche en
progression permanente.
Parmi les paramètres ayant une influence sur le
comportement thermique des disques de frein, on a le mode de freinage qui
dépend du conducteur et des conditions de circulation. Certains modes de
freinage peuvent entrainer la destruction du disque et par conséquent
causer des accidents graves de circulation. Un mode de freinage est
représenté sous forme de cycles de freinage, lesquels
décrivent la variation de la vitesse du véhicule en fonction du
temps (v= f(t)). Ces cycles peuvent être constitués d'une
série de freinages d'urgence ou de cycles comportant des phases de
freinage suivies d'un temps d'arrêt.
IV.6.7.1 Freinage répété
Lors de l'exploitation des véhicules automobiles, le
système de freinage est soumis à des actions
répétées du conducteur. On a envisagé deux types de
freinage dont la durée totale de simulation est égale à
135 [s]. La figure IV.52 montre un cycle de freinage de quatorze freinages
successifs, sous forme de dents de scie.
Chapitre IV Résultats et Discussions
-1
Vitesse [m s ]
3 0
2 5
2 0
1 5
1 0
5
0
81
0 2 0 4 0 6 0 8 0 1 0 0 1 2 0
Temps [ s ]
Fig. IV.52 : Cycle avec quatorze
freinages
successifs (mode 1).
La figure IV.53 montre un autre mode de freinage où
après chaque phase de freinage on dispose d'un temps d'arrêt ou de
ralenti.
0 2 0 4 0 6 0 8 0 1 0 0 1 2 0
Temps [ s ]
-1
Vitesse [m s ]
3 0
2 5
2 0
1 5
1 0
5
0
Fig. IV.53 : Cycle de freinage
avec phase de ralenti
après chaque freinage (mode 2).
Les figures IV.54 et 55 montrent la distribution
tridimensionnelle de la température maximale atteinte dans le disque
pour les deux modes de freinage, On observe une augmentation normale de
température dans les pistes de frottement et la couronne
extérieure. Les ailettes s'échauffent très violement et
tendent à se dilater et se déformer jusqu'à la
solidification complète du disque. Cette déformation provoquera
la mise en parapluie du disque.
La figure IV.56 montre l'évolution de la
température du disque pour un freinage cyclique respectivement selon le
premier mode et le deuxième mode. Pour les deux modes de freinage, on
constate que les températures dans le disque s'élèvent
fortement après chaque freinage, puis elles commencent à
décroitre d'une manière exponentielle. Plus le nombre de
répétitions de freinage augmente, plus les températures
maximales augmentent. L'état initial du disque change après
chaque cycle, les temps d'arrêt ne permettent qu'un refroidissement
partiel. Après chaque phase de refroidissement, le disque commence de
nouveau à
Chapitre IV Résultats et Discussions
s'échauffer. Lors des freinages successifs la
capacité de refroidissement du disque est insuffisante pour abaisser la
température de surface à une valeur proche de la
température initiale ; ceci entraîne un cumul d'énergie et
donc une température de surface plus élevée. Ces
résultats montrent que le comportement thermique transitoire d'un disque
de frein dépend du cycle de freinage imposé, lequel est
prépondérant car il dicte la durée de refroidissement du
disque. Selon la figure IV.56, on remarque que dans le cas du cycle de freinage
du mode 2, une réduction de la température d'environ 535°C,
soit 45,19% par rapport au premier cycle. On conclût que le mode de
freinage avec une phase de refroidissement influe très positivement sur
les échanges de la chaleur dans le disque. Il en résulte une
diminution de la température maximale d'interface. Cette chute de
température permet d'éviter le phénomène de
fissuration et de l'usure mécanique. Par ailleurs, cette tendance
permettra d'assurer une sécurité et une durée de vie plus
grande de l'organe de freinage. Enfin, il serait intéressant de
réaliser ces modes de freinage sur un banc d'essais de frein pour
pouvoir valider les résultats de cette simulation numérique.
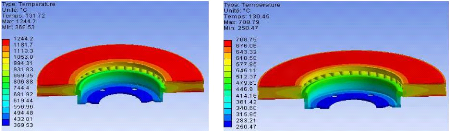
Fig. IV.54 : Carte thermique du
disque en mode de freinage 1 à l'instant t=131,72 [s].
Fig. IV.55 : Carte thermique du
disque en mode de freinage 2 à l'instant t=130,45 [s].

Température [°C]
1 2 0 0
1 1 0 0
1 0 0 0
9 0 0
8 0 0
5 0 0
4 0 0
3 0 0
2 0 0
6 0 0
1 0 0
7 0 0
0
Mode d e freinage 2 Mode d e freinage 1
0 2 0 4 0 6 0 8 0 1 0 0 1 2 0
Temps [s]
82
Fig.IV.56 : Evolution de la
température des deux modes de freinage en fonction du temps.
Chapitre IV Résultats et Discussions
83
IV.7 RESULTATS DE CALCUL MECANIQUE ET DISCUSSIONS
Le code de calcul ANSYS permet également la
détermination et la visualisation des déformations de la
structure dues au contact glissant entre le disque et les plaquettes. Les
résultats des calculs de contact décrits dans cette partie
concernent les déplacements ou bien la déformée totale au
cours de la séquence de chargement, le champ des contraintes
équivalentes de Von Mises sur le disque, les pressions de contact de la
plaquette intérieure et extérieure à différents
instants de la simulation. On procède ensuite l'influence de quelques
paramètres sur les résultats de calcul.
IV.7.1 Maillage du modèle
Le modèle d'éléments finis du rotor est
réalisé avec un maillage de 20351 éléments
pour un total de 39208 noeuds. Le maillage du disque et
plaquette issu du logiciel ANSYS est présenté
sur la figure IV.57.

Fig. IV.57 : Maillage volumique du
disque et plaquettes (Noeuds 39208, Eléments 20351).
IV.7.2 La déformée totale
La figure IV.58 montre différentes configurations des
déplacements de l'ordre du
modèle en fonction du temps, tout en gardant la forme
symétrique par rapport au plan médian
vertical. La déformée totale est atteinte à
la fin du freinage et elle varie entre 0 à
52,829 . Sur le modèle de la plaquette
intérieure non-déformée on a une dégradation des
couleurs allant du jaune et vert vers la rouge où la
valeur critique se situe sur le bord radial supérieure de la plaquette
déformée, représentée sur la figure IV.59 par la
couleur rouge. Ceci est du au module d'élasticité de plaquette
qui est inférieur à celui du disque. Pour le disque, on constate
que les déplacements se localisent uniquement sur les pistes de
frottement et sa
couronne extérieure ; ils atteignent une valeur
maximale égale à 19,108 à l'instant t= 45
[s] soit 36 % de la déformée totale de la
plaquette intérieure, Fig. IV.60. Sur la figure IV.61 on remarque que la
plaquette extérieure a le même comportement que la plaquette
intérieure au niveau de la zone de contact, mais sa
déformée totale chute de 67,43 %, soit l'équivalent
de 35,62 .
Chapitre IV Résultats et Discussions

-a- : à l'instant t= 0,25
[s]. -b- : à l'instant t= 1 [s]. c- :
à l'instant t= 2 [s].
-d- : à l'instant t=3 [s].
-e- : à l'instant t= 3,5 [s].
-j- : à l'instant t= 45 [s].
Fig.IV.58 : Variation de la
déformée totale du modèle ( échelle
réelle).

-a- : vue de face. -b-
: vue de dessous. -c- : vue de droite.
Fig.IV.59 : La
déformée totale de la plaquette intérieure à la fin
de freinage t=45 [s].

84
Fig.IV.60 : La
déformée totale du disque Fig.IV.61 : La
déformée totale de la plaquette
à la fin de freinage t=45 [s]. extérieure
à la fin de freinage t=45 [s].
Chapitre IV Résultats et Discussions

Déformée totale [um]
5 0
4 0
3 0
2 0
6 0
1 0
0
Plaquette intérieure Plaquette extérieure
Disque
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [ s ]
Fig.IV.62: Variation de la
déformée totale en fonction du temps.
Sur la figure IV.62 on a la variation de la
déformée totale en fonction du temps respectivement du disque,
des plaquettes intérieures et extérieures. On constate que la
partie la plus sollicitée en chargement donne des déplacements
plus importants que les autres régions . La plaquette intérieure
soumise à la pression hydraulique a une déformation plus grande
que le disque . Ce comportement est valable également pour le disque et
la plaquette extérieure.
IV.7.3 Contraintes équivalentes de Von
Mises
La figure IV.65 présente la répartition de la
contrainte équivalente de Von Mises en fonction du temps de simulation.
Les valeurs de la contrainte équivalente de Von Mises varient de 0
MPa à 31.441 MPa. La valeur maximale
enregistrée lors de cette simulation se situe au niveau du bol (du
côté interne ou externe du disque). Les concentrations de
contraintes les plus importantes naissent dans la zone du bol du disque au
début de freinage à l'instant t= 0,25 [s] et elles se propagent
vers la piste de frottement intérieure avec des niveaux faibles au cours
du freinage .Ce comportement est dû à l'application de pression de
contact qui en présente de la rotation du disque produisent des efforts
de torsion et de cisaillements .Notons que, le disque comporte des
perçages de fixation constituant des zones de concentration de
contraintes lesquelles peuvent provoquer une rupture du bol, Fig.IV.64.

85
Fig.IV.63 : Concentration des
contraintes de Fig.IV.64 : Détail de concentration
des
Von Mises dans les trous de fixation. Contraintes.
Chapitre IV Résultats et Discussions

-a- : à l'instant t= 0,25
[s]. -b- : à l'instant t= 1 [s]. -c-
: à l'instant t= 2 [s].
86
-d- : à l'instant t=3 [s].
-e- : à l'instant t= 3,5 [s].
-j- : à l'instant t= 45 [s].
Fig.IV.65 : Distribution des
contraintes de Von Mises dans le modèle disque-plaquette.
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0

Contraintes de Von Mises [MPa]
35
30
25
20
15
10
5
0
D isq ue
Plaquette intérieure Plaquette
extérieure
Temps [s]
Fig. IV.66 : Évolution
des contraintes de Von Mises selon le temps de simulation.
La figure IV.66 représente les contraintes de Von
Mises en fonction du temps. Les contraintes pour les trois
éléments du couple disque-plaquettes croît avec le temps et
se stabilisent à partir de t= 3.5s. Ce résultat est d'autant plus
satisfaisant, lorsqu'on le compare à ceux trouvés dans la
littérature.
Chapitre IV Résultats et Discussions
87
IV.7.4 Champ de contraintes sur les plaquettes de
frein
IV.7.4.1 Plaquette intérieure
IV.7.4.1.1 Répartition du champ des contraintes
équivalentes de Von Mises
Dans la figure IV.67, on constate que la contrainte
équivalente de Von Mises atteint à l'instant t= 45 [s] une valeur
maximale à l'extrémité gauche du contact (à la
sortie du contact) .Elle varie de 0,3682 MPa à 5,2839 MPa
; la plus faible valeur se situe sur le bord intérieur de la
plaquette intérieure. La distribution du champ des contraintes reste
symétrique par rapport à la rainure indépendamment du
temps de simulation.

-a- : à l'instant t= 0,25
[s]. -b- : à l'instant t= 0,5 [s]. -c-
: à l'instant t= 1 [s].
-d- : à l'instant t=2 [s].
-e- : à l'instant t= 2,5 [s].
-j- : à l'instant t= 3 [s].

-g- : à l'instant t= 3,5
[s]. -h- : à l'instant t= 45 [s].
Fig.IV.67 : Distribution des
contraintes de Von Mises dans la plaquette intérieure.
La figure IV.68 montre l'évolution des contraintes de
Von Mises de la plaquette intérieure suivant la position angulaire
à l'instant t=45 [s]. Les trois courbes comportent des points
extrémaux, car le contact frottant génère localement des
instabilités de type adhérence-glissement-décollement
résultant des vibrations du disque. Ces zones d'instabilités se
déplacent de la sortie vers l'entrée de contact. On observe aussi
qu'il ya presque une symétrie par rapport à l'angle (
è=30°) qui correspond à la position de la rainure de la
plaquette. On
Chapitre IV Résultats et Discussions
88
note que la contrainte est maximale au niveau de la sortie du
contact ce qui est conforme à la réalité.
1 0 2 0 3 0 4 0 5 0 6 0

Contrainte de Von Mises [MPa]
4
3
2
6
5
1
0
Bord supérieur
Centre
B o rd in fé r ie u r
L 'angle circulaire
Fig. IV.68 : Variation des
contraintes Von Mises en fonction de l'angle circulaire dans la
plaquette
intérieure.
IV.7.4.1.2 Répartition du champ de pression de
contact
La figure IV.69 donne la répartition de la pression de
contact de la plaquette intérieure pour différents temps de
simulation. La pression de contact augmente progressivement et atteint sa
valeur maximale pmax = 1,7927 MPa à la fin du freinage. La
répartition de la pression n'est pas homogène au sein de chaque
partie de la plaquette, elle a symétrique par rapport à la
rainure. Cette élévation de la pression sur la surface de contact
provoque une élévation de la température du disque et
également l'usure des plaquettes. A l'entrée de contact, la
répartition de la pression de contact tend vers des valeurs maximales au
niveau du bord inférieur de la plaquette, alors qu'à la sortie de
contact à des pressions basses. Cette augmentation est due à la
diminution de l'aire de contact. Ce phénomène perdure tant que la
vitesse de rotation du disque et la force appliquée resteront
constantes.

-a- : à l'instant t= 0,25
[s]. -b- : à l'instant t= 0,5 [s]. -c-
: à l'instant t= 1 [s].
Chapitre IV Résultats et Discussions

-d- : à l'instant t=2 [s].
-e- : à l'instant t= 2,5 [s].
-j- : à l'instant t= 3 [s].
-g- : à l'instant t= 3,5
[s]. -h- : à l'instant t= 45 [s].
89
Fig. IV.69 : Distribution des
pressions de contact dans la plaquette intérieure.
La figure IV.70 représente l'évolution des
pressions de contact en fonction de l'angle de rotation respectivement au bord
inférieur, au bord extérieur et au milieu de la plaquette. La
valeur maximale de la pression de contact se situe au niveau du bord
inférieur à l'entrée en contact. Au-delà de la
rainure vers la sortie de contact (la partie droite de la plaquette), les trois
zones ont le même comportement mécanique (mêmes pressions).
Ceci est dû au serrage des plaquettes et à la présence des
forces centrifuges qui agissent sur le disque lors de la rotation.
0 1 0 2 0 3 0 4 0 5 0 6 0

Pression de contact [MPa]
1 .8
1 .6
1 .4
1 .2
1 .0
0 .8
0 .6
0 .4
Bord i
C e n tr e Bord s
n fé r ie u r
u p é r ie u r
L'angle c ir c u la ir e
Fig. IV.70 : Variation des
pressions de contact en fonction de l'angle circulaire dans la
plaquette
intérieure.
Chapitre IV Résultats et Discussions
Les figures IV.71 et IV.72 représentent respectivement
la répartition des contraintes de frottement et la répartition de
la distance de glissement en fin de simulation. On remarque une symétrie
de distribution par rapport à la rainure ; les valeurs maximales se
localisent toujours dans le bord supérieur de la plaquette.

90
Fig.IV.71: Répartition de la
contrainte Fig.IV.72: Répartition de la
distance
de frottement. de glissement.
IV.7.4.2 Plaquette extérieure
IV.7.4.2.1 Répartition du champ des contraintes
équivalentes de Von Mises
La figure IV.73 montre la répartition des pressions de
contact dans les plaquettes
(face extérieure) pour différents instants de
simulation. On remarque une distribution régulière des
contraintes et symétrique par rapport la rainure le long du temps de
freinage. La valeur maximale de la contrainte égale à 1,77
MPa est atteinte à l'instant t=45[s] ; elle est plus petite que
celle obtenue dans la plaquette intérieure. La plaquette
extérieure a tendance à engendrer des pressions locales
élevées sur le bord supérieur dans la zone proche de la
rainure.

-a- : à l'instant t= 0,25
[s]. -b- : à l'instant t= 0,5 [s]. -c-
: à l'instant t= 1 [s].

-d- : à l'instant t=2 [s].
-e- : à l'instant t= 2,5 [s]. -f- :
à l'instant t= 3 [s].

Chapitre IV Résultats et Discussions
91
-g- : à l'instant t= 3,5
[s]. -h- : à l'instant t= 45 [s].
Fig.IV.73 : Distribution des
contraintes de Von Mises dans la plaquette extérieure.
IV.7.4.2.2 Répartition du champ de pression de
contact
La figure IV.74 donne la répartition de pression de
contact obtenue pour différentes instants de simulation dans le cas
d'une plaquette extérieure. On constate que la pression de contact
maximale est atteinte sur le milieu de la plaquette (1,33 MPa) et elle
est bien inférieure à celle obtenue pour la plaquette
inférieure.

-a- : à l'instant t= 0,25
[s]. -b- : à l'instant t= 0,5 [s]. -c-
: à l'instant t= 1 [s].

-d- : à l'instant t=2 [s].
-e- : à l'instant t= 2,5 [s].
-j- : à l'instant t= 3 [s].

-g- : à l'instant t= 3,5
[s]. -h- : à l'instant t= 45 [s].
Fig.IV.74: Distribution des
pressions de contact dans la plaquette extérieure.
Les courbes de la figure IV.75 qui donnent les pressions de
contact en fonction de l'angle circulaire confirment les résultats
précédents de la plaquette intérieure.
Chapitre IV Résultats et Discussions

B o r d in fé r ie u r Centre
Bord supérieur
1 .8
1 .6
Pression de contact [MPa]
1 .4
1 .2
1 .0
0 .8
0 .6
0 .4
1 0 2 0 3 0 4 0 5 0 6 0
L 'angle circulaire
Fig. IV.75 : Variation des
pressions de contact en fonction de l'angle circulaire dans la
plaquette
extérieure.
Les figures IV.76, IV.77 donnent respectivement le champ de
contraintes de frottement et la distance de glissement observées
à la fin du freinage. Les deux plaquettes ont les mêmes valeurs
maximales atteintes à l'instant t= 45 [s], la répartition des
contraintes de frottement et de la distance de glissement sont
différentes.

92
Fig.IV.76: Répartition de
contrainte Fig.IV.77: Répartition de la
distance
de frottement. de glissement.
IV.7.5 Contraintes de traction/compression et
contraintes de cisaillement dans le disque
Les contraintes de traction/compression et les contraintes de
cisaillement dans le disque sont présentées dans la figure IV.78.
Lors de la rotation du disque, on remarque une concentration de contraintes au
niveau des perçages de fixation et dans la zone de raccordement des
pistes au bol. Les contraintes se propagent ensuite sur les pistes de
frottement en fonction du temps. La valeur maximale des contraintes de
compression est de l'ordre de 22,574 MPa et celle des
contraintes de traction de 22,713 MPa. Les contraintes de
cisaillement varient de 0,336 MPa à 5,71 MPa.
Ce chargement a une influence sur les déformations globales du disque
qui pourrait prendre la forme d'un cône.
Chapitre IV Résultats et Discussions

-a- : Contraintes normales
-b-: Contraintes normales -c- : Contraintes
normales
93
-d-:Contraintes
-e-:Contraintes -f-: Contraintes

de cisaillement de cisaillement de cisaillement
Fig.IV.78: Contraintes normales
et contraintes de cisaillement à t=45 [s].
.IV.7.6 Cas d'un disque sans rotation
En supposant le cas d'un disque au repos, on remarque selon la
figure IV.79 que la concentration de contraintes de Von Mises se localise
uniquement au niveau du bol, mais elle ne se propage pas sur les pistes de
frottement contrairement au cas du disque avec rotation. La
déformée totale varie selon la figure IV.80 de 0
à 49,58 ; on a une différence de 3,24
par rapport à celle d'un disque mobile. Les
déplacements sont situés généralement sur la
couronne extérieure du disque et atteignent la valeur
maximale de 17,68 au niveau de
périphérie de la couronne.

Fig.IV.79: Contraintes de Von
Mises. Fig.IV.80: Déformée totale.
Chapitre IV Résultats et Discussions
94
Les déplacements des noeuds situés sur le rayon
extérieur moyen et sur la couronne extérieure du disque avec et
sans rotation sont présentés dans la figure IV.81. On constate
que les deux courbes suivent la même allure. La valeur maximale de
déplacement est atteinte à l'angle è = 90°
qui correspond à la position de serrage du disque par les plaquettes. Le
comportement des déplacements avec ou sans rotation est tout à
fait conforme aux observations faites habituellement avec les disques de
frein.
0 5 0 1 0 0 1 5 0 2 0 0 2 5 0 3 0 0 3 5 0

Déplacements [u m]
2 0
1 8
1 6
1 4
1 2
1 0
4
2
8
6
0
Rayon moyen (avec rotation)
Rayon moye
Couron
C o u r o n
n e extérieure ( a v e c rotation)
n e e x té r ie u r e ( s a n s rotation)
n (sans rotation)
Position angulaire( degrés)
Fig.IV.81: Déplacements
sur le rayon extérieur moyen et sur la couronne extérieure
du
disque en fonction de l'angle.
Réaction de force [KN]
|
6
5
4
3
2
1
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Piste
|
|
extérieure
|
|
(avec
|
|
rotation)
|
|
|
|
|
|
|
|
|
Piste
|
|
intérieure
|
|
( avec
|
r o t
|
a ti o
|
n)
|
|
|
|
|
|
|
|
e x
|
intérieure té r ie
|
u r e
|
(s a n (s a n s
|
s r o t r o ta
|
a tio tio n
|
n )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [ s ]
Fig.IV.82: Variation de l'effort
de réaction sur le disque en fonction du temps.
Sur la figure IV.82 sont représentés les
efforts de réaction sur les deux parties qui se trouvent en
vis-à-vis de la plaquette intérieure et extérieure
respectivement pour le cas du disque avec et sans rotation. L'introduction de
la rotation du disque engendre une augmentation de l'effort de frottement
quelque que soit la piste de contact. Pour la piste
Chapitre IV Résultats et Discussions
extérieure, on constate que dans le cas du disque en
rotation la force de réaction augmente de 2,1 KN à 5,1
KN et pour la piste intérieure de 2.1N à 5.9N. Les
écarts des efforts de réaction (avec et sans rotation) sont
très visibles ; ils atteignent une valeur maximale de l'ordre de 4 N. La
figure IV.83 donne la répartition de l'effort de contact en trois
dimensions pour les deux cas (avec et sans rotation).

3
2
1
10
8
-1
2
4
6
4 2
6
5
0,7500
6
6,000
8
10
4
1,625
2,500
3,375
4,250
5,125
0
-1,000
-0,1250

1
0
-1
-2
10
-3
6
4
3
-1,625
8
2
4
4
2
10
6
8
2
-3,500
-2,563
-0,6875
0,2500
1,188
2,125
3,063
4,000
95
-a- : Avec rotation -b- :
Sans rotation
Fig.IV.83: Forces de
réaction sur la piste intérieure du disque.

-a-:Contraintes normales
-b-:Contraintes normales -c-: Contraintes
normales

-d-: Contraintes -e-:
Contraintes -f-: Contraintes
de cisaillement de cisaillement de cisaillement
Fig.IV.84: Contraintes normales
et contraintes de cisaillement à t=45[s].
Chapitre IV Résultats et Discussions
96
Les contraintes de traction/compression et de cisaillement
apparaissent aussi dans le modèle sans rotation. On obtient des
contraintes de compression de 22,99 MPa (Fig. IV.84 - c). Les
contraintes de cisaillement varient de 3,75 MPa à 16,357
MPa. La prise en compte de la rotation du disque est donc essentielle
puisqu'elle a plusieurs effets :
· Les contraintes maximales sur les pistes du disques
augmente de manière notable, mais elles concernent une zone
dissymétrique.
· Les contraintes de cisaillement apparaissent au niveau
du bol.
Le tableau IV.6 résume les résultats de la
simulation, lorsqu'on élimine la rotation du disque. En comparaison avec
les résultats obtenus pour le cas du disque en rotation,on constate une
augmentation des contraintes et une diminution des déplacements , des
pressions et des contraintes de frottement .
|
Min
|
Max
|
Déformée totale ( )
|
0
|
49,587
|
(MPa)
|
-11,252
|
18,176
|
(Mpa)
|
-15,798
|
11,514
|
(Mpa)
|
-22,992
|
21,642
|
(Mpa)
|
-11,977
|
9,540
|
(Mpa)
|
-16,357
|
3,755
|
(Mpa)
|
-5,671
|
7,267
|
Von Mises (Mpa)
|
1,70e-011
|
33,251
|
Contraintes de frottement (Mpa)
|
0
|
0,281
|
Distance de glissement ( )
|
0
|
3,560
|
Pression (Mpa)
|
0
|
1,755
|
Temps (CPU) (s)
|
586.656
|
|
Tableau. IV.6 : Résultats
de la simulation numérique.
Les figures IV.85 et 86 montrent respectivement la
déformée totale et les contraintes équivalentes de Von
Mises pour les deux cas (avec et sans rotation) en fonction du temps de la
simulation .On constate que l'allure des courbes est la même, mais les
écarts augmentent avec le temps. La déformée du disque en
rotation est plus grande que celle sans rotation et inversement pour le cas des
contraintes de von mises.
Chapitre IV Résultats et Discussions

Disque sans rotation Disque avec rotation
Déformée totale [um]
|
6 0 5 0 4 0 3 0
2 0
1 0
0
|
|
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [ s ]
Fig.IV.85: Effet de rotation du
disque sur les déplacements.

Contrainte de Von Mises [MPa]
3 5
3 0
2 5
2 0
1 5
1 0
5
0
D is q u e sans rotation D is q u e avec rotation
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [ s ]
97
Fig.IV.86: Effet de rotation du
disque sur le champ des contraintes. IV.7.7 Cas d'un étrier
à double piston
Pour une étude comparative, on a choisi le cas d'un
étrier fixe (disque à double pression) décrit
précédemment dans l'étude bibliographique, mais tout en
maintenant les mêmes conditions aux limites du cas d'un étrier
à simple piston.
La figure IV.87 présente les niveaux de contraintes
équivalentes de Von Mises dans une section dans un disque à la
fin du freinage t=45 [s]. Contrairement au cas du disque avec étrier
à simple piston, on remarque que les contraintes se propagent sur la
totalité du disque et sur les pistes de frottement selon la
dégradation en couleurs et que l'échelle des contraintes
équivalentes de Von Mises varie de 0,048 MPa à 8,28
MPa. On obtient une chute de contraintes d'environ 73,66% par rapport
au dispositif de freinage avec étrier à simple piston. La valeur
la plus grande se situe au niveau de la partie extérieure des ailettes
du disque où les plaquettes exercent le serrage, Fig.IV.88. Ces
concentrations peuvent entrainer des
Chapitre IV Résultats et Discussions
98
endommagements, car elles s'additionnent aux contraintes
thermiques. Ce phénomène dépend de la
géométrie intérieure du disque, des conditions aux limites
appliquées et du type de l'étrier.
Les résultats de la déformée totale du
modèle sont illustrés par la figure IV.89. La distribution de la
déformée totale se distingue par la forme symétrique
indépendamment du
temps de simulation ; elle atteint une valeur maximale
égale à 38,09 qui se situe les
bords des deux plaquettes
(intérieure et extérieure). On a une diminution de 28 % de la
déformée par rapport à celle trouvée
précédemment. Les déplacements ont une distribution
symétrique par rapport au plan médian vertical aux plaquettes,
Fig.89-b.
En conclusion, la meilleure répartition des
contraintes équivalentes de Von Mises a lieu pour un chargement
appliqué aux plaquettes à double pression.

Fig.IV.87: Contraintes de Von
Mises. Fig.IV.88 : Détail de concentration des
contraintes.

-a- : Vue de face. -b-
: Vue de dessous. -e- : Section au milieu.
Fig.IV.89:
Déformées totales.
IV.7.8 Résultats des modèles
maillés
Un test de convergence est prévu pour évaluer
l'influence du maillage sur la précision de la simulation
numérique. On a essayé quatre cas de maillage (grossier, fin,
hexaédrique et quadrilatère) dont les caractéristiques
sont présentés dans le tableau IV.7.
Chapitre IV Résultats et Discussions
Type de maillage
|
Noeuds
|
Eléments
|
Type d'élément
|
Temps CPU (s)
|
Grossier
|
39208
|
20351
|
SOLID 187
|
644,234
|
Quadrilatère
|
90680
|
31879
|
SOLID 186-SOLID 187
|
3030,047
|
Hexaédrique
|
103098
|
36901
|
SOLID 186-SOLID 187
|
4477,625
|
Fin
|
160918
|
88625
|
SOLID 187
|
1982,203
|
|
Tableau. IV.7: Résultats
des différents cas de maillage.
Les figures IV.90, 91, 92 et 93 montrent les modèles
de maillage du couple disque-plaquettes.

Fig.IV.90 : Maillage volumique du
disque Fig.IV.91 : Maillage à éléments
quadrilatères
(Noeuds 39208, Eléments 20351). (Noeuds 90680,
Eléments 31879).

99
Fig.IV.92 : Maillage à
éléments hexaédriques Fig.IV.93: Maillage
fin
(Noeuds 103098, Eléments 36901). (Noeuds160918,
Eléments 88625).
D'après le tableau IV.8, on remarque que les
contraintes maximales équivalentes de Von Mises augmentent en fonction
du nombre d'éléments du maillage. La valeur maximale de la
contrainte équivalente de Von Mises ainsi que la déformée
totale atteintes correspondent au maximum d'éléments du maillage
sont pratiquement celles qu'on rencontre dans la littérature. Il est
donc judicieux de choisir un maillage raffiné, car la solution devient
plus exacte en augmentant le nombre de noeuds du maillage.
Chapitre IV Résultats et Discussions
Méthode du
maillage
|
Nombre de
|
Nombre
d'éléments
|
Déformée totale
|
Contraintes
|
Temps
CPU (s)
|
|
Max
|
Min
|
Max
|
|
Noeuds
39208
|
20351
|
0
|
52,829
|
1,79e-011
|
31,441
|
644,234
|
Quadrilatère
|
90680
|
31879
|
0
|
55,247
|
1,99e-002
|
54,337
|
3030,047
|
Hexaédrique
|
103098
|
36901
|
0
|
55,443
|
1,93e-002
|
96,434
|
4477,625
|
Fin
|
160918
|
88625
|
0
|
54,817
|
5,27e-012
|
44,603
|
1982,203
|
|
Tableau. IV.8 : Contraintes de Von
Mises et déformées totales. IV.7.8.1 Influence de la
finesse du maillage
Pour cela, on a considéré un second type de
maillage, plus fin et raffiné dans les pistes de frottement, figure
IV.94. L'élément utilisé dans ce maillage est SOLID 187 et
le temps total de simulation est égal à 8 331.328 (s). Ce nouveau
maillage (type M2) est constitué de 11 3367 éléments TE
à 4 noeuds, soit 18 5901 noeuds. Il est donc bien plus fin que le
maillage M1 (Fig. IV.93) utilisé jusque-là.

Fig.IV.94 : Maillage plus
raffiné
(Noeuds 185901, Eléments 113367).
Le tableau IV.9 présente les résultats
numériques pour les deux types de maillage (grossier et fin). On observe
que toutes les valeurs extrêmes de résultats augmentent en
fonction du nombre des noeuds et du nombre d'éléments du maillage
.On constate ainsi que l'effet de raffinement du maillage influence d'une
manière importante sur la précision de la simulation
numérique adoptée.
Maillage fin
|
Maillage plus raffiné
|
Noeuds
|
Eléme
|
Noeuds
|
Eléments
|
160918
|
88625
|
185901
|
113367
|
Min
|
Max
|
Min
|
Max
|
|
0
5,27e-12
0
1,8e-11
Déformée totale ( )
Von Mises (MPa)
Temps (CPU) (s)
54,82
44,603
54,81
32,476
100
Tableau. IV.9 : Comparaison entre
les résultats du maillage fin et maillage raffiné.
Chapitre IV Résultats et Discussions
IV.7.9 Influence du matériau des plaquettes
On étudie ici la sensibilité des
résultats par rapport à deux paramètres, le module de
Young des garnitures et le coefficient de frottement entre le disque et les
plaquettes. Ce dernier paramètre varie fortement avec la pression, la
vitesse de glissement, la température ce qui rend difficile de lui
attribuer une valeur exacte. L'étude de sensibilité permettra
d'évaluer la pertinence des calculs qui ne prennent pas en compte la
variation du coefficient de frottement.
IV.7.9.1 Influence du module de Young des
plaquettes
L'étude bibliographique montre que le module de Young
du matériau des plaquettes actuelles varie généralement
entre 0, 5 GPa et 1, 5 GPa. Dans cette
partie, on a choisi deux matériaux dont les propriétés
mécaniques et tribologiques sont données dans le tableau
IV.10.
|
Matériau 1
|
Matériau 2
|
Module de Young E (GPa)
|
1
|
1,5
|
Coefficient de Poisson ( )
|
0,25
|
0,25
|
Masse volumique
|
1400
|
2595
|
coefficient de frottement ( )
|
0,2
|
0,2
|
|
Tableau. IV.10 :
Propriétés mécaniques des plaquettes de
frein.
Les figures IV.95 montrent l'état de contact, la
pression de contact, les contraintes de frottement et la distance de glissement
de la plaquette intérieure.

-a-:Etat -b-
:Pression -c-:Contraintes
-d-:Distance
du contact de contact de frottement de glissement
Fig.IV.95: Comportement de la
plaquette intérieure.
101
Les résultats de cette simulation sont
récapitulés dans le tableau IV.11.
Chapitre IV Résultats et Discussions
102
|
Matériau de plaquette de frein
|
|
Matériaux 2
|
|
Max
|
Min
|
Max
|
Déformée totale ( )
|
0
|
52,829
|
0
|
37,488
|
(MPa)
|
-11,012
|
17,23
|
-8,101
|
11,344
|
(MPa)
|
-13,946
|
11,1
|
-8,669
|
7,424
|
(MPa)
|
-22,574
|
22,713
|
-15,511
|
16,468
|
(MPa)
|
-11,05
|
8,891
|
-7,146
|
5,827
|
(MPa)
|
-15,346
|
2,988
|
-10,104
|
1,683
|
(MPa)
|
-5,650
|
7,188
|
-4,382
|
4,934
|
Von Mises (MPa)
|
1,7e-011
|
31,441
|
2,0e-011
|
20,882
|
Contraintes de frottement (MPa)
|
0
|
0,300
|
0
|
0,3081
|
Distance de glissement ( )
|
0
|
4,138
|
0
|
3,359
|
Pression (MPa)
|
0
|
1,792
|
0
|
2,0846
|
Temps (CPU) (s)
|
644.234
|
577.000
|
|
Tableau. IV.11 : Influence du
matériau de plaquettes de frein (valeurs extrêmes).
Du tableau IV.11, on remarque que l'augmentation du module de
Young des plaquettes de frein entraine une diminution de la
déformée totale, des contraintes (Von Mises, normale et
cisaillement), et de la distance de glissement, mais un accroissement des
contraintes de frottement et des pressions de contact. La figure IV.96 montre
la variation des contraintes en fonction du module de Young. On constate que
les contraintes de Von Mises, les contraintes normales et les contraintes de
cisaillement varient d'une manière linéaire décroissante
avec le module de Young.
Contraintes (MPa)
|
3 0 2 5 2 0 1 5 1 0 5 0
|
|
|
|
|
|
|
Contrainte
|
(xx)
|
|
|
|
|
|
|
|
|
|
Contrainte
Contrainte
|
(yy)
(zz)
|
|
|
|
|
|
|
|
|
|
Contrainte
|
(xy)
|
|
|
|
|
|
|
|
|
|
Contrainte Contrainte
|
(yz)
(zx)
|
|
|
|
|
|
|
|
|
|
Contrainte
|
Von
|
Mises
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .0 1 .1 1 .2 1 .3 1 .4 1 .5
Module d e Young E (G P a )
Fig. IV.96: Résultats des
contraintes en fonction du module de Young
Chapitre IV Résultats et Discussions
D'après le tableau IV.13, on peut conclure que :
· Dans le cas statique, plus les plaquettes sont souples
et plus les déplacements sont élevés ;
· En présence de rotation, les
déplacements du disque ne varient que légèrement
(de 19,10 à 13,95 ) ;
· Les contraintes normales, les contraintes de cisaillement
et les contraintes Von Mises diminuent avec le module de Young.
· La pression de contact et les contraintes de frottement
augmentent par contre avec le module de Young des plaquettes,
IV.7.9.2 Influence du coefficient de frottement
Nous allons maintenant, nous intéresser à
l'étude de sensibilité des résultats par rapport au
coefficient de frottement ; pour cette raison ; on faisant varier ce
paramètre de 0,2 jusqu'à 0,4 au niveau de la zone de contact
disque-plaquette à chaque simulation. La figure IV.97 montre
différentes configurations de la déformée totale du
modèle en phase finale du freinage. Nous pouvons clairement identifier
l'effet du frottement dans cette nouvelle simulation.
En l'absence de rotation, les résultats varient
très peu avec le coefficient de frottement. En revanche, avec la
rotation du disque, les déplacements, la surface réelle de
contact mais surtout les efforts tangentiels subissent une forte variation.

-a- : =0,25 -b- :
=0,30 -e- : =0,35
103
Fig.IV.97: Déformée
totale à la fin de freinage.
La figure IV.98 donne la répartition du champ des
contraintes de Von mises à l'instant t=3,5 [s] pour deux valeurs du
coefficient de friction. On constate que le coefficient de frottement n'exerce
aucune influence sur la contrainte.
Chapitre IV Résultats et Discussions
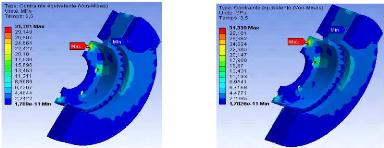
104
-a- : =0,25 -b- :
=0,35
Fig.IV.98: Contraintes de Von
Mises à l'instant t=3,5 [s].

-a- : =0,20 -b- :
=0,30 -e- : =0,40
Fig.IV.99: Champs de pression de
contact d'interface à l'instant t = 2 [s].
La figure IV.99 montre que l'augmentation de coefficient de
frottement s'accompagne par une diminution des pressions de contact des
plaquettes.
Dans les figures IV.100 et 101, on a présenté
respectivement l'évolution de la contrainte et la distance de glissement
en fonction du temps pour différentes valeurs du coefficient de
frottement. On note une augmentation de la contrainte de frottement avec
l'accroissement du coefficient de frottement. La distance de glissement est par
contre inversement proportionnelle au coefficient de frottement.
Chapitre IV Résultats et Discussions

Contrainte de frottement [MPa]
0 .4 5
0 .4 0
0 .3 5
0 .3 0
0 .2 5
0 .2 0
0 .1 5
0 .1 0
0 .0 5
0 .0 0
u = 0 ,2 u = 0 ,2 5 u = 0 ,3 u = 0 ,3 5 u = 0 ,4
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
105
Temps [ s]
Fig. IV.100:Evolution de
contrainte de frottement pour différentes valeurs de .
Distance de glissement [um]
4
3
2
1
0

u = 0 ,2 u = 0 ,2 5 u = 0 ,3 u = 0 ,3 5 u = 0 ,4
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [ s ]
Fig. IV.101: Evolution de distance
de glissement pour différentes valeurs de . IV.7.9.3
Influence de la vitesse de rotation du disque
La figure IV.102 représente le champ de pressions de
contact à l'instant t=45 [s] où les pressions maximales sont
atteintes pour ce type de freinage en fin de freinage. On constate que la
répartition de la pression est quasiment identique dans les trois cas et
elle augmente avec l'accroissement de la vitesse angulaire du disque [44], la
localisation de cette dernière se situe sur le bord inférieur de
la plaquette. On observe que cette augmentation peut créer l'usure des
plaquettes où elles peuvent laisser des dépôts sur le
disque, donnant lieu à ce qu'on appelle « le troisième corps
». On note que la pression maximale de contact dans la plaquette est
produite à l'entrée et descend vers la sortie de la région
de frottement.

Chapitre IV Résultats et Discussions
106
-a- : w =60 rad/s -b- :
w =90 rad/s -c- : w =120 rad/s
Fig. IV.102: Distributions de
pression de contact d'interface.
La figure IV.103 représente la distribution du champ de
contraintes de frottement à l'instant t=45[s], on note qu'à
mesure que la distribution de ce champ est symétrique par rapport
à la rainure et sa valeur augmente légèrement quand la
vitesse de rotation du disque augmente.
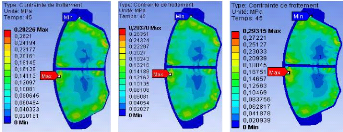
-a- : w =60 rad/s -b- :
w =90 rad/s -c - : w =120 rad/s
Fig. IV.103: Distributions de
contrainte de frottement d'interface.
La figure IV.104 donne la répartition du champ des
contraintes équivalentes de Von Mises à la fin de freinage
lorsqu'on varie la vitesse angulaire du disque. On observe que la
densité de distribution des contraintes augmente au niveau des
plaquettes intérieures avec l'accroissement de la vitesse du disque.

-a- : w =60 rad/s -b- :
w =90 rad/s -c - : w =120 rad/s
Fig. IV.104: Champs de contrainte
Von Mises de frottement d'interface.
Chapitre IV Résultats et Discussions
107
L'évolution des contraintes de Von Mises de surface du
disque pour différentes valeurs de vitesse de rotation est
présentée par la figure IV.105. On note que la contrainte du
disque reste quasi-identique et elle est inversement proportionnelle à
la vitesse de rotation.
3 5
3 0
2 5
2 0
1 5
1 0
5
Contrainte de Von Mises [MPa]
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
ro ta
|
tio n
|
6 0 ra
|
d /s
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
rotation
|
|
9 0 ra
|
d /s
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
rotation
|
|
1 2 0
|
ra d
|
/s
|
|
|
|
|
|
|
|
|
|
Vitesse
|
d e
|
rotation
|
|
1 5 7
|
,8 9
|
ra d /s
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [s]
Fig. IV.105: Influence de la
vitesse de rotation sur la distribution du champ de contrainte de
Von Mises.
IV.7.9.4 Cas d'un disque en acier inoxydable
Pour un but comparatif, on a choisi un autre matériau du
disque en acier inoxydable tout en gardant le même matériau de la
plaquette. Les caractéristiques mécaniques de deux pièces
en contact sont résumées dans le tableau IV.12.
|
Disque
|
Plaquette
|
|
Module de Young E (Gpa)
|
203
|
1
|
|
Coefficient de Poisson
|
0 ,3
|
0,25
|
|
Masse volumique
|
7900
|
1400
|
|
Coefficient de frottement
|
0 ,2
|
0,2
|
Tableau .IV.12 : Tableau des
caractéristiques mécaniques des deux pièces.
IV.7.9.4.1 Comparaison entre le champ des
déplacements
D'après la figure IV.106, on constate que les
résultats des déplacements du modèle en Acier inoxydable
coïncident exactement avec celui du Fonte Grise. On observe que la
valeur maximale atteinte est diminue légèrement de
52,829 à 51 ,407 (un écart de
déplacement négligeable).

Chapitre IV Résultats et Discussions
108
(a) Disque en acier inoxydable
(b) Disque en fonte grise
Fig.IV.106:
Déformée totale à la fin de
simulation.
IV.7.9.4.2 Comparaison entre le champ des
contraintes
D'après la figure IV.107, on constate la
répartition des contraintes sont très différentes avec des
singularités au niveau du corps du disque et des pistes de frottement et
du bol. Dans un disque en acier inoxydable, les contraintes varient de 0
MPa à 43,048 MPa, alors que dans le disque en fonte
grise de 0 MPa à 31,441 MPa. L'écart est assez
important soit de l'ordre de 12 MPa. La plus grande valeur de
contrainte maximale équivalente apparaît dans le disque en acier
inoxydable (Fig.IV.107-a), tandis que la plus faible est celle du
disque en fonte grise (Fig.IV.107-b). C'est pour cette raison
que la fonte grise est la plus couramment utilisée dans l'industrie
automobile et qui assure d'ailleurs un bon comportement thermique et
mécanique (une bonne résistance mécanique et une faible
usure).

-a- : Disque en Acier Inoxydable
-b- : Disque en Fonte Grise
Fig.IV.107: Contraintes Von Mises
à la fin de simulation.
D'après les résultats obtenus de la simulation,
on constate que l'acier inoxydable (module de Young supérieur à
celui de la fonte grise) influe sur les valeurs de la déformée
totales (inversement proportionnelle) et également sur les contraintes
maximales équivalentes de Von Mises, figures IV.108 et IV.109.
Chapitre IV Résultats et Discussions

Déformée totale [um]
4 0
2 0
6 0
5 0
3 0
1 0
0
Acier Inoxydable Fonte Grise
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
109
Temps [ s]
Fig.IV.108: Variation de la
déformée totale en fonction du temps
pour les deux
disques.
Contrainte de Von Mises [MPa]
20
50
40
30
10
0

Acier In oxydable (Fonte Grise)
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Temps [s]
Fig.IV.109: Variation de la
contrainte de Von Mises en fonction du temps
pour les deux disques.
IV.7.9.5 Etude de l'influence de la rainure
Les plaquettes de frein automobile comportent
généralement des rainures médianes. Outre leur rôle
d'évacuation des poussières et de l'eau, ces rainures peuvent
avoir une influence sur le comportement mécanique du système de
freinage. Pour cela on a procédé à une comparaison des
contraintes de Von Mises et de la déformée totale d'une plaquette
avec et sans rainure, Fig.IV.110 et 111.
Chapitre IV Résultats et Discussions

110
Fig. IV.110:Plaquette sans rainure.
Fig.IV.111: Plaquette avec rainure.
D'après les figures IV.112 et IV.113, on constate que
la présence de la rainure influe positivement sur les
déplacements de la plaquette et sur les contraintes équivalentes
de Von Mises. Les variations ne sont néanmoins assez faibles.
Contrainte de Von Mises [MPa]
2 5
2 0
3 5
3 0
1 5
1 0
5
0

Plaquette avec rainure Plaquette sans rainure
0 .0 0 .5 1 .0 1 .5 2 .0 2 .5 3 .0 3 .5 4 .0
Temps [s]
Fig. IV.112: Influence de la
rainure sur la variation du champ de contrainte de Von Mises.
Déformée totale [um]
20
50
40
30
10
60
0

Plaquette avec rainure Plaquette sans rainure
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Temps [s]
Fig. IV.113: Influence de la
rainure sur la variation de la déformée totale.
Chapitre IV Résultats et Discussions
111
IV.8 RESULTATS DU CALCUL THERMOELASTIQUE
L'objectif de l'analyse thermoélastique à l'aide
du code de calcul ANSYS Multiphysics est de déterminer les niveaux des
contraintes et des déformations globales du modèle
étudié (disque-plaquette) durant la phase de freinage sous
l'effet de la température.
Le problème physique rencontré ici est un
couplage de transfert de chaleur (problème thermique) et
d'évolution mécanique. Le couplage thermoélastique peut
être formulé par un système d'équations aux
dérivées partielles et d'équations ordinaires dans un
domaine en fonction du temps, en respectant les conditions aux limites.
Sur la figure IV.114 qui représente la distribution
issue de code de calcul en 3 D de la température du modèle
disque-plaquette, on a choisi l'instant qui correspond à la
température maximale Tmax= 346,31 °C à t= 1,7271
[s]. On constate la montée rapide de la température du disque sur
les deux pistes de frottement qui amène une augmentation de stockage de
chaleur au niveau du zone de contact, on observe que la partie
supérieure de la plaquette est totalement refroidie par l'effet de
convection à l'air ambiant.

Fig. IV.114: Distribution de la
température du disque
et plaquettes à l'instant t=1,7271
[s].
IV.8.1 Déformée totale et contraintes de
Von Mises du modèle
Dans cette .partie, on présente une deuxième
modélisation mécanique du contact qui tient compte de la
température. Le but est de mieux comprendre les déformations
totales du disque lorsque celui-ci est soumis à la pression des
plaquettes mais aussi aux dilatations induites par les élévations
de température.
La figure IV.115 montre les déplacements des noeuds
situés sur le rayon moyen et la couronne extérieure du disque. On
a une nette différence entre les déformées pour la
couronne extérieure et le rayon moyen du disque. Les courbes ont une
allure identique (même
Chapitre IV Résultats et Discussions
comportement). Sous l'effet du serrage du disque, il apparait
un phénomène de mise en parapluie qui résulte de
l'échauffement des pistes de frottement non-parallèles par
rapport à la position initiale.
Déplacements (um)
2 8 0
2 7 0
2 6 0
2 5 0
2 4 0
2 3 0
2 2 0
2 1 0
2 0 0
1 9 0
1 8 0
1 7 0
1 6 0
1 5 0

Couronne extérieure d u disque
Périphérie moyenne d u disque
0 4 5 9 0 1 3 5 1 8 0 2 2 5 2 7 0 3 1 5 3 6 0
Position angulaire (degrés)
Fig. IV.115: Déplacements du
rayon moyen et la couronne extérieure du disque en
fonction de la position angulaire à l'instant t=3,5
[s].
La variation de déformée totale maximale de la
piste de frottement croit linéairement en fonction du rayon du disque
comme le montre visiblement la figure IV.116

Déplacements (um)
280
260
240
220
200
180
160
140
120
100
è= 90 è= 0 è=180 è=270
112
70 80 90 100 110 120 130
Rayon (m m )
Fig.IV.116: Variation des
déplacements de piste en fonction du rayon pour
différentes
positions angulaires à l'instant t=3,5 [s].
Les figures IV.117 et 118 montrent clairement l'écart
important entre le modèle mécanique et thermoélastique. La
température a une forte influence sur la réponse
thermomécanique du modèle.
Chapitre IV Résultats et Discussions
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Problème
|
|
mécanique
|
sec
|
|
|
|
|
Problème
|
|
therm
|
omécanique
|
couplé
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
300 250 200 150 100 50 0
Déformée totale [um]
113
0 10 20 30 40
Temps [s]
Fig. IV.117: Comparaison pour les
résultats des déplacements entre les deux
modèles
traités

500
400
Problème thermomécanique couplé
Problème mécanique sec
0
0 10 20 30 40
Contrainte de Von Mises [MPa]
300
200
100
Temps [s]
Fig. IV.118: Comparaison pour les
résultats des contraintes Von Mises entre les deux
modèles traités.
IV.8.2 Champ des contraintes de Von Mises dans la
plaquette intérieure
Dans cette partie, on présente l'influence de la
rainure dans les plaquettes de frein et le mode de chargement à double
piston sur la distribution des contraintes équivalentes de Von Mises. La
figure IV.119 montre que la contrainte de Von Mises atteinte par exemple
à l'instant t= 3,5 [s] chute d'environ de 1%, lorsque la
plaquette comporte une rainure. D'une manière analogue, on observe une
diminution des contraintes de 5%, dans le cas du dispositif à double
piston. La présence de la rainure et du mode à double piston
influent donc positivement sur les contraintes en surface de la plaquette.
Chapitre IV Résultats et Discussions

-a- : à l'instant t= 1,7271
[s].
-b- : à l'instant t= 3,5 [s].
-d- : à l'instant t= 20 [s].
-c- : à l'instant t= 10 [s].
114
-e-
Chapitre IV Résultats et Discussions
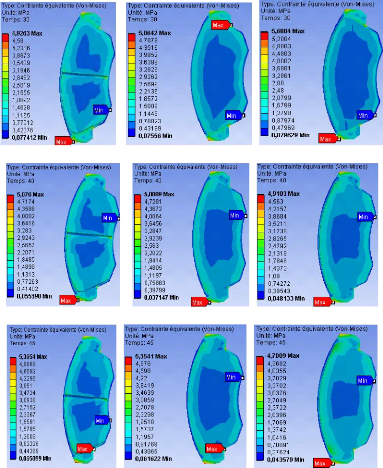
-e- : à l'instant t= 30 [s].
-g- : à l'instant t= 40 [s].
: à l'instant t= 45 [s].
115
Fig.IV.119 : Distribution des
contraintes de Von Mises dans la plaquette intérieure. simple piston
(à gauche et au centre), à double piston (à
droite).
IV.8.3 Pression de contact
En procédant à des sondages le long des bords
inférieurs, supérieurs et du rayon moyen de la plaquette à
l'instant t= 1.7271 [s] où la température du modèle est
maximale (T=346.46 °C), on obtient la variation de la pression de contact
en fonction de l'angle de rotation représentée par la figure
IV.120. On remarque une symétrie des pressions par rapport à la
rainure.
Chapitre IV Résultats et Discussions
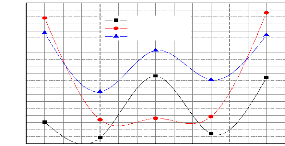
Pression [MPa]
0 ,9 0
0 ,8 5
0 ,8 0
0 ,7 5
0 ,7 0
0 ,6 5
0 ,6 0
0 ,5 5
0 ,5 0
0 ,4 5
0 ,4 0
Bord supérieur Moyen
Bord inférieur
0 1 0 2 0 3 0 4 0 5 0 6 0
116
L'angle circulaire
Fig.IV.120 : Distribution de
pression de contact le long des bords inférieur, supérieur
et
moyen de la plaquette à l'instant t= 1.7271 [s].
Contrainte Von Mises [MPa]
400
300
200
500
100
0
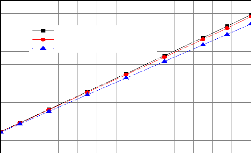
Plaquette rainurée 1 P Plaquette non rainurée 1
P Plaquette non rainurée 2 P
0,5 1,0 1,5 2,0 2,5 3,0 3,5
Temps [S]
Fig.IV.121 : Variation de
contrainte de Von Mises en fonction du temps
dans le couplage
thermomécanique.
Sur la figure IV.121, on constate que la présence de la
rainure influe négativement sur la contrainte sur la surface du disque,
contrairement à l'utilisation du dispositif à double piston.

Chapitre IV Résultats et Discussions
117
Fig.IV.122 : Contrainte de
frottement et distance de glissement de la plaquette intérieure à
l'instant t= 3.5 [s].
La figure IV.122 montre que les contraintes de frottement et
des distances de glissement de la plaquette intérieure sont
symétriques par rapport à la rainure et sont maximales sur les
bords.
IV.8.4 Déformation du disque
Lors d'une manoeuvre de freinage, le température
maximale atteinte sur les pistes dépend de la capacité de
stockage de l'énergie thermique dans le disque. On constate sur la
figure IV.123 que le déplacement maximum se localise sur les pistes de
frottement, les ailettes et la couronne extérieure. Ce
phénomène s'explique par le fait que la déformation du
disque est due à la chaleur (l'effet parapluie) qui peut engendrer un
endommagement par fissuration. Dans ce cas, le couplage thermomécanique
est assez important. Les gradients thermiques et les dilatations
génèrent des contraintes thermiques qui s'ajoutent aux
contraintes mécaniques.

Fig. IV.123:
Déformée totale maximale en couplage
thermomécanique.
IV.8.5 Effet parapluie
L'échauffement d'un disque de frein provoque un
déplacement des pistes de frottement par rapport à l'état
initial. Cette déformation est appelée effet parapluie,
figure IV.124.

Chapitre IV Résultats et Discussions
118
Fig. IV.124: Effet parapluie d'un
disque.
La déformée totale maximale se trouve au niveau
de la couronne extérieure du disque, elle atteint 284,55 um
à l'instant t =3,5 s. Une élévation de la pression et
donc de la température sur une surface de contact réduite peut
créer ce phénomène (déformation due à la
chaleur), une fatigue locale du matériau et parfois une fissuration du
disque. L'effet parapluie du disque n'est pas souhaité car il a une
influence négative sur l'efficacité des freins.
Le fonctionnement correct d'un frein sous l'influence d'une
charge thermique est limité par certains phénomènes
thermomécaniques tels que :
- la fissuration due au gradient de température sur les
pistes de frottement, pouvant causer la rupture du disque,
- la déformation du disque due à la chaleur
(1'effet parapluie) qui influence la surface de contact, réduisant ainsi
l'efficacité du frein,
- l'usure du disque et des plaquettes de frein,
- l'influence sur l'environnement du disque (les étriers,
l'état de l'huile ...).
119
Conclusion générale et perspectives
CONCLUSION GENERALE ET PERSPECTIVES
L'analyse du comportement thermomécanique des disques
de frein est une étape incontournable dans la conception des
systèmes de freinage, car la température et les contraintes
conditionnent le comportement thermomécanique des matériaux du
disque et des plaquettes qui peuvent subir dans des situations critiques de
freinage des dommages sévères. Durant la phase de freinage, les
températures et les gradients thermiques sont très
élevées. Celles-ci génèrent des contraintes et des
déformations qui se manifestent par l'apparition de fissures. Ce
phénomène n'est pas nouveau dans le domaine des transports
ferroviaires, aéronautiques ou automobile. Un nombre important de
travaux de modélisation et expérimentaux a été
mené ces dernières décennies pour essayer de comprendre
les mécanismes de contact sec frottant. La modélisation du
contact sec demeure un sujet d'actualité, surtout lorsqu'il s'agit des
organes de freinage.
En raison de la sécurité des passagers, la
construction optimale des disques de freins est actuellement l'objet de
nombreuses études. Le contact disque - plaquettes implique de nombreux
phénomènes, tels que l'élévation de la
température, l'usure des pièces et les vibrations.
Vu que les essais expérimentaux, bien qu'indispensables
avant toute production en série d'un système de freinage, sont
relativement coûteux et longs à mettre en place, les constructeurs
font appel lors de la phase de conception à la simulation
numérique.
Dans ce travail de recherche, on a présenté une
modélisation numérique du contact disque - plaquettes en
utilisant le code de calcul ANSYS 11.0, basé sur la méthode des
éléments finis, pour analyser le comportement sous l'aspect
purement thermique et mécanique ainsi que sous l'aspect
thermoélastique et pour prédire la tenue en fatigue des
pièces en contact glissant.
Dans la première partie de ce travail, on a
présenté une simulation numérique de l'écoulement
de l'air autour du disque en utilisant le code de calcul CFX ( méthode
des volumes finis ). On a débuté cette étape par le calcul
de la valeurs du transfert de chaleur (h) en régime transitoire . Ce
paramètre a été exploité pour l'analyse du
comportement thermique du disque plein et ventilé pour un freinage
d'arrét du véhicule . On a étudié l'influence de 3
types de fontes ( FG 25 AL , FG 20 , FG 15 ).
120
Conclusion générale et perspectives
D'après les résultats de simulation obtenus , on
a pu constater que le système de ventilation joue un role
non-négligeable dans la réduction de la température du
disque dans la phase de freinage.
A travers les résultats des différentes
simulations, on a remarqué que la qualité des résultats
concernant la répartition de la température est influencée
par plusieurs paramètres :
· Paramètres technologiques illustrés par la
conception,
· Paramètres numériques
représentés par le nombre d'élément et le pas du
temps.
· Paramètres physiques exprimés par le type
de matériaux.
· Mode de freinage mis en jeu.
Dans la deuxième partie de ce travail, on a
présenté une étude purement mécanique du contact
entre disque de frein et la plaquette. A l'aide du modèle
développée, on a pu examiner la sensibilité de certains
paramètres sur les résultats de calcul, qui se résume
comme suit :
· Les parties à forte concentration de
contraintes se trouvent généralement dans le disque au niveau du
bol, les pistes de frottement, les pieds des ailettes. causant des
phénomènes mécaniques (fissures radiales, l'usure,
rupture,...etc.).
· La vitesse de rotation initiale du disque a une grande
influence sur le comportement mécanique.
· L'étrier à double pression constitue le
chargement le plus favorable.
· La finesse du maillage augmente la précision de
la solution.
· Le bon choix du matériau des plaquettes
dépend de son module de Young. Le matériau ayant le plus grand
module d'élasticité diminue les contraintes maximales et donne
des bons résultats.
· Le choix d'un matériau des plaquettes est
dépend d'un bon coefficient de frottement (le plus élevé
possible).
· L'augmentation de la vitesse de rotation de disque
entraîne la diminution des contraintes équivalentes de Von Mises,
les contraintes de cisaillement du disque, et entraîne l'augmentation des
contraintes normaux du disque et les pressions et contraintes de frottement
ainsi la déformée totale des plaquettes
· L'emploi de la fonte grise pour les disques de frein
influe positivement sur la contrainte en surface du disque. Elle se distingue
par un meilleur comportement mécanique.
121
Conclusion générale et perspectives
· La présence de rainures dans les plaquettes influe
défavorablement sur le comportement mécanique d'un système
de freinage.
· Les contraintes de Von Mises et les déformations
globales du disque et les pressions de contact des plaquettes augmentent d'une
manière notable lorsque l'aspect thermique et mécanique sont
couplés.
· Les résultats obtenus pour le calcul
numérique sont comparable à ceux qu'on trouve dans la
littérature spécialisée.
Concernant les perspectives, on peut citer certains axes de
recherche :
· Etude expérimentale pour vérifier
l'exactitude du modèle numérique développé,
· Etude tribologique et vibratoire du contact disque -
plaquettes.
· Etude du contact sec glissant sous l'aspect macroscopique
(état macroscopique des surfaces du disque et plaquettes)
BIBLIOGRAPHIE
[1] SCHMITT. Emmanuelle, GAGNE .Wilfrid. " Etude sur le
freinage automobile ". Préparation à l'agrégation
de mécanique 2002-2003.
[2] M. AUBLIN, R .BONCOMPAIN ,M .BOULATON,D.CARON,E.JEAY,B.
LALAGE, J. REA : " Systèmes mécaniques - Théorie
et dimensionnement " , 2 ème édition, Editions DUNOD,
2004
[3] J-J.Carré. "Technique d'Ingénieur
,Technologie de Freinage ,Frein à Disque ".BD.4-5574.
11-1993.
[4] M. Benramdane1 , Y. Khadraoui1 et N. Bibi-Triki2
" Analyse de la contribution du transfert thermique des disques
tournants (disque de frein) uniformément chauffés "
Département de Génie Mécanique, Faculté
des Sciences de l'Ingénieur Université Abou Bekr Belkaïd,
Tlemcen, Algérie
[5] J. Guichard, "Freinage à très Hautes
Performances, Techniques de l'Ingénieur, B-5580, pp. 1 - 21,
2000. Le freinage
[6] FAUQUERT Gaétan.LE PICHOURON Erwan
"Modélisation et calculs sur un étrier de frein
automobile" Projet CAO - Calculs 2003 Maîtrise IUP GMP option
MPC
[7] " Etude de positionnement de la branche
composants automobiles " Cahier du CEPI N°9 - API décembre
2000
[8] Carneiro E.A., Winocq L., Berthaud J. : "Disc
brakes of trucks : a technical innovation for heavy vehicles",
Warrendale SAE, 1992
[9] Jimbo Y. et al. : " Development of high thermal
conductivity cast iron for brake disc rotor", Warrendale SAE,
pp.22-28, 1990
[10] Kim S.S., Lee S.H., Lee S.M. :"Thermomechanical
wear mecanism of friction brake", Proceedings of the international
tribology conference, Tokohama, pp.1567-1572, 1995
[11] Kennedy F.E., Ling F.F. : "A thermal,
thermoelastic and wear simulation of a high-energy sliding contact problem
", Journal of lubrification Technology, vol.23, pp.276-296,2000
[12] Tirovic M., Day A.J. : "Disc brake interface
pressure distributions", Instn.Mech.Engrs., vol.205, pp.137-146,
1991
[13]
http://seigneurienet.free.fr/travaux/Disquedefreins.htm
123
Conclusion générale et perspectives
[14] H.Dittrich et R.Lang. "Finite
Element Analysis of the Thermal Loads Acting on a Passenger Car Brake
Disk". Automobiltechnische Zeitschrift. Vol 86, N°
6,pp,265-269, 1984.
[15] Michel Houdé. "Introduction aux
phénomènes de transfert". Université de
Technologie Compiègne. France (1994-1998)
[16] YVES JANNOT. " Transferts Thermiques "
Ecole des mines Nancy 2009
[17] PHILIPPE MARTY . " cours de transferts thermiques
conduction et rayonnement" Université Joseph fourier Grenoble
septembre 2001.
[18] Claude SAINT-BLANQUET. Bernard FOURCHER "Conduction
de la chaleur" Université de Nantes 2001.
[19] F. KREITH "Transmission de la chaleur et
Thermodynamique" Université du Colorado,1967
[20] Oschwald Martin. "Development of a Methodology
for Design and Optimization of Multi-Material Objects for enhanced Thermal
Behavior Application: Brake Disk Rotor" Mechanical Engineering
Department College of Engineering & Science Clemson University South
Caroline March 12, 2004
[21] Yves Debard . "Méthode des
éléments finis : thermique Master Modélisation
Numérique et Réalité Virtuelle" Université
du Maine mars 2006
[22] K.-J. Bathe - "Finite element procedures in
engineering analysis", Prentice Hall, 1996.
[23] K. H. Huebner , E. A. Thornton et T. G. Byron " The
finite element method for engineers", Wiley,1995.
[24] R.W.Lewis, K.Morgan, H.Thomas and K.N.Seetharamu
"The finite element method in heat transfer analysis", Wiley,
1996.
[25] NGUYEN-TAJAN Thi Mac-Lan"Modélisation
thermomécanique des disques de frein par une approche
eulérienne"Thèse de doctorat de l'école
polytechnique-spécialité mécanique des solides , janvier
2002.
[26] Y. YILDIZ and M. DUZGUN" Stress analysis of
ventilated brake discs using the finite element method " International
Journal of Automotive Technology, Mechanical Department, Faculty of Technical
Education, Gazi University, Ankara 06500, Turkey 21 January 2009
124
Conclusion générale et perspectives
[27] Benoît MAGNAIN
"Développement d'algorithmes et d'un code de calcul pour
l'étude des problèmes de l'impact et du choc
"Thèse de doctorat de l'université d'évry -val
d'essonne , novembre 2006
[28] Thomas J. Mackin , Steven C .Noe, K.J .Ball, B.C. Bedell
," Thermal cracking in disc brakes"Department of Mechanical
and Industrial Engeneering,The university of Illinois at Urbana -Champaign.USA
September 2000.
[29] Oder, G.; Reibenschuh, M.; Lerher, T.; raml, M.; amec,
B.; Potrè, I. "Thermal and stress analysis of brake discs in
railway vehicules"Advanced Engineering 3(2009)1, ISSN 1846-5900
[30] Nicolas COUDEYRAS"Analyse non-linéaire
des instabilités multiples aux interfaces frottantes : application au
crissement de frein " Thèse de doctorat de l'école
centrale de Lyon-spécialité : mécanique, décembre
2009.
[31] M.M.Mayuram, R.Vasudevan " Simulation of
Thermoelastic Instability in Disc Brakes through Finite Element Programming "
Department of Mechanical Engineering, Indian Institute of Technology
Madras. Chennai 600036.(India)
[32] J.H.Choi, I.Lee " Finite Element Analysis of
Transient Thermoelastic Behaviors in Disk Brakes " Department of
Aerospace Engineering, Korea Advanced Institute of Science and Technology.
South Korea July 2003.
[33] P Hwang, X Wu , Y B Jeon " Thermal Mechanical
coupled simulation of a solid brake disc in repeated braking cycles "
Proceedings of the Institution of Mechanical Engineers, Part J:
Journal of Engineering Tribology 2009 223: 1041 .Yeungnam University, Gyongsan,
Republic of Korea 1May 2009.
[34] Kim, J. Y. " Ansys thermal analysis " 2002
( Teasung S & E Inc., Seoul, Republic of Korea).
[35] Arpaci,V. S. " Conduction heat transfer "
1991 ( Ginn Press, Nedham Heights, MA).
[36] R.Kumar,V.K.Jadon " Transient Thermoelastic
Analysis of Disk Brake using Ansys Software "Master of Engineering .
Department of Mechanical Engineering, Thapar University, Patalia-147004, India
,June 2008.
[37] Y.B.Ko,J.T.Hwang,S.H.Cho,Ch.K.Kim " The Analysis
for Thermal Behaviors of Disc Brakes Using Disc-Pad Contact Model "
Tribology Research Center, Hongik University
[38] H.Jianmeng,G.Chenghui , T.Xusheng, L.Xiezhao "
Numerical Modeling and Analysis of the Thermal - structure coupling of the Disc
Brake " College of Mechanical
125
Conclusion générale et perspectives
Engineering and Automation, Fuzhou University, Fuzhou 350002 ,
Vol 44 N°02, Feb 2008.
[39] CHEVEREAU Edouard.COSSON Yves
"Simulation de l'échauffement d'un disque de frein d'une moto de
compétition sous Star-CD"Projet de formation Université
de Maine
[40] Carlos H. Galindo-Lopez " Evaluating new ways of
conducting convective heat dissipation experiments with ventilated brake discs"
Cranfield University, Bedfordshire, MK43 OAL, UK
[41] ANSYS Analysis User's Manual , Version 11.0
[42] T. Bouache, A. Baïri, J.G. Bauzin, N.
Laraqi "Evolution transitoire 3D des températures d'un disque de
frein" Laboratoire d'Energétique et Economie d'Energie,
Université de Paris X ; Mai 2006.
[43] JONATHAN WONG"Analyse de l'endommagement par
fatigue thermique et modélisation du comportement thermomécanique
de couples disques-garnitures de type TGV frottantes " Thèse de
doctorat de l'école centrale de Lille-spécialité :
mécanique, décembre 2007.
[44] A. R. Abu Bakar, H. Ouyang and Q. Cao "
Interface Pressure Distributions through Structural Modifications
«Department of Engineering University of Liverpool ,Liverpool
.L69 3GH, U.K. 2003
| 


