La gestion des risques dans le cadre des assurances- vie. Cas de la compagnie TRUST Assurances de Personnes (Alger )

Ecole Nationale Supérieure de statistique et d'Economie Appliquée ex (INPS)

Mémoire de fin de cycle en vue de l'obtention du diplôme d'ingénieur d'Etat en économie
et statistique appliquée option ; Finance et Actuariat

La gestion des risques dans le

cadre des assurances vie

Cas de la compagnie TRUST Assurances de Personnes

Présenté par : REKOUCHE Kais

Sous la direction de : BENKHLIFA Brahim

(ENSSEA)

Promoteur : TIBAOUI Mehdi (TRUST Assurances de personnes)

Année 2011

Remerciements

En premier lieu, je tiens à remercier mon promoteur de mémoire Mr Mehdi TIBAOUI, pour le soutien et la confiance qu'il m'a accordée. Je remercie aussi vivement mon encadreur Mr Brahim BENKHLIFA.

Je présente mes sincères remerciements à Mr ZERROUKI et Mlle TAGMOUNTE, de m'avoir fait l'honneur d'accepter de participer à mon jury.

Je remercie tous les membres de l'équipe de la Trust assurance de personnes pour leur accueil chaleureux, leur aide tout au long de mes six mois de stage. Je les remercie pour les nombreux conseils qu'ils m'ont donnés ainsi que l'intérêt qu'ils ont montré à mes travaux de recherche.

Je remercie l'ensemble de mes professeurs, de mes amis ainsi que tous mes camarades de ENSSEA.

Une pensée particulière à la mémoire de mon ami Nassim DALI.

Je tiens aussi à remercier mes proches, ma tante Naima, ma cousine Meriem, un remerciement particulier à ma soeur Soumia, un affectueux remerciement à Lina pour son soutien sa gentillesse et sa patience.

Enfin, je veux dédier ce travail à mon père, à la mémoire de ma mère. Les mots que je pourrais écrire ne sont pas à la hauteur de ce que je peux ressentir à leur égard. Je les aime du fond du coeur et les remercie pour l'amour et le soutien qu'ils m'ont donné tout au long de ma vie. Je les remercie surtout de m'avoir inculqué les valeurs morales qui m'ont permis de devenir la personne que je suis.

1

Introduction

Les définitions du mot risque sont nombreuses, selon le domaine étudié, l'application ou encore les époques. Dans un premier temps, le mot "risque" n'apparaissait même pas alors qu'il était question de jeux de hasard. Plus tard, les mathématiques se sont explicitement penchées sur le calcul de risques. Cependant, une définition indéniable émerge, à savoir que le risque est un danger potentiel. Pour l'assureur, il représente la probabilité du sinistre encouru, ou encore l'espérance mathématique de ce dernier.

Les mathématiciens furent les premiers à employer le mot "risque" dans son sens abstrait, complètement dégagé de connotations normatives, à l'instar de Bernoulli, attribuant une mesure du sort. Ce dernier mot désigne les conséquences de la participation aux jeux de hasard que les mathématiciens ont dénommé "variable aléatoire". A partir de là, les probabilistes vont se délecter de résoudre des questions liées à des jeux de société, ou d'inventer des jeux qui illustrent des problèmes mathématiques.

On confond donc, généralement, le risque avec sa mesure. Ces métonymies, qui vont de l'objet à sa représentation, ou de l'objet au sujet, permettent une grande variété d'emplois du mot "risque". On peut rappeler que si la signification principale du risque reste inchangée, seule sa désignation s'élargit, à travers les époques, ainsi que les domaines d'applications.

Les assurances, qui touchent, par nature, des phénomènes aléatoires, offraient dès l'origine un domaine d'application pour le calcul des probabilités. Il s'agissait de déterminer avec une certaine précision les primes. Les assurances sur la vie vont susciter une abondante littérature. C'est ainsi qu'avec la question de l'évaluation des assurances-vie que se développent véritablement les mathématiques actuarielles. En effet, il y a là un enjeu à la fois pour les gestionnaires qui ne peuvent évaluer les rentes à vue de nez, et pour les mathématiciens qui s'intéressent au formalisme des séries.

Assurance vie, l'expression est trompeuse, car elle confond assurance décès et assurance contre le risque de vivre, au-delà d'un âge préalablement déterminé entre l'assuré et l'assureur. L'évaluation des primes d'assurance décès nécessite de connaître la probabilité de décéder dans l'année. En revanche, l'assurance vie, à proprement parler, couvre un grand nombre de possibilités qui consistent en général à échanger un montant certain (la prime) contre une somme hypothétique (le sinistre). Dans le cas d'une rente viagère, cette somme hypothétique est un revenu annuel régulier payé au contractant qui peut ainsi se garantir un revenu régulier jusqu'à la fin de ses jours (dont la date est, à l'évidence, inconnue à la signature du contrat).

2

Aujourd'hui, la mathématique actuarielle est l'un des domaines les plus importants de la recherche appliquée en finance. Nous verrons dans le présent document qu'une compagnie d'assurances vie dont l'activité présente une singularité, implique des outils de gestion spécifiques. Ces outils ont pour objectifs l'évaluation du risque encouru par la compagnie d'assurances et sont à la base de la détermination des primes demandées aux assurés, ainsi que l'évaluation des provisions mathématiques.

~Comment une compagnie d'assurances peut-elle fixer le montant d'une prime, alors que les éléments ou les paramètres constituant cette dernière sont aléatoires ?~

Nous tenterons de dépasser cette vison simplicite qui consiste à penser qu'une compagnie d'assurances est une entreprise comme une autre vendant des polices d'assurances ; ce qui est loin d'être le cas. En effet, au-delà de vendre des polices d'assurances, une compagnie prend en charge des risques, les gère, les couvre, les transfère, et parfois les revend.

Nous chercherons à modéliser le risque. Dans ce cadre, nous pouvons noter que le risque est partout et concerne aussi bien les individus que les entreprises. Quant aux compagnies d'assurances elles sont aussi confrontées à un risque, nécessitant parfois le recours à la réassurance. Aujourd'hui, il est impensable de gérer une compagnie d'assurances sans recourir, de façon systématique, à des études de modélisation du risque encouru et l'optimisation sous contraintes.

Cependant, il est important d'aller au-delà de simples résultats élémentaires de probabilités et de concepts de base des mathématiques financières, car elles se fondent sur des modalisations liées à la vie humaine, d'où l'importance d'en saisir toute la portée mais aussi les limites.

Pour comprendre la gestion des risques ou bien la politique de gestion du risque d'une compagnie d'assurance, nous devons, au préalable, répondre à un certain nombre de questions.

> Quels sont les différents risques liés à l'assurance-vie ?

> Quels sont les outils utilisés pour mesurer ces risques ?

> Quelle est le lien entre ces différents risques ?

> Quels sont les moyens adéquats pour modéliser ce risque ?

Le présent mémoire va traiter, dans sa première partie, la notion de risque dans le but d'appréhender les mécanismes qui régissent la gestion du risque en assurance vie et plus précisément le risque lié à l'assurance de personnes.

Dans le premier chapitre de ce mémoire nous allons nous intéresser à la partie névralgique de l'assurance de personnes dénommée la production, ou la couverture du risque moyennant une prime de risque en faisant une analogie avec une entreprise. Cette partie représente la production pour une compagnie d'assurances dont la police

3

d'assurance est le produit. Elle comporte un risque dit technique ou risque viager (lié à la durée de vie), et qui est le propre de l'assurance de personnes. A l'évidence, ce risque existe dès lors que le contrat d'assurance prévoit une prestation d'un montant différent ou une date différente de versement de la prestation selon que l'assureur survit ou décède.

Nous verrons quelles sont les méthodes et les techniques utilisées par les compagnies d'assurance pour mesurer, quantifier et modéliser ce risque afin de calculer une prime de risque qui respecte le principe d'équité.

Dans le deuxième chapitre, nous examinerons les risques encourus par la compagnie d'assurances ainsi que les risques que l'on pourra qualifier de collatéraux, car assimilés à des risques indirects liés à l'activité de l'assurance. Aussi, nous nous intéresserons à la Direction financière où demeure le risque financier qui est lié aux variables économiques telles que le taux d'intérêt, et par conséquent au risque de taux, puisque l'essentiel de ses placements est constitué de produits obligataires, et qui peuvent créer un décalage préjudiciable entre la valeur des actifs et celle des passifs.

Une de ces spécificités majeures de la compagnie d'assurances reste l'inversion du cycle de production, par rapport à un cycle de production dit classique. En effet, celui de la compagnie d'assurances est inversé, c'est-à-dire que le prix du produit (l'assurance) est déterminé avant que les charges (le coût du sinistre) ne le soient. Cette spécificité propre à l'assurance nécessite de recourir à la gestion de l'actif-passif, dans l'établissement de leurs bilans, ainsi que dans le calcul des différentes provisions liées à leur activité, dans le but de se soumettre aux exigences réglementaires (comptables et prudentielles) imposées par les autorités compétentes en la matière.

Dans le dernier chapitre, nous allons nous intéresser au cas de la Trust assurance de personnes, avec une vision globale de l'environnement de l'assurance vie en Algérie, nous élaborerons une table de mortalité, en se basant sur le modèle Gompertz-Makeham aussi au travers d'une étude non exhaustive du portefeuille de contrats de la Trust nous verrons, les spécificités des différents contrats.

L'anticipation des coûts de gestion liés à la production, ainsi que la maitrise des risques du portefeuille d'assurés reste une condition nécessaire à l'activité de l'assureur, et qui ne peut être envisageable sans ces prérequis. Le rôle prédominant des compagnies d'assurances dans l'économie, mais aussi le risque qu'elles représentent, implique qu'elles soient en permanence contrôlées et encadrées.

Comme nous pouvons le constater l'assurance de personnes est sujet, à un certain nombre de risque sans compter celui, prédominant à son activité (risque viager). Nous verrons que ces risques ne sont pas cloisonnés, par chaque direction de la compagnie d'assurance, mais liés entre eux, ce qui nous conduit à adapter une vision plus globale de la compagnie d'assurances.

4

Ainsi nous devons concevoir les risques, liés à chaque direction, non pas comme des éléments indépendants mais comme un ensemble régie par un mécanisme transversal, aux différentes directions, qui consiste en "la gestion du risque". Toute la problématique de l'assurance vie réside dans l'optimisation de ce processus.

La Direction générale a pour rôle d'adopter une stratégie qui pilote la gestion risque, régulièrement alimentée en indicateurs, nécessaire à cette gestion, qui sont transmis par les différentes directions, d'où une nécessité d'une communication claire et directe.

Chapitre I

Les Risques liés à l'assurance-vie

Section 1 : Une approche méthodologique face à un évènement aléatoire

Section 2 : Etude des fonctions probabilistes de l'assurance vie Section 3 : Modélisation du risque en assurance vie

5

Chapitre I : Les Risques liés à l'assurance-vie

Section 1 Une approche méthodologique face à un événement aléatoire :

1 les probabilités liées aux événements aléatoires

Face à un évènement aléatoire, nous devons toujours nous poser la question de savoir si les probabilités liées à cet évènement sont connues.

Cette information est cruciale dans notre tentative de comprendre l'évènement aléatoire, car en l'absence de cette information, nous serons face à un évènement aléatoire non probabilisé. Une première approche keynésienne consistait purement et simplement à ignorer l'évènement aléatoire, du fait de l'impossibilité de l'intégrer faute de moyens ou d'informations. C'est loin d'être le cas aujourd'hui, car les outils actuariels nous offrent la possibilité de le faire comme c'est le cas, notamment, le cas de la théorie de jeux et la simulation de probabilité.

Figure 1 Modélisation dans un avenir incertain source (Thiriez 2004)

La procédure indiquée par le schéma ci-dessus nous montre que même en l'absence de probabilité, il est toujours possible d'estimer le risque. Sans rentrer dans un antagonisme, nous pouvons poser des probabilités qu'elles soient objectives ou subjectives, dont les principales théories sont :

1) La méthode des scénarios connue aussi sous le nom de modèles déterministes ou des outils de2^ème génération utilisés dans la gestion du risque financier.

2) La théorie des jeux utilisée souvent dans les études de marché et de Benchmarking est un modèle de pris de la décision dans un environnement incertain non probabilisable.

3) La théorie de la décision est une approche utilisable dès que l'on peut associer une probabilité à l'événement aléatoire. Elle est objective quand elle repose sur des données statistiques et subjectives dans le cas d'une estimation élaborée, l'assurance repose sur cette dernière.

6

Chapitre I : Les Risques liés à l'assurance-vie

4) La simulation de probabilité est utilisée dans certaines situations où il est impossible d'avoir les probabilités relatives à l'événement (Thiriez 2004) ; ce qui ne nous empêche pas d'en affecter en utilisant un générateur de nombres aléatoires. Cet outil nécessite des calculs importants et le modèle construit doit aussi avoir une structure mathématique que l'on peut optimiser ; ce qui n'est pas toujours le cas. En revanche il possède un avantage majeur car il n'y a aucune limite à ce que l'on peut modéliser grâce à la simulation qui est statique (sans dimension temporelle) ou stochastique (avec une dimension temporelle).

2 La théorie de l'assurance

La théorie de l'assurance s'inscrit dans le cadre de la théorie des choix en avenir incertain probabilisable. Plus explicitement c'est la théorie de la décision objective car elle repose sur des données statistiques non seulement fiables mais aussi particulièrement abondantes en assurance vie.

Dans le cas pratique, on distingue deux catégories d'opération d'assurance : l'assurance dommage, essentiellement accidents et incendies, et l'assurance de personnes relative à la vie humaine (au sens large : décès, invalidité, épargne retraite...).

3 Modélisation du risque et prime d'assurance

Une logique simple que nous allons développer tout au long de ce mémoire, consiste à ce qu'un assureur doit faire face à un sinistre qui est pour lui des dépenses probables futures, en se basant sur les primes d'assurance qui sont des recettes certaines.

Cette prime d'assurance comporte trois parties :

3.1 La prime pure

Elle représente l'espérance mathématique E(x) et permet, en théorie, à l'assureur de faire face aux sinistres futurs.

3.2 Le chargement technique (CT)

C'est le montant qui vient compléter la prime pure, afin de prémunir l'assureur contre les fluctuations des sinistres plus précisément de l'espérance mathématique. Il existe plusieurs façons de calculer le chargement technique selon les critères de l'assureur, en utilisant un des indicateurs par rapport au coefficient proportionnellement positif ë, CT = A E(x) ou bien par rapport à la variance CT = A Var(x)

3.3 Le chargement commercial (CC)

Il permet à l'assureur de couvrir l'ensemble des frais liés à la gestion et la commercialisation des contrats d'assurances. L'assureur doit prendre porter une attention particulière à l'estimation de ce chargement, car celui-ci contribue au résultat de la compagnie d'assurance. Les chargements sont définis en fonction des frais qu'ils couvrent

7

Chapitre I : Les Risques liés à l'assurance-vie

Le chargement d'acquisition : destiné à couvrir les frais d'acquisition Le chargement de gestion : destiné à couvrir les frais de gestions

4 La Mutualisation des risques

La mutualisation des risques reste un des principes fondamentaux de l'assurance et consiste en un regroupement d'un nombre de risques indépendants permettant une compensation statistique.

Conséquence de la loi des grands nombres : pour une suite de variables aléatoires x1,x2,...,x_n indépendantes, de même loi de probabilité et de moyenne ou espérance mathématique commune (u), la variable (x1,x2,...,x_n) / n converge l'espérance mathématique commune ou la moyenne (m) des variables aléatoires x1,x2,...,x_n.

V > 0,1imn,+oe (1"1+"2+--+"nn

p -- E(X) >_ &= 0.

Ce phénomène crée une compensation qui, si elle n'apparait pas à l' instant t, est une compensation temporelle, ce qui signifie que si certaine années sont déficitaires, elles pourront être compensées par d'autres qui seront bénéficiaires.

Fort heureusement, les compagnies d'assurance n'ont pas qu'un seul bénéfice qui est le bénéfice technique, résultat uniquement des opérations d'assurance.

En effet, l'assureur a la possibilité de placer le montant des primes dans les valeurs de son choix et ce en accord avec la réglementation. Le bénéfice qu'il produit n'a rien à voir avec l'opération d'assurance car c'est un bénéfice purement financier.

8

Chapitre I : Les Risques liés à l'assurance-vie

Section 2 Etude des fonctions probabilistes de l'assurance vie

1 Repères historiques

L'assurance vie apparut surtout sous la forme de l'assurance maritime et couvrait les voyageurs. Elle présentait le caractère d'une spéculation, notamment en Italie, ce qui entraina inévitablement de nombreux abus. Aussi fut-elle interdite par les autorités religieuses en 1589 et par l'ordonnance de la marine française.

Elle réapparut sous une forme complètement différente appelée les Tontines qui constituaient une sorte d'assurance d'épargnants. Le fonds commun constitué par le groupe d'adhérents est capitalisé et le produit des placements, réparti entre les seuls survivants. Ce qui est incontestablement le principe de l'assurance vie.

En 1818, le Conseil d'Etat dut se prononcer sur les statuts des sociétés d'assurance-vie et adopta une démarche constructive et mit l'accent sur l'aspect positif du contrat d'assurance-vie en tant qu'opération de prévoyance permettant au père de famille de préserver, du coup du sort, les êtres qui lui sont chers.

2 Les facteurs influant la mortalité

Le risque pris en charge par la compagnie d'assurances peut être modélisé par une ou plusieurs variables aléatoires. Nous allons présenter brièvement le modèle probabiliste sur lequel sont basés les calculs actuariels de l'assurance vie. Au préalable et afin de justifier le modèle, nous indiquerons les principaux facteurs influant sur la mortalité humaine. En actuariat on distingue deux types de circonstances qui conditionnent la mortalité.

a) L'âge

A l'évidence, le premier facteur, est l'âge de l'assuré. Ainsi pour tout assuré pris à l'époque (t=0), il est clair que sa probabilité de survie à l'époque (t=n) décroit avec le temps. Cependant, les statistiques nous apprennent bien plus que cette Lapalissade (Petauton 1996).

b) La profession

Bien que ce paramètre influence indéniablement la durée de vie, il n'est pas systématiquement pris en compte par les assureurs à défaut de statistiques car il n'est pas facilement mis sous forme numérique. Néanmoins, ce critère est utilisé pour certains types de risques, notamment l'assurance groupe.

c) Le sexe

Étant cratérisé par une variable binaire, ce paramètre peut aisément être introduit dans les calculs de probabilités ; la mortalité des hommes est nettement supérieure à celle des femmes et avoisine le double, entre 30 et 60 ans.

9

Chapitre I : Les Risques liés à l'assurance-vie

d) Le pays

Le niveau et le mode de vie influent sur la mortalité d'un pays à un autre. Il s'ensuit que la table de mortalité varie en fonction de ce paramètre géographique.

e) Evolution de la mortalité au cours des époques

Il est incontestable que la mortalité évolue est plutôt diminue au cours des époques. On observe, spécialement dans les pays développés, une augmentation de la longévité. Cette évolution est récemment prise en compte par les compagnies d'assurances au moyen des tables de mortalités prospectives.

3 Cadre juridique de l'assurance de personnes et ses déclinaisons

ART. 2. (MODIFIE PAR L'ART. 2 L 06-04) - L'assurance est, au sens de l'article 619 du code civil algérien, un contrat par lequel l'assureur s'oblige, moyennant des primes ou autres versements pécuniaires, à fournir à l'assuré ou au tiers bénéficiaire au profit duquel l'assurance est souscrite, une somme d'argent, une rente ou une autre prestation pécuniaire, en cas de réalisation du risque prévu au contrat (Code des Assurances s.d.).

ART. 60 (MODIFIE PAR L'ART. 10 L 06-04) - L'assurance de personnes est une convention de prévoyance contractée entre le souscripteur et l'assureur et par laquelle l'assureur s'oblige à verser, à l'assuré ou au bénéficiaire désigné, une somme déterminée, sous forme de capital ou de rente, en cas de réalisation d'événement ou au terme prévu au contrat (Code des Assurances s.d.).

Le souscripteur s'oblige à verser des primes suivant un échéancier convenu.

ART. 232 - Les éléments constitutifs de tarification des risques se déterminent comme suit :

> la nature du risque ;

> la probabilité de survenance du risque ;

> les frais de souscription et de gestion du risque ;

> tout autre élément technique de tarification propre à chaque opération d'assurance

(Code des Assurances s.d.).

ART. 232 BIS. (AJOUTE PAR L'ART. 44 L 06-04) - En matière d'assurance de personnes, les tables de mortalité applicables ainsi que le taux minimum garanti aux contrats (Code des Assurances s.d.).

En résumé

L'opération d'assurance donne lieu à un contrat qui lie la compagnie d'assurances dénommée l'assureur, à une personne l'assuré ou souscripteur. Ce contrat impose à l'assuré le versement d'une prime. L'assureur en échange cette dernière doit verser un capital, une rente ou une autre prestation pécuniaire, en cas de réalisation du sinistre tout au long de la durée de validité du contrat.

10

Chapitre I : Les Risques liés à l'assurance-vie

Le sinistre étant un événement futur aléatoire du moins quant à sa date (concernant l'assurance décès), nous allons tenter de définir les probabilités qui régissent cet événement.

3.1 Les différentes risques couverts en assurance de personnes

ART. 63. Les risques qui peuvent être couverts en assurance de personnes sont notamment :

> Les risques dépendant de la durée de la vie humaine

> Le décès accidentel

> L'incapacité permanente partielle ou totale

> L'incapacité temporaire de travail

> Le remboursement de frais médicaux, pharmaceutiques et chirurgicaux

3.2 Les assurances de personnes

Par opposition aux assurances de biens, d'autres assurances couvrent les personnes. On peut les distinguer selon leurs couvertures deux types de contrats :

1) En cas de vie, en cas de décès ou par une combinaison des deux dénommées contrat mixtes ; ce sont des contrats qui combinent assurance et épargne,

2) En cas de maladie ou d'accident corporel, ce sont des contrats d'assurance classiques (assurances maladie et accident).

a) Assurance en cas de vie a.1 Assurance retraite

C'est une épargne souscrite à titre individuel ou par adhésion à un groupe. Le contrat peut prévoir, au choix de l'assuré, le versement d'une retraite complémentaire à 60 ans sous forme de rente viagère, ou sous forme de capital.

Dans les deux cas (rente ou capital), le contrat comprend une clause permettant de rembourser les cotisations versées ou l'épargne acquise lors du décès prématuré de l'assuré.

a.1.1.1 La retraite anticipée

Une retraite anticipée avant l'âge de 60 ans est possible pour les assurés âgés de 50 ans. a.1.1.2 La réversion de la rente

Une pension de réversion égale à 60 % de la pension de l'assuré décédé peut être versée au bénéficiaire désigné dans le contrat. (M.Douakh 2006)

11

Chapitre I : Les Risques liés à l'assurance-vie

a.1.1.3 La cotisation

La cotisation en cause dépendra de la rente choisie, de la durée du contrat et de l'âge au moment de la souscription. Elle peut être unique ou périodique. Dans le dernier cas, elle est payable, à terme échu, le premier jour du trimestre civil.

a.2 Les assurances de groupe

a.2.1 Le risque

Le contrat d'assurance de groupe est souscrit par une personne morale ou chef d'entreprise en vue de l'adhésion d'un ensemble de personnes répondant aux conditions définies au contrat pour la couverture d'un ou plusieurs risques relatifs aux assurances de personnes.

Elle peut être contractée dans le cadre d'une convention collective couvrant par exemple une catégorie de personnel (cadres, cadres supérieurs, etc.), peut être une couverture d'activité commune de caractère non professionnel ou encore une couverture à caractère économique telle que les opérations de crédit.

a.2.2 Les garanties de base a.2.2.1 Le décès :

En cas de décès de l'assuré, le paiement d'un capital est garanti au(x) bénéficiaire(s) désigné(s).

a.2.2.2 L'invalidité permanente totale :

Est considéré comme atteint d'une invalidité permanente et totale, tout assuré classé par la Sécurité sociale dans la catégorie du troisième groupe. La compagnie verse à l'assuré, par anticipation, le capital prévu en cas de décès.

a.2.3 Les garanties complémentaires

Le décès consécutif à un accident : dans ce cas, un capital supplémentaire sera versé au(x) bénéficiaire(s).

Le décès consécutif à un accident de la circulation : dans cette situation, il sera réglé un capital supplémentaire cumulable aux garanties citées ci-dessus.

La rentes éducation : suite au décès de l'assuré, ces rentes sont destinées à faire face à l'entretien des orphelins jusqu'à l'âge de 18 ou 21 ans ou jusqu'à la fin des études.

L'incapacité temporaire : l'assurance garantit le paiement d'une indemnité quotidienne à l'assuré qui, par suite d'une maladie ou d'accident, est dans l'obligation de cesser son activité.

L'invalidité : lorsque l'assuré est atteint d'une incapacité permanente de travail qui ne lui permet plus de tirer un revenu de son travail, l'assurance lui garantit une rente d'invalidité.

12

Chapitre I : Les Risques liés à l'assurance-vie

La maladie et soins annexes : cette assurance garantit le remboursement des frais de traitements médicaux occasionnés par une maladie ou un accident dont l'assuré pourrait être atteint ou victime.

b) Assurance temporaire décès

Ce contrat prévoit le versement au bénéficiaire désigné d'un capital au décès de l'assuré, le décès devant survenir avant une date déterminée.

L'invalidité permanente et totale de l'assuré entraîne le paiement anticipé du capital si elle survient avant le terme du contrat et avant l'âge de 60 ans.

Cette assurance répond au besoin de préserver la famille pendant quelques années, par exemple aussi longtemps que les enfants ne sont pas élevés.

Il existe également des assurances temporaires décès au capital décroissant, particulièrement indiquées lorsque le contrat est souscrit en garantie d'une dette amortissable.

b.1 Individuelle voyages

Il s'agit d'une assurance qui couvre le décès, la maladie et une assistance à l'étranger pour le rapatriement de la personne ou du corps. C'est une assurance qui n'est pas obligatoire mais qui s'impose en fait. A titre d'exemple, l'entrée sur le territoire Schengen ne peut se faire que sur la production d'une attestation d'assurance spécifique couvrant les frais médicaux et le rapatriement.

b.1.1 Le risque

C'est un contrat qui garantit l'assuré en cas d'accidents survenus en cours de voyages, privés ou d'affaires. C'est une assurance qui est de fait limitée dans le temps.

b.1.2 La couverture

Décès : si l'assuré décède suite à un accident, soit immédiatement soit dans un délai maximum d'un an à compter de l'accident, la compagnie verse le capital convenu au(x) bénéficiaire(s) désigné(s) au contrat.

Infirmité permanente : lorsque l'accident entraîne une infirmité permanente dans les douze mois qui suit l'accident, il est versé à l'assuré, selon le degré de cette infirmité, le capital convenu ou une proportion de ce capital déterminée d'après le barème des invalidités fixé au contrat.

Frais de rapatriement : la compagnie garantit les frais de rapatriement du corps de l'assuré décédé à la suite d'un accident couvert et dans les limites fixées au contrat.

13

Chapitre I : Les Risques liés à l'assurance-vie

b.2 Individuelle accident

b.2.1 Le risque

Ce contrat a pour objet de garantir le paiement des sommes assurées dans les cas où l'assuré serait victime d'accidents tant au cours de sa vie professionnelle qu'en dehors de celle-ci.

Il importe de souligner que l'événement dommageable est défini comme toute atteinte corporelle non intentionnelle de la part de l'assuré, et provenant de l'action soudaine d'une cause extérieure.

La garantie est valable, dans le monde entier, pour les indemnités dues en cas de décès ou d'incapacité permanente.

b.2.2 La couverture

Décès : si l'assuré meurt des suites d'un accident, soit immédiatement soit dans un délai maximum d'un an à compter de l'accident, la compagnie verse le capital convenu au(x) bénéficiaire(s) désigné(s) au contrat.

Infirmité permanente : lorsque l'accident entraîne une infirmité permanente, dans les douze mois qui suivent l'accident, il est versé à l'assuré, selon le degré de cette infirmité, le capital convenu ou une proportion de ce capital déterminée d'après le barème des invalidités fixé au contrat.

Incapacité temporaire : lorsque l'assuré est dans l'impossibilité d'exercer son activité, il lui sera versé l'indemnité journalière convenue, à compter du point de départ stipulé et jusqu'à guérison ou consolidation, mais au plus jusqu'au 365^e jour qui suit l'accident.

Frais médicaux : la compagnie assure le remboursement à l'assuré des dépenses engagées jusqu'à concurrence des limites fixées.

14

Chapitre I : Les Risques liés à l'assurance-vie

Section 3 Modélisation du risque en Assurance vie

1 Définition du taux instantané de mortalité

Le taux instantané de mortalité résulte de la probabilité conditionnelle que l'individu d'âge x décède entre ' et ' ( ) (avec h strictement positifs). On désigne q_x cette probabilité conditionnelle *+,' - T₊ - ' ( ). = *+,T+ > '. " *+,T+ > ' ( ).. On pose ) = 1 ce qui

nous donne *+,' - T₊ - ' ( 1. et qui représente le taux annuel de mortalité. ₀*₊ =

1231245	7 7 7 912 9 :~ 12 ? 0 Si ) ? 0 on a lim0?6 * 0*+ ~ lim0?6 * 1231245 ~ " * ~ " ~ 0 12 0 12 9+ 9+
12

;+ (Taux instantané de mortalité).

a) Relation entre probabilité de survie et taux instantané de mortalité

;++< =

9 :~ 124= ? 9< , Integral: > ;+~< ~ "@ln B+~<CD ? ~ "ln B+? " ln B+ ~ " ln 124E 12 6

>

? ;+~< ~ "ln 0F+ 6 2 Lissage des taux instantanés de mortalité

Les estimations des taux de décès annuels forment une courbe de mortalité qui se révèle, en général, assez irrégulière. Ces irrégularités sont dues aux fluctuations d'échantillonnage et ne sont pas représentatives de la réalité. Alors que les taux de décès évoluent avec l'âge et afin d'améliorer les estimations brutes, il est possible d'utiliser les connaissances que nous avons a priori sur la forme des courbes de mortalité. De nombreuses méthodes permettent de répondre à cet objectif ; les estimations corrigées sont nommées estimations lissées des taux de décès.

Même si la plupart des données que nous avons sont des taux de mortalité annuel il est évident que la mortalité est un phénomène continu dans le temps ce qui nous amené a au taux instantané de mortalité.

2.1 Estimations lissées des taux de décès

Pour des commodités de calculs d'assurance, il convient souvent d'avoir une formule dans le but de déterminer l_x en fonction de x (l'âge). Toutefois cet ajustement par une loi analytique des observations, doit se faire sur les taux annuels de mortalité q_x plutôt que l_x (Petauton 1996).

Nous présentons quatre catégories de méthodes permettant d'obtenir des estimations lissées des taux de décès et, ainsi, de construire une table de mortalité :

> les modèles paramétriques

> les lissages paramétriques

> les lissages non paramétriques

> les modèles relationnels

15

Chapitre I : Les Risques liés à l'assurance-vie

2.2 Modèle paramétrique

Une hypothèse est posée a priori sur la forme de la courbe de mortalité. Pour cette raison, la fonction mathématique qui exprime le taux de mortalité en fonction de l'âge doit être une fonction dont la capacité à retracer la courbe de mortalité a déjà été éprouvée sur d'autres populations.

Elle doit permettre de capturer des caractéristiques fondamentales et persistantes des courbes de mortalité ; ce qui conduit à privilégier les fonctions contenant peu de paramètres.

Cette particularité conduit à un certain manque de souplesse dans la fidélité aux données. En contrepartie elle permet théoriquement d'étendre l'estimation des taux de mortalité à des âges où il n'y a pas encore d'observations. La partie II de ce chapitre présente plusieurs modèles paramétriques de référence.

2.3 Les méthodes de lissage paramétriques ou non-paramétriques

Elles permettent un ajustement assez fidèle aux données d'expérience. Contrairement aux modèles paramétriques, elles ne reposent pas sur l'hypothèse que la courbe de mortalité a une forme connue a priori et, à ce titre, ne sont pas prévues pour obtenir une estimation des taux de mortalité en dehors de la plage de lissage. On peut même noter qu'une extrapolation est par nature impossible pour les méthodes de lissages non-paramétriques étant donné que les taux de mortalité ne sont pas représentés à l'aide d'une fonction mathématique.

2.4 Modèles relationnels

Ils partent du même principe que la modélisation paramétrique, à la seule différence que le taux de mortalité est désormais exprimé en fonction non plus de l'âge, mais du taux de mortalité donné par une autre table. Ainsi, une table de mortalité connue est prise comme référence et il est supposé que l'on peut, à l'aide d'une fonction comprenant un petit nombre de paramètres, transformer cette table de mortalité de référence pour obtenir celle de la population étudiée.

Les modélisations paramétriques et les méthodes relationnelles permettent d'estimer les taux de mortalité même en dehors des plages d'âge d'expérience ; ce qui est une propriété intéressante. Il faut toutefois rappeler que ces approches font prendre un risque de modèle.

Pour limiter ce risque, nous allons analyser graphiquement les taux bruts de mortalité avant de sélectionner le modèle paramétrique ou relationnel.

Quand il y a trop de fluctuations dans les estimations brutes, il est intéressant d'effectuer un lissage non-paramétrique, préalablement à l'analyse graphique.

16

Chapitre I : Les Risques liés à l'assurance-vie

A l'inverse, les méthodes de lissage paramétrique ou non-paramétrique permettent une plus grande fidélité dans l'ajustement aux taux bruts mais ne sont pas conçues pour être utilisées en dehors de la plage d'estimation.

Soulignons également l'intérêt des méthodes de lissages paramétriques ou non paramétriques pour le lissage en deux dimensions.

2.5 La modélisation paramétrique

La modélisation paramétrique repose sur l'hypothèse que la courbe de mortalité peut être représentée par une fonction mathématique.

Démographes et actuaires ont étudié de nombreux modèles potentiels et identifié ceux qui sont les plus adaptés à retracer ces caractéristiques.

Une attention particulière doit être accordée au nombre de paramètres contenus dans le modèle. En effet, si l'augmentation du nombre de paramètres permet un meilleur ajustement aux taux bruts, elle se fait au détriment de la robustesse du modèle, c'est-à-dire de sa capacité à refléter des caractéristiques générales des courbes de mortalité. Un modèle qui n'est pas robuste, donne de bons estimateurs s'il est adapté aux données. En revanche, s'il n'est pas approprié, il peut donner de très mauvaises estimations.

Nous présentons dans ce chapitre quelques modèles paramétriques, en commençant par l'une des plus anciennes la loi de Gompertz. Viennent ensuite les formules de Makeham, de Weibull, finalement la fonction logistique et la formule de Kannisto.

Ces modèles paramétriques ont été largement validés pour des données de population générale.

Pour une utilisation sur des données d'assurance, il est important de s'assurer au préalable que la population étudiée est relativement homogène. Citons, comme exemple de source d'hétérogénéité, la sélection effectuée à la souscription du contrat : la sélection peut influencer le risque de décès différemment selon l'âge de l'assuré. Ainsi la courbe de mortalité sera déformée de façon différente selon les âges. Plus généralement, les modèles paramétriques décrits ici s'appliquent à des tables unidimensionnelles.

Enfin, il ne faut pas négliger le risque qu'un modèle ne soit pas adapté aux données. Pour éviter cet écueil, il est nécessaire de procéder à toutes les vérifications usuelles, à commencer par une analyse graphique des estimations brutes des taux de décès en fonction de l'âge pour déterminer si la fonction choisie pour la modélisation paramétrique semble acceptable. Il est également nécessaire de procéder aux vérifications usuelles de la qualité d'une régression.

17

Chapitre I : Les Risques liés à l'assurance-vie

a) Modèle de Gompertz (2 paramètres)

Sur de nombreuses populations, il a été observé que le taux instantané de mortalité augmente d'une manière quasi-exponentielle avec l'âge. Gompertz (1825) a proposé un modèle paramétrique simple qui traduit cette tendance : u_x = B * C^x avec B>0, C>1

> B varie en fonction du niveau de mortalité,

> C mesure l'augmentation du risque de décès avec l'âge.

Cette fonction peut permettre de modéliser la courbe de mortalité car le taux augmente de façon exponentielle Il faut cependant savoir qu'elle tend à sous-estimer la mortalité avant 40 ans et à la surestimer au-delà de 80 ans.

La formule de Gompertz rend compte sous la forme u_x = B * C^x du seul processus de vieillissement, mais il négligeait le faite qu'une partie des décès qui surviennent est due à des accidents. (Petauton 1996).

À l'instar de la loi normale, il s'agit d'une modélisation de phénomènes naturels qui s'applique à diverses situations en marketing par exemple, elle est utilisée pour connaitre la durée de vie d'un produit sur le marché nommée aussi courbe de vie, ou bien dans le domaine des ressource humaines pour estimer l'efficacité d'une formation courbe d'apprentissage, etc.

b) Modèle de Makeham (3 paramètres)

L'idée de Makeham est d'améliorer l'évolution de mortalité, pour y parvenir il a ajouté à la loi de Gompertz un paramètre a indépendant de l'âge, appelée mortalité extérieure à l'individu. Pour améliorer l'évaluation de la mortalité, Makeham (1960) a enrichi la formule de Gompertz d'un paramètre u_x = A + B * C^x Avec A>0, B>0, C>1

On considère usuellement que le paramètre A rend compte de la mortalité accidentelle, indépendante de l'âge. Cette interprétation peut poser question car il arrive d'obtenir des valeurs négatives pour A.

La formule de Makeham ne résout pas le problème de la surestimation du risque aux âges supérieurs à 80 ans déjà rencontré avec la formule de Gompertz, l'utilisation de ce modèle sera liée à l'âge limite d'assurance du produit étudié

Ces formules ont pendant très longtemps eu la faveur des compagnies d'assurance du fait des propriétés simples qu'elles présentent dans les calculs d'assurances sur plusieurs têtes (Petauton 1996)

18

Chapitre I : Les Risques liés à l'assurance-vie

c) Modèle de Heligman-Pollard (8 paramètres)

Cette loi a été introduite par L. Heligman et J.H. Pollard. Ce modèle, composé de trois courbes et de huit paramètres, prend en considération la mortalité infantile.

*+ = H~+~I)J ( K L _e3N(:~ +3:1 O)Z ( PQ+

1 ( PQ+

H(+~I)J :La Première composante de la fonction Heligman-Pollard, représente la mortalité infantile C<0, le premier composant diminue rapidement.

K L _e3N~:~ +3:n O)2 : La deuxième partie représente la mortalité accidentelle Makeham

PQ⁺/1 ( PQ⁺: La dernière composante représente la mortalité due au processus de vieillissement introduite par Gompertz. Contrairement à cette dernière, cette composante est représentée par un modèle logistique.

On peut montrer que, dans ce modèle, la mortalité tend asymptotiquement vers une droite, alors qu'elle a une forme exponentielle dans le modèle de Gompertz.

Ainsi, aux âges les plus élevés, le modèle de Gompertz donnera usuellement des estimations supérieures à celles du modèle de Heligman-Pollard.

d) Le modèle logistique et l'approximation de Kannisto (de 2 à 4 paramètres)

Les trois premiers modèles présentés précédemment (Gompertz, Makeham, Weilbull) impliquent que la probabilité de décès (q_x), tende asymptotiquement vers (1) quand l'âge augmente.

Une autre possibilité est que la probabilité de décès augmente avec l'âge mais tend vers une limite inférieure à (1). C'est l'hypothèse qui est contenue dans le modèle logistique (le modèle de Kannisto est une simplification du modèle logistique), où :

G * UV+

*+ =
	1 ( G * UV+

D'après ce modèle, il n'existe pas de limite maximale à la durée de vie humaine étant donné que, à aucun âge, la probabilité de survivre jusqu'à l'âge suivant ne devient négligeable.

Le modèle logistique présente donc une approche relativement différente des précédents modèles quant à la mortalité aux âges les plus élevés.

Ainsi une divergence entre les modèles est toujours observée aux âges très élevés (même avec un ajustement très similaire sur la plage 80- 100 ans, on observe une divergence au-delà de 100 ans).

19

Chapitre I : Les Risques liés à l'assurance-vie

Le modèle le plus général comporte 4 paramètres : ;+ = H ( ^I*WJ2 HYUZ H > 0, G > 0. Il

7~X*WJ²

inclut le modèle de Makeham, dans le cas où (D=0). 2.6 Lissages paramétriques

Le lissage paramétrique consiste à trouver une courbe paramétrique qui représente bien l'évolution des taux de décès en fonction de l'âge. Contrairement à la modélisation paramétrique, il ne s'agit pas de postuler a priori une forme bien précise pour la courbe de mortalité mais de déterminer, celle qui s'adapte le mieux aux taux bruts parmi une famille de fonctions mathématiques.

Les fonctions utilisées doivent être suffisamment flexibles pour permettre d'obtenir une courbe de taux lissés qui soit proche de celle des taux bruts.

Nous présentons ici deux familles de fonctions qui peuvent être utilisées pour effectuer un lissage paramétrique. Nous commençons par les splines. Pour effectuer un lissage paramétrique, on a recours aux techniques de régression linéaire généralisée quand la variable expliquée est une fonction linéaire des variables explicatives, ou bien aux techniques de régression non linéaire quand cette fonction n'est pas linéaire.

Dans ce dernier cas, il est fait appel à des techniques itératives qui nécessitent de choisir des valeurs initiales pour les paramètres de la fonction. Le choix de ces valeurs initiales est un élément crucial car elles doivent être suffisamment proches de leurs vraies valeurs pour que la procédure de régression converge.

a) Méthode des splines :

Le terme spline tire son origine d'une technique utilisée autrefois pour construire les coques des navires. Cette technique permettait d'obtenir, entre les points d'attache, la forme la plus lisse possible. Les mathématiciens ont étudié cette forme à partir de 1946 et en ont dérivé la fonction spline. Dont les restrictions aux intervalles [\ , [_\+7 , ] = 0, ... ,1

sont des polynômes de degré _ > 0 par convention [₆ = 8 et [\ = (8

Lissage par un spline L'ajustement d'une fonction spline aux estimations brutes des taux de décès se fait par la méthode des moindres carrés pondérés (minimisation de la somme pondérée des écarts quadratiques entre les estimations brutes et lissées.

aC = ? c₊ *

+ +g+\?h i₊ " *j₊~^k.
def

Pour les poids, on peut par exemple utiliser les effectifs sous risque ou l'inverse des variances des estimateurs bruts.

Dans l'objectif de minimiser SC, le déplacement d'un noeud est parfois plus intéressant que l'ajout d'un noeud supplémentaire. Pour déterminer les valeurs des noeuds, plusieurs approches sont envisageables.

20

Chapitre I : Les Risques liés à l'assurance-vie

Une première consiste à les fixer préalablement à la minimisation et à comparer les résultats obtenus avec plusieurs choix différents. Une analyse graphique de la courbe de mortalité peut aider à déterminer les valeurs et le nombre de noeuds. Une approche alternative serait d'inclure les valeurs des noeuds dans les paramètres de la minimisation.

b) Méthode des moyennes mobiles pondérées (MMP)

La méthode des moyennes mobiles centrées symétriques pondérées, est l'une des premières méthodes de lissage à avoir été développée.

Dans ce cadre, citons en particulier, les travaux d'E.L. De Forest dans les années 1870. La méthode MMP est assez peu utilisée aujourd'hui car des méthodes plus efficaces lui ont succédé.

La valeur lissée du taux de mortalité est obtenue en prenant la moyenne mobile pondérée de 2[ ( 1 des estimations initiales consécutives (taux de décès estimés bruts), indicées de x " ]

m

La formule générale pour un lissage de degré 2[ ( 1 est i₊ = ? Z\ *

\g3m *^j+~\

c) Méthode de Whittaker-Henderson

Cette méthode de lissage doit son nom à E. T. Whittaker (1923), et à R. Henderson (1924). La méthode de Whittaker-Henderson consiste à rechercher le meilleur compromis entre l'adéquation aux données brutes et la régularité de la courbe de mortalité. Les taux de mortalité lissés sont obtenus en minimisant la mesure n = o ( )a, où :

· o = ? c₊ *

+ +g+\?h (i₊ " *j₊~^k, o est la somme pondérée des carrés des écarts entre
def

les valeurs lissées et les valeurs brutes, elle mesure la fidélité des taux de mortalité lissés aux taux bruts. Plus les taux lissés se rapprochent des taux bruts, plus la valeur de o diminue.

· a = ? ~p^q * i₊)²

+ def3q , S est la somme des carrés des différences d'ordre z des

+g+\?h

taux lissés, elle permet d'évaluer la régularité de la courbe lissée. Plus l'aspect de la courbe est régulier, plus la valeur de S diminue.

· z est un entier positif. En pratique, les valeurs les plus utilisées sont z = 2, 3 ou 4.

· h est un réel positif qui permet de contrôler l'influence que l'on souhaite donner à chacun des deux critères précédents. Plus h est grand, plus la minimisation porte sur le terme S et impose à la courbe une allure régulière. Plus h est petit, plus la minimisation accorde de l'importance au terme F et impose à la courbe lissée de se rapprocher des données brutes. Soulignons que si 0 = h, aucun lissage n'est effectué.

· c₊ sont les poids donnés à chaque âge (c₊=0).

21

Chapitre I : Les Risques liés à l'assurance-vie

3 Structure de la population de l'assureur

La population assurée est différente de la population générale, de par sa structure, son étendue, ou bien de par les choix des différents acteurs que sont l'assureur qui accepte ou non la souscription et l'assuré qui sélectionne le type d'assurance, cela donne à la population assurée une structure différente de celle de la population générale, car nous devons prendre en considération les annulations, les nouveaux contrats, les avenants modifiant le type de contrat.

Ainsi, pour un groupe d'individus d'âge x, en début d'année, on à N(x) est l'effectif présent, et si on a E(x) entrées, D(x) décès et S(x) départs, le taux annuel brut de mortalité est habituellement évalué par la fraction :

D(x)

Q_x _

N(x)+E(x) /2-S(x) /2

4 Calcul d'une prime fixe dans un environnement aléatoire

L'aléa est le propre des opérations d'assurance, il doit être pris en charge par l'assureur. C'est pourquoi, aux mécanismes d'actualisation habituels, doivent s'ajouter des éléments probabilistes. Les paiements envisagés dans le futur doivent être non seulement actualisés, mais aussi affectés de probabilités convenables. On est donc conduit à la notion d'échéancier aléatoire, présente dans tous les contrats d'assurance.

4.1 Variable aléatoire, la durée de vie de l'assuré

Contrairement à l'assurance non-vie on ne se pose pas la question de l'avènement du sinistre, il est certain en assurance vie. Il en découle que la seule variable aléatoire à étudier est la durée de vie de l'assuré T_x définie dans un espace probabilisé.

L'assureur prend des engagements financiers aléatoires à long terme qui sont par définition liés à la durée de vie humaine. C'est un événement stochastique autrement dit d'une famille de variables aléatoires indexées par le temps (l'âge de l'assuré).

C'est cet aléa qui doit être pris en charge par l'assureur. Aussi, aux mécanismes d'actualisation habituels, nous devons ajouter des éléments probabilistes. Les paiements envisagés dans le futur doivent être, non seulement actualisés, mais aussi affectés de probabilités calculées.

4.2 Le principe de l'actualisation en avenir aléatoire

En mathématiques financières déterministes, la valeur actuelle d'un capital différé de montant unité payable dans n années, s'écrit(1 + i)^-n, ou i désigne le taux t'intérêt annuel, car dans cette optique on suppose que le capital sera payé de façon certaine.

Par contre, en assurance vie, en plus de faire intervenir le mécanisme d'actualisation, s'ajoute une probabilité liée à la variable aléatoire qui est la durée de vie de l'assuré.

22

Chapitre I : Les Risques liés à l'assurance-vie

a) Valeur actuelle aléatoire et valeur actuelle probable :

La Valeur actuelle aléatoire (vaa), d'un capital unité payable à l'époque n associée à la réalisation de l'événement, est représentée par la valeur w_? actualisée avec une prime dont

7

les valeurs peuvent être réalisés ou non à la fin de chaque année, soit w_? = (7+\)E ou

w_? = 0 (Hess 2000). On peut conclure que cette valeur suit une loi de Bernoulli.

La Valeur actuelle probable consiste à envisager tous les paiements possibles, à les actualiser financièrement au taux annuel i, puis les pondérer par les probabilités (Petauton 1996).

b) Capital différé et annuités viagère

Comme on l'a déjà vu, le propre des opérations d'assurance est la présence d'un aléa qui doit être pris en charge par l'assureur. C'est pourquoi, aux éléments probabilistes, doivent s'ajouter des mécanismes d'actualisation. Les paiements envisagés dans le futur doivent être non seulement actualisés, mais aussi affectés de probabilités convenables. On est donc conduit à la notion d'échéancier aléatoire, présente dans tous les contrats d'assurance lié à la durée de vie.

Dans ce qui suit, nous examinerons d'abord l'un élément simple de l'assurance vie (capital différé), le but étant de comprendre les mécanismes, ou plutôt, l'interaction entre les probabilistes et le mécanisme d'actualisation. Le capital diffère est un exemple probant et

7

très explicite du principe de la valeur actuelle probable w_? = 7\ E .

On pourra par la suite calculer les annuités qui s'expriment comme une somme de capitaux différés. Cela sera fait en distinguant les modèles en temps discret et ceux en temps continu.

Figure 2 Principe fondamental de l'assurance vie

Le capital obtenu au terme par les survivants est égal à leur mise initiale augmentée par

> l'effet de levier, dû à la mortalité : B+? - B₊

> la capitalisation financière, à travers le taux d'intérêt technique : (1 ( ]~?

23

Chapitre I : Les Risques liés à l'assurance-vie

Le taux d'intérêt, supposé constant sur la période considérée. Le capital différé sera payé de façon probable, car il est lié à la réalisation éventuelle, il est alors nécessaire de faire intervenir, en plus du mécanisme d'actualisation, la probabilité pour que le capital soit effectivement payé. Cette probabilité (p_x) concernant l'état viager de l'individu ou du groupe d'assurés est susceptible de se réaliser ou non à l'époque (n). Par définition la valeur actuelle probable d'un capital unité payable à l'époque n et associée à la réalisation de l'événement, est l'espérance mathématique E(w_n).

Capital différé payable en cas de vie après n années : _nE_x = ilzn ' (1 + i)^-n, que l'on peut écrire, _nE_x = _nP_x ' Vn

c) Les fonctions de commutation

Dans le but de simplifier les calculs numériques de l'assurance vie, des fonctions dites de commutation ont été introduites dès le dix-huitième siècle. Elles permettent aussi des expressions plus condensées des (vap), valeurs actuarielles probables les plus couramment utilisées. On distingue deux types de commutations selon leur domaine d'application, celui de l'assurance en cas de vie ou celui de l'assurance décès. Plus brièvement, on utilise l'appellation "commutations vie" et "commutations décès", (voir Annexe 8 page 115).

4.3 Prime pure et prime annuelle

La prime pure représente l'espérance mathématique E(x) de la variable x, coût des sinistres sur la période de référence (Hess 2000).

Elle représente ce que doit l'assuré à l'assureur, et comporte un payement unique pour couvrir le risque pour la durée contractuelle. rc(x) = E(x)

Il convient de rappeler un principe simple mais fondamental relatif à l'assurance où les primes encaissées au titre du contrat doivent, en toute logique, financer le coût des prestations futures garanties. Là où les primes résultent d'un principe d'équilibre financier entre l'assuré et l'assureur, à la souscription du contrat.

Le fait que l'assuré verse à l'assureur une prime périodique (généralement annuelle), plutôt qu'une prime unique présente l'avantage. Les engagements de l'assureur, les engagements de l'assuré seront aussi étalés dans le temps, ce qui conduit à une situation plus équilibrée entre les deux parties.

Cela présente, aussi, un avantage commercial et psychologique importait. Par exemple, dans le cas d'une assurance décès, cette modalité permet à l'assureur d'éviter de demander à l'assuré une prime croissante, compte tenu de l'aggravation de ce risque au cours du temps.

Remarque On a calculé une prime annuelle constante, ou prime nivelée, bien que le risque de décès augmente avec le temps. La prime de risque (non constante), qui couvrirait exactement le risque de l'année est appelée prime naturelle.

24

Chapitre I : Les Risques liés à l'assurance-vie

De manière générale, et conformément à la notation actuarielle internationale, nous désignons par _(nðx) la prime pure unique pour un contrat temporaire de n années, et _(nPx) la prime pure annuelle constante pour le même type de contrat.

La relation entre ces deux primes pures est d'écrite, par l'égalité en t = 0, autrement dit à la signature du contrat, entre la (vap) de la prime pure unique (_nð_x), et la (vap) de l'échéancier constitué de (n) versements égaux à (_nP_x).

C'est en utilisant cette relation générale, adaptée à chaque situation particulière, que l'on obtient les primes pures annuelles à partir de la prime pure unique.

Il est quelquefois nécessaire d'introduire la durée (p) de paiement des primes, en la distinguant de la durée (n) du contrat. En effet, il peut arriver que ces deux valeurs ne soient pas égales. Cependant, rappelons que (p) ne peut être supérieur à (n), puisque l'assuré n'aurait aucun intérêt à payer pour des prestations, passées.

~ Comment fait l'assureur pour honorer ses prestations futures, garanties par le contrat, dans un environnement aléatoire ? ~

Au sens juridique, la prime pure est déterminée essentiellement d'une part, par la probabilité de survenance du sinistre, et d'autre part, par le coût moyen des sinistres.

DECRET EXECUTIF N° 96-47 DU 17 JANVIER 1996 RELATIF A LA TARIFICATION DES RISQUES EN MATIERE D'ASSURANCE. (J.O. N° 5 DU 21 JANVIER 1996).

1) Probabilité de survenance du sinistre est relative à la table de mortalité, donc comme paramètre unique l'âge de l'assuré.

2) Le cout moyen du sinistre résulte des deux paramètres que sont le type de contrat d'assurance et le montant assuré.

Ce principe d'équivalence financière repose sur l'hypothèse que les primes sont placées jusqu'au moment où il faudra payer les prestations, bien que en pratique l'assureur diversifie ses placements afin de maximiser ces gains dans le cadre réglementaire comme nous le verrons.

L'assureur prend ainsi, en charge un ensemble de risques sans se mettre lui-même en situation de risque par la mutualisation des risques car, même si l'assurance prend en charge un nombre (n) risques, le plus important, est que ces risques restent indépendants ; ce qui est le cas en assurance de personnes. En effet, il n'y a aucune corrélation entre eux. De ce fait nous aurons ce que l'on pourra nommer une compensation statistique qui résulte de leur indépendance.

Dans notre approche de calcul de la prime, nous allons prendre en compte seulement l'aléa viager ; sans prendre en compte la probabilité d'annulation du contrat par l'assuré, qui n'ont pas fait l'objet d'étude dans le présent document, dans le but définir et de mesurer les valeurs de rachat, car ces annulations de contrat dépendent uniquement de la volonté du

25

Chapitre I : Les Risques liés à l'assurance-vie

souscripteur qui a la possibilité d'annuler ou de racheter son contrat d'assurance. ART. 90 BIS (AJOUTE PAR L'ART. 22 L 06-04)

Il est possible d'avoir différentes combinaisons de police d'assurance. A l'évidence, le calcul des primes diffère selon le type de police d'assurance. En ce qui nous concerne, nous allons nous attacher à segmenter les types d'assurance par rapport à trois paramètres :

> le type de risque ou de couverture de risque > la durée

> la population à assurer

4.4 Le type de risque

Il est vrai que l'assurance de personne couvre tous les risques relatifs à la personne. Dans ce cadre, le paramètre le plus influant reste bien évidemment l'âge de l'assuré, alors que dans d'autres types d'assurance que sont l'assurance accident corporel et l'assurance voyage, nous devons prendre en compte d'autres paramètres qui seront la catégorie socioprofessionnelle pour l'assurance accident, le pays de destination et la durée, pour l'assurance voyage.

4.5 La durée d'assurance

Elle influe sur la prime d'assurance en toute logique. Il y aura une différence entre une prime pure pour les contrats vie entière c'est à dire illimités dans le temps, bien que le terme illimité est relatif à une durée probable (la durée de vie de l'assuré) d'où le nom de ce type de contrats et les contrats temporaires à savoir à durée déterminée qui sont limités dans le temps, ce qui le cas pour l'ensemble des contrats de la Trust Assurance.

4.6 La population assurée

L'assureur couvre le risque non pas d'un individu mais d'un ensemble, constituant de ce fait un groupe d'assurés qui peuvent souscrire en un seul contrat représenté par une personne morale (entreprises, syndicats, associations, etc.)

Le calcul de la prime du contrat groupe n'est pas fondamentalement différent de celui du contrat individuel. En effet, la prime d'un contrat groupe est théoriquement égale à la somme des primes individuelles de chaque membre du groupe. Ici les taux de chargements que nous aborderons dans ce qui suit est nettement inférieur à celui prévus dans les contrats individuels. L'assureur pourra tenir compte des éléments particuliers du groupe à tarifer et s'appuyer sur les statistiques du groupe.

Chapitre II

Réassurance & gestion actif-passif

Section 1 : Couverture du risque par la réassurance Section 2 : Gestion actif-passif

Section 3 : Outils de nouvelle génération

26

Chapitre II : Réassurance & Gestion actif-passif

Section 1 Couverture du risque par la réassurance

Quand on parle de la réassurance, on pense souvent, en premier lieu, à la réassurance de biens et souvent au moment des catastrophes naturelles (tempêtes, tremblements de terre...etc.). Il est vrai qu'une des raisons d'être de la réassurance est d'assumer les risques de pointe, en les mutualisant.

La réassurance de personnes est moins exposée sur le plan médiatique et constitue néanmoins une branche très dynamique du secteur ; elle est moins volatile que la réassurance non-vie ce qui conduit à un intérêt accru des investisseurs, même si le marché mondial de la réassurance dommages est aujourd'hui plus important en volume que celui de la réassurance de personnes.

Le recours à la réassurance est une volonté certaine de la compagnie d'assurances, qui se focalise plus sur la distribution de ces produits, laissant le développement, l'expertise technique, la conception, ainsi que la prise de risque à leurs réassureurs.

La réassurance est la technique de gestion des risques qui permet le transfert du risque, dans le but de diminuer la volatilité du résultat de la compagnie d'assurance, en contrepartie d'une réduction bénéfice. Pour schématiser, la réassurance est l'assurance des assurances, aussi parfois appelée assurance secondaire.

Celle-ci ne peut pas exister sans l'étape préalable du transfert de risque que représente l'assurance primaire et joue un rôle fondamental dans la gestion du risque des compagnies d'assurance. La cédante est liée au réassureur par un traité de réassurance, souvent un choix stratégique, et demeure souvent une nécessitée.

1 Traité de réassurance

Le traité de réassurance relève du droit commun du contrat, donc peu réglementé. Les pratiques de marché enferment la réassurance dans un cadre coutumier assez strict qui permet d'effectuer une classification systématique des traités. La principale ligne de partage est entre les traités de réassurance dite "proportionnelle" ou "non proportionnelle".

Avant, d'entrer dans le détail technique des différents mécanismes, nous énumérons les clauses communes à tous les traités de réassurance.

A l'instar du contrat d'assurance, un traité de réassurance doit tout d'abord définir clairement les risques dont la réalisation est susceptible de déclencher le paiement de la part du réassureur. Il y a lieu de définir le portefeuille d'assurance directe de l'assureur en fonction de :

> Nature technique des risques couverts

> Situation géographique des risques couverts

27

Chapitre II : Réassurance & Gestion actif-passif

> Période de couverture (fréquemment une année civile, parfois plusieurs). (Deelstra et Plantin 2005).

Les réassureurs paient des montants importants sur la foi de bordereaux de relevés de sinistres parfois succincts car la confiance mutuelle entre les parties est un élément essentiel de la relation de réassurance.

Elle est largement entretenue par le caractère restreint de l'offre. Aussi tout comportement indélicat, entrainera sans doute une publicité rapide dans le marché et rendrait le renouvellement des traités à la prochaine échéance très délicat, ainsi qu'une pérennité compromise.

Bien que relativement peu importantes en général, les obligations de la cédante en matière d'information des réassureurs sont précisément stipulées dans les traités de réassurance. Pour les portefeuilles jeunes, évoluant rapidement, ou constitués de grands risques, la composition du portefeuille doit être fournie au réassureur.

Un récapitulatif des sinistres, en mentionnant les charges les plus importantes dans le cas des garanties traditionnelles doit être établi. Pour les sinistres dépassant un certain seuil, une déclaration périodique en général mensuelle ou trimestrielle devra être transmise au réassureur.

2 La réassurance proportionnelle

Les traités de réassurance proportionnelle sont ainsi dénommés car ils sont construits de telle sorte que :

Sinistres cédés

Primes cédées

~

Primes brutes

Sinistres bruts

Elle consiste en une participation proportionnelle du réassureur aux gains et pertes de la cédante. Dans le cadre de la réassurance proportionnelle, le réassureur, en contrepartie d'une portion ou partie prédéterminée de la prime d'assurance, indemnise cette dernière contre une portion déterminée des sinistres couverts par la cédante au titre des polices.

Les taux de primes et sinistres cédés sont égaux. Les deux types de traités proportionnels sont le traité en quote-part et le traité en excédent de plein.

2.1 Quote-part ou QP

Il s'agit du traité de réassurance le plus simple. Le réassureur cède un pourcentage (1-á) de ses primes ainsi que de ses sinistres bruts où (1-á) est le taux de cession et (á) le taux de rétention.

28

Chapitre II : Réassurance & Gestion actif-passif

Le traité en quote-part est la forme la plus simple de cession de réassurance obligatoire et consiste à partager proportionnellement les primes et les sinistres d'une branche ou une catégorie selon un pourcentage fixé d'avance.

Dans ce genre de traité, il n'y a pas d'homogénéité dans la réassurance, mais un partage proportionnel du risque entre la cédante et le réassureur, car ils ont exactement le même

v

ratio (sinistre/prime).

É

Cette propriété, même si elle facilite la mise en place du mécanisme de la gestion du risque, est à double tranchant.

> Elle atténue les problèmes d'aléa moral, car le fait d'être couvert ne doit pas inciter la cédante à adopter un comportement défavorable pour le réassureur si son taux de rétention est suffisant.

> Cette identité de sort n'est pas le moyen le plus efficace de réduire la volatilité du portefeuille.

Les traités présentés ci-après, brisent cette symétrie en laissant la partie la plus risquée à la charge du réassureur.

2.2 Excédent de plein ou XP

Le réassureur va intervenir uniquement sur les polices dépassant un certain montant de garantie dénommé le plein de réassurance. Ce dernier, fixé par un conseil d'administration, représente le montant du capital conservé par la cédante pour son propre compte sur chaque affaire et varie selon sa capacité de souscription dans une catégorie déterminée.

Les traités en excédent de plein s'appliquent dans le cas où la valeur assurée est définie sans ambiguïté. Pour simplifier, il s'agit d'une quote-part dont le taux de cession n'est pas connu à la signature du traité mais calculé risque par risque, une fois les affaires souscrites. Le traité fonctionne comme une quote-part pour chaque police.

L'avantage de l'excédent de plein sur la quote-part est de permettre de modeler le profil du risque de la rétention avec plus de précision ; la cédante cède d'autant plus que ses risques unitaires sont élevés.

Ce type de traités est toutefois relativement peu utilisé, car il entraîne une gestion administrative plus importante que dans le cas de la quote-part. En effet, les taux de cession sont déterminés police par police entrainant une complexité déraisonnable.

La réassurance non proportionnelle permet d'atteindre cet objectif de cession des pointes de sinistralité avec plus d'efficacité et moyennant une mise en oeuvre administrative significativement, plus légère.

29

Chapitre II : Réassurance & Gestion actif-passif

3 Réassurance non proportionnelle

La réassurance non proportionnelle regroupe l'ensemble des traités qui ne vérifient pas par construction S/P, la propriété d'identité entre taux de cession des primes et taux de cession des sinistres. Dans ce cas, le réassureur n'intervient qu'à un certain seuil de sinistre de la cédante. Le réassureur touchera pour cela un pourcentage de la prime. Le sort de la cédante et du réassureur sont beaucoup moins liés. Ainsi au cours d'une année d'exercice, l'assurance pourra être en perte, mais pas forcément le réassureur.

3.1 Excédent de sinistre ou XS

Il est déterminé par un seuil d'intervention sur le sinistre, appelé la priorité du traité qui est la limite d'intervention du réassureur. Le réassureur protège une catégorie du portefeuille de la cédante à la survenance de tout sinistre dépassant cette priorité. L'année de survenance du sinistre généralement une année ferme, et une portée dénommée portée du traité est la limite à régler par sinistre, fixée d'avance.

Pour un traité en excess loss a-XS-b, l'indemnisation du réassureur est la fonction suivante du coût x d'un événement, entrant dans le champ du traité : min(max (x - b, 0), a.

Ainsi, le réassureur intervient que si l'événement a un coût supérieur à b. Il paie alors le coût de l'événement, diminué de la franchise b, sans toutefois verser un montant supérieur à a. La notation a-XS-b signifie donc que le réassureur paie au maximum a sur la partie du coût qui excède b. Dans la terminologie de la réassurance :

> b est la priorité du traité

> a est la portée du traité

> a + b est le plafond du traité

3.2 Excédent de perte (stop-loss ou SL)

Le réassureur intervient lorsque l'assureur est en perte. Le seuil et la limite d'intervention du réassureur sont définis en fonction d'un pourcentage du total des primes perçues par la cédante. En outre, l'assureur peut protéger le résultat d'une branche par une couverture en Stop-loss. Ce genre de traité permet l'équilibre du bilan technique annuel de cette dernière.

Le stop-loss est identique à excess loss, à la seule différence que portée et priorité ne sont pas exprimées en numéraires, mais le sont en pourcentage des primes brutes. Les traités stop-loss sont notés u(%)-XL-t(%).

L'avantage du stop-loss provient du fait que les traités de réassurance sont en général souscrits avant que le chiffre d'affaires de l'exercice ne soit connu. Ce mécanisme d'indexation permet d'obtenir une portée et une priorité adaptées au volume d'affaires.

30

Chapitre II : Réassurance & Gestion actif-passif

4 Rétrocession

Il arrive souvent qu'un réassureur se réassure lui-même auprès d'autres réassureurs. Cela s'appelle la rétrocession. Le réassureur sera alors appelé rétrocédant et il rétrocède tout ou partie de son risque auprès d'un rétrocessionnaire. Les rétrocessionnaires se réassurent parfois eux-mêmes, et le cercle d'assurance / réassurance peut continuer sur plusieurs échelons, et sur plusieurs exercices comptables. On parle alors d'une spirale.

Section 2 Gestion actif-passif

La gestion actif-passif existe ailleurs que dans l'assurance. Les institutions financières sont confrontées, à divers degrés, aux risques de fluctuation des marchés. Particulièrement les banques ont créé depuis longue date des départements de gestion actif-passif.

La similarité entre l'activité bancaire et l'activité d'assureur a la particularité de l'inversion du cycle de production. En raison de cette similarité, les outils de contrôle des risques utilisés par les banques peuvent souvent être adaptés aux assurances.

La profession bancaire disposant d'une certaine préexistence dans l'analyse des risques de bilan, les assureurs se sont souvent inspirés de ses méthodes.

La problématique des investisseurs institutionnels que sont les sociétés d'assurance, diffère pourtant de celle des banquiers sur plusieurs points importants :

> Le passif des assureurs vie est principalement composé d'engagements contractuels. Ces engagements conduisent à ce que le passif moyen ou long terme d'un assureur évolue plus lentement que celui d'un banquier qui peut modifier, quasiment de manière instantanée, la structure de son passif en recourant à des instruments financiers à terme.

> Le passif des assureurs vie est particulièrement homogène et long. L'homogénéité du passif est un handicap, car elle conduit à une concentration de certains risques.

Par ailleurs, les règles comptables et fiscales de l'assurance freinent la gestion active des valeurs mobilières, particulièrement des obligations détenues en direct, qui représentent la majorité des placements des assureurs vie. Les outils de la gestion actif-passif en assurance vie sont donc spécifiques de cette activité et diffèrent des outils bancaires, même s'ils en sont souvent inspirés. Il est possible de les classer, approximativement, en trois générations de sophistication croissante, tout en gardant à l'esprit les points suivants :

> une génération n'en remplace pas une autre, mais vient compléter la palette opérationnelle des analystes actif-passif

> certains modèles opérationnels ont des caractéristiques mixtes entre deux ou trois générations

31

Chapitre II : Réassurance & Gestion actif-passif

> certains modèles sont intégrés dans des outils actuariels classiques, dont ils constituent des modules complémentaires

> au sein d'une même génération d'outils, le stade de développement, l'intégration des différents types d'actifs et de passifs et le caractère opérationnel peuvent être très inégaux d'un modèle à un autre.

Les outils de 1^re génération, sont directement inspirés des premiers outils bancaires de contrôle des risques de taux et de liquidité. Ils ont pour base la projection et la comparaison des flux financiers à l'actif et au passif. Ces projections sont généralement effectuées sur une base statique, c'est-à-dire à partir des stocks d'actifs et de passifs arrêtés à une date donnée, sans tenir compte de la production et des investissements ultérieurs.

Les outils de 2^e génération, sont des modèles de simulation de bilan. Ces modèles permettent la projection des résultats financiers et comptables, et de l'évolution du bilan, en fonction d'un jeu d'hypothèses détaillées fixées par l'utilisateur. Ces jeux d'hypothèses, dénommés scénarii, portent tant sur l'environnement économique et financier que sur la production et le comportement des clients.

Les modèles actifs passifs déterministes peuvent être plus ou moins complets et détaillés. Dans leur plus grande généralité, ils permettent, de projeter l'ensemble du bilan dans une approche dynamique, c'est-à-dire en tenant compte de la production future, de simuler l'interaction active passive et les provisions mathématiques, et de tester différentes politiques financières.

L'usage principal des modèles déterministes est la projection des résultats dans une optique budgétaire, mais aussi le stress testing, ou test de résistance du bilan à des conditions financières adverses. A signaler que le stress testing est un sujet d'actualité dans la zone euro, eu égard aux crises d'endettement de certains pays (la Grèce, l'Espagne...).

Par rapport aux outils de première génération, la recherche ne porte plus sur l'indicateur unique du risque de taux, mais sur un éventail beaucoup plus vaste de risques d'actif-passif.

Les outils de 3^e génération, sont les modèles stochastiques. Ils utilisent des techniques de simulation semblables à celles des modèles déterministes, mais ou les scénarios économiques et financiers ne sont plus directement déterminés par l'utilisateur. Le modèle génère lui-même un grand nombre de scénarios aléatoires, et calcule les résultats sur l'ensemble des scénarios. Le principe de base de ces tirages, dite méthode de Monte-Carlo, est de considérer les scénarios tirés aléatoirement comme équiprobables.

On peut calculer ensuite, pas à pas, des résultats moyens espérés, des intervalles de confiance et mesurer la dispersion des résultats. Différents indicateurs de risque, tels que la probabilité que le résultat d'exploitation soit inférieur à un certain seuil, peuvent être obtenus. Il existe également pour ces modèles, de nombreux degrés de développement,

32

Chapitre II : Réassurance & Gestion actif-passif

notamment en matière de description des scénarios financiers. Les méthodes de tirage aléatoire peuvent être très variées, des plus simples aux plus sophistiquées.

Les méthodes d'optimisation ne peuvent être utilisées avec profit que si les scénarios financiers stochastiques utilisés sont raisonnablement représentatifs des risques moyen et long terme.

1 Outil de 1re génération (l'analyse des flux de trésorerie)

Les outils de 1^re génération se fondent exclusivement sur la projection et la comparaison des flux de trésorerie (cash-flows) générés par les actifs financiers d'une part, et par les engagements d'assurance d'autre part. La comparaison directe de ces flux sous forme de séries annuelles ou mensuelles, fait apparaître des excédents ou des insuffisances de trésorerie dites impasses de trésorerie. Dans l'activité bancaire traditionnelle c'est-à-dire le crédit, ces excédents doivent être placés et ces insuffisances doivent être comblées en recourant au marché interbancaire ou à d'autres marchés. Dans les deux cas, le résultat d'exploitation se révèle étroitement dépendant de l'évolution des taux.

Dans le secteur de l'assurance, la situation est un peu plus complexe, mais on peut assimiler le coût des engagements (les taux servis à la clientèle) au coût des ressources bancaires, et symétriquement, assimiler les revenus du portefeuille financier au taux de rendement des emplois bancaires.

Au-delà de la comparaison des cash-flows issus de l'actif et du passif, il est possible de calculer séparément la valeur actuelle de chacune des séries et de comparer ces valeurs par la méthode de la valeur actuelle nette.

En particulier l'examen de la sensibilité de ces deux valeurs par rapport à l'évolution des taux permet de tirer des conclusions sur les risques de taux encourus par l'assureur. Les outils de 1^re génération présentent cependant des limites du fait qu'ils ne traitent que du risque lié aux variations des taux d'intérêt.

1.1 Projection des flux de trésorerie

On distingue deux approches pour le calcul des flux de trésorerie : a) L'approche statique

Elle consiste à effectuer les projections de cash-flows à partir des stocks d'actifs et de passifs arrêtés à une certaine date, sans prendre en compte aucune opération créant ultérieurement de nouveaux passifs.

b) L'approche dynamique

Elle consiste à projeter la totalité des cash-flows issus des actifs et passifs présents à la date de l'étude, ou constitués ultérieurement en fonction d'hypothèses sur l'activité future de la société.

33

Chapitre II : Réassurance & Gestion actif-passif

Les outils de 1^re génération se limitent généralement à l'analyse statique, en effet celle-ci est beaucoup plus simple, précisément parce qu'elle dispense d'effectuer des hypothèses sur l'activité future. Il est d'ailleurs possible de limiter la recherche de l'adéquation actif-passif aux seuls stocks existants, à condition toutefois de veiller à maintenir cette adéquation pour les futurs contrats.

c) Projection des flux de l'actif

Concrètement, la projection des cash-flows de l'actif consiste à additionner par période, pour l'ensemble du portefeuille financier, les éléments de revenus futurs (intérêts, loyers, dividendes, coupons) et les éléments d'amortissement des obligations (remboursements au terme). Seuls comptent les cash-flows, c'est-à-dire les revenus ou remboursements échus et encaissés.

d) Projection des flux du passif

Pour garantir leurs engagements envers les assurés, les compagnies d'assurances doivent gérer leurs passifs à l'intérieur d'un cadre prudentiel strict. La réglementation impose en effet toute une série de provisions dont les mécanismes de constitution s'avèrent particulièrement complexes, d'où la nécessité d'établir des projections. Ces dernières reposent sur deux piliers, essentielle à savoir :

> le taux minimum garanti

> la durée du contrat

> le coefficient de participation aux bénéfices financiers > le comportement du client (rachat anticipé, prorogation)

Les caractéristiques du contrat, sont en principe connues de l'assureur, par contre le comportement du client l'est moins. L'élaboration de ces statistiques demeure néanmoins indispensable à toutes les phases ultérieures à l'analyse du passive, ainsi qu'au calcul des différentes provisions. Les données statistiques sont essentiellement constituées par :

> la table mortalité qui reflète la mortalité observée de la population des assurés > la cadence des règlements.

1.2 Mesure des impasses de trésorerie

a) Impasses et excédents de trésorerie

L'analyse de la série des impasses de trésorerie a pour but de contrôler l'adéquation entre actif et passif, en termes de cash-flows mensuels ou annuels. Le contrôle de cette adéquation consiste précisément à comparer entre eux, et période par période, les flux projetés de l'actif et du passif.

Sur une base statique, les flux financiers de l'actif sont toujours positifs, les cash-flows et flux des passifs toujours négatifs. La somme des deux donne les flux financiers nets, et fait

34

Chapitre II : Réassurance & Gestion actif-passif

apparaître pour chaque période un excédent ou une impasse de trésorerie selon le signe positif ou négatif du flux net.

La confrontation des flux financiers devrait idéalement être prolongée jusqu'à l'extinction du stock de contrats. Même si elle est menée sur une période plus courte, l'intérêt de cette approche réside dans la possibilité pour l'assureur de prévoir, à l'avance, les montants qu'il devra investir en cas de flux nets positifs dus, ou au contraire, le montant des actifs qu'il devra liquider pour faire face à ses engagements en cas de flux nets négatifs.

En fonction de ces informations, l'assureur peut procéder à des ajustements de son portefeuille financier ou mettre en oeuvre une couverture financière appropriée des risques liés au réinvestissement ou à la liquidation des actifs.

b) Notion d'adossement

Lorsque sur chaque période les flux nets obtenus sont toujours positifs ou nuls, l'actif est dit adossé au passif. Il est dit exactement ou parfaitement adossé si les flux nets sont nuls.

Dans le cas où les flux de trésorerie sont fixes et parfaitement connus, l'adossement de l'actif et du passif permet de garantir entièrement la marge de l'assureur, puisque celle-ci est alors indépendante de l'évolution des marchés. En effet l'assureur n'a, a priori, aucun besoin de recourir au marché financier, ni pour emprunter ou vendre des actifs, ni pour effectuer des placements, puisque ses engagements d'assurance sont naturellement couverts par les cash-flows issus de son stock d'actifs.

c) Analyse par type de passif

Aux origines de la recherche en matière d'équilibre actif-passif des banques, la méthode des cash-flows était utilisée de la façon qui consiste à répartir les ressources par groupe de taux, puis de trouver un adossement pour chaque groupe par des actifs de taux de rendement équivalent, sauf dans le cas où les cash-flows sont exactement identiques entre actif et passif. Il était, en outre, nécessaire de vérifier l'égalité des valeurs actuelles pour disposer de quantités égales d'actifs et de passifs dans chaque groupe.

Une fois que tous les passifs ont été couverts par cette méthode, les actifs excédentaires sont alors considérés comme libres et représentatifs de la situation nette réelle de l'assurance.

Cette approche est toujours utilisée par les assureurs, avec la différence que les passifs peuvent être regroupés sur d'autres critères que le seul rendement.

Les engagements au passif des assureurs sont généralement répartis par famille de contrats, puis les provisions correspondantes et les cash-flows associés sont calculés. L'adéquation actif-passif doit être assurée indépendamment pour chacune des familles de contrats ainsi constituées, qui sont parfois dénommés cantons.

35

Chapitre II : Réassurance & Gestion actif-passif

Un canton est le résultat de l'affectation d'actifs et de passifs à une section distincte du bilan. Le cantonnement d'actifs et de passifs peut être décidé pour en permettre une gestion particulière. (Le Vallois, Palsky et Tosetti 2003)

La répartition des actifs par type de passif permet de vérifier, outre l'adossement des cash-flows, la bonne adéquation des actifs en termes de taux de rendement financier et comptable comparé au taux garanti moyen du passif correspondant.

1.3 Calcul de la Valeur Actuelle Nette

Les actifs ou les passifs financiers n'ont pas d'autre valeur que celle des flux monétaires futurs qui doivent en découler. En principe, il est donc possible de recalculer la valeur financière des actifs et des passifs de l'assureur en partant de la séquence des cash-flows projetés. Le calcul consiste simplement à actualiser les flux avec des taux de marché appropriés.

En pratique, ce n'est pas si simple, puisque les cash-flows ne peuvent être prévus qu'avec une marge d'erreur très variable selon les actifs ou les passifs étudiés. A cette réserve près, il est possible de calculer la valeur actualisée des cash-flows de l'actif et du passif et, par différence, d'obtenir la valeur actualisée de la situation nette de l'assureur. L'équation de base est : Valeur Actuelle Nette =Valeur Actuelle Actif -Valeur Actuelle Passif.

a) Valeur actuelle des actifs

Dans le cas général, on se dispense de calculer la valeur actuelle nette des actifs pour prendre leur valeur de marché, si elle est connue. Pour les immeubles, il faut utiliser une valeur à dire d'expert. Pour les prêts, on peut effectivement recourir à l'actualisation des cash-flows.

Pour les actifs non cotés ou peu liquides, il n'est plus possible de se référer à la valeur de marché. On peut toujours utiliser une valeur à dire d'expert mais cela n'est acceptable que si la proportion de ces actifs est faible dans le portefeuille. C'est généralement le cas dans les bilans des sociétés d'assurance.

En effet, les actifs de taux, à l'exemple des obligations ou titres assimilés, représentent une part prépondérante dans le portefeuille de placements, des compagnies d'assureurs vie.

a.1 Valeur actuelle des actifs obligataires

En pratique, nous l'avons dit, il n'est pas nécessaire de calculer la valeur actuelle des actifs obligataires, puisqu'il est plus simple d'observer leur valeur de marché.

Cependant, dans le cas des obligations à taux fixe, la séquence des cash-flows futurs associés à un titre est parfaitement connue. On considère même généralement, que dans le cas des emprunts d'Etat, cette séquence est certaine, ne présentant aucun risque de défaillance de l'émetteur.

36

Chapitre II : Réassurance & Gestion actif-passif

En suivant une démarche inverse à celle du calcul de la valeur actuelle, il est donc possible de calculer, à partir du prix de marché, un taux d'actualisation des cash-flows correspondants.

Pour chaque obligation, il existe un taux de rendement actuariel R tel que :

> Prix de marché = Valeur Actuelle = ? O=

?

<g7 (7~‡)=

> Avec Fi = flux de l'obligation (coupon ou amortissement à l'époque t). a.2 Courbe des taux zéro-coupon

Le calcul effectué dans l'encadré précédent fait apparaître un taux de rendement actuariel différent pour chaque obligation observée. Ceci n'est pas satisfaisant pour l'esprit et demande une analyse plus approfondie pour déterminer le juste prix ou le taux de rendement normal d'une obligation comparée à l'ensemble des titres de même nature.

Bien entendu, le marché demande aux émetteurs privés un taux d'intérêt supérieur à celui des émetteurs souverains des pays développés, pour compenser le risque de défaillance. Mais même si on limite l'analyse aux emprunts d'Etats, tous identiques en termes de risque, on constate encore des différences entre les taux de rendement actuariels de différents titres.

L'étude du prix des obligations sans risque, ou emprunts d'Etat, fait immédiatement apparaître que les taux de rendement actuariels sont à un moment donné essentiellement dépendants de la durée résiduelle des obligations correspondantes.

En réalité, il faudrait utiliser un taux d'actualisation différent pour chaque échéance. Les obligations restent cependant difficiles à comparer entre elles parce qu'elles correspondent à un mélange de différentes maturités (une pour chaque coupon, et une pour l'amortissement final).

Le seul cas où le taux de rendement actuariel observé correspond, sans ambiguïté, à une seule maturité, est le cas où il n'y a qu'un seul cash-flow.

Ce cas existe puisqu'il correspond aux titres dits zéro-coupon, pour lesquels les intérêts sont versés en une seule fois au moment de l'échéance finale. L'observation des prix des zéro-coupon permettrait donc de bâtir une courbe des taux zéro-coupon en fonction des maturités.

A l'aide de cette structure par terme des taux (notée r_t), il est possible de reconstituer le prix de l'obligation (ou de toute séquence de flux fixes) sans risque, en utilisant toujours la même fonction ci-après :

> Prix de marché Prix estimé = ? O=

? (7+‡)= <g7

37

Chapitre II : Réassurance & Gestion actif-passif

L'intérêt de disposer d'une courbe des taux zéro-coupon est aussi de permettre un calcul d'actualisation sur les cash-flows du passif, en tenant compte de façon cohérente de la maturité des flux.

a.3 Compensation du risque de défaillance

A maturité égale, le marché demande aux émetteurs privés un taux d'intérêt supérieur à celui des émetteurs souverains. Ce supplément de rendement porte le nom de marge de signature. Cette marge correspond donc à une prime de risque, pour les emprunts obligataires émis par des emprunteurs publics ou privés.

En effet, chaque émetteur et à chaque émission, et évolue au cours du temps en fonction de l'appréciation des marchés quant au risque représenté par le titre. Il est usuel de classer les émetteurs en fonction de leur rating, attribué par les agences de notation financière et de classer les titres émis par les notations (AAA, AA, A, BBB,...) (voir Annexe 17 Principales notations financières page 130).

On peut ensuite distinguer, dans l'analyse du risque de taux, ce qui est de la variation générale des taux sans risque représentée par la courbe des taux zéro-coupon et ce qui provient de la variation des marges, en sachant que parfois les taux sans risque et les marges de signature évoluent de façon totalement divergente.

b) Valeur actuelle des passifs

Il est logique d'envisager la valorisation des cash-flows du passif en utilisant la courbe des taux zéro coupon étudiée ci-dessus. Elle permet, en effet, de tenir compte de la maturité de chacun des flux pour lui attribuer un taux d'actualisation précis. Par analogie avec la valorisation des actifs, il faudrait ajouter à cette courbe des taux sans risque, une prime de risque.

Néanmoins, le calcul de la valeur actuelle du passif peut être réalisé avec une prime de risque arbitrairement choisie, éventuellement nulle. Ce calcul est riche d'enseignements, car il permet d'aborder la question de l'adéquation actif-passif, de façon nouvelle en considérant les variations potentielles de la valeur actuelle nette en fonction des variations des taux de marché retenus pour l'actualisation des actifs et des passifs. (Le Vallois, Palsky et Tosetti 2003)

Le calcul de la valeur actuelle diffère nettement du calcul des provisions mathématiques, pour lequel on utilise des taux d'actualisation des tables de mortalité réglementaires, et qui ne comporte pas d'hypothèses de rachats anticipés ou de participations aux bénéfices au-delà des taux garantis contractuellement.

38

Chapitre II : Réassurance & Gestion actif-passif

1.4 Mesures de la sensibilité de la Valeur Actuelle Nette

La recherche de l'adéquation actif-passif est d'abord passée par la répartition des engagements par groupe de taux de rendement, puis par la construction de groupes d'actifs de taux de rendement équivalent et de valeur actuelle identique. Pour chacun des groupes ainsi constitués, la valeur actuelle nette est donc nulle.

Malheureusement, il est rapidement apparu que cet équilibre était instable, car susceptible de fortes variations en fonction de l'évolution des marchés. A l'évidence cette situation était peu satisfaisante, et les économistes et actuaires précurseurs de la gestion actif-passif se consacrèrent donc à l'étude et à l'explication des variations de la valeur actuelle nette.

a) Sensibilité de l'Actif

Calcul d l d' ?VA(r) VA() En=1--t Ft

e a dérivée

?

premiere

R = r = t *

(1+R)t+i

La variation de la valeur actuelle pour une petite variation du taux d'actualisation est donnée par le

La sensibilité de la valeur actuelle nette est la variation de prix relative ÔVA(r)/ÔR. ¹Sensibilité = -- vA * (rtL1 t * (1+R)t+i)

Lorsque les cash-flows _Ft, sont tous positifs, la sensibilité de la valeur actuelle aux variations du taux d'actualisation est nécessairement négative. Il en est bien sûr ainsi dans le cas des obligations, dont la valeur de marché baisse quand les taux sont à la hausse et réciproquement.

a.1 Duration de Macaulay

Frédérick Macaulay, en 1938, définit la duration comme étant la durée moyenne de l'obligation, chaque durée t étant pondérée par la valeur actuelle des cash-flows correspondants F_t/(1 + R)^t+1

Sensibilité = -- (1

1+R) * (^'1t= * vA*(+tR)t+l).

L'expression(L ₁ t * vA*(+tR)t+l), représente la duration d'une série du flux fixes (Ft).

La sensibilité et la duration d'une série de flux fixes sont donc reliées par la formule de

dua<\o?

John Richard Hicks, (1946), à savoir Sensibilité ~ --

(1+R) .

a.2 Duration d'une rente perpétuelle

La duration d'une rente fixe annuelle dont l'arrérage vaut 1 et dont la durée est n années est

donnée par la formule D_n = VAn¹ * Ey ₁1 * 1

(1+R)i

39

Chapitre II : Réassurance & Gestion actif-passif

b) Sensibilité du Passif

Des résultats encourageants dans l'analyse de l'actif avec l'application des concepts de duration et de convexité, sont obtenus. Certes, ces concepts ne s'appliquent pas universellement, mais ils sont simples et utiles pour des calculs approchés. Néanmoins, nous avons constaté qu'il existait deux limites importantes :

> le domaine d'utilisation de ces concepts est limité aux variations parallèles de la courbe des taux

> les calculs de la duration et de la convexité ne sont valides que pour les flux fixes, indépendants des taux de marché.

La première limite n'est pas sans conséquence, mais elle n'invalide pas totalement l'analyse du risque de taux. En effet, les variations parallèles de la courbe des taux représentent la principale source de risque pour la plupart des portefeuilles obligataires.

Ceci est démontrable, statistiquement, en analysant la variance des taux. Une analyse statistique, en composante principale des mouvements de la courbe des taux, permet d'identifier le premier facteur comme la variation générale du niveau des taux.

L'analyse des portefeuilles obligataires par la duration ou la convexité reste donc réellement pertinente, même si elle est limitée aux variations parallèles de la courbe des taux. En revanche, la seconde limite (cash-flows fixes) est très contraignante pour l'analyse des passifs en assurance vie.

Dans l'exercice de ces options, le comportement du client sera fréquemment influencé par l'évolution des taux de marché. Les cash-flows du passif sont donc, dans le cas général, dépendants du niveau des taux. Pour effectuer l'analyse des engagements avec les outils de 1^ergénération, nous devons nécessairement assimiler les cash-flows du passif à des flux fixes, au moins en première analyse.

L'actuaire peut envisager un pourcentage de rachat minimum incompressible et indépendant de la conjoncture des taux de marché. Il peut également, mais avec moins de certitude, proposer un taux de rachat maximal dans un contexte de hausse des taux.

c) Notion d'immunisation

La notion de sensibilité est un indicateur de l'exposition au risque de taux. En effet, on peut calculer l'exposition de la Valeur Actuelle Nette au risque de taux :

dVA nette	dVA actif =	dVA passif

dR dR dR

Si on considère le cas où la Valeur Actuelle Nette initiale est égale à zéro, et où la sensibilité de l'actif et du passif sont identiques, alors la variation de taux est sans influence

sur la Valeur Actuelle Nette dVA nette₌

0.

dR

40

Chapitre II : Réassurance & Gestion actif-passif

On parle dans ce cas d'immunisation du risque de taux. En effet, la Valeur Actuelle Nette devient insensible, sinon à toute variation de taux, du moins à une petite variation parallèle de la courbe des taux ; cet effet est obtenu en alignant les sensibilités de l'actif et du passif.

1.5 Limite des outils de 1re génération

a) Cas où l'approche statique est inadaptée

D'une façon générale, l'approche statique privilégiée par les outils de 1^re génération introduit des distorsions dans la perception des risques :

> D'une part, elle ne prend pas en compte les bénéfices générés par les versements futurs ou par l'activité de production des futurs contrats. Ceci peut sembler conforme au principe de prudence comptable, mais nous ne sommes pas ici dans l'optique de l'enregistrement du passé, mais bien dans celle de l'analyse prospective de l'équilibre du bilan.

> D'autre part, l'approche statique sous-évalue ou ignore entièrement certains risques financiers associés, non pas aux stocks d'épargne déjà constitués, mais aux versements futurs effectués sur les contrats existants.

Dans ce cas (très fréquent), les caractéristiques de l'actif constitué face au contrat vont être modifiées en fonction du niveau et du contexte financier des versements futurs. En particulier, les versements effectués par les clients dans un contexte de baisse des taux auront pour effet de diminuer le rendement global des portefeuilles obligataires.

b) Limitation au seul risque de taux

Lorsque les contrats d'assurance étudiés relèvent bien de l'analyse statique, les outils de 1re génération proposent une approche simple et compréhensible, mais entièrement focalisée sur le risque de taux. A la limite, la recherche tend à réduire la question de l'adéquation actif-passif, à la sensibilité de la Valeur Actuelle Nette (VAN) au risque de taux.

Cette analyse est pertinente s'il est possible d'assimiler actifs et passifs à des échéanciers de taux fixe ; ce qui peut être envisagé pour une activité d'assurance limitée aux produits les plus simples (bons d'épargne vie ou bons de capitalisation), et dont les placements seraient effectués presque exclusivement en obligations.

Les risques liés au comportement de la clientèle, notamment en matière d'exercice des options cachées, ne peuvent pas être décelés ou traités par les outils de 1^re génération. Les risques de marché non directement liés aux taux obligataires (risque boursier ou immobilier, risque d'inflation) ne peuvent pas être non plus analysés par ces outils.

41

Chapitre II : Réassurance & Gestion actif-passif

c) Inadaptation aux passifs des assureurs vie

La recherche d'immunisation du risque de taux est fondée sur un concept mathématique : la sensibilité ou la duration du passif. Mais en toute rigueur. La duration n'est définie que pour des séries de flux financiers fixes et indépendants des taux.

Or les engagements des assureurs vie ne présentent que rarement cette caractéristique de fixité. On peut, certes, définir une sensibilité locale du passif aux petites variations de taux, en faisant l'hypothèse que de faibles variations ne peuvent pas modifier le comportement de rachat ou de prorogation de la clientèle. Il faut alors conserver à l'esprit que cette immunisation ne protégera pas réellement l'assureur contre de fortes variations des taux.

Mais pour que cette sensibilité locale ait un sens, il faut encore faire une hypothèse plus forte. Il faut supposer que le taux servi par l'assureur reste indépendant des taux de marché jusqu'au terme du contrat.

d) Risques comptables ignorés

Les problèmes comptables ne sont pas envisagés par les outils de 1^re génération. Or les différentes provisions prudentielles relatives à la gestion des actifs qui sont les :

> provisions pour risque d'exigibilité > provisions pour aléas financiers > provisions globales de gestion,

Constituent un souci majeur pour les assureurs puisqu'elles impactent le niveau des fonds propres, et donc la marge de solvabilité. Il est pratiquement indispensable d'utiliser des outils complémentaires pour mesurer ces risques.

e) Conclusion sur l'utilisation des outils de 1^re génération

En conclusion, les outils de 1^re génération sont utiles pour mesurer approximativement les enjeux de l'adéquation actif-passif. Mais ils ont été créés par les banques, dans les années 30 à 70, dans un contexte où les ressources et les emplois bancaires étaient pratiquement assimilables à des titres à taux fixes. Pour les sociétés d'assurance vie (ainsi d'ailleurs que pour les banques), la situation actuelle est bien différente.

Les outils d'analyse des flux financiers ne peuvent traiter exhaustivement car :

> seuls les risques de taux sont étudiés

> les flux du passif sont rarement fixes et se prêtent mal aux calculs de duration

> certains risques de bilan ne peuvent pas du tout être étudiés avec une vision statique.

A des degrés divers, tous ces points seront abordés et traités plus efficacement par les outils de 2^ème génération, à savoir les modèles déterministes.

42

Chapitre II : Réassurance & Gestion actif-passif

Section 3 Outils de nouvelle génération

1 Outils de 2ème génération (les scénarios déterministes)

Les outils de 1^re génération analyse des flux de trésorerie ne permettent de résoudre qu'une petite partie des problèmes d'adéquation actif-passif auxquels sont confrontés les assureurs vie. L'analyse des flux de trésorerie ne permet pas de résoudre des problèmes tels que :

> les flux du passif ne sont généralement pas fixes mais dépendent du comportement des assurés et de la politique de l'assureur

> l'analyse statique ne peut pas rendre compte des risques d'actif-passif liés aux versements futurs

> les provisions prudentielles et la vision comptable des résultats ne peuvent pas être intégrées dans les calculs de la valeur actuelle nette.

Pour contourner la première de ces difficultés, il apparaît nécessaire de traiter la variabilité des flux du passif en testant différentes hypothèses de taux de rachat ou de taux de prorogation, elles-mêmes corrélées avec des variations des taux obligataires.

Pour dépasser l'analyse statique, il faut utiliser une projection dynamique des flux financiers, qui tienne compte des primes futures et qui permet d'en mesurer l'impact sur le rendement financier des actifs. En outre, les versements futurs dépendent du comportement de l'assuré, lui-même lié la conjoncture économique. La simulation des primes doit être effectuée en fonction de différentes hypothèses concernant principalement l'évolution des taux obligataires.

Enfin, le modèle doit traduire les éléments financiers en comptes prévisionnels de façon à calculer les principales provisions prudentielles, notamment la provision pour risque d'exigibilité (PRE), qui est destinée à faire face à une insuffisante de liquidité due notamment à une modification du rythme de règlement des sinistres.

Les outils de 2^e génération permettent de projeter l'évolution des actifs et des passifs selon les différents périodes en fonction des scénarios déterministes décrivant l'évolution de ces derniers. À la différence des outils de 1^re génération, la valeur actuelle nette n'est pas la seule à déterminer cette évolution.

Après avoir présenté la notion de scénario et de stress testing, nous examinerons les composantes d'un modèle déterministe, puis les problèmes de conception de scénario. Ensuite, nous indiquerons les domaines d'application de l'outil déterministe et nous évoquerons les inévitables difficultés d'application.

43

Chapitre II : Réassurance & Gestion actif-passif

1.1 Scénarios et stress testing

Les outils de simulation de 1^re génération limitaient l'analyse des risques financiers aux petites variations parallèles de la courbe des taux. Avec les modèles de simulation déterministe, il devient possible d'examiner un éventail de scénarios beaucoup plus vaste.

Cette approche porte le nom de stress testing. Comme pour mesurer la résistance d'un matériau, le stress testing permet de contrôler la résistance du bilan à des scénarios économiques adverses. L'approche par scénarios contrastés apporte de précieuses informations sur les conditions limites dans lesquelles l'activité de l'assureur reste viable.

Avec un modèle de simulation suffisamment détaillé, on peut tester, pour chaque scénario, différentes allocations d'actifs, mais aussi différentes politiques de taux servis à la clientèle. Les simulations sont les éléments permettant de définir une politique de compromis raisonnable, assurant le maintien de la solvabilité de la compagnie d'assurances dans différents scénarios qui lui sont défavorables.

1.2 Eléments d'un modèle déterministe (simulation)

La réalisation d'un modèle détaillé de l'activité de production de l'assureur, ainsi que l'évolution de son portefeuille de contrats et des investissements n'est pas une tâche aisée, pas plus d'ailleurs que la traduction de cette activité en termes de résultats comptables prévisionnels. Dès que l'on demande une certaine précision dans la simulation des actifs et des passifs, la capacité des tableurs est dépassée. Aussi faut-il recourir à un développement informatique plus conséquent.

Les modèles de 2^ème génération sont donc en général des programmes informatiques appartenant à la famille des logiciels de simulation. Nous aurons donc deux types de variables dans la simulation, des variables endogènes et exogènes :

> Une variable exogène est une information ou un paramètre dont la valeur est connue, et introduite dans la simulation.

> Une variable endogène est un résultat ou un paramètre calculé auto-généré par le modèle.

a) Autres éléments modélisables

Certain éléments dans la simulation restent cependant nécessaires pour construire un modèle global opérant l'activité de l'assureur vie. Ces éléments sont :

> les frais généraux

> les mouvements des capitaux propres

> la politique de réalisation de plus-values

> la politique de dotation à la provision pour participation aux excédents

44

Chapitre II : Réassurance & Gestion actif-passif

a.1 Frais généraux

Pour une modélisation à court terme, les frais généraux peuvent être introduits à partir des prévisions budgétaires de la compagnie, en tant qu'hypothèse exogène. Pour une modélisation à long terme, il n'existe pas de prévision budgétaire et, en tout état de cause, les scénarios économiques contrastés sont incompatibles avec une hypothèse de frais invariants.

Il est donc préférable de traiter les frais généraux de façon endogène, en simulant des frais variables proportionnels au montant des engagements, au chiffre d'affaires et au montant des sinistres.

a.2 Mouvements des capitaux propres

Les mouvements des capitaux propres sont constitués par les augmentations de capital, par les émissions ou les amortissements des emprunts subordonnés, et enfin par les versements de dividendes aux actionnaires de la compagnie. Tous ces éléments peuvent faire l'objet d'hypothèses exogènes. Le modèle peut calculer, la marge de solvabilité minimale réglementaire, et le comparer au total des principaux éléments constitutifs de la marge :

> les fonds propres,

> la réserve de capitalisation,

> les plus-values latentes sur valeurs mobilières.

a.3 Réalisation de plus-values

Si le modèle est suffisamment détaillé à l'actif, il est possible de simuler une politique de réalisation de plus ou moins-values. Il ne s'agit plus ici de stratégie financière, mais plutôt de tactique comptable. Cependant l'importance de cet aspect tactique ne doit pas être négligée, car la réalisation de plus-values permet à l'assureur de manoeuvrer en fonction des différentes provisions et réserves prudentielles imposées par la réglementation.

b) Modèles statiques et dynamiques

Il existe de nombreuses variantes de ces modèles. Dont les caractéristiques usuelles permettent de les classer en deux modèles opérationnels. Les modèles statiques, qui ne traitent que des stocks du bilan existants, à partir d'une situation initiale arrêtée à une date donnée. Ils simulent le vieillissement des contrats en stock, mais ils ne tiennent pas compte des nouveaux contrats, ni des primes ou cotisations supplémentaires versées au titre des contrats existants.

Au contraire, les modèles dynamiques incluent des hypothèses sur la production de contrats futurs, ainsi que sur les investissements correspondants. L'activité est donc simulée sur la base de la poursuite de l'exploitation normale de la société. Un modèle dynamique peut toujours fonctionner en statique. Il suffit de faire des hypothèses de production nulle.

45

Chapitre II : Réassurance & Gestion actif-passif

Nous avons déjà observé que l'analyse statique ne peut pas traiter tous les risques d'actif-passif. De plus, les provisions comptables et les ratios réglementaires ne peuvent être projetés de façon réaliste que par l'approche dynamique.

Les modèles dynamiques sont donc préférables pour une analyse actif-passif exhaustive. Ils sont, en revanche, plus complexes que les modèles statiques et dépendent d'hypothèses plus nombreuses.

b.1 Les micros et macros modèles

i. Le macro-modèle calcule globalement l'évolution des provisions mathématique sur la base d'une représentation matricielle du stock de passif et le montant des provisions mathématiques par type de contrats et par année de souscription.

Dans ce modèle, nous calculons le montant des prestations, en cas de décès, en appliquant un taux de décès moyen spécifique pour chaque ligne de la matrice de description des provisions mathématiques.

ii. Le micro-modèle calcule l'évolution du passif contrat individuel par contrat individuel. Les données sont tirées directement de l'inventaire des contrats. Dans ce modèle, chaque contrat est examiné séparément et le décès du souscripteur peut être simulé par tirage aléatoire en fonction de l'âge précis du souscripteur et d'une table de mortalité adaptée.

Les micro-modèles simulent donc individuellement l'évolution des contrats et cumulent les résultats obtenus pour obtenir les projections du passif. Le stock contrats est mis à jour fictivement à chaque période.

L'approche des micro-modèles peut sembler complexe, mais en réalité ces modèles sont rarement créés ex nihilo pour la gestion actif-passif. Ils sont issus de modèles actuariels existants déjà, qui servent à calculer et vérifier les provisions mathématiques. Ils bénéficient donc des développements déjà effectués par les actuaires et offrent, en principe, une bonne précision dans la projection des provisions techniques.

Il suffit de rajouter à ces modèles actuariels des fonctionnalités spécifiques de modélisation des actifs pour construire un outil actif-passif de 2^e génération. Les choses se compliquent cependant pour passer à une modélisation dynamique, car un micro-modèle doit alors générer des contrats fictifs pour représenter la production future.

Par ailleurs, les micro-modèles consomment beaucoup de ressources informatiques. Le coût de ces ressources est aujourd'hui raisonnable, mais c'est le temps de traitement qui constitue un écueil pour les analystes actif-passif, en effet difficile de tester de multiples scénarios.

46

Chapitre II : Réassurance & Gestion actif-passif

1.3 Conception des scénarios

Les modèles déterministes sont conçus pour simuler l'évolution du bilan et des résultats des assureurs vie en fonction de scénarios économiques exogènes. Il s'agit bien de scénarios au pluriel, car il n'est pas question d'utiliser un scénario unique, ce qui ramènerait en pratique aux outils de 1^re génération.

Les scénarios envisageables sont littéralement innombrables, de nombreuses variantes pouvant être envisagées tant pour les hypothèses économiques et financières que pour les hypothèses de production et de comportement des assurés.

Il faut pourtant sélectionner un nombre limité de scénarios représentatifs, faute de quoi le comité actif-passif se trouverait rapidement noyé sous les résultats du modèle.

Le premier scénario qui vient à l'esprit est celui de la continuité, les marchés financiers conservant leur position ou leur tendance sans forte variation. Par rapport à ce scénario de référence, généralement qualifié de scénario central, il faut ensuite étudier des scénarios contrastés dont la conception est beaucoup moins évidente.

a) Scénario central

Le scénario central correspond à une situation moyenne et stable des marchés financiers pour autant qu'on puisse parler de stabilité dans ce domaine. Son utilité principale est de constituer une référence pour mesurer la variation des résultats en fonction des scénarios contrastés étudiés ultérieurement. Cette durée en assurance vie est généralement située entre 5 et 15 ans.

b) Scénarios contrastés (stress testing)

Il existe des prévisions budgétaires dont l'objectif est bien de prévoir l'avenir aussi exactement que possible. Mais en gestion actif-passif, il s'agit seulement de projeter les résultats associés à des scénarios arbitraires, dont certains peuvent être particulièrement défavorables. Il n'y a là aucune prévision, mais seulement une méthode de contrôle des risques.

Cette approche est d'ailleurs utilisée dans le risque management liée à l'assurance ou la réassurance des grands risques, dont la fonction est d'évaluer les coûts et d'imaginer les réponses à apporter dans le cas de réalisation du sinistre.

La conception de ces scénarios découle de la variation de plusieurs paramètres. Le résultat de la compagnie d'assurances vie est très sensible aux hypothèses retenues. Par conséquent, la conception des scénarios se pose donc avec acuité.

La faiblesse essentielle des scénarios déterministes réside dans les variations qui sont arbitrairement retenus. Cependant, en pratique ces questions ne font pas l'objet de grands débats, car l'objet premier du scénario est de tenter d'avoir une estimation. On utilise de

47

Chapitre II : Réassurance & Gestion actif-passif

préférence des scénarios économiques très simples, dans lesquels les variations des taux sont standardisées, alors que le scénario central est basé sur une philosophie de continuité du présent et des scénarios contrastés en nombre limité. (Le Vallois, Palsky et Tosetti 2003)

Les conséquences de ces scénarios sur la valeur des différents actifs financiers, et le comportement des assurés, font que la conception du scénario reste très délicate. L'actuaire est libre d'utiliser autant de scénarios de stress qu'il le juge nécessaire, par conséquent son expérience joue ici un rôle déterminant.

c) Comparaison des résultats

Comment comparer les résultats obtenus entre différents scénarios ?

La question peut sembler triviale. Les modèles ont précisément pour objet de projeter les résultats comptables et financiers. Il suffit donc de comparer les résultats relatifs à différents scénarios, ou pour un même scénario économique, comparer les résultats des différentes politiques financières.

En outre, un modèle déterministe complet permet de déceler, pour chaque scénario, les écueils comptables ou réglementaires, tels que l'insuffisance de la marge de solvabilité ou le seuil de déclenchement de la provision pour aléas financiers.

Cependant, dans certains cas il est intéressant de réduire ces séquences de résultats à un indicateur de rentabilité unique, notamment pour pouvoir classer les politiques financières entre elles. Différents indicateurs peuvent être employés à cet effet, proches dans leur principe des notions financières de marge actualisée ou de retour sur capital investi.

1.4 Cohérence des hypothèses

Le choix des scénarios de stress est arbitraire. Ce point faible des outils de 2^e génération est cependant moins important qu'il n'y paraît. Le réalisme ou la vraisemblance d'un scénario de stress testing ne constitue qu'un aspect de l'objectif du scénario qui est le calcul d'une provision prudentielle.

En revanche, il est nécessaire que le scénario financier soit combiné avec des hypothèses cohérentes concernant la politique de l'assureur et le comportement des assurés. Dans le cas contraire, les problèmes actif-passif potentiels liés à la hausse des taux ne seront pas convenablement identifiés, et l'exercice de simulation deviendra sans intérêt et susceptible de produire des conclusions erronées.

Les hypothèses cohérentes dont il est question portent sur :

> la politique financière de l'assureur,

> la politique de rémunération des contrats (taux servis),

> le comportement des assurés (souscription, rachats anticipés, prorogations, etc.).

48

Chapitre II : Réassurance & Gestion actif-passif

a) Politique financière

Dans le cadre des outils de 2^e génération, la question financière n'est plus limitée au choix de la durée des investissements obligataires.

a.1 Allocation d'actifs

Selon la sophistication du modèle, la description de la politique financière peut être plus ou moins détaillée. Au minimum, il faut traiter, canton par canton, des éléments suivants :

> la répartition par grandes classes d'actifs (immobilier, monétaire, obligations, actions),

> la durée des investissements obligataires.

Ces éléments sont véritablement représentatifs de la stratégie de l'assureur, et globalement désignés sous l'appellation de politique d'allocation d'actifs, ou d'allocation stratégique des actifs.

Il est important de ne pas oublier que la durée et la structure des placements obligataires fait intégralement partie de la stratégie financière, même si elle n'est pas l'unique objet de la recherche de l'adéquation actif-passif.

Cependant, la notion d'allocation d'actifs est plus complexe que ne le laisse entendre la définition ci-dessus car elle présente en fait deux aspects :

> Elle est représentée implicitement par la composition initiale des actifs de chaque canton, qui est une donnée du modèle,

> Il faut préciser la politique d'investissement (ou de désinvestissement) liée aux cash-flows du canton.

a.2 Restructuration d'un portefeuille financier

La mise en oeuvre d'une allocation d'actifs est un aspect tactique important, pour lequel les modèles de 2^e génération peuvent apporter une aide précieuse. Si la modélisation de l'actif est suffisamment détaillée, il est possible, non seulement, de tester si telle allocation est meilleure que telle autre, mais aussi de projeter les conséquences comptables du passage de l'allocation actuelle à une allocation préconisée.

Il est rarement possible de modifier radicalement la composition de son portefeuille sans créer une cascade de conséquences comptables parfois significatives. Les simulations permettent de mesurer si ces conséquences sont supportables. Le cas échéant, elles donnent des indications conduisant à reporter la restructuration du portefeuille.

b) Le comportement des assurés

Le comportement des clients est un facteur clé, dans la projection des résultats. Ce comportement intervient naturellement dans un modèle dynamique via l'hypothèse de

49

Chapitre II : Réassurance & Gestion actif-passif

production, qui détermine les primes futures. Mais même dans le cadre d'une analyse purement statique, le comportement des clients en matière de rachat, de transfert ou de prorogation, influence considérablement les résultats et les cash-flows du passif.

On peut constater statistiquement, que le comportement de la clientèle diffère fortement selon ses caractéristiques socioprofessionnelles, patrimoine, âge, profession, ainsi que le mode de commercialisation des contrats. La difficulté est que ce comportement des assurés est fluctuant et dépendant du contexte des marchés.

Toute l'expérience de l'analyste actif-passif doit donc être mobilisée pour bâtir des hypothèses cohérentes. Il faut commencer par l'étude statistique du comportement normal des assurées. Il s'agit par exemple de mesurer régulièrement les taux de rachats anticipés en fonction :

> du type de contrat,

> de l'ancienneté du contrat,

> de l'âge du client,

> du montant de l'épargne,

> et du réseau de commercialisation.

On peut en déduire un classement des clients selon leur degré plus ou moins élevé de sensibilité supposée à un écart entre les taux servis et les taux concurrentiels.

Les conséquences des scénarios économiques sur les comportements des assurés de la compagnie d'assurance, dans le cas d'une hausse des taux, se traduisent par la dégradation de la situation concurrentielle de la compagnie, avec comme conséquence la baisse de la production ainsi qu'une hausse des rachats anticipés. Une baisse aura l'effet inverse.

1.5 Domaines d'utilisation

L'allocation d'actifs est assurément le problème central de la gestion actif-passif et le stress testing apporte un éclairage particulier sur ce problème, orienté vers le contrôle des risques comptables et financiers. Les modèles de simulation déterministes ont aussi d'autres usages en matière de tactique financière et comptable, ainsi que pour l'étude des garanties et options attribuées à la clientèle.

a) Etude de l'allocation d'actifs

La politique financière peut être prédéterminée, ou tout simplement constatée, d'après la composition actuelle des actifs en portefeuille. Dans ce cas, les outils de simulation sont parfaitement adaptés pour choisir la politique financière qui assure le meilleur rapport rendement/risque.

50

Chapitre II : Réassurance & Gestion actif-passif

Pour cela, nous devons effectuer un travail théorique considérable, pour définir les notions de rendement et de risque dans le cadre de l'activité d'assurance, avant même de l'aborder au plan pratique.

En fait, la modélisation déterministe ne permet pas de trouver le meilleur rapport rendement/risque. Elle permet surtout de rejeter ou de transmettre certaines allocations d'actifs dont le risque perçu apparaît trop élevé dans l'un ou l'autre des scénarios testés. Plus simplement trouver un compromis convenable entre la rentabilité mesurée avec le scénario central et les risques mesurés avec les différents scénarios du stress testing.

Intuitivement, il serait tentant de rechercher une solution optimale selon l'exemple des modèles de la frontière efficiente, inspirés des travaux de Harry Markowitz. Malheureusement la complexité des problèmes d'adéquation actif-passif de l'assureur vie est bien trop grande pour être réduite à une simple analyse (espérance/variance) des gains financiers.

Il n'est pas non plus possible de greffer des outils d'optimisation sur les modèles déterministes, car toute méthode d'optimisation demande la définition d'une mesure de probabilité sur un ensemble de scénarios économiques possibles. Or il n'est pas réaliste d'attribuer aux scénarios déterministes des poids de probabilité.

Dans le cas d'attribution de probabilité aux divers scénarios, cette distribution sera une distribution arbitraire. Cependant, on peut se poser la question de savoir sur quelle base ont été attribuées ces probabilités, les outils d'optimisation ne pouvant être utilisés qu'avec des scénarios stochastiques.

b) Tactique financière et comptable

Si le modèle utilisé est suffisamment détaillé en ce qui concerne les actifs financiers, les rendements et les valeurs de marché d'un portefeuille de valeurs mobilières sont calculés ligne à ligne. Une telle précision n'est pas nécessaire pour l'analyse de l'allocation stratégique des placements, mais elle s'avère très utile en matière de tactique comptable.

En effet, la complexité de la comptabilité des opérations financières de l'assureur est telle que la gestion courante des actifs ne peut pas être effectuée sans étude systématique ; tout mouvement financier impacte de très nombreux agrégats comptables et modifie la situation de l'assureur vis-à-vis des risques d'actif-passif et des provisions prudentielles exigées par le code des assurances ART. 224. (MODIFIE PAR L'ART. 39 L 06-04).

b.1 Actifs-obligataires et assimilés

En cas de baisse des taux, les obligations en portefeuille présentent généralement des plus-values latentes par rapport à leur prix de revient historique, même après correction de ce prix de revient par l'amortissement des surcotes ou des décotes. Quelles sont les conséquences de la réalisation de plus-values sur des titres obligataires ?

51

Chapitre II : Réassurance & Gestion actif-passif

> Les plus-values réalisées sont neutralisées par la dotation à la réserve de capitalisation.

Elles ne peuvent ni augmenter les résultats comptables de l'assureur, ni contribuer à la participation distribuée aux assurés.

> La réserve de capitalisation augmente. à terme, la réserve de capitalisation contribue à améliorer la marge de solvabilité de l'assureur, car elle est un élément constitutif de la marge.

Cependant, l'effet instantané est nul, puisque le stock des plus-values latentes sur valeurs mobilières qui diminue lui aussi est un élément du calcul.

c) Etude des garanties

Lors des études préalables au lancement d'un produit nouveau, il est particulièrement intéressant de contrôler, pour chaque scénario contrasté, la rentabilité attendue. Il est important de signaler que, de même la diversification des actifs améliore la sécurité des investissements, la diversification des contrats et des garanties peut contribuer à la stabilité des résultats des assureurs vie. Du point de vue de la gestion actif-passif, la rentabilité d'un contrat ne peut être estimée indépendamment et doit être évaluée par rapport à l'ensemble des activités de la compagnie.

1.6 Difficultés opérationnelles

a) Risque de modèle

Les modèles de simulation déterministes sont d'autant plus utiles qu'ils sont détaillés et exhaustifs dans la description des actifs et des passifs. Cependant, ces qualités se traduisent nécessairement par une complexité importante, pour assurer la conception, l'évolution et l'utilisation régulière des outils de 2^ème génération.

Le risque de modèle n'est pas négligeable. Il s'agit du risque que le modèle soit mal spécifié ou mal utilisé, et donne des indications largement erronées sur les conséquences des scénarios étudiés. Ce risque peut également provenir de défauts dans la cohérence des hypothèses utilisées.

Seules l'expérience et la qualification des analystes actif-passif permettent de contenir le risque de modèle. Il faut également procéder à des contrôles et des pointages rigoureux des résultats, notamment pour rapprocher périodiquement les projections du modèle avec les résultats enregistrés en comptabilité générale.

b) Communication a la Direction Générale de l'assurance

Par essence, les méthodes de stress testing se prêtent assez mal à la communication vers le Direction générale et encore moins vers l'extérieur de l'entreprise. Le principe de ces méthodes n'est pas toujours bien compris, et l'analyste actif-passif se trouve accusé de pessimisme, voire même d'alarmisme.

52

Chapitre II : Réassurance & Gestion actif-passif

Mais, par ailleurs, il est difficile de présenter sous une forme simple les résultats de simulations effectuées chaque trimestre sur un panel de 5 ou 10 scénarios d'une durée de 15 ans, d''autant plus que cette présentation n'est complète que si les hypothèses de politique de taux servis et de comportement des assurés sont expliquées.

Il est préférable de limiter strictement le nombre de scénarios étudiés, sinon la confusion s'installe inévitablement entre les trop nombreuses simulations. Les modèles déterministes sont donc avant tout des outils d'étude et d'aide à la décision, mais pas des outils de reporting (rapport actuariel) très efficaces.

Ce défaut est loin d'être mineur, car il est très important que les analyses actives passives soient correctement intégrées dans les chaînes de décision. Cette intégration concerne des fonctions stratégiques des différentes directions, et ne peut être obtenue qu'avec l'implication de la Direction générale, qui demande naturellement en retour à être informée et alimentée régulièrement en indicateurs de gestion.

2 Outils de 3e génération (les modèles stochastiques)

Pour évaluer les scénarios d'une manière objective, il faudrait pouvoir pondérer, les scénarios contrastés utilisés dans l'approche déterministe. Car ils sont considérés implicitement comme représentatifs de l'ensemble des scénarios de hausse ou de baisse possibles ; toutefois il n'est pas envisageable d'accorder un poids de probabilité d'une manière arbitraire.

Les modèles stochastiques permettent de donner un sens conventionnel à la notion de probabilité des scénarios et d'obtenir, de ce fait une mesure des risques cohérente. Les premiers modèles de ce type sont qualifiés de modèles de 3^ème génération.

Ils ne sont pas conceptuellement très éloignés des modèles déterministes préexistants. Les modèles stochastiques examinent de nombreux scénarios tirés aléatoirement et évaluent statistiquement les risques, ce qui permet d'ajouter à la boîte à outils actif-passif de nouvelles applications.

A l'exemple de la Value at Risk, qui représente la perte potentielle maximale, à l'intérieur d'un intervalle de confiance donné. Supportée par une compagnie d'assurances sur son portefeuille, dans l'hypothèse d'un scénario défavorable du marché.

VaR = x * loi. normal. inverse(a, u, a)

2.1 Processus stochastiques

Un processus stochastique est une série de variables aléatoires (xt) indexée au temps et peut être défini en temps continu ou en temps discret (hebdomadaire, mensuel, annuel, etc.). Pour une variable aléatoire (x), chaque tirage est un point unique (x) appartenant à l'ensemble de définition de x pour la modélisation financière.

53

Chapitre II : Réassurance & Gestion actif-passif

Les variables utilisées sont définies sur l'ensemble des réels R ou sur Rⁿ. Mais pour le processus stochastique, chaque tirage est une série chronologique x(t) définie sur R x T ou Rn x T, est désigné comme étant une trajectoire. Moyennant le choix de processus adaptés, il est possible de générer à volonté des trajectoires pour représenter des scénarios économiques et financiers (inflation, taux, etc.).

Contrairement aux scénarios déterministes, les scénarios stochastiques ne sont pas créés arbitrairement par l'analyste ou l'actuaire. Cependant, ils dépendent de choix effectués à un autre niveau :

> du type de processus stochastique,

> des paramètres retenus pour le processus,

> du générateur de nombres aléatoires utilisé pour la simulation.

En effet, il n'est pas entièrement décrit par les densités de probabilité de x à chaque instant t. Il faut de plus connaître pour tout intervalle de temps d_t les probabilités de transition d'une valeur de x à une autre, soit donc la distribution de Xt+dt /X_t = X_t (Le Vallois, Palsky et Tosetti 2003)

2.2 Méthode de Monte-Carlo

Considérons une fonction d'une variable aléatoire F(x) qui peut, par exemple, représenter un résultat d'exploitation en fonction de l'état des marchés financiers, représenté par (x).

La méthode de Monte-Carlo est une procédure numérique qui permet d'estimer les caractéristiques de la loi de probabilité de F(x) (telle que la moyenne, l'écart-type, les quantiles, etc.) à partir de la densité de probabilité de (x).

Elle consiste à générer des tirages aléatoires indépendants x1, x2, x3,..., x_n en fonction de la densité de probabilité de (x), puis à estimer les caractéristiques de la loi de probabilité de F(X) à partir de statistiques établies sur l'échantillon des n résultats F (x1), F (x2), F (x3),...., F (x_n).

Cette technique porte le nom de Monte-Carlo en référence aux jeux de hasard pratiqués dans les casinos monégasques. Mais en dépit de cette association avec l'univers du jeu, la méthode de Monte-Carlo est un outil mathématique utilisé pour toutes sortes d'applications professionnelles dans des domaines variés (tels que la finance stochastique, la recherche opérationnelle ou la physique quantique...). (Thiriez 2004)

a) Application à la gestion actif-passif

En gestion actif-passif, les scénarios stochastiques peuvent être substitués aux scénarios déterministes. La technique consiste à tirer aléatoirement de nombreux scénarios économiques, puis à utiliser pour chacun d'eux un modèle de simulation analogue aux modèles de 2^e génération.

54

Chapitre II : Réassurance & Gestion actif-passif

On peut alors calculer sur l'échantillon obtenu divers indicateurs tels que l'espérance de la valeur des fonds propres à un horizon donné ou la probabilité de constater une provision pour risque d'exigibilité.

La méthode de Monte-Carlo reste un outil d'exploration ; l'objectif n'est pas seulement de calculer un des indicateurs, mais d'observer la distribution de nombreuses variables comptables et financières dans un large éventail de scénarios

2.3 Passage d'un modèle déterministe à un modèle stochastique

Les fonctionnalités d'un modèle déterministe ou d'un modèle stochastique sont identiques, du moins en ce qui concerne la philosophe qui consiste à projeter les actifs et les passifs en fonction de plusieurs scénarios économiques et financiers. Il suffirait donc de générer des scénarios stochastiques et de les injecter dans un modèle de simulation déterministe déjà existant.

L'expérience des modèles déterministes a démontré qu'il était difficile de communiquer efficacement les résultats des simulations effectuées périodiquement sur un éventail limité de scénarios de stress-testing. Avec un modèle stochastique, il faut imaginer des techniques d'analyse nouvelles pour traiter les nombreux scénarios ; il faut également synthétiser les résultats pour la direction générale.

2.4 Fonctions de comportement des clients

Dans un modèle déterministe, les cash-flows du passif sont calculés à partir d'hypothèses plus ou moins détaillées sur le comportement des assurées ; ces hypothèses portent sur les éléments suivants :

> les souscriptions,

> les versements libres ou programmés,

> les prorogations,

> les transferts ou les arbitrages,

> les rachats partiels ou totaux,

> les avances, etc.

En fonction du scénario étudié, l'analyste actif-passif introduit manuellement des hypothèses sur le comportement conjoncturel des clients.

Chapitre III

Elaboration et étude du cas

Trust Algérie

Section 1 : Environnement de l'assurance vie en Algérie Section 2 : Modélisation de la mortalité

Section 3 : Etude du portefeuille de contrats de la Trust Assurance de Personnes

55

Chapitre III : Elaboration et étude du cas Trust Algérie

Section 1 Environnement de l'assurance vie en Algérie

1 Le marché algérien en chiffres 1.1 Caractéristiques du marché

L'assurance algérienne occupe le 68^e rang mondial avec une part de 0,016 % du marché mondial.

L'Algérie participe seulement à hauteur de 1,3 % du marché de l'assurance du continent africain qui lui-même ne pèse guère plus de 1,1 % du marché mondial de l'assurance.

Sans tenir compte de l'Afrique du Sud qui totalise à elle seule 82 % du marché continental, l'Algérie représente 7 % du marché africain.

Les 16 sociétés du marché algérien des assurances totalisent un chiffre d'affaires annuel de 460 millions d'euros en 2006, faible dans l'absolu, mais en croissance soutenue et régulière (13 % en 2006, avec une moyenne supérieure à 10 % sur les cinq dernières années). L'année 2007 voit se poursuivre cette croissance avec un chiffre d'affaires de l'ordre de 538 millions d'euros (+ 16 %). L'assurance automobile (obligatoire) prédomine avec 46 % du total.

Les assurances de personnes ne représentent, en Algérie que 7 % de ce total pour 2007, contre plus de 50 % sur les marchés européen, nord-américain ou japonais. Cela s'explique par la présence d'une couverture sociale, couvrant près de 5.767.000 assurés, sans oublier de tenir compte des ayants droit, ce qui nous ramène à environ 26,403 millions de personnes à raison de 4 ayants droit par assuré (conjoint et trois enfants à charge). Pour une population totale, avoisinant les 30 millions, anis un taux de couverture de 87,4 % en 1999 (C.N.E.S 2001). En conséquence une assurance personnes atténuée (3 milliards de dinars, soit moins de 30 millions d'euros).

Les assurances de crédit ont connu une évolution de plus de 156 % par rapport à 2006. De 23 millions d'euros en 2006 à environ 60 millions d'euros en 2007, les assurances crédits ne représentent encore que 1 % des parts du marché des assurances (KPMG 2009).

1.2 Densité d'assurance et taux de pénétration:

Au niveau européen, l'assurance est une activité relativement importante de l'économie, puisqu'elle représente entre 4 % (Luxembourg) et 12 % (Royaume-Uni) du P11B de ces pays. On parle d'ailleurs de «l'industrie des assurances», tant son rôle est prépondérant dans l'activité financière.

En Algérie, le taux de pénétration (primes d'assurance en pourcentage du P11B) est voisin de 0,6 % et reste quasiment invariable depuis 2001.

56

Chapitre III : Elaboration et étude du cas Trust Algérie

En 2007, la part des assurances dans le PIB reste inférieure à 1 %. Elle est de 0,55 % en 2006 et de 0,57 % en 2007.

Quant à la densité d'assurance (prime d'assurance par habitant), elle est inférieure à 16 euros. Les chiffres publiés par le ministère des finances dénotent une légère amélioration de la densité. En 2007, les primes payées par habitant sont de 1561 DA contre 1373 DA en 2006.

Les raisons communément admises sont avant tout l'absence d'une culture assurantielle dans le pays, le faible niveau de revenu des ménages ainsi que l'absence de marché financier structuré ne font qu'accentuer cet état de fait.

1.3 La réassurance :

La Compagnie Centrale de Réassurance (CCR) bénéficie d'une cession obligatoire de 5 ou 10 % suivant les risques et d'une priorité pour les autres cessions, qui ne peuvent être cédées qu'à des réassureurs classés au moins BBB(ou notation équivalente), et de la garantie de l'Etat dans ses opérations de réassurance des risques de catastrophes naturelles.

33 % des primes encaissées par le marché sont cédées en réassurance (15,2 milliards de dinars en 2006). 67 % de ces cessions sont réalisées directement sur le marché international et 33 % sur le marché national, dont 30 % au réassureur national, la CCR. Ces données restent pratiquement inchangées en 2007.

Le fait marquant de ces trois dernières années est l'augmentation de la conservation de la CCR, signe d'une meilleure maîtrise des risques et d'une solidité financière accrue en 2007. Le taux de rétention représente 54 % de son portefeuille. L'augmentation de la rétention de la CCR est liée au type de traité utilisé, qui passe du proportionnel au non proportionnel, du système basé sur les primes à celui basé sur les sinistres.

La tendance est nettement en faveur de la branche traditionnelle qu'est la branche automobile. Les autres risques, notamment ceux de l'assurance de personnes, bien qu'enregistrant une légère hausse, restent loin derrière la branche automobile. Cependant, il est à noter que ce sont là des produits récents sur le marché algérien des assurances, leur part dans le marché des assurances étant amenée à se développer.

57

Chapitre III : Elaboration et étude du cas Trust Algérie

2 Les acteurs du marché de l'assurance

2.1 Ministre des Finances

a) Direction des Assurances

Celui-ci intervient pour délivrer l'autorisation préalable pour l'ouverture en Algérie de succursales d'assurances étrangères et pour l'ouverture de bureaux de représentation des sociétés d'assurances et/ou de réassurance. L'ouverture de succursales étrangères est soumise à l'autorisation préalable sous réserve du principe de réciprocité.

C'est également le ministre qui agrée une association professionnelle d'assureurs de droit algérien à laquelle les sociétés d'assurances et/ou de réassurances étrangères sont tenues d'adhérer. Les sociétés d'assurances et/ou de réassurance ne peuvent exercer leur activité qu'après avoir obtenu l'agrément du ministre.

Le ministre des Finances agrée pareillement une association professionnelle des agents généraux et des courtiers, comme il établit la liste des documents que les sociétés d'assurances et/ou de réassurance doivent fournir à la Commission de Supervision des Assurances (CSA).

b) Centrale des risques

Le décret exécutif n° 07-138 précise les contours de sa mission : la centrale collecte et centralise les informations relatives aux contrats d'assurances souscrits auprès des sociétés d'assurances et de réassurance et les succursales d'assurances étrangères.

c) Organe de tarification

Aux fins d'élaborer des projets de tarifs, d'étudier et d'actualiser les tarifs en vigueur, il a été institué un organe de tarification.

En plus de ces attributions, cet organe peut émettre des avis sur tout litige en matière de tarifs pour permettre à l'administration de contrôle, de se prononcer.

2.2 Fonds de garantie des assurés

Ce fonds a pour charge de supporter, toute ou une partie de l'insolvabilité des sociétés d'assurances, des dettes envers les assurés et les bénéficiaires des contrats d'assurance.

(ARTICLE 213 BIS - AJOUTE PAR LA LOI 06-04).

Le financement de ce fonds est assuré par une cotisation annuelle des sociétés d'assurances et/ou de réassurance et des succursales d'assurances étrangères.

Le montant de ce financement ne peut dépasser 1 % des primes émises nette d'annulation.

La loi de finances complémentaire 2008 apporte des modifications de formes. Ainsi, ce fonds n'est plus rattaché au ministère des Finances.

58

Chapitre III : Elaboration et étude du cas Trust Algérie

2.3 Commission de supervision des assurances (CSA)

a.1 Missions

La Commission de supervision des assurances, par dispositions de L'ARTICLE 209 DE L'ORDONNANCE (MODIFIE PAR LA LOI 06-04), est l'organe qui exerce le contrôle de l'Etat sur l'activité des assurances. Ses fonctions sont de :

> Protéger les intérêts des assurés et bénéficiaires de contrat d'assurance, en veillant à la régularité des opérations d'assurance ainsi qu'à la solvabilité des sociétés d'assurances.

> Promouvoir et développer le marché national des assurances, en vue de son intégration dans l'activité économique et sociale.

LE DECRET EXECUTIF N° 08-113 DU 9 AVRIL 2008 reprend ces fonctions et les fait suivre de l'obligation, pour elle, de vérifier les informations sur l'origine des fonds qui ont servi à la constitution ou à l'augmentation du capital social de la société d'assurances et/ou de réassurance.

Cette Commission est assistée par des inspecteurs d'assurance assermentés. Ceux-ci sont habilités à vérifier sur pièce et/ou sur place toutes les opérations relatives à l'activité d'assurance et/ou de réassurance.

2.4 Conseil national des assurances (CNA)

Le CNA se définit comme le cadre de concertation entre les diverses parties impliquées dans l'activité de l'assurance : les assureurs et intermédiaires d'assurance, les assurés, les pouvoirs publics et enfin le personnel exerçant dans le secteur. Mais aussi comme force de réflexion et de proposition, organe consultatif des pouvoirs publics et centre de conception et de réalisation des études techniques.

a) Organisation du CNA

Les attributions, l'organisation, la composition et le fonctionnement du CNA sont définis par les dispositions du DECRET EXECUTIF N° 95-339, modifié et complété par le DECRET EXECUTIF N° 07-137 DU 19 MAI 2007.

Le CNA est présidé par le ministre des Finances. Le Conseil comprend une assemblée délibérante et quatre commissions techniques. Le Conseil a compétence pour en instituer d'autres. Enfin, le Conseil est financé par les sociétés et intermédiaires d'assurances.

b) Missions :

b.1 Organe consultatif

Le Conseil, conformément aux textes, délibère sur toutes questions relatives à la situation, l'organisation et le développement de l'activité d'assurances et de réassurance, soit par son président le ministre des Finances, soit à la demande de la majorité de ses membres.

59

Chapitre III : Elaboration et étude du cas Trust Algérie

Par ailleurs, il peut être saisi, par le président du Conseil, d'avant-projets de textes législatifs ou règlementaires qui relèvent de ses compétences. Il peut se saisir lui-même, de sa propre initiative.

b.2 Organe de concertation

Le Conseil propose aux pouvoirs publics toutes actions ou toutes propositions qui ont pour objectifs de mettre en oeuvre des mesures propres à rationaliser le fonctionnement de l'activité ou de sa promotion.

De la même façon, il peut proposer des mesures relatives aux règles techniques et financières qui visent à améliorer les conditions générales de fonctionnement des sociétés d'assurances et de réassurance ainsi que celles des intermédiaires ; des mesures qui ont trait aux conditions générales des contrats d'assurances et des tarifs ; des mesures qui tiennent à l'organisation de la prévention des risques.

2.5 Associations professionnelles

Les sociétés d'assurances, sont tenues par la loi d'adhérer à une association qui a pour objet de représenter et de gérer les intérêts collectifs de ses membres, l'information et la sensibilisation de ses membres et du public. (ARTICLE 214, ORD. 95-07, MODIFIE PAR L'ART. 33 L. 06-04).

a) Union algérienne des sociétés d'assurances et de réassurance (UAR)

Elle est régie par la LOI N° 90-31 et qui regroupe toutes les sociétés d'assurances exerçant en Algérie. Son rôle est reconnu comme important par les professionnels et les institutions du secteur. Elle est représentée à la Commission juridique, à la Commission des agréments et à l'assemblée du CNA. Par ses statuts, elle a pour missions de développer l'activité de l'assurance, d'améliorer la qualité de prestation des assureurs, de coordonner les actions communes des membres et de représenter les intérêts de la corporation aux niveaux national et international.

2.6 Le système national de sécurité sociale

Le système de sécurité sociale algérien se caractérise par :

> l'unification des régimes basée sur les principes de la solidarité et de la répartition > l'affiliation obligatoire de tous les travailleurs, salariés, non-salariés, assimilés à des salariés

> l'affiliation est également obligatoire pour d'autres catégories de personnes dites catégories particulières

> l'unification des règles relatives aux droits et aux obligations des bénéficiaires > l'unicité du financement

Le système comprend toutes les branches de la sécurité sociale prévues par les conventions internationales, à savoir l'assurance maladie, l'assurance maternité, l'assurance invalidité,

60

Chapitre III : Elaboration et étude du cas Trust Algérie

l'assurance décès, la branche accidents du travail et maladies professionnelles, la retraite (l'assurance vieillesse), l'assurance chômage et les prestations familiales. (M.T.E.S.S 2010)

Le système national de sécurité sociale se compose de cinq (05) caisses nationales qui ont le statut d'établissement public à gestion spécifique :

> La Caisse Nationale des Assurances Sociales des travailleurs salariés (CNAS) : Compétente pour les travailleurs salariés en matière d'assurances sociales, d'accidents du travail et de maladies professionnelles et des allocations familiales ;

> La Caisse Nationale des Retraites (CNR) : Gère la retraite des travailleurs salariés et la retraite anticipée ;

> La Caisse Nationale de l'Assurance Chômage (CNAC) : Gère l'assurance chômage et le dispositif de création de micro-entreprises pour les personnes âgées de 30 à 50ans ;

> La Caisse Nationale de sécurité sociale des Non-Salariés (CASNOS) : Gère la sécurité sociale des non-salariés.

> La Caisse Nationale de Recouvrement des cotisations de Sécurité Sociale (CNRSS) : dont l'achèvement de sa mise en place est prévu en 2011, aura pour mission le recouvrement des cotisations de sécurité sociale des travailleurs salariés, mission assurée actuellement par la CNAS.

Le système national de sécurité sociale a dépensé plus de 170 Milliards de DA en 1999 (4,58% du PIB) soit plus 6,4 % par rapport à l'année 1998 et ce, pour assurer notamment un revenu de remplacement à plus de un million de ménages et couvrir plus de 80 % de la population en termes d'assurance maladie. Les dépenses de la sécurité sociale pour l'année 2000 s'élèvent à près de 186 milliards de DA, soit 4,52 % du PIB.

En comparaison, le budget social de l'Etat, - constitué par des transferts à caractère social (en espèce et en nature) en direction des ménages - pour la même année est de l'ordre de 221,6 milliards de DA soit 5,4 % par rapport au PIB et de 206 milliards de DA, soit 6,5 % du PIB en 1999. Ces chiffres placent les dépenses de la sécurité sociale à un niveau proche des dépenses de l'action sociale consenties par l'Etat.

Avec un taux global de cotisation est fixé, depuis le 1er janvier 1999, à 34,5% dont 9% à la charge du travailleur, 25% à la charge de l'employeur et 0,5% prélevés sur la part travailleur des oeuvres sociales.

On rappellera par ailleurs que les lois de 1983 portantes refontes du système ont étendu le bénéfice de la sécurité sociale à des catégories de non actifs. La cotisation due par ces catégories particulières est à la charge de l'Etat, ce qui (théoriquement) préserve le caractère contributif du système.

61

Chapitre III : Elaboration et étude du cas Trust Algérie

3 Présentation de la Trust Assurance

La Trust Assurances, Société par actions a été créée le 25 Octobre 1997, lors de l'assemblée générale constitutive tenue par les actionnaires la Trust International Insurance Corporation Bahreïn (TIIC) et la Qatar General insurance (Qatar).

La Trust Assurance a obtenu du Ministre des Finances l'agrément en date du 18 novembre 1997, pour pratiquer l'ensemble des branches d'assurances contenues dans la nomenclature officielle et a commencé ses activités dès janvier 1998.

La Trust Assurance fait partie du Groupe « Trust International Insurance Group of Companies » qui dispose d'une organisation Internationale implantée à travers certains pays, qui sont :

> Qatar General, Jordanie,

> TIIC Bahreïn,

> Compass insurance (Liban),

> TIIC Ramallah (Palestine).

> TIIC Gaza (Palestine),

> Trust Yemen Insurance. TIIC (Syria).

> TIIC (Libya),

> MIB (Market insurance Broker) Londres.

La Trust Assurance est une société par actions mixte de droit algérien dont le siège social est fixé à Alger, son capital a été fixé à 2.050.000.000 DA, réparti entre les actionnaires Trust Bahreïn et Qatar General.

Trust Re Bahreïn est classé BBB stable par l'Agence de notation Standard & Poor's, (voir Annexe 17) page 130. Le Trust Groupe dispose d'une capacité d'intervention très importante au niveau des pays où sont installées les sociétés filiales et au plan international en matière d'activité de réassurance.

La Direction AP (Assurance de personnes) ou Life insurance, point de départ mais aussi le pivot qui nous permettra ensuite de lier et de comprendre le cheminement du processus de la gestion du risque de l'assurance vie. Nous pouvons constater que parfois il arrive de nommer cette direction assurance vie en référence à la dénomination anglaise et par opposition Insurance no life. C'est tout simplement un jeu de sémantique car l'assurance de personnes englobe aussi l'assurance vie.

3.1 Assurance dépendant de la durée de la vie humaine

L'assurance sur la vie est un contrat par lequel, en échange d'une prime, l'assureur s'engage à verser, au souscripteur, une somme déterminée (une rente ou un capital) en cas de mort de la personne assurée à une époque déterminée.

62

Chapitre III : Elaboration et étude du cas Trust Algérie

> Assurance en cas de décès

> Assurances mixtes

a) Assurance en cas de décès

a.1 Assurance vie entière

L'assureur s'engage à verser un certain capital aux bénéficiaires, au décès de l'assuré et cela quelle qu'en soit l'époque.

Cette formule d'assurance est la meilleure façon pour un assuré voulant transmettre un capital qui pourra être payé soit sous forme de rentes, à un bénéficiaire quel qu'il soit, au moment du décès de l'assuré, soit pour lui garantir des revenus. Prime pure unique (n) :

H₊ = ? mF + · *+m L Ym~~

~ ~ , en utilisant la table de commutation (voir Annexe 9 page
mg6

118), H₊ = ^ú2, (La Trust assurance ne propose pas ce genre de police).

2

a.2 Assurance temporaire décès à capital fixe

Elle garantit le versement d'un capital aux bénéficiaires désignés dans le contrat si l'assuré décède avant la date fixée par le contrat. Dans le cas contraire, aucune prestation n'est due et les primes restent acquises par l'assureur qui a couvert le risque.

Ce type de contrat ne peut faire l'objet de rachat ART. 90 (MODIFIE PAR L'ART. 21 L 06-04) C'est le cas des polices d'assurance suivantes :

> Le plan de protection familiale

> Le plan de protection constant

> Le plan de protection caractérisé

Ces contrats sont conclus généralement, moyennant des primes annuelles, avec une spécification pour le plan de protection caractérisé par la possibilité de récupérer une partie

des primes et non pas du capital, la prime pure unique (n) : H+:?····· = ú23D2+E, en utilisant la

_x

?37

table de commutation (voir Annexe 9 page 118), H+:?····· ~ ? mF+ · *+m L Ym~~ ~ .

mg6

a.3 Assurance temporaire décès à capital variable

Tout comme la précédente, cette police d'assurance garantit le versement d'un capital variable, généralement pour un crédit. C'est le cas du plan de protection du crédit où le capital suit une progression arithmétique décroissante car l'assureur doit rembourser le montant du crédit restant dû à la banque créditrice, en cas de décès de l'assuré. Prime pure unique (n) : |? (KH) + = ? ô (... " [) · 124cents31124cents4~ · (1 ( ])³(^m

_x+2&

m~~n = |?(KH)+ = ? ~... " [~ ·

3+ mF+ · *+m L _Y~
mg6

63

Chapitre III : Elaboration et étude du cas Trust Algérie

|? (KA) X = Rx4E4~-Rx4~~?
·Mx

En utilisant, la table de commutation (voir Annexe 9 page 118), ð =

D_x

b) Assurances mixtes et combinées

Dans le but de proposer des polices d'assurance toujours plus attractives, l'assurance propose des produits qui offrent à la fois les avantages d'une garantie, en cas de décès, et d'une garantie en cas de vie.

b.1 Assurance mixte classique

Comme pour l'assurance temporaire décès, l'assureur s'engage à verser un capital décès aux ayants droit au décès de l'assuré, s'il intervient durant la période d'assurance. En outre, si l'assuré est en vie à l'échéance du contrat, il recevra un capital identique.

Dans le cas où l'assuré choisit de régler sa dette à l'assureur par le paiement des primes périodiques (ce qui est presque toujours le cas en pratique) la durée de versement de ces primes, est aléatoire, car il y a toujours un aléa à la charge de l'assureur, ce qui est une condition incontestable aux opérations d'assurance (Hess 2000). Cette formule d'assurance marie la prévoyance à l'épargne.

b.2 Assurance mixte combinée

C'est une assurance mixte dans laquelle le capital assuré en cas de décès n'est pas nécessairement égal à celui garanti en cas de vie. Lorsque le capital décès est supérieur au capital vie, elle est dénommée mixte prévoyance ; dans le cas où le capital vie est supérieur au capital décès, c'est une assurance mixte d'épargne. (Foukroun 2008).

C'est le cas des plans ci-après :

> Le plan de protection épargne

> Le plan de protection prospérité

> Le plan de protection croissance

Pour les différents plans cités ci-dessus, le capital versé en cas de vie est supérieur au capital versé en cas de décès car il subit une majoration de 2% annuel par rapport au capital initial.

Les modalités de payement sont versées en trois (3) tranches pour le plan protection prospérité et en cinq (5) tranches pour le plan de protection croissance.

64

Chapitre III : Elaboration et étude du cas Trust Algérie

c) Assurance contre les accidents corporels

L'assurance contre les accidents corporels est un contrat par lequel, en échange d'une prime, l'assureur s'engage, au cas où, durant la période garantie, un accident corporel atteindrait l'assuré, ou en cas de décès, à verser au bénéficiaire désigné un capital, et à rembourser tout ou une partie des frais médicaux ou pharmaceutiques engagés par suite dudit accident.

Quatre (4) conséquences de l'accident corporel peuvent être garanties :

> Décès

> Incapacité permanente totale

> Incapacité permanente partielle > Incapacité temporaire

Les prestations sont alors fonction du capital assuré, du degré de l'incapacité suivant un barème prévu.

L'assurance contre les accidents corporels peut couvrir une seule personne ou plusieurs, comme elle peut garantir les accidents de la vie privée uniquement ou incluant aussi les accidents corporels.

Nous avons deux types de contrats pour cette assurance. c.1 Individuelle accidents

L'assurance individuelle accident (Trust1) comme son nom l'indique, couvre une seule personne contre les accidents corporels.

c.1.1 Garantie de base

La garantie de base accordée est le versement d'un capital fixé dans le contrat au bénéficiaire désigné en cas de décès de l'assuré par suite d'accident couvert.

c.1.2 Incapacité Permanente Totale ou Partielle (IPT) ou (IPP)

L'incapacité permanente est constatée médicalement après consolidation des blessures subies lors de l'accident par l'assuré. Ainsi il sera versé à l'assuré ou à la personne ayant droit, un capital invalidité, égal au produit du capital de base pondéré par le taux d'invalidité qui est déterminé sur la base d'un barème conventionnel annexé au contrat.

Le capital décès et le capital incapacité permanente ne se cumulent pas. En effet, si l'assuré venait à décéder des suites de l'accident après avoir touché un capital incapacité permanente, celui-ci est déduit du capital décès qui sera versé aux bénéficiaires.

Des règles contractuelles prévoient le mode de calcul des indemnités en cas d'infirmités multiples atteignant le même membre ou plusieurs membres. Les assureurs appliquent la méthode du cumul des indemnités ou méthode Balthazar qui tient compte de la capacité

65

Chapitre III : Elaboration et étude du cas Trust Algérie

restante après chacune des incapacités constatées (sans évidemment dépasser le capital total assuré, ni le taux maximal prévu pour le seul membre infirme).

Exemple :

> Un premier accident conduit à un taux d'IPP de 5 % : la capacité restante = 100 % - 5% = 95 %.

> Si un deuxième accident conduit à un IPP de 7 % : la nouvelle capacité restante est 95 %, donc (7%.100%)/95% = 87.64 %, soit un taux de 12.36 %.

Cette incapacité restante sera la même quel que soit l'ordre de prise en compte des déficiences. Ainsi le cumul de 2 taux d'IPP de 5%, en appliquant le règle de Balthazar n'est pas de 10% mais de 10,26 %.

c.1.3 Incapacité Temporaire Totale de travail (ITT)

Par suite d'accident, il sera versé à l'assuré des indemnités journalières pour une incapacité temporaire totale de travail, pour lui éviter des chutes de revenus. Elles peuvent être versées à tout assuré pendant la durée de son hospitalisation consécutive à un accident. Elles ont alors moins pour but de compenser une perte de revenus que d'indemniser les frais directs.

c.1.4 Frais médicaux et pharmaceutiques

Cette garantie permet à l'assuré d'obtenir le remboursement, sur remise des pièces justificatives des frais de traitement exposés à la suite d'un accident garanti, dans la limite du maximum prévu au contrat.

Contrairement aux trois premières garanties qui sont soumises au principe forfaitaire (et peuvent donc se cumuler éventuellement avec d'autres indemnités) le remboursement des frais et des soins est soumis au principe indemnitaire et intervient en complément des régimes sociaux.

d) Assurance santé

L'assurance santé prévoit des indemnités en cas de maladie ou de maternité et couvre les frais engagés à la suite d'une maladie, soit :

> sur la base du complément de ceux pris en charge par la sécurité sociale > sur la base d'un barème conventionnel d'indemnisation

En raison de sa sinistralité enregistrée, cette assurance est incluse dans les contrats d'assurance groupe. C'est notamment le cas pour les contrats proposés par la Trust assurance de personnes.

Il est à noter que ce type d'assurance intègre aussi la plupart des plans de protection et d'assurance individuel accident, à l'exception du plan protection crédit et du plan de

66

Chapitre III : Elaboration et étude du cas Trust Algérie

protection famille. Elles ne prévoient pas le remboursement des frais occasionnés en complément de la prise en charge par la sécurité sociale, mais des indemnités forfaitaires et souvent plafonnées liées aux frais d'hospitalisation, ou à une intervention chirurgicale.

Dans ce type d'assurance, les garanties proposées sont :

> remboursement des frais médicaux, pharmaceutiques et d'hospitalisation

> incapacité temporaire ou permanente : incapacité non seulement due à un accident, mais également la conséquence d'une maladie

> indemnité journalière pour hospitalisation

> maladie redoutée nouvelle forme d'assurance santé mise en place par certains assureurs vie pour répondre aux besoins d'une partie de leurs clients ayant souscrit un capital décès et regretteraient de ne pas pouvoir en disposer pour se soigner, alors qu'ils sont atteints d'une maladie grave et devraient faire face à des frais médicaux importants, c'est le cas notamment de l'individuel (Trust 3)

> le versement d'une rente pour l'incapacité liée à l'accident. Cette rente a pour but de permettre à l'assuré de faire face aux frais d'une assistance à domicile ou aux frais de séjour en établissement. L'individuel (Trust 2) couvre ce type de d'indemnité.

3.2 Assurance d'assistance aux personnes en déplacement (Assurance voyage) :

Cette assurance est généralement couplée, soit à une assurance contre les accidents corporels au cours de voyage, soit à une assurance automobile. Elle prévoit des prestations servies en nature et/ou pécuniairement.

L'assurance la plus répandue en Algérie est l'assurance voyage exigée par les ambassades de l'espace Schengen.

Les prestations prévues sont :

1) Garanties de base (Décès -Invalidité Totale - Invalidité Partielle - Frais Médicaux).

2) Garanties complémentaires (Assistance aux personnes - Annulation et retour anticipé - Départ retardé - Perte de bagages).

3.3 Assurance collective ou assurance groupe

Le public ne ressent pas toujours comme indispensable la souscription d'un contrat d'assurance sur la vie (contrairement à certaines assurances dommages obligatoires). Par conséquent les assureurs de personnes ont conçu des méthodes de commercialisation originales pour attirer le grand public vers les produits d'assurance vie.

L'assurance groupe est donc un contrat souscrits par une personne morale au profit d'un groupe, généralement une entreprise, une association, ce type de contrat est étudié en fonction

67

Chapitre III : Elaboration et étude du cas Trust Algérie

des besoins de ces derniers. Elle couvre un grand nombre de personnes par la signature d'une seule et même police.

Dans l'article 62, l'ordonnance 95-07 modifiée et complétée, définit le contrat d'assurance groupe qui est souscrit par une personne morale ou un chef d'entreprise en vue de l'adhésion d'un ensemble de personnes répondant aux conditions définies au contrat pour la couverture d'un ou de plusieurs risques relatifs aux assurances de personnes. Les adhérents doivent avoir un lien de même nature avec le souscripteur.

Les garanties généralement accordées en assurance groupe sont :

a.1 Décès invalidité Absolue et Définitive

C'est la garantie de base de ce contrat. Les employeurs la souscrivent en faveur de leurs employés en vue de leur garantir un capital en cas de décès ou en cas d'invalidité absolue et définitive.

L'invalidité définitive et absolue est l'invalidité qui rend l'assuré incapable d'accomplir des tâches les plus ordinaires de la vie, allant jusqu'à l'assujettir à une tierce personne.

a.2 Décès accidentel

En cas de décès d'un assuré suite à un accident couvert, l'assureur verse un capital supplémentaire venant s'ajouter au capital décès de base.

a.3 Rente éducation

En cas de décès d'un assuré laissant des enfants mineurs scolarisés, il leur sera versé une rente temporaire jusqu'à 18 ans ou un autre âge, à condition qu'ils soient vivants, payable trimestriellement à terme échu.

a.4 Rente d'incapacité permanente et partielle

En cas d'incapacité permanente et partielle de l'assuré, suite à un accident ou à une maladie, il lui sera versé une rente temporaire jusqu'à son 60ème anniversaire à condition qu'il soit vivant.

a.5 Exonération du paiement de primes

En cas d'incapacité temporaire de travail de plus de 30 à 90 jours, ou d'invalidité en cours de consolidation, l'assuré sera exonéré du paiement des primes d'assurance tout en restant couvert au même titre que les autres adhérents.

68

Chapitre III : Elaboration et étude du cas Trust Algérie

Section 2 Modélisation de la mortalité

1 Elaboration d'une table de mortalité

Les tables de mortalité nous fournissent, pour chaque individu d'âge x, le nombre moyen de survivants l_x d'une population comportant initialement l0 individus d'âge 0. Par

différence on déduit la valeur d_x du nombre moyen de décès d = B - 1x+1 et la ê₂

1_x

Il est important de noter que les chiffres présentés dans les tables de mortalité sont des estimations de valeurs théoriques inconnues.

probabilité de décès q =

L'étude de recensement général de la population et de l'habitat en Algérie réalisé en 1998 et un traitement des données par une des méthodes de lissages et d'ajustement des données cité précédemment, vont nous permettre d'établir une table de mortalité relative à l'Algérie.

Par convention, il est à noter que la table TD est utilisée pour les assurances décès, tandis que la table TV sera utilisée pour l'assurance en cas de vie (rentes viagères, paiement de capital en cas de vie,..).

1.1 Prérequis

Au préalable nous allons poser les hypothèses suivantes sous-jacentes à la table de mortalité.

1) La population d'individus est fermée, c'est-à-dire qu'elle diminue par le seul fait de la mortalité ; le phénomène migratoire n'affecte pas cette population.

2) Les individus composant cette population meurent selon un calendrier de mortalité préétabli, constitué par la série des taux de mortalité observés pour une année ou pour une période déterminée.

3) La population d'individus est fictive. Son effectif est fixé par convention à 100 000 individus. Cet effectif constitue ce que l'on appelle la racine de la table de mortalité. Le choix d'un chiffre rond à deux avantages, faciliter le calcul et la lecture des résultats et permettre aisément la comparabilité des tables de mortalité.

4) Les décès à l'exception des premières années de la vie, sont par hypothèse, répartis de façon linéaire dans chaque groupe d'âge.

Le quatrième recensement général de la population et de l'habitat a été réalisé en été 1998 avec pour date de référence, le 25 juin 1998. La structure par âge et par sexe de la population algérienne résidente recensée au milieu de l'année 1998 est fournie dans le tableau, voir (Annexe 1) page 109.

69

Chapitre III : Elaboration et étude du cas Trust Algérie

C'est sur la base de ces données (ONS, DONNEES STATISTIQUES N° 305, DECEMBRE 2000) qu'il sera possible de calculer les taux de mortalité nécessaires à l'élaboration de la table de mortalité abrégée. Nous avons estimé plus prudent d'utiliser la moyenne des décès sur trois années, à savoir 1997, 1998 et 1999 plutôt que de prendre directement les décès de l'année 1998 afin d'atténuer les fluctuations, voir (Annexe 3) page 110, avec une répartition d'âge quinquennale, que nous devons repartir en âge unitaire.

Pour ce faire, nous utiliserons une méthode d'interpolation avec jonctions lisses la méthode Karup-King, (Monotonic Karup-King Osculatory Interpolation), voir (Annexe 7) page 114.

1.2 Ajustement de la table de mortalité

La table interpolée par la méthode de Karup-King est limitée à l'âge de 85 ans, alors qu'en assurance vie, on a besoin de tables dont l'âge limite dépasse 100 ans. L'ajustement de la table obtenue au-delà de cet âge est nécessaire.

a) L'ajustement

L'ajustement de la table complète obtenue, se fait par la méthode de Makeham u(x) = a + b X c^X, ou de Gompertz u(x) = b. c^X Le calcul des constantes se fait en 2 étapes :

· La première étape consiste à déterminer une première évaluation des constantes a, b, c par la méthode de King Hardy

Pour l'ajustement des tables algériennes, on considère 20 ans comme âge d'entrée et que la table au-delà l'âge de 75 ans suit une exponentielle de Makeham.

b) Résultats

Une première méthode consiste à donner une table Makehamisée, ajustée comme suit :

1) Pour la tranche d'âge [0-20 ans [, on ajuste, en général, par un polynôme de degrés 6 ou un polynôme de degrés 3 par intervalle. Mais comme les observations sont interpolées par la méthode de Karup-King, et lissées par cette dernière, il est préférable de garder les observations comme telles.

2) Pour la tranche d'âge [20-75 ans], les deux formules de Makeham et Gompertz ont été tentées, mais celle de Makeham a donné de meilleurs résultats.

3) Comme les données de la tranche d'âge [20-75 ans] ont été ajustées par une loi de Makeham, les données de 75 ans et plus seront ajustées par une exponentielle de Makeham, (voir Table de mortalité Tv97-99 des (q_x) ajusté Annexe 5 page 111).

70

Chapitre III : Elaboration et étude du cas Trust Algérie

b.1 Comparaison des tables de mortalité :

Dans cette étape, on compare les tables utilisées dans le secteur des assurances-vie, à savoir la table TV 88-90, voir (Annexe 11) page 122, et la table TV et TD 97-99 Algérienne, voir (0) page 111.

b.1.1 Comparaison des tables TV88-90 et TV97-99 Algérienne :

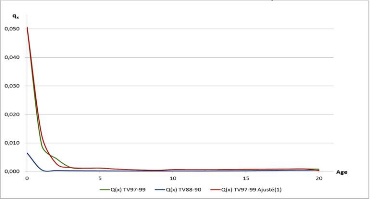
Figure 3 Comparaison des qx des tables TV88-90 et TV97-99 Algérienne âge de [0-20ans [

1) La tranche [0-20 ans [ : nous pouvons constater qu'il n'y a pas de grande divergence entre les deux tables, à l'exception d'un TMI plus élevé. TMI (Taux de mortalité infantile) = 55.99

TM! =	Décès d'age 0		* 1000

Figure 4 Comparaison des qx des tables TV88-90 et TV97-99 Algérienne âge de [20-80 ans [

2) La tranche [20-75 ans [ : on remarque que les taux de la table Algérienne sont nettement plus élevés, que ceux de la TV88-90.

71

Chapitre III : Elaboration et étude du cas Trust Algérie

Q(x) TV97-99 Ajusté ^(1)		Q(x) TD97-99 Ajusté ^(1)
Moyenne	0,00293	Moyenne	0,00472
Écart-type	0,00290	Écart-type	0,00347
Variance	0,0000084	Variance	0,0000121
Minimum	0,00032	Minimum	0,00163
Maximum	0,01078	Maximum	0,01420

Table 1 Statistique descriptive des Tables TV et TD 97-99 Algériennes Ajusté tranche [20-75 ans [

Les observations font apparaitre que le taux de mortalité des hommes est plus élevé que celui des femmes. En effet entre [30-60 ans [ et selon la table TVTD 97-99 Algérienne, on observe que la moyenne q_x de la table TV=0,00293, et celle de la table TD =0,00472.

Figure 5 Comparaison des qx des tables TV97-99 et TD97-99

Ce qui nous permet d'établir l'approximation que pour un âge x compris entre 30 et 60 ans, le q₊(homme) ? 1,6 * q₊(femme).

En conséquence, le fait que la table TD reflète la mortalité masculine et la table TV la mortalité féminine, favorise l'assureur pour les contrats d'assurance décès souscrits par les femmes, ou pour les contrats d'assurance en cas de vie souscrits par les hommes, lui procure un gain moyen positif systématique que l'on peut assimiler à un chargement technique implicite, (Petauton 1996).

Ce chargement implicite est justifié si on le considère comme une mesure prudentielle.

2 Modélisation de Lx et du taux instantané de mortalité en utilisant le

Modèle de Makeham (3 paramètres)

Le Modèle Makeham nommé aussi modèle de Gompertz et Makeham, va nous permettre de lisser les taux instantanés de mortalité ; il fait partie des modélisations dites paramétriques (voir page 16).

Nous allons modéliser les taux instantanés de mortalité de la population algérienne grâce à une régression non linéaire afin d'estimer les 3 paramètres du modèle de Makeham. Cette

Chapitre III : Elaboration et étude du cas Trust Algérie

modélisation présente bon nombres d'avantages dont celui de sa facilité d'utilisation, une logique explicative ainsi qu'une commodité certaine dans le calcul de la prime d'assurance sur deux têtes. Cependant, ce modèle présente aussi certains inconvenants, car la modélisation ne représente pas des phénomènes tels que la mortalité infantile. Néanmoins, c'est l'une des modélisations les plus utilisées par les compagnies d'assurance, du fait que les assurés sont âgés de plus de 18 ans.

Pour ce faire, nous utiliserons le logiciel XLstat? Modélisation des données ? Régression non linéaire, pour ne pas fausser notre modélisation, et dans le but d'avoir une modélisation robuste (sans bais). Nous allons sélectionner la variable explicative (Age) à partir de 6 ans dans la Table de commutation Algérienne TD97-99 voir (Annexe 9 page 118) car, comme nous l'avons souligné, la fonction du Modèle de Makeham ne prend pas en compte la mortalité infantile, et ne fait pas partie de la bibliothèque des fonctions prédéfinies dans XLstat, donc il nous reste à éditer cette dernière.

Nous avons le taux instantané de mortalité du modèle Gompertz Makeham U_x = A + B
·

_Cx

Nous chercherons à définir les paramètres A, B, C pour la population Algérienne. Pour cela nous utiliserons plutôt L_x

-B
·CX

1nL_x = --(A + B
· C^x) ? L_x = k
· e-A
·x
· e

d dx

1n C

72

Dans XLstat nous allons formuler différemment cette expression, et nous poserons aussi k=92784, qui correspond à l'âge x=6, l'âge de départ de notre modélisation. Comme nous l'avons souligné plus haut, nous utiliserons la table TD97-99 Algérienne (voir Annexe 9 page 118).

Y = 92784 * Exp(--pr1 * X1 -- (pr2 * (pr3^X1)/Ln(pr3) ))

Figure 6 Régression non linéaire des Lx (modèle Gompertz Makeham)

Chapitre III : Elaboration et étude du cas Trust Algérie

2.1 Coefficients d'ajustement de la Régression non linéaire des Lx

la somme des carrés des résidus du modèle

la moyenne des carrés des résidus du modèle

la racine de la moyenne des carrés des résidus du modèle

Observations

			100
DDL			97
R^2			1,000
SCE	58	886	853,54
MCE		607	080,96
RMCE			779,15

nombre d'observations le nombre de degrés de liberté le coefficient de détermination

73

Table 2 Coefficients d'ajustement de la Régression non linéaire des Lx (modèle Gompertz Makeham)

Comme nous pouvons le constater, la modélisation est fidèle avec un coefficient de détermination égal à 1.

2.2 Qualité de la régression non linéaire modèle de Gompertz Makeham

Figure 7 Lx Observés/Estimés par la Régression non linéaire modèle (Gompertz Makeham) et Histogramme des résidus

Y = 92784 * Exp(--pr1 * X1 - (pr2 * (pr3^X1)/Ln(pr3) )) 2.3 Paramètres du modèle Gompertz Makeham

Paramètre	Valeur	Ecart-type
pr1: A	1,207E-03	2,807		pr2: B
3,056E-05	1,602E-02	pr3: C
1,104	8,663

Table 3 Paramètres du modèle Gompertz Makeham

La fonction de modélisation des Lx concernant la population Algerienne

L₊ 92784 * F ·"1,207 * 10³⁶ * ~ " 13,056 * 10^36» * 1,104+

L...~1,104)¼½

Ou bien en utilisant la le Taux instantané de mortalité

U, = 1,207 * 10³⁶ + (3,056 * 10^36» * 1,104^x)

3 Modélisation des (dx) en utilisant le Modèle de Makeham (3 paramétrés)

Dans ce qui suit, nous allons modéliser non pas la probabilité de décès (qx), que nous examinerons plus loin, mais la mortalité (dx). Cette modélisation s'impose à nous comme

74

Chapitre III : Elaboration et étude du cas Trust Algérie

une approche préliminaire dans la modélisation des (qx). Même si nous utilisons toujours les (qx) dans le calcul des primes, cela va nous permettre, néanmoins, de constater les âges où se situent les écarts les plus importants entre les observations et le modèle de Makeham. Il y a de noter que d_x = lx+i -- l_x. Pour ce faire nous allons utiliser tout simplement les

-B
·cX

estimations des (lx), à savoir lx = k · e--A ·x · e
	in c ; ce qui nous donne

-B
·c(x+i) -B
·cX

d_x = k
· e-A
·(x+1)
· e inc -- (k
· e--A
·x
· e hE c )

Nous écrirons la formule pour l'estimation des paramètres, toujours dans XLstat :

Y = 100000 * Exp(--pr1 * X1-- (pr2 * (pr3^X1)/Ln(pr3) )) -- 100000

* Exp(--pr1 * (X1+1) -- (pr2 * ((pr3^(X1 + 1))/Ln(pr3) )))

Figure 8 Régression non linéaire des dx (modèle Makeham)

Remarque : contrairement au point de départ utilisé dans l'estimation des qx par le Modèle de Makeham ou l6=92784, nous utiliserons, comme point de départ l0 ou k =100.000 ; car dans le cas contraire cela aura pour conséquence de décaler le modèle par rapport aux observations.

Toujours dans le but d'avoir un modèle robuste (sans biais), nous ne prendrons pas en considération les âges inférieurs à 6 ans qui représentent la mortalité infantile.

Chapitre III : Elaboration et étude du cas Trust Algérie

3.1 Coefficients d'ajustement

Observations			100
DDL			97
R^2			0,987
SCE	1	639	962,53
MCE		16	906,83
RMCE			130,03

nombre d'observations

le nombre de degrés de liberté

le coefficient de détermination

la somme des carrés des résidus du modèle

la moyenne des carrés des résidus du modèle

la racine de la moyenne des carrés des résidus du modèle

75

Table 4 Coefficients d'ajustement de la Régression non linéaire des dx (modèle Makeham)

Figure 9 dx Observés/Estimés par la Régression non linéaire modèle (Makeham) et Histogramme des résidus

3.2 Paramètres du modèle

Paramètre	Valeur	Ecart-type
pr1	2,36E-04	0,002
pr2	1,50E-04	0,000
pr3	1,080	0,000

Table 5 Paramètres dx du modèle Makeham

d₊ 100000 * ExF ·"2,36E " 04 * x " 11,50E " 04 * 1,08x

#172;...~1,08~¼½ - 100000

* ExF Á"2,36E " 04 * x ( 1 " ·1,50E " 04 * ¾ 1,08+7

Ln(1,08)½Â

4 Modélisation des (qx) probabilités de décès par le modèle de Gompertz Makeham

La modélisation des probabilités de décès annuels, par le modèle de Gompertz Makeham reste l'une des méthodes les plus simples d'utilisation, de ce fait l'une des plus utilisées en assurance de personnes, même si d'autres modélisations ont vu le jour depuis cette dernière, à l'instar du modèle de Heligman-Pollard et Kannisto, que nous avons appliqué à la table TVTD 97-99 Algérienne voir (Annexe 14) et (Annexe 15) page 127 et 128 respectivement.

Chapitre III : Elaboration et étude du cas Trust Algérie

Observations	104,000
DDL	101,000
R^2	0,998
SCE	0,006
MCE	0,000
RMCE	0,008

Observations

la somme des carrés des résidus du modèle

la moyenne des carrés des résidus du modèle

la racine de la moyenne des carrés des résidus du modèle

le nombre de degrés de liberté le coefficient de détermination

76

Table 6 Coefficients d'ajustement de la Régression non linéaire des qx (modèle Makeham)

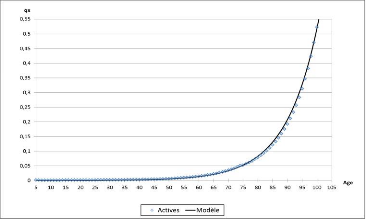
Figure 10 Régression non linéaire des qx (modèle Makeham)

u₊ = a + b c^X La fonction représente le taux instantané de mortalité (voir page 17)

Paramètre	Valeur	Ecart-type
a	3,38E-05	4,17E-03
b	5,41E-05	0,00
c	1,10	0,00

Table 7 Paramètres qx du modèle Makeham

u₊ = 3,38 10^36» + 5,41 10^36» x 1,10⁺

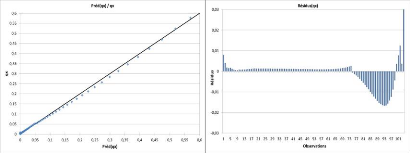
Figure 11 qx Observés/Estimés par la Régression non linéaire modèle (Makeham) et Histogramme des résidus

77

Chapitre III : Elaboration et étude du cas Trust Algérie

La mortalité est un phénomène continu dans le temps. Il nous sera donc possible de passer d'une écriture d'une variable discrète qui est le taux annuel de mortalité (q_x) à une variable continue (u_x) qui est le taux instantané de mortalité, ou inversement (voir page 14).

9

;+~< = " 9 ln _<F₊, ou alors F₊ = 1 " *+ = 1 " UxF(">;₊+< _<).

(qx) TD 97-99 Ajusté par le Modèle de Gompertz Makeham
Moyenne	0,08228
Écart-type	0,16037
Variance de l'échantillon	0,02572
Minimum	0,00009
Maximum	0,74950
Médiane	0,00671
Nombre d'échantillons	104
Niveau de confiance(95%)	0,03119

Table 8 Statistique descriptive des (q_x) table TD 97-99 Ajustés par le Modèle le Gompertz Makeham

78

Chapitre III : Elaboration et étude du cas Trust Algérie

Section 3 Etude du portefeuille de contrats de la Trust assurance de personnes

1 Analyse du portefeuille de contrats du point de vue quantitatif

Nous allons comparer les différentes polices d'assurances afin de voir la composition du portefeuille de contrats de la Trust assurance. Dans ce cadre nous posons l'hypothèse de deux aspects, l'un quantitatif, en comparant la production par le montant des primes pour les différentes polices d'assurances, et l'autre qualitatif en comparant le nombre de contrats qui sont gérés par la compagnie d'assurance, étant entendu que les termes quantitatif pour les montants et qualitatif pour le nombre de contrats, ne sont pas des indicateurs suffisants. Néanmoins, ils nous permettent d'avoir une idée de la composition ainsi de la structure du portefeuille de contrats.

Nous avons, dans un premier temps, établi un tableau représentatif de la production de la Trust assurance de personnes, après avoir consolidé les données relatives aux différentes années (voir Annexe 12 Production de la Trust Assurance de personnes par police d'assurance de 2007 à 2010 page 124). Le tableau qui suit est tiré de ce dernier, et

représente les primes nettes.

Primes nettes = (primes des nouvelles affaires + primes des contrats renouveles + les avenant au contrat "augmentation ou diminution du capital assure"- annulations).

Police d'assurance		2007			2008			2009			2010		Moyenne			En %
Assurance voyage Assistance	35	174	320	43	873	263	45	653	056	52	745	183	44	361	455	40,17%
Groupe	14	559	627	21	979	235	25	186	857	41	811	612	25	884	333	23,44%
Individuel accident (Trust 1)	13	183	155	11	326	997	8	204	401	9	091	227	10	451	445	9,46%
Individuel accident (Trust 2)	2	384	511		19	880		22	008		209	648		659	012	0,60%
Individuel accident (Trust 3)			-		19	345			-		1	935		5	320	0,00%
Individuel accident Collectif			-	3	736	923	5	019	445	5	546	706	3	575	769	3,24%
Plan de protection Caractérisé		88	173		79	357		102	564		8	126		69	555	0,06%
Plan de protection Constant		167	222		380	105		118	208		342	112		251	912	0,23%
Plan de protection Epargne		872	014		466	123		280	909		397	786		504	208	0,46%
Plan de protection Familiale		163	277		615	994		337	763		299	028		354	016	0,32%
Plan de protection Prospérité	1	749	043		346	298		840	661		529	899		866	475	0,78%
Temporaire Décès (Crédit)	17	644	766	24	086	269	15	865	200	36	260	275	23	464	128	21,24%
Total général	85	986	108	106	929	789	101	631	072	147	243	537	110	447	626	100%

Table 9 Moyenne du montant des primes nettes par police d'assurance, période de 2007 à 2010 (Unité DA)

Après une rapide lecture du tableau de la production par police d'assurance pour la période 2007 à 2010, nous remarquons que :

> l'assurance voyage représente de 40,17%, soit une moyenne de production de 44.361.455DA

> l'assurance groupe représente 23,44% de la production soit une moyenne de 25.884.333DA

> l'assurance temporaire décès représente 21,24% soit une moyenne de 23.464.128DA

79

Chapitre III : Elaboration et étude du cas Trust Algérie

> l'assurance individuelle accident (Trust 1) représente 9,46% de la production soit 10.451.445DA

Nous pouvons ainsi en déduire que l'assurance voyage, l'assurance groupe, l'assurance temporaire décès et l'individuel accident (Trust 1) représentent plus de 94% soit (104.161.360DA) d'une production globale de 110.447.626DA, qui a été estimée sur la moyenne de la période allant de 2007 à 2010.

Cette première estimation nous renseigne sur la composition du portefeuille de contrats de la Trust assurance, qui est un portefeuille hétérogène, dont le principal facteur de production reste l'assurance voyage.

Nous pouvons expliquer cela par le fait que l'assurance voyage, dans le domaine de l'assurance de personnes, reste une obligation, contrairement aux autres polices d'assurances qui restent un choix de l'assuré.

La quantité de production représente un aspect du portefeuille de contrats. Cette information ne suffit pas à nous renseigner sur la composition du portefeuille de contrats gérés par la compagnie d'assurance, comme nous l'avons indiqué dans notre hypothèse. Certes, nous avons là une information, ou plutôt une indication sur le portefeuille, mais celle-ci demeure, néanmoins, insuffisante. Aussi il est nécessaire de la compléter par une analyse d'un point de vue qualitatif.

2 Analyse du portefeuille de contrat d'un point de vue qualitatif

Nous allons comparer la production en nombre de contrats gérés par l'entreprise. En effet, si les primes représentent les montants annuels encaissés par la compagnie d'assurance, le nombre représente les contrats qui sont à l'origine de ces primes.

Police d'assurance	2007	2008	2009	2010	Moyenne		En %	Assurance voyage Assistance
13 942	17 691	18 747	19 447	17 457	60,24%		Groupe
36	53	35	52	44	0,15%		Individuel accident (Trust 1)
10 708	7 758	7 440	8 021	8 482	29,27%		Individuel accident (Trust 2)
1 111	1	2	12	282	0,97%		Individuel accident (Trust 3)
-	11	-	6	4	0,01%		Individuel accident Collectif
-	639	418	386	361	1,24%		Plan de protection Caractérisé
12	16	3	2	8	0,03%		Plan de protection Constant
8	27	9	10	14	0,05%		Plan de protection Epargne
52	176	40	44	78	0,27%		Plan de protection Familiale
26	106	40	39	53	0,18%		Plan de protection Prospérité
87	109	30	22	62	0,21%		Temporaire Décès (Crédit)
2 216	3 641	2 486	196	2 135	7,37%		Total général
28 198	30 228	29 250	28 237	28 978	100%

Table 10 Moyenne du nombre de contrats par police d'assurance, période de 2007 à 2010

Du point de vue du nombre de contrats, l'assurance voyage représente 60,24% des contrats souscrits en moyenne soit 17.457 contrats pour la période 2007- 2010, engendrant 40,17% de la production en termes de primes, confortant ainsi notre première estimation du

80

Chapitre III : Elaboration et étude du cas Trust Algérie

portefeuille contrats, basée sur le montant des primes. Par ailleurs il y a lieu de noter que l'assurance groupe qui ne représente que 0,15% du total du nombre de contrats, engendre plus de 23% de la production en termes de montant.

Ainsi, nous pouvons dire qu'un portefeuille de contrats ne se mesure pas exclusivement par le montant des primes. En effet, il est impératif d'introduire une dimension qui représente le nombre de contrats, car se fier uniquement au montant des primes, engendrerait une erreur inéluctable d'estimation, d'où l'analyse du nombre de contrats qui, rappelons-le, sont à l'origine des primes. Ainsi nous pouvons dire que l'estimation d'un portefeuille de contrats n'est pas une discipline unidimensionnelle.

3 Evolution du portefeuille de contrats

Nous pouvons approfondir d'avantage cette analyse du portefeuille de contrats en introduisant une autre dimension. A cet effet, nous allons observer l'évolution des polices d'assurances, qui sont prépondérantes dans ce portefeuille de contrats, tant au point de vue quantitatif (montants des primes), que qualitatif (nombres de contrats).

Police d'assurance	Variation 07/08	Variation 08/09	Variation 09/10		Tendance	Assurance voyage Assistance
+24,73%	+4,06%	+15,53%			Groupe
+50,96%	+14,59%	+66,01%			Individuel accident (Trust 1)
-14,08%	-27,57%	+10,81%			Temporaire Décès (Crédit) Globle
+36,51% +24,36%	-34,13% -4,96%	+128,55% +44,88%

Table 11 Evolution du montant des primes entre 2007 et 2010

Nous pouvons constater que le montant des primes de l'assurance voyage a connu une augmentation de 24,73% entre 2007 et 2008, par rapport à une variation globale de 24,36% (toutes polices d'assurance confondues). L'augmentation la plus importante reste celle de l'assurance groupe estimée à 50,96%.

Pour l'exercice 2008-2009, on remarque une diminution du montant des primes (-4,96%), due vraisemblablement, à une diminution du montant des primes de l'assurance temporaire décès (-34,13%), ainsi que l'individuel accident (Trust 1) (-27,57%).

L'exercice 2009-2010 reste, à l'évidence, une année où la production connait un essor considérable, avec une augmentation de près de 44,88% pour l'ensemble des polices d'assurance de la Trust assurance de personnes, avec au premier plan l'assurance temporaire décès (+128,55%), et l'assurance groupe (+66,01%).

Police d'assurance	Variation 07/08	Variation 08/09	Variation 09/10		Tendance	Assurance voyage Assistance
+26,89%	+5,97%	+3,73%			Groupe
+47,22%	-33,96%	+48,57%			Individuel accident (Trust 1)
-27,55%	-4,10%	+7,81%			Temporaire Décès (Crédit)
+64,31%	-31,72%	-92,12%			Globale
+7,20%	-3,24%	-3,46%

81

Chapitre III : Elaboration et étude du cas Trust Algérie

Table 12 Evolution du nombre de contrats entre 2007 et 2010

Le tableau ci-dessus, représente l'évolution du nombre de contrats, avec une augmentation, pour l'année 2008 de près de 7,2% ; cette augmentation est due en premier lieu, à l'assurance temporaire décès (+64,31%) et à l'assurance groupe (+47,22%), ainsi qu'une diminution du nombre de contrats individuel accident (Trust1) de (-27,55%) ; ceci explique sa diminution en termes de montants.

Pour l'exercice 2009, on observe une diminution globale (-3,24%), du fait de la diminution du nombre de contrats pour l'assurance temporaire décès (-31,72%), et l'assurance groupe (-33,96%).

L'exercice 2010 marque des changements d'ordre stratégique, car nous pouvons constater une augmentation du montant des primes (+44,88%) inversement non-proportionnelle à la diminution du nombre de contrats (-3,46%).

L'assurance temporaire décès enregistre une diminution importante en termes de nombre de contrats de (-92,12%) qui passe de 2486 contrats en 2009 à 196 contrats, en 2010 (voir Table 12 page 81). Paradoxalement, nous constatons l'augmentation du montant des primes en 2010 (+128,55%) soit un montant de 36.260.275DA (voir Table 9 page 78).

Nous pouvons ainsi conclure que l'augmentation du nombre de contrats ne se traduit pas nécessairement par l'augmentation du montant des primes généré. A l'inverse, une augmentation du montant des primes ne signifie pas une augmentation du nombre de contrats. Pour pallier cela, nous devons prendre en considération le montant des primes générées pour chaque contrat en calculant, à titre indicatif, le montant moyen généré par type de contrat.

Police d'assurance	2007		2008		2009		2010			Assurance voyage Assistance
2	523	2	480	2	435	2	712		Groupe
404	434	414	703	719	624	804	069		Individuel accident (Trust 1)
1	231	1	460	1	103	1	133		Temporaire Décès (Crédit)
7	962	6	615	6	382	185	001		Globale
3	049	3	537	3	475	5	215

Table 13 Moyenne de la prime par police d'assurance de 2007 à 2010

L'examen du tableau ci-dessus, indique, sans aucune surprise, que les contrats qui génèrent la prime la plus importante sont les contrats assurance groupe. En moyenne, chaque contrat groupe génère une prime de 404.434 DA en 2007 et qui double en quatre(4) ans pour passer à 804.096 DA en 2010. Nous pouvons ainsi constater que la Trust assurance adopte une stratégie adéquate concernant l'assurance groupe.

L'assurance temporaire décès avec une prime de 7.962DA et l'assurance voyage avec une prime de 2.523DA pour 2007 représentent, au côté de l'assurance groupe la tête de file du portefeuille de contrats de la Trust assurance de personnes, comme nous avons eu l'occasion de le constater au préalable, car elles s'imposent par le nombre (voir Table 10).

82

Chapitre III : Elaboration et étude du cas Trust Algérie

Cela va nous inciter à examiner l'évolution de la moyenne de ces primes, comprendre les paramètres qui influencent cette dernière.

Table 14 Evolution de la prime moyenne par police d'assurance par rapport à 2007

La moyenne par police d'assurance ainsi que l'évolution de cette dernière représente un bon indicateur. La variation non pas année par année mais par rapport à l'année de référence (2007), nous permet de constater une augmentation considérable de la prime moyenne de l'assurance temporaire décès (+2223,43%) par rapport à 2007 ?

Cela est dû à la conjugaison de deux effets, une augmentation du montant des primes (+128,55%) voir (Table 11), et une diminution du nombre de contrats (-92,12%) voir (Table 12).

Cette augmentation est due en grande partie à l'accord conclu avec la Société Générale car ce dernier même si il a toutes les qualités d'un contrat groupe ne l'est pas, ce type de contrat est dénommé contrat groupe ouvert à l'adhésion, et d'autre part l'augmentation est justifiée par une convention ( les contrats temporaires décès bénéficies des mêmes avantages liés à un contrat groupe avec un taux similaire).

Par ailleurs, on constate une augmentation de la prime moyenne pour l'assurance groupe (+98,81%) par rapport à 2007 et de l'assurance voyage (+7,51%). Globalement, la prime d'assurance connait une augmentation en 2010 par rapport à 2007 de +71% toutes branches confondues.

3.1 Taux d'annulation

Juridiquement les deux parties peuvent rompre le contrat d'assurance dans le cas où l'un ou l'autre ne respecte pas les obligations liées à ce dernier (Code des Assurances Art. 109).

Le taux d'annulation reste très important dans la détermination de la population de l'assureur et en conséquence de son portefeuille de contrat (voir

Chapitre III : Elaboration et étude du cas Trust Algérie

Structure de la population de l'assureur, page 21). Il reste indispensable dans l'élaboration de la population de l'assureur et la conception d'une loi de chute, aussi dénommé "S(x), taux de départ". (Petauton 1996)

Police d'assurance Assurance voyage Assistance	2007 12,96%	2008 15,62%	2009 16,96%	2010 11,09%		Moyenne 14,16%	Groupe
-	6,511%	4,175%	0,840%	3,84%		Individuel accident (Trust 1)
0,029%	0,085%	0,052%	0,059%	0,06%		Temporaire Décès (Crédit)
0,207%	0,408%	0,311%	1,053%	0,49%		Global
6,56%	9,15%	11,09%	6,75%	8,39%

Table 15 Taux d'annulation par police d'assurance pour la période 2007 à 2010

nouvelles affaires

Le taux d'annulation = annulation

x 100, voir (Annexe 12 page 124).

83

Nous pouvons ainsi constater que la baisse de la production pour l'exercice 2009 est due à une augmentation du taux d'annulation global (11,09%) du fait, en grande partie de l'augmentation du taux d'annulation de l'assurance voyage (16,96%).

4 Provisions mathématiques

Dans le but de calculer les provisions mathématiques, nous allons utiliser un modèle dit statique, qui ne traite que les contrats en cours à partir d'une situation, et une date initiale. Ce modèle simule un vieillissement des contrats en stock ; mais à la différence du modèle dynamique, il ne tient pas compte des nouveaux contrats.

Aussi, et afin d'avoir une projection du développement de ces contrats, nous utiliserons la base de données dont nous disposons et qui contient un descriptif de 294 contrats, dont 45 contrats d'assurance temporaire décès à capital fixe, représentent par les différents plans de protections, ces types de contrats ne peuvent faire l'objet de rachat ART. 90 (MODIFIE PAR L'ART. 21 L 06-04). Nous extrairons de cette base et pour chaque assuré, les informations nécessaires à l'élaboration des provisions mathématiques pour les contrats d'assurance temporaire décès, à savoir l'âge de l'assuré, la durée du contrat d'assurance.

Nous posons l'hypothèse de travail que l'application d'un modèle statique, (voir page 44) et que le calcul de ces provisions mathématiques que nous allons élaborer sur cette base de données et qui représente pour nous l'échantillon, est loin de refléter la réalité qui nécessiterait d'avoir une base de données de tous les contrats en cours et actualisés au moment de l'estimation et que le calcul doit être effectué contrat par contrat.

Cependant, cela ne vas pas nous empêcher d'exploiter cette base de données dans le but de calculer les provisions mathématiques (PM). A cet effet, nous utiliserons ce qui pourrait donner, éventuellement, matière à une controverse, à savoir la moyenne du portefeuille, à laquelle nous appliquerons pour le calcul des (PM) la méthode rétrospective,

84

Chapitre III : Elaboration et étude du cas Trust Algérie

xV k = ( _Ep ₂* _E' ₂ )- _EOE 2

_EE 2

A l'évidence, cette méthode n'a pas la prétention de calculer des provisions mathématiques (PM) à des fins de comptables, mais seulement de pouvoir constater l'évolution de ces dernières dans le temps.

Il y a lieu de rappeler que dans la pratique, les modèles utilisés pour calculer les provisions mathématiques, sont issus de modèles actuariels existants et qui bénéficient d'un développement effectués par les actuaires, en la matière.

	Moyenne de l'Age		Moyenne de la duree Moyenne du Capital Deces		Mixte
45,81	15,55		529 318,84	Plan de protection Epargne
48,23	16,19		551 063,83	Plan de protection Prospérité
40,64	14,18		482 863,64	Temporaire Décès
40,92	11,04		4 528 040,35	Plan de protection Caractérisé
43,67	5,00		550 000,00	Plan de protection Constant
37,44	6,89		4 111 111,11	Plan de protection Familiale
37,91	14,39		386 363,64	Temporaire Décès (Crédit)
41,61	10,73		5 374 494,88	Total général
42,07	12,10		3 589 564,89

Table 16 Moyenne de l'âge de la durée et du capital décès des assurés de l'échantillon étudié pour l'année 2010

Le tableau ci-dessus, met en évidence, un certain nombre d'informations indispensables à notre étude. Ainsi nous pouvons dire que pour la branche de l'assurance temporaire décès (capital fixe) , l'âge moyen de l'assuré est de 38,2ans, et qu'il assure une somme moyenne de 1.142.222,22DA pour une durée moyenne de 12,27ans. Aussi nous utiliserons pour le calcul des (PM) la table de mortalité Algérienne TD 97-99, pour (i=3,5).

Ce qui nous donne la distribution suivante des (PM) pour chaque année

k	nAx	nax	nEx	nPx	xVk		PM	0
0,0000	0,0000	1,0000	0,0040	0,0000	0,00		1
0,0029	1,0000	0,9634	0,0040	0,0011	1 292,87		2
0,0058	1,9634	0,9279	0,0040	0,0021	2 452,68		3
0,0087	2,8913	0,8936	0,0040	0,0030	3 459,75		4
0,0118	3,7849	0,8604	0,0040	0,0037	4 280,06		5
0,0149	4,6454	0,8283	0,0040	0,0043	4 891,05		6
0,0180	5,4737	0,7972	0,0040	0,0046	5 255,44		7
0,0212	6,2709	0,7671	0,0040	0,0047	5 347,22		8
0,0246	7,0379	0,7378	0,0040	0,0045	5 111,62		9
0,0280	7,7758	0,7095	0,0040	0,0040	4 517,63		10
0,0315	8,4853	0,6821	0,0040	0,0031	3 504,67		11
0,0352	9,1674	0,6554	0,0040	0,0018	2 021,70		12
0,0389	9,8228	0,6296	0,0040	0,0000	0,00

Table 17 Provision mathématique d'une assurance temporaire décès, prime et durée moyenne estimée

85

Chapitre III : Elaboration et étude du cas Trust Algérie

> _xVk = (nPP* nax )- nAx, (PM) "méthode rétrospective" nEx

> A+:?····· = ú23ú24E

X2 (Prime pure d'une assurance décès temporaire de n années)

> a^Êx:n = u23u24E X2

(Annuité viagère temporaire de n années payable à terme anticipé).

> _?E₊ ~ X24E

X (Capital différé de n années)

> 7k+ ~ OE2:~~ ······ '^Ê2:12 ······

(Prime annuelle)

> Dans notre cas l'âge de l'assuré (x)=38,2 au moment de la souscription, ... = [ /k E {1,2, ...,12}

> (Voir aussi Annexe 16 Fonctions Commutations page 129).

Figure 12 Courbe de répartition des Provisions Mathématiques assurance temporaire décès

Le graphe ci-dessus nous donne déjà une première vision de ce qu'est, ou plutôt de ce que sera la distribution des provisions mathématique pour un contrat temporaire décès. Rappelons que nous avons utilisé pour cela la moyenne pour estimer les différents paramètres nécessaires au calcul des (PM), et que nous estimons dans ce cas, être le plus représentatif de ce type de police.

Aussi, nous poserons un interval de confiance pour (á=0,05), car rappelons-le, les observations sont réalisées sur un échantillon de contrats temporaire décès.

A des fins pratiques, et en utilisant un raisonnement empirique, nous pourrions user de ce type de raisonnement pour calculer les (PM). Cependant, cela suppose qu'il n'y a pas de distorsion entre les contrats de même type, ce qui n'est jamais le cas. Cela dit, nous posons ici, un niveau de confiance supportable pour un échantillon de cette ampleur.

Chapitre III : Elaboration et étude du cas Trust Algérie

Le tableau ci-dessous représente l'interval de confiance supérieur et inferieur pour notre estimateur de la (PM)

Moyenne	3	241,13
Ecart.type			1	849,21
I.C 95%			1	005,22
k		PM			IC Inf				IC Sup
0		0,00			-1			005,22	1	005,22
1	1	292,87						287,65	2	298,10
2	2	452,68			1			447,46	3	457,90
3	3	459,75			2			454,53	4	464,98
4	4	280,06			3			274,84	5	285,28
5	4	891,05			3			885,83	5	896,27
6	5	255,44			4			250,22	6	260,66
7	5	347,22			4			342,00	6	352,44
8	5	111,62			4			106,40	6	116,84
9	4	517,63			3			512,41	5	522,85
10	3	504,67			2			499,45	4	509,89
11	2	021,70			1			016,48	3	026,93
12		0,00			-1			005,22	1	005,22

Table 18 Provisions mathématique assurance temporaire décès IC 95%

86

Figure 13 Provisions mathématique assurance temporaire décès IC95%

87

Chapitre III : Elaboration et étude du cas Trust Algérie

5 Assurance voyage

Comme nous avons eu l'occasion de le remarquer (voir page 78), l'assurance voyage représente une part importante de la production ; ce qui va susciter note intérêt dans un premier temps. D'un autre coté l'assurance voyage est une particularité de l'assurance de personnes, car elle couvre l'assuré mais aussi ses biens, les retards et les annulations, qui n'ont rien à voir avec l'âge de l'assuré. Aussi nous pouvons constater que la prime d'assurance est le fruit d'un facteur lié à l'âge (ce qui est le propre de l'assurance de personnes), mais aussi d'autres facteurs qui ne sont pas liés à l'âge.

Cela nous amène à nous intéresser aux modalités de la tarification liée à cette police d'assurance qui, vraisemblablement, varie selon deux critères à savoir l'âge de l'assuré et la durée du séjour. Nous déterminerons aussi le facteur le plus influent sur la prime de l'assurance voyage.

Pour ce faire, nous allons reporter les données du tableau de contingence sur un nouveau tableau représentant les primes en fonction des deux facteurs, à savoir la durée et l'âge dans le but de déterminer la matrice de corrélation.

Table 19 Matrice de corrélation variable dépendante (la prime), variables explicatives (âge et nombre de jours)

Comme nous le montre la matrice de corrélation, nous pouvons remarquer que le montant de la prime est expliqué par la durée du séjour et l'âge de l'assuré :

> la durée du séjour explique 75,31% du montant de la prime > l'âge de l'assuré explique 24,68% du montant de la prime

Là réside la spécificité de cette police d'assurance qui fait partie de l'assurance de personnes, même si en réalité 75,31% du montant de cette dernière peut être assimilé à de l'assurance non-vie, car l'évènement aléatoire n'est pas lié à l'âge de l'assuré. A titre d'exemple, il n'y a aucun lien entre la perte de bagage ou la prolongation du séjour et l'âge de l'assuré. Cependant les indemnités liées à cette police d'assurance sont forfaitaires ; ce qui est le propre de l'assurance de personnes. Cela implique que l'assurance voyage est un produit hybride ; c'est pour cette raison que nous allons la décomposer et étudier chaque facteur à part. Nous allons examiner, respectivement, l'évolution de la prime d'assurance par rapport à l'âge et à la durée du séjour.

88

Chapitre III : Elaboration et étude du cas Trust Algérie

5.1 Variation de la prime par rapport à l'âge

Figure 14 Régression non linéaire de la prime par rapport à l'âge de l'assuré

Table 20 Coefficients d'ajustement de la régression non linéaire (prime par âge de l'assuré)

Nous pouvons constater que la moyenne de la prime est de 2790,47 Da, et qu'elle évolue de façon exponentielle ; ce qui est caractéristique d'une police d'assurance liée à l'âge de l'assuré.

Figure 15 Prime observée par rapport à la prime estimer par le modèle non linéaire et histogramme des résidus

89

Chapitre III : Elaboration et étude du cas Trust Algérie

Table 21 Statistiques descriptives de l'âge et de la prime

Table 22 Paramètres du modèle de la régression non linéaire

Prime = 1941,763 + 1,467 * Exp(0,101 * Age)

Figure 16 Régression linéaire de la prime par rapport à la durée du séjour

Table 23 Coefficients d'ajustement de la régression linéaire de la prime par la durée du séjour

5.2 Variation de la prime par rapport à la durée de séjour

Figure 17 Prime observée par rapport à la prime estimer par le modèle linéaire et histogramme des résidus

Prime = 1688,75 + 61,52 * Nbr Jours

Table 24 Statistiques descriptives de la durée du séjour et de la prime

Table 25 Paramètres du modèle de la régression linéaire

90

Chapitre III : Elaboration et étude du cas Trust Algérie

91

Chapitre III : Elaboration et étude du cas Trust Algérie

6 Comparaison de deux assurances groupes

Pour bien appréhender le risque lié à l'assurance groupe, nous allons comparer deux assurances groupe (voir page11). Ces échantillons vont nous permettre, dans un premier temps, de voir la composition du portefeuille des assurés, et à travers ceci de voir les étapes nécessaire à l'estimation du risque d'un portefeuille de contrats. Pour ce faire nous comparons le portefeuille de contrat de Wataniya Telecom Algérie composé de 1855 assurés, et celui de Société Générale composé de 9099 assurés.

La première étape consiste à calculer l'âge de chaque assuré pour l'année 2011 et de calculer dans une deuxième étape, les fréquences pour chaque âge.

6.1 Etude de l'assurance groupe de la Société Générale

D'après l'histogramme de distribution des effectifs, nous pouvons poser l'hypothèse que la distribution de l'effectif suit une loi normale. A cet effet, nous utilisons dans XLstat dans modélisation des données, l'ajustement d'une loi de probabilité.

a) Paramètres estimés des assurés de la Société Générale

Table 26 Paramètres estimés de la distribution des assurés de la Société Générale

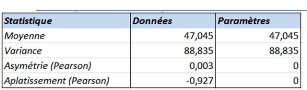
a.1 Statistiques estimées des paramètres de la loi Normale

Table 27 Statistiques estimées à partir des données Société Générale et calculées à partir des estimateurs des paramètres de la loi Normale

Le test non paramétrique de Kolmogorov-Smirnov (K-S), consiste à mesurer l'écart maximum qui existe entre la fonction de densité cumulée observée (ou tout simplement les fréquences cumulées), et la fonction de répartition théorique qui nécessite l'utilisation de la table de Kolmogorov. Sous l'hypothèse nulle (H0), cet écart est faible et la répartition des observations s'intègre dans une distribution théorique.

Dans notre cas, les observations représentent l'âge des assurés de la Société Générale, comparé à la répartition théorique de la loi normale pour (á=0,05). Nous avons préalablement estimé les paramètres nécessaires au test (K-S), à savoir la moyenne (47,04), et l'écart-type (9,42). (Il y a lieu de signaler que le test de (K-S) a été effectué avec SPSS? test non paramétrique).

Chapitre III : Elaboration et étude du cas Trust Algérie

a.2 Test de Kolmogorov-Smirnov

Table 28 Test de Kolmogorov-Smirnov de sur la distribution de la Société Générale pour une loi Normale

a.3 Interprétation du test de K-S

> Hypothèse nulle _(H0), l'échantillon suit une loi Normale

> Hypothèse alternative (H1), l'échantillon ne suit pas une loi Normale

Etant donné que la valeur de signification asymptotique bilatérale est inférieure au niveau de signification (á=0,05), on doit retenir l'hypothèse nulle (H0) et rejeter l'hypothèse alternative (H1).

Nous pouvons donc conclure que la distribution testée suit une loi gaussienne de paramètre (47,04 ; 9,42) pour (á=0,05)

L'âge moyen arithmétique du groupe dénommé âge moyen actuariel du groupe, sera d'une grande utilité, pour établir une tarification adéquate.

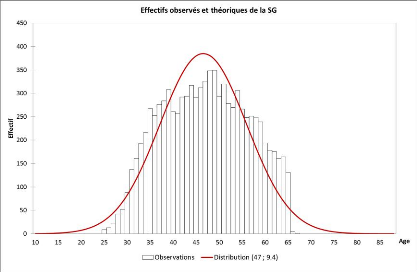
92

Figure 18 Effectif observés et théorique des assurés de la Société Général

93

Chapitre III : Elaboration et étude du cas Trust Algérie

Figure 19 Histogramme de densité et fonction de répartition des fréquences cumulés des assurés de la Société Générale

6.2 Etude de l'assurance groupe de Wataniya Telecom Algérie

De même, nous estimons préalablement les paramètres de la distribution nécessaires au test (K-S), à savoir la moyenne et l'écart-type et nous utiliserons SPSS? test non paramétrique? test de (K-S). Les observations représentent l'âge des assurés de la Wataniya Télécom Algérie, comparé à la répartition théorique d'une loi normale (á=0,05).

Table 29 Paramètres estimés de la distribution des assurés de Wataniya Télécom Algérie

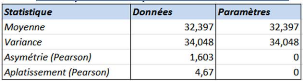
a.1 Statistiques estimées paramètres de la loi Normale

Table 30 Statistiques estimées à partir des données Wataniya Télécom Algérie et calculées à partir des estimateurs des paramètres de la loi Normale

94

Chapitre III : Elaboration et étude du cas Trust Algérie

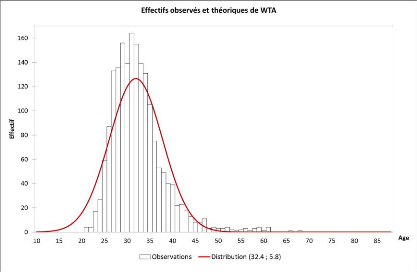
Figure 20 Effectif observés et théorique des assurés de Wataniya Telecom Algérie

Figure 21 Histogramme de densité et fonction de répartition des fréquences cumulés des assurés de la Wataniya Telecom Algérie

a.2 Test de Kolmogorov-Smirnov

Table 31 Test de Kolmogorov-Smirnov de sur la distribution de Wataniya Telecom Algérie pour une loi Normale

95

Chapitre III : Elaboration et étude du cas Trust Algérie

a.3 Interprétation du test de K-S

> Hypothèse nulle _(H0), l'échantillon suit une loi Normale

> Hypothèse alternative (H1), l'échantillon ne suit pas une loi Normale

Etant donné que la valeur de signification asymptotique bilatérale est inférieure au niveau de signification (á=0,05), on doit retenir l'hypothèse nulle (H0) et rejeter l'hypothèse alternative (H1).

Nous pouvons donc conclure que la distribution testée suit une loi gaussienne de paramètre (32,39 ; 5,83)

6.3 Mesurer et comparer le risque

L'estimation ci-dessus nous renseigne sur les distributions des âges pour chaque assurance groupe, mais ne permet toujours pas de mesurer le risque affecté. En effet, même si nous connaissons cette distribution, nous devons y affecter une probabilité de décès (d_x), lui correspondant.

Pour cela, nous utiliserons le modèle Makeham étudié précédemment (voir Figure 8 Régression non linéaire des dx (modèle Makeham) page 74), afin d'établir une fonction de risque pour chaque portefeuille de contrat, qui représente le produit de la distribution des assurés par âge, par la probabilité de décès (d_x).

Pour mesurer le risque du contrat groupe Société Générale, nous utiliserons les âges représentés par une loi gaussienne de paramètres N-'(47,04 ; 9,42) pondéré par leurs probabilités. Il en est de même pour Wataniya Telecom Algérie représenté par la loi gaussienne de paramètre N-'(32,39 ; 5,83).

	Wta	SG
i de x	32,40	47,05
o de x	5,84	9,43		i de qx
2,60E-05	7,74E-05	o de qx
4,51E-05	9,64E-05
qx^(1)	2,01E-03	5,56E-03

qx ⁽¹⁾ la probabilité de décès correspondant à la moyenne d'âge pour les deux distributions respectivement (2,01^E-03) pour un âge x=32,4 et (5,56^E-03) pour l'âge x=47,05. Nous pouvons constater que l'assurance groupe de la Société Générale représente un risque plus important que celui de Wataniya Telecom Algérie. Cependant on ne peut se contenter de cette estimation du risque, du fait que la distribution n'est pas équiprobable, les probabilités qui y sont affectées suivant une loi de type exponentielle (Gompertz Makeham).

Avant de calculer la moyenne du risque pour chaque contrat assurance groupe, nous devons pondérer les deux distributions avec les probabilités correspondantes. Ce n'est que

96

Chapitre III : Elaboration et étude du cas Trust Algérie

par la suite que nous calculerons la moyenne pour obtenir les résultats suivants u (q_x) de WTA égale 2,60^E-05, celui de SG correspond à 7,74^E-05. Cela conforte la première estimation toute en relevant que le risque pour chaque portefeuille de contrat est inferieur à notre première estimation qui prenait en compte uniquement la probabilité correspondante à la moyenne de la distribution u (qx) de chaque contrat groupe ; cette dernière sera utile pour pouvoir établir une prime correspondante.

Aussi, après avoir étudié et comparé les moyennes de chaque distribution, nous devons nous tourner vers l'étude de la variance, tout en sachant que plus une distribution est étendue, plus le risque d'avoir des évènements qui seront éloignés de l'estimation de la moyenne, augmentera.

En outre, nous avons aussi pu constater que la structure de la population assurée diffère de la population générale.

Cela doit nécessairement être pris en considération par l'assureur lors de l'établissement du contrat et de la prime d'assurance. En effet, cette différence de structure crée inexorablement une différence de paramètre, et une prime groupe qui sera calculée en conséquence. Aussi nous constatons une différence entre la moyenne (qx) de la population assurée et celle de la population générale ajustée par le modèle de Gompertz Makeham (voir Table 8 page 77).

Nous pouvons alors noter que la moyenne q_x (probabilité de décès) pour les différents contrats assurance groupe, à savoir la moyenne pour WTA et la SG respectivement u(q_x) =2.60^E-05 et u(q_x)=7.74^E-05, est nettement inférieure à la moyenne u(q_x)=0,08228 de la population générale.

Ces informations relatives à la composition de la population pour chaque contrat groupe, nous permettent de pouvoir établir une tarification adéquate. Cependant, dans la pratique il arrive que ces informations ne soient pas toujours disponibles. Aussi en l'absence d'informations détaillées, l'actuaire pourra employer l'âge moyen arithmétique du groupe qu'il majorera de 4 à 8 ans en fonction des capitaux garantis, et établir une tarification globale, en se basant sur l'âge moyen actuariel (Bakayoko 2007).

97

Conclusion

Nous avons constaté que même en l'absence de probabilité, il est toujours possible d'estimer le risque. Sans rentrer dans un antagonisme, nous pouvons poser des probabilités qu'elles soient objectives ou subjectives.

La théorie de l'assurance s'inscrit dans le cadre de la théorie des choix en avenir incertain probabilisable et objectif car elle repose sur des données statistiques non seulement fiables mais aussi particulièrement abondantes en assurance vie.

Nous sommes arrivés à la conclusion que les personnes s'assurent pour deux raisons, qui sont la prévoyance et l'épargne ; même si au sens large, ces deux raisons sont analogues, tels des contrats temporaires décès, vie entière, ou les contrats prévoyances tels l'assurance emprunteur qui verse le capital restant dû, du prêt en cas de décès.

Aussi, l'épargne retraite produit des types de rentes viagères pour des contrats individuels ou collectifs, toujours calculés par les tables de mortalité, et garantis a un taux d'intérêt technique. Dans ce cas, l'assureur garantit à l'assuré une performance annuelle minimale de son épargne (Taux Minimum Garanti). Celle-ci augmentée de la participation aux bénéfices. Ce type de contrat est structurellement peu risqué en raison de la garantie de taux et de la faculté de rachat. Ils sont essentiellement investis en obligations, dans le but de se protéger d'une baisse des marchés financiers tout en se constituant une épargne progressive, le but étant toujours de créer un produit innovant qui puisse offrir un rendement supérieur, tout en étant moins risqué.

D'où la nécessité d'avoir des tables de mortalité algérienne qui présentent un taux de mortalité supérieur à celui de la table Tv88-90 de ce fait une sous-évaluation des primes, sans oublier le côté pratique de l'utilisation d'une modélisation paramétrique, tel que le modèle Makeham, et d'estimer les paramètres de cette dernière et d'aboutir à une loi qui modélise la mortalité de la population algérienne ; nous utiliserons éventuellement cette dernière pour le calcul des provisions mathématiques.

Il reste important d'estimer non seulement la population générale mais encore plus important d'estimer la population de l'assuré, car cette dernière diffère sensiblement de la population générale. Il est d'une importance cruciale, d'avoir le plus d'informations sur la population assurée qui nous permet d'évaluer le portefeuille de contrat d'une compagnie d'assurances mais l'appréciation d'un portefeuille de contrats ne s'arrête pas au montant des primes.

Il faut aller au-delà d'une vision unidimensionnelle qui considère le montant des primes pour qualifier un portefeuille de contrats, car si les primes représentent le montant généré par la production, ce sont les contrats qui sont à l'origine de ces dernières. Ce qui ressort de notre étude, c'est que l'assurance voyage reste au premier plan, que ça soit d'un point

98

de vu de montant ou bien d'un point de vue de nombre de contrats cela s'explique par le fait que cette dernière est obligatoire.

Les outils actuariels aident la compagnie d'assurances à fixer le montant des primes d'assurances sur la base d'éléments et de paramètres qui sont incertains. De ce fait une activité qui au départ semble simple, apparentée à celle d'une entreprise vendant des produits (d'assurances), et visant à faire un profit, dans le cadre d'une compagnie d'assurances cela est plus complexe, car le risque est à la base de ce produit ; de ce fait tous les autres éléments, doivent s'y adapter.

Les modèles que nous utilisons, n'ont pas de limite ; seule l'erreur qu'ils génèrent désigne un bon d'un mauvais modèle. Dans ce cadre, nous pouvons dire que le risque est partout et concerne aussi bien les individus que les entreprises. C'est la raison pour laquelle aujourd'hui, il est impensable de gérer une compagnie d'assurances sans recourir, de façon systématique, à des études de modélisation du risque en amont et en aval.

L'anticipation des coûts de gestion liés à la production, ainsi que la maitrise des risques du portefeuille d'assurés reste une condition certaine dans l'activité de l'assureur. Elle ne peut être envisageable sans ces prérequis. Aussi une projection dans la conception de produit d'assurance doit se faire au préalable du lancement d'un nouveau produit d'assurance, et cela tout en considérant les spécificités liées à l'activité de l'assurance. Cette projection des flux futurs (primes), et des risques encourus reste primordiale pour la compagnie d'assurance.

Dans le cadre du lancement d'un nouveau produit, nous recommandons une étude en amont et en aval, c'est-à-dire une projection de tous les éléments étudies dans notre présent mémoire et cela avant tout lancement du produit, avec en premier lieu une étude qui porterait sur le besoin client, la population ciblée, l'étude des garanties, la définition du risque et les réserves, pour pouvoir tarifier le produit d'assurances.

C'est le rôle de l'actuaire produit, qui a pour mission la conception et la tarification du produit. Nous pourrons ainsi dire que pour la compagnie d'assurances l'actuaire est tel un alchimiste concevant des produits d'assurances, qui s'adaptent à une demande d'une clientèle toujours plus exigeante, estimant les risques, ainsi que les réserves de ces produits d'assurance, s'accommodant de contraintes réglementaires toute en étant rentables.

L'assurance de personnes est sujette à un certain nombre de risques sans compter celui, prédominant à son activité. Nous avons vu que ces risques ne sont pas cloisonnés, par chaque direction de la compagnie d'assurances, mais liés entre eux ; ce qui nous oblige à avoir une vision plus globale de la compagnie d'assurances.

Ce qui nous amène à établir les risques non pas comme des éléments indépendants mais comme un ensemble régi par un mécanisme transversal aux différentes directions qui consiste en la gestion du risque, ainsi qu'une stratégie formulée par la direction générale, et

99

adoptée par toutes les structures de la compagnie d'assurance. L'assurance vie réside dans l'optimisation de ce mécanisme, l'économie du risque apparaît essentiellement comme duale. D'un côté, une théorie, abstraite, réductrice, fortement mathématisée. De l'autre, des études éparses sans véritable unité conceptuelle.

Pour autant, ce n'est pas une économie de théoriciens confrontée, à une économie de praticiens, il existe des praticiens du calcul stochastique dans l'assurance, la finance, la recherche opérationnelle. L'assurance de personnes particulièrement les compagnies du secteur privé devront être considérées, comme des laboratoires car elles usent de techniques de méthodes pointues, dont le secteur public peut ou pourrait s'inspirer.

En offrant une perspective historique l'extension, de la désignation du mot "risque", très spécifique à l'âge classique, est désormais universellement prévalente. Nous avons également essayé de montrer les outils du calcul avaient connu une évolution remarquablement voisine, et voient, leur utilisation se répandre dans de nouveaux domaines.

Toutefois, l'approche statistique de la question permet enfin de traiter le risque de manière purement probabiliste. Cependant l'usage du calcul doit être distancié et certainement accompagné par une réflexion sur le statut épistémologique de la probabilité et des théories de la décision.

100

Bibliographie

Annamaria, Olivier, et Ermanno Pitacco. Assurance vie, Évaluer les contrats et les portefeuilles. Village Mondial, 2008.

Bakayoko, Saliou. Fonctionnement technique et actuariel de l'assurance vie. Bamako: Seminaire Conjoint FANAF, 2007.

C.N.E.S, Conseil National Economique et Social. «Evolution des systèmes de protection sociale, perspectives, conditions et modalités permettant d'assurer leur équilibre financier.» Conseil National Economique et Social, 2001.

Cassabalian, Jean-Louis. Mathematiques et Calculs Financiers sur Tableur. Eska, 2000. Cayatte, Jean-Louis. Introduction à l'économie de l'incertitude. De Boeck, 2004.

Code des Assurances. «Ordonnance n° 95-07 du 23 chaabane 1415 correspondant au 25 janvier 1995 relative aux assurances et ses textes d'application.» s.d.

Deelstra, Griselda, et Guillaume Plantin. Théorie du risque et de la réassurance. Economica, 2005.

Delwarde, Antoine. Construction de tables de mortalite periodiques et prospectives. Economica, 2005.

Denuit, Michel, et Arthur Charpentier. Mathematiques de l'assurance non-vie ; principes fondamentaux de theorie du risque. Economica, 2004.

Denuit, Michel, et Christian Robert. Actuariat des assurances de personnes modélisation, tarification et provisionnement. Economica, 2007.

Esch, Louis, Robert Kieffer, et Thierry Lopez. Asset & Risk Management. De Boeck, 2003. Foukroun. «Actuariat IAHEF.» 2008.

Henriet, Dominique, et Jean-Charles Rochet. Microeconomie de l'assurance. Economica, 1999.

Hess, Christian. Méthodes Actuarielles de l'Assurance Vie. Paris: Economica, 2000. KPMG. Guide des Assurances en Algérie. KPMG, 2009.

Langmeier, Robert. Etude de différentes méthodes d'ajustement. Université de Lausanne, 2000.

101

Le Vallois, Franck, Patrice Palsky, et Alain Tosetti. Gestion actif passif de l'assurance-vie Réglementation, outils, méthodes. Economica, 2003.

M.Douakh. «Cours Assurance vie master .» Alger , 2006. 4.

M.T.E.S.S, Ministère du Travail de l'Emploi et de la Sécurité Social. «Présentation du système de sécurité sociale algérien.» 2010.

Octave, Jokung. Microéconomie de l'incertain. Dunod, 2001.

Petauton, Pierre. Théorie et pratique de l'Assurance Vie . Paris: Dunod, 1996.

Planchet, Frédéric. Modèles de durée ; Applications actuarielles. Economica, 2006.

Poincelin, Thierry. Calculs élémentaires de l'assurance-vie. Economica, 2003.

Pradier, Pierre-Charles. La notion de Risque en Economie. La Découverte, 2006.

Thiriez, Hervé. La Modélisation du Risque ; simulations de monte carlo. Economica, 2004.

Tosetti, Alain. Les outils de l'actuariat vie. Economica, 2003.

Tosetti, Alain, Thomas Béhar, et Michel Fromenteauet. Assurance. Comptabilité, Réglementation, Actuariat. Economica, 2002.

Viviani, Jean-Laurent. Gestion De Portefeuille. 2e. Dunod, 2006.

102

Liste des tableaux

Statistique descriptive des Tables TV et TD 97-99 Algériennes Ajusté tranche [20-75 ans [ 71

Coefficients d'ajustement de la Régression non linéaire des Lx (modèle Gompertz Makeham) 73

Paramètres du modèle Gompertz Makeham 73

Coefficients d'ajustement de la Régression non linéaire des dx (modèle Makeham) 75

Paramètres dx du modèle Makeham 75

Coefficients d'ajustement de la Régression non linéaire des qx (modèle Makeham) 76

Paramètres qx du modèle Makeham 76

Statistique descriptive des (q_x) table TD 97-99 Ajustés par le Modèle le Gompertz Makeham 77

Moyenne du montant des primes nettes par police d'assurance, période de 2007 à 2010 (Unité DA) 78

Moyenne du nombre de contrats par police d'assurance, période de 2007 à 2010 79

Evolution du montant des primes entre 2007 et 2010 80

Evolution du nombre de contrats entre 2007 et 2010 81

Moyenne de la prime par police d'assurance de 2007 à 2010 81

Evolution de la prime moyenne par police d'assurance par rapport à 2007 82

Taux d'annulation par police d'assurance pour la période 2007 à 2010 83

Moyenne de l'âge de la durée et du capital décès des assurés de l'échantillon étudié pour l'année 2010 84

Provision mathématique d'une assurance temporaire décès, prime et durée moyenne estimée 84

Provisions mathématique assurance temporaire décès IC 95% 86

Matrice de corrélation variable dépendante (la prime), variables explicatives (âge et nombre de jours) 87

Coefficients d'ajustement de la régression non linéaire (prime par âge de l'assuré) 88

Statistiques descriptives de l'âge et de la prime 89

Paramètres du modèle de la régression non linéaire 89

Coefficients d'ajustement de la régression linéaire de la prime par la durée du séjour 89

Statistiques descriptives de la durée du séjour et de la prime 90

Paramètres du modèle de la régression linéaire 90

Paramètres estimés de la distribution des assurés de la Société Générale 91

Statistiques estimées à partir des données Société Générale et calculées à partir des estimateurs des

paramètres de la loi Normale 91

Test de Kolmogorov-Smirnov de sur la distribution de la Société Générale pour une loi Normale 92

Paramètres estimés de la distribution des assurés de Wataniya Télécom Algérie 93

Statistiques estimées à partir des données Wataniya Télécom Algérie et calculées à partir des estimateurs

des paramètres de la loi Normale 93

Test de Kolmogorov-Smirnov de sur la distribution de Wataniya Telecom Algérie pour une loi Normale 94

Population Algérienne Résidente au 01/07/1998 (Unité en millier) source O.N.S 109

Taux de mortalité par âge (sexe masculin) 1997-1999 sources C.N.A 110

Table de mortalité TV97-99 des qx Ajusté 112

Table de mortalité TD97-99 des qx Ajusté 113

Table de commutation Algérienne TV97-99 117

Table de commutation Algérienne TD97-99 120

Modélisation des dx par la loi de Gompertz Makeham 122

Table de mortalité TV TD88-90 des qx 123

Production Trust Assurance par police d'assurance 2007-2010 125

Coefficients d'ajustement de la RNL des Lx (modèle Logistique) 126

Paramètres du modèle Logistique 126

Coefficients d'ajustement de la RNL des qx (Modèle de Kannisto) 128

Paramètres du modèle de Kannisto 128

Notations financières Standard & Poor's 130

103

Liste des figures

Figure 1 Modélisation dans un avenir incertain source (Thiriez 2004) 5

Figure 2 Principe fondamental de l'assurance vie 22

Figure 3 Comparaison des qx des tables TV88-90 et TV97-99 Algérienne âge de [0-20ans [ 70

Figure 4 Comparaison des qx des tables TV88-90 et TV97-99 Algérienne âge de [20-80 ans [ 70

Figure 5 Comparaison des qx des tables TV97-99 et TD97-99 71

Figure 6 Régression non linéaire des Lx (modèle Gompertz Makeham) 72

Figure 7 Lx Observés/Estimés par la Régression non linéaire modèle (Gompertz Makeham) et Histogramme

des résidus 73

Figure 8 Régression non linéaire des dx (modèle Makeham) 74

Figure 9 dx Observés/Estimés par la Régression non linéaire modèle (Makeham) et Histogramme des résidus

75

Figure 10 Régression non linéaire des qx (modèle Makeham) 76

Figure 11 qx Observés/Estimés par la Régression non linéaire modèle (Makeham) et Histogramme des

résidus 76

Figure 12 Courbe de répartition des Provisions Mathématiques assurance temporaire décès 85

Figure 13 Provisions mathématique assurance temporaire décès IC95% 86

Figure 14 Régression non linéaire de la prime par rapport à l'âge de l'assuré 88

Figure 15 Prime observée par rapport à la prime estimer par le modèle non linéaire et histogramme des

résidus 88

Figure 16 Régression linéaire de la prime par rapport à la durée du séjour 89

Figure 17 Prime observée par rapport à la prime estimer par le modèle linéaire et histogramme des résidus

90

Figure 18 Effectif observés et théorique des assurés de la Société Général 92

Figure 19 Histogramme de densité et fonction de répartition des fréquences cumulés des assurés de la

Société Générale 93

Figure 20 Effectif observés et théorique des assurés de Wataniya Telecom Algérie 94

Figure 21 Histogramme de densité et fonction de répartition des fréquences cumulés des assurés de la

Wataniya Telecom Algérie 94
Figure 22 Pyramide des âges de la Population Algérienne Résidente au 01/07/1998 source O.N.S (Unité en

millier) 109

Figure 23 Vision globale de l'assurance 110

Figure 24 Monotonic Karup-King Osculatory Interpolation 114

Figure 25 Karup-King Fonction de densité 114

Figure 26 Régression non linéaire des Lx (modèle Logistique) 126

Figure 27 Lx Observés/Estimés par la Régression non linéaire modèle (Logistique) et Histogramme des

résidus 126

Figure 28 Régression non linéaire des qx (modèle de Heligman-Pollard) 127

Figure 29 qx Observés/Estimés par la Régression non linéaire modèle (Heligman-Pollard) et Histogramme

des résidus 127

Figure 30 Régression non linéaire des qx (modèle de Kannisto) 128

Figure 31 qx Observés/Estimés par la Régression non linéaire modèle (Kannisto), Histogramme des résidus

128

104

Table des matières

INTRODUCTION 0

CHAPITRE I LES RISQUES LIES A L'ASSURANCE-VIE 5

SECTION 1 UNE APPROCHE METHODOLOGIQUE FACE A UN EVENEMENT ALEATOIRE : 5

1 les probabilités liées aux événements aléatoires 5

2 La théorie de l'assurance 6

3 Modélisation du risque et prime d'assurance 6

3.1 La prime pure 6

3.2 Le chargement technique (CT) 6

3.3 Le chargement commercial (CC) 6

4 La Mutualisation des risques 7

SECTION 2 ETUDE DES FONCTIONS PROBABILISTES DE L'ASSURANCE VIE 8

1 Repères historiques 8

2 Les facteurs influant la mortalité 8

3 Cadre juridique de l'assurance de personnes et ses déclinaisons 9

3.1 Les différentes risques couverts en assurance de personnes 10

3.2 Les assurances de personnes 10

SECTION 3 MODELISATION DU RISQUE EN ASSURANCE VIE 14

1 Définition du taux instantané de mortalité 14

2 Lissage des taux instantanés de mortalité 14

2.1 Estimations lissées des taux de décès 14

2.2 Modèle paramétrique 15

2.3 Les méthodes de lissage paramétriques ou non-paramétriques 15

2.4 Modèles relationnels 15

2.5 La modélisation paramétrique 16

2.6 Lissages paramétriques 19

3 Structure de la population de l'assureur 21

4 Calcul d'une prime fixe dans un environnement aléatoire 21

4.1 Variable aléatoire, la durée de vie de l'assuré 21

4.2 Le principe de l'actualisation en avenir aléatoire 21

4.3 Prime pure et prime annuelle 23

4.4 Le type de risque 25

4.5 La durée d'assurance 25

4.6 La population assurée 25

CHAPITRE II REASSURANCE & GESTION ACTIF-PASSIF 26

SECTION 1 COUVERTURE DU RISQUE PAR LA REASSURANCE 26

1 Traité de réassurance 26

2 La réassurance proportionnelle 27

2.1 Quote-part ou QP 27

105

2.2 Excédent de plein ou XP 28

3 Réassurance non proportionnelle 29

3.1 Excédent de sinistre ou XS 29

3.2 Excédent de perte (stop-loss ou SL) 29

4 Rétrocession 30

SECTION 2 GESTION ACTIF-PASSIF 30

1 Outil de 1^re génération (l'analyse des flux de trésorerie) 32

1.1 Projection des flux de trésorerie 32

a) L'approche statique 32

b) L'approche dynamique 32

1.2 Mesure des impasses de trésorerie 33

1.3 Calcul de la Valeur Actuelle Nette 35

1.4 Mesures de la sensibilité de la Valeur Actuelle Nette 38

1.5 Limite des outils de 1^re génération 40

SECTION 3 OUTILS DE NOUVELLE GENERATION 42

1 Outils de 2^ème génération (les scénarios déterministes) 42

1.1 Scénarios et stress testing 43

1.2 Eléments d'un modèle déterministe (simulation) 43

1.3 Conception des scénarios 46

1.4 Cohérence des hypothèses 47

1.5 Domaines d'utilisation 49

1.6 Difficultés opérationnelles 51

2 Outils de 3^e génération (les modèles stochastiques) 52

2.1 Processus stochastiques 52

2.2 Méthode de Monte-Carlo 53

2.3 Passage d'un modèle déterministe à un modèle stochastique 54

2.4 Fonctions de comportement des clients 54

CHAPITRE III ELABORATION ET ETUDE DU CAS TRUST ALGERIE 55

SECTION 1 ENVIRONNEMENT DE L'ASSURANCE VIE EN ALGERIE 55

1 Le marché algérien en chiffres 55

1.1 Caractéristiques du marché 55

1.2 Densité d'assurance et taux de pénétration: 55

1.3 La réassurance : 56

2 Les acteurs du marché de l'assurance 57

2.1 Ministre des Finances 57

2.2 Fonds de garantie des assurés 57

2.3 Commission de supervision des assurances (CSA) 58

2.4 Conseil national des assurances (CNA) 58

2.5 Associations professionnelles 59

2.6 Le système national de sécurité sociale 59

3 Présentation de la Trust Assurance 61

106

3.1 Assurance dépendant de la durée de la vie humaine 61

3.2 Assurance d'assistance aux personnes en déplacement (Assurance voyage) : 66

3.3 Assurance collective ou assurance groupe 66

SECTION 2 MODELISATION DE LA MORTALITE 68

1 Elaboration d'une table de mortalité 68

1.1 Prérequis 68

1.2 Ajustement de la table de mortalité 69

2 Modélisation de Lx et du taux instantané de mortalité en utilisant le Modèle de

Makeham (3 paramètres) 71

2.1 Coefficients d'ajustement de la Régression non linéaire des Lx 73

2.2 Qualité de la régression non linéaire modèle de Gompertz Makeham 73

2.3 Paramètres du modèle Gompertz Makeham 73

3 Modélisation des (dx) en utilisant le Modèle de Makeham (3 paramétrés) 73

3.1 Coefficients d'ajustement 75

3.2 Paramètres du modèle 75

4 Modélisation des (qx) probabilités de décès par le modèle de Gompertz

Makeham 75

SECTION 3 ETUDE DU PORTEFEUILLE DE CONTRATS DE LA TRUST ASSURANCE DE PERSONNES 78

1 Analyse du portefeuille de contrats du point de vue quantitatif 78

2 Analyse du portefeuille de contrat d'un point de vue qualitatif 79

3 Evolution du portefeuille de contrats 80

3.1 Taux d'annulation 82

4 Provisions mathématiques 83

5 Assurance voyage 87

5.1 Variation de la prime par rapport à l'âge 88

5.2 Variation de la prime par rapport à la durée de séjour 89

6 Comparaison de deux assurances groupes 91

6.1 Etude de l'assurance groupe de la Société Générale 91

6.2 Etude de l'assurance groupe de Wataniya Telecom Algérie 93

6.3 Mesurer et comparer le risque 95

CONCLUSION 97

BIBLIOGRAPHIE 100

LISTE DES TABLEAUX 102

LISTE DES FIGURES 103

TABLE DES MATIERES 104

LES ANNEXES 109

A

Actifs de taux	34,	35,	38
Age moyen actuariel		92,	96
Aléa moral			28
Analyse statique 33,	40,	42,	45
B
Benchmarking			5
Bordereaux de relevés de sinistres			27
C
Canton	34,	35,	48
Cash-flows 32, 33, 34, 35, 36,	37,	38,	54
Cession des pointes de sinistralité			28
Chaînes de décision			52
Chargement technique implicite			71
Commission de Supervision des Assurances			57
Compagnie Centrale de réassurance			56
Compensation statistique			24
Composition du portefeuille 27,	78,	79,	91
Convexité			39
Courbe d'apprentissage			17
Courbe de vie			17
Courbe des taux zéro-coupon		36,	37
D
Duration	38,	39,	41
E
E.L. De Forest			20
Emetteurs privés		36,	37
Emetteurs souverains		36,	37
Estimations lissées des taux de décès			14
Excess loss			29
F
Frédérick Macaulay			38

G

Gompertz	16,	17,	18,	69
H
Harry Markowitz				50
Heligman-Pollard				18
Hypothèses de rachat				37
I
Immunisation du risque de taux				40
Insurance no life				61
J
John Richard Hicks				38

K

Kannisto 16, 18, 126, 128 Karup-King		69
L
Lapalissade		8
Life insurance		61
Lissage non-paramétrique	14,	15
Lissage paramétrique	14, 16,	19
Loi de Bernoulli		22
M
Makeham 16, 17,	18, 19,	69
Mesure prudentielle		71
Méthode Balthazar		64
Méthode de Karup-King	69, 114
Méthode de King Hardy		69
Méthode de Monte-Carlo	31, 53,	54
Méthode de Whittaker-Henderson		20
Méthode des moyennes mobiles pondérées		20
Méthode des splines		19
Mixte d'épargne		63
Mixte prévoyance		63

MMP Voir Méthode des moyennes mobiles pondérées

Modèle de Gompertz 17

Modèle de Heligman-Pollard 18, 127

Modèle de Makeham 17, 71

Modèle logistique 18, 126, 128

107

108

Modèle paramétrique 15

Modèle relationnel 15

Modélisation paramétrique 15, 16, 19

Monotonic Karup-King Osculatory Interpolation 69

Mortalité accidentelle 17, 18

P

Plafond du traité 29

PM Voir Provisions mathématique

Portée du traité 29

PRE Voir Provision pour risque d'exigibilité

Prime naturelle 23

Prime nivelée 23

Priorité du traité 29

Provision pour risque d'exigibilité 42, 54

Q

QP Voir Quote-part

Quote-part 27, 28

R

Régression non linéaire 19, 88, 89

Rétrocession 30

Risque de défaillance 35, 36, 37

Risque de modèle 15, 51

Risque de taux 3, 31, 37, 39, 40, 41

Risque d'exigibilité 41

Risque viager 3

S

Schengen 12, 66

Simulation de probabilité 6

Sinistre 6, 9, 10, 21, 24, 46

SL

Excédent de perte 29

Souscripteur 9, 25, 45, 61, 67

Spline 19

Standard & Poor's 61, 130

Stress testing 31, 42, 43, 46, 47, 49, 50, 51

T

Tables de mortalités prospectives 9

Taux d'invalidité 64

Taux de cession 27

Taux de décès annuel 14

Taux de décès estimés bruts 20

Taux de mortalité 14, 15, 20, 68, 69, 71

Taux de mortalité infantile 70

Taux de pénétration 55

Taux de prorogation Voir taux de rachat

Taux de rachat 39, 42

Taux de rendement actuariel 36

Taux de rendement financier 35

Taux de rétention 27, 28, 56

Taux garanti contractuellement 37

Taux garanti moyen 35

Taux instantané de mortalité 14, 17

Taux minimum garanti aux contrats 9

Taux obligataire 40, 42

Taux sans risque 37

Taux zéro-coupon 36

Test de Kolmogorov-Smirnov 91, 92, 94

Test de résistance 31

Théorie de la décision 5

Théorie des jeux 5

TMI Voir Taux de mortalité infantile

Tontines 8

V

Valeur actuelle 21, 22, 23, 32, 35, 36, 37, 38, 42

Valeur actuelle nette 32, 35, 37, 38, 39, 40, 42

Value at Risk 52

W

Weibull 16

Whittaker-Henderson 20

X

XP Voir Excédent de plein XS

Excédent de sinistre 29

109

Les Annexes

Annexe 1 Population Algérienne Résidente par groupe d'âge au 01/07/1998 source

O.N.S

Table 32 Population Algérienne Résidente au 01/07/1998 (Unité en millier) source O.N.S

Annexe 2 Pyramide des âges de la Population Algérienne Résidente au 01/07/1998

source O.N.S

Figure 22 Pyramide des âges de la Population Algérienne Résidente au 01/07/1998 source O.N.S (Unité en millier)

Annexe 3 Taux de mortalité par âge (sexe masculin) 1997-1999

110

Table 33 Taux de mortalité par âge (sexe masculin) 1997-1999 sources C.N.A C.N.A : Conseil national des assurances (CNA) voir page 58

Annexe 4 Vision globale de l'assurance

Figure 23 Vision globale de l'assurance

Annexe 5 Table de mortalité TV97-99 des Q_x Ajusté

111

Age	Q(x) TV97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)	Age	Q(x) TV97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)
0	0,05061	0,05061	0,05061	39	0,00255	0,00157	0,00255
1	0,00931	0,01280	0,00931	40	0,00276	0,00171	0,00276
2	0,00455	0,00279	0,00455	41	0,00301	0,00188	0,00301
3	0,00139	0,00139	0,00139	42	0,00321	0,00205	0,00320
4	0,00113	0,00113	0,00113	43	0,00334	0,00225	0,00334
5	0,00118	0,00118	0,00118	44	0,00342	0,00246	0,00342
6	0,00086	0,00086	0,00086	45	0,00348	0,00270	0,00348
7	0,00063	0,00063	0,00063	46	0,00362	0,00296	0,00362
8	0,00047	0,00047	0,00047	47	0,00381	0,00324	0,00381
9	0,00039	0,00039	0,00039	48	0,00389	0,00355	0,00389
10	0,00066	0,00066	0,00066	49	0,00431	0,00389	0,00431
11	0,00063	0,00063	0,00063	50	0,00456	0,00427	0,00456
12	0,00062	0,00062	0,00062	51	0,00484	0,00468	0,00484
13	0,00064	0,00064	0,00064	52	0,00521	0,00513	0,00521
14	0,00069	0,00069	0,00069	53	0,00567	0,00563	0,00567
15	0,00074	0,00074	0,00074	54	0,00620	0,00618	0,00620
16	0,00077	0,00077	0,00077	55	0,00659	0,00678	0,00659
17	0,00081	0,00081	0,00081	56	0,00696	0,00744	0,00696
18	0,00085	0,00085	0,00085	57	0,00754	0,00816	0,00754
19	0,00089	0,00089	0,00089	58	0,00840	0,00895	0,00839
20	0,00082	0,00032	0,00082	59	0,00953	0,00983	0,00953
21	0,00086	0,00034	0,00086	60	0,01065	0,01078	0,01065
22	0,00090	0,00037	0,00090	61	0,01166	0,01184	0,01166
23	0,00093	0,00040	0,00093	62	0,01283	0,01299	0,01283
24	0,00096	0,00043	0,00096	63	0,01422	0,01426	0,01422
25	0,00113	0,00047	0,00113	64	0,01595	0,01565	0,01595
26	0,00115	0,00051	0,00115	65	0,01814	0,01718	0,01814
27	0,00120	0,00055	0,00120	66	0,02049	0,01886	0,02049
28	0,00125	0,00060	0,00125	67	0,02269	0,02071	0,02269
29	0,00133	0,00065	0,00133	68	0,02472	0,02273	0,02472
30	0,00204	0,00071	0,00204	69	0,02652	0,02496	0,02652
31	0,00153	0,00078	0,00153	70	0,02875	0,02740	0,02875
32	0,00138	0,00084	0,00138	71	0,03172	0,03008	0,03172
33	0,00140	0,00092	0,00140	72	0,03486	0,03303	0,03486
34	0,00160	0,00101	0,00160	73	0,03808	0,03626	0,03808
35	0,00193	0,00110	0,00193	74	0,04132	0,03981	0,04132
36	0,00208	0,00120	0,00208	75	0,03991	0,05045	0,05045
37	0,00224	0,00131	0,00224	76	0,03855	0,05661	0,05661
38	0,00239	0,00143	0,00239	77	0,04668	0,06338	0,06338

112

Age	Q(x) TV97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)	Age	Q(x) TV97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)
78	0,06427	0,07082	0,07082	95		0,35106	0,35106
79	0,08693	0,07896	0,07896	96		0,38002	0,38002
80	0,10358	0,08787	0,08787	97		0,41077	0,41077
81	0,09763	0,09759	0,09759	98		0,44337	0,44337
82	0,13295	0,10817	0,10817	99		0,47787	0,47787
83	0,14745	0,11967	0,11967	100		0,51435	0,51435
84	0,15880	0,13215	0,13215	101		0,55286	0,55286
85		0,14566	0,14566	102		0,59346	0,59346
86		0,16026	0,16026	103		0,63621	0,63621
87		0,17602	0,17602	104		0,68116	0,68116
88		0,19299	0,19299	105		0,72836	0,72836
89		0,21124	0,21124	106		0,77787	0,77787
90		0,23082	0,23082	107		0,82974	0,82974
91		0,25181	0,25181	108		0,88401	0,88401
92		0,27426	0,27426	109		0,94072	0,94072
93		0,29825	0,29825	110		0,99993	0,99993
94		0,32382	0,32382

34 Table de mortalité TV97-99 des qx Ajusté

Ajusté(1) : Ajustement par la fonction polynomial de [0,20] et par l'exponentielle de Makeham de [0,75] Ajusté(2) : Ajustement par l'exponentielle de Makeham de [0,75]

Annexe 6 Table de mortalité TD97-99 des Q_x Ajusté

Age	Q(x) TD97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)	Age	Q(x) TD97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)
0	0,05599	0,05599	0,05599	21	0,00211	0,00166	0,00211
1	0,00800	0,00800	0,00800	22	0,00226	0,00169	0,00226
2	0,00411	0,00411	0,00411	23	0,00232	0,00173	0,00232
3	0,00185	0,00185	0,00185	24	0,00227	0,00176	0,00227
4	0,00152	0,00152	0,00152	25	0,00224	0,00181	0,00224
5	0,00177	0,00177	0,00177	26	0,00228	0,00185	0,00228
6	0,00127	0,00127	0,00127	27	0,00230	0,00190	0,00230
7	0,00091	0,00091	0,00091	28	0,00230	0,00195	0,00230
8	0,00068	0,00068	0,00068	29	0,00228	0,00202	0,00228
9	0,00057	0,00057	0,00057	30	0,00223	0,00208	0,00223
10	0,00098	0,00098	0,00098	31	0,00219	0,00215	0,00219
11	0,00094	0,00094	0,00094	32	0,00220	0,00223	0,00220
12	0,00096	0,00096	0,00096	33	0,00227	0,00232	0,00227
13	0,00102	0,00102	0,00102	34	0,00240	0,00242	0,00240
14	0,00113	0,00113	0,00113	35	0,00254	0,00253	0,00254
15	0,00124	0,00124	0,00124	36	0,00265	0,00265	0,00265
16	0,00132	0,00132	0,00132	37	0,00279	0,00277	0,00279
17	0,00142	0,00142	0,00142	38	0,00290	0,00292	0,00290
18	0,00153	0,00153	0,00153	39	0,00309	0,00307	0,00309
19	0,00168	0,00168	0,00168	40	0,00330	0,00325	0,00329
20	0,00189	0,00163	0,00189	41	0,00352	0,00344	0,00352

113

Age	Q(x) TD97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)	Age	Q(x) TD97-99	Q(x) Ajusté^(1)	Q(x) Ajusté^(2)
42	0,00370	0,00365	0,00370	75	0,05099	0,05189	0,05189
43	0,00381	0,00388	0,00381	76	0,05142	0,06191	0,05628
44	0,00391	0,00413	0,00391	77	0,06032	0,06980	0,06108
45	0,00390	0,00441	0,00390	78	0,07787	0,07853	0,06635
46	0,00395	0,00472	0,00395	79	0,10036	0,08815	0,07215
47	0,00414	0,00505	0,00414	80	0,11814	0,09874	0,07851
48	0,00432	0,00543	0,00432	81	0,13406	0,11037	0,08552
49	0,00505	0,00583	0,00505	82	0,15176	0,12312	0,09323
50	0,00579	0,00629	0,00579	83	0,16772	0,13706	0,10174
51	0,00661	0,00678	0,00661	84	0,17979	0,15228	0,11112
52	0,00743	0,00733	0,00743	85		0,16886	0,12149
53	0,00814	0,00793	0,00814	86		0,18689	0,13294
54	0,00856	0,00859	0,00856	87		0,20645	0,14561
55	0,00873	0,00931	0,00873	88		0,22764	0,15965
56	0,00910	0,01011	0,00910	89		0,25055	0,17521
57	0,00984	0,01099	0,00984	90		0,27528	0,19248
58	0,01099	0,01196	0,01099	91		0,30193	0,21166
59	0,01261	0,01303	0,01261	92		0,33058	0,23299
60	0,01447	0,01420	0,01446	93		0,36135	0,25673
61	0,01614	0,01549	0,01614	94		0,39434	0,28317
62	0,01771	0,01692	0,01771	95		0,42964	0,31267
63	0,01917	0,01848	0,01916	96		0,46736	0,34561
64	0,02047	0,02020	0,02047	97		0,50760	0,38242
65	0,02175	0,02210	0,02175	98		0,55046	0,42360
66	0,02322	0,02418	0,02322	99		0,59605	0,46973
67	0,02505	0,02648	0,02505	100		0,64447	0,52146
68	0,02736	0,02900	0,02736	101		0,69581	0,57952
69	0,03042	0,03178	0,03042	102		0,75017	0,64478
70	0,03479	0,03484	0,03479	103		0,80766	0,71819
71	0,03975	0,03821	0,03975	104		0,86837	0,80088
72	0,04456	0,04191	0,04456	105		0,93239	0,89412
73	0,04876	0,04599	0,04876	106		0,99981	0,99939
74	0,05183	0,05047	0,05183

35 Table de mortalité TD97-99 des qx Ajusté

Ajusté⁽¹⁾ : Ajustement par la fonction polynomial de [0,20] et par l'exponentielle de Makeham de [0,75] Ajusté⁽²⁾ : Ajustement par l'exponentielle de Makeham de [0,75]

Annexe 7 Méthode de Karup-King

Figure 24 Monotonic Karup-King Osculatory Interpolation

La méthode d'interpolation de Karup-King a une élégante structure symétrique, établie grâce à un polynôme du troisième degré à quatre points de passage tout le principe de cette méthode repose sur la manière de sélectionner ces points de passage, nommés points-pivots, dans des groupes quinquennaux en sommant cinq valeurs centrées sur l'âge

++k ++k

E₊^») = Ï E\ , _+~»~ = Ï _\

\g+3k \g+3k

De ces données groupées, nous obtenons les points-

pivots en utilisant la formule de Karup-King qui est correcte jusqu'à la cinquième différence.

Figure 27 Karup-King Fonction de densité

+ = 0.2

	· c+ " 0.008 ·	(c+3»	" 2c+ ( c++»)	(
0.000896	· (c+376 " 4	· c+3»	( 6 · c+ " c++»	(
c++76)

En pratique, nous n'utiliserons que les 2 premiers termes _x = 0.2 · c_x " 0.008 · (cx"5 " 2c_x ( cx(5)

Un traitement particulier est appliqué aux extrémités Si a w est le premier groupe quinquennal, on obtient

' = 0.2 · c_' " 0.008 · (c'3» " 2c_' ( c'+») Si b w est le dernier groupe quinquennal, on a que

Ð = 0.2 · cÐ " 0.008 · (cÐ3» " 2cÐ ( cÐ+»)

(Langmeier 2000).

114

Se reporter à Geoffrey Crofts, A Karup-King Formula «Actuarial Research Clearing House»,1998 vol. 1.

115

Annexe 8 Table de commutation Algérienne TV97-99

Age		Lx		Dx		Nx			Sx			dx		Cx		Mx		Rx
0	100	000	100	000,00	2	500	072,39	57	794	796,42	5	061	4	973,73	14	778,14	533	282,16
1	94	939	91	693,07	2	400	072,39	55	294	724,03		884		839,05	9	804,41	518	504,02
2	94	055	87	733,52	2	308	379,33	52	894	651,63		428		392,35	8	965,35	508	699,61
3	93	627	84	348,36	2	220	645,81	50	586	272,31		130		115,10	8	573,00	499	734,26
4	93	497	81	351,40	2	136	297,45	48	365	626,50		106		90,64	8	457,91	491	161,25
5	93	391	78	480,94	2	054	946,05	46	229	329,05		110		90,84	8	367,27	482	703,34
6	93	281	75	708,43	1	976	465,10	44	174	383,00		80		63,81	8	276,42	474	336,08
7	93	201	73	057,27	1	900	756,68	42	197	917,90		59		45,45	8	212,61	466	059,65
8	93	142	70	514,80	1	827	699,40	40	297	161,22		43		31,99	8	167,16	457	847,04
9	93	099	68	072,48	1	757	184,60	38	469	461,82		37		26,59	8	135,17	449	679,88
10	93	062	65	718,97	1	689	112,13	36	712	277,22		61		42,33	8	108,58	441	544,71
11	93	001	63	430,46	1	623	393,15	35	023	165,09		59		39,55	8	066,25	433	436,12
12	92	942	61	222,93	1	559	962,69	33	399	771,94		57		36,90	8	026,70	425	369,88
13	92	885	59	093,47	1	498	739,77	31	839	809,25		60		37,51	7	989,80	417	343,17
14	92	825	57	036,22	1	439	646,30	30	341	069,48		64		38,65	7	952,29	409	353,37
15	92	761	55	048,19	1	382	610,08	28	901	423,19		68		39,66	7	913,64	401	401,08
16	92	693	53	127,13	1	327	561,89	27	518	813,11		72		40,56	7	873,98	393	487,44
17	92	621	51	270,88	1	274	434,76	26	191	251,21		75		40,80	7	833,43	385	613,46
18	92	546	49	477,84	1	223	163,89	24	916	816,45		78		40,98	7	792,63	377	780,03
19	92	468	47	745,94	1	173	686,04	23	693	652,57		83		42,12	7	751,65	369	987,40
20	92	385	46	072,13	1	125	940,11	22	519	966,52		75		36,76	7	709,53	362	235,76
21	92	310	44	460,81	1	079	867,98	21	394	026,42		80		37,87	7	672,77	354	526,23
22	92	230	42	903,50	1	035	407,17	20	314	158,44		83		37,94	7	634,90	346	853,46
23	92	147	41	399,35		992	503,67	19	278	751,27		85		37,53	7	596,96	339	218,56
24	92	062	39	947,03		951	104,33	18	286	247,59		89		37,95	7	559,43	331	621,60
25	91	973	38	543,96		911	157,29	17	335	143,27		104		42,83	7	521,48	324	062,17
26	91	869	37	184,06		872	613,33	16	423	985,97		105		41,77	7	478,64	316	540,69
27	91	764	35	871,70		835	429,27	15	551	372,64		110		42,26	7	436,88	309	062,05
28	91	654	34	603,73		799	557,57	14	715	943,37		115		42,67	7	394,62	301	625,17
29	91	539	33	378,71		764	953,84	13	916	385,81		121		43,36	7	351,95	294	230,56
30	91	418	32	194,89		731	575,13	13	151	431,97		187		64,72	7	308,59	286	878,61
31	91	231	31	030,55		699	380,24	12	419	856,84		139		46,46	7	243,87	279	570,02
32	91	092	29	923,96		668	349,69	11	720	476,60		126		40,68	7	197,41	272	326,15
33	90	966	28	860,90		638	425,73	11	052	126,90		127		39,60	7	156,73	265	128,74
34	90	839	27	835,23		609	564,84	10	413	701,17		145		43,67	7	117,13	257	972,02
35	90	694	26	840,64		581	729,60	9	804	136,33		175		50,90	7	073,46	250	854,89
36	90	519	25	872,95		554	888,96	9	222	406,73		188		52,81	7	022,57	243	781,42
37	90	331	24	936,46		529	016,01	8	667	517,77		202		54,80	6	969,76	236	758,86
38	90	129	24	030,04		504	079,54	8	138	501,76		215		56,33	6	914,95	229	789,10
39	89	914	23	153,09		480	049,51	7	634	422,22		229		57,95	6	858,62	222	874,15
40	89	685	22	304,55		456	896,41	7	154	372,71		248		60,61	6	800,67	216	015,53

116

Age		Lx		Dx	Nx			Sx			dx	Cx		Mx		Rx
41	89	437	21	482,39	434	591,87	6	697	476,30		268	63,26	6	740,06	209	214,86
42	89	169	20	685,74	413	109,47	6	262	884,44		286	65,20	6	676,79	202	474,80
43	88	883	19	914,43	392	423,73	5	849	774,96		297	65,40	6	611,59	195	798,01
44	88	586	19	169,29	372	509,30	5	457	351,23		304	64,65	6	546,19	189	186,42
45	88	282	18	450,36	353	340,01	5	084	841,93		307	63,05	6	481,54	182	640,23
46	87	975	17	757,58	334	889,65	4	731	501,92		319	63,28	6	418,49	176	158,68
47	87	656	17	088,27	317	132,07	4	396	612,27		334	63,99	6	355,21	169	740,19
48	87	322	16	441,14	300	043,79	4	079	480,20		340	62,91	6	291,22	163	384,98
49	86	982	15	817,20	283	602,65	3	779	436,41		375	67,02	6	228,31	157	093,76
50	86	607	15	210,55	267	785,46	3	495	833,75		395	68,18	6	161,29	150	865,45
51	86	212	14	623,51	252	574,91	3	228	048,30		417	69,51	6	093,12	144	704,16
52	85	795	14	055,22	237	951,40	2	975	473,39		447	71,97	6	023,60	138	611,04
53	85	348	13	503,95	223	896,18	2	737	521,99		484	75,26	5	951,64	132	587,44
54	84	864	12	968,29	210	392,23	2	513	625,81		526	78,99	5	876,38	126	635,80
55	84	338	12	447,28	197	423,94	2	303	233,59		556	80,64	5	797,39	120	759,42
56	83	782	11	942,46	184	976,66	2	105	809,65		583	81,67	5	716,74	114	962,04
57	83	199	11	453,89	173	034,20	1	920	832,99		627	84,83	5	635,07	109	245,29
58	82	572	10	978,92	161	580,31	1	747	798,80		693	90,55	5	550,24	103	610,22
59	81	879	10	514,56	150	601,39	1	586	218,49		781	98,56	5	459,69	98	059,98
60	81	098	10	058,21	140	086,83	1	435	617,10		864	105,31	5	361,13	92	600,29
61	80	234	9	610,82	130	028,63	1	295	530,26		936	110,19	5	255,82	87	239,17
62	79	298	9	173,95	120	417,80	1	165	501,63	1	017	115,63	5	145,63	81	983,35
63	78	281	8	746,66	111	243,86	1	045	083,83	1	113	122,22	5	030,00	76	837,72
64	77	168	8	327,51	102	497,20		933	839,97	1	231	130,55	4	907,79	71	807,72
65	75	937	7	914,49	94	169,69		831	342,78	1	378	141,14	4	777,24	66	899,93
66	74	559	7	505,19	86	255,20		737	173,09	1	527	151,06	4	636,09	62	122,70
67	73	032	7	100,13	78	750,01		650	917,89	1	657	158,31	4	485,03	57	486,61
68	71	375	6	701,80	71	649,88		572	167,88	1	765	162,87	4	326,72	53	001,57
69	69	610	6	312,60	64	948,08		500	518,00	1	846	164,52	4	163,85	48	674,86
70	67	764	5	935,10	58	635,48		435	569,91	1	948	167,67	3	999,33	44	511,01
71	65	816	5	567,40	52	700,38		376	934,43	2	088	173,58	3	831,66	40	511,68
72	63	728	5	206,46	47	132,99		324	234,05	2	221	178,32	3	658,08	36	680,02
73	61	507	4	853,21	41	926,53		277	101,06	2	343	181,69	3	479,76	33	021,94
74	59	164	4	508,72	37	073,32		235	174,54	2	444	183,04	3	298,07	29	542,19
75	56	720	4	174,69	32	564,59		198	101,22	2	862	207,02	3	115,03	26	244,12
76	53	858	3	828,51	28	389,91		165	536,62	3	049	213,00	2	908,01	23	129,09
77	50	809	3	488,29	24	561,39		137	146,72	3	220	217,26	2	695,01	20	221,07
78	47	589	3	155,51	21	073,11		112	585,32	3	370	219,60	2	477,76	17	526,06
79	44	219	2	831,81	17	917,59		91	512,22	3	492	219,77	2	258,15	15	048,30
80	40	727	2	519,01	15	085,78		73	594,63	3	578	217,49	2	038,38	12	790,15
81	37	149	2	219,15	12	566,77		58	508,84	3	626	212,87	1	820,89	10	751,77

117

Age		Lx	Dx	Nx		Sx			dx	Cx	Mx		Rx
82	33	523	1 934,08	10	347,63	45	942,07	3	626	205,59	1 608,02	8	930,88
83	29	897	1 665,91	8	413,55	35	594,44	3	578	195,93	1 402,43	7	322,86
84	26	319	1 416,39	6	747,64	27	180,90	3	478	183,95	1 206,50	5	920,43
85	22	841	1 187,19	5	331,25	20	433,25	3	327	169,94	1 022,55	4	713,93
86	19	514	979,59	4	144,06	15	102,00	3	127	154,27	852,61	3	691,38
87	16	387	794,49	3	164,47	10	957,94	2	885	137,46	698,34	2	838,77
88	13	502	632,24	2	369,98	7	793,48	2	605	119,88	560,88	2	140,43
89	10	897	492,81	1	737,74	5	423,50	2	302	102,31	441,00	1	579,55
90	8	595	375,41	1	244,93	3	685,76	1	984	85,16	338,69	1	138,54
91	6	611	278,88		869,51	2	440,83	1	665	69,03	253,53		799,85
92	4	946	201,51		590,63	1	571,32	1	356	54,29	184,50		546,33
93	3	590	141,27		389,11		980,70	1	071	41,42	130,21		361,82
94	2	519	95,73		247,85		591,58		816	30,48	88,79		231,62
95	1	703	62,51		152,12		343,73		598	21,57	58,31		142,83
96	1	105	39,17		89,61		191,62		420	14,63	36,74		84,51
97		685	23,45		50,44		102,01		281	9,45	22,11		47,77
98		404	13,36		26,98		51,57		179	5,82	12,65		25,66
99		225	7,19		13,62		24,59		108	3,39	6,84		13,01
100		117	3,61		6,44		10,97		60	1,82	3,45		6,17
101		57	1,70		2,83		4,53		32	0,94	1,63		2,72
102		25	0,72		1,13		1,70		15	0,42	0,69		1,09
103		10	0,28		0,41		0,57		6	0,16	0,27		0,40
104		4	0,11		0,13		0,16		3	0,08	0,10		0,13
105		1	0,03		0,03		0,03		1	0,03	0,03		0,03

36 Table de commutation Algérienne TV97-99

118

Annexe 9 Table de commutation Algérienne TD97-99

Age		Lx		Dx		Nx			Sx			dx		Cx		Mx		Rx
0	100	000	100	000,00	2	478	933,33	56	803	224,03	5	599	5	503,52	16	451,90	567	733,27
1	94	401	91	208,70	2	378	933,33	54	324	290,70		755		717,03	10	948,38	551	281,37
2	93	646	87	419,54	2	287	724,63	51	945	357,37		385		353,27	10	231,36	540	332,98
3	93	261	84	116,08	2	200	305,09	49	657	632,74		172		152,49	9	878,08	530	101,63
4	93	089	81	121,69	2	116	189,01	47	457	327,64		141		120,78	9	725,59	520	223,54
5	92	948	78	259,72	2	035	067,33	45	341	138,63		164		135,73	9	604,82	510	497,95
6	92	784	75	479,84	1	956	807,61	43	306	071,31		118		94,36	9	469,09	500	893,13
7	92	666	72	834,64	1	881	327,76	41	349	263,70		84		64,90	9	374,73	491	424,04
8	92	582	70	307,84	1	808	493,12	39	467	935,94		63		47,03	9	309,83	482	049,31
9	92	519	67	884,06	1	738	185,28	37	659	442,82		53		38,22	9	262,81	472	739,48
10	92	466	65	550,89	1	670	301,23	35	921	257,53		91		63,41	9	224,58	463	476,67
11	92	375	63	271,86	1	604	750,34	34	250	956,31		87		58,57	9	161,17	454	252,09
12	92	288	61	074,66	1	541	478,48	32	646	205,97		89		57,89	9	102,60	445	090,91
13	92	199	58	952,42	1	480	403,82	31	104	727,49		94		59,08	9	044,70	435	988,32
14	92	105	56	900,79	1	421	451,40	29	624	323,67		104		63,15	8	985,62	426	943,61
15	92	001	54	914,53	1	364	550,61	28	202	872,27		114		66,89	8	922,47	417	957,99
16	91	887	52	991,78	1	309	636,07	26	838	321,66		121		68,59	8	855,59	409	035,52
17	91	766	51	132,36	1	256	644,30	25	528	685,59		130		71,20	8	786,99	400	179,93
18	91	636	49	333,26	1	205	511,93	24	272	041,29		140		74,09	8	715,79	391	392,94
19	91	496	47	592,17	1	156	178,67	23	066	529,35		154		78,74	8	641,71	382	677,14
20	91	342	45	905,37	1	108	586,51	21	910	350,68		149		73,61	8	562,97	374	035,44
21	91	193	44	280,67	1	062	681,14	20	801	764,17		152		72,55	8	489,36	365	472,47
22	91	041	42	711,94	1	018	400,47	19	739	083,04		154		71,02	8	416,82	356	983,10
23	90	887	41	197,77		975	688,53	18	720	682,57		157		69,95	8	345,80	348	566,28
24	90	730	39	735,85		934	490,75	17	744	994,04		160		68,88	8	275,85	340	220,48
25	90	570	38	324,42		894	754,90	16	810	503,29		163		67,80	8	206,97	331	944,64
26	90	407	36	961,79		856	430,48	15	915	748,39		167		67,11	8	139,17	323	737,67
27	90	240	35	645,90		819	468,69	15	059	317,90		171		66,40	8	072,06	315	598,50
28	90	069	34	375,22		783	822,79	14	239	849,21		176		66,03	8	005,67	307	526,43
29	89	893	33	147,88		749	447,56	13	456	026,42		181		65,61	7	939,64	299	520,77
30	89	712	31	962,45		716	299,69	12	706	578,86		187		65,49	7	874,03	291	581,13
31	89	525	30	817,22		684	337,24	11	990	279,17		193		65,30	7	808,55	283	707,09
32	89	332	29	710,90		653	520,02	11	305	941,94		200		65,38	7	743,24	275	898,55
33	89	132	28	641,92		623	809,11	10	652	421,92		207		65,38	7	677,86	268	155,30
34	88	925	27	609,08		595	167,19	10	028	612,81		215		65,61	7	612,48	260	477,44
35	88	710	26	610,95		567	558,11	9	433	445,62		224		66,05	7	546,86	252	864,97
36	88	486	25	646,14		540	947,16	8	865	887,51		234		66,66	7	480,81	245	318,10
37	88	252	24	713,35		515	301,02	8	324	940,34		245		67,44	7	414,15	237	837,29
38	88	007	23	811,34		490	587,67	7	809	639,32		257		68,35	7	346,71	230	423,14
39	87	750	22	938,95		466	776,33	7	319	051,65		270		69,38	7	278,36	223	076,43
40	87	480	22	095,04		443	837,38	6	852	275,31		284		70,51	7	208,99	215	798,07

119

Age		Lx		Dx	Nx			Sx			dx	Cx		Mx		Rx
41	87	196	21	278,56	421	742,34	6	408	437,93		300	71,96	7	138,48	208	589,08
42	86	896	20	488,26	400	463,78	5	986	695,59		317	73,47	7	066,52	201	450,60
43	86	579	19	723,21	379	975,52	5	586	231,81		336	75,24	6	993,05	194	384,09
44	86	243	18	982,28	360	252,32	5	206	256,28		356	77,02	6	917,81	187	391,04
45	85	887	18	264,66	341	270,03	4	846	003,97		379	79,22	6	840,79	180	473,23
46	85	508	17	569,15	323	005,37	4	504	733,93		403	81,39	6	761,57	173	632,43
47	85	105	16	895,02	305	436,22	4	181	728,56		430	83,91	6	680,18	166	870,86
48	84	675	16	241,21	288	541,20	3	876	292,34		459	86,54	6	596,27	160	190,69
49	84	216	15	606,93	272	299,99	3	587	751,14		491	89,44	6	509,73	153	594,42
50	83	725	14	991,24	256	693,06	3	315	451,14		526	92,58	6	420,29	147	084,69
51	83	199	14	393,30	241	701,82	3	058	758,08		564	95,91	6	327,72	140	664,39
52	82	635	13	812,29	227	308,52	2	817	056,26		605	99,40	6	231,81	134	336,68
53	82	030	13	247,51	213	496,23	2	589	747,74		650	103,18	6	132,41	128	104,87
54	81	380	12	698,10	200	248,72	2	376	251,51		699	107,21	6	029,23	121	972,46
55	80	681	12	163,32	187	550,62	2	176	002,78		751	111,29	5	922,02	115	943,24
56	79	930	11	642,61	175	387,30	1	988	452,16		808	115,69	5	810,73	110	021,22
57	79	122	11	135,18	163	744,70	1	813	064,86		870	120,35	5	695,04	104	210,49
58	78	252	10	640,33	152	609,51	1	649	320,17		936	125,10	5	574,69	98	515,45
59	77	316	10	157,54	141	969,18	1	496	710,65	1	007	130,04	5	449,59	92	940,76
60	76	309	9	686,23	131	811,64	1	354	741,47	1	084	135,25	5	319,55	87	491,17
61	75	225	9	225,73	122	125,41	1	222	929,83	1	166	140,56	5	184,30	82	171,62
62	74	059	8	775,59	112	899,68	1	100	804,42	1	253	145,94	5	043,74	76	987,32
63	72	806	8	335,37	104	124,09		987	904,75	1	345	151,36	4	897,80	71	943,58
64	71	461	7	904,72	95	788,71		883	780,66	1	444	157,01	4	746,44	67	045,79
65	70	017	7	483,09	87	883,99		787	991,94	1	547	162,52	4	589,43	62	299,35
66	68	470	7	070,29	80	400,90		700	107,95	1	656	168,08	4	426,91	57	709,92
67	66	814	6	665,98	73	330,61		619	707,05	1	769	173,48	4	258,83	53	283,01
68	65	045	6	270,04	66	664,63		546	376,43	1	886	178,70	4	085,35	49	024,18
69	63	159	5	882,35	60	394,60		479	711,80	2	007	183,74	3	906,65	44	938,83
70	61	152	5	502,83	54	512,24		419	317,21	2	130	188,40	3	722,91	41	032,18
71	59	022	5	131,56	49	009,41		364	804,96	2	255	192,71	3	534,51	37	309,27
72	56	767	4	768,60	43	877,86		315	795,55	2	379	196,44	3	341,80	33	774,76
73	54	388	4	414,26	39	109,26		271	917,70	2	501	199,53	3	145,36	30	432,96
74	51	887	4	068,86	34	695,00		232	808,44	2	619	201,87	2	945,84	27	287,60
75	49	268	3	732,83	30	626,14		198	113,44	2	557	190,43	2	743,96	24	341,77
76	46	711	3	419,42	26	893,31		167	487,30	2	629	189,17	2	553,53	21	597,81
77	44	082	3	117,84	23	473,89		140	593,99	2	693	187,22	2	364,36	19	044,27
78	41	389	2	828,38	20	356,04		117	120,11	2	746	184,45	2	177,14	16	679,91
79	38	643	2	551,43	17	527,66		96	764,06	2	788	180,94	1	992,69	14	502,77
80	35	855	2	287,29	14	976,24		79	236,40	2	815	176,51	1	811,75	12	510,09
81	33	040	2	036,44	12	688,94		64	260,16	2	826	171,21	1	635,23	10	698,34

120

Age		Lx	Dx	Nx		Sx			dx	Cx	Mx		Rx
82	30	214	1 799,28	10	652,50	51	571,22	2	817	164,90	1 464,02	9	063,11
83	27	397	1 576,35	8	853,22	40	918,72	2	787	157,62	1 299,13	7	599,09
84	24	610	1 368,11	7	276,86	32	065,50	2	735	149,45	1 141,50	6	299,96
85	21	875	1 174,95	5	908,75	24	788,64	2	657	140,28	992,05	5	158,46
86	19	218	997,33	4	733,80	18	879,89	2	555	130,33	851,77	4	166,41
87	16	663	835,49	3	736,48	14	146,08	2	426	119,57	721,44	3	314,63
88	14	237	689,71	2	900,98	10	409,61	2	273	108,24	601,88	2	593,19
89	11	964	560,00	2	211,27	7	508,63	2	096	96,43	493,64	1	991,31
90	9	868	446,27	1	651,27	5	297,36	1	899	84,42	397,20	1	497,68
91	7	969	348,20	1	205,00	3	646,08	1	687	72,46	312,79	1	100,47
92	6	282	265,21		856,80	2	441,08	1	464	60,75	240,33		787,69
93	4	818	196,52		591,59	1	584,28	1	237	49,60	179,58		547,35
94	3	581	141,13		395,07		992,68	1	014	39,28	129,98		367,77
95	2	567	97,74		253,94		597,61		803	30,05	90,70		237,79
96	1	764	64,90		156,20		343,67		610	22,06	60,65		147,09
97	1	154	41,02		91,30		187,47		441	15,41	38,59		86,44
98		713	24,49		50,28		96,17		302	10,19	23,18		47,85
99		411	13,64		25,79		45,89		193	6,29	12,99		24,66
100		218	6,99		12,16		20,09		114	3,59	6,69		11,68
101		104	3,22		5,17		7,94		60	1,83	3,10		4,98
102		44	1,32		1,95		2,77		28	0,82	1,27		1,88
103		16	0,46		0,63		0,82		11	0,31	0,45		0,61
104		5	0,14		0,17		0,19		4	0,11	0,14		0,16
105		1	0,03		0,03		0,03		1	0,03	0,03		0,03

37 Table de commutation Algérienne TD97-99

121

Annexe 10 Modélisation des d_x par la loi de Gompertz Makeham

Age	dx	Préd(dx)	Résidus	Age	dx	Préd(dx)	Résidus
8	63	44,69	18,31	47	430	561,06	-131,06
9	53	47,03	5,97	48	459	600,98	-141,98
10	91	49,55	41,45	49	491	643,50	-152,50
11	87	52,27	34,73	50	526	688,76	-162,76
12	89	55,20	33,80	51	564	736,85	-172,85
13	94	58,37	35,63	52	605	787,90	-182,90
14	104	61,79	42,21	53	650	842,00	-192,00
15	114	65,47	48,53	54	699	899,24	-200,24
16	121	69,45	51,55	55	751	959,70	-208,70
17	130	73,74	56,26	56	808	1 023,45	-215,45
18	140	78,37	61,63	57	870	1 090,51	-220,51
19	154	83,36	70,64	58	936	1 160,89	-224,89
20	149	88,74	60,26	59	1007	1 234,57	-227,57
21	152	94,54	57,46	60	1084	1 311,50	-227,50
22	154	100,79	53,21	61	1166	1 391,56	-225,56
23	157	107,53	49,47	62	1253	1 474,60	-221,60
24	160	114,80	45,20	63	1345	1 560,39	-215,39
25	163	122,63	40,37	64	1444	1 648,66	-204,66
26	167	131,06	35,94	65	1547	1 739,05	-192,05
27	171	140,15	30,85	66	1656	1 831,10	-175,10
28	176	149,94	26,06	67	1769	1 924,29	-155,29
29	181	160,48	20,52	68	1886	2 017,97	-131,97
30	187	171,82	15,18	69	2007	2 111,40	-104,40
31	193	184,04	8,96	70	2130	2 203,73	-73,73
32	200	197,18	2,82	71	2255	2 293,97	-38,97
33	207	211,31	-4,31	72	2379	2 381,05	-2,05
34	215	226,51	-11,51	73	2501	2 463,75	37,25
35	224	242,85	-18,85	74	2619	2 540,75	78,25
36	234	260,41	-26,41	75	2557	2 610,64	-53,64
37	245	279,27	-34,27	76	2629	2 671,93	-42,93
38	257	299,53	-42,53	77	2693	2 723,07	-30,07
39	270	321,26	-51,26	78	2746	2 762,48	-16,48
40	284	344,58	-60,58	79	2788	2 788,59	-0,59
41	300	369,58	-69,58	80	2815	2 799,90	15,10
42	317	396,37	-79,37	81	2826	2 795,04	30,96
43	336	425,05	-89,05	82	2817	2 772,79	44,21
44	356	455,74	-99,74	83	2787	2 732,21	54,79
45	379	488,56	-109,56	84	2735	2 672,66	62,34
46	403	523,63	-120,63	85	2657	2 593,89	63,11

122

Age	dx	Préd(dx)	Résidus	Age	dx	Préd(dx)	Résidus
86	2555	2 496,11	58,89	96	610	888,88	-278,88
87	2426	2 380,04	45,96	97	441	734,12	-293,12
88	2273	2 246,96	26,04	98	302	593,48	-291,48
89	2096	2 098,71	-2,71	99	193	468,82	-275,82
90	1899	1 937,68	-38,68	100	114	361,23	-247,23
91	1687	1 766,79	-79,79	101	60	270,94	-210,94
92	1464	1 589,37	-125,37	102	28	197,40	-169,40
93	1237	1 409,09	-172,09	103	11	139,37	-128,37
94	1014	1 229,74	-215,74	104	4	95,13	-91,13
95	803	1 055,15	-252,15

Table 38 Modélisation des dx par la loi de Gompertz Makeham

Annexe 11 Table de mortalité TV TD88-90 des Qx

Age	Q(x) TV88-90	Q(x) TD88-90	Age	Q(x) TV88-90	Q(x) TD88-90
0	0,006480	0,008710	17	0,000343	0,000872
1	0,000584	0,000726	18	0,000424	0,001157
2	0,000332	0,000474	19	0,000445	0,001311
3	0,000252	0,000333	20	0,000465	0,001425
4	0,000222	0,000293	21	0,000455	0,001528
5	0,000202	0,000273	22	0,000445	0,001602
6	0,000171	0,000243	23	0,000456	0,001564
7	0,000161	0,000212	24	0,000497	0,001566
8	0,000161	0,000212	25	0,000507	0,001548
9	0,000161	0,000202	26	0,000538	0,001551
10	0,000171	0,000212	27	0,000558	0,001563
11	0,000161	0,000213	28	0,000548	0,001586
12	0,000151	0,000223	29	0,000579	0,001620
13	0,000192	0,000263	30	0,000620	0,001674
14	0,000212	0,000334	31	0,000641	0,001739
15	0,000232	0,000456	32	0,000662	0,001804
16	0,000293	0,000618	33	0,000723	0,001912

123

Age	Q(x) TV88-90	Q(x) TD88-90	Age	Q(x) TV88-90	Q(x) TD88-90
34	0,000815	0,002009	73	0,019929	0,042352
35	0,000908	0,002107	74	0,022515	0,046051
36	0,000929	0,002226	75	0,025524	0,050764
37	0,001002	0,002367	76	0,028681	0,055495
38	0,001074	0,002520	77	0,032666	0,061491
39	0,001167	0,002642	78	0,037325	0,068037
40	0,001241	0,002850	79	0,042950	0,074924
41	0,001345	0,003112	80	0,049060	0,082401
42	0,001480	0,003334	81	0,056150	0,092285
43	0,001616	0,003761	82	0,064492	0,101421
44	0,001763	0,004085	83	0,073040	0,111499
45	0,001942	0,004359	84	0,082370	0,122564
46	0,002049	0,004659	85	0,093101	0,134109
47	0,002136	0,005006	86	0,104249	0,146109
48	0,002318	0,005456	87	0,116540	0,160898
49	0,002531	0,006066	88	0,130774	0,177457
50	0,002757	0,006687	89	0,146342	0,192344
51	0,002995	0,007319	90	0,163103	0,207796
52	0,003256	0,008044	91	0,180883	0,225195
53	0,003499	0,008785	92	0,199245	0,245185
54	0,003648	0,009612	93	0,216789	0,261839
55	0,003895	0,010601	94	0,236743	0,279041
56	0,004273	0,011421	95	0,253880	0,293737
57	0,004634	0,012257	96	0,277200	0,318043
58	0,005042	0,013395	97	0,292828	0,336323
59	0,005349	0,014431	98	0,294574	0,387838
60	0,005725	0,015656	99	0,322802	0,419426
61	0,006217	0,016861	100	0,350237	0,448669
62	0,006718	0,018121	101	0,376691	0,475862
63	0,007261	0,019433	102	0,402337	0,513158
64	0,007905	0,020644	103	0,427374	0,540541
65	0,008452	0,022016	104	0,448780	0,588235
66	0,009260	0,023387	105	0,477876	0,714286
67	0,010251	0,025320	106	0,491525	1,000000
68	0,011455	0,027372	107	0,533333
69	0,012652	0,029650	108	0,571429
70	0,014081	0,032080	109	0,666667
71	0,015796	0,035535	110	1,000000
72	0,017721	0,038737

Table 39 Table de mortalité TV TD88-90 des qx

2007 Individuel accident 15 326 576,46 - 244 899,00 - 3 810,00 15 567 665,46

2008 Individuel accident 10 799 303,00 6 299,00 569 725,00 - 9 105,00 11 366 222,00

2009 Individuel accident 8 139 344,00 15 800,50 75 490,40 - 4 226,00 8 226 408,90

2010 Individuel accident 9 220 795,00 87 379,00 - - 5 364,00 9 302 810,00

124

Annexe 12 Production de la Trust Assurance de personnes par police d'assurance de 2007 à 2010

Nouvelles Renouveles Avenants Annulations Total
Assurance voyage
2007	40	411	222,80			-			-	- 5 236	903,00	35	174	319,80
2008	51	997	100,00			-			-	- 8 123	837,00	43	873	263,00
2009	54	975	687,00			-			-	- 9 322	631,00	45	653	056,00
2010	59	322	810,00			-			-	- 6 577	627,00	52	745	183,00
Groupe
Groupe
2007	4	841	230,03			-	9	718	396,92		-	14	559	626,95
2008	3	499	230,00	10	067	141,00	8	640	682,00	- 227	818,00	21	979	235,00
2009	6	507	500,00	13	153	647,47	5	797	374,00	- 271	664,00	25	186	857,47
2010	23	937	930,00	13	773	789,00	4	301	048,00	- 201	155,00	41	811	612,00
Individuel accident Collectif
2007			-			-			-		-			-
2008	1	615	178,00		26	750,00	2	096	670,00	- 1	675,00	3	736	923,00
2009	1	531	317,00	1	098	416,00	2	397	869,00	- 8	157,00	5	019	445,00
2010	3	054	058,00		98	650,00	2	521	252,00	- 127	254,00	5	546	706,00

2007 Groupe 4 841 230,03 - 9 718 396,92 - 14 559 626,95

2008 Groupe 5 114 408,00 10 093 891,00 10 737 352,00 - 229 493,00 25 716 158,00

2009 Groupe 8 038 817,00 14 252 063,47 8 195 243,00 - 279 821,00 30 206 302,47

2010 Groupe 26 991 988,00 13 872 439,00 6 822 300,00 - 328 409,00 47 358 318,00

Individuel accident

Individuel accident (Trust 1)

2007 2008 2009 2010

	12 10 8 9		986 760 125 073		514,50 078,00 904,00 932,00	6 7 22			- 299,00 232,50 659,00	200 569 75			450,00 725,00 490,40 -	- 3 810,00 - 9 105,00 - 4 226,00 - 5 364,00		13 11 8 9		183 326 204 091		154,50 997,00 400,90 227,00
Individuel accident (Trust 2)
2007	2		340		061,96				-	44			449,00	-		2		384		510,96
2008			19		880,00				-				-	-				19		880,00
2009			13		440,00	8			568,00				-	-				22		008,00
2010			144		928,00	64			720,00				-	-				209		648,00
Individuel accident (Trust 3)
2007					-				-				-	-						-
2008			19		345,00				-				-	-				19		345,00
2009					-				-				-	-						-
2010			1		935,00				-				-	-				1		935,00

125

Mixte

Plan de protection Epargne
2007		810	423,00			-		61	590,86		-		872	013,86
2008		142	885,00		338	358,00			-	- 15	120,00		466	123,00
2009			-		226	625,00		54	284,00		-		280	909,00
2010		99	283,00		193	712,00		104	791,00		-		397	786,00
Plan de protection Prospérité
2007	1	667	650,70			-		124	490,45	- 43	097,96	1	749	043,19
2008		5	960,00		333	125,00		7	213,00		-		346	298,00
2009		261	600,00		227	554,00		351	507,00		-		840	661,00
2010			-		320	343,00		209	556,00		-		529	899,00
2007 Mixte 2		478	073,70			-		186	081,31 - 43		097,96 2		621	057,05
2008 Mixte		148	845,00		671	483,00		7	213,00 - 15		120,00		812	421,00
2009 Mixte		261	600,00		454	179,00		405	791,00		- 1		121	570,00
2010 Mixte		99	283,00		514	055,00		314	347,00		-		927	685,00
Temporaire Décès
Plan de protection Caractérisé
2007		88	172,70			-			-		-		88	172,70
2008		62	009,00		17	348,00			-		-		79	357,00
2009		37	200,00		65	363,50			-		-		102	563,50
2010		8	126,00			-			-		-		8	126,00
Plan de protection Constant
2007		167	222,20			-			-		-		167	222,20
2008		17	545,00		362	560,00			-		-		380	105,00
2009		28	290,00		89	918,00			-		-		118	208,00
2010		252	142,00		89	970,00			-		-		342	112,00
Plan de protection Familiale
2007		163	277,20			-			-		-		163	277,20
2008		485	974,00		85	444,00		44	576,00		-		615	994,00
2009		91	155,00		242	528,00		4	080,00		-		337	763,00
2010		127	172,00		164	531,00		7	325,00		-		299	028,00
Temporaire Décès (Crédit)
2007	17	669	670,98			-		11	738,40	- 36	643,20	17	644	766,18
2008	24	024	032,00		152	537,00		7	750,00	- 98	050,00	24	086	269,00
2009	15	505	361,00		361	153,00		46	880,00	- 48	194,00	15	865	200,00
2010	7	554	320,00	12	722	071,00	16	063	454,00	- 79	570,00	36	260	275,00
2007 Temporaire Décès 18		088	343,08			-		11	738,40 - 36		643,20 18		063	438,28
2008 Temporaire Décès 24		589	560,00		617	889,00		52	326,00 - 98		050,00 25		161	725,00
2009 Temporaire Décès 15		662	006,00		758	962,50		50	960,00 - 48		194,00 16		423	734,50
2010 Temporaire Décès 7		941	760,00 12		976	572,00 16		070	779,00 - 79		570,00 36		909	541,00
Total 2007	81	145	446,07			-	10	161	115,63	- 5 320	454,16	85	986	107,54
Total 2008	92	649	216,00	11	389	562,00	11	366	616,00	- 8 475	605,00	106	929	789,00
Total 2009	87	077	454,00	15	481	005,47	8	727	484,40	- 9 654	872,00	101	631	071,87
Total 2010	103	576	636,00	27	450	445,00	23	207	426,00	- 6 990	970,00	147	243	537,00

Table 40 Production Trust Assurance par police d'assurance 2007-2010

126

Annexe 13 Régression non linéaire des Lx (modèle Logistique)

OE

L = 1+exp(B+Cx) , le modèle logistique reste la base, de l'approximation de Kannisto, voir

Le modèle logistique et l'approximation de Kannisto (de 2 à 4 paramètres) page 18.

Figure 28 Régression non linéaire des Lx (modèle Logistique)

Observations	106,00 Observations
DDL R^2 SCE MCE RMCE	103,00 le nombre de degrés de liberté 0,99 le coefficient de détermination 723793071,55 la somme des carrés des résidus du modèle 7027117,20 la moyenne des carrés des résidus du modèle 2650,87 la racine de la moyenne des carrés des résidus du modèle

Table 41 Coefficients d'ajustement de la RNL des Lx (modèle Logistique)

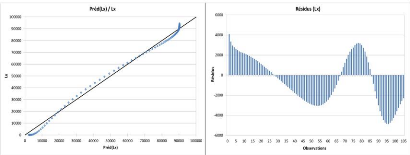
Figure 29 Lx Observés/Estimés par la Régression non linéaire modèle (Logistique) et Histogramme des résidus

Paramètre	Valeur	Ecart-type
pr1	9,343	0,237
pr2	-0,124	0,003
pr3	90333,09	387,76

Table 42 Paramètres du modèle Logistique

127

l_x =

	90333,092
	1 + e-9,343+0,123*x

Annexe 14 Régression non linéaire des qx (modèle de Heligman-Pollard)

q_x = A(x+e)c + D x _e-E(lnx-ln F)2 + ^GHxx (Voir Modèle de Heligman-Pollard (8

1+GH

paramètres) page 18).

Figure 30 Régression non linéaire des qx (modèle de Heligman-Pollard)

Figure 31 qx Observés/Estimés par la Régression non linéaire modèle (Heligman-Pollard) et Histogramme des résidus

q_x = (10-9*(xt0,21)0,09) + (9,11 · 10^-» * e(8,60*Ln(x)-Ln(0,003)2) + ( ^0,003+ \) J\1 + 0,003x)

128

Annexe 15 Régression non linéaire de qx (modèle de Kannisto)

Le modèle de Kannisto est une simplification du modèle logistique), où :

B*e^Cx

q₊ =

1+B*eCx voir Le modèle logistique et l'approximation de Kannisto (de 2 à 4 paramètres), page 18.

Figure 32 Régression non linéaire des qx (modèle de Kannisto)

Observations DDL R^2 SCE MCE RMCE	102,000 Observations 100,000 le nombre de degrés de liberté
	0,982 le coefficient de détermination 0,049 la somme des carrés des résidus du modèle 0,000 la moyenne des carrés des résidus du modèle 0,022 la racine de la moyenne des carrés des résidus du modèle

Table 43 Coefficients d'ajustement de la RNL des qx (Modèle de Kannisto)

Figure 33 qx Observés/Estimés par la Régression non linéaire modèle (Kannisto), Histogramme des résidus

Paramètre	Valeur	Ecart-type
pr1	0,183	0,015
pr2	1,376E-08	0,000

Table 44 Paramètres du modèle de Kannisto

129

1,376 · 10^36Ú * U6,7Ú*+

*+ = 1 ( 1,376 · 10³⁶Ú * U6,7Ú*+

Annexe 16 Fonctions Commutations

1) Commutations vie

K₊ = B₊ · Y+

s₊ = Ï 3+

mg6 +

B · Y++m

3+

mg6

3+

s₊ = Ï K++m = K₊ ( _K++7 ( _K++k ( ? ( K

mg6

3+

a₊ = Ï[ ( 1 · B₊ · Y+~m

mg6

3+

a₊ = Ï[ ( 1 · K+~m ~ K₊ ( 2 · K+7 ( 3 · K+~k ( ? ( " ~ ( 1 · K

s++m = s₊ ( _s++7 ( _s++k ( ?( s

mg6

1) Commutations décès

a₊ ~ Ï

C+ = (B+ " B++7) · Y++		7 k
C+ = _+ · Y++	7 k

n₊ ~ Ï B₊ " B+~m~7~ · Y+~m~7

3+

k

mg6

n₊ ~ Ï _+ · Y+7

3+

k

mg6

3+

n₊ ~ Ï _+m ~+ ( ₊₇ ( _+k ( ? ( ~

mg6

+ = Ï	^3+([ ( 1) · (B+ " B++m+7) · Y++m+7k mg6
+ = Ï	^3+([ ( 1) · _+m · Y+~m~7 k mg6

3+

+ = Ï ([ ( 1) · C++m= C₊ ( 2 · C++7 ( 3 · C++k ( ?( ( " x ( 1) · C mg6

+ = Ï

3+ n++m = n+ ( n++7 ( n++k ( ?( n mg6

130

Annexe 17 Principales notations financières

Standard & Poor's (S&P) est une filiale de McGraw-Hill qui publie des analyses financières sur des actions et des obligations, ses origines remontent aux activités de son fondateur Henry Poor en 1860. C'est l'une des trois principales sociétés de notation financière, avec ses deux concurrents Moody's et Fitch Ratings.

Elle est connue sur le marché américain pour son indice boursier S&P 500, avec des publications hebdomadaire d'analyse du marché boursier. Intitulée The Outlook, littéralement "Perspectives".

Moody's		Standard & Poor's		Fitch Ratings		Commentaire
Long terme	Court terme	Long terme	Court terme	Long Terme	Court terme
Aaa	P-l	AAA	A-1+	AAA	F1+	Sécurité maximale.
Aa1 Aa2 Aa3		AA+ AA AA-		AA+ AA AA-		Qualité haute ou bonne.
A1 A2 A3	P-2	A+ A A-	A-l A-2	A+ A A-	F1 F2	Qualité moyenne.
Baal Baa2 Baa3	P-3	BBB+ BBB BBB-	A-3	BBB+ BBB BBB-	F3	Qualité moyenne inférieure.
Bal Ba2 Ba3	Not Prime	BB+ BB BB-	B	BB+ BB BB-	B	Spéculatif.
B1 B2 B3		B+ B B-		B+ B B-		Hautement spéculatif.
Caa		CCC	C	CCC	C	Risque substantiel, mauvaise condition.
Ca		CC		CC		Extrêmement spéculatif.
C		C		C		Peut être déjà en défaut.
		D	D	DDD DD D	D	En défaut (sur une ou plusieurs obligations).

Table 45 Notations financières Standard & Poor's