|

REMERCIEMENTS
Ce mémoire sanctionne la fin du second cycle de notre
formation d?études d?Ingénieur Civil à la faculté
Polytechnique de l?Université de Kinshasa ; il ne serait pas
réalisé si certaines personnes ne nous avaient apporté
leur contribution. Nous nous acquittons ici de l?agréable devoir de leur
exprimer notre gratitude.
Nous remercions sincèrement tous les Professeurs, Chefs de
Travaux et Assistants de la faculté Polytechnique pour notre
formation.
De façon particulière, notre mot de remerciement
s?adresse au Professeur Docteur Ingénieur Jean Marie BEYA, directeur du
présent travail, pour ses conseils, critiques ainsi que ses orientations
pertinentes.
A vous mes chers parents Jean MINGASHANGA et Marceline
MBULAKAMA, vous qui avez eu à assumer correctement vos
responsabilités avec tant de sacrifices, pour nous stimuler à
donner le meilleur de nous ; voilà le précieux fruit de votre
amour. Merci.
A papa Théophile KWETE et notre exceptionnelle maman
Nancy KAYOWA pour leur soutien si important ; qu?ils trouvent à travers
cette phrase l?expression de notre sentiment de reconnaissance.
A papa Constantin MBENGELE et à papa Daniel MANTSHUMA,
pour tous les bienfaits.
Nous apprécions à sa juste valeur, l?amour, le
soutien moral que nous ont accordé tous nos frères et soeurs,
Monique MBOKASHANGA, Alain MBOMONINGA, Judith MBULAKAMA, Séraphin MISHA,
Pierrot MISHA, Gisèle MBEK, Sophie INAYENGE, sans oublier
Félicien BOPE, Bienvenue MIKOBI, George MIKOBI, Alice BULAPE,
Noëlla MWELA, Blandine PELENGE, Divine KWETE et Emmanuel KWETE, trouvez
ici l?expression de notre amour fraternel.
A Charlot MIKOBI, Honoré MBANTSHI et Jean Calvin
MINGASHANGA pour leurs conseils et soutien tant moral que financier.
A notre grand-mère Jacqueline MWELA pour son affection.
A Narcisse MIKOBI, toi qui as réussi à passionner
mes pensées, trouve ici l?expression réelle de mon amour.

Nous remercions nos amis et collègues pour les moments
difficiles passés ensemble et nous vous souhaitons un avenir plein
d?espoir ; nous citons : Eric KABANGA, Patrick BUKASA, Freddy MUKENDI,
Gérard KANDE, Bertin KUBANANGIDI, Louis LUENGA, Elvis TSHILUMBA, Claver
MFUAMBA, Léandre MISHALEIYA, Roger MILAMBO, Christian BIDUAYA, Martin
KABANTU, Aimé MUFUNGIZI, Bruno MUKENGESHAYI, Guélord EZUA,
Norbert PAYOU BELL et Philippe BUJINGO.
Que tous ceux et celles que nous n?avons pas pu citer
nommément qui, de près ou de loin nous ont aidé à
atteindre notre objectif, trouvent à travers ces lignes l?expression de
notre gratitude.

LISTE DES FIGURES
Figure 1.1 : Illustration d?un réseau radial ou en
antenne
Figure 1.2 : Illustration d?un réseau maillé
Figure 1.3 : Illustration d?un réseau bouclé
Figure 1.4 : Charge couplée en étoile
Figure 1.5 : Schéma équivalent monophasé
d?un alternateur à pôles lisses Figure 1.6 : Schéma
équivalent monophasé d?un alternateur à pôles
saillants Figure 1.7 : Schéma équivalent des réactances
d?une machine synchrone Figure 1.8 : Schéma équivalent
triphasé d?un alternateur
Figure 1.9 : Schémas équivalents direct (a),
inverse (b) et homopolaire (c) d?un alternateur
Figure 1.10 : Schémas équivalents d?un
transformateur à deux enroulements Figure 1.11 : Schéma
équivalent d?un transformateur à trois enroulements
Figure 1.12 : Schémas équivalents homopolaires d?un
transformateur à deux enroulements
Figure 1.13 : Schéma équivalent d?une ligne
courte
Figure 1.14 : Modèle en d?une ligne moyenne
Figure 1.15 : Modèle d?une ligne à
paramètres distribués longue de km Figure 1.16 : Modèle
équivalent en d?une ligne longue
Figure 2.1 : Réseau à n noeuds
indépendants
Figure 2.2 : Illustration d?un défaut triphasé au
noeud k
Figure 2.3 : Schéma équivalent sur la phase «
a » d?un réseau avec un défaut triphasé
impédant au noeud k
Figure 2.4 : Illustration d?un défaut monophasé au
noeud k
Figure 2.5 : Schéma équivalent du réseau
avec un défaut monophasé au noeud k
Figure 2.6 : Illustration d?un défaut biphasé au
noeud k
iv
Figure 2.7 : Schéma équivalent du réseau
avec un défaut biphasé au noeud k Figure 2.8 : Illustration d?un
défaut biphasé-terre au noeud k
Figure 2.9 : Schéma équivalent du réseau
avec un défaut biphasé-terre au
noeud k
Figure 2.10 : Schéma équivalent du réseau
avec un défaut biphasé au noeud k Figure 2.11 : Schéma
équivalent du réseau avec un défaut franc
biphasé-terre
au noeud k
Figure 3.1 : L?espace de travail MATLAB 7.9.0
Figure 3.2 : L?éditeur MATLAB 7.9.0
Figure 3.3 : Interface graphique fault_program
Figure 3.4 : Diagramme unifilaire du réseau à 4
noeuds de l?exemple 1 Figure 3.5 : Diagramme unifilaire du réseau
à 7 noeuds de l?exemple 2 Figure 3.6 : Réseau connecté
à un jeu de barres infini
Figure 3.7 : Diagramme unifilaire de l?exemple 4

TABLE DES MATIERES
REMERCIEMENTS i
LISTE DES FIGURES iii
INTRODUCTION 1
Chapitre I. GENERALITES SUR LES RESEAUX ELECTRIQUES 3
1.1. Introduction 3
1.2. Production de l?énergie électrique 3
1.3. Interconnexion, transport et distribution de
l?énergie électrique 4
1.4. Structures topologiques des reseaux electriques 5
1.4.1. Reseaux radiaux [2] 5
1.4.2. Reseaux mailles 6
1.4.3. Reseaux boucles 6
1.5. Systèmes polyphases [9] 7
1.6. Matrices d?admittances et d?impédances d?un
réseau électrique [2] 8
1.7. Système triphase desequilibre [2], [3], [9] 9
1.7.1. Transformation de Fortescue d?un système
triphasé déséquilibré 10
1.7.2. Effet de la transformation de Fortescue sur les impedances
11
1.7.3. Puissance en fonction des composantes symetriques 13
1.8. Modèles des composants d?un réseau
électrique 13
1.8.1. Machine synchrone triphasee [2], [9] 13
1.8.1.1. Circuit équivalent d?un alternateur à
pôles lisses 14
1.8.1.2. Circuit équivalent d?un alternateur à
pôles saillants 14
1.8.1.3. Machine synchrone en regime transitoire [1], [6] 15
1.8.1.4. Composantes de Fortescue des impédances d?une
machine synchrone [2],
[4] ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~.16
1.8.2. Transformateurs triphases [9], [10] 17
1.8.2.1. Schémas équivalents d?un transformateur
à deux enroulements 18
1.8.2.2. Transformateur à trois enroulements 18
1.8.2.3. Schemas equivalents simplifies 19
1.8.2.4. Composantes de Fortescue des impédances d?un
transformateur 19
1.8.3. Lignes de transmission [3], [4] 20
1.8.3.1. Lignes courtes 21
1.8.3.2. Lignes moyennes 21

1.8.3.3. Lignes longues 21
1.8.3.4. Composantes de Fortescue des impédances d?une
ligne de
transmission~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
23
1.8.4. Bancs de condensateurs et d?inductances [3] 23
1.8.5. Charges [1] 23
1.9. Representation en grandeurs reduites [2] 24
Chapitre II. MODELISATION DES DEFAUTS DANS UN RESEAU ELECTRIQUE
26
2.1. Introduction 26
2.2. Methodes de calcul 26
2.3. Situation du réseau avant l?apparition d?un
quelconque défaut 28
2.4. Tensions aux noeuds pendant le défaut 30
2.5. Modelisation des differents types de defauts [2], [3], [4]
32
2.5.1. Defaut triphase impedant 33
2.5.2. Defaut phase-terre impedant 34
2.5.3. Defaut biphase impedant 35
2.5.4. Defaut biphase-terre impedant 37
2.6. Calcul des courants de défaut via l?interconnexion
des réseaux direct, inverse et
homopolaire 39
2.6.1. Cas du defaut monophase 40
2.6.2. Cas du defaut biphase 42
2.6.3. Cas du defaut biphase-terre 44
2.7. Court-circuit symetrique [1], [7], [8] 45
NORMES ET CALCULS DES COURANTS DE COURT-CIRCUIT 47
2.8. Les effets des courants de defaut dans les equipements
electriques [1], [11] 48
Chapitre III. CALCUL DE DEFAUTS DANS UN RESEAU ELECTRIQUE SOUS
MATLAB 49
3.1. Introduction 49
3.2. Presentation de MATLAB 49
3.3. Programmation dans MATLAB [12], [13] 51
3.4. Donnees du programme 52
3.5. Fichier de donnees 53
3.6. Utilisation du programme de calcul de defauts 55
3.7. Exemples d?application 57
3.7.1. Exemple 1 [5, p 274 à 280] 57
3.7.2. Exemple 2 [5, p 298 à 309] 59
3.7.3. Exemple 3 [4, p 274] 62

3.7.4. Exemple 4 [2, p 271 à 274] 64
3.7.5. Exemple 5 [5, p 285, 292, 293, 294] 66
3.7.6. Exemple 6 68
3.8. Comparaison des tensions obtenues en p.u de deux
méthodes de calcul des
défauts 70
3.8.1. Comparaison sur l?exemple 2 70
a) Méthode ordinaire 70
b) Méthode d?interconnexion des réseaux D, I et O
71
3.8.2. Comparaison sur l?exemple 3 en considérant un défaut
biphasé au noeud
222222 entre les phases b et c 71
a) Méthode ordinaire 72
b) Méthode d?interconnexion des réseaux D et I
72
CONCLUSION 74
REFERENCES 76
ANNEXES 77
Résultats du calcul de défaut de l'exemple 1
pendant la période transitoire 78
Hill lillts du calcul de défaut de l'exemple 1 pendant
la période permanente 79
Résultats du calcul de défaut de l'exemple 2
80

INTRODUCTION
Un défaut dans un réseau électrique est tout
état de fonctionnement anormal du réseau.
La plupart des défauts sont des défauts
déséquilibrés souvent via une impédance de
défaut.
En considérant le réseau en régime
permanent, la méthode des composantes symétriques nous permet de
calculer tant les courants que les tensions résultant des défauts
équilibrés ou non [3].
Les défauts peuvent être soit d?origine
mécanique, soit électrique (dégradation d?isolant,
surtension), ou encore humaine (erreur de l?exploitant), etc..
Le dimensionnement du réseau ainsi que des
équipements de protection à mettre en oeuvre, résultent
aussi du calcul des puissances de court-circuit en tout point du
réseau.
Pendant longtemps, l?analyse des réseaux
électriques n?a pas été accessible au calcul par suite
d?un nombre élevé de variables mises en jeu.
Le développement des ordinateurs tant en capacité
de calcul que de mémoire permet à présent de traiter par
calcul les réseaux les plus étendus.
Dans ce travail, nous nous proposons d?utiliser le logiciel
MATLAB (MATrix LABoratory) ; outil mathématique orienté
essentiellement sur les calculs matriciels, et qui connait un succès
sans cesse grandissant auprès des étudiants, des chercheurs et
des ingénieurs grâce à des aspects tels que son mode
interactif, ses capacités graphiques, sa multitude de fonctions
intégrées dans des boites à outils ou Toolbox, avec son
langage de programmation simple. Ce qui permet la résolution des
problèmes numériques complexes en moins de temps.
Le présent travail se propose de calculer les courants
tant dans un défaut que dans le reste des branches du réseau,
à la suite d?un défaut équilibré ou non, pour un
réseau électrique de n?importe quelle topologie, avec des
transformateurs connectés en triangle et/ou en étoile, avec ou
sans mise à la terre, en utilisant la méthode des composantes
symétriques et MATLAB.
Ce travail s?intègre dans un projet global de mise en
oeuvre d?un outil de
simulation des réseaux multi-machines
actuellement en développement au

département de génie électrique et
informatique de la faculté Polytechnique de l?Université de
Kinshasa sous la supervision du Professeur JM Beya Kamba.
Nous nous limitons au cas d?un seul défaut à la
fois, susceptible de se produire soit sur un jeu de barres, ou soit sur une
ligne de transmission.
Etant donné que les courts-circuits sont les
défauts les plus susceptibles de causer le plus des dégâts
dans un réseau, nous nous proposons de nous intéresser dans ce
travail plus particulièrement aux courts-circuits francs et
impédants triphasé, monophasé, biphasé isolé
et biphasé-terre.
Pour atteindre cet objectif, nous avons adopté la
méthode documentaire consistant à consulter des ouvrages (livres,
syllabus, etc.) et avons pris l?option d?articuler le travail autour de trois
chapitres suivants :
> Chapitre I : Généralités sur les
réseaux électriques
> Chapitre II : Modélisation des défauts dans un
réseau électrique
> Chapitre III : Calcul de défauts dans un
réseau électrique sous MATLAB
Enfin, une conclusion résumant l?essentiel du travail sera
faite.

Chapitre I. GENERALITES SUR LES
RESEAUX
ELECTRIQUES
1.1. Introduction
Un réseau électrique est un ensemble de composants
électriques interconnectés d?une manière quelconque.
Une distribution électrique, importante et complète
comprend les diverses parties suivantes :
> Les usines de production de l?énergie
électrique ou
centrales électriques;
> Un réseau de lignes de transport à
(très) haute tension ;
> Des postes de transformation, d?interconnexion, de
répartition ; > Des réseaux de lignes de distribution en
moyenne tension ;
> Des postes de transformation (cabines), associés
à des lignes d?utilisation à basse tension.
Dans ce chapitre nous passerons en revue quelques
différents moyens de production de l?énergie électrique,
la variété des structures topologiques des réseaux, les
systèmes polyphasés, plus particulièrement les
systèmes triphasés équilibrés et
déséquilibrés, la modélisation des
différents composants et la représentation en grandeurs
réduites d?un réseau électrique.
1.2. Production de l'énergie
électrique
La production consiste à utiliser des énergies
diverses de manière à entrainer des alternateurs qui souvent,
produisent des tensions et des courants électriques triphasés.
On distingue ainsi des centrales de production : thermiques,
nucléaires, hydrauliques, éoliennes, solaires,
géothermiques, etc. Les avantages et inconvénients de chaque type
proviennent principalement de la facilité d'exploitation et d'entretien
des ressources et surtout du rendement de la transformation
d'énergie.

1.3. Interconnexion, transport et distribution de
l'énergie électrique
L?énergie électrique peut etre
transportée soit par courant alternatif mono ou polyphase à des
differents niveaux de tension avec une frequence donnee, soit par courant
continu.
Les systèmes à courant alternatif sont
universellement employes à cause d?importants avantages qu?ils
présentent et ceux à courant continu sont reserves pour certaines
applications particulières.
Pour des raisons techniques et economiques, les centres de
production de l?énergie electrique sont concentres sur un nombre
relativement reduit des sites ; quant aux nombreux consommateurs, ils sont
repartis sur l?ensemble du territoire.
Afin de pouvoir assurer les differentes liaisons des uns avec
les autres, il importe d?établir des lignes electriques qui permettent
le transit de puissance electrique.
Ces lignes sont raccordees entre elles au travers des postes
electriques qui sont des noeuds comprenant particulièrement les
appareillages électriques, les transformateurs, les appareils de mesure,
de commande et de contrôle, etc.
Les reseaux sont donc constitues des branches (maillees ou en
antennes) formees par des lignes electriques et des postes.
L?ensemble du réseau assure le transit de
l?énergie des centres de production aux differents centres de
consommation et realise aussi une certaine mise en commun (interconnexion) des
moyens de production. Les quantités d?énergie transportees vont
en decroissant des generateurs, relativement peu nombreux, aux millions de
consommateurs.
Pratiquement, un certain nombre de reseaux assurent diverses
fonctions specifiques entre lesquelles les frontières ne sont pas
toujours precises et sont susceptibles de varier dans le temps avec les
modalités d?exploitation.
On distingue :
> Les réseaux de
transport et d'interconnexion ;
> Les réseaux de
répartition ;
> Les réseaux de
distribution.

1.4. Structures topologiques des réseaux
électriques
La structure topologique d?un réseau électrique est
celle qui apparait sur une carte ; elle ne suffit pas pour caractériser
le schéma d?exploitation du réseau.
Nécessité de topologies variées
Les réseaux doivent assurer le transit de
l?énergie avec le maximum de sécurité malgré les
atteintes diverses dont ils peuvent être victimes (foudre, pollution,
chocs mécaniques, etc.) et les avaries qui peuvent en
résulter.
On peut accroitre la sécurité :
> En améliorant la fiabilité du matériel
;
> En assurant un entretien préventif adéquat
;
> En améliorant les dispositions constructives ;
> En augmentant le nombre de circuits, de transformateurs,
..., cela est particulièrement onéreux.
Il est donc important de trouver un compromis entre le
coût des investissements supplémentaires et celui de la
défaillance éventuelle, que l?on peut tirer par l?énergie
risquant de n?être pas distribuée. Ce compromis ne peut être
le même suivant les fonctions assurées par les réseaux,
leur tension, le type d?usagers raccordés à ceux-ci.
Cela conduit à des différentes topologies de
réseaux dont nous pouvons citer les réseaux radiaux,
bouclés et ceux maillés.
Chaque branche entre deux noeuds consécutifs i et j
sera représentée par son schéma équivalent et il
est fréquent dans la pratique de connaître la charge en un noeud i
par sa puissance et son facteur de puissance .
1.4.1. Réseaux radiaux [2]
Leur configuration est celle rencontrée dans
l?exploitation des réseaux de distribution dont les sources de tension
sont constituées d?un ou plusieurs transformateur(s) abaisseur(s).
La tension fournie par chacune de ces sources peut être
variable, en suivant les fluctuations du réseau haute tension auquel est
branché le transformateur, ou réglable si le rapport de
transformation peut être modifié.
La figure 1.1 ci-après illustre le schéma d?un
réseau radial. Le calcul d?un tel réseau est
particulièrement aisé.


Fig.1.1 : Illustration d'un réseau radial ou en
antenne
1.4.2. Réseaux maillés
Ce sont des réseaux dans lesquels les liaisons forment
des boucles dont la majorité a des côtés communs,
réalisant ainsi une structure semblable aux mailles d?un filet.
Dans ces réseaux, les transits d?énergie dans les
différentes branches peuvent facilement échapper à tout
contrôle précis.
Cette structure est généralement utilisée
pour le transport ; la figure 1.2 ciaprès donne la structure
maillée d?un réseau électrique.

Fig.1.2 : Illustration d'un réseau maillé
1.4.3. Réseaux bouclés
Un réseau bouclé est un réseau maillé
simplifié présentant un certain nombre de boucles fermées.
Chacune de boucle contient un nombre limité de sources.


Fig.1.3 : Illustration d'un réseau bouclé
1.5. Systèmes polyphasés [9]
Généralement l?énergie électrique
est distribuée à la plupart d?installations industrielles par des
systèmes polyphases et particulièrement par des systèmes
triphases qui sont composes de trois phases.
Un système polyphase se definit comme etant un ensemble
de grandeurs sinusoïdales de même frequence, dephasees les unes par
rapport aux autres. Le système polyphase de grandeurs est alors appele
« système -phasé ».
Un système -phase est dit « symétrique
ou équilibré » si les valeurs efficaces de ses
grandeurs sinusoïdales sont egales et si le dephasage entre deux grandeurs
consecutives vaut , sinon le système -phase est dit « non
symétrique ou déséquilibré ».
Les differents systèmes polyphases sont :
> Système diphasé : c?est un
système non conforme à la définition d?un
système polyphase car il exigerait un dephasage de entre
les
grandeurs. Dans ce système particulier on prend pour le
calcul du
dephasage et pour le nombre de phases.
> Système triphasé:
> Système tétraphasé :
> Système hexaphasé :
Dans la suite, nous nous interessons particulièrement au
système triphase.
On définit l?opérateur de déphasage ou de
rotation pour un système triphasé par :
p (
~ ) ? --
Avec .

Les phaseurs tensions ~ ~ ~ ) sur les trois phases en un noeud
d?un système triphasé symétrique direct sont
définies par les phaseurs suivants :
Le système symétrique est complètement
défini par un seul phaseur de référence ~.
Les phaseurs tensions ~ ~ ~ ) sur les trois phases en un noeud
d?un système triphasé symétrique inverse sont
définies par les phaseurs suivants :
Ce système symétrique est aussi
complètement défini par un seul phaseur de
référence ~.
1.6. Matrices G'DGPLAADCFI-R I-A G'RPStoGDCFI-M GpC
ttoseau électrique [2]
D?après la théorie de l?analyse des circuits
électriques linéaires, les équations de tensions aux
différents noeuds conduisent aux représentations standards
suivantes sous forme matricielle condensée pour un système
à n noeuds indépendants.
[~~ [ ~ [ ] [ ] [ ] [V] (1.3)
[I/ vecteur colonne composé de phaseurs tensions aux n
noeuds du réseau ; [ ~ vecteur colonne composé de phaseurs
courants injectés aux n noeuds ;
[ ] matrice symétrique d?impédances du
réseau passif ;
[ ~ matrice symétrique d?admittances du réseau
passif.
[ ~ [ ~
·
·
·
|
·
·
·
|
·
·
·
|
·
·
·
|
~
|
|
|
|
|
|
~
|
|
|
|
·
·
·
|
·
·
·
|
·
·
·
|
·
·
·
|
|
|
[ ]
|
·
·
·
·
·
·
|
·
·
·
·
~
|
~ [ ]
|
·
·
·
·
·
·
|
·
·
·
...
|
~ [V]
|
~
~
|
; [ ]
|
(1.3a) ]
|
Il est plus facile de construire la matrice d?admittances du
réseau que celle d?impédances ; chaque séquence de
fonctionnement (directe, inverse et homopolaire) du réseau aura sa
propre matrice d?admittances ou d?impédances par le fait que les
impédances directe, inverse et homopolaire des composants du
réseau ne sont pas nécessairement identiques.

L?obtention de la matrice d?impédances est facile par
inversion de la matrice d?admittances si l?on se sert d?un calculateur
numérique requis.
Cette matrice d?impédances est très importante
pour les calculs des défauts comme nous le verrons au deuxième
chapitre traitant de la modélisation des défauts dans un
réseau électrique.
Les éléments et des matrices [ ] et [ ] sont
respectivement appelés
impédances et admittances mutuelles
ou de transfert entre les noeuds et ; chaque admittance mutuelle est
égale à l?opposé de la somme de toutes admittances
mutuelles entre ces deux noeuds.
Les éléments et sont respectivement
appelés impédances et admittances propres ou
ponctuelles aux noeuds ; chaque admittance propre à un noeud
est égale à la somme des admittances qui aboutissent à ce
noeud.
L?expression générale, pour une source de courant
débitant en un noeud d?un réseau à n noeuds
indépendants en dehors du noeud de référence est :
? ~
= (1.4)
Cette relation peut s?écrire pour chacun de n noeuds
auxquels la tension est inconnue.
1.7. Système triphasé
déséquilibré [2], [3], [9]
Les réseaux de transport et de distribution de
l?énergie électrique sont conçus de sorte qu?ils
fonctionnent dans des conditions très proches d?une parfaite
symétrie quand ils sont en fonctionnement normal.
Les impédances propres et celles mutuelles des toutes
les trois phases des alternateurs, transformateurs et lignes électriques
dans un système triphasé, ont des valeurs approximativement
égales.
Une part importante de la consommation industrielle est quasi
équilibrée sur les trois phases, mais cela n?est pas le cas pour
les consommations domestiques et professionnelles.
Statistiquement, la répartition de ces nombreuses
consommations monophasées est supposée balancée au niveau
des réseaux de distribution à haute et à basse tension.
Il est donc important d?analyser certaines situations
(défauts monophasé, biphasé, ...) pouvant conduire le
réseau à pouvoir fonctionner dans un
déséquilibre.
Pour cela, il a été introduit des
méthodes de calcul permettant une transformation d?un système
polyphasé déséquilibré à n vecteurs en un
système polyphasé équilibré à n vecteurs
également.
La transformation de Fortescue est une des transformations
couramment utilisée pour ce fait ; l?application de cette théorie
d?analyse des réseaux publiée en 1918 par Fortescue montrant
comment un système de tensions (ou de courants)
déséquilibré peut être transformé en trois
ensembles des composantes triphasés équilibrés, est d?une
importance capitale.
1.7.1. Transformation de Fortescue d'un systt(me
triphasé déséquilibré
Les n phaseurs de chaque ensemble des composantes sont de
même longueur et la phase entre elles a une valeur identique.
Dans le cas présent, nous nous intéressons aux
systèmes triphasés même si la méthode des
composantes symétriques est valable pour n?importe quels systèmes
polyphasés.
Selon le théorème de Fortescue, trois phaseurs
déséquilibrés ~ ~ ~ d?un système de tension
triphasé peuvent être représentés par trois
systèmes de phaseurs équilibrés :
> Direct
Composé de trois phaseurs ~ ~ ~ égaux en modules,
déphasés de 120°
et ayant la même séquence que le système
original ;
Les composantes symétriques directes sont données
à la relation (1.1) ; l?indice peut être remplacé par
l?indice pour exprimer la séquence directe.
> Inverse
Composé de trois phaseurs ~ T ~ égaux en modules,
déphasés de
120° et ayant la séquence opposée au
système original ;
Les composantes symétriques inverses sont données
à la relation (1.2) ; l?indice peut être remplacé par
l?indice pour exprimer la séquence inverse.
> Homopolaire
Composé de trois phaseurs ~ " ' égaux en modules et
en phases ;
Les composantes symétriques homopolaires sont ~ ~ ~ ; les
grandeurs
de cette séquence peuvent écrites avec l?indice ou
.
La relation de la transformation de Fortescue pour le
système de tension est :
~ ~
[ ~ ] ~ ~ [ ~ ] (1.5)
~ ~
La matrice de transformation de Fortescue est :
[ [
avec - (1.6)
La transformation inverse de Fortescue est régie par la
relation matricielle :
~ ~
[ ~ ] ~ ~ ~ [ ~ ] (1.7)
~ ~
Toutes les relations précédentes sont aussi
valables pour le système des courants :
[ ]
lag
1 a2 a
] ~ ~ [
] et [ [ ] [ ] (1.8)
Comme la somme des trois courants de ligne est égale au
courant de terre, cela implique que le courant de terre vaut trois fois le
courant homopolaire.
(1.9)
Une charge connectée en triangle n?ayant pas de connexion
à la terre, les courants de cette charge n?ont pas de composante
homopolaire.
1.7.2. Effet de la transformation de Fortescue sur les
impédances
Pour déterminer cet effet, on part du circuit de la figure
1.4 pour lequel, les couplages mutuels entre les phases a, b et c sont
admis.

Fig.1.4 : Charge couplée en étoile
Pour ce circuit, les tensions sont liees aux courants par la
relation matricielle suivante :
~
[ ~ ] ~ ~ [ ] (1.10)
~
Compte tenu des relations (1.5) et (1.8), on obtient la relation
(1.11), cela après avoir pose que :
~ ~ ~ ~ ~ ~ ~ ~
20 Z21 Z22 1 a a2 Zca Zcb Zcc 1 a
a2
(1.10a)
~
[ ~ ] ~ ~ [ ] (1.11)
~
Avec : [ ] ~ 1 [ ] ~ ~ (1.11a)
La symetrie de la matrice [ ] peut être telle que la
matrice [ ] soit
diagonale, cela simplifie considerablement les calculs.
La matrice [ ] est diagonale sous les conditions suivantes d?une
parfaite
symetrie entre les trois phases ( ) [9].
Le type de matrice [ ] souvent rencontre est celui où les
elements de la
diagonale sont egaux ( ) et où tous les autres
elements (avec # )
sont aussi egaux ( ~ .
La matrice [ ~ devient :
[ ~ ~ ~ [ ] ~ ~ ~ ~ (1.12)
-- -- (1.13)
La matrice [ ] diagonale exprime qu?il n?y a pas couplage mutuel
entre les
schemas equivalents des composantes direct, inverse et
homopolaire.
Dans ce cas, les impedances et sont respectivement les
impedances
homopolaire, directe et inverse dont les definitions pour un
circuit symetrique sont les suivantes :
> L?impédance directe est l?impédance que
présente une phase lorsqu?un
système direct de courants est appliqué au circuit
; elle est donnée par :
V (1.14)
> L?impédance inverse est
l?impédance que présente une phase lorsqu?un
système inverse de courants est appliqué au circuit
;
~ (1.15)
> L?impédance homopolaire est
l?impédance vue par les courants
homopolaires, elle est donnée par :
V (1.16)
L?analyse des défauts déséquilibrés
consiste à déterminer les composantes symétriques des
courants déséquilibrés circulant dans le circuit.
1.7.3. Puissance en fonction des composantes
symétriques La puissance apparente complexe totale vaut :
|
[~ ~ ~ 1 [ ] [~ ~ ~ ] [ ] (1.17)
|
Il n?y a pas couplage des composantes et le facteur 3 provient
du fait qu?il y a neuf composantes de tension et neuf composantes de courant (3
pour chacune de trois phases).
1.8. Modèles des composants d'un réseau
électrique
Il n?est pas aisé d?établir un schéma
équivalent triphasé complet d?un système
électro-énergétique étant donné que celui-ci
est généralement triphasé.
Dans la pratique, il est de coutume de représenter un
système électroénergétique par l?utilisation des
schémas équivalents monophasés de chacun de ses
composants.
Dans la suite, les transformateurs et les lignes sont
supposés en régime permanent de sorte qu?ils soient
représentés par leurs schémas équivalents en et en
.
1.8.1. Machine synchrone triphasée [2], [9]
La machine synchrone est l?un des éléments
importants qui influent sur le comportement d?un réseau
électrique dans les régimes permanent ou transitoire.
Cette machine transforme l?énergie mécanique en
énergie électrique (alternateur) et réciproquement
(moteur), à l?exception du cas de fonctionnement en compensateur
synchrone.
1.8.1.1. Circuit équivalent d'un alternateur
à pôles lisses
Le schéma équivalent par phase tenant compte de
la résistance d?induit et de la réactance synchrone d?un
générateur synchrone à pôles lisses se
présente comme sur la figure 1.5.
|
V
|
: Respectivement phaseurs tensions simple aux bornes de la
machine chargée et à vide ;
|
: Tension générée dans une phase par le
flux d?entrefer ; : Courant d?armature (de charge);
: Respectivement réactances inductives due à la
réaction d?armature et de dispersion ; Leur somme représente la
réactance synchrone

Er
'a
Ra
Xar X1
V
E
Fig.1.5 : Schéma équivalent monophasé
d'un
alternateur à pôles lisses
1.8.1.2. Circuit équivalent d'un alternateur
à pôles saillants
Pour une machine synchrone à pôles lisses, la
réactance de l?axe direct est égale à la réactance
de l?axe en quadrature ; par contre avec la machine synchrone à
pôles saillants, il faudra faire la différence entre le flux d?axe
direct et celui d?axe en quadrature par le fait de l?anisotropie
magnétique de cette machine.
et (1.18)
Où est la réactance de dispersion pour la phase
« a » et
respectivement réactances de magnétisation d?axe
direct et d?axe en quadrature.
Selon la convention en générateur, le
schéma équivalent de la machine synchrone à pôles
saillants en régime permanent est celui illustré à la
figure 1.6.

????
????
?????? ????
???? : Force électromotrice
??
????
de Joubert.
????
Fig.1.6 : Schéma équivalent monophasé
d'un
alternateur à pôles saillants
La résistance d?armature est généralement
très faible vis-à-vis de la
réactance synchrone de telle manière que l?on
peut la négliger sans conséquence appréciable dans une
étude qualitative aussi bien pour l?alternateur à pôles
lisses que celui à pôles saillants.
1.8.1.3. Machine synchrone en régime transitoire
[1], [6]
Les modèles des machines synchrones ci-dessus se
rapportent au régime permanent où les réactances sont
mises en série avec des forces électromotrices constantes.
Lorsqu?il se produit par exemple un défaut dans un
réseau sur lequel sont connectées les machines synchrones, le
courant qui circule aux premiers instants immédiatement après est
différent du courant en régime permanent de défaut.
Dans la modélisation des machines, on utilisera les
réactances soit subtransitoire , soit transitoire ou synchrone selon que
le calcul se fait pour la période subtransitoire, transitoire ou
permanente.
Pour un défaut se produisant aux bornes d?une machine
à vide (figure 1.7), on obtient ainsi les relations qui permettent de
calculer le courant de défaut si l?on connaît la valeur de la
réactance :
Les trois composantes du courant de défaut sont telle que
.
étant respectivement les courants subtransitoire,
transitoire et permanent de défaut.
La grandeur E représente la force
électromotrice à vide.


Fig.1.7. schéma équivalent des
réactances d'une machine synchrone
Le comportement de la machine synchrone en régime
transitoire est entièrement déterminé par les
équations électriques, magnétiques et mécaniques
disponibles en théories de machines électriques.
1.8.1.4. Composantes de Fortescue des impédances
d'une machine synchrone [2], [4]
Dans une machine synchrone, les impédances directe et
inverse ne sont pas les mêmes par le fait que le sens du champ tournant
dû au courant direct d?induit est le même que celui du rotor alors
que le courant inverse d?induit produit un champ qui tourne à la
même vitesse que le rotor mais, dans le sens opposé de ce dernier.
Les deux flux ne rencontreront donc pas la même opposition.
En négligeant l?influence de l?inductance d?excitation,
la valeur de la réactance inverse varie entre la réactance
subtransitoire d?axe en quadrature et la réactance subtransitoire d?axe
direct, et on utilise la valeur moyenne pour la réactance inverse.
d (1.20)
Une valeur typique de la réactance inverse est de l?ordre
de .
L?impédance homopolaire d?une machine synchrone est encore
plus faible que la réactance inverse, soit de l?ordre de .
Considérant une machine synchrone avec une
impédance de mise à la terre schématisée par la
figure 1.8, alimentant une charge triphasée, ses schémas
équivalents direct, inverse et homopolaire sont donnés à
la figure 1.9.
De la figure 1.8, on obtient la relation (1.21) et par rapport
à la figure 1.9, on écrit la relation matricielle (1.22).
~ [ ] (1.21)
~
[ ~ ] ~ ~ ~ ~ ~ [ ] (1.22)
000Z2
~

????
????
????
(a) (b) (c)
???? ????
????
????
????
????
????
????
????
????
????
????
????
????
????
?? ????
?? ????
?? ????
Fig.1.8 : Schéma équivalent triphasé
Fig.1.9 : Schémas équivalents direct (a), inverse (b)
d'un alternateur et homopolaire (c) d'un alternateur
: Force électromotrice à vide entre la phase
« a » et le neutre ;
: Respectivement impédances directe, inverse et
homopolaire de
l?alternateur ; Avec .
Les trois équations de la relation (1.22) sont
d?application pour n?importe quel alternateur parcouru par des courants
déséquilibrés et sont un point de départ pour
l?établissement des équations des composantes du courant de
défaut dans différents types de défauts.
Lorsque le calcul se fait dans les conditions transitoires ou
subtransitoires, ces
équations seront d?application mais en
remplaçant par ~ ou selon le
|
cas ;
|
~
|
et étant les forces électromotrices
respectivement derrière les
|
réactances transitoire et subtransitoire.
Généralement la liaison au réseau de la
machine synchrone est assurée via un ou des transformateur(s) de
puissance.
1.8.2. Transformateurs triphasés [9], [10]
Un transformateur reçoit l?énergie par un
enroulement primaire et la transmet à son enroulement secondaire par le
biais d?un champ magnétique au travers d?un noyau magnétique fait
des tôles empilées.
On peut le retrouver dans les postes d?interconnexion pour
permettre le transit
d?énergie entre deux réseaux dont les
niveaux de tensions sont différents
selon que l?on veut élever ou abaisser la tension, dans
les postes de transformation pour élever le niveau de tension pour
pouvoir transporter l?énergie électrique à des longues
distances et pour rabaisser la tension au centre de consommation.
1.8.2.1. Schémas équivalents d'un
transformateur à deux enroulements
Une modélisation complète du transformateur
réel à deux enroulements distincts est donnée par la
figure 1.10.a illustrant le schéma équivalent en T par phase vu
du primaire.

??
??
?? ?? ??
?? ??
?? ??fe g ??mi ??
??
??
??
??
?? ?????? ??????
??
??
a. modèle complet (en grandeurs réelles) b.
modèle simplifié (en
grandeurs réelles)
Figure 1.10 : Schémas équivalents d'un
transformateur à deux
enroulements
Les indices 1 et 2 correspondent respectivement au primaire et au
secondaire du transformateur.
Les et sont respectivement les résistances et
réactances des
enroulements ; est une résistance traduisant les pertes en
fer et
réactance de magnétisation.
; : Respectivement résistance et réactance de
court-
circuit.
1.8.2.2. Transformateur à trois enroulements
Ce transformateur porte sur son circuit magnétique trois
enroulements : un enroulement primaire (1), un enroulement secondaire (2), et
un enroulement tertiaire (3).
Il permet d?alimenter deux réseaux de tensions respectives
et à partir d?un réseau de tension à l?aide d?un appareil
unique.

Figure 1.11 : Schéma équivalent d'un
transformateur à trois enroulements
Les paramètres de ce transformateur sont donnés par
les relations suivantes :
|
|
|
3 3 ; 3 3
3 3 ; 3 3
|
|
|
|
|
(1.23)
|
|
|
|
|
|
3 3
; ~ ~ ~
|
|
|
|
3
|
|
|
|
Lesparamètres e entre deuxnoeuds et
jétanttdéterminéssexpérimentalementtàa
partir de trois essais de court-circuit.
1.8.2.3.Schémasséquivalentsssimplifiéss
Unepremièree simplification consisteàa
déplacer la branche shunt du milieu duschémaa en T
vers les bornes primaires ou secondaires ; on obtient leschémaa
e et la branche horizontale comprendl?impédancee de
court-circuit, qui a
pour expression :
) )) (1.24)
Leschémaa e introduit une erreurnégligeablee pour
les transformateurs de
puissance.
Pour les transformateurs de
puissancesupérieureeàa 100 kVA, le
courantmagnétisantt estinférieurràa 2% du
courant nominal ; parconséquentt on peut omettre la branche shunt
duschémaaéquivalentt (fig.1.10.b) etfréquemmentt
larésistance estnégligéee vis-à-vis de
laréactance .. 1.8.2.4.Composantes de Fortescue des
impédances d'un transformateur U
Dans un transformateur, lesparamètressréactancess
directe, inverse et homopolaire sontégaux..
Pour un transformateuràa deux enroulements,
leschémaaéquivalentt direct est celui donnée à la
figure 1.10 ;ilt reste aussi valable pour laséquencee inverseàa
la seuledifférencee que le rapport de transformation complex
duschémaa inverse estl?opposéé de celui duschémaa
direc ..
Selon le groupe de couplage, les commutateurs de la figure
1.12 illustrant les schémas équivalents homopolaires d?un
transformateur triphasé à deux enroulements, peuvent être
aux positions :
> YN ou yN pour le couplage étoile avec neutre
relié à la terre au primaire via l?impédance
Zn1 et au secondaire via l?impédance Z?n2 ;
> Y ou y pour le couplage étoile sans liaison à
la terre ;
> D ou d pour le couplage triangle.

Fig.1.12 : Schémas équivalents homopolaires
d'un transformateur à deux enroulements
Pour de grandes puissances, la branche transversale de la
figure 1.12 peut être omise et on peut aussi négliger la
résistance de court-circuit (Rcc=R1h+R?2h) du transformateur
par rapport à la réactance de court-circuit
(Xcc=X1h+X?1h).
1.8.3. Lignes de transmission [3], [4]
La résistance, la réactance inductive, la
réactance capacitive et la conductance, sont les quatre
paramètres qui affectent la capacité d?une ligne de transmission
de pouvoir remplir correctement sa fonction.
Généralement la conductance est
négligée dans les lignes (aériennes) de transport de
l?énergie électrique lorsqu?il s?agit de calculer les courants et
les tensions.
Selon la longueur de la ligne, on distingue les lignes
courtes, moyennes et longues ; leurs limites de longueur qui seront
données dans la suite concernent les réseaux dont la
fréquence est de 50 Hz.
La modélisation de toutes ces lignes où une
exactitude poussée est exigée dans les calculs, doit tenir compte
du fait que leurs paramètres ne sont pas regroupés, mais
plutôt repartis uniformément le long de chaque ligne.
Les lignes de longueurs courtes et moyennes peuvent être
représentées par des paramètres concentrés et
celles dites longues sont nécessairement représentées par
des paramètres repartis.
1.8.3.1. Lignes courtes
Ce sont des lignes dont la longueur est inférieure
à 100 km ; les capacités sont tellement petites qu?elles peuvent
être négligées sans perte de précision.
Une ligne courte est représentée par une
résistance R mise en série avec une inductance L, pour une
phase.
|
???? ???? : tension et courant à la source
???? ???? : tension et courant à l?extrémité
réceptrice
|
|
Fig.1.13 : Schéma équivalent d'une ligne courte
1.8.3.2. Lignes moyennes
|
|
Toutes les lignes dont les longueurs sont comprises entre 100 km
et 300 km sont considérées comme étant des lignes
moyennes.
Leur schéma équivalent en est celui de la figure
1.14 ; il comprend en plus d?une résistance mise en série avec
une inductance longitudinalement, la moitié de la capacité par
rapport au neutre à ses deux bouts.

Fig.1.14 : Modèle en ?? d'une ligne moyenne
1.8.3.3. Lignes longues
Les lignes longues sont celles dont la distance est
supérieure à 300 km ; leurs paramètres doivent être
considérés distribués et non concentrés comme dans
la modélisation des lignes courtes et moyennes.
Sur la figure 1.15, z est l?impédance longitudinale
linéique, l?admittance transversale linéique pour
l?élément de ligne de distance t considéré, et la
longueur de la ligne.

Fig.1.15 : Modèle d'une ligne a paramètres
distribués longue de ?? km
Un élément de la ligne est
caractérisé par le système d?équations
différentielles (1.25) suivant :
(1.25)
dx dl
= VZ
dx
I V
Z
La solution à ce système d?équations est
la relation matricielle (1.26) qui lie les tensions et courants au point
situé à la distance x de l?extrémité
réceptrice de la ligne.
[~ ~
~] [ ~ ~
~ ~ ] [~
] (1.26)
et sont des termes complexes qui expriment respectivement
l?impédance caractéristique de la ligne et la constante de
propagation ou l?atténuation complexe linéique donnés par
:
~
v~ v ~ (1.27)
v et étant respectivement la
tension et le courant à l?extrémité réceptrice
de
la ligne.
Pour obtenir la tension et le courant à l?entrée de
la ligne, il suffit de remplacer la distance par la longueur de ladite ligne
dans la relation (1.26).
~ ~
[~
] ~ ~
~ ~ [~
] (1.28)
Le circuit équivalent en d?une ligne longue est celui de
la figure 1.16.

???? ?? ????
?? ??
????
????
Fig.1.16 : Modèle équivalent en ð d'une
ligne longue
~ i ) )
) ;
t ) ) ; avec z ; (1.29)
1.8.3.4. Composantes de Fortescue des impédances
d'une ligne de transmission
Les réactances directe et inverse d?une ligne sont
égales.
La réactance homopolaire pour une disposition
symétrique des conducteurs sur leurs supports vaut :
(1.30)
1.8.4. Bancs de condensateurs et d'inductances [3]
Dans un réseau électrique nous pouvons aussi
retrouver les bancs de condensateurs ou d?inductances ; ils sont comptés
parmi les moyens utilisés pour l?amélioration du plan de tensions
d?un réseau électrique. Ce sont des dispositifs utilisés
dans les cas suivants :
> Si les puissances active P et réactive Q
demandées sont élevées, les tensions tendent à
diminuer vers des niveaux inacceptables. Dans ces conditions, des bancs de
condensateurs peuvent être mis en service, ce qui relève le niveau
de tension ;
> Par contre lorsque la demande est trop faible, la
capacité du réseau (des lignes) peut être suffisante pour
augmenter les tensions vers des valeurs inacceptables. Dans ces conditions, les
inductances shunt peuvent être mises en service pour rabaisser le niveau
de tension.
1.8.5. Charges [1]
La consommation de l'énergie électrique est le fait
de tous les secteurs de la vie : industries, services, ménages.
Les charges se présentent sous des formes très
diverses : moteurs
synchrones et asynchrones, appareils de chauffage, lampes
d?éclairage.
Contrairement au cas des générateurs, il
n?est pas toujours évident
d?individualiser chaque consommation ; c?est l'agrégat
de consommation en un noeud du réseau qui constitue la charge
caractérisant ce noeud.
On distingue les charges résistive, inductive et
capacitive. Chaque charge est caractérisée par la puissance
apparente qu?elle consomme sous une tension et un courant absorbé ,
avec un facteur de puissance donné.
Une représentation élaborée de la charge
est nécessaire là où la sensibilité à la
fréquence ou à la tension du réseau est importante.
1.9. Représentation en grandeurs réduites
[2]
Dans un réseau électrique existent plusieurs
niveaux de tension et en grandeurs réelles la comparaison de ces
différentes tensions n?est pas évidente ; il est donc important
de choisir les grandeurs de base pour l?ensemble du système
électro-énergétique.
La valeur d?une grandeur donnée en pour un ou per unit
[p.u] est égale au rapport de la valeur exprimée en unité
donnée sur la valeur de base dans la même unité.
Les grandeurs de base du système sont :
~ v~ ~
v~
~
s
YB = GB = BB = 1
, 4 = 3 * 4
zB
(1.31)
Avec :
> v respectivement tensions de ligne et de
phase de base ;
> respectivement puissances apparente, active
et réactive de
base ;
> respectivement impédance,
résistance et réactance de base ;
> B respectivement admittance, conductance
et susceptance de
base.
Fréquemment, les équipements disposent de
valeurs en p.u qui sont définies par rapport à leurs valeurs
nominales [ B ~ ] mais, pour le réseau d?étude on peut choisir
une certaine base d?étude [ B B ]; d?où la
nécessité d?opérer un changement de base au moyen de la
relation :
~ [~ ~ ~ [~ ~ ~
~
(1.32)
Avantages de la représentation en p.u :
> Une bonne perception des valeurs de certains
paramètres avec les grandeurs exprimées en p.u, d?où la
facilité de détecter une erreur dans les calculs ;
> Pour les transformateurs, un bon choix de la base (
) permet d?éliminer le transformateur parfait dans le
schéma
équivalent d?analyse, ce qui simplifie
considérablement les calculs.
Inconvénients de la représentation en p.u
:
> Les chiffres deviennent abstraits quand on n?a aucune
idée de la base de calcul ;
> Pour certaines relations on est habitué à
travailler avec le facteur 3 ou v prêtant confusion quand on est en p.u (
[p ] v[p ] 3 [p ]
[p ] z ~ z ).
Chapitre II. MODELISATION DES DEFAUTS DANS UN
RESEAU
ELECTRIQUE
2.1. Introduction
Le calcul des courants de défaut en tout point d?un
réseau est un des principaux points dont il faut tenir compte dans le
dimensionnement rationnel d?un réseau électrique et des
matériels à mettre en oeuvre, dans la détermination des
protections des personnes et des biens.
Les défauts peuvent être monophasés (80%
de cas) ou biphasés (15% de cas) qui dégénèrent
souvent en défauts triphasés (5% seulement dès l?origine)
[8] ; ils peuvent présenter une impédance de défaut
(défauts impédants) ou non (défauts francs).
Dans le dimensionnement des matériels, les calculs
s?opèrent avec un défaut franc triphasé étant
donné que c?est ce type de défaut qui conduit aux contraintes les
plus sévères.
Dans ce chapitre, il sera question de montrer comment
procéder pour calculer différents types de défauts dans un
réseau par utilisations des matrices d?impédances.
Les relations de ce chapitre montreront que pendant le
défaut les transits des courants sont fonction des forces
électromotrices internes des machines en service, de leurs
impédances et des impédances des éléments du
réseau situés entre les machines et le point de défaut.
Le calcul des courants de défaut via l?interconnexion des
réseaux direct, inverse et homopolaire sera aussi abordé dans ce
chapitre.
2.2. Méthodes de calcul
Dans ce chapitre, nous traitons les cas des défauts
pouvant se produire dans un réseau électrique simple ou beaucoup
plus complexe par utilisation des matrices d?impédances de
séquences directe, inverse et homopolaire de ce réseau.
La première méthode consiste à utiliser
les trois matrices de façon indépendante ; tandis que la seconde
tient compte de l?interconnexion des réseaux direct, inverse et
homopolaire pour obtenir une matrice globale d?admittances et celle
d?impédances ; la manière d?interconnecter étant fonction
du type de défaut.
n
.
.
.
k
.
.
.
2
1
0

Pour cela, nous considérons un réseau à n
noeuds indépendants (1, 2, ..., k, ~, n, avec 0 comme noeud de
référence) schématisé par la figure 2.1.
C?est au travers de certains noeuds qu?il y a injection ou
soutirage des puissances dans le réseau.
Tout point de défaut sera considéré comme
étant un noeud ; ainsi un défaut apparaissant sur une ligne
donnera naissance à un nouveau noeud qui sera connecté aux noeuds
adjacents de la ligne par des impédances dont les valeurs sont
proportionnelles à la localisation du défaut.
|
SCHEMA EQUIVALENT DU
RESEAU PASSIF
|
Fig.2.1 : Réseau à n noeuds
indépendants
Hypothèses de base:
Pour les calculs des courants de défaut, des
hypothèses précisant le domaine de validité des formules
données sont nécessaires. Souvent simplificatrices et
accompagnées d?approximations justifiées, ces hypothèses
rendent plus aisée la compréhension des phénomènes
physiques et ainsi le calcul des courants de défaut, tout en gardant une
précision acceptable.
Les hypothèses retenues dans ce travail sont :
> Nous considérons initialement un réseau
triphasé équilibré alimentant des charges balancées
;
> Ce réseau alimenté en courant alternatif
par des machines synchrones triphasées, fonctionne en régime
permanent avant l?apparition du défaut ;
> Pendant la durée du défaut, le nombre de
phases concernées n?est pas modifié : un défaut
triphasé reste triphasé, de même un défaut
phaseterre reste phase-terre, etc. ;
> L?impédance de défaut est prise en compte si
elle existe ;
> Nous considérons le modèle en pour les lignes
si leurs capacités doivent être prises en compte;
> Nous considérons le modèle en T pour les
transformateurs si leurs branches shunts doivent être prises en compte
;
> Les conductances des lignes sont négligées
;
> Les courants de charge sont pris en compte si le calcul de
load flow est fait au préalable ;
> Toutes les impédances de séquence directe,
inverse et homopolaire sont prises en compte.
Il est impérieux de connaitre les différentes
tensions en module et en phase aux noeuds du réseau faisant objet de
l?étude.
C?est par le calcul de l?écoulement des charges (load
flow) que nous avons la
possibilité de trouver les phaseurs tensions ~ , ~ , ...,
~ ... ~ respectivement
aux noeuds 1, 2, ..., k, ..., n du réseau pendant le
régime permanent avant l?apparition du défaut en un noeud
donné.
2.3. Situation du réseau avant l'apparition d'un
quelconque défaut
Ecrivons premièrement les équations liant les
tensions et les courants injectés aux noeuds relatives à la phase
« a » dans les trois séquences de fonctionnement tout sachant
que :
> Les premiers indices des phaseurs tensions et courants
indiquent les numéros des noeuds (noeuds 1, 2, ..., k, ... et n);
> Les deuxièmes indices des phaseurs tensions et
courants précisent la phase en fonction de laquelle les équations
sont écrites (phases a, b et c) ;
> Les troisièmes indices (après la virgule) de
ces phaseurs, des
impédances et des admittances précisent la
séquence de
fonctionnement du réseau (h, d, et i respectivement pour
les séquences homopolaire, directe et inverse).
Le fonctionnement de l?ensemble du réseau en régime
permanent est régi par les équations (2.1), (2.2) et (2.3).
Séquence directe
|
V ~
V ~
V ~
V ~
Séquence inverse
V ~
V ~
V ~
V ~
Séquence homopolaire
V ~
V ~
V ~
V ~
|
~
~
~
~
~
~
~
~
~
~
~
~
|
|
(2.1)
(2.2)
(2.3)
|
Rappelons que les indices , , et expriment respectivement les
séquences homopolaire, directe, et inverse ; on peut aussi utiliser les
indices , , et pour exprimer ces trois séquences.
Les tensions aux noeuds de la phase « a » s?obtiennent
en additionnant les trois vecteurs tensions direct, inverse et homopolaire.
Nous pouvons poser que :
|
·
·
·
|
·
·
·
|
|
|
|
·
·
·
|
·
·
·
|
|
|
·
·
·
|
·
·
·
|
|
|
|
·
·
·
|
·
·
·
|
|
[ ]
|
·
·
·
|
·
·
·
|
; [
|
~
|
|
·
·
·
|
·
·
·
|
|
|
·
·
·
|
~
|
·
·
·
|
|
·
·
·
|
·
·
·
|
~
|
(2.4)
|
|
|
|
·
·
·
|
|
·
·
·
|
|
|
|
|
[ ]
|
|
·
·
·
|
|
·
·
·
|
|
|
|
|
|
|
·
·
·
|
|
~
|
|
|
|
|
Les matrices [ ] [ ] et [ ] sont celles des impedances des
circuits passifs de Thevenin respectivement des sequences directe, inverse et
homopolaire du reseau dans lesquelles toutes les machines synchrones sont
remplacees par leurs reactances synchrones pour le fonctionnement en regime
permanent, et par leurs reactances subtransitoires ou transitoires respectives
dans le cas des calculs des defauts avec leurs forces electromotrices
court-circuitees.
2.4. Tensions aux noeuds pendant le défaut
Elles s?obtiennent en partant des composantes symetriques
donnees par les relations (2.5), (2.6), (2.7) et les groupes de relations
(2.8), (2.9) ; L?exposant f? des phaseurs courants de trois
premières relations indique qu?il s?agit des composantes symetriques des
courants de defaut. Hormis les phaseurs courants de défaut relatifs au
noeud k en defaut, les autres phaseurs courants en rapport avec tous les autres
noeuds sont nuls dans les relations (2.5), (2.6) et (2.7). L'exposant
o' dans ces relations indique qu'il s'agit des phaseurs tensions aux
noeuds avant l'apparition du defaut pour eviter la confusion avec les phaseurs
qui seront calcules pendant le defaut par les relations (2.10).
> Composantes de Fortescue des
tensions de la phase « a » :
V
V
|
V
V
|
·
·
·
·
·
·
|
·
·
·
·
·
·
|
|
|
(2.5)
·
·
·
~ ] [
V
|
V
|
|
·
·
·
|
·
·
·
|
·
|
·
|
|
~
|
|
|
|
|
|
|
V
|
|
·
·
·
|
·
·
·
|
·
|
·
|
|
~
V
|
~
V
|
~ [
|
·
·
·
·
·
·
|
·
·
· ~
|
|
(2.6)
|
|
V
V
V
F
V
V
V
V
V
V
V
1
V
V
V
1
V
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
> Composantes de Fortescue des
tensions des phases « b » et « c » :
V
V
V (2.8)
~
|
|
|
|
|
|
|
|
V
V
|
V
V
|
|
V
V
|
V
V
|
|
V
V
|
V
|
V
|
;
[
|
|
V
|
;
|
V
|
1
|
~
|
|
~
|
|
1
|
|
(2.9)
Les tensions aux noeuds pendant le défaut pour les trois
phases « a », « b » et « c » sont alors
données par les relations (2.10) :
V
V
V
V
|
V
V
V
V
|
V
V
V
V
|
V
V
V
V
|
;
|
V
V
V
V
|
V
V
V
1
|
|
|
|
|
|
|
|
|
V
V
V
1
|
V
V
V
V
|
;
|
V
V
V
~
|
V
V
V
V
|
V
V
V
V
|
V
V
V
V
|
(2.10)
|
|
Les phaseurs courants de défauts sur les phases « a
», « b » et « c » sont :
; et (2.11)
;
et
(2.11)
Avec :
|
~ ~
[
|
;
]
|
|
[
~
[
|
|
(2.12)
|
|
Composantes de Fortescue des courants transitant du noeud
j au noeud l sur
la phase « a » pendant le défaut :
~ (~ ~ ~ ) ~
{ (2.13)
~ (~ ~ ~ ) ~
~ ~ ~ ~ ~ ~ ~
Avec et respectivement admittances de transfert directe,
homopolaire et inverse entre les noeuds et ; les sont
les admittances
shunts des équivalents en ð des branches .
Courants transitant de à sur les trois phases (a,
b, c) pendant le défaut :
2.5. Modélisation des différents types
de défauts [2], [3], [4]
Tous les défauts sont analysés par utilisation
des composantes de Fortescue et indépendamment du type de défaut,
on peut toujours appliquer les équations (2.15) dérivées
pour les alternateurs à l?endroit du défaut en associant les
conditions de défaut ; on obtient ainsi les schémas
équivalents exprimant chaque type de défaut.
~
|
~
|
|
|
|
[ ~
|
~
|
] ~ ~ ~ ~ ~ ~ [
|
|
] (2.15)
|
~
|
V
|
|
|
|
|
~ étant le phaseur tension de Thevenin au noeud en
défaut avant l?apparition dudit défaut.
Dans la suite, après avoir déterminé les
composantes symétriques du courant de défaut au noeud k sur la
phase « a », il faudra recourir aux relations (2.12) pour obtenir les
composantes symétriques des courants de défaut sur les phases
« b » et « c ».
Pour chaque type de défaut se produisant au noeud k
traité dans la suite, les composantes symétriques des tensions
aux différents noeuds sur la phase « a » se déterminent
par les relations (2.5), (2 .6) et (2.7) tandis que celles des phases « b
» et « c » se calculent au moyen des relations (2.8) et (2.9)
tout en sachant que
* . Quant aux phaseurs tensions aux noeuds sur les trois
phases, on utilisera les relations (2.10).
Les composantes symétriques des courants transitant
dans les différentes branches sur la phase « a » se
calculeront à l?aide des relations (2.13) et les courants réels
correspondants sur les trois phases se détermineront par la relation
(2.14).
2.5.1. Défaut triphasé impédant
Soit un défaut triphasé se produisant au noeud k
au travers d?une impédance de défaut par phase.
?
Vka
Noeud k
?
Vkb
?
Vkc

??f ?
'kc
?
'kb
?
'ka
?
Fig.2.2 : Illustration d'un défaut triphasé au
noeud k
CONDITIONS DE DEFAUT
' ' ; ' ' ; ; (2.16)
> Phase « a »
Le courant de défaut sur la phase « a » est
donné par :
~
(2.17)
V
d
Ses composantes de Fortescue sont :
[

Fig.2.3 : Schéma équivalent sur la phase
« a » d'un réseau avec un défaut triphasé
impédant au noeud k
Vkb
Vkc
?
?
?
'kb
?

Noeud k
Vka
z???
'kc ?
Pour un défaut symétrique les courants et
tensions inverses et homopolaires n?existent pas ; donc les réseaux
inverse et homopolaire ne sont pas pris en compte. Pour un défaut franc
(court-circuit) symétrique, il suffit de remplacer l?impédance
par zéro dans la relation (2.17) afin d?obtenir le courant de
défaut.
Le schéma équivalent de la figure 2.3 est
obtenu à partir de la relation (2.17) ; les schémas similaires
peuvent être trouvés pour les deux autres phases b et c.
2.5.2. Défaut phase-terre impédant
Soit un défaut phase-terre (monophasé) se
produisant au noeud entre la phase « a » et la terre via une
impédance .

Fig.2.4 : Illustration d'un défaut monophasé
au noeud k
CONDITIONS DE DEFAUT
> Phase « a »
Les composantes de Fortescue du courant de défaut sur la
phase « a » sont données par :
ka,hka,d ka,i
V
d i 3
(2.19)
Le courant de défaut sur la phase « a » est
La relation (2.19) permet d?obtenir le circuit
équivalent de la figure 2.5 où les trois réseaux direct D,
inverse I et homopolaire O sont mis en série avec le triple de
l?impédance de défaut.

f If If
Ika ka d ka i
k
D
Vka
3Zf
O
k n
I
k n
Fig.2.5 : Schéma équivalent du réseau
avec un défaut monophasé au noeud k
> Pour un défaut phase-terre se produisant au noeud k
entre la phase
« b » et la terre, les conditions de défauts
sont :
On obtient :
d i 3 (2.21)
> Pour un défaut phase-terre se produisant au noeud k
entre la phase
« c » et la terre, les conditions de défauts
sont :
On obtient :
~
~ ~ ~
|
(2.23)
|
|
2.5.3. Défaut biphasé impédant
Soit un défaut phase-phase (biphasé isolé)
se produisant au noeud k entre les phases « b » et « c » au
travers d?une impédance .
???

?
??
????
??????
?
?????? ?
?????? ?
?????? ?
???? ?
Fig.2.6 1 XXWIEURCO'XI dIfEXIENKE*1EX11oeXd k
CONDITIONS DE DEFAUT
; -- ; v -- ~ (2.24)
>
Phase « a »
Les composantes de Fortescue du courant de défaut sur la
phase « a » sont données par :
~
;
(2.25)
~
~
~
d i
Les relations (2.25) indiquent qu?il y a insertion de
l?impédance de défaut entre les réseaux direct et inverse
si elle existe et que le réseau homopolaire n?est pas pris en compte.
D?où l?obtention du schéma équivalent de la figure 2.7.
Si le défaut est franc ( ), les réseaux direct et
inverse se retrouvent en
parallèle.
k+n

k
Fig.2.7: Schéma équivalent du réseau
avec un
défaut biphasé au noeud k
> Pour un défaut phase-phase se
produisant au noeud k entre les phases « a » et « b », les
conditions de défauts sont :
; -- ; v -- 1 (2.26)
On obtient :
?
;
(2.27)
?
~
~
d i
> Pour un défaut phase-phase se
produisant au noeud k entre les phases « a » et « c », les
conditions de défauts sont :
; -- ; v -- V (2.28)
On obtient :
;
(2.29)
?
~
~
d i
??kN ?
Zf?


?
V
kb
??kb ?
Tr?
v kc
??kc ?
??ka ?
Vka
?
Noeud k
2.5.4. Défaut biphasé-terre
impédant
Soit un court-circuit franc entre les phases b et c se produisant
au noeud k et relié à la terre via une impédance .

Figure 2.8 : Illustration d'un défaut
biphasé-terre au noeud k CONDITIONS DE DEFAUT
> Phase « a »
Les composantes de Fortescue du courant de défaut sur la
phase « a » sont données par :
?
~
|
~
|
|
3 )
i 3 ~
|
|
|
i 3 )
? i 3 )
|
?
|
(2.31)
|
i 3 )
Les relations (2.31) indiquent que les réseaux direct
et inverse sont en parallèle et, l?ensemble est en parallèle avec
la mise en série du réseau homopolaire avec le triple de
l?impédance de défaut. D?où l?obtention du schéma
équivalent de la figure 2.9.
Si le défaut est franc ( ), les réseaux direct,
inverse et homopolaire sont
en parallèle.

Fig.2.9 : Schéma équivalent du réseau
avec un défaut biphasé-terre au noeud k
> Pour un défaut phase-phase-terre se
produisant au noeud k entre les phases « a », « b » et la
terre, les conditions de défauts sont :
Les composantes symétriques du courant de défaut
au noeud k sont :
|
~
|
|
3 ) ~ ~ ~
|
|
~
|
~
|
|
|
i 3 )
? i 3 )
|
(2.33)
|
i
?
·
·
·
·
~ ~ ~
> Pour un défaut phase-phase-terre se
produisant au noeud k entre les phases « a », « c » et la
terre, les conditions de défauts sont :
Les composantes symétriques du courant de défaut au
noeud k sont :
|
~
|
|
|
3 )
~ ~ )
|
|
|
~
|
~
|
|
|
|
i 3 )
~ i 3 )
|
|
(2.35)
|
|
i
|
~
~ ~ ~
2.6. CalFXl 13IW CFRXLDCtW 13H
13
·IDXIMiDINCIeLFRQ2e IR( )13FW réseaux direct, inverse et
homopolaire
La plupart des défauts sont dissymétriques ou
déséquilibrés ; ils sont soit monophasé, soit
biphasé isolé ou biphasé-terre francs ou impédants
et un réseau donné a toujours les schémas
équivalents direct (D), inverse (I) et homopolaire (O).
Il a été montré à la section
précédente que ces trois schémas peuvent s?interconnecter
d?une certaine manière selon le type de défaut
étudié ; cette interconnexion se fait au niveau du noeud k sur
lequel se produit un court-circuit.
Il est possible de reconstituer le nouveau réseau en
termes de matrice Y d?admittances tenant compte de l?interconnexion des trois
réseaux équivalents D, I et O.
Les éléments de cette matrice peuvent se
calculer soit en appliquant les définitions respectives des admittances
ponctuelles et de transfert données au premier chapitre, soit en
combinant d?une certaine manière les éléments bien
déterminés des matrices d?admittances directes , inverses et
homopolaires
déjà calculées pour chaque réseau ;
ces matrices sont données par les relations (2.36).
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
~
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
|
|
|
·
·
·
|
·
·
|
(2.36)
|
|
·
·
·
|
·
·
·
|
·
|
·
|
·
|
·
·
·
·
·
·
·
·
·
|
·
·
·
·
·
·
·
·
|
|
Quant à la matrice Z d?impédances du nouveau
réseau, il suffit d?inverser la matrice Y d?admittances calculée
au préalable.
2.6.1. Cas du défaut monophasé
Pour un défaut monophasé se produisant au noeud k
sur la phase « a », les réseaux D, I et O s?interconnectent
comme sur la figure 2.5.
Le nouveau réseau comprend 3n noeuds dont :
> 1, 2, ..., k, ~, n pour le réseau D ;
> 1+n, 2+n, ~, k+n, ~, 2n pour le réseau I ;
> 1+2n, 2+2n, ~, k+2n, ~, 3n pour le réseau O.
Nous calculons la matrice globale d?admittances en partant des
matrices d?admittances des réseaux D, I et O.
Les matrices d?admittances et d?impédances du nouveau
réseau obtenu sont des matrices carrées d?ordre 3n.
(2.37)
La matrice du nouveau réseau sera donnée par la
relation (2.38) dont certains de ses éléments sont donnés
par les relations (2.37).
) ~ ~ ) ?
~ ~ ~ ~ ~ ~ ?
; ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ?
~ ~ ~ ~ ~ ?
~
~ ~ ~ ~ ~ ?
~ ~ ~ ~ ~ ~ ?
~ ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ?
~ ~ ~ ~ ~ ?
) ~ ? ?
~
{ ~ ~ ? ?
Les autres éléments sont effectivement ceux des
matrices et de départ
des réseaux D, I et O.
|
~
|
·
·
·
·
·
·
·
·
·
·
·
·
|
|
·
·
·
·
·
·
·
·
· ~ ~
|
|
|
|
|
|
|
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
|
|
)
)
)
)
|
)
)
)
)
|
~
~
~
·
·
·
|
|
|
|
·
·
·
|
·
·
·
·
·
·
·
·
·
·
·
·
)
|
·
·
·
·
·
·
·
·
·
·
~o
) ~
|
|
) )
|
) )
|
"'
|
)
|
)
|
"'
|
)
|
)
|
|
|
|
·
·
·
|
|
|
|
·
·
·
|
|
|
|
·
·
·
|
)
|
~
|
~
|
|
|
·
·
·
|
|
|
|
~
|
|
|
|
|
|
·
·
·
|
|
)
|
)
|
~
|
|
|
|
·
·
·
|
)
|
~
|
~
|
(2.38)
|
|
·
·
·
|
|
|
|
~
|
|
|
|
|
|
·
·
·
|
|
|
|
·
|
|
|
|
·
·
·
|
)
|
~
|
~
|
|
|
|
·
·
·
|
·
·
·
|
|
|
|
|
|
|
|
·
|
|
|
|
·
|
|
|
|
·
·
·
|
|
|
·
·
·
|
|
|
|
·
·
·
|
·
·
·
|
|
|
|
|
)
|
)
|
)
|
)
|
~
|
|
)
|
)
|
|
)
|
)
|
·
·
·
|
|
|
·
·
·
|
|
|
|
·
·
·
|
·
·
·
|
|
|
|
|
|
|
·
·
·
|
|
|
|
|
|
~
|
|
|
·
·
·
|
)
|
)
|
~
|
|
|
|
|
|
|
·
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
·
·
·
|
...
|
|
|
|
|
|
|
|
|
|
|
|
|
~
|
|
|
·
·
·
|
|
|
~
|
|
|
·
·
·
Dans ce cas, la composante directe du courant de défaut
sur la phase « a » est donnée par :
Les tensions aux noeuds de la figure 2.5 se
déterminent par la relation (2.40) et il suffit de les combiner pour
retrouver les tensions aux noeuds du réseau réel à n
noeuds.
V
V V
V
V
V
V
V
V V
V V
V V ~ (2.40)
V V
V
V V
V
V [
V V
V
2.6.2. Cas du défaut biphasé
Pour un défaut biphasé se produisant au noeud k
entre les phases « b » et « c », les réseaux D, I
peuvent s?interconnecter comme sur la figure 2.10.
Après interconnexion des réseaux D et I, le nouveau
réseau comprend 2n noeuds dont :
> 1, 2, ..., k, ..., n pour le réseau D ;
> 1+n, 2+n, ..., k+n, ..., 2n pour le réseau I ;
Les matrices des admittances et des impédances du nouveau
réseau obtenu sont des matrices carrées d?ordre 2n.

k
k+n
Fig.2.10: Schéma équivalent du réseau
avec un
défaut biphasé au noeud k
Partant des matrices d?admittances des réseaux direct
et inverse de la relation (2.36), la matrice du nouveau réseau sera
donnée par la relation (2.42) dont certains de ses
éléments sont donnés par les relations (2.41).
|
~
|
|
~
|
|
~
|
~
|
~
|
|
?
~
|
~
|
~
|
~
|
|
~
|
~ ~ ?
|
~
|
~
|
~ ~
|
|
|
|
)
~
|
)
|
|
)
|
)
|
|
|
)
|
)
|
~ ?
|
~
|
~ ~
|
~
|
~
|
~
|
~
|
~
|
~ ?
|
~
|
|
|
(2.41)
|
|
|
|
|
|
|
|
|
~
|
~
|
|
? ~
|
?
|
~
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
·
·
·
|
|
|
·
·
·
|
|
|
|
|
|
·
·
·
|
|
)
|
)
|
·
·
·
|
|
|
|
|
|
|
|
|
·
·
·
|
|
|
·
·
·
|
|
|
|
|
|
·
·
·
|
|
)
|
)
|
·
·
·
|
|
|
|
|
|
|
|
|
·
·
·
|
|
|
·
·
·
|
|
|
|
|
|
·
·
·
|
|
)
|
)
|
·
·
·
|
|
|
|
|
|
|
|
|
|
|
|
|
·
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
·
·
·
|
·
·
·
|
|
|
·
·
·
~
|
|
|
|
|
|
·
·
·
·
·
·
|
|
)
|
)
|
|
·
·
·
|
(2.42)
|
|
|
|
) )
|
|
)
|
)
|
"'
|
|
|
) )
|
"'
|
)
|
)
|
|
|
·
·
·
|
|
|
|
|
·
·
·
|
|
|
|
|
|
|
·
·
·
|
|
|
|
|
~
|
|
|
|
|
·
|
|
)
|
|
)
|
·
·
·
|
|
|
|
|
|
|
·
|
|
|
|
|
~
|
|
|
|
|
·
·
·
|
|
|
|
|
~
|
|
La composante directe de Fortescue du courant de défaut
sur la phase « a » est donnée par :
Les tensions aux noeuds de la figure 2.10 se
déterminent par la relation (2.44) et il suffit de les combiner pour
retrouver les tensions aux noeuds du réseau réel à n
noeuds.
|
V
~
~
v
|
V
V
V1
v,
|
|
[
|
(2.44)
|
|
|
~
|
|
V
V
V
v
|
V
~
VI
~
|
|
2.6.3. Cas du défaut biphasé-terre
Pour un défaut biphasé-terre franc se produisant
au noeud k entre les phases « b » et « c », les
réseaux D, I et O peuvent s?interconnecter comme sur la figure 2.11.
Les éléments de cette matrice globale
d?admittances peuvent se calculer en appliquant les définitions
respectives des admittances ponctuelles et de transfert en rapport avec la
figure 2.11.
Après interconnexion des réseaux D, I et O, le
nouveau réseau comprend (3n1) noeuds dont :
> 1, 2, ..., k, ..., n pour le réseau D ;
> 1+n, 2+n, ..., k+n, ..., 2n pour le réseau I ;
> 1+n, 2+2n, ..., k+2n, ..., 3n-1 pour le réseau O.
Les matrices d?admittances et d?impédances du nouveau
réseau obtenu sont des matrices carrées d?ordre (3n-1).

Fig.2.11 : Schéma équivalent du réseau
avec un défaut biphasé-terre au noeud k
La composante directe de Fortescue du courant de défaut
sur la phase « a » est donnée par :
~
v (2.45)
Les tensions aux noeuds de la figure 2.11 se
déterminent par la relation (2.46) et il suffit de les combiner pour
retrouver les tensions aux noeuds du réseau réel à n
noeuds.
V
V V
V
V
V
V
V
V V
V V
V V ~ (2.46)
V V
V
V V
V
V [
V - V
V
2.7. Court-circuit symétrique [1], [7], [8]
L?analyse des conditions de défaut permet d?obtenir un
certain nombre de paramètres importants dont les principaux sont :
> les courants maximum et minimum d?un court-circuit
triphasé (condition sévère d?un défaut) ;
v [ ] (2.47)
est le courant initial (courant subtransitoire) de court-circuit
et un
coefficient qui est fonction du rapport entre la
résistance et la réactance de Thevenin vue de l?endroit du
court-circuit (tableau 2.1).
> le courant de coupure qui est le courant symétrique
lors de l?ouverture d?un disjoncteur ;
~ [ ] (2.48)
Où est un coefficient dépendant du rapport entre
le courant symétrique de court-circuit et la somme des courants nominaux
de tous les alternateurs en service dans le réseau (tableau 2.1).
> le mode de fonctionnement des relais de protection ;
> la capacité (pouvoir de coupure symétrique)
des disjoncteurs, la répartition du courant de défaut et les
tensions aux différents noeuds du réseau au moment du
défaut ;
~ v ~ (2.48)
~ = puissance de coupure et = tension nominale. > la puissance
de court-circuit
La puissance de court-circuit complexe en per unit vaut :
[p ] V [p ] [p ] (2.49)
Elle est équivalente au courant de court-circuit si la
tension nominale correspond à la tension de base et elle est l?inverse
de l?impédance de court-circuit (impédance de Thevenin) du
réseau vue de l?endroit du court-circuit. Le réseau peut
être représenté par l?équivalent de Thevenin
constitué de cette impédance mise en série avec une source
de tension valant la tension nominale ~ [p ].
[p ] [p ] (2.50)
Plus la puissance de court-circuit est élevée, plus
le réseau est insensible aux perturbations [7].
Tableau 2.1

NORMES ET CALCULS DES COURANTS DE COURT-CIRCUIT
Les normes proposent plusieurs méthodes de calculs des
courants de court-circuit.
> Le guide pratique C 15-105, qui complète la NF C
15-100(installations BT alimentées en courant alternatif),
présente les trois méthodes suivantes :
- La méthode des " impédances » qui permet
de calculer les courants de défaut en tout point d?une installation avec
une bonne précision en totalisant différentes impédances
de la boucle de défaut, de la source jusqu?au point
considéré ;
- La méthode de " composition » utilisable lorsque
les caractéristiques de l?alimentation ne sont pas connues.
L?impédance amont du circuit considéré est calculée
à partir de l?estimation du courant de court-circuit à son
origine ;
- La méthode " conventionnelle », qui permet sans
connaître les impédances ou les courants de court-circuit de la
partie d?installation en amont du circuit considéré, de calculer
les courants de court-circuit minima et les courants de défaut à
l?extrémité d?une canalisation. Elle est basée sur
l?hypothèse que la tension à l?origine du circuit est
égale à 80% de la tension nominale de l?installation pendant la
durée du court-circuit ou du défaut.
> La norme CEI 60909 (VDE 0102) s?applique à tous
les réseaux, radiaux et maillés, jusqu?à 550 kV.
Basée sur le théorème de Thevenin, elle consiste à
calculer une source de tension équivalente au point de court-circuit
pour ensuite déterminer le courant en ce même point. Toutes les
alimentations du réseau et les machines synchrones et asynchrones sont
remplacées par leurs impédances (directe, inverse et
homopolaire).
2.8. Les effets des courants de défaut dans les
équipements électriques [1], [11]
Les effets du courant de défaut sont multiples et
variables selon la nature et la durée de défaut, le point
concerné du réseau et l?intensité du courant. Parmi ces
effets, on peut citer :
> les efforts électrodynamiques de courant de
défaut dans les équipements (déformation des jeux de
barres, arrachement des câbles, ~);
> les effets thermiques (suréchauffements par
augmentation des pertes par effet Joules, avec risque de
détérioration des isolants);
> les creux de tensions ;
> l?instabilité dynamique et/ou la perte de
synchronisme des machines ;
> les effets d?induction dans le réseau de
télécommunication (réseau à câbles et lignes
aériennes).
Chapitre III. CALCUL DE DEFAUTS DANS UN RESEAU
ELECTRIQUE SOUS MATLAB
3.1. Introduction
MATLAB est un logiciel optimisé pour le
traitement des matrices, d?où son nom MATrix LABoratory.
Pour les calculs numériques, MATLAB est
beaucoup plus concis que les «vieux» langages (C, Pascal, Fortran,
Basic) [13]. Il contient également une interface graphique puissante,
ainsi qu?une grande variété d?algorithmes scientifiques.
On peut l?enrichir en ajoutant des «boîtes à
outils» (toolbox) qui sont des ensembles de fonctions
supplémentaires, profilées pour des applications
particulières (traitement de signaux, analyses statistiques,
optimisation, etc.).
Dans ce dernier chapitre, nous ferons une brève
présentation du logiciel MATLAB, et nous dirons un mot sur l?utilisation
des scripts et fonctions qui calculent les courants de court-circuit que nous
avons écrits, cela sera suivi d?une série d?exemples
d?application et une comparaison des résultats de deux méthodes
de calcul précitées sera faite.
3.2. Présentation de MATLAB
MATLAB est un logiciel interactif essentiellement basé
sur le calcul matriciel. Il est utilisé dans les calculs scientifiques
et les problèmes d?ingénierie étant donné qu?il
permet la résolution des problèmes numériques complexes en
moins de temps requis par les langages de programmation, et ce grâce
à une multitude de fonctions intégrées et à
plusieurs programmes outils testés et regroupés selon usage
(boites à outils ou Toolbox).
Après que le logiciel soit installé, on peut
démarrer MATLAB en doublecliquant sur son icône ou saisir
l?instruction matlab dans l?invite de commande de Windows. Une ou
plusieurs fenêtres identifiables par leurs noms affichés dans les
barres de titre respectives apparaissent.
L?interface de la version de MATLAB que nous avons utilisé
dans ce travail se présente comme sur la figure 3.1.
Fig.3.1 : L'espace de travail MATLAB 7.9.0
Les déclarations et les commandes peuvent être
introduites ligne par ligne dans la fenêtre de commande (Command Window)
ou sous forme d?un script dans un éditeur (figure 3.2) qui peut
être évoqué par la commande edit.
L?exécution du script (le fichier des commandes une
après une) se fait à l?aide du bouton Save and Run ou avec le
menu debug/Save File and Run ou bien, simplement, en appuyant sur la touche
fonction F5.
Les résultats d?exécution sont affichés dans
la fenêtre de commande de la même manière que si les
commandes sont entrées dans cette fenêtre.
Fig.3.2 :L'éditeur MATLAB 7.9.0
MATLAB fonctionne essentiellement avec un seul type d?objets :
des matrices rectangulaires avec des éléments pouvant être
réels, complexes ou symboliques.
Les scalaires sont interprétés comme des matrices
1×1.
Une matrice peut être introduite dans MATLAB de plusieurs
façons :
> Entrée explicitement par liste des
éléments (>> A = [1 2;3 4]); >
Générée par une fonction interne (>> B = zeros(2,2))
;
> Entrée à partir d?un fichier script avec
l?éditeur ;
> Chargée à partir d?un fichier de
données ou importée d?une application (ce qui est le cas pour le
présent travail).
Les aspects élémentaires de MATLAB sont : les
aides (help, doc, whos, ...), les variables scalaires, workspace, les
opérations élémentaires (+, -, *, /, \, ^), les
commentaires, les variables spéciales (i, j, inf, pi, eps,...), les
nombres complexes, les fonctions mathématiques, le format d?affichage et
les entrées-sorties.
3.3. Programmation dans MATLAB [12], [13]
Il est possible d?enregistrer des séquences de commandes
MATLAB dans des fichiers portant l?extension .m qui sont nommés
M-files.
L?exécution de toutes ces commandes se fait
automatiquement dès que le nom du fichier est saisi et validé.
Dans leur forme la plus simple, de tels fichiers sont
nommés script files. Après l?introduction des
premières lignes du programme, il est recommandé de sauvegarder
le travail et d?attribuer un nom au fichier en utilisant l?option du menu File
de l?éditeur.
MATLAB offre à son utilisateur la possibilité de
programmer ses propres fonctions. Tout comme les scripts, les fichiers de
fonctions sont également des fichiers M-files ; pour cela le premier
terme (après d?éventuels commentaires) doit être function.
Les fichiers de fonctions prennent des arguments externes, placés entre
parenthèses, immédiatement après le nom de la fonction.
3.4. Données du programme
Toutes les données sont en per unit et doivent
être introduites dans un fichier de données avec une extension
.top, qui doit contenir les informations suivantes :
> Le nombre de noeuds, de lignes, de transformateurs, de
machines synchrones, d?éventuels éléments shunts (bancs de
condensateurs + bancs d?inductances) ;
> La période de calcul de défaut
(subtransitoire, transitoire, ou permanente) ;
> La puissance (MVA) et différentes tensions (kV) de
base ;
> Les caractéristiques des composants du
réseau d?étude (machines synchrones, transformateurs, lignes,
bancs de condensateurs ou d?inductances éventuels) en per unit avec une
base commune de puissance pour tout le réseau ;
> Les phaseurs tensions aux noeuds avant l?apparition d?un
quelconque défaut. Ces tensions sont les sorties du programme de load
flow qui dépasse le cadre de ce travail ;
> Le type de défaut à calculer (défaut
monophasé, défaut biphasé, défaut
biphasé-terre, défaut triphasé) ;
> Préciser le noeud en défaut et les phases
concernées par le défaut ; > L?impédance de
défaut.
Après introduction de toutes ces informations dans le
fichier de données, le script les importe dans MATLAB sous forme
matricielle grâce à la commande textscan et c?est cette matrice
qui est exploitée pour opérer les calculs qui font l?objet de ce
travail.
Il faudra prendre soin de mettre la virgule après la
saisie de chaque donnée.
Les données lues sont alors mises en forme, ensuite les
scripts calculent pour le noeud concerné le courant de défaut de
chaque séquence de fonctionnement (directe, inverse et homopolaire) du
réseau après avoir calculé les matrices d?admittances et
d?impédances des réseaux direct, inverse et homopolaire, cela en
tenant bien sûr compte de la tension de Thevenin en ce noeud avant
l?apparition dudit défaut.
Les phaseurs tensions aux noeuds du réseau pendant le
défaut se calculent par l?utilisation des relations (2.10) du
deuxième chapitre et les différents transits de courants se
calculent à partir de leurs composantes symétriques
données par les relations (2.13).
3.5. Fichier de données
Un exemplaire d?un fichier de données nommé
donneesexemple0.top et contenant une légende qui
fournit les détails sur les informations à inscrire dans ce
fichier est le suivant :

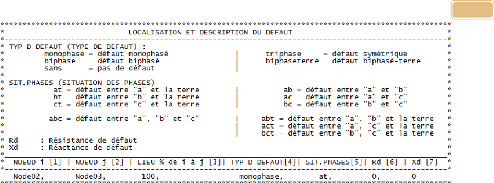
54
C?est fichier texte qui peut s?ouvrir soit avec le bloc-notes,
soit par le command window avec l?instruction edit donneesexemple0.top.
Pour une machine synchrone qui n?est pas reliée à
la terre, Rgn=inf et Xgn=inf.
Dans la colonne de noeuds auxquels sont connectées les
machines, un noeud ayant plus d?une machine sera saisi autant de fois qui
correspondent au nombre de machines connectées à ce noeud ; il en
est de même pour la colonne de noeuds auxquels sont connectées les
bancs de condensateurs et/ou d?inductances.
Le champ en rapport avec les informations sur le SHUNT doit
être vide si Nsh=0 ; on pourra le constater avec la série
d?exemples.
En ce qui concerne les colonnes de noeuds qui constituent les
branches (lignes ou transformateurs), si le réseau dispose de lignes
et/ou de transformateurs en parallèle, il vaut mieux saisir les noeuds
concernés par le groupement parallèle autant de fois qu?il y a
des transformateurs et/ou des lignes en parallèle.
Si une ligne est à deux ternes et que ses
paramètres sont donnés par terne, dans notre programme nous
considérons qu?il s?agit de deux lignes en parallèle ; mais s?ils
sont donnés par phase, on considère que c?est une seule ligne.
Pour un transformateur dont une étoile n?est pas
reliée à la terre, Rn=inf et Xn=inf.
3.6. Utilisation du programme de calcul de
défauts
Les possibilités permettant de lancer notre programme de
calcul des défauts sont :
> La première se fait par une interface graphique
à travers la fonction fault_program qui, à son
tour appelle le script calcul_defaut_dans_reseau.m ; pour
cela, il convient de saisir fault_program dans le command
window. Dès que cela est validé, une fenêtre de la figure
3.3 apparait, et il suffit de cliquer sur le bouton
Défaut pour lancer le programme.

> La seconde possibilité se fait par la fonction
CalculDefaut ; l?argument de cette fonction est le nom du
fichier de données que l?on doit saisir avec son extension entre les
apostrophes ; on écrit par exemple :

On utilise la première syntaxe lorsqu?on n?a pas besoin
de stocker les variables dans le workspace et la seconde si on veut
mémoriser les variables indiquées pour faire un autre calcul tel
que la détermination des matrices globales d?admittances et
d?impédances ; Avec : Yreseau1=Yd , Yreseau2=Yi, Yreseau0 = Yh, Zd=Zf ,
Vf=Vecteur tension avant l?apparition du défaut.
Il faudra saisir ces variables comme indiqué dans la
deuxième syntaxe.
Fig.3.3 : Interface graphique fault_program
Avant le lancement de notre programme, pour que les
résultats s?affichent correctement, il faudra prendre soins de maximiser
la fenêtre Command Window de l?interface Matlab soit en cliquant
sur le bouton Maximize Command Window, soit en cliquant sur l?onglet
Desktop, puis sur Desktop Layout et enfin sur Command
Window only.
La fonction fault_program.m ou la fonction
CalculDefaut.m lance automatiquement le script
calcul_defaut_dans_reseau_suite1.m qui appellera aussi
calcul_defaut_dans_reseau2.m.
Les autres fonctions que nous avons créées sont
:
> lignetfo : qui permet la séparation
des données de lignes et celles de transformateurs qui sont tous les
branches ;
> admittance_globale_mono : qui
génère les matrices globales d?admittances et d?impédances
résultant de l?interconnexion des réseaux D, I et O due au
défaut monophasé ;
> admittance_global_biphase : qui
génère les matrices globales d?admittances et d?impédances
résultant de l?interconnexion des réseaux D et I due au
défaut biphasé ;
Les autres scripts sont :
> admittance_globale_biphaseterre.m : qui
génère les matrices globales d?admittances et d?impédances
résultant de l?interconnexion des réseaux D, I et O due au
défaut monophasé ; pour ce script, il faut lancer le programme
des défauts par le script calcul_defaut_dans_reseau.m
;
> tensions_cas_monophase.m : qui calcule
les tensions aux pendant le défaut monophasé par la
méthode de la matrice globale d?impédances ;
> tensions_cas_biphase.m : qui calcule les
tensions aux pendant le défaut biphasé par la méthode de
la matrice globale d?impédances.
L?utilisation des scripts tensions_ cas_monophase.m et
tensions_cas_biphase.m nécessite que les matrices
globales
d?impédances soient calculées au préalable.
3.7. Exemples d'application 3.7.1. Exemple 1 [5,
p 274 a 280]
On considère le réseau électrique de la
figure 3.4. Supposons qu?un court-circuit symétrique se produit du
côté haute tension (Node04) du transformateur T2.
Supposant que le réseau est initialement à vide avec la tension
de ? pu au niveau de tous les noeuds, déterminons le courant de
défaut, les tensions aux noeuds pendant le défaut et
différents transits de courants dans ce réseau pendant la
période subtransitoire.
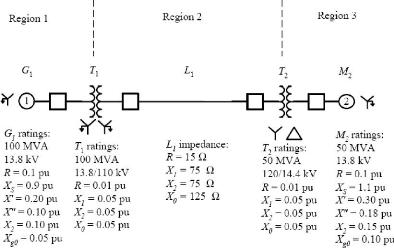
NodeO1 NodeO2 NodeO3 NodeO4
Fig.3.4 : Diagramme unifilaire du réseau a 4 noeuds de
l'exemple 1
On inscrit les données dans le fichier nommé
donneesexemple1.top suivant :
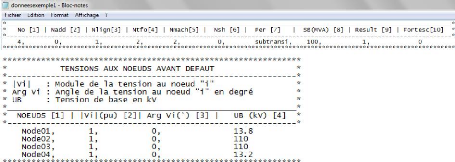
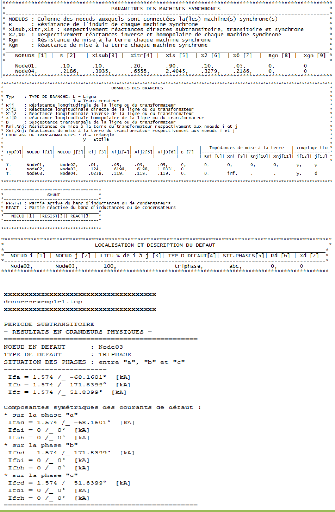
> Résultats du programme :
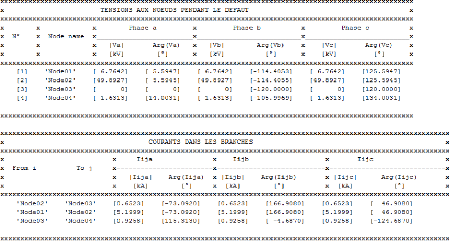
3.7.2. Exemple 2 [5, p 298 a 309]
Les informations du réseau de la figure 3.5 dans lequel
a lieu un court-circuit monophasé au noeud 4 sont données
ci-après. Supposant que le réseau est initialement à vide
( ? pu), déterminons le courant de défaut, les tensions aux
noeuds pendant le défaut et différents transits de courants dans
ce réseau pendant la période subtransitoire, toutes les
résistances sont à négliger.

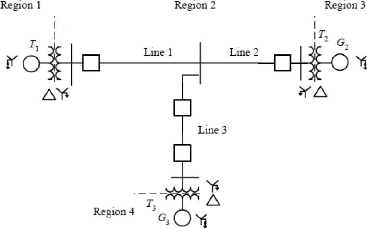
Kwilu Kimwenza Liminga
Lingwala
Fig.3.5 : Diagramme unifilaire du réseau a 7 noeuds de
l'exemple 2 Admettons que sur ce réseau de la figure 3.5 :
> Le noeud sur lequel est connecté le groupe G1 se
nomme Maluku ; > Le noeud sur lequel est connecté le groupe
G2 se nomme Utexco ; > Le noeud sur lequel est connecté le
groupe G3 se nomme Funa.
On inscrit les données dans le fichier nommé
donneesexemple2.top comme suit :
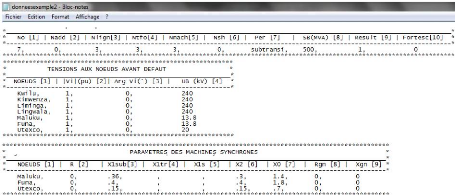
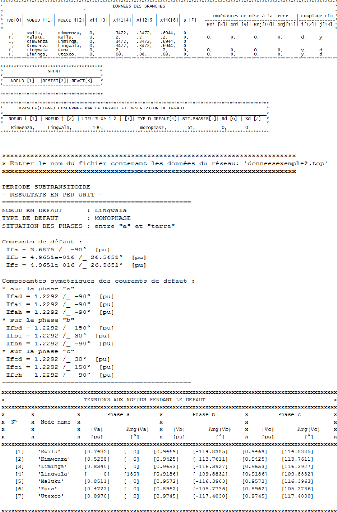
> Résultats du programme :
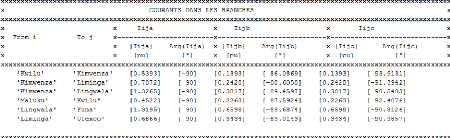
3.7.3. Exemple 3 [4, p 274]
Les données en pu du réseau connecté
à un jeu de barres infini de la figure 3.6 sont les suivantes :

Soit à déterminer le courant de défaut
dû à un court-circuit monophasé se produisant du
côté où le transformateur T1 est couplé en
étoile (noeud 222222) au moment où aux bornes de deux
générateurs et au jeu de barres infini nous avons une tension de
? pu.

111111
444444
222222 333333
Fig.3.6 : Réseau connecté à un jeu de
barres infini
On inscrit les données dans le fichier nommé
donneesexemple3.top comme suit :

> Résultats


3.7.4. Exemple 4 [2, p 271 a 274]
Un réseau comprend deux alternateurs fonctionnant en
parallèle et alimentant un moteur synchrone recevant une puissance de 60
MW à un facteur de puissance arrière de 0.8 sous une tension de 6
kV.
Soit à déterminer le courant de défaut,
les tensions aux noeuds pendant le défaut et différents transits
de courant si un défaut monophasé a lieu au milieu de la ligne
à travers d?une résistance de 4.033 Ù.
Le schéma unifilaire de ce réseau est donné
par la figure 3.7 dont les données sont les suivantes :


Kwilu Kimw1
Kimw2
Fig.3.7 : Diagramme unifilaire de l'exemple 4
Inga

> Résultats


3.7.5. Exemple 5 [5, p 285, 292, 293, 294]
Soit un alternateur triphasé de 200 MVA, 20 kV, 60 Hz,
couplé en étoile et directement relié à la terre.
Il est connecté à une ligne 138 kV au travers d?un transformateur
de 200 MVA, 20/138 kV, Y-Y.
Se référant à la base de 200 MVA, 20 kV,
les réactances de l?alternateur sont Xs = 1.40 pu, X? = 0.30
pu, X?? = 0.15 pu, X2 = 0.15 pu, Xg0 = 0.10 pu et pour le transformateur dont
les neutres sont directement mis à la terre, les réactances
séries directe, inverse et homopolaire sont identiques et égalent
à 0.10 pu. Les résistances de l?alternateur et du transformateur
peuvent être négligées.
Supposons qu?un court-circuit biphasé-terre se produit
au jeu de barres 138 kV alimenté par le transformateur.
Déterminer le courant de court-circuit, les tensions aux deux noeuds
pendant la période subtransitoire.
Données :

> Résultats du programme :


3.7.6. Exemple 6
Supposons à présent que toutes les
résistances des composants du réseau de l?exemple 1 (figure 3.4)
soient négligées pour déterminer l?écart des
courants dans le défaut de ce cas et celui du cas où les
résistances sont prises en compte ; les conditions de défaut
étant les mêmes que celles de l?exemple 1.
Le fichier de données nommé
donneesexemple1_Ro.top est le suivant :


Résultats :


Il est à remarquer que le module du courant dans le
défaut vaut 1.574 kA dans le cas où les résistances sont
prises en compte et 1.7059 kA lorsque les résistances sont
ignorées ; l?écart relatif vaut :
9 - 1.574)
1.7059
3.8. Comparaison des tensions obtenues en p.u de deux
méthodes de calcul des défauts
3.8.1. Comparaison sur l'I-xI-P SlI-i2 a)
Méthode ordinaire


b) Méthode d?interconnexion des réseaux D, I et
O

3.8.2. Comparaison sur l'exemple 3 en considérant un
défaut biphasé au noeud 222222 entre les phases b et c

a) Méthode ordinaire

b) Méthode d?interconnexion des réseaux D et I

La matrice globale d?impédances du nouveau réseau
est :

Nous remarquons que ces deux méthodes de calcul conduisent
aux mêmes résultats.
CONCLUSION
Le fonctionnement d?un réseau électrique peut
être sujet à l?apparition des défauts occasionnant des
courants élevés, avec de lourdes conséquences qui peuvent
se révéler néfastes tant pour les équipements que
pour la suite de l?exploitation.
Ce travail a pour objectif la détermination des
courants des défauts, du plan de tensions et des différents
courants dans toutes les branches lors d?un défaut et plus
particulièrement les cas de court-circuit en un noeud quelconque d?un
réseau multi-machines.
Pour ce faire, en supposant le cas d?un régime
permanent, il possible d?utiliser tant le concept des phaseurs que la
méthode des composantes de Fortescue.
Les machines sont modélisées par la mise en
série de leurs résistances d?induit et réactances, selon
le cas, subtransitoire, transitoire ou synchrone ; les transformateurs et les
lignes de transmissions sont modélisés respectivement par leurs
schémas équivalents en T et en ð.
Les éventuels bancs de condensateurs ou d?inductances aux
jeux de barres étant modélisés par leurs impédances
équivalentes.
Les défauts susceptibles de se produire dans un
réseau peuvent être soit des ouvertures des phases, soit des
courts-circuits ; dans le cadre de ce travail, nous n?avons traité que
les cas des courts-circuits francs ou impédants qui peuvent être
soit monophasé, soit biphasé, soit biphasé-terre ou encore
triphasé et pouvant se localiser sur un noeud existant ou sur une ligne
de transmission ; et dans ce dernier cas, un noeud supplémentaire sera
ajouté au reste du réseau. Ce noeud se connectera aux noeuds
adjacents de la ligne concernée par des impédances dont les
valeurs sont proportionnelles à la localisation du défaut.
Sur ce, le calcul des courants des courts-circuits a
été traité par deux méthodes ; la première
qui a consisté à déterminer toutes les composantes
symétriques du courant de court-circuit par utilisation
séparée des matrices d?impédances directe, inverse et
homopolaire. Quant à la seconde méthode, elle a consisté
à calculer les courants de court-circuit via l?interconnexion des
réseaux direct, inverse et homopolaire en combinant les matrices
précitées en fonction du type de court-circuit.
Les exemples traités indiquent que les résultats
correspondent à ceux des références, et nous permettent
d?affirmer que ces deux méthodes sont équivalentes.
Les calculs indiquent aussi que les plus grands courants sont
ceux avec les réactances subtransitoires des machines, et le
réseau offre alors le plus mauvais plan de tensions lors du
défaut.
L?écart relatif entre le courant dans le défaut
lorsque les résistances de tous les composants du réseau sont
prises en compte, et celui du cas où toutes ces résistances
seraient négligées est généralement
inférieur à 10%.
Notre programme de calcul de court-circuit est d?application pour
un réseau électrique à n?importe topologie et peut servir
à :
- Déterminer l?équivalent de Thevenin d?un
réseau vu d?un noeud quelconque ;
- Faire des réglages des relais de protection de par le
fait qu?il calcule les courants dans toutes les branches et les tensions sur
tous les noeuds tant de phases que des composantes symétriques lors d?un
défaut.
Les résultats de ce programme constituent une sorte de
solution pour le dimensionnement et le choix de l?appareillage
électrique, et tant d?autres équipements d?un réseau.
Il serait prétentieux pour nous de dire que le ce
travail répond à tous les besoins, certains aspects du
présent projet peuvent faire l?objet d?une étude poussée
que nous recommandons aux générations futures.
Parmi les points restants et pouvant contribuer au projet, plus
particulièrement à l?aspect modélisation et calcul des
courants de défaut, nous indiquons :
- La possibilité de traiter plusieurs défauts de
divers types à la fois;
- La modélisation de l?ouverture d?une ou plusieurs
phase(s) étant donné que cela fait partie des défauts
déséquilibrés ;
- L?intégration du programme des calculs de
défauts au projet global de mise oeuvre d?un outil de simulation des
réseaux multi-machines ; et plus particulièrement au programme de
load flow devant calculer les tensions initiales qui sont utilisées dans
le programme développé dans ce travail.
REFERENCES
[1] Pr.Dr.Ir. KITOKO SENGHI, Centrales et Réseaux
électriques, Cours, Université de Kinshasa,
Faculté Polytechnique, 2008.
[2] Pr.Dr.Ir. KITOKO SENGHI, Réseaux
électriques, Cours, Université de Kinshasa,
Faculté Polytechnique, 2008.
[3] Pr.Dr.Ir. J.M. BEYA, Statique et Dynamique des
Réseaux électriques, Cours, Université de
Kinshasa, Faculté Polytechnique 2011.
[4] Prof. DEBAPRIYA DAS, Electrical Power
Systems, India Institute of Technology, 2006.
[5] Stephen J. Chapman, Electric Machinery and Power
System Fundamentals, First Edition, 2001.
[6] Prof William D.STEVEN, Elements of Power Systems
analysis, Fourth Edition, 1988.
[7] Prof. Jean-Louis LILIEN, Transport et Distribution de
l'énergie électrique, Université de
Liège, Faculté des Sciences Appliquées, 2000
[8] B. de METZ-NOBLAT, F. DUMAS et C. POULIN, Calcul
des courants de court-circuit, Schneider Electric, Cahier
Technique 158, édition Septembre 2005.
[9] Pr.Dr.Ir. KAMABU TSONGO, Machines
électriques, Cours, Université de Kinshasa,
Faculté Polytechnique, 2008
[10] Pr.Dr.Ir. KAMABU TSONGO, Compléments des
machines électriques, Cours, Université de
Kinshasa, Faculté Polytechnique, 2008.
[11] B. de METZ-NOBLAT, Les calculs sur les
réseaux électriques BT et HT, Schneider Electric,
Cahier Technique 213, édition Décembre 2004.
[12] Adrian BIRAN et Moshe BREINER, Matlab pour
l'Ingénieur, Versions 6 et 7, Paris, 2004.
[13] Alfred A. MANUEL, Eléments de
Matlab, Université de Genève, 2004.
ANNEXES
Résultats du calcul de défaut de l'exemple 1
pendant la période transitoire

Résultats du calcul de défaut de l'exemple 1
pendant la période riiiiiianiin ii

Résultats du calcul de défaut de l'exemple 2
pendant la période subtransitoire
avec les composantes symétriques des tensions aux
noeuds et celles des courants dans les branches



| 


