La théorie de la gravité quantique de Bohm dans l'approximation linéaire du champ

RÉPUBLIQUE DU CAMEROUN REPUBLIC OF CAMEROON

Paix - Travail - Patrie Peace - Work - Fatherland



UNIVERSITÉ DE YAOUNDE I UNIVERSITY OF YAOUNDE I

Ecole Normale Supérieure Higher Teacher's Training School

DÉPARTEMENT DE PHYSIQUE DEPARTMENT OF PHYSICS



La théorie de la gravité quantique de BOHM
Dans l'approximation linéaire du champ

MÉMOIRE
Présenté en vue de l'obtention du
Diplôme de Professeur de L'enseignement secondaire deuxième grade
(DI.P.E.S II)

1ffI

Lucien MANDENG MANDENG

Elève - professeur en 5^ème année physique

P.C.E.G / Maître es sciences

Matricule : 02Y497

Option : Mécanique Matricule : 02Q076

Jury

Président : Professeur Timoléon Crépin KOFANE, Labo de Mécanique, Université de Yaoundé I Rapporteur : Docteur Jean - Marie MBOUNGA, E.N.S de Yaoundé, Université de Yaoundé I Examinateur : Docteur Edmond GNOKAM, E.N.S de Yaoundé, Université de Yaoundé I

Année académique 2006 - 2007

Dédicace

Ce mémoire est dédié à toute ma famille en partant des lointains ancêtres aux descendants à venir, particulièrement à la mémoire de feu mon frère MANDENG Clément Hervé.

Remerciements

Mes remerciements s'adressent à tous ceux qui de près ou de loin m'ont soutenu, encouragé, contribué (et continuent à le faire) à mon évolution scolaire, ainsi qu'à la réalisation de ce mémoire : Je tiens à leur témoigner ici mon éternelle reconnaissance à ce moment, où se « s'achève » un long périple de 5 ans passés en formation l'E.N.S de Yaoundé. Périple n'ayant pas été des plus faciles, avec tous les désagréments, écueils, difficultés de toutes sortes mais qui heureusement grâce à la justice Divine finit ici avec la réalisation de ce travail. Tout ce que je souhaite , c'est que ce beau monde continue dans cette voie en soutenant les générations à venir dans cette voie de la valorisation de la pensée qui place l'Homme égal d'une Entité Supérieure, car comme le dit si couramment l'un de mes proches « On peut tout refuser à l'Homme ,mais certainement pas le chemin qui le mène vers la connaissance » ; Du monde auquel s'adresse ses remerciements , je pense particulièrement :

-A la justice Divine, qui permet que je sois encore animé dans ce plan de la réalité objective de l'espace -- temps quadridimensionnelle correspondant à la source de matière qu'est la planète Terre.

- - A ma famille (frères et soeurs proches ou lointains), qui m'a toujours soutenu et a toujours cru en moi et participe grandement à l'organisation concernant à la présentation de ce travail

- A mon grand -- mère maternel pour ses bénédictions.

- - A mon père M. MANDENG Emmanuel, et à ma mère Mme MANDENG Marie - Claire, je témoigne ici le profond attachement que j'éprouve pour eux, compte tenu des sacrifices qu'ils ont dû concéder sur leur bien -- etre matériel et spirituel afin que je puisse arriver jusqu'ici.

- A mon encadreur M. MBOUNGA Jean -- Marie, dont le savoir, les encouragements, la disponibilité, les critiques, les remarques judicieuses ont contribué à l'achèvement de ce travail et à ma formation à l'E.N.S de Yaoundé.

- A Monsieur le Pr. Timoléon Crépin KOFANE, pour l'aide qu'il a eu à m'apporter quant aux difficultés que j'ai rencontrées dans le calcul tensoriel, aussi au Dr. BOUETOU pour ses judicieux conseils quant à la démarche à entreprendre dans la quête d'informations sur l'article utilisé.

- A mes Professeurs à l'E.N.S : Dr. OWONO, Dr. GNOKAM, Dr. BEGUIDE, Dr. MUKAM, Dr. FOUPOUAGNIGNI, les Professeurs de Chimie...

-A ma soeur Ngo MANDENG Sylvie, pour son soutien continuel, et pour m'avoir aidé à éditer ce

travail.

-A la famille TOUKO pour tout ce qu'elle a fait pour moi. Je remercie particulièrement M. POUGOUE TOUKO pour son assistance technique à la présentation de ce travail.

- A Mlle Dora ANDEME, pour avoir bien voulu consacrer de son précieux temps à la relecture de ce travail et à l'organisation de la présentation de ce travail.

- A M. BAYIHA

- A mes professeurs de Collège et Lycée qui ont cru en moi : M. Prosper BAYEBECK, M. Philippe MAEMBLE, M. Thomas KANGA, M. Ruben BIKOÏ, M. Joachim DJOMGANG, M. BABE bref à tous ceux qui ont eu la bienveillance de partager leur connaissance avec moi.

- - A tous mes camarades d'études et amis , je pense à : NKOT BALEGUEL François , William LANG , Jacques Christian KOTTA, Laurent FOTSE, Rémy TAKOGUE , Fredy FEZEU, bref à tous mes camarades promotionnaires depuis l' école maternelle Groupe 1 ,2^ème section d'Abong -- Mbang (1990 -- 1991) à la 5^ème année physique E.N.S (06 -- 07 )

- A ceux dont les aides particulières en documentation m'ont facilité la tache dans mes études jusqu'ici , je pense à : M. Joachim DJOMGANG ( Précis de chimie Paul Arnaud) , M. POUGOUE TOUKO (Mécanique , Fondements et applications J.P Perez) , M. Gabriel MINYEMECK ( Relativité restreinte , Electromagnétisme , et cours divers ...) , M. Désiré (Electrotechnique , cours divers...) , M. Jacques DJON ( Documents en mathématiques ...) .

- A mes encadreurs de stages pratiques (3ème et 5^ème année) pour avoir partager avec moi leur expérience professionnelle en matière d'enseignement : M. Michel DONFOUET, Mme Cécile TSAMO.

- - Aux mathématiciens J.B PATENOU et son collègue pour m'avoir aidé à surmonter les difficultés concernant le formalisme mathématique assez ardu utilisé dans ce travail. Je pense également aux étudiants en mathématiques Patrick et Placide pour leur soutien logistique aidant dans la présentation de ce travail sans oublier Mlle NIETCHA Merline (étudiante en informatique) pour avoir bien voulu prendre de son temps pour la réalisation des différentes courbes apparaissant dans ce travail.

- A mon amie Sandrine HUET pour ses encouragements et son soutien moral.

En somme je remercie ainsi, tous ceux et celles dont les noms ne figurent certainement pas ici mais qui n'en sont pas moins pour quelque chose dans mon évolution et dans la réalisation de ce travail.

Une fois de plus, merci a tous.

Avant - Propos

Il y a près de deux ans que j'ai eu à réaliser un travail (Projet de mémoire [5]) sur « Le déterminisme en physique », un sujet qui débattait sur les fondements conceptuels du duel entre les théories déterministes et les théories indéterministes (probabilistes) en physique [6]. J'avais voulu dans le cadre ce travail là, toucher du doigt les points clé de la divergence entre ces deux méthodes de la prévision en physique, principalement, ceux qui rendaient incompatibles la théorie de la mécanique quantique d'avec les théories classiques telles que la relativité générale. Puisque les pensées de la grande synthèse unitaire concourent actuellement à vouloir établir un pont entre ces deux enfants terribles des physiciens du début du 20^ème siècle et d'après ce que j'ai pu lire [3 -- 16], le sujet principal de la physique fondamental tourne autour de cet improbable pont conduisant vers l'unité. Aussi c'est dans un souci de continuer dans cette lancée que, j'ai voulu inscrire mon travail de fin formation à l'ENS de Yaoundé. Pour cela j'ai dl chercher à formuler mon sujet moimême, ce qui certainement vous le pensez aurait été une prétention de ma part ; toujours est -- il que quand mon encadreur, m'a présenté la revue « Physica scripta 2003. Vol. 68) afin que je choisisse un sujet qui m'intéresserait, étant tombé sur un article traitant non seulement d'un des phénomènes physiques fondamentaux (gravitation) rentrant en ligne de compte de la continuité de mon travail antérieur, et utilisant un formalisme qui m'a véritablement émerveillé (calcul tensoriel) un an auparavant, je n'ai pas hésité un seul instant à choisir ce sujet surtout que j'avais déjà eu sous la main des notes concernant la théorie de BOHM.

Dites vous que la gravitation est avant tout un phénomène à priori décrit classiquement , la première fois par le premier physicien à être érigé à un haut piédestal , corrigé et généralisé par celui qui osa se juché sur les épaules du premier. Comme j'ai eu à le montrer dans mon précédent travail et comme il est actuellement clamé en physique : celle -- ci se divise en deux, d'une théorie de l'infiniment petit (mécanique quantique) incompatible dans ses axiomes avec celle de l'infiniment grand (Relativité générale). Très loin est donc le reve du physicien de 1905 qui croyait en une synthèse unitaire des théories de la physique. Pourtant le reve n'est tout de meme pas mort avec lui, puisque nous l'avons déjà dit, il se situe au coeur meme des problèmes de la physique fondamentale actuelle. C'est donc dans une tentative de la grande synthèse que s'inscrit la gravité quantique : théorie susceptible d'établir un pont entre le monde quantique (probabiliste) et celui de l'infiniment grand ou règnent en maîtres les phénomènes gravitationnels (déterministes). Il est à noter comme nous le verrons tout au long de ce travail qu'il n'existe pas

actuellement de théorie à proprement parler de la gravitation quantique. Seules sont développées des approches qui sont plus ou moins satisfaisantes mais pas totalement convaincantes au sens où elles s'érigeraient en véritable théorie. C'est donc comme cela que l'approche de David BOHM de la gravité quantique sera présenté dans le cadre de l'approximation linéaire du champ, comme une approche qui doit faire ses preuves face aux tests expérimentaux vérifiables afin de passer du statut d'approche à celui de théorie véritable, celle là que sont si impatients (les théoriciens de la physique) de découvrir. Ce que nous ferons dans cet ouvrage, c'est reprendre les investigations des physiciens Fatimah et Ali SHOJAI, concernant la théorie de BOHM de la gravité quantique, en retrouvant les intermédiaires du formalisme et les fondements de cette théorie dans leurs détails [1].

Il est donc clair qu'au terme de ce travail nous devrions donner notre idée, appréciation de cette approche de BOHM, en faisant référence aux possibilités de développements conceptuels qu'elle offre, si possible apporter notre modeste contribution à l'approche en particulier, et au problème de l'établissement de la théorie de la gravité quantique en général.

Par Lucien MANDENG le 24 Septembre 2008

Table des Matières

Dédicace 2

Remerciements 3

Avant -- propos 5

Table des matières 7

Résumé .. 9

Abstract 10

Constantes et abréviations 11

Chapitre I : INTRODUCTION ET GENERALITES 12

I.1 THEORIE DE NEWTON DE LA GRAVITATION.........................................................12 I.1.1 Loi d'attraction gravitationnelle ...............................................................13 I.1.2 Lois Newtoniennes de la dynamique .............................. ............................14

I.2 THEORIE METRIQUE DE LA GRAVITATION........................................................ 14

I. 2.1 Espace -- temps einsteinien 16

I.2.2 Formalisme Lagrangien dans le cas d'un champ classique ... 17

I.3 ELEMENTS DE LA THEORIE D'EINSTEIN DE LA GRAVITATION OU RELATIVITE

GENERALE................................................................................................18 I.3.1 Equations d'EINSTEIN de la gravitation....................................................18

I.4 QUELQUES NOTIONS SUR LA THEORIE LINEARISEE DE LA RELATIVITE GENERALE..20 I.4.1 Champ gravitationnel à l'approximation linéaire.........................................20 I.4.2 Equations d'EINSTEIN linéarisées ....................................................... 21

I.5 NOTIONS SUR LA GRAVITE QUANTIQUE DE BOHM..............................................22 I.5.1 Généralités ....................................................................................22 I.5.2 Mécanique Bohmienne ......................................................................22 I.5.3 Gravité quantique de BOHM ........................................................................23

I.6 CONCLUSION DU CHAPITRE I...........................................................................26

Chapitre II : LA THEORIE DE LA GRAVITE QUANTIQUE DE BOHM DANS L'APPROXIMATION LINEAIRE DU CHAMP GRAVITATIONNEL ..27

II.1 CAS DE L'APPROXIMATION NEWTONIENNE ~~~~~~~~~~~~~~~~~.. 30

II.2 METRIQUE STATIQUE ET A SYMETRIE SPHERIQUE ...............35

II.2.1 Solution aux équations d'EINSTEIN du vide ............. .............................35

II.2.2 Cas de la Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ 36

II.3 CONCLUSION DU CHAPITRE II~~~~~~~~~~~~~~~~~~~~~.39

Chapitre III : APPLICATIONS DES THEORIES 40

- RELATIVITÉ GENERALE

- GRAVITE QUANTIQUE DE BOHM

III.1 LA DEVIATION DE LA LUMIERE~~~~~~~~~~~~~~~~~~~~~~~..40 III.1.1 Théorie de la relativité générale~~~~~~~~~~~~~~~~~~~~~~.40 III.1.2 Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ 43

III.2 MIRAGES GRAVITATIONNELS~~~~~~~~~~~~~~~~~~~~~~~~.45 III.2.1 Théorie de la relativité générale ~~~~~~~~~~~~~~~~~~~~~..45 III.2.2 Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ....46

III.3 DÉCALAGE SPECTRAL DES FREQUENCES 46

III.3.1 Théorie de la relativité générale~~~~~~~~~~~~~~~~~~~~~~ 46

III.3.2 Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ 48

III.4 CONCLUSION DU CHAPITRE III ~~~~~~~~~~~~~~~~~~~~~~~...49

CONCLUSION GENERALE 50

ANNEXE DES EQUATIONS 51

LEXIQUE 61

NOTICE 63

BIBLIOGRAPHIE 66

Résumé

Dans ce mémoire, il est question d'appliquer la théorie de la gravité quantique de BOHM A l'approximation du champ linéaire gravitationnel [1].

Il s'agit du développement de l'article de Fatimah SHOJAI et Ali SHOJAI tous deux du département de physique à l'Université de TEHERAN, paru dans la revue scientifique « Physica Scripta Vol.68, 207-212, 2003 » comme article numéro 1. Ce sujet est intéressant dans la mesure où il est situé au coeur des débats, recherches en physique théorique [2 -- 16]. Cela dit, l'unification des deux théories inconciliables que sont la mécanique quantique et la relativité générale dans le cadre des phénomènes gravitationnels peut trouver ici un fil conducteur intéressant, nécessaire pour son établissement. La théorie sera alors appliquée A quelques problèmes spécifiques comme l'approximation newtonienne et la solution statique, et A symétrie sphérique ;

Quelques effets observables (en cosmologie, astrophysique) de la théorie seront alors étudiés, il s'agit de :

n La déviation de la lumière.

n Mirage gravitationnel.

n Le décalage spectral des fréquences.

Abstract

In this work, it is question to apply the Bohmian Quantum Gravity in the linear field approximation [1].

In fact, it is a development of the paper of Fatimah SHOJAI and Ali SHOJAI both of

physic's department of TEHERAN University appeared in the year 2003 in the scientific review of
«Physica Scripta Vol.68, 207 -- 212 «like first paper». This research subject is very important in the

case that, it is currently placed in the hearth of debates of the physics basis [2 -- 16]. Then, the unification of the two opposed theories which are the quantic mechanic and the general relativity in the case of gravitational phenomenas can find here one conductor file necessary for its establishment. The theory will be applied to some specifics problems like the Newtonian limit and the static, symmetrical and spherical solution;

Some observable effects are investigated (in cosmology, astrophysics), they are:

· The light deflection

· The gravitational mirage.

· Spectral variation of frequencies.

Constantes et Abréviations

1. Constante gravitationnelle de NEWTON:

2. Grandeurs à l'échelle de PLANCK



3. solution SSS : Solution statique, et à symétrie sphérique.

4. Célérité de la lumière dans le vide :

5. Constante de couplage gravitationnelle dans la théorie de la relativité générale :

6. Constante cosmologique :

7. Constante de la théorie de gravité quantique de BOHM donnant un caractère évanescent à la

fonction d'onde : dans le cas relativiste

8. Caractéristiques du Soleil : ;

9. Caractéristiques de la terre : M_T = 6x 10²⁴ kg ^rPolaire = ^635?

10. Rayon de SCHWARZSCHILD :

CHAPITRE I Introduction et Généralités

Il convient de noter que le cadre dans lequel se développe notre mémoire est la gravitation¹. La force de gravitation est l'une des quatre forces fondamentales de la physique. NEWTON² l'introduit en 1687 pour interpréter le mouvement des planètes, le mouvement de la lune et le mouvement des corps dans le voisinage de la terre, cette interprétation est connue sous le nom de la « Mécanique de NEWTON ». Malgré le formidable succès de cette dernière, EINSTEIN³ a rebondi sur le sujet en 1916 dans le cadre de la relativité générale⁴ A cause du rôle décisif joué par la gravitation en astrophysique⁵. Bien que les deux interprétations des phénomènes gravitationnels continuent de rencontrer du succès (particulièrement la relativité générale), il a paru nécessaire d'introduire une approche quantique de la gravitation .Puisque nous savons que les principaux outils que possèdent le physicien sont la mécanique quantique, celle de NEWTON, les relativités restreintes et générales d'Albert EINSTEIN ..., tous pour décrire la réalité physique. La question qui se pose est la suivante : « Si la mécanique Newtonienne, la relativité générale ont pu chacune donner une interprétation de la gravité pourquoi n'en serait --il pas de même de la mécanique quantique ? » (Bien que celle-ci soit incompatible avec les deux premières). Et surtout que l'on a constaté avec la relativité générale que la description effective des trous noirs devrait être faite par une théorie quantique de la gravitation. C'est donc une approche quantique de la gravité établie par David BOHM que nous utiliserons ici dans l'approximation linéaire du champ gravitationnel⁶ pour cela il faudrait faire certains rappels nécessaires A cette investigation [1 -- 2].

I.1 THEORIE DE NEWTON DE LA GRAVITATION7

Pour des raisons de simplifications, nous utiliserons les éléments du calcul tensoriel⁸ pour établir les relations mathématiques décrivant les phénomènes physiques correspondant A notre étude (cela est valable également pour la suite).

¹ Voir Lexique

² Voir Lexique

³ Voir Lexique

⁴ Voir Lexique

⁵ Voir Lexique

⁶ Voir Lexique

⁷ Du paragraphe I.1 au paragraphe I.4, les relations proviennent majoritairement de la référence [2]

Traditionnellement, on présente la gravitation (dans la théorie de NEWTON), en soulignant la ressemblance entre la force de gravitation et la force électrostatique entre deux particules chargées [3].

I.1.1 Loi d'attraction gravitationnelle

La loi d'attraction gravitationnelle, publiée par NEWTON en 1987 dans les « Principia i i

stipule que la force exercée sur une particule par une particule est donnée par [2] :

(I.1) Où est la masse grave passive de la particule et où est le champ gravitationnel de

la particule .On a qui est donnée par :

	ga		) U			(I.2)

où est la masse grave active de la particule b, G⁹ étant la constante de couplage

gravitationnel (Constante de NEWTON). Le champ gravitationnel, on le sait dérive d'un potentiel scalaire : le potentiel de NEWTON qui s'écrit pour le corps :

(I.3) L'énergie d'interaction de nature potentielle pour la particule est

(I.4)

⁸ Voir lexique.

⁹ Voir constantes et abréviations.

dans l'approximation linéaire du champ

I.1.2 Lois Newtoniennes de la dynamique

La dynamique est l'étude des mouvements des corps en relation avec les causes, appelées forces qui les produisent [3].

C'est par rapport à la classe privilégiée des observateurs inertiels de l'espace -- temps galiléen que les lois Newtoniennes de la dynamique sont formulées :

(a) La premi~re loi stipule qu'une particule soumise à aucune force est en mouvement de translation uniforme pour un observateur inertiel¹⁰. C'est le principe d'inertie qui caractérise justement les observateurs inertiels. Une autre façon de le dire est que sa ligne d'univers est une droite dans l'espace-temps galiléen.

(b) La deuxième loi est la loi fondamentale de la dynamique pour une particule de masse inerte m soumise à un champ de forces extérieures :

(I.5)

(c) La troisiqme loi est celle de l'action et de la réaction dans un systdme de particules ponctuelles en interaction .Si un corps q exerce une force sur un corps p alors la force

exercée par le corps p sur le corps q est telle que :

= - (I.6)

I.2 THEORIE METRIQUE DE LA GRAVITATION

La théorie de NEWTON de la gravitation présente des difficultés conceptuelles comme celle de l'action à distance. Ce qui veut qu'une variation du champ gravitationnel est transmise instantanément dans tout l'espace -- temps galiléen¹¹.

Depuis 1905, l'espace -- temps galiléen est rejeté à la lumière de la relativité restreinte car l'équation fondamentale de la dynamique et la loi d'attraction gravitationnelle sont invariantes sous une transformation de GALILEE. Il faut donc une théorie relativiste de la gravitation.

¹⁰ Voir lexique

¹¹ Voir lexique

dans l'approximation linéaire du champ

Ladite théorie relativiste de la gravitation est construite dans l'espace - temps de MINKOWSKI¹² ; On définit par , ì = les coordonnées minkowskiennes d'un événement M (c'est aussi sa ligne d'univers).

La théorie relativiste de la dynamique est formulée pour un observateur inertiel. Soit un champ de

Quadri - forces extérieures , celles - ci dérivent d'un potentiel Ö . Alors la loi relativiste

de la dynamique s'écrit

F ? ( x ? ( s

(I.7)

où est la quadri - vitesse, s est le temps propre et la ligne d'univers de la particule La

quadri - accélération est orthogonale à :

(I.8) Pour assurer la compatibilité, on admet la condition algébrique suivante :

(I.9)

La quadri - quantité de mouvement : F

(I.10)

Comme	dérive du potentiel Ö (car ) on sait par ailleurs que



; le théorème de Gauss pour le champ de composantes est :

¹² Voir lexique

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(I.11)

Il en ressort l'équation de poisson :

(I.12) Où G est la constante de NEWTON, est la masse grave volumique.

II. 2.1 Espace - temps einsteinien¹³

La géométrie de l'espace-temps minkowskien est tout à fait satisfaisante pour décrire la réalité physique tant que les effets gravitationnels ne sont pas pris en compte. Le fait qu'il

faille nécessairement décrire globalement les phénomènes physiques dans l'univers implique que nous devons considérer les effets de la gravitation sur ceux-ci .Pour cela nous admettons que ces effets résultent uniquement de la structure géométrique l'espace-temps minkowskien, pour adopter l'espace-temps Einsteinien dont la géométrie est Lorentzienne caractérisée par une métrique¹⁴ g de signature¹⁵ et de la connexion riemannienne¹⁶ associe à la métrique

g. L'espace-temps einsteinien décrit un véritable champ de gravitation si le tenseur de RIEMANN¹⁷ est non nul, donc si l'espace-temps est courbe et non localement plat .Le principe de covariance stipule qu'il n'existe pas de systèmes privilégiés de coordonnées, alors les champs physiques sont des champs de tenseurs et les lois physiques s'écrivent de façon tensorielle dans n'importe quel système de coordonnées, éventuellement limites à ceux de la matrice Jacobienne de déterminant positif nécessitant que l'espace-temps soit orientable. Donc pour un champ tenseur T on a :

(I.14)

¹³ Voir lexique

¹⁴ Voir lexique

¹⁵ Voir lexique

¹⁶ Voir lexique

¹⁷ Voir lexique

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

I.2.2 Formalisme Lagrangien dans le cas d'un champ classique

Dans l'espace-temps minkowskien, les champs classiques (scalaire, électromagnétique,...) ont des équations de champ quoi dérivent d'un Lagrangien. En notant contenant de

façon générique et ses dérivées , on sait que est un scalaire. Dans l'espace -- temps

einsteinien, d'après le principe d'équivalence d'EINSTEIN, on remplace par et a_lYI_M



par dans l'expression du Lagrangien noté qui reste donc un scalaire. L'action

associée au Lagrangien L est l'intégrale de la densité lagrangienne L = dans un domaine

Ù de l'espace -- temps Einsteinien :

(I.15)

s_M ^??est indépendante du choix du système de coordonnées .La variation de s_m par rapport à

??

donne les équations de champs :

(I.16) La variation de l'action de par rapport à ou par rapport à définit le tenseur
énergie -- impulsion symétrique :

(I.17)	(I.18)	(I.19)	(I.20)	(I.21)		(I.22)		(I.23)	(I.17)
n'est possible qu'à l'approximation quasi-classique où							dans la limite .

suivant que l'on fait apparaître ou dans la densité Lagrangienne en faisant attention au

signe puisque . On peut donc voir ici que l'espace -- temps Einsteinien ^étantdonné, les champs classiques peuvent titres quantifiés, comme nous le verrons dans la suite de

notre travail.

Dans le cas d'un champ scalaire, la description quantique d'une seule particule par une onde

dans l'approximation linéaire du champ

La phase de l'onde est gouvernée par une équation¹⁸ que nous verrons dans la suite.

I.3. ELEMENTS DE LA THEORIE D'EINSTEIN DE LA GRAVITATION OU RELATIVITE GENERALE

I.3.1 Equations d'EINSTEIN de la gravitation

On admet que l'espace -- temps est une variété différentiable munie d'une métrique Lorentzienne g, la gravitation étant une manifestation de la structure géométrique de l'espace -- temps.

Les idées suivantes conduisent aux équations d'EINSTEIN de la gravitation :

a) les équations de la gravitation devront être tensorielles. On peut les écrire dans n'importe quel système de coordonnées ; c'est le principe de covariance déjà invoqué. Pour déterminer les composantes de la métrique, il faut une source de même

nature tensorielle .Le tenseur énergie - impulsion qui contient la densité de masse ñ

semble tout indiqué (également respectivement le principe de covariance

).

b) ,Il est rEOonnIIle MLgIr qN lAffpquaVINQ VIR Mamp gravMIonnel soiHJ des équations aux dérivées partielles du second ordre de façon à généraliser les équations de POISSON de la théorie de NEWTON de la gravitation ( ).

On doit donc trouver un tenseur géométrique deux fois covariant dépendant

uniquement de et de ses dérivées jusqu'au second ordre qui satisfasse .

On a :

(I.18)

et qui sont les deux tenseurs possibles.

¹⁸ Voir lexique

dans l'approximation linéaire du champ

Les équations d'EINSTEIN de la gravitation sont :

(I.19)

c

où ÷ est la constante couplage gravitationnel de dimension ; Ë est la constante

cosmologique de dimension .

Ces équations non linéaires relient la géométrie de l'espace - temps et la distribution

énergétique de la matière, déterminent les composantes de la métrique dans un certain

système de coordonnées ( ). Elles nécessitent des conditions aux limites : en dehors de la

matière , les solutions sont celles du vide ; pour

la métrique Minkowskienne alors l'espace - temps Minkowskien est une solution

particuliJqre du vide lorsque Ë = 0 .

Donc hors du champ cosmologique

_p

(I.20)

La valeur de ÷ est fixée :

(I.21) On constate généralement que la théorie d'EINSTEIN de la gravitation n'est plus valable à





des distances de l'ordre de , pour des masses de l'ordre de

, pour des temps



de l'ordre , pour des énergies d'interaction de l'ordre de

(Qui sont tous respectivement la distance, masse, temps, énergie de PLANCK)¹⁹ puisqu'il faudrait une théorie quantique de la gravitation pour décrire ces domaines. Ce qui fera l'objet du paragraphe sur la théorie de BOHM de la gravitation.

¹⁹ Voir constantes et abréviations

dans l'approximation linéaire du champ g ? ? ? h avec

I.4. LA THEORIE LINEARISEE DE LA RELATIVITE GENERALE

h

I.4.1 Champ gravitationnel à l'approximation linéaire

Dans le paragraphe précédent , il a été clair qu'il fallait déterminer simultanément la métrique et le tenseur énergie - impulsion pour résoudre les équations d'EINSTEIN

puisque nous avons la loi de conservation covariante ? ?T .La méthode a décrit un milieu

matériel auto - gravitant spatialement borné dont l'espace - temps Einsteinien est asymptotiquement Minkowskien .La méthode a permis de trouver l'approximation Newtonienne de la théorie d'EINSTEIN. Ce qui implique que selon NEWTON les forces de gravitation sont du même ordre de grandeur que les autres forces agissant sur le milieu.

Toutefois, il existe des situations physiques où les forces de gravitation sont beaucoup plus faibles que les autres forces dues aux tensions dans le milieu ; alors les équations du mouvement du milieu matériel ne sont pas affectées par le champ gravitationnel engendré par celui - ci .Elles se réduisent aux équations de MINKOWSKI du mouvement définies par en

coordonnées Minkowskiennes.

En tenant compte des équations d'Albert EINSTEIN, la métrique engendrée sera une perturbation linéaire en G de la métrique Minkowskienne. Il existe alors une classe de coordonnées privilégiées appelées « quasi - Minkowskiennes », telles que les composantes de la

métrique diffèrent peu de la métrique Minkowskienne. Nous posons :

(I.22)

où sont considérées comme les potentiels gravitationnels dans un espace - temps

Minkowskien dans lequel satisfait . Les constituent les composantes pour un
type de transformation de POINCARE.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

I.4.2 Equations d'EINSTEIN linéarisées

Avec l'expression linéarisée du tenseur de RICCI et de la relation les

équations d'EINSTEIN linéarisées s'écrivent :

(I.23) Choisissons une jauge qu'on appellera la jauge harmonique :

(I.24)

condition . Une





Or

transformation de jauge supplémentaire permet aux fonctions de satisfaire l'équation :

(I.25)

Ce qui implique que donc les équations d'EINSTEIN linéarisées et

simplifiées sont équivalentes au système :



(I.26)

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

I.5 NOTIONS SUR LA GRAVITE QUANTIQUE DE BOHM

I.5.1 Généralités [1, 4]

Nous insistons sur le fait qu'il n'existe actuellement aucune théorie quantique de la gravitation dans le sens où on l'entend c'est -- à -- dire une théorie quantique des champs de jauge. La théorie de la gravité quantique est simplement une plage ouverte à toute théorie ou éventuellement toutes les théories susceptibles d'unifier ou de réunir ensemble notre théorie de l'infiniment petit : « la mécanique quantique » et notre théorie de l'infiniment grand : « la relativité générale » .Il s'agit donc pour la théorie de la gravité quantique de réconcilier ces deux visions qui sont à priori incompatibles.

Nous avons signalé précédemment²⁰ que pour les domaines de l'ordre de grandeurs des quantités de PLANCK, il fallait une théorie quantique de la gravitation.

Nous n'allons pas débattre ici sur les fondements philosophiques de la nécessité de

« quantiser » le champ gravitationnel afin d'obtenir une théorie universelle de la gravité quantique qui pour « certains » relève des divagations abstraites du théoricien de la physique sans aucune utilité pratique immédiate. Toutes ces questions métaphysiques sortent du cadre de ce travail.

Touj ours est -- il, que comme nous le disions tantôt, bien qu'il n'existat pas de

« véritable » théorie quantique de la gravité, quelques approches font l'objet d'âpres
investigations. Les plus importantes sont : la théorie des supercordes, la gravité quantique canonique (ou formalisme canonique ou encore formalisme de WDW²¹), l'approche de NARLIKAR et PADMANABHAN sur la quantisation du degré de liberté formel de la métrique de l'espace -- temps²² , la gravitation quantique à boucles, la gravité quantique de BOHM une nouvelle approche reliant la mécanique quantique et la géométrie de l'espace -- temps. Bien évidemment nous nous intéressons uniquement à la gravité quantique de BOHM.

I.5.2 Mécanique bohmienne

Selon David BOHM, la description du mouvement d'un système de n particules définies ensemble par la fonction d'onde ø dudit système avec sa configuration

sont les positions de ces particules .La fonction d'onde, qui évolue

²⁰ Paragraphe I.3.1°)

²¹ Voir bibliographie [1]

²² Voir bibliographie [1]

dat564approximatioCAéEIreBSu chCEm S

k

selon l'équation non stationnaire de SCHRÖDINGER :

(I.27)

(où est le Hamiltonien du système) représente le mouvement des particules qui évoluent dans la plus simple des manières possibles selon l'équation différentielle ordinaire de premier ordre :

(I.28)

Où le second membre²³ est régénéré par la fonction d'onde. En considérant la simplicité et la symétrie de l'espace -- temps, on détermine alors la forme , donnant ainsi la définition des équations²⁴ de la mécanique de BOHM :

(I.29) et l'équation (I.27) où le Hamiltonien usuel contient comme paramètres les masses

des particules aussi bien que la fonction énergie potentielle V du système .Les équations (I.27) et (I.29) forment une spécification de la théorie sans besoin d'autres axiomes.

I.5.3 Gravité quantique de BOHM

La transition de la mécanique quantique à celle de BOHM est très simple sinon triviale : On incorpore simplement l'actuelle configuration dans la théorie comme variable de base et on stipule qu'elle évolue dans un cadre naturel suggéré par la symétrie et par l'équation de SCHRÖDINGER. Le champ de vitesse est en fait, relié à la probabilité quantique courante

par :

²³ C'est - à - dire le champ de vecteur vitesse sur la configuration de l'espace

²⁴ Voir Bibliographie [4].

at564EESERIVEORCAPEILIBSKAICEP S

suggérant, quand

satisfait l'équation de continuité avec , que les

prédictions empiriques de la mécanique de BOHM , pour les positions et ultimement en fait , pour d'autres « observables » , agrée avec celles de la mécanique quantique.

Pour comprendre comment la théorie de la gravité quantique de BOHM fonctionne,

A h

revenons à l'équation de SCHRÖDINGER (I.27) ; en exprimant par on

obtient :

(I.31) Si on décompose²⁵ la fonction d'onde en sa norme et sa phase :

(I.32)

ici R est la norme de obtient le système :					,remplaçons (I.32) dans (I.31), on
	h V			(I.33)

On posera pour la suite comme étant le potentiel quantique de BOHM. La

?

première équation de (I.33) est l'équation de continuité provenant du fait qu'on adopte que la

m

relation classique donne la trajectoire de la particule :

(I.34)

²⁵ Voir paragraphe I.2.4°).

dans l'approximation linéaire du champ

La deuxième équation de (I.33) est l'équation d' HAMILTON -- JACOBI modifiée. Prenons le gradient de cette dernière on aura :

(I.35) Or d'après (I.34) on aura :

(I.36)

On obtient ainsi l'équation du mouvement de NEWTON. Ainsi l'interprétation de BOHM s'énonce comme suit :

«Pour quantiser n'importe quel syst~me classique, on ajoute un potentiel quantique à l'équation classique de HAMILTON -- JACOBI ; le potentiel quantique est donnée en terme de la densité d'un ensemble hypothétique du syst~me (R²) et alors on doit ajouter l'équation de continuité pour avoir un systqme d'équations adéquats. »

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

I.6 CONCLUSION DU CHAPITRE I

Bien que rencontrant des succès, la théorie quantique de BOHM de la gravitation se heurte également à des difficultés .La plus importante est le fait qu'elle ignore complètement la

covariance générale²⁶.

Etant muni de tous ces rappels nécessaires pour la suite, nous nous engageons à appliquer la théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ gravitationnel, comme nous avons eu à le faire pour les autres théories de la gravitation²⁷.

²⁶ Alors que c'est l'un des piliers fondamentaux des théories métriques de la gravitation (La relativité générale d'EINSTEIN en occurrence, et certaines autres approches quantiques de la gravitation.

²⁷ Théories de NEWTON et celle d'El NSTEl N

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

CHAPITRE II La théorie de la gravité quantique de BOHM dans

l'approximation linéaire du champ gravitationnel [1]

Dans ce cadre, la métrique de l'espace -- temps est développée dans l'espace -- temps plat de MINKOWSKI²⁸.

On ne considère que les termes linéaires en . La densité de LAGRANGE²⁹ pour un

champ gravitationnel linéaire s'écrit :

(II.1)

Ici sont les composantes respectivement covariantes et contravariantes du champ

classique gravitationnel. Pour simplifier, selon la relation (I.24), introduisons comme suit :

(II.2)

Ce qui signifie d'après (I.24), que la jauge harmonique s'écrira :

?

(II.3)

Définissons le moment canonique ³⁰; on sait que dans le formalisme classique du

Lagrangien on a au regard de (I.17) on aura :

28 Comme d'après la relation (I.22).

²⁹ Celle dont on a parlée dans le paragraphe I.2.2°).

³⁰ Communément appelé impulsion ou quantité de mouvement.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(II.4)

Or l'énergie potentielle est donnée par :

(II.5)

Et la densité du Hamiltonien :

(II.6)

La transition A la théorie quantique peut être réalisée par le principe de correspondance suivant le schéma de quantisation canonique³¹ de DIRAC :

(II.7)

Or l'équation d'évolution de SHCRÖDINGER est :

(II.8)

Où est la fonctionnelle d'onde. L'interprétation de BOHM de cette équation d'onde peut être réalisée en prenant comme A la relation (I.32) ; ce qui mène A la deuxième équation de (I.33), , on a la correspondance :

(II.9)

31

Dans le principe de correspondance on utilise généralement ó or suivant le schéma de quantisation de DIRAC on utilise ä.

dans l'approximation linéaire du champ

Et ici V a la valeur de la relation (II.5). Ce conduit à la relation suivante :
			(II.10)
	? )

Et la première équation de (I.33) qui est celle de continuité³² on obtient :

(II.11)

avec Q' le potentiel quantique de BOHM :

							(II.12)
Les trajectoires de BOHM s'obtiennent à partir de la relation (I.34) :
	01W _ OS ?							(II.13)

Bien évidemment l'invariance générale de la transformation des coordonnées du champ gravitationnel linéaire est garantie par la jauge harmonique (II.3). L'équation de champ peut etre dérivée en prenant la variation de l'équation d'HAMILTON -- JACOBI modifiée (II.10) selon

et on aboutit à la relation suivante :

(II.14)

³² Selon (II.8) , ce qui permet d'écrire que

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

II.1 CAS DE L'APPROXIMATION NEWTONIENNE

Dans le cas où l'on applique ces résultats à l'approximation newtonienne, on aura la métrique donnée par :

(II.15)

Où est le potentiel gravitationnel de NEWTON. Le champ est donné par

; ; (II.16)

et nous avons les identités :

. (II.17)

On a :

(II.18)

Cette dernière équation est l'équation d' HAMILTON - JACOBI modifiée sous forme simplifiée³³. Et on a l'équation de continuité qui simplifiée de la meme façon que l'équation précédente comme suit :

(II.19)

Ainsi le potentiel quantique s'écrira donc :



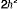
(II.20)

Pour ce qui est des équations des trajectoires de BOHM on obtient :

³³ Ici on fait partir les indices des tenseurs, on reste avec les simples grandeurs scalaires usuelles.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(II.21)

Dans l'approximation newtonienne, le potentiel gravitationnel est constant dans le temps donc 0 # f(t) ao = 0 , ceci à cause de la j auge harmonique : aPo_i,= 0 pour la relation (II.21),cela implique que :

(II.22)

C'est le cas où le potentiel quantique est du même ordre de grandeur que le potentiel classique, ainsi ce potentiel³⁴ est non négligeable.

(II.22) dans (II.18) . On se souvient que l'on a pris



en (I.32) or on sait qu'en mécanique quantique la fonction d'onde non



stationnaire s'écrit , en se référant à cela on peut poser : ceci parce

1 que dans le domaine Newtonien, les grandeurs physiques ne doivent pas dépendre du temps
(puisqu'ici on considère des cas stationnaires pour l'approximation Newtonienne). Pour ce la
l'équation de continuité (II.19) est donc identiquement satisfaite si on considère (II.22) et le fait

que De même comme en (II.14) on peut obtenir l'équation du champ :

(II.18) au regard de (II.22) devient : or

Nous obtenons l'équation de champ, de l'approximation Newtonienne provenant de la théorie de BOHM :

(II.23)

Ici nous avons juste considéré le champ linéaire de la gravité quantique de BOHM, en ignorant celui créé par source de matière. D'après l'idée de BOHM de la gravitation quantique on

³⁴ Il s'agit du potentiel quantique.

dans l'approximation linéaire du champ

doit donc introduire ce terme³⁵, l'équation de POISSON s'écrira dans l'approximation Newtonienne de la manière suivante :

(II.24)

Dans ce cadre de l'approximation Newtonienne de la gravité quantique de BOHM, déterminons l'expression du potentiel quantique ; Pour cela choisissons R la norme du paquet d'onde autour de la solution classique de l'équation du champ gravitationnel :

(II.25)



où et sont respectivement un paramètre d'extinction et le champ quantique ; On a la

fonction d'onde ; Le terme R est équivalent à celui de la fonction

d'onde d'un oscillateur harmonique quantique, sauf qu'ici la variable est le champ gravitationnel, ? ?
au lieu de la position comme dans le cas de l'oscillateur.

D'après BOHM le champ total est 0 donné par :

(II.26)

où est le potentiel gravitationnel classique solution de l'équation de POISSON, on a
en remplaçant dans l'expression de R on a :

(II.27)

Bien sûr la constante « » rassure sur le fait que l'on n'ait pas une fonction d'onde dont
la norme tend vers l'infini à mesure que le champ tend vers l'infini.

³⁵ On doit ajouter le terme classique de la source de matière .

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Si on omet Q dans l'équation (II.24), satisfera celle -- ci. Si on remplace cette expression

de R dans celle de Q :

(II.28)

Ici on considère que . On sait que l'équation de champ dans la théorie de BOHM est :



(II.29)

Prenons le cas où on a comme source de matière, un point matériel alors on peut écrire

(II.30)

Alors pour résoudre (II.29) on se sert de (II.26). On doit avoir :

(II.31)

Où M, r sont respectivement la masse de la source de matière et la distance entre elle et le point où le champ dérivant de Oc est créé. L'équation (II.29) s'écrit :

		(II.32)
En explicitant le Laplacien on aura :

En coordonnées sphériques³⁶ :



(II.33)

³⁶ Dans un système de coordonnées sphériques correspondant à une base orthonormée.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Pour résoudre (II.33) utilisons la méthode de séparation des variables et on obtient le système suivant :



(II.34)





En considérant une source de matière à symétrie sphérique et statique seule la première équation de (II.34) nous intéresse :

				(II.35)

Cette équation (II.35) est une équation de la forme de celles de BESSEL de première espèce³⁷. Ici

d²U dU

on aura , a= 2 et b = ot² . La solution sera donc :

(II.36)

La solution est donc :

(II.37)

OA Ces constantes ont la même unité que le champ gravitationnel
classique. La solution sera alors :

(II.38)

Certains points de cette solution sont intéressants :

³⁷ Qui est de la forme :

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

ü Par exemple aux grandes distances r de la source de matière, le comportement asymptotique des fonctions sphériques de BESSEL :

(II.39)

On constate bien que la solution quantique est inversement proportionnelle à r aux grandes distances de la source.

ü Si la masse de la source de matière est négligeable ( --> 0 ), on a , ainsi on a une

pure solution quantique dans laquelle on a une petite source de gravité .Cela signifie que les fluctuations quantiques de la gravité peuvent produire une gravité observable.

Il doit etre noté que l'approximation du champ faible est seulement applicable aux grandes distances .Ainsi cette solution ne donne aucune information concernant les cas des singularités et horizons gravitationnels.

ü A cause de la nature oscillatoire des fonctions sphériques de BESSEL, le potentiel gravitationnel est aussi oscillatoire .Ainsi nous avons un ensemble de points stables et périodiques, où le potentiel est minimum et une particule -- test peut etre au repos à d'autres positions³⁸. Il doit etre noté que, si nous choisissons un fin paquet d'ondes³⁹, la fréquence des oscillations est très grande.

II.2 METRIQUE STATIQUE ET A SYMETRIE SPHERIQUE

II.2.1 Solution aux équations d'EINSTEIN du vide40

Elle est caractérisée par un paramètre m, elle s'écrit :

(II.40)

³⁸ Ceci est aussi vrai pour le cas .

³⁹ dans l'équation (II.27).

40 Métrique statique de SCHWARZSCHILD.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAKEPp

[

ce qui correspond au tenseur métrique⁴¹ : dans un

r r

système de coordonnees ? _?(x^° ,r,0 , 0) définies pour (avec rS étant le rayon de

SCHWARZSCHILD , dont la valeur est ; cette métrique de SCHWARZSCHILD

c²

décrit l'espace -- temps extérieur de tout corps massif statique et à symétrie sphérique. Le domaine de validité est avec la condition .

II.2.2 Cas de la Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ

Les relations (II.10) et (II.11) deviendront :

(II.41)

Et

? ? ? ^?x??^? ? c · ( p ) x

(II.42)

L'équation de continuité qui est la deuxième équation s'écrit ainsi parce que nous avons mentionnés ; déjà que les grandeurs physiques telle que la norme de la fonction d'onde ne

dépendent pas du temps. Les trajectoires de BOHM peuvent être obtenues par la relation (II.13) ? ^?ainsi que la condition de jauge.

En dérivant la première équation des deux par on obtient :

(II.43)

Comme dans le cas de l'approximation Newtonienne, on prend :

(II.44)

⁴¹ Car

.

dans l'approximation linéaire du champ

avec donc en remplagant (II.44) dans (II.27) on obtient :

(II.45)

En remplaçant R dans l'expression⁴² de Q' :



(II.46)

Introduisons (II.46) dans l'équation de champ (II.43) précédente :



(II.47)

La condition de jauge est ; On a vu que , on

peut prendre la solution classique⁴³ ; On retrouve (car on doit ajouter la solution

classique) :



(II.48)

Pour obtenir la solution de cette équation, on procède comme précédemment⁴⁴ ; On retrouve une équation de BESSEL de première espèce. La solution de l'équation (II.48) est la même

en que de la relation (II.37) ; On aura : or et



xmat

N ce qui conduit à :

⁴² L'expression (II.12) de Q'.

43

44 Comme dans le cas de l'approximation Newtonienne.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(II.49)

Avec ; On a vu que⁴⁵ d'où le système

suivant :

(II.50)



² ?Soit h_p. = dia+^r s+ ¹ q, ^7-s+^{0 q,dx71} s+⁰ q ,-^7- s +0 d 3 et r 2 r ? r 2 ? 2 2 r 2 r 2

Ainsi la métrique de la théorie de la gravité quantique de BOHM dans

l'approximation du champ linéaire :

Soit

(II.51)

(II.52)

⁴⁵ Voir relation (II.2).

.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

II.3 CONCLUSION DU CHAPITRE 2

Nous venons ainsi de présenter la théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ gravitationnel, on a pu déterminer la métrique correspondante qui s'écrit comme celle de la théorie classique plus un terme représentant les corrections quantiques. Il s'avère donc que la théorie de BOHM dans ce cadre généralise les résultats obtenus dans le cas classique en décrivant avec plus de précision la réalité (elle fait intervenir des fluctuations quantiques autour de la métrique classique, des fluctuations qui ont été négligées dans cette dernière). A l'aide de puissant outil qu'est la métrique de BOHM, nous appliquerons la théorie dans le cas de certains phénomènes observables (déviation de la lumière par un corps massif, statique et à symétrie sphérique, le mirage gravitationnel et enfin le décalage spectral des fréquences...), histoire de montrer que l'on peut (à l'instar de la relativité générale) obtenir des résultats réalistes à l'aide de celle -- ci.

dans l'approximation linéaire du champ

CHAPITRE III Applications des théories :

- relativité générale

- gravite quantique de BOHM

Après tout ce périple, il est nécessaire de nous attarder sur des résultats observables de la solution statique et à symétrie sphérique dans le cadre des différentes théories de gravitation dont nous avons parlées. La théorie de NEWTON de la gravitation étant généralisée par celle d'EINSTEIN nous nous limiterons à cette dernière pour le cas classique de la gravitation.

III.1 LA DEVIATION DE LA LUMIERE

III.1.1 Théorie de la relativité générale

Quand on étudie un mouvement qui n'est pas lent en particulier la lumière, il faut renoncer à un développement en de la métrique .Toutes les composantes de la métrique doivent être

connues au même ordre, en fait en puissance de G . On a la providence que l'approximation linéaire en G, la métrique post -- newtonienne donne la métrique désirée :

avec , (III.1)

Où ã=1 dans la théorie de la relativité générale. La déviation (voir fig. 1 page suivante) des rayons lumineux par un corps massif statique et à symétrie sphérique relève de l'étude des géodésiques⁴⁶ du genre lumière de cette métrique linéarisée.

⁴⁶ Lexique.

dans l'approximation linéaire du champ

Soit la géodésique du genre lumière de vecteur -- dérivée pour un paramètre affine

ë. L'équation de la géodésique s'écrit sous la forme simplifiée :

(III.2)

Nous considérons une perturbation de la trajectoire de l'espace -- temps

minkowskien dont le vecteur de propagation a pour composantes (1, 1, 0, 0). Le vecteur de

propagation est une perturbation sous la forme . La perturbation satisfait
donc l'équation :

(III.3)



Déplacement apparent

A

Observateur

Figure 1 (prise dans la référence [1])

Cette relation (III.3) s'intègre comme ceci :

(III.4)

Avec la condition que ; la déviation Ä pour une trajectoire d'impact x²=b

est égale à äk2 à ë=8. Donc :

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(III.5)

On peut tracer avec valeur adimensionnée de ( = ) comme sur

la courbe suivante pour le cas du Soleil ( = 2x 1 O^mkg , c = 3x 1 0⁸m
· sH )



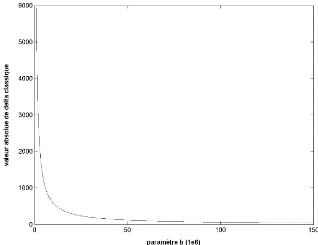
Courbe 1 (tracée dans MATLAB)

On remarque la déviation de la lumière au alentour d'une masse statique, et à symétrie sphérique (exemple cas du Soleil), est inversement proportionnelle au paramètre d'impact de cette masse. On assiste donc à une décroissance de la déviation au fur et mesure qu'on s'éloigne de la masse. On note donc que la valeur maximale de la déviation est obtenue lorsque la lumière frôle pratiquement la masse, comme on le voit sur la figure suivante :



Figure 2 (Voir bibliographie [16])

dans l'approximation linéaire du champ

? ? ? ? ?

Les rayons lumineux sont fortement déviés au voisinage de la masse.

On constate donc que pour b rayon du Soleil, on trouve [2] (résultat vérifié par

EDDINGTON dès 1919 lors d'une éclipse totale du Soleil). Dans le cas newtonien on a .

III.1.2 Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ

Comme dans le cadre de la théorie précédente, on suppose qu'un rayon lumineux approche un corps massif à symétrie sphérique et statique à partir de l'infini le long de la direction du paramètre affine ë (dans le même plan que le précédent (x¹,x²)) avec pour paramètre d'impact b. L'équation de la géodésique (III.2) est également valable ici et toujours est le vecteur de

propagation. Donc on a : ; on est ici dans les mêmes conditions que dans le

¹

paragraphe précédent :

(III.6)

or . Pour simplifier, nous considérons seulement⁴⁷ le terme

a00 comme contribution de Ö_q : or on a vu que quand

ici quand , et l=0 :

(III.7)

Si on remplace (III.7) dans (III.6) :

⁴⁷ Si on veut une métrique qui ne dépend pas des angles sphériques à l'infini, seuls les coefficients de sont non

nuls. Les comportements de et sont similaires, ainsi nous considérons le premier (en considérant le second

ne change pas l'interprétation physique.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(III.8)

Bien sûr le premier terme est le terme classique de la déviation classique, le second représente celui des corrections quantiques. Nous représentons également sur la

courbe 2 suivante :



Courbe 2 (Tracée dans MATLAB)

On a tracé ici sur un même graphique, le cas classique précédant et la déviation selon la théorie de la gravité quantique de BOHM. On constate que la prédiction quantique de BOHM, indique que la déviation de la lumière oscille autour du résultat classique (à cause de sa dépendance à b à l'aide de fonctions sinus et cosinus). Lorsque le paramètre d'impact est pratiquement égal (en rapport 1) au rayon de la masse, la déviation est maximale et diffère très peu du résultat classique (effet quantique pratiquement négligeable). Mais plus, on s'éloigne de la masse (b de plus en plus grand), plus les effets quantiques deviennent significatifs face à la déviation classique jusqu'à ce qu'ils soient presque observables aussi important que la déviation classique. On observe alors des oscillations de la déviation de BOHM autour de celle d'EINSTEIN. On peut donc dire ici que la déviation de BOHM généralise celle d'EINSTEIN en rendant compatible la prédiction de la relativité générale à celle de la mécanique quantique.

dans l'approximation linéaire du champ

III.2 MIRAGES GRAVITATIONNELS

III.2.1 Théorie de la relativité générale

Le phénomène précédent conduit à la possibilité des mirages gravitationnels. Il y a

l ? d

? 1 ? ? 1 ? ? 0 ?

formation de deux images :



Ä1

Ä2

l d

? Figure 3 Mirage gravitationnel

? ?

l

0 ?

voir [2]

Pour chaque trajectoire 1 et 2 de la lumière, nous notons Ä1 et Ä2 les angles de déviations. A cette approximation, la géométrie dans le plan des rayons lumineux donne :

(III.9 a)

Et

(III.9.b)

Vu l'expression de la déviation Ä^(c) , nous avons à résoudre l'équation suivante pour trouver â prenons : , on aboutit à l'équation suivante :

dans l'approximation linéaire du champ

(III.10)

			et

Posons les solutions seront données par :

(III.11)

et sont les deux valeurs représentant le mirage gravitationnel.

III.2.2 Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ

Si nous reprenons l'expression		, on obtient l'équation du mirage

gravitationnel, décrit par la théorie de la gravitation Bohmienne dans l'approximation du champ linéaire :

(III.12)

Cette équation peut être résolue numériquement, bien sûr dans un cas concret dans lequel les constantes .

III.3 DÉCALAGE SPECTRAL DES FREQUENCES

III.3.1 Théorie de la relativité générale

Considérons du décalage vers le rouge des raies spectrales d'un atome en position r_e , de quadri -- vitesse et un observateur statique en ro de quadri -- vitesse .

D'après la formule de l'effet DOPPLER générale, nous avons :			est le

vecteur de propagation de la lumière. Il satisfait l'équation des géodésiques du genre lumière pour un paramètre affine A , que nous écrivons sous la forme simplifiée :

dans l'approximation linéaire du champ

(III.13)

Puisque la métrique n'est pas fonction de x^° nous avons , qui n'est rien

d'autre que où î désigne le vecteur de KILLING orienté dans le temps . La formule se

simplifie, nous avons dans un champ gravi tationnel fort, statique et à symétrie sphérique :

							(III.14)
Car				; La relation (III.14) représente donc le décalage spectral

des fréquences dans le cadre de la relativité générale.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

III.3.2 Théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ En tenant compte des résultats obtenus dans cas précédent on applique la théorie de

BOHM. Du champ linéaire : donc la relation traduisant le





décalage spectral pour le cas de la théorie de BOHM dans l'approximation du champ linéaire s'écrit :

0 = 0 =

(III.15)

2 /⁴: ₁ rs ₊0^,7(0)

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

III.4 CONCLUSION DU CHAPITRE 3

Nous constatons donc qu'il est bel et bien possible d'effectuer des observations réelles, prévues par la gravité quantique de David BOHM dans l'approximation linéaire du champ , ceci , pour certaines expériences qui ont servies de tests à la relativité générale. Le formalisme de la théorie quantique de la gravitation Bohmienne a été appliqué au cas de la solution SSS. Il est observé que la solution est constituée du résultat classique (relevant de la relativité générale) plus quelques corrections quantiques (pour un paquet d'onde gaussien) autour dudit résultat. Dans le cas de la déviation de la lumière par un corps massif, statique et à symétrie sphérique la théorie de BOHM module quelques fluctuations oscillatoires (dues à la nature des fonctions de BESSEL). Compte tenu de la remarque que nous avons faite sur la solution SSS, nous l'avons appliquée⁴⁸ à des problèmes simples comme celui du mirage gravitationnel (dans lequel on aboutit à une équation dont la solution peut être obtenue numériquement pour un problème concret) et celui du décalage spectral des fréquences. On en conclut que les prédictions de la gravité quantique de BOHM dans l'approximation du champ linéaire pourraient englober celle d'EINSTEIN. On peut également noter que la théorie a été validée⁴⁹ par une simulation numérique sur le phénomène des forces des marées. Pour un développement futur, on doit étendre la théorie aux termes non linéaires du champ gravitationnel⁵⁰.

⁴⁸ Ceci est notre propre calcul, il n'apparaît pas sur l'article utilisée, voir bibliographie [1], on a tenu compte des résultats obtenus par la théorie (la métrique) pour postuler ces applications. Nous aurions voulu appliquer également la théorie pour le phénomène de l'avance du périhélie de MERCURE , le problème qui s'est posé est que la théorie classique utilise les termes non linéaires du champ , nous laissons donc ce cas et les autres phénomènes gravitationnels (explication de l'effondrement des trous noirs , observateur en chute libre dans la métrique , trou de ver , Big Bang flèche temporelle , ondes gravitationnelles et gravitions bref toute l'astrophysique , cosmologie et mécanique céleste) pour un développement ultérieur puisqu'ils englobent un vaste champ de recherche fondamentales en physique.

⁴⁹ Il s'agit de la simulation apparue dans l'article utilisé, voir bibliographie [1].

50 Qui sait ? Peut -- être verrait t -- on apparaître des solitons du type pulses ou enveloppes relevant de l'utilisation d'une équation de SCHRÖDINGER non linéaire.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Conclusion Générale

En définitive, dans ce mémoire, il était question de présenter la théorie de la gravité quantique de BOHM dans l'approximation linéaire du champ, tout en la comparant à l'actuelle théorie classique de la gravitation. Cette comparaison a été faite en faisant l'approximation newtonienne de chacune de ces théories, et en les appliquant chacune au cas de la solution SSS. Pour conforter la théorie de BOHM, la solution SSS a été utilisée pour décrire le phénomène de la déviation de la lumière (auquel nous avons ajouté les applications du mirage gravitationnel et du décalage spectral des fréquences ceci en fonction de la solution SSS). On a vu que des observations concrètes pouvaient être possibles, ce qui est un succès de la théorie de BOHM. Compte tenu de tout ceci, nous pensons que cette théorie devrait être prise au sérieux en tant qu'approche de la gravité quantique au même titre que les autres [1, 4]. Toutefois, avant d'acquérir le statut de véritable théorie de gravitation quantique, certains points encore obscurs devront être résolus. Nous pensons qu'il faille davantage la formaliser, l'étendre aux termes non linéaires du champ. Nous devront alors l'utiliser pour avoir une véritable explication des phénomènes gravitationnels et de l'Univers dans son ensemble (comme toute bonne théorie de la gravitation quantique, c'est à ce titre que les autres approches prétendent). La théorie de la gravitation quantique de BOHM en unifiant les quatre (04) interactions fondamentales réalise ainsi le rêve des théoriciens de la physique comme Albert EINSTEIN (théorie unitaire déterministe) tout en constituant un vaste champ fertile de la recherche fondamentale qu'il faut explorer par des expériences concrètes et surtout par celle de la pensée.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Annexe des équations I- Chapitre 1

1. Obtention de l'équation (I.12)





(I.12)

2. Obtention de l'équation (I.23)



or



Donc on aura :

(I.23)

3. Obtention de l'équation (I.33)



? ? ?

R ? exp i at

?

e ? ?2 2 ? ? VR e



R

?





ih

t

i ? e

1

?

²
1







e

aS i ? ² i S i S ?

?

? ? R e

( )

?



? ?

m
h

? 2

R ? V e i ? ?



? ? ?

R S 2m 2m h

? ? ? ?? ? ?

i ? ? ? ? ? ? ? ?

?

On effectue touts les simplifications possibles, notamment on simplifie par

? ?

e i R

? e ² R e ? ? ? ?

?

? ? ? ? R S e ? VR e i

? ? ? ? ?

R S e dans les deux

? ?? ?? ? ? ? 2

membres de cette relation on obtient :

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

m

S

m ]

S

;

? ?Ras m2

m

? S ? hi2 ? VR S

Rm(

R m

m m

Si on divise cette dernière relation par R on obtient :

Regroupons à gauche les termes imaginaires et à droite les autres :

Pour que cette dernière relation soit solvable, il faut que ses deux membres soient identiquement nulles :





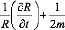
Multiplions la première équation de ce système par 2R :



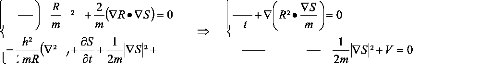
aS 2

m

SV =o L ? ? ? ?

S V ? t m

at

2

(I.33)

S

+ ? ? ?

RV

S S ?

P:

S

R

t

4. Obtention de l'équation (I.36)

· m or v d e f (t) ?	dt ? ? ? m	m V		+



?² ?

^m V(v")+VV v ? ? ?

V Q or 0

?

dt 2

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

On donc :

(I.34)

II- Chapitre 2

?

1. Obtention de l'équation (II.5)

La densité du Hami ltoni en en fonction de celle du Lagrangien : ? ?

or d'après (II.3),

[

O fivaR.Ogv = 2 _fiv^iiv tell_A.

1 [ u
· # v 00

P tel





(II.5)

12. Obtention de l'équation (II.8)

? ? ? ^?

d'après (II.5)

De (II.6) on a:

?

V ?	? 8 8 1 3 ?? 1 ?

L'équation s'écrit alors :

(II.8)

3. Obtention de l'équation (II.10)

3 dans l'approximation linéaire du champ

x ' ' ? ? ? ?

? ??

? ? x ' '

? ? x '

? ?



S S

? 1' = ¹ f d³ xv o_' ,,(xi)v e^v'(x^{i 2}

4. Obtention de l'équation (II.13) On sait d'après (II.4)

<=> Thy

(II.13)

5. Obtention de l'équation (II.14)

Or

S

? 0

? a

at ? ?

? ?

x ??

? ??

De même ?



		pression=d (cx nditioi de jauge)		? ? ?
1
? 60 ? ?			V

6

? ?

f ^d3x ' [0 i ' iv ' .^j cr]

2 _iew p J P ₍50Pv

d Dansle premier membre on fait : 6Q

³

? ? ?? ?

On doit faire



, est symétrique de signature

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

? q

si l' ?

? ' d³ x'V''² O_{p 2} ? + 0

(II.14)

6. Obtention de l'équation (I1.18)

(II.18)

7. Obtention de l'équation (II.19)

Rx 6 ? ? ax S ? ? ? ? +4 8 [R2 8 S .1cPx' at 80(xx 80(.0 ? x = 0 ? 8. Obtention de l'équation II.21

(II.19)



qti srira





e Bx H M (11' 13) s'écrit. Op. _ d 31 äö x' 2 ?

²:



? 4 ? d x ?

RCe qui conduit à

?ä '

? ?

?

(II.21)

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

9. Obtention de l'équation (II.23)



(II.23)

10. Obtention de l'équation (II.28)

^R 80(x)2 2 ?R ^?801⁸0 ?







2







? ?

Q'= R - 1 80 d³x x a Q 0c )R}en R fér³tint pa( ?

) R

? 1

?

? Q= 2ah²[1- 04 ?

(II.28)

?cY

11. Obtention de l'équation (II.29)

-a

2

V²0= -4A^-G + a^{2 2 8}(0^-0

? 2 80 ?

?



(II.29)



(II.32)

(II.34)

aB (sin Y +

Théorie de la gravité quantique de BOHM Par MANDENG .M. Lucien (E.N.S 06 #177;07)

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

12. Obtention de l'équation (II.31)

14. Obtention de l'équation (II.32)

1 [0c 2 0,₇q = ^--4A^-1 Ma( X) ^--ia^{2 2} (q ^--0^c ) V²0^c #177; V²q,₇ ? ? ? ? ? ?

^{2 2}

? d " ?II r ₃₁ sin V2 ? -- ^?2 2 r ² ? ?V2 2 ?

16. Obtention de l'équation (II.33)

d 1 U ? ?

r 2 1^,.2 sinr

ao

1+ ^{s a 1.2sin° a°}aO q)#177; 1 a rUsY ?

r2 sin O ar arsin

(II.33)

15. Obtention du système (II.34)

? ? 0 0

? ? ? ?U(r)Y(9 ) ( ^{d (}r²ⁿ Uj+ U a i_sine²sin + U n ay) r r2sint9 ?

at9L ? ¹ ? ?

e ) r sin B app app

16. Obtention de l'équation (II.43) ? ? ? ? ?

(II.31)

57

dans l'approximation linéaire du champ

(II.43)

17. Obtention de l'équation (II.46)







? ?v ( ) v

(oF - 8 " )



(II.46)

18. Obtention de l'équation (II.47)



a r 2a a 2 2

?

1¹ a

?

R

8 80

			(II.47)
	V

?

? ? ?

? ? ? ?

( _q

1 ?

4 19. Obtention de l'équation (II.48)

? ? ?

? ?? ?

??

? ² ?

or donc

	(II.48)

III- Chapitre 3

1. Obtention de l'équation (III.3)

&h_a

?k	? (k0 ? ? 2 8k^a, 1 ^a (Ike, + dl
&ha		o
			O

Nous négligeons dans ce deuxième membre les termes en ä :

of, 4 2

(III.3)

dans l'approximation linéaire du champ

2. Obtention de l'équation (III.5)



? ?

1d t ^{a d2rs} )⁺y^{a (rrs} )¹
2 -- ab r b r i

or







(III.5)



3. Obtention de l'équation (III.6)

hoo ^20^2 hii =^20^(c^) + ^22b

= ^S + 3 ? ?^2 ? = il ?2 22 ay (2hoo)ka ka d ?



; de même quand x²=y=b à



(III.6)

y=oo ;

4. Obtention de l'équation (III.8)

? ?A

+ .)

a s ? a			? ? ? ? ^2 ? ? ) ? 0 ? ? ? ?			= uoo r ? ? sn ? ? ?+ ah "3 + ?
										? 2	A ?
? (	1 !I (	A ?						1

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(III.8)

5. Obtention de l'équation (III.10)

(III.10)

6. Obtention de l'équation (III.12)















(III.12)

GaLs l'aSSrR[iPatiRL liLéaire Gu AhaPS

Lexique

Approximation linéaire du champ

gravitationnel : elle consiste à ignorer les termes d'ordre supérieur à un dans le développement en G (Constante de NEWTON) de l'expression du champ gravitationnel.

Astrophysique : partie de l'astronomie (science qui étudie la position, les mouvements et la constitution des corps célestes) qui étudie la constitution, les propriétés physiques et l'évolution des astres et des divers milieux qui les composent).

Calcul tensoriel : partie des mathématiques qui traite de l'algèbre des tenseurs, des opérations sur les tenseurs....

Composante covariante d'un tenseur : Composante d'un tenseur avec des indices en position basse : par exemple.

Composante contravariante d'un tenseur : Composante d'un tenseur avec des indices en position haute.

Connexion riemannienne : il s'agit d'une
connexion linéaire sur une variété

différentiable í, sans torsion qui conserve le produit scalaire défini par la métrique riemannienne, elle est noté :

;

Cosmologie : branche de l'astronomie qui étudie la structure et l'évolution de l'Univers dans son ensemble.

Espace - temps : c'est la réunion de tous les évènements possibles, un évènement étant ce qui peut survenir en un lieu et à un instant .C'est donc un ensemble de points dont les coordonnées de localisation sont au « nombre de 4 »(il peut en exister d'autres selon les nouvelles théories de la gravitation) :la première est celle du temps et les trois autres sont celles de l'espace physique ordinaire.

Espace - temps einsteinien : C'est une géométrie lorentzienne caractérisée par la métrique lorentzienne g_m, et muni de la connexion riemannienne associée à g. Il est courbe car il est décrit à l'aide d'une géométrie non euclidienne.

Espace - temps galiléen : espace - temps de géométrie euclidienne.

Espace - temps minkowskien : espace affine à 4 dimensions dont l'espace vectoriel réel associé est muni d'un produit scalaire lorentzien ; cela signifie qu'il existe une base

de l'espace vectoriel telle que

,

Cette base constitue une tétrade lorentzienne. Cet espace - temps est plan car défini à l'aide d'une géométrie euclidienne.

Géodésique : c'est la ligne d'Univers la plus courte joignant deux points sur une surface.

Géométrie Riemannienne : c'est une géométrie non euclidienne donc courbe, différentielle, muni de la connexion riemannienne.

Gravitation : phénomène physique par lequel deux corps matériels s'attirent avec une force proportionnelle au produit de leur masse et inversement proportionnelle au carré de leur distance (D'après NEWTON).

Gravité : force de gravitation exercée par un astre sur un corps quelconque (NEWTON).

Gravité quantique : La gravité quantique est la branche de la physique théorique tentant d'unifier la mécanique quantique et la relativité générale ;

Relativité générale : actuelle théorie

classique et déterministe de la gravitation (Théorie de l'infiniment grand) , fondée par EINSTEIN en 1916 , et dont la théorie de NEWTON de la gravitation n'est qu'une approximation pour des champs gravitationnels faibles.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Le champ d'action de la relativité générale part des systèmes d'étoiles, en passant par les

galaxies jusqu'à l'Univers pris dans son ensemble.

Masse grave : masse traduisant la propriété qu'elle a d'attirer d'autres masses ou d'être attirer par d'autres masses. Suivant le cas, on parlera respectivement de masse grave active ou de masse grave passive.

Masse inerte : masse traduisant la propriété qu'elle a de résister à sa mise en mouvement par des forces. En fait la masse inerte et la masse grave pour un même corps matériel sont égales d'après le principe de

l'équivalence.

Métrique : c'est un champ de tenseur g deux fois covariant, symétrique et non dégénéré.

avec et .

Métrique de SCHWARZSCHILD : métrique permettant de décrire le champ gravitationnel autour d'une masse sphérique et statique (ie qui n'est pas en rotation). Cette masse peut être une étoile, une planète ou un trou noir de SCHWARZSCHILD.

Métrique lorentzienne : C'est une métrique décrite pour l'espace - temps einsteinien ou espace - temps lorentzien. Elle est notée

de signature .

Métrique minkowskienne : on définit

comme la métrique décrite dans l'espace - temps minkowskien et dont la signature est
ou .

Observateur : possède une horloge pour mesurer le temps d'un évènement et une règle graduée dans son voisinage immédiat pour mesurer la localisation spatiale dudit évènement. Si deux évènements peuvent être reliés par l'intermédiaire de cette règle alors ils sont dits simultanés pour cet observateur.

Observateur inertiel : c'est un observateur dont la ligne d'Univers est une droite de l'espace - temps galiléen non incluse dans l'espace. Il conserve une direction d'espace fixe au cours du temps.

Signature d'une métrique : Ensemble ordonné des signes des composantes de la diagonale

( ² 1) / 2

principale d'une métrique.

Symboles de CHRISTOFFELL : Ils sont de première espèce et de deuxième

espèce on a les relations

g ._ar_ka =F_icji et , Iki= k

,

Tenseur : être mathématique (géométrique) Représentant une grandeur physique intervenant dans des lois qui doivent avoir

Une forme à caractère universel c'est - à - dire que cette forme ne doit pas dépendre du système de coordonnées (critère tensoriel). Dans un système de coordonnées à 3 dimensions, le tenseur est défini par un nombre entier n, on lui associe alors une matrice à 3ⁿ composantes, qu'on identifie généralement sous forme indicée selon leur position dans la matrice du tenseur considéré.

Tenseur anti - symétrique : un tenseur est ainsi appelé lorsque : .

Tenseur de RIEMANN : c'est le tenseur de courbure pour la connexion riemannienne. Il possède des propriétés d'antisymétrie en tant que tenseur de courbure : = --R₁₁₀ , et

d'autres propriétés de symétries :

.Ce tenseur

vérifie également la première identité de BIANCHI : ainsi que la

deuxième : . Il

permet de calculer la commutation des dérivées

covariantes : . Ce

tenseur a composantes
indépendantes.

Tenseur de RICCI : il est obtenu en effectuant
une contraction d'indices sur le tenseur de

RIEMANN . Il est symétrique et

possède n(n+1)/2 composantes indépendantes. Tenseur symétrique : un tenseur est ainsi dit lorsque :

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Notice [16(4)]

1. Approches candidates à la gravitation quantique Un certain nombre de propositions ont ete avancees pour aborder le problème :

· La première tentative de guérir la non-renormalisabilite de la gravitation a ete de rajouter l'ingredient de la supersymetrie afin de relier le comportement du graviton à celui des autres particules de spin plus petit et adoucir ainsi les divergences de la theorie. Le resultat porte le nom de theorie de supergravite. Malheureusement, malgre un comportement en effet meilleur les divergences restent et ces theories ne sont donc pas bien definies quantiquement.

· La theorie des cordes ou bien, plus precisement dans sa version supersymetrique, la theorie des supercordes est une tentative non seulement de description quantique de la gravite mais egalement des autres interactions fondamentales presentes dans le modèle standard de la physique des particules. Les differents modèles de la theorie des cordes sont parfaitement definis d'un point de vue quantique et de façon remarquable admettent les theories de supergravite comme theories effectives à basse energie. En ce sens les theories de cordes fournissent une description microscopique, on parle aussi de completion ultraviolette, aux theories de supergravite. C'est la branche de ce domaine la plus active par le nombre des chercheurs et des publications. Une partie des chercheurs travaillant sur la gravitation quantique à boucles critiquent neanmoins la theorie des cordes dont la place qui lui est accordee est selon eux hegemonique et empêche le developpement normal de theories alternatives en l'absence de confirmations experimentales.

· La gravitation quantique à boucles introduite par Lee Smolin et Carlo Rovelli sur la base du formalisme d'Ashtekar s'attache à presenter une formulation quantique de la gravite explicitement independante d'une eventuelle metrique de fond (contrairement à la description actuelle de la theorie des cordes même si elle inclut egalement la symetrie de reparametrisation comme sous ensemble de ses symetries) ce qui est un effort naturel conforme à l'esprit de la relativite generale. Contrairement à la theorie des cordes, la gravitation quantique à boucle ne se donne pas comme but de decrire egalement les autres interactions fondamentales. Elle ne se veut donc pas une theorie du tout. La viabilite de ce projet est contestee par une partie de la communaute des chercheurs en theorie des cordes (voir Lubos Motl à ce sujet).

· Alain Connes a recemment propose l'utilisation de sa geometrie non commutative pour reconstruire le modèle standard par reduction dimensionnelle de la relativite generale sur une variete non-commutative dans l'esprit de la theorie de Kaluza-Klein cherchant à reproduire l'electromagnetisme par reduction dimensionnelle de la relativite generale sur un cercle. Cependant son analyse se base sur une description classique du modèle standard et la quantification de son modèle n'est pas encore developpee ce n'est donc pas encore à proprement parler une description quantique de la gravite.

· La theorie des twisteurs de Roger Penrose introduite dans les annees 70 a introduit un nouveau formalisme permettant l'etude des solutions des equations de la relativite generale et à ce titre aurait pu

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

offrir un meilleur point de départ pour la quantification de celle-ci. Mais les efforts dans ce sens n'ont pas abouti et le projet de quantification par cette voie a été abandonné aujourd'hui. Par contre le formalisme de twisteur reste utile dans le cadre de la relativité et a même retrouvé un regain d'intérêt récemment dans le cadre de l'étude de la théorie de Yang-Mills via la théorie des cordes (travaux de Witten sur ce dernier point).


· Théorie de la gravité quantique de David BOHM incluant le potentiel quantique et récemment testé

sur les résultats de la relativité générale. Elle apporte des termes correctifs sur la déviation de la lumière par un corps massif á symétrie sphérique, résultat obtenue par simulation numérique (Déviation déjá calculée á l'aide de la relativité générale) et donne une image corrective des lignes des forces des marées. La théorie de BOHM est déterministe, ne respecte pas le principe de covariance générale mais inclut également une vision métrique de la gravitation, á l'aide la fonction d'onde du système. Je pense qu'avec la métrique obtenue dans le cadre de cette théorie, l'on peut prévoir également des phénomènes comme l'effondrement gravitationnel d'une étoile, les mirages gravitationnels, les ondes gravitationnels.... Physica Scripta 2003, Vol.68,207-212, Bohmian quantum gravity in the linear field approximation de Fatimah SHOJAI et Ali SHOJAI )

2. Unification des interactions

Les physiciens ont recensé quatre interactions fondamentales dans la nature. Il n'est pas impossible que d'autres interactions existent sans que les moyens expérimentaux dont nous disposons aujourd'hui ne nous permettent de les mettre en évidence. En tout état de cause, qu'il y ait 4, 10 ou 20 interactions fondamentales, aucune indication dans la nature ne nous renseigne sur les raisons pour lesquelles il y en aurait 4, 10 ou 20 ! Quelque soit le véritable nombre d'interactions, leur multiplicité est inexplicable et la contingence de ce nombre soulève de graves difficultés d'ordre épistémologique et philosophique. Finalement, il est tout á fait légitime de se demander pourquoi la nature compte quatre interactions fondamentales et non 3 ou 5. Pourquoi n'en existe-t-il pas une seule ? Les physiciens aiment la simplicité qu'ils ont presque élevée en principe universel. Or quatre interactions, cela fait désordre et compliqué, alors que le principe de simplicité nous ferait plutôt pencher vers une interaction unique, synthèse parfaite de toutes celles observées á ce jour. Cette recherche de la simplicité a permis de débroussailler, avec un grand succès, la multitude des particules (les hadrons). Alors pourquoi ne pas tenter la même aventure avec les interactions ?

Pour unifier les interactions, deux approches sont possibles :

1. Une approche synthétique : les interactions seraient des manifestations différentes d'un même phénomène plus global qui pourrait être décrit par un seul cadre théorique á très haute énergie,

2. Une approche "historique" : les interactions étaient unifiées au moment du "big bang" et elles se

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

seraient différenciées au fil du temps, un peu à la manière des cellules d'un embryon.

La beauté de la chose réside dans le fait, qu'au fond, ces deux approches sont équivalentes. En effet, augmenter l'énergie mise en jeu dans les interactions revient à se rapprocher des conditions qui prévalaient lors du Big Bang. Augmenter l'énergie est donc équivalent à remonter le cours de l'histoire de l'univers. S'il existe effectivement une interaction unique à très haute énergie, synthèse des interactions observées à notre niveau d'énergie, alors cela signifie que cette interaction était celle qui existait au moment du Big Bang.

Certains faits expérimentaux tendent à laisser soupçonner l'existence d'une telle synthèse à très haute énergie. Notamment, les expériences ont montré que les valeurs des constantes de couplage des diverses interactions se modifient avec l'augmentation de l'énergie et semblent, en première approximation, converger vers une valeur unique (à l'exception de la gravitation, toutefois).

3. La théorie de BOHM

(Mécanique quantique de BOHM)

Elle est déterministe, tandis que la mécanique quantique standard admet une interprétation non déterministe. A la différence d'un potentiel de la physique classique, le potentiel quantique de BOHM ne diminue pas nécessairement avec la distance spatiale. De plus la manière dont il détermine la trajectoire d'un système quantique peut dépendre de façon immédiate de facteurs éloignés dans l'espace. Il s'agit donc d'un nouveau type d'interaction, caractéristique du domaine quantique : une interaction à distance qui contrairement aux autres interactions, ne respecte pas la vitesse finie de la lumière comme vitesse limite. Elle conduit aux mêmes résultats que la mécanique quantique standard mais inclut comme EINSTEIN des variables cachées non locales. L'opposition entre la mécanique quantique standard et la mécanique quantique de BOHM est un exemple paradigmatique de la thèse philosophique de la sous -- détermination de la théorie par l'expérience. Trois points permettent néanmoins de fonder une critique à l'adresse de la théorie de BOHM : La mécanique quantique est la déclinaison d'une théorie quantique plus large qui inclut la théorie des champs quantiques. La théorie de BOHM peut -- elle être étendue à la théorie des champs quantiques ? Peut -- elle en reproduire toutes les prédictions expérimentales ?

- Est -- il cohérent d'accorder à la position le statut de propriété privilégiée, la valeur numérique définie de la position étant la variable cachée ? Toutes les autres propriétés n'acquièrent, d'après la théorie de BOHM, comme d'après la mécanique quantique standard, une valeur numérique définie que lors du processus de la mesure.

- L'hypothèse d'un potentiel quantique étant, semble t -- il une hypothèse ad hoc, supposer qu'un tel potentiel existe repose sur l'argument de reproduire les prédictions de la mécanique quantique standard. Source voir bibliographie [11].

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Bibliographic

[1] Bohmian Quantum Gravity in the Linear Field Approximation Ali SHOJAI and Fatimah SHOJAI, Physica scripta .Vol. 68,207-212, 2003.

[2] Note de cours de RELATIVITE GENERALE (D.E.A de physique théorique) Paris VI, Paris VII, Paris IX, E.N.S, X

Bernard LINET, 2004 - 2005, [e-mail]

[3] Mécanique, Fondements et applications J.-P. PEREZ, 5^ème édition, MASSON 1997.

[4] Physics meets philosophy at the PLANCK scale, contemporary theories in quantum gravity

By Craig CALLENDER (University of California at San Diego)

And Nick HUGETT (University of ILLINOIS at Chicago)

CAMBRIDGE University Press, 2001 Printed in U.S.A.

[5] Le déterminisme en physique

Par Lucien MANDENG, Projet de mémoire (E.N.S 04 - 05) , sous la direction du Docteur Jean Marie MBOUNGA, 2005.

[6] La physique du Hasard de Blaise Pascal à Niels Bohr Ch. RUHLA, Liaisons scientifiques, Hachette 1989.

[7] La décohérence, espoir du calcul quantique Article d'Harold Ollivier et Philippe Pajot, La recherche Septembre 2004, N°378, Pages 34 - 37.

[8] « A la une, Dépasser EINSTEIN » : L'héritage infernal Science et vie, Avril 2005, Pages 50 - 55.

[9] « A la une, Le monde existe - t - il vraiment ? »

1. Aux limites de la matiAre, la réalité n'est plus une certitude.

2. Et si tout n'était qu'information ?

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Science et vie, Octobre 2005, (1) Pages 70 - 77 et (2) Pages 78 - 83.

[10] La gravité est - elle illusion ?

Article de Juan Maldacena, Pour la science, Janvier 2006, N°339

[11] Un problème de physique : interpréter ou expérimenter ? Article de Nicolas Gisin et Valerio Scarani , Hors - série sciences et avenir , Octobre / Novembre 2006, Pages 66 - 71.

[12] Les univers cachés

1. Des cordes pour unir les forces de la nature

Par Emile Martin, Ciel et espace, Mai 2006, Pages 40 - 42.

2. « Notre univers serait une brane parmi d'autres »

Interview de Pierre Binétry, cosmologiste, Ciel et espace, Mai 2006, Pages 43 - 45.

3. Le rêve : la théorie qui résout tout

Par Stéphane Fay , Ciel et espace , Mai 2006 , Pages 46 - 48 .

[13] L'Univers, un monstre informatique

Article de Seth Llyod et Y. Jack Ng, Pour la science, Novembre 2004, N°325, Pages 31 - 37.

[14] Einstein et la théorie unitaire : 40 ans perdus ?

Article de C. Goldstein et Jim Ritter, Pour la science, Décembre 2004, N°326.

[16] L'évolution des idées en physique

Albert EINSTEIN, Léopold INFELD, traduit par Maurice SOLOVINE, Champs (Flammarion), 1982

[16] Liens des pages web visitées :

1. http://jac_leon.club.fr/gravitation/article-francais/f-38.html

2. http://jac_leon.club.fr/gravitation/article-francais/f-39.html

3. http://jac_leon.club.fr/gravitation/article-francais/f-310.html

4. fr.wikipedia.org/wiki/Gravité_quantique

5. fr.wikipedia.org/wiki/Gravitation_quantique_à_boucles

6. http://www.peiresc.org/2004/Cosmologie.htm

7. www.cieletespace.com/cat/quiseralenouveleinsteinversunenouvelletheorie de_la_gravitation.html

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

8. http://depire.free.fr/publique/THC/Cordes12.html

9. www.linternaute.com/science/espace/dossiers/06/theorie-du-tout/7.shtml

10. www.lpt.ens.fr/~gervais/activites/node35.html

11. www.webastro.net/forum/showthread.php?t=2282

12. http://www.mad-jarova.org/francais/gal13.htm

13. http://fr.wikipedia.org/wiki/Horizon_(trou_noir)

14. http://fr.wikipedia.org/wiki/Singularit%C3%A9_gravitationnelle

15. http://dept-info.labri.fr/~gavoille/divers.html

16. http://www.cpt.univ-mrs.fr/~coque/book/node221.html

17. http://jac_leon.club.fr/gravitation/article-francais/f-37.html

18. http://perso.orange.fr/michel.hubin/celebres/chap_cel4.htm

19. http://www.outre-vie.com/vieapresvie/chercheurs/bohm.htm

20. http://www.arikah.net/encyclopedie-francaise/Elwin Bruno Christoffel

21. http://fr.wikipedia.org/wiki/G%C3%A9om%C3%A9trie diff%C3%A9rentielle

22. http://fr.wikipedia.org/wiki/G%C3%A9om%C3%A9trie_riemannienne

23. http://fr.wikipedia.org/wiki/G%C3%A9om%C3%A9trie_non_euclidienne

Version reconstituée, adaptée pour la mise en ligne le 24 Septembre 2008

Edité par Lucien M.MANDENG

Contact de l'Auteur :

Tel. Fixe: ([phone] Cell. : ([phone]

Email: [e-mail] ,

B.P: 30815 Biyem - assi YAOUNDE CAMEROUN

Toute remarque ou suggestion serait la bienvenue