Modélisation hydraulique et de la qualité d'eau dans les réseaux d'adduction d'eau potable par EPANET

UNIVERSITÉ DE TUNIS EL MANAR

MEMOIRE DE MASTERE EN

MODELISATION EN HYDRAULIQUE ET ENVIRONNEMENT

Élaboré par : Jalel KHELIL
Soutenu le devant le jury composé de :

Président Membre

Membre

Mr. Khlifa MAALEL Encadreur

Mr Hedi CHANNOUFI Invité

S O M M A I R E

L I S T E D E S F I G U R E S

L I S T E D E S T A B L E A U X

LISTE DES ANNEXES

R E S U M É

INTRODUCTION GENERALE

Chapitre I: Concepts de bases de la modélisation hydraulique 1

I-1 / Principales phases de la modélisation 1

I-2/ Equations d'équilibrage hydraulique 1

I-3/ Méthodes numériques pour la résolution des équations d'équilibrage hydraulique 4

I-3-1/ Principe de l'approche hybride noeud-maille 4

I-3-2/ Algorithme de simulation 5

I-4/ Conclusion 8

Chapitre II: La dégradation du chlore dans l'eau : Processus et approches de modélisation 9

II-1/ Généralités 9

II-1-1/ Conservation de la masse 9

II-1-2/ Mélange aux noeuds 11

II-1-2-1/ Noeud sans injection de constituant 11

II-1-2-2/ Noeud avec injection de constituant 11

II-1-3/ La cinétique des réactions 12

II-1-4/ Les processus de transport dans un fluide 13

II-1-4-1/ Le mécanisme d'advection 13

II-1-4-2/ La diffusion moléculaire 13

II-1-4-3/ La diffusion turbulente 14

II-1-4-4/ La dispersion 14

II-1-4-5/ L'impact de la diffusion et la dispersion 14

II-2/ Processus de dégradation du chlore dans l'eau 15

II-2-1/ Différentes formes du chlore 15

II-2-2/ Réactions chimiques du chlore dans l'eau 15

II-2-3/ Notion de demande en chlore 16

I-2-4/ Principaux facteurs physicochimiques influençant la dégradation du chlore dans l'eau 16

II-2-4-1/ pH et minéralisation 17

II-2-4-2/ Température 18

II-2-4-3/ Oxygène dissous 18

II-2-4-4/ Turbidité 18

II-2-4-5/ Matière organique 18

II-2-4-6/ Dureté 18

II-2-4-7/ Ions fer 19

II-2-4-8/ La nitrite 19

II-3/ Approches pour la modélisation de la dégradation du chlore 19

II-3-1/ Modèles de dégradation de chlore à coefficients invariables 20

II-3-2/ Modèles de dégradation de chlore à coefficients paramétrés 21

II-4/ L'algorithme de simulation de la qualité d'eau par EPANET2 22

II-4-1/ Principe 22

II-4-2/ L'algorithme 22

II-5/ Conclusion 24

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'adduction d'eau potable. Cas de la région de Bizerte 25

III-1/ Construction du modèle hydraulique 25

III-2/ Construction du modèle de dégradation paramétré du chlore : Cas général 27

III-2-1/ Détermination du coefficient de dégradation du chlore dans la masse d'eau 28

III-2-2/ Couplage du modèle qualité d'"EPANET2"avec le tableur Excel 30

III-2-2-1/ Hypothèse 30

III-2-2-2/ Exportation des informations du modèle EPANET vers Excel 30

III-2-2-3/ Mise en place de la feuille de calcul EXCEL 30

III-2-2-4/ Importation des informations par le modèle EPANET a partir de la feuille Excel 30 III-2-3/ Calage du modèle qualité : cas général 31
III-4/ Modèle hydraulique et de qualité d'eau : cas du réseau d'adduction de la région de Bizerte3 1

III-4-1/ Etendue de l'étude 31

III-4-2/ Mise en place du modèle hydraulique du réseau de la région de Bizerte 35

III-4-2-1/ Modélisation et consignes d'asservissement des pompes du modèle 37

III-4-2-2/ Modélisation et consignes d'asservissement des vannes du modèle 38

III-4-2-3/ Calage du modèle hydraulique 39

III-4-3/ Construction du modèle qualité 40

III-4-3-1/ Gestion de la qualité d'eau dans le réseau d'étude 40

III-4-3-2/ Détermination de la constante de dégradation de masse du chlore résiduel libre

dans l'eau 41

III-4-3-2-1/ Méthodologie 41

III-4-3-2-2/ Résultats statistiques des analyses et discussions 42

III-4-3-3/ Elaboration du fichier Input de qualité pour "EPANET2" 43

III-4-3-4/Calage du modèle qualité 47

III-5/ Conclusion 49

Chapitre IV: Exploitation des modèles hydraulique et de qualité du réseau d'adduction d'eau potable
de la région de Bizerte 50

IV-1/ Exploitation du modèle hydraulique développé 50

IV-2/ Exploitation du modèle de qualité développé 51

IV-3/ Exemples d'Amélioration de la qualité d'eau dans le réseau 55

IV-4/Impact des ouvrages de stockage sur la qualité d'eau 58

IV-5/ Conclusion 58

CONCLUSION GENERALE ET PERSPECTIVES LISTE BIBLIOGRAPHIQUE

L I S T E D E S F I G U R E S

Figure II.1 :Demande en chlore (Cockx, 2005) 16

Figure II.2:Description schématique du modèle de transport 2-D de chlore 17

Figure II.3: Comparaison entre des études de dégradation du chlore (Ozdemir et Ger, 1998) 20

Figure III.1 Appareil de mesure du chlore dans l'eau "Le Comparateur" 28

Figure III.2: Plan schématique du réseau d'adduction de Bizerte 33

Figure III.3: Schéma du réseau d'adduction du modèle "EPANET2" 37

Figure III.4: Sélection des pompes 44

Figure III.5:Sélection des vannes de régulation des mélanges d'eaux 44

Figure III.6: Localisation des points d'échantillonnage 47

Figure IV. 1: Graphique type" balance en eau" 50

Figure IV.2: Profil en long de la conduite d'adduction à partir de la station de traitement jusqu'au réservoir de "Rhézala" 51

Figure IV.4: Distribution du chlore résiduel libre dans la conduite d'adduction de la station de traitement de Mateur en périodes estivale et hivernale pour les pics et les creux de consommation. 52

Figure IV. 5: Distribution du temps de séjour en période hivernale et estivale 53

Figure IV.6: Distribution du coefficient Kb en période hivernale et estivale 54

Figure IV.7: Modulation du taux de chlore (à droite) et de la vitesse d'écoulement (à gauche) au niveau de la station de reprise Roumadia pour les périodes hivernale et estivale. 55

Figure IV.8:Représentation schématique de la formation et de la structure d'un biofilm au sein d'un réseau d'eau potable (Gauthier,2001) 56

Figure IV.9:Distribution modifié du chlore résiduel libre dans la conduite d'adduction de la station de traitement de Mateur 57

Figure IV.10: Impact des ouvrages de stockage sur la qualité d'eau 58

L I S T E D E S T A B L E A U X

Tableau I.1: Formules de perte de charge totale (exprimée en mce et le débit en m³/s) 3

Tableau II.2: Quelques ordres de grandeurs du coefficient de dégradation de chlore dans l'eau (Frederick L et al, 1992) 21

Tableau III.1: Equation de corrélation entre Kb, T et C_o 43

Tableau III.2: Exemple du fichier "input" de débits moyens des pompes et vannes de régulations 45

Tableau III.3: Exemple de coefficients Kb, mélange (en mn-1) et K_w (avant calage) 46

Tableau III.4: Chlore résiduel libre mesuré et calculé 48

LISTE DES ANNEXES

Annexe 1 : Technique de détermination de la concentration du chlore résiduel libre.

Annexe 2 : Logiciel de calcul statistique REGRESS 1.0

Annexe 3 : Données d'exploitations (SONEDE/District de Bizerte) Annexe 4 : Courbes de modulations horaires

Annexe 5 : Résultats d'analyses physico-chimiques (Laboratoire Ghdir Golla)

Annexe 6 : Etude de régression du chlore résiduel total.

Annexe 7 : Détermination des équations de corrélation entre Kb, Co et T pour chaque groupe de sources d'eau.

Annexe 8 : Générateur des coefficients Kb, mélange Annexe 9 : Calage du modèle qualité d'EPANET Annexe 10: Base de données du modèle EPANET Annexe 11 : Logiciel de modélisation EPANET

1

R E S U M É

Cette étude a pour objectif l'analyse expérimentale et l'élaboration d'un modèle hydraulique et de dégradation du chlore pour les réseaux d'adduction d'eau potable. La partie principale de notre travail a consisté à concevoir, réaliser et exploiter un modèle hydraulique et de dégradation du chlore spécifique pour le réseau d'adduction de la région de Bizerte. Ce modèle devrait refléter le mieux la réalité du terrain tout en restant simple.

L'outil informatique utilisé pour l'élaboration des modèles hydraulique et de qualité est le logiciel EPANET2. Ce logiciel est distribué gratuitement par l'agence américaine E.P.A. (U.S. Environmental Protection Agency) depuis le mois de septembre 1993. Depuis, il est largement utilisé dans le monde entier grâce à ses algorithmes de calcul les plus avancés, son interface graphique conviviale et intuitive et grâce aux possibilités de liaisons avec d'autres logiciels d'application (Rossman, 2000).

Au cours de l'étude de l'éventuel corrélation entre les coefficients de la cinétique chimique de la dégradation du chlore dans l'eau avec certains paramètres choisis de la bibliographie, on a supposé que :

- les réactions chimiques du chlore à l'intérieur des réseaux et les mélanges aux interconnexions sont ceux qui définissent la qualité d'eau à chaque point du réseau et à tout moment

- l'origine et la température d'eau ainsi que la consigne de chloration au niveau des points d'injection du chlore dans le réseau sont les paramètres qui participent à la détermination des cinétiques des réactions de dégradation du chlore dans l'eau.

Les coefficients ainsi déterminés, sont exploités dans la mise en place du modèle qualité du logiciel EPANET2.

En se basant sur un total de 84 échantillons, nous avons étudié, pour des conditions initiales différentes, l'évolution de la concentration du chlore dans chacun d'eux dans le temps et dans des conditions initiales différentes par le moyen de l'appareil de mesure du chlore "chloromètre". Un total de 831 mesures a été réalisé pour constituer la base de données de l'étude statistique où on a évalué la corrélation entre les coefficients de la cinétique chimique de la dégradation du chlore et certains paramètres tel que la température, la matière organique et la concentration initiale du chlore. Les résultats statistiques ont donné des coefficients de dégradation R² compris entre 0,65 et 0,95.

Pour tenir compte de cette dépendance dans le modèle qualité d'EPANET2, traduite par les coefficients de dégradation du chlore - coefficients primordiaux pour la simulation de la qualité des eaux, nous avons développé une interface entre "EXCEL" et EPANET2. Cette interface matérialisée

2

par une feuille de calcul EXCEL renferme les résultats de l'étude statistique présentés sous forme d'équations de corrélation pour chaque tronçon de conduite. En effet, après avoir élaborer et ajuster le modèle hydraulique, les débits moyens sur un intervalle de temps prédéfini, résultants de la simulation hydraulique, sont exportés vers la feuille de calcul EXCEL où les coefficients sus indiqués sont par la suite générés et transmise au modèle de qualité d'EPANET2.

Les résultats de la simulation du comportement du chlore dans le réseau étudié traduit bien la réalité du terrain en comparant les concentrations mesurés et calculés.

Mots clés : réseau adduction, eau potable, modélisation hydraulique, dégradation du chlore résiduel libre, EPANET2.

2

INTRODUCTION GENERALE

On défini l'adduction des eaux comme étant le transport des eaux brutes des zones de captage aux zones d'utilisation. Les réseaux d'adduction sont caractérisés par :

- Une étendu importante : les conditions climatiques peuvent changer d'une zone à une autre du réseau.

- La diversité de ses composantes : réservoirs volumineux, pompes immergées, pompes horizontales, brises charges, vannes de régulations, stations de traitements,...

- Des diamètres relativement importants des conduites de transfert.

L'un des indicateurs de la qualité d'eau dans ces réseaux est le taux du désinfectant, principalement le chlore libre. Il renseigne sur les risques de la contamination d'eau. Son absence est la cause de l'accroissement de la densité bactérienne au niveau du biofilms sur les parois internes des conduites, ce qui engendre la diminution de la section de passage de l'eau et par la suite la débitance des conduites.

Les gestionnaires des réseaux d'adduction d'eau potable sont sensés assurer un service satisfaisant sur les plans disponibilité et qualité d'eau. Ce n'est pas un objectif facile en raison de la complexité de ces réseaux.

Ces difficultés éprouvées par les responsables font de la modélisation un outil d'aide pour la bonne gestion hydraulique et de qualité de tels réseaux. Cette modélisation est rendue possible grâce aux progrès de l'informatique traduit par le développement spectaculaire des moyens informatiques.

Dans le cadre de ce travail de mémoire de mastère, notre intérêt sera consacré à la conception d'un modèle hydraulique et de qualité pour les réseaux d'adduction d'eau potable, en focalisant sur la dégradation du chlore dans l'eau transporté appelé aussi "DECAY" et en se rapprochant au mieux de la réalité du terrain.

Contrairement au réseau de distribution d'eau potable et vu le caractère dynamique des mélanges des eaux, les coefficients de la cinétique de la dégradation du chlore dans l'eau, ne peuvent pas être considérés comme des valeurs statiques. Pour cela, ce travail stipule que les coefficients de la cinétique de la dégradation du chlore dans l'eau pourraient être influencés par des paramètres à déterminer et à étudier au cas par cas pour tenir compte de la variabilité de ces coefficients.

3

Dans le cadre de ce master nous proposons de développer, de tester et de valider cette approche de modélisation sur un cas réel qui est le réseau d'adduction de la région de Bizerte par trois moyens :

- Moyen expérimental : prélèvement de 84 échantillons au niveau des sources d'eau soumis à des conditions initiales prédéfinis et la réalisation de 831 mesures du chlore dans l'eau par le moyen de l'appareil "Chloromètre". Ces mesures sont la base de données de l'étude expérimentale.

- Moyen statistique : à partir des mesures suscitées, on étudie la corrélation qui pourrai exister entre d'une part les coefficients de la cinétique de la dégradation du chlore et d'autre part l'origine d'eau, la température et la concentration initiale du chlore.

- Moyen de modélisation : pour ce faire on a opté pour le logiciel EPANET2 vu qu'il est largement utilisé dans le monde et que ses algorithmes de calcul les plus avancés, et que son interface graphique est conviviale et intuitive avec des possibilités de couplage avec d'autres logiciels d'application (Rossman, 2000).

Après avoir élaborer le modèle hydraulique du réseau d'étude, les résultats de la simulation hydraulique en terme de débit moyens transité dans chaque tronçon sont transmises à la feuille de calcul EXCEL où sont introduits les équations de corrélations suscitées pour chaque tronçon. Les coefficients de dégradations du chlore sont alors générés automatiquement et par la suite exportés vers le modèle qualité d'EPANET2 pour simuler la distribution spatio-temporelle du chlore résiduel dans l'eau.

Dans ce qui suit on présente un aperçu sur l'organisation de ce mémoire et sur la contribution de chaque chapitre aux objectifs recherchés. Ce mémoire est organisé en Quatre chapitres :

Le premier chapitre est une introduction aux concepts de base de la modélisation hydraulique. En effet, les processus de réaction-transport à l'intérieur des conduites d'un réseau sont gouvernés par les vitesses et les pressions. Ainsi, la validité des résultats obtenus par le modèle de qualité dépendra en grande partie de la fiabilité des calculs hydrauliques. Trois sections forment ce chapitre. La première s'intéresse à de la définition de la modélisation en général et la modélisation hydraulique en particulier en énumérant les phases de son déroulement. La deuxième section s'intéresse à la formulation des équations qui régissent les écoulements en charges et aux équations d'équilibrage hydraulique. La dernière section est consacrée à la méthode numérique pour la résolution de ces équations utilisé par le logiciel EPANET2, appelée la méthode du gradient.

4

Le deuxième chapitre est consacré à l'étude de la dégradation du chlore dans l'eau : ses processus ainsi que des approches pour sa modélisation. Une synthèse des aspects théorique et bibliographique de la modélisation du chlore résiduel libre dans l'eau au niveau des réseaux sous pression est exposée. Trois sections forment ce chapitre. La première s'intéresse aux processus de réaction-transport nécessaires pour la compréhension des phénomènes liés à la modélisation de la qualité d'eau en général. La deuxième section, s'intéresse à une présentations bibliographique de deux approches pour la modélisation de la dégradation du chlore libre. La troisième section est un exposé de l'algorithme de simulation de la qualité d'eau par l'outil informatique EPANET2.

Le troisième chapitre, est consacré à l'attribution de ce travail dans le domaine de la modélisation hydraulique et de la qualité d'eau pour les réseaux d'adduction d'eau potable. Il commence par une présentation générale de notre approche de modélisation hydraulique et de la dégradation du chlore résiduel libre.

Parmi les données d'entrées nécessaires pour cette approche :

- Pour le modèle hydraulique : les dimensions des conduites et des réservoirs, les cotes NGT des extrémités des conduites, les caractéristique techniques des groupes électropompes ainsi que leurs modes d'asservissement, les niveaux statiques des nappes et les modulations de la demande au noeuds.

- Pour le modèle qualité : les coefficients de dégradation du chlore avec la masse d'eau et avec les parois des conduite pour chaque tronçon. Ces coefficients sont déterminés suite à l'étude expérimentale et statistique menée dans le cadre de cette recherche.

Parmi les données de sortie des modèles hydrauliques et de qualité developpés:

- Pour le modèle hydraulique : les débits dans chaque tronçon ainsi que la vitesse des écoulements, la pression aux noeuds et la variation des niveaux d'eau dans les réservoir.

- Pour le modèle de qualité : la concentration en chlore à chaque endroit et à chaque pas de temps de l'eau transité par le réseau de transport.

Ce chapitre s'achève par l'application de notre approche sur un réseau existant qui est le réseau de transport d'eau potable de la région de Bizerte

Le quatrième chapitre de ce rapport s'intéresse à l'aspect exploitation des modèles construits. En effet ces modèles permettent le suivi du comportement des réseaux envers des situations prédéterminées (débits, températures, concentrations...) par l'utilisateur, en se basant sur les résultats des simulations.

1

Chapitre I

Concepts de bases de la modélisation hydraulique

Dans ce chapitre, une synthèse des aspects théoriques et bibliographique de la modélisation hydraulique dans les réseaux d'adduction d'eau potable est présentée. On définira la modélisation et on décrira l'approche numériques utilisé par le logiciel EPANET2 pour la résolution des équations d'équilibrage hydraulique après avoir exposer les équations qui régissent les écoulements. Ensuite, on exposera l'algorithme de simulation hydraulique du logiciel EPANET2 basé sur l'approche numérique hybride noeud-maille.

I-1/ Principales phases de la modélisation

Le terme "modèle" est un terme générique. On le défini comme étant une conceptualisation de la réalité, une certaine image de la réalité que nous nous créons- une image incomplète et partielle, comprenant des caractéristiques, des attributs de la réalité qui nous intéressent en particulier ou que nous avons la possibilité de connaître (Cunge,1988 ).

On distingue deux régimes de modélisation :

- Modélisation en régime statique : c'est la représentation d'une situation stationnaire pour des conditions définies déterminées et constantes dans le temps.

- Modélisation en régime dynamique : c'est la représentation dans l'espace et dans le temps du fonctionnement de l'ensemble des éléments du réseau

La construction d'un modèle hydraulique pour les réseaux d'eau potable se réalise selon les phases présentées ci-dessous (Générale des Eaux, 2005) :

- Choix du réseau à modéliser : étape préalable permettant de décider du niveau de détail du modèle, en fonction des objectifs visés par la modélisation ;

- Construction de la base de données : collecte, synthèse des données sur les conduites, les ouvrages, la topographie, les volumes produits et distribués ;

-- Compagne de mesures en vue de calage pour ajuster les paramètres du modèle (rugosité des conduites, pertes de charges singulières, profils de demande, ...).

I-2/ Equations d'équilibrage hydraulique

Le modèle hydraulique représente, de façon mathématique, le réseau d'eau potable et permet de connaître, après équilibrage hydraulique, les paramètres de fonctionnement de ce réseau, en particulier le débit, le sens de circulation et la perte de charge dans les conduites ainsi que la pression

en chaque point par la résolution d'équations différentielles ou intégrales souvent non linéaires. En régime dynamique, il renseigne également sur le marnage des réservoirs et le mode de fonctionnement des pompes et organes de régulation.

En effet, l'équilibrage hydraulique d'un réseau revient à rechercher, pour une distribution des diamètres fixés sur les tronçons, la distribution des débits qui vérifie l'équation de continuité aux noeuds et l'équation d'équilibre des charges aux mailles (Rossman, 2000).

L'équation de continuité au noeud i peut s'écrire :

(I.1)

mi

?

j = 1

Q D

ij i

=

2

Qij : débit qui entre au noeud i provenant du noeud j. D_i : tirage au noeud i.

mi : nombre de conduite connectée au noeud i.

L'équation d'équilibre des charges aux mailles et pseudo mailles peut s'écrire :

ml pl ? -?= J H dh wl pkl l

( 1,2 , ... ) l L = (I.2)

i k

= =

1 1

Jwl : perte de charge dans la w ^ième conduite à la l ^ième maille.

Hpkl : charge hydraulique fournie par la k ^ième pompe dans le l ^ième maille.

dh_l : différence de charge hydraulique entre les points de charge constante d'une maille l.

ml : nombre de conduites de la l ^ième maille.

pl : nombre de pompes de la l ^ième maille.

La perte de charge dans la w ^ième conduite au l ^ième maille délimitée par les noeuds i et j peut être décomposée en perte de charge linéaire et perte de charge singulière et s'écrit :

J wl = Hi - Hj = h ij = rQ il + mQ il n 2

(I.3)

H_i : la charge au noeud i.

hij : la perte de charge dans la conduite entre les noeuds i et j

r : le coefficient de résistance (tableau n°I.1).

Q : le débit.

n : l'exposant du débit.

m : le coefficient de pertes singulière.

La valeur du coefficient de résistance dépend de la formule de perte de charge utilisée. Les formules les plus utilisées sont :

3

8L Q ²

[ ] L [ ] L [ ] L

(I.4) (I.5) (I.6)

ij ij

Formule de Darcy Weisbach : rQij n = ë

D g

5 2

ð

4 L Q 1,852

10.67

Formule de Hazen-Williams : rQ n ij ij

C D

1,8524,871

HW

ij =

2 2

1 0.29 4 N L Q

Formule de Chezy-Manning : rQn ij ij

=

ij _D5,33

CHW : coefficient de rugosité de Hazen-Williams

N : coefficient de rugosité de Manning.

L : longueur totale de la conduite entre les noeuds i et j (en m).

ë: coefficient de perte de charge qui est fonction du nombre de Reynolds "Re" et la rugosité relative ks/D avec :

Re = UD/í

U étant la vitesse moyenne de l'écoulement

ks : la rugosité de la conduite

í : la viscosité cinématique d'eau (í ? 10^-6 m²/s).

Tableau I.1: Formules de perte de charge totale (exprimée en mce et le débit en m³/s)

Formule	r	n
Darcy Weisbach	8L ë	2
	5 2 D g ð
Hazen-Williams	10.674 × L	1.852
	1,852 4,871 × C D HW
Chezy-Manning	2 × × 10.294 n L	2
	D 5,33

Pour les pompes, la perte de charge (valeur négative du gain de charge) peut être calculée avec une formule de la forme suivante:

Hpkl = - h o - rQ ij ( ) n

(I.7)

dans laquelle h_o est la charge de la pompe à débit nul et r et n sont des coefficients de la courbe caractéristique.

Résoudre les équations des débits implique la résolution simultanée d'un grand nombre d'équations non linéaires. Il y a deux étapes pour résoudre ces équations :

· installation des équations de continuité à chaque noeud et des équations d'équilibre des charges à chaque maille du réseau de sorte qu'il y ait autant d'équations indépendantes que d'inconnues,

4

· résoudre le système d'équations en utilisant des procédés numériques appropriés.

Dans le paragraphe suivant, une illustration de quelques méthodes numériques pour la résolution de ces systèmes d'équation.

I-3/ Méthodes numériques pour la résolution des équations d'équilibrage hydraulique

L'objectif premier, au niveau de la gestion d'un réseau, est la rapidité de calcul en fonction de l'état des dispositifs (vannes) et de la demande qui est variable afin de fournir au gestionnaire la répartition des débits et des pressions Une fois le système d'équations décrivant le réseau est développé, un ensemble de techniques numériques peuvent être exploités pour trouver la répartition des débits et des pressions. Ci-après on exposera le principe de la méthode utilisé par le logiciel EPANET2 appelé l'approche hybride noeud-maille (Rossman, 2000) ainsi que l'algorithme de simulation basé sur cette méthode. En effet le logiciel EPANET2 sera l'outil informatique de modélisation utilisé dans la partie expérimentale.

I-3-1/ Principe de l'approche hybride noeud-maille

C'est la méthode de résolution utilisée par le logiciel EPANET2 pour résoudre les équations de perte de charge et de conservation de la masse, qui caractérisent l'état hydraulique du réseau à un instant donné. Elle est développée par Todini et Pilati en 1978 (Rossman, 2000). Ci-après un extrait du manuel d'utilisation d'EPANET2 où la méthode sus-indiqué est explicitée.

Cette méthode commence par une estimation initiale des débits dans chaque conduite, qui peut ne pas répondre à l'équation de continuité au noeud (éq. I.1). À chaque itération de cette méthode, des nouvelles charges aux noeuds sont générés en résolvant l'équation matricielle suivante:

AH=F (I.8)

dans laquelle A est une matrice Jacobienne (NxN), H est un vecteur (Nx1) représentant les charges inconnues aux noeuds et F un vecteur (Nx1) contenant les termes du côté droit.

Les éléments diagonaux de la matrice Jacobienne sont:

A = ? P (I.9)

ii iJ

J

Tandis que les éléments non-nuls, qui ne se trouvent pas sur la diagonale s'expriment de la manière suivante:

A iJ = - P iJ (I.10)

avec _pij l'inverse de la dérivée de la perte de charge dans une conduite, une pompe ou une singularité (vanne , clapet...), appelées aussi "arc", entre les noeuds i et j, en respectant le débit.

Pour les conduites :

1

p ij n

= - 1

ij

nr Qm Q

ij ij ij

+ 2

(I.11)

Pour les pompes fonctionnant à leurs régimes nominal:

1

1

(I.12)

p = nr Q -

ij n

( )

ij

5

Tous les termes du côté droit sont dus au déséquilibre de flux en un noeud et à un facteur de correction:

? ? F Q D y p H i ij i ij if f = ? - ? + + ? ? ? ? ? j j f

(I.13)

Le dernier terme de l'expression s'applique à tous les tronçons qui relient le noeud i à un noeud de hauteur fixe f. Le facteur de correction _yij s'exprime ainsi:

y ij = p _ij r _ij Q _ij + m Q ij Q ij (I.14)

( ² ) sgn( )

n

Pour les conduites, avec sgn(x) égal à 1 si x > 0 et à -1, autrement , et:

y ij = - p _ij h - r Q ij (I.15)

( 0 ( ) )

n

Pour les pompes _Qij est toujours positif.

Après avoir trouvé les nouvelles charges en résolvant les équations (I.8), les nouveaux débits s'obtiennent en résolvant l'équation suivante:

Q ij = Q ij - (y_ij - p _ij (H i - H_j)) (I.16)

Si la somme des variations absolues de débits dans tous les tronçons, divisée par la somme de tous les débits dans tous les tronçons est supérieure à la tolérance préétablie (par exemple, 0,001), les équations (I.8) et (I.16) et sont recalculées.

I-3-2/ Algorithme de simulation

Le logiciel EPANET2 applique l'approche hybride noeud-maille en suivant les étapes suivantes :

1. Pour la première itération, le débit dans une conduite est choisi de telle sorte que la vitesse est
égale à une unité (1 pied/sec), tandis que le débit à travers une pompe est égal au débit nominal. (Les

6

unités utilisées pour les calculs sont le pieds pour la charge et le pieds au cubes par seconde pour le débit).

2. Le coefficient de résistance des conduites (r) est calculé comme décrit dans le tableau I.1.

3. Le facteur de pertes singulières "m" est calculé selon la formule ci-après :

8 K

m = (I.17)

gðd

2 4

Dans laquelle K est le coefficient de perte de charge singulière, et d le diamètre.

Une valeur r est assignée aux vannes. On suppose qu'une vanne (arc) ouverte se comporte comme une conduite lisse (ë= 0,02) dont la longueur est deux fois le diamètre de la vanne. Cependant, une vanne fermée est soumise à une relation de perte de charge avec un facteur de résistance (ë) très élevé, par exemple h= 10⁸Q alors p=10^-8 et y=Q

Pour les "arcs" vérifiant la condition suivante : (r+m) Q < 1 0^-7 c'est-à-dire un coefficient "n" (exposant du débit) égal à 2, on a p = 10⁷ et y = Q/2.

4. Le logiciel contrôle l'état des pompes, la consigne des vannes anti-retour et des vannes de contrôle et l'état des conduites connectées à des réservoirs pleins ou vides après chaque itération jusqu'à la dixième itération. En effet les pompes sont arrêtées si la pression est supérieure à la charge à débit nul (pour éviter l'écoulement inverse). De même, les clapets anti-retour sont fermés si leur perte de charge est négative. Si ces conditions ne sont pas remplies lors du contrôle suivant, l'arc est rouvert. Un contrôle similaire est effectué pour les arcs reliés aux réservoirs vides ou pleins. Ces arcs sont fermés si la différence de charge entraîne la vidange d'un réservoir au niveau minimale ou le remplissage d'un réservoir plein. Si ces conditions ne sont pas remplies lors du contrôle suivant, l'arc est rouvert. Suite à la dixième itération, l'état est contrôlé après que le logiciel a atteint la convergence, à l'exception des vannes de régulation de la pression (vannes stabilisatrices aval et vannes stabilisatrices amont), dont l'état est contrôlé après chaque itération.

5. Si une pompe, un clapet anti-retour ou une conduite est fermé, son débit est mis à 10^-6 pieds cubes par seconde. A la réouverture d'une pompe, son débit est déterminé en cherchant la valeur qui correspond à la charge présente selon sa courbe caractéristique. A la réouverture d'une conduite ou d'un clapet anti-retour, son débit est calculé avec l'Equation I.3 pour la perte de charge h actuelle, ignorant les pertes singulières.

6. Les coefficients de la matrice Jacobienne qui correspondent aux vannes stabilisatrices aval, vannes stabilisatrices amont et vannes régulatrices de débit sont calculés après l'analyse de tous les

7

autres arcs. Le contrôle de l'état des Vannes Stabilisatrices Aval et des Vannes Stabilisatrices Amont se fait comme décrit dans le point 5 ci-dessus. Ces vannes peuvent être entièrement ouvertes, entièrement fermées ou actives dans leur consigne de débit ou de charge.

7. Les coefficients de la matrice Jacobienne pour les Vannes Brise- Charge sont mis aux valeurs suivantes: p = 10⁸ et y = 10⁸Hfixe ^où _Hfixe est la perte de charge fixe de la vanne (en pieds). Les Vannes Diaphragme sont traitées comme des conduites, le coefficient r est calculé de la façon décrite dans le point 4 ci-dessus et m est la transformation du coefficient de fonctionnement de la vanne (voir le point 3 ci-dessus).

8. Le débit à travers une vanne stabilisatrice aval active est maintenu constant au noeud en aval, celle à travers une vanne stabilisatrice amont est maintenu constant au noeud en amont. Pour maintenir la pression de sortie dans une Vanne Stabilisatrice Aval active entre les noeuds i et j, on pose : Pij = 0

Fj = Fj + 10⁸ Hset

Ajj= Ajj+ 10⁸

Où _Hset est la consigne de pression convertie en charge. Ainsi la pression au noeud en aval est maintenue à la valeur _Hset. Une détermination équivalente est effectuée pour les vannes stabilisatrices amont, à l'exception des cas où le suffixe de F et de A sont ceux du noeud en amont i. Les coefficients des vannes stabilisatrices aval et des vannes stabilisatrices amont ouvertes ou fermées sont les mêmes que pour les conduites.

9. Pour une Vanne Régulatrice de Débit active entre les noeuds i et j avec une consigne de débit Qset, cette valeur est ajoutée au débit qui sort du noeud i et au débit qui entre au noeud j, c'est à dire, est soustraite de Fi et ajoutée à Fj. Si la charge au noeud i est inférieure à celle au noeud j, la vanne ne peut pas maintenir ce débit et fonctionne comme une conduite normale.

10. Pour les simulations de longue durée, le logiciel suit la procédure suivante:

a. après qu'une solution a été trouvée pour la période présente, le laps de temps jusqu'au prochain calcul de solution est le plus court des intervalles de temps suivants:

- le laps de temps jusqu'au nouvel intervalle de demande

- le laps de temps le plus court pendant lequel un réservoir se vide ou se remplit

- le laps de temps le plus court pendant lequel le niveau d'un réservoir provoque un changement d'état d'un arc (par exemple, une pompe qui se met en marche) comme décrit par une commande simple.

8

- le laps de temps jusqu'au prochain instant de la simulation où une commande simple ou élaborée modifie l'état d'un arc.

b. une fois l'intervalle déterminé, l'heure de la simulation est ajustée et le logiciel calcule les nouvelles demandes, les nouveaux niveaux des bâches et les nouveaux états des arcs.

c. Le programme commence une nouvelle série d'itérations avec les équations I.8 et I.16 et les débits actuels.

I-4/ Conclusion

Une modélisation hydraulique d'un réseau, est un résultat de la résolution d'un système d'équations algébriques pré-établi au niveau des noeuds et des mailles de ce réseau par le moyen d'un outil numérique de résolution. Dans le plus part des cas, le recours aux méthodes classiques de résolution numérique pour étudier ces distributions au niveau des réseaux étendus et diversifiés est limité. Un certain nombre d'approche numérique récente est développé pour la résolution de ces systèmes tel que l'approche numérique hybride noeud-maille. Cette approche est utilisée par le logiciel de modélisation hydraulique EPANET2 qui sera le support informatique au niveau de la partie expérimentale de ce travail.

9

Chapitre II

La dégradation du chlore dans l'eau :

Processus et approches de modélisation

La qualité d'eau fournie par un réseau d'eau potable dépend directement de sa concentration en chlore résiduel libre. Transporté par l'eau dans le réseau, le chlore réagit avec la matière organique pouvant y être présente pour assurer une bonne désinfection. La modélisation du chlore est la première cause du développement des modèles de qualité d'eau potable. C'est pourquoi, un grand nombre de recherches essayent de comprendre son mécanisme pour mieux modéliser cette substance dans les systèmes hydraulique. Dans ce contexte, dans ce chapitre, on essaye de présenter un aperçu sur la cinétique chimique de la réaction du chlore dans l'eau véhiculée dans les réseaux d'eau potables ainsi qu'un certain nombre de méthodes numériques pour connaître sa distribution au sein de ces réseaux. Ce chapitre commence par une synthèse des aspects théoriques et bibliographique de la modélisation du chlore résiduel libre dans l'eau au niveau des réseaux sous pression est présenté. Il s'achève par une description de l'algorithme de simulation de qualité du logiciel EPANET2 basé sur l'algorithme de transport de Lagrange après avoir exposer les équations régissant l'évolution de la concentration du chlore résiduel libre ..

I I-1/ Généralités

La qualité d'eau est un paramètre important dans la gestion des systèmes d'adduction d'eau potable. Elle devient même très importante lorsque l'eau potable provient de sources de qualités différentes. De même lorsqu'on se trouve devant une pollution partielle de la ressource ; il s'agit alors de protéger rapidement l'usager en suivant l'évolution de la qualité d'eau dans le temps et dans l'espace. Un tel suivi constitue un défi pour les gestionnaires des réseaux d'eau potable car il nécessite une maîtrise totale de l'hydraulique et de la qualité.

La difficulté de la gestion de la qualité d'eau sur les réseaux d'eau potable a conduit au développement de modèles de simulations décrivant les lois de réaction de transport des polluants ou désinfectants. Il est à noter que la validité des résultats obtenu à l'aide de ces modèles dépendra en partie de la fiabilité hydraulique donc de la finesse de son calage. La modélisation des phénomènes liés à la qualité d'eau nécessite une connaissance approfondie des processus chimique dont ci après les principaux processus :

II-1-1/ Conservation de la masse

L'expression de la loi de conservation de masse, le long d'un tronçon i peut s'écrire selon deux

expressions définies comme suite:

ä ä

C C

i i

= - × +

u R

t x

i

ä ä

( ) C(II.1)

i

C_i : la concentration au tronçon i à la position x et temps t. u_i: la vitesse moyenne de l'écoulement dans le tronçon i. R(C_i): taux de réaction.

?

dt dt

dm d

C Q C Q

entrée entrée sortie sortie

c

× - × +

?

entrée sortie

( )

CV eau(II.2)

dm avec m C Q = = c inj entrée entrée l ? dt l? J entrée

(II.3)

Avec :

Centrée : concentration volumique à l'entrée du volume de contrôle

Csortie: concentration volumique à la sortie du volume de contrôle

C entrée : concentration effective résultant de l'injection d'une masse de constituant défini

inj

Q entrée : débit du fluide à l'entrée du volume de contrôle Qsortie : débit du fluide à la sortie du volume de contrôle Veau : le volume d'eau dans le volume de contrôle

m

m_c : la masse du constituant (désinfectant...) injecté à l'eau par unité de temps c

m =

t

Pour l'équation (II.2), le terme gauche exprime le transport de masse du constituant vers ou à partir du volume de contrôle. Les deux premiers termes sont le transport avec le fluide. Le dernier terme est un terme de réaction qui quantifie les transformations de dégradation ou de croissance du constituant dans le volume de contrôle.

Le terme droit exprime le taux de variation de masse du constituant avec le volume de contrôle. L'injection du chlore est spécifiquement de l'ordre de mg/l. Alors que les bactéries sont dans l'intervalle de ug/l qui est équivalente à mg/m³.

Au niveau des noeuds, une autre relation de conservation de masse est la suivante :

=

j I

? k

=

0

Ci_x

(II.4)

Q C Q C

j j S S

+ ×

x Lf

=

?

10

?

j I ? k

Q Q j S +

I : tronçon avec un débit quittant le noeud K

IK : ensemble de tronçons avec des flux entrants le noeud K LF : longueur du tronçon j

Qj : débit dans le tronçon j

CS : concentration de la source extérieure entrant le noeud K.

QS : débit de la source extérieure entrant le noeud K.

II-1-2/ Mélange aux noeuds

II-1-2-1/ Noeud sans injection de constituant

Aux noeuds de jonction dans un réseau de conduite, la qualité d'eau change à cause de l'injection et la dilution. La conservation de la masse est appliquée aux noeuds pour déterminer l'effet d'associer le débit avec différentes concentrations de constituants. Un mélange complet et total est supposé se produire dans la conduite résultant de l'uniformité des concentrations au delà de la section aval de la conduite. Dés qu'un noeud ne peut stocker d'eau, la masse du constituant au noeud est constante et le terme gauche de l'équation (II.2) est égal à 0. Aussi, dés que les longueurs de conduites au noeud sont très petites, il n'y a pas de temps de séjour au noeud, pour cela il n'y a ni dégradation ni croissance du constituant qui peut se produire. Pour une simple jonction, il n'y a pas de constituant demandé en ce noeud. Les deux derniers cas impliquent que :

dmc = dt

0 (II.5)

Sous ces conditions l'équation (II. 2) devient : d CV

( ) dm

eau= ? × - ? × + ? × - ? × =

C Q C Q C Q C Q

^c 0 (II.6)

entrée entrée sortie sortie entrée entrée sortie sortie

entrée sortie entrée sortie

dtdt

L'équation (II.2) peut être écrite pour un noeud comme suit :

?

C Q C Q

l l entrée entrée

+

C sortie

? l J ? sortie

Q q l sortie +

l J

? entrée

(II.7)

Ici, le débit entrant au noeud à partir des conduites _Jentrée est comme une injection externe (débit), Qentrée Chacun de ces débits peut avoir différentes concentrations du constituant, C_l et C _entrée ,

respectivement. Les débits sortant consistes en le tirage au noeud, _qsortie et l'ensemble des débits dans

les _Jsortie conduites amenant l'eau à partir du noeud. Avec un mélange complet, tous les débits sortant ont la même concentration,C_sorti_e. L'équation (II.7), montre que la concentration du débit sortant est une moyenne pondérée des concentrations entrantes.

II-1-2-2/ Noeud avec injection de constituant

Pour ce cas, dmc

dt

dans l'équation (II.2) n'est pas égal à 0. Dans la majorité des modèles de

11

qualité, la concentration pour tous les débits externes entrant au noeud peut être spécifiée. Le débit
est typiquement une demande négative au noeud ou un débit à partir d'un réservoir ou station de

traitement d'eau. La concentration d'entrée d'eau, _Centrée dans l'équation (II.7) est décrite comme la source de concentration.

Substituons l'équation (II.3) dans l'équation (II.7), on trouve :

? ? ?

C Q C Q m C Q C Q C Q

inj

l l entrée entrée entrée l l entrée entrée entrée l

+ + + +

l J

Csortie

(II.8)

? l J

? l J

?

entrée entrée entrée

= =

? ?

Q q

l sortie

+ Q q

l sortie

+

l J

? l J

?

sortie sortie

II-1-3/ La cinétique des réactions

Chaque substance dans un réseau hydraulique réagie avec la masse d'eau et avec les parois des conduites et des réservoirs. Ces réactions doivent être représenté dans l'équation de la conservation de la masse (II.2). Les substances réagissent suivant différentes relations. La cinétique des réactions est utilisée pour décrire ces relations. La forme générale du terme de la vitesse de réaction r(C) pour les processus de dégradation et de formation est respectivement :

* 1

n c -

r C k C C C
( ) ( )

= - (II.9)

r C k C C C

* 1

n c -

( ) (

= - - )(II.10)

C* est respectivement la concentration limite ou la portion non réactive de la substance, k est la constante de réaction et n_c est l'ordre de la réaction.

Pour une réaction d'ordre 0, 1 ou 2 le terme r(C) devient respectivement :

( )

C k

=(II.11)

( )

C kC =(II.12)

(II.13)

( ) =

12

C* est supposé nul.

D'autre part le changement d'état d'un constituant, dans un système hydraulique, dépend du temps passé dans ce système, un long séjour peut causer des problèmes de qualité. Alors, le temps de séjour est souvent utilisé comme un indicateur supplémentaire de la qualité d'eau.

Il est à préciser que dans les réservoirs, la zone d'échange avec les parois est négligeable devant le volume du réservoir pour ceci la réaction au niveau des parois est comptabilisé dans la réaction avec la masse d'eau. Par contre, dans les conduites, elle est traitée séparément. A cause de leur complexité et variabilité entre conduites, les ordres cinétiques des réactions avec les parois sont représentés par l'ordre un ou l'ordre zéro.

Généralement pour tenir compte de la réaction avec la masse d'eau et celle avec les parois, une constante de réaction dite globale est utilisée :

k=k_b+k_w (II.14)

kb et k_w sont respectivement les coefficients de réaction dans la masse d'eau et avec la paroi.

II-1-4/ Les processus de transport dans un fluide

Le transport, au sein d'un fluide, d'une entité se fait selon cinq processus : l'advection, la diffusion moléculaire, la diffusion turbulente, la dispersion et la radiation. La radiation est limitée au transport d'énergie par les ondes électromagnétiques. Ce mécanisme reste toujours négligé par les modèles de transport dans les conduites d'eau. Au contraire, l'advection est considérée comme le mécanisme dominant parmi ces processus. La diffusion moléculaire et la diffusion turbulente sont négligées dans les réseaux d'eau potable dés que l'écoulement est généralement turbulent.

II-1-4-1/ Le mécanisme d'advection

L'advection est le mouvement d'un constituant avec l'eau en direction de l'écoulement et est proportionnel à l'intensité de la vitesse. Dans l'équation de conservation de la masse (éq.II.2), l'advection est représentée par les deux premiers termes à gauche de l'égalité. Un écoulement parfait et advective est un écoulement piston.

L'équation de conservation de la masse (éq.II.2) peut être écrite pour un système à volume (Veau) constant et un écoulement stationnaire :

? =

V eau

C dm c

( ) (

CQ CQ

- +

) (II.15)

entrée sortie

? t dt

Pour un élément ?x de la conduite, on peut écrire que :

( )

CQ CQ Q C C

entrée sortie

- -? ?

( ) ( )

= = -V (II .16)

V V x

?

eau eau

En substituant ce résultat dans l'équation (II.15), on trouve l'équation d'advection suivante:

? ?

C C

tx V dt

eau

1 dm c (II.17)

13

Le transport advective est le mécanisme de transport le plus dominant. Cependant autres processus de transport peuvent être important sous des conditions dont l'écoulement n'est pas suffisamment turbulent. La non uniformité de la distribution de la vitesse se produisant dans l'écoulement laminaire donne naissance à un mélange longitudinal ou dispersion qui n'existe pas dans l'écoulement turbulent. Le mélange diminue avec le degré de turbulence.

II-1-4-2/ La diffusion moléculaire

La diffusion moléculaire est le transport de masse causé par le mouvement moléculaire connu sous le non du mouvement Brownien (Chahed, 2005). Ce mécanisme existe quant l'écoulement est

laminaire. La redistribution d'un constituant dans un réservoir ou dans une conduite où l'écoulement est lent est causée par la conduction. La conduction est tenue en compte dans le dernier terme à gauche de l'égalité de l'équation (II. 2). L taux de conduction est lié à la magnitude du déséquilibre de la concentration par la loi de Fick's (Cockx, 2005). La loi de Fick's énonce que le taux de transferts de masse est lié au gradient de concentration de masse :

C C

2

? ?

2

=D _m

? ?

t y

(II.18)

(Dm) est le coefficient de la diffusion moléculaire qui est de l'ordre de 1 0^-5 (cm²/s). II-1-4-3/ La diffusion turbulente

La diffusion turbulente existe dans la conduite durant l'écoulement turbulent. La turbulence dans le mouvement d'eau crée des tourbillons. Mathématiquement, la diffusion turbulente est décrite par l'équation suivante :

C C

? 2

(II.19)

? =Dt

2

? ?

t y

(Dt) est le coefficient de la diffusion turbulente qui est de l'ordre de 10⁰ -10⁵ (cm²/s).

II-1-4-4/ La dispersion

Dans les écoulements turbulents, la vitesse est presque uniforme à travers la section et presque égal à la valeur de la vitesse moyenne alors la propagation d'un constituant dans la masse d'eau dans la direction de l'écoulement est faible. Dans le cas des écoulements laminaire, la distribution non uniforme de la vitesse va causer des variations dans le transport axial à travers la conduite. Le centre de la conduite a une vitesse plus grande que la moyenne. Si l'advection est uniquement considérée alors le transport additionnel au dessus de la moyenne peut ne pas être considéré. La propagation axiale et longitudinale d'un constituant à cause de la non uniformité de l'écoulement est appelée la dispersion. Elle s'exprime par la loi de Fickian :

C C

? 2

(II.20)

? = D disp

2

? ?

t y

(Ddisp) est le coefficient de dispersion qui est de l'ordre de 10⁶ (cm²/s).

II-1-4-5/ L'impact de la diffusion et la dispersion

14

En résumé, la diffusion affecte le transport de masse dans la direction radial et axiale. La dispersion est un mécanisme de transport dans l'écoulement laminaire qui affect seulement le transport axial. La diffusion moléculaire est généralement négligé si le l'eau est en écoulement. La

15

diffusion turbulente existe dans les écoulements turbulents. L'équation de transport advective peut être généralisé pour tenir compte de la diffusion et la dispersion :

? ? ? ?

C C C C

2 2

+ - + - + =

V D D D D r C

( ) ( ) ₂ ( )

m t m t (II.21)

? ? ? ?

t x r x

2

Pour un écoulement laminaire, Dt est ignoré et la dispersion est ajoutée à cette expression pour obtenir :

? ? ? ?

C C C C

2 2

+ - - + =

V D D D r C

m m disp (II.22)

( ) ₂ ( )

? ? ? ?

t x r x

2

Au niveau des modèles informatiques, il existe deux familles. Une première famille qui néglige l'effet du phénomène de dispersion sur les résultats, tel que EPANET2 (Rossman, 2000) et une seconde famille qui tient compte de ce phénomène (Tzatchkov, 2003). Pour les réseaux d'adduction d'eau potable, le logiciel EPANET2 est préconisé (Tzatchkov, 2003). En effet, la négligence du phénomène de dispersion par le modèle EPANET2 n'a pas d'effets sur les résultats vu que ces réseaux sont le siége d'écoulements turbulents (fort nombre de Reynolds).

II-2/ Processus de dégradation du chlore dans l'eau II-2-1/ Différentes formes du chlore

Les formes les plus utilisées du chlore sont (Cockx, 2005) :

· Le chlore gazeux Cl2 est majoritaire en traitement d'eau potable et est stocké sous forme liquide,

· Les hypochlorites de sodium ou de calcium NaOCl et Ca (OCI) ₂ dites aussi eau de Javel,

· Les monochloramines, NH2Cl peu utilisés à cause de leurs cinétiques lentes,

· Le dioxyde de chlore, ClO2 qui est un gaz instable d'où dangereux. Il doit être produit sur site.

II-2-2/ Réactions chimiques du chlore dans l'eau

Au cours d'une réaction de désinfection par le chlore, on mesure le chlore résiduel libre, le chlore résiduel combiné et le chlore résiduel total. Le chlore résiduel libre est le chlore qui demeure dans l'eau après une période de séjour donnée et qui est capable de réagir comme acide hypochloreux (HClO) ou ion hypochlorite (ClO^-). Sa présence est l'indicateur de qualité d'une eau. Le chlore résiduel combiné est une partie du chlore résiduel total qui persiste à la fin d'un temps de séjour donné et qui réagir comme la chloramine qui est un produit résultant de la combinaison du chlore et d'ammoniac d'origine organique ou inorganique. Le chlore résiduel total est la somme du chlore résiduel libre et le chlore résiduel combiné.

L'acide hypochloreux est l'espèce active pour la désinfection. Les réactions chimiques possibles du chlore dans l'eau sont :

16

Pour le chlore gazeux : Cl2 2

+ ? + +

H O HOCl Cl H (II.23)

- +

Pour l'hypochlorite de sodium: 2

NaOCl H O HOCl Na OH (II.24)

+ ? + +

+ -

Pour l'hypochlorite de calcium Ca OCl 2 H O 2 HOCl Ca 2 OH (II.25 )

2 + -

( ) + ? + +

2 2

II-2-3/ Notion de demande en chlore

Lorsque le chlore est introduit dans l'eau, une première réaction instantanée se produit entre le l'acide hypochloreux HOCl et la matière organique présente dans l'eau pour donner les chloramines (Cockx, 2005):

· Monochloramine : HOCl + NH₃ ? NH₂Cl + H₂O (II.26)

· Dichloramine : HOCl + NH₂Cl ? NHCl₂ + H₂O (II.27)

· Trichloramine : HOCl + NHCl₂ ? NCl₃ + H₂O (II.28)

Il est à préciser que le chlore consommé par la matière organique n'a aucun rôle désinfectant : c'est ce qu'on appelle demande en chlore. Lorsque la matière organique est épuisée, la formation du chlore libre peut commencer pour amorcer la désinfection. La figure ci-dessous décrit les transformations successives engendrées par l'ajout de doses croissantes de chlore à une eau faible en matière organique (graphique gauche) et pour une eau riche en matière organique (graphique droit). A partir du point d'origine les doses ajoutées réagissent avec la matière organique ce qui engendre la production des monochloramines et ce jusqu'au point maximum de la courbe « Demande ». Au-delà de ce pont les monochloramines sont transformées en dichloramines et en acide chlorhydrique HCl. Le point PC est un point de changement de l'allure de la courbe appelé point critique, il est atteint lorsque la demande en chlore est satisfaite. Au-delà de ce point, le chlore ajouté est du chlore libre efficace pour la désinfection et qui croit à la même allure que les doses de chlore appliquées.

Figure II.1:Demande en chlore (Cockx, 2005)

I-2-4/ Principaux facteurs physicochimiques influençant la dégradation du chlore dans l'eau

17

Savoir les aspects physico-chimiques derrière la dégradation de chlore est indispensable si nous devons développer une stratégie capable de désinfecter un système d'adduction d'eau potable, en même temps, de préserver la qualité d'eau jusqu'au point de distribution, sans employer plus désinfectant que nécessaire. Dans ce sens, la modélisation du taux de dégradation du chlore est essentielle pour projeter correctement de nouveaux systèmes ou pour faire des changements de celles existantes.

La dégradation du taux de chlore et les modèles de propagation traitent le tronçon de conduite comme s'il était un réacteur chimique. Pour ce réacteur, on supposé que le chlore entre d'une extrémité, se consomme dans l'eau (dégradation en bloc) par les micros organismes et par les biofilms fixé à ces parois et transporté à l'autre extrémité de la conduite par la convection. Le chlore peut également réagir avec la conduite elle-même. Le mécanisme de dégradation (réaction) et de transport de chlore est schématiquement décrit sur le schéma au dessous. Par conséquent, le phénomène de réaction du désinfectant avec l'eau dans les tronçons du réseau se produit aussi bien dans la veine liquide qu'au niveau de la paroi.

Concentration importante

Convection et dégradation axiale par la masse d'eau

Diffusion Radial et dégradation par les biofilms

Concentration moins
importante

Biofilms

Figure II.2:Description schématique du modèle de transport 2-D de chlore

II-2-4-1/ pH et minéralisation

Dans le réseau, le pH et la minéralisation sont importants pour le contrôle de la corrosion, l'agressivité d'eau, l'action du désinfectant et la précipitation des éléments dissous. Mais le pH peut

18

varier le long de la distribution du fait d'une évolution de la concentration de CO2 dissous, ou bien parce que l'eau traitée n'était pas forcément à l'équilibre calcocarbonique en sortie de la station. Une aération dans un réservoir peut rendre une eau dure et incrustante par une perte de CO2, ce qui risque alors d'obturer les conduites par dépôt de tartre. La solution est l'addition de CO2 et/ou l'extraction de CaCO3, qui sert à restaurer l'équilibre. Inversement, une eau chargé CO2 agressif (avec un pH bas) a tendance à attaquer les matériaux qu'elle rencontre avec des conséquences importantes: dissolution de ciments, attaque des métaux ferreux (corrosion) ou attaque de métaux toxiques tels que le plomb. Des solutions envisageables sont l'élimination de CO2 agressif, l'addition de chaux pour la mise à l'équilibre calcocarbonique ou un traitement de reminéralisation.

II-2-4-2/ Température

Une température élevée peut favoriser des goûts ou odeurs désagréables. De plus, elle accélère la plupart des réactions physico-chimiques et biologiques dans le réseau, influence la croissance bactérienne, dissipe l'effet du désinfectant résiduel en agissant sur les constantes d'équilibre et accélère la corrosion. L'activité bactérienne s'accroît nettement lorsque la température dépasse 15°C.

II-2-4-3/ Oxygène dissous

Toute baisse de la teneur en oxygène dissous détectée sur le réseau peut être interprétée comme un signe de croissance biologique. Dans le cas où le réseau est correctement entretenu, une anaérobiose répandue ne se produit qu'avec des temps de séjour très longs.

II-2-4-4/ Turbidité

Si la turbidité d'eau est supérieure à 0.4 NTU, l'action des désinfectants est ralentie, voire annulée. Les colloïdes responsables de la turbidité peuvent protéger les bactéries des oxydants. Ainsi, un traitement de chlore libre à 0.4 mg/l pendant une heure, qui donne normalement une garantie bactériologique à l'eau, n'est actif que si la turbidité est inférieure à 0.4 NTU.

II-2-4-5/ Matière organique

Elle représente une source nutritive essentielle pour la prolifération bactérienne, le contenu en éléments organiques carbonés est aujourd'hui considéré comme un facteur primordial dans la maîtrise de la qualité microbiologique d'eau dans le réseau. En effet une consommation de la matière organique s'accompagne d'un accroissement de la densité bactérienne au niveau du biofilm.

II-2-4-6/ Dureté

19

Une eau trop douce a un effet corrosif sur les canalisations et peut amener dans l'eau une présence excessive de métaux (tel le plomb) provenant des canalisations. La dureté d'eau n'a pas d'incidence sur la santé (observatoire régional de l'environnement Poitou-Charentes). Elle se calcule en degré français (°F) correspondant à 4 mg de calcium ou 2,4 mg de magnésium par litre d'eau. La valeur idéale est de 15°F.

II-2-4-7/ Ions fer

L'influence des ions de fer sur la dégradation du chlore existe au cours de l'oxydation des ions Fe²⁺ (sous forme de bicarbonate) en ions Fe³⁺ (sous forme d'hydroxyde de fer) en milieu alcalin et dure (présence de la molécule de carbonate de magnésium ou de calcium), qui est une réaction très rapide en solution, où le chlore réagit avec le calcium ou magnésium.

I I-2-4-8/ La nitrite

Le chlore libre oxyde les ions nitrites en ions nitrates.

I I-3/ Approches pour la modélisation de la dégradation du chlore

Un certain nombre de recherches scientifiques ont conduit au développement des modèles qui s'intéressent à la dégradation du chlore dans l'eau potable. Parmi les premières tentatives figure le modèle développé par Feben et Taras en 1951 qui est le suivant :

D t = D t

₁(II.29)

n

Où D_t est la quantité de chlore qui a réagit à l'instant t (heures), D₁ la quantité de chlore qui à réagit

après une heure et n un paramètre déterminé expérimentalement pour une eau donnée.

La plus part de ces recherches (Ozdemir et Ger, 1998) considèrent, pour les écoulements entièrement turbulents auxquels les gradients de vitesse ne sont pas importants, que :

- le mécanisme de dégradation du chlore est bi-dimentionnel : une première dimension qui est l'axe longitudinal de la conduite le long de laquelle le chlore est transporté et affaibli et une seconde qui est la direction radiale le long de laquelle le chlore est transporté par diffusion radiale.

- la dégradation la plus importante de chlore se produit pour les écoulements à nombre de Reynolds inférieur à 30 000 pour lesquels on ne peut pas dire que l'écoulement est entièrement turbulent, comme représenté sur le schéma ci-dessous. La valeur de C a été obtenue par la normalisation de la concentration en chlore à la sortie de la conduite par la concentration en chlore à l'entrée de la conduite. Cependant, les écoulements dans les réseaux d'adduction d'eau ont des nombres de Reynolds nettement supérieurs à 30 000.

20

Figure II.3: Comparaison entre des études de dégradation du chlore (Ozdemir et Ger, 1998)

Deux démarches de modélisation de la dégradation du chlore existent. Une première qui attribue à chaque tronçon des coefficients de dégradation qui négligent les paramètres qui pourraient les influencer. Ces coefficients sont établis pour un état significatif du réseau. Une deuxième qui attribue à chaque tronçon de conduite des coefficients de dégradation paramétrés. Dans ce qui suit, on optera pour la deuxième démarche.

II-3-1/ Modèles de dégradation de chlore à coefficients invariables

- L'étude réalisée par Frederick L et al, présentée au NEWWA Computer Symposium en 1992, intitulé " La distribution du chlore résiduel dans le réseau de distribution d'eau " décrit des méthodes pour conduire des simulations d'une distribution de chlore dans un réseau d'eau potable. Des résultats de cette étude peuvent être récapitulés comme suit :

· L'évaluation, au laboratoire, des eaux prouve que l'eau a une dégradation très faible du chlore. Ils assument que la perte du chlore résiduel dans le réseau est due au temps de séjour excessif d'eau dans le réseau et/ou des matériaux des canalisations.

· Une évaluation du temps de séjour d'eau d'un réseau n'a pas soutenu la spéculation que l'âge excessif d'eau peut être une cause significative du taux faible du chlore résiduel dans le réseau. Ils concluent donc que les causes les plus susceptibles pour interpréter la perte de chlore sont la nature et l'état des matériaux des canalisations. Ils expliquent ceci par le fait qu'une conduite vieillit, sa rugosité augmente en raison de l'incrustation et de la tuberculisation des produits de corrosion aux

parois, ce qui rend sa paroi plus réactive à certains agents chimiques, plus particulièrement au chlore et à d'autres désinfectants.

- Un ensemble de coefficients sont présentés dans le tableau issu de quelques études. On voit bien que ces coefficients dépendent du type et état des canalisations.

Tableau II.2: Quelques ordres de grandeurs du coefficient de dégradation de chlore dans l'eau (Frederick L et al,
1992)

Chercheurs	k (l/min)	Temps séjour moyen (heure)	Observations
Tracy et al	0,0135	0,25	conduite en fonte
	0,0059-0,0075	2,0
	0,0019	8,0
	0,002	16,0
	0,001	40,0
	0,00074	44,0
	0,00033	45,0
	0,00047	50,0
O'Connor et	0,0019	4,0	conduite en amiante ciment
	0,0036	11,0
	0,0032	16,0
	0,0021	18,0
Martin et al	0,0056	8,0
	0,0048	9,0
	0,00015	45,0
Rose	0,036	0,55
	0,0067	0,83
	0,0034	1,25
	0,0014	1,38
	0,0194	1,73	avant nettoyage
	0,0058	1,73	après nettoyage
	0,023	2,0	avant nettoyage
	0,012	2,0	après nettoyage
Olivieri et al	0,005	2,3	chlore libre

21

II-3-2/ Modèles de dégradation de chlore à coefficients paramétrés

- Chambers et al. (1995) a réalisé une étude pour examiner la validité de l'expression de dégradation exponentielle pour le chlore résiduel libre et total. Ses résultats ont prouvé que le modèle dégradation exponentiel est approprié pour modéliser le chlore résiduel libre dans les réseaux d'eau potable et qu'il est possible de produire des modèles réussis de qualité d'eau.

- Vieira et al. (2004) estime que les facteurs les plus appropriés pour l'étude de la dégradation du chlore suite aux réactions avec la masse d'eau sont la température, la concentration initiale du chlore, la concentration en fer et la matière organique.

- Pour estimer les paramètres inconnus de leur modèle, Clark et Sivaganesan ont utilisé des échantillons d'eau potable pour développer un modèle général. L'étude statistique faite par ces deux chercheurs a prouvé que les paramètres de ce modèle dépendent de : TOC, UVA, la concentration initiale du chlore, pH, la concentration en Bromure, la température en °C, l'alcalinité en mg/L. Ce modèle a été testé dans divers cas pour voir sa crédibilité. Généralement, il reflète bien les mesures expérimentales (Clark et Sivaganesan, 1998).

I I-4/ L'algorithme de simulation de la qualité d'eau par EPANET2

Si on considère un réseau entier, les équations régissant la qualité d'eau, comme la conservation de la masse, aboutissent à un système complexe d'équations algébriques différentielles partielles. Une solution analytique du système est impossible. A cet effet, nombreuses méthodes de résolution ont été exposées en bibliographie, dont la méthode lagrangienne basée sur le temps (Time Driven Method -TDM) qui est l'algorithme de simulation qualité du logiciel EPANET2.

II-4-1/ Principe

L'idée principale de cette approche consiste à subdiviser chaque tronçon du réseau en segment et ce en tenant compte des débits relatifs au pas de temps hydraulique considéré et de supposer que la taille du segment le plus en amont augmente au cours du temps pendant qu'une perte dans la taille du segment le plus en aval se produit quand l'eau quitte le tronçon mais la taille des segments intermédiaires reste inchangée. Pour chacun des pas de temps de qualité et après le phénomène de réaction dans le tronçon, les concentrations au niveau des noeuds sont calculées par le moyen d'un comptage cumulatif et des nouveaux segments seront crées à l'amont de chaque tronçon tout en tenant compte des débits qui y rentrent. L'exactitude de cette méthode dépend du pas de temps de qualité et du seuil adopté à la génération des segments à l'amont de chaque tronçon et au début de chaque pas de temps de qualité (Ayari, 2003).

22

II-4-2/ L'algorithme

23

Le simulateur de la qualité d'eau d'EPANET2 utilise l'approche lagrangienne pour détecter des changements subis par des volumes d'eau élémentaires qui circulent dans les conduites et qui se mélangent entre eux aux noeuds de demande entre deux intervalles déterminés (Rossman, 2000). Ces intervalles de mesure de qualité sont normalement beaucoup plus courts que les intervalles utilisés pour calculer le comportement hydraulique (généralement, plutôt des minutes que des heures), parce que le temps de séjour d'eau dans une conduite peut être très court. Lorsque l'eau entre dans une conduite, la taille du volume élémentaire d'eau amont croît, et la taille du volume élémentaire en aval décroît dans la même proportion. La taille des éléments de volume intermédiaires reste inchangée.

À la fin de chaque pas de temps, EPANET2 entreprend les actions suivantes:

1. La qualité d'eau dans chaque segment est mise à jour conformément aux réactions qui ont eu lieu dans la conduite.

2. L'eau qui entre dans le noeud de demande en amont, et qui provient d'autres conduites, est mélangée pour calculer la nouvelle qualité d'eau. Le volume fourni par chaque volume élémentaire d'eau est égal au produit du débit dans la conduite d'origine et du laps de temps de l'intervalle. Si ce volume est supérieur à celui du segment, celui-ci est détruit et le prochain élément de volume commence à fournir son volume d'eau.

3. Les substances provenant de sources extérieures sont ajoutées dans les noeuds de demande. La façon dont la qualité dans les réservoirs est mise à jour dépend du type de mélange appliqué.

4. De nouveaux segments d'eau sont créés dans les conduites qui sortent du noeud de demande, du réservoir ou de la bâche. Le volume de chaque segment est égal au produit du débit par l'intervalle de temps, et sa qualité égale à la nouvelle qualité d'eau dans le noeud.

Pour réduire le nombre de segments, l'étape 4 n'est exécutée que si la différence entre la nouvelle qualité dans le noeud et celle du dernier segment est supérieure à une tolérance définie par l'utilisateur. Si la différence de qualité est inférieure à cette tolérance, le volume qui entre dans la conduite au cours de l'intervalle est simplement ajouté au dernier segment.

Ensuite, ce processus est répété pour l'intervalle de temps suivant. Au début de l'intervalle hydraulique suivant, l'ordre des volumes élémentaires est inversé dans les arcs où le sens de l'écoulement a changé. Initialement, chaque tuyau du réseau est constitué d'un unique élément de volume dont la qualité est égale à la qualité assignée au noeud en amont.

24

II-5/ Conclusion

Un aperçu sur la cinétique chimique de la réaction du chlore dans l'eau véhiculée dans les réseaux d'adduction d'eau potables est présenté au cours de ce chapitre. On en déduit ce qui suit :

- le chlore résiduel libre est le chlore qui demeure dans l'eau après une période de séjour donnée. Sa présence est l'indicateur de qualité.

- Le phénomène de dégradation de ce type de chlore se produit aussi bien dans la veine liquide qu'au niveau de la paroi des conduites.

- Le mécanisme de dégradation est considéré bi-dimentionnel pour des écoulements turbulents.

- Les facteurs les plus appropriés pour l'étude de cette dégradation peuvent être la nature de la conduite comme ils peuvent être la température, la concentration initiale en chlore, la concentration en fer et la matière organique, etc.

Dans ce qui suit, on met en place un modèle de dégradation du chlore en se basant sur des résultats tirés de la bibliographie.

25

26

27

Chapitre III

Mise en place d'un modèle de dégradation du chlore pour les

réseaux d'adduction d'eau potable. Cas de la région de Bizerte

Dans ce chapitre, une nouvelle approche de modélisation des réseaux d'adduction d'eau potable en terme de distribution spatio-temporelle de la concentration du chlore résiduel libre où la cinétique chimique de la réaction de cette entité est supposée liée à des différents paramètres tel que la température et la matière organique (Vieira, 2004 et Clark et Sivaganesan, 1998).

L'influence de ces paramètres est déterminé en se basant sur des mesures de l'évolution temporelle de la concentration du chlore résiduel libre, réalisée dans le cadre de ce master, sur des échantillons pris à partir des sources d'eau qui alimentent le réseau. Ces échantillons sont traités dans des conditions expérimentales initiales bien définies. Les mesures sont étudiées statistiquement afin de formaliser ces éventuelles corrélations entre les paramètres expérimentaux.

III-1/ Construction du modèle hydraulique

Pour la construction du modèle hydraulique d'un réseau d'adduction d'eau potable par le logiciel EPANET 2, nous avons adopté la démarche suivante :

- Sélectionner la formule de perte de charge afin de saisir le coefficient de perte de charge adéquat pour chaque tronçon.

- Fixer une période de simulation et un pas de temps de calcul hydraulique.

- Dessiner les noeuds et leur attribuer une cote NGT, le débit distribué moyen et la courbe de modulation horaire de distribution du réservoir qui alimente chacun d'eux. En absence d'enregistrements, on affecte la courbe disponible du réservoir le plus proche.

Compte tenu des variations saisonnières de consommation liées à l'activité touristique et aux modifications des rythmes de travail (passage à la journée continue en été) et pour s'approcher de la réalité du terrain, il faut faire la différence entre un modèle estival et un modèle hivernal en établissement des courbes de variation hivernale et estivale de consommations à l'aval des réservoirs afin de mettre en évidence l'influence de ces facteurs sur la répartition journalière de la consommation. Ces courbes ont un rôle important pour la réussite d'un modèle hydraulique.

La démarche adoptée pour la détermination des courbes saisonnières de modulation horaire comprend 3 étapes :

1. critique des données disponibles : pour l'analyse, on choisi comme période de référence Janvier (pour la saison hivernale) et Juillet ou Août (pour la saison estivale) lorsque ces données étaient disponibles.

2. choix d'une semaine type et calcul des courbes de modulation horaire : à l'issue de la critique des données, on retenu les journées qui me semblaient les plus caractéristiques et calculé pour chacune d'elles la courbe de modulation horaire.

3. Détermination d'une courbe de tendance : A partir des courbes de modulation horaire calculées pour différents jour, on défini la courbe de tendance des variations horaires par la méthode des moyennes mobiles.

Ainsi, les courbes de modulation horaire des différents jours ont permis d'établir une courbe moyenne qui est obtenue en faisant la moyenne arithmétique des coefficients de modulation pour chaque pas de temps.

La méthode des moyennes mobiles est ensuite utilisée pour lisser la courbe obtenue. A chaque pas de temps, la valeur Vi calculée est remplacée par la moyenne arithmétique des n valeurs qui l'entourent, comme illustré par le schéma ci-dessous pour n= 3.

Courbe à lisser Courbe après lissage

V1 V1

V2 V2'= (V1+V2+V3)/3

V3 V3'= (V2+V3+V4)/3

V4 .

- Dessiner et associer à chaque pompe une courbe caractéristique donnant le débit en fonction de la hauteur manométrique totale.

- Dessiner et attribuer à chaque réservoir la cote du radier, du bas niveau, du haut niveau et le diamètre. Pour modéliser l'alimentation par le haut des réservoirs, l'entrée est constitué d'une vanne stabilisatrice amont, suivie par un tronçon très court de conduite de grand diamètre. La pression de consigne de la vanne est mise à 0 m et l'altitude du noeud de sortie est égale à la cote de déversement d'eau dans le réservoir.

- Dessiner et attribuer pour chaque tronçon de conduite sa longueur, son diamètre et le coefficient de rugosité

En dernier lieu, on procède au calage du modèle obtenu. Le paramètre de calage pour les conduites de refoulement est la consigne opérationnelle des vannes de régulation des débits. Le but de ce calage étant d'obtenir des débits de refoulement proches de la réalité. Par contre, le paramètre de calage pour les conduites gravitaires est le coefficient de rugosité de la formule de perte de charge de Hazen-

Williams. Le but de ce calage étant d'obtenir des débits d'écoulements gravitaires proches de la réalité. Au cours de la tournée de collecte de données de calage, les débits suivants sont mesurés:

- Le débit de refoulement pour chaque groupe électropompe au niveau des forages et stations de pompages afin d'ajuster, au niveau du modèle hydraulique, le coefficient de perte de charge de la vanne fictive en aval de ces pompes. En effet la pompe est caractérisé par un point de fonctionnement contractuel qui change au cours du temps par usure des roues ce qui entraîne la diminution de leurs performances. D'autre part des pertes de charge singulières indéterminées peuvent avoir lieu sur les conduites de refoulement. Tous ces paramètres sont comptabilisés dans les coefficients des vannes fictives.

- Les débits à l'entrée et à la sortie de chaque réservoir pour les eaux issues des conduites gravitaires en respectant le temps de séjour, afin d'ajuster les coefficients de perte de charge de la formule Hazen Williams de ces conduites.

Il est à préciser que :

- Les brises charges sont modélisés par des vannes stabilisatrice aval ayant pour consigne une pression nul.

- Les forages sont modélisés comme des bâches dont la charge hydraulique est égale au niveau dynamique de la nappe, puis ils sont connectés avec le reste du réseau par les pompes.

I II-2/ Construction du modèle de dégradation paramétré du chlore : Cas général

Une fois que le modèle hydraulique est mis en place, on construit le modèle de qualité du réseau d'adduction d'eau potable. Le paramètre de qualité à étudier est le chlore résiduel libre. Pour chaque tronçon on attribue un coefficient de dégradation du chlore avec les parois (K_w) et un coefficient de dégradation dans la masse d'eau (Kb) du chlore.

En se référant aux résultats des recherches présentées dans le paragraphe (II-3), les ordres cinétiques des réaction seront pris comme suit :

- On modélise les réactions dans la masse d'eau avec une cinétique d'ordre 1 ou 2 selon les résultats de l'étude statistique.

- On modélise les réactions aux parois avec une cinétique d'ordre 1

On supposera que le mélange dans les réservoirs sont parfais. En effet l'opération de la chloration se réalise au niveau de la bâche d'entrée des réservoirs où le mélange est parfaitement assuré.

Le coefficient de dégradation dans la masse d'eau au niveau de chaque tronçon sera déterminé à partir des relations statistiques. Ces relations sont établies suite à des analyses de laboratoire et une étude

28

statistique de corrélation qui pourrait exister entre ce coefficient et des éventuels paramètres. Le coefficient de dégradation avec les parois sera pris comme paramètre de calage lors de la comparaison entre les valeurs mesurée et calculées. Il sera déterminé en se basant sur les mesures des concentrations du chlore résiduel libre dans des noeuds situés entre des points d'injection de chlore.

III-2-1/ Détermination du coefficient de dégradation du chlore dans la masse d'eau

Le coefficient de dégradation du chlore dans la masse d'eau d'une source donnée et dans des conditions bien définies, sera déterminée en laboratoire : des échantillons sont pris des différents forages. Les analyses sont réalisées selon la méthodologie adoptée par la SONEDE basée sur l'utilisation d'un "comparateur" (figure III.1) capable d'indiquer directement le taux, en mg/l, du chlore résiduel libre dans l'eau (Annexe n°1).

Figure III.1 : Appareil de mesure du chlore dans l'eau "Le Comparateur"

Sachant que la matière organique, le fer et la nitrite sont parmi les facteurs les plus appropriés pour l'étude de la dégradation du chlore (Vieira et al, 2004), le nombre d'échantillons peut être réduit en regroupant les points d'eau ayant des concentrations proches en fer et en nitrite et en supposant que les eaux de forages, appartenants à une même nappe, ont la même quantité de matière organique.

Dans le but d'évaluer l'influence du dosage initial de chlore et de la température, des températures ambiantes de 15, 20 et 25 °C et des concentrations initiales de chlore résiduel libre prédéterminés seront étudiés. Afin de se rapprocher des conditions trouvées dans les réseaux d'eau potable, la gamme de concentration en chlore résiduel libre choisie est 1 à 3 mg/l

Le mode opératoire est le suivant :

- le contenu de chaque bouteille est devisé dans 4 bouteilles remplis et fermés. Ces bouteilles seront conditionnées dans des milieux ayant des températures respectivement égales à 15, 20 et 25°C.

- Le contenu de chaque bouteille sera divisé dans 4 autres auquel on ajoute une solution diluée de chlore préparé à partir d'une solution commerciale d'hypochlorite de sodium afin d'avoir une

concentration initiale en chlore résiduel libre respectivement égale à 1, 1.5, 2 et 3 mg/l. Au total, on aura 12 bouteilles pour chaque source d'eau.

- On analysera chaque échantillon pour déterminer une équation de corrélation entre la concentration du chlore résiduel libre dans ces échantillons et le temps. Les mesures seront réalisées par le "comparateur" et les calculs de corrélation seront faits par le logiciel d'analyse de corrélation statistique "REGRESS 1.0" (Annexe n°2). Le choix de la cinétique d'ordre 1 pour les réactions de dégradations du chlore dans la masse d'eau implique une équation de forme exponentielle. Dans le cas où le coefficient d'erreur R² sera inférieur à 0.5, l'hypothèse d'une cinétique d'ordre 1 sera alors remplacé par une cinétique d'ordre 2.

- Pour chaque couple de température (T) et de concentration initiale en chlore résiduel libre (C_o), on déterminera une équation de type :

C C e-

= 0 (III.1)

a T

Où C est la concentration en chlore résiduel libre à une instant t. Le coefficient (a) n'est autre que le coefficient Kb.

A partir des coefficients de dégradations Kb pour chaque couple (C_o, T) et source d'eau, on détermine une équation de corrélation double entre Kb C_o et T et ceci pour chaque source d'eau de type :

K_b C T (III.2)

= á × ×

â ã

0

Où á, â et ã sont des coefficients d'ajustement obtenus par un programme de calcul des dégradations doubles développé dans le cadre de ce master sous Excel et présenté dans l'annexe 7 Ce programme donne en plus des coefficientsá, â, ã et le coefficient de corrélation R².

Ainsi, l'équation III.2 rende la détermination du coefficient Kb , pour chaque source d'eau, une tache aisée en sachant la température et la concentration initiale en chlore résiduel libre.

Au niveau du modèle, on affectera à chaque conduite un coefficient _Kb,mélange comme suit.:

? q C T q K

?

â ã

× á × × ×

i i i i i b i

0 ,

Kb

= , mélange

i i ? ? = (III.3) q q i i

29

30

i i

En effet, pour s'approcher de la réalité, on doit considérer la variabilité des mélanges d'eau transitée dans les conduites d'adduction. Ainsi, le coefficient _Kb,mélange pour une conduite n'est autre qu'une moyenne pondérée de débit (qi) des coefficients élémentaires Kb .

Le logiciel EPANET2 n'envisage pas de tels coefficients. Effectivement des coefficients sont affectés
initialement aux tronçons de conduites par le manipulateur du modèle et y demeures. Pour lever cette

limite, on présentera dans ce qui suit une alternative en exploitant la possibilité d'importer et d'exporter des donner sous format Excel par EPANET2.

III-2-2/ Couplage du modèle qualité d'"EPANET2"avec le tableur Excel

Afin de tenir compte de la dépendance du coefficient Kb avec le mélange, la température et la concentration initiale en chlore, on peut exploiter la possibilité de coupler le modèle classique d'" EPANET2" avec une feuille de calcul du tableur Excel. Le moyen proposé sera la suivante :

III-2-2-1/ Hypothèse

Pour commencer, on choisir une période pendant laquelle on supposera que l'influence de la variation dans le temps des paramètres influence la présence du chlore dans l'eau est négligeable. D'une autre manière, le coefficient Kb est supposé relativement constant.

III-2-2-2/ Exportation des informations du modèle EPANET vers EXCEL

Pour calculer les coefficients pondérés de l'équation III.3, on doit savoir les débits de production moyens de chaque source d'eau sur la période prédéfinie. Pour ce faire, au niveau du modèle EPANET du réseau d'étude, on choisira comme information statistique figurant dans le rapport de la simulation de longue durée l'option "AVERAGE" (rapporte les moyennes des résultats sur une période de simulation), on lance ensuite une simulation hydraulique sur cette période. Les débits de chaque source d'eau et de chaque vanne de régulation des mélanges d'eaux sont exportés vers une feuille de calcul Excel.

Pour que les résultats seraient meilleurs, on choisit le "REPORT START", qui est l'heure à laquelle les résultats commencent à être rapportés, supérieur à 48 heures afin que le comportement du réseau se stabilise.

III-2-2-3/ Mise en place de la feuille de calcul EXCEL

La feuille de calcul où sont stockés les débits sera un fichier input pour le modèle qualité d'EPANET. En respectant la syntaxe exigé pour les fichier d'Input d'EPANET, on affecte pour chaque tronçon du modèle ce qui suit :

- l'expression de l'équation paramétrée (III.2).

- la température d'eau, la consigne de chloration dans le réservoir et le débit de chaque source qui l'alimente. Ces paramètres seront affectés automatiquement à l'équation de Kb _mélange .

III-2-2-4/ Importation des informations par le modèle EPANET a partir de la

feuille EXCEL

31

32

Les coefficients Kb _mélange ainsi trouvés, seront regroupés suivant la syntaxe exigée dans la feuille Excel qui sera par la suite exporté vers "EPANET2" comme "SCENARIO" en changeant l'extension du fichier 'scn' au lieu de 'xls' .

Après avoir remplacer l'option "AVERAGE" par "NONE" dans le modèle EPANET de qualité au niveau 'informations statistiques', on lance la simulation dynamique du modèle du réseau d'adduction sur la période de l'étude.

Ainsi les coefficients Kb assignés aux tronçons seront réellement fonctions des mélanges, des températures et des consignes de chloration dans les réservoirs pendant la période initialement choisie.

I II-2-3/ Calage du modèle qualité : cas général

Comme le calage hydraulique, le calage de qualité d'eau représente l'étape complémentaire de la modélisation qualitative. Il consiste à collecter les résultats de calcul provenant de la résolution des lois mathématiques et à analyser les écarts entre ces résultats et les valeurs réellement enregistrés in situ à fin d'ajuster les paramètres concernés dans le calcul. Les mesures de concentration sont faites dans des conduites à caractéristiques connues. Pour notre cas, le coefficient de réaction avec la paroi "Kw" sera utilisé comme paramètre de calage du modèle qualité. Sa valeur est généralement comprise entre -5 et 0 pied/jour et inversement proportionnel avec le diamètre de la conduite (voir paragraphe II-3). Nous pouvons prendre comme valeurs initiales de ce coefficient :

- -1 pied/jour pour les conduites à diamètre 1000 et 1200

- -3 pied /jour pour les conduites ayant un diamètre égale à 600 mm

- -5 pied/jour pour les conduites ayant un diamètre inférieur à 600 mm.

Les résultats de calage permettront d'affirmer que le modèle de qualité ainsi établi reflète convenablement le comportement du chlore résiduel dans le réseau d'étude.

I II-4/ Modèle hydraulique et de qualité d'eau : cas du réseau d'adduction de la région de Bizerte

Afin de mettre en évidence notre approche de modélisation du comportement du chlore résiduel libre dans l'eau d'un réseau d'adduction, on prendra le réseau d'adduction de la région de Bizerte comme cas concret. Les composantes physiques et les données d'exploitation nécessaires pour la mise en place d'un tel modèle sont détaillées en annexe 3.

III-4-1/ Etendue de l'étude

La zone d'étude (figure 5) s'étend sur les délégations de Mateur, Menzel Bourguiba, Bizerte sud, Bizerte Nord, Menzel Djemil, Menzel Abderrahman, El Alia, Rive Sud du gouvernorat de Bizerte. Elle comptait environ 419 303 habitants en 2004 (INS, 2004)

L'alimentation en eau potable de cette zone est assurée à partir de :

· La station de traitement des eaux de surface des barrages Joumine et Sejnéne. situés à Mateur

· La nappe de Mateur

· La nappe d'El Azib

· La nappe d'El Alia

Cette zone est subdivisée en deux sous zones :

· La rive Nord : c'est la zone située au Nord de canal de Bizerte, elle comporte les villes de Bizerte ville, Menzel Bourguiba, Tinja et Mateur.

· La rive sud : c'est la zone située au sud de canal de Bizerte, elle comporte les villes de Menzel Abderrahman, Jarzouna, Menzel Jemil, El Alia, Ras Djebal Ghar El Meleh, Metline et RafRaf.

33

34

Les ouvrages pris en compte dans le cadre de l'étude sont localisés sur le schéma des adductions. Ce schéma a été établi à partir des documents remis par la SO.N.E.D.E et corrigés lors des visites des ouvrages effectuées durant le mois de Juin 2006.

Les documents ci-après ont été exploités afin de définir les caractéristiques physiques du réseau d'adduction étudié :

- Le schéma général des adductions du district de Bizerte, en ce qui concerne la structure générale du réseau entre les localités,

- Les plans de recollement des différentes composantes du réseau en question.

- L'inventaire des stations de pompage et forages du district de Bizerte, en ce qui concerne les caractéristiques dimensionnelles (débit nominaux, HMT, nombre de pompes, etc..) de ces ouvrages.

- Les profils en long en format « xls » des conduites suivantes pour vérifier leurs cotes, longueurs et diamètres :

o DN 600 entre le réservoir de Ras el Ain et le réservoir de Rhézala

o DN 1200 entre la station de traitement de Mateur et le réservoir de Koudia o DN 1200 entre la station de traitement et le brise charge en ligne de Tinja o DN 1200 entre la station de traitement et le réservoir de Faroua

o DN 1000 et DN 800 du brise charge de Faroua et le brise charge de koudiat La consistance du réseau est la suivante :

1. Station de pompage à vitesse variable ayant un débit nominal de 1 m³/s, refoulant l'eau de la conduite Joumine-Medjerdah DN 1800 mm vers une station de traitement. L'eau traitée est collectée dans un réservoir de tête 2 x 5 000 m3 pour être transitée gravitairement vers Menzel Bourguiba et Bizerte.

2. Une adduction DN 1250/1000/800 mm de 40 km de longueur appelé adduction de Joumine, et constituée de deux biefs séparés par un brise charge en ligne situé sur la colline de Tinja. Cette adduction est également utilisée en appoint pour alimenter le réservoir de Rhézala (5 000 m3). Elle permet aussi d'assurer un appoint à l'ancienne adduction de Mateur au niveau du réservoir de Ras El Ain qui alimente Bizerte et Ml Bourguiba.

3. Cette adduction est à commande hydraulique par l'aval. Les biefs débouchent dans des chambres brise charge équipées de vannes cylindriques qui ferment l'arrivée dès que les réservoirs de tête des conduites de distribution sont remplis.

4. La stérilisation des eaux est effectuée à l'amont de la station de traitement et l'injections du chlore est effectuée au niveau des brises charges à l'entrée des réservoirs.

5.

35

Les zones hautes de Bizerte sont alimentées par une conduite DN300 de refoulement desservie par la station de reprise Koudiat (100 l/s) qui refoule vers le réservoir de Baccar (2 500 m³)

6. Une conduite DN 500 mm a été posée dans le canal de Bizerte pour alimenter la station de reprise (300 l/s) et le réservoir de Roumadia (2 x 1000 m3). Ce réservoir dessert la ville de Ml Abderrahmen et par une conduite gravitaire DN 300 mm le réservoir de Ml Jemil. Le réservoir de Roumadia assure également un appoint pour toute la Rive Sud de Bizerte. Sur le même réservoir sera piquée la conduite DN 500 mm qui alimente la station de reprise Hriza de la rive Sud de Bizerte.

7. La ville de Mateur est alimentée à partir de la nappe de Mateur avec un appoint de la conduite d'adduction de Joumine.

8. L'alimentation en eau de la Rive Sud de Bizerte est assurée par la nappe d'El Azib et d'El Alia. Les eaux des forages d'El Azib (au nombre de huit) ayant un débit total de 90 l/s sont collectées soit directement, soit par l'intermédiaire de la station de reprise SGR9, vers le réservoir d'Ain Bouras (250 m³)

Le périmètre du réseau étudié comprend l'ensemble des reseaux d'adduction depuis la station de refoulement de Joumine et les champs captant de Mateur, El Azib et El Alia jusqu'aux réservoir de distribution ci- après :

- Réservoirs de Mateur

- Réservoir de Ras Ain

- Réservoirs de Ml Bourguiba

- Réservoir de Beni Nafaa

- Réservoir de Rhézala

- Réservoir de Koudiat

- Réservoir de Baccar

- Réservoir de Roumadia

- Réservoir de Ml Djémil

- Réservoir de Hriza

- Les réservoir tête alimentant la rive Sud à savoir le réservoir Ain Bouras et El Alia. Ces réseaux d'adduction sont partiellement maillés.

III-4-2/ Mise en place du modèle hydraulique du réseau de la région de Bizerte

36

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

Le réseau modélisé est composé de 17 forages, 24 pompes, 44 vannes, 17 réservoirs, 105 conduites, et 135 noeuds. Il comprend les ouvrages principaux des adductions ci-après :

· L'adduction de Joumine, depuis la station de reprise de Joumine jusqu'aux réservoirs CE6, de Beni Nafaa, de Koudiat et de Rhézala.

· Le réseau d'adduction de la ville de Mateur, depuis le forage de Mateur ville jusqu'au réservoir de Mateur.

· L'adduction de Koudiat, depuis le réservoir de Rhézala jusqu'aux réservoir de Baccar.

· L'adduction de Roumadia depuis le réservoir de Rhézala jusqu'aux réservoirs de Roumadia et de Ml Djemil.

· L'adduction depuis le réservoir de Roumadia et la nappe d'El Alia jusqu'aux réservoirs d'El Alia et Ain Bouras.

· L'adduction depuis le champ captant d'El Azib.

Dans ce modèle, on considère une période de deux journées avec un pas de temps de calcul hydraulique de 15 minutes. On se base sur les données hydrauliques suivantes :

- Formule de perte de charge : Hazen- Williams

- Coefficient de rugosité initial 85 pour les conduites de diamètre supérieur à 300 mm - Coefficient de rugosité initial 100 pour les conduites de diamètre inférieur à 300 mm - Unité de débit : litre/seconde

En se basant sur les données concernant les volumes journaliers moyens produits par la station de traitement de Mateur et les forages de la nappe de Mateur, Azib et El Alia, les volumes journaliers moyens distribués au niveau de l'ensemble des réservoirs de la région de Bizerte et les consignes de régulations pendant le mois de septembre 2005, on ajuste :

- la demande aux noeuds de consommation en aval des réservoirs

- les consignes de marche des vannes de régulation de débit (CFV) et des vannes diaphragmes (TCV) pour retrouver les débits pompés en septembre 2005, avec les niveaux dynamique des nappes de Mateur, El Alia et El Azib de septembre 2005.

- les consignes d'asservissement des groupes de pompage à partir des heures de pompages mentionnés dans les feuilles de marche et les rapports mensuels d'exploitation. Les pompes des forages ont été asservies au niveau d'eau dans les réservoirs de collecte. Même si elles ne sont pas actuellement asservies, leur arrêt et leur redémarrage sont en effet commandés manuellement par un gardien en fonction des niveaux d'eau dans les réservoirs de collecte.

Le schéma du modèle "EPANET2" du réseau d'adduction de la région de Bizerte retenu est ci dessous.

37

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

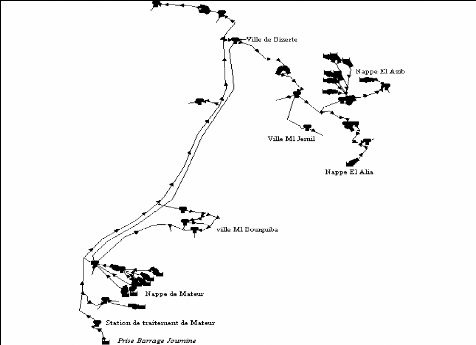
Figure III.3: Schéma du réseau d'adduction du modèle "EPANET2"

III-4-2-1/ Modélisation et consignes d'asservissement des pompes du modèle

L'objectif primordial d'un modèle est de refléter la réalité du terrain. Pour ce faire, on essayera de traduire le fonctionnement des stations de pompage par des bâches dont la charge hydraulique est égale au niveau dynamique de la nappe. Ces bâches sont connectées avec le reste du réseau par les pompes. Les consignes d'asservissement des groupes électropompes sont comme suit:

- Si le niveau d'eau dans la bâche de collecte des eaux de la nappe El Azib, nommé«Bache SGR09«, dépasse les 4 m alors les groupes électropompes immergés des forages suivants s'arrêtent : SGR08, SGR10, SGR01, SGR13, SGR12, SGR1 1 et SGR09. Au dessous de 2m, tous ces groupes démarrent.

- Si le niveau d'eau dans le réservoir Ain Bourass dépasse 2,5 m alors les groupes électropompes dans la station SGR09 s'arrêtent. Au dessous de la valeur de 2 m, ils démarrent.

- Si le niveau d'eau dans le réservoir El Alia dépasse 4,1 m ou descend au dessous de 1m dans le réservoir Hriza alors les groupes électropompes de la station de reprise de Hriza s'arrêtent.

- Si le niveau d'eau dans le réservoir El Alia descend au dessous 3,6 m alors les groupes électropompes de la station de reprise de Hriza démarrent.

38

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

- Si le niveau d'eau dans le réservoir Roumadia dépasse 4 m ou descend au dessous de 1m dans le réservoir Rhézala alors les groupes électropompes de la station de reprise de Roumadia s'arrêtent.

- Si le niveau d'eau dans le réservoir Roumadia descend au dessous 3,3 m alors les groupes électropompes de la station de reprise de Roumadia démarrent.

- Si le niveau d'eau dans la bâche de collecte des eaux de la nappe de Mateur, nommé«Bache Mateur Basse«, dépasse les 3,5 m alors les groupes électropompes immergés des forages suivants s'arrêtent : FM08, FM04, FM02, FM09. Au dessous de 1,7m, tous ces groupes démarrent.

- Si le niveau d'eau dans la bâche de collecte des eaux de la nappe de Mateur «Bâche Mateur Basse« descend au dessous 0,8 m alors les groupes électropompes de la station de reprise de Mateur Basse s'arrêtent. Au dessus du niveau de 3m, ils démarrent.

- Si le niveau d'eau dans le réservoir Ras Ain dépasse 5,5 m alors les groupes électropompes de la station de Mateur Basse et les forages FM05 et FM1 1 s'arrêtent. Lorsque ce niveau descend au dessous de 5m, tous ces groupes démarrent.

- Si le niveau d'eau dans le réservoir Baccar descend au dessous 3,8 m alors les groupes électropompes de la station de reprise de Koudia démarrent. Au dessus de la valeur de 4,5 m, ils s'arrêtent.

III-4-2-2/ Modélisation et consignes d'asservissement des vannes du modèle

L'ignorance d'un certain nombre d'informations liées au fonctionnement d'un réseau d'adduction d'eau potable tel que les consignes d'asservissement des vannes de régulation, peut induire au manque de crédibilité des résultats du modèle hydraulique et par conséquent du modèle qualité. Dans ce contexte, on a procédé comme suit :

- Pour modéliser l'alimentation par le haut d'un réservoir, l'entrée de ce dernier est modélisé par une vanne stabilisatrice amont suivie par un tronçon de conduite très court et un grand diamètre. La pression de consigne de la vanne est mise à zéro mètre et l'altitude du noeud de sortie du réservoir est égale à la côte de déversement d'eau dans le réservoir.

- Les brises charges sont modélisés par des vannes stabilisatrice aval ayant pour consigne une pression nul. Les consignes d'asservissement des groupes électropompes des forages et stations de reprise du réseau d'étude sont :

· Si le niveau d'eau dans le réservoir "Mateur ville" dépasse 4,5m alors l'alimentation à partir de l'adduction DN1200 est arrêtée.

· Si le niveau d'eau dans le réservoir "Mateur ville" descend au dessous de 3m alors le débit d'alimentation à partir de l'adduction DN1200 peut atteindre 115 l/s.

39

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

· Si le niveau d'eau dans la bâche de collecte "SGR09" descend au dessous de 1 ,7m alors l'alimentation à partir du réservoir de "Roumadia" est ouverte.

· Si le niveau d'eau dans la bâche de collecte "SGR09" dépasse de 2m alors l'alimentation à partir du réservoir de "Roumadia" est fermée.

· Si le niveau d'eau dans le réservoir de "Rhézala" dépasse 4,3 m alors l'alimentation à partir du "BC5" est fermée.

· Si le niveau d'eau dans le réservoir de "Rhézala" est compris entre 3,8 m et 4,3 m alors le débit d'alimentation à partir du "BC5" peut atteindre 100l/s.

· Si le niveau d'eau dans le réservoir de "Rhézala" est compris entre 3,3 m et 3,8 m alors le débit d'alimentation à partir du "BC5" peut atteindre 200l/s.

· Si le niveau d'eau dans le réservoir de "Rhézala" est compris entre 2,8 m et 3,3 m alors le débit d'alimentation à partir du "BC5" peut atteindre 250l/s.

· Si le niveau d'eau dans le réservoir de "Rhézala" est inférieur à 3,8 m alors le débit d'alimentation à partir du "BC5" peut atteindre 350l/s.

· Si le niveau d'eau dans le réservoir de "Ras Ain" est inférieur à 3,5 m et l'alimentation à partir de la nappe de Mateur est ouverte alors le débit d'alimentation à partir de la conduite DN1200 peut atteindre 30 l/s.

· Si le niveau d'eau dans le réservoir de "Ras Ain" est inférieur à 3,5 m et l'alimentation à partir de la nappe de Mateur est fermé alors le débit d'alimentation à partir de la conduite DN1200 peut atteindre 100 l/s.

· Si le niveau d'eau dans le réservoir de "Ras Ain" est supérieur à 3,5 m et l'alimentation à partir de la nappe de Mateur est ouverte alors le débit d'alimentation à partir de la conduite DN1200 est nul.

· Si le niveau d'eau dans le réservoir de "Koudia" est supérieur à 4 m alors le débit d'alimentation à partir de la conduite DN1000 peut atteindre 100 l/s.

· Si le niveau d'eau dans le réservoir de "Koudia" est compris entre 3,2 et 4m alors le débit d'alimentation à partir de la conduite DN1000 peut atteindre 150 l/s.

· Si le niveau d'eau dans le réservoir de "Koudia" est inférieur à 3,2 alors le débit d'alimentation à partir de la conduite DN1000 peut atteindre 200 l/s.

III-4-2-3/ Calage du modèle hydraulique

Le paramètre de calage est le coefficient de perte de charge dans le réseau. La spécificité des réseaux d'adduction d'eau potable rende l'opération de mesure sur terrain de la pression pour le calage

40

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

inutile, contrairement aux réseaux de distributions d'eau potable. En effet, il suffit de prendre des mesures de débits (débitance), au niveau des stations de pompages et des réservoirs tout en tenant compte du temps de séjour, pour ajuster les coefficients de perte de charge des conduites du modèle du réseau. Les résultats de calage sont comme suit :

1- La débitance enregistré pour la conduite gravitaire DN 350 mm entre le réservoir de Ras El Ain et celui CE1 est de l'ordre de 47 l/s. Le coefficient retenu de perte de charge de la formule Hazen Willliams pour les tronçons de cette conduite est 110 _{(débitmodèle=47} l/s).

2- La débitance enregistré pour la conduite gravitaire DN 300 mm entre le réservoir de Roumadia et celui Ml Jemil est de l'ordre de 97 l/s. Le coefficient retenu de perte de charge de la formule Hazen Willliams pour les tronçons de cette conduite est 130 _{(débitmodèle=1} 03 l/s).

3- Pour le reste des conduites, l'adduction est en charge. Le calage des débits transités dans ces conduites est réalisé en ajustant les coefficients de perte de charge des vannes fictives à l'aval des pompes.

Il est à noter qu'on a attribué pour chaque noeud de demande d'eau la courbe de modulation horaire Eté du réservoir qui l'alimente. En absence d'enregistrements pour certains réservoirs, on a affecté la courbe disponible du réservoir le plus proche. Alors, pour modéliser une situation donnée, il suffira d'introduire des coefficients correctifs pour corriger ces débits

III-4-3/ Construction du modèle qualité

L'objectif de ce chapitre est de construire un modèle qualité de la région de Bizerte qui tient en compte la dépendance du coefficient de dégradation du chlore résiduel libre"Kb" avec la température, la concentration initiale en chlore résiduel libre et de l'origine d'eau. A la suite d'une étude expérimentale, un fichier "INPUT" du logiciel "EPANET 2" sera crée par le tableur "Excel" où seront calculés et assignés les valeurs de Kb pour chaque tronçon du modèle hydraulique déjà établi.

III-4-3-1/ Gestion de la qualité d'eau dans le réseau d'étude

La chloration est l'unique traitement sanitaire appliqué à l'eau du réseau d'adduction d'eau potable de la région de Bizerte. Elle est effectuée au niveau des brises charges à l'entrée des réservoirs afin d'assurer une bonne homogénéité d'eau. Cette chloration est assurée par des bacs contrôlés par des robinets manuels. Entre autre, pour optimiser le bon dosage de chlore, des pompes doseuses à fonctionnement automatique associé aux impulsions délivrées par les compteurs d'eau ont pris la place de ces bacs dans certains ouvrages. La forme de chlore utilisé pour la désinfection d'eau est la solution d'hypochlorite de sodium (eau de javel). La quantité de ce désinfectant dépend du degré mesuré du produit en stock et du volume d'eau à traiter compte tenu du dosage souhaité à la sortie de l'ouvrage

41

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

(Besbes, 1997). La formule suivante illustre le débit à injecter en litre par heure où dj est le degré d'eau de javel en stock.

V j	Q m h Dosage g m ( / )* ( / ) 3 3 (III.4) dj *3,17

III-4-3-2/ Détermination de la constante de dégradation de masse du chlore résiduel libre dans l'eau

III-4-3-2-1/ Méthodologie

On assignera à chaque source d'eau un coefficient Kb fonction de la température et de la concentration initiale en chlore C_o (éq.III.2). Ce coefficient sera déterminé expérimentalement, il traduit le comportement de cette eau avec le chlore qui y sera injecté au niveau des stations de chloration dans le réseau.

Etant donnée que les facteurs les plus appropriés pour l'étude de la cinétique de la réaction du chlore résiduel libre avec l'eau sont la matière organique, le fer et la nitrite (Paula Vieira, 2004), le nombre d'échantillon peut être alors réduit en regroupant les points d'eau ayant des concentrations proches en fer et en nitrite et en supposant que les eaux des forages avoisinants et appartenants à la même nappe ont la même quantité de matière organique. A partir des résultats d'analyse physico- chimique effectués par la SONEDE en septembre 2006 (Annexe n°5), on note la faible concentration en ions nitrite de toutes les eaux. On peut ressortir 7 groupes :

· Groupe 1 : station de traitement de Mateur

· Groupe 2 (nappe Mateur, [Fe] <0,1 mg/l): forages Mateur 11, Mateur 8, Mateur ville, Mateur 2 et Mateur 5.

· Groupe 3 (nappe Mateur, [Fe]>0,34 mg/l): forages Mateur 4, Mateur 9

· Groupe 4 (nappe Azib, [Fe] <0,1 mg/l): forages SGR 12, SGR 13, SGR 8, SGR 10 et SGR9

· Groupe 5 (nappe Azib, [Fe]>0,42 mg/l): forage SGR 1, SGR 11

· Groupe 6 (nappe Alia): forage SGR 6

· Groupe 7 : forage SGR 4

Dans un total de 84 échantillons et dans le but d'évaluer l'influence du dosage initial de chlore et de la température, une température ambiante de 15 à 25 °C et des concentrations initiales de chlore résiduel libre (1 à 3 mg/l) ont été simultanément étudiés afin de se rapprocher des conditions trouvées dans le réseau.

On rappelle que le mode opératoire est le suivant :

42

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

- le contenu de chaque bouteille est devisé dans 4 nouvelles bouteilles remplis et fermés. Ces bouteilles seront conditionnées dans des milieux ayant des températures respectivement égale à 15, 20 et 25°C.

- Le contenu de chaque bouteille sera divisé dans 4 autres à qui on ajoute une solution diluée de chlore préparé à partir d'une solution commerciale d'hypochlorite de sodium afin d'avoir une concentration initiale en chlore résiduel libre respectivement égale à 1 - 1,5 - 2 et 3 mg/l. En total, on aura 12 bouteilles pour chaque source d'eau.

- On analysera chaque échantillon pour déterminer une équation de corrélation entre la concentration du chlore résiduel libre dans ces échantillons et le temps. Les mesures seront réalisées par le "comparateur" et les calculs de corrélation seront faits par le logiciel d'analyse de corrélation statistique "REGRESS 1.0" (Annexe n°6). Le choix de la cinétique d'ordre 1 pour les réactions de dégradations du chlore dans la masse d'eau implique une équation de forme exponentielle. Dans le cas où le coefficient d'erreur R² sera faible, l'hypothèse d'une cinétique d'ordre 1 sera alors remplacé par une cinétique d'ordre 2.

- Pour chaque couple de température (t) et de concentration initiale en chlore résiduel libre (C_o), on déterminera une équation de type même type que l'équation (III.1)

Où le coefficient (a) n'est autre que le coefficient Kb.

A partir des coefficients de dégradations Kb pour chaque couple (C_o, T) et source d'eau, on détermine une équation de corrélation double entre Kb C_o et T et ceci pour chaque source d'eau de type (éq. III.2). Cette équation généralisera le calcule Kb pour chaque source d'eau: en sachant la température et la concentration initiale en chlore résiduel libre pour une source donnée on calculera Kb.

On affectera à chaque conduite un coefficient Kb qui dépendra du mélange d'eau. On supposera que le coefficient global pour une conduite sera la moyenne pondérée de débit (qi) des coefficients élémentaires (éq. III.3)

III-4-3-2-2/ Résultats statistiques des analyses et discussions

Les résultats des analyses effectués sur les différents échantillons sont présentés en annexe n°7. Le modèle cinétique d'ordre un a donné des résultats satisfaisants. Les équations de corrélation exponentielle entre le coefficient Kb, la température et la concentration initiale du chlore sont les suivantes :

43

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

Tableau 3Tableau III.1: Equation de corrélation entre Kb, T et Co

N° Groupe		Equation: Kb (min^-1) = f (T,Co)						R^2	1
Kb =	-0.000031	* Co	-1.1789	* T	1.38955	0.88		2
Kb =	-0.000057	* Co	-1.1474	* T	1.50166	0.92		3
Kb =	-0.000021	* Co	-1.2368	* T	1.78502	0.90		4
Kb =	-0.000129	* Co	-1.3509	* T	1.0841	0.65		5
Kb =	-0.000402	* Co	-1.2965	* T	0.8128	0.66		6
Kb =	-0.000082	* Co	-0.6310	* T	1.00088	0.66		7
Kb =	-0.000215	* Co	-1.1597	* T	1.04978	0.74

A partir de ce tableau, on note que :

- Le coefficient Kb est proportionnel à la température et inversement proportionnel à la concentration initiale du chlore résiduel libre.

- Les coefficients de corrélation R² indiquent bien la dépendance du coefficient Kb vis-à-vis des paramètres C_o et T. Ainsi, l'approche classique de modélisation de la dégradation du chlore dans les réseaux d'eau potable où les coefficients Kb sont fonction uniquement de la nature et de la rugosité des conduites donnera une distribution non précise du chlore résiduel libre pour les réseaux d'adduction d'eau potable.

Vu que pour le logiciel EPANET2 les coefficients Kb sont affectés au tronçon de chaque conduite, on essayera dans ce qui suit de mettre en place un fichier input permettent de tenir en compte des résultats sus-mentionnés.

Dans ce qui suit, on développe l'approche proposée.

III-4-3-3/ Elaboration du fichier Input de qualité pour "EPANET2"

Une feuille de calcul Excel est mise en place pour générer, pour chaque tronçon du réseau, des coefficients Kb obéissants aux équations ci-dessus (Tableau III.1). Pour ce faire, il est nécessaire d'avoir les valeurs des paramètres "C_o" et "T" pour chaque tronçon ainsi que la répartition des débits, nécessaire pour la pondération (éq.III.3).

Les valeurs des paramètres "C_o" et "T" sont introduites dans la feuille de calcul manuellement. Alors que les débits sont déterminés par l'intermédiaire des résultats de la simulation hydraulique (tableau III.2).

44

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

Cette approche se fera alors en deux étapes : la première étape permettra la détermination des débits "qi" de l'équation III.3, alors que la deuxième étape permettra la génération des coefficients "Kb,mélanges de la même équation.

Dans ce qui suit le développement de l'approche adoptée :.

- A partir des débits moyens, sur une période prédéfinie, de refoulement de chaque pompe, de produit par la station de traitement de mateur et de la consigne de chaque vanne de régulation de débit on détermine la proportion de chaque source d'eau dans les mélanges dans les réservoirs du réseau.

Ces débits résultes de la simulation hydraulique du réseau en choisissant initialement "AVERAGE" comme OPTIONS/TIMES /STATISTIC (tableau III.2) et en précédant comme suit :

* Pour voir que les débits relatifs aux pompes, il suffit de sélectionner les arcs (links) ayant un coefficient de friction égal à zéro et un diamètre inférieur à 1 (figure III.4).

Figure III.4: Sélection des pompes

* Pour avoir que les débits des vannes qui contrôlent les mélanges des eaux, il suffit d'assigner une valeur fictive (dans notre cas égale à 555) comme diamètre de vannes (figure III.5).

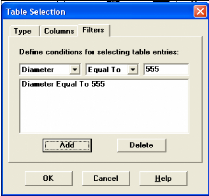
Figure III.5:Sélection des vannes de régulation des mélanges d'eaux

45

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

- Les débits moyens collectés sont stockés dans une feuille de calcul Excel (Tableau III.2). Ces débits seront primordiaux pour le calcul des coefficients Kb, mélange pour chaque tronçon (éq.III.3).

Tableau III.2: Exemple du fichier "input" de débits moyens des pompes et vannes de régulations

Network Table - Links			Network Table - Links
Flow			Flow	Link ID
LPS	Link ID		LPS	Pump FM1 1
42.00	Valve BC6		0.00	Pump FM02
26.97	Valve BC4		136.12	Pump FM05
26.66	Valve BC5		87.13	Pump FM04
29.32	Valve 38		0.00	Pump FM08
32.49	Valve 12		36.12	Pump R_mateur_basse
119.97	Valve 22		5.27	Pump roumadia1
53.05			Pump koudia
43.77
51.69
0.00
12.54
13.74
10.22
7.09
6.56
7.67
9.05
8.31
2.43
8.75
36.90
15.52
30.52
24.45

- Pour chaque tronçon, sachant la température d'eau, la consigne de chloration dans le réservoir qui l'alimente et le débit et le coefficient de dégradation du chlore résiduel libre dans la masse d'eau de chaque source d'eau qui en y transite, la feuille de calcule génère automatiquement le coefficient Kb,mélange en tenant compte des équations de corrélations figurants dans le tableau III.1.

4Ainsi chaque tronçon aura son propre coefficient pendant un axe de temps prédéfini.

46

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

Tableau III.3: Exemple de coefficients Kb, mélange (en mn-1) et K_w (avant calage)

[REACTIONS]			Bulk	127	0.001549	Bulk	157	0.0034299	Bulk	185		0.001903	Bulk
100	0	Wall	127	0	Wall	157	0	Wall	185	0		Wall
100	0	Bulk	129	0.001903	Bulk	158	0.000576	Bulk	186	0		Bulk
101	0.004969	Wall	129	0	Wall	158	0	Wall	186	0		Wall
101	0	Bulk	130	0.001903	Bulk	159	0.0036847	Bulk	187	0		Bulk
102	0	Wall	130	0	Wall	159	0	Wall	187	0		Wall
102	0	Bulk	131	0.001903	Bulk	160	0.0014174	Bulk	188	0.004897		Bulk
103	0	Wall	131	0	Wall	160	0	Wall	188	0		Wall
103	0	Bulk	132	0.002173	Bulk	161	0	Bulk	189	0.004969		Bulk
104	0	Wall	132	0	Wall	161	0	Wall	189	0		Wall
104	0	Bulk	133	0.001549	Bulk	162	0	Bulk	190	0		Bulk
105	0	Wall	133	0	Wall	162	0	Wall	190	0		Wall
105	0	Bulk	134	0	Bulk	163	0.004969	Bulk	191	0		Bulk
106	0	Wall	134	0	Wall	163	0	Wall	191	0		Wall
106	0	Bulk	135	0.000576	Bulk	164	0.004969	Bulk	192	0		Bulk
107	0	Wall	135	0	Wall	164	0	Wall	192	0		Wall
107	0	Bulk	136	0	Bulk	165	0.0048969	Bulk	193	0		Bulk
108	0	Wall	136	0	Wall	165	0	Wall	193	0		Wall
108	0	Bulk	137	0.003763	Bulk	166	0.0048969	Bulk	194	0		Bulk
109	0.004969	Wall	137	0	Wall	166	0	Wall	194	0		Wall
109	0	Bulk	138	0	Bulk	167	0.004969	Bulk	195	0		Bulk
110	0.0048969	Wall	138	0	Wall	167	0	Wall	195	0		Wall
110	0	Bulk	139	0	Bulk	168	0.004969	Bulk	196	0		Bulk
111	0.0007854	Wall	139	0	Wall	168	0	Wall	196	0		Wall
111	0	Bulk	140	0.004969	Bulk	169	0.0048969	Bulk	197	0.001077		Bulk
112	0.0021726	Wall	140	0	Wall	169	0	Wall	197	0		Wall
112	0	Bulk	141	0.004969	Bulk	170	0.0048969	Bulk	198	0		Bulk
113	0.004969	Wall	141	0	Wall	170	0	Wall	198	0		Wall
113	0	Bulk	142	0.004897	Bulk	171	0.0048969	Bulk	199	0.004969		Bulk
114	0.004969	Wall	142	0	Wall	171	0	Wall	199	0		Wall
114	0	Bulk	143	0.001992	Bulk	172	0.004969	Bulk	200	0.001903		Bulk
115	0.000576	Wall	143	0	Wall	172	0	Wall	200	0		Wall
115	0	Bulk	144	0.001992	Bulk	173	0.004969	Bulk	201	0.004969		Bulk
116	0.0032487	Wall	144	0	Wall	173	0	Wall	201	0		Wall
116	0	Bulk	145	0.001992	Bulk	174	0.0048969	Bulk	202	0.001992		Bulk
117	0.0032487	Wall	145	0	Wall	174	0	Wall	202	0		Wall
117	0	Bulk	146	0.001903	Bulk	175	0.004969	Bulk	203	0.001992		Bulk
118	0.0032487	Wall	146	0	Wall	175	0	Wall	203	0		Wall
118	0	Bulk	148	0.003763	Bulk	176	0.0048969	Bulk	204	0.000576		Bulk
119	0.0032487	Wall	148	0	Wall	176	0	Wall	204	0		Wall
119	0	Bulk	149	0	Bulk	177	0.004969	Bulk	147	0.001903		Bulk
120	0.0032487	Wall	149	0	Wall	177	0	Wall	147	0		Wall
120	0	Bulk	150	0	Bulk	178	0.0048969	Bulk	128	0.001903		Bulk
121	0.0032487	Wall	150	0	Wall	178	0	Wall	128	0		Wall
121	0	Bulk	151	0	Bulk	179	0		Bulk
122	0.004969	Wall	151	0	Wall	179	0
122	0	Bulk	152	0	Bulk	180	0.004969
123	0.004969	Wall	152	0	Wall	180	0
123	0	Bulk	153	0	Bulk	181	0.004969
124	0.0010768	Wall	153	0	Wall	181	0
124	0	Bulk	154	0	Bulk	182	0.0014045
125	0.0010768	Wall	154	0	Wall	182	0
125	0	Bulk	155	0	Bulk	183	0.0032487
126	0.000576	Wall	155	0	Wall	183	0
126	0	Bulk	156	0.00343	Bulk	184	0.0019033
		Wall	156	0	Wall	184	0

47

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

Ainsi chaque tronçon possède deux coefficients pour la réaction de dégradation du chlore résiduel dans l'eau. Un exemple, le tronçon N° 110 a un coefficient Kb noté "BULK" égale à 0.0048969mn^-1 et un coefficient K_w noté "WALL" égale à 0.

- Les valeurs trouvées du coefficient Kb, mélange pour chaque tronçon dans la feuille Excel seront exportés vers "EPANET2" comme fichier Input de qualité sous la forme de SCENARIO en changeant l'extension du fichier (scn au lieu de xls) et en respectant la mise en page des données.

- Après avoir choisir "NONE" comme OPTIONS/TIMES/STATISTIC, on lance de nouveau la simulation hydraulique et qualité du réseau d'adduction.

Ainsi les coefficients _Kb,mélange assignés au tronçon sont fonctions des mélanges, des températures et des consignes de chloration dans les réservoirs.

III-4-3-4/Calage du modèle qualité

Comme le calage hydraulique, le calage de qualité d'eau (Annexe n°9) représente l'étape complémentaire de la modélisation qualitative. Le débit et la température sont considérés constants au cours du temps. Les mesures sont faites dans des pas de temps fixés, dans les bâches d'arrivées et de mise en charge des différents réservoirs du réseau (figure III.6).

Figure III.6: Localisation des points d'échantillonnage

48

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

Le coefficient de réaction avec la paroi "K_w" est utilisé comme paramètre de calage du modèle qualité. Sa valeur est généralement comprise entre -5 et 0 pied/jour et inversement proportionnel au diamètre de la conduite. On prendra comme valeurs initiales de ce coefficient :

· -1 pied/jour (0,3 m/jour) pour les conduites à diamètre 1000 et 1200

· -3 pied /jour (0,9 m/jour) pour les conduites ayant un diamètre égale à 600 mm

· -5 pied/jour (1 ,5 m/jour) pour les conduites ayant un diamètre inférieur à 600 mm. Dans le tableau comparatif suivant, les concentrations calculées par "EPANET2" sont proches des mesures effectuées sur le terrain.

On peut conclure que le modèle de qualité reflète convenablement le comportement du chlore résiduel libre dans le réseau d'étude.

Tableau III.4: Chlore résiduel libre mesuré et calculé

			Concentration du chlore (mg/l)			OUVRAGE
Débits (l/s) Entrée/Sortie		mesuré à l'arrivée	calculé à l'arrivée	mesuré à la sortie	Station de traitement de Mateur 5000 m3
500/500		-	-	0.5	Réservoirs"Mateur ville" 4500 m3
113/-		0.1	0.09	-	Réservoir"Ras Ain" 3000 m3
92/		0	0	1	Réservoirs"CE1" 3000 m3
40/-		0	0	0	Réservoirs"CE2" 3000 m3
20/-		0	0	0	Réservoir"CE6" 2500 m3
55/-		0	0	0	Réservoirs"Beni Nafaa" 3000 m3
-		0	0	-	Réservoir"Rhézala" 5000 m3
(137+105)/173		0	0	1.12	Réservoirs"Koudiat" 10000 m3
125/-		0	0	1.41	Réservoir"Baccar" 2500 m3
-		0.7	0.7	-	Station de reprise"Roumadia"
175/1 75		0.4	0.4	0.4	Réservoirs"Roumadia" 2000 m3
225/118		0.3	0.22	1.7	Réservoirs"Menzel Jemil" 1000 m3
95/-		0.9	0.89	-	Bâche. SGR09 (Roumadia)
10		0.4	0.37	0	Réservoir .Ain Bouras 250 m3
-		0	0	-	Reprise Hriza
140/140		0.1	0.05	0.1	Réservoir Alia 1500 m3
-		0	0	0

49

Chapitre III: Mise en place d'un modèle de dégradation du chlore pour les réseaux d'AEP. Cas de la région de Bizerte HELIL Jalel

III-5/ Conclusion

Ce chapitre avait comme objectif la formulation et la validation sur un cas réel d'une approche pour la modélisation de la distribution spatio-temporelle de la concentration du chlore résiduel libre dans les réseaux d'adduction d'eau potable où les coefficients de dégradation du chlore dans la masse d'eau sont fonctions des propriétés de cette eau (température, matière organique, composition ionique...).

Les résultats de l'étude expérimentale effectué sur des échantillons des différentes sources d'eau du réseau d'adduction d'eau potable de la région de Bizerte ont constitué une preuve en faveur de l'approche de modélisation qui stipule la dépendance du coefficient Kb et des paramètres tel que la température, la concentration initiale C_o et l'origine d'eau. Le modèle du réseau d'adduction mis en place sera exploité dans le chapitre suivant.

50

Chapitre IV

Exploitation des modèles hydraulique et de qualité du réseau

d'adduction d'eau potable de la région de Bizerte

IV-1/ Exploitation du modèle hydraulique développé

Les résultats d'une simulation ainsi que certains paramètres, peuvent être visualisés en utilisant différents types de graphiques.

Le graphique type "balance en eau" montre l'évolution de la quantité totale d'eau qui est demandée dans le temps (Figure IV.1) : un maximum de 1000 l/s et un minimum de 340 l/s sont enregistrés, le coefficient de pointe horaire globale du réseau est alors de l'ordre de 2,95.

Figure IV.1: Graphique type" balance en eau"

- Le graphique "profil longitudinal" peut être utilisé pour dessiner le profil en long d'une conduite. Les figures IV.2 et IV.3 sont les profils relatifs à l'adduction gravitaire depuis la station de traitement de Mateur vers le réservoir de "Rhézala" et à l'adduction par pompage depuis le réservoir "Rhézala" vers le réservoir "Alia".

51

Avec : - noeud ST_Mateur : station de traitement de Mateur à la cote 83,76 mNGT - noeud 1026 : piquage vers le réservoir Mateur ville à la cote 63,66 mNGT - noeud 1000 : piquage vers le réservoir Ras Ain à la cote 60,4 mNGT

- noeud 1113 : piquage vers le réservoir CE6 à la cote 65,7 mNGT

- noeud 1009 : piquage vers le réservoir Beni Nafaa à la cote 46,9 mNGT - noeud Rhézala : réservoir Rhézala à la cote 42,7 mNGT

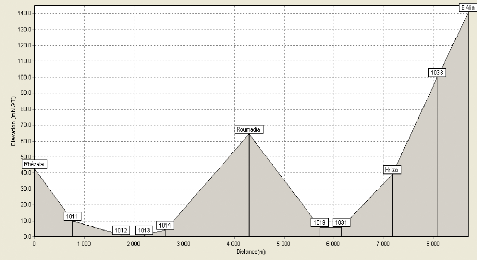
Figure IV.2: Profil en long de la conduite d'adduction à partir de la station de traitement jusqu'au réservoir de
"Rhézala"

Avec :- noeud Rhézala : réservoir Rhézala à la cote 42,7 mNGT

- noeuds 1012 et 1013 : amont et aval passage sous pont mobile de Bizerte - noeud 1014 : station de pompage de "Roumadia" à la cote 4,34 mNGT

- noeud Roumadia : réservoir "Roumadia" à la cote 64,3 mNGT

- noeud 1019 : piquage vers la station de reprise SGR09 à la cote 7 mNGT - noeud Hriza : station de reprise "Hriza" à la cote 41,0 mNGT

- noeud El Alia : réservoir El Alia à la cote 140,8 mNGT

IV-2/ Exploitation du modèle de qualité développé

- De même le graphique type "profil longitudinal" peut être utilisé pour analyser la distribution du
chlore résiduel libre dans une conduite d'eau. Les figures suivantes illustrent cette distribution dans la

52

conduite issue de la station de traitement de Mateur (DN 1 250mm) vers le réservoir de Rhézala en période estivale et hivernale et pendant les pics et les creux de consommation.

On observe que :

- pour tous les cas, le chlore résiduel libre disparaît totalement au niveau du brise charge de Tinja (piquage réservoir CE6).

- pour la période estivale et hivernale, la dégradation du chlore résiduel libre est plus importante en période de consommation creuse qu'en période de pic de consommation.

- pour un pic ou un creux de consommation, la dégradation du chlore résiduel libre est plus importante en période hivernale qu'en période estivale.

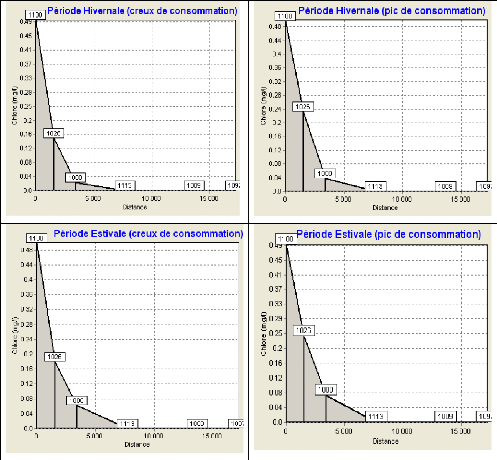
Figure IV.4: Distribution du chlore résiduel libre dans la conduite d'adduction de la station de traitement de
Mateur en périodes estivale et hivernale pour les pics et les creux de consommation.

Avec :

·

53

54

noeud 1100: départ station de traitement de Mateur

· noeuds 1026: piquage vers le réservoir de Mateur ville

· noeuds 1000: piquage vers le réservoir de Ras Ain

· noeuds 1113: brise charge Tinja (piquage vers le réservoir CE6)

· noeuds 1009: piquage vers le réservoir de Beni Nafaa

· noeuds 1097: arrivée réservoir Rhézala

Le graphe de distribution dans le logiciel "EPANET2" représente sur l'axe Y la fraction des noeuds ou tous les arcs, à un instant donné, de valeur inférieur à la valeur de l'axe X. Dans notre cas, on peut exploiter ce type de graphique pour savoir la répartition spatial du temps de séjour dans le réseau en périodes estivale et hivernale. Il a révélé les résultats suivants :

En période estivale (température=25 °C) :

· 53 % d'eau transitée présente un temps de séjour inférieur à 24 heures

· 37 % d'eau transitée présente un temps de séjour entre 24 et 48 heures.

· 10 % d'eau transitée présente un temps de séjour supérieur à 48 heures.

En période hivernale (température=20 °C) :

· 46 % d'eau transitée présente un temps de séjour inférieur à 24 heures

· 15 % d'eau transitée présente un temps de séjour entre 24 et 48 heures.

· 39% d'eau transitée présente un temps de séjour supérieur à 48 heures.

Le faible marnage des réservoirs de régulation et de stockage explique ces ordres de grandeur pour les deux périodes. En effet le renouvellement d'eau dans un réservoir asservie entre deux cotes extrêmes proches engendre la stagnation et le "vieillissement" d'eau en dedans.

La différence entre la distribution du temps de séjour en période estivale et hivernale s'explique par l'augmentation de la demande en eau en été.

Figure IV.5: Distribution du temps de séjour en période hivernale et estivale

- Ce même type de graphe peut être utilisé pour étudier la distribution du coefficient de dégradation du chlore résiduel libre avec la masse d'eau (figure IV.6). Il a révélé les résultats suivants :

En période estivale (température=25 °C) :

· Kb maximal = 10 jour^-1

· 33 % des conduites présente un coefficient compris entre 10 et 7 (jour^-1)

· 25 % des conduites présente un coefficient compris entre 7 et 3 (jour^-1)

· 42 % des conduites présente un coefficient inférieur à 3 (jour^-1) En période hivernale (température=20 °C) :

· Kb maximal = 7,1 jour^-1

· 45 % des conduites présente un coefficient compris entre 7 et 3 (jour^-1)

· 55 % des conduites présente un coefficient inférieur à 3 (jour^-1)

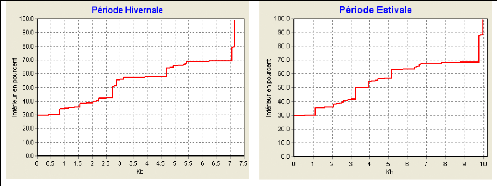
Figure IV.6: Distribution du coefficient Kb en période hivernale et estivale

On constate que les valeurs de Kb sont plus faibles l'hiver puisque la vitesse de dégradation du chlore résiduel libre est moins rapide en eau froide.

- Le graphe d'évolution dans le temps du taux de chlore résiduel libre au niveau du noeud témoin "station de reprise Roumadia" (figure IV.7) montre que ce taux atteint une valeur maximale aux premières heures et enregistre une nette diminution aux heures creuses de consommation. Cette diminution est due à la stagnation d'eau dans le réseau (arrêt du pompage) et la poursuite des processus de réaction du chlore résiduel libre avec la masse d'eau et les parois des conduites.

- Cette même figure montre que le taux du chlore résiduel libre, à chaque instant, en période estivale est supérieur à celui enregistré en période hivernale. Ceci montre bien que le temps de séjour joue un rôle plus important dans le processus de dégradation du chlore résiduel libre que la température d'eau.

55

56

57

Figure IV.7: Modulation du taux de chlore (à droite) et de la vitesse d'écoulement (à gauche) au niveau de la station
de reprise Roumadia pour les périodes hivernale et estivale.

-On peut étudier aussi l'influence des variations des mélanges des eaux dans la dégradation du chlore résiduel libre dans l'eau. On suppose, en période hivernale où la température est proche de 10°C, que la consigne de chloration dans la station de traitement de Mateur est de 2.5mg/l et que cette consigne est de 2 mg/l au niveau du réservoir de Ras El Ain. On simule le fonctionnement hydraulique et de qualité d'eau lorsque la vanne de régulation du débit alimentant la conduite de diamètre 1250 mm à partir du réservoir Ras Ain est totalement ouverte puis totalement fermé. Comme résultats, on comparera la distribution du chlore résiduel libre dans cette conduite.

IV-3/ Exemples d'Amélioration de la qualité d'eau dans le réseau

La formation d'un biofilm bactérien est un phénomène complexe impliquant le milieu, les bactéries et les surfaces colonisées. Il est la résultante des propriétés énergétiques entre les surfaces du matériau et des micro-organismes et de leur réponse à l'adhésion et à l'augmentation de leur densité cellulaire. La formation d'une matrice polymérique extra cellulaire est impliquée dans l'accélération des phénomènes de bio-corrosion en créant une zone anoxique où des bactéries anaérobies se

développent et en piégeant des produits de dégradation anodique des surfaces métalliques (D.Haras, 2005). Ce phénomène est plus important en absence de chlore dans l'eau.

Figure IV.8:Représentation schématique de la formation et de la structure d'un biofilm au sein d'un réseau d'eau
potable (Gauthier,2001)

La figure IV.9 montre que la concentration du chlore résiduel libre s'annule à partir de la brise charge de Tinja. Par le moyen du modèle qualité d'"EPANET2" on essayera d'avoir une concentration en chlore résiduel libre supérieur à 0.2 mg/l.

On se propose alors de simuler la création de points d'injections de chlore au niveau du piquage vers le réservoir "Ras Ain" (noeud 1000) et le noeud de piquage du réservoir "Béni Nafaa" (noeud 1009). La consigne de sortie de ces points sera optimisée à l'issue de quelques simulations. Le scénario de référence correspond à un fonctionnement automatique du réseau en temps normal. Les

consommations de base sont modélisées par une consommation de base estimée égale à la valeur moyenne des consommations en période hivernale et une température d'eau égale à 18°C. La simulation s'étend sur 124 heures et débute à 06 heures du matin.

Les résultats des simulations sont comme suit :

- Pour une consigne de concentration de chlore résiduel libre en sortie égale à 2mg/l et 1 mg/l relative au noeuds 1000 et 1009, on arrive à avoir une concentration supérieur à 0.1 mg/l en tout points de la conduite (figure IV.9)

Figure IV.9:Distribution modifié du chlore résiduel libre dans la conduite d'adduction de la station de traitement de
Mateur

- noeud 1100: départ station de traitement de Mateur

- noeuds 1026: piquage vers le réservoir de Mateur ville

- noeuds 1000: piquage vers le réservoir de Ras Ain

- noeuds 1113: brise charge Tinja (piquage vers le réservoir CE6)

- noeuds 1009: piquage vers le réservoir de Beni Nafaa

- noeuds 1097: arrivée réservoir Rhézala

Autre avantage de ce modèle est l'assurance en terme de qualité d'eau distribuée par le réservoir CE6 en cas de rupture de l'approvisionnement en eau de Javel pour cet ouvrage. En effet, vu l'accès difficile à ce réservoir, ce cas de rupture est fréquent en période hivernale. Ce modèle permettra d'avoir une concentration moyenne à la sortie du réservoir égale à 0,27 mg/l.

58

IV-4/Impact des ouvrages de stockage sur la qualité d'eau

On étudiera l'impact des ouvrages de stockage sur la qualité d'eau en simulant la dégradation du chlore libre entre l'entrée et la sortie d'un réservoir du réseau. En prend le réservoir "CE6" comme exemple.

On considère une concentration à l'entrée du réservoir CE6 identique à celle du modèle décrit ci-dessus (figure IV.9). La figure ci-après décrit la variation horaire de la concentration du chlore résiduel libre à l'entrée et à la sortie de ce réservoir.

On remarque que la différence entre l'état à l'entrée et celui à la sortie du réservoir en terme de chlore résiduel peut atteindre :

- 0,15 mg/l en terme de concentration (figure IV. 10)

- 60% en terme de perte.

Figure IV.10: Impact des ouvrages de stockage sur la qualité d'eau

IV-5/Conclusion :

Les modèles hydraulique et de la qualité d'eau des réseaux d'adduction d'eau potable sont des outils d'aide à la décision nécessaire pour assurer respectivement un bon service hydraulique et une sécurité alimentaire des installations.

C O N C L U S I O N G E N E R A L E

Et PERSPECTIVES

La connaissance du comportement hydraulique et de qualité d'un réseau d'eau potable à chaque instant nécessite en premier lieu la mise en place d'un modèle hydraulique de ce réseau. Pour ce faire, on a besoin au recours à des approches numérique permettant la résolution d'un ensemble d'équations différentielles basées sur des principes hydraulique tel que la continuité au noeuds et les équilibres des charges aux mailles. L'approche numérique adopté dans ce travail est l'approche hybride noeud-maille utilisée par le logiciel EPANET2. Suite à la mise en place du modèle hydraulique, le modèle qualité comme la distribution de la concentration du chlore résiduel libre peut être entamé.

Le chlore résiduel libre est le chlore qui demeure dans l'eau après une période de séjour donnée. Sa présence est l'indicateur de qualité. Le phénomène de dégradation de ce chlore dans l'eau se produit aussi bien dans la veine liquide qu'au niveau de la paroi des conduites. Une étude expérimentales sur des échantillons d'eau prises des sources du réseau d'adduction d'eau potable de la région de Bizerte, ont constitué une preuve en faveur de l'approche de modélisation adopté dans ce travail qui stipule la dépendance du coefficient de dégradation de chlore résiduel libre dans la masse d'eau (Kb ) avec la température d'eau, la concentration initiale en chlore au niveau des points de chloration dans le réseau, la concentration en fer, la matière organique, etc.

Ce modèle vient remplacer les modèles classiques où les coefficients de dégradations du chlore résiduel libre dans la masse d'eau sont des coefficients statiques. Ces derniers modèles pourraient être validés dans le cas des réseaux de distributions d'eau potable. En effet, pour ces réseaux, la dégradation du chlore avec les parois des conduites est plus importante que celle dans la masse d'eau.

Ainsi, les modèles élaborés reflètent au mieux la réalité du terrain et peuvent constituer un outil d'aide pour la gestion des réseaux d'adduction de point de vue hydraulique et de qualité. Un exemple d'application de ces modèles est le maintien d'une concentration minimale en chlore résiduel libre en tout point du réseau en optimisant le lieu et la quantité à injecté dans le réseau. Ceci pourrait éviter au niveau des parois des conduites la formation des biofilms qui constituent une menace pour le bon fonctionnement du réseau d'adduction.

Il a été prouvé, selon le site web ( www.Lenntech.com), que le dioxyde de chlore détruit les biofilms dans les systèmes d'adduction d'eau potable, et prévient également leur formation, lorsque

celui-ci est utilisé de façon continue à de faibles concentrations et que cette forme de chlore a plus d'effet sur les biofilms que l'eau de Javel, utilisé à notre stade comme forme de chlore.

Toutefois, il est possible, à un stade plus avancé, d'utiliser le dioxyde de chlore au lieu d'eau de Javel comme désinfectant et de modéliser sa distribution spatio-temporelle dans les réseaux d'adduction d'eau potable. Cependant, ceci reste tributaire de la disponibilité d'une instrumentation spéciale pour effectuer des analyses et des mesures expérimentales sachant que le dioxyde de chlore est une substance nocive.

L I S T E B I B L I O G R A P H I Q U E

1 .Ayari.A 2003. Essai de modélisation de la propagation du chlore dans les réseaux sous pression. Mémoire DEA, INAT.

2.Besbes 1997. Guide de calcul du volume d'eau de javel à injecter. Note interne SONEDE. 3.Celerier.J et FABY.J. 2000. La dégradation de la qualité d'eau potable dans les réseaux. Document technique FNDAE.

4.Chahed. 2005. Module "Mécanique des fluides environnementale". ENIT.

5.Chambers et Joy. 1995. "Modelling free and total chlorine decay in potable water distribution systems". Journal of Water Supply, and Technology.

6.Clark .Sivagesean. 1998. Modeling chlorine decay and formation of Disinfection By Products (DBPs) in drinking water. EPA.

7.Cockx. A. 2005. Désinfection en traitement des eaux. Cours Master LMHE/ENIT.

8.Cunge.J. 1988. Modèles mathématiques en hydraulique et en hydrologie. Traité construction, volume C--180 (pp. 1-18). Techniques de l'ingénieur.

9.Haras. 2005. Biofilms et altérations des matériaux : de l'analyse du phénomène aux stratégies de prévention. Matériaux et Techniques 93, s.27-s.41 université de Bretagne Sud

10. Frederick L et al. 1992. Chlorine Residual Distribution in a Municipal Water Network. NEWWA Computer Symposium.

11. Gauthier, F.2001: Biofilms et qualité biologique d'eau potable au cours de sa distribution. Mémoire de DESS : Qualité et gestion d'eau. Université de Picardie Jules Verne.

12. Générale des eaux. 2005. Modélisation du réseau d'eau potable du SIAEP de FrontignanBalaruc. Etude.

13. Haddad, R., 2001. Calage et simulation du fonctionnement hydraulique et qualitatif d'un réseau d'AEP - Cas de l'étage 50 Sud. Projet de Fin d'Etudes du Cycle Ingénieur INAT.

14. Nouiri. I et al. 2000: La modulation de la chloration aux départs des conduites de distribution : Une approche pour la désinfection optimale.

15. Nouiri I., 2007. Optimisation multi-objectifs de la chloration dans les réseaux d'alimentation en eau potable par algorithmes génétiques. Thèse de doctorat, INAT 2007.

16. PROLOG ingénierie/CISE/OTH 1997. Etude pour le projet de gestion du réseau de distribution d'eau de Bizerte. Rapport de la mission A.

17. Ozdemir et Ger.1999. "Dynaq: A chlorine decay simulator in water supply networks", Turk J Engin Environ Sci, 24(2000), 401-412.

18. Shayeb. 2005. Module "Procédés et traitement d'eau", ENIT 2005.

19. SONEDE (1993): AEP la rive sud de Bizerte /Projet de renforcement du réseau d'adduction DEH. Nord.

20. Robert.Jean-Loup.Ph.D .2007: GCI-20552- Cours d'Hydraulique urbaine. Département de génie civil. Université Laval

21. Rossman. 2000. EPANET2 user's manual.EPA/600/R-00/057. National risk management research laboratory/U.S. Environmental protection agency, Cincinnati, USA.

22. Tzatchkov. 2003: A domain decomposition strategy for the numerical simulation of contaminant transport in pipe networks. Fourteenth international conference on domain decomposition methods.

23. Walski. M.1992 Analysis of water distribution systems. U.S Army Corps of Engineers, Mississippi.

24. Vieira. P et al 2004. Accounting for the influence of initial chlorine concentration, TOC, iron and temperature when modelling chlorine decay in water supply. Journal of Water Supply: Research and technology-AQUA, 53.7.

LES ANNEXES

Annexe n°1 : Technique de détermination du chlore résiduel libre

Remplir un tube colorimétrique jusqu'au premier trait (5-mL) avec l'échantillon d'eau. Ceci est le blanc.

Placer ce tube dans l'ouverture supérieure gauche du comparateur.

Remplir un autre tube jusqu'au premier trait (5-mL) avec l'échantillon d'eau.

Ajouter le contenu d'un sachet de réactif DPD chlore libre au second tube. Terminer l'essai et lire le résultat en moins d'une minute après l'addition du réactif.

Agiter pour mélanger. Attendre trois minutes. Lire le résultat en moins de 3 minutes après l'addition du réactif.

Placer le second tube dans l'ouverture supérieure droite du comparateur.

Tenir le comparateur face à une surface uniformément éclairée (ciel, lampe, fenêtre) et regarder par les ouvertures de la face antérieure du comparateur.

Tourner le disque jusqu'à égalité des teintes dans les deux ouvertures.

Lire la concentration du chlore libre en mg/L dans la fenêtre de l'échelle.

ANNEXE 2: Logiciel de calcul statistique REGRESS 1.0

ANNEXE : DONNEES D'EXPLOITATION
(SONEDE/ District de Bizerte)

Composantes physiques du modèle hydraulique

1/ Ressources en eau

Les ressources en eaux de la zone d'étude comportent :

· La station de traitement de Mateur

· La nappe de Mateur

· La nappe d'El Azib et El Alia

2/ La station de traitement de Mateur

L'approvisionnement en eau brute de la station de traitement de Mateur (Bâche d'arrivée des eaux brutes) est assuré soit à partir du barrage Joumine ou du barrage Sedjnane par le moyen d'une station de pompage existante calée à la côte TN 40 mNGT et équipée par trois groupes électropompes à vitesse variables identiques de débit unitaire chacune 500 l/s suite à la variation de la hauteur de l'eau dans les barrages.

Les eaux brutes sont refoulées vers la bâche d'arrivée de la station de traitement à travers une conduite de caractéristique :

- Longueur (L) : 1500 ml

- Diamètre nominal (D) : 1200 mm

- Débit Max (Qmax) : 1400 l/s

Les principales caractéristiques des eaux brutes provenant de ces deux barrages sont résumées dans le tableau suivant :

Tableau 1: caractéristiques des eaux brutes

Désignation	Barrage Joumine		Barrage Sedjnane	Turbidité (NTU)
3,55	39,6		pH
8,09	7,61		Cl résiduel (mg/l)
1,46	1,37		Oxy KMnO4 (mgO2/l)
4,53	4		Ta (mg/l)
0	0		TAC (mg/l)
10,8	74		DH (mg/l)
23,9	53		TH Ca (mg/l)
67,13	41		TH Mg (mg/l)
19,12	12

Avec:

- Ta : Le titre alcalimétrique, il représente l'alcalinité due aux carbonates et aux ions OH^-

- TAC : Le titre alcalimétrique complet, il représente l'alcalinité totale des eaux due aux carbonates (CO3), bicarbonates (HCO3) et bases libres (OH^-).

- DH : Le titre hydrotimétrique, c'est la dureté de l'eau due aux sels de Ca et Mg.

- TH Ca : Le titre hydrotimétrique de Ca, il mesure la dureté de l'eau due au Ca.

- TH Mg : Le titre hydrotimétrique de Mg, il mesure la dureté de l'eau due au Mg.

On remarque bien que la turbidité des eaux du barrage Sedjnane est six fois plus élevée que celle du barrage Joumine ce qui induit un coût de production plus élevé pour les eaux de barrage Sedjnane. Toute fois un problème sanitaire (problème de larve qui est en cours d'étude et de recherche) est détectées dans les eaux du barrage Joumine, a induit des instructions d'exploitation des eaux du barrage Sedjnane avec un coût plus élevé.

On note aussi qu'une injection de chlore sous forme gazeuse s'effectue au niveau de la station de refoulement vers la station de traitement avec une consigne de 4 mg/l.

Les eaux traitées de la station de traitement présentent les caractéristiques suivantes :

Tableau 2: caractéristiques qualitatifs des eaux traités

Désignation		Valeur	Turbidité (NTU)
4,3		pH
6,93		Cl résiduel (mg/l)
0,46		Oxy KMnO4 (mgO2/l)
4		Ta (mg/l)
<3		TAC (mg/l)
74		DH (mg/l)
51		TH Ca (mg/l)
40		TH Mg (mg/l)
11		Résidu sec (mg/l)
0,325

(SONEDE - S.LA, Septembre 2006) Le schéma suivant présente les principales composantes de station de traitement.

Figure 1: Composantes de la station de traitement de Mateur

3/ La nappe de Mateur

Cette nappe est emmagasinée dans les calcaires blancs fissurés du crétacé supérieur (campanien), elle est en continuité hydraulique avec la nappe phréatique de quaternaire.

Les ressources en eaux de cette nappe épaisse de 75 m sont importantes d'après le débit du pompage actuel, son substratum est formé par la partie basale de campanien inférieur qui est le sénonien supérieur. Cette nappe à une capacité importante, elle est captée par 9 forages dont les caractéristiques sont résumées dans le tableau suivant :

Tableau 3: Caractéristiques des forages Mateur

Forage	Niveau statique m/TN	Niveau dynamique m/TN	Q(l/s)	Résidu sec (g/l)			Nitrate(mg/l)		Mateur ville
		50	1,34	Norme nationale NT.0914 <2.5 g/l		66	Norme nationale NT.0914 <45 mg/l	Mateur 9
		40	1,22
14,48	16	27	1,26
		25	0,9
25,5	29,5	42	1,1
6,5	9,5	46	1,9
3	11	30	1,6
17	23	30	1,68
13,48	13,48	27	1,51
	295

(SONEDE - DP/DTPN - DPNE/SPB, Octobre 2006) Le débit d'exploitation des ces forages est actuellement (Octobre 2006) compris entre 27 et 50 l/s. Le débit total est de 317 l/s. Les résidus secs sont supérieurs à 1 g/l sauf pour le forage Mateur 12 qui est de 0.9 g/l. La concentration en nitrate est très aléatoire et varie d'un forage à un autre pour atteindre 66 mg/l pour le forage de Mateur ville. Elle est de 3 mg/l pour le forage Mateur 5,6.

Etant donnée que la concentration maximale en nitrate admise par la norme tunisienne NT. 0914 est de 45 mg/l, les eaux des forages Mateur ville ne peuvent être potables qu'après leurs mélanges en quantités suffisantes avec les eaux de station de traitement.

4/ La nappe d'El Azib et Alia

Elle est exploitée par une batterie de 9 forages destinés à l'alimentation en eau potable des localités de la rive sud de la région de Bizerte.

Les débits moyens d'exploitation de ces forages ainsi que le résidu sec de l'eau par forage sont représentés dans les tableaux suivants :

Tableau 4:Caractéristique des forages El Azib en 2003

Forages	Année mise en service	Cote TN (m NGT)	Résidu sec (g/l)	Débit d'exploitation (l/s)	Niveau statique (m/TN)		Niveau Dynamique (m/TN)	SGR 1 Q
1999	8,35	0,28	15,1	-37	-42		SGR 4 bis
1983	48,10	0,450	10,9	-31	-42		SGR 8 bis
2002	7,00	0,275	16,7	-78	-81		SGR 9
1979	5,00	0,37	9	-38	-66		SGR 10
1979	7,00	0,300	5	-51	-61		SGR 11
1979	2,00	0,53	5,6	-39	-55		SGR 12
1979	8,00	0.33	14,3	-40	-79		SGR 13
1979	8,00	0.32	15,3	-40	-54

(SONEDE - DP/DTPN - DPNE/SPB et S.La, Octobre 2006)

Tableau 5: Caractéristiques des forages de la nappe d'El Alia

Forages	Q (l/s)		Résidu sec (g/l)	SGR 14(El Alia)
25	1,168		SGR 6Q(El Alia)
15,5	0,370		Total
40,5	-

(SO.N.E.D.E/Résultat des essais de débit sur les forages de nappe El Azib, Octobre 2006)

Les ressources dégagées par l'ensemble de ces forages s'élèvent à 136,5 l/s avec un résidu sec qui ne dépasse pas 0,5 g/l sauf pour le forage SGR 14 ce qui permet de conclure qu'il s'agit d'une nappe de bonne qualité.

5/ Total des ressources

Les ressources totales sont représentées dans le tableau suivant :

Tableau 6: Total des ressources

Désignation	Débit d'exploitation (l/s)		Total (l/s)	Station de traitement
1000 (Q nominal)	1431		Nappe de Mateur
295
136,5

Il ressort de ce tableau que les ressources totales disponibles en régime d'exploitation nominal de la station de traitement sont de 1431 l/s. Ces ressources seront portées à 1631 l/s en régime d'exploitation maximale de la station de traitement.

Les Ouvrages de Stockage

Le réseau modélisé est doté actuellement de 41250 m³ de réserves réparties dans 15 réservoirs. Il comprend les réservoirs dont les caractéristiques hydrauliques sont ci - après :

Tableau 7: Caractéristiques des réservoirs

Désignation		Capacité (m^3)	Côte radier (m/NGT)	Côte PHE (m/NGT)	Côte TN (m/NGT)		Côte arrivée (m/NGT)	Mateur
500		67.52	72.27	68.77	72.30
		64.50	69.00	65.75	68.15
		63.40	69.00	65.75			Ras El Ain
3000		60.40	66.10	67.82	66.10		MLBourguiba
CE1	2*500+2000	45.00	49.70		50.75
	3*1000	46.84	51.49		51.60
	2500	65.70	70.40	67.00	66.70		Beni Nafaa
3*1000		46.90	51.60				Rhézala
5000		42.70	49.00	48.00	46.50		Koudiat
2*5000		41.00	46.50	44.30			Baccar
2500		84.36	89.65	86.50	88.41		Roumadia
2*1000		64.30	69.00	67.00	69.00		ML Jamil
2*500		48.00	52.50	50.76	52.75		El Alia tête
1500		140.80	145.10	141.00	145.55		Ain Bouras
250		146.27	154.18	148.20	149.30

1/ Ouvrage de tête : station de traitement de Mateur

- Caractéristiques principales :

La station de traitement, mise en service en 1984, a été complétée en 1986 pour produire 1,2 m3/s. Elle comprend :

· 2 bassins de stockage de l'eau brute de 400 m3 chacun

· 2 étages de traitement :

o Pré-traitement physico-chimique : coagulation-floculation-décantation dans deux décanteurs installés en parallèle.

o Filtration comprenant 6 filtres à stable installés en parallèle de capacité normale égale à 200l/s.

· 2 réservoirs de stockage de l'eau traité de 5 000 m3 et de 6.3 de hauteur chacun calés à la cote 83.76 mNGT.

Les réservoirs de l'eau traitée alimentent la conduite d'adduction DN1250 qui dessert gravitairement :

o Mateur

o Menzel Bourguiba

o Bizerte

Il est à noter qu'au niveau de la station de traitement, l'eau traitée n'est pas rechloré. Seulement l'injection du chlore gazeux à une consigne de 4 mg/l est réalisée au niveau de la station de surpression à l'amont de la station.

- Principes d'exploitation

La station de traitement, alimentée par les eaux superficielles du barrage de Joumine, et Sejnène est à commande par l'aval : son débit est fonction de la demande. La régulation fine des adductions est faites sur la base des relevés des index en tête des distributions de 15 localités comptées ainsi que les niveaux dans les réservoirs principaux de ces mêmes localités tout les jours. Les consignes de production sont :

o 0.4 m3/s en hiver

o 0.75 m3/s en été (juin, juillet, août et septembre)

Les consignes sont appliquées sur le terrain en régulant le débit en 4 points qui sont :

· Le brise charge de Ras El Ain (BC3)

· Le brise charge de Faroua (BC1)

· Le brise charge de Koudiat (B)

· Le brise charge de Rhézala

Les variations du débit de demande sont répercutées vers l'amont sur les différents brises charges et vannes de régulation jusqu'aux réservoirs de tête de l'adduction situés à l'aval de la station de traitement. Ces réservoirs battent, en marche normale, entre la cote +6.3 (trop plein) et les cotes +4 m (consigne hivernale) et +4.5 m (consigne estivale) de manière à conserver une réserve de sécurité. Au dessous de la cote +1.80, la vanne « Stop » en tête de l'adduction se déclenche et ferme l'alimentation de l'adduction. En cas de crise , le brise charge de l'adduction à Ras El Ain (BC3) est fermé et la production des forages de la nappe de Mateur est augmentée pour maintenir un niveau élevé dans le réservoir de Ras El Ain.

2/ Ouvrage de tête : Réservoir de Ras El Ain

- Caractéristiques principales :

Il s'agit d'un réservoir enterré de capacité nominale 5000 m3 dont la cote du radier est 60,40 mNGT et la cote du trop plein 66,10 mNGT. Il est alimenté par le haut à partir des forages du

champ captant de Mateur et une brise charge (BC6) piqué sur l'adduction de Joumine. Ce réservoir assure les 4 fonctions principales suivantes :

· Régulation et stockage de sécurité en tête de l'adduction Mateur-Bizerte

· Alimentation de la Cité Ras El Ain

· Alimentation de Mateur lorsque la demande journalière moyenne dépasse la capacité des forages qui alimentent directement le réseau d'adduction-distribution de la ville de Mateur qui sont Mateur10 et Mateur ville.

· Alimentation de Menzel Bourguiba qui est alimenté par la conduite DN350 de El Fouledh et par un piquage sur l'adduction Mateur-Bizerte. Une partie du réseau de cette localité est alimenté également par l'adduction Joumine à partir du complexe CE6.

· Le débit de l'adduction de Joumine est régulé manuellement, en fonction de la demande à Ml Bourguiba et à Mateur et de la capacité de production des forages.

Les différentes manoeuvres de régulation du brise charge sont déclenchées lorsque le niveau dans le réservoir de Ras El Ain est inférieur à 3 m.

- Principes d'exploitation

Lorsque le niveau dans le réservoir est inférieur à 3,5 mètre, le débit en tête de l'adduction DN 600 est égal au débit refoulé par la station de pompage de Mateur Basse augmenté du débit de l'adduction de Joumine. Les consignes adoptées par le gardien sont les suivantes : agir sur les vannes de régulation du brise charge pour maintenir le niveau du réservoir au dessus de la cote +3,5 mètre sur le radier en augmentant progressivement, le débit de l'adduction de Joumine.

En été, lorsque le tirage est plus important, on alimente les réservoirs à la fois avec les eaux des forages de Mateur et les eaux de l'adduction de Joumine.

En hiver, quand le tirage diminue, on réduit les apports de l'adduction de Joumine voire même on ferme les conduites de la brise charge et on travaille avec les réservoirs à niveau élevé. Pendant cette saison, les réservoirs de Mateur ayant un niveau plus élevé, l'adduction Mateur-Ras El Ain est arrêtée à fin d'éviter de vider les réservoirs de Mateur vers Ras El Ain. Au cas où on atteint le trop plein dans le réseau Ras El Ain, le gardien des réservoirs ferme la brise charge de l'adduction de Joumine, puis si le niveau continue d'augmenter, il arrête un ou plusieurs forages. Une javellisation est réalisé au niveau de la bâche d'arriver du réservoir en continu par l'intermédiaire d'un bac contrôlé par une pompe doseuse qui à pour consigne 1.4 mg/l.

3/ Réservoirs de Mateur

- Caractéristiques principales :

Les trois réservoirs de Mateur sont regroupés sur le même site et assurent la distribution de l'eau de la ville de Mateur, un appoint pouvant être assuré par le réservoir de Ras El Ain via une conduite DN 300 de longueur environ 3 Kms.

Ce sont des réservoirs circulaires, semi enterrés en béton armé de capacité 500, 1500 et 2500 m3 et de profondeur respectives 4.7 m, 4.9 m et 5.6 m.

Les forages « Mateur1 0 » et « MateurVille » alimentent successivement par le haut les réservoirs 1, 2 et 3 par l'intermédiaire d'une conduite de refoulement DN 300.

Les trois réservoirs jouent un rôle de régulation des volumes distribués et de réserve de sécurité. La distribution s'effectue par l'intermédiaire de trois antennes principales :

· Une antenne DN 300 partant du réservoir 500 m3

· Une antenne DN 400 partant du réservoir 1500 m3

· Une antenne DN 500 partant du réservoir 2500 m3

- Principes d'exploitation

Un niveau de l'eau minimal de 1.5 m est maintenu dans les réservoirs pour conserver une réserve de sécurité d'environ 1500 m3.

Le remplissage des réservoirs 1500 et 2500 m3 nécessite de fermer quotidiennement la vanne d'alimentation du réservoir 500 m3 lorsque celui-ci est plein à fin d'éviter qu'il ne déborde. Si le niveau du trop plein du réservoir 1500 m3 est en passe d'être atteint, le gardien peut demander l'arrêt des forages. Une javellisation est effectuée en continu dans les réservoirs 500 et 1500 par l'intermédiaire d'un bac contrôlé par une pompe doseuse qui à pour consigne 1 mg/l.

4/ Réservoir de Rhézala

- Caractéristiques principales :

Le réservoir est de forme circulaire en béton en béton armé semi enterré de capacité nominale 5 000 m3. Il est alimenté par le brise charge BC5 piqué sur l'adduction DN 1000 de Joumine qui alimente également la zone haute Rhézala et le réservoir de Koudiat. La cote du radier 42.7 mNGT et la cote du trop plein 49 mNGT. Ce réservoir dessert l'étage bas de la ville de Bizerte ainsi que Zarzouna et la Pêcherie. Il joue le rôle de réserve de sécurité en tête de ces réseaux de distribution. Il est aussi alimenté à partir de l'adduction de Mateur. Ainsi au niveau de cet ouvrage, un mélange entre les eaux de la station de traitement de Mateur et les eaux de la nappe de Mateur s'effctue. Une javellisation est réalisé au niveau de la bâche d'arriver du réservoir par l'intermédiaire d'une réserve de l'eau de Javel dont l'écoulement est contrôlé par pompe doseuse réglé à 1.2 mg/l.

- Principes d'exploitation

Le réservoir de Rhézala est alimenté en priorité à partir de le brise charge BC5, le brise charge BC4 servant d'appoint en cas de fort tirage lorsque la station de reprise de Roumadia est en service. La liaison entre les deux brises charges est toujours ouverte. La régulation du débit de le brise charge BC4 est effectuée par des manoeuvres manuelles. Il est fermé lorsque le niveau du réservoir de Rhézala dépasse environ 3.7 m en hiver et 4.7 m en été pour éviter le débordement du réservoir. Au dessus de ces niveaux, le réservoir n'est donc alimenté qu'à partir de le brise charge BC5 (adduction de Mateur). La vanne à flotteur du brise charge BC5 se ferme automatiquement lorsque la station de reprise de Roumadia s'arrête et que le réservoir de Rhézala est plein.

5/ Réservoir de Ml Djémil

- Caractéristiques principales :

Ce réservoir comprend deux cuves circulaires en béton armé semi enterrées de capacité nominal total 1 000 m3. La cote du radier est 48 mNGT et la cote du trop plein 52.5 mNGT. Il est alimenté gravitairement par la conduite DN300 en provenance du réservoir de Roumadia. Ce réservoir alimente :

- La ville de Ml Djémil

- L'étage haut de Ml Djémil

- La station de reprise SGR9 en appoint

- La zone industrielle de Ml Djémil

Une javellisation est réalisé au niveau de la bâche d'arriver du réservoir et est contrôlé par un robinet manuel.

- Principes d'exploitation

La vanne de sectionnement sur la conduite d'arriver DN 300 est manoeuvrée manuellement par le gardien du réservoir à fin :

- D'éviter le débordement du réservoir

- D'éviter que le niveau de l'eau du réservoir ne descende en dessous d'une hauteur de 3 m sur le radier.

6/ Réservoirs de Koudiat et de Baccar et station de reprise de Koudiat

- Caractéristiques principales :

Le réservoir de Koudiat est alimenté à partir du brise charge BC3 à l'aval de l'adduction de Joumine. Il comprend 2 cuves semi enterrées en béton armé de capacité totale 10 000 m3. La cote du radier est 41 mNGT et la cote du trop plein 46.5 mNGT. Il alimente la ville de Bizerte et la station de reprise de Koudiat vers les étages hauts de Bizerte et de Koudiat.

La station de reprise de Koudiat, située à la cote 41.20 mNGT, refoule vers le réservoir de Baccar par l'intermédiaire d'une conduite DN 300 d'une longueur de 1 700 m. Elle comprend deux groupe électropompes en parallèle. En fonctionnement normal, une seule pompe refoule un débit de 60 l/s avec une HMT de l'ordre de 45 m.

Le réservoir de Baccar est constitué d'une cuve semi enterrée en béton armé de capacité nominal de 2 500 m3. La cote de radier est 84.36 mNGT et la cote de trop plein 89.65 mNGT.

Une javellisation est effectuée dans le brise charge de Koudiat (BC3) par l'intermédiaire d'un bac de javellisation contrôlé par pompe doseuse.

- Principes d'exploitation

- Alimentation du réservoir de Koudiat :

La vanne à flotteur dans le brise charge BC3 est réglé de tel sorte de garder une hauteur de l'eau supérieure à 3 mètre dans le réservoir de Koudiat.

- Exploitation de la station de reprise de Koudiat :

Lorsque la pression de refoulement dépasse une valeur de 6 bars le groupe électropompe s'arrête. Une horloge commande le redémarrage de la pompe au bout de 1h45min.

- Alimentation du réservoir de Baccar :

Lorsque le niveau du réservoir de Baccar approche du trop plein, le robinet flotteur fermer la conduite d'alimentation et provoque l'arrêt de la station de reprise. Au bout de 1h45 m la station de reprise de Koudiat redémarre.

7/ Réservoir de Beni Nafaa

- Caractéristiques principales :

Ce réservoir est composé de trois cuves circulaires en béton enterrées, de capacité total nominal de 3000 m3. La cote du radier est 46.9 mNGT et la cote du trop plein 51.6 m NGT. Il est alimenté par une conduite DN 200 mm piqué de l'adduction de Joumine.

Ce réservoir assure une fonction de stockage de sécurité et de régulation en tête des réseaux de distribution des localités avoisinantes (Beni Nafaa, Mohr ...) et les bases navale et aérienne de Bizerte.

Une javellisation est réalisé au niveau de la bâche d'arriver du réservoir et est contrôlé par un robinet manuel.

- Principes d'exploitation

Les vannes d'alimentation des cuves sont manoeuvrés manuellement et quotidiennement par le gardien du réservoir de manière à :

s Eviter le débordement du réservoir

s Eviter un niveau de l'eau du réservoir au dessous d'une hauteur sur le radier de 3m. 8/ Station de reprise et réservoir de Roumadia

- Caractéristiques principales :

La station de reprise de Roumadia alimente le réseau de Roumadia à partir du réservoir de Rhézala. Sa cote TN est à 5mNGT. Elle comprend deux groupes électropompes en parallèles de débit nominal 150 l/s avec une hauteur de refoulement HMT = 43 m.

La station est piqué et refoule dans la conduite d'adduction DN600 du réservoir de Roumadia (2x 1000 m3) sur une longueur de 1432 m. En fonctionnement normal, une pompe refoule un débit de 140 l/s à une pression de 6.8 bar avec une pression à l'aspiration de 32 m. La réserve de Roumadia comprend 2 cuves circulaires en béton armé semi enterré de capacité nominal total de 2000 m3. La cote du radier est 64.3 mNGT et la cote de trop plein 69 mNGT. Il alimente 3 antennes de distributions principales :

- Antenne DN 350 de Ml Abdelrahmen

- Antenne DN 350 vers la caserne, où serai piqué la conduite d'adduction DN 500 de la station de reprise de la rive sud (Hriza) qui refoule vers le réservoir de tête d'El Alia (1500 m3)

- Antenne DN300 de Ml Djemil, la station de reprise SGR9, STIR et la zone industrielle de Zarzouna.

- Principes d'exploitation

Actuellement le fonctionnement des pompes est alternatif. Une pompe est démarrée manuellement lorsque le niveau dans le réservoir de Roumadia est en dessous de 3 m environ. Elle est arrêté lorsque le niveau dans le niveau dans le réservoir approche du trop plein. Le gardien du réservoir communique ses indicateurs par téléphone à la station de reprise. La station fonctionne actuellement pendant la journée. La durée moyenne de pompage s'élève à 8 à 10 heures par jour en base saison et 4 heures par jour en haute saison. Une javellisation est réalisé au niveau de la bâche d'arriver du réservoir et est contrôlé par un robinet manuel.

9/ Refoulement d'El Azib et réservoir Ain Bouras

- Caractéristiques principales :

Le champ captant d'El Azib est exploité avec un débit d'environ 91 l/s par huit forages. Les eaux de ces forages sont colletées dans la station de reprise SGR9 puis refoulées dans le réservoir Aïn BouRas moyennant une conduite 0 300 mm (Amiante Ciment L=5263 m, et fonte L=93 1

m).Le réservoir Aïn Bou Ras (250 m³), reçoit aussi l'eau du forage SGR4 par une conduite de refoulement 0 150 mm AC de longueur 2730 m.

Pendant la saison estivale, la station de refoulement reçoit un appoint par une conduite DN300 gravitairement en provenance du réservoir de Roumadia. Un piquage sur cette conduite permet d'alimenter l'adduction DN500 de la Rive Sud vers la station de reprise de Hriza.

La station de refoulement est équipé avec trois groupes électropompes en parallèle identiques de débit nominal Qn= 45 l/s et de hauteur manométrique HMTn = 180 m.

Le bassin de reprise d'El Azib comprend une bâche d'aspiration de 100 m3 qui reçoit les quatre conduites alimentées par les forages et la conduite de Roumadia.

- Principes d'exploitation

a) Forages :

Les forages peuvent fonctionner soit en manuel, soit en automatique en fonction des hauteurs de remplissage de la bâche de reprise de la station de pompage. Ils ont été asservis par groupes à 3 couples de niveau de l'eau dans la bâche d'aspiration de la station de reprise :

- N1 : forages SGR8 et SGR12

- N2 : forages SGR9 et SGR10

- N3 : forages SGR1, SGR1 1 et SGR1 3

Pour les niveaux N1: arrêt des forages à la cote TP-0.3m/ démarrage des forages à la cote R+1 .2m Pour les niveaux N2: arrêt des forages à la cote TP-0.35 m/ démarrage des forages à la cote R+0.65m

Pour les niveaux N3: arrêt des forages à la cote TP-0.7m/ démarrage des forages à la cote R+0.65m Actuellement l'ensemble des forages fonctionne en continu avec un appoint complémentaire du réservoir de Roumadia (20 l/s).

b) Station de refoulement :

La station a été conçue pour fonctionner automatiquement. Les pompes de refoulement sont asservies d'une part au niveau de l'eau dans le réservoir d'Ain Bouras et d'autre part au niveau de la bâche de reprise de la station.

En marche normal, un groupe de pompage fonctionne en permanence, le deuxième en discontinu. Le troisième sert uniquement de secours. Le démarrage de la deuxième pompe (pompe en appoint) est automatique lorsque le niveau dans la bâche atteint une cote proche du niveau du trop plein et la première pompe est en marche.

Les pompes sont asservies :

- D'une part, à la cote du réservoir de Ain Bouras :

· la pompe n°1 démarre lorsque le niveau de l'eau atteint le niveau bas (cote radier + 0.4 m)

· la pompe n°2 démarre après deux minutes si le niveau bas persiste.

· La pompe n°2 s'arrête lorsque le niveau de l'eau atteint le niveau haut (cote trop plein - 0.55 m)

· La pompe n°1 s'arrête lorsque le niveau de l'eau atteint le niveau cote trop plein - 0.3 m) - D'autre part, à la cote de niveau de l'eau dans la bâche d'aspiration des groupes :

· La pompe n°1 démarre lorsque le niveau atteint est à la cote trop plein -0.9 m.

· La pompe n°2 démarre après 2 minutes si le niveau haut reste atteint.

· La pompe n°2 s'arrête lorsque le niveau de la bâche atteint la cote radier + 0.75m.

· La pompe n°1 s'arrête lorsque le niveau dans la bâche atteint la cote radier +0.3 5m.

Les Conduites d'adduction

Le réseau modélisé comprend les conduites d'adduction ci - après. Il est à noter qu'il n'existe aucun point de rechloration intermédiaire sur ces conduites.

1/ Tronçon : la station de traitement - BC Faroua (RSE CE6)

Les eaux traitées sont véhiculées gravitairement vers le brise charge existant sur la colline de Faroua (Tinja) à travers une conduite de caractéristique :

· Longueur (L) : 21660,43 ml

· Diamètre nominal (DN) : 1250 mm béton précontraint

· La côte de départ : 90 m NGT

· La côte d'arrivée : 64 m NGT

Cette conduite assure en cours de route :

- L'alimentation en eau potable de la ville de Mateur par un piquage en DN 400 mm fonte dont les besoins de pointe journalière s'élève actuellement à environ 100 l/s.

- Le renforcement des réservoirs de Ras El Ain de capacité 6000 m³ pour assurer le mélange avec les eaux des forages de la nappe de Mateur, par un piquage DN 600 mm béton.

Dans le même site du brise charge El Faroua (réservoir semi enterré CE6) un réservoir semi enterré de capacité 2500 m³ est calé pour la desserte des villes Menzel Bourguiba et Tinja. Ce réservoir reçoit les eaux à partir de la conduite DN 1250 mm.

2/ Tronçon RSE CE6 - RSE de Koudiat

A partir du réservoir CE6, les eaux sont véhiculées gravitairement vers le réservoir semi enterré d'El Koudiat à travers une conduite de caractéristique :

· Longueur (L) : 16771,12 ml

· Diamètre nominal (DN) : 1000 mm béton précontraint et DN 800

· La côte de départ : 64 m NGT

· La côte d'arrivée : 43,32 m NGT

Cette conduite assure en cours de route l'alimentation en eau potable du réservoir de Rhézala, calé à la même côte que le réservoir El Koudia

3/ Tronçon réservoir de Ras El Ain - Réservoir Rhézala

Les eaux de la nappe Mateur sont collectées au niveau de réservoir Ras El Ain et sont acheminées gravitairement vers le réservoir de Rhézala par une conduite dont les principales caractéristiques sont :

· Longueur (L) : 32398 ml

· Diamètre nominal (DN) : 600 mm béton précontraint

· La côte de départ : 60m NGT

· La côte d'arrivée : 42m NGT

4/ Tronçon réservoir Rhézala - Station de reprise Roumadia

Après satisfaction des besoins de Bizerte et de Jarzouna, le reliquat des eaux collectées au niveau du réservoir Rhézala (côte TN 45 m NGT) est acheminé gravitairement vers la station de reprise Roumadia calée à la côte TN 5 m NGT par une conduite de longueur totale 5106 ml composée comme suit :

·	L= 708 ml	DN = 600 mm		béton	·
L= 1968 ml	DN = 500 mm	fonte		·
L= 280 ml	DN = 500 mm	acier		·
L= 150 ml	DN = 500 mm	fonte		·
L= 2000 ml	DN = 600 mm	béton

5/ Tronçon station de reprise Roumadia - Réservoir Roumadia

La station de reprise de Roumadia calée à la côte TN 5m NGT et refoule vers le réservoir 2Õ1000 m³ de Roumadia implantés à la côte 64 m NGT

Cette station est équipée par deux groupes électropompes de caractéristique chacune :

· Q = 85 l/s à HMT= 30m

Les caractéristiques de la conduite de refoulement reliant cette station et le RSE Roumadia sont comme suit :

· Longueur (L) :1400 ml

· Diamètre nominal (DN) : 600 mm Béton armé (BA).

Deux régimes du fonctionnement de la station de reprise sont possibles

· Le fonctionnement d'un seul groupe électropompe nous donne :

Q = 84 l/s à HMT= 28 m

· Le fonctionnement en parallèle de deux groupes électropompes donne les résultats suivants :

Q = 178 l/s à HMT= 37 m

6/ Tronçon: Réservoir Roumadia - Station de reprise Hariza

Les caractéristiques de ce tronçon sont les suivantes :

· Longueur (L) : 14992 ml

· Diamètre nominal (DN) : 500 mm Amiante ciment classe C

· La côte de départ Hd : 64,7 m NGT

· La côte d'arrivée H_a : 39,47 m NGT

7/ Tronçon: Station de reprise Hariza - Réservoir 1500m3 El Alia

La station de pompage de Hariza est calé à la côte 38 m NGT assure le remplissage du réservoir 1500 m³ d'El Alia qui se trouve sur la côte 140 m NGT.

Cette station est équipée par deux groupes électropompes dont les principales caractéristiques sont :

· Q = 75 l/s à HMT= 111 m

La conduite reliant la station de pompage au réservoir est une conduite télescopique constituée par deux tronçons de diamètre et de nature différentes :

· L : 2916 ml DN : 600 mm fonte

· L : 876 ml DN : 500 mm Amiante ciment

Deux régimes de fonctionnement sont possibles :

* Le régime de fonctionnement à un seul groupe électropompe nous donne : Q = 75 l/s * Le régime de fonctionnement à deux groupes électropompes nous donne : Q = 140 l/s

Données d'exploitations

Pour le réseau d'adduction de l'eau potable de la région de Bizerte, les données d'exploitation disponibles concernant les mesures des volumes produits et distribués sont les suivantes (Annexe n°3) :

- Les volumes mensuels distribués par réservoir de 2000 à 2006 pour l'ensemble des réservoirs. - Les volumes journaliers distribués par réservoir en Juillet et Août 2005 et Janvier 2006

- Les mesures permanentes de débit au pas de temps de 15 mn en 2006 à l'aval des réservoirs de Mateur, Ras El Ain, CE6, Koudiat, Rhézala, Ml Jémil, CE2, Ml Abderrahmen et El Alia.

- Les mesures des débits horaires au niveau de la station de traitement de Mateur

- Les feuilles de marche matériel au niveau des forages de Mateur, d'El Azib, El Alia et stations de reprises des mois de Janvier 2006 et Juillet 2006

-- Suivi mensuel des niveaux des nappes et relèves des points de fonctionnement des forages de la nappe de Mateur, El Alia et El Azib.en 2005.

1/ Analyse des Volumes produits

Une analyse statistique des mesures des débits produits par les forages et la station de traitement a été réalisée afin d'étudier les mélanges de l'eau dans les canalisations.

1-1/ Station de traitement de Mateur

La plus grande partie des besoins en eaux potable des localités de la zone d'étude, 85% en 2004 et 86% en 2005, est couverte par la production de la station de traitement de Mateur via l'adduction de Joumine.

Tableau 8: Evolution de la production en eau de la région de Bizerte de 1999 à 2005 (SONEDE)

ANNEE	PRODUCTION ANNUELLE						TOTAL				EVOLUTION
				Forages
11	384	130	3	093	800	14	477		930		2000
12	777	380	2	735	575	15	512		955	0,07	2001
12	878	852	3	065	204	15	944		056	0,03	2002
11	914	850	3	514	407	15	429		257	-0,03	2003
13	043	400	3	648	747	16	692		147	0,08	2004
14	245	700	2	597	400	16	843		100	0,01	2005
14	658	870	3	397	618	18	056		488	0,07

1700000

1600000

1500000

1400000

1300000

1200000

1100000

1000000

900000

700000

800000

Janv Févr Mars Avril Mai Juin Juill Aout Sept Oct Nov Déc
Mois

2005
2004
2003

Figure 4: Production de la station de traitement de Mateur

La figure précédente illustre l'évolution saisonnière de la production qui connaît une pointe marquée en Août et un creux situé de Novembre à Février selon les années. Le coefficient de pointe mensuel varie de 1,91 en 2005 à 1,65 en 2003 Le rapport entre la production du mois le plus faible et la production mensuelle moyenne est plus stable autour de 0,74

Le rapport entre la production du mois le plus chargé et la production mensuelle moyenne est 1,34. Une analyse détaillé du fonctionnement hydraulique de la station de traitement de Mateur en Janvier et Août 2005 à été effectuée sur la base du cahier d'exploitation, sur lequel sont consignées heure par heure les caractéristiques principales de fonctionnement, en particulier :

- Le débit à l'entrée de la station

- Le débit à la sortie de la station

- La variation horaire du niveau dans les réservoirs de tête de l'adduction de Joumine Ces principales indications sont reportées en annexe 3

En hiver les constatations ci-après peuvent être faites :

- Le débit de fonctionnement varie

- Le niveau de l'eau dans les réservoirs de tête varie, en moyenne entre 3,0 m et 5,5 m

- La station fonctionne durant en moyenne 14 heures par jour à un débit variant de 300 à 400l/s selon la demande.

Ce fonctionnement hivernal dure jusqu'en Avril

Entre Avril et Juin, la station de traitement fonctionne en moyenne 23 heures par jour à un débit variant de 350 à 750 l/s selon la demande.

Pendant le mois de Juillet et Aout, la station fonctionne en moyenne 23 heures par jour à un débit
moyen de 575 l/s. Le débit de traitement varie fortement selon les jours (500 à 700 l/s), de ce fait le

marnage des réservoirs de tête était très faible : entre 5,9 en moyenne à 4 heures et 4,4 m en moyenne à 24 heures soit un marnage de 1,5 m.

1-2/ Nappe de Mateur

L'évolution saisonnière et interannuelle de la production des forages de la nappe de Mateur est représentée sur la figure suivante :

450000

400000

250000

200000

500000

350000

300000

150000

100000

Janv Févr Mars Avril Mai Juin Juill Aout Sept Oct Nov Déc

Mois

2003
2004
2005

Figure 5: Production de la nappe de Mateur

Les variations saisonnières de la production sont importantes puis que le coefficient de pointe mensuel est de 1,81 en 2005 et 2,57 en 2003.

Le mode de gestion est l'exploitation de la nappe de Mateur tout au long de l'année, l'adduction de "Joumine" étant utilisée en appoint pour couvrir les besoins non satisfaits par l'adduction de Mateur.

Une analyse de fonctionnement horaire des forages de la nappe de Mateur est faite sur la base des feuilles de marche des groupes de pompage des mois de Janvier, Juillet 2006 et les rapport mensuel de production des années 2003, 2004,2005 et 2006 montre bien que :

- Les forages sont exploités différemment, le temps de fonctionnement varie de 10 heures par

jour (forage M10) à 24 heures par jour (forage M8) en Janvier contre 16 heures et 23 heures par

jour pour ces deux même forage en Août. Ceci peut être expliqué par des arrêts fréquents de

certains forages pour des problèmes techniques. Ces arrêts sont compensés par les autres forages.

- On note par ailleurs une forte baisse des débits instantanés pompés sur certains forages : o Pour le forage M2, le débit pompé serait passé de 30.9 l/s en 2003 à 26.7 l/s en 2004. o Pour le forage M4, le débit pompé serait passé de 37.25 l/s en 2003 à 29 l/s en 2004. o Pour le forage M5, le débit pompé serait passé de 30.79 l/s en 2003 à 27.5 l/s en 2004. o Pour le forage M8, le débit pompé serait passé de 34.6 l/s en 2003 à 29.5 l/s en 2004.

260000

240000

220000

200000

180000

160000

140000

120000

100000

Janv Fev Mars Avril Mai Juin Juil Aout Sept. Oct. Nov. Dec.

mois

2003
2004
2005

Cette baisse peut s'expliquer en partie par une baisse de niveau de la nappe. Elle a été compensée par une hausse de la durée moyenne de pompage sur les différents forages.

La station de reprise de Mateur Basse qui reprend les débits des forages suit le même régime de fonctionnement que ces forages avec une durée de pompage légèrement inférieur puisque son débit, de l'ordre de 125 l/s est supérieur au débit cumulé instantané des forages.

1-3/ Nappe d'El Azib et El Alia

L'évolution saisonnière et interannuelle de la production des forages de la nappe de Mateur est représentée sur les deux figures au dessous. Les variations saisonnières de la production sont importantes en 2003 et 2004 puis que le coefficient de pointe mensuel est de 1,44 en 2003 et 1,88 en 2004 pour la nappe d'El Azib et de 2,40 en 2003 et 2,32 pour la nappe d'El Alia.

En 2005, les volumes produits sont élevés à :

- 1,731 Mm3 à partir de la nappe d'El Azib

- 0,3 97 Mm3 à partir de la nappe d'El Alia

- La plus part des forages des nappes en question sont exploités en continu prés de 24 h/24h durant toute l'année

- Trois forages sont exploités en continu l'été et fonctionnent 10 à 14 heures par jour en hiver (SGR4 et SGR9 et SGR14).

- Les deux pompes de la station de reprise SGR9 fonctionnent généralement en alternance à un débit de l'ordre de 92 l/s pendant un plus de 20 heures sur 24 heures. Toute fois pendant l'été 2005, les deux pompes fonctionnaient simultanément environ 15 heures par jour.

45000

25000

95000

85000

75000

65000

55000

35000

Janv Fev Mars Avril Mai Juin Juil Aout Sept. Oct. Nov. Dec.

mois

2003
2004
2005

Figure 7: Production de la nappe d'El Alia

L'analyse des volumes produits montre bien que la part de chaque source et de la station de traitement de Mateur dans le mélange de l'eau dans les canalisations est variable d'une année à l'autre et d'une saison à l'autre.

2/ Analyse des Volumes distribués à l'amont des localités

Une analyse statistique des mesures des débits distribués par la SONEDE en aval des réservoirs (source : district SO.N.E.D.E Bizerte) a été réalisée afin de définir :

- Les volumes journaliers distribués en aval des réservoirs pour trois situations de référence (volume moyen, minimum et maximum),

- Les courbes de modulation horaire des consommations à l'aval des réservoirs pour deux situations de référence (consommation de pointe estivale et consommation minimale hivernale),

Les données de base disponibles pour cette analyse sont les suivantes :

- Les volumes mensuels distribués par réservoir de 2003 à 2005

- Les volumes journaliers distribués en Janvier, juillet et août 2005 pour les réservoirs de Ras El Ain, Mateur, Ml Bourguiba, Bizerte, Roumadia et Ml Jemil.

- Les mesures permanentes de débit au pas de 15 mn en 2005 et 2006, à l'aval des réservoirs CE6, Mateur, Rhézala e Koudiat

2-1/ Analyse des volumes journaliers distribués

Pour chaque réservoir on détermine :

- Le volume moyen journalier distribué

- Le volume maximum distribué. Il a été défini comme le volume moyen distribué durant le mois de plus grande consommation. Dans la plupart des cas, il s'agit du mois de Juillet ou Août

- Le volume minimum distribué. Il a été défini comme le volume moyen distribué durant le mois

de plus faible consommation. Dans la plupart des cas, il s'agit du mois de Janvier ou de Février Ces calculs ont été effectués en s'appuyant sur les volumes journalières distribués en Janvier, Juillet et Août 2005 ou bien sur les volumes mensuels distribués où le débit du jour de pointe a été estimé à partir du débit moyen observé pour le mois de plus forte consommation. En effet, l'analyse des rapport entre le volume distribué pour le jour de pointe et le volume distribué pour le mois correspondant pour les réservoirs sur lesquels les deux volumes sont disponibles fait ressortir un coefficient moyen de 1,4. Les résultats de ces calculs sont récapitulés dans tableau ci-après :

Tableau 9:Volumes distribués pour l'année 2005

Réservoir	Vtotal (m^3)	Vmoy^(m3/j)	Vmin^(m3/j)	Vmax^(m3/j)	Vmin/Vmoy		Vmax/Vmoy	Mateur
1 981 400	5 428,5	2 474,2	6 864,5	0,46	1,26		Ras Ain
360 104	986,6	971,32	1 726,7	0,98	1,75		CE1
869 371	2 381,8	2 348	2 663	0,98	1,12		CE2
210 407	576	463	627	0,80	1,09		CE6
2 603 500	7 132,9	5 077,4	9 187,1	0,71	1,29		Beni Nafaa
248 900	681,9	426,7	990,3	0,63	1,45		Rhézala
4 111 200	11 263,5	8 693,5	13 674	0,77	1,21		Koudiat
4 167 900	11 419	9 790,3	14 616,1	0,86	1,28		Baccar
1 633 596	4 475 ,6	3 278,3	5 767,7	0,73	1,29		Roumadia
4 523 500	12 393,1	7 261,3	17 606,5	0,59	1,42		Ml Jemil
952 712	2 610,1	2 161,9	3 466,2	0,83	1 ,33		El Alia
2 766 937	7 580,65	5 590,4	10 230,9	0,74	1.35		Ain Bouras
1 815 744	4 974,6	4 748 ,2	5 516,1	0,95	1,11

Le coefficient de pointe journalier varie entre 1,09 et 1,75 avec une moyenne de 1,3. Le coefficient minimum varie entre 0,46 et 0,98 avec une moyenne de 0,77.

En ce qui concerne l'appoint de l'eau fourni à El Azib, le coefficient minimum et le coefficient de pointe sont tout à fait irréguliers dans la mesure où la fourniture de l'eau s'effectue essentiellement en été. Il en résulte des fluctuations saisonnières importantes du débit fourni.

2-2/ Analyse des variations horaires de débit distribué

Cette analyse a été effectuée à partir des mesures instantanées de débit au pas de temps de

15 minutes qui m'a été fournie par le district de la SONEDE de Bizerte.

Les résultats obtenus sur les réservoirs pour lesquels des données existent et ont pu être exploitées sont présentés dans l'annexe n° 4.

SONEDE Mateur le, 05/02/2005

DP/DTPN

DPNE/SPB

SPB DPNE

Suivi de Rabattement des Niveaux des Nappes de champ
captant de Mateur

Mois:Février 2005

Désignation Forages	Niveau statique	Niveau dynamique		Débit	Forage Mateur 2
-23.5	-25.5	31		Forage Mateur 4
-23.48	-23.48	32		Forage Mateur 5
-30.5	-31.5	32		Forage Mateur 8
-14.48	-12.48	34		Forage Mateur 10
-8	-10	27		Forage Mateur 11
-16	-16.5	43

Chef sèrvice de Production Bizèrte
A.Hamdi

Sonede / Sce Etudes Régulation Année: 2005

Stations	Janvier		Février		Mars		Avril		Mai		Juin		Juillet		Aôut		Septembre		Octobre		Novembre			Décembre
	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures	Volume	heures		Volume	heures	Rep Koudiat
117654	464	112660	368	113472	419	113472	419	166183	540	180272	608	213786	854	223292	487.5	132691	842	202034	817	90247	641		85074	552	Rep Roumadia
261000	390	250000	414	270000	477.25	290000	477.25	414400	629	454000	745	574100	1074	606500	1055	488000	795	434200	741	291200	634		200600	462	For SGR 11
15990	742	14364	646	16026	743	16026	743	13474	571	16617	720	17419	707	19194	731	20248	720	20215	718	20283	718		17520	642	Rep SGR 9
	777		755		847		740		856		376		950		944		759		787		745			730	For SGR 9
19786	585	17304	528	17310	559	17310	559	17253	633	17063	673	17226	719	17130	728	14760	690	14286	715	13306	696		12024	686	For SGR 12
21348	382	20337	391	18432	354	16955	325	23018	444	27361	563	31816	640	31247	651	30944	646	32000	682	28900	597		30058	610	For SGR 13
16846	338	19608	395	17418	348	16262	324	21991	443	23697	490	30195	638	30066	641	30347	640	32375	682	29987	626		29520	610	For SGR 1
30510	581	27224		22574	229	14916	285	5436	104	0		En arrêt		0		En arrêt		En ârret		En arrêt			0		For SGR 8
43954	744	38360	648	43764	744	41930	714	43532	734	39541	653	37655	640	15485	266	0		0		42344	696		28566	471	For SGR 10
0		0		19932	551	14546	489	22128	738	17663	591	18485	640	16706	576	19000	648	20329	711	18201	620		17859	602	For SGR 4
7334	238	6167	199	6726	232	6496	234	5383	178	6318	234	19440	720	En panne	En panne	En panne				En arrêt			0		Rep Hriza
141441	568	126476	463	144286	524	149526	576	207843	742	223780	858	304816	1236	285528	1192	227641	498	218280	897	169894	600		170000	653	For SGR 14
0	0	0	0	0	0															En arrêt			0		For SGR 6
31860	665	31750	648	35450	0	33310	693	35150	744	34080	720	33680	733	31630	670	32290	707	32950	721	33000	720		32276	730	For Mat 10
0	0	0	0	0	0																				For Mat ville
0	0	0	0	0	0							24318	167	35567	236

Date		Indèx CTR Volume		01/08/2005
442 086		202	02/08/2005
442 292		206	03/08/2005
442 497		205	04/08/2005
442 681		184	05/08/2005
442 882		201	06/08/2005
443 089		207	07/08/2005
443 277		188	08/08/2005
443 472		195	09/08/2005
443 668		196	10/08/2005
443 875		207	11/08/2005
444 085		210	12/08/2005
444 297		212	13/08/2005
444 412		115	14/08/2005
444 712		300	15/08/2005
444 911		199	16/08/2005
445 114		203	17/08/2005
445 319		205	18/08/2005
445 506		187	19/08/2005
445 711		205	20/08/2005
445 925		214	21/08/2005
446 118		193	22/08/2005
446 311		193	23/08/2005
446 487		176	24/08/2005
446 672		185	25/08/2005
446 853		181	26/08/2005
447 032		179	27/08/2005
447 228		196	28/08/2005
447 420		192	29/08/2005
447 606		186	30/08/2005
447 777		171	31/08/2005
447 949		172

Date	Indèx CTR				Volume	01/08/2005
7	008		482	17 252	02/08/2005
7	025		210	16 728	03/08/2005
7	040		646	15 436	04/08/2005
7	056		375	15 729	05/08/2005
7	071		782	15 407	06/08/2005
7	087		615	15 833	07/08/2005
7	103		221	15 606	08/08/2005
7	118		978	15 757	09/08/2005
7	134		860	15 882	10/08/2005
7	151		010	16 150	11/08/2005
7	168		438	17 428	12/08/2005
7	185		960	17 522	13/08/2005
7	202		167	16 207	14/08/2005
7	218		472	16 305	15/08/2005
7	234		448	15 976	16/08/2005
7	250		090	15 642	17/08/2005
7	265		500	15 410	18/08/2005
7	281		086	15 586	19/08/2005
7	297		642	16 556	20/08/2005
7	313		185	15 543	21/08/2005
7	327		988	14 803	22/08/2005
7	342		609	14 621	23/08/2005
7	356		523	13 914	24/08/2005
7	371		402	14 879	25/08/2005
7	385		939	14 537	26/08/2005
7	401		224	15 285	27/08/2005
7	416		123	14 899	28/08/2005
7	431		397	15 274	29/08/2005
7	445		984	14 587	30/08/2005
7	451		919	5 935	31/08/2005
7	473		600	21 681

Station : Roumadia Station : elkoudia

Indèx début du mois : 441 884 Indèx début du mois : 6991230

Date	Indèx CTR		Volume	01/08/2005
900 441	15 326		02/08/2005
916 350	15 909		03/08/2005
931 884	15 534		04/08/2005
946 556	14 672		05/08/2005
960 898	14 342		06/08/2005
976 420	15 522		07/08/2005
990 720	14 300		08/08/2005
1 005 592	14 872		09/08/2005
1 020 490	14 898		10/08/2005
1 036 002	15 512		11/08/2005
1 051 968	15 966		12/08/2005
1 066 498	14 530		13/08/2005
1 081 316	14 818		14/08/2005
1 096 212	14 896		15/08/2005
1 111 116	14 904		16/08/2005
1 126 682	15 566		17/08/2005
1 141 262	14 580		18/08/2005
1 156 614	15 352		19/08/2005
1 171 494	14 880		20/08/2005
1 186 444	14 950		21/08/2005
1 201 227	14 783		22/08/2005
1 218 084	16 857		23/08/2005
1 231 055	12 971		24/08/2005
1 244 402	13 347		25/08/2005
1 258 400	13 998		26/08/2005
1 272 117	13 717		27/08/2005
1 286 912	14 795		28/08/2005
1 301 106	14 194		29/08/2005
1 314 640	13 534		30/08/2005
1 327 790	13 150		31/08/2005
1 340 974	13 184

Date	Indèx CTR				Volume		01/08/2005
5	804		634	18	319	02/08/2005
5	823		151	18	517	03/08/2005
5	841		466	18	315	04/08/2005
5	858		306	16	840	05/08/2005
5	874		961	16	655	06/08/2005
5	892		536	17	575	07/08/2005
5	909		916	17	380	08/08/2005
5	926		836	16	920	09/08/2005
5	941		990	15	154	10/08/2005
5	960		063	18	073	11/08/2005
5	978		921	18	858	12/08/2005
5	998		767	19	846	13/08/2005
6	017		322	18	555	14/08/2005
6	034		454	17	132	15/08/2005
6	051		320	16	866	16/08/2005
6	067		054	15	734	17/08/2005
6	086		080	19	026	18/08/2005
6	103		598	17	518	19/08/2005
6	120		354	16	756	20/08/2005
6	135		666	15	312	21/08/2005
6	150		430	14	764	22/08/2005
6	171		148	20	718	23/08/2005
6	184		650	13	502	24/08/2005
6	199		030	14	380	25/08/2005
6	214		000	14	970	26/08/2005
6	229		282	15	282	27/08/2005
6	244		106	14	824	28/08/2005
6	261		662	17	556	29/08/2005
6	276		390	14	728	30/08/2005
6	290		400	14	010	31/08/2005
6	303		830	13	430

Station : Rézala (dist) Station : Rézala (1000)

Indèx début du mois : 885115 Indèx début du mois : 5786315

Date	Indèx CTR				Volume	01/08/2005
3	337		027	12 536	02/08/2005
3	349		330	12303	03/08/2005
3	361		870	12 540	04/08/2005
3	374		316	12 446	05/08/2005
3	386		826	12 510	06/08/2005
3	399		368	12 542	07/08/2005
3	411		898	12 530	08/08/2005
3	424		150	12 252	09/08/2005
3	436		610	12 460	10/08/2005
3	448		961	12 351	11/08/2005
3	461		334	12 373	12/08/2005
3	473		831	12 497	13/08/2005
3	486		348	12 517	14/08/2005
3	498		990	12 642	15/08/2005
3	511		479	12 489	16/08/2005
3	513		981	2 502	17/08/2005
3	536		530	22 549	18/08/2005
3	548		876	12 346	19/08/2005
3	561		327	12 451	20/08/2005
3	574		069	12 742	21/08/2005
3	586		596	12 527	22/08/2005
3	599		115	12 519	23/08/2005
3	611		606	12 491	24/08/2005
3	624		106	12 500	25/08/2005
3	636		554	12 448	26/08/2005
3	649		001	12 447	27/08/2005
3	661		452	12 451	28/08/2005
3	673		821	12 369	29/08/2005
3	686		210	12 389	30/08/2005
3	698		640	12 430	31/08/2005
3	711		089	12 449

Date	Indèx CTR				Volume	01/08/2005
1	477		628	818	02/08/2005
1	478		573	945	03/08/2005
1	479		465	892	04/08/2005
1	480		205	740	05/08/2005
1	480		823	618	06/08/2005
1	481		452	629	07/08/2005
1	482		072	620	08/08/2005
1	482		651	579	09/08/2005
1	483		451	800	10/08/2005
1	484		655	1 204	11/08/2005
1	485		820	1 165	12/08/2005
1	486		656	836	13/08/2005
1	487		390	734	14/08/2005
1	488		116	726	15/08/2005
1	488		885	769	16/08/2005
1	489		721	836	17/08/2005
1	490		556	835	18/08/2005
1	491		532	976	19/08/2005
1	492		394	862	20/08/2005
1	493		218	824	21/08/2005
	0			0	22/08/2005
1	494		192	974	23/08/2005
1	494		721	529	24/08/2005
1	495		300	579	25/08/2005
1	496		065	765	26/08/2005
1	496		997	932	27/08/2005
1	497		832	835	28/08/2005
1	498		412	580	29/08/2005
1	498		991	579	30/08/2005
1	499		653	662	31/08/2005
1	500		151	498

Station : Rézala (600) Station : Bni Nefaa (250)

Indèx début du mois : 3224491 Indèx début du mois : 1476810

VOLUME DISTRIBUER JOURNALIER

Mois de: Juillet 2005

ML JEMIL	ROUMADIA CTR CTR général CTR CTR millitaire add vers STIR Ml Abder (add Ml millitaire ben Hriza jemil) nouveau nigrou				date
ville	millitaire	Azib (ain bouras)	^surpresseur
3891	156				2790	4930	229			2
3796	113				2700	4360	229			3
3075	92				2655	4460	229			4
3829	83				2755	4225	230			5
3214	117				2740	4370	229			6
3738	133				2780	4590	229			7
3881	129				2630	4480	230			8
3469	121				2635	4350	229			9
3660	120				2635	4685	229			10
3648	87				2730	4080	230			11
3281	69				2800	4730	229			12
3570	111				2700	4130	229			13
3558	116				2610	4805	230			14
3935	160				2730	4820	229			15
4046	151				2775	4830	229			16
3959	106				2815	4820	230			17
3846	92				2765	4690	229			18
4015	96				2845	4765	229			19
4251	96				3085	5145	230			20
3670	152				3140	5325	229		CB	21
3766	146				2950	5035	229			22
3881	126				2880	6410	229			23
3446	134				3085	5400	177			24
3494	128				2610	4915	290			25
3469	119				2950	4905	230			26
3808	119				2955	4315	208			27
3841	154				3015	5730	212			28
3831	134				3180	5500	280			29
3894	125				3160	5770	225			30
3920	146				3190	5780	217			31
3496	125				2660	5370	225			Total
115 178	3756	0	0	0 87 950 151720 7109 0 0

Volume distribué de reservoir de KOUDIAT 'MOIS:Juillet 2005

Jour	VA Koudiat	V.P. Koudiat vers baccar	H Koudiat	Vd Baccar calculé	Vd koudiat par débitmètre	VD Rhézala	Arrivé 1000 Débitmétre		Rhézala Arri 600	1
		613
	7516	601		8377	14119	16040	12522		2
14152	6756	580		8014	14560	17179	12504		3
14525	6173	621		8085	11985	16084	12636		4
14404	6640	616		8201	13080	12296	12556		5
15793	6820	619		8375	13413	15636	12567		6
14518	6385	614		8427	13747	15309	12438		7
14302	6414	620		8310	12403	14958	12472		8
14128	6876	565		8181	11063	15229	12474		9
14956	6473	611		8107	10684	12522	12545		10
14789	6480	615		8345	10310	16305	12505		11
14465	6689	615		8397	10355	13661	12631		12
14024	5705	616		8069	10200	13601	12525		13
14156	6272	612		8198	10435	14183	12455		14
14752	7395	614		8520	10738	13410	12500		15
14657	6683	615		8103	10898	16543	12491		16
14683	6724	610		8289	10768	15037	12419		17
15444	7716	610		8532	11006	16490	12560		18
16116	7662	596		9008	11207	16280	12350		19
15701	7606	569		8869	11865	15050	12452		20
15455	6614	612		8372	11247	16775	12384		21
15368	7129	613		8673	15500	16670	12333		22
15036	6908	610		8334	16391	17573	12451		23
15272	7003	615		7451	16113	19518	12587		24
15583	7160	610		8643	14541	16592	12363		25
16075	7540	595		8915	14547	16953	12380		26
17033	7910	594		9377	15319	17789	12329		27
16047	7737	614		8890	16210	19230	12454		28
16123	7197	615		9110	15955	19574	12627		29
16072	7177	616		8955	15035	17256	12546		30
16315	7709	599	209289	9075	16026	18632	12518		31
17650	7178	565		9075	15299	17853	12617		Total 472925 216247 209289 263277 308299 500228
387191

VA: Volume d'arrivée au reservoir de KOUDIAT VP: Volume pompé vers le reservoir de BACCAR H: Hauteur d'eau dans le reservoir de KOUDIAT VD: Volume distribué par le reservoir de KOUDIAT

	MATEUR VILLE				RAS EL AIN		date
Rr 2500	Rr 1500		Arrivé400	vers Mateur	vers village	1
3201	3708		7748		68	2
2941	3814		7670		107	3
3225	3711		7417		63	4
3102	3616		7462		75	5
2963	3606		7322		78	6
2873	3636		7027		148	7
3160	3656		7760		69	8
2832	3704		7523		69	9
2864	3664		6973		71	10
2877	3510		7283		65	11
2723	3605		7139		71	12
2882	3636		5400		99	13
3000	3656		6176		86	14
2906	3694		4669		70	15
3064	3855		6620		56	16
3050	3725		5877		64	17
3166	3833		6080		57	18
3593	3442		6817		67	19
3327	4234		6036		107	20
2959	3537		5839		104	21
3090	3704		6000		115	22
3090	3772		6201		130	23
3057	3757		6111		126	24
3183	3301		6121		134	25
3399	3980		6871		138	26
3380	4015		6517		128	27
3442	4040		6544		103	28
3389	4055		6828		86	29
3299	4978		8015		126	30
3324	3659		8051		134	31
3507	3558		6242		134	Total
96868 116661 208339 0 2948

		ML BOURGUIBA						date
CE1 Arrivée		CE1 Distribué	CE2 Arrivée	CE2 Distribué	Rr CE6	CTR Faroua	1
2814			566	494		606	2
2282			446	443		580	3
2117			473	443		460	4
2234			0	461		448	5
2428			895	514		580	6
2186			447	512		551	7
2269			422	595		585	8
2012			550	537		576	9
2149			664	533		571	10
2171			0	456		634	11
1997			838	448		568	12
1936			0	431		590	13
2075			609	561		611	14
2038			523	468		617	15
1816			832	430		635	16
1940			0	464	9913	670	17
2843			340	417	11047	587	18
1678			1052	502	9432	573	19
1461			630	563	10881	621	20
2192			0	319	10103	602	21
1719			659	594		682	22
2264			0	574		720	23
1679			0	511		711	24
2009			368	555		689	25
2380			361	415		721	26
2227			1197	526		760	27
2248			638	475		674	28
2046			130	510		636	29
3228			1050	576		721	30
2342			0	483		722	31
1882			772	452		636	Total 66662 70000 14462 15262 197373.14 20965

arr CE1 de Ras el ain 17924

DR2 TABLEAU RECAPITULATIF

PRODUCTION ET DISTRIBUTION D'EAU

Mois : juillet 2005

ACHAT
EAU

PRODUCTION
CENTRE

LOCALITES

0

NADHOUR+AIN EL OUCH

1 550 113

BENI NEFAA ET MELITAIRE

405 391

Production Forages Mateur

CASERNE SIDI HMED

Rep ROUMADIA

OBSERV.

BIZERTE+ZARZOUNA

ML. BOURGUIBA ET TINJA

ZAAROUR

FAROUA + LOUATA+BENI TOUN

RAS EL AIN VILLAGE

0

Production Forages Mateur ville et 10

MATEUR+C,NACER+C,HACHED

PRODUCTION
TOTALE

DISTRIBUTION
TOTALE

PERTE
%

1 550 113

405 391

0

0

1 381 404

752 192

28 600

45 910

285 598

4 009

20 965

2 948

213 529

5 312

1 359 063

S/total adduction St.Traitement - Bizerte

1 381 404

1.6%

0

-574 100

SONEDE DISTRICT: BIZERTE

ML JEMIL

						115 178 87 950 7 248					ML ABDERRAHMEN
											BEJOU
											EL AZIB (AIN BOURAS)*
	172 236 33 680	50 222		172 236 33 680 50 222		11 450 39 586 14 802 145 518 86 715 4 606				Piquages sur conduites	METLINE
											BENI ATTA + CAP ZEBIB+Chatt Mami
											RAS JEBEL
											RAF RAF VILLE+PLAGE+ SOUNINE
											SIDI ALI CHEBEB
											Production Forages SGR6 et 14
											EL ALIA + HRIZA+KHETMINE+JOUAOUDA+MZATA+Tella+Tsella
											AOUSJA + ZOUAOUINE + TOUIBIA
											GHAR EL MELH
											BACH HAMBA + MABTOUH
											ZHANA+ UTIQUE
											S/TOTAL adduction Rive Sud
		50 222

DR2 TABLEAU RECAPITULATIF

PRODUCTION ET DISTRIBUTION D'EAU

Mois : Janvier 2006

ACHAT
EAU

PRODUCTION
CENTRE

-270 000

997 384

0

PERTE
%

OBSERV.

LOCALITES

BIZERTE+ZARZOUNA

NADHOUR+AIN EL OUCH

BENI NEFAA ET MELITAIRE

Production Forages Mateur

BORJ CHALLOUF

ML. BOURGUIBA ET TINJA

ZAAROUR

FAROUA + LOUATA+BENI TOUN

RAS EL AIN VILLAGE

Production Forages Mateur ville et 10

MATEUR+C,NACER+C,HACHED

CASERNE SIDI HMED

Rep ROUMADIA

S/total adduction St.Traitement - Bizerte

PRODUCTION
TOTALE

276 164

991 220

0

0

997 384

DISTRIBUTION
TOTALE

490 556

24 309

27 529

0

236 369

2 663

10 384

2 702

148 305

3 480

946 297

0

991 220

276 164

0

ML JEMIL

91 461 38 230 3 327

ML ABDERRAHMEN

BEJOU

EL AZIB (AIN BOURAS)*

143 141 34 286

26 248

143 141 34 286 26 248

9 688 26 975 7 438 102 980 42 966 2 709

Piquages sur conduites

METLINE

BENI ATTA + CAP ZEBIB+Chatt Mami

RAS JEBEL

RAF RAF VILLE+PLAGE+ SOUNINE

SIDI ALI CHEBEB

Production Forages SGR6 et 14

EL ALIA + HRIZA+KHETMINE+JOUAOUDA+MZATA+Tella+Tsella

AOUSJA + ZOUAOUINE + TOUIBIA

GHAR EL MELH

BACH HAMBA + MABTOUH

ZHANA+ UTIQUE

26 248

5.1%

SONEDE DISTRICT: BIZERTE

Volume distribué de reservoir de KOUDIAT

MOIS:janvier 2006

Vd koudiat Jour VA Koudiat V.P. VD Koudiat Vd Baccar Arrivé 1000 Rhézala Arri 600 pomp ain el par VD Rhézala Koudiat calculé calculé Débitmétre berda débitmètre											1
9152		4255			4592	10649	8920	11598		2
8048		5033			4574	10686	7689	11627		3
9510		4724			4161	10205	7679	11361		4
7961		3945			4015	10039	6792	11690		5
8138		4107			4223	10247	7500	11532		6
8686		3997			4609	9371	7210	11518		7
8730		4176			4870	10264	7208	11627		8
9127		4340			4840	10479	5911	11165		9
9108		4297			4944	9374	7333	11675		10
9340		4359			4971	10829	10896	11517		11
11815		5611			6197	19816	15630	11970		12
9685		4406			5289	9697	6146	11874		13
9346		4477			5048	9854	6268	11662		14
8891		4136			4765	9595	7250	11684		15
9195		4440			4848	9078	6231	11590		16
9663		4614			5411	10323	7736	11790		17
9044		4229			4890	9581	6619	11583		18
8146		4251			4654	9703	6044	11674		19
9715		4405			4835	9590	6230	11563		20
8842		4104			4772	9488	8498	11561		21
8498		3885			4541	9305	6303	11522		22
8886		4021			4533	9416	6040	11600		23
9584		4493			5301	9421	6589	11082		24
8745		4181			4725	9410	6400	11525		25
7883		3776			4421	9169	5892	11610		26
8862		4297			4544	9577	5601	11744		27
8570		4058			4667	9392	5017	11602		28
9087		4418			4750	10065	7074	11652		29
8761		3942			4942	9520	7170	11611		30
9586		4849		133796	5105	10584	7686	11600	24654	31
8081		3970			4214	8436	4772	11595		Total 278685 133796 0 109142 148251 233163 222334
359404									24654

VA: Volume d'arrivée au reservoir de KOUDIAT VP: Volume pompé vers le reservoir de BACCAR VD: Volume distribué par le reservoir de KOUDIAT

	MATEUR VILLE					RAS EL AIN		date
Rr 2500	Rr 1500		Surp	Arrivé400	vers Mateur	vers village	1
2051	2728		23	5567			2
2188	2462		18	6450			3
2052	2777		12	5508			4
2030	2541		12	5567			5
2108	2606		12	5380			6
2162	2736		14	5708			7
2035	2732		15	5462			8
2100	2741		17	5864			9
2100	2771		16	6503			10
2711	3284		25	5778			11
2152	2822		17	5910			12
2426	2786		18	5850			13
2180	2777		15	5873			14
2106	2801		18	6061			15
2275	2861		18	5591			16
2228	2777		20	5765			17
2185	2716		15	5601			18
2318	2802		15	6101			19
2210	3002		16	5958			20
2044	2376		13	5221			21
2016	2344		13	5069			22
2054	2436		17	5685			23
2131	2412		13	5178			24
2027	2327		11	5030			25
2140	2397		12	5289			26
2072	2397		14	5669			27
2199	2517		15	5316			28
2128	2440		16	5282			29
2183	2485		19	5469			30
1993	2249		11	5103			31
2147	2452		16	5357			Total 66751 81554 486 174165 0 0

		ML BOURGUIBA						date
CE1 Arrivée		CE1 Distribué	CE2 Arrivée	CE2 Distribué	Rr CE6	CTR Faroua	1
1380			1010	339	7239	189	2
1440			990	411	6599	321	3
1160			990	386	5988	272	4
1120			951	407	5382	297	5
1172			729	381	6812	278	6
1123			980	1023	6391	321	7
1475			970	897	6868	334	8
1490			422	835	7054	314	9
1150		1099	552	618	7120	366	10
2033		1286	765	645	10581	451	11
910			262	702	7129	373	12
1097		1189	950	878	6506	339	13
1203		1331	1015	1119	6302	328	14
1400		1300	990	850	6843	309	15
1450		1380	170	730	7416	375	16
1430		1370	980	928	7103	396	17
1430		1376	1000	1008	7574	449	18
980		1310	900	1136	7255	352	19
1062		1337	1011	1170	7134	332	20
1058		1033	949	977	6614	299	21
1090		980	1010	1020	6768	301	22
1100		1200	960	1211	7500	340	23
1900		1290	980	1229	7878	357	24
960		1180	1045	1132	7000	306	25
1050		1230	993	1050	7761	303	26
1393		1110	980	1073	7274	329	27
1077		1430	1000	987	7398	369	28
1152		1268	1000	1015	7613	335	29
1033		1152	800	729	7729	388	30
1075		839	900	893	6457	300	31
1290			1000	854	7592	361	Total 38 683 37 923 27 254 26 633 171 813 10 384

ML JEMIL	ROUMADIA CTR CTR général CTR CTR millitaire add vers STIR Ml Abder (add Ml millitaire ben Hriza jemil) nouveaunigrou				date
ville	millitaire	Azib (ain bouras)	^surpresseur
3061	27		346		1315		180			2
2959	32		365		1280		130			3
2965	38		321		1080		125			4
3172	47		273		1120		133			5
2987	57		277		1050		130			6
3000	50		200		1100		125			7
3034	55		210		1130		97			8
2887	34		329		1120		160			9
2868	25		329		1025		146			10
2970	27		326		1340		155			11
3513	23		409		1410		115			12
3065	23		475		1340		105			13
2892	46		316		1160		137			14
2926	41		347		1170		118			15
2864	30		352		1130		158			16
3127	31		408		1290		107			17
2742	54		320		1420		135			18
2685	50		317		1435		110			19
2746	60		275		1360		150			20
2740	57		277		1555		135			21
2792	50		264		1310		140			22
2725	28		264		1220		135			23
3140	42		354		1165		133			24
2920	55		281		1165		136			25
2866	55		257		1105		141			26
2866	55		256		1080		144			27
2850	57		290		990		141			28
3045	56		310		1150		140			29
3210	44		331		1160		145			30
3127	34		386		1265		138			31
2717	35		320		1790		139			Total
91 461	1318	0	9785	0 38 230 0 4183 0 0

Annexe n°4: Courbes de modulation horaires

1,60

1,40

1,20

1,00

0,80

0,60

0,40

Heure

1,65

1,45

1,25

1,05

0,85

0,65

0,45

0,25

0 6 12 18 24

1 7 13 19

heure

Courbe de modulation horaire hiver Rhézala

Courbe de modulation horaire été Rhézala

2,2

2

1,8

1,6

1,4

1,2

1

0,8

0,6

0,4

0,2

heure

0 6 12 18 24

Courbe de modulation horaire été El Alia

Courbe de modulation horaire hiver CE6

1,8

1,6

1,4

1,2

1

0,8

0,6

0,4

1 6 11 16 21

heure

Modulation horaire été CE6

1,6

1,4

1,2

1

0,8

0,6

0,4

0 6 12 18 24

heure

Courbe de modulation horaire été de Mateur

1,6

1,4

1,2

1

0,8

0,6

0,4

0 6 12 18 24

heure

2

1,8

1,6

1,4

1,2

1

0,8

0,6

0,4

0,2

heure

2

1,8

1,6

1,4

1,2

1

0,8

0,6

0,4

0,2

0 6 12 18 24

heure

1 7 13 19

Courbe de modulation horaire été Ml Jemil

Courbe de modulation horaire hiver CE1

2

1,8

1,6

1,4

1,2

1

0,8

0,6

0,4

0,2

0

heure

1 7 13 19

Courbe de modulation horaire hiver Koudiat

Composant	Unité	Prélèvement 24/01/06	Prélèvement		Mesure max.admissible	Turbidité
NTU	2.1		5		Temp,mesure de pH
°C	12.8				pH
	7.33		6,5-8,5		Dureté totale
°F	16		100		Calcium
mg/l	41		300		Magnésium
mg/l	13		150		Sodium
mg/l	46				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	73				Chlorure
mg/l	74		600		Sulfate
mg/l	81		600		Nitrate
mg/l	2.5		45		Nitrite
mg/l	0.013				Résidu sec
mg/l	322		2500		Fluor
mg/l	0.36		1.7		Fer
mg/l	0.17		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	0.32				Silicium
mg/l	<2,00				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	3.5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,5		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 24/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	2.2	2.6	5		Temp,mesure de pH
°C	12.9	24.1			pH
	7.22	7.09	6,5-8,5		Dureté totale
°F	14.5	14.5	100		Calcium
mg/l	44	36	300		Magnésium
mg/l	8	13	150		Sodium
mg/l	46	48			Potassium
mg/l	<5	2.44			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	72	96			Chlorure
mg/l	73	76	600		Sulfate
mg/l	64	65	600		Nitrate
mg/l	<0,5	<0,5	45		Nitrite
mg/l	0.011	<0,01			Résidu sec
mg/l	374	285	2500		Fluor
mg/l	0.24	0.28	1.7		Fer
mg/l	0.06	<0,05	0,5-1		Manganèse
mg/l	<0,03	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	0.27	0.34			Silicium
mg/l	<2,0	-			Zinc
mg/l	<0,2	<0,20	5		Chrome
j.tg/l	<1,5	2			Argent
j.tg/l	<0,012	<0,012	0.02		Arsenic
j.tg/l	<3,5	<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

ANNEXE n°5: Résultats d'analyses physico-chimiques

( Laboratoire de contrôle de qualité de l'eau à Guédir El Golla - SO.N.E.D.E ) Réservoir Roumadia Réservoir Koudiat

Réservoir Rézala Forage SGR 11 El Azib

Composant	Unité	Prélèvement 24/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	1.4	1.6	5		Temp,mesure de pH
°C	13.2	23.7			pH
	7.14	7.37	6,5-8,5		Dureté totale
°F	40.5	46.5	100		Calcium
mg/l	119	126	300		Magnésium
mg/l	26	37	150		Sodium
mg/l	121	145			Potassium
mg/l	<5	4.11			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	170	205			Chlorure
mg/l	249	288	600		Sulfate
mg/l	156	155	600		Nitrate
mg/l	1.9	3	45		Nitrite
mg/l	<0,01	<0,01			Résidu sec
mg/l	1010	1010	2500		Fluor
mg/l	2.2	0.42	1.7		Fer
mg/l	0.43	<0,05	0,5-1		Manganèse
mg/l	<0,03	<0,03	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	0.31	<0,25			Silicium
mg/l	2.2	-			Zinc
mg/l	<0,20	<0,20	5		Chrome
j.tg/l	<1,5	<1,5			Argent
j.tg/l	<0,012	<0,012	0.02		Arsenic
j.tg/l	<3,50	<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 23/05/06		Mesure max.admissible	Turbidité
NTU	3.2	4.1	5		Temp,mesure de pH
°C	13.2	29.7			pH
	7.37	7.63	6,5-8,5		Dureté totale
°F	25.5	26.5	100		Calcium
mg/l	71	74	300		Magnésium
mg/l	19	20	150		Sodium
mg/l	113	108			Potassium
mg/l	<5	4.17			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	310	315			Chlorure
mg/l	125	127	600		Sulfate
mg/l	49	49	600		Nitrate
mg/l	<0,5	<0,5	45		Nitrite
mg/l	0.013	<0,01			Résidu sec
mg/l	495	650	2500		Fluor
mg/l	0.35	0.34	1.7		Fer
mg/l	0.43	0.49	0,5-1		Manganèse
mg/l	<0,030	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	<0,25	<0,25			Silicium
mg/l	6.28	-			Zinc
mg/l	<0,20	<0,20	5		Chrome
j.tg/l	2.5	<1,5			Argent
j.tg/l	<0,012	<0,012	0.02		Arsenic
j.tg/l		<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 23/05/06		Mesure max.admissible	Turbidité
NTU	0.72	0.59	5		Temp,mesure de pH
°C	13	26.8			pH
	7.32	7.39	6,5-8,5		Dureté totale
°F	22	23	100		Calcium
mg/l	64	68	300		Magnésium
mg/l	15	14	150		Sodium
mg/l	30	37			Potassium
mg/l	<5	2.03			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	220	220			Chlorure
mg/l	49	51	600		Sulfate
mg/l	25	60	600		Nitrate
mg/l	2.5	1.6	45		Nitrite
mg/l	<0,01	<0,01			Résidu sec
mg/l	290	380	2500		Fluor
mg/l	0.34	0.34	1.7		Fer
mg/l	<0,05	0.09	0,5-1		Manganèse
mg/l	<0,030	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	<0,25	<0,25			Silicium
mg/l	4.72	-			Zinc
mg/l	0.3	<0,20	5		Chrome
j.tg/l	4.6	2.8			Argent
j.tg/l	<0,012	0.015	0.02		Arsenic
j.tg/l	<3,5	<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.71		5		Temp,mesure de pH
°C	13				pH
	7.13		6,5-8,5		Dureté totale
°F	25.5		100		Calcium
mg/l	68		300		Magnésium
mg/l	21		150		Sodium
mg/l	45				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	240				Chlorure
mg/l	61		600		Sulfate
mg/l	24		600		Nitrate
mg/l	2.9		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	370		2500		Fluor
mg/l	0.33		1.7		Fer
mg/l	0.05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	4.94				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	2.5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 23/05/06		Mesure max.admissible	Turbidité
NTU	0.6	0.8	5		Temp,mesure de pH
°C	13.4	26.9			pH
	7.25	7.41	6,5-8,5		Dureté totale
°F	22.5	26.5	100		Calcium
mg/l	65	68	300		Magnésium
mg/l	15	23	150		Sodium
mg/l	41	48			Potassium
mg/l	<5	2.11			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	285	235			Chlorure
mg/l	55	58	600		Sulfate
mg/l	36	50	600		Nitrate
mg/l	1.5	<0,5	45		Nitrite
mg/l	<0,01	<0,01			Résidu sec
mg/l	320	455	2500		Fluor
mg/l	0.33	0.37	1.7		Fer
mg/l	<0,05	<0,05	0,5-1		Manganèse
mg/l	<0,03	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	<0,25	<0,25			Silicium
mg/l	5.03	-			Zinc
mg/l	<0,20	<0,20	5		Chrome
j.tg/l	2.8	1.6			Argent
j.tg/l	<0,012	<0,012	0.02		Arsenic
j.tg/l	<3,5	<3,50	50		Plomb
j.tg/l	<2,5	7.2	50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.54		5		Temp,mesure de pH
°C	13.3				pH
	7.05		6,5-8,5		Dureté totale
°F	25.5		100		Calcium
mg/l	68		300		Magnésium
mg/l	20		150		Sodium
mg/l	37				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	290				Chlorure
mg/l	55		600		Sulfate
mg/l	29		600		Nitrate
mg/l	0.8		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	310		2500		Fluor
mg/l	0.39		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,03		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	4.96				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	2.7				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,5		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 23/05/06		Mesure max.admissible	Turbidité
NTU	1.8	0.38	5		Temp,mesure de pH
°C	13.3	27.3			pH
	7.24	7.48	6,5-8,5		Dureté totale
°F	28.5	24	100		Calcium
mg/l	73	73	300		Magnésium
mg/l	25	14	150		Sodium
mg/l	45	62			Potassium
mg/l	<5	2.69			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	255	215			Chlorure
mg/l	71	50	600		Sulfate
mg/l	67	35	600		Nitrate
mg/l	<0,5	<0,5	45		Nitrite
mg/l	<0,01	<0,01			Résidu sec
mg/l	330	400	2500		Fluor
mg/l	0.39	0.28	1.7		Fer
mg/l	0.23	0.06	0,5-1		Manganèse
mg/l	<0,030	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	<0,25	<0,25			Silicium
mg/l	5.5	-			Zinc
mg/l	0.2	0.45	5		Chrome
j.tg/l	<1,5	<1,5			Argent
j.tg/l	<0,012	0.015	0.02		Arsenic
j.tg/l	<3,5	<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

Composant	Unité	Prélèvement 03/01/06	Prélèvement 23/05/06		Mesure max.admissible	Turbidité
NTU	1.1	0.65	5		Temp,mesure de pH
°C	13.6	27			pH
	7.63	7.48	6,5-8,5		Dureté totale
°F	36	25	100		Calcium
mg/l	89	78	300		Magnésium
mg/l	34	13	150		Sodium
mg/l	45	54			Potassium
mg/l	<5	2.54			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	285	250			Chlorure
mg/l	81	77	600		Sulfate
mg/l	45	22	600		Nitrate
mg/l	2	2	45		Nitrite
mg/l	<0,01	<0,01			Résidu sec
mg/l	415	510	2500		Fluor
mg/l	0.4	0.34	1.7		Fer
mg/l	0.05	0.08	0,5-1		Manganèse
mg/l	<0,030	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	<0,25	<0,25			Silicium
mg/l	5.21	-			Zinc
mg/l	0.33	<0,20	5		Chrome
j.tg/l	2.9	<1,5			Argent
j.tg/l	<0,012	0.019	0.02		Arsenic
j.tg/l	<3,5	<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

Composant	Unité	Prélèvement 24/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.3		5		Temp,mesure de pH
°C	13.1				pH
	7.23		6,5-8,5		Dureté totale
°F	74		100		Calcium
mg/l	225		300		Magnésium
mg/l	43		150		Sodium
mg/l	174				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	345				Chlorure
mg/l	397		600		Sulfate
mg/l	256		600		Nitrate
mg/l	11.7		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	1520		2500		Fluor
mg/l	0.6		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	4.63				Zinc
mg/l	0.49		5		Chrome
j.tg/l	<1,5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 24/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	64		5		Temp,mesure de pH
°C	13.7				pH
	7.14		6,5-8,5		Dureté totale
°F	78		100		Calcium
mg/l	236		300		Magnésium
mg/l	48		150		Sodium
mg/l	191				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	335				Chlorure
mg/l	440		600		Sulfate
mg/l	296		600		Nitrate
mg/l	45		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	1750		2500		Fluor
mg/l	0.63		1.7		Fer
mg/l	0.05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	4.95				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	<1,5				Argent
j.tg/l	0.015		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Forage Mateur 11 Forage Mateur 4

Composant	Unité	Prélèvement 24/01/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.41	0.35	5		Temp,mesure de pH
°C	13.9	24			pH
	7.06	7.26	6,5-8,5		Dureté totale
°F	66	65	100		Calcium
mg/l	203	179	300		Magnésium
mg/l	38	48	150		Sodium
mg/l	150	176			Potassium
mg/l	<5	3.83			Alcalinité (Carb)
mg/l	<3	<3			Alcalinité (Bicarb)
mg/l	350	350			Chlorure
mg/l	312	306	600		Sulfate
mg/l	239	210	600		Nitrate
mg/l	42.5	16.2	45		Nitrite
mg/l	<0,01	<0,01			Résidu sec
mg/l	1140	1210	2500		Fluor
mg/l	0.57	0.61	1.7		Fer
mg/l	<0,05	<0,05	0,5-1		Manganèse
mg/l	<0,030	<0,030	0.5		Cuivre
mg/l	<0,05	<0,05	1		Aluminium
mg/l	<0,25	<0,25			Silicium
mg/l	4.88	-			Zinc
mg/l	<0,20	<0,20	5		Chrome
j.tg/l	<1,5	2			Argent
j.tg/l	<0,012	<0,012	0.02		Arsenic
j.tg/l	<3,50	<3,50	50		Plomb
j.tg/l	<2,5	<2,5	50

Composant	Unité	Prélèvement 21/02/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	1.1		5		Temp,mesure de pH
°C	19				pH
	7.38		6,5-8,5		Dureté totale
°F	39		100		Calcium
mg/l	110		300		Magnésium
mg/l	28		150		Sodium
mg/l	153				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	181				Chlorure
mg/l	277		600		Sulfate
mg/l	125		600		Nitrate
mg/l	6.8		45		Nitrite
mg/l	0.011				Résidu sec
mg/l	870		2500		Fluor
mg/l	0.32		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	3.55				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	3.3				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	-		50

Composant	Unité	Prélèvement 21/02/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	1.5		5		Temp,mesure de pH
°C	19.3				pH
	7.38		6,5-8,5		Dureté totale
°F	37		100		Calcium
mg/l	105		300		Magnésium
mg/l	27		150		Sodium
mg/l	130				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	171				Chlorure
mg/l	250		600		Sulfate
mg/l	120		600		Nitrate
mg/l	4.7		45		Nitrite
mg/l	0.011				Résidu sec
mg/l	830		2500		Fluor
mg/l	0.36		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	3.6				Zinc
mg/l	0.42		5		Chrome
j.tg/l	11.8				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	-		50

Composant	Unité	Prélèvement 06/03/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	161		5		Temp,mesure de pH
°C	15.4				pH
	7.49		6,5-8,5		Dureté totale
°F	13.5		100		Calcium
mg/l	39		300		Magnésium
mg/l	9		150		Sodium
mg/l	46				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	84				Chlorure
mg/l	69		600		Sulfate
mg/l	82		600		Nitrate
mg/l	2.3		45		Nitrite
mg/l	0.011				Résidu sec
mg/l	285		2500		Fluor
mg/l	<0,1		1.7		Fer
mg/l	0.1		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	13.6				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	<1,5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 06/03/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	1.6		5		Temp,mesure de pH
°C	15.7				pH
	6.78		6,5-8,5		Dureté totale
°F	12.5		100		Calcium
mg/l	40		300		Magnésium
mg/l	6		150		Sodium
mg/l	39				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	46				Chlorure
mg/l	64		600		Sulfate
mg/l	88		600		Nitrate
mg/l	1.9		45		Nitrite
mg/l	0.013				Résidu sec
mg/l	3.5		2500		Fluor
mg/l	0.14		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	<2				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	3.8				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 15/05/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	1.5		5		Temp,mesure de pH
°C	24				pH
	7.14		6,5-8,5		Dureté totale
°F	66		100		Calcium
mg/l	186		300		Magnésium
mg/l	49		150		Sodium
mg/l	176				Potassium
mg/l	3.87				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	350				Chlorure
mg/l	306		600		Sulfate
mg/l	210		600		Nitrate
mg/l	15.2		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	1180		2500		Fluor
mg/l	0.6		1.7		Fer
mg/l	0.22		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	-				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	<1,5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Station Mateur Eau Traitée Forage Mateur 8

Composant	Unité	Prélèvement 23/05/06	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.82		5		Temp,mesure de pH
°C	26.3				pH
	7.58		6,5-8,5		Dureté totale
°F	21		100		Calcium
mg/l	63		300		Magnésium
mg/l	13		150		Sodium
mg/l	41				Potassium
mg/l	2.01				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	215				Chlorure
mg/l	50		600		Sulfate
mg/l	35		600		Nitrate
mg/l	<0,5		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	400		2500		Fluor
mg/l	0.28		1.7		Fer
mg/l	0.06		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	-				Zinc
mg/l	0.45		5		Chrome
j.tg/l	<1,5				Argent
j.tg/l	0.015		0.02		Arsenic
j.tg/l	<3,50		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 28/02/05 *	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.55		5		Temp,mesure de pH
°C	24.2				pH
	7.44		6,5-8,5		Dureté totale
°F	39		100		Calcium
mg/l	115		300		Magnésium
mg/l	24.8		150		Sodium
mg/l	187				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	80				Chlorure
mg/l	378		600		Sulfate
mg/l	175		600		Nitrate
mg/l	26.5		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	1120		2500		Fluor
mg/l	0.61		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	5.74				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	2.5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	-		50		Plomb
j.tg/l	<2,5		50

* date analyse: 26/09/2005

Forage SGR1 bis R1500+Ras El Ain

R1 500 Mateur CE6 Tinja

Composant	Unité	Prélèvement 28/02/05 *	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	0.38		5		Temp,mesure de pH
°C	24.1				pH
	7.41		6,5-8,5		Dureté totale
°F	36		100		Calcium
mg/l	109		300		Magnésium
mg/l	21.1		150		Sodium
mg/l	300				Potassium
mg/l	30				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	69				Chlorure
mg/l	364		600		Sulfate
mg/l	450		600		Nitrate
mg/l	18		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	1270		2500		Fluor
mg/l	0.4		1.7		Fer
mg/l	<0,05		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	6.67				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	2.6				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	-		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 21/02/05 *	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	2.6		5		Temp,mesure de pH
°C	25.9				pH
	7.58		6,5-8,5		Dureté totale
°F	29		100		Calcium
mg/l	90		300		Magnésium
mg/l	16		150		Sodium
mg/l	89				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	108				Chlorure
mg/l	164		600		Sulfate
mg/l	145		600		Nitrate
mg/l	24.5		45		Nitrite
mg/l	0.02				Résidu sec
mg/l	640		2500		Fluor
mg/l	1.3		1.7		Fer
mg/l	0.62		0,5-1		Manganèse
mg/l	0.11		0.5		Cuivre
mg/l	<0,030		1		Aluminium
mg/l	<0,05				Silicium
mg/l	<0,25				Zinc
mg/l	3.72		5		Chrome
j.tg/l	<0,20				Argent
j.tg/l	1.7		0.02		Arsenic
j.tg/l	<0,012		50		Plomb
j.tg/l	<2,5		50

* date analyse: 26/09/2005 * date analyse: 15/08/2005

CE2 Ml Bourguiba CE1 Ml Bourguiba

Composant	Unité	Prélèvement 21/02/05 *	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	2.4		5		Temp,mesure de pH
°C	25.7				pH
	8.04		6,5-8,5		Dureté totale
°F	12		100		Calcium
mg/l	40		300		Magnésium
mg/l	5		150		Sodium
mg/l	45				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	<3				Alcalinité (Bicarb)
mg/l	69				Chlorure
mg/l	69		600		Sulfate
mg/l	41		600		Nitrate
mg/l	8.5		45		Nitrite
mg/l	<0,01				Résidu sec
mg/l	250		2500		Fluor
mg/l	0.21		1.7		Fer
mg/l	0.1		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	<0,25				Silicium
mg/l	6.12				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	<1,5				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	-		50		Plomb
j.tg/l	<2,5		50

Composant	Unité	Prélèvement 23/02/05 *	Prélèvement 15/05/06		Mesure max.admissible	Turbidité
NTU	3.3		5		Temp,mesure de pH
°C	28.3				pH
	7.94		6,5-8,5		Dureté totale
°F	32.5		100		Calcium
mg/l	103		300		Magnésium
mg/l	17		150		Sodium
mg/l	80				Potassium
mg/l	<5				Alcalinité (Carb)
mg/l	0				Alcalinité (Bicarb)
mg/l	166				Chlorure
mg/l	161		600		Sulfate
mg/l	130		600		Nitrate
mg/l	21		45		Nitrite
mg/l	0.019				Résidu sec
mg/l	690		2500		Fluor
mg/l	0.63		1.7		Fer
mg/l	0.15		0,5-1		Manganèse
mg/l	<0,030		0.5		Cuivre
mg/l	<0,05		1		Aluminium
mg/l	0.25				Silicium
mg/l	2.36				Zinc
mg/l	<0,20		5		Chrome
j.tg/l	3.1				Argent
j.tg/l	<0,012		0.02		Arsenic
j.tg/l	-		50		Plomb
j.tg/l	<2,5		50

* date analyse: 15/08/2005 * date analyse: 29/08/2005

Annexe n°6 : Etude de la régression du chlore résiduel libre.

Model premier ordre

	Point X	Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	0.995			2
20.000	1.000	0.981			3
40.000	0.950	0.966		Y = 1.00 * e'(-0.000751719 * X)	4
60.000	0.950	0.952			5
80.000	0.950	0.937		Value Variance	6
120.000	0.900	0.910			7
180.000	0.850	0.869		Bo: 0.9954 0.0000	8
240.000	0.850	0.831		B1: -0.0008 0.0000	9
300.000	0.800	0.794			10
360.000	0.750	0.759			11
450.000	0.700	0.710			12
570.000	0.650	0.649		Correlation (R'2) = .9921142	13
800.000	0.550	0.546

Y = 1.00 * e'(-0.000751719 * X)

1.0 0.8 0.6 0.4 0.2 0.0

0 200 400 600 800

X

Y

Actual Data

Curve Fit

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.700 1.742

2 20.000 1.700 1.679

3 40.000 1.650 1.618

4 60.000 1.600 1.559

5 80.000 1.550 1.502

6 120.000 1.350 1.395

7 180.000 1.200 1.248

8 240.000 1.100 1.117

9 300.000 1.000 1.000

10 360.000 0.900 0.895

11 450.000 0.770 0.757

Coefficients for Equation:

Y = 1.7 * e'(-0.00185114 * X)

Value Variance

Bo: 1.7421 0.0001

B1: -0.0019 0.0000

Correlation (R'2) = .9894923

Y = 1.7 * e'(-0.00185114 * X)

X

2.0

0.5

0.0

1.5

1.0

0 100 200 300 400 500

Y

Actual Data

Curve Fit

2.5

2.0

1.5

1.0

0.5

0.0

1.5

1.0

0.5

0.0

STATION DE TRAITEMENT T=25°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.003

2 20.000 1.950 1.951

3 40.000 1.900 1.901

4 60.000 1.850 1.852

5 80.000 1.800 1.804

6 120.000 1.700 1.713

7 180.000 1.600 1.584

8 240.000 1.500 1.465

9 300.000 1.400 1.354

10 360.000 1.150 1.252

11 450.000 1.150 1.114

Coefficients for Equation:

Y = 2.0 * e'(-0.00 1304235 * X)

Value Variance

Bo: 2.0029 0.0002

B1: -0.0013 0.0000

Correlation (R'2) = .9832647

Y = 2.0 * e'(-0.001304235 * X)

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

STATION DE TRAITEMENT T=25°C - Co=1 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	1.001		Y = 1.00 * e'(-0.00264957 * X)	2
20.000	0.950	0.950		Value Variance	3
40.000	0.900	0.901			4
60.000	0.800	0.854		Bo: 1.0014 0.0001	5
80.000	0.800	0.810		B1: -0.0026 0.0000	6
120.000	0.700	0.729			7
180.000	0.600	0.622			8
240.000	0.600	0.530			9
300.000	0.500	0.452		Correlation (R'2) = .98807 13	10
360.000	0.400	0.386			11
450.000	0.300	0.304			12
570.000	0.200	0.221			13
720.000	0.150	0.149

Y = 1.00 * e'(-0.00264957 * X)

0 200 400 600 800

X

Y

Actual Data

Curve Fit

3.0

2.5

2.0

1.5

1.0

0.5

0.0

2.5

2.0

1.5

1.0

0.5

0.0

STATION DE TRAITEMENT T=25°C - Co=3 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	3.000	3.000			2
20.000	3.000	2.983		Y = 3.0 * e'(-0.0002709016 * X)	3
40.000	2.950	2.967			4
60.000	2.950	2.951		Value Variance	5
80.000	2.950	2.935			6
120.000	2.900	2.904		Bo: 2.9996 0.0000	7
180.000	2.850	2.857		B1: -0.0003 0.0000	8
240.000	2.800	2.811			9
300.000	2.750	2.765			10
360.000	2.750	2.721		Correlation (R'2) = .9846 827	11
450.000	2.650	2.655

Y = 3.0 * e'(-0.0002709016 * X)

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

STATION DE TRAITEMENT T=15°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.014

2 20.000 2.000 2.002

3 40.000 2.000 1.990

4 60.000 2.000 1.979

5 80.000 1.950 1.967

6 120.000 1.950 1.944

7 180.000 1.900 1.910

8 240.000 1.900 1.877

9 300.000 1.850 1.844

10 360.000 1.800 1.812

11 450.000 1.750 1.765

12 570.000 1.700 1.704

13 800.000 1.600 1.592

Coefficients for Equation:

Y = 2.0 * e'(-0.0002935617 * X)

Value Variance

Bo: 2.0138 0.0000

B1: -0.0003 0.0000

Correlation (R'2) = .9892726

Y = 2.0 * e'(-0.0002935617 * X)

0 200 400 600 800

X

Y

Actual Data

Curve Fit

2.0

1.5

Y

1.0

0.5

0.0

Actual Data

Curve Fit

STATION DE TRAITEMENT T=15°C - Co=1.7 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.700	1.690			2
20.000	1.700	1.675		Y = 1.7 * e'(-0.000442 1945 * X)	3
40.000	1.700	1.661			4
60.000	1.600	1.646		Value Variance	5
80.000	1.600	1.632			6
120.000	1.600	1.603		Bo: 1.6904 0.0001	7
180.000	1.600	1.561		B1: -0.0004 0.0000	8
240.000	1.500	1.520			9
300.000	1.500	1.480			10
360.000	1.400	1.442			11
450.000	1.400	1.385		Correlation (R'2) = .9666 152	12
570.000	1.300	1.314			13
800.000	1.200	1.187

Y = 1.7 * e'(-0.0004421945 * X)

0 200 400 600 800

X

STATION DE TRAITEMENT T=20°C - Co=1 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	0.997			2
20.000	1.000	0.965		Y = 1.00 * e'(-0.00163749 * X)	3
40.000	0.950	0.934			4
60.000	0.900	0.904		Value Variance	5
80.000	0.900	0.875			6
120.000	0.800	0.820		Bo: 0.9975 0.0001	7
180.000	0.800	0.743		B1: -0.0016 0.0000	8
240.000	0.700	0.673			9
300.000	0.600	0.610			10
360.000	0.500	0.553		Correlation (R'2) = .9758092	11
450.000	0.400	0.477			12
570.000	0.400	0.392			13
800.000	0.300	0.269

Y = 1.00 * e'(-0.00163749 * X)

0 200 400 600 800

X

0.8

0.6

0.4

0.2

0.0

1.0

Y

Actual Data

Curve Fit

4

3

2

1

0

STATION DE TRAITEMENT T=15°C - Co=3 mg/l

Model premier ordre

Point X		Actual Y Predicted Y		Coefficients for Equation:			1
0.000	3.000	3.010				2
20.000	3.000	3.005	Y = 3.0 * e'(-0.00009323701 * X)	3
40.000	3.000	2.999				4
60.000	3.000	2.994	Value	Variance		5
80.000	3.000	2.988				6
120.000	3.000	2.977	Bo: 3.0103	0.0000		7
180.000	2.950	2.960	B1: -0.0001	0.0000		8
240.000	2.950	2.944				9
300.000	2.900	2.927				10
360.000	2.900	2.911	Correlation (R'2) = .9612 171			11
450.000	2.900	2.887				12
570.000	2.850	2.855				13
800.000	2.800	2.794

Y = 3.01 * e'(-0.00009324 * X)

0 200 400 600 800

X

Y

Actual Data

Curve Fit

STATION DE TRAITEMENT T=20°C - Co=2 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.000	2.005			2
20.000	2.000	1.970		Y = 2.0 * e'(-0.000877733 * X)	3
40.000	2.000	1.936			4
60.000	1.900	1.902		Value Variance	5
80.000	1.900	1.869			6
120.000	1.800	1.805		Bo: 2.0052 0.0002	7
180.000	1.700	1.712		B1: -0.0009 0.0000	8
240.000	1.600	1.624			9
300.000	1.500	1.541			10
360.000	1.400	1.462			11
450.000	1.300	1.351		Correlation (R'2) = .982 1355	12
570.000	1.300	1.216			13
800.000	1.000	0.994

Y = 2.0 * e'(-0.000877733 * X)

X

2.5

2.0

0.5

0.0

1.5

1.0

0 200 400 600 800

Y

Actual Data

Curve Fit

STATION DE TRAITEMENT T=20°C - Co=1,7 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.700 1.679

2 20.000 1.700 1.636

3 40.000 1.600 1.594

4 60.000 1.600 1.553

5 80.000 1.500 1.513

6 120.000 1.400 1.436

7 180.000 1.300 1.329

8 240.000 1.200 1.229

9 300.000 1.100 1.137

10 360.000 1.000 1.051

11 450.000 1.000 0.935

12 570.000 0.800 0.800

13 800.000 0.600 0.594

Coefficients for Equation:

Y = 1.7 * e'(-0.001299566 * X)

Value Variance

Bo: 1.6786 0.0001

B1: -0.0013 0.0000

Correlation (R'2) = .9874441

Y = 1.7 * e'(-0 .001299566 * X)

X

2.0

0.5

0.0

1.5

1.0

0 200 400 600 800

Y

Actual Data

Curve Fit

STATION DE TRAITEMENT T=20°C - Co=3 mg/l

Model premier ordre

Coefficients for Equation:

3.012					2.994
Y = 3.0 *	e'(-0.0003052603 * X)	2.976
				2.958
	Value	Variance		2.940
				2.904
Bo:	3.0122	0.0001		2.851
B1:	-0.0003	0.0000		2.799
				2.749

Correlation (R'2) = .9753059

Y = 3.0 * e'(-0.0003052603 * X)

Point X Actual Y Predicted Y

1 0.000 3.000

2 20.000 3.000

3 40.000 3.000

4 60.000 3.000

5 80.000 2.900

6 120.000 2.900

7 180.000 2.900

8 240.000 2.800

9 300.000 2.700

10 360.000 2.700 2.699

11 450.000 2.600 2.626

12 570.000 2.500 2.531

13 800.000 2.400 2.360

4 3 2 1 0

0 200 400 600 800

X

Y

Actual Data

Curve Fit

1.0

0.8

0.6

Y

0.4

0.2

0.0

Actual Data

Curve Fit

Mateur 5 T=15°C - Co=0.80 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	0.800	0.799			2
20.000	0.750	0.767		Y = 0.80 * e'(-0.00204813 * X)	3
40.000	0.700	0.736			4
60.000	0.700	0.707		Value Variance	5
80.000	0.700	0.678			6
120.000	0.600	0.625		Bo: 0.7992 0.0001	7
180.000	0.600	0.553		B1: -0.0020 0.0000	8
240.000	0.500	0.489			9
300.000	0.500	0.432			10
360.000	0.400	0.382			11
450.000	0.300	0.318		Correlation (R'2) = .9785718	12
570.000	0.200	0.249			13
1050.000	0.100	0.093

Y = 0.80 * e'(-0.00204813 * X)

0 500 1000 1500

X

Mateur 5 T=15°C - Co=2 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.000	2.002			2
20.000	1.950	1.952		Y = 2.0 * e'(-0.00 1269522 * X)	3
40.000	1.900	1.903			4
60.000	1.800	1.856		Value Variance	5
80.000	1.800	1.809			6
120.000	1.700	1.720		Bo: 2.0025 0.0001	7
180.000	1.600	1.593		B1: -0.0013 0.0000	8
240.000	1.500	1.477			9
300.000	1.400	1.368			10
360.000	1.300	1.268			11
450.000	1.200	1.131		Correlation (R'2) = .9877587	12
570.000	0.900	0.971

Y = 2.0 * e'(-0.001269522 * X)

0 100 200 300 400 500 600

X

2.5

2.0

1.0

0.5

0.0

1.5

Y

Actual Data

Curve Fit

Point X Actual Y Predicted Y

1 0.000 1.500 1.502

2 20.000 1.450 1.448

3 40.000 1.400 1.396

4 60.000 1.300 1.345

5 80.000 1.300 1.296

6 120.000 1.200 1.204

7 180.000 1.000 1.078

8 240.000 1.000 0.965

9 300.000 0.900 0.864

10 360.000 0.800 0.773

11 450.000 0.700 0.655

12 680.000 0.400 0.429

Coefficients for Equation:

Y = 1.50 * e'(-0.00184433 * X)

Value Variance

Bo: 1.5025 0.0001

B1: -0.0018 0.0000

Correlation (R'2) = .9892111

Y = 1.50 * e'(-0.00184433 * X)

0 200 400 600 800

X

2.0

0.5

0.0

1.5

1.0

Y

Actual Data

Curve Fit

Point X Actual Y Predicted Y

1 0.000 3.000 2.975

2 20.000 3.000 2.946

3 40.000 3.000 2.917

4 60.000 2.900 2.888

5 80.000 2.900 2.860

6 120.000 2.800 2.803

7 180.000 2.700 2.721

8 240.000 2.600 2.642

9 300.000 2.500 2.564

10 360.000 2.400 2.489

11 450.000 2.300 2.380

12 800.000 2.100 2.001

Coefficients for Equation:

Y = 3.0 * e'(-0.000495 8928 * X) Value Variance

Bo: 2.9754 0.0004

B1: -0.0005 0.0000

Correlation (R'2) = .9551933

Y = 3.0 * e'(-0.000495893 * X)

3.0 2.5 2.0 1.5 1.0 0.5 0.0

0 200 400 600 800

X

Y

Actual Data

Curve Fit

1.5

1.0

0.5

0.0

1.5

1.0

0.5

0.0

Mateur 5 T=20°C - Co=1 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	1.001			2
20.000	0.950	0.900		Y = 1.00 * e'(-0.0053159 * X)	3
40.000	0.800	0.809			4
60.000	0.700	0.728		Value Variance	5
80.000	0.600	0.654			6
120.000	0.500	0.529		Bo: 1.0011 0.0001	7
180.000	0.400	0.385		B1: -0.0053 0.0000	8
240.000	0.300	0.280			9
300.000	0.250	0.203			10
400.000	0.100	0.119		Correlation (R'2) = .987 835

Y = 1.00 * e'(-0 .0053159 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

Mateur 5 T=20°C - Co=1,5 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.500	1.499			2
20.000	1.400	1.393		Y = 1.50 * e'(-0.00364948 * X)	3
40.000	1.300	1.295		Value Variance	4
60.000	1.200	1.204			5
80.000	1.100	1.119		Bo: 1.4987 0.0003	6
120.000	1.000	0.967		B1: -0.0036 0.0000	7
180.000	0.900	0.777			8
240.000	0.600	0.624			9
300.000	0.400	0.501		Correlation (R'2) = .9877521	10
600.000	0.200	0.168			11
720.000	0.100	0.108

Y = 1.50 * e'(-0.00364948 * X)

0 200 400 600 800

X

Y

Actual Data

Curve Fit

2.5

2.0

1.5

1.0

0.5

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

Mateur 5 T=20°C - Co=2 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.000	2.045		Y = 2.0 * e'(-0.00250048 * X)	2
20.000	1.900	1.945			3
40.000	1.900	1.850		Value Variance	4
60.000	1.900	1.760			5
80.000	1.600	1.674		Bo: 2.0447 0.0007	6
120.000	1.400	1.515		B1: -0.0025 0.0000	7
180.000	1.300	1.304			8
240.000	1.200	1.122			9
300.000	1.000	0.966			10
550.000	0.500	0.517		Correlation (R'2) = .976 1243

Y = 2.0 * e'(-0.00250048 * X)

0 100 200 300 400 500 600

X

Y

Actual Data

Curve Fit

Mateur 5 T=20°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 2.980

2 20.000 3.000 2.903

3 40.000 2.900 2.829

4 60.000 2.700 2.756

5 80.000 2.700 2.686

6 120.000 2.500 2.549

7 180.000 2.300 2.358

8 240.000 2.100 2.181

9 300.000 2.000 2.017

10 420.000 1.800 1.726

Coefficients for Equation:

Y = 3.0 * e'(-0.001300521 * X)

Value Variance

Bo: 2.9800 0.0005

B1: -0.0013 0.0000

Correlation (R'2) = .97722 18

Y = 3.0 * e'(-0.001300521 * X)

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

1.0

0.8

0.6

0.4

0.2

0.0

2.0

1.5

1.0

0.5

0.0

Mateur 5 T=25°C - Co=1 mg/l

Model premier ordre

Point X		Actual Y Predicted Y		Coefficients for Equation:					1
0.000	1.000	0.996						2
20.000	0.800	0.803	Y = 1.00 *	e'(-0.0107722 * X)				3
40.000	0.700	0.647						4
60.000	0.400	0.522		Value	Variance	5
80.000	0.400	0.421						6
120.000	0.400	0.273	Bo:	0.9958		0.0010		7
200.000	0.100	0.115	B1:	-0.0108		0.0000

Correlation (R'2) = .9416605

Y = 1.00 * e'(-0.010772 * X)

0 50 100 150 200

X

Y

Actual Data

Curve Fit

Mateur 5 T=25°C - Co=1,5 mg/l

Model premier ordre

Point X		Actual Y Predicted Y		Coefficients for Equation:					1
0.000	1.500	1.511						2
20.000	1.400	1.293	Y = 1.51 *	e'(-0.0077999 * X)				3
40.000	1.100	1.106						4
60.000	1.000	0.947		Value	Variance	5
80.000	0.800	0.810						6
120.000	0.600	0.593	Bo:	1.5115		0.0004		7
180.000	0.300	0.371	B1:	-0.0078		0.0000		8
360.000	0.100	0.091

Correlation (R'2) = .9876705

Y = 1.51 * e'(-0.0077999 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

2.5

2.0

1.5

1.0

0.5

0.0

4

3

2

1

0

Mateur 5 T=25°C - Co=2 mg/l

Model premier ordre

Point X		Actual Y Predicted Y		Coefficients for Equation:				1
0.000	2.000	2.032					2
20.000	1.800	1.883	Y = 2.0 * e'(-0.003 80603 * X)				3
40.000	1.700	1.745					4
60.000	1.600	1.617	Value	Variance	5
80.000	1.500	1.499					6
120.000	1.500	1.287	Bo: 2.032 1		0.00 12		7
180.000	1.000	1.024	B1: -0.003 8		0.0000		8
360.000	0.500	0.516

Correlation (R'2) = .9682665

Y = 2.0 * e'(-0.00380603 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

Mateur 5 T=25°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 3.023

2 20.000 2.900 2.835

3 40.000 2.700 2.659

4 60.000 2.500 2.494

5 80.000 2.400 2.340

6 120.000 2.100 2.058

7 180.000 1.500 1.699

8 360.000 1.000 0.955

Coefficients for Equation:

Y = 3.0 * e'(-0.00320205 * X)

Value Variance

Bo: 3.0228 0.0011

B1: -0.0032 0.0000

Correlation (R'2) = .9835948

Y = 3.0 * e'(-0.00320205 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

1.0

0.8

0.6

0.4

0.2

0.0

Mateur 9 T=25°C - Co=1 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 0.943

2 10.000 0.800 0.856

3 20.000 0.800 0.778

4 30.000 0.750 0.706

5 40.000 0.700 0.642

6 60.000 0.400 0.529

7 100.000 0.400 0.360

8 120.000 0.300 0.297

Coefficients for Equation:

Y = 0.94 * e'(-0.0096242 * X)

Value Variance

Bo: 0.9429 0.0007

B1: -0.0096 0.0000

Correlation (R'2) = .92381

Y = 0.94 * e'(-0.0096242 * X)

0 50 100 150

X

Y

Actual Data

Curve Fit

1.5

1.0

0.5

0.0

Mateur 9 T=25°C - Co=1.5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.382

2 10.000 1.300 1.286

3 20.000 1.200 1.196

4 30.000 1.000 1.113

5 40.000 1.000 1.035

6 60.000 0.900 0.896

7 100.000 0.700 0.671

Coefficients for Equation:

Y = 1.38 * e'(-0.0072211 * X)

Value Variance

Bo: 1.3822 0.0009

B1: -0.0072 0.0000

Correlation (R'2) = .923 8272

Y = 1.38 * e'(-0.0072211 * X)

0 20 40 60 80 100

X

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

Mateur 9 T=25°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 1.790

2 10.000 1.800 1.681

3 20.000 1.700 1.578

4 30.000 1.500 1.481

5 40.000 1.200 1.391

6 60.000 1.000 1.226

7 100.000 0.900 0.952

8 150.000 0.800 0.694

Coefficients for Equation:

Y = 1.8 * e'(-0.0063133 * X)

Value Variance

Bo: 1.7903 0.0037

B1: -0.0063 0.0000

Correlation (R'2) = .8486004

Y = 1.8 * e'(-0.0063133 * X)

0 50 100 150

X

Y

Actual Data

Curve Fit

3.0

2.5

2.0

1.5

1.0

0.5

0.0

Mateur 9 T=25°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 2.890

2 10.000 2.900 2.816

3 20.000 2.700 2.744

4 30.000 2.600 2.674

5 40.000 2.500 2.605

6 60.000 2.500 2.473

7 100.000 2.200 2.229

8 150.000 2.000 1.958

Coefficients for Equation:

Y = 2.9 * e'(-0.00259694 * X)

Value Variance

Bo: 2.8903 0.0009

B1: -0.0026 0.0000

Correlation (R'2) = .945055

Y = 2.9 * e'(-0.0025969 * X)

0 50 100 150

X

Y

Actual Data

Curve Fit

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	0.991			2
10.000	1.000	0.969		Y = 0.99 * e'(-0.00225532 * X)	3
20.000	0.950	0.947		Value Variance	4
30.000	0.950	0.926			5
40.000	0.900	0.905		Bo: 0.9907 0.0001	6
60.000	0.900	0.865		B1: -0.0023 0.0000	7
100.000	0.700	0.791			8
150.000	0.700	0.706			9
200.000	0.600	0.631			10
250.000	0.600	0.564		Correlation (R'2) = .9577044	11
310.000	0.500	0.492

Y = 0.99 * e'(-0 .00225532 * X)

0 100 200 300 400

X

0.8

0.6

0.4

0.2

0.0

1.0

Y

Actual Data

Curve Fit

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.500	1.470			2
10.000	1.450	1.458		Y = 1.47 * e'(-0.000847880 * X)	3
20.000	1.400	1.446		Value Variance	4
30.000	1.400	1.433			5
40.000	1.400	1.421		Bo: 1.4704 0.0001	6
60.000	1.400	1.397		B1: -0.0008 0.0000	7
100.000	1.400	1.351			8
150.000	1.300	1.295			9
200.000	1.300	1.241			10
320.000	1.100	1.121		Correlation (R'2) = .9533 083	11
440.000	1.000	1.013

Y = 1.47 * e'(-0.00084788 * X)

0 100 200 300 400 500

X

0.5

0.0

1.5

1.0

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

Mateur 9 T=15°C - Co=2 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.000	1.984		Y = 2.0 * e^(-0.00083 1700 * X)	2
10.000	2.000	1.967		Value Variance	3
20.000	2.000	1.951			4
30.000	1.900	1.935		Bo: 1.9838 0.0001	5
40.000	1.900	1.919		B1: -0.0008 0.0000	6
60.000	1.900	1.887			7
100.000	1.800	1.826			8
150.000	1.700	1.751			9
200.000	1.700	1.680		Correlation (R^2) = .9753298	10
320.000	1.500	1.520			11
440.000	1.400	1.376

Y = 2.0 * e^(-0.000831700 * X)

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

Mateur 9 T=15°C - Co=3 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	3.000	2.997			2
10.000	3.000	2.980		Y = 3.0 * e^(-0.000569 870 * X)	3
20.000	2.900	2.963		Value Variance	4
30.000	2.900	2.946			5
40.000	2.900	2.929		Bo: 2.9970 0.0002	6
60.000	2.900	2.896		B1: -0.0006 0.0000	7
100.000	2.900	2.831			8
150.000	2.800	2.751			9
200.000	2.700	2.674			10
320.000	2.500	2.497		Correlation (R^2) = .9669 161	11
440.000	2.300	2.332

Y = 3.0 * e^(-0.000569870 * X)

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

Mateur 9 T=20°C - Co=1 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 0.983

2 10.000 1.000 0.946

3 20.000 0.900 0.911

4 30.000 0.900 0.876

5 40.000 0.800 0.844

6 60.000 0.800 0.781

7 100.000 0.700 0.670

8 150.000 0.500 0.554

9 200.000 0.400 0.457

10 260.000 0.400 0.363

11 320.000 0.300 0.289

Coefficients for Equation:

Y = 0.98 * e'(-0.003 82872 * X)

Value Variance

Bo: 0.983 1 0.0001

B1: -0.003 8 0.0000

Correlation (R'2) = .9765593

Y = 0.98 * e'(-0.003 8287 * X)

0 100 200 300 400

X

0.8

0.6

0.4

0.2

0.0

1.0

Y

Actual Data

Curve Fit

Mateur 9 T=20°C - Co=1.5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.454

2 10.000 1.400 1.425

3 20.000 1.400 1.396

4 30.000 1.300 1.368

5 40.000 1.300 1.340

6 60.000 1.300 1.286

7 100.000 1.200 1.185

8 150.000 1.100 1.069

9 200.000 1.000 0.965

10 260.000 0.900 0.854

11 320.000 0.700 0.755

Coefficients for Equation:

Y = 1.45 * e'(-0.00204932 * X)

Value Variance

Bo: 1.4543 0.0002

B1: -0.0020 0.0000

Correlation (R'2) = .9729976

Y = 1.45 * e'(-0.00204932 * X)

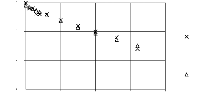
0 100 200 300 400

X

0.5

0.0

1.5

1.0

Y

Actual Data

Curve Fit

Mateur 9 T=20°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.012

2 10.000 2.000 1.978

3 20.000 2.000 1.945

4 30.000 1.900 1.912

5 40.000 1.900 1.879

6 60.000 1.700 1.817

7 100.000 1.700 1.697

8 150.000 1.600 1.559

9 200.000 1.500 1.431

10 260.000 1.200 1.293

11 320.000 1.200 1.167

Coefficients for Equation:

Y = 2.0 * e'(-0.00170178 * X)

Value Variance

Bo: 2.0119 0.0003

B1: -0.0017 0.0000

Correlation (R'2) = .9623561

Y = 2.0 * e'(-0 .00170178 * X)

0 100 200 300 400

X

2.5

2.0

0.5

0.0

1.5

1.0

Y

Actual Data

Curve Fit

Mateur 9 T=20°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 2.990

2 10.000 3.000 2.966

3 20.000 3.000 2.943

4 30.000 2.900 2.920

5 40.000 2.900 2.897

6 60.000 2.800 2.851

7 100.000 2.800 2.763

8 150.000 2.600 2.656

9 200.000 2.500 2.553

10 260.000 2.400 2.435

11 320.000 2.400 2.322

Coefficients for Equation:

Y = 3.0 * e'(-0.000789417 * X)

Value Variance

Bo: 2.9896 0.0002

B1: -0.0008 0.0000

Correlation (R'2) = .9600464

Y = 3.0 * e'(-0.000789417 * X)

3.0 2.5 2.0 1.5 1.0 0.5 0.0

0 100 200 300 400

X

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

2.5

2.0

1.5

1.0

0.5

0.0

SGR01 T=25°C - Co=1.50 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.500	1.524			2
20.000	1.500	1.428		Y = 1.52 * e'(-0.00324535 * X)	3
40.000	1.300	1.338			4
60.000	1.200	1.254		Value Variance	5
80.000	1.200	1.175			6
120.000	1.000	1.032		Bo: 1.5239 0.0007	7
180.000	1.000	0.850		B1: -0.0032 0.0000	8
240.000	0.600	0.699			9
300.000	0.600	0.576		Correlation (R'2) = .95 13041

Y = 1.52 * e'(-0.00324535 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=25°C - Co=2.5 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.500	2.486			2
20.000	2.300	2.348		Y = 2.5 * e'(-0.00286395 * X)	3
40.000	2.300	2.217			4
60.000	2.200	2.094		Value Variance	5
80.000	1.800	1.977			6
120.000	1.800	1.763		Bo: 2.4864 0.00 14	7
180.000	1.400	1.485		B1: -0.0029 0.0000	8
240.000	1.400	1.250			9
300.000	1.000	1.053		Correlation (R'2) = .9588651

Y = 2.5 * e'(-0.00286395 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

1.5

1.0

0.5

0.0

4

3

2

1

0

SGR01 T=25°C - Co=1 mg/l

Model premier ordre

Point X	Actual Y Predicted Y			Coefficients for Equation:	1 0.000
1.000	1.029			2 20.000
0.900	0.911		Y = 1.03 * e'(-0.0060735 * X)	3 40.000
0.800	0.807			4 60.000
0.600	0.715		Value Variance	5 80.000
0.600	0.633			6 120.000
0.600	0.496		Bo: 1.0288 0.0008	7 180.000
0.500	0.345		B1: -0.0061 0.0000	8 240.000
0.200	0.239			9 300.000
0.150	0.166		Correlation (R'2) = .9337565

Y = 1.03 * e'(-0.0060735 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=25°C - Co=3 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	3.000	3.030			2
20.000	2.900	2.948		Y = 3.0 * e'(-0.001363849 * X)	3
40.000	2.900	2.869			4
60.000	2.800	2.792		Value Variance	5
80.000	2.700	2.717			6
120.000	2.700	2.573		Bo: 3.0300 0.0004	7
180.000	2.300	2.370		B1: -0.0014 0.0000	8
240.000	2.200	2.184			9
300.000	2.000	2.013		Correlation (R'2) = .9744996

Y = 3.0 * e'(-0.001363849 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

1.5

1.0

0.5

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

SGR01 T=15°C - Co=1,5 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.500	1.499			2
20.000	1.500	1.445		Y = 1.50 * e'(-0.00183307 * X)	3
40.000	1.400	1.393			4
60.000	1.400	1.343		Value Variance	5
80.000	1.300	1.294			6
120.000	1.100	1.203		Bo: 1.4989 0.0004	7
180.000	1.000	1.078		B1: -0.0018 0.0000	8
240.000	1.000	0.965			9
300.000	0.900	0.865		Correlation (R'2) = .9386421

Y = 1.50 * e'(-0.00183307 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=15°C - Co=2,5 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.500	2.503			2
20.000	2.500	2.454		Y = 2.5 * e'(-0.000986044 * X)	3
40.000	2.400	2.406			4
60.000	2.400	2.360		Value Variance	5
80.000	2.300	2.313			6
120.000	2.200	2.224		Bo: 2.5033 0.0003	7
180.000	2.000	2.096		B1: -0.0010 0.0000	8
240.000	2.000	1.976			9
300.000	1.900	1.862		Correlation (R'2) = .9616582

Y = 2.50 * e'(-0.00098604 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=15°C - Co=1 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 1.001

2 20.000 0.900 0.938

3 40.000 0.900 0.880

4 60.000 0.800 0.824

5 80.000 0.800 0.773

6 120.000 0.700 0.679

7 180.000 0.600 0.559

8 240.000 0.400 0.460

9 300.000 0.400 0.379

Coefficients for Equation:

Y = 1.00 * e'(-0.00323789 * X)

Value Variance

Bo: 1.0011 0.0002

B1: -0.0032 0.0000

Correlation (R'2) = .9755 875

Y = 1.00 * e'(-0.00323789 * X)

1.5 1.0 0.5 0.0

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=15°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 3.036

2 20.000 3.000 3.009

3 40.000 3.000 2.982

4 60.000 3.000 2.956

5 80.000 2.900 2.930

6 120.000 2.900 2.878

7 180.000 2.800 2.803

8 240.000 2.700 2.729

9 300.000 2.700 2.657

10 420.000 2.500 2.519

Coefficients for Equation:

Y = 3.0 * e'(-0.000443 9525 * X) Value Variance

Bo: 3.0357 0.0001

B1: -0.0004 0.0000

Correlation (R'2) = .9699631

Y = 3.0 * e'(-0.0004439525 * X)

4 3 2 1 0

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

SGR01 T=20°C - Co=1,5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.566

2 20.000 1.400 1.469

3 40.000 1.400 1.378

4 60.000 1.200 1.292

5 80.000 1.200 1.212

6 120.000 1.200 1.067

7 180.000 1.000 0.880

8 240.000 0.800 0.727

9 300.000 0.500 0.600

Coefficients for Equation:

Y = 1.57 * e'(-0.00319924 * X)

Value Variance

Bo: 1.5659 0.0011

B1: -0.0032 0.0000

Correlation (R'2) = .9326589

Y = 1.57 * e'(-0.00319924 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=20°C - Co=2,5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.500 2.519

2 20.000 2.500 2.402

3 40.000 2.200 2.291

4 60.000 2.200 2.185

5 80.000 2.000 2.084

6 120.000 2.000 1.896

7 180.000 1.600 1.645

8 240.000 1.500 1.428

9 300.000 1.200 1.239

Coefficients for Equation:

Y = 2.5 * e'(-0.00236603 * X)

Value Variance

Bo: 2.5189 0.0007

B1: -0.0024 0.0000

Correlation (R'2) = .9724 153

Y = 2.5 * e'(-0.00236603 * X)

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=20°C - Co= 1 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 1.020

2 20.000 0.900 0.941

3 40.000 0.900 0.869

4 60.000 0.800 0.802

5 80.000 0.800 0.741

6 120.000 0.600 0.631

7 180.000 0.500 0.497

8 240.000 0.400 0.391

9 300.000 0.300 0.307

Coefficients for Equation:

Y = 1.02 * e'(-0.00399751 * X)

Value Variance

Bo: 1.0198 0.0001

B1: -0.0040 0.0000

Correlation (R'2) = .9846 83

Y = 1.02 * e'(-0 .0039975 * X)

1.5 1.0 0.5 0.0

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR01 T=20°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 3.017

2 20.000 3.000 2.960

3 40.000 2.900 2.903

4 60.000 2.800 2.848

5 80.000 2.800 2.793

6 120.000 2.700 2.687

7 180.000 2.500 2.536

8 240.000 2.500 2.393

9 300.000 2.200 2.259

Coefficients for Equation:

Y = 3.0 * e'(-0.000965710 * X)

Value Variance

Bo: 3.0175 0.0003

B1: -0.0010 0.0000

Correlation (R'2) = .9643 35

Y = 3.0 * e'(-0.000965710 * X)

4 3 2 1 0

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

2.5

2.0

1.5

1.0

0.5

0.0

1.5

1.0

0.5

0.0

SGR4 T=25°C - Co=2mg/l

Model premier ordre

Point X		Actual Y Predicted Y		Coefficients for Equation:			1
0.000	2.000	2.039				2
20.000	1.900	1.868	Y = 2.0 * e'(-0.0043 865 * X)			3
40.000	1.700	1.711	Value	Variance		4
60.000	1.600	1.567				5
80.000	1.600	1.435	Bo: 2.0388	0.0010		6
100.000	1.200	1.315	B1: -0.0044	0.0000		7
120.000	1.100	1.204				8
180.000	1.000	0.926				9
240.000	0.700	0.711	Correlation (R'2) = .9610 102

Y = 2.0 * e'(-0.0043865 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=25°C - Co=1mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	1.009			2
20.000	0.900	0.895		Y = 1.01 * e'(-0.0059845 * X)	3
40.000	0.800	0.794		Value Variance	4
60.000	0.700	0.705			5
80.000	0.600	0.625		Bo: 1.0092 0.0005	6
100.000	0.500	0.555		B1: -0.0060 0.0000	7
120.000	0.500	0.492			8
180.000	0.500	0.344			9
230.000	0.200	0.255		Correlation (R'2) = .94046 16

Y = 1.01 * e'(-0.0059845 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

SGR4 T=25°C - Co=2.7mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.700 2.728

2 20.000 2.600 2.562

3 40.000 2.500 2.406

4 60.000 2.200 2.260

5 80.000 2.000 2.123

6 120.000 2.000 1.872

7 180.000 1.500 1.551

8 240.000 1.300 1.285

Coefficients for Equation:

Y = 2.7 * e'(-0.003 13465 * X)

Value Variance

Bo: 2.7276 0.00 10

B1: -0.0031 0.0000

Correlation (R'2) = .972783

Y = 2.7 * e'(-0 .00313465 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=25°C - Co=1,5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.517

2 20.000 1.300 1.358

3 40.000 1.300 1.215

4 60.000 1.100 1.087

5 80.000 1.000 0.973

6 100.000 1.000 0.871

7 120.000 0.600 0.779

8 180.000 0.600 0.558

9 240.000 0.400 0.400

Coefficients for Equation:

Y = 1.52 * e'(-0.0055528 * X)

Value Variance

Bo: 1.5172 0.0010

B1: -0.0056 0.0000

Correlation (R'2) = .9446918

Y = 1.52 * e'(-0.0055528 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=15°C - Co=1mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 1.005

2 20.000 0.900 0.942

3 40.000 0.900 0.884

4 60.000 0.800 0.829

5 80.000 0.800 0.778

6 100.000 0.700 0.730

7 120.000 0.700 0.685

8 180.000 0.700 0.565

9 240.000 0.400 0.466

Coefficients for Equation:

Y = 1.00 * e'(-0.00319648 * X)

Value Variance

Bo: 1.0046 0.0004

B1: -0.0032 0.0000

Correlation (R'2) = .8999045

Y = 1.00 * e'(-0.00319648 * X)

1.5 1.0 0.5 0.0

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=15°C - Co=2mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.010

2 20.000 2.000 1.964

3 40.000 1.900 1.919

4 60.000 1.900 1.875

5 80.000 1.800 1.832

6 100.000 1.800 1.791

7 120.000 1.700 1.750

8 180.000 1.700 1.632

9 240.000 1.500 1.523

Coefficients for Equation:

Y = 2.0 * e'(-0.001155508 * X)

Value Variance

Bo: 2.0099 0.0002

B1: -0.0012 0.0000

Correlation (R'2) = .9470767

Y = 2.0 * e'(-0.001155508 * X)

2.5 2.0 1.5 1.0 0.5 0.0

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

3.0

2.5

2.0

1.5

1.0

0.5

0.0

2.0

1.5

1.0

0.5

0.0

SGR4 T=20C - Co=2,7mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.700 2.717

2 20.000 2.700 2.662

3 40.000 2.600 2.609

4 60.000 2.500 2.556

5 80.000 2.500 2.505

6 100.000 2.500 2.454

7 120.000 2.400 2.405

8 180.000 2.300 2.262

9 240.000 2.100 2.129

Coefficients for Equation:

Y = 2.7 * e'(-0.001016780 * X)

Value Variance

Bo: 2.7169 0.0002

B1: -0.0010 0.0000

Correlation (R'2) = .9688563

Y = 2.7 * e'(-0 .001016780 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=20°C - Co=1,5 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.500	1.514			2
20.000	1.400	1.410		Y = 1.51 * e'(-0.00355374 * X)	3
40.000	1.300	1.313			4
60.000	1.300	1.223		Value Variance	5
80.000	1.100	1.139			6
100.000	1.000	1.061		Bo: 1.5137 0.0004	7
120.000	1.000	0.988		B1: -0.0036 0.0000	8
180.000	0.900	0.798			9
240.000	0.600	0.645		Correlation (R'2) = .963519

Y = 1.51 * e'(-0 .00355374 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

1.5

1.0

0.5

0.0

SGR4 T=20°C - Co=2 mg/l

Model premier ordre

Point X	Actual Y Predicted Y			Coefficients for Equation:	1 0.000
2.000	1.998			2 20.000
2.000	1.929		Y = 2.0 * e'(-0.00 174687 * X)	3 40.000
1.800	1.863		Value Variance	4 60.000
1.800	1.799			5 80.000
1.700	1.737		Bo: 1.9978 0.0002	6 100.000
1.700	1.678		B1: -0.0017 0.0000	7 120.000
1.600	1.620			8 180.000
1.500	1.459			9 240.000
1.300	1.314		Correlation (R'2) = .9675541

Y = 2.0 * e'(-0 .00174687 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=20°C - Co=1 mg/l

Model premier ordre

Point X	Actual Y Predicted Y			Coefficients for Equation:	1 0.000
1.000	1.006		Y = 1.01 * e'(-0.0046221 * X)	2 20.000
0.900	0.917		Value Variance	3 40.000
0.800	0.836			4 60.000
0.800	0.762		Bo: 1.0062 0.0002	5 80.000
0.700	0.695		B1: -0.0046 0.0000	6 100.000
0.600	0.634			7 120.000
0.600	0.578			8 180.000
0.500	0.438			9 240.000
0.300	0.332		Correlation (R'2) = .9757414

Y = 1.01 * e'(-0.0046221 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

2.0

1.5

1.0

0.5

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

SGR4 T=15°C - Co=1,5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.523

2 20.000 1.400 1.448

3 40.000 1.400 1.376

4 60.000 1.300 1.308

5 80.000 1.300 1.244

6 100.000 1.200 1.182

7 120.000 1.100 1.124

8 180.000 1.000 0.965

9 240.000 0.800 0.829

Coefficients for Equation:

Y = 1.52 * e'(-0.00253495 * X)

Value Variance

Bo: 1.523 1 0.0002

B1: -0.0025 0.0000

Correlation (R'2) = .9769 105

Y = 1.52 * e'(-0.00253495 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR4 T=15°C - Co=2,7 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.700 2.698

2 20.000 2.600 2.642

3 40.000 2.600 2.588

4 60.000 2.500 2.535

5 80.000 2.500 2.483

6 100.000 2.500 2.432

7 120.000 2.400 2.381

8 180.000 2.200 2.238

9 240.000 2.100 2.102

Coefficients for Equation:

Y = 2.7 * e'(-0.001039382 * X)

Value Variance

Bo: 2.6978 0.0002

B1: -0.0010 0.0000

Correlation (R'2) = .9677081

Y = 2.7 * e'(-0.001039382 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

1.0

0.8

0.6

0.4

0.2

0.0

4

3

2

1

0

SGR6 T=25°C - Co=0.8mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	0.800	0.800		Y = 0.80 * e'(-0.0056032 * X)	2
20.000	0.700	0.715		Value Variance	3
40.000	0.600	0.639			4
60.000	0.600	0.571		Bo: 0.7998 0.0001	5
80.000	0.500	0.511		B1: -0.0056 0.0000	6
100.000	0.500	0.457			7
120.000	0.400	0.408			8
180.000	0.300	0.292		Correlation (R'2) = .98423	9
240.000	0.200	0.208

Y = 0.80 * e'(-0.0056032 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=25°C - Co=3mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	3.000	3.006			2
20.000	2.900	2.916		Y = 3.0 * e'(-0.00153210 * X)	3
40.000	2.800	2.828			4
60.000	2.700	2.742		Value Variance	5
80.000	2.700	2.660			6
100.000	2.600	2.579		Bo: 3.0064 0.0004	7
120.000	2.500	2.502		B1: -0.0015 0.0000	8
180.000	2.400	2.282			9
240.000	2.000	2.081		Correlation (R'2) = .9656297

Y = 3.0 * e'(-0.001532097 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=15°C - Co=3mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 3.027

2 20.000 3.000 2.984

3 40.000 2.900 2.941

4 60.000 2.900 2.898

5 80.000 2.900 2.857

6 100.000 2.800 2.816

7 120.000 2.800 2.775

8 180.000 2.700 2.657

9 240.000 2.500 2.544

Coefficients for Equation:

Y = 3.0 * e^(-0.000724611 * X)

Value Variance

Bo: 3.0272 0.0001

B1: -0.0007 0.0000

Correlation (R^2) = .9550076

Y = 3.0 * e^(-0 .000724611 * X)

4 3 2 1 0

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=15°C - Co=1.6mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.600 1.622

2 20.000 1.600 1.594

3 40.000 1.600 1.567

4 60.000 1.500 1.540

5 80.000 1.500 1.514

6 100.000 1.500 1.488

7 120.000 1.500 1.463

8 180.000 1.400 1.390

9 240.000 1.300 1.320

Coefficients for Equation:

Y = 1.62 * e^(-0.000857625 * X) Value Variance

Bo: 1.6217 0.0001

B1: -0.0009 0.0000

Correlation (R^2) = .9334002

Y = 1.6 * e^(-0.000857625 * X)

2.0 1.5 1.0 0.5 0.0

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=25°C - Co=1,6mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.600 1.582

2 20.000 1.500 1.506

3 40.000 1.500 1.434

4 60.000 1.400 1.365

5 80.000 1.200 1.299

6 100.000 1.200 1.237

7 120.000 1.200 1.177

8 180.000 1.000 1.015

9 240.000 0.900 0.876

Coefficients for Equation:

Y = 1.58 * e'(-0.00246350 * X)

Value Variance

Bo: 1.5820 0.0003

B1: -0.0025 0.0000

Correlation (R'2) = .9576998

Y = 1.58 * e'(-0.00246350 * X)

2.0 1.5 1.0 0.5 0.0

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=25°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.029

2 20.000 2.000 1.961

3 40.000 1.900 1.896

4 60.000 1.800 1.832

5 80.000 1.800 1.771

6 100.000 1.700 1.711

7 120.000 1.600 1.654

8 180.000 1.600 1.493

9 240.000 1.300 1.348

Coefficients for Equation:

Y = 2.0 * e'(-0.00 170629 * X)

Value Variance

Bo: 2.0295 0.0003

B1: -0.0017 0.0000

Correlation (R'2) = .9487936

Y = 2.0 * e'(-0.00170629 * X)

2.5 2.0 1.5 1.0 0.5 0.0

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

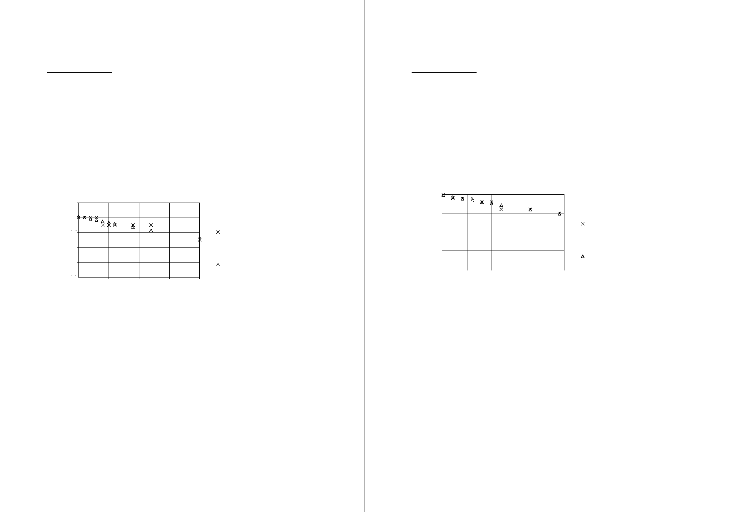
1.0

0.8

0.6

0.4

0.2

0.0

2.0

1.5

1.0

0.5

0.0

SGR6 T=20°C - Co=0,8 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	0.800	0.816			2
20.000	0.800	0.799		Y = 0.82 * e'(-0.001078665 * X)	3
40.000	0.800	0.782			4
60.000	0.800	0.765		Value Variance	5
80.000	0.700	0.749			6
100.000	0.700	0.733		Bo: 0.8162 0.0002	7
120.000	0.700	0.717		B1: -0.0011 0.0000	8
180.000	0.700	0.672			9
240.000	0.700	0.630			10
400.000	0.500	0.530		Correlation (R'2) = .8498659

Y = 0.82 * e'(-0.001078665 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

SGR6 T=20°C - Co=2mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.000	1.984			2
20.000	1.900	1.936		Y = 2.0 * e'(-0.00 1220284 * X)	3
40.000	1.900	1.889			4
60.000	1.900	1.844		Value Variance	5
80.000	1.800	1.799			6
100.000	1.800	1.756		Bo: 1.9837 0.0003	7
120.000	1.600	1.714		B1: -0.0012 0.0000	8
180.000	1.600	1.593			9
240.000	1.500	1.480		Correlation (R'2) = .9133528

Y = 2.0 * e'(-0.001220284 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

4

3

2

1

0

2.0

1.5

1.0

0.5

0.0

SGR6 T=20°C - Co=3 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	3.000	3.009			2
20.000	3.000	2.977		Y = 3.0 * e'(-0.000527 1208 * X)	3
40.000	3.000	2.946			4
60.000	2.900	2.915		Value Variance	5
80.000	2.900	2.885			6
100.000	2.800	2.854		Bo: 3.0088 0.0002	7
120.000	2.800	2.824		B1: -0.0005 0.0000	8
180.000	2.700	2.736			9
240.000	2.700	2.651		Correlation (R'2) = .9048 173

Y = 3.0 * e'(-0.000527121 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=20°C - Co=1,6mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.600	1.600			2
20.000	1.600	1.569		Y = 1.60 * e'(-0.000958051 * X)	3
40.000	1.500	1.539		Value Variance	4
60.000	1.500	1.510			5
80.000	1.500	1.482		Bo: 1.5996 0.0001	6
100.000	1.500	1.453		B1: -0.0010 0.0000	7
120.000	1.400	1.426			8
180.000	1.300	1.346			9
240.000	1.300	1.271		Correlation (R'2) = .911517

Y = 1.6 * e'(-0.0009580507 * X)

0 50 100 150 200 250

X

Y

Actual Data

Curve Fit

SGR6 T=15°C - Co=0,8 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 0.800 0.816

2 20.000 0.800 0.799

3 40.000 0.800 0.782

4 60.000 0.800 0.765

5 80.000 0.700 0.749

6 100.000 0.700 0.733

7 120.000 0.700 0.717

8 180.000 0.700 0.672

9 240.000 0.700 0.630

10 400.000 0.500 0.530

Coefficients for Equation:

Y = 0.82 * e'(-0.001078665 * X) Value Variance

Bo: 0.8162 0.0002

B1: -0.0011 0.0000

Correlation (R'2) = .8498659

Y = 0.82 * e'(-0.001078665 * X)

1.0 0.8 0.6 0.4 0.2 0.0

0 100 200 300 400

X

Y

Actual Data

Curve Fit

SGR6 T=15°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.011

2 20.000 2.000 1.994

3 40.000 2.000 1.977

4 60.000 2.000 1.960

5 80.000 1.900 1.944

6 100.000 1.900 1.927

7 120.000 1.900 1.911

8 180.000 1.900 1.863

9 240.000 1.800 1.816

10 400.000 1.700 1.697

Coefficients for Equation:

Y = 2.0 * e'(-0.0004241281 * X) Value Variance

Bo: 2.0106 0.0001

B1: -0.0004 0.0000

Correlation (R'2) = .924647

Y = 2.01 * e'(-0.000424128 * X)

2.5 2.0 1.5 1.0 0.5 0.0

0 100 200 300 400

X

Y

Actual Data

Curve Fit

4

3

2

1

0

1.5

1.0

0.5

0.0

SGR08 T=25°C - Co=3mg/l

Model premier ordre

Point X	Actual Y Predicted Y			Coefficients for Equation:	1 0.000
3.000	3.010			2 20.000
3.000	2.934		Y = 3.0 * e'(-0.00 1286063 * X)	3 40.000
2.900	2.859			4 60.000
2.800	2.787		Value Variance	5 80.000
2.700	2.716			6 100.000
2.700	2.647		Bo: 3.0103 0.0015	7 160.000
2.500	2.450		B1: -0.0013 0.0000	8 220.000
2.000	2.268			9 400.000
1.900	1.800		Correlation (R'2) = .9256509

Y = 3.0 * e'(-0.001286063 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

SGR08 T=25°C - Co=1.4mg/l

Model premier ordre

Point X	Actual Y Predicted Y			Coefficients for Equation:	1 0.000
1.400	1.409			2 20.000
1.300	1.335		Y = 1.41 * e'(-0.00270335 * X)	3 40.000
1.300	1.265			4 60.000
1.200	1.198		Value Variance	5 80.000
1.200	1.135			6 100.000
1.100	1.075		Bo: 1.4089 0.0002	7 160.000
0.900	0.914		B1: -0.0027 0.0000	8 220.000
0.700	0.777			9 400.000
0.500	0.478		Correlation (R'2) = .9803976

Y = 1.41 * e'(-0.00270335 * X)

0 100 200 300 400

X

Y

Actual Data

Curve Fit

SGR08 T=25°C - Co=2.5mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.500 2.536

2 20.000 2.450 2.424

3 40.000 2.300 2.316

4 60.000 2.300 2.213

5 80.000 2.000 2.115

6 100.000 2.000 2.021

7 160.000 1.800 1.763

8 220.000 1.600 1.538

9 400.000 1.000 1.022

Coefficients for Equation:

Y = 2.5 * e'(-0.00227253 * X)

Value Variance

Bo: 2.5364 0.0005

B1: -0.0023 0.0000

Correlation (R'2) = .9845521

Y = 2.5 * e'(-0.00227253 * X)

3.0 2.5 2.0 1.5 1.0 0.5 0.0

0 100 200 300 400

X

Y

Actual Data

Curve Fit

SGR08 T=25°C - Co=1 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 1.016

2 20.000 0.900 0.938

3 40.000 0.900 0.866

4 60.000 0.800 0.799

5 80.000 0.700 0.738

6 100.000 0.700 0.681

7 160.000 0.600 0.536

8 220.000 0.400 0.421

9 300.000 0.300 0.306

Coefficients for Equation:

Y = 1.02 * e'(-0.00399809 * X)

Value Variance

Bo: 1.0157 0.0001

B1: -0.0040 0.0000

Correlation (R'2) = .980055

Y = 1.02 * e'(-0.00399809 * X)

1.5 1.0 0.5 0.0

0 50 100 150 200 250 300

X

Y

Actual Data

Curve Fit

SGR08 T=15°C - Co=3 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 3.000 3.033

2 20.000 3.000 3.018

3 40.000 3.000 3.004

4 60.000 3.000 2.989

5 80.000 3.000 2.974

6 100.000 3.000 2.960

7 160.000 2.900 2.917

8 220.000 2.900 2.874

9 300.000 2.800 2.818

10 420.000 2.700 2.736

11 540.000 2.700 2.657

12 600.000 2.600 2.618

Coefficients for Equation:

Y = 3.0 * e'(-0.0002450622 * X) Value Variance

Bo: 3.033 1 0.0001

B1: -0.0002 0.0000

Correlation (R'2) = .9635967

Y = 3.03 * e'(-0.00024506 * X)

4 3 2 1 0

0 100 200 300 400 500 600

X

Y

Actual Data

Curve Fit

SGR08 T=15°C - Co=2 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 2.000 2.032

2 20.000 2.000 2.013

3 40.000 2.000 1.995

4 60.000 2.000 1.976

5 80.000 2.000 1.958

6 100.000 1.900 1.940

7 160.000 1.900 1.887

8 220.000 1.800 1.835

9 300.000 1.800 1.768

10 420.000 1.700 1.673

11 540.000 1.600 1.582

12 600.000 1.500 1.539

Coefficients for Equation:

Y = 2.0 * e'(-0.0004631875 * X) Value Variance

Bo: 2.0319 0.0001

B1: -0.0005 0.0000

Correlation (R'2) = .9697314

Y = 2.0 * e'(-0.000463 1875 * X)

Y

2.5 2.0 1.5 1.0 0.5 0.0

Actual Data Curve Fit

0 100 200 300 400 500 600

X

2.0

1.5

1.0

0.5

0.0

1.5

1.0

0.5

0.0

SGR08 T=15°C - Co=1.5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.532

2 20.000 1.500 1.483

3 40.000 1.400 1.436

4 60.000 1.400 1.390

5 80.000 1.300 1.346

6 100.000 1.300 1.303

7 160.000 1.200 1.182

8 220.000 1.100 1.073

9 300.000 1.000 0.943

10 420.000 0.800 0.777

11 540.000 0.600 0.640

Coefficients for Equation:

Y = 1.53 * e'(-0.00161680 * X)

Value Variance

Bo: 1.5315 0.0001

B1: -0.0016 0.0000

Correlation (R'2) = .9875838

Y = 1.53 * e'(-0.001616804 * X)

0 100 200 300 400 500 600

X

Y

Actual Data

Curve Fit

SGR08 T=15°C - Co=1 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	1.000	1.032			2
20.000	1.000	0.978		Y = 1.03 * e'(-0.00270303 * X)	3
40.000	0.900	0.926			4
60.000	0.900	0.877		Value Variance	5
80.000	0.800	0.831			6
100.000	0.800	0.788		Bo: 1.0320 0.0002	7
160.000	0.600	0.670		B1: -0.0027 0.0000	8
220.000	0.600	0.569			9
300.000	0.500	0.459			10
420.000	0.400	0.332			11
540.000	0.200	0.240		Correlation (R'2) = .9760901

Y = 1.03 * e'(-0.00270303 * X)

0 100 200 300 400 500 600

X

Y

Actual Data

Curve Fit

4

3

2

1

0

SGR08 T=20°C - Co=3 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	3.000	3.044			2
20.000	3.000	2.987		Y = 3.0 * e'(-0.000946981 * X)	3
40.000	2.900	2.931			4
60.000	2.900	2.876		Value Variance	5
80.000	2.800	2.822			6
100.000	2.800	2.769		Bo: 3.0443 0.0009	7
160.000	2.800	2.616		B1: -0.0009 0.0000	8
220.000	2.500	2.472			9
300.000	2.100	2.291			10
420.000	2.000	2.045			11
540.000	1.900	1.826		Correlation (R'2) = .95 10534

Y = 3.0 * e'(-0.000946981 * X)

0 100 200 300 400 500 600

X

Y

Actual Data

Curve Fit

SGR08 T=20°C - Co=2 mg/l

Model premier ordre

Point X		Actual Y Predicted Y			Coefficients for Equation:	1
0.000	2.000	2.033			2
20.000	1.900	1.957		Y = 2.0 * e'(-0.00192159 * X)	3
40.000	1.900	1.883			4
60.000	1.800	1.812		Value Variance	5
80.000	1.700	1.744			6
100.000	1.700	1.678		Bo: 2.0333 0.0002	7
160.000	1.600	1.495		B1: -0.0019 0.0000	8
220.000	1.300	1.332			9
300.000	1.200	1.142			10
420.000	0.900	0.907		Correlation (R'2) = .9882973	11
540.000	0.700	0.720

Y = 2.0 * e'(-0 .00192159 * X)

0 100 200 300 400 500 600

X

Y

2.5

2.0

0.5

0.0

1.5

1.0

Actual Data

Curve Fit

SGR08 T=20°C - Co=1,5 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.500 1.540

2 20.000 1.500 1.491

3 40.000 1.400 1.442

4 60.000 1.400 1.396

5 80.000 1.300 1.350

6 100.000 1.300 1.307

7 160.000 1.200 1.184

8 220.000 1.200 1.073

9 300.000 1.000 0.940

10 420.000 0.700 0.772

Coefficients for Equation:

Y = 1.54 * e'(-0.00164579 * X)

Value Variance

-

Bo: 1.5404 0.0004

B1: -0.0016 0.0000

Correlation (R'2) = .9482356

Y = 1.54 * e'(-0.00164579 * X)

2.0 1.5 1.0 0.5 0.0

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

SGR08 T=20°C - Co=1 mg/l

Model premier ordre

Point X Actual Y Predicted Y

1 0.000 1.000 1.030

2 20.000 1.000 0.969

3 40.000 0.900 0.911

4 60.000 0.900 0.857

5 80.000 0.800 0.807

6 100.000 0.800 0.759

7 160.000 0.600 0.632

8 220.000 0.500 0.526

9 300.000 0.400 0.412

10 420.000 0.300 0.286

Coefficients for Equation:

Y = 1.03 * e'(-0.00305353 * X)

Value Variance

Bo: 1.0298 0.0001

B1: -0.0031 0.0000

Correlation (R'2) = .9864305

Y = 1.03 * e'(-0.00305353 * X)

1.5 1.0 0.5 0.0

0 100 200 300 400 500

X

Y

Actual Data

Curve Fit

ANNEXE n°7 : Détermination des équations de corrélation entre Kb, C0 et T pour chaque
groupe

Co	T		Abs(Kb)	1.00
15	0.000752		1.00
20	0.001637		1.00
25	0.002649		1.70
15	0.000442		1.70
20	0.001300		1.70
25	0.001851		2.00
15	0.000294		2.00
20	0.000878		2.00
25	0.001304		3.00
15	0.000093		3.00
20	0.000305		3.00
25	0.000271

Groupe 1 :

moy(LogCo#X)=	0.580597					moy(LogT#Z)=
2.974219					moy(LogKb#Y)=
-7.300507					rXZ=
0.000000					rYZ=
0.575075					rXY=
-0.740727					Sx=
0.41 1405					Sz=
0.218395					Sy=
0.994071					a=
-1.789807					b=
1.389545					c=
-10.394163
	-1.7898		1.38955		Kb =
-0.000031 *Co		*T

R²= 0.879387

Co	T		Abs(Kb)	0.80
15	0.002048		1.00
20	0.005315		1.00
25	0.010770		1.50
15	0.001844		1.50
20	0.003649		1.50
25	0.007800		2.00
15	0.001269		2.00
20	0.002500		2.00
25	0.003800		3.00
15	0.000495		3.00
20	0.001300		3.00
25	0.003200

Groupe 2 :

moy(LogCo#X)=	0.530711					moy(LogKb#Y)=
2.974219					moy(LogT#Z)
-5.913046					rXY=
0.054967					rYZ=
0.761382					rXZ=
-0.563609					Sx=
0.449783					Sy=
0.218395					Sz=
0.849841					a=
-1.147449					b=
1.501661					c=
-9.770352
	-1.1474		1.50166		Kb =
-0.000057 * Co		* T

R²= 0.923138

Co	T		Abs(Kb)	1.00
15	0.002255		1.00
20	0.003828		1.00
25	0.009620		1.50
15	0.000847		1.50
20	0.002049		1.50
25	0.007221		2.00
15	0.000832		2.00
20	0.001701		2.00
25	0.0063 13		3.00
15	0.000570		3.00
20	0.000789		3.00
25	0.002590

Groupe 3 :

moy(LogCo#X)=	0.549306					moy(LogKb#Y)=
2.974219					moy(LogT#Z)
-6.133641					rXY=
0.000000					rYZ=
0.791583					rXZ=
-0.548476					Sx=
0.419368					Sy=
0.218395					Sz=
0.945673					a=
-1.236811					b=
1.785017					c=
-10.763286
	-1.2368		1.78502		Kb =
-0.000021 *Co		*T

R²= 0.896205

Co	T		Abs(Kb)	1.00
15	0.002703		1.00
20	0.003054		1.00
25	0.003998		1.50
15	0.001616		1.50
20	0.001646		1.40
25	0.002703		2.00
15	0.000463		2.00
20	0.001922		2.50
25	0.002273		3.00
15	0.000245		3.00
20	0.000947		3.00
25	0.001286

Groupe 4 :

moy(LogCo#X)=	0.562152					moy(LogKb#Y)=
2.974219					moy(LogT#Z)
-6.494114					rXY=
0.036179					rYZ=
0.551155					rXZ=
-0.69832 1					Sx=
0.433923					Sy=
0.218395					Sz=
0.8 15029					a=
-1.350865					b=
1.084096					c=
-8.959064
	-1.3509		1.0841		Kb =
-0.000129 *Co		*T

R²= 0.649813

Co	T		Abs(Kb)	1.00
15	0.003237		1.00
20	0.003998		1.00
25	0.006074		1.50
15	0.001833		1.50
20	0.003199		1.50
25	0.003245		2.50
15	0.000986		2.50
20	0.002366		2.50
25	0.002863		3.00
15	0.000444		3.00
20	0.000966		3.00
25	0.001363

Groupe 5 :

moy(LogCo#X)=	0.605092					moy(LogKb#Y)=
2.974219					moy(LogT#Z)
-6.185105					rXY=
0.000000					rYZ=
0.496664					rXZ=
-0.792202					Sx=
0.451179					Sy=
0.218395					Sz=
0.738396					a=
-1.296513					b=
0.812838					c=
-7.818153
	-1.2965		0.81284		Kb =
-0.000402 * Co		* T

R²= 0.662366

Co	T		Abs(Kb)	0.80
15	0.001078		0.80
20	0.001078		0.80
25	0.005603		1.60
15	0.000857		1.60
20	0.000958		1.60
25	0.002464		2.00
15	0.000424		2.00
20	0.001220		2.00
25	0.001706		3.00
15	0.000724		3.00
20	0.000527		3.00
25	0.001532

Groupe 6 :

moy(LogCo#X)=	0.509655					moy(LogKb#Y)=
2.974219					moy(LogT#Z)
-6.748051					rXY=
0.000000					rYZ=
0.723926					rXZ=
-0.456389					Sx=
0.500665					Sy=
0.218395					Sz=
0.692204					a=
-0.630990					b=
1.000878					c=
-9.403294
	-0.6310		1.00088		Kb =
-0.000082 * Co		* T

R²= 0.661946

Co	T		Abs(Kb)	1.00
15	0.003196		1.00
20	0.004622		1.00
25	0.005985		1.50
15	0.002535		1.50
20	0.003553		1.50
25	0.005553		2.00
15	0.001155		2.00
20	0.001746		2.00
25	0.004386		2.70
15	0.001039		2.70
20	0.001016		2.70
25	0.003 135

Groupe 7 :

1.04978

moy(LogCo#X)=

0.522966		moy(LogKb#Y)=
2.974219		moy(LogT#Z)
-5.926866		rXY=
0.000000		rYZ=
0.622560		rXZ=
-0.687773		Sx=
0.382847		Sy=
0.218395		Sz=
0.645571		a=
-1.159748		b=
1.049784		c=
-8.442644
	-1.1597	Kb =
-0.000215 *Co	*T	R^2=
0.735491

Co concentration initiale du chlore (mg/l)

T température de l'eau °C

Kb coefficient de régression du chlore dans la masse d'eau min ^-1

Annexe n° 8 : Générateur des coefficients Kb,mélange

						Selection des vannes: Diamétre=555 Selection des pompes: (Longueur< 0)& (Diamétre = 0)
Flow			Flow
LPS		Link ID	LPS			Pump FM1 1
	38,3	Valve BC6		0		Pump FM02
	21,15	Valve BC4		139,48		Pump FM05
	24,31	Valve BC5		173,97		Pump FM04
	23,04	Valve 38		0		Pump FM08
	26,54	Valve 12		30,82		Pump R_mateur_basse
	113,1	Valve 22		3,11		Pump roumadia1
	95,46					Pump koudia
	66,64					Pump roumadia2
	95,46					Pump FMville
	0					Pump R_Hriza
	58,69					Pump SGR06
	13,74					Pump SGR04
	10,06					Pump SGR09
	7,03					Pump SGR1 1
	6,5					Pump SGR12
	7,6					Pump SGR13
	8,98					Pump SGR01
	8,24					Pump SGR10
	2,41					Pump SGR08
	8,67					Pump R_SGR09
	29,43					Pump R_SGR09bis
	29,43					Pump FM09
	44,35					Pump R_Hrizabis
	58,25

				0.002
	127
Wall	127	0.000
Bulk	129	0.002
Wall	129	0.003
Bulk	130	0.002		1.50166
Wall	130	0.003
Bulk	131	0.002
Wall	131	0.001
Bulk	132	0.003		1.78502
Wall	132	0.003
Bulk	133	0.002
Wall	133	0.000
Bulk	134	0.000		1.0841
Wall	134	0.003
Bulk	135	0.001
Wall	135	0.003
Bulk	136	0.000		0.81284
Wall	136	0.000
Bulk	137	0.005
Wall	137	0.002
Bulk	138	0.000		1.00088
Wall	138	0.000
Bulk	139	0.000
Wall	139	0.000
Bulk	140	0.007		1.04978
Wall	140	0.001
Bulk	141	0.007
Wall	141	0.003
Bulk	142	0.007
Wall	142	0.003
Bulk	143	0.003
Wall	143	0.002		0.6
Bulk	144	0.003
Wall	144	0.003		1
Bulk	145	0.003
Wall	145	0.003		1.2
Bulk	146	0.002
Wall	146	0.001		1.2
Bulk	148	0.005
Wall	148	0.000		1.7
Bulk	149	0.000
Wall	149	0.000		0
Bulk	150	0.000
Wall	150	0.000		0
Bulk	151	0.000
Wall	151	0.000		1.41
Bulk	152	0.000
Wall	152	0.000
Bulk	153	0.000
Wall	153	0.000
Bulk	154	0.000
Wall	154	0.000
Bulk	155	0.000
Wall	155	0.000
Bulk	156	0.004
Wall	156	0.003

[REACTIONS]	100		0.000	Bulk
100	0.00 1		Bulk
101	0.007		Wall
101	0.00 1		Bulk
102	0.000		Wall
102	0.003		Bulk
103	0.000		Wall
103	0.003		Bulk
104	0.000		Wall
104	0.003		Bulk
105	0.000		Wall
105	0.003		Bulk
106	0.000		Wall
106	0.003		Bulk
107	0.000		Wall
107	0.003		Bulk
108	0.000		Wall
108	0.002		Bulk
109	0.007		Wall
109	0.00 1		Bulk
110	0.007		Wall
110	0.003		Bulk
111	0.001		Wall
111	0.003		Bulk
112	0.003		Wall
112	0.003		Bulk
113	0.007		Wall
113	0.000		Bulk
114	0.007		Wall
114	0.000		Bulk
115	0.001		Wall
115	0.000		Bulk
116	0.004		Wall
116	0.002		Bulk
117	0.004		Wall
117	0.002		Bulk
118	0.004		Wall
118	0.002		Bulk
119	0.004		Wall
119	0.002		Bulk
120	0.004		Wall
120	0.001		Bulk
121	0.004		Wall
121	0.000		Bulk
122	0.007		Wall
122	0.001		Bulk
123	0.007		Wall
123	0.001		Bulk
124	0.001		Wall
124	0.003		Bulk
125	0.001		Wall
125	0.003		Bulk
126	0.001		Wall
126	0.000

Co
(mg/l)

1.41

1.41

0.6 25

0.6 25

0.6 25

0.6 25

0.6 25

0.6 25

1.2 25

1.2 25

1.2 25

1.2 25

1.2 25

1.2 25

2 25

2 25

2 25 source : station de traitement Mateur

2 25

1

T
(°C

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25 R²= 0.74

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

Grp 1 Kb = R^2=	0.000031 * Co 0.88	-1 .7898		* T
	-1.1474			Grp 2 Kb =
0.000057 * Co		* T		R^2=
0.92
	-1.2368			Grp 3 Kb =
0.000021 * Co		* T		R^2=
0.9
	-1 .3509			Grp 4 Kb =
0.000129* Co		* T		R^2=
0.65
	-1.2965			Grp 5 Kb =
0.000402 * Co		* T		R^2=
0.66
	-0.63 1			Grp 6 Kb =
0.000082 * Co		* T		R^2=
0.66
	-1.1597			Grp 7 Kb =
0.000215* Co		* T

source: Réservoir Ras Ain

source CE6

source Rhézala

source Roumadia

source Bache_SGR09

source Hriza

source Koudia

0.6 25

0.6 25

1.7 25

1.7 25

1.7 25

1.7 25

2 25

2 25

2 25

2 25

1

1

1

1

1

1

1

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

			0.004	Bulk
157
157	0.003		Bulk
158	0.001		Wall
158	0.000		Bulk
159	0.005		Wall
159	0.000		Bulk
160	0.002		Wall
160	0.000		Bulk
161	0.000		Wall
161	0.000		Bulk
162	0.000		Wall
162	0.000		Bulk
163	0.007		Wall
163	0.00 1		Bulk
164	0.007		Wall
164	0.00 1		Bulk
165	0.007		Wall
165	0.002		Bulk
166	0.007		Wall
166	0.002		Bulk
167	0.007		Wall
167	0.00 1		Bulk
168	0.007		Wall
168	0.00 1		Bulk
169	0.007		Wall
169	0.002		Bulk
170	0.007		Wall
170	0.002		Bulk
171	0.007		Wall
171	0.002		Bulk
172	0.007		Wall
172	0.00 1		Bulk
173	0.007		Wall
173	0.00 1		Bulk
174	0.007		Wall
174	0.002		Bulk
175	0.007		Wall
175	0.00 1		Bulk
176	0.007		Wall
176	0.002		Bulk
177	0.007		Wall
177	0.00 1		Bulk
178	0.007		Wall
178	0.002		Bulk
179	0.000		Wall
179	0.00 1		Bulk
180	0.007		Wall
180	0.002		Bulk
181	0.007		Wall
181	0.00 1		Bulk
182	0.007		Wall
182	0.000		Bulk
183	0.004		Wall
183	0.000		Bulk
184	0.002		Wall
184	0.000

1

25

25

2 25

25

1 25

25

2 25

25

25

25

25

25

0.6 25

25

0.6 25

25

1

25

25

1

25

25

0.6 25

25

0.6 25

25

1

25

25

1

25

25

1

25

25

0.6 25

25

0.6 25

25

1

25

25

0.6 25

25

1

25

25

0.6 25

25

1

25

25

25

25

0.6 25

25

0.6 25

25

1

25

25

1.2 25

25

1.7 25

25

			0.002	Bulk
185
185	0.000		Bulk
186	0.000		Wall
186	0.003		Bulk
187	0.000		Wall
187	0.000		Bulk
188	0.007		Wall
188	0.003		Bulk
189	0.007		Wall
189	0.000		Bulk
190	0.000		Wall
190	0.002		Bulk
191	0.000		Wall
191	0.003		Bulk
192	0.000		Wall
192	0.003		Bulk
193	0.000		Wall
193	0.000		Bulk
194	0.000		Wall
194	0.003		Bulk
195	0.000		Wall
195	0.002		Bulk
196	0.000		Wall
196	0.001		Bulk
197	0.001		Wall
197	0.002		Bulk
198	0.000		Wall
198	0.001		Bulk
199	0.007		Wall
199	0.003		Bulk
200	0.002		Wall
200	0.000		Bulk
201	0.007		Wall
201	0.001		Bulk
202	0.003		Wall
202	0.003		Bulk
203	0.003		Wall
203	0.003		Bulk
204	0.001		Wall
204	0.003		Bulk
147	0.002		Wall
147	0.001		Bulk
128	0.002		Wall
128	0.001

1.7 25

25

25

25

25

25

1

25

25

0.6 25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

25

1.41

25

25

25

25

0.6 25

25

1.7 25

25

0.6 25

25

1

25

25

1

25

25

2 25

25

1.7 25

25

1.7 25

ANNEXE n°9: Calage du modèle qualité d'"EPANET"

Point N°2 : l'amont du réservoir "Baccar"

Point N°1 : l'amont du réservoir "Mateur ville"

Point N°4 : l'amont du réservoir "Roumadia"

Point N°3 : l'amont de la station de pompage "Roumadia"

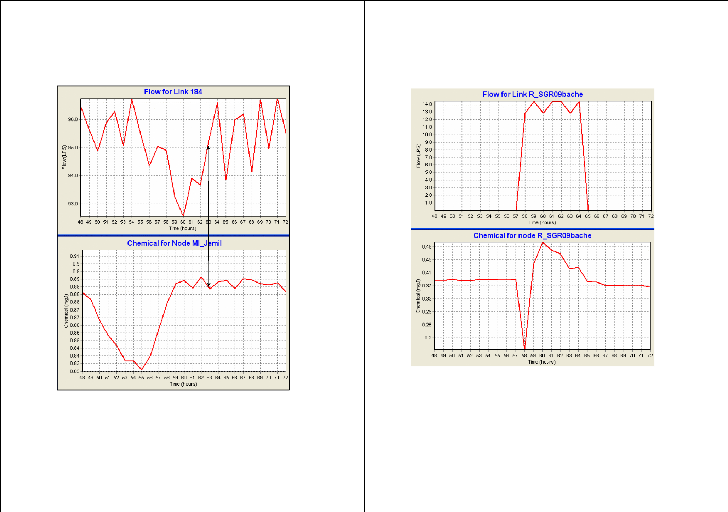
Point N°5 : l'amont du réservoir "Ml Jemil"

Point N°6 : l'amont du réservoir "Bache SGR09"

Point N°7 : l'amont de la station de "Hriza"

	ANNEXE n°10: Base de données du modèle EPANET		1040	7	0
		1041	9	0			[JUNCTIONS]
		1042	100	0			;ID
Elevation	Demande au noeud	1043	62.1	0			1000
5	0	D_bizerte2	38	99	Mod_E_Rhézala		1001
6	0	D_rive _sud1	100	127	Mod_E_Alia		1002
11.09	0	D_rive _sud2	90	65	Mod_E_Rive _Sud		1003
14.09	0	1044	8.35	0			1004
10.48	0	1045	8	0			1005
17.76	0	1046	83	0			1006
12.5	0	1047	1.13	0			D_zaarour
46	13.50	1048	4.05	0			1007
10.14	0	1049	26.48	0			1008
46	0	1050	25.58	0			D_CE2
45	7 Mod_E_CE6	D _localités	1.42	25	;		D_CE1
38	27 Mod_E_CE6	1051	44.36	0			1009
36.5	0	1052	1.23	0			D_beni_nafaa
45	18 Mod_E_Rhézala	1053	4.9	0			1010
43.42	0	1054	5.73	0			1011
10	0	1055	42.48	0			1012
1.15	0	1056	42	0			1013
1.15	0	1057	15.53	0			1014
4.34	0	1058	7.06	0			1015
4.5	0	1059	83	0			D_bizerte1
35	116 Mod_E_Rhézala	1060	44	0			1016
44	0	1061	70	0			1017
35	0	1062	52.75	0			D_baccar
70	68 Mod_E_Rhézala	1063	150	0			D_roumadia
55	33 Mod_E_Mljemil	1064	146.57	0			1018
50.76	0	1065	50.8	0			1019
6.1	0	1066	35	0			D_mateur1
62	2 Mod_E_Mateur	1067	64.18	0			D_Ml_Jemil
47.5	43 Mod_E_Mljemil	1068	66.11	0			1020
12.64	0	1069	12	0			D_mateur2
55	80 Mod_E_Mateur	1070	66.6	0			1021
39.32	0	1071	13	0			1022
34.38	0	1072	8	0			1023
34.8	0	1073	11.09	0			1024
42.28	0	1074	10.48	0			1025
48.7	0	1075	17.76	0			1026
11.5	0	1076	10.14	0			1027
11.5	0	1077	13.13	0			1028
46	0	1078	13.13	0			1029
46	0	1079	6	0			1030
46	0	1080	14.09	0			1031
6.1	0	1081	62.1	0			1032
7.5	0	1082	8	0			1033
100	0	1083	7	0			1034
8	0 ;	1084	8.35	0			1035
8	0	1085	8	0			1036
8	0	1086	8	0			1037
7.5	0	1087	8	0			1038
8	0	1088	48	0			1039
8.35	0	1089	39.32	0
		1090	9	0

1091 4.5 1092 35 1093 39.32		0 0 0		[TANKS] ;ID Elevation VolCurve	InitLevel MinLevel		MaxLevel	Diameter		MinVol		1094 146
	0		ST_Mateur 83.76	5 1.8		6.3	44.96	0			1095 90
	0		Ras _Ain 60.4	5 1.5		5.7	39	0			1096 44
	0		Mateur 9.5 _basse	3.5	0	4.5	9.21			0	1097 44
	0		CE1 45	4 1		4.4	28.82	0			1098 47
	0		CE2 46.84	4 1		4.65	29.7	0			1099 83.7
	0		CE6 65.7	4 1.8		4.7	26.03	0			1100 83.7
	0		Beni_Nafaa 46.9	3.5 1		4.7	28.5	0			1101 69.7
	0		Roumadia 64.3	3 0		4.7	23.29	0			1102 70.41
	0		Rhézala 42.7	4 1		5	31.8	0			1103 7.6
	0		Koudia 41	3 2		5.2	48.12	0			1104 148.5
	0		Baccar 84.36	4 1		5.29	24.53	0			1105 41
	0		Ml_Jemil 48	3.5 1		4	17.845	0			1106 41
	0		Mateurville 63.66	4 1.7		5.33	30.7	0			1107 66
	0		ElAlia 140.8	3.5 0.5		4.3	21.1	0			1108 143.5
	0		Ain_Bouras 146.57	2.5 0		3	10.3	0			1109 52.75
	0		Bache_SGR09 7	1 0.5		6	26.6	0			1110 44
	0		Hriza 39	2 1		3	3	0			1111 51.61
	0										1112 88.4
	0		[PIPES]								1113 64.18
	0		;ID Node1	Node2 Length		Diameter	Roughness				1114 48.8
	0		100 1059	ST_Mateur 10		1200	126				1115 48.8
	0		101 1026	1000 3488		1250	126	0			1116 49.8
	0		102 1079	1068 554		315	126	0			1117 49.8
	0		103 1073	1069 1914		300	126	0			1118 45
	0		104 1003	1068 920		315	126	0			D_louata 40
	82	Mod_E _CE6	105 1005	1006 1914		400	126	0
			106 1006	1069 1717		400	126	0
			107 1004	1069 101		300	126	0			[RESERVOIRS]
			108 1076	1068 659		600	110	0			;ID
Head			109 1000	1050 9394		1250	126	0			ND_FMville
-11.36			110 1118	CE1 10		300	110	0			ND_FM1 1
-4			111 CE2	D_CE2 10		300	126	0			ND_FM05
-13.5			112 CE1	D_CE1 10		300	126	0			ND_FM02
-14.9 1			113 1113	1102 10		500	126	0			ND_FM04
-9			114 1009	1111 192		200	126	0			ND_FM08
2.28			115 Beni_Nafaa	D_beni_nafaa 10		250	126	116			ND_SGR01
-36.65			Rhézala 1011	709 600		126	0	117			ND_SGR10
-61.3			1011 1012	1968 500		126	0	118			ND_SGR08
-81			1012 1013	260 500		126	0	119			ND_SGR13
-50.29			1013 1014	2003 600		126	0	120			ND_SGR12
-68.79			1091 1061	1432 600		126	0	121			ND_SGR11
-48.8			Rhézala D_bizerte1	10 800		126					ND_SGR09
-55.4			122 1010	1098 1916		800	80	0			ND_SGR04
11.93			123 1016	Koudia 2		800	126	0			ND_SGR06
3.5			124 Koudia	1017 45		500	126	0			ND_BARRAGE
150			125 1092	1095 1700		300	126	0			ND_FM09
2.13			126 Baccar	D_baccar 10		300	126	0
			127 Roumadia	D_roumadia 10		300	126
			129 Roumadia	1018 1819		300	116
			130 1018	1109 268		300	116	0
			131 Roumadia	1019 5308		500	116
			132 Ras_Ain	D_mateur1 10		300	126

133	Ml_Jemil	D_Ml_Jemil	100	300	126		189	1065	Beni_Nafaa	2	200		126			134
1020	1070	287	300	126	0	190	1068	Ras _Ain	10	600		126	0		135
Mateurville	D_mateur2	1000	400	126		191	1069	Mateur _basse	10	800		126			136
1022	1024	526	200	126	0	192	1070	Mateurville	10	300		126			137
1089	1033	2908	600	126	0	193	1103	Bache_SGR09	10	1000		126			138
1024	1094	331	300	126	0	194	1078	Mateur _basse	1717	400		126			139
1088	1064	2730	150	126	0	195	1081	Ras _Ain	10	600		126	0		140
1100	1026	2850	1250	126	0	196	1108	ElAlia	5	800		126	0		141
1027	Mateurville	2696	400	126		197	1112	Baccar	10	300		126	0		142
Ras_Ain	D_zaarour	16103	350	110		198	ST_Mateur	1099	10	1250		80			143
CE6	1028	6020	600	126	0	199	1101	CE6	5	500		126	0		144
1029	1116	600	200	126	0	200	1106	Hriza	5	500		126	0		145
1030	1115	1360	200	126	0	201	1010	1110	68	1000		100	0		146
1031	1105	8107	500	116	0	202	1114	CE1	10	200		126	0		148
1033	1094	876	500	126	0	203	1117	CE2	10	200		126	0		149
1087	1071	11	200	100	10	204	CE6	D_louata	1000	300		126	0		150
1072	1071	1600	150	100	0	147	1019	1	1500	100		126	0		151
1036	1071	561	200	100	0	128	1032	Bache_SGR09	5	300		126			152
1037	1071	1000	200	126	0										153
1082	1037	2042	250	126	0	[VALVES]									154
1083	1039	254	250	126	0	;ID	Node1	Node2	Diameter	Type	Setting		MinorLoss		155
1039	1037	3250	200	126	0	prise_barrage	1046	1059	800	PRV	5		0 ;		156
1090	1042	5263	300	126	0	BC1	1113	1067	500	PRV	5		0 ;		157
1042	1063	931	300	126	0	1	1026	1027	400	FCV			0 ;		158
Koudia	D_bizerte2	10	300	126		18	1035	1072	100	TCV	50		0 ;		159
Ain_Bouras	D_rive _sud2 1000	200		126		23	1002	1073	150	TCV	120		0 ;		160
ElAlia	D_rive _sud1	1000	200	126		29	1004	1074	150	TCV	65		0 ;		161
1084	1039	10	250	126	0	30	1075	1005	150	TCV	40		0 ;		162
1086	1036	10	200	126	0	31	1007	1076	200	TCV	12		0 ;		163
1067	1047	5388	1000	126	0	32	1077	1078	400	TCV	40		0 ;		164
1047	1053	5579	1000	126	0	33	1001	1079	150	TCV	0		0 ;		165
Ras_Ain	1048	713	600	100	0	35	1080	1003	100	TCV	50		0 ;		166
1048	1049	9087	600	126	0	BC6	1043	1081	555	FCV			0 ;		167
1050	D _localités	5171	1250	126	0	43	1028	1030	250	FCV	0		0 ;		168
D _localités	1113	737	1250	126	0	48	1028	1029	250	FCV			0 ;		169
1049	1051	6716	600	100	0	49	1038	1082	100	TCV	0		0 ;		170
1051	1052	4633	600	100	0	50	1040	1083	100	TCV	0		0 ;		171
1052	1054	5533	600	100	0	59	1044	1084	100	TCV	0		0 ;		172
1053	1009	2424	1000	126	0	60	1085	1036	100	TCV	10		0 ;		173
1009	1055	920	1000	126	0	63	1045	1086	100	TCV	0		0 ;		174
1054	1056	3334	600	100	0	73	1034	1087	100	TCV	100		0 ;		175
1055	1057	2733	1000	126	0	74	1025	1088	100	TCV	80		0 ;		176
1056	1058	1104	600	100	0	76	1021	1089	350	TCV	0		0 ;		177
1057	1010	648	1000	126	0	77	1023	1022	150	TCV	5		0 ;		178
1058	1096	1278	600	100	0	78	1041	1090	250	TCV	0		0 ;		179
ND_BARRAGE1046	1422		1200	126		82	1015	1091	350	TCV	0		0 ;		180
1000	1043	507	600	126	0	83	1066	1092	250	TCV	60		0 ;		181
1097	Rhézala	10	1000	126	0	89	1093	1089	350	TCV	20		0 ;		182
1060	Rhézala	2	600	126	0	BC4	1096	1060	555	FCV			0 ;		183
1107	Roumadia	10	800	126		BC5	1110	1097	555	FCV			0 ;		184
1062	Ml_Jemil	2	300	130	0	BC3	1098	1016	500	FCV	200		0 ;		185
1019	1031	2	500	116	0	7	1099	1100	500	FCV	1000		0 ;		186
1104	Ain_Bouras	2	500	126		88	1102	1101	500	FCV			0 ;		187
1064	Ain_Bouras	2	150	126		10	1071	1103	400	PSV	0		0 ;		188
D_zaarour	1008	1000	350	110		13	1063	1104	300	PSV	0		0 ;

11 1105 1106 500 PSV 0 0 ; 14 1061 1107 600 PSV 0 0 ; 15 1094 1108 600 PSV 0 0 ; 16 1109 1062 300 PSV 0 0 ; 28 1111 1065 200 FCV 18 0 ; 19 1095 1112 300 PSV 0 0 ; 38 1115 1114 555 PSV 0 0 ; 98 1116 1117 300 PSV 0 0 ; 12 1008 1118 555 FCV 0 ; 22 1 1032 555 FCV 0 ; [PATTERNS] ;ID Multipliers ;Courbe Modulation Eté Ras El Ain Mod_E_Ras_Ain 0.33 0.3 0.27 0.33 0.45 0.55 Mod_E_Ras_Ain 0.77 0.85 1.04 1.07 2.75 2.72 Mod_E_Ras_Ain 2.64 1.04 0.96 1.04 1.32 1.31 Mod_E_Ras_Ain 1.17 0.91 0.76 0.55 0.49 0.41 ;Courbe été El Alia Mod_E_Alia 0.37 0.36 0.4 0.65 0.46 0.47 Mod_E_Alia 0.76 1.2 1.66 2 1.71 1.58 Mod_E_Alia 1.4 1.17 1.17 1.21 1.2 1.35 Mod_E_Alia 1.22 1.16 0.95 0.68 0.46 0.43 ;Courbe été Rhézala Mod_E_Rhézala 0.64 0.63 0.58 0.65 0.59 0.72 Mod_E_Rhézala 0.8 0.94 1.14 1.29 1.45 1.48 Mod_E_Rhézala 1.43 1.36 1.22 1.23 1.23 1.05 Mod_E_Rhézala 1.02 1.04 0.99 0.93 0.84 0.75 ;Courbe Modulation Eté CE6 Mod_E_CE6 0.48 0.48 0.5 0.54 0.6 0.82 Mod_E_CE6 1.15 1.4 1.5 1.54 1.52 1.43 Mod_E_CE6 1.32 1.18 1.25 1.32 1.25 1.07 Mod_E_CE6 1.12 0.96 0.81 0.68 0.57 0.51 ;Courbe Modulation Eté Ml Jemil Mod_E_Mljemil 0.42 0.39 0.36 0.38 0.45 0.51 Mod_E_Mljemil 0.69 1 1.4 1.63 1.83 1.89 Mod_E_Mljemil 1.63 1.42 1.16 1.16 1.2 1.07 Mod_E_Mljemil 0.99 1.05 1.12 1.02 0.74 0.52 ;Courbe été Mateur Mod_E_Mateur 0.44 0.44 0.49 0.59 0.75 0.99 Mod_E_Mateur 1.14 1.23 1.33 1.38 1.39 1.38 Mod_E_Mateur 1.21 1.07 1.17 1.24 1.24 1.25 Mod_E_Mateur 1.29 1.08 0.97 0.84 0.63 0.48 ;Courbe été Rive Sud Mod_E_Rive_Sud 0.37 0.35 0.34 0.38 0.42 0.61 Mod_E_Rive_Sud 0.86 1.22 1.46 1.79 1.88 1.8 Mod_E_Rive_Sud 1.59 1.39 1.21 1.09 1.14 1.11 Mod_E_Rive_Sud 1.34 1.15 0.9 0.67 0.53 0.44 [CURVES] ;ID x-Value Y-Value ;PUMP: Courbe caractéristique pompe forage M4 M04 30 30 ;PUMP: Courbe caractéristique pompe forage M8 M08 30 20		;PUMP: Courbe caractéristique pompe forage M9 M09 32 40 ;PUMP: Courbe caractéristique pompe forage M2 M02 30 40 ;PUMP: Courbe caractéristique pompe Mateur basse R_Mateur_Basse 125 61 ;PUMP: Courbe caractéristique pompe reprise Koudiat koudiat 0 75 koudiat 13.89 69 koudiat 27.78 67 koudiat 4 1.67 66 koudiat 55.56 65 koudiat 83.33 63 koudiat 90 62 koudiat 97.22 60 koudiat 125 50 koudiat 128.89 41 ;PUMP: Courbe caractéristique pompe Roumadia Roumadia 150 38 ;PUMP: Courbe caractéristique pompe reprise SGR9 R_SGR09 0 219 R_SGR09 14 216 R_SGR09 30 210 R_SGR09 55 198 R_SGR09 85 180 R_SGR09 120 150 R_SGR09 132 132 ;PUMP: Courbe caractéristique pompe forage SGR6 SGR06 12 160 ;PUMP: Courbe caractéristique de la pompe forage M11 M11 37.5 90 ;PUMP: Courbe caractéristique pompe forage M5 M05 30 120 ;PUMP: Courbe caractéristique pompe forage SGR4 SGR04 9 165 ;PUMP: Courbe caractéristique pompe forage SGR9 SGR09 12 80 ;PUMP: Courbe caractéristique pompe forage SGR1 1 SGR11 6.67 94.5 SGR11 7.5 90.3 SGR11 8.33 86.8 SGR11 9.17 83.3 SGR11 10 79.8 SGR11 10.83 76 SGR11 12 71 SGR11 13.33 66 SGR11 14.3 62.3 SGR11 15.12 58.31 SGR11 16.67 49.7 SGR11 17.68 42 ;PUMP: Courbe caractéristique pompe forage SGR12 SGR12 15 79 ;PUMP: Courbe caractéristique pompe forage SGR13 SGR13 15 70 ;PUMP: Courbe caractéristique pompe forage SGR1

SGR01 15 60 ;PUMP: Courbe caractéristique pompe forage SGR10 SGR10 8 70 ;PUMP: Courbe caractéristique pompe forage SGR8 SGR08 15 100 ;PUMP: M10 30.55 23 ;PUMP: FMville 37.87 69.8 ;EFFICIENCY: Courbe caractéristique R. Koudia E_koudia 55.56 66.84 E_koudia 69.44 72.67 E_koudia 83.33 76.9 E_koudia 90 78.2 E_koudia 97.22 77.8 E_koudia 111.11 75.1 E_koudia 125 70.55 E_koudia 138.89 63.48 ;EFFICIENCY: Courbe rendement SGR1 1 E_SGR11 6.67 58 E_SGR11 7.5 62 E_SGR11 8.33 65 E_SGR11 9.17 68 E_SGR11 10 70 E_SGR11 10.83 72 E_SGR11 12 73 E_SGR11 13.33 73.7 E_SGR1 1 14.3 73 E_SGR11 15.12 71.5 E_SGR11 16.67 66.5 E_SGR11 17.68 60 ;EFFICIENCY: Courbe rendement SGR13 E_SGR13 8.33 36 E_SGR13 9.17 51 E_SGR13 10.03 59 E_SGR13 10.88 64.2 E_SGR13 11.67 66.5 E_SGR13 12.5 69 E_SGR13 15 71 E_SGR13 16.67 70.8 E_SGR13 18.33 69.5 E_SGR13 20.1 67 E_SGR13 20.83 65 E_SGR13 22.22 61 ;EFFICIENCY: Courbe Rdt. SGR10 E_SGR10 6.67 52.8 E_SGR10 7.5 56.2 E_SGR10 8 58 E_SGR10 8.33 59.3 E_SGR10 9.17 62 E_SGR10 10 64 E_SGR10 10.83 65 E_SGR10 11.67 66.1 E_SGR10 12.5 66.7 E_SGR10 13.33 67 E_SGR10 14.32 66.2		E_SGR10 16.11 63 E_SGR10 17.68 57.5 ;EFFICIENCY: Courbe de rendement Hriza E_Hriza 27.78 71.53 E_Hriza 34.72 76.41 E_Hriza 41.67 81.75 E_Hriza 48.61 85.83 E_Hriza 55.56 88.75 E_Hriza 69.44 89 E_Hriza 75 87.81 E_Hriza 83.33 85.41 E_Hriza 90.28 82.32 E_Hriza 97.22 76.3 ;EFFICIENCY: Courbe de rendement R. SGR9 E_R_SGR09 18 42 E_R_SGR09 30 57 E_R_SGR09 36 62.5 E_R_SGR09 45 67.5 E_R_SGR09 52 69 E_R_SGR09 62 69 E_R_SGR09 68 68 E_R_SGR09 74 65 E_R_SGR09 80 61 E_R_SGR09 88 55 ;PUMP: FM09 32 40 ;PUMP: Hriza 70 107 ;PUMP: Courbe caractéristique forage FM Ville Mville 9.1 118.8 Mville 18.2 114 Mville 25 108 Mville 27.78 103.5 Mville 30 100 Mville 33.33 92 Mville 36.11 84 Mville 39 76.3 Mville 41.67 70 Mville 44.44 64.5 [CONTROLS] LINK 200 CLOSED IF NODE Hriza ABOVE 3 LINK 200 OPEN IF NODE Hriza BELOW 3 LINK 88 80 IF NODE CE6 ABOVE 3 LINK 88 140 IF NODE CE6 BELOW 2 LINK 88 0 IF NODE CE6 ABOVE 4.5 LINK 48 50 IF NODE CE2 ABOVE 3 LINK 48 70 IF NODE CE2 BELOW 2 LINK 48 0 IF NODE CE2 ABOVE 4 [RULES] RULE 1

IF TANK Bache _SGR09 LEVEL ABOVE 4 THEN PUMP SGR08 STATUS IS CLOSED AND PUMP SGR10 STATUS IS CLOSED AND PUMP SGR01 STATUS IS CLOSED AND PUMP SGR13 STATUS IS CLOSED AND PUMP SGR12 STATUS IS CLOSED AND PUMP SGR1 1 STATUS IS CLOSED AND PUMP SGR09 STATUS IS CLOSED RULE 2 IF TANK Bache _SGR09 LEVEL BELOW 2 THEN PUMP SGR08 STATUS IS OPEN AND PUMP SGR10 STATUS IS OPEN AND PUMP SGR01 STATUS IS OPEN AND PUMP SGR13 STATUS IS OPEN AND PUMP SGR12 STATUS IS OPEN AND PUMP SGR1 1 STATUS IS OPEN AND PUMP SGR09 STATUS IS OPEN RULE 3 IF TANK Ain _Bouras LEVEL ABOVE 2.5 THEN PUMP R_SGR09 STATUS IS CLOSED RULE 4 IF TANK Ain _Bouras LEVEL ABOVE 2.5 THEN PUMP R _SGR09bis STATUS IS CLOSED RULE 5 IF TANK Ain _Bouras LEVEL BELOW 2.0 THEN PUMP R_SGR09 STATUS IS OPEN AND PUMP R _SGR09bis STATUS IS OPEN RULE 6 If Tank ElAlia level ABOVE 4.1 OR TANK Hriza LEVEL BELOW 1 THEN Pump R_Hriza STATUS IS CLOSED AND Pump R_Hrizabis STATUS IS CLOSED RULE 7 If Tank ElAlia level BELOW 3.6 THEN Pump R_Hriza STATUS IS OPEN AND Pump R_Hrizabis STATUS IS OPEN RULE 9 IF TANK Roumadia LEVEL ABOVE 4 OR TANK Rhézala LEVEL BELOW 1 THEN PUMP roumadia1 STATUT IS CLOSED AND PUMP roumadia2 STATUT IS CLOSED RULE 10 IF TANK Roumadia LEVEL BELOW 3.3 AND TANK Rhézala LEVEL ABOVE 1 THEN PUMP roumadia1 STATUT IS OPEN AND PUMP roumadia2 STATUT IS OPEN RULE 11 IF TANK Mateur _basse LEVEL ABOVE 3.5 THEN PUMP FM08 STATUS IS CLOSED AND PUMP FM04 STATUS IS CLOSED AND PUMP FM02 STATUS IS CLOSED AND PUMP FM09 STATUS IS CLOSED RULE 12 IF TANK Mateur _basse LEVEL BELOW 1.7 THEN PUMP FM08 STATUS IS OPEN		AND PUMP FM04 STATUS IS OPEN AND PUMP FM02 STATUS IS OPEN AND PUMP FM09 STATUS IS OPEN RULE 13 IF TANK Mateur_basse LEVEL BELOW 0.8 THEN PUMP R _mateur _basse STATUS IS CLOSED RULE 14 IF TANK Mateur_basse LEVEL ABOVE 3 THEN PUMP R _mateur _basse STATUS IS OPEN RULE 15 IF TANK Ras _Ain LEVEL ABOVE 5.5 THEN PUMP R _mateur _basse STATUS IS CLOSED AND PUMP FM05 STATUS IS CLOSED AND PUMP FM1 1 STATUS IS CLOSED PRIORITY 15 RULE 16 IF TANK Ras _Ain LEVEL BELOW 5 THEN PUMP R _mateur _basse STATUS IS OPEN AND PUMP FM05 STATUS IS OPEN AND PUMP FM1 1 STATUS IS OPEN RULE 17 IF TANK Mateurville LEVEL ABOVE 4.5 THEN VALVE 1 SETTING IS 0 RULE 18 IF TANK Mateurville LEVEL BELOW 3 THEN VALVE 1 SETTING IS 115 RULE 19 IF TANK Baccar LEVEL BELOW 3.8 THEN PUMP koudia STATUS IS OPEN RULE 39 IF TANK Baccar LEVEL ABOVE 4.5 THEN PUMP koudia STATUS IS CLOSED RULE 20 IF TANK Bache _SGR09 LEVEL BELOW 2 THEN VALVE 22 STATUS IS OPEN RULE 21 IF TANK Bache _SGR09 LEVEL ABOVE 2 THEN VALVE 22 STATUS IS CLOSED RULE 23 IF TANK Rhézala LEVEL ABOVE 4.3 THEN VALVE BC5 SETTING IS 0 RULE 24 IF TANK Rhézala LEVEL ABOVE 3.8 AND TANK Rhézala LEVEL BELOW 4.3 THEN VALVE BC5 SETTING IS 100 RULE 25 IF TANK Rhézala LEVEL ABOVE 3.3 AND TANK Rhézala LEVEL BELOW 3.8 THEN VALVE BC5 SETTING IS 200 RULE 26 IF TANK Rhézala LEVEL ABOVE 2.8 AND TANK Rhézala LEVEL BELOW 3.3 THEN VALVE BC5 SETTING IS 250 RULE 28

IF TANK Rhézala LEVEL BELOW 2.8		Bulk	110		-9.991060135	THEN VALVE BC5 SETTING IS 350
	Wall	110	-5		RULE 30
	Bulk	111	-1.130962588		IF TANK Ras _Ain LEVEL BELOW 3.5
	Wall	111	-5		AND LINK 108 STATUS IS OPEN
	Bulk	112	-4.413016496		THEN VALVE BC6 STATUS IS 30
	Wall	112	-5		RULE 31
	Bulk	113	-9.756557694		IF TANK Ras _Ain LEVEL ABOVE 3.5
	Wall	113	0		AND LINK 108 STATUS IS OPEN
	Bulk	114	-9.756557694		THEN VALVE BC6 SETTING IS 0
	Wall	114	0		RULE 32
	Bulk	115	-1.130962588		IF LINK 108 STATUS IS CLOSED
	Wall	115	0		AND TANK Ras _Ain LEVEL BELOW 3.5
	Bulk	116	-5.15179705		THEN VALVE BC6 STATUS IS 100
	Wall	116	-3		RULE 33
	Bulk	117	-5.15179705		IF TANK Koudia LEVEL ABOVE 4
	Wall	117	-3		THEN VALVE BC3 SETTING IS 100
	Bulk	118	-5.15179705		RULE 34
	Wall	118	-3		IF TANK Koudia LEVEL BELOW 4
	Bulk	119	-5.15179705		AND TANK Koudia LEVEL ABOVE 3.2
	Wall	119	-3		THEN VALVE BC3 SETTING IS 150
	Bulk	120	-5.15179705		RULE 35
	Wall	120	-2		IF TANK Koudia LEVEL BELOW 3.2
	Bulk	121	-5.15179705		THEN VALVE BC3 SETTING IS 200
	Wall	121	0
	Bulk	122	-9.756557694		[SOURCES]
	Wall	122	-2		;Node Type Quality
Pattern	Bulk	123	-9.756557694		ST_Mateur SETPOINT 0.5
	Wall	123	-2		Ras _Ain MASS 1
	Bulk	124	-2.114264692		Roumadia SETPOINT 1.7
	Wall	124	-5		Rhézala SETPOINT 1.12
	Bulk	125	-2.114264692		Koudia SETPOINT 1.3
	Wall	125	-5
	Bulk	126	-1.130962588		[REACTIONS]
	Wall	126	0		;Type Pipe/Tank Coefficient
	Bulk	127	-2.591421605		Bulk 100 0
	Wall	127	0		Wall 100 -1
	Bulk	129	-3.217830912		Bulk 101 -9.756557694
	Wall	129	-5		Wall 101 -1
	Bulk	130	-3.217830912		Bulk 102 0
	Wall	130	-5		Wall 102 -5
	Bulk	131	-3.217830912		Bulk 103 0
	Wall	131	-1		Wall 103 -5
	Bulk	132	-4.413016496		Bulk 104 0
	Wall	132	-5		Wall 104 -5
	Bulk	133	-2.591421605		Bulk 105 0
	Wall	133	0		Wall 105 -5
	Bulk	134	0		Bulk 106 0
	Wall	134	-5		Wall 106 -5
	Bulk	135	-1.130962588		Bulk 107 0
	Wall	135	-5		Wall 107 -5
	Bulk	136	0		Bulk 108 0
	Wall	136	0		Wall 108 -3
	Bulk	137	-6.6 16244592		Bulk 109 -9.756557694
	Wall	137	-3		Wall 109 -1
	Bulk	138	0

Wall	138	0	Bulk	167		-9.756557694	Bulk
139	0	Wall	167	-1		Wall
139	0	Bulk	168	-9.756557694		Bulk
140	-9.756557694	Wall	168	-1		Wall
140	-1	Bulk	169	-9.991060135		Bulk
141	-9.756557694	Wall	169	-3		Wall
141	-5	Bulk	170	-9.991060135		Bulk
142	-9.991060135	Wall	170	-3		Wall
142	-5	Bulk	171	-9.991060135		Bulk
143	-3.91049491	Wall	171	-3		Wall
143	-3	Bulk	172	-9.756557694		Bulk
144	-3.91049491	Wall	172	-1		Wall
144	-5	Bulk	173	-9.756557694		Bulk
145	-3.91049491	Wall	173	-1		Wall
145	-5	Bulk	174	-9.991060135		Bulk
146	-3.217830912	Wall	174	-3		Wall
146	-1	Bulk	175	-9.756557694		Bulk
148	-6.6 16244592	Wall	175	-1		Wall
148	0	Bulk	176	-9.991060135		Bulk
149	0	Wall	176	-3		Wall
149	0	Bulk	177	-9.756557694		Bulk
150	0	Wall	177	-1		Wall
150	0	Bulk	178	-9.991060135		Bulk
151	0	Wall	178	-3		Wall
151	0	Bulk	179	0		Bulk
152	0	Wall	179	-1		Wall
152	0	Bulk	180	-9.756557694		Bulk
153	0	Wall	180	-3		Wall
153	0	Bulk	181	-9.756557694		Bulk
154	0	Wall	181	-1		Wall
154	0	Bulk	182	-9.991060135		Bulk
155	0	Wall	182	0		Wall
155	0	Bulk	183	-5.15179705		Bulk
156	-6.376635758	Wall	183	0		Wall
156	-5	Bulk	184	-3.217830912		Bulk
157	-6.376635758	Wall	184	0		Wall
157	-5	Bulk	185	-3.217830912		Bulk
158	-1.130962588	Wall	185	-0.5		Wall
158	0	Bulk	186	0		Bulk
159	-6.771982509	Wall	186	-5		Wall
159	0	Bulk	187	0		Bulk
160	-2.5 19943387	Wall	187	0		Wall
160	0	Bulk	188	-9.991060135		Bulk
161	0	Wall	188	-5		Wall
161	0	Bulk	189	-9.756557694		Bulk
162	0	Wall	189	0		Wall
162	0	Bulk	190	0		Bulk
163	-9.756557694	Wall	190	-3		Wall
163	-1	Bulk	191	0		Bulk
164	-9.756557694	Wall	191	-5		Wall
164	-1	Bulk	192	0		Bulk
165	-9.991060135	Wall	192	-5		Wall
165	-3	Bulk	193	0		Bulk
166	-9.991060135	Wall	193	0		Wall
166	-3	Bulk	194	0

[REACTIONS]			Order Bulk
1		Order Tank
1		Order Wall
1		Global Bulk
0		Global Wall
0		Limiting Potential
0

Wall		194	Bulk
195		Wall
195		Bulk
196		Wall
196		Bulk
197		Wall
197		Bulk
198		Wall
198		Bulk
199		Wall
199		Bulk
200		Wall
200		Bulk
201		Wall
201		Bulk
202		Wall
202		Bulk
203		Wall
203		Bulk
204		Wall
204		Bulk
147		Wall
147		Bulk
128		Wall
128

[MIXING]

;Tank Model

[TIMES]

Duration 144

Hydraulic Timestep 1

Quality Timestep 0:05

Pattern Timestep 1:00

Pattern Start 0:00

Report Timestep 1

Report Start 72

Start ClockTime 12 am

Statistic None

[REPORT]

Status No

Summary No

Page 0

[OPTIONS]

Roughness Correlation

-5	Units		LPS	0
Headloss	H-W		-3
Specific Gravity	1		0
Viscosity	1		-2
Trials 35			-2.114264692
Accuracy	0.01		-3
Unbalanced	Continue 10		0
Pattern	1		-1
Demand Multiplier	1.0		-9.756557694
Emitter Exponent	0.1		-5
Quality	Chlore mg/l		-3.217830912
Diffusivity	1		-0.5
Tolerance	0.01		-9.756557694
			-1
			-3.91049491
[END]			-5
			-3.91049491
			-5
			-1.130962588
			-5
			-3.217830912
			-1
			-3.217830912
			-1
			0

ANNEXE 11
Logiciel "EPANET2 "

L'outil informatique utilisé pour la modélisation est le logiciel "EPANET". Il est développé par l'agence pour la protection de l'environnement des Etats-Unis. C'est un logiciel gratuit de simulation du comportement hydraulique et de la qualité de l'eau sur de longues durées dans les réseaux sous pression.

A-1/ Composantes physiques

"EPANET" modélise un système hydraulique sous pression comme un ensemble d'arcs reliés à des noeuds. Les arcs représentent des conduites, des pompes, et des vannes de contrôle. Les noeuds représentent des noeuds de demande, des réservoirs et des bâches.

A-1-1/ Les bâches

Les bâches infinies sont des noeuds représentant une source externe de capacité infinie. Elles sont utilisées pour modéliser des éléments tels que les couches aquifères souterraines ou les arrivées de réseaux extérieurs. Les bâches infinies peuvent également servir de point d'injection d'une substance entrant dans le réseau. Les données de base pour une bâche sont la charge totale (égale au niveau de la surface de l'eau si la bâche infinie n'est pas sous pression) et la qualité initiale de l'eau dans le cas où l'on exécuterait une analyse de qualité de l'eau. Puisqu'une bâche est un élément de frontière d'un réseau, la qualité et la charge hydraulique de l'eau ne peuvent pas être affectées par ce qui se produit dans le réseau. Par conséquent, aucune propriété n'est calculée au cours de la simulation.

A-1-2/ Les conduites

Les conduites sont des arcs qui transportent l'eau d'un point du réseau à l'autre "EPANET" suppose que tous les tuyaux sont pleins à tout instant. L'eau s'écoule de l'extrémité qui a la charge hydraulique la plus élevée (altitude + pression, ou énergie interne par poids d'eau) à celle qui a la charge hydraulique la plus faible. Les données de base pour les conduites sont:

· Les noeuds initial et final;

· Le diamètre;

· La longueur;

· Le coefficient de rugosité (pour déterminer la perte de charge);

· L'état (ouvert, fermé, ou avec un clapet anti-retour).

Le paramètre d'état permet à des conduites de contenir implicitement des vannes de sectionnement et de contrôler les clapets anti-retour.

Les données de qualité de l'eau pour les conduites sont :

· Le coefficient de réaction dans la masse d'eau ;

· Le coefficient de réaction aux parois.

Les valeurs calculées pour les conduites incluent :

· Le débit

· La vitesse d'écoulement

· La perte de charge

· Le facteur de friction de Darcy-Weisbach

· La vitesse moyenne de réaction (le long du tuyau)

· La qualité moyenne de l'eau (le long du tuyau)

A-1-3/ Les réservoirs

Les Réservoirs sont des noeuds avec une capacité de stockage, dont le volume d'eau stocké peut varier au cours du temps. Les données de base pour des réservoirs sont les suivantes:

· L'altitude du radier (où le niveau d'eau est zéro)

· Le diamètre (ou sa forme s'il n'est pas cylindrique)

· Les niveaux initial, minimal et maximal de l'eau

· La qualité initiale de l'eau.

Les principaux éléments calculés dans la simulation sont les suivants:

· La charge (altitude de l'eau)

· La pression (niveau de l'eau)

· La qualité de l'eau.

Le niveau dans les réservoirs doit rester entre les niveaux minimal et maximal. "EPANET" arrête la sortie d'eau si un réservoir est à son niveau minimal et arrête l'arrivée s'il est à son niveau maximal. Les réservoirs peuvent également servir de source pour une substance entrant dans le réseau (injection de chlore).

A-1-4/ Les vannes

Les vannes sont modélisées comme des arcs qui limitent la pression ou le débit en un point précis du réseau. Leurs principaux paramètres d'entrée sont:

· Les noeuds d'entrée et de sortie

· Le diamètre

· La consigne de fonctionnement

· L'état de la vanne.

Les éléments calculés en sortie de simulation pour une vanne sont le débit et la perte de charge hydraulique.

Les différents types de vannes qu'offre "EPANET" sont:

· La vanne stabilisatrice aval limite la pression au noeud en aval

· La vanne stabilisatrice amont maintient une pression prédéterminée au noeud en amont

· La vanne brise charge ou réducteur de pression provoque une perte de pression spécifique au passage de la vanne

· La vanne régulatrice de débit ou limiteur de débit limite le débit à une valeur spécifiée

· La vanne diaphragme simule une vanne partiellement fermée en ajustant le coefficient de perte de charge singulière de la vanne

· La vanne d'usage général utilisée pour représenter des arcs où l'utilisateur prévoit une relation spécifique entre le débit et la perte de charge, au lieu de suivre une des formules hydrauliques standard

On peut choisir la consigne de fonctionnement d'une vanne en spécifiant qu'elle est entièrement ouverte ou fermée. La consigne d'une vanne peut être modifiée pendant la simulation en utilisant des commandes de contrôle

A-1-5/ Les pompes et les forages

Les principaux paramètres d'entrée pour une pompe sont ses noeuds d'aspiration et de décharge et sa courbe caractéristique. Les pompes peuvent être mises en route et arrêtés à des heures préétablies ou quand certaines conditions existent dans le réseau parmi des commandes.

Les forages sont modélisés comme des bâches dont la charge hydraulique sont égales au niveau piézométrique de l'aquifère et connectés au reste du réseau par des pompes. Si le débit de pompage est connu, une alternative plus simple consiste à représenter la combinaison source-pompe par un noeud avec une demande négative, égale au débit de pompage.

A-2/ Composantes non physiques

En plus des composants physiques, "EPANET" utilise trois types d'objets non physiques:

· Les courbes qui sont la courbe caractéristique et la courbe de rendement pour une pompe, courbe de volume pour un réservoir et courbe de perte de charge pour une vannes ou une conduite

· Les courbes de modulation qui peuvent être assignées à la demande d'un noeud, au niveau d'une bâche, à la qualité de l'eau dans une source.

· Les commandes de contrôle qui sont des instructions qui déterminent comment le réseau est géré pendant la simulation. Elles indiquent l'état des arcs déterminés en fonction du temps, l'état des niveaux d'eau aux réservoirs et la valeur de la pression à certains points du réseau. Deux catégories de commandes peuvent être utilisées: les commandes simples et les commandes élaborées.

A-3/ Modèle de simulation hydraulique d'"EPANET"

Le modèle hydraulique de simulation d'"EPANET" calcule l'évolution des charges hydrauliques dans les noeuds et l'écoulement dans les arcs, en fonction des niveaux initiaux des réservoirs, des variations dans le temps des niveaux des bâches et des demandes en eau aux noeuds de demande. D'un intervalle à l'autre, les niveaux des bâches et les demandes dans les noeuds de demande sont mis à jour selon les courbes de modulation entrées comme paramètres du calcul, tandis que les niveaux des réservoirs sont mis à jour selon les débits qui entrent et qui sortent. La détermination des charges et des débits à un instant donné implique de résoudre simultanément les équilibres de masse dans les noeuds et les pertes de charges dans chaque arc du réseau. Ce procédé, appelé équilibre hydraulique du réseau, utilise une technique itérative pour résoudre les équations non linéaires en jeux. "EPANET" utilise l' "Algorithme du Gradient" (II-19).

A-4/ Modèle de simulation de la qualité d'eau d'"EPANET"

Le simulateur de la qualité de l'eau d'"EPANET" utilise une approximation Lagrangienne pour suivre, à intervalles définis, ce qui se passe dans des portions d'eau discrètes, lorsqu'elles circulent dans les tuyaux et se mélangent aux noeuds de demande.

A-4-1/ Modélisation du transport

"EPANET" a un noyau qui utilise un modèle de transport d'advection-réaction. La négligence du phénomène de dispersion par le modèle EPANET n'a pas d'effets sur l'éxactitude des résultats de la modélisation de la qualité d'eau des réseaux d'adduction. En effet ces réseaux sont le siége d'écoulements turbulents (fort nombre de Reynolds).

A-4-2/ Réactions modifiant la qualité de l'eau

"EPANET" peut suivre l'accroissement ou la régression d'une substance dans l'eau suite à des réactions dans le réseau sous pression. Ces réactions peuvent se produire dans la masse d'eau et aux parois des conduites. "EPANET" modélise les réactions dans la masse d'eau avec une cinétique d'ordre n, le coefficient de régression ou d'accroissement dans la masse d'eau "Kb" s'exprimera comme une concentration élevée à la puissance (1-n) divisée par le temps. Pour les réactions aux parois, "EPANET" autorise uniquement des réactions d'ordres 0 ou 1, par conséquent les unités du

coefficient de régression ou d'accroissement K_w seront en masse/surface/temps (ordre 0) ou bien longueur par unité de temps (ordre 1). Ces coefficients auront des signes positifs dans le cas d'un accroissement et un signe négatif dans le cas contraire.

A-4-3/ Temps de séjour et dépistage des sources

En plus du transport chimique, "EPANET" peut modéliser le temps de séjour de l'eau dans un système de distribution. "EPANET" peut également effectuer un dépistage des sources : pour cela "EPANET" calcule pour l'instant « t » le pourcentage d'eau arrivant à un noeud donné du réseau, en fonction de différentes origines d'eau.

A-4-4/Qualité de source

La source peut être l'installation principale de traitement, une installation de chloration ou un réservoir intermédiaire de retraitement. Elle peut simuler aussi l'injection d'une substance contaminante. Une source de type concentration en sortie est le meilleur choix pour modéliser l'injection d'un désinfectant additionnel ou l'injection d'un contaminant dans le réseau.