II.2.4 MODELE D'ANALYSE D'INTERVENTIONS
II.2.4.1 INTRODUCTION
Il arrive fréquemment que les séries
chronologiques soient affectées par des interventions : changement de
définition de la grandeur étudiée, changement de
réglementation qui affecte sa valeur, circonstances particulières
(accidents, grèves, promotion, etc.). Ces phénomènes se
traduisent par des données atypiques ou aberrantes dans les
séries statistiques.
Ces données conduisent généralement
à des estimations erronées des paramètres du modèle
pouvant à leur tour conduire à des mauvaises prévisions.
Face à ces données atypiques, bien d'auteurs
préconisent soit leur élimination, soit leur lissage. Ces
opérations ont comme conséquence le perte ou la
déformation de l'information contenue dans les séries.
Pour palier ce problème, on utilise le modèle
d'interventions ou modèle ARMA incluant des variables binaires.
II.2.4.2 ANALYSE DES INTERVENTIONS
Les modèles d'analyse d'interventions permettent de
représenter l'influence d'information qualitative en plus de
l'information quantitative. En fait, dans leur démarche, ces
modèles utilisent les variables binaires pour saisir l'information
qualitative supposée contenue dans les données atypiques.
II.2.4.3 FORMES D'INTERVENTIONS
Il existe plusieurs formes d'interventions dont le choix et
l'identification de l'instant s'effectuent à partir du graphe de la
série chronologique. Il est aussi possible de combiner sur une
même série différentes formes d'interventions.
Plus généralement, on définit quatre
formes d'impacts :
1. Impulsion de o au temps
· Définition de la variable à
introduire
 ; la
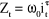fonction de la variable est  avec  la variable
binaire telle que  .
Z
0
0
t
- 1 + 1
· Insertion des effets des interventions dans le
modèle ARMA :
2. Saut de o au temps
· Définition de la variable à
introduire
 , la
fonction de la variable est :
Z
0
0
t
- 1 + 1
· Insertion des effets des interventions dans le
modèle ARMA :
3. Accroissement o au temps ,
exponentiellement dégressif au taux
· Définition de la variable à
introduire
 ; la
fonction de la variable est :
Z
0
t
0
- 1 + 1
· Insertion des effets des interventions dans le
modèle ARMA :
4. Rampe de pente 1 au temps
· Définition de la variable à
introduire
 ; la
fonction de la variable est :
Z
0
1
0
- 1 + 1
t
· Insertion des effets des interventions dans le
modèle ARMA :
| 
