|
N° d'ordre : 2776
THÈSE
présentée à
L'UNIVERSITÉ BORDEAUX I
ÉCOLE DOCTORALE DES SCIENCES PHYSIQUES ET DE
L'INGÉNIEUR
par
Christophe GACHET
POUR OBTENIR LE GRADE DE
DOCTEUR
SPÉCIALITÉ : SCIENCES DU BOIS
INVENTAIRE ET HIÉRARCHISATION DE PARAMÈTRES
STRUCTURAUX ET ULTRASTRUCTURAUX FACTEURS DE VARIABILITÉ INTRA
SPÉCIFIQUE
DE CERTAINES PROPRIÉTÉS MÉCANO
PHYSIQUES DES TISSUS LIGNEUX
Soutenue le 16 décembre 2003
Après avis de :
MM. B. CHARRIER, Maître de Conférences, HDR- IUT
de PAU et des Pays de l'Adour Rapporteurs
J. GRIL, Directeur de Recherche CNRS-LMGC, Montpellier
Devant la commission d'examen formée de :
MM. B. DE JESO, Professeur-LCSV, Institut du Pin, Univ.
Bordeaux 1 Président
J.R. PUIGGALI, Professeur-LEPT-ENSAM, Univ. Bordeaux 1
Rapporteur
B. CHARRIER, Maître de Conférences, HDR-IUT de PAU
et des Pays de l'Adour
J. GRIL, Directeur de Recherche CNRS-LMGC, Montpellier
Examinateurs
D. GUITARD, Professeur-LEPT-ENSAM, Univ. Bordeaux 1
A. ZOULALIAN, Professeur-LERMAB, Univ. Nancy 1
- 2003 -
Ce travail a été réalisé au
Laboratoire Energétique et Phénomènes de Transferts,
unité mixte
de recherche associée au CNRS, à
l'Université de Bordeaux 1 et à l'Ecole Nationale
Supérieure d'Arts et Métiers; il a été soutenu par
un financement du Ministère de l'Education Nationale de la Recherche et
des Technologies.
Je souhaite tout d'abord remercier sincèrement
Monsieur le Professeur Bernard De
Jeso pour avoir accepté de présider mon jury de
thèse.
C'est un grand honneur que m'ont fait Messieurs Bertrand
Charrier, Maître de
Conférences, Joseph Gril, Directeur de Recherche au CNRS
et André Zoulalian, Professeur, en s'intéressant à mes
travaux de recherche et en acceptant de les rapporter.
Tout au long de ce travail, les conseils avisés de
Monsieur Joseph Gril, Directeur de Recherche au CNRS, m'ont permis
d'appréhender toute la complexité du comportement
rhéologique du matériau bois.
Je voudrais tout particulièrement remercier
Monsieur Jean Rodolphe Puiggali, Professeur et Directeur du LEPT - ENSAM
pour ses remarques, ses conseils avisés comme pour son soutien
indéfectible.
Monsieur Daniel Guitard, Professeur et Directeur de
Thèse a eu la lourde tache d'initier (ou de re-initier) aux
rudiments de la Mécanique des Solides et de la Résistance des
Matériaux, un physico chimiste de formation. Qu'il en soit ici
sincèrement remercié ; la mission n'ayant pas toujours
été facile. Durant ces trois années j'ai pu
également bénéficier
de son expérience à l'origine de nombreuses
discussions particulièrement enrichissantes.
L'équipe du CIRAD Forêt de Montpellier a
mis a ma disposition de nombreux moyens expérimentaux et a su me
consacrer une partie de son temps, ô combien précieux ; je tiens
donc ici à remercier Anne et Bernard Thibaut ainsi que Gilles Calcheras.
Votre aide a été plus qu'appréciable.
Monsieur Philippe Rozenberg, Chargé de Recherches
INRA (station d'Olivet), a su m'orienter et me guider dans le domaine bien
spécifique des études microdensitométriques.
Enfin, je désire remercier les miens, Béa, mes
Parents et Valérie pour leur réconfort permanent.
TABLE DES MATIERES
Introduction
.................................................................................................................................................
3
1 Inventaire des facteurs essentiels de la
variabilité intra arbre des propriétés
mécaniques des tissus ligneux
.......................................................................................................
5
1.1 La cellule ligneuse
........................................................................................................................
5
1.1.1 Description cytologique sommaire de la cellule ligneuse
dite de « bois normal »............ 5
1.2 Des macromolécules au comportement mécanique de
la paroi cellulaire .................................... 6
1.2.1 Les polymères fondamentaux de la paroi cellulaire
.......................................................... 6
1.2.2 Les microfibrilles de cellulose : des
éléments essentiels de renfort pariétal
..................... 7
1.2.3 La matrice ligno-cellulosique
..........................................................................................
12
1.2.4 L'angle des microfibrilles dans la sous couche S2 : un
paramètre micromécanique primordial
........................................................................................................................
14
1.2.5 Prise en compte du caractère multicouche de la paroi
cellulaire ..................................... 17
1.2.6 Description du comportement mécanique de sous couche
.............................................. 18
1.2.7 La double cloison, un passage obligé vers le tissu
ligneux ............................................. 18
1.3 L'anisotropie élastique à l'échelle du
tissu ligneux
.................................................................... 22
1.3.1 La morphologie
cellulaire................................................................................................
23
1.4 Facteurs explicatifs de l'anisotropie élastique
à l'échelle du cerne de croissance ...................... 26
1.4.1 Le cerne assimilé à un bicouche
......................................................................................
26
1.4.2 Le rayon ligneux : un élément de renfort
radial .............................................................. 27
1.5 Conclusion
..................................................................................................................................
29
2 Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV) ................ 30
2.1 Modèles multi échelles retenus pour
décrire l'anisotropie élastique du bois de résineux
.......... 30
2.1.1 Le concept de modélisation multi
échelles......................................................................
30
2.1.2 Modèles à parois cellulaires multicouche
(Multicouche) ................................................ 30
2.1.3 Modèle à squelette de microfibrilles
(Squelette) ............................................................. 40
2.1.4 Nombre total de paramètres structuraux retenus
............................................................. 41
2.2 Construction du Résineux Standard
Virtuel................................................................................
45
2.2.1 Validation des modèles prévisionnels de
l'anisotropie élastique .................................... 45
2.2.2 Résultats et discussions
...................................................................................................
46
2.2.3 Situation des paramétres du modèle RSV
vis-à-vis de ceux de trois essences résineuses ..
.........................................................................................................................................
54
2.3 Conclusion
..................................................................................................................................
59
3 Hiérarchisation des paramètres
descriptifs de l'anisotropie élastique du bois normal 63
3.1 La porosité, facteur de l'anisotropie élastique
du réseau cellulaire nid d'abeille ....................... 63
3.1.1 Comparaison au modèle de Gibson et al et
influence de l'élément de paroi fléchie .......... 66
3.1.2
Conclusion.......................................................................................................................
69
3.2 Hétérogénéité tissulaire
et anisotropie élastique du bois normal
................................................ 69
3.2.1 Différence de morphologique cellulaire entre le bois
initial et le bois final ................... 70
3.2.2 Distinction densitométrique entre le bois initial et
le bois final ...................................... 72
3.2.3 La texture, facteur d'anisotropie élastique dans le
plan transverse .................................. 73
3.3 Rôle des rayons ligneux dans l'anisotropie
élastique du cerne ...................................................
82
3.4 Influence des paramètres ultrastructuraux sur
l'anisotropie élastique tissulaire ......................... 83
3.4.1 Sensibilité de l'anisotropie tissulaire L/T à
l'angle des microfibrilles ............................ 83
3.4.2 Incidence du module d'élasticité des
microfibrilles ........................................................ 86
3.4.3 Influence du module élastique de la matrice
................................................................... 86
3.4.4 Anisotropie tissulaire L/T d'un bois normal imputable
à l'AMF dans S2 ....................... 89
1
3.4.5
Conclusion.......................................................................................................................
91
3.5 Différences et complémentarités entre
les modélisations Multicouches et Squelette ................. 91
3.5.1 Paramètres d'entrées des modélisations
confrontées....................................................... 91
3.6 Valeurs de modules élastiques de double paroi
présentés dans la littérature
.............................. 92
3.6.1 Choix des valeurs cibles
..................................................................................................
93
3.7 Propriétés élastiques prévues par
les différentes
modélisations.................................................. 93
3.7.1 Le bicouche M1
...............................................................................................................
94
3.7.2 Le multicouche M2
.........................................................................................................
95
3.7.3 Modules élastiques de double paroi virtuelle obtenus
via le modèle M3 ........................ 96
3.7.4 Degrés d'anisotropie pariétale
.........................................................................................
98
3.8 Comportement en flexion torsion du stratifié
pariétal
................................................................ 98
3.8.1 Influence d'une modification de l'épaisseur de S1
.......................................................... 99
3.8.2 Influence de l'angle des microfibrilles
............................................................................
99
3.9 Conclusion
................................................................................................................................
100
4 Vers une description de l'anisotropie élastique
du bois de réaction................................ 101
4.1 Existence de plusieurs bois de compression
.............................................................................
101
4.1.1 Description sommaire des caractères anatomiques
généraux du bois de compression . 101
4.2 Etude
expérimentale..................................................................................................................
103
4.2.1 Mise en oeuvre de l'étude
..............................................................................................
103
4.2.2 Synthèses des différents résultats
..................................................................................
111
4.2.3 Influence de modifications anatomiques sur les
caractéristiques élastiques prédites.... 124
4.2.4
Conclusion.....................................................................................................................
129
5 Conclusion et
perspectives.........................................................................................................
130
2
Introduction
Depuis longtemps (tels Carrington en 1922, Kollmann
et al en 1941 et 1960 rapportés dans Kollmann et
Coté, 1984), ou plus récemment (Bodig, 1984, Guitard et
al, 1987), de nombreux auteurs, se sont préoccupés
d'analyser et même de modéliser l'influence de
paramètres physiques tels que la masse volumique, le taux
d'humidité, ou encore la température sur les
propriétés élastiques du matériau bois.
Des modèles prévisionnels des
caractéristiques élastiques anisotropes (Guitard et
al, 1987), s'appuyant sur des indicateurs tels que la nature feuillue ou
résineuse de l'essence considérée, la masse volumique, le
taux d'humidité et la température ont ainsi
démontré leur pertinence quand
à l'évaluation, à priori, des
constantes élastiques anisotropes ou des coefficients de retraits
hydriques (Presioza et al, 1986).
Plus de quatre vingt pour cent de la variabilité inter
spécifique, et même intra spécifique, de ces
propriétés technologiques du bois normal sont ainsi
largement expliqués par ces seuls indicateurs.
Les modèles précités, très
certainement efficaces pour élucider la variabilité inter
spécifique des modules élastiques et des retraits pour le
bois « normal », sont pourtant mis en défaut pour
décrire la variabilité intra arbre de ces mêmes
caractéristiques mécano physiques. Tout au long
de sa croissance, outre le bois dit « normal
», l'arbre élabore en effet une grande variété
de tissus ligneux (bois juvénile, bois adulte, bois initial,
bois final, bois de réaction, bois duraminisé), ceci en
réponse à des impératifs de développement de
la plante, notamment en réaction à des stimuli
extérieurs variés (gravitropiques, héliotropiques,
climatiques, attaques fongiques ou d'insectes).
Cette diversité tissulaire, s'exprimant tant au
niveau de la macrostructure (moelle excentrée, largeur de cernes,
texture, duramen) que de la structure cellulaire (formes et
diamètres des cellules, épaisseurs de paroi, présence
d'une sous couche gélatineuse) voire de l'ultra structure
(nature des bio polymères, angle des microfibrilles,
taux de cristallinité de la cellulose) peut donc être
considérée à l'origine du caractère
hétérogène et fortement variable du matériau.
La plupart des propriétés mécano
physiques observées à l'échelle du bois massif
(échelle macroscopique) résulte donc d'une imbrication
à priori étroite de plusieurs niveaux
d'hétérogénéité : échelle
supramoléculaire (microfibrilles de cellulose, polymères
amorphes), échelle pariétale (orientation des microfibrilles
dans les sous-couches), échelle de la cellule
(morphologie cellulaire), échelle du tissu ligneux
(différenciation en bois initial / final) et échelle du
cerne d'accroissement (présence de rayons ligneux).
De façon quasi systématique, la sensibilité
de l'anisotropie élastique transverse macroscopique
(caractérisée par le rapport des modules
d'élasticité radial et tangentiel) a, de fait, souvent (et
« naturellement ») été
analysée par l'anisotropie de la paroi cellulaire, par la
géométrie cellulaire, par l'agencement cellulaire (en
quinconce, aligné,...) ou encore par la présence de rayons
ligneux.
L'objectif de ce travail, limité au seul cas des
résineux, est donc, à travers une étude transversale
pluridisciplinaire (cytologie, anatomie, mécanique des
composites), d'énumérer et de
3
hiérarchiser, les paramètres les plus
pertinents susceptibles de conditionner l'anisotropie élastique du
bois normal aux différentes échelles d'observations.
In fine, il s'agit, par un cheminement plus
déterministe que statistique, d'établir un jeu de
paramètres strictement utiles, capables, de par les intervalles
de variations qu'une étude documentaire leur assigne, de rendre
compte de la variabilité intra arbre des propriétés
mécano physiques du bois normal des résineux.
Cette démarche s'appuie en particulier sur
l'exploitation de modèles explicatifs proposés par
différents auteurs et sur leur confrontation éventuelle à
des jeux de données expérimentales.
4
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
1 Inventaire des facteurs essentiels de la
variabilité intra arbre des
propriétés mécaniques des tissus
ligneux
Les différents niveaux de description et
d'hétérogénéité de la matière
ligneuse sont ici successivement explorés, depuis l'ultrastructure
moléculaire, jusqu'à la macrostructure du bois massif sans
défaut, dans une perspective mécanicienne. Les
éléments bibliographiques essentiels sont évoqués
en appui des choix qui sont, in fine, retenus, dans l'objectif
d'alimenter une succession de modèles micro-macro (non
nécessairement les plus sophistiqués) explicatifs et
descriptifs du comportement élastique anisotrope du bois massif.
Quelques indications succinctes de la variabilité des paramètres
susceptibles de conditionner l'anisotropie élastique sont
également précisées.
1.1 La cellule ligneuse
1.1.1 Description cytologique sommaire de la cellule
ligneuse dite de « bois normal »
Une fois différenciée, la cellule ligneuse
présente plusieurs parois (couches) constitutives,
inégales en proportion. Une description des couches
externes vers les couches cellulaires plus internes permet de distinguer :
une couche intercellulaire qui joue le rôle d'un ciment
entre deux cellules mitoyennes,
une paroi primaire tapissant la couche
précédente,
une paroi secondaire se déposant sur la paroi
primaire.
La paroi secondaire, par sa structure et son volume, constitue la
partie de la cellule ligneuse la plus résistante
mécaniquement.
Les études cytologiques classiques distinguent au
sein de cette paroi secondaire trois sous couches superposées,
appelées S1, S2, et S3, se déposant successivement au
cours de la maturation, (Dunning, 1968), et se singularisant, non seulement
par leur dimension et par leur composition chimique (proportion de
macromolécules), mais aussi par l'inclinaison des microfibrilles
par rapport au grand axe cellulaire (angle des microfibrilles noté AMF,
Figure
1.1).
La sous couche externe S1, formation intermédiaire
entre la paroi primaire et les sous couches plus internes de la paroi
secondaire, présente une structure lamellaire (3 à 6 lamelles).
Dans cette sous couche, qui représente entre 5 et 10% de
l'épaisseur totale de la paroi cellulaire
(soit au maximum 0.35 um, d'après Keller, 1999),
l'inclinaison des microfibrilles de cellulose
est de l'ordre de 60 à 80 degrés. Le renfort
cellulosique de cette sous couche est constitué de deux enroulements de
microfibrilles croisés et superposés (treillis de fibres).
La sous couche centrale S2 (75 à 85% de
l'épaisseur totale et au maximum 10 um d'après
Keller, 1999) est formée d'une organisation nettement plus
dense de lamelles de microfibrilles
de cellulose, quasi parallèles et inclinées
d'au minimum 5 degrés chez les résineux. Comparativement
aux autres sous couches, c'est au sein de S2 que l'angle des microfibrilles
varie le plus selon le « type » de bois observé (bois initial
et final, constitutifs du bois normal, mais aussi bois juvénile ou
encore bois de compression). La valeur maximale de cet angle des microfibrilles
est assez variable ; nous envisagerons ici, dans le cadre
d'un bois dit
« normal », et comme de nombreux auteurs
mécaniciens (Mark, 1967, 1980, Barrett, 1973,
5
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Koponen et al, 1989, Navi et al, 1995), une
valeur maximale de 40 degrés attribuée à la sous
couche S2 du bois initial ou à celle des rayons
ligneux.
Composante essentielle de la paroi secondaire, la sous
couche S2 est considérée (Mark, 1967,
1980, Barrett, 1973, Gillis, 1972, Bodig et al, 1982,
Norimoto, 1986 dans Gril, 1987) comme
principale responsable du comportement mécanique
global de la cellule ligneuse de bois normal.
La sous couche interne S3, relativement mince (entre 0,5 et
1,10um), possède également une structure en lamelle mais les
microfibrilles sont moins strictement parallèles entre elles que dans
S2. L'inclinaison des microfibrilles y est de l'ordre de 60 à 90
degrés d'après Kollman et
al (1984).

Figure 1.1 Vue schématique d'une paroi cellulaire
typique d'une trachéide de conifère, tiré et adapté
de Siau (1984)
P : paroi primaire, P', P'' paroi primaire de cellules
adjacentes
M : lamelle moyenne
S1 : sous couche externe de la paroi secondaire S2 : sous
couche centrale de la paroi secondaire S3 : sous couche interne de la paroi
secondaire
1.2 Des macromolécules au comportement
mécanique de la paroi cellulaire
1.2.1 Les polymères fondamentaux de la paroi
cellulaire
La matière constitutive de la paroi de la cellule
ligneuse est généralement assimilée à un
mélange de macromolécules de plusieurs bio
polymères, pour l'essentiel de la lignine (ou plutôt des
lignines), des hémicelluloses et de la cellulose. De récents
travaux ont montré qu'il n'existe pas réellement de
différence significative au niveau de la composition chimique
massique entre les conifères et les feuillus (Tsoumis, 1991 sur
153 espèces de zones tempérées). La proportion de
cellulose est, de plus, remarquablement uniforme dans les deux
« catégories » d'essences (Chow, 1946).
La teneur en macromolécules des sous couches
constitutives de la paroi cellulaire (comme celle de la paroi dans
son ensemble) étant connue depuis longtemps, la plupart des
mécaniciens du bois (Barrett, 1973, Cave, 1975, Mark, 1980, Bodig et
al, 1982, Kollmann et
6
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
al, 1984, Guitard, 1987) adoptent des valeurs
comparables quand à la proportion des
polymères essentiels de la paroi.
1.2.1.1 Les substances cristallines
De par sa structure, la cellulose, offre de nombreuses
possibilités de liaisons inter et intra moléculaires (son
Degré de Polymérisation peut aller jusqu'à 10000).
Cet homopolymère linéaire, fondamental du point de vue du
comportement mécanique, représente de 40 à 45 %
de la masse de la matière ligneuse (Kollmann et
al, 1984).
Dans la cellule de bois, la cellulose I, forme native
de la cellulose, est majoritaire. Ce composé, fortement
cristallin, est généralement présent sous la forme d'un
mélange de deux isomères ; la forme triclinique (cellulose
á) et la forme monoclinique (cellulose â). Si la
proportion de chaque isomère est fortement dépendante de
l'espèce, la forme monoclinique demeure néanmoins majoritaire
dans la cellule ligneuse (VanderHart et al, 1984). La cellulose
I est avant tout le constituant essentiel des microfibrilles
qui confèrent à la fibre sa rigidité. Pour rendre compte
de la proportion de ce renfort filamentaire cellulosique dans la
paroi cellulaire, la fraction volumique en microfibrilles est
généralement considérée par les
mécaniciens comme un paramètre descriptif suffisant.
1.2.1.2 Les substances amorphes
Les hémicelluloses (représentant de 7
à 15% en masse) sont quant à eux des polymères
à chaînes plus courtes présentant un Degré de
Polymérisation moyen compris entre 50 et 300. Ces polysaccharides
ramifiés forment, avec les lignines polyphénoliques
réticulées (24 à 36%
en masse), une matrice amorphe, thermo et hygro
sensible, autour de structures cristallines appelées
microfibrilles. Contrairement à la cellulose, les structures
et proportions des hémicelluloses et des lignines, dépendent
très sensiblement de la nature résineuse ou feuillue
de l'essence ligneuse.
De part leur caractère très hydrophile, et leur
capacité à se replier sur elles mêmes (faibles longueurs de
chaîne), les hémicelluloses sont les principales responsables des
phénomènes de retrait - gonflement de la paroi avec les
variations des teneurs en eau (Siau, 1984). Les lignines, quant à
elles, majoritairement localisées au sein de la lamelle mitoyenne,
jouent le rôle d'un adhésif intercellulaire hydrophobe.
D'autres substances, appelées pectines
(polysaccharides), sont rencontrées, plus
anecdotiquement, dans les parties externes de la paroi cellulaire.
Pour les mécaniciens, la matière ligneuse est
assimilée à un matériau composite simplifié dont
la structure est censée décrire « la
paroi cellulaire » dans son intégralité. Cette
approche schématique de l'organisation pariétale fait donc
abstraction de la variabilité naturelle des teneurs en
macromolécules dans la paroi cellulaire ligneuse (celles des lignines a
notamment
été décrite par Boutelje, 1962,
Ruel, 1984, Donaldson, 2001 et Monties 2003, celle des polysaccharides
l'a été par Bergander et al, 2001) comme de la
variabilité des agencements mutuels (supramoléculaires) des bio
polymères essentiels.
1.2.2 Les microfibrilles de cellulose : des
éléments essentiels de renfort pariétal
Le regroupement en « bâtonnets » rigides
rectangulaires des chaînes linéaires cellulosiques est
fortement favorisé par la présence de
groupements hydroxyles périphériques sur chaque maillon
(monomère) cellobiose. Cette association supramoléculaire est
appelée « microfibrille
de cellulose ». La taille de ces « segments
» cellulosiques, quasi cristallins, varie
généralement en fonction de l'espèce ligneuse
considérée. En dépit de cette variabilité
de
7
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
dimension, il est possible de donner une estimation de
la longueur de la microfibrille de
l'ordre de 1,5 à 5 nm. Les faisceaux de
microfibrilles, séparés les uns des autres par des couches
de cellulose (plus ou moins organisée) ou
d'hémicelluloses, se regroupent pour former des agrégats,
nommés fibrilles, dont l'épaisseur est
généralement comprise entre la dizaine et la vingtaine de nm
(Hult et al, 2000).
1.2.2.1 Prise en compte des différents caractères
de la structure microfibrillaire dans une perspective mécanicienne
Un renfort filamentaire régulier en dépit d'une
structure discontinue
Depuis longtemps, des études, menées à
l'échelle sub-microscopique (Mark, 1967, Fengel et
al, 1984) ont souligné le caractère
discontinu des microfibrilles. Par diffraction des rayons X puis par
microscopie électronique, la présence systématique de
zones amorphes désordonnées distribuées sur la longueur de
la microfibrille a été montrée. Les cristallites de
cellulose ne représentent ainsi pas une phase continue. De
surcroît, ces éléments cristallins apparaissent fortement
variables dans leurs dimensions (Mark, 1967). L'organisation exacte des
cristallites dans la microfibrille n'a, jusqu'alors, pas
été parfaitement élucidée (nombre, disposition
spatiale). Elle a donc été sujette à de multiples
interprétations et a donné lieu à plusieurs
modélisations (en particulier celles de Fengel, 1968, et de Mark,
1980).
Diverses techniques expérimentales (localisation de
l'accessibilité de la cellulose amorphe à certaines
molécules, diffraction rayons X, ...) conduisent à une
évaluation du taux de cristallinité de la cellulose du bois de
l'ordre de 60 à 70% (Preston, 1964 dans Panshin et al,
1980). Devant une telle proportion de cristallites, et une
longueur de segment cristallin bien supérieure à celle de la
zone amorphe, les descriptions mécaniciennes envisagées
à cette échelle considèrent que les microfibrilles
assurent un renfort filamentaire régulier et continu à
la sous couche S2. La justification de cette
approximation de continuité a été décrite
par
Salmèn et al (1985, 1986) avec son modèle
de fibre aplatie. Celui-ci, reprenant les équations
de Halpin Tsai (évaluation des
caractéristiques élastiques d'un composite renforcé
par des fibres courtes), a montré, expérimentalement
(fibres mercerisées et régénérées),
qu'une diminution de la rigidité axiale de la fibre n'est
observée que dans le cadre de modifications simultanées du taux
de cristallinité et de la longueur des zones cristallines. Des
modifications locales (ponctuelles) de cristallinité le long de la fibre
ne conduisent pas à des changements majeurs de rigidités. En
quantifiant l'impact d'une modification de la longueur des renforts
cellulosiques, sur les modules élastiques de sous couche
(méthode « auto cohérente »), Vieville (1992) est
également arrivé, de manière plus théorique,
à la même conclusion.
Des fibres cellulosiques aux propriétés
mécaniques homogènes
Bien que de nombreux travaux (Mark, 1967, Fengel
et al, 1984) aient montré d'une part l'existence
d'incrustations lenticulaires (lignines mêlées
d'hémicelluloses) séparant les microfibrilles, et d'autre
part la présence de liens désordonnés entre
microfibrilles d'une même lamelle (ou entre lamelles adjacentes
d'une même sous couche, Boyd et al, 1975, Figure 1.2), le
renfort cellulosique pariétal est très généralement
décrit comme étant assuré par des fibres
mécaniquement homogènes.
Certaines modélisations d'effet mécano sorptif
survenant lors de la morphogenèse cellulaire
(déformations résiduelles de maturation) ne
négligent pas l'incidence de ces interactions
« fibres - matrice » sur les propriétés
mécaniques du réseau microfibrillaire.
8
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Ainsi, la modélisation monodimensionnelle de Gril (1987),
inspirée de celle de Boyd et al,
(1975), schématise la nappe microfibrillaire par un
réseau de poutres cellulosiques élastiques encastrées, au
sein duquel les incrustations lenticulaires de matrice, localisées aux
noeuds du milieu périodique, sont assimilées, par leur fonction,
à des ressorts. Ces ressorts, schématisant
le rôle joué par la lignine lors de la
maturation cellulaire, tendraient à « dilater » le
réseau cellulosique dans les directions transverses aux
microfibrilles et à le raccourcir dans la direction axiale,
à la manière d'un « vérin mécanique ».
Un comportement élastique anisotrope
L'hypothèse d'un comportement élastique
anisotrope de la microfibrille, imputé à une orientation
spécifique des cristallites par rapport au grand axe
microfibrillaire a déjà été avancée
(Mark, 1975). La prise en compte d'un tel comportement mécanique
anisotrope de la fibre dans le comportement mécanique de la
paroi n'est cependant pas unanime. Généralement
intégré dans les modèles de paroi multicouches à
fibres parallèles (Bergander,
2001), il n'intervient sur les modules élastiques de
paroi que comme un paramètre de second ordre. Ce degré de
sophistication n'est en conséquence pas retenu, dans d'autres approches
sélectives du rôle mécanique de chaque sous couche (Guitard
et al, 1999).
Superposition « locale » des microfibrilles dans la
sous couche S2
Récemment (Daniel et al, 1998, dans Bergander,
2001), des microphotographies électroniques
de microfibrilles dans la direction longitudinale de la
cellule ont montré l'existence de structures ondulantes dans la
paroi secondaire assez semblables à la configuration en
« treillis » observée en son temps par Boyd
et al (1975) (Figure 1.2).
D'autres auteurs (Kataoka et al, 1992),
considèrent que la construction de la sous couche S2
est assurée par des dépôts successifs et
croisés de faisceaux microfibrillaires (Figure 1.3).

Figure 1.2 Micrographie électronique montrant la
configuration en forme de treillis observée entre les
microfibrilles de lamelles adjacentes lors de la
lignification, tiré de Boyd et al (1975). L'intervalle entre les deux
repères correspond à 0.3 m
Cet empilement ordonné conduirait, selon ces derniers,
à l'existence d'une architecture locale
en treillis dans l'épaisseur de S2. Les angles de
croisement des microfibrilles relevés par
Kataoka et al sur Cryptomeria Japonica D (Sugi) sont
périodiques et leurs valeurs vont de 11
à 35 degrés. Cette configuration en
treillis semble assez semblable à celle relevée
habituellement dans la sous couche S1 (les angles de croisement dans S2 sont
néanmoins plus faibles que ceux obtenus dans S1). Bien que l'AMF ait
été souvent mesuré, les mécanismes
9
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
cellulaires à l'origine de sa mise en place ne sont encore
pas, à l'heure actuelle, bien élucidés
(Chaffey et al, 2000).

Figure 1.3 Croisement et superposition des microfibrilles
(mis en évidence par microscopie électronique)
dans les parois radiales de la sous couche S2
.
Dans l'ensemble des travaux cherchant à
modéliser les voies de passage micro-macro, les microfibrilles
dans la sous couche S2 (et dans les autres sous couches) sont
néanmoins considérées comme étant strictement
parallèles entre elles. On notera que l'observation des architectures
des différentes sous couches (de type treillis ou proche de celles des
feutres) est fortement dépendante de la technique expérimentale
utilisée (effet de contraste).
Disparité bibliographique des caractéristiques
élastiques de la microfibrille de cellulose
Dans leurs propositions de modèles, visant
à évaluer les propriétés élastiques de
la paroi cellulaire, les mécaniciens du bois utilisent
très généralement un module élastique
longitudinal de microfibrille (dit « module d'Young des microfibrilles
») assimilé à celui des chaînes de cellulose purement
cristalline (cellulose I). Les paragraphes précédents ont
évoqué
la structure discontinue de cet élément
essentiel du renfort filamentaire de la paroi. Il convient donc de
préciser les « limites » de la prise en compte de
telles valeurs dans les différents modèles
proposés.
Une banque de données assez variée
La littérature, qu'elle soit issue d'études
ultrastructurales ou plus mécaniciennes, fait état, de diverses
valeurs numériques caractérisant, à priori, la
rigidité axiale des microfibrilles. L'examen de cet ensemble
d'éléments bibliographiques, assez
hétérogène, amène quelques commentaires.
Des valeurs représentatives de la structure
microfibrillaire ?
La valeur de 137 GPa, obtenue par Sakurada et al (1962)
est à l'heure actuelle, la référence la plus couramment
utilisée dans les modélisations du comportement
mécanique de la paroi
(Salmèn et al, 1985, 1986, 1998,
Yamamoto et al, 1998,1999, Guitard et al, 1999). Elle
y représente la rigidité supposée des microfibrilles
(Tableau 1.1). Pourtant, l'insertion de telles rigidités de
microfibrilles au sein de descriptions « composite multicouche» du
comportement élastique de la paroi, conduit à une surestimation
des rigidités transverses pariétales en regard
de certaines observations expérimentales (Bergander,
2001).
10
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Ce module d'élasticité expérimental a
été établi par Sakurada et al sur une fibre
de Ramie
blanchie soumise à une traction sous charge.
L'exploitation d'un ensemble de spectres de diffraction des rayons X (plan
réticulaire 040), a fourni une évaluation de l' « extension
» du réseau cristallin de la cellulose I, puis a permis
aux auteurs l'estimation indirecte du déplacement de la fibre. Il
s'agit donc d'un module d'élasticité de la « région
cristalline » de
la microfibrille. Des évaluations plus directes
de la rigidité microfibrillaire n'ont malheureusement pas
encore été mentionnées dans la littérature.
Il existe en outre, quelques désaccords entre les
mesures micromécaniques de l'élasticité de certaines
fibres de cellulose et celles obtenues via des « mesures » du
déplacement des plans réticulaires. L'exemple de la cellulose II
(isomère de conformation de la cellulose I) est assez significatif. De
récents essais de traction sur ce type de fibre (Kompella et
al, 2002) ont en effet montré que le module
d'élasticité longitudinal déterminé par
exploitation de courbes force - déplacement est très
éloigné (2 GPa) de celui calculé par la méthode de
diffraction rayons X (valeur de 70-90 GPa obtenue par Bledzki et al,
1999).
En employant la même technique (sur le même type de
fibres) que Sakurada et al, Ishikawa et
al (1997), ont fait état, via l'utilisation
d'un méthode inverse (zones amorphes et cristallines associées
en série comme Sakurada et al, ou plus originalement
en série et parallèle) de valeurs de module élastique
de la cellulose I de 114 GPa et 90 GPa.
L'ensemble de ces résultats suggèrent donc que si
le module d'élasticité de la cellulose I est sans aucun doute
proche de la centaine de GPa, l'alternance de zones amorphes et cristallines
au sein d'une même microfibrille, peut lui
conférer un module élastique axial sensiblement inférieur
à la valeur de Sakurada et al. Bledzki et al
(1999), proposent ainsi un module de microfibrilles situé
entre 61 et 130 GPa tandis que Michell (1989) et Fink et al
(1994) adoptent une valeur moyenne de 70 GPa (Tableau 1.1).
|
Références
|
Module d'élasticité longitudinal de la
cellulose I
(GPa)
|
|
Cités dans Sakurada et al
(1962)
|
Meyer et al (1936)
|
79-123 et 80-110
|
|
Lyons (1959)
|
180
|
|
Cités dans Salmèn et al
(1984)
|
Treloar (1960)
|
56,5
|
|
Jaswon et al (1968)
|
56,6
|
|
Gillis (1969)
|
246
|
|
Gillis (1969) : valeur admise comme majorant
|
319
|
|
Sakurada et al (1962)
|
134
|
|
Mark (1967-1970-1980)
|
137
|
|
Ishikawa et al (1997)
|
90
|
|
Michell (1989), Fink et al, (1994) dans Bledzki
(1999)
|
70
|
Tableau 1-1Modules élastiques longitudinaux de la
cellulose I considérés comme représentatifs de la
rigidité microfibrillaire axiale
11
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
D'après les résultats de Mott et al
(1996), suggérant des variations ponctuelles de rigidité
le
long de la microfibrille, les valeurs affichées
ne peuvent, en outre, représenter que des estimations moyennes,
résultant de l'intégration sur toute la microfibrille de
modules d'élasticité supposés plus « locaux
».
Enfin, d'autres auteurs estiment qu'assimiler le
déplacement des chaînes de cellulose, lors d'un essai
micromécanique, au seul déplacement des plans réticulaires
conduit à majorer la rigidité des fibres. Ils soulignent en
effet que le déplacement d'une fibre de cellulose sous charge
résulte non seulement d'une élongation des
chaînes cristallines (donc d'un déplacement monodimensionnel
des plans réticulaires) mais aussi d'une rotation des chaînes
autour de l'axe de la fibre (Northolt et al, 2001).
1.2.3 La matrice ligno-cellulosique
Composée pour 50% de lignines tridimensionnelles et de 50%
de polysaccharides, la matrice
est généralement rendue responsable du
comportement mécanique différé
(viscoélasticité) du matériau bois. Elle suscite
néanmoins encore beaucoup d'interrogations quand à ses
propriétés mécaniques propres.
1.2.3.1 Propriétés mécaniques des
constituants macromoléculaires de la matrice
Les modules d'élasticité des
polymères constitutifs de la matrice (lignines,
hémicelluloses pour l'essentiel) sont clairement identifiés
dans la littérature. Ils doivent néanmoins être
considérés, comme des caractéristiques élastiques
de polymères obtenus très généralement par des
techniques d'extraction, c'est-à-dire mesurés sur des
molécules isolées de leur contexte structurel (organisation
dans un éventuel réseau, structure chimique différente
dans le milieu originel). Leur représentativité quant aux
caractéristiques élastiques des polymères in situ
(non encore mesurées) est donc encore à
démontrer.
Pour Cousin (1978), dont les résultats sont très
largement repris, les hémicelluloses ont une rigidité (à
l'état sec) de l'ordre de 8 GPa, tandis que les lignines ont un module
de l'ordre de 5
à 7 GPa.
1.2.3.2 Une isotropie élastique supposée
A l'intérieur des sous couches S1 et S2, certains des
polymères constitutifs de la matrice (une partie des
hémicelluloses et quelques lignines) sont en contact étroit
avec les microfibrilles
(Salmèn et al, 1998). Au sein de ces associations
supramoléculaires quelque peu complexes,
regroupées sous le terme de matrice et assimilables
à un véritable enchevêtrement, les lignines
généralement qualifiées de tridimensionnelles (elles ne le
sont en toute rigueur que dans la lamelle moyenne) apparaissent pour
certains auteurs comme des éléments importants du
comportement mécanique pariétal (Donaldson, 2003, Gindl et al
2002, 2003).
La présence de liens covalents entre lignine et
hémicellulose (Kerr et al, 1975 dans Salmèn
et
al, 1985), ou encore l'existence d'une orientation
privilégiée des hémicelluloses par rapport à l'axe
des chaînes de cellulose (Liang et al, 1960 dans
Salmèn et al, 1985, Cave, 1972, Hackney et al,
1994) suggèrent assez naturellement un comportement élastique
anisotrope de
la matrice ligno cellulosique.
Chez les essences feuillues, de tels liens entre lignines et
hémicelluloses ont d'ailleurs conduit certains auteurs (Yamamoto
et al, 2003) à modéliser le comportement
élastique pariétal du
12
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
bois de tension par celui d'un matériau composite
formé par un squelette de matrice amorphe
renforcé par des microfibrilles parallèles.
Néanmoins, une récente simulation du
comportement mécanique de la paroi des résineux
(Bergander et al, 2000, Bergander 2001), menée
via une modélisation multicouche à fibres parallèles a
montré, d'une part que l'arrangement des lignines et
hémicelluloses n'a pas d'influence majeure sur les
propriétés élastiques transverses de la paroi, et plus
généralement que la matrice ne joue pas un rôle
prépondérant dans le comportement élastique
pariétal global.
Pour ces raisons, mais aussi devant le manque de
données utiles à une évaluation de l'éventuel
degré d'anisotropie de la matrice et le caractère amorphe des
unités monomères des lignines, bon nombres de
mécaniciens du bois sont conduits à admettre l'existence
d'une matrice quasi amorphe au comportement mécanique isotrope.
Un module d'élasticité de la matrice de 2 GPa est alors
unanimement envisagé (Mark, 1967, 1980, Barrett, 1973, Bodig
et
al, 1982, Gril, 1987, Yamamoto 2001).

On notera enfin que, les homogénéisations
mécaniciennes rencontrées dans la littérature, font
nécessairement appel à une organisation spatiale
simplifiée du milieu bi phasique matrice- microfibrilles (Figure
1.4). La matrice ligno-cellulosique est ainsi assimilée à
un ensemble amorphe enveloppant les microfibrilles (elle se place sur
leur pourtour pour Mark 1980, Norimoto et al, 1985) à la
manière d'une gaine. Bien qu'assez éloignée de la stricte
réalité microfibrillaire, cette schématisation
permet néanmoins d'apprécier le comportement
mécanique global de la matière ligneuse à l'échelle
de la sous couche. Ainsi, Salmèn (2001) a montré que les
dispositions respectives des hémicelluloses en regard des microfibrilles
et des hémicelluloses en regard des lignines ne jouent qu'un
rôle mineur sur le comportement mécanique de la paroi.
Figure 1.4 : Schématisation du milieu bi phasique
constituant chaque sous couche pariétale
1.2.3.3 Perspective ultrastructurale envisagée
Dans le travail ici mené, il s'agit moins de prendre en
compte, dans le modèle adopté in fine,
de données ultrastructurales précises (qui
assureraient une description moléculaire stricte de la matière
ligneuse pariétale), que de traduire mécaniquement le
rôle du renfort filamentaire cellulosique. La matière
constitutive de la paroi cellulaire pourra donc être
assimilée, en première approximation, à un milieu bi
phasique constitué d'une matrice amorphe entourant
13
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
des fibres de renfort quasi cristallines. Dans le terme de module
élastique de microfibrilles,
comme dans celui de module élastique de matrice
ligno cellulosique, il conviendra donc d'entendre plutôt des «
grandeurs » caractérisant un matériau mécaniquement
« équivalent » à une microfibrille non
homogène et à l'agrégat moléculaire quasi
amorphe (lignine, hémicelluloses, pectines,
éventuellement extractibles) qui comble l'interstice entre
les microfibrilles. Les deux phases de ce matériau devront être
vues comme étant parfaitement
« confondues » l'une dans l'autre (Sassus,
1998). L'échelle de description « moléculaire »
sera, par soucis de simplicité, ignorée (peu de travaux
atteignent un tel degré de finesse descriptive).
1.2.4 L'angle des microfibrilles dans la sous couche S2 :
un paramètre micromécanique primordial
Comme cela a été évoqué, l'AMF
caractérise, au sein de chaque sous couche pariétale,
l'inclinaison des microfibrilles par rapport au grand axe
cellulaire. Ces fibres cellulosiques, qui assurent l'essentiel du renfort de la
paroi, permettent à cette dernière, de résister à
toutes sortes de sollicitations mécaniques. Leur inclinaison
constitue donc un critère déterminant dans la tenue
mécanique de la paroi cellulaire, voire dans les
propriétés élastiques « globales »
du matériau bois. Nous nous proposons donc de
faire un inventaire succinct de quelques sources majeures de
variabilité des mesures de l'AMF dans S2, puis de préciser, pour
chacune d'elles, comment les modélisations mécaniciennes les
plus « usuelles » les prennent en compte.
1.2.4.1 Une distribution uniforme de l'AMF dans la sous couche S2
?
Perturbations dues à la présence de
ponctuations
Certains auteurs, ont montré que la présence de
ponctuations dans la sous couche S2 engendre des déviations locales
de l'AMF relevé par diffraction rayons X (Sahlberg et
al, 1997). Cependant, la longueur de la trachéide
relevée sur les résineux (4 mm et plus, Keller dans
Jodin, 1994), comparée aux dimensions des ponctuations (diamètre
de 0,2 à 4 m, Siau, 1984) permet de considérer l'influence de
cette réorganisation ultrastructurale de la paroi comme non
strictement essentielle dans le comportement mécanique global
pariétal. Il est donc possible d'admettre, en première
approximation et uniquement sous un angle de vision
« mécanicien », une distribution homogène
de l'angle des microfibrilles dans la sous couche
S2.
Variations internes de l'AMF dans la sous couche S2
Des études ultrastructurales (Roland et
al, 1982) ont évoqué l'existence d'une distribution
gaussienne de l'AMF dans l'épaisseur de la sous couche S2. D'autres
observations montrent une répartition non uniforme de l'AMF le long de
la sous couche S2 de quelques Pins (Khalili
et al, 2001).
En dépit de ces deux types d'observations, la
grande majorité des auteurs mécaniciens se contente
d'assimiler, par soucis de simplicité, la sous couche S2 à une
enveloppe cylindrique
de composite dans lequel l'inclinaison des microfibrilles est
sensiblement constante aussi bien
dans l'épaisseur (directions transverses
cellulaire) que dans la longueur (direction longitudinale de la
cellule).
14
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Une différence d'inclinaison des microfibrilles entre
les parois d'une même cellule ?
Dans la plupart des modélisations
mécaniques du comportement pariétal, l'inclinaison des
microfibrilles entre les parois cellulaires radiales et tangentielles d'une
même cellule ligneuse n'est pas distinguée, et ce, contrairement
à des propositions déjà anciennes (Frey-Wissling,
1940, cité dans Botosso, 1997, Boutelje, 1962,
Boyd, 1974, Boyd et al, 1975). Cette différence d'angle
microfibrillaire (de 0 à 15 degrés, Preston, 1934,
Boutelje, 1962), initialisée durant la lignification de la paroi
secondaire (Boyd, 1974), constituerait pour Boutelje (1962) un facteur
explicatif de l'anisotropie élastique transverse pariétale
des résineux. Pour d'autres auteurs (Mark, 1967, Barrett, 1973),
la prise en compte de cette distinction entre les deux parois
transverses ne serait pas, à elle seule, suffisante pour
expliciter l'anisotropie transverse pariétale.
Ces différences, particulièrement délicates
à mettre en évidence expérimentalement,
s'avèrent
au demeurant assez faibles dans des travaux plus récents
(inférieures à 5 degrés pour Kataoka
et al, 1992, Khalili et al, 2001).
Elles ne sont généralement pas prises en compte par les
mécaniciens. Certains auteurs (Barrett, 1973) évoquent, sans la
modéliser, l'éventualité d'une anisotropie transverse
élastique pariétale due à une topo chimie des lignines
différente dans
les deux parois (Bosshard, 1956). Des
évaluations micromécaniques directes (nano indentation) de
la rigidité dans S2 montrent, cependant sur Picea abies, qu'il n'est
pas certain que les propriétés élastiques des parois
radiales et tangentielles différent significativement
(Wimmer et al, 1997).
1.2.4.2 Influence de la technique expérimentale sur la
disparité des mesures d'AMF
rapportées
La variabilité biologique de l'inclinaison des
microfibrilles (AMF), peut s'exprimer sur un ensemble de cernes
immédiatement voisins comme à l'intérieur d'un
même cerne de croissance, i.e. entre le bois initial et le bois final
(Sahlberg et al, 1997, Bergander 2001).
Les valeurs mesurées sur un même tissu
(bois initial, bois final) varient, en outre, très sensiblement
avec les techniques expérimentales mises en oeuvre (Tableau 1.2, mesures
sur Picea abies).
Avec la technique fondée sur l'exploitation des
spectres de diffraction des rayons X, des différences sensibles
d'AMF relevé peuvent même apparaître selon le plan
réticulaire (002 ou
040) sujet de l'étude. Sahlberg et al (1997)
soulignent ainsi que bien que le plan (002) ait été
le plus souvent étudié (diffraction
présentant la plus grande intensité), il ne fournit
qu'une mesure indirecte nécessitant une calibration. La
détermination de l'AMF à partir du plan
(040) ne présente pas, pour l'auteur, ce genre
d'inconvénient technique.
Sahlberg et al (1997), ont comparé les
résultats obtenus via des méthodes expérimentales
distinctes (Tableau 1.2). Ils expliquent les différences entre
les AMF caractérisés via des déviations d'une
lumière polarisée et celles obtenues par l'exploitation de
spectre de diffraction rayons X, par des perturbations locales de l'AMF
autour des ponctuations.
Pour ces auteurs, la technique utilisant une
lumière polarisée, lorsqu'elle est appliquée aux
parois cellulaires tangentielles, prend uniquement en compte la portion
de microfibrilles présentes en dehors de l'environnement local
des ponctuations. La valeur moyenne alors obtenue n'intègre donc
pas les singularités ponctuelles. La méthode
d'interprétation des
15
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
spectres de diffraction rayons X, en plus d'être la plus
rapide, présente quant à elle l'avantage
d'évaluer l'AMF tout autour de la paroi. Cette
technique permet donc d'accéder à une information globale.
Toujours selon Sahlberg et al (1997), la dispersion des mesures
d'angle dans les parois radiales est directement attribuée à un
nombre important de ponctuations.
|
Auteurs
|
Nature de la fibre testée
|
AMF
|
Technique employée
|
|
Ollinma
(1961) dans
Sahlberg et al (1997)
|
Moyenne dans le cerne
|
25,5
|
Lumière polarisée
|
|
Marton
(1970) dans
Sahlberg et al (1997)
|
BI
|
20,4
|
Lumière polarisée
|
|
BF
|
18,1
|
Lumière polarisée
|
|
BI
|
11,5
|
Diffraction R.X (002)
|
|
BF
|
12,0
|
Diffraction R.X (002)
|
|
Paakkari
(1984)
|
BI
|
4,9
|
Diffraction R.X (002)
|
|
BF
|
4,3
|
Diffraction R.X (002)
|
|
Sahlberg et al
(1997)
|
BI
|
9,7
|
Diffraction R.X (040)
|
|
BF
|
8,3
|
Diffraction R.X (040)
|
|
Moyenne sur le cerne
|
5,1
|
Cristaux d'iodes
(Senft et al, 1985)
|
|
BI en
moyenne
|
9,0
|
Diffraction R.X (040)
|
|
BF en moyenne
|
8,1
|
Diffraction R.X (040)
|
|
Bergander
et al (2001)
|
BI normal
en moyenne
|
10
|
Polarisation confocale (CLSM)
|
|
8
|
Diffraction R,X,
|
|
Ruelle
(2003)
|
Bois normal en moyenne
|
20,18
|
Cristaux d'iodes (Senft et al,
1985)
|
Tableau 1-2 Valeurs d'AMF relevées sur le bois
initial (BI) et le bois final (BF) de Picea abies
1.2.4.3 Une distinction parfois délicate des AMF dans les
cellules de bois initial et de bois final
Les différences d'AMF relevés entre les sous
couches S2 des cellules de bois initial et de bois final sont aussi (et a
fortiori) très fortement dépendants de la technique
expérimentale mise en
16
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
oeuvre (Sahlberg et al, 1997). Certaines mesures
laisseront donc apparaître une différence
nette dans l'inclinaison microfibrillaire de ces deux tissus
tandis que d'autres ne permettront aucune distinction (valeur globale
commune).
Des résultats établis via la technique de
diffraction des rayons X, montrent ainsi des différences minimes
entre l'AMF du bois initial et celui du bois final (1 à 2
degrés pour Paakkari et al, 1984, Sahlberg et al,
1997, Bergander et al, non publié). D'autres, fournis par des
mesures plus « locales » (lumière polarisée,
orientation des cristaux d'iodes, Senft et al,
1985), suggèrent de plus grands écarts entre les
deux tissus (jusqu'à 30 degrés pour McMillin,
1973, Herman et al, 1999).
L'utilisation directe, dans une modélisation, des
résultats rapportés dans la littérature, exige donc une
connaissance précise des conditions expérimentales :
précision de la mesure effectuée, technique
expérimentale employée, mesure individuelle sur une
trachéide (fibre unique) ou mesure plus globale (paquet de fibres). La
littérature ne présente que très rarement
de telles informations ce qui conduit bon nombre d'auteurs
à insérer des valeurs médianes au sein de leurs
modèles. Une étude numérique parait indispensable
pour élucider le rôle de l'inclinaison des microfibrilles
sur l'anisotropie pariétale tout en s'affranchissant des
difficultés expérimentales de sa détermination.
Nous admettrons ici, comme certains auteurs mécaniciens
(Barrett, 1973, Mark, 1967, 1980, Mark et al, 1970, Navi et
al, 1995), une distinction nette entre l'angle des microfibrilles du bois
initial et celui du bois final.
1.2.5 Prise en compte du caractère multicouche de
la paroi cellulaire
Si toutes les modélisations du comportement
mécanique pariétal de la cellule de bois normal
accordent un rôle prépondérant
à la sous couche S2, la hiérarchisation des
éléments micro anatomiques participant au comportement
mécanique de la paroi cellulaire ne fait pas l'unanimité.
Certains auteurs, s'inspirant de constatations cytologiques
avérées (microscopie électronique pour la plupart),
proposent des modèles à fibres parallèles faisant
intervenir d'autres sous couches (trois sous couches pour Yamamoto,
1998, 1999, Yamamoto et al,
2001, prise en compte de S1 en particulier dans le comportement
mécanique transverse de la paroi de bois initial dans le cas de Mark,
1972, Cave, 1975, Salmèn et al, 1985, Bergander et
al, 2000a, 2000b).
Ces dernières propositions, traduisant le
caractère stratifié de la paroi cellulaire par un
empilement multicouches, apparaissent belles et bien réalistes en
regard de la diversité des épaisseurs de sous couches
(Dunning, 1968) et de la structure cellulaire déjà
évoquée
(paragraphe 1.1.1). Elles permettent en outre d'exprimer
directement (parfois au prix d'un nombre élevé de
paramètres descriptifs) la variabilité intra cerne des
épaisseurs pariétales (S1
est jusqu'à 3 fois plus importante dans le bois
initial que dans le bois final, Panshin et al,
1980, Kollmann et al, 1984, Koponen et al,
1989, Bergander, 2000) ainsi qu'une part de la variabilité intra cerne
des teneurs en macromolécules de la paroi (Fukuzawa et
al, 1981). Néanmoins, de telles modélisations multicouches,
n'amènent pas d'amélioration significative aux résultats
de modèles prédictifs des déformations de maturation
attribuant à la sous couche
S2 l'essentiel du comportement élastique de la paroi
cellulaire (Guitard et al, 1999).
Pour ces raisons, d'autres auteurs (Guitard et
al, 1999, 2002) préfèrent donc décrire le
comportement mécanique d'un ensemble de parois par celui
d'une couche composite unique
17
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
dont les caractéristiques ultrastructurales (en
particulier l'AMF) sont empruntées à la sous
couche S2.
L'origine d'une telle simplification est plus une
schématisation du renfort filamentaire,
conféré à la paroi par les microfibrilles
orientées, qu'une description stricte de l'architecture
de la sous couche pariétale S2.
Cette unique prise en compte de la sous couche S2
dans le comportement mécanique global
de la paroi, envisagée uniquement pour les
résineux, trouvera sans doute des limites dans le
cas des feuillus (structure pariétale plus complexe,
Clair, 2001) et plus encore si on sort du cadre d'étude du bois
normal (sous couche S3 du bois de réaction riche en cellulose
cristalline).
1.2.6 Description du comportement mécanique de sous
couche
Si la prise en compte du caractère multicouche de la paroi
cellulaire dans le comportement
mécanique de la cellule ligneuse ne fait pas
l'unanimité, la transition en terme mécanique du passage de
l'échelle ultrastructurale à l'échelle de la sous couche,
est en revanche assurée, de manière unanime, par
l'assimilation du comportement du milieu bi phasique « matrice
fibres » à celui d'une couche composite à renfort
filamentaire.
Au sein de ce milieu bi phasique, décrivant la
matière constitutive de chaque sous couche, l'état
mécanique moyen de chaque phase peut être
considéré comme décrit par un même champ de
déformation (le réseau microfibrillaire s'intrique dans la
matrice).
Pour permettre l'évaluation des composantes du
tenseur des rigidités dans chaque sous couche, la matrice et
les fibres cellulosiques sont associées en parallèle dans
la direction longitudinale, en série dans les directions
transverses.
1.2.7 La double cloison, un passage obligé vers le
tissu ligneux
Dans la très grande majorité des
modélisations proposées afin d'évaluer les
propriétés
élastiques tissulaires, la juxtaposition des
parois ligneuses adjacentes de deux cellules contiguës est prise en
compte par la création d'un multicouche (ou stratifié), plus ou
moins complexe, élaboré par l'assemblage d'un nombre
variable (selon les modèles) de sous couches composites (Figure
1.5). Chaque pli ou sous couche est principalement
caractérisé,
par une orientation microfibrillaire propre
(paramétrée par l'AMF), de signe opposé à celle de
son homologue située de l'autre coté de la lamelle mitoyenne.
Ainsi élaboré, ce stratifié
antisymétrique rend notamment compte, du comportement
élastique
de membrane (discuté plus loin) de deux parois
élémentaires tissulaires attenantes. La quantité
de matière ligneuse comprise entre deux lumens
immédiatement voisins sera appelée, par la suite, la double
cloison cellulaire ou double cloison.
Il convient ici de préciser la différence
essentielle entre l'étape descriptive précédente et
celle
ici évoquée. A travers l'assimilation du milieu
bi phasique à celui d'un composite renforcé par des fibres,
l'étape antérieure visait la description du comportement
mécanique d'une unique sous couche (voire d'une paroi si seule la sous
couche S2 est considérée). Par l'assemblage de deux sous
couches voisines, le formalisme évoqué maintenant a pour
objectif essentiel de transcrire le comportement mécanique d'un
ensemble de parois ; il se situe donc plus sous l'angle de
description des propriétés mécaniques tissulaires que
sous celui des propriétés mécaniques de la paroi
isolée.
18
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
1.2.7.1 La double paroi cellulaire décrite par un
empilement multicouche de sous couches à
fibres parallèles.

Figure 1.5 Transition du comportement mécanique
d'une sous couche à celui de la double paroi par la création d'un
multicouche à plis anti symétriques (tiré et adapté
de Salmèn et al, 1986). La notation ö représente ici l'AMF
propre à
la sous couche S2.
Ce type de modélisation (Carlsson et al,
1986, Frey-Wyssling, 1968 dans Bodig, 1982, Barrett, 1973, Gillis,
1972, Cave, 1975,1976, Mark, 1980, Koponen et al, 1989, 1991,
Norimoto, 1986, Salmén, 1986), visant à décrire le
comportement élastique de la double paroi cellulaire, fait appel
à la théorie classique des stratifiés (Tsai et
al, 1980, Daviaud et al, 1983, Guitard et al, 1987).
Cette deuxième étape de la
modélisation intégrative micro-macro, assure la transition
mécanique de l'échelle de la sous couche à celle de la
double cloison. Elle permet notamment d'exprimer les rigidités de
membrane (sous l'hypothèse de contraintes planes) et conduit, in fine,
à des estimations des modules bipariétaux longitudinal et
transverses (double paroi).
Les modèles multicouches les plus simples
définissent ainsi ce même passage par un assemblage de deux
sous couches S2 (à fibres parallèles) parfaitement
collées. D'autres, plus complexes et certainement cytologiquement
plus réalistes, autorisent diverses distinctions
(épaisseurs, composition chimique, AMF) entre les
différentes sous couches envisagées.
Par l'empilement de sous couches (plis) à inclinaison de
fibres de renforts antisymétrique, la double cloison est décrite
par un stratifié non équilibré. Par conséquent, on
notera la présence
de termes de couplages non nuls entre les rigidités de
membrane et les moments de flexion torsion.
Nous reviendrons sur les expressions des
différentes caractéristiques élastiques des
multicouches pariétaux au cours des chapitres suivants (chapitres 2 et
3).
19
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
La restriction de cisaillement
Dans le réseau cellulaire propre à un
tissu ligneux, les mouvements de torsion de chaque cellule
imbriquée sont fortement gênés (blocages par les
cellules immédiatement voisines). Un tel environnement implique donc
la nullité des déformations de cisaillement,
phénomène mécanique souvent appelé "restriction de
cisaillement" (Bodig et al, 1982, Gril, dans Perré,
1998). Dans une telle situation, la double paroi cellulaire
présente alors une rigidité nettement supérieure à
celle d'une double paroi de même structure extraite de son
environnement histologique.
Néanmoins, la prise en compte de cette
restriction de cisaillement dans les modèles multicouches, ne
fait pas l'unanimité. Norimoto et al (1986) considèrent
ainsi que sa prise en compte amène à des prédictions en
désaccord avec leurs résultats expérimentaux.
Description mécanique du renfort cellulosique de
la double cloison par un squelette de microfibrilles
entrecroisées.
La sous couche S2 étant la plus épaisse et la plus
riche en cellulose (exception faite de la sous couche S3, dite couche
gélatineuse, du bois de réaction des feuillus), certaines
modélisations
du comportement mécanique de la double paroi
cellulaire (Guitard et al, 1999, 2002) résument le
comportement mécanique de la cellule à celui d'une unique sous
couche virtuelle dont les caractéristiques ultrastructurales sont
empruntées essentiellement à la sous couche S2.
La cellule ligneuse vue comme une structure cylindrique de
matériau composite
La cellule, réduite à une unique sous
couche S2, (schématisation proposée initialement par Barber
et al, 1964 afin de prédire le retrait longitudinal), est
assimilée à un cylindre à paroi fine constitué
d'un matériau composite fibres cristallines isotropes - matrice
amorphe très spécifique.
La matière constitutive de la cellule virtuelle
est en effet décrite par une matrice amorphe, élastique et
isotrope, de lignine et d'hémicelluloses, renforcée par un
réseau de microfibrilles cristallines isotropes parfaitement
interconnectées (double enroulement croisé, Figure 1.6).
Dans ce type de modélisation (Guitard et al,
1999), initialement proposée pour rendre compte des déformations
de maturation, la composition chimique pariétale de la sous couche S2
n'est pas distinguée selon le type (bois initial, bois final)
de cellule considérée, conformément à certaines
récentes constatations chimiques (Bergander, 2001,
Salmèn communication personnelle, sur Picea abies).
Contrairement aux modèles multicouches
précédents (paragraphe 1.2.7.1), ce modèle à
squelette de fibres, décrivant une double cloison virtuelle, assure
directement la restriction de cisaillement interpariétale par
l'intermédiaire d'un réseau dense de microfibrilles
entrecroisées.
Il n'a en outre pas pour vocation de rendre compte
du comportement mécanique de deux parois mitoyennes (double cloison)
mais plutôt de décrire celui d'un ensemble de cinq cellules
ligneuses par le comportement d'une cellule virtuelle,
énergétiquement équivalente. Ce faisant, il s'agit plus
d'un modèle de tissu cellulaire homogène qu'un modèle de
cellule isolée.
20
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux

Figure 1.6 Passage de deux cellules adjacentes à
enroulement hélicoïdal de microfibrilles
à une cellule unique virtuelle avec double
enroulement croisé, d'après le modèle de Yamamoto
cité dans Guitard et al, 1999.
Enfin, contrairement aux stratifiés
pariétaux les caractéristiques élastiques de la
double cloison virtuelle sont, par construction, indépendantes de
l'épaisseur du composite i.e. des caractéristiques
géométriques de la cellule ligneuse (Guitard et
al, 1999). Les propriétés élastiques de double
pariétale fournies par ce modèle seront détaillées
dans le chapitre 2.
Le modèle proposé par Guitard et al
(1999) a prouvé sa pertinence quand à la prédiction
des déformations résiduelles de maturation (variations
dimensionnelles de la paroi au cours du processus de maturation
cellulaire) tant longitudinales (DRLM) que tangentielles (DRTM) et
ce à partir des mesures d'angles des
microfibrilles dans S2. Il n'a pas été nécessaire
d'envisager une paroi cellulaire multicouche pour simuler le passage du retrait
au gonflement pour des angles inférieurs à 30 degrés.
Cette modélisation rend ainsi compte de l'inversion de
la DRLM prévue pour un angle situé entre 20 et
30 degrés, et se révèlent apte à la
prédiction simultanée des DRLM et DRTM sur deux essences
résineuses japonaises (Cryptomeria Japonica D. Don, Chamaecyparis
obtusa Endl).
Contrairement à des propositions de
schématisation multicouche de la paroi, il n'a en outre pas
été nécessaire de modifier la constitution chimique
des sous couches cellulaires avec l'angle des microfibrilles pour rendre
compte du comportement de la cellule virtuelle lors du processus de
maturation.
21
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
1.3 L'anisotropie élastique à
l'échelle du tissu ligneux

Figure 1.7 Organisation cellulaire d'un bois de
résineux (Guitard, 1987)
a : trachéide dans le bois de printemps b :
trachéide dans le bois d'été
c : canal résinifère d : rayon
ligneux
e : rayon ligneux avec canal
résinifère
f : ponctuation.
La nature, le nombre et l'organisation spatiale des
cellules du bois peuvent être décrits par l'observation de
trois coupes matérielles (LR, RT, TL) identifiées en
définissant la base
r r r
( R , T , L ) comme le repère d'orthotropie du
matériau bois (Figure 1.7). Ces plans de
référence décrivent le « plan
ligneux » d'une espèce. Bien que l'architecture du cerne
soit considérée comme un caractère systématique,
quasiment invariable pour une même essence, puisque
génétiquement prédéterminée, la
proportion des différentes cellules qui constituent
« le plan ligneux » est très fortement
dépendante des conditions de croissance de l'arbre
(substrat, climat,...).
A partir de différentes observations
(microphotographies) et dans le cas des résineux présentant
une organisation du plan ligneux relativement simple, il est possible
d'assimiler le matériau bois à une structure
alvéolée de type nid d'abeille.
22
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Sous l'hypothèse d'une masse volumique de la
matière ligneuse constante (i.e. assimilée à
celle des parois cellulaires), le module d'Young macroscopique
longitudinal (noté par la suite
EL) peut être alors évalué à partir du
module élastique pariétal correspondant et de la
porosité
(Gibson et al, 1988). Ce passage micro-macro
s'avère bien plus délicat dans le plan transverse. A
cette échelle, et dans ce même plan de description
(où les démarches d'homogénéisations apparaissent
relativement complexes), la morphologie cellulaire joue un rôle important
et conduit à une importante anisotropie élastique (Farruggia,
1998, Farruggia et
al, 1996, 2000).
1.3.1 La morphologie cellulaire
Selon divers auteurs (Gillis, 1972, Gibson et al, 1988,
Koponen et al, 1989, 1991, Perré et al,
1994, Farruggia, 1998, Farruggia et al, 1996, 2000,
Perré, 1998, Holmberg et al, 1999), pour une même
porosité, les propriétés élastiques
transverses macroscopiques de structures tubulaires de type nids
d'abeilles sont fortement variables (modules élastiques). Gillis
(1972)
a ainsi montré que des bois de densité
proches pourront posséder des modules élastiques transverses
(ER et ET) très différents s'ils se distinguent les uns
des autres par la forme
(morphologie cellulaire) ou par la disposition
spatiale de leurs cellules (arrangement cellulaire).

R

Figure 1.8 : Deux morphologies cellulaires
envisagées : (a) modèle de Gibson et al (1988), (b) modèle
de Guitard et al (2002)
Figure1.9 : Micrographie
électronique (ESEM) montrant le cas d'une
cellule hexagonale sur P. radiata, (d'après Donaldson, 2003)
Barre d'échelle 16 um
Figure 1.10 : Cellule de

forme quasi rectangulaire de P. abies observée par
double coloration safranine/ bleu alcyan (Ruelle, 2003). Barre d'échelle
25 um
Le tissu ligneux est ici défini comme un ensemble
de cellules identiques, regroupées en
réseau, et assurant dans l'arbre, la même
fonction physiologique (conduction de la sève brute, fonction
mécanique de support, conduction et renfort radial respectivement
pour les trois cellules essentielles constituant le bois initial, le bois
final et les rayons ligneux).
Pour prédire le comportement macroscopique
élastique d'une structure aussi hétérogène dans
sa constitution que le bois, et ce à partir de sa
morphologie et des propriétés microscopiques
de ses constituants, la littérature fait
généralement état de nombreuses démarches
de changement d'échelles (Gillis, 1972, Farruggia, 1998, Badel 1999,
Badel et al, 1999, Perré,
23
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
1998) consistant en la représentation d'un milieu
équivalent et en la construction d'un modèle
applicable à ce même milieu.
De telles approches, impliquent la désignation d'une
cellule ou d'un ensemble de cellules
(Volume Elémentaire Représentatif) comme
élément(s) unitaire(s) du milieu périodique, ce qui
apparaît, à priori, assez délicat compte tenu de la
variabilité intra et interspécifique de la forme
géométrique de la cellule ligneuse constatée
habituellement chez les résineux comme chez les feuillus (Venet et
al, 1986, Watanabe et al, 1999, 2000).
1.3.1.1 Choix de la cellule unitaire comme élément
architectural représentatif du tissu ligneux
Une grande variabilité de formes cellulaires
La forme microscopiquement observable des cellules de
résineux peut être tour à tour approximativement
rectangulaire (Keller, 1999), hexagonale (Decoux et al, non
publié), ou variable selon le type de tissu ligneux (hexagonal
et rectangulaire respectivement pour les cellules initiales et finales
du bois normal de Picea abies, Bergander, 2001, voire presque
circulaire pour les cellules de bois de compression de plusieurs essences
résineuses, Timell,
1986, Ruelle, 2003). Les Figures 1.9 et 1.10 illustrent
ainsi, pour deux essences résineuses
(Pinus radiata et Picea abies), un exemple de morphologie
cellulaire rencontrée dans le bois final dit « normal ».
Certains récents travaux (Marion, 2001, Sarèn
et al, 2001), menés sur Picea abies, ont montré, par
analyse d'images, une importante variabilité inter cerne de la
morphologie cellulaire.
L' « indice de circularité » des cellules de
bois normal décroît ainsi avec l'âge de la couche
d'accroissement ; la forme des lumens est proche de l'ovale
prés de la moelle et devient progressivement rectangulaire au fur
et à mesure d'une progression radiale vers le cambium. Des
précisions complémentaires sur ces évolutions
morphologiques intra cerne seront fournies ultérieurement
(chapitre 3).
Devant un tel éventail de formes cellulaires
possibles, les modélisations du comportement mécanique
tissulaire admettent donc nécessairement une morphologie
cellulaire simplifiée
(moyenne), n'ayant pour but que de préciser les
éléments de la cellule ligneuse susceptibles
de répondre à des sollicitations mécaniques
spécifiques (traction, compression, flexion).
Des paramètres géométriques communs aux
différents modèles de cellule ?
Les modules d'élasticité des
différents tissus étant le reflet direct du comportement
de la cellule à une sollicitation spécifique (traction et/ou
compression, éventuellement flexion), à modules
élastiques de double paroi identiques, les différences les
plus notables entre les propriétés élastiques
tissulaires rencontrées dans la bibliographie, proviennent
donc, essentiellement, de la géométrie cellulaire adoptée
dans chaque modèle.
Des modèles assimilant la morphologie cellulaire à
un rectangle (modèles proposés par Navi
et al, 1995, Holmberg et al, 1999, Guitard
et al, 2002) ou à une structure hexagonale (modèles
de Gibson et al, 1988, Koponen et al,
1991) conduisent ainsi chacun à des évaluations de
modules élastiques de tissu sensiblement différentes
(respectivement par excès et par défaut). Dans le cadre de
schématisation du plan ligneux par différents
réseaux de cellules hexagonales, l'épaisseur
pariétale dans le coin cellulaire constitue de plus un
paramètre essentiel (rôle de renfort) dans
l'évaluation du module élastique tissulaire
tangentiel
(Watanabe et al, 2000).
24
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Néanmoins, et même s'ils apparaissent de
prime abord différents, les paramètres
géométriques traduisant la forme
générale de la cellule « moyenne » sont
généralement communs (le lien est plus ou moins direct) aux
schématisation de forme envisagées.
Ainsi la variable , du modèle hexagonal de
Gibson et al (1988), (Figure 1.8a), ou son équivalent
RCW fixé à 30 degrés dans la modélisation
proposée par Koponen et al (1991), fournissent tous les deux
une indication de l'angle entre la direction radiale R du bois et celle
de l'élément de paroi soumis à une
flexion lors d'un chargement tangentiel. Avec une description du plan
ligneux par un nid d'abeille à élément
rectangulaire (Figure 1.8b), les facteurs de forme précédents
sont pris égaux à zéro dans le modèle de Guitard
et al (2002). L'influence de ce même paramètre angulaire
n'est néanmoins pas ignorée dans ce dernier modèle, elle
est prise en compte de façon indirecte en considérant que
l'épaisseur (eR) de la paroi radiale peut être différente
de l'épaisseur (eT ) de la paroi tangentielle.
On notera enfin une autre singularité du modèle
à cellules rectangulaires envisagé par Guitard
et al (2002). La longueur de paroi fléchie prise
en compte est égale au diamètre (DR) diminué
de deux fois l'épaisseur de paroi
(eT), contrairement au modèle proposé par Gibson
et al,
(1988) considérant le diamètre cellulaire,
indépendamment de l'épaisseur pariétale. A
porosité
fixée, cette différence conférera, a
priori, une plus grande rigidité au nid d'abeille tissulaire, puisque
les dimensions de l'élément cellulaire soumis à la flexion
sont moindres. Une étude complémentaire sur la part d'anisotropie
tissulaire imputable à la flexion des parois sera donc menée plus
loin (chapitre 3).
1.3.1.2 Disposition spatiale des cellules dans le plan transverse
: l'arrangement cellulaire
Admettant une organisation bidimensionnelle du cerne,
Khale et al (1994), ont décrit l'architecture du plan
ligneux de résineux, à partir de microphotographies. Dans la
direction radiale, les cellules (provenant de la division d'une même
initiale cambiale) sont globalement alignées (elles forment en fait de
petits « zig zag », combinaison de paroi orientées dans la
direction radiale et dans la direction tangentielle), tandis qu'une
distribution bien plus anarchique est constatée dans la direction
tangentielle. Le long d'une même disposition « zig zag », les
auteurs précisent que le faible nombre de paroi tendant à
s'éloigner de la direction radiale permet de supposer que lors d'un
chargement radial tous les efforts sont supportés par
les parois disposées en prolongement les unes des
autres (soumises à une telle sollicitation, les parois tangentielles
ne joueraient le rôle que d'entretoise, Bergander et al,
2000a, 2000b, Guitard et al, 2002).
D'autres travaux essentiels, visant à obtenir
un maillage numérique de tissu ligneux, aboutissent, sur les
résineux, à ces mêmes conclusions (Perré et
al, 98, Farruggia, 1998). On notera ici que les équations
développées par l'ensemble des auteurs, à partir
des théories classiques de la résistance des matériaux,
ne sont que des approximations du comportement mécanique complexe du
plan ligneux (lors de tout chargement, l'absence d'alignement dans la direction
tangentielle induit l'existence de régions à haute concentration
de contraintes).
Les Figures 1.11 et 1.12 illustrent, dans le plan transverse de
deux résineux (Pinus pinaster et
Pinus radiata), l'existence d'une disposition quasi
ordonnée des parois cellulaires dans la
r r
direction radiale R et d'une orientation bien plus
aléatoire dans la direction tangentielle T .
25
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux

R
T
Figure 1.11 : Microscopie confocale associée
à l'auto fluorescence de la lignine sur Pinus
radiata (site internet www.forestresearch.co.nz).
Fenêtre de 160*160 um.

R
T
Figure 1.12 : Double coloration à la safranine
bleu alcyan sur Pinus pinaster, (Ruelle, 2003). Barre d'échelle, 25
um
1.3.1.3 Une estimation des modules élastiques tranverses
tissulaires par excès ?
Dans leurs appréciations du comportement
mécanique tissulaire, la plupart des modélisations admettent le
collage parfait par la lignine de deux parois cellulaires
contiguës (double cloison). Dans le cadre de la cohésion de
l'ensemble des cellules disposées en réseau, excluant tout
mouvement entre parois voisines, la rigidité à la flexion est
nettement supérieure
(flexion réduite d'un facteur 4 pour une
porosité de 0,64, Perré et al, 1994) à celle
obtenue en autorisant un glissement sans frottement entre les parois de deux
cellules adjacentes (permis par une lamelle mitoyenne hypothétique).
La réalité, en terme de rigidité
tissulaire en flexion, se situe sans doute entre ces deux
dernières propositions « limites », en raison d'une part d'une
morphologie moyenne cellulaire
de résineux plus fréquemment proche de
l'ovale (Marion, 2001, Hunter, 2001) ou de l'hexagonal (Decoux et
al, non publié) que du rectangulaire (Navi et al, 1995,
Guitard et al,
2002), et de l'existence de lignifications différentes
entre les parois radiales et tangentielles
(Bosshard, 1956).
1.4 Facteurs explicatifs de l'anisotropie
élastique à l'échelle du cerne de croissance
1.4.1 Le cerne assimilé à un bicouche
Sur les résineux, une coupe transversale suivant
les directions radiale et tangentielle de la
grume permet généralement d'observer, à
l'oeil nu, les cernes de croissance dans lesquels se distingue (sur les
essences de zones non tropicales) le bois initial du bois final plus dense.
Divers clichés radiographiques, illustrent ainsi, par
un profil microdensitométrique (Figure
1.13), l'alternance, dans la direction radiale, de
couches de bois de printemps de masse volumique moyenne voisine de
0,35 g/cm3 et de bois d'été de masse volumique
moyenne pouvant atteindre, voire dépasser, 0,75 g/cm3 (chez
les résineux, la masse volumique du bois initial est deux à trois
fois inférieure à celle du bois final, Kramer et al,
1979).
26
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux

Figure 1.13 : Exemple de profil
microdensitométrique obtenu sur un bois adulte de Douglas Fir
(données numériques
fournies par P. Rozenberg)
Une grande partie de l'anisotropie mécanique
à l'échelle de la couche d'accroissement est
attribuée à la présence de ces deux tissus
physiologiquement spécifiques (Ylinen et al, 1967, Keller,
1999, Dumail, 1995, Farruggia, 1998).
1.4.1.1 Une discrétisation du cerne essentiellement
fondée sur des critères technologiques
Admettant la spécificité propre des
propriétés mécaniques du bois initial et final, les
mécaniciens du bois utilisent un critère appelé
texture, et généralement employé pour
l'appréciation des qualités technologiques du matériau.
D'après la norme NF B 50-002 n°42,
la texture définit « le rapport de la
largeur de bois d'été à la largeur totale de la
couche d'accroissement ». D'un point de vue biologique, ce
même paramètre est le reflet des conditions de croissance de
l'arbre au cours de la saison de végétation.
Ainsi discrétisé, le cerne de croissance est
assimilé à un bicouche composite, figurant la
stratification en deux couches de bois initial et de bois final. Ce
matériau équivalent au cerne
est élaboré à partir des
propriétés de ces deux tissus ligneux constitutifs,
supposés biologiquement homogènes (Schniewind, 1959, 1972,
Guitard et al, 1987, Koponen et al,
1991). Pour ce faire, ces deux tissus ligneux essentiels sont
considérés comme deux milieux orthotropes.
1.4.2 Le rayon ligneux : un élément de
renfort radial
Aux deux tissus différenciés que sont le bois
initial et le bois final, il convient d'adjoindre un
troisième tissu constitué des rayons ligneux,
qui, bien que moins important en terme de poids relatif dans le cerne,
intervient de manière essentielle dans le comportement
mécanique macroscopique du matériau.
De récents travaux expérimentaux sur Picea
abies (Farruggia et al, 2000 : isolement des rayons ligneux dans
un échantillon de bois initial, Bergander, 2001) ont en effet
confirmé le rôle mécanique des rayons ligneux à
l'échelle de la couche d'accroissement comme à
l'échelle du bois massif.
27
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
1.4.2.1 Mise en évidence du rôle mécanique
des rayons ligneux
En associant des essais de traction sur des
éprouvettes de petites dimensions, à une
extensomètrie optique, Schniewind (1959) a pu étudier l'influence
de paramètres macroscopiques et microscopiques sur l'anisotropie
élastique. Ses travaux l'ont amené à proposer une
liste d'équations (inspirés de celles de Ylinen et
al, 1967, et des travaux de Barkas, 1941), prédictives de
l'anisotropie élastique macroscopique. Le formalisme introduit
lui a notamment permis d'obtenir les caractéristiques
élastiques du bois massif sans défaut en prenant comme
variables, l'humidité, la texture et la proportion en rayons
ligneux dans le cerne.
Schniewind (1959) est ainsi un des premiers auteurs à
considérer que les rayons ligneux sont responsables de la
rigidité radiale macroscopique. Selon lui, le module
d'élasticité du cerne de croissance, exprimé dans cette
même direction, peut être considéré comme une
fonction linéaire de la proportion de rayons ligneux.
S'inspirant de l'hypothèse du rôle des rayons
ligneux sur l'anisotropie de retrait proposée par Barkas (1941) et
appuyée par Schniewind (1959), des recherches sur leur
rôle dans l'anisotropie élastique ont également
étés menées par Guitard et al (1987). Ces auteurs
ont repris les modèles antérieurs (Ylinen, 1954, Schniewind,
1959) en y ajoutant la contribution des rayons ligneux placés en
quadrature par rapport à la disposition des tissus bois initial et
final.
Pour Guitard et al (1987), la fraction
volumique (n) en rayons ligneux est utilisée comme indicateur du
degré d'anisotropie macroscopique car reliée aux modules
d'élasticités du bois massif (ER, ET, EL) par la relation (1.1)
donnée par Barkas (1941) :
(1.1)
n = E R E T
(E R
E T ) + (E L
E T )
Cette même prise en compte de la fraction volumique en
rayons ligneux a permis à Guitard et
al (1987) d'améliorer une relation statistique
entre les modules d'Young macroscopiques et la masse volumique (ñ) tant
en ce qui concerne les résineux que les feuillus.
Deux modèles prévisionnels (résineux,
feuillus) ont ainsi étés établis en se basant sur
l'hypothèse selon laquelle une fraction volumique en rayons
ligneux importante induit un renfort radial au détriment de la
rigidité longitudinale.
Chez les résineux, les modules
d'élasticité du bois propre dans les directions radiale (ER) et
longitudinale (EL), exprimés en MPa sont ainsi liés
à la fraction volumique (n) en rayons ligneux et à la
masse volumique ñ (en g/cm3) par les relations
statistiques (Guitard et al,
|
1987) :
|
|
|
|
(1.2)
|
EL = -663 +37200 ñ -282n
|
avec R = 0,939
|
|
(1.3)
|
ER = -875 + 3250 ñ + 39,6n
|
avec R= 0,932
|
28
Inventaire des facteurs essentiels de la variabilité intra
arbre des propriétés mécaniques des tissus ligneux
Insertion du renfort radial des rayons ligneux dans le
bicouche bois initial / bois final
Pour rendre compte, à l'échelle du cerne
d'accroissement, du rôle mécanique de ces cellules essentielles,
la démarche d'homogénéisation usuelle, consiste à
les inclure sous la forme d'un renfort radial dans le bicouche bois
initial / bois final. Pour ce faire, les rayons ligneux
simplifiés sont assimilés à un tissu dont
les propriétés mécano physiques (modules
d'élasticité, densité) sont localement
homogènes et aux caractéristiques anatomiques
parfaitement identifiées.
Ce type d'hypothèse, naturellement indispensable
à la détermination du solide homogène
mécaniquement équivalent, fait, ipso facto, abstraction d'une
partie de la nature réelle de la structure des rayons ligneux
(section non régulière, distribution aléatoire dans
le cerne, existence de gradient de propriétés
mécaniques internes, Bodig et al, 1982, gradient
intra
(faible) et inter cerne de densité des rayons
rapportée sur le Chêne, Guilley, 2000).
La variabilité des caractéristiques anatomiques
des rayons ligneux est d'ailleurs telle qu'elle a donnée lieu à
la création d'une échelle de classification (Venet et
al, 1986) s'appuyant principalement sur leurs dimensions (longueur,
diamètre).
Pour les mécaniciens, les rayons (disposés
essentiellement dans la direction radiale) donc sont assimilés à
des cellules homogènes dont les microfibrilles sont fortement
inclinées par rapport
à leur axe longitudinal propre (40 degrés, Barkas,
1941 ; 30 degrés, Barrett, 1973 ; Koponen
et al, 1991). On leur attribue en outre des
épaisseurs de paroi faibles (Barrett, 1973; Venet et
al, 1986).
1.5 Conclusion
Les facteurs de variabilité de l'anisotropie
élastique du bois normal, classiquement cités dans
la littérature, ont été
évoqués depuis l'échelle ultrastructurale (bio
molécules) jusqu'à l'échelle du cerne. S'inspirant de
cet inventaire « orienté », tout en en extrayant des
paramètres jugés essentiels, une modélisation multi
échelles prédictive de l'anisotropie élastique peut
être proposée dans la suite de l'étude.
29
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
2 Modèles multi échelles et
construction du Résineux Standard Virtuel
(RSV)
Un grand nombre des paramètres évoqués au
chapitre précèdent, susceptibles de conditionner
le comportement mécanique macroscopique du bois, sont
intégrés dans ce qui suit dans une modélisation
prédictive déterministe. Il s'agit de modèles multi
échelles permettant les Passages successifs, en terme de
propriétés mécaniques (élastiques) entre les
différents
« angles » d'observations des
hétérogénéités de la matière
ligneuse ; les macromolécules essentielles, les sous couches
pariétales, la double paroi cellulaire, le tissu ligneux, le cerne
d'accroissement.
Dans une première partie, les éléments
constitutifs d'un modèle micromécanique relativement classique,
assimilant la paroi cellulaire à un assemblage multicouches,
sont présentés. Une variante plus originale, faisant passer
directement des macromolécules à la double paroi
cellulaire virtuelle en privilégiant certains paramètres
essentiels de l'ultrastructure
(supramoléculaire) est proposée. Cette alternative
est privilégiée dans la suite du travail.
Dans un second temps, le modèle retenu est alimenté
par un jeu de paramètres dont les valeurs
de départ sont suggérées par la
bibliographie analysée au chapitre précédent
(chapitre 1). C'est à travers un processus d'optimisation contrainte
qu'est dégagé un jeu de valeurs de ces paramètres
associés au « Résineux Standard Virtuel »
noté RSV. Les valeurs cibles sont les trois
modules d'élasticité traduisant l'anisotropie élastique
ainsi que la masse volumique du résineux standard définis par
Guitard (1987).
La carte d'identification du bois normal de résineux
standard est discutée en fin de chapitre dans la perspective d'une
extension de la démarche vers la description de bois particuliers : bois
juvénile, bois de compression, ...etc.
2.1 Modèles multi échelles retenus
pour décrire l'anisotropie élastique du bois de
résineux
2.1.1 Le concept de modélisation multi
échelles
L'objectif est de décrire les propriétés
élastiques anisotropes macroscopiques du bois massif
sans défaut de résineux, ceci à travers une
succession de changements d'échelles :
Passage 1 : des macromolécules à la sous couche
pariétale ;
Passage 2 : de la sous couche pariétale à la
double cloison cellulaire ; Passage 3 : de la double paroi cellulaire au tissu
ligneux homogène ; Passage 4 : des tissus ligneux au bois massif sans
défaut.
Deux modélisations sont présentées
dans les deux sous paragraphes suivants. La seconde comporte un
raccourci par rapport à la première qui minimise le
nombre de paramètres retenus.
2.1.2 Modèles à parois cellulaires
multicouche (Multicouche)
Le modèle gigogne « Multicouche » comporte les
quatre changements d'échelle, ou Passages,
évoqués ci-dessus. A chaque changement
d'échelle, les expressions analytiques, donnant des estimations des
propriétés élastiques du solide homogène
équivalent à l'échelle considérée
30
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
sont proposées en fonction des
caractéristiques élastiques de l'échelle
immédiatement
inférieure et des paramètres retenus comme
étant caractéristiques de la transition envisagée.
Les techniques d'homogénéisations restent
simples, voire simplistes, elles sont basées essentiellement
sur la loi des mélanges. Elles considèrent des
assemblages en série ou en parallèles des sous-ensembles,
l'objectif étant de prendre en compte les
paramètres considérés, au mieux de ce que permettent
les techniques utilisées. Chaque Passage de la
modélisation gigogne constitue un « tiroir »
alimenté par un jeu de paramètres d'entrée et
délivrant un ensemble de paramètres de sortie. Sans changer le
principe de la méthode, l'un des « tiroirs » peut être
changé au profit d'un sous modèle plus performant
(éventuellement plus réaliste). Le paragraphe 2.1.3, relatif au
modèle Squelette, illustra ce propos.
2.1.2.1 Passage 1 : des macromolécules à la sous
couche pariétale
Le Passage 1 traduit les propriétés
élastiques d'une sous couche pariétale, en l'occurrence,
chacune des composantes du tenseur des modules élastiques Cijkl,
ceci en fonction des propriétés élastiques des
polymères constitutifs.
Une sous couche pariétale « s » est
assimilée à un composite à renfort filamentaire
constitué d'une matrice amorphe de lignine et
d'hémicelluloses, supposée homogène et isotrope,
renforcée par un faisceau de fibres parallèles ; les
microfibrilles de cellulose fortement cristallines.
Les propriétés des constituants pris en compte sont
donc : Propriétés élastiques isotropes de la matrice
ligno-cellulosique :
Em : Module d'Young de la matrice
õm : Coefficient de Poisson de la matrice
Propriétés élastiques des microfibrilles de
cellulose :
Ef : Module d'élasticité longitudinal
õf : Coefficient de Poisson des fibres de
cellulose
Une grandeur caractéristique de ce premier changement
d'échelle, quantifiant la proportion de renfort filamentaire dans le
milieu bi phasique est adoptée :
V : Fraction volumique en microfibrilles.
Le solide équivalent, correspondant à la sous
couche pariétale, est supposé homogène,
élastique, orthotrope, et à isotropie transverse.
L'expression matricielle associée au tenseur
r r r r
des complaisances élastiques Sijkl
dans un repère
(1 , 2, 3)
dont l'axe
(1 )
est colinéaire au
renfort filamentaire est notée sous la forme suivante
(2.1) :
31
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
S
S
S
0
s s s
11 12 12
0 0
s s s
S 12
Ss
S 22
s
S 12 0
s
0 0
(2.1) (Ss ijkl ) = 12
0
0
S 23
0
0
S 22
0
0
0
Ss 44
0
0 0
0 0
Ss 55 0
0 0
0 0 0
Ss 55
Dans la direction longitudinale
r
(1 )
de la sous couche envisagée, une association «
en
parallèle » de la matrice amorphe et des fibres
cristallines conduit à :
S
(2.2)
s 1
=
11 V Ef + (1 V) Em
Compte tenu de la relation d'ordre entre la
rigidité des fibres cristallines (quasi
r r
indéformables) et celle de la matrice ligno cellulosique,
dans les directions transverses
un arrangement de type « série » conduit
à l'expression (2.3) :
(2, 3)
s s =V (1 V) (1 V)
(2.3)
S 22
= S 33 = +
E f E m E m
En raison de cette même relation d'ordre, les
composantes Ss23 et Ss44 de la matrice des
complaisances sont évaluées par les expressions
(2.4) et (2.5):
(2.4)
Ss 23
m
Ss 23
= í
(2.5)
Ss44
E m
(1 V) 2 (1 + ím )
=
Em
r r
La souplesse au cisaillement dans le plan
(1 , 2)
est estimée par la somme pondérée
des
souplesses au cisaillement des fibres et de la matrice :
(2.6)
Ss66
= Ss55
2 (1 + íf )
= V +
Ef
(1 V)
2 (1 + ím )
Em
Les seules autres composantes non nulles sont alors
Ss12 et Ss13, complaisances élastiques
toutes les deux identiques sous l'hypothèse d'une
isotropie transverse de sous couche (2.7) :
(2.7)
s
S 12
s
= S 13
í f
= V
(1 V) í
m
E f E m
32
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Les formules permettant d'exprimer les composantes
Cij de la matrice des rigidités en
fonction des composantes Sij de la matrice des souplesses sont
reproduites dans le Tableau
2.1.
|
2 2 2
D = S11 S22 S33 + 2 S12 S23 S31 -S11 S23 -S22
S31 - S33 S12
|
|
C11= 1 (S S S2 )
D 22 33 23
|
1 2
C = S S - S
22 D 33 11 31
|
C33= S11 S22 - S
1 2
D 12
|
|
1
C32 = C23 = D (S31 S12 - S32 S11)
|
1
C23 = C32 = D (S12 S23 - S13 S22)
|
|
1
C21 = C12 = D (S23 S31 - S21 S33)
|
|
1
C44 =
|
1
C55 =
|
1
C66 =
|
S44
S55
S66
Tableau 2-1 Expression des modules élastiques
Cij en fonction des complaisances Sij
2.1.2.2 Passage 2 : de la sous couche à la double paroi
Le Passage 2 conduit à l'expression des modules
d'élasticité longitudinal ELp et transverses ETp de la
double paroi. Ces mêmes modules élastiques, appelés
par la suite modules élastiques bipariétaux,
représentent des caractéristiques élastiques de tissus
ligneux (chapitre
1, paragraphe 1.2.5) et non des modules élastiques de
paroi.
La double paroi représente la quantité de
matière comprise entre deux lumens constitutifs, elle est, dans ce
premier modèle, assimilée à un stratifié
multicouches comportant un nombre N de sous couches empilées.
La sous couche de rang « p » est
caractérisée par :
les modules élastiques ELp et ETp déduits du
paragraphe précédent,
l'orientation AMF öP, angle des
microfibrilles de la sous couche (p) par rapport au grand axe de la
cellule (Figure 1.1),
l'épaisseur ep de la sous couche
considérée.
Le calcul des caractéristiques élastiques de la
double paroi comporte deux étapes :
a) expressions des modules élastiques de chaque sous
couche dans le référentiel de paroi
(2.8)
C P ijkl
= Cs pqrs .á P pi .á P
qj .á P rk .á P sl
Les composantes áij sont celles de
la matrice de changement de base faisant passer du
référentiel de sous couche au
référentiel de cellule :
c P
(2.9) [á P ij ] = s P
0
s P 0
c P 0
0 1
33
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
b) l'assemblage des N sous couches permet de dégager
notamment les rigidités de membranes
Aij du multicouche, auxquelles sont associées
les modules d'élasticité longitudinal et transverses de
double paroi notés respectivement ELp et ETp :
N
en posant c = cos ( ), s = sin ( ), avec h=
e(p)
p = 1
l'épaisseur de la double cloison et avec
z(p) la côte du plan moyen de rang (p) par
rapport au plan du stratifié, il vient :
1 N (p)
( p ) p 4
12 66
( p )
( p )
p2 p2
22
( p ) p4
(2.10) ELp h
e {C 11 c
p =1
+ (2C + 4C ) s
c + C s
(C(p) c p2 + C (p) s p2
) 2
- 13 32 }
C
(p)
33
1 N (p)
22
( p ) p4
( p )
( p )
p2 p2
( p ) p4
(2.11) ETp h
e {C c
p = 1
+ (2C 12 +4C 66 ) s c
+ C 11 s
(C(p) s p2 + C (p) c p2
) 2
- 13 23 }
C
(p)
33
Cette même construction permet également
d'expliciter (via les rigidités de flexion torsion)
les modules équivalents de flexion torsion E11 et
E22 des structures multicouches. Leurs évolutions avec certains
paramètres essentiels seront détaillées plus loin
(chapitre 3).
12 N
(p)
(p) 2
e(p) 3
( p )
12 66
( p )
( p )
p2 p2
22
( p ) p4
3
(2.12) E11 {
h
e z
p =1
+ } {C 11 c
12
+ (2C + 4C ) s
c + C s
N (p) 3
(C(p) c p2 + C (p) s p2
) 2
- 13 32 }
C
(p)
33
D11
12
(p)
(p) 2 e
( p ) p4
( p )
( p )
p2 p2
(2.13) E22 12
3
h
{ e z
h 3 p =1
+ } {C c
12
+ (2C 12 +4C 66 ) s c
(p) p2
(p)
p2 2
22
11 s
+ C ( p ) p4 -
(C13 s + C 23 c ) }
C
(p)
33
Remarque : cette présentation du modèle ne
préjuge pas du nombre N de sous couches prises
en compte.
2.1.2.3 Passage 3 : de la double paroi cellulaire au tissu
ligneux homogène
Le Passage 3 correspond au changement d'échelle
permettant l'évaluation de la masse
X
volumique ñx ainsi que les modules
d'élasticité longitudinal EL
X
, radial ER
et tangentiel
34
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
X
ET d'un tissu cellulaire « x »
élaboré à partir d'un ensemble de cellules jointives
supposées
localement identiques.
La représentation schématique d'un tissu
ligneux retenue Figure 2.1, est un nid d'abeille à cellules
rectangulaires. Les données d'entrée de ce troisième
changement d'échelle sont :
les modules d'élasticité longitudinal ELp et
transverse ETp, ERp de la double paroi considérée,
les caractéristiques géométriques du tissu
ligneux représentées par les diamètres radial
(DR) et tangentiel (DT) ainsi que les
épaisseurs de parois radiales (eR) et tangentielles
(eT) de la cellule représentative du
tissu.

Figure 2.1 Schéma en perspective retenu pour un
tissu ligneux de résineux
Quatre grandeurs sont déduites, la masse volumique
tissulaire ñx, les modules d'élasticité
X X X
tissulaire mésoscopique, longitudinal EL
, radial ER
et tangentiel ET .
Nb : à cette étape de la modélisation, le
qualificatif mésoscopique est employé pour distinguer
les deux « catégories » de modules
élastiques tissulaires ; les modules élastiques
bipariétaux évoqués précédemment et les
modules élastiques d'un V.E.R de chaque tissu du plan ligneux.
a) Porosité et masse volumique d'un tissu ligneux
Sous l'hypothèse couramment retenue selon laquelle la
masse volumique du matériau ligneux constituant les parois
cellulaires est une constante ñm = 1,51 kg/m3, la
donnée des quatre paramètres cellulaires
géométriques (DR, DT, eR, eT), retenus ici, fixe la
porosité P0 du
matériau, et en conséquence la masse
volumique ñx du tissu ligneux « x »
considéré. On prendra garde dans la suite que les données
géométriques tissulaires et la masse volumique ne sont pas des
paramètres indépendants.
Vol.lumen
(D
2e
)(D
2e )
e e
e e
(2.14)
P0 = = R T T R = 1
2 T + R 2 T R
Vol.Total
D R D T
D R D T
D R D T
e e
e e
(2.15)
ñ x = ñ m (1 P0 ) = 2ñ m T
+ R 2 T R
D R D T
D R D T
35
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
X
b) Evaluation du module élastique longitudinal
EL
d'un tissu « x »
Un effort longitudinal est distribué sur une
surface égale à celle de la section droite de la
X
cellule représentative. En conséquence, le
module d'élasticité longitudinale EL
du solide
homogène équivalent au nid d'abeille,
s'évalue à partir de ELp et en proportion de l'aire de
la
surface « mécaniquement » active de la
paroi par rapport à l'aire de la section droite de cellule,
soit :
D D
(D
2e
)(D
2e )
e e
e e
(2.16)
E L x
= R T R T T R E Lp
= 2 T
+ R
2 T R E Lp
E
E
D R D T
D R D T
D R D T
Compte tenu de l'avant dernière expression (2.14) de
la masse volumique tissulaire ñx, (2.15)
devient :
=
(2.17)
E L x
ñ x
Lp
ñ
m
=
Cette relation exprime la dépendance des paramètres
géométriques évoquée ci-dessus en a).
X
c) Evaluation du module d'élasticité radial
ER
d'un tissu « x »
Un effort appliqué suivant la direction radiale,
comme représenté sur la Figure 2.2, se
transmet par les parois radiales des cellules, supposées
positionnées dans le prolongement les unes des autres (Khale et
al, 1994).
X
En conséquence, le module élastique radial
ER
, du solide homogène équivalent se déduit
du
module d'élasticité transverse ETp de la
double paroi dans le rapport de l'épaisseur de la double paroi
radiale (2 eR) au diamètre tangentiel (DT) :
(2.18)
E R x
2e R
Tp

D
T
Figure 2.2 Illustration de la distribution des efforts
dans le cas d'un chargement radial
36
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
X
d) Evaluation du module élastique tangentiel
ET
d'un tissu « x »
Un effort appliqué suivant la direction tangentielle
comme précisé sur la Figure 2.3, se
transmet par les parois radiales mais aussi par les parois
tangentielles des cellules, du fait de la disposition en quinconces de
celles-ci. Les éléments de paroi tangentiels (AB, CD, EF,
Figure
2.3) travaillent en traction compression de façon analogue
aux sollicitations décrites dans le paragraphe précédent.
De plus, l'élément de paroi radiale (BCE, Figure 2.3)
travaille en
« flexion trois points ».

Figure 2.3 Illustration de la distribution des efforts
dans le cas d'un chargement tangentiel
Les assemblages de rigidités sont
réalisés de la façon suivante ; les
éléments AB et EF, assemblés en parallèles sont
associés en série avec les éléments BCE et CD. En
conséquence,
X
le module élastique tangentiel ET
somme de deux termes :
du solide homogène élastique équivalent
s'écrit comme la
(2.19)
1 = 1 D R +
x
1 D R (D
R 2e T )3
3
E T 2E Tp e T
128.E Rp D T e R
Le premier terme du second membre, comparable à
l'expression (2.18), correspond aux
éléments travaillant en traction compression,
tandis que le second terme est relatif à l'élément
travaillant en flexion (poutre de largeur unité et de hauteur
2eR « encastrée » aux deux extrémités).
(2.20)
1 = 1 D R
1 E Tp eT
(D R 2eT )3
1 +
E T x
2.E Tp
e T
64 E Rp D T
e R 3
Les configurations cellulaires choisies (directement
inspirées de microphotographies de
résineux), illustrées sur les Figures 2.1,
2.2 et 2.3, correspondent respectivement à des alignements des
parois radiales et à des dispositions en quinconce des parois
tangentielles
(Bodig et al, 1982, Khale et al, 1994,
Bergander et al, 2000). Il s'agit de situations extrêmes
X
qui donnent des estimations respectives par
excès du module radial ER
X
et par défaut du
module tangentiel ET .
37
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
2.1.2.4 Passage 4 : des tissus ligneux au bois propre
Le cerne de croissance d'un résineux est assimilé
à un composite de trois tissus ligneux ; le bois initial (bois de
printemps), le bois final (bois d'été) et les rayons ligneux.

Figure 2.4 : Schéma d'un volume
élémentaire de cerne de croissance : a) constitué de trois
tissus ; b) en
deux tissus après homogénéisation
des bois initial et final.
La maille élémentaire représentative d'un
cerne de croissance est constituée d'un cube, limité
r r r
par les faces perpendiculaires respectivement à
chacun des axes d'orthotropie
matériau. L'arête du cube élémentaire
est égale à la largeur de cerne.
(R, T, L) du
Le Passage 4 assure donc le changement d'échelle entre les
trois tissus ligneux constitutifs et
le cerne de croissance.
Les variables d'entrée sont les
caractéristiques élastiques de chacun des trois
tissus
X X
constitutifs, à savoir : les trois modules
d'élasticité longitudinal EL
X
, radial ER
et tangentiel
ET .
Les paramètres complémentaires sont
spécifiques de l'organisation des tissus ligneux dans le
cerne :
· la texture TX, rapport de l'épaisseur de bois
final à la largeur de cerne, caractérise la proportion bois
initial et de bois final,
· la fraction volumique en rayon ligneux, notée
n, définie la proportion de ce tissus par rapport à l'ensemble
des tissus constitutifs.
Le Passage 4 est assuré en deux phases successives :
a) Homogénéisation selon le sens radial du bois
initial et du bois final
L'épaisseur du cerne (e) est assimilée
à un bicouche, de bois initial formé en début de
croissance, suivi d'une couche de bois final.
38
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Le solide homogène élastique anisotrope
équivalent est noté « infi », les modules
élastiques
correspondants sont évalués par la loi des
mélanges, en considérant des assemblages série et des
assemblages parallèles.
Suivant la direction radiale, les rigidités radiales
ERini, ERfin du bois initial et du bois final sont en
série, en conséquence, les souplesses s'additionnent au prorata
des épaisseurs :
(2.21)
1 = (1 Tx )
Tx
+
E R infi
E R ini
E R fin
Suivant la direction tangentielle, les rigidités
tangentielles ETini, ERfin du bois initial et
du
bois final sont en parallèle, en conséquence, les
rigidités s'additionnent également au prorata des
épaisseurs :
(2.22)
E T infi = (1 Tx ) E T
ini + Tx E T fin
Suivant la direction longitudinale, les rigidités
longitudinales ELini, ELfin du bois initial et
du
bois final sont en parallèle, en conséquence,
les rigidités s'additionnent au prorata des épaisseurs :
(2.23)
E L infi
= (1 Tx ) E L ini
+ Tx E L fin
b) Homogénéisations selon le sens tangentiel du
bois « infi » et des rayons ligneux
Il s'agit de caractériser l'assemblage du tissu «
infi » décrit au paragraphe précédent et des rayons
ligneux considérés comme un tissu ligneux spécifique.
Suivant la direction radiale, la disposition en
parallèle des tissus entraîne que la rigidité
E
radiale
selon:
infi
R
R
du bois « infi » et la rigidité radiale
E Rayon des rayons ligneux s'additionnent
(2.24) ER = (1-n) E infi + n E Rayon
R R
Suivant la direction tangentielle, la disposition en
série des tissus fait que la souplesse
E
tangentielle
1
du bois « infi » et la
souplesse tangentielle
inf i
T
1
des rayons ligneux
E
Rayon
T
E
s'additionnent selon :
E
(2.25)
1 (1 n) n
= +
inf i
T T
Rayon
E
T
39
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Suivant la direction longitudinale, la disposition en
parallèle des tissus fait que la rigidité
L
longitudinale E inf i
du bois « infi » et la rigidité
longitudinale des rayons ligneux
Rayon
E
L
s'additionnent selon :
(2.26) EL = (1-n) E inf i + n E Rayon
L L
Les relations (2.24), (2.25) et (2.26) expriment ainsi
les modules d'élasticité homogénéisés
ER , ET et EL du Bois propre en fonction des modules
d'élasticité homogénéisés du bicouche
«infi», E inf i , E infi , inf i
Rayon
Rayon
R
Rayon
T E L
et des modules d'élasticité du tissu rayon
ligneux, E R
, E T et
E L compte tenu de la fraction volumique en
rayons ligneux n.
Trois tissus ligneux constituent le cerne de croissance dont la
composition est réglée par deux
paramètres, la texture (TX) qui fixe la proportion de
bois initial et de bois final et la fraction volumique (n) en rayon ligneux. A
l'instar des tissus bois initial et bois final, les cellules de rayons sont
caractérisées ici par un jeu de quatre paramètres
géométriques ; épaisseurs
(radiale et tangentielle) et diamètres (radial et
tangentiel).
2.1.2.5 Conclusion sur les modélisations M1 et M2
Les relations (2.1) à (2.26) assurent les quatre
changements d'échelles (Passages) considérées
au paragraphe 2.1.1. On remarquera que la double paroi
cellulaire est un multicouche dont le nombre N de sous couches est
laissé à l'appréciation de l'utilisateur. Nous discuterons
par la suite et dans le chapitre 3, de deux configurations
particulières de la modélisation Multicouche:
le modèle M1 comportant deux sous couches S2,
le modèle M2 comportant neuf sous couches (neuf plis).
2.1.3 Modèle à squelette de microfibrilles
(Squelette)
Le modèle M3 à squelette de microfibrilles
est directement inspiré des travaux discutés
précédemment. Cette modélisation
diffère de la précédente (paragraphe 2.1.2) en ce que les
deux premiers Passages (Passage 1, des macromolécules à la sous
couche pariétale ; Passage
2, de la sous couche à la double paroi
cellulaire) sont fusionnés en un seul changement d'échelle
noté Passage 1-2. Le Passage 1-2 conduit directement
des propriétés des macromolécules à celles de
la double paroi cellulaire. Les caractéristiques de la sous couche
S2 sont ici privilégiées, notamment en ce qui
concerne l'orientation des microfibrilles (ö). Les
caractéristiques et la vocation de cette modélisation ont
été évoquées au chapitre 1.
2.1.3.1 Passage 1-2 : des macromolécules à la
double paroi virtuelle
Comme au paragraphe précédent, (2.1.2.1), les
propriétés des constituants pris en compte sont :
les propriétés élastiques isotropes de la
matrice (Module d'Young Em, coefficient de
Poisson õm),
40
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
les propriétés élastiques des
microfibrilles de cellulose (Module d'élasticité
longitudinal Ef, coefficient de Poisson
õf),
la proportion de renfort filamentaire décrite par la
fraction volumique en microfibrilles
V,
l'angle des microfibrilles (noté dans ce
modèle ö) de la sous couche S2 du tissu ligneux
considéré.
Les modules élastiques bipariétaux longitudinal
ELp et transverse ETp sont évalués en fonction de ces
paramètres micromécaniques, comme indiqué par les
relations (2.27) et
(2.28).
Lp
(2.27) E = (1 V) (1 í) E m + V (1- s4)Ef
(1 + í)(1 2í)
Tp Rp
(2.28) E = E = (1 V) (1 í) E m + V (1-
c4)Ef
(1 + í)(1 2í)
2.1.4 Nombre total de paramètres structuraux
retenus
A chaque niveau de description (ultra structural, tissulaire ou
à l'échelle du cerne) est associé
un jeu de paramètres bio mécaniques et/ou
bio structuraux. Lorsqu'ils sont pris en compte dans chacune des
différentes modélisations détaillées ici, ces
ensembles de paramètres se révèlent aptes à
rendre compte, localement, de l'anisotropie élastique. A
l'échelle macroscopique, l'anisotropie élastique du bois
sans défaut est décrite, par un empilement gigogne de
différents niveaux d'hétérogénéités
(démarche micro macro, synopsis Figure 2.5). Dans ce cadre, il est
possible de dresser un inventaire du nombre total de paramètres
nécessaires à la modélisation pyramidale envisagée
(Tableau 2.2).
2.1.4.1 Recensement du nombre de paramètres utiles
à une description de l'anisotropie élastique
bipariétale
La première partie du Tableau 2.2 (colonnes A et
B), fait l'inventaire du nombre de paramètres
micromécaniques ou microstructuraux nécessaires aux Passages 1, 2
et 1-2.
L'examen des deux colonnes A et B, montre que le nombre de
variables d'entrées, utiles à une description du comportement
élastique de la double cloison par celui d'un Multicouches à
fibres parallèles est directement lié aux nombres N de sous
couches pariétales empilées (7N pour N sous couches). Un bicouche
simple (M1) formé de l'empilement de deux sous couches
S2 fera ainsi appel à 14 paramètres
descriptifs, un 9 couches (M2) plus complexe (4 sous couches S1 pour
traduire au mieux l'existence d'un réseau de microfibrilles
croisées dans une sous couche S1, 2 sous couches S2, 2 sous couches S3
et une lamelle mitoyenne composée) ne nécessitera pas moins de 67
paramètres micromécaniques.
On rappelle de plus ici que le comportement isotrope des fibres
cellulosiques, envisagé dans
de tels modèles, tend bien évidemment à
minimiser le nombre de paramètres micromécaniques.
41
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
2.1.4.2 Importance du Passage 2 sur le nombre total de
paramètres bio structuraux retenus
dans une description gigogne de l'anisotropie élastique du
bois normal
La colonne C récapitule le nombre de paramètres
nécessaires à la description de l'anisotropie élastique
tissulaire, tandis que la colonne D du Tableau 2.2 résume le nombre de
paramètres nécessaires à une description de l'anisotropie
élastique macroscopique du matériau bois.
L'étape de transition d'un comportement
mécanique de sous couche à celui de la double cloison
(Passage 2, colonne B) se révèle particulièrement
importante. Pour les deux derniers Passages, dans le cadre de
l'utilisation d'un multicouche « N-couches » à fibres
parallèles disjointes, le nombre total de paramètres utiles
à la description de l'anisotropie élastique tissulaire est
7N+ 4, il s'élève à 21N+14 à l'étape finale
macroscopique (colonne D).
Dans le cadre du modèle bicouche M1 l'anisotropie
élastique macroscopique est alors décrite par un jeu de 56
éléments, ce jeu de paramètres passe à 189 pour un
9 couches M2. Le modèle Squelette M3 ne nécessite quand à
lui « que » 22 paramètres.
Pour cette raison le choix de telle ou telle option de
description de la double paroi
(Multicouches ou Squelette), en regard de critères
spécifiques (valeurs cibles de modules longitudinal ELp et
transverse ETp, ERp, réalisme cytologique) sera discuté
plus loin
(chapitre 3).
42
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
|
A
|
B
|
C
|
D
|
|
Passage
1
|
Passage
2
|
Passage
3
|
Passage
4
|
|
Sous
couche
|
Double
paroi à N
sous
couches
|
Tissu
ligneux
|
Bois
propre
|
|
Paramètres ultrastructuraux
|
Module d'Young de la matrice
|
m
E
|
1
|
N
|
N
|
3N
|
|
Coefficient de Poisson de la matrice
|
m
|
1
|
N
|
N
|
3N
|
|
Module d'Young des microfibrilles
|
Ef
|
1
|
N
|
N
|
3N
|
|
Coefficient de Poisson des microfibrilles
|
f
|
1
|
N
|
N
|
3N
|
|
% de microfibrilles
|
V
|
1
|
N
|
N
|
3N
|
|
Paramètres de la sous couche
pariétale
|
Angle des microfibrilles dans S2
|
ö
|
|
N
|
N
|
3N
|
|
Epaisseurs de sous couches
|
(p)
e
|
|
N
|
N
|
3N
|
|
Paramètres de la géométrie
cellulaire dans un tissu
|
Diamètres cellulaires
|
DR
|
|
|
2
|
6
|
|
DT
|
|
Epaisseurs pariétales
|
eR
|
|
|
2
|
6
|
|
eT
|
|
Paramètres caractéristiques du
cerne
|
Texture
|
TX
|
|
|
|
1
|
|
% en rayons ligneux
|
n
|
|
|
|
1
|
|
Nombre de paramètres nécessaires à
la modélisation gigogne
|
Nombre total de paramètres pour N sous couches
à fibres parallèles
|
|
5
|
7N
|
7N+4
|
21N+14
|
|
Hypothèse du bicouche M1
|
|
|
14
|
18
|
56
|
|
Hypothèse du 9
couches M2
|
|
|
63
|
67
|
189
|
|
Hypothèse du Squelette de fibres
entrecroisées M3
|
|
5
|
6
|
10
|
22
|
Tableau 2-2 Tableau récapitulatif du nombre de
paramètres nécessaires à une modélisation multi
échelles
de l'anisotropie élastique
43
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
|
|
|
Bio polymères constitutifs de la matière
Microfibrilles cristallines (fraction
ligneuse : lignines, cellulose et volumique V) et matrice amorphe
:
hémicelluloses milieu bi phasique
Approche composite d'une sous couche (p): matrice
(Em,m) renforcée par des microfibrilles
orientées (Ef , ím)
Sous couche S2
Sous couche S1 Sous
couche S3 Lamelle Moyenne
e(S ), (S ), V S S e(S
), (S ),V S e(LM),
(LM),VLM
1 1 1 e(S2), (S2),V
2 3 3 3
Modélisation d'une sous couche par des Multicouches
à fibres parallèles
Homogénéisation 2 D
Squelette
de Double
microfibrilles cloison Prise en
compte de la
restriction de cisaillement
Nid d'abeille Géométrie tissulaire
différenciée bois initial, bois final et rayons
ligneux (épaisseurs de parois, eT, eR
diamètres cellulaires DR,
DT)
Texture :
Milieu bicouche TX
équivalent (bois
initial final)
Renfort radial des rayons
Solide homogène ligneux ; fraction
équivalent volumique n
au cerne annuel
BOIS MACROSCOPIQUE, EL, ER ET, ñ
|
|
|
|
|
|
|
|
|
|
|
Figure 2.5 : Voies de passages micro macro et «
options » de la modélisation gigogne envisagée

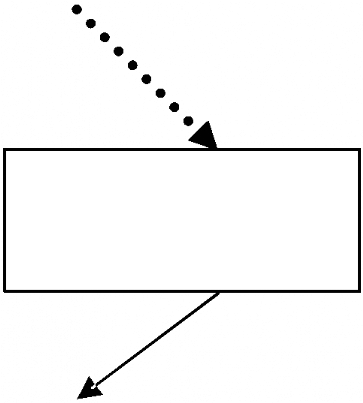





44
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
2.2 Construction du Résineux Standard
Virtuel
On soulignera ici, que les homogénéisations
prédictives mises en oeuvre à chaque niveau
d'hétérogénéité du matériau bois, ne
constituent certainement pas des solutions optimales à la recherche des
propriétés élastiques des solides homogènes
équivalents. Elles répondent toutefois à l'objectif
de ce travail qui est moins de prévoir, avec une
précision sévère, les propriétés du
matériau bois à partir de celles de ses constituants, que de
rendre compte avec pertinence de l'influence des différents
paramètres pris en compte, sur le comportement macroscopiquement
observable, ceci à des fins de hiérarchisation de
l'influence de ces paramètres.
2.2.1 Validation des modèles prévisionnels de
l'anisotropie élastique
Valider la pertinence de la pyramide des modèles
introduits précédemment pose deux classes
de problèmes. Il convient, d'une part, de disposer de
valeurs cibles cohérentes des propriétés macroscopiques
élastiques que la modélisation est sensée simuler
et il faut, d'autre part, choisir un jeu réaliste de l'ensemble des
paramètres utilisés par les différents modèles.
2.2.1.1 Des propriétés matérielles cibles
La masse volumique du bois résineux standard
Conformément aux propositions de Guitard (1987), la
masse volumique ñ du résineux standard, première
valeur cible de l'optimisation, est fixée à
0,45g/cm3.
Sachant que la masse volumique de chacun des tissus
(ñinitial, ñfinal, ñrayon) est fixée par la
donnée des paramètres géométriques de chacun
de ceux-ci, la contrainte sur la masse volumique du bois ñb est
satisfaite en considérant que la fraction volumique en rayons ligneux
(n) et la texture (Tx) sont tels que :
(2.29) ñb = (1-n) ñinfi + n ñrayon
(2.30) ñinfi = (1-Tx) ñinitial + Tx
ñfinal
Etant donnée que la masse volumique du bois ñb
est fixée, que (n) est donnée et que ñrayon est
calculé, la relation (2.29) implique ñinfi. De plus,
ñinitial et ñfinal ayant été calculées,
alors la relation (2.30) implique la texture (Tx). Tout ceci suppose
que les données choisies soient réalistes «
biologiquement » pour conduire à des résultats
cohérents.
Des propriétés élastiques cibles
Les caractéristiques élastiques utilisées
comme cibles pour valider la modélisation sont celles
du « résineux standard ». Il s'agit des
propriétés élastiques d'un bois résineux,
stabilisé à un taux d'humidité de 12 % et de masse
volumique ñ = 0,45 g/cm3, statistiquement
représentatif d'une banque de données expérimentales
relatives à 38 essences résineuses (Guitard, 1987).
Les caractéristiques retenues sont les modules
d'élasticité suivant les trois directions d'orthotropie
du bois, soit :
ER = 1,00 GPa Module d'élasticité radial
ET = 0,636 GPa Module d'élasticité tangentiel
EL = 13,1 GPa Module d'élasticité longitudinal
45
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Les rapports d'anisotropie élastique EL /
ER =13,1 et ER / ET = 1,57, bien que
redondants,
sont de même considérés.
A des fins de comparaison, avec les modules élastiques
du résineux standard, les propriétés élastiques
modélisées, correspondant à un bois vert, sont
corrigées en humidité et ramenées du point de saturation
des fibres, estimé ici à HPSF = 30% à
l'humidité de référence H= 12%, moyennant les
relations données dans Guitard (1987).
Une base de données de paramètres
structuraux
Le Tableau 2.3 regroupe, pour des essences résineuses,
une partie des valeurs de différents paramètres
considérés, extraites des travaux discutés au
chapitre 1. D'autres données, tirés d'examens
microdensitométriques ou par planimétrie sont reportées
dans le Tableau 2.6. Sur cette base pluridisciplinaire, un jeu de
paramètres de départ a été défini. Les
valeurs initiales choisies sont reportées dans la colonne A des Tableaux
2.4 et 2.5
L'optimisation dont il est ici rendu compte a été
conduite sous deux types de contraintes :
Les angles des microfibrilles (ö) de la sous couche
S2 des tissus ligneux présents à l'intérieur
du cerne ont été forcés, de telle sorte
qu'ils différent et soient situés dans l'intervalle compris
entre 5 et 10 degrés pour le bois final et
supérieurs à 20 degrés pour le bois initial (Barrett,
1973, Sahlberg et al, 1997, Herman et al,
1999).
La masse volumique doit être celle choisie comme
représentative du résineux standard.
2.2.2 Résultats et discussions
2.2.2.1 Procédures d'optimisation des paramètres
structuraux
L'ensemble des relations introduites dans les
paragraphes précédents sont aisément saisies puis
traitées sur un tableur numérique de type Excel. Les
différentes estimations de propriétés élastiques
arrondies à trois chiffres significatifs, ainsi que les valeurs des
paramètres qui ont permis de les obtenir sont
répertoriées dans les colonnes A à F des Tableaux
2.4 et 2.5. L'analyse des résultats obtenus à chaque
étape, suggère des modifications des valeurs
numériques assignées aux paramètres pour
l'étape suivante. Cette procédure d'optimisation empirique,
quelque peu archaïque, a été
préférée à une méthode
mathématique qui aurait conduit plus rapidement mais en aveugle, au
jeu de paramètres optimisés. Elle a été
facilitée par une automatisation complémentaire issue d'un
programme élémentaire réalisé sous MATLAB.
Les discussions et commentaires qui suivent, illustrent
l'intérêt de la démarche, notamment sur le plan
pédagogique et méthodologique.
46
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Tableau 2-3 : Paramètres structuraux et
ultrastructuraux issus de la littérature. * signifie données ne
permettant pas de distinguer le bois initial (BI) du bois final
(BF).
Paramètres
de
l'ultra
structure
ligneuse
Em
GPa 2 - -
|
-
|
-
|
-
|
0,3
|
-
|
0,3
|
0,3
|
-
|
-
|
|
|
|
|
|
|
-
|
-
|
-
|
-
|
-
|
0,3
|
-
|
-
|
-
|
0,3
|
|
-
|
-
|
-
|
50
|
-
|
-
|
-
|
-
|
-
|
|
|
|
|
|
|
-
|
-
|
-
|
-
|
-
|
40
|
-
|
-
|
40
|
50
|
|
-
|
-
|
137
|
137
|
-
|
246
|
27
|
-
|
-
|
|
|
|
|
|
|
-
|
-
|
-
|
-
|
-
|
40
|
-
|
-
|
40
|
62
|
|
|
|
30 à
|
|
|
|
15 à
|
10
|
|
|
|
|
|
|
10 à
|
|
30 à
|
20
|
|
-
|
|
|
|
22
|
ím
V
%
Ef
GPa
i
1,23
et
2,04
- - 2 - -
- - - - - 1,2 - - 1,2 2
Paramètres
de sous
B (°) -
- -
I
50 - - 40
30 à 30
40 - 50 -
- - -
couche S2 B F
f
(°)
- - -
10 à
30
10 à
30 - 10 15 à
30
10 à
|
2
|
-
|
-
|
2
|
-
|
1,8
|
|
0,3
|
-
|
-
|
-
|
0,3
|
0,3
|
|
-
|
-
|
-
|
50
|
-
|
50
|
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
10
|
30
|
-
|
20
|
-
|
|
-
|
10
|
10
|
-
|
20
|
-
|
30
0 à -
30
15 à 20
30
|
-
|
-
|
20 à
60
|
-
|
30
|
|
-
|
-
|
-
|
-
|
37,5
|
- - - - - 5,9
DTi
(m)
- - - - 25 à
38
15 à
80
- - - - - 38 - 25
Paramètres
du
réseau
cellulaire
DRi
B m
I eTi
(m)
eRi
(m)
DTf
(m)
DRf
B
(m)
F eTf
(m)
eRf
(m)
- - - - 30 à
50
- - - - -
|
-
|
36
|
-
|
30 à
45
|
-
|
-
|
|
-
|
34
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
- - - - -
|
-
|
36
|
-
|
30 à
45
|
-
|
-
|
|
-
|
16
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
- - - - 23 à
38
- - - - 13 à
24
- - - - -
- - - - -
35 - - - 30 - 53 - 34
|
-
|
1-5*
|
-
|
1 à 2
|
-
|
3,4
|
-
|
3
|
-
|
-
|
-
|
-
|
1,07
|
|
-
|
1-5*
|
-
|
1 à 2
|
-
|
3,4
|
-
|
4
|
-
|
-
|
-
|
-
|
0,85
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
|
-
|
-
|
30
|
-
|
36
|
-
|
60
|
-
|
-
|
1 à
2
1 à
2
15 à
80
35 - - - 10 - 25 - 18
3 à
8
3 à
8
20 à
60
- 35
Paramètres
du
n - 17 - - - - 6 - 7 5 - - - - - 5 -
- - 6 - 3 à
% 12
|
-
|
1-5*
|
-
|
4 à 5
|
-
|
4,4
|
-
|
9
|
-
|
-
|
-
|
-
|
2,87
|
|
-
|
1-5*
|
-
|
4 à 5
|
-
|
4,4
|
-
|
9
|
-
|
-
|
-
|
-
|
2 ,87
|
- - 2
cerne Tx
%
- - - - - - - - - - - - - - - - 20 - - - - 50 30
- 51 ,2
47
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Vers un jeu de paramètres caractéristiques du
résineux standard
La colonne A du Tableau 2.4 correspond au jeu initial
des paramètres structuraux. Ces premiers résultats
suggèrent trois remarques essentielles :
le module d'élasticité longitudinal EL = 8,16 GPa
est 40% plus faible que la valeur cible,
la texture (Tx) de l'ordre de 4% est anormalement basse
en regard de la biologie
(Keller, 1999) bien que déjà
rencontrées dans des propositions plus mécaniciennes
(Khale et al, 1994),
les rapports d'anisotropie obtenus ne sont pas
réalistes.
Un premier ajustement a été d'augmenter la
rigidité (Ef) des microfibrilles, en proportion du
déficit constaté sur la valeur de EL. L'efficacité de ceci
est traduite dans la colonne B ou la valeur de EL est fixée à
12,9 GPa.
Une masse volumique de bois initial de ñinitial
= 0,44 g/cm3est trop élevée. En
référence à divers profils microdensitométriques
(fournis par P. Rozenberg) qui indiquent une valeur inférieure
à 0,3g/cm3 (un exemple sur le Sapin de Douglas est
illustré sur la Figure 1.13 du chapitre 1), la seconde modification
a porté sur une diminution de l'épaisseur pariétale
du bois initial, à diamètre cellulaire inchangé.
L'incidence de cette seconde modification est illustrée en
colonne C. Il en résulte une texture plus réaliste et la
relation d'ordre entre les modules d'élasticité (EL, ER,
ET) est maintenant respectée. Si l'estimation de EL est
satisfaisante, celle de ET et surtout ER sont encore
très supérieures aux valeurs cibles, respectivement, de 20 et
de 75 %.
A travers les résultats de la colonne D, c'est la
sensibilité de la modélisation à l'angle des
microfibrilles (ö) dans S2 qui est illustrée. La
troisième modification envisagée porte sur l'AMF de la seule
paroi de bois final, qui passe de ö = 10 à 8,5
degrés.
La sensibilité des caractéristiques
élastiques à ce paramètre est très forte. Une
réduction de 1,5
degré de l'AMF dans S2, (depuis 10 degrés), induit
une diminution de 11% de ER et de 18%
de ET. Le module EL est en revanche pratiquement insensible
à cette modification.
2.2.2.2 Commentaires sur les paramètres
optimisés.
La colonne E des Tableaux 2.4 et 2.5 rend compte
d'un jeu de paramètres structuraux optimisés, obtenus
moyennant le critère d'un écart relatif de chaque
constante élastique calculée à la valeur cible
correspondante, inférieur à 1%. Les contraintes
étant celles indiquées au paragraphe 2.2.1.1, à savoir
une masse volumique du bois fixée et un AMF (ö)
significativement différent dans le bois initial et dans le bois
final.
Une première remarque porte sur le module
d'élasticité des microfibrilles, dont la valeur
optimisée est sensiblement la moitié du module
d'élasticité de 134 GPa affiché par Sakurada
et al (1962). Deux commentaires explicatifs permettent
de justifier cette différence.
En premier lieu, la modélisation micromécanique du
renforcement de la paroi cellulaire par des microfibrilles de cellulose que
nous utilisons ici (Guitard et al, 1999, 2002), défini par
les
48
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
relations (2.25) et (2.26), diffère des modèles
classiquement mis en oeuvre pour évaluer les
propriétés des fibres, par méthode
inverse, à partir de mesures de rigidité de tissus ligneux. Notre
modèle assure la « restriction » du cisaillement induit
entre deux cellules voisines vraies, en envisageant une cellule
élémentaire fictive constituée d'un squelette
tridimensionnel de microfibrilles noyé dans une matrice amorphe. Ce
modèle est rigidifiant en regard de celui d'une structure
multicouche renforcée par des nappes de fibres parallèles
disjointes. Il assure notamment la rigidification du module
d'élasticité transverse avec l'augmentation de l'AMF (ce point
sera discuté dans le chapitre 3).
En second lieu, on rappellera ici qu'un module de 130 GPa est
une évaluation des propriétés élastiques de la
cristallite de cellulose obtenue par des mesures de déplacement
de plans réticulaires par diffraction rayons X, mesure dont la
représentativité à déjà été
évoquée au chapitre 1.
Ces deux arguments convergent ici pour expliquer que le module
élastique apparent optimisé des microfibrilles soit plus faible
que le module de fibrilles purement cristallines.
Le bois « virtuel » correspondant à ce jeu de
paramètres est fortement hétérogène quand à
la masse volumique des tissus constitutifs, avec 0,73 g/cm3
pour le bois final et 0,167 g/cm3 pour le bois initial,
en accord avec les divers profils microdensitométriques
déjà évoqués.
Une seconde hétérogénéité
tient à la différence d'angle des microfibrilles, avec
une valeur d'AMF de 22 degrés pour le bois initial contre 5,9
degrés pour le bois final. Notons que ceci répond à l'une
des contraintes imposées lors du processus d'optimisation.
La différence d'ovalisation des cellules entre bois
initial et bois final est un troisième facteur
d'hétérogénéité. Le rapport
géométrique DR / DT évolue en effet de 1,25 pour le bois
initial à
0,43 pour le bois final. Ce résultat est sensiblement
conforme à ce que suggère la littérature
(Marion, 2001, Sarèn et al, 2001).
Les paramètres de cerne, une texture de l'ordre de 50 %
et une fraction volumique en rayons ligneux de 2%, fixent les proportions
des tissus ligneux constitutifs du cerne. Avec 2%, la proportion en
rayons ligneux (n) est probablement une valeur un peu faible.
En conclusion, le jeu de paramètres optimisés de la
colonne E constitue un ensemble cohérent susceptible de
caractériser un bois résineux virtuel de
référence.
On remarque ici, en référence aux relevés
planimétriques du Tableau 2.6, que les différentes masses
volumiques tissulaires ñinitial et ñfinal affichées
par cette optimisation doivent être considérées comme
des valeurs extrêmes qui demeurent néanmoins admissibles par la
prise
en compte, dans le modèle RSV d'une texture fixée
à 0,512.
2.2.2.3 Multiplicité des solutions
Un second jeu de paramètres optimisés,
présenté dans la colonne F, a été obtenu en levant
la contrainte précédente sur l'AMF, l'orientation des
microfibrilles est dans ce cas identique dans les trois tissus
constitutifs de l'ordre de 12,3 degrés.
L'expérience numérique confirme la
possibilité d'une multiplicité de solutions optimales. Il
est en conséquence possible de fixer un certain nombre
de contraintes d'optimisation devant conduire aux différents jeux de
paramètres associés à chacun des types de bois observables
au sein d'un même arbre (bois juvénile, bois adulte, bois de
réaction).
49
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
2.2.2.4 Conclusions
Un jeu cohérent de paramètres
optimisés a été obtenu pour décrire le
« Résineux Standard Virtuel», sous deux types de contraintes
; une masse volumique du bois fixée à 0,45 g/cm 3 et
des angles de microfibrilles différenciées entre bois initial (10
degrés) et bois final
(20 degrés).
Cet outil de simulation ouvre des possibilités
d'expérimentation numérique en appui aux campagnes
expérimentales traditionnelles de caractérisation du
matériau bois, en permettant notamment:
une analyse détaillée de la
sensibilité des propriétés élastiques
macroscopiques à la variabilité des différents
paramètres structuraux et ultrastructuraux,
d'associer à la diversité des bois,
présent au sein d'une même grume, des jeux de
paramètres microstructuraux spécifiques, en tenant compte de
contraintes d'optimisations découlant d'observations
expérimentales,
d'étendre la démarche vers un champ
d'investigation beaucoup plus complexe, celui des essences feuillues.
On rappellera enfin que sur la plan
méthodologique, la démarche de modélisation micro-
macro, à plusieurs étages et proposée ici, est
parfaitement adaptable, en procédant, à l'une ou l'autre des
échelles de description, à des substitutions de
modèles élémentaires jugées plus opportunes.
50
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
|
A
|
B
|
C
|
D
|
E
|
|
F
|
|
|
|
|
|
|
|
|
|
Paroi de cellule bois initial
|
|
|
|
|
|
|
|
|
Em matrice en GPa
|
1,2
|
1,2
|
1,2
|
1,2
|
2
|
|
0,55
|
|
ím coefficient de Poisson de la matrice
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
|
0,35
|
|
Ef fibrilles en GPa
|
40
|
64
|
64
|
64
|
62
|
|
61,5
|
|
AMF dans S2 en degrés
(öi)
|
25
|
25
|
25
|
25
|
22
|
|
12,3
|
|
V taux de microfibrilles
|
0,5
|
0,5
|
0,5
|
0,5
|
0,5
|
|
0,5
|
|
|
|
|
|
|
|
|
|
Tissu de bois initial
|
|
|
|
|
|
|
|
|
DTi diamètre tangentiel en um
|
30
|
30
|
30
|
30
|
30
|
|
50
|
|
eTi épaisseur paroi tangentielle en um
|
2
|
2
|
1
|
1
|
1,068
|
|
2,35
|
|
OV paramètre d'ovalisation Dri/Dti
|
1,166
|
1,166
|
1,166
|
1,166
|
1,25
|
|
1
|
|
ei= eRi/eTi paramètre d'épaisseur
pariétale
|
1,5
|
1,5
|
1,5
|
1,5
|
0,8
|
|
1
|
|
ñinitial masse volumique en g/cm3
|
0,44
|
0,44
|
0,229
|
0,229
|
0,167
|
|
0,271
|
|
|
|
|
|
|
|
|
|
Paroi de cellule bois final
|
|
|
|
|
|
|
|
|
Em matrice en GPa
|
1,2
|
1,2
|
1,2
|
1,2
|
2
|
|
0,55
|
|
ím coefficient de Poisson de la matrice
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
|
0,35
|
|
Ef fibrilles en GPa
|
40
|
64
|
64
|
64
|
62
|
|
61,5
|
|
AMF dans S2 en degrés
(öf)
|
10
|
10
|
10
|
8,5
|
5,9
|
|
12,3
|
|
V taux de microfibrilles
|
0,5
|
0,5
|
0,5
|
0,5
|
0,5
|
|
0,541
|
|
|
|
|
|
|
|
|
|
Tissu de bois final
|
|
|
|
|
|
|
|
|
DTf diamètre tangentiel en um
|
35
|
35
|
35
|
35
|
35
|
|
50
|
|
eTf épaisseur paroi tangentielle en um
|
3
|
3
|
3
|
3
|
2,87
|
|
4,5
|
|
OV paramètre d'ovalisation DRf/DTf
|
0,514
|
0,514
|
0,514
|
0,514
|
0,43
|
|
0,44
|
|
ef= eRf/eTf paramètre d'épaisseur
pariétale
|
1
|
1
|
1
|
1
|
1
|
|
1
|
|
ñfinal masse volumique en
g/cm3
|
0,676
|
0,676
|
0,676
|
0,676
|
0,729
|
|
0,778
|
Tableau 2-4 Données pariétales et
géométrie cellulaire des tissus bois initial et bois
final
51
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
|
A
|
B
|
C
|
D
|
E
|
|
F
|
|
Paroi de cellule de rayon
|
|
|
|
|
|
|
|
|
Em matrice en GPa
|
1,2
|
1,2
|
1,2
|
1,2
|
2
|
|
0,55
|
|
ím coefficient de Poisson de la matrice
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
|
0,35
|
|
Ef microfibrilles en GPa
|
40
|
64
|
64
|
64
|
60
|
|
61,5
|
|
AMF dans S2 en degrés
|
40
|
40
|
40
|
40
|
46
|
|
12,3
|
|
V taux de microfibrilles
|
0,5
|
0,5
|
0,5
|
0,5
|
0,5
|
|
0,5
|
|
|
|
|
|
|
|
|
|
Tissu de rayon
|
|
|
|
|
|
|
|
|
DTr diamètre tangentiel en um
|
30
|
30
|
30
|
30
|
34,5
|
|
50
|
|
eTr épaisseur paroi tangentielle en um
|
2
|
2
|
2
|
2
|
1,032
|
|
2,4
|
|
OV paramètre d'ovalisation DRr/DTr
|
1,166
|
1,166
|
1,166
|
1,166
|
1,18
|
|
1
|
|
eR= eRr/eTr paramètre d'épaisseur
pariétale
|
1,5
|
1,5
|
1,5
|
1,5
|
1,5
|
|
1
|
|
ñrayon masse volumique en g/cm3
|
0,44
|
0,44
|
0,44
|
0,44
|
0,202
|
|
0,276
|
|
|
|
|
|
|
|
|
|
Paramètres de cerne
|
|
|
|
|
|
|
|
|
Tx texture
|
0,043
|
0,043
|
0,495
|
0,495
|
0,512
|
|
0,36
|
|
n fraction volumique en rayons en %
|
2
|
2
|
2
|
2
|
2
|
|
1,75
|
|
|
|
|
|
|
|
|
|
Les critères cibles
|
|
|
|
|
|
|
|
|
Masse volumique ñ = 0,45 g/cm3
|
0,45
|
0,45
|
0,45
|
0,45
|
0,45
|
|
0,45
|
|
ER = 1,00 GPa
|
2,95
|
4,46
|
1,75
|
1,55
|
1
|
|
0,995
|
|
ET = 0,636 GPa
|
0,36
|
0,545
|
0,758
|
0,621
|
0,635
|
|
0,634
|
|
EL = 13,1 GPa
|
8,16
|
12,9
|
13,1
|
13,1
|
13,1
|
|
13,2
|
|
EL/ER = 13,1
|
2,76
|
2,89
|
7,5
|
8,47
|
13,1
|
|
13,3
|
|
ER/ET = 1,57
|
8,2
|
8,17
|
2,31
|
2,5
|
1,57
|
|
1,57
|
|
|
|
|
|
|
|
|
Tableau 2-5 Données pariétales et
géométrie cellulaire des rayons ligneux, paramètres de
cerne et les critères cibles
52
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
|
South Finland Pine
|
54 ans
|
Relevés planimétriques
|
North Finland Pine
|
52 ans
|
Relevés planimétriques
|
Finland spruce
|
36 ans
|
Relevés planimétriques
|
France spruce
|
35 ans
|
Relevés planimétriques
|
France
Fir
|
49 ans
|
Relevés planimétriques
|
|
N°
cerne
|
Densité
[kg/m3]
|
ep. de paroi
[um]
|
DR
en
[um]
|
DT
en
[um]
|
N°
cerne
|
Densité
[kg/m3]
|
ep. de paroi
[um]
|
DR
en
[um]
|
DT
en
[um]
|
N°
cerne
|
Densité
[kg/m3]
|
ep. de paroi
[um]
|
DR
en
[um]
|
DT
en
[um]
|
N°
cerne
|
Densité
[kg/m3]
|
ep. de paroi
[um]
|
DR
en
[um]
|
DT
en
[um]
|
N°
cerne
|
Densité
[kg/m3]
|
ep. de paroi
[um]
|
DR
en
[um]
|
DT
en
[um]
|
|
1
|
508
|
3,046
|
38,76
|
30,37
|
1
|
433
|
3,791
|
35,14
|
28,09
|
1
|
363
|
2,878
|
47,39
|
31,05
|
1
|
351
|
3,081
|
41,36
|
32,8
|
1
|
330
|
2,642
|
42,87
|
29,25
|
|
2
|
374
|
2,83
|
43,3
|
30,74
|
2
|
371
|
3,652
|
35,31
|
27,35
|
2
|
285
|
2,808
|
48,24
|
30,8
|
2
|
286
|
2,853
|
41,98
|
33,19
|
2
|
287
|
2,471
|
43,25
|
29,65
|
|
3
|
355
|
2,808
|
43,63
|
31,64
|
3
|
352
|
3,538
|
36,88
|
27,86
|
3
|
299
|
2,852
|
44,38
|
30,84
|
3
|
289
|
2,864
|
39,19
|
33,28
|
3
|
286
|
2,511
|
42,73
|
29,93
|
|
4
|
346
|
2,896
|
39,06
|
31,2
|
4
|
361
|
3,454
|
37,37
|
28,36
|
4
|
307
|
2,889
|
40,59
|
30,75
|
4
|
288
|
2,884
|
38,67
|
33,69
|
4
|
303
|
2,564
|
42,55
|
29,91
|
|
5
|
348
|
2,96
|
38,91
|
30,9
|
5
|
362
|
3,435
|
37,82
|
27,19
|
5
|
319
|
2,942
|
41,18
|
30,94
|
5
|
300
|
2,948
|
36,95
|
33,62
|
5
|
314
|
2,661
|
41,88
|
30,94
|
|
6
|
360
|
2,999
|
41,32
|
30,63
|
6
|
354
|
3,565
|
37,19
|
27,99
|
6
|
317
|
2,962
|
40,11
|
30,09
|
6
|
306
|
2,974
|
35,83
|
33,23
|
6
|
327
|
2,796
|
40,91
|
31,25
|
|
7
|
383
|
3,13
|
39,56
|
29,99
|
7
|
366
|
3,785
|
39,23
|
28
|
7
|
316
|
2,991
|
39,33
|
29,9
|
7
|
318
|
3,221
|
40,15
|
32,89
|
7
|
337
|
2,962
|
41,58
|
30,79
|
|
8
|
398
|
3,244
|
38,43
|
30,2
|
8
|
376
|
3,875
|
42,09
|
28,01
|
8
|
328
|
3,037
|
40,48
|
30,02
|
8
|
338
|
3,504
|
40,96
|
32,09
|
8
|
351
|
3,132
|
39,34
|
30,52
|
|
9
|
406
|
3,288
|
39,56
|
30,13
|
9
|
375
|
3,991
|
39,69
|
28,01
|
9
|
340
|
3,07
|
39,21
|
29,37
|
9
|
364
|
3,674
|
39,89
|
31,95
|
9
|
382
|
3,186
|
35,86
|
30,44
|
|
10
|
427
|
3,251
|
36,75
|
30,6
|
10
|
378
|
4,064
|
37,82
|
28,38
|
10
|
361
|
3,138
|
38,1
|
29,25
|
10
|
396
|
3,717
|
36,51
|
31,64
|
10
|
420
|
3,381
|
36,11
|
30,7
|
|
11
|
453
|
3,423
|
35,86
|
30,28
|
11
|
396
|
4,213
|
39,05
|
28,35
|
11
|
397
|
3,191
|
36,56
|
29,09
|
11
|
420
|
4,197
|
34,12
|
31,31
|
11
|
453
|
3,616
|
34,83
|
30,66
|
|
12
|
530
|
3,648
|
35,8
|
29,51
|
12
|
425
|
4,599
|
35,06
|
28,37
|
12
|
433
|
3,465
|
34,24
|
29,4
|
12
|
442
|
4,065
|
35,66
|
31,6
|
12
|
505
|
3,868
|
31,49
|
30,61
|
|
13
|
706
|
3,972
|
32,84
|
29,56
|
13
|
479
|
5,642
|
35,24
|
28,3
|
13
|
455
|
3,68
|
33,63
|
28,96
|
13
|
456
|
4,26
|
36,04
|
31,06
|
13
|
552
|
4,251
|
30,51
|
31,24
|
|
14
|
817
|
4,224
|
27,76
|
29,95
|
14
|
530
|
6,09
|
33,93
|
28,26
|
14
|
498
|
4,156
|
33,07
|
29,31
|
14
|
479
|
4,288
|
36,04
|
31,47
|
14
|
620
|
4,566
|
27,59
|
30,46
|
|
15
|
845
|
4,613
|
26,98
|
28,54
|
15
|
628
|
6,334
|
28,55
|
28,6
|
15
|
554
|
4,203
|
32,14
|
29,07
|
15
|
516
|
4,766
|
34,26
|
31,59
|
15
|
700
|
4,74
|
25,83
|
28,96
|
|
16
|
859
|
5,36
|
25,21
|
29,66
|
16
|
746
|
6,11
|
24,68
|
27,47
|
16
|
642
|
4,925
|
29,47
|
29,74
|
16
|
592
|
5,086
|
30,9
|
31
|
16
|
716
|
4,833
|
26,54
|
29,35
|
|
17
|
975
|
5,796
|
25,15
|
31,8
|
17
|
826
|
6,914
|
23,08
|
27,1
|
17
|
713
|
5,295
|
26,02
|
28,95
|
17
|
685
|
5,253
|
27,51
|
30,79
|
17
|
783
|
5,108
|
23,66
|
28,86
|
|
18
|
997
|
5,96
|
25,87
|
31,8
|
18
|
921
|
6,867
|
23,11
|
27,5
|
18
|
765
|
5,743
|
25,34
|
29,17
|
18
|
827
|
5,855
|
25,97
|
30,49
|
18
|
814
|
5,273
|
23,98
|
28,45
|
|
19
|
998
|
5,992
|
24,05
|
30,03
|
19
|
959
|
6,58
|
22,39
|
26,62
|
19
|
864
|
6,422
|
24,04
|
29,56
|
19
|
962
|
6,121
|
22,6
|
31,24
|
19
|
842
|
5,325
|
22,64
|
28,65
|
|
20
|
862
|
4,647
|
19,85
|
31,06
|
20
|
875
|
5,824
|
19,35
|
27,04
|
20
|
867
|
5,823
|
19,12
|
31,1
|
20
|
1027
|
6,145
|
19,21
|
32,5
|
20
|
861
|
5,074
|
18,28
|
28,73
|
Tableau 2-6 Relevés planimétriques de
dimensions cellulaires de cinq essences résineuses (Leban). La
densité est mesurée par l'absorption d'un rayonnement
X.
53
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
2.2.3 Situation des paramétres du modèle RSV
vis-à-vis de ceux de trois essences résineuses
2.2.3.1 Méthodologie
Ruelle (2003) a relevé l'angle des microfibrilles
(ö) et certains paramètres de forme des cellules de
bois initial et de bois final sur trois essences résineuses. Les
différentes méthodes expérimentales utilisées
seront détaillées dans le chapitre 4. L'étude anatomique a
porté sur 2 échantillons de bois normal d'Epicéa commun
(Picea abies) de Pin maritime (Pinus pinaster)
et de Pin sylvestre (Pinus sylvestris). Les paramètres
mesurés par l'auteur sont les diamètres radial et tangentiel de
lumens (FLDR) et (FLDT), ainsi que les épaisseurs de double paroi, dans
les directions radiales (FePR) et tangentielle (FePT). Les formules
exprimant les caractéristiques géométriques
relevées par l'auteur en fonction des paramètres de forme (DR,
DT, eR, eT) envisagés dans notre modèle de tissu ligneux sont
:
e T =
e R =
FePR
2
FePT
2
D R =
FLDR
+ 2 e T
D T =
FLDT + 2 e R
Les écarts types sur l'AMF (ö) et sur
ces mêmes paramètres (DR, DT, eR,
eT) ont été calculés
à partir de ceux relevés par Ruelle (ils sont
reportés sur les Figures 2.6 à 2.12 sous la forme de barres
d'erreurs).
Les moyennes des dimensions cellulaires (DR, DT, eR, eT) pour
chaque tissu et pour un cerne ont été fournies sur chaque
échantillon. Par application de la formule (2.14) on calcule la
porosité moyenne puis la masse volumique moyenne de chaque
tissu et du cerne. Une approximation de la texture (Tx) est alors
déduite (méthode inverse) à partir des masses
volumiques tissulaires et de celle du cerne (l'intervention de la masse
volumique des rayons ligneux dans la masse volumique du cerne est
négligée).
x
T = ñ cerne ñ
initial
ñ final ñ
initial
On notera que la masse volumique des éprouvettes
(complètes) relevée par l'auteur n'a pas
été utilisée, pour déterminer la
texture par cette méthode, puisque le nombre de cernes dans chaque
éprouvette n'est pas précisé.
Pour chaque essence et chaque tissu, l'AMF
(ö) (Figures 2.6 à 2.8), et les paramètres
géométriques des cellules de bois normal (noté BN sur les
Figures 2.9 à 2.11) sont comparés à ceux du modèle
RSV.
La Figure 2.12 permet, pour chaque essence, de comparer les
valeurs moyennes de la texture, des masses volumiques du bois initial, du bois
final et du cerne aux valeurs correspondantes
du RSV.
54
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Les faibles écarts types des valeurs d'AMF
(ö) mesurées par Ruelle (2003), suggèrent que
les
AMF ne différent pas significativement dans le
bois initial et final. Pour cette raison sont représentés
sur chacune des Figures 2.6 à 2.11, les paramètres ayant servi
à la construction d'un RSV (i=f) ayant le même
AMF(ö) dans les bois initial et final (colonne F des Tableaux
2.4 et 2.5).
2.2.3.2 Situation du modèle RSV en regard des trois
essences.
A l'échelle de la double cloison
La valeur de 22 degrés attribuée à l'AMF
(ö) des tissus bois initial dans le modèle RSV est assez
proche de celles relevées par Ruelle sur le bois initial des trois
essences. La valeur de ce même paramètre (ö)
envisagée dans le bois final du RSV (5,9 degrés) demeure bien
inférieure
à celle relevée expérimentalement (Figures
2.6 à 2.8).
A l'échelle tissulaire
Pour les trois essences (Figures 2.9 à 2.12), les
épaisseurs de paroi tangentielles et radiales qu'elles
caractérisent un bois initial (eRi, eTi) ou un bois final (eRf, eTf)
sont systématiquement supérieures à celle
insérées dans le modèle RSV. En revanche, les
diamètres radial et tangentiel de tissus (DRi, DTi, DRf, DTf)
sont assez proches des valeurs moyennes relevées
expérimentalement.
Une conséquence directe de la faiblesse de ces
épaisseurs pariétales optimisées réside en une
masse volumique de tissu (ñinit) et (ñfin) du bois RSV
inférieure ou égale (cas du Pin maritime, Figure 2.12) à
celles estimées par une assimilation du plan ligneux des trois
essences à un réseau de cellules rectangulaires.
Devant les écarts types des autres
paramètres il est délicat de rapprocher, en terme de
paramètres géométriques comme en terme d'AMF
(ö), le modèle RSV de telle ou telle essence.
2.2.3.3 Situation en regard des 3 essences d'un cas particulier
du RSV ; le RSV (i=f)
L'AMF (ö) de 12,3 degrés envisagé
dans le modèle RSV (i=f) est assez proche des valeurs relevées
par l'auteur sur les trois essences. Deux différences essentielles
distinguent le modèle RSV (i=f) du modèle RSV; des
diamètres cellulaires (DRi = DTi = DTf = 50 um) élevés et
un angle des microfibrilles communs au deux tissus.
La nécessité de cette forte augmentation des
valeurs de diamètres cellulaires (DRi, DTi, DTf ) pour des faibles
variations d'angle (ö) laisse présager que les
caractéristiques élastiques ayant servies de cible pour la
construction du RSV sont très sensibles aux variations de l'angle des
microfibrilles.
55
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)

Figure 2.6 Comparaison des AMF relevés sur les
bois initial et final de l'Epicéa aux AMF du RSV et RSV
(i=f)
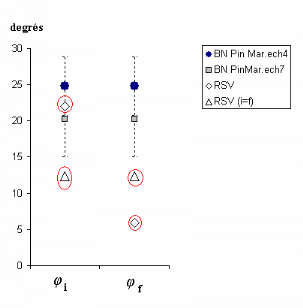
Figure 2.7 Comparaison des AMF relevés sur les
bois initial et final du Pin maritime aux AMF du RSV et
RSV (i=f)
56
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
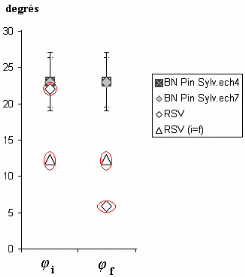
Figure 2.8 Comparaison des AMF relevés sur les
bois initial et final de Pin Sylvestre aux AMF du RSV et
RSV (i=f)
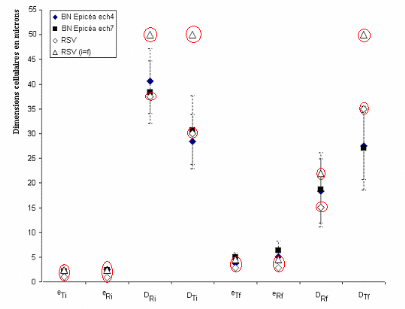
Figure 2.9 Comparaison des paramètres structuraux
et ultrastructuraux relevés sur un bois normal
d'Epicéa aux paramètres optimisés du
RSV et RSV (i=f))
57
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
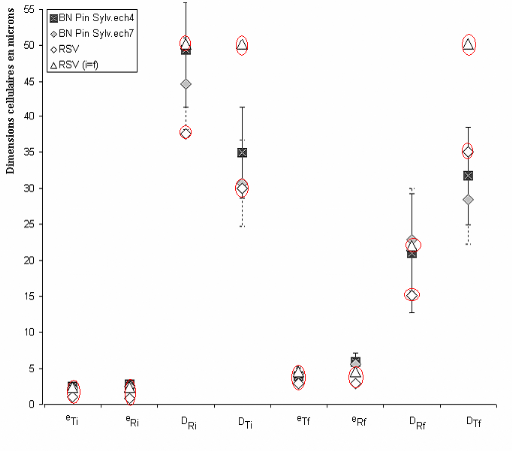
Figure 2.10 Comparaison des paramètres structuraux
et ultrastructuraux obtenus sur un bois normal de
Pin sylvestre aux paramètres optimisés du
RSV et RSV (i=f).
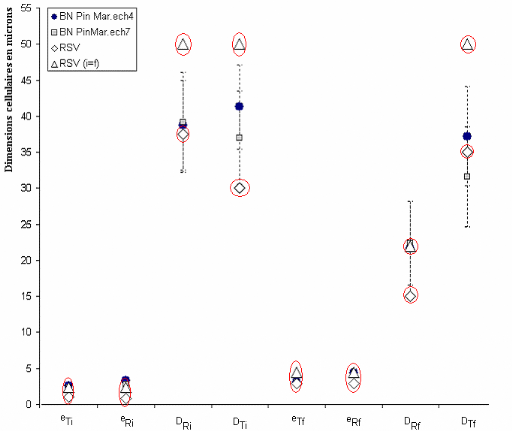
Figure 2.11 Comparaison des paramètres structuraux
et ultrastructuraux obtenus sur un bois normal de
Pin maritime aux paramètres optimisés du
RSV et du RSV (i=f))
58
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
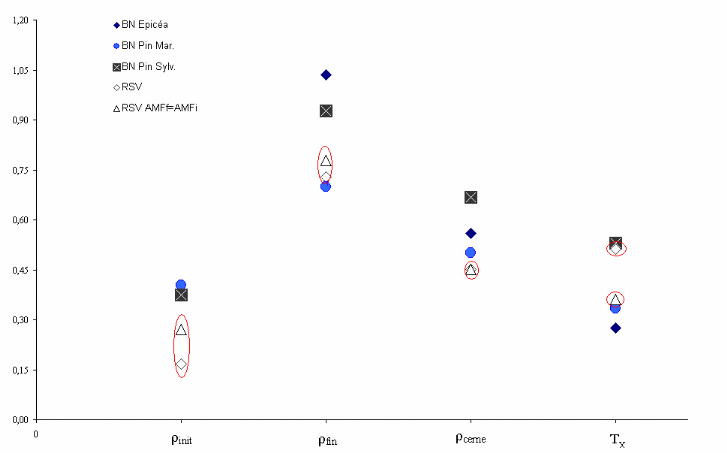
Figure 2.12 Comparaison de paramètres tissulaires
et paramètres de cerne déduits sur un bois normal de
trois essences résineuses à ceux
résultants de l'optimisation (RSV et RSV (i=f))
2.3 Conclusion
A partir d'un ensemble de valeurs probables
assignées, via une étude documentaire, aux différents
paramètres susceptibles de conditionner l'anisotropie
élastique du résineux standard, un bois virtuel de
résineux (RSV) a été construit. Aux
propriétés élastiques du résineux standard
(Guitard, 1987) est maintenant assigné un ensemble de 22
paramètres structuraux descriptifs. La confrontation à posteriori
de certaines de valeurs optimisées à des jeux
expérimentaux déterminés sur trois essences
résineuses confirme le réalisme biologique
de cette essence « virtuelle ». Sur cette base
de travail, une hiérarchisation des paramètres
insérés peut être proposée.
59
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
ANNEXE 1
Caractéristiques élastiques du modèle
Squelette de microfibrilles (Guitard et al, 1999) Rigidités des
microfibrilles de cellulose
La forme générale des complaisances
élastiques exprimées selon les axes principaux de chacune
des nappes de revêtement des microfibrilles est en premier lieu
écrite en fonction des constantes élastiques des fibres
cellulosiques et sous l'hypothèse d'une symétrie orthotrope.
1 í f
í f
f
21
13 0
0 0
E
f
1 E2f E3
f f
í21 1
í23 0
0 0
E
f
f E f E
1 2 3
31
í f
f
í12f 1
f f
0 0 0
f*
E1 E2 E3
S =
(A1.1)
ijkl 0 0
1
0 G f 0 0
0 0
23
0 0 1 0
G f
0 0
31
0 0 0
= 1
G12f
Il est supposé que les efforts longitudinaux selon les
fibres et les efforts de cisaillement entre
les fibres ne peuvent être transmis que par
l'intermédiaire des nappes de microfibrilles.
Les seuls paramètres élastiques
considérés comme non nuls ne sont donc que E3f,
G23f et
G31f
Les modules d'élasticité au cisaillement sont
arbitrairement estimés à partir du module longitudinal des
microfibrilles E3f,
E3f
31
(A1.2)
G 23f = G f =
2
Les effets Poisson ne sont pas pris en compte :
(A.1.3)
í f 12
= í f 21
= í f 23
= í f 32
= í f 31
= í f 13 = 0
Le tenseur des rigidités Cf*ijkl est
obtenu par inversion du tenseur des complaisances
Sf*ijkl précédemment
exprimé.
Sous ces conditions, les composantes non nulles de
Cf*ijkl sont :
60
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
C f * 3333
f *
= E 3 f
E 3 f
(A.1.4)
C 2323 = 2
f
C f *
3131
= E 3
2
ijkl
Les composantes du tenseur des rigidités de l'une des
nappes de microfibrilles Cf (+ö)
sont
en premier lieu exprimées dans le système des axes
principaux de la cellule et déduites des
r
Cf*ijkl par une rotation d'angle
(ö) autour du grand axe cellulaire (1)
Les composantes du tenseur des rigidités
Cfijkl du squelette de microfibrilles, exprimées suivant
les axes principaux de la cellule sont calculées par
superposition pondérée des caractéristiques de chacune
des deux nappes d'orientations symétriques, les termes en
puissances impaires de sin (ö) sont ainsi
éliminés.
(A.1.5)
Cf ijkl
Cf(+ ) ijkl
= +
2
Cf( )
2
ijkl
Les axes associés aux coordonnées cylindriques
(r, è, z) définissent ainsi les directions
principales du tenseur des rigidités du squelette des
microfibrilles.
La forme du tenseur des rigidités du squelette des
microfibrilles est:
(A.1.6)
C f rrrr
( f C
C f èèrr
C f rrèr
C f èèèè
C f rrzz 0
C f èèrr 0
0 0
0 0
C ijkl )=
f
zzrr
0
0
C f zzèz
0
0
C f zzzz
0
0
0
C f èzèz
0
0 0
0 0
C f zrzr 0
0 0 0
0 0 C f rèèr
61
Modèles multi échelles et construction du
Résineux Standard Virtuel (RSV)
Cf rrrr = C
f
f *
1111
f * 4 f *
f * 2 2 f *
C èèèè = C
2222c
+ 2 (C
2233 + 2C
3232 )c s + C
3333s4
Cf zzzz = C
f * 4
3333c
f
+ 2 (C
*
2233 + 2Cf *
3232 )c2s2
f
*
+ C 2222s4
Cf zèèz = C
f * 2
3232 (c
s2 )2
f
+ (C
*
f
2222 + C
*
3333 2C
f * 2 2
2233 )c s
(A.1.7)
Cf rèèt = C
f
f * 2
1212c
f * 2
*
f 2
+ C 3131s
f *
C rzrz = C
f f
1313c
+ C 1212s2
f * 2 f * 2
C rrèr
f
= C èèrr = C
f
2211c + C
f * 4
3311s
4 f * f * f *
C zzèè = C
f f
èèzz = C
f *
2233 (c
2
+ s ) + (C
f * 2
2222 + C
3333 4C
3232 )s2c2
C zz rr = C
rrzz = C
3311c + C
2211s
Les composantes non nulles du tenseur sont donc :
Cf èèèè = E
3f
s 2 (1 + c 2 )
Cf zzzz = E 3f
c 2 (1 + s 2 )
Cf zèèz = E 3f
(c 2
s 2 ) 2
(A.1.8)
Cf è èzz = Cf zzèz
f
Cf rzrz = E 3 c 2
2
= E 3f c 2s 2
f
Cf rèèr = E 3 s
2
2
Les modules élastiques longitudinal et transverses de la
double paroi virtuelle notés
respectivement ELp et ETp sont alors :
(2.27) ELp C = (1 V) E m +
V(1 s 4 )E f
(1 )
zzzz
(1 + )(1 2 )
Tp Rp ( ) m 4 f
(1 )
(2.28) E = E C = 1 V E +
V(1 c )E
(1 + )(1 2 )
62
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
3 Hiérarchisation des paramètres
descriptifs de l'anisotropie élastique du
bois normal
Le chapitre 1 a permis de dresser l'inventaire, via une
étude documentaire pluridisciplinaire, des paramètres
essentiels rendus responsables de la variabilité intra arbre de
l'anisotropie élastique du bois normal. Les valeurs
numériques assignées à chacun de ces mêmes
paramètres, via une technique simple d'optimisation
associant calculs et propositions bibliographiques, ont conduit à
la définition d'un résineux standard virtuel RSV (chapitre 2).
Cette essence fictive a été considérée comme «
médiane » en terme de propriétés mécaniques
élastiques. L'objectif de ce chapitre est de préciser
numériquement, en s'appuyant sur des banques de données
structurelles ou des tendances générales issues de la
bibliographie, l'influence de chacun des paramètres clés,
sur les rapports d'anisotropie élastique du bois massif sans
défaut.
3.1 La porosité, facteur de l'anisotropie
élastique du réseau cellulaire nid d'abeille
Par soucis de simplification, et devant la
disparité des valeurs des rigidités de parois cellulaires
présentées dans la littérature, les études
numériques sont menées dans ce chapitre, sous l'hypothèse
d'une isotropie transverse de la double paroi (ETp = ERp).
Dans la modélisation présentée
précédemment (chapitre 2), la masse volumique (stabilisée
à l'humidité de référence de 12%) est liée
aux paramètres géométriques tissulaires
épaisseurs
(eT, eR) et diamètres (DR, DT) comme à la masse
volumique de la matière ligneuse par les deux expressions (2.12) et
(2.13) données dans le chapitre 2.
A cette première étape de la discussion, les
épaisseurs pariétales, radiale et tangentielle
(posées égales à e), ainsi que les
diamètres radial DR et tangentiel DT, ne seront pas distingués
(DR = DT = D). Le facteur de forme des cellules (supposées
en premier lieu carrées) est alors exprimé par le rapport
adimensionnel e/D.
Les rapports directionnels d'anisotropie élastique L/R et
L/T du tissu ligneux élémentaire sont
alors liés aux rapports d'anisotropie élastique
ELp
ERp
de la double paroi par les relations (3.1),
(3.2) via les coefficients d'anisotropie définis par les
relations (3.3) à (3.5):
(3.1)
E L
E R
e
= 2 1
D
E Lp
=
E Rp
a LR
E Lp
E Rp
E L
e
=1 =e (D 2e)3
E Lp
E Lp
(3.2)
= 2 1
D
E T
1 +
64 D
e3
E Tp
= a LT
E Tp
(3.3)
1 e
=
a F
64 D
(D 2e)3
e3
63
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(3.4)
a LR
e
2
= 1
D
e
1 e (D 2e)3
(3.5)
a LT
= 2 1 1 +
=
3
a LR (1 + a F )
D
64 D e
Le rapport aF représente ainsi la
proportion d'anisotropie élastique L/T résultant de la mise
en
flexion de la double paroi cellulaire, tandis que le rapport
aLR fournit une estimation de la proportion d'anisotropie élastique
L/R résultant du renfort radial crée par l'alignement des
parois dans le sens R. Le produit aLT exprime enfin la proportion
d'anisotropie élastique résultant d'un alignement dans le sens
T.
Il convient ici de préciser qu'à cette
étape du travail, la discussion fait état de sens R et de sens T
et non des directions d'orthotropie radiale et tangentielle du matériau
bois, tout ceci afin de caractériser l'influence des
différences disposition en alignement (sens T) ou en quinconces
(sens T) du tissu ligneux sur les caractéristiques du nid d'abeille.
Considérant un échelonnement des masses volumiques
du matériau bois compris entre 0,2 et
1,5 (masse volumique de la matière ligneuse), il est
possible, pour différentes porosités, de déduire les
valeurs du facteur de forme e/D des cellules, supposées, en premier
lieu, carrées
(Tableau 3.1).
On calcule les valeurs du coefficient
d'anisotropie géométrique aLR correspondant à
l'arrangement cellulaire d'alignement sens R, à l'aide de (3.4),
ainsi que les valeurs du coefficient d'anisotropie
géométrique, aLT correspondant à l'arrangement cellulaire
d'alignement sens T (3.5). On accède enfin au coefficient sans dimension
aF à l'aide de (3.3), représentant la proportion d'anisotropie
résultant de la mise en flexion de certains éléments de
la paroi cellulaire. Les valeurs numériques
correspondantes sont reportées dans le Tableau
3.1.
Un premier examen du Tableau 3.1 montre que la porosité Po
varie dans un large intervalle de
86% à 1%, lorsque les masses volumiques ñ de la
structure considérée sont comprises dans l'intervalle 0,2
à 1,5 g/cm3. A une porosité quasi nulle correspond
bien une masse volumique proche de la valeur admise pour la matière
ligneuse (ñm= 1,51 g/cm3).
Les résultats affichés dans le Tableau 3.1,
permettent de conclure que, dans le cadre de l'étude
(i.e. cellules carrées), la porosité
intervient, via le rapport de forme e/D, dans l'anisotropie
élastique apparente du matériau bois assimilé à une
structure nid d'abeille.
Dans le cas des arrangements en alignement suivant la
direction R, la porosité Po intervient directement (Po = (aLR
-1)2) par l'intermédiaire du coefficient multiplicatif aLR
dont la valeur numérique reste comprise dans l'intervalle de 1 à
2.
Dans le cas des arrangements en quinconces faisant
intervenir un comportement en
« flexion » de certains éléments de la
paroi cellulaire (portion BCE soumise à une flexion 3 points, Figure 2.3
du chapitre 2), on constate (Tableau 3.1) d'une part que le coefficient aLT
varie dans une plus large gamme allant de 23 à 1, et d'autre
part que des anisotropies classiques L/T, exprimées par une valeur
du facteur aLT de l'ordre de 20, (valeurs courantes
64
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
dans le bois initial et final, Bodig et al, 1982, comme
dans le bois massif, Guitard et al 1987),
ne peuvent être atteintes que pour des masses volumiques
inférieures ñ à 0,25 g/cm3 (Figure
3.1). Cette dernière valeur de masse volumique
apparaît bien restrictive en regard de l'intervalle des variations
de cette même grandeur classiquement observable sur la majorité
des essences résineuses (Venet et al, 1986, Keller, 1999).

Figure 3.1 Evolutions des rapports
géométriques avec la masse volumique ñ
|
(g/cm3)
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
|
Po (%)
|
0,86
|
0,80
|
0,73
|
0,66
|
0,60
|
0,53
|
0,47
|
0,40
|
0,33
|
0,27
|
0,20
|
0,13
|
0,07
|
0,01
|
|
e/D
|
0,03
|
0,05
|
0,07
|
0,09
|
0,11
|
0,13
|
0,16
|
0,18
|
0,21
|
0,24
|
0,27
|
0,31
|
0,37
|
0,46
|
|
aF
|
10,73
|
4,07
|
1,93
|
1,03
|
0,58
|
0,34
|
0,20
|
0,12
|
0,06
|
0,03
|
0,01
|
0,01
|
0,00
|
0,00
|
|
aLR
|
1,93
|
1,89
|
1,85
|
1,81
|
1,77
|
1,73
|
1,68
|
1,63
|
1,58
|
1,52
|
1,45
|
1,37
|
1,26
|
1,08
|
|
aLT
|
22,67
|
9,62
|
5,45
|
3,69
|
2,81
|
2,32
|
2,02
|
1,83
|
1,69
|
1,57
|
1,48
|
1,38
|
1,27
|
1,08
|
Tableau 3-1 Comparaison de l'évolution des
coefficients d'anisotropie avec la porosité Po
L'étendue de l'intervalle de variations du coefficient
d'anisotropie aLT pourrait laisser penser que le fonctionnement en flexion
des parois cellulaires est une des raisons de la très forte
anisotropie L/T observée expérimentalement sur le bois initial
comme sur le bois final.
Pourtant, d'après la Figure 3.1, construite à
partir des données présentées au Tableau 3.1, la prise en
compte de la flexion des parois, traduite par la valeur du facteur aF, est peu
justifiée
dés que la masse volumique est supérieure
à 0,6 g/cm3. En effet, pour une telle valeur du
paramètre, au facteur de forme des cellules e/D = 0,58, correspond un
facteur de forme de l'élément sollicité en flexion
très faible L/h = (D-e) /2e = 3,5. Pour des cellules assimilables
à des cellules de bois final (parois épaisses et diamètres
cellulaires assez faibles), une partie de l'anisotropie L/T, est donc
directement imputable à un effet « quantité de
matière ».
65
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Pour évaluer le degré d'anisotropie induit dans le
plan transverse du nid d'abeille par la seule
différence des arrangements en alignement radial et en
quinconces, les variations du rapport aRT d'anisotropie transverse
tissulaire ER / ET exprimé en (3.6), en fonction de la masse
volumique, sont reportées dans le Tableau 3.2 et la Figure 3.2.
E 1
e (D 2e)3 E E E
(3.6)
R
= 1 +
Rp
F
= (1 + a
) Rp = a Rp
E T
64 D
e3
E Tp
E Tp
RT
E
Tp
L'examen simultané de la Figure 3.2 et du Tableau 3.2
permet de constater qu'une anisotropie

transverse macroscopique R/T classique (Guitard et al, 1987)
supérieure ou égale à 2 ne peut être attribué
à la seule différence d'arrangement en quinconce ou en alignement
que pour des masses volumiques inférieures à 0,5
g/cm3.
|
(g/cm3)
|
Po (%)
|
e/D
|
aRT
|
|
0,20
|
0,86
|
0,03
|
15,42
|
|
0,30
|
0,80
|
0,05
|
5,56
|
|
0,40
|
0,73
|
0,07
|
3,03
|
|
0,50
|
0,66
|
0,09
|
2,06
|
|
0,60
|
0,60
|
0,11
|
1,61
|
|
0,70
|
0,53
|
0,13
|
1,37
|
|
0,80
|
0,47
|
0,16
|
1,19
|
|
0,90
|
0,40
|
0,18
|
1,13
|
|
1,00
|
0,33
|
0,21
|
1,07
|
|
1,10
|
0,27
|
0,24
|
1,04
|
|
1,20
|
0,20
|
0,27
|
1,02
|
|
1,30
|
0,13
|
0,31
|
1,01
|
|
1,40
|
0,07
|
0,37
|
1,00
|
|
1,50
|
0,01
|
0,46
|
1,00
|
Tableau 3-2 Variations des rapports de forme
e/D
et du rapport d'anisotropie aRT avec la
masse volumique
Figure 3.2 Evolutions du facteur aRT
avec la masse volumique
3.1.1 Comparaison au modèle de Gibson et al et
influence de l'élément de paroi fléchie
Afin d'élucider l'influence de la morphologie
cellulaire sur les rapports d'anisotropie
élastique du tissu ligneux, la modélisation de
Guitard et al (2002), retenue ici, est confrontée
à celle formulée par Gibson et al
(1988) (et reprise par Koponen et al en 1991), décrivant
le matériau bois comme une structure nid d'abeille
hexagonale non régulière. Cette confrontation est d'autant
plus aisée que les dispositions alignées et en quinconces
évoquées dans le modèle de Guitard et al
(2002) représentent deux cas « limites » de la
géométrie tissulaire décrite et admise par Gibson et
al (1988).
Ainsi, si la configuration des cellules en alignement (sens R)
envisagée ici est à rapprocher
(en terme de réponse mécanique) de la
configuration en carré, proposée par ces derniers auteurs,
la disposition en quinconce (sens T, Figure 1.8b du chapitre 1),
correspond à la structure nid d'abeille hexagonale (sens 2),
rappelée sur la Figure 1.8a du chapitre 1.
66
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Les particularités géométriques du
modèle (b), proposé par Guitard et al, (Figure 1.8b)
sont
les suivantes: la valeur du paramètre angulaire è
est prise nulle (è = 0), tandis que les valeurs numériques
assignées aux paramètres géométriques
(paramètres de forme) l et h, caractérisant
la cellule rectangulaire (b) sont DR /2 et h = DT.
La différence essentielle entre le modèle (a) et
le modèle (b), réside ainsi dans le choix de la longueur utile
des éléments de paroi sollicités en flexion. Selon
Gibson et al (1988), la longueur des éléments
fléchis, notée l, n'est pas liée à
l'épaisseur de la paroi. Dans le cas du modèle (b), la
longueur utile de l'élément fléchi, noté (DR
- 2eT), est, de façon évidente, fonction décroissante
de cette même épaisseur de paroi. En conséquence, pour un
diamètre
DR de cellule fixé, le modèle (b) sera plus
rigide que le modèle (a) au fur et à mesure que l'on
considère des parois plus épaisses, c'est à dire
des masses volumiques plus élevées. Ceci rejoint la remarque
faite au paragraphe précédent (paragraphe 3.1).
L'estimation du module d'Young du tissu ligneux, soumis à
une sollicitation dans la direction
2, proposée par Gibson et al (1988) est
donnée par la relation suivante (3.7):
E t 3 (h
+ sinè)
(3.7)
2
E 2paroi
=
l
l
cos3è
Cette relation appliquée à la configuration
géométrique (b), envisagée notamment par Guitard
et al (2002) et présentée sur la
Figure 1.8 b, en utilisant les notations propres à la cellule
rectangulaire devient (3.8):
3
(3.8)
ET = 128 DT
eR
ERp
DR DR
Cette dernière expression est à comparer
à la relation (3.9), résultant de l'inversion de la
relation (2.19) du chapitre 2, qui peut se mettre sous la forme
suivante:
(3.9)
E T
= E Tp eT 1
2
E E D 1
e D
2e
3
Rp Rp
R
1 +
E Tp T
R T
64
E Rp
D T e R
L'expression (3.9) diffère de (3.8) par
l'intermédiaire de deux termes. Le "1", premier terme à
l'intérieur du crochet au dénominateur,
représente la contribution des éléments de paroi
sollicités en traction compression à la rigidité du nid
d'abeille. Ce terme est négligé a priori par les auteurs du
modèle (a). Le second terme du crochet au dénominateur
est lié à la contribution des éléments de paroi
sollicités en flexion (Figure 2.3, chapitre 2).
Comme évoqué dans le début de ce paragraphe,
la différence entre les deux expressions porte
sur la correction en (2eT) de la longueur des
éléments fléchis (DR-2 eT). En négligeant chacun
de ces deux effets, c'est à dire en annulant chacun des
deux termes, (3.9) se réduit strictement
à (3.8).
67
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Pour apprécier l'incidence de la correction de
la longueur des éléments fléchis sur
l'anisotropie tissulaire L/T, il convient de comparer
numériquement les valeurs du coefficient aLT défini en (3.5)
à son équivalent aG (3.10) déduit de (3.8).
1 E Tp e
(D 2e
)3
e D e
(3.5)
a LT
= 1 + T
R T 1 2 R +
R R
64
E Rp D T
e R 3
D T D T eT
1 E
e D
3
e D e
(3.10)
= = Tp T R
1 2 R +
R R
a
G 64
E Rp
D T e R
D T D T
eT
Remarque : les expressions précédentes
(3.6) à (3.10), faisant intervenir le rapport
d'anisotropie transverse bipariétal
E Rp
, ont été laissées
en l'état pour « montrer »
E Tp
l'influence des propriétés mécaniques
de la double cloison sur les différents coefficients
d'anisotropie tissulaires. Comme précisé en début de ce
chapitre, les applications numériques sont néanmoins
menées, faute d'information sur le degré d'anisotropie transverse
de la paroi, sous l'hypothèse d'une isotropie transverse de la double
cloison.
Sous les conditions précisées, une application
numérique est présentée dans le Tableau 3.3.

Figure 3.3 Comparaison de l'évolution des
coefficients géométriques d'anisotropie
(aLT) du modèle de Guitard et al
et
du coefficient équivalent
(aG) du modèle proposé par Gibson
et al
|
ñ (g/cm3)
|
0,2
|
0,3
|
0,4
|
0,5
|
0,7
|
1
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
|
aLT
|
22,67
|
9,62
|
5,45
|
3,69
|
2,32
|
1,69
|
1,57
|
1,48
|
1,38
|
1,27
|
1,08
|
|
aG
|
25,67
|
10,78
|
5,71
|
3,42
|
1,51
|
0,56
|
0,41
|
0,30
|
0,22
|
0,15
|
0,08
|
Tableau 3-3 Evolution des valeurs numériques
des coefficients d'anisotropie (aLT) et (aG) avec
la masse volumique
68
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
La Figure 3.3 représente, en fonction de la masse
volumique ñ, les valeurs du coefficient
géométrique d'anisotropie aLT du modèle
(b) de Guitard et al et du coefficient équivalent aG
correspondant au modèle (a) de Gibson et al. On constate que
pour des masses volumiques faibles, inférieures à 0,5
g/cm3, les deux schématisations sont quasi
équivalentes et prévoient
des anisotropies L/T d'autant plus élevées que la
valeur de la masse volumique est faible.
Pour des structures de densité supérieure
à 0,5, le modèle de Guitard et al (2002) (sens T)
indique une anisotropie géométrique tissulaire L/T
supérieure à celle prévue par le modèle
proposé par Gibson et al (1988). Néanmoins, pour
de telles valeurs de densité, le niveau d'anisotropie
prévue par le modèle (b) à cellules rectangulaires est peu
supérieur à 3 et tout à fait insuffisant pour rendre
compte des rapports L/T observés expérimentalement.
3.1.2 Conclusion
L'ordre de grandeur du coefficient d'anisotropie L/T du bois,
observé expérimentalement et
voisin de 15 à 20, n'est expliqué que
partiellement par la géométrie de l'organisation cellulaire,
assimilée à une structure nid d'abeille. La porosité (et
son corollaire e/D) ne peut donc constituer qu'un facteur explicatif
partiel de l'anisotropie élastique du tissu ligneux. Pour des
masses volumiques comprises entre 0,4 et 0,8 g/cm3, il
apparaît que, selon les modèles, le coefficient
géométrique d'anisotropie L/T prend des valeurs comprises entre 6
et
1. Une part importante de l'anisotropie L/T observable
à l'échelle « mésoscopique » tissulaire est, en
conséquence, directement imputable à l'anisotropie
élastique microscopique L/T de la double paroi (donc de la
paroi) cellulaire, laquelle s'explique essentiellement par le
renforcement de la sous-couche S2 par les renforts
filamentaires que constituent les microfibrilles orientées de
cellulose. Compte tenu de la démarche d'analyse multi
échelle adoptée dans ce travail, il convient maintenant de
quantifier la proportion d'anisotropie tissulaire imputable à la
différenciation des cellules en cellules dites de bois initial
et bois final.
3.2 Hétérogénéité
tissulaire et anisotropie élastique du bois normal
Pour rendre compte de l'anisotropie élastique
macroscopique du cerne, les homogénéisations prédictives
évoquées au chapitre 1 et mises en oeuvre au chapitre 2 (Passage
3), assimilent le cerne d'accroissement à un ensemble composite de
couches (strates) élaborées à partir de tissus
ligneux (bois initial et final) supposés morphologiquement parfaitement
différenciés (en terme d'épaisseurs de paroi comme en
terme de diamètres cellulaires).
Pourtant, la bibliographie relative aux
différences morphologiques expérimentalement observables
entre des cellules de bois initial et de bois final, présente un
caractère fortement contradictoire. Une des raisons de cette
disparité tient en une variabilité inter spécifique
et intra spécifique de forme cellulaire fortement
dépendante des conditions de croissances
(Botosso, 1997) auquel s'ajoute l'effet « âge du cerne
». Il a ainsi été montré sur Picea abies
(Sarèn et al, 2001) que la morphologie
cellulaire varie selon la position de l'examen microphotographique par
rapport à la moelle ; de cellules quasi circulaires proches du
centre,
on arrive à des cellules approximativement
rectangulaires au fur et à mesure d'une progression
centrifuge radiale vers le cambium.
Par conséquent, seront évoquées par la
suite, des informations se référant à un cerne de bois
adulte d'essence résineuse, et ce, pour des conditions de croissance
fixées. Ces éléments, pour
la plupart bibliographiques, n'auront alors pour
objectif que d'expliciter les tendances générales
accompagnant, en terme de modifications morphologiques, la transition d'un bois
initial à un bois final dans un ensemble de cernes proches en
âge.
69
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Ces informations seront ensuite employées pour
étayer, via deux simulations analytiques intra
cerne, une discussion du rôle de la morphologie cellulaire
sur l'anisotropie élastique du cerne dépourvu de rayons
ligneux.
3.2.1 Différence de morphologique cellulaire entre
le bois initial et le bois final
3.2.1.1 Une distinction visuelle parfois délicate
Des tentatives de définitions des limites entre le bois
initial et final en termes géométriques ont été
réalisées mais souvent discutées. Parmi elles, le
critère de Mork (1928, cité dans Denne, 1988 et
illustré sur la Figure 3.4), liant épaisseurs de paroi (e) et
largeur des lumens
(LL), a été très souvent employé afin
de « formaliser » analytiquement une distinction entre bois initial
et final qui n'était jusqu'alors que visuelle (et donc entachée
d'une incertitude liée
à l'observation humaine). Néanmoins, une
récente synthèse (Denne, 1988) a montré la
nécessité de rediscuter certains
résultats admis par Mork (1928) et repris en l'état par de
très nombreux auteurs (représentativité des
dimensions de cellules relevées en regard des variations
inter cerne, interprétation des formules initialement
proposées).
Denne (1988) fait ainsi état de l'existence,
dans la littérature, de deux définitions
géométriques différentes des trachéides de bois
final (Figure 3.4, Formules 1 et 2).
Utilisant tour à tour les deux formulations du
critère avancé par Mork (1928), ce dernier auteur montre,
sur quelques Pins (Tableau 3.4), d'une part que la proportion calculée
de bois final dans un cerne diffère notablement selon l'expression
employée, et d'autre part, que les deux formules
précitées ne peuvent être appliquées à
toutes les espèces (Pinus contorta et Pinus strobus
présentent alors une texture nulle !).
Dans le cas ou les deux inéquations (Formules 1 et 2,
Tableau 3.4) conduisent à des résultats plausibles,
l'écart entre les deux prédictions est d'autant plus
sensible que les différences morphologiques relevées entre le
bois initial et final sont faibles (Tableau 3.4, Pinus pinaster, cas c).

Figure 3.4 : Les deux interprétations du
critère de définition du bois final proposé par Mork
(1928)
L : double épaisseur cellulaire,
LL : largeur de lumen, e : épaisseur de
paroi
Tiré et adapté de Denne
(1988)
70
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
|
Pinus
|
% de bois final calculé par application de
|
|
Formule 1
|
Formule 2
|
|
a) taeda
|
30
|
28
|
|
b) pinaster
|
27
|
13
|
|
c) contorta
|
29
|
0
|
|
d) strobus
|
0
|
0
|
Tableau 3-4 : Pourcentage de bois final calculé
à partir des deux interprétations du critère de Mork sur 4
essences
résineuses, tiré et adapté de Denne
(1988).
3.2.1.2 Tendances générales
D'après Ferrand (1982), dans le bois normal des
conifères, c'est l'épaisseur de paroi qui augmente le plus
fortement lors de la transition physiologique bois initial bois final
; le diamètre (essentiellement radial) des cellules varie
également, mais sans changer d'ordre de grandeur. Decoux et al
(non publié) relient, quant à eux, l'augmentation de
densité observée par micro densitométrie, essentiellement
à des augmentations d'épaisseurs pariétales.
Des études microphotographiques ont montré sur
quelques résineux, que les changements de dimensions cellulaires
(diamètres comme épaisseurs) sont plus prononcés
dans la direction radiale que dans la direction tangentielle du cerne (Picea
abies, Erickson et al, 1974, Latix laricina, Picea glauca, Picea
mariana, Marguerie et al, 2000, Picea abies, Douglas Fir, Pinus
sylvestris, Decoux et al, non publié).
Les recherches menées par Marion (2001), sur
Picea abies, établissent, par construction analytique de
cellules moyennes de bois initial et final (à partir
d'un ensemble de photographies de plan ligneux et analyse d'images), que le
diamètre tangentiel évolue peu lors
du passage d'un bois de printemps à un bois
d'été. Pour cet auteur, l'expansion cellulaire
(ovalisation) du bois normal se fait principalement dans la
direction radiale.
Admettant la conservation du diamètre tangentiel
à l'intérieur du cerne de croissance, et assimilant
à un carré la morphologie de la cellule de bois initial, Fengel
et al (1973), Boyd
(1974b), considèrent pour leur part, que
l'essentiel des modifications géométriques accompagnant la
transition morphologique bois initial bois final peut être
résumée à un doublement de l'épaisseur de la
paroi radiale.
Pour Bergander (2001), le passage bois initial bois final sur
Picea abies, s'accompagne d'une modification majeure et plus complexe de la
géométrie cellulaire ; d'un bois initial présentant des
cellules de forme hexagonale on arrive, dans le bois final, à
des cellules de forme rectangulaire. Les variations de l'épaisseur et
des diamètres ne sont pas explicitées dans ses travaux.
L'examen de ces tendances générales,
présentées dans la littérature, et leur comparaison aux
valeurs caractéristiques des cellules virtuelles dites de bois
initial et final, élaborées au chapitre 2, suggère
quelques commentaires.
Les paramètres géométriques des cellules
dites de bois initial et de bois final, (Tableau 2.4 du chapitre 2) obtenus via
la démarche d'optimisation précédemment explicitée
(construction du RSV), répondent assez bien aux propositions
bibliographiques avancées par l'ensemble des auteurs
précités.
71
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Le passage d'une cellule de bois initial à une cellule de
bois final est ainsi caractérisé par :
une relative constance du diamètre tangentiel cellulaire
(de DTi = 30 um à DTf = 35
um, valeurs optimisées),
une augmentation au moins double de l'épaisseur radiale
(eRi = 0.85 um, eTi = 1.06
um ; eRf = eTf =2.8 um),
une diminution importante (plus de 50%) du diamètre
radial (de DRi = 37.5 um à DRf
= 15 um).
S'il est ainsi possible, pour chacun des types de
cellules rencontrées dans le cerne de bois normal, de disposer
d'un jeu de paramètres géométriques (DR, DT, eR,
eT) spécifiques, la simulation analytique du passage d'une
catégorie de cellule (bois initial, bois final) à l'autre
est délicate. En effet, devant l'actuelle absence
d'étude faisant état des liens biologiques reliant les
variations d'un paramètre géométrique à celles
d'un autre, il apparaît délicat d'adopter un pas de
variation relative pour un paramètre géométrique,
dont seules sont connues les valeurs bornes.
Pour ces raisons, et avec objectif unique de rendre compte de
l'effet d'une ovalisation sur les caractéristiques élastiques
tissulaires, nous serons conduits à simuler le passage d'une cellule
de bois initial à une cellule de bois final par
un ensemble de modifications géométriques simples (deux types
de simulation).
La cellule de bois initial sera en premier lieu
assimilée à une cellule carrée, d'épaisseur
constante, ne subissant de modifications géométriques qu'en
terme de diamètre radial (conformément aux propositions de
Fengel et al, 1973 et de Boyd,
1974b, 1977).
Dans un second temps, la transition d'une cellule de bois
initial à celle d'un bois final sera simulée par des variations
simultanées simples de diamètre radial et d'épaisseurs.
3.2.2 Distinction densitométrique entre le bois
initial et le bois final
Les profils de densité intra cerne ne laissent
généralement pas apparaître de transition abrupte
lors du passage bois initial bois final (Holmberg
et al, 1999, Leban, 1999a, 1999b). La pertinence d'une
démarche de discrétisation du cerne (bois initial/bois
final) en terme de densité demande donc à être
évaluée en regard de quelques résultats
proposés dans la littérature.
Des modélisations prédictives des variations
intra cerne de la masse volumique du bois ont été
présentées pour différentes espèces de
gymnospermes (Leban, 1999a, 1999b). Si ces descriptions analytiques
sont belles et bien spécifiques à chaque genre de
résineux, elles présentent néanmoins l'avantage
d'être assez proches les unes des autres au niveau de leur
formulation.
Ces modèles segmentés, considèrent ainsi que
l'évolution de la densité dans le cerne, peut être traduite
par un raccordement de 3 fonctions affines « densité,
position dans le cerne »
(correspondant aux zones dites de bois initial, zone de
transition, bois final).
72
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Les meilleures estimations (corrélations statistiques) de
l'évolution de la densité intra cerne
sont obtenues (Leban 1999a, 1999b) en associant des
paramètres caractéristiques de chacune des zones
précédentes à l'âge et à la largeur de cerne,
comparativement à celles associant une variation de masse volumique
moyenne à la largeur des cernes et à leur âge. La
discrétisation
du cerne, en terme de densité (bois initial, final, zone
de transition) est donc envisageable.
Pour établir « numériquement » une
limite entre le bois initial et final, la méthode la plus
couramment utilisée, et employée dans la suite de
ce chapitre (utilisation de profils microdensitométriques),
consiste à définir la frontière entre les deux
types de bois, par la moitié de la différence entre le
maximum et le minimum de densité de chaque cerne, ce qui permet
alors, de s'affranchir des variations de densité inter cerne
(Mäkinen et al, 2002, Leban,
1999b).
En conclusion, s'il apparaît difficile d'établir un
critère géométrique reproductible permettant
de distinguer, pour toutes les essences résineuses, les
deux types de cellules dites initiales et finales, la discrétisation
possible du cerne d'accroissement en terme de densité ainsi que
l'examen microphotographique confirment l'existence d'une réelle
hétérogénéité tissulaire. Les paragraphes
précédents ayant montré l'importance de la
porosité et de la morphologie cellulaire respectivement sur les
rapports d'anisotropie élastique à l'échelle du
cerne et à l'échelle tissulaire, il apparaît
nécessaire d'évaluer l'influence, sur ces mêmes rapports,
de la présence des deux catégories de cellules (bois
initial et final) et de caractériser
« mécaniquement » la transition de l'une
à l'autre.
3.2.3 La texture, facteur d'anisotropie élastique dans
le plan transverse
Comme cela a été indiqué
précédemment (chapitre 1), le bois présente une
hétérogénéité
selon la direction radiale à l'intérieur d'un
même cerne de croissance ; ceci s'explique par le passage progressif d'un
tissu ligneux, de porosité élevée, adapté à
la conduction de la sève, vers un tissu plus dense à parois
cellulaires plus épaisses, mieux adapté à la
fonction mécanique de support.
Les modèles mécaniques tissulaires
présentés dans le deuxième chapitre (Passage
3) permettent de préciser les effets de l'ovalisation des
cellules et de la modification de l'épaisseur de paroi, sur
l'anisotropie élastique transverse. L'ovalisation des cellules est
schématisée sur la Figure 3.5a, par la diminution du
diamètre radial DR par rapport au diamètre tangentiel DT,
lorsque l'on progresse vers le bois final. Ceci correspond assez bien,
d'après la bibliographie présentée au paragraphe
précédent, à ce qui est observable, en
première approximation, sur la majorité des plans ligneux de
résineux (la Figure 3.5 b en est
un exemple sur Picea abies).
Pour apprécier l'influence de l'ovalisation cellulaire,
l'analyse est menée en premier lieu en se plaçant dans les
conditions particulières suivantes.
3.2.3.1 Ovalisation radiale
La cellule de départ est choisie carrée et
représentative (via la masse volumique fixée à
0,35g/cm3 d'un tissu de bois initial. Le passage du
bois initial au bois final, est alors, à cette étape de la
discussion, simulé par une unique variation continue du
diamètre radial. Cette transition aboutit donc à une
morphologie cellulaire rectangulaire dont les caractéristiques sont
précisées par la relation 3.11
73
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(3.11) ETp= ERp , eT =
eR= e
DT = D DR= ë D avec ë = 1
Les paramètres géométriques épaisseur
de paroi et diamètre tangentiel sont fixés, d'une part, avec le
soucis d'être réalistes en regard de la bibliographie (Tableaux
2.3 et 2.6 du chapitre 2)
et d'autre part de manière à obtenir une
masse volumique cohérente en regard de divers profils
microdensitométriques.


R
T
Figure 3.5 (a) Ovalisation selon la direction
radiale, (b) coupe transversale de P. abies colorée à
la
safranine et au bleu alcyan, Ruelle (2003),
montrant un quasi alignement des parois radiales
(grossissement x 500, barre d'échelle 25
um)
Sous ces restrictions, les relations (2.15 du
chapitre 2), (3.1) et (3.2) deviennent respectivement (3.12), (3.13)
et (3.14):
e 1
e
(3.12) = m (1-Po) = 2 m D + 1 - 2 D
E 2e
1 E E
(3.13)
L =
1
+ Lp
= a LR Lp
ER
ëD ë ETp
ERp
E 1
e ëD
3
e E E
(3.14)
L
= 1 +
2
1 2
+ ë
Lp
Lp
a LT
E T
64 D e
D E Tp
E Tp
Le rapport d'anisotropie transverse tissulaire
(mésoscopique) s'écrit enfin (3.15)
E 1
e ëD
3 E
(3.15)
R
= 1 +
2 Rp
E T
64 D e
E Tp
=
74
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Les trois coefficients aLR, aLT
et aRT ainsi définis, caractérisent
l'influence de l'ovalisation
des cellules sur l'anisotropie élastique du tissu
ligneux.
Les Figures 3.6 et 3.7 illustrent les modifications des
coefficients géométriques d'anisotropie associées à
une diminution du diamètre radial DR par rapport au diamètre
tangentiel DT. Les applications numériques sont conduites à
partir d'un facteur de forme e/D= 0,06, qui correspond pour des cellules
carrées à une masse volumique de 0,35 g/cm3 (bois
initial).
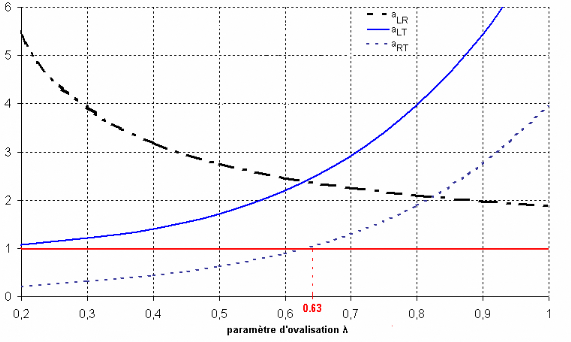
Figure 3.6 : Variations des coefficients d'anisotropie
tissulaires en fonction du paramètre d'ovalisation ë

Figure 3.7 : Evolution du paramètre d'ovalisation
ë en fonction de la densité
Dans ces conditions, on constate que, pour des valeurs
de DR décroissantes, la masse volumique augmente, d'où une
diminution de la porosité et d'autre part, que les facteurs aLT et aLR
évoluent en sens opposés. Ceci se traduit (Figure 3.6)
par un coefficient géométrique
75
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
d'anisotropie dans le plan transverse aRT qui
devient inférieur à 1, pour ë = 0,63, c'est à
dire
une masse volumique de 0,43 g/cm3 (Figure
3.7), avec pour conséquence directe une inversion de l'anisotropie
dans le plan transverse.
Sous l'effet de ce seul paramètre
géométrique ë (on rappelle ici l'absence des rayons ligneux,
éléments essentiels de renfort radial), le module
d'élasticité tangentiel ET d'un tissu, assimilable par
la forme de ses cellules à un tissu de bois final,
deviendrait supérieur au module ER, contrairement à des
propositions bibliographiques statistiques (modèles
prévisionnels l'anisotropie élastique, Guitard, 1987).
En outre, des rapports d'anisotropie élastique L/T
(facteur aLT) de l'ordre de 20 ne peuvent être obtenus par seul effet
de l'ovalisation résultant d'une transition d'une cellule de
bois initial vers une cellule de bois final.
3.2.3.2 Etablissement d'un lien entre variations
d'épaisseurs pariétales et diamètre radial
Associant microphotographies et études
microdensitométriques sur Picea abies, Holmberg et
al (1999), suggèrent une croissance lente
de la densité dans le bois initial liée à une
augmentation modérée de l'épaisseur, à
diamètre radial constant. Pour ces derniers auteurs, dans la zone de
transition, l'épaisseur pariétale augmente rapidement (avec pour
conséquence directe une croissance rapide de la densité), tandis
que le diamètre radial décroît. Dans le bois final, si la
densité croit lentement, le diamètre radial demeure constant
alors que l'épaisseur de paroi augmente.
Pour compléter l'étude précédente, en
tenant compte des liens probables (non explicités dans
la littérature) entre les variations
d'épaisseurs pariétale et celles du diamètre radial,
une simulation analytique des modifications des rapports d'anisotropie
tissulaire est réalisée à partir de profils
microdensitométriques sur du bois adulte de Picea abies fournis
par P. Rozenberg (INRA Orléans, Unité d'Amélioration,
Génétique et Physiologie Forestière).
Le choix de l'accroissement annuel utilisé (zone B) s'est
fait :
d'une part avec la volonté de ne pas avoir un profil de
densité trop irrégulier (reprise
de croissance, zone A sur la Figure 3.8)
afin de disposer de la plus large gamme de
relevés densitométrique (la zone B est
préférée à la zone C).
76
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
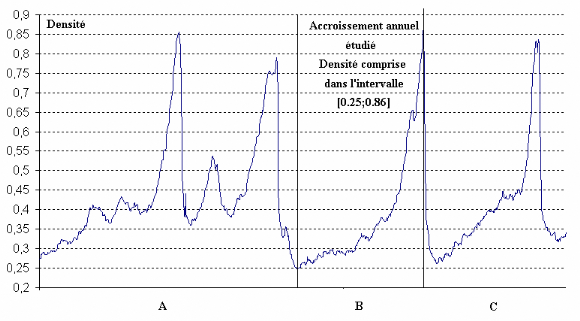
Figure 3.8 Exemple de profil microdensitométrique
d'étude sur P.abies (données numériques fournies
par
Rozenberg). Densité mesurée par absorption
d'un rayonnement X
3.2.3.2.1 Lien entre l'épaisseur et le diamètre
radial via la masse volumique
La morphologie de la cellule initiale est choisie comme
carrée. Une fois cette conformation adoptée, les
paramètres géométriques cellulaires, épaisseur
pariétale (e) et diamètre tangentiel
(D), sont fixés sous les trois contraintes suivantes
(Figure 3.8).
La masse volumique initiale , liée au facteur
de forme cellulaire e0/D (3.12) est choisie via un ensemble de profils
microdensitométriques pour être représentative du bois
initial (méthode de la moyenne décrite par Leban, 1999b). La
valeur retenue est
0.25 g/ cm3.
L'épaisseur pariétale initiale (eT = eR
= e0) doit répondre à des propositions bibliographiques
déjà présentées (valeur comprise au centre
d'un intervalle apte à rendre compte d'une variabilité intra
arbre, Guitard et al, 2002).
Le diamètre cellulaire tangentiel D est
calculé, puis sa valeur déduite est re- confrontée
à des références bibliographiques (Boyd, 1974).
Les caractéristiques de chaque type de cellule sont donc
:
Pour la cellule dite de bois initial :
épaisseurs radiale et tangentielle non distinctes et fixées
à
e0 =1 um, diamètre tangentiel fixé à D =23
um, facteur de forme e0/D =0.04, diamètre radial
DR = D.
Pour la cellule dite de bois final :
épaisseurs radiale et tangentielle variables e, diamètre
tangentiel fixe D, diamètre radial DR variable.
77
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.9 : Modifications de la géométrie
tissulaire envisagées lors de la transition d'une cellule de bois
initial à une cellule de bois final
Dans cette simulation, le diamètre radial DR est
soumis à une décroissance linéaire : les bornes (DR
min =15 um et DR max = 23 um) de l'intervalle de variations sont conformes aux
valeurs rencontrées dans la littérature (dont quelques exemples
ont été donnés dans le Tableau
2.3 du chapitre 2), le pas de variations est
déterminé en fonction des bornes précédemment
définies et du nombre de relevés
microdensitométriques disponibles (245 valeurs relevées tous
les 24um). La valeur du pas de variations de DR est donc directement obtenue en
divisant
l'écart entre les extrema (valeurs bornes) par
le nombre de relevés microdensitométriques. Une telle
procédure permet d'éviter une transition abrupte d'un bois
initial à un bois final conformément à des
constatations anatomiques (passage progressif du bois initial au bois final sur
ce résineux, Venet et al, 1986).
Moyennant les hypothèses précédentes, la
relation (2.13) du chapitre 2 devient (3.16) :
ñ e
e 2e 2
(3.16)
= +
2ñ m
D R
D D.D R
Posant
ñ
A = , cette dernière expression
devient :
2ñ m
2
2
A.D R .D = e.D + e.D R 2e
En posant de plus B tel que : A.D = B, l'unique
solution (biologiquement acceptable) de
l'équation du second degré (3.16) est alors
exprimée selon (3.17) :
(3.17)
e1 =
(D + D R ) +
(D + D R )
4
8.B.D R
Le Tableau 3.5 résume ainsi pour quelques valeurs
remarquables de densité relevées
expérimentalement (microdensitométrie), les
diamètres radial DR et épaisseurs de paroi (e1) calculés,
ainsi que les différents coefficients d'anisotropie
géométriques aLR, aLT et aRT précédemment
définis (relations 3.4, 3.4 et 3.6).
La Figure 3.9 représente, de manière
plus exhaustive et ce pour chaque relevé
microdensitométrique, les variations des valeurs attribuées aux
paramètres diamètre radial et épaisseur de paroi en
fonction de la densité relevée.
78
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Tableau 3-5 : Simulation intra cerne de
l'évolution du diamètre radial et de l'épaisseur en
fonction de la densité sur l'Epicéa ; conséquences sur les
rapports d'anisotropie tissulaire
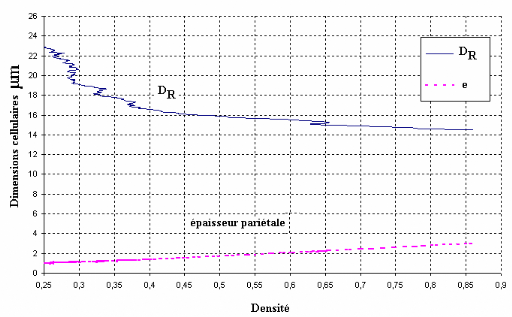
Figure 3.10 Variations simultanées des
paramètres diamètre radial et épaisseur de paroi dans le
cadre d'une simulation basée sur un relevé
microdensitométrique réalisé sur du bois adulte d'
Epicéa (Picea abies)
Une première remarque est que le rapport d'anisotropie
élastique L/T traduit par la valeur du coefficient aLT n'est toujours
pas de l'ordre de la valeur suggérée (L/T = 20) par
Guitard
(1987). L'allure générale des
évolutions (Tableau 3.5) des coefficients d'anisotropie
géométriques aLR, aLT et aRT avec la densité est
semblable à celle établie en ne faisant pas
varier l'épaisseur de paroi (paragraphe
précèdent). A une augmentation de la densité sont
simultanément associées une augmentation de
l'anisotropie L/R (facteur aLR) et une diminution de l'anisotropie
L/T (aLT).
79
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Une différence notable par rapport à la
précédente simulation (Figure 3.7) réside en
l'impossibilité d'une inversion de l'anisotropie
transverse (facteur aRT du Tableau 3.5) pour
la gamme de densité explorée (de 0,25 à
0,86). Cette dernière remarque montre le réalisme du
modèle ici décrit et alimenté par un jeu, en partie
expérimental, de données structurelles.
En second lieu, et ce conformément à des
propositions bibliographiques tirées d'examens microphotographiques
(Panshin et al, 1980), la Figure 3.9, comme le Tableau 3.5
font apparaître des variations relatives intra cerne d'épaisseurs
pariétales (e) plus importantes que celles du diamètre radial DR.
Dans la simulation analytique, si DR décroît de 23 um à 14
um, l'épaisseur pariétale varie du simple au triple (de 1
à 3 um). Les sens de variations avec la densité intra cerne
des paramètres géométriques cellulaires
diamètres et épaisseurs, observables sur la Figure (3.9),
sont comparables aux résultats obtenus à partir des
données numériques fournis par J.M. Leban (INRA, Nancy, LERFORB,
ERQB) sur du bois adulte de
5 essences résineuses (Figures 3.11 3.12, 3.13,
mesures des paramètres DR, DT, par planimétrie et
relevés microdensitométriques par absorption des rayons X). Si,
conformément
à la littérature évoquée
précédemment, la diminution du diamètre radial DR
accompagnant la
transition d'une cellule de bois initial à une cellule de
bois final est relativement bien admise, l'épaisseur de paroi ne peut
être considérée comme un paramètre constant.
Ces deux variations simultanées de
diamètre radial et d'épaisseur doivent donc
être hiérarchisées afin d'évaluer les
modifications des coefficients d'anisotropie géométriques
(rapportées dans le Tableau 3.5) accompagnant le
passage d'un bois initial à un bois final. Une simulation est
tentée (Tableau 3.6) avec, dans le cas 1, pour une cellule de bois
initial, une variation du diamètre DR à épaisseur
de paroi e fixée, tandis que dans le cas 2, seule
l'épaisseur e varie de 1 um à 3 um. Dans les deux cas les valeurs
bornes de chaque paramètre sont issues du Tableau 3.5.
La première partie du Tableau 3.6 (cas 1) montre les
évolutions des différents rapports avec une diminution de DR
(valeurs bornes tirées de la simulation) à épaisseur de
paroi constante. Ces résultats sont conformes aux évolutions des
différents facteurs d'anisotropie aLR, aLT et aRT, rapportées
sur la Figure 3.7.
La seconde partie (cas 2, Tableau 3.6) montre les variations des
mêmes rapports d'anisotropie aLR, aLT et aRT avec une augmentation de
l'épaisseur à diamètre radial DR constant.
On remarque que les rapports d'anisotropies aLT et aRT
évoluent dans le même sens pour les deux modifications
géométriques cellulaires envisagées, ceci
conformément aux résultats plus généraux de la
simulation intra cerne (diminution des rapports aLT et
aRT).
Pour le rapport aLR, les évolutions
sont différentes suivant la modification géométrique
envisagée (à épaisseur constante, une diminution
du paramètre DR conduit à une augmentation de
aLR tandis qu'une augmentation d'épaisseur de paroi,
à diamètre constant, entraîne une diminution de ce
même facteur). Une comparaison avec l'évolution intra cerne
du rapport d'anisotropie aLR (augmentation lors du
passage d'un bois initial à un bois final) rapporté dans le
Tableau 3.5 confirme que la diminution de diamètre radial constitue,
dans notre modélisation, la première modification
géométrique explicative de l'augmentation de
l'anisotropie L/R.
80
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
|
Densité
|
D (um)
|
DR
(um)
|
e (um)
|
aLR
|
aLT
|
aRT
|
|
Cas 1
|
|
|
|
|
|
|
|
|
0,25
|
22,92
|
22,92
|
1
|
1,91
|
13,85
|
7,24
|
|
0,28
|
22,92
|
18
|
1
|
2,16
|
6,44
|
3,79
|
|
0,35
|
22,92
|
15
|
1
|
2,39
|
3,92
|
2,5
|
|
|
|
|
|
|
|
|
|
Cas 2
|
0,25
|
22,92
|
22,92
|
1
|
1.91
|
13.85
|
7.24
|
|
0,48
|
22,92
|
22,92
|
2
|
1.83
|
3.93
|
2.15
|
|
0,69
|
22,92
|
22,92
|
3
|
1.74
|
2.38
|
1.37
|
Tableau 3-6 : Simulation de l'impact des modifications
univoques de l'épaisseur pariétale et du
diamètre
radial sur l'anisotropie élastique
tissulaire
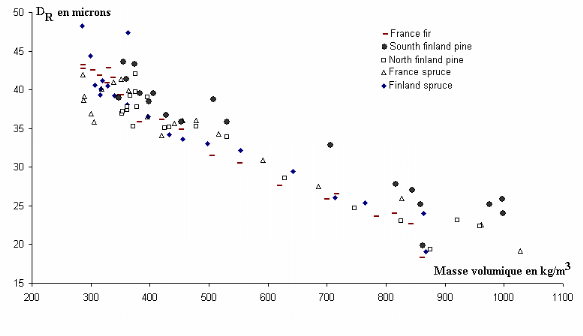
Figure 3.11 Evolutions intra cerne du diamètre
radial pour différentes essences résineuses

Figure 3.12 Evolutions intra cerne du diamètre
tangentiel pour différentes essences résineuses
81
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.13 Evolutions intra cerne de l'épaisseur
pariétale pour différentes essences résineuses
3.3 Rôle des rayons ligneux dans l'anisotropie
élastique du cerne
L'association bois « infi » et rayons ligneux
du chapitre 2 a notamment été établie en se basant
sur l'hypothèse selon laquelle une fraction volumique en rayons ligneux
(n) importante induit un renfort radial au détriment de la
rigidité longitudinale (Barkas, 1941).
On notera que la qualité des régressions
linéaires entre les modules d'Young macroscopiques
EL et ER de plusieurs essences et leurs masses volumiques
(ñ) a été améliorée (Guitard et
al,
1987) par la prise en compte du paramètre (n).
Comme le montrent la Figure 3.14 et le Tableau 3.7, le
paramètre (n) est donc un facteur qui intervient essentiellement sur
l'anisotropie L/R (facteur aLR) et L/T (aLT). Une valeur
élevée
de (n) conduit à une réduction de
l'anisotropie L/R (par une augmentation de ER et une diminution de
EL) et à une augmentation de l'anisotropie L/T (diminution de
ET plus
« rapide » que celle de EL).
|
n (%)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EL
(GPa)
|
13,30
|
13,18
|
13,10
|
12,92
|
12,80
|
12,67
|
12,55
|
12,42
|
12,30
|
12,17
|
12,04
|
|
ER
(GPa)
|
0,88
|
0,95
|
1,00
|
1,08
|
1,15
|
1,22
|
1,29
|
1,35
|
1,42
|
1,49
|
1,56
|
|
ET(GPa)
|
0,73
|
0,68
|
0,64
|
0,60
|
0,56
|
0,53
|
0,51
|
0,48
|
0,46
|
0,44
|
0,42
|
|
aLR
|
15,12
|
13,91
|
13,10
|
11,94
|
11,13
|
10,41
|
9,76
|
9,18
|
8,66
|
8,18
|
7,74
|
|
aLT
|
18,34
|
19,46
|
20,60
|
21,63
|
22,67
|
23,70
|
24,70
|
25,67
|
26,62
|
27,54
|
28,44
|
|
aRT
|
1,21
|
1,40
|
1,57
|
1,81
|
2,04
|
2,28
|
2,53
|
2,80
|
3,07
|
3,37
|
3,67
|
Tableau 3-7 Variations des coefficients d'anisotropie
avec le paramètre (n). Le bois étudié est le
RSV.
82
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.14 : Evolutions avec la fraction volumique en
rayons ligneux des différents facteurs d'anisotropie
3.4 Influence des paramètres ultrastructuraux
sur l'anisotropie élastique tissulaire
Les paragraphes précédents ont montré
que des coefficients d'anisotropie tissulaire L/T classiquement
rencontrés dans le bois normal, ne peuvent être expliqués
que partiellement par l'influence de la géométrie cellulaire et
de ses modifications (évolutions du rapport e/D via des variations de
porosité ou par une ovalisation radiale).
La masse volumique contribue à une rigidification
du matériau par effet « quantité de matière
». L'hétérogénéité tissulaire
densitométrique du cerne est un paramètre de second ordre
qui joue un rôle contradictoire à l'anisotropie élastique
R/T observée sur les résineux.
La fraction volumique en rayons ligneux est un paramètre
sensible tel qu'à une valeur élevée
de ce paramètre correspond une réduction du rapport
d'anisotropie L/R
L'objet de ce paragraphe est donc d'une part, de
préciser, numériquement, l'influence de quelques
caractéristiques ultrastructurales de la matière ligneuse
(module d'élasticité de la matrice, des fibres, inclinaison
(ö) des microfibrilles dans la sous couche S2) sur
l'anisotropie
élastique bipariétale (modélisation
de type Squelette) et d'autre part, de déterminer leur
influence directe sur les caractéristiques
élastiques tissulaires mésoscopiques.
3.4.1 Sensibilité de l'anisotropie tissulaire L/T
à l'angle des microfibrilles
Afin d'évaluer le rôle de l'inclinaison
des microfibrille (ö) sur l'anisotropie des
caractéristiques élastiques tissulaires, une
estimation de l'influence d'un accroissement autour
de valeurs particulières d'AMF (ö0) sur les
modules élastiques mésoscopiques de tissus est menée.
L'influence de l'ovalisation ayant déjà été
montrée (par l'intermédiaire du facteur aLT
lui-même dépendant du paramètre
d'ovalisation ë), il convient de rechercher les facteurs
complémentaires de variabilité de l'anisotropie élastique
du tissu à une échelle d'observation inférieure.
Posant c = cos (ö), s = sin (ö) et E
= VEf, le rapport d'anisotropie bipariétale L/T,
défini à partir des relations (2.27) et (2.28)
présentées au chapitre 2, s'écrit (3.17)
83
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(3.17)
E Lp
=
E Tp
D Es 4
= F (ö)
D Ec 4
En ayant posé, pour alléger l'écriture ;
D = (1 V) (1 ) E m
(1 + )(1 2 )
+ VE f
|
Variation relative de l'anisotropie tissulaire L/T, pour des
variations d'angle (ö) exprimées en °
|
|
(ö0)
exprimé en°
|
Coefficient
S (ö0)
|
Valeurs de
F (ö0)
|
[+1]LT
|
[+2 ]LT
|
[1]LT
|
[2 ]
LT
|
|
5
|
-104,912
|
17,817
|
-0,115
|
-0,259
|
0,093
|
0,170
|
|
10
|
-65,618
|
10,139
|
-0,127
|
-0,292
|
0,101
|
0,184
|
|
15
|
-32,809
|
6,008
|
-0,105
|
-0,235
|
0,087
|
0,160
|
|
20
|
-17,381
|
3,905
|
-0,084
|
-0,184
|
0,072
|
0,134
|
|
25
|
-10,104
|
2,743
|
-0,069
|
-0,148
|
0,060
|
0,114
|
|
30
|
-6,410
|
2,040
|
-0,058
|
-0,123
|
0,052
|
0,099
|
|
35
|
-4,394
|
1,577
|
-0,051
|
-0,108
|
0,046
|
0,089
|
|
40
|
-3,228
|
1,248
|
-0,047
|
-0,099
|
0,043
|
0,083
|
|
45
|
-2,521
|
1,000
|
-0,046
|
-0,096
|
0,042
|
0,081
|
Tableau 3-8 : Variations relatives de l'anisotropie
tissulaire L/T autour de quelques valeurs d'AMF
ö0
choisies

Figure 3.15 Incidence sur l'anisotropie tissulaire L/T
d'un ajout de 1° et 2° autour de quelques valeurs d'AMF
ö0 choisies
84
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
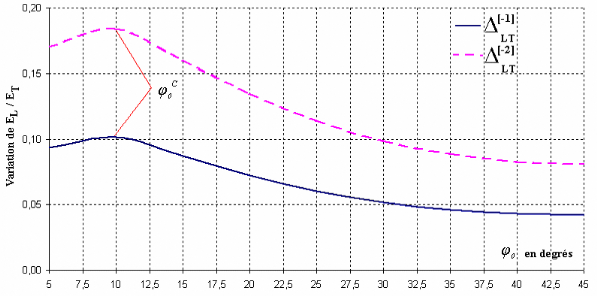
Figure 3.16 Incidence sur l'anisotropie tissulaire L/T
d'une soustraction de 1° et 2° autour de quelques
valeurs d'AMF ö0
Au voisinage d'un angle (ö0), le rapport
d'anisotropie L/T de la double paroi s'écrit
(développement limité de Taylor au premier ordre)
:
(3.18)
E Lp
D E s 4 ( )
4 E c (
) s (
) [(Ec 4 (
)s 2 (
) + Ec 2 (
)s 4 (
) - D)]
= 0
+ (
0 ) 0 0 0 0 0 0
E Tp
+ è ( 2 )
D E c 4 ( 0 )
(D Ec 4 ( 0
)) 2
La sensibilité de ce rapport à l'angle des
microfibrilles (ö) dans S2, autour d'un angle
(ö0) est
donc exprimée (3.19) par le second terme du
deuxième membre de l'équation (3.18), noté
S(ö0)
4Ec (
)s (
) [(Ec 4 (
)s 2 (
) + Ec 2 (
)s 4 (
) - D) ]
(3.19)
S(
) = 0 0 0 0 0 0
0 (D Ec 4 (
0
)) 2
Le rapport d'anisotropie tissulaire mésoscopique L/T peut
donc s'écrire sous la forme (3.20)
0
E L
D E s 4 ( )
(3.20)
= a LT
E T D E c 4
( 0 )
+ (
0 ) S( 0 )
Il est alors possible de définir la variation relative,
LT
[ ]
0
du même rapport d'anisotropie
0
tissulaire L/T pour des variations positives ou
négatives [ ]
autour de chaque valeur
d'angle (ö0) (Tableau 3. 7, ou les divers angles
sont exprimées en degrés)
85
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
(
).S( )
(3.21)
? LT[ 0 ] = 0 0
( 0 ).S( 0 ) + F(
0 )
Les valeurs numériques attribuées aux
« coefficients de sensibilité »
S(ö0) permettent de
montrer (Tableau 3.8) l'existence d'une zone de
sensibilité maximale de l'anisotropie L/T du
tissu, située aux alentours de 10 degrés (angle
correspondant à un bois final).
0
L'examen du Tableau 3.8 et des Figures 3.15 et 3.16,
définit comme valeur critique ( ö c
)du
paramètre (ö), la valeur de 10
degrés, autour de laquelle les variations de l'anisotropie L/T sont les
plus importantes. Ainsi une augmentation de 1 degré autour de 10
degrés conduit à une diminution de plus de 12% de l'anisotropie
L/T, une augmentation de 2 degrés conduit à une chute de plus de
29% du rapport L/T.
On remarque également (Figures 3.15 et 3.16) que plus
l'angle des microfibrilles dans S2 (ö)
est élevé, moins l'anisotropie tissulaire
mésoscopique L/T en est dépendante. Dans notre
modélisation, un bois caractérisé par une
valeur élevée d'angle des microfibrilles (ö) dans
S2
(bois initial, bois juvénile, éventuellement
bois de compression) verra donc son rapport
d'anisotropie tissulaire L/T moins sensible à ce
même paramètre qu'un bois possédant une plus faible
inclinaison microfibrillaire (bois final) dans la même sous couche.
L'angle (ö) des microfibrilles dans la sous couche S2
constitue cependant une composante essentielle de
l'anisotropie élastique tissulaire.
3.4.2 Incidence du module d'élasticité des
microfibrilles
A l'échelle de la sous couche
élémentaire, les différentes modélisations du
comportement
élastique bipariétal (Multicouches ou
Squelette) considèrent, une association en série
« matrice - fibres » dans la direction
longitudinale de la cellule et une association parallèle dans
les directions transverses. Compte tenu de la relation d'ordre entre
les modules longitudinaux de microfibrille employés (supérieurs
à la centaine de GPa) et les modules de matrice
généralement admis (de l'ordre de 2 GPa), le module
d'élasticité longitudinal des microfibrilles constitue, quelque
soit la modélisation, un paramètre déterminant de
l'élasticité
(longitudinale ou transverse) de la double paroi.
Une étude de l'influence du module
d'élasticité des microfibrilles sur les
caractéristiques élastiques de la double paroi sera menée
plus loin.
3.4.3 Influence du module élastique de la
matrice
Divers auteurs (Salmèn et al, 1985,
Bergander, 2001), ont montré que les propriétés
mécaniques des hémicelluloses et lignines,
influencent, de manière significative, les modules transverses de
double paroi fournis par des modélisations multicouches à
fibres parallèles anisotropes et très peu le module
bipariétal longitudinal.
Pour hiérarchiser les paramètres
ultrastructuraux responsables à priori de l'anisotropie des deux
doubles cloisons envisagées (M2 et M3), une comparaison de
l'influence du module d'élasticité de la matrice sur
les modules de double cloison est menée. Ces deux
modélisations font toutes les deux appel à la valeur
optimisée du module de microfibrille (62
GPa, présentée au chapitre 2) et attribuent un
comportement isotrope aux fibres.
L'étude est menée à partir d'un
composite stratifié à 9 couches dont les
caractéristiques micromécaniques ultrastructurales sont
rappelées au Tableau 3.9.
86
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Pour chaque modèle (M2 et M3), et pour
différents modules de matrice, les variations des
modules élastiques homogénéisés ELp
et ETp avec l'AMF (ö) sont traduites dans le Tableau
3.10 et sur les Figures 3.17 et 3.18.
|
Sous couche
|
S1
|
S2
|
S3
|
LM
|
|
Em (GPa)
|
variable
|
variable
|
variable
|
variable
|
|
Ef
|
62
|
62
|
62
|
62
|
|
V
|
0,3
|
0,5
|
0,5
|
0,1
|
|
ím
|
0,3
|
0,3
|
0,3
|
0,3
|
|
íf
|
0,1
|
0,1
|
0,1
|
0,1
|
|
AMF ö (en °)
|
+/- 60°
|
variable
|
60
|
90
|
Tableau 3-9 Paramètres ultrastructuraux du
modèle multicouche M2
|
Em = 1GPa
|
Em = 2GPa
|
Em = 3GPa
|
|
AMF (ö) dans
S2 (en °)
|
Multicouche
M2
|
Squelette
M3
|
Multicouche
M2
|
Squelette
M3
|
Multicouche
M2
|
Squelette
M3
|
|
ELp
|
ETp
|
ELp
|
ETp
|
ELp
|
ETp
|
ELp
|
ETp
|
ELp
|
ETp
|
ELp
|
ETp
|
|
5
|
22,56
|
5,11
|
31,67
|
1,14
|
24,32
|
8,39
|
32,34
|
1,82
|
24,32
|
8,39
|
33,02
|
2,49
|
|
10
|
21,65
|
5,12
|
31,64
|
2,51
|
23,49
|
8,41
|
32,32
|
3,19
|
23,49
|
8,41
|
32,99
|
3,86
|
|
15
|
20,19
|
5,20
|
31,53
|
4,69
|
22,17
|
8,49
|
32,21
|
5,36
|
22,17
|
8,49
|
32,88
|
6,03
|
|
20
|
18,31
|
5,39
|
31,25
|
7,50
|
20,45
|
8,67
|
31,92
|
8,17
|
20,45
|
8,67
|
32,60
|
8,85
|
|
25
|
16,13
|
5,77
|
30,68
|
10,76
|
18,47
|
9,02
|
31,36
|
11,43
|
18,47
|
9,02
|
32,03
|
12,10
|
|
30
|
13,81
|
6,41
|
29,74
|
14,24
|
16,35
|
9,61
|
30,41
|
14,91
|
16,35
|
9,61
|
31,08
|
15,58
|
|
35
|
11,48
|
7,36
|
28,32
|
17,72
|
14,22
|
10,48
|
28,99
|
18,39
|
14,22
|
10,48
|
29,66
|
19,06
|
|
40
|
9,28
|
8,66
|
26,38
|
21,00
|
12,22
|
11,67
|
27,05
|
21,67
|
12,22
|
11,67
|
27,73
|
22,34
|
|
45
|
7,33
|
10,31
|
23,92
|
23,92
|
10,43
|
13,17
|
24,60
|
24,60
|
10,43
|
13,17
|
25,27
|
25,27
|
|
50
|
5,68
|
12,26
|
21,00
|
26,38
|
8,93
|
14,96
|
21,67
|
27,05
|
8,93
|
14,96
|
22,34
|
27,73
|
Tableau 3-10 : Comparaisons des variations des modules
élastiques du multicouche M2 avec l'AMF(ö)
87
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.17 Evolutions des modules élastiques de
double paroi prévus par le modèle M2 avec l'angle des
microfibrilles (ö) et influence du module
de la matrice ligno cellulosique
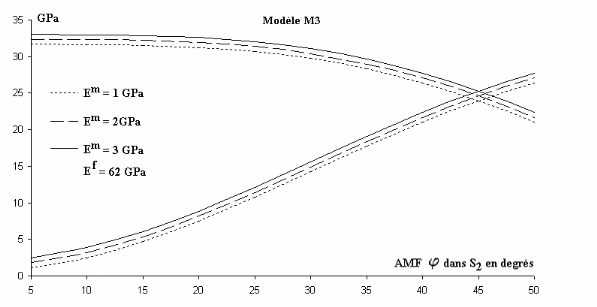
Figure 3.18 Evolutions des modules élastiques
prédits par le modèle M3 avec l'angle des microfibrilles
(ö).
Influence du module élastique de la matrice ligno
cellulosique.
L'examen du Tableau 3.10 et de la Figure 3.17 permet de noter
l'importante sensibilité des
ELp et ETp du modèle M2
au module élastique Em de la matrice. Cette tendance
est
particulièrement marquée sur le module
transverse ETp. Elle s'explique essentiellement par l'association en
série de la matrice et des microfibrilles dans les directions
transverses des différentes plaques composites (relation 2.3 du
chapitre 2). L'association en parallèle des mêmes
éléments conduit à une moindre sensibilité du
module longitudinal ELp du modèle M2.
Le paramètre Em est donc un
paramètre sensible pour une modélisation multicouche de la
double paroi.
Les modules homogénéisés ELp et ETp du
Squelette M3 sont quant à eux, bien moins dépendants des
valeurs de Em employées (Tableau 3.9 et Figure 3.18).
L'expression des ELp
et ETp (fonction affine de Em, à
(ö) fixé, relations 2.27 et 2.28 du chapitre 2)
constitue
88
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
l'explication de cette quasi insensibilité. Le
modèle M3 accorde en effet un rôle majeur au
renfort filamentaire et donc à un de ses
paramètres descriptifs essentiel l'angle des microfibrilles
dans S2 (ö). Puisque les transferts d'efforts ne sont pris en
charge, dans M3, que par le squelette de fibres cellulosique, il
n'apparaît pas nécessaire de faire appel à un
paramètre descriptif de l'état mécanique de la matrice.
3.4.4 Anisotropie tissulaire L/T d'un bois normal imputable
à l'AMF dans S2
La Figure 3.19 résume, pour 8 inclinaisons
microfibrillaires (ö) et pour différentes
densités,
les valeurs du rapports de l'anisotropie L/T de la double
paroi (ELp / ETp noté ici aLTp pour alléger
l'écriture) sur l'anisotropie élastique tissulaire L/T
(facteur aLT). A l'échelle de la double paroi le modèle
considéré est M3 (Squelette).
Le produit de aLTp par aLT conduit à l'expression de
l'anisotropie élastique tissulaire définie par la relation (3.2).
La cellule initiale est supposée au départ carrée (son
diamètre cellulaire initial est fixé à 30um, son
épaisseur de paroi est 2 um, soit e/D = 0,06) puis elle subit une
ovalisation radiale durant laquelle seul le diamètre DR varie.
L'ovalisation radiale entraîne donc une modification de la
densité du tissu. La Figure 3.20 rappelle l'évolution du facteur
de flexion des parois avec la densité.
Pour des valeurs de (ö) usuelles, situés
entre 5 et 10 degrés, et quelque soit la densité de la structure
nid d'abeille, la part d'anisotropie L/T imputable au paramètre
(ö) prédomine sur l'anisotropie tissulaire attribuable
à la « géométrie du réseau» au sens large
(aLT).
L'anisotropie tissulaire L/T d'un bois que nous avons
défini comme final sera donc due uniquement au paramètre
(ö). Pour un bois de densité 0,75 (bois final) la part
d'anisotropie due à la flexion des parois est en effet quasi nulle
(Figure 3.20).
Pour un (ö) supérieur ou égal
à 10 degrés, l'anisotropie élastique tissulaire
liée à la morphologie et à l'arrangement cellulaire
entre en « compétition » avec l'anisotropie
attribuée
au paramètre (ö). Cette tendance est
d'autant plus marquée que la densité est faible ou que l'angle
(ö) est élevé. Un bois initial,
présentant à la fois une faible densité et un angle
(ö) important aura donc une anisotropie L/T plus sensible
à la flexion des parois qu'un bois final.
Plus généralement sur un bois RSV (densité
0,45), la Figure 3.19 montre que l'essentiel de l'anisotropie élastique
L/T est imputable à l'angle des microfibrilles (ö).
89
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.19 Comparaison de l'influence sur l'anisotropie
élastique macroscopique de l'anisotropie
« géométrique » et de
l'anisotropie imputée à l'AMF dans S2

Figure 3.20 Evolutions avec la densité du terme de
flexion des parois
90
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
3.4.5 Conclusion
Une étude de la sensibilité de l'anisotropie
élastique tissulaire du bois normal a permis de
montrer, avec le modèle adopté (modèle
squelette M3), l'existence d'une zone de sensibilité maximale (autour
de 10 degrés) de cette même anisotropie L/T
à l'inclinaison des microfibrilles (ö) dans la sous
couche S2.
La comparaison, pour différentes densités, de la
part d'anisotropie tissulaire L/T imputable au
paramètre (ö) montre :
qu'un bois RSV devra l'essentiel de son anisotropie L/T l'angle
(ö),
qu'un bois assimilable, par sa masse volumique et son AMF
(ö), à un bois final à une anisotropie L/T due
uniquement à l'angle des microfibrilles (ö),
que l'anisotropie tissulaire L/T d'un bois présentant un
angle (ö) et une densité proche d'un bois initial est
l'anisotropie la plus sensible à la flexion des parois.
L'AMF dans S2 ne constitue donc certainement pas le seul
paramètre à prendre en compte dans l'explication de l'anisotropie
élastique du bois initial.
Cette dernière tendance va dans le sens de ce que
suggèrent divers auteurs mécaniciens
(Mark, 1972, Cave, 1975, Salmèn et al, 1985,
Bergander et al, 2000a, 2000b) à l'échelle de la double
paroi. Pour ces derniers, le paramètre (ö) n'est en effet
pas à lui seul suffisant pour expliquer le comportement
mécanique de la double paroi de bois initial. L'intervention du
comportement mécanique de la sous couche S1 est donc souvent
évoquée.
Des observations microscopiques montrent par ailleurs, que le
passage d'une cellule de bois
final à une cellule de bois initial s'accompagne
d'une augmentation assez singulière de l'épaisseur de la sous
couche S1 (triplement de l'épaisseur pour Schniewind, 1972, Panshin
et
al, 1980, Kollmann et al, 1984, Koponen et
al, 1989, Keller, 1999).
3.5 Différences et
complémentarités entre les modélisations Multicouches et
Squelette
Il ne s'agit pas ici de tester (et d'affirmer) la pertinence
d'une modélisation Multicouche (M1
et M2) du comportement élastique de la double paroi par
rapport à celle du Squelette (M3) puisque les deux types de
modélisation n'ont pas la même vocation (chapitre1). L'objet de ce
paragraphe est plutôt de préciser, en regard de quelques
éléments bibliographiques, la situation des modules
élastiques de double paroi évalués par les deux types de
modélisations
3.5.1 Paramètres d'entrées des
modélisations confrontées
Les valeurs numériques (Tableau 3.11)
assignées aux paramètres micromécaniques retenus
ont été considérées comme
caractéristiques d'une paroi cellulaire de bois normal de
résineux, elles sont issues dans leur grande majorité d'une large
banque de données bibliographiques déjà
présentée (Tableau 2.3 du chapitre 2, Guitard et al,
2002).
L'utilisation simultanée, au sein des deux types de
modèles, de la valeur optimisée (62 GPa)
du module élastique longitudinal des microfibrille, ainsi
que l'attribution d'un comportement
91
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
élastique isotrope à ces mêmes fibres
de renfort permettent une analyse comparative des
différents modules pariétaux équivalents
obtenus au travers de ces modélisations parentes.
|
Modèles M1
et M2
|
Sous couche S1
|
Sous couche S2
|
Sous couche S3
|
Lamelle Mitoyenne composée
|
Modèle
M3
|
Références
|
|
Ef (GPa)
|
62
|
62
|
62
|
62
|
62
|
Guitard et al (2002)
|
|
íf
|
0,1
|
0,1
|
0,1
|
0,1
|
-
|
Mark (1967)
|
|
V (%)
|
30
|
50
|
50
|
10
|
50
|
Bergander et al
(2000)
|
|
Em (GPa)
|
2
|
2
|
2
|
2
|
2
|
Barrett, (1973), Bodig et al (1982)
|
|
ím
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
Gillis, (1972), Koponen et al (1991)
|
|
AMF ö (en degrés)
|
+/- 60
|
10
|
60
|
90
|
10
|
Keller (1999)
|
|
Epaisseur relative (%)
|
10
|
70
|
10
|
10
|
*
|
Keller (1999)
|
Tableau 3-11 Paramètres micromécaniques
employées dans les multicouches M1, M2 et dans le
modèle
squelette M3
*les modules élastiques obtenues via M3,
sont intrinsèques à la matière ligneuse de la sous couche
S2 et indépendants des caractéristiques
géométriques cellulaires (épaisseurs)
|
Bois initial
|
Bois final
|
|
Modèles
|
M1
|
M2
|
M3
|
M1
|
M2
|
M3
|
|
Nombres de sous couches
|
2
|
9
|
1 sous couche virtuelle
|
2
|
9
|
1
|
|
AMF ö (en degrés)
|
35
|
35
|
35
|
10
|
10
|
10
|
|
ELp (en GPa)
|
16,7
|
14,2
|
29
|
30,6
|
23,5
|
32
|
|
ETp(en GPa)
|
7
|
10,48
|
18
|
4
|
8,4
|
3,19
|
|
Degré d'anisotropie ELp/
ETp
|
2,4
|
1,4
|
1,6
|
7,8
|
2,8
|
10
|
Tableau 3-12 Degrés d'anisotropie de la double
paroi pour le bois initial et final, prédits par les
modèles
M1, M2 et M3 employant un module de microfibrilles de 62
GPa
Les expressions des modules élastiques de membrane (2.10
et 2.11) et de flexion torsion (2.12
et 2.13) des multicouches, comme les modules élastiques du
modèle Squelette (2.27 et 2.28)
ont été présentées dans le chapitre
2.
Pour évaluer les situations des modules élastiques
de double paroi définis par les deux types
de modélisations aux résultats de la
littérature, il convient de disposer de valeurs dites
« cibles ».
3.6 Valeurs de modules élastiques de double
paroi présentés dans la littérature
A cette échelle, les investigations sur le comportement
mécanique de la paroi sont délicates.
La littérature fait donc état de nombreuses
valeurs de modules élastiques de double paroi, obtenues par
méthode inverse et donc fortement conditionnées par le
modèle envisagé.
92
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Les valeurs maximales de ELp, obtenues via
l'expérimentation (fibres isolées) sont bien
souvent inférieures à celle
déterminées par méthode inverse (i.e. ; passage
macro-micro longitudinal intégrant la restriction de cisaillement).
Dans le premier cas elles sont proches de 30 GPa, (24 GPa sur le
bois initial de Sugi, Bodig et
al, 1982 ; 30 GPa pour Norimoto et
al, 1986 ; 25 GPa sur le bois initial de Picea rubens, Wimmer
et al, 1997) alors que dans le deuxième, elles se rapprochent
de 50 GPa (Cave, 1968, Khale et al, 1994 sur Picea abies).
Sur des fibres aplaties de Picea mariana, Salmèn
et al (1985) obtiennent un module longitudinal de double paroi de
l'ordre de 70 GPa. Cette valeur leur semble représentative de
la rigidité d'une double cloison dont les mouvements de
torsion sont bloqués (restriction de cisaillement).
L'écart entre les évaluations de ETp
par méthode inverse et les quelques mesures
expérimentales est tout aussi important.
Obtenus par méthode inverse, les modules
élastiques transverses de double paroi ETp sont
généralement de l'ordre de la dizaine de GPa (10 GPa pour Cave,
1968, 9 GPa pour Khale et
al, 1994, 15 GPa sur le bois initial de Picea abies,
Farruggia 1998).
Une récente expérimentation sur Picea
abies (microscopie électronique utilisée pour
déterminer le déplacement sous charge), attribue à la
double paroi isolée un ETp transverse de
1,5 à 3 GPa (Bergander et al, 2000).
3.6.1 Choix des valeurs cibles
L'examen de la littérature conduit, pour la
discussion qui va suivre, à l'adoption de deux
valeurs cibles médianes ELpC et
ETpC. Ces deux valeurs seront utilisées pour
évaluer la
« position » des modules élastiques
prédits par les modèles M1, M2 et M3 (chapitre 2), en fonction de
l'AMF (ö) et du module de fibres Ef. Cette comparaison
sera envisagée pour une inclinaison des fibres allant de 5 à 40
degrés (valeur minimale dans Keller 1999, 7 degrés).
ELpC = 30GPa
ETpC = 10GPa
3.7 Propriétés élastiques
prévues par les différentes modélisations
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
|
Modèles
|
M1
|
M1
|
M2
|
M2
|
M1
|
M2
|
M1
|
M2
|
M1
|
M3
|
|
Ef (GPa)
|
62
|
120
|
62
|
90
|
62
|
62
|
120
|
120
|
120
|
62
|
|
ö (en °)
|
10
|
10
|
10
|
10
|
5
|
5
|
5
|
5
|
35
|
10
|
|
ELp (GPa)
|
30,6
|
57,9
|
22,6
|
31,9
|
31,8
|
23,4
|
60,4
|
43,7
|
29,8
|
32
|
|
ETp (GPa)
|
3,9
|
4
|
6,8
|
8,4
|
3,9
|
6,8
|
3,9
|
10
|
10,2
|
2
|
Tableau 3-13 Modules élastiques de double paroi
prévus par les trois types de modélisations
93
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal

Figure 3.21 Evolutions des modules élastiques de
double paroi en fonction de (ö) pour le modèle
M1.
Influence du module de microfibrilles
3.7.1 Le bicouche M1
Pour une valeur de Ef de 62 GPa et un AMF
(ö) de 10 degrés (valeur en référence
à un bois de résineux dit normal) le modèle M1
fournit des estimations des rigidités bipariétales
longitudinales et transverses (Figure 3.21 et Tableau 3.13, colonne A) :
E Lp
E Tp
M1 (10) = 30,5 GPa
M1 (10) = 3,9 GPa
Si pour un tel AMF (ö), le module
d'élasticité pariétale longitudinal ELpM1
(10°) correspond
bien à la valeur cible ELp C, le module
pariétal transverse ETpM1 (10°) demeure bien
inférieur
à la valeur cible ETpC qui n'est atteinte
que des AMF (ö) supérieurs à 45 degrés
(Figure 3.21).
M1
Ce faisant, la valeur ELp
(45°) correspondante reste néanmoins trop faible
puisque proche de
la dizaine de GPa (Figure 3.21).
Pour une valeur double de Ef (i.e. :120 GPa) et
pour un AMF(ö) de 10 degrés, ELpM1 (10°)
est sensiblement le double de ELpC tandis que ETpM1
(10°) est plus de deux fois inférieure à la valeur
cible ETpC (Tableau 3.13, colonne B):
E Lp
E Tp
M1 (10) = 57,8 GPa
M1 (10) = 4 GPa
Avec ce même module, les valeurs cibles
ELpC et ETpC sont simultanément atteintes pour
un
AMF (ö) de 35 degrés (Figure 3.21).
94
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
E Lp M1 (35) = 29,8 GPa
E Tp M1 (35) = 10,2 GPa
Pour rendre compte simultanément des valeurs cibles
choisies, le modèle M1 doit donc faire
appel à un module Ef de 120 GPa et
un AMF (ö) supérieur à 35 degrés
(angle pouvant correspondre à un bois initial, en admettant que la sous
couche S2 assure encore l'essentiel du comportement mécanique dans ce
type de bois, colonne I du Tableau 3.13).
Pour assurer une rigidité pariétale
transverse supérieure, de nombreux auteurs sont donc amenés
à considérer pour ce type de modélisation multicouches,
l'intervention des autres sous couches dans le comportement
élastique de la paroi cellulaire (Mark, 1972, Barrett 1973,
Cave, 1975, Yamamoto 1998,1999, Yamamoto et al, 2001).

Figure 3.22 Evolutions des modules élastiques de
double paroi en fonction de (ö) pour le modèle M2.
Influence du module de microfibrilles
3.7.2 Le multicouche M2
Avec un module de microfibrille Ef de 62 GPa et pour
un AMF de 10 degrés, le modèle M2
prévoit (Figure 3.22, colonne C du Tableau 3.13)
ELpM2 (10°) = 22,6 GPa
ETpM2 (10°) = 6,8 GPa
ELpC n'est jamais atteinte tandis que ETpC
n'est obtenue que pour des angles (ö) supérieurs
à
40 degrés (Figure 3.22).
Atteindre, dans la gamme d'AMF (ö) choisie, avec M2
la valeur cible ELpC nécessite donc l'emploi d'un module
d'élasticité des microfibrilles supérieur à la
valeur de Ef = 62 GPa.
95
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
Ainsi (Figure 3.22) un module d'élasticité de
microfibrille sensiblement double (120 GPa),
permet d'atteindre, dés 5 degrés
ETpC, mais confère une valeur trop importante à
ELpM2 (27
degrés devient l'angle minimal à partir duquel
il est possible d'atteindre ELpC) en regard de
notre valeur cible. Une solution intermédiaire,
réside alors dans l'adoption d'un Ef situé aux
alentours de 90 GPa (colonne D du Tableau 3.13).

Figure 3.23 Comparaison des modules élastiques
bipariétaux obtenus via les modélisations M1 et M2
L'examen de la Figure 3.23, permettant la comparaison des
différents modules de double paroi prévus par M1 et M2
amène une remarque supplémentaire.
Pour une inclinaison des microfibrilles (ö) de 5
degrés et Ef = 62 GPa, ETpM1 (5°) = 4 GPa
et ETpM2 (5°) = 7 GPa
Tandis qu'avec un Ef fixé à 120 GPa,
ETpM1 (5°) = 4 GPa et ETpM2
(5°)= 10 GPa.
Ajouter des sous couches, au sein d'un modèle multicouches
à fibres parallèles (M2) permet donc d'assurer un renfort
transverse supérieur à celui permis par le modèle
bicouche M1
(colonnes E et F, Tableau 3.13, marque sur la Figure 3.23).
3.7.3 Modules élastiques de double paroi virtuelle
obtenus via le modèle M3
Pour un Ef de 62 GPa, et pour 10 degrés
(Figure 3.23, colonne J du Tableau 3.12); ELpM3 (10°) = 32
GPa
ETpM3 (10°) = 2 GPa
La valeur cible ETpC ne peut
être atteinte qu'à partir d'un angle de 24 degrés (Figure
3.23).
96
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
ETpM3 (24°) =
ETpC
L'emploi d'un module de microfibrille Ef double (120
GPa) ne permet d'atteindre ETpC qu'à partir d'un AMF
(ö) de 17 degrés.
L'examen de la Figure 3.23 permet de noter d'une part la
faible sensibilité de ELpM3 à l'AMF
(ö) par rapport à son homologue
ELpM1, mais aussi le caractère rigidifiant, dans la
direction
longitudinale de la modélisation M3 par rapport à
la modélisation M1. Ainsi, si pour 5 degrés
les ELpM1(5°) et ELpM3(5°),
sont sensiblement égaux à 32 GPa, un angle (ö) de
20 degrés fait
chuter ELpM1(20°) à 26 GPa tandis que
ELpM3 (20°) demeure très proche de 32 GPa.
Certains modules expérimentaux ETp, singulièrement
inférieurs à la dizaine de GPa (1,5- 3
GPa bois initial de Picea abies, Bergander et
al, 2000b), demeurent accessibles par les modélisation de
type squelette (M3) ou bicouche (M1), mais pas par une
approche multicouche (M2) (Figure 3.23) attribuant à la double
paroi isolée une rigidité transverse minimale ( pour un
ö = 5°) proche de la dizaine de GPa (colonne H du Tableau
3.13).
L'obtention de modules élastiques pariétaux
longitudinaux de résineux, aussi bien théoriques
(Cave, 1968, Khale et al, 1994, Farruggia, 1998,
Bergander et al, 2000b), qu'expérimentaux
(Suzuki, 1969 dans Bodig et al, 1982, Bergander et
al, 2000a) par une approche multicouche, nécessite alors l'emploi
d'un module longitudinal des microfibrille de cellulose Ef
supérieur
(120 GPa) à celui rendu nécessaire dans une
modélisation de type squelette (62 GPa). Pour rendre compte de la
restriction de cisaillement, les modèles multicouches doivent faire
appel à une rigidité microfibrillaire importante et proche
de celle de la cellulose I purement cristalline.

Figure 3.24 : Evolutions comparées des modules de
double paroi prédits par les 3 modèles M1, M2 et M3
en fonction de l'AMF dans la sous couche
S2
97
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
3.7.4 Degrés d'anisotropie pariétale
Le Tableau 3.12 fournit les valeurs ELp et ETp obtenues par les
modèles M1, M2 et M3 et ce pour des cellules dites de bois final et bois
initial (définis respectivement par un AMF (ö) de
10 degrés, et un AMF (ö) de 35
degrés). L'anisotropie de la paroi cellulaire est alors
caractérisée par le rapport ELp / ETp appelé «
degré d'anisotropie de la paroi cellulaire ».
Dans le cas du bois final, le degré
d'anisotropie donné par le modèle squelette M3 est
particulièrement élevé, avec une valeur de ELp / ETp =
10, prés de 1,5 fois supérieure à la valeur prédite
par M1 (ELp / ETp =7,8) et plus de 3 fois plus importante que le
résultat obtenu
via le modèle M2 (ELp / ETp
=2,8).
L'explication de la différence entre les deux
modèles multicouches à fibres disjointes M1 et
M2 résulte de l'augmentation de la quantité de sous
couche S1 présentant un large angle (ö =
60°), ce faisant ELp décroît de
30 à 23 GPa, tandis que ETp augmente de 4 à 7
GPa.
Pour le bois initial, et en comparaison au bois final
(passage d'un AMF de 10° à 35°), l'anisotropie
pariétale diminue drastiquement, en particulier pour le modèle M3
(division par
7 du degré d'anisotropie). Cette diminution du
degré d'anisotropie résulte plus d'une forte augmentation de
ETp (de 2 à 18 GPa) que d'une diminution, somme toute peu importante de
ELp (de 32 à 29 GPa).
Le coefficient d'anisotropie devient naturellement égal
à 1 pour une inclinaison de 45 degrés, dans le cadre des
modèles M1 et M3. On remarque que pour le modèle M2 cette valeur
est obtenue pour un angle (ö) légèrement
inférieur (41°) en raison de la présence d'une plus
grande proportion de sous couche S1 à fibres particulièrement
inclinées.
On rappelle enfin que quelque soit le modèle
envisagé, les modules élastiques longitudinaux d'une double paroi
de bois initial sont toujours inférieurs à ceux d'une double
paroi de bois final. Les modules transverses de double paroi d'un bois
initial sont eux supérieurs à ceux d'un bois final. Ces
résultats sont conformes à diverses observations (Wimmer et
al, 1997, Farruggia, 1998) expliquées respectivement par une teneur
en cellulose plus important dans la paroi de bois final (Panshin et
al, 1980) et un AMF (ö) plus important dans le bois
initial.
3.8 Comportement en flexion torsion du stratifié
pariétal
La détermination des rigidités de flexion torsion
d'un stratifié, par l'application de la théorie des plaques
minces, n'est valable que sous l'hypothèse d'une épaisseur totale
faible en regard
du rayon de courbure que présente le multicouche
sollicité.
Appliquée à la paroi de la cellule ligneuse, cette
théorie prédictive doit donc être manipulée avec
précaution dans le cadre de cellule à parois épaisses
(bois à forte densité ou bois final) ou
de section particulièrement circulaire (bois de
compression par exemple).
Utilisant la théorie des plaques minces, nous nous sommes
intéressés dans la première partie
de ce chapitre au comportement de membrane du
stratifié, conduisant à l'évaluation de modules
élastiques équivalents de double paroi indépendants du
rayon de courbure.
98
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
L'objet de ce paragraphe est de comparer l'influence, sur les
modules équivalents de flexion
torsion du stratifié M2, définis en (2.12) et
(2.13), de quelques modifications microstructurales majeures, pouvant
être assimilées au passage d'une double paroi de bois
final à une double paroi de bois initial (augmentation de
l'épaisseur de S1 dans la cellule de bois initial, angle
(ö) des microfibrilles notablement plus élevé dans
le bois initial que dans le bois final).
3.8.1 Influence d'une modification de l'épaisseur de
S1
Pour évaluer, l'influence d'une augmentation de
la proportion de S1 dans la paroi sur le
comportement en flexion torsion de la double paroi, les
épaisseurs de la sous couche S3 et de
la lamelle moyenne composée sont fixées
à 10%, conformément au Tableau 3.11.
L'évaluation porte ainsi sur les modules
équivalents en flexion torsion (notés E11 et E22), d'un
multicouche de type M2 à fibres isotropes, dans lequel
l'épaisseur totale est constante. Les évolutions des E11 et E22
en fonction de la proportion de sous couche S1 sont reportées dans le
Tableau 3.14. On rappelle que la direction 1 correspondant à
l'axe normal au multicouche tandis que la direction 2 est une direction
transverse (dans le plan de la plaque).
|
Proportion de sous couche S1 dans la double cloison
(%)
|
E11 (GPa)
|
E22 (GPa)
|
|
10
|
23,61
|
8,31
|
|
20
|
23,10
|
8,47
|
|
30
|
22,11
|
8,78
|
|
40
|
20,48
|
9,30
|
|
50
|
18,04
|
10,07
|
Tableau 3-14 : Valeurs numériques
attribuées aux modules équivalents de flexion torsion de M2
en
fonction de la proportion de sous couche S1
L'examen du Tableau 3.14 amène quelques commentaires.
Les sens de variation des rigidités E11 et E22 avec
la proportion relative de sous couche S1 sont opposés. Le passage de
10% à 50% de S1 se traduit respectivement pour E11 par une
diminution de 33% (de 23,61 à 18,04 GPa) et pour E22 par une
augmentation de 21% (de 8,31
à 10,07 GPa). Augmenter le pourcentage de sous
couche S1 tend donc renforcer la double paroi dans les directions
transverses et à l'affaiblir dans la direction longitudinale. Le poids
relatif de sous couche S1 dans la double paroi semble donc à priori un
paramètre important du comportement mécanique en flexion
torsion de la cellule. Il convient alors de comparer l'influence de
ce paramètre « épaisseur de S1 » à celle
du paramètre (ö) rendu responsable jusqu'alors de
l'essentiel du comportement mécanique de la double paroi.
3.8.2 Influence de l'angle des microfibrilles
Pour rendre compte de la variabilité intra arbre de
l'angle (ö), l'intervalle de variations choisi
est [10°, 40°].
99
Hiérarchisation des paramètres descriptifs de
l'anisotropie élastique du bois normal
|
AMF ö dans S2 en degrés
|
E11
|
E22
|
|
10
|
23,6
|
8,3
|
|
20
|
20,3
|
8,6
|
|
30
|
15,9
|
9,6
|
|
40
|
11,5
|
11,8
|
Tableau 3-15 Valeurs numériques des modules
équivalents en flexion torsion en fonction de l'AMF dans
S2
La simulation d'une transition d'un bois final à un bois
initial par le passage d'un angle de 10
à 40° dans la sous couche S2 se traduit par une
diminution drastique de plus de 100% de E11
(de 23,6 GPa à 11,5 GPa) et une augmentation de
42 % de E22 (de 8,3 GPa à 11,8 GPa)
(Tableau 3.15).
Le comportement en flexion torsion de la double
cloison modélisée par un multicouche à fibres
parallèles est plus sensible à une modification de l'angle des
microfibrilles dans la sous couche S2 qu'à une augmentation de
l'épaisseur relative de la sous souche S1.
Il a été montré dans les
paragraphes précédents qu'une modélisation de type
Squelette attribuant un rôle majeur à l'angle des
microfibrille de la sous couches S2 était apte à la
prédiction des modules d'élasticité de double paroi.
Les derniers résultats présentés ici confirment, par
les évaluations du comportement de membrane et de flexion
torsion, que l'essentiel du comportement mécanique de la paroi
cellulaire peut être imputé à la sous couche S2 et
à son paramètre descriptif essentiel ; l'angle des microfibrilles
(ö).
3.9 Conclusion
L'anisotropie élastique des résineux est souvent
attribuée à l'influence d'une ou de plusieurs séries de
paramètres structuraux. Par une hiérarchisation de leur
influence, il a été montré dans ce chapitre, sur
un bois RSV, qu'elle est au premier chef la conséquence de
l'angle d'orientation des microfibrilles de cellulose dans la sous couche S2.
Les différentes variations
du rapport de forme cellulaire e/D ne sont, en effet,
pas en elles mêmes suffisantes pour
expliquer les valeurs d'anisotropie L/T observées dans le
bois normal.
Le chapitre 2 a en outre souligné l'importance du
passage de l'échelle de la sous couche à l'échelle de la
double paroi en ce qui concerne le nombre de paramètres rendus
nécessaires à une description de l'anisotropie élastique
macroscopique.
A ce même niveau de description, au moins deux
options de modélisation, fortement complémentaires peuvent
être envisagées.
Les modèles Multicouches prenant en compte le
caractère stratifié de la paroi reflètent assez
fidèlement la structure pariétale des résineux. Ils
doivent employer, pour rendre compte de la restriction de cisaillement, des
modules d'élasticité de microfibrille élevés
(proches de celui
de la cellulose I) bien souvent obtenus par méthode
inverse.
Le modèle Squelette assimile le renfort filamentaire
cellulosique à un réseau de microfibrilles entrecroisées
parfaitement interconnectées. Cette première étape de
modélisation se démarque des précédentes par la
prise en compte d'une unique sous couche, assimilable à la sous
couche
S2.
Autorisant, pour rendre compte de la restriction de
cisaillement, l'emploi d'un module
d'élasticité des microfibrilles bien
inférieur à celui nécessaire aux Multicouches, le
Squelette
de microfibrilles présente l'avantage majeur de ne faire
appel qu'à un nombre très restreint de paramètres
descriptifs.
100
Vers une description de l'anisotropie élastique du bois de
réaction
4 Vers une description de l'anisotropie
élastique du bois de réaction
Dans les chapitres précédents, la
possibilité d'une prédiction de l'anisotropie élastique du
bois normal à partir d'un nombre, somme toute assez limité de
paramètres a été montrée. Un des champs
d'application de la démarche envisagée dans ce travail consiste
en sa mise en oeuvre sur le bois de réaction des résineux
appelé bois de compression. L'objectif premier de ce chapitre est
d'évaluer expérimentalement certaines propriétés
mécano physiques du bois de compression. Les
caractéristiques élastiques obtenues via
l'expérimentation seront ensuite confrontées à celle
prévues par la modélisation adoptée.
4.1 Existence de plusieurs bois de compression
Il est possible, en s'appuyant, sur un ensemble de
caractères anatomiques de distinguer plusieurs classes de bois de
compression (Singh et al, 1999, Fioravanti et al, 2003).
Le premier type de bois de compression est désigné
par les auteurs précédents comme
« sévèrement » comprimé ; il est
notamment caractérisé par des épaisseurs de parois
importantes, la quasi absence de sous couche S3 et des teneurs
élevées en lignine dans
les sous couches S2 et S1. Des coupes anatomiques
transversales montrent de nombreux espaces inter cellulaires entre les
trachéides. La majorité des études cytologiques
rencontrées dans la littérature se réfère au bois
sévèrement comprimé.
La seconde catégorie, de bois de compression,
beaucoup moins étudiée, est appelée par les
mêmes auteurs, bois de compression « moyennement »
comprimé. Les espaces intercellulaires (Singh et al, 1999)
n'y sont pas systématiques. Pour ces derniers auteurs, ce type
de bois de compression est un bois dont les
caractéristiques ultrastructurales sont intermédiaires entre
celles d'un bois de compression sévèrement comprimé et un
bois normal.
Le troisième type, qualifié de bois de
compression peu comprimé, se distingue des précédents
par l'absence quasi-totale d'espaces intercellulaires et de sous couche S3. Ses
caractéristiques structurales et ultrastructurales ne sont que rarement
explicitées.
Certains auteurs relient directement l'inclinaison des
microfibrilles dans la sous couche S2 au
« degré » de compression du bois ; plus le bois
est comprimé, plus l'angle des microfibrilles
(ö) est important (Singh et al, 1999).
4.1.1 Description sommaire des caractères
anatomiques généraux du bois de compression
Compte tenu du peu d'information disponible sur les
caractéristiques anatomiques des bois de
compression dits « moyennement et
sévèrement » comprimés, les tendances
générales évoquées par la suite devront
être considérées comme celles définissant
un bois de compression « fortement » comprimé au sens de
Singh et al (1999) et Fioravanti et al (2003).
4.1.1.1 Des teneurs en macromolécules différentes
de celles du bois normal
Comparativement à la paroi de bois normal, la
teneur en cellulose de la paroi du bois de compression est fortement
diminuée (taux de cellulose de la paroi entre 20 et 30%). La teneur
en lignines est quant à elle généralement
supérieure (aux alentours de 40% d'après Kolmann
101
Vers une description de l'anisotropie élastique du bois de
réaction
et al, 1984, Keller, 1999). En associant microscopie
électronique et auto fluorescence de la
lignine, sur du bois de compression de Pinus radiata,
une variabilité significative de lignification dans la lamelle
mitoyenne et la sous couche S2 (Singh et al, 1999) a été
montrée.
4.1.1.2 Une paroi cellulaire spécifique
Les sous couches pariétales sont réduites à
S1 et S2, la sous couche S3 est généralement très mince
(Singh et al, 1999 sur Pinus radiata) voire inexistante (Timell,
1986).
La distinction tissulaire entre le bois initial et le
bois final du bois de compression est généralement
délicate en terme d'inclinaison des microfibrilles dans la sous
couche S2. Un AMF (ö) maximum de l'ordre de 45 degrés,
commun au bois initial et final, est généralement admis (Panschin
et al, 1980, Cloutier, communication personnelle, Bodig et
al, 1984, Keller,
1994, Sahlberg et al, 1997).
4.1.1.3 Modifications des paramètres
géométriques cellulaires
Timell (1986) a établi des tendances
générales en compilant un grand nombre de données
anatomiques issues de la littérature :
Les diamètres cellulaires :
dans le bois initial de compression, les diamètres
radial et tangentiel ne sont pas
significativement différents de ceux observés sur
le bois initial normal.
dans le bois final de compression, le diamètre radial
est égal ou faiblement inférieur à celui du bois final
normal. Le diamètre tangentiel est inférieur à
celui de bois final normal.
Les épaisseurs de paroi :
Les trachéides de bois initial de compression
présentent des épaisseurs de parois identiques à
celles de bois initial de bois normal (Kramer et al,
1979, Panshin et al, 1980, synthèse des résultats
présentés dans Timell, 1986, Ruelle, 2003), mais sont de
10 à 40% plus courtes
(Keller, 1999). Dans la cellule de bois final de compression il
est vraisemblable d'admettre une épaisseur de paroi cellulaire double de
celle constatée sur une cellule de bois final normal
(Keller, 1999). Les épaisseurs pariétales ne sont
en revanche pas distinguées selon la direction radiale ou transverse de
l'observation.
Les différences de géométrie
cellulaire entre le bois de compression et le bois normal se situent
essentiellement au niveau des trachéides de bois final ; celles-ci ont
une forme plutôt arrondie dans le bois de compression alors qu'elles
présentent une géométrie nettement plus rectangulaire dans
le bois normal.
Dans le plan transverse, des espaces intercellulaires
apparaissent. Ils sont particulièrement marqué dans le bois
final de compression (Panshin et al, 1980, Keller, 1999).
Certains auteurs rapportent une masse volumique du bois final
de compression deux fois plus élevée que celle de bois final
« normal » (Keller, 1999, Necesany et al, 1967,
rapportés dans Timell, 1986). Timell (1986) attribue cette forte valeur
à une épaisseur de paroi dans le bois final de compression double
de celle du bois final normal
102
Vers une description de l'anisotropie élastique du bois de
réaction
L'anatomie des rayons ligneux du bois de compression ne se
démarque généralement pas de
celle observée sur le même type de cellule du bois
normal (Kramer et al, 1979, Keller, 1994). Certains pins
présentent néanmoins des rayons plus gros et en plus grand nombre
dans le bois
de compression (Venet et al, 1986, Keller, 1994).
4.1.1.4 A l'échelle du cerne ; une organisation assez
semblable à celle du bois normal
La texture (TX) du bois de compression est, pour certains
auteurs, supérieure à celle du bois normal (Cloutier
communication personnelle, Panshin et al, 1980, Ruelle, 2003). Si le
bois normal présente un bois final distinct et marqué,
dans le bois de compression, il est généralement difficile
d'identifier une transition nette entre les deux tissus bois initial et
final
(Keller, 1994 cite l'exemple de Pinus strobus).
La fraction volumique en rayons ligneux (n) dans le
bois de compression est pour certains auteurs légèrement
supérieure (Timell, 1986) à celle du bois normal.
D'autres travaux rapportent une tendance inverse (Onaka, 1949 dans Ruelle,
2003).
4.1.1.5 Propriétés mécano physiques du bois
de compression
Contrairement au bois normal dont les caractéristiques
mécano physiques ont été largement étudiées
et modélisées, les propriétés du bois de
réaction des résineux restent assez mal identifiées.
Seules des tendances générales directement liées à
l'anatomie (épaisseurs de paroi importante, angle des microfibrilles
particulièrement ouvert) peuvent être évoquées.
a) La masse volumique
La masse volumique du bois de compression est
généralement plus importante que celle du bois normal (de 10
à 20% supérieure à celle du bois normal pour
Panshin et al, 1980, Cloutier, non publié).
b) Des modules élastiques cibles ?
Très peu de références sont
disponibles dans la bibliographie. Le bois de compression est
considéré un bois de qualité mécanique assez
médiocre. Il constitue d'ailleurs du point de vue industriel un
défaut.
Son module d'élasticité longitudinal est
inférieur à celui du bois normal, les modules transverses
sont peu ou pas identifiés.
4.2 Etude expérimentale
4.2.1 Mise en oeuvre de l'étude
4.2.1.1 Matériel végétal et
préparation des échantillons
3 Résineux ont été prélevés
dans la région de Bordeaux. Il s'agit de 3 arbres jeunes (21 ans pour
l'Epicéa, 18 ans pour le Pin sylvestre, 13 ans pour le Pin
maritime) très fortement inclinés par une tempête (1999)
et ayant basculé droit par déficience du système
raçinaire. Sur
les trois essences, la partie haute du tronc avait
retrouvé sa verticalité.
103
Vers une description de l'anisotropie élastique du bois de
réaction
Le pin sylvestre présentait deux axes (axe
réitéré) n'appartenant pas au même plan.
4.2.1.2 Mesures in situ
Mesures des Indicateurs de Contrainte de Croissance (A. et B.
Thibaut)
Après écorçage jusqu'au cambium, une
couronne de 8 points de mesures (espacés chacun de
45 degrés) d'indicateurs de contrainte de croissance
(ICC) a été réalisée à une hauteur
de
1,30m sur chaque essence. La méthode de mesure des ICC,
dite du trou unique, consiste en la mesure des déplacements par un
capteur électronique autour d'un trou foré à la
surface écorcée. Les déplacements mesurés
résultent d'une modification du champ de contraintes induite par
le perçage (Bailleres, 1994).
Un disque a été tronçonné au
niveau des mesures des ICC et les distances de chacun des points de
mesure d'ICC relevées. Simultanément des billons ont
été découpés juste en dessous
de ces disques afin d'en extraire des jeux d'éprouvettes
utiles à des essais mécaniques ou des mesures de retrait.

Figure 4.1 Billon d'Epicéa E3

Figure 4.2 Billon de Pin maritime (PM)
104
Vers une description de l'anisotropie élastique du bois de
réaction

Figure 4.3 Billon de Pin sylvestre (PS2)
4.2.1.3 Mesures en laboratoire
Mesures des retraits longitudinal et tangentiel
(A.Thibaut)
Les mesures de retrait radial (RR), tangentiel (RT) et
longitudinal (RL) ont étés réalisées sur des
éprouvettes (extraites des rondelles précédente) de
dimensions 20x20x50mm (+/-1%). Les dimensions et masse des
éprouvettes ont étés relevées à
l'état vert puis pour différentes stabilisation en ambiance
régulée en température et humidité relative HR
(30° et 80% HR, 20°
et 30%HR, 0% HR). Par différence entre la masse humide
et la masse anhydre, pour chaque ambiance, le taux d'humidité des
éprouvettes a été déterminé. Les retraits
totaux sont ensuite calculés, pour les directions radiale, tangentielle
et longitudinale par différence de dimensions entre l'état vert
et l'état anhydre. Nous ne présenterons ici que les retraits
totaux calculés par
le CIRAD entre l'état vert et l'état anhydre.
Certains retraits n'ont pas été calculés en raison
de la présence de noeud. D'autres, réalisés
uniquement sur des éprouvettes plus petites ne sont pas figurés
pas soucis d'homogénéité dans la présentation.
Etudes anatomiques (J. Ruelle)
a) Préparation des échantillons
Des couples d'échantillons correspondant aux fortes
valeurs d'ICC et de retrait longitudinal et aux faibles valeurs d'ICC et
de retrait longitudinal ont étés prélevés.
Sur ces mêmes échantillons, des coupes d'épaisseurs 15
um, ont étés réalisées au microtome, puis une
double coloration safranine (colorant des parois lignifiées) / bleu
alcian (colorant de la cellulose) a
été appliquée.
b) Observations microphotographiques (dimensions cellulaires et
AMF ö)
Les coupes microtomées ont ensuite été
montées en lame mince pour pouvoir être observées par
microscopie (grossissements 100X et 500X) puis photographiées
numériquement. Les critères géométriques
mesurés et fournis par l'auteur sont :
diamètre radial (FLDR) et tangentiel (FLDT) des lumens
des fibres (exprimés en um)
105
Vers une description de l'anisotropie élastique du bois de
réaction
épaisseur de la double paroi radiale (FepPR),
tangentielle (FepPT) calculées par
l'auteur, sur chaque cellule, par la différence
entre le diamètre externe de la fibre
(non fourni) et le diamètre du lumen dans la direction
donnée.
L'ensemble des mesures de ces critères anatomiques a
étés réalisé par un traitement d'images
(routines écrites en Analytical Language for Images et
logiciel de traitement Optimas).
L'inclinaison des microfibrilles dans la sous couche S2 des
cellules de bois initial et final de chaque échantillon a
également été mesurée. La méthode de mise en
évidence et de mesures des microfissures est celle mise au point et
décrite dans Senft et al (1985). Pour chaque coupe
mince sont déterminés les angles dans S2 d'environ
80 microfibrilles.
Mesures des modules élastiques longitudinaux par
méthode vibratoire (A.Thibaut)
Des éprouvettes sèches à l'air de
25x25x500mm (+/-1%), en appui sur des supports élastiques ont
été percutées radialement (PR) et tangentiellement
(PT) (méthode mise au point par Bordonné en 1989). Les
vibrations libres du signal résultant ont été, une fois
acquises par un microphone, numérisées puis traitée par le
logiciel Bing 2000 du CIRAD Forêt (transformées
de Fourrier puis analyse spectrale). Par calcul, est
déduite une appréciation du module élastique.
Essais de compression longitudinale jusqu'à rupture
(A. Thibaut)
Des éprouvettes (20x20x60mm) ont été
taillées selon la direction longitudinale dans chacune des zones
définies dans la rondelle (Figures 4.2 et 4.3).
Les données numériques (fichiers txt)
relatives aux essais de compression longitudinale jusqu'à rupture
ainsi que les dimensions des éprouvettes testées ont
été fournies par l'équipe Bois du CIRAD Montpellier.
a) Dispositif expérimental
La machine de traction compression (à plateau
inférieur rotulé) est une machine hydraulique Adhamel Lomargy DY
36 équipée du logiciel d'acquisition et de pilotage Testworks
(société MTS). Des précharges de 10 N ont
été appliquées avant essai sur des
éprouvettes de
20x20x60cm. La vitesse de sollicitation est de 0,01 mm/s et le
capteur de force est de 100 kN
(+/-10 N), la position de traverse est estimée avec une
incertitude de 1/100 mm.
b) Procédure d'exploitation des résultats
A partir des courbes expérimentales, et
après identification du domaine de comportement linéaire,
des rigidités longitudinales équivalentes (pente) sont
calculées par régression linéaire. A partir des
dimensions de l'éprouvette, les modules d'élasticité
longitudinaux de chaque échantillon ont été
déduits. La sélection des points de mesure pris en
compte s'est faite avec le souci d'un coefficient de régression
linéaire le plus proche de l'unité. La longueur de chaque
éprouvette est de 60mm, l'ordre de grandeur de la section carrée
est de 4
cm2 (mesurée au 1/100 de mm).
106
Vers une description de l'anisotropie élastique du bois de
réaction
Essais préliminaires de compression sur des
échantillons cubiques centimétriques
a) De l'arbre sur pied aux cubes
Sur chacune des rondelles issues des billons
prélevés in situ (Figures 4.1, 4.2 et 4.3), des zones
d'études (zones 1, 2, 3, 4) espacées chacune de 90 degrés
ont été définies. Les zones 1
et 2 correspondent à des échantillons
situés dans la zone la plus colorée de chaque rondelle les zones
3 et 4 sont diamétralement opposées respectivement aux zones 2 et
1. De chacune de ces zones (quartiers) ont étés extraits des
barreaux qui ont été amené à l'état sec
à l'air après séchage à l'étuve
(80°C progressivement durant 6 jours jusqu'à ce que la
masse soit stabilisée). Ce premier séchage a été
réalisé afin de faciliter la découpe.
Une barrette verticale a ensuite été
taillée dans la profondeur disponible de chacun des barreaux. A
partir de cette barrette, des échantillons de forme cubique ont
été découpés. Suivant les conditions techniques
de la découpe (épaisseur disponible dans la rondelle), 2 ou 3
éprouvettes grossièrement cubiques ont été
extraites. Ces éprouvettes ont ensuite étés
fraisées pour leur donner des arrêtes de 2cm. Avant les essais,
les échantillons ont été soumis à un nouveau
séchage à l'étuve (80°C durant 6 jours). La
pesée des échantillons (+/- 0,01g) à été
réalisée avant chaque série d'essais. La mesure de chacune
des faces (+/-1% répétées deux fois) a été
faite en sortie de l'étuve.
Les essais mécaniques, réalisés sur les
cubes, ne peuvent en toute rigueur être qualifiés d'essais
de compression. Ils n'obéissent en effet pas aux règles de
normalisation classiques
(entre autre la longueur de l'éprouvette sur le
coté de sa section carrée doit être compris entre
3 et 4 (Martin, 1984)). L'ambition initiale était moins de
déterminer des modules d'élasticité normalisés que
d'évaluer des rapports d'anisotropie élastique du bois de
compression.
b) Dispositif expérimental utilisé
Les essais mécaniques ont été conduits,
à l'ENSAM Talence, sur une machine hydraulique de traction compression
Adhamel Lomargy DY 36 pilotée en force et à plateaux non
rotulés. Les compressions réalisées selon les directions
radiale et tangentielle ont été menées en utilisant la
partie haute de la machine (capteur de force 1kN +/-10-1N),
les essais de compression longitudinaux font appel à une utilisation
de la partie basse (capteur 10kN+/-10N).
La vitesse de sollicitation, commune aux deux types d'essais, est
de 0,1mm/min. L'incertitude
sur le déplacement de traverse (acquis par le
logiciel Autotrack) est de 10-2mm (cette incertitude
correspond à chaque « palier » horizontal sur les
Figures 4.4 et 4.5). Des prés charges de 1N pour les essais
transverses et de 10N pour la compression longitudinale sont
appliquées.
c) Déroulement des essais
Les cubes ont ensuite été soumis chacun à
une sollicitation dans des directions correspondant approximativement aux
directions d'orthotropie du bois. Chaque essai a été
mené avec le souci de ne conduire qu'à une déformation
maximale de 2% tout en étant dans le domaine de comportement
linéaire du matériau.
Compte tenu du fait que le déplacement est un
déplacement de traverse et non un déplacement mesuré sur
les faces, nous parlerons plus de déformation apparente ou de
déplacement de
107
Vers une description de l'anisotropie élastique du bois de
réaction
traverse que de déformation ou déplacement
d'échantillons. La même remarque est valable
pour les caractéristiques élastiques
calculées. d) Procédure d'exploitation des résultats
Après acquisition des fichiers numériques
et identification d'une partie du domaine de
comportement linéaire de chaque échantillon, un
traitement manuel des courbes conduit, pour chaque direction de compression,
à la sélection d'une gamme de points de mesures :
pour les directions transverses de compression ; les
déplacements considérés seront ceux correspondant
à une valeur de force appliquée comprise dans l'intervalle
[300N,
500N] soit une contrainte appliquée comprise dans
l'intervalle [0.75MPa, 1.25MPa]
(Figure 4.4, Epicéa A4, compression radiale).
dans la direction longitudinale les déplacements
sélectionnés correspondront à une valeur de force
appliquée comprise dans l'intervalle [1000N, 2500N] soit une
contrainte appliquée située dans l'intervalle [2.5MPa,
7.5MPa] (Figure 4.4, Epicéa A4, compression longitudinale).
Une régression linéaire permet, de
déterminer une estimation des raideurs (ou rigidités)
apparentes Kapp.ech de chaque échantillon.
Le coefficient de régression linéaire
minimal obtenu sur l'ensemble des échantillons correspond
à l'exploitation de l'essai longitudinal de E1A1, sa valeur est de
0,93.
Nb : Pour chaque essence et chaque « type de bois
», des compressions d'un cube jusqu'à rupture ont
été menées afin de vérifier que l'essai
correspondait bien au domaine de comportement linéaire.
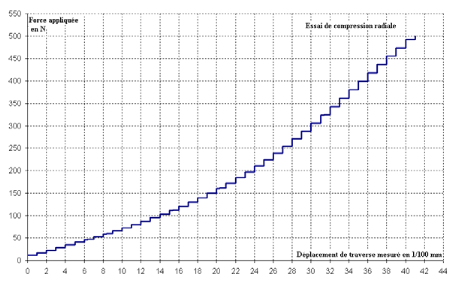
Figure 4. 4 Essai de compression radiale sur
l'Epicéa
Les courbes force déplacements obtenues montrent
toutes un important pieds de courbe, imputable au rattrapage de jeu de la
machine (contact échantillon plateau).
108
Vers une description de l'anisotropie élastique du bois de
réaction

Figure 4.5 Essai de compression longitudinale sur
l'Epicéa
Estimation de la rigidité apparente du dispositif
expérimental
Pour chaque configuration du montage (partie haute pour les
compressions transverses, partie
basse pour une compression longitudinale) et avant
chaque série d'essais (plusieurs
utilisateurs de la machine), une estimation de la
rigidité apparente
K app.Dispo. du dispositif
expérimental, a été fournie par une
compression à « blanc » des deux plateaux.
Pour les essais de compression longitudinale la rigidité
apparente du dispositif est évaluée à
3,09.107 N/m. Pour les essais de compression
transverses, réalisés en deux temps, elle est
estimée à 4,06.106 N/m ou 4,20.106 N/m
(plusieurs utilisateurs de la machine).
Nb : ces estimations ont été
réalisées dans la gamme de forces utilisée pour les essais
sur les cubes.
A titre de comparaison, les rigidités apparentes
expérimentales des cubes dans la direction longitudinale sont de
l'ordre de 2,00.107 N/m et de l'ordre de 3,00.106 N/m
pour les directions transverses.
Une fois ces valeurs estimées, des corrections sur les
raideurs apparentes des échantillons ont étés
apportées en modélisant le système (dispositif -
échantillon) par l'association en série de
deux ressorts de raideur
K app.Dispo. et Kapp.ech . La raideur apparente
corrigée
Kech .corr de
chaque échantillon testé est donc donnée par
la relation (4.1):
(4.1)
Kech.corr =
Kapp.ech K
app.Dispo
Kapp.Dispo
Kapp.ech
Incertitudes sur la détermination des
différentes caractéristiques élastiques
Pour un essai de compression selon une direction z, notant F, la
valeur de la force appliquée,
d le déplacement de traverse relevé,
module d'Young apparent s'écrit (4.2)
L x , L y , L z les dimensions de l'échantillons
testé, le
F L
(4.2)
E = z
z Lx L y d
109
Vers une description de l'anisotropie élastique du bois de
réaction
L'incertitude sur le module d'élasticité dans
la direction z, E z est alors (4.3)
(4.3)
?E z
?F ?L x ?L y ?L z
+ ?d
+ + +
E z F L x
L y L z d
nb : pour les éprouvettes du Cirad
Forêt, l'incertitude
?L z sur la dimension
L z de
l'échantillon est distincte des deux autres
déterminées au pieds à coulisse. Essai de compression
jusqu'à rupture (Montpellier)
Dans les conditions expérimentales des essais
réalisés à Montpellier, l'ensemble des relations
définies en (4.4) fournit une estimation par excès de
l'incertitude sur les modules d'élasticité apparents des
échantillons (4.5) :
3
?F
= 4 10
F
= 3 10
?L x = ?L y 3
L x L y
(4.4)
?d
2
= 4 10
d
?L z
L z
= 4 10 2
(4.5)
?E z
E z
0,09
De manière analogue, l'ensemble des relations
définies en (4.6) et (4.7) fournit des
estimations des différentes incertitudes (dans la gamme de
points de mesure choisie) pour les essais de compression radiale et
tangentielle sur les éprouvettes cubiques :
3
?F
= 3 10
F
(4.6)
?L x,
L x
= ?L y,
L y
= ?L z
L z
= 10 2
?d
2
= 3 10 .
d
(4.7)
?E x, y
0,09
E x, y
Pour l'essai de compression longitudinale, l'incertitude est
110
Vers une description de l'anisotropie élastique du bois de
réaction
2
?F
= 10
F
(4.8)
?L x,
L x
= ?L y,
L y
= ?L z
2
L z
= 10 2
?d
= 8 10 .
d
(4.9)
?E z
E z
0,15
4.2.2 Synthèses des différents
résultats
Les différentes mesures évoquées
précédemment sont présentées dans les Tableaux 4.1,
4.2,
4.3. Les qualificatifs « bois normal », (BN), «
bois opposé » (BO) et « bois de compression »
(BC) sont attribuées en premier lieu sur des
critères uniquement visuels (excentrement et coloration plus
foncée).
Indicateurs de contrainte de croissance
Les mesures d'ICC (colonne A) réalisées in
vivo permettent de confirmer la classification visuelle bois de
compression / bois normal. Les secteurs les plus comprimés de
chaque essence présentent systématiquement des valeurs
fortement négatives d'ICC. Les zones correspondantes à la
limite entre le bois de compression et le bois normal
présentent des valeurs d'ICC positives dans le cas du Pin maritime (PM
3.10 et PM 7.6) et négatives pour l'Epicéa (E3.12, 5).
Mesures anatomiques
Pour les trois essences résineuses (Tableau 4.4) les
valeurs d'angle moyen des microfibrilles pour les coupes relatives au bois de
compression (BC) sont systématiquement supérieures à celle
du bois dit « normal » (BN), l'écart le plus
important (de l'ordre de 24 degrés) entre l'AMF (ö)
de bois normal et AMF (ö) de bois de compression est
observé sur le Pin maritime
(Pinus pinaster).
L'examen des écarts types faibles associés
aux mesures des AMF sur l'ensemble du cerne suggère que l'AMF
dans le bois initial de compression est peu différent de celui dans le
bois normal. Ce résultat est conforme aux mesures par
diffraction rayons X menée sur Larix decidua (Fioravanti et
al, 2003).
111
Vers une description de l'anisotropie élastique du bois de
réaction
|
E3
|
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
|
Secteur
|
Distance à la moelle
(cm)
|
Nature
|
ICC
(udef)
|
AMF ö
en degrés
|
d
(12%)
|
RR
en %
|
RT
en %
|
RL
en %
|
EL(CPR)
en MPa
|
EL(PT)
en MPa
|
Fn en N
|
D en mm
|
W en kJ
|
|
1
|
16
|
BC
|
-110
|
32,4
|
0,69
|
2,18
|
4,83
|
1,55
|
3942
|
8172
|
17784
|
1,557
|
19198
|
|
2
|
9
|
noeud
|
|
|
0,61
|
|
|
|
3877
|
7260
|
14642
|
1,172
|
11471
|
|
2
|
12,5
|
fin du
BC
|
-18
|
30,5
|
0,6
|
2,16
|
5,99
|
1,04
|
4068
|
7582
|
15028
|
1,119
|
11106
|
|
3
|
8
|
BN
|
65
|
|
0,54
|
3,76
|
9,74
|
0,11
|
4291
|
11744
|
15450
|
1,219
|
11366
|
|
4
|
5
|
BO
|
17
|
17,7
|
0,49
|
4,61
|
9,90
|
0,07
|
3737
|
8220
|
13057
|
1,206
|
7846
|
|
5
|
|
BO
|
10
|
|
0,52
|
3,37
|
8,48
|
0,14
|
3293
|
6388
|
11643
|
0,806
|
5751
|
|
6
|
4
|
moelle
|
|
|
0,46
|
4,08
|
8,68
|
0,19
|
|
|
|
|
|
|
6
|
7,5
|
BN
|
21
|
|
0,55
|
4,63
|
9,50
|
0,19
|
3473
|
8666
|
10737
|
0,781
|
4469
|
|
7
|
13
|
BN
|
21
|
22,6
|
0,56
|
4,43
|
10,03
|
0,14
|
4074
|
11496
|
|
|
|
|
8
|
13
|
BC
|
|
|
0,82
|
|
|
|
2844
|
7221
|
21219
|
2,626
|
38547
|
|
8
|
17
|
cambium
|
35
|
|
0,79
|
3,30
|
7,47
|
0,51
|
3665
|
7424
|
21235
|
2,298
|
34860
|
Tableau 4. 1 Synthèse des différents
résultats expérimentaux sur l'Epicéa
|
PM
|
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
|
Secteur
|
Distance à la moelle
(cm)
|
Nature
|
ICC
(udef)
|
AMFö en degrés
|
d
(12%)
|
RR
en %
|
RT
en %
|
RL
en %
|
EL(CPR)
en MPa
|
EL(PT)
en MPa
|
Fn en
N
|
D en mm
|
W en kJ
|
|
1
|
7
|
BC
|
|
|
0,56
|
1,87
|
3,17
|
3,43
|
1695
|
2800
|
11743
|
3,051
|
27417
|
|
1
|
4
|
BC
|
|
|
0,49
|
2,10
|
3,80
|
2,70
|
1423
|
2562
|
9595
|
2,633
|
18673
|
|
1
|
10
|
BC
|
|
|
0,67
|
1,88
|
2,80
|
3,85
|
1295
|
3420
|
12542
|
2,455
|
19059
|
|
1
|
11
|
BC
|
-127
|
44,6
|
0,66
|
2,08
|
3,03
|
4,13
|
1655
|
3247
|
12970
|
2,092
|
16277
|
|
2
|
9
|
BC
|
|
|
0,57
|
2,14
|
4,06
|
2,85
|
1784
|
2473
|
13025
|
3,201
|
29475
|
|
2
|
11,5
|
BC
|
-177
|
44,8
|
0,64
|
2,21
|
2,58
|
3,99
|
1776
|
2933
|
12032
|
2,196
|
8877
|
|
3
|
4
|
BN+BC
|
|
|
0,42
|
1,78
|
4,31
|
2,78
|
1586
|
2820
|
8395
|
2,017
|
12780
|
|
3
|
7
|
BN+BC
|
|
|
0,41
|
3,25
|
6,33
|
0,47
|
2577
|
4914
|
9644
|
1,341
|
9443
|
|
3
|
8
|
BN
|
|
|
0,43
|
3,74
|
6,23
|
0,31
|
2778
|
5442
|
9460
|
0,776
|
3854
|
|
3
|
10
|
fin BC
|
70
|
|
0,43
|
2,81
|
6,21
|
0,65
|
1949
|
4944
|
9353
|
1,344
|
7691
|
|
4
|
6
|
BN
|
20
|
24,8
|
0,41
|
4,04
|
6,84
|
0,21
|
2363
|
5629
|
9824
|
1,093
|
6472
|
|
5
|
2
|
BN
|
|
|
0,36
|
3,66
|
6,57
|
0,36
|
1651
|
3955
|
7340
|
1,321
|
6158
|
|
5
|
5
|
BO
|
-15
|
|
0,39
|
4,11
|
6,51
|
0,31
|
2104
|
5504
|
6439
|
0,717
|
3233
|
112
Vers une description de l'anisotropie élastique du bois de
réaction
|
PM
|
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
|
Secteur
|
Distance à la moelle
(cm)
|
Nature
|
ICC
(udef)
|
AMFö en degrés
|
d
(12%)
|
RR
en %
|
RT
en %
|
RL
en %
|
EL(CPR)
en MPa
|
EL(PT)
en MPa
|
Fn en
N
|
D en mm
|
W en kJ
|
|
6
|
4,5
|
BO
|
|
20,2
|
0,39
|
4,12
|
6,12
|
0,19
|
2050
|
5678
|
7701
|
0,927
|
4864
|
|
7
|
6
|
fin BC
|
|
|
0,45
|
2,60
|
4,31
|
1,37
|
2315
|
4356
|
10720
|
1,407
|
10303
|
|
8
|
8,5
|
BC
|
|
|
0,63
|
2,16
|
2,92
|
3,13
|
1972
|
3626
|
13463
|
2,624
|
26197
|
Tableau 4 -2 Synthèse des différents
résultats expérimentaux sur le Pin maritime
|
PS2
|
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
|
Secteur
|
Distance à la moelle
(cm)
|
Nature
|
ICC
(udef)
|
AMF en degrés
|
d
(12%)
|
RR
en %
|
RT
en %
|
RL
en %
|
EL(CPR)
en MPa
|
EL(PT)
en MPa
|
Fn en
N
|
D en mm
|
W en kJ
|
|
1
|
4,5
|
BC
|
|
|
0,65
|
|
|
|
1822
|
4201
|
12896
|
1,963
|
15884
|
|
1
|
7,5
|
BC
|
|
|
0,65
|
|
|
|
2305
|
4222
|
14363
|
2,299
|
22562
|
|
1
|
10,5
|
BC
|
|
|
0,65
|
|
|
|
2203
|
4807
|
13929
|
1,751
|
16613
|
|
1
|
13,5
|
milieu du
BC
|
-100
|
35,7
|
0,65
|
1,57
|
4,16
|
1,97
|
2445
|
5082
|
14728
|
1,605
|
16063
|
|
2
|
13
|
fin du BC
|
-90
|
32,7
|
0,52
|
1,41
|
4,77
|
1,33
|
3017
|
6436
|
13415
|
1,597
|
14846
|
|
3
|
5
|
BN+BC
|
|
|
0,48
|
|
|
|
3806
|
9026
|
13001
|
0,753
|
5936
|
|
3
|
8,5
|
BN+BC
|
|
|
0,45
|
|
|
|
2635
|
6925
|
11730
|
0,964
|
6954
|
|
3
|
11
|
BN
|
31
|
|
0,49
|
4,31
|
8,98
|
0,27
|
3998
|
9870
|
14705
|
0,797
|
6142
|
|
4
|
8
|
BN
|
33
|
23,0
|
0,48
|
3,63
|
9,07
|
0,07
|
3806
|
9026
|
13001
|
0,753
|
5936
|
|
5
|
3,5
|
BN
|
2
|
|
0,51
|
|
8,61
|
0,14
|
2753
|
6743
|
10314
|
0,825
|
4711
|
|
6
|
5,5
|
BO
|
24
|
|
0,52
|
|
8,49
|
0,26
|
2674
|
7661
|
9753
|
0,968
|
5572
|
|
7
|
7,5
|
BN +BC
|
44
|
23,0
|
0,49
|
4,71
|
9,33
|
0,14
|
3678
|
9030
|
10035
|
0,895
|
5665
|
|
8
|
11
|
BC
|
-76
|
|
0,64
|
2,59
|
6,84
|
0,42
|
2507
|
5612
|
14481
|
2,063
|
20221
|
Tableau 4 -3 Synthèse des résultats
expérimentaux sur le Pin sylvestre
113
Vers une description de l'anisotropie élastique du bois de
réaction
Angles des microfibrilles (ö)
|
Espèces
|
Echantillon
|
Nature
|
AMF ö en degrés
|
Ecart type en degrés
|
|
Epicéa (E3)
|
1.16
|
BC
|
32,40
|
3,87
|
|
2.12,5
|
BC
|
30,46
|
3,46
|
|
4.5
|
BN
|
17,74
|
3,83
|
|
7.13
|
BN
|
22,62
|
3,62
|
|
|
|
|
|
|
Pin sylvestre (PS2)
|
1.13,5
|
BC
|
35,67
|
3,74
|
|
2.13
|
BC
|
32,73
|
4,21
|
|
4.8
|
BN
|
23,02
|
4,04
|
|
7.7,5
|
BN
|
22,96
|
3,37
|
|
|
|
|
|
|
Pin maritime (PM)
|
1.11
|
BC
|
44,59
|
4,88
|
|
2.11,5
|
BC
|
44,80
|
3,29
|
|
4.6
|
BN
|
24,77
|
4,05
|
|
6.4,5
|
BN
|
20,19
|
5,18
|
Tableau 4-4 Comparaison pour trois essences
résineuses des mesures de l'angle des microfibrilles ö
du
bois normal et du bois de compression
(J.Ruelle)

AMF
Figure 4.6 Détail d'une coupe radiale dans la
sous couche S2 de Pin maritime, traitement par
l'iodure de
potassium et l'acide nitrique (Senft et al ,1985). Barre
d'échelle : 25 um. Grossissement 500X. Ruelle
(2003).
L'examen des différentes colonnes (C à K)
des Tableaux 4.1 à 4.3 permet de dégager très
nettement les particularités mécano physiques des
éprouvettes de bois de compression.
La densité à 12%
Pour une même essence, la densité (colonne
C) à 12% des éprouvettes BC est toujours supérieure
à celles des éprouvettes BN. Les valeurs les plus fortes de
densité des éprouvettes BN et BC sont obtenues sur
l'Epicéa commun. Elles sont respectivement de 0,56 et 0,82 pour
les éprouvettes E3 7.13 et E3.8.13.
114
Vers une description de l'anisotropie élastique du bois de
réaction
Les retraits
La relation d'ordre classique entre les différents
retraits des éprouvettes de bois normal (retrait transverses très
supérieurs au retrait longitudinal) est vérifiée à
travers les résultats consignés dans les Tableaux 4.1, 4.2 et
4.3. Cette relation est fortement modifiée sur les éprouvettes de
bois de compression. En effet, le retrait longitudinal est, sur ce type
d'échantillon, toujours supérieur aux deux retraits
transverses
Ce résultat est d'ailleurs bien connu dans la
littérature ; de forts retraits longitudinaux sont attribués
(notamment) à un angle des microfibrilles particulièrement ouvert
(Yamamoto et al,
2001). Des éprouvettes taillées dans une zone
proche de la limite bois de compression/ bois normal (PM 3.4, PM 3.7, PS
2.13, E3.12.5) présentent encore des retraits longitudinaux
supérieurs à ceux du bois normal.
Propriétés mécaniques des
éprouvettes de bois de compression
a) Modules élastiques longitudinaux
Nous avons choisi de ne faire figurer dans les Tableaux 4.1
à 4.3 que les modules d'élasticité longitudinaux EL(PT)
tirées d'une percussion tangentielle (colonne H). Comparativement
à une percussion radiale, une sollicitation tangentielle
permet en effet de s'affranchir d'une surestimation de la
rigidité dans un milieu particulièrement rigide (bois final par
exemple).
Quelque soit la méthode utilisée, les modules
d'élasticité longitudinaux (colonnes G et H des Tableaux 4.1
à 4.3) des éprouvettes de bois de compression sont
toujours plus faibles que ceux obtenus sur le bois normal (BN).
Ces résultats marquent la différence
nette des propriétés élastiques entre le bois
de compression et le bois normal ; le bois de compression bien que nettement
plus dense que le bois normal présente un module élastique
longitudinal plus faible.
Les écarts les plus importants entre les modules
élastiques longitudinaux du bois de compression et ceux du bois
normal sont obtenus par la méthode vibratoire (Tableau, colonnes
H des Tableaux 4.1 à 4.3).
b) Comparaisons des modules d'élasticité
longitudinaux obtenus par méthode vibratoire et par compression
jusqu'à rupture
Les écarts les plus importants entre les modules
élastiques longitudinaux du bois de compression et ceux du bois
normal sont obtenus par la méthode vibratoire (Tableaux 4.1 à
4.3, colonnes G et H).
Les mesures des modules élastiques, obtenues sur des
éprouvettes de même origine (BC ou
BN) sont significativement différentes selon la
méthode utilisée (méthode vibratoire ou essai
de compression, Tableaux 4.1 à 4.3, colonnes G et H,
Figures 4.7, 4.8 et 4.9). Un rapport de l'ordre de deux entre la mesure par
méthode vibratoire EL(PT) et la mesure tirée de l'essai de
compression EL(CPR) est observé. Ce rapport n'est pas spécifique
à la nature (BN ou BC) de l'éprouvette testée.
115
Vers une description de l'anisotropie élastique du bois de
réaction

Figure 4.7 Comparaison sur le Pin sylvestre du module
élastique longitudinal obtenu par méthode
vibratoire au module tiré de l'essai de
compression
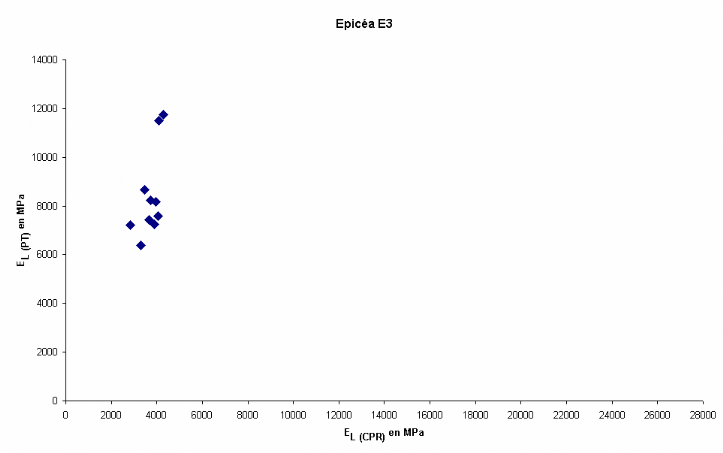
Figure 4.8 Comparaison sur l'Epicéa du module
élastique longitudinal obtenu par méthode vibratoire
au
module tiré de l'essai de compression
116
Vers une description de l'anisotropie élastique du bois de
réaction
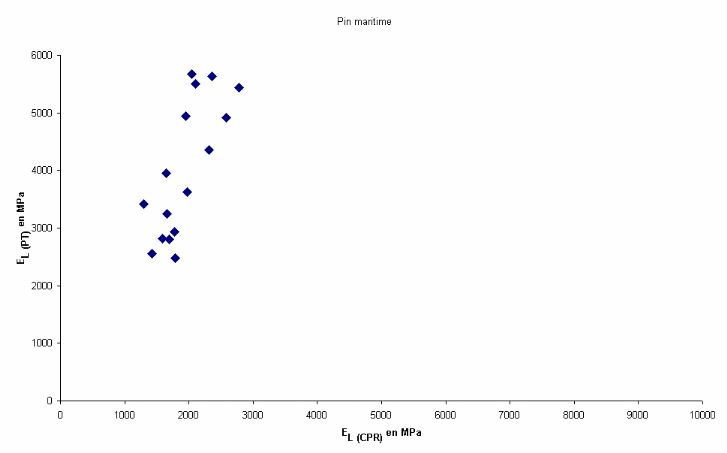
Figure 4.9 Comparaison sur le Pin maritime du module
élastique longitudinal obtenu par méthode
vibratoire au module tiré de l'essai de
compression
c) Travail jusqu'à la force maximale appliquée
durant l'essai
Lors des essais mécaniques, la force maximale Fn
relevée sur les éprouvettes BC est systématiquement
supérieure à celle relevée sur les éprouvettes BN
(Figures 4.10). Le module élastique longitudinal calculé sur les
éprouvettes BC est quand à lui toujours inférieur à
celui des éprouvettes BN.
Pour rendre compte de ces deux tendances constatées
sur les trois essences, le travail W
nécessaire à une déformation maximale de
chaque type d'éprouvette été évalué en
calculant
l'aire de chaque courbe située entre l'origine et la force
maximale
Fn . En notant di chaque
déplacement élémentaire et Fi chaque force
relevée le travail W est donc
(4.10)
n -1
w =
i = 0
1
(d
2
i +1
d i
)(Fi +1
+ Fi )
Les résultats présentés en colonne K des
Tableaux 4.1 à 4.3 confirment que le travail W est
plus important pour des éprouvettes de bois de compression
que pour des éprouvettes de bois normal.
Compte tenu du rôle bio mécanique du bois de
compression dans l'arbre (gravitropisme), ce résultat apparaît
cohérent. Le bois de compression est moins rigide que le bois normal et
se déforme plus avant de rompre.
117
Vers une description de l'anisotropie élastique du bois de
réaction

Figure 4.10 Comparaison des courbes expérimentales
(essai de compression) obtenues sur le bois de
compression et le bois normal
c) Modules d'élasticité des échantillons
cubiques
Les résultats obtenus sur les échantillons cubiques
sont reportés dans le Tableau 4.5.
Les modules élastiques longitudinaux
déterminés sur les cubes sont tous inférieures aux
modules élastiques évalués par méthode vibratoire
ou à ceux tirés des essais de compression jusqu'à
rupture.
Si la zone 1 peut être à coup sur qualifiée
de zone de bois de compression sur les 3 essences
en regard des densités mesurées, la zone 2 bien
que fortement colorée correspond plus à un mélange de bois
de compression et de bois normal. Les modules élastiques longitudinaux
de cette zone 1 sont tous inférieurs aux modules élastiques des
zones 2, 3 et 4. Cette même zone
2 présente sur les 2 essences des modules
élastiques longitudinaux légèrement supérieurs
à celle de la zone 1, la classification de la zone 2 comme
mélange BC+BN est donc vraisemblable. Une distinction des
différents types de bois dans la rondelle ne peut être
tentée sur un seul critère de coloration.
Les modules transverses sont fortement disperses, il
apparaît difficile de distinguer le bois de compression des autres
types de bois. On remarque néanmoins que le module radial est
supérieur au module tangentiel (excepté pour les deux
échantillons de E1A1 et pour le premier échantillon de
E1A4). Dans ces trois échantillons la tangente aux cernes n'est
pas parfaitement parallèle à la face radiale du cube. Ce
défaut est particulièrement marqué pour
les échantillons de E1A1 (angle de 35 degrés entre
la tangente au cerne et la face radiale du cube). Pour le premier
échantillon de E1A4, le même angle n'est « que » de 10
degrés.
Ces résultats partiels montrent que la procédure
de découpe des cubes demande à être revue. Plusieurs
échantillons ont présenté des coins fortement
ébréchés, voire cassés, en particulier ceux du Pin
maritime.
118
Vers une description de l'anisotropie élastique du bois de
réaction
|
Echantillons
|
Zone
|
Densité
|
Nature
|
EL en
GPa
|
ER en
GPa
|
ET en
GPa
|
|
|
|
|
|
|
|
|
E1A1
|
1
|
0,88
|
BC
|
2,68
|
0,63
|
0,95
|
|
|
0,67
|
BC
|
2,22
|
0,56
|
0,66
|
|
|
|
|
|
|
|
|
E1A2
|
2
|
0,39
|
BC+BN
|
3,83
|
0,51
|
0,29
|
|
|
0,41
|
BC+BN
|
4,69
|
0,57
|
0,32
|
|
|
|
|
|
|
|
|
E1A3
|
3
|
0,40
|
BO
|
4,36
|
0,12
|
0,33
|
|
|
0,45
|
BO
|
4,06
|
0,33
|
0,25
|
|
|
|
|
|
|
|
|
E1A4
|
4
|
0,39
|
BO
|
3,40
|
0,46
|
0,24
|
|
|
0,37
|
BO
|
4,55
|
0,16
|
0,12
|
|
|
|
|
|
|
|
|
PS21
|
1
|
0,52
|
BC
|
2,27
|
0,74
|
0,21
|
|
|
0,51
|
BC
|
1,44
|
1,20
|
0,26
|
|
|
0,48
|
BC
|
1,42
|
0,90
|
0,28
|
|
|
|
|
|
|
|
|
PS22
|
2
|
0,38
|
BC+BN
|
2,21
|
1,61
|
0,25
|
|
|
0,40
|
BC+BN
|
3,20
|
-
|
-
|
|
|
0,40
|
BC+BN
|
3,39
|
1,30
|
0,28
|
|
|
|
|
|
|
|
|
PS23
|
3
|
0,45
|
BO
|
1,81
|
1,33
|
0,41
|
|
|
0,48
|
BO
|
4,01
|
2,97
|
0,42
|
|
|
0,46
|
BO
|
3,54
|
1,88
|
0,42
|
|
|
|
|
|
|
|
|
PS24
|
4
|
0,45
|
BO
|
5,04
|
0,96
|
0,60
|
|
|
0,47
|
BO
|
2,74
|
0,58
|
0,57
|
|
|
0,52
|
BO
|
2,82
|
1,08
|
0,44
|
Tableau 4-5 Résultats partiels obtenus sur les
échantillons cubiques
119
Vers une description de l'anisotropie élastique du bois de
réaction
Paramètres géométriques cellulaires
A partir des résultats fournis par Ruelle, nous
avons calculé les valeurs de nos paramètres
géométriques DR, DT, eR, eT (Tableau 4.9) à partir des
valeurs FLDR, FLDT, FePR, FePT
(Tableau 4.6).
L'examen des valeurs portées dans le Tableau 4.9
permet de comparer les valeurs des paramètres
géométriques du bois initial normal à ceux de bois initial
de compression.
Comparaison entre le bois initial normal et le bois initial de
compression
Conformément à la littérature, quelque
soit l'espèce il n'y a pas de différences notables en terme de
diamètre radial et tangentiel ou en terme d'épaisseur
entre les deux tissus. Les diamètres radial et tangentiel et les
épaisseurs pariétales déduits ne sont pas
différents
Comparaison entre le bois final normal et le bois final de
compression
La différence essentielle entre le bois final de
compression et le bois final normal réside dans les épaisseurs de
parois qui sont toujours supérieures dans le bois final de
compression
Les diamètres radial et tangentiel déduits ne
peuvent être considérés comme significativement
différents de ceux du bois final normal
120
Vers une description de l'anisotropie élastique du bois de
réaction
|
Espèce
|
Echantillon
|
|
Nature
|
FLDR
|
|
FLDT
|
|
FepPR
|
|
FepPT
|
|
|
|
|
|
moyenne
|
écart-type
|
moyenne
|
écart-type
|
moyenne
|
écart-type
|
moyenne
|
écart-type
|
|
Epicea
|
1.16
|
Tot_cerne
|
BC
|
17,30
|
9,72
|
18,12
|
6,04
|
8,82
|
2,95
|
10,80
|
3,95
|
|
E3
|
|
Bois initial
|
|
31,14
|
5,44
|
24,76
|
4,60
|
4,81
|
0,38
|
6,29
|
3,69
|
|
|
Bois final
|
|
6,86
|
2,77
|
12,97
|
4,35
|
11,31
|
2,56
|
14,75
|
1,83
|
|
2.12,5
|
Tot_cerne
|
BC
|
18,36
|
10,43
|
18,12
|
6,58
|
8,14
|
2,50
|
9,70
|
3,06
|
|
|
Bois initial
|
|
34,95
|
5,69
|
25,24
|
5,22
|
4,35
|
0,43
|
5,46
|
0,85
|
|
|
Bois final
|
|
7,04
|
3,19
|
12,02
|
4,80
|
10,45
|
1,93
|
13,44
|
2,11
|
|
4.5
|
Tot_cerne
|
BN
|
26,75
|
10,23
|
21,76
|
4,94
|
5,09
|
1,52
|
6,38
|
2,45
|
|
|
Bois initial
|
|
36,83
|
6,27
|
23,52
|
4,75
|
3,82
|
0,34
|
4,87
|
0,75
|
|
|
Bois final
|
|
11,00
|
5,41
|
17,36
|
4,16
|
7,39
|
1,13
|
10,11
|
2,63
|
|
7.13
|
Tot_cerne
|
BN
|
26,02
|
10,60
|
22,55
|
6,55
|
6,58
|
2,26
|
7,00
|
3,46
|
|
|
Bois initial
|
|
34,10
|
5,98
|
25,89
|
6,38
|
4,25
|
0,39
|
4,83
|
0,59
|
|
|
Bois final
|
|
8,75
|
5,61
|
14,42
|
4,56
|
9,88
|
1,95
|
12,65
|
3,93
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pin maritime
|
1.11
|
Tot_cerne
|
BC
|
17,84
|
6,19
|
20,13
|
5,27
|
6,97
|
2,13
|
9,42
|
2,46
|
|
PM
|
|
Bois initial
|
|
19,21
|
4,40
|
22,98
|
4,76
|
3,91
|
0,97
|
5,46
|
0,99
|
|
|
Bois final
|
|
20,96
|
9,72
|
21,65
|
4,86
|
6,26
|
1,39
|
8,96
|
1,33
|
|
2.11,5
|
Tot_cerne
|
BC
|
16,65
|
4,42
|
18,67
|
5,23
|
8,19
|
1,21
|
10,24
|
1,28
|
|
|
Bois initial
|
|
20,19
|
4,41
|
19,71
|
5,55
|
7,91
|
0,81
|
9,31
|
0,95
|
|
|
Bois final
|
|
14,74
|
4,90
|
17,34
|
5,09
|
7,80
|
1,30
|
10,11
|
1,07
|
|
4. 6
|
Tot_cerne
|
BN
|
26,20
|
8,77
|
29,12
|
6,56
|
5,71
|
0,97
|
7,08
|
1,31
|
|
|
Bois initial
|
|
33,46
|
5,79
|
34,61
|
5,35
|
5,25
|
0,43
|
6,69
|
0,50
|
|
|
Bois final
|
|
15,56
|
5,43
|
28,46
|
5,73
|
6,12
|
1,02
|
8,77
|
1,18
|
|
6. 4.5
|
Tot_cerne
|
BN
|
25,55
|
9,47
|
28,51
|
7,15
|
5,15
|
1,11
|
6,56
|
2,01
|
|
|
Bois initial
|
|
34,35
|
6,43
|
31,35
|
5,90
|
4,84
|
0,51
|
5,67
|
0,54
|
|
|
Bois final
|
|
16,14
|
4,65
|
23,00
|
5,67
|
6,22
|
1,15
|
8,60
|
1,24
|
Tableau 4-6 Critères anatomiques mesurés
par Ruelle sur les bois initial et final du bois normal (BN) et du bois de
compression (BC) d'Epicéa et de Pin maritime
121
Vers une description de l'anisotropie élastique du bois de
réaction
|
Espèce
|
Echantillon
|
|
Nature
|
eT(um)
|
|
DT(um)
|
|
eR(um)
|
|
DR(um)
|
|
|
|
|
|
|
écart type
|
|
écart type
|
moy
|
écart type
|
|
écart type
|
|
Epicea
|
1.16
|
Tot_cerne
|
BC
|
4,41
|
1,48
|
28,92
|
9,99
|
5,40
|
1,98
|
26,13
|
12,67
|
|
E3
|
|
Bois initial
|
|
2,40
|
0,19
|
31,05
|
8,29
|
3,15
|
1,85
|
35,95
|
5,82
|
|
|
Bois final
|
|
5,65
|
1,28
|
27,73
|
6,18
|
7,38
|
0,91
|
18,17
|
5,32
|
|
2.12,5
|
Tot_cerne
|
BC
|
4,07
|
1,25
|
27,81
|
9,64
|
4,85
|
1,53
|
26,49
|
12,93
|
|
|
Bois initial
|
|
2,18
|
0,21
|
30,70
|
6,07
|
2,73
|
0,43
|
39,30
|
6,12
|
|
|
Bois final
|
|
5,23
|
0,97
|
25,46
|
6,90
|
6,72
|
1,05
|
17,49
|
5,12
|
|
4.5
|
Tot_cerne
|
BN
|
2,54
|
0,76
|
28,14
|
7,39
|
3,19
|
1,22
|
31,84
|
11,75
|
|
|
Bois initial
|
|
1,91
|
0,17
|
28,39
|
5,51
|
2,43
|
0,38
|
40,64
|
6,61
|
|
|
Bois final
|
|
3,69
|
0,56
|
27,47
|
6,79
|
5,05
|
1,31
|
18,39
|
6,54
|
|
7.13
|
Tot_cerne
|
BN
|
3,29
|
1,13
|
29,55
|
10,01
|
3,50
|
1,73
|
32,60
|
12,86
|
|
|
Bois initial
|
|
2,13
|
0,20
|
30,72
|
6,97
|
2,41
|
0,29
|
38,36
|
6,37
|
|
|
Bois final
|
|
4,94
|
0,97
|
27,07
|
8,49
|
6,32
|
1,97
|
18,63
|
7,56
|
|
Pin maritime
|
1.11
|
Tot_cerne
|
BC
|
3,48
|
1,06
|
29,54
|
7,73
|
4,71
|
1,23
|
24,81
|
8,32
|
|
PM
|
|
Bois initial
|
|
1,95
|
0,49
|
28,44
|
5,75
|
2,73
|
0,50
|
23,11
|
5,37
|
|
|
Bois final
|
|
3,13
|
0,70
|
30,62
|
6,19
|
4,48
|
0,66
|
27,21
|
11,12
|
|
2.11, 5
|
Tot_cerne
|
BC
|
4,09
|
0,61
|
28,91
|
6,51
|
5,12
|
0,64
|
24,84
|
5,63
|
|
|
Bois initial
|
|
3,96
|
0,41
|
29,02
|
6,50
|
4,66
|
0,47
|
28,10
|
5,22
|
|
|
Bois final
|
|
3,90
|
0,65
|
27,44
|
6,16
|
5,05
|
0,54
|
22,54
|
6,20
|
|
4.6
|
Tot_cerne
|
BN
|
2,86
|
0,48
|
36,20
|
7,87
|
3,54
|
0,65
|
31,91
|
9,74
|
|
|
Bois initial
|
|
2,62
|
0,22
|
41,30
|
5,86
|
3,34
|
0,25
|
38,71
|
6,23
|
|
|
Bois final
|
|
3,06
|
0,51
|
37,23
|
6,90
|
4,39
|
0,59
|
21,68
|
6,45
|
|
6.4, 5
|
Tot_cerne
|
BN
|
2,58
|
0,56
|
35,07
|
9,15
|
3,28
|
1,00
|
30,71
|
10,58
|
|
|
Bois initial
|
|
2,42
|
0,26
|
37,02
|
6,44
|
2,83
|
0,27
|
39,19
|
6,94
|
|
|
Bois final
|
|
3,11
|
0,58
|
31,60
|
6,91
|
4,30
|
0,62
|
22,37
|
5,80
|
Tableau 4.7 Paramètres géométriques
cellulaires du réseau nid d'abeille d'Epicéa et de Pin maritime
déduits des mesures de Ruelle
122
Vers une description de l'anisotropie élastique du bois de
réaction
|
Espèce
|
Echantillon
|
|
Nature
|
FLDR
|
|
FLDT
|
|
FepPR
|
|
FepPT
|
|
|
|
|
|
moyenne
|
écart-type
|
moyenne
|
écart-type
|
moyenne
|
écart-type
|
moyenne
|
écart-type
|
|
Pin sylvestre
|
1.13.5
|
Tot_cerne
|
BC
|
22,09
|
9,16
|
20,30
|
5,50
|
7,70
|
2,38
|
8,85
|
2,09
|
|
PS2
|
|
Bois initial
|
|
34,90
|
7,26
|
23,60
|
4,57
|
6,01
|
2,76
|
7,02
|
1,06
|
|
|
Bois final
|
|
15,10
|
5,42
|
18,50
|
4,73
|
6,77
|
1,97
|
8,31
|
1,38
|
|
2.13
|
Tot_cerne
|
BC
|
26,19
|
11,63
|
21,45
|
5,51
|
7,06
|
2,21
|
8,14
|
2,32
|
|
|
Bois initial
|
|
41,48
|
6,49
|
25,75
|
5,66
|
5,10
|
0,65
|
5,47
|
0,87
|
|
|
Bois final
|
|
13,40
|
4,97
|
17,97
|
4,11
|
7,45
|
1,95
|
9,31
|
1,33
|
|
4.8
|
Tot_cerne
|
BN
|
27,98
|
13,04
|
23,38
|
6,49
|
7,71
|
3,22
|
8,33
|
3,05
|
|
|
Bois initial
|
|
44,25
|
7,47
|
29,35
|
5,33
|
4,97
|
0,55
|
5,62
|
0,99
|
|
|
Bois final
|
|
13,11
|
5,99
|
19,85
|
4,33
|
7,88
|
2,29
|
11,85
|
2,47
|
|
7.7.5
|
Tot_cerne
|
BN
|
24,88
|
11,78
|
20,22
|
6,57
|
7,39
|
2,85
|
8,75
|
3,32
|
|
|
Bois initial
|
|
39,91
|
5,96
|
25,64
|
5,19
|
4,58
|
0,37
|
5,06
|
0,79
|
|
|
Bois final
|
|
14,26
|
5,09
|
17,35
|
4,49
|
8,56
|
2,06
|
11,12
|
1,74
|
Tableau 4-8 Critères anatomiques mesurés
par Ruelle sur le Pin sylvestre
|
Espèce
|
Echantillon
|
|
Nature
|
eT (um)
|
|
DT (um)
|
|
eR (um)
|
|
DR (um)
|
|
|
|
|
|
|
écart type
|
|
écart type
|
moy
|
écart type
|
|
écart type
|
|
Pin sylvestre
PS2
|
1.13, 5
|
Tot_cerne
|
BC
|
3,85
|
1,19
|
29,15
|
7,59
|
4,42
|
1,05
|
29,79
|
11,54
|
|
|
Bois initial
|
|
3,00
|
1,38
|
30,61
|
5,63
|
3,51
|
0,53
|
40,90
|
10,02
|
|
|
Bois final
|
|
3,39
|
0,99
|
26,81
|
6,11
|
4,16
|
0,69
|
21,88
|
7,39
|
|
2.13
|
Tot_cerne
|
BC
|
3,53
|
1,10
|
29,59
|
7,83
|
4,07
|
1,16
|
33,25
|
13,83
|
|
|
Bois initial
|
|
2,55
|
0,32
|
31,22
|
6,52
|
2,74
|
0,43
|
46,58
|
7,13
|
|
|
Bois final
|
|
3,72
|
0,97
|
27,28
|
5,45
|
4,66
|
0,67
|
20,84
|
6,92
|
|
4.8
|
Tot_cerne
|
BN
|
3,86
|
1,61
|
31,71
|
9,54
|
4,16
|
1,53
|
35,70
|
16,26
|
|
|
Bois initial
|
|
2,49
|
0,27
|
34,96
|
6,32
|
2,81
|
0,50
|
49,22
|
8,02
|
|
|
Bois final
|
|
3,94
|
1,14
|
31,70
|
6,80
|
5,92
|
1,23
|
20,99
|
8,27
|
|
7.7, 5
|
Tot_cerne
|
BN
|
3,70
|
1,43
|
28,98
|
9,89
|
4,38
|
1,66
|
32,28
|
14,63
|
|
|
Bois initial
|
|
2,29
|
0,18
|
30,69
|
5,98
|
2,53
|
0,40
|
44,49
|
6,33
|
|
|
Bois final
|
|
4,28
|
1,03
|
28,47
|
6,23
|
5,56
|
0,87
|
22,82
|
7,15
|
Tableau 4-9 Paramètres géométriques
du nid d'abeilles déduits des mesures de Ruelle sur le Pin
sylvestre
123
Vers une description de l'anisotropie élastique du bois de
réaction
4.2.3 Influence de modifications anatomiques sur les
caractéristiques élastiques prédites.
L'objet de ce paragraphe est d'évaluer l'influence
sur les caractéristiques élastiques du
RSV de certaines modifications structurales essentielles entre
un bois normal et un bois de compression. Cette estimation s'est faite en
faisant varier les valeurs des paramètres descriptifs de
l'anisotropie élastique du Résineux Standard Virtuel selon
les tendances générales évoquées dans la
littérature. La cohérence des valeurs numériques
attribuées aux paramètres descriptifs de cette distorsion du
RSV a de plus été vérifiée en regard des
résultats anatomiques obtenus par Ruelle.
A l'échelle du cerne : une masse volumique cible de
0,65 g/ cm3
En regard des différents résultats obtenus par
A.THIBAUT, une valeur de 0,65 g/cm3 a
été choisie comme masse volumique cible pour le
bois de compression. La texture et la fraction volumique en rayons ligneux
du bois de compression n'ont pas été modifiées,
elles ne sont en outre pas identifiées dans la littérature.
A l'échelle tissulaire.
Conformément à la littérature
(Timell, 1986), la structure anatomique des tissus bois initial et
rayon ligneux du bois de compression a été
considérée comme strictement identique à celle des
mêmes tissus du RSV.
Les modifications envisagées ont donc porté sur les
paramètres géométriques cellulaires
du bois final RSV.
Les diamètres radial et tangentiel doivent être
respectivement égal et légèrement inférieur aux
mêmes paramètres décrivant le bois final RSV.
Compte tenu de ces deux dernières contraintes,
l'application de la relation 3.12 du chapitre 3, permet d'envisager
une épaisseur de paroi de bois final de 4,60 um plus de
60% supérieure à celle décrivant le
bois final du RSV (2,87 um). La conséquence immédiate de
cette modification est une augmentation de plus de 50% de la masse
volumique de ce même tissu (de 0.73 à 1.10 g/cm3,
colonne A Tableau 4.10).
Sous l'ensemble de ces conditions, les colonnes A des Tableaux
4.10 et 4.11 représentent des jeux de paramètres cellulaires
possibles ainsi que les caractéristiques élastiques
calculées.
Il est alors possible d'évaluer l'impact de ces
modifications sur les modules élastiques prédits par la
modélisation.
Le module élastique le plus sensible à une
augmentation de 50% de la masse volumique
du bois final est le module longitudinal EL qui passe d'une
valeur de 13,1 GPa pour le RSV à 18,47 GPa dans le bois de compression
(colonnes RSV et A, Tableau 4.11). Cette modification exprime directement la
sensibilité du modèle à une diminution de la
porosité
(i.e à une augmentation de la densité). La
deuxième modification particulièrement notable concerne le module
élastique tangentiel ET dont la valeur passe de 0,635 GPa à 1,05
GPa ;
124
Vers une description de l'anisotropie élastique du bois de
réaction
cette rigidification est directement imputable à la
réduction du terme de flexion des parois
par une forte augmentation de l'épaisseur
pariétale. A l échelle ultrastructurale
Conformément à des constatations cytologiques
déjà évoquées, le taux de microfibrilles a
été abaissé (colonnes B des Tableaux 4.10 et 4.11)
à 30%. La modification la plus remarquable a lieu sur le
module élastique longitudinal EL qui passe d'une valeur de
18,47 GPa à 11,70 GPa. Les modules transverses
sont assez peu sensibles à cette modification.
Une modification de l'angle des microfibrilles a
ensuite été envisagée (colonnes C des Tableaux 4.10
et 4.11) dans les deux tissus bois initial et bois final. L'angle adopté
a été fixé initialement à 45 degrés,
valeur pouvant être considérée comme maximale dans
le bois de compression.
La modification la plus sensible des
caractéristiques élastiques a porté sur les modules
transverses. Le module ER passe ainsi d'une valeur de 1,15 GPa
à 3,36 GPa, dans le même temps le module tangentiel passe de
1,15 GPa à 3,16 GPa. Cette modification des caractéristiques
élastiques macroscopiques est directement imputable à une
rigidification transverse de la double paroi par une augmentation de l'angle
des microfibrilles (ö).
Le module longitudinal EL dont la valeur est de 9,08 GPa à
cette étape de la construction apparaît comme une valeur possible
pour un bois de compression.
La valeur de 45 degrés de l'angle des
microfibrilles doit être considérée comme une valeur
maximale. Pour cette raison les évolutions des différents modules
élastiques avec la valeur de l'angle des microfibrilles
insérée dans la modélisation sont reportées
sur la Figure 4.12.
On remarque qu'une diminution de l'angle des microfibrilles a
pour conséquence majeure une augmentation forte du module longitudinal
et une diminution des modules élastiques transverses. Ces mêmes
modules élastiques sont en outre assez proches l'un de l'autre et
ce quelque soit l'angle des microfibrilles (on tend vers une
isotropie transverse).
Pour une valeur d'AMF (ö) de 30 degrés le
module longitudinal passe d'une valeur de
9,08 GPa à 11,07 GPa, les modules transverses
évoluent quant à eux de 3,35 GPa à 2,17
GPa pour ER et de 3,15 à 2,7 GPa pour ET. Plusieurs
facteurs explicatifs de tels résultats peuvent être
évoqués.
Module d'élasticité longitudinal
Le module longitudinal est a priori surestimé par la
modélisation appliquée. Directement
liée à la porosité (relation 2.17
du chapitre 2), l'évaluation du module longitudinal suppose que
les tissus ligneux peuvent être considérés comme des
structures nids d'abeilles à cellules rectangulaires. La
présence dans le plan transverse du bois de compression,
d'espaces intercellulaires quasi systématiques est ici ignorée,
elle conduit de fait à une évaluation par excès du module
longitudinal.
125
Vers une description de l'anisotropie élastique du bois de
réaction
Modules d'élasticité transverses
Dans le bois de compression, la modélisation
prévoit une quasi isotropie transverse
(Figure 4.12). Cette tendance est explicable (relation 3.6 du
chapitre 3) par une diminution
du terme de flexion aF provenant d'une épaisseur
pariétale particulièrement importante
(Figure 4.11). La forme arrondie des cellules contribue sans
doute à un renforcement de la résistance en flexion
(élément BCE envisagé dans le chapitre 2, Figure 2.3).

Figure 4.11 Coupe transversale de Pinus pinaster (bois
final de compression) colorée à la safranine. Grossissement 500X.
Barre d'échelle 25um. Ruelle (2003).
. 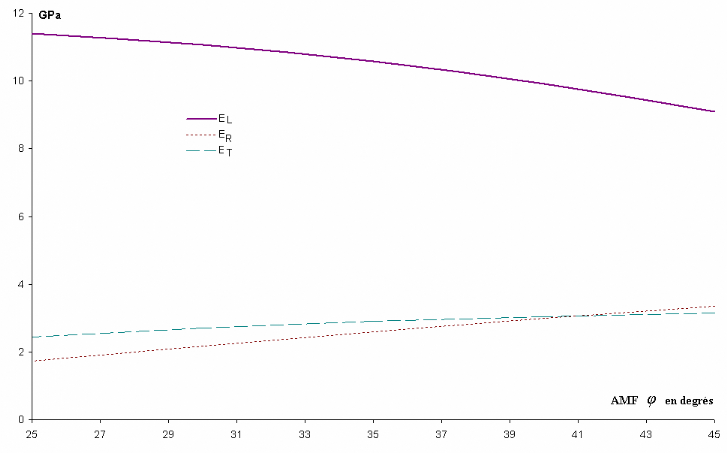
Figure 4.12 Evolutions des différents modules
élastiques d'une distorsion du bois RSV avec l'angle des
microfibrilles
126
Vers une description de l'anisotropie élastique du bois de
réaction
|
RSV
|
VERS UN BOIS DE COMPRESSION
|
|
|
A
|
B
|
C
|
D
|
|
Paroi de cellule bois initial
|
|
|
|
|
|
|
Em matrice en GPa
|
2
|
2
|
2
|
2
|
2
|
|
ím coefficient de Poisson de la matrice
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
|
Ef fibrilles en GPa
|
62
|
62
|
62
|
62
|
62
|
|
AMF dans S2 en degrés
(öi)
|
22
|
22
|
22
|
45
|
30
|
|
V taux de microfibrilles
|
0,5
|
0,5
|
0,3
|
0,3
|
0,3
|
|
|
|
|
|
|
|
Tissu de bois initial
|
|
|
|
|
|
|
DTi diamètre tangentiel en um
|
30
|
30
|
30
|
30
|
30
|
|
eTi épaisseur paroi tangentielle en um
|
1,068
|
1,068
|
1,068
|
1,068
|
1,068
|
|
OV paramètre d'ovalisation Dri/Dti
|
1,25
|
1,25
|
1,25
|
1,25
|
1,25
|
|
ei= eRi/eTi paramètre d'épaisseur
pariétale
|
0,8
|
0,8
|
0,8
|
0,8
|
0,8
|
|
ñinitial masse volumique en g/cm3
|
0,167
|
0,167
|
0,167
|
0,167
|
0,167
|
|
|
|
|
|
|
|
Paroi de cellule de bois final
|
|
|
|
|
|
|
Em matrice en GPa
|
2
|
2
|
2
|
2
|
2
|
|
ím coefficient de Poisson de la matrice
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
|
Ef fibrilles en GPa
|
62
|
62
|
62
|
62
|
62
|
|
AMF dans S2 en degrés
(öf)
|
5,9
|
5,9
|
5,9
|
45
|
30
|
|
V taux de Microfibrilles
|
0,5
|
0,5
|
0,3
|
0,3
|
0,3
|
|
|
|
|
|
|
|
Tissu de bois final
|
|
|
|
|
|
|
DTf diamètre tangentiel en um
|
35
|
31
|
31
|
31
|
31
|
|
eTf épaisseur paroi tangentielle en um
|
2,87
|
4,60
|
4,60
|
4,60
|
4,60
|
|
OV paramètre d'ovalisation DRf/DTf
|
0,43
|
0,485
|
0,485
|
0,485
|
0,485
|
|
ef= eRf/eTf paramètre d'épaisseur
pariétale
|
1
|
1
|
1
|
1
|
1
|
|
ñfinal masse volumique en
g/cm3
|
0,729
|
1,1
|
1,1
|
1,1
|
1,1
|
Tableau 4.10 Paramètres ultrastructuraux et
tissulaires envisagés pour les bois initial et final de
compression
127
Vers une description de l'anisotropie élastique du bois de
réaction
|
RSV
|
A
|
B
|
C
|
D
|
|
Paroi de cellule de rayon
|
|
|
|
|
|
|
Em matrice en GPa
|
2
|
2
|
2
|
2
|
2
|
|
ím coefficient de. Poisson de la matrice
|
0,3
|
0,3
|
0,3
|
0,3
|
0,3
|
|
Ef microfibrilles en GPa
|
60
|
60
|
60
|
60
|
60
|
|
AMF dans S2 en degrés
|
46
|
46
|
46
|
46
|
46
|
|
V taux de microfibrilles
|
0,5
|
0,5
|
0,5
|
0,5
|
0,5
|
|
|
|
|
|
|
|
Tissu de rayon
|
|
|
|
|
|
|
DTr diamètre tangentiel en um
|
34,5
|
34,5
|
34,5
|
34,5
|
34,5
|
|
eTr épaisseur paroi tangentielle en um
|
1,032
|
1,032
|
1,032
|
1,032
|
1,032
|
|
OV paramètre d'ovalisation DRr/DTr
|
1,18
|
1,18
|
1,18
|
1,18
|
1,18
|
|
eR= eRr/eTr paramètre d'épaisseur
pariétale
|
1,5
|
1,5
|
1,5
|
1,5
|
1,5
|
|
ñrayon masse volumique en g/cm3
|
0,202
|
0,202
|
0,202
|
0,202
|
0,202
|
|
|
|
|
|
|
|
Paramètres de cerne
|
|
|
|
|
|
|
Tx texture
|
0,512
|
0,512
|
0,512
|
0,512
|
0,512
|
|
n fraction volumique en rayons en %
|
2
|
2
|
2
|
2
|
2
|
|
|
|
|
|
|
|
Les critères cibles
|
|
|
|
|
|
|
Masse volumique ñ = 0,45 g/cm3
|
0,45
|
0,65
|
0,65
|
0,65
|
0,65
|
|
ER = 1,00 GPa
|
1
|
1,36
|
1,15
|
3,36
|
2,17
|
|
ET = 0,636 GPa
|
0,635
|
1,05
|
1,15
|
3,16
|
2,70
|
|
EL = 13,1 GPa
|
13,1
|
18,47
|
11,70
|
9,08
|
11,07
|
|
EL/ER = 13,1
|
13,1
|
13,6
|
10,19
|
2,70
|
5,101
|
|
ER/ET = 1,57
|
1,57
|
1,29
|
0,99
|
1,06
|
0,80
|
|
|
|
|
|
|
Tableau 4.11. Paramètres ultrastructuraux et
tissulaires des rayons ligneux et paramètres de cerne
envisagés pour le bois de compression
128
Vers une description de l'anisotropie élastique du bois de
réaction
4.2.4 Conclusion
Une campagne expérimentale a permis d'identifier
certaines caractéristiques mécano
physiques du bois de compression de trois essences
résineuses. Le bois de réaction bien que plus dense que le bois
normal montre un module d'élasticité longitudinal bien
inférieur à celui
du bois normal. Des échantillons de ce type de bois
montrent en outre un retrait longitudinal important. Ces singularités
sont attribuées depuis longtemps à un angle des
microfibrilles particulièrement ouvert (pouvant aller jusqu'à 45
degrés).
Des essais de compression jusqu'à rupture ont
montré que ce type de bois se distingue singulièrement du
bois normal par son aptitude à se déformer avant de rompre. Ces
résultats apportent une justification bio mécanique à la
formation du bois de compression dans l'arbre.
L'évaluation des modules élastiques
équivalent apparaît fortement dépendante de la
méthode envisagée. Les plus fortes valeurs sont
déterminées par la méthode vibratoire.
Les résultats des essais de compression sur les
échantillons cubiques montrent que des éprouvettes de bois
de compression présentent un module d'élasticité
longitudinal apparent inférieur à celui d'éprouvettes de
bois opposé et à celui d'éprouvettes constituées
à la fois de bois normal et de bois de compression. Les modules
équivalents transverses déterminés par notre
expérimentation ne permettent pas de distinction nette entre le bois
normal et le bois de compression.
Une distorsion du modèle Résineux Standard Virtuel
a été envisagée afin de tester l'aptitude
du modèle (envisagé jusqu'alors pour le
bois normal) à la prédiction des
propriétés mécaniques élastiques du bois de
compression. Dans le cas du module élastique longitudinal,
la modélisation est apte à décrire la
diminution des propriétés mécaniques avec l'angle des
microfibrilles et prévoit une isotropie dans le plan transverse.
129
Conclusion et perspectives
5 Conclusion et perspectives
Le comportement élastique du matériau bois est
habituellement expliqué par la combinaison des comportements
individuels de multiples éléments structuraux
attachés à chacune des échelles
d'hétérogénéités. Partant de cette
constatation, l'objectif principal de ce travail était
de préciser les paramètres les plus
pertinents susceptibles de conditionner la variabilité de
l'anisotropie élastique du bois des résineux.
Dans ce but, un certain nombre de propositions bibliographiques
ont été intégrées selon une
« intuition » mécanicienne, au sein d'une
modélisation globale multi échelles de l'anisotropie
élastique.
Sur la base d'une étude documentaire
pluridisciplinaire, les sources principales de variabilité intra arbre
de l'anisotropie élastique sont inventoriées dans le
chapitre 1. Les échelles
d'hétérogénéités et de descriptions
envisagées à l'issu de ce recensement sont strictement
limitées à l'essentiel ; l'échelle de la sous
couche pariétale, l'échelle de la double cloison
cellulaire, l'échelle du tissu ligneux et l'échelle du cerne.
Un ensemble de modélisations mécaniques,
basées sur la recherche du solide élastique homogène
équivalent, assure le passage de la microstructure au
comportement mécanique macroscopique du bois sans défaut.
Utilisant essentiellement des lois des mélanges, ces
homogénéisations ne font appel qu'à un nombre
limité de paramètres structuraux (jugés strictement
utiles). Les cheminements intermédiaires amenant à la simulation
de l'anisotropie élastique d'un bois de résineux sont alors
résumés à 4 transitions fondamentales,
appelées Passages.
Le Passage 1 introduit l'anisotropie élastique
à l'échelle de la sous couche par la prise en compte
d'un renfort filamentaire de la matière ligneuse assuré
par des microfibrilles de cellulose quasi cristallines. Il permet
la transition des propriétés mécaniques des
bio polymères essentiels au comportement mécanique de la sous
couche élémentaire.
Le Passage 2 établit un lien entre le comportement de
sous couche et la première étape vers un comportement
mécanique tissulaire appelée comportement de double cloison
cellulaire. Le paramètre majeur expliquant l'anisotropie
élastique à cette échelle est l'inclinaison des
microfibrilles dans la sous couche S2 (paramétrée par l'angle des
microfibrilles AMF (ö)).
Le Passage 3 permet l'expression des
propriétés élastiques d'un tissu ligneux
homogène, assimilé à une structure nid d'abeille, à
partir des propriétés mécaniques de la double cloison.
La prise en compte de la géométrie
(diamètres radial et tangentiel, épaisseurs de paroi radiale
et tangentielle) et de l'arrangement cellulaires (parois
en quinconces ou alignées) autorise alors l'expression des
propriétés élastiques de trois tissus ligneux ; le bois
initial, le bois final
et enfin le rayon ligneux.
Le Passage 4 conduit enfin à l'expression du
comportement mécanique du cerne par son assimilation à un
bicouche bois initial-bois final renforcé radialement par des rayons
ligneux homogènes. Les paramètres descriptifs utilisés
à cette échelle sont la texture (épaisseur relative
de bois final dans le cerne) et la fraction volumique en rayons ligneux.
130
Conclusion et perspectives
La méthodologie employée autorise la
substitution éventuelle, à chaque Passages, de
modélisations prédictives plus
sophistiquées.
La seconde partie du chapitre 2 illustre cette
alternative par la mise en place d'une schématisation du
renfort filamentaire cellulosique par un squelette de
microfibrilles entrecroisées (modélisation Squelette M3).
Les Passages 1 et 2 sont, à cette étape et dans
la suite du travail, remplacés par un Passage 1-2 qui assure la
transition directe des propriétés mécaniques des bio
polymères cellulose, hémicelluloses et lignines à celles
du tissu ligneux.
Une des originalités de cette modélisation
réside dans la schématisation de la double cloison par une
couche unique renforcée par un réseau de
microfibrilles entrecroisées dont l'orientation est empruntée
à l'angle des microfibrilles dans S2.
Une étude documentaire puis une optimisation contrainte
conduisent, en fin de chapitre 2, à la construction d'un Résineux
Standard Virtuel (RSV). Les propriétés mécano physiques
cibles adoptées pour la construction de cette essence fictive sont la
masse volumique ñ et les trois modules élastiques ER, ET, EL
du résineux standard (Guitard, 1987) stabilisé à un
taux d'humidité de 12%. L'essence RSV, élaborée par
l'assemblage de trois tissus ligneux (bois initial, bois final et rayons
ligneux), est alors décrite par un jeu total de 22
paramètres structuraux. Le réalisme biologique du RSV est
testé par la confrontation, à posteriori, de certains de
ses paramètres descriptifs à leurs équivalents
obtenus expérimentalement sur 3 essences résineuses.
L'outil de modélisation RSV est ensuite
employé dans le chapitre 3 afin d'analyser la sensibilité
des propriétés élastiques du bois normal à
la variabilité de l'ensemble des paramètres architecturaux
retenus.
Quelque soit l'option de modélisation
envisagée à l'échelle de la double cloison
(Multicouches M1, M2 ou Squelette M3), l'anisotropie
élastique globale du matériau est fortement
dépendante de l'anisotropie élastique de la double paroi.
Il est ainsi montré que l'essentiel du comportement élastique
macroscopique du bois RSV (densité de 0,45 et AMF
(ö) compris entre 5 et 25 degrés)
résulte des variations de l'angle des microfibrilles dans la double
cloison virtuelle. L'influence de l'angle des microfibrilles sur l'anisotropie
élastique macroscopique est particulièrement marquée
sur un bois final présentant une forte densité
(0,75) et un AMF (ö) compris entre 5 et 10
degrés. Pour un bois initial présentant de faibles
épaisseurs pariétales et un AMF (ö)
supérieur, un terme de flexion de paroi vient concurrencer l'influence
de l'inclinaison des microfibrilles sans toutefois bousculer la
hiérarchie précitée.
La comparaison des évolutions des modules
élastiques de double cloison prédits par les deux types de
modélisations (M2 et M3) montre que pour le modèle Multicouche
M2, un angle des microfibrilles (ö) usuel (i.e : compris
entre 5 et 35 degrés) conditionne essentiellement le module
élastique longitudinal de la double cloison. Dans le cadre
d'une modélisation Squelette M3, ce même paramètre
(ö) n'intervient fondamentalement que sur les modules
transverses de la double cloison. Il est également montré
à cette étape que le choix du module d'élasticité
des fibres cellulosiques à prendre en compte est directement
lié à l'option de modélisation envisagée pour la
double cloison.
L'outil RSV mis en oeuvre dans le cadre du bois normal
est ensuite envisagé pour décrire l'anisotropie
élastique du bois de compression (chapitre 4). Devant le manque de
références
131
Conclusion et perspectives
concernant les caractéristiques élastiques
(ER, ET et EL) et l'anisotropie
élastique de ce type
de bois, une expérimentation sur trois essences
résineuses est mise en place. Les modules élastiques
longitudinaux obtenus sur des éprouvettes
parallélépipédiques s'avèrent sensiblement
différents selon l'essai mis en oeuvre pour les déterminer
(méthode vibratoire ou essais de compression jusqu'à
rupture). Ils demeurent néanmoins bien inférieurs à
ceux du bois normal.
L'exploitation des courbes expérimentales des essais de
compression jusqu'à rupture montre par ailleurs que des
éprouvettes de bois de compression ont plus tendance à se
déformer avant
de rompre que des éprouvettes de bois normal.
Des expériences préliminaires visant
l'identification des modules élastiques équivalents ER
ET et EL du bois de compression ont été
tentées sur des éprouvettes cubiques centimétriques
sèches à l'air. Ici encore, le module longitudinal du bois de
compression est inférieur à celui
du bois normal.
Les modules transverses ER et ET obtenus ne sont pas
différents et ce quelque soit la nature
de l'éprouvette testée (bois de
compression, bois opposé). Les dimensions de telles
éprouvettes impliquent la mise au point d'une
expérimentation plus soignée passant notamment par un
dispositif expérimental parfaitement approprié (entre autre
mesure de déplacements sur les faces des échantillons) et
la définition d'un volume élémentaire
représentatif (effet largeur et nombre de cernes). La
géométrie des échantillons se doit en outre
d'être irréprochable (uniformité du champ de contraintes).
Une lubrification à l'interface échantillon plateau devra
également être mise en place (film de téflon).
Une étude bibliographique, présentée en
première partie du chapitre 4, permet de faire état de quelques
transformations structurales majeures accompagnant la transition d'un bois
normal à
un bois de compression. Sur cette base, une distorsion
du Résineux Standard Virtuel est ensuite présentée.
L'impact de certaines modifications (augmentation d'épaisseur
pariétale, diminution de diamètre cellulaire, diminution
du taux de cristallinité de la cellulose augmentation de
l'angle des microfibrilles dans la sous couche S2) sur les
caractéristiques élastiques prédites par la
modélisation gigogne est alors évalué.
Certaines hypothèses de construction du
modèle, valables pour le bois normal (cellules rectangulaires et
de forme régulière), conduisent à une
légère surestimation du module longitudinal par une
évaluation par défaut de la porosité. La
diminution du degré d'anisotropie élastique transverse du
bois de compression (rapport ER / ET) est constatée à cette
étape. Cette tendance est expliquée par des épaisseurs de
parois importantes conduisant à une forte diminution du terme de flexion
des parois.
Une campagne expérimentale plus large devra
être menée prochainement pour acquérir certaines
données anatomiques manquantes (texture, fraction volumique en rayons
ligneux) et afin de disposer d'un ensemble plus large de mesures de modules
élastiques.
Sans remettre en cause la hiérarchisation introduite au
chapitre 3, le réalisme biologique de certains « tiroirs » de
modélisation pourrait sans doute, par de nouvelles investigations,
être amélioré.
132
Conclusion et perspectives
Les interactions biologiques entre certaines variables
structurales demandent à être
explicitées :
à l'échelle du tissu ligneux, les variations
d'épaisseurs pariétales ne sont sans doute pas physiologiquement
indépendantes des variations des diamètres cellulaires,
à l'échelle de la couche d'accroissement,
le réalisme de la discrétisation bois initial bois final
est biologiquement discutable ; les évolutions de densité
intra cerne sont sans doute plus proches d'une sigmoïde que d'une
fonction échelon.
Le premier champ d'application du concept de
modélisation multi échelles, concerne la prédiction
des propriétés de transferts en dessous et au dessus du
point de saturation des fibres. Les ponctuations, constituent en effet les
éléments structuraux essentiels conditionnant
la variabilité des coefficients de transports
(Comstock, 1970, Siau, 1986). Le nombre d'échelles de
modélisations à prendre en compte devrait être
inférieur à celui envisagé pour une modélisation
de l'anisotropie élastique (l'échelle de la sous couche
est généralement ignorée).
Un deuxième champ d'application vise
l'explication structurelle de l'anisotropie des coefficients de
retraits hydriques. Ainsi l'anisotropie transverse des retraits a
souvent été analysée par l'influence de la
combinaison de plusieurs facteurs associés à l'anatomie
(alternance de bois initial bois final, présence
de rayons ligneux, morphologie cellulaire, structure et topo chimie des
parois, angle des microfibrilles). Les échelles de modélisations
à envisager seront, dans ce dernier cas, identiques à celles
prises en compte dans ce travail.
133
Bibliographie
Bibliographie
BADEL E., PERRE P. (1999) : Détermination des
propriétés élastiques d'éléments
individuels du plan ligneux du chêne par des essais de traction sur
micro éprouvettes, Ann. For. Sci. 56 467-478.
BADEL E. (1999) : Détermination des
propriétés élastiques et du retrait transverse d'un
cerne annuel de chêne dans le plan transverse: description de la
morphologie, mesures des propriétés microscopiques et
calcul d'homogénéisation, thèse ENGREF- Nancy 1, 176
pp.
BAILLERES H. (1994) : Précontraintes de
croissance et propriétés mécano physiques de
clones d'Eucalyptus (Pointe - Noire , Congo) :
hétérogénéités, corrélations et
interprétations histologiques. Thèse Université Bordeaux
1, spécialité Sciences du Bois, 161 pp.
BARBER N.F., MEYLAN B.A. (1964) : The anisotropic
shrinkage of wood: a theorical model. Holzforschung 18 (5):
146-155.
BARKAS W.W. (1941) : The influence of ray cells on the shrinkage
of wood. in Wood Water Relationships
IV. Trans Faraday Soc. 37. 535.
BARRETT J.D. (1973) : Theorical models of wood shrinkage and
elasticity. Ph.D University of California, Berkeley, 276 pp.
BERGANDER A., SALMEN L. (2000) : a The transverse elastic modulus
of the native wood fibre wall, J. Pulp. Paper. Sci. 26: 234-238.
BERGANDER A., SALMEN L. (2000) : b Variations in
Transverse Fibre Wall Properties: relations between Elastic Properties and
Structure: Holzforschung.54: 654-660.
BERGANDER A., (2001) : Local variability in chemical and physical
properties of spruce wood fibers. Doctoral thesis. Stockolm 77 pp.
BERGANDER A., BRANDSTROM J., DANIEL G., SALMEN L. : Fibril
angle variability in earlywood of Norway spruce using soft rot cavities and
polarization confocal microscopy. Submitted to Journal of Wood Science.
BLEDSKY A.K, GASSAN J. (1999) : Composites reinforced with
cellulose based fibres, Prog. Polym. Sci
24: 221-274.
BODIG J, JAYNE B.A (1982) : Mechanics of wood and wood
composites, Van Nostrand Reinhold, New
York, NY.
BOTOSSO P.C. (1997) : Une méthode de mesure du
retrait microscopique du bois : App.lication à la
prédiction du retrait tangentiel d'éprouvettes de bois massif de
Sapin pectiné (Abies alba Mill.), thèse en Sciences du
Bois, Université Nancy 1, 247 pp.
BOUTELJE J.B. (1962) a : The relationship of structure to
transverse anisotropy in wood with reference to shrinkage and elasticity.
Holzforschung 30.
BOUTELJE J.B (1962) b : On shrinkage and change in
microscopic void volume during drying, as calculated from measurements
on microtome cross sections of Swedish pine. Svensk papp.erstidning
65,
209-215.
BOUTELJE J.B (1972) : On the relation ship between structure and
the shrinkage and swelling of the wood
in Swedish pine (Pinus sylvestris L.) and Spruce
(Picea abies). Svensk papp.erstidning 755, 1-6.
BOYD J.D. (1974) a :Relating lignification to microfibril angle
differences between tangential and radial faces of all layers in wood cells.
Drev. Visk 19: 41-54.
134
Bibliographie
BOYD J.D. (1974) b : Anisotropic shrinkage of wood:
identification of the dominant determinants. Journal
of the Japan Wood Research Society 20 (10): 473-482.
BOYD J.D, FOSTER J.C. (1975) : Microfibrils in primary
and secondary wall growth develop trellis configurations, Can.J.Bot. 53
(23): 2687-2701.
BOYD J.D.(1977) : Relationship between fibre morphology and
shrinkage of wood, Wood Sci.Technol. 11 :
3-22.
BRISTOW J.A, KOLSETH P. (1986) : Paper. Structure and
properties. International Fiber Science and
Technology Series 8, 390 pp. Editions Marcel Dekker, inc/ New
York. Basel.
BURGERT I., FRUHMANN K. (2003) : Micromechanics of wood
-structure - function relationships on the tissue and fiber level. Proceedings
of the second International Conference of the European Society for Wood
Mechanics. Stockholm, Sweden, May 25th-28th 2003, pp 85-94.
CARLSSON L., SALMEN L. (1986) : Basic Relations for Laminated
Orthotropic Plates, in : Bristow J.A. Editions Marcel Dekker, inc/ New York.
Basel, Paper. Structure and properties. International Fiber Science and
Technology Series 8, pp. 369-375
CAVE I.D. (1968) : The anisotropic elasticity of the plant cell
wall, Wood Sci.Technol. 2: 268-278.
CAVE I.D. (1972) : Swelling of a fibre reinforced composite in
which the matrix is water reactive. Wood
Sci. Technol. 6 : 157-161.
CAVE I.D. (1975) : Wood substance as a water reactive fibre
reinforced composite. J. Microscopy. 104: 47-
52.
CAVE I.D. (1976) : Modelling the structure of softwood cell wall
for computation of mechanical properties. Wood Sci. Technol. 10: 19-28.
CHAFFEY, I. (2000) : Microfibril orientation in wood cells: new
angles on an old topic. Trends in Plant
Sciences, 5: 360-362.
CHARRON S., JOUREZ B., MARCHAL M., HEBERT J. (2003) : Etude
comparative des caractéristiques physiques et mécaniques des
mélèzes d'Europe (Larix decidua Mill.), du Japon (Larix kaempferi
(Lambert) Carr.) et de leur hybride (Larix x eurolepis Henry).
Biotechnol.Agron. Soc. Environ. 7 (1) : 5-16.
CHOW K.Y. (1946) : A comparative study of the structure and
chemical composition of tension wood and normal wood in beech (Fagus
sylvatica L.), Forestry 20 : 60-77.
CLAIR B., DESPAUX G., CHANSON B., THIBAUT B. (2000) : Utilisation
de la microscopie acoustique pour l'étude des propriétés
locales du bois: étude préliminaire de paramètres
expérimentaux, Ann. For. Sci.
57 : 335-343.
CLAIR B. (2001) : Etude des propriétés
mécaniques et du retrait au séchage du bois à
l'échelle de la paroi cellulaire : essai de compréhension du
comportement macroscopique paradoxal du bois de tension à couche
gélatineuse. Thèse ENGREF, spécialité Sciences
Forestières et du Bois, 165 pp.
COMSTOCK G.L. (1970) : Directional permeability of softwoods.
Wood Fiber 1 : 283-289.
COUSINS W.J. (1978) : Young's Modulus of Hemicellulose as related
to moisture content. Wood Science and Technology, 10 : 1.9-17.
DAVIAUD R., FILLIATRE C. (1983) : Introduction aux
matériaux composites. Editions du CNRS. 452 p. DECOUX V., VARCIN E.,
LEBAN J.M. : Relationships between the intra rings wood density assessed by
X ray densitometry and optical anatomical measurements
in conifers. Consequences for the cell wall
app.arent density. Non publié.
135
Bibliographie
DENNE M.P. (1988) : Definition of latewood according to Mork
(1928). IAWA Bulletin n.s.10 (1): 59-62.
DONALDSON L.A. (2001) : Lignification and lignin
topochemistry- an ultrastructural view. Phytochemistry 57:
859-873.
DUMAIL J.F. (1995) : Caractéristiques physiques et
mécaniques du bois juvénile de pin maritime (Pinus
pinaster), thèse de Mécanique, Université Bordeaux
1,229 pp.
DUNNING C.E. (1968) : Cell- wall morphology of longleaf pine
latewood. Wood Sci. Technol. 1: 65-76. ERICKSON H.D., HARRISSON A.T. (1974) :
Douglas Fir Wood Quality Studies, Part I: Effects of Age
and Stimulated Growth on Wood Density an Anatomy. Wood
Sci.Technol. 8: 207-225
FARRUGGIA F., LAHBABI R., PERRE P. (1996) : Détermination
des propriétés mécaniques des résineux
à l'échelle microscopique du plan ligneux, Cahiers
Lorrains du Bois ARBOLOR.
FARRUGGIA F. (1998) : Détermination du comportement
élastique d'un ensemble de fibres de bois à partir
de son organisation cellulaire et d'essais mécaniques sous
microscope. Thèse ENGREF, spécialité Sciences
Forestières et du Bois, 93 pp.
FARRUGGIA F., PERRE P. (2000) : Microscopic tensile tests
in the transverse plane of earlywood and latewood parts of spruce. Wood
Sci.Technol. 34: 65-82.
FENGEL D. (1968) : The ultrastructure of wood. Wood Sci. Technol
2 (2): 73-83.
FENGEL D., STOLL M.(1973) : On the Variation of the Cell Cross
Area, The Thickness of the Cell Wall and of the Wall Layers of Spruce wood
Tracheids within an Annual Ring, Holzforshung 27: 1-7.
FENGEL D., WEGENER G. (1984) : The Internal Structure of Fibrils,
Wood: Chemistry, Ultrastructure, Reactions. De Gruyter, Berlin - New York.
97-98.
FERRAND J.C. (1982) : Réflexions sur la Densité du
Bois. 1ere partie : Définition de la densité du bois.
Holzforshung 36: 99-105.
FIORAVANTI M., FEDERICI S. (2003) : Determination of Microfibril
Angle in Compression Wood by Means of X-ray Diffraction Technique. Proceedings
of the second International Conference of the European Society for Wood
Mechanics. Stockholm, Sweden, May 25th-28th 2003. pp 223-229.
FUKUZAWA K., IMAGAWA H. (1981) : Quantitative analysis of lignin
using an UV microscopic image analyser. Variation within one growth increment.
Wood Sci. Technol 15: 45-55.
GACHET C., GUITARD D., GRIL J. (2003) : The importance of S2
sub- layer in the description of cell wall anisotropy in softwood. Proceedings
of the second International Conference of the European Society for Wood
Mechanics. Stockholm, Sweden, May 25th-28th 2003. pp 319-324.
GIBSON L.J., ASHBY M.F.(1988) : Cellular solids, Pergamon
Press.
GILLIS P.P. (1972) : Orthotropic elastic constant of wood. Wood
Sci. Technol. 6: 138-156.
GINDL W., GUPTA H.S., GUNWALD C. (2002) : Lignification of spruce
tracheids secondary cells walls related to longitudinal hardness and modulus of
elasticity using nano-indentation. Can.J.Bot 80 : 1029-1033.
GINDL W., WIMMER R., GUPTA H., SCHOBERL T. (2003) :
Nanoindentation technique-mechanical analysis at the sub- micron scale.
Proceedings of the second International Conference of the European
Society for Wood Mechanics. Stockholm, Sweden, May 25th-28th 2003. p
285-290.
GRIL J. (1987) : Une modélisation du
comportement hygro-rhéologique du bois à partir de
sa microstructure, thèse de Sciences Physiques, Université Paris
VI, 268 pp.
GUILLEY E. (2000) : La densité du bois de
Chêne sessile (Quercus petraea Liebl.) : Elaboration d'un
modèle pour l'analyse des variabilités intra et inter arbre ;
Origine et évaluation non destructive de l'effet
136
Bibliographie
« arbre » ; interprétation anatomique du
modèle proposé, thèse ENGREF, spécialité
Sciences Forestières et
Sciences du Bois, 207 pp.
GUITARD D. (1987) : Mécanique du matériau bois et
composites, Editions C.E.P.A.D.U.E.S. 220 p
GUITARD D., EL AMRI F. (1987) : "La fraction volumique en rayons
ligneux comme paramètre explicatif
de la variabilité de l'anisotropie élastique
du matériau bois.". Actes du 2éme Colloque des
Sciences et
Industries du Bois". 22-24 Avril 1987. Nancy.
GUITARD D., MASSE H., YAMAMOTO H., OKUYAMA T. (1999) : Growth
stress generation: a new mechanical model of the dimensional change of wood
cells during maturation, J.Wood Sci 45: 384-391.
GUITARD D., GACHET C. (2002) : Paramètres
structuraux et/ou ultrastructuraux facteurs de variabilité intra
arbre de l'anisotropie élastique du bois, Annals of Forest Science,
accepté.
HACKNEY J. M., ATALLA H., VANDERHART D.L. (1994) : Int.J.
Biol.Macromol 16 : 215.
HERMAN M., DUTILLEUL P., SHAW T.A. (1999) : Growth rate
effects on intra ring and inter ring trajectories of microfibril angle in
Norway spruce (Picea abies) IAWA J. 20: 3-21.
HOLMBERG S., PERSSON K., PETERSSON H. (1999) : Non linear
behaviour and analysis of wood and fibre materials. Computers and Structures
72. 459-480.
HULT E.L, LARSSON P.T., IVERSEN T. (2000) : A comparative CP/MAS
13 C-NMR study of cellulose structure in spruce wood and kraft pulp. Cellulose
7: 35-55.
HUNTER A.J. (2001) : The distribution of mechanical stresses in
the cell wall of wood induced by capillary tension in the lumen water- an
approximate analysis. Wood Sc. & Technol.35: 283-296.
ISHIKAWA A., OKANO T., SUGIYAMA J. (1997) : Fine structure and
tensile properties of ramie fibres in the crystalline form of cellulose I, II,
III1 and IV1 . Polymer 38 (2): 463-468.
JODIN P. (1994) : Le bois, matériau d'ingénierie,
Editions A.R.B.O.L.O.R. 433 p.
KATAOKA Y., SAIKI H., FUJITA M. (1992) : Arrangement and
Superimposition of Cellulose Microfibrils
in the Secondary Walls of Coniferous Trachéids. Mokuzai
Gakkaishi 38 (4) : 327-335.
KELLER R. (1999) : Cours de DEA Sciences du Bois: structure,
composition, formation du bois. ENGREF. KHALE E., WOODHOUSE J. (1994) : The
influence of cell geometry on the elasticity of softwood, Journal
of Materials Science 29: 1250-1259.
KHALILI S., NILSSON T., DANIEL G. (2001) : The use of soft rot
fungi for determining the microfibrillar orientation in the S2 layer of pine
tracheids. Holz Roh Werkst. 58: 439-447.
KOLLMANN F.P., COTE W.A.(1984) : Principles of wood
sciences and technology.1. Solid wood. Springer -Verlag, New York.
KOMPELLA M.K., LAMBROS J.(2002) : Micromechanical
characterization of cellulose fibers. Polymer
Testing 21 : 523-530.
KOPONEN S., TORATTI T., and KANERVA P. (1989) :
Modelling elastic and shrinkage properties of wood. Wood Sci.Technol. 23:
55-63.
KOPONEN S., TORATTI T., and KANERVA P. (1991) : Modelling
longitudinal elastic and shrinkage of wood based on cell structure. Wood Sci.
Technol. 25: 25-32.
KRAMER P.J., KOZLOWSKI T.T. (1979) : Physiology of Woody Plants.
Academic Press New York San
Francisco London. 811 p.
137
Bibliographie
LAHBABI R. (1995) : Mesure par analyse d'image de
paramètres microscopiques requis pour une
prédiction déterministe des
propriétés du bois. Thèse ENGREF, Nancy, 141 pp.
LARTIGUE C. (1987) : Mécanismes élémentaires
mis en jeu lors du séchage du pin maritime. Thèse de
Mécanique, Université Bordeaux I, 150 pp.
LEBAN J.M. (1999) a : Un modèle de profil
microdensitométrique pour le Pin Laricio. Rapport final de la convention
DERF INRA n° 01.40.27/98 : Modélisation : croissance,
branchaison, qualité des bois et intégration logicielle.
Dreyfus PH.ed .p 16-22.
LEBAN J.M. (1999) b: Un modèle de profil
microdensitométrique pour le Cèdre de l'Atlas. Rapport final
de
la convention DERF INRA n° 01.40.27/98 :
Modélisation : croissance, branchaison, qualité des bois et
intégration logicielle. Novembre 1999.
MAKINEN H., SARANPAA P., LINDER S. (2002) : Wood density of
Norway spruce in relation to nutrient optimization and fibre dimensions. Can.
J. For. Res. 32: 185-194.
MARGUERIE D., BEGIN Y., COURNOYER L. (2000) : Distinction
anatomique du bois du Mélèze (Larix laricina [Du Roi] K.
Koch), de l'Epinette blanche (Picea glauca [Moench.] Voss), et de
l'Epinette noire
(Picea mariana [Mill.] B.S.P.), en vue de l'analyse des
macrorestes. Géographie physique et Quaternaire.
54(3) : 317-325.
MARION C. (2001) : «Caractérisation de
l'agencement cellulaire du bois à l'aide de
critères morphologiques mesurables par analyse d'images», rapport
de DEA Sciences du Bois, 30 pp.
MARK R.E. (1967) : Cell wall mechanics of tracheids. New Haven
and London, Yale University Press. MARK R.E, GILLIS P.P. (1970) : New models in
cell wall mechanics. Wood and Fiber 2 : 79-95.
MARK R.E. (1972) : Mechanical behaviour of the molecular
components of fibers in: Eds. Jayne, B.A, Syracuse University Press,
Syracuse: Theory and design of wood and fiber composite materials. pp.
49-82.
MARK R.E. (1980) : Molecular and cell wall structure of wood.
Adhesion in Cellulosic and Wood-Based
Composites. Plenum Press pp. 7-51.
MARTIN P. (1984) : Propriétés technologiques
pp. B1-1-B1-28, dans Le matériau bois. Propriétés.
Technologie. Mise en oeuvre. (1984) Editions ARBOLOR.
MCMILLIN C.W. (1973) : Fibril angle of Loblolly Pine wood as
related to specific gravity, growth rate and distance from pith. Wood Sci
Technol 7(4): 251-255.
MICHELL AJ. (1989) : Wood cellulose organic polymer composites.
Composite Asia Pacific, Adelaide.89:
19-21.
MONTIES B. (2003) : Biological variability of
lignification and mechanical behaviour of woody plants. Proceedings of
the second International Conference of the European Society for Wood
Mechanics. Stockholm, Sweden, May 25th-28th 2003. p 1-14.
MOTT L., SHALER S.M. GROOM L.H. (1996) : A technique to measure
strain distribution in single wood pulp fibres. Wood Sci. Technol.28
429-437.
NAVI, P., RASTOGI P.K., GRESSE V., TOLOU A. (1995) :
Micromechanics of wood subjected to axial tension. Wood Sc. & Technol.29:
411-429.
NORIMOTO M., TAKABE K. (1985) : On noncrystalline structure of
wood. Wood Research and Technical
Notes, 21 : 96-101.
NORTHOLT M.G., BOERSTOEL H., MAATMAN H., HUISMAN R.,
VEURINK J., ELZERMAN H.
(2001) : The structure and properties of cellulose fibres spun
from a anisotropic phosphoric acid solution. Polymer 42: 8249-8264.
138
Bibliographie
ONAKA F. (1949) : Studies on compression and tension
wood. Wood research, Bulletin of the Wood
research Institute, Kyoto University, Japan, 24: 3. 1-88.
PAAKKARI T. SERIMAA R. (1984) : A study of structure of wood
cells by X-ray diffraction. Wood Sci. Technol 18: 79-85.
PANSHIN A.J., DE ZEEUW C. (1980) : "Textbook of wood technology"
- Fourth edition -Mc Graw Hill
Book Company - 722 p.
PERRE P. (1994) : « Le séchage du bois » pp.
202-290 dans Le bois, matériau d'ingénierie, recueil de textes
par P. JODIN, Editions A.R.B.O.L.O.R. 433 p.
PERRE P., KELLER R. (1994) : La prédiction des
propriétés macroscopiques du bois à partir de sa structure
anatomique: besoin ou moyen de caractériser la paroi? Journal of trace
and Microprobe Techniques 12(4) :
277-288.
PERRE P. (1998) : Relations structure- propriétés
et comportement haute température dans le bois: compte- rendu de la
réunion conjointe de deux projets financés par la DERF, 145 p.
PERRE P. (1998) : The use of homogeneisation to simulate
heat and mass transfert in wood: towards a double porosity app.roach,
Keynote adress, IDS.
PRESIOZA M., GUITARD D. et SALES C. (1986) :
«Contraintes internes de séchage dans le matériau
bois: Le tenseur des coefficients de contraintes de séchage
comme caractéristique isotrope de la matière ligneuse».
Bois et forêts des tropiques. Cahiers scientifiques n°8, p.
91-109.
PRESTON R.D. (1934) : The organization of the cell wall of the
coniferous tracheid. Phil. Trans.Roy.Soc. CCXXIV : 131-174.
PLUVINAGE G. (1992) : La rupture du bois et de ses composites,
Editions CEPADUES, 319 p
ROLAND J.C., MOSINIAK M., CZANINSKY Y., VIAN B. (1982) :
«Précisions ultra structurales sur les modalités
d'oscillation dans l'orientation de la cellulose des parois du bois»,
Colloque Sciences et Industries
du Bois, Groupe 1 Grenoble 20-22 septembre 1982.
RUEL K. (1984) : Etudes en microscopie électronique des
inter relations cellulose - hémicelluloses- lignine dans les parois
végétales, thèse d'état, Grenoble, 194 pp.
RUEL K., IMAI T., PILATE T., BAILLERES H., JOSELEAU J.P.
(2003) : Microstructural diversity of cell walls in wood revealed by
immuno- electron microscopy. Proceedings of the second International
Conference of the European Society for Wood Mechanics. Stockholm, Sweden, May
25th-28th 2003.
RUELLE J. (2003) : Anatomie comparative bois
normal/bois de réaction et observation des relations
structure/propriétés du bois de six espèces d'angiospermes
de forêt tropicale humide et de trois espèces de gymnospermes de
zone tempérée. Rapport de DEA Sciences du Bois. 39 p.
SAKURADA I., NUKUSHINA Y., ITO T. (1962) : Experimental
determination of the elastic modulus of crystalline regions in oriented
polymers, J. Polymer Sci. 57: 651- 660.
SAHLBERG U., SALMEN L., OSCARSSON A. (1997): «The fibrillar
orientation in the S2 layer of wood fibres as determined by X-ray diffraction
analysis». Wood Sci. Technol.31:77-86.
SALMEN L., DE RUVO A. (1985) : A model for the prediction of
fiber elasticity. Wood and Fiber Science,
17 (3): pp 336-350.
SALMEN L. (1986) : The cell wall as a composite structure, in :
Bristow J.A. Editions Marcel Dekker, inc/ New York. Basel, Paper. Structure and
properties. International Fiber Science and Technology Series 8, pp
51-73.
139
Bibliographie
SALMEN L., KOLSETH P. (1986) : A mechanical model of softwood. ,
in : Bristow J.A. Editions Marcel
Dekker, inc/ New York. Basel, Paper. Structure and properties.
International Fiber Science and Technology
Series 8, pp. 377-380.
SALMEN L., OLSSON A.M. (1998) : Interaction between
hemicelluloses, lignin and cellulose : structure- property relationships.
J.Pulp Paper Sci. 24 : 99-103.
SALMEN L. (2001) : Micromechanics of the wood cell
wall : a tool for a better understanding of its structure. Proceedings
of the First International Conference of the European Society for Wood
Mechanics. Lausanne, Switzerland.
SAREN M.T, SERIMAA R., ANDERSSON S., PAAKKARI T., SARANPAA P.
(2001) : PESONEN E.: Structural variation of tracheids in Norway Spruce
(Picea abies [L.] Karst.). Journal of Structural Biology
136:101-109.
SASSUS F. (1998) : Déformations de maturation et
propriétés du bois de tension chez le hêtre et le
peuplier
: mesures et modèles. Thèse ENGREF,
spécialité Sciences Forestières et du Bois.
SCHNIEWIND A.P.(1959) : Transverse anisotropy of wood: A function
of gross anatomic structure. Forest products journal.350-359.
SCHNIEWIND A.P.(1972) : Elastic behavior of the wood fiber,
Theory and design of wood fiber composite materials. B.A. Jayne Editor.
SEICHEPINE J.L. (1980) : Mise au point d'une méthode
expérimentale destinée à l'identification de la matrice
des complaisances élastiques de solides anisotropes : application au
matériau bois, thèse de l'I.N.P.L, 186 pp.
SENFT J.F., BENDSEN B.A.(1985) : Measuring microfibrillar angles
using light microscopy. Wood Fiber
Sci 17(4): 564-567.
SIAU J.F.(1984): «Transport processes in wood»,
Springer-Verlag Berlin N.Y. 254p.
SINGH A.P., DONALDSON L.A. (1999) : Ultrastructure of
tracheid cell walls in Radiata Pine (Pinus radiata) mild
compression wood. Can. J. Bot. 77: 32-40.
TIMELL. T.E. (1986) : Compression wood in Gymnosperms.
(vol.I). Bibliography, Historical Background, Determination, Structure,
Chemistry, Topochemistry, Physical Properties, Origin and Formation
of Compression Wood. Springer -Verlag, Berlin 706 p.
TSAI S.W., HAHN H.T. (1980) : «Introduction to composite
materials» Technomic Publishing Company, Wesport.
TSOUMIS G. (1991). Science and technology of wood :
structure, properties, utilization. Van Nostran
Reinhold, New York, 494 p.
VANDERHART D.L., ATALLA R.J. (1984) : Studies of
microstructure in native celluloses using solid- state 13 C NMR.
Macromolecules 17 : 1465-1473.
VENET J., KELLER R. (1986) : Identification et classement des
bois français. Editions de l'Ecole Nationale
du Génie Rural, des Eaux et des Forêts, 2ième
édition revue par R. KELLER, 310 p.
VIEVILLE P. (1992) : Influence des paramètres
architecturaux sur les caractéristiques viscoélastiques du
bois à ses différentes échelles
d'hétérogénéité, thèse de
Mécanique et Energétique, I.N.P.L., 197pp.
WATANABE U., NORIMOTO M, OHGAMA T, FUJITA M. (1999) :
Tangential Young's modulus of coniferous earlywood investigated using cell
models. Holzforschung 53 : 209-214.
WATANABE U., NORIMOTO M., MOROOKA T. (2000) : Cell wall
thickness and tangential Young's modulus in coniferous earlywood. J. Wood
Sci. 46 : 109-114.
140
Bibliographie
WIMMER R., LUCAS B.N., TSUI T.Y., OLIVER W.C. (1997) :
Longitudinal hardness and Young's
Modulus of spruce tracheid secondary walls using nanoindentation
technique. Wood Sc. Technol, 31: 131-
141.
YAMAMOTO H. (1998) : Generation mechanism of growth
stresses in wood cell walls: role of lignin deposition and cellulose
microfibril during cell wall maturation. Wood Sc. Technol, 32: 171-182.
YAMAMOTO H. (1999) : A model of the anisotropic swelling
and shrinking process of wood. Part1. Generalization of Barber's wood
fiber model Wood Sc.Technol, 33: 311-325.
YAMAMOTO H., SASSUS F., NINOMOIYA M., GRIL J. (2001) : A model of
anisotropic swelling and shrinking process of wood .Wood Sc.Technol, 35:
167-181.
YAMAMOTO H., OKUYAMA T., GRIL J. (2003) : Role of the
Gelatinous Layer (G-Layer) on the Physical Properties Peculiar to the
Tension Wood. Proceedings of the second International Conference of the
European Society for Wood Mechanics. Stockholm, Sweden, May 25th-28th 2003. p
23-29.
YLINEN A., JUMPPANEN P. (1967) : Theory of the shrinkage of wood.
Wood Sc. Technol, 1 : 241-252.
141
|
|



