Impact du taux de change sur l'inflation en RDC de 2000-2020

c) Validation économétrique

Elle porte essentiellement sur l'estimation du modèle. Pour effectuer cette estimation du modèle, nous avons recouru à la méthode de moindres carrés ordinaires (MCO), à travers le logiciel Eviews 6. Les résultats issus de cette estimation ont pu être validés économiquement, statistiquement et économétriquement avant de conclure de la qualité explicative du modèle.

Pour la validation économétrique, nous avons apprécié la qualité des résidus de l'estimation de notre modèle, la multi-colinéarité et la forme fonctionnelle de notre modèle. De ce fait, nous avons appliqué le test de JarqueBera pour la normalité des résidus, le LM-test de Breush-Godfrey pour l'autocorrélation des erreurs sur les résidus, le test de white pour l'hétéroscedasticité des erreurs, le test de Klein pour la multi colinéarité et le Reset-test de Ramsey pour la forme fonctionnelle du modèle.

Pour avoir une bonne compréhension et interprétation de résultats lors du traitement des données, il est nécessaire de recourir aux différents tests économiques, statistiques et économétriques.

Ø Tests économiques :

§ Test de la stationnarité des variables du modèle (test de racine unitaire)

Une série est dite stationnaire si elle ne comporte ni tendance ni saisonnalité et plus généralement aucun facteur n'évoluant avec le temps.

Pour faire, ce test nous pouvons passer par :

ü Test de Philips-Perron

Avec l'application sur Eviews, les hypothèses suivantes sont retenues :

H₀ : la série n'est pas stationnaire

H₁ : la série est stationnaire

PP : PP Test Statistiques (Test Philips-Perron)

CV :Critical Value (Valeur critique)

- Si la valeur de PP est inférieure à la valeur de CV au seuil de 5%, alors on accepte l'hypothèse H1 donc la série est stationnaire.

- Si la valeur de PP est supérieure ou égale à la valeur de CV au seuil de 5%, alors on accepte l'hypothèse H0 donc la série est non stationnaire.

ü Test de stationnarité de Dickey Fuller Augmenté (ADF)

Les tests de Dickey - Fuller et Dickey - Fuller Augmenté (ADF) permettent non seulement de mettre en évidence le caractère stationnaire ou non d'une chronique par la détermination d'une tendance déterministe ou stochastique, mais aussi de déterminer la bonne manière de stationnariser cette chronique.

Avec l'application sur Eviews, les hypothèses suivantes sont retenues :

H₀ : la série est stationnaire

H₁ : la série n'est pas stationnaire

On accepte l'hypothèse nulle si la valeur ADF prise en valeur absolue est supérieure à la valeur critique de MAKINNON considérée aussi en valeur absolue au seuil de 5% ; au cas contraire, on la rejette au profit de H1.

Tous ces tests sont faits au seuil de 5%.

Ø Tests statistiques

§ Impact des variables explicatives sur la variable expliquée (Test Individuel ou de Student)

On effectue le test de signification des paramètres à l'aide de la statistique de student. Il permet de déterminer la significativité de paramètre au seuil de signification de 5%.

Pour ce faire, on émet les hypothèses suivantes :

H₀ : ai = 0, le paramètre n'est pas significatif ;

H₁ : ai ? 0, le paramètre est significatif.

Si la valeur de t statistique est inférieure à 1.96 (au seuil de 5 pourcent), on valide hypothèse nulle. Le contraire est valable pour l'hypothèse alternative.

Avec l'application sur Eviews, si la probabilité associée à chaque paramètre est supérieure à 0.05, on accepte l'hypothèse nulle. Par contre, si elle est inférieure à 0.05, on rejette l'hypothèse nulle au profit de l'hypothèse alternative.

ü Degré d'explication du modèle

Pour mesurer ce degré, nous faisons recours au coefficient de déterminationdonné par l'équation ci-après :

R²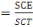

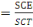
Parfois, R² a tendance à croître avec le nombre de variables explicatives du modèle, même si ces variables n'ont rien à voir avec le phénomène étudié, Pour pallier à cet inconvénient, certains chercheurs ont proposé d'introduire un R² corrigé.

§ Test de significativité du modèle (Test de Fischer)

On pose comme hypothèses :

H₀ : R2=0, le modèle n'est pas significatif,

H₁ : R2?0, le modèle est significatif.

Décision : Si FCal>Fth ; on rejette l'hypothèse nulle et on accepte l'hypothèse alternative.

2. Tests économétriques

Ces tests se fondent sur les tests des résidus et sur leurs stabilités.

§ Tests sur les résidus

Examiner les résidus est un des moyens les plus utilisés pour évaluer la qualité de la régression. Dans ce cadre, nous allons nous intéresser aux tests suivants :

ü Test de normalité de résidus de JARQUE-BERA

Le principe de ce test repose sur le calcul des coefficients d'asymétrie A et d'aplatissement K.

Cette statistique suit une loi de Khi-carré avec 2 degrés de liberté. Le test se formule en posant :

H₀ : il y a normalité des résidus ;

H₁ : pas de normalité des résidus.

Règle de décision :

ü Si la valeur de JB calculée est supérieure à la valeur du Khi-carré de la table(5,99 à 5%), on rejette alors l'hypothèse nulle. Par conséquent, la distribution des résidus n'est pas normale.

Avec l'application sur Eviews, la statistique de Jarque-Bera doit être inférieure à 5,99 ou soit sa probabilité doit être supérieure à 0,05, pour valider l'hypothèse nulle. Sinon, on valide l'hypothèse alternative.

ü Test de Multiplicateur de Lagrange :

Ce test examine la corrélation entre les résidus et la probabilité des valeurs retardées à un degré supérieur. Le critère de validation repose sur les hypothèses ci-après :

H₀ : il y a absence d'autocorrélation des erreurs ;

H₁ : il y a présomption d'auto corrélation des erreurs.

La probabilité de NR2 doit être supérieure à 0,05 pour que H₀ soit validée, au cas contraire, on valide l'hypothèse alternative.

ü Test d'auto corrélation des erreurs de Durbin-Watson

Ce test permet de vérifier s'il y a l'auto corrélation d'ordre 1 des erreurs.

Il repose sur les hypothèses suivantes :

H₀ : il y a absence d'auto corrélation d'ordre 1

H₁ : il y a présomption d'auto corrélation d'ordre 1

On lit dans la table de Durbin-Watson. Au seuil de 5%,Durbin-Watson doit être à l'intervalle de 1.5 à 2.4.il doit être proche de 2 pour validerH₀ dans le cas contraire on valide H₁.

ü Test de l'hétéroscedasticité

Pour vérifier l'hétéroscedasticité, nous faisons recours au test de WHITE et ou de celui d'ARCH.

Ces deux tests posent les mêmes hypothèses et le même critère de validation :

H₀ : il y a homoscédasticité ;

H₁ : il y a hétéroscedasticité.

On accepte H₀ si la probabilité de NR2 est supérieure à 0,05. L'inverse est valable pour accepter H₁.

ü Test de colinéarité (test deKlein)

Ce test permet de voir s'il y a multicolinéarité entre les variables exogènes ou pas. Il y a multicolinéarité entre les variables dans un modèle de régression lorsqu'il existe une relation linéaire parfaite ou presque parfaite entre quelques-unes ou toutes les variables explicatives.

Elle résulte dans un modèle où les variables exogènes sont liées. La liaison entre les variables exogènes peut être relative. C'est le cas qu'on rencontre fréquemment. Elle peut être absolue. C'est le cas qu'on rencontre si le modèle a été mal spécifié.

On évalue R² :

· Si r²x_j>R² : on admet qu'il y a colinéarité entre x_i et x_j ;

· Si r₂x_j<R² : on admet qu'il n'y a pas colinéarité.

ü Test de stabilité du modèle

Ces tests permettent de voir au seuil d'erreur de 5%, si le modèle est stable à travers le temps.

Pour effectuer ce test on peut passer par :

ü Test de Chow

H_o : SCR = SCR1 + SCR2, le modèle est stable ;

H₁ : SCR ? SCR1 + SCR2, le modèle est instable.

Si Fcal>Fth, on rejette H_o.

Lorsque les données ne sont pas suffisamment élevées par sous échantillon, on utilise le test de Chow réduit. Il s'agit du test sur un seul sous échantillon : le sous échantillon ayant plus ou moins 15 données.

On construit dans ce cas la statistique F du test comme suit :

Où n₁ = taille de l'échantillon total

n₂ = taille du sous échantillon

Cette statistique suit une distribution F de Fisher à n₂ et (n₁ - k) degrés de liberté. Si FC>FT, on rejette H_o.

Avec l'application sur le logiciel Eviews, les coefficients du modèle sont stables si probabilité est supérieur à 5%.

Les coefficients du modèle sont instables si probabilité est inférieure ou égale à 5%. On choisit les dates de rupture.

ü Test de Cusum (Brown, Durbin, Ewans)

Pour Cusum on fait un modèle de cadrage. Les résidus vont se présenter dans un cadrant.

H_o : si la courbe ne coupe pas le corridor : modèle est stable

H₁ : si la courbe coupe le corridor : le modèle est instable.

ü Test de Cusum

Ce test permet de détecter les instabilités structurelles.

ü Test de Cusum Carré

Ce test permet de détecter les instabilités ponctuelles.

- Si la courbe ne coupe pas le corridor : le modèle est stable

- Si la courbe coupe le corridor : le modèle est instable.

- Le corridor est en pointillés.

§ Test de spécification du modèle (test de Ramsey)

Le test de Ramsey consiste à vérifier si la forme fonctionnelle est correcte.Nous vérifions cela en utilisant les hypothèses suivantes :

H_o : P>0,05 : le modèle est bien spécifié ;

H₁ : P<0,05 : le modèle est mal spécifié.