2. Répartitions spatiales des stations de la
zone étudiée.
Suite à la configuration spatiale des stations
pluviométriques retenues dans l'étude, nous pouvons dire que la
distribution couvre bien les grands ensembles topographiques de la zone
d'étude.
Chapitre III :
Méthodes d'Approche et
Données
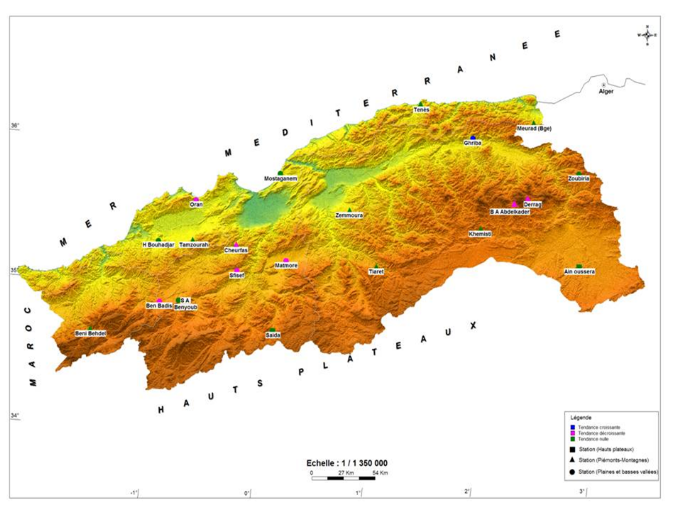
Figure.6 : Répartition spatial des
stations de la zone d'étude. Source :
Medjerab .2005.
3. Les méthodes utilisées dans
l'étude des changements climatiques.
3.1Méthodes d'étude de la variabilité
pluviométrique.
3.1.1 Indicateurs Statistiques.
L'objectif essentiel de la statistique est de maitriser au
mieux cette incertitude, pour mieux extraire des informations des
données, par l'intermédiaire de l'analyse des variations dans les
observations, dans notre cas d'étude de nos séries sont
indicées par le temps ce qu'on appel des séries
chronologiques.
Les représentations graphiques ne permettent qu'une
analyse visuelle de la répartition des paramètres
étudiés. Pour des variables quantitatives, il est
intéressant de donner des indicateurs numériques, permettant de
caractériser au mieux ces paramètres. On donne en
général deux indicateurs : des indicateurs de
localisation et des indicateurs de dispersion.
3.1.1.1 Indicateur de localisation ou de tendance
centrale.
Le but est de donner un ordre de grandeur général
des observations, un nombre unique qui résume au mieux les
données. On pense immédiatement à la moyenne de la
série des données de mesures.
3.1.1.1.1 La moyenne.
La moyenne de l'échantillon est la moyenne
arithmétique des observations. Aussi est-il important de disposer
d'indicateurs qui ne soient pas trop sensibles aux valeurs aberrantes. Or la
moyenne est très sensible : si une des observations est
extrêmement grande, elle va tirer la moyenne vers le haut. Par contre La
médiane est un indicateur de localisation construit pour ne pas
être insensible aux valeurs aberrantes.
Chapitre III :
Méthodes d'Approche et
Données

3.1.1.1.2 Médiane.
La médiane de l'échantillon, notée Xn ou
X1/2, est un réel, qui partage l'échantillon ordonné en
deux parties de même effectif. La moitié des observations sont
inferieures à Xn et l'autre moitié lui sont
supérieures.
3.1.1.2 Indicateur de Pression.
3.1.1.2.1 L'écart-type.
L'écart-type de l'échantillon est la racine
carrée de la variance : Il s'exprime dans la même unité que
les données, ce qui rend son interprétation plus facile que celle
de la variance. Cependant, la variabilité doit toujours se comparer
à la valeur moyenne.
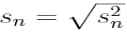
3.1.1.2.2 Le coefficient de
variation.
L'intérêt de cet indicateur est qu'il est
sans dimension. Une pratique empirique courante est de considérer que
l'échantillon possède une variabilité significative si CV
> 0,15. Si CV < 0,15, les données présentent peu de
variabilité.

| 


