Conception d'idéotypes de tomate adaptés au stress hydrique.

Université Montpellier 2 Faculté des Sciences et Techniques Département Informatique Bât 16, RC Place Eugène Bataillon 34095 Montpellier cedex 05

MASTER 2 INFORMATIQUE

Spécialité-MOCA : Modélisation, Optimisation, Combinatoire, Algorithme Année universitaire 2013-2014

RAPPORT DE STAGE

Effectué à :

INRA UR 1115 Plantes et systèmes de culture Horticoles Domaine St Paul, 84914 Montfavet cedex 9

Du 10 Mars 2014 au 31 août 2014
Sous le thème :

Conception d'idéotypes de tomate

adaptés au stress hydrique

Par:

Ould Mohamed Abdellahi Cheikh Mehdi

Devant le jury : Maître de stage : Mme. Bertin NADIA Tuteur universitaire : M. Rodolphe GIROUDEAU Rapporteur: M. Philippe JANSSEN

Soutenu à Montpellier le 05/09/2014

1

Table des matières

1	Introduction 1.1 Problématique ................................. 1.2 Présentation de l'entreprise .......................... 1.3 Contexte général du stage .......................... 1.3.1 Les données observées ........................ 1.3.2 Présentation du modèle ....................... 1.3.3 L'objectif: ajustement des paramètres génotype-dépendants . . .			10 10 11 12 12 12 14
2	Méthodologie			17
	2.1		L'optimisation mono-objectif .........................	17
			2.1.1 Construction de la fonction objectif .................	17
	2.2		L'optimisation multi-objectif .........................	18
			2.2.1 Construction des fonctions multi-objectif à minimiser .......	19
	2.3		NSGA-II ....................................	19
			2.3.1 Notion de domination et le front de Pareto ............	19
			2.3.2 Historique ...............................	20
			2.3.3 Le principe de la distance de Crowding ...............	20
			2.3.4 Les différentes étapes de NSGA-II ..................	21
	2.4		La somme pondérée ..............................	23
			2.4.1 Utilisation de la somme pondérée ..................	25
	2.5		Utilisation de NSGA-II ............................	25
			2.5.1 La recherche du meilleur compromis sur le front de Pareto . . .	26
			2.5.1.1 Tracer le front de Pareto pour les meilleurs compromis .	26
			2.5.1.2 Critère de sélection par la distance minimale .......	27
			2.5.1.3 Critère de sélection par la distance maximale ......	27
			2.5.1.4 Critère de sélection par seuil ................	29
3	Les résultats sur les génotypes			30
	3.1		Les résultats d'ajustement indépendant ...................	31
	3.2		Les résultats d'ajustement parallèle .....................	41
	3.3		Analyse de la variabilité des paramètres ...................	46
			3.3.1 L'analyse avec la fonction pairs ...................	46
			3.3.2 L'analyse avec ACP ..........................	46
			3.3.3 Le critère de décision sur une corrélation forte ...........	47
			3.3.4 Analyser sur six paramètres .....................	47
	3.4		Les résultats finaux ..............................	48

2

4

5	Synthèse de la solution apportée Conclusions		62 65
	5.1	Résultats obtenus ...............................	65
	5.2	Difficultés rencontrées ............................	65
	5.3	Apports ....................................	65
		5.3.1 Pour l'entreprise ...........................	65
		5.3.2 Apport personnel ...........................	66
6	Bibliographie		67
	6.1	Références bibliographiques .........................	67
	6.2	Webographies .................................	68

3

Table des figures

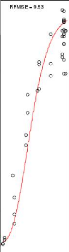
1.1 L'ensemble des nuages de points qui présentent l'évolution de MFobs et de

MSobs. Chaque point représente un fruit prélevé à un stade donné. . . . 13
1.2 Le fonctionnement du modèle croissance de fruit..............14

1.3 L'évolution de MFpred et de MSpred pour le génotype SSD45. ...... 15

1.4 Illustration du problème sur un génotype dans une condition donnée. . . 16

2.1 Le principe de regroupement par cluster...................18 2.2 La notion de domination et le front de Pareto................20 2.3 Le principe de distance de crowding.....................21

2.4 Comparaison basée sur la dominance pour la population R(t). ...... 23

2.5 Le scénario général de NSGA-II....................... 24

2.6 Les compromis construisant le front de Pareto se trouvent sur la courbe

rouge, comment choisir le meilleur ?. . . . . . . . . . . . . . . . . . . . . 28

2.7 Critère de sélection par la distance maximale ................ 28

3.1 La teneur en matière sèche prédite par le modèle au cours de 24H..... 31

3.2 L'ajustement indépendant des paramètres du génotype Levovil. ..... 33

3.3 L'ajustement indépendant des paramètres du génotype Cervil. ...... 34

3.4 L'ajustement indépendant des paramètres du génotype CervXLev..... 35

3.5 L'ajustement indépendant des paramètres du génotype SSD106. ..... 36

3.6 L'ajustement indépendant des paramètres du génotype SSD133. ..... 37

3.7 L'ajustement indépendant des paramètres du génotype SSD45....... 38

3.8 L'ajustement indépendant des paramètres du génotype SSD18....... 39

3.9 L'ajustement indépendant des paramètres du génotype SSD173. ..... 40

3.10 L'ajustement parallèle des paramètres des génotypes Cervil et Levovil. . . 42
3.11 L'ajustement parallèle des paramètres des génotypes CervXLev et SSD106. 43 3.12 L'ajustement parallèle des paramètres des génotypes SSD133 et SSD45. . 44 3.13 L'ajustement parallèle des paramètres des génotypes SSD18 et SSD173. . 45

3.14 Les graphes des corrélations entre les huit paramètres par génotype. . . . 49
3.15 Les graphes des corrélations entre les huit paramètres par génotype et sur

l'ensemble des génotypes............................50 3.16 Les graphes d'analyse en composantes principales entre les huit paramètres

par génotype et sur l'ensemble des génotypes................51

3.17 Les histogrammes obtenus pour num et pi_f0. ............... 52

3.18 La convergence des num et pi_f0....................... 53
3.19 Les graphes des corrélations entre les six paramètres par génotype et sur l'ensemble des génotypes............................54

4

3.20 Les graphes d'analyse en composantes principales entre les six paramètres par génotype et sur l'ensemble des génotypes................55

3.21 La convergence des ph_max, Y_param, el et tstar. ............ 56

3.22 Les 20 meilleurs compromis pour SSD45. .................. 58

3.23 Le meilleur des 20 meilleurs compromis pour SSD45. ........... 59
3.24 Les graphes des corrélations et d'analyse en composantes principales entre les six paramètres sur 37 génotypes......................60 3.25 La convergence des ph_max, Y_param, el et tstar dans les résultats finaux. 61

4.1 Les schémas d'illustrations sur les objectifs atteints dans ce travail. . . . 64

5

List of Algorithms

1	La fonction multi-objectifs à minimiser . . . . . . . . . . . . . . . . . . .	19
2	Calcul de la distance de Crowding d'un individu i sur un front F .....	21
3	Solution-non-dominées(P) [Deb et al, 2002] .................	22
4	NSGA-II ....................................	25
5	Tracer le front de Pareto à partir des nuages des points des compromis .	27
6	Sélection par seuil ...............................	29

6

Liste des tableaux

2.1 Les compromis à traiter par le critère de seuil................29

3.1 Tableau des valeurs de paramètres de NSGA-II pour analyser sur 8 para-

mètres......................................32 3.2 Les valeurs des RRMSE(s) trouvées salon les critères de sélection pour le

génotype SSD173 en condition témoin....................32 3.3 Les 50 estimations trouvées par génotype pour faire une analyse sur huit

paramètres...................................48 3.4 Tableau des valeurs de paramètres de NSGA-II pour analyser sur six pa-

ramètres.....................................48

3.5 Tableau des valeurs de paramètres de NSGA-II pour les résultats finaux. 57

7

Résumé:

Dans ce rapport de stage, nous allons aborder les chapitres suivants :

> Une introduction qui aboutira à l'identification du problème posé.

> Une méthodologie où nous étudierons en détail la solution adaptée pour ce problème.

> Des résultats sur les génotypes où nous présenterons et analyserons les résultats obtenus selon la solution adaptée.

> Une synthèse de la solution apportée où nous donnerons une description synthétique de la solution proposée.

> Et une conclusion sur les résultats obtenus.

Mots clés : génotype, ajustement, NSGA-II, front de Pareto, compromis, corrélation.

8

Remerciements :

Durant mon stage, j'ai bénéficié du soutient moral et technique de plusieurs personnes ce qui a rendu mon environnement de travail très agréable.

J'adresse tout particulièrement mes plus chaleureux remerciements à mon responsable de stage Madame Nadia Bertin, pour m'avoir permis d'intégrer l'équipe de recherche dans le cadre de ce stage, pour son écoute, sa disponibilité et ses conseils précieux.

Mes remerciements les plus chaleureux vont également aux membres de mon équipe pour m'avoir bien accueilli, intégré et de leurs aides illimités. Chacun d'eux a permis de son niveau, le bon déroulement de ce stage, je tiens à les remercier sincèrement :

> Gilles Vercambre > Michel Génard

> Pierre Valsesia

> Valentina Baldazzi

J'adresse une attention particulière à Monsieur Gilles Vercambre grâce à lui, j'ai pu dépasser tous les défis techniques rencontrés durant ce travail.

Mes plus chaleureux remerciements s'adressent également à mon tuteur universitaire et responsable de ma formation Monsieur Rdlphe GIROUDEAU, pour avoir accepté de diriger ce travail.

Mes remerciements vont également à Monsieur Philippe JANSSEN pour avoir accepté être le rapporteur de ce travail.

Je tiens aussi à remercier sincèrement les membres du jury qui me font le grand honneur d'évaluer ce travail.

Enfin, je tiens à remercier mes parents qui m'ont soutenu et aidé tout au long de mes études, en particulier mes frères Bah et Elhusseine, qui veillaient sur mes études, je vous remercie infiniment.

9

Lexique :

MF : Matière fraiche (poids total du fruit)

MS : Matière sèche (poids du fruit après séchage)

MFobs : Matière fraiche observée expérimentalement

MSobs : Matière sèche observée expérimentalement

MFpred : Matière fraiche prédite par le modèle

MSpred : Matière sèche prédite par le modèle

Condition : Soit témoin, soit stress

Anthèse (la floraison) : la période fonctionnelle pour la pollinisation de la fleur

RMSE : Root-Mean-Square Error

RRMSE : Relative Root Mean-Squared Error

Les huit paramètres à ajuster :

> phi_max : utilisé pour le calcul de l'extensibilité de la paroi cellulaire

> Y _param : correspond au seuil de la pression de turgescence pour la croissance > pi_f0 : utilisé pour le calcul de la pression osmotique du fruit

> Lp : conductivité de la membrane composite pour le transport de l'eau

> nu_m : vitesse maximale de transport du carbone par unité de masse sèche utilisé dans le calcul de U_a (absorption active de sucre).

> tstar : utilisé dans le calcul de U_a (absorption active de sucre) > tau_a : utilisé dans le calcul de U_a (absorption active de sucre) > el : utilisé dans le calcul de U_a (absorption active de sucre)

10

Chapitre 1

Introduction

1.1 Problématique

Depuis plusieurs années, les météorologistes constatent des modifications des conditions climatiques à l'échelle mondiale, et surtout régionale, allant vers un réchauffement de la planète. Ce changement climatique entraîne une fréquence accrue d'évènements climatiques extrêmes, parmi lesquels des périodes de sècheresse provoquant un stress hydrique important sur les plantes cultivées avec pour conséquence une diminution des rendements et une modification de la qualité des produits (Seki et col. , 2003; Farooq et col. ;2009a,b et 20011). En effet, l'eau est l'un des principaux facteurs qui influent sur la croissance et le développement des plantes, car elle constitue la force motrice de la multiplication et de l'élongation cellulaire qui sont les mécanismes clés de la croissance des plantes. Pour croître, les plantes ont besoin d'un apport régulier d'eau. Un manque d'eau au niveau du sol peut affecter le contenu en eau des feuilles, le transport et l'accumulation des éléments nutritifs et par là même la croissance des plantes cultivées. Le déficit hydrique peut donc être définit comme un manque d'eau par rapport aux besoins de la plante pour une croissance et un développement optimal durant son cycle de vie (Manivannan et al., 2008).

La tomate est l'une des plus importantes plantes cultivées à travers le monde ainsi qu'une source importante de vitamines et d'antioxydants (H.K Klee et col., 2011). Comme toute plante, la tomate est aussi sensible au déficit hydrique, qui provoque une perte de rendement et une modification de la qualité des fruits. La qualité du fruit est un objectif de recherche majeur chez la tomate et un caractère complexe car de nombreux critères doivent être pris en compte. Pour l'industrie, la taille des fruits, le contenu en matière sèche, la couleur et la viscosité sont des critères importants. Plus récemment, des critères de qualité pour la valeur santé et le plaisir des consommateurs sont aussi pris en compte. Pour le marché de frais, la taille des fruits, leur texture et leur composition en sucres et acides sont des critères très importants.

Aujourd'hui, les agriculteurs doivent se conformer à un nombre croissant de réglementations afin de réduire l'impact des productions sur l'environnement et la santé humaine. Dans ce contexte, des exigences de qualité des aliments et de régularité de la production les obligent à envisager toutes les alternatives possibles pour pallier à ces questions. Pour cela les systèmes de production doivent s'adapter au contexte climatique, mais aussi faire

11

face à la demande sociale croissante en termes de qualité organoleptique, nutritionnelle et environnementale des produits alimentaires. Par conséquent, une question cruciale pour l'avenir est de savoir comment mieux exploiter la variabilité génétique pour concevoir de nouvelles variétés plus adaptées au nouveau contexte climatique et à des pratiques culturales respectueuses de l'environnement notamment la réduction des apports d'eau. Une approche intégrée est nécessaire pour gérer les liens et les antagonismes entre les processus biologiques sous l'influence du génotype et des pratiques culturelles. Dans cet objectif, un modèle de simulation décrivant les interactions entre les principaux processus de croissance du fruit pourrait éventuellement être utilisé pour analyser la variabilité génétique et aider à la conception de génotypes adaptés aux contraintes environnementales (on parle d'idéotype, c'est-à-dire de génotype ideal dans des conditions données). Les modèles peuvent également permettre la construction de systèmes de production innovants, en appliquant une méthodologie d'optimisation.

Durant ces dernières années, des approches de modélisation écophysiologique ont été développées pour comprendre les interactions entre les processus clés impliqués dans le contrôle génétique de caractères complexes et prédire les interactions génotypeXenvironnement Xpratiques culturales et pour la conception de nouveaux idéotypes adaptés aux environnements cibles (Génard et col., 2007). Pour la tomate, plusieurs modèles ont été développés pour prédire le développement et la croissance du fruit, sa concentration en sucre ainsi que l'endoréduplication ou endomitose de l'ADN (Bertin et col., 2003; Bertin et col., 2007; Bussières, 2002; Liu et col. 2007). Ces modèles sont des outils potentiels d'analyse de la variabilité génétique et des interactions génotypeXenvironnement ainsi que des outils de phénotypage (Genard et col., 2010).

La conception de systèmes de production durable combinant idéotypes est un problème multicritères, car il y a beaucoup des critères antagonistes à remplir et de nombreuses contraintes à respecter. Lorsque les critères sont choisis et les contraintes définies, la sélec-tion/conception à base de modèles de systèmes intégrés de production peut-être formulée comme un problème d'optimisation multi-objectifs. Par conséquent, nous devons recourir à des méthodes d'évaluation multicritères "efficaces", des algorithmes d'optimisation multi-objectifs pour la conception elle-même et des techniques multicritères d'évaluation afin d'évaluer la pertinence des systèmes de culture conçus.

1.2 Présentation de l'entreprise

Le centre Inra Provence-Alpes-Côte d'Azur est un centre de recherche tourné vers l'agroécologie des systèmes de culture sous serres et en vergers et la modélisation de l'impact régionalisé du changement climatique à l'échelle du paysage. Parmi ses unités des recherches, l'unité PSH (Plantes et Systèmes de culture Horticoles) travaille sur les productions horticoles alimentaires, et principalement les fruits et légumes consommés en frais. Ses objectifs finalisés sont de contribuer à la mise au point de scénarios techniques et paysagers permettant de promouvoir la qualité des produits récoltés et le respect de l'environnement. La réalisation de ces objectifs s'appuie sur des études au niveau de la plante, de ses fruits, et de populations de bioagresseurs, destinées à mieux comprendre

12

leurs réponses à l'environnement. Elle s'appuie également sur des études au niveau des systèmes de culture permettant de représenter le fonctionnement des plantes en interaction avec l'environnement physique et biotique et les interventions culturales.

1.3 Contexte général du stage

L'unité PSH est structurée en 2 équipes de recherches dont l'équipe (Ecophysiologie de la Plante Horticole). Ce stage se déroule au sein de cette équipe et s'inscrit dans un projet plus vaste sur l'adaptation de la tomate au déficit hydrique, financé par le CTPS (Comité Technique Permanent de la Sélection).

1.3.1 Les données observées

Une expérimentation a été menée en 2013 sur une population de 120 lignées cultivées en condition témoin et en condition de stress hydrique. Cette population est issue du croisement entre une lignée (le génotype Cervil) à petits fruits mais aux qualités orga-noleptiques remarquables et une lignée (le génotype Levovil) à gros fruits (Causse et al. 2002). On traite tout génotype (élément de la population précédente) sous deux conditions (témoin et stress), sous chaque condition donnée, on s'intéresse aux variables MF (la matière fraiche) et MS (la matière sèche) qui varient en fonction de l'âge (des jours après anthèse de la fleur) de ce génotype.

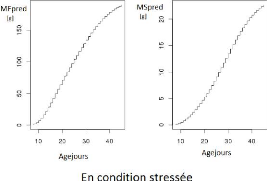
Deux types de données : les premières issues de l'expérimentation, ce qui a permis de mesurer la MF et la MS, ce qu'on appelle dans ce cas, la MFobs (matière fraiche observée) et la MSobs (matière sèche observée) pour tout génotype et dans chaque condition. Le deuxième type de données est issu de la simulation qu'on fait grâce au modèle (la sous section suivante). Au niveau des axes, l'axe X = »des_jours» (il n'est considéré qu'à partir du jour=8) et sur l'axe Y =(MF ou MS). La Figure1.1 illustre pour l'un des génotypes (appelé SSD45) les mesures de matière fraiche observée et matière sèche observée obtenues pour les 2 conditions de culture (témoin et stress). On voit que les stress hydrique a réduit la croissance du fruit.

1.3.2 Présentation du modèle

Le modèle développé pour la tomate permet de simuler un ensemble des variables [Lui et al.2007]. On se concentrera dans ce travail uniquement sur l'un des modules du modèle VirtualFruit, appelée "modèle croissance du fruit", liée aux flux d'eau et de carbone et à l'expansion cellulaire. Ce modèle nous permet d'obtenir le deuxième type de données, en simulant à un pas de temps horaire, la croissance du fruit, en matière fraîche et sèche qu'on appelle dans ce cas : MFpred (matière fraiche prédite) et MSpred (matière sèche prédite) . Pour faire une simulation avec le modèle de croissance du fruit, il faut donner le jour de début, le jour de fin de la simulation et deux fichiers sont nécessaires : > Un fichier des entrées : il contient les informations suivantes renseignées à un pas de temps horaire :

c des données climatiques : température, humidité de l'air dans la serre.

c des données plantes : potentiel hydrique de tige et concentration en sucre dans le phloème.

En condition témoin

I

MFobs [g] e? - N 0 4 -

a (c) o a a CO o o a o O O IP

MSobs [g] c~ - N -- 4 -

o o O 0 a o o O

I I I I I I I I

10 20 30 40 10 20 30 40

Agejours Agejours

		i		En condition stressée			i
0
	o ca
ua --

a O

O

o

D _o O

0 Ô	cip	o
	D O O

0.1

MFobs [g]

Q _ N

U)

MSobs [g] _L _

o

o

o

o

13

p O

O --

O

I

I I I I f

10 20 30 40 10 20 30 40

Agejours Agejours

FIGURE 1.1 L'ensemble des nuages de points qui présentent l'évolution de MFobs et de MSobs. Chaque point représente un fruit prélevé à un stade donné.

14

~ une donnée fruit : la conductance de la cuticule du fruit à la vapeur d'eau (rho) .

> Un fichier des paramètres : il contient tous les paramètres nécessaires au modèle croissance avec :

~ des paramètres correspondant à des constantes physiques (constantes des gaz parfait, masse molaire des sucres et de l'eau . . .)

~ des paramètres plantes fixés quel que soit le génotype (taux de respiration, effet de la température sur la respiration . . .)

~ des paramètres plantes génotype-dépendants

A la fin de la simulation, le modèle génère un fichier de sorties, contenant toutes les informations calculées par le modèle au cours de la simulation, et en particulier la MF-pred et la MSpred qui nous concerneront dans ce qui suit. La Figure 1.2 illustre l'idée générale du fonctionnement du modèle de croissance du fruit.

FIGURE 1.2 Le fonctionnement du modèle croissance de fruit.

1.3.3 L'objectif: ajustement des paramètres génotype-dépendants

Pour que le modèle simule correctement l'évolution au cours du temps des deux variables MF et MS, il est nécessaire d'ajuster huit paramètres ayant un fort impact sur ces variables. On considère que ces paramètres sont génotype dépendants, mais ne dépendent pas de l'environnement. Pour un même génotype, les plants en condition témoin et stressé partagent les mêmes valeurs de paramètres (voir la Figure1.3). Le travail du stage va donc consister dans un premier temps à ajuster ces paramètres pour un génotype quelconque dans chacune des conditions (témoin ou stress hydrique) pour simuler le mieux possible l'évolution mesurée au cours du temps de la matière fraîche et de la matière sèche. La Figure1.4 montre un exemple où la valeur des paramètres ne permet pas une simulation correcte de la dynamique de croissance du fruit. Cette question sera appelée "ajustement indépendant", dans le sens où pour un même génotype, les paramètres peuvent être différents dans les 2 conditions de culture. Dans un deuxième temps, on cherchera à ajuster les paramètres d'un génotype dans les deux conditions simultanément,

c'est-à-dire que la valeur des paramètres sera identique dans les 2 conditions de culture. On parlera dans cette étape "d'ajustement parallèle".

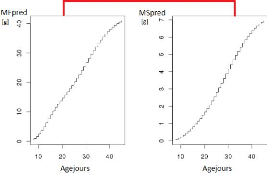
15

FIGURE 1.3 L'évolution de MFpred et de MSpred pour le génotype SSD45.

Si on résume, les objectifs du stage sont les trois points suivants :

i) Recalibrer le modèle de croissance du fruit existant (Liu et al. 2007) sur la population de lignées recombinantes et éventuellement le modifier pour qu'il soit capable de prédire les effets du stress hydrique :

- Faire l'ajustement indépendant sur huit génotypes de la population.

- Faire l'ajustement parallèle sur huit génotypes de la population.

ii) Analyser la variabilité génétique des paramètres du modèle.

iii) Proposer au final la meilleur combinaison de paramètres permettant d'avoir le meilleur ajustement parallèle par génotype pour toute la population.

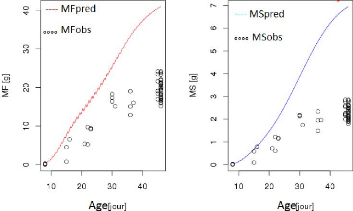
16

FIGURE 1.4 Illustration du problème sur un génotype dans une condition donnée.

17

Chapitre 2

Méthodologie

Résumé : Nous proposons dans ce chapitre de présenter les méthodes (algorithmes) principalement utilisées pour arriver aux objectifs proposés. Dans les deux premières sections, nous allons montrer comment l'ajustement des paramètres du modèle peut se transformer en un objectif d'optimisation mono-objectif et éventuellement multi-objectifs, en profitant de méthodes (algorithme) existant dans le domaine de l'optimisation. Et dans les trois sections suivantes, nous présentons un algorithme évolutionnaire multi-objectif et une méthode classique choisis pour résoudre notre problème et des critères pour traiter l'ensemble des solutions trouvées.

2.1 L'optimisation mono-objectif

En optimisation mono-objectif, on cherche à minimiser/maximiser une fonction objectif unique. Cette fonction objectif varie en fonction d'un ou plusieurs paramètres chacun de ces paramètres étant borné (contraintes). On va présenter dans la sous section suivante comment construire nos fonctions objectifs à partir des données observées et prédites par le modèle de la croissance du fruit.

2.1.1 Construction de la fonction objectif

Pour toute condition donnée, le modèle permet la simulation de la matière fraîche et de la matière sèche pendant la croissance du fruit à un pas de temps horaire. Les mesures ont été réalisées au cours du temps. Comme ces mesures sont destructives, plusieurs fruits ont été récoltés à des âges après anthèse variable. En général, le nombre de mesures à la récolte est très important alors qu'à contrario, peu de fruit ont été récoltés au cours de la croissance pouvant aller jusqu'à 1 seule mesure à certaine date. De plus, les fruits n'ont pas été cueillis toujours au même âge, mais plutôt sur certaines plages d'âges. Au vu du jeu de donnée (âge variable, nombre de mesures très variable entre les différents âges), nous avons, donc construit des clusters permettant à la fois de regrouper différentes mesures réalisés dans des fenêtres d'âge proche et permettant de donner un poids identique à ces différentes dates en prenant pour chaque cluster la moyenne des différences entre les données observées et prédites (illustration avec la Figure2.1 : chaque cluster est illustré par une couleur). Dans un deuxième temps, il a fallu définir une fonction objectif pour chacune des variables MF et MS. Pour chacune de ces variables, il est nécessaire de

(2.1)

(2.2)

18

construire une fonction objectif qui nous permettra d'optimiser la valeur des paramètres. L'objectif de cette fonction doit être de nous permettre de minimiser les écarts entre les données simulées et les données observées.

nCluster_{P P}n

1 1

RMSE = (Dobsi,j - Dpredi_,j)²

nCluster n

i=1 j=1

Les variables de l'équation (équatin2.1) sont :

Dobs : (MF ou MS).

Dpred :(MFpred ou MSpred).

nCluster : nombre de culster.

n : nombre de points des données observées au niveau de culster i.

RRMSE = 100 × RMSE

MFobs

La fonction à minimiser est le RRMSE (équatin2.2), aussi bien pour la matière fraîche que pour la matière sèche. L'objectif est bien de trouver la meilleure combinaison de paramètre permettant de simuler le mieux possible la matière fraîche et la matière sèche, donc de minimiser simultanément RRMSEMF et RRMSEMS. Nous nous trouvons donc dans la situation d'avoir à optimiser sur deux critères, et nous nous plaçons dans le cadre général de l'optimisation multi-objectifs (voir section suivante).

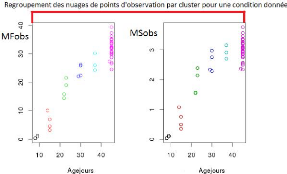
FIGURE 2.1 Le principe de regroupement par cluster.

2.2 L'optimisation multi-objectif

La plupart des problèmes du monde réel nécessitent l'optimisation selon plusieurs objectifs, ces objectifs pouvant potentiellement être contradictoires et/ou dépendants les

19

Algorithm 1 La fonction multi-objectifs à minimiser

1: k : le nombre des fonctions objectifs et défini selon la procédure d'ajustement.

2: Initialisation :

~ Initialiser x=(Les_paramètres_à_ajuster) // un vecteur contenant ces paramètres.

3: Calcul des fonctions objectifs

for (i=1; i<=k; i++) {Calculer la fonction objectif fi(x)}

4: Remplir le vecteur de fonctions objectifs f : f(x) = (f1(x), f2(x), ..., fk(x))

5: Retourner f(x).

uns des autres. Pour l'optimisation à objectif unique (ou à critère unique ou encore mono-objectif), la solution optimale est généralement clairement définie. Pour les problèmes à objectifs multiples (ou à critères multiples ou encore multi-objectifs), il n'y a généralement pas une solution optimale, mais plutôt un ensemble de solutions qui sont des compromis. Dans la sous-section suivante, on va créer une fonction multi-objectifs qui regroupera nos fonctions objectifs à minimiser.

2.2.1 Construction des fonctions multi-objectif à minimiser

Notre problème se présente donc comme un problème d'optimisation multi-objectif, avec deux fonctions à minimiser RRMSEMF et RRMSEMS, qui seront notées fMF ^et fMS. Ces fonctions dépendent des valeurs des paramètres à ajuster, x=(Les_paramètres_à_ajuster). La minimisation de ces fonctions doit être réalisée sous contrainte, les valeurs des paramètres étant bornées. L'objectif est de minimiser ces fonctions en respectant les contraintes sur les paramètres. L'algorithme1 résume la création des fonctions multi-objectifs à minimiser. Un algorithme d'optimisation multi- objectifs évolutionnaire NSGA-II et une méthode classique la somme pondérée sont utilisés à ces fins (les sections suivantes).

2.3 NSGA-II

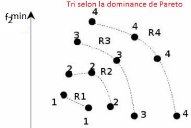
2.3.1 Notion de domination et le front de Pareto

Sur la Figure2.2, on illustre la notion de domination et le front de Pareto tel que, le point noir :

> domine chacun des carrés.

> est dominé par chacun des triangles.

> n'est pas comparables avec les cercles.

Le front de Pareto représente l'ensemble des points de l'espace de recherche tels qu'il n'existe aucun point qui est strictement meilleur qu'eux (les domine) sur tous les objectifs simultanément. Il s'agit de l'ensemble des meilleurs compromis réalisables entre les objectifs contradictoires, et l'objectif de NSGA-II va être d'identifier cet ensemble de compromis optimaux.

20

FIGURE 2.2 La notion de domination et le front de Pareto.

2.3.2 Historique

NSGA-II (Non-dominated Sorting Genetic Algorithm) a été proposé par [Deb et al, 2002] et est classé comme l'un des algorithmes phares dans le domaine de l'optimisation évolutionnaire multi-objectif. Il tient son appellation de l'algorithme NSGA qui a été proposé auparavant par [Srinvas et Deb, 1994]. L'algorithme NSGA reprend l'idée proposée par Goldberg sur l'utilisation du concept de classement par dominance (sous-section précédente) dans les algorithmes génétiques [Goldberg 1989]. Dans plupart des aspects NSGA-II est très différent de NSGA, cependant le nom a été gardé pour indiquer les origines de cette approche. NSGA-II intègre un opérateur de sélection d'un individu (solution), basé sur un calcul de la distance de "Crowding" (voir sous-section suivante). Comparativement à NSGA, NSGA-II obtient de meilleurs résultats sur toutes les instances présentées dans les travaux de [Deb et al, 2002], ce qui fait que cet algorithme est l'un des algorithmes les plus efficaces pour trouver l'ensemble optimal de Pareto avec une excellente variété des solutions.

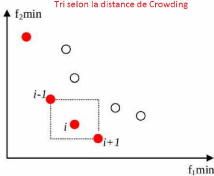
2.3.3 Le principe de la distance de Crowding

La distance de Crowding (ou surpeuplement) est un opérateur de sélection, utilisé pour estimer la densité au voisinage d'un individu (solution) j dans l'espace de recherche. Il calcule la distance moyenne sur chaque objectif, entre les deux points les plus proches situés de part et d'autre de la solution j. Cette distance notée di sert d'estimateur de taille du plus large hypercube incluant le point j sans inclure un autre point de la population et formé par les solutions du même front de Pareto les plus proches de j (voir la Figure2.3, les points rouges appartiennent du même front de Pareto). L'algorithme2 montre les étapes nécessaires pour calculer cette distance (di) pour un individu j.

21

FIGURE 2.3 Le principe de distance de crowding.

Algorithm 2 Calcul de la distance de Crowding d'un individu j sur un front F

1: Initialiser :

l : le nombre d'individus de front F.

di = 0 : pour tout individu j se trouve sur F.

in = 1 : un compteur sur les objectifs.

2: Réordonner l'ensemble F de façon que les valeurs de l'objectif f_m sur ses éléments diminuent. Notons I^m = sort[f_m>](F) le vecteur des indices, c'est à dire I^m_i dénote l'indice de la solution j dans la liste ordonnée selon l'objectif f_m

3: Mettre à jour la valeur de di

Pour chaque solution j telle que 2 I^m_i (l - 1) :

~fm[Im ~

i +1]-fm[Im _i -1]

di = di + max(fm)-min(fm)

2.3.4 Les différentes étapes de NSGA-II

Soient deux populations de même taille N, P(t) (des parents) générée aléatoirement et Q(t) (des enfants) créée à partir de la population P(t), en utilisant les opérateurs génétiques (sélection-croisement-mutation) (voir le projet TER). Ensuite, elles sont réunies en ensemble pour former la population mixte R(t) = P(t) U Q(t), qui est triée selon le principe de dominance en un nombre des fronts de Pareto distincts Rj de la façon suivante : tous les individus non-dominés de R appartiennent à l'ensemble R1 (premier front) ; ensuite, tous les éléments non-dominés de R\R1 sont placés dans l'ensemble R2 (deuxième front) et ainsi de suite jusqu'à ce que tous les individus (solutions) de R(t) soient attribués à un front (voir la Figure2.4, L'algorithme3 montre les étapes nécessaires pour faire un tri de dominance pour une population donnée). Notons que entre deux solutions de même front, aucune ne peut être considérée meilleure que l'autre.

Quand toute la population R(t) est triée, la population suivante P(t + 1) est remplie

22

Algorithm 3 Solution-non-dominées(P) [Deb et al, 2002]

1: for each p E P // P : une population à trier selon le principe de dominance

S_p = O // S_p : une liste ayant contenu tous les individus(solutions) dominés par p

n_p = 0 // n_p : le nombre d'individus(solutions) qui dominent p

for each q E P

if (p -< q) then // si p domine q

S_p = S_p U {q} // mettre q dans S_p

else if (q -< p) then // si q domine p

n_p = n_p + 1

if (n_p = 0) then //p appartient au premier front

pfront = 1

F1 = F1 U {p}

2: i = 1 // Initialize the front counter

while (Fi =6 O)

Q = O // Used to store the members of the next front

for each p E Fi

for each q E S_p

n_q = n_q - 1

if (n_q = 0) then // q appartient au front suivant

qfront = i + 1

Q=QU{q}

i = i + 1

Fi = Q

par les solutions des sous-ensembles non-dominé de R(t) l'un après l'autre en ajoutant les fronts, en commençant par le premier front R1, second front R2, ... etc. Pour choisir les solutions du front qui vont survivre dont seulement une partie peut être placée dans la population suivante, l'opérateur de sélection utilise la distance de Crowding (l'algo-rithme2). Tant que |P(t + 1)| ne dépassent pas N, un tri selon la distance de Crowding est appliqué sur les individus du premier front suivant, non inclus dans P(t+1). Ce tri a pour objectif d'insérer les (N-|P(t+1)|) meilleurs individus (solutions) qui manquent dans la population P(t + 1).

Une fois que les individus appartenant à la population P(t + 1) sont identifiés, une nouvelle population enfant Q(t + 1) est créée. La sélection des individus pour la création de Q(t + 1) à partir de P(t + 1) se fait en utilisant un opérateur sélection appelé de tournoi qui est appliqué entre n individus tirés au hasard dans P(t + 1). Un individu i gagne un tournoi contre un individu j si et seulement si une des deux conditions suivantes est vraie :

> Front(i) < Front(j)

> Ou Front(i) = Front(j) et di > dj

Étant donné que ce tournoi permet à NSGA-II d'éviter le problème de non élitisme, c'est-à-dire perdre le meilleur individu de la population P(t) dans la population P(t + 1).

23

FIGURE 2.4 Comparaison basée sur la dominance pour la population R(t).

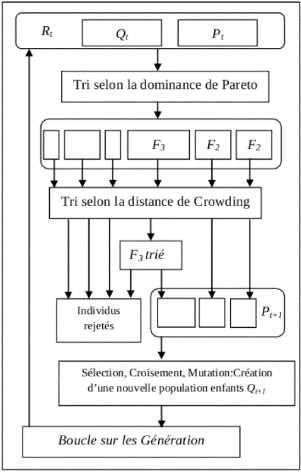
Le processus continue, d'une génération à la suivante, jusqu'à la dernière. Le scénario général de NSGA-II est illustré dans la Figure2.5 et résumé dans l'algrithme4.

Remarque 2.1. [Deb et al, 2002] ont montré que la complexité du NSGA-II est de l'ordre de O(MN²) où M est le nombre d'objectifs (critères) et N la taille de la population. Cette complexité est induite par la procédure du tri (l'algrithme3) des solutions non dominées de l'algorithme.

Remarque 2.2. NSGA-II a un problème pour résoudre les problèmes ayant un grand nombre des critères, ses performances se détériorent au delà de 3 critères, la plupart des individus (solutions) de la population sont des solutions non dominées, ils ne peuvent pas se déplacer vers la région optimale au sens de Pareto. La taille de la population peut être augmentée pour surmonter ce problème, mais ce qui rend le travail de l'algorithme très lent. Donc une méthode classique "la somme pondérée" a été utilisée pour limiter le nombre de nos critères (les sorties de l'algrithme1) à 2. Elle sera traité dans la section suivante.

2.4 La somme pondérée

Cette méthode de résolution est la plus évidente et la plus largement utilisée en pratique parmi toutes les méthodes classiques. Elle consiste à ramener le problème multi-objectif à un problème d'optimisation mono-objectif, il s'agit d'associer à chaque fonction objectif un coefficient de pondération et à faire la somme des fonctions objectifs pondérées pour obtenir une nouvelle et unique fonction objectif (l'équatin2.3). Ces coefficients sont généralement choisis en fonction de l'importance relative que le décideur attribue à l'objectif.

F = min k i=1 wifi(x), k = 2 (2.3)

Où les poids 0 < wi < 1 sont tels que k i=1 wi = 1

24

FIGURE 2.5 Le scénario général de NSGA-II.

25

Algorithm 4 NSGA-II

1: Initialiser les populations P(0), Q(0) de taille N, L : nombre de génération, t = 0.

2: while t < L do

3: R(t) = P(t) ? Q(t) ;//Création de R(t), P(t) et Q(t) désignent respectivement la population et la progéniture à la génération t.

4: F=Algorithme3(R(t)) //Trier R(t) selon le principe de dominance, F = (F1, F2, F3, ...).

5: P(t + 1) = Ø, i = 1 ;// La nouvelle population

6: while |P(t + 1)| + |Fi| < N do

7: P(t + 1) = P(t + 1) ? Fi ;

8: Algorithme2(Fi);

9: i + +;

10: end while

11: P(t+1) = P(t+1)?Fi[1 : (N-|P(t+1)|)]//Ordonner l'ensemble Fi selon la distance de Crowding et inclure les N -|P(t+1)| solutions ayant les valeurs di les plus grandes.

12: Q(t + 1) = mak_new_pop(P(t + 1))//Créer la population des enfants Q(t + 1) à partir de la population des parents P(t + 1).

13: t + +;

14: end while

2.4.1 Utilisation de la somme pondérée

Il est à noter que la variable k (le nombre des fonctions objectifs dans l'algorithme1) ne prend que deux valeurs dans ce travail :

> 2 si on fait un ajustement indépendant (ajuster sous une seule condition (témoin ou stress) la MFobs et la MSobs d'où deux fonctions objectifs seulement).

> 4 si on fait un ajustement parallèle (les deux conditions témoin et stress d'où deux fonctions objectifs par condition). Pour cet ajustement la somme pondérée est utilisée pour fusionner les 2 fonctions objectifs par condition à une seule par condition (l'équation2.4).

fCondition = w × fMF + (1 - w) × fMS (2.4)

Avec w=0.50 : l'importance relative attribuée aux fonctions objectifs fMF ^et fMS est identique, chacune de ces fonction ayant importance identique.

2.5 Utilisation de NSGA-II

L'algorithme NSGA-II est déjà implémenté sous R (l'outil utilisé pour la programmation) et appeler de la façon suivante :

nsga2(fn, idim, odim, generations, popsize,lower.bounds, upper.bounds, cprob , cdist,mprob , mdist ) avec,

fn : la fonction à minimiser (l'algorithme1 (section2.2.1) pour nous).

idim : la taille des entrées de la fonction fn (le nombre de nos paramètres à ajuster) odim : la taille des sorties de la fonction fn (la taille de vecteur des sorties de l'algorithme1, qui est 2 pour nous et quelque soit la procédure d'ajustement).

26

generations : le nombre de générations souhaitées et aussi le critère d'arrêt à respecter.

popsize : la taille de la population, il présente aussi le nombre des compromis qu'on

pourra avoir.

lower.bounds : les bornes inférieures des entrées de la fonction fm (les bornes inférieures

de nos paramètres )

upper.bounds : les bornes supérieures des entrées de la fonction fm (les bornes supé-

rieures de nos paramètres )

cprob : Crossover probability

cdist : Crossover distribution index

mprob : Mutation probability

mdist : Mutation distribution index

Lorsqu'on fait un appel de l'algorithme NSGA-II sur un génotype pour un ajustement (indépendant ou parallèle), les sorties sont stockées dans un fichier contenant des colonnes pour les valeurs obtenues des nos paramètres à ajuster et deux colonnes particulières représentant les valeurs des fonctions objectifs à minimiser f1 et f2 (les sorties de l'algorithme1 (section2.2.1)). Cet algorithme va donc donner en sortie les "popsize : nombre de compromis" meilleurs compromis obtenus. Et la question posée est comment choisir le compromis ayant des valeurs minimales à la fois de f1 et puis f2 ?, cette question sera traitée dans la sous section suivante.

2.5.1 La recherche du meilleur compromis sur le front de Pareto

Comme toute méthode d'optimisation multi-objectif, l'algorithme NSGA-II vise à déterminer le front de Pareto ayant contenu l'ensemble des meilleurs compromis optimaux. NSGA-II nous propose donc les valeurs de fonctions objectifs (f1, f2), pour les meilleurs compromis trouvés. Pour lesquels, il faut tracer le front de Pareto.

2.5.1.1 Tracer le front de Pareto pour les meilleurs compromis

Pour qu'un compromis (une solution) A, ayant les coordonnées (xA, yA) soit sur le front de Pareto, il ne faut pas qu'il existe un autre compromis B ayant les coordonnées (xB, yB), qui vérifie la contrainte suivante :

xB < xA et yB < yA (2.5)

L'algorithme5 résume les étapes nécessaires pour sélectionner les compromis formant le front de Pareto, tel qu'à l'étape2 (while), on fait les tests sur les compromis, s'il existe un compromis B qui vérifie la contrainte2.5 contre un compromis A, cela veut dire que A est rejeté sinon retenu et stocké dans le tableau Pareto[k,2]. Nous obtenons donc un tableau qui récapitule l'ensemble des solutions minimisant les fonctions objectifs (f1, f2). La Figure2.6 donne un exemple sur l'application du critère.

Maintenant la question devient comment sélectionner le meilleur compromis se trouvant sur le front de Pareto?. Trois critères de sélection ont été développés pour répondre à cette question.

27

Algorithm 5 Tracer le front de Pareto à partir des nuages des points des compromis

1: Initialiser :

k = 0;

Pareto[k, 2] : Il prendra les compromis ayant construit le front de Pareto. i = 1;

2: while(i<= f1 )) // Notons que, f1 = f2

{

for(j = 1; j <= f1 ; j++)

{

if((f1[j]<f1[i]) and (f2[j]<f2[i]))

{

boule=False;

break;

}

else{boule=True ;}

}

if(boule==True)

{

k=k+1;

Pareto[k,] =(f1[i],f2[i])

}

i=i+1;

}

3: Tracer les éléments de Pareto.

Remarque 2.3. La cntrainte2.5 traduit juste le principe de dominance entre deux individus (solutions) dans l'espace de recherche (vu en sectin2.3.1 et algrithme3).

2.5.1.2 Critère de sélection par la distance minimale

On calcule la distance de chaque compromis se trouvant sur le front de Pareto par rapport au point d'origine du repère (f1, f2) et on sélectionne comme choix final le compromis ayant une distance minimale (l'équation2.6).

\/dmin = f2 1 + f2 ₂ (2.6)

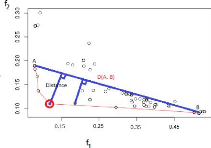
2.5.1.3 Critère de sélection par la distance maximale

L'idée de ce critère est de partir des deux points A(min(f1), max(f2)) et B(max(f1), min(f2)),

les extrêmes du front de Pareto et de calculer la distance de chaque compromis (solution)

se trouvant sur le front de Pareto par rapport à la droite D(A, B) passant par les points

A et B. Le compromis (solution) retenu est celui présentant la distance maximale à la

droite D (voir la Figure2.7).

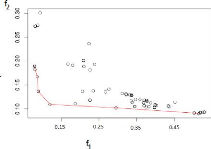
FIGURE 2.6 Les compromis construisant le front de Pareto se trouvent sur la courbe rouge, comment choisir le meilleur?.

28

FIGURE 2.7 Critère de sélection par la distance maximale

29

f1

a1 a2 a3 .. ai .. an

f2 b1 b2 b3 .. bi .. bn

TABLE 2.1 Les compromis à traiter par le critère de seuil.

Algorithm 6 Sélection par seuil

1: Initialiser :

Lmax = {Ø} : // La liste ayant contenu les maximums des couples (ai, bi)

2: for(i=1; i<=|f1| ; i++)

{

Lmax = {max(ai, bi)}

}

3: Lk = min(Lmax)

4: Sélectionner (ak, bk)

2.5.1.4 Critère de sélection par seuil

Les critères de sélection par la distance minimale/maximale peuvent amener à choisir une solution (compromis) très bonne pour une des fonctions objectif mais beaucoup moins bonne pour la seconde fonction objectif. Ce critère a été développé de façon à trouver la solution étant le meilleur compromis sur les 2 fonctions simultanément. Sur les deux colonnes associées aux f1 et f2 dans le fichier des sorties (voir la Table2.1), on sélectionne le maximum de chaque couple (ai, bi), on le met dans une liste Lmax, puis on choisit le compromis associé à la valeur minimale de cette liste (voir l'algorithme6).

30

Chapitre 3

Les résultats sur les génotypes

Résumé : Il est à noter que les résultats de ce travail seront illustrés dans ce rapport sur huit génotypes, qui ont été choisis parmi les 120 génotypes à traiter. Les 112 génotypes restants seront traités dans un autre document. Ceci est du au fait que pour chaque génotype, il faudrait 4 à 5 figures (soit au moins deux pages par génotype pour rendre les figures visibles), ce qui prendrait plus de 200 pages dans le rapport. Donc pour illustrer la qualité du travail et diminuer le volume du rapport, nous nous bornerons à présenter seulement les résultats pour ces 8 génotypes. Rappelons aussi qu'on applique le même traitement sur les 120 génotypes. Trois documents seront préparés pour contenir les résultats sur les 120 génotypes :

-Le rapport (document actuel), contiendra les 8 génotypes choisis.

-Un grand document, contiendra les résultats finaux sur toute la population (les 112 Génotypes restants + aussi les 8 génotypes choisis).

-Un fichier des valeurs des paramètres des 120 génotypes.

Comme dit à la sectin1.3.3, on va ajuster selon deux procédures, la première consiste à ajuster indépendamment sur les deux conditions (témoin et stress). Cette procédure aboutit donc à deux vecteurs de paramètres différents pour les deux conditions et la deuxième procédure consiste à ajuster les paramètres simultanément pour les deux conditions. On aboutit alors à une combinaison de paramètres communes aux deux conditions. Dans les deux premières sections, on traitera ces deux procédures d'ajustement, puis en troisième section on fera une analyse sur la variabilité des paramètres ajustés et à la dernière section on présentera les résultats finaux.

Il est à noter aussi que dans toute procédure d'ajustement, l'heure de récolte prise en compte au niveau de modèle de croissance du fruit est 10H qui correspond à l'heure moyenne des prélèvements de fruits pour les valeurs observées (sur par exemple la Fi-gure3.1, on voit bien que la teneur en matière sèche pour un génotype dans une condition donnée commence à croitre à partir de l'heure 10H) et les huit paramètres seront ajustés sur les bornes suivantes :

> phi_max E [2.0e - 03, 3.0e - 01] et Y_param E [0.1, 20.0]

> Lp E [2.0e - 04, 1.0] et tstar E [1.0, 1500.0]

> tau_a E [100.0, 400.0] et el E [0.0, 0.30]

> pi_f0 E [0.0, 30.0] et nu_m E [1.0e - 03, 0.050]

31

FIGURE 3.1 La teneur en matière sèche prédite par le modèle au cours de 24H.

3.1 Les résultats d'ajustement indépendant

Dans cette section, on illustre les résultats selon la première procédure d'ajustement sur les 8 génotypes choisis représentatifs de la population (120 génotypes). Pour avoir ces résultats, l'algorithme NSGA-II a été appelé sur les valeurs de la Table3.1 (revoir la sectin2.5) par génotype. Les paramètres cprob et mprob sur cette table, représentent respectivement la probabilité d'appliquer les opérateurs de croisement et de mutation sur l'ensemble des individus de la population dans l'espace de recherche. L'opérateur de croisement a pour but d'enrichir la diversité de la population en manipulant la structure des individus. L'opérateur de mutation a pour but de garantir l'exploration de l'espace de recherche, c'est-à- dire le fait que tout point de l'espace de recherche peut être atteint en un nombre fini de mutations.

Sur l'ensemble des figures (Figure3.2, ..., Figure3.9) de ces résultats, l'axe X représente l'age des fruits (jours) et l'axe Y représente soit MF(observée-point ou prédite-ligne) soit MS(observée-point ou prédite-ligne). Et comme indiqué sur les graphiques chaque courbe représente le meilleur compromis choisi par l'un des trois critères de choix :

-dist min : Critère de sélection par la distance minimale.

-dist max : Critère de sélection par la distance maximale

-seuil :Critère de sélection par seuil

Il apparaît aussi que certains compromis sont identiques ou très proches ne permettant pas de les distinguer sur les courbes.

32

Les paramètres de NSGA-II	Les valeurs des paramètres de NSGA-II
idim	8
odim	2
generations	50
popsize	100
cprob	0.7
cdist	5
mprob	0.1
mdist	10

TABLE 3.1 Tableau des valeurs de paramètres de NSGA-II pour analyser sur 8 paramètres.

Critère de sélection	Le RRMSE de MF	Le RRMSE de MS
Distance minimale	12.54	12.80
Seuil	12.54	12.80
Distance maximale	28.86	12.25

TABLE 3.2 Les valeurs des RRMSE(s) trouvées salon les critères de sélection pour le génotype SSD173 en condition témoin.

Sur l'ensemble des génotypes, on voit bien que chaque compromis trouvé par chacun des critères de sélection simule correctement les données observées pour le génotype désigné. Pour choisir un seul compromis parmi ces trois trouvés par génotype, on choisit celui ayant des valeurs minimales à la fois de RRMSE de MF et puis de RRMSE de MS (revoir la sectin2.5). Par exemple sur la Table3.2, on choisit pour le génotype SSD173 en condition témoin le compromis trouvé par les critères de sélection par distance minimale et seuil (même compromis). Nous allons donc voir dans ce qui suit qu'un seul critère de sélection sera adapté. Donc d'une manière globale, le modèle simule correctement l'évolution au cours temps des deux variables MF et MS sur l'ensemble des génotype. Nous allons maintenant voir les résultats selon la deuxième procédure (section suivante).

Remarque 3.1. La courbe médiane est la courbe passant par les médianes des clusters et tracer pour voir la qualité d'ajustement pour le meilleurs compromis choisi au final par génotype.

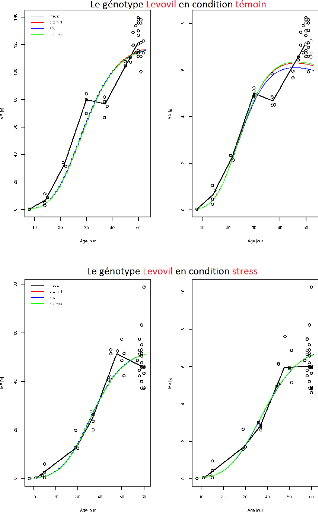
FIGURE 3.2 L'ajustement indépendant des paramètres du génotype Levovil.

33

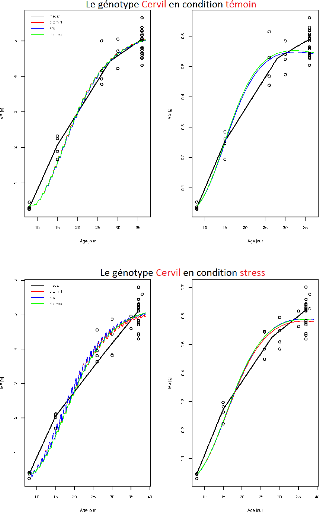
FIGURE 3.3 L'ajustement indépendant des paramètres du génotype Cervil.

34

FIGURE 3.4 L'ajustement indépendant des paramètres du génotype CervXLev.

35

FIGURE 3.5 L'ajustement indépendant des paramètres du génotype SSD106.

36

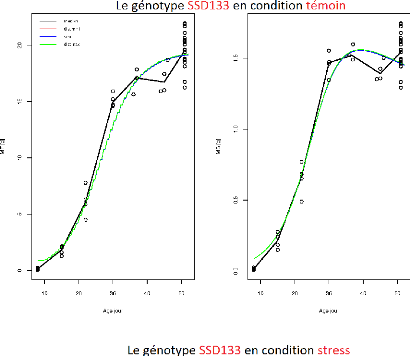
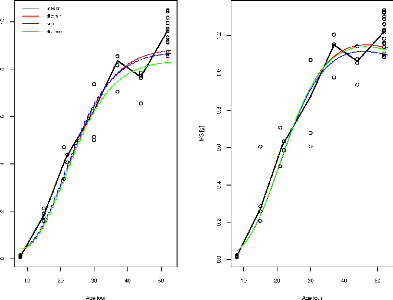
FIGURE 3.6 L'ajustement indépendant des paramètres du génotype SSD133.

37

Le génotype SSD45 en condition témoin

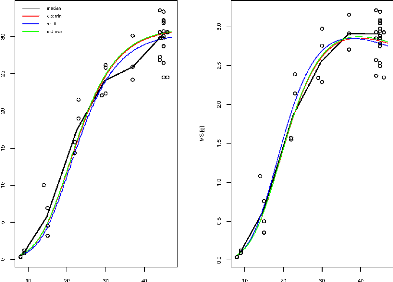
Age jour Age jour

Le génotype SSD45 en condition stress

N(V

FIGURE 3.7 L'ajustement indépendant des paramètres du génotype SSD45.

Age jour Age jour

38

FIGURE 3.8 L'ajustement indépendant des paramètres du génotype SSD18.

39

FIGURE 3.9 L'ajustement indépendant des paramètres du génotype SSD173.

40

41

3.2 Les résultats d'ajustement parallèle

Dans la section précédente, pour chaque génotype, 8 paramètres ont été ajustés indépendamment suivant les conditions donnant donc 8 valeurs de paramètres en conditions témoin et 8 en conditions stress, soit 16 valeurs par génotype. Avec la procédure d'ajustement parallèle, nous allons ajuster tous les génotypes avec un seul jeu de paramètre, quelques soient les conditions (témoin ou stress). Avec toujours les mêmes huit génotypes, on illustre les résultats selon cette procédure. Ces résultats ont été obtenus après avoir appelé l'algorithme NSGA-II sur encore la même Table3.1 par génotype. Sur l'ensemble des figures (Figure3.10, ..., Figure3.13) de ces résultats deux génotypes par figures, les informations indiquées sont :

> Le nom de génotype.

> Les.val.of.param : Les valeurs des paramètres trouvées pour ce génotype.

> sum.of.RRMSE : le somme des valeurs des RRMSE(s) de MF(respectivement, MS) en condition témoin (respectivement, stress).

La valeur de RRMSE est relative avec la qualité d'ajustement de la courbe associée, c'est-à-dire que si cette valeur est petite, alors la courbe va beaucoup mieux ajuster les données observées sinon elle sous-ajuste. D'une manière générale, on trouve que le modèle simule l'évolution au cours temps des deux variables MF et MS sur l'ensemble des génotype selon cette procédure, ce qui nous permet d'aller faire une analyse sur la variabilité des paramètres (section suivante).

Vu que cette procédure est celle choisie pour cette analyse et éventuellement les résultats finaux, il a fallu faire un seul choix sur les critères de sélections et comme dit à la sectin2.5.1.4, c'est le critère de seuil qui est le plus performant par rapport aux critères de sélection par distance suivi du critère de la distance minimale. En effet le critère de sélection par la distance minimale est forte pour deux critères quand on minimise les RRMSE(s) seulement mais vu que cette procédure a ajouté la somme pondérée (sectin2.4), ce critère se détériore parfois en amenant à choisir un compromis très bonne pour une des fonctions objectif mais beaucoup moins bonne pour la seconde fonction objectif. Ainsi que avec la minimisation de quatre critères avant découvrir la Remarque2.2 de NSGA-II. Donc dans tout ce qui suit, seule la procédure d'ajustement parallèle couplée au critère de sélection par seuil sera utilisée.

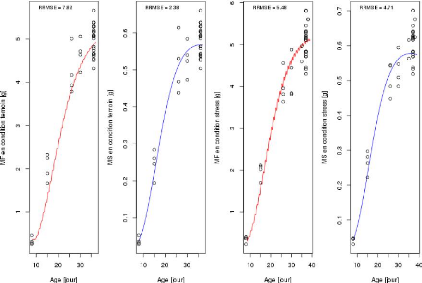
Le gneotype Cervil ; Les.val.of.param: phimax = 0.1609 Y_param = 10.64766 Lp = 0.81023

tstar = 29.31592 tau a = 1 E0.66633 el = 0.28917 pi f0 = 6.87033 nu_m = 0.04017 Sum.of.RRMSE = 20.39

40

I I I I 1

10 20 30

Age Dour]

Age Dour]

10 20 30

Age []our]

10 20 30 40

Age []our]

MS en condition stress [g]

a

MF en condition temoin [g]

N

O

o

MS en condition temoin [g]

C)

nd tion stress [g]

m LL

Cd

O

ô

ô

o

N

ô

RRMSE -4.71

o

O

6 a

a 0

a

Age [Our]

Age [Our]

Age []our]

Age []our]

Le genotype Levovil ; Les.val.of.param: phi_max = 0.06724 Y_ cram = 4.30963 Lp = 0.42637

tatar = 218.47987 tau a = 277.57125 el = 0.14175 pi 0= 7.79146 nu_m = 0.03971 Sum.of.RRMSE = 55.36

1 1 I I I

10 30 50

1 1

10 30 50

MFen condition temoin [g]

ME en condition stress [g]

RRMSE- 10137

0

0

RRMSE - 1933

O

N

O

o -

10

a

MS en condition stress [g]

o a

O N

10 20 30 40 50

10 20 30 40 50

42

FIGURE 3.10 L'ajustement parallèle des paramètres des génotypes Cervil et Levovil.

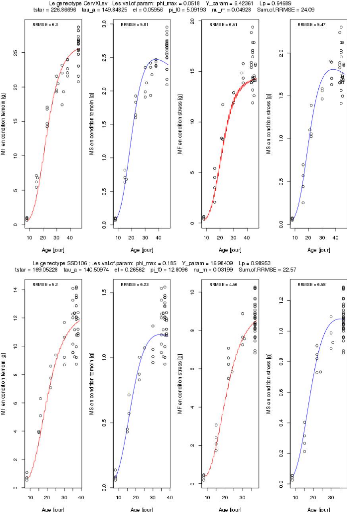
43

FIGURE 3.11 L'ajustement parallèle des paramètres des génotypes CervXLev et SSD106.

MS en co nd do n te mo in [g]

ME en condition stress [g]

MS en condition stress [g]

MFen condition temoin [g]

Le wmotype SSD133 Les.val.of.param: phimax = 0.07864 Y_ram = 5.82745 Lp = 0.99707

tstar = 401.77526 tau a = 186.68099 el = 0.14069 pi f0 = 6.60399 nu_m = 0.01725 Sum.of.RRMSE = 35.87

Age [Our]

Age [Our]

Age [pur]

Age [pur]

MF en condition temoin [g]

10 20 30 40 50

MS en condition temoin [g]

10 20 30 40 50

MF en cond fion stress [g]

MS en condition stress [g]

N

N

O

10 20 30 40 50

10 20 30 40 50

Le gneotype SSO45: Les.val.of.param: phi_max = 0.04307 Y_ram = 10.83638 Lp = 0.71487

tstar = 203.84713 tau a = 178.54754 el = 0.06858 pi f0= 10.93544 nu_m = 0.04633 Sum.of.RRMSE = 31.67

RRMSE-959

O

o

LP N

N

I 1 I

10 20 30 40

Age [pur]

I I I

10 20 30 40

Aga [pur]

I

10 20 30 40

Age [Our]

I 1 I

10 20 30 40

Age [pur]

44

FIGURE 3.12 L'ajustement parallèle des paramètres des génotypes SSD133 et SSD45.

50

I 1 I

10 20 30 40

RRMSE- 12.1 0₀

0

,

b b°

o

4 00

O

O

Le geneotype 55018 ; Les.val.of.param: phi_max = 0.15587 Y_param = 3.71011 Lp = 0.9E031

tstar = 35.27268 tau a = 217.59222 el = 0.27496 pi f0 = 5.19321 nu_m = 0.04434 Sum.of.RRMSE = 38.21

o -

Age []our]

I I I

10 20 30 40 50

Age []our]

10 20 30 40

Age []our]

10 20 30 40

Age []our]

MF-i7 condition stress [g]

MS en condition stress [g]

o

o

In

o

rI

In

o

MS en condition temoin [g]

o

o

N

MF en coud tion temoin [g]

RRMSE-222

4

0

o

a

00

0⁰

O

_°

O

b

Le geneotype 550173: Les.val.of.param: phi_rnax = 0.04503 Y_ram = 4.74944 Lp = 0.35584

tstar = 231.03342 tau a = 207.55825 el = 0.16539 pi f0 = 6.33521 nu_m = 0.03257 Sum.of.RRMSE = 51.19

I I

10 20 30 40

Age []our]

MS en condition stress [g]

-r

MFen condition temoin [g]

ms en .:o nd tio n te mo in

o

I 1 I

10 20 30 40

I I I

10 20 30 40

10 20 30 40

Age [Our]

Age [pur]

Age [pur]

RRMSE-1255

a

a °

°

45

FIGURE 3.13 L'ajustement parallèle des paramètres des génotypes SSD18 et SSD173.

46

3.3 Analyse de la variabilité des paramètres

Après avoir obtenu les différentes combinaisons pour les valeurs des paramètres, il était nécessaire de faire une analyse graphique et statistique des relations entre ces paramètres. L'objectif est éventuellement de pouvoir réduire le nombre de paramètres à ajuster, si certains paramètres sont très fortement corrélés. Pour faire cette analyse, nous avons fait 50 estimations selon l'ajustement parallèle (section précédente) sur chacun de nos 8 génotypes, ce qui a donné 50 valeurs par paramètre sur tous les génotypes. Chaque estimation a été trouvée après avoir appelé NSGA-II sur toujours la même Table3.1 par génotype. Sur la Table3.3, les paramètres sont les colonnes et les estimations (compromis) sont les lignes. Deux méthodes d'analyses ont été utilisées à savoir, la fonction "pairs" et la méthode ACP (analyse composant principale), elle seront traitées dans les sous sections suivantes.

3.3.1 L

'analyse avec la fonction pairs

pairs est une fonction graphique sous R de haut niveau qui utilise un ensemble de fonctions et paramètres par défaut pour faire des graphes de corrélations de variables 2 à 2. Elle peut être appelée par génotype sur la Table3.3 (voir les Figure3.14 et Figure3.15) et pour l'ensemble des génotypes (voir la sous-figure "l'ensemble des génotypes" en bas sur la Figure3.15).

Sur ces graphiques, le nom des paramètres sont indiqués sur la diagonale, les coefficients de corrélations au-dessus de la diagonale. Trois couples de paramètres sont corrélés entre eux 2 à 2, (tstar et tau_a), (tstar et nu_m) et (Y _param et pi_f0). Ces deux derniers couples sont les plus fortement corrélés aussi bien au niveau de l'analyse par génotype que dans l'analyse globale. Les valeurs des paramètres nu_m et pi_f0 seront fixés dans ce qui suit et seuls les paramètres tstar et Y_param peuvent être ajustés parmi ces deux couples.

3.3.2 L

'analyse avec ACP

La méthode ACP (analyse en composantes principales), consiste à transformer des variables liées entre elles (dites "corrélées" en statistique) en nouvelles variables décorrélées les unes des autres. Ces nouvelles variables sont nommées "composantes principales", ou axes principaux. Elle permet au praticien de réduire le nombre de variables et de rendre l'information moins redondante [wikipedia]. Elle peut être appelée par génotype sur la Table3.3 (voir la Figure3.16) ou pour l'ensemble des génotypes (voir la sous-figure "l'ensemble des génotypes" en bas sur la Figure3.16).

Sur les sous figures, ACP sélectionne les deux axes qui explique en pourcentage le plus de variance. Dans les cercles si deux paramètres forment :

> Un angle inférieur à 90^°, ils sont en corrélation positive. Plus l'angle est fermé (l'angle converge vers 0^°) plus la corrélation positive est forte,

> Un angle supérieur à 90^°, ils sont en corrélation négative. Plus l'angle est ouvert (l'angle converge vers 180^°), plus la corrélation négative est forte,

47

> Un angle proche de 90^?, ils ne sont pas corrélés,

La partie à gauche des sous figures représente la distribution des estimations sur les axes choisis. On trouve encore les mêmes couples (tstar et n_m), en très fortement corrélation négative et (Y _param et pi_f0), très fortement corrélés positivement, aussi bien sur l'analyse par génotype et que pour l'ensemble des génotypes. Donc les résultats de cette méthode confirment bien ceux de la fonction pairs. La question maintenant, est de savoir à quelles valeurs fixer les paramètres n_m et pi_f0?

A partir des 400 valeurs trouvées (50 valeurs pour chacun des huit génotypes) pour les paramètres n_m et pi_f0, on dessine les histogrammes associés (la Figure3.17). Chaque histogramme présente la distribution des valeurs prises par le paramètre désigné et la médiane "median" associée se trouve dans l'intervalle le plus fréquenté dans cette distribution. On va fixer les paramètres aux valeurs de leurs médianes, soient donc 0.030 pour n_m et 7.36 pour pi_f0. Cependant le fait de fixer un paramètre peut dégrader la qualité d'ajustement et très probablement certains génotypes deviennent quasiment non ajustables sur une des courbes (MF ou MS) en condition témoin ou stressée. Pour éviter ce problème, il a fallu construire un critère permettant de prendre une décision sur une corrélation forte. La décision soit oui (la corrélation sera prise en compte) soit non (la corrélation ne sera pas prise en compte), (voir la sous section suivante).

3.3.3 Le critère de décision sur une corrélation forte

Pour ce faire, on trie les n (50 ici) compromis trouvés par génotype du meilleur jusqu'au moins bon. Dès que ce tri est fait par le critère de sélection par seuil (sectin2.5.1.4), on dessine les valeurs des paramètres à fixer en fonction des compromis triés et une droite horizontale représentant la valeur de la médiane pour laquelle, il faut fixer le paramètre désigné (la Figure3.18). Rappelons que la valeur de la médiane est bien celle trouvée sur 400 valeurs (pour les huit génotypes), donc c'est une valeur globale pour les histogrammes de paramètre associé et non locale. La décision est oui, si la droite (la valeur de la médiane) simule au moins une partie de l'ensemble des nuages des points de son paramètre sur tous les huit génotypes et non en cas d'existence d'un génotype qui ne vérifie pas cette contrainte. Donc d'après la Figure3.18, la décision est oui pour les couples de corrélations (tstar et n_m) et (Y _param et pi_f0).

Remarque 3.2. La variable (Val_de_critère_de_seuil) sur la Figure3.18 représente les valeurs de la somme pondérée (car on applique l'ajustement parallèle) dans la liste L_max (revoir encore la sectin2.5.1.4).

Maintenant, on fixe les paramètres n_m et pi_f0 à leurs valeurs indiquées à la section précédente, puis on ajuste les six paramètres restants avec éventuellement la recherche des nouvelles corrélations.

3.3.4 Analyser sur six paramètres

Cette analyse a été faite de la même manière que celle sur huit paramètres, nous avons fait 50 estimations selon l'ajustement parallèle sur chacun de nos 8 génotypes. Chaque estimation a été trouvée après avoir appelé NSGA-II sur la Table3.4 (juste

48

??????????????? Paramètres Estimation

	phi_max	Y_param	Lp	tstar	tau_a	el	pi_f0	n_m
Estimation1	a1,1	a1,2	..	..	..	...	...	a1,8
Estimation2	a2,1	a2,2	..	..	..	..	..	a2,8
..	..	..	..	..	..	..	..	..
Estimationi	ai,1	ai,2	..	..	..	..	..	ai,8
..	..	..	..	..	..	..	..	..
Estimation50	a50,1	a50,2	..	..	..	..	..	a50,8

TABLE 3.3 Les 50 estimations trouvées par génotype pour faire une analyse sur huit paramètres.

Les paramètres de NSGA-II	Les valeurs des paramètres de NSGA-II
idim	6
odim	2
generations	50
popsize	100
cprob	0.7
cdist	5
mprob	0.1
mdist	10

TABLE 3.4 Tableau des valeurs de paramètres de NSGA-II pour analyser sur six paramètres.

le paramètre idim qui a changé) par génotype. D'après l'appel de la fonction pairs (la Figure3.19) et la méthode ACP (la Figure3.20), deux nouveaux couples fortement corrélés aussi bien au niveau de l'analyse par génotype que dans l'analyse globale sont apparus, (phi_max et Y _param) et (tstar et el). Pour ces deux couples de corrélations, il n'apparait pas possible de fixer l'un des paramètres à la valeur de sa médiane sans prendre en compte la qualité d'ajustement (voir la Figure3.21, la décision du critère est non). Sur cette figure, deux génotypes ne vérifient pas la contrainte du critère de décision sur les quatre paramètres des ces deux couples des corrélations fortes. Rappelons encore que la valeur de la médiane est globale (la médiane sur les 400 valeurs des huit génotypes).

Pour résumer, aucun paramètre n'a alors été fixé dans cette analyse et les résultats finaux (section suivante) sont obtenus en ajustant les six paramètres restants.

3.4 Les résultats finaux

La tâche principale de ce travail est de proposer au final la meilleure combinaison de paramètres permettant d'avoir le meilleur ajustement parallèle par génotype. Pour trouver la meilleure combinaison paramétrique par génotype, il faut donner des tailles de

49

FIGURE 3.14 Les graphes des corrélations entre les huit paramètres par génotype.

FIGURE 3.15 Les graphes des corrélations entre les huit paramètres par génotype et sur l'ensemble des génotypes.

50

Varlablea factor map (PCA)		Y -		individuels factor map (PCA)
				39 0 42 · GB ^-1·I-~8-_ . 23 · P	1.0 -0.5 0.0 0.5

-4 -2 0 2 4

Dim 1 (32.37%)

Dim1 (3022%)

CeNI I Variables factor map (PCA)

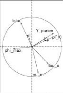
-1.0 -0.5 0.0 0.5 1.0

Dim 1 (30.22%)

Celle-ci est une sous figure

Individuals factor map (PCA) Levovil

Dim 1 (32.37%)

-2 0 2 4

1,0 -0.5 0.0 0.5 1.0

-1,0 -0.5 0.0 0.5 1.0 4 -2 0 2 4

Dim 1 (37.21%)

Dim 1 (37.21%)

Dim, (37.18%)

Dim 1 (37.18%)

48

¹ 8 7

31 ₃:

a2 12 4

· as'₂ ).^6° âti

5073

.2 0 2 4

Dim, (41.80%)

1.0 -2 5 0.0 0.5

Dim 1 (38.99%)

1.0

1.0 -0.5 OD 0.s 1.0 4 -2 0 2

Dim, (41.80%) Dim1 (38.99%)

Individuals factor map (PCA) ^SSD45 Variables factor map (PCA)

Individual, factor map (PCA) ^SSD18 Variables factor map (PCA)

SSD173

Individual, factor map (PCA) Variables factor map (PCA)

CervXLev

Individual, factor map (PCA) Variables factor map (PCA)

Individuals factor map (PCA)^SSD133 Variables factor map (PCA)

Individuels factor map (PCA) ^SSD1Oâyariablea factor map (PCA)

Dim 1 (38.83%)

21⁹94 10 23 ⁴.0_.t

9~~ 42

2145 3

· 33 u^.

I

2 0 2 4

Dim, (35 00%)

1.0 -05 0.0 0.5 1'0

Dim 1 (35.00%)

24

É

E

~0 iT843

21 22
·

·

25 50

45 27

· ~°
· 33

qqaa

1 zz y

3fi2 2
·reeïT
·9 14b2i~ 7s ~
·

· ⁴ 35³
·

·
·

·

· 34 2, 2

Al2 ₆ 32 a§

,,p4,~~ L+tA9

₅
· 41

L'ensemble des génotypes

Individual, factor map (PCA) Variables factor map (PCA)

p\(2

_tau_ Y.peram

51

FIGURE 3.16 - Les graphes d'analyse en composantes principales entre les huit paramètres par génotype et sur l'ensemble des génotypes.

I l I l

4 -2 0 2 4

Dire 1 (27.87%)

phi_ max

Istar

1.0 -0.5 0.0 0.5 1.0

Dim 1 (27.87%)

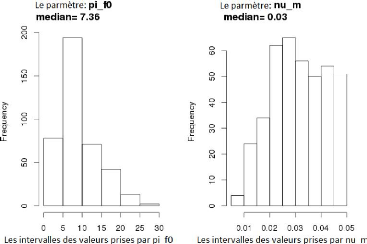
52

FIGURE 3.17 Les histogrammes obtenus pour num et pi_f0.

génération/population permettant à l'algorithme NSGA-II de bien explorer l'espace de recherche vers le meilleur front de Pareto possible. Après plusieurs tests, qui ont été faits durant ce travail sur l'ensemble des génotypes, le choix le plus judicieux qui a été défini est d'appeler NSGA-II sur une génération de taille 250 et une population de taille 400 par génotype. Avec ces tailles (voir la Table3.5), on a fait 20 estimations par génotype (la Figure3.22 pour le génotype SSD45).

Pour faire le graphique associé à ces 20 meilleurs compromis, on a appliqué le principe de cluster (vu en sectin2.1.1) sur les nuages de points de données observées (MFobs, MSobs) en remplaçant chaque cluster par sa moyenne et son écart-type (le point segment) puis on trace les 20 courbes associées aux MFpred et MSpred. Même chose pour les sous graphiques associés aux teneurs en matière sèche (MS/MF) en condition témoin et stress.

Sur le graphique associé à ces 20 meilleurs compromis, on trouve que les courbes simulent presque les points-segment des données observées de la même manière, ce qui prouve la convergence de ces compromis vers la même zone du meilleur compromis possible.

Au niveau des courbes des teneurs, on voit qu'elles n'ajustent pas bien les données dans un premier temps et cela vient du fait que les poids du fruit (MF, MS) sont très petits au début (assez proches). Mais dès que ces poids commencent à croître, les teneurs prédites simulent relativement bien les teneurs observées.

Sur chacun des sous graphiques associés à la convergence des paramètres (toujours la Figure3.22), on voit bien que chaque paramètre converge presque vers la même valeur (ou disons reste restreint dans le même petit intervalle), ce qui nous permet de

ol	Levovll		Levovll			Coral!	ô		Cervll
	o -- median so o o °o 0 ° ô 0 0 tô		° --maan 0 0 0 00 °°° ° 0 0 0 ° ^°o a o0			-- median ô ^00 0 0 0 0 ° 0 0 ° o 0 0 0			oe -- median oao 0 0 0 ° o 0 o$
						o
	8 10 12 14 18		8 10 12 14 18			11 12 13 14			11 12 13 14
Val de critere de seuil Val de critere de seuil					Val_de_critere_de_seu I I			Vol_de_critere_de_seu I I

SSD173 SSD173 CervXLev CervXLev

median

median

₀ 0° o 0
o_° 0 8
°°
_p0 0 0

00 0

° o

0 0

⁰8 ° ZP°⁰ o ^g2/0 0 00

0 ⁰

median

o

00 8 ₀

o ^o A

°° O

0

0

0 00ô0ô

~o

° 0
.0.4%

_GO ° ° o0 0

° ° o

13 14 15 16 17 18 19

Vol_de_critare_de_seu i l

13 14 15 18 17 18 19

V al_de_critere_de_seuil

9 8 10 12 14 8 8 10 12 14

Val_de_critere_de_seu i l Vol_de_critere_de_seu i l

^E o

SSD133

-- madian

oYd g~o

moo_®

° 0 0

9 10 11 12 13

Val_de_critere_de_seu I I

SSD133

0₀ 0

ô °

0 0

o ^°9 0 0o 0ô 0 0

o 0

0 o

o

median

9 10 11 12 13

V al_de_critere_de_sauil

SSD106

median

04 o° °

° ° o

0

10 12

Val_de_critere_de_seu I I

SSD106

median

0 °

8 10 12

Val_de_critere_de_seu il

53

FIGURE 3.18 La convergence des num et pi f0.

Levavll

Cervll

50 150 250

0 05 0 15

0 05 0 20

0.83

phi_max

phi_max

0.62

0.34

:fl

Y_param

0.70

Y_param

0.51

KIM

Lp

Lp

0.99

0.93

0.87

0.86

tatar

tatar

0.81

tau_a

tau_a

0.62

el

el

0 05 0 15

SSD45

SSD18

0.87

phi_max

0.81

phi_max

0.48

0.50

com

0.40

0 35

Y_param

Y_param

0.61

0.50

0.52

0.54

044

0.44

0.49

8 ° m8

;bEA^{e a} Wi-rr~-rr

Lp

Lp

0.98

0.91

0.98

0.77

tatar

tatar

0.83

tau_a

tau_a

0.63

el

el

SSD173

CervXLev

150 250 950

005 0 15 025

0.81

phi_max

phi_max

0.71

054

0.43

0.40

0.43

0.40

Y_param

Y_param

0.49

0.59

0.55

0.57

v ldI

^°ôd

oo 8

o. o. o oo t,o o

Lp

Lp

054

0.46

ria

0.99

0.98

0.88

0.83

tatar

tatar

0.81

tau_a

tau_a

0.72

el

el

SSD133

SSD106

100 200

0 15 0 25

0.88

phi_max

phi_max

0.44

0,42

0.49

0.40

Y_param

0.71

0.70

Y_param

0.61

0.64

052

0.47

044

Lp

Lp

0.52

0.46

â

· e

002 001 014 04 Od 01 10

0.93

0.84

0.83

0.80

tatar

tatar

tau_a

tau_a

r

el

el

200 240

120 150 200

L'ensemble des genotypes

phi_max

0.64

Y_param

0.58

0 07

!>

i

Lp

0.80

tatar

rr 7¹1

tau_a

el

·

00 04 08

54

FIGURE 3.19 Les graphes des corrélations entre les six paramètres par génotype et sur l'ensemble des génotypes.

Individuals factor map (PCA) CONS Variables factor map (PCA)

		Dim 1 (44. 59%)

Individual. factor map (PCA) sols Variable. factor map (PCA)

			Dim 1 (80.78%)
		Dim 1 (83.]5%)

Individuals factor map (PCA) Levovil Variables factor map (PCA)

38 31

.43
·

24 10
·

· 512 54)^,
4^,21

331.- 1,_! -2 - 3.
·zé
·

1 ..138

48
· 4 ⁰⁸ .0

· ,Ar5
·
r

.25

-4 -2 0 2

Dlm 1 (48.94%)

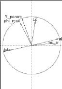
1.0 -05 00 0.5 1.0

Dim 1 (48. 94%)

Indlvlduala factor map (PCA) 555 ° Variables factor map (PCA)

1.0 -0.5 00 0.5 1.0

Dim 1 (5792%) Dim 1 (5792%)

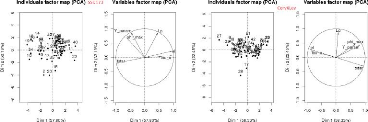
1.0 -0.9 00 0.5 110

Dim 1 (58.33%)

8 -0 -2 0 2 4 Dim 1 (58.33%)

Indlvlduala factor map (PCA) 55 c^ Variables factor map (PCA)

Individual. factor map (PCA) Variable. factor map (PCA)

EervxLev

Dim 1 (57.80%)

Dim 1 (5].80%)

10 -5 5 00 0.5 1.8

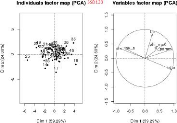
Indlvlduala factor map (PCA) 554133 Variables factor map (PCA)

Individuals factor map (PCA) OSE100 Variable. factor map (PCA)

E ô 9

-8 -4 -2 0 2 4 Dim 1 (59.29%)

1.0 -0.5 0.0 0.s 10

Dim 1 (59.29%)

-4 -2 0 2 4

Dim 1 (52.83%)

Yyera

E

1.0 -0.s 00 5.s 10

Dim 1 (52 83%)

_N

5-

L'ensemble des génotypes

Indlvlduala factor map (PCA) Variables factor map (PCA)

E o

FIGURE 3.20 - Les graphes d'analyse en composantes principales entre les six paramètres par génotype et sur l'ensemble des génotypes.

-4 -2 0 2 4

Dim 1 (3829%)

55

1.0 -0.5 0.0 0.5 1.0 Dlm l (38.29%)

SSD106

I I I I

6 7 8 9 10 11

Val de critere de seuil Val de critere de seuil

SSD106 Levovil

a

0 D -- median

o

C}

in

C1--

6 e ₀0D o0

Q ₀0 O

N - 0 0

d 0 O

o o

0

a -

d Î I I I I I

6 7 8 9 10 11

14.0 14.5 15.0 15.5 16.0 16.5

Val de critere de seuil Val de critere de seuil

FIGURE 3.21 -- La convergence des ph max, Yparam, el et tstar.

56

1

9

6 7 8

SSD106

Q

median

·

⁰o

o

CV

Q

a

{V --

m ⁰

D 00

0 p0

Q

0 0 00

o

00

a

d

o

a

d

114^-7

d

LU

a

0

d

edia0

Vie: Opt

0 _O OD

ç
·

2 POP

_a,

cv

0

CO -

a --

0₆, 0

o

c

o

o

o

0 a -

mediar

o

0

m 0 0 0

· 0 ki₀

o ⁰ _co

o

CV

a

a -

0 a -

57

Les paramètres de NSGA-II	Les valeurs des paramètres de NSGA-II
idim	6
odim	2
generations	250
popsize	400
cprob	0.9
cdist	20
mprob	0.1
mdist	20

TABLE 3.5 Tableau des valeurs de paramètres de NSGA-II pour les résultats finaux.

sélectionner le meilleur de ces 20 compromis ayant la meilleure combinaison possible de paramètres, c'est-à-dire qui permet d'avoir le meilleur ajustement parallèle (Figure3.23).

Pour résumer, on appliquera le même traitement (20 estimations par génotype, puis la sélection du meilleur des 20 meilleurs) sur l'ensemble des génotypes, qui seront traités dans le grand document.

Remarque 3.3. Sur les résultats finaux de 37 génotypes qui ont été déjà traités, on a refait encore l'analyse de la variabilité des paramètres et la Figure3.25 confirme l'invalidité des corrélations trouvées dans la Figure3.24. Ce qui nous confirme encore ce qui a été trouvé en sectin3.3 pour ces corrélations.

Le graphique associe aux 20 estimations pour le genotype SSD45

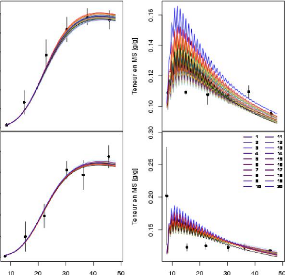
10 20 30 40 50

10 20 30 40

50

O

o

N

O

Teneur en MS [gig]

O

o

o O

If1

0 N

o

Teneur en MS [gr'g]

o

o N LL · - 0
u-
O
			I I I I
		10 20 30 40 50

o ri

N

o

_ N co 0

^T2 r

o

o

O

o

N

o

N

~
^{· r}

o

o

o

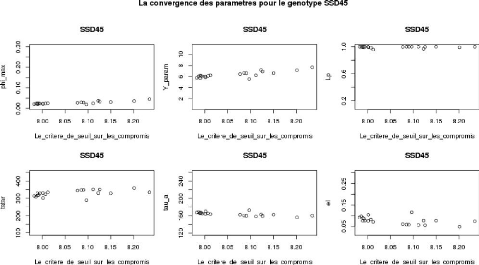
o

aari D ₆ O O 4

La convergence des pa ra metres pour le genotype SSD45

o

o

O

o

E m

N -

₀% ô^°%

o

0 N

o

^o

I

E

E

SSD45

SSD45

6.00 8.05 8.10 8.15 8.20

Le_crite re_de_se u il_su r_les_co m pro m s

SSD45

D

o

o -

6.00 8.05 2.10 8.15 8.20

Le_crite re_de_se u il_su r_les_co m pro m s

O

N -

8.00 6.05 6.10 6.15 8.20

Le_crite re_de_se u il_su r_les_ca m prom s

8.00 6.05 6.10 6.15 8.20

Le_crite re_de_se u il_su r_les_ca m prom s

SSD45

N

O

o

40 0on 0

p^dD 0

o

ow O 4 O 0 o

cktEtop

SSD45

8.00 2.05 8.10 8.15 8.20

Le_crite re_de_se u il_su r_les_ca m prom s

SSD45

8.00 8.05 8.10 8.15 8.20

.131

Le_crite re_de_se u il_su r_les_ca m prom s

O

6

N -

0

0

0 -

o

m

0 4 O a

m

0

N _ ô

58

FIGURE 3.22 Les 20 meilleurs compromis pour SSD45.

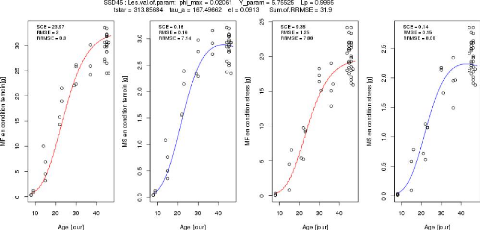
00

4 d

SCE-L35RMSE-125 RRMSE-71!

55045 : Les.val.of.param: phi_rrax = 0.02061 Yjram = 5.75525 Lp = 0.9995

tstar = 313.85684 tau a = 16749662 el = 0.0913 Sum.of.RRMSE = 31.9

10 20 30 40

Age [our]

10 20 30 40 10 20 30 40

Auge []our] Age Dur]

MF en condition temoin[g]

MS en condition temoin [g]

MF en condition stress [g]

Age [pur]

MS en condition stress [g]

10 20 30 40

D

u_

u_ en^-

teneur simule

0 ô I I
	I I

Le genotype 991345 en condition temoin

Le genotype SSD45 en condition stress

teneur simule

tn

o _

a I I I I

59

10 20 30 40 50 60 10 20 30 40 50 60

Temps [jour] Temps [jour]

FIGURE 3.23 Le meilleur des 20 meilleurs compromis pour SSD45.

Sur 37 genotypes

phi_max

0 4 e

I I L

0.62

Y_param

0.00 0.15 0.30

0.89

__o

0.0 0.4 0.8

150 250 350

tstar

0.27

el

0.00 0.15 0.30

I

0.46

0.49

O

O

0 200 400

11 I I I 1

0.37

0.47

Lp

5 15

aiG

Individuals factor map (PCA) Variables factor map (PCA)

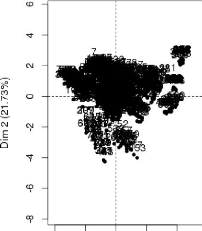
I I I I

Dim 2 (21.73%)

0

cv

00 --

L(

rn

L(.

Lp

Y_param

tstar

ph.iimax

ta __a

I I

-4 -2 Cl 2 4 -1.0 -0.5 0.0 0.5 1.0

OH 1 (44,47%) Dim 1 (44.47%)

60

FIGURE 3.24 -- Les graphes des corrélations et d'analyse en composantes principales entre les six paramètres sur 37 génotypes.

61

SSD1O6

					SSD1O6
- ô u, N -- O O N -- O ce E _ ç O Q O O u, 4 --O O O 0	medi	E a Q }		0 03 m N -- O -		(=MO ® n media
						I I I 1 I I
5.94 5.98 6.02				5.94 5.98 6.02
Val de critere de seuil				Val de critere de seuil
SSD1O6				Levovil
0 en --ô u,				0 O --Ln
	q 0 median q 0 c7					median
N --
O
				O -		D
0						0
-- O
				O
				O -
Ln		ce
O		.^N.
				O
O				O -- N
4 u, O --				O O -
O
4
O -				O -
O
						I I I I I

5.94 5.98 6.02 13.80 13.90 14.00

Val de critere de seuil Val de critere de seuil

FIGURE 3.25 -- La convergence des ph max, Yparam, el et tstar dans les résultats finaux.

62

Chapitre 4

Synthèse de la solution apportée

Dans le cadre de ce projet, nous avons vu que le modèle de croissance du fruit ne permettait pas de simuler correctement l'évolution au cours du temps des deux variables MF et MS de manière simultanée en condition témoin et stress. Par conséquent, le premier objectif du stage était de réaliser la procédure d'ajustement indépendant (sectin3.1) sur les huit paramètres ayant un fort impact sur les variables à prédites pour l'ensemble des génotypes.

Pour cela, nous avons défini une fonction objectif (sectin2.1.1) pour chacune des variables MF et MS. L'objectif de cette fonction était de nous permettre de minimiser les écarts entre les données simulées et les données observées. Par la suite, nous avons construit une fonction multi-objectif (sectin2.2.1) ayant comme sortie ces deux fonctions objectifs. Pour minimiser cette dernière, nous avons utilisé l'algorithme NSGA-II (sectin2.3) qui nous permettait de trouver le front de Pareto contenant les meilleurs compromis entre les deux fonctions objectifs de MF et MS. Enfin, nous avons développé trois critères (sectin2.5.1) permettant de sélectionner le meilleur des meilleurs compromis se trouvant sur le front de Pareto et ajustant les données observées.

Dès que cet objectif était atteint, le deuxième objectif a consisté à développer une procédure d'ajustement parallèle (sectin3.2). Pour cela, on a appliqué le même principe que pour la procédure précédente mais il a fallu régler auparavant trois problèmes majeurs : > Faire que le modèle puisse être appelé parallèlement sur les deux conditions en même temps. En effet le modèle pour l'instant ne peut être appelé que pour une seule condition et la solution la mieux adaptée à ce problème est de faire deux appels successifs pour les deux traitements témoin et stress dans le corps de la fonction multi-objectif, ce qui a augmenté fortement le temps de calcul.

> Un problème au niveau d'une équation dans le corps du modèle liée à l'évolution de la variable MSpred, qui a été réglé par l'équipe et nous a fait changer la version du modèle. > Et le problème de NSGA-II (Remarque2.2), qu'on a résolut grâce à la somme pondérée (sectin2.4.1).

Le schéma1 sur la Figure4.1 illustre les étapes nécessaires pour arriver à ces deux objectifs (les deux procédures d'ajustements).

63

Ensuite un troisième objectif est l'analyse de la variabilité des paramètres (sectins3.3). Étant donné que cette analyse visait à réduire le nombre de paramètres à ajuster mais aussi à déterminer les paramètres génétiques du modèle. Pour ce faire, on a travaillé sur la recherche de l'existence de corrélations fortes entre ces paramètres en utilisant la fonction pairs (sectin3.3.1) et la méthode ACP (sectin3.3.2). On vérifie tout d'abord si les deux méthodes indiquent une corrélation forte entre les paramètres. Si la corrélation est forte, un critère de décision (sectin3.3.3) a été construit pour voir si la fixation d'un des paramètres n'engendrait pas une forte dégradation de la qualité de l'ajustement. La corrélation forte est rejetée dans deux cas, un cas de désaccord entre les méthodes (pairs et ACP) ou un cas d'une réponse négative au test du critère de décision. Le schéma2 sur la Figure4.1 résume les étapes nécessaires pour faire cette analyse.

Enfin ces trois objectifs se résument à un seul objectif principal, trouver la meilleure combinaisons de paramètres, qui permet d'avoir le meilleur ajustement parallèle par génotype (sectin3.4). En effet, cet objectif nous a permis d'aboutir aux résultats finaux sur l'ensemble des génotypes de la manière suivante, appliquant sur tout génotype un ajustement parallèle couplé au critère de sélection par seuil (sectin2.5.1.4), qui fait l'appel à NSGA-II sur une génération de taille 250 et une population de taille 400 (revoir la Table3.5). Ensuite le critère de sélection par seuil, nous permet de sélectionner le meilleur des meilleurs compromis, après avoir atteint 20 estimations (une seule estimation donne un meilleur compromis) par génotype. Le schéma3 sur la Figure4.1 illustre les processus permettant d'atteindre ce dernier objectif.

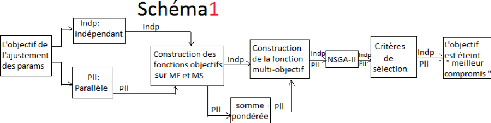
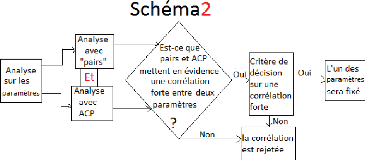
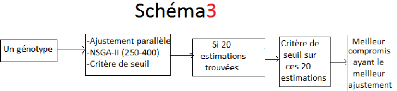
64

FIGURE 4.1 Les schémas d'illustrations sur les objectifs atteints dans ce travail.

65

Chapitre 5

Conclusions

5.1 Résultats obtenus

L'objectif principal du stage a été suivi dans un premier temps via l'ajustement indépendant (sectin3.1) de 8 paramètres en obtenant 16 valeurs par génotype. Dans un deuxième temps un ajustement parallèle (sectin3.2) a permis de réduire le nombre de paramètres de 16 à 8 par génotype. Ensuite grâce à l'analyse de la variabilité des paramètres (sectin3.3), on a pu réduire encore le nombre des paramètres à ajuster de 8 à 6. Et au final l'objectif principal du stage à savoir, estimer les paramètres du modèle de croissance du fruit pour simuler correctement l'évolution au cours du temps des deux variables MF et MS pour l'ensemble des génotypes a été atteint via l'ajustement parallèle de six paramètres.

5.2 Difficultés rencontrées

Les principales difficultés du stage étaient de pouvoir s'adapter aux situations de la vie en laboratoire de recherche, découvrir et exploiter les travaux précédents sur le modèle dans un court laps de temps, comprendre le vocabulaire de biologie et travailler avec l'outil de programmation R (exigé par l'équipe) que je n'aurais jamais utilisé auparavant. Du coté technique les trois problèmes évoqués en chapitre4, m'ont pris la majorité du temps. Il a fallu découvrir chacun d'eux après un long temps et éventuellement chercher la solution la mieux adaptée.

5.3 Apports

5.3.1 Pour l'entreprise

Le bilan de ce stage est positif, les principaux objectifs (sectin1.3.3) du projet sont accomplis. Désormais, le modèle de croissance du fruit permet de simuler correctement l'évolution au cours du temps des deux variables MF et MS pour l'ensemble des génotypes via l'ajustement parallèle (sectin3.2) de six paramètres. En conséquence, nous pouvons dire, sans aucune prétention, que le modèle développé est un outil efficace pour remplir plusieurs objectifs envisagés dans le cadre du projet TOMSEC (conception d'idéotypes

66

culturaux adaptés à la contrainte hydrique et améliorés sur des critères de qualité gustative et nutritionnelle), notamment les deux objectifs suivants :

> Utiliser le modèle pour prédire le comportement de différentes combinaisons allé-liques/paramètres génétiques dans des conditions d'alimentation en eau variables. On suppose que les valeurs des paramètres du modèle dépendent des allèles présents chez les génotypes.

> Proposer des combinaisons de paramètres génétiques permettant d'optimiser le rendement (MS/MF) et la qualité des fruits dans des conditions variables d'environnement. Il s'agit de trouver par l'optimisation multi-objectif les combinaisons de paramètres qui permettent un calibre et une teneur en MS répondant aux exigences du consommateur et ce, dans des conditions respectueuses de l'environnement.

5.3.2 Apport personnel

Ce stage était l'occasion de me plonger dans un milieu professionnel où j'ai eu la chance de travailler au sein d'une équipe de recherche très accueillante et chaleureuse, ce qui me permettait de rencontrer des chercheurs et de partager leurs expériences. Ce stage m'a ainsi permis de mettre en pratique les connaissances théoriques et pratiques acquises lors de ma formation, et d'acquérir un nouvel outil de programmation R qui est très utilisé dans le monde professionnel et surtout les centres de recherche et de calcul là où ma formation est orientée. Il m'a permis également d'approfondir mes connaissances dans le domaine de l'optimisation multi-objectif qui est aussi très demandée aujourd'hui dans la plupart des secteurs, soit il peut s'agir de minimiser un coût de production, d'optimiser le parcours d'un véhicule, d'améliorer les performances d'un circuit électronique, d'affiner un modèle de calcul, de fournir une aide à la décision à des managers, etc. Enfin ce stage est une expérience enrichissante, qui me donne un aperçu du travail dans le milieu de la recherche.

67

Chapitre 6

Bibliographie

6.1 Références bibliographiques

[R1] : J.BONNEFOI (2013). Phénotypage d'une population de tomate dans deux conditions d'alimentation en eau pour le calibrage d'un modèle de qualité du fruit et l'analyse QTL de paramètres de modèles: Mémoire fin d'étude. UR 1115 PSH, INRA d'Avignon, France.

[R2] : M-M.Ould-Sidi, F.Lescourret (2010). Model-based design of integrated production systems : a review. PSH, INRA d'Avignon, France.

[R3] : B.Quilot-Turnion, M-M.Ould-Sidi, A.Kadrani, N.Hilgert, M.Génard, F.Lescourrt (2012). Optimization of parameters of the "Virtual Fruit" model ton design peach genotype of sustainable production systems. INRA-Avignon-Montpellier, France.

[R4] : K. Deb and A. Pratap and S. Agarwal and T. Meyarivan, A fast and elitist mul-tiobjective genetic algorithm : NSGA-II, IEEE T. Evolut. Computat. 6, 182197, 2002.

[R5] : X.Li, L.Amodeo, F.Yalaoui, H.Chehade (210).METAHEURISTIQUES MULTIOB-JECTIF POUR UN PROBLEME D'ORDONNANCEMENT DE MACHINES PARAL-LELES. Institut Charles Delaunay, LOSI, STMR. Page5.

[R6] : M.MÈndez, D.Greiner, B.Galvan (2010). Algorithme Èvolutionnaire multi-objectif qui surélève la région d'intérêt. Toulouse.

[R7] : C.Chatelain, Y.Oufella, S.Adam, Y.Lecourtier, L.Heutte (2008). Optimisation multi-objectif pour la sélection de modèles SVM. Laboratoire LITIS, Université de Rouen, Avenue de l'université, France.

[R8] : Y.OUAZENE, H.CHEHADE, A.YALAOUI. Approches mono et multi-objectives pour la conception d'un système de production à deux machines et un stock-tampon. Université de Technologie de Troyes, 10010 Troyes cedex, FRANCE. Page19.

[R9] : S.Amédée, R.Francois-Gérard (2004). ALGORITHMES GENETIQUES : TE de

68

fin d'année.

[R10] : T.Gräbener, A.Berro (2008). Optimisation multiobjectif discrète par propagation de contraintes. IRIT-Université de Toulouse

[R11] : M.Yagoubi (2012). Optimisation évolutionnaire multi-objectif parallèle : application à la combustion Diesel. Université de Paris Sud XI

[R12] : M.Schoenauer (2009). Techniques avancées. Equipe TAO -INRIA Futurs et LRI . Page48.

[R13] : A.Berro (2008). Algorithmeévolutionnaire Algorithme évolutionnaire pour l'optimisation multiobjectif. Toulouse, France.

[R14] : M-M.Ould-Sidi, B.Quilot-Turion, A.Rolland. Méthodes multicritères pour le tri de fruits virtuels. INRA-Avignon, Bron Cedex, France.

[R15] : P-L.GONZALEZ. L'analyse en composantes principales (A.C.P).

[R16] : D.Puthier (2009). Introduction au logiciel d'analyse statistique R. MARSEILLE cedex 09, FRANCE. Les pages 34-35.

6.2 Webgraphies

[W1] : http :// fr.wikipedia.org/wiki/

[W2] : http :// pinville.com/algorithmes-evolutionnistes.php

[W3] : http :// fr.slideshare.net/paskorn/rnsgaii-presentation. Le point3.

[W4] : http :// www.recherche.enac.fr/opti/papers/thesis/HABIT/main002.html

[W5] : http :// www.r-project.org/other-docs.html

[W6] : http :// www.unige.ch/ses/sococ/cl/r/scatmat.f.html

[W7] : http ://www.lirmm.fr/ rgirou/enseignement/pageenseignement.html

[W8] : http :// www.inside-r.org/packages/cran/mco/docs/nsga2