Approche statistique sur l'étude des rendements financiers et applications.

REPUBLIQUE DU SENEGAL
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA
RECHERCHE SCIENTIFIQUE
UNIVERSITÉ GASTON BERGER DE SAINT-LOUIS
U.F.R DES SCIENCES APPLIQUÉES ET TECHNOLOGIES

Section de Mathématiques Appliquées

Maitrise Mathématiques Appliquées et Informatique
Option : Probabilités-Statistique

SUJET : APPROCHE STATISTIQUE SUR L' ETUDE DES
RENDEMENTS FINANCIERS ET APPLICATIONS
Présenté par :
Babacar DJITTE
Sous la direction de :
Pr Ali Souleymane DABYE
Dr El'hadji Dème

1

Année Universitaire 2013-2014

2

Table des matières

	Dédicace Remerciements Introduction				4 5 6
1	Généralités sur les rendements financiers				7
	1.1		Définition		7
	1.2		Les différents types de rendements		8
			1.2.1 le rendement arithmétique		8
			1.2.2 Le Log-rendement et le taux de rendement		8
			1.2.3 Le rendement moyen		9
			1.2.4 Le rendement cumulé		11
2	Approche statistique				13
	2.1		Définitions et modélisation		13
			2.1.1 Notion de processus stochastique		13
			2.1.2 Exemples de processus AR(p)		16
	2.2		Utilisation des modèles de régression linéaire		17
	2.3		Estimation des paramètres du modèle AR(p)		20
			2.3.1 Méthode de Yule-Walker		21
			2.3.2 La méthode des moindres carrés		22
			2.3.3 La méthode du maximum de vraisemblance exacte . .		24
			2.3.4 La méthode du maximum de vraisemblance conditionnel 25

3

	2.4 2.5	2.3.5 Propriétés statistiques des estimateurs Choix d'un modèle 2.4.1 Critère d'information 2.4.2 Définition Prévision 2.5.1 Prévision d'un modèle AR(p)	28 28 28 28 29 30
3	Simulations		32
	3.1	Exemples de processus AR	32
		3.1.1 Les processus AR(1)	32
		3.1.2 Les processus AR(2)	35
	3.2	Estimation	37
		3.2.1 Estimation des paramètres d'une modélisation AR(1) .	37
		3.2.2 Estimation des paramètres d'une modélisation AR(2) .	38
4	Application du modèle AR sur l'indice boursier S&P 500		40
	4.1	Le S&P 500	40
	4.2	Présentation des données	41
	4.3	Applications	41
		4.3.1 Allure de la série S&P 500	42
		4.3.2 L'ACF et la PACF de la série S&P 500	42
		4.3.3 Estimation	44
		4.3.4 Choix du modèle	46
	Conclusion		47
	Bibliographie		48

4

DÉDICACE

Je dédie ce modeste travail

A mon défunt père Pathé, que le Tout Puissant l'accueille dans Ses jardins

les plus hauts.

A ma chère mère Ndella DJITTE qui a fait de nombreux sacrifices pour que

mes études se passent dans de très bonnes conditions.

A nos Etres chers qui ne sont plus dans ce monde. Qu' Allah(swt) les

accueille dans Son paradis.

A mes chéres soeurs Amy et Mame Diarra .

A tous les membres du Dahira Mafaatihoul Bichri des étudiants et

ex-étudiants de l'Université Gaston BERGER

A mes chérs fréres plus particulièrement à Mor DJITTE, Baye Ibra...

A mes amis d'enfance Khone DJITTE, Modou CISSE, Sangue CISSE,

Mbaye DJITTE...

A mes camarades Aliou SAME, Maty Cheikh MBAYE, Moulaye DIOUSS,

Touba SALL, Babacar MBENGUE...

A ma nièce Aissatou DJITTE et à tous les habitants de mon village natal

NDJITTE

A mes voisins de chambre Lamine NDOYE, Babacar SIGNATE et Serigne

Mounirou THIOUNE

A tous les Méckhois et Méckhoises.

A tous les étudiants de l'UFR SAT.

Mention spéciale à mes camarades de promo.

5

REMERCIEMENTS

Aprés avoir rendu grâce à ALLAH, le tout Puissant et son Prophête Mouha-med (PSL), nous rendons gràce à Cheikh Ahmadou Bamba notre guide vers le droit chemin.

Je remercie chaleureusement mon encadreur, le docteur El'hadji DEME de l'Unité de Formation et de recherches des Sciences Appliquées et Technologies de l'Université Gaston Berger de St-Louis de sa disponibilité, sa courtoisie, sa compréhension, son soutien mais aussi pour m' avoir disposé des sujets si intéressants.

Je remercie aussi le professeur Ali Souleymane DABYE qui n'a jamais cessé de me donner de bons conseils.

Je tiens à remercier tous ceux qui ont durant mon séjour universitaire contribué pour la bonne marche de mes études.

Mes plus profonds remerciements vont à mes parents et surtout ma mère, tout au long de mon cursus, ils m' ont toujours soutenu, encouragé et aidé. Je remercie mon oncle Souleymane DJITTE pour tous les efforts qu'il a fourni afin que mes études se déroulent dans de très bonnes conditions.

Je salue de passage mes tantes Adama DIAKHATE et Ndeye DJITTE, qui m'ont soutenu depuis mon enfance.

Et à toutes les personnes que nous avons eu l'inélégance de mentionner, sachez que sans vous, ce modeste travail ne verrait pas le jour.

6

INTRDUCTIN

L'utilisation des modèles autoregressifs dans le cadre de la modélisation des rendements financiers est de plus en plus courante dans les milieux académiques et pratiques. La principale motivation derrière le travail de recherche et de synthèse présenté dans ce texte a été de faire une approche statistique sur l'etude des rendements financiers et leurs applications.

Ce travail se subdivise en quatre chapitres à savoir :

Au chapitre 1, on introduit la notion de rendements financiers. On introduit aussi les différents types de rendements puis les relations qui existent entre ces rendements.

Au chapitre 2, on présente une approche statistique. Apres avoir défini la notion de processus stochastique, on présente les processus autoregréssifs à p dimensions notés AR(p) qui sont des outils très essentiels pour étudier les rendements financiers. On va développer certains outils qui permettent d'estimer les paramètres du modèle AR mais aussi certains outils qui nous guident à choisir un bon modéle. Enfin on introduit les notions de prévisions Au chapitre 3, on présente un exemple d'application via le logiciel R des outils développés au chapitre 2 avec un ensemble de données.

On terminera avec le chapitre 4 qui présente une application statistique du modèle AR pour les rendements de la série S&P 500.

CHAPITRE1

Généralités sur les rendements finan- ciers

1.1 Définition

Le rendement est défini comme étant le gain ou la perte de valeur d'un actif sur une période donnée. Il est constitué des revenues occasionnés et des gains en capitaux d'un investissement et est habituellement représenté sous la forme d'un pourcentage. Ces derniers peuvent prendre la forme de coupons pour les titres à revenus fixes et de dividendes pour les actions échangées sur les marchés boursiers. Le rendement consite à mesurer la performance d'un actif ou d'un produit . Dans beaucoup de problémes d'intérét en finance, le point de départ est une série chronologique de prix. Pour un certain nombres de prix, il est préférable de ne pas travailler directement avec des séries de prix, de sortes que ces derniers seront souvent converties en séries de rendements. Ainsi par exemple si un rendement annuel est de 10 % alors l'investisseur sait qu'il aura gagné 71500 francs cfa ou bien 715000 francs cfa pour un investissement de 650000 francs cfa et ainsi de suite.

Deux méthodes sont utilisées pour calculer les rendements à partir d'une série de prix donnée. Celles-ci impliquent l'existence de rendement discret (ou rendement simple ou encore rendement arithmétique ), de rendement

8

(1.2)

continu (ou log-rendement), de rendement cumulé et de rendement moyen.

1.2 Les différents types de rendements

Dans toute la suite on considère une suite de n prix d'un titre financier (X1, X2, . . . , X_n). On définit le prix Xt > 0 d'un titre financier observé au temps t.

1.2.1 le rendement arithmétique

On appelle rendement arithmétique (ou le rendement discret) la quantité définie par:

Rarith _t = Xt-Xt_1

Xt_1

1.2.2 Le Log-rendement et le taux de rendement

Implicitement le prix considèré est celui de la fermeture. On définit aussi le taux de rendement effectif Rt sur une période comprise dans l'intervalle de temps [t - 1, t]. C'est le taux composé continument, aussi appelé force d'intérét, qui aurait occasionné les mêmes gains ou pertes sur un montant déposé en banque au cours de la période concernée. Le taux de rendement est la variable d'intérét dans le contexte de la modélisation financière.

On associe le taux de rendement effectif à la différence entre le logarithme du prix initial et final. Dans la situation où le taux de rendement est déterministe et non aléatoire, on obtient l'équation différentielle suivante :

dXt

dt

= Rt.Xt

On peut interpréter cette équation en affirmant que la variation du prix dXt sur un intervalle de temps infiniment petit dt est proportionnelle à la valeur

9

actuelle Xt. Cette équation différentielle a pour solution générale :

Xt = X0e^Rt.t (1.1)

Afin de définir les propriétés de l'échantillon sélectionné, on pose comme hypothèse:

Hypothèse 1.1 : Le rendement R(t) est constant durant la période définie par l'intervalle de temps [t - 1, t], mais il est différent d'une à l'autre : R_s =6 Rt pour s =6 t.

On peut alors représenter le rendement R(t) comme étant la différence entre les logarithmes des prix observés au temps t et t - 1, ou encore le logarithme du quotient de ces mêmes prix :

Rt = ln(Xt) - ln(Xt_1) = ln Xt ?

Xt-1

Un développement limité de Rt nous donne:

Rt = ln

Xt ?~ Xt-Xt-1 Xt-1 Xt_1

Le terme ln(Xt) - ln(Xt_1) est appelé le log-rendement.

La formule du log-rendement souvent plus utilisé en économétrie, est aussi appelé le "log-price" car c'est le logarithme du ratio (rapport) entre le prix pour la présence période au prix de la période précédente. D'une manière générale si Lt représente la variation de temps, alors le rendement continu de la période qui va de t à t + Lt est défini par :

R(t,Ät) = ln(Xt+Ät) - ln(Xt) (1.3)

1.2.3 Le rendement moyen

Le rendement continu a une propriété qui le rend très maniable. En effet, si l'on s'intéresse non plus au rendement continu du marché en 2014 mais au

(1.4)

rendement continu de t = 2010 a` t + T = 2014, il nous suffit de combiner la

moyenne arithmétique des différentes années :

Ainsi le rendement moyen est défini par :

1

=

T

T log?Xt+T

1

Rm Xt
(t,t+T ) =

logXt+T ?

.Xt+T-1 . ... Xt+2 _.Xt+1

Xt+1 Xt

Xt+T-1 XT+t-2

T ?log Xt+T

1 ?+ logXt+T -1 ?+ . . . + logXt+2 ?+ log?^Xt+1

_Xt ?

= Xt+T -1 XT +t-2 Xt+1

= donc on a :	1 T	?T k=1	Rt+k-1,t+k
1 ?T Rm t,t+T = Rt+k-1,t+k T k=1

Et on s'aperçoit bien que le rendement moyen est la moyenne arithmétique des rendements continus.

Par exemple pour t = 2010 et t + T = 2014 on obtient comme rendement

_4P4

moyen de 2010 à 2014, Rm 2010,2014 = 1 k=1 R2009+k,2010+k. Par conséquent le

rendement moyen est bien la moyenne arithmétique des rendements continus. les deux tableaux ci-dessous résume un exemple de calculs du log-rendement

_rln

t et le rendement arithmétique Rarith

t pour quelques valeurs de t. Pt repré-

sente le prix de l'actif à l'instant t.

t	1	2	3
Pt	100	102	100

Tableau 1 : Prix de l'actif en fonction du temps

At	(2 - 1)	(3 - 2)	(2 - 1) + (3 - 2)	(3 - 1)
Rarith t	2.00%	-1.96%	0.04%	0.00%
rln t	1.98%	-1.98%	0.00%	0.00%

10

(1.5)

11

Tableau 2 : Calcul du log-rendement et de rendement arithmétique

1.2.4 Le rendement cumulé

Le rendement de t-jours pour une période menant de 0 à t est appelé le rendement cumulé noté Lt et se définit comme étant la somme des rendements effectifs observés (rendement continus quotidiens) sur l'intervalle [0, t]. Ce dernier représente une propriété utile dans le domaine de la statistique.

Lt = =

?t i=1 ?t i=1

Ri [ln(Xi) - ln(Xi_1)]

= ln(Xt) - ln(X0)

= ln?^Xt

X0

donc on a finalement:

Lt = ln?^Xt

X0

Cette représentation permet d'exprimer le prix actuel Xt en fonction de la valeur initiale X0 sous une forme similaire á la solution (1.1), mais tenant compte de l'hypothèse mise précédemment :

eLt = Xt

X0 = Xt = X0e^Lt

Ce qui entraine en substituant Lt par sa valeur:

Xt = X0 _exp?t?i=1 Ri (1.6)

On suppose l'hypothèse suivante :

Hypothèse 1.2 : Les rendements Ri ; i=1, 2, . . . , t ( ou rendement quotidien) sont indépendants, mais pas nécessairement identiquement distribués.

On peut alors obtenir la distribution du rendement cumulé Lt en utilisant le produit de convolution. Notons _öRi la fonction caractéristique d'un rendement Ri et _öLt celle du cumulé Lt. On obtient alors que cette dernière est égale au produit des fonctions caractéristiques des rendements effectifs sur chacune des périodes de l'intervalle [0, t] :

öL_t(u) = _?t öR_i(u) Vu E [0,t]. (1.7)

i=1

12

On considére la situation où l'on posera plutôt l'hypothèse suivante :

Hypothèse 1.3 : Les rendements Ri pour i=1 ,..., t sont à la fois indépendants et identiquement distribués.

Alors, la fonction caractéristique des rendements est égale pour chaque période :

öR(u) = öR₁(u) = . . . = öR_t(u) (1.8)

La formule (1.7) s'écrit ainsi :

öL_t(u) = [öR(u)]ⁿ Vu E[0,t] . (1.9)

Considérer une distribution qui est fermée sous la convolution pour modéliser les rendements sur une période Ri peut alors étre intéressant. Le rendement cumulé Lt pourra aussi être modélisé à l'aide de la méme distribution. Pour ce faire, on modifie un paramétre d'échelle en fonction de la longueur t de l'intervalle de temps considéré.

CHAPITRE2

Approche statis- tique

2.1 Définitions et modélisation

En statistique, toute tentative de modélisation se fait en introduisant la notion de variable aléatoire. L'approche statistique des rendements d'un actif financier se déroule en plusieurs phases qui englobent chacune en soi un processus. Aussi de l'appréciation, de l'évolution de ces rendements à l'estimation, nous aurons à étaler plusieurs aspects à la fois statistiques et financiers.

2.1.1 Notion de processus stochastique

L'approche statistique d'une série de rendement consiste a` mettre en place un modéle statistique qui considère chaque observation xt pour t=1,. .. ,T comme la réalisation d'une variable aléatoire Xt(w) , telle que

Xt : (Ù , F , P) -+ (R , B(R))

où B( R) est la tribu des Boréliens de R et ( , F , P) est un espace probabilisé. Dans la pratique Xt représente le prix et le rendement se modélise comme étant une variable aléatoire St définies par :

St : (Ù , F, P) -+ (R , B(R))

14

Définition 2.1.1.1 (Processus stochastique) Un processus stochastique est une famille de variables aléatoires (Xt) indéxée par un ensemble T, en général infini, à valeurs dans un espace mesurable (E, 5).

Un élément de T sera appelé un temps ou une date.

Pour une valeur de w fixée dans I, la fonction qui associe à chaque date t la réalisation Xt(w) est la trajectoire du processus au point w. De même, pour une date t fixée dans T, la fonction qui associe à chaque w la réalisation Xt(w) est l'état du processus à la date t.

(Xt) et (St) définissent dans la section 2.1.1 sont des processus stochastiques.

Définition 2.1.1.2 (Processus autorégressif) Un processus stochastique (Xt) est dit autorégressif d'ordre p, noté AR(p) s'il est défini, pour p t par la relation de récurrence

Xt = 1Xt_1 + _{ç2Xt_2} + ... + _{çbpXt_p} + Et (2.1)

V t E Z

où les variables aléatoires X0, X1, . . . , _{Xp_1} sont fixées arbitrairement. Les valeurs çbi pour i=1,. . .,p sont les paramètres de ce processus AR(p), tandis que (Et) est un bruit blanc associé à (Xt), c'est à dire une suite de variables aléatoires indépendantes et de même loi centrées et de carré intégrable. Le polynôme A(X) = 1-çb1X -. . .-çb_pXp définit le polynôme caractéristique du processus.

Définition 2.1.1.3 (Processus stationnaire) Un processus autorégressif (Xt) est asymptotiquement stationnaire si et seulement si son polynôme caractéristique a toutes ses racines à l'exterieur du disque unité.

Définition 2.1.1.4 Un processus (Xt) est stationnaire au second ordre si i) pour t, E(X2 _t ) < +00,

15

ii)pour tout t, E(Xt) = u, constante indépendante de t,

iii)pour tout t et pour tout h, cov(Xt, Xt+h)=E([Xt - u][Xt+h - u]) = ã(h), est indépendant de t

Définition 2.1.1.5 La fonction ã(.) sera appelée fonction d'autocovariance.

On peut montrer aisément que ã(.) est une fonction paire, au sens où ã(h)=ã(-h)

Définition 2.1.1.6 (Corrélation) Etant donnés deux processus (Xt, t E T) et (Yt, t E T)) avec t E T et t + h E T.(T est l'espace des temps).

La corrélation est définie par

Cov(Xt, Yt+h)

Xt)ó

Yt

(

(

+h

ãh(Xt, Yt+h) = (2.2)
ó

oú ó(Xt) et ó(Yt) sont les écart-types respectifs des processus Xt, Yt et _{ó(Xt)ó(Yt+h)} 0.

Définition 2.1.1.7 (fonction d'autocorrélation) On se donne un processus stationnaire (Xt, t E T). On définit le coefficient d'autocorrélation ou fonction d'autocorrélation par

Cov(Xt, Xt+h)

h 7? ãX(h) = ó(Xt)ó(Xt+h) .(2.3)

La fonction ãX prend ses valeurs dans [-1; 1] et on a aussi ãX(0) = 1

Définition 2.1.1.8 (Autocorrélogramme) La matrice d'autocorrélation ou matrice de Toeplitz du vecteur (Xt, _Xt+1, ... , _Xt+h) est définie par :

1 ã(1) ··· ã(h - 1)

ã(1) ... ... ...

ã(1)

ã(h - 1) ··· ã(1) 1

????????

? ???????

...

...

. ..

A(h) =

2.1.2 Exemples de processus AR(p)

Exemple 2.1.2.1 (Processus stationnaire) Soit Xt le processus AR(1) dit de Markov définit par :

2 Xt = 5

Xt_1 + Et.

Puisque Xt_1 = LXt donc on a Xt(1 - ²₅L) = Et

le polynome caracteristique du processus est donc P(z)=1 - ²₅z , qui a pour racine z = 52 . Or |z| > 1 , donc le processus de Markov est bien un processus stationnaire.

Exemple 2.1.2.2 (Processus non stationnaire) On se donne Xt le processus AR(1) définit par :

Xt = Xt_1 + Et.

On a Xt_1 = LXt ce qui donne Xt(1 - L) = Et

le polynome caracteristique du processus est donc P(z) = 1 - z, qui a pour racine z = 1 . De |z| = 1, on en déduit que notre processus est donc non stationnaire.

Considérons maintenant le processus AR(3) définit par :

Zt = 3Zt_1 4

3

Zt_2 + 4

11

Zt_3 + Et

La première étape sera encore d'exprimer cette équation en utilisant l'opérateur retard L et en factorisant par Zt

11

Zt = 3LZt 4

L²Zt + ³₄L³Zt + Et

16

11

(1-3L+ ₄ L²-³ ₄L³)Zt=Et.

17

L'équation caractéristique est donc

11

1 - 3z + 4 z2 - 3 ₄z³ = 0

Une factorisation de l'équation précédente donne :

3 1

(1 - z)(1 - ₂z)(1 - ₂z) = 0.

Ainsi les racines d'une telle équations sont z1 = 1, z2 = ²₃, z3 = 2.

Or la racine z2 = 2 est en dehors du cercle unité car |z2| > 1, ce qui implique la non stationnarité du processus Zt.

NB : la série de rendement est un processus autoregressif AR(p) où p est la taille de l'échantillon. On l'appelle l'ordre du processus

2.2 Utilisation des modèles de régression linéaire

On dispose d'une suite d'observations (X1, X2, ... , X_p) de prix d'actif financier. A partir de ces observations, on définit l'echantillon de rendement (R1, R2, ... , R_p). Puisque la série de rendement (Rt) est un processus auto-régressif d'odre p donc elle peut se mettre sous la forme :

Rt = '1Rt-1 + _ç2Rt-2 + ... + _OpRt-p + Et, Vt E Z (2.4)

V t E Z L'équation (2.1) est equivalent à l'écriture :

A(L)Rt = Et oú A(L) = 1 - çb1L - ... - ç_pLp

Prédire ou expliquer les valeurs de Rt á partir des valeurs de Rt-1, Rt-2, ... , R1 et (Et) est le terme d'erreur ou encore résidus du modèle ou encore bruit blanc : Et ti N (0,u²) c'est à dire une loi normale, elle résume tout ce que le modéle n'explique pas.Les (Et) sont indépendantes.

- Rt est dite "variable endogène", c'est la variable dont on essaie de prédire les valeurs (variable expliquée) ;

- Rt-1, Rt-2, ... , R1 sont les " variables exogènes ", ce sont les variables qui servent à prédire les valeurs de Rt (variables explicatives).

- Les çi pour i=1, ... , p sont les paramètres positifs ou négatifs à estimer Les variables de _Rt-i, pour i=1 , ... , p sont donc connues (ou mesurées rapidement, facilement) elles servent à prédire les valeurs des Rt qui sont inconnues (ou connues avec retard).

La régression linéaire multiple utilise deux méthodes de résolution :

- La connaissance des coefficients de corrélations linéaire simple de toutes les paires de variables entre elles, de la moyenne arithmétique et des écarts-types de toutes les variables.

- La seconde repose sur des calculs matriciels.

Nous nous intéresserons de cette dernière méthode de résolution dans la suite. Ecrivons l'équation (2.1) sous la forme matricielle. Pour t = p+ 1 , ... , n on a :

Rp+1 = O1Rp + _02Rp-1 + ... + _OpR1 + Ep+1 Rp+2 = ç2Rp-1 + _ç3Rp-2 + . . . + _çpR2 + Ep+2 R_n = ç1Rn-1 + _02Rn-2 + . . . + _OpRn-p + E_n

???????

Rp+1

Rp+2

...

R_n

? ??????

Posons :

Y = R(p+1):n =

18

un vecteur de (n - p) rendements.

02

...

0_p

01

Ö=

???????

???????

Ep+1

Ep+2

...

???????

E_n

???????

01

02

0n

_u2

???????????

...

???????????

19

un vecteur de p nombres réels.

E = E(p+1):n =

un vecteur de (n - p) termes d'erreur E ti N (0,cr²T[).

Donc en regroupant les (n - p) on obtient l'expression du modèle linéaire suivante :

Y = RÖ + E (2.5)

où R est la matrice de rendements de taille (n - p) * p définie par :

R = ???????

???????

R_p Rp-1 ··· R1

Rp+1 R_p ··· R2

...

...

. ..

Rn-1 Rn-2 · · · Rn-p

Les paramètres à estimer sont le vecteur Ö et la variance ci² du bruit blanc E, Autrement dit le vecteur défini ci-dessous :

20

Pour ce faire différentes méthodes ont été proposées.

2.3 Estimation des paramètres du modèle AR(p)

A cette étape, on se donne un modèle AR(p) où l'ordre p est supposé connu. Il convient alors d'estimer les paramètres ' et ó². Sous l'hypothèse E suit la loi normale de moyenne 0 et de variance ó², on usera la méthode de Yule-Walker, la méthode des moindres carrés, la méthode du maximum de vraisemblance conditionnel et la méthode du maximum de vraisemblance exacte . Nous allons, dans ce paragraphe, présenter la démarche de l'estima-tion par ces différentes méthodes.

Equations de Yule-Walker

Considérons la série de rendement (Rt) définie dans l'équation (2.4)

En multipliant les deux membres par _Rt-j et en prenant l'espérance on obtient

E(Rt-iRt-j) = E( _?p öiRtRt-i) + E(EtRt-j) i=1

or E(RtRt-j) = ãj par définition de la fonction d'autocovariance. Les termes du bruit blancs sont indépendants les uns des autres et, de plus _Rt-j est indépendant de Et pour tout j positif ou nul.

Donc pour je N^* on a E(EtRt-j) = 0 et pour j = 0 on a :

E(EtRt) = E[~t( _?p öiRt-i + Et)

i=1

= _?p öiE(EtRt-i) + E(4) i=1

= 0 + ó2

21

Donc E(ctRt) = ó2 Maintenant pour j > 0 on a : ?p ãj = E[ i=1

öiRt-iRt-j] + ó^2äj

äj = ????

où äj est le symbole de Kronecker définit par :

1 si j = 0 0 sinon

Par ailleurs ,

?p E[ i=1

p p j p Rt-iRt-jJ = ? i=1

p p öiE(RtRt-j+i) = ? i=1

öiãj-i

Ce qui donne les équations de Yule-Walker

ãj = _?p öiãj-i + ó²äj pour j E N i=1

et ãj = ã-j _?p öiã|j|-i + ó²äj pour j N i=1

2.3.1 Méthode de Yule-Walker

La méthode consiste à reprendre les équations de Yule-Walker en inversant les relations : on exprime les coefficients en fonction des autocovariances. On applique alors le raisonnement de la Méthode des moments et ensuite on trouve les paramètres estimés d'après les autocovariances estimées. En prenant l'equation sous forme matricielle :

r = or' (2.6)

avec :

22

Ö=

???????????

ö1 ö2 ... öP ó2

? ??????????

p1 ã-2 ã-3 ' ' ' 1

ã-1 ã-2 ' ' ' 0

, = ã0 ã-1 ' ' ' 0 ã1 ã0 ''' 0

1

ãP-2 ã0 ' '' 0

et

???????????

_???ã¹

ã2

= ã3

? ...

ã_P

Et on en déduit les estimateurs attendus.

èà =

???????????

^àö1 ^àö2 ... ^àöP àó2

? ??????????

2.3.2 La méthode des moindres carrés

On utilise ici les équations de Yule-Walker qui consiste à substituer les autocorrélations théoriques par leurs estimateurs afin de retrouver les esti-

mateurs de la méthode des moindres carrés du modèle par la résolution des équations de Yule-Walker.

On considère toujours l'équation définie en (2.4) dans laquelle on ajoute une constante c. On a donc :

Rt = c+ _ö1Rt-1+ ...+ _öpRt-p + Et

= Z^'_tâ^' + Et avec Et ~ N(0, ó²)

où Z^'_t = (1, Rt-1, Rt-2, . . . , _Rt-p) et â^' = (c, ö1, ö2, ... , ö_p)

Notons par Zt et â respectivement les transposées de Z^'_t et â^'.

L'estimation des paramètres ó² et â, du modèle Rt = Z^'_tâ^'+Et par la méthode des moindres carrés donne

âà =(ZtZ't)-1ZtRt

1

àó2 =

et

âà est

T - (p + ₁₎?(Rt - Z't 4)2

Les résultats usuels d'économétrie ne sont pas vérifiés ici, en particulier

biaisé(i.e E(0) =6 â). Il est toutefois possible de montrer le résultat suivant :

Propriété 2.3.2.1 Si le processus AR(p)est stationnaire alors

âà asymptotiquement sans biais c est á dire âà ?P â

et

_a2 P? ó2,

de plus

vT (â^à - â) ? ^loiN(0, ó²V)

oú

1

V = p lim

T ?+8 T

ZtZ^'_t.

23

Remarque 2.3.2.1 Si la méthode des moindres carrées peut être utilisée pour estimer les paramètres d'un modèle AR(p), elle ne marche plus dès lors que l'on a des termes autorégressifs sur les résidus.

2.3.3 La méthode du maximum de vraisemblance exacte

L'estimation d'un modéle AR(p) par la méthode du maximum de vraisemblance est délicate car la fonction de vraisemblance est très complexe et n'a pas de dérivée analytique. Cette difficulté provient de l'interdépendance des valeurs , ainsi que du fait que les observations antérieures ne sont toutes disponibles pour les p premiers valeurs. Pour determiner la vraisemblance, il est nécessaire de supposer connue la loi des erreurs. Nous supposerons les erreurs normalements distribuées. Cette méthode fait appel à la fonction d'autocorrélation pour déterminer la fonction d'autocorrélation de toutes les données de la série; ce qui permet d'évaluer la vraisemblance conjointe. Soit

_r

?

?????????????

? ?????????????

Yt

Yt-1

Y=

Yt-2

...

Y2 Y1

24

et soit la matrice T × T de covariance Y (T le nombre d'observations de l'échantillon). La vraisemblance de Y est

2 exp?-Y '-1Y

f(Y |ö, ó²) = (2ð)-T ² ||-T

2

On en déduit la forme de la log-vraisemblance (exacte, et non conditionnelle), L(ö,ó²;Y) = -T 2 ln(2ð) - T 2 ln || - 1 ₂Y ^0-1Y

25

avec F la matrice des autocovariances ,

?

F= ?????????????

Y0 Y1 ... ... _YT-1 YT

Y1 Y0 ... ... YT-2 YT-1 Y2 Y1 ... ... YT-3 YT-2 ... ... ... ... ... ... YT-1 YT-2 ... ... Y0 Y1 YT YT-1 ... ... Y1 Y0

?? ?????????????

Ces autocovariances sont données par les paramètres du modèle (exceptées les constantes) ö et ó². Souvent on a recours à un algorithme de maximisation pour trouver le vecteur de paramètre maximisant la log-vraisemblance. D'une manière générale, cette méthode est considérée comme étant plus précise que celle du maximum de vraissemblance approché ou conditionel. On peut noter que la maximisation de la vraisemblance exacte est un problème d'optimisation non-linéaire.

2.3.4 La méthode du maximum de vraisemblance conditionnel

Une manière de simplifier la complexité de la fonction de vraisemblance est de conditionner cette fonction aux p premières observations c'est â dire on utilise la densité de Rt sachant Rt-1, Rt-2, ... , pour estimer les paramétres du modele AR(p). Ces données sont supposées suivre conditionnellement une loi normale. En considérant l'équation (2.4), cette densité est donc :

2 exp-~2 ⁱ

f(Rt|Rt-1, Rt-2, ... , ö, ó²) = (2ðó2)-1 2ó2

2 1 _-(Rt -i=1 öiRt-i)²

= (2ðó) ² exp

2ó²

Et étant un bruit blanc, on a la vraissemblance conjointe qui s'exprime comme suit :

f(Rt|Rt-1,Rt-2,... ,ö,ó^2) =

?t i=1

- 2 (2ðó2) ^21 exp i 2ó^2?

la fonction log-vraissemblance est définit par

2 _i

1

L(ö, ó²; Rt|Rt-1, Rt-2, ...) = - ? ln(2ð) - ? ln(ó²) - 1 t?i=1ó2 .

2 2 2

NB :

La condition du premier ordre pour la moyenne des paramètres d'une log-vraisemblance normale ne dépend pas de ó². Ainsi l'estimateur du maximum de vraisemblance de la variance est :

àó2 = T-1

?T t=1

(Rt - ö0 - ö1Rt-1 - ... - öpRt-p)^2

= -

1 2

?T t=1

?T 1 ln?T^-1 t- T PT t t=1 2 ln(2ð) - T?t=1 2PT 2 2 t=1 2 t=1 t

= -

1 2

?T t=1

?T 1 ln?T-1 ln(2ð) - T?t=1 t- T 2 2 2 t=1

= -

1 2

?T t=1

?T T 1 ln?T-1 t ln(2ð) - T?t=1 2 2 - 2 t=1

= -

1 2

?T t=1

T T ln(2ð) - 2 - 2 ln(àó2).

26

= T-1

?T t=1

E2 t

L(Rt|Rt

Ceci introduit dans la log-vraisemblance fait que

? 1

T

Et 2

-1, Rt-2, ... ; ö, ó²) = - ln(2ð) + ln?T-1

E_t +

2 t=1 t=1 T^-1Pt^T=1 E_t²

= -

1 2

?T t=1

?T 1 2 ln?T^-1 t- T t ln(2ð) - T?t=1 2 T?t=1 T-1PT 2 2 t=1 2 t=1 t

27

La maximisation de cette fonction par rapport aux paramètres ö correspond à la minimisation des erreurs du modèle.

Autrement dit

max L(Rt|Rt-1, Rt-2, . . . ; ö, ó²) = -^T₂ ln àó²

avec

àEt = Rt - ö0 - ö1Rt-1 - ö2Rt-2 - . . . - öpRt-p

L'estimateur du maximum de vraisembance conditionnel correspond ainsi à celui des moindres carrés. L'estimateur obtenu sera équivalent à l'estimateur inconditionnel dans de grands échantillons et tous deux ont la même distribution asymptotique ¹. Il peut être biaisé²

NB : Ces estimations nous permettent de faire des prévisions.

2.3.5 Propriétés statistiques des estimateurs

Davidson et McKinnon (1993) rapportent que l'estimateur des moindres carrés conditionnel est biaisé, mais néanmoins convergent. Cryer et Chan (2008) proposent une simulation Monte-Carlo pour tester les différents estimateurs.

2.4 Choix d'un modèle

2.4.1 Critère d'information

Cette approche a été introduite par Akaike en 1969. Cette mesure de l'ecart entre le modèle proposé et la vraie loie peut être obtenue à l'aide de la quantité de Kullback.

1. Hamilton 1994, p. 126

2. voir Greene (2005, p. 256)

28

2.4.2 Définition

On se donne f0 la densité inconnue d'observations et ?f(.), f E F_? la famille des densités parmi lesquelles on a fait l'estimation. L'écart entre la vraie loi et le modèle est donné par

fEF? log f0(x)

I(f0, F) = min f(x) f(x)dx

Cette quantité est toujours et s'annule seulement si f0 appartient F. Cette quantité étant inconnue car f0, on essaiera de minimiser un estimateur de I, ^àI. Plusieurs estimateurs de la quantité d'information ont été proposés, dans le cas de modèles AR(p), à partir de T observations. Dans la suite on supposera disposer d'un modèle AR(p).

Nous avons vu jusqu'á maintenant que les fonctions d'autocorrélation et d'au-tocorrélation partielle nous permettent de determiner l'ordre d'un modèle autorégressif.Maintenant, l'idée est de créer des critères statistiques qui choisiront l'ordre du mod`ele.

Critère AIC et BIC pour processus autorégressif

L'idée du critère AIC, appelé encore le critère d'Akaike est de créer une fonction qui nous permettra de calculer la qualité de l'ajustement .On sait que le nombre de paramétres augmente, la variance àó² diminue. Dans le but de ne pas se retrouver avec une surparamétrisation du modèle, on ajoute un facteur qui permettra de faire un compromis entre le nombre de paramètre et la variance minimale. Dans les paragraphes qui suivent, on considère un modèle AR(p) et on calcule àó² a` l'aide du maximum de vraisemblance pour plusieurs valeurs positives de p. Le critére AIC consiste à calculer

AIC(p) = log(àó²) + 2 p

T

où T représente le nombre d'observations En utilisant ce critère, on remarque que si pà est le paramètre obtenu de la minimisation et que p est le paramètre

du vrai modèle, on a la proprièté suivante

P(àp ~ p) -+ 1 lorsque T -+ oc

Le critère a donc tendance à choisir un nombre de paramètres plus grand que celui du vrai modèle, ce qui nous conduit à un plus petit terme d'erreur àó². Si l'on désire avoir un meilleur choix de l'ordre p, il existe le critère BIC qui utilise une plus forte pénalité. Le critére BIC (Critère d'Information Bayé-sien) sélectionne le paramètre p qui minimise la quantité suivante :

BIC(p) = log(àó²) + p T log(T)

.

2.5 Prévision

Une fois que l'on a spécifié et estimé un processus AR, qui a passé avec succés les tests de validation, on désire l'utiliser pour effectuer des prévisions sur la série. On dispose donc des donnèes X1, . . . , XT observé entre 1 et T, et on désire prédire la valeur de la série à l'horizon h avec h ~ 0 , à savoir XT+h. On note TX* T +h ce prédicteur et on suppose que tous les processus AR seront mis sous forme canonique, et n'avoir aucune racine unité.

2.5.1 Prévision d'un modèle AR(p)

On considére toujours l'équation (2.4). Le modèle s'écrit donc,

Rt = ö1Rt_1 + ... + _{öpRt_p} + Et oh (L)Rt = Et

La prévision optimale (horizon h = 1) à la date T + 1, faite à la date T est

29

TR* T+1 = E[L(RT+1|RT,RT_1 ...)]

30

Aussi,

TR*T+1 = ö1RT + ... + öpRT-p De mani`ere analogue,

RT+h = ö1RT+h-1 + . . . + _öpRT+h-p + ET+h

Et donc,

_T R* T+h = E[L(RT+h|RT, RT-1 ...)] est donné, de façon récursive par

_T R* T+h = ö1.T RT+h-1 + . . . + öh-1.T RT+1 + _öhRT + . . . + _öpRT+h-p pour tout h < p et TRz,+h = ö1.TRT+h-1 + . . . + _öh-1.TRT+1 sinon

Exemple 2.5.1.1 Dans le cas d'un processus AR(1), (Xt) défini par :

Xt = öXt-1 + u + Et

alors :

i) TXi',+1 = öXT + u (horizon h=1)

ii) TXT+2 = ö.TX^*T+1 + u = u + ö[u + öXT]=u[1 + ö] + ö²XT (horizon h=2)

iii) TXT+3= ö.TX^*T+2 + u = u + ö[u + ö(u + öXT)]=u[1 + ö + ö²] + ö³XT (horizon h=3)

et récursivement on peut obtenir _TX7,+h de la forme

TXT+h = ö.TX4^,+h-1 + u = u[1 + ö + ö² + ... + +ö^h-1] + ö^hXT

Exemple 2.5.1.2 Une méthode alternative est de considérer le processus centré Yt = Xt - uó alors Yt = öYt-1 + Et.

31

Alors de facon réçursive TYT*+h = ö.T Y *-1

T +het donc TY T * +h = ö^hYT . Aussi on

peut écrire

_T X* T +h = u ö + ö^h[XT - u ö]

= u

1 - öh

1 - ö + ö^hXT

= u(1 + ö + ö² + . . . + ö^h-1) + ö^hXT .

CHAPITRE3
	Simulations

Dans cette partie, on va essayer de simuler les fonctions définies dans les paragraphes précédents.

3.1 Exemples de processus AR

3.1.1 Les processus AR(1)

Un processus AR(1) : Xt = çXt_1 + Et sera autocorrélé positivement si 0 < ç < 1, et autocorrélé négativement si -1 < ç < 0. Cette série va osciller autour de 0, en s'ecartant suivant la valeur Et du processus d'innovation (si -1 < ç < +1). Si ç = +1, on obtient une marche aléatoire et ç > +1 ou ç < -1 le processus n'est pas stationnaire, et on obtient un modèle qui explo-sera(à moyen terme). La valeur ç dans le cas où le proccessus est stationnaire, est la corrélation entre deux dates consécutives. ç=Corr(Xt, Xt_1)

Exemple 3.1.1.1 ( Processus AR(1) avec ç1 > 0)

Considérons un processus AR(1) noté (AR1t) stationnaire avec ç1 = 0.6 c'est-à-dire

AR1t = 0.6AR1t-1 + Et

On obtient donc le code R et le résultat ci-dessous pour la simulation de la série (AR1t) :

33

FIGURE 3.1 - La série AR1

Les trois courbes représentent respectivement l'allure de la série AR1 (en noire), la fonction d'autocorrélation (ACF) (en rouge) et la fonction d'auto-corrélation partielle (PACF) (en vert) de la série AR1.

La courbe de l'ACF a une décroissance exponentielle et pour le PACF on note un un Pic significatif pour le premier retard. Notre processus est donc correlé positivement .

Exemple 3.1.1.2 (La série AR(1) avec ç1 < 0)

Soit à etudier la série AR(1) notée (AR11t) stationnaire avec ö1 = -0.6

c'est-à-dire

AR11t = -0.6AR11t_1 + Et

Le code ci-dessus nous fournit le resultat suivant:

34

FIGURE 3.2 - La série AR11

Ces allures représentent respectivement celle de la série AR1 (en noire), celle de la fonction d'autocorrélation (ACF)(en rouge) et celle de la fonction d'au-tocorélation partielle (PACF) (en vert) de la série AR11.

On a constaté que l'ACF a une décroissance sinusoïdale et pour la PACF

35

on note un un Pic significatif pour le premier retard . On peut aussi remarquer que cette série est corrélée négativement .

3.1.2 Les processus AR(2)

Le comportement d'un processus AR(2) :Xt = ç1Xt_1 + _{ç2Xt_2} + ct dépendra fortement des racines de son équation caractéristique 1 - ç1.z - ç1.z² =0. Le cas le plus intéressant est celui où l'équation caractéristique a deux racines complexes conjuguées et reⁱ⁹ et re_ⁱ⁹ pour r<1 : le processus est alors stationnaire (et oscille alors autour de 0, sans exploser, de la même facon que les processus AR(1) dans le cas où |ç| < 1). Le processus est alors quasi-cyclique, de fréquence , avec un bruit aléatoire.

Exemple 3.1.2.1 (AR(2) avec ç1 > 0 et ç2 < 0)

Considérons le processus AR(2) noté (X1t) avec ç1 = 0.6, ç2 = -0.4. Autrement dit X1t = 0.6X1t_1 - 0.4X1t_2 + ct. On a le code R suivant:

Le code ci-dessus nous permet de visualiser l' ACF et la PACF de la série (X1t) :

36

FIGURE 3.3 - La série X1 : ACF(rouge) et PACF(vert)

On a une décroissance sinusoïdale pour l'ACF et on a des pics de signification pour le premier retard et le second retard pour la PACF.

Exemple 3.1.2.2 (AR(2) avec ç1 < 0 et ç2 < 0)

On se donne la série AR(2) noté (X2t) avec ç1 = -0.6, ç2 = -0.4. Autrement dit X2t = -0.6X2t_1 - 0.4X2t_2 + ct. On a le code R suivant:

Le code ci-dessus nous permet de visualiser l' ACF et la PACF de la série (X2t) :

37

FIGURE 3.4 - La série X2 : ACF(rouge) et PACF(vert)

D'une manière générale que pour un processus AR(p), la fonction d'auto-corrélation décroit exponentiellement et/ou sinusoïdalement rapide et pour la la fonction d'autocorrélation partielle les pics sont significatifs pour les premiers retards, les autres coefficients sont nuls pour des retards supérieurs à p.

3.2 Estimation

Pour estimer l'ordre p, on utilise les propriétés vues précédemment sur les formes des autocorrélogrammes 'TX(h) ou des autocorrélogrammes partiels. En particuliers pour les processus AR(p) l'autocorrélogramme partiel s'annule à partir de p ( à gauche).

38

3.2.1 Estimation des paramètres d'une modélisation

AR(1)

Considérons la série AR1 définie précedemment i.e AR1t = 0.6AR1t_1+ct. Pour estimer ses paramétres, on a l'algorithme suivant :

Un estimateur de (ö1, ó²) est donc ( ^àö1, ^àó²) tel que ^àö1 = 0.5697 et ^àó² =0.9677

Remarque 3.2.1.1 sigma² estimated as, loglikelihood et aic représentent respectivement la variance des erreurs, le maximum de vraisemblance et l'aic du modèle donné en argument.

3.2.2 Estimation des paramètres d'une modélisation

AR(2)

Considérons la série AR(2), (X2t) définie précedemment c'est - à - dire définie par X2t = -0.6X2t_1 - 0.4X2t_2 + ct . L'algorithme suivant nous permet de faire une estimation des paramétres de ladite série.

Un estimateur de (ö1, ö2, ó²) est donc ( ^àö1, ^àö2, ^àó²) tel que ^àö1 =-0.6233 ^àö1 =-0.3976 et ^àó² =0.999

39

CHAPITRE4

Application du mo- dèle AR sur l'indice boursier S&P 500

4.1 Le S&P 500

Le S&P 500 (SPX) est un indice boursier basé sur 500 grandes sociétés cotées sur les bourses américaines. Parmi ces sociétés on peut citer Nucor Corp, Oracle Corp, Phillips 66, etc... . L'indice est possédé et géré par Standard & Poor's, l'une des trois principales sociétés de notation financière. L'indice S&P 500 a été créé en 1950. Il a détrôné le Dow Jones Industrial Average comme indice le plus représentatif du marché boursier américain parce qu'il est composé d'un plus grand nombre de compagnies et que sa valeur tient compte de la capitalisation boursière des compagnies contenues dans l'indice. De son côté, le Dow Jones Industrial Average est basé sur seulement 30 compagnies. La pondération des valeurs au sein du Dow ne s'effectue ni en fonction des capitalisations boursières, ni du flottant (comme pour les indices francais), mais en fonction des cours de bourse. Une variationd'un dollar dans la valeur de la plus petite compagnie de l'indice a le même impact sur l'indice qu'une variation d'un dollar dans la valeur de la plus grosse compagnie.

41

4.2 Présentation des données

On va utliser les données mensuelles de la série S&P 500 datant du 19 Août 2005 au 17 décembre 2013, soit un echantillon de 108 valeurs. Ces données ont été extraites à partir du site de Yahoo France.

FIGURE 4.1 - moyennes mensuelles de S&P 500

4.3 Applications

Pour visualiser les allures de la s 'erie, de l' ACF et de la PACF, on doit créer à partir des données du S&P 500, la série X. L'algorithme de création de cette sèrie est donné par :

42

4.3.1 Allure de la série S&P 500

Grâce à la commande ci-dessus, la série S&P 500 s'illustre graphiquement par la figure suivante.

FIGURE 4.2 - Allure de la série S&P500

4.3.2 L'ACF et la PACF de la série S&P 500

Pour la PACF on a :

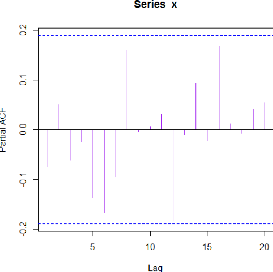
FIGURE 4.3 - PACF de la série

43

Et pour l'ACF on obtient:

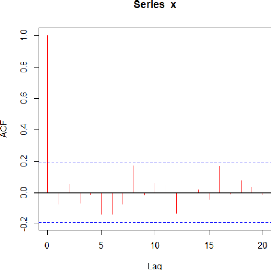
44

FIGURE 4.4 - ACF de la série

On note ici pour l'ACF, un pic significatif de premier retard, cela signifie donc que la série S&P 500 est correlé positivement.

4.3.3 Estimation

Les algorithmes ci-dessous nous permettent d'estimer les paramétres du modèle.

45

46

4.3.4 Choix du modèle

Pour choisir le modéle adéquat pour modéliser la série, on doit selec-tionner celui qui a le plus petit AIC. Pour cela on regroupe les resultats précédents dans le tableau ci-dessous :

modèle	u^2	logL	AIC
AR(1)	0.9782	-152.06	310.12		AR(2)
0.9758	-151.93	311.85	AR(3)
0.9720	-151.72	313.44	AR(4)
0.9712	-151.68	315.36	AR(5)
0.9530	-150.62	315.23

Ces résultats nous montrent que le modèle AR(1) a le plus faible AIC. Donc il sera pris en compte pour la modélisation de la série S&P 500.

47

CNCLUSIN

La réalisation de ce document nous a permis de savoir bien appliquer la statistique dans le domaine de la finance, grâce à ses différentes riches méthodes. Vu que les séries de rendements financiers peuvent étre assimilées à des processus autorégressifs donc aprés quelques généralités sur les rendements financiers et sur les processus stochastiques, le modèle autorégressif (modèle AR) , y a été aussi développé. Différentes techniques d'estimations et de prévisions avec ce modèle y sont également traitées.

Nous avons profité de la dernière partie de ce travail pour appliquer la théorie sur des données réelles plus précisément sur l'indice boursier S&P 500. Et c'est grâce au logiciel R que ces traitements de données ont eu lieu.

Enfin, avec les méthodes développées, il sera possible de les utliser afin de pouvoir les appliquer avec d'autres données telles que le CAC40, etc...

48

Bibliographie

[1] Russel DAVIDSON et James G. MACKINNON : Estimation and Inference in Econometrics. , New York,Oxford University Press,1994 p.874

[2] James DOUGLAS HAMILTON: Times Series Analysis. Princeton University Press,1994 p.799

[3] Arthur CHARPENTER : Cours de séries temporelles : Théorie et application. DESS actuariat et DESS mathématiques de la Décision.

[4] Steven FORTIER, département de mathématiques, Université de Sherbrooke: Les mod`ele MA, AR et ARMA multidimensinnels : estimation et causalité. CaMUS 4,112-136.

[5] Arthur CHARPENTER : Modeles de prévision : Séries temporelles ,15 mai 2012 UQAM, ACT6420,Hivers 2011

[6] Russel DAVIDSON et James G. MACKINNON (1993)

[7] Cryer et Chan (2008)

[8] Akaike (1969)